История комбинаторики — Википедия

История комбинаторики освещает развитие комбинаторики — раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные проблемы. Начав с анализа головоломок и азартных игр, комбинаторика оказалась исключительно полезной для решения практических задач почти во всех разделах математики. Кроме того, комбинаторные методы оказались полезными в статистике, генетике, лингвистике и многих других науках.

Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо^[1]

. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.

Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.)^[2]. Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона^[2]. Во II веке до н. э. индийцы знали, что сумма всех биномиальных коэффициентов степени n равна 2n{\displaystyle 2^{n}}.

Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло. Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000^[3]. Аристотель при изложении своей логики безошибочно перечислил все возможные типы трёхчленных силлогизмов. Аристоксен рассмотрел различные чередования длинных и коротких слогов в стихотворных размерах.^[3] Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).

В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.

В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра подсчитывал число размещений с перестановками в огласовках имени Бога^[4] и обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.

Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

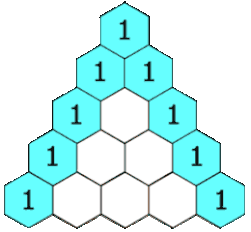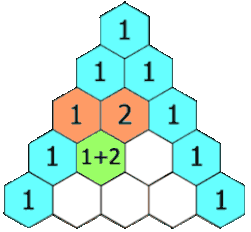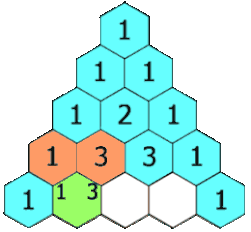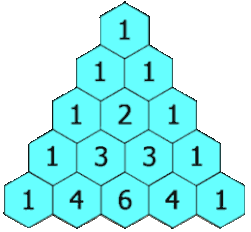
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику^[5]. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.^[6]

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

В начале XX века начала развиваться комбинаторная геометрия: были доказаны теоремы Минковского — Радона, Радона, Хелли, Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана. Во второй четверти XX века были поставлены проблема Борсука и проблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

1. ↑ Виленкин Н. Я., 1975, с. 7.
2. ↑ ^{1 2} Amulya Kumar Bag. Binomial theorem in ancient India. Indian J. History Sci., 1:68-74, 1966.
3. ↑ ^{1 2} Виленкин Н. Я., 1975, с. 9.
4. ↑ Краткий комментарий к Исход, 3:13.
5. ↑ Виленкин Н. Я., 1975, с. 19.
6. ↑ O’Connor, John; Edmund Robertson. Abraham de Moivre (неопр.). The MacTutor History of Mathematics archive (06 2004). Дата обращения 31 мая 2010. Архивировано 27 апреля 2012 года.

Алгебраическая комбинаторика — Википедия

Матроид Фано, полученный из плоскости Фано. Матроиды — одна из многих областей, изучаемых в алгебраической комбинаторике.

Алгебраическая комбинаторика — это область математики, использующая методы общей алгебры, в особенности теории групп и теории представлений, в различных комбинаторных контекстах и, наоборот, применяющая комбинаторные техники к задачам в алгебре.

В начале или середине 1990-х типичные комбинаторные объекты, которые рассматривались в алгебраической комбинаторике, либо имели большое число общепризнанных симметрий (схема отношений^[en], сильно регулярные графы, частично упорядоченные множества с действием группы), либо обладали богатой алгебраической структурой, как правило, имеющей теоретические источники (симметрические функции, диаграммы Юнга). Этот период отражён в разделе 05E, «

Алгебраическая комбинаторика», математической предметной классификации AMS, предложенной в 1991 году.

Алгебраическую комбинаторику можно рассматривать как область математики, где взаимодействие комбинаторных и алгебраических методов особенно сильно и существенно. Такими комбинаторными темами могут быть перечисления по свойствам или области, вовлекающие матроиды, многогранники, частично упорядоченные множества или конечные геометрии. Со стороны алгебры, кроме теории групп и теории представлений, часто используются решётки и коммутативная алгебра. Журнал «Journal of Algebraic Combinatorics^[en]», выпускаемый издательством Springer-Verlag, является интернациональным журналом для статей из этой области.

Симметрические функции[править | править код]

Кольцо симметрических функций^[en] является своеобразным пределом колец симметрических многочленов от n переменных при n, стремящемся к бесконечности. Это кольцо служит универсальной структурой, в которой связи между симметрическими многочленами могут быть выражены без привязки к числу переменных (но элементы кольца не являются ни многочленами, ни функциями). Кроме всего прочего, это кольцо играет важную роль в теории представлений симметрических групп

[en].

Схемы отношений[править | править код]

Схема отношений^[en] — это набор бинарных отношений, удовлетворяющих определённым условиям совместимости. Схемы отношений дают единообразный подход ко многим разделам, например, комбинаторным схемам и теории кодирования^[1][2]. В алгебре схемы отношений обобщают группы, а теория схем отношений обобщает теорию характеров линейных представлений групп^[3][4][5].

Сильно регулярные графы[править | править код]

Сильно регулярный граф определяется следующим образом. Пусть G = (V,E) — регулярный граф с v вершинами и степенью k. Говорят, что G сильно регулярен, если существуют целые числа λ и μ, такие, что:

• Любые две смежные вершины имеют λ общих соседей.
• Любые две несмежные вершины имеют μ общих соседей.

Графы такого вида иногда обозначаются srg(v, k, λ, μ).

Некоторые авторы исключают графы, которые удовлетворяют определению тривиально, а именно те графы, которые являются объединением непересекающихся (одного и более) одинаковых полных графов^[6][7], и их дополнения, графы Турана.

Диаграммы Юнга[править | править код]

Диаграммы Юнга — комбинаторные объекты, полезные в теории представлений и исчислении Шуберта^[en]. Они дают удобный способ описания представлений симметрических групп и полных линейных групп и позволяют изучать свойства этих объектов. Диаграммы были предложены Альфредом Юнгом^[en], математиком Кембриджского университета, в 1900 году. В 1903 году они были применены для изучения симметрических групп Фердинандом Георгом Фробениусом. Позднее их теория была развита многими математиками, включая Перси Макмагона

[en], В. В. Д. Ходжа, Г. де Б. Робинсона^[en], Д.-К. Рота^[en], Алена Ласку^[en], М.-П. Шютценберже^[en] и Ричарда Стэнли.

Матроиды[править | править код]

Матроид — это структура, которая вбирает и обобщает понятие линейной независимости в векторных пространствах. Имеется много эквивалентных путей определения матроида, и наиболее важные из них — в терминах независимых множеств, баз, замкнутых множеств или плоскостей, операторов замыкания и функций ранга.

Теория матроидов в значительной степени заимствует терминологию из линейной алгебры и теории графов, в основном потому, что в ней используются абстракции различных центральных понятий из этих областей, из топологии, комбинаторной оптимизации, теории сетей^[en] и теории кодирования^[8][9].

Конечные геометрии[править | править код]

Конечная геометрия — это любая геометрическая система, имеющая лишь конечное число точек. Привычная Евклидова геометрия не конечна, поскольку евклидова прямая содержит бесконечно много точек. Геометрию, основанную на графике компьютерного экрана, где пиксели считаются точками, можно считать конечной геометрией. Хотя существует много систем, которые можно было бы считать конечными геометриями, в основном внимание уделяется конечным проективным и аффинным пространствам ввиду их регулярности и простоты. Другие существенные типы конечных геометрий — конечные плоскости Мёбиуса или инверсные плоскости и плоскости Лагерра

[en], которые являются примерами более общих объектов, называемых плоскостями Бенца^[en], и их аналогами в более высоких размерностях, таких как конечные инверсионные геометрии^[en].

Конечные геометрии могут быть построены с помощью линейной алгебры, начиная с векторных пространств над конечными полями. Аффинные и проективные плоскости, построенные таким образом, называются геометриями Галуа. Конечные геометрии могут также быть определены чисто аксиоматически. Самые распространенные конечные геометрии — геометрии Галуа, поскольку любое конечное проективное пространство размерности три и более изоморфно проективному пространству над конечным полем. Однако в размерности два имеются аффинные и проективные плоскости, которые не изоморфны геометриям Галуа, а именно, недезарговы плоскости. Похожие результаты имеют место для других видов конечных геометрий.

1. ↑ Bannai, Ito, 1984.
2. ↑ Godsil, 1993.
3. ↑ Bailey, 2004, с. 387.
4. ↑ Zieschang, 2005b.
5. ↑ Zieschang, 2005a.
6. ↑ Brouwer, Haemers, 2010, с. 116.
7. ↑ Godsil, Royle, 2001, с. 218.
8. ↑ Neel, Neudauer, 2009, с. 26–41.
9. ↑ Kashyap, Soljanin, Vontobel, 2009.

• Bailey, Rosemary A. (2004), Association Schemes: Designed Experiments, Algebra and Combinatorics, Cambridge University Press, ISBN 978-0-521-82446-0, <http://www.maths.qmul.ac.uk/~rab/Asbook> .
• Andries E Brouwer, Willem H Haemers.
  Spectra of Graphs. — New York, Dordrecht, Heidelberg, London: Springer-Verlag, 2010. — (Universitext). — ISBN 9781461419389. — DOI:10.1007/9781461419396. Архивная копия от 16 марта 2012 на Wayback Machine
• David L. Neel, Nancy Ann Neudauer. Matroids you have known // Mathematics Magazine. — 2009. — Т. 82, вып. 1. — С. 26—41. — DOI:10.4169/193009809×469020.
• Navin Kashyap, Emina Soljanin, Pascal Vontobel. Applications of Matroid Theory and Combinatorial Optimization to Information and Coding Theory. — 2009.
• Eiichi Bannai, Tatsuro Ito. Algebraic combinatorics I: Association schemes. — Menlo Park, CA: The Benjamin/Cummings Publishing Co., Inc., 1984. — С. xxiv+425. — ISBN 0-8053-0490-8.
• New Perspectives in Algebraic Combinatorics / L. J. Billera, A. Björner, C. Greene, R. Simion, R. P. Stanley. — MSRI Publications. — Cambridge University Press, 1999. — Т. 38.
• Chris Godsil, Gordon Royle. Algebraic Graph Theory. — New York: Springer-Verlag, 2001. — Т. 207. — (Graduate Texts in Mathematics). — ISBN 0-387-95220-9. — ISBN 0-387-95241-1.
• C. D. Godsil. Algebraic Combinatorics. — New York: Chapman and Hall, 1993. — ISBN 0-412-04131-6.
• Takayuki Hibi. Algebraic combinatorics on convex polytopes. — Glebe, Australia: Carslaw Publications, 1992.
• Melvin Hochster. Ring theory, II (Proc. Second Conf., Univ. Oklahoma, Norman, Okla., 1975). — New York: Dekker, 1977. — Т. 26. — С. 171—223. — (Lecture Notes in Pure and Appl. Math.).
• Ezra Miller, Bernd Sturmfels. Combinatorial commutative algebra. — New York, NY: Springer-Verlag, 2005. — Т. 227. — (Graduate Texts in Mathematics). — ISBN 0-387-22356-8.
• Richard Stanley. Combinatorics and commutative algebra. — 2nd. — Boston, MA: Birkhäuser, 1996. — Т. 41. — (Progress in Mathematics). — ISBN 0-8176-3836-9.
• Bernd Sturmfels. Gröbner bases and convex polytopes. — Providence, RI: American Mathematical Society, 1996. — Т. 8. — (University Lecture Series). — ISBN 0-8218-0487-1.
• Doron Zeilberger. The Princeton Companion to Mathematics^[en]. — Princeton University Press, 2008. — ISBN 978-0-691-11880-2.
• Zieschang, Paul-Hermann (2005a), «Association Schemes: Designed Experiments, Algebra and Combinatorics by Rosemary A. Bailey, Review», Bulletin of the American Mathematical Society Т. 43 (02): 249–253, doi:10.1090/S0273-0979-05-01077-3, <http://www.ams.org/bull/2006-43-02/S0273-0979-05-01077-3/S0273-0979-05-01077-3.pdf> 
• Zieschang, Paul-Hermann (2005b), Theory of association schemes, Springer, с. xii+283, ISBN 3-540-26136-2 
• Zieschang, Paul-Hermann (2006), «The exchange condition for association schemes», Israel Journal of Mathematics Т. 151 (3): 357–380, ISSN 0021-2172, DOI 10.1007/BF02777367 

Комбинаторика — это… Что такое Комбинаторика?

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

• Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
• Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
• Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
• Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
• Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примерами комбинаторных задач являются:

1. Сколькими способами можно разместить n предметов по m ящикам так, чтобы выполнялись заданные ограничения?
2. Сколько существует функций из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
3. Сколько существует различных перестановок из 52 игральных карт?

   Ответ: 52! (52 факториал), то есть, 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8,0658 × 10⁶⁷.

4. При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати?

   Решение: Каждый возможный исход соответствует функции (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

Топологическая комбинаторика

Топологическая комбинаторика (англ.) применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

Инфинитарная комбинаторика

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.

Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).^[1]

Исторический очерк

См. также

Примечания

Литература

• Андерсон Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8
• Виленкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975.
• Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
• Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
• Раизер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
• Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.
• Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
• Риордан Дж. Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
• Р. Стенли. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2
• Р. Стенли. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — С. 767. — ISBN 978-5-03-003476-8

Ссылки

Арифметическая комбинаторика — Википедия

Материал из Википедии — свободной энциклопедии

Арифметическая комбинаторика — раздел математики, возникший на стыке теории чисел, комбинаторики, эргодической теории и гармонического анализа.

Пусть N{\displaystyle \mathbb {N} } — множество натуральных чисел, E{\displaystyle \mathbb {E} } — чётных, P{\displaystyle \mathbb {P} } — простых, а S{\displaystyle \mathbb {S} } — множество всех квадратов натуральных чисел.

Знаменитую теорему Лагранжа можно компактно сформулировать как равенство S+S+S+S=N{\displaystyle \mathbb {S} +\mathbb {S} +\mathbb {S} +\mathbb {S} =\mathbb {N} }, а не менее знаменитую гипотезу Гольдбаха — как P+P⊇E{\displaystyle \mathbb {P} +\mathbb {P} \supseteq \mathbb {E} }. Изучением поведения подмножеств целых чисел (а также более сложных алгебраических структур) относительно имеющихся операций занимается (в тесном сотрудничестве с традиционной теорией чисел) арифметическая комбинаторика.

Аддитивная комбинаторика относится к специальному случаю арифметической комбинаторики, когда во внимание берутся только операции сложения и вычитания.

Изучаемые множества могут быть подмножествами алгебраических структур, отличных от целых чисел, например, групп, колец или полей.^[1]

Арифметическая комбинаторика объясняется в рецензии Грина на книгу «Аддитивная комбинаторика» Тао и Ву.

Эта статья или раздел описывает ситуацию лишь применительно к частным случаям. Необходимо переработать изложение или добавить информацию, чтобы статья описывала более общий случай.

Пусть A — множество, содержащее n целых чисел, каков будет размер множества сумм

A+A:={x+y:x,y∈A}{\displaystyle A+A:=\{x+y:x,y\in A\}},

множества разностей (не путать с разностью множеств)

A−A:={x−y:x,y∈A}{\displaystyle A-A:=\{x-y:x,y\in A\}},

или множества произведений (не путать с произведением множеств)

A×A:={xy:x,y∈A}{\displaystyle A\times A:=\{xy:x,y\in A\}}

Как связаны размеры этих множеств?

• Łaba, Izabella (англ.)русск.. From harmonic analysis to arithmetic combinatorics (англ.) // Bull. Amer. Math. Soc. : journal. — 2008. — Vol. 45, no. 01. — P. 77—115. — DOI:10.1090/S0273-0979-07-01189-5.
• Additive Combinatorics and Theoretical Computer Science, Luca Trevisan, SIGACT News, June 2009
• Additive combinatorics with a view towards computer science and cryptography: An exposition, Khodakhast Bibak, 2012
• Open problems in additive combinatorics, E Croot, V Lev
• From Rotating Needles to Stability of Waves: Emerging Connections between Combinatorics, Analysis, and PDE, Тао, Теренс, AMS Notices March 2001
• Tao, Terence (англ.)русск.; Vu, Van H. (англ.)русск.. Additive combinatorics (неопр.). — Cambridge: Cambridge University Press, 2006. — Т. 105. — (Cambridge Studies in Advanced Mathematics). — ISBN 0-521-85386-9.
• Additive Combinatorics (неопр.) / Granville, Andrew (англ.)русск.; Nathanson, Melvyn B.; Solymosi, József. — American Mathematical Society, 2007. — Т. 43. — (CRM Proceedings & Lecture Notes). — ISBN 978-0-8218-4351-2.
• Mann, Henry (англ.)русск.. Addition Theorems: The Addition Theorems of Group Theory and Number Theory (англ.). — Corrected reprint of 1965 Wiley. — Huntington, New York: Robert E. Krieger Publishing Company, 1976. — ISBN 0-88275-418-1.
• Melvyn B. Nathanson. Additive Number Theory: the Classical Bases (англ.). — Springer-Verlag, 1996. — Vol. 164. — (Graduate Texts in Mathematics). — ISBN 0-387-94656-X.
• Melvyn B. Nathanson. Additive Number Theory: Inverse Problems and the Geometry of Sumsets (англ.). — Springer-Verlag, 1996. — Vol. 165. — (Graduate Texts in Mathematics). — ISBN 0-387-94655-1.
• Теренс Тао, Some Highlights of Arithmetic Combinatorics
• K Soundararajan, Additive Combinatorics: Winter 2007
• Luca Trevisan, Earliest Connections of Additive Combinatorics and Computer Science

Аддитивная комбинаторика — Википедия

Аддитивная комбинаторика (от англ. addition — сложение) — междисциплинарная^[1] область математики, изучающая взаимозависимость различных количественных интерпретаций понятия структурированности подмножества группы (как правило, конечной), а также аналогичные свойства производных от множества структур, использующихся при этих интерпретациях. Кроме того, аддитивная комбинаторика изучает структурированность в различных смыслах некоторых специфических множеств или классов множеств (например, подмножеств простых чисел или мультипликативных подгрупп).

Таким образом, основным объектом изучения являются конечные множества, по возможности как можно более абстрактные, ограниченные иногда только в своих размерах, что делает эту науку похожей на комбинаторику. Однако, в отличие от комбинаторики как таковой, где элементы множеств идентифицируются только отличием друг от друга и принадлежностью к тем или иным рассматриваемым множествам, в аддитивной комбинаторике у каждого элемента множества есть чёткое значение, и между элементами появляются дополнительные взаимосвязи, вытекающие из их значений и свойств операции группы (и, возможно, специфических законов, характерных для заданной группы).

Аддитивная комбинаторика тесно связана с арифметической комбинаторикой, где предметом изучения является соотношение подмножества поля (а не просто группы, как здесь) сразу с двумя операциями — сложением и умножением.

Аддитивная теория чисел[править | править код]

Вопросы представления чисел через суммы элементов из небольшого числа заданных множеств рассматривались математиками ещё с древних времён. Классическими примерами являются задачи представимости любого числа суммой четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов) или любого чётного числа, которое больше трёх, суммой двух простых (проблема Гольдбаха). Если обозначить через Q={0}∪{n2:n∈N}{\displaystyle {\mathbb {Q} }=\left\lbrace {0}\right\rbrace \cup \left\lbrace {n^{2}:n\in {\mathbb {N} }}\right\rbrace } множество всех квадратов неотрицательных чисел, то в терминах аддитивной комбинаторики (см. раздел с обозначениями ниже) теорему Лагранжа можно записать как

Q+Q+Q+Q=N{\displaystyle {\mathbb {Q} }+{\mathbb {Q} }+{\mathbb {Q} }+{\mathbb {Q} }={\mathbb {N} }}

В ходе решения подобных задач возникали и другие аналогичные, с другими множествами, но похожими формулировками. Всё это сформировало область математики, называемую аддитивной теорией чисел^[en].

Однако аддитивную комбинаторику не следует воспринимать как обобщение или развитие аддитивной теории чисел — хотя задачи последней могут быть удобно записаны в терминах аддитивной комбинаторики, но её общие методы к ним, как правило, не применимы. Теория чисел всегда рассматривает множества специального вида — простые числа, квадраты, другие степени, числа с малым количеством делителей и т. д. Аддитивная же комбинаторика пытается понять структуру сложения как таковую, вывести как можно более общие результаты.

Тем не менее, первые результаты, которые можно по духу отнести к аддитивно-комбинаторным, зарождались в начале XX века именно как часть теории чисел (называемая также комбинаторной теорией чисел).^[1] Таким, например, является метод Шнирельмана для решения проблемы Гольдбаха (который был также применён Линником для проблемы Варинга) — он основан на теореме Шнирельмана о множестве сумм чисел из двух произвольных множеств, о которых известна только их плотность^[2] (следует заметить, что при этом само специфическое определение плотности по Шнирельману, использовавшееся в этой теореме, в аддитивной комбинаторике как объект для изучения не прижилось).

Теория Рамсея[править | править код]

Возникшая в первой половине XX века теория Рамсея также анализировала различные представления о структурированности. Утверждения теории Рамсея касаются наличия хотя бы малого «островка» структурности в достаточно сложных (по количеству элементарных частей) объектах.^[3]

Однако теория Рамсея рассматривает не подмножества, а разбиения заданного множества (например, множества рёбер графа, натуральных чисел или части булеана конечного множества), и результат о структуре имеет в виду наличие структурированности у одного из элементов разбиения, и, как правило, непонятно, у какого. Следовательно, о каком-то отдельном подмножестве ничего сказать нельзя.

Наглядным примером является теорема ван дер Вардена^[en]* — она говорит, что при любом разбиении натуральных чисел на конечное число классов хотя бы в одном из классов будет присутствовать арифметическая прогрессия (любой заданной длины). При этом очевидно, что в любом разбиении есть класс, плотность чисел в котором больше, чем в других, и интуитивно кажется, что прогрессия должна находится в этом множестве — ведь здесь больше всего элементов, то есть больше всего возможностей. Очевидно также, что самое большое множество будет иметь положительную (ненулевую) плотность. Однако доказать, что абсолютно любое бесконечное множество натуральных чисел положительной плотности содержит в себе арифметическую прогрессию, не получается просто через теорему ван дер Вардена — по ней прогрессия может оказаться в любом классе, даже самом маленьком. Для доказательства наличия прогрессии в любом плотном множестве приходится привлекать намного более сложные средства — решение этой задачи получило название теоремы Семереди, которая как раз считается классическим аддитивно-комбинаторным результатом.

Тригонометрические суммы[править | править код]

Гибким инструментом для оценки упорядоченности множества, сыгравшим значительную роль и в аддитивной теории чисел, являются тригонометрические суммы (суммы корней из единицы, соответствующих числам множества). Они стали инструментом и объектом для изучения и в аддитивной комбинаторике, поскольку допускают довольно общее применение.

Ещё Гаусс, первым исследовавший тригонометрические суммы, обнаружил через них связь распределения всех возможных разностей чисел из заданного множества и самого множества. Исследуя квадратичные вычеты, Гаусс рассматривал сумму

S(a)=∑x=0p−1e2πax2pi{\displaystyle S(a)=\sum \limits _{x=0}^{p-1}{e^{2\pi {\frac {ax^{2}}{p}}i}}}

и выводил оценку для квадрата её модуля:

|S(a)|2=∑x,ye2πa(x2−y2)pi{\displaystyle |S(a)|^{2}=\sum \limits _{x,y}{e^{2\pi {\frac {a(x^{2}-y^{2})}{p}}i}}}

Оценка на эту сумму получалась чисто комбинаторно из свойств выражения x2−y2{\displaystyle x^{2}-y^{2}} при замене переменной x=y+h{\displaystyle x=y+h}.^[4] Таким образом, мультимножество разностей давало информацию о структуре множества самих квдаратичных вычетов. В аддитивной комбинаторике действует похожий по идее подход, когда уже множество, а не мультимножество разностей (или сумм, произведений и т. д.) элементов из заданного множества даёт информацию о структуре этого множества. Такой переход — от мультимножества ко множеству — связан с переходом от количества решений того или иного уравнения (например, a1+b1=a2+b2,ai∈A,bi∈B{\displaystyle a_{1}+b_{1}=a_{2}+b_{2},a_{i}\in A,b_{i}\in B}) к представлению чисел в том или ином виде (например, в виде a+b,a∈A,b∈B{\displaystyle a+b,a\in A,b\in B}), который в принципе характерен для метода тригонометрических сумм.

Теорема Фреймана[править | править код]

Отдельным фундаментом для развития новой науки о поэлементных суммах множеств (множествах сумм A+B={a+b:a∈A,b∈B}{\displaystyle A+B=\left\lbrace {a+b:a\in A,b\in B}\right\rbrace }) стала доказанная Григорием Фрейманом теорема о строении множеств с малым удвоением (то есть множеств, множество сумм двух элементов которых имеет малый размер, или проще говоря, суммы элементов из которых часто совпадают).^[5]

Вопросы о суммах элементов из того или иного множества рассматривались также Эрдёшем и Семереди без введения специальной символики для обозначения суммирования множеств.^[6]

Множество сумм[править | править код]

Важным понятием аддитивной комбинаторики является множество сумм

A+B={a+b:a∈A,b∈B}{\displaystyle A+B=\left\lbrace {a+b:a\in A,b\in B}\right\rbrace }

для конечных множеств A,B∈G{\displaystyle A,B\in \mathrm {G} }, где (G,+){\displaystyle (\mathrm {G} ,+)} — группа. Размер такого множества определяется структурой A{\displaystyle A} и B{\displaystyle B} относительно операции +{\displaystyle +}. Если A{\displaystyle A} и B{\displaystyle B} — арифметиеские прогрессии, то |A+B|{\displaystyle |A+B|} мало. А если, например, A,B∈Zn{\displaystyle A,B\in {\mathbb {Z} }_{n}} выбраны случайно по схеме Бернулли, то |A+B|{\displaystyle |A+B|} очень велико. Промежуточные случаи между указанными двумя как раз и представляют аддитивно-комбинаторный интерес.

Кроме того, интересна сама по себе структура множеств A+B{\displaystyle A+B}. В частности, по состоянию на 2018 год нет общих критериев (кроме прямого перебора), позволяющих определить, представляется ли заданное множество в виде A+A{\displaystyle A+A}.

Связываемые характеристики множеств[править | править код]

В таблице ниже представлены теоремы и неравенства аддитивной комбинаторики, связывающие различные характеристики подмножеств групп. Утверждение, указанное в ячейке, связывает характеристики, указанные в её строке и столбце. Приведены лишь некоторые, наиболее известные, из таких теорем.

Для краткости в заголовках используются следующие сокращения:

• Плотность множества A⊂G{\displaystyle A\subset {\mathbb {G} }} для конечной группы G{\displaystyle {\mathbb {G} }} — это величина |A||G|{\displaystyle {\frac {|A|}{|{\mathbb {G} }|}}} или закон её асимптотического роста с ростом размера G{\displaystyle {\mathbb {G} }}, а для бесконечных G{\displaystyle {\mathbb {G} }} — асимптотическая плотность (или закон распределения) A{\displaystyle A} в G{\displaystyle {\mathbb {G} }},
• ОАП (от «обобщённая арифметическая прогрессия») — присутствие во множестве больших арифметических прогрессий, нетривиальных обобщённых арифметических прогрессий или их больших частей, а также, наоборот, возможность покрыть множество (или большую его часть) не сликом большой арифметической прогрессией;
• A1+⋯+Ak{\displaystyle A_{1}+\dots +A_{k}} — размер и строение множества сумм (а также разностей и комбинаций сумм и разностей) — в частности, возможность представить любой элемент группы как сумму заданного количества элементов данного множества;
• X=A1+⋯+Ak{\displaystyle X=A_{1}+\dots +A_{k}} — представимость множества или большой его части как множества сумм (а также разностей и комбинаций сумм и разностей) чисел из небольшого числа множеств, то есть разрешимость уравнения множеств X=A1+⋯+Ak{\displaystyle X=A_{1}+\dots +A_{k}} для заданного X{\displaystyle X}, возможно, даже при определённых условиях на A1,…,Ak{\displaystyle A_{1},\dots ,A_{k}} (например, A1=⋯=Ak{\displaystyle A_{1}=\dots =A_{k}}), где +{\displaystyle +} означает сумму Минковского
• коэффициенты Фурье имеются в виду для характеристической функции множества и функций, определяемых через неё, а также их статистика — разного рода нормы, количесттво элементов с большим значением и структура их множества;
• ЧРУ (от «число решений уравнения») — число решений различных линейных уравнений (в частности, аддитивная энергия) или систем уравнений, в которых переменные принимают значения из заданных множеств, а также соотношение количества их решений

Также в ячейках используется несколько специфических обозначений:

	Плотность	ОАП	A1+⋯+Ak{\displaystyle A_{1}+\dots +A_{k}}	X=A1+⋯+Ak{\displaystyle X=A_{1}+\dots +A_{k}}	Коэффициенты Фурье	ЧРУ
Плотность
ОАП	Теорема Семереди
A1+⋯+Ak{\displaystyle A_{1}+\dots +A_{k}}	Неравенство Шнирельмана, Теорема Фюрстенберга — Саркози[en]	Теорема Фреймана[en]
X=A1+⋯+Ak{\displaystyle X=A_{1}+\dots +A_{k}}		A+B{\displaystyle A+B} при больших |A|{\displaystyle |A|} и |B|{\displaystyle |B|} содержат длинную а. п.[7][8]	Неравенство Плюннеке — Ружа
Коэффициенты Фурье	Принцип неопределённости[9]	Если A⊂ZN{\displaystyle A\subset {\mathbb {Z} }_{N}}, ||ρA^||∞{\displaystyle ||{\widehat {\rho _{A}}}||_{\infty }} мало, то A{\displaystyle A} содержит а. п. длины 3[10]	Если ||A^||∞{\displaystyle ||{\widehat {A}}||_{\infty }} и ||B^||∞{\displaystyle ||{\widehat {B}}||_{\infty }} малы, то |A+B|{\displaystyle |A+B|} велико
ЧРУ	Теорема Рота	Если A{\displaystyle A} — а. п., то E(A,A)≥Ω(|A|3){\displaystyle E(A,A)\geq \Omega (|A|^{3})}	|A|2|B|2≥|A+B|E(A,B){\displaystyle |A|^{2}|B|^{2}\geq |A+B|E(A,B)}[11]	Из соотношений аддитивных энергий можно сделать выводы о структуре множества[12]	Если A,B∈ZN{\displaystyle A,B\in {\mathbb {Z} }_{N}}, то E(A,B)=∑r=0N−1|A^(r)|2|B^(r)|2{\displaystyle E(A,B)=\sum \limits _{r=0}^{N-1}{|{\widehat {A}}(r)|^{2}|{\widehat {B}}(r)|^{2}}}

Некоторые используемые понятия[править | править код]

Норма Гауэрса^[en] — обобщение понятия коэффициентов Фурье, придуманное Уильямом Гауэрсом в ходе доказательства теоремы Семереди.

Изоморфизм Фреймана — это отображение из подмножества одной группы в подмножество другой, сохраняющее отношение равенства сумм заданного количества элементов множества.

Конечное множество A={a1≤⋯≤an}{\displaystyle A=\left\lbrace {a_{1}\leq \dots \leq a_{n}}\right\rbrace } вещественных чисел называется строго выпуклым множеством если ai+1−ai<ai+2−ai+1{\displaystyle a_{i+1}-a_{i}<a_{i+2}-a_{i+1}} для i=1,…,n−2{\displaystyle i=1,\dots ,n-2}, то есть если A{\displaystyle A} является образом отрезка {1,…,n}{\displaystyle \left\lbrace {1,\dots ,n}\right\rbrace } для некоторой строго выпуклой функции.^[13] Свойства таких множеств широко изучаются в аддитивной комбинаторике.^{[14][15][16][17]} Это понятие не стоит путать с выпуклым множеством в обычном смысле.

Множество Бора — структура с малым удвоением, используемая иногда в доказательствах как ослабленный аналог понятия подпространства.^[18]. Определяется как множество элементов поля, на которых все аддитивные характеры из заданного семейства имеют малое значение. Множества Бора содержат в себе большие обобщённые арифметические прогрессии, так что наличие во множестве прогрессий иногда доказывается через наличие в нём нужного множества Бора.

Почти периодичная функции^[en] — функция f{\displaystyle f} такая, что норма ||f(x+t)−f(x)||p{\displaystyle ||f(x+t)-f(x)||_{p}} достаточно мала для некоторого p{\displaystyle p} и для всех t∈T{\displaystyle t\in T}, где T{\displaystyle T} — некоторое множество (например, множество Бора). На таких множествах построено одно из доказательств теоремы Рота.^[19]

Множество больших тригонометрических сумм (иногда называется также спектром) множества A⊂Zp{\displaystyle A\subset {\mathbb {Z} }_{p}} — это множество вычетов r{\displaystyle r}, для которых сумма ∑a∈Aep(ar){\displaystyle \sum \limits _{a\in A}{e_{p}(ar)}} (коэффициент Фурье) имеет большой модуль.^[20]

Диссоциативным множеством называется множество, у которого суммы элементов из двух различных подмножеств всегда различны, то есть сумма вида ∑a∈Aεaa,∀a∈A:εa∈{−1,0,1}{\displaystyle \sum \limits _{a\in A}{\varepsilon _{a}a},\forall a\in A:\varepsilon _{a}\in \left\lbrace {-1,0,1}\right\rbrace } никогда не равна нулю.^[20]

Элементарные методы[править | править код]

Конечно, несмотря на существование мощных и сложных методов изучения теорем аддитивной комбинаторики, некоторые приёмы и задачи поддаются элементарному описанию. Из неравенства Коши (∑i=1nai)2≤n∑i=1nai2{\displaystyle \left({\sum \limits _{i=1}^{n}{a_{i}}}\right)^{2}\leq n\sum \limits _{i=1}^{n}{{a_{i}}^{2}}} выводятся свойства аддитивной энергии, применяемые почти повсеместно. Вообще при элементарном подходе часто анализируется число решений тех или иных уравнений. Также часто применяется аргумент среднего^[en] — например, при разложении числа решений уравнения на сумму числа решений при том или ином значении отдельной переменной.^[21]

Элементарными методами можно доказать теорему Рота^[22] и теорему Коши — Давенпорта^[23].

Однако многие доказательства, полученные другими методами, не имеют элементарных аналогов.

Комбинаторные методы[править | править код]

Одним из самых знаковых комбинаторных доказательств аддитивной комбинаторики является первое из появившихся доказательство теоремы Семереди^[24] — в нём Семереди сформулировал и использовал так называемую лемму о регулярности, касающуюся чистой теории графов. Графовые аналогии применяются и при доказательстве особых версий неравенства Плюннеке-Ружа или оценок типа Балога-Семереди-Гауэрса^[25].

Алгебраические методы[править | править код]

Алгебраические методы в аддитивной комбинаторике используют свойства многочленов, которые строятся на основе тех или иных множеств. Степени таких многочленов, как правило, зависят от размеров изучаемых множеств, а множество корней многочленов может дать ту или иную информацию о суммах, пересечениях и т. д. исходных множеств.

Примером инструмента для применения такого метода является комбинаторная теорема о нулях. С помощью неё может доказываться теорема Коши-Давенпорта и некоторые её обобщения.^[23]

Другие применения алгебраического метода можно найти в доказательствах теоремы Рота для некоторых групп специального вида^[26][27][28] или в оценке размера пересечений сдвигов мультипликативных подгрупп полей Fp{\displaystyle {\mathbb {F} }_{p}} и доказательстве проблемы Варинга для простого поля (для этого используется, в частности, метод Степанова).^[29]

Аналитические методы[править | править код]

Основным аналитическим инструментом в аддитивной комбинаторике являются коэффициенты Фурье. Это обусловлено тесной связью операции взятия коэффициента Фурье с операцией свёртки функций. Коэффициенты Фурье были применены ещё при первом доказательстве теоремы Рота.^[30] Их обобщением являются нормы Гауэрса, науку о которых также называют анализом Фурье высших порядков.^[20]

На примере коэффициентов Фурье (в частности, их применения к доказательству теоремы Рота) лучше всего иллюстрируется так называемый итеративный аргумент, когда рассмотрение произвольного множества разбивается на два случая — когда у множества нет больших (относительно размера множества) коэффициентов Фурье и когда есть. В первом случае можно напрямую воспользоваться свойствами коэффициентов Фурье, а во втором — найти подструктуру множества с большей плотностью в бесконечной арифметической прогрессии, причём с настолько большей, что количество таких возможных шагов до достижения предельной плотности будет ограничено величиной, зависящей от общей плотности начального множества. Это обнаруживает идею разделения на случай псевдослучайного множества и множества с некой глобальной структурой. Такая идея нашла отражение и в других методах.^[1][10]

Другой аналитический подход заключается в исследовании почти периодичности функций, связанных с характеристическими функциями исследуемых множеств.^[31]

Эргодические методы[править | править код]

Эргодический подход предполагает применение к задачам аддитивной комбинаторики результатов из теории динамических систем. Впервые этот подход был применён Хиллелем Фюрстенбергом к теореме Семереди^[32], но вскоре оказалось, что он допускает обобщение на намного более широкий круг задач.

Теория динамических систем часто позволяет доказать результаты, недоступные для переформулировки другими методами, но при этом не способна дать никаких количественных оценок (например, оценок на плотность множества в теореме Семереди).^[33]

Сочетание — Википедия

Материал из Википедии — свободной энциклопедии

В комбинаторике сочетанием из n{\displaystyle n} по k{\displaystyle k} называется набор k{\displaystyle k} элементов, выбранных из данного множества, содержащего n{\displaystyle n} различных элементов.

Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-элементные сочетания, подмножества, k=3{\displaystyle k=3}) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6{\displaystyle n=6}) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать k{\displaystyle k} элементов из множества, содержащего n{\displaystyle n} различных элементов, стоит на пересечении k{\displaystyle k}-й диагонали и n{\displaystyle n}-й строки треугольника Паскаля.^[1]

3х элементные подмножества 5 элементного множества

Число сочетаний из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

(nk)=Cnk=n!k!(n−k)!.{\displaystyle {n \choose k}=C_{n}^{k}={\frac {n!}{k!\left(n-k\right)!}}.}

При фиксированном n{\displaystyle n} производящей функцией последовательности чисел сочетаний (n0){\displaystyle {\tbinom {n}{0}}}, (n1){\displaystyle {\tbinom {n}{1}}}, (n2){\displaystyle {\tbinom {n}{2}}}, … является:

∑k=0n(nk)xk=(1+x)n.{\displaystyle \sum _{k=0}^{n}{\binom {n}{k}}x^{k}=(1+x)^{n}.}

Двумерной производящей функцией чисел сочетаний является

∑n=0∞∑k=0n(nk)xkyn=∑n=0∞(1+x)nyn=11−y−xy.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}{\binom {n}{k}}x^{k}y^{n}=\sum _{n=0}^{\infty }(1+x)^{n}y^{n}={\frac {1}{1-y-xy}}.}

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз. В частности, количество монотонных неубывающих функций из множества {1,2,…,k}{\displaystyle \{1,2,\dots ,k\}} в множество {1,2,…,n}{\displaystyle \{1,2,\dots ,n\}} равно числу сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k}.

Число сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} равно биномиальному коэффициенту

C(n)k=((nk))=(n+k−1n−1)=(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!⋅(n−1)!.{\displaystyle C_{(n)}^{k}=\left(\!\!{\binom {n}{k}}\!\!\right)={\binom {n+k-1}{n-1}}={\binom {n+k-1}{k}}=(-1)^{k}{\binom {-n}{k}}={\frac {(n+k-1)!}{k!\cdot (n-1)!}}.}

Доказательство

Пусть имеется n{\displaystyle n} типов объектов, причём объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше k{\displaystyle k}) количество объектов каждого типа. Из этого ассортимента выберем k{\displaystyle k} объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через xj{\displaystyle x_{j}} количество выбранных объектов j{\displaystyle j}-го типа, xj≥0{\displaystyle x_{j}\geq 0}, j=1,2,…,n{\displaystyle j=1,2,\dots ,n}. Тогда x1+x2+⋯+xn=k{\displaystyle x_{1}+x_{2}+\dots +x_{n}=k}. Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд k{\displaystyle k} шаров и n−1{\displaystyle n-1} перегородок так, чтобы между (j−1){\displaystyle (j-1)}-й и j{\displaystyle j}-й перегородками находилось ровно xj{\displaystyle x_{j}} шаров. Но таких расстановок в точности (n+k−1k){\displaystyle {\tbinom {n+k-1}{k}}}, что и требовалось доказать.■

При фиксированном n{\displaystyle n} производящей функцией чисел сочетаний с повторениями из n{\displaystyle n} по k{\displaystyle k} является:

∑k=0∞(−1)k(−nk)xk=(1−x)−n.{\displaystyle \sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}=(1-x)^{-n}.}

Двумерной производящей функцией чисел сочетаний с повторениями является:

∑n=0∞∑k=0∞(−1)k(−nk)xkyn=∑n=0∞(1−x)−nyn=1−x1−x−y.{\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{\infty }(-1)^{k}{-n \choose k}x^{k}y^{n}=\sum _{n=0}^{\infty }(1-x)^{-n}y^{n}={\frac {1-x}{1-x-y}}.}

• Р. Стенли. Перечислительная комбинаторика. — М.: Мир, 1990.

Реферат по математике на тему «Комбинаторика»

Реферат

По дисциплине: Математика

„ Комбинаторика “

Комбинаторика

Комбинаторика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

• Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.

• Перестановкой из n элементов (например, чисел 1,2,…,n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.

• Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

• Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.

• Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примеры комбинаторных задач:

1. Сколькими способами можно разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?

2. Сколько существует функций из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?

3. Сколько существует различных перестановок из 52 игральных карт?

Ответ: 52! (52 факториал), то есть, 80658175170943878571660636856403766975289505440883277824000000000000 или примерно 8,0658 × 10⁶⁷.

4. При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?

Решение: Каждый возможный исход соответствует функции 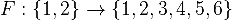(аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчёт количества перестановок. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определённым свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства у заданного множества.

Топологическая комбинаторика

Топологическая комбинаторика (англ.) применяет идеи и методы комбинаторики в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

Инфинитарная комбинаторика

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам.

Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).^[1]

Исторический очерк

Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

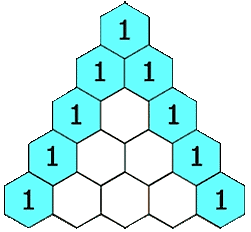
Треугольник Паскаля

Блёз Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Комбинаторика в языкознании

Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.

Литература

• Андерсон Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — С. 960. — ISBN 0-13-086998-8.

• Виленкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975.

• Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.

• Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.

• Раизер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.

• Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.

• Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.

• Риордан Дж. Введение в комбинаторный анализ — пер. с англ. — М., 1963.

• Р. Стенли. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — С. 440. — ISBN 5-03-001348-2.

• Р. Стенли. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — С. 767. — ISBN 978-5-03-003476-8.