Решение пропорций | Математика
Рассмотрим решение пропорций на конкретных примерах.
Решить уравнения с пропорцией:
1) 25 : x = 10 : 18
Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:
25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.
Ответ: 45.
Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:
Ответ: 13,5.
При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.
Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:
В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Сокращаем 24 и 6 на 6, 10 и 45 — на 5:
Еще раз сокращаем 4 и 2 на 2:
Ответ: 18.
Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.
Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:
Смешанные числа переводим в неправильные дроби:
Ответ: 28.
При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.
Произведение крайних членов пропорции равно произведению средних членов:
Здесь удобно упростить уравнение, разделив обе части на 5:
Ответ: 10,5.
Произведение крайних членов пропорции равно произведению ее средних членов:
Для упрощения вычислений удобно умножить каждую часть уравнения на 10:
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 1,12.
www.for6cl.uznateshe.ru
Пропорции
Вопросы занятия:
· вспомнить, что называют отношением двух чисел, или величин;
· ввести понятие «пропорция»;
· вспомнить прямо пропорциональную и обратно пропорциональную зависимости.
Материал урока
Прежде чем мы приступим к повторению темы «Пропорции», следует вспомнить, что называют отношением.
Определение.
Отношение двух чисел a и b — это их частное или дробь с числителем а и знаменателем b.

Эти записи читают так: «Отношение числа а к числу b», или «отношение чисел а и b», или же просто «отношение а к b».
Сами числа, а и b, называют членами отношения.
Напомню, что значение отношения двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого
.Например,

Это значит, что 12 в 3 раза больше четырёх.

Это означает, что 4 составляет одну треть от числа 12.
Посмотрим, как знания об отношениях можно применять при решении задач.
Пример.

Пример.

Сделаем важное замечание:
Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.
Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.
Вот, к примеру, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи. Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.
А теперь давайте разберемся, почему отношение разноименных величин – это новая величина.

Теперь следует вспомнить основное свойство отношения:

Теперь, освежив в памяти знания об отношении чисел и величин, перейдём к повторению пропорции.
Определение.
Пропорцией называется верное равенство двух отношений.
В буквенном виде пропорцию записывают так:

Первая буквенная запись пропорции – общий вид пропорции, где: a, b, c и d – называют членами пропорции. Договариваются, что все члены пропорции отличны от нуля.
a и d – это крайние члены пропорции, b и c – средние члены пропорции.
Что очень хорошо видно из равенства на экране.

Эти названия сохраняются и тогда, когда пропорция записана в виде дробей.
Пример.

Сейчас вспомним очень важное свойство: основное свойство пропорции.
В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции.

Это утверждение и есть основное свойство пропорции. С его помощью очень легко определять, является ли равенство отношений пропорцией.
Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов, то пропорция верна.

Это утверждение называется признаком пропорции.
Кстати, если в верной пропорции поменять местами средние члены и крайние члены, то получившиеся новые пропорции также верны.

Пример.

Самым важным является то, что с помощью основного свойства пропорции не составит никакого труда по трём известным членам пропорции найти её неизвестный член.
Сформулируем правило для нахождения неизвестного крайнего члена пропорции:
Чтобы найти неизвестный крайний член пропорции, нужно произведение ее средних членов разделить на известный крайний член пропорции.

Совершенно аналогично формируется правило для нахождения неизвестного среднего члена пропорции:
Чтобы найти неизвестный средний член пропорции, нужно произведение ее крайних членов разделить на известный средний член.

Пример.

Вы помните, что между двумя величинами имеется зависимость, если для вычисления одной из них нужно знать вторую.
Например,

Определение.

Определение.

Определение.


Определение.

Определение.

Определение.


Задача.

Задача.

Итоги урока
На этом уроке мы рассмотрели такую тему, как «Пропорции». Вспомнили, что называют отношением двух чисел, или величин. Поговорили о пропорциях. А затем вспомнили прямо пропорциональную и обратно пропорциональную зависимости.

videouroki.net
Отношения и пропорции в математике
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.
Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия «деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.п. При этом многие отношения величин однородных принято выражать в процентах.
ПримерВ супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?
400 – общее число товара
200 – РФ
Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.
200 : 400 = 0,5 или 50%
В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.
Два равных отношения образуют пропорцию
В современной математике принято считать, что пропорцией является два равным между собой отношения. К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:
1.Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов
200 : 400 = 0,5 или 50%
2.Триста разделить на шестьсот равняется ноль целых пять десятых, то есть пятьдесят процентов
300 : 600 = 0,5 или 50%
В данном случае имеется пропорция, которую можно записать следующим образом:
Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.
Произведение средних членов пропорции
Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:
Двести умноженное на шестьсот равняется сто двадцать тысяч;
200 × 600 = 120 000
Триста умноженное на четыреста равняется сто двадцать тысяч.
300 × 400 = 120 000
Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.
Если вернуться к приведенному выше примеру пропорции, то:
Двести равняется четыреста умноженное на триста и деленное на шестьсот.
Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.
simple-math.ru
Пропорция. Основное свойство пропорции — 6 класс
Головач Александр Григорьевич
ГУО «Средняя школа №18 г. Бреста»
Тема: Пропорция. Основное свойство пропорции. (6 класс)
Тип урока: изучения и первичного закрепления новых знаний
Образовательная: познакомить учащихся с понятиями: пропорция и члены пропорции; научить чтению пропорции и составлению пропорций из отношений; познакомить учащихся с основным свойством пропорции и сформировать навык по определению верной пропорции.
Развивающая: активизировать познавательную деятельность учащихся; развивать память, логическое мышление;
Воспитательная: воспитывать уважение к труду, работе в коллективе.
Литература: Математика: учеб. пособие для 6 кл. общеобразоват. учреждений с рус. яз. обучения / Е. П. Кузнецова [и др.]; под ред. Л. Б. Шнепермана. – Минск: Нац. ин-т образования, 2010. — 320 с.: ил.
Оборудование: учебник, доска, мел, презентация, компьютер, проектор.
Ход урока:
Организационный момент (2 мин)
Проверка домашнего задания (3 мин)
Актуализация знаний (8 мин)
Изучение нового материала (12 мин)
Физкультминутка (2 мин)
Первичное закрепление (13 мин)
Задание на дом (1 мин)
Рефлексия. Подведение итого. (4 мин)
1. Организационный момент
Организую внимание учащихся. Предлагаю сесть. Отмечаю отсутствующих на уроке учеников.
Здороваются. Садятся.
2. Проверка домашнего задания
— Сегодня у нас на уроке новая тема «Пропорция. Основное свойство пропорции».
И цели нашего урока: познакомиться с определение «Пропорция»; из каких элементов состоит пропорция; изучить основное свойство пропорций.
Но перед тем, как приступить к изучению новой темы, давайте проверим домашнее задание.
3. Актуализация знаний
/*фронтальный опрос*/
— На прошлом уроке у нас была тема «Отношение чисел и величин».
1. Давайте вспомним, что же называется отношением?
2. А как называются сами эти числа или величины?
3. Скажите, что будет с отношением, если его члены умножить или разделить на одно и тоже число, отличное от нуля?
А теперь давайте вспомним, как читаются отношения и найдем их значение.
1. 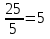
2. 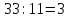
3. 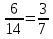
4. 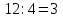
5. 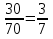
6. 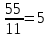
1. Частное двух чисел (или двух величин) называется отношением.
2. Эти числа или величины называются членами отношения.
3. Отношение не изменится, если его члены умножить или разделить на одно и тоже число, не равное нулю.
1. Отношение числа 25 к 5 равно 5.
2. Отношение числа 33 к 11 равно 3.
3. Отношение числа 6 к 14 равно 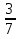 .
.
4. Отношение числа 12 к 4 равно 3.
5. Отношение числа 30 к 70 равно 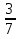
6. Отношение числа 55 к 11 равно 5.
4. Изучение нового материала
— Ребята скажите, под какими номерами у наших отношений получились одинаковые значения.
У нас получились записи равных отношений:
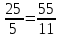
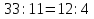
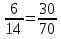
— Так вот равенство двух отношений называют пропорцией.
Пропорцию записывают:
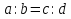
или
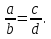
Прочитать такую пропорцию можно по-разному:
— отношение a к b равно отношению c к d;
— a относится в b, как c относится к d;
— a, деленное на b, равно c, деленное на d.
Т.к. в записи 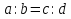 числа a и d стоят с краю, то их принято называть крайними членами пропорции. Ну а т.к. числа b и c находятся в середине, то и называются они соответствующе – средними членами пропорции.
числа a и d стоят с краю, то их принято называть крайними членами пропорции. Ну а т.к. числа b и c находятся в середине, то и называются они соответствующе – средними членами пропорции.
Эти названия сохраняются и тогда, когда пропорция записана в виде 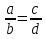 .
.
Давайте вернемся к получившимся у нас пропорциям и назовем их крайние и средние члены.
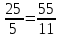
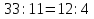
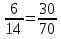
А теперь немного посчитаем. Перемножьте в наших пропорциях крайние и средние члены
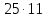
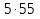
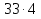
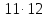
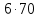
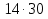
Какой вывод можно сделать?
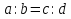 , то
, то 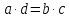
Верно. Это утверждение называется основным свойством пропорции.
Отношение 1 равно отношению 6.
Отношение 2 равно отношению 4.
Отношение 3 равно отношению 5.
Крайние 25 и 11, средние 5 и 55.
Крайние 33 и 4, средние 11 и 12.
Крайние 6 и 70, средние 14 и 30.
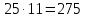
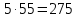
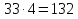
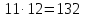
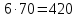
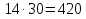
Произведение крайних членов пропорции равно произведению ее средних членов.
5. Физкультминутка
— Ну а теперь немного отдохнем. Проведем физкультминутку для глаз. Т.к. уже зима, то на экране будут появляться снежинки, а ваша задача внимательно следить за их движениями.
6. Первичное закрепление
— А теперь с новыми силами начнем выполнение заданий.
№ 5.27 (устно)
5.29 (1;3)
5.30 (1;3)
5.31 (1;3) (доп. 5.32)
№ 5.27
1) 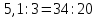 ;
;
2) 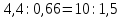 ;
;
3) 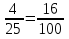 ;
;
4) 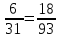 .
.
№5.29 (1;3)
Составьте пропорцию, если m и n – ее крайние члены, а x и y – средние:
1) 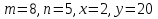 ;
;
3) 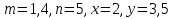 ;
;
№ 5,30 (1;3)
Определите, является ли пропорцией равенство.
1) 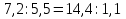
3) 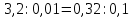
№ 5,31 (1;3)
1) 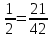
3) 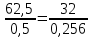
№ 5.27
1) 5,1 относится к 3, как 34 относится к 20. Крайние члены: 5,1 и 20. Средние члены: 3 и 34.
2) 4,4 относится к 0,66, как 10 относится к 1,5. Крайние члены: 4,4 и 1,5. Средние члены: 0,66 и 10.
3) 4 относится к 25, как 16 относится к 100. Крайние члены: 4 и 100. Средние члены: 25 и 16.
1) 6 относится к 31, как 18 относится к 93. Крайние члены: 6 и 93. Средние члены: 31 и 18.
№5.29
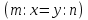
1) 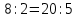 или
или 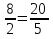
3) 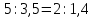 или
или 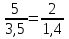
№ 5,30 (1;3)
1) нет
3) нет
№ 5,31 (1;3)
1) да
3) да
7. Задание на дом
— Откройте дневники и запишите задание на дом: п.5.2 №5.29-5.31 (2;4)
8. Рефлексия. Подведение итого
Подведение итогов.
1. С каким новым определение Вы сегодня познакомились?
2. Что такое «Пропорция»?
3. Какие члены пропорции бывают?
4. Как звучит основное свойство пропорции?
Выставляю отметки за урок.
Рефлексия.
Предлагаю учащимся продолжить фразу:
“Сегодня на уроке я узнал…”,
“Было интересно…”,
“Было трудно…”,
“Меня удивило…”,
“Я хотел бы узнать…”,
“Сегодня на уроке я научился…”.
Ответы:
1. С определением «Пропорция».
2. Пропорция – это равенство двух отношений.
3. У пропорции бывают крайние и средние члены.
4. Произведение крайних членов пропорции равно произведению ее средних членов.
infourok.ru