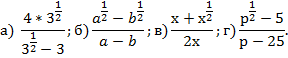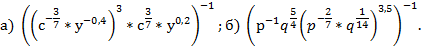Задачи со степенями и радикалами. Видеоурок. Алгебра 11 Класс
На данном уроке мы рассмотрим более сложные задачи со степенями и радикалами, решение которых базируется на определении и свойствах степени с рациональным показателем.
Напомним основное определение.
Степенью неотрицательного числа а с рациональным положительным показателем 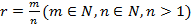 называется число
называется число 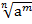 .
.
Степенью положительного числа а с рациональным отрицательным показателем 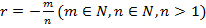 называется число
называется число 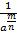 .
.
Для 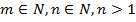 выполняется равенство:
выполняется равенство:
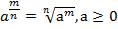
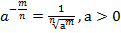 .
.
Например: 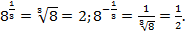
Напомним свойства степеней с рациональными показателями.
Здесь 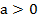 ,
,  , s и r – рациональные числа.
, s и r – рациональные числа.
1. 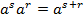 ;
;
2. 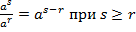
3. 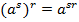 ;
;
4. 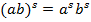 ;
;
5. 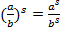 .
.
Пример 1 – вычислить:
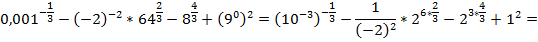
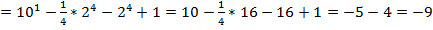 .
.
Пример 2 – сократить дробь:
 .
.
Чтобы сократить заданную дробь, нужно разложить знаменатель на множители:
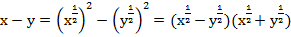 .
.
В результате преобразований получили дробь:
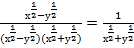 .
.
Данный ответ справедлив при условии, что 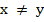 , иначе дробь не имеет смысла.
, иначе дробь не имеет смысла.
Сделаем некоторые замечания:
- При
 замена
замена  допустима,
допустима,  (по определению степени с положительным рациональным показателем).
(по определению степени с положительным рациональным показателем).
Пример 3 – сократить дробь:
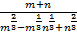 .
.
ОДЗ:
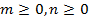 .
.
В данном случае для разложения нужно применить другую формулу сокращенного умножения и разложить числитель:
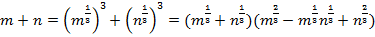 .
.
В результате преобразования получили дробь:
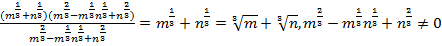 .
.
Ответ справедлив в том случае, если m и n одновременно не равны нулю, данный факт часто записывают следующим образом:
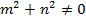 .
.
Пример 4 – упростить выражение:
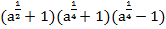 .
.
Несложно заметить, что произведение второй и третьей скобок можно свернуть по формуле разности квадратов:

В результате преобразования получили произведение двух скобок, которое также можно свернуть по формуле разности квадратов:
 .
.
Отметим, что в данном случае значения а ограничены: 
Пример 5 – решить уравнение:
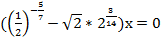 .
.
Скобка – это конкретное число, не зависящее от х, имеем право на нее сократить и получить 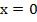 , но только в том случае, если выражение в скобках не равно нулю. Проверим:
, но только в том случае, если выражение в скобках не равно нулю. Проверим:
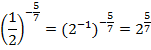
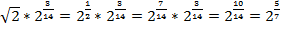 .
.
В результате преобразований получили скобку:
 .
.
Пример 6 – решить уравнение:
а) 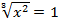 .
.
Возводим уравнение в куб:
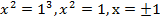 .
.
б) 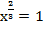

Ответ: 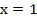 .
.
в) 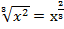

Ответ: 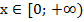 .
.
Пример 7 – решить уравнение:
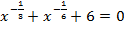 .
.
При решении данного уравнения следует не забыть про область определения и ввести замену переменных:
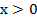 ,
, 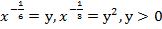 .
.
После введения замены получили уравнение:
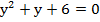
Решаем полученное квадратное уравнение любым удобным способом, например по теореме Виета:
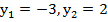 .
.
Первый корень не входит в ОДЗ, остается корень  , отсюда находим ответ:
, отсюда находим ответ:
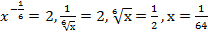 .
.
Пример 8 – решить уравнение:
а) 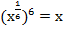

Ответ: 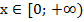 .
.
б) 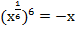

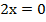
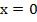 .
.
Ответ: 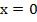 .
.
в) 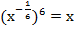


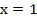 .
.
Ответ: 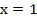 .
.
Итак, мы рассмотрели различные типовые задачи со степенями и радикалами, на следующем уроке мы перейдем к изучению степенных функций.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Домашнее задание
- Алгебра и начала анализа, 10–11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 438, 439, 444.
- Сократить дробь:

- Упростить выражение:

Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Математика (Источник).
- Интернет-портал Nado5.ru (Источник).
- Интернет-портал Terver.ru (Источник).
interneturok.ru
Умножение и деление степеней с одинаковыми показателями (продолжение)
На этом уроке мы продолжим изучение умножения и деления степеней с одинаковыми показателями. В начале урока сделаем краткую сводку уже известных нам формул действий со степенями. Далее будем решать примеры на все действия со степенями.
Тема: Степень с натуральным показателем и ее свойства
Урок: Умножение и деление степеней с одинаковыми показателями (продолжение)
Напоминание:
Основные определения:
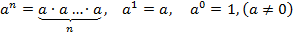
Здесь a — основание степени,
n — показатель степени,
 — n-ая степень числа.
— n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:
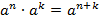
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
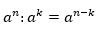
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:
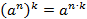
Теорема 4.
Для любых чисел а и b и любого натурального n справедливо равенство:
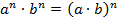
Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.
Теорема 5.
Для любого числа а и b (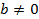 ) и любого натурального n справедливо равенство:
) и любого натурального n справедливо равенство:

Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.
Пример 1: Возвести дробь в степень.
Для решения следующих примеров воспользуемся теоремой 5.
а) 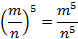
б)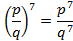
Для решения следующего примера вспомним формулы:
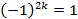

в) 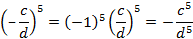
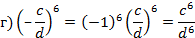
д) 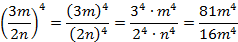
Замечание: 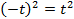 ,
, 
е) 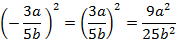
ж) 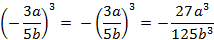
Пример 2: Вычислите.
а) 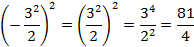
б) 
Пример 3: Представить выражение в виде степени с показателем больше 1.
а) 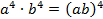
б) 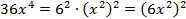
б) 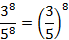
б) 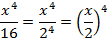 или по-другому:
или по-другому: 
Пример 4: Вычислить наиболее рациональным способом.
а) 
б) 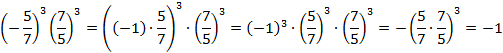
в) 
г) 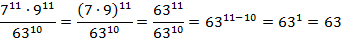
д) 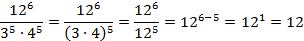
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Школьный помощник (Источник).
2. Школьный помощник (Источник).
Рекомендованное домашнее задание
1. 583, 584, 585 стр. 152. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Вычислить наиболее рациональным способом.
а) 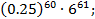 б)
б)  в)
в) 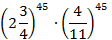
3. Представить выражение в виде степени с показателем больше 1.
а)  б)
б)  в)
в) 
interneturok.ru
Свойства степени с натуральным показателем. Примеры с решениями
Возведение произведения в степень
Выражение (ab)n является степенью произведения множителей a и b. Это выражение можно представить в виде произведения степеней anbn. Докажем это на примере.
По определению степени:

Раскрываем скобки, а затем, используя переместительный закон умножения, переставляем сомножители так, чтобы одинаковые буквы стояли рядом:

Группируем отдельно множители a и множители b и получаем:

Воспользовавшись определением степени, находим:

Следовательно:
(ab)n = anbn
Свойство степени произведения распространяется на степень произведения двух и более множителей:
(3a2b)2 = 9a4b2
Отсюда следует правило:
Чтобы возвести произведение в степень, можно отдельно возвести в эту степень каждый множитель и полученные результаты перемножить.
Возведение частного в степень
Для возведения в степень частного надо возвести в степень отдельно делимое и делитель.
Если говорить иначе, то степень частного равна частному степеней:

Так как частное в алгебре часто записывается в виде дроби (знак деления заменяется дробной чертой), то правило возведения частного в степень можно переформулировать так, чтобы оно подходило и для дробей:
Чтобы возвести дробь в степень надо возвести в эту степень отдельно её числитель и знаменатель.
Общая формула возведения в степень частного будет выглядеть так:

Возведение степени в степень
Для возведения степени числа в степень, надо перемножить показатели степеней, а основание оставить без изменений.
Например, нам нужно возвести 72 в третью степень:
(72)3
Чтобы нам не возводить 7 сначала во вторую степень, а после этого ещё в третью, вспоминаем, что степень числа это сокращённая форма умножения одинаковых сомножителей, а это значит, что:
(72)3 = 72 · 72 · 72 = 72+2+2 = 72·3 = 76
Следовательно, при возведении степени в степень показатели степеней перемножаются.
Общая формула возведения степени в степень:
(ax)y = axy
Примеры на свойства степеней
Пример 1. Выполните действия:
а) (x5)3; б) 2(n3)5; в) -4(a4)2
Решение:
а) (x5)3 = x5 · 3 = x15
б) 2(n3)5 = 2n3 · 5 = 2n15
в) -4(a4)2 = -4a4 · 2 = -4a8
Пример 2. Возведите в степень:
а) (-2mn)4; б) (3bc)3; в) (-6a4b)2
Решение:
а) (-2mn)4 = (-2)4 · m4 · n4 = 16m4n4
б) (3bc)3 = 33 · b3 · c3 = 27b3c3
в) (-6a4b)2 = (-6)2 · (a4)2 · b2 = 36 · a8 · b2 = 36a8b2
Пример 3. Возведите дробь в степень:
| а) ( | 2a | )2; б) (- | xy | )5; в) ( | a2b | )3 |
| 5 | z | 2c3 |
Решение:
| а) ( | 2a | )2 = | (2a)2 | = | 4a2 |
| 5 | 52 | 25 |
| б) (- | xy | )5 = — | (xy)5 | = — | x5y5 |
| z | z5 | z5 |
| в) ( | a2b | )3 = | (a2b)3 | = | (a2)3 · b3 | = | a6b3 |
| 2c3 | (2c3)3 | 23 · (c3)3 | 8c9 |
naobumium.info
Калькулятор степеней онлайн: формула, примеры с решением
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
am × an = a(m+n).
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
(13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 132. Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:
am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:
(am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 150? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 154 на 154, что запишется как дробь:
154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:
154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:
a0 = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
a-m = 1 / am
При этом для значения -1 правило трансформируется в элегантную формулу:
a-1 = 1 / a.
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:
a(m/n) есть корень n-ной степени из am.
Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e(kt),
где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Заключение
Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.
bbf.ru
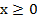 замена
замена 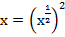 допустима,
допустима, 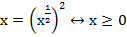 (по определению степени с положительным рациональным показателем).
(по определению степени с положительным рациональным показателем).