Нестандартные методы решения уравнений от эксперта TutorOnline

Пример 1. Решить уравнение

                      .                     (1)

 

       Решение. Нетрудно убедиться, что раскрытие модуля или возведение в квадрат обеих частей данного уравнения не приводит к его решению. Решить уравнение (1) можно только на основе использования нестандартных рассуждений.

    Уравнение (1) перепишем как

                             .                     (2)

    Поскольку  , то из уравнения (2) получаем неравенство  .  Отсюда следует

,   ,  

 или   .

    Так как  , то   или  .  Подстановкой в уравнение (1) убеждаемся, что   является его корнем.

    Ответ: .

Пример 2. Решить уравнение

                                   .                                     (3)

 

   Решение. Уравнение (3) можно решить обычным методом: сначала обе части уравнения умножим на  выражение . Затем после несложного преобразования возведем обе части уравнения в квадрат. Решая биквадратное уравнение, получим единственный корень. Однако  уравнение (3) можно решить нестандартно, используя для этого тригонометрическую подстановку.

    Поскольку переменная в уравнении (3) может принимать произвольные значения, то произведем замену  ,  где   .   

    В  таком  случае       (так как  , то  )  и уравнение (3) принимает вид тригонометрического уравнения    .

    Отсюда получаем   ,    или  . Корнями квадратного уравнения являются     и  .

    Однако  , поэтому .  Если  , то     и   .   Следовательно, имеем корень   .

Ответ:  . 

Пример 3. Решить систему уравнений

                                                          (4)

 

    Решение.  Знакомство с системой уравнений (4) не может вызвать у школьника особого энтузиазма, поскольку совсем непонятно, как решать эту систему. Ниже предлагается метод решения заданной системы, основанный на использовании известного числового неравенства Коши.

    Из второго уравнения системы (4) следует, что   и . Воспользуемся неравенством Коши  , в котором   и  .

    Имеет место

  или   .

    Аналогично получаем   

  или   .

    В таком случае имеет место неравенство

                                                .                                         

    Если полученное неравенство сравнить со вторым уравнением системы (4), то можно сделать вывод о том, что примененные выше (дважды) неравенства Коши превратились в равенства, а это возможно только тогда, когда   и  , т.е.    и  .

    Подставляя полученные значения   и в первое уравнение системы (4) убеждаемся,  что    и   являются корнями системы.

    Ответ:  , . 

Пример 4. Решить уравнение

 

                                   .                                 (5)

 

    Решение. Заданное уравнение решить обычными методами весьма затруднительно, поскольку в его левой части находятся корни четвертой и восьмой степеней. Кроме того, совсем непонятно, какую следует делать замену. В этой связи предлагается нестандартный метод, основанный на использовании свойства монотонности аналитических функций.

    Первоначально устанавливаем, что областью допустимых значений уравнения (5) являются   .    

    Перепишем уравнение (5) в виде   

                                         .                                        (6)

    Рассмотрим функции   и . Так как функция является монотонно убывающей на отрезке  , а функция    – монотонно возрастающей, то уравнение (6) имеет не более одного корня. Непосредственным подбором несложно определить, что    является искомым корнем.

    Ответ: .

Пример 5. Решить систему уравнений

                                                                                    (7)

 

    Решение.  Система уравнений (7) относится к числу трудно решаемых и поэтому ее корни можно найти только в том случае, если использовать нестандартный подход, основанный на сведении системы (7) к функциональному уравнению.

    Перепишем систему (7) следующим образом

                                                                                             (8)

    Очевидно, что здесь  , и .  Введем в рассмотрение аналитическую функцию . В таком случае уравнения системы (8) принимают вид   и поэтому систему уравнений можно  задать посредством функционального уравнения

                                             .                                           (9)

    Известно, если функция   отрезке    строго возрастает, то уравнение (9) на этом отрезке равносильно уравнению  .

    Так как  функция является возрастающей на своей области определения, то  уравнение (9) эквивалентно уравнению .

    Далее, после возведения в квадрат обеих частей уравнения получаем квадратное уравнение  , корнями которого  являются   .  Поскольку ,  то  уравнение (9) имеет корень  .  

    Так как уравнение (9) имеет единственный корень , а переменные   входят в уравнения системы (7) симметрично, то    и   .

    Ответ:    .

Пример 6. Решить уравнение 

                         .                         (10)

 

  Решение.  Решение уравнения (10) стандартным методом заключается в следующем: первоначально один из радикалов переносится в правую часть уравнения, а затем обе части его части дважды возводятся в квадрат. Однако ниже предлагается несколько необычный метод решения уравнения (10), основанный на применении основных свойств векторного исчисления.

    Перепишем уравнение (10) в виде

                                   .                           (11)

    Предположим, что вектор   имеет координаты , а вектор    –  координаты  . В таком случае

 и  .

Пусть  ,  тогда координаты вектора   будут вычисляться по формулам:  и  . Следовательно, здесь  ,     и   .

Так как , то выполняется неравенство треугольника . Если в данное неравенство подставить выражения и  , то получим неравенство   .

    Отсюда и из уравнения (11) следует,  что  . Это равенство означает, что векторы    и   коллинеарные.  

Используя основное свойство коллинеарных векторов, получаем уравнение  ,  т.е.  .

    Ответ:  .

Пример 7. Решить уравнение

                             .                              (12)

        

    Решение. Найти подбором хотя бы один корень уравнения четвертой степени (12) весьма затруднительно. Метод группировки также не дает положительных результатов. Однако существует нестандартный метод решения уравнения (12), основанный на введении параметра и последующего решения квадратного уравнения относительно введенного параметра.

    Перепишем уравнение (12) в виде уравнения с параметром , которое совпадает с (12) при , т.е. получаем квадратное уравнение относительно параметра   вида

                                    .                                 (13)

    Квадратное уравнение (13)  имеет два корня

                                                                                                                    ,

т.е.    и  . Так как  , то получаем два уравнения относительно переменной   вида

  и  .

    Ответ:      и  .  

Пример 8. Решить уравнение

 

                       .                            (14)

        

    Решение. Уравнение (14) можно решить обычным образом: перенести один из радикалов вправо, а затем дважды возвести в квадрат. Ниже предлагается нестандартный метод решения уравнения (14), основанный на использовании одного очень известного равенства.

    Преобразуем исходное уравнение (14), используя известное равенство  , где  , тогда получим  

                                   .

    Отсюда вытекает уравнение

                                 .                   (15)

    Если уравнение (14) сложить с уравнением (15), то получим

                                        .                                      (16)

    Поскольку левая часть уравнения (16) неотрицательна, то  . Возведем обе части уравнения (16) в квадрат и получим квадратное уравнение , корнями которого являются   и . Непосредственной подстановкой в (14) убеждаемся, что найденные значения   являются корнями исходного уравнения.

    Ответ:  ,  .

Пример 9. Решить уравнение 

                                 .                                   (17)

        

    Решение. Уравнение (17) можно решать стандартным образом

blog.tutoronline.ru

Уравнение

Цели урока:

1) Обучающая: формировать представления об уравнении, корне уравнения, решении уравнений; организовать деятельность, направленную на выполнение учебных заданий, связанных с решением уравнений вида: х + а = b, x — a = b, a — x = b и приводимых к ним; создать условия для расширения знаний математических понятий и формирования новых знаний.

2) Развивающая: содействовать развитию и обогащению словарного запаса.

3) Воспитывающая: содействовать расширению кругозора.

Тип урока: изучение нового материала с первичным закреплением.

План урока:

1. Организационный этап.

2. Актуализация опорных знаний.

3. Этап получения новых знаний.

4. Этап обобщения и закрепления нового материала.

5. Рефлексия.

6. Заключительный этап.

Форма урока: Видеоматериал с элементами практикума.

Ход урока:

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы узнать, ваше настроение и как вы настроены к работе на уроке.

2. Актуализация опорных знаний:

На предыдущих уроках мы с вами решали задачи способом моделирования условия задачи отрезками, и в ходе решения составляли выражения для нахождения неизвестного числа.

3. Этап получения знаний:

Скачать видеоурок «Уравнение»

Тема нашего урока «Уравнение». На этом уроке мы узнаем такие понятия как уравнение, корень уравнения. А также научимся составлять и решать уравнения.

В математике принято и очень удобно обозначать неизвестное число буквой, затем составлять равенство и решать это равенство. Рассмотрим задачу: Лере задали прочитать рассказ. Она прочитала этот рассказ за два дня. В первый день Лера прочитала 40 страниц. Сколько страниц прочитала Лера за второй день, если известно, что весь рассказ состоял из 65 страниц?

Решение: Для наглядности внесем известные нам данные в таблицу. Мы знаем, что за первый день Лера прочитала 40 страниц, и знаем, что всего 65 страниц в рассказе. Обозначим буквой х неизвестное количество страниц, которые Лера прочитала за второй день. Составим равенство по известным нам данным. Мы к страницам, прочитанным за первый день (40), прибавим количество прочитанных страниц за второй день (х), и это будет равно количеству всех страниц в рассказе (65). Получили равенство: 40 + х = 65. Нам надо найти такое значение х, при котором будет выполняться это равенство. По смыслу вычитания, чтобы найти неизвестное слагаемое мы должны от известной суммы отнять известное слагаемое. Т. е. получаем х = 65 — 40. Вычислим правую часть получившегося равенства, получим х = 25. Значит, Лера прочитала 25 страниц рассказа за второй день. Ответом задачи будет: Лера прочитала 25 страниц за второй день.

Равенство 40 + х = 65 называют уравнением.

Уравнение — это равенство, содержащее букву, значение которой надо найти.

Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.

Например, корнем уравнения 40 + х = 65 является число 25.

Если в равенство входит буква, то оно может быть верным при одних значениях этой буквы и неверным при других ее значениях. Например, уравнение 40 + х = 65 при х = 25 — верно, подставим вместо х значение 25, видим, что равенство выполняется верно. А при х = 15 — это равенство будет уже неверным, т.к. при замене х на число 15 равенство 40 + 15 никак не может быть равно 65.

Иногда надо узнать, является ли данное число корнем уравнения или нет. Тогда его не надо решать, нужно просто подставить предлагающиеся числа вместо неизвестного числа. Если получится верное равенство, то это данное число и есть корень уравнения, если равенство неверно — число не является корнем. Например, выполним задание: какое из чисел 3, 5 или 7, является корнем уравнения х + 7 = 12? Подставим по очереди каждое данное нам число. При х = 3 получаем равенство 3+7 равно оно 10, что в свою очередь не равно 12. При х = 5, получаем 5+7=12. При х = 7, получаем 7+7=14 и ≠12. При подстановке чисел мы убедились, что только число 5 дает в сумме с числом 7 верное равенство.

Решить уравнение — значит найти все его корни, или убедиться, что уравнение не имеет корней.

Запишите полезные правила для решения некоторых уравнений:

1. Нахождение неизвестного слагаемого:

a + x = b, где a и b — любые натуральные числа. Если нам неизвестно второе слагаемое, то мы должны из суммы вычесть первое слагаемое, т. е. x = b — a.

x + a = b. Если нам неизвестно первое слагаемое, то мы должны от суммы отнять второе слагаемое, т. е. x = b — a.

2. Нахождение неизвестного уменьшаемого:

x — a = b. Если нам неизвестно уменьшаемое, то мы должны к разности прибавить вычитаемое, т. е. x = b + a.

3. Нахождение неизвестного вычитаемого:

a — x = b. Если нам неизвестно вычитаемое, то мы должны от уменьшаемого отнять разность, т. е. x = а — b.

4. Этап обобщения и закрепления нового материала.

Итак, сделаем основные выводы: на этом уроке мы узнали, что такое уравнение, корень уравнения. Научились составлять уравнения и решать их.

Для закрепления материала ответьте на вопросы:

— Какое равенство называют уравнением?

— Какое число называют корнем уравнения?

— Что означает требование Решить уравнение?

— Как проверить, является ли определенное число корнем данного уравнения?

— Как найти неизвестное слагаемое (уменьшаемое, вычитаемое)?

5. Рефлексия.

Были ли трудности при работе на уроке? Если да, то какие?

videouroki.net

УРАВНЕНИЯ — это… Что такое УРАВНЕНИЯ?

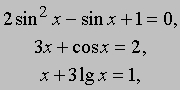
где lg — логарифм по основанию 10.
Дифференциальные уравнения. Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы.
Интегральные уравнения. Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения. Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x — 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения. Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом. 1. Если равные величины увеличить на одно и то же число, то результаты будут равны. 2. Если из равных величин вычесть одно и то же число, то результаты будут равны. 3. Если равные величины умножить на одно и то же число, то результаты будут равны. 4. Если равные величины разделить на одно и то же число, то результаты будут равны. Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения. Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения. Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители. Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 — x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю: Таким образом, корни равны x = -1,
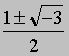
, т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений. Два линейных уравнения с двумя неизвестными можно записать в виде
Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей
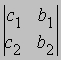
и
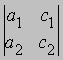
отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации — система

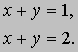
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений. Общая теория рассматривает m линейных уравнений с n переменными:
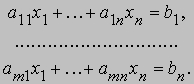
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
где Aji — алгебраическое дополнение элемента aij в матрице (aij). В более общем плане существуют следующие теоремы. Пусть r — ранг матрицы (aij), s — ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца из чисел bi. Тогда: (1) если r = s, то существует n — r линейно независимых решений; (2) если r См. также АЛГЕБРА.

Энциклопедия Кольера. — Открытое общество. 2000.

• ЧИСЛО e
• КОНЕЧНЫЕ РАЗНОСТИ

Смотреть что такое «УРАВНЕНИЯ» в других словарях:

• Уравнения — Уравнение равенство вида или , где f и g функции (в общем случае векторные) одного или нескольких аргументов, а также задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут… …   Википедия

• уравнения — решать дифференциальные уравнения • решение …   Глагольной сочетаемости непредметных имён

• Уравнения Эйлера — Лагранжа — Уравнения Эйлера  Лагранжа (в физике также уравнения Лагранжа Эйлера или уравнения Лагранжа) являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти… …   Википедия

• Уравнения Навье — Стокса — Механика сплошных сред Сплошная среда Классическая меха …   Википедия

• Уравнения Рейнольдса — (англ. RANS (Reynolds averaged Navier Stokes))  уравнения Навье Стокса (уравнения движения вязкой жидкости) осредненные по Рейнольдсу. Используются для описания турбулентных течений. Метод осреднения Рейнольдса заключается в замене случайно… …   Википедия

• Уравнения Эйлера-Лагранжа — Уравнения Эйлера  Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации, и, совместно с принципом действия,… …   Википедия

• Уравнения Прока — Уравнения Прока  обобщение уравнений Максвелла, призванное описывать массивные частицы со спином 1. Уравнения Прока обычно записываются в виде , где   антисимметричный тензор электромагнитного поля …   Википедия

• Уравнения Петерсона ― Кодацци — Уравнения Петерсона ― Майнарди ― Кодацци ― уравнения, составляющие вместе с уравнением Гаусса необходимые и достаточные условия интегрируемости системы, к которой сводится задача восстановления поверхности по её первой и второй квадратичным… …   Википедия

• Уравнения Рауса — Уравнения Рауса  дифференциальные уравнения движения механической системы в переменных Рауса. Предложены Э. Раусом (англ.)русск. в 1867 г. Для системы с s степенями свободы, находящейся под действием потенциальных сил, уравнения… …   Википедия

• Уравнения Фаддеева — Уравнения Фаддеева  это уравнения, которые описывают все возможные взаимодействия в системе трёх частиц в полной квантовомеханической формулировке. Установлены Л. Д. Фаддеевым. Уравнения могут быть решены итерационным способом. В… …   Википедия

dic.academic.ru