Приклади:
Приклад №1.
Обчислити детермінант
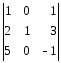
Розв’язання.
1-й спосіб. Скористаємося формулою для обчислення детермінанта третього порядку:
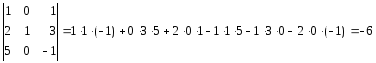
2-й спосіб. Відмітимо, що в другому стовпці всі елементи, крім одного, дорівнюють нулю. Тоді розкладемо детермінант за елементами другого стовпця:
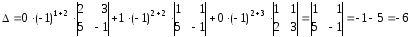
Зауваження. Перший і третій доданки в розкладі можна було не вписувати.
Приклад №2.
Обчислити детермінант
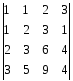
Розв’язання.
Якщо детермінант розкласти за елементами якого-небудь рядка або стовпця, то його обчислення зводиться до обчислення чотирьох детермінантів третього порядку. Очевидно, що це не кращий шлях. Застосуємо спосіб одержання в якому-небудь рядкові або стовпцеві нулів: якщо із другого рядка відняти перший, із третього – подвоєний перший, із четвертого – потроєний перший, то одержимо детермінант
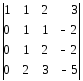 ,
,
рівний даному. Розкладемо його за елементами першого стовпця:
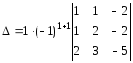
Тепер треба обчислити лише один детермінант третього порядку.
Якщо продовжити процес «одержання нулів» (наприклад, із другого рядка відняти перший), то
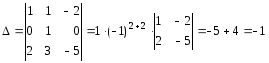
Приклад №3.
Не обчислюючи детермінанта, знайти член детермінанта, який утримує x2:
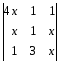
Розв’язання.
За означенням детермінанта це буде алгебраїчна сума наступних трьох елементів: 4x2—x2-12x2=-9x2
Приклад №4.
Розв’язати рівняння.
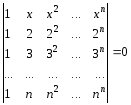
Розв’язання. За третьою властивістю детермінанта коренями даного рівняння будуть числа: x1=2, x2=3,…, xn=n
Обернена матриця
Матриця А-1називається оберненою по відношенню до матриці А, якщо АА-1=А-1А=Е, де Е – одинична матриця.
Для того, щоб для матриці
Квадратна матриця, детермінант якої відмінний від нуля, називається невиродженою (або неособливою), в противному випадку – виродженою (або особливою). Вироджені матриці обернених матриць не мають. Будь-яка невироджена матриця А має єдину обернену матрицю А-1:
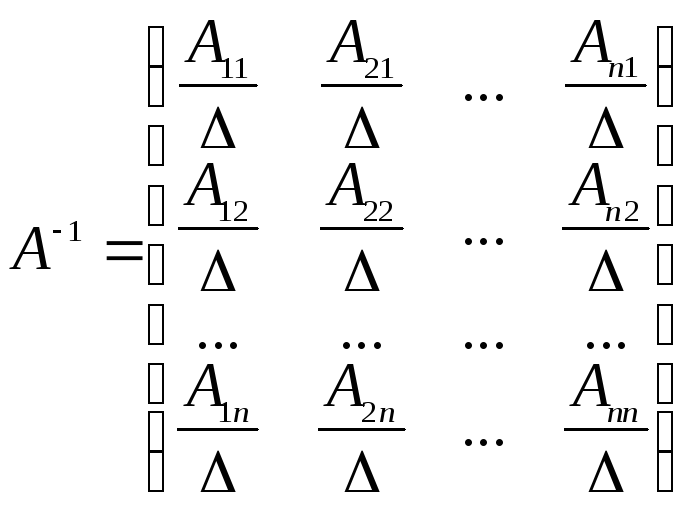
де А, Аij— алгебраїчні доповнення елемента аij матриці А, утворену за правилом: кожен елемент матриці А заміняється його алгебраїчним доповненням, потім одержана матриця транспонується і кожен її елемент ділиться на детермінант матриці А.
Для невироджених матриць вірне співвідношення:
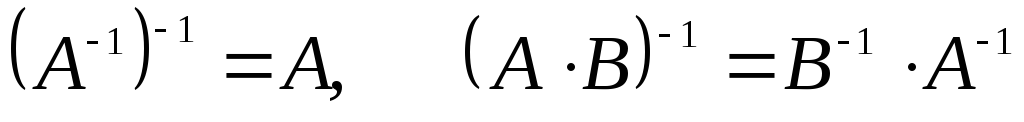
Приклад №1.
Обчислити матрицю
А-1, обернену до матриці А 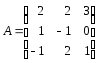
Розв’язання.
Відомо, що обернена матриця існує тоді і тільки тоді, коли задана матриця неособлива. Оскільки
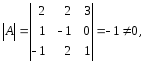
то А – неособлива матриця і А-1 існує. Відомо також, що
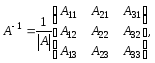
де Аij – алгебраїчне доповнення елемента аij. Знаходимо послідовно
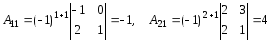
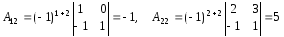
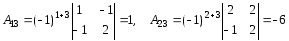
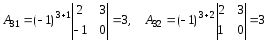
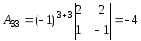

Зауваження Найпростішою перевіркою правильності знаходження оберненої матриці є множення заданої і знайденої матриць: якщо добуток їх дорівнює одиничній матриці, то обернену матрицю знайдено правильно.
Зробимо перевірку:
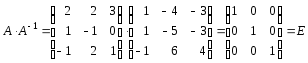
Матричні рівняння
Приклад.
Розв’язати матричне рівняння
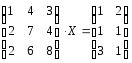
Розв’язання.
Позначимо матрицю 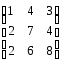 через А,
а матрицю
через А,
а матрицю 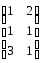
Матричне рівняння набуває вигляду: AX=B X=A-1B.
Обчислимо детермінант матриці А:
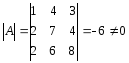
Отже, матриця А має обернену матрицю А-1. Знаходимо А-1, для чого обчислимо алгебраїчне доповнення елементів А:
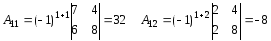
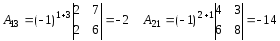
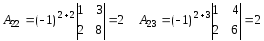
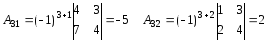
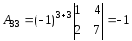
Матриця

Зробимо перевірку:
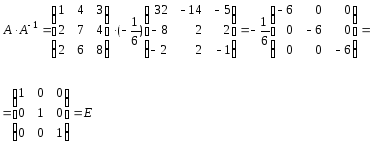
Матриця А-1 обчислена вірно.
Знайдемо матрицю X:
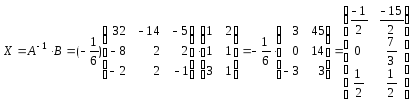
Перевірка:
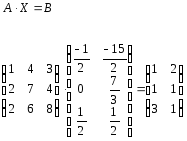
Матриця X знайдена вірно.
Система лінійних рівнянь. Матричний метод
Маричний метод обчислення СЛАР не такий поширений як метод Крамера, однак він присутній в авчальній програмі з лінійної алгебри і його вивчають як один із способів розв’язання системи рівнянь.
Нехай маємо систему N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x1, x2,…, xN.,коефіцієнтами при яких є елементи матриці A(aij), а вільними членами є числа b1, b2,…, bN.
Позначимо через X – матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:
A*X=B
Якщо квадратна матриця A має відмінний від нуля визначник , то для неї існує обернена A-1. Помноживши зліва в цьому рівнянні на A-1, одержимо
Враховуючи, що добуток оберненої матриці на саму матрицю дає одиничну , а також формулу , одержимо матричний розв’язок системи
X=A-1*B
Знаходження матричного розв’язку називається матричним способом розв’язування системи лінійних алгебраїчних рівнянь (СЛАР).
Приклад 1. Розв’язати систему лінійних рівнянь матричним методом.
Розв’язок. Маємо систему з трьох рівнянь. Позначимо матрицю і вектори літерами
Матричний розв’язок системи алгебраїчних рівнянь шукаємо за формулою X=A-1*B. Для знаходження оберненої матриці A-1 обчислимо визначник
Оскільки він відмінний від нуля , то задана система рівнянь сумісна і має єдиний розв’язок.
Знайдемо транспоновану матрицю A
Обчислимо алгебраїчні доповнення до елементів заданої матриці:
Обернену матрицю отримаємо за формулою
Знайдемо розв’язок СЛАР
Розв’язок системи рівнянь x1=3; x2=-5; x3=-7.
Розрахунки для системи із трьох рівнянь достатньо прості і зводяться на практиці до обчислень оберненої матриці, що теж не складно. У випадку системи чотирьох рівнянь обчислень буде куда більше і для визначення оберненої матриці доведеться шукати 16 визначників матриць розміром 3×3. Для системи рівнянь 5 порядку при визначенні оберненої матриці необхідно знаходити 25 визначників 4 порядку, або методом розкладу куда більше визначників 3 порядку. Перемножити обернену матрицю на праву частину рівняння після всіх операцій досить просто, і з цим справляються усі. Труднощі лише у обчисленні обернених матриць!
Матричний метод розв’язання однорідних лінійних систем з постійними коефіцієнтами, страница 5
Розглянемо питання приведення до канонічного виду за допомогою
матричного методу лінійної однорідної системи з постійними коефіцієнтами. Нехай
дана лінійна однорідна система (2.101) з матрицею коефіцієнтів 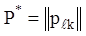 . Тоді відповідне їй матричне рівняння має
вигляд (2.102), де
. Тоді відповідне їй матричне рівняння має
вигляд (2.102), де 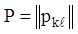
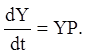 (2. 117)
(2. 117)
Введемо замість інтегральної матриці Y нову інтегральну матрицю Z за допомогою підстановки:
Z = YU, (2.118)
де U — невироджена постійна матриця. Диференціюючи (2.118) по t з урахуванням (2.117), одержуємо:
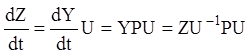
або:
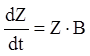 (2. 119)
(2. 119)
де:
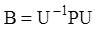 (2. 120)
(2. 120)
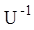 .
.Виберемо тепер матрицю U так, щоб матриця B мала жорданову нормальну форму, тобто:
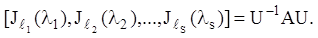 (2.
121)
(2.
121)
Тоді підстановкою (2.118) приведемо рівняння (2.117) до виду:
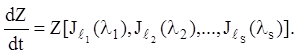 (2.
122)
(2.
122)
Рівняння (2.122) називається рівнянням канонічного виду, що відповідає даному рівнянню (2.117). Інтегральною матрицею матричного рівняння (2.122) буде, згідно (2.95), матриця:
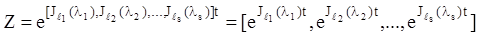 (2. 123)
(2. 123)
Тоді інтегральна матриця Y даного матричного рівняння (2.117) відповідно до (2.118) має вигляд:
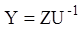 ,
(2.124)
,
(2.124)
де Z — квазідіагональна матриця (2.123), тобто має вигляд (2.112).
Цим самим визначається фундаментальна система розв’язань даної системи (2.101), що складається з s груп розв’язань структури (2.115). Система диференціальних рівнянь, що відповідає матричному рівнянню канонічного виду (2.124), називається канонічним видом даної системи (2.101).
Розглянемо тепер канонічний вид системи диференціальних рівнянь, що відповідає матричному рівнянню (2.122), з огляду на при цьому, що перехід від системи рівнянь до матричного рівняння й навпаки супроводжується транспонуванням матриці коефіцієнтів системи. Тому, транспонуючи матрицю
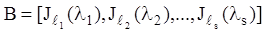
матричного рівняння (2.122), замість останнього одержимо відповідну систему диференціальних рівнянь або ж рівносильне їй векторно-матричне рівняння виду:
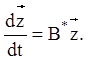 (2. 125)
(2. 125)
Якщо врахувати (2.40), можна легко встановити структуру складових
частин (верхніх жорданових кліток) матриці 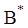 й
структуру її в цілому. Очевидно, що:
й
структуру її в цілому. Очевидно, що:
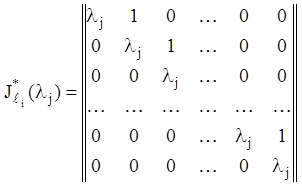 ,
(2.126)
,
(2.126)
і тому, записуючи векторно-матричне рівняння (2.125) у координатній формі, одержимо наступний канонічний вид вихідної системи (2.101):
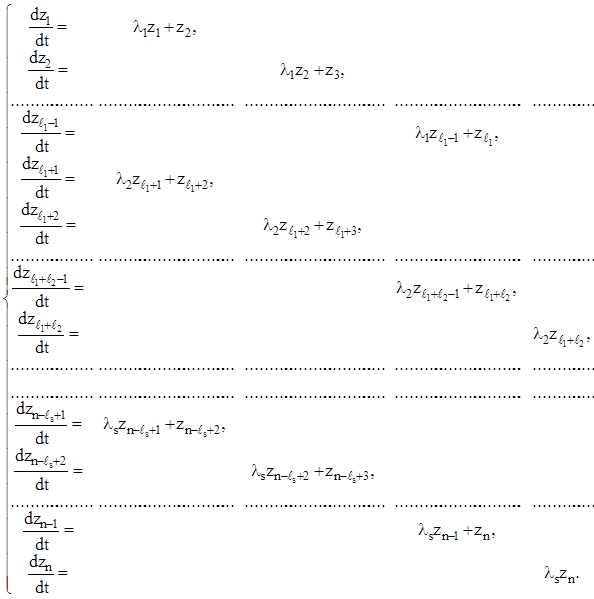
Дамо останній системі номер (2.127).
Отже, канонічним видом системи (2.101) є однорідна система n лінійних рівнянь (2.125), що складається з s груп. З огляду на те, що матриця B, обумовлена виразом (2.120), подібна до транспонованої матриці коефіцієнтів P системи (2.101), укладаємо про рівність елементарних дільників цих матриць. Тому, можна сказати, що канонічна система рівнянь (2.127) розбивається на таку кількість груп рівнянь, що дорівнює числу s всіх елементарних дільників матриці P, а число рівнянь кожної групи дорівнює степеня елементарного дільника, що відповідає цій групі. Структура канонічної системи рівнянь (2.127) наочна: діагональні коефіцієнти в кожній групі рівнянь рівні відповідному характеристичному числу, а коефіцієнти, що стоять у кожній групі на паралельній верхній діагоналі, рівні одиниці, все-таки інші коефіцієнти дорівнюють нулю.
Відзначимо, що у випадку простих елементарних дільників (це має місце завжди при простих характеристичних числах матриці P, а також може бути й при кратних характеристичних числах цієї матриці) матриця B має діагональний вигляд:
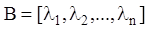 , (2.128)
, (2.128)
а векторно-матричне рівняння (2.125) запишеться так:
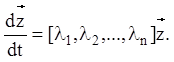 (2. 129)
(2. 129)
Матричний метод розв’язання систем лінійних алгебраїчних рівнянь — Вікіпедія
Метод розв’язання систем лінійних алгебраїчних рівнянь заданих матричним способом.
Зміст
- 1 Суть методу
- 2 Див. також
- 3 Джерела
- 4 Посилання
Якщо
- A{\displaystyle \ A} — основна матриця системи,
- b{\displaystyle \ b} — вектор-стовпчик вільних членів,
- x{\displaystyle \ x} — вектор-стовпчик невідомих;
то має місце рівність:
- Ax=b{\displaystyle \ Ax=b}
Якщо матриця A{\displaystyle \ A} є квадратною та невиродженою, то для неї існує обернена матриця. Помноживши обидві частини рівняння зліва на A−1{\displaystyle \ A^{-1}}, отримаємо
- A−1Ax=A−1b{\displaystyle \ A^{-1}Ax=A^{-1}b}.
оскільки A−1A=I{\displaystyle A^{-1}A=I} та Ix=x{\displaystyle Ix=x}, то отримаємо формулу:
- x=A−1b{\displaystyle \ x=A^{-1}b}
- Обернена матриця
- Одинична матриця
- Метод Крамера
- Метод Гауса
- Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — Москва : Наука, 1971. — 271 с. — ISBN 5791300158.(рос.)
- Мальцев А. И. Основы линейной алгебры. — 3-е изд. — Новосибирск : Наука, 1970. — 400 с.(рос.)
- Конспект лекций по высшей математике: полный курс / Дмитрий Письменный.– 5-е изд.– М.: Айрис-пресс, 2007.–608 с.: ил. –(Высшее образование). ISBN 978-5-8112-2374-9
- Матричний метод // Вища математика в прикладах і задачах: Навчальний посібник. 2-ге видання. – К.: Центр учбової літератури / Клепко В.Ю., Голець В.Л.. — 2009. — С. 31. — 594 с.
Метод оберненої матриці (матричний метод). Знаходження розв’язку системи лінійних рівнянь використовуючи метод оберненої матриці.
Автор: admin | Дата: 12.06.2014 | Переглядів : 25,342 | Коментарів немає
Нехай маємо систему лінійних алгебраїчних рівнянь з невідомими :
Для зручності систему (1) запишемо у матрично-векторній формі , де — матриця, елементами якої є коефіцієнти при невідомих системи (1), — вектор-стовпець вільних членів, — вектор-стовпець невідомих. Далі, при умові, що визначник матриці відмінний від нуля (), переходимо до обчислення елементів оберненої матриці .
Зауваження: для знаходження оберненої матриці можна використовувати один з насутпних методів:
- Знаходження оберненої матриці методом Гаусса.
- Знаходження оберненої матриці з допомогою алгебраїчних доповненень.
- Обчислення елементів оберненої матриці з допомогою розв’язку відповідних систем лінійних алгебраїчних рівнянь.
Після того, помножимо обидві частини рівняння (2) на знайдену обернену матрицю зліва. В результаті будемо мати: . Cкориставшиць асоціативною властивістю множення матриць, останнє рівняння перепишемо в насутпному вигляді: .
Далі, враховуючи що та , отримуємо формулу методу оберненої матриці (також відомий як матричний метод) для знаходження розв’язку системи (1):
Розв’язок системи лінійних рівнянь методом оберненої матриці — приклад:
Розв’язати систему лінійних алгебраїчних рівнянь матричним методом:
Запишем задану систему у матрично-векторінй формі:
Далі, виходячи з того, що вище розглянутий алгоритм для знаходження розв’язку СЛАР вимагає знаходження оберненої матриці, то на першому кроці, для матриці коефіцієнтів при невідомих обчислюємо визначник:
Оскільки він відмінний від нуля, то задана система рівнянь сумісна і має єдиний розв’язок. На наступному кроці, приступимо до знаходження оберненої матриці. Для цього скористаємось другим з перерахованих вище методів, а саме методом алгебраїчних доповнень, та, слідуючи його алгоритму, до матриці коефіцієнтів знайдемо транспоновану матрицю, після чого до елементів отриманої матриці обчислимо алгебраїчні доповнення:
Після того, як алгебраїчні доповнення відомі, обернену матрицю знаходимо за наступною формулою:
Далі, скориставшись формулою (3) знаходимо шуканий розв’язок заданої системи:
Тобто, .
Блок-схема програмної реалізації методу оберненої матриці (матричний метод):
Початкове рівняння напишемо в матричній формі

ТОП 10: |
, де , .
Матричне рівняння виду має розв’язки, якщо матриці
Для даної матриці . Тогда и
. Відповідь:
2) Зайти невідому матрицю з рівняння
Розв’язання. Початкове рівняння напишемо в матричній формі , де
Матричне рівняння виду має розв’язки, якщо матриці
Для даної матриці
Тоді
Відповідь: .
Індивідуальні завдання
Варіант № 1
1.1. 1.2.
1.4.
1.5.
Варіант № 2
2.1.
2.4.
2.5. ,
Варіант № 3
3.1 3.2.
3.4.
3.5.
Варіант № 4
4. 1. 4.2.
4.4.
4.5. , 4. 6.
Варіант № 5
5.1. 5.2.
5.4.
5.5. ,
Варіант № 6
6.1.
6.4.
6.5. ,
Варіант № 7
7.1.
7.4.
7.5.
Варіант № 8
8.1. 8.2.
8.4.
8.5.
Варіант № 9
9.1. 9.2.
9.4.
9.5. ,
Варіант № 10
10.1.
10.4.
10.5. ,
Варіант № 11
11.1.
11.4.
11.5.
Варіант № 12
12.1.
12.4.
12.5.
Варіант № 13
13.1.
13.4.
13.5.
Варіант № 14
14.1.
14.4.
14.5. , 14.6.
Варіант № 15
15.1. 15.2.
15.4.
15.5.
Варіант № 16
16.1.
16.4.
16.5.
Варіант № 17
17.1.
17.4.
17.5.
Варіант № 18
18.1.
18.4.
18.5. ,
Варіант № 19
19.1.
19.4.
19.5. ,
Варіант № 20
20.1. 20.2. 20.3.
20.4.
20.5.
Варіант № 21
21.1.
21.4.
21.5.
Варіант № 22
22.1.
22.4.
22.5.
Варіант № 23
23.1. 23.2.
23.4.
23.5.
Варіант № 24
24.1. 24.2.
24.4.
24.5. , 24.6.
Варіант № 25
25.1. 25.2. 25.3.
25.4.
25.5.
Варіант № 26
26.1.
26.4.
26.5. ,
Варіант № 27
27.1.
27.4.
27.5.
Варіант № 28
28.1.
28.4.
28.5. ,
Варіант № 29
29.1.
29.4.
29.5.
Варіант № 30
30.1.
30.4.
30.5.
1.2 СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ Завдання 1.2 Методом Крамера знайти розв’язання системи лінійних алгебраїчних рівнянь. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці. Методом Гауса (або методом виключення невідомих) знайти розв’язання системи лінійних алгебраїчних рівнянь. Знайти загальний розв’язок однорідної системи лінійних алгебраїчних рівнянь. 5. При яких значеннях Зразок розв’язання. Методом Крамера знайти розв’язок системи лінійних алгебраїчних рівнянь. . Розв’язання. Розв’язок системи знаходимо за формулами Крамера . Обчислимо визначник системи
Послідовно замінивши в ;
. Відповідь:
Задана система з трьох рівнянь з трьома невідомими. Встановити, що система рівнянь має єдиний розв’язок, і знайти його за допомогою оберненої матриці.
Розв’язання. Якщо визначник системи відмінний від нуля, то система має єдиний розв’язок (теорема Крамера). Обчислимо визначник даної системи:
отже, система має єдиний розв’язок. Дану систему можна записати у матричній формі:
Оскільки Знайдем обернену матрицю за формулою
де алгебраїчне доповнення елемента .
, .
Тоді
Відповідь:
|
Системи лінійних алгебраїчних рівнянь. — Вища математика — Меню сайту — Каталог статей
Лекція 3
Системи лінійних алгебраїчних рівнянь.
План
- Системи m лінійних рівнянь з n невідомими.
- Матричний метод розв’язування систем лінійних рівнянь.
- Розв’язування систем лінійних рівнянь за формулами Крамера.
Системи m лінійних рівнянь з n невідомими.
Розглянемо систему m лінійних рівнянь, які містять n невідомих.
(1)
Розв’язком системи (1) називається сукупність чисел , що задовольняють усі рівняння системи (1).
Система рівнянь (1) називається сумісною, якщо вона має принаймні один розв’язок, і несумісною, коли вона не має розв’язків.
Система рівнянь (1) називається визначеною, якщо вона має лише один розв’язок, і невизначеною, якщо вона має безліч розв’язків.
Розглянемо дві матриці, які відповідають системі (1):
А називають матрицею системи (1), В – розширеною матрицею системи (1).
Приведемо матрицю В за допомогою елементарних перетворень і відкидання нульових рядків до матриці ступінчастого виду .
Потрібно розуміти, що все, що ми робимо з рядками матриці В, ми робимо з рівняннями системи (1). Тому, очевидно, системи, які відповідають матриці В або , рівносильні або еквівалентні.
Зрозуміло, що при приведенні В до , матриця А також приводиться до матриці ступінчатого виду, крім випадку, коли останній рядок матриці має вигляд 0 0 0 C, С=0. У цьому випадку, щоб отримати ступінчасту матрицю до матриці А, потрібно відкинути останній рядок. Це означає, що ранг А буде на 1 меншим за ранг матриці В. З іншого боку, коли останній рядок матриці має вигляд 0 0 0 C, С=0, то це рівносильно тому, що в системі буде відповідне рівняння виду:
.
Зрозуміло, що таке рівняння розв’язку не має. Отже, система буде несумісною.
На цій основі доводиться і теорема.
Теорема. (Кронекера-Капеллі). Система (1) сумісна тоді і тільки тоді, коли ранг матриці системи дорівнює рангу розширеної матриці системи.
Якщо rang A = rang B = n, то система визначена, коли rang A = rang B — система невизначена.
Нехай rang A = rang B = .
Якщо , ( — кількість рівнянь системи), то це говорить про те, що в системі є лише лінійно незалежних рівнянь. Решта рівнянь отримується з тих рівнянь шляхом алгебраїчних перетворень. Такими рівняннями, які лінійно незалежні, будуть саме ті рівнянь, на коефіцієнтах яких можна побудувати визначник порядку, відмінний від нуля. Тільки ці рівняння і потрібно розглядати в системі, решта рівнянь відкидається.
Оскільки в ступінчастій матриці рядків не більше ніж стовпців, то лінійно незалежних рівнянь не може бути більше ніж кількості змінних.
Якщо rang A = rang B =, то система визначена.
Розглянемо випадок, коли rang A = rang B = . Тут виділяють змінних, які називаються головними, а решта — змінних називаються вільними. За головні змінні потрібно брати саме ті змінні на коефіцієнтах, при яких можна побудувати визначник порядку, відмінний від нуля. Таких комбінацій може бути одна або декілька.
Для того, щоб отримати загальний розв’язок системи, потрібно головні змінні виразити через вільні. Розв’язок, отриманий при конкретних значеннях вільних змінних, називається частковим або окремим.
Матричний метод розв’язування систем
Нехай кількість рівнянь системи (1) дорівнює числу невідомих, тобто m = n. Тоді матриця системи буде квадратною , а її визначник називають основним визначником системи.
Припустимо, що матриця А невироджена, тобто її визначник . У цьому разі існує обернена матриця .
Запишемо систему у матричному вигляді (2). Помноживши зліва обидві частини матричної рівності на матрицю , дістанемо:
.
Оскільки , то розв’язком системи буде матриця-стовпець
. (3)
Приклад 1. Розв’язати систему рівнянь матричним методом:
Розв’язання:
Запишемо дану систему у матричному вигляді:
, ,
Спочатку обчислимо визначник цієї матриці:
Отже, матриця А невироджена й для неї існує обернена матриця . Обчислимо всі алгебраїчні доповнення матриці :
Складемо нову матрицю: і транспонуємо її .
Запишемо обернену матрицю .
Відповідно .
Розв’язування систем лінійних рівнянь за формулами Крамера.
Нехай маємо систему n лінійних рівнянь з n невідомими (1).
Визначник, елементами якого є коефіцієнти при невідомих у системі (1) називається визначником цієї системи і позначається :
.
Теорема. Якщо визначник системи лінійних алгебраїчних рівнянь (1) відмінний від нуля, то ця система має єдиний розв’язок:
Тут – визначник, утворений з визначника системи (1) заміною -го стовпчика на стовпчик вільних членів.
Розглянемо випадки, коли визначник системи дорівнює нулю.
- =0 і кожен визначник =0. Це має місце лише тоді, коли коефіцієнти при невідомих пропорційні, тобто кожне рівняння системи отримуємо з першого рівняння множенням обох його частин на деяке число. Очевидно, що при цьому система має безліч розв’язків.
2. =0 і хоча б один з визначників . Це має місце лише тоді, коли коефіцієнти при всіх невідомих, крім , пропорційні. Тоді система не має розв’язків.
Приклад 2.
Розв’язати систему рівнянь за формулами Крамера:
Розв’язання: Запишемо і обчислимо відповідні визначники:
, , .
Знайдемо значення та за формулами Крамера:
, .
Відповідь: , .
Приклад 3. Розв’язати систему рівнянь за формулами Крамера:
Розв’язання: Запишемо і обчислимо відповідні визначники:
=3 ;
= ;
=;
=.
Знайдемо значення , та за формулами Крамера:
; .
Відповідь: , ,.
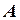 і – квадратні матриці однакового порядку і матриця
і – квадратні матриці однакового порядку і матриця 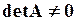 . У цьому випадку для матриці
. У цьому випадку для матриці 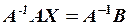 , де
, де 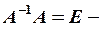 одинична матриця,
одинична матриця,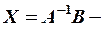 шукана матриця.
шукана матриця.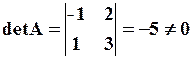 . Отже, існує . Знайдемо її за формулою , де алгебраїчне доповнення елемента матриці
. Отже, існує . Знайдемо її за формулою , де алгебраїчне доповнення елемента матриці 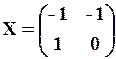 .
.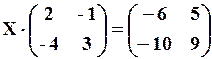 .
.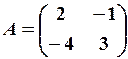 ,
, 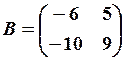 .
.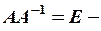 одинична матриця, або
одинична матриця, або 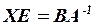 , або
, або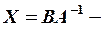 шукана матриця.
шукана матриця.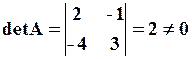 . Отже, існує . Знайдемо її за формулою, вказаною у прикладі 1), маємо:
. Отже, існує . Знайдемо її за формулою, вказаною у прикладі 1), маємо: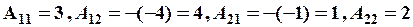 и
и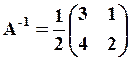 .
.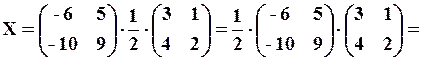
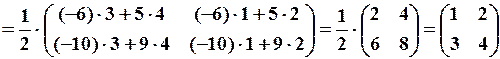 .
.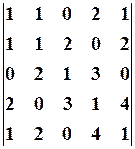 1.3.
1.3. 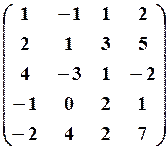
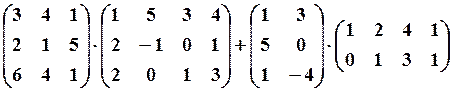
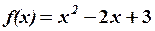 ,
, 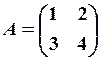 1.6.
1.6. 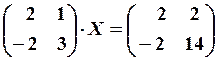
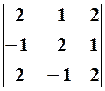 2.2. 2.3.
2.2. 2.3. 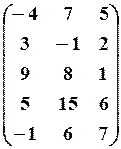
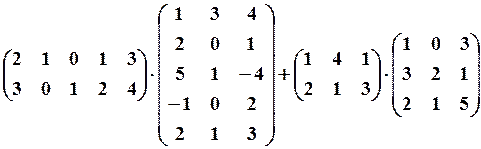
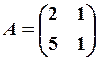 2.6.
2.6. 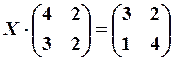
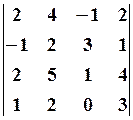 3.3.
3.3. 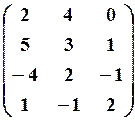
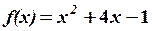 ,
, 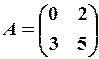 3.6.
3.6. 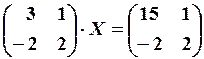
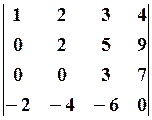 4.3.
4.3.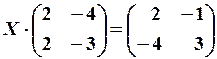
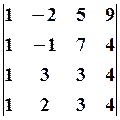 5.3.
5.3.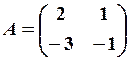 5.6.
5.6. 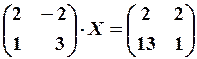
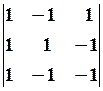 6.2.
6.2. 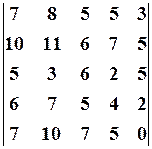 6.3.
6.3.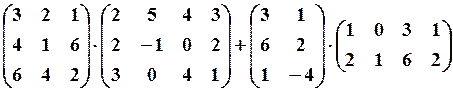
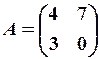 6.6.
6.6.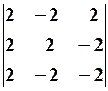 7.2.
7.2. 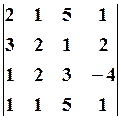 7.3.
7.3. 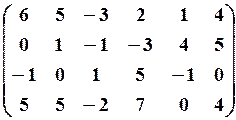
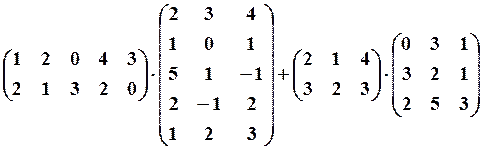
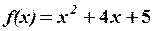 ,
, 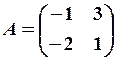 7. 6.
7. 6.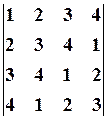 8.3.
8.3.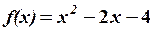 , 8.6.
, 8.6. 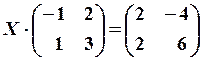
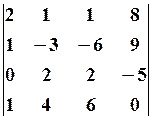 9.3.
9.3. 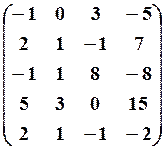
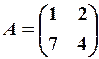 9.6.
9.6.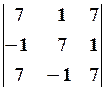 10.2. 10.3.
10.2. 10.3. 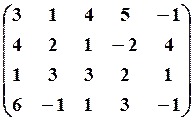
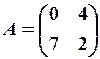 10.6.
10.6. 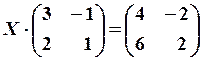
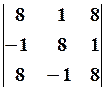 11.2.
11.2. 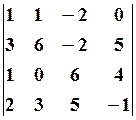 11.3.
11.3. 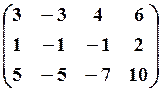
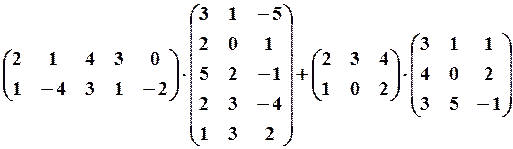
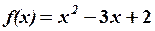 ,
, 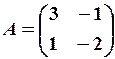 11. 6.
11. 6.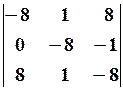 12.2.
12.2. 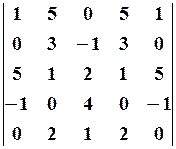 12.3.
12.3. 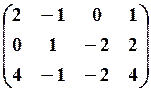
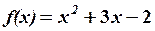 , 12.6.
, 12.6.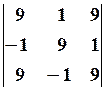 13.2.
13.2. 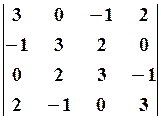 13.3.
13.3. 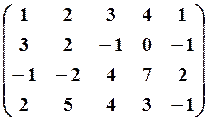
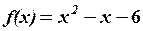 ,
, 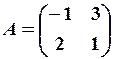 13.6.
13.6. 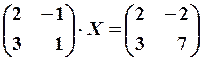
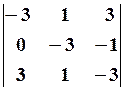 14.2.
14.2. 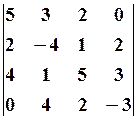 14.3.
14.3. 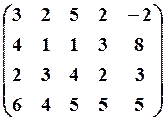
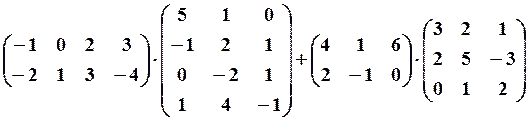
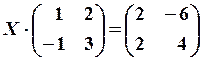
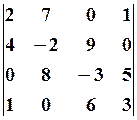 15.3.
15.3. 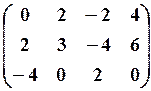
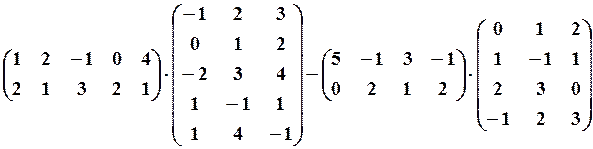
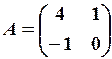 15.6.
15.6.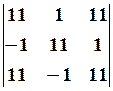 16.2.
16.2. 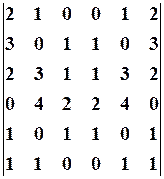 16.3.
16.3.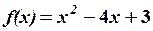 , 16.6.
, 16.6. 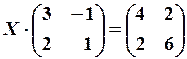
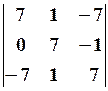 17.2. 17.3.
17.2. 17.3.
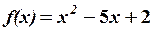 ,
, 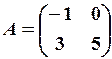 17.6.
17.6.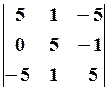 18.2. 18.3.
18.2. 18.3. 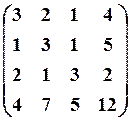
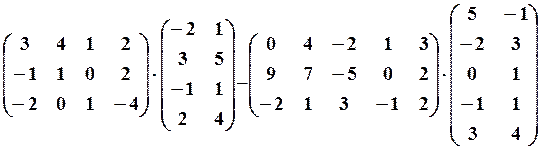
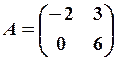 18.6.
18.6. 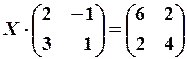
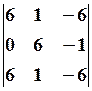 19.2.
19.2. 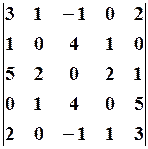 19.3.
19.3. 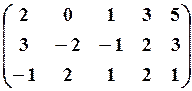
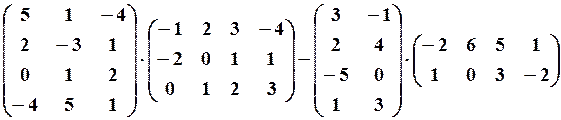
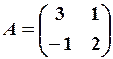 19.6.
19.6. 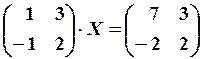
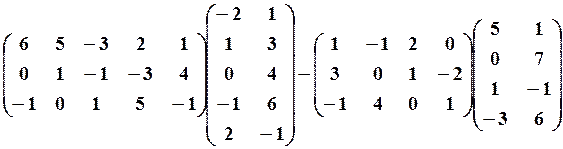
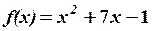 ,
, 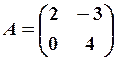 20.6.
20.6. 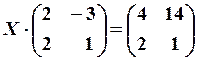
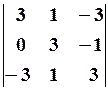 21.2.
21.2. 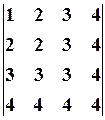
 21.3.
21.3.
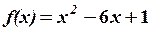 ,
, 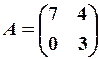 21.6.
21.6. 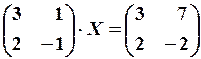
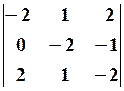 22.2.
22.2. 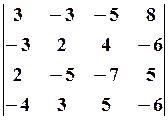 22.3.
22.3.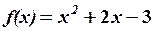 ,
, 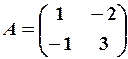 22.6.
22.6.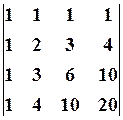 23.3.
23.3. 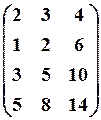
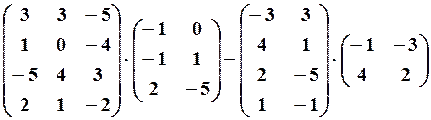
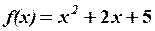 ,
, 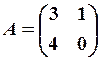 23.6.
23.6. 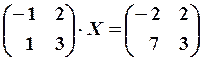
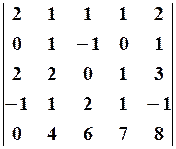 24.3.
24.3. 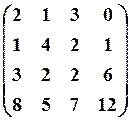
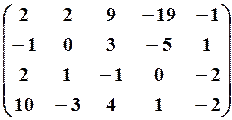
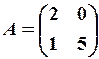 25.6.
25.6. 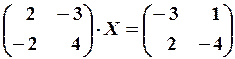
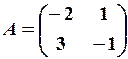 26.6.
26.6. 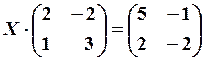
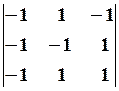 27.2.
27.2. 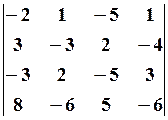 27.3.
27.3. 
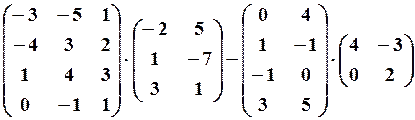
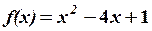 , 27.6.
, 27.6.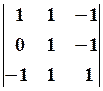 28.2.
28.2. 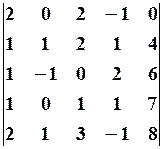 28.3.
28.3. 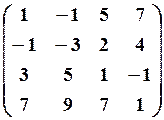
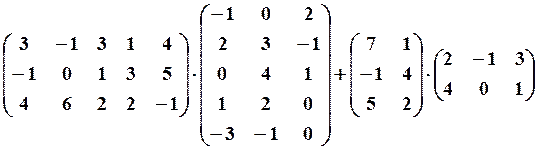
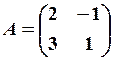 28.6.
28.6. 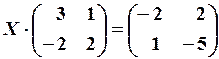
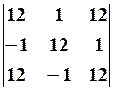 29.2.
29.2. 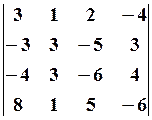 29.3.
29.3. 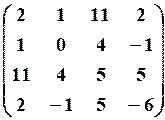
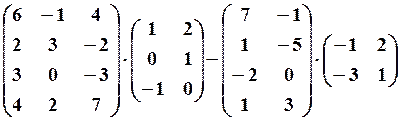
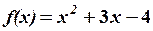 ,
, 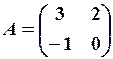 29.6.
29.6. 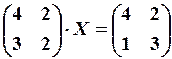 .
.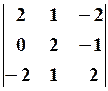 30.2.
30.2. 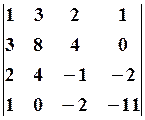 30.3.
30.3. 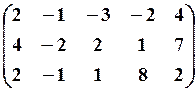
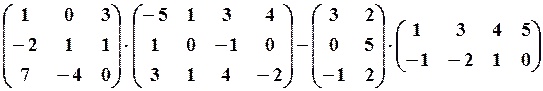
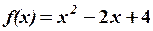 ,
, 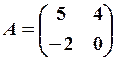 30.6. .
30.6. . система рівнянь має нетривіальні (ненульові) розв’язки? Знайти ці розв’язки.
система рівнянь має нетривіальні (ненульові) розв’язки? Знайти ці розв’язки.
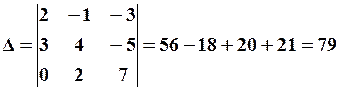 .
.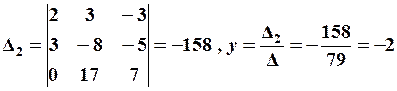 ;
;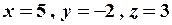 .
.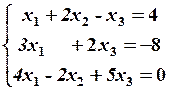 .
.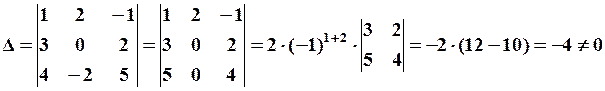 ,
,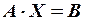 , де
, де 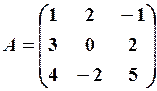 ,
, 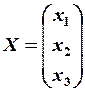 , .
, .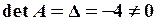 , то для матриці
, то для матриці 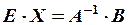 , або
, або 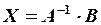 .
.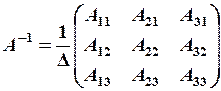 ,
,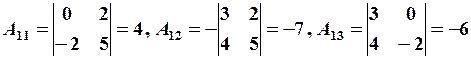 ,
,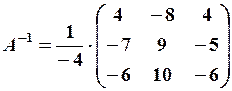 .
.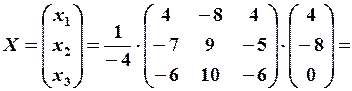
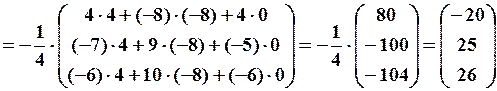 .
.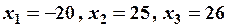 .
.