Свойства трапеции, с примерами
Параллельные стороны называются основаниями трапеции. Две другие стороны называются ее боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Трапеция, у которой боковые стороны равны, называется равнобокой (равнобедренной) трапецией. Трапеция, у которой при одной боковой стороне прямые углы называется прямоугольной.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
- Треугольники, образованные при пересечении диагоналей и лежащие на основаниях трапеции, подобные:
- Треугольники, образованные при пересечении диагоналей и лежащие на боковых сторонах трапеции, равновеликие:
- Если трапеция равнобокая, то ее диагонали равны и углы при основании равны.

- Если трапеция равнобокая, то около нее можно описать окружность.
- Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.
- Площадь трапеции вычисляется по формуле
где – основания трапеции, – высота трапеции.
- Если в трапецию вписана окружность радиуса и она делит боковую сторону точкой касания на два отрезка длины и , то .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Диагонали трапеции
Свойства диагоналей трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.
Данный отрезок параллелен основаниям трапеции.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).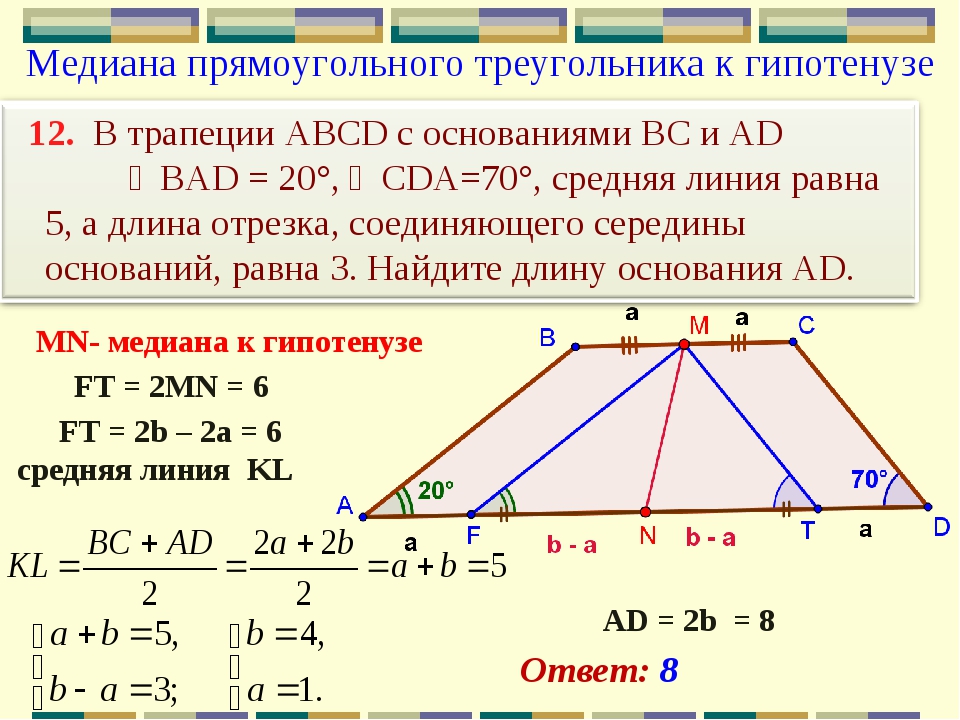
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.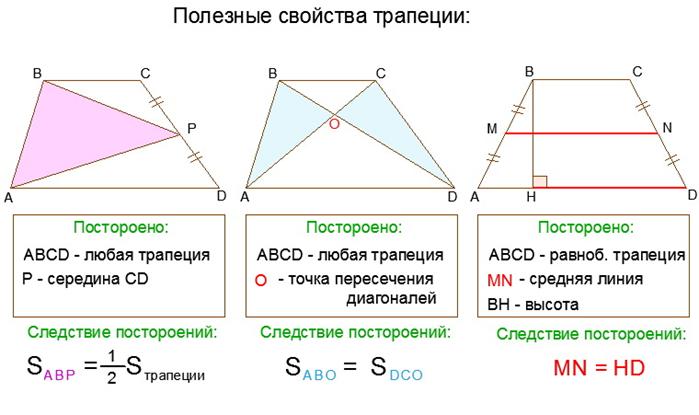
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание.
 В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.
Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ: 16 см
Задача.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
h2 + (24 — a)2 = (5√17)2
и
h2 + (24 — b)2 = 132
Учтем, что a = 16 — b , тогда в первом уравнении
h2 + (24 — 16 + b)2 = 425
h2 = 425 — (8 + b)2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
Получим:
425 — (8 + b)2 + (24 — b)2 = 169
-(64 + 16b + b)2 + (24 — b)2 = -256
-64 — 16b — b2 + 576 — 48b + b2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h2 = 425 — (8 + b)2 = 425 — (8 + 12)2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см2
Ответ: площадь трапеции равна 80 см2.
Трапеция (задачи про основания) | Описание курса | Прямоугольная трапеция
Трапеция
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. \circ\).
\circ\).
2) Т.к. \(AD\parallel BC\) и \(BD\) – секущая, то \(\angle DBC=\angle
BDA\) как накрест лежащие.
Также \(\angle BOC=\angle AOD\) как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\).
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\). Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\). Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle COD}\]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN’\parallel AD\) (\(N’\in CD\)). Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
Тогда по теореме Фалеса (т.к. \(MN’\parallel AD\parallel BC, AM=MB\)) точка \(N’\) — середина отрезка \(CD\). Значит, точки \(N\) и \(N’\) совпадут.
2) Докажем формулу.
Проведем \(BB’\perp AD, CC’\perp AD\). Пусть \(BB’\cap MN=M’, CC’\cap MN=N’\).
Тогда по теореме Фалеса \(M’\) и \(N’\) — середины отрезков \(BB’\) и \(CC’\) соответственно. Значит, \(MM’\) – средняя линия \(\triangle ABB’\), \(NN’\) — средняя линия \(\triangle DCC’\). Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]
Т.к. \(MN\parallel AD\parallel BC\) и \(BB’, CC’\perp AD\), то \(B’M’N’C’\) и \(BM’N’C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B’M’=M’B\). Значит, \(B’M’N’C’\) и \(BM’N’C\) – равные прямоугольники, следовательно, \(M’N’=B’C’=BC\).
Таким образом:
\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\), \(N\) и \(M\) лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\)). Пусть она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
Рассмотрим \(\triangle BPN\) и \(\triangle APM\). Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\). Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\). Но \(BN=NC\), следовательно, \(AM=DM\).
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\) – середина \(BC\), \(O\) – точка пересечения диагоналей. Проведем прямую \(NO\), она пересечет сторону \(AD\) в точке \(M\). Докажем, что \(M\) – середина \(AD\).
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\). Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\). Но \(BN=CN\), следовательно, \(AM=MD\).
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.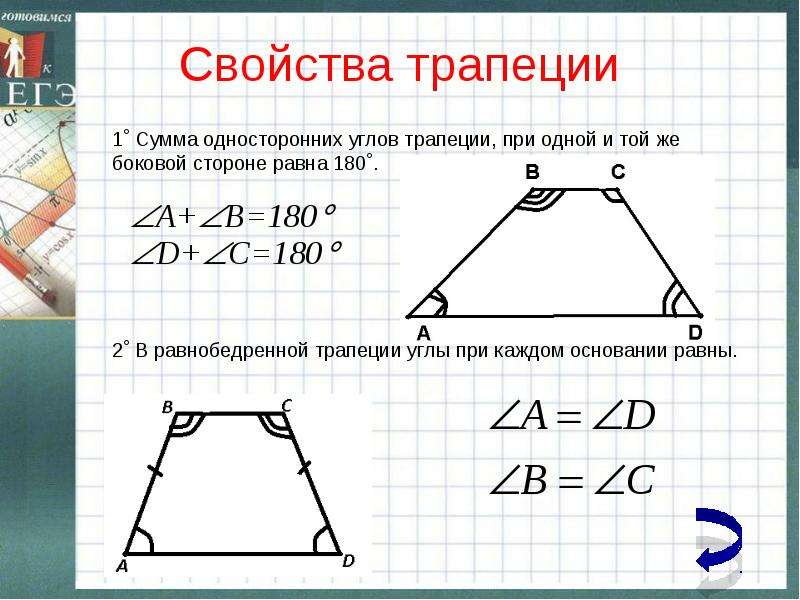
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\).
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\), то \(BM\parallel CN\); \(AD\parallel BC\), тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\).
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\). Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\), то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\).
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку \(\triangle ABD=\triangle ACD\). Следовательно, \(AC=BD\).
3) Т.к. \(\triangle ABD=\triangle ACD\), то \(\angle BDA=\angle CAD\). Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\), такую что \(\angle A = \angle D\).
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\), то треугольник \(AED\) равнобедренный и \(AE = ED\). Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\). Аналогично равны углы \(2\) и \(4\), но \(\angle 1 = \angle 2\), тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\).
В итоге \(AB = AE — BE = DE — CE = CD\), то есть \(AB = CD\), что и требовалось доказать.
2) Пусть \(AC=BD\). Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).
Т.к. \(\triangle AOD\sim \triangle BOC\), то обозначим их коэффициент подобия за \(k\). Тогда если \(BO=x\), то \(OD=kx\). Аналогично \(CO=y \Rightarrow AO=ky\).
Т.к. \(AC=BD\), то \(x+kx=y+ky \Rightarrow x=y\). Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\).
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\), чтд.
Замечательное свойство трапеции | Треугольники
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.
Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.
Сформулируем это свойство иначе:
Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.
Дано:
ABCD- трапеция, AD||BC,
AB∩CD=F, AC∩BD=O,
FO∩AD=K, FO∩BC=P
Доказать: K- середина AD,
P- середина BC
Доказательство:
Рассмотрим треугольники AOK и COP.
∠AOK=∠COP (как вертикальные),
∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).
Значит, треугольники AOK и COP подобны (по двум углам).
Следовательно,
Аналогично, треугольники DOK и BOP подобны и
Так как правые части этих равенств равны, то левые также равны:
Рассмотрим треугольники AFK и BFP.
∠F- общий,
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).
Следовательно, треугольники AFK и BFP подобны (по двум углам).
Отсюда,
Аналогично, треугольники DFK и CFP подобны и
Правые части равенств равны, приравниваем левые части:
Так как
то
По основному свойству пропорции,
а значит, CP=BP, то есть P — середина BC.
Аналогично,
AK=DK, K — середина AD.
Что и требовалось доказать.
Альтернативный вариант.
- Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
- Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания
В нашем случае докажем, что точки O и P лежат на прямой FK.
FK — медиана треугольника AFD.
Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.
BC||AD (как основания трапеции), QL||AD (по построению).
О — середина QL.
Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.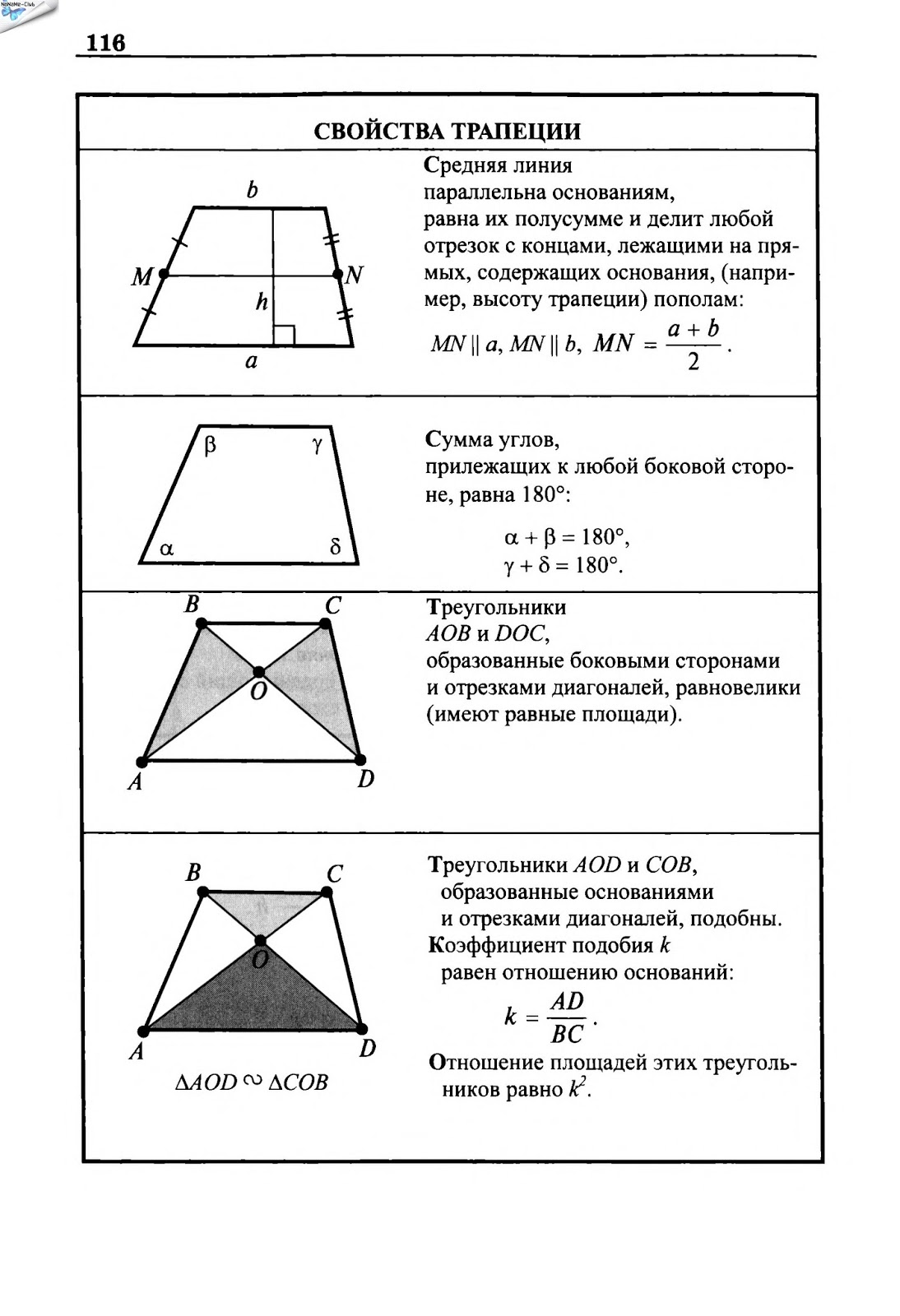
И ещё.
Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:
Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.
Трапеция, Средняя линия трапеции, треугольник
Четырёхугольник, у которого только две стороны параллельны называются трапецией.
Параллельные стороны трапеции называются её основаниями, а те стороны, которые не параллельны, называются боковыми сторонами. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции.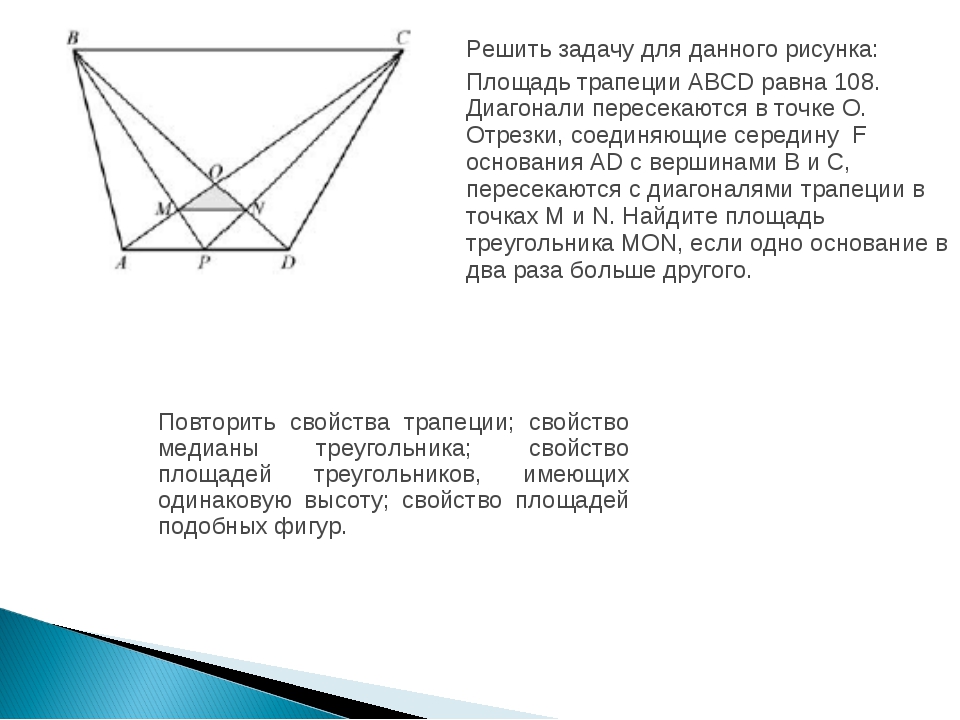 Средняя линия трапеции параллельна её основаниям.
Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.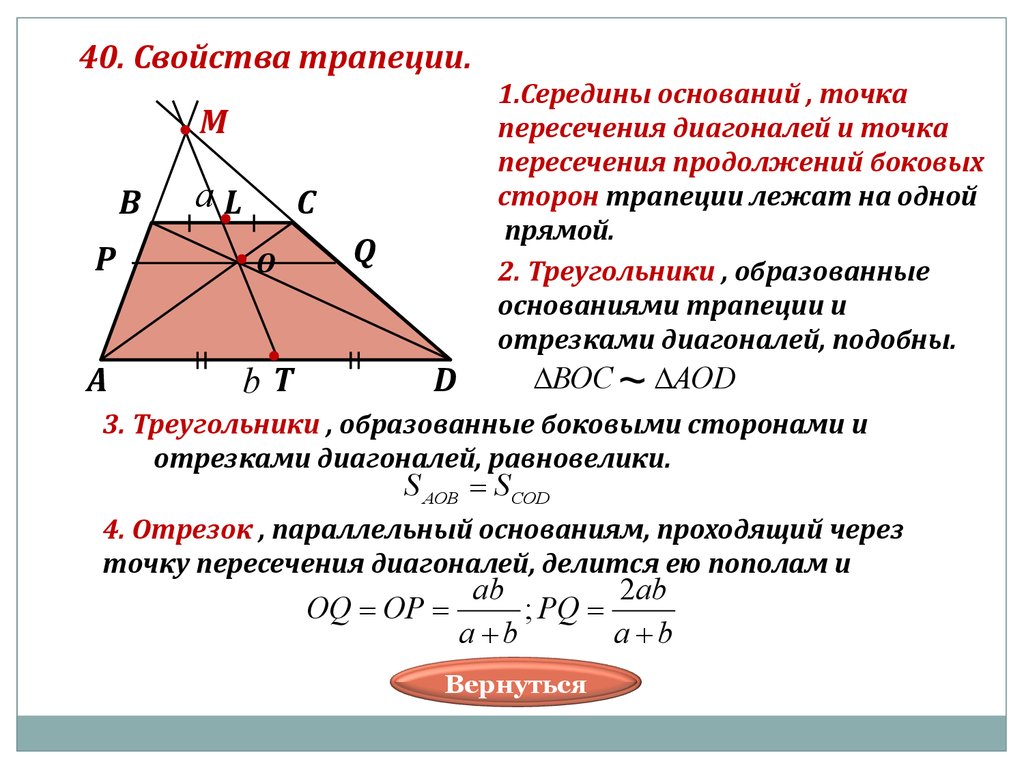
AM = MC and BN = NC =>
MN || AB
MN = AB/2
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA1 = A1A2 = A2A3 = A3A4 = A4A5
Мы соединяем A5 с B и проводим такие прямые через A4, A3, A2 и A1, которые параллельны A5B. Они пересекают AB соответственно в точках B4, B3, B2 и B1. Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB3A3A5 мы видим, что BB4 = B4B3. Таким же образом, из трапеции B4B2A2A4 получаем B4B3 = B3B2
В то время как из трапеции B3B1A1A3, B3B2 = B2B1.
Тогда из B2AA2 следует, что B2B1 = B1A. В заключении получаем :
AB1 = B1B2 = B2B3 = B3B4 = B4B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
то
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
откуда
Биссектрисы трапеции
Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.
I. Биссектрисы углов при боковой стороне трапеции пересекаются.
1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).
2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).
3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.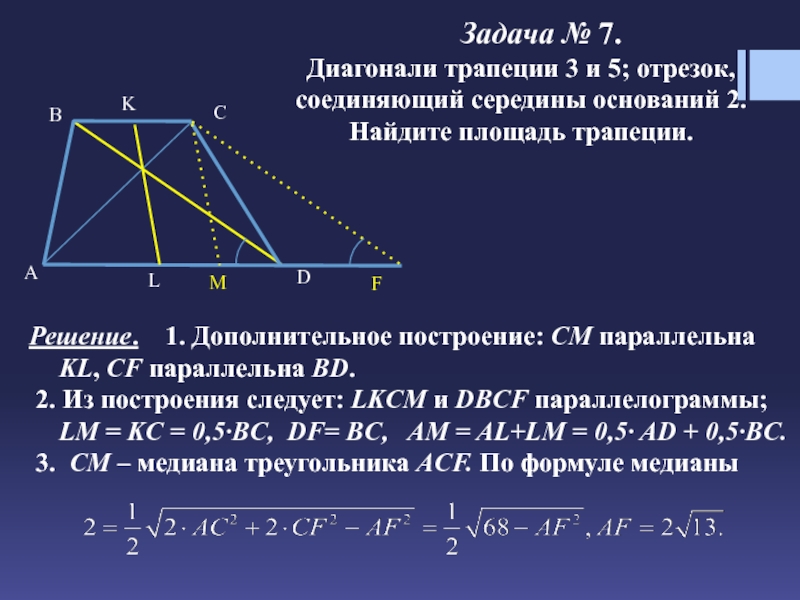
Вывод:
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Вывод:
Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.
Таким образом, BC=BK+KC=AB+CD.
Вывод:
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.
Отсюда AD=AF+FD=AB+CD.
Вывод:
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Трапеция
(Перейти к области трапеции или периметру трапеции)
Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечены стрелками ниже):
| Трапеция | Равнобедренная трапеция |
Трапеция:
| имеет пару параллельных сторон | |
— это равнобедренная трапеция , когда она имеет равных углов с параллельной стороны | |
| называется « трапеция » в Великобритании (см. Ниже) |
Люфт трапецией:
Параллельные стороны — это «основания»
Две другие стороны — «ножки»
Расстояние (под прямым углом) от одной базы до другой называется «высотой»
Площадь трапеции
Площадь — это среднее значение для двух базовых длин, в раз превышающее высоту : Площадь = a + b 2 × h |
Пример: два основания трапеции — 6 м и 4 м, а высота — 3 м.
 Какова его площадь?
Какова его площадь?Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м 2
Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.
Периметр трапеции
Периметр — это расстояние по краям.
Периметр — сумма длин всех сторон : Периметр = a + b + c + d |
Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см. Каков ее периметр?
Периметр = 5 см + 12 см + 4 см + 15 см = 36 см
Медиана трапеции
Медиана (также называемая средней линией или средним сегментом) — это линейный сегмент на полпути между двумя основаниями. Средняя длина — это среднее значение двух базовых длин: м = а + б 2 |
Вы можете рассчитать площадь, зная медианное значение, это просто медиана, умноженная на высоту:
Площадь = mh
Трапеция
Трапеция (UK: trapezoid) — четырехугольник без параллельных сторон.
Определения США и Великобритании поменялись местами, например:
| Трапеция | Трапеция | |
| США: | Пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | Пара параллельных сторон |
Медиана трапеции: определение и теорема — видео и стенограмма урока
Медиана трапеции — это линия, параллельная основанию, которая простирается от середины одной ноги до середины другой.Здесь фиолетовая линия — это медиана. Это та же линия, которая представляет опорную балку на нашем воображаемом мосту; опорная балка — это середина трапеции. Вы можете увидеть, как он разрезает каждую ногу пополам; часть ноги выше середины такой же длины, как часть ноги ниже середины. Две синие фишки равны друг другу, а две красные равны друг другу.
Вы можете увидеть, как он разрезает каждую ногу пополам; часть ноги выше середины такой же длины, как часть ноги ниже середины. Две синие фишки равны друг другу, а две красные равны друг другу.
Это не обязательно означает, что синие фигуры равны красным.Ноги не обязательно должны быть одинаковой длины. Например, предположим, что длина красной ножки составляет 7 единиц, а синей ножки — 8 единиц. Тогда вы получите это. Это все еще медиана, потому что оба синих участка равны друг другу, а оба красных участка равны друг другу.
Во многих математических задачах вам будет предложено найти медиану трапеции. Для этого можно использовать простую формулу: медиана — это среднее значение оснований. Например, предположим, что верхнее основание нашей трапеции имеет длину 10 единиц, а нижнее основание — 18 единиц.В этом случае медианой будет среднее значение 10 и 18.
Помните, что среднее значение группы чисел — это сумма всех чисел, деленная на число чисел. Чтобы найти среднее значение, вы складываете все числа и делите их на то количество, которое у вас есть. В этом случае у вас есть два числа, 10 и 18, поэтому вы должны взять (10 + 18) / 2. Это дает вам 28/2 или 14 в качестве среднего. Длина медианы этой трапеции будет равна 14.
В нашем примере с мостом мы знаем, что его верхняя часть имеет длину 500 футов, а нижняя — 750 футов.Таким образом, мы можем найти медианное значение, взяв среднее значение от 500 до 750: (500 + 750) / 2 = 1250/2 = 625 футов. Итак, если вы заказывали опорные балки, вам нужно было бы заказать достаточно, чтобы покрыть 625 футов.
Резюме урока
В этом уроке вы узнали о медиане трапеции. Трапеция — это четырехсторонняя форма, в которой по крайней мере две стороны параллельны. Две параллельные стороны называются основаниями, а две другие стороны — ногами. Медиана представляет собой прямую линию, параллельную основанию, проходящую от середины одной ноги до середины другой.
Длина медианы — это среднее значение двух оснований, поэтому вы можете найти ее по формуле: ((длина одного основания) + (длина другого основания)) / 2.
Много реальных- В приложениях life используются трапеции, например мосты, столы, здания и другие архитектурные конструкции. Оглянитесь вокруг и посмотрите, заметите ли вы кого-нибудь в своей комнате, а затем попробуйте свои силы в вопросах викторины.
Трапеция : четырехсторонняя форма, по крайней мере, с одной парой параллельных сторон.
Основания трапеции : две параллельные стороны трапеции.
Ножки трапеции : Непараллельные стороны трапеции.
Медиана : линия, параллельная основанию, которая проходит от середины одной ноги до середины другой.
Среднее значение : сумма всех номеров группы, деленная на количество номеров в этой группе.
Нахождение медианы : медиана — это среднее значение оснований.Медиана = (более длинное основание + более короткое основание) / 2.
Результаты обучения
Определите, сможете ли вы достичь этих целей по окончании урока:
- Распознать трапецию
- Понять определение медианы трапеции
- Расчет медианы трапеции
Площадь трапеции с медианой
В дополнение к стандартной формуле для площади трапеции с использованием ее оснований, мы также можем вычислить площадь трапеции с ее серединой и ее высотой.Медиана — это линия, соединяющая две средние точки ног трапеции — непараллельные стороны трапеции. Медиана также называется срединным сегментом или средней линией.
Задача
BCD — трапеция, AB || CD . EF — это линия, соединяющая середины ног AD, и BC , AE = ED и BF = FC . h — высота трапеции. Найдите формулу для его площади, используя h и | EF |
Стратегия
Давайте посмотрим, как мы можем связать то, что мы знаем о медиане трапеции, с формулой, которая у нас уже есть для площади трапеции. Площадь трапеции составляет (короткое основание + длинное основание) · высота / 2, или A = ½ ( AB + DC ) · h.
Площадь трапеции составляет (короткое основание + длинное основание) · высота / 2, или A = ½ ( AB + DC ) · h.
В этой задаче у нас есть высота и средний или средний сегмент. Из теоремы о срединном сегменте трапеции мы получаем связь между средним сегментом и основаниями: | EF | = ½ ( AB + DC ). Глядя на две формулы, мы видим, что можем просто заменить EF на ½ ( AB + DC ) в формуле для площади и получить A = | EF | · h
Решение
(1) A = ½ ( AB + DC ) · h // Площадь трапеции
(2) AE = ED , BF = FC // задано
(3) EF — средний сегмент // (2), Определение среднего сегмента
(4) | EF | = ½ ( AB + DC ) // (3), теорема о среднем сегменте трапеции
(5) A = | EF | · H // (1), (4), замена
Другой способ решения этой проблемы
В предыдущем разделе мы полагались на признание того, что формула для площади трапеции — A = ½ ( AB + DC ) · h очень похожа на формулу для длины мидсегмента — | EF | = ½ ( AB + DC ) и произвела замену, которая привела к очень компактному и элегантному решению.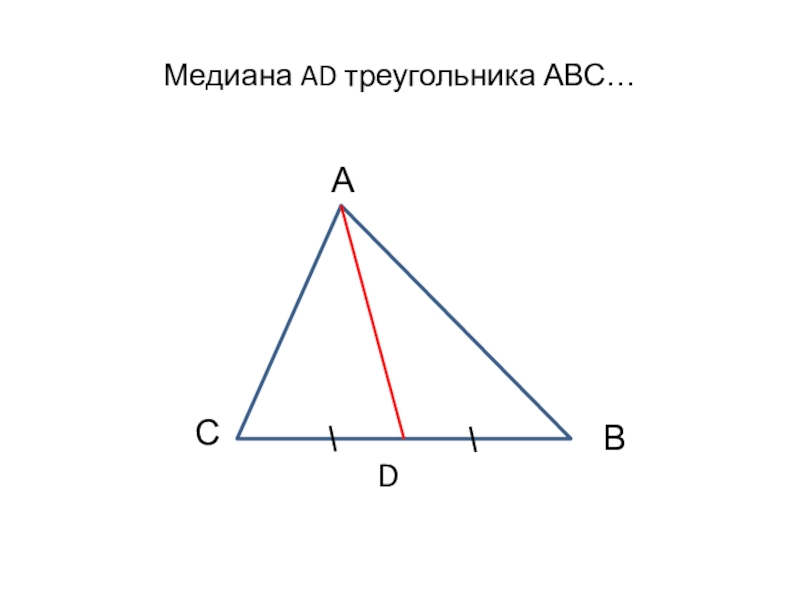
Но что, если мы не сразу узнаем, что формулы похожи, или не вспомним, что средний сегмент равен половине суммы оснований? Давайте посмотрим на другой способ решить эту проблему, не полагаясь на это.
Поскольку EF — это линия, соединяющая середины сторон, мы могли бы использовать теорему о треугольнике середины отрезка, но для этого нам понадобится треугольник. Итак, давайте нарисуем один, используя диагональ AC:
Решение, используя теорему о среднем сегменте треугольника
В треугольнике ΔACD, | EG | — это линия, параллельная основанию CD, которая начинается от середины стороны AD, поэтому согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания.Положим | EG | = x. Если x равен половине базы, то CD базы должен быть равен 2x.
Теперь посмотрим на другой треугольник ΔACB. Используя те же рассуждения, что и выше, | GF | начинается от середины стороны BC и параллельна AB — так что, согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания.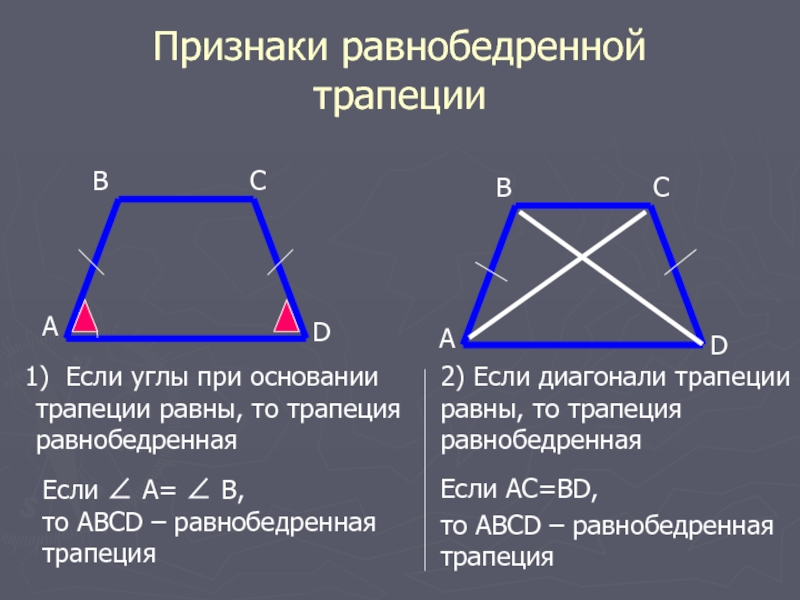 Длина | GF | равно | EF | -x, поэтому основание AB равно 2 · (| EF | -x) или 2 · | EF | -2x.
Длина | GF | равно | EF | -x, поэтому основание AB равно 2 · (| EF | -x) или 2 · | EF | -2x.
Теперь давайте подставим эти значения в формулу для площади трапеции:
(1) A = ½ ( AB + CD ) · h
(2) AB = 2 · | EF | — 2x
(3) CD = 2x
(4) A = ½ (2 · | EF | -2x + 2x) · h = ½ (2 · | EF |) · h = | EF | · h
| ||
Трапеция, средняя линия и средний сегмент трапеции и треугольника
Четырехугольник с двумя противоположными параллельными сторонами называется трапецией (трапеция) .
Параллельные стороны трапеции называются основаниями (AB и CD), а те, которые не параллельны, называются ногами (AD и BC).
Если ноги равны по длине, трапеция называется равнобедренная .
DE и CF — высот .
Средняя линия трапеции
Линия, соединяющая середины сторон, которые не параллельны, называется средней линией (или средним сегментом) трапеции.
Линия MN является средней линией ABCD. А сегмент MN — это средний сегмент ABCD.
AM = MD
BN = NC
Средняя линия трапеции параллельна ее сторонам.
В нашем случае — MN || AB || ОКРУГ КОЛУМБИЯ.
Теорема 1:
Если линия, проходящая через середину отрезка трапеции, параллельна ее основаниям, затем линия проходит через середину другой ноги.
Теорема 2:
Средний отрезок трапеции составляет половину длины двух параллельных сторон.
Другими словами:
$ \ overline {MN} = \ frac {\ overline {AB} + \ overline {DC}} {2} $
Середина треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средним сегментом треугольника.
Он параллелен третьей стороне, а его длина вдвое меньше длины третьей стороны.
Теорема : Если отрезок прямой пересекает середину одной стороны треугольника и параллелен другой стороне того же треугольника, то этот отрезок делит третью сторону пополам.
$ \ overline {AM} = \ overline {MC} $ и $ \ overline {BN} = \ overline {NC} $ =>
$ MN || AB $
$ \ overline {MN} = \ frac {\ overline {AB}} {2} $
Применение свойств средних сегментов
Разделите отрезок на равные отрезки без измерения.
Задание: Разделите данный сегмент $ \ overline {AB} $ на 5 равных сегментов без измерения.
Решение:
Пусть p — произвольный луч с началом A, не лежащий на AB. На п. Рисуем последовательно пять равных отрезков.
$ \ overline {AA_1} = \ overline {A_1A_2} = \ overline {A_2A_3} = \ overline {A_3A_4} = \ overline {A_4A_5} $
Соединяем A 5 с B и проводим линии через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B.
Они пересекают AB в точках B 4 , B 3 , B 2 и B 1 соответственно.
Эти точки делят отрезок $ \ overline {AB} $ на пять равных отрезков.
Действительно, из трапеции BB 3 A 3 A 5 мы видим, что $ \ overline {BB_4} = \ overline {B_4B_3} $. Таким же образом из трапеции B 4 B 2 A 2 A 4 , получаем $ \ overline {B_4B_3} = \ overline {B_3B_2} $
При этом от трапеции B 3 B 1 A 1 A 3 ,
$ \ overline {B_3B_2} = \ overline {B_2B_1} $.
Тогда из B 2 AA 2 следует, что $ \ overline {B_2B_1} = \ overline {B_1A} $. В итоге получаем:
$ \ overline {AB_1} = \ overline {B_1B_2} = \ overline {B_2B_3} = \ overline {B_3B_4} = \ overline {B_4B} $
Понятно, что если AB нужно разделить на другое количество равных отрезков, мы должны спроецировать такое же количество равных отрезков на p. Далее поступаем так же.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 калькулятора трапеций Прокрутите вниз для получения инструкций и определений.  Щелкните здесь, чтобы просмотреть информацию обо всех четырехугольниках.Чтобы получить калькулятор воздушных змеев, щелкните здесь.
Для калькулятора параллелограммов щелкните здесь параллелограммы.
Для калькулятора ромбов щелкните здесь ромбы.
Для калькулятора квадратов и прямоугольников щелкните здесь квадраты. Щелкните здесь, чтобы просмотреть информацию обо всех четырехугольниках.Чтобы получить калькулятор воздушных змеев, щелкните здесь.
Для калькулятора параллелограммов щелкните здесь параллелограммы.
Для калькулятора ромбов щелкните здесь ромбы.
Для калькулятора квадратов и прямоугольников щелкните здесь квадраты.Площадь трапеции = ((сумма оснований) ÷ 2) • высота Линии BC и AD параллельны и называются основаниями. Линии AB и DC являются непараллельными сторонами и называются участками . Линии AC (или q ) и BD (или p ) называются диагоналями Линия, перпендикулярная линиям AD и BC, называется высотой или высотой. Прямая, параллельная линиям AD и BC, находится в середине линий AB и DC. и называется средним или средним сегментом . Длина медианы = (Линия AD + Линия BC) ÷ 2 Трапеции имеют 2 пары из смежных углов (A и B) и (B и C), которые являются дополнительными (добавить 180 °). 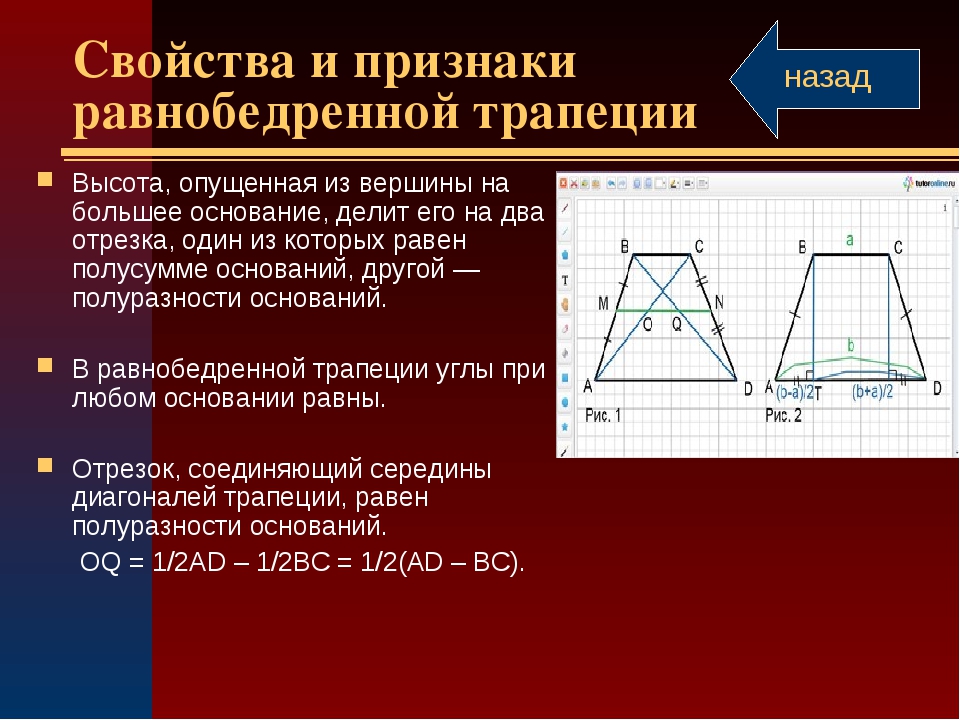
|


 Четырехугольник, Средние точки, Внешняя линия,
Перпендикулярные линии.
Четырехугольник, Средние точки, Внешняя линия,
Перпендикулярные линии.  Треугольник, Центроид, Поперечный, Перпендикулярный
линий.
Треугольник, Центроид, Поперечный, Перпендикулярный
линий.  Ромб, перпендикуляры, среднее арифметическое.
Ромб, перпендикуляры, среднее арифметическое.  Трапеция,
Середина, треугольник, площадь. Медиана трапеции.
Трапеция,
Середина, треугольник, площадь. Медиана трапеции.

 (линия BC).
(линия BC).