Эратосфен — Википедия

Эратосфе́н Кире́нский (др.-греч. Ἐρατοσθένης ὁ Κυρηναῖος; 276 год до н. э.—194 год до н. э.) — греческий математик, астроном, географ, филолог и поэт. Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки. Первый известный учёный, вычисливший размеры Земли.

Сын Эглаоса, уроженец Кирены.

Начальное образование Эратосфен получил в Александрии под руководством своего учёного земляка Каллимаха. Другим учителем Эратосфена в Александрии был философ Лизний. Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена; кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом.

В 245 году до н. э. царь Птолемей III Эвергет пригласил Эратосфена приехать из Афин, чтобы работать в Александрийской библиотеке, где уже трудились его учитель Каллимах и Аполлоний Родосский. Эратосфен откликнулся на приглашение, в возрасте около тридцати лет он приехал в Александрию, где и остался до самой смерти. Через пять лет после приезда он сменил Аполлония Родосского на посту главы Александрийской библиотеки. Как глава библиотеки, Эратосфен занимался обучением детей монарха — будущего правителя Птолемея IV и его сестры (а впоследствии и жены) Арсинои

[4].

На посту главы библиотеки активно занимался её расширением и развитием, стремясь поддержать репутацию библиотеки в соперничестве с Пергамской библиотекой. По его просьбе александрийские портовые власти изымали все книги с приходящих кораблей для изучения и копирования^[5]. Эратосфен приобретал аутентичные копии трагедий великих греческих авторов — Эсхила, Софокла и Эврипида, а также учредил в библиотеке целый отдел, занимавшийся изучением творчества Гомера.

В старости у Эратосфена воспалились глаза, что в дальнейшем привело к слепоте. Невозможность читать и наблюдать за природой сильно угнетала его и в 194 год до н. э. он принял решение уморить себя голодом.

Отголоски признания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатлос» (греч. Πένταθλος) — пятиборец, то есть всесторонне развитый человек, оно было ему дано за одарённость в самых разных областях знания^[5].

В честь Эратосфена назван кратер на Луне, один из периодов геологической истории Луны, а также подводная гора в Средиземном море, близ Кипра.

По математике[править | править код]

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда «О шаре и цилиндре». В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего «Собрания» называет сочинение Эратосфена «О средних величинах», замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена «Платоник», посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во «Введении в арифметику» Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена). Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000.

По астрономии[править | править код]

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно: «Катастеризмы» — перечисление созвездий и заключающихся в них звёзд, где указывается до 700 объектов. Определения положений этих звёзд сочинение не даёт.

Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярные сферы.

Эратосфен определил угловое расстояние от экватора до тропика: он нашёл его равным 11/83 от 180°.

По геодезии и географии[править | править код]

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу. Теперь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к северу от Сиены. Эти города лежат на одном меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны. Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5 000 стадиев. Поэтому весь круг будет равен 250 000 стадиям. Таков метод Эратосфена.

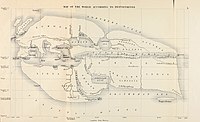Измерение Земли по Эратосфену Карта мира по Эратосфену (около 194 года до н. э.). Реконструкция XIX века

Позднее полученное Эратосфеном число было увеличено до 252 000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. При значении стадия от 209,4 метров (стадий системы фараонов) до 178 (греческого) и 172,5 (египетский) значения радиуса могли колебаться от 8 397 км до 6 916 км. Также упоминают использования стадия в размере 157,2 метра, при котором радиус Земли равнялся бы 6 302 км^[6]. Современные измерения дают для усреднённого радиуса Земли величину 6 371 км, что в любом случае делает вышеописанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

Считается, что именно Эратосфен создал первую карту мира, которая давала примерное представление о взаимной удаленности городов и стран. Он утверждал, что точное отображение мира, даже в двух измерениях, зависит только от установления точных линейных размеров. Его великие достижения в области картографии сразу стали использоваться в качестве новой методики для построения карт с меридианами, и параллелями. Эти осевые линии были размещены на карту Земли из места своего происхождения — Родоса, и с тех пор мир стал разделен на сектора. Затем Эратосфен стал использовать эти участки земли для определения мест на карте.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша.

Эратосфена называют «отцом географии» за его заслуги в развитии географических идей, а также за то, что ему принадлежит и сам термин «география» (землеописание).

Литературные сочинения[править | править код]

В античном мире Эратосфен был известен не только как естествоиспытатель, но и как эпический и элегический поэт. В поэме «Гермес» он вкладывает в уста Гермеса рассказ о гармонии сфер. В элегии «Эригона» (дочь Икара), написанной на одном из ионийских диалектов, наиболее знаменит отрывок, в котором повествуется о введении в обиход нового танца, с которым связано возникновение трагедии. По легенде впервые это танец исполнялся после того, как Икар убил козла (др.-греч. τράγος, отсюда tragoedia), забравшегося в его виноградник. В поэме «Гесиод» пересказывается легенда о поэте Гесиоде, якобы соблазнившем чужую жену и за это убитом её братьями. Упомянутые литературные сочинения сохранились во фрагментах. Полностью сохранилась лишь эпиграмма Эратосфена, посвящённая Птолемею III.

Прочие труды[править | править код]

Эратосфен является основателем научной хронологии. В своём труде «Хронографии» он попытался установить даты, связанные с историей Эллады, составил список победителей Олимпийских игр. Кроме того, Эратосфен написал филологический трактат «О древней комедии».

Согласно Страбону, Эратосфен (в неназванном труде) считал, что в каждом народе есть хорошее и дурное, и критиковал Аристотеля за то, что тот делил человечество на греков и варваров и настаивал на сохранении расовой чистоты греков^[7].

1. ↑ Berry A. A Short History of Astronomy — John Murray, 1898.
2. ↑ ^{1 2} Бобынин В. В. Эратосфен // Энциклопедический словарь — СПб.: Брокгауз — Ефрон, 1904. — Т. XLа. — С. 947–949.
3. ↑ Любкер Ф. Eratosthenes // Реальный словарь классических древностей по Любкеру / под ред. Ф. Ф. Зелинский, А. И. Георгиевский, М. С. Куторга и др. — СПб.: Общество классической филологии и педагогики, 1885. — С. 492–493.
4. ↑ Chambers, James T. «Eratosthenes of Cyrene» Dictionary Of World Biography: The Ancient World, January 1998.
5. ↑ ^{1 2} Magill,, Frank Northen. Dictionary of World Biography (неопр.). — Taylor & Francis, 2003. — С. 403. — ISBN 9781579580407.
6. ↑ Edward Gulbekian. The origin and value of the stadion unit used by Eratosthenes in the third century B.C (англ.) // Archive for History of Exact Sciences. — 1987-12-01. — Vol. 37, iss. 4. — P. 359—363. — ISSN 1432-0657. — DOI:10.1007/BF00417008.
7. ↑ Kaldellis,, Anthony. Hellenism in Byzantium: The Transformations of Greek Identity and the Reception of the Classical Tradition (англ.). — Cambridge University Press, 2008. — P. 24—25. — ISBN 9781139468428.

На иностранных языках

• Aujac G. Eratosthène de Cyrène, le pionier de la geographie. — Paris: Édition du CTHS, 2001. — 224p.
• Cameron McPhail. Reconstructing Eratosthenes’ Map of the World: a Study in Source Analysis. A Thesis Submitted for the Degree of Master of Arts at the University of Otago. — Dunedin, New Zealand, 2011.
• Dicks D.R. Eratosthenes // Dictionary of Scientific Biography. — Vol. IV. — New York: C. Schribner’s Sons, 1971. — P. 388—393.
• Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. — 1934. — Bd. 27. — Heft 3. — S. 258—269.
• Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
• Fischer I. Another look at Eratosthenes’ and Posidonius’ determinations of the Earth’s circumference. // Quarterly Journal of the Royal Astronomical Society. — Vol. 16. — 1975. — P. 152—167.
• Fraser P. M. Ptolemaic Alexandria. — Oxford: Clarendon Press, 1972.
• Geus K. Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftgeschichte. — München: Verlag C.H. Beck, 2002. (Münchener Beiträge zur Papyrusforschung und antiken Rechtsgeschichte. — Bd. 92) — X, 412 S.
• Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
• Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
• Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
• Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
• Shcheglov D.A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21-37.
• Shcheglov D.A. Eratosthenes’ Parallel of Rhodes and the History of the System of Climata // Klio. — Bd. 88. — 2006. — P. 351—359.
• Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
• Wolfer E.P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

Решето Эратосфена | Научные парадоксы Wiki

Эта статья является статьёй проекта «Простые числа» Вы можете помочь проекту, развив и дополнив её.

Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа $ n $, который приписывают древнегреческому математику Эратосфену Киренскому.

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
2. Пусть переменная p изначально равна двум — первому простому числу.
3. Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)
4. Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.
5. Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
6. Все не вычеркнутые числа в списке — простые числа.

На практике, алгоритм можно немного улучшить следующим образом. На шаге №3, числа можно вычеркивать, начиная сразу с числа $ p^2 $, потому что все составные числа меньше его уже будут вычеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда $ p^2 $ станет больше, чем $ n $.

Эратосфен.

Эратосфен Киренский / math5school.ru

 

ок. 276–194 до н.э.

 

Поэтому весь круг будет равен 250000 стадиям. Таков метод Эратосфена.

Клеомед

  

Эратосфен Киренский (276 год до н.э. – 194 год до н.э.) – один из самых разносторонних ученых античности, греческий математик, основатель физической географии, астроном и поэт.

Эратосфен родился в Африке, в Кирене, одном из величайших городов античности, располагавшемся на территории современной Ливии. Учился сначала в Александрии, а затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания, а также философов – стоика Аристона и платоника Аркесилая. Вероятно, именно благодаря столь широкому образованию и разнообразию интересов, около 235 года до нашей эры, после смерти Каллимаха, Эратосфен получил от Птолемея III Эвергета приглашение вернуться в Александрию, чтобы стать воспитателем наследника престола, впоследствии Птолемея IV Филопатра, и возглавить Александрийскую библиотеку. Эратосфен принял это предложение и занимал должность библиотекаря около сорока лет, почти до самой смерти.

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда «О шаре и цилиндре». В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия, простого механического прибора, предназначенного для извлечения кубических корней.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп Александрийский, греческий математик и механик эпохи позднего эллинизма, так же живший и работавший в Александрии,  в двух местах своего Собрания называет сочинение Эратосфена «О средних величинах», замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена «Платоник», посвящённом пропорциям, говорит греческий философ Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.  

Отрывок из ещё одного сочинения Эратосфена приводит во «Введении в арифметику» Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел, не превосходящих некоторое целое число, так называемое решето Эратосфена.

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

1. Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
2. Пусть переменная p изначально равна двум – первому простому числу.
3. Считая от p шагами по p, зачеркнуть в списке все числа от 2p до n кратные p (то есть числа 2p, 3p, 4p, …).
4. Найти первое незачеркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
5. Повторять шаги 3 и 4, пока возможно.

Теперь все незачеркнутые числа в списке – простые.

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, «Катастеризмы» – перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт. Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярную сферу (астрономический инструмент, употреблявшийся для определения экваториальных или эклиптических координат небесных светил) изобретение которой приписывается ему.

 

Согласно Энциклопедическому словарю Брокгауза и Ефрона:

Древние астрономы: Эратосфен, за ним Гиппарх и Птоломей пользовались армиллярной сферой и для производства наблюдений, которые хотя и не могли быть весьма точны при сравнительно грубой конструкции этого инструмента, но все же доставили некоторые результаты, ценные даже для современной науки. Употребление армиллярной сферы как инструмента для астрономических наблюдений удержалось весьма долго. Даже Тихо Браге произвел большую часть своих наблюдений над планетами при помощи этого инструмента…

Еще древние китайцы и вавилоняне открыли, что плоскости эклиптики и экватора расположены под некоторым углом друг к другу. В Китае его значение еще примерно в 1100 году до нашей эры установил Чу Конг (23°52′). Во времена Эратосфена угол составлял 23°44′, а он получил значение, равное 22/83 от прямого угла, т. е. 23°51′ (ошибка около 7′).

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода».

Каким методом была получена Аристотелем и его учениками более ранняя оценка – 400000 стадиев, истории науки остается неизвестным. О методе, примененном Эратосфеном, сведения остались; более того, считается, что ему помогал не кто иной, как сам великий Архимед.

Давно было известно, что в городе Сиене на юге Египта в полдень дня летнего солнцестояния, тогда он приходился именно на 19 июня, предметы не отбрасывают тени, т.е. Солнце стоит точно в зените и его лучи падают на Землю вертикально. Согласно легенде, туда прибыл Архимед с помощниками, имея при себе солнечные и песочные часы. Они нашли глубокий колодец и возле него забили в землю вертикальный шест. В день летнего солнцестояния в полдень светило оказалось в зените, т. е. тень шеста исчезла, а лучи Солнца осветили воду на дне колодца. В Александрии, расположенной на одном меридиане с Сиеной, находился Эратосфен с помощниками. Строго в полдень они измерили угол между шестом и падающими солнечными лучами, поскольку там шест отбрасывал короткую тень. Угол оказался равным 7°12′, и осталось провести только математические вычисления.

Поскольку оба города находятся на одном меридиане, дуга земной окружности между ними также соответствует углу 7°12′. Земной окружности соответствует полный угол 360°, т. е. измеренный угол составляет примерно его 1/50 часть. Расстояние между Александрией и Сиеной было измерено, исходя из средней скорости движения верблюжьего каравана и времени, за которое он проходил весь путь, и оказалось равным 5 000 стадиев. Оставалось только решить простую пропорцию 

7°12′ : 360° = 5000 : х

откуда получилась длина земной окружности 250000 стадиев (позднее результат несколько уточнили, получив значение 252000 стадиев). В то время в измерениях применялись как египетский (185 м), так и греческий (157,5 м) стадии. Скорее всего, Эратосфен использовал греческий стадий, поскольку александрийская школа многое позаимствовала из культуры древней Эллады. В таком случае длина земной окружности по меридиану получается примерно 39690 км (по египетской мере примерно 46620 км). По современным измерениям длина окружности составляет около 40000 км, т.е. погрешность результата, полученного Эратосфеном, составляла всего 1%! Источники погрешности заключались как в неточном измерении малого угла падения солнечных лучей в Александрии, так и в оценке расстояния между двумя городами.

После Эратосфена подобные же измерения длины меридиана проводили арабы, но их точность была невелика. И лишь примерно 2000 лет спустя ученые французской академии наук и В.Я. Струве в России достигли в этом деле очень высокой точности и превзошли древнегреческого астронома.

Эратосфеном были рассмотрены и другие астрономические задачи, такие, как оценка размера Солнца и Луны и расстояния до них, солнечные и лунные затмения и продолжительность дня в зависимости от географической широты.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера (Эратосфен понимал, что Гомер был поэтом, поэтому он выступал против трактовки «Илиады» и «Одиссеи» как кладезя географических сведений) до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша. Эратосфен также высказал предположение, что если плыть от Гибралтара на запад, то можно доплыть до Индии (это положение косвенным путем достигло Колумба и подсказало ему идею его путешествия). Эратосфен снабдил свое произведение географической картой мира. Именно Эратосфен ввёл в обращение термин «география».

Эратосфена можно считать также основателем научной хронологии. В своих «Хронографиях», в девяти книгах, он пытался установить даты, связанные с политической и литературной историей Древней Греции. Эратосфен составил список победителей Олимпийских игр, определил дату Троянской войны (1194–1184 годы до н.э.). Рассмотренный им период охватывал время от разрушения Трои (датированного Эратосфеном 1184–1183 годами до н.э.) до смерти Александра (323 год до н.э.). Эратосфен опирался на составленный им список олимпийских победителей и разработал точную хронологическую таблицу, в которой все известные ему политические и культурные события датировал по олимпиадам (то есть, четырехлетними периодами между играми). «Хронографии» Эратосфена стали основой позднейших хронологических исследований Аполлодора Афинского.

В трактате «О древней комедии», где анализировались произведения афинских драматургов, Эратосфен выступил как литературный критик и филолог. Эратосфен написал также поэму «Гермес», повествующую о рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий эпос, «Гесиод», посвящен смерти поэта и каре, постигшей его убийц. Эратосфен написал также трактат «Катастеризмы» – описание созвездий и изложение посвященных им мифов (сохранившееся сочинение под таким названием вызывает сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по истории и философии, которые не сохранились.

Эратосфен был энциклопедически разносторонен. Кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом. Отголоски призвания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатл» – пятиборец или многоборец, – так как прославился он во многих науках – астрономии, географии, математике, успешно трудился в области филологии, поэзии, музыки и философии.

Научные таланты учёного удостоились высокой оценки современника Эратосфена, Архимеда, который посвятил ему свою книгу «Эфодик» («Метод»).

Эратосфен прожил долгую жизнь и несколько десятилетий возглавлял знаменитую Александрийскую библиотеку. В знаменитой библиотеке хранилось более 700000 свитков, которые содержали все сведения о мире, известные людям той эпохи. При содействии своих помощников Эратосфен первым рассортировал свитки по темам. Удалённый в старости от этой должности, Эратосфен впал в крайнюю нищету и, страдая болезнью глаз или даже совсем ослепнув, уморил себя голодом. Он не представлял себе жизни без возможности работать со своими любимыми книгами.

Именем Эратосфена назван кратер на Луне.

Имя Эратосфена носят следующие математические объекты:

• решето Эратосфена.

 

По материалам Википедии и сайтов: elite-astronomy.narod.ru, www.astro-cabinet.ru и www.geografia.ru.

 

Эратосфена решето — это… Что такое Эратосфена решето?



Эратосфена решето

        метод в теории чисел, назван по имени Эратосфена, заключающийся в отсеивании (например, путём зачёркивания) тех целых чисел заданной последовательности а₁, a₂,…, a_N (например, натурального ряда чисел), которые делятся хотя бы на одно из простых чисел, меньших N^α (0 1/₂). Э. р. как теоретический метод исследования в теории чисел был введён в 1920 норвежским математиком В. Вруном.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Эратосфен Киренский
• Эрб Вильгельм Генрих

Смотреть что такое «Эратосфена решето» в других словарях:

• Эратосфена решето — Решето Эратосфена простой алгоритм нахождения всех простых чисел до некоторого целого числа n. Он был создан древнегреческим математиком Эратосфеном. Содержание 1 Пример для n = 20 2 См. также 3 Примеры реализации …   Википедия

• ЭРАТОСФЕНА РЕШЕТО — метод, разработанный Эратосфеном (3 в. до н. э.) и позволяющий отсеивать составные числа из натурального ряда. Сущность Э. р. заключается в следующем. Зачеркивается единица. Число 2 простое. Зачеркиваются все натуральные числа, делящиеся на 2.… …   Математическая энциклопедия

• Решето Аткина — В математике решето Аткина  быстрый современный алгоритм нахождения всех простых чисел до заданного целого числа N. Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде ax²+by²).… …   Википедия

• Решето Сундарама — В математике решето Сундарама детерминированный алгоритм нахождения всех простых чисел до некоторого целого числа . Разработан индийским студентом С. П. Сундарамом в 1934 году. Содержание 1 Описание 2 Обоснование …   Википедия

• Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа n, который приписывают древнегреческому математику Эратосфену Киренскому. Содержание 1 Алгоритм …   Википедия

• Решето Эратосфена — этим именем называют следующий способ получения ряда простых чисел. Из ряда чисел 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14… вычеркивают кратные двум; 4, 6, 8, 10, 12,… кратные трем: 6, 9, 12, 15,… кратные пяти: 10, 15, 20, 25, 30,…… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• БРУНА РЕШЕТО — один из решета методов в элементарной теории чисел, созданный В. Вруном [1]; является развитием Эратосфена решета. Метод Б. р. заключается в следующем: из последовательности натуральных чисел высеиваются (выбрасываются) числа с малыми простыми… …   Математическая энциклопедия

• Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и …   Википедия

• Программируемые алгоритмы —       Служебный список статей, созданный для координации работ по развитию темы.   Данное предупреждение не устанавл …   Википедия

• Тест Миллера (теория чисел) — У этого термина существуют и другие значения, см. Тест Миллера. Не следует путать с «Тестом Миллера Рабина»  вероятностным полиномиальным тестом простоты. Тест Миллера  детерминированный полиномиальный тест простоты. В 1976 году Миллер… …   Википедия

Обсуждение:Решето Эратосфена — Википедия

Материал из Википедии — свободной энциклопедии

Представьте, что по числовой прямой слева направо катится колесо с длиной окружности, равной 2. На ободе колеса имеется радиальный выступ, которым оно «выталкивает» из числовой прямой каждое второе число. Затем по числовой прямой катится похожее колесо с длиной окружности, равной 3. Это колесо убирает каждое третье число и т.д. Все сохранившиеся на числовой прямой числа будут простыми. Можете представить себе ее вид, после того, как по ней проедет n колес с разной длиной окружности? 86.57.146.226 16:01, 22 октября 2018 (UTC)

А почему 4-ка не вычеркивается? Это ж не простое число. Updated: А вот теперь все видно 🙂 UnSigned 20:34, 4 Дек 2004 (UTC) 4-ка вычеркиваеццо! превед медведам

Зачем убрали модель Сундарама? Она изящна и проста для понимания. Siberex 05:48, 28 июля 2007 (UTC)

Иллюстрация весит 200 кб, может, ее лучше уменьшить или убрать(переместить). —CaesarIII 12:25, 25 мая 2008 (UTC)

Удаление параграфа внесенного участником Pro100SOm[править код]

Поддерживю удаление [1]. Удаленный «алгоритм» попросту неверен — после удаления кратных 2-м и 3-м, числа кратные 5-ти вовсе не будут каждым 5-тым числом среди оставшихся. Решето Ератосфена не удаляет сразу, а метит, и только потом удаляет все составные числа за один проход. Удаляя по одному, превращаем массив в список, и прямая адресация становится невозможной.

Вы видимо описывали постепенный алгоритм, но он вынужден сравнивать значения для их удаления, а это чревато ухудшением алгоритмической сложности (но кстати все-же не на квадрат, а к чуть меньше полуторной степени, в линейном варианте). В любом случае в начальном параграфе нужно описывать базисный, простейший вариант алгоритма. При желании можно будет добавить новую главку в статью. WillNess 21:27, 15 октября 2011 (UTC)

Спасибо за ваши исправления. Из новых изменений надо будет взять «историю». Но: безнадежно испорчено главное — описание алгоритма. Пример в статье необходим, чтобы она была понятна — в главном — и детям. Примерам кода в статье не место («не репозитарий»). Иллюстрация должна быть нормально видна. В уменьшенном виде её было плохо видно.

Пока что возвращаю прежнюю версию. — WillNess 18:01, 26 марта 2014 (UTC)

Вернул часть вашего текста из раздела «история», без повторов других статей Википедии, а именно — статьи о Эратосфене. Эта статья посвящена алгоритму, а к статье о его авторе дается отсылка в предисловии. — WillNess 18:34, 26 марта 2014 (UTC)

Тогда верните еще раздел с модификациями метода. — Shishkinii 03:52, 27 марта 2014 (UTC)

Считаю, что примеры реализаций должны быть. Они присутствуют практически во всех статьях по алгоритмам (Быстрая сортировка, Сортировка перемешиванием и т.п.). Добавил ссылку на репозиторий http://rosettacode.org/, где можно посмотреть реализацию на других языках. — Shishkinii 09:25, 27 марта 2014 (UTC)

Не возражаю; главное, сохраните пожалуйста описание алгоритма и псевдокод (и пример тоже). — WillNess 18:37, 27 марта 2014 (UTC)

Эратосфен — это… Что такое Эратосфен?

Эратосфе́н Кире́нский (Ἐρατοσθένης ὁ Κυρηναῖος; 276 год до н. э.—194 год до н. э.) — греческий математик, астроном, географ и поэт. Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки.

Биография

Сын Эглаоса, уроженец Кирены.

Начальное образование Эратосфен получил в Александрии под руководством своего учёного земляка Каллимаха. Другим учителем Эратосфена в Александрии был философ Лизний. Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена; кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом.

Царь Птолемей III Эвергет после смерти Каллимаха вызвал Эратосфена из Афин и поручил ему заведование Александрийской библиотекой. Удалённый в старости от этой должности, Эратосфен впал в крайнюю нищету и, страдая болезнью глаз или даже совсем ослепнув, уморил себя голодом.

Отголоски призвания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатл» — пятиборец.

В честь Эратосфена назван кратер на Луне.

Работы и сочинения Эратосфена

Работы по математике

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда О шаре и цилиндре. В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего Собрания называет сочинение Эратосфена О средних величинах, замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена Платоник, посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во Введении в арифметику Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена).

Работы по астрономии

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, Катастеризмы — перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт.

Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярные сферы.

Эратосфен определил угловое расстояние от экватора до тропика: он нашёл его равным 11/83 от 180°.

Работы по геодезии и географии

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Измерение Земли по Эратосфену

«Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу. Теперь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к северу от Сиены. Эти города лежат на одним меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны. Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5.000 стадиев. Поэтому весь круг будет равен 250.000 стадиям. Таков метод Эратосфена.»

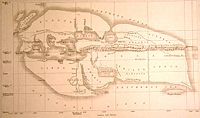Карта Эратосфена

Позднее полученное Эратосфеном число было увеличено до 252000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7,082 км, если египетским (157,5), то 6,287 км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. Что делает выше описанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша.

Другие работы Эратосфена

Эратосфен является основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с историей Эллады, составил список победителей Олимпийских игр.

Сохранились отрывки из сочинения Эратосфена О древней комедии и из двух его поэм; в одной он вкладывает в уста Гермеса рассказ о строении неба, светил и гармонии сфер, в другой передаётся легенда об Эригоне, дочери Икара.

См. также

Издания и переводы

Литература

• Античная география. М., 1953.

На иностранных языках

• Aujac G. Eratosthène de Cyrène, le pionier de la geographie. – Paris: Édition du CTHS, 2001. – 224p.
• Cameron McPhail. Reconstructing Eratosthenes’ Map of the World: a Study in Source Analysis. A Thesis Submitted for the Degree of Master of Arts at the University of Otago. — Dunedin, New Zealand, 2011.
• Dicks D.R. Eratosthenes // Dictionary of Scientific Biography. – Vol. IV. – New York: C. Schribner’s Sons, 1971. – P. 388–393.
• Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. – 1934. – Bd. 27. – Heft 3. – S. 258–269.
• Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
• Fischer I. Another look at Eratosthenes’ and Posidonius’ determinations of the Earth’s circumference. // Quarterly Journal of the Royal Astronomical Society. — Vol. 16. — 1975. — P. 152—167.
• Fraser P. M. Ptolemaic Alexandria. – Oxford: Clarendon Press, 1972.
• Geus K. Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftgeschichte. – München: Verlag C.H. Beck, 2002. (Münchener Beiträge zur Papyrusforschung und antiken Rechtsgeschichte. – Bd. 92) – X, 412 S.
• Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
• Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
• Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
• Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
• Shcheglov D.A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21–37.
• Shcheglov D.A. Eratosthenes’ Parallel of Rhodes and the History of the System of Climata // Klio. — Bd. 88. — 2006. — P. 351–359.
• Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
• Wolfer E.P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

Ссылки

Эратосфен — это… Что такое Эратосфен?

Эратосфе́н Кире́нский (Ἐρατοσθένης ὁ Κυρηναῖος; 276 год до н. э.—194 год до н. э.) — греческий математик, астроном, географ и поэт. Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки.

Биография

Сын Эглаоса, уроженец Кирены.

Начальное образование Эратосфен получил в Александрии под руководством своего учёного земляка Каллимаха. Другим учителем Эратосфена в Александрии был философ Лизний. Перебравшись затем в Афины, он так тесно сблизился со школой Платона, что обыкновенно называл себя платоником. Результатом изучения наук в этих двух центрах была энциклопедическая эрудиция Эратосфена; кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом.

Царь Птолемей III Эвергет после смерти Каллимаха вызвал Эратосфена из Афин и поручил ему заведование Александрийской библиотекой. Удалённый в старости от этой должности, Эратосфен впал в крайнюю нищету и, страдая болезнью глаз или даже совсем ослепнув, уморил себя голодом.

Отголоски призвания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатл» — пятиборец.

В честь Эратосфена назван кратер на Луне.

Работы и сочинения Эратосфена

Работы по математике

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда О шаре и цилиндре. В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего Собрания называет сочинение Эратосфена О средних величинах, замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена Платоник, посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во Введении в арифметику Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена).

Работы по астрономии

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, Катастеризмы — перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт.

Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярные сферы.

Эратосфен определил угловое расстояние от экватора до тропика: он нашёл его равным 11/83 от 180°.

Работы по геодезии и географии

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Измерение Земли по Эратосфену

«Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу. Теперь он говорит, что Сиена лежит на круге летнего тропика. И если бы летнее солнцестояние в созвездии Рака происходило ровно в полдень, то солнечные часы в этот момент времени с необходимостью не отбрасывали бы тени, поскольку Солнце находилось бы точно в зените; дела и в самом деле обстоят таким образом в [полосе шириной] в 300 стадиев. А в Александрии в этот же час солнечные часы отбрасывают тень, поскольку этот город лежит к северу от Сиены. Эти города лежат на одним меридиане и на большом круге. На солнечных часах в Александрии проведём дугу, проходящую через конец тени гномона и основание гномона, и этот отрезок дуги произведёт большой круг на чаше, поскольку чаша солнечных часов расположена на большом круге. Далее, вообразим две прямые, опускающиеся под Землю от каждого гномона и встречающиеся в центре Земли. Солнечные часы в Сиене находятся отвесно под Солнцем, и воображаемая прямая проходит от Солнца через вершину гномона солнечных часов, производя одну прямую от Солнца до центра Земли. Вообразим ещё одну прямую, проведённую от конца тени гномона через вершину гномона к Солнцу на чаше в Александрии; и она будет параллельна уже названной прямой, поскольку уже сказано, что прямые от разных частей Солнца к разным частям Земли параллельны. Прямая, проведённая от центра Земли к гномону в Александрии, образует с этими параллельными равные накрестлежащие углы. Один из них — с вершиной в центре Земли, при встрече прямых, проведённых от солнечных часов к центру Земли, а другой — с вершиной на конце гномона в Александрии, при встрече с прямой, идущей от этого конца к концу его же тени от Солнца, там где эти прямые встречаются наверху. Первый угол опирается на дугу от конца тени гномона до его основания, а второй — на дугу с центром в центре Земли, проведённую от Сиены до Александрии. Эти дуги подобны между собой, поскольку на них опираются равные углы. И какое отношение имеет дуга на чаше к своему кругу, такое же отношение имеет и дуга от Сиены до Александрии [к своему кругу]. Но найдено, что на чаше она составляет пятидесятую часть своего круга. Поэтому и расстояние от Сиены до Александрии с необходимостью будет составлять пятидесятую часть большого круга Земли. Но оно равно 5.000 стадиев. Поэтому весь круг будет равен 250.000 стадиям. Таков метод Эратосфена.»

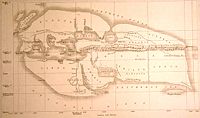Карта Эратосфена

Позднее полученное Эратосфеном число было увеличено до 252000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7,082 км, если египетским (157,5), то 6,287 км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. Что делает выше описанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша.

Другие работы Эратосфена

Эратосфен является основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с историей Эллады, составил список победителей Олимпийских игр.

Сохранились отрывки из сочинения Эратосфена О древней комедии и из двух его поэм; в одной он вкладывает в уста Гермеса рассказ о строении неба, светил и гармонии сфер, в другой передаётся легенда об Эригоне, дочери Икара.

См. также

Издания и переводы

Литература

• Античная география. М., 1953.

На иностранных языках

• Aujac G. Eratosthène de Cyrène, le pionier de la geographie. – Paris: Édition du CTHS, 2001. – 224p.
• Cameron McPhail. Reconstructing Eratosthenes’ Map of the World: a Study in Source Analysis. A Thesis Submitted for the Degree of Master of Arts at the University of Otago. — Dunedin, New Zealand, 2011.
• Dicks D.R. Eratosthenes // Dictionary of Scientific Biography. – Vol. IV. – New York: C. Schribner’s Sons, 1971. – P. 388–393.
• Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. – 1934. – Bd. 27. – Heft 3. – S. 258–269.
• Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
• Fischer I. Another look at Eratosthenes’ and Posidonius’ determinations of the Earth’s circumference. // Quarterly Journal of the Royal Astronomical Society. — Vol. 16. — 1975. — P. 152—167.
• Fraser P. M. Ptolemaic Alexandria. – Oxford: Clarendon Press, 1972.
• Geus K. Eratosthenes von Kyrene. Studien zur hellenistischen Kultur- und Wissenschaftgeschichte. – München: Verlag C.H. Beck, 2002. (Münchener Beiträge zur Papyrusforschung und antiken Rechtsgeschichte. – Bd. 92) – X, 412 S.
• Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
• Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
• Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
• Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
• Shcheglov D.A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21–37.
• Shcheglov D.A. Eratosthenes’ Parallel of Rhodes and the History of the System of Climata // Klio. — Bd. 88. — 2006. — P. 351–359.
• Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
• Wolfer E.P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

Ссылки