метод сита Эратосфена, для вычисления простого числа
script1adsense2code
script1adsense3code
Список Python: Упражнение — 34 с решением
Напишите программу на Python, используя метод Sieve of Eratosthenes для вычисления простых чисел до заданного числа.
Примечание. В математике сито Эратосфена (древнегреческое: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous), одно из множества сит с простыми числами, представляет собой простой древний алгоритм поиска всех простых чисел вплоть до любого заданного предела.
Из Википедии Сито Эратосфена: шаги алгоритма для простых чисел ниже 121 (включая оптимизацию, начиная с простого числа).
Пример решения : —
Код Python:
def prime_eratosthenes(n):
prime_list = []
for i in range(2, n+1):
if i not in prime_list:
print (i)
for j in range(i*i, n+1, i):
prime_list. append(j)
print(prime_eratosthenes(100))';
append(j)
print(prime_eratosthenes(100))';
Пример вывода:
2 3 5 7 11 ------- 79 83 89 97 Никто
Блок — схема:
Редактор кода Python:
Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.
Предыдущий: Напишите программу на Python для генерации всех подсписков списка.
Далее: Напишите программу на Python для создания списка путем конкатенации данного списка, диапазон которого варьируется от 1 до n.
Опыт Эратосфена для вычисления размеров Земли
Размеры Земли были впервые определены более двух тысяч лет назад греческим учёным Эратосфеном.
Древнегреческий астроном и географ Эратосфен жил в Александрии, там и проводил свои наблюдения. Как-то он узнал, что в месте, находящимся на расстоянии 5 000 стадий (одна греческая стадия примерно равна 157,5 м) от Александрии в день летнего солнцестояния Солнце освещает дно колодца.
Учитывая то, что по наблюдениям самого Эратосфена в этот день лучи Солнца падали под углом 7,2
Выполним чертёж к этой задаче, учитывая, то что солнечные лучи падают на Землю параллельно, так как Солнце находится по сравнению с размерами Земли на очень большом расстоянии, (на чертеже они изображены оранжевым цветом)
1) Рассчитаем расстояние от А до В:
5 000 стадий · 157,5 м = 787 500 м
2) Так как центральному углу АОВ = 7,2о соответствует дуга
АВ = 787 500 м, то составим пропорцию:
360о / 7,2о = длина всей окружности / 787 500 м.
Решив эту пропорцию, получаем длину всей окружности
360о · 787500 м / 7,2о = 39 375 000 м.
3) Помня о том, что длина всей окружности = 2∏R, где R – радиус окружности, находим
R = 39 375 000 м / 2∏ = 6269904,4586 м.
Сравним полученные данные с размерами Земли, рассчитанными другими, более современными способами, где минимальный радиус Земли у полюсов 6 356 863 м, максимальный радиус на экваторе 6 378 245 м, а средний радиус Земли – 6 371 302 м.
Рассчитаем погрешность вычисления в опыте Эратосфена
(6 371 302 м – 6 269 904 м) / 6 371 302 м = 0,0159 = 1,59 % .
Это очень маленькая погрешность для данного способа определения размеров Земли. А какие способы определения размеров Земли и других небесных тел Вы знаете?
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Измеритель Земли – Наука – Коммерсантъ
О том, кто, когда и как измерил Землю, мы знаем из дошедших до нас трудов древнегреческого ученого Клеомеда. Клеомед был современником Христа, то есть жил спустя почти три века после Эратосфена, но насчет точности даты первого измерения земного шара можно не беспокоиться. Иного дня для измерения нашей планеты не могло быть, да и метод ее измерения в то время мог быть только одним — по длине тени гномона (вертикального шеста солнечных часов) в полдень 19 июня. Именно этот день в III веке до н. э. был днем летнего солнцестояния.
Ход мысли Эратосфена Клеомед восстановил по своему разумению, но и тут было трудно ошибиться, потому что это была единственно возможная логика ученого того времени. Прежде всего, для Эратосфена, который занимал пост хранителя Александрийской библиотеки, главного научного учреждения Древней Греции, шарообразность Земли была не предположением, а фактом. Это экспериментально доказали греческие ученые еще за сто лет до Эратосфена.
Эратосфен исходил из двух допущений. Во-первых, он считал, что Александрия в дельте Нила, где он проводил измерения, и город Сиен (Асуан) в верховьях Нила находятся на одном меридиане. Во-вторых — что Сиен находится под тропиком Рака, то есть в полдень дня летнего солнцестояния вертикальный шест в Сиене не отбрасывает вообще никакой тени, он строго перпендикулярен Солнцу. Оставалось измерить длину тени вертикального шеста (гномона) в солнечных часах в Александрии в полдень 19 июня, что и сделал Эратосфен.
По длине тени можно определить угол, под которым шест направлен к Солнцу в зените. Угол оказался равен 1/50 от всего круга солнечных часов (360 градусов). Расстояние от Александрии до Сиена было известно — 5000 стадиев. Дальше все сводилось к геометрии, в которой греки были сильны. Если дуга окружности Земли в 1/50 ее длины равна 5 тыс. стадиев, то вся окружность Земли равна 250 тыс. стадиев (43 тыс. км). А радиус Земли у Эратосфена получился равным 6287 км в наших мерах длины.
Современные измерения дают окружность нашей планеты по меридиану 40 008 км, радиус — 6371 км. Точность измерений Эратосфена была почти абсолютная. Небольшие расхождения связаны с погрешностями его допущений. Александрия и Асуан лежат не на одном меридиане, Асуан на 2,5 градуса западнее. Кроме того, Асуан лежит все-таки не под тропиком Рака, а на полградуса севернее.
Сергей Петухов
XPOHOCВВЕДЕНИЕ В ПРОЕКТФОРУМ ХРОНОСАНОВОСТИ ХРОНОСАБИБЛИОТЕКА ХРОНОСАИСТОРИЧЕСКИЕ ИСТОЧНИКИБИОГРАФИЧЕСКИЙ УКАЗАТЕЛЬПРЕДМЕТНЫЙ УКАЗАТЕЛЬГЕНЕАЛОГИЧЕСКИЕ ТАБЛИЦЫСТРАНЫ И ГОСУДАРСТВАЭТНОНИМЫРЕЛИГИИ МИРАСТАТЬИ НА ИСТОРИЧЕСКИЕ ТЕМЫМЕТОДИКА ПРЕПОДАВАНИЯКАРТА САЙТААВТОРЫ ХРОНОСАРодственные проекты:РУМЯНЦЕВСКИЙ МУЗЕЙДОКУМЕНТЫ XX ВЕКАИСТОРИЧЕСКАЯ ГЕОГРАФИЯПРАВИТЕЛИ МИРАВОЙНА 1812 ГОДАПЕРВАЯ МИРОВАЯСЛАВЯНСТВОЭТНОЦИКЛОПЕДИЯАПСУАРАРУССКОЕ ПОЛЕ |
ЭратосфенЭратосфен (ок. Эратосфен родился в Африке, в
Кирене. Учился сначала в Александрии, а
затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания,
а также философов – стоика Аристона и платоника Аркесилая. Вероятно, именно
благодаря столь широкому образованию и разнообразию интересов ок. 245 до
н.э. Эратосфен получил от Птолемея III Эвергета приглашение вернуться в
Александрию, чтобы стать воспитателем наследника престола и возглавить
Александрийскую библиотеку. Сочинения Эратосфена не сохранились, мы имеем от них лишь фрагменты.
Трактаты Эратосфена Удвоение куба и О среднем были посвящены решению
геометрических и арифметических задач, в Платонике он обращается к
математическим и музыкальным основам платоновской философии. Самым
знаменитым математическим открытием Эратосфена стало т.н. «решето», с
помощью которого находятся простые числа. Эратосфен является
основоположником научной географии. В его Географии в 3 книгах содержалась
история географических открытий, а также рассматривался ряд физических и
математических проблем, связанных с географией, включая указание на
сферическую форму Земли и описание ее поверхности. Однако самым известным достижением Эратосфена в области географии был изобретенный им способ измерения величины земного шара, изложению которого был посвящен трактат Об измерении Земли. Здесь было описано впервые отмеченное в науке одновременное наблюдение и проведение измерений в столь отдаленных точках, как Александрия и Сиена (совр. Асуан, Египет). Хотя остается спорным, получилось ли у Эратосфена в итоге 250 000 стадий (согласно Клеомеду) или 252 000 (по сообщению Страбона и Теона Смирнского), в любом случае этот результат замечателен – диаметр Земли оказывается всего лишь на 80 км меньше, чем фактический полярный диаметр. В этой же работе были рассмотрены и астрономические задачи, такие, как размер Солнца и Луны и расстояния до них, солнечные и лунные затмения и продолжительность дня в зависимости от географической широты. Эратосфена можно считать также основателем научной хронологии. Использованы материалы энциклопедии «Мир вокруг нас». Литература:Дитмар А.
|
Эратосфен Киренский / math5school.ru
ок. 276–194 до н.э.
Поэтому весь круг будет равен 250000 стадиям. Таков метод Эратосфена.
Клеомед
Эратосфен Киренский (276 год до н.э. – 194 год до н.э.) – один из самых разносторонних ученых античности, греческий математик, основатель физической географии, астроном и поэт.
Эратосфен родился в Африке, в Кирене, одном из величайших городов античности, располагавшемся на территории современной Ливии. Учился сначала в Александрии, а затем в Афинах у известных наставников, поэта Каллимаха, грамматика Лисания, а также философов – стоика Аристона и платоника Аркесилая. Вероятно, именно благодаря столь широкому образованию и разнообразию интересов, около 235 года до нашей эры, после смерти Каллимаха, Эратосфен получил от Птолемея III Эвергета приглашение вернуться в Александрию, чтобы стать воспитателем наследника престола, впоследствии Птолемея IV Филопатра, и возглавить Александрийскую библиотеку. Эратосфен принял это предложение и занимал должность библиотекаря около сорока лет, почти до самой смерти.
Эратосфен принял это предложение и занимал должность библиотекаря около сорока лет, почти до самой смерти.
Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда «О шаре и цилиндре». В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия, простого механического прибора, предназначенного для извлечения кубических корней.
Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп Александрийский, греческий математик и механик эпохи позднего эллинизма, так же живший и работавший в Александрии, в двух местах своего Собрания называет сочинение Эратосфена «О средних величинах», замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.
О сочинении Эратосфена «Платоник», посвящённом пропорциям, говорит греческий философ Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.
Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.
Отрывок из ещё одного сочинения Эратосфена приводит во «Введении в арифметику» Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел, не превосходящих некоторое целое число, так называемое решето Эратосфена.
Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум – первому простому числу.
- Считая от p шагами по p, зачеркнуть в списке все числа от 2p до n кратные p (то есть числа 2p, 3p, 4p, …).

- Найти первое незачеркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4, пока возможно.
Теперь все незачеркнутые числа в списке – простые.
Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, «Катастеризмы» – перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт. Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярную сферу (астрономический инструмент, употреблявшийся для определения экваториальных или эклиптических координат небесных светил) изобретение которой приписывается ему.
Согласно Энциклопедическому словарю Брокгауза и Ефрона:
Древние астрономы: Эратосфен, за ним Гиппарх и Птоломей пользовались армиллярной сферой и для производства наблюдений, которые хотя и не могли быть весьма точны при сравнительно грубой конструкции этого инструмента, но все же доставили некоторые результаты, ценные даже для современной науки.
Употребление армиллярной сферы как инструмента для астрономических наблюдений удержалось весьма долго. Даже Тихо Браге произвел большую часть своих наблюдений над планетами при помощи этого инструмента…
Еще древние китайцы и вавилоняне открыли, что плоскости эклиптики и экватора расположены под некоторым углом друг к другу. В Китае его значение еще примерно в 1100 году до нашей эры установил Чу Конг (23°52′). Во времена Эратосфена угол составлял 23°44′, а он получил значение, равное 22/83 от прямого угла, т. е. 23°51′ (ошибка около 7′).
В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода».
Каким методом была получена Аристотелем и его учениками более ранняя оценка – 400000 стадиев, истории науки остается неизвестным. О методе, примененном Эратосфеном, сведения остались; более того, считается, что ему помогал не кто иной, как сам великий Архимед.
Давно было известно, что в городе Сиене на юге Египта в полдень дня летнего солнцестояния, тогда он приходился именно на 19 июня, предметы не отбрасывают тени, т.е. Солнце стоит точно в зените и его лучи падают на Землю вертикально. Согласно легенде, туда прибыл Архимед с помощниками, имея при себе солнечные и песочные часы. Они нашли глубокий колодец и возле него забили в землю вертикальный шест. В день летнего солнцестояния в полдень светило оказалось в зените, т. е. тень шеста исчезла, а лучи Солнца осветили воду на дне колодца. В Александрии, расположенной на одном меридиане с Сиеной, находился Эратосфен с помощниками. Строго в полдень они измерили угол между шестом и падающими солнечными лучами, поскольку там шест отбрасывал короткую тень. Угол оказался равным 7°12′, и осталось провести только математические вычисления.
Поскольку оба города находятся на одном меридиане, дуга земной окружности между ними также соответствует углу 7°12′. Земной окружности соответствует полный угол 360°, т. е. измеренный угол составляет примерно его 1/50 часть. Расстояние между Александрией и Сиеной было измерено, исходя из средней скорости движения верблюжьего каравана и времени, за которое он проходил весь путь, и оказалось равным 5 000 стадиев. Оставалось только решить простую пропорцию
е. измеренный угол составляет примерно его 1/50 часть. Расстояние между Александрией и Сиеной было измерено, исходя из средней скорости движения верблюжьего каравана и времени, за которое он проходил весь путь, и оказалось равным 5 000 стадиев. Оставалось только решить простую пропорцию
7°12′ : 360° = 5000 : х
откуда получилась длина земной окружности 250000 стадиев (позднее результат несколько уточнили, получив значение 252000 стадиев). В то время в измерениях применялись как египетский (185 м), так и греческий (157,5 м) стадии. Скорее всего, Эратосфен использовал греческий стадий, поскольку александрийская школа многое позаимствовала из культуры древней Эллады. В таком случае длина земной окружности по меридиану получается примерно 39690 км (по египетской мере примерно 46620 км). По современным измерениям длина окружности составляет около 40000 км, т.е. погрешность результата, полученного Эратосфеном, составляла всего 1%! Источники погрешности заключались как в неточном измерении малого угла падения солнечных лучей в Александрии, так и в оценке расстояния между двумя городами.
После Эратосфена подобные же измерения длины меридиана проводили арабы, но их точность была невелика. И лишь примерно 2000 лет спустя ученые французской академии наук и В.Я. Струве в России достигли в этом деле очень высокой точности и превзошли древнегреческого астронома.
Эратосфеном были рассмотрены и другие астрономические задачи, такие, как оценка размера Солнца и Луны и расстояния до них, солнечные и лунные затмения и продолжительность дня в зависимости от географической широты.
В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера (Эратосфен понимал, что Гомер был поэтом, поэтому он выступал против трактовки «Илиады» и «Одиссеи» как кладезя географических сведений) до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша. Эратосфен также высказал предположение, что если плыть от Гибралтара на запад, то можно доплыть до Индии (это положение косвенным путем достигло Колумба и подсказало ему идею его путешествия). Эратосфен снабдил свое произведение географической картой мира. Именно Эратосфен ввёл в обращение термин «география».
Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша. Эратосфен также высказал предположение, что если плыть от Гибралтара на запад, то можно доплыть до Индии (это положение косвенным путем достигло Колумба и подсказало ему идею его путешествия). Эратосфен снабдил свое произведение географической картой мира. Именно Эратосфен ввёл в обращение термин «география».
Эратосфена можно считать также основателем научной хронологии. В своих «Хронографиях», в девяти книгах, он пытался установить даты, связанные с политической и литературной историей Древней Греции. Эратосфен составил список победителей Олимпийских игр, определил дату Троянской войны (1194–1184 годы до н.э.). Рассмотренный им период охватывал время от разрушения Трои (датированного Эратосфеном 1184–1183 годами до н.э.) до смерти Александра (323 год до н.э.). Эратосфен опирался на составленный им список олимпийских победителей и разработал точную хронологическую таблицу, в которой все известные ему политические и культурные события датировал по олимпиадам (то есть, четырехлетними периодами между играми). «Хронографии» Эратосфена стали основой позднейших хронологических исследований Аполлодора Афинского.
«Хронографии» Эратосфена стали основой позднейших хронологических исследований Аполлодора Афинского.
В трактате «О древней комедии», где анализировались произведения афинских драматургов, Эратосфен выступил как литературный критик и филолог. Эратосфен написал также поэму «Гермес», повествующую о рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий эпос, «Гесиод», посвящен смерти поэта и каре, постигшей его убийц. Эратосфен написал также трактат «Катастеризмы» – описание созвездий и изложение посвященных им мифов (сохранившееся сочинение под таким названием вызывает сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по истории и философии, которые не сохранились.
Эратосфен был энциклопедически разносторонен. Кроме сочинений по математическим наукам, он писал ещё трактаты «о добре и зле», о комедии и др. Из всех своих сочинений Эратосфен придавал особенное значение литературным и грамматическим, как это можно заключить из того, что он любил называть себя филологом. Отголоски призвания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатл» – пятиборец или многоборец, – так как прославился он во многих науках – астрономии, географии, математике, успешно трудился в области филологии, поэзии, музыки и философии.
Отголоски призвания обширной учёности Эратосфена звучат и в прозвищах, которые он получил от современников. Называя его «бета», они, по предположению многих исследователей, желали выразить свой взгляд на него, как на второго Платона, или вообще как на учёного, который только потому занимает второе место, что первое должно быть удержано за предками. Другим прозвищем Эратосфена было «пентатл» – пятиборец или многоборец, – так как прославился он во многих науках – астрономии, географии, математике, успешно трудился в области филологии, поэзии, музыки и философии.
Научные таланты учёного удостоились высокой оценки современника Эратосфена, Архимеда, который посвятил ему свою книгу «Эфодик» («Метод»).
Эратосфен прожил долгую жизнь и несколько десятилетий возглавлял знаменитую Александрийскую библиотеку. В знаменитой библиотеке хранилось более 700000 свитков, которые содержали все сведения о мире, известные людям той эпохи. При содействии своих помощников Эратосфен первым рассортировал свитки по темам. Удалённый в старости от этой должности, Эратосфен впал в крайнюю нищету и, страдая болезнью глаз или даже совсем ослепнув, уморил себя голодом. Он не представлял себе жизни без возможности работать со своими любимыми книгами.
Удалённый в старости от этой должности, Эратосфен впал в крайнюю нищету и, страдая болезнью глаз или даже совсем ослепнув, уморил себя голодом. Он не представлял себе жизни без возможности работать со своими любимыми книгами.
Именем Эратосфена назван кратер на Луне.
Имя Эратосфена носят следующие математические объекты:
- решето Эратосфена.
По материалам Википедии и сайтов: elite-astronomy.narod.ru, www.astro-cabinet.ru и www.geografia.ru.
Учение о Земле как о шаре. Определение радиуса Земли по методу Эратосфена
Оглавление
Введение……………………………………………………………………………3
1 Учение о Земле как о шаре. Определение радиуса Земли по методу Эратосфена…………………………………………………………………………5
2 Создание первых карт…………………………………………………………..7
3 Градусные измерения……………………………………………………………9
Заключение…………………………………………………………………………11
Список литературы………………………………………………………………. ..12
..12
Введение
Представление о фигуре и размерах Земли создавалось постепенно, на основе наблюдений, измерений и расчетов. Уже в VII в до н.э. древнегреческие ученые высказали предположение о шарообразности Земли. В IV веке до н.э. Аристотель собрал уже имеющиеся доказательства шарообразности Земли, дополнил и обосновал их. Эратосфен Киренский во II веке до н.э. определил близкую к действительной длину большого круга (40 000 км) и одного градуса меридиана (110,6 м − действительная 111,2 м.). В настоящее время окружность Земли можно измерить с помощью спутников и другой измерительной аппаратуры. Однако более 2000 лет назад не имея современных измерительных приборов, Эратосфен вычислил размеры Земли, не покидая стен библиотеки, где работал. Эратосфен был греческим ученым, который жил в египетском городе Александрия с 276 года по 196 год до нашей эры. Эратосфен заведовал библиотекой, в которой хранилось около 100 тысяч книг, написанных на свитках папируса. Он изучал историю, философию, естественные науки, был театральным критиком. Эратосфена особенно прославили труды по математике, астрономии, географии, а так же у него есть успешные труды в философии, музыке, филологии и поэзии, за которые, современники дали ему прозвище Пентатл, то есть Многоборец. Эратосфен считается основателем научной географии [1].
Эратосфена особенно прославили труды по математике, астрономии, географии, а так же у него есть успешные труды в философии, музыке, филологии и поэзии, за которые, современники дали ему прозвище Пентатл, то есть Многоборец. Эратосфен считается основателем научной географии [1].
Известно, что от проезжих путешественников Эратосфен услышал о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко к югу от Александрии. Путешественники рассказали, что в полдень первого дня лета − в самый тельный день в году − в Сиене исчезали тени. Солнце в это время стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно вглядываясь в воду водоема или в глубокие колодцы, можно было рассмотреть отражение Солнца на дне.
Эратосфен съездил в Сиену и сам убедился в этом. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены здания, где он работал, продолжали отбрасывать тень на землю. Основываясь на таком простом наблюдении, он смог вычислить окружность Земли [2].
В данной работе будет подробно рассмотрен метод Эратосфена по определению формы и размеров Земли, определение радиуса Земли по методу Эратосфена, его вклад в создание первых карт, а также геометрические основы градусных измерений.
1 Учение о Земле как о шаре. Определение радиуса Земли по методу Эратосфена
Ученый Аристотель полагал, что Земля имеет шарообразную форму. В качестве доказательства он приводил форму земной тени во время лунных затмений. Круглую форму тени может отбрасывать только шар, освещаемый Солнцем с любой стороны. Доказать шарообразность Земли математическим способом удалось египетскому математику и географу Эратосфену. При этом Эратосфен использовал принцип «градусных измерений», который применялся геодезистами до конца XX века [1].
В 240-ом году 19 июня он в Александрии использовал чашу с длинной иглой, которая в то время называлась «скафис», с помощью которой стало возможно определить угол, под которым Солнце располагается на небе. Эратосфен установил, что в городе Сиене (в настоящее время этот город называется Асуан) Солнце в полдень освещало дно самых глубоких колодцев, а в городе Александрия его лучи отклонялись от вертикали на 7 градусов 12 минут (1/50 окружности). Такой итог привел к выводу: Сиена отстоит от Александрии на 1/50 окружности. Расстояние между исследуемыми городами составило 5,000 стадий, из чего следует, что окружность Земли – 250 000 стадий, а радиус составляет 39 тысяч 790 стадий. Каким именно стадием руководствовался Киренский не известно, но по тем временам, если греческим в 178 метров, то радиус Земли – 7 082 км, а если египетским, то 6 287 км. На сегодняшний день радиус Земли равен 6 371 км. Несмотря на то, что исходные данные были недостаточно точные, Эратосфен вычислил длину окружности экваториальной области Земли, а затем и радиус [3]. То есть, методика определения радиуса Земли была предложена правильная. На рисунке 1 показан метод Эратосфена по определению радиуса Земли.
Эратосфен установил, что в городе Сиене (в настоящее время этот город называется Асуан) Солнце в полдень освещало дно самых глубоких колодцев, а в городе Александрия его лучи отклонялись от вертикали на 7 градусов 12 минут (1/50 окружности). Такой итог привел к выводу: Сиена отстоит от Александрии на 1/50 окружности. Расстояние между исследуемыми городами составило 5,000 стадий, из чего следует, что окружность Земли – 250 000 стадий, а радиус составляет 39 тысяч 790 стадий. Каким именно стадием руководствовался Киренский не известно, но по тем временам, если греческим в 178 метров, то радиус Земли – 7 082 км, а если египетским, то 6 287 км. На сегодняшний день радиус Земли равен 6 371 км. Несмотря на то, что исходные данные были недостаточно точные, Эратосфен вычислил длину окружности экваториальной области Земли, а затем и радиус [3]. То есть, методика определения радиуса Земли была предложена правильная. На рисунке 1 показан метод Эратосфена по определению радиуса Земли.
Математик оптимизировал решето Эратосфена, чтобы искать простые числа с меньшим расходом памяти
38-летний перуанский математик Харальд Хельфготт три года назад доказал тернарную гипотезу Гольдбаха, а сейчас сумел оптимизировать компьютерный алгоритм для расчёта решета Эратосфена. Фото: Matías Loewy
Фото: Matías Loewy
В III в. до нашей эры древнегреческий математик, астроном, географ, филолог и поэт Эратосфен Киренский придумал гениальный способ поиска простых чисел. Очень эффективный и быстрый метод, который используется до сих пор, получил название решето Эратосфена.
Суть понятна из названия. Решето Эратосфена означает поиск простых чисел методом исключения. Берём список чисел, исключаем из него все составные числа — и получаем список простых чисел, словно просеяв список через решето.
В виде алгоритма решето Эратосфена формализуется следующим образом:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум — первому простому числу.
- Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).
- Найти первое незачёркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4, пока возможно.

После выполнения этой операции незачёркнутыми в списке остаются только простые числа.
Очевидно, что компьютерная реализация решета Эратосфена требует большого объёма памяти. Так оно и было, пока своё решение проблемы не предложил 38-летний перуанский математик Харальд Хельфготт.
Харальд Хельфготт
Харальд Хельфготт привлёк всеобщее внимание в 2013 году, когда ему удалось решить тернарную проблему Гольдбаха. Тернарная проблема Гольдбаха — более слабое утверждение основной бинарной проблемы Гольдбаха — одной из самых известных открытых математических проблем, которая до сих пор остаётся нерешённой. Это утверждение о том, что любое чётное число, начиная с 4, можно представить в виде суммы двух простых чисел.
Тернарная гипотеза Гольдбаха напрямую следует из бинарной гипотезы. Тернарная гипотеза утверждает, что любое нечётное число, начиная с 7, можно представить в виде суммы трёх простых чисел. Эта гипотеза была доказана для чисел от 1 до N Иваном Виноградовым в 1937 году, за что он получил Сталинскую премию и звание Героя Социалистического Труда. Советские математики думали, что Виноградов доказал гипотезу для всех чисел, но на самом деле позже выяснилось, что граница N в работе Виноградова составляет всего лишь 106 846 168.
Советские математики думали, что Виноградов доказал гипотезу для всех чисел, но на самом деле позже выяснилось, что граница N в работе Виноградова составляет всего лишь 106 846 168.
Перуанский математик Харальд Хельфготт сумел окончательно доказать эту гипотезу — уже действительно для всех чисел. Его доказательство опубликовано в журнале Science 24 мая 2013 года (doi: 10.1126/science.340.6135.913). Оно подтверждено другими квалифицированными математиками, способными понять доказательство, например, Теренсом Тао.
Сейчас талантливый математик Харальд Хельфготт, чьи предки происходят из Черновицкой области, направил свои усилия на ещё одну важную задачу современной науки — оптимизацию поиска простых чисел. Ему удалось предложить улучшенный вариант решётки Эратосфена — метода поиска простых чисел, сформулированного примерно в 240 г до н.э. Новый вариант в компьютерной реализации требует меньше оперативной памяти, что означает меньший объём подкачки страниц из виртуальной памяти — следовательно, процесс существенно ускоряется.
«Как и многие другие 10-летние дети, я изучал решето Эратосфена в начальной школе», — говорит Харальд Хельфготт, который сейчас работает в Национальном центре научных исследований Франции и Гёттингенском университете.
Харальд признался, что начал думать «даже слишком много» о решётке Эратосфена ещё во время работы над тернарной проблемой Гольдбаха. В частности, об объёме данных в памяти. Он понимал, что именно ограниченный объём памяти является бутылочным горлышком, которое снижает максимально возможную скорость вычислений в данном случае.
Специалисты говорят, что эффективность алгоритма определяется двумя факторами:
- Количество операций на один бит входных данных.
- Количество бит в памяти во время выполнения инструкций.
По количеству операций на бит решётка Эратосфена относительно эффективна. Оно растёт пропорционально размеру интервала от 1 до N. А вот если посмотреть, что нужно хранить в памяти для каждого шага алгоритма на больших интервалах, то ни о какой эффективности не идёт и речи.
Оптимизация решета Эратосфена
Для оптимизации компьютерного алгоритма решета Эратосфена математик применил вариант того же метода, который использовал при работе над тернарной проблемой Гольдбаха. Речь идёт о круговом методе Харди-Литтлвуда. Том самом методе, который в начале прошлого века великолепно усовершенствовал математик Иван Виноградов, в результате чего почти сумел доказать гипотезу Гольдбаха.
Согласно методу Харди-Литтлвуда, решение задачи задаётся интегралом по единичной окружности от некоторого ряда. Этот интеграл разбивается на два, один из которых оценивается, а про другой доказывается его относительная малость. Составляющие первую сумму называются большими дугами, а вторую — малыми.
Сам математик объясняет метод следующим образом:
«Анализ количества решений производится, по сути, посредством преобразования Фурье. Представьте себе, что простые числа — это звуки на некоторой записи, скажем, в моменты времени 2, 3, 5, 7, 11 и так далее микросекунд.
После преобразования у вас получается своего рода шум, в котором вы пытаетесь услышать какие-то ноты. Среди них есть такие, которые слышны достаточно хорошо, — это и есть большие дуги. А есть частоты, которые просто являются шумовыми фрагментами, — это малые дуги. Весь метод распадается на две части — выделение нот и доказательство того, что остальное на самом деле шум. За первую часть метода отвечают оценки на большие дуги, за второй — на малые».
На основе метода Харди-Литтлвуда учёный разработал подход, который позволяет вместо объёма оперативной памяти N использовать объём памяти ∛N (кубический корень из N).
Образно говоря, вместо 1 гигабайта памяти, т.е. 109 байт (не путать с гибибайтом 230) нужен всего лишь 1 мегабайт (∛109 = 103 байт).
Гигабайт и мегабайт — большая разница, согласитесь.
Такая оптимизация в каком-то смысле стала побочным эффектом решения проблемы Гольдбаха.
Тезисы своей работы Харальд Хельфготт представил на 21-м Латиноамериканском коллоквиуме по алгебре в Буэнос-Айресе 25-29 июля 2016 года, а также на мероприятии Sinapsis 2016 в Париже — неформальной встрече перуанских учёных, проживающих в Европе.
Есть разные алгоритмы для поиска простых чисел, но Хельфготт обращает внимание, что решето Эратосфена имеет важное качество — оно совместимо с другими математическими операциями, такими как факторизация, а ведь именно на факторизации (разложении больших простых чисел на множители) базируется криптография. «Факторизация стала ключевым элементом современной цивилизации», — констатирует Хельфготт.
Автор: alizar
Источник
Как Эратосфен вычислил окружность Земли
В середине 20 века мы начали запускать в космос спутники, которые помогли нам определить точную окружность Земли: 40 030 км. Но более 2000 лет назад человек в Древней Греции придумал почти такую же фигуру, используя всего лишь палку и свой мозг. Ниже приводится стенограмма видео.
Как древнегреческий математик рассчитал длину окружности Земли. В середине 20 века мы начали запускать в космос спутники, которые помогли бы нам определить точную окружность Земли — 40 030 км.
Но более 2000 лет назад в Древней Греции человек получил почти такую же фигуру, воткнув палку в землю. Этим человеком был Эратосфен. Греческий математик и глава Александрийской библиотеки.
Эратосфен слышал, что в Сиене, городе к югу от Александрии, в полдень летнего солнцестояния не отбрасывались вертикальные тени. Солнце стояло прямо над головой. Он задавался вопросом, верно ли это и в Александрии.
Итак, 21 июня он воткнул палку прямо в землю и ждал, не отбросит ли тень в полдень.Оказывается, один был. И это было около 7 градусов.
Итак, если солнечные лучи входят под одним и тем же углом в одно и то же время дня, и палка в Александрии отбрасывает тень, а палка в Сиене — нет, это должно означать, что поверхность Земли изогнута. И Эратосфен, вероятно, уже знал это.
Идея сферической Земли была выдвинута Пифагором около 500 г. до н.э. и подтверждена Аристотелем пару столетий спустя. Если бы Земля действительно была сферой, Эратосфен мог бы использовать свои наблюдения, чтобы оценить окружность всей планеты.
Поскольку разница в длине тени составляет 7 градусов в Александрии и Сиене, это означает, что два города находятся на расстоянии 7 градусов друг от друга на 360-градусной поверхности Земли. Эратосфен нанял человека, чтобы измерить расстояние между двумя городами, и узнал, что они находятся на расстоянии 5000 стадий друг от друга, что составляет около 800 километров.
Затем он мог бы с помощью простых пропорций найти окружность Земли — 7,2 градуса составляют 1/50 от 360 градусов, так что 800 умножить на 50 равно 40 000 километров. И вот так 2200 лет назад человек нашел окружность всей нашей планеты с помощью всего лишь палки и своего мозга.
Это видео снял Алекс Кузоян.
Это видео было первоначально опубликовано 3 июля 2016 года.
Этот месяц в истории физики
Июнь, прибл. 240 г. до н. Э. Эратосфен измеряет Землю
| Эратосфен |
Примерно к 500 году до нашей эры большинство древних греков считали Землю круглой, а не плоской. Но они понятия не имели, насколько велика планета, примерно до 240 г. до н. Э.C., когда Эратосфен изобрел хитроумный метод оценки его окружности.
Но они понятия не имели, насколько велика планета, примерно до 240 г. до н. Э.C., когда Эратосфен изобрел хитроумный метод оценки его окружности.
Это было около 500 г. до н. Э. что Пифагор первым предложил сферическую Землю, в основном из эстетических соображений, а не из каких-либо физических доказательств. Как и многие греки, он считал, что сфера имеет наиболее совершенную форму. Возможно, первым, кто предложил сферическую Землю на основе реальных физических доказательств, был Аристотель (384-322 до н.э.), который перечислил несколько аргументов в пользу сферической Земли: корабли сначала исчезают, когда они плывут над горизонтом, Земля отбрасывает круглую тень на Луну. во время лунного затмения, и на разных широтах видны разные созвездия.
Примерно в это же время греческие философы начали верить, что мир можно объяснить естественными процессами, а не призывом к богам, и ранние астрономы начали проводить физические измерения, отчасти чтобы лучше предсказывать времена года. Первым, кто определил размер Земли, был Эратосфен из Кирены, который произвел удивительно хорошие измерения, используя простую схему, сочетающую геометрические вычисления с физическими наблюдениями.
Первым, кто определил размер Земли, был Эратосфен из Кирены, который произвел удивительно хорошие измерения, используя простую схему, сочетающую геометрические вычисления с физическими наблюдениями.
Эратосфен родился около 276 г. до н. Э.C., ныне Шаххат, Ливия. Учился в Афинах в лицее. Около 240 г. до н. Э. Король Александрийский Птолемей III назначил его главным библиотекарем Александрийской библиотеки.
Известный как один из выдающихся ученых того времени, Эратосфен написал впечатляющие работы по астрономии, математике, географии, философии и поэзии. Современники дали ему прозвище «Бета», потому что он был очень хорош, хотя и не совсем первоклассным, во всех этих областях науки. Эратосфен особенно гордился своим решением проблемы удвоения куба, и теперь он хорошо известен разработкой решета Эратосфена, метода нахождения простых чисел.
Самым известным достижением Эратосфена является измерение окружности Земли. Он записал детали этого измерения в рукописи, которая сейчас утеряна, но его техника была описана другими греческими историками и писателями.
Эратосфен был увлечен географией и планировал составить карту всего мира. Он понял, что ему нужно знать размер Земли. Очевидно, что невозможно обойтись вокруг, чтобы понять это.
Эратосфен слышал от путешественников о колодце в Сиене (ныне Асуан, Египет) с интересным свойством: в полдень во время летнего солнцестояния, которое происходит примерно 21 июня каждого года, солнце освещает все дно этого колодца, не забрасывая его. любые тени, указывающие на то, что солнце находилось прямо над головой.Затем Эратосфен измерил угол тени, отбрасываемой палкой в полдень во время летнего солнцестояния в Александрии, и обнаружил, что она составляет около 7,2 градуса, или около 1/50 полного круга.
Он понял, что если бы он знал расстояние от Александрии до Сиены, он мог бы легко вычислить окружность Земли. Но в те времена было крайне сложно определить расстояние с какой-либо точностью. Некоторые расстояния между городами измерялись временем, за которое караван верблюдов переместился из одного города в другой. Но верблюды имеют тенденцию бродить и ходить с разной скоростью. Итак, Эратосфен нанял бематистов, профессиональных геодезистов, обученных ходить шагами одинаковой длины. Они обнаружили, что Сиена находится примерно в 5000 стадиях от Александрии.
Но верблюды имеют тенденцию бродить и ходить с разной скоростью. Итак, Эратосфен нанял бематистов, профессиональных геодезистов, обученных ходить шагами одинаковой длины. Они обнаружили, что Сиена находится примерно в 5000 стадиях от Александрии.
Эратосфен затем использовал это, чтобы вычислить окружность Земли, которая составляет около 250 000 стадий. Современные ученые расходятся во мнениях относительно длины стадиона, на котором находился Эратосфен. Были предложены значения от 500 до примерно 600 футов, в результате чего рассчитанная Эратосфеном окружность составляла от примерно 24 000 до примерно 29 000 миль.Теперь известно, что Земля имеет длину около 24 900 миль вокруг экватора, немного меньше вокруг полюсов.
Эратосфен сделал предположение, что солнце находится так далеко, что его лучи по существу параллельны, что Александрия находится к северу от Сиены и что Сиена находится точно на тропике рака. Хотя эти предположения не совсем верны, они достаточно хороши, чтобы провести довольно точное измерение с использованием метода Эратосфена. Его основной метод надежен, и сегодня он используется даже школьниками во всем мире.
Его основной метод надежен, и сегодня он используется даже школьниками во всем мире.
Другие греческие ученые повторили подвиг измерения Земли, используя процедуру, аналогичную методу Эратосфена. Спустя несколько десятилетий после измерения Эратосфена Посидоний использовал звезду Канопус в качестве источника света и города Родос и Александрию в качестве базовой линии. Но поскольку у него было неправильное значение расстояния между Родосом и Александрией, он придумал значение окружности Земли около 18 000 миль, что почти на 7 000 миль меньше.
Птолемей включил это меньшее значение в свой трактат по географии во втором веке нашей эры.D. Более поздние исследователи, включая Христофора Колумба, поверили в ценность Птолемея и пришли к убеждению, что Земля достаточно мала, чтобы плавать вокруг нее. Если бы вместо этого Колумб знал Эратосфена более крупную и точную ценность, возможно, он никогда бы не отплыл.
5.4: Измерение Земли с помощью Эратосфена
- Последнее обновление
- Сохранить как PDF
- Комплексные концепции
- Стандарты науки нового поколения
- Для преподавателя
- Факты, которые вам необходимо знать
- Преподавание и педагогика
- Результаты учащихся
- Что откроет для себя учащийся?
- Что ваши ученики узнают о науке?
- Проведение деятельности
- Материалы
- Измерение Земли с помощью Эратосфена
- Дополнительные материалы
- Углубляясь вглубь
- Быть астрономом
- Быть ученым:
- Продолжение
Древнегреческий астроном по имени Эратосфен был первым человеком, точно измерившим размер Земли. Его метод был очень прост: он измерял угол, образованный тенью от вертикальной палки в двух разных городах в один и тот же день и время. С помощью другого учителя вы можете воссоздать эксперимент Эратосфена, и ваши ученики смогут сами измерить размер Земли! Все, что вам понадобится, — это два мерила, транспортир, магнитный компас и немного веревки.
Его метод был очень прост: он измерял угол, образованный тенью от вертикальной палки в двух разных городах в один и тот же день и время. С помощью другого учителя вы можете воссоздать эксперимент Эратосфена, и ваши ученики смогут сами измерить размер Земли! Все, что вам понадобится, — это два мерила, транспортир, магнитный компас и немного веревки.
Академические стандарты
Наука и инженерная практика
- Задавать вопросы и определять проблемы.
- Планирование и проведение расследований.
- Анализ и интерпретация данных.
- Используя математику.
- Построение объяснений.
- Аргумент из доказательств.
- Получать, оценивать и передавать информацию.
Общие концепции
- Масштаб, пропорции и количество.
- Системы и системные модели.
Научные стандарты нового поколения
- Инжиниринг и дизайн (К-5, 6-8, 9-12).

- Система Земля-Луна (6-8, 9-12).
Для педагога
Факты, которые вам необходимо знать
- Окружность Земли была впервые точно измерена более 2200 лет назад греческим астрономом по имени Эратосфен.
- Метод Эратосфена был очень прост; он измерил длину тени от вертикальной палки известной высоты в двух городах в один и тот же день. Соотношение между расстоянием север-юг между двумя городами и измеренными углами дало соотношение, которое позволило Эратосфену вычислить размер Земли.
Учебно-педагогическая деятельность
Это прекрасный пример практической геометрии и мощное введение в древние культуры; это не только STEM, но и межучебная программа. Это распространенное заблуждение, что только потому, что культуры были древними, они должны были быть примитивными или упрощенными. Мы часто путаем технологическую сложность с обучением и знаниями. Мероприятие, когда ученики фактически работают вместе с детьми из другой школы, является живым доказательством того, что это не так.
Это упражнение также является еще одним примером практического применения математики. Математика не должна быть сложной или полностью оторванной от реальности; дети действительно реагируют и учатся лучше, когда математика представлена в реальном мире. Я не могу придумать более драматичного ответа на извечный вопрос: «В любом случае, для чего мы будем использовать этот математический мусор?» чем сказать: «Мы собираемся измерить размер Земли сегодня!»
Результаты учащихся
Что откроет для себя студент?
- Это прекрасный проект по многим причинам; Как и в случае с заданиями № 10 и № 11, учащиеся могут использовать простые методы для выполнения удивительных вещей, в данном случае для измерения всей Земли.
- Эратосфен измерил Землю с точностью до 2% от современного измеренного значения. Студенты тоже могут легко сделать это с помощью палки, транспортира и веревки.
Что ваши ученики узнают о естественных науках?
- Наука — совместное предприятие.
 Без помощи студентов-ученых из другой школы это мероприятие невозможно. Несмотря на то, что сама деятельность чрезвычайно проста (измерьте один угол в определенное время дня), без сотрудничества ничего не получится.
Без помощи студентов-ученых из другой школы это мероприятие невозможно. Несмотря на то, что сама деятельность чрезвычайно проста (измерьте один угол в определенное время дня), без сотрудничества ничего не получится.
Материалы
- Метр
- Нить или шпагат
- Точный транспортир
Измерение Земли с помощью Эратосфена
- Первый шаг — связаться с другим учителем того же уровня, который живет не менее чем в 100 милях к северу или югу от вас — для этого эксперимента лучше подальше друг от друга. Прямая линия север-юг между городами также важна для этого, вам нужно будет как можно точнее знать, сколько миль к северу или югу от вас находится другая школа, в отличие от прямого расстояния между городами.Посмотрите на карту и выберите подходящий город, поищите информацию об их школах в Интернете, свяжитесь с кем-нибудь по электронной почте и отправьте им приглашение присоединиться к вашему классу в этом захватывающем проекте.
 Это может занять одну или две попытки, но я уверен, что вы сможете найти партнера без особых трудностей!
Это может занять одну или две попытки, но я уверен, что вы сможете найти партнера без особых трудностей! - Когда наступит знаменательный день, отправьте электронное письмо утром, чтобы быть уверенным, что в обоих городах будет солнечная погода. За несколько минут до полудня установите дворовые палки на детской площадке. Одну палку нужно держать вертикально (используйте для этого небольшой плотницкий уровень).С помощью компаса положите второй эталон на земле так, чтобы он указывал строго на север. Вы сделали простые солнечные часы! Смотрите, как тень движется по часовой стрелке; когда тень лежит прямо вдоль плоского мерила, измерьте и запишите положение, в котором падает кончик тени. В зависимости от вашего местоположения и времени года тень может выходить за край плоской шкалы — ничего страшного, просто отметьте ее положение тротуарным мелом.
- Теперь, когда вы отметили кончик тени, протяните кусок веревки от вершины вертикального мерила вниз до того места, где кончик тени коснулся земли.
 Как можно точнее измерьте угол между вертикальной палкой и веревкой с помощью транспортира и запишите его. Отправьте эту информацию друг другу по электронной почте — разница в между углами будет важна для этого упражнения!
Как можно точнее измерьте угол между вертикальной палкой и веревкой с помощью транспортира и запишите его. Отправьте эту информацию друг другу по электронной почте — разница в между углами будет важна для этого упражнения! - Эратосфен считал, что Земля круглая, и поэтому угол наклона Солнца в небе будет разным в зависимости от того, насколько далеко вы находитесь на севере от экватора — и он был прав! Установив простое соотношение и пропорцию между разницей двух углов и расстоянием между городами, он впервые смог точно измерить окружность Земли около 2300 лет назад.Расчет размеров Земли Эратосфеном был точен в пределах 2% от наших современных значений. Насколько близко могут подойти ваши ученики? Настройте расчет, как показано ниже!
5. Фактическая длина окружности Земли составляет 24 900 миль. Приведенный выше пример был сделан моими собственными учениками несколько лет назад и показывает значение в пределах 4% от истинного размера Земли — очень хорошо для детей, использующих веревку и транспортир! Как близко подойдут ваши ученики!
Вопросы для обсуждения
- У Эратосфена, очевидно, не было телефона или Интернета, как вы думаете, как ему удавалось заниматься этим в Древнем Египте? (Египет тогда был частью Греко-Македонской империи.
 )
)- Ответ: Эратосфен не сделал оба измерения в один и тот же день! Астроном измерил солнечный угол в городе Сиена на юге Египта в день летнего солнцестояния. Затем он пошел в город Александрию на севере Египта, тщательно измерил расстояние по пути и снова измерил солнечный угол во время летнего солнцестояния в следующем году.
- Иногда мы думаем о древних людях как о «примитивных» или даже «невежественных».Что вы думаете о древнегреческой культуре Эратосфена теперь, когда вы знаете, что люди в эту эпоху могли измерить размер Земли и Луны и даже точно измерить расстояние между ними?
- Ответ: Не все древние культуры были невежественными или примитивными! Во многих культурах были «темные века», когда обучение не было продвинутым, но древние культуры были во многих отношениях значительно продвинутыми!
Идем глубже
Понимание того, что происходит, когда мы измеряем угол Солнца в двух разных местах, и как это помогает нам измерять Землю, является шедевром научного мышления. Иногда трудно понять силу простого эксперимента или аргумента.
Иногда трудно понять силу простого эксперимента или аргумента.
Один из способов понять мышление Эратосфена — нарисовать Землю и Солнце, показывая углы между ядром Земли и линиями, представляющими лучи Солнца. Посмотрите, сможете ли вы таким образом понять идеи Эратосфена!
В Интернете есть множество рисунков идей Эратосфена, которые помогут вам!
Быть астрономом
Измерение солнечного угла с помощью палки, веревки и транспортира — еще одно упражнение, которое может показать, как небо меняется в зависимости от времени года.Если ваши ученики могут измерять солнечный угол один раз в неделю и вести постоянный учет результатов, вы обнаружите, что солнечный угол заметно меняется в зависимости от времени года.
Можете ли вы найти связь между солнечным углом и временем года?
Быть ученым: Климатические изменения — горячая тема для исследований и политических дебатов в наши дни, но климат не просто меняется медленно на протяжении веков. Климатическое изменение сезонной погоды, вызванное изменением солнечного угла, является одновременно мощным и измеримым.
Климатическое изменение сезонной погоды, вызванное изменением солнечного угла, является одновременно мощным и измеримым.
Если ваши ученики будут вести постоянный учет солнечного угла и средней высокой температуры каждую неделю, вы увидите интересную взаимосвязь.
Создайте два графика: один показывает угол солнечного света с течением времени, а другой показывает среднюю высокую температуру за неделю с течением времени. Сравните два графика; что ты найдешь?
Солнце — самый мощный фактор в наших климатических изменениях. Сравнивая угол наклона Солнца с колебаниями температуры, мы можем найти прочную связь между количеством получаемого солнечного света и нашими местными температурами.
Продолжение
Древние ученые, такие как Эратосфен, Пифагор, Аристотель и многие другие, внесли свой вклад в наши современные научные знания. Изучите некоторые идеи и открытия этих древних мастеров и посмотрите, что вы сможете найти!
Эратосфен измеряет окружность Земли
Эратосфен измеряет окружность Земли Ast 350L У вас может быть один партнер для этого занятия, или вы можете делать это в одиночку. Если у вас есть партнер, укажите оба имени в листе для ответов.
Если у вас есть партнер, укажите оба имени в листе для ответов.
Напишите дату, два места и покажите всю работу на листе для ответов.
Папирус 230 г. до н. Э. :
Эратосфен нашел диаметр Земли!
Александрия Эратосфен заглянул в колодецвот в полдень и придумал диаметр и
окружность нашей планеты! Летнее солнцестояние
г. солнце и поездка в Сиену — все, что потребовалось ………..
Цели-
- Оценить диаметр и окружность Земли
- путем повторения эксперимента Эратосфена.
- Используйте Интернет для обмена данными и результатами измерений. .
- путем повторения эксперимента Эратосфена.
- Компьютер с доступом в Интернет и электронной почтой.
- Метрическая палка или шест сопоставимой длины
- Измерительная лента (или вторая измерительная линейка)
- Научный калькулятор
Эратосфен с удивительной точностью измерил размер
Земля. Он знал, что в день летнего солнцестояния солнце светит прямо
в полдень в колодец в Сиене. Он обнаружил, что в то же время в
Александрия, Египет, примерно в 787 км к северу от Сиены (ныне Асуан),
угол наклона солнечных лучей был около 7,2. С этими
измерения он вычислил диаметр и окружность земли
как и мы будем делать.
Он знал, что в день летнего солнцестояния солнце светит прямо
в полдень в колодец в Сиене. Он обнаружил, что в то же время в
Александрия, Египет, примерно в 787 км к северу от Сиены (ныне Асуан),
угол наклона солнечных лучей был около 7,2. С этими
измерения он вычислил диаметр и окружность земли
как и мы будем делать.
Деятельность-
1) Как Эратосфен получил результат?
2) Твоя очередь!
- Найдите человека, с которым вы можете связаться по электронной почте, который находится не менее 500 км либо на север, либо на
юг.
 .
Например, из Хьюстона можно выбрать Талсу, штат Оклахома. Используя атлас, чтобы измерить расстояние между ними, можно найти, что они находятся на расстоянии 705 км друг от друга.
.
Например, из Хьюстона можно выбрать Талсу, штат Оклахома. Используя атлас, чтобы измерить расстояние между ними, можно найти, что они находятся на расстоянии 705 км друг от друга. - Вбить столб в землю под углом 90 градусов. Убедитесь, что он находится в солнечном месте. Измерьте длину шеста от земли до самой верхней точки. Запишите это число.
- Следите за полюсом в полдень по местному времени, то есть когда тень самая маленькая.Отправьте электронное письмо партнеру, чтобы он измерил угол наклона солнца. наклон от тени, отбрасываемой его / ее шестом, и вернуть результат. Убедитесь, что ваш партнер включает в себя длину шеста от земли до самой верхней точки. (Воспользуйтесь подсказкой внизу страницы, чтобы сообщить им, когда проводить измерение.) См. Схему ниже для измерений.
- Используя значение расстояния и измеренный угол, вычислите
окружность и диаметр, как в упражнении 1.
 6 мес.
6 мес. - Вычислить процент ошибки для результата Эратосфена. ______________%
- Вычислите процент ошибки для вашего результата. ______________%
4) Вопросы для обсуждения:- Как вы думаете, почему нам нужно выбрать два города, которые лежат примерно на такая же продольная линия? Почему мы не могли использовать Нью-Йорк и Лос-Анджелес?
- Как Эратосфен измерил расстояние между Александрией и Сиене более 2000 лет назад?
- Откуда Эратосфен мог знать, что в полдень во время летнего солнцестояния в Сиене солнечные лучи падали прямо на дно колодца, в то время как при этом в Александрии их не было?
Подсказка
Чтобы узнать время, когда солнце находится на самом высоком уровне в любой день и в любом месте, поищите «время прохождения солнца» на веб-сайте Военно-морской обсерватории США.
Автор:
Деннис П. Донован в
Университет Райса 1996
Донован в
Университет Райса 1996
Адаптировано Мэри Кей Хеменуэй, Техасский университет в Остине, сентябрь 2003 г. - Вычислить процент ошибки для результата Эратосфена. ______________%
Эратосфен: Измерение невозможного | OpenMind
Примерно за 1700 лет до знаменитой экспедиции Магеллана и Элькано, которой потребовалось более трех лет, чтобы облететь Землю, чтобы убедиться, что она не плоская, а круглая, греческий эрудит Эратосфен сумел сделать ту же находку , а также оценить ее диаметр с прямым математическим рассуждением, не покидая города Александрии и с удивительной точностью.Сила математики, разработанной классическими греками, была ключом к совершению этого замечательного подвига и умению измерить невозможное.
Эратосфен родился в Кирене, городе, расположенном на территории современной Ливии, около 276 г. до н. Э. и в 236 г. до н. э. стал главным библиотекарем престижной Александрийской библиотеки . Он внес вклад в такие очевидно разрозненные области, как поэзия, философия, математика, астрономия, история и география, среди других. Как математик, он хорошо известен благодаря так называемому решету Эратосфена, которое позволяет выделить и определить все простые числа вплоть до данного натурального числа и которое используется до сих пор.
Он внес вклад в такие очевидно разрозненные области, как поэзия, философия, математика, астрономия, история и география, среди других. Как математик, он хорошо известен благодаря так называемому решету Эратосфена, которое позволяет выделить и определить все простые числа вплоть до данного натурального числа и которое используется до сих пор.
Кроме того, он знал, как применять базовые математические знания, такие как вычисление длины дуги окружности, которое сейчас изучается в средней школе, чтобы очень точно приблизить радиус Земли, используя только элементарные инструменты. В частности, Эратосфен наблюдал тень, создаваемую лучами Солнца во время летнего солнцестояния в двух местах , достаточно далеко друг от друга: Сиене (ныне египетский город Асуан) и Александрии, расположенной к северу от Сиены по тому же меридиану. .
В солнечный полдень того дня в глубоком колодце Сиены на очень короткое время можно было увидеть отражение содержащейся в нем воды, что показывало, что солнечные лучи падают перпендикулярно. Это верно во время летнего солнцестояния и в тропике Рака (Эратосфен поместил Сиену на этой земной параллели). Однако в тот же момент в Александрии (расположенной примерно на 7 градусов севернее) лучи падали под слегка поперечным углом. , , поскольку обелиски или простая трость, воткнувшаяся в землю, отбрасывают небольшую, но заметную тень .Это уже само по себе является простым доказательством того, что Земля не может быть плоской, потому что, если бы это было так, в тот же момент в Александрии солнечные лучи также должны были бы падать перпендикулярно и не давать никакой тени.
Это верно во время летнего солнцестояния и в тропике Рака (Эратосфен поместил Сиену на этой земной параллели). Однако в тот же момент в Александрии (расположенной примерно на 7 градусов севернее) лучи падали под слегка поперечным углом. , , поскольку обелиски или простая трость, воткнувшаяся в землю, отбрасывают небольшую, но заметную тень .Это уже само по себе является простым доказательством того, что Земля не может быть плоской, потому что, если бы это было так, в тот же момент в Александрии солнечные лучи также должны были бы падать перпендикулярно и не давать никакой тени.
Простое правило трех
Эратосфен начал с модели круглой Земли в форме сферы, поэтому он знал, что кривизна Земли вызовет этот эффект. Он разработал метод расчета диаметра сферы только по двум точкам данных : углу падения солнца в Александрии в день летнего солнцестояния (который совпадает с участком окружности, определяемым двумя городами) и расстояние между ними. Таким образом, с помощью простого правила трех он мог вычислить длину окружности Земли. Если угол падения дает длину дуги окружности, равную расстоянию между Александрией и Сиеной, то общая длина будет соответствовать 360 градусам (полная окружность).
Таким образом, с помощью простого правила трех он мог вычислить длину окружности Земли. Если угол падения дает длину дуги окружности, равную расстоянию между Александрией и Сиеной, то общая длина будет соответствовать 360 градусам (полная окружность).
В этом видео рассказывается, как Эратосфен рассчитал длину окружности Земли. Кредит: Business Insider
Чтобы рассчитать угол падения солнечных лучей в Александрии в день летнего солнцестояния, ему пришлось использовать концепции тригонометрии, которые уже были известны греческим математикам, хотя и с использованием методов, сильно отличающихся от используемых сегодня.В современной терминологии этот угол падения — это значение арктангенса деления тени объекта и его высоты (см. Рисунок 2). Эратосфен получил значение, близкое к 7,2 градуса , или 1/50 окружности круга.
Для завершения расчетов ему требовалась достаточно точная оценка расстояния между двумя городами. Легенда гласит, что Эратосфен знал, что верблюду требуется пятьдесят дней, чтобы добраться из одного города в другой, путешествуя около ста стадий в день, поэтому он оценил расстояние примерно в пять тысяч стадий.Точность его расчета неизвестна, поскольку стадион — это не единица измерения с четкой величиной. Но если принять за меру стадиона тот, который соответствует египетскому стадиону (157,5 метра), мы получим приблизительное расстояние 787,5 км. Подставляя эти значения в правило трех выше, , мы получаем длину окружности 39 375 км . Это отличное приближение к фактическому значению, которое составляет около 40 075 км на экваторе.
Довольно удачная модель Земли
У Эратосфена была модель Земли и Солнечной системы, которая оказалась весьма успешной.Несмотря на то, что он сделал ряд предположений, которые не совсем точны ( Земля не является сферой, солнечные лучи не параллельны, Сиена не находится прямо на тропике Рака …), объединив современные возможности с той же техникой , можно получить результат, максимально близкий к реальному. В настоящее время эта величина оценивается с помощью спутников и систем геолокации. Эти точные измерения позволяют обнаруживать даже небольшие изменения (в сантиметрах) на поверхности Земли.
В настоящее время эта величина оценивается с помощью спутников и систем геолокации. Эти точные измерения позволяют обнаруживать даже небольшие изменения (в сантиметрах) на поверхности Земли.
Однако, много веков назад, почти без каких-либо технологий, используя изобретательность и математику, развитую их предшественниками (Пифагор, Архимед, Евклид, Фалес Милетский …), другие классические греки сделали удивительные вычисления, такие как вычисление расстояния от Земли до Солнца, предсказание затмений и движения известных планет и даже предположение, что Солнце было центром Вселенной, а не Земля, как это делал Аристарх Самосский.Благодаря этим достижениям они вышли за рамки экспериментального знания, основанного только на прямых измерениях, к гораздо более амбициозной концепции научного знания, которая позволила нам знать вещи, выходящие за рамки нашего непосредственного восприятия.
Иллюстративная математика
Задача
Древнегреческий ученый Эратосфен разработал следующий эксперимент для оценки окружности Земли, которую он предположил сферической по форме.На фото ниже солнечные лучи падают в два разных места на поверхности земли. Точка $ P $ на рисунке ниже находится в тропиках, и в это время солнечные лучи падают на эту точку перпендикулярно. В точке $ Q $ солнечные лучи встречаются с Землей под углом, который можно измерить, определив длину тени, отбрасываемой объектом в точке $ Q $.
- Предполагая, что солнечные лучи, попадающие в точки $ P $ и $ R $, параллельны, как на картинке, объясните, почему угол $ POQ $ конгруэнтен углу $ QRS $.
- Для двух местоположений, использованных Эратосфеном, тень, отбрасываемая десятифутовым шестом в местоположении $ Q $, составляла около 1,26 фута. Используя эту информацию, найдите $ a $, меру угла $ POQ $.

- Согласно Эратосфену, расстояние от точки $ P $ до точки $ Q $ было приблизительно 2 584 000 $ футов. Используя эту информацию и расчет из части (b), какую оценку это дает для окружности земли в футах и милях?
- Текущие оценки окружности Земли составляют около 24 900 миль.В пределах какой ошибки в процентах от этого текущего значения находится оценка Эратосфена?
Комментарий IM
Картинка нарисована с $ a = 20 $, потому что угол $ 7,2 $ градуса что точно отражало бы измерения, сделанные Эратосфеном был слишком мал, чтобы оставить место для всех обозначенных точек. Также, конечно, точки $ R $ и $ S $ не предназначены для «реалистичности», поскольку на практике высота объекта, отбрасывающего тень, будет очень мало по сравнению с окружностью земли.
В
точность и простота этого эксперимента поразительны. Замечательный проект
для студентов, что обязательно предполагает совместную работу с другой школой
и, скорее всего, школа в другом штате или регионе страны будет
попытаться повторить эксперимент Эратосфена. Поскольку континентальная часть США не
есть земля в тропиках, студентам придется либо сотрудничать с
школа на Гавайях или по другому методу Эратосфена. Что происходит с этим методом
если точка $ P $ переместится на другую сторону от $ Q $?
Поскольку континентальная часть США не
есть земля в тропиках, студентам придется либо сотрудничать с
школа на Гавайях или по другому методу Эратосфена. Что происходит с этим методом
если точка $ P $ переместится на другую сторону от $ Q $?
Учителя могут обсудить некоторые гипотезы, лежащие в основе этого метода.Например, разумно ли предположить, что солнечные лучи достигают точек $ P $ и
$ Q $ параллельны? Как измерить расстояние от $ P $ до $ Q $? С GPS
Сегодня это не так важно, но для Эратосфена это, должно быть, стало серьезной проблемой. Учителя могут также пожелать дать больше исторического
контекст этой проблемы. Два города, в которых проводились измерения, были
Сиена (современный Асуан на юге Египта) и Александрия (также в Египте)
в полдень летом
солнцестояние: таким образом, в этот момент солнце находилось прямо над головой в одном из двух мест, а именно в Сиене.Поскольку Александрия находится прямо к северу от Сиены, Эратосфен оценил
полярная окружность Земли, которая немного меньше экваториальной
длина окружности.
Это задание предназначено в основном для учебных целей, давая интересный контекст для реализации идей из геометрии и тригонометрии.
Эратосфен и тайна стадионов
Примечание редактора: Эта статья стала победившей в конкурсе на лучшую историю математики 2005 года, проведенном студентом, спонсором которого является история математики SIGMAA Американской математической ассоциации.
В третьем веке до нашей эры блестящий библиотекарь Эратосфен из Кирены (276–195 до н.э.) изобрел остроумный метод измерения окружности Земли. Используя геометрию и Солнце, Эратосфен совершил невозможное. Хотя его оригинальные произведения давно утеряны, легендарная история пересказывается уже более двух тысяч лет. Как и во всех легендах, стало трудно отделить факт от вымысла. Некоторые ученые утверждают, что размер Земли Эратосфена приближался к 2% от ее фактического значения; в то время как другие считают, что точность его измерения сильно преувеличена. Ключ к разгадке этой древней загадки — нестандартная древняя единица длины — стадия. Существует большая неуверенность относительно реальной длины стадиона, который использовал Эратосфен. Также неясно, проводил ли он измерения, использованные в расчетах, или полагался на информацию других. Возможно, самый загадочный вопрос заключается в том, почему Эратосфен необъяснимым образом добавил 2000 стадиев к своей первоначальной величине окружности Земли. Загадка — это та самая загадка, которая движет учеными даже сегодня.
Ключ к разгадке этой древней загадки — нестандартная древняя единица длины — стадия. Существует большая неуверенность относительно реальной длины стадиона, который использовал Эратосфен. Также неясно, проводил ли он измерения, использованные в расчетах, или полагался на информацию других. Возможно, самый загадочный вопрос заключается в том, почему Эратосфен необъяснимым образом добавил 2000 стадиев к своей первоначальной величине окружности Земли. Загадка — это та самая загадка, которая движет учеными даже сегодня.
Эратосфен был человеком большой известности среди ученых древнего мира. Он был хорошим другом известного греческого ученого Архимеда Сиракузского (287–212 гг. До н. Э.). Фактически, одна из величайших работ Архимеда, «Метод», была посвящена Эратосфену [12, с.104].
Я уже однажды отправлял вам некоторые из обнаруженных мною теорем, просто записав их формулировки и пригласив вас найти доказательства, которых я в тот момент не приводил.
[…] Доказательства этих теорем я отправил вам. Более того, видя в вас, как я уже сказал, серьезного ученика, выдающегося философа и почитателя […] [13, с.12-13]
Поскольку Эратосфен был хорошо осведомлен во всех областях науки, но не был «Альфой» (величайшим) ни в одной из ветвей, его сверстники дали ему прозвище «Бета» [12, с.104]. Эратосфен получил образование, эквивалентное высшему образованию в Афинах, а затем отправился в египетский город Александрия [1, с.388]. Привлекая ученых и студентов со всего древнего мира, большая библиотека в Александрии стала центром научных достижений. Написано, что в библиотеке было более 500 000 свитков [15, с.59]. Около 235 г. до н. Э. Эратосфен был назначен главным библиотекарем Александрийской библиотеки [1, с.388]. Именно в этот период Эратосфен разработал свой метод определения длины окружности Земли.
Все работы-победители студенческого конкурса HOM SIGMAA опубликованы в Convergence ; многие из них также доступны в архивах HOM SIGMAA по адресу http: // homsigmaa. net / письменные призы /.
net / письменные призы /.
Конвергенция других статей студенческого конкурса HOM SIGMAA
2020: Джеффри Пауэрс (Общественный колледж Гранд-Рапидса), «Архимед проводил вычисления?»
2019: Аманда Нетингтон (Университет Миссури — Канзас-Сити), «Достижение философского совершенства: успешная замена параллельного постулата Евклида Омаром Хайямом».
2018: Первое место — Калли Лейн (Университет Миссури — Канзас-Сити), «Гонка за преломление: повторное открытие закона Снеллиуса»; Второе место — Кристен Петерс (Университет Ли), «Реальность комплекса: открытие и развитие мнимых чисел» и Рэйчел Талмадж (Университет Миссури, Канзас-Сити), «Франсуа Виет использует геометрию для решения трех задач.«
2017: Победители — Аманда Акин (Университет Ли), «В бесконечность и дальше: историческое путешествие к созерцанию бесконечности», Иоганн Геблер (Гарвардский университет), «Традиционализм: 1894–1925» и Натан Оттен ( Университет штата Миссури — Канзас-Сити), «Гюйгенс и . Ценность всех шансов в играх на удачу».
Ценность всех шансов в играх на удачу».
2016: Со-победители — Бриттани Энн Карлсон (Общественный колледж Солт-Лейк-Сити), «Скрытый элемент деятельности Алисы в стране чудес: консервативная викторианская математика» и Уильям Коул (Университет Ли), «Эволюция метода круга в Аддитивная теория простых чисел.”
2015: Победители — Сэмюэл Паттерсон (Университет Миссури, Канзас-Сити), «Бернард Больцано, гений, незамеченный в свое время» и Бриана Янки (Университет Ли), «Изучение опровергнутых математических идей через призму философии. . »
2014: Первое место — Дженна Миллер (Университет Миссури, Канзас-Сити), «Проливая свет на статистическую жизнь Флоренс Найтингейл» и Анна Рифф (Университет Миссури, Канзас-Сити), «Невозможное доказательство: анализ. о попытках Адриана-Мари Лежандра доказать Пятый постулат Евклида »; Второе место — Пол Айерс (Университет Миссури — Канзас-Сити), « Габриэль Крамер: Более 260 лет сокрушения неизвестных, » и Мэри Рафф (Университет штата Колорадо — Пуэбло), «Вероятность до 1750 года. «
«
2013: Мэтью Шивс (Колледж Худ), «Парадигмы и математика: творческая перспектива».
2012: Первое место — Джесси Хамер (Университет Миссури — Канзас-Сити), «Неделимые и циклоида в начале 17 века»; Второе место — Кевин Л. Винингер (Университет Оттербайна), «Об основах рентгеновской компьютерной томографии в медицине: фундаментальный обзор« преобразования радона »и дань уважения Иоганну Радону».
2011: Первое место — Пол Шталь (Университет Миссури, Канзас-Сити), «Развитие математической астрономии Кеплером»; Второе место — Сара Кострелл (Университет Брандейса), «Математика и математическая мысль в квадривиуме Исидора Севильского» и Рик Хилл (Университет Миссури, Канзас-Сити), «Томас Харриот Artis Analyticae Praxis и корни современной алгебры. .”
2010: Со-победители — Дженнифер Нильсен (Университет Миссури, Канзас-Сити), «Сердце — это доска для пыли: Абу’л Вафа аль-Бузджани, Рассмотрение, строительство и диалог между искусством и математикой в средневековом исламе». Культура », Палмер Рэмпелл (Академия Филлипса и Гарвардский университет),« Использование сходства в древней вавилонской математике »и Стефани Стрек (Тихоокеанский лютеранский университет),« Проблема Ферма ».
Культура », Палмер Рэмпелл (Академия Филлипса и Гарвардский университет),« Использование сходства в древней вавилонской математике »и Стефани Стрек (Тихоокеанский лютеранский университет),« Проблема Ферма ».
2009: Первое место — Натан Маклафлин (Университет Монтаны), «Математическая оптика сэра Уильяма Гамильтона: коническое преломление и кватернионы»; Второе место — Тим Чалберг (Тихоокеанский лютеранский университет), «Регрессионный анализ: мощный инструмент и захватывающая драма»; Почетное упоминание — Эми Бухманн (Университет Чепмена), «Краткая история кватернионов и теория голоморфных функций от кватернионных переменных.”
2008: Первое место — Мэйм Мэлони (Чикагский университет), «Конструктивизм: реалистичный подход к математике?»; Второе место — Вуди Берчетт (Джорджтаунский колледж), «Мышление внутри коробки: геометрическая интерпретация квадратичных задач в BM 13901» и Коул МакГи (Государственный университет Колорадо — Пуэбло), «Жан Ле Ронд Д’Аламбер: биография математика, Философ и писатель »; Почетное упоминание — Мэйм Мэлони (Чикагский университет), «Патологические функции в 18-19 веках.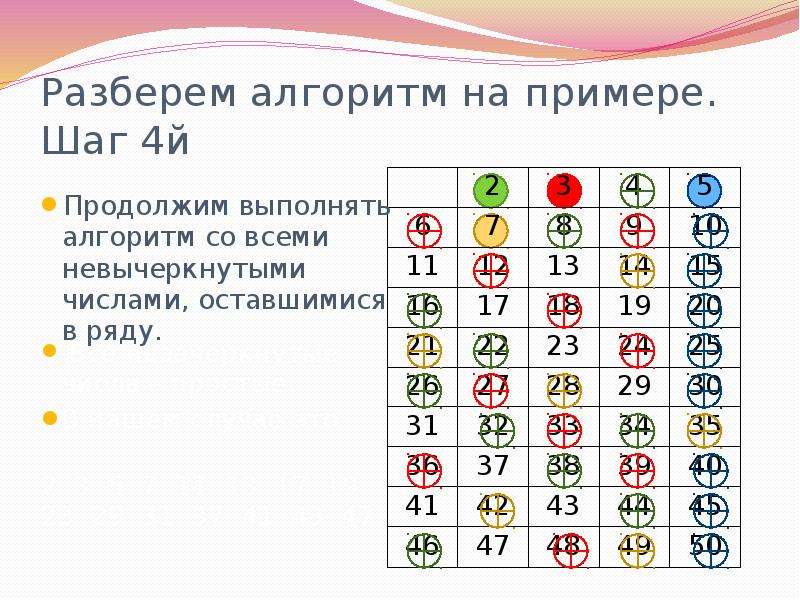 ”
”
2007: Победители — Рори Плант, « Libra Astronomica и ее математика» и Дуглас Смит (Университет Майами, Огайо), «Теорема Лукаса: великая теорема».
2006: Победители — Дженнифер Вигерт, «Проницательность кругов: история изопериметрической проблемы» и Саманта Рейнольдс (Университет Миссури, Канзас-Сити), «Мария Гаэтана Агнеси: женщина-математик и блестящий исследователь 18 -е Век ».
2005: Первое место — Ньюлин Уолкап (Университет Миссури — Канзас-Сити), «Эратосфен и Тайна стадионов»; Второе место — Джеймс Коллингвуд (Университет Дрейка), «Тщательность в анализе: от Ньютона до Коши.”
2004: Победители — Марк Уолтерс, «Кажется, что четырех цветов достаточно: исторический обзор теоремы четырех цветов» и Хит Йейтс (Университет Миссури, Канзас-Сити), «Табличка из храма Эманджи».
.
 append(j)
print(prime_eratosthenes(100))';
append(j)
print(prime_eratosthenes(100))';
 275 – 194 до н.э.), один из
самых разносторонних ученых античности. Особенно прославили Эратосфена труды
по астрономии, географии и математике, однако он успешно трудился и в
области филологии, поэзии, музыки и философии, за что современники дали ему
прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. «второй»,
возможно, также не содержит ничего уничижительного: им желали показать, что
во всех науках Эратосфен достигает не высшего, но превосходного результата.
275 – 194 до н.э.), один из
самых разносторонних ученых античности. Особенно прославили Эратосфена труды
по астрономии, географии и математике, однако он успешно трудился и в
области филологии, поэзии, музыки и философии, за что современники дали ему
прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. «второй»,
возможно, также не содержит ничего уничижительного: им желали показать, что
во всех науках Эратосфен достигает не высшего, но превосходного результата. Эратосфен принял это предложение и занимал
должность библиотекаря вплоть до своей кончины. Его научные таланты
удостоились высокой оценки современника Эратосфена, Архимеда, который
посвятил ему свою книгу Эфодик (т.е. Метод).
Эратосфен принял это предложение и занимал
должность библиотекаря вплоть до своей кончины. Его научные таланты
удостоились высокой оценки современника Эратосфена, Архимеда, который
посвятил ему свою книгу Эфодик (т.е. Метод).
 В своих
Хронографиях он пытался установить даты, связанные с политической и
литературной историей Древней Греции, составил список победителей
Олимпийских игр. В трактате О древней комедии, где анализировались
произведения афинских драматургов, Эратосфен выступил как литературный
критик и филолог. Эратосфен написал также поэму Гермес, повествующую о
рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий
эпос, Гесиод, посвящен смерти поэта и каре, постигшей его убийц. Эратосфен
написал также трактат Катастеризмы – описание созвездий и изложение
посвященных им мифов (сохранившееся сочинение под таким названием вызывает
сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по
истории и философии, которые не сохранились.
В своих
Хронографиях он пытался установить даты, связанные с политической и
литературной историей Древней Греции, составил список победителей
Олимпийских игр. В трактате О древней комедии, где анализировались
произведения афинских драматургов, Эратосфен выступил как литературный
критик и филолог. Эратосфен написал также поэму Гермес, повествующую о
рождении, подвигах и гибели бога, до нас дошли ее фрагменты. Другой короткий
эпос, Гесиод, посвящен смерти поэта и каре, постигшей его убийц. Эратосфен
написал также трактат Катастеризмы – описание созвездий и изложение
посвященных им мифов (сохранившееся сочинение под таким названием вызывает
сомнения в смысле подлинности). Эратосфену принадлежал еще ряд работ по
истории и философии, которые не сохранились. Б. Родосская параллель. Жизнь и деятельность Эратосфена. М.,
1965
Б. Родосская параллель. Жизнь и деятельность Эратосфена. М.,
1965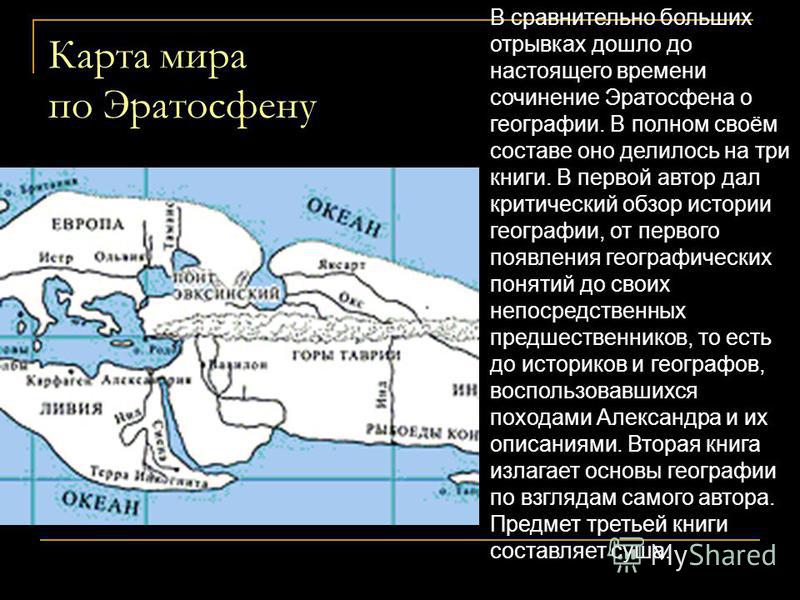
 Употребление армиллярной сферы как инструмента для астрономических наблюдений удержалось весьма долго. Даже Тихо Браге произвел большую часть своих наблюдений над планетами при помощи этого инструмента…
Употребление армиллярной сферы как инструмента для астрономических наблюдений удержалось весьма долго. Даже Тихо Браге произвел большую часть своих наблюдений над планетами при помощи этого инструмента…
 После преобразования у вас получается своего рода шум, в котором вы пытаетесь услышать какие-то ноты. Среди них есть такие, которые слышны достаточно хорошо, — это и есть большие дуги. А есть частоты, которые просто являются шумовыми фрагментами, — это малые дуги. Весь метод распадается на две части — выделение нот и доказательство того, что остальное на самом деле шум. За первую часть метода отвечают оценки на большие дуги, за второй — на малые».
После преобразования у вас получается своего рода шум, в котором вы пытаетесь услышать какие-то ноты. Среди них есть такие, которые слышны достаточно хорошо, — это и есть большие дуги. А есть частоты, которые просто являются шумовыми фрагментами, — это малые дуги. Весь метод распадается на две части — выделение нот и доказательство того, что остальное на самом деле шум. За первую часть метода отвечают оценки на большие дуги, за второй — на малые».
 Без помощи студентов-ученых из другой школы это мероприятие невозможно. Несмотря на то, что сама деятельность чрезвычайно проста (измерьте один угол в определенное время дня), без сотрудничества ничего не получится.
Без помощи студентов-ученых из другой школы это мероприятие невозможно. Несмотря на то, что сама деятельность чрезвычайно проста (измерьте один угол в определенное время дня), без сотрудничества ничего не получится. Это может занять одну или две попытки, но я уверен, что вы сможете найти партнера без особых трудностей!
Это может занять одну или две попытки, но я уверен, что вы сможете найти партнера без особых трудностей! Как можно точнее измерьте угол между вертикальной палкой и веревкой с помощью транспортира и запишите его. Отправьте эту информацию друг другу по электронной почте — разница в между углами будет важна для этого упражнения!
Как можно точнее измерьте угол между вертикальной палкой и веревкой с помощью транспортира и запишите его. Отправьте эту информацию друг другу по электронной почте — разница в между углами будет важна для этого упражнения! )
) .
Например, из Хьюстона можно выбрать Талсу, штат Оклахома. Используя атлас, чтобы измерить расстояние между ними, можно найти, что они находятся на расстоянии 705 км друг от друга.
.
Например, из Хьюстона можно выбрать Талсу, штат Оклахома. Используя атлас, чтобы измерить расстояние между ними, можно найти, что они находятся на расстоянии 705 км друг от друга. 6 мес.
6 мес.  Донован в
Университет Райса 1996
Донован в
Университет Райса 1996 
 […] Доказательства этих теорем я отправил вам. Более того, видя в вас, как я уже сказал, серьезного ученика, выдающегося философа и почитателя […] [13, с.12-13]
[…] Доказательства этих теорем я отправил вам. Более того, видя в вас, как я уже сказал, серьезного ученика, выдающегося философа и почитателя […] [13, с.12-13]