Метод Крамера
Пусть дана система трех линейных уравнений:
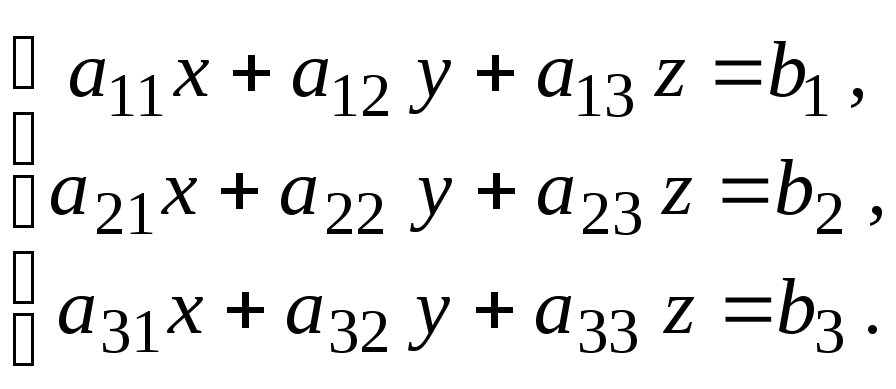 (1)
(1)
Для
решения системы линейных уравнений
методом Крамера из коэффициентов при
неизвестных составляется главный
определитель
системы .
Для системы (1) главный определитель
имеет вид 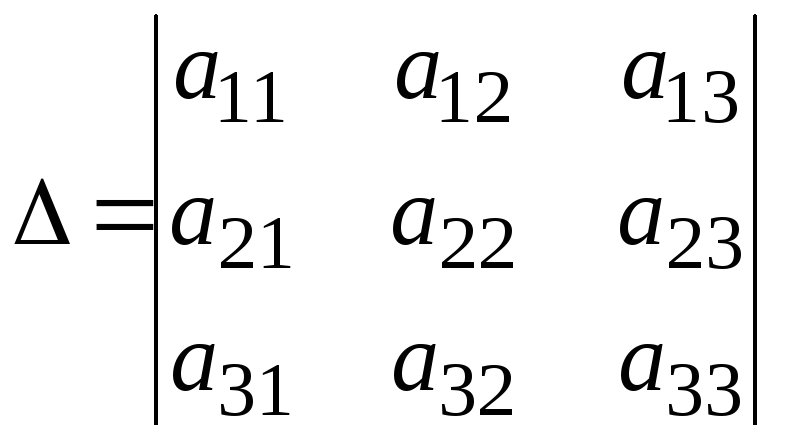 .
.
Далее
составляются определители по переменным 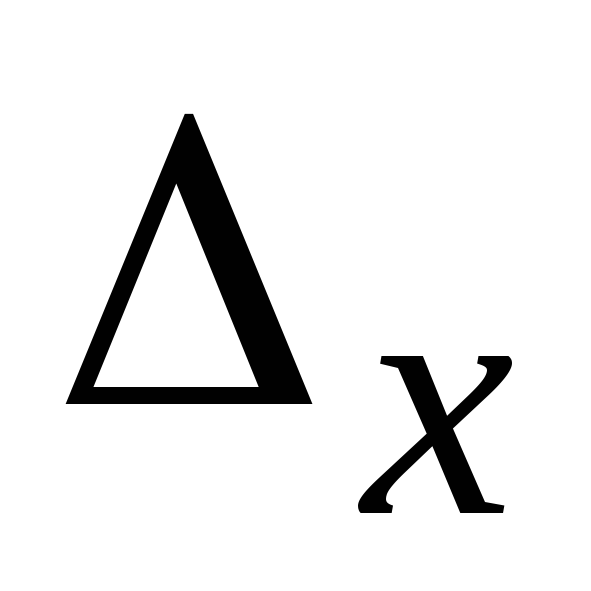 ,
,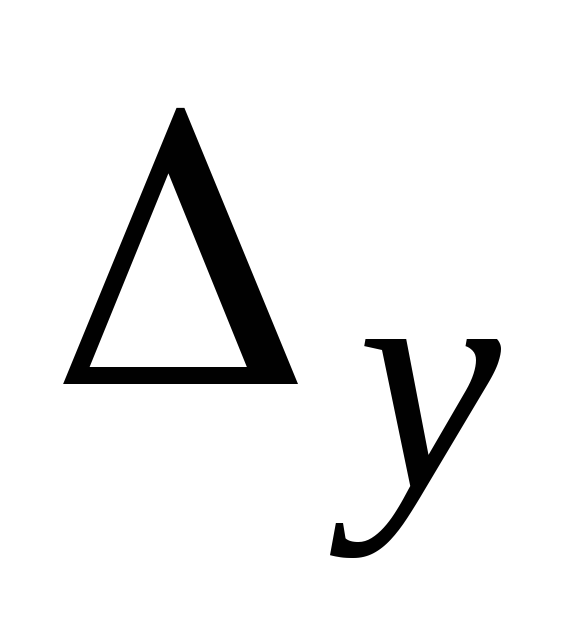 ,
, .
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
.
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
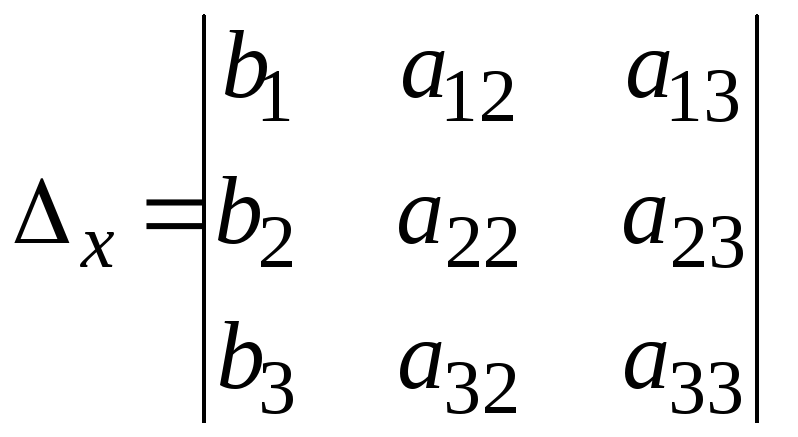 ,
, 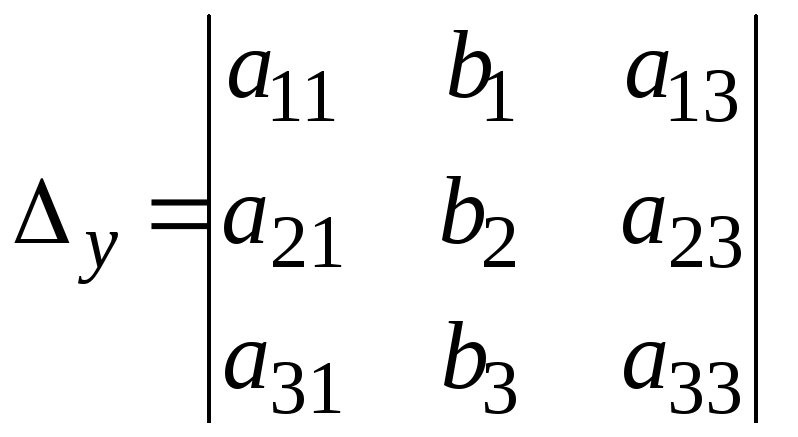 ,
,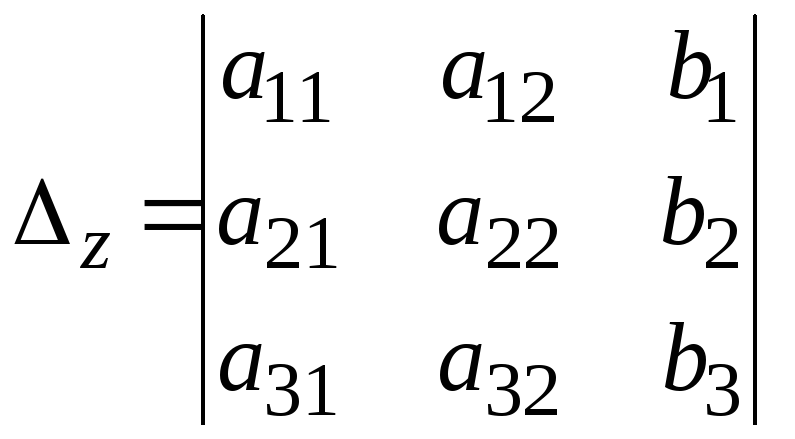 .
.
Тогда решение системы находится по формулам Крамера
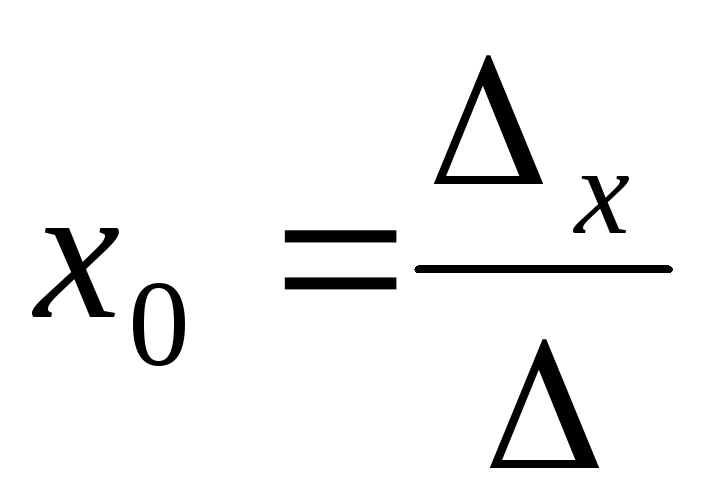 ,
, 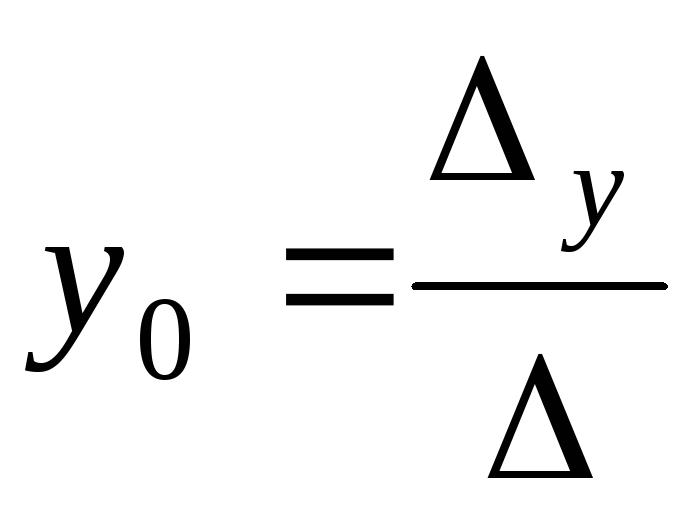 ,
, 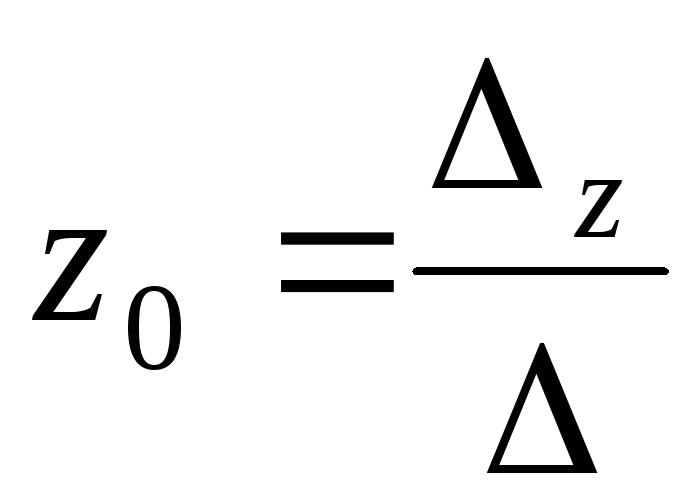
Следует
отметить, что система имеет единственное
решение 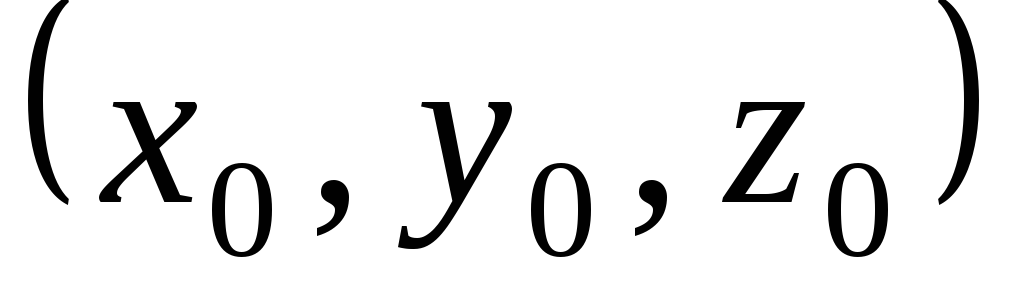 ,
если главный определитель
,
если главный определитель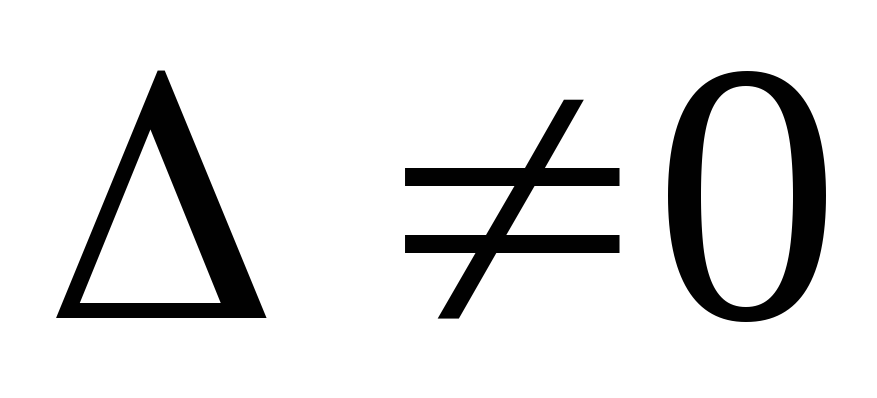 .Если же
.Если же 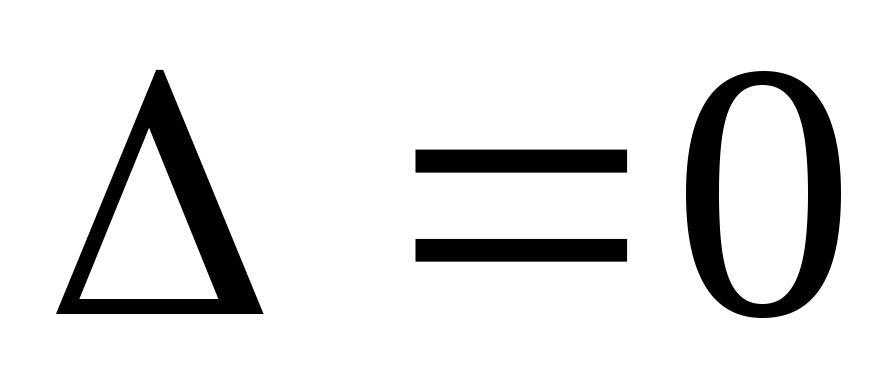 и
и 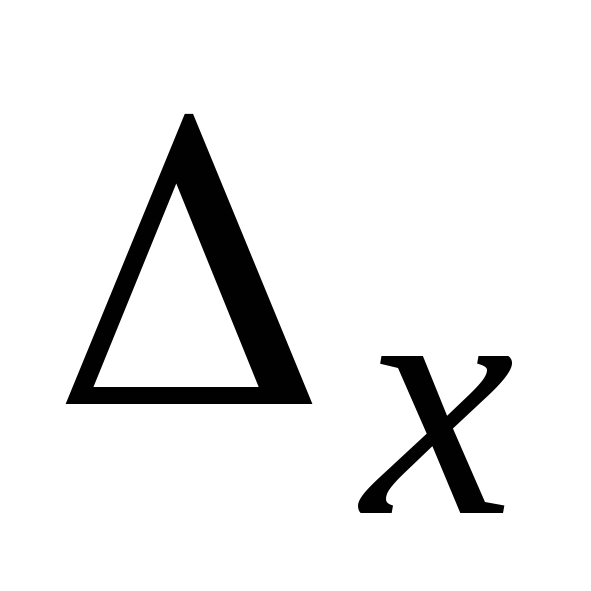 =
0,
=
0,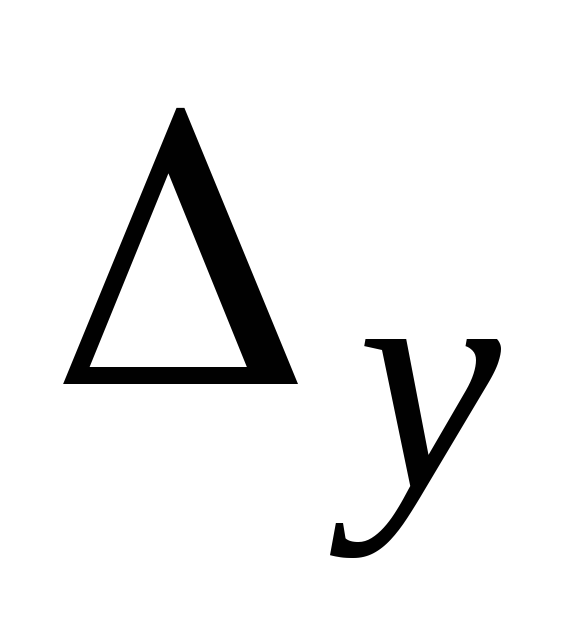 =
0,
=
0, =
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же
=
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же 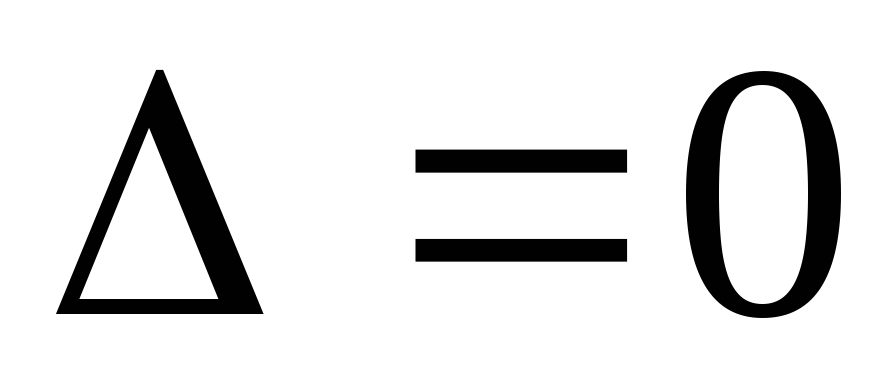 и
и 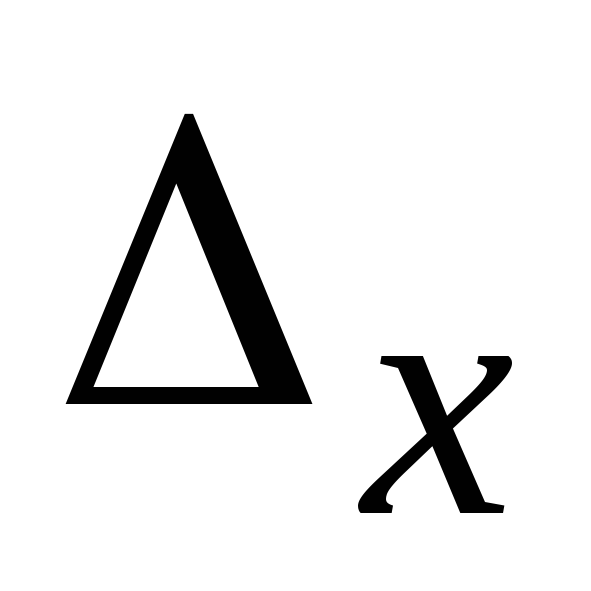
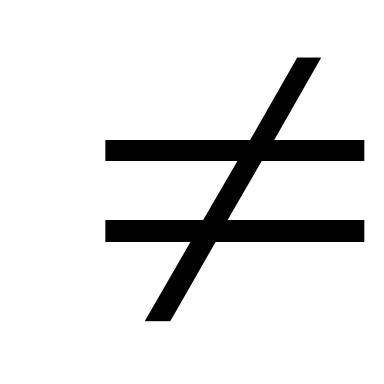 0,
или
0,
или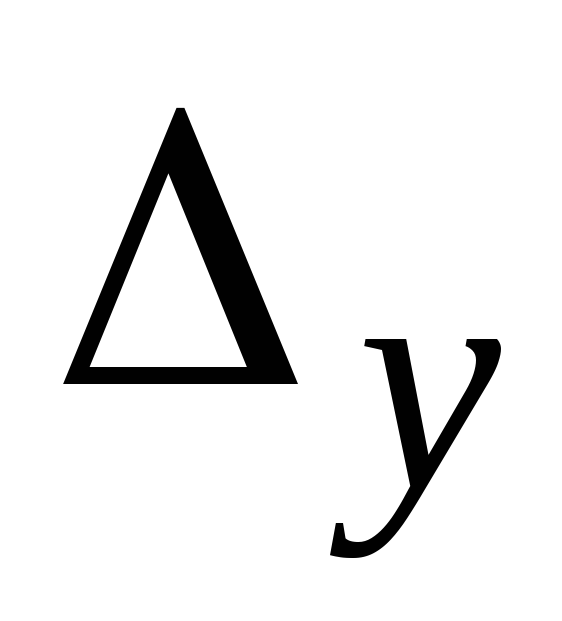
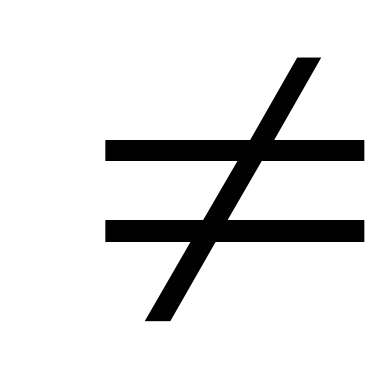

 0,
то система уравнений несовместна, то
есть решений не имеет.
0,
то система уравнений несовместна, то
есть решений не имеет.Пример
Решить
систему уравнений методом Крамера: 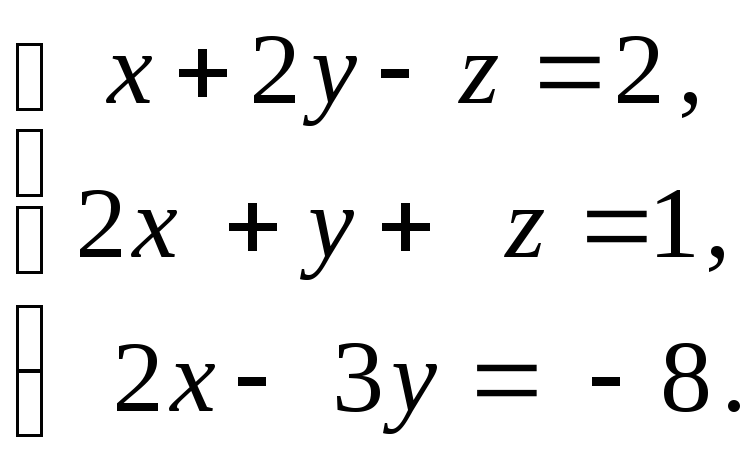
Решение:
1) Составим и вычислим главный определитель системы, состоящий из коэффициентов при неизвестных.
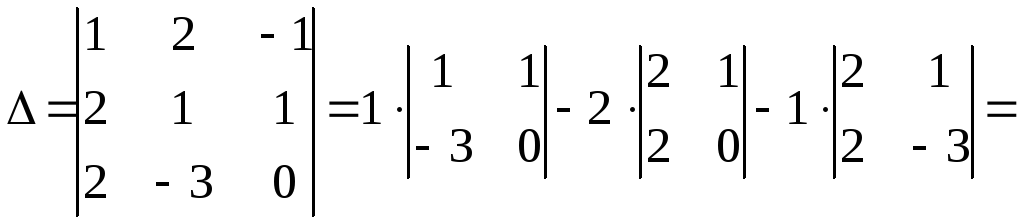
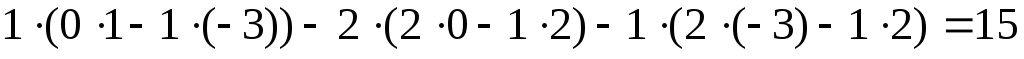 .
.
Следовательно, система имеет единственное решение.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов.
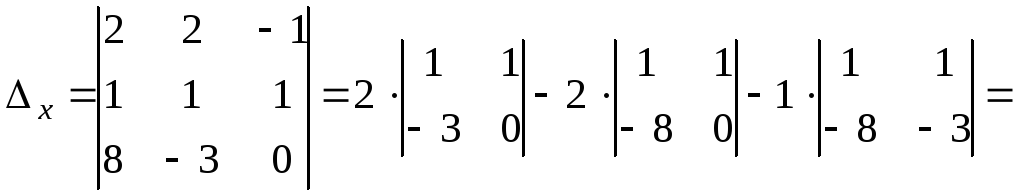
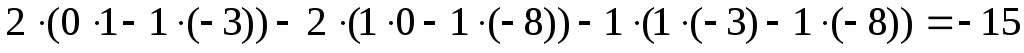
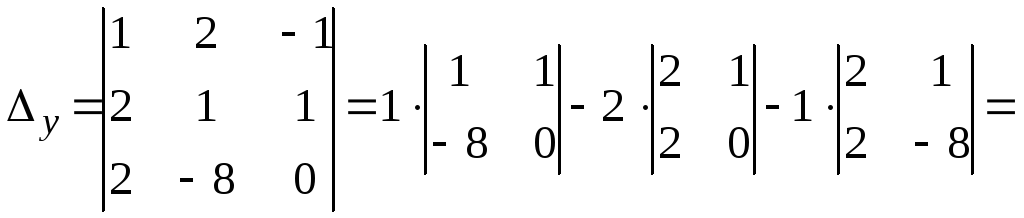
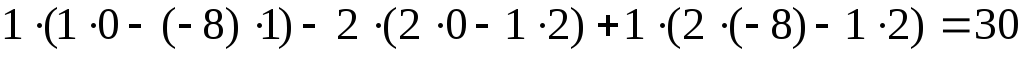
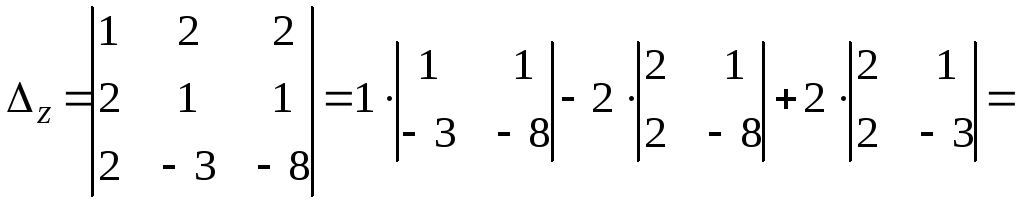
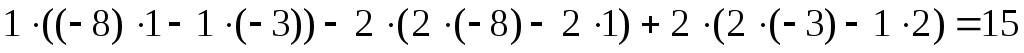
По формулам Крамера находим неизвестные:
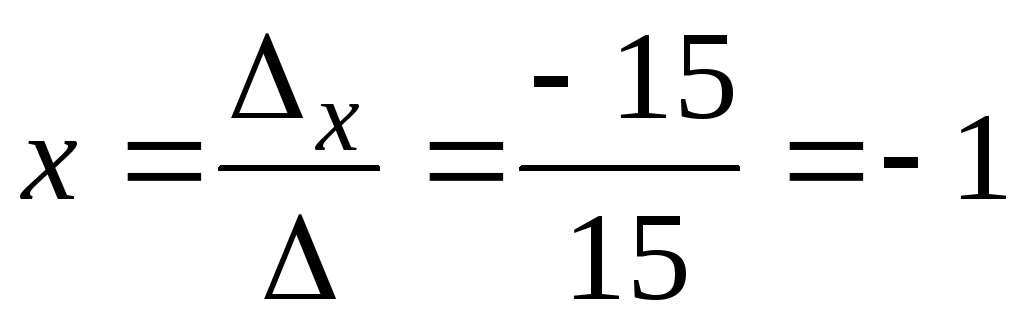 ,
, 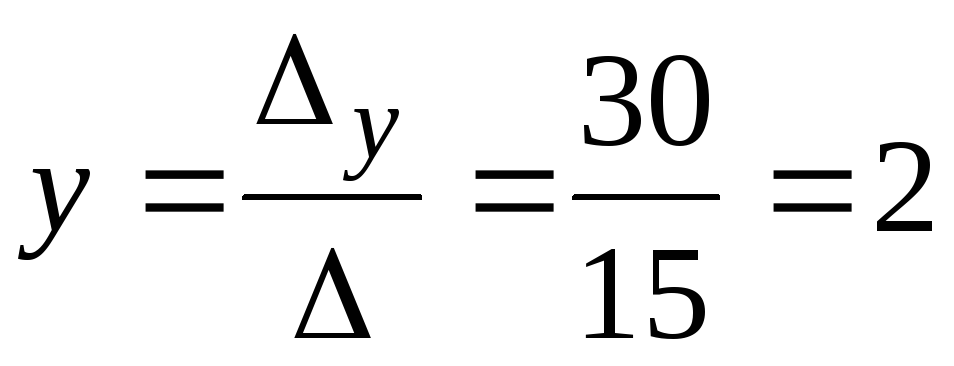
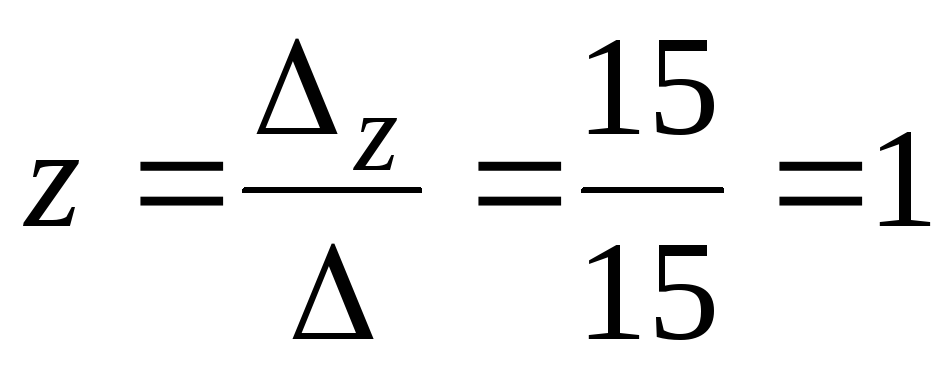 .
.Сделаем проверку, чтобы убедиться в правильности решения
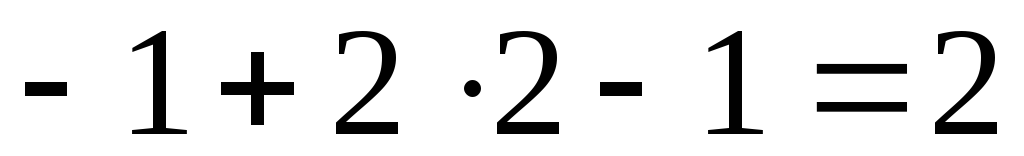 ,
т.е.
,
т.е. 
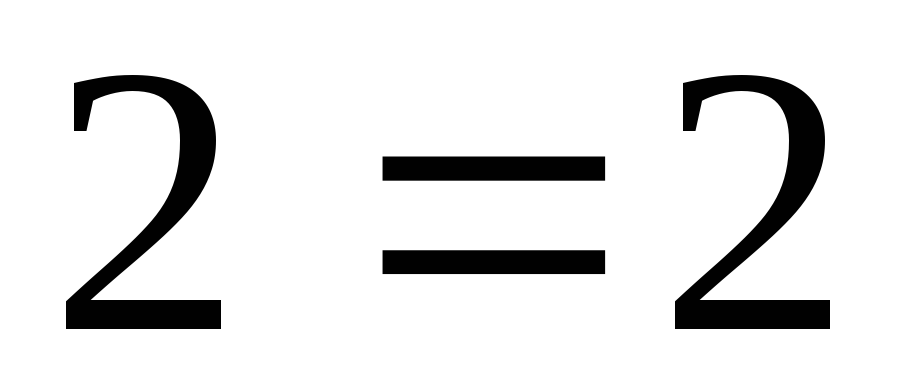 .
.
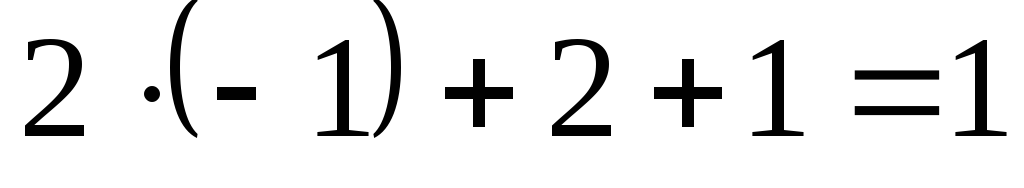 ,
т.е.
,
т.е. 
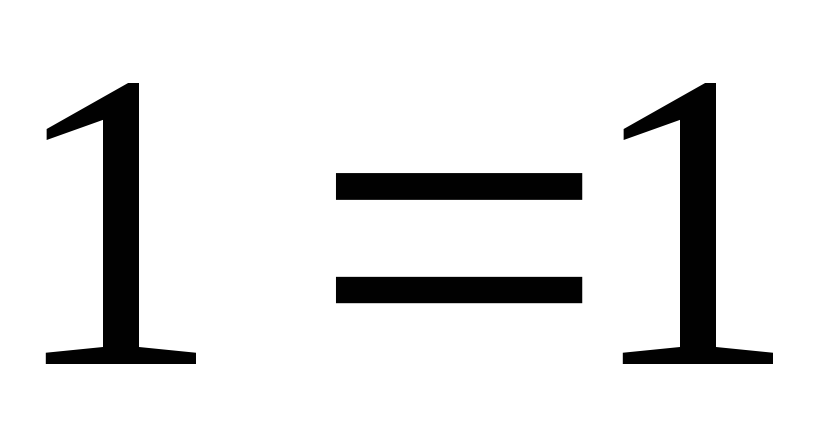
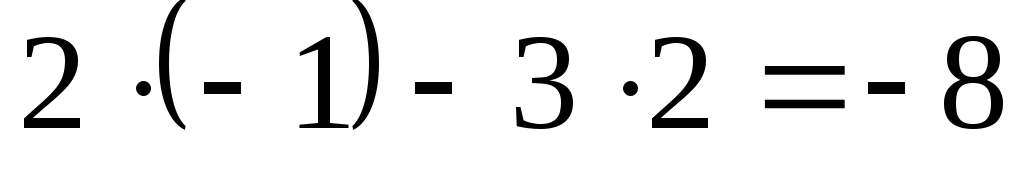 ,
т.е.
,
т.е. 
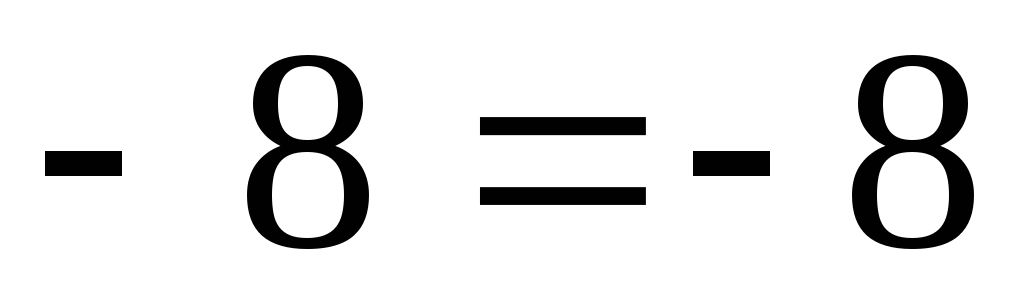
Ответ: 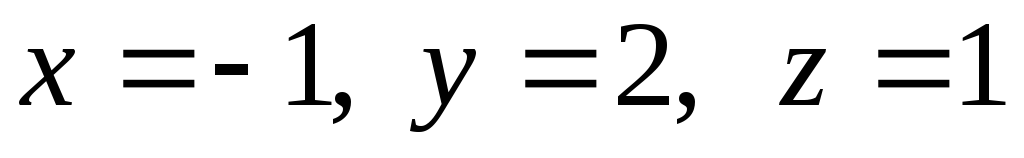 .
.
Пример
Решить систему уравнений методом Крамера:
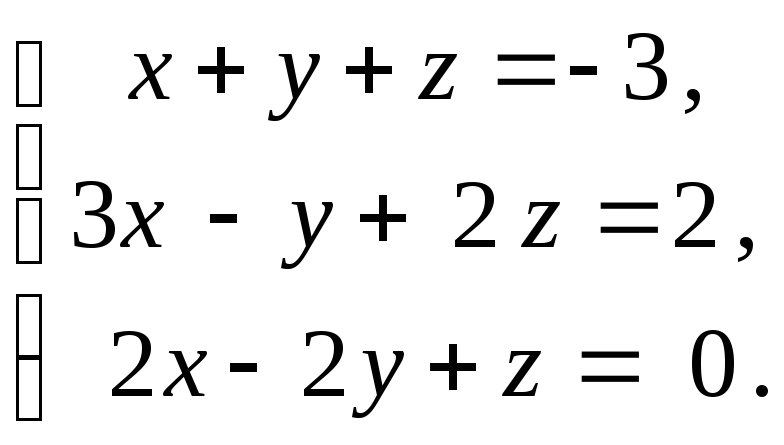
Решение:
1) Составим и вычислим главный определитель системы из коэффициентов при неизвестных:
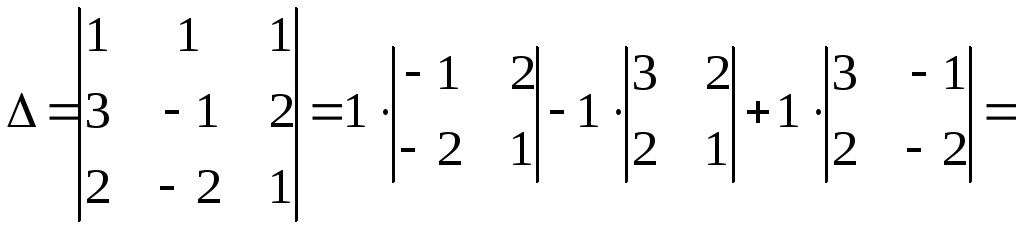
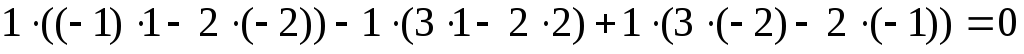 .
.
Следовательно, система не имеет единственного решения.
2) Составим и вычислим вспомогательные определители, заменяя соответствующий столбец в столбцом из свободных членов:
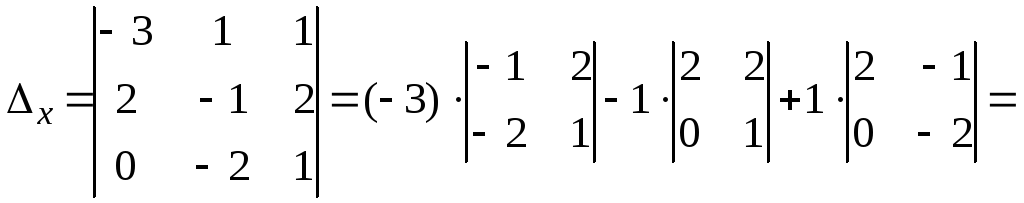
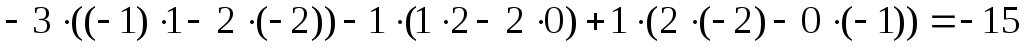 .
.
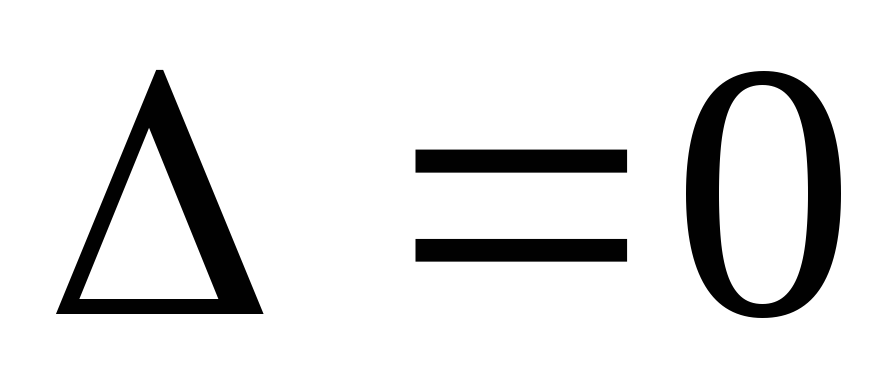 ,
, 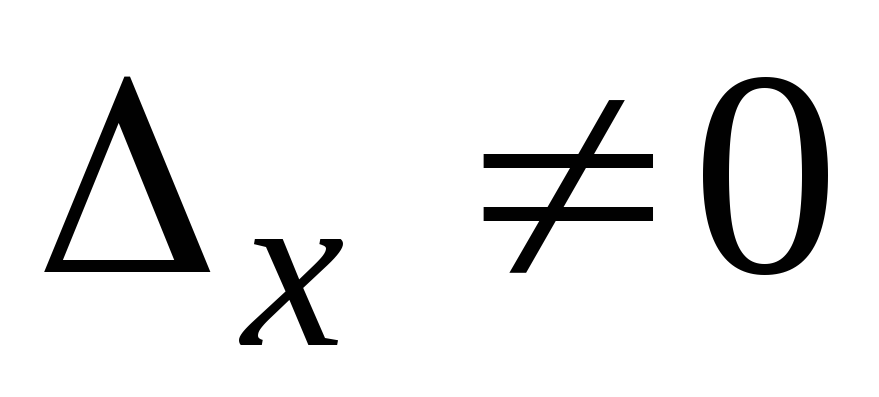 ,
следовательно, система несовместна.
,
следовательно, система несовместна.
Ответ: система несовместна.
Метод Гаусса
Метод Гаусса состоит из двух этапов. Первый этап заключается в последовательном исключении переменных из уравнений системы при помощи действий, не нарушающих равносильности системы. Например, рассмотрим два первых уравнения системы (1).
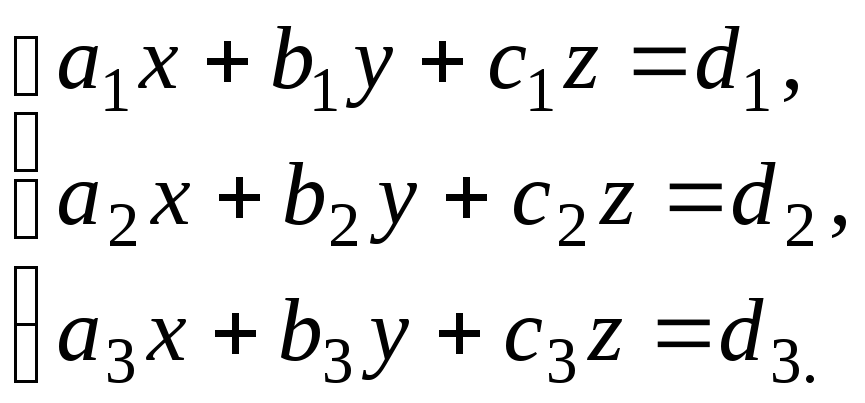
Необходимо
путем сложения этих двух уравнений
получить уравнение, в котором отсутствует
переменная 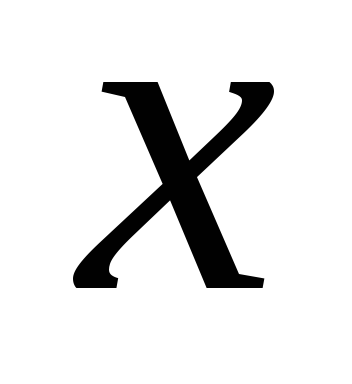 .
Умножим первое уравнение на
.
Умножим первое уравнение на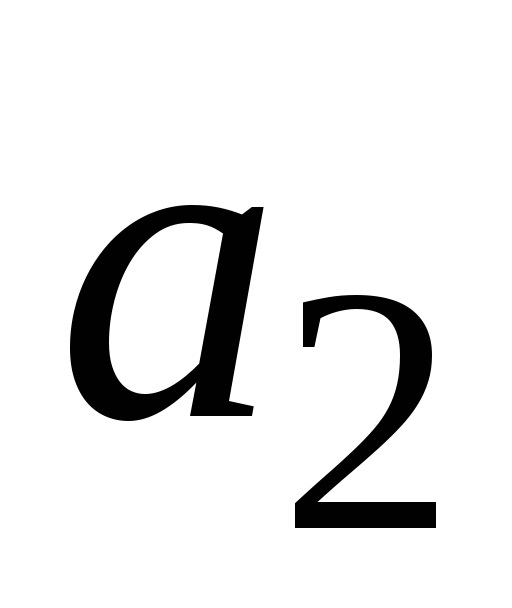 ,
а второе на (
,
а второе на (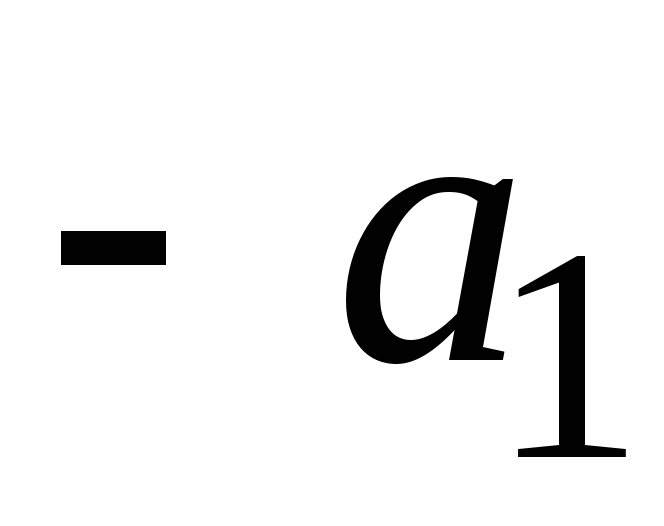 )
и сложим полученные уравнения
)
и сложим полученные уравнения
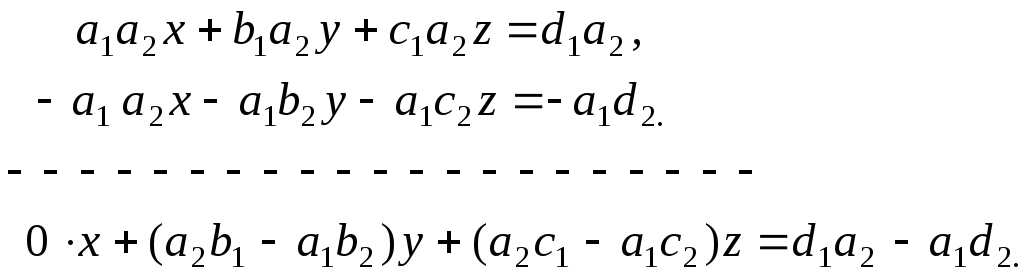
+
Заменим
коэффициент перед y, z и свободный член на 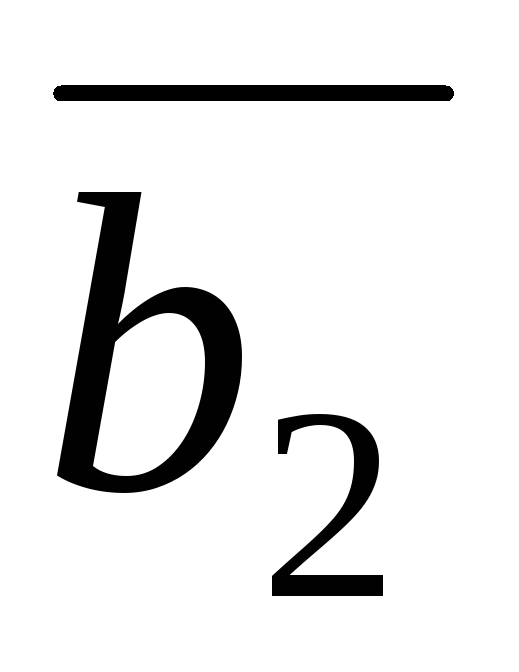 ,
,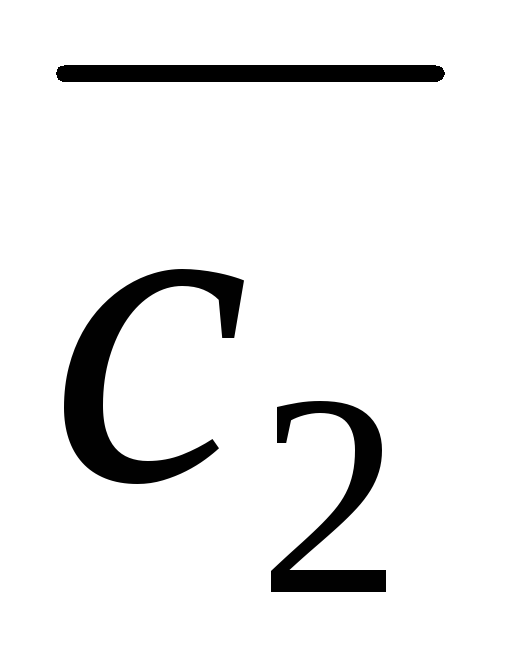 и
и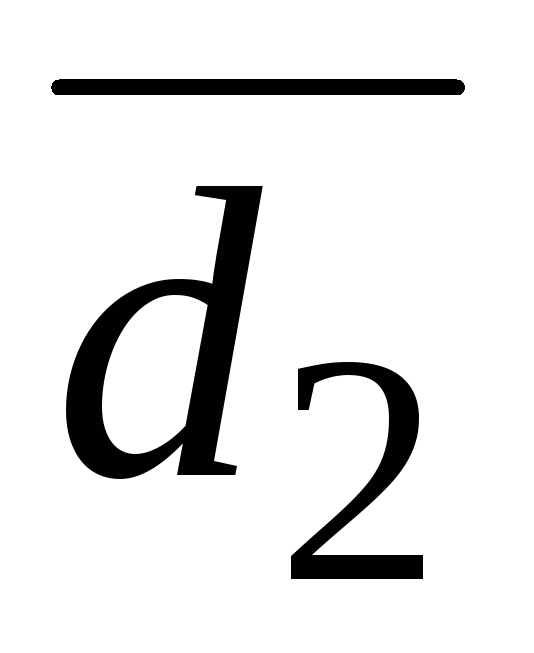
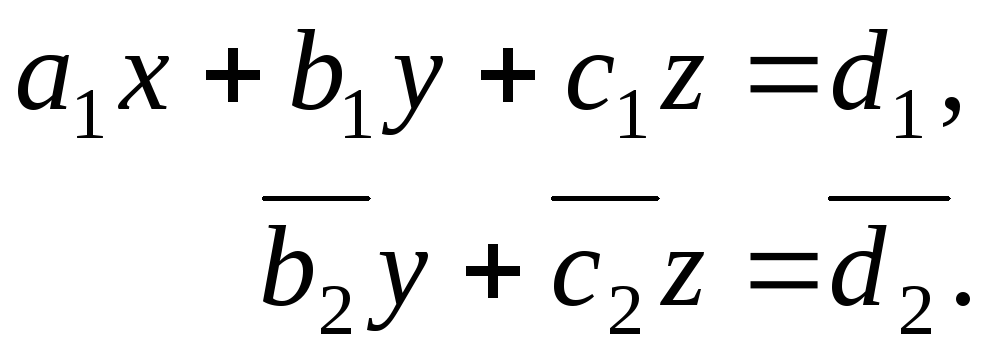
Заметим, что во втором уравнении отсутствует переменная x.
Проведя аналогичные действия над первым и третьим уравнениями системы (1), а затем над полученными в результате сложения вторым и третьим уравнениями, преобразуем систему (1) к виду

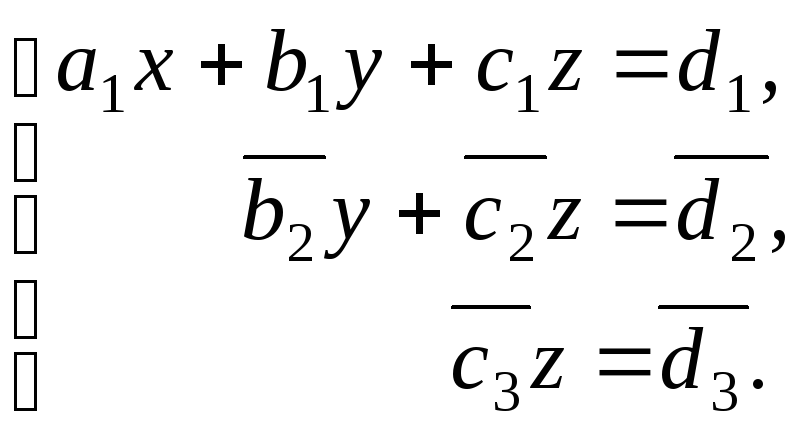 (2)
(2)
Такой результат возможен, если система имеет единственное решение. В этом случае решение находится при помощи обратного хода метода Гаусса (второй этап). Из последнего уравнения системы (2) находим неизвестную переменную z, затем из второго уравнения находим y, а x соответственно из первого, подставляя в них уже найденные неизвестные.
Иногда в результате сложения двух уравнений суммарное уравнение может принять один из видов:
А) 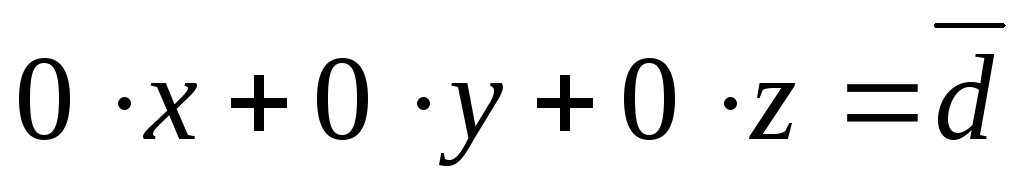 ,
где
,
где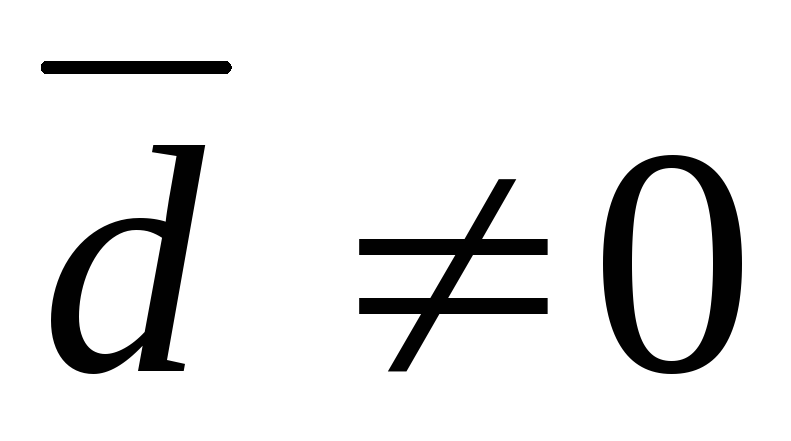 .
Это означает, что решаемая система
несовместна.
.
Это означает, что решаемая система
несовместна.
Б) 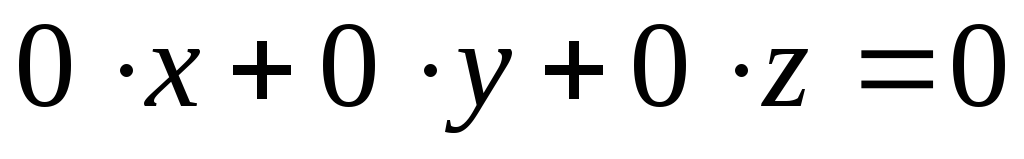 ,
то есть
,
то есть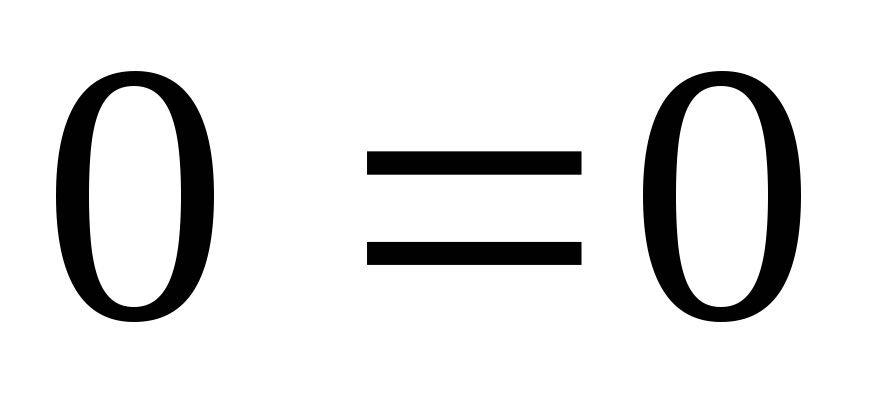 .
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
.
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
Пример
Решить
систему методом Гаусса: 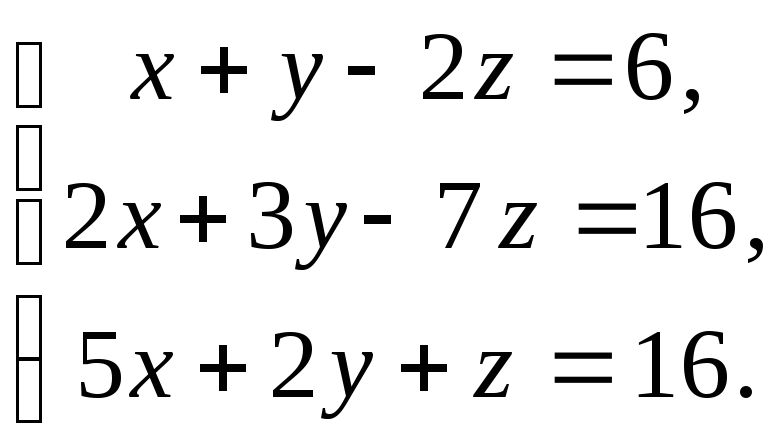
Решение:
Рассмотрим следующий способ осуществления первого этапа решения методом Гаусса. Запишем три строки коэффициентов при неизвестных и свободных членов, соответствующих трем уравнениям системы. Свободные члены отделим от коэффициентов вертикальной линией, а под третьей строкой проведем горизонтальную прямую.
Первую
строку, которая соответствует первому
уравнению системы, обведем – коэффициенты
в этом уравнении останутся неизменными.
Вместо второй строки (уравнения) надо
получить строку (уравнение), где
коэффициент при 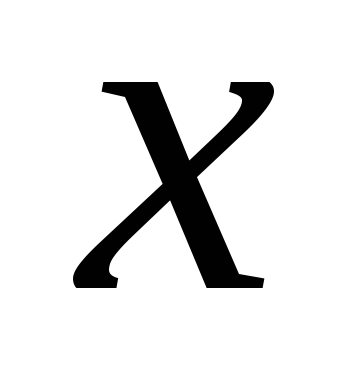 равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при
равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при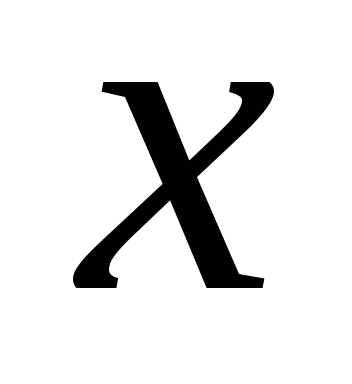 равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.
равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.
Все описанные действия изображены в таблице 1 при помощи арифметических знаков и стрелок. Обведенные в таблице строки запишем снова в виде уравнений (3) и, применив обратный ход метода Гаусса, найдем значения переменных x, y и z.
Таблица 1
1 | 1 | -2 | 6 | *(-2) | *(-5) |
2 | 3 | -7 | 16 | ||
5 | 2 | 1 | 16 | ||
0 | 1 | -3 | 4 | *( 3) | |
0 | -3 | 11 | -14 | ||
0 | 0 | 2 | -2 |
Восстанавливаем систему уравнений, полученную в результате наших преобразований:
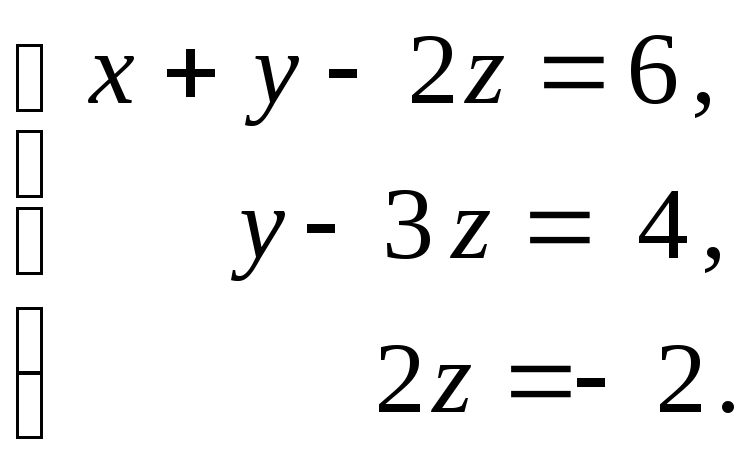 (3)
(3)
Обратный ход метода Гаусса
Из
третьего уравнения 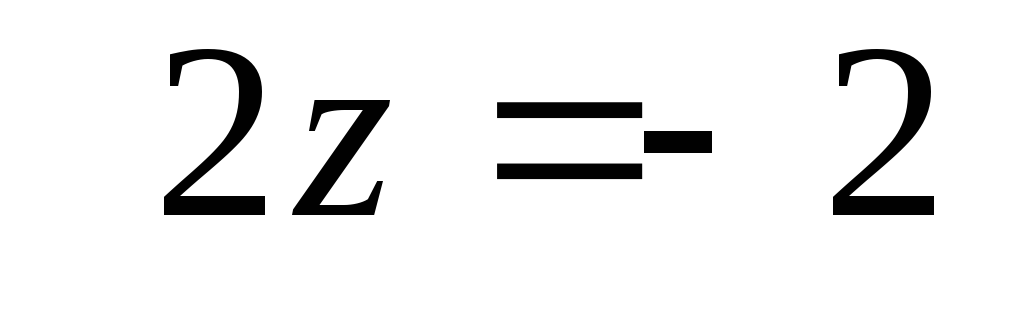 находим.
находим.
Во
второе уравнение системы 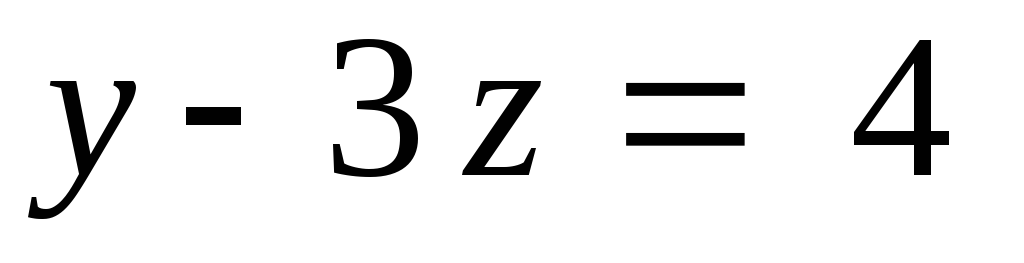 подставим найденное значение
подставим найденное значение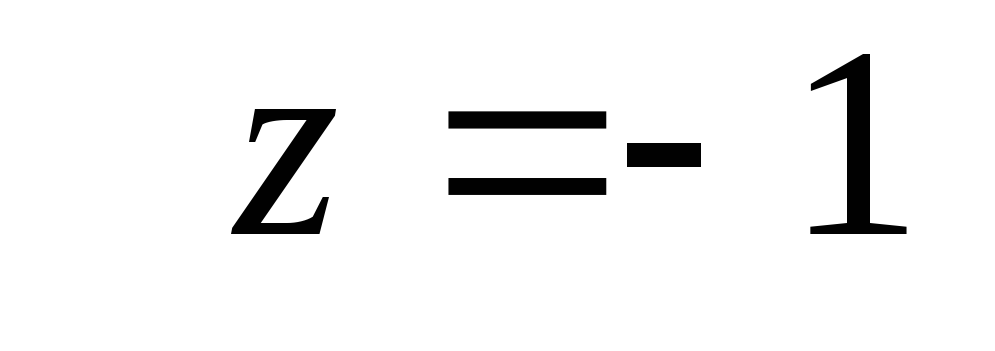 ,
получим
,
получим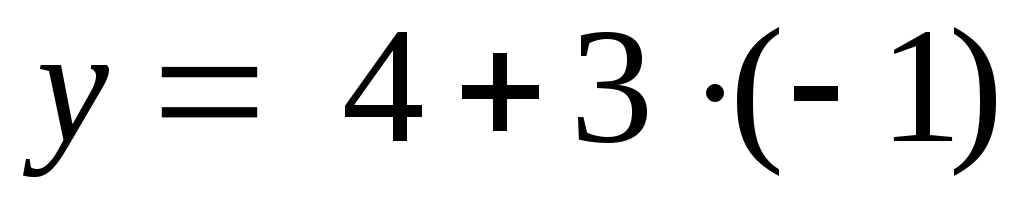 или
или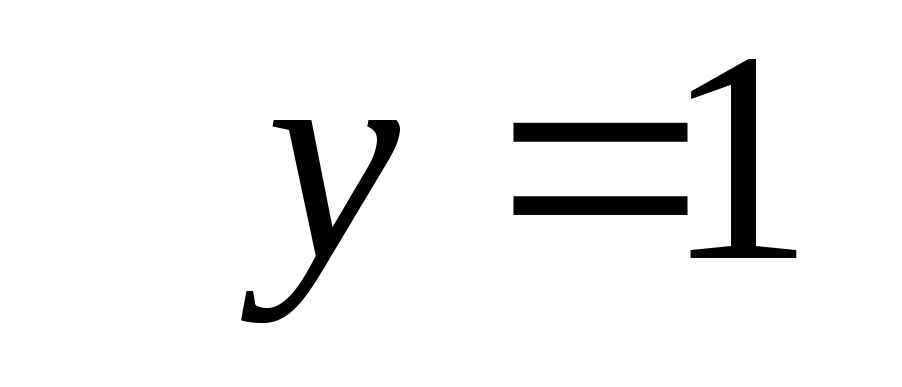 .
.
Из
первого уравнения 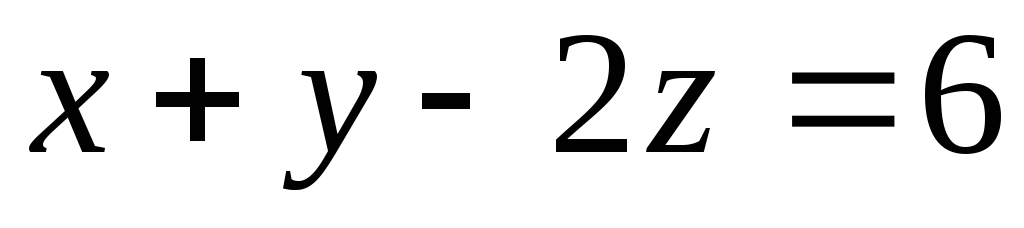 ,
подставляя уже найденные значения
переменных, получаем
,
подставляя уже найденные значения
переменных, получаем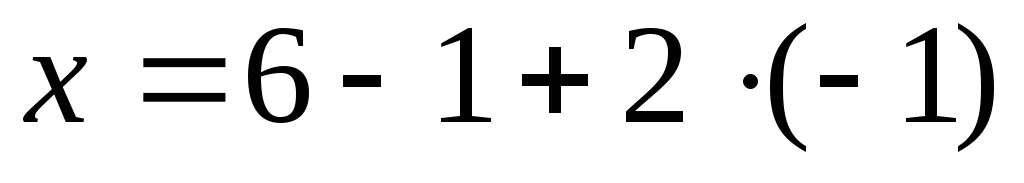 ,
то есть
,
то есть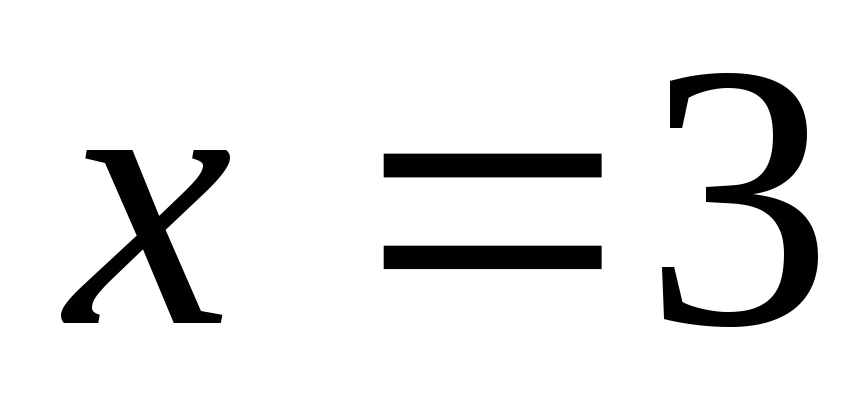 .
.
Чтобы убедиться в правильности решения, проверку необходимо сделать во всех трех уравнениях системы.
Проверка:
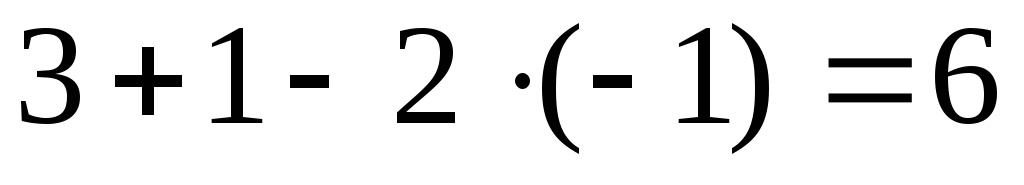 ,
получим
,
получим 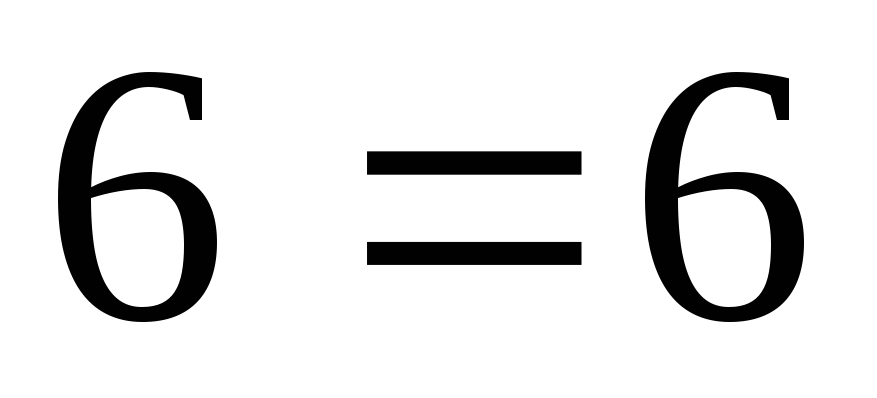
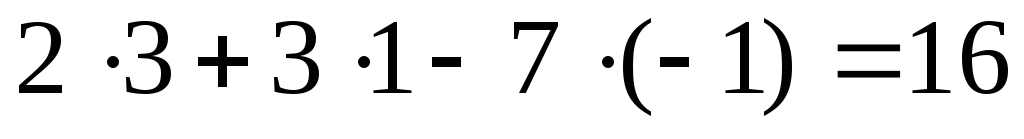 ,
получим
,
получим 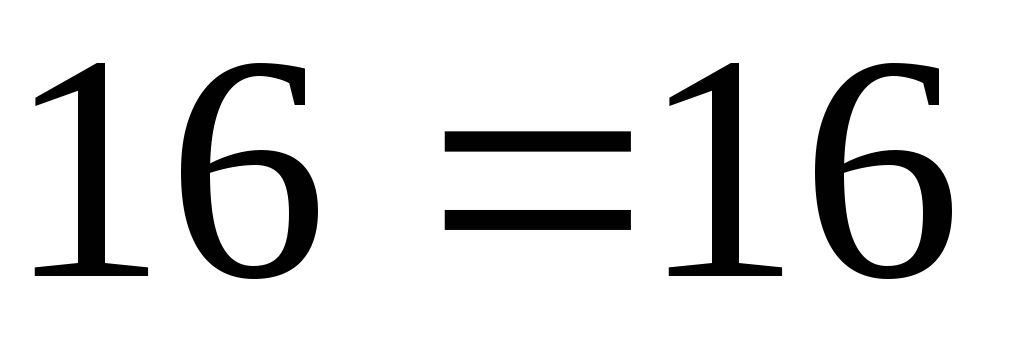
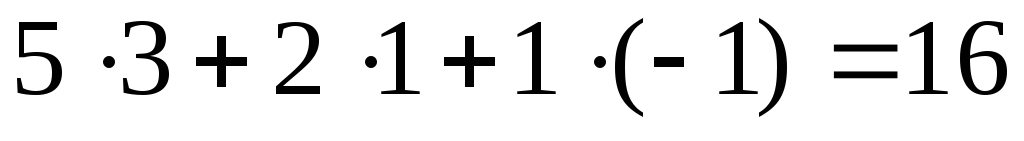 ,
получим
,
получим 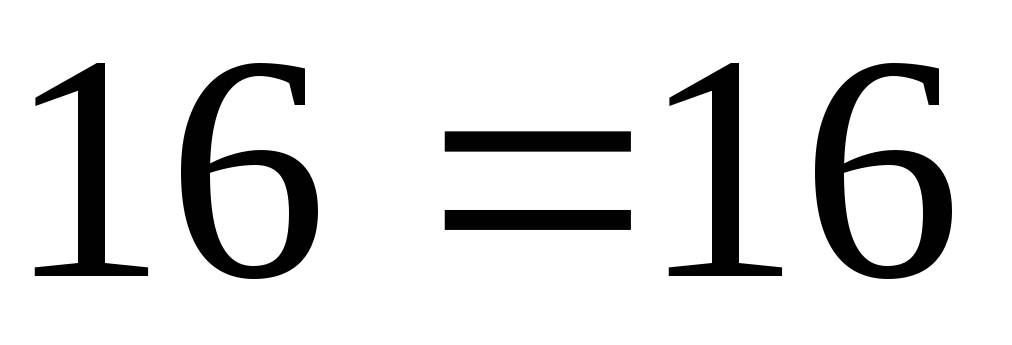
значит, система решена верно.
Ответ: 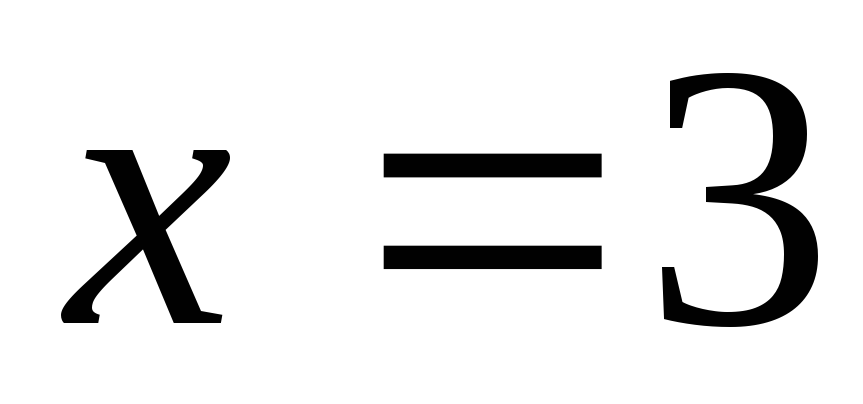 ,
,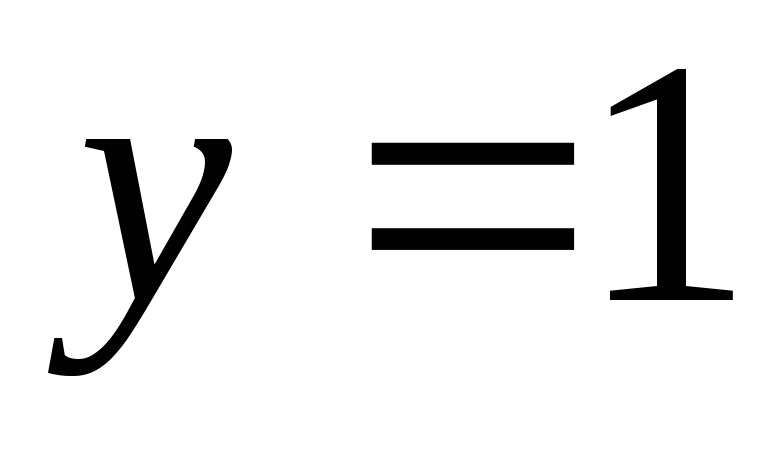 ,
,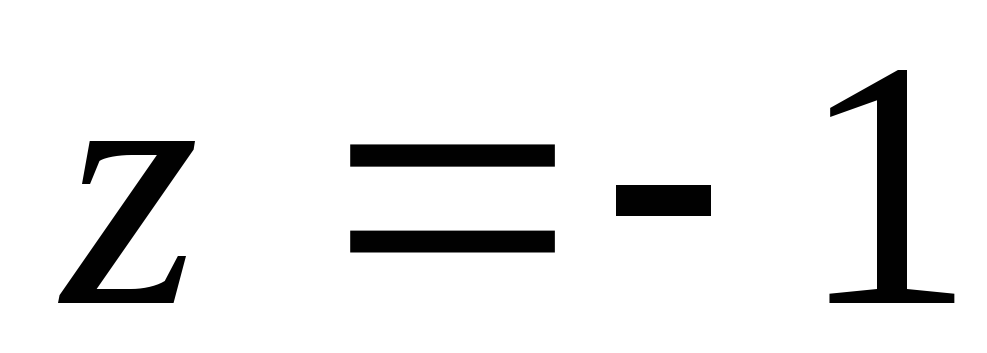 .
.
Пример
Решить
систему методом Гаусса: 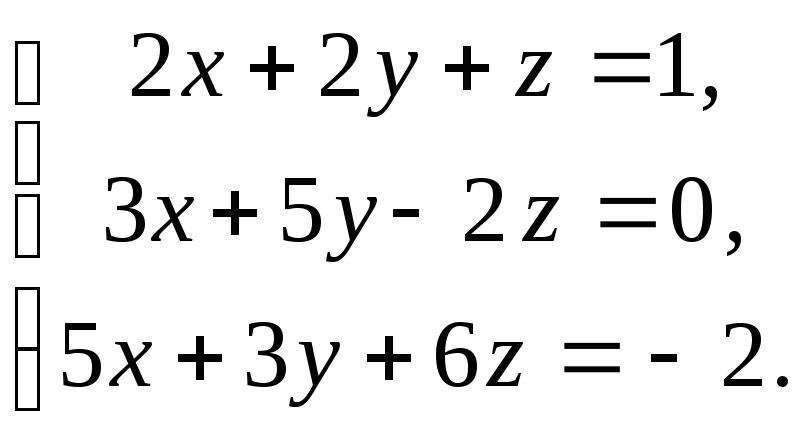
Решение:
Порядок действий в этом примере аналогичен порядку в предыдущем примере, а конкретные действия указаны в таблице 2.
Т аблица2
аблица2
2 | 2 | 1 | 1 | *(-3) | *(-5) |
3 | 5 | -2 | 0 | *2 | |
5 | 3 | 6 | -2 | *2 | |
0 | 4 | -7 | -3 | ||
0 | -4 | 7 | -9 | ||
0 | 0 | 0 | -12 |
В
результате преобразований получим
уравнение вида 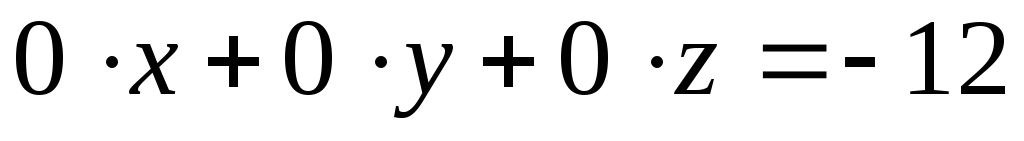 ,
следовательно, заданная система
несовместна.
,
следовательно, заданная система
несовместна.
Ответ: система несовместна.
Пример
Решить
систему методом Гаусса: 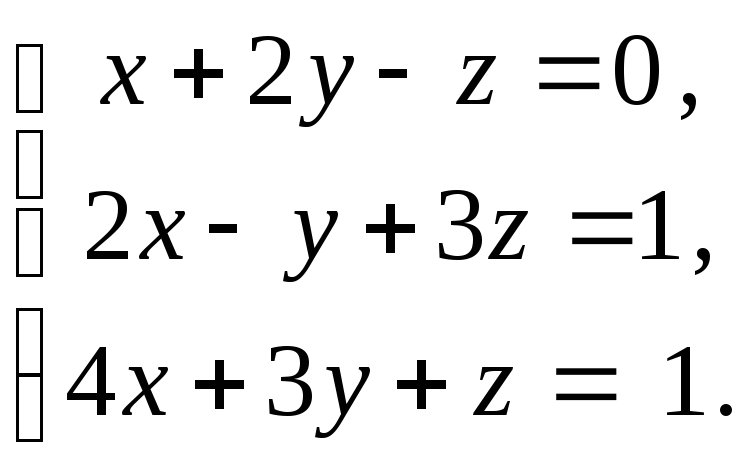
Решение:
Таблица 3
1 | 2 | -1 | 0 | *(-2) | *(-4) |
2 | -1 | 3 | 1 | ||
4 | 3 | 1 | 1 | ||
0 | -5 | 5 | 1 | *(-1) | |
0 | -5 | 5 | 1 | ||
0 | 0 | 0 | 0 |
В
результате преобразований получим
уравнение вида 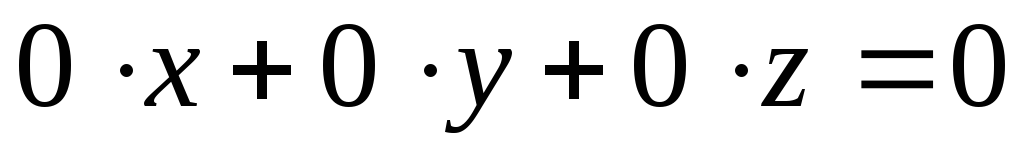 ,
которое исключается из рассмотрения.
Таким образом, имеем систему уравнений,
в которой число неизвестных 3, а число
уравнений 2.
,
которое исключается из рассмотрения.
Таким образом, имеем систему уравнений,
в которой число неизвестных 3, а число
уравнений 2.
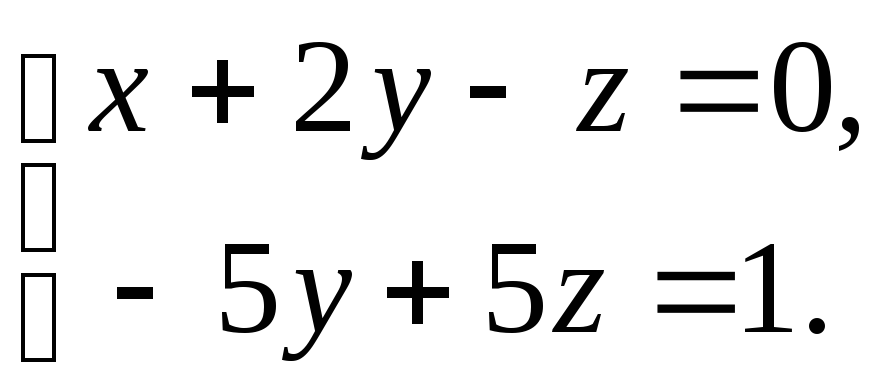
Система имеет бесчисленное множество решений. Чтобы отыскать эти решения, введем одну свободную переменную. (Число свободных переменных всегда равно разности между числом неизвестных и числом уравнений, оставшихся после преобразования системы. В нашем случае 3 – 2 = 1).
Пусть 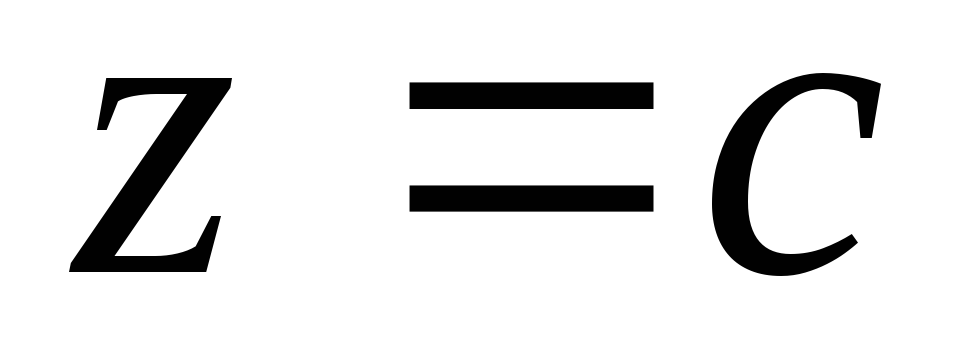 – свободная переменная.
– свободная переменная.
Тогда
из второго уравнения найдем 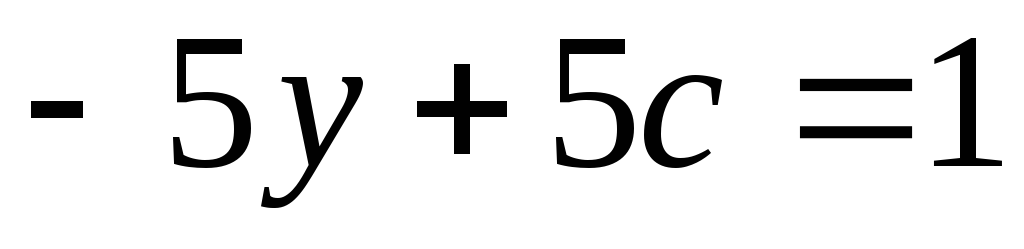 ,
откуда
,
откуда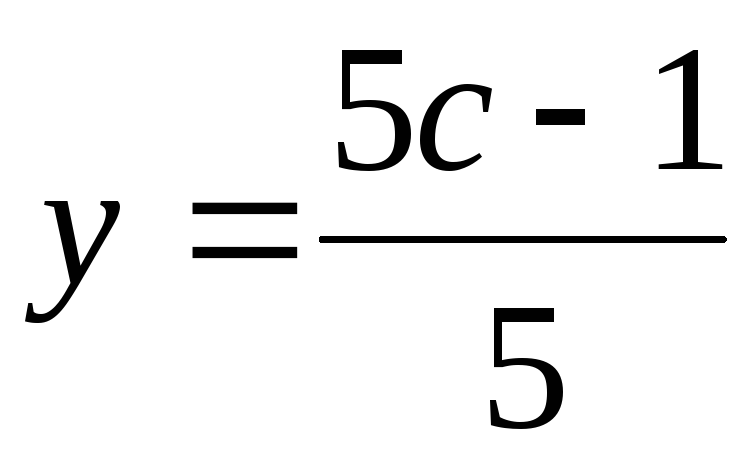 ,
а затем найдемx из первого уравнения
,
а затем найдемx из первого уравнения 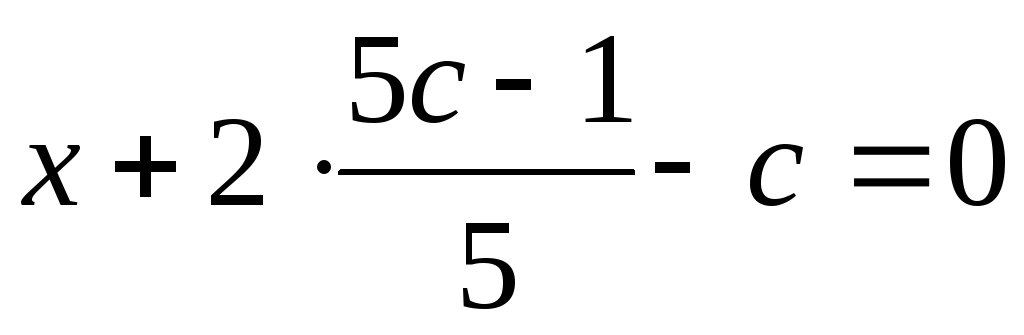 или
или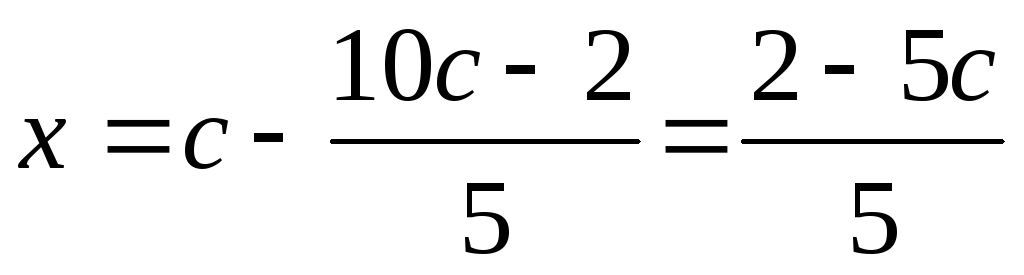 .
.
Таким
образом, 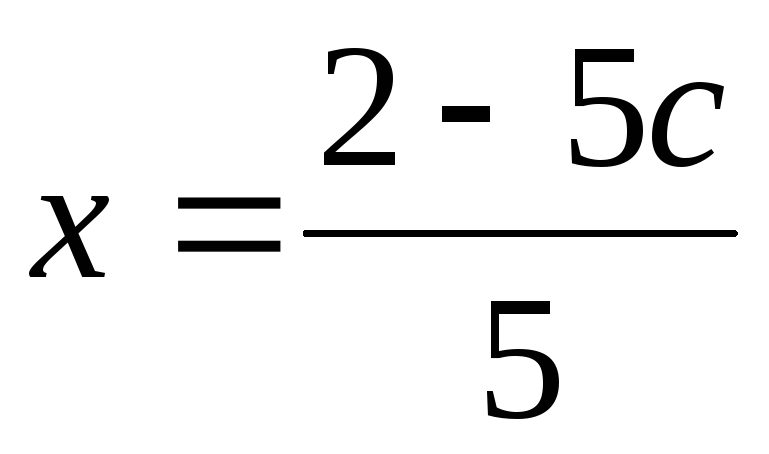 ;
;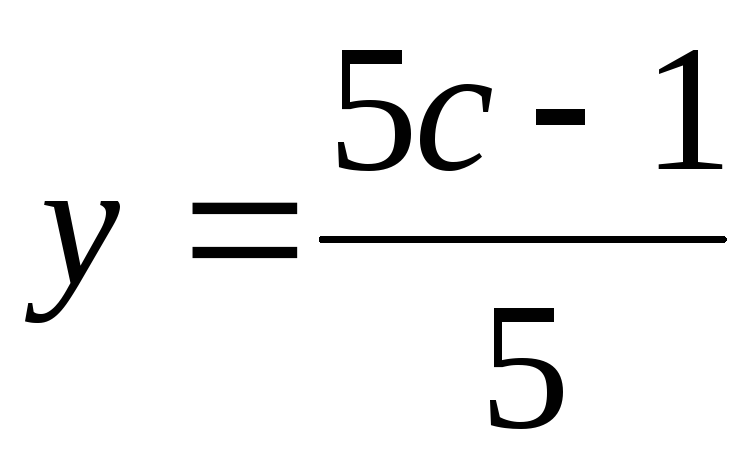 ;
;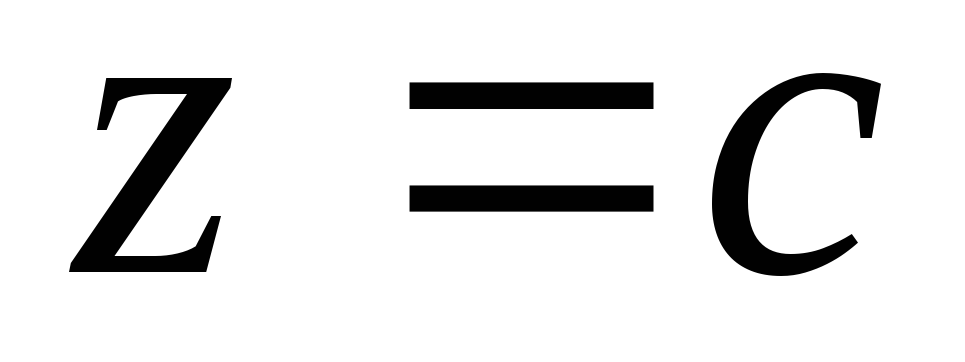 .
.
Сделаем
проверку в уравнениях, которые не
участвовали в нахождении  и
и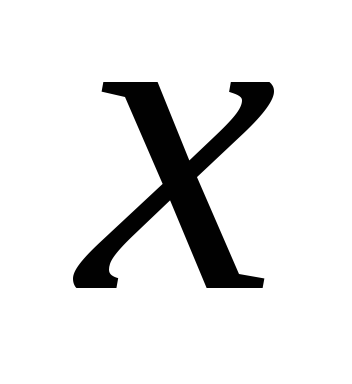 ,
то есть во втором и в третьем уравнениях
первоначальной системы.
,
то есть во втором и в третьем уравнениях
первоначальной системы.
Проверка:
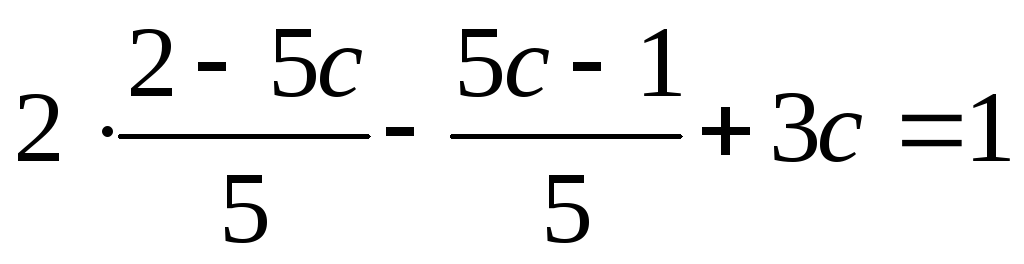 или
или 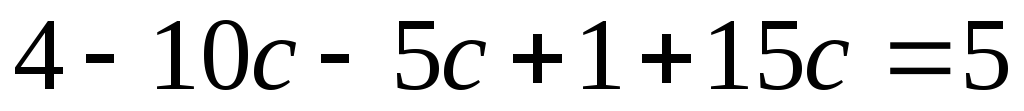 ,
получаем
,
получаем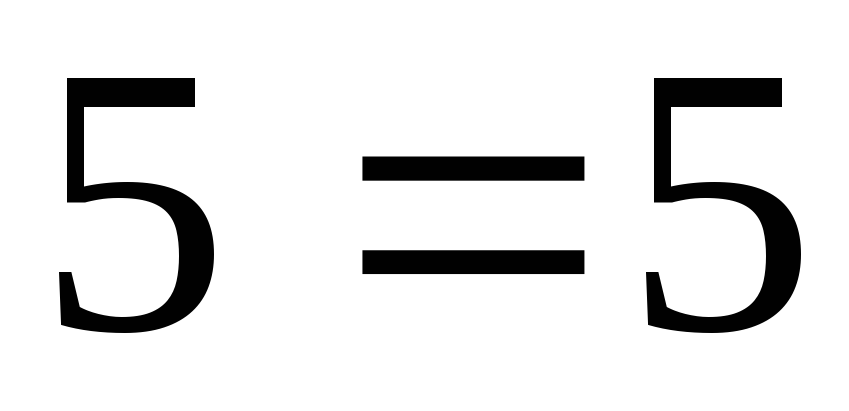 .
.
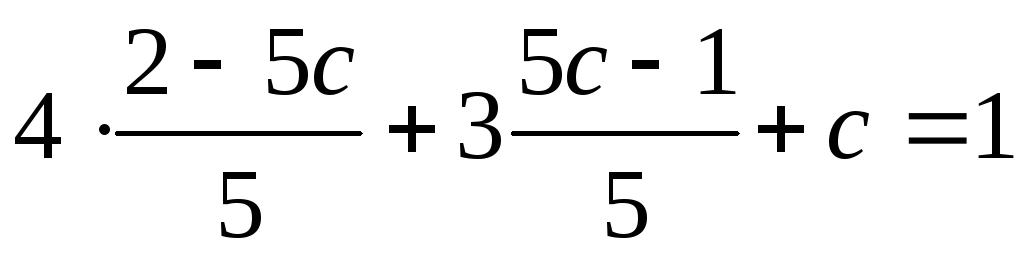 или
или 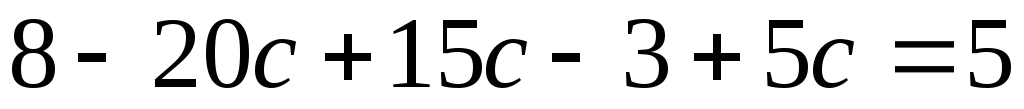 ,
получаем
,
получаем .
.
Система
решена верно. Давая произвольной
постоянной  различные значения, будем получать
различные значенияx, y и z.
различные значения, будем получать
различные значенияx, y и z.
Ответ: 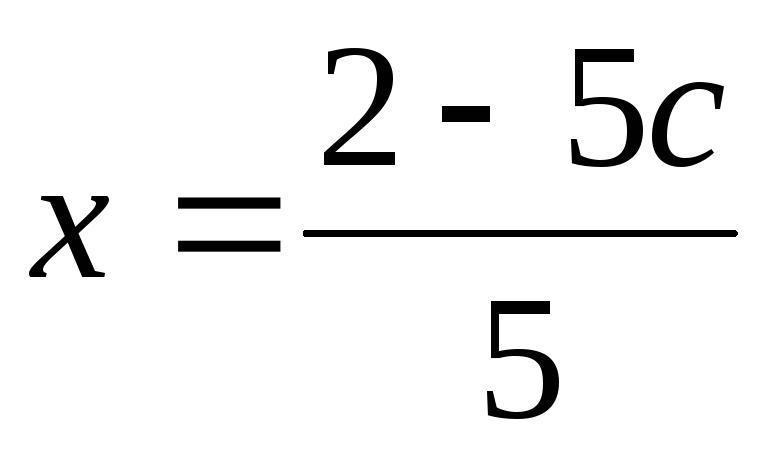 ;
;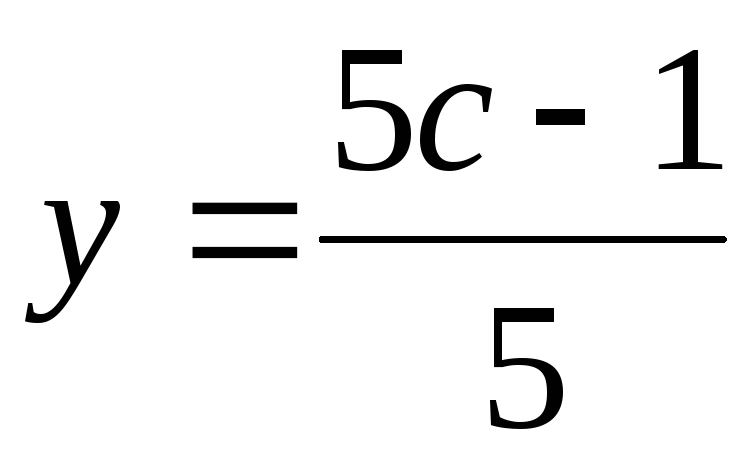 ;
;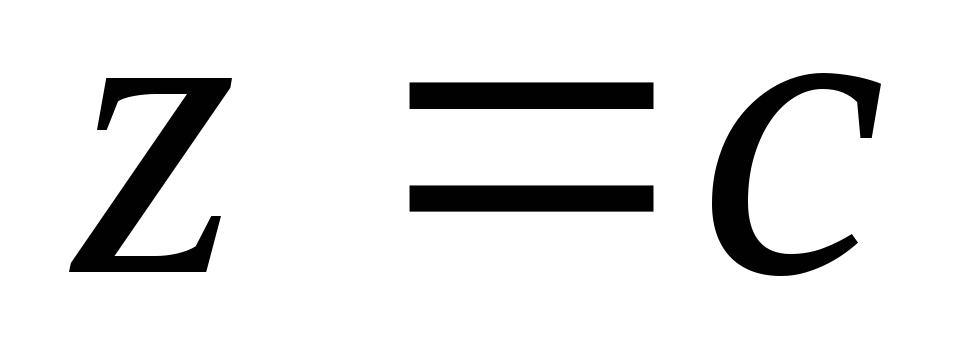 .
.
21
studfile.net
Метод Гаусса и Крамера

Матрицы
Метод Гаусса
Формулы Крамера

Матрица Определение
Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента а i j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:

Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

Метод Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Система т линейных уравнений с п неизвестными имеет вид:
x 1 , x 2 , …, x n – неизвестные.
a i j — коэффициенты при неизвестных.
b i — свободные члены (или правые части)

Типы уравнений
Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.
Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными , если они имеют одно и то же множество решений.

Элементарные преобразования
К элементарным преобразованиям системы отнесем следующее:
- перемена местами двух любых уравнений;
- умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Общий случай
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
1-ый шаг метода Гаусса
На первом шаге исключим неизвестное х 1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а 11 . Получим уравнение:
где
Исключим х 1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х 1 (соответственно а 21 и а 31 ).
Система примет вид:
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
(1)
(2)
(3)

2-ой шаг метода Гаусса
На втором шаге исключим неизвестное х 2 из третьего уравнения системы (3) . Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3) , получим уравнение:
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
(4)

В результате преобразований система приняла вид:
Система вида (5) называется треугольной .
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2 ) называют прямым ходом метода Гаусса .
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х 3 подставляют во второе уравнение системы (5) и находят х 2 . Затем х 2 и х 3 подставляют в первое уравнение и находят х 1 .
(5)

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b , где b 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное
решение, которое находится в
результате проведения обратного хода метода Гаусса.
Ступенчатая система имеет вид:
Такая система имеет бесчисленное
множество решений.

Рассмотрим на примере
- Покажем последовательность решения системы из трех уравнений методом Гаусса
- Поделим первое уравнение на 2, затем вычтем его из второго (a 21 =1, поэтому домножение не требуется) и из третьего, умножив предварительно на a 31 =3
- Поделим второе уравнение полученной системы на 2, а затем вычтем его из третьего, умножив предварительно на 4,5 (коэффициент при x 2 )
Тогда
x 3 =-42/(-14)=3;
x 2 =8-2×3=2
x 1 =8-0,5×2-2×3=1

Метод Крамера
Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Создан Габриэлем Крамером в 1751 году.

Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)

Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает с числом неизвестных:
Теорема. Cистема
a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1
a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2
… …
a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
- a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n

Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:
a 11 a 12 … a 1n
a 21 a 22 … a 2n
… …
a n1 a n2 … a nn
- a 11 a 12 … a 1n a 21 a 22 … a 2n … … a n1 a n2 … a nn
≠ 0

В этом случае решение можно вычислить по формуле Крамера

Для получения значения x k в числитель ставится определитель, получающийся из det(A) заменой его k- го столбца на столбец правых частей
- Пример. Решить систему уравнений :

Решение.

Найдите оставшиеся компоненты решения.
- Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления (n+1)-го определителя порядка n , в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка n . Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат
- Решение системы линейных уравнений с квадратной матрицей A является непрерывной функцией коэффициентов этой системы при условии, что det A не равно 0 .

Найдите оставшиеся компоненты решения.
- Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра.
- зависящей от параметра , определить предел отношения компонент решения:

Решение.
- В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при . Для случая применением метода Гаусса убеждаемся, что система несовместна. Тем не менее, указанный предел существует. Формулы Крамера дают значения компонент решения в виде
и, хотя при каждая из них имеет бесконечный предел, их отношение стремится к пределу конечному.

Ответ.
Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной: при стремлении параметра к какому-то критическому значению (обращающему в нуль определитель матрицы системы) хотя бы одна из компонент решения «уходит на бесконечность».

Использованные источники
- В.С. Щипачев, Высшая математика
- Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов.
- Волков Е.А. Численные методы.
- В.Е. Шнейдер и др., Краткий курс высшей математики,том I.
multiurok.ru
Правило Крамера и метод Гаусса. Лекция
ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
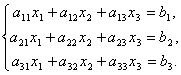
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
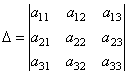
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
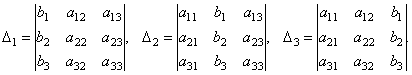
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
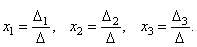
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
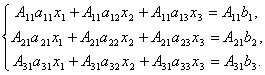
Сложим эти уравнения:
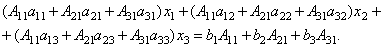
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
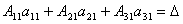 .
.
Далее рассмотрим коэффициенты при x2:
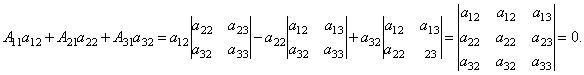
Аналогично можно
показать, что и 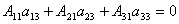 .
.
Наконец несложно
заметить, что 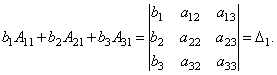
Таким образом,
получаем равенство: 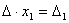 .
.
Следовательно, 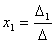 .
.
Аналогично выводятся
равенства 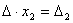 и
и 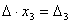 ,
откуда и следует утверждение теоремы.
,
откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений
Итак, х=1, у=2, z=3.
Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.
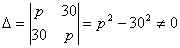 .
Поэтому
.
Поэтому 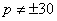 .
.
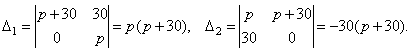
При

При p = 30 получаем систему уравнений
 которая
не имеет решений.
которая
не имеет решений.При p = –30 система принимает вид
 и,
следовательно, имеет бесконечное
множество решений x=y, yR.
и,
следовательно, имеет бесконечное
множество решений x=y, yR.
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
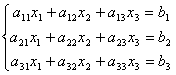 .
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
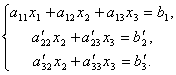
Теперь из последнего
уравнения исключим слагаемое, содержащее x2.
Для этого третье уравнение разделим на 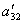 ,
умножим на
,
умножим на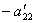 и сложим со вторым. Тогда будем иметь
систему уравнений:
и сложим со вторым. Тогда будем иметь
систему уравнений:
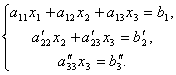
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
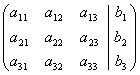
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.
Вернувшись к системе уравнений, будем иметь
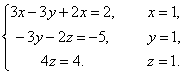
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
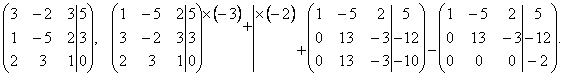
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
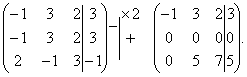
Вернемся к системе
уравнений. 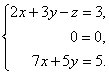
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
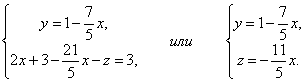
Таким образом, система имеет бесконечное множество решений.
studfile.net
1.3. Системы линейных уравнений. Метод Крамера
Рассмотрим систему 3-х уравнений с тремя неизвестными
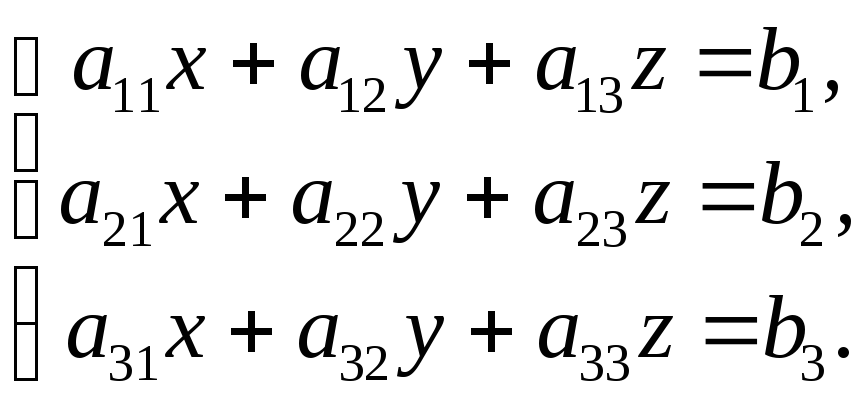 (1.3)
(1.3)
Используя определители 3-го порядка, решение такой системы можно записать в таком виде:
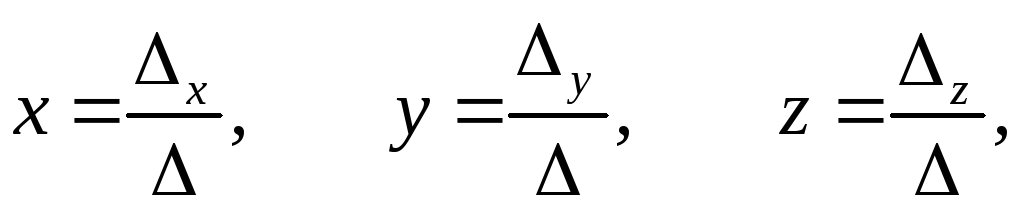 (1.4)
(1.4)
если 0. Здесь
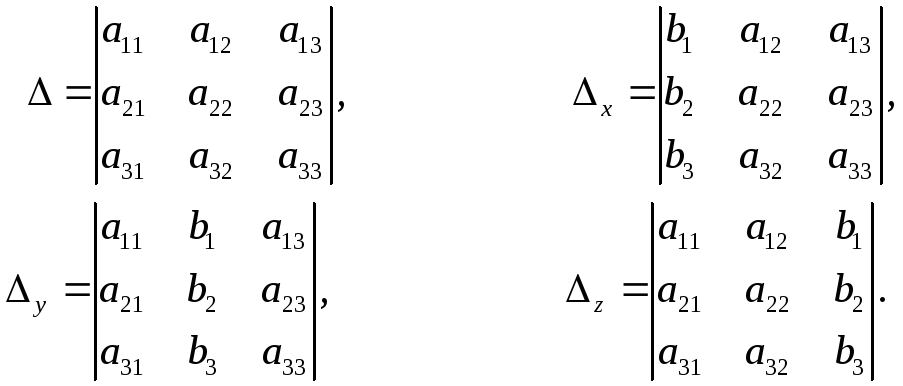 (1.5)
(1.5)
Это есть формулы Крамерарешения системы трех линейных уравнений с тремя неизвестными.
Пример 1.6.Решить систему линейных уравнений методом Крамера:
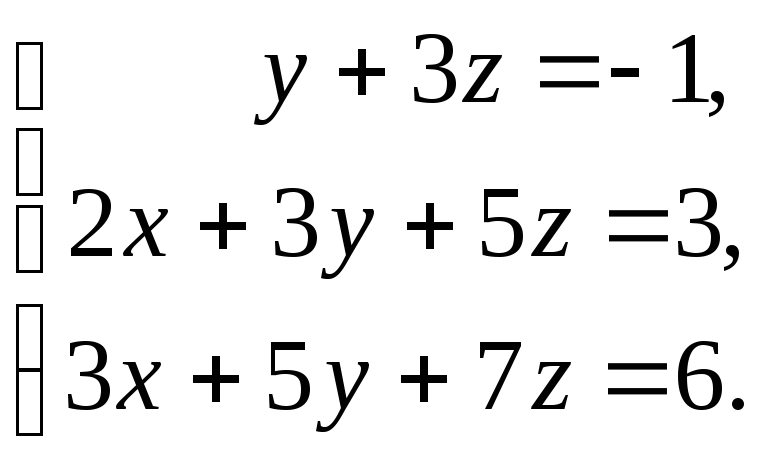
Решение. Находим определитель основной матрицы системы:
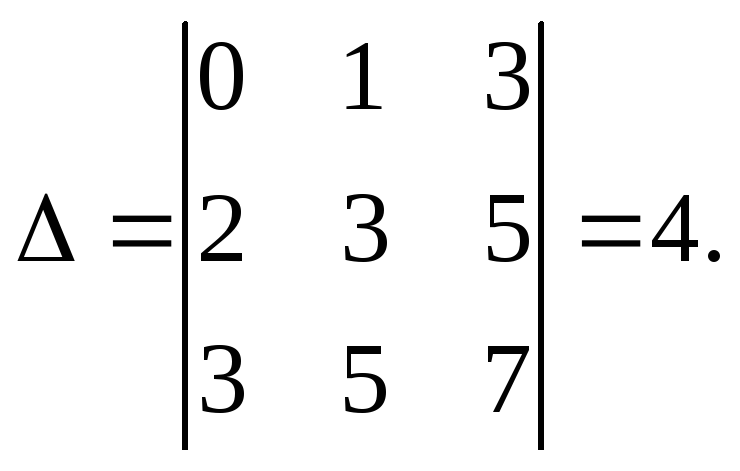
Поскольку 0, то для нахождения решения системы можно применить метод Крамера. Вычислим остальные определители:

Тогда
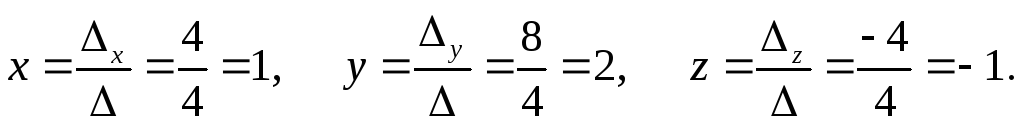
Проверка:
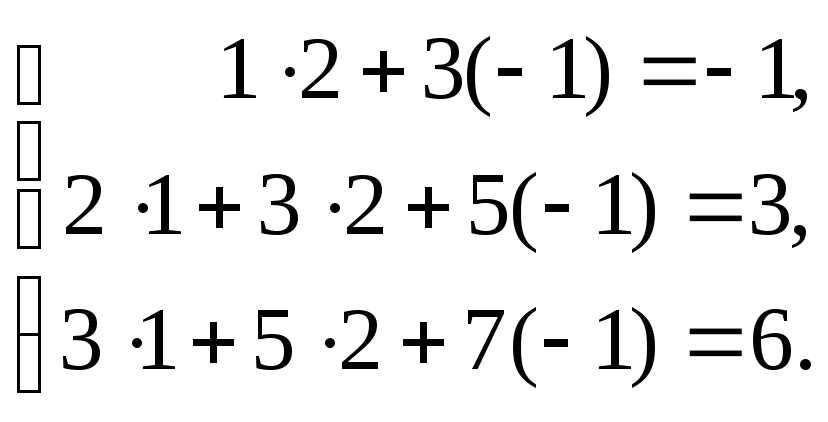
Следовательно, решение найдено правильно.
Теорема Крамера.Квадратная система линейных неоднородных уравнений n-го порядка с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение, и это решение вычисляется по формулам:
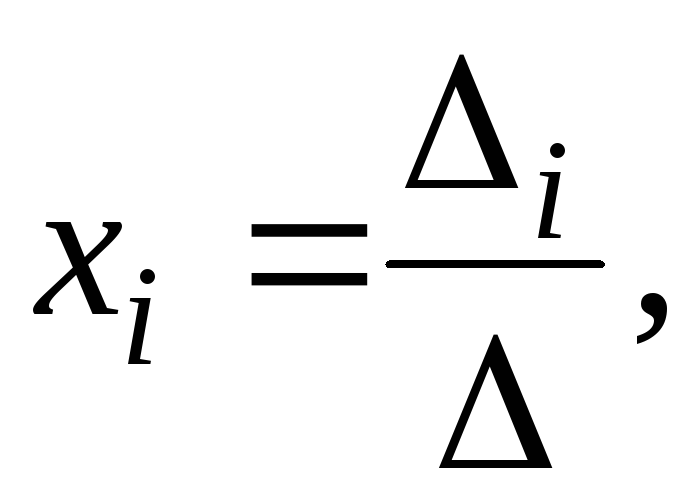
где – определитель основной матрицы, i – определитель матрицы, полученной из основной, заменой i-го столбца столбцом свободных членов.
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо вообще не имеет решений, либо имеет бесконечное множество решений.
1.4. Матричный метод. Обратная матрица
Матрица А–1называетсяобратнойматрицей по отношению к матрицеА, если выполняется равенствоAA–1=A–1A=E. Только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрицаАимела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля:detA0.
Пример 1.7.Решить систему линейных уравнений матричным методом (при помощи обратной матрицы).
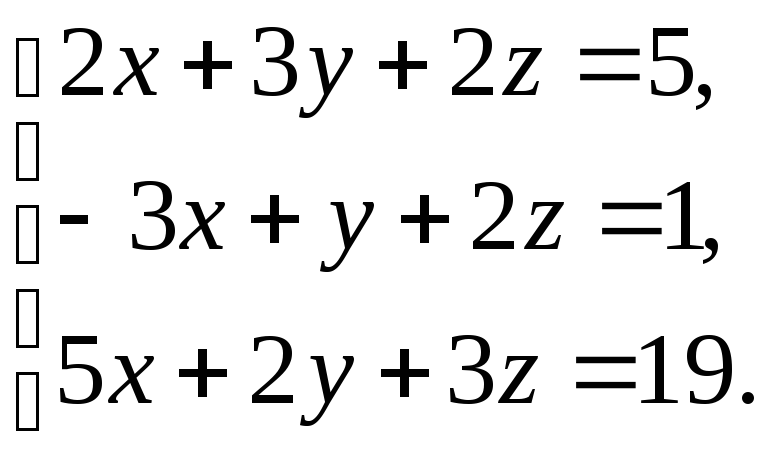
Решение. Запишем исходную систему уравнений в матричном виде:
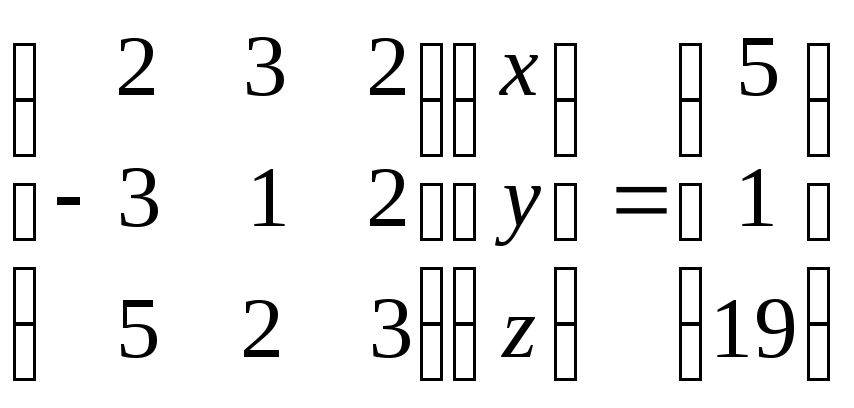 .
.
Тогда решение можно формально записать в виде:
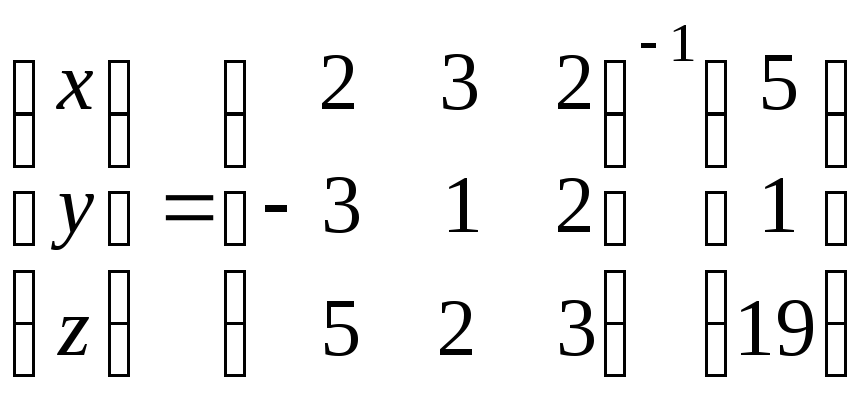 .
.
Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу
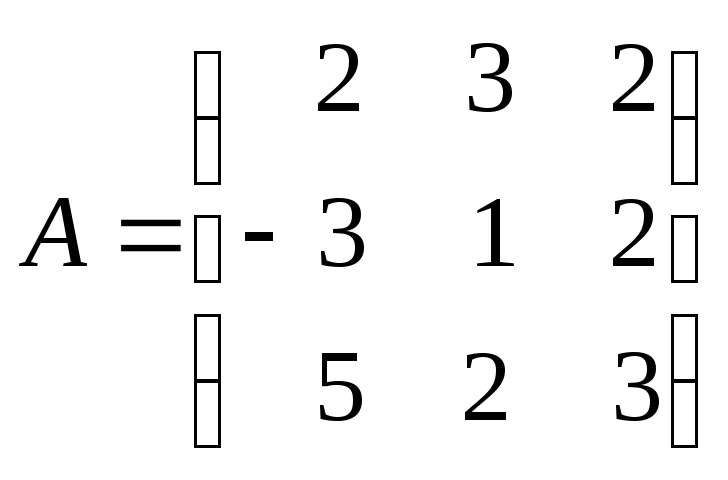 .
.
Найдем ее
1) Вычисляем
определитель исходной матрицы: 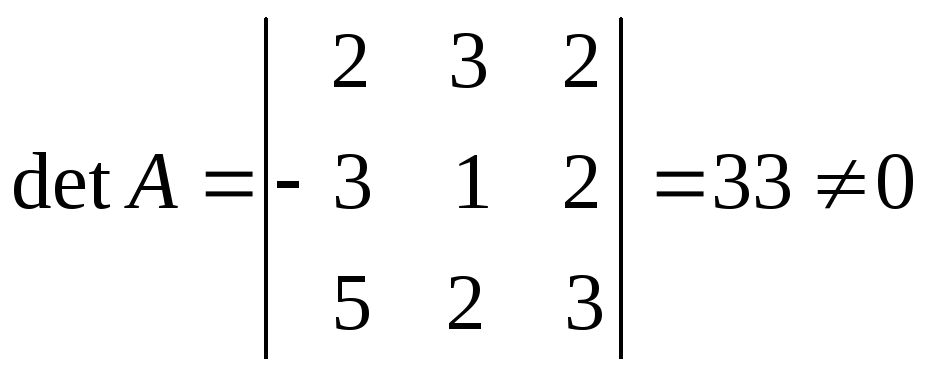 .
.
2) Транспонируем
матрицу 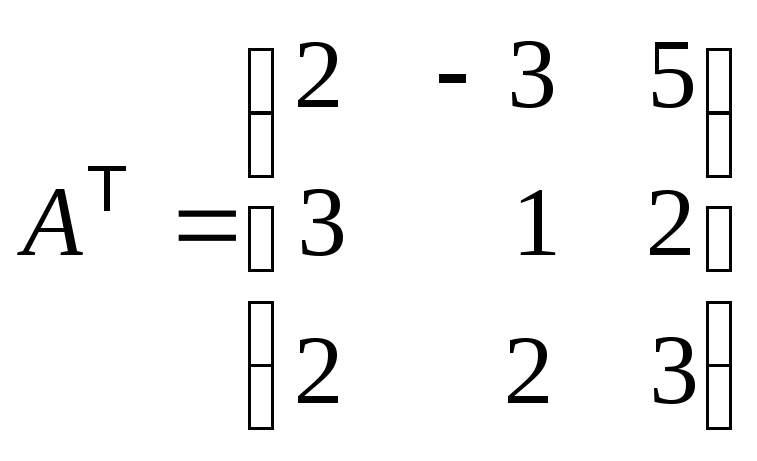 .
.
3) Находим все алгебраические дополнения транспонированной матрицы:
4) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:
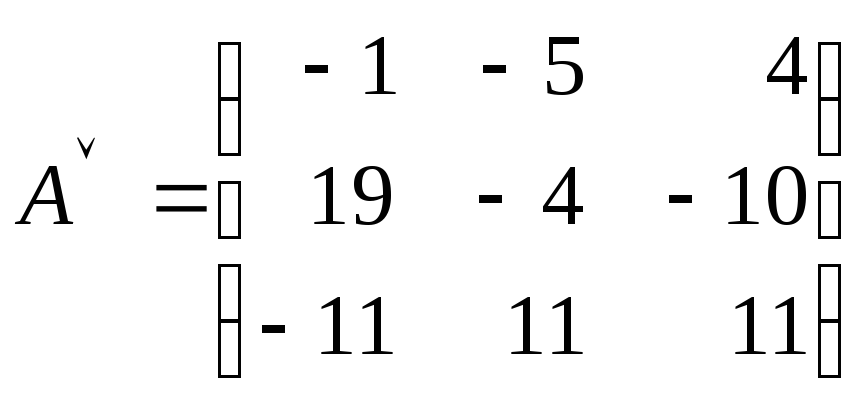
5) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:
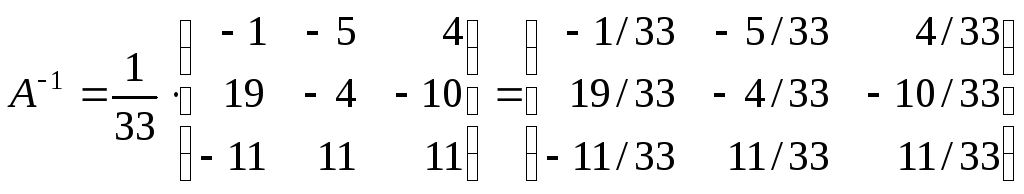 .
.
6) Сделаем проверку:
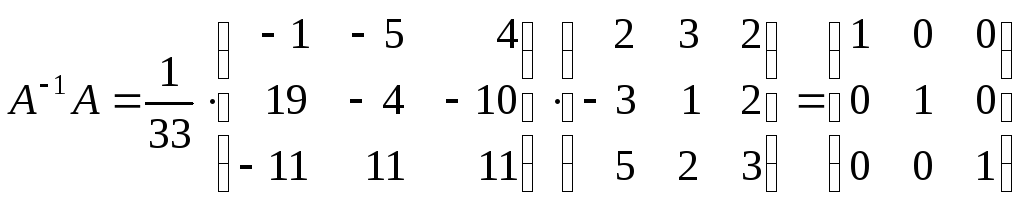 .
.
Следовательно, обратная матрица найдена правильно.
Теперь, используя найденную обратную матрицу можно найти решение исходной системы:
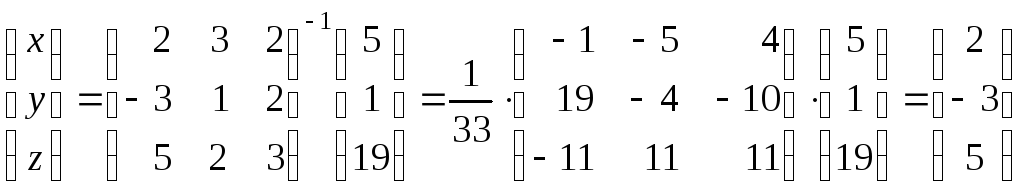 .
.
1.5. Метод Гаусса
Рассмотрим произвольную систему линейных уравнений
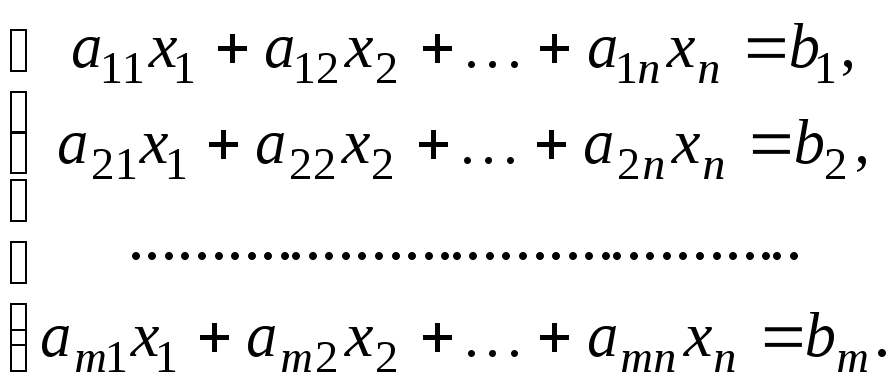 (1.5)
(1.5)
В общем случае nm.
Задача теории систем линейных уравнений состоит в том, чтобы найти все решения системы. При этом возможны три случая. 1) Система вообще не имеет решений. Системы линейных уравнений, не имеющие ни одного решения, называются несовместными. 2) Система имеет хотя бы одно решение. такие системы называютсясовместными. 3) Система имеет только одно решение. Такие системы называютсяопределёнными.
Метод Гаусса (метод последовательного исключения неизвестных)заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Рассмотрим метод Гаусса на конкретных примерах.
Пример 1.8. Решить систему линейных уравнений методом Гаусса.

Решение.Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее к треугольному виду:

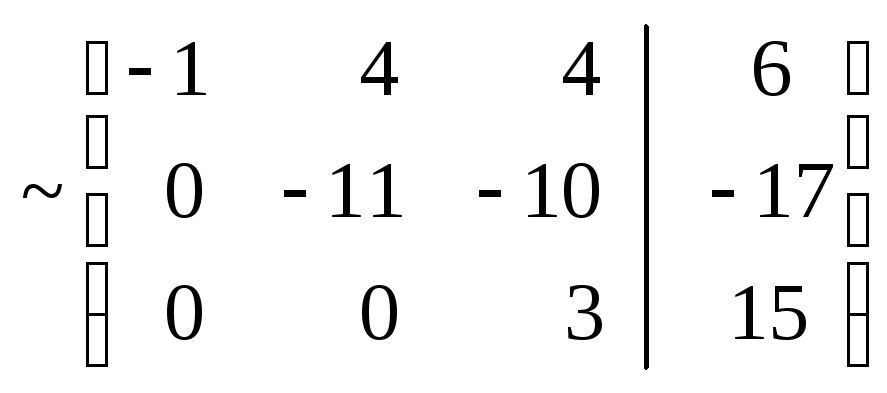 .
.
Теперь выписываем соответствующую укороченную систему уравнений. Из последнего уравнения находим значение z и подставляем его во второе уравнение. После этого из второго уравнения находим y. Найденные значения y и z подставляем в первое уравнение, из которого затем находим значение x:
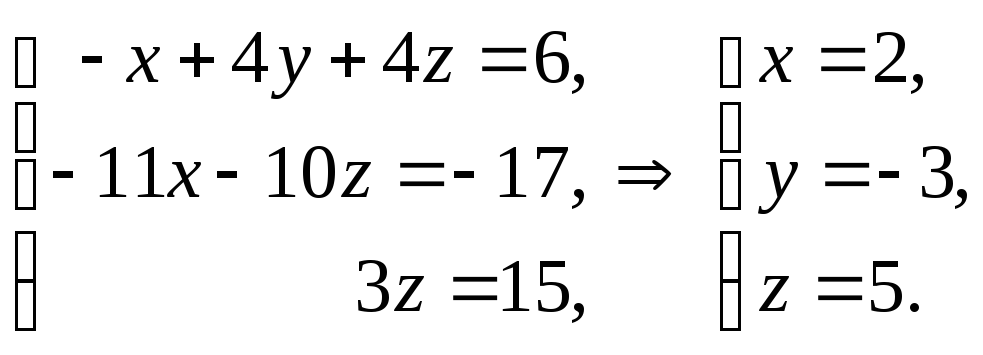
Эта тройка чисел будет являться единственным решением системы.
Пример 1.9.Решить систему методом Гаусса:
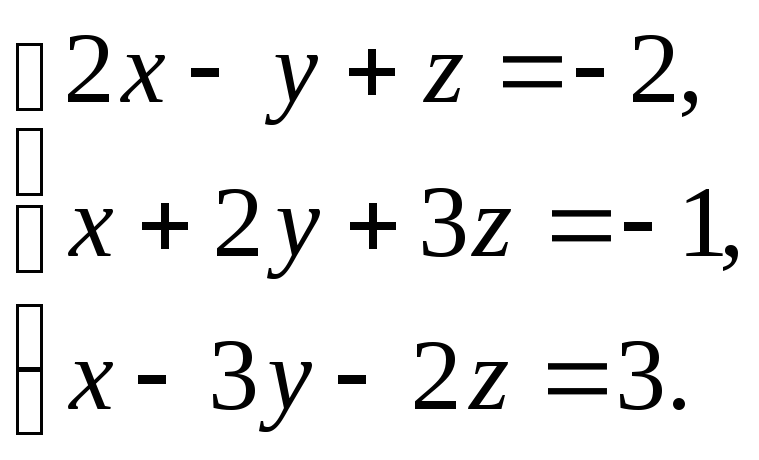
Решение. Выписываем и преобразуем расширенную матрицу системы

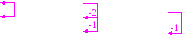
Записываем упрощенную систему уравнений:
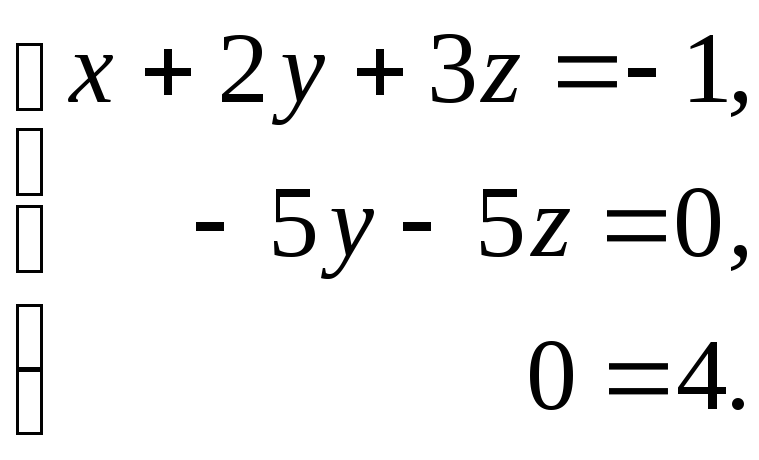
Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна.
Пример 1.10. Найти общее решение методом Гаусса
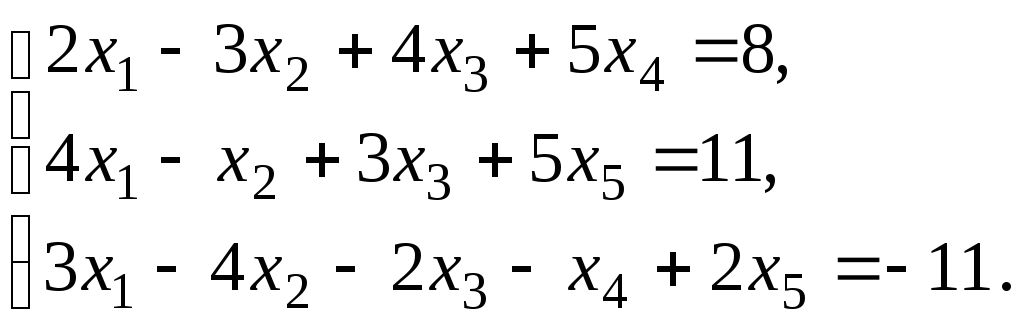
Решение. Выпишем расширенную матрицу системы, а затем при помощи элементарных преобразований строк приведем ее трапециевидной форме:
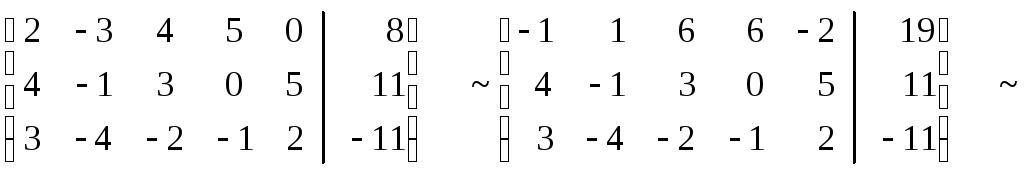







-1
4
3







3

:15
.Теперь выписываем соответствующую укороченную систему уравнений:
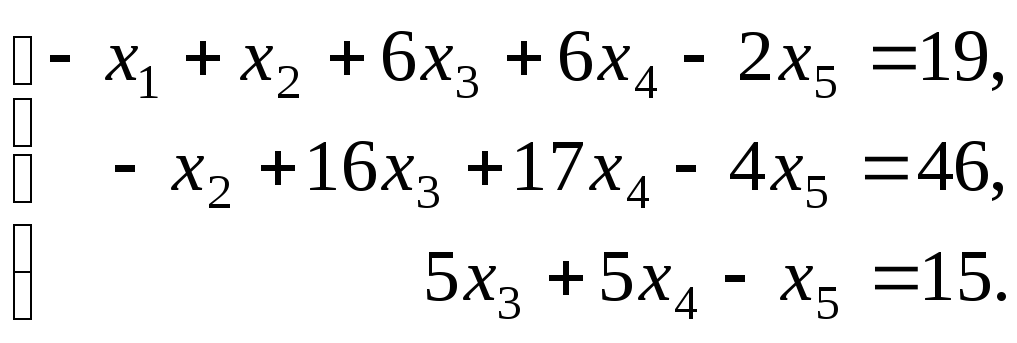
Пусть переменные x4 и x5 будут свободными, тогда переменные x1, x2 и x3 будут основными (или базисными). Их мы оставим в левой части:
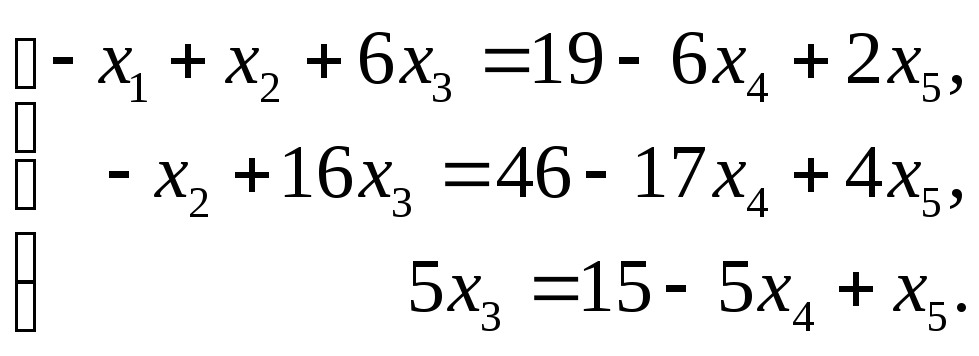
Разрешая эту систему относительно x1, x2 и x3 получим
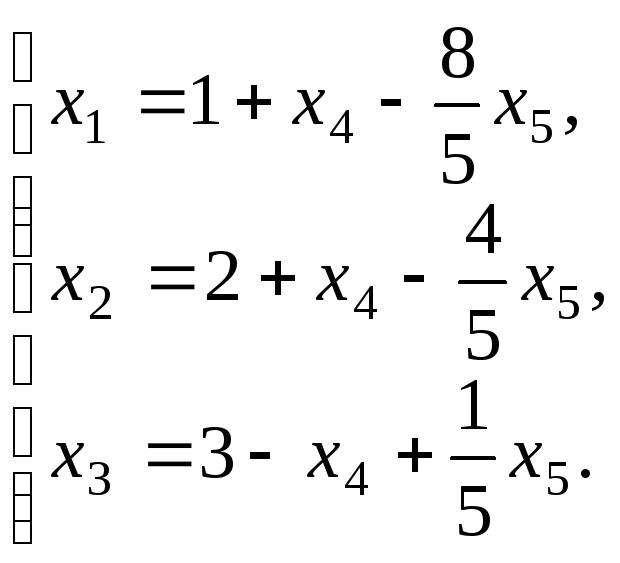
Это есть общее решение системы. Запишем это решение в параметрическом виде. Пусть x4=a и x5=5b. Тогда общее решение системы запишется в виде:
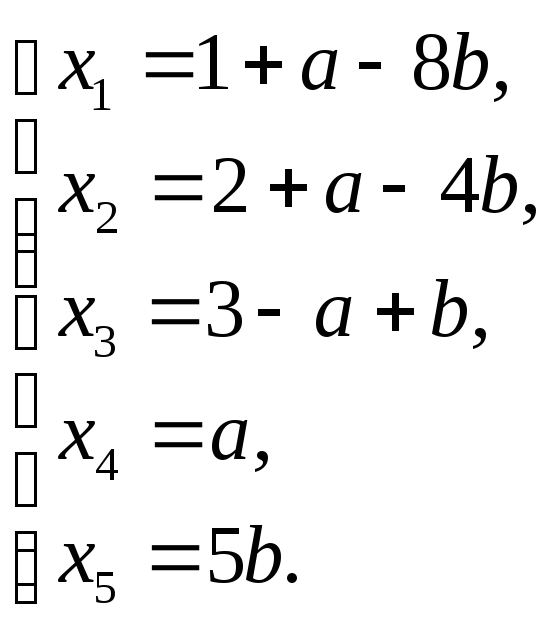
Давая числам a и b различные значения, будем получать частные решения. Например, если a=0, b=1, то x1=–7, x2=–2, x3=4, x4=0, x5=5.
studfile.net
Тема 3 системы линейных уравнений. Правила крамера. Метод гаусса конспект 3
3.1 Правило крамера
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными, которые ждут вас в электротехнике на 2 курсе!
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Теорема
Система nуравнений сnнеизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.
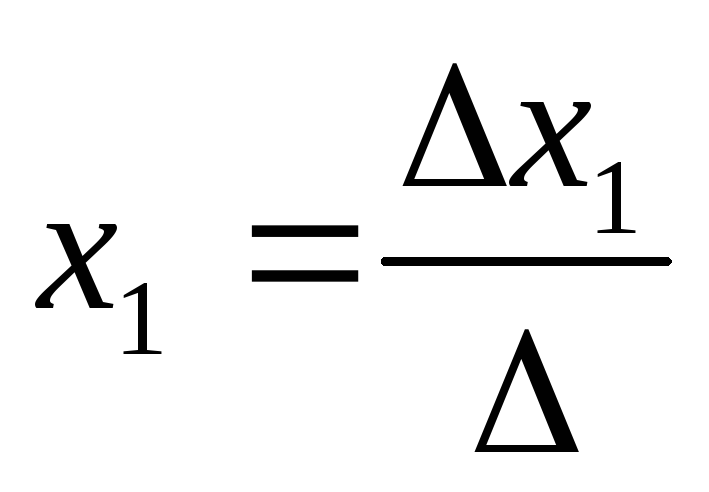
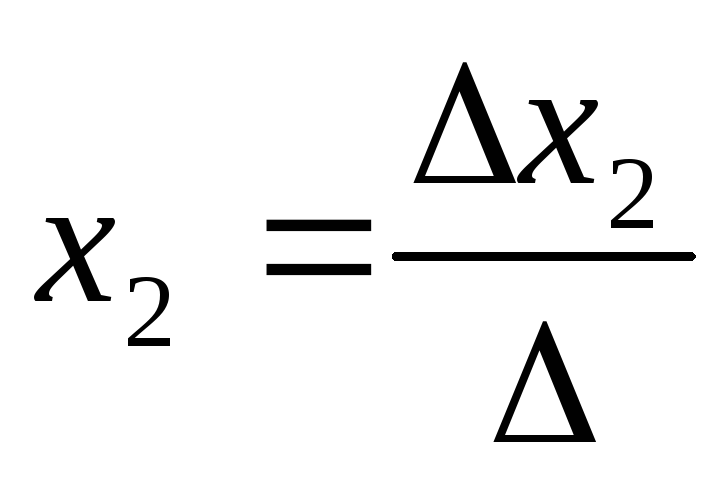 …
…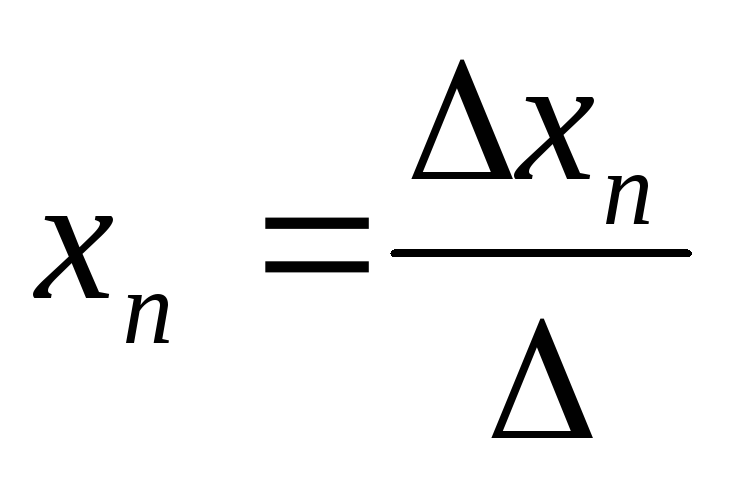

Рассмотрим систему уравнений 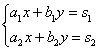
На
первом шаге вычислим определитель 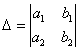 ,
его называютглавным определителем
системы.
,
его называютглавным определителем
системы.
Если 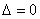 ,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать метод
Гаусса.
,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать метод
Гаусса.
Если 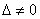 ,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя: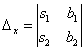 и
и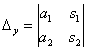
На
практике вышеуказанные определители
также могут обозначаться латинской
буквой 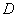 .
.
Корни
уравнения находим по формулам: 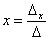 ,
,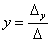
Пример 1
Решить систему уравнений: 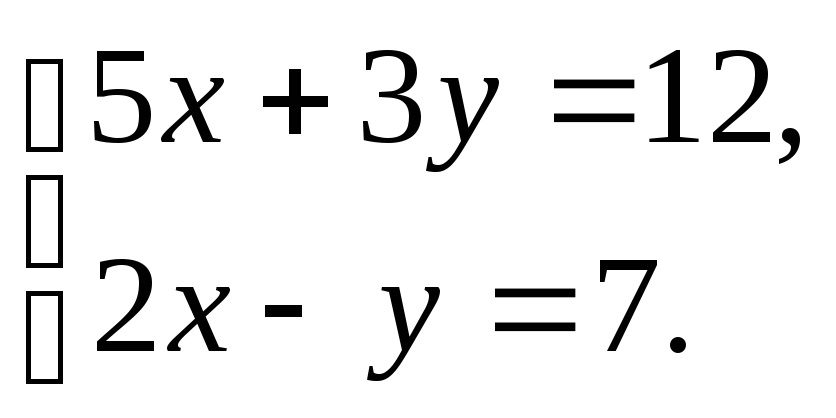
Решение
Составим и вычислим определитель
 :
: — система имеет одно решение, можно
применить теорему Крамера
— система имеет одно решение, можно
применить теорему Крамера
2) Составим и вычислим определитель 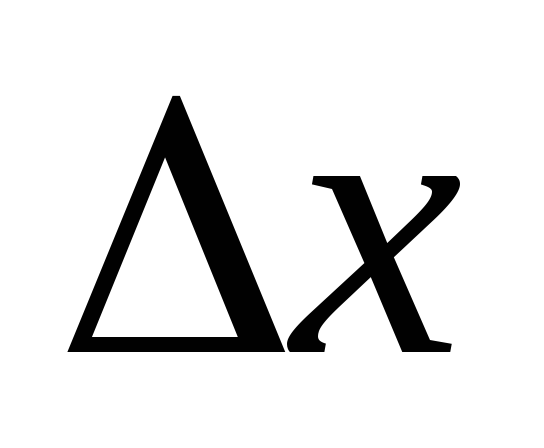 :
: 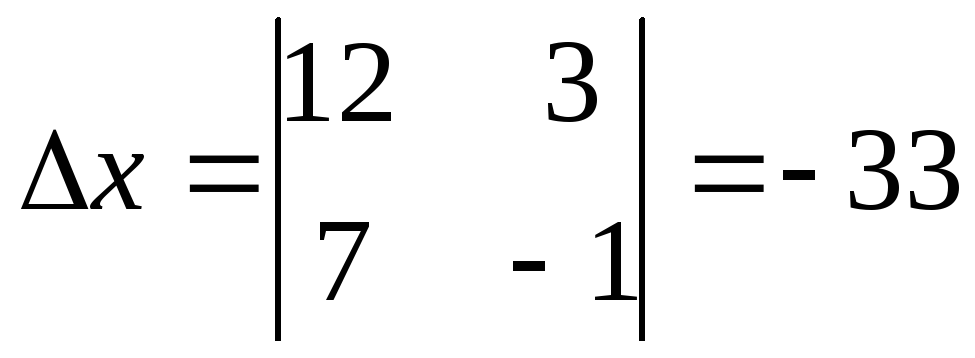
Составим и вычислим определитель
 :
:Найдем значения xиyпо формулам Крамера
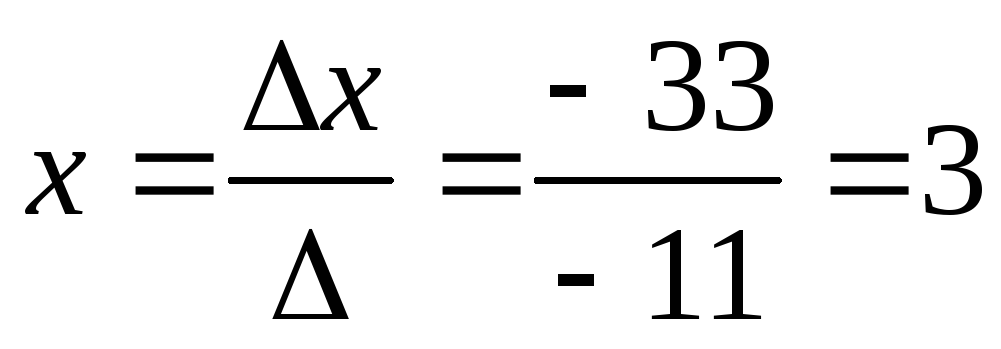
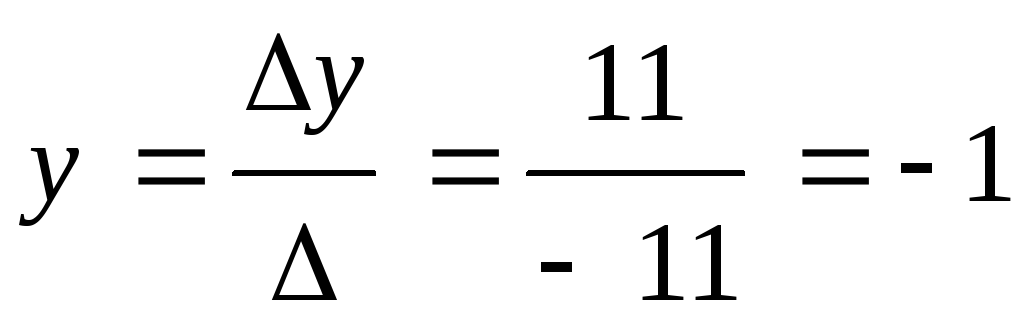
Ответ: (3; -1)
Пример 2
Решить систему линейных уравнений 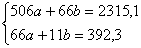
Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему мы взяли из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
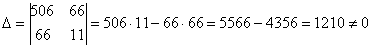 ,
значит, система имеет единственное
решение.
,
значит, система имеет единственное
решение.
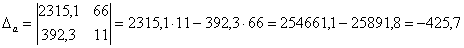 ;
;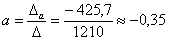
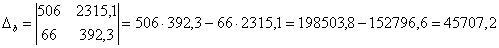 ;
;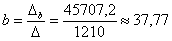
Ответ: 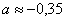 ,
,
3.2 МЕТОД ГАУССА
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Вернемся к простейшей системе 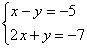 и
решим ее методом Гаусса.
и
решим ее методом Гаусса.
На
первом этапе нужно записать расширенную
матрицу системы: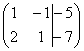 .
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
.
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица
системы – это матрица,
составленная только из коэффициентов
при неизвестных, в данном примере матрица
системы: 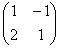 . Расширенная матрица системы – это та же матрица системы плюс столбец
свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец
свободных членов, в данном случае: 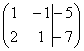 .
Любую из матриц можно для краткости
называть просто матрицей.
.
Любую из матриц можно для краткости
называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строкиматрицыможнопереставлятьместами. Например,
в рассматриваемой матрице можно
безболезненно переставить первую и
вторую строки: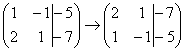
2)
Строку матрицы можно умножить
(разделить)на любое число,отличное
от нуля. Рассмотрим, например, матрицу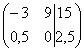 .
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2:
.
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2: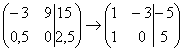 .
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
.
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
3) Это
преобразование вызывает наибольшие
затруднения, но на самом деле ничего
сложного тоже нет. К строке матрицы
можно прибавить другую строку,
умноженную на число, отличное от
нуля. Рассмотрим нашу матрицу из
практического примера: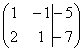 .
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на –2:
.
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на –2: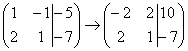 ,
ико второй строке прибавляем первую
строку умноженную на –2:
,
ико второй строке прибавляем первую
строку умноженную на –2: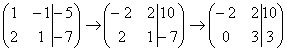 .
Теперь первую строку можно разделить
«обратно» на –2:
.
Теперь первую строку можно разделить
«обратно» на –2: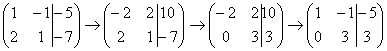 .
.
Как видите, строка, которую ПРИБАВЛЯЛИ–не изменилась.Всегдаменяется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На
практике так подробно, конечно, не
расписывают, а пишут короче: 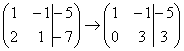 Еще
раз: ко второй строкеприбавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
Еще
раз: ко второй строкеприбавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
«Переписываю
матрицу и переписываю первую строку: 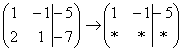 »
»
«Сначала
первый столбец. Внизу мне нужно получить
ноль. Поэтому единицу вверху умножаю
на –2: 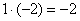 ,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку:
,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку: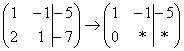 »
»
«Теперь
второй столбец. Вверху –1 умножаю на
–2: 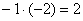 .
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую строку:
.
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую строку: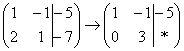 »
»
«И
третий столбец. Вверху –5 умножаю на
–2: 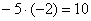 .
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку:
.
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку: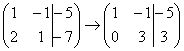 »
»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ:рассмотренные
манипуляциинельзя использовать,
если Вам предложено задание, где матрицы
даны «сами по себе». Например, при
«классических»действиях с матрицамичто-то переставлять внутри матриц ни в
коем случае нельзя! Вернемся к нашей
системе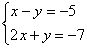 .
Она уже почти решена.
.
Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
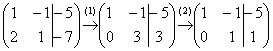
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель
элементарных преобразований –привести матрицу к ступенчатому виду: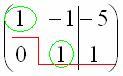 .
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто называетсятрапециевидный видилитреугольный
вид.
.
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто называетсятрапециевидный видилитреугольный
вид.
В
результате элементарных преобразований
получена эквивалентнаяисходной
система уравнений: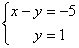
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В
нижнем уравнении у нас уже готовый
результат: 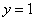 .
.
Рассмотрим
первое уравнение системы 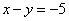 и
подставим в него уже известное значение
«игрек»:
и
подставим в него уже известное значение
«игрек»: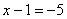
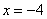
Ответ: 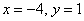
Пример 1
Решить
методом Гаусса систему уравнений: 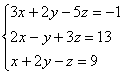
Запишем
расширенную матрицу системы: 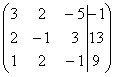
Сейчас
я сразу нарисую результат, к которому
мы придём в ходе решения: 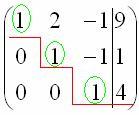 И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
Сначала
смотрим на левое верхнее число: 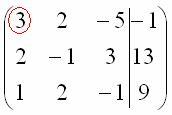 Почти
всегда здесь должна находитьсяединица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки:
Почти
всегда здесь должна находитьсяединица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки:
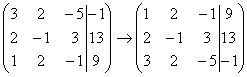
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица
в левом верхнем углу организована.
Теперь нужно получить нули вот на этих
местах: 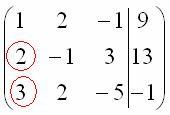
Нули
получаем как раз с помощью «трудного»
преобразования. Сначала разбираемся
со второй строкой (2, –1, 3, 13). Что нужно
сделать, чтобы на первой позиции получить
ноль? Нужно ко второй строке прибавить
первую строку, умноженную на –2.
Мысленно или на черновике умножаем
первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же
мысленно или на черновике) сложение,ко
второй строке прибавляем первую строку,
уже умноженную на –2: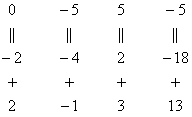
Результат
записываем во вторую строку: 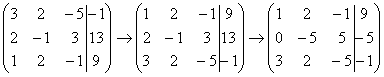 Аналогично
разбираемся с третьей строкой (3, 2, –5,
–1). Чтобы получить на первой позиции
ноль, нужнок третьей строке прибавить
первую строку, умноженную на –3.
Мысленно или на черновике умножаем
первую строку на –3: (–3, –6, 3, –27). Ик
третьей строке прибавляем первую строку,
умноженную на –3:
Аналогично
разбираемся с третьей строкой (3, 2, –5,
–1). Чтобы получить на первой позиции
ноль, нужнок третьей строке прибавить
первую строку, умноженную на –3.
Мысленно или на черновике умножаем
первую строку на –3: (–3, –6, 3, –27). Ик
третьей строке прибавляем первую строку,
умноженную на –3: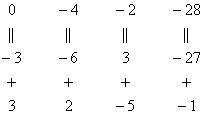
Результат
записываем в третью строку: 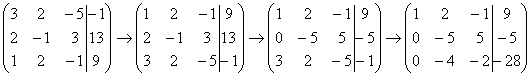
На
практике эти действия обычно выполняются
устно и записываются в один шаг: 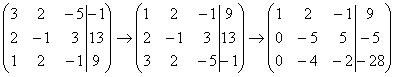
Не
нужно считать всё сразу и одновременно.
Порядок вычислений и «вписывания»
результатовпоследователени обычно такой: сначала переписываем
первую строку, и пыхтим себе потихонечку
– ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: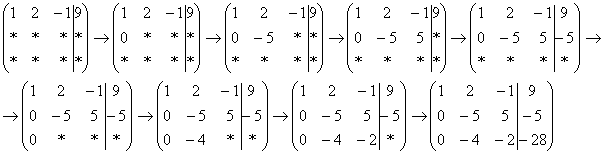 Далее
нужно получить единицу на следующей
«ступеньке»:
Далее
нужно получить единицу на следующей
«ступеньке»: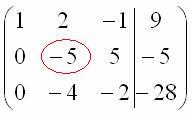
В
данном примере это сделать легко, вторую
строку делим на –5 (поскольку там все
числа делятся на 5 без остатка). Заодно
делим третью строку на –2, ведь чем
меньше числа, тем проще решение: 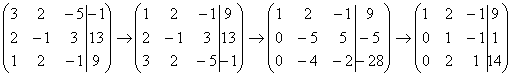
На
заключительном этапе элементарных
преобразований нужно получить еще один
ноль здесь: 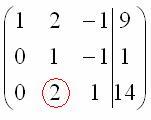
Для
этого к третьей строке прибавляем
вторую строку, умноженную на –2: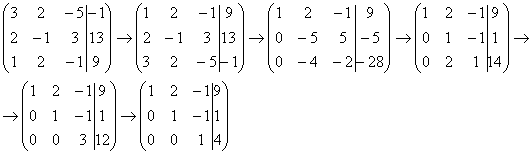 Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В
результате элементарных преобразований
получена эквивалентная исходной система
линейных уравнений: 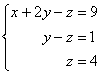 Теперь
в действие вступает обратный ход метода
Гаусса. Уравнения «раскручиваются»
снизу вверх.
Теперь
в действие вступает обратный ход метода
Гаусса. Уравнения «раскручиваются»
снизу вверх.
В
третьем уравнении у нас уже готовый
результат: 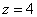
Смотрим
на второе уравнение: 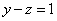 .
Значение «зет» уже известно, таким
образом:
.
Значение «зет» уже известно, таким
образом: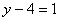
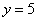
И,
наконец, первое уравнение: 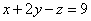 .
«Игрек» и «зет» известны, дело за
малым:
.
«Игрек» и «зет» известны, дело за
малым: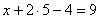
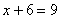
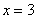
Ответ: 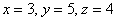
ПРАКТИКУМ 3
ЗАДАНИЕ N 1
Систему 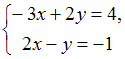 решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)
решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)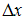 2)
2)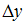 3)x 4)y
3)x 4)y
Решение:Решение системы линейных
уравнений по правилу Крамера находится
по формулам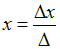 и
и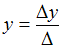 ,
где
,
где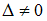 .
Здесь
.
Здесь –
главный определитель системы, в котором
первый столбец состоит из коэффициентов
приx,
а второй столбец – из
коэффициентов приy. В нашем случае
–
главный определитель системы, в котором
первый столбец состоит из коэффициентов
приx,
а второй столбец – из
коэффициентов приy. В нашем случае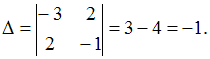 Если
Если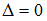 ,
то правило Крамера для решения системы
уравнений не применяют.
,
то правило Крамера для решения системы
уравнений не применяют.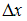 –
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приxна столбец, состоящий из
соответствующих свободных членов. Имеем
–
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приxна столбец, состоящий из
соответствующих свободных членов. Имеем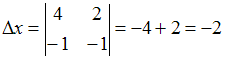 ,
тогда
,
тогда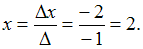 Аналогично
Аналогично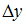 –
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приy, на столбец, состоящий из
соответствующих свободных членов. Получим
–
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приy, на столбец, состоящий из
соответствующих свободных членов. Получим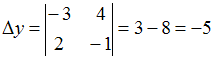 ,
тогда
,
тогда
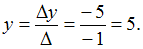
ЗАДАНИЕ N 2
Тема: Правило КрамераСистему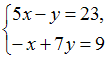 решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)
решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1) 2)
2)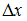 3)
3)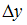 4)y
4)y
Решение:Решение системы линейных
уравнений по правилу Крамера находится
по формулам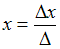 и
и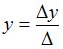 ,
где
,
где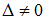 .
Здесь–
главный определитель системы, в котором
первый столбец состоит из коэффициентов
приx,
а второй столбец – из
коэффициентов приy. В нашем случае
.
Здесь–
главный определитель системы, в котором
первый столбец состоит из коэффициентов
приx,
а второй столбец – из
коэффициентов приy. В нашем случае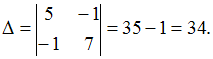 Если
Если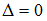 ,
то правило Крамера для решения системы
уравнений не применяют.
,
то правило Крамера для решения системы
уравнений не применяют.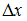 –
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приxна столбец, состоящий из
соответствующих свободных членов. Имеем
–
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приxна столбец, состоящий из
соответствующих свободных членов. Имеем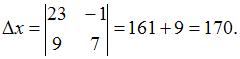 Аналогично
Аналогично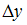 –
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приy, на столбец, состоящий из
соответствующих свободных членов.
Получим
–
это определитель, который получается
из главного определителя системы путем
замены столбца, состоящего из коэффициентов
приy, на столбец, состоящий из
соответствующих свободных членов.
Получим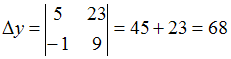 ,
тогда
,
тогда
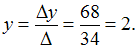
ЗАДАНИЕ N 3Тема: Системы линейных уравненийСистема линейных уравнений
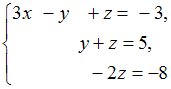 имеет
решение …
имеет
решение …
Решение:Из третьего уравнения
системы найдем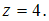 Из
второго уравнения легко получить, что
Из
второго уравнения легко получить, что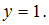 Зная
значенияyиz, из первого уравнения
системы получим
Зная
значенияyиz, из первого уравнения
системы получим Решение
данной системы:
Решение
данной системы: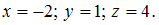
ЗАДАНИЕ N 4
Тема: Системы линейных уравненийСистема линейных уравнений
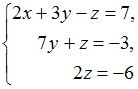 имеет
решение …
имеет
решение …
Решение:Из третьего уравнения
системы найдем, что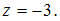 Из
второго уравнения системы получим
Из
второго уравнения системы получим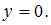 Зная
значенияyиz, из первого уравнения
системы найдем
Зная
значенияyиz, из первого уравнения
системы найдем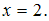 Решение
данной системы:
Решение
данной системы: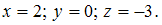
ЗАДАНИЕ N 5
Тема: Системы линейных уравненийСистема линейных уравнений
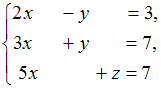 имеет
решение …
имеет
решение …
Решение:Найдем сумму первого и
второго уравнений системы, получим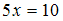 ,
тогда
,
тогда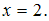 Найдемyиз первого или второго уравнений
системы, получим
Найдемyиз первого или второго уравнений
системы, получим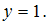 Из
третьего уравнения имеем
Из
третьего уравнения имеем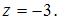 Решение
данной системы:
Решение
данной системы: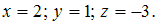
ЗАДАНИЕ 6
Тема: Системы линейных уравнений
Решить систему по формулам Крамера. 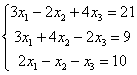
Решение:
Решим систему по формулам Крамера. 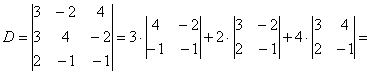
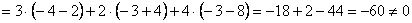 ,
значит, система имеет единственное
решение.
,
значит, система имеет единственное
решение.
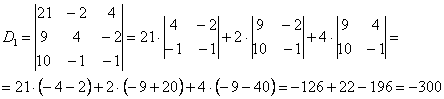
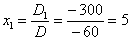
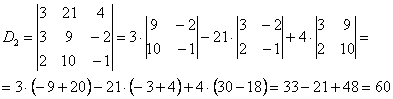
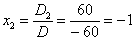
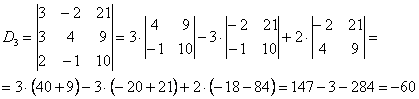
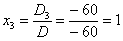
Ответ: 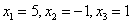 .
.
ЗАДАНИЕ 7
Решить
систему линейных уравнений методом
Гаусса 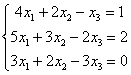
Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду: 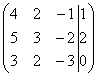
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
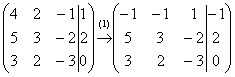
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше
алгоритм работает уже по накатанной
колее: 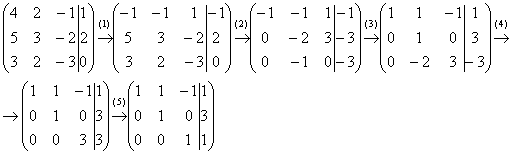
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным
признаком, который свидетельствует об
ошибке в вычислениях (реже – об опечатке),
является «плохая» нижняя строка. То
есть, если бы у нас внизу получилось
что-нибудь вроде 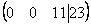 ,
и, соответственно,
,
и, соответственно,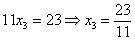 ,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
Заряжаем
обратный ход, в оформлении примеров
часто не переписывают саму систему, а
уравнения «берут прямо из приведенной
матрицы». Обратный ход, напоминаю,
работает, снизу вверх:
Да тут подарок
получился: 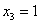
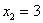
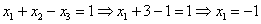
Ответ: 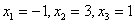 .
.
САМОСТОЯТЕЛЬНАЯ РАБОТА 3
ЗАДАНИЕ N 1
Тема: Правило КрамераСистему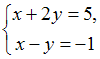 решают
по правилу Крамера.
Вычислите: 1)
решают
по правилу Крамера.
Вычислите: 1) 2)
2)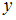 3)
3)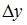 4)x
4)x
ЗАДАНИЕ N 2
Тема: Правило
Крамера Систему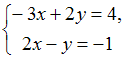 решают
по правилу Крамера.
Вычислите: 1)
решают
по правилу Крамера.
Вычислите: 1)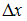 2)
2)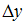 3)x 4)y
3)x 4)y
ЗАДАНИЕ N 3
Правило КрамераСистему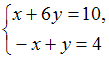 решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)
решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)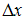 2)
2)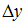 3)x 4)y
3)x 4)y
1 | 2 | 3 | 4 | 5 |
— 14 | 14 | — 2 | 2 | 1 |
ЗАДАНИЕ N 4
Правило КрамераСистему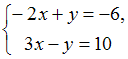 решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1)
решают
по правилу Крамера.
Установите
соответствие между названиями величин
и их значениями.
1) 2)
2)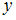 3)
3)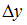 4)x
4)x
ЗАДАНИЕ N 5Тема: Системы линейных уравненийСистема линейных уравнений
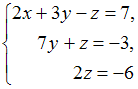 имеет
решение …
имеет
решение …
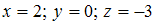
ЗАДАНИЕ N 6Тема:
Системы линейных уравнений Система
линейных уравнений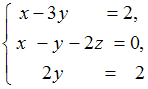 имеет
решение …
имеет
решение …
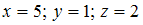
ЗАДАНИЕ N 7
Тема: Системы линейных уравненийСистема
линейных уравнений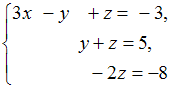 имеет
решение …
имеет
решение …
ЗАДАНИЕ N 8Тема:
Системы линейных уравненийСистема
линейных уравнений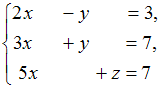 имеет
решение …
имеет
решение …
ЗАДАНИЕ N 9
Тема: Системы линейных уравненийСистема
линейных уравнений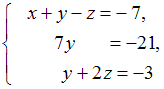 имеет
решение …
имеет
решение …
ЗАДАНИЕ N 10
Решить
систему линейных уравнений методом
Гаусса 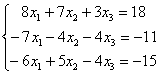
studfile.net
Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера
Пусть m=n.
Тогда матрица системы является квадратной
, а ее определитель 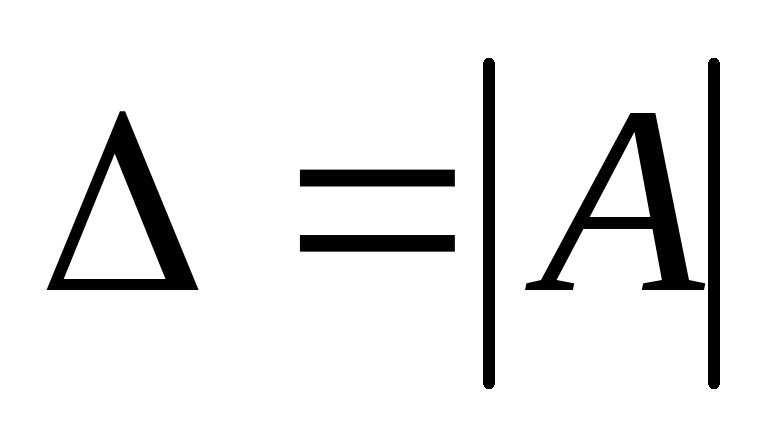 называетсяопределителем
системы.
называетсяопределителем
системы.
Предположим, что
квадратная матрица 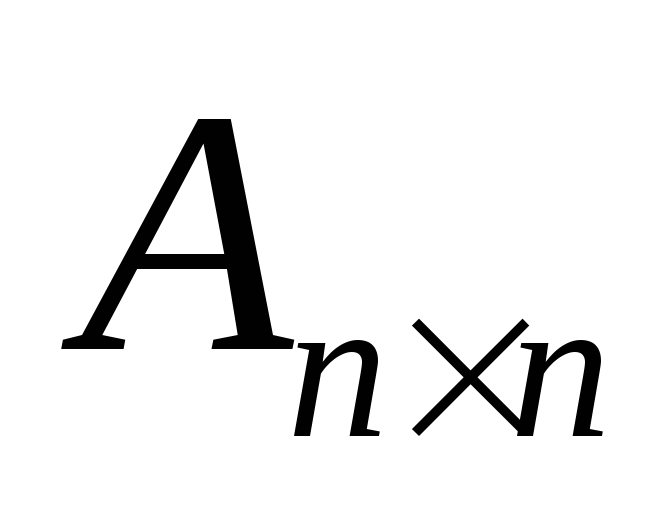 невырожденная, т.е.
невырожденная, т.е.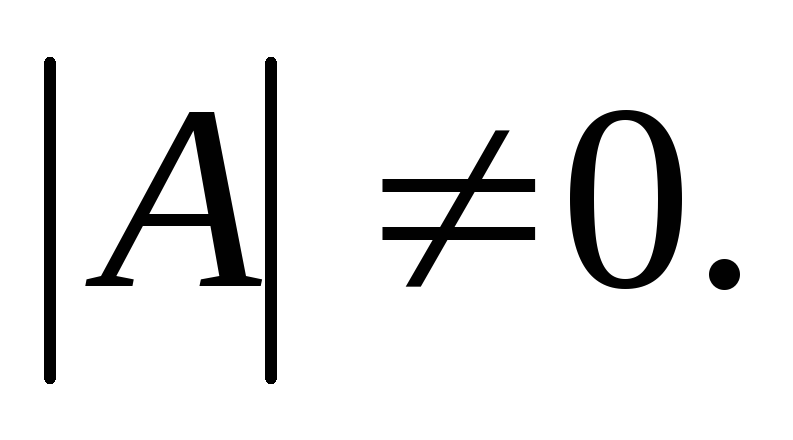
В этом случае
существует 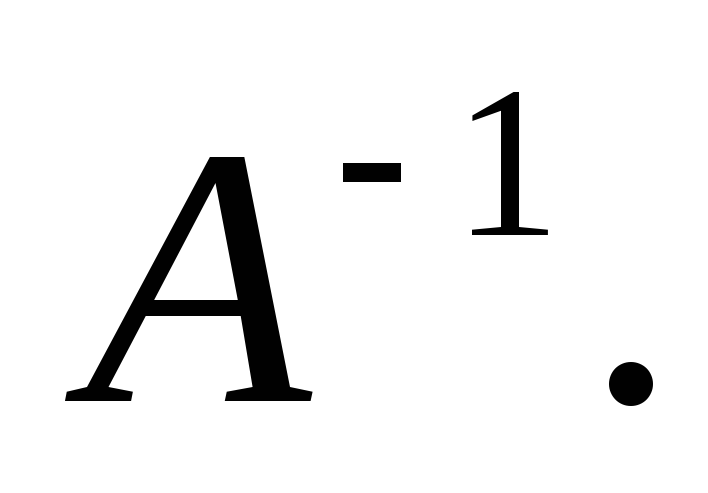
Умножим слева обе
части (3) на матрицу 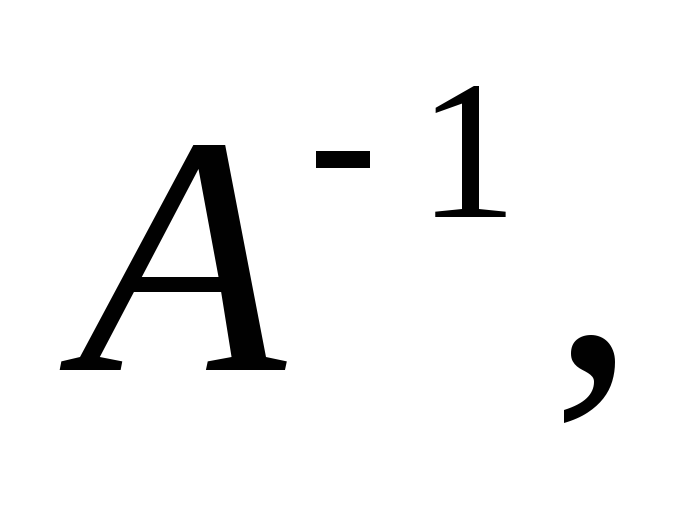 получим
решение системы методом обратной
матрицы:
получим
решение системы методом обратной
матрицы:
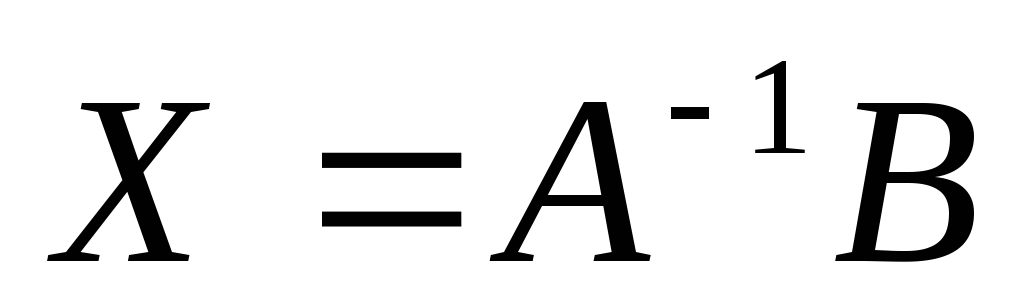
Отсюда видно, что вектор решения системы уравнений получается, если вектор свободных членов умножить слева на матрицу, обратную к матрице системы. Поэтому в методе обратной матрицы главным является обращение матрицы.
Другим способом решения системы уравнений с квадратной матрицей является использование формул Крамера.
Теорема Крамера.
Пусть  -определитель
матрицы системы А, а
-определитель
матрицы системы А, а -определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если
-определитель
матрицы, получаемый из А заменойj-го
столбца столбцом свободных членов.
Тогда, если 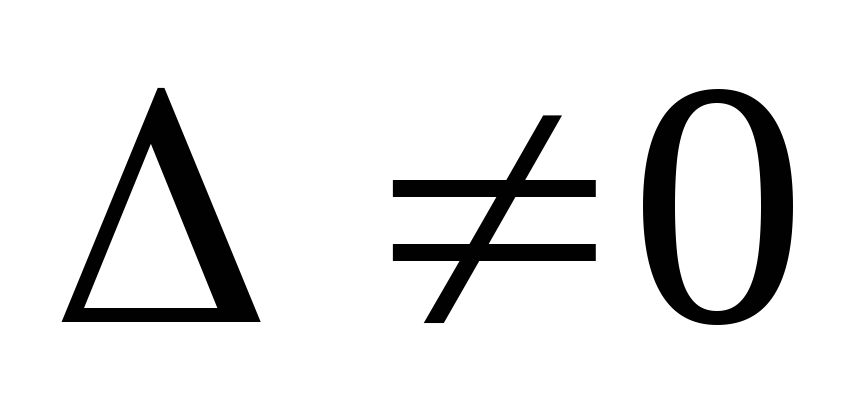 ,
то система имеет единственное решение,
определяемое по формулам:
,
то система имеет единственное решение,
определяемое по формулам:
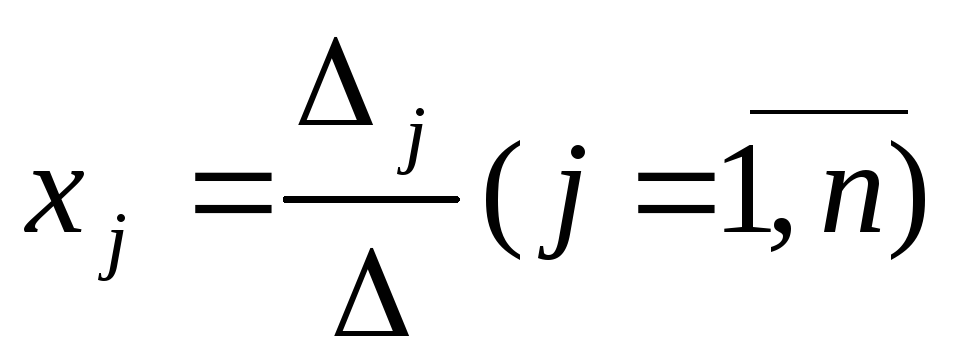 (5)
(5)
Формулы (5) называются формулами Крамера.
Недостаток формул Крамера и метода обратной матрицы- их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных задач.
П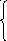 ример.
Решить по формулам Крамера и методом
обратной матрицы следующую систему
уравнений:
ример.
Решить по формулам Крамера и методом
обратной матрицы следующую систему
уравнений:
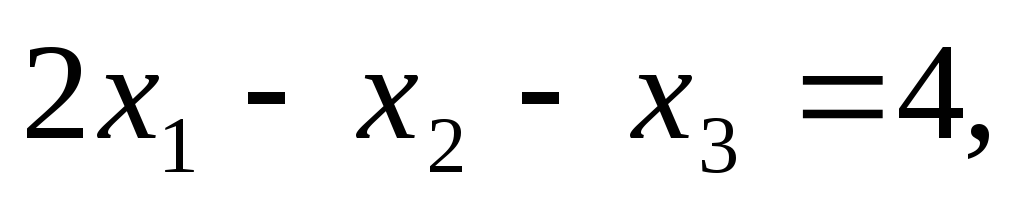
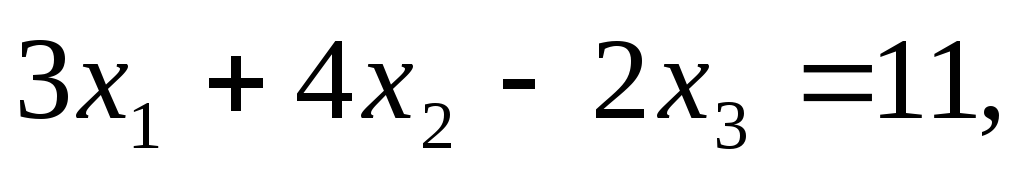
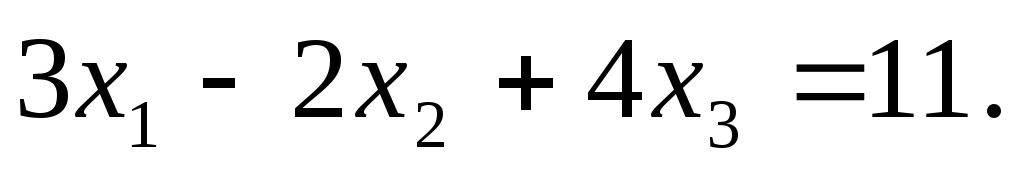
Для применения формул Крамера вычислим определитель системы :


2 -1 -1
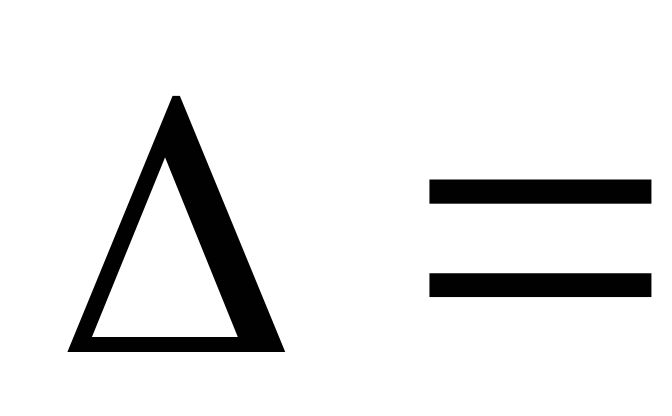 3 4 -2 = 60
3 4 -2 = 60
3 -2 4
Заменим в определителе системы первый столбец на столбец свободных членов, вычислим полученный определитель:


4 -1 -1
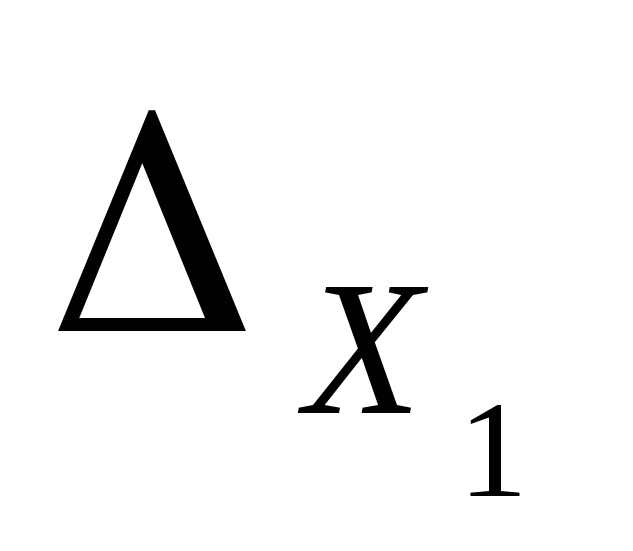 =11 4 -2 =180
=11 4 -2 =180
11 -2 4
Заменим в определителе системы второй столбец на столбец свободных членов, вычислим полученный определитель:

 2 4
-1
2 4
-1
3 11 -2
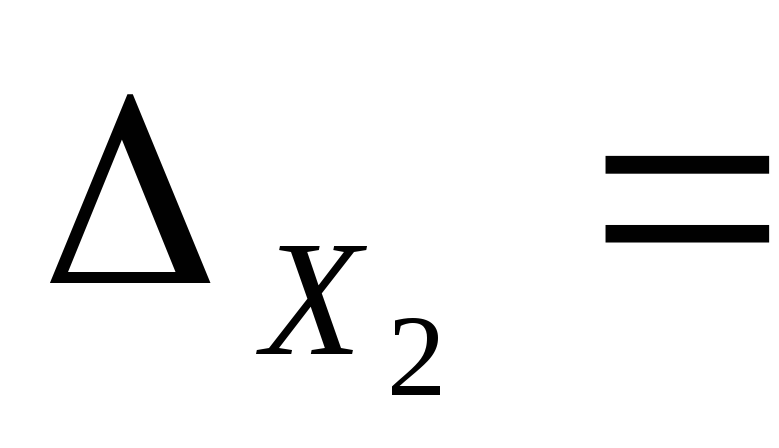 3 11 4 =60
3 11 4 =60
Заменим в определителе системы третий столбец на столбец свободных членов, вычислим полученный определитель:


2 -1 4
3 4 11
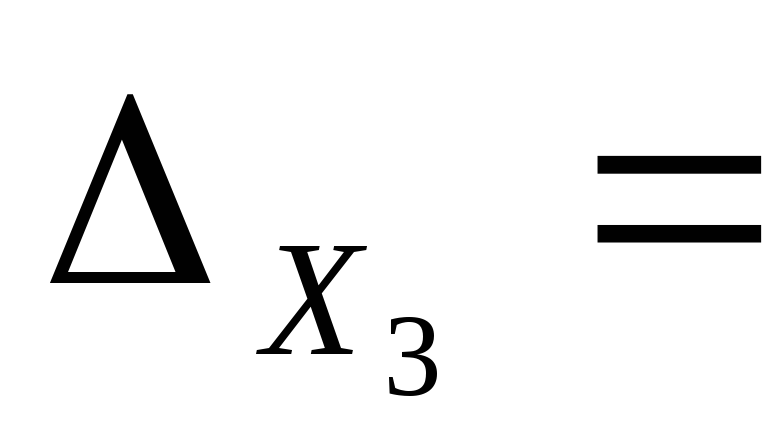 3 -2 11 =60.
3 -2 11 =60.
Вычислим значения неизвестных:
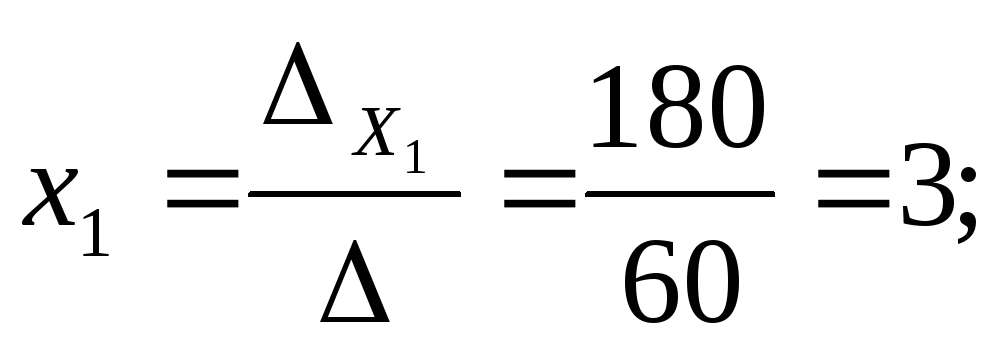
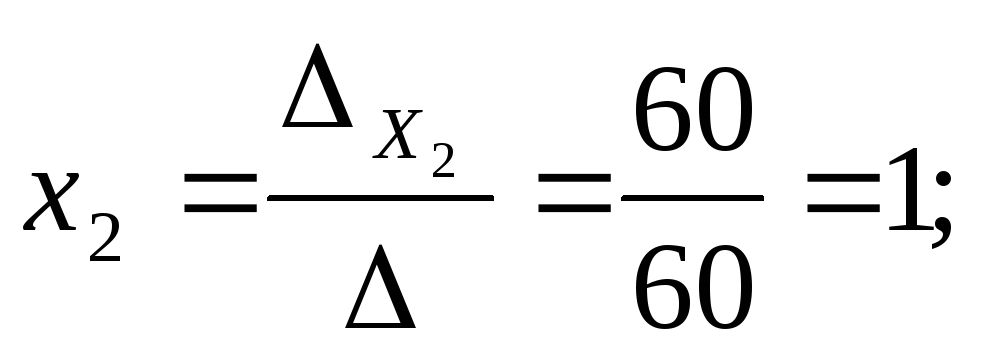
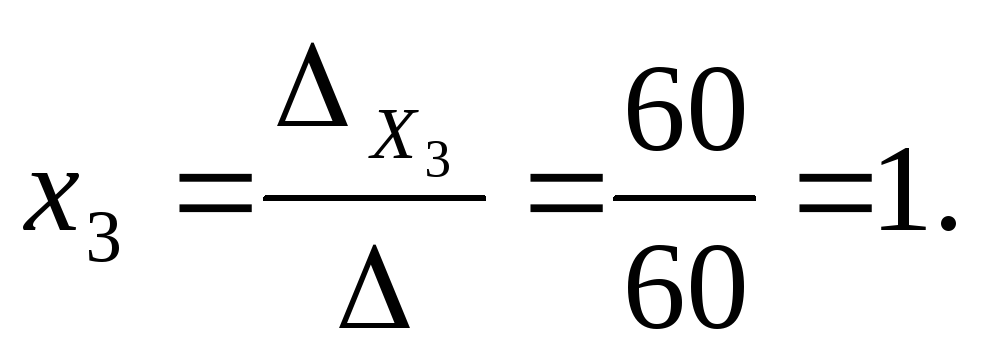
Для применения метода обратной матрицы представим систему уравнений в матричной форме:
2




 -1 -1
-1 -1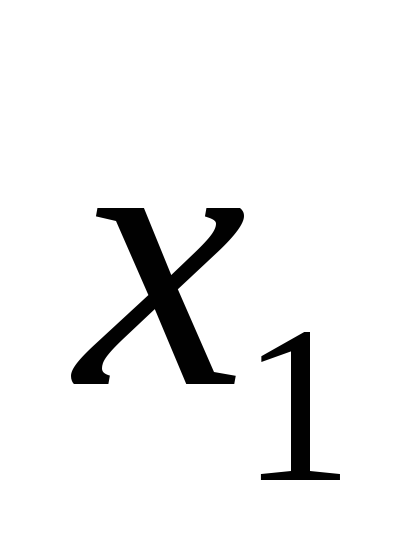 4
4
3
4 -2 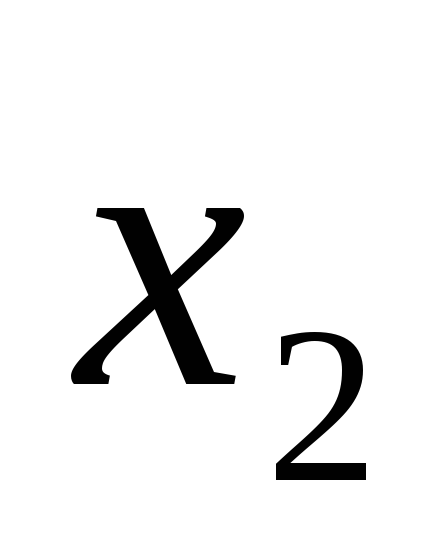 = 11
= 11
3 -2
4 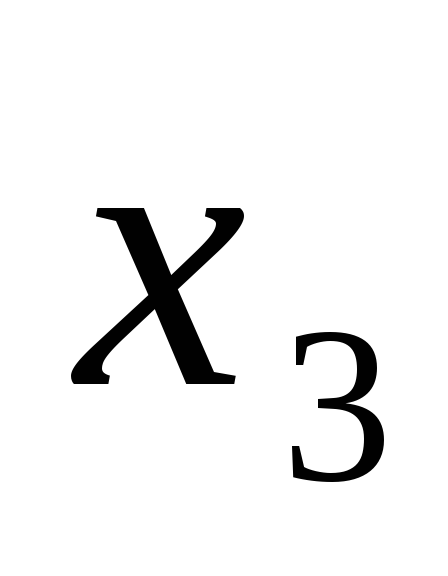 11
11
Далее рассчитываем обратную матрицу:


12 6 6

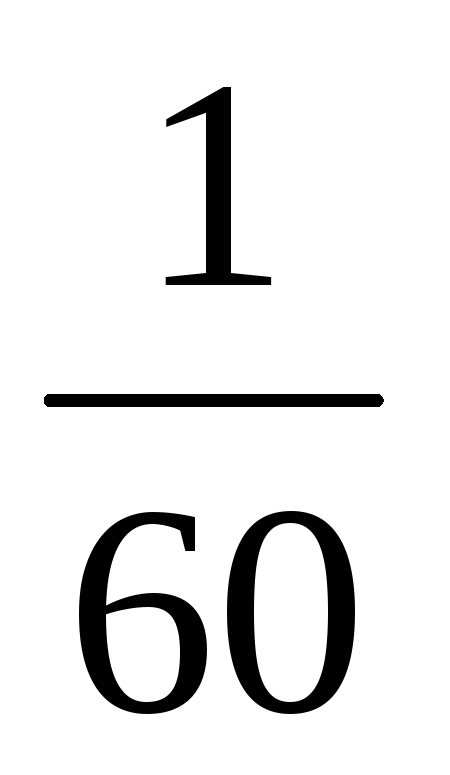 -18 11 1
-18 11 1
-18 1 11
По формуле (4) получаем решение:
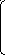

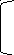



12 6 6 4 3
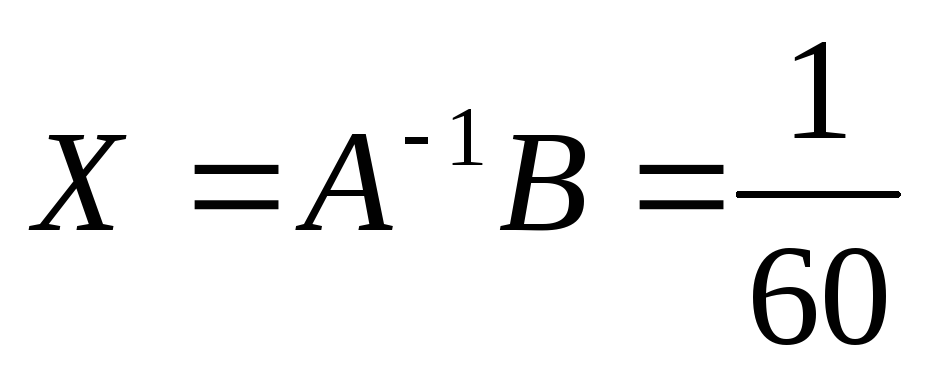 -18 11 1 11
= 1
-18 11 1 11
= 1
-18 1 11 11 1
Метод Гаусса
Метод Гаусса— метод последовательного исключения неизвестных- заключается в том, что с помощью элементарных преобразований система уравнений приводиться к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних переменных, находятся все остальные переменные.
Предположим, что
в системе (1) 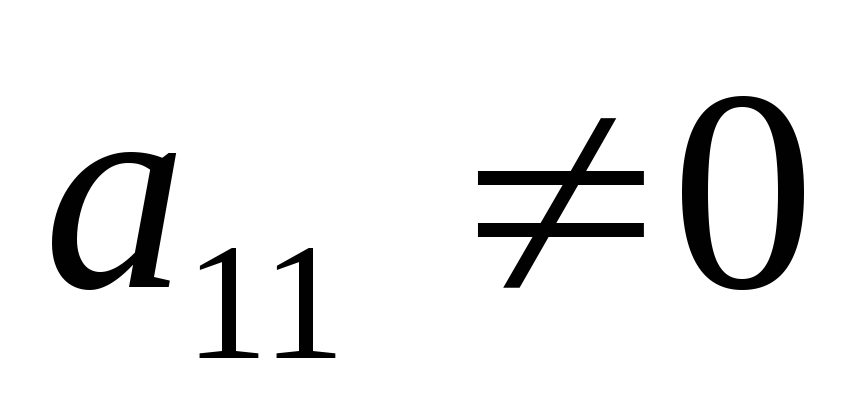 ( этого всегда можно добиться перестановкой
уравнений)
( этого всегда можно добиться перестановкой
уравнений)
Шаг
1. Умножим
1-ое уравнение на 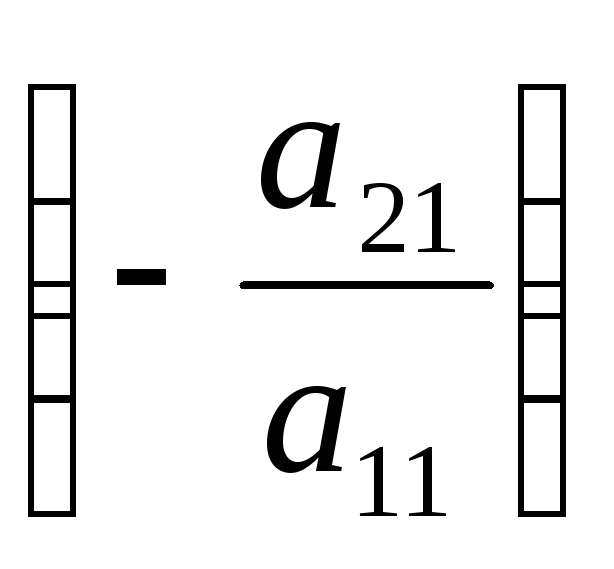 и прибавим ко второму; затем умножим
1-ое уравнение на
и прибавим ко второму; затем умножим
1-ое уравнение на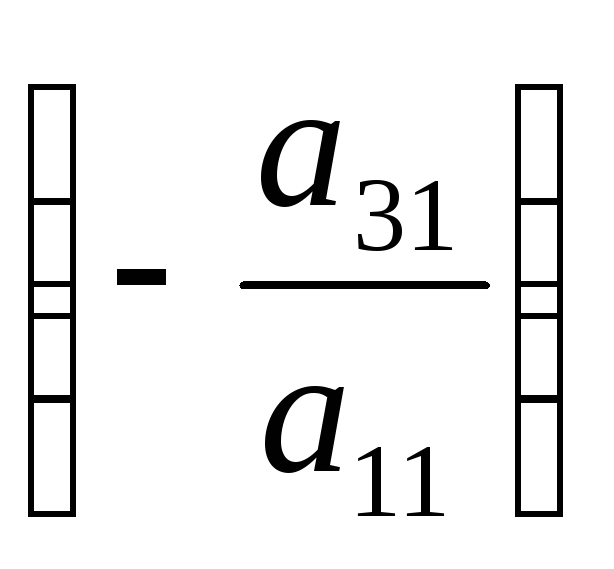 и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на
и прибавим к третьему, и т.д., и , наконец,
умножим 1-ое уравнение на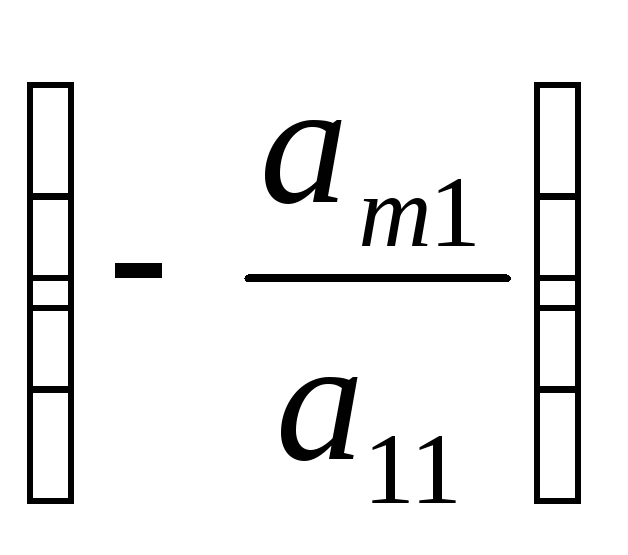 и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой
и прибавим кm-му
уравнению. Получим преобразованную
систему уравнений, в которой 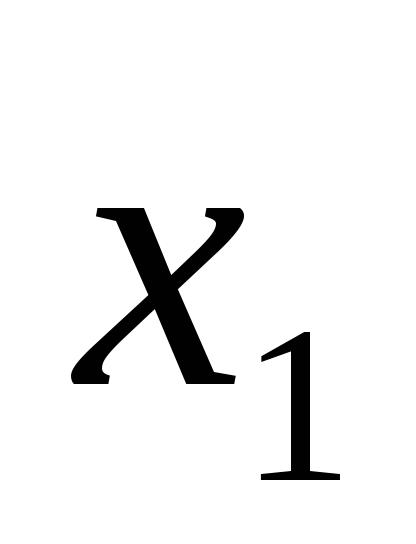 исключено
из всех уравнений, кроме первого:
исключено
из всех уравнений, кроме первого:
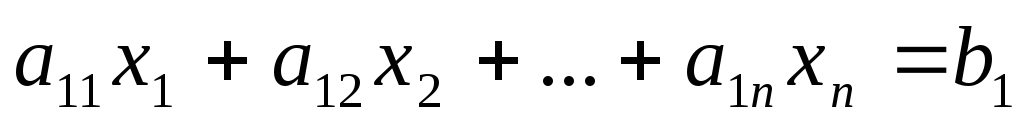
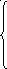
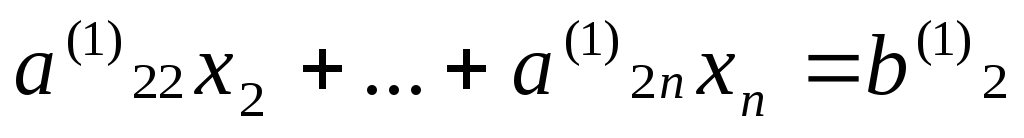
……………………….. ( 6)
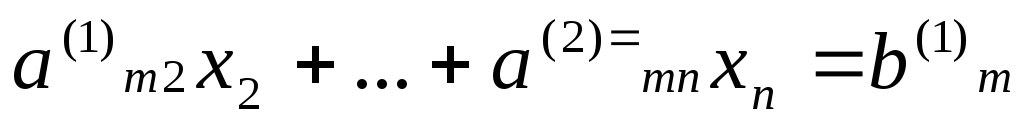
Здесь коэффициенты с верхним индексом (1) получены после 1-ого шага.
Шаг
2. Предположим,
что 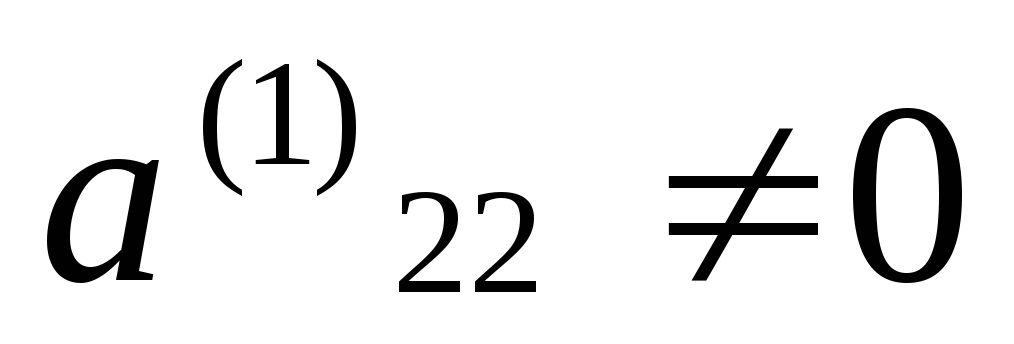 .(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
.(этого
всегда можно добиться перестановкой
уравнений с перенумерацией).
У




 множаем
2-ое уравнение на числа —
множаем
2-ое уравнение на числа —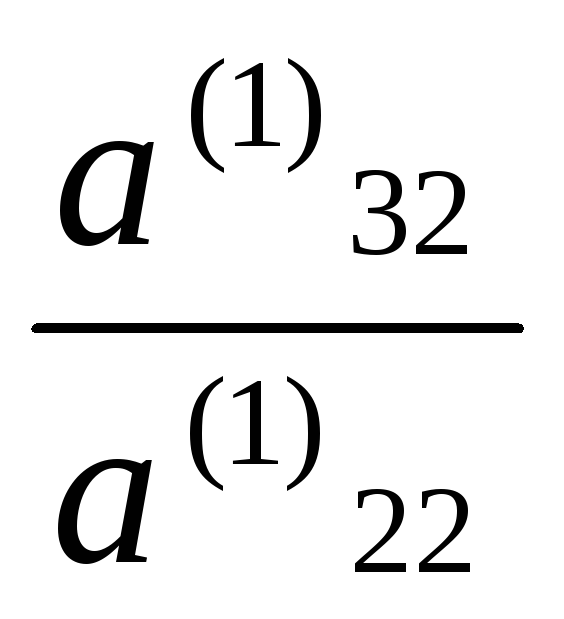 ,
,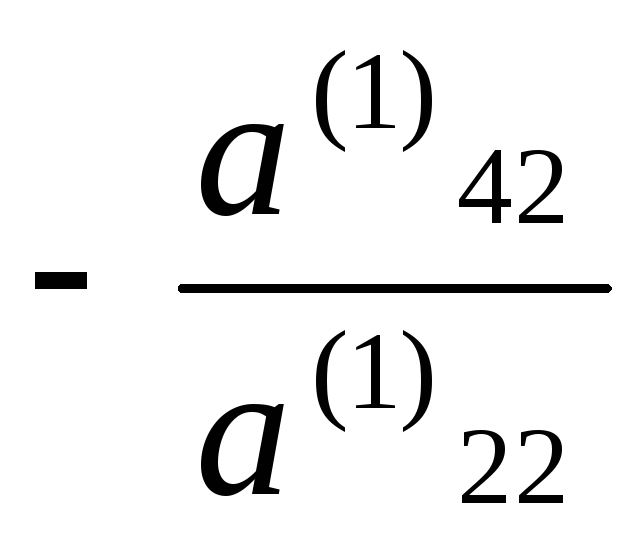 , …,
, …,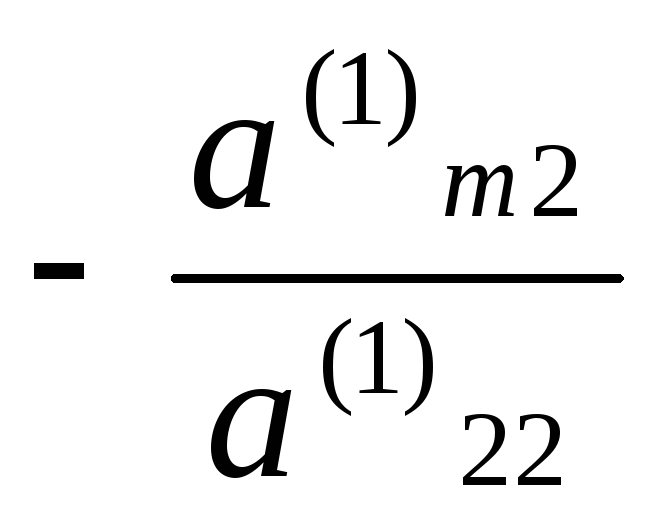 и прибавим полученные уравнения
соответственно к третьему, четвертому,
и прибавим полученные уравнения
соответственно к третьему, четвертому,
…,m-му
уравнению системы (6), исключая 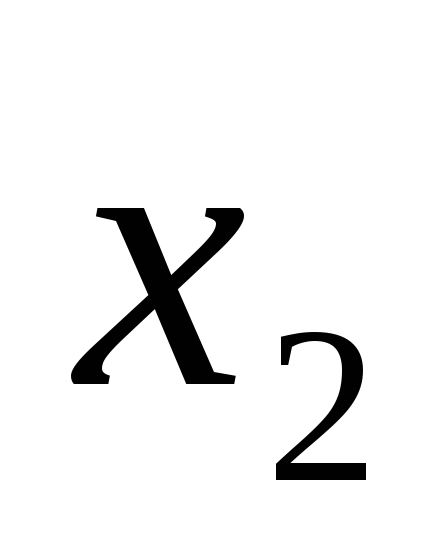 из всех уравнений, начиная с третьего.
из всех уравнений, начиная с третьего.
Продолжая процесс последовательного исключения переменных, после (r-1)- го шага получим систему:
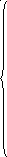
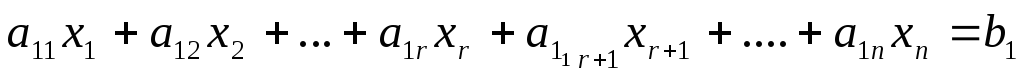
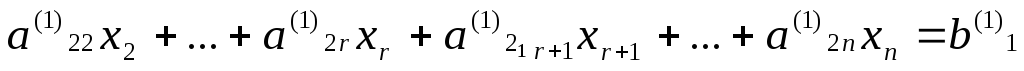
………………………………….
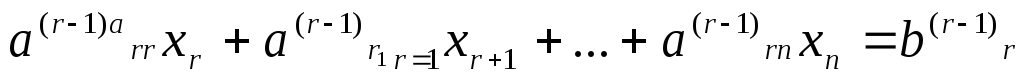 (7)
(7)
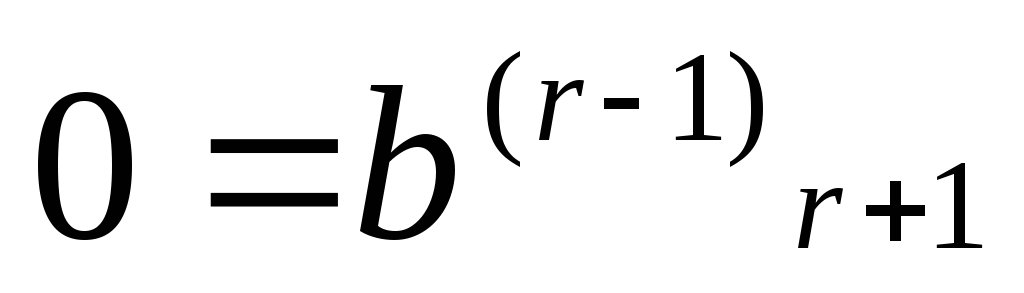
…………
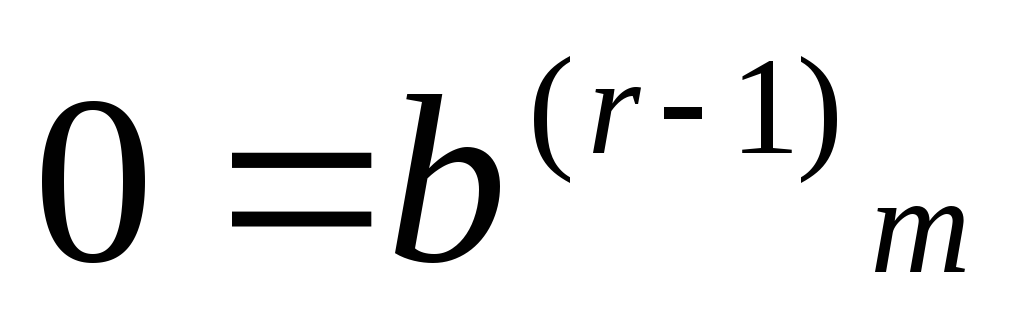
Если хотя бы одно
из чисел 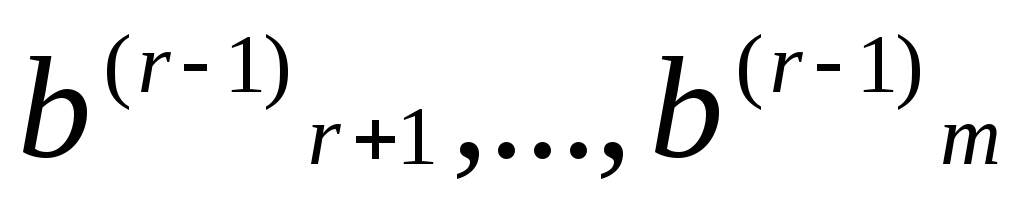 не равно нулю, то соответствущее равенство
противоречиво, и система (1) несовместна.
Для любой совместной системы (m-r)
уравнений в системе (7) являются
тождествами, и их можно не принимать во
внимание при решении системы (1). После
отбрасывания « лишних» уравнений
возможны два случая:
не равно нулю, то соответствущее равенство
противоречиво, и система (1) несовместна.
Для любой совместной системы (m-r)
уравнений в системе (7) являются
тождествами, и их можно не принимать во
внимание при решении системы (1). После
отбрасывания « лишних» уравнений
возможны два случая:
А) r=n , и в этом случае система (7) имеет треугольный вид;
Б) r<n, и система (7) имеет ступенчатый вид.
Переход системы (1) к равносильной системе (7) называется прямым ходом метода Гаусса, а нахождение переменных из системы (7)- обратным ходом .
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы (1), в которую, кроме матрицы А, дополнительно включен столбец свободных членов.
Пример. Решить методом Гаусса систему уравнений:
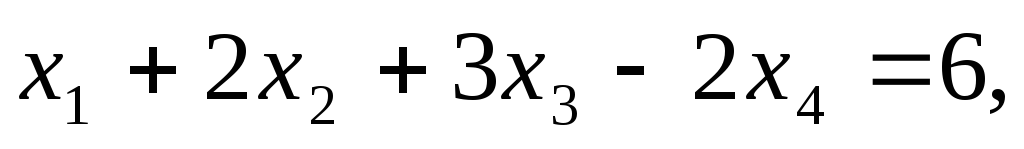
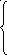
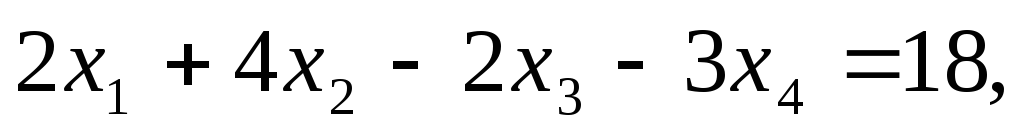
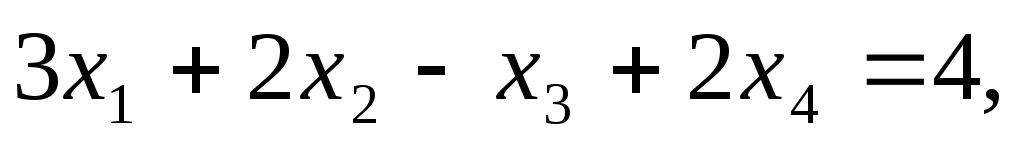
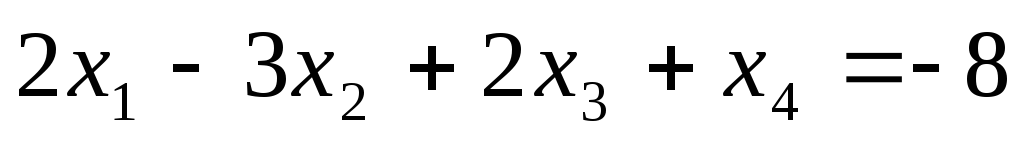
Расширенная матрица системы имеет вид:
1

 2 3 -2 6
2 3 -2 6
2 4 -2 -3 18
3 2 -1 2 4
2 –3 2 1 -8
Т


 еперь
все действия над уравнениями будут
эквивалентны действиям над строками
матрицы. Умножаем 1-ую строку на —
еперь
все действия над уравнениями будут
эквивалентны действиям над строками
матрицы. Умножаем 1-ую строку на —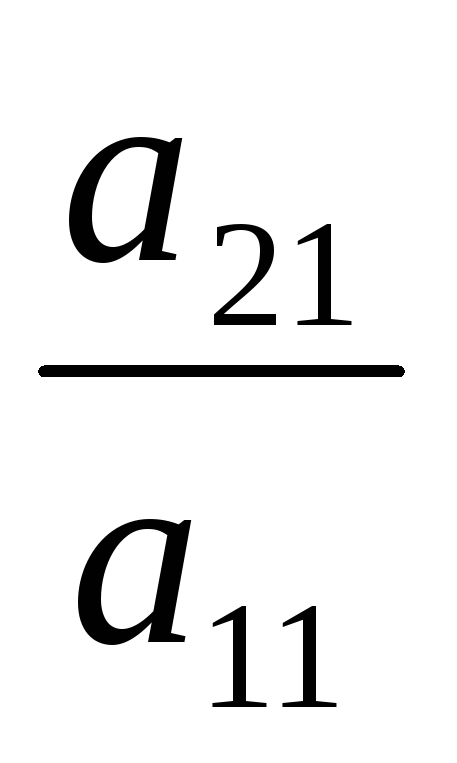 , т.е. на —
, т.е. на —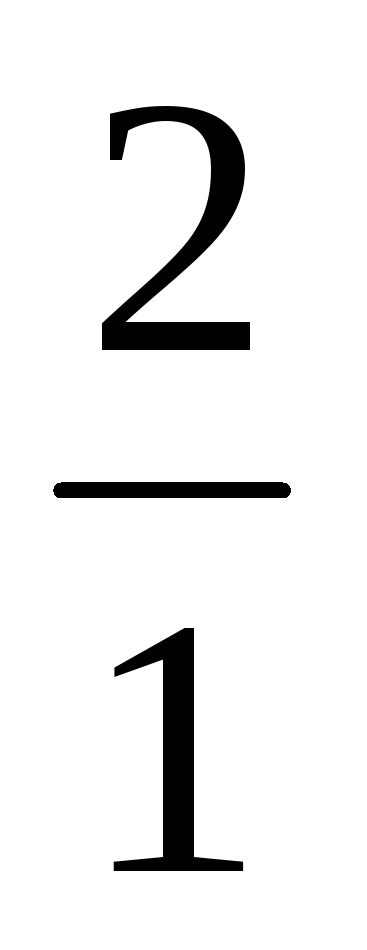 = -2, получаем
= -2, получаем
(-2 -4 -6 4 -12)
эту строку прибавляем ко второй строке, получаем новую 2-ю строку:
0 -8 1 6).
Аналогично умножим 1-ую строку на (-3) и сложим с третьей строкой; умножим 1-ую строку на (-2) и сложим с 4-ой строкой. Расширенная матрица после 1-ого шага имеет вид:
2


 3 -2 6
3 -2 6
0 0 -8 1 6
-4 -10 8 -14
0 -7 -4 5 -20
Первая
строка при преобразованиях Гаусса
остается без изменений. Для дальнейшего
хода необходимо переставить 2-ую и 3-ю
строки ,чтобы 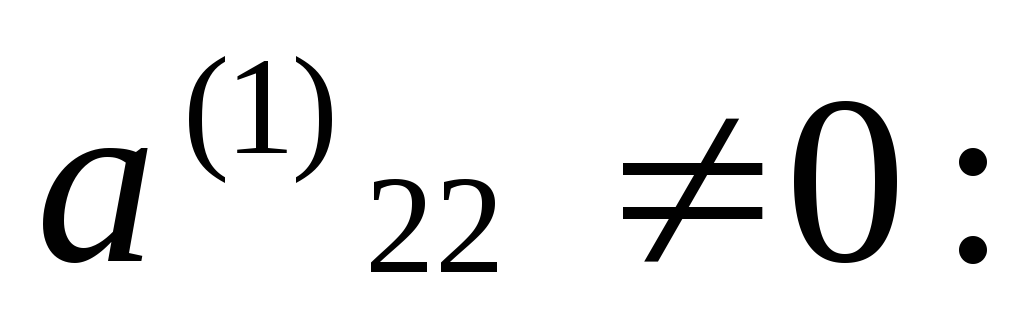



2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 -7 -4 5 -20
На
2-ом шаге, поскольку 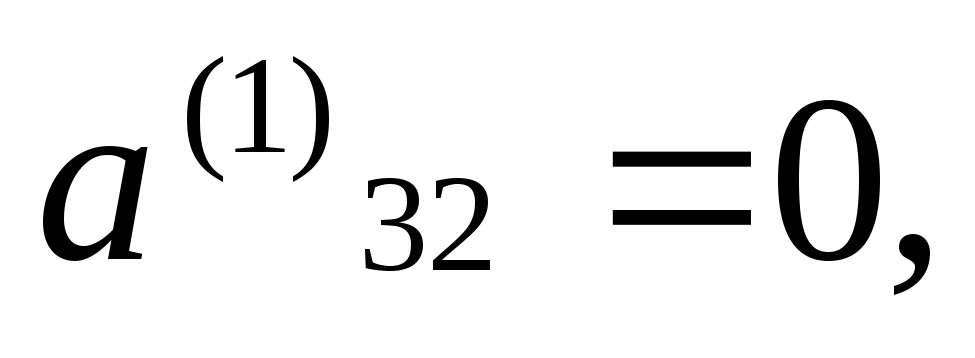 требуется
только обнулить элемент
требуется
только обнулить элемент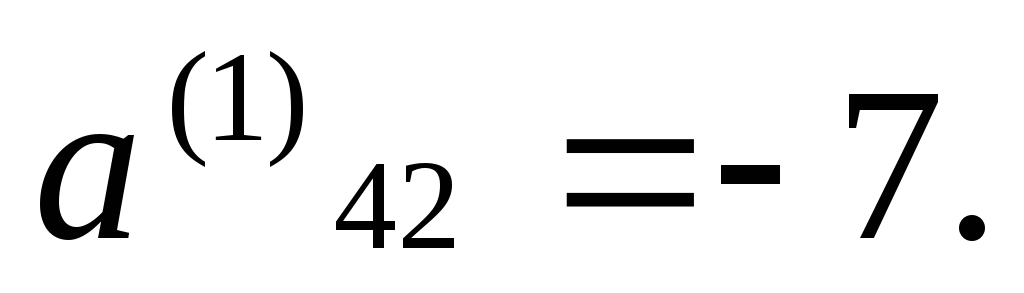 Для
этого 2-ое уравнение умножим на
Для
этого 2-ое уравнение умножим на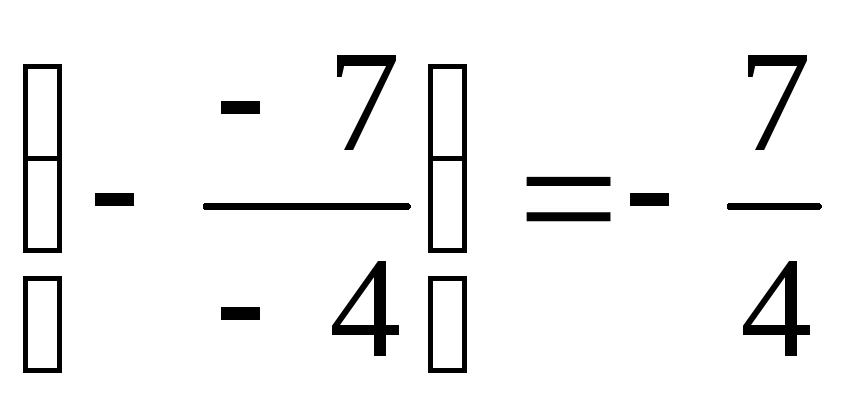 и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
и сложим с 4-м уравнением. 2-ое уравнение
после умножения выглядит так:
(
0 7 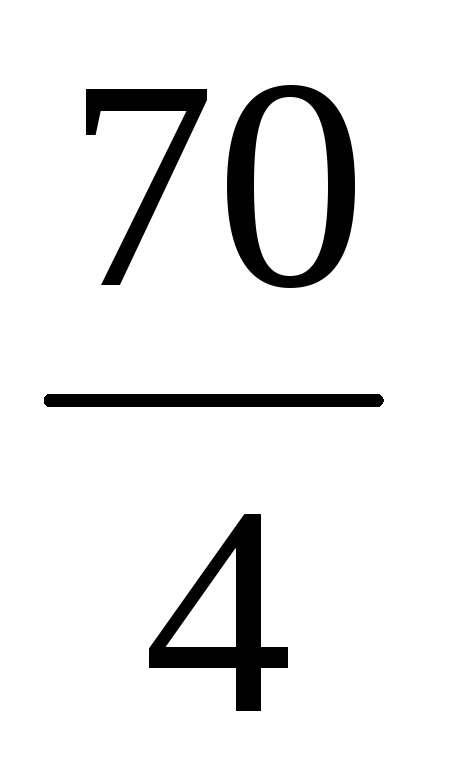 —
—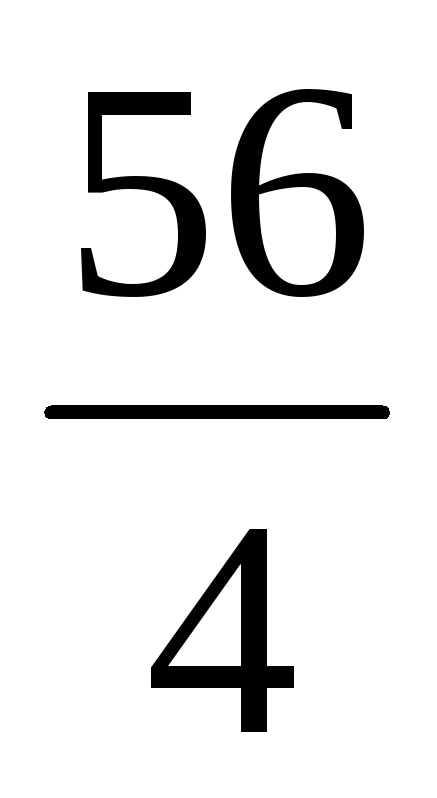
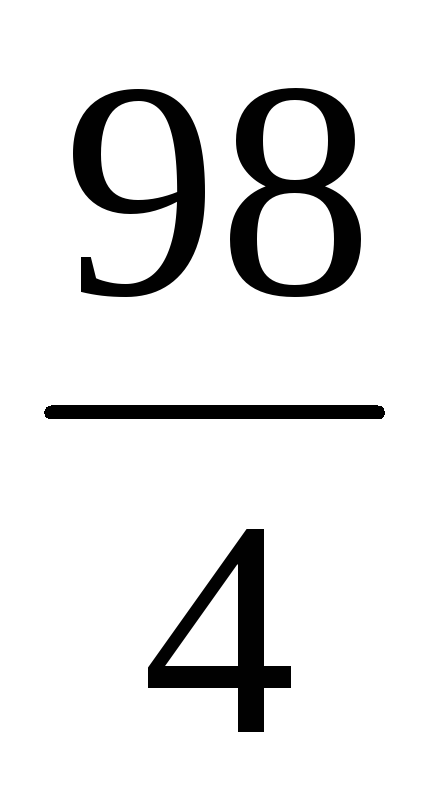 )
)
После 2-го шага матрица имеет вид:
1

 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 54/4 -36/4 -18/4
Поскольку в элементах последней строки одинаковый знаменатель, исключаем его; кроме того, можно сократить всю 4-ую строку на общий множитель 18:
1

 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 3 -2 1
Н
 а
3-м шаге исключаем
а
3-м шаге исключаем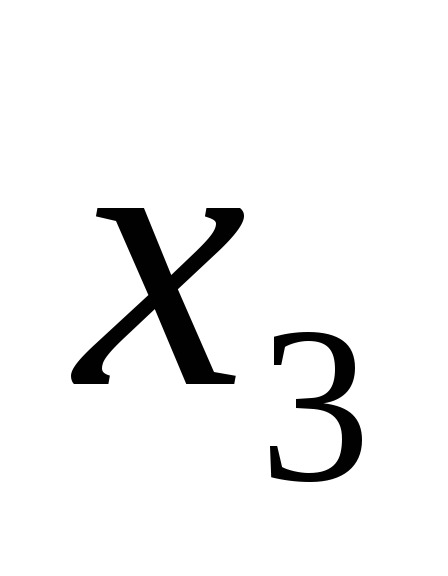 из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
из 4-ого уравнения; для этого умножим
3-ю строку на 3/8 и сложим с 4-ой строкой:
1 2 3 -2 6
2 3 -2 6
0 -4 -10 8 -14
0 0 -8 1 6
0 0 0 -13/8 26
Теперь матрица системы имеет треугольный вид: все элементы ниже главной диагонали равны нулю.
Далее совершаем обратный ход метода Гаусса. 4-ое уравнение системы можно записать так:
оно
имеет решение: 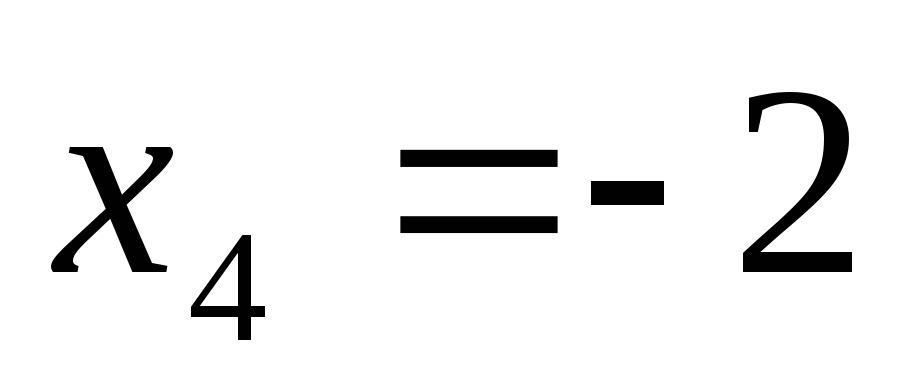 .
.
Подставляем полученное значение в 3-е уравнение:
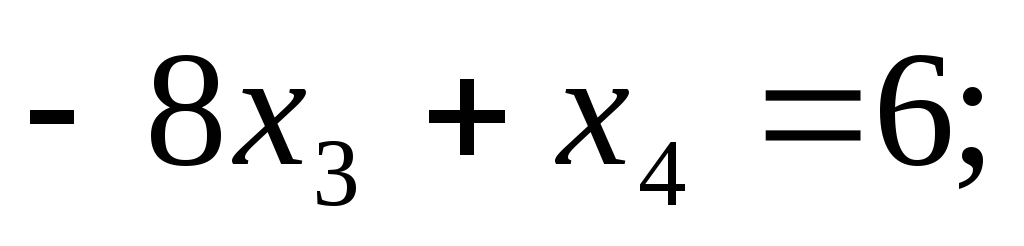
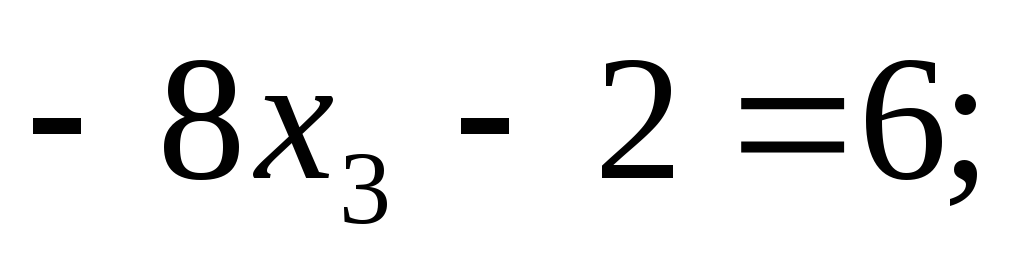
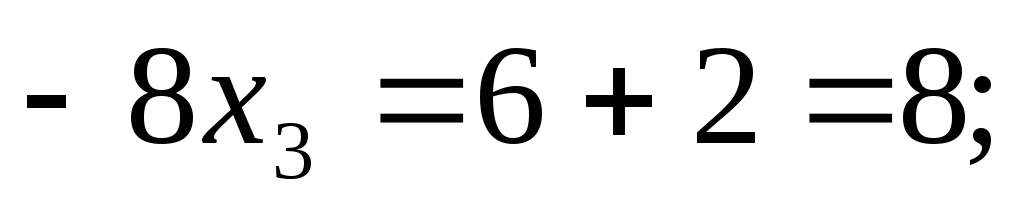
Теперь
в 3-м уравнении только одно неизвестное 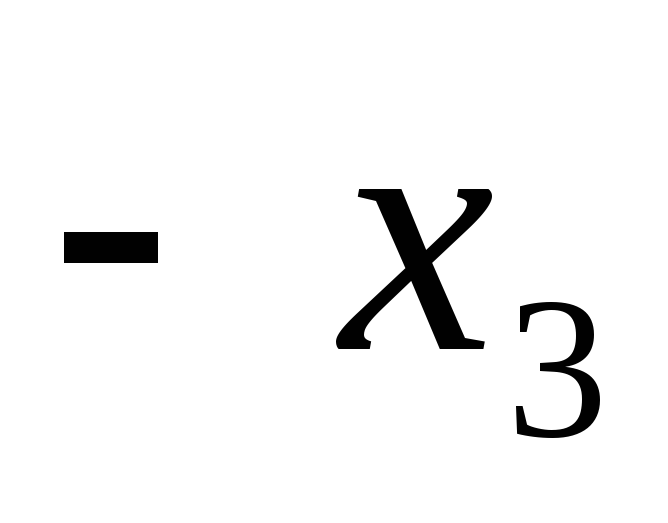 .Решаем
уравнение, получаем
.Решаем
уравнение, получаем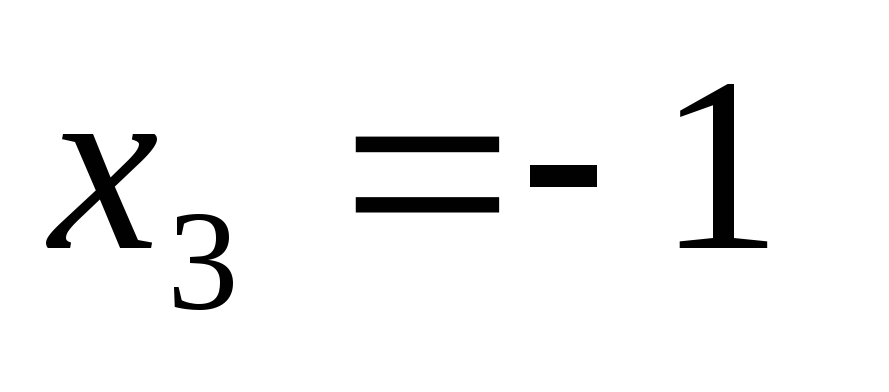 .
Далее подставим известные
.
Далее подставим известные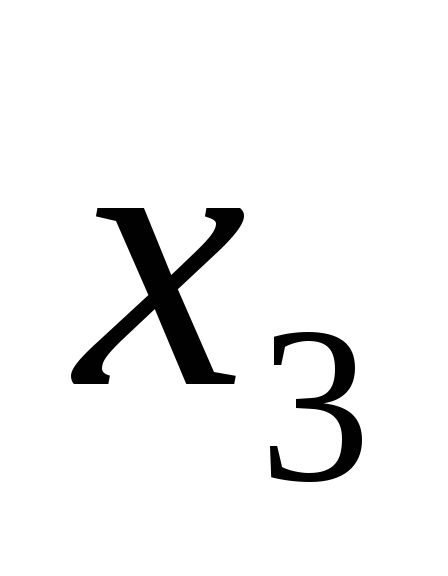 и
и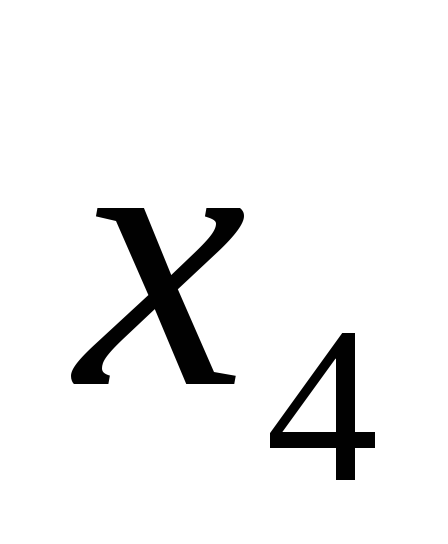 во
второе уравнение:
во
второе уравнение:
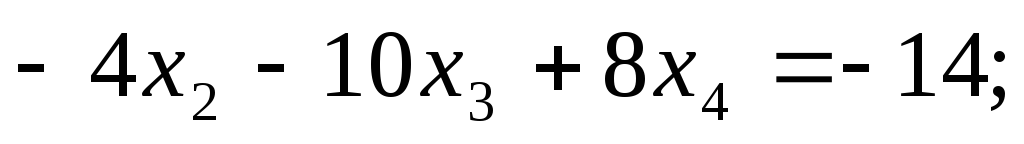
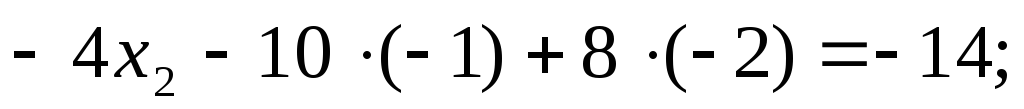
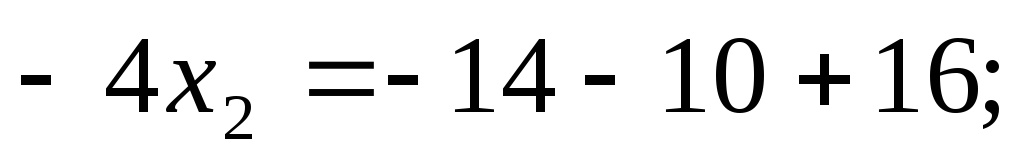
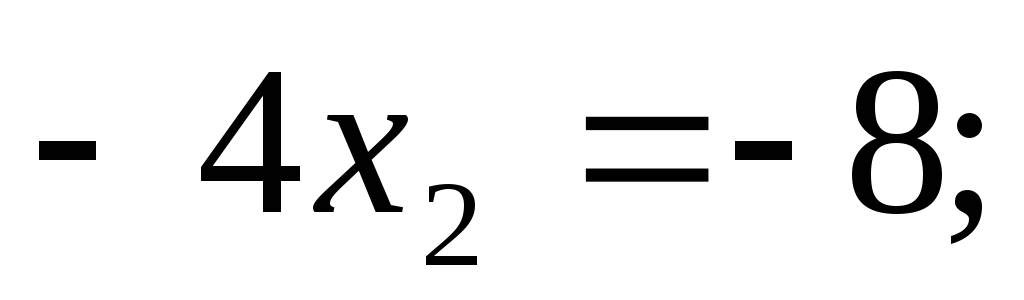
Отсюда 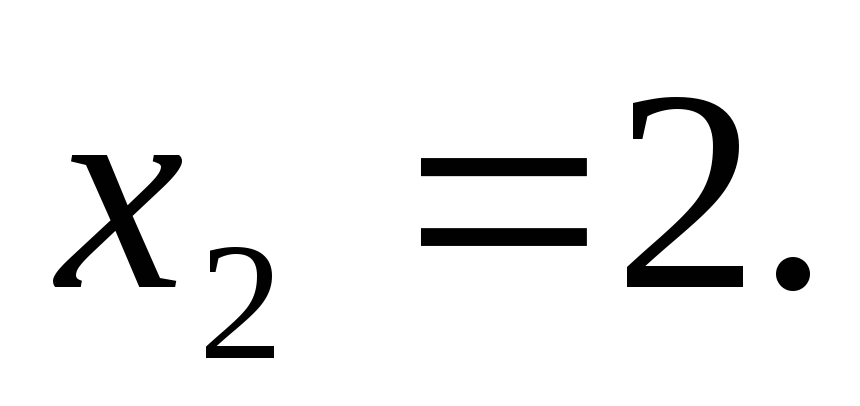
Подставляем
в 1-ое уравнение известные 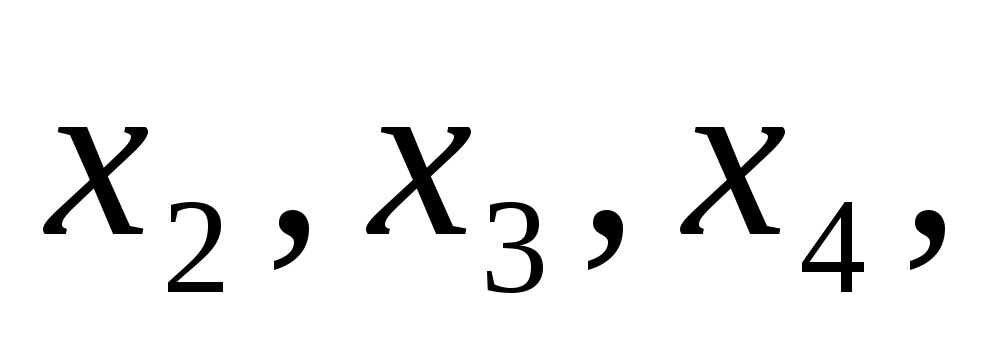 получаем
решение:
получаем
решение:
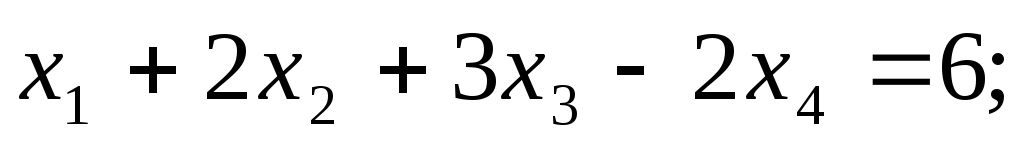
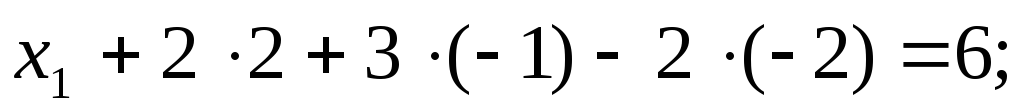
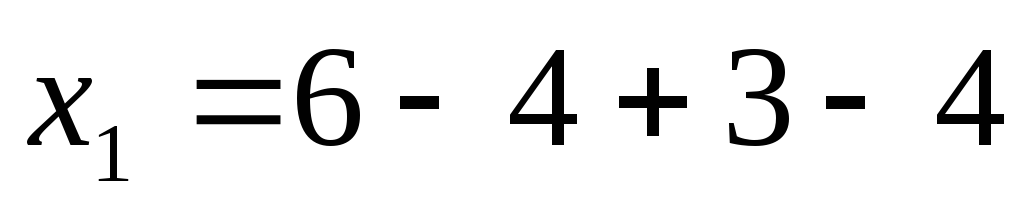
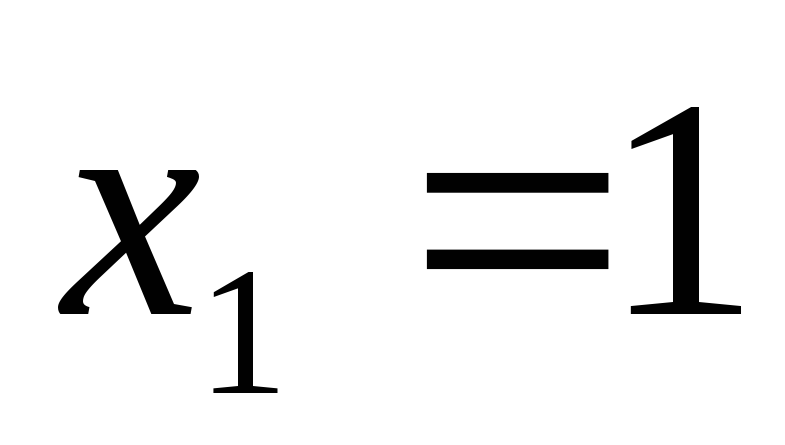
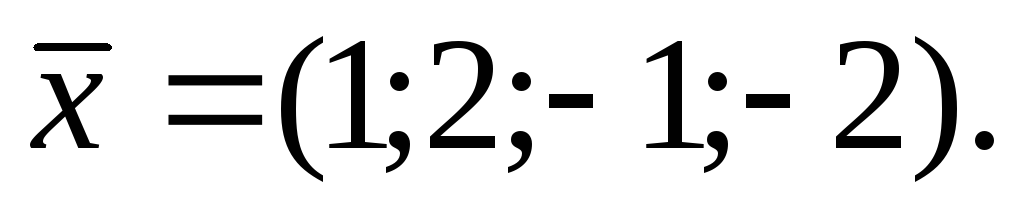
Вопросы для самоконтроля:
Чем отличается СЛАУ от систем произвольных уравнений?
Привести примеры определенной и неопределенной СЛАУ.
Какие основные методы решения СЛАУ?
studfile.net
Системы линейных уравнений. Правило Крамера. Метод Гаусса. Матричный способ
Пример 1. Решить систему:
1—й способ. По формулам Крамера:
где -главный определитель системы, столбцы которого есть коэффициенты при неизвестных
-вспомогательный определитель, который получается из главного заменой 1-го столбца (коэффициентов при x) столбцом свободных членов.
Аналогично получаем и :
Если , то система имеет единственное решение, если , а хотя бы один из не равен 0, то система не имеет решений. Если , то система имеет множество решений.
2-й способ. Метод Гаусса, или метод исключения неизвестных.
Рассмотрим сначала несколько понятий.
Определение. Рангом матрицы называется наивысший порядок её минора, отличного от нуля.
Пример.
Вычислим все миноры третьего порядка:
Вычислим минор второго порядка:
поэтому ранг матрицы A равен 2:
.
Рассмотрим более простой способ вычисления ранга матрицы, основанный на приведении матрицы к ступенчатому виду.
Определение. Матрицу А называют ступенчатой, если
а) любая её строка имеет хотя бы один отличный от нуля элемент,
б) первый отличный от нуля элемент каждой её строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.
Пример.
Определение. Элементарными преобразованиями матрицы называются следующие преобразования её строки:
а) перестановка двух каких-нибудь строк;
б) умножение элементов какой-либо строки на число, отличное от нуля;
в) прибавление к элементам какой-либо строки соответствующих элементов другой строки, умноженных на некоторое число.
Пример.
Из последней матрицы (ступенчатый вид) видно, что .
Приведем несколько утверждений без доказательств.
Теорема 1. При элементарных преобразованиях и отбрасывании нулевой строки ранг матрицы не изменяется.
Теорема 2. Всякую ненулевую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований и выбрасывания нулевых строк.
Теорема 3. Ранг ненулевой матрицы равен числу строк её ступенчатого вида.
Рассмотрим систему:
Определение. Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.
Определение. Матрица называется расширенной матрицей системы, если к матрице присоединить столбец из свободных членов системы.
.
Расширенная матрица- это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями мы можем заменить работой со строками матрицы.
Эффективным методом решения и исследования системы линейных уравнений является метод исключения неизвестных, называемый также методом Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида (или, в частности, треугольную систему), которая легко исследуется и решается. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.
Рассмотрим систему линейных уравнений с неизвестными ,которую запишем в виде расширенной матрицы:
.
Заметим, что иногда могут встречаться уравнения, все коэффициенты которых (т.е. соответствующая строка матрицы) равны 0:
.
Если в этом уравнении , то ему, очевидно, не удовлетворяют никакие значения неизвестных, и система, содержащая хотя бы одно такое уравнение, несовместна, т.е. не имеет решения. Если же , то ему удовлетворяют любые решения неизвестных, т.е. рассматриваемое уравнение является тождеством и его можно удалить из системы.
Элементарные преобразования матрицы, рассмотренные ранее, можно производить и над расширенной матрицей системы, поэтому в дальнейшем будем говорить об элементарных преобразованиях, не делая различий между уравнениями системы и строками расширенной матрицы.
Разберём идею метода Гаусса на конкретных примерах.
Пример 2.
Решение.
I этап: запишем систему в виде расширенной матрицы
II этап: исключим с помощью первого уравнения x из остальных уравнений. Для этого домножим первую строку на –3 и сложим её со второй, затем умножим первую строку на –2 и сложим её с третьей.
Получим
.
Последняя строка состоит из нулей, если её расписать в виде уравнения, то получим
.
Это уравнение является тождеством, поэтому его нет смысла оставлять в системе.
Раскодируем полученную матрицу:
Выразим из второго уравнения :
Подставим в первое уравнение вместо его выражение через и выразим :
,
Ответ:
Получим так называемое общее решение системы, которое является формулой для получения конкретных её решений. Эти конкретные решения системы называются частными решениями. Получают их следующим образом: придавая переменным , произвольные значения и находя по этим значениям и , всякий раз находят решение системы. Так как и можно придавать произвольные значения, то эти переменные называются свободными. Неизвестные и , значения которых вычисляются по значениям и , называются базисными.
Получим одно из частных решений в предыдущем примере. Пусть , а , тогда , .
Ответ: -частное решение.
Пример 3.
Решение.
Закодируем систему и приведем матрицу к треугольному виду
Таким образом, заданная система равносильна следующей:
Находим из последнего уравнения, затем из второго, и наконец, из первого:
Ответ: .
Пример 4.
Выпишем расширенную матрицу и упростим её:
Полученная система
несовместна, так как её последнее уравнение не имеет смысла. Следовательно, исходная система также несовместна.
cyberpedia.su


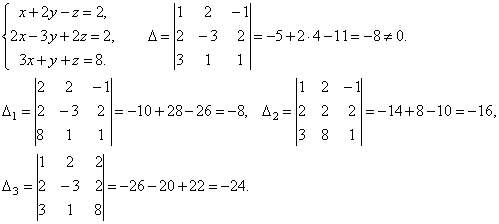
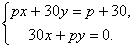
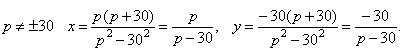
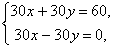 которая
не имеет решений.
которая
не имеет решений.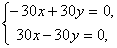 и,
следовательно, имеет бесконечное
множество решений x=y, yR.
и,
следовательно, имеет бесконечное
множество решений x=y, yR.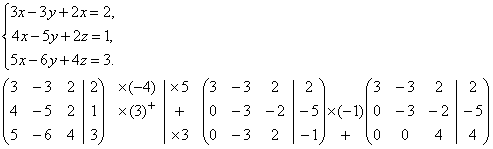
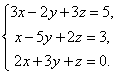
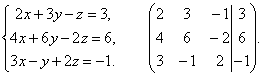
 :
: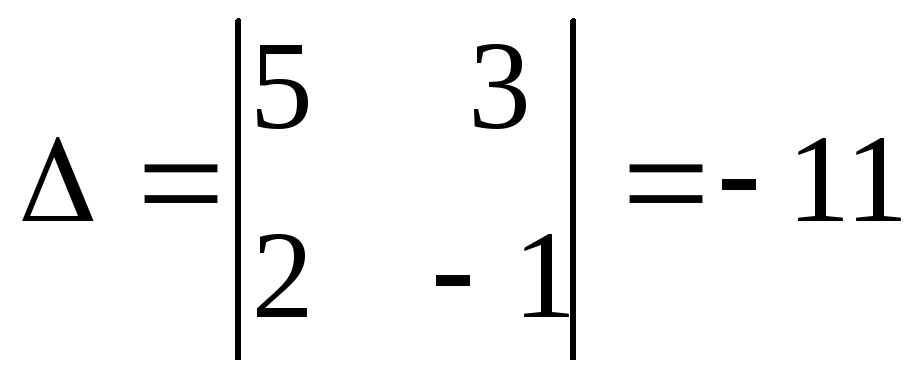 — система имеет одно решение, можно
применить теорему Крамера
— система имеет одно решение, можно
применить теорему Крамера :
:

 3 -2 6
3 -2 6