Обратная матрица — Википедия
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
- AA−1=A−1A=E{\displaystyle AA^{-1}=A^{-1}A=E}
Квадратная матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Способы нахождения обратной матрицы[править | править код]
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы[править | править код]
Метод Жордана—Гаусса[править | править код]
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi{\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
- Λ1⋅⋯⋅Λn⋅A=ΛA=E⇒Λ=A−1{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}.
- Λm=[1…0−a1m/amm0…0…0…1−am−1m/amm0…00…01/amm0…00…0−am+1m/amm1…0…0…0−anm/amm0…1]{\displaystyle \Lambda _{m}={\begin{bmatrix}1&\dots &0&-a_{1m}/a_{mm}&0&\dots &0\\&&&\dots &&&\\0&\dots &1&-a_{m-1m}/a_{mm}&0&\dots &0\\0&\dots &0&1/a_{mm}&0&\dots &0\\0&\dots &0&-a_{m+1m}/a_{mm}&1&\dots &0\\&&&\dots &&&\\0&\dots &0&-a_{nm}/a_{mm}&0&\dots &1\end{bmatrix}}}.
Вторая матрица после применения всех операций станет равна Λ{\displaystyle \Lambda }, то есть будет искомой. Сложность алгоритма — O(n3){\displaystyle O(n^{3})}.
С помощью матрицы алгебраических дополнений[править | править код]
Матрица, обратная матрице A{\displaystyle A}, представима в виде
- A−1=adj(A)det(A){\displaystyle {A}^{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj(A){\displaystyle {\mbox{adj}}(A)} — присоединенная матрица (матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы).
Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Использование LU/LUP-разложения[править | править код]
Матричное уравнение AX=In{\displaystyle AX=I_{n}} для обратной матрицы X{\displaystyle X} можно рассматривать как совокупность n{\displaystyle n} систем вида Ax=b{\displaystyle Ax=b}. Обозначим i{\displaystyle i}-й столбец матрицы X{\displaystyle X} через Xi{\displaystyle X_{i}}; тогда AXi=ei{\displaystyle AX_{i}=e_{i}}, i=1,…,n{\displaystyle i=1,\ldots ,n}, поскольку i{\displaystyle i}-м столбцом матрицы In{\displaystyle I_{n}} является единичный вектор ei{\displaystyle e_{i}}. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)[1].
Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA=LU{\displaystyle PA=LU}. Пусть PA=B{\displaystyle PA=B}, B−1=D{\displaystyle B^{-1}=D}. Тогда из свойств обратной матрицы можно записать: D=U−1L−1{\displaystyle D=U^{-1}L^{-1}}. Если умножить это равенство на U и L то можно получить два равенства вида UD=L−1{\displaystyle UD=L^{-1}} и DL=U−1{\displaystyle DL=U^{-1}}. Первое из этих равенств представляет собой систему из n² линейных уравнений для n(n+1)2{\displaystyle {\frac {n(n+1)}{2}}}, из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для n(n−1)2{\displaystyle {\frac {n(n-1)}{2}}}, из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно рекуррентно определить все n² элементов матрицы D. Тогда из равенства (PA)−1 = A−1P−1 = B−1 = D получаем равенство A−1=DP{\displaystyle A^{-1}=DP}.
В случае использования LU-разложения не требуется перестановки столбцов матрицы D, но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
Итерационные методы[править | править код]
Методы Шульца[править | править код]
{Ψk=E−AUk,Uk+1=Uk∑i=0nΨki{\displaystyle {\begin{cases}\Psi _{k}=E-AU_{k},\\U_{k+1}=U_{k}\sum _{i=0}^{n}\Psi _{k}^{i}\end{cases}}}
Оценка погрешности[править | править код]
Выбор начального приближения[править | править код]
Проблема выбора начального приближения U0{\displaystyle U_{0}} в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору U0{\displaystyle U_{0}}, обеспечивающие выполнение условия ρ(Ψ0)<1{\displaystyle \rho (\Psi _{0})<1} (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы AAT{\displaystyle AA^{T}} (а именно, если A — симметричная положительно определённая матрица и ρ(A)≤β{\displaystyle \rho (A)\leq \beta }, то можно взять U0=αE{\displaystyle U_{0}={\alpha }E}, где α∈(0,2β){\displaystyle \alpha \in \left(0,{\frac {2}{\beta }}\right)}; если же A — произвольная невырожденная матрица и ρ(AAT)≤β{\displaystyle \rho (AA^{T})\leq \beta }, то полагают U0=αAT{\displaystyle U_{0}={\alpha }A^{T}}, где также α∈(0,2β){\displaystyle \alpha \in \left(0,{\frac {2}{\beta }}\right)}; можно конечно упростить ситуацию и, воспользовавшись тем, что ρ(AAT)≤kAATk{\displaystyle \rho (AA^{T})\leq {\mathcal {k}}AA^{T}{\mathcal {k}}}, положить U0=AT‖AAT‖{\displaystyle U_{0}={\frac {A^{T}}{\|AA^{T}\|}}}). Во-вторых, при таком задании начальной матрицы нет гарантии, что ‖Ψ0‖{\displaystyle \|\Psi _{0}\|} будет малой (возможно, даже окажется ‖Ψ0‖>1{\displaystyle \|\Psi _{0}\|>1}), и высокий порядок скорости сходимости обнаружится далеко не сразу.
Матрица 2 × 2[править | править код]
- A−1=[abcd]−1=1detA[d−b−ca]=1ad−bc[d−b−ca]{\displaystyle \mathbf {A} ^{-1}={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}^{-1}={\frac {1}{\det \mathbf {A} }}{\begin{bmatrix}d&-b\\-c&a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}d&-b\\-c&a\\\end{bmatrix}}}[2]
Обращение матрицы 2 × 2 возможно только при условии, что ad−bc=detA≠0{\displaystyle ad-bc=\det A\neq 0}.
ru.wikipedia.org
Нахождение обратной матрицы: три алгоритма и примеры
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1. Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.

Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
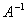 ,
,
произведение на которую матрицы А справа является единичной матрицей, т.е, 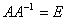 . (1)
. (1)

Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Нахождение обратной матрицы — задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
На сайте есть онлайн калькулятор для нахождения обратной матрицы. Вы можете открыть его в новом окне уже сейчас, если держите перед собой ваши собственные задания. А мы разберём несколько разминочных.
Для неособенной квадратной матрицы А обратной является матрица
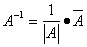 , (2)
, (2)
где 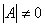
 — матрица, союзная с матрицей А.
— матрица, союзная с матрицей А.Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
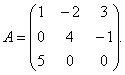
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
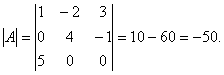
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу
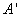 ,
транспонированную относительно матрицы A:
,
транспонированную относительно матрицы A:
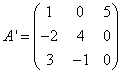
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
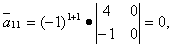
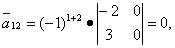
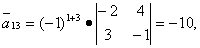
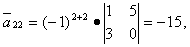
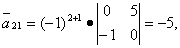
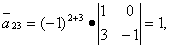
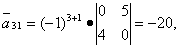
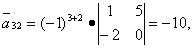
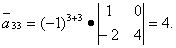
Следовательно, матрица
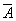 ,
союзная с матрицей A, имеет вид
,
союзная с матрицей A, имеет вид
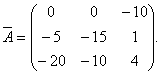
Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы
Применяя формулу (2), находим матрицу, обратную матрице А:
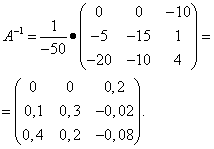
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
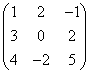
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
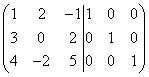
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
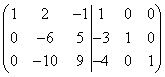 .
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
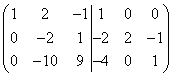 .
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
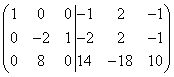 .
.
Разделим третью строку на 8, тогда
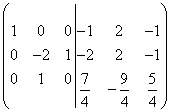 .
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
 .
.
Переставим местами вторую и третью строку, тогда окончательно получим:
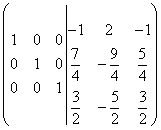 .
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части
получилась обратная матрица 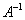 .
Таким образом:
.
Таким образом:
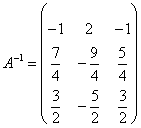 .
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
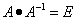 .
.
В результате должна получиться обратная матрица.
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Пример 3. Для матрицы
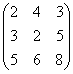
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
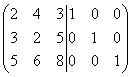
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
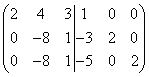 .
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
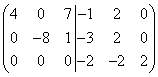 .
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование — это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование — систему линейных уравнений вида
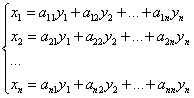 ,
,
где aij — элементы матрицы A.
2. Решить полученную систему относительно y — найти для предыдущего линейного преобразование обратное линейное преобразование
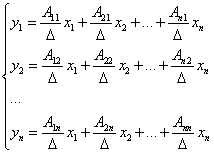 ,
,
в котором Aij — алгебраические дополнения элементов матрицы A, Δ — определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки — в столбце, а для элементов столбца — в строке.
3. Находим коэффициенты при y: 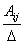 ,
которые и будут элементами матрицы, обратной для матрицы A.
,
которые и будут элементами матрицы, обратной для матрицы A.
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований — это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы
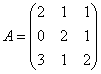 .
.
Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:
 .
.
Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
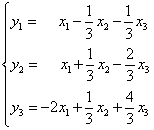
Коэффициенты при иксах в обратном линейном преобразовании — это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
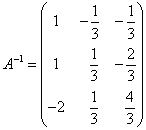
Проверить решение можно с помощью онлайн калькулятора для нахождения обратной матрицы.

Начало темы «Матрицы»
Другие темы линейной алгебры
function-x.ru
Алгоритм вычисления обратной матрицы методом элементарных преобразований (метод Гаусса)
Приписываем справа к матрице А размера
 единичную матрицу того же размера,
получим прямоугольную матрицу
единичную матрицу того же размера,
получим прямоугольную матрицу размера
размера .
.С помощью элементарных преобразований над строками матрицы Г сначала приведем ее к ступенчатому виду
 ,
где матрица А1 – треугольная.
,
где матрица А1 – треугольная.Затем, так же, с помощью элементарных преобразований приведем Г1 к виду
 .
.
Пример
2. Найти
матрицу, обратную к данной методом
Гаусса: 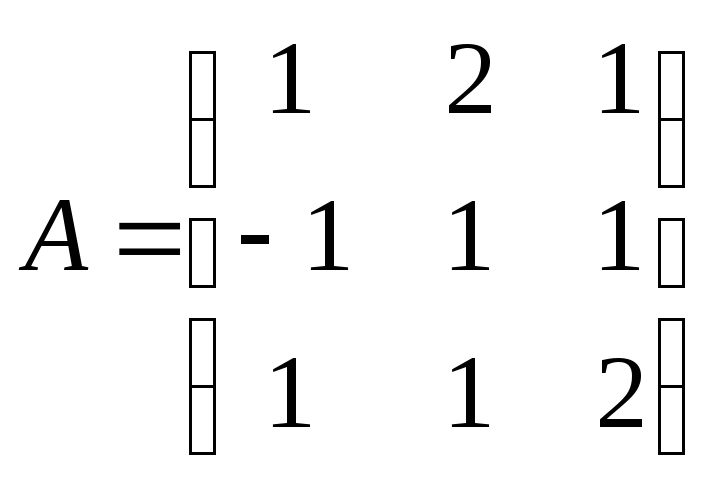
1. 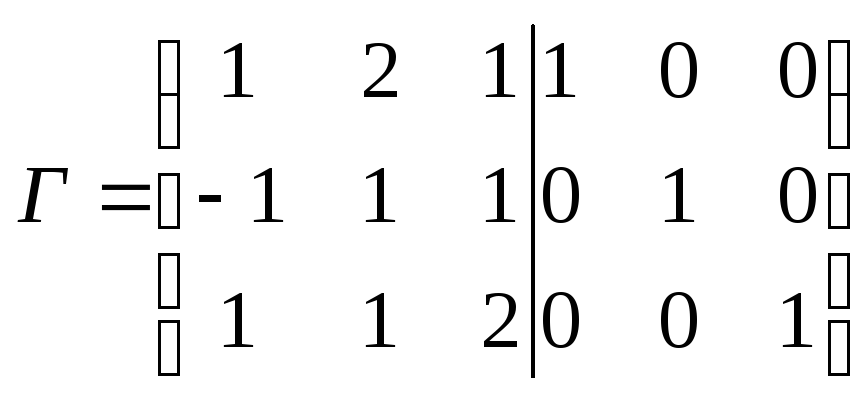 .
.
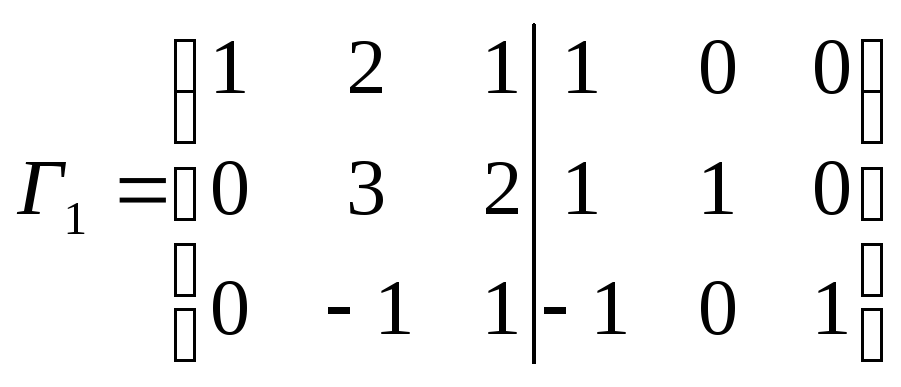
2. 
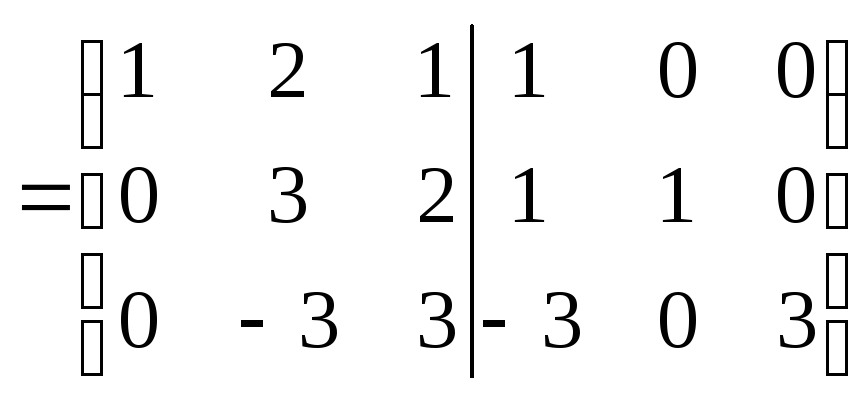
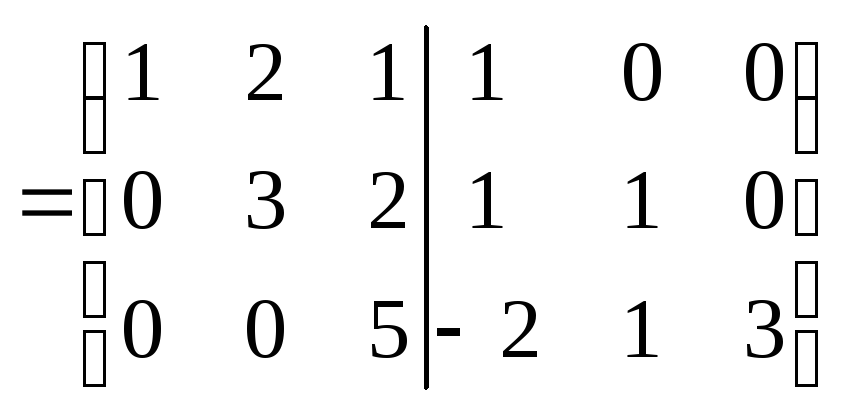 .
.
3.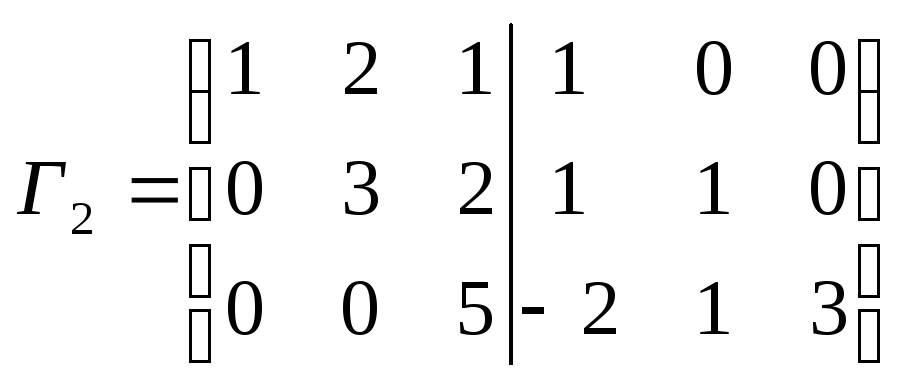
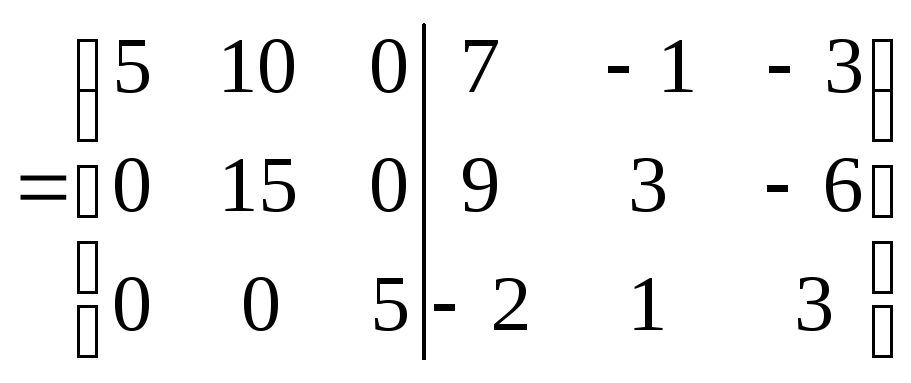
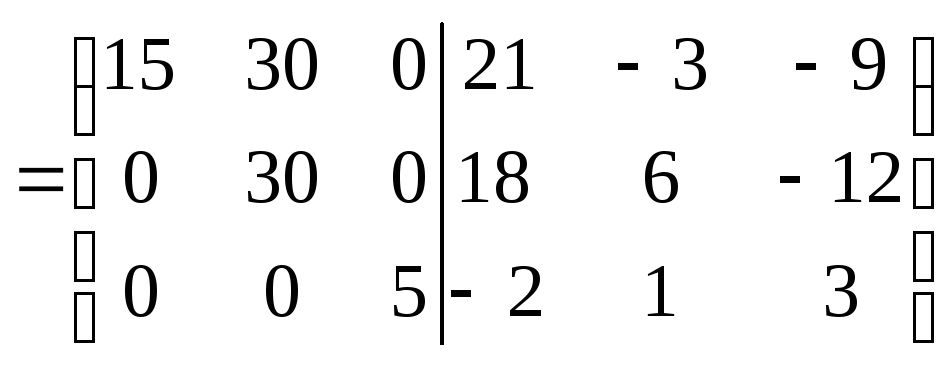
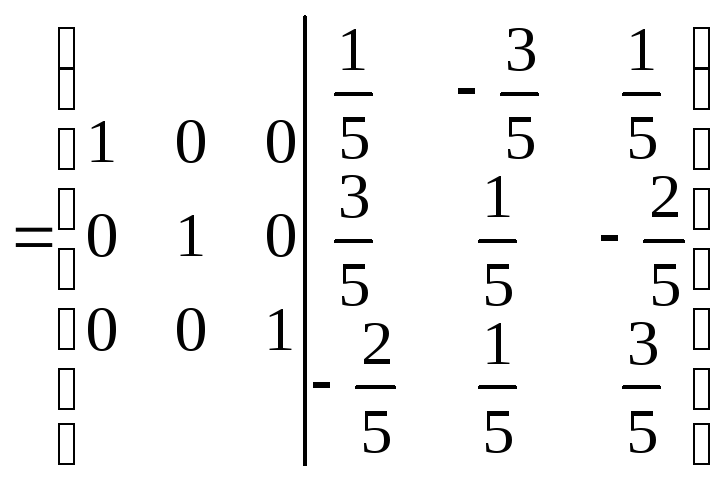
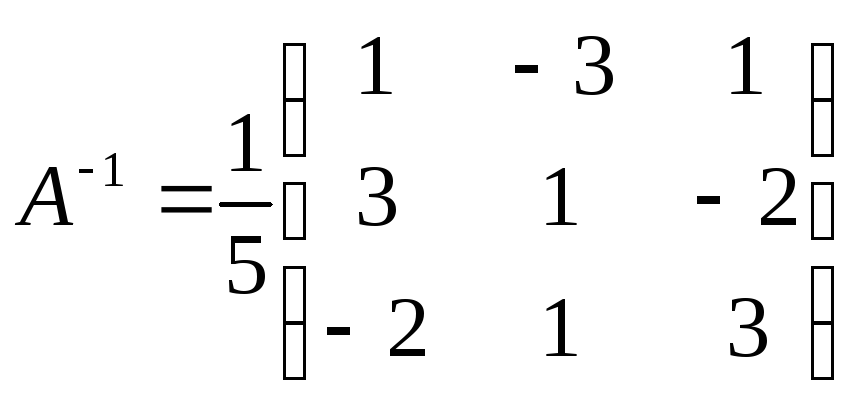 .
.
Ранг матрицы. Совместность систем.
Пусть задана система m линейных уравнений с n неизвестными:
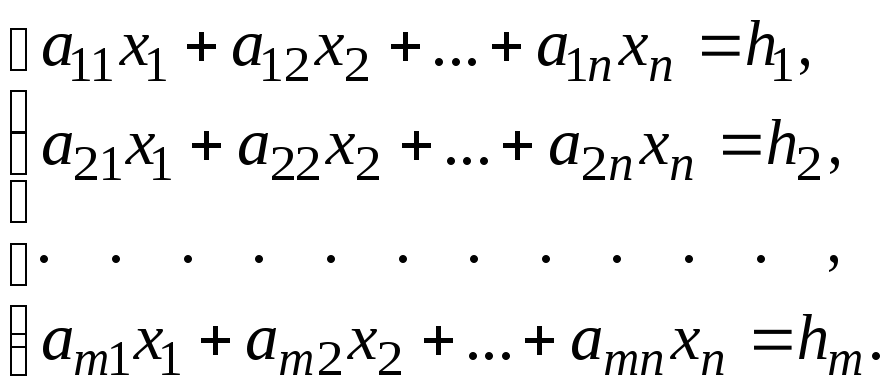 (1)
(1)
Определение 4. Если 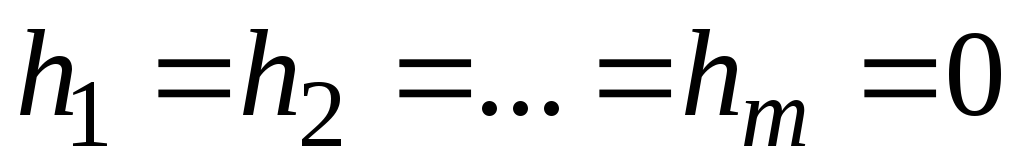 ,
то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично
от нуля, то система неоднородная.
,
то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично
от нуля, то система неоднородная.
Для
исследования данной системы составим
матрицу 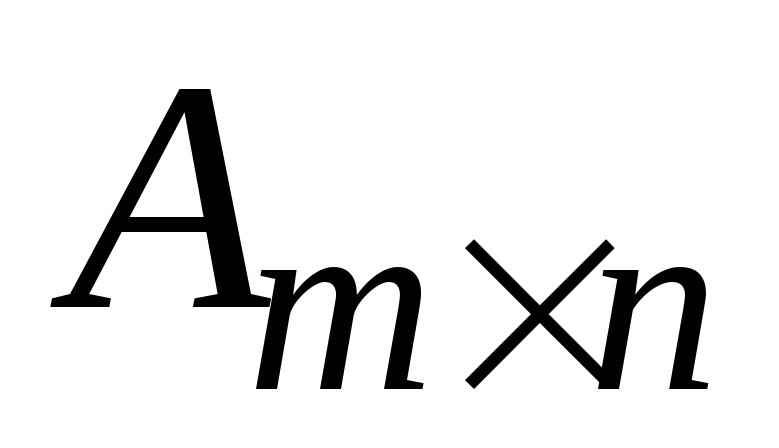 из коэффициентов при неизвестных. Для
решения многих задач важное значение
имеет понятие ранга матрицы.
из коэффициентов при неизвестных. Для
решения многих задач важное значение
имеет понятие ранга матрицы.
Определение 5. В матрице Amn вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где kmin(m;n). Определители таких матриц называются минорами k-го порядка матрицы Amn.
Определение 6. Рангом матрицы Amn называется наивысший порядок ненулевых миноров этой матрицы.
Обозначается rang A или r(A).
Из определения следует:
ранг матрицы Amn не превосходит меньшего из её размеров;
r(A) = 0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А нулевая матрица.
Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А имеет определитель отличный от нуля.
Определение 7. Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.
Пример
2. Вычислить ранг матрицы 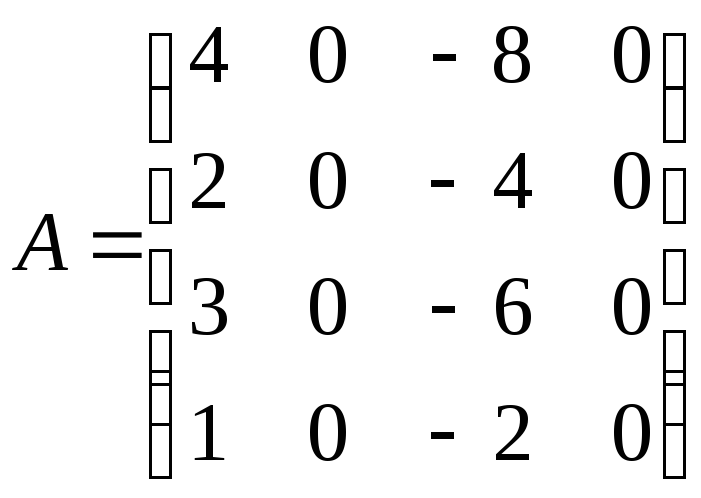 и указать какой-либо ее базисный минор.
и указать какой-либо ее базисный минор.
Решение:
матрица имеет четвертый порядок, но detА =
0. Все миноры 3-го порядка тоже равны
нулю, так как содержат хотя бы один
нулевой столбец (свойство 50 определителя). Все миноры 2-го порядка
тоже равны нулю, тек как содержат либо
нулевой столбец, либо пропорциональные
столбцы (свойство 60).
Значит r(A)
= 1, т.к. есть элементы отличные от нуля.
Любой такой элемент можно принять за
базисный минор, к примеру, 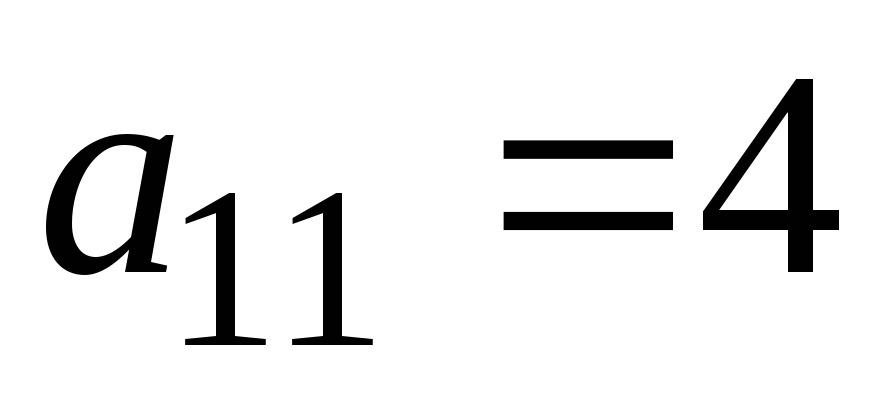 .
.
Пример
3. Вычислить ранг матрицы  и указать какой-либо ее базисный минор.
и указать какой-либо ее базисный минор.
Решение: А34 значит r(A) 3. Среди миноров третьего порядка лишь один не содержит нулевого столбца. Вычислим его:
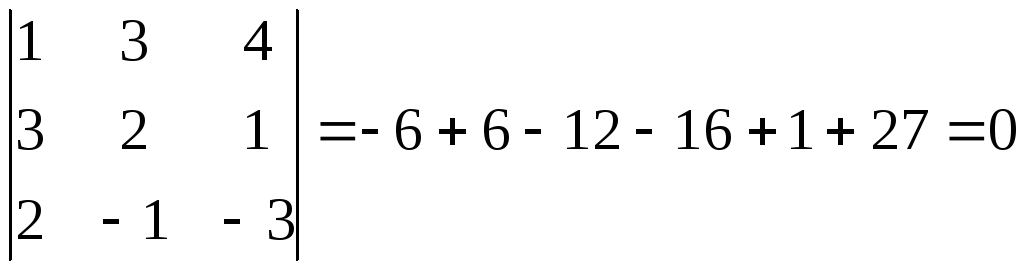
Итак,
все миноры третьего порядка равны нулю.
Среди миноров второго порядка есть
ненулевые, например, 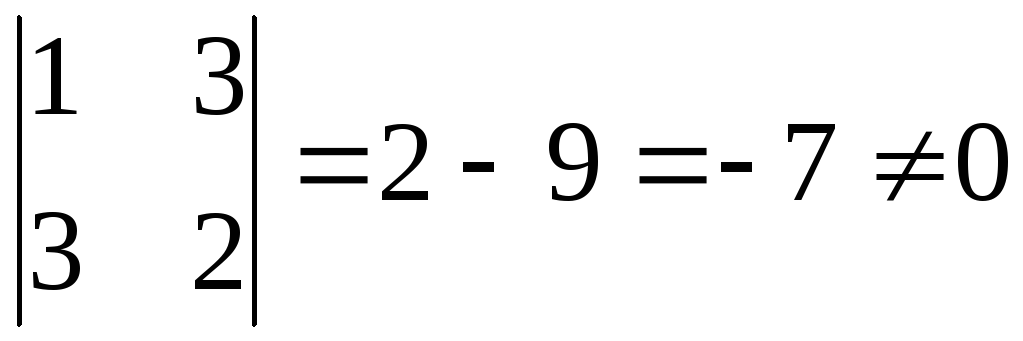 .
Следовательно,r(A)
= 2.
.
Следовательно,r(A)
= 2.
Для облегчения нахождения ранга матрицы используются элементарные преобразования матриц, которые сохраняют её ранг. Напомним, что к элементарным преобразованиям матриц относятся:
1) Умножение всех элементов строк или столбцов матрицы на число, отличное от нуля.
2) Изменение порядка строк или столбцов матрицы.
3) Прибавление к каждому элементу одной строки или столбца соответствующих элементов другой строки или столбца, умноженных на любое число.
С помощью элементарных преобразований строк и перестановки столбцов можно привести матрицу к трапециевидному или ступенчатому виду, когда определение её ранга не составляет труда.
Определение 8. Трапециевидной или ступенчатой называется матрица вида:
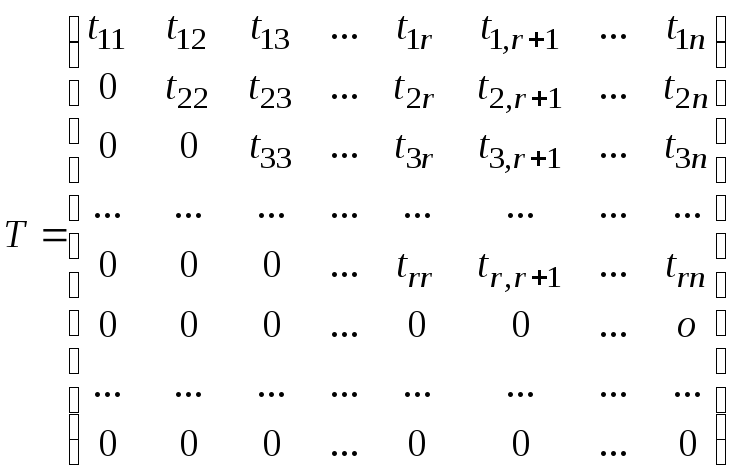 ,
,
где 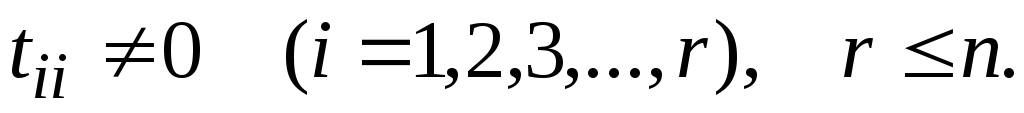
Ранг трапециевидной или ступенчатой матрицы равен количеству ненулевых строк.
Пример 4. Найти ранг матрицы
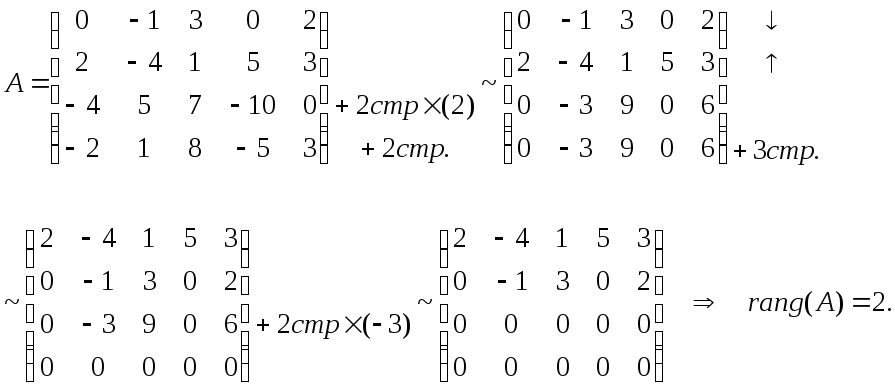
Лекция 5. Матричные уравнения. Системы линейных уравнений.
studfile.net
Обратная матрица и методы ее вычисления
Запишем вспомогательную матрицу
и приведем её, с помощью элементарных преобразований, к матрице, в которой единичная матрица будет слева. Переставим местами первую и вторую строки
Прибавим ко второй строке первую строку, умноженную на а к третьей строке первую, умноженную на
Прибавим ко второй строке третью, умноженную на
Умножим вторую строку на
Прибавим к первой строке вторую, умноженную на а к третьей вторую, умноженную на
Разделим третью строку на 3
К первой строке прибавим третью, умноженную на
Тогда обратная матрица равна
ru.solverbook.com
Метод Жордана-Гаусса
Определение 1
Метод Жордана-Гаусса – это метод решения линейных уравнений путём полного исключения неизвестных. Данный метод является модификацией метода Гаусса, только в случае метода Жордана-Гаусса элементарные преобразования проводятся дальше.
История возникновения метода
Исторически метод Гаусса возник достаточно давно. Решение систем уравнений подобным способом было изложено ещё в древнем китайском математическом трактате под названием “Математика в девяти книгах”, представляющим собой разрозненное собрание решений различных прикладных математических задач.
Некоторые главы этого трактата датируются 150 г. до н.э.
В Европе же первым, кто занимался изучением этого метода, был Исаак Ньютон. Учёный изучил много книг по алгебре того времени и обнаружил, что ни в одной из них не предложено решений систем уравнений со множеством переменных, после чего он предложил свой способ решения.
Его работа на эту тему была опубликована в 1707 г., в это время Ньютон уже больше не работал в Кембридже. После этого в течение века метод появился во многих книгах и учебниках по алгебре.
В 1810 году известный немецкий учёный и математик К. Ф. Гаусс опубликовал свои дополнения к этому методу вместе с другими своими работами по линейной алгебре, после чего метод с получением верхней треугольной матрицы стал широко известен под его именем.
Затем в в конце XIX века геодезист и математик Жордан разработал на основе метода Гаусса свой усовершенствованный вариант с получением диагональной матрицы.
Примечательно, что он сделал это практически одновременно с другим учёным, тем не менее, в названии усовершенствованного метода отразилось только имя геодезиста Жордана.
Практическое применение метода Жордана-Гаусса
Метод Жордана и Гаусса используется для решения систем линейных уравнений, а также для получения обратных матриц и нахождения ранга матрицы. Также этот метод весьма полезен и часто применяем для решения технических задач со множеством неизвестных.
Для решения получаемых на основе технических задач систем уравнений выделяют наибольшие по модулю переменные для уменьшения ошибки погрешности, а затем производят поочередное удаление лишних переменных из строчек матрицы.
Для решения технических задач методом Жордана-Гаусса также используются реализации на различных языках программирования, они позволяют получать более точные значения переменных.
Объяснение сущности метода Жордана-Гаусса
Обычно матрица, полученная с помощью метода Жордана-Гаусса выглядит как диагональ с единицами, вот например:
$A = \begin{array}{ccc|c} 1& 0 &0 &a_1 \\ 0& 1 &0 &a_2 \\ 0 & 0 & 1 &a_3 \end{array}$
Разница между методом Гаусса и методом Жордана-Гаусса состоит в том, что в случае метода Гаусса необходимо привести только нижнюю часть матрицы к нулям, тогда как в случае метода Жордана-Гаусса в каждой строчке матрицы остаётся лишь один коэффициент при переменной.
С помощью метода Гаусса можно найти базисное и общее решение системы уравнений, также как и с помощью метода Жордана-Гаусса.
Базисное решение системы уравнений – это решение, при котором все свободные переменные равны нулю.
Общее решение системы уравнений – это решение, при котором основные переменные выражаются через свободные переменные.
Также методом Жордана-Гаусса производят получение обратных матриц.
Получение обратной матрицы методом Жордана-Гаусса
Обратная матрица – это такая матрица, при умножении на которую из исходной матрицы получается единичная матрица. Обратные матрицы существуют только для квадратных и невырожденных матриц.
Сущность метода нахождения обратной матрицы состоит в том, чтобы записать рядом исходную матрицу и единичную, и затем, производить элементарные преобразования по методу Жордана-Гаусса одновременно к двум матрицам.
В результате мы получим диагональную единичную матрицу из исходной, а рядом с ней будет её обратная матрица, полученная из единичной матрицы.
Получение обратной матрицы методом Жордана-Гаусса.
Исходная матрица:
$\begin{array}{cc} 1& 2 \\ 3 & 4 \\ \end{array}$
Запишем рядом единичную матрицу и исходную:
$ \begin{array}{cc|cc} 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end{array}$
Теперь к нижней строчке прибавляем верхнюю строчку, умноженную на $-3$:
$ \begin{array}{cc|cc} 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end{array}$
Прибавляем к верхней строчке нижнюю:
$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end{array}$
Делим вторую строку на $-2$:
$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end{array}$
Обратной исходной будет следующая матрица:
$\begin{array}{cc} -2& 1 \\ 3/2 & -1/2 \\ \end{array}$
Чтобы решить СЛАУ методом Жордана-Гаусса, к матрице возможно применить те же элементарные преобразования, что и в случае решения методом Гаусса, а именно:
- умножение любой строчки на константу, отличную от нуля;
- вычитание или сложение двух любых строчек;
- перестановка любых двух строчек местами;
- удаление строчек, состоящих из одних нулей;
- удаление лишних строк, пропорциональных друг другу.
Соответственно, чтобы решить систему линейных уравнений методом Гаусса-Жордана, необходимо выполнить ряд преобразований над получающейся после применения метода Гаусса матрицей.
Общий алгоритм решения системы уравнений методом Жордана-Гаусса
- Выбирают строчку, в которой первый элемент имеет ненулевое значение максимально приближенное к единице и ставят её на место первой строки. Такой элемент называют также “разрешающим”
- Приводят значение верхней левой ячейки к $1$ посредством деления или умножения всей верхней строки.
- Из оставшихся строчек вычитают верхнюю строчку, помноженную на коэффициент, стоящий на первом месте в строчке, над которой ведутся преобразования.
- Далее тоже самое проделывают необходимое количество раз с целью получения треугольной матрицы, в которой все элементы ниже главной диагонали, проходящей слева направо сверху вниз, равны нулю. Последовательность действий, описанных выше, называется прямым ходом преобразования матрицы.
- После получения треугольной матрицы затем вычитают последнюю строку из предпоследней, помножив последнюю строку на элемент из предпоследней. На данном этапе в последней и предпоследней строке остаётся по одному коэффициенту. Эту операцию повторяют пока не дойдут до верха матрицы, получив диагональную матрицу. Эти действия носят название обратного хода преобразования матрицы.
Пример 1
Задача. Решить систему линейных уравнений методом Гаусса-Жордана
$\begin{cases} 3x_1 + 2x_2 – 5x_3 = -1 \\ 2x_1 – x_2 + 3x_3 = 13 \\ x_1 + 2x_2 – x_3 = 9 \end{cases}$
Теперь запишем эту систему в виде расширенной матрицы:
$ \begin{array}{ccc|c} 3& 2 & -5 & -1\\ 2 & -1& 3 & 13 \\ 1 & 2 & -1 & 9 \\ \end{array}$
Путём элементарных преобразований методом Гаусса получим следующую матрицу:
$ \begin{array}{ccc|c} 1& 2 & -1 & 9\\ 0 & 1& -1 & 1 \\ 0 & 0& 1 & 4 \\ \end{array}$
Теперь начнём использовать обратный ход и преобразуем эту матрицу чтобы получить диагональ из единиц.
Сначала к средней и верхней строчкам необходимо добавить последнюю строчку, получается:
$ \begin{array}{ccc|c} 1& 2 & 0 & 13\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$
А теперь к верхней строчке прибавим среднюю, умноженную на $-2$:
$ \begin{array}{ccc|c} 1& 0 & 0 & 3\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$
Получаем следующую систему:
$\begin{cases} x_1 = 3 \\ x_2 = 5 \\ x_3 = 4 \end{cases}$
Пример 2
Решить систему линейных уравнений методом Жордана-Гаусса:
$\begin{cases} x_1 – 8x_2 + x_3 — 9x_4 = 6 \\ x_1 – 4x_2 – x_3 — 5x_4 = 2 \\ -3x_1 + 2x_2 + 8x_3 + 5x_4 = 4 \\ 5x_1 + 2x_2 + 2x_3 + 3x_4 = 12 \end{cases}$
Сначала запишем систему в матричном виде:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ -1 & -4& -1 & -5 & 2 \\ -3 & 2 & 8 & 5 & 4 \\ 5& 2 & 2 & 3 & 12 \\ \end{array}$
Затем преобразуем до треугольной:
К самой верхней строчке прибавляем вторую строчку, домноженную на $-1$. К третьей строчке прибавляем утроенную самую верхнюю строчку, затем к последней строчке прибавляем самую верхнюю, помноженную на $-5$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 4& -2 & 4 & -4 \\ 0 & -22 & 11 & -22 & 22 \\ 0& 42 & -3 & 48 & -18 \\ \end{array}$
Теперь вторую строчку необходимо поделить на $2$, третью строчку на на $11$, а самую нижнюю строку делим на 3:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0 & -2 & 1 & -2 & 2 \\ 0& 14 & -1 & 16 & -6 \\ \end{array}$
Удаляем третью строчку, так как она пропорциональна со второй. А к последней строке прибавляем вторую, предварительно домноженную на $-7$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 6 & 2 & 8 \\ \end{array}$
Теперь сокращаем последнюю строчку с $2$:
$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
В полученной матрице количество строк и столбцов неодинаково, а значит, она имеет бесконечное множество решений. Продолжаем дальнейшее преобразование системы, для этого необходимо в третьем столбце получить числа с равным модулем, поэтому сначала верхнюю строку умножаем на $-3$, а среднюю на $3$:
$ \begin{array}{cccc|c} -3& 24 & -3 & 27 & -18 \\ 0 & 6& -3 & 6 & -6 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Складываем поочередно первую строчку с третьей, а затем вторую с третьей:
$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & 6 & 0 & 7 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Домножаем вторую строчку на $-4$ чтобы получить одинаковые по модулю числа во втором столбце нашей матрицы:
$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Складываем верхнюю строчку со второй:
$ \begin{array}{cccc|c} -3& 0 & 0 & 0 & -6 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$
Теперь необходимо разделить верхнюю строчку на $-3$, среднюю строчку на $-24$, а последнюю строчку нужно разделить на 3:
$ \begin{array}{cccc|c} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 7/6 & -1/3 \\ 0& 0 & 1 & 1/3 & 4/3 \\ \end{array}$
Если переписать в виде системы, получим следующее:
$\begin{cases} x_1 = 2 \\ x_2 + \frac{7}{6}x_4 = -\frac{1}{3} \\ x_3 + \frac{1}{3}x_4 = \frac{4}{3} \\ \end{cases}$
А теперь просто выражаем базисные переменные:
$\begin{cases} x_1 = 2 \\ x_2 = -\frac{7}{6}x_4 — \frac{1}{3} \\ x_3 = -\frac{1}{3}x_4 + \frac{4}{3} \\ \end{cases}$
Данная система является общим решением уравнения.
spravochnick.ru
Обратная матрица онлайн
Для любой невырожденной квадратной матрицы (т.е. такой определитель которой отличен от нуля), существует обратная матрица, такая, что её произведение на исходную матрицу равно единичной:
A∙A−1 = A−1∙A = E
Наш калькулятор поддерживает два различных способа вычисления обратной матрицы: по методу Гаусса-Жордана и при помощи построения алгебраических дополнений к исходной матрице.
Для нахождения обратной матрицы по методу Гаусса-Жордана, к исходной матрице справа дописывают единичную матрицу:
( A | E )
Затем, с помощью элементарных преобразований приводят исходную матрицу к единичной, выполняя теже самые операции и над единичной матрицей, записанной справа. В результате таких действий исходная матрица приводится к единичной, а единичная к обратной:
( A | E) → ( E | A−1)
Метод довольно простой, удобный и не очень трудоемкий.
Для нахождения обратной матрицы при помощи метода алгебраических дополнений используют следующую формулу:
где
| A |
— определитель матрицы
A,
Ai j
— алгебраическое дополнение элемента
ai j
матрицы
A.
По определению:
Ai j = (-1) i+j Mi j
где Mi j — минор элемента ai j матрицы A.
По определению — минор элемента ai j матрицы A — это определитель, полученный путем вычеркивания i строки, j столбца матрицы A.
Таким образом, метод алгебраических дополнений для вычисления обратной матрицы порядка n является достаточно трудоемким, поскольку помимо определителя исходной матрицы, нужно вычислить n2 определителей n-1 порядка.
mathforyou.net
Обратная матрица с помощью элементарных преобразований
Для того что бы найти обратную матрицу можно использовать два метода: с помощью алгебраических дополнений (метод присоединённой (союзной) матрицы) или элементарных преобразований (метод Жордано-Гаусса). Рассмотрим как найти обратную матрицу с помощью элементарных преобразований.
Обратной матрицей называется матрицы A-1 при умножении на исходную матрицу A получается единичная матрица E.
A·A-1 = A-1 · A = E
Алгоритм нахождения обратной матрицы с помощью элементарных преобразований:
- Найти определитель (детерминант) матрицы A. Если определитель ≠ 0, то обратная матрица существует. Если определитель = 0, то обратная матрица не существует.
- Дописываем справа единичную матрицу
- Делаем прямой ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей под ее главной диагонали.
- Делаем обратный ход. Обнуляем все элементы (с помощью элементарных преобразований) левой матрицы стоящей над ее главной диагонали.
- Элементы главной диагонали левой матрицы, преобразуем в единицы.
Пример
Рассмотрим данный метод на примере. Дана матрицы 3х3:
Найдем определитель (детерминант) матрицы, detA = 8 обратная матрица существует.
Допишем к нашей матрице слева единичную матрицу.
Чтобы сделать нули под элементом a11, вычтем 1-ую строку из всех строк, что расположены ниже её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a11.
Чтобы сделать нули над элементом a33, вычтем 3-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a33.
Чтобы сделать нули над элементом a22, вычтем 2-ую строку с всех строк, что расположены выше её, при чём, для того, чтобы работать с меньшими числами, поделим каждую из этих строк на a22.
Поделим каждую строку на элемент, который стоит на главной диагонали.
Вот мы и нашли обратную матрицу.
www.mozgan.ru
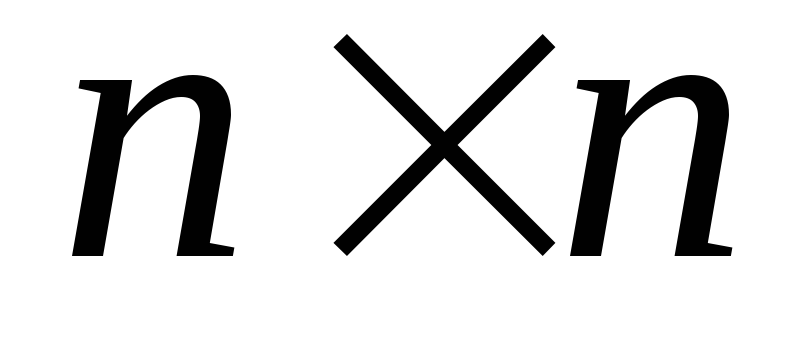 единичную матрицу того же размера,
получим прямоугольную матрицу
единичную матрицу того же размера,
получим прямоугольную матрицу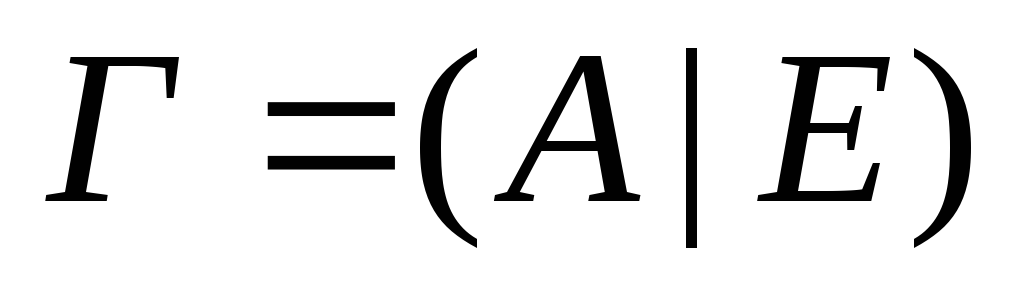 размера
размера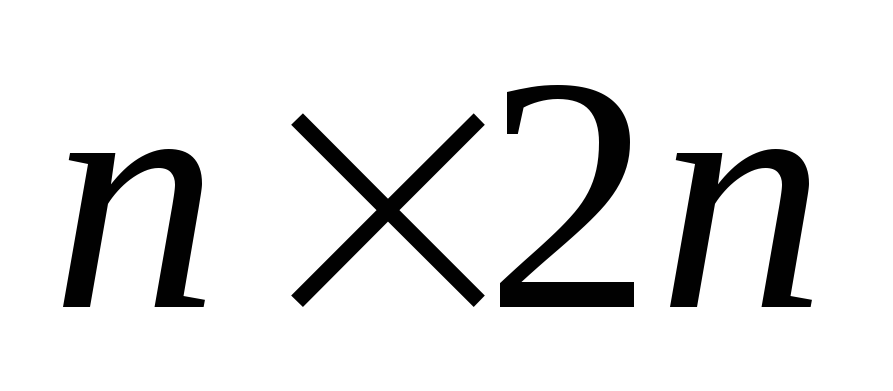 .
.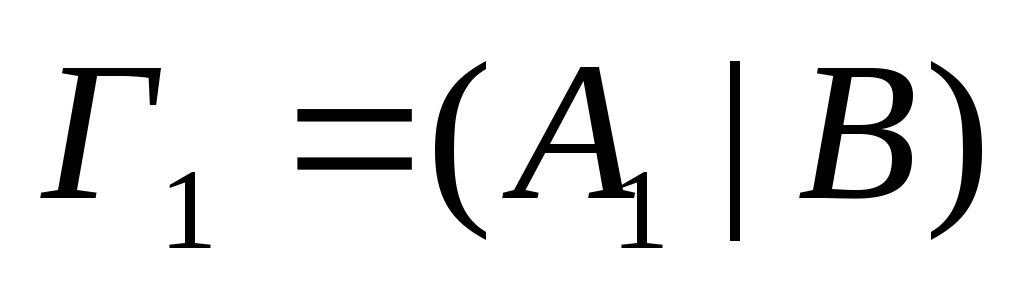 ,
где матрица А1 – треугольная.
,
где матрица А1 – треугольная.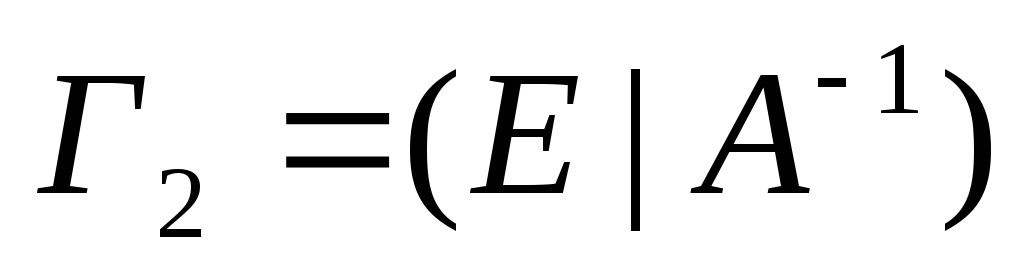 .
.