Обратный ход метода Гаусса — Мегаобучалка
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Метод Гаусса решения систем линейных
уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Метод Гаусса решения систем линейных уравнений
Эквивалентные системы уравнений
Две системы линейных уравнений называются эквивалентными, если каждое решение одной из них является решением другой. Процесс решения системы линейных уравнений состоит в последовательном преобразовании её в эквивалентную систему с помощью так называемых элементарных преобразований, которыми являются:
1) перестановка любых двух уравнений системы;
2) умножение обеих частей любого уравнения системы на отличное от нуля число;
3) прибавление к любому уравнению другого уравнения, умноженного на любое число;
4) вычёркивание уравнения, состоящего из нулей, т.е. уравнения вида .
Гауссовы исключения
Рассмотрим систему m линейных уравнений с n неизвестными:
Суть метода Гаусса или метода последовательного исключения неизвестных состоит в следующем.
Вначале с помощью элементарных преобразований исключается неизвестная из всех уравнений системы, кроме первого. Такие преобразования системы называются шагом гауссового исключения. Неизвестная называется разрешающей переменной на первом шаге преобразований. Коэффициент называется разрешающим коэффициентом, первое уравнение называется разрешающим уравнением , а столбец коэффициентов при разрешающим столбцом.
При выполнении одного шага гауссового исключения нужно пользоваться следующими правилами:
1) коэффициенты и свободный член разрешающего уравнения остаются неизменными;
2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;
3) все прочие коэффициенты и свободные члены при выполнении первого шага вычисляются по правилу прямоугольника:
, где i=2,3,…,m; j=2,3,…,n.
Аналогичные преобразования выполним и над вторым уравнением системы. Это приведёт к системе, у которой во всех уравнениях, кроме первых двух, будет исключена неизвестная . В результате таких преобразований над каждым из уравнений системы (прямой ход метода Гаусса) исходная система приводится к эквивалентной ей ступенчатой системе одного из следующих видов.
Обратный ход метода Гаусса
Ступенчатая система
имеет треугольный вид и все (i=1,2,…,n). Такая система имеет единственное решение. Неизвестные определяются, начиная с последнего уравнения (обратный ход метода Гаусса).
Ступенчатая система имеет вид
где , т.е. число уравнений системы меньше либо равно числу неизвестных. Эта система не имеет решений, так как последнее уравнение не будет выполняться ни при каких значениях переменной .
Ступенчатая система вида
имеет бесчисленное множество решений. Из последнего уравнения неизвестная выражается через неизвестные . Затем в предпоследнее уравнение вместо неизвестной подставляется её выражение через неизвестные . Продолжая обратный ход метода Гаусса, неизвестные можно выразить через неизвестные . В этом случае неизвестные называются свободными и могут принимать любые значения, а неизвестные базисными.
При практическом решении систем удобно выполнять все преобразования не с системой уравнений, а с расширенной матрицей системы, состоящей из коэффициентов при неизвестных и столбца свободных членов.
Пример 1. Решить систему уравнений
Решение. Составим расширенную матрицу системы и выполним элементарные преобразования:
.
В расширенной матрице системы число 3 (оно выделено) является разрешающим коэффициентом, первая строка является разрешающей строкой, а первый столбец – разрешающим столбцом. При переходе к следующей матрице разрешающая строка не изменяется, все элементы разрешающего столбца ниже разрешающего элемента заменяются нулями. А все другие элементы матрицы пересчитываются по правилу четырёхугольника. Вместо элемента 4 во второй строке запишем , вместо элемента -3 во второй строке будет записано и т.д. Таким образом, будет получена вторая матрица. У этой матрицы разрешающим элементом будет число 18 во второй строке. Для формирования следующей (третьей матрицы) вторую строку оставляем без изменения, в столбце под разрешающим элементом запишем нуль и пересчитаем оставшиеся два элемента: вместо числа 1 запишем , а вместо числа 16 запишем .
В результате исходная система свелась к эквивалентной системе
Из третьего уравнения находим . Подставим это значение во второе уравнение: y=3. В первое уравнение подставим найденные значения y и z: , x=2.
Таким образом, решением данной системы уравнений является x=2, y=3, .
Пример 2. Решить систему уравнений
Решение. Выполним элементарные преобразования над расширенной матрицей системы:
Во второй матрице каждый элемент третьей строки разделили на 2.
В четвёртой матрице каждый элемент третьей и четвёртой строки разделили на 11.
. Полученная матрица соответствует системе уравнений
Решая данную систему, найдём , , .
Пример 3. Решить систему уравнений
Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования:
.
Во второй матрице каждый элемент второй, третьей и четвёртой строк разделили на 7.
В результате получена система уравнений
эквивалентная исходной.
Так как уравнений на два меньше, чем неизвестных, то из второго уравнения . Подставим выражение для в первое уравнение: , .
Таким образом, формулы дают общее решение данной системы уравнений. Неизвестные и являются свободными и могут принимать любые значения.
Пусть, например, Тогда и . Решение является одним из частных решений системы, которых бесчисленное множество.
Вопросы для самоконтроля знаний
1) Какие преобразования линейных систем называются элементарными?
2) Какие преобразования системы называются шагом гауссова исключения?
3) Что такое разрешающая переменная, разрешающий коэффициент, разрешающий столбец?
4) Какими правилами нужно пользоваться при выполнении одного шага гауссова исключения?
megaobuchalka.ru
Обратный ход метода Гаусса
Запишем линейную систему, получившуюся в результате прямого хода метода Гаусса, с расширенной матрицей, приведенной в табл. 3.3.:
 (3.2.10)
(3.2.10)
Система
(3.2.10) равносильна исходной системе
(3.2.1) и ее решение получить несложно. Из
последнего уравнения системы можно
сразу найти  ,
из предпоследнего
,
из предпоследнего 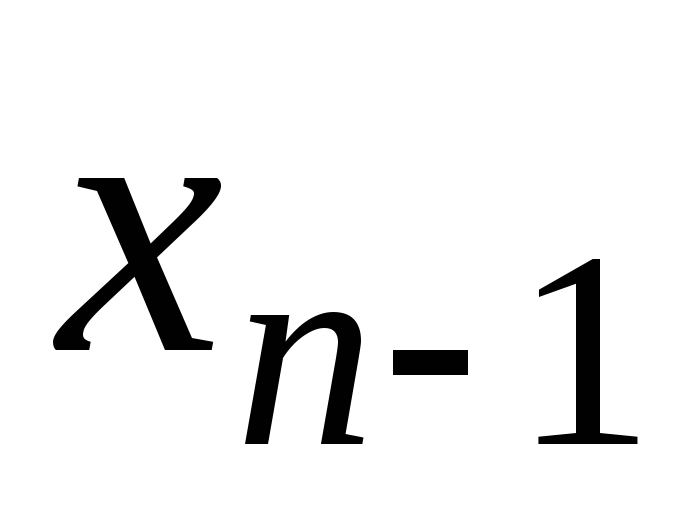
Алгоритм и расчетные формулы для обратного хода метода Гаусса
Приближенная проверка невырожденности матрицы системы. Если
 ,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия
,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия модуль определителя матрицы системы
будет меньше
модуль определителя матрицы системы
будет меньше и близок к нулю.
и близок к нулю.Вычисление решения по рекуррентным формулам
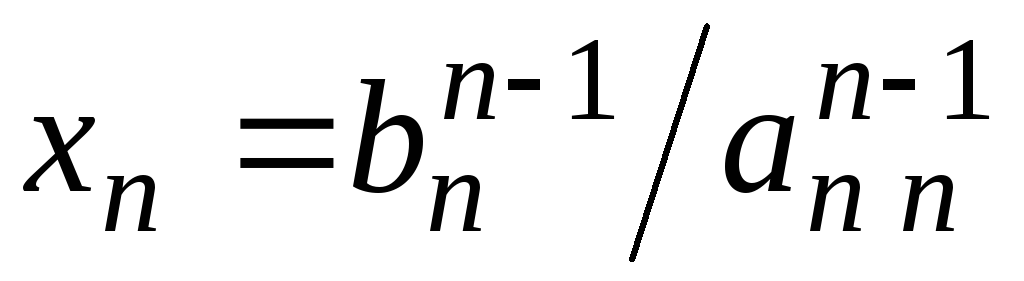 ,
(3.2.11)
,
(3.2.11)
 ,
, 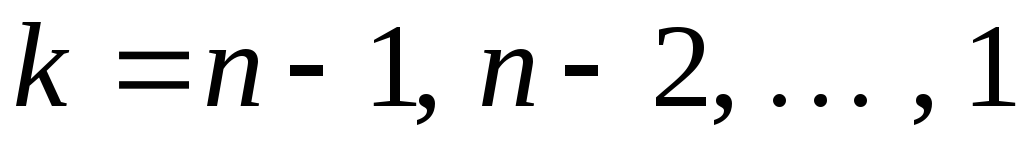
На
этом можно было бы завершить алгоритмическую
схему метода Гаусса с выбором главных
элементов в столбцах. Осталось только
сделать последнее замечание. В
процессе обратного хода метода Гаусса
используются только элементы матрицы,
стоящие выше главной диагонали и  .
Нули, стоящие под главной диагональю,
и единицы, стоящие на главной диагонали,
для получения решения не нужны. Поэтому
их можно не вычислять. А для того чтобы
не делать эти лишние операции, можно исключить
из алгоритма прямого хода вычисления
по формулам (3.2.6), (3.2.8) при
.
Нули, стоящие под главной диагональю,
и единицы, стоящие на главной диагонали,
для получения решения не нужны. Поэтому
их можно не вычислять. А для того чтобы
не делать эти лишние операции, можно исключить
из алгоритма прямого хода вычисления
по формулам (3.2.6), (3.2.8) при  .
.
Применение метода Гаусса для вычисления определителей Теоретические основы
При вычислении определителя квадратной матрицы А можно использовать прямой ход метода Гаусса. Применение метода Гаусса для вычисления определителей основано на их свойствах:
Если поменять местами две строки матрицы, то ее определитель поменяет свой знак, а абсолютная величина определителя не изменится
 .
.Если какую-либо строку матрицы разделить на некоторую постоянную с, не равную нулю, то определитель матрицы уменьшится в с раз
 .
.Если из какой-либо строки матрицы вычесть другую строку, умноженную на некоторое число, не равное нулю, то определитель не изменится
 .
.Если матрица является верхней треугольной (все ее элементы, лежащие ниже главной диагонали, равны 0), то её определитель будет равен произведению диагональных элементов этой матрицы.
В
результате преобразований прямого хода
метода Гаусса матрица А превратится в верхнюю треугольную
матрицу  .
На главной диагонали матрицы
.
На главной диагонали матрицы будут стоять единицы на всех строчках,
кроме последней. А в последней строке
на главной диагонали будет стоять
будут стоять единицы на всех строчках,
кроме последней. А в последней строке
на главной диагонали будет стоять 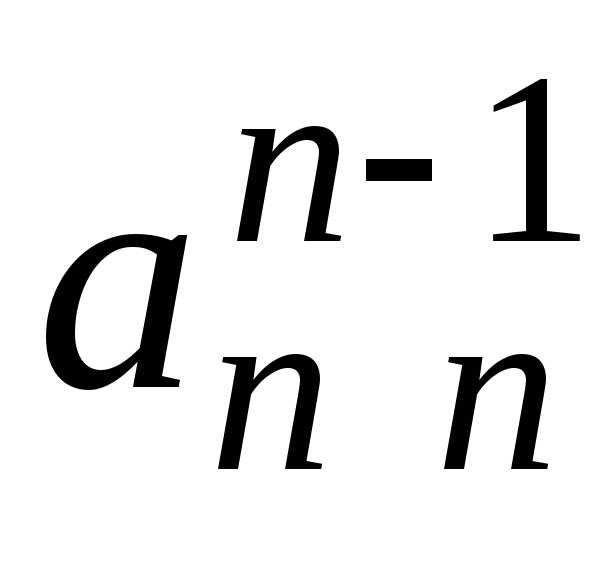 .
Поэтому определитель преобразованной
матрицы
.
Поэтому определитель преобразованной
матрицы  будет равен
будет равен  (произведению диагональных элементов).
В процессе прямого хода метода Гаусса
используются перестановки строк,
меняющие знак определителя, но не
меняющие его модуль. Обозначим через s число перестановок строк, совершаемых
в процессе прямого хода. Кроме того, в
процессе прямого хода производятся
деления строк матрицы на элементы
(произведению диагональных элементов).
В процессе прямого хода метода Гаусса
используются перестановки строк,
меняющие знак определителя, но не
меняющие его модуль. Обозначим через s число перестановок строк, совершаемых
в процессе прямого хода. Кроме того, в
процессе прямого хода производятся
деления строк матрицы на элементы 
 ,
которые приводят к тому, что величина
определителя будет разделена на
произведение
,
которые приводят к тому, что величина
определителя будет разделена на
произведение .
Причемздесь
используются значения этих величин
после перестановки строк, если она
производится.
Таким образом,
.
Причемздесь
используются значения этих величин
после перестановки строк, если она
производится.
Таким образом, 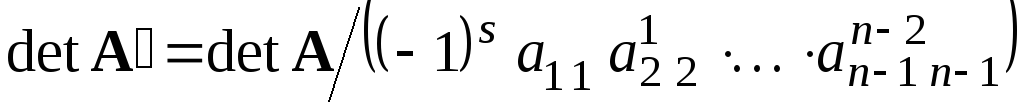 .
Отсюда
.
Отсюда
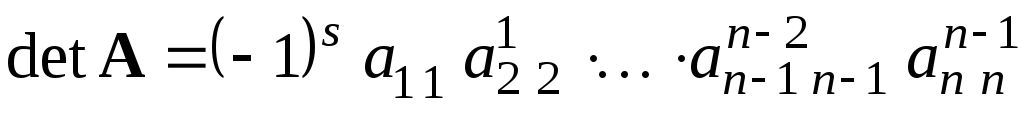 .
(3.2.13)
.
(3.2.13)
Все величины, входящие в эту формулу, кроме s, вычисляются в процессе прямого хода метода Гаусса, а вычислить величину s не составляет труда.
studfile.net
Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников
Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случаеприведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статьяНесовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся
к простейшей системе с урока Как
решить систему линейных уравнений? 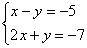 и
решим ее методом Гаусса.
и
решим ее методом Гаусса.
На
первом этапе нужно записать расширенную
матрицу системы: 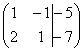 .
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
.
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
Справка: рекомендую
запомнить термины линейной
алгебры. Матрица
системы –
это матрица, составленная только из
коэффициентов при неизвестных, в данном
примере матрица системы: 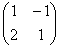 . Расширенная
матрица системы –
это та же матрица системы плюс столбец
свободных членов, в данном случае:
. Расширенная
матрица системы –
это та же матрица системы плюс столбец
свободных членов, в данном случае: 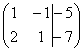 .
Любую из матриц можно для краткости
называть просто матрицей.
.
Любую из матриц можно для краткости
называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами.
Например, в рассматриваемой матрице
можно безболезненно переставить первую
и вторую строки: 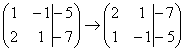
2)
Если в матрице есть (или появились)
пропорциональные (как частный случай
– одинаковые) строки, то следует удалить из
матрицы все эти строки кроме одной.
Рассмотрим, например матрицу 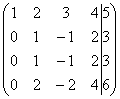 .
В данной матрице последние три строки
пропорциональны, поэтому достаточно
оставить только одну из них:
.
В данной матрице последние три строки
пропорциональны, поэтому достаточно
оставить только одну из них: 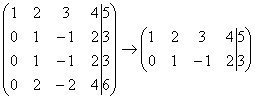 .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.
4)
Строку матрицы можно умножить
(разделить) на
любое число, отличное
от нуля.
Рассмотрим, например, матрицу  .
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2:
.
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2:  .
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
.
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
5)
Это преобразование вызывает наибольшие
затруднения, но на самом деле ничего
сложного тоже нет. К строке матрицы
можно прибавить
другую строку, умноженную на число,
отличное от нуля. Рассмотрим нашу матрицу
из практического примера: 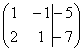 .
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на
–2:
.
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на
–2: 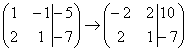 ,
и ко
второй строке прибавляем первую строку
умноженную на –2:
,
и ко
второй строке прибавляем первую строку
умноженную на –2: 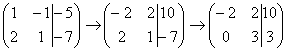 .
Теперь первую строку можно разделить
«обратно» на –2:
.
Теперь первую строку можно разделить
«обратно» на –2: 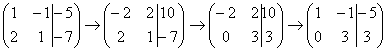 .
Как видите, строка, которую ПРИБАВЛЯЛИ – не
изменилась. Всегда меняется
строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
.
Как видите, строка, которую ПРИБАВЛЯЛИ – не
изменилась. Всегда меняется
строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На
практике так подробно, конечно, не
расписывают, а пишут короче: 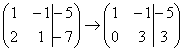 Еще
раз: ко второй строке прибавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
Еще
раз: ко второй строке прибавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
«Переписываю
матрицу и переписываю первую строку: 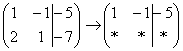 »
»
«Сначала
первый столбец. Внизу мне нужно получить
ноль. Поэтому единицу вверху умножаю
на –2:  ,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку:
,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку: 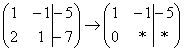 »
»
«Теперь
второй столбец. Вверху –1 умножаю на
–2: 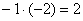 .
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую
строку:
.
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую
строку: 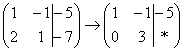 »
»
«И
третий столбец. Вверху –5 умножаю на
–2: 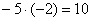 .
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку:
.
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку: 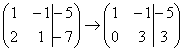 »
»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
!
ВНИМАНИЕ:
рассмотренные манипуляции нельзя
использовать,
если Вам предложено задание, где матрицы
даны «сами по себе». Например, при
«классических» действиях
с матрицами что-то
переставлять внутри матриц ни в коем
случае нельзя! Вернемся к нашей
системе 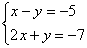 .
Она практически разобрана по косточкам.
.
Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
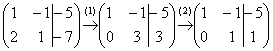
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель
элементарных преобразований – привести
матрицу к ступенчатому виду:  .
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто
называется трапециевидный
вид или треугольный
вид.
.
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто
называется трапециевидный
вид или треугольный
вид.
В
результате элементарных преобразований
получена эквивалентная исходной
система уравнений: 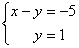
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В
нижнем уравнении у нас уже готовый
результат: 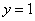 .
.
Рассмотрим
первое уравнение системы  и
подставим в него уже известное значение
«игрек»:
и
подставим в него уже известное значение
«игрек»: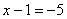
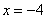
Ответ: 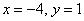
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить
методом Гаусса систему уравнений: 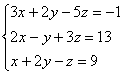
Запишем
расширенную матрицу системы: 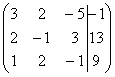
Сейчас
я сразу нарисую результат, к которому
мы придём в ходе решения: 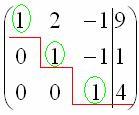 И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
Сначала
смотрим на левое верхнее число:  Почти
всегда здесь должна находиться единица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки:
Почти
всегда здесь должна находиться единица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки: 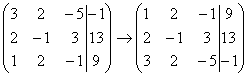
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица
в левом верхнем углу организована.
Теперь нужно получить нули вот на этих
местах: 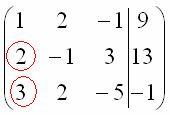
Нули
получаем как раз с помощью «трудного»
преобразования. Сначала разбираемся
со второй строкой (2, –1, 3, 13). Что нужно
сделать, чтобы на первой позиции получить
ноль? Нужно ко
второй строке прибавить первую строку,
умноженную на –2.
Мысленно или на черновике умножаем
первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же
мысленно или на черновике) сложение, ко
второй строке прибавляем первую строку,
уже умноженную на –2: 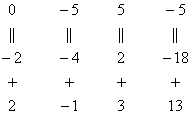
Результат
записываем во вторую строку: 
Аналогично
разбираемся с третьей строкой (3, 2, –5,
–1). Чтобы получить на первой позиции
ноль, нужно к
третьей строке прибавить первую строку,
умноженную на –3.
Мысленно или на черновике умножаем
первую строку на –3: (–3, –6, 3, –27). И к
третьей строке прибавляем первую строку,
умноженную на –3: 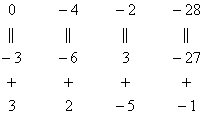
Результат
записываем в третью строку: 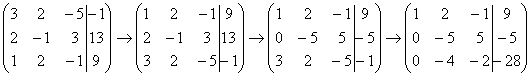
На
практике эти действия обычно выполняются
устно и записываются в один шаг: 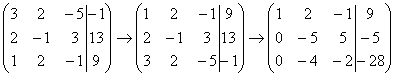
Не
нужно считать всё сразу и одновременно.
Порядок вычислений и «вписывания»
результатов последователен и
обычно такой: сначала переписываем
первую строку, и пыхтим себе потихонечку
– ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: 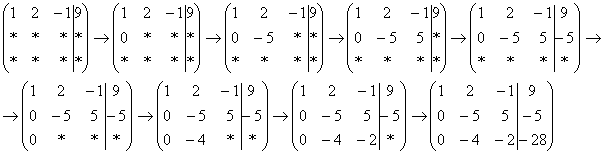 А
мысленный ход самих расчётов я уже
рассмотрел выше.
А
мысленный ход самих расчётов я уже
рассмотрел выше.
Далее
нужно получить единицу на следующей
«ступеньке»: 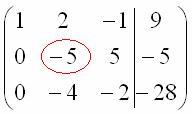
В
данном примере это сделать легко, вторую
строку делим на –5 (поскольку там все
числа делятся на 5 без остатка). Заодно
делим третью строку на –2, ведь чем
меньше числа, тем проще решение: 
На
заключительном этапе элементарных
преобразований нужно получить еще один
ноль здесь: 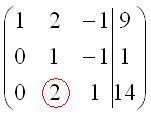
Для
этого к
третьей строке прибавляем вторую строку,
умноженную на –2: 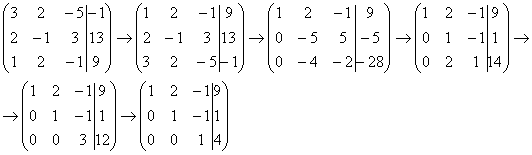 Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В
результате элементарных преобразований
получена эквивалентная исходной система
линейных уравнений: 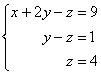 Круто.
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В
третьем уравнении у нас уже готовый
результат: 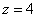
Смотрим
на второе уравнение:  .
Значение «зет» уже известно, таким
образом:
.
Значение «зет» уже известно, таким
образом: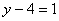
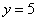
И,
наконец, первое уравнение:  .
«Игрек» и «зет» известны, дело за
малым:
.
«Игрек» и «зет» известны, дело за
малым:
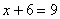

Ответ: 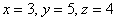
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Решить
систему линейных уравнений методом
Гаусса 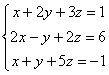
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить
систему линейных уравнений методом
Гаусса 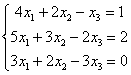
Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду: 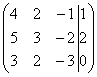
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
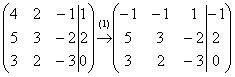
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше
алгоритм работает уже по накатанной
колее: 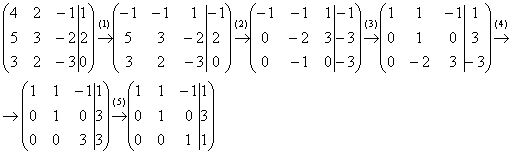
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным
признаком, который свидетельствует об
ошибке в вычислениях (реже – об опечатке),
является «плохая» нижняя строка. То
есть, если бы у нас внизу получилось
что-нибудь вроде 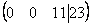 ,
и, соответственно,
,
и, соответственно, 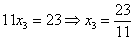 ,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
Заряжаем
обратный ход, в оформлении примеров
часто не переписывают саму систему, а
уравнения «берут прямо из приведенной
матрицы». Обратный ход, напоминаю,
работает, снизу вверх. Да тут подарок
получился: 
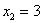
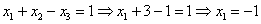
Ответ: 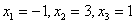 .
.
Пример 4
Решить
систему линейных уравнений методом
Гаусса 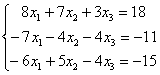
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В
последней части рассмотрим некоторые
особенности алгоритма Гаусса.
Первая
особенность состоит в том, что иногда
в уравнениях системы отсутствуют
некоторые переменные, например: 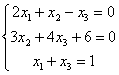 Как
правильно записать расширенную матрицу
системы? Об этом моменте я уже рассказывал
на уроке Правило
Крамера. Матричный метод.
В расширенной матрице системы на месте
отсутствующих переменных ставим
нули:
Как
правильно записать расширенную матрицу
системы? Об этом моменте я уже рассказывал
на уроке Правило
Крамера. Матричный метод.
В расширенной матрице системы на месте
отсутствующих переменных ставим
нули: 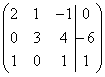 Кстати,
это довольно легкий пример, поскольку
в первом столбце уже есть один ноль, и
предстоит выполнить меньше элементарных
преобразований.
Кстати,
это довольно легкий пример, поскольку
в первом столбце уже есть один ноль, и
предстоит выполнить меньше элементарных
преобразований.
Вторая
особенность состоит вот в чём. Во всех
рассмотренных примерах на «ступеньки»
мы помещали либо –1, либо +1. Могут ли там
быть другие числа? В ряде случаев могут.
Рассмотрим систему: 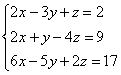 .
.
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или
еще такой условный пример: 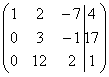 .
Здесь тройка на второй «ступеньке» тоже
нас устраивает, поскольку 12 (место, где
нам нужно получить ноль) делится на 3
без остатка. Необходимо провести
следующее преобразование: к третьей
строке прибавить вторую строку, умноженную
на –4, в результате чего и будет получен
нужный нам ноль.
.
Здесь тройка на второй «ступеньке» тоже
нас устраивает, поскольку 12 (место, где
нам нужно получить ноль) делится на 3
без остатка. Необходимо провести
следующее преобразование: к третьей
строке прибавить вторую строку, умноженную
на –4, в результате чего и будет получен
нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить
методом Гаусса систему 4-х линейных
уравнений с четырьмя неизвестными. 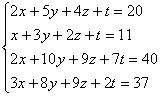
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример
2: Решение: Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду. 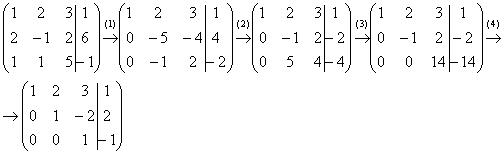 Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Обратный
ход: 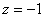

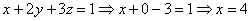
Ответ:  .
.
Пример
4: Решение: Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду: 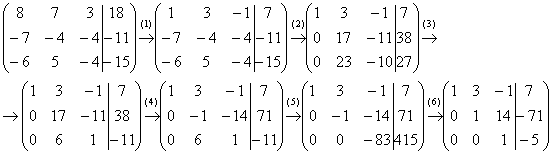
Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена. (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.
Обратный
ход: 

Ответ: 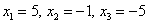
Пример
5: Решение: Запишем
матрицу системы и с помощью элементарных
преобразований приведем ее к ступенчатому
виду: 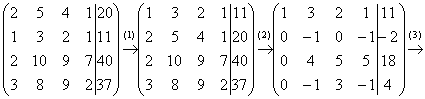
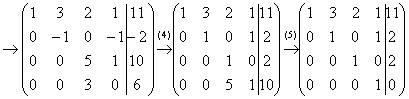
Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный
ход: 
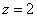
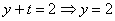
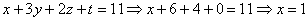
Ответ: 
\
studfile.net
2. Метод Гаусса
Пусть
дана система  линейных уравнений с
линейных уравнений с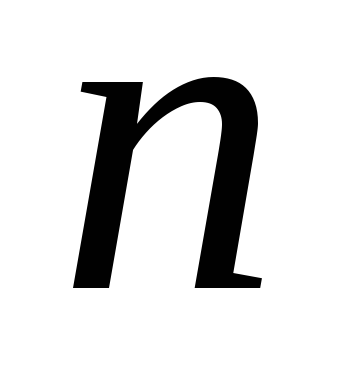 неизвестными:
неизвестными:
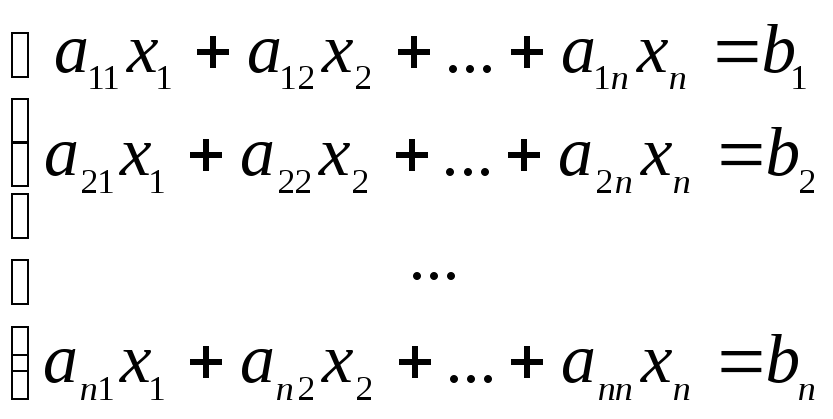 (1)
(1)
Запишем систему (1) в матричном виде:
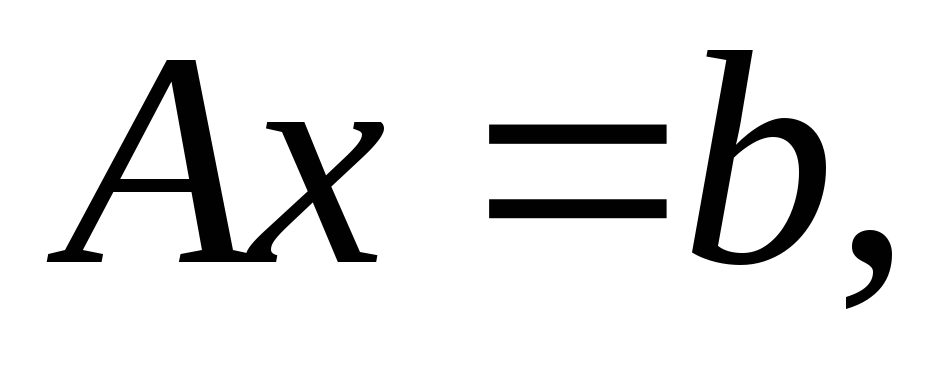 (2)
(2)
где 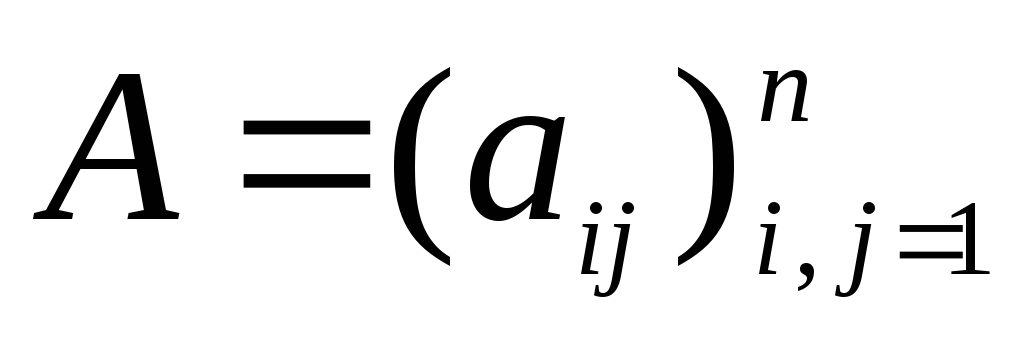 —
—  — матрица;
— матрица;
 —
вектор – столбец неизвестных;
—
вектор – столбец неизвестных;
 —
вектор – столбец правых частей.
—
вектор – столбец правых частей.
Метод Гаусса состоит в последовательном исключении неизвестных системы путем ее равносильного преобразования. При этом в численных методах с целью хорошей алгоритмизации задачи преобразованию подвергаются не сами уравнения, а исходные данные – матрица A и вектор правых частей b, соединенных в одну расширенную матрицу. Метод имеет прямой и обратный ход.
Прямой ход состоит в исключении элементов, расположенных ниже элементов главной диагонали матрицы A, т.е приведение матрицы А к верхнетреугольному виду с единицами на главной диагонали. Преобразование включает в себя следующие действия:
каждый элемент строки, в которой находится ведущий элемент (a11 – в первой строке на первом шаге, a22 – во второй строке на втором шаге…) делится на ведущий элемент. При этом предполагается, что ведущие элементы отличны от нуля.
исключаются элементы столбцов, лежащие ниже ведущих строк. Для исключения элементов первого столбца используется первая ведущая строка, для элементов второго столбца – вторая…
Формулы пересчета прямого хода:
 (3)
(3)
где k=1,2,…,n-1, k – номер шага,
i=k+1,…,n;
j=k+1,…,n.
По определению полагаем
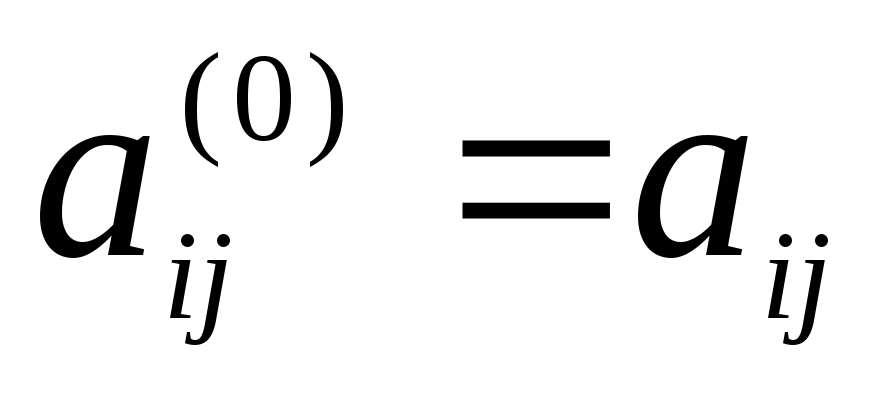 ,
, 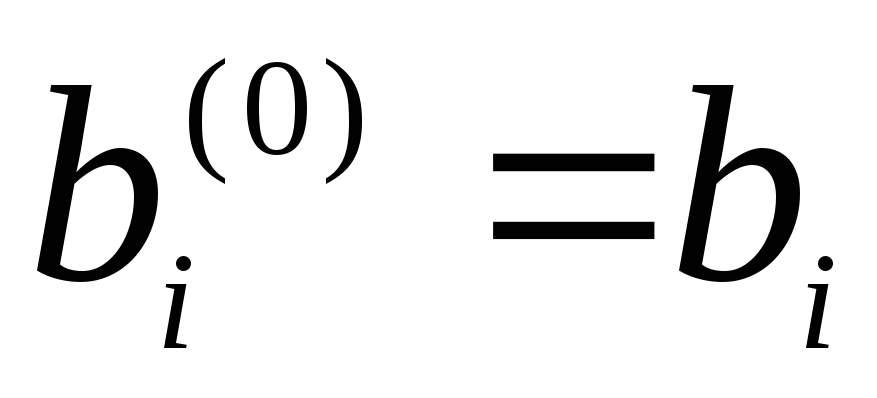 .
.
Обратный ход позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего. Для этого переходим к системе, включающей х1, х2,…,хn.
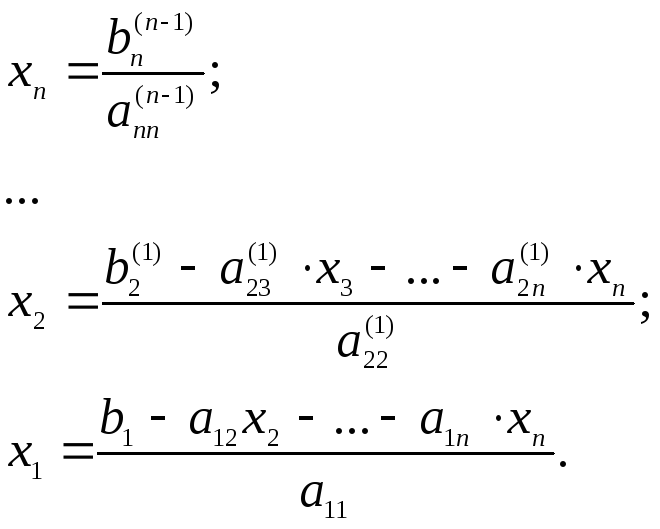 (4)
(4)
3. Метод Гаусса с постолбцовым выбором главного элемента
Реальные математические расчеты производятся с приближенными числами, т.е. неизбежны ошибки округлений. Знаменатель дроби в формуле (3) может оказаться равным нулю или очень маленьким числом. В результате выполнение алгоритма может прекратиться или будет получен результат, далекий от реального. Чтобы избежать этой ситуации, на каждом шаге прямого хода строки рассматриваемой матрицы переставляют так, чтобы деление производилось на наибольший по модулю в обрабатываемом подстолбце элемент. Числа, на которые производится деление, называются ведущими или главными элементами. Соответственно, метод Гаусса, исключающий деление на ноль и уменьшающий влияние ошибок округлений, — это метод Гаусса с постолбцовым выбором главного элемента.
УТОЧНЕНИЕ КОРНЕЙ, ПОЛУЧЕННЫХ МЕТОДОМ ГАУССА
Пусть
для системы 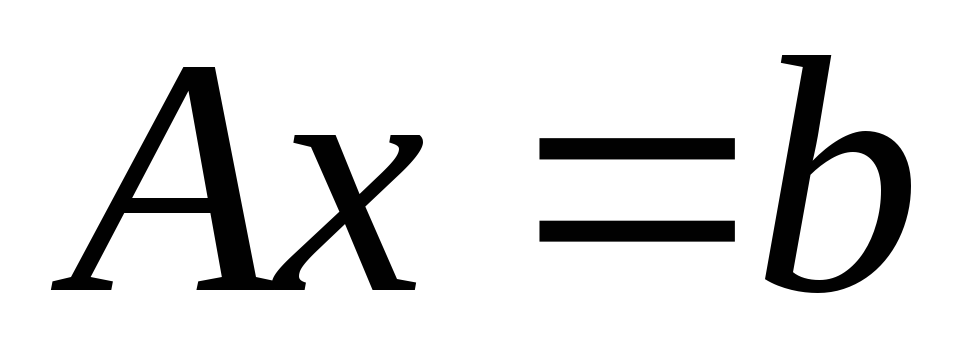 найдено приближенное решениех0.
найдено приближенное решениех0.
Полагая
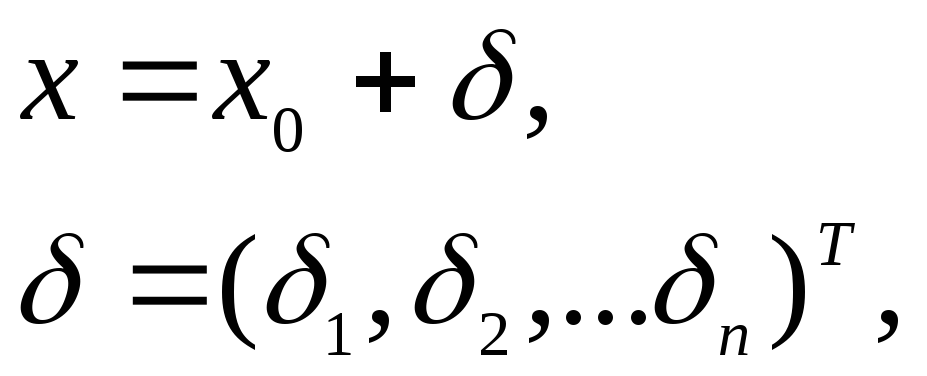
для уточнения корня будем иметь уравнение:
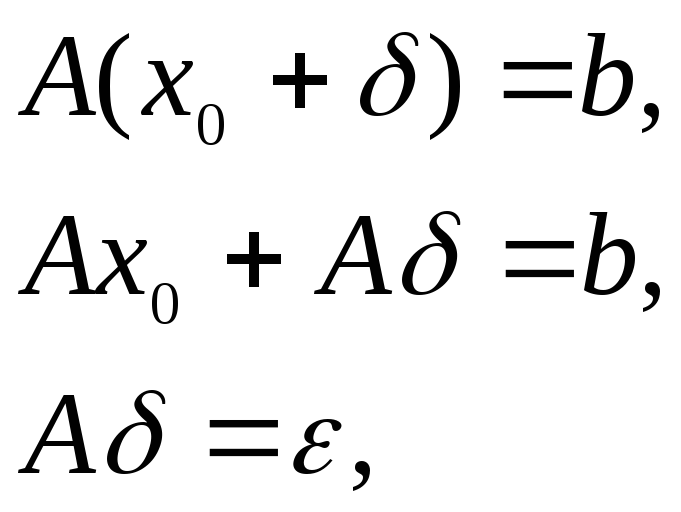 (5)
(5)
где 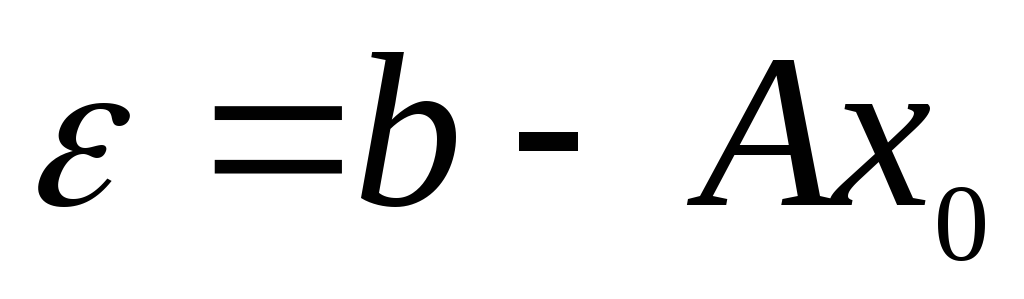 — (6)
— (6)
невязка для приближенного решения х0.
Таким
образом, чтобы найти  ,
нужно решить СЛАУ с прежней матрицейА и новым свободным членом
,
нужно решить СЛАУ с прежней матрицейА и новым свободным членом 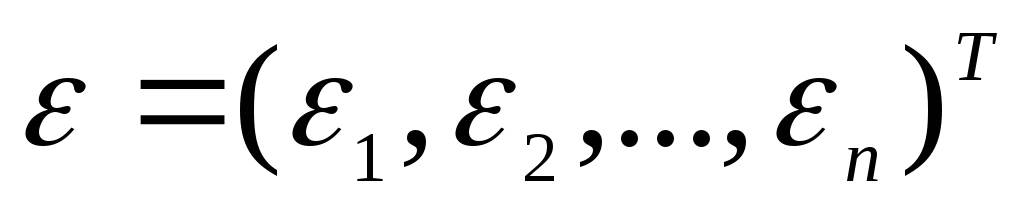 .
Для этого к основной схеме вычислений
нужно присоединить столбец
.
Для этого к основной схеме вычислений
нужно присоединить столбец свободных членов, преобразовать его по
прежним правилам, получая поправки
свободных членов, преобразовать его по
прежним правилам, получая поправки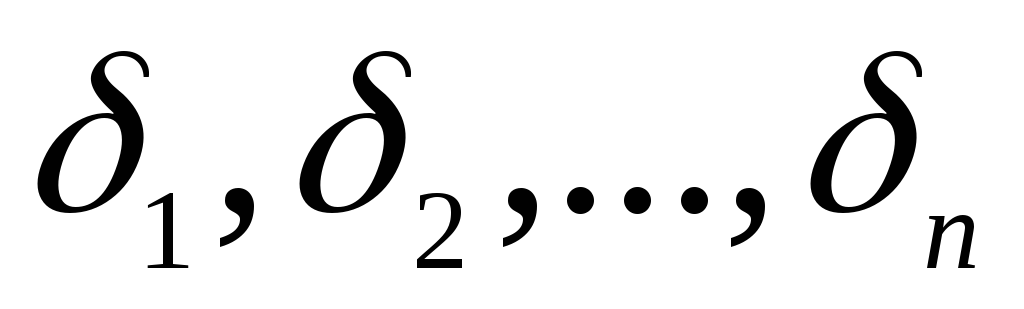 неизвестных. Далее находят уточненные
значения неизвестных, прибавляя к
приближенному значениюх0 соответствующие поправки
неизвестных. Далее находят уточненные
значения неизвестных, прибавляя к
приближенному значениюх0 соответствующие поправки  :
: .
.
Пример 1. Найти решение СЛАУ методом Гаусса с постолбцовым выбором главного элемента. Произвести уточнение решения.
 ;
; 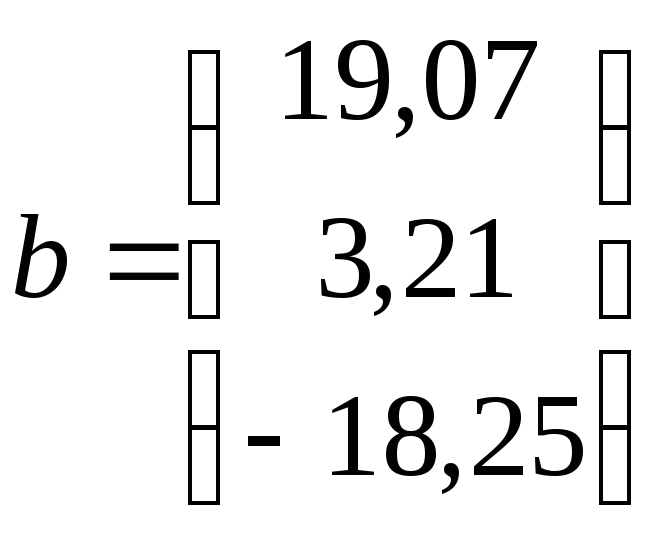 .
.
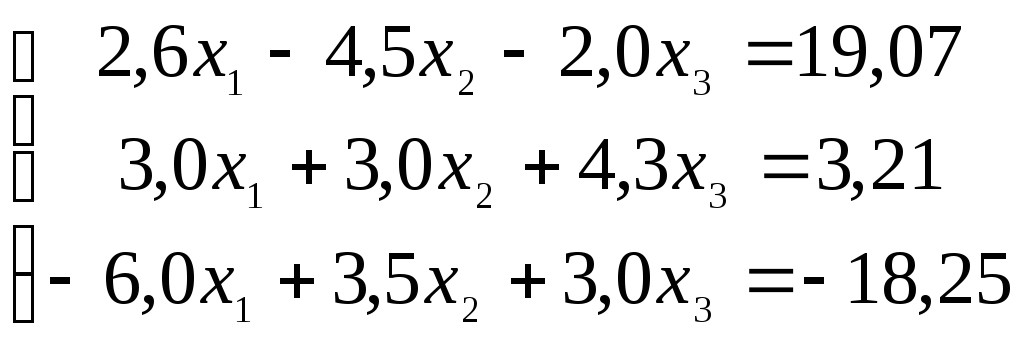
Решение произведем в табличном виде:
ai1 | ai2 | ai3 | bi |
|
2,6 3,0
| -4,5 3,0 3,5 | -2,0 4,3 3,0 | 19,07 3,21 -18,25 | -0,007 -0,011 0,016 |
3,0 2,6 | 3,5 3,0 -4,5 | 3,0 4,3 -2,0 | -18,25 3,21 19,07 | 0,016 -0,011 -0,007 |
1 0 0 | -0,583
-2,983 | -0,5 5,8 -0,7 | 3,042 -5,915 11,162 | -0,0027 -0,003 -0,0001 |
1 0 0 | -0,583 1 0 | -0,5 1,221
| 3,042 1,245 7,447 | -0,0027 0,0006 -0,002 |
1 0 0 | -0,583 1 0 | -0,5 1,221 1 | 3,042 -1,245 2,531 | -0,0027 -0,0006 -0,0007 |
Для обратного хода перейдем к системе, включающей неизвестные хi , и последовательно одно за другим вычисляем их значения, начиная с х3.
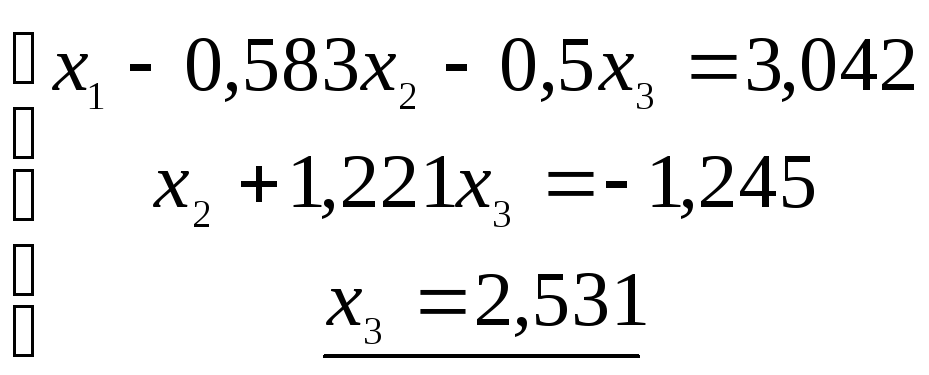
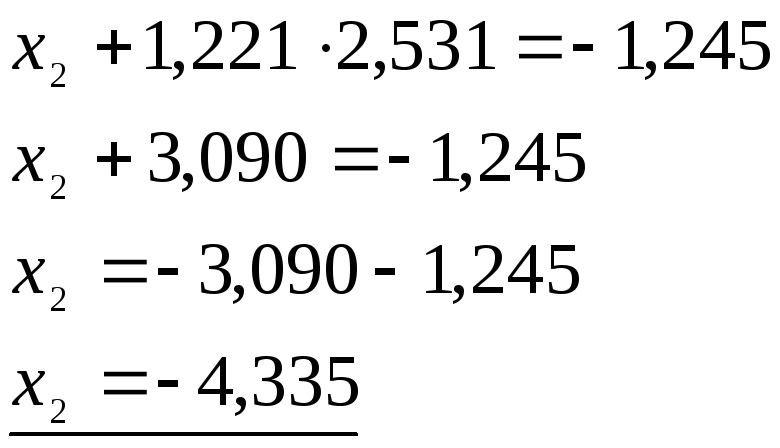
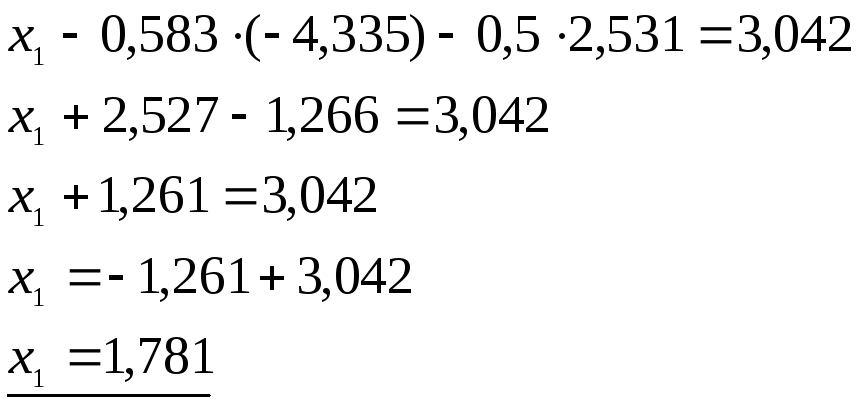
Итак, вектор решения:
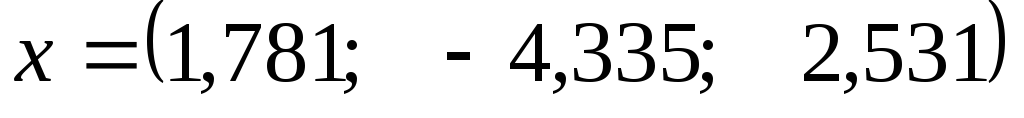
Уточним
решение. Для этого полученный вектор
решения х будем считать
начальным приближение х0.Подставим
его в исходную схему и найдем невязку  по формуле (6).
по формуле (6).
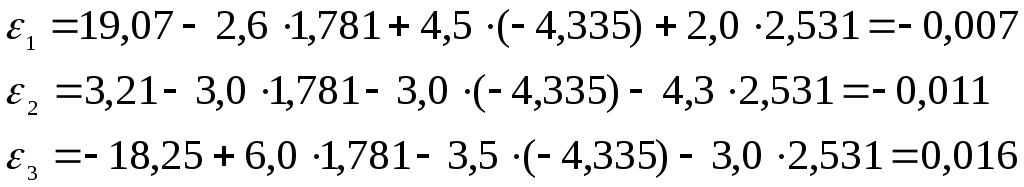

Полученный
вектор невязок 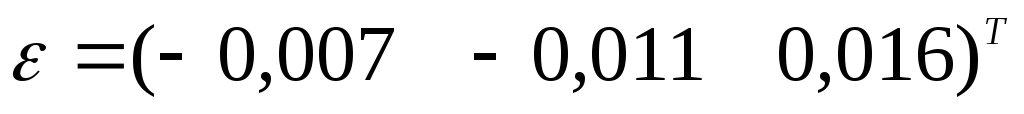 используем как новый свободный член
системы Аδ= ε, приписывая его как столбец
к основной схеме вычислений. Решая СЛАУ
с прежней матрицей А и новым свободным
членом
используем как новый свободный член
системы Аδ= ε, приписывая его как столбец
к основной схеме вычислений. Решая СЛАУ
с прежней матрицей А и новым свободным
членом ,
получаем вектор поправок
,
получаем вектор поправок неизвестных:
неизвестных:
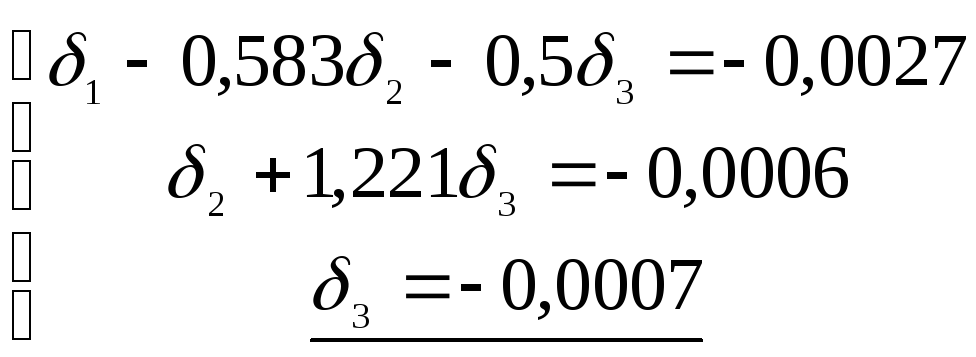
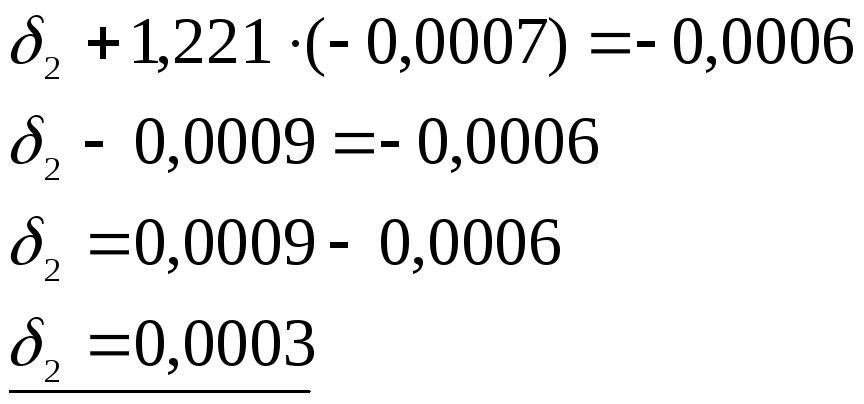

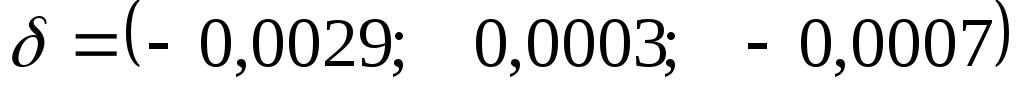
Уточняем решение по формуле
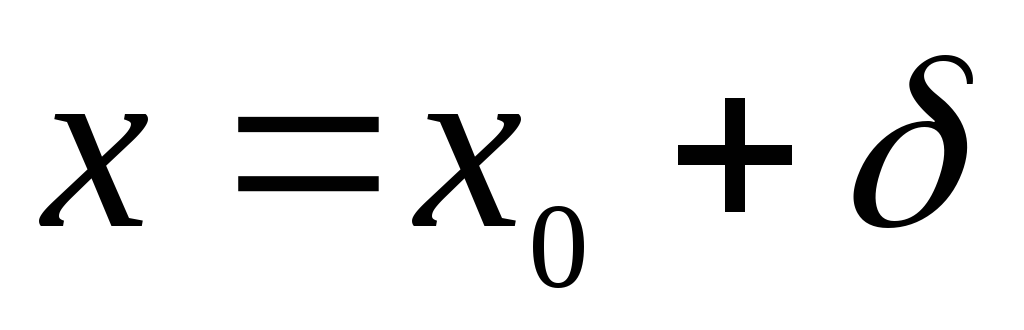 :
:
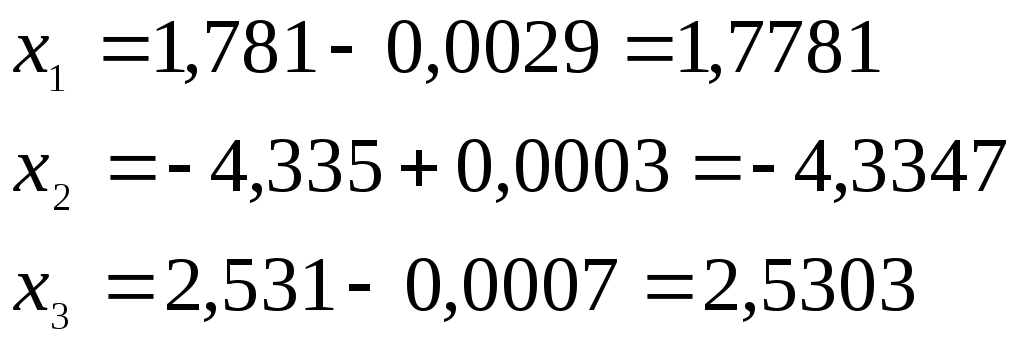
Уточненный вектор решения:
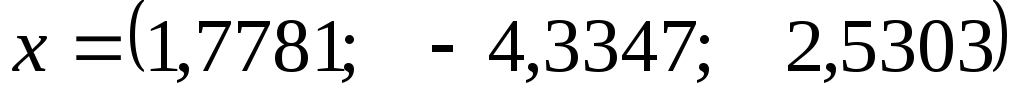
ПРИМЕНЕНИЕ МЕТОДА ГАУССА К ВЫЧИСЛЕНИЮ ОПРЕДЕЛИТЕЛЕЙ
Метод Гаусса может быть использован при вычислении определителей. Преобразования прямого хода, приводящие матрицу А к верхнетреугольному виду, не изменяют определителя матрицы А. Учитывая, что определитель треугольной матрицы равен произведению диагональных элементов, имеем:
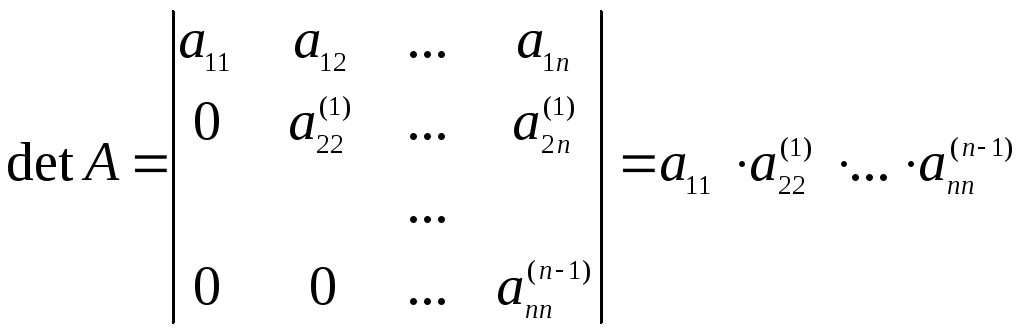 .
.
Таким образом, detA равен произведению всех ведущих элементов.
При использовании модификации метода Гаусса с постолбцовым выбором главного элемента производится перестановка строк матрицы, что может изменить знак detА. Поэтому в результате нужно учесть четность количества перестановок:
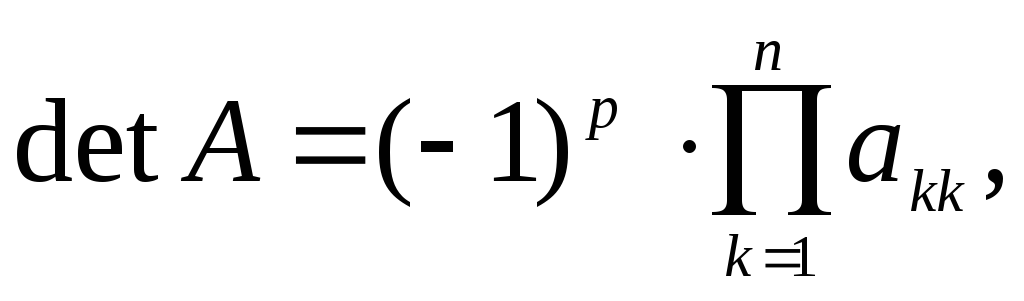 где
где  — количество перестановок строк.
— количество перестановок строк.
Найдем определитель для матрицы А из Примера 1 главы 4:
det A = (-1)1*(-6,0)*4,75*2,942= 83,847
ПРИМЕНЕНИЕ МЕТОДА ГАУССА К ВЫЧИСЛЕНИЮ ОБРАТНОЙ МАТРИЦЫ
Пусть
дана матрица 
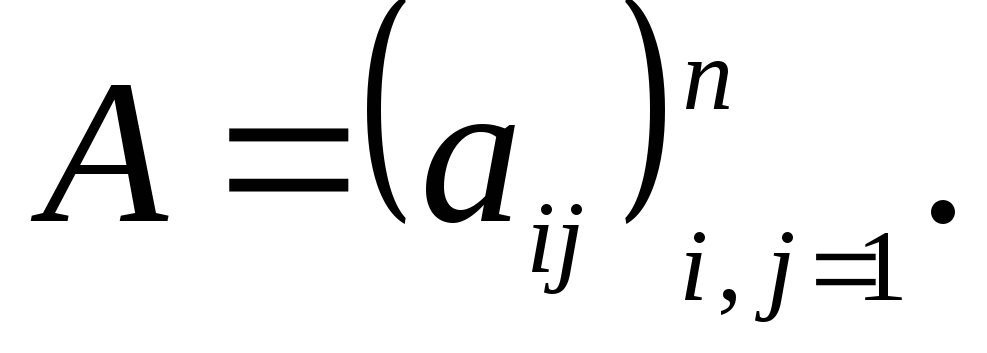 Для нахождения обратной матрицы
Для нахождения обратной матрицы будем использовать основное соотношение
будем использовать основное соотношение ,
гдеЕ –
единичная матрица n-го
порядка. Т.е. будем исходить из того, что
обратная матрица
,
гдеЕ –
единичная матрица n-го
порядка. Т.е. будем исходить из того, что
обратная матрица 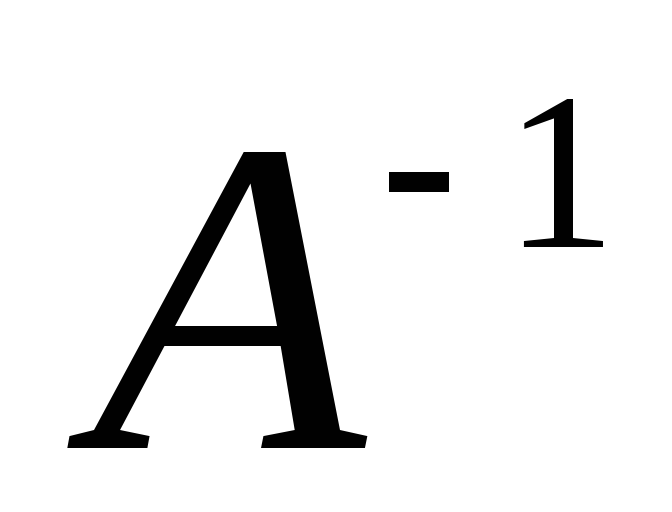 является решением матричного уравнения:
является решением матричного уравнения:
 (7)
(7)
Представляя
искомую матрицу  ,
как набор векторов-столбцов:
,
как набор векторов-столбцов:
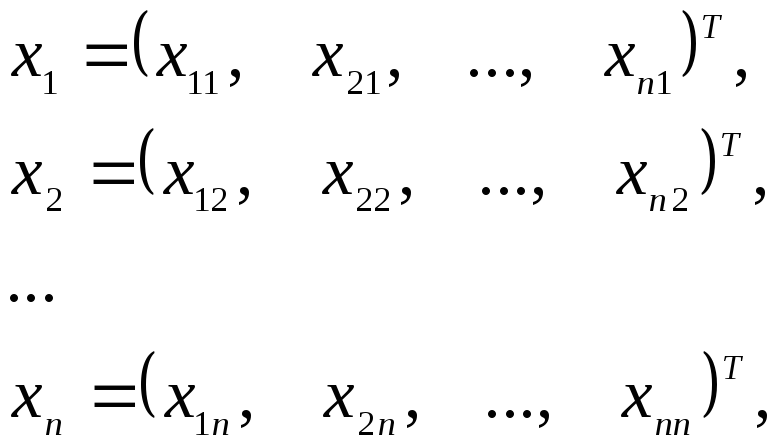
а единичную матрицу Е как набор единичных векторов:
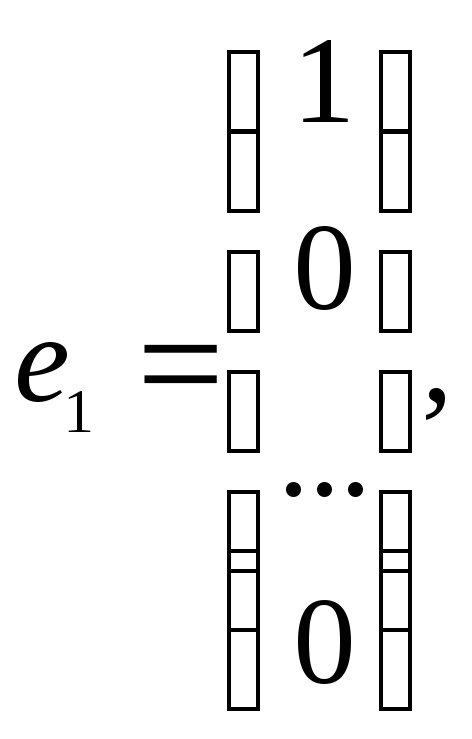
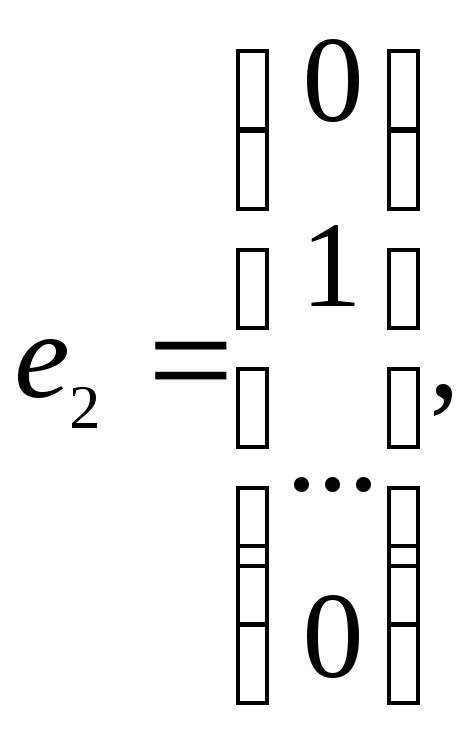 …,
…, 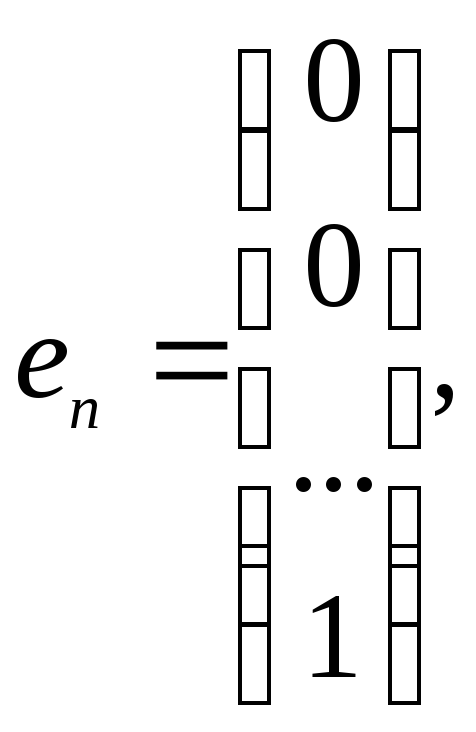
матричное уравнение (7) в соответствии с правилами умножения матриц заменяем эквивалентной системой векторно-матричных уравнений:
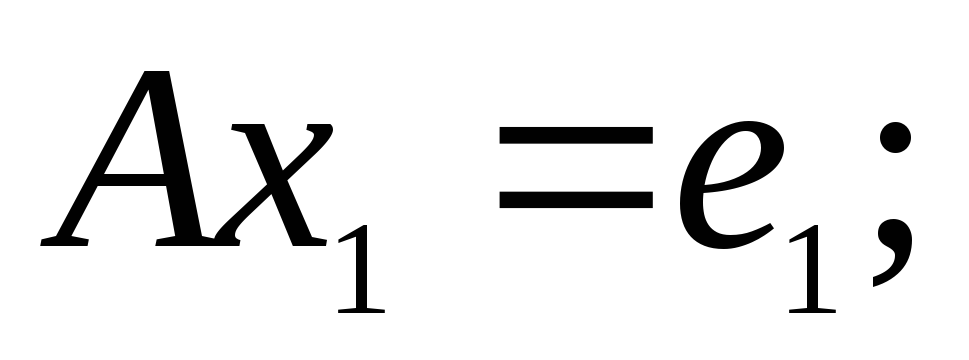
 …,
…, 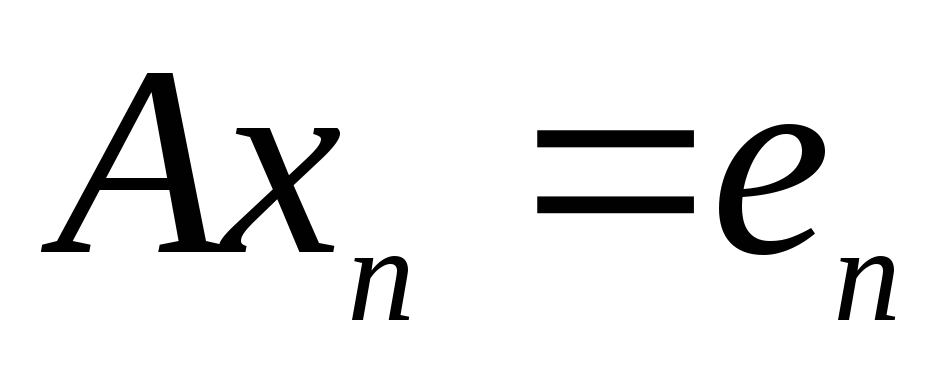 .
(8)
.
(8)
Каждое
из последних уравнений имеет вид (1) и
может быть решено методом Гаусса. Все
СЛАУ (8) имеют одну и ту же матрицу
коэффициентов, но разные правые части,
составляющие единичную матрицу. В
результате завершения работы алгоритма
будут получаться столбец за столбцом
элементы обратной матрицы 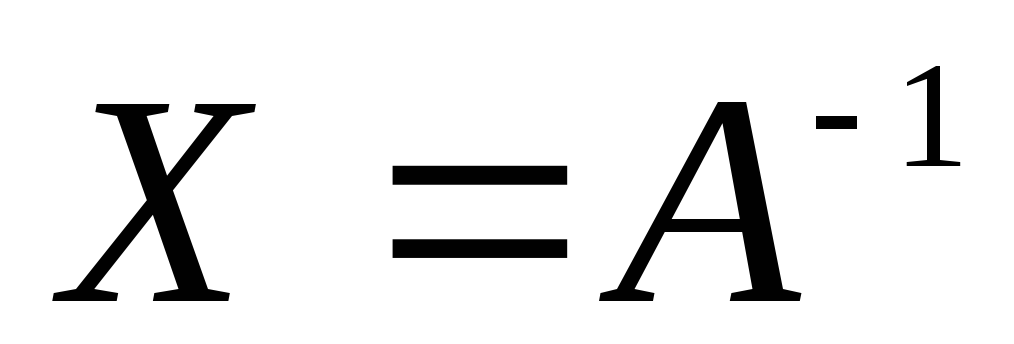 .
Заметим, что элементы строк обратной
матрицы получаются в обратном порядке.
.
Заметим, что элементы строк обратной
матрицы получаются в обратном порядке.
Пример
2. Решить
систему линейных уравнений методом
Гаусса. Уточнить решение. Найти
определитель и обратную матрицу 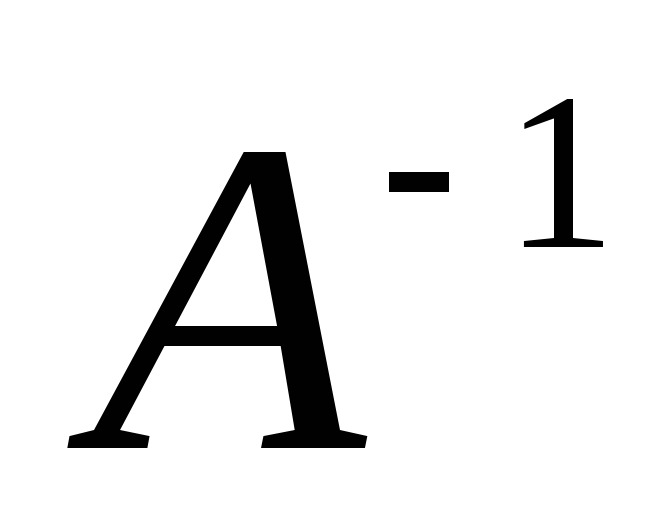 ,
включив процесс в общий алгоритм метода
Гаусса.
,
включив процесс в общий алгоритм метода
Гаусса.
НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА.
ai1 | ai2 | ai3 | bi | Ei | e1 | e2 | e3 |
1,15
1,00 | 0,42 0,55 0,35 | 100,71 0,32 3,00 | -198,70 2,29 -0,65 | 0,00035 0,00014 -0,00000 | 1 0 0 | 0 1 0 | 0 0 1 |
1 0 0 | 0,46218 -0,11151
| 0,26891 100,40076 2,73109 | 1,92437 -200,91303 -2,57437 | 0,00012 0,00021 -0,00012 | 0 1 0 | 0,84034 -0,96639 -0,84034 | 0 0 1 |
1 0 0 | 0,46218 1 0 | 0,26891 -24,34141
| 1,92437 22,94486 -198,35474 | 0,00012 0,00107 0,00033 | 0 0 1 | 0,84034 7,49100 -0,13107 | 0 -8,91424 -0,99403 |
1 0 0 | 0,46218 1 0 | 0,26891 -24,34561 1 | 1,92437 22,94856 -2,03053 | 0,00012 0,00107 0,00000 | 0 0 0,01024 | 0,84034 7,49100 -0,00134 | 0 -8,91424 -0,01018 |
*Используя постолбцовый выбор главного элемента:
Решение:
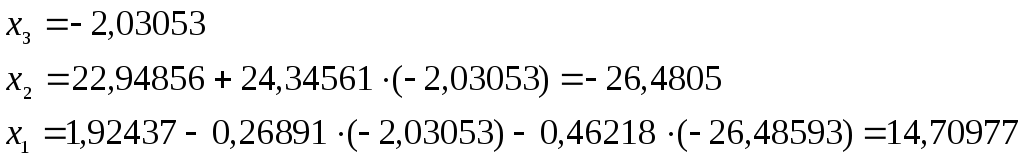
Определитель:

Вектор поправок:

Уточненное решение:

Находим
обратную матрицу 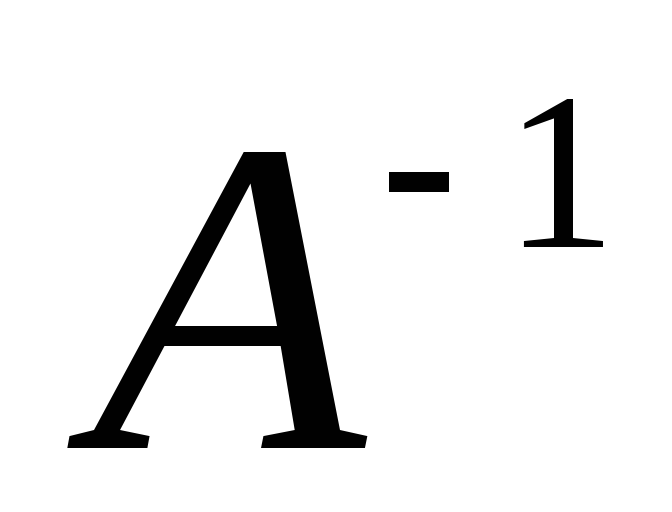 :
:

Обратная
матрица 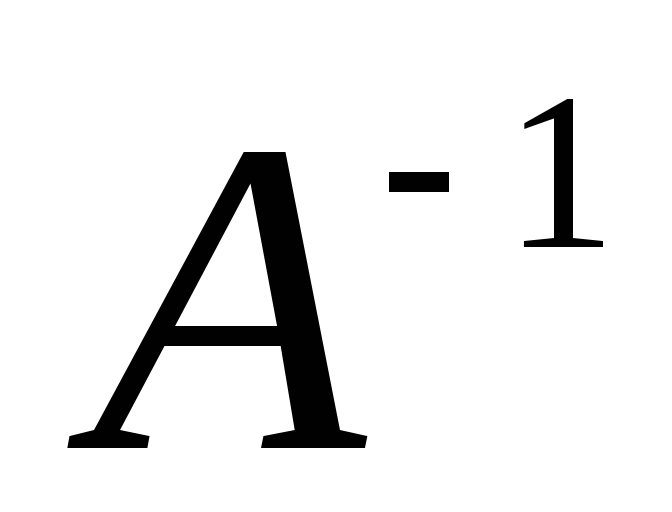 :
:

studfile.net
Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.
Как
бы мы поступили в школе, если бы получили
задание найти решение системы уравнений  .
.
Некоторые сделали бы так.
Заметим,
что прибавив к левой части второго
уравнения левую часть первого, а к правой
части — правую, можно избавиться от
неизвестных переменных x2 и x3 и
сразу найти x1: 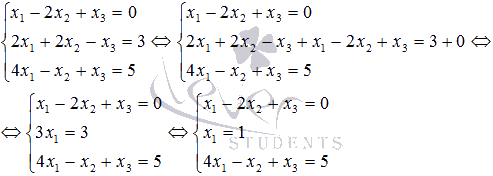
Подставляем
найденное значение x1=1 в
первое и третье уравнение системы: 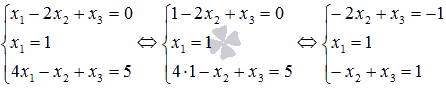
Если
умножить обе части третьего уравнения
системы на -1 и
прибавить их к соответствующим частям
первого уравнения, то мы избавимся от
неизвестной переменной x3 и
сможем найти x2: 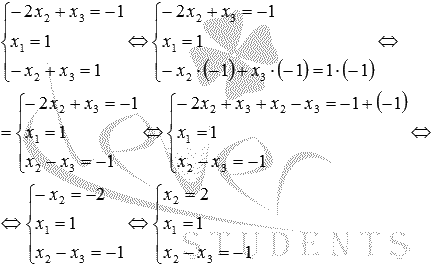
Подставляем
полученное значение x2=2 в
третье уравнение и находим оставшуюся
неизвестную переменную x3: 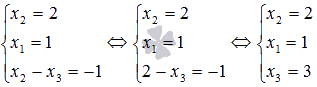
Другие поступили бы иначе.
Разрешим
первое уравнение системы относительно
неизвестной переменной x1 и
подставим полученное выражение во
второе и третье уравнение системы, чтобы
исключить из них эту переменную: 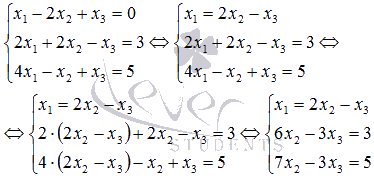
Теперь
разрешим второе уравнение системы
относительно x2 и
подставим полученный результат в третье
уравнение, чтобы исключить из него
неизвестную переменную x2: 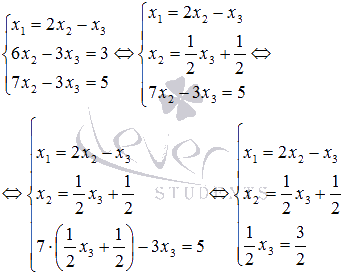
Из
третьего уравнения системы видно,
что x3=3.
Из второго уравнения находим 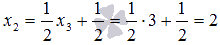 ,
а из первого уравнения получаем
,
а из первого уравнения получаем 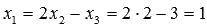 .
.
Знакомые способы решения, не правда ли?
Самое интересное здесь то, что второй способ решения по сути и есть метод последовательного исключения неизвестных, то есть, метод Гаусса. Когда мы выражали неизвестные переменные (сначала x1, на следующем этапе x2) и подставляли их в остальные уравнения системы, мы тем самым исключали их. Исключение мы проводили до того момента, пока в последнем уравнении не осталась одна единственная неизвестная переменная. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса.
Следует заметить, что когда мы выражаем x1 через x2 и x3 в первом уравнении, а затем подставляем полученное выражение во второе и третье уравнения, то к такому же результату приводят следующие действия:
к левой и правой частям второго уравнения прибавляем соответствующие части первого уравнения, умноженные на
 ,
,к левой и правой частям третьего уравнения прибавляем соответствующие части первого уравнения, умноженные на
 .
.
Действительно,
такая процедура также позволяет исключить
неизвестную переменную x1 из
второго и третьего уравнений системы: 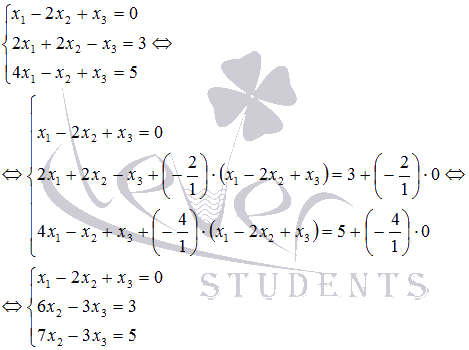
Нюансы с исключением неизвестных переменных по методу Гаусса возникают тогда, когда уравнения системы не содержат некоторых переменных.
Например,
в СЛАУ 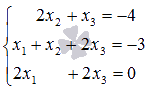 в
первом уравнении отсутствует неизвестная
переменная x1 (иными
словами, коэффициент перед ней равен
нулю). Поэтому мы не можем разрешить
первое уравнение системы относительно x1,
чтобы исключить эту неизвестную
переменную из остальных уравнений.
Выходом из этой ситуации является
перестановка местами уравнений системы.
Так как мы рассматриваем системы линейных
уравнений, определители основных матриц
которых отличны от нуля, то всегда
существует уравнение, в котором
присутствует нужная нам переменная, и
мы это уравнение можем переставить на
нужную нам позицию. Для нашего примера
достаточно поменять местами первое и
второе уравнения системы
в
первом уравнении отсутствует неизвестная
переменная x1 (иными
словами, коэффициент перед ней равен
нулю). Поэтому мы не можем разрешить
первое уравнение системы относительно x1,
чтобы исключить эту неизвестную
переменную из остальных уравнений.
Выходом из этой ситуации является
перестановка местами уравнений системы.
Так как мы рассматриваем системы линейных
уравнений, определители основных матриц
которых отличны от нуля, то всегда
существует уравнение, в котором
присутствует нужная нам переменная, и
мы это уравнение можем переставить на
нужную нам позицию. Для нашего примера
достаточно поменять местами первое и
второе уравнения системы 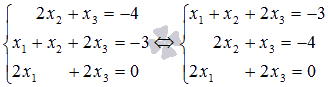 ,
дальше можно разрешить первое уравнение
относительно x1 и
исключить ее из остальных уравнений
системы (хотя во втором уравнении x1 уже
отсутствует).
,
дальше можно разрешить первое уравнение
относительно x1 и
исключить ее из остальных уравнений
системы (хотя во втором уравнении x1 уже
отсутствует).
Надеемся, что суть Вы уловили.
Опишем алгоритм метода Гаусса.
Пусть
нам требуется решить систему из n линейных
алгебраических уравнений с nнеизвестными
переменными вида 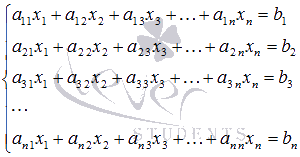 ,
и пусть определитель ее основной матрицы
отличен от нуля.
,
и пусть определитель ее основной матрицы
отличен от нуля.
Будем
считать, что  ,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на 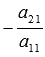 ,
к третьему уравнению прибавим первое,
умноженное на
,
к третьему уравнению прибавим первое,
умноженное на  ,
и так далее, к n-омууравнению
прибавим первое, умноженное на
,
и так далее, к n-омууравнению
прибавим первое, умноженное на  .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид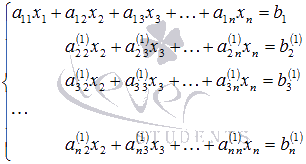 где
где 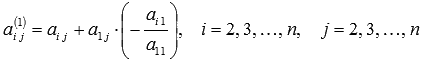 ,
а
,
а  .
.
К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке 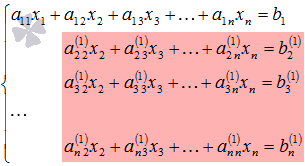
Будем
считать, что 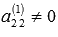 (в
противном случае мы переставим местами
вторую строку с k-ой,
где
(в
противном случае мы переставим местами
вторую строку с k-ой,
где 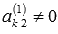 ).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на  ,
к четвертому уравнению прибавим второе,
умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на  ,
и так далее, к n-омууравнению
прибавим второе, умноженное на
,
и так далее, к n-омууравнению
прибавим второе, умноженное на 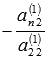 .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид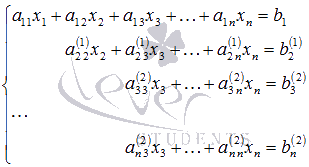 где
где  ,
а
,
а 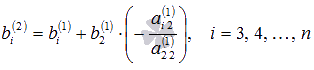 .
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
.
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы 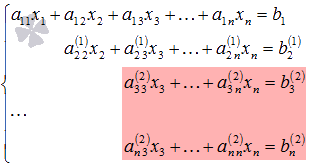
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид 
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как 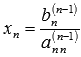 ,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Разберем алгоритм на примере.
Пример.
Найдите
решение системы уравнений 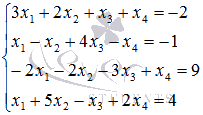 методом
Гаусса.
методом
Гаусса.
Решение.
Коэффициент a11 отличен
от нуля, так что приступим к прямому
ходу метода Гаусса, то есть, к исключению
неизвестной переменной x1 из
всех уравнений системы, кроме первого.
Для этого к левой и правой частям второго,
третьего и четвертого уравнения прибавим
левую и правую части первого уравнения,
умноженные соответственно на 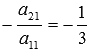 ,
,  и
и  :
: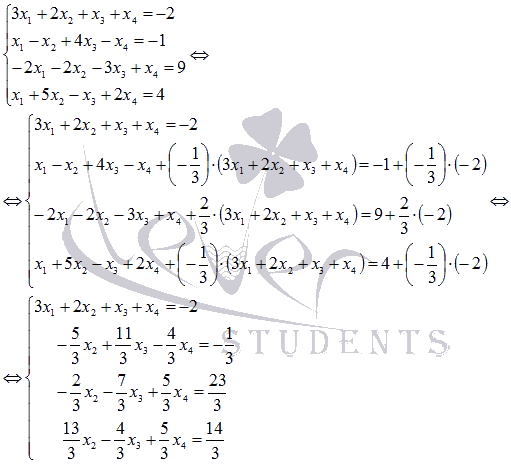
Неизвестную
переменную x1 исключили,
переходим к исключению x2.
К левым и правым частям третьего и
четвертого уравнений системы прибавляем
левую и правую части второго уравнения,
умноженные соответственно на 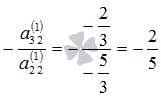 и
и 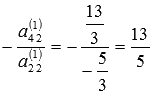 :
:
Для
завершения прямого хода метода Гаусса
нам осталось исключить неизвестную
переменную x3 из
последнего уравнения системы. Прибавим
к левой и правой частям четвертого
уравнения соответственно левую и правую
часть третьего уравнения, умноженную
на  :
: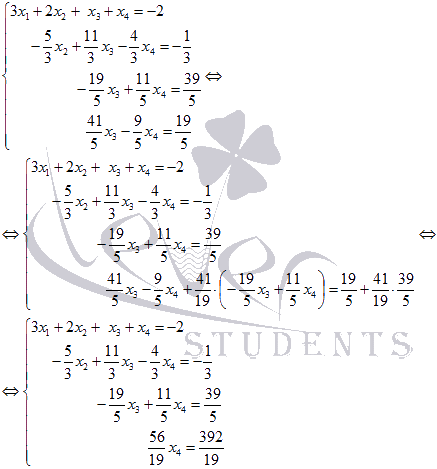
Можно начинать обратный ход метода Гаусса.
Из
последнего уравнения имеем 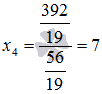 ,
из
третьего уравнения получаем
,
из
третьего уравнения получаем 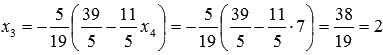 ,
из
второго
,
из
второго  ,
из
первого
,
из
первого 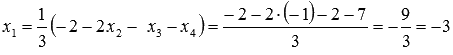 .
.
Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно.
Ответ:
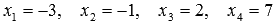 .
.
А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи.
Пример.
Найдите
решение системы уравнений  методом
Гаусса.
методом
Гаусса.
Решение.
Расширенная
матрица системы имеет вид 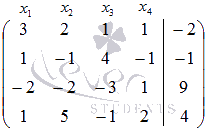 .
Сверху над каждым столбцом записаны
неизвестные переменные, которым
соответствуют элементы матрицы.
.
Сверху над каждым столбцом записаны
неизвестные переменные, которым
соответствуют элементы матрицы.
Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь.
Преобразуем
матрицу так, чтобы все элементы в первом
столбце, начиная со второго, стали
нулевыми. Для этого к элементам второй,
третьей и четвертой строк прибавим
соответствующие элементы первой строки
умноженные на , 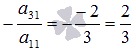 и
на
и
на 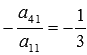 соответственно:
соответственно: 
Далее
полученную матрицу преобразуем так,
чтобы во втором столбце все элементы,
начиная с третьего стали нулевыми. Это
будет соответствовать исключению
неизвестной переменной x2.
Для этого к элементам третьей и четвертой
строк прибавим соответствующие элементы
первой строки матрицы, умноженные
соответственно на  и
и  :
: 
Осталось
исключить неизвестную переменную x3 из
последнего уравнения системы. Для этого
к элементам последней строки полученной
матрицы прибавим соответствующие
элементы предпоследней строки, умноженные
на 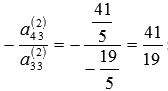 :
: 
Следует
отметить, что эта матрица соответствует
системе линейных уравнений  которая
была получена ранее после прямого хода.
которая
была получена ранее после прямого хода.
Пришло
время обратного хода. В матричной форме
записи обратный ход метода Гаусса
предполагает такое преобразование
полученной матрицы, чтобы матрица,
отмеченная на рисунке  стала
диагональной, то есть, приняла
вид
стала
диагональной, то есть, приняла
вид 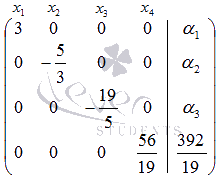 где
где  —
некоторые числа.
—
некоторые числа.
Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой.
Прибавим
к элементам третьей, второй и первой
строк соответствующие элементы последней
строки, умноженные на 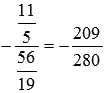 ,
на
,
на 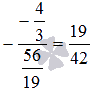 и
на
и
на  соответственно:
соответственно: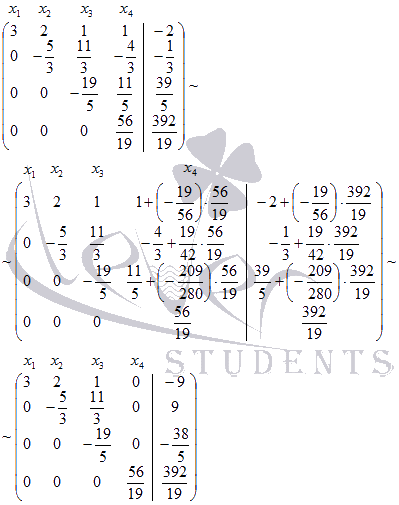
Теперь
прибавим к элементам второй и первой
строк соответствующие элементы третьей
строки, умноженные на 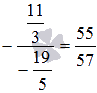 и
на
и
на 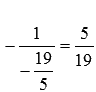 соответственно:
соответственно: 
На
последнем шаге обратного хода метода
Гаусса к элементам первой строки
прибавляем соответствующие элементы
второй строки, умноженные на 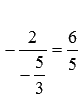 :
: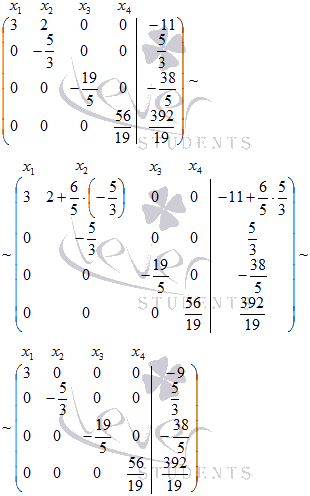
Полученная
матрица соответствует системе уравнений 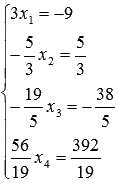 ,
откуда находим неизвестные переменные.
,
откуда находим неизвестные переменные.
Ответ:
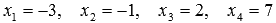 .
.
ОБРАТИТЕ ВНИМАНИЕ.
При использовании метода Гаусса для решения систем линейных алгебраических уравнений следует избегать приближенных вычислений, так как это может привести к абсолютно неверным результатам. Рекомендуем не округлять десятичные дроби. Лучше от десятичных дробей переходить к обыкновенным дробям.
Пример.
Решите
систему из трех уравнений методом
Гаусса 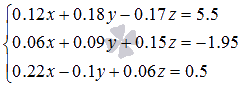 .
.
Решение.
Отметим,
что в этом примере неизвестные переменные
имеют другое обозначение (неx1,
x2,
x3,
а x,
y, z).
Перейдем к обыкновенным дробям: 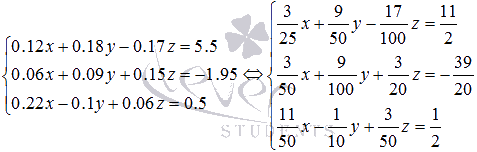
Исключим
неизвестную x из
второго и третьего уравнений системы: 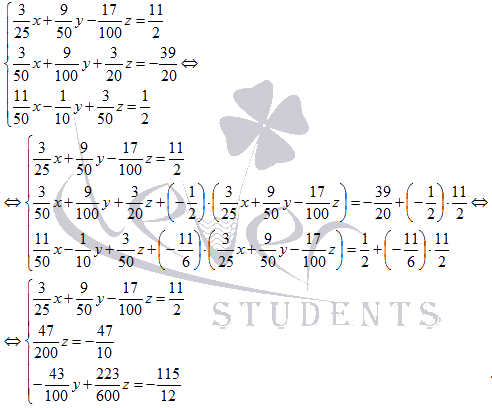
В
полученной системе во втором уравнении
отсутствует неизвестная переменная y,
а в третьем уравнении y присутствует,
поэтому, переставим местами второе и
третье уравнения: 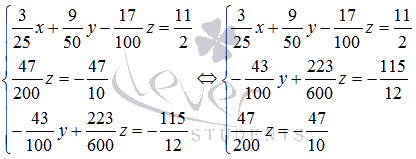
На этом прямой ход метода Гаусса закончен (из третьего уравнения не нужно исключать y, так как этой неизвестной переменной уже нет).
Приступаем к обратному ходу.
Из
последнего уравнения находим  ,
из
предпоследнего
,
из
предпоследнего 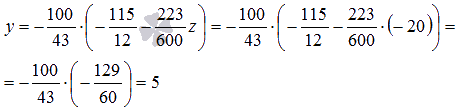 из
первого уравнения имеем
из
первого уравнения имеем 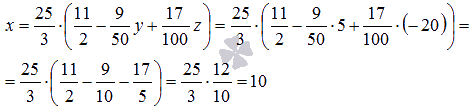
Ответ:
x = 10, y = 5, z = -20.
К началу страницы
studfile.net
С++ программная реализация метода Гаусса
Вычислительная схема метода Гаусса состоит из двух этапов. Первый этап заключается в приведении системы к трапециевидной. Этот этап называется прямым ходом. Второй этап — определение неизвестных — называется обратным ходом.
Прямой ход метода Гаусса состоит в последовательном исключении коэффициентов при неизвестных начиная с первого столбца.
Прямой ход реализуется по следующим формулам (индекс k в круглых скобках означает номер цикла — номер столбца).
Умножение k-й строки на число
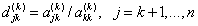 . (1)
. (1)
Вычитание k-й строки из j-й строки
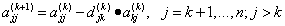 . (2)
. (2)
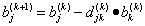 . (3)
. (3)
Обратный ход — вычисление неизвестных — реализуется по следующим формулам, начиная с последнего уравнения системы
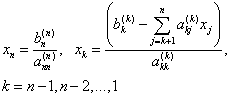 . (4)
. (4)
Код C++
#include <iostream>
using namespace std;
int n, i, j, k;
double d, s;
int main()
{
cout «Poryadok: »
cin >> n;
double **a = new double *[n];
for (i = 0; i
a[i] = new double [n];
double **a1 = new double *[n];
for (i = 0; i
a1[i] = new double [n];
double *b = new double [n];
double *x = new double [n];
cout «Vvedite koefficienty i svobodnye chleny »
for (i = 1; i
{
for (j = 1; j
{
cout «a[ » «,» «]= «;
cin >> a[i][j];
a1[i][j] = a[i][j];
}
cout «b,[ » «]= «;
cin >> b[i];
}
for (k = 1; k // прямой ход
{
for (j = k + 1; j
{
d = a[j][k] / a[k][k]; // формула (1)
for (i = k; i
{
a[j][i] = a[j][i] — d * a[k][i]; // формула (2)
}
b[j] = b[j] — d * b[k]; // формула (3)
}
}
for (k = n; k >= 1; k—) // обратный ход
{
d = 0;
for (j = k + 1; j
{
s = a[k][j] * x[j]; // формула (4)
d = d + s; // формула (4)
}
x[k] = (b[k] — d) / a[k][k]; // формула (4)
}
cout «Korni sistemy: »
for( i = 1; i
cout «x[» «]=» » »
return 0;
}
function-x.ru
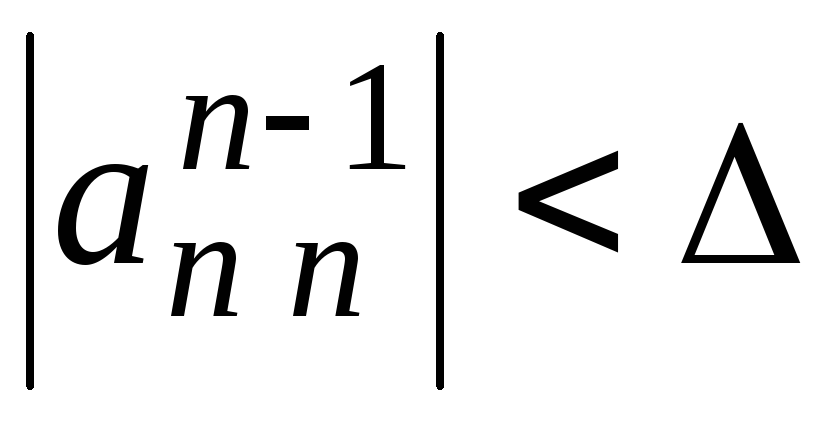 ,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия
,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия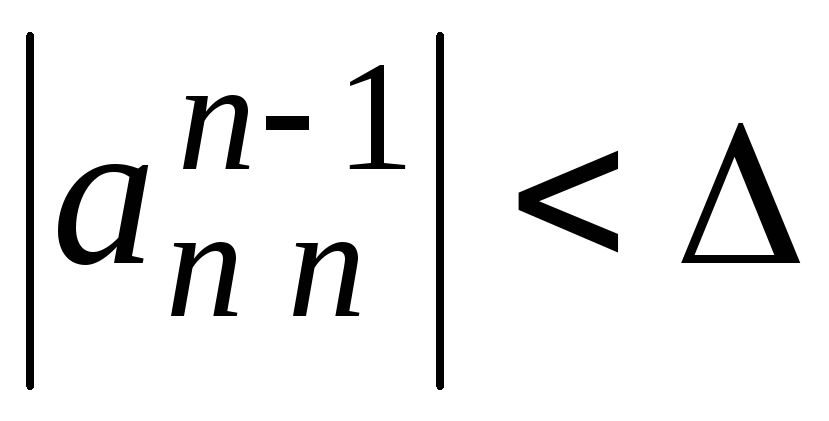 модуль определителя матрицы системы
будет меньше
модуль определителя матрицы системы
будет меньше и близок к нулю.
и близок к нулю. .
.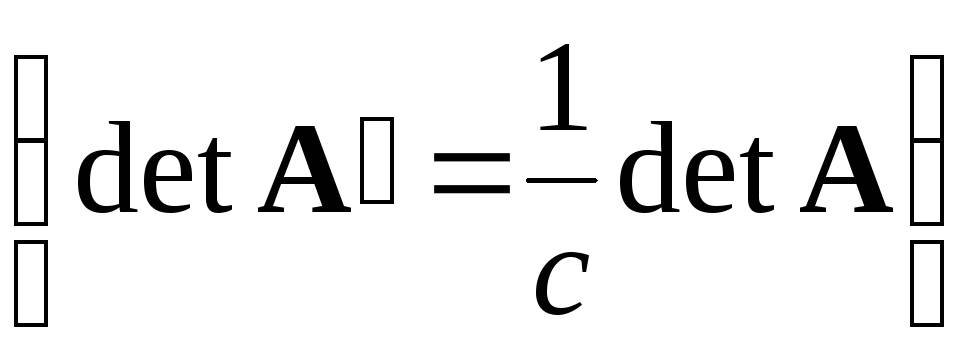 .
. .
.

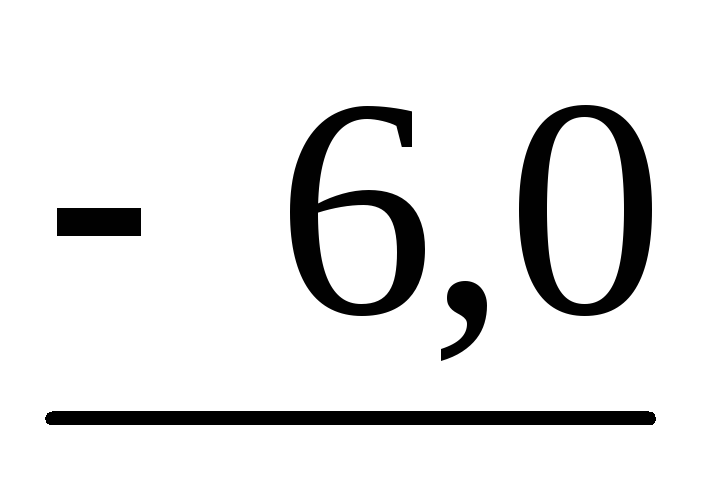
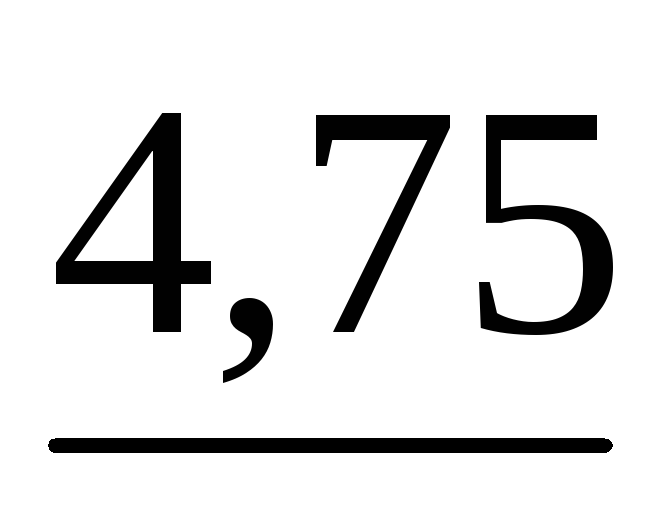
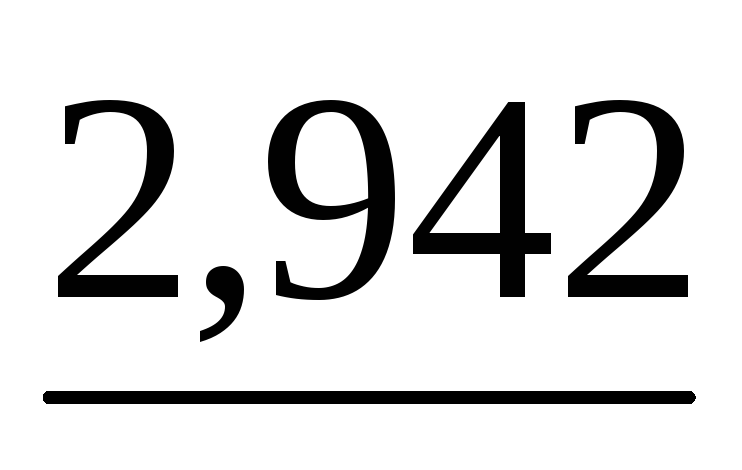
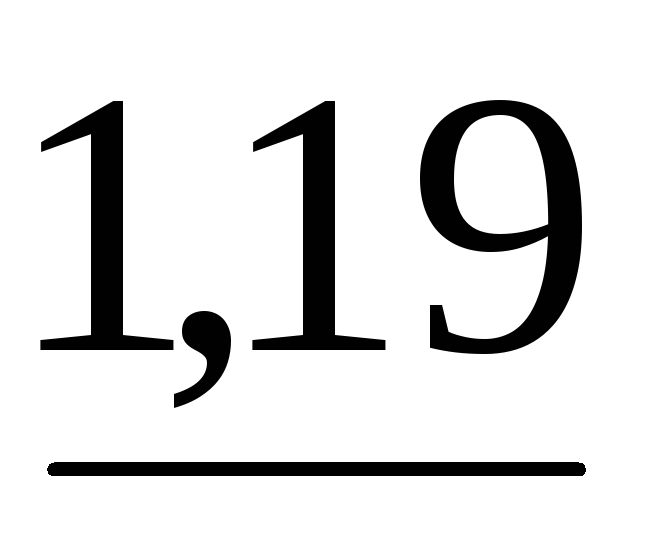
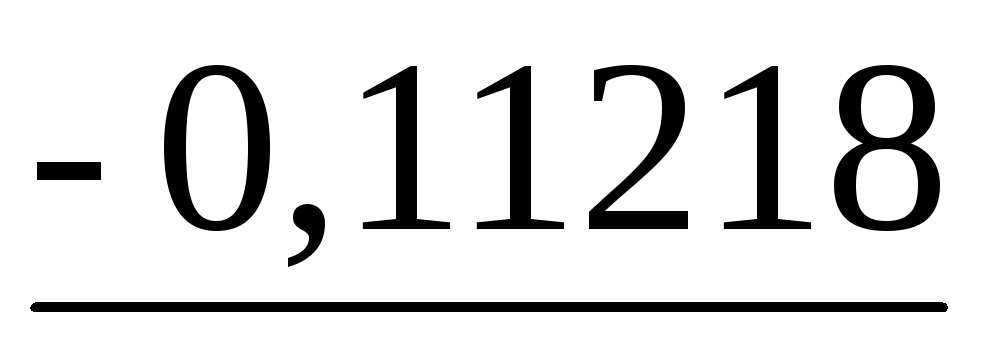
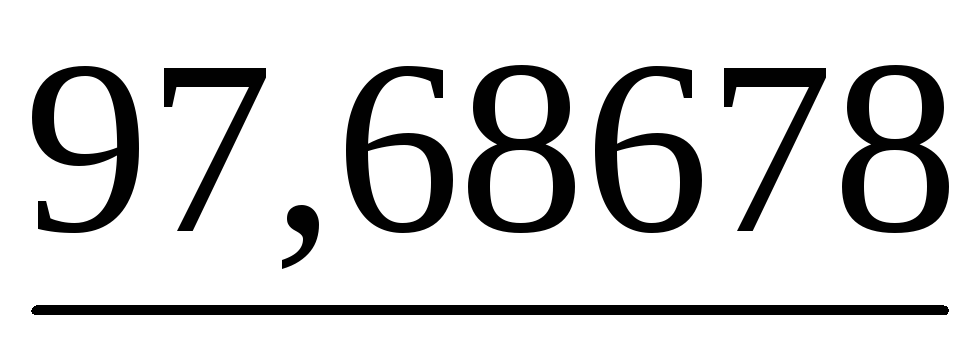
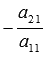 ,
,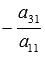 .
.