Метод подстановки (С.М.Слупко). Видеоурок. Алгебра 7 Класс
Продолжаем разговор о том, как решать системы линейных уравнений с двумя неизвестными.
Повторим основные мысли:
- Уравнение – это условие, наложенное на переменные. Или – это та информация, которая нам известна про переменные. Нам известно, что сумма
 и
и  равна
равна  :
:  .
. - Объединение двух уравнений в систему означает, что эти условия выполняются одновременно. Или, иными словами, информация нам известна про одни и те же переменные. Нам известно, что сумма

 равна
равна  , а также что
, а также что  минус
минус  равно
равно  :
:  .
. - Решение системы – это пара чисел, являющаяся решением каждого уравнения. Если коротко, то это общее решение для обоих уравнений. Пара
 является решением каждого уравнения, а значит, и всей системы.
является решением каждого уравнения, а значит, и всей системы.
Рассмотрим систему уравнений: 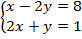 .
.
Первое уравнение нам сообщает, что 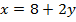 . Тогда запишем, что
. Тогда запишем, что 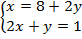 .
.
Говорят: «мы выразили переменную 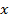
Так как уравнения объединены в систему, значит, речь в каждом идет про одни и те же 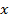 и
и 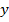 . Значит, все, что мы знаем про
. Значит, все, что мы знаем про 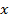 из первого уравнения, мы можем использовать во втором.
из первого уравнения, мы можем использовать во втором.
Заменим во втором уравнении 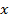 на равное ему выражение. Вот именно здесь и появляется метод подстановки. Информацию из одного уравнения подставляем в другое. Получим:
на равное ему выражение. Вот именно здесь и появляется метод подстановки. Информацию из одного уравнения подставляем в другое. Получим: 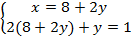
Получили уравнение с одной переменной 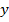 , которое мы уже умеем решать:
, которое мы уже умеем решать:
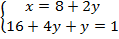
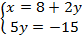
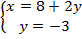
Теперь эту информацию, про 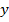 , используем в первом уравнении.
, используем в первом уравнении.
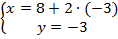
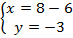
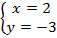
Решение системы – это пара чисел 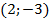 .
.
Метод подстановки, когда одно условие подставляется в другое, мы часто используем в обычной жизни. Кто хочет, может изучить пример использования этого принципа при поиске человека в социальных сетях.
Поиск в социальных сетях
Представьте такую ситуацию. Вы в гостях у своего друга Пети познакомились с девочкой Женей и, уже вернувшись домой, решили найти ее в социальной сети.
Вот что вы знаете:
1. Она подруга Пети
2. Она тоже учится в 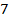
3. Зовут Женя
4. Живет тоже в Москве
Каждое из этих условий имеет очень много решений по отдельности. Друзей у Пети много, 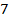 -классниц огромное количество, девочек с именем Женя тоже и так далее.
-классниц огромное количество, девочек с именем Женя тоже и так далее.
Но так как все эти условия относятся к одному человеку, то это система: 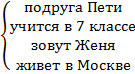 , а решением системы является такой человек, который соответствует сразу всем условиям. И решаем эту систему мы методом подстановки. Выбираем одно условие, потом туда подставляем другое и так далее.
, а решением системы является такой человек, который соответствует сразу всем условиям. И решаем эту систему мы методом подстановки. Выбираем одно условие, потом туда подставляем другое и так далее.
Итак:
Открываете страничку Пети и выбираете список всех его друзей. Это решения первого условия. Их 
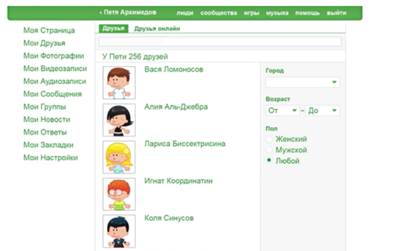
Рис. 1. Решение первого условия системы
Подставляем сюда второе условие. Раз в 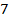 классе, то ее возраст от
классе, то ее возраст от  до
до  лет. Количество решений уменьшилось до
лет. Количество решений уменьшилось до  . (См. Рис. 2.)
. (См. Рис. 2.)
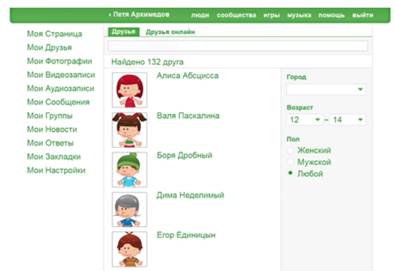
Рис. 2. Выполнение первых двух условий системы
Добавляем условие, которое мы изначально забыли, но нам его подсказала сеть – пол. Женский. Осталось 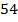 . (См. Рис. 3.)
. (См. Рис. 3.)
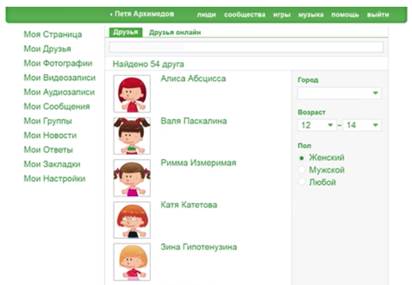
Рис. 3. Еще одно условие
Город Москва. Осталось 37 человек (См. Рис. 4.)
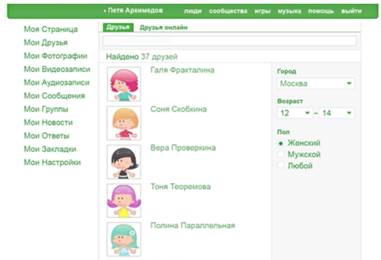
Рис. 4. Выполнение еще одного условия
Имя Женя. Осталось два человека. (См. Рис. 5.)
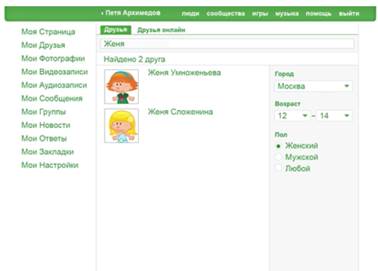
Рис. 5. Итог после выполнения всех условий
Итак, система имеет 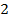 решения, из них несложно выбрать нужного нам человека.
решения, из них несложно выбрать нужного нам человека.
Мы последовательно в одно условие подставляли другое и так 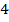 раза, то есть решили задачу методом подстановки.
раза, то есть решили задачу методом подстановки.
Решить систему: 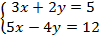 .
.
Решение
Выражать переменную легче ту, коэффициент перед которой равен единице. Если нет переменной с таким коэффициентом, то выражаем любую переменную из любого уравнения.
Выразим из первого уравнения переменную 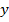
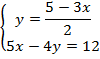
Подставим во второе уравнение вместо 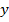 полученное выражение:
полученное выражение:
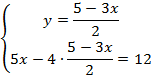
Получили уравнение только с переменной 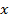 . Решим его:
. Решим его:
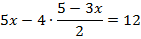
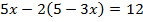
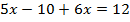
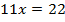
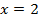
Так, 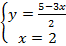 .
.
Подставим найденное значение 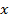 в выражение для
в выражение для 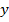 :
:
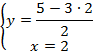
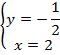
Поменяем местами первое и второе уравнение:
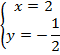
Сделаем проверку, подставив решение в каждое уравнение.
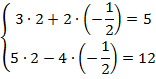
Получаем верные равенства:
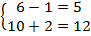
Проиллюстрируем решение системы графически.
Для каждого уравнения системы выберем по два решения. Например, 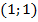 и
и 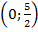 для
для 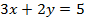 и
и 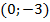 и
и 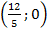 для
для 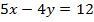
Отметим эти решения в виде точек и проведем через них прямые. (См. Рис. 6.)
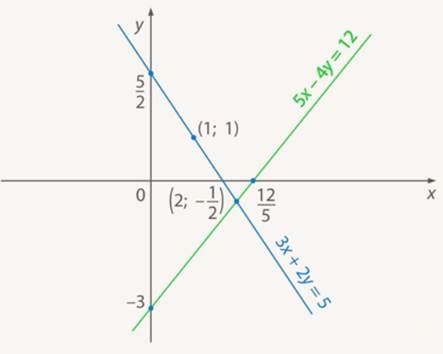
Рис. 6. Графики уравнений
Получили графики (множество решений) каждого уравнения. Точка пересечения и есть решение системы.
1. Выразить одну (любую) переменную из любого уравнения.
2. Подставить полученное выражение во второе уравнение.
3. Решить уравнение с одной переменной.
4. Найденное значение переменной подставить в первое уравнение и найти значение второй переменной.
1. Решить 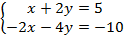 .
.
Решение
Выразим 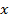 из первого уравнения:
из первого уравнения: 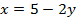
И подставим во второе: 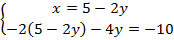
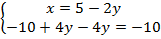
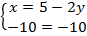
Во втором уравнении получили очевидный факт, верное равенство. Эта запись не несет никакой полезной информации для нас, мы ее можем исключить. Остается только первое уравнение.
Система эквивалента одному уравнению: 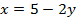 , а ее решение – это решение данного уравнения, которых бесконечно много.
, а ее решение – это решение данного уравнения, которых бесконечно много.
Проиллюстрируем решение системы графически.
Возьмем два решения для первого уравнения: 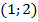 и
и 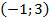 .
.
Но они же являются решениями и для второго. Два графика совпадают. (См. Рис. 7.)
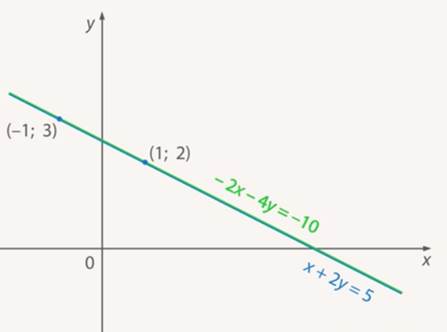
Рис. 7. Графики совпадают
Решение уравнения и есть решение системы. То есть решений у системы бесконечно много – вся прямая.
Итак, если после подстановки мы получили верное числовое равенство, то система имеет бесконечно много решений.
2. Решить 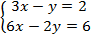 .
.
Решение
Выразим 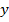 из первого уравнения:
из первого уравнения: 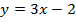 .
.
Подставим выражение во второе уравнение: 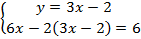 .
.
Решим полученное уравнение с одной переменной:
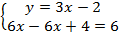
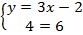
Получили неверное числовое равенство. То есть уравнение, полученное после подстановки, не имеет решения. Задаем себе вопрос – при каких значениях 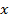 и
и 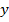 :
: 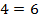 ? Не существует таких значений. Делаем вывод: система не имеет решений.
? Не существует таких значений. Делаем вывод: система не имеет решений.
Построим графики уравнений этой системы. Выбираем по два решения для каждого уравнения и строим графики. (См. Рис. 8.) Например, 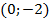 и
и 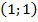 для
для 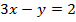 и
и 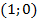 и
и 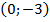 для
для 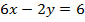 .
.
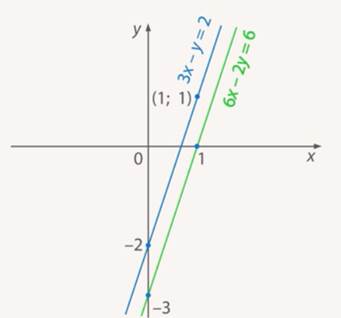
Рис. 8. Графики уравнений
Они параллельны друг другу. То есть нет общих точек (общих решений) у этих графиков. Вывод: решений у системы нет.
Таким образом, если после подстановки мы получили неверное числовое равенство, то решений у системы нет.
3. Решить: 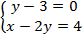
Решение
Одно из уравнений содержит только одну переменную. Задача становится только проще. Выражаем 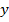 и подставляем во второе уравнение:
и подставляем во второе уравнение:
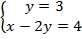
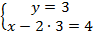
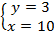
Получаем решение: 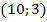 .
.
Построим графики этих уравнений. График первого уравнения – прямая, параллельная оси 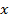 , проходящая через отметку
, проходящая через отметку 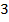 на оси
на оси 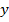 . Второй график проходит, например, через точки
. Второй график проходит, например, через точки 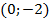 и
и 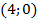 . Точка пересечения – решение системы. (См. Рис. 9.)
. Точка пересечения – решение системы. (См. Рис. 9.)
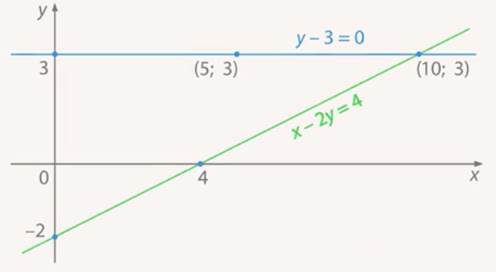
Рис. 9. Графики уравнений
Итак, повторим.
1. Уравнения системы – это информация про одни и те же переменные. Поэтому информацию из одного уравнения можно использовать в другом, подставлять в другое уравнение: 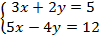 .
.
2. Для решения системы выражаем одну (любую) переменную из любого уравнения и подставляем во второе уравнение: 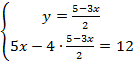 .
.
3. Получим уравнение с одной переменной. Решаем его: 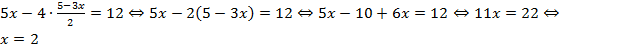
4. Полученное значение переменной подставим в первое и находим оставшуюся переменную: 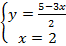 ;
; 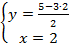 ;
; 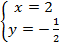 .
.
5. Если в ходе решения в одном уравнении пропали все переменные и получилось ВЕРНОЕ числовое равенство: 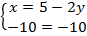 , это значит, что уравнения были эквивалентны друг другу, решениями системы являются решения любого из них. Их бесконечно много.
, это значит, что уравнения были эквивалентны друг другу, решениями системы являются решения любого из них. Их бесконечно много.
6. Если в ходе решения мы получили НЕВЕРНОЕ числовое равенство: 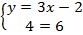 , это означает, что одно уравнение не имеет общих решений со вторым. У системы нет решений.
, это означает, что одно уравнение не имеет общих решений со вторым. У системы нет решений.
Список литературы
1. М.И. Башмаков. Алгебра. Рабочая тетрадь для 7 класса. – М.: БИНОМ. Лаборатория знаний, 2014 – 224 с.
2. Гельфман Э.Г., Демидова Л.Н., Терре А.И. Алгебра. Практикум для 7 класса. – М.: БИНОМ. Лаборатория знаний, 2014 – 184 с.
3. Э.Г. Гельфман и др. Алгебра. Учебник для 7 класса. – М.: БИНОМ. Лаборатория знаний, 2013 – 264 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт «Школьный помощник» (Источник)
3. Интернет-сайт mathematics-repetition.com (Источник)
Домашнее зада
interneturok.ru
Примеры решения систем методом подстановки
Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.
В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:
Первое уравнение — уравнение с одной переменной y. Решаем его:
5(7-3y)-2y = -16
35-15y-2y= -16
-17y= -51
y=3.
Полученное значение y подставляем в выражение для x:
Ответ: (-2; 3).
В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:
Второе уравнение — уравнение с одной переменной x. Решим его:
3x-4(-1,5-3,5x)=23
3x+6+14x=23
17x=17
x=1.
В выражение для y вместо x подставляем x=1 и находим y:
Ответ: (1; -5).
Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):
Решаем первое уравнение:
4x-9(1,6-0,3x)= -1
4x-14,4+2,7x= -1
6,7x=13,4
x=2.
Подставляем x=2 и находим y:
Ответ: (2; 1).
Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:
Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:
Решаем первое уравнение системы:
3(21,5 + 2,5b) — 7b = 63
64,5+7,5b-7b=63
0,5b= -1,5
b= -3.
Осталось найти значение a:
Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
Ответ: (14; -3).
Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.
В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:
9x-4(43-4x)=78
9x-172+16x=78
25x=250
x=10.
Ответ: (10;1).
Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.
www.algebraclass.ru
Метод подстановки — методическая рекомендация. Алгебра, 7 класс.
| 1. | Выразить одну переменную через другую | 1 вид — рецептивный | лёгкое | 1 Б. | Выразить одну переменную через другую в линейном уравнении. |
| 2. | Выразить переменную a через переменную b | 1 вид — рецептивный | лёгкое | 1 Б. | Выразить переменную a через переменную b. |
| 3. | Система линейных уравнений | 2 вид — интерпретация | лёгкое | 2 Б. | Решение системы линейных уравнений методом подстановки. |
| 4. | Вычисление одной переменной системы, если известна вторая переменная (обыкновенные дроби) | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление одной переменной системы, если известна вторая переменная. |
| 5. | Вычисление одной переменной системы, если известна вторая переменная (целые числа) | 2 вид — интерпретация | среднее | 3 Б. | Вычисление одной переменной системы, если известна вторая переменная. Перенесение слагаемых из одной части уравнения в другую, умножение обеих частей уравнения на -1. |
| 6. | Прямая пропорциональность и линейная функция (коэффициент — отрицательная десятичная дробь) | 2 вид — интерпретация | среднее | 3 Б. | Нахождение точки пересечения графиков без построения. Решение системы уравнений, умножение десятичных дробей с разными знаками. |
| 7. | Система двух уравнений (число, противоположное отрицательному) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений, нахождение одночлена, противоположного отрицательному. |
| 8. | Система линейных уравнений (переменная во втором уравнении выражена) | 2 вид — интерпретация | среднее | 5 Б. | Решение системы линейных уравнений, раскрытие скобок, перед которыми стоит знак « — ». |
| 9. | Система двух линейных уравнений (распределительный закон умножения) | 2 вид — интерпретация | среднее | 5 Б. | Решение системы уравнений, применение распределительного закона умножения. |
| 10. | Система линейных уравнений, раскрытие скобок | 2 вид — интерпретация | сложное | 8 Б. | Решение системы линейных уравнений, раскрытие скобок, перед которыми стоит знак « — », применение распределительного закона умножения. |
| 11. | Система дробных уравнений | 2 вид — интерпретация | сложное | 8 Б. | Решение системы дробных уравнений, сводимых к линейным (знаменатели — целые числа). |
| 12. | Система двух дробных уравнений | 2 вид — интерпретация | сложное | 8 Б. | Решение системы двух дробных уравнений (знаменатель — число), сводимых к линейным: приведение дробей к общему знаменателю, применение распределительного закона умножения. |
www.yaklass.ru
Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты
Тестирование онлайн
Система линейных уравнений
Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
Решение системы линейных уравнений способом подстановки
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.
Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
Метод введения новых переменных
Замена переменных может привести к решению более простой системы уравнений, чем исходная.
Рассмотрим решение системы
Введем замену , тогда
Переходим к первоначальным переменным
Особые случаи
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система
1) Если , то система имеет единственное решение.
2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.
3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.
Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.
fizmat.by
Онлайн урок метод подстановки при решении систем уравнений.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
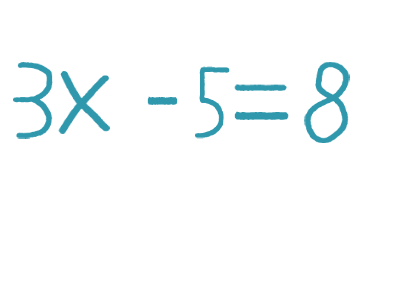
Уравнение — это равенство, содержащее одну или несколько переменных, значения которых нужно найти.
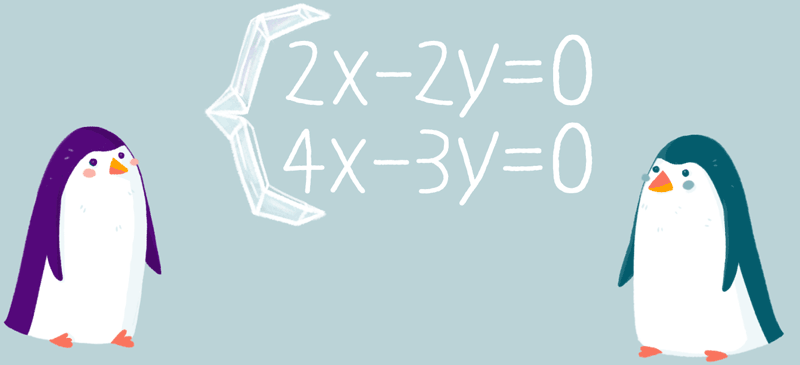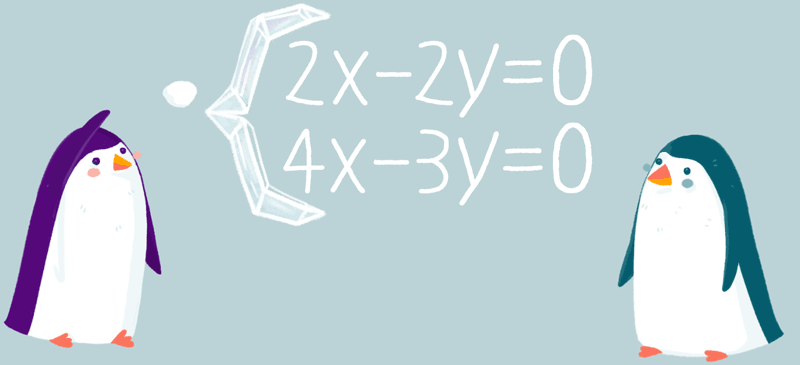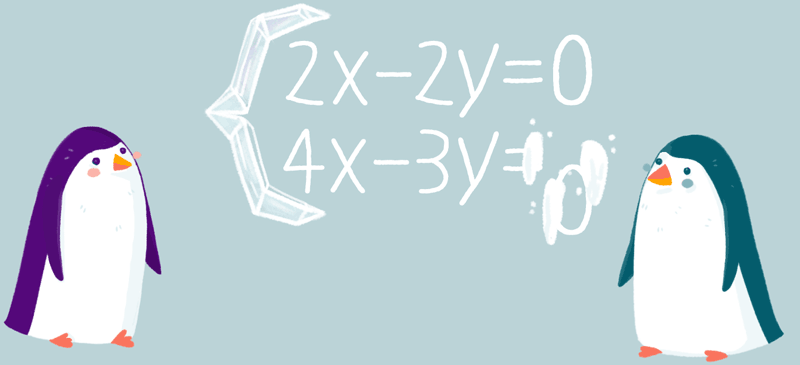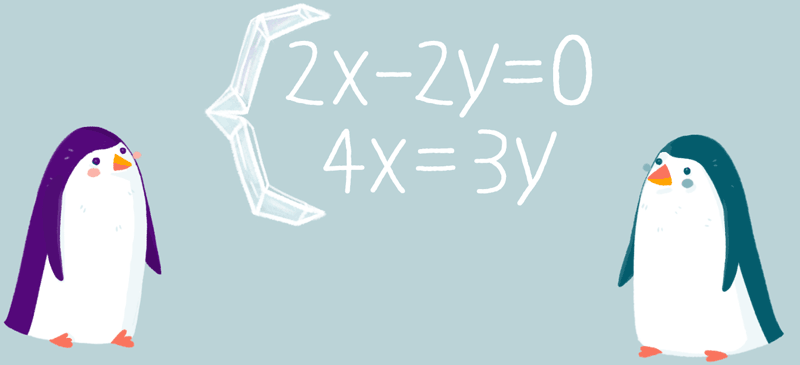
Если одно уравнение системы оставить без изменения, а другое уравнение заменить равносильным уравнением, то полученная система будет равносильна заданной.
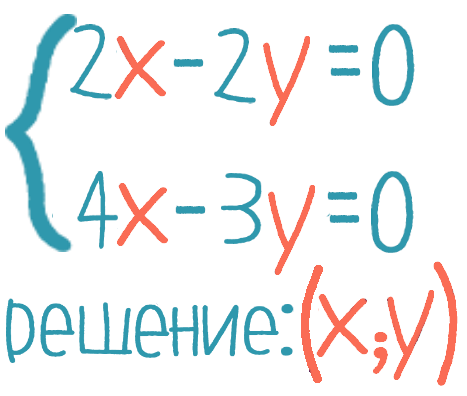
Пара решений, обращающая каждое уравнение в верное равенство, называется решением системы уравнений.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.
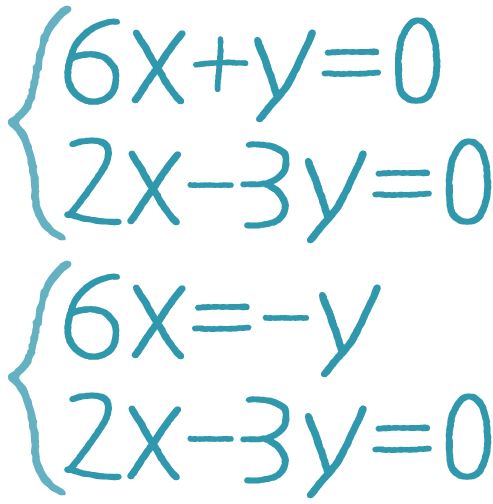
равносильные системыне равносильные системыпохожие уравненияравносильные уравнения

x = 1, y = 7x = 6, y = 14x = 3, y = -7x = 5, y = 12
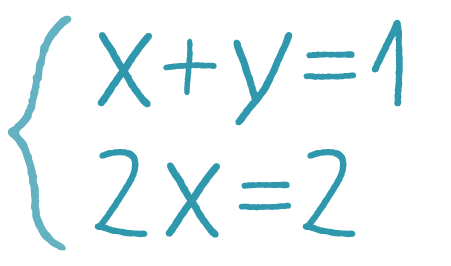
(x, y) = (1, 1)(x, y) = (0, 1)(x, y) = (2, 0)(x, y) = (1, 0)
Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Преобразования уравнений системы.
2. Метод подстановки при решении систем уравнений.
2. Системы, не имеющие решений.
myalfaschool.ru
Решение систем линейных уравнений методом подстановки онлайн
Самым простым методом решения системы линейных алгебраических уравнений (СЛУ) является метод подстановкиили метод исключения. Рассмотрим его более подробно, предположим, нам дана СЛУ вида:
Требуется её решить, т.е. найти такие значения переменных x1, x2, чтобы при подстановке их в исходную СЛУ, последняя обращалась в верное тождество. Метод подстановки заключается в следующем:
1. Решим первое уравнение относительно переменной x1:
2. Подставим полученное для переменной x1 выражение во второе уравнение системы:
3. Упростим второе уравнение системы:
4. Решим второе уравнение системы относительно x2:
5. Подставим полученное для переменной x2 выражение в первое уравнение системы:
6. Упростим первое уравнение системы:
Данный онлайн калькулятор решает СЛУ методом методом подстановки с описанием пошагового хода решения на русском языке. Коэффициенты СЛУ могут быть не только числами или дробями, но также и параметрами. Для работы калькулятора необходимо ввести уравнения и выбрать переменные СЛУ, которые необходимо найти.
mathforyou.net
Метод подстановки | Алгебра
Метод подстановки решения систем линейных уравнений первый раз изучается в курсе алгебры 7 класса. В дальнейшем этот метод встречается ещё не раз, поскольку с помощью подстановки можно решать и другие виды систем уравнений.
Алгоритм решения систем линейных уравнений методом подстановки
1) В одном из уравнений выражаем одну переменную через другую.
2) Полученное выражение подставляем вместо этой переменной в другое уравнение системы и решаем уравнение с одной переменной.
3) Найденное значение переменной подставляем в выражение и вычисляем значение другой переменной.
Ответ системы записывают в круглых скобках через точку с запятой в алфавитном порядке. Для системы уравнений из двух переменных ответ схематически выглядит так:
(x; y),
из трёх — (x; y; z).
Как определить, из какого уравнения выразить одну переменную через другую?
При решении систем линейных уравнений способом подстановки выразить одну переменную через другую можно из любого уравнения, но желательно лучше выбирать для этого путь, который проще.
- Как правило, удобнее всего брать переменную, коэффициент при которой равен единице. В этом случае, чтобы выразить такую переменную через другую, нужно просто перенести остальные слагаемые в правую часть, изменив при переносе их знаки на противоположные.
Например, в системе
во втором уравнении коэффициент при переменной y равен 1 (b2=1), поэтому удобно выразить из второго уравнения y через x:
y=с2 — a2x
и подставить получившееся выражение вместо y в первое уравнение:
a1x+b1(с2 — a2x)=с1.
Записывают эти действия коротко:
- Следующий по удобству вариант — коэффициент -1 перед переменной.
Например, в системе
коэффициент при y в первом уравнении равен -1, поэтому удобно выразить из первого уравнения y через x.
Это можно сделать так: оставив y со знаком «-«в левой части, первое слагаемое перенести в правую часть
-y=с1 -a1x,
после чего умножить обе части уравнения на -1:
y= a1x — с1 .
Также можно y перенести в правую часть, изменив его знак на «+», а a1x — в левую, изменив знак на «-«:
a1x — с1=y.
Можно сразу же поменять местами правую и левую части:
y= a1x — с1 .
Записывают эти действия кратко:
- Поскольку удобно делить на 2, 5, 10, при наличии одного из таких коэффициентов перед переменной удобно выразить такую переменную через другую.
Например, в системе
можно выразить из первого уравнения x через y:
- В общем виде план решение систем линейных уравнений способом подстановки можно записать, например, так:
Из второго уравнения находим значение x. Подставив это значение в 1-е уравнение, находим y.
В следующий раз рассмотрим решение систем линейных уравнений методом подстановки на конкретных примерах.
www.algebraclass.ru
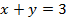 .
.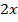 минус
минус  :
: 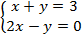 .
.