Дифференциальные уравнения | Математика, которая мне нравится
1. Уравнения в полных дифференциалах
Уравнение
называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции . Это имеет место, если
Чтобы решить исходное уравнение, нужно найти функцию , полный дифференциал которой равен левой части уравнения. Тогда общее решение уравнения можно записать в виде , где — произвольная постоянная.
Задача 1. Решить уравнение
Решение. Это — уравнение в полных дифференциалах. Действительно,
Найдем функцию , такую, что .
Интегрируем по первое из этих уравнений, считая постоянным, при этом вместо постоянной интегрирования нужно поставить — неизвестную функцию от : Подставляя это
выражение для во второе уравнение, найдем :
Следовательно, можно взять , и общее решение исходного уравнения может быть записано в виде
2. Интегрирующий множитель
Интегрирующим множителем для уравнения
называется такая функция , после умножения на которую уравнение превращается в уравнение в полных дифференциалах. Если функции и в уравнении имеют непрерывные частные производные и не обращаются в нуль одновременно, то интегрирующий множитель существует. Однако нет общего метода для его отыскания (когда общее решение уравнения неизвестно).
Для решения некоторых уравнений можно применять метод выделения полных дифференциалов, используя известные формулы:
Если в уравнении можно выделить полный дифференциал некоторой функции , то иногда уравнение упрощается, если от переменных перейти к переменным или , где .
Задача 2. Решить уравнение
Решение. Сгруппируем члены так, чтобы выделить полные дифференциалы:
Разделив на и сделав замену , , получим уравнение
которое легко решается.
3. Уравнения, не разрешенные относительно производной
Уравнения вида можно решать следующими методами.
3.1. Разрешить уравнение относительно , то есть из уравнения выразить через и . Получится одно или несколько уравнений вида . Каждое из них нужно решить.
3.2. Метод введения параметра
Пусть уравнение можно разрешить относительно , то есть записать в виде . Введя параметр
получим
Взяв полный дифференциал от обеих частей равенства выше и заменив через , получим уравнение вида
Если решение этого уравнения найдено в виде , то, воспользовавшись равенством, выражающим через и , получим решение исходного уравнения в
параметрической записи .
Уравнения вида решаются тем же методом.
Задача 3. Решить уравнение
Берем полный дифференциал от обеих частей равенства и заменяем на :
Делим на .
а) Если , то делим на , получаем уравнение в полных дифференциалах
Решаем его:
И удовлетворяет уравнению
тогда . Отсюда , .
б) Если , то получаем решение .
4. Уравнения, допускающие понижение порядка
4.1. Если в уравнение не входит искомая функция , т.е. оно имеет вид , то порядок уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных, входящих в уравнение, т.е. сделав замену .
4.2. Если в уравнение не входит независимая переменная , т.е. уравнение имеет вид , то порядок уравнения можно понизить, взяв за новую независимую переменную , а за неизвестную функцию .
Задача 4. Решить уравнение .
Решение. В уравнение не входит . Полагаем . Тогда
Подставляя в уравнение, получим . Отсюда и . Далее решаем уравнения
4.3. Если уравнение однородно относительно и его производных, т.е. не меняется при одновременной замене на , то порядок уравнения понижается подстановкой , где — новая неизвестная функция.
Задача 5. Решить уравнение
Решение. Сделаем замену , получим
Подставим и в исходное уравнение:
4.4. Порядок уравнения понижается, если оно является однородным относительно и в обобщенном смысле, т.е. не меняется от замены на , — на (при этом заменяется на , — на и т.д.). Чтобы узнать, будет ли уравнение однородным, и найти число , надо приравнять друг другу показатели степеней, в которых число будет входить в каждый член уравнения после указанной замены. Если полученные уравнения для будут несовместными, то дифференциальное уравнение не является однородным в указанном смысле.
После того как число найдено, нужно сделать замену переменных , где — новая неизвестная функция, а — новая независимая переменная. Получим уравнение, в которое не входит независимая переменная . Порядок такого уравнения можно понизить одним из указанных выше способом.
Задача 6. Решить уравнение
Решение. Приравниваем показатели степеней:
Делаем замену , получаем далее
Отсюда получаем
4.5. Порядок уравнения понижается, если можно привести его к такому виду, чтобы обе его части являлись полными производными по от каких-нибудь функций.
Задача 7. Решить уравнение .
Решение. Разделим обе части уравнения на , получим
Порядок уравнения понижен. Решаем полученное уравнение:
Задачи.
1. Решить уравнения
а) ;
б) ;
в) ;
г) ;
д) .
2. Решить уравнения
а) ;
б) ;
в) .
3. Решить уравнения
а) ;
б) ;
в) .
4. Найдите все решения дифференциального уравнения
проходящие через точку .
5. Решите уравнение
6. Решить краевую задачу
— ограничено,
7. Решить систему дифференциальных уравнений
с начальными данными .
8. Пусть — решение дифференциального уравнения .
Докажите, что ограничено.
9.
с начальными условиями . Докажите, что если , то ни при каком не выполняется равенство , а если , то для любого можно выбрать такое , что .
дифференциальные уравнения метод введения параметра
Вы искали дифференциальные уравнения метод введения параметра? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и метод введения параметра дифференциальные уравнения, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дифференциальные уравнения метод введения параметра».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как дифференциальные уравнения метод введения параметра,метод введения параметра дифференциальные уравнения. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и дифференциальные уравнения метод введения параметра. Просто введите задачу в окошко и нажмите «решить» здесь (например, дифференциальные уравнения метод введения параметра).
Где можно решить любую задачу по математике, а так же дифференциальные уравнения метод введения параметра Онлайн?
Решить задачу дифференциальные уравнения метод введения параметра вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
4. Особые решения дифференциальных уравнений. Огибающая семейства интегральных кривых. Уравнения клеро и лагранжа. Другие типы дифференциальных уравнений, решаемых методом введения параметра
Решение 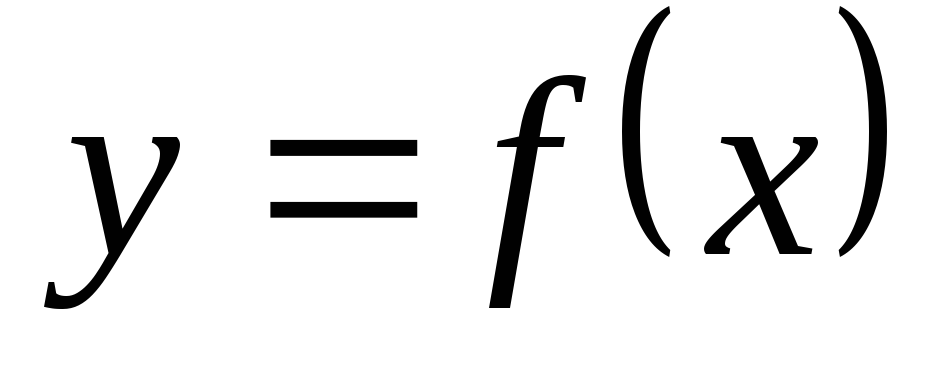 дифференциального уравнения
дифференциального уравнения
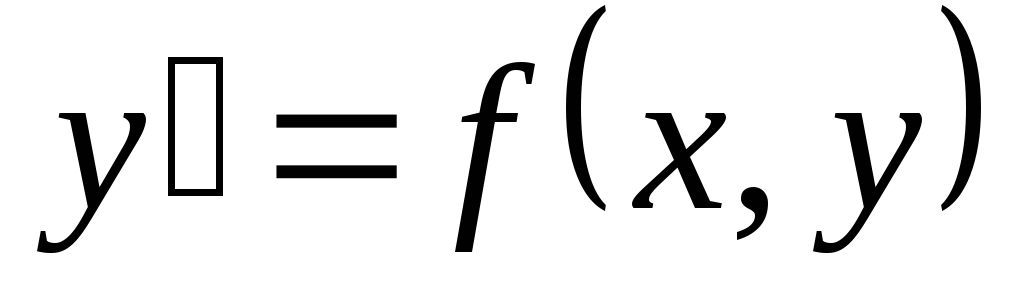
называется
особым, если в каждой его точке нарушается
свойство единственности, т.е. если через
каждую его точку 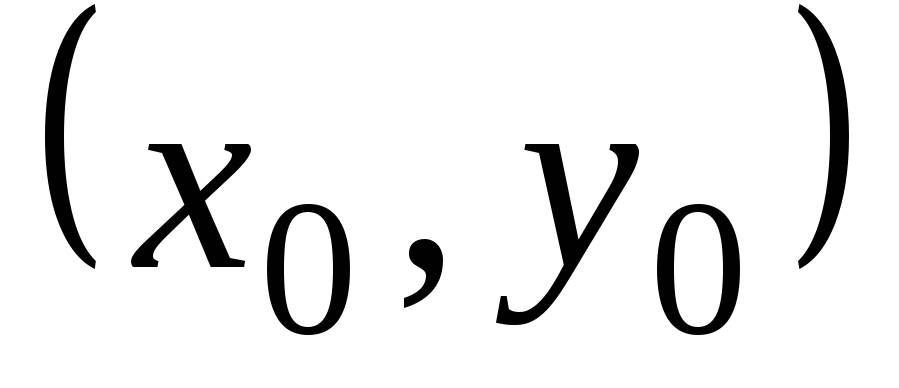 ,
кроме этого решения, проходит и другое
решение, имеющее в точке
,
кроме этого решения, проходит и другое
решение, имеющее в точке  ту же касательную, но не совпадающее с
решением
ту же касательную, но не совпадающее с
решением 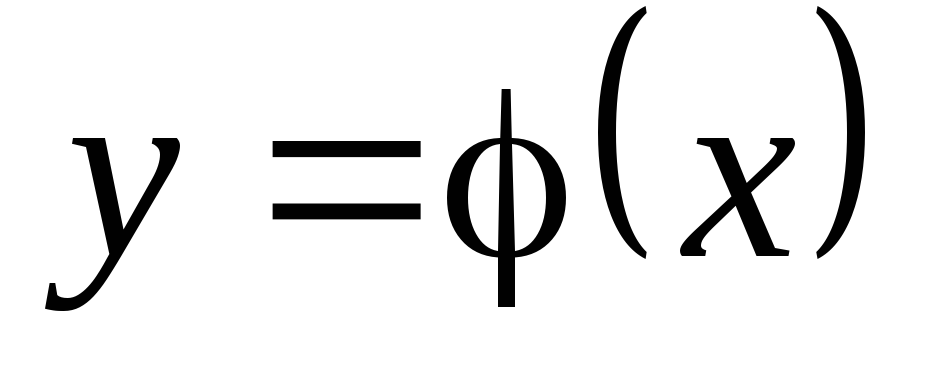 в сколь угодно малой окрестности точки
в сколь угодно малой окрестности точки 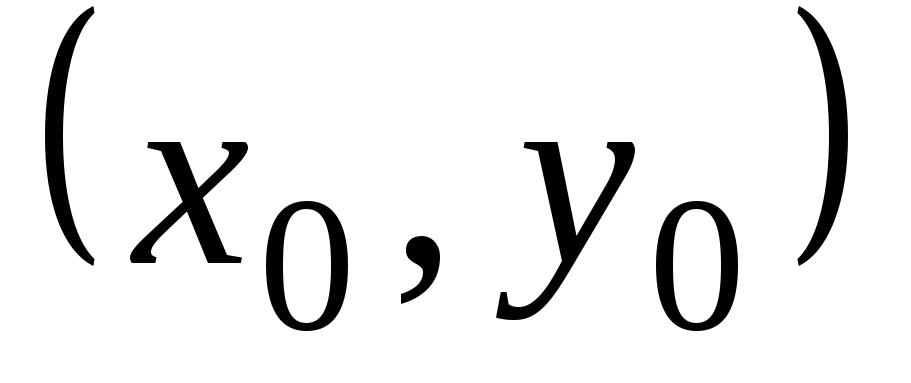 .
График особого решения будем называть
особой интегральной кривой.
.
График особого решения будем называть
особой интегральной кривой.
Если две кривые 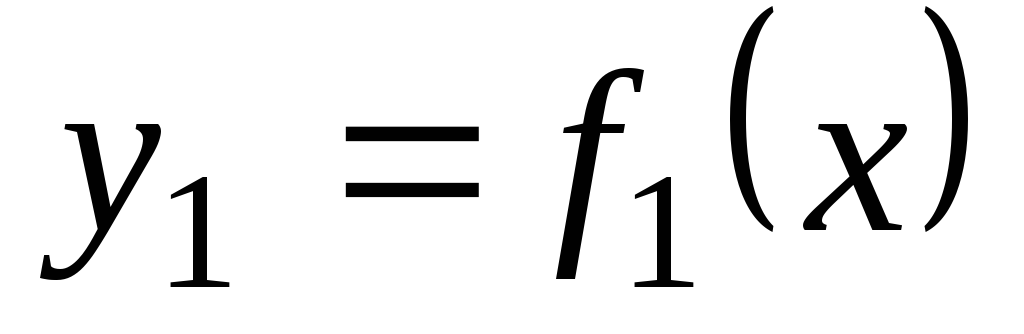 и
и 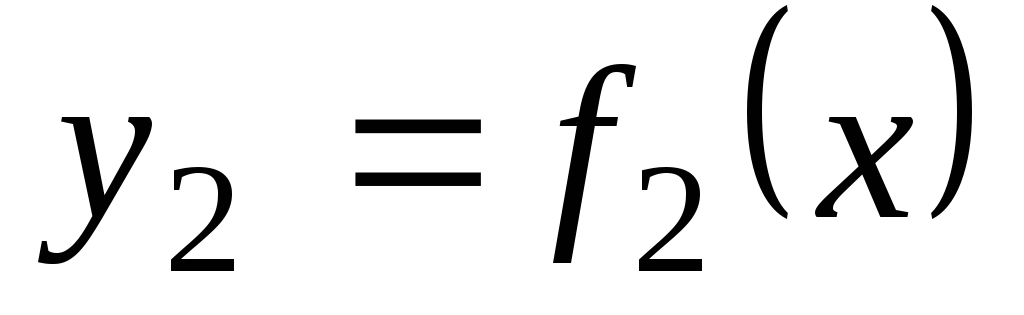
Условия касания кривыx:

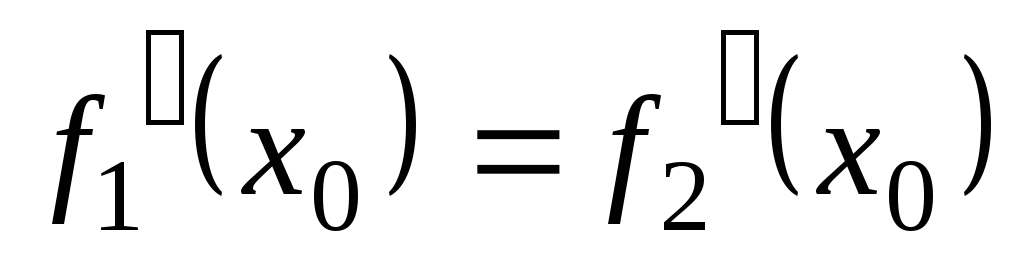 .
.
Кривая, которая касается каждой кривой семейства
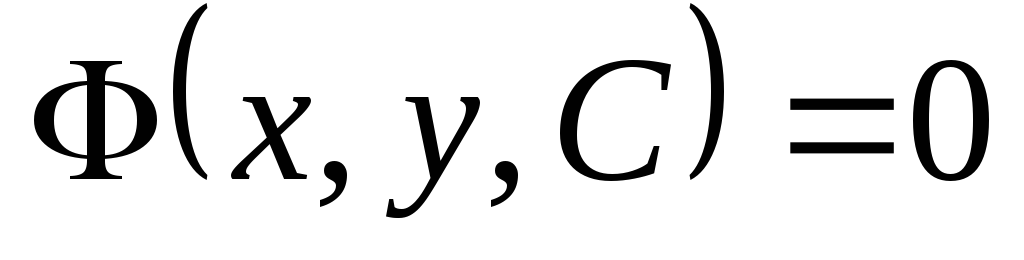
в одной или
нескольких точках и притом вся состоит
из точек касания, называется огибающей
данного семейства. (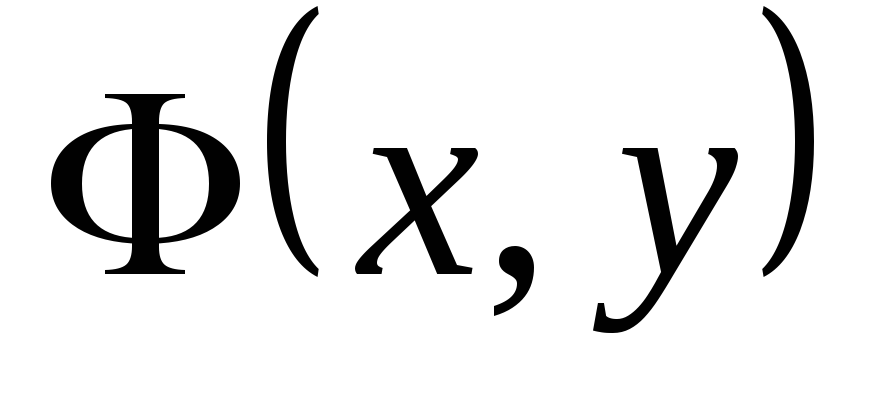 — непрерывно дифференцируемая функция.)
— непрерывно дифференцируемая функция.)
Теорема. Пусть  — семейство кривых, причем
— семейство кривых, причем
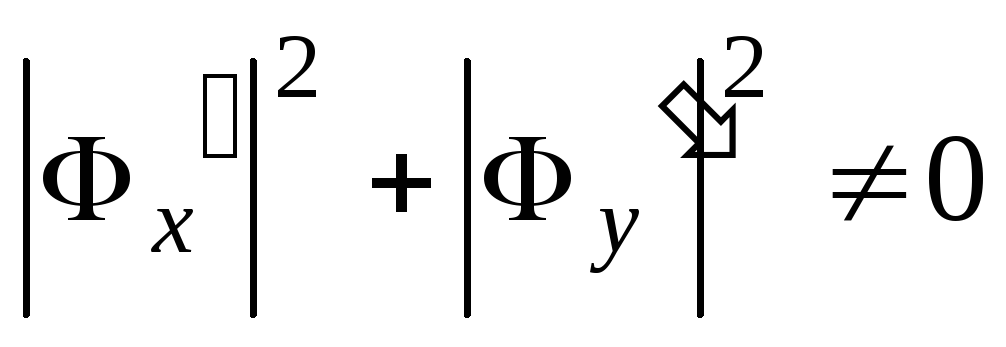 в точке
в точке 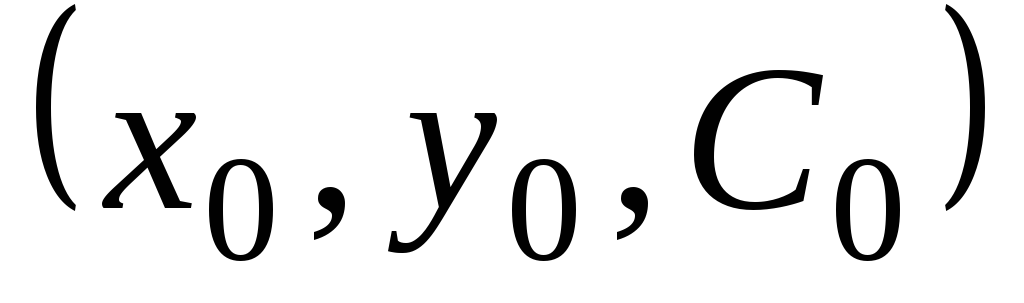 .
.
Тогда в
некоторой окрестности точки 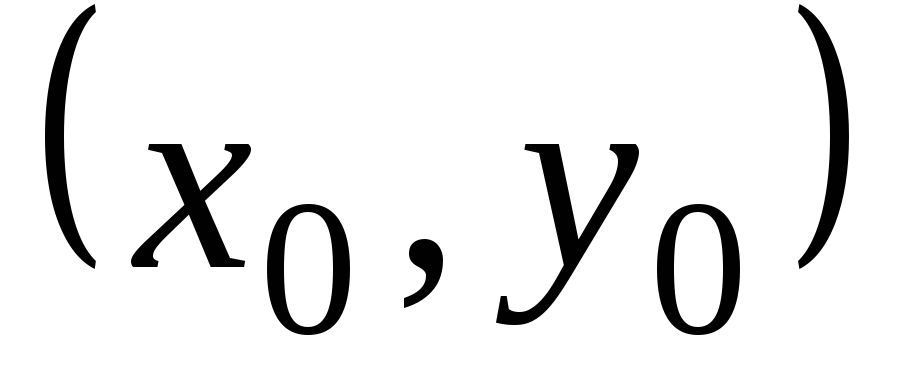 ,
точки, лежащие на огибающей
,
точки, лежащие на огибающей  этого семейства кривых, удовлетворяют
системе:
этого семейства кривых, удовлетворяют
системе:
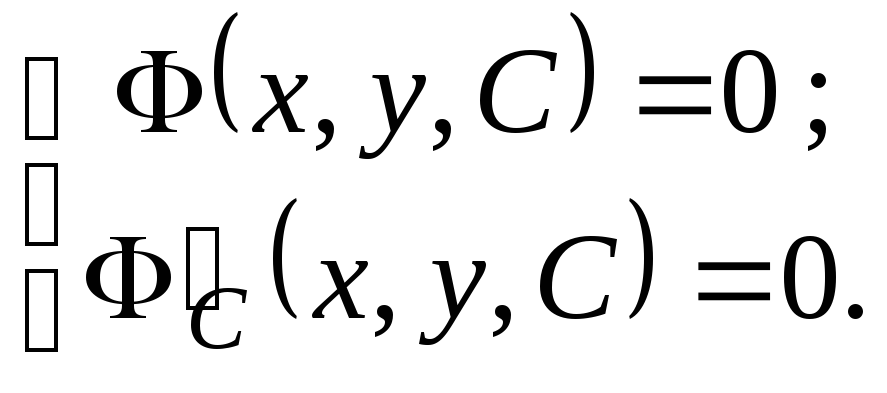 (4.2)
(4.2)
Замечание. Теорема утверждает, что
если  — огибающая, то всякая её точка удовлетворяет
(4.2). Обратное неверно, т.е. определяемая
(4.2) кривая может и не быть огибающей.
(Теорема даёт лишь необходимое условие
огибающей.) Из решений системы (4.2)
огибающие отбираются непосредственной
проверкой условий касания.
— огибающая, то всякая её точка удовлетворяет
(4.2). Обратное неверно, т.е. определяемая
(4.2) кривая может и не быть огибающей.
(Теорема даёт лишь необходимое условие
огибающей.) Из решений системы (4.2)
огибающие отбираются непосредственной
проверкой условий касания.
Если из уравнений системы (4.2) удается
исключить параметр C,
то уравнение огибающей получается в
явном виде, как 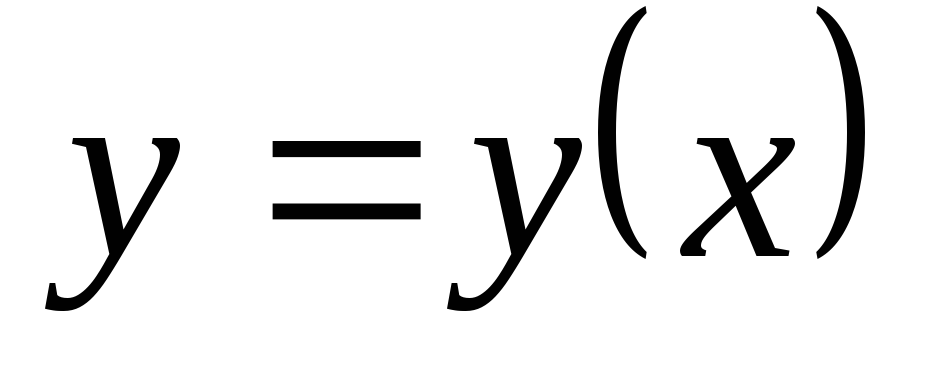 .
.
Пример 4.1. 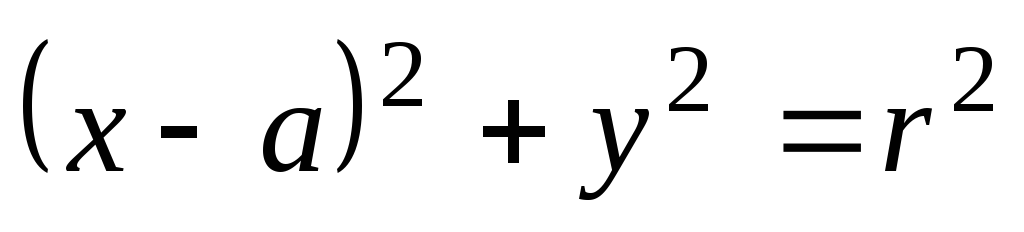 .
.
Это уравнение описывает семейство
окружностей радиуса 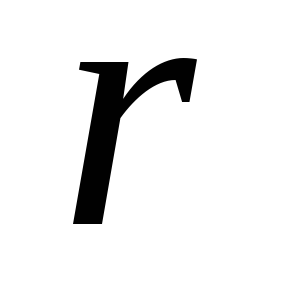 ,
центры которых лежат на оси OX, а
параметр
,
центры которых лежат на оси OX, а
параметр  есть смещение центров относительно
начала координат.
есть смещение центров относительно
начала координат.
Продифференцировав уравнение по
параметру  ,
получим
,
получим 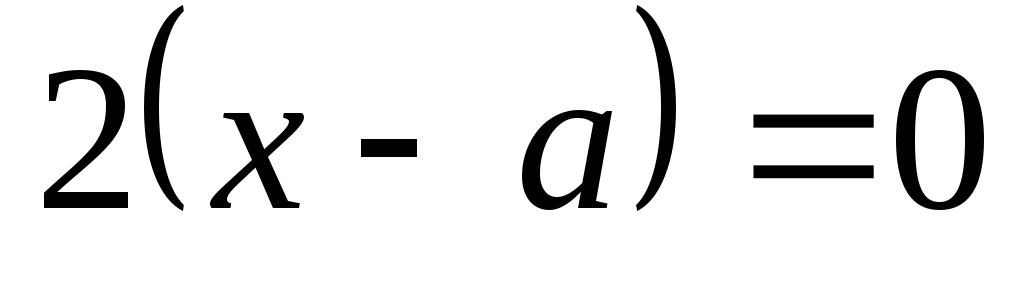 .
Подставив в уравнение
.
Подставив в уравнение  и исключив тем самым параметр
и исключив тем самым параметр  ,
получим
,
получим  , или иначе
, или иначе 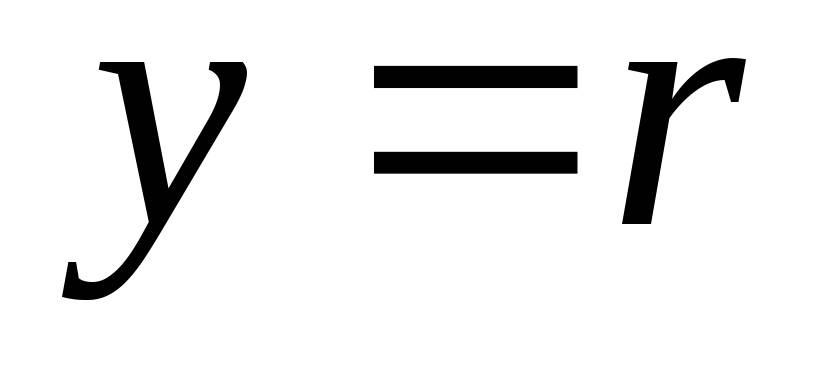 и
и  — уравнения двух огибающих семейства
кривых.
— уравнения двух огибающих семейства
кривых.
Красивый наглядный пример особого решения дает уравнение Клеро, имеющее вид
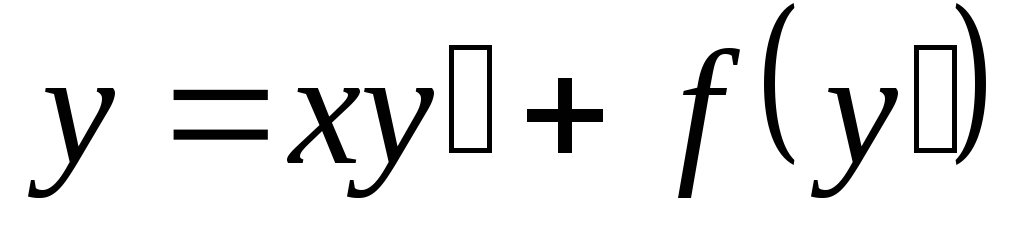 . (4.3)
. (4.3)
При интегрировании его применим метод введения параметра. Приняв y’= p и подставив в (4.3), получим
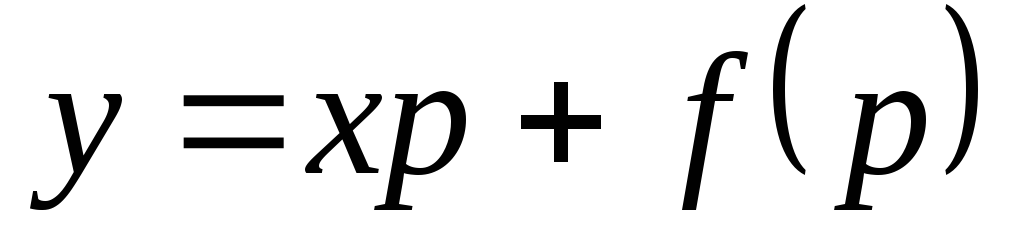 . (4.4)
. (4.4)
Далее,
продифференцировав уравнение (4.4) по
переменной 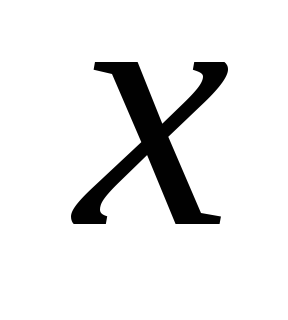 ,
получим
,
получим
 ,
,
откуда
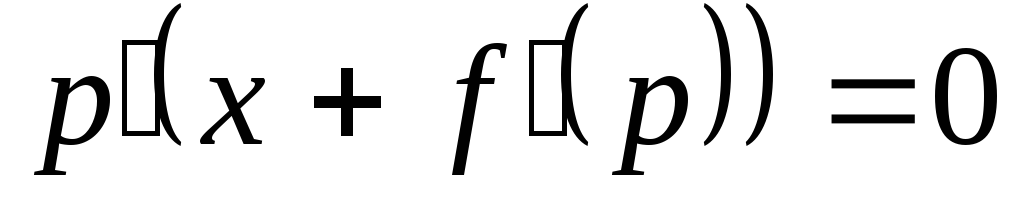 .
.
Здесь либо 1)
,
либо 2)  .
.
Из 1) следует 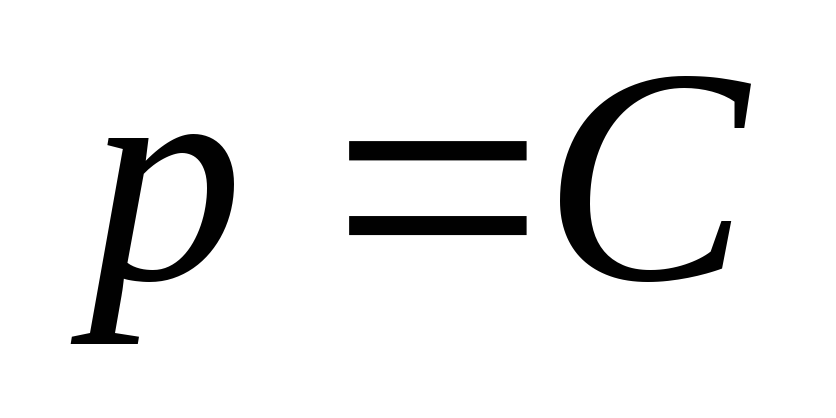 .
Подставив это в уравнение (4.4), получим
.
Подставив это в уравнение (4.4), получим 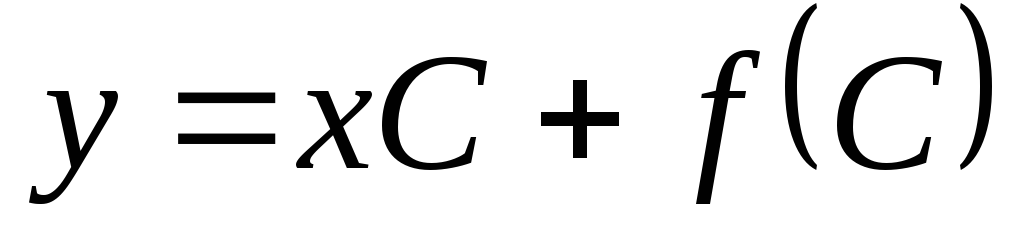 — уравнение семейства прямых с угловым
коэффициентом
— уравнение семейства прямых с угловым
коэффициентом  ,
пересекающих ось OY в точках
,
пересекающих ось OY в точках 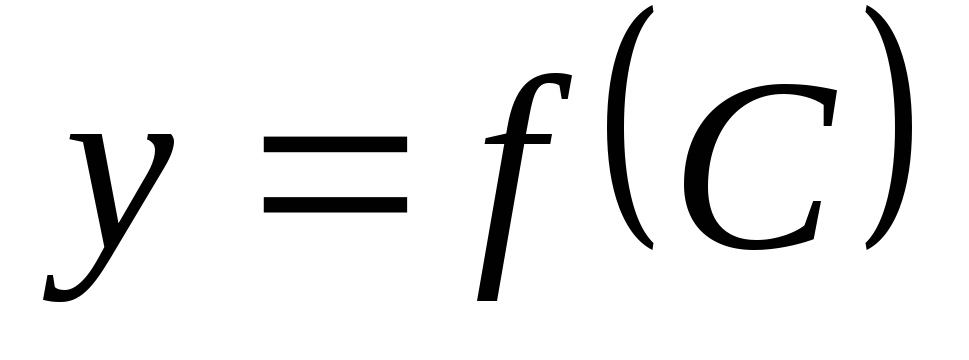 .
.
 и решение можно представить в
параметрическом виде:
и решение можно представить в
параметрическом виде:
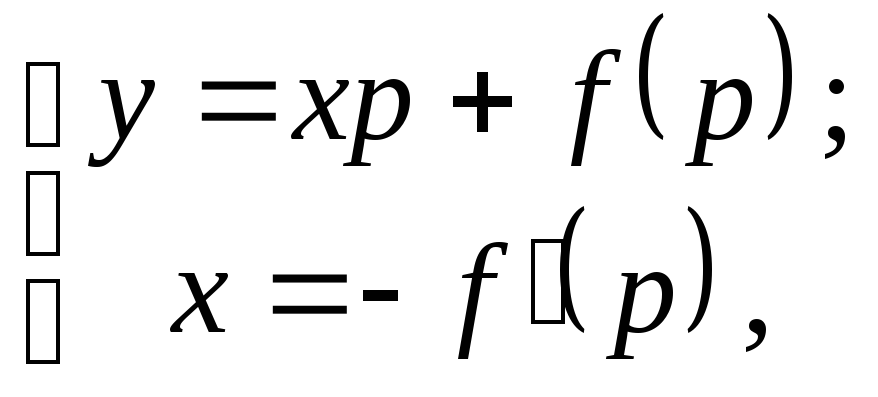 (4.5)
(4.5)
где  .
Нетрудно увидеть, что интегральная
кривая, определяемая (4.5), является
огибающей семейства прямых
.
Нетрудно увидеть, что интегральная
кривая, определяемая (4.5), является
огибающей семейства прямых  .
.
Действительно, в этом случае 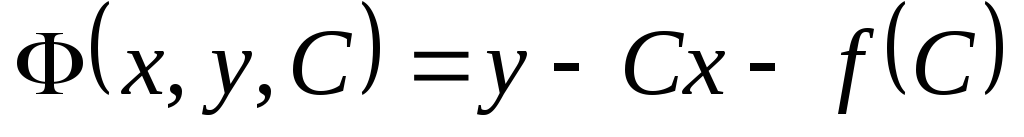 и огибающая определяется уравнениями
и огибающая определяется уравнениями  и
и  ,
или
,
или
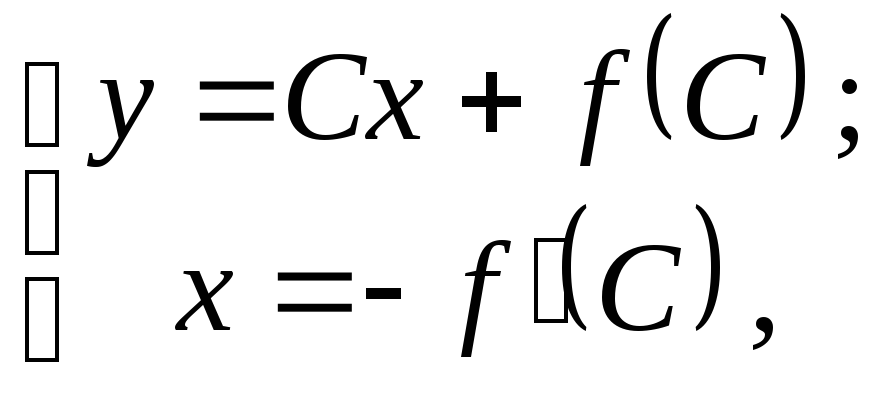 (4.5′)
(4.5′)
где 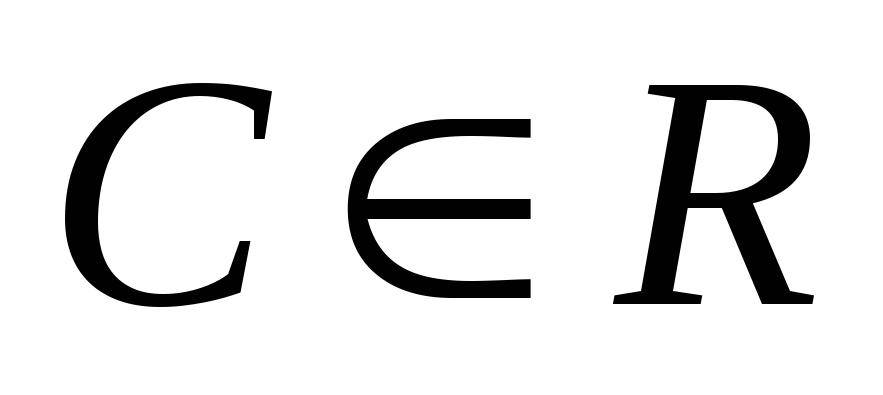 ,
что отличается от (4.5) лишь обозначениями.
,
что отличается от (4.5) лишь обозначениями.
Если удается исключить С из (5′), то особое решение можно получить в явном виде.
Пример Б 4119
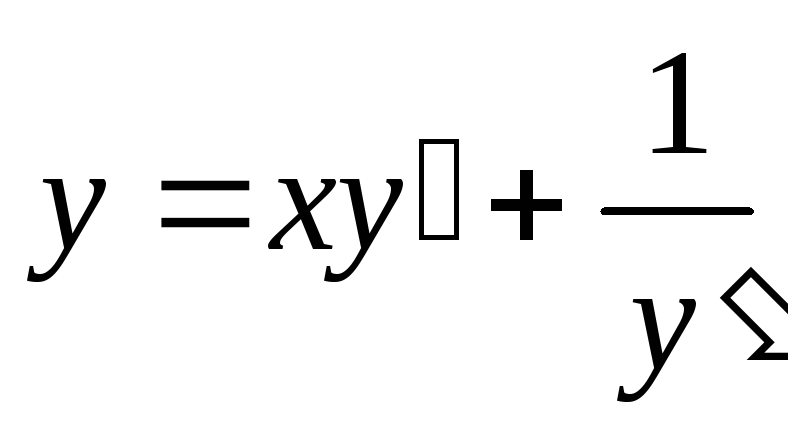 .
(4.6)
.
(4.6)
Решение. Подставим 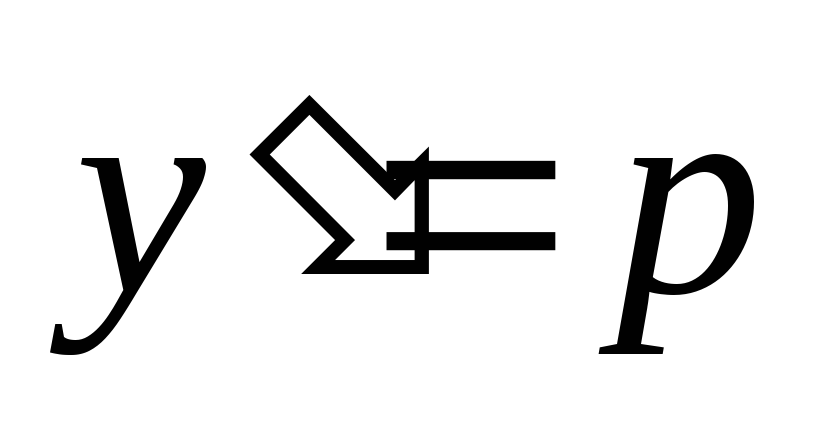 ,
получим
,
получим
 . (4.6′)
. (4.6′)
Продифференцировав
по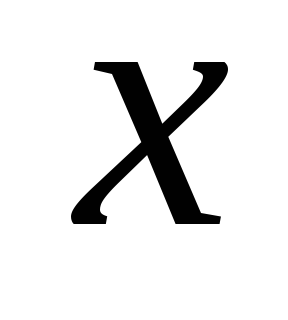 ,
имеем
,
имеем
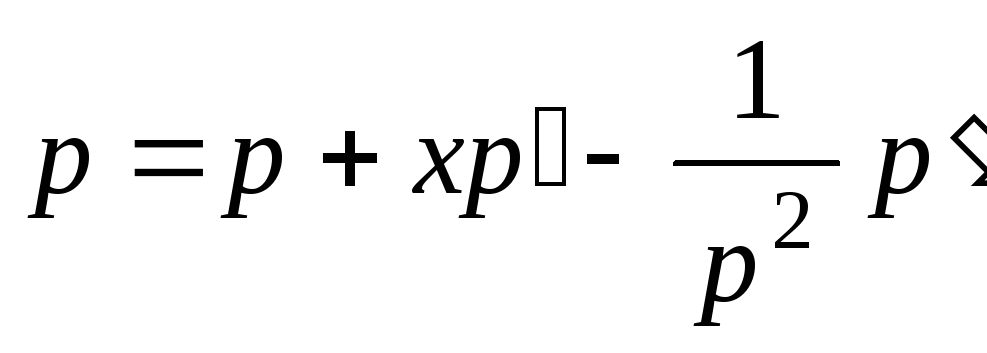 ,
,
откуда
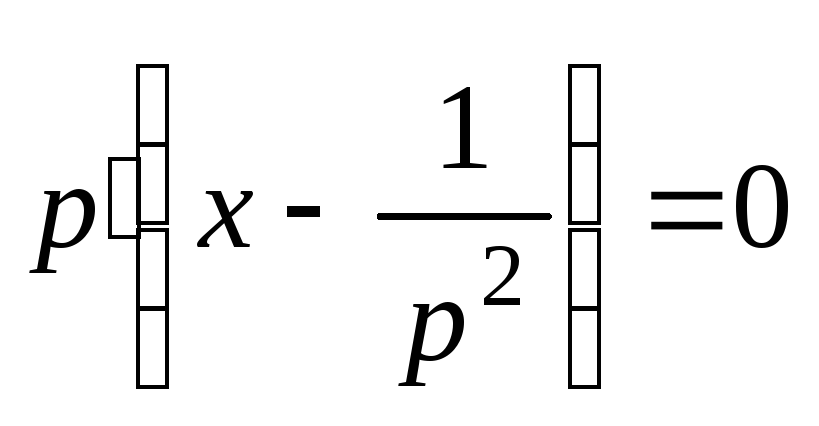 ;
;  ;
; 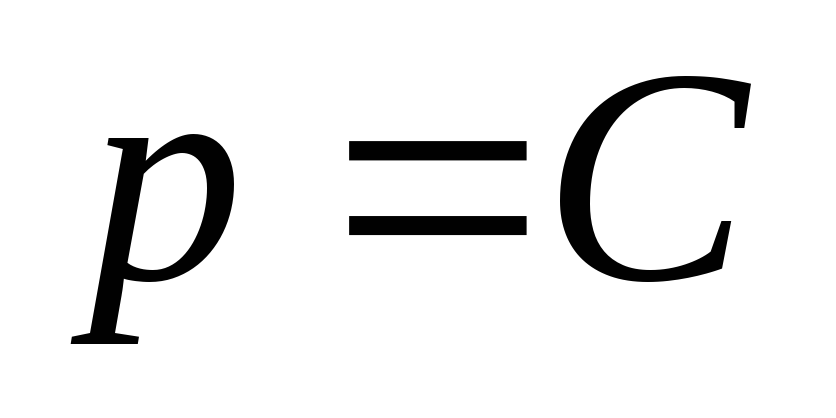 ;
;  .
.
Подставив в
выражения для  и
и 
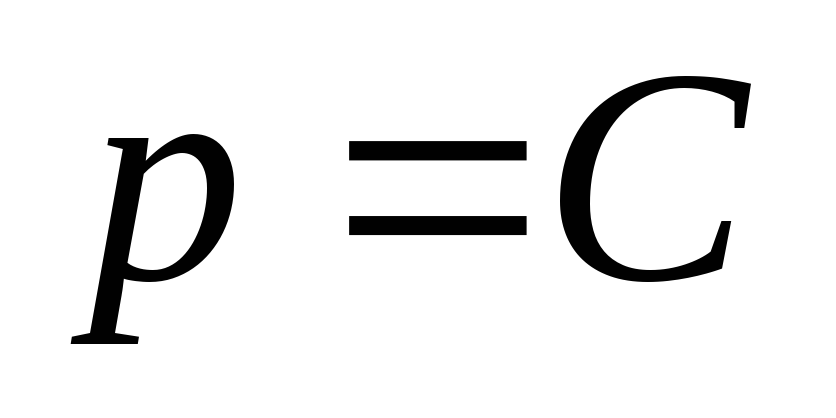 ,
получим систему уравнений:
,
получим систему уравнений:
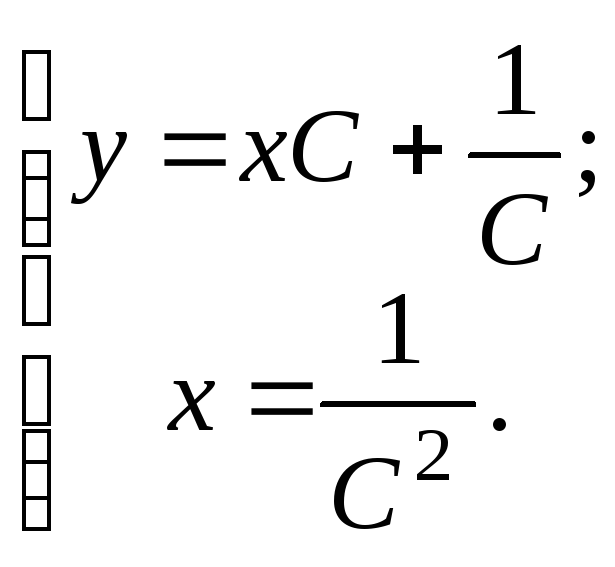 (4.7)
(4.7)
подставив 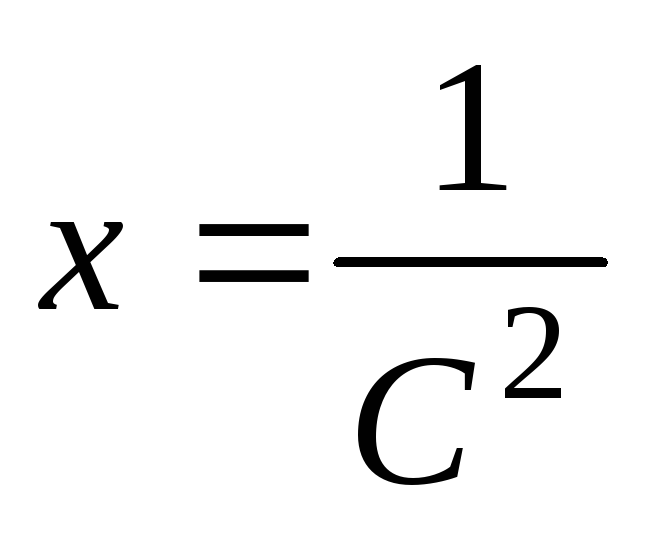 в первое уравнение, найдем
в первое уравнение, найдем
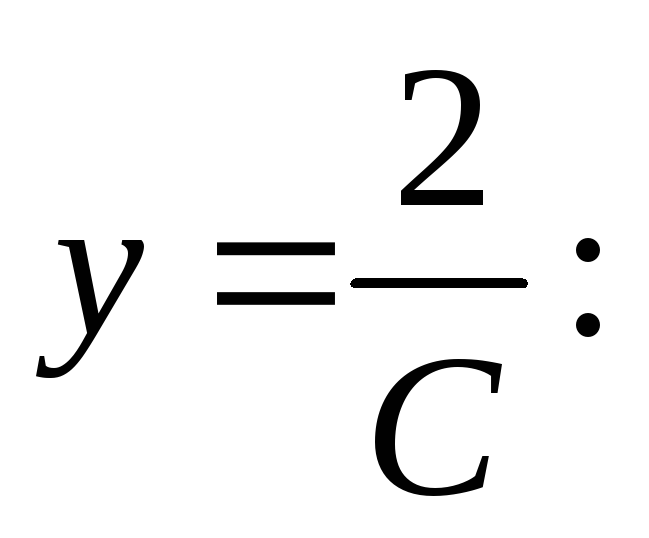
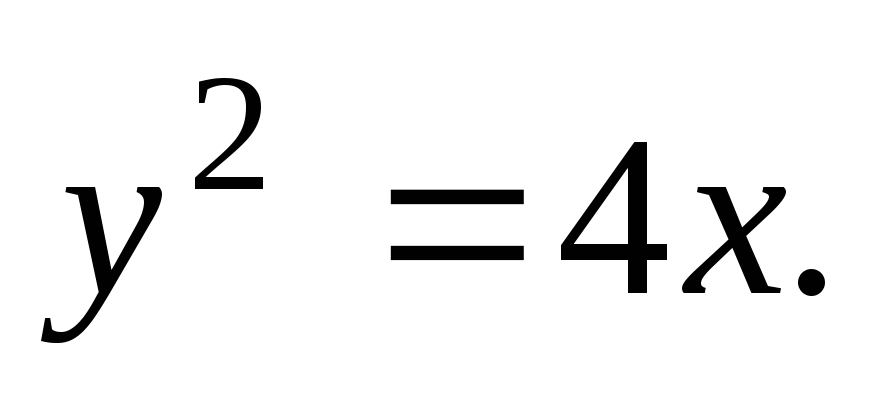 (4.8)
(4.8)
Это – уравнение параболы, симметричной относительно оси OX. Семейство прямых, описываемых первым уравнением системы (4.7), есть семейство касательных к этой параболе. Таким образом, парабола (4.8) может рассматриваться как огибающая семейства собственных касательных. Такое геометрическое истолкование характерно для уравнения Клеро.
Пример 4.3.  .
.
Это — уравнение Лагранжа. Его канонический вид
 .
.
Решаем его
методом введения параметра 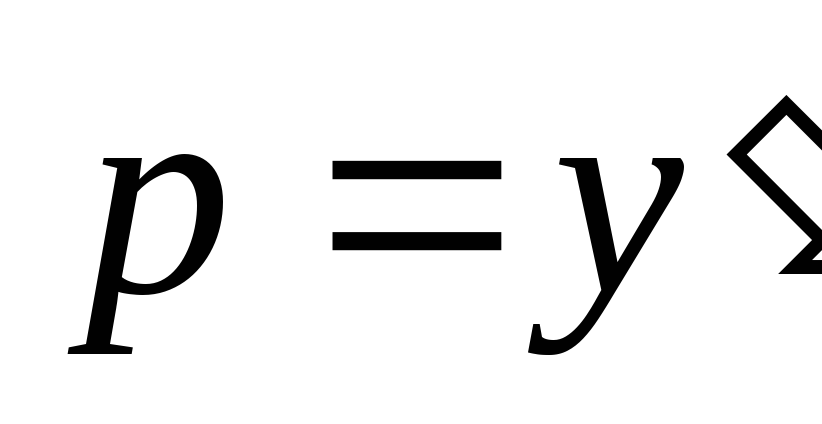 с последующим дифференцированием по
переменной
с последующим дифференцированием по
переменной 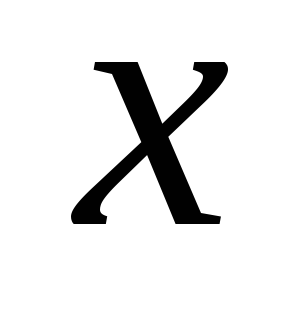 .
Получаемое соотношение оказывается
линейным неоднородным уравнением
первого порядка относительно функции
.
Получаемое соотношение оказывается
линейным неоднородным уравнением
первого порядка относительно функции 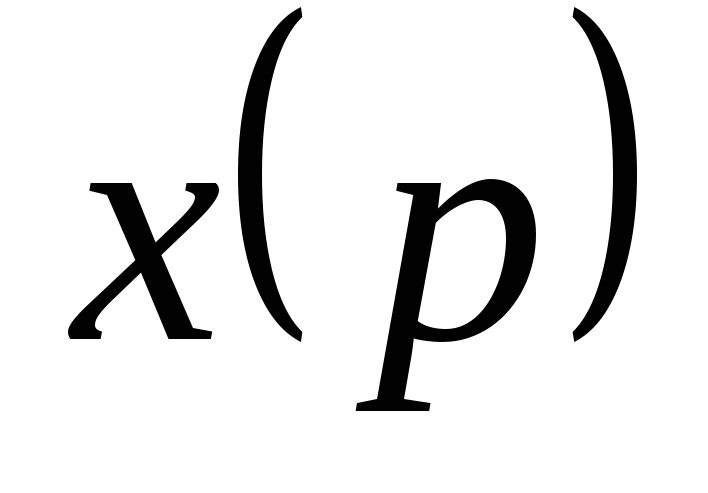 и её производной
и её производной 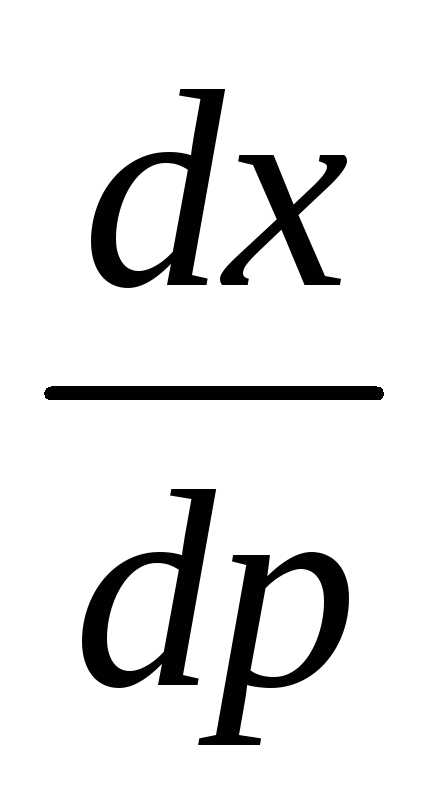 .
.
В результате интегрирования этого уравнения общее решение получается в параметрической форме, как система функций
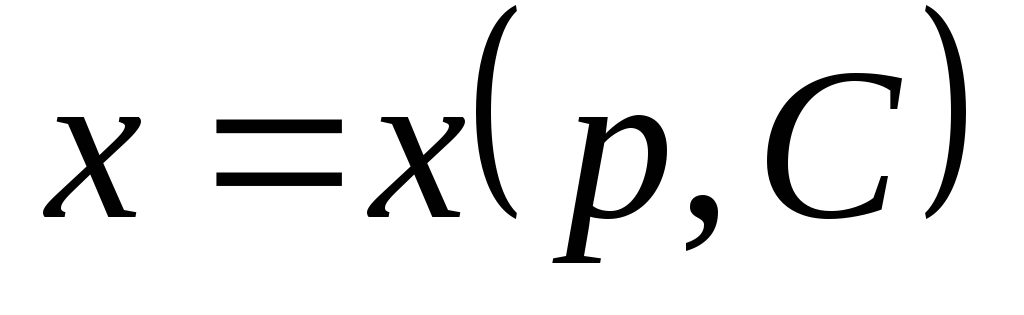 ,
,  .
.
Решение. Полагаем  ,
тогда
,
тогда
 . (4.9)
. (4.9)
Дифференцируя,
находим 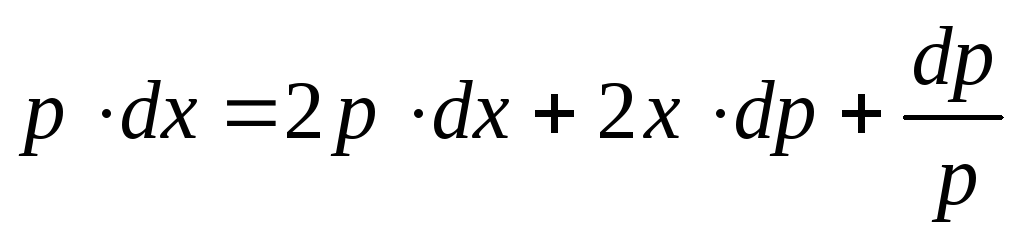 ,
, откуда
откуда
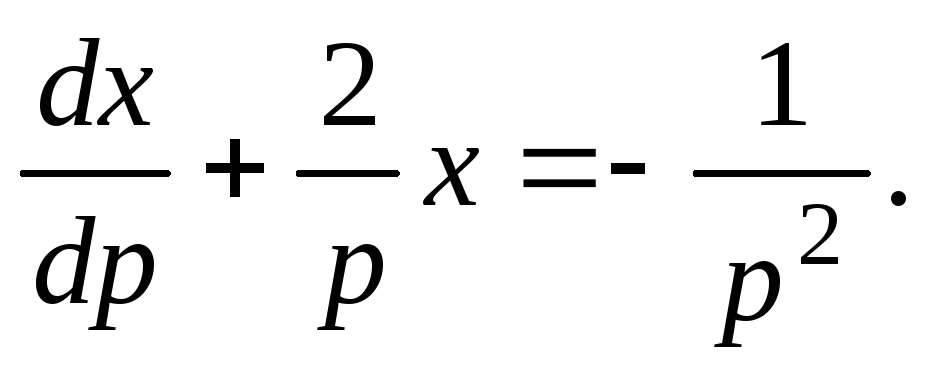 (4.10)
(4.10)
Это — линейное неоднородное дифференциальное
уравнение первого порядка относительно
функции  и её производной
и её производной  .
Однородное уравнение
.
Однородное уравнение
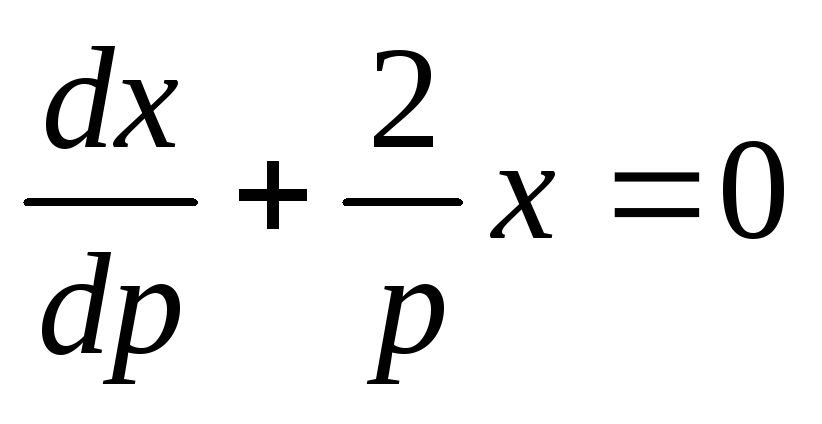
решаем методом разделения переменных. Получаем:
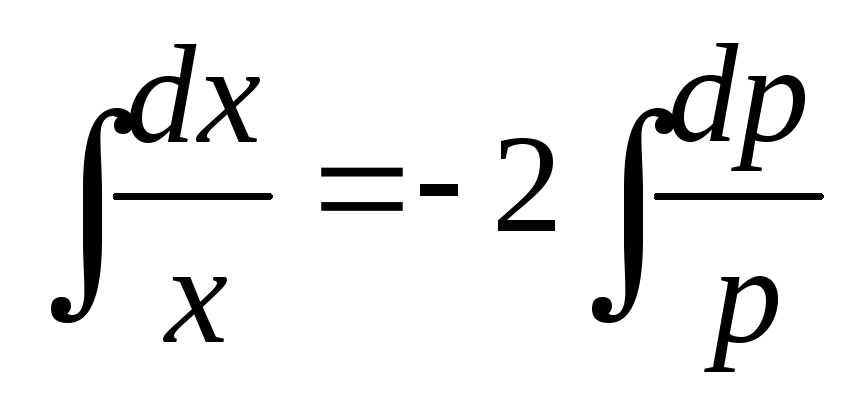 ;
;  ;
; 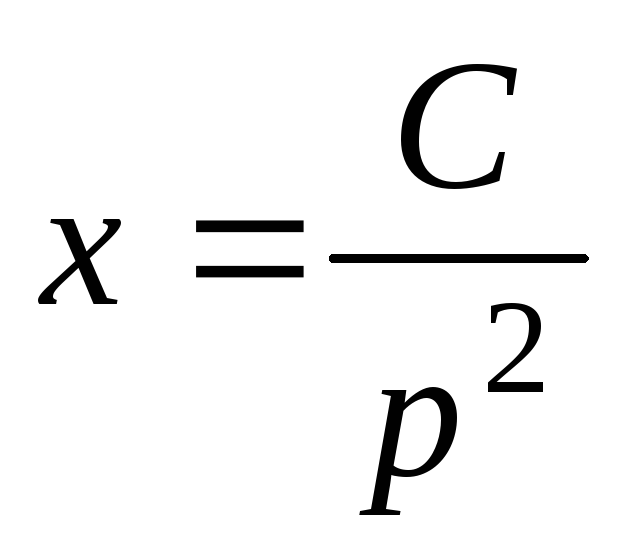 .
.
Решение
неоднородного уравнения находим методом
вариации произволь-ной постоянной в
виде 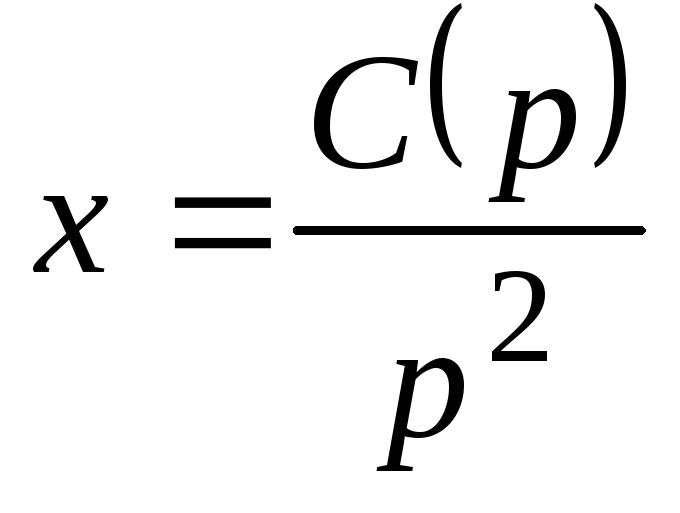 .
Подставив последнее в неоднородное
уравнение (4.10), имеем:
.
Подставив последнее в неоднородное
уравнение (4.10), имеем:
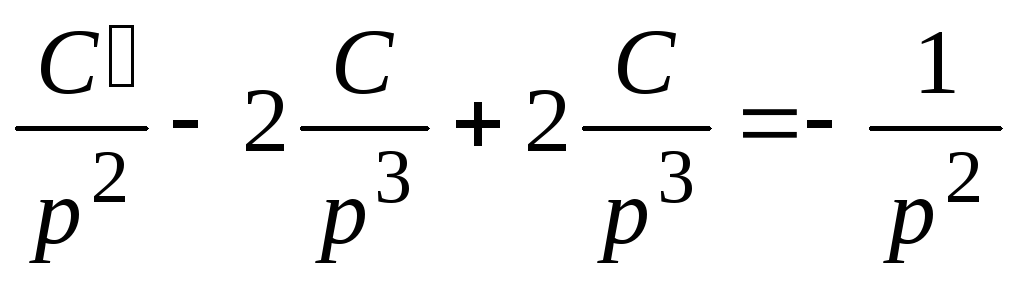 ;
;
после сокращений
 ,
, 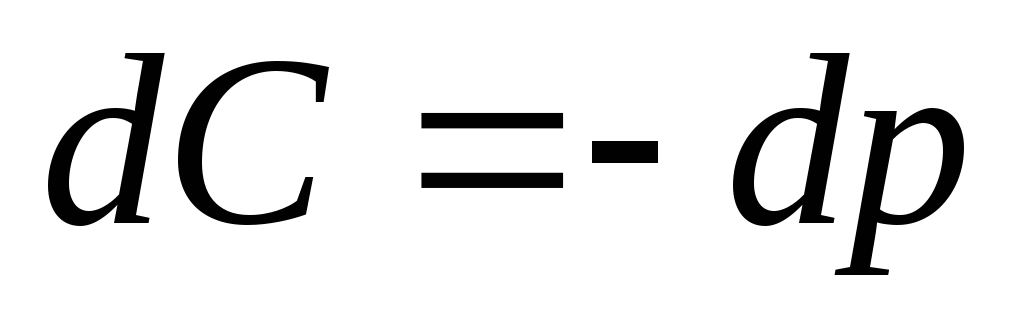 ,
, 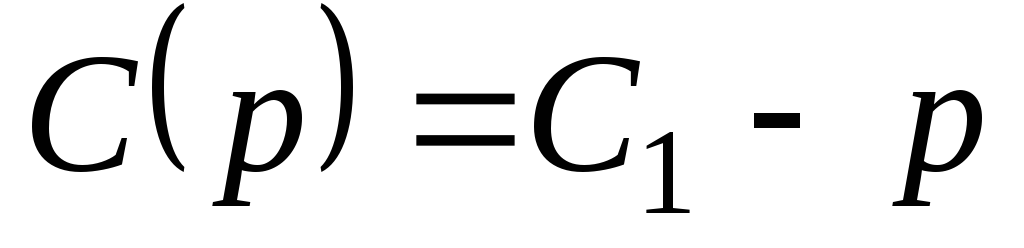 ,
, 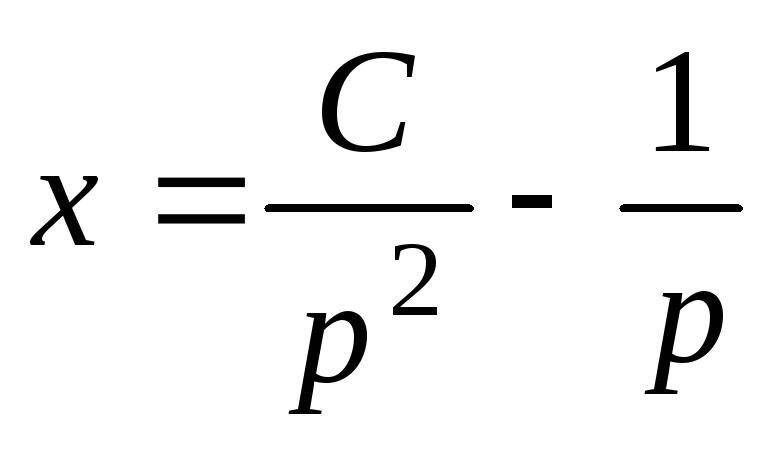 .
(Здесь
.
(Здесь  .)
.)
Подставив найденное выражение для 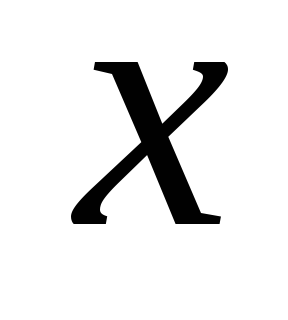 в выражение для
в выражение для  (4.9), найдем общее решение уравнения
Лагранжа в параметрической форме:
(4.9), найдем общее решение уравнения
Лагранжа в параметрической форме:
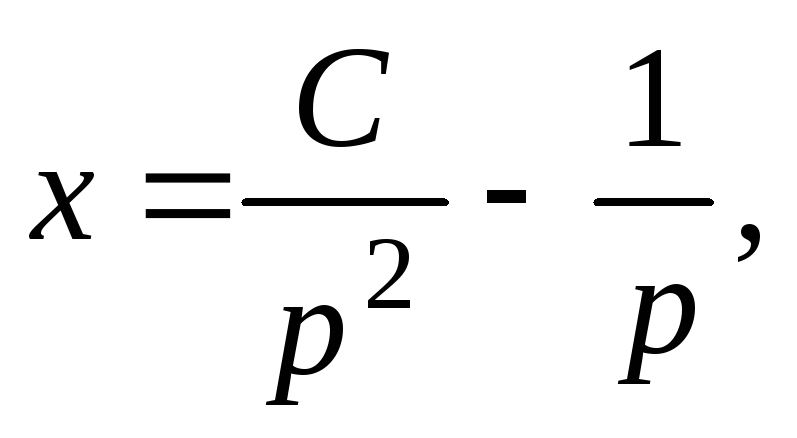
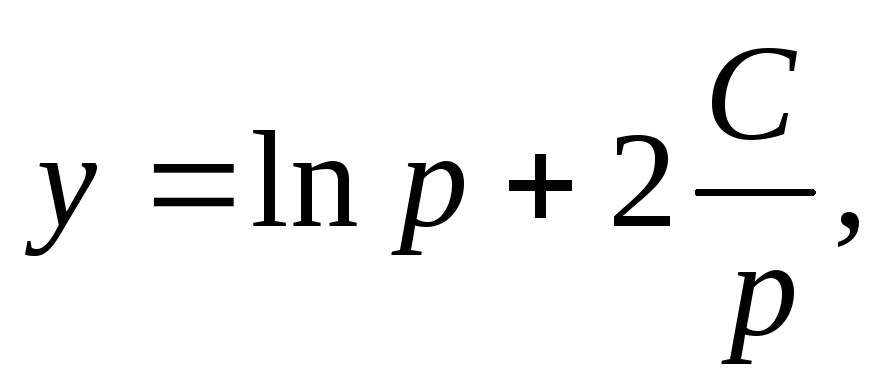
 .
.
Методом введения параметра удаётся интегрировать и другие типы дифференциальных уравнений, например, вида
 или
или 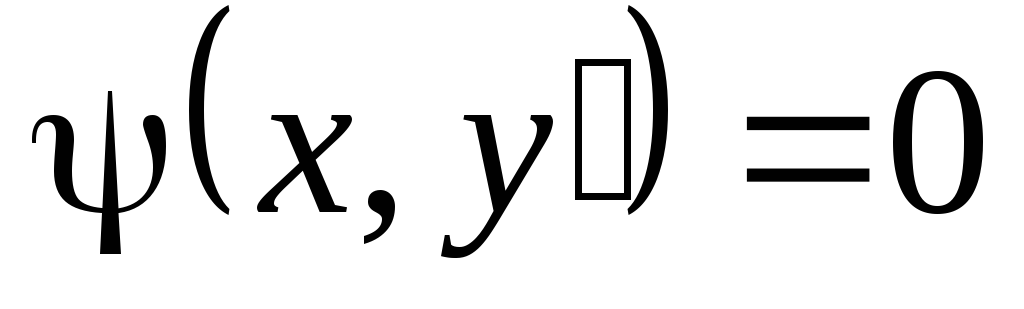 .
.
Если эти уравнения можно разрешить
относительно  ,
то получаются уравнения с разделяющимися
переменными. В противном случае
проинтегрировать уравнения иногда
возможно методом введения параметра.
,
то получаются уравнения с разделяющимися
переменными. В противном случае
проинтегрировать уравнения иногда
возможно методом введения параметра.
А. Уравнение вида 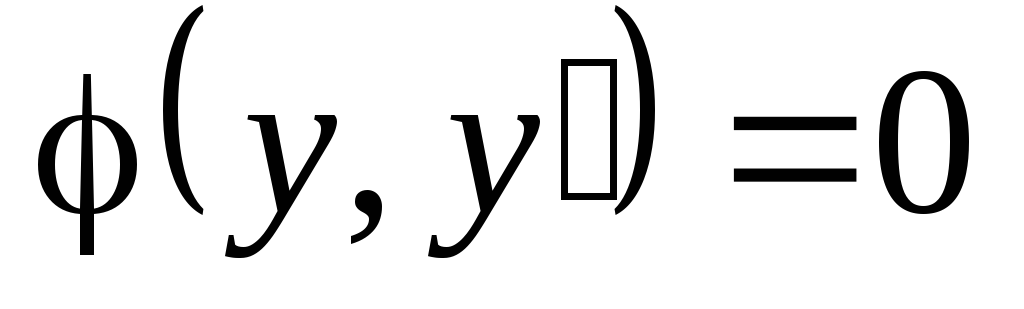 разрешимо относительно y:
разрешимо относительно y:
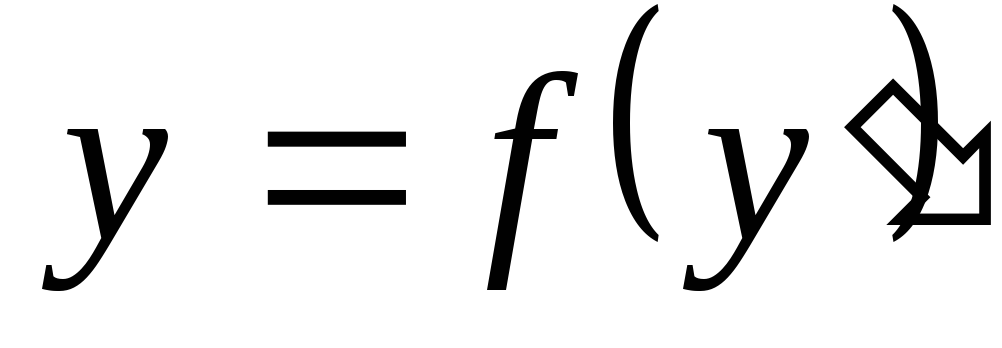 .
.
Полагаем 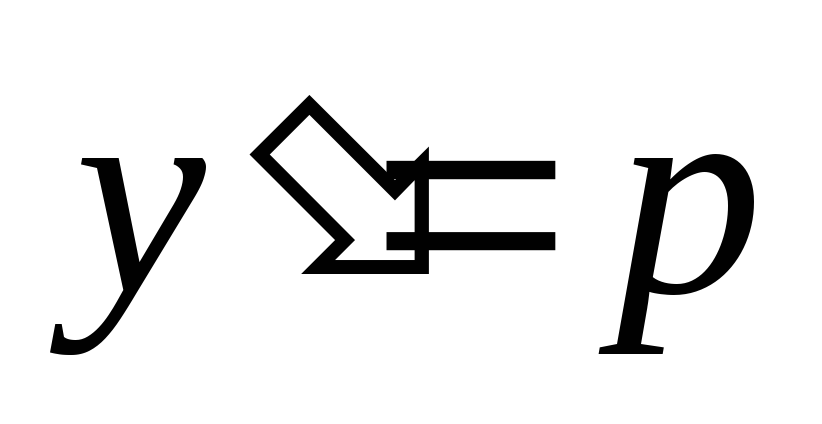 ,
тогда
,
тогда  .
Дифференцируем последнее урав-нение и
, заменив dy на p dx,
получаем
.
Дифференцируем последнее урав-нение и
, заменив dy на p dx,
получаем 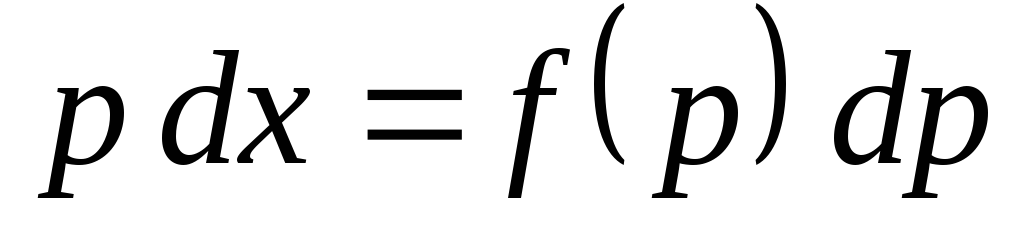 ,
откуда
,
откуда

 и
и 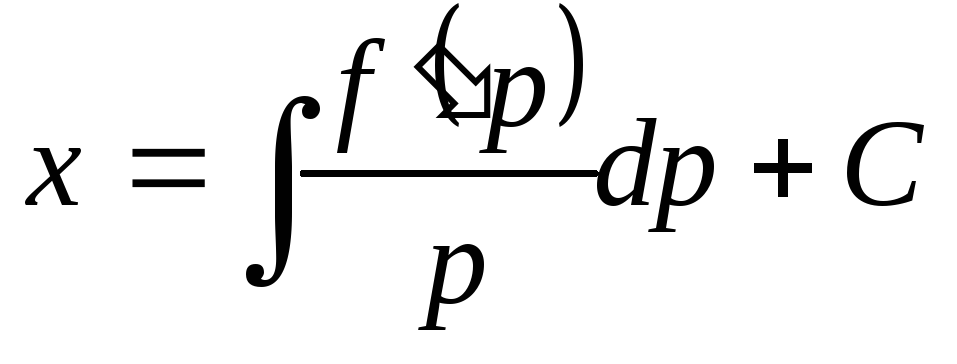 ,
, 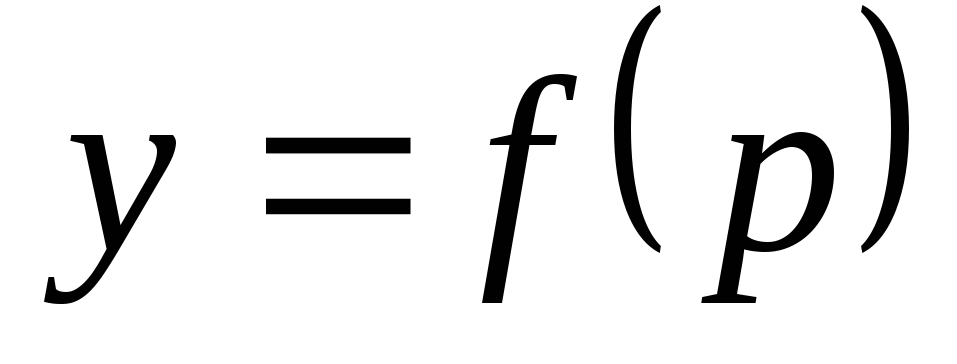 .
.
Это — общее решение дифференциального уравнения в параметрической форме.
Пример 4.4.
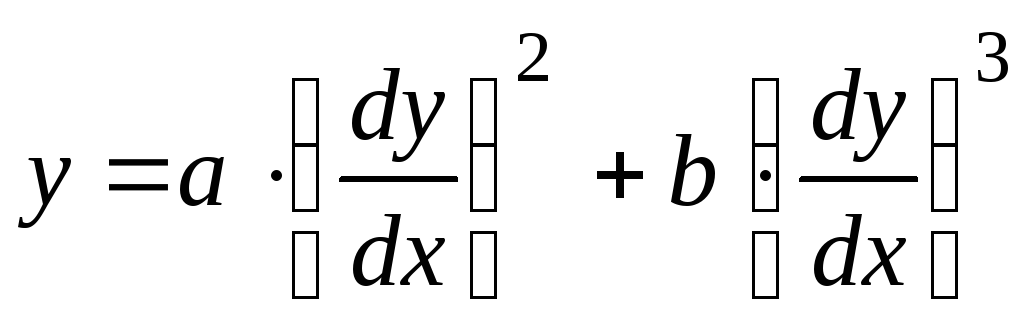 (a и b –
постоянные).
(a и b –
постоянные).
Решение. Положим 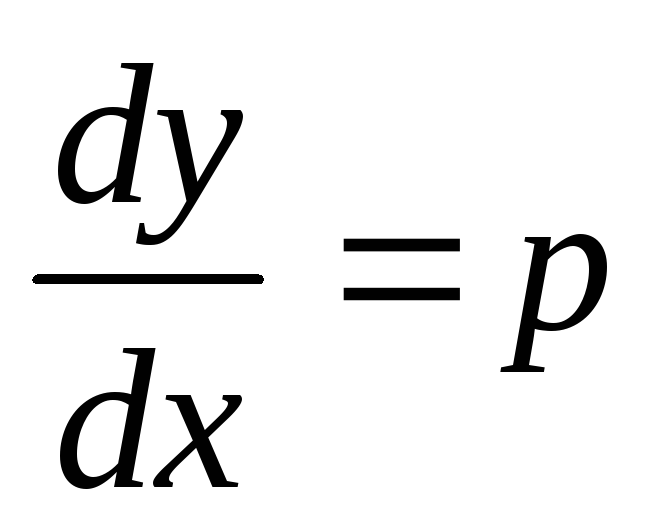 ,
тогда
,
тогда 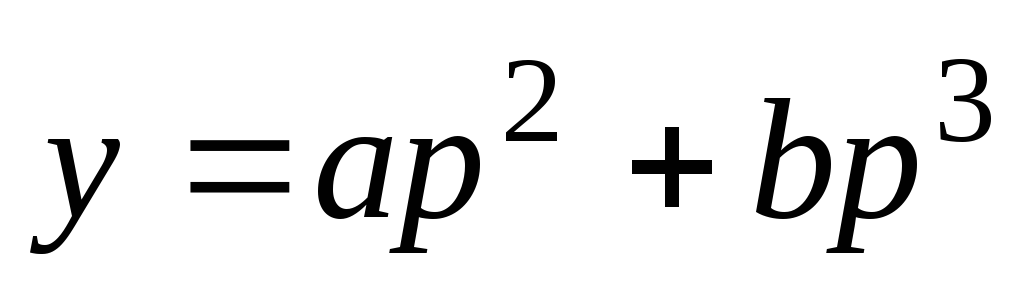 .
.
 или
или 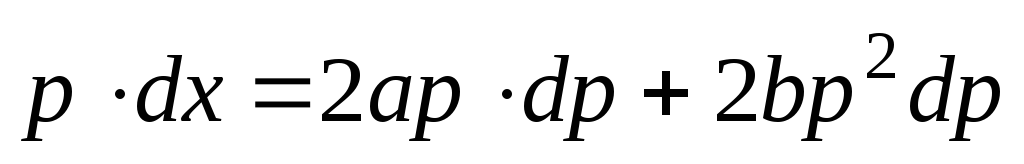 ,
,
откуда
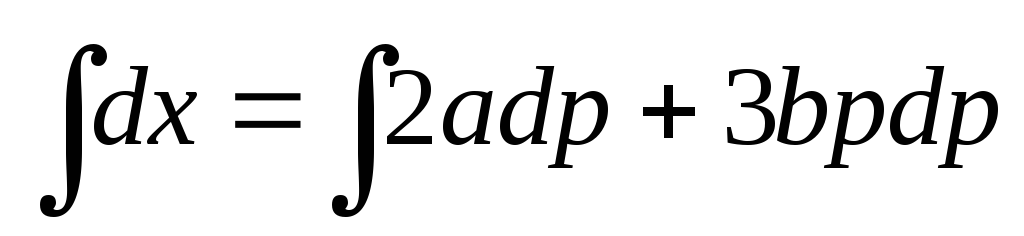 и
и  .
.
Общее решение будет иметь вид:
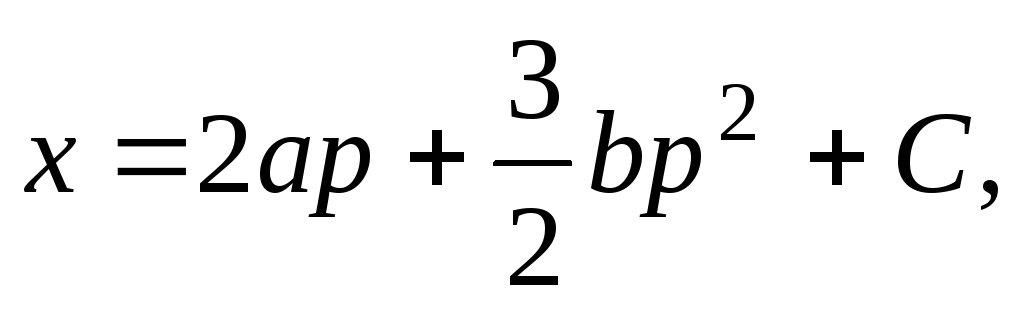
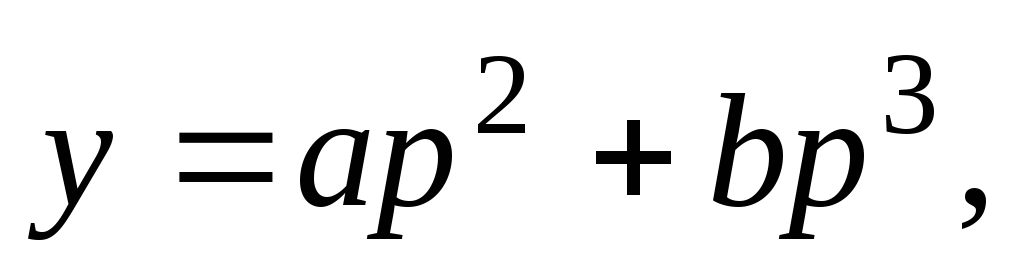
 .
.
В. Уравнение вида 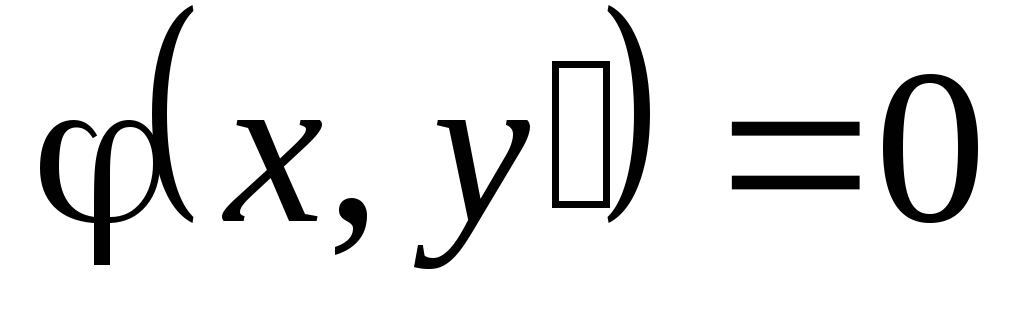 разрешимо относительно
разрешимо относительно  ,
т.е.
,
т.е. 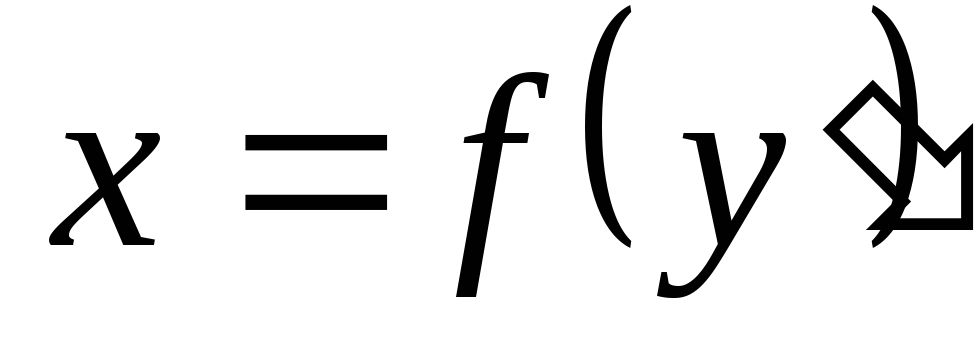 .
Полагая
.
Полагая 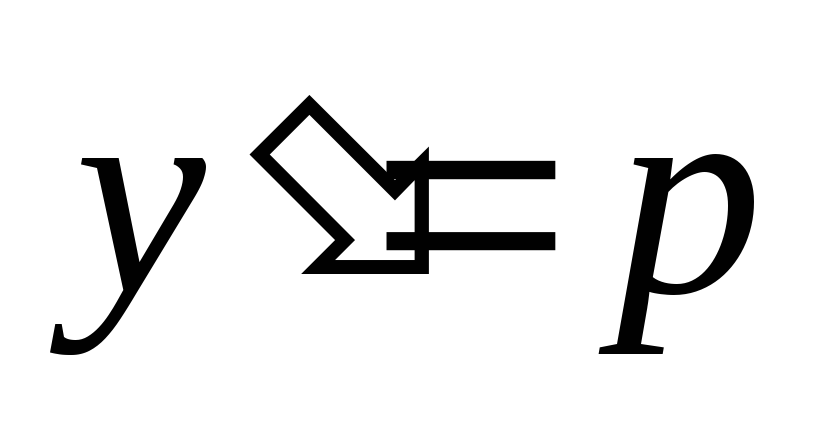 ,
получим
,
получим 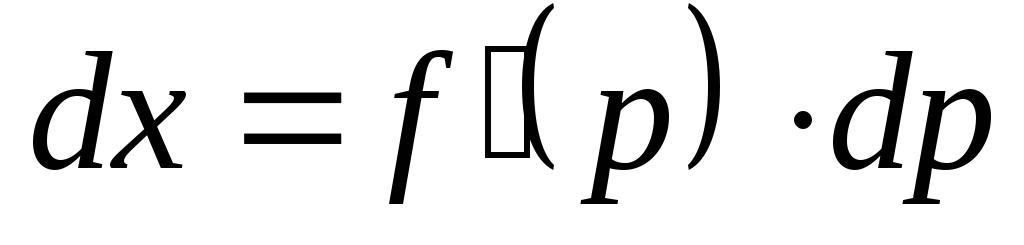 .
Кроме того,
.
Кроме того,  т.е.
т.е.  и
и 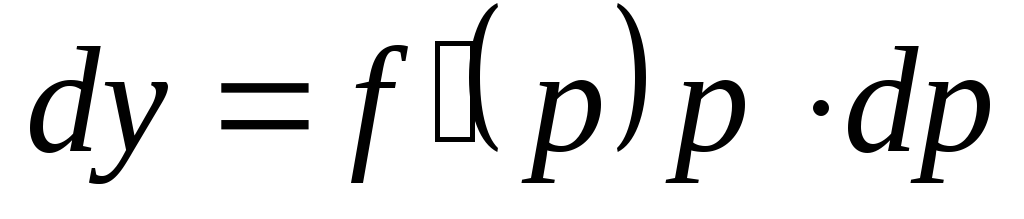 .
Проинтегрировав, найдем общее
решение дифференциального уравнения
в параметри-ческой форме:
.
Проинтегрировав, найдем общее
решение дифференциального уравнения
в параметри-ческой форме:
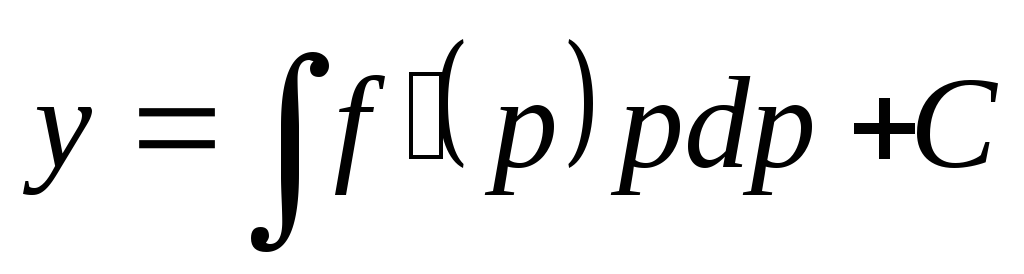 ,
, 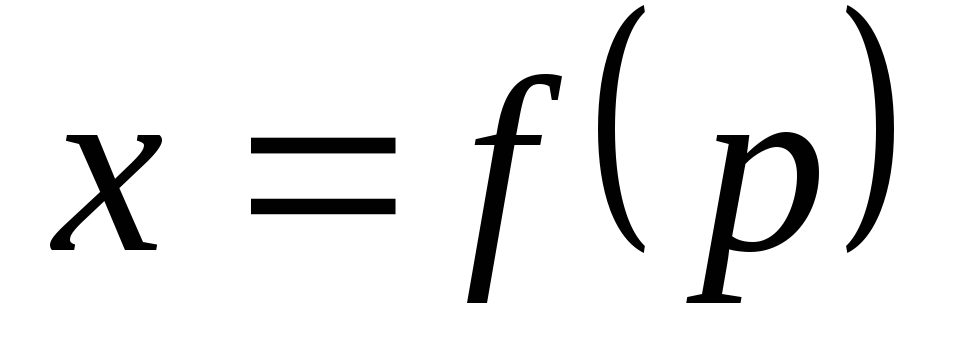 .
.
Пример 4.5. 
Решение. Положим 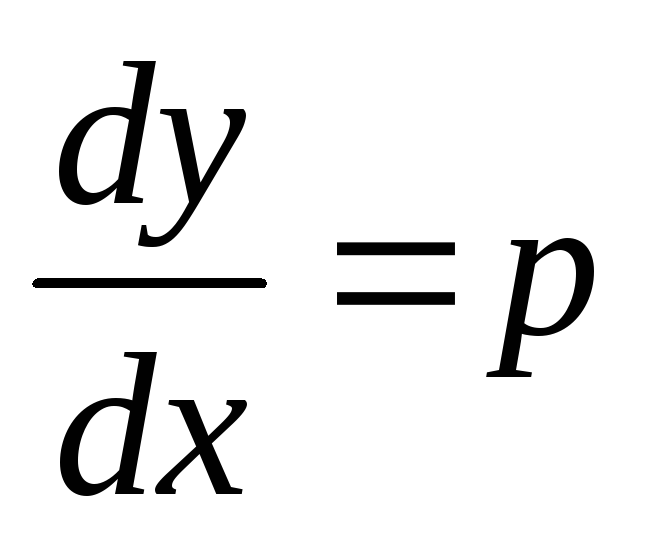 ,
тогда
,
тогда 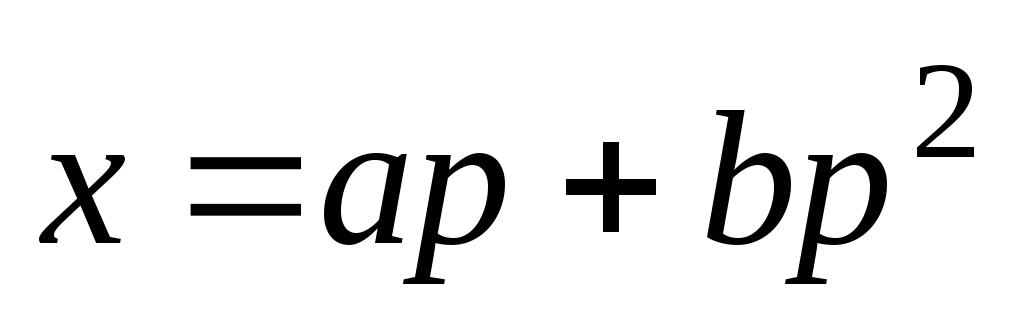 ,
,
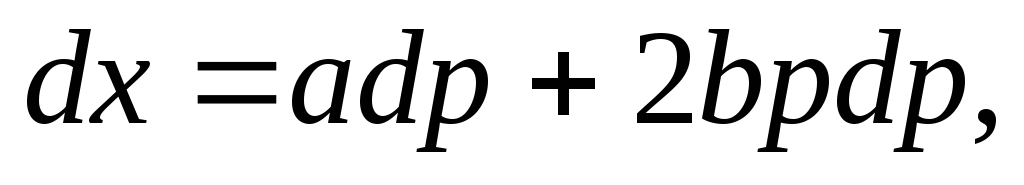
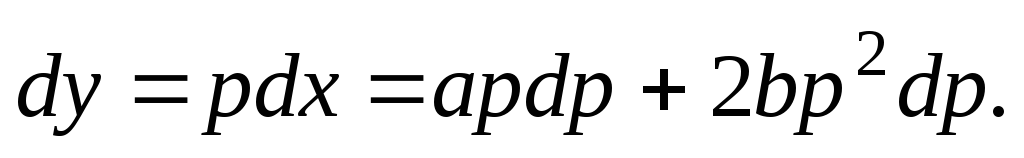
В итоге
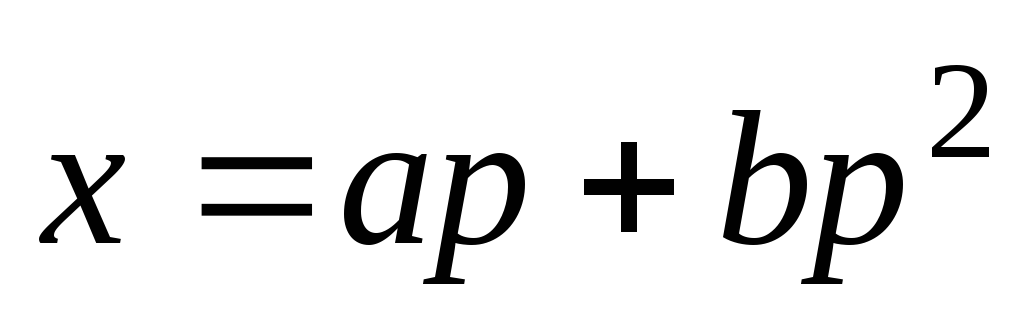 ,
, 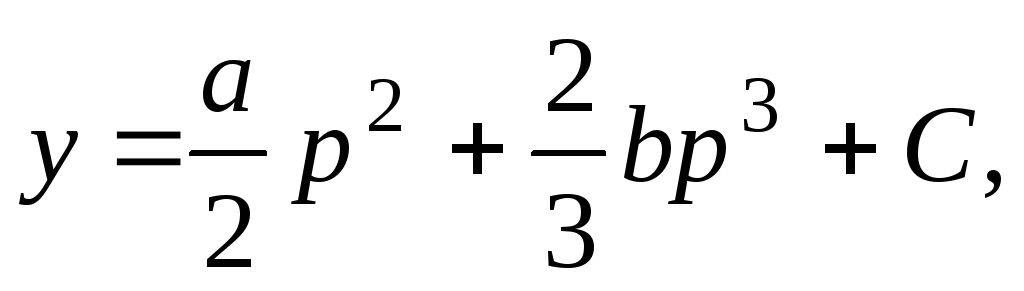
 .
.
Б. 4117. 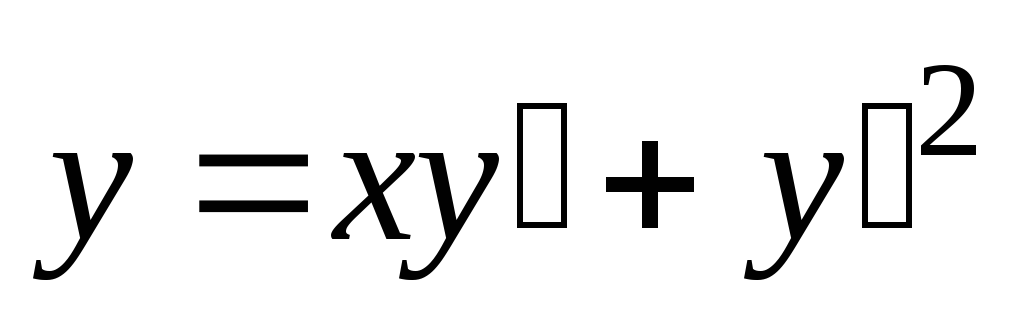 .
.
Решение. Это — уравнение Клеро. После
введения параметра 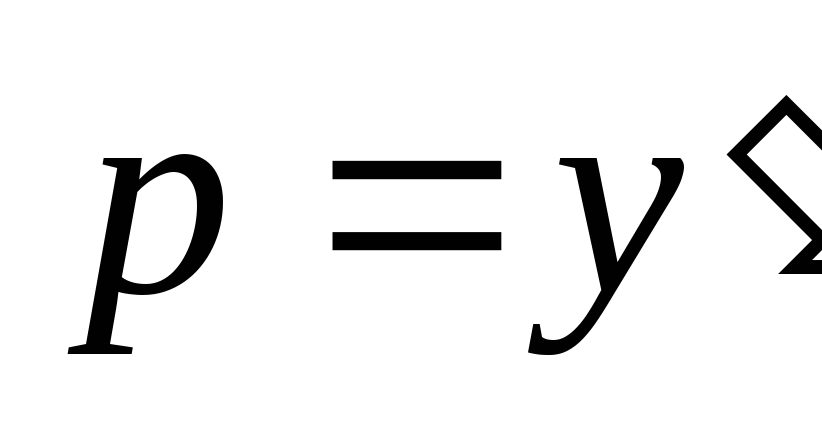 уравнение имеет вид:
уравнение имеет вид:
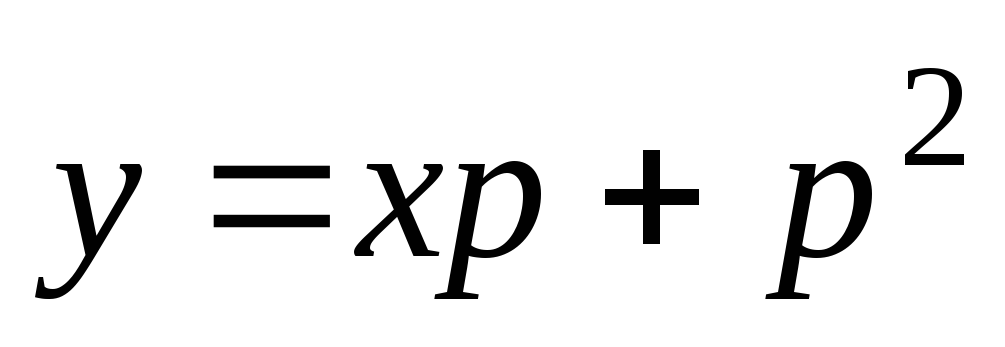 .
(4.11)
.
(4.11)
Взяв полный
дифференциал и заменив  на
на  ,
получим:
,
получим:
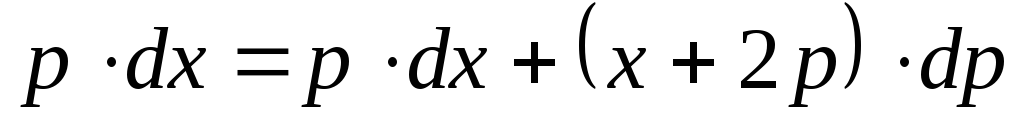 ,
откуда
,
откуда 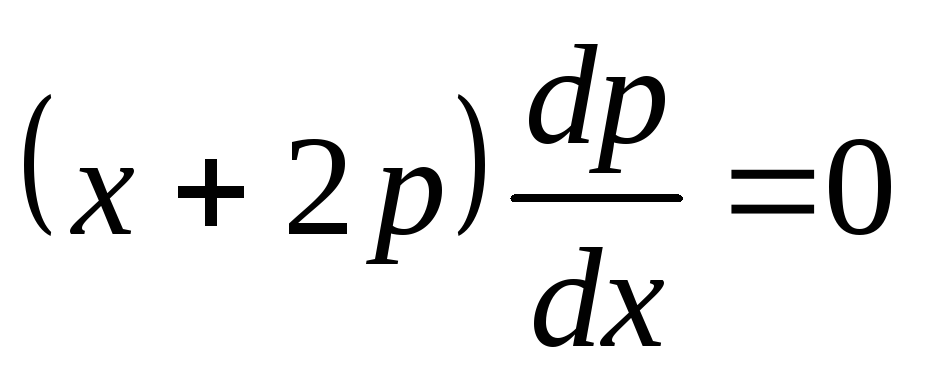 .
.
Если 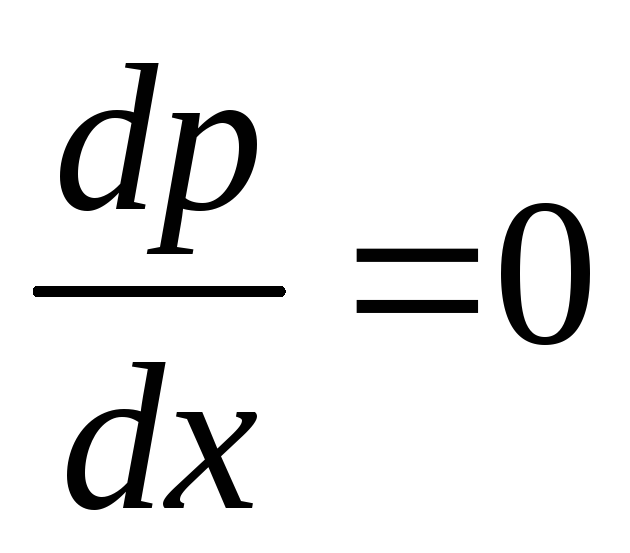 ,
то
,
то 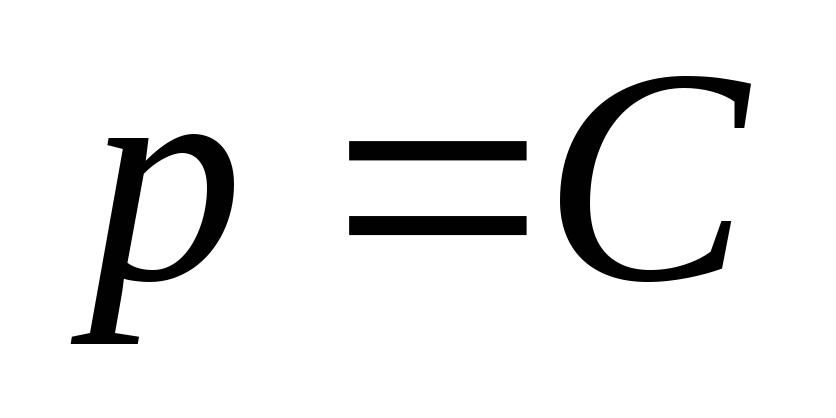
 .
.
Подставив 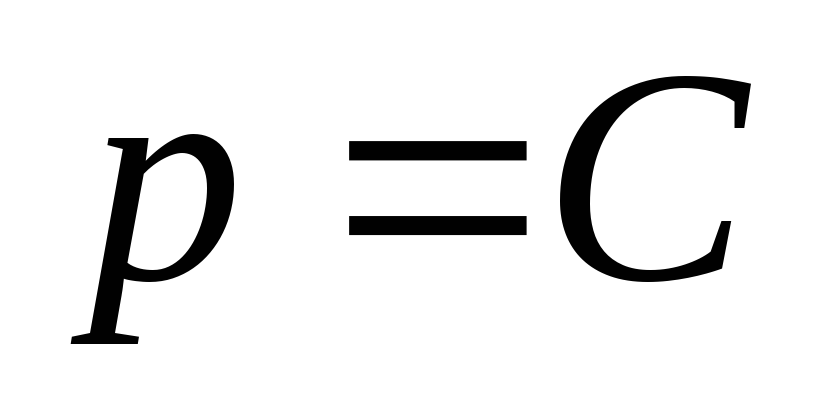 в (4.11), получаем
в (4.11), получаем
 , (4.12)
, (4.12)
подставив  в уравнение
в уравнение 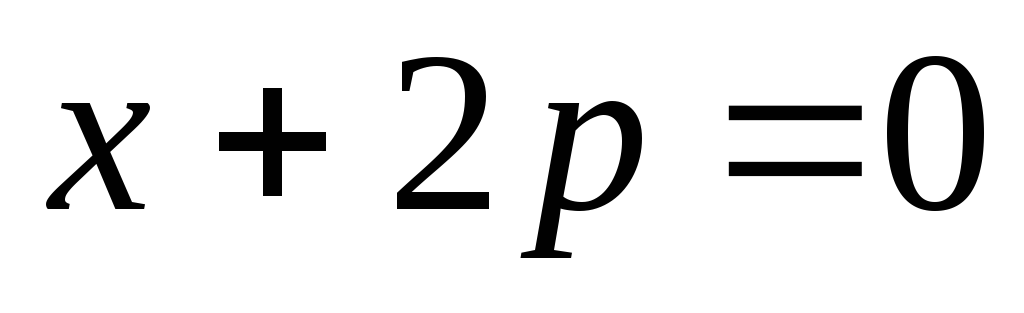 ,
имеем
,
имеем
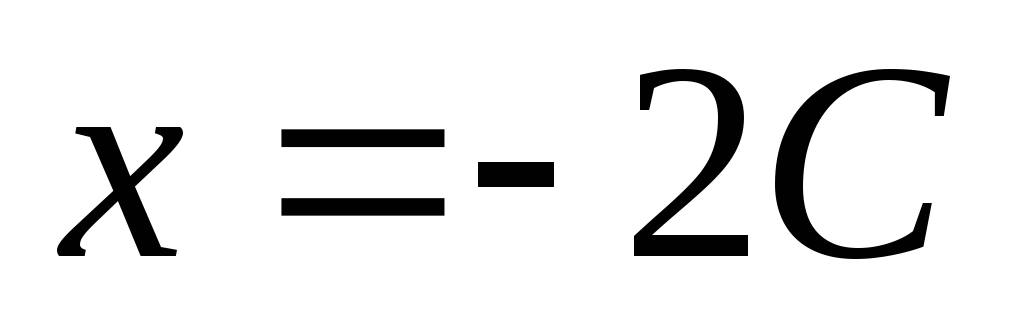 . (4.13)
. (4.13)
Очевидно, что (4.13) может быть получено из (4.12) дифферен-цированием по параметру C, следовательно, в соответствии с изложенным ранее, система уравнений (4.12), (4.13) в параметрической форме описывает особое решение уравнения, графиком которого является огибающая семейства прямых, заданных общим решением (4.12).
Исключив параметр C из системы уравнений (4.12), (4.13), найдем урав-нение огибающей в явном виде:
 .
.
Б. 4123. 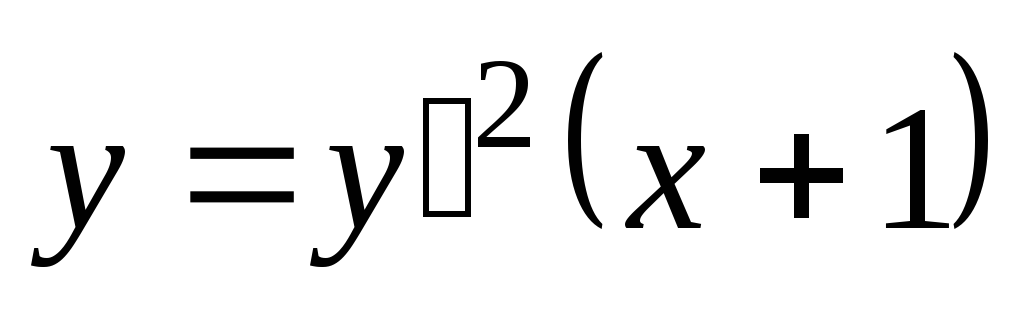 .
.
Решение. Введем параметр 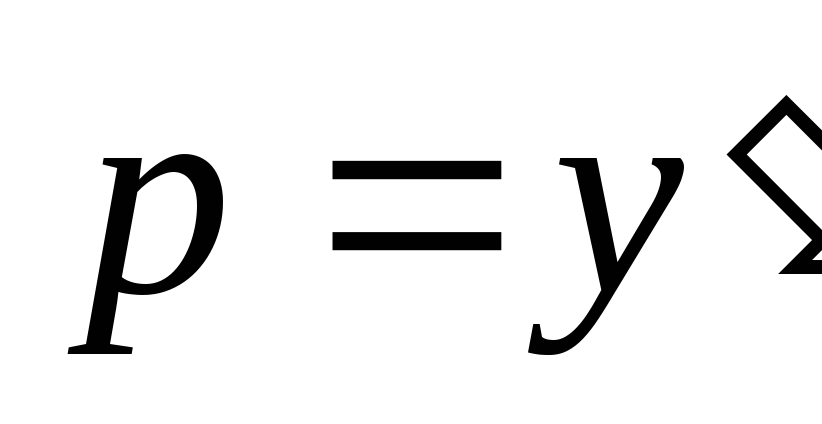 ,
получим
,
получим
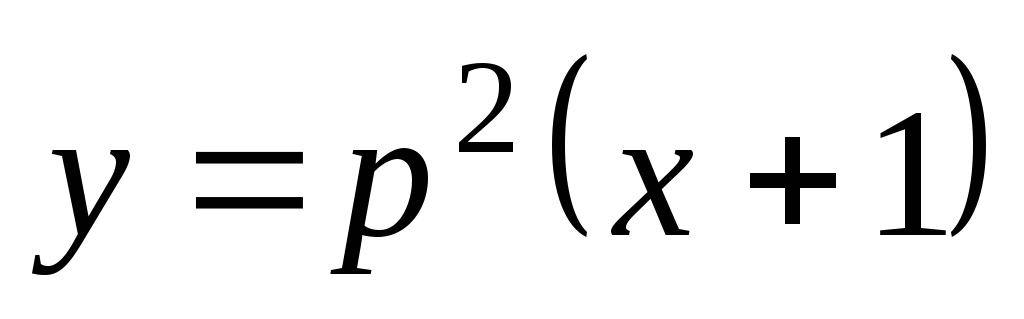 . (4.14)
. (4.14)
Дифференциал последнего
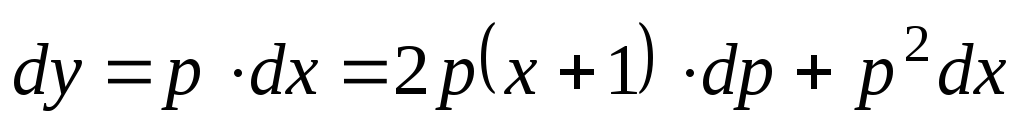 ,
,
откуда
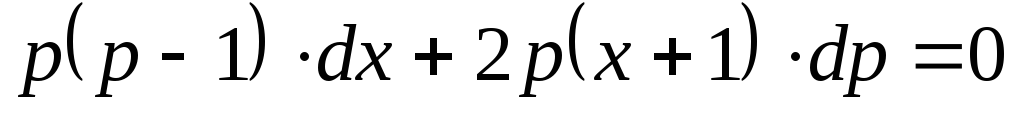 .
.
Если 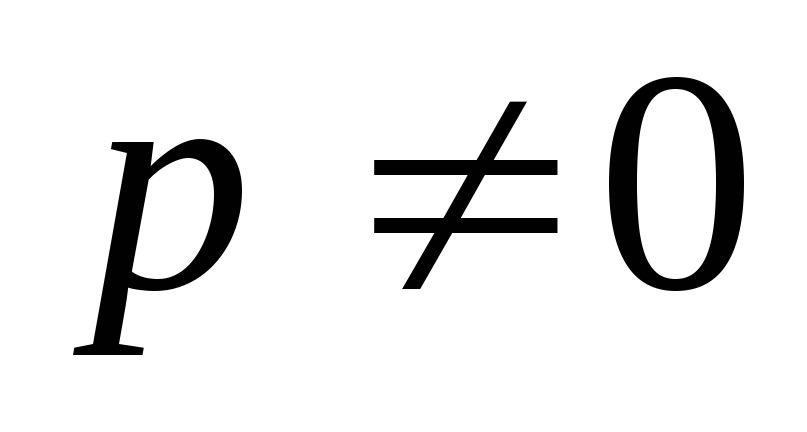 ,
то, сократив на
,
то, сократив на 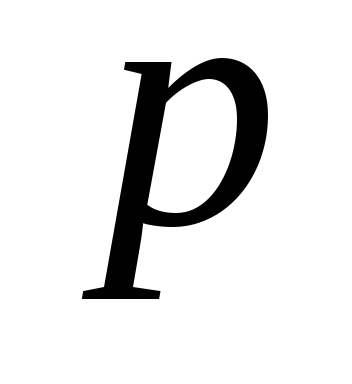 ,
получим уравнение:
,
получим уравнение:
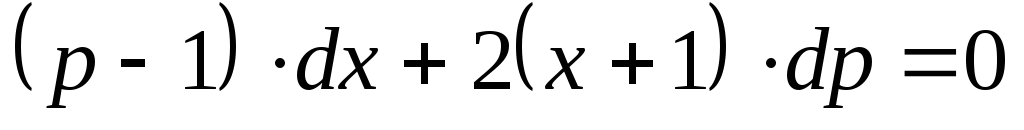
с разделяющимися переменными. Далее
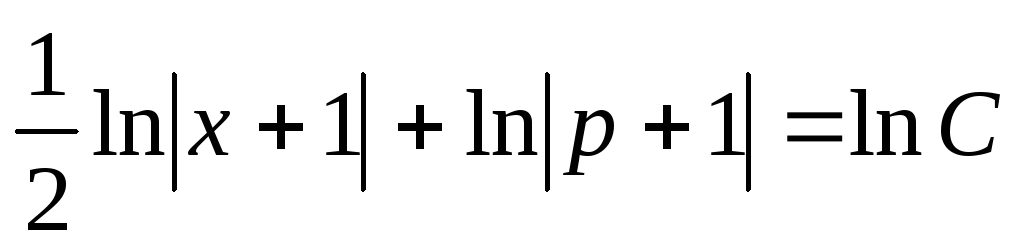 ,
, 
откуда

Подставив p в (4.14), находим:
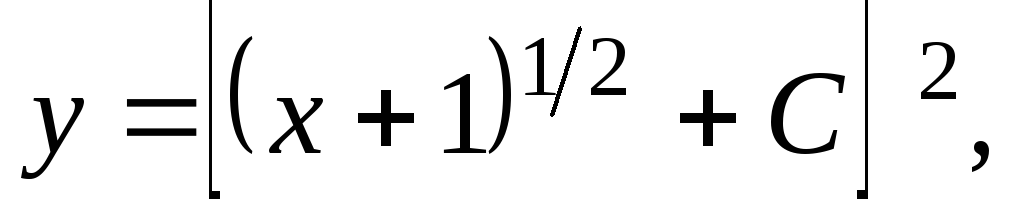
 . (4.15)
. (4.15)
Если 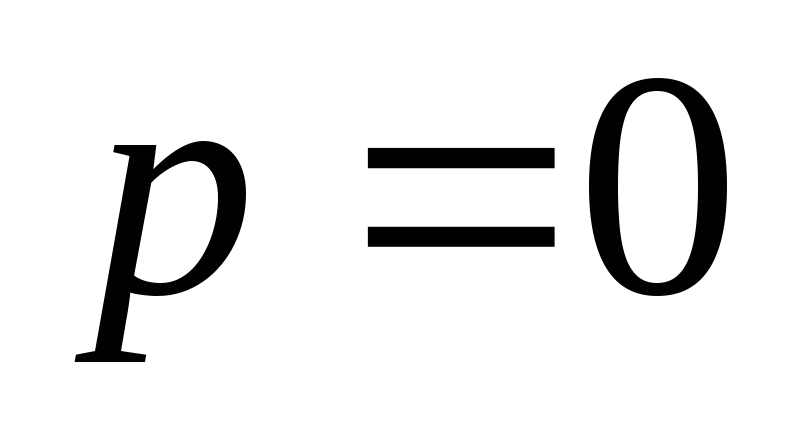 ,
то из соотношения (4.14) очевидно, что
,
то из соотношения (4.14) очевидно, что 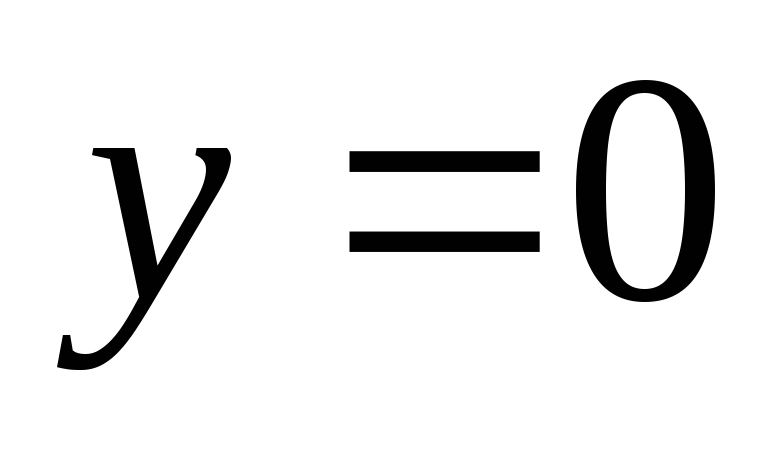 есть частное решение уравнения. Оно
является и особым решением. Графиком
решения
есть частное решение уравнения. Оно
является и особым решением. Графиком
решения 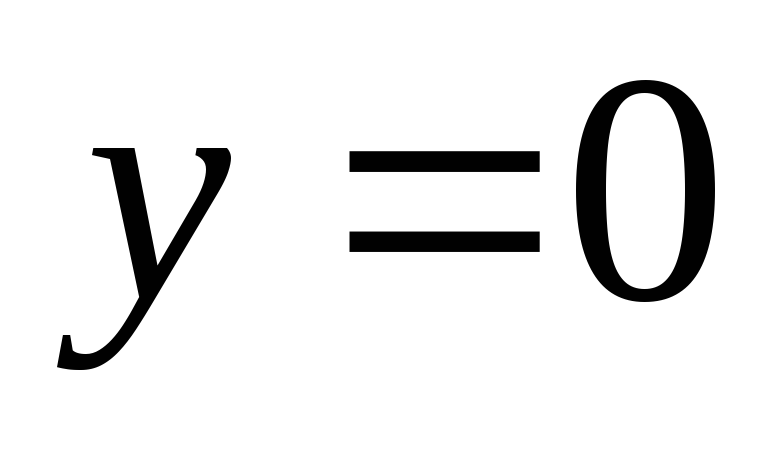 является ось OX, и в каждой точке
графика нарушается условие единственности
решения, так как каждая из интегральных
кривых, определяемых общим решением
(4.15), пересекает ось OX.
является ось OX, и в каждой точке
графика нарушается условие единственности
решения, так как каждая из интегральных
кривых, определяемых общим решением
(4.15), пересекает ось OX.
Примеры для самостоятельного решения: Б. 4118, Б. 4120, Б. 4122, Б. 4125
Уравнения, не разрешенные относительно производной
Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.
241. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
y’2 — y2 = 0.
242. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
8y’3 = 27y.
243. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
(y’ + 1)3 = 27(x + y)2.
244. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
y2(y’2 + 1) = 1.
245. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
y’2 — 4y3 = 0.
246. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
y’2 = 4y3(1 — y).
247. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
xy’2 = y.
249. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
y’3 + y2 = yy'(y’ + 1).
250. Найти все решения данного уравнения. Выделить особые решения (если они есть). Дать чертеж.
4(1 — y) = (3y — 2)2y’2.
251. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y’2…
252. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
xy'(xy’ + y) =…
254. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
xy’2…
256. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y’3…
257. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y’2…
259. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y’2…
260. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y'(2y — y’) =…
261. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y’4…
263. Уравнение разрешить относительно y’, после этого общее решение искать обычными методами (§§ 2, 4, 5, 6). Найти также особые решения, если они есть.
y(xy’ — y)2…
267. Решить уравнение методом введения параметра.
x = y’3 + y’.
268. Решить уравнение методом введения параметра.
x(y’2 — 1) = 2y’.
269. Решить уравнение методом введения параметра.
x = y’ sqrt(y’2 + 1).
270. Решить уравнение методом введения параметра.
y'(x — ln y’) = 1.
271. Решить уравнение методом введения параметра.
y = y’2 + 2y’3.
272. Решить уравнение методом введения параметра.
y = ln(1 + y’2).
273. Решить уравнение методом введения параметра.
(y’ + 1)3 = (y’ — y)2.
274. Решить уравнение методом введения параметра.
y = (y’ — 1)ey’.
275. Решить уравнение методом введения параметра.
y’4 — y’2 = y2.
276. Решить уравнение методом введения параметра.
y’2 — y’3 = y2.
277. Решить уравнение методом введения параметра.
y’4 = 2yy’ + y2.
278. Решить уравнение методом введения параметра.
y’2 — 2xy’ = x2 — 4y.
279. Решить уравнение методом введения параметра.
5y + y’2 = x(x + y’).
280. Решить уравнение методом введения параметра.
x2y’2 = xyy’ + 1.
281. Решить уравнение методом введения параметра.
y’3 + y2 = xyy’.
282. Решить уравнение методом введения параметра.
2xy’ — y = y’ ln yy’.
283. Решить уравнение методом введения параметра.
y’ = exy’/y.
284. Решить уравнение методом введения параметра.
y = xy’ — x2y’3.
285. Решить уравнение методом введения параметра.
y = 2xy’ + y2y’3.
286. Решить уравнение методом введения параметра.
y(y — 2xy’)3 = y’2.
287. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y = xy’ — y’2.
288. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y + xy’ = 4 sqrt(y’).
289. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y = 2xy’ — 4y’3.
290. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y = xy’ — (2 + y’).
291. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y’3 = 3(xy’ — y).
292. Решить уравнения Лагранжа и Клеро (задачи 287–296).
y = xy’2 — 2y’3.
293. Решить уравнения Лагранжа и Клеро (задачи 287–296).
xy’ — y = ln y’.
294. Решить уравнения Лагранжа и Клеро (задачи 287–296).
xy'(y’ + 2) = y.
295. Решить уравнения Лагранжа и Клеро (задачи 287–296).
2y’2(y — xy’) = 1.
296. Решить уравнения Лагранжа и Клеро (задачи 287–296).
2xy’ — y = ln y’.
297. Найти особое решение дифференциального уравнения, если известно семейство решений этого уравнения: а) у = Сх2 — C2, б) Су = (х — C)2, в) у = С(х — C)2,…
298. Найти кривую, каждая касательная к которой образует с осями координат треугольник площади 2a2.
299. Найти кривую, каждая касательная к которой отсекает на осях координат такие отрезки, что сумма величин, обратных квадратам длин этих отрезков, равна 1.
300. Найти кривую, проходящую через начало координат и такую, что отрезок нормали к ней, отсекаемый сторонами первого координатного угла, имеет постоянную длину, равную 2.
Метод разделения переменных — Википедия
Метод разделения переменных — метод решения дифференциальных уравнений, основанный на алгебраическом преобразовании исходного уравнения к равенству двух выражений, зависящих от разных независимых переменных.
В применении к уравнениям в частных производных схема разделения переменных приводит к нахождению решения в виде ряда или интеграла Фурье. В этом случае метод также называют методом Фурье (в честь Жана Батиста Фурье, построившего решения уравнения теплопроводности в виде тригонометрических рядов[1]) и методом стоячих волн[2][3].
Обыкновенные дифференциальные уравнения[править | править код]
Рассмотрим обыкновенное дифференциальное уравнение, правая часть которого есть произведение функции только от x{\displaystyle x} на функцию только от y{\displaystyle y} [4]:
dydx=g(x)h(y).(1){\displaystyle {\frac {dy}{dx}}=g(x)h(y).\qquad (1)}
При h(y)≠0{\displaystyle h(y)\neq 0} это уравнение можно переписать в виде
dyh(y)=g(x)dx{\displaystyle {\frac {dy}{h(y)}}=g(x)dx}.
Пусть y(x){\displaystyle y(x)} — некоторое решение уравнения (1). Из равенства дифференциалов следует, что их неопределённые интегралы отличаются лишь произвольным постоянным слагаемым:
∫dyh(y)=∫g(x)dx+C{\displaystyle \int {\frac {dy}{h(y)}}=\int g(x)dx+C}.
Вычисляя интегралы, получим общий интеграл уравнения (1).
Если уравнение задано в виде[5]:
M(x)N(y)dx+P(x)Q(y)dy=0,{\displaystyle M(x)N(y)dx+P(x)Q(y)dy=0,}
то для разделения переменных не нужно приводить его к виду (1). Достаточно разделить обе части на N(y)P(x){\displaystyle N(y)P(x)}:
M(x)dxP(x)+Q(y)dyN(y)=0,{\displaystyle {\frac {M(x)dx}{P(x)}}+{\frac {Q(y)dy}{N(y)}}=0,}
откуда получится общий интеграл
∫M(x)dxP(x)+∫Q(y)dyN(y)=C.{\displaystyle \int {\frac {M(x)dx}{P(x)}}+\int {\frac {Q(y)dy}{N(y)}}=C.}
Пример[править | править код]
Пусть
xdy−ydx=0{\displaystyle xdy-ydx=0}[6].
Разделяя переменные, получим
dyy=dxx.{\displaystyle {\frac {dy}{y}}={\frac {dx}{x}}.}
Интегрируя обе части последнего равенства, будем иметь
ln|y|=ln|x|+lnC1,{\displaystyle \ln |y|=\ln |x|+\ln C_{1},}
где C1{\displaystyle C_{1}} — положительная постоянная. Отсюда
|y|=C1|x|{\displaystyle |y|=C_{1}|x|}
или
y=Cx,{\displaystyle y=Cx,}
где C=±C1{\displaystyle C=\pm C_{1}} — произвольная постоянная, которая может принимать как положительные, так и отрицательные значения.
Решениями данного дифференциального уравнения являются также функции x=0{\displaystyle x=0} и y=0{\displaystyle y=0}. Последнее решение получается из общего решения y=Cx{\displaystyle y=Cx} при C=0{\displaystyle C=0}.
Метод разделения переменных применяется для решения краевых задач для линейных уравнений второго порядка гиперболического, параболического и эллиптического типов, а также для некоторых классов нелинейных уравнений и уравнений высших порядков [7].
Однородное уравнение[править | править код]
Приведем схему метода для задачи о колебаниях струны, закрепленной на концах[8]:
utt=a2uxx,(2){\displaystyle u_{tt}=a^{2}u_{xx},\qquad (2)}
u(0,t)=0,u(l,t)=0,(3){\displaystyle u(0,t)=0,\quad u(l,t)=0,\qquad (3)}
u(x,0)=φ(x),ut(x,0)=ψ(x).(4){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x).\qquad (4)}
Будем искать тождественно не равные нулю решения уравнения (2), удовлетворяющие краевым условиям (3) в виде произведения
u(x,t)=X(x)T(t).(5){\displaystyle u(x,t)=X(x)T(t).\quad (5)}
Подставим предполагаемый вид решения в уравнение (2) и поделим на a2X(x)T(t){\displaystyle a^{2}X(x)T(t)}:
X″(x)X(x)=T″(t)a2T(t).(6){\displaystyle {\frac {X»(x)}{X(x)}}={\frac {T»(t)}{a^{2}T(t)}}.\qquad (6)}
Левая часть равенства (6) является функцией только переменного x{\displaystyle x}, правая — только t{\displaystyle t}. Следовательно, обе части не зависят ни от x{\displaystyle x}, ни от t{\displaystyle t} и равны некоторой константе −λ{\displaystyle -\lambda }. Получаем обыкновенные дифференциальные уравнения для определения функций X(x){\displaystyle X(x)} и T(t){\displaystyle T(t)}:
X″(x)+λX(x)=0,X(x)≢0,(7){\displaystyle X»(x)+\lambda X(x)=0,\quad X(x)\not \equiv 0,\qquad (7)}
T″(t)+a2λT(t)=0,T(t)≢0,(8){\displaystyle T»(t)+a^{2}\lambda T(t)=0,\quad T(t)\not \equiv 0,\qquad (8)}
Подставляя (5) в краевые условия (3), получаем
X(0)=X(l)=0.(9){\displaystyle X(0)=X(l)=0.\qquad (9)}
Приходим к задаче Штурма-Лиувилля (7),(9). Эта задача имеет нетривиальные решения (собственные функции)
Xn(x)=sinπnlx,{\displaystyle X_{n}(x)=\sin {\frac {\pi n}{l}}x,}
определяемые с точностью до произвольного множителя только при значениях λ{\displaystyle \lambda }, равных собственным значениям
λn=(πnl)2,n=1,2,3,…{\displaystyle \lambda _{n}=\left({\frac {\pi n}{l}}\right)^{2},\quad n=1,2,3,\dots }
Этим же значениям λn{\displaystyle \lambda _{n}} соответствуют решения уравнения (8)
Tn(t)=Ancosπnlat+Bnsinπnlat,{\displaystyle T_{n}(t)=A_{n}\cos {\frac {\pi n}{l}}at+B_{n}\sin {\frac {\pi n}{l}}at,}
где An{\displaystyle A_{n}} и Bn{\displaystyle B_{n}} — произвольные постоянные.
Таким образом, функции
un(x,t)=Xn(x)Tn(t){\displaystyle u_{n}(x,t)=X_{n}(x)T_{n}(t)}
являются частными решениями уравнения (2), удовлетворяющими условиям (3). Решение задачи (2)-(4) получается в виде бесконечной суммы частных решений
u(x,t)=∑n=1∞un(x,t)=∑n=1∞(Ancosπnlat+Bnsinπnlat)sinπnlx,{\displaystyle u(x,t)=\sum _{n=1}^{\infty }u_{n}(x,t)=\sum _{n=1}^{\infty }\left(A_{n}\cos {\frac {\pi n}{l}}at+B_{n}\sin {\frac {\pi n}{l}}at\right)\sin {\frac {\pi n}{l}}x,}
где константы An{\displaystyle A_{n}} и Bn{\displaystyle B_{n}} могут быть найдены из начальных условий (4) как коэффициенты Фурье функций φ(x){\displaystyle \varphi (x)} и ψ(x){\displaystyle \psi (x)}:
An=2l∫0lφ(x)sinπnlxdx,Bn=2πna∫0lψ(x)sinπnlxdx.{\displaystyle A_{n}={\frac {2}{l}}\int _{0}^{l}\varphi (x)\sin {\frac {\pi n}{l}}xdx,\quad B_{n}={\frac {2}{\pi na}}\int _{0}^{l}\psi (x)\sin {\frac {\pi n}{l}}xdx.}
Метод разделения переменных также применим к уравнению колебаний струны общего вида
∂∂x[k(x)∂u∂x]−q(x)u=ρ(x)∂2u∂t2,{\displaystyle {\frac {\partial }{\partial x}}\left[k(x){\frac {\partial u}{\partial x}}\right]-q(x)u=\rho (x){\frac {\partial ^{2}u}{\partial t^{2}}},}
где k{\displaystyle k}, q{\displaystyle q} и ρ{\displaystyle \rho } — непрерывные положительные на отрезке 0<x<l{\displaystyle 0<x<l} функции[9]. В этом случае решение строится в виде ряда по собственным функциям задачи Штурма-Лиувилля
ddx[k(x)dXdx]−q(x)X+λρ(x)X=0,X(0)=X(l)=0.(10){\displaystyle {\frac {d}{dx}}\left[k(x){\frac {dX}{dx}}\right]-q(x)X+\lambda \rho (x)X=0,\quad X(0)=X(l)=0.\qquad (10)}
Основополагающие работы по обоснованию метода Фурье принадлежат В. А. Стеклову[10]. Теорема Стеклова утверждает, что при определенных условиях любая функция единственным образом разлагается в ряд Фурье по собственным функциями краевой задачи (10).
Неоднородное уравнение[править | править код]
Метод разделения переменных для неоднородных уравнений иногда называют методом Крылова в честь А. Н. Крылова[2]. При решении краевой задачи для уравнения неоднородного уравнения колебаний струны
utt=a2uxx+f(x,t)(11){\displaystyle u_{tt}=a^{2}u_{xx}+f(x,t)\quad (11)}
функции u{\displaystyle u} и f{\displaystyle f} разлагаются в ряды Фурье по системе собственных функций задачи Штурма-Лиувилля для соответствующего однородного уравнения (2):
u(x,t)=∑n=1∞Tn(t)sinπnlx,{\displaystyle u(x,t)=\sum _{n=1}^{\infty }T_{n}(t)\sin {\frac {\pi n}{l}}x,}
f(x,t)=∑n=1∞fn(t)sinπnlx.{\displaystyle f(x,t)=\sum _{n=1}^{\infty }f_{n}(t)\sin {\frac {\pi n}{l}}x.}
Подстановка полученных рядов в уравнение (11) с учетом ортогональности системы {sinπnlx}{\displaystyle \left\{\sin {\frac {\pi n}{l}}x\right\}} даёт уравнение относительно Tn(t){\displaystyle T_{n}(t)}:
Tn″(t)+a2λnTn(t)=fn(t).(12){\displaystyle T»_{n}(t)+a^{2}\lambda _{n}T_{n}(t)=f_{n}(t).\qquad (12)}
Функции Tn(t){\displaystyle T_{n}(t)} могут быть найдены как решения задач Коши для уравнений (12) с начальными условиями, полученными из начальных условий исходной краевой задачи.
- ↑ Клейн Ф. Лекции о развитии математики в XIX столетии. — М.-Л.: ГОНТИ, 1937. — Т. I. — С. 103.
- ↑ 1 2 Юрко В. А. Уравнения математической физики, 2004.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 88.
- ↑ Смирнов В. И. Курс высшей математики, 1974, Т. 2, с. 14.
- ↑ Степанов В. В. Курс дифференциальных уравнений, 1950, с. 24.
- ↑ Демидович Б. П., Моденов В. П. Дифференциальные уравнения, 2008, с. 19.
- ↑ Зайцев В. Ф., Полянин А. Д. Метод разделения переменных в математической физике, 2009.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 82.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 113.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 119.
- Смирнов В. И. Курс высшей математики. — 21-е издание. — Наука, 1974. — Т. 2.
- Степанов В. В. Курс дифференциальных уравнений. — Изд. 6-е. — 1950.
- Демидович Б. П., Моденов В. П. Дифференциальные уравнения: учебное пособие. — 3-е изд.. стер.. — СПб.: Лань, 2008. — 288 с.
- Зайцев В. Ф., Полянин А. Д. Метод разделения переменных в математической физике. — СПб., 2009. — 92 с. — ISBN 978–5–94777–211–1.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики: Учебное пособие.. — 6-е изд., испр. и доп.. — М.: Изд-во МГУ, 1999. — 798 с. — ISBN 5-211-04138-0.
- Юрко В. А. Уравнения математической физики: учеб. пособие для студентов механико-математического и физического факультетов. — Саратов: Изд-во Сарат. ун-та, 2004. — 118 с. — ISBN 5-292-03022-8.
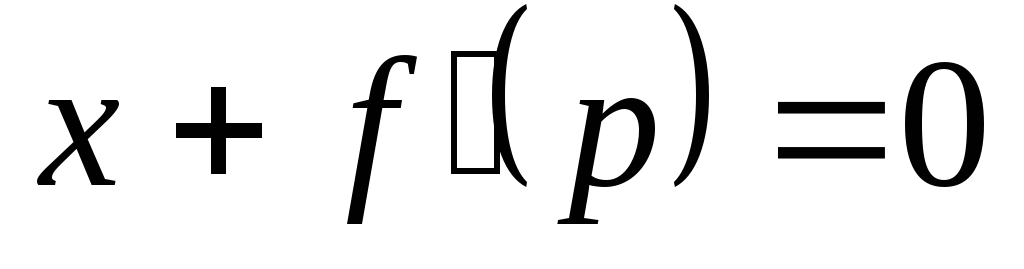 и решение можно представить в
параметрическом виде:
и решение можно представить в
параметрическом виде: