Методом гаусса решать онлайн: Метод Гаусса онлайн — Детская игровая комната «Волшебный лес»

Posted on 30.01.202026.04.2021 by alexxlab

Содержание

Онлайн решение системы комплексных линейных уравнений

Вы ввели следующую систему уравнений

Решение системы следующее

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

— иметь только одно верное решение;

— иметь бесконечное множество корней;

— иметь несовместный тип (когда решений быть не может).

Метод Гаусса, используемый нашим АБАК-ботом — самое мощное и безотказное средство для поиска решения любой системы уравнений линейного типа.

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т. н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Наш бот умеет молниеносно выдавать решения системы линейных уравнений с неограниченным количеством переменных!

Практическое применение решение таких систем находит в электротехнике и геометрии: расчетах токов в сложных контурах и выведение уравнения прямой при пересечении трех плоскостей а также в множестве специализированных задач.

Данный сервис позволяет решать неограниченную по размерам систему линейных уравнений с комплексными коэффициентами.

Ну, раз бот умеет считать решения комплексных систем, то для него не составит труда считать частный случай, когда элементы системы являются вещественные числа.

Второе, в школе Вам это наверняка не понадобится, но вот в институте, особенно институтах связи, при расчетах токов в сложных контурах в электротехнике, наверняка пригодится.

Рассчитаем комплексную систему линейных уравнений такого вида

Записываем все элементы в поле ввода. Как видите, данные могут быть не только числовые но и быть произвольным выражением, включающее в себя комплексные числа.

И получаем следующий результат.

Вы ввели следующую систему уравнений

Решение системы следующее

Успехов в расчетах !

Метод Гаусса — решение систем линейных уравнений, пример — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Линейная алгебра

В этом видео уроке рассказывается о том, как использовать метод Гаусса при решении систем линейных уравнений, пример. Метод Гаусса является универсальным методом решения систем линейных уравнений. Он основан на последовательном исключении неизвестных. Здесь будет рассмотрен простейший случай, т.е. когда система имеет единственное решение. При решении, системе уравнений сопоставляется, так называемая, расширенная матрица, состоящая из коэффициентов при неизвестных и свободных членов. Суть Метода Гаусса заключается в том, что по определенным правилам выполняется преобразование этой матрицы к виду, в котором ниже главной диагонали располагаются только нули. Элементарные преобразования матрицы выполняются по таким правилам как перемена местами двух строк, умножение (деление) строки на число, добавление к строке другой строки, умножение на число и вычеркивание строки из нулей. После такого преобразования система уравнений легко решается. В качестве примера практического применения метода Гаусса, будет рассмотрено задание с решением системы линейных уравнений с тремя неизвестными. Видео урок «Метод Гаусса — решение систем линейных уравнений, пример» вы можете смотреть онлайн в любое время совершенно бесплатно.

Удачи Вам!

Автор: alWEBra
Длительность: 5:32
Дата: 22.11.2013
Смотрели: 504
Рейтинг: 5.0/1

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

Решение уравнений методом сложения. Калькулятор онлайн

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»

Центр дистанционного образования

Урок алгебры в 7 классе

Тема урока: Метод алгебраического сложения.

Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.

Задачи урока:

Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.

Метапредметные: Познавательные УУД : анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД : излагать своё мнение, аргументируя его. Личностные УУД: ф ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.

Форма работы: индивидуальная

Этапы урока:

1) Организационный этап.

организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.

2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.

Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.

3. Изучение нового материала.

1). формировать умение решать системы линейных уравнений способом сложения;

2). развивать и совершенствовать имеющиеся знания в новых ситуациях;

3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.

http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html

Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.

5. Закрепление изученного материала

Цель: проверить знания, умения и навыки, полученные на уроке

6. Итог урока, информация о домашнем задании, рефлексия.

Ход урока (работа в электронном документе Google):

1. Сегодня урок я хотела начать с философской загадки Вальтера.

Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?

Время

Вспомним основные понятия по теме:

Перед нами система двух уравнений.

Вспомним, как мы решали системы уравнений на прошлом уроке.

Методом подстановки

Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?

Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.

Только получив уравнение с одной переменной нам удалось решить систему уравнений.

3. Мы приступаем к решению следующей системы:

Выберем уравнение, в котором удобно одну переменную выразить через другую.

Такого уравнения нет.

Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?

Найти новый метод.

Попытаемся сформулировать цель урока.

Научиться решать системы новым методом.

Что нам необходимо сделать, чтобы научиться решать системы новым методом?

знать правила (алгоритм) решения системы уравнения, выполнить практические задания

Приступим к выведению нового метода.

Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.

Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.

Сложить уравнения.

Что значит сложить уравнения?

По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.

Попробуем. Работаем вместе со мной.

13x+14x+17y-17y=43+11

Получили линейное уравнение с одной переменной.

Решили систему уравнений?

Решение системы — пара чисел.

Как найти у?

Найденное значение х подставить в уравнение системы.

Имеет значение, в какое уравнение подставим значение х?

Значит найденное значение х можно подставить в…

любое уравнение системы.

Мы познакомились с новым методом — методом алгебраического сложения.

Решая систему, мы проговорили алгоритм решения системы данным методом.

Алгоритм мы рассмотрели. Теперь применим его к решению задач.

Умение решать системы уравнений может пригодится в практике.

Рассмотрим задачу:

В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?

Зная, что всего кур и овец 19, составим первое уравнение: х + у =19

4х — число ног у овец

2у — число ног у кур

Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46

Составим систему уравнений:

Решим систему уравнений, применяя алгоритм решения методом сложения.

Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?

Рассмотрим ещё один пример!

Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.

4. Электронная физкультминутка для глаз: http://zhakulina20090612. blogspot.ru/2011/06/blog-post_25.html

5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.

Дополнительные задания:

Рефлексия.

Я за свою работу на уроке ставлю оценку — …

6. Использованные ресурсы-интернет:

сервисы Google для образования

Учитель математики Соколова Н. Н.

Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:

{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2

Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Пример решения способом сложения

Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

{3*x + 2*y = 10;
{5*x + 3*y = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2

Получим следующую систему уравнений:

{9*x+6*y = 30;
{10*x+6*y=24;

Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

10*x+6*y — (9*x+6*y) = 24-30; x=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

{3*(-6) + 2*y =10;
{2*y=28; y =14;

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

{3*x + 2*y = 10;
{5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Как видите, получились два верных равенства, следовательно, мы нашли верное решение.

Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.

Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:

1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.

2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.

Решение системы — это точки пересечения графиков функции.

Рассмотрим на примерах.

Пример 1.

Дана система:

Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:

Действия, которые обведены красным цветом, выполняем в уме.

Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.

-4 — y + 5 = 0 → y = 1,

В виде системы решение выглядит где-то так:

Ответ: x = -4 , y = 1.

Пример 2.

Дана система:

В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.

Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:

Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .

Следующий шаг:

1-е уравнение умножаем на ,

3-е уравнение умножаем на ,

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.

Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y.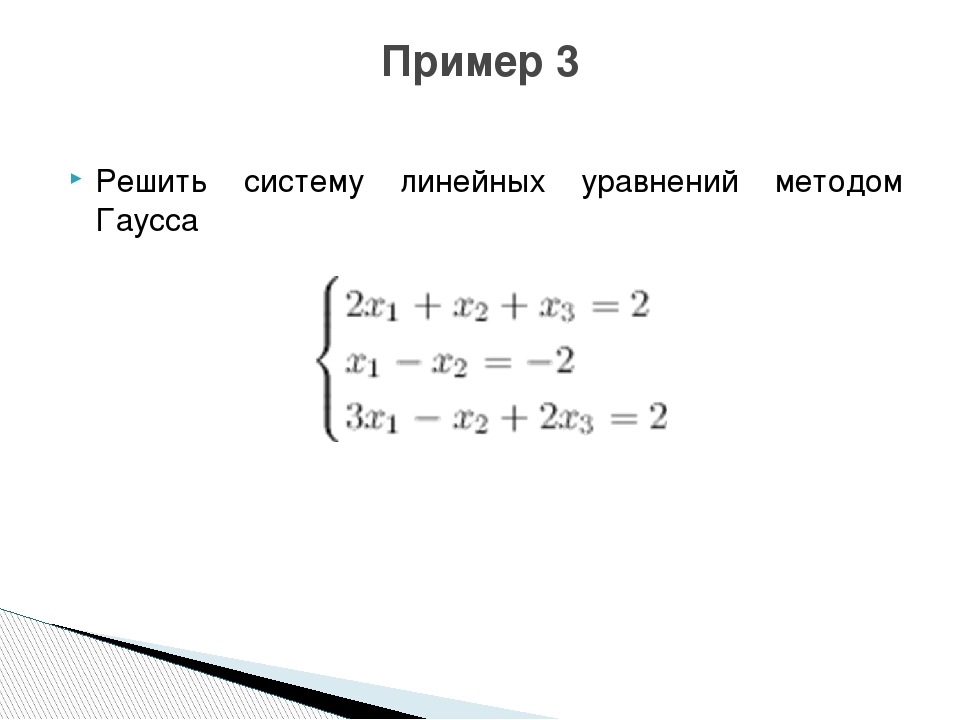 Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
Почленно сложить полученное выражение и найти одно из неизвестных.
Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.

Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.

Решение для полученных в итоге системы находят методом сложения.

Наглядный метод решения систем

Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.

Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.

Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.

В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.

Матрица и ее разновидности

Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.

Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.

Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Решение примеров систем линейных уравнений матричным методом

Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

Решение систем линейных уравнений методом Гаусса

Линейная и квадратичная интерполяция

Интерполяция с помощью многочлена Лагранжа.

Численное дифференцирование методом конечных разностей.

Численное интегрирование методом прямоугольников и трапеции

Численное решение интегралов методом прямоугольников.

Делим на равные части. Шаг следования точек разбиения равен h=(b-a)/n. Заменим каждый интеграл ri площадью прямоугольников с основанием h и высотой f(xi), то есть hf(xi).

Численное решение интегралов методом трапеции.

Заменим каждый интеграл площадью трапеции с высотой h и основаниями длины и , то есть .

Численное интегрирование методом Симпсона

Делим на четное количество отрезков. Шаг следования h=(b-a)/2n.

Численное интегрирование методом Монте-Карло.

Решение нелинейных уравнений методом деления отрезка пополам.

Метод деления отрезка пополам позволяет найти корень уравнения f(x)=0 на отрезке [a, b] при условии, что функция f(x) непрерывна и на концах отрезка принимает значения разных знаков: f(a)f(b)<0.

Суть метода деления отрезка пополам заключается в следующем. Находим середину отрезка [a, b], содержащего корень данного уравнения, и проверяем условие f(a)f(с)<0. Если условие есть True, то корень уравнения принадлежит отрезку [a, c], который и принимаем за новый отрезок, полагая b=c, а если False, то корень уравнения принадлежит отрезку [c, b], поэтому полагаем a=c. Проверяем условие остановки |b-a}<e. Если оно верно, то с и есть корень с данной погрешностью. Если оценка не верна, о повторяем процесс деления пополам для нового отрезка [a, b]. Вариант f(c)=0 сразу определяет корень.

Решение нелинейных уравнений методом Ньютона.

Метод Ньютона (или метод касательных) является итерационным методом решения уравнения с одной неизвестной f(x)=0 и характеризуется способом приведения этого уравнения к виду x=ф(x). Метод Ньютона заключается в следующем: пусть функция f(x), имеет единственный корень e на отрезке [a, b]. Возьмем точку х0 принадлежит [a, b].

Пусть касательная к графику функции y=f(x) в точке с абсциссой x0 пересекает ось х-ов в точке x1. Пусть касательная к графику функции y=f(x) в точке с абсциссой x1 пересекает ось х-ов в точке x2. Продолжая такие построения, получим последовательность точек {xn}n=0,1,2,… При соблюдении некоторых условии такая последовательность точек будет сходится к корню е.

Приведем формулу для вычисления элементов последовательности. Для этого напишем уравнение касательной к графику функции y=f(x) в точке ( , f( )): .

Решение нелинейных уравнений методом хорд.

Уравнение прямой через две точки

Решение систем линейных уравнений методом Гаусса

Рассмотрим систему линейных алгебраических уравнений (СЛАУ)

Прямой ход. Пусть коэффициент а11 не равен нулю. Поделим первое уравнение системы (ведущая строка) на элемент а11 (ведущий элемент):

Здесь и далее индексами вида «(1)» обозначены соответствующие изменения коэффициентов. Исключим из такой системы переменную х1 из второго, третьего и так далее до n-го уравнения. Для этого из i-го уравнения системы вычитаем первое уравнение, умноженное на коэффициент .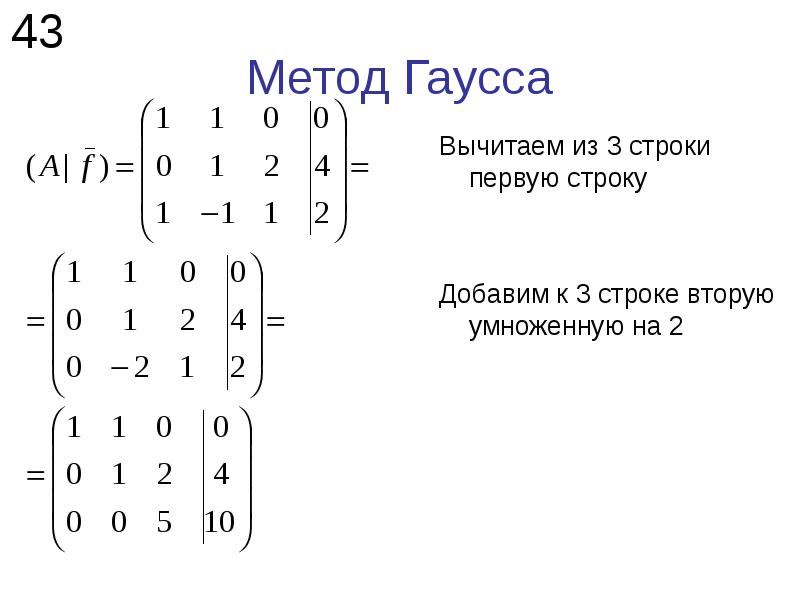 В результате приведем систему к следующему виду:

Далее, делим второе уравнение на коэффициент при х2 и исключаем переменную х2 из третьего и так далее до n-го уравнения. Повторяем этот процесс до последнего уравнения. Последнее уравнение поделим на коэффициент при неизвестной. Тем самым, равносильными преобразованиями, система уравнения будет приведена к треугольному виду.

Обратный ход. Из последнего уравнения системы, содержащего одну переменную, находим . Найденное подставляем в последнее уравнение и находим , и так далее.

Метод Гаусса для решения систем линейных уравнений | Математика

Пусть задана система из линейных уравнений с неизвестными:

(1.27)

Допустим, что в системе коэффициент при в первом уравнении Разделив обе части этого уравнения на , получим равносильную данной систему:

(1.

28)

где

Получить решение

Исключим с помощью первого уравнения системы (1.28) неизвестное из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последовательно на и в том же порядке вычтем полученное из второго, третьего и последующих уравнений системы (1.28). В результате получим равносильную систему вида

(1.29)

где

Допустим, что коэффициент при во втором уравнении системы (1.29) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.

Исключим неизвестное с помощью второго уравнения из всех последующих уравнений. Для этого разделам второе уравнение на . Затем умножим последовательно полученное второе уравнение на и вычтем эти результаты из третьего, четвертого и всех оставшихся уравнений.

В итоге получим очередную систему уравнений:

где

Продолжая этот процесс исключения неизвестных, получим либо несовместную, либо совместную систему уравнений. В первом случае в системе будет содержаться уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, т.е. уравнение вида , где . Во втором случае получим либо систему треугольной формы

(1.30)

либо систему трапециевидной (ступенчатой) формы

(1.31)

В случае треугольной системы из последнего уравнения (1.30) следует, что Подставляя это значение в предпоследнее уравнение системы (1.30), найдем неизвестное . Подставляя значения и в предыдущее уравнение, найдем значение неизвестного и т.д.

Таким образам, если данная система (1. 27) с помощью элементарных преобразований приводится к системе треугольной формы, то система имеет единственное решение (т.е. система совместна и определенна).

В случае системы ступенчатой формы (1.31), перенося все слагаемые, содержащие неизвестные в правую часть уравнений, получим систему вида

(1.32)

Из (1.32) следует, что значения неизвестных выражаются через значения неизвестных . Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.32), а вместе с ней и данная система (1.27), имеет бесконечное множество решений.

Итак, если данная система приводится к трапециевидной форме, то она имеет бесконечное множество решений (т.е. система совместна и неопределенна). Найденные решения, записанные в форме

где любые числа, называются общими решениями системы. Решения, полученные из общих решений при конкретных значениях свободных неизвестных , называются частными решениями.

Заключение

Матричный способ решения систем линейных уравнений, как и решение методом Крамера, применим только для особых систем линейных уравнений, в которых количество неизвестных совпадает с количеством уравнений. Метод Гаусса применим для решения произвольных систем линейных уравнений и, следовательно, является универсальным методом. Этот метод позволяет существенно упростить и сам процесс поиска решений, если все промежуточные преобразования осуществить над специальной матрицей составленной из коэффициентов системы (1.27) и ее свободных членов.

Матрица В называется расширенной матрицей системы. Она позволяет заменить элементарные преобразования системы уравнений на соответствующие элементарные преобразования над своими строками, что существенно сокращает процесс поиска решении.

Примеры решения методом Гаусса

ПРИМЕР 1. 1.15

Решить систему уравнений методом Гаусса.

Построим расширенную матрицу системы

Исключая с помощью первой строки неизвестное из всех оставшихся строк матрицы , получим

где символ есть символ элементарного преобразования матрицы.

Исключая с помощью второй строки неизвестное из всех последующих строк матрицы , получим

Исключая с помощью третьей строки неизвестное из четвертой строки, получим:

Матрица имеет треугольную форму. Следовательно, заданная система эквивалентна системе

Последовательно вычисляя из последнего уравнения, далее из третьего, из второго и из первого уравнения этой системы найдем, что =2, =1, =0, =1. Итак, заданная система имеет единственное решение =1, =0, =1, =2.

ПРИМЕР 1.1.16

Решить систему уравнений

Построим расширенную матрицу системы

Таким образом, заданная система эквивалентна системе,

которая имеет ступенчатый вид, и, следовательно, имеет бесконечное множество решений. Выразим переменные через :

;

Итак, общим решением данной системы будет

любое число.

Полагая, в частности, найдем, что . Тогда , будет одним из частных решений системы.

Система комплексных линейных уравнений

Вы ввели следующую систему уравнений

Решение системы следующее

Решение системы линейных уравнений

Наборы линейных уравнений довольно часто встречаются в повседневных расчетах, поэтому методов их решения придумано великое множество. Но перед рассмотрением самого простого алгоритма нахождения неизвестных стоит вспомнить о том, что вообще может иметь система таких уравнений:

— иметь только одно верное решение;

— иметь бесконечное множество корней;

— иметь несовместный тип (когда решений быть не может).

Возвращаясь к терминам высшей математики, метод Гаусса можно сформулировать так: с помощью элементарных преобразований система уравнений должна быть приведена к равносильной системе треугольного типа (или т.н. ступенчатого типа), из которой постепенно, начиная с самого последнего уравнения, находятся оставшиеся переменные. При всем этом элементарные преобразования над системами — ровно то же самое, что и элементарные преобразования матриц в переложении для строк.

Практическое применение:

Синтаксис

Для пользователей XMPP клиентов: linur_i <список элементов системы>

список элементов системы — является список значений перечисленных в одну или несколько строк разделенными пробелами между собой

linur_i 5:2 3 10 2 -11:3 0:-30

Примеры

linur_i 5:2 3 10 2 -11:3 0:-30

Корни системы линейных уравнений равны следующим значениям.

Переменные считаются слева направо

1.4389598942265:-1.941383869546

-0.3591890700749:2.2763331864257

то есть x1=1.4389598942265 — 1.941383869546 i

x2=-0.3591890700749+2.2763331864257 i

Рассчитаем комплексную систему линейных уравнений

такого вида

И получаем следующий результат.

Вы ввели следующую систему уравнений

Решение системы следующее

Успехов в расчетах !

Скалярное произведение двух матриц >>

Метод Гаусса

Пользователи также искали:

метод гаусса 5 класс, метод гаусса — — это, метод гаусса, пример 3 порядка, метод гаусса пример 4 порядка, метод гаусса примеры с ответами, метод гаусса с++, метод гаусса задачи, метод гаусса — жордана, Гаусса, метод, гаусса, Метод, Метод Гаусса, примеры, порядка, пример, метод гаусса с, метод гаусса задачи, метод гаусса класс, задачи, жордана, ответами, класс, метод гаусса — — это, метод гаусса — жордана, метод гаусса примеры с ответами, метод гаусса пример 4 порядка, метод гаусса 5 класс, метод гаусса пример 3 порядка, метод гаусса пример порядка, метод гаусса, методы решения слау. метод гаусса,

3.3: Решение систем с исключением Гаусса-Джордана

Цели обучения

Напишите расширенную матрицу системы уравнений.
Напишите систему уравнений из расширенной матрицы.
Решите систему линейных уравнений с помощью матриц и графического калькулятора.
Решайте финансовые приложения с помощью матриц и графического калькулятора.

Необходимые навыки

Прежде чем начать, пройдите предварительный тест.

Введите в калькулятор следующие матрицы и затем выполните указанные операции. Если операция не может быть проведена, укажите причину.

\ (A = \ begin {bmatrix} 5 & 1 & -2 \\ 2 & 6 & 7 \\ 4 & 1 & −5 \ end {bmatrix} \), \ (B = \ begin {bmatrix} 3 & -7 \\ 0 & 1 \\ 2 & −8 \ end {bmatrix} \), \ (C = \ begin {bmatrix} 9 & 4 \\ 6 & -5 \\ 7 & −1 \ end {bmatrix} \)

а. \ (А \ cdot B \)

г. \ (B \ cdot A \)

г. \ (4B-2C \)

г.\ (А + С \)

Нажмите здесь, чтобы проверить свой ответ

а. \ (\ begin {bmatrix} 11 & -18 \\ 20 & -64 \\ 2 & 13 \ end {bmatrix} \)

г. Не определено, поскольку количество столбцов в матрице \ (B \) не соответствует количеству строк в матрице \ (A \).

г. \ (\ begin {bmatrix} -6 & -36 \\ — 12 & 14 \\ — 6 & −30 \ end {bmatrix} \)

г. Не определено, поскольку размер матрицы \ (A \) не соответствует размерам матрицы \ (C \).{th} \) века, но он по-прежнему считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.

Рисунок \ (\ PageIndex {1} \): немецкий математик Карл Фридрих Гаусс (1777–1855).

Ранее в этой главе мы исследовали методы решения систем уравнений.В этом разделе мы изучим другую технику решения систем, на этот раз с использованием матриц.

Расширенные матрицы

Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства. Когда система написана в такой форме, мы называем ее расширенной матрицей .

Например, рассмотрим следующую систему уравнений \ (2 × 2 \).

\ [\ begin {align *} 3x + 4y & = 7 \\ 4x-2y & = 5 \ end {align *} \]

Мы можем записать эту систему в виде расширенной матрицы:

\ (\ left [\ begin {array} {cc | c} 3 & 4 & 7 \\ 4 & -2 & 5 \ end {array} \ right] \)

Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов .

\ (\ begin {bmatrix} 3 & 4 \\ 4 & −2 \ end {bmatrix} \)

Трехмерная система уравнений типа , например

\ [\ begin {align *} 3x-y-z & = 0 \\ x + y & = 5 \\ 2x-3z & = 2 \ end {align *} \]

имеет матрицу коэффициентов

\ (\ begin {bmatrix} 3 & −1 & −1 \\ 1 & 1 & 0 \\ 2 & 0 & −3 \ end {bmatrix} \)

и представлена расширенной матрицей

\ (\ left [\ begin {array} {ccc | c} 3 & −1 & −1 & 0 \\ 1 & 1 & 0 & 5 \\ 2 & 0 & −3 & 2 \ end {array} \ right] \)

Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: \ (x \) — члены идут в первый столбец, \ (y \) — термины во втором столбце, и \ (z \) — термины в третьем столбце.Очень важно, чтобы каждое уравнение было записано в стандартной форме \ (ax + by + cz = d \), чтобы переменные совпадали. Когда в уравнении отсутствует член переменной, коэффициент равен \ (0 \).

Как: по системе уравнений написать расширенную матрицу

Запишите коэффициенты членов \ (x \) как числа в первом столбце.
Запишите коэффициенты членов \ (y \) в виде чисел во втором столбце.
Если есть \ (z \) — члены, запишите коэффициенты как числа в третьем столбце.
Нарисуйте вертикальную линию и напишите константы справа от нее.

Пример \ (\ PageIndex {1} \): написание расширенной матрицы для системы уравнений

Напишите расширенную матрицу для данной системы уравнений.

\ [\ begin {align *} x + 2y-z & = 3 \\ 2x-y + 2z & = 6 \\ x-3y + 3z & = 4 \ end {align *} \]

Решение

Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.

\ (\ left [\ begin {array} {ccc | c} 1 & 2 & −1 & 3 \\ 2 & −1 & 2 & 6 \\ 1 & −3 & 3 & 4 \ end {array} \ right] \)

Упражнение \ (\ PageIndex {1} \)

Запишите расширенную матрицу данной системы уравнений.

\ [\ begin {align *} 4x-3y & = 11 \\ 3x + 2y & = 4 \ end {align *} \]

Ответ: \ (\ left [\ begin {array} {cc | c} 4 & −3 & 11 \\ 3 & 2 & 4 \ end {array} \ right] \)

Написание системы уравнений из расширенной матрицы

Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не обременены переменными.Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.

Пример \ (\ PageIndex {2} \): Написание системы уравнений из расширенной матричной формы

Найдите систему уравнений из расширенной матрицы.

\ (\ left [\ begin {array} {ccc | c} 1 & −3 & −5 & -2 \\ 2 & −5 & −4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \)

Решение

Когда столбцы представляют переменные \ (x \), \ (y \) и \ (z \),

\ [\ left [\ begin {array} {ccc | c} 1 & -3 & -5 & -2 \\ 2 & -5 & -4 & 5 \\ — 3 & 5 & 4 & 6 \ end {array} \ right] \ rightarrow \ begin {align *} x-3y-5z & = -2 \\ 2x-5y-4z & = 5 \\ -3x + 5y + 4z & = 6 \ end {align *} \]

Упражнение \ (\ PageIndex {2} \)

Напишите систему уравнений из расширенной матрицы.

\ (\ left [\ begin {array} {ccc | c} 1 & -1 & 1 & 5 \\ 2 & -1 & 3 & 1 \\ 0 & 1 & 1 & -9 \ end {array} \ right] \)

Ответ: \ (\ begin {align *} x-y + z & = 5 \\ 2x-y + 3z & = 1 \\ y + z & = -9 \ end {align *} \)

Форма пониженного ряда

Чтобы решить систему уравнений, мы хотим преобразовать ее матрицу в сокращенную форму строки , в которой единицы по главной диагонали от верхнего левого угла до нижнего правого угла, а нули в каждое положение выше и ниже главной диагонали, как показано.

Уменьшенная форма строки-эшелона \ (\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)

Следующие расширенные матрицы представлены в сокращенной форме строки-эшелона.

\ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)

Следующие расширенные матрицы не являются сокращенными строками.

\ (\ left [\ begin {array} {cc | c} 2 & 4 & -6 \\ 4 & 0 & 7 \ end {array} \ right] \), \ (\ left [\ begin {array} {ccc | c} 0 & 2 & 3 & 3 \\ 1 & 5 & 0 & 2 \\ 0 & 0 & 1 & 0 \ end {array} \ right] \)

Пример \ (\ PageIndex {3} \): матрицы в сокращенной форме строки-эшелон

Запишите систему уравнений из каждой из матриц в приведенной строчно-эшелонированной форме сверху. В чем преимущество этой формы?

а. \ (\ left [\ begin {array} {cc | c} 1 & 0 & -2 \\ 0 & 1 & 5 \ end {array} \ right] \)

г.\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 4 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \)

Решение

а. \ (\ begin {align *} x = -2 \\ y = 5 \ end {align *} \)

г. \ (\ begin {align *} x = 4 \\ y = 3 \\ z = 2 \ end {align *} \)

Преимущество сокращенной формы строки-эшелон состоит в том, что решение системы уравнений приводится в правом столбце.

УСТРАНЕНИЕ ПО ГАУСС-ИОРДАНИИ

Метод исключения Гаусса-Жордана относится к стратегии, используемой для получения уменьшенной строковой формы матрицы.Цель состоит в том, чтобы записать матрицу \ (A \) с числом \ (1 \) в качестве записи вниз по главной диагонали и иметь все нули сверху и снизу.

\ (A = \ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \ end {bmatrix} \ xrightarrow {После \ space Gauss-Jordan \ space elimination} A = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} \)

Мы можем выполнить операции со строками над матрицей, такие как сложение, умножение на константу и перестановку строк, чтобы создать сокращенную форму строки-эшелон.Процесс выполнения этих шагов вручную выходит за рамки этого класса. Тем не менее, вы можете найти дополнительную информацию о методе Гаусса-Джордана ЗДЕСЬ.

Решение систем уравнений с исключением Гаусса-Жордана

В рамках этого курса мы продемонстрируем, как найти сокращенную форму строки-эшелон в графическом калькуляторе.

Как: решить систему уравнений с помощью матриц с помощью калькулятора

Сохранить расширенную матрицу как матричную переменную \ ([A], [B], [C] ,… \)
1. Press 2 ^nd MATRIX. На экране отобразится меню матрицы. Дважды нажмите кнопку со стрелкой вправо, чтобы выбрать меню ПРАВКА. В меню EDIT используйте стрелку вниз для перемещения курсора, чтобы выбрать желаемое имя матрицы из меню, и нажмите ENTER. Появится экран ввода матрицы.
2. Введите размеры общего размера матрицы в виде строк \ (\ times \) столбцов. Введите количество строк, нажмите ENTER, введите количество столбцов и снова нажмите ENTER.Форма матрицы настраивается на экране, чтобы отобразить требуемое количество строк и столбцов. Убедитесь, что форма соответствует желаемой матрице; в противном случае вернитесь в верхний ряд и отрегулируйте размеры. Если матрица слишком велика для экрана, используйте клавиши со стрелками для прокрутки вправо или вниз, чтобы увидеть оставшиеся строки и столбцы.
3. Введите элементы матрицы, нажимайте ENTER после каждого. Курсор прокручивает матрицу, перемещаясь по каждой строке слева направо, а затем вниз к следующей строке.Использование клавиш со стрелками для перемещения курсора вместо нажатия ENTER может привести к тому, что значение не будет сохранено в памяти калькулятора.
4. Нажмите 2 ^nd QUIT, чтобы завершить процесс сохранения и вернуться на главный экран.
Используйте функцию rref (в калькуляторе, чтобы найти сокращенную форму строки-эшелона матрицы.
1. На главном экране нажмите 2 ^nd MATRIX.Используйте стрелку вправо один раз, чтобы перейти в меню МАТЕМАТИКА.
2. Прокрутите вниз (или вверх) до rref (, стараясь не выбрать ref (, и нажмите ENTER.
3. Снова нажмите 2 ^nd MATRIX и используйте стрелку вниз (при необходимости), чтобы выбрать имя матрицы, и нажмите ENTER.
4. Нажмите ENTER, чтобы завершить операцию.
Если существует сокращенная форма строки-эшелона матрицы, калькулятор отобразит ее на главном экране. ×

Пример \ (\ PageIndex {4} \): решение систем уравнений с матрицами с помощью калькулятора

Решите систему уравнений.

\ [\ begin {align *} 6x + 4y + 3z & = -6 \\ x + 2y + z & = \ dfrac {1} {3} \\ -12x-10y-7z & = 11 \ end {align *} \ ]

Решение

Напишите расширенную матрицу для системы уравнений.

\ (\ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).

\ ([A] = \ left [\ begin {array} {ccc | c} 6 & 4 & 3 & -6 \\ 1 & 2 & 1 & \ dfrac {1} {3} \\ — 12 & -10 & -7 & 11 \ end {array} \ right] \)

Используйте в калькуляторе функцию rref (, вызывающую матричную переменную \ ([A] \).

rref ([A])

Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.

Оценить

\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & — \ dfrac {2} {3} \\ 0 & 1 & 0 & \ dfrac {5} {2} \\ 0 & 0 & 1 & — 4 \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = — \ dfrac {2} {3} \\ y + 0z & = \ dfrac {5} {2 } \\ z & = -4 \ end {align *}} \ end {array} \]

Таким образом, решение, которое легко найти в правом столбце приведенной строковой формы матрицы, будет \ (\ left (- \ dfrac {2} {3}, \ dfrac {5} {2}, −4 \ справа) \).

Упражнение \ (\ PageIndex {3} \)

Решите систему уравнений.

\ [\ begin {align *} 4x-7y + 2z & = -5 \\ -x + 3y-8z & = -10 \\ -5x-4y + 6z & = 19 \ end {align *} \]

Ответ

Напишите расширенную матрицу для системы уравнений.

\ (\ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)

На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную \ ([A] \).

\ ([A] = \ left [\ begin {array} {ccc | c} 4 & -7 & 2 & -5 \\ -1 & 3 & -8 & -10 \\ -5 & -4 & 6 & 19 \ end {array} \ right] \)

Используйте в калькуляторе функцию rref (, вызывающую матричную переменную \ ([A] \).

rref ([A])

Используйте опцию MATH -> FRAC в калькуляторе, чтобы выразить матричные элементы в виде дробей.

Оценить

\ [\ begin {array} {cc} {\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & \ dfrac {3} {2} \ end {array} \ right] \ rightarrow} & {\ begin {align *} x + 0y + 0z & = -2 \\ y + 0z & = 0 \\ z & = \ dfrac {3} {2} \ end {align *}} \ end {array} \]

Таким образом, решение, которое можно легко прочитать из правого столбца приведенной строковой формы матрицы, будет \ (\ left (-2, 0, \ dfrac {3} {2} \ right) \).

Пример \ (\ PageIndex {5} \): применение матриц \ (2 × 2 \) к финансам

Кэролайн инвестирует в общей сложности \ (12 000 долларов) в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил \ (1335 долларов). Сколько было вложено по каждой ставке?

Решение

У нас есть система двух уравнений с двумя переменными. Пусть \ (x = \) сумма, инвестированная под 10,5% годовых, а \ (y = \) сумма, инвестированная под 12%.

\ [\ begin {align *} x + y & = 12,000 \\ 0,105x + 0,12y & = 1,335 \ end {align *} \]

В качестве матрицы имеем

\ (\ left [\ begin {array} {cc | c} 1 & 1 & 12,000 \\ 0.105 & 0.12 & 1335 \ end {array} \ right] \)

Введите эту матрицу как матричную переменную \ ([A] \). Используйте функцию rref (, вызывающую матричную переменную \ ([A] \).

rref ([A])

\ (\ left [\ begin {array} {cc | c} 1 & 0 & 7000 \\ 0 & 1 & 5000 \ end {array} \ right] \)

Таким образом, \ ($ 7000 \) было инвестировано по ставке 10.5% годовых и \ (5000 долларов \) под 12% годовых.

Пример \ (\ PageIndex {6} \): применение матриц \ (3 × 3 \) к финансам

Ava инвестирует в общей сложности \ (10 000 долларов США) в три счета, один из которых платит 5% годовых, другой — 8%, а третий — 9%. Годовой процент, полученный по трем инвестициям в прошлом году, составил \ (770 долларов). Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?

Решение

У нас есть система трех уравнений с тремя переменными.Пусть \ (x \) будет сумма, инвестированная под 5% годовых, пусть \ (y \) будет суммой, инвестированной под 8%, и пусть \ (z \) будет суммой, инвестированной под 9%. Таким образом,

\ [\ begin {align *} x + y + z & = 10,000 \\ 0,05x + 0,08y + 0,09z & = 770 \\ 2x-z & = 0 \ end {align *} \]

В качестве матрицы имеем

\ (\ left [\ begin {array} {ccc | c} 1 & 1 & 1 & 10,000 \\ 0,05 & 0,08 & 0,09 & 770 \\ 2 & 0 & -1 & 0 \ end {array} \ right] \)

Введите эту матрицу как матричную переменную \ ([A] \).Используйте функцию rref (, вызывающую матричную переменную \ ([A] \).

rref ([A])

\ (\ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 0 & 3000 \\ 0 & 1 & 0 & 1000 \\ 0 & 0 & 1 & 6000 \ end {array} \ right] \)

Ответ: \ (3000 долларов \) вложены под 5%, \ (1000 долларов \) вложены под 8%, и \ (6000 долларов \) инвестированы под 9%.

Упражнение \ (\ PageIndex {4} \)

Небольшая обувная компания взяла ссуду в размере \ (1 500 000 долларов) на расширение своих запасов.Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла \ (130 500 долларов США). Используйте матрицы, чтобы найти сумму займа по каждой ставке.

Ответ: \ (150 000 долларов \) под 7%, \ (750 000 долларов \) под 8%, \ (600 000 долларов \) под 10%

Медиа

Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в решении систем линейных уравнений с использованием метода исключения Гаусса.

Ключевые понятия

Расширенная матрица — это матрица, которая содержит коэффициенты и константы системы уравнений. См. Пример \ (\ PageIndex {1} \).
Матрица, дополненная постоянным столбцом, может быть представлена как исходная система уравнений. См. Пример \ (\ PageIndex {2} \).
Мы можем использовать метод исключения Гаусса-Жордана для решения системы уравнений. См. Пример \ (\ PageIndex {4} \).
Многие реальные проблемы можно решить с помощью расширенных матриц.См. Пример \ (\ PageIndex {5} \) и Пример \ (\ PageIndex {6} \).

Авторы и авторство

Матрицы

и исключение Гаусса

Назад Замена

Напомним, что линейная система уравнений состоит из двух или более линейных уравнений с одинаковыми переменными. Линейная система, состоящая из трех уравнений стандартной формы, расположенных так, чтобы переменная x не появлялась ни в одном уравнении после первого, а переменная y не появлялась ни в одном уравнении после второго, называется верхнетреугольной формой. линейная система, состоящая из уравнений с тремя переменными в стандартной форме, расположенная так, что переменная x не появляется после первого уравнения, а переменная y не появляется после второго уравнения.. Например,

Обратите внимание, что система образует треугольник, в котором каждое последующее уравнение содержит на одну переменную меньше. В целом

Линейные системы в верхней треугольной форме {a1x + b1y = c1b2y = c2 {a1x + b1y + c1z = d1b2y + c2z = d2c3z = d3

Если линейная система находится в этой форме, мы можем легко найти одну из переменных, а затем произвести обратную замену, чтобы найти оставшиеся переменные.

Пример 1

Решить: {3x − y = 72y = −2.

Решение:

Напомним, что решения линейных систем с двумя переменными, если они существуют, представляют собой упорядоченные пары ( x , y ). Мы можем легко определить значение y , используя второе уравнение.

2у = −2у = −1

Затем используйте первое уравнение 3x − y = 7 и тот факт, что y = −1, чтобы найти x .

3x − y = 73x — (- 1) = 73x + 1 = 73x = 6x = 2

Ответ: (2, −1)

Пример 2

Решите: {x − 6y + 2z = 163y − 9z = 5z = −1.

Решение:

Напомним, что решения линейных систем с тремя переменными, если они существуют, являются упорядоченными тройками ( x , y , z ). Воспользуйтесь вторым уравнением 3y − 9z = 5 и тем фактом, что z = −1, чтобы найти y .

3y − 9z = 53y − 9 (−1) = 53y + 9 = 53y = −4y = −43

Затем подставьте y и z в первое уравнение.

x − 6y + 2z = 16x − 6 (−43) +2 (−1) = 16x + 8−2 = 16x + 6 = 16x = 10

Ответ: (10, −43, −1)

Попробуй! Решить: {4x − y + 3z = 12y − 9z = −23z = 2.

Ответ: (14, 2, 23)

Матрицы и исключение Гаусса

В этом разделе цель — разработать метод, упрощающий процесс решения линейных систем. Мы начинаем с определения матрицы — прямоугольного массива чисел, состоящего из строк и столбцов., Который представляет собой прямоугольный массив чисел, состоящий из строк и столбцов. Учитывая линейную систему в стандартной форме, мы создаем матрицу коэффициентов Матрицу коэффициентов линейной системы в стандартной форме, записанную так, как они выглядят выстроенной, без переменных или операций.записывая коэффициенты в том виде, в каком они кажутся выстроенными, без переменных или операций, как показано ниже.

Матрица коэффициентов линейной системы {a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3 ⇒ [a1b1c1a2b2c2a3b3c3]

Строки представляют коэффициенты в уравнениях, а столбцы представляют коэффициенты каждой переменной. Кроме того, если мы включим столбец, представляющий константы, мы получим так называемую расширенную матрицу — матрицу коэффициентов с включенным столбцом констант.. Для линейной системы с двумя переменными

Расширенная матрица линейной системы {a1x + b1y = c1a2x + b2y = c2 ⇔ [a1b1 | c1a2b2 | c2]

А для линейной системы с тремя переменными имеем

Расширенная матрица линейной системы {a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3 ⇔ [a1b1c1 | d1a2b2c2 | d2a3b3c3 | d3]

Примечание : Пунктирная вертикальная линия обеспечивает визуальное разделение между матрицей коэффициентов и столбцом констант.В других ресурсах по алгебре, с которыми вы можете столкнуться, это иногда опускается.

Пример 3

Постройте расширенную матрицу, которая соответствует: {9x − 6y = 0 − x + 2y = 1.

Решение:

Эта система состоит из двух линейных уравнений стандартной формы; следовательно, коэффициенты в матрице отображаются так же, как и в системе.

{9x − 6y = 0 − x + 2y = 1 ⇔ [9−6 | 0−12 | 1]

Пример 4

Постройте расширенную матрицу, которая соответствует: {x + 2y − 4z = 52x + y − 6z = 84x − y − 12z = 13.

Решение:

Поскольку уравнения даны в стандартной форме, коэффициенты появляются в матрице так же, как и в системе.

{x + 2y − 4z = 52x + y − 6z = 84x − y − 12z = 13 ⇔ [12−4 | 521−6 | 84−1−12 | 13]

Матрица имеет верхнюю треугольную форму, если все элементы ниже ведущего ненулевого элемента в каждой последующей строке равны нулю. Например,

Обратите внимание, что элементы ниже главной диагонали равны нулю, а коэффициенты выше образуют треугольную форму.В целом

Верхняя треугольная форма [a1b10b2] [a1b1c10b2c200c3]

Это важно, потому что в этом разделе мы очерчиваем процесс, с помощью которого можно выполнить определенные операции для создания эквивалентной линейной системы в верхней треугольной форме, чтобы ее можно было решить с помощью обратной подстановки. Обзор процесса представлен ниже:

Когда система принимает форму верхнего треугольника, мы можем использовать обратную замену, чтобы легко ее решить.Важно отметить, что представленные здесь расширенные матрицы представляют собой линейные системы уравнений в стандартной форме.

Следующие элементарные операции со строками Операции, которые могут быть выполнены для получения эквивалентных линейных систем. приводят к расширенным матрицам, которые представляют эквивалентные линейные системы:

Любые две строки можно поменять местами.
Каждый элемент в строке можно умножить на ненулевую константу.
Любая строка может быть заменена суммой этой строки и кратной другой.

Примечание: Эти операции согласуются со свойствами, используемыми в методе исключения.

Чтобы эффективно решить систему линейных уравнений, сначала постройте расширенную матрицу. Затем примените соответствующие элементарные операции со строками, чтобы получить расширенную матрицу в форме верхнего треугольника. В этой форме эквивалентная линейная система может быть легко решена с помощью обратной подстановки. Этот процесс называется гауссовским устранением. Шаги, используемые для получения эквивалентной линейной системы в верхней треугольной форме, чтобы ее можно было решить с помощью обратной подстановки., названный в честь Карла Фридриха Гаусса (1777–1855).

Рисунок 3.1

Карл Фридрих Гаусс (Википедия)

Шаги решения линейного уравнения с двумя переменными с использованием исключения Гаусса перечислены в следующем примере.

Пример 5

Решить, используя матрицы и метод исключения Гаусса: {9x − 6y = 0 − x + 2y = 1.

Решение:

Перед началом этого процесса убедитесь, что уравнения в системе имеют стандартную форму.

Шаг 1 : Постройте соответствующую расширенную матрицу.

{9x − 6y = 0 − x + 2y = 1 ⇔ [9−6 | 0−12 | 1]

Шаг 2 : Примените операции элементарной строки, чтобы получить верхнюю треугольную форму. В этом случае нам нужно только удалить первый элемент второй строки, −1. Для этого умножьте вторую строку на 9 и прибавьте ее к первой строке.

Теперь используйте это, чтобы заменить вторую строку.

[9−6 | 0012 | 9]

В результате получается расширенная матрица в форме верхнего треугольника.

Шаг 3 : Преобразуйте обратно в линейную систему и решите, используя обратную подстановку. В этом примере у нас

[9−6 | 0012 | 9] ⇒ {9x − 6y = 012y = 9

Решите второе уравнение относительно y ,

12y = 9y = 912y = 34

Подставьте это значение вместо y в первое уравнение, чтобы найти x ,

9x − 6y = 09x − 6 (34) = 09x − 92 = 09x = 92x = 12

Ответ: (12, 34)

Шаги по использованию исключения Гаусса для решения линейного уравнения с тремя переменными перечислены в следующем примере.

Пример 6

Решить, используя матрицы и метод исключения Гаусса: {x + 2y − 4z = 52x + y − 6z = 84x − y − 12z = 13.

Решение:

Перед началом этого процесса убедитесь, что уравнения в системе имеют стандартную форму.

Шаг 1 : Постройте соответствующую расширенную матрицу.

{x + 2y − 4z = 52x + y − 6z = 84x − y − 12z = 13 ⇒ [12−4 | 521−6 | 84−1−12 | 13]

Шаг 2 : Примените операции элементарной строки, чтобы получить верхнюю треугольную форму.Начнем с исключения первого элемента второй строки, в данном случае 2. Для этого умножьте первую строку на −2, а затем добавьте ее во вторую строку.

[12−4 | 521−6 | 84−1−12 | 13] ⇒ × (−2) −2−48−10 + 21−680−32−2

Используйте это, чтобы заменить вторую строку.

[12−4 | 50−32 | −24−1−12 | 13]

Затем удалите первый элемент третьей строки, в данном случае 4, умножив первую строку на −4 и прибавив ее к третьей строке.

[12−4 | 50−32 | −24−1−12 | 13] ⇒ × (−4) −4−816−20 + 4−1−12130−94−7

Используйте это для замены третьей строки.

[12−4 | 50−32 | −20−94 | −7]

Это приводит к расширенной матрице, в которой элементы под первым элементом первой строки равны нулю. Затем удалите второй элемент в третьей строке, в данном случае −9. Умножьте вторую строку на −3 и прибавьте ее к третьей строке.

Используйте это, чтобы заменить третью строку, и мы видим, что мы получили матрицу в форме верхнего треугольника.

[12−4 | 50−32 | −200−2 | −1]

[12−4 | 50−32 | −200−2 | −1] ⇒ {x + 2y − 4z = 5−3y + 2z = −2−2z = −1

Ответ: Читателю остается убедиться, что решение (5,1,12).

Примечание: Обычно работа по замене строки путем умножения и сложения выполняется на стороне с использованием бумаги для заметок.

Пример 7

Решить, используя матрицы и метод исключения Гаусса: {2x − 9y + 3z = −18x − 2y − 3z = −8−4x + 23y + 12z = 47.

Решение:

Начнем с преобразования системы в расширенную матрицу коэффициентов.

{2x − 9y + 3z = −18x − 2y − 3z = −8−4x + 23y + 12z = 47 ⇒ [2−93 | −181−2−3 | −8−42312 | 47]

Операции с элементарными строками упрощаются, если ведущий ненулевой элемент в строке равен 1.По этой причине начните с замены первого и второго ряда местами.

Заменить вторую строку суммой −2, умноженной на первую и вторую строку.

Заменить третью строку суммой четырех строк первой и третьей.

Далее разделите 3-ю строку на 15.

Поменяйте местами третий ряд со вторым.

Затем замените строку 3 суммой, умноженной на 5 строк второй и третьей.

В результате получается матрица в форме верхнего треугольника. Матрица находится в виде эшелона строк Матрица в треугольной форме, где ведущий ненулевой элемент каждой строки равен 1., если она находится в верхней треугольной форме, где ведущий ненулевой элемент каждой строки равен 1. Мы можем получить эту форму, заменив третью строку на результат деления на 9.

Преобразуйте в систему линейных уравнений и решите обратной подстановкой.

[1−2−3 | −8010 | 1001 | 13] ⇒ {x − 2y − 3z = −8y = 1z = 13

Здесь y = 1 и z = 13. Подставляем в первое уравнение, чтобы найти x .

x − 2y − 3y = −8x − 2 (1) −3 (13) = — 8x − 2−1 = −8x − 3 = −8x = −5

Ответ: Следовательно, решение — (−5, 1, 13).

Технологическое примечание : Многие современные калькуляторы и системы компьютерной алгебры могут выполнять метод исключения Гаусса. Сначала вам нужно узнать, как войти в матрицу.Затем используйте функции калькулятора, чтобы найти форму эшелона строки. Предлагаем вам провести исследование по этой теме для вашей конкретной модели калькулятора.

Попробуй! Решить, используя исключение Гаусса: {x − 3y + 2z = 164x − 11y − z = 692x − 5y − 4z = 36.

Ответ: (6, −4, −1)

Напомним, что некоторые непротиворечивые линейные системы зависимы, то есть у них бесконечно много решений.А некоторые линейные системы не имеют одновременного решения; это несовместимые системы.

Пример 8

Решить, используя матрицы и метод исключения Гаусса: {x − 2y + z = 42x − 3y + 4z = 74x − 7y + 6z = 15.

Решение:

Начнем с преобразования системы в расширенную матрицу коэффициентов.

{x − 2y + z = 42x − 3y + 4z = 74x − 7y + 6z = 15 ⇒ [1−21 | 42−34 | 74−76 | 15]

Заменить строку два на −2 (строка 1) + (строка 2) и заменить строку три на −4 (строка 1) + (строка 3).

[1−21 | 4012 | −1012 | −1]

Заменить третью строку на −1 (строка 2) + (строка 3).

[1-21 | 4012 | -1000 | 0]

Последняя строка указывает, что это зависимая система, потому что преобразование расширенной матрицы обратно в уравнения, которые у нас есть,

{x − 2y + z = 4y + 2z = −10x + 0y + 0z = 0

Обратите внимание, что строка нулей соответствует следующему тождеству,

0x + 0y + 0z = 00 = 0 ✓

В этом случае мы можем выразить бесконечно много решений через z .Из второго ряда имеем:

y + 2z = −1y = −2z − 1

И из первого уравнения,

x − 2y + z = 4x − 2 (−2z − 1) + z = 4x + 5z + 2 = 4x = −5z + 2

Решения имеют вид (x, y, z) = (- 5z + 2, −2z − 1, z), где z — любое действительное число.

Ответ: (−5z + 2, −2z − 1, z)

Зависимые и несовместимые системы могут быть идентифицированы в расширенной матрице коэффициентов, когда все коэффициенты в одной строке равны нулю.

Если строка нулей имеет соответствующую константу, равную нулю, тогда матрица представляет зависимую систему. Если константа отлична от нуля, матрица представляет собой несовместимую систему.

Попробуй! Решить, используя матрицы и метод исключения Гаусса: {5x − 2y + z = −310x − y + 3z = 0−15x + 9y − 2z = 17.

Ответ: Ø

Основные выводы

Линейная система в верхней треугольной форме может быть легко решена с помощью обратной подстановки.
Расширенная матрица коэффициентов и метод исключения Гаусса могут использоваться для упрощения процесса решения линейных систем.
Чтобы решить систему с использованием матриц и исключения Гаусса, сначала используйте коэффициенты для создания расширенной матрицы. Примените операции с элементарными строками как средство для получения матрицы в форме верхнего треугольника. Преобразуйте матрицу обратно в эквивалентную линейную систему и решите ее, используя обратную подстановку.

Тематические упражнения

Часть A: Обратная замена

Решите, используя обратную замену.

{5x − 3y = 2y = −1
{3x + 2y = 1y = 3
{x − 4y = 12y = −3
{x − 5y = 310y = −6
{4x − 3y = −167y = 0
{3x − 5y = −104y = 8
{2x + 3y = −13y = 2
{6x − y = −34y = 3
{х-у = 02у = 0
{2x + y = 23y = 0
{x + 3y − 4z = 1y − 3z = −2z = 3
{x − 5y + 4z = −1y − 7z = 10z = −2
{x − 6y + 8z = 23y − 4z = −42z = −1
{2x − y + 3z = −92y + 6z = −23z = 2
{10x − 3y + z = 1311y − 3z = 92z = −6
{3x − 2y + 5z = −244y + 5z = 34z = −12
{x − y + 2z = 12y + z = 13z = −1
{x + 2y − z = 2y − 3z = 16z = 1
{x − 9y + 5z = −32y = 103z = 27
{4x — z = 33y − 2z = −12z = −8

Часть B: Матрицы и исключение Гаусса

Построить соответствующую расширенную матрицу (не решать).

{х + 2у = 34х + 5у = 6
{6x + 5y = 43x + 2y = 1
{x − 2y = 12x − y = 1
{х-у = 2-х + у = -1
{−x + 8y = 32y = 2
{3x − 2y = 4 − y = 5
{3x − 2y + 7z = 84x − 5y − 10z = 6 − x − 3y + 2z = −1
{x − y − z = 02x − y + 3z = −1 − x + 4y − 3z = −2
{x − 9y + 5z = −32y = 103z = 27
{4x − z = 33y − 2z = −12z = −8
{8x + 2y = −13−2y + z = 112x − 5z = −18
{x − 3z = 2y + 6z = 42x + 3y = 12

Решите, используя матрицы и метод исключения Гаусса.

{x − 5y = 22x − y = 1
{x − 2y = −1x + y = 1
{10x − 7y = 15−2x + 3y = −3
{9x − 10y = 23x + 5y = −1
{3x + 5y = 82x − 3y = 18
{5x − 3y = −147x + 2y = −1
{9x + 15y = 53x + 5y = 7
{6x − 8y = 1−3x + 4y = −1
{х + у = 0х-у = 0
{7x − 3y = 03x − 7y = 0
{2x − 3y = 4−10x + 15y = −20
{6x − 10y = 20−3x + 5y = −10
{x + y − 2z = −1 − x + 2y − z = 1x − y + z = 2
{x − y + z = −2x + 2y − z = 6 − x + y − 2z = 3
{2x − y + z = 2x − y + z = 2−2x + 2y − z = −1
{3x − y + 2z = 7 − x + 2y + z = 6x + 3y − 2z = 1
{x − 3y + z = 6 − x − y + 2z = 42x + y + z = 3
{4x − y + 2z = 12x − 3y + 2z = 7−2x + 3y + 4z = −16
{2x − 4y + 6z = −43x − 2y + 5z = −25x − y + 2z = 1
{3x + 6y + 9z = 62x − 2y + 3z = 0−3x + 18y − 12z = 5
{−x + y − z = −23x − 2y + 5z = 13x − 5y − z = 3
{x + 2y + 3z = 43x + 8y + 13z = 212x + 5y + 8z = 16
{2x − 4y − 5z = 3 − x + y + z = 13x − 4y − 5z = −4
{5x − 3y − 2z = 43x − 6y + 4z = −6 − x + 2y − z = 2
{−2x − 3y + 12z = 44x − 5y − 10z = −1 − x − 3y + 2z = 0
{3x − 2y + 5z = 104x + 3y − 3z = −6x + y + z = 2
{x + 2y + z = −3x + 6y + 3z = 7x + 4y + 2z = 2
{2x − y + z = 14x − y + 3z = 52x + y + 3z = 7
{2x + 3y − 4z = 03x − 5y + 3z = −105x − 2y + 5z = −4
{3x − 2y + 9z = 2−2x − 5y − 4z = 35x − 3y + 3z = 15
{8x + 2y = −13−2y + z = 112x − 5z = −18
{x − 3z = 2y + 6z = 42x + 3y = 12
{9x + 3y − 11z = 62x + y − 3z = 17x + 2y − 8z = 3
{3x − y − z = 4−5x + y + 2z = −36x − 2y − 2z = 8
{2x − 4y + 3z = 153x − 5y + 2z = 185x + 2y − 6z = 0
{3x − 4y − 3z = −144x + 2y + 5z = 12−5x + 8y − 4z = −3

Часть C: Обсуждение

Изучите и обсудите историю метода исключения Гаусса.Кто первым разработал этот процесс? Опубликуйте что-нибудь, что вам показалось интересным из этой истории
Изучите и обсудите историю современной матричной записи. Кому засчитывается разработка? В каких сферах они используются сегодня? Разместите свои выводы на доске обсуждений.

ответов

(-15, -1)
(-5, -32)
(-32,23)
(−6, −2, −12)
(85,0, −3)
(73,23, −13)

[12 | 345 | 6]
[1-2 | 12-1 | 1]
[−18 | 302 | 2]
[3−27 | 84−5−10 | 6−1−32 | −1]
[1−95 | −3020 | 10003 | 27]
[820 | −130−21 | 1120−5 | −18]
(13, −13)
(32,0)
(х, 23x − 43)
(12,12, −12)
(1,0,12)
(−8, −12z + 52, z)
(-32, -12, 0)

Линейная алгебра

— зачем использовать метод исключения Гаусса-Джордана вместо исключения Гаусса, различия

Следующий пример, часть Поиск последовательности элементарных матриц дополняет идею @ Xoque55

Целевая матрица $$ \оставил[ \ begin {array} {cc | cc} 2 и 4 \\ 1 и 1 \\ \ end {массив} \верно] $$

Используйте элементарные операции со строками для исключения Гаусса.$ \ color {blue} {Blue} $ окрашивание обозначает измененные элементы в выходной матрице.

Рядная форма

Формируют расширенную матрицу

$$ \оставил[ \ begin {array} {c | c} \ mathbf {A} & b \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | c} 2 и 4 и b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно]

Нормализовать строку 1: $$ \оставил[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | c} 2 и 4 и b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | c} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно]

Очистить столбец 1 $$ \оставил[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | c} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} b_ {1} \\ 1 & 1 & b_ {2} \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cr | c} 1 и 2 & \ frac {1} {2} b_ {1} \\ \ color {blue} {0} & \ color {blue} {- 1} & b_ {2} — \ frac {1} {2} b_ {1} \\ \ end {массив} \верно]

Система может быть решена обратной заменой.

Редукционная форма ступени

Процесс восстановления $$ % \оставил[ \ begin {array} {c | c} \ mathbf {A} & \ mathbf {I} \ end {массив} \верно] % \ qquad \ Rightarrow \ qquad % \оставил[ \ begin {array} {c | c} \ mathbf {E_ {A}} и \ mathbf {R} \ end {массив} \верно]

Формируют расширенную матрицу

$$ \оставил[ \ begin {array} {c | c} \ mathbf {A} & \ mathbf {I} \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | cc} 2 и 4 и 1 и 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно]

Нормализовать строку 1: $$ \оставил[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | cc} 2 и 4 и 1 и 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | cc} \ color {blue} {1} & \ color {blue} {2} & \ frac {1} {2} & 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно]

Очистить столбец 1 $$ \оставил[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | cc} 1 и 2 & \ frac {1} {2} & 0 \\ 1 и 1 и 0 и 1 \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cr | rc} 1 и 2 & \ frac {1} {2} & 0 \\ \ color {blue} {0} & \ color {blue} {- 1} & — \ frac {1} {2} & 1 \\ \ end {массив} \верно]

Нормализовать строку 2 $$ \оставил[ \ begin {array} {cr} 1 & 0 \\ 0 & -1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ \ color {blue} {0} & \ color {blue} {1} & \ frac {1} {2} & -1 \\ \ end {массив} \верно]

Очистить столбец 2 $$ \оставил[ \ begin {array} {cr} 1 & -2 \\ 0 и 1 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {cc | cr} 1 и 2 & \ frac {1} {2} & 0 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | rr} \ color {blue} {1} & \ color {blue} {0} & — \ frac {1} {2} & 2 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно] $$ Результат $$ \оставил[ \ begin {array} {c | c} \ mathbf {E_ {A}} и \ mathbf {R} \ end {массив} \верно] знак равно \оставил[ \ begin {array} {cc | rr} 1 & 0 & — \ frac {1} {2} & 2 \\ 0 & 1 & \ frac {1} {2} & -1 \\ \ end {массив} \верно]

Решение $$ \ mathbf {A} x = b \ quad \ Rightarrow \ quad х = \ mathbf {A} ^ {- 1} б \ quad \ Rightarrow \ quad x = \ frac {1} {2} \ left [ \ begin {array} {rr} -1 и 4 \\ 1 & -2 \\ \ end {массив} \верно] % \оставил[ \ begin {array} {c} б_ {1} \\ Би 2} \\ \ end {массив} \верно] \ quad \ Rightarrow \ quad х = \оставил[ \ begin {array} {l} — \ frac {1} {2} b_ {1} + 2b_ {2} \\ \ phantom {-} \ frac {1} {2} b_ {1} — b_ {2} \\ \ end {массив} \верно]

Произведение редукционных матриц

Произведение последовательности матриц редукции является обратным: $$ % четыре \оставил[ \ begin {array} {cr} 1 & -2 \\ 0 и 1 \\ \ end {массив} \верно] % в третьих \оставил[ \ begin {array} {cr} 1 & 0 \\ 0 & -1 \\ \ end {массив} \верно] % второй \оставил[ \ begin {array} {rc} 1 & 0 \\ -1 и 1 \\ \ end {массив} \верно] % первый \оставил[ \ begin {array} {cc} \ frac {1} {2} & 0 \\ 0 и 1 \\ \ end {массив} \верно] знак равно \оставил[ \ begin {array} {rr} — \ frac {1} {2} & 2 \\ \ frac {1} {2} & -1 \\ \ end {массив} \верно] знак равно \ mathbf {A} ^ {- 1}

$ Форма

Row Echelon Form и сокращенная форма Row Echelon Form

Содержание (Щелкните, чтобы перейти к этому разделу:

Форма эшелона?
Форма эшелона
Форма пониженного эшелона
Исключение по Гауссу
Ранг матрицы

Что такое форма эшелона?

Форма

Echelon означает, что матрица находится в одном из двух состояний:

Форма рядного эшелона.
Уменьшенная форма рядного эшелона.

Это означает, что матрица удовлетворяет следующим трем требованиям:

Первое число в строке (называемое ведущим коэффициентом) — 1. Примечание: некоторые авторы не требуют, чтобы ведущий коэффициент был равен 1; это могло быть любое число. Вы можете узнать у своего инструктора, какой версии этого правила они придерживаются).
Каждая ведущая 1 находится справа от первой.
Любые ненулевые строки всегда находятся над строками со всеми нулями.

Следующие примеры представляют собой матрицы в эшелонированной форме:

Следующие примеры представляют собой , а не в эшелонированной форме:

Матрица A не имеет строк со всеми нулями ниже ненулевых строк.
Матрица B имеет 1 во второй позиции в третьем ряду. Для формы эшелона строки он должен быть справа от ведущего коэффициента над ним. Другими словами, он должен быть на четвертой позиции вместо 3.
Матрица C имеет 2 в качестве ведущего коэффициента вместо 1.
Матрица D имеет -1 в качестве ведущего коэффициента вместо 1.

Другой способ думать о матрице в форме эшелона — это то, что матрица подверглась гауссовскому исключению, которое представляет собой серию операций со строками.

Уникальность и формы эшелона

Эшелонированная форма матрицы не уникальна, что означает, что при сокращении строк возможно бесконечное количество ответов. Уменьшенная форма эшелона строки находится на другом конце спектра; он уникален на , что означает, что сокращение строк в матрице даст один и тот же ответ независимо от того, как вы выполняете одни и те же операции со строками.
Вернуться к началу.

Что такое форма эшелона строк?

Матрица находится в форме эшелона строк, если она соответствует следующим требованиям:

Первое ненулевое число слева («ведущий коэффициент») всегда находится справа от первого ненулевого числа в строке выше.
Строки, состоящие из нулей, находятся внизу матрицы.

Форма рядного эшелона. «А» может представлять любое число.

Технически, ведущий коэффициент может быть любым числом.Однако в большинстве учебников линейной алгебры утверждается, что ведущим коэффициентом должно быть число 1. Чтобы добавить путаницы, в некоторых определениях формы эшелона строк говорится, что должны быть нули как выше , так и на ниже ведущего коэффициента. Поэтому лучше всего следовать определению, данному в учебнике, которому вы следуете (или тому, что дал вам ваш профессор). Если вы не уверены (то есть сейчас воскресенье, у вас должна быть домашняя работа, и вы не можете связаться с профессором), безопаснее всего использовать 1 в качестве ведущего коэффициента в каждой строке.

Если ведущий коэффициент в каждой строке — это только ненулевое число в этом столбце, матрица называется уменьшенной эшелонированной строкой.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Строковые формы эшелона обычно встречаются в линейной алгебре, когда вас иногда просят преобразовать матрицу в эту форму. Форма эшелона строк может помочь вам увидеть, что представляет собой матрица, а также является важным шагом к решению систем линейных уравнений.

Онлайн-калькулятор формы эшелона строк

Этот онлайн-калькулятор преобразует любую матрицу, и предоставляют операции со строками, которые помогут вам от шага к шагу.На следующем изображении (из калькулятора Университета Старого Доминиона показано, как матрица [01, 00, 59] приводится к форме эшелона строк с помощью двух простых операций со строками:

Back to Top.

Что такое форма сокращенного эшелона строк?

Уменьшенная форма эшелона строк — это тип матрицы, используемой для решения систем линейных уравнений. Форма сокращенного ряда имеет четыре требования:

Первое ненулевое число в первой строке (, ведущая запись ) — это число 1.
Вторая строка также начинается с цифры 1, которая находится правее первой записи в первой строке. В каждом последующем ряду цифра 1 должна быть правее.
Начальная запись в каждой строке должна быть единственным ненулевым числом в ее столбце.
Любые ненулевые строки помещаются внизу матрицы.

Матрица 3 × 5 в сокращенной форме эшелона строк.

Преобразование матрицы в форму сокращенного эшелона строк

Любая матрица может быть преобразована в сокращенную форму эшелона строк с помощью метода, называемого исключением Гаусса.Это особенно полезно для решения систем линейных уравнений. Большинство графических калькуляторов (например, TI-83) имеют функцию rref, которая преобразует матрицу в сокращенную форму эшелона строк. См. Эту статью на веб-сайте Университета штата Колорадо, где приведены инструкции по использованию TI-89 и TI-83 для расчета формы сокращенного эшелона строки.
Этот онлайн-калькулятор на веб-сайте Университета Старого Доминиона преобразует введенную вами матрицу в сокращенную форму эшелона строк.

Расчет вручную требует знания операций с элементарными строками, а именно:

Менять местами одну строку другой.
Умножьте одну строку на ненулевую константу.
Заменить одну строку на: одну строку плюс константу, умноженную на другую строку.

Кроме того, недостаточно просто знать правила, вы должны уметь взглянуть на матрицу и принять логическое решение о том, какое правило вы собираетесь использовать и когда. Вы пытаетесь преобразовать матрицу в сокращенный ряд строк, поэтому вам также нужно будет обратиться к четырем требованиям, приведенным в начале этой статьи. Если вам нужно вручную преобразовать матрицу в сокращенную форму эшелона строк, рекомендуется использовать один из приведенных выше калькуляторов, чтобы проверить свою работу.Фактически, если вы используете онлайн-калькулятор ODU, он даже предоставит вам операции со строками. На изображении ниже показано преобразование калькулятором матрицы [204,923]:

Вернуться к началу.

Что такое метод исключения Гаусса?

Метод исключения Гаусса — это способ найти решение системы линейных уравнений. Основная идея состоит в том, что вы выполняете математическую операцию над строкой и продолжаете, пока не останется только одна переменная. Например, некоторые возможные операции со строками:

Поменять местами любые два ряда
Сложите две строки вместе.
Умножить одну строку на ненулевую константу (например, 1/3, -1, 5)

Одновременно можно выполнять несколько операций со строками. Например, умножьте одну строку на константу, а затем добавьте результат к другой строке.

После этого цель состоит в том, чтобы получить матрицу в сокращенной форме эшелона строк, где ведущий коэффициент, 1, в каждой строке находится справа от ведущего коэффициента в строке над ней. Другими словами, вам нужно получить 1 в верхнем левом углу матрицы.В следующей строке должен быть 0 в позиции 1 и 1 в позиции 2. Это дает вам решение системы линейных уравнений.

Пример исключения Гаусса

Решите следующую систему линейных уравнений методом исключения Гаусса:

х + 5у = 7
-2x — 7y = -5

Шаг 1: Преобразуйте уравнение в форму матрицы коэффициентов . Другими словами, просто возьмите коэффициент для чисел и забудьте пока о переменных:

Шаг 2. Превратите числа в нижней строке в положительные, прибавив 2 раза первую строку:

Шаг 3: Умножьте вторую строку на 1/3.Это дает вам второе ведущее значение 1:

Шаг 4: Умножьте строку 2 на -5, а затем добавьте это к строке 1:

Вот и все!
В первой строке у вас x = -8, а во второй строке y = 3. Обратите внимание, что x и y находятся в тех же положениях, что и при преобразовании уравнения на шаге 1, поэтому все, что вам нужно сделать, это прочтите решение:

Вернуться к началу.

Что такое ранг матрицы?

Ранг матрицы равен количеству линейно независимых строк.Линейно независимая строка — это строка, которая не является комбинацией других строк.

Следующая матрица имеет две линейно независимых строки (1 и 2). Однако, когда в смесь добавляется третья строка, вы можете видеть, что первая строка теперь равна сумме второй и третьей строк. Следовательно, ранг этой конкретной матрицы равен 2, поскольку есть только две линейно независимых строки.

Ранг матрицы всегда будет на меньше, чем числа ненулевых строк или числа столбцов в матрице.Если все строки в матрице линейно независимы, матрица имеет ранг , полный ранг строки . Для квадратной матрицы она имеет полный ранг только в том случае, если ее определитель не равен нулю.

Выяснить ранг матрицы, пытаясь определить на глаз, сколько строк или столбцов линейно независимы, может быть практически невозможно. Более простой (и, возможно, очевидный) способ — преобразовать в форму эшелона строк.

Как найти матрицу Рейтинг

Найти ранг матрицы просто, если вы знаете, как найти матрицу эшелона строк.Чтобы найти ранг любой матрицы:

Найдите матрицу эшелона строк.
Подсчитать количество ненулевых строк.

Преобразование матрицы в форму эшелона строк.

Вышеупомянутая матрица была преобразована в форму эшелона строк с двумя ненулевыми строками. Следовательно, ранг матрицы равен 2.

Вы также можете найти отличный инструмент для конвертации на сайте Old Dominion University.

Вернуться к началу.

Список литературы

Эверитт, Б.S .; Скрондал А. (2010), Кембриджский статистический словарь, Cambridge University Press.
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Сирл, С. (2017). Матричная алгебра, полезная для статистики (серия Уайли по вероятности и статистике), 2-е издание. Вайли.

————————————————— —————————-

Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

Исключение Гаусса Джордана

путем поворота

Исключение Гаусса Джордана путем поворота

Система линейных уравнений может быть помещены в матричную форму. Каждый уравнение становится строкой, и каждое переменная становится столбцом. An добавлен дополнительный столбец для справа. Система показаны линейные уравнения и результирующая матрица.

Система линейных уравнений …

 3x + 2y - 4z = 3
2x + 3y + 3z = 15
5x - 3y + z = 14

становится расширенной матрицей …

х	y	z	справа
3	2	-4	3
2	3	3	15
5	-3	1	14

Цель при решении системы уравнений состоит в том, чтобы преобразовать расширенную матрицу в сокращенную форму строки-эшелона, если это возможно.

Есть три элементарные операции со строками, которые вы можете использовать для размещения матрицы в приведенная строчно-эшелонированная форма.

Каждое из требований сокращенной матрицы строка-эшелон может быть удовлетворено с использованием элементарной строки операции.

Если есть строка со всеми нулями, то она находится внизу матрицы.
Поменяйте местами две строки матрицы, чтобы переместить строку со всеми нулями вниз.
Первый ненулевой элемент любой строки — это единица.Этот элемент называется ведущим.
Умножьте (разделите) строку на ненулевую константу, чтобы превратить первый ненулевой элемент в один.
Первая строка любой строки находится справа от первой строки предыдущей строки.
Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку. В Смысл этой элементарной операции со строками состоит в том, чтобы преобразовать числа в нули. Сделав числа под ведущими в ноль, это заставляет первый ненулевой элемент любой строки быть справа от ведущей предыдущей строки.
Все элементы выше и ниже ведущего равны нулю.
Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку. В Суть этой элементарной операции со строками состоит в том, чтобы преобразовать числа в ноль. Разница здесь в что вы очищаете (обнуляете) элементы выше ведущего, а не чуть ниже ведущий.

Что такое поворот?

Цель поворота — сделать элемент выше или ниже ведущего. в ноль.

«Поворотный элемент» или «сводный элемент» — это элемент в левой части матрицы. что вы хотите элементы сверху и снизу равны нулю.

Обычно это единица. Если вы найдете книгу, в которой упоминается поворот, они обычно сказать вам, что вы должны повернуться на один. Если ограничиться тремя элементарными рядами операций, то это верное утверждение.

Однако, если вы хотите объединить вторую и третью элементарные операции со строками, вы придумать другую строковую операцию (не элементарную, но все еще действующую).

Вы можете умножить строку на ненулевую константу и добавить ее к ненулевому кратному другому. row, заменив эту строку.

И что? Если вам нужно повернуться на одном, то вам иногда придется использовать второй. элементарная операция со строкой и разделите строку на ведущий элемент, чтобы превратить ее в единицу. Деление приводит к дробям. Хотя дроби — ваши друзья, у вас меньше шансов ошибиться если вы их не используете.

В чем прикол? Если вы не остановитесь на одном, вы, вероятно, столкнетесь с большими числами.Большинство люди готовы работать с большими числами, чтобы избежать дробей.

Процесс поворота

Pivoting работает, потому что общее кратное (не обязательно наименьшее общее кратное) двух чисел всегда можно найти, умножив два числа вместе. Возьмем предыдущий пример и очистить первый столбец.

х	y	z	справа
3	2	-4	3
2	3	3	15
5	-3	1	14

Полезные советы

Хотя вам не нужно поворачиваться на единицу, это очень желательно.Переход на единицу означает, что вы умножаете на 1 (что легко сделать).
Поворот по главной диагонали — это хорошо, но не обязательно. Некоторым людям нравится начинать с левого верхнего угла и продвигаться вниз к Нижний правый.
Пока вы выполняете поворот только один раз для каждой строки и столбца, столбцы, которые были очищены, останутся очищенными.
Поскольку целью поворота является очистка столбца вращения, выбор столбец, в котором уже есть нули, экономит время, потому что у вас нет чтобы изменить строку, содержащую ноль.

Выбор оси

Выберите столбец с наибольшим количеством нулей.
Использовать строку или столбец только один раз
Если возможно, установите единицу
Поворот по главной диагонали
Никогда не поворачивайтесь на ноль
Никогда не поворачивайте вправо

Поскольку в первом ряду никого нет, у нас есть два варианта: либо мы первую строку делим на три и работаем дробями, либо делаем поворот на три и получите большие числа.Это вариант, который я собираюсь использовать. Я поверну на трех в R ₁ C ₁. Обведите его как стержневой элемент. В зависимости от вашего браузера вы элементы поворота могут быть обведены красным кружком или просто отмечены знаком * перед ним.

х	y	z	справа
* 3	2	-4	3
2	3	3	15
5	-3	1	14

Идея состоит в том, чтобы превратить числа в рамке (желтые) в ноль.Использование комбинированного рядная операция (это не элементарная операция), это может сделать 3R ₂ — 2R ₁ → R ₂ и 3R ₃ — 5R ₁ → R ₃.

Единственная строка, которая не изменяется, — это строка, содержащая элемент поворота ( 3). Весь смысл процесса поворота состоит в том, чтобы обнулить значения в рамке. Перепишите сводную строку и очистите (сделайте ноль) сводный столбец.

х	y	z	справа
* 3	2	-4	3
0
0

Для замены значений в строке 2 каждый новый элемент получается путем умножения элемент, заменяемый во второй строке на 3 и вычитающий в 2 раза элемент в первой строка из того же столбца, что и заменяемый элемент.

Чтобы выполнить поворот, приложите один палец к оси поворота (обведено кружком). номер) и один палец на заменяемом элементе. Умножьте эти два числа вместе. Теперь поместите один палец на номере в рамке в той же строке, что и элемент, который вы заменяя и другой палец в поворотном ряду и такой же столбец как номер, который вы заменяете. Умножьте эти два числа вместе. Возьмите изделие за шарнир и вычесть произведение без оси.

х	y	z	справа
* 3	2	-4	3
2	3	3	15
5	-3	1	14

Чтобы заменить 3 в R ₂ C ₂, вы должны взять 3 (3) — 2 (2) = 9-4 = 5.

Чтобы заменить 3 в R ₂ C ₃, вы должны взять 3 (3) — 2 (-4) = 9 +8 = 17.

Чтобы заменить 15 в R ₂ C ₄, вы должны взять 3 (15) — 2 (3) = 45-6 = 39.

Чтобы заменить -3 в R ₃ C ₂, вы должны взять 3 (-3) — 5 (2) = -9-10 = -19.

Чтобы заменить 1 в R ₃ C ₃, вы должны взять 3 (1) — 5 (-4) = 3 + 20 = 23

Чтобы заменить 14 в R ₃ C ₄, вы должны взять 3 (14) — 5 (3) = 42-15 = 27.

Вот как выглядит процесс.

х	y	z	справа
поворотный ряд, копия 3	поворотный ряд, копия 2	поворотный ряд, копия -4	поворотный ряд, копия 3
поворотная стойка, прозрачная 0	3 (3) — 2 (2) 5	3 (3) — 2 (-4) 17	3 (15) — 2 (3) 39
поворотная стойка, прозрачная 0	3 (-3) — 5 (2) -19	3 (1) — 5 (-4) 23	3 (14) — 5 (3) 27

Или, если убрать комментарии, матрица после первого поворота выглядит так.

х	y	z	справа
3	2	-4	3
0	5	17	39
0	-19	23	27

Пришло время повторить весь процесс.Мы проходим и выбираем другое место для поворота. Мы хотел бы, чтобы он был на главной диагонали, с единицей или с нулями в столбце. К сожалению, у нас не может быть ничего из этого. Но так как мы должны все умножить другие числа у оси, мы хотим, чтобы она была маленькой, поэтому мы перейдем к 5 в R ₂ C ₂ и очистите 2 и -19.

х	y	z	справа
3	2	-4	3
0	* 5	17	39
0	-19	23	27

Начните с копирования вниз сводной строки (2-я строка) и очистки сводного столбца (2-я строка). столбец).Ранее очищенные столбцы останутся очищенными.

х	y	z	справа
	0
0	* 5	17	39
0	0

Вот вычисления, чтобы найти следующее взаимодействие.Обратите особое внимание в 3-ю строку, где мы вычитаем значение -19 раз. Поскольку мы вычитаем отрицательный, я записал его как плюс 19.

х	y	z	справа
5 (3) — 2 (0) 15	поворотная стойка, прозрачная 0	5 (-4) — 2 (17) -54	5 (3) — 2 (39) -63
сводная строка, копия 0	поворотный ряд, копия 5	поворотный ряд, копия 17	поворотный ряд, копия 39
ранее погашено 0	поворотная стойка, прозрачная 0	5 (23) + 19 (17) 438	5 (27) + 19 (39) 876

И получившаяся матрица.

х	y	z	справа
15	0	-54	-63
0	5	17	39
0	0	438	876

Обратите внимание, что все элементы в первой строке кратны 3 и все элементы в последней строке кратны 438.Разделим, чтобы сократить ряды.

х	y	z	справа
5	0	-18	-21
0	5	17	39
0	0	1	2

Это имело дополнительное преимущество, давая нам 1, именно там, где мы хотим, чтобы он был вращаться.Итак, мы переместимся на 1 в R ₃ C ₃ и уберем -18 и 17. Обведите свою точку поворота и поместите остальные числа в рамку. этот столбец очистить.

х	y	z	справа
5	0	-18	-21
0	5	17	39
0	0	* 1	2

Скопируйте сводную строку и очистите сводный столбец.Ранее очищенные столбцы будет оставаться очищенным до тех пор, пока вы не повернете строку или столбец дважды.

х	y	z	справа
	0	0
0		0
0	0	* 1	2

Обратите внимание, что каждый раз приходится выполнять меньше вычислений.Вот расчеты для этой оси. Опять же, поскольку значение в сводном столбце в первая строка -18, и мы вычитаем, я записал это как + 18.

х	y	z	справа
1 (5) +18 (0) 5	ранее погашено 0	поворотная стойка, прозрачная 0	1 (-21) + 18 (2) 15
ранее погашено 0	1 (5) — 17 (0) 5	поворотная стойка, прозрачная 0	1 (39) — 17 (2) 5
сводная строка, копия 0	сводная строка, копия 0	поворотный ряд, копия 1	поворотный ряд, копия 2

И получившаяся матрица.

х	y	z	справа
5	0	0	15
0	5	0	5
0	0	1	2

Обратите внимание, что первая и вторая строки кратны 5, поэтому мы можем уменьшить их ряды.

х	y	z	справа
1	0	0	3
0	1	0	1
0	0	1	2

И окончательный ответ: x = 3, y = 1 и z = 2.Вы также можете написать это как упорядоченный триплет {(3,1,2)}.

Надеюсь, вы заметили, что когда я работал над этим примером, я не следовал подсказкам Я дал. Это потому, что я хотел, чтобы вы увидели, что произойдет, если вы не повернетесь на один. В исходной матрице был один на главной диагонали, и Лучше было бы начать с этого.

Сводка

Выбирайте поворотный элемент с умом.
Выбор столбца с нулями означает меньший поворот.
Выбор единицы в качестве оси поворота уменьшает числа, упрощает умножение и оставляет ненулевые элементы в очищенном столбце такие же (без поворота)
Поворот по главной диагонали означает, что вам не придется переключать строки, чтобы поместить матрицу в приведенная строчно-эшелонированная форма.
Не поворачивайтесь на ноль.
Не поворачивайте вправо.
Используйте строку или столбец только один раз
Возьмите продукт с шарниром за вычетом продукта без шарнира

Особые случаи

Если вы получите строку из всех нулей, кроме правой части, то система не имеет решения.

Если вы получили строку со всеми нулями, а количество ненулевых строк меньше, чем количество переменных, то система зависима, у вас будет много ответов, и вам нужно написать свой ответ в параметрической форме.

Обращение матрицы с использованием элементарных операций со строками (Гаусс-Джордан)

Также называется методом Гаусса-Жордана.

Это интересный способ найти обратную матрицу:

Поиграйте со строками (сложение, умножение или замена местами) пока мы не превратим Matrix A в Identity Matrix I

И ТАКЖЕ внесение изменений в матрицу идентичности, она волшебным образом превращается в инверсию!

«Элементарные операции со строками» — это простые вещи, такие как добавление строк, умножение и замена местами… но давайте посмотрим на примере:

Пример: найти обратную букву «А»:

Мы начинаем с матрицы A и записываем ее с Матрицей идентичности I рядом с ней:

(это называется «Расширенная матрица»)

Матрица идентичности

«Матрица идентичности» является матричным эквивалентом числа «1»:

Матрица идентификации 3×3

Это «квадрат» (в нем столько же строк, что и столбцов),
Он имеет 1 с по диагонали и 0 с по всей остальной части.
Его символ — заглавная буква I .

Теперь мы делаем все возможное, чтобы превратить «А» (Матрица слева) в Матрицу Идентичности. Цель состоит в том, чтобы матрица A имела 1 с по диагонали и 0 с в другом месте (матрица идентичности) … и правая сторона используется для поездки, и с ней также выполняется каждая операция.

Но мы можем выполнять только эти «Элементарные операции со строками» :

поменять местами строк
умножить или разделить каждый элемент в строке на константу
заменить строку на , прибавив к ней или вычтя из нее число, кратное другой строке

И мы должны сделать это для всей строки , вот так:

Начните с A рядом с I

Добавить строку 2 к строке 1,

, затем разделите строку 1 на 5,

Затем возьмите 2 раза первую строку и вычтите ее из второй строки,

Умножить вторую строку на -1/2,

Теперь поменяйте местами вторую и третью строки,

Наконец, вычтите третью строку из второй строки,

И готово!

И матрица преобразована в Матрицу идентификации…

… и в то же время идентификационная матрица превратилась в A ^-1

СДЕЛАНО! Как по волшебству, и так же весело, как решать любую головоломку.

И обратите внимание: не существует «правильного способа» сделать это, просто продолжайте экспериментировать, пока у нас не получится!

(Сравните этот ответ с тем, который мы получили об обратной матрице с использованием младших, сомножителей и адъюгата. Это то же самое? Какой метод вы предпочитаете?)

Большие матрицы

Мы можем сделать это с матрицами большего размера, например, попробуйте эту матрицу 4×4:

Начать как это:

Посмотри, сможешь ли ты сделать это сам (я бы начал с деления первой строки на 4, но ты делаешь это по-своему).

Вы можете проверить свой ответ с помощью калькулятора матрицы (используйте кнопку «inv (A)»).

Онлайн решение системы комплексных линейных уравнений

Метод Гаусса — решение систем линейных уравнений, пример — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Линейная алгебра

Решение уравнений методом сложения. Калькулятор онлайн

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Алгоритм решения способом сложения

Пример решения способом сложения

Линейное уравнение

Виды систем линейных уравнений

Простые и сложные методы решения систем уравнений

Решение систем методом подстановки

Решение с помощью алгебраического сложения

Способ решения введением новой переменной

Наглядный метод решения систем

Матрица и ее разновидности

Правила преобразования системы уравнений в матрицу

Варианты нахождения обратной матрицы

Решение примеров систем линейных уравнений матричным методом

Решение систем методом Гаусса

Решение систем линейных уравнений методом Гаусса

Метод Гаусса для решения систем линейных уравнений | Математика

Заключение

Примеры решения методом Гаусса

Система комплексных линейных уравнений

Решение системы линейных уравнений

Синтаксис

Примеры

Метод Гаусса

Пользователи также искали:

3.3: Решение систем с исключением Гаусса-Джордана

Расширенные матрицы

Написание системы уравнений из расширенной матрицы

Форма пониженного ряда

Решение систем уравнений с исключением Гаусса-Жордана

Ключевые понятия

Авторы и авторство

и исключение Гаусса

Назад Замена

Пример 1

Пример 2

Матрицы и исключение Гаусса

Пример 3

Пример 4

Пример 5

Пример 6

Пример 7

Пример 8

Основные выводы

Тематические упражнения

Часть A: Обратная замена

Часть B: Матрицы и исключение Гаусса

Часть C: Обсуждение

ответов

— зачем использовать метод исключения Гаусса-Джордана вместо исключения Гаусса, различия

Row Echelon Form и сокращенная форма Row Echelon Form

Что такое форма эшелона?

Уникальность и формы эшелона

Что такое форма эшелона строк?

Онлайн-калькулятор формы эшелона строк

Что такое форма сокращенного эшелона строк?

Преобразование матрицы в форму сокращенного эшелона строк

Что такое метод исключения Гаусса?

Пример исключения Гаусса

Что такое ранг матрицы?

Как найти матрицу Рейтинг

Список литературы

путем поворота

Что такое поворот?

Процесс поворота

Полезные советы

Выбор оси

Сводка

Особые случаи

Обращение матрицы с использованием элементарных операций со строками (Гаусс-Джордан)

Пример: найти обратную букву «А»:

Матрица идентичности

Большие матрицы

Добавить комментарий Отменить ответ