Методом математической индукции докажите формулу общего: Докажите методом математической индукции ,что общий член геометрической прогрессии {bn} вычисляется по формуле bn=b1q^n-1 — Детская игровая комната «Волшебный лес»

Posted on 01.12.201808.04.2021 by alexxlab

Содержание

Метод математической индукции

Математическая индукция лежит в основе одного из самых распространенных методов математических доказательств. С его помощью можно доказать большую часть формул с натуральными числами n, например, формулу нахождения суммы первых членов прогрессии Sn=2a1+n-1d2·n, формулу бинома Ньютонаa+bn=Cn0·an·Cn1·an-1·b+…+Cnn-1·a·bn-1+Cnn·bn.

В первом пункте мы разберем основные понятия, потом рассмотрим основы самого метода, а затем расскажем, как с его помощью доказывать равенства и неравенства.

Понятия индукции и дедукции

Для начала рассмотрим, что такое вообще индукция и дедукция.

Определение 1

Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному.

Например, у нас есть утверждение: 254 можно разделить на два нацело. Из него мы можем сделать множество выводов, среди которых будут как истинные, так и ложные. Например, утверждение, что все целые числа, которые имеют в конце цифру 4, могут делиться на два без остатка – истинное, а то, что любое число из трех знаков делится на 2 – ложное.

В целом можно сказать, что с помощью индуктивных рассуждений можно получить множество выводов из одного известного или очевидного рассуждения. Математическая индукция позволяет нам определить, насколько справедливы эти выводы.

Допустим, у нас есть последовательность чисел вида 11·2, 12·3, 13·4, 14·5,…, 1n(n+1), где n обозначает некоторое натуральное число. В таком случае при сложении первых элементов последовательности мы получим следующее:

S1=11·2=12, S2=11·2+12·3=23, S3=11·2+12·3+13·4=34,S4=11·2+12·3+13·4+14·5=45,…

Используя индукцию, можно сделать вывод, что Sn=nn+1. В третьей части мы докажем эту формулу.

В чем заключается метод математической индукции

В основе этого метода лежит одноименный принцип. Он формулируется так:

Определение 2

Некое утверждение будет справедливым для натурального значения n тогда, когда 1) оно будет верно при n=1 и 2) из того, что это выражение справедливо для произвольного натурального n=k, следует, что оно будет верно и при n=k+1.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Применение метода математической индукции осуществляется в 3 этапа:

Для начала мы проверяем верность исходного утверждения в случае произвольного натурального значения n (обычно проверка делается для единицы).
После этого мы проверяем верность при n=k.
И далее доказываем справедливость утверждения в случае, если n=k+1.

Как применять метод математической индукции при решении неравенств и уравнений

Возьмем пример, о котором мы говорили ранее.

Пример 1

Докажите формулу Sn=11·2+ 12·3+…+1n(n+1)=nn+1.

Решение

Как мы уже знаем, для применения метода математической индукции надо выполнить три последовательных действия.

Для начала проверяем, будет ли данное равенство справедливым при n, равном единице. Получаем S1=11·2=11+1=12. Здесь все верно.
Далее делаем предположение, что формула Sk=kk+1 верна.
В третьем шаге нам надо доказать, что Sk+1=k+1k+1+1=k+1k+2, основываясь на справедливости предыдущего равенства.

Мы можем представить k+1 в качестве суммы первых членов исходной последовательности и k+1:

Sk+1=Sk+1k+1(k+2)

Поскольку во втором действии мы получили, что Sk=kk+1, то можно записать следующее:

Sk+1=Sk+1k+1(k+2).

Теперь выполняем нужные преобразования. Нам потребуется выполнить приведение дроби к общему знаменателю, приведение подобных слагаемых, применить формулу сокращенного умножения и сократить то, что получилось:

Sk+1=Sk+1k+1(k+2)=kk+1+1k+1(k+2)==k(k+2)+1k+1(k+2)=k2+2k+1k+1(k+2)=(k+1)2k+1(k+2)=k+1k+2

Таким образом, мы доказали равенство в третьем пункте, выполнив все три шага метода математической индукции.

Ответ: предположение о формуле Sn=nn+1 является верным.

Возьмем более сложную задачу с тригонометрическими функциями.

Пример 2

Приведите доказательство тождества cos2α·cos4α·…·cos2nα=sin 2n+1α2nsin 2α.

Решение

Как мы помним, первым шагом должна быть проверка верности равенства при n, равном единице. Чтобы это выяснить, нам надо вспомнить основные тригонометрические формулы.

cos 21=cos 2αsin 21+1α21sin 2α=sin 4α2sin 2α=2sin 2α·cos 2α2sin 2α=cos 2α

Следовательно, при n, равном единице, тождество будет верным.

Теперь предположим, что его справедливость сохранится при n=k, т.е. будет верно, что cos 2α·cos 4α·…·cos 2kα=sin 2k+1α2ksin 2α.

Доказываем равенство cos 2α·cos 4α·…·cos 2k+1α=sin 2k+2α2k+1sin 2α для случая, когда n=k+1, взяв за основу предыдущее предположение.

Согласно тригонометрической формуле,

sin 2k+1α·cos 2k+1α==12(sin(2k+1α+2k+1α)+sin(2k+1α-2k+1α))==12sin(2·2k+1α)+sin 0=12sin 2k+2α

Следовательно,

cos 2α·cos 4α·…·cos 2k+1α==cos 2α·cos 4α·…·cos 2kα·cos 2k+1α==sin 2k+1α2k sin 2α·cos 2k+1α=12·sin 2k+1α2ksin 2α=sin 2k+2α2k+1sin 2α

Ответ: На этом тождество можно считать доказанным. Мы успешно применили для этого метод математической индукции. Точно так же мы можем доказать справедливость формулы бинома Ньютона.

Пример решения задачи на доказательство неравенства с применением этого метода мы привели в статье о методе наименьших квадратов. Прочтите тот пункт, в котором выводятся формулы для нахождения коэффициентов аппроксимации.

9 класс. Алгебра. Геометрическая прогрессия. — Геометрическая прогрессия.

Комментарии преподавателя

Посмотрев этот видеоурок, пользователи смогут получить представление о теме «Определение и свойства геометрической прогрессии, формула n-го члена». В ходе занятия учитель познакомит с понятием геометрической прогрессии, расскажет о ее свойствах. Кроме того, на уроке будет дана формула n-го члена и будет показано, как правильно применять ее на практике.

Тема: Геометрическая прогрессия

Урок: Определение и свойства геометрической прогрессии, формула n–го члена

На уроке дается определение геометрической прогрессии, выводится формула общего члена, решаются типовые задачи.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией. При этом число q называют знаменателем прогрессии.

Математическая запись.

геометрическая прогрессия, ее члены , при этом:

Иная запись:, т.е. .

Рассмотрим примеры геометрических прогрессий:

здесь каждый следующий член получается из предыдущего умножением на 2; полученная последовательность при этом возрастает (

2. здесь каждый следующий член получается из предыдущего умножением на ; полученная последовательность при этом убывает (

Теперь выведем формулу n–го члена геометрической прогрессии.

Рассмотрим геометрическую прогрессию , при этом

Тогда,

. . . . . . . . . . .

n=1,2,3,…

Докажем полученную формулу методом полной математической индукции.

Дано:геометрическая прогрессия,

Доказать:.

Доказательство.

1. Проверим справедливость формулы дляn =1:

2. Предположим, что формула справедлива для n=k:

3. Докажем, что из справедливости формулы для n=k следует справедливость формулы для n=k+1:

Вывод: формула верна для всех

Рассмотрим геометрическую прогрессию как функцию натурального аргумента и построим ее график.

Обозначим, тогда

, это показательная функция натурального аргумента.

Рассмотрим примеры.

Перейдя к функции, имеем

Составим таблицу значений функции.

И построим ее график.

Рис. 1.

, поэтому график – это только отдельные точки, которые лежат на показательной кривой.

2. ;

Перейдя к функции, имеем

Составим таблицу значений функции.

И построим ее график.

Рис. 2

Снова график – это отдельные точки, лежащие на показательной кривой.

Из графиков видно, что если геометрическая прогрессия возрастает, то возрастает очень быстро, а если убывает, то убывает тоже быстро (как показательная функция).

Далее рассмотрим типовые задачи, для решения которых понадобится формула общего члена геометрической прогрессии:

1. Дано:геометрическая прогрессия, . Найти: . Решение: Ответ:

2. Дано:геометрическая прогрессия,. Проверить, является ли число 1536 членом этой прогрессии, если да, найти его номер. Решение: Ответ:

3. Дано:геометрическая прогрессия, . Найти: Решение: Ответ:

4. Дано:геометрическая прогрессия, . Найти: Решение: Ответ:

Если известны два члена геометрической прогрессии то справедлива формула:

Действительно, Рассмотрим еще одну задачу.

5. Дано:геометрическая прогрессия, . Найти: Решение: Ответ:

нта.

Выведем далее формулу суммы конечного числа членов геометрической прогрессии.

Дано: геометрическая прогрессия.

Найти:

Решение:.

Умножим обе части этого равенства на q:

И вычтем из первого равенства второе:

В полученной формуле , рассмотрим частный случай

Геометрическая прогрессия имеет nравных членов, поэтому ее сумма

Итак, , при ; при .

Далее рассмотрим типовые задачи, для решения которых понадобится формула суммы членов геометрической прогрессии:

1. Дано:геометрическая прогрессия, . Найти: Решение: . Ответ:

2. Дано:геометрическая прогрессия, . Найти: . Решение: Ответ:

3. «Легенда об изобретателе шахмат». Дано:геометрическая прогрессия, . Найти: Решение: Ответ: А теперь легенда. Восточный правитель захотел наградить мудреца за то, что он научил правителя играть в шахматы. Мудрец попросил на первую клетку шахматной доски положить одно зернышко пшеницы, а на каждую следующую в 2 раза больше зерен, чем на предыдущую. Шахматная доска имеет 64 клетки, поэтому общее количество зерен на доске – это сумма 64 членов геометрической прогрессии, у которой . Мы только что нашли, что Оказалось, что это число настолько огромно, что у правителя не нашлось столько пшеницы. Возрастающая геометрическая прогрессия возрастает очень быстро и сумма даже не очень большого числа членов – огромное число.

1. Дано:геометрическая прогрессия, . Найти: Решение: Ответ:

2. Найдите сумму Решение:Данная сумма является суммой геометрической прогрессии, действительно, ,отношение не зависит от n, т.е. это геометрическая прогрессия. В этой прогрессии , тогда . Ответ:.

3. Докажите тождество Доказательство: Притождество справедливо. При имеем геометрическую прогрессию (). В предыдущей задаче мы вычислили , тогда Тождество доказано.

Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/progressii/opredelenie-i-svoystva-geometricheskoy-progressii-formula-n-go-chlena?konspekt&chapter_id=38

Источник видео: http://www.youtube.com/watch?v=vl47O6_MPtY

Задачи для самостоятельного решения Группа а

1. Найти наибольший общий делитель чисел 882; 1008 и 1334. (Ответ: 126.)

2. Найти наименьшее общее кратное чисел 40; 64 и 112 (Ответ: 2240.)

3. Произведение двух чисел равно 3042, а их наибольший общий делитель равен 78. Найти наименьшее общее кратное этих чисел. (Ответ: 9.)

4. Найти два натуральных числа, сумма которых равна 35, а наименьшее общее кратное равно 42. (Ответ: (14; 21).)

5. Найти пары натуральных чисел, разность квадратов которых равна 45.

(Ответ: (23; 22), (9; 6), (7; 2).)

6. При каких целых значениях дробьявляется натуральным числом?

(Ответ:;;5.)

7. Найти все пятизначные числа вида (- цифра сотен,- цифра единиц), которые делятся на 15. В ответ записать их количество. (Ответ: 7.)

8. Доказать, что — иррациональное число.

9. Доказать, что — иррациональное число.

10. Запишите число в виде обыкновенной несократимой дроби: а) ; б); в). (Ответ: а) , б) , в) .)

Группа b

1. Найти значение выражения . (Ответ: 1.)

2. Найти значение выражения . (Ответ: 3,08.)

3. Существуют ли такие натуральные и, что последняя цифра разности указанных двух степеней равна нулю: а); б)?

(Ответ: а) Да, например, 6 и 2; б) да, например, 2 и 1.)

4. Методом математической индукции докажите формулу общего члена арифметической прогрессии .

5. Методом математической индукции докажите формулу суммы первых членов арифметической прогрессии.

6. Методом математической индукции докажите формулу общего члена геометрической прогрессии .

7. Докажите, что при любом натуральном значении выполняется равенство:

8. Докажите, что для любого натурального значения справедливо утверждение:.

9. Докажите, что .

10. Докажите, что для любого натурального числа.

Группа с

1. Методом математической индукции докажите неравенство: , где.

2. Методом математической индукции докажите неравенство: , где,.

3. Методом математической индукции докажите, что для любого натурального значения справедливо утверждение:.

4. Методом математической индукции докажите, что для любого натурального числа выполняется неравенство.

5. Методом математической индукции докажите, что для любого натурального числа справедливо неравенство.

2. Функции действительного переменного

2.1. Понятие функции

Изучение различных явлений связано с использованием переменных величин. Например, объем конуса зависит от радиуса его основания и высоты, цена покупки от веса товара, оценка на экзамене – от количества решенных задач и т. д.

Определение 2.1. Пусть заданы некоторые непустые числовые множества и. Если каждому числуставится в соответствие по некоторому законуединственное значение, то говорят, что на множествезаданафункция или.

Переменную называют независимой переменной(аргументом), а переменную – зависимой переменной (функцией от аргумента ). Множество – областью определения функции, а множество всех значений , таких, что,, называютмножеством значений (областью значений) функции.

Для функции приняты обозначения:– область определения функции,- множество значений функции,– значение функции в точке.

Если и , то функцию называют числовой.

Элементы множества также называютзначениями аргумента, а соответствующие им элементы –значениями функции.

Таким образом, символ обозначает число, которое в силу законасоответствует значению. Например,есть значение функциив точке, если. Если жене принадлежит(), то говорят, что функцияне определена в точке .

Существуют функции, для которых всем значениям соответствует одно и то же значение. В этом случае функции называютконстантами.

Если функция задана формулой и область определения не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл. В этом случае говорят о естественной области определения функции.

Например, область определения функции состоит из всех чисел, кроме числа.

Пример 2.1. Найти область определения функции .

Решение. Область определения данной функции задается условием

Ответ: .

Пример 2.2. Найти область определения функции .

Решение. Учитывая, что для функции ,, получаем область определения данной функции:

Ответ: .

Пример 2.3. Найти область определения функции

Решение. Область определения функции задается неравенством

, ,.

Ответ: ,.

Пример 2.4. Найти множество значений функций

а) ; б).

Решение. а) Преобразуем подкоренное выражение, выделив полный квадрат

Учитывая ограниченность функции :, и, умножая, все части неравенства на положительное число, получаем. Вычтем из всех частей неравенства:, тогда. Продолжим преобразования:

б) Множество значений функции состоит из таких чисел , для каждого из которых существует число, являющееся решением уравнения. Рассмотрим уравнениеотносительно неизвестнойи выясним, при какихоно имеет решение:

При получаем линейное уравнение.

При получаем квадратное уравнение, имеющее решение только в случае неотрицательного дискриминанта:

Ответ: а) ; б) .

Пример 2.5. Найти множество значений функции

Решение. При получаем. Приполучаем, тогда имеем .

Ответ: .

Определение 2.2. Функции и называютсятождественно равными на множестве , если они определены на данном множестве и для каждогосправедливо числовое равенство(при этом пишут ).

Например: 1) для всех; 2),.

Определение 2.3 Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

4. Доказательство формулы общего члена последовательности, заданной рекуррентно

4.3.5. Домашняя контрольная работа «30 задач на индукцию»

Подобрать и решить 30 задач на доказательства методом полной математической индукции по следующим темам:

1. Доказательства равенств.

2. Доказательства неравенств.

3. Доказательства делимости.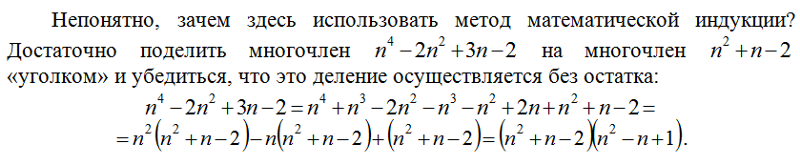

4. Доказательство формулы общего члена рекуррентной последовательности.

5. Доказательство геометрических утверждений.

Срок сдачи – октябрь.

Примерный перечень задач

1. Доказательство равенств

1) Докажите, что сумма первых натуральных чисел равна .

2) Докажите, что сумма квадратов первых натуральных чисел равна .

3) Докажите, что .

4) Докажите, что .

5) Докажите, что

6) Докажите тождества

;

7) Найдите и докажите формулы:

, , , .

2. Доказательство неравенств

Докажите неравенства: 1) при любом натуральном ;

2) при любом натуральном ;

3) при любом натуральном ;

4) при любом натуральном ;

5) при ; 6)

7) ; 8) ;

9) .

10) , .

3. Доказательство делимости

Докажите, что для любого натурального числа :

1) ; 2) ; 3) ; 4) ; 5) ; 6) кратно 17.

4. Доказательство формулы общего члена последовательности, заданной рекуррентно

1) Дано: , . Докажите, что .

2) Дано: , , . Докажите, что .

3) Дано: , , . Докажите, что .

4) Дано: , , . Докажите, что .

5) Последовательность Фибоначчи задана рекуррентно: , , . Докажите, что: , .

6) Последовательность задана рекуррентно: , , . Выразите через .

7) Последовательность задана рекуррентным соотношением с начальными значениями , . Докажите, что: все члены последовательности делятся на 3;

все члены последовательности с четными номерами делятся на 5.

5. Доказательства по индукции в геометрии

1) На сколько частей разделят плоскость прямых плоскости, проходящих через одну точку?

2) На сколько интервалов разделят прямую ее точек?

3) Докажите, что плоскостей пространства, из которых каждые три пересекаются и никакие четыре не имеют общей точки, делят пространство на частей.

4) В плоскости проведено окружностей так, что каждые две из них пересекаются в двух точках и никакие три не имеют общей точки. Докажите, что при этом плоскость разбивается на частей.

5) Докажите, что сторона правильного -угольника выражается через радиус описанной окружности выражается формулой: .

6) На сколько треугольников -угольник может быть разбит своими непересекающимися диагоналями?

7) Докажите, что сумма внутренних углов выпуклого -угольника равна .

Используемые источники:

1. М.Л.Галицкий, М.М.Мошкович, С.И.Шварцбурд, Углубленное изучение курса алгебры и математического анализа. М.: «Просвещение», 1990.

2. Н.Я.Виленкин, Г.С.Сурвилло, Ф.С.Симонов, А.И.Кудрявцев Алгебра 9. М.: «Просвещение», 1998.

3. М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич, Сборник задач по алгебре 8-9. М.: «Просвещение», 1997.

4. И.С.Соминский, Л.И.Головина, И.М.Яглом, О математической индукции. М.: «Наука», 1967.

Метод математической индукции — презентация онлайн

Метод
математической
индукции
Содержание:
1.Введение.
2.Основная часть и примеры.
3.Заключение.
Знаменитый математик XVII в.

П.Ферма
проверив, что числа
20
2 1 1 3
2
2 2 1 5
2
2
2
,
2
23
1 17
, 1 257
24
1 65537
простые, сделал по индукции
предположение, что для всех
n=1,2,3,… числа вида
2
простые.
2
n
1
В XVIII веке Л.Эйлер нашел, что при n=5
2
25
1 4294967297 641 6700417
составное число
Введение
В основе всякого математического исследования
лежат дедуктивный и индуктивный методы.
Дедуктивный метод рассуждений — это
рассуждение от общего к частному, т.е.
рассуждение, исходным моментом которого
является общий результат, а заключительным
моментом – частный результат. Индукция
применяется при переходе от частных результатов
к общим, т.е. является методом, противоположным
дедуктивному.
Основная часть
По своему первоначальному смыслу слово
“индукция” применяется к рассуждениям,
при помощи которых получают общие
выводы, опираясь на ряд частных
утверждений. Простейшим методом
рассуждений такого рода является полная
индукция. Вот пример подобного
рассуждения.
Пусть требуется установить, что каждое
натуральное чётное число n в пределах
4
простых чисел. Для этого возьмём все такие
числа и выпишем соответствующие
разложения:
4=2+2; 6=3+3; 8=5+3;
10=7+3; 12=7+5; 14=7+7;
16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое
из интересующих нас чисел действительно
представляется в виде суммы двух простых
слагаемых.
Таким образом, полная индукция заключается
в том, что общее утверждение доказывается
по отдельности в каждом из конечного числа
возможных случаев.
Иногда общий результат удаётся предугадать
после рассмотрения не всех, а достаточно
большого числа частных случаев (так
называемая неполная индукция).
Полная индукция имеет в математике
лишь ограниченное применение.

Многие
интересные математические утверждения
охватывают бесконечное число частных
случаев, а провести проверку для
бесконечного числа случаев мы не в
состоянии. Неполная же индукция часто
приводит к ошибочным результатам.
Во многих случаях выход из такого рода
затруднений заключается в обращении к
особому методу рассуждений,
называемому методом математической
индукции.
Принцип математической
индукции.
Если предложение А(n), зависящее от
натурального числа n, истинно для n=1 и из
того, что оно истинно для n=k (где k-любое
натуральное число), следует, что оно истинно и
для следующего числа n=k+1, то
предположение А(n) истинно для любого
натурального числа n.
Если предложение А(n) истинно при n=p и
если А(k) >А(k+1) для любого k>p, то
предложение А(n) истинно для любого n>p.
Док-во по методу математической индукции
проводиться следующим образом. Сначала
доказываемое утверждение проверяется для
n=1, т.е. устанавливается истинность
высказывания А(1). Эту часть
доказательства называют базисом
индукции. Затем следует часть док-ва,
называемая индукционным шагом. В этой
части доказывают справедливость
утверждения для n=k+1 в предположении
справедливости утверждения для n=k ,т.е.
доказывают, что А(k) >A(k+1).

12. Алгоритм доказательства методом математической индукции

Проверяют справедливость гипотезы для наименьшего
из натуральных чисел при котором гипотеза имеет смысл
(базис индукции).
1.
Сделав предположение, что гипотеза верна для
некоторого значения k, стремятся доказать
справедливость ее для k+1 (индукционный шаг).
2.
Если такое доказательство удалось довести до конца,
то, на основе принципа математической индукции можно
утверждать, что высказанная гипотеза справедлива для
любого натурального числа n.
3.
Метод математической индукции
в решении задач на делимость.

Пример 1
Доказать, что при любом n , 7 n-1 делится на
6 без остатка.
Решение:
1)Пусть n=1, тогда Х1 =71-1=6 делится на 6
без остатка. Значит при n=1 утверждение
верно.
2) Предположим, что при n=k ,7k-1 делится
на 6 без остатка.
3) Докажем, что утверждение справедливо
для n=k+1.
X k+1 =7 k+1 -1=7
7 k -7+6=7(7 k -1)+6.
Первое слагаемое делится на 6, поскольку
7 k-1 делится на 6 по предположению, а
вторым слагаемым является 6. Значит 7 n-1
кратно 6 при любом натуральном n. В силу
метода математической индукции
утверждение доказано.
Применение метода к
суммированию рядов.
Пример 2
Доказать, что
1+х+х
2
+х
3
+…+х
n
=(х
n+1
-1)/(х-1), где х (1)
Решение:
1) При n=1 получаем
2
1+х=(х -1)/(х-1)=(х-1)(х+1)/(х-1)=х+1
следовательно, при n=1 формула верна; А(1)
истинно.
2) Пусть k-любое натуральное число и пусть
формула верна при n=k, т.е.
1+х+х 2 +х 3 +…+х k =(х k+1 -1)/(х-1).
Докажем, что тогда выполняется равенство
2
3
k
k+1
k+2
1+х+х +х +…+х +x
=(x
-1)/(х-1).
В самом деле
2
3
k
k+1
2
3
1+х+х +x +…+х +x
=(1+x+x +x +…+x
k
)+x k+1 = (x k+1 -1)/(x-1)+x k+1 =
=(x k+2 -1)/(x-1).
Итак, А(k) > A(k+1).
На основании принципа математической
индукции заключаем, что формула верна для
любого натурального числа n.
Применения метода к
доказательству неравенств.
Пример 3
Доказать, что при n>2 справедливо неравенство
1+(1/2
2
)+(1/3
2
)+…+(1/n
2
)
Решение:
1) При n=3 неравенство верно
1+(1/2 2 )+(1/3 2 )=245/180
2)Предположим, что при n=k
1+(1/2
2
)+(1/3
2
)+…+(1/k 2 )=1,7-(1/k).
3) Докажем справедливость неравенства при n=k+1
(1+(1/2
2
)+…+(1/k
2
))+(1/(k+1)
2
)

Докажем, что
1,7-(1/k)+(1/(k+1) 2 )
(1/(k+1) 2 )+(1/k+1)
k(k+2)
Последнее очевидно, а поэтому
1+(1/2
2
)+(1/3
2
)+…+(1/(k+1) 2 )
В силу метода математической индукции неравенство
доказано.

Метод в применение к другим
задачам.
Пример 4
Доказать, что число диагоналей выпуклого nугольника равно n(n-3)/2.
Решение:
1) При n=3 утверждение справедливо, ибо в
треугольнике
А 3 =3(3-3)/2=0 диагоналей;
А 2 А(3) истинно.
2) Предположим, что во всяком
выпуклом k-угольнике имеет ся А k =k(k-3)/2
диагоналей.
3)Докажем, что тогда в выпуклом
А k+1 (k+1)-угольнике число
диагоналей А k+1 =(k+1)(k-2)/2.
Пусть А 1 А 2 А 3 …A k A k+1 -выпуклый (k+1)угольник. Проведём в нём диагональ A 1 A k . Чтобы
подсчитать общее число диагоналей этого (k+1)угольника нужно подсчитать число диагоналей в kугольнике A 1 A 2 …A k , прибавить к полученному
числу k-2, т.е. число диагоналей (k+1)-угольника,
исходящих из вершины А k+1 , и, кроме того, следует
учесть диагональ А 1 А k. Таким образом,
k+1=k+(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.
Итак, А(k) > A(k+1). Вследствие принципа математической
индукции утверждение верно для любого выпуклого
n-угольника.
Заключение
В частности изучив метод математической
индукции, я повысила свои знания в этой
области математики, а также научилась
решать задачи, которые раньше были мне
не под силу.
В основном это были логические и
занимательные задачи, т.е. как раз те,
которые повышают интерес к самой
математике как к науке. Решение таких
задач становится занимательным занятием
и может привлечь в математические
лабиринты всё новых любознательных. Помоему, это является основой любой науки.
«Понимание и умение
правильно применять
принцип математической
индукции, является хорошим
критерием логической
зрелости, которая
совершенно необходима
математику»
А.Н. Колмогоров

23. Ханойские башни

Есть три стержня и колец
разного размера. Класть
можно
только
кольцо
меньшего
размера
на
кольцо большего размера.

Можно ли переместить
пирамидку
с
одного
стержня на другой?

24. Пересечение прямых

Докажите, что любые n
прямых, расположенных на
одной плоскости, никакие
две
из
которых
не
параллельны, и никакие
три не пересекаются в
одной точке, пересекаются
ровно в
точках.

25. Докажите тождество

1. [БАЗА]Проверим, работает ли эта формула при n=1:
2.[ПРЕДПОЛОЖЕНИЕ] Предположим, что тождество верно при n=k, то есть
3.[ШАГ] Шаг индукции будет соответствовать проверке этого тождества
при n=k+1, то есть нужно доказать, что
4.[ВЫВОД] Тождество верно для любого .
Группа 1.
Задача 1. Докажите, что при каждом
натуральном , начиная с , существует
выпуклый -угольник, имеющий ровно
три острых угла.
Задача 2. Доказать, что 1+3+5+…+(2n1)=n 2 .
Задача 3.Доказать, что (11 n+2 +12 2n+1 )
делится на 133 без остатка.
Группа 3.
Задача 1. Докажите что сумма углов
выпуклого n-угольника равна
(или
радиан). В частности для
треугольника получаем
а для четырехугольника
Задача 2. Доказать, что при любом n
справедливо утверждение:
1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.
Задача 3.Доказать, что 3 3n-1 +2 4n-3 при
произвольном натуральном n делится на
11.
Группа 2.
Задача 1. Плоскость разделена на части n
прямыми. Докажите, что эти части
можно раскрасить в два цвета так, что
соседние куски будут раскрашены в
разные цвета.
Задача 2. Доказать, что
1+х+х 2 +х 3 +…+х n =(х n+1 -1)/(х-1).
Задача 3.Доказать, что при любом n 7 n -1
делится на 6 без остатка.
Группа 4.
Задача 1. Чему равно количество
кусочков, на которые n прямых (не
проходящих через одну точку) делят
плоскость на части? Одна прямая — на две
части, две — на четыре. А пятнадцать
прямых?
Задача 2. Доказать, что 1 3 -2 3 +3 3 4 3 +…+(2n-1) 3 -(2n) 3 =-n 2 (4n+3) для
любого натурального n.

Задача 3.Доказать, что 11 2n -1 при
произвольном натуральном n делится на 6
без остатка.

27. Рефлексия

Доказательство индукцией

Доказательство индукцией Доказательства по индукции Доказательство по индукции похоже на обычное доказательство, в котором каждый шаг должно быть оправдано. Однако в нем используется хитрый прием, который позволяет вам доказать утверждение о произвольном числе n, предварительно доказав это верно, когда n равно 1, а затем предполагая, что это верно для n = k и показывая это верно для n = k + 1. Идея в том, что если вы хотите показать это кому-то может подняться на n-й этаж пожарной лестницы, вам нужно только показать, что вы можете подняться по лестнице на пожарную лестницу (n = 1), а затем показать, что умеешь подниматься по лестнице с любого уровня пожарной лестницы (n = k) на следующий уровень (n = k + 1).

Если вы сделали доказательство по индукции до того, как вас, возможно, попросили предположим случай n-1 и покажем случай n, или предположим случай n и покажем случай n + 1. Это то же самое, что я объясняю здесь, но я используйте другую букву, потому что я думаю, это позволяет избежать путаницы, когда пытаясь выяснить, в чем заключается каждый случай.

Пример 1. Докажите 1 + 2 + … + n = n (n + 1) / 2, используя доказательство по индукции.

n = 1: 1 = 1 (2) / 2 = 1 проверка.

Предположим, что выполняется n = k: 1 + 2 +… + k = k (k + 1) / 2 (индукционная гипотеза)
Показать n = k + 1: 1 + 2 + … + k + (k + 1) = (k + 1) ((k + 1) +1) / 2
Я просто подставляю k и k + 1 в формулу, чтобы получить эти строки. Обратите внимание, что я записываю то, что хочу доказать.

Теперь я начну с левой части уравнения, которое хочу показать. и продолжаем, используя предположение индукции и алгебру, чтобы достичь правая часть уравнения. 1 + 2 + … + (к + 1) = 1 + 2 + … + к + (к + 1)
= k (k + 1) / 2 + (k + 1) по гипотезе индукции
= (k (k + 1) +2 (k + 1)) / 2 на 2/2 = 1 и распределение деления по сложению
= (k + 2) (k + 1) / 2 по распределению умножения над сложением
= (k + 1) (k + 2) / 2 по коммутативности умножения

QED

Пример 2: Докажите, что если P1 P2. ..Pn — коллинеарные точки в пространстве, удовлетворяющие аксиомам инцидентности и промежуточности, так что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 … (n-1), тогда Pj находится между P1 и Pn для любого j = 2 … (n-1).

Это другой вид доказательства по индукции, потому что в нем нет смысла. пока n = 3. Итак, мы начинаем с n = 3, а затем показываем, что если n = k, мы получаем n = (k + 1), таким образом доказывая утверждение для n = 3,4,5,6, …

n = 3: P2 находится между P1 и P3, подразумевает, что P2 находится между P1 и P3.Сделанный

Предположим, что n = k: , если P1 P2 … Pk коллинеарные точки такой, что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 … (k-1), тогда Pj находится между P1 и Pk для любого j = 2 … (k-1). Гипотеза индукции.

Показать n = k + 1: , если P1 P2 … P (k + 1) коллинеарные точки такой, что каждый Pj находится между P (j-1) и P (j + 1) для j = 2 … k, тогда Pj находится между P1 и P (k + 1) для любого j = 2 … (k).

K точек P1, P2, … P (k-1) P (k + 1) удовлетворяют условиям индукции гипотеза, чтобы мы знали Pj находится между P1 и P (k + 1) для любого j = 2… (к-1).

K точек P1, P3, P4 … Pk P (k + 1) также удовлетворяют условиям индукции гипотеза, поэтому мы знаем, что Pj находится между P1 и P (k + 1) для любого j = 3 … (k).

QED

Пример 3: Докажите, что любое пространство, удовлетворяющее аксиомам инцидентности и Промежуток, содержащий точку, имеет бесконечное количество различных коллинеарные точки.

Если я могу показать, что пространство содержит n точек для любого числа n, тогда он должен иметь бесконечное количество точек.Так Я проведу доказательство индукцией по количеству точек n.

n = 1: Содержит ли пробел хотя бы одну точку? Да, это делает гипотеза («которая содержит точку»)

Предположим, мы нашли n = k коллинеарных точек (гипотеза индукции)
Покажите, что мы можем найти n = k + 1 коллинеарных точек. Нам нужно найти еще одну точку.

А теперь нарисуем картинку. Если мы поставим все точки на линию тогда легко добавить еще одну точку в конце.Сделать это проще если баллы в порядке. Другими словами было бы проще доказать: любое пространство, удовлетворяющее Аксиомам инцидентности и Промежуток, содержащий точку, имеет бесконечное количество различных коллинеарные точки P1, P2, … такие, что каждая Pi находится между P (i + 1) и P (i-1) для i> 1. Итак, мы изменим нашу гипотезу индукции.

Предположим, что n = k: , что у нас есть n = k коллинеарных точек P1, P2, … Pk таких, что P2 находится между P1 и P3, P3 находится между P4 и P2… P (k-1) находится между P (k-2) и Pk. (Новая гипотеза индукции)

Показать n = k + 1: что у нас есть n = k + 1 коллинеарных точек P1, P2, … P (k + 1) таких, что P2 находится между P1 и P3, P3 находится между P4 и P2, … P (k) находится между P (k-1) и P (k + 1).

По предположению индукции мы имеем k коллинеарных точек. Находим k + 1 точку, используя аксиому B2, которая гласит, что при B = P (1) и D = Pk мы можем найти новая точка E = P (k + 1) такая, что Pk находится между P (1) и P (k + 1). *

Теперь нам нужно показать, что P (k + 1) отличается от Pj для любого j = 1,2…к.

По примеру 2. мы знаем, что Pj находится между P1 и Pk для j = 2,3 … k-1. *

Однако P (k) находится между P1 и P (k + 1), поэтому по аксиоме B3 P (k + 1) не может быть Pj для j = 2,3 … k-1.

Поскольку P (k + 1) уже отличался от P1 и Pk, мы закончили.

QED?

В этом доказательстве есть две ошибки! Когда мы цитировали Пример 2, мы могли сделать это, только если k было больше или равно 3! Также на самом первом шаге мы предполагаем, что k было больше или равно 2! См. * В доказательстве.

Затем мы должны выполнить эти случаи в начале в дополнение к n = 1.

n = 2: Согласно аксиоме I3 существуют три точки, которые не являются коллинеарными. Пусть P1 и P2 — две из этих точек. Эти пункты «по порядку» потому что их всего двое.

n = 3: В случае n = 2 мы знаем, что у нас есть две коллинеарные точки P1 и P2. По аксиоме B3 мы можем найти P3 такое, что P2 находится между P1 и P3. Они уже в порядке только Axiom B3.(n-1) используя определение производная.

3) Докажите, что пространство с n точками чьи прямые — это любая пара различных точек удовлетворяет аксиомам инцидентности.

4) Докажите, что в пространстве, удовлетворяющем аксиомам инцидентности и между двумя точками A и B бесконечно между ними много точек.

Математическая индукция

Математическая индукция — это особый способ доказательства. В нем всего 2 ступени:

Шаг 1.Покажите, что это верно для первый
Шаг 2. Покажите, что если любое истинно, то следующее истинно

Тогда все верны

Вы слышали об «эффекте домино»?

Шаг 1. Первое падение домино
Шаг 2. Когда выпадает любого домино, выпадает следующих домино

Итак … все домино упадут!

Так работает математическая индукция.

В мире чисел мы говорим:

Шаг 1. Покажите, что это верно для первого случая, обычно n = 1
Шаг 2. Покажите, что если n = k верно, то n = k + 1 также верно

Как это сделать

Шаг 1 обычно прост, нам просто нужно доказать, что он верен для n = 1

Шаг 2 лучше всего выполнить так:

Предположим, что верно для n = k
Докажите, что истинно для n = k + 1 (мы можем использовать случай n = k как факт .)

Это все равно что сказать «ЕСЛИ мы можем заставить домино упасть, упадет ли следующая?»

Шаг 2 часто может быть сложным , нам, возможно, придется использовать творческие уловки, чтобы заставить его работать!

Как в этом примере:

Пример: 3

ⁿ −1 делится на 2?
Это правда? Давайте узнаем.
1. Покажите, что это верно для n = 1
3 ¹ −1 = 3−1 = 2
Да 2 делится на 2.Это было просто.
3 ¹ −1 верно
2. Предположим, что это верно для n = k
3 ^k −1 верно
(Погодите! Откуда мы это знаем? Мы этого не делаем!
Это предположение … что мы рассматриваем
как факт для остальной части этого примера)
Теперь докажем, что 3 ^{k + 1} −1 делится на 2
3 ^{k + 1} также 3 × 3 ^k
Затем разделите 3 × на 2 × и 1 ×
И каждое из них кратно 2
Потому что:
2 × 3 ^k делится на 2 (мы умножаем на 2)
3 ^k −1 верно (мы сказали, что в предположении выше)
Итак:
3 ^{k + 1} −1 верно
СДЕЛАНО!
Вы видели, как мы использовали случай 3 ^k −1 как истинный , хотя мы этого и не доказали? Это нормально, потому что мы полагаемся на Domino Effect …
… мы спрашиваем , если упадет любое домино, упадет ли следующий ?
Итак, мы принимаем это как факт (временно), что домино « n = k » падает (т.е. 3 ^k −1 верно), и посмотрим, означает ли это « n = k + 1 ». «Домино тоже упадет.
Уловки
Я уже говорил, что нам часто нужно использовать творческие уловки.
Обычный трюк — переписать случай n = k + 1 на 2 части:
одна часть представляет собой случай n = k (который предполагается верным)
затем можно проверить другую часть, чтобы убедиться, что она также верна
Мы сделали это в примере выше, а вот еще один:
Пример: сложение нечетных чисел
1 + 3 + 5 +… + (2n − 1) = n ²
1. Покажите, что это верно для n = 1
1 = 1 ² верно
2. Предположим, что это верно для n = k
1 + 3 + 5 + … + (2k − 1) = k ² верно
(Предположение!)
Теперь докажите, что это верно для «k + 1»
1 + 3 + 5 + … + (2k − 1) + (2 (k + 1) −1) = (k + 1) ² ?
Мы знаем, что 1 + 3 + 5 +… + (2k − 1) = k ² (предположение выше), поэтому мы можем сделать замену для всех членов, кроме последнего:
к ² + (2 (к + 1) −1) = (к + 1) ²
Теперь разверните все термины:
к ² + 2 к + 2 — 1 = к ² + 2 к + 1
И упростить:
к ² + 2k + 1 = к ² + 2k + 1
Они такие же! Так что это правда.
Итак:
1 + 3 + 5 +… + (2 (k + 1) −1) = (k + 1) ² верно
СДЕЛАНО!
Твоя очередь
А теперь еще два примера , на которых вы можете попрактиковаться.
Сначала попробуйте сами, а затем посмотрите наше решение ниже.
Пример: треугольные числа
Треугольные числа — это числа, которые могут образовывать треугольный точечный узор.
Докажите, что n-ое треугольное число равно:
Т _п = п (п + 1) / 2
Пример: сложение чисел куба
Числа куба — это кубы натуральных чисел
Докажите, что:
1 ³ + 2 ³ + 3 ³ +… + n ³ = ¼n ² (n + 1) ²
. . . . . . . . . . . . . . . . . .
Пожалуйста, не читайте решения, пока не попробуете сами, это единственные вопросы на этой странице, над которыми вы можете попрактиковаться!
Пример: треугольные числа
Докажите, что n-ое треугольное число равно:
Т _п = п (п + 1) / 2
1. Показать, что это правда для n = 1
T ₁ = 1 × (1 + 1) / 2 = 1 истинно
2. Предположим, что это верно для n = k
T _k = k (k + 1) / 2 Верно (предположение!)
Теперь докажите, что это верно для «k + 1»
Т _{к + 1} = (к + 1) (к + 2) / 2?
Мы знаем, что T _k = k (k + 1) / 2 (предположение выше)
T _{k + 1} имеет дополнительный ряд из (k + 1) точек
Итак, T _{k + 1} = T _k + (k + 1)
(к + 1) (к + 2) / 2 = к (к + 1) / 2 + (к + 1)
Умножьте все члены на 2:
(к + 1) (к + 2) = к (к + 1) + 2 (к + 1)
(к + 1) (к + 2) = (к + 2) (к + 1)
Они такие же! Так что правда .
Итак:
T _{k + 1} = (k + 1) (k + 2) / 2 истинно
СДЕЛАНО!
Пример: сложение чисел куба
Докажите, что:
1 ³ + 2 ³ + 3 ³ + … + n ³ = ¼n ² (n + 1) ²
1. Покажите, что это верно для n = 1
1 ³ = ¼ × 1 ² × 2 ² верно
2. Предположим, что это верно для n = k
1 ³ + 2 ³ + 3 ³ + … + k ³ = ¼k ² (k + 1) ² верно (предположение!)
Теперь докажите, что это верно для «k + 1»
1 ³ + 2 ³ + 3 ³ + … + (k + 1) ³ = ¼ (k + 1) ² (k + 2) ²?
Мы знаем, что 1 ³ + 2 ³ + 3 ³ +… + k ³ = ¼k ² (k + 1) ² (предположение выше), поэтому мы можем заменить все, кроме последнего члена:
¼k ² (k + 1) ² + (k + 1) ³ = ¼ (k + 1) ² (k + 2) ²
Умножьте все члены на 4:
к ² (к + 1) ² + 4 (к + 1) ³ = (к + 1) ² (к + 2) ²
Все термины имеют общий множитель (k + 1) ², поэтому его можно отменить:
к ² + 4 (к + 1) = (к + 2) ²
И упростить:
к ² + 4 к + 4 = к ² + 4 к + 4
Они такие же! Так что это правда.
Итак:
1 ³ + 2 ³ + 3 ³ + … + (k + 1) ³ = ¼ (k + 1) ² (k + 2) ² верно
СДЕЛАНО!
Математическое доказательство правильности и эффективности алгоритма
Введение
При разработке совершенно нового алгоритма необходим очень тщательный анализ его правильности и эффективности .
Меньше всего вам хотелось бы, чтобы ваше решение было неадекватным для проблемы, для решения которой изначально был разработан .
В этой статье речь пойдет о следующих предметах:
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ : как вы можете видеть из заголовков разделов, это никоим образом не предназначено для прямого применения. Это Computer Science Theory , и он предназначен только для более глубокого понимания определенных областей практического программирования.
Математическая индукция
Математическая индукция (MI) — важный инструмент для доказательства утверждения, которое доказывает правильность алгоритма.Общая идея MI состоит в том, чтобы доказать, что утверждение верно для любого натурального числа n .
Что это на самом деле означает?
Это означает, что мы должны пройти 3 шага:
Гипотеза индукции : Определите правило, которое мы хотим доказать для каждого n , давайте назовем правило F (n)
База индукции : Доказательство того, что правило действительно для начального значения, или, скорее, для отправной точки — это часто подтверждается решением гипотезы индукции F (n) для n = 1 или любого подходящего начального значения
Шаг индукции : Доказательство того, что, если мы знаем, что F (n) истинно, мы можем сделать шаг на один шаг вперед и предположить, что F (n + 1) верно
Если вы выполнили эти шаги, теперь у вас есть возможность зацикливаться! Нет, правда, это дает нам возможность делать что-то вроде этого:
для (i в диапазоне (n)): T [i] = Верно
Базовый пример
Задача :
Если мы определим S (n) как сумму первых n натуральных чисел, например, S (3) = 3 + 2 + 1 , докажите, что следующая формула может быть применена к любому n :
$$
S (n) = \ frac {(n + 1) * n} {2}
$$
Проследим наши шаги:
Гипотеза индукции : S (n) определяется формулой выше
Индукционная база : На этом этапе мы должны доказать, что S (1) = 1 :
$$
S (1) = \ frac {(1 + 1) * 1} {2} = \ frac {2} {2} = 1
$$
Шаг индукции : На этом шаге нам нужно доказать, что если формула применима к S (n) , она также применима к S (n + 1) следующим образом:
$$ S (n + 1) = \ frac {(n + 1 + 1) * (n + 1)} {2} = \ frac {(n + 2) * (n + 1)} {2} $$
Это известно как импликация (a => b), что просто означает, что мы должны доказать правильность b при условии, что мы знаем, что a правильное.2 + 3n + 2} {2} = \ frac {(n + 2) * (n + 1)} {2}
$$
Обратите внимание, что S (n + 1) = S (n) + (n + 1) просто означает, что мы рекурсивно вычисляем сумму. Пример с литералами:
S (3) = S (2) + 3 = S (1) + 2 + 3 = 1 + 2 + 3 = 6
Q.E.D.
Подтверждение правильности
Поскольку метод, который мы используем для доказательства правильности алгоритма, основан на математике, или, скорее, на основе функции , чем больше решение похоже на реальную математическую функцию, тем проще доказательство.
Почему это спросите вы? Ну, в практическом императивном программировании есть такая вещь, которая называется состоянием , это означает, что вывод программы зависит от 3 вещей:
Его последовательность инструкций
Его входные значения
его состояние , точнее, все ранее инициализированные переменные, которые могут каким-либо образом изменить выходное значение
Пример состояния программы
def foo (x): х = у + 1 вернуть х
Если бы я попросил вас дать мне выходное значение этой функции для x = 1 , вы, естественно, сказали бы:
Ну, боже, сэр, как бы нам узнать выходное значение, если бы мы не знали, черт возьми, значение y .
Видите ли, именно в этом суть, эта (императивная) программа, как и любая другая, имеет состояние , которое определяется списком переменных и их соответствующими значениями. Только тогда результат этой программы действительно будет детерминированным .
Детерминированный — система без случайных факторов
Это открывает совершенно новую историю о парадигмах программирования, которые имеют полностью прозрачное состояние или, другими словами, не имеют ПЕРЕМЕННЫХ .Это может показаться безумием, но оно существует и используется нечасто, особенно функциональное программирование в Haskell .
Но поскольку в императивном программировании в нашем распоряжении традиционно отсутствуют функциональные концепции, мы выбираем следующий лучший способ доказательства правильности — рекурсию . Рекурсия очень проста для математической интерпретации, потому что она эквивалентна рекуррентным отношениям (подробнее о рекуррентных отношениях в следующих разделах).
Пример рекурсии
def factorial (n): если (n == 0): возврат 1 еще: вернуть n * факториал (n-1)
Преобразовано в повторную форму:
$$
Факториал (n) = n * Факториал (n-1)
$$
Инварианты цикла
Все это звучит хорошо и модно, но до сих пор мы ничего не говорили о представлении циклов и состояний программы в виде математических формул.Переменные в состоянии программы создают проблему, потому что все они должны постоянно контролироваться, на случай, если кто-то выйдет из строя.
Кроме того, петли создают проблему, потому что им очень мало математических эквивалентов. Это означает, что мы должны включить математическую индукцию в нашу модель анализа алгоритмов , потому что это единственный известный нам метод, который может итеративно инкриминировать значения в математике, как в реальном коде.
Самый простой способ решения обеих задач (с помощью математической индукции) — это Инварианты цикла :
Инвариант цикла — это логическая формула или просто набор правил, которые истинны до, во время и после рассматриваемого цикла (поэтому он не зависит от итераций).Крайне важно, чтобы он содержал правила для всех переменных, которые встречаются в указанном цикле, потому что нам нужно привязать их все к набору значений, которые мы хотим, чтобы они были.
Выбор инварианта цикла
Инвариант цикла может быть настолько сложным и простым, насколько вы хотите. Однако суть в том, что она должна быть сконструирована так, чтобы как можно точнее походить на рассматриваемую проблему.
Например, я всегда могу сказать, что следующий инвариант цикла:
(x> y) ∨ (x Но, используя тавтологию (логическая формула, которая всегда верна) в качестве инварианта цикла, мы на самом деле ничего не достигаем, Единственная причина, по которой он технически классифицируется как инвариант цикла, заключается в том, что он соответствует всем трем требованиям:
Формула верна ДО выполнения цикла
Формула верна ВО ВРЕМЯ выполнения цикла, включая все шаги между
Формула верна ПОСЛЕ выполнения цикла
Пример:
Давайте посмотрим на следующий код и определим оптимальный инвариант цикла:
х = 10 у = 4 г = 0 п = 0 в то время как (n
Логически этот код просто вычисляет значение x * y и сохраняет его в z, это означает, что z = x * y .Еще одно условие, которое, как мы знаем, всегда будет истинным, - это n <= x (подробнее о равенстве в примере). Но действительно ли эти два аспекта применимы только после того, как программа завершила вычисления?
Значение n - это, по сути, количество циклов, которые уже были выполнены, но также это количество раз, когда значение z было увеличено на y .
Таким образом, это означает, что и z = n * y , и n <= x могут всегда применять .Осталось только проверить, действительно ли они могут использоваться в качестве инварианта цикла.
Пример инварианта цикла - индукционное доказательство
Во-первых, нам нужно доказать, что инвариант цикла истинен до того, как войдет в цикл (что эквивалентно доказательству и основанию индукции ):
# <=> - логическая эквивалентность, левая и правая части уравнения имеют одинаковое логическое значение (Истина или Ложь) # <= - меньше или равно (не путать с подтекстом, который также выглядит как стрелка влево) х = 10 у = 4 г = 0 п = 0 # ПРАВИЛО 1: z == n * y # 0 == 0 * 4 = 0 <=> Верно # поэтому применяется ПРАВИЛО 1 # ПРАВИЛО 2: n <= x # 0 <= 10 <=> Верно # поэтому применяется ПРАВИЛО 2, поэтому инвариант действителен до входа в цикл
Во-вторых, нам нужно проверять истинность инварианта после каждого завершенного цикла (исключая последний), мы делаем это, наблюдая за переходом от z, n к z ', n' , где z ' и n ' - значения z и n после выполнения следующего цикла.
Следовательно, z '= z + y и n' = n + 1 . По сути, нам нужно доказать, что если мы знаем, что инвариант верен для z и n , он также верен для z ' и n' :
. z ′ = z + yz = n ∗ yn ′ = n + 1 Если справедливо следующее утверждение, верен инвариант: z ′ = n ′ ∗ y? z ′ = (n + 1) ∗ y = n ∗ y + y = z + y В-третьих, нам нужно проверить, верен ли инвариант после последней итерации цикла. Поскольку n является целым числом, и мы знаем, что n-1 истинно, но n ложно, это означает, что n = x (это причина, по которой инвариант должен включать n <= x , а не n ). Следовательно, мы знаем, что z = x * y . Q.E.D. Анализ эффективности: отношения повторяемости Когда говорят об эффективности алгоритма, первое, что приходит на ум, - это рекуррентные отношения. Это просто означает, что функция, такая как f (n) , зависит от ее предшествующих и последующих значений, таких как f (n-1) и f (n + 1) . Простейшим примером такой функции может быть последовательность Фибоначчи: $$ Фибоначчи (n) = Фибоначчи (n-1) + Фибоначчи (n-2) $$ Вы можете узнать эту концепцию из моей статьи о динамическом программировании.И да, проблема очень похожа, но метод решения очень другой. При анализе эффективности алгоритма вы будете решать в основном два типа отношений: Линейные однородные рекуррентные соотношения Нелинейные рекуррентные отношения - пример использования основной теоремы Решение однородных линейных рекуррентных отношений Читая заголовок выше, вы можете спросить себя "Черт побери, что это за математическая чушь?!?!" Ну, сначала давайте посмотрим на общую формулу: F (n) = a1F (n - 1) + a2F (n - 2) +. 5 = i, \ end {align} $$ это означает, что i имеет цикл длиной = 5 другие комплексные числа могут быть адаптированы для получения точного цикла, в котором нет двух одинаковых элементов (кроме начального и конечного элементов) Используя указанную выше замену, получаем характеристический многочлен : rk − a1rk − 1 − a2rk − 2−...− ak = 0 Это очень удобное уравнение, где r может иметь k возможных решений (корней). Кроме того, мы можем представить F (n) как линейную комбинацию всех его предшественников (доказательство правильности этой формулы не будет показано ради вашего и моего собственного здравомыслия): F (n) = ∑i = 1kcirin ci - неизвестные коэффициенты, которые указывают, какой r имеет наибольшее влияние при вычислении значения F (n) Кроме того, если значение корня (например, r ) встречается более одного раза, мы говорим, что r имеет кратность ( m ) больше 1. Это немного изменяет предыдущее уравнение: (2) F (n) = ∑i = 1shi (n) hi , являющийся элементом, может содержать ri , которое вычисляется (с учетом множественности) по формуле: (3) hi (n) = (Ci, 0 + Ci, 1n + Ci, 2n2 + ... + Ci, mi − 1nmi − 1) rin Поздравляем, теперь мы можем решить голых рекуррентных уравнений. Давайте проверим! Магистр теоремы информатики Помните, когда я сказал, что выше было только голых костей повторяющихся отношений? Что ж, теперь мы рассмотрим более сложный, но гораздо более полезный тип рекуррентного отношения.к $$ из которых все константы равны или больше нуля a, b, c, k> = 0 и b = / = 0 Это гораздо более распространенное рекуррентное отношение , потому что оно воплощает принцип разделяй и властвуй (он вычисляет T (n) , вычисляя гораздо меньшую задачу, например T (n / b) ). Формула, которую мы используем для вычисления T (n) в случае такого рекуррентного соотношения, выглядит следующим образом: T (n) = {O (nlogba) для a> bkO (nklog n) для a = bkO (nk) для a Поскольку приведенная выше формула достаточно логична, , и поскольку доказательство на самом деле нетривиально, Я бы посоветовал просто запомнить его как есть... но если вы все еще хотите увидеть доказательство, прочтите доказательство теоремы 5.1 1-2 в этой статье. Пример: двоичный поиск Если у нас есть отсортированный массив A длиной n , и мы хотим узнать, сколько времени нам потребуется, чтобы найти конкретный элемент, назовем его, например, z . Сначала нам нужно взглянуть на код, который мы будем использовать, чтобы найти указанный элемент с помощью двоичного поиска: # leftIndex и rightIndex указывают, какая часть исходного массива # мы сейчас исследуем, начальный вызов функции - find (A, z, 1, n) импортная математика def find (A, z, leftIndex, rightIndex): # если наш диапазон поиска сужен до одного элемента, # мы просто проверяем, равно ли оно z, где target является индексом желаемого элемента # A [цель] = z если leftIndex == rightIndex: если A [leftIndex] == z: вернуть leftIndex еще: возврат -1 еще: middlePoint = математика.ceil ((leftIndex + rightIndex) / 2) print ("{} {} {}". формат (leftIndex, rightIndex, middlePoint)) # поскольку массив отсортирован, мы знаем, что если z = X [middlePoint] и мы вызываем # find (A, z, leftIndex, middlePoint - 1) # если z == A [middlePoint]: # return middlePoint если z = A [средняя точка] # оставление средней точки в этом вызове намеренно # потому что нет проверки средней точки # кроме случаев, когда leftIndex == rightIndex вернуть find (A, z, middlePoint, rightIndex) def main (): A = [1, 3, 5, 7, 8, 9, 12, 14, 22] г = 12 цель = найти (A, z, 0, len (A)) print ("Целевой индекс: {}".формат (цель)) если __name__ == "__main__": основной() Наиболее трудоемкой частью этого поиска является рекурсия, это означает, что мы можем представить время, необходимое алгоритму двоичного поиска для поиска в массиве длиной n , используя следующее рекуррентное соотношение: $$ T (n) = T (\ frac {n} {2}) + 1 $$ 1 представляет постоянную операцию, такую как проверка значения (например, leftIndex == rightIndex , эта константа на самом деле не так важна, учитывая, что она намного меньше, чем T (n) и T (n \ b ) ). Из сопоставления основной формулы основной теоремы и формулы двоичного поиска мы знаем: $$ a = 1, b = 2, c = 1, k = 0 \ $$ Используя формулу основной теоремы для T (n) , мы получаем: $$ T (n) = O (log \ n) $$ Итак, двоичный поиск действительно более эффективен, чем стандартный линейный поиск. Пример: динамическое программирование против рекурсии Давайте в последний раз взглянем на последовательность Фибоначчи (обещаю, в последний раз): $$ Фибоначчи (n) = Фибоначчи (n-1) + Фибоначчи (n-2) $$ Динамическое программирование, как мы знаем из моей последней статьи, имеет временную сложность O (n) , потому что оно использует запоминание и генерирует массив линейно , без ретроспективных данных (он строит массив с нуля). ). Теперь давайте докажем, что использование динамического программирования намного эффективнее. Анализ временной сложности Фибоначчи Предположим, что T (n) представляет собой время, необходимое для вычисления n-го элемента последовательности Фибоначчи. Тогда мы знаем, что применима следующая формула: $$ T (n) = T (n-1) + T (n-2) $$ Во-первых, нам нужно получить неявную форму уравнения ( math talk для размещения всего с одной стороны, чтобы на другой стороне был только ноль): $$ T (n) -T (n-1) -T (n-2) = 0 $$ Теперь воспользуемся стандартной заменой (формула (1)): $$ r ^ n-r ^ {n-1} -r ^ {n-2} = 0 $$ Чтобы еще больше упростить уравнение, разделим обе части с r на степень наименьшей степени, присутствующей в уравнении (в данном случае это n-2 ): rn − rn − 1 − rn − 2 = 0 / rn − 2rn− (n − 2) −rn − 1− (n − 2) −rn − 2− (n − 2) = 0r2 − r1 − r0 = 0r2− r − 1 = 0 Этот шаг сделан для того, чтобы мы могли свести проблему к квадратному уравнению . Используя формулу квадратного уравнения, мы получаем следующие возможные значения для r : r1 = 1 + 52, r1 = 1−52 Теперь, используя формулу (2) , мы определяем основную формулу для Фибоначчи (n) : T (n) = C1 ∗ r1n + C2 ∗ r2n Поскольку мы знаем, что Фибоначчи (0) = 0 и Фибоначчи (1) = 1 , поэтому T (0) = 0 и T (1) = 1 (технически T (0) и T (1) может быть любым постоянным числом операций, необходимых для вычисления их значений, но на самом деле это не так сильно влияет на результат, поэтому для простоты , они 0 и 1 , точно так же, как Fib (0) и Fib (1) ), мы можем использовать их для решения приведенного выше уравнения для C1 и C2 : T (0) = 0 = C1 ∗ r10 + C2 ∗ r20 = C1 + C2 Что означает: C1 = −C2 Их, используя T (1) : T (1) = 1 = C1 ∗ r11 + C2 ∗ r21 = C1 ∗ r1 + C2 ∗ r2 Поскольку нам известны значения `r1` и` r2`, а также следующее: C1 = −C2 Мы можем подставить их в основное уравнение : 1 = −C2 ∗ 1 + 52 + C2 ∗ 1−52 Когда мы решаем вышеуказанное уравнение для C2 , мы получаем: C1 = −15 C2 = 15 Это означает, что теперь у нас есть окончательное решение рекуррентного соотношения: T (n) = - 15 ∗ (1 + 52) n + 15 ∗ (1−52) n Выведение сложности алгоритма из отношения повторяемости Поскольку T (n) представляет количество шагов, необходимых программе для вычисления n-го элемента в последовательности, n также является входным значением или, чаще всего, размером ввода в битах.n) (рекурсивная - экспоненциальная временная сложность) намного выше, чем O (n) (динамическое программирование - линейная временная сложность), теперь у нас есть окончательный ответ , почему динамическое программирование превосходит по времени традиционное рекурсия . Заключение Я знаю, что эта статья может показаться несколько лишней. Но доказательства правильности и эффективности являются краеугольными камнями современной теории компьютерных наук и основной причиной того, что эта область продолжает быстро развиваться. Компьютерные науки - это не то же самое, что программирование, это лишь один из множества вариантов использования. И я думаю, что людям было бы неплохо лучше понять, что это такое на самом деле, по крайней мере, только через эту статью. Биномиальная теорема: доказательство математической индукцией Видео от Мигеля Á. Padriñán from Pexels Этот мощный метод теории чисел, примененный к биномиальной теореме Математическая индукция, представляет собой метод доказательства, который позволяет нам проверить теорему для всех натуральных чисел.Мы применим эту технику к биномиальной теореме и покажем, как она работает. Индуктивный процесс Рисунок 1: Индуктивный процесс Индуктивный процесс требует 3 шагов. Базовый шаг Мы делаем общее утверждение относительно всех целых чисел. На базовом этапе мы проверяем, верна ли теорема для одного конкретного целого числа. Индуктивная гипотеза Мы предполагаем, что теорема верна для некоторого целого числа, t . Индуктивный шаг Мы показываем, что , если теорема применима к некоторому целому числу t , она также должна применяться к целому числу t +1. В нашем примере мы применяем базовый шаг к n = 3. Поскольку это верно для n = 3, индуктивный шаг говорит нам, что это должно быть верно для n = 3 + 1 = 4. Логика продолжается для всех следующих целых чисел. Мы опрокидываем одно домино; остальные следуют их примеру. Базовый шаг: n = 3 Биномиальная теорема говорит нам, как разложить бином в некоторой неотрицательной целой степени.(Это выходит за рамки этого, но нам не нужно прямо сейчас преследовать эту белку.) Уравнение 1: формулировка биномиальной теоремы Например, когда n = 3: Уравнение 2: биномиальная теорема применительно к n = 3. Мы можем проверить это, вручную умножив ( a + b ) ³. Мы используем n = 3, чтобы лучше всего продемонстрировать теорему в действии. Мы могли бы использовать n = 0 в качестве базового шага. Хотя результат тривиален, его достаточно. Читателю следует проверить теорему для n = 0, 1 и 2. Мы хотим доказать, что эта теорема применима для любого неотрицательного целого числа , n . Индуктивная гипотеза и индуктивный шаг Мы показываем, что , если биномиальная теорема верна для некоторой экспоненты, t , то она обязательно истинна для экспоненты t +1. Уравнение 3: индуктивная гипотеза и ее предполагаемое следствие Мы предполагаем, что у нас есть некоторое целое число t , для которого теорема работает.Это предположение индуктивная гипотеза . Затем мы доводим это предположение до его логического завершения. Очевидно следующее утверждение: Уравнение 4: Утверждение, основанное на установленных правилах арифметики. На основе индуктивной гипотезы и уравнения 4: Уравнение 5. Уравнение 6: Мы будем обрабатывать части A и B по отдельности. Мы хотим добавить серию A и серию B (уравнение 6), но у нас есть проблема. Когда мы выстраиваем их по очереди, показатели не совпадают. Уравнение 7: Серии A и B, по срокам. Это потому, что в серии A в каждом термине есть дополнительные a . Серия B имеет дополнительный b . Решаем задачу сдвигом рядов друг относительно друга. Уравнение 8: То же, что и уравнение 7, но слагаемые, сдвинутые друг относительно друга. Вместо того, чтобы пытаться различить детали, обратите внимание на форму в уравнении 8. Первый член серии A выступает влево. Последний член серии B распространяется вправо. Чтобы рассмотреть это расположение более наглядно, мы перепишем обе серии, используя обозначение суммирования.Однако мы извлекаем первый член из серии A и последний член из серии B. Серия A проста. Выпишите первый член, затем начните индекс с k = 1 вместо k = 0. Equation 8 Series B требует небольшой настройки. Уравнение 9 Серия B считает от k = 0 до k = t-1 . Чтобы сместить его вправо, отсчитайте от k = 1 до k = t. Чтобы учесть это, уменьшите каждый из членов k на 1.Вот что мы получаем: Уравнение 10: Серия A, как в Уравнении 8; Серия B, немного скорректированная по уравнению 9. Когда мы складываем серии A и серию B, мы можем объединить два суммирования. Мы можем вынести за скобки члены с показателями, ведущие к двум биномиальным коэффициентам. Уравнение 11: Серии A и B вместе. Правило Паскаля Два биномиальных коэффициента в уравнении 11 необходимо суммировать. Мы делаем это с помощью правила Паскаля . Вместо того, чтобы ссылаться на Правило, мы выведем его для этого конкретного случая. Возможно, это самая сложная часть вывода. Начнем с расширения биномиального коэффициента. Затем мы берем каждый из трех элементов и расширяем их дальше. Уравнение 12 показывает каждый элемент с его развернутым аналогом. Элементы рекомбинируются для получения нового биномиального коэффициента, умноженного на оставшиеся элементы. Уравнение 12. Мы проделываем ту же операцию со следующим биномиальным коэффициентом (уравнение 13). Уравнение 13. Мы объединяем уравнения 12 и 13, чтобы получить один биномиальный коэффициент (уравнение 14). Уравнение 14. Читатель может найти полезным видео-обзор Правила Паскаля. Видео 1: Самая утомительная часть этого доказательства - применение правила Паскаля. Вот прогон видео. Результатом всех этих усилий является уравнение 15. Здесь у нас есть сумма t членов с дополнительными членами, прикрепленными спереди и сзади. Уравнение 15 Если последний член становится неожиданностью, мы применили только следующее самоочевидное тождество: Уравнение 16 Чтобы повторно вставить первый член в формулу суммирования, мы меняем k = 0 на k = 1. Уравнение 17 Наконец, мы повторно интегрируем последний член в суммирование, заменяя t на t + 1 (над сигмой). Уравнение 18 На этом индуктивный шаг завершен. Мы начали с предположения, что биномиальная теорема применима к некоторому числу, t . Теперь мы показали, что из этого предположения следует, что теорема должна применяться к t +1. Мы уже проверили теорему для t = 3, поэтому мы знаем, что она применима к t = 3 + 1. Мы оставляем читателю возможность подтвердить тривиальный случай t = 0, чтобы завершить доказательство. Для дальнейшего размышления Применима ли биномиальная теорема к отрицательным целым числам? Как можно применить математическую индукцию к этому вопросу? Без заголовка Без заголовка Индукционная Использование математической индукции Предметы для изучения угадывание и проверка с помощью индукции Содержание Иногда, когда вы видите повторяющийся узор в значении некоторого математического выражения, например, сумма некоторых членов, вы можете угадать общую формулу для значения.Чтобы проверить или опровергнуть свое предположение, вы можете использовать математическую индукцию. Пример приведен ниже. Мы видели, что для любого натурального числа n 1 + 2 + ... + n = n (n + 1) / 2 и 1 ² + 2 ² + ... + n ² = п (п + 1) (2 п + 1) / 6 удерж. Тогда можно задаться вопросом, что 1 ³ + 2 ³ +... + n ³ будет равно. Один из способов выяснить это - сделать предположение (то есть обоснованное предположение) и доказать его. Давайте сначала предположим. Посмотрев на суммы 1 + 2 + ... + n = n (n + 1) / 2 --- функция n ² и 1 ² + 2 ² + ... + n ² = п (п + 1) (2 п + 1) / 6 --- функция n ³ , можно догадаться, что 1 ³ + 2 ³ +... + n ³ равно некоторой функции от n ⁴ , то есть 1 ³ + 2 ³ + ... + n ³ = an ⁴ + bn ³ + cn ² + dn + e ---- (1) для некоторых констант a, b, c, d и e . Теперь, чтобы определить значение a, b, c, d и e , мы сравниваем стоимость обе части уравнения (1) для пяти значений n . Для n = 0 , LHS = 0 и RHS = e . Отсюда получаем e = 0 . Аналогично для n = 1 , 1 = a + b + c + d , для n = 2 , 9 = 16a + 8b + 4c + 2d , для n = 3 , 36 = 81a + 27b + 9c + 3d , и для n = 4 , 100 = 256a + 64b + 16c + 4d . Решая эту систему уравнений, получаем a = c = 1/4, b = 1/2 и d = 0 . Следовательно, наша гипотеза 1 ³ + 2 ³ + ... + n ³ = 1/4 n ² (n ² + 2n + 1) = (1/2 n (n + 1)) ² . Далее мы попытаемся доказать это с помощью математической индукции. Доказательство математической индукцией: Базовый шаг: Для n = 0 , LHS = 0 ³ = 0 , и RHS = (1/2 * 0 (0 + 1)) ² = 0 . Следовательно, LHS = RHS. Индукция: Предположим, что 1 ³ + 2 ³ + ... + n ³ = (1/2 п (п + 1)) ² для произвольной n . --------- Гипотеза индукции Тогда для n + 1 , LHS = 1 ³ + 2 ³ + ... + n ³ + (n + 1) ³ = ( 1 ³ + 2 ³ +... + n ³ ) + (n + 1) ³ = ( 1/2 n ( n + 1 )) ² + (n + 1) ³ по предположению индукции. = ( 1/4 (п + 1) ² (п ² + 4 * (п + 1)) = (1/2 (п + 1) (п + 2)) ² , , что равно RHS. Конец проверки Таким образом, теперь мы точно знаем, что 1 ³ + 2 ³ +... + n ³ = (1/2 n (n + 1)) ² . Далее - Корректность программы с использованием индукции Далее - Второй принцип математической индукции Вернуться к расписанию Вернуться к содержанию математическая индукция | Определение, принцип и доказательство Математическая индукция , один из различных методов доказательства математических утверждений, основанный на принципе математической индукции. Принцип математической индукции Класс целых чисел называется наследственным, если всякий раз, когда любое целое число x принадлежит классу, наследник x (то есть целое число x + 1) также принадлежит к этому классу. Принцип математической индукции таков: если целое число 0 принадлежит классу F и F является наследственным, каждое неотрицательное целое число принадлежит классу F . В качестве альтернативы, если целое число 1 принадлежит классу F и F является наследственным, тогда каждое положительное целое число принадлежит F .Принцип формулируется иногда в одной форме, иногда в другой. Поскольку любая форма принципа легко доказывается как следствие другой, нет необходимости проводить различие между ними. Принцип также часто формулируется в интенсиональной форме: свойство целых чисел называется наследственным, если всякий раз, когда какое-либо целое число x имеет свойство, его наследник имеет свойство. Если целое число 1 обладает определенным свойством, и это свойство является наследственным, каждое положительное целое число обладает этим свойством. Доказательство математической индукцией Примером применения математической индукции в простейшем случае является доказательство того, что сумма первых n нечетных натуральных чисел равна n ², то есть (1.) 1 + 3 + 5 + ⋯ + (2 n - 1) = n ² для каждого натурального числа n . Пусть F будет классом целых чисел, для которого выполняется уравнение (1.) ; тогда целое число 1 принадлежит F , поскольку 1 = 1 ².Если любое целое число x принадлежит F , то (2.) 1 + 3 + 5 + ⋯ + (2 x - 1) = x ². Следующее нечетное целое число после 2 x - 1 равно 2 x + 1, и, когда это добавляется к обеим частям уравнения (2.) , результат (3.) 1 + 3 + 5 + ⋯ + (2 x + 1) = x ² + 2 x + 1 = ( x + 1) ². Уравнение (2.) называется гипотезой индукции и утверждает, что уравнение (1.) выполняется, когда n равно x , тогда как уравнение (3.) утверждает, что уравнение (1.) выполняется, когда n равно x + 1. Поскольку уравнение (3.) было доказано как следствие уравнения (2.) , было доказано, что всякий раз, когда x принадлежит F преемник x принадлежит F .Следовательно, по принципу математической индукции все натуральные числа принадлежат F . Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас Вышеизложенное является примером простой индукции; иллюстрацией многих более сложных видов математической индукции является следующий метод доказательства с помощью двойной индукции. Чтобы доказать, что конкретное бинарное отношение F выполняется среди всех положительных целых чисел, достаточно сначала показать, что отношение F выполняется между 1 и 1; во-вторых, всякий раз, когда F находится между x и y , он находится между x и y + 1; и, в-третьих, всякий раз, когда F находится между x и определенным положительным целым числом z (которое может быть фиксированным или может зависеть от x ), оно находится между x + 1 и 1. Логический статус метода доказательства с помощью математической индукции до сих пор вызывает разногласия среди математиков. Джузеппе Пеано включил принцип математической индукции в качестве одной из пяти аксиом арифметики. Многие математики соглашаются с Пеано в том, что он рассматривает этот принцип как один из постулатов, характеризующих конкретную математическую дисциплину (арифметику), и как фундаментально не отличающийся от других постулатов арифметики или других разделов математики. Пеано, Джузеппе Джузеппе Пеано. MacTutor Архив истории математики / Школа математики и статистики, Университет Сент-Эндрюс, Шотландия Анри Пуанкаре утверждал, что математическая индукция является синтетической и априорной, то есть она не сводится к принципу логики или не может быть доказана только на основе логических оснований, и тем не менее известна независимо от опыта или наблюдения. Таким образом, математическая индукция занимает особое место как составляющая математического рассуждения par excellence и позволяет математике исходить из своих предпосылок к действительно новым результатам, что, по общему мнению, невозможно с помощью одной лишь логики.В этой доктрине Пуанкаре следует школе математического интуиционизма, которая рассматривает математическую индукцию как окончательное основание математической мысли, не сводимое ни к чему предшествующему и синтетическое a priori в смысле Иммануила Канта. Анри Пуанкаре, 1909. Х. Роджер-Виолле Прямо противоположно этому - предприятие Готтлоба Фреге, за которым позже последовали Альфред Норт Уайтхед и Бертран Рассел в Principia Mathematica , чтобы показать, что принцип математической индукции является аналитическим в том смысле, что он сводится к принципу чистой логики. подходящими определениями задействованных терминов. Трансфинитная индукция Обобщение математической индукции, применимое к любому хорошо упорядоченному классу или области D , вместо области положительных целых чисел, является методом доказательства с помощью трансфинитной индукции. Домен D считается хорошо упорядоченным, если элементы (числа или объекты любого другого типа), принадлежащие ему, находятся или были помещены в такой порядок, что: 1. нет элемент предшествует самому себе по порядку; 2. , если x предшествует y по порядку, а y предшествует z , то x предшествует z ; 3. в каждом непустом подклассе D есть первый элемент (тот, который предшествует всем остальным элементам в подклассе). Из , 3. , следует, в частности, что сам домен D , если он не пустой, имеет первый элемент. Когда элемент x предшествует элементу y в только что описанном порядке, можно также сказать, что y следует за x .Преемник элемента x хорошо упорядоченного домена D определяется как первый элемент, следующий за x (так как по 3. , если есть какие-либо элементы, следующие за x , там должен быть первым среди них). Точно так же преемник класса E элементов D является первым элементом, который следует за всеми элементами E . Класс F элементов D называется наследственным, если всякий раз, когда все члены класса E элементов D принадлежат к F , наследник E , если таковой имеется, также принадлежит на F (и, следовательно, в частности, когда элемент x из D принадлежит F , преемник x , если таковой имеется, также принадлежит F ).Доказательство трансфинитной индукцией затем зависит от принципа, что если первый элемент хорошо упорядоченной области D принадлежит наследственному классу F , все элементы D принадлежат F . Один из способов трактовать математическую индукцию - рассматривать ее как частный случай трансфинитной индукции. Например, в некотором смысле простая индукция может рассматриваться как трансфинитная индукция, примененная к области D положительных целых чисел.Фактическое сведение простой индукции к этому частному случаю трансфинитной индукции требует использования принципов, которые сами по себе обычно доказываются математической индукцией, особенно упорядочения положительных целых чисел, и принципа, который является наследником класса положительных целых чисел, если существует равно единице, должно быть преемником определенного целого числа (последнего или наибольшего целого числа) в классе. Следовательно, в некотором смысле математическая индукция не сводится к трансфинитной индукции. Точка зрения трансфинитной индукции, однако, полезна при классификации более сложных видов математической индукции. В частности, двойную индукцию можно рассматривать как трансфинитную индукцию, применяемую к области D упорядоченных пар ( x , y ) положительных целых чисел, где D хорошо упорядочивается по правилу, что пара ( x ₁, y ₁) предшествует паре ( x ₂, y ₂), если x ₁ < x ₂ 90 или 903 ₁ = x ₂ и y ₁ < y ₂. Эта статья была последней отредактированной и обновленной Майклом Рэем, редактором. Узнайте больше в этих связанных статьях Britannica: Математическая индукция | Математика вики Математическая индукция - это метод доказательства, с помощью которого можно продемонстрировать, что утверждение о переменной истинно для всех целых значений этой переменной, больших или равных заданному целому числу (обычно 0 или 1). Пример такого заявления: Количество возможных пар из n различных объектов равно (для любого положительного целого числа n ). Доказательство индукцией происходит следующим образом: Утверждение доказано для первого возможного значения n (обычно 0 или 1, но возможны и другие «начальные значения»). Утверждение предполагается, что истинно для некоторого фиксированного, но неуказанного значения n , и это предположение используется, чтобы доказать, что утверждение истинно для (последнее утверждение является просто исходным утверждением с заменой n на) . Утверждение затем считается истинным для всех соответствующих значений n (все неотрицательные значения или все положительные значения, в зависимости). То, что вывод шага 3 выше следует из шагов 1 и 2, это принцип математической индукции . Более формально, учитывая утверждение о целочисленной переменной n , для которого необходимо доказать, необходимо доказать следующее. Вывод тогда для. История Ранние неявные следы математической индукции можно найти в доказательстве Евклида, что число простых чисел бесконечно, и в «циклическом методе» Бхаскары. ^[1] Противоположный повторный метод, считая вниз, на , а не вверх, можно найти в парадоксе Сорита, где один утверждал, что если 1 000 000 песчинок образуют кучу, а удаление одного зерна из кучи оставляет ее кучей, тогда одна песчинка (или даже не песчинка) образует кучу. Самое раннее доказательство математической индукции для арифметических последовательностей было представлено в Al-Fakhri , написанном Аль-Караджи около 1000 г. н.э., который использовал его для доказательства биномиальной теоремы, треугольника Паскаля и формулы суммы для целых кубов.Формула суммы для целых кубов - это (истинное) утверждение, что каждое целое число может быть выражено суммой натуральных чисел в кубе. Это частный случай того, что называется проблемой Варинга. ^[2] Его доказательство было первым, в котором использовались два основных компонента индуктивного доказательства. Во-первых, он отмечает истинность утверждения для n = 1. То есть 1 - это сумма одного куба, потому что 1 = 1 ³ . Во-вторых, он выводит истину для n = k из истины для n = k - 1.Например, когда n = 2, верно, что 2 = 1 ³ + 1 ³ . Когда n = 3, верно, что 3 = 1 ³ + 1 ³ + 1 ³ . Истинность утверждения может быть экстраполирована таким образом без ограничений. Конечно, по мере роста n некоторые суммы 1 ³ можно переписать как кубики других натуральных чисел: например, когда n = 8 , тогда 8 = 2 ³ = [ 1 ³ × 8] .Конечно, этот второй компонент не является явным, поскольку в некотором смысле аргумент аль-Караджи обратный; то есть он начинает с n = 10 и опускается до 1, а не идет вверх ». ^[3] ^[4] Вскоре после этого Ибн аль-Хайтам (Альхазен) использовал индуктивный метод, чтобы доказать сумма четвертых степеней и, в более широком смысле, сумма любых целых степеней ^[5] ^[6] Он сформулировал это только для конкретных целых чисел, но его доказательство для этих чисел было индукционным и обобщаемым.^[5] Ибн Яхья аль-Магриби ас-Самав'ал ближе всего подошел к современному доказательству с помощью математической индукции в досовременные времена, которую он использовал для расширения доказательства биномиальной теоремы и треугольника Паскаля, ранее данного аль-Караджи . Индуктивный аргумент аль-Самавала был всего в нескольких шагах от полного индуктивного доказательства общей биномиальной теоремы. ^[7] Самое раннее строгое использование индукции и иллюстрации доказательств с ее использованием было сделано Герсонидом. ^[8] Другой подобный случай (вопреки тому, что написал Вакка, как тщательно показал Фройденталь) произошел с Франческо Моролико в его Arithmeticorum libri duo (1575), который использовал эту технику, чтобы доказать, что сумма первые n нечетных целых чисел n ².Явная формулировка принципа индукции была дана Паскалем в его работе Traité du треугольник арифметической (1665). Другой француз, Ферма, широко использовал родственный принцип - косвенное доказательство бесконечным спуском. Индуктивная гипотеза также использовалась швейцарцем Якобом Бернулли, и с тех пор она стала более или менее известной. Современная строгая и систематическая трактовка этого принципа появилась только в XIX веке у Джорджа Буля, ^[9] Джузеппе Пеано и, прежде всего, у Ричарда Дедекинда.^[1] См. Также Банкноты ↑ ^1,0 ^1,1 Каджори (1918), стр. 197 «Процесс рассуждений, называемый« математическая индукция », имеет несколько независимых источников. Он восходит к швейцарцу Якобу (Джеймсу) Бернулли, французу Б. Паскалю и П. Ферма и итальянцу Ф. Маволику. [...] Читая немного между строк, можно найти следы математической индукции еще раньше, в трудах индусов и греков, как, например, в «циклическом методе» Бхаскары и в доказательстве Евклида. что количество простых чисел бесконечно." ↑ Кац (1998), стр. 255: «Еще одна важная идея, предложенная аль-Караджи и продолженная ас-Самав'алом и другими, заключалась в индуктивном аргументе для работы с определенными арифметическими последовательностями. Таким образом, аль-Караджи использовал такой аргумент, чтобы доказать результат на суммы целых кубов, уже известные Арьябхате [...] аль-Караджи, однако, не сформулировали общий результат для произвольных n . Он сформулировал свою теорему для конкретного целого числа 10 [...] Тем не менее, свое доказательство был явно разработан с возможностью расширения до любого другого целого числа. ↑ Кац (1998), стр. 255: "Аргументы аль-Караджи включают, по существу, два основных компонента современного аргумента по индукции, а именно истинность утверждения для n = 1 (1 = 1 ³) и вывод истины для n = k от n = k - 1. Конечно, этот второй компонент не является явным, поскольку, в некотором смысле, аргумент аль-Караджи обратный, то есть он начинает с n = 10 и уменьшается до 1, а не увеличивается.Тем не менее, его аргумент в аль-Фахри является самым ранним из сохранившихся доказательств формулы суммы для целых кубов ». ↑ О'Коннор, Джон Дж .; Робертсон, Эдмунд Ф., «Абу Бекр ибн Мухаммад ибн аль-Хусейн аль-Караджи», Архив истории математики MacTutor , Университет Сент-Эндрюс, http://www-history.mcs.st-andrews.ac.uk /Biographies/Al-Karaji.html. "Аль-Караджи также использует форму математической индукции в своих аргументах, хотя он, конечно, не дает строгого изложения принципа." ↑ ^5,0 ^5,1 Виктор Дж. Кац (1995), стр. 165–169. «Центральной идеей доказательства формул суммы ибн аль-Хайсама был вывод уравнения [...] Естественно, он не сформулировал этот результат в общей форме. Он сформулировал его только для определенных целых чисел, [.. .], но его доказательство для каждого из этих k проводится индукцией по n и немедленно обобщается на любое значение k ». ↑ Кац (1998), стр.255–259. ↑ Кац (1998), стр. 259: «Подобно доказательствам аль-Караджи и ибн аль-Хайсама, аргумент аль-Самавала содержит два основных компонента индуктивного доказательства. Он начинает со значения, для которого известен результат, здесь n = 2, а затем использует результат для данного целого числа, чтобы получить результат для следующего. Хотя ас-Самав'ал не имел никакого способа сформулировать и, следовательно, доказать общую биномиальную теорему для современных читателей, существует только короткий шаг от аргумента ас-Самавала к полному индуктивному доказательству биномиальной теоремы." ↑ Rabinovitch, Nachum. L. Раввин Леви Бен Гершон и истоки математической индукции , Архив истории точных наук , 6, 237–248 (1970) [1]. ↑ «Иногда требуется доказать теорию, которая будет верной всякий раз, когда определенное количество n , которое она включает, должно быть целым или целым числом, и метод доказательства обычно имеет следующий вид. 1st . Теорема подтверждается при n = 1. 2-е место . Доказано, что если теорема верна, когда n является заданным целым числом, она будет верна, если n является следующим большим целым числом. Следовательно, теорема верна для всех. . .. Этот вид аргумента может быть назван продолжением соритов »(Бул около 1849 г. Элементарный трактат по логике, а не математике стр. 40–41, перепечатанный в Grattain-Guinness, Ivor and Bornet, Gérard (1997), George Boole: Избранные рукописи по логике и ее философии , Birkhäuser Verlag, Berlin, ISBN 3-7643-5456-9 Список литературы Введение История Acerbi, F.(2000). «Платон: Парменид 149a7-c3. Доказательство полной индукции?». Архив истории точных наук 55 : 57–76. DOI: 10.1007 / s004070000020.
Бусси, У. Х. (1917). «Происхождение математической индукции». Американский математический ежемесячник 24 (5): 199–207. DOI: 10.2307 / 2974308. http://links.jstor.org/sici?sici=0002-9890%281
%2924%3A5%3C199%3ATOOMI%3E2.0.CO%3B2-Y.
Каджори, Флориан (1918). «Происхождение названия« Математическая индукция »». Американский математический ежемесячник 25 (5): 197–201. DOI: 10.2307 / 2972638. http://links.jstor.org/sici?sici=0002-9890%281%2925%3A5%3C197%3AOOTN%22I%3E2.0.CO%3B2-2.
«Могли ли греки использовать математическую индукцию? Использовали ли они ее?». Physis XXXI : 253–265. 1994.
Фройденталь, Ганс (1953). "Zur Geschichte der vollständigen Induction". Архивы международной истории наук 6 : 17–37.
Кац, Виктор Дж. (1998). История математики: введение . Эддисон-Уэсли. ISBN 0321016181.
Рабинович, Начум Л. (1970). «Раби Леви Бен Гершон и истоки математической индукции». Архив истории точной науки 6 : 237–248. DOI: 10.1007 / BF00327237.
Рашед, Рошди (1972). "L'induction mathématique: аль-Караджи, ас-Самав'ал". Архив истории точных наук 9 : 1–12.DOI: 10.1007 / BF00348537.
Ungure, S. (1991). "Греческая математика и математическая индукция".

Метод математической индукции

Понятия индукции и дедукции

В чем заключается метод математической индукции

Как применять метод математической индукции при решении неравенств и уравнений

9 класс. Алгебра. Геометрическая прогрессия. — Геометрическая прогрессия.

Задачи для самостоятельного решения Группа а

Группа b

Группа с

2. Функции действительного переменного

2.1. Понятие функции

4. Доказательство формулы общего члена последовательности, заданной рекуррентно

Метод математической индукции — презентация онлайн

12. Алгоритм доказательства методом математической индукции

23. Ханойские башни

24. Пересечение прямых

25. Докажите тождество

27. Рефлексия

Доказательство индукцией

Математическая индукция

Как это сделать

Пример: 3

Уловки

Пример: сложение нечетных чисел

Твоя очередь

Пример: треугольные числа

Пример: сложение чисел куба

Пример: треугольные числа

Пример: сложение чисел куба

Математическое доказательство правильности и эффективности алгоритма

Введение

Математическая индукция

Базовый пример

Подтверждение правильности

Пример состояния программы

Пример рекурсии

Инварианты цикла

Выбор инварианта цикла

Пример:

Пример инварианта цикла - индукционное доказательство

Анализ эффективности: отношения повторяемости

Решение однородных линейных рекуррентных отношений

Магистр теоремы информатики

Пример: двоичный поиск

Пример: динамическое программирование против рекурсии

Анализ временной сложности Фибоначчи

Выведение сложности алгоритма из отношения повторяемости

Заключение

Биномиальная теорема: доказательство математической индукцией

Этот мощный метод теории чисел, примененный к биномиальной теореме

Индуктивный процесс

Базовый шаг: n = 3

Индуктивная гипотеза и индуктивный шаг

Для дальнейшего размышления

Без заголовка

Предметы для изучения

Содержание

математическая индукция | Определение, принцип и доказательство

Принцип математической индукции

Доказательство математической индукцией

Трансфинитная индукция

Узнайте больше в этих связанных статьях Britannica:

Математическая индукция | Математика вики

История

См. Также

Банкноты

Список литературы

Добавить комментарий Отменить ответ

`Пример инварианта цикла - индукционное доказательство`

`Анализ эффективности: отношения повторяемости`

`Решение однородных линейных рекуррентных отношений`