6.9.3. Решение систем линейных уравнений методом сложения.   математика-повторение

Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:

1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;

2) сложить почленно полученные уравнения и найти значение одной из переменных;

3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.

Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).

Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.

Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24.  Вторым уравнением системы можно записать любое уравнение исходной системы.

 

Найдём х и подставим его значение во 2-ое уравнение.

 

Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.

Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.

Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.

 

Ответ: (3; -5).

 

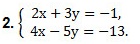Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:

Сложим эти равенства почленно.

Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):

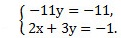Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.

 

Решаем последнее уравнение системы и получаем х = -2.

Ответ: (-2; 1).

Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.

Подставим значение х=4 во 2-ое уравнение.

3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.

Ответ: (4; -3).

 

www.mathematics-repetition.com

9 класс. Алгебра. Системы уравнений. — Решение систем уравнений методом сложения.

Комментарии преподавателя

На этом уроке мы продолжим изучение метод решения систем уравнений, а именно: метода алгебраического сложения. Вначале рассмотрим применение этого метода на примере линейных уравнений и его суть. Также вспомним, как уравнивать коэффициенты в уравнениях. И решим ряд задач на применение этого метода.

 

 

Тема: Си­сте­мы урав­не­ний

Урок: Метод ал­геб­ра­и­че­ско­го сло­же­ния 

Рас­смот­рим метод ал­геб­ра­и­че­ско­го сло­же­ния на при­ме­ре ли­ней­ных си­стем.

При­мер 1. Ре­шить си­сте­му 

Ре­ше­ние:

Если мы сло­жим эти два урав­не­ния, то y вза­им­но уни­что­жат­ся, и оста­нет­ся урав­не­ние от­но­си­тель­но x.

Если же вы­чтем из пер­во­го урав­не­ния вто­рое, вза­им­но уни­что­жат­ся x, и мы по­лу­чим урав­не­ние от­но­си­тель­но y. В этом и за­клю­ча­ет­ся смысл ме­то­да ал­геб­ра­и­че­ско­го сло­же­ния.

  

Ответ: 

Мы ре­ши­ли си­сте­му и вспом­ни­ли метод ал­геб­ра­и­че­ско­го сло­же­ния. По­вто­рим его суть: мы можем скла­ды­вать и вы­чи­тать урав­не­ния, но при этом необ­хо­ди­мо обес­пе­чить, чтобы по­лу­чи­лось урав­не­ние толь­ко с одним неиз­вест­ным.

При­мер 2. Ре­шить си­сте­му 

Ре­ше­ние:

Член  при­сут­ству­ет в обоих урав­не­ни­ях, по­это­му удо­бен метод ал­геб­ра­и­че­ско­го сло­же­ния. Вы­чтем из пер­во­го урав­не­ния вто­рое.

 

 

Ответ: (2; -1).

Таким об­ра­зом, про­ана­ли­зи­ро­вав си­сте­му урав­не­ний, можно уви­деть, что она удоб­на для ме­то­да ал­геб­ра­и­че­ско­го сло­же­ния, и при­ме­нить его.

Рас­смот­рим еще одну ли­ней­ную си­сте­му.

При­мер 3. Ре­шить си­сте­му 

Ре­ше­ние:

Мы хотим из­ба­вить­ся от y, но в двух урав­не­ни­ях ко­эф­фи­ци­ен­ты при y раз­ные. Урав­ня­ем их, для этого умно­жим пер­вое урав­не­ние на 3, вто­рое – на 4.

 

Ответ: 

При­мер 4. Ре­шить си­сте­му 

Ре­ше­ние:

Урав­ня­ем ко­эф

www.kursoteka.ru

Пожалуйста объясните поподробней как решать системы уравнений способом сложения!!!!

1.надо выбрать переменную от которой хотите избавиться. если х или у (в двух уравнениях) уже имеют равные по модулю и противоположные по знаку коэфициенты то переходим к пункту 3 2 допустим выбрали х .в 1 урав он имеет коэф 2 а во втором коэф 5 тогда приводим к одному коэф с противопол знаками .для этого 1 урав умнож на (-5) а второе на 2 . в 1 получаем (-10х) во втором 10х 3 складываем оба уравнения иксы с иксами, у с у-ами, число с числом . приэтом х изчезнет останется уравнение с одним неизвестным у. 4.решаем находим у 5.подставляем найденное значение в одно из первоначальных уравн и находим х

Сложение или вычитание. Этот метод состоит в следующем. система уравнений (1): ах + by=c dx + ey = f 1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их: система уравнений -axd — bdy = — cd adx + aey = af ______________ — bdy + aey = — cd + af Отсюда получаем: y = ( af – cd ) / ( ae – bd ). 2) Подставляем найденное для y значение в любое уравнение системы (1): ax + b( af – cd ) / ( ae – bd ) = c. 3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ). П р и м е р . Решить систему уравнений: 3x — 2y = — 4 x+3y = 5 методом сложения или вычитания. Умножаем первое уравнение на –1, второе – на 3 и складываем их: — 3x + 2y = — 4 3x + 9y = 15 ___________ 11y = 11 отсюда y = 1. Подставляем это значение во второе уравнение (а в первое можно?) : 3x + 9 = 15, отсюда x = 2.

Я ТУПОЙ, МЕНЯ ВЫГОНЯЮТ ИЗ ШКОЛЫ.

touch.otvet.mail.ru

Урок на тему » Алгоритм решения систем линейных уравнений методом сложения»

Урок №

ТЕМА: Алгоритм решения систем
линейных уравнений способом сложения

Задачи: создать условия для развития умения решать системы двух линейных уравнений с двумя переменными методом сложения
Планируемые результаты
Предметные: познакомятся с алгоритмом решения системы двух линейных уравнений с двумя переменными методом сложения; научатся решать системы двух линейных уравнений с двумя переменными методом сложения	Метапредметные: познавательные ‒ ориентироваться на разнообразие способов решения задач; регулятивные ‒ учитывать правило в планировании и контроле способа решения; коммуникативные ‒ учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве	Личностные: формировать интерес к изучению темы и желание применять приобретенные знания и умения
Образовательные ресурсы: 1) Видеоуроки. URL: http://interneturok.ru/ 2) Школьный помощник. URL: http://school-assistant.ru/

Ход урока

I. Устная работа.

1. Является ли пара чисел (4; –1) решением системы уравнений:

а) б) в)

2. Являются ли данные системы уравнений равносильными:

и

II. Объяснение нового материала.

Объяснение проводить согласно пункту 44 учебника в несколько этапов:

1. На примере 1 выявить суть способа сложения решения систем линейных уравнений.

2. Рассмотреть вопрос о равносильности систем уравнений и его геометрическую интерпретацию.

3. Рассмотреть пример 2 из учебника.

4. Вывести алгоритм решения систем линейных уравнений способом сложения.

Так же, как был записан алгоритм решения систем уравнений способом подстановки, учащиеся должны занести в тетради новый алгоритм вместе с примером.

Алгоритм

1-й шаг.

Умножить почленно уравнения системы на такие множители, чтобы коэффициенты при одной
из переменных стали противоположными

2-й шаг.

Сложить почленно левые и правые части
уравнений системы

3-й шаг.

Решить получившееся уравнение с одной
переменной

–х = –1,

х = 1.

4-й шаг.

Найти соответствующее значение второй
переменной

3·1+2у=–1,

2у=–4,

у=–2.

Ответ: (1; –2)

Системы, в которых нужно подбирать множители к обоим уравнениям, на этом уроке решать не нужно, поэтому пример 3 также лучше разобрать на следующем уроке.

III. Формирование умений и навыков.

В течение урока учащиеся должны запомнить алгоритм решения систем линейных уравнений способом сложения.

1. Умножьте одно из уравнений системы на какое-нибудь число так, чтобы с помощью сложения можно было исключить одну из переменных.

а) б) в)

2. № 1082.

Для решения каждой системы следует вызывать к доске по одному учащемуся. Требовать, чтобы они вслух комментировали все шаги решения.

Необходимо показать учащимся вариант оформления решения системы уравнений способом сложения.

Решение:

в)

2у = 60;

у = 30;

4х – 5 · 30 = 90;

4х = 240;

х = 60.

Ответ: (60; 30).

3. № 1084 (а, б, в).

Этот номер несколько сложнее предыдущего.

Учащимся придётся подбирать множитель, который сделает коэффициенты противоположными. Множитель лучше не «держать в уме», а записывать справа от уравнения.

Решение:

а)

15у = 0;

у = 0;

20х – 7 · 0 = 5;

20х = 5;

х = .

Ответ: .

IV. Итоги урока.

– Какие существуют способы решения систем уравнений?

– Сформулируйте алгоритм решения систем линейных уравнений способом сложения.

– Сколько решений может иметь система линейных уравнений?

Домашнее задание: № 1083; № 1085 (а, б).

infourok.ru

Уроки №8-9 Системы уравнений. Решение систем линейных уравнений. Способ сложения 7 класс

Цель уроков: Ввести понятие функции, функциональной зависимости и как частный случай, линейная функция. Подведение под понятие системы с помощью построения пересекающихся прямых.

I этап. Вопросы по домашнему заданию и подведение итогов СР( урок №7). (15 мин)

Основные ошибки и непонимание:

• Не смогли построить график функции:

• Не ответили на вопрос задания №1:

• При подстановке в №2 не поставили скобки или неверно раскрыли скобки, не учтя минус перед скобками:

• Не поняли задание №3.

II этап. Введение алгоритма Решения систем линейных уравнений. Способ сложения.

Решим систему уравнений:

СПОСОБ СЛОЖЕНИЯ.

ЗАМЕТИМ!

В обоих уравнениях есть , но в одном , а в другом .

При сложении

1. Сложим почленно уравнения (левая часть одного + левая часть другого и правые части отдельно.

Второе уравнение допишем неизменно.

2. При сложении одно уравнение получилось с одной переменной, значит можем найти его корень.

Найденное неизвестное из первого уравнения, подставляем в другое уравнение.

Находим второе неизвестное

Записываем ответ.

Иногда, чтобы применить этот способ, необходимо сделать преобразование уравнений. Рассмотрим пример№2

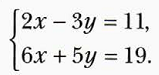
Данная система «НЕ ГОТОВА» к применению способа сложения.

Но мы можем домножить обе части уравнения на одно и то же число, чтобы в обоих уравнениях получилось одно неизвестное с противоположными коэффициентами!

1. УМНОЖИМ ОБЕ ЧАСТИ ПЕРВОГО УРАВНЕНИЯ НА (-3), чтобы получить противоположные числа при x

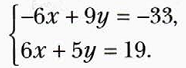
2. ДАЛЕЕ ПО АЛГОРИТМУ

ОТВЕТ: (-1;4)

ПРИМЕЧАНИЕ! Для подставки неизвестного можно выбирать любое из данных уравнений.

ОТВЕТ получился тот же самый

III этап. Решение систем линейных уравнений. Способ сложения.

IV этап. Разминка в начале следующего урока (устно).

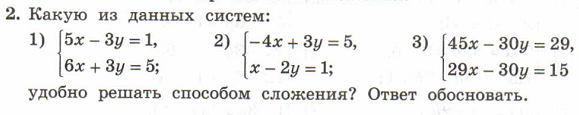
ДАЛЕЕ … ПРОДОЛЖАЕМ РЕШАТЬ СИСТЕМЫ СПОСОБОМ СЛОЖЕНИЯ.

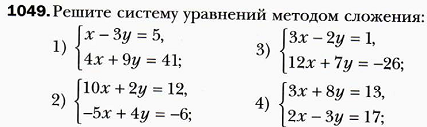
Дополнительно:

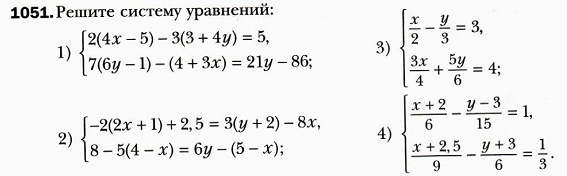
Домашнее задание (записать в тетрадь).

Лебединцева Е.А., Беленкова Е.Ю. Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие. — М.: Интеллект-Центр, 2013. – 176 с.

Изучение алгебры в 7-9 классах: Кн. Для учителя / Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М. : Просвещение, 2002. – 287 с.: — ISBN 5-09-010414-X.

Алгебра. Дидактические материалы. 8 класс / М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. – 2-е изд., дораб. – М.: Просвещение, 2013. – 96 с. : ил. – ISBN 978-5-09-028132-4

Мерзляк А.Г. Алгебра: 9 класс: учебник для учащихся общеобразовательных организация/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2014. – 304 c.: ил. ISBN 978-5-360-05308-8

Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И. АЛГЕБРА. Рабочая тетрадь. 8 класс. Пособие для учащихся общеобразовательных организаций в двух частях. Издательство «Просвещение», 2013 ISBN 978-5-09-032404-5(общ.) ISBN 978-5-09-032403-8(1)

Лебединцева Е.А., Беленкова Е.Ю. Алгебра 7 класс. Задания для обучения и развития учащихся. Учебное пособие.

infourok.ru

Тренажёр по алгебре (7 класс) на тему: Алгоритм решения систем уравнений методом подстановки и сложения .Алгебра 7 класс.

	Образец  решения системы уравнений методом подстановки	АЛГОРИТМ (последовательность шагов при работе)
1.	3х + у = 7    -5х + 2у =3	Выразить из первого уравнения  у через  х, т.е.перенести  3х  в другую часть с противоположным знаком ( т.к. у записан в уравнении без числа(коэффициента)).  Получится  у = 7 – 3х
2.	у = 7 – 3х	Выделить в рамочку выраженную переменную у. Написать её в той же строчке в системе уравнений.
3.	у = 7 – 3х   — 5х + 2(7 – 3х) = 3	Подставить  во второе уравнение  вместо у выражение (7 – 3х), взяв его в скобки !
4.	х =    у =	Приготовить знак системы уравнений и место для будущих ответов х  у
5.	-5х + 2·(7 – 3х) = 3 -5х + 14 -6х = 3	«Выйти из системы» и решить отдельно только уравнение с одной переменной х : 1) раскрыть скобки, умножив число перед  скобкой на всё что в скобках;
6.	-5х + 14  -6х = 3 -5х — 6х = 3 — 14	2)Перенести число 14 в правую часть уравнения с противоположным знаком, т.е. сделать «сортировку» — буквы к буквам, числа к числам.
7.	— 11х= -11	3)Посчитать значение в левой и правой части уравнения
8.	х = -11:(-11)    х = 1	4)Вычислить х как неизвестный множитель, вспомнив простой пример    2 · 3  = 6
9.	х = 1   у =	Заполнить место в системе уравнений для  х
10.	у = 7 – 3х = 7 — 3·1 = 7-3 = 4	Найти значение второй переменной   у
11.	х = 1  у = 4	Заполнить место в системе уравнений для  у
12.	Ответ: (1;4)	Записать ответ в виде координат точки  (х;у)

             Решить систему уравнений методом подстановки

выбирая удобную переменную для её выражения, когда она записана без  числа.

№1.     у – 2х = 1                                                       №4.       2х + у = 12   

             6х – у = 7                                                                      7х – 2у = 31    

№2.     х + у =6                                                          №5.       4х – у = 11

             3х – 5у = 2                                                                    6х – 2у = 13          

№3.     7х – 3у = 13                                                  №6.        8у – х = 4 

             х – 2у = 5                                                                       2х – 21у = 2

Карточка составлена учителем математики Головлянициной Лидией Вадимовной

nsportal.ru