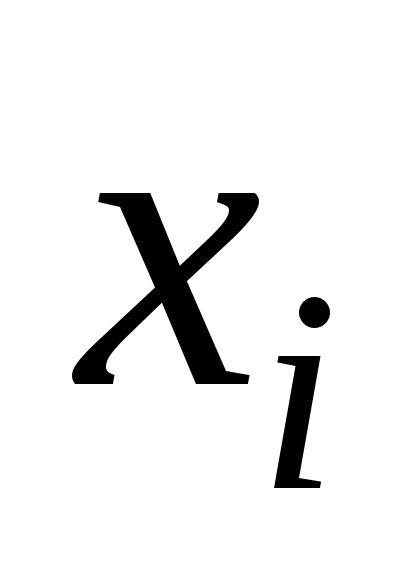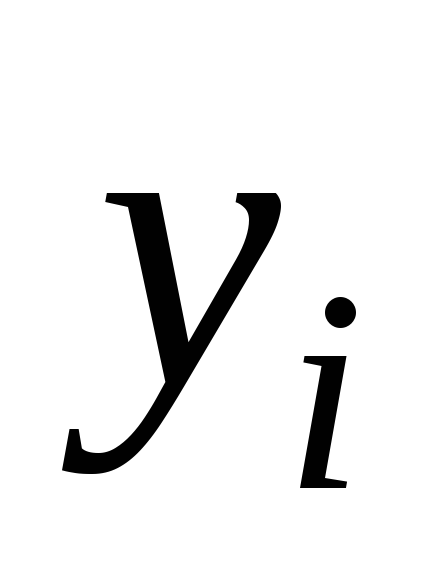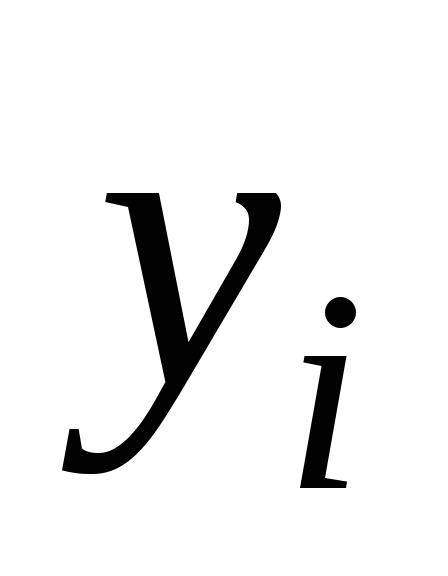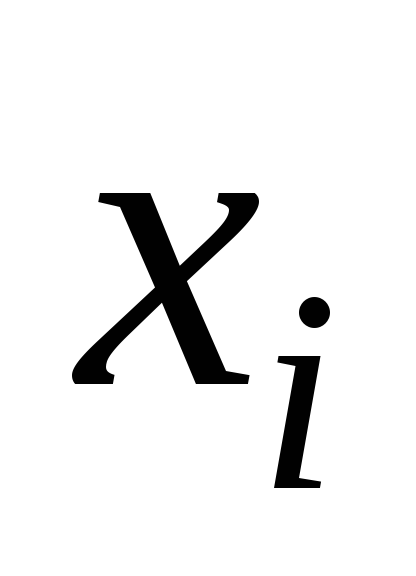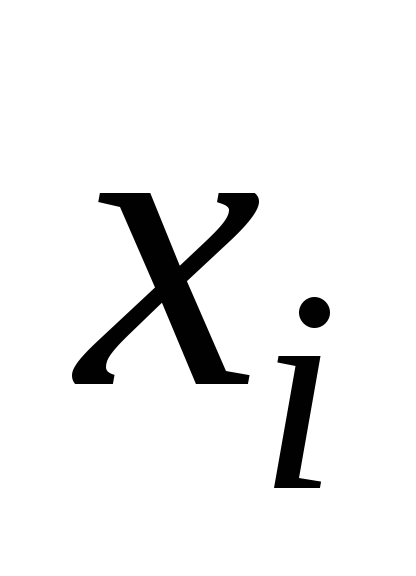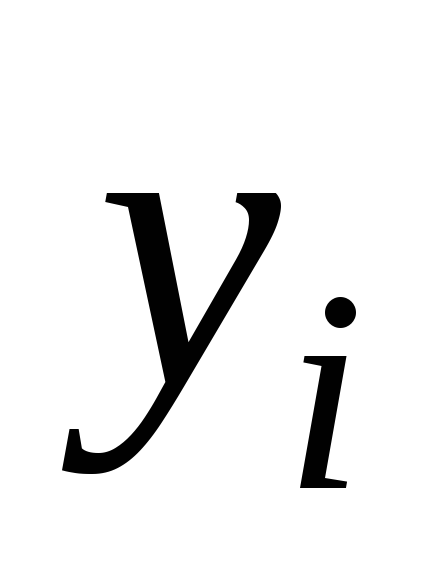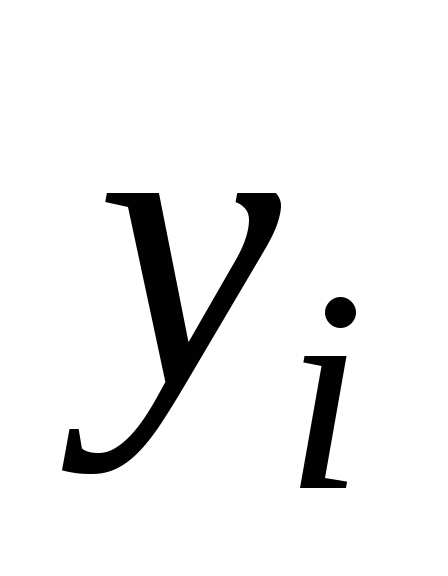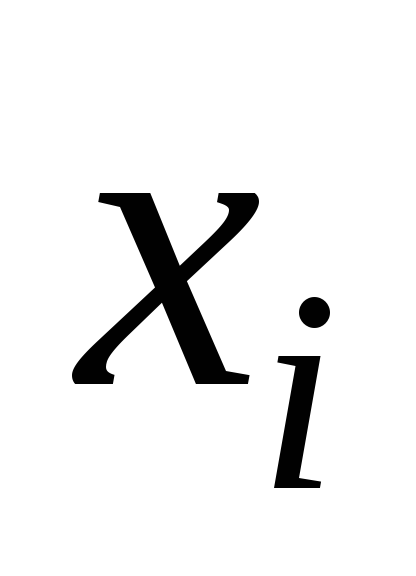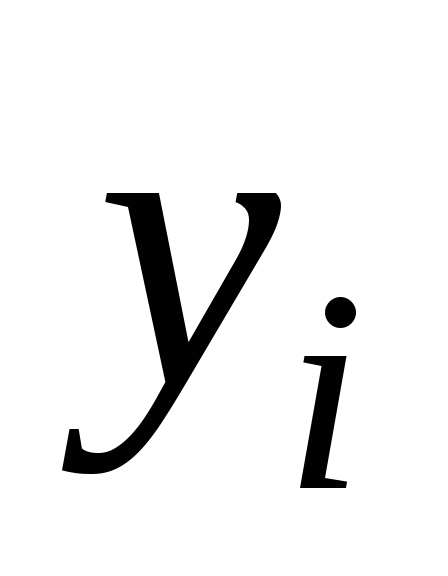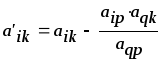Прямые методы решения систем линейных уравнений.
Цель работы
Цель работы – научиться решать системы линейных алгебраических уравнений, используя прямые методы решения
Задание
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.
Решить систему линейных уравнений методом прогонки для систем с трехдиагональной матрицей
Математическое описание
1. Метод Крамера
Требуется найти решение системы линейных уравнений
Ax = b, (1.1)
где  – квадратная матрица коэффициентов
при неизвестных;
– квадратная матрица коэффициентов
при неизвестных;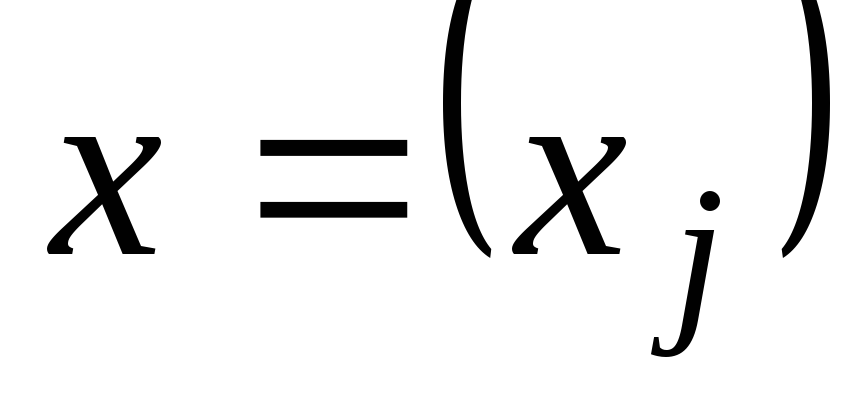
 и
значение каждого из неизвестных
вычисляется как отношение двух
определителей порядкаn,
т. е.
и
значение каждого из неизвестных
вычисляется как отношение двух
определителей порядкаn,
т. е.  j =1, …, n. (1.2)
j =1, …, n. (1.2)
Здесь 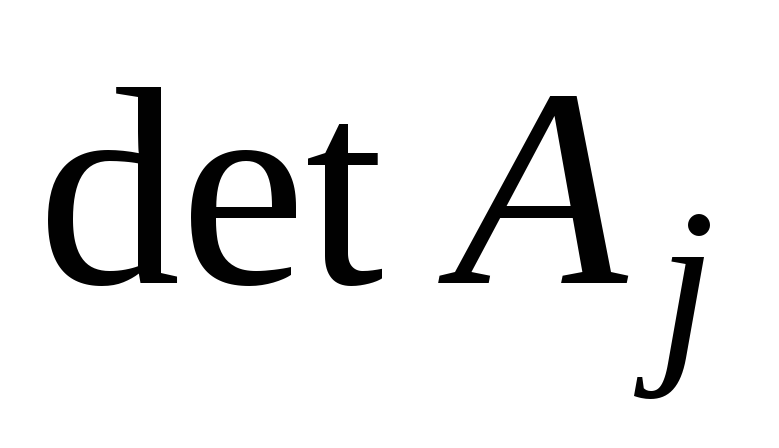 –
определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом
правых частей.
–
определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом
правых частей.
2. Метод Гаусса
Систему уравнений (1.1) представим в виде
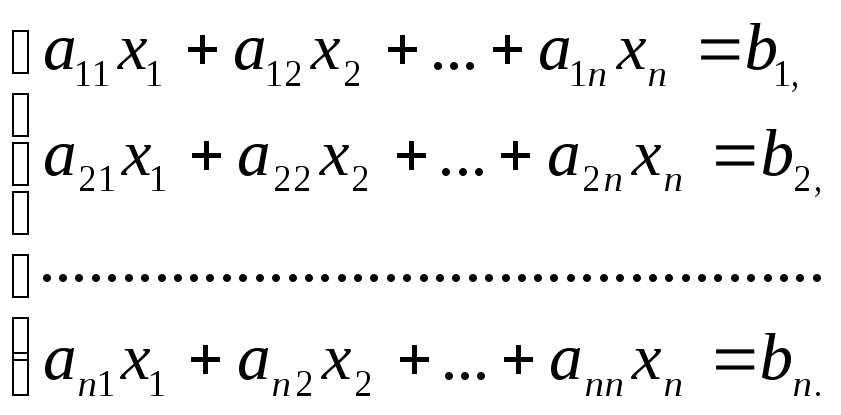
или
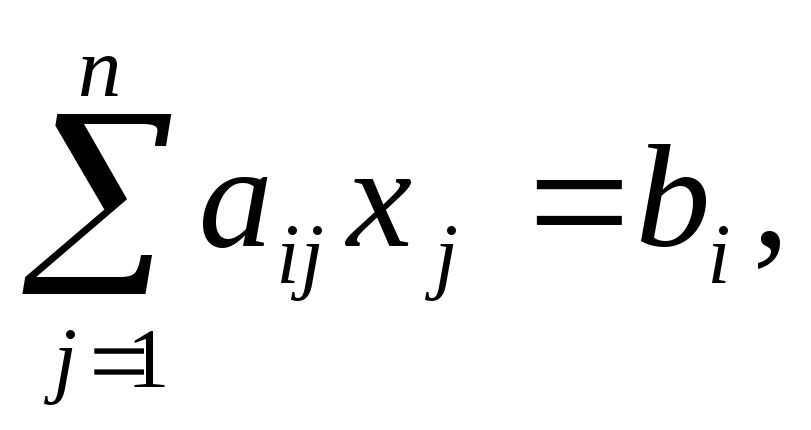 i = 1,…, n.
i = 1,…, n.
Метод Гаусса можно интерпретировать как метод, в котором первоначально матрица приводится к верхней треугольной форме (прямой ход), а далее – к единичной (обратный ход).
Пусть
матрица система (2.1) – верхняя треугольная,
поэтому  приi > j, т. е. все
элементы ниже главной диагонали равны
нулю. Тогда из последнего уравнения
сразу определяем
приi > j, т. е. все
элементы ниже главной диагонали равны
нулю. Тогда из последнего уравнения
сразу определяем 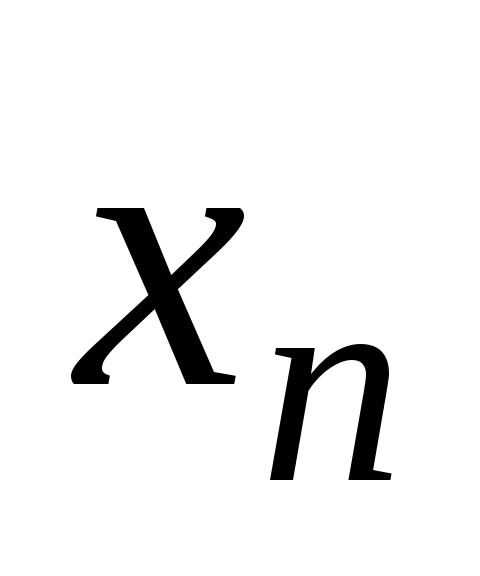 .
Подставляя
.
Подставляя
 и т. д.
и т. д. Общие формулы имеют вид
 при k = n (2.2)
при k = n (2.2)
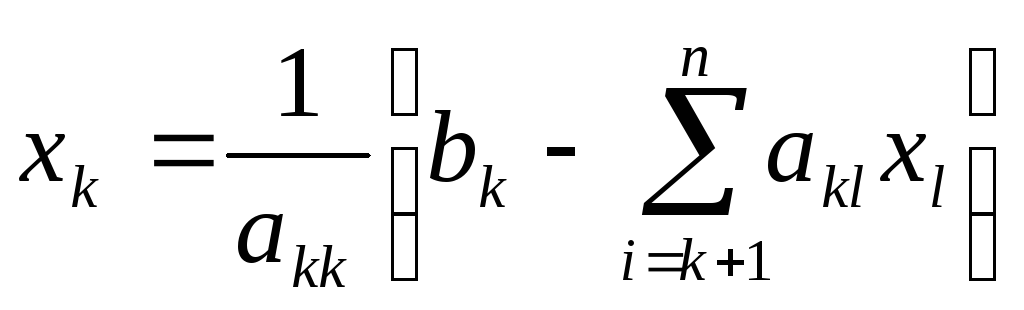 при k = n – 1, n – 2, …, 1.
при k = n – 1, n – 2, …, 1.
При k > l коэффициенты  .
.
Приведем
матрицу системы (1.3) к верхней треугольной.
Вычтем из второго уравнения системы
(1.3) первое, умноженное на такое число,
при котором коэффициент при 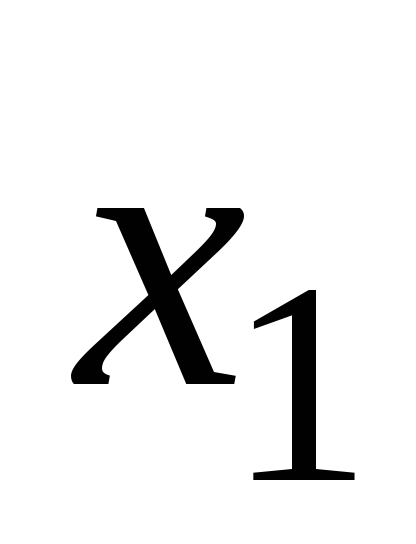
Запишем общие формулы метода Гаусса. Пусть проведено исключение коэффициентов из (k-1)-го столбца. Тогда останутся уравнения с ненулевыми элементами ниже главной диагонали:


Умножим k-ю строку на
число 
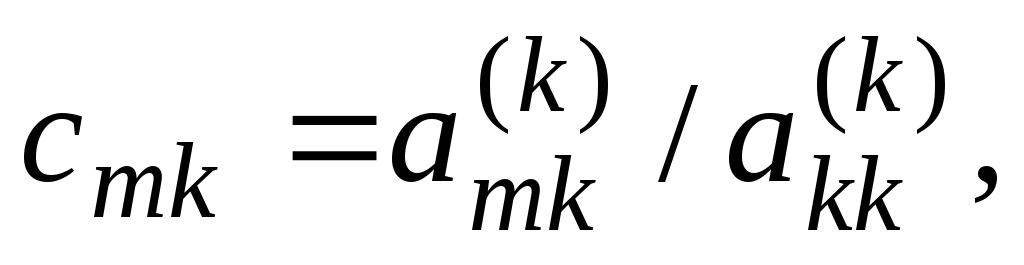

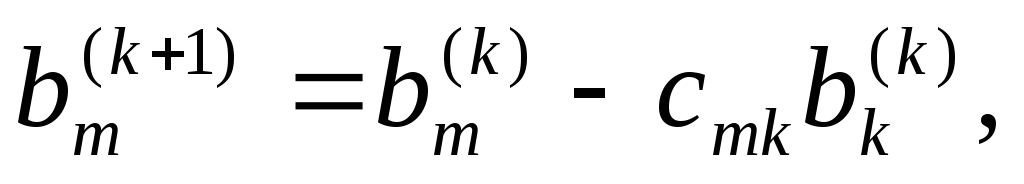 k
< m.
k
< m.
Весь процесс приведения называется ПРЯМЫМ ХОДОМ МЕТОДА ГАУССА. Вычисление неизвестных по формулам (1.4) называют ОБРАТНЫМ ХОДОМ метода.
3. Метод прогонки для решения систем линейных уравнений с трехдиагональной матрицей
Метод прогонки принадлежит к числу прямых методов решения систем линейных уравнений и используется в тех случаях, в которых многие коэффициенты матрицы равны нулю. В методе прогонки применительно к системе линейных уравнений, имеющих трехдиагональную матрицу, можно выделить следующие этапы.
• Приведение трехдиагональной матрицы к верхней треугольной (прямой ход), В случае трехдиагональной матрицы это означает приведение к двухдиагональной, т. е. приведение исходной системы к системе, содержащей по два неизвестных в каждом уравнении, кроме последнего, в котором содержится только одно неизвестное.
• Запись
обратного хода в виде  ,
так как преобразованная матрица –
двухдиагональная.
,
так как преобразованная матрица –
двухдиагональная.
•Вывод
рекуррентного соотношения для 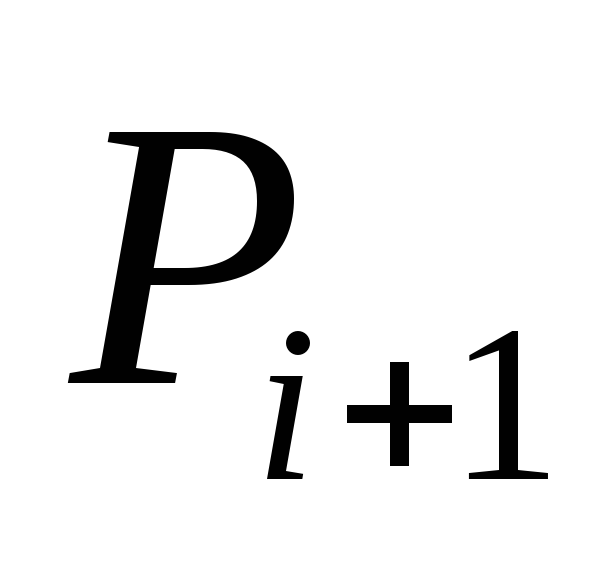 и
и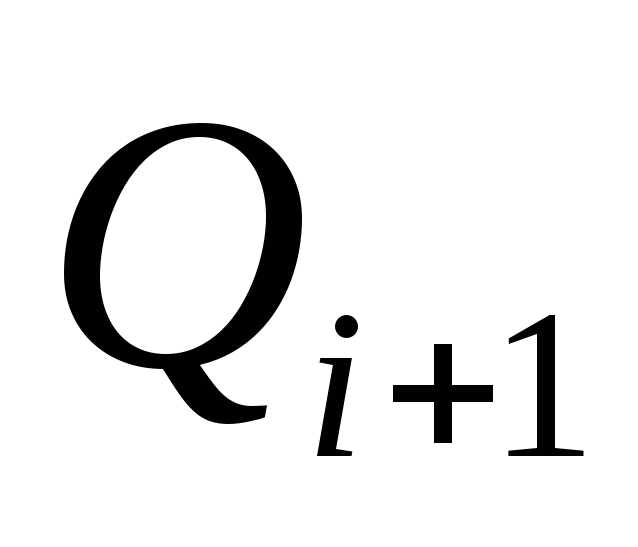 через
через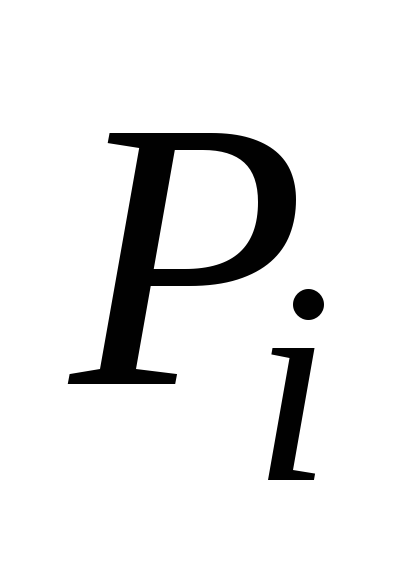 и
и и получение соотношения для
и получение соотношения для

 .
.• Осуществление обратного хода метода прогонки и определение всех неизвестных.
Запишем систему линейных алгебраических уравнений с трехдиагональной матрицей в виде
 i = 1,2,…, n, (3.1)
i = 1,2,…, n, (3.1)
Матрица системы (1.6) имеет вид:
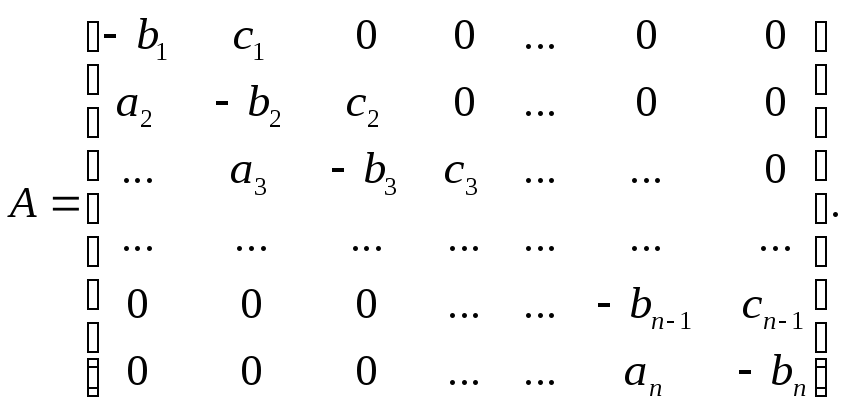
Прямой
ход метода прогонки сводится к исключению
неизвестного  в каждом уравнении системы. Получаемая
в результате прямого хода система
содержит в каждом уравнении только два
неизвестных
в каждом уравнении системы. Получаемая
в результате прямого хода система
содержит в каждом уравнении только два
неизвестных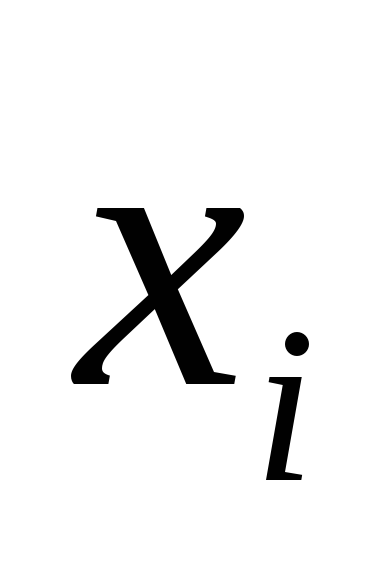
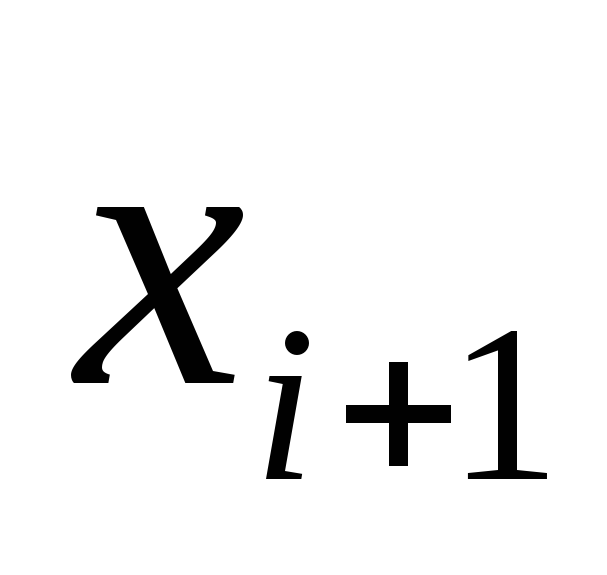 ,
и матрица ее – верхняя треугольная с
двумя диагоналями. Запишемi-ю строку
преобразованной двухдиагональной
матрицы в виде
,
и матрица ее – верхняя треугольная с
двумя диагоналями. Запишемi-ю строку
преобразованной двухдиагональной
матрицы в виде  (3.2)
(3.2)
Если система (3.1) приведена к виду (3.2), то обратный ход метода Гаусса очевиден. Однако использование общих алгоритмов прямого и обратного хода нецелесообразно. Построим эффективную вычислительную схему, которая и составляет суть метода прогонки. Для этого, уменьшив в (3.2) индекс на единицу, запишем
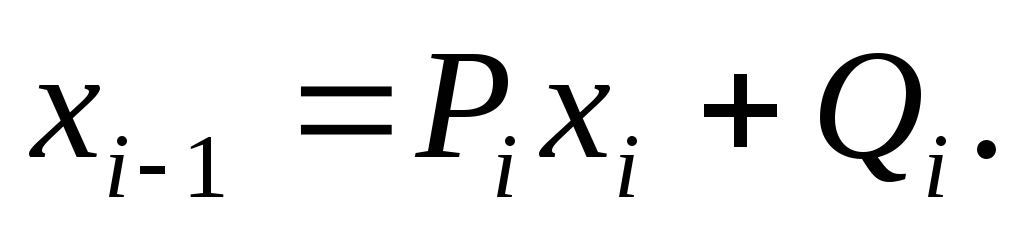
Подставляя 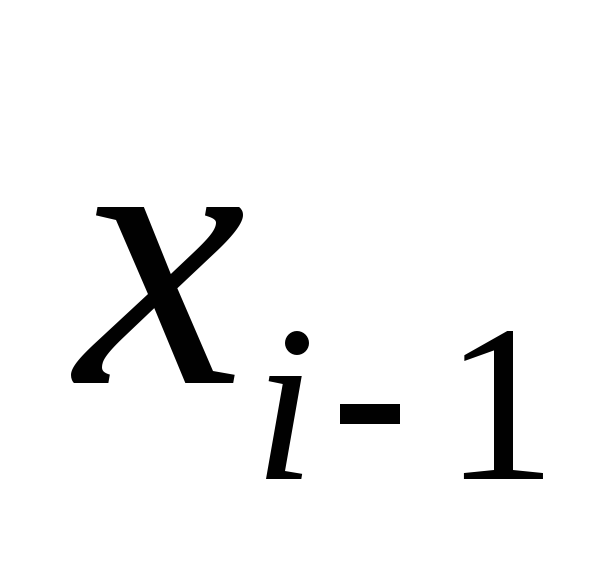
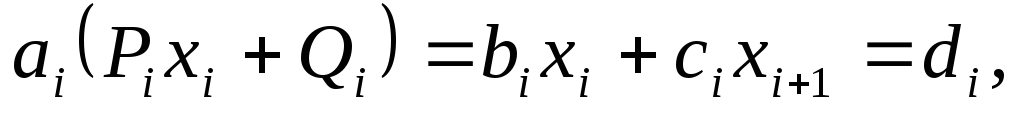
из которого нетрудно получить
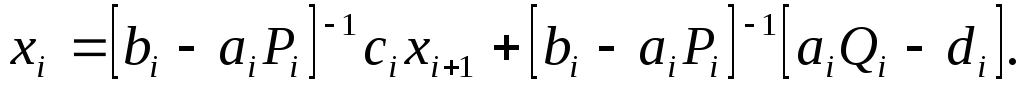
Сравнивая это соотношение с (3.2), можем записать рекуррентные соотношения

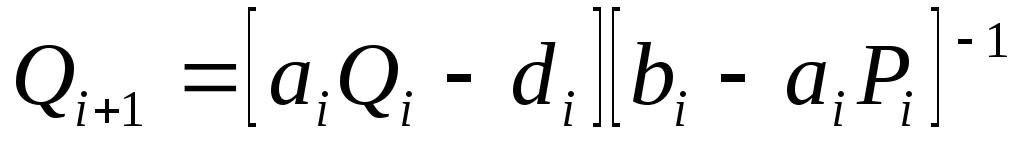 (3.3)
(3.3)
для вычисления так называемых ПРОГОНОЧНЫХ КОЭФФИЦИЕНТОВ.
Для
начала прямого хода метода прогонки
необходимо задать начальные (стартовые)
значения прогоночных коэффициентов,
например,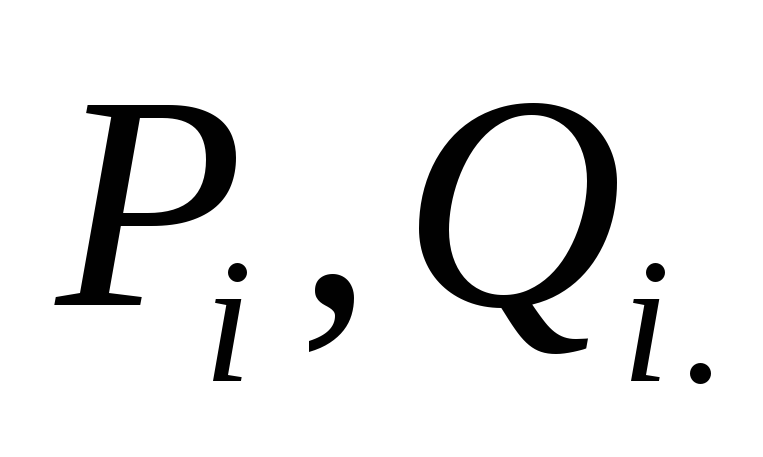
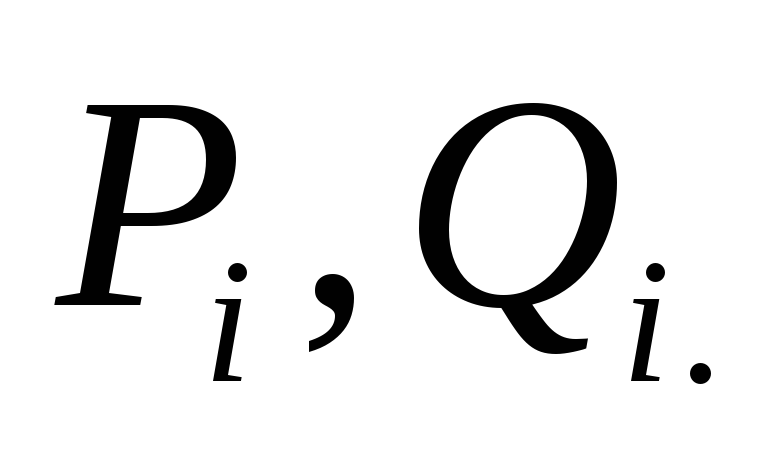 в рассмотренной схеме вычислений не
требуются, так как значения коэффициентов
в рассмотренной схеме вычислений не
требуются, так как значения коэффициентов вычисляются
только через коэффициенты первого
уравнения системы (3.1): приi = 1 из (3.1)
получаем соотношение
вычисляются
только через коэффициенты первого
уравнения системы (3.1): приi = 1 из (3.1)
получаем соотношение  Сравнивая это выражение с (3.2) приi =1, получаем
Сравнивая это выражение с (3.2) приi =1, получаем 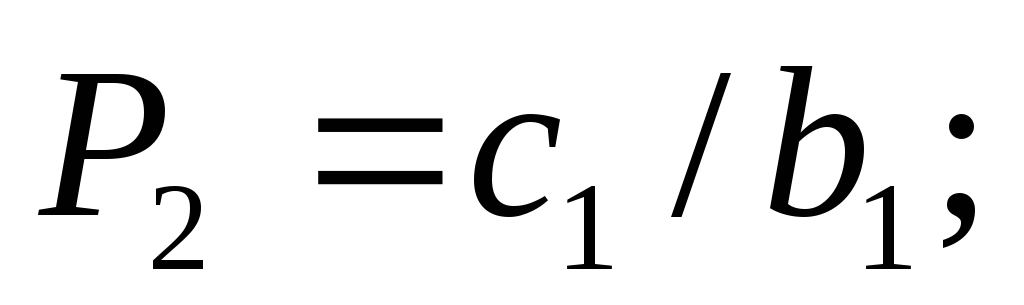
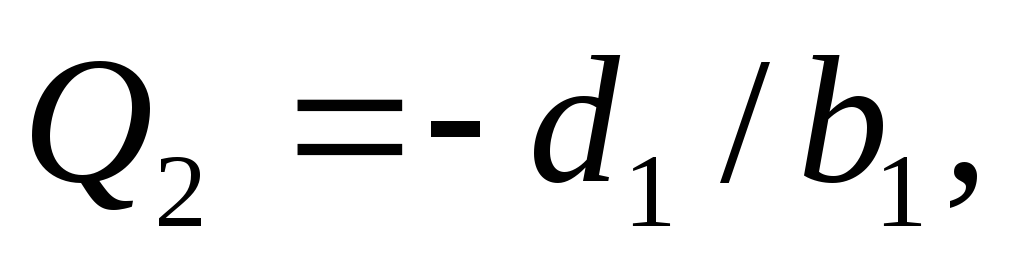 а значение
а значение в обратном ходе вычисляем по соотношению
в обратном ходе вычисляем по соотношению Для начала обратного хода метода прогонки
необходимо для вычисления
Для начала обратного хода метода прогонки
необходимо для вычисления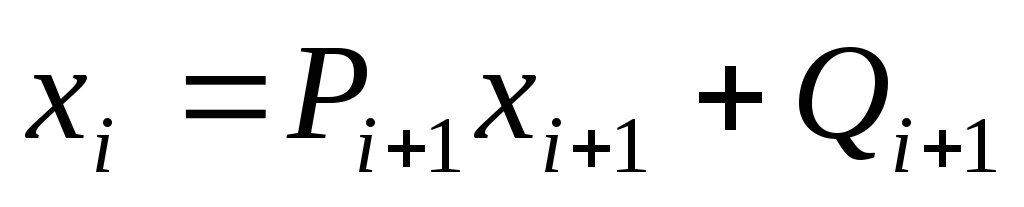
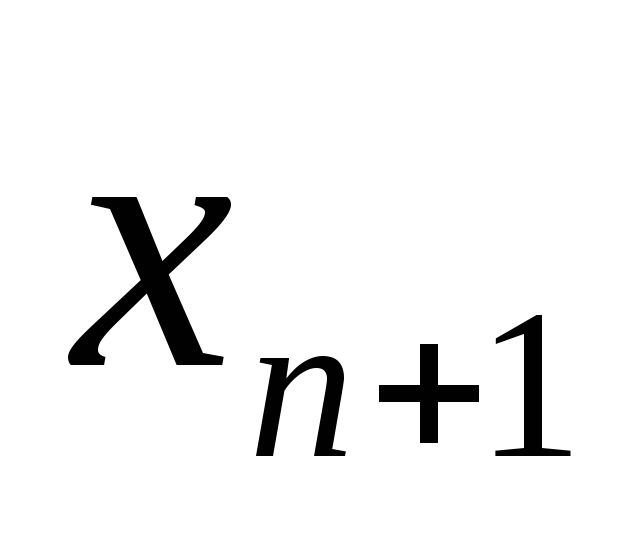 .
Так как
.
Так как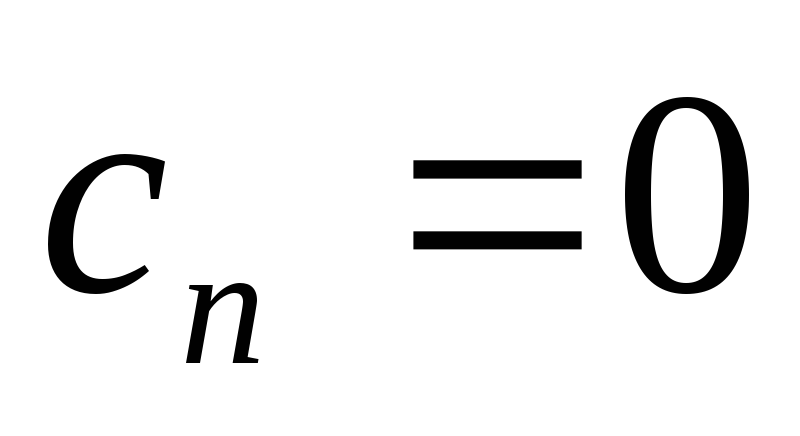 ,
то из первого соотношения (3.3) вытекает,
что
,
то из первого соотношения (3.3) вытекает,
что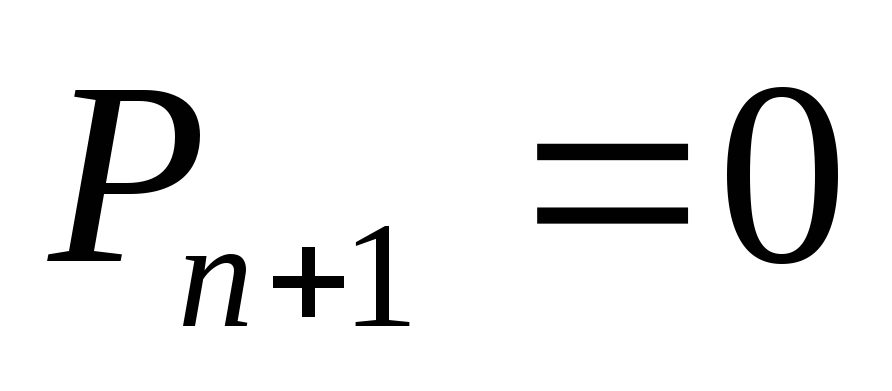 и, следовательно, можно задать любое
значение для
и, следовательно, можно задать любое
значение для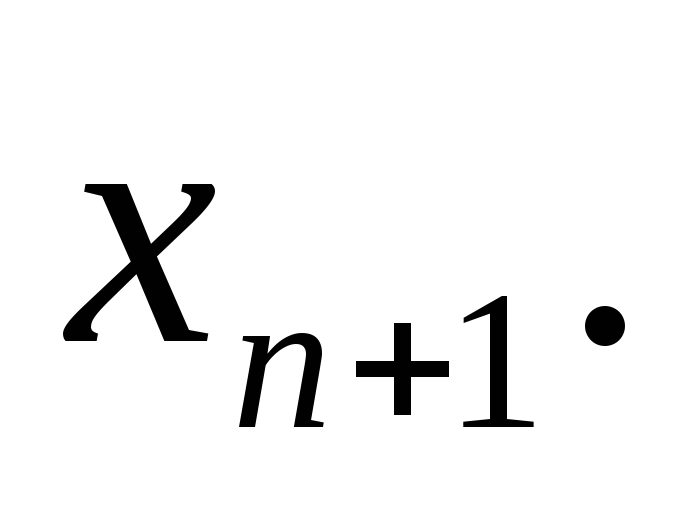 Обычно полагают
Обычно полагают 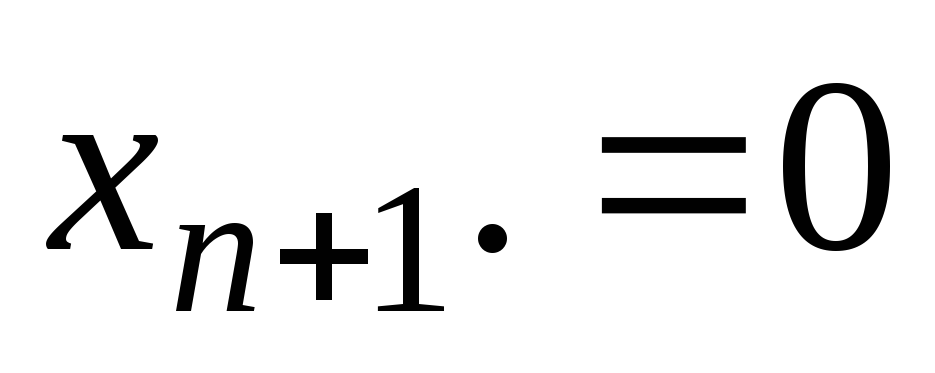 ,и тогда
,и тогда 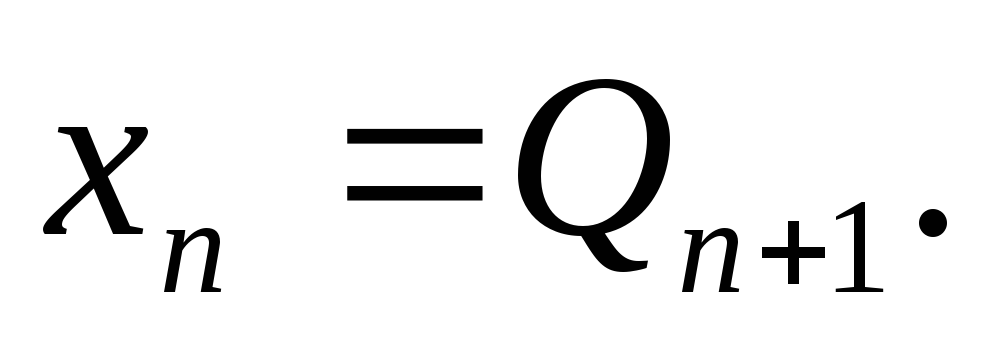
Методы решения систем линейных уравнений.
Решение
систем трех линейных уравнений с тремя
неизвестными x,y,z 
можно найти с помощью формул Крамера.
х =  ;y =
;y =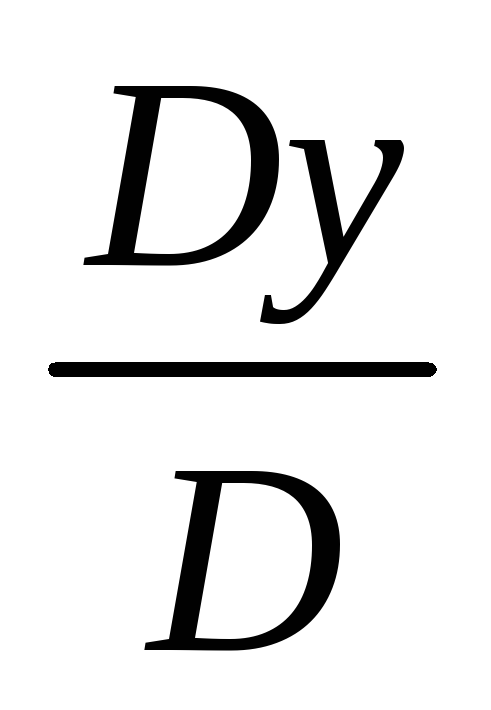 ; z =
; z =  ,
,
где D =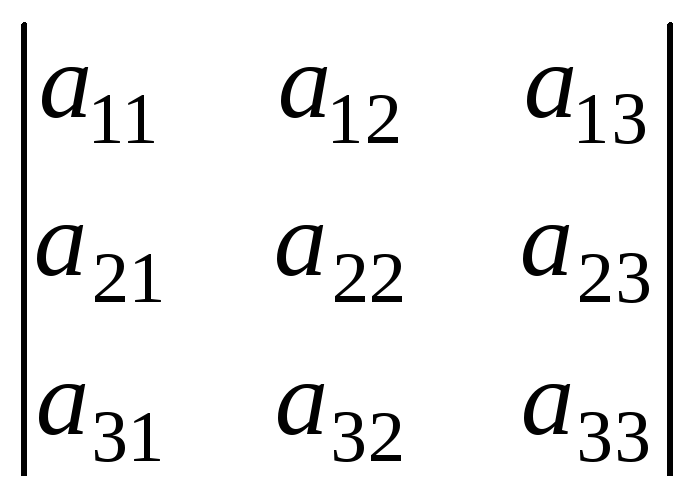 ,Dx =
,Dx =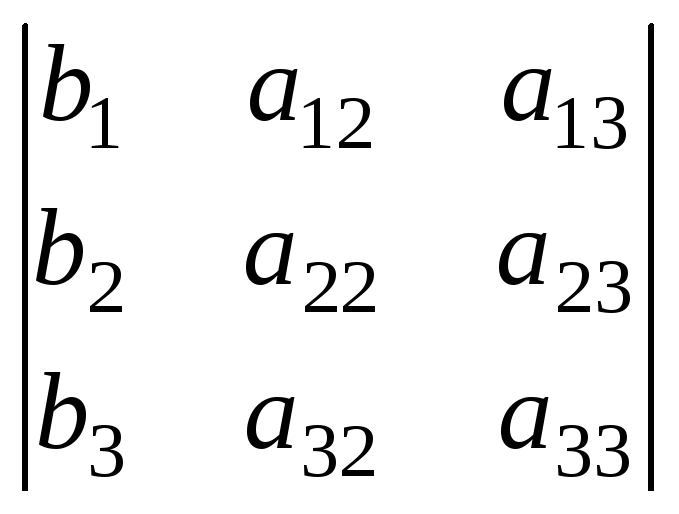 ;Dу=
;Dу=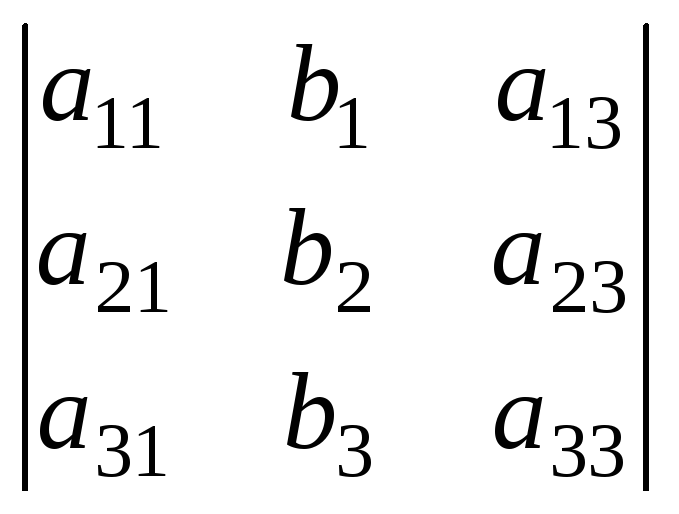 ;Dz=
;Dz=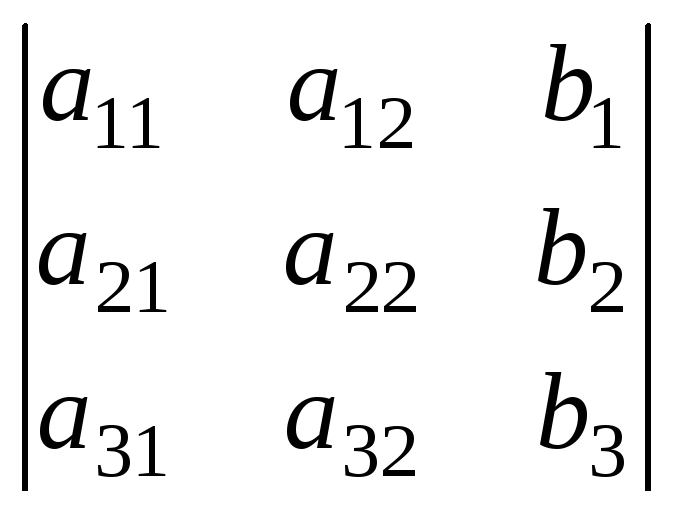 ,
,
При D 0 система имеет единственное решение. Если D = 0 ,то исходная система либо неопределенная, либо несовместная.
Пример. Решить систему линейных уравнений.
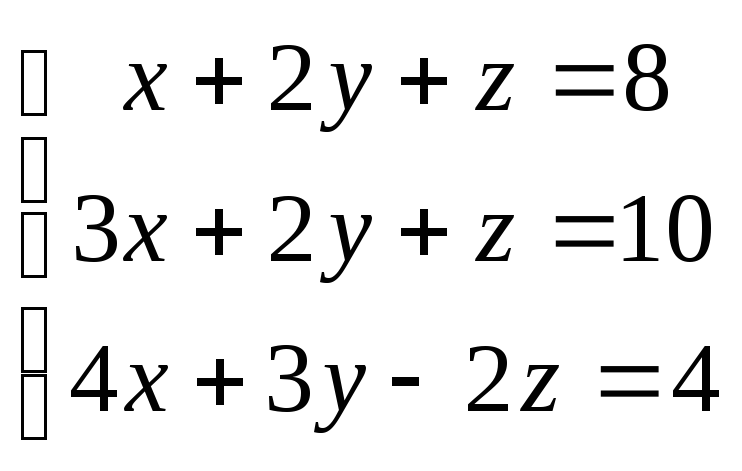
Решение:
D
=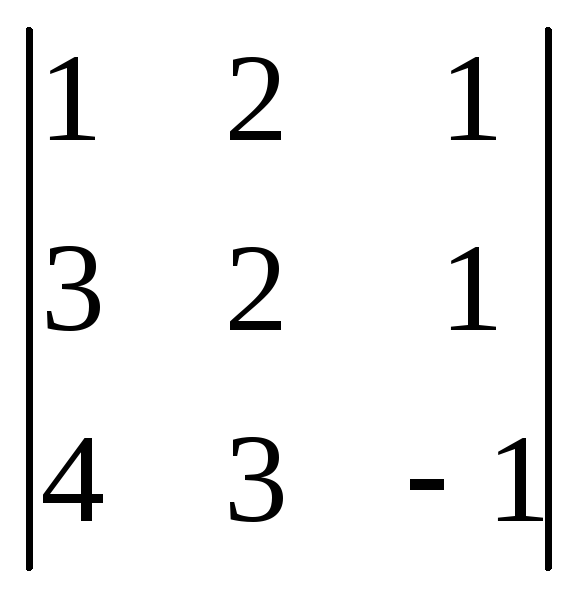 =14, Dx=
=14, Dx=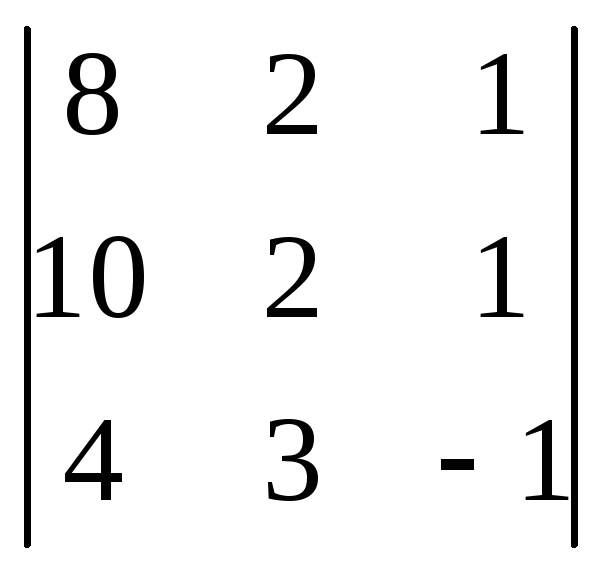 = 14,
Dу =
= 14,
Dу =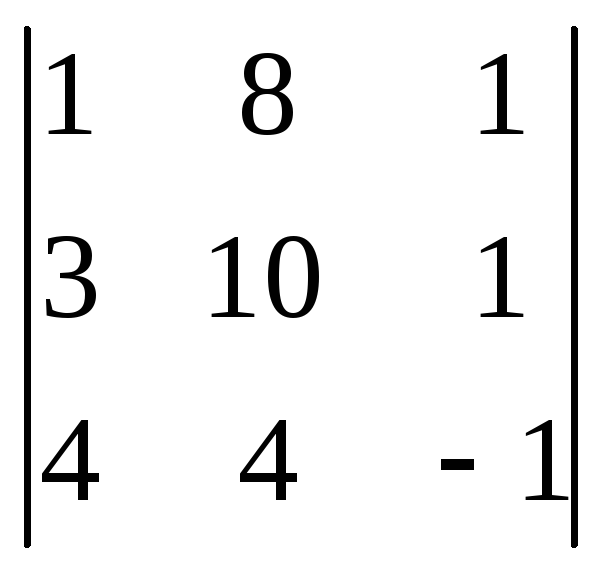 =28, Dz
=
=28, Dz
=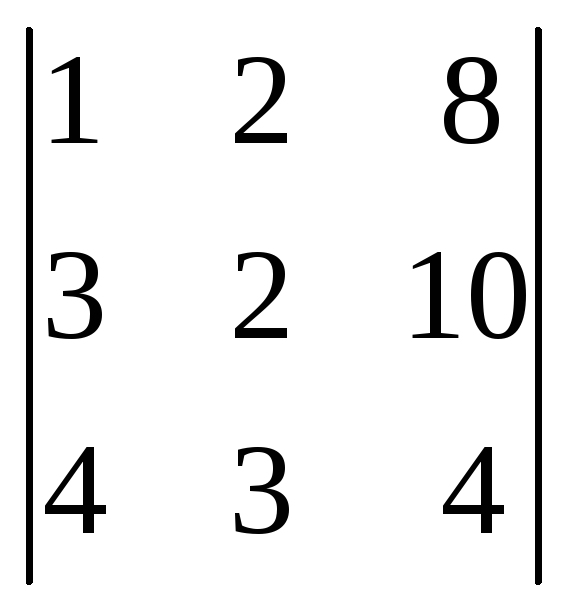 =42.
=42.
х =  = =1; y
=
= =1; y
= =
=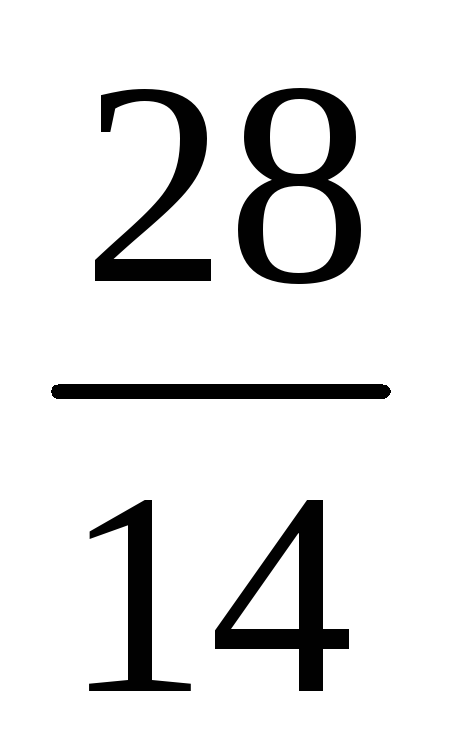 = 2;
z =
= 2;
z = 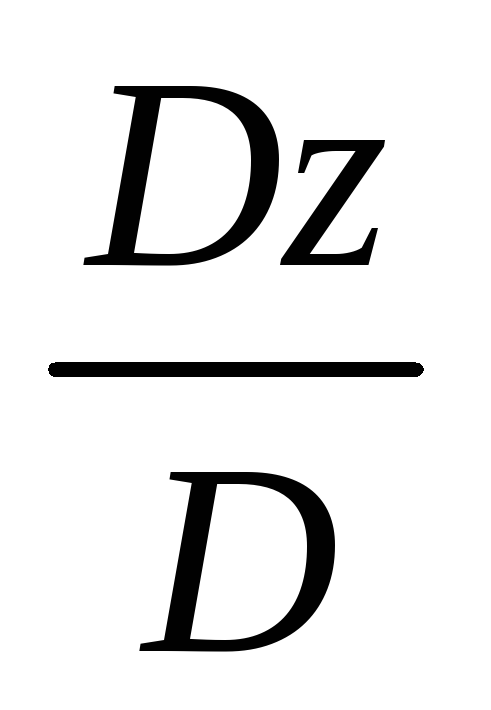 =
=  =3.
=3.
Метод Гаусса. Одним из способов решения линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных. Этот метод заключается в преобразовании системы линейных уравнений к такому виду, где все элементы, лежащие по одну сторону от главной диагонали равны нулю. Удобнее приводить к ступенчатому виду не саму систему, а матрицу из коэффициентов и свободных членов. Переход от одной матрицы к другой будем осуществлять при помощи знака эквивалентности «~». Если система имеет единственное решение, то ступенчатая система уравнений приведется к треугольной, т.е. к такой, в которой последнее уравнение содержит одно неизвестное. В случае неопределенной – более одного неизвестного.
Общее решение строят из исходной системы уравнений с помощью элементарных преобразований, под которыми понимается любое из следующих действий:
1) вычеркивание уравнения, у которого все коэффициенты при неизвестных и свободный член равны нулю;
2) умножение обеих частей какого-либо уравнения системы на отличное от нуля число;
3) замена 1-го уравнения системы уравнением, которое получается путем прибавления к 1-му уравнению системы ее n-го уравнения, умноженного на число.
Пример. Решить систему уравнений методом Гаусса.
 .
.
Решение:
 ~
~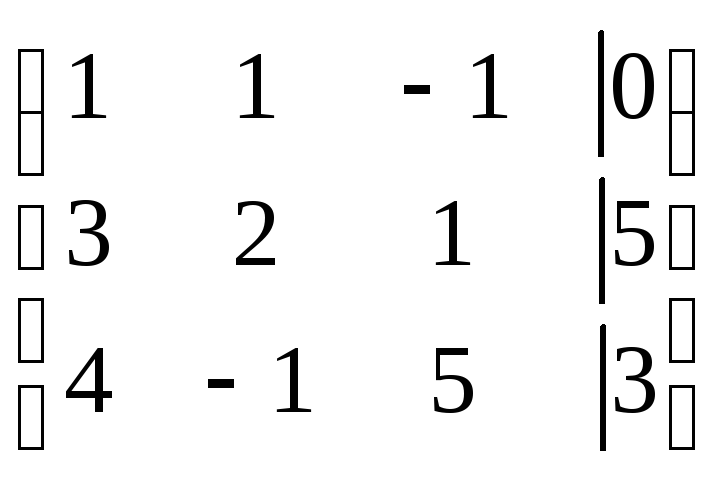 ~
~ ~
~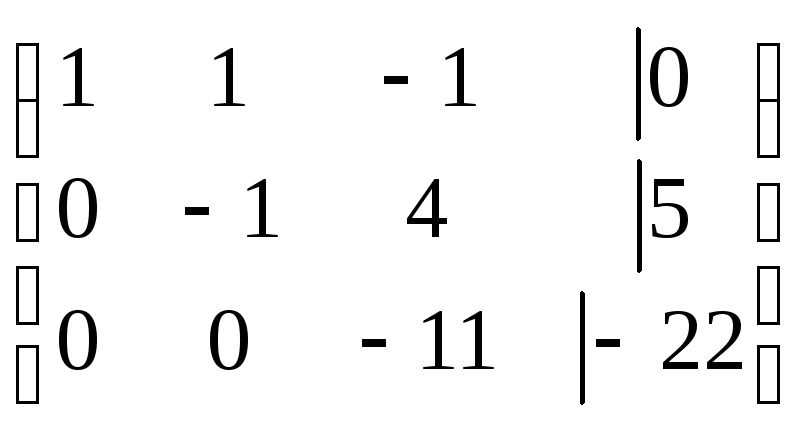 ~
~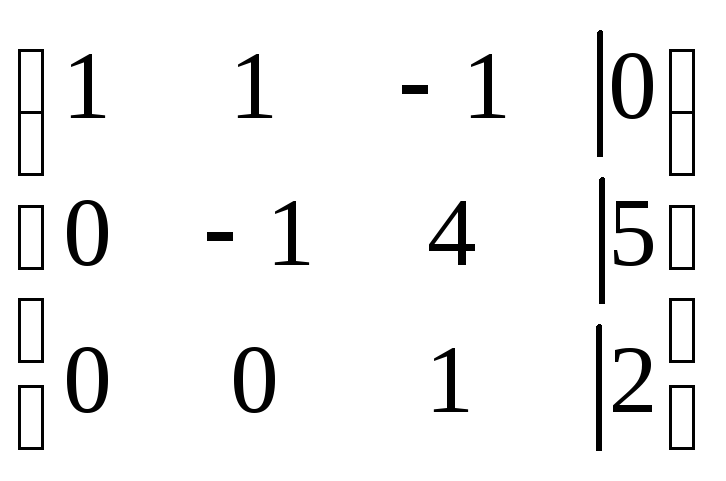
Система приведена к треугольному виду. Запишем полученную систему:
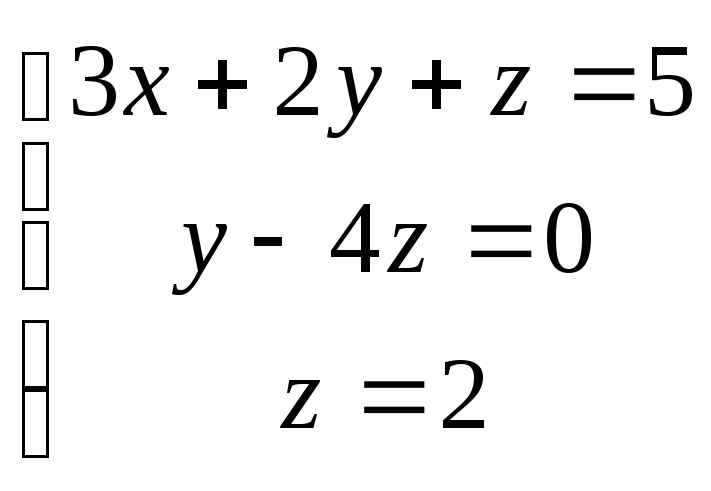
 .
.
Обратная матрица.
Обратной матрицей А-1 для матрицы А называется матрица, для которой выполняется равенство АА-1= А-1А=Е и которая имеет вид:
А-1 =  .
.
Для того, чтобы найти обратную матрицу А-1 для матрицы А, нужно:
вычислить определитель матрицы А;
найти алгебраические дополнения ко всем элементам матрицы А;
записать обратную матрицу по формуле, обратив внимание, на то, что матрица, составленная из алгебраических дополнений транспонированна;
сделать проверку, перемножив данную и обратную матрицы. В результате должна получится единичная матрица.
Пример.
Дана матрица А= .
Найти обратную матрицу для данной.
.
Найти обратную матрицу для данной.
Решение:
Вычислим
определитель матрицы А. 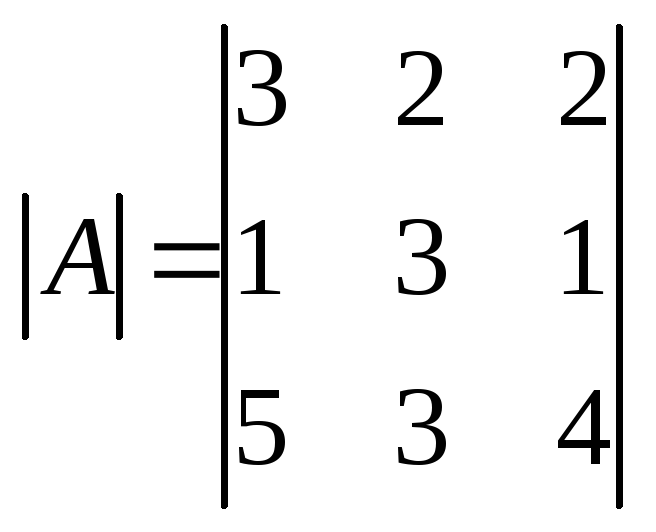 =
27 + 2 – 24 = 5.
=
27 + 2 – 24 = 5.
Найдем алгебраические дополнения:
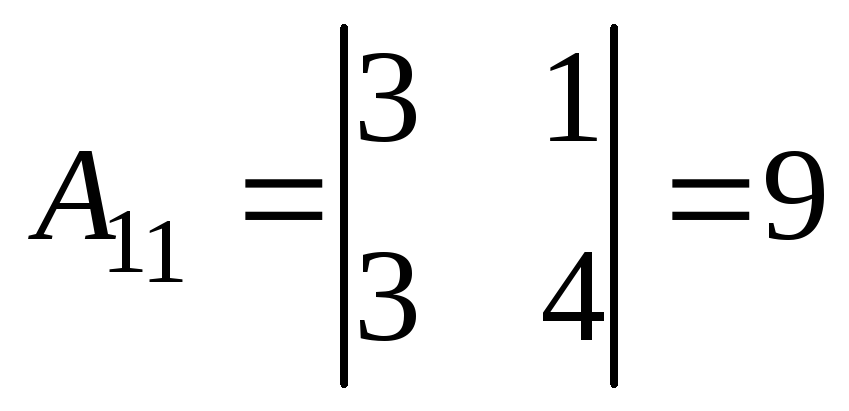 ;
; 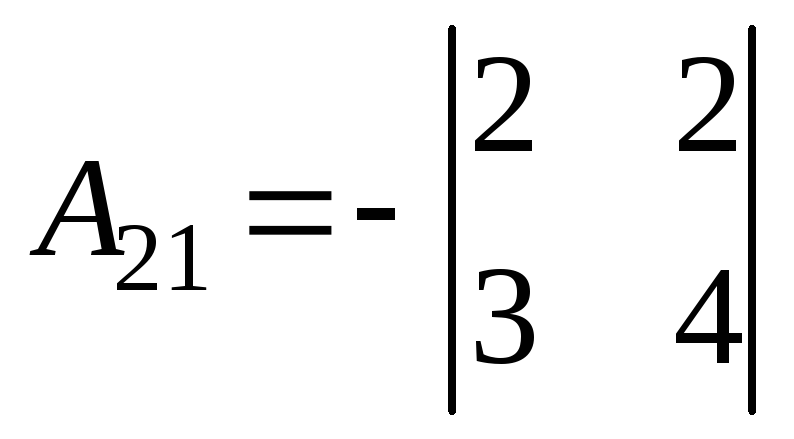 =
-2;
=
-2;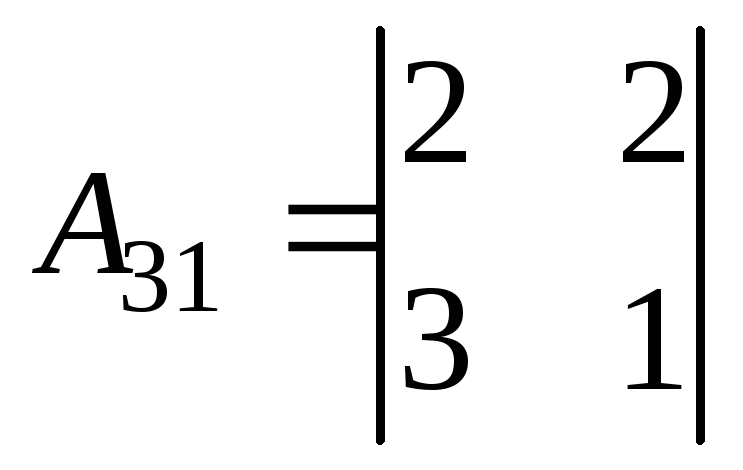 = 4
= 4
 = 1;
= 1;  ;
;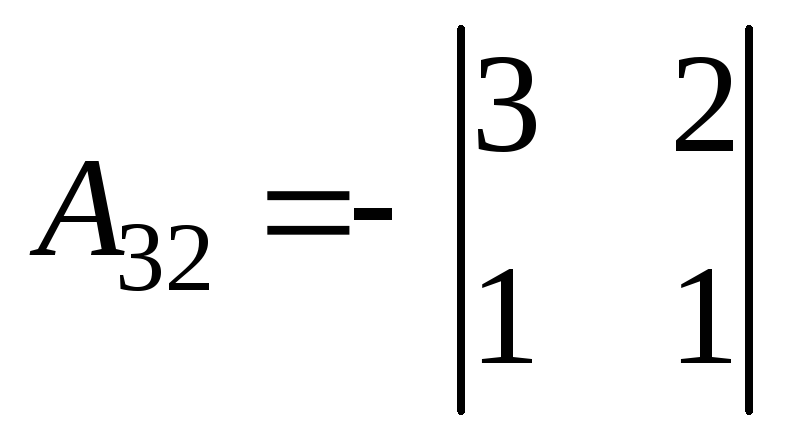 = -1
= -1
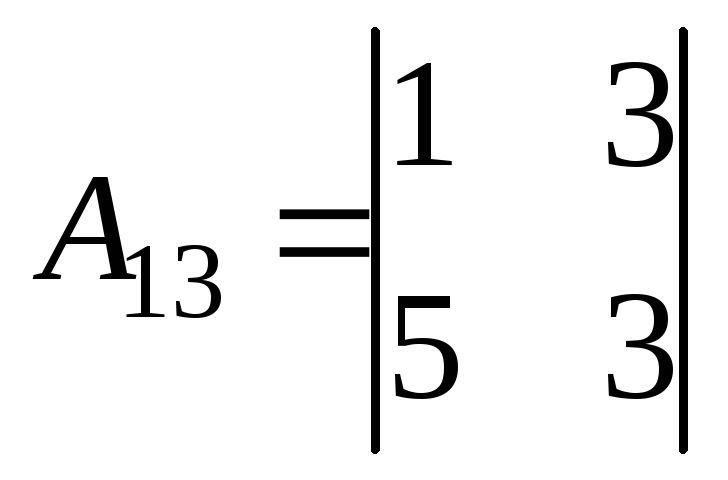 = -12;
= -12; 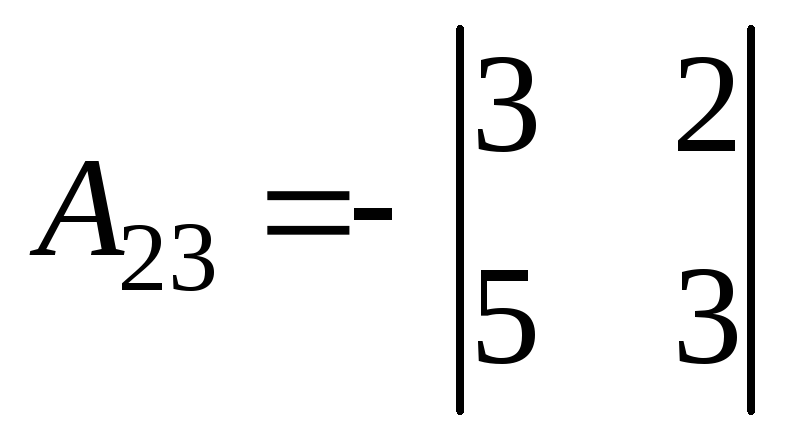 = 1;
= 1;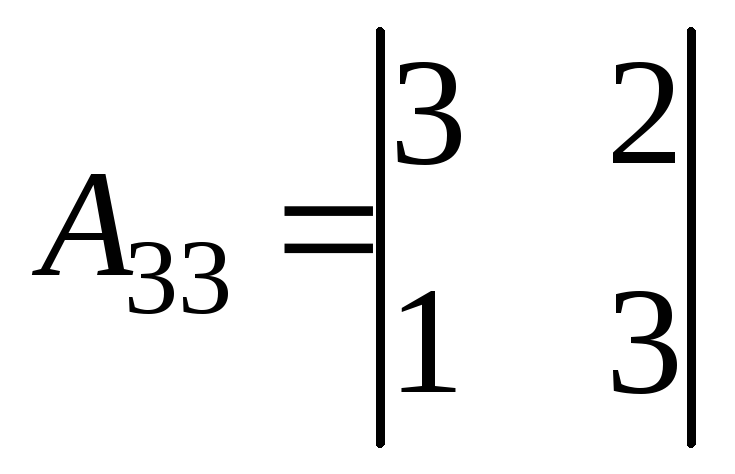 = 7
= 7

Решение систем уравнений матричным методом.
Система
уравнений  может быть записана в виде
может быть записана в виде
АХ
= В, где А
=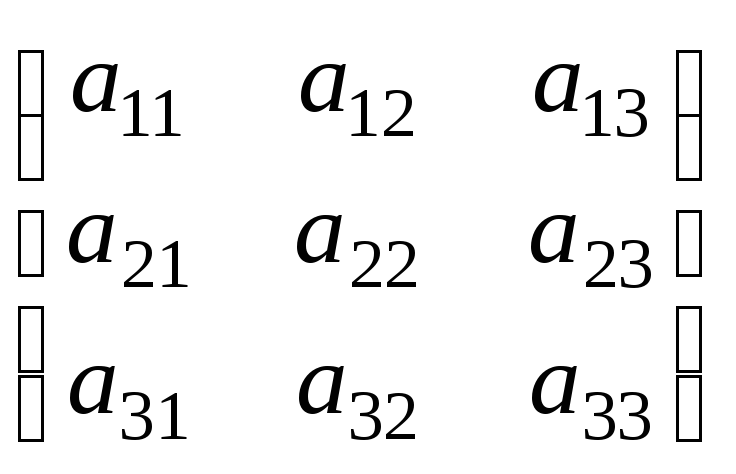 ,Х =
,Х =  ,В =
,В = 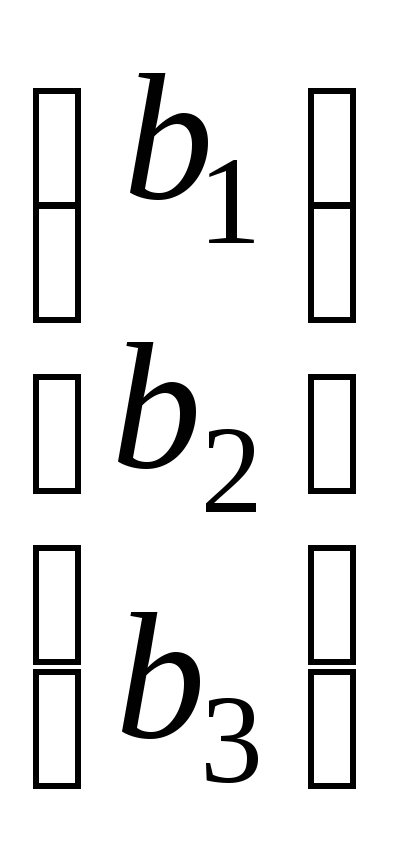 .
.
Решение
этой системы имеет вид: Х
=А-1 В (если 
0).
0).
Пример.
Решить систему  ,
представив ее в виде матричного уравнения.
,
представив ее в виде матричного уравнения.
Решение: Перепишем систему в виде АХ = В.
А
=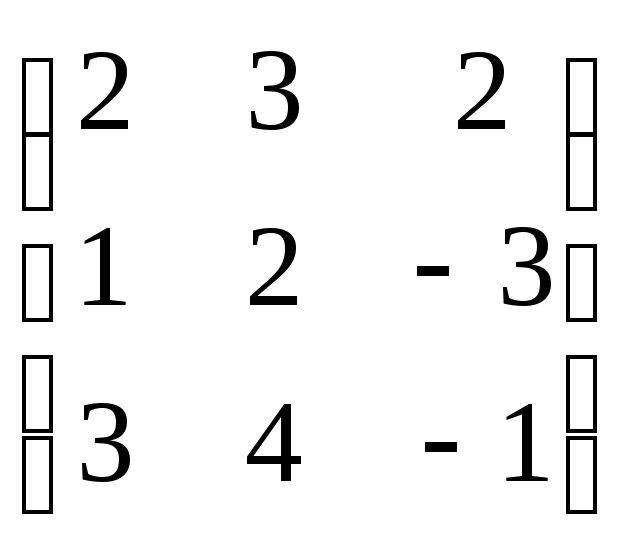 ,Х =
,Х = 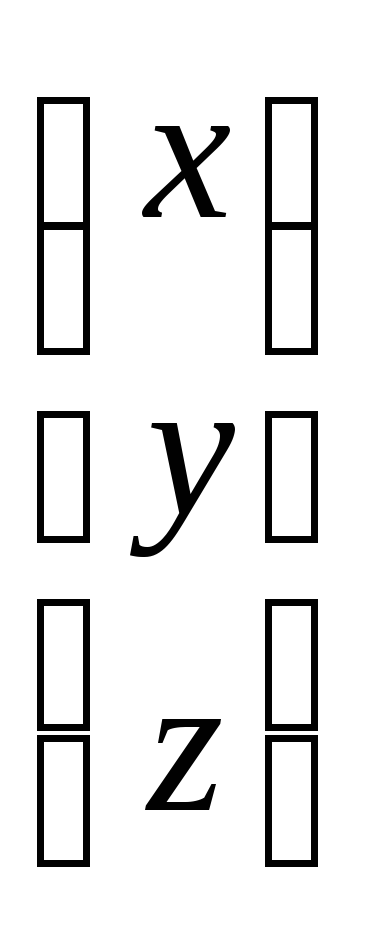 ,В =
,В = 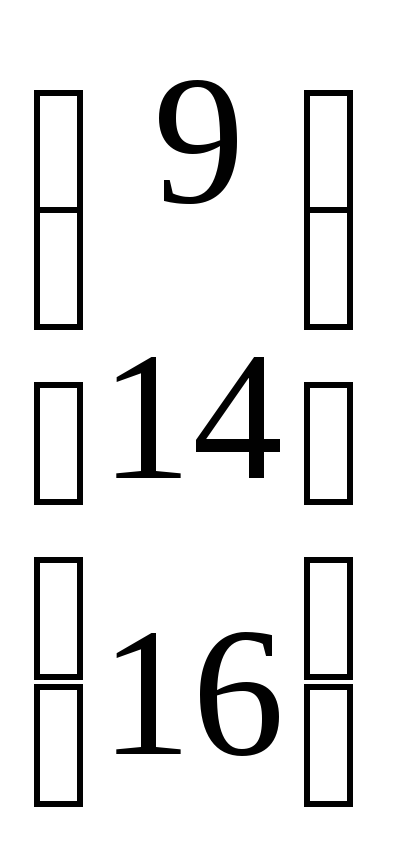 .
.
Решение матричного уравнения имеет вид: Х =А-1 В . Найдем А-1:
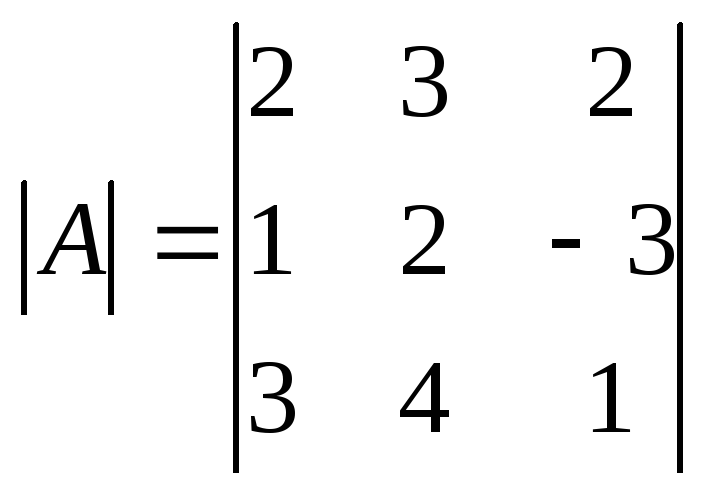 =
-6.
=
-6.
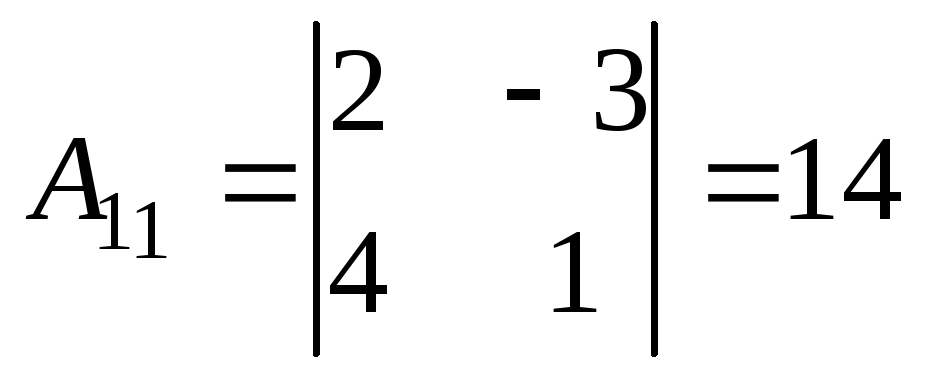 ;
; 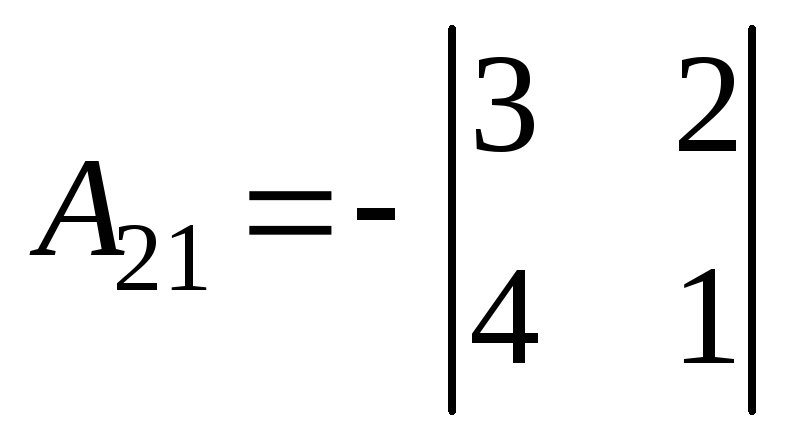 =
5;
=
5;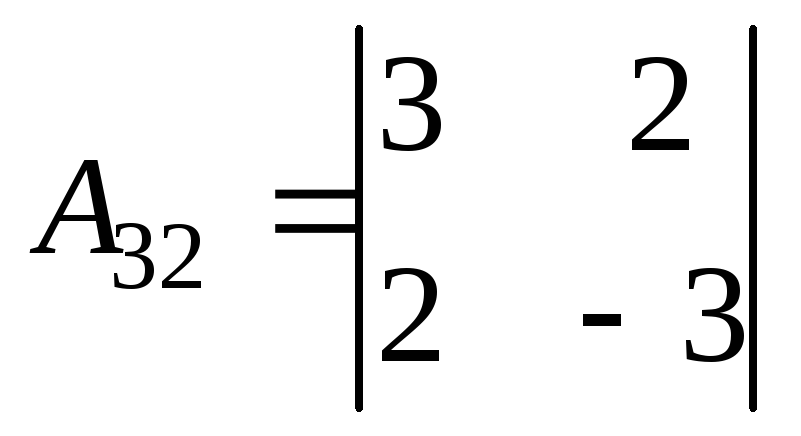 = -13
= -13
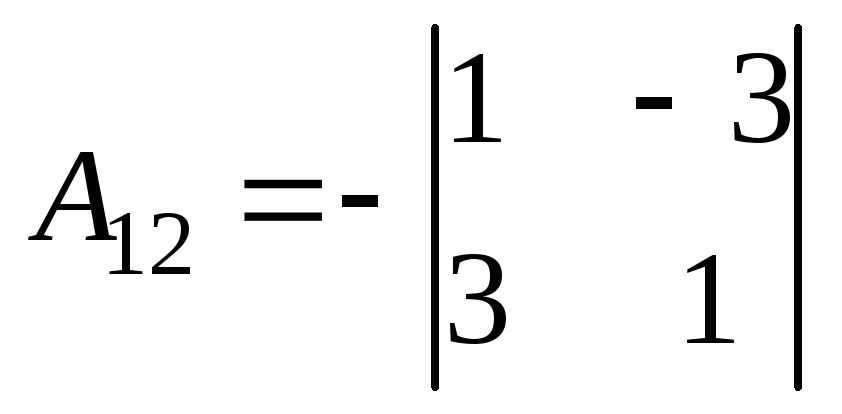 = -10;
= -10;  ;
;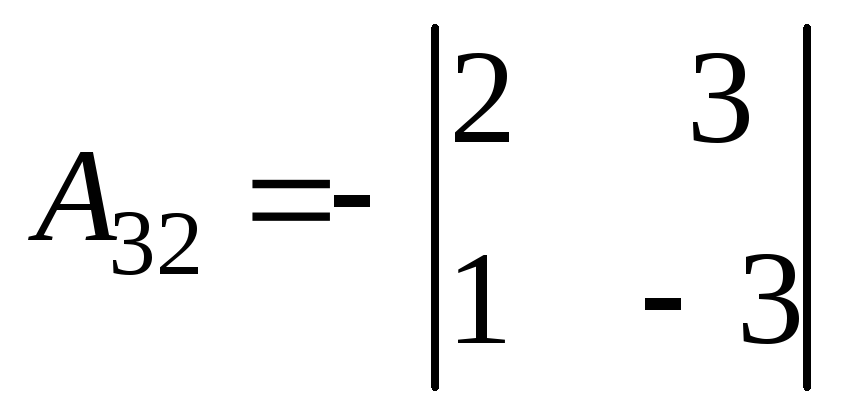 = 8
= 8
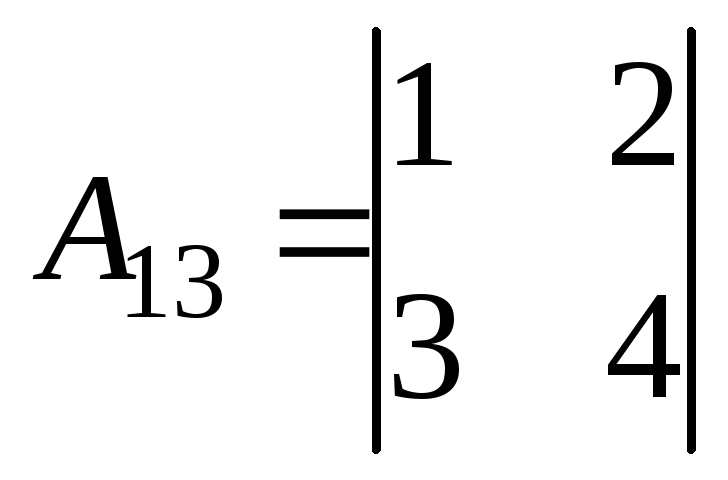 = -2;
= -2;  = 1;
= 1;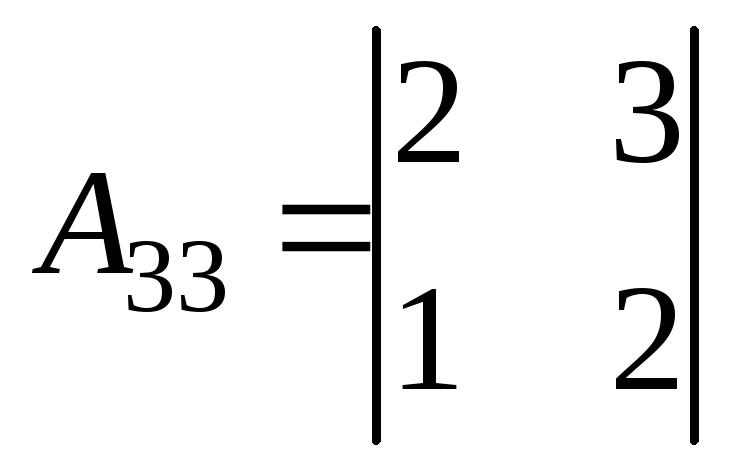 = 1
= 1
Откуда
Х
=  ,
,
следовательно, х = 2, y = 3, z = -2.
Ранг матрицы.
Дана прямоугольная матрица
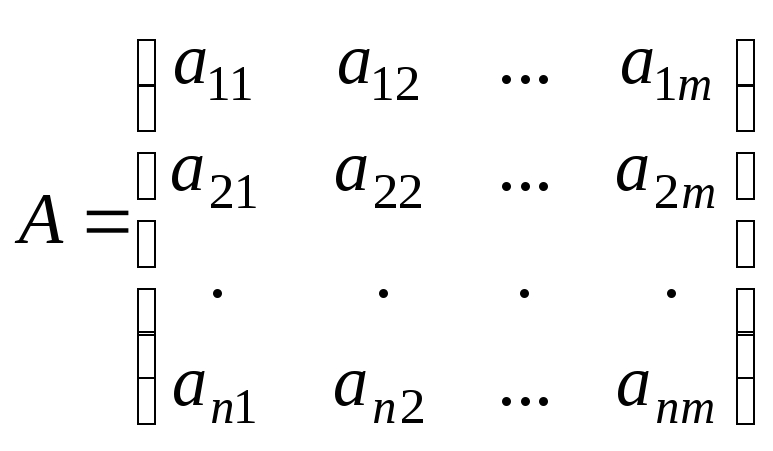
Выделим
в этой матрице k произвольных строк и k произвольных столбцов (k  т,
т,
k 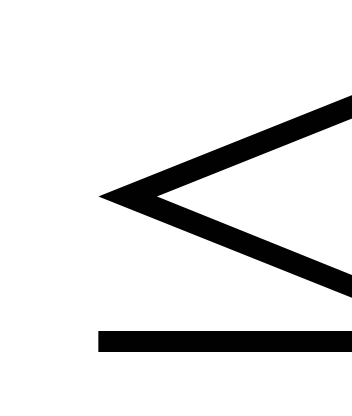 n). Определитель k—го
порядка, составленный из элементов
матрицы А,
расположенных на пересечении выделенных
строк и столбцов, называем минором
k-го порядка
матрицы А. Рассмотрим всевозможные миноры матрицы А. Рангом матрицы А называется
наибольший порядок минора этой матрицы,
отличный от нуля. Если все элементы
матрицы равны нулю, то ранг этой принимают
равным нулю.
n). Определитель k—го
порядка, составленный из элементов
матрицы А,
расположенных на пересечении выделенных
строк и столбцов, называем минором
k-го порядка
матрицы А. Рассмотрим всевозможные миноры матрицы А. Рангом матрицы А называется
наибольший порядок минора этой матрицы,
отличный от нуля. Если все элементы
матрицы равны нулю, то ранг этой принимают
равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы А будем обозначать через Dk (А). Если Dk (А)=Dk (В), то матрицы А и В называются эквивалентными. Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимают:
1) замену строк столбцами, а столбцов — соответствующими строками;
2) перестановку строк матрицы;
3) вычерчивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой строки.
Пример.
Определить ранг матрицы:  .
.
Решение: Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры же первого порядка (сами элементы матриц) отличен от нуля. Следовательно, ранг матрицы равен 1.
Практически удобно пользоваться следующим приемом: если найден минор k— го порядка Dk, то остается вычислить только те миноры (k+1)го порядка, которые представляют собой «окаймление» Dk.
Пример.
Определить
ранг матрицы: А =  .
.
D2 = 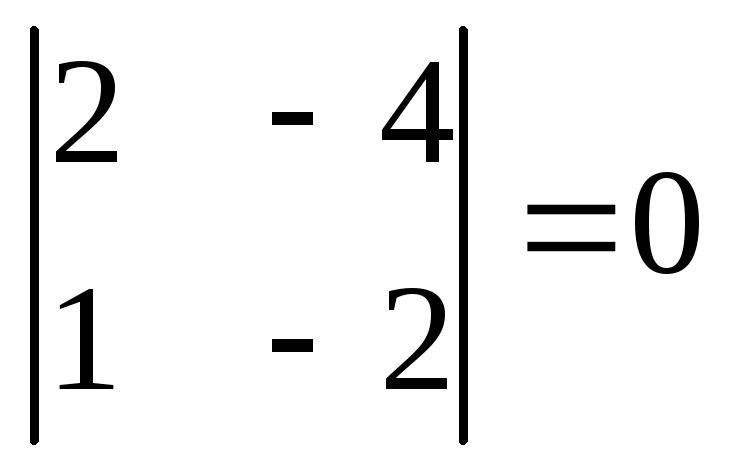 ; D2=
; D2=  .
.
Обзор методов решения систем линейных алгебраических уравнений
Параллельные алгоритмы решения систем линейных алгебраических уравнений
Содержание
Введение
Обзор методов решения систем линейных алгебраических уравнений
Прямые методы решения
Итерационные методы
Вариационные методы
Метод Якоби
Решение на однопроцессорных компьютерах
2.2 Решение на многопроцессорных компьютерах
Основные функции MPI.
Численный эксперимент
Расчет на однопроцессорных компьютерах
Расчет на многопроцессорных компьютерах
Литература
1.1 Прямые методы решения
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) [1,2]
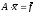 ,
(1)
,
(1)
где 
матрица
матрица 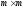 ,
,
искомый вектор,
искомый вектор, 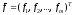
заданный вектор. Будем предполагать,
что определитель матрицы
заданный вектор. Будем предполагать,
что определитель матрицы 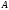 отличен
от нуля, т.е. решение системы (1) существует.
отличен
от нуля, т.е. решение системы (1) существует.
Методы численного решения системы (1) делятся на две группы: прямые методы («точные») и итерационные методы.
Прямыми методами называются методы, позволяющие получить решение системы (1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Итерационные
методы (методы последовательных
приближений) состоят в том, что решение
системы (1) находится как предел
последовательных приближений  при
при ,
гдеn номер итерации. При использовании
методов итерации обычно задается
некоторое малое число 0
и вычисления проводятся до тех пор, пока
не будет выполнена оценка
,
гдеn номер итерации. При использовании
методов итерации обычно задается
некоторое малое число 0
и вычисления проводятся до тех пор, пока
не будет выполнена оценка 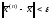 .
К этим методам относятся метод Зейделя,
Якоби, метод верхних релаксаций и т.д.
.
К этим методам относятся метод Зейделя,
Якоби, метод верхних релаксаций и т.д.
Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.
Метод Гаусса
Запишем систему Ax=f, в развернутом виде
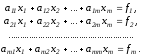
Метод
Гаусса состоит в последовательном
исключении неизвестных из этой системы.
Предположим, что  .
Последовательно умножая первое уравнение
на
.
Последовательно умножая первое уравнение
на и складывая сi-м
уравнение, исключим
и складывая сi-м
уравнение, исключим 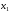 из всех уравнений кроме первого. Получим
систему
из всех уравнений кроме первого. Получим
систему
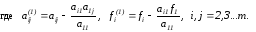
Аналогичным
образом из полученной системы исключим 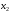 .
Последовательно, исключая все неизвестные,
получим систему треугольного вида
.
Последовательно, исключая все неизвестные,
получим систему треугольного вида
Описанная
процедура называется прямым ходом
метода Гаусса. Заметим, что ее выполнение
было возможно при условии, что все  ,
, не равны нулю.
не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
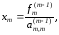
 .
.
Эта процедура получила название обратный ход метода Гаусса..
Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы А. Поэтому численная реализация метода сводится к преобразованию элементов массива размерности (m×(m+1)), где m+1 столбец содержит элементы правой части системы.
Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.
Один
из основных недостатков метода Гаусса
связан с тем, что при его реализации
накапливается вычислительная погрешность.
В книге [ Самарский, Гулин показано, что
для больших систем порядка m число действий умножений и делений
близко к 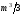 .
.
Для того, чтобы уменьшить рост вычислительной погрешности, применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и следовательно относительная погрешность будет наименьшей.
Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы1. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета. Поэтому целесообразность выбора того или иного метода определяется непосредственно программистом2.
Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду, позволяют вычислить определитель матрицы
.
Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение
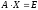 ,
,
где Е единичная матрица. Его решение сводится к решению m систем

у
вектора 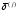 j –я компонента равна единице, а остальные
компоненты равны нулю.
j –я компонента равна единице, а остальные
компоненты равны нулю.
LU–метод
LU-метод основан на том, что если главные миноры матрицы А отличны от нуля, тогда матрицу А можно представить, причем единственным образом, в виде произведения
А=LU,
где L–нижняя треугольная матрица с ненулевыми диагональными элементами и U–верхняя треугольная матрица с единичной диагональю.
Рассмотрим СЛАУ Ax=f.

A=LU
где


или
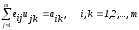 ,
,
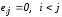

Окончательно запишем



Полагая  получим следующие рекуррентные формулы
для вычисления элементов матрицы L и U
получим следующие рекуррентные формулы
для вычисления элементов матрицы L и U
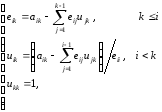
Если найдены матрицы L и U, то решение исходной системы (1)ID_1 сводится к последовательному решению двух систем уравнений с треугольными матрицами

LU – метод позволяет вычислить определитель матрицы А
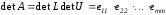 .
.
Метод квадратного корня
Метод квадратного корня по своему идейному содержанию близок к LU-методу. Основное отличие в том, что он дает упрощение для симметричных матриц.ID_1
Этот метод основан на разложении матрицы А в произведение
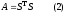
где
S–верхняя
треугольная матрица с положительными
элементами на главной 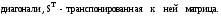

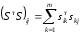
Из условия (2) получаются уравнения

Так как матрица А симметричная, не ограничивая общности, можно считать, что в системе (3) выполняется неравенство i≤j. Тогда (3) можно переписать в виде
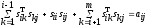
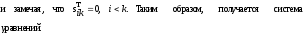
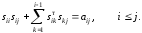
В частности, при i=j получится
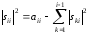
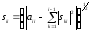 (4)
(4)
Далее, при i<j получим

По формулам (4) и (5) находятся рекуррентно все ненулевые элементы матрицы S.
Обратный ход метода квадратного корня состоит в последовательном решении двух систем уравнений с треугольными матрицами.
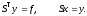
Решения этих систем находятся по рекуррентным формулам
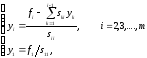

Всего
метод квадратного корня при факторизации
A=SтS
требует примерно 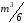 операций умножения и деления иm операций извлечения квадратного
корня.[1]
операций умножения и деления иm операций извлечения квадратного
корня.[1]
Метод вращений решения линейных систем
Как и в методе Гаусса, цель прямого хода преобразований в этом методе–приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.
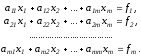
Умножим первое уравнение исходной системы (1) на с1 ,второе на s1 и сложим их ; полученным уравнением заменим первое уравнение системы. Затем первое уравнение исходной системы умножаем на –s1 , второе на c1 и результатом их сложения заменим второе уравнение . Таким образом, первые два уравнения (1) заменяются уравнениями
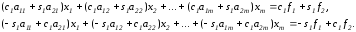
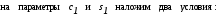
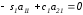
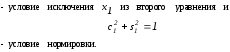
Отсюда  .
Эти числа можно интерпретировать как
косинус и синус некоторого угла
.
Эти числа можно интерпретировать как
косинус и синус некоторого угла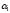 (отсюда
названиеметод
вращения,
каждый шаг такого преобразования можно
рассматривать как вращение расширенной
матрицы системы в плоскости обнуляемого
индекса).
(отсюда
названиеметод
вращения,
каждый шаг такого преобразования можно
рассматривать как вращение расширенной
матрицы системы в плоскости обнуляемого
индекса).
В результате преобразований получим систему

где
Далее первое уравнение системы заменяется новым, полученным сложением результатов умножения первого и третьего уравнений соответственно на

а
третье–уравнением, полученное при
сложении результатов умножения тех
же 
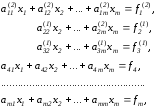
где

Выполнив преобразование m-1 раз, придем к системе
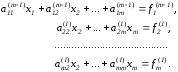
Вид полученной системы такой же, как после первого этапа преобразований методом Гаусса. Эта система обладает следующим свойством: длина любого вектора-столбца (эвклидова норма) расширенной матрицы остается такой же, как у исходной матрицы. Следовательно, при выполнении преобразований не наблюдается рост элементов.
Далее по этому же алгоритму преобразуется матрица
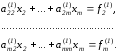
и т.д.
В результате m-1 этапов прямого хода система будет приведена к треугольному виду.
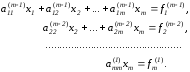
Нахождение неизвестных не отличается от обратного хода метода Гаусса.
Всего
метод вращения требует примерно 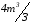 операций умножения и деления.
операций умножения и деления.
Системы линейных уравнений
Система m линейных уравнений с n переменными в общем виде записывается следующим образом:
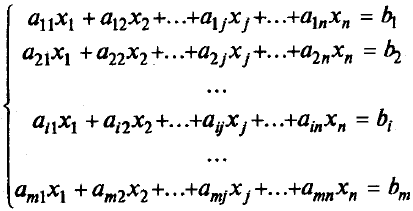
где xj– переменные,aij,bi–
константы,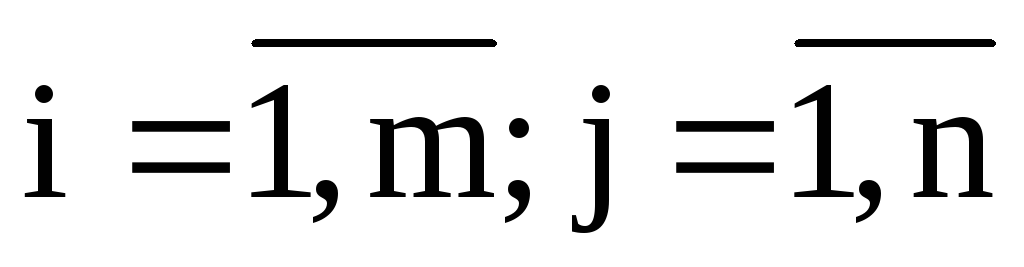 .
.
При этом величины aij(те константы, которые умножаются на переменные) принято называтькоэффициентамипри переменных, а правые части уравненийbi(те константы, которые не умножаются на переменные) —свободными членами.
Более кратко ту же систему можно записать в виде:
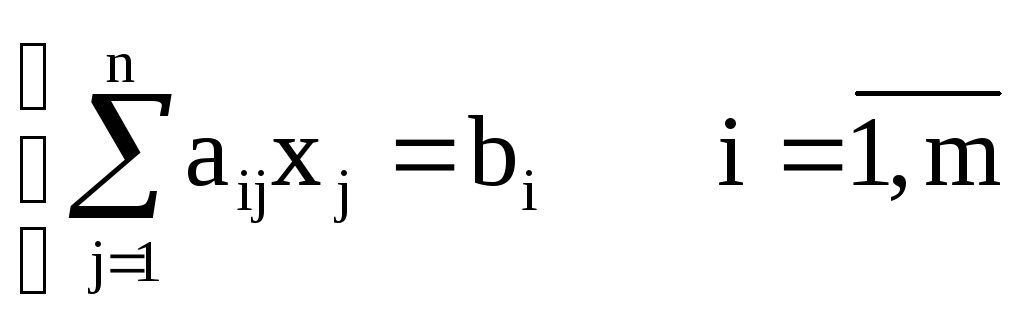
Отметим, что в последней
записи тоже записана именно система
уравнений, хотя на первый взгляд создается
впечатление, что уравнение только одно
(запись 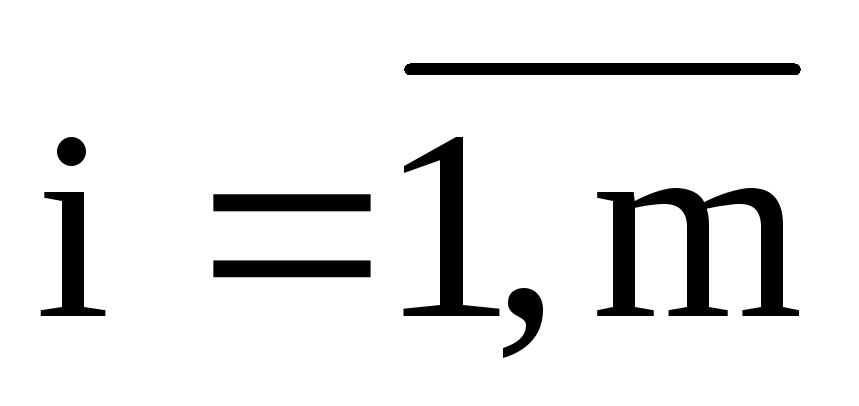 означает,
что такие уравнения записываютсяmраз для разныхi).
означает,
что такие уравнения записываютсяmраз для разныхi).
Решением такой системы называют совокупность n числовых значений переменных xj, при подстановке которых в систему каждое уравнение обращается в истинное равенство.
Систему уравнений называют совместной, если она имеет хотя бы одно решение (т.е. хотя бы один такой набор из n чисел), инесовместной, если она не имеет решений.
Совместную систему уравнений называют определенной, если она имеет единственное решение, инеопределенной, если она имеет более одного решения.
Например, рассмотрим
систему уравнений 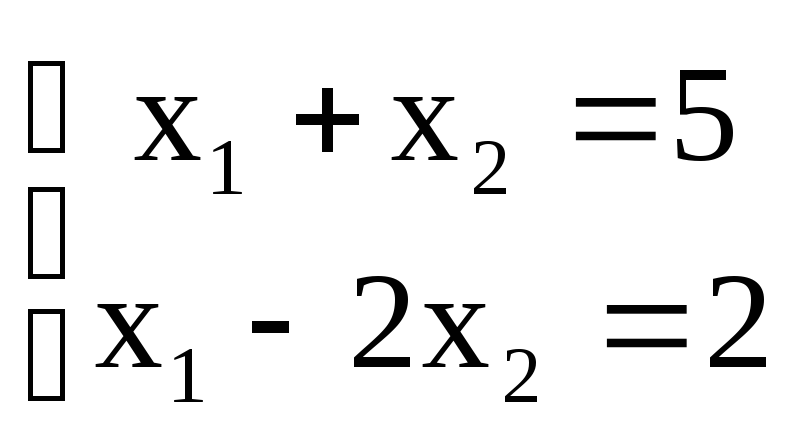 .
.
Чтобы решить эту систему, вычтем из верхнего уравнения нижнее. Получим 3х2= 3. Отсюда х2= 1; и из любого уравнения х1= 4. Таким образом, эта система имеет только одно решение – (4; 1). Это означает, что она — совместная и определенная.
Рассмотрим другую
систему: 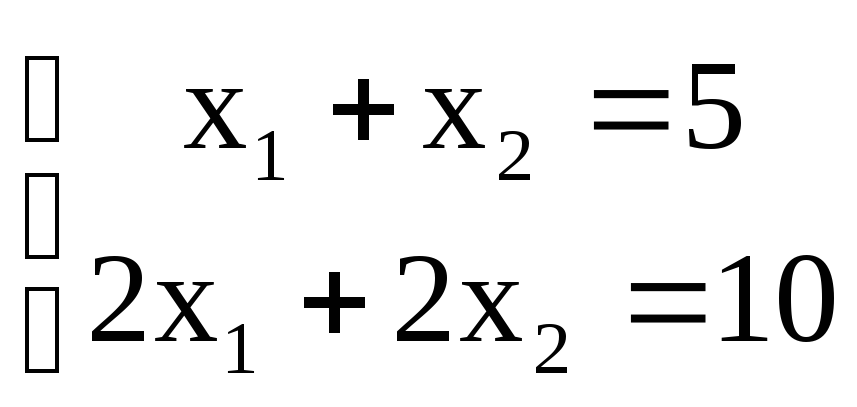 .
Легко убедиться, что значения (4; 1) будут
решением и этой системы тоже. Значит,
она тоже совместная. Однако, у нее есть
и другие решения, например (2; 3). Значит,
она неопределенная. Более того, у этой
системы бесконечно много решений. На
самом деле, решением здесь будут любые
два числа, которые в сумме дают пять,
потому что в левой части второго уравнения
стоит удвоенная левая часть первого
уравнения (если в левой части первого
уравнения получено число 5, то во втором
всегда будет 10, и оно тоже будет истинным
равенством). Таким образом, решение этой
системы в общем виде можно записать как
( с; 5 – с), где с – любое число.
.
Легко убедиться, что значения (4; 1) будут
решением и этой системы тоже. Значит,
она тоже совместная. Однако, у нее есть
и другие решения, например (2; 3). Значит,
она неопределенная. Более того, у этой
системы бесконечно много решений. На
самом деле, решением здесь будут любые
два числа, которые в сумме дают пять,
потому что в левой части второго уравнения
стоит удвоенная левая часть первого
уравнения (если в левой части первого
уравнения получено число 5, то во втором
всегда будет 10, и оно тоже будет истинным
равенством). Таким образом, решение этой
системы в общем виде можно записать как
( с; 5 – с), где с – любое число.
Приведем пример
несовместной системы: 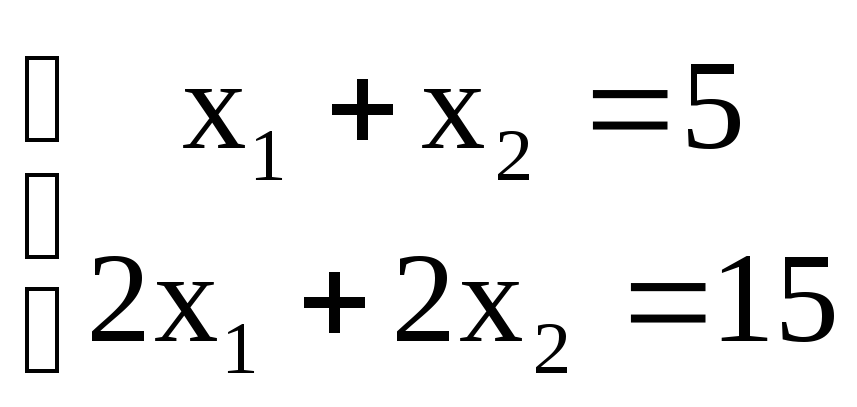 .
У этой системы, очевидно, нет решений,
так как если сумма переменных равна 5,
то эта же удвоенная сумма не может
равняться 15.
.
У этой системы, очевидно, нет решений,
так как если сумма переменных равна 5,
то эта же удвоенная сумма не может
равняться 15.
Две системы уравнений называются равносильными, илиэквивалентными, если они имеют одно и то же множество решений.
Запишем систему линейных уравнений в общем виде в матричной форме. Обозначим:


Кроме того, для решения систем линейных уравнений используют также понятие расширенной матрицы системы, которую получают, приписав кматрице системысправа столбец свободных членов:

Задумаемся, что будет, если подвергнуть расширенную матрицу системы рассмотренным ранее элементарным преобразованиям строк матрицы:
а) отбрасыванию нулевых строк;
б) умножению всех элементов строки на число, отличное от нуля;
в) изменению порядка строк;
г) прибавлению к каждому элементу строки соответствующих элементов другой строки, умноженных на любое число.
Применительно к системе уравнений они сведутся к умножению обеих частей уравнений на одинаковые числа, сложению уравнений друг с другом и перестановке уравнений местами (ну а нулевая строка означает, что соответствующее уравнение вообще исключено из системы). Таким образом, применяя к системе уравнений элементарные преобразования строк, мы получим равносильную систему.
Столбцы матрицы системы тоже можно менять местами. По сути это сведется к перемене местами слагаемых в уравнениях. Впоследствии следует не забыть, что соответствующие переменные поменялись местами (т.е. при умножении преобразованной матрицы на столбец переменных последний тоже надо изменить).
1. Итерационные методы решения систем линейных уравнений
К решению систем линейных уравнений сводятся многочисленные практические задачи. Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространённых и важных задач вычислительной математики.
Запишем систему из nуравнений сnнеизвестными:
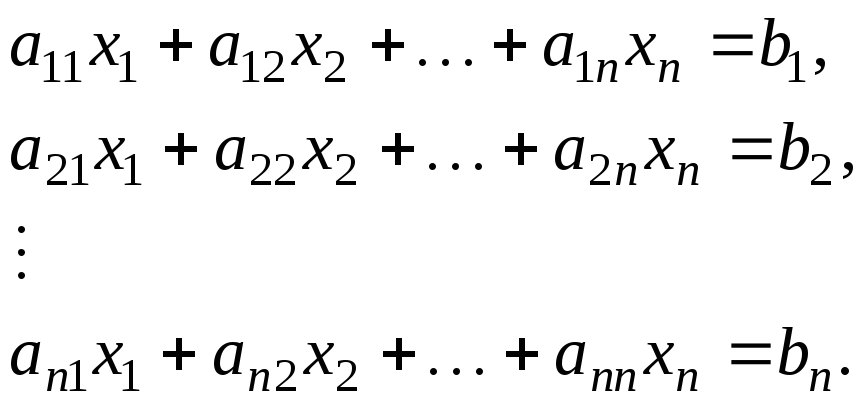 (1)
(1)
здесь  и
и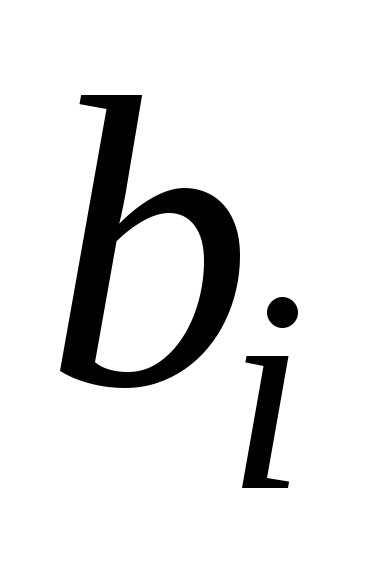 (
(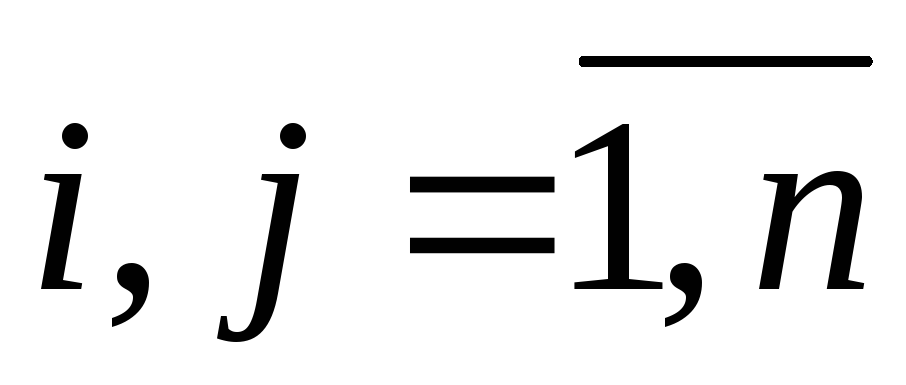 )
– числовые коэффициенты,
)
– числовые коэффициенты,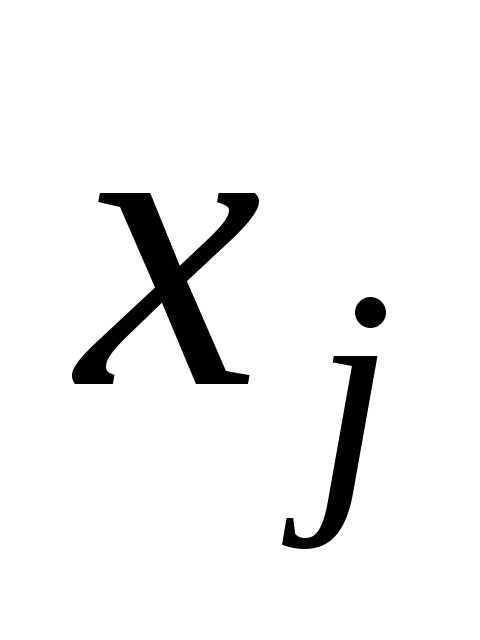 – неизвестные.
– неизвестные.
Методы решения систем линейных уравнений делятся на две группы – прямые и итерационные. Прямые методы используют конечные соотношения (формулы) для вычисления неизвестных. Они дают решение после выполнения заранее известного числа операций. Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближённое решение – начальное приближение. После этого с помощью некоторого алгоритма проводится один цикл вычислений, называемых итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с требуемой точностью. Одним из самых распространенных итерационных методов является метод Гаусса-Зейделя.
Метод Гауcса–Зейделя
Достаточным условием сходимости метода Гаусса-Зейделя является
 при i=1,
2,…, n.
при i=1,
2,…, n.
Следующая последовательность шагов представляет метод Гаусса-Зейделя.
Шаг 1. Проверить
выполнение условия  0,
0,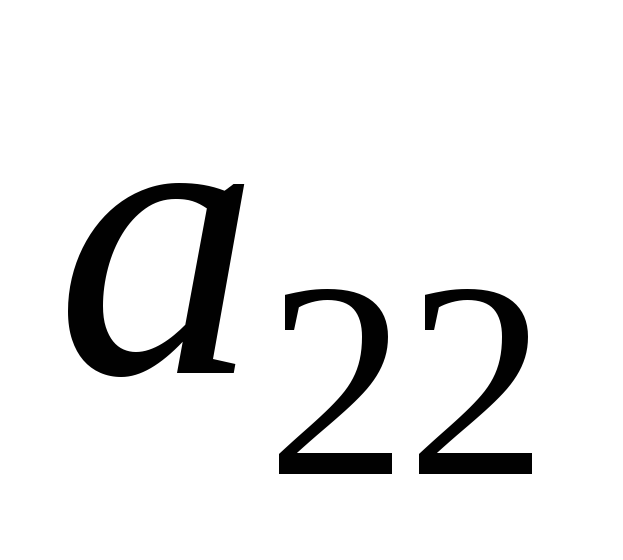 0, …,
0, …,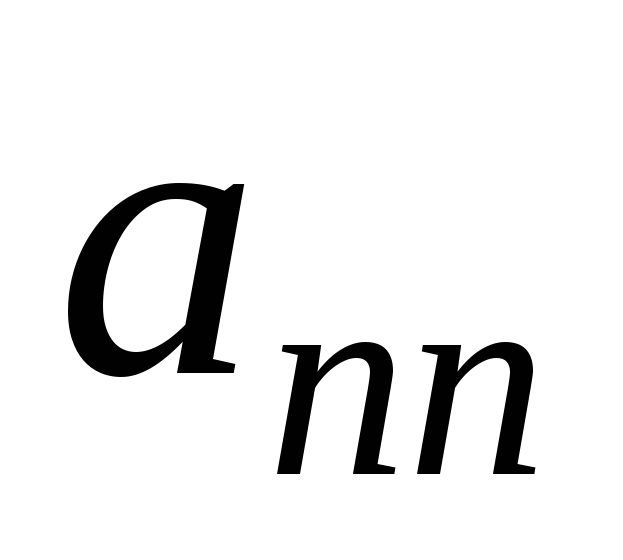 0. Если оно не выполняется, переставить
уравнения так, чтобы оно выполнялось.
0. Если оно не выполняется, переставить
уравнения так, чтобы оно выполнялось.
Шаг 2. Выразить j-ю переменную изj-го уравнения для каждогоj=1,…,n. Получим
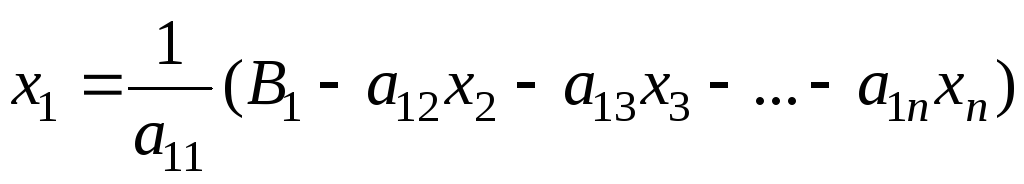

…………………………………………
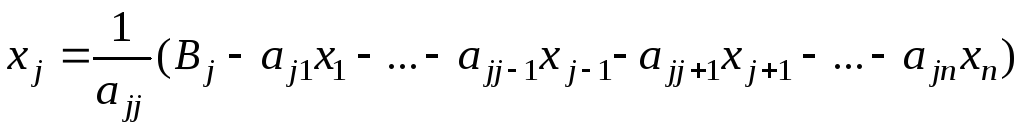 (2)
(2)
…………………………………………
Шаг 3. Выбрать
произвольным образом начальное
приближение  .
.
Шаг 4. Подставить 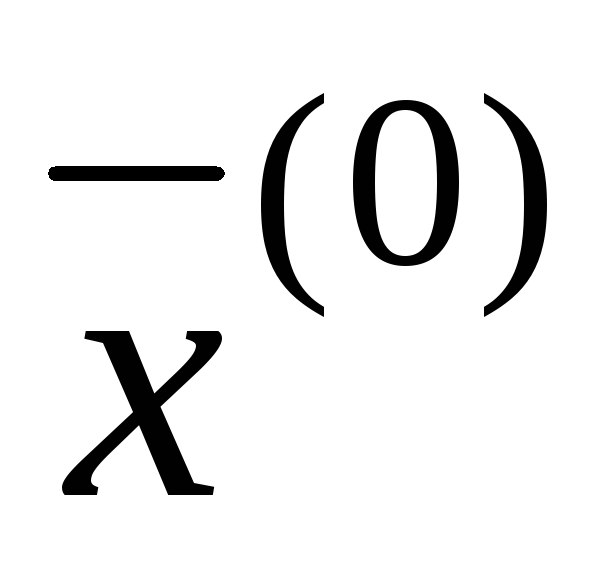 в правую часть системы (2), тогда в левой
её части получится первое приближение
в правую часть системы (2), тогда в левой
её части получится первое приближение


…………………………………………

…………………………………………
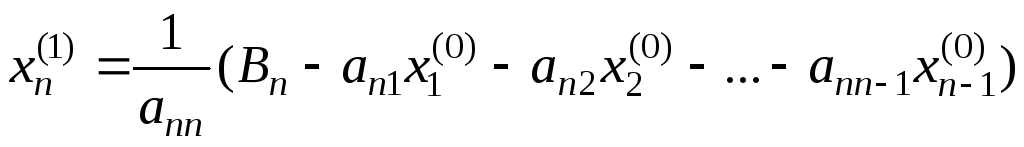
Шаг 5. Вычислить
=max|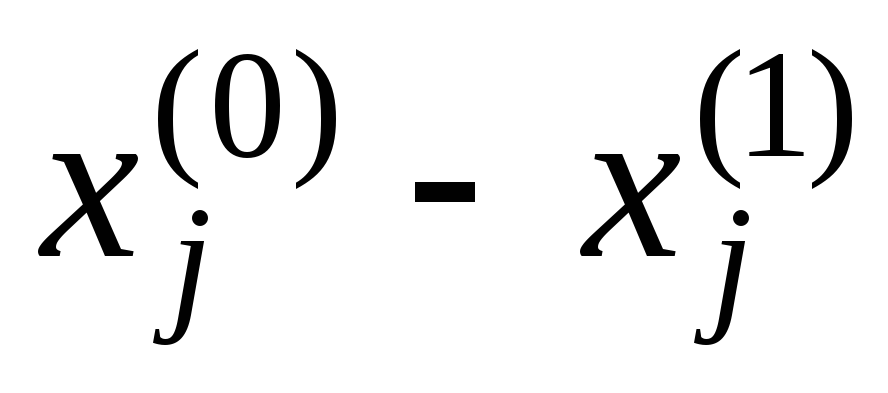 |,
1jn.
|,
1jn.
Шаг 6. Если  меньше заданной точности, то
меньше заданной точности, то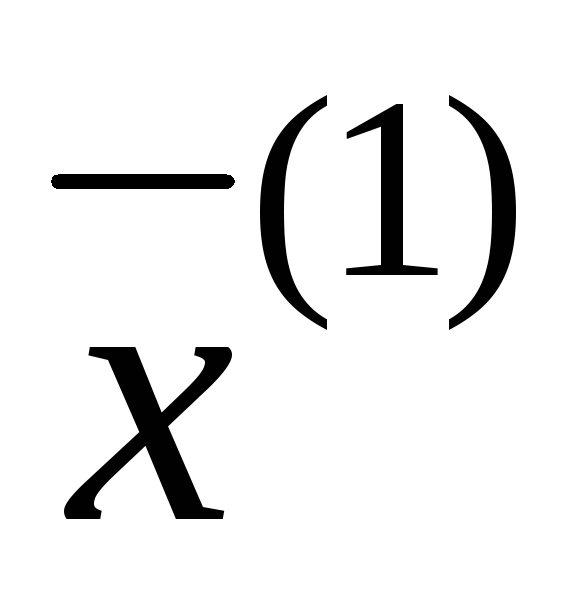 — приближенное решение, в противном
случае подставить
— приближенное решение, в противном
случае подставить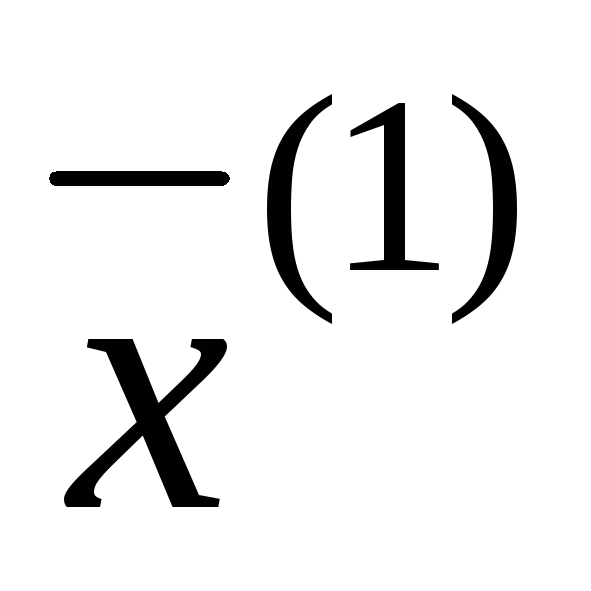 в правую часть системы (2), тогда в левой
части получим второе приближение
в правую часть системы (2), тогда в левой
части получим второе приближение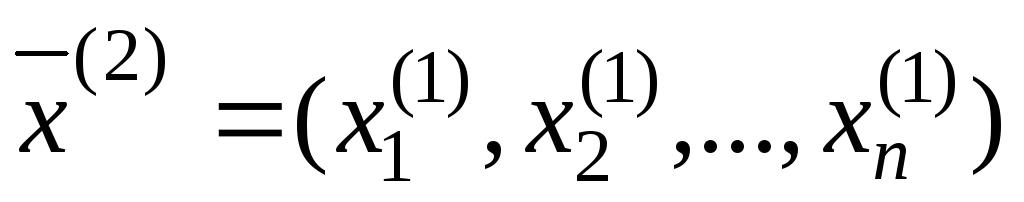 .
Снова вычислить=max|
.
Снова вычислить=max|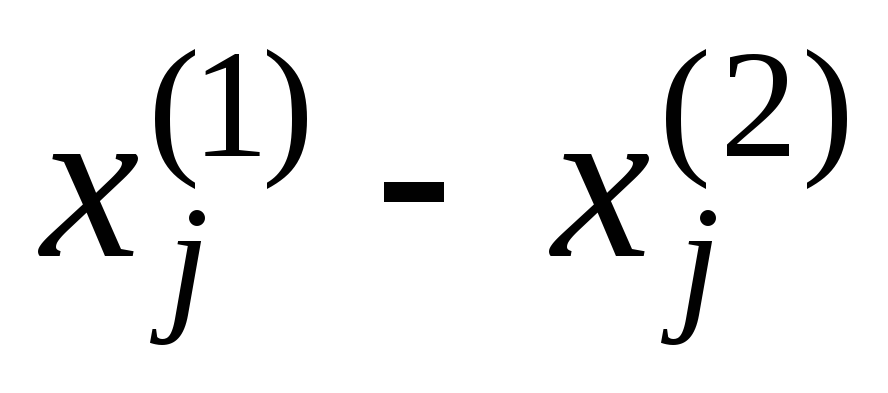 |
и поступать таким образом до тех пор,
пока
|
и поступать таким образом до тех пор,
пока станет меньше заданной точности.
станет меньше заданной точности.
Переход от k-ого приближения к (k+1)-му осуществляется по формулам

………………………………….. (3)
 ,
,
а выход из цикла происходит при выполнения условия
 ,
,
где — заданная точность приближения.
Пример. Решить с точностью 0,001 систему

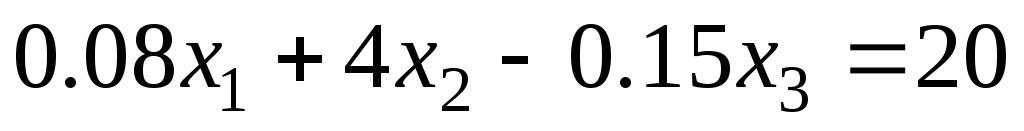
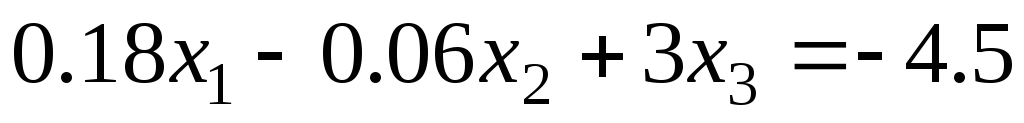 .
.
Решение. Диагональные элементы отличны от нуля, поэтому можно применить метод Гаусса-Зейделя. Приведем систему к виду (3):

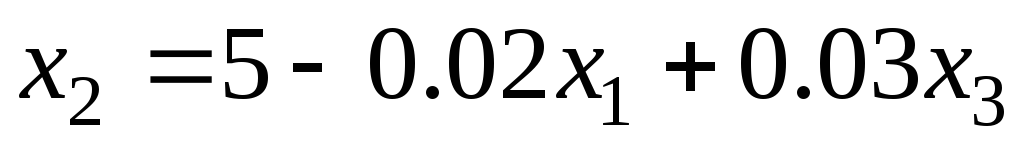
 .
.
Выберем начальное
(нулевое) приближение 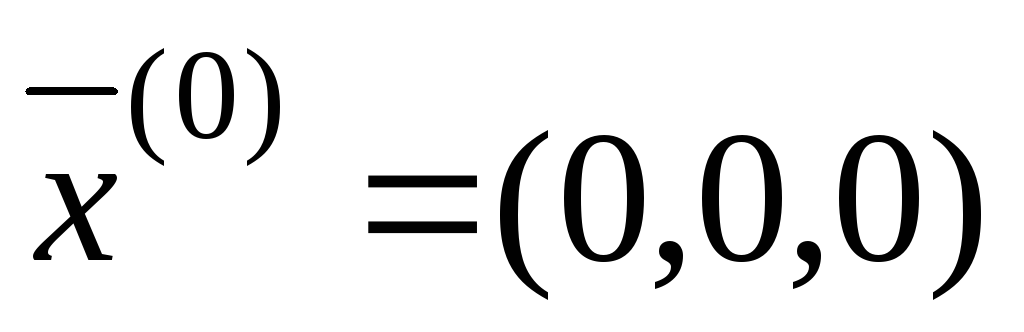 и найдем
и найдем :
:


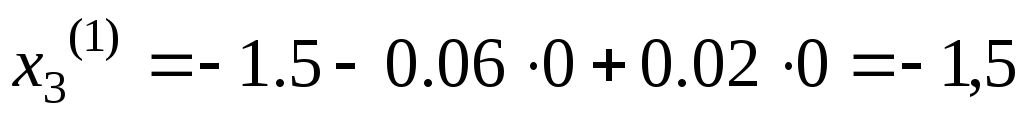 .
.
Найдем второе
приближение 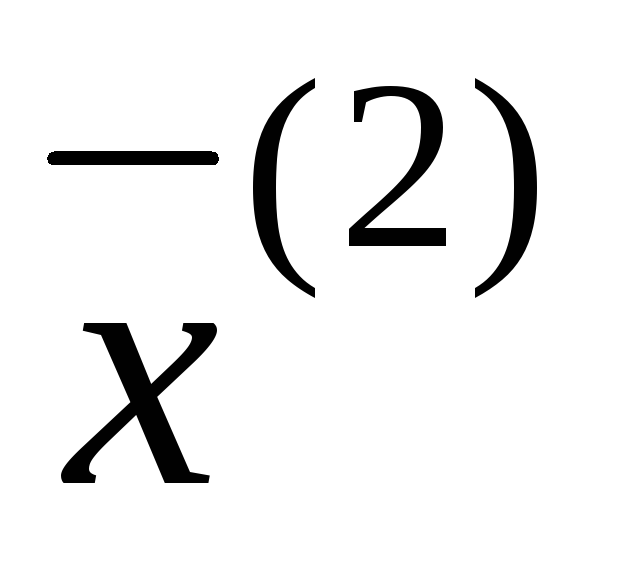 :
:
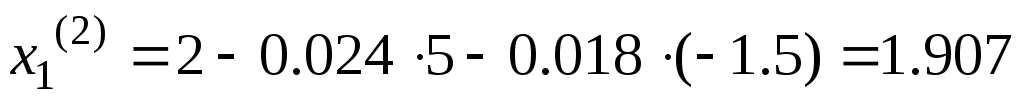

 .
.
Найдем третье
приближение 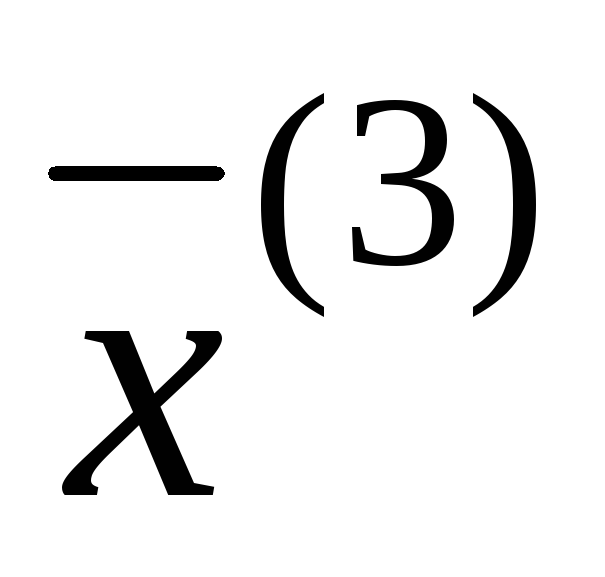 :
:

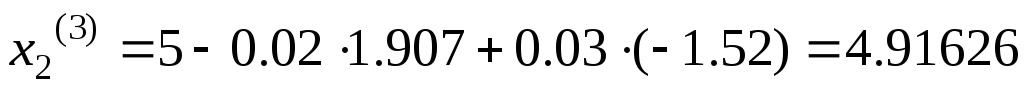
 .
.
Найдем четвертое
приближение 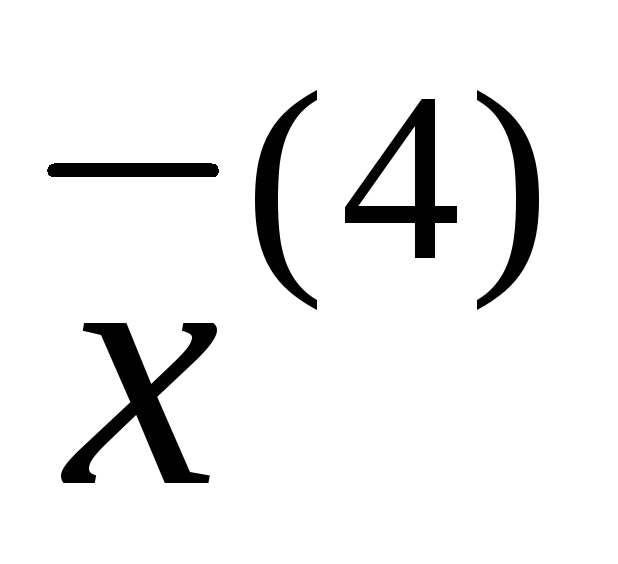 :
:

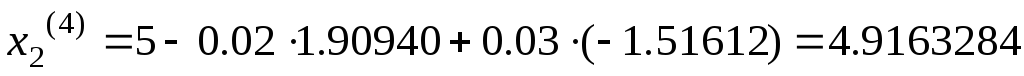
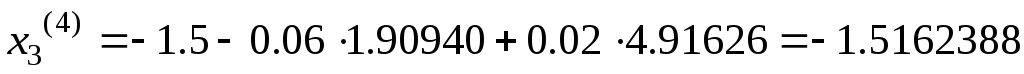 .
.
Первые
три знака после запятой в  и
и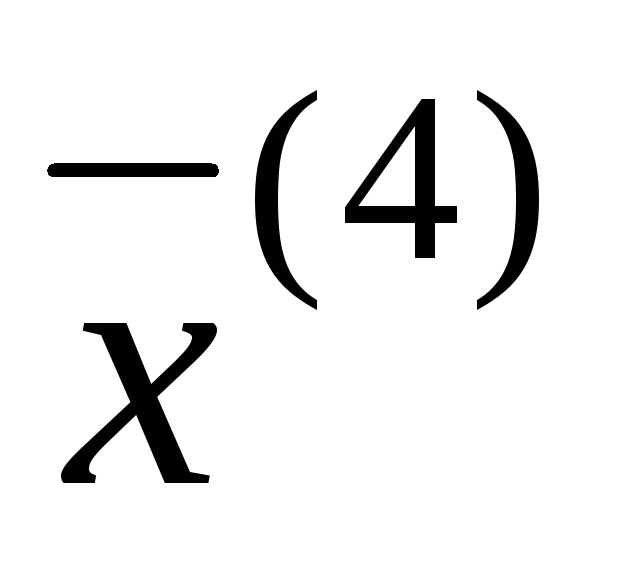 одинаковы, поэтому приближенным решением
с заданной точностью является вектор
одинаковы, поэтому приближенным решением
с заданной точностью является вектор
 .
.
Задание 1 Решить методом Гаусса-Зейделя систему уравнений с точностью 0.001.
Варианты
0.  1.
1.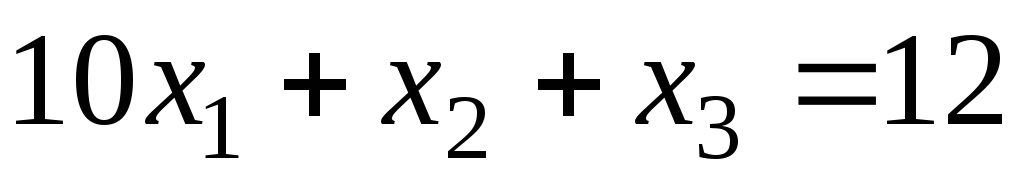

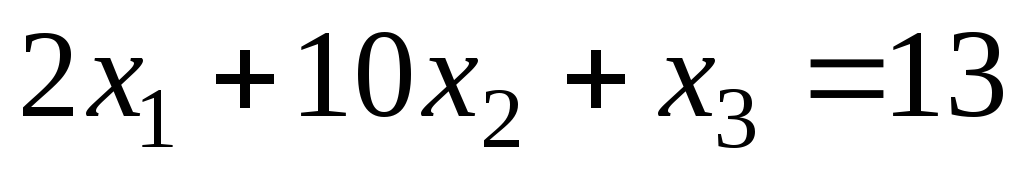
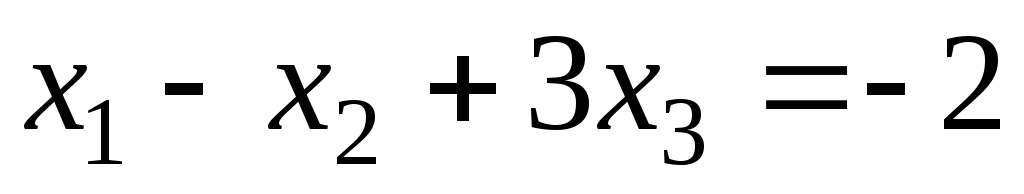 .
.  .
.
2. 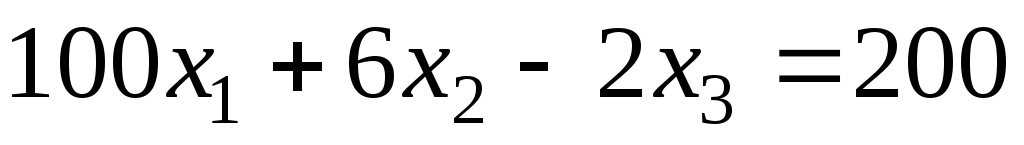
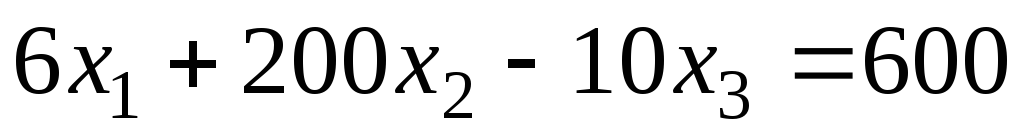
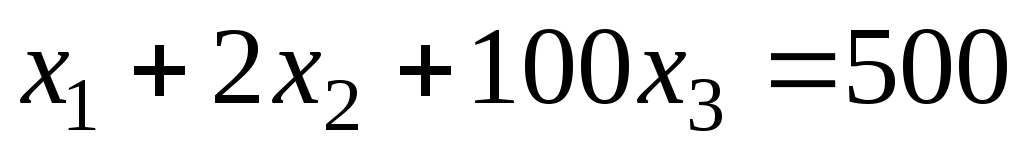 .
.
3.
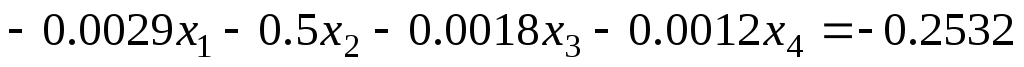
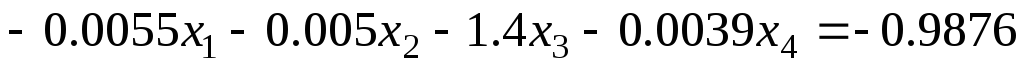
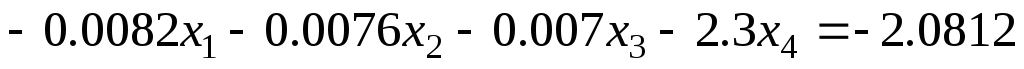
4. 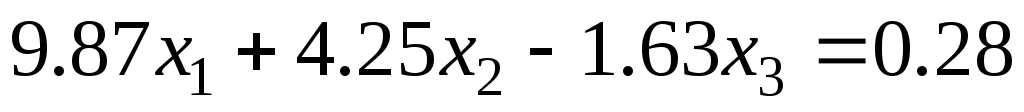
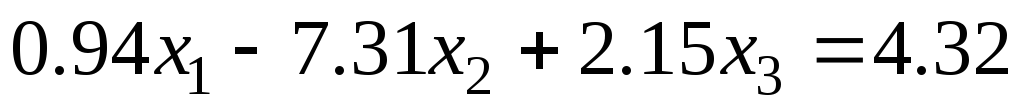
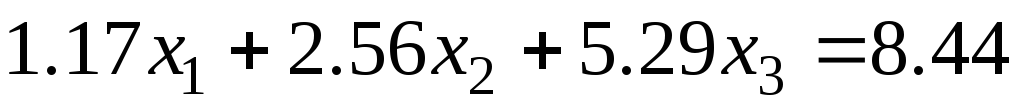 .
.
5. 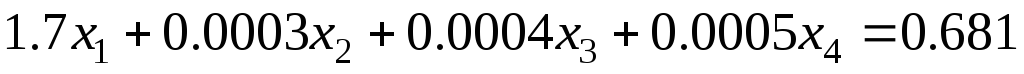
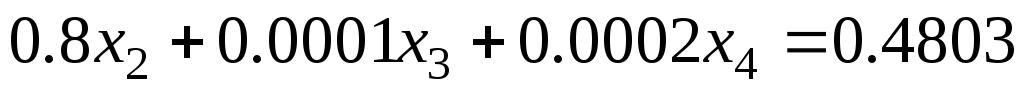
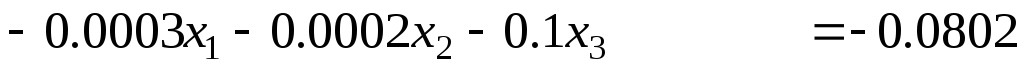

6. 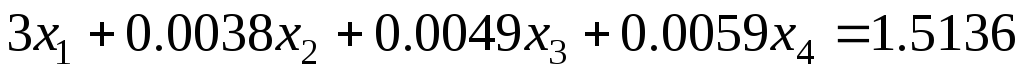
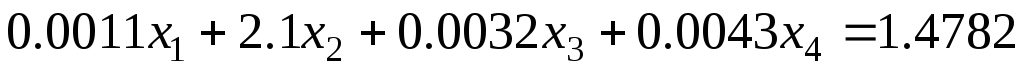

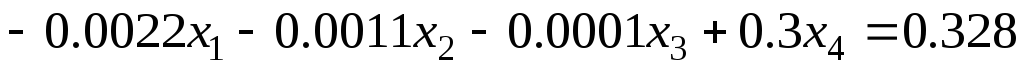
7. 
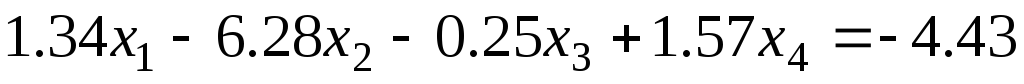
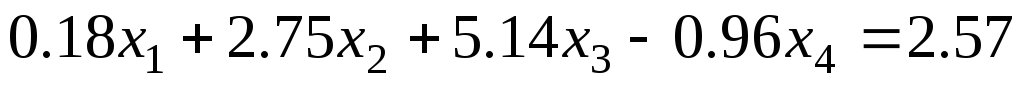
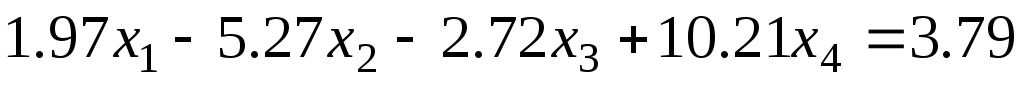
8. 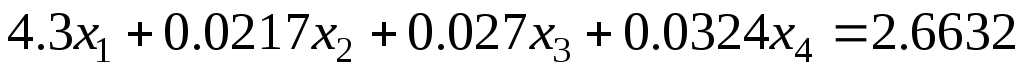
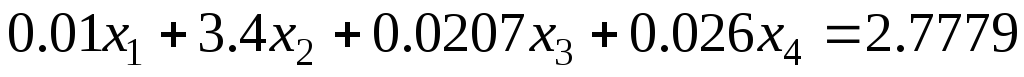
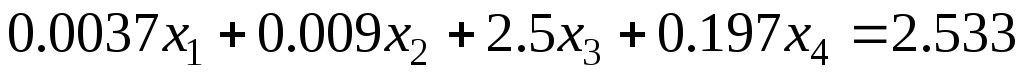
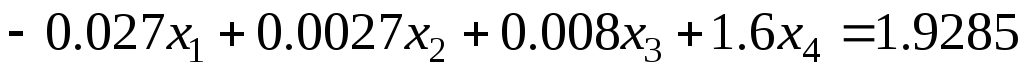
9. 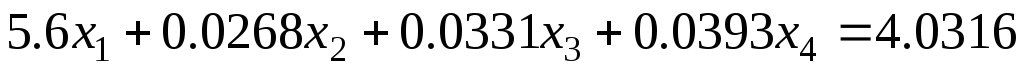
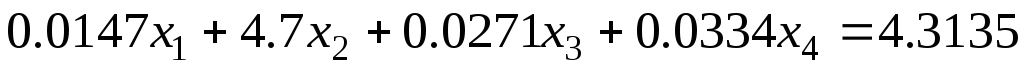
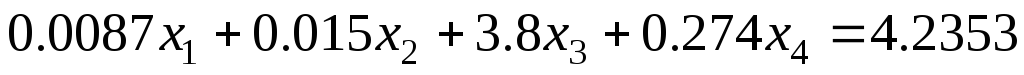
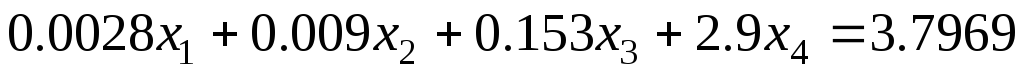
2. Интерполирование функции многочленом Лагранжа
Постановка
задачи.Пусть величинауявляется
функцией аргументах. Это означает,
что любому значениюхиз области
определения поставлено в соответствие
значениеу. Вместе с тем на практике
часто неизвестна явная связь междууих, т.е. невозможно записать эту
связь в виде некоторой зависимости .
В некоторых случаях даже при известной
зависимости
.
В некоторых случаях даже при известной
зависимости она настолько громоздка (например,
содержит трудно вычисляемые выражения,
сложные интегралы и т.д.), что её
использование в практических расчетах
затруднительно.
она настолько громоздка (например,
содержит трудно вычисляемые выражения,
сложные интегралы и т.д.), что её
использование в практических расчетах
затруднительно.
Наиболее
распространенным и практически важным
случаем, когда вид связи между параметрами хиунеизвестен, является задание
этой связи в виде некоторой таблицы .
Это означает, что дискретному множеству
значений аргумента
.
Это означает, что дискретному множеству
значений аргумента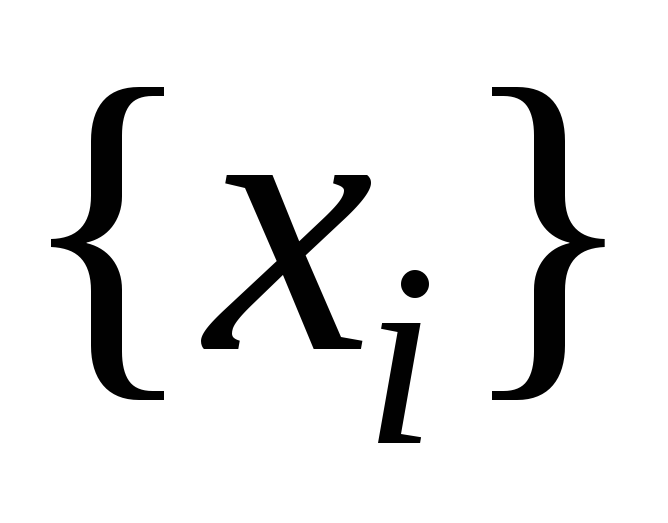 поставлено в соответствие множество
значений функции
поставлено в соответствие множество
значений функции Эти значения — либо результаты расчетов,
либо экспериментальные данные. На
практике нам могут понадобиться значения
величиныуи в других точках, отличных
от узлов
Эти значения — либо результаты расчетов,
либо экспериментальные данные. На
практике нам могут понадобиться значения
величиныуи в других точках, отличных
от узлов .
Таким образом, необходимо использовать
имеющиеся табличные данные для
приближенного вычисления искомого
параметра
.
Таким образом, необходимо использовать
имеющиеся табличные данные для
приближенного вычисления искомого
параметра при любом значении (из некоторой области)
определяющего параметра
при любом значении (из некоторой области)
определяющего параметра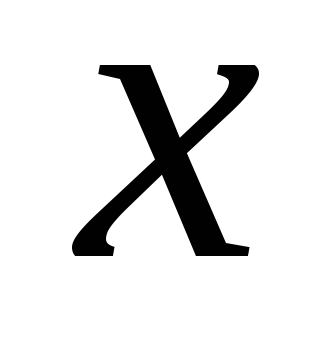 ,
поскольку точная связь
,
поскольку точная связь неизвестна.
неизвестна.
Этой цели и служит
задача о приближении (аппроксимации)
функций: данную функцию 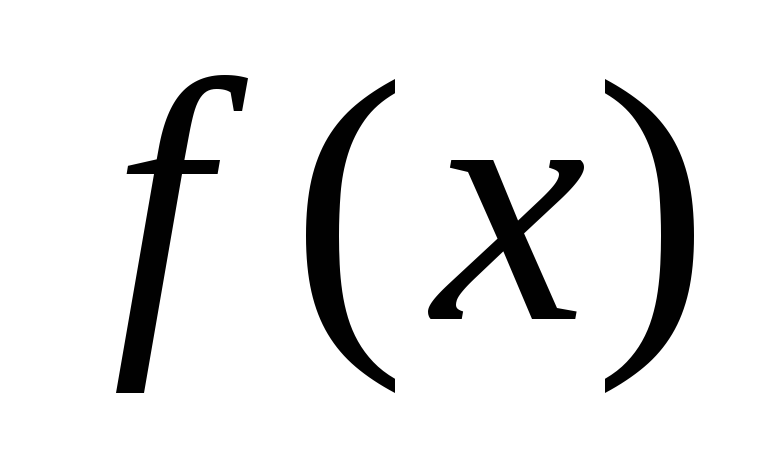 требуется приближенно заменить
(аппроксимировать) некоторой функцией
требуется приближенно заменить
(аппроксимировать) некоторой функцией так, чтобы отклонение (в некотором
смысле)
так, чтобы отклонение (в некотором
смысле)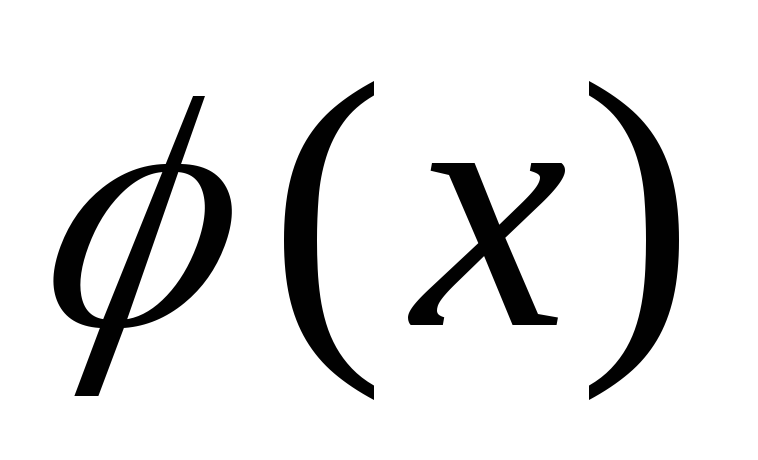 от
от в заданной области было наименьшим.
Функция
в заданной области было наименьшим.
Функция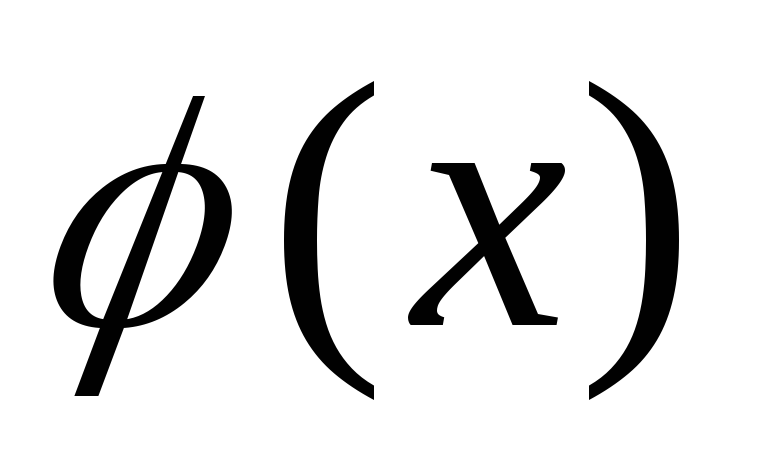 при этом называется аппроксимирующей.
при этом называется аппроксимирующей.
Для практики весьма важен случай аппроксимации функции многочленом
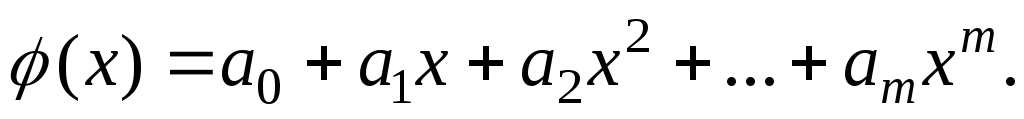 (4)
(4)
При этом коэффициенты  будут подбираться так, чтобы достичь
наименьшего отклонения многочлена от
данной функции.
будут подбираться так, чтобы достичь
наименьшего отклонения многочлена от
данной функции.
Одним из основных
типов аппроксимации является
интерполирование. Оно состоит в следующем:
для данной функции 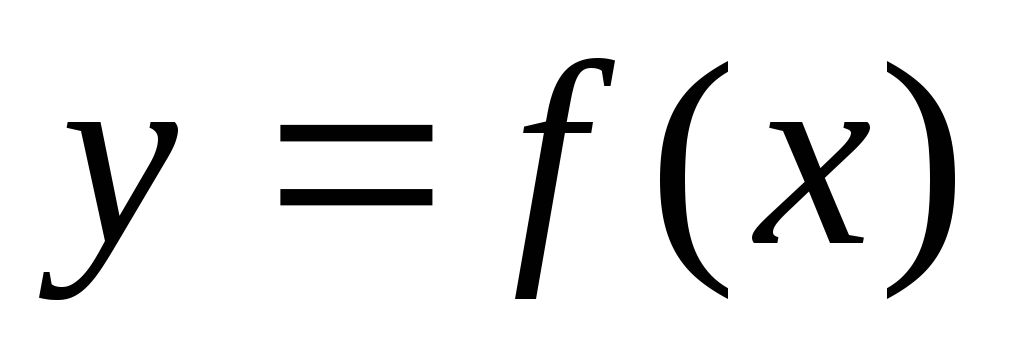 строим многочлен (4), принимающий в
заданных точках
строим многочлен (4), принимающий в
заданных точках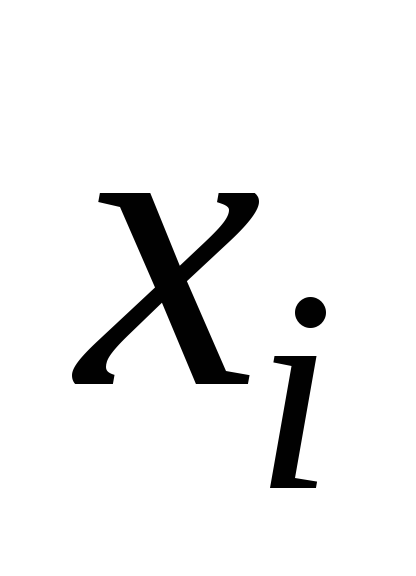 те же значения
те же значения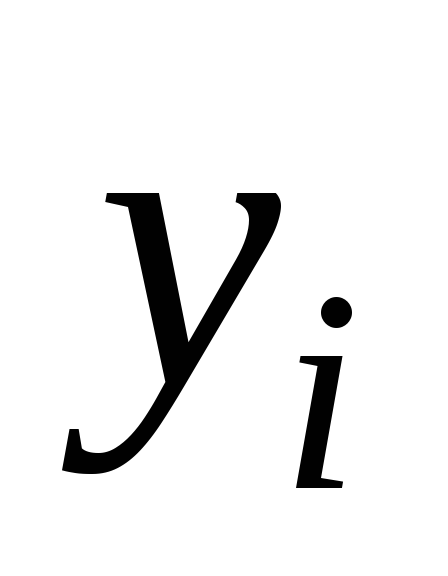 что и функция
что и функция ,
т.е.
,
т.е.
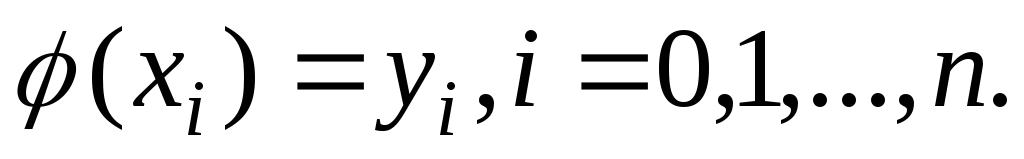 (5)
(5)
При этом
предполагается, что среди значений 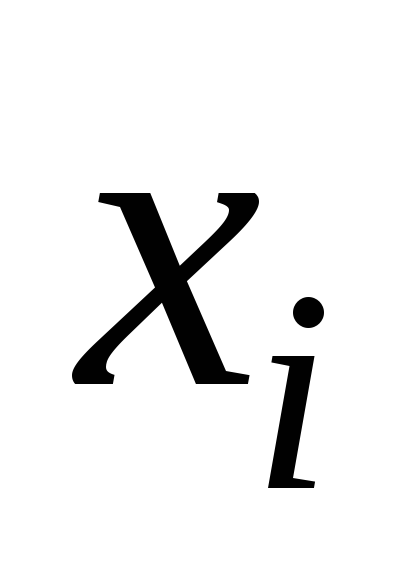 нет одинаковых, т.е.
нет одинаковых, т.е.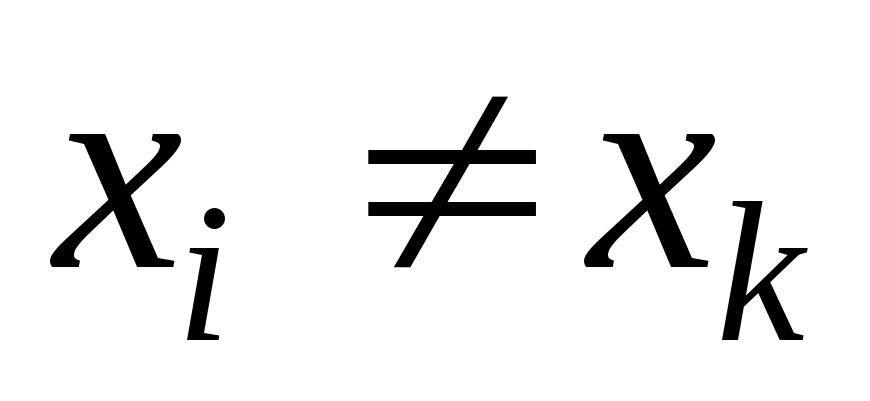 при
при Точки
Точки называются узлами интерполяции, а
многочлен
называются узлами интерполяции, а
многочлен — интерполяционным многочленом.
— интерполяционным многочленом.
Пусть
функция 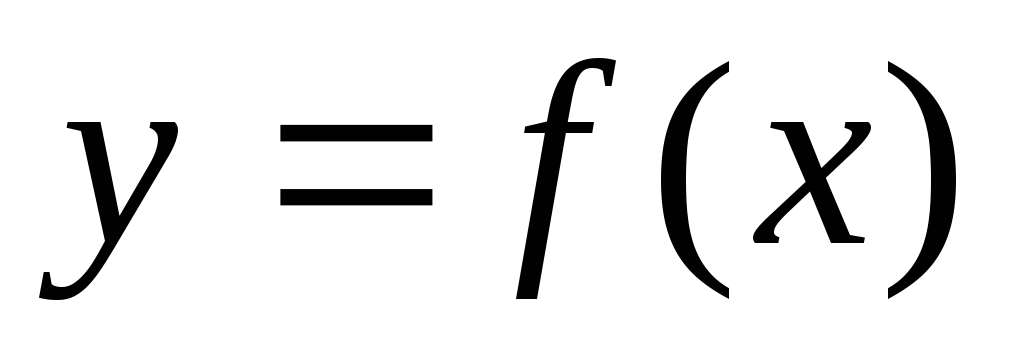 определена таблицей
определена таблицей
Задачей
интерполяции является построение
многочлена  ,
значения которого в узлах интерполяции
{xi}
равны соответствующим значениям
заданной функции, т.е.
,
значения которого в узлах интерполяции
{xi}
равны соответствующим значениям
заданной функции, т.е.
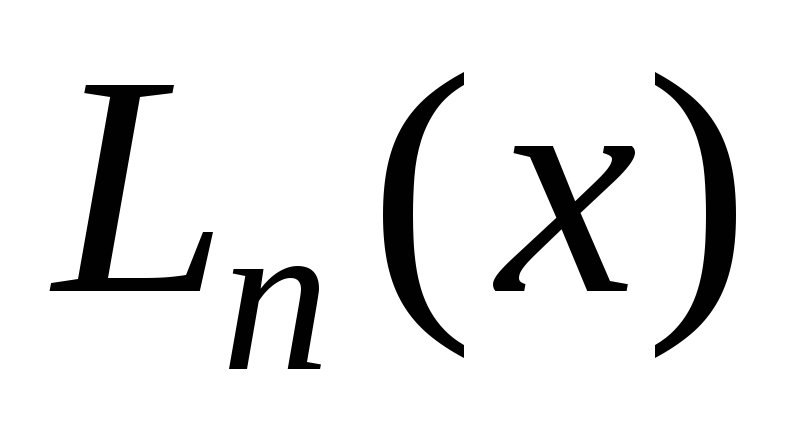 =yi (i=0,1,…,n).
=yi (i=0,1,…,n).
Интерполяционной
формулой Лагранжа называется формула,
представляющая многочлен 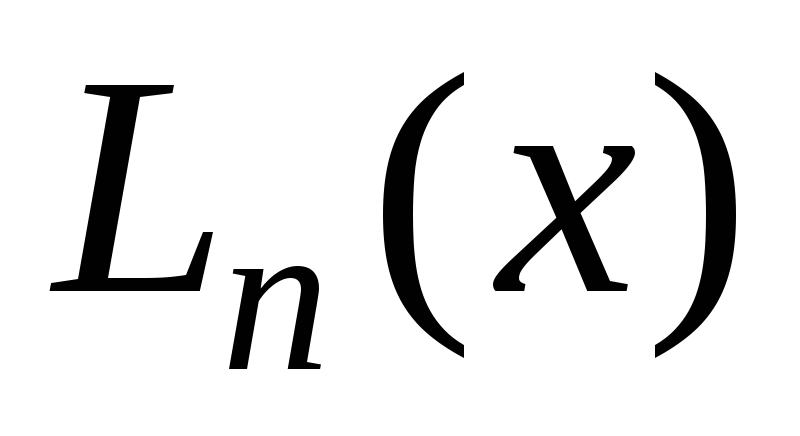 в виде
в виде

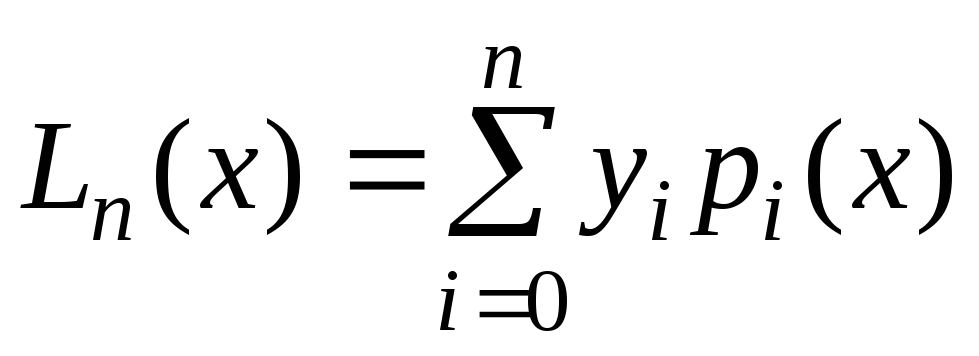 ,
(6)
,
(6)
где 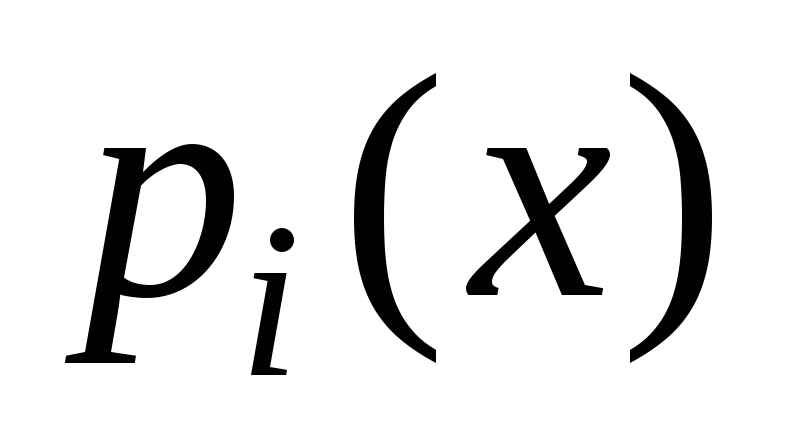 — многочлен степениn,
принимающий значение, равное единице
в узле
— многочлен степениn,
принимающий значение, равное единице
в узле 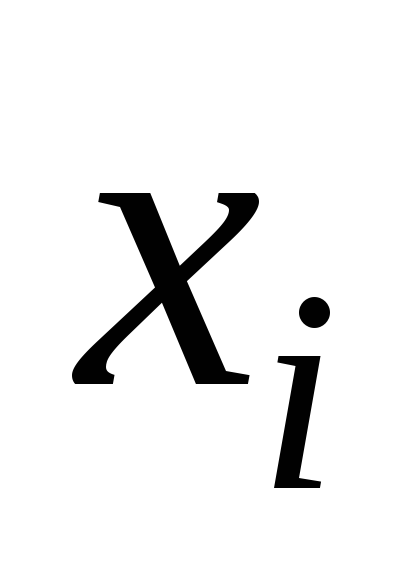 ,
и равные нулю значения в остальных узлах
,
и равные нулю значения в остальных узлах (
(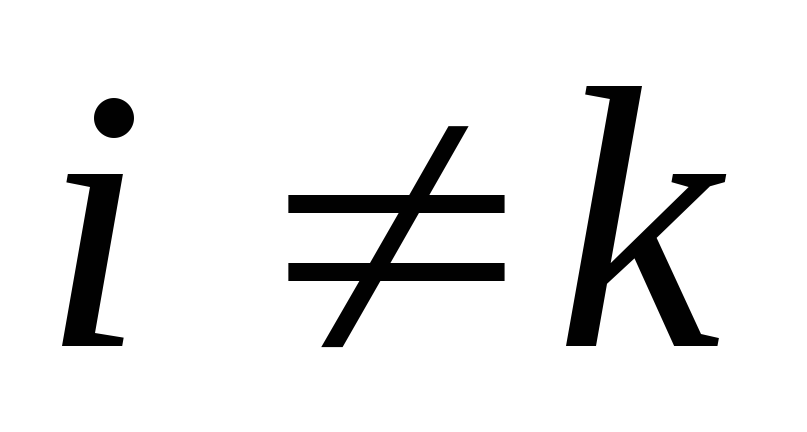 ),
(i,k=0,1,…,n).
Многочлен
),
(i,k=0,1,…,n).
Многочлен 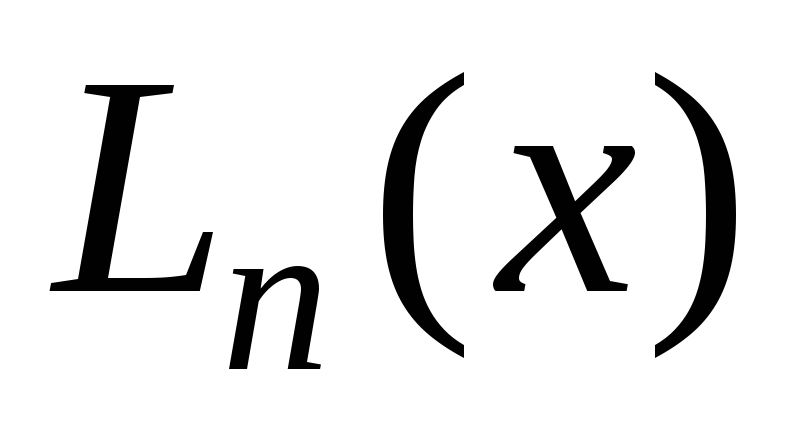 называется интерполяционным многочленом
Лагранжа. Следует отметить, что степень
многочлена Лагранжа не превышает числаn.
называется интерполяционным многочленом
Лагранжа. Следует отметить, что степень
многочлена Лагранжа не превышает числаn. 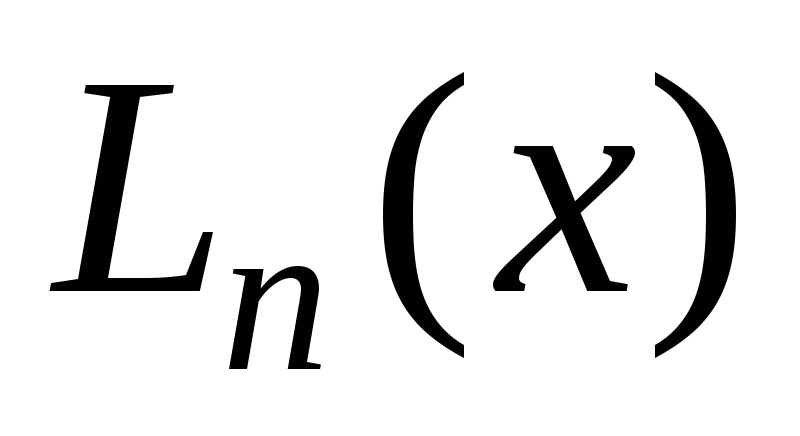 определяется по следующей формуле
определяется по следующей формуле
 .
(7)
.
(7)
Пример. Для функции, заданной таблицей, построить интерполяционный многочлен Лагранжа.
| -1 | 0 | 1 |
| 3 | 2 | 5 |
Решение. Многочлен Лагранжа для трех узлов интерполирования запишется так:
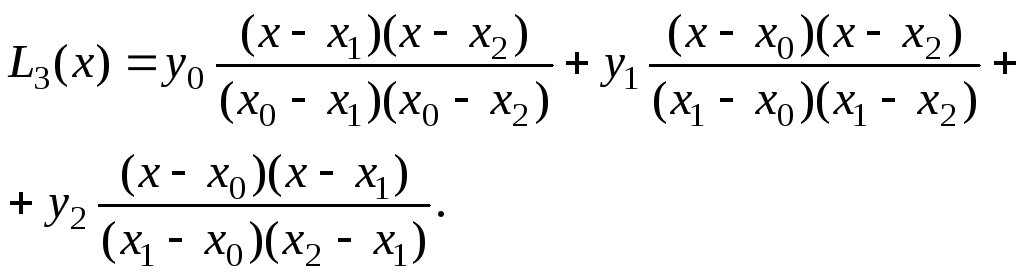
Применяя формулу Лагранжа, получим
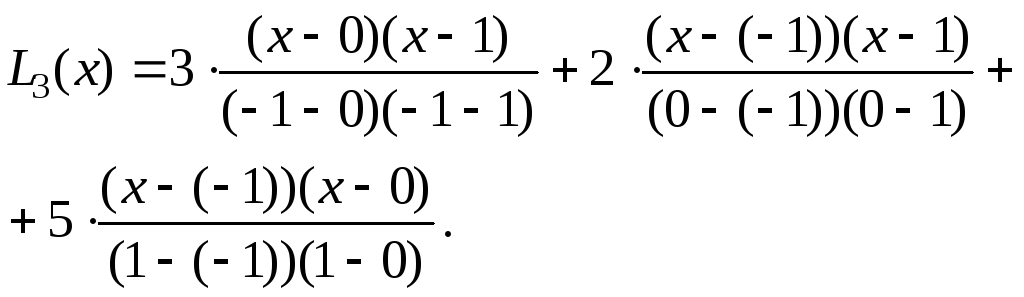
После
элементарных преобразований получаем
интерполяционный многочлен Лагранжа
второй степени 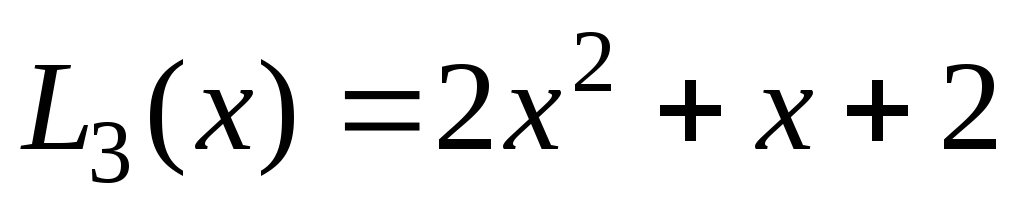 .
.
Задание 2
Для
функции 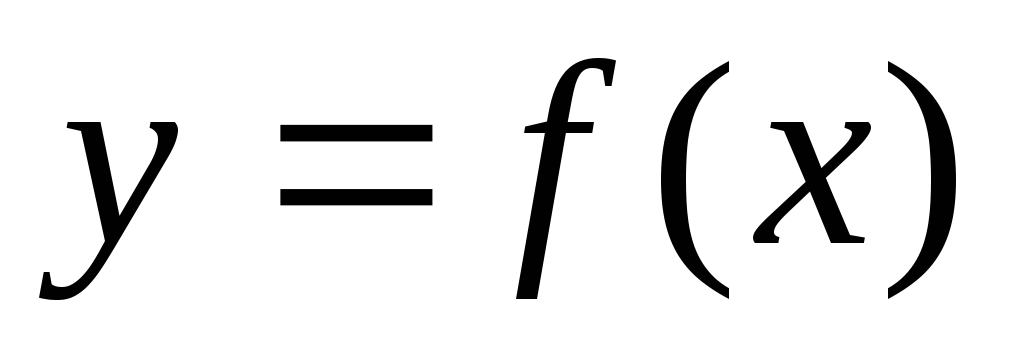 , заданной
таблицей, построить интерполяционный многочлен
Лагранжа.
, заданной
таблицей, построить интерполяционный многочлен
Лагранжа.
Варианты
0.
| 2.5 | 3.0 | 3.5 | 4.0 |
| 1.4981 | 1.4675 | 1.4323 | 1.3931 |
1.
| 0.0 | 0.5 | 1.0 | 1.5 | 2.0 |
| 1.5708 | 1.5738 | 1.5828 | 1.5981 | 1.62 |
2.
| 2.5 | 3.0 | 3.5 | 4.0 |
| 1.649 | 1.6858 | 1.7313 | 1.7868 |
3.
| 0.3 | 0.4 | 0.50 | 0.6 | 0.7 |
| 0.29131 | 0.37995 | 0.46212 | 0.53705 | 0.60437 |
4.
| 0.8 | 0.9 | 1.0 |
| 0.66404 | 0.7163 | 0.76159 |
5.
| 0.0 | 0.5 | 1.0 | 1.05 | 2.0 |
| 1.5708 | 1.5678 | 1.5589 | 1.5442 | 1.5238 |
6.
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 0.11246 | 0.2227 | 0.32863 | 0.42839 | 0.5205 |
7.
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 0.17469 | 0.35031 | 0.52773 | 0.70765 | 0.89054 |
8.
| 0.1 | 0.2 | 0.3 | 0.4 |
| 1.07657 | 1.26548 | 1. 45663 | 1.649 |
9.
| 0.60 | 0.65 | 0.70 | 0.75 | 0.80 |
| 0.912 | 0.897 | 0.881 | 0.864 | 0.846 |
Тема 1. Методы решения систем линейных уравнений
нейной или нелинейной в зависимости от математической природы входящих в нее уравнений.
Решение линейного уравнения с одним неизвестным получается достаточно просто и здесь не рассматривается.
Концепция методов
Способы решения систем линейных уравнений делятся на две группы:
•точные (прямые) методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, метод Крамера, метод Гаусса и др.), т.е. при использовании таких методов за конечное число действий получаем точное решение системы. Точное реше-
ние получается в том случае, если вычисления проводить без округлений, т.е. понятие точное относится к алгоритму решения 1.
•итерационные (приближенные) методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов
(метод итерации, метод Зейделя и др.).
Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.
Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.
В общем виде линейная система уравнений записывается следующим образом:
a | 11 | x | 1 | + a | 12 | x | 2 | + a | 13 | x | 3 | + …+ a | 1n | x | n | = b |
| |||||||||
|
|
|
|
|
|
|
|
|
| 1 |
| |||||||||||||||
a21 x1 + a22 x2 + a23 x3 | + …+ a2n xn | = b2 | , | |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
………………………………………………………….. |
| |||||||||||||||||||||||||
a | n1 | x | 1 | + a | n2 | x | 2 | + a | n3 | x | 3 | + …+ a | nn | x | n | = b |
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
| ||||||||||
или чаще в матричном виде: a x = B , где а – квадратная матрица размером n x n, B и x – векторы размером n (n – размерность системы).
Метод Гаусса
Рассмотрим систему n линейных алгебраических уравнений относительно
n неизвестных х1, х2, …, хn: |
|
|
|
|
|
|
|
| |||||||||||
a | 11 | x | 1 | + a | 12 | x | 2 | + …+ a | 1n | x | n | = b |
| ||||||
|
|
|
|
|
|
| 1 |
| |||||||||||
a21 x1 + a22 x2 + …+ a2n xn | = b2 | (1.1) | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
………………………………………… |
| ||||||||||||||||||
a | n1 | x | 1 | + a | n2 | x | 2 | + …+ a | nn | x | n | = b |
| ||||||
|
|
|
|
|
|
|
|
|
|
| n |
| |||||||
Метод Гаусса, его еще называют методом Гауссовых исключений (методом последовательных исключений), состоит в том, что систему (1.1) приво-
1 Метод Крамера для ЭВМ не всегда удобен. Ведь чтобы вычислить определитель nго порядка нужно сделать (n-1)·n! вычислений. Тогда, при n=20 получаем 19·20!=4,5·1019 действий, что для ЭВМ с быстродействием в 1 млн. операций в секунду потребует 1,4·106 лет!
Метод Гаусса дает 2n3/3+0(n2) операций, что гораздо меньше и вполне приемлемо.
2. Численные методы решения системы линейных уравнений
2.1. Постановка задачи
Рассмотрим систему
линейных алгебраических уравнений:  ,
где
,
где 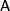 матрица m×m,
матрица m×m,  — искомый вектор, — заданный вектор. Будем
предполагать, что определитель матрицы
— искомый вектор, — заданный вектор. Будем
предполагать, что определитель матрицы 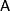 отличен от нуля, т.е. решение
системы существует.
отличен от нуля, т.е. решение
системы существует.
Методы численного
решения системы делятся на две группы:
прямые методы («точные») и итерационные
методы.
Прямыми методами
называются методы, позволяющие
получить решение системы за конечное
число арифметических операций. К этим
методам относятся метод Крамера,
метод Гаусса,
LU-метод
и т.д.
Итерационные методы
(методы последовательных
приближений) состоят в том, что решение
системы находится как предел
последовательных приближений 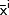 при
при  ,
где
,
где 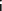 — номер итерации. При использовании
методов итерации обычно задается
некоторое малое число
— номер итерации. При использовании
методов итерации обычно задается
некоторое малое число  и вычисления проводятся до тех
пор, пока не будет выполнена оценка
и вычисления проводятся до тех
пор, пока не будет выполнена оценка  .
К этим методам относятся
метод Зейделя,
Якоби,
метод верхних релаксаций
и т.д.
.
К этим методам относятся
метод Зейделя,
Якоби,
метод верхних релаксаций
и т.д.
Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.
В нашем случае необходимо решить следующую систему линейных алгебраических уравнений.

2.2. Метод Гаусса
Запишем систему в развернутом виде:
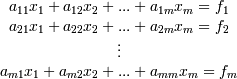
Метод Гаусса состоит
в последовательном исключении неизвестных
из этой системы. Предположим, что  .
Последовательно умножая первое уравнение
на
.
Последовательно умножая первое уравнение
на 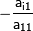 и складывая сi-м уравнением,
исключим
и складывая сi-м уравнением,
исключим 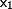 из всех уравнений кроме первого.
Получим систему:
из всех уравнений кроме первого.
Получим систему:

где 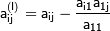 ,
, 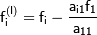 ,
, 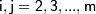 .
.
Аналогичным образом
из полученной системы исключим  .
Последовательно, исключая все неизвестные,
получим систему треугольного вида:
.
Последовательно, исключая все неизвестные,
получим систему треугольного вида:
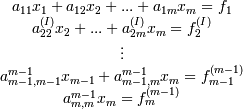
Описанная процедура
называется
прямым ходом метода Гаусса.
Заметим, что ее выполнение было возможно
при условии, что все 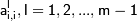 ,
не равны нулю.
,
не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
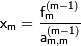 ,
, 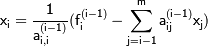
Эта процедура получила название обратный ход метода Гаусса.
Метод Гаусса может
быть легко реализован на компьютере.
При выполнении вычислений, как правило,
не интересуют промежуточные значения
матрицы  .
Поэтому численная реализация метода
сводится к преобразованию элементов
массива размерности (
.
Поэтому численная реализация метода
сводится к преобразованию элементов
массива размерности ( ×(
×( )),
где
)),
где  столбец
содержит элементы правой части системы.
столбец
содержит элементы правой части системы.
Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается.
Один из основных
недостатков метода Гаусса связан с тем,
что при его реализации накапливается
вычислительная погрешность. Для больших
систем порядка  число действий умножений и
делений близко к
число действий умножений и
делений близко к 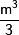 .
.
Для того, чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и следовательно относительная погрешность будет наименьшей.
Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы . Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета.
Алгоритм Гауссовских преобразований с выбором главного элемента по всей матрице:
Выберем ведущий элемент в какой-либо строке (для простоты расчетов лучше, если он будет равен 1).
Разделим ведущую строчку на ведущий элемент.
Обнулим элементы ведущего столбца
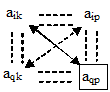
Остальные элементы пересчитаем по правилу прямоугольника


Столбец-контроль используется для контроля правильности вычислений. В первой таблице в нем собираются суммы по строкам. Пересчитывается, он также как и все остальные элементы. Если после пересчета в нем все равно остались суммы по строкам, значит, вычисления были проведены верно.
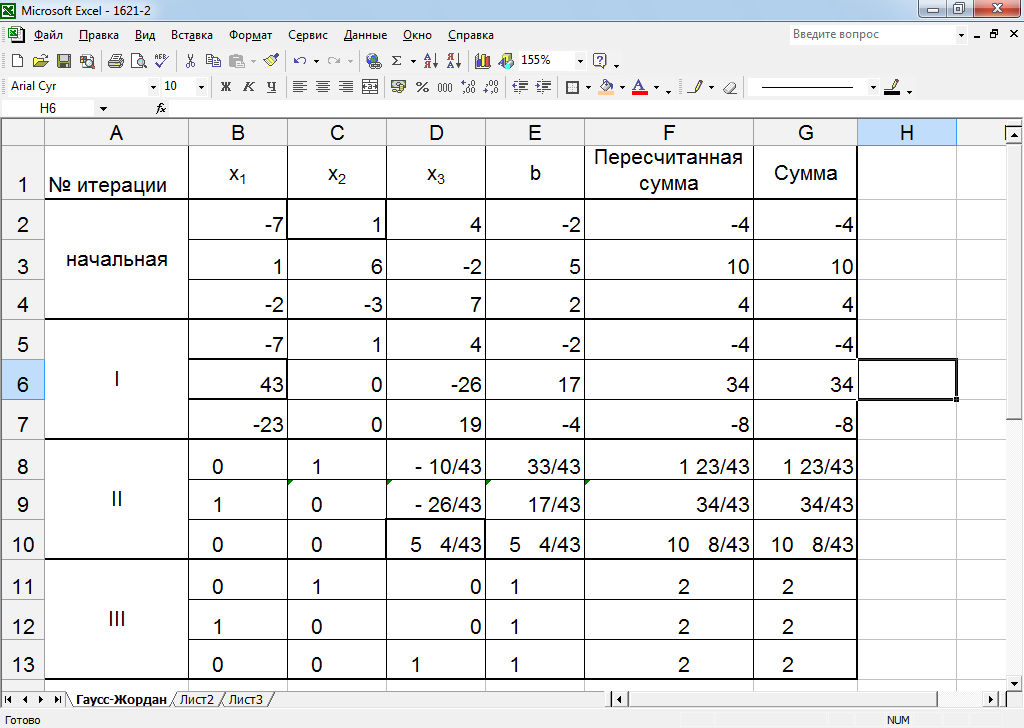
Рисунок 13 – Реализация алгоритма методом Жордана-Гаусса
Опишем механизм создания листа Excel с реализацией метода Гаусса.
На лист Excel занесем значения на начальной итерации. При столбцах х1, х2, х3 запишем основную матрицу системы. В столбце bзапишем столбец свободных коэффициентов. В столбцах «пересчитанная сумма» и «сумма» (они пока не отличаются способом расчета) автосуммируем все значения по строкам исходной матрицы.
На следующих итерациях «пересчитанная сумма» будет пересчитываться так же, как и все остальные элементы, а в «сумме» по-прежнему будут автосуммы по строкам. Если значения в 2 этих столбцах будут равны, значит, вычисления проведены верно.
Приведем пример пересчета элемента 1 (ячейка B3)

В ячейку D3 будет записано значение 43.
Чтобы эффективно использовать формулы Excel, создавая их только один раз, и затем копируя их, будем использовать абсолютные и относительные адреса ячеек. Если в адресе ячейки проставить знаки $ перед строкой или перед столбцом, то имя столбца или номер строки не будут смещаться в направлении копирования при копировании. Используем это свойство для создания рабочих формул Excel. Для перехода между относительными и абсолютными адресами ячеек используем клавишу F4.

Рисунок 14 – Рабочие формулы реализации метода Жордана-Гаусса
Если ведущий элемент не равен 1, то при пересчете возникают дробные значения, поэтому выделим ячейки, содержащие дробные значения и в меню Формат, команда Ячейки выберем вкладку Число и применим Дробный форма. Выберем тип «Дробями до двух цифр» поскольку именно столько цифр было в ведущем элементе, на который делились элементы (в нашем случае ведущий элемент на первой итерации был равен 43).

Рисунок 15 –установка дробного формата.
Продолжаем итерации пока не получим матрицу с единичными столбцами. Снова выпишем преобразованную систему линейных алгебраических уравнений.
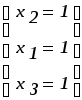
Фактически, на последней итерации получаем точное решение.
Жордано-Гауссовские преобразования избавляют от необходимости ведения обратного хода Гаусса.