План-конспект урока по алгебре (10 класс) на тему: «Способы решения логарифмических уравнений».

Тема:    «Способы решения логарифмических уравнений».

ФИО	Плотникова Татьяна Владимировна
Место работы	МБОУ «СОШ №1 г.Суздаля»
Должность	Учитель математики
Предмет	Алгебра и начала математического анализа
Класс	10
Тема урока	«Способы решения логарифмических уравнений», 2 часа
Базовый учебник	Ш.А. Алимов, Ю.М. Колягин и др. / М. Просвещение 2014

Цель  урока: повторить знания учащихся о логарифме числа, его свойствах; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений.

Задачи:

— обучающие: повторить определение и основные свойства логарифмов, уметь применять их в вычислении логарифмов, в решении логарифмических уравнений;

-развивающие: формировать умение решать логарифмические уравнения;

-воспитательные: воспитывать настойчивость, самостоятельность; прививать интерес к предмету

Тип урока:  урок изучения нового материала.  

Необходимое техническое оборудование: компьютер, проектор, экран.

Структура и ход  урока:

1. Организационный момент.

Учитель.

— Здравствуйте, садитесь!        Сегодня тема нашего урока «Решение логарифмических уравнений», на котором мы познакомимся со способами их решения, используя определение и свойства логарифмов. (слайд № 1)

2. Устная работа.

Закрепление понятия логарифма, повторение его основных свойств и свойств логарифмической функции:

1. Разминка по теории:

 1. Дайте определение логарифма. (слайд № 2)

 2. От любого ли числа можно найти логарифм?

 3. Какое число может стоять в основании логарифма?

 4.  Функция y=log0,8 x является возрастающей или убывающей?Почему?

 5.  Какие значения может принимать логарифмическая функция?

 6. Какие логарифмы называют десятичными, натуральными?

7. Назовите основные свойства логарифмов. (слайд № 3)

8. Можно ли перейти от одного основания логарифма к другому? Как это сделать? (слайд № 4)

2. Работа по карточка(3-4 ученика):

Карточка №1:  Вычислить: а) log64 + log69 =

                                               б) log1/336 – log1/312 =

                            Решить уравнение: log5х = 4 log53 – 1/3 log527

Карточка №2:  

                           Вычислить: а) log211 – log244 =

                                                б) log1/64 + log1/69 =

                          Решить уравнение: log7х = 2 log75 + 1/2 log736 – 1/3 log7125.

Фронтальный опрос класса (устные упражнения)

 Вычислить: (слайд № 5)

log216 lоg3 √3 log71   log5 (1/625) log211  — log 244

log814 + log 832/7 log35  ∙ log53 5 log5 49  8 lоg 85 — 1 25 –log 510

Сравнить числа: (слайд № 6)

1. log½ е и log½π;
2. log2 √5/2 и log2√3/2.

Выяснить  знак выражения log0,83 · log62/3. (слайд № 7)

3. Проверка домашнего задания:

На дом были задания следующие упражнения: №327(неч.), 331(неч.), 333(2) и 390(6). Проверить ответы к данным заданиям и ответить на вопросы учащихся.

4. Изучение нового материала:

Определение: Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.

Простейшим примером логарифмического уравнения служит уравнение
 loga х =с (а > 0, а≠ 1)
Способы решения логарифмических уравнений: (слайд № 8)

1. Решение уравнений на основании определения логарифма. (слайд № 9)

loga х = с (а > 0, а≠ 1) имеет решение  х = ас.

На основе определения логарифма решаются уравнения, в которых:

• по данным основаниям и числу определяется логарифм,
• по данному логарифму и основанию определяется  число,
• по данному числу и логарифму определяется основание.

Примеры:

log2 128= х,         log16х = ¾,                 logх 27= 3,

2х= 128,               х =16 ¾   ,                   х3 =27,

2х = 27,                 х =2 3  ,                       х3 = 33   ,

х =7  .                   х = 8.                          х =3.

С классом решить следующие уравнения:

а) log7(3х-1)=2 (ответ: х=3 1/3)

б) log2(7-8х)=2 (ответ: х=3/8).

2. Метод потенцирования. (слайд № 10)

Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их т.е.

 loga f(х) = loga g(х), то f(х) = g(х), при условии, что f(х)>0, g(х)>0 , а > 0, а≠ 1.

Пример:

Решите уравнение   =

ОДЗ:

3х-1>0;                     х>1/3

6х+8>0.

3х-1=6х+8

-3х=9

х=-3

-3 >1/3 — неверно

Ответ: решений нет.

С классом решить следующее уравнение:

lg(х2-2) = lg х (ответ: х=2)

3. Уравнения, решаемые с помощью применения основного логарифмического тождества. (слайд №11)

Пример:

Решите уравнение  =log2(6-х)

ОДЗ:

6-х>0;

х>0;

х≠1;

log2х2>0;

х2>0.

Решение системы: (0;1)Ụ (1;6).

 = log2(6-х)

х2 = 6-х

х2+х-6=0

х=-3 не принадлежит ОДЗ.

х=2 принадлежит ОДЗ.

Ответ: х=2

 С классом решить следующее уравнение:

 =  (ответ: х=1)

4. Метод приведения логарифмов к одному и тому же основанию. (слайд № 12)

Пример:

Решите уравнение  log16х+ log4х+ log2х=7

ОДЗ: х>0

¼ log2х+½ log2х+ log2х=7

7/4 log2х=7

log2х=4

х=16 – принадлежит ОДЗ.

Ответ: х=16.

С классом решить следующее уравнение:

 +  =3 (ответ: х=5/3)

5. Уравнения, решаемые с помощью применения свойств логарифма. (слайд № 13)

Пример:

Решите уравнение  log2 (х +1)  —  log2 (х -2 ) = 2.

ОДЗ:

х+1>0;

х-2>0.         х>1.

Воспользуемся формулой преобразования разности логарифмов логарифм частного, получаем   log2 = 2, откуда следует  = 4.

Решив последнее уравнение, находим х = 3, 3>1 — верно

Ответ: х = 3.

С классом решить следующие уравнения:

а)log5  (х +1) + log5 (х +5) = 1 (ответ: х=0).

б)log9( 37-12х ) log7-2х 3   =  1,

37-12х >0,                 х

7-2х >0,                     х

7-2х≠ 1;                     х≠ 3;                         х≠ 3;

       log9( 37-12х ) / log3 (7-2х )  =  1,

       ½ log3( 37-12х ) = log3 (7-2х ) ,

        log3( 37-12х ) = log3 (7-2х )2 ,

        37-12х= 49 -28х +4х2  ,

        4х2-16х +12 =0,

         х2-4х +3 =0,   Д=19,   х1=1,   х2=3,  3 –посторонний корень .

Ответ: х=1 корень уравнения.

    в) lg(х2-6х+9) — 2lg(х — 7) = lg9.

 (х2-6х+9) >0,     х≠ 3,

 х-7 >0;               х  >7;             х  >7.

        lg ((х-3)/(х-7))2 = lg9

((х-3)/(х-7))2    = 9,

(х-3)/(х-7) = 3,                                 (х-3)/(х-7)= — 3 ,

х- 3 = 3х -21 ,                                    х -3 =- 3х +21,

х =9.                                                       х=6 —   посторонний корень.

Проверка показывает 9 корень уравнения.              

  Ответ : 9

6. Уравнения, решаемые введением новой переменной. (слайд № 14) 

 Пример:

Решите уравнение    lg2х — 6lgх+5 = 0.

ОДЗ: х>0.

Пусть lgх = р, тогда р2-6р+5=0.

р1=1, р2=5.

Возвращаемся к замене:

lgх = 1,                                                 lgх =5

х=10, 10>0 – верно                              х=100000, 100000>0 – верно

Ответ: 10, 100000

С классом решить следующее уравнение:

   log62 х  + log6 х  +14 = (√16 – х2)2 +х2,

      16 – х2  ≥0  ;      — 4≤ х ≤ 4;

       х >0 ,                    х >0,                О.Д.З. [ 0,4).    

    log62 х  + log6 х  +14 = 16 – х2 +х2,        

      log62 х  + log6 х  -2 = 0

      заменим log6 х  = t

   t 2 + t -2 =0 ;        D = 9 ;      t1 =1 ,  t2 = -2.

 log6 х = 1 , х = 6  посторонний корень .

 log6 х = -2, х = 1/36 , проверка показывает  1/36 является корнем .

                                                Ответ : 1/36.

7. Уравнения, решаемые с помощью разложения на множители. (слайд № 15)

Пример:

Решите уравнение log4(2х-1)∙ log4х=2 log4(2х-1)

ОДЗ:

 2х-1>0;

  х >0.      х>½.

log4(2х-1)∙ log4х — 2 log4(2х-1)=0

log4(2х-1)∙(log4х-2)=0

log4(2х-1)=0    или    log4х-2=0

2х-1=1                        log4х = 2

х=1                             х=16

1;16 – принадлежат ОДЗ

Ответ: 1;16

С классом решить следующее уравнение:

log3х ∙log3(3х-2)= log3(3х-2) (ответ: х=1)

8. Метод логарифмирования обеих частей уравнения. (слайд № 16)

Пример:

Решите уравнения                    

                     

Прологарифмируем обе части  уравнения  по основанию 3.

Получим      log3                     =  log3 (3х)

                                               .

получаем :    log3 х2 log3 х   =  log3 (3х),

                      2log3 х log3 х   =  log3 3+ log3 х,

                      2 log32 х    =  log3 х +1,

                      2 log32 х   —  log3 х -1=0,

заменим log3 х  = р ,     х >0

  2 р 2 + р -2 =0 ;     D = 9 ;   р1 =1 ,  р2 = -1/2

 log3 х  = 1 ,  х=3,

log3 х  = -1/ 2 , х= 1/√3.                      

Ответ: 3 ;  1/√3

С классом решить следующее уравнение:

    log2 х  — 1                      

х             =   64 (ответ:  х=8 ; х=1/4)

9. Функционально – графический метод. (слайд № 17)

Пример:

Решите уравнения:   log3 х = 12-х.

Так как функция у= log3 х возрастающая , а функция у =12-х убывающая на (0; + ∞ ) то заданное уравнение на этом интервале имеет один корень.

Построим в одной системе координат графики двух функций: у= log3 х и  у =12-х.

При  х=10  заданное уравнение обращается в верное числовое равенство 1=1. Ответ х=10.

С классом решить следующее уравнение:

1-√х =ln х (ответ : х=1).

5. Подведение итогов, рефлексия (раздать кружочки, на которых ребята отмечают свое настроение рисунком). (слайд № 18,19)

Определить метод решения уравнения:

6. Домашнее задание: 340(1), 393(1), 395(1,3), 1357(1,2), 337(1), 338(1), 339(1)

Литература

1. Рязановский, А.Р. Математика. 5 – 11 кл.: Дополнительные материалы  к уроку математики/ А.Р.Рязановский, Е.А.Зайцев. – 2-е изд., стереотип. – М.: Дрофа,2002
2. Математика. Приложение к газете «Первое сентября». 1997. № 1, 10, 46, 48; 1998. № 8, 16, 17, 20, 21, 47.
3. Скоркина, Н.М. Нестандартные формы внеклассной работы. Для средних и старших классов/ Н.М. Скоркина.  – Волгоград: Учитель, 2004
4. Зив, Б.Г., Гольдич,В.А. Дидактические материалы по алгебре и началам анализа для 10 класса./Б.Г.Зив, В.А.Гольдич. – 3-е изд., исправленное. – СПб.: «ЧеРо-на-Неве», 2004
5. Алгебра и начала анализа: математика для техникумов/под ред. Г.Н.Яковлева.-М.: Наука, 1987

«Методы решения логарифмических уравнений»

Алгебра и начала анализа, 11-й класс. «Методы решения логарифмических уравнений»

Цели урока:

• образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;

• развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;

• воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку.

«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь».
Французский математик и астроном П.С. Лаплас

Ход урока

I. Постановка цели урока

Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.

Запишите в тетради тему урока: «Методы решения логарифмических уравнений». Приглашаю всех к сотрудничеству.

II. Актуализация опорных знаний

Подготовимся к изучению темы урока. Каждое задание вы решаете и записываете ответ, условие можно не писать. Работайте в парах.

(Демонстрируется слайды с заданиями для устной работы).

1) При каких значениях х имеет смысл функция:

а)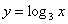

б)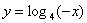 

в)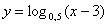

д)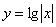

(По каждому слайду сверяются ответы и разбираются ошибки)

2) Совпадают ли графики функций?

а) y = x и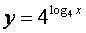

 

б) 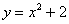 и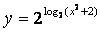

3) Перепишите равенства в виде логарифмических равенств:

 

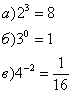
4) Запишите числа в виде логарифмов с основанием 2:

4 =

— 2 =

0,5 =

1 =

5) Вычислите: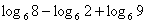

III. Ознакомление с новым материалом

Демонстрируется на экране высказывание:

«Уравнение – это золотой ключ, открывающий все математические сезамы».
Современный польский математик С. Коваль

Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).

Рассмотрим простейшее логарифмическое уравнение:logax = b (где а>0, a ≠ 1 ). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.

Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х

). Из определения логарифма сразу следует, что аb является таким решением.

Запишите заголовок: Методы

1. По определению логарифма.

Так решаются простейшие уравнения вида .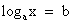

 

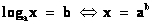
Рассмотрим № 514(а): Решить уравнение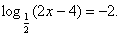

Как вы предлагаете его решать? (По определению логарифма)

Решение.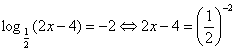

, Отсюда 2х – 4 = 4; х = 4.

Ответ: 4.

В этом задании 2х – 4 > 0, так как 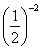> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.

2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).

Рассмотрим пример 2(стр. 242):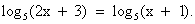

Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).

При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.

Решение 1. ОДЗ: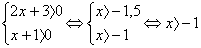

Потенцируем исходное уравнение 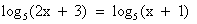, получим уравнение 2x + 3 = х + 1. Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.

Можно решить это уравнение иначе – переходом к равносильной системе:

Уравнение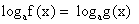

(Система содержит избыточное условие – одно из неравенств можно не рассматривать).

Решение 2. Уравнение 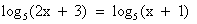 равносильно системе:

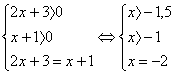
Эта система решений не имеет.

Есть еще один вариант решения – переход к следствию из данного уравнения. При неравносильных преобразованиях найденное решение необходимо проверить подстановкой в исходное уравнение.

Решение 3. 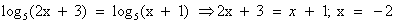. Сделаем проверку: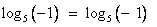

неверно, так как не имеет смысла.

Ответ: корней нет.

Вопрос классу: Какое из этих трех решений вам больше всего понравилось? (Обсуждение способов).

Вы имеете право решать любым способом.

3. Введение новой переменной.

Рассмотрим № 520(г). .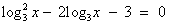

Что вы заметили? (Это квадратное уравнение относительно log3x) Ваши предложения? (Ввести новую переменную)

Решение. ОДЗ: х > 0.

Пусть 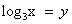, тогда уравнение примет вид: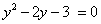

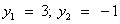. Дискриминант D > 0. Корни по теореме Виета:.

Вернемся к замене: 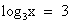или .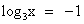

Решив простейшие логарифмические уравнения, получим:

;

.

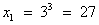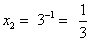
Ответ: 27;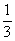

4. Логарифмирование обеих частей уравнения.

Решить уравнение:.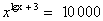

Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:

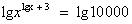. Применим свойство логарифма степени:

(lgx + 3) lgx =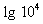

(lgx + 3) lgx = 4

Пусть lgx = y, тогда (у + 3)у = 4

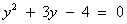, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.

Вернемся к замене, получим: lgx = -4,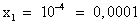; lgx = 1, .

Ответ: 0,0001; 10.

5. Приведение к одному основанию.

№ 523(в). Решите уравнение: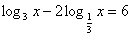

Решение: ОДЗ: х>0. Перейдем к основанию 3.

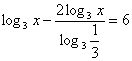 или ;.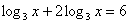

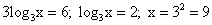Ответ: 9.

6. Функционально-графический метод.

№ 509(г). Решить графически уравнение: 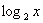= 3 – x.

Как вы предлагаете решать? (Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков).

Посмотрите ваше решение на слайде.

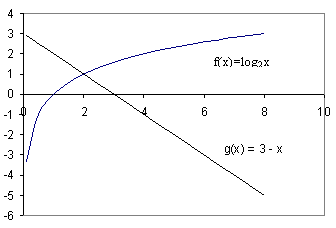
Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

В нашем случае функция 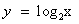возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 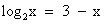имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .

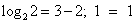Ответ: 2

IV. Первичное закрепление

Демонстрируется высказывание:

«Правильному применению методов можно научиться,
только применяя их на различных примерах».
Датский историк математики Г. Г. Цейтен

Предложите метод решения уравнений:

1) № 520 (в).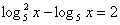

2) № 514 (в).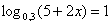

3) № 522 (а).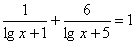

4) № 519 (в).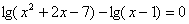

5) № 509(в).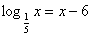

6) № 523(а).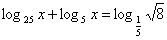

V. Домашнее задание

П. 39 рассмотреть пример 3, решить № 514, № 520 (в).

VI. Подведение итогов урока

Какие методы решения логарифмических уравнений мы рассмотрели на уроке?

На следующих уроках рассмотрим более сложные уравнения. Для их решения пригодятся изученные методы.

Демонстрируется последний слайд:

«Что есть больше всего на свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого».
Фалес

Желаю всем достичь желаемого. Благодарю за сотрудничество и понимание.

Подведение итогов (рефлексия).

Продолжите фразу:

“Сегодня на уроке я узнал…”
“Сегодня на уроке я научился…”
“Сегодня на уроке я познакомился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…”

Урок-лекция по теме «Логарифмические уравнения. Основные методы их решения»

Урок-лекция по теме «Логарифмические уравнения.

Работу выполнила учитель математики высшей категории Курылева Э. Р.

МОУ «СОШ № 42» г. Воркуты Республики Коми.

В моём календарно-тематическом планировании на тему «Логарифмические уравнения» отводится 3 часа. Я их разбиваю следующим образом:

1урок — лекция «Логарифмические уравнения. Основные методы их решения». В конце лекции задаю блок уравнений обязательного уровня.

2 урок – решение уравнений различного типа и сложности (это зависит от уровня математической подготовки класса, использую индивидуальный подход).

3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.

1урок — лекция «Логарифмические уравнения. Основные методы их решения», но только два метода – на основании определения и потенцирования. Решение уравнений на применение этих методов.

2 урок – лекция «Логарифмические уравнения. Основные методы их решения», два других метода – подстановки и логарифмирования. Решение уравнений на применение этих методов.

3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.

Вариант подачи темы зависит от подготовленности класса.

1 урок.

Лекция «Логарифмические уравнения. Основные методы их решения».

Слайд 1.

Эпиграфом своей сегодняшней лекции я привожу слова Ричарда Олдингтона (1892 – 1962гг., английский поэт, прозаик, критик): «Ничему тому, что важно знать, научить нельзя, — всё, что может сделать учитель, это указать дорожки».

Слайд 2.

А так же – русскую народную пословицу: «Кто говорит – тот сеет, кто слушает – тот собирает».

В самом начале моей лекции я хотела бы обратить ваше внимание на следующее. При решении логарифмических уравнений применяют преобразования, которые не приводят к потере корней, но могут привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений. Здесь возможны два подхода:

В своей лекции я буду использовать оба этих подхода, а ваше право уже самим выбирать, какой лично вам больше нравится. Следует отметить, что при решении логарифмических неравенств возможен только один из них: ОДЗ!

Основные методы решения логарифмических уравнений.

Слайд 3.

Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.

Определение логарифма: Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. Т. е.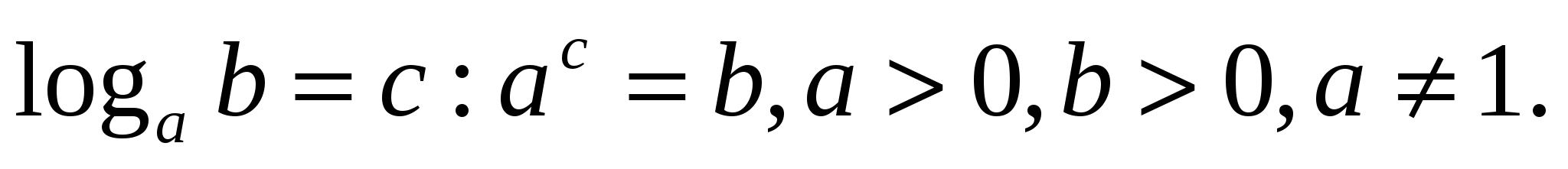

Таким образом, применяя его к нашей теме, мы получим следующее:

А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид 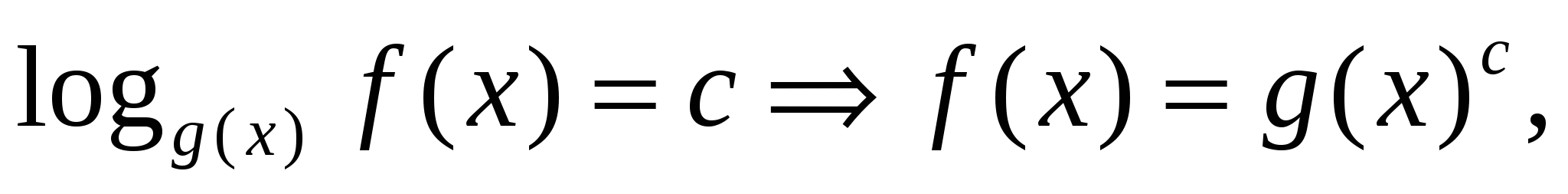при этом Хочу отметить особо, что рассуждения НЕ ИЗМЕНИЛИСЬ!

Пример 4: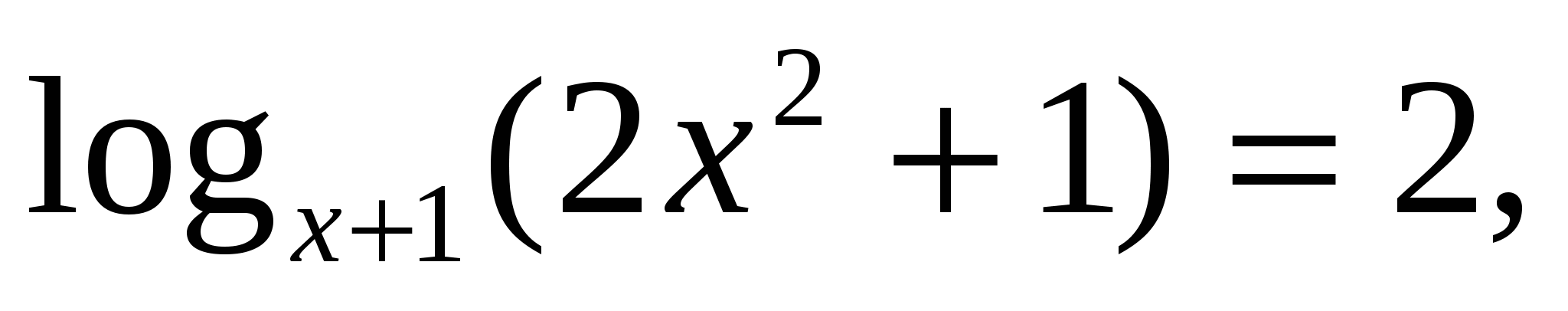

ОДЗ:.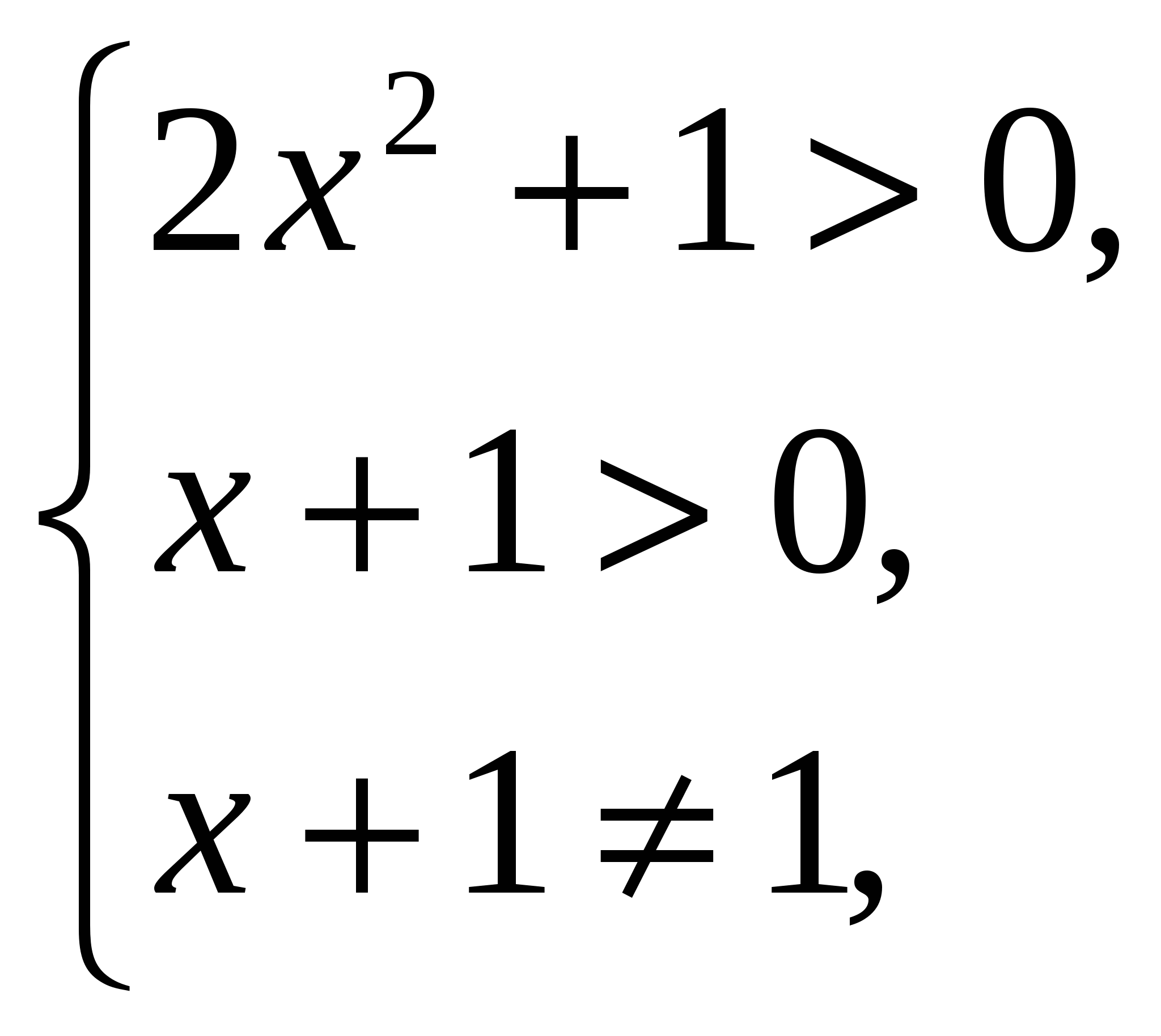

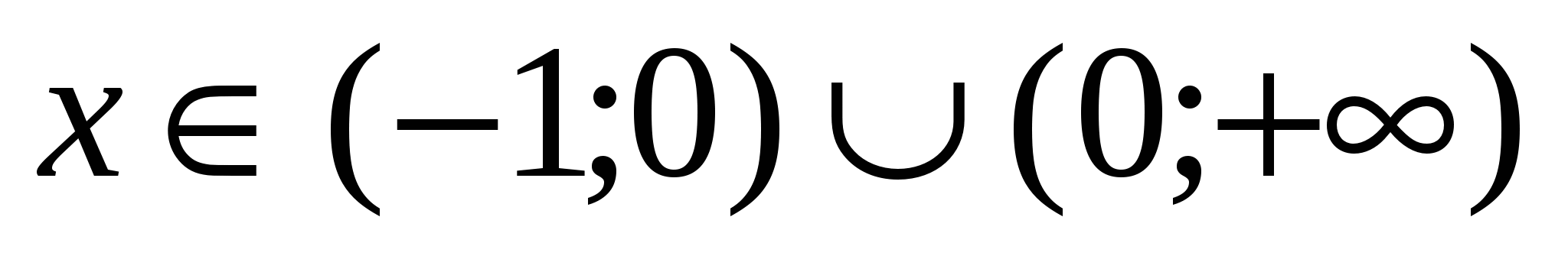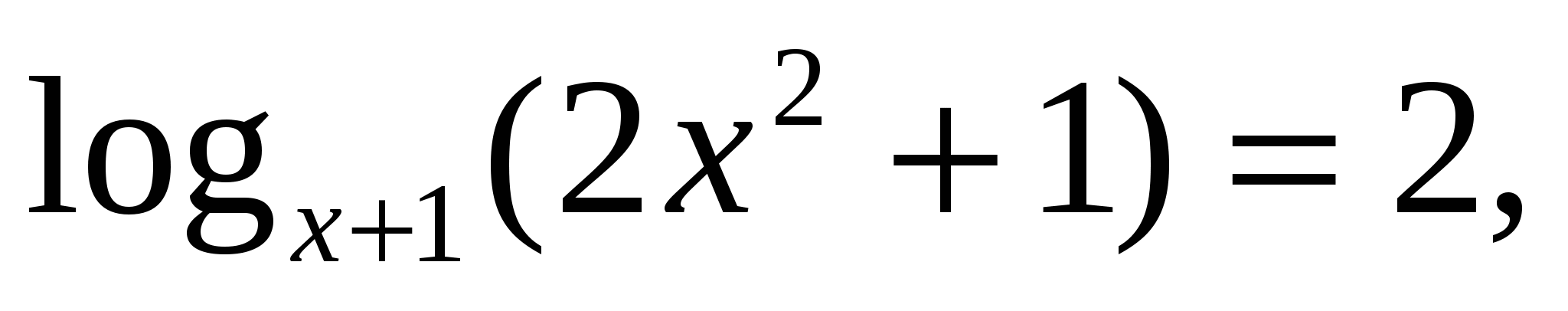
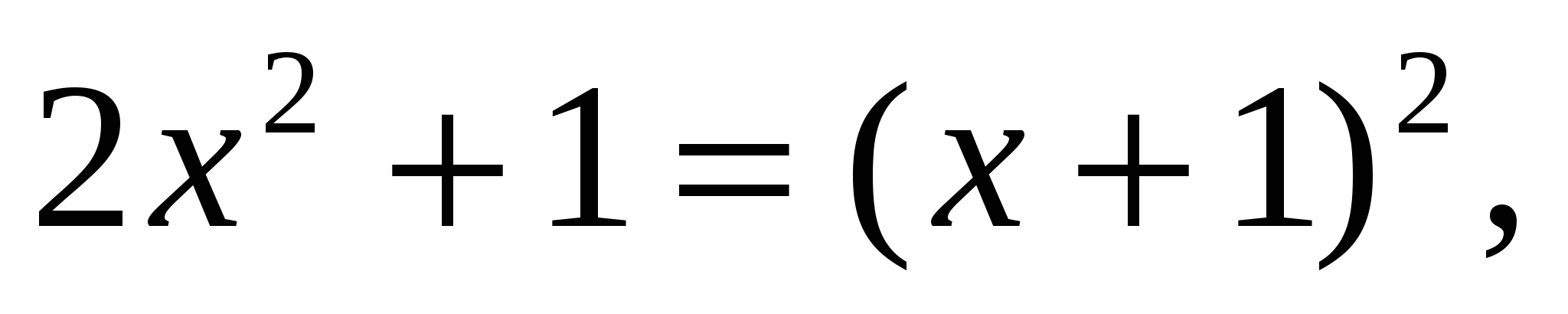
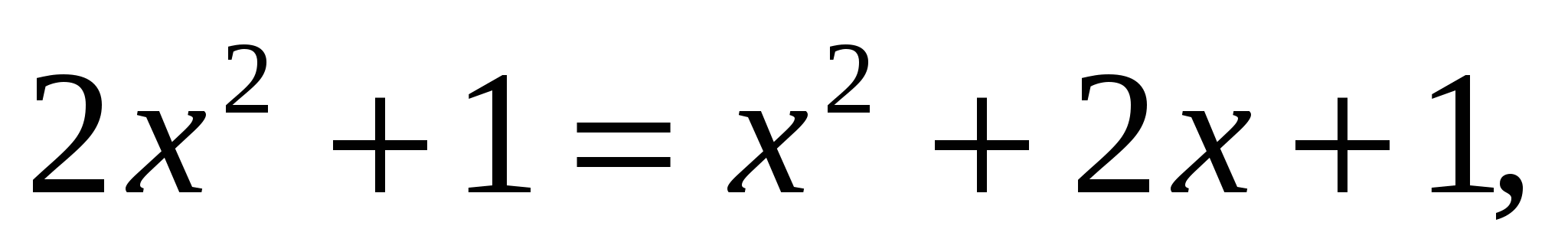
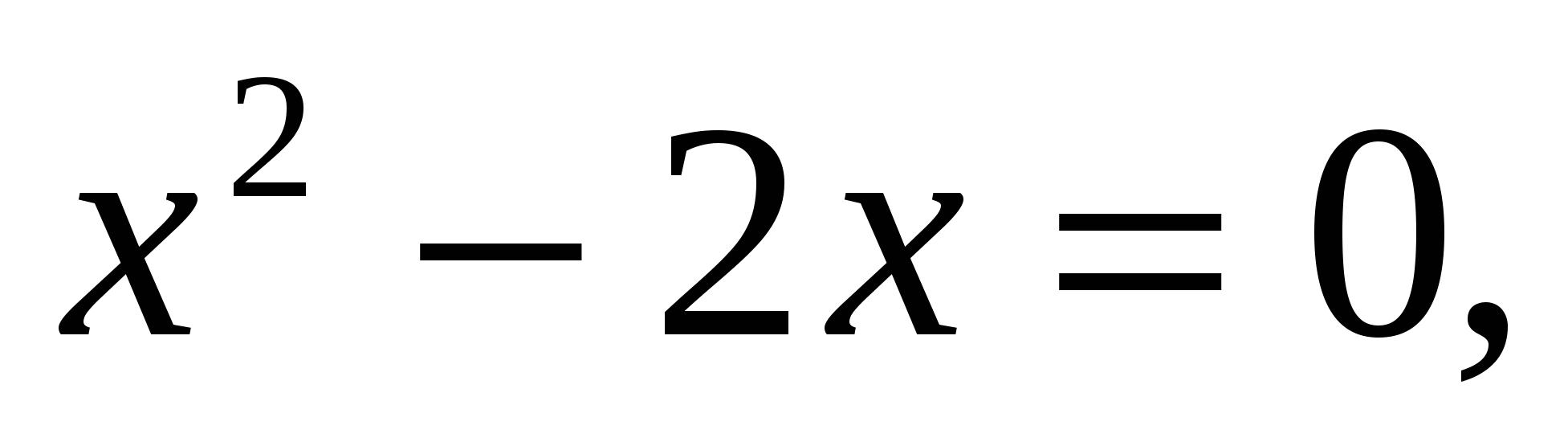
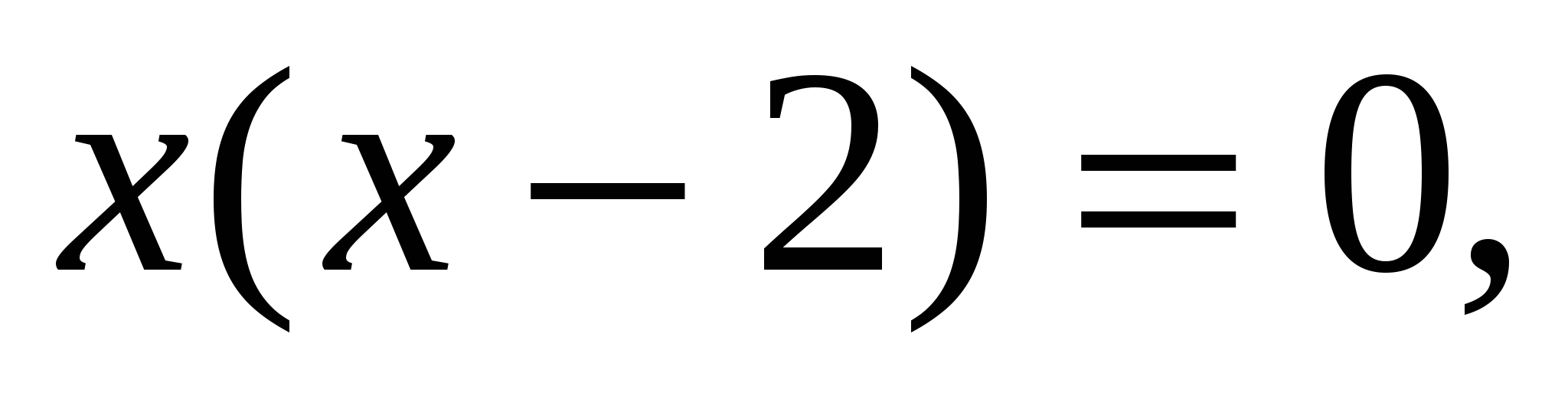
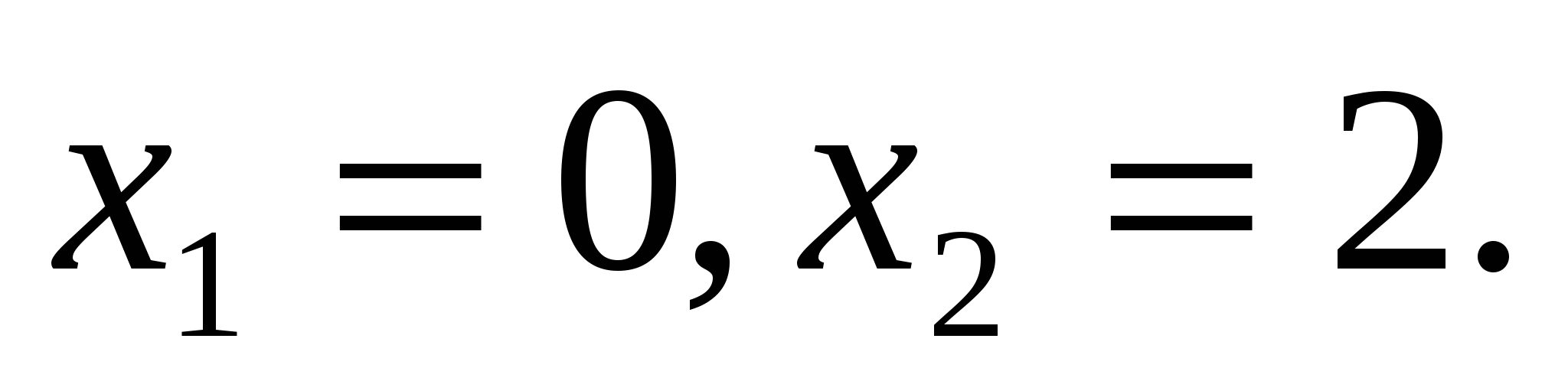
С учётом ОДЗ получим, что решением данного уравнения является число 2.

Ответ: 2.

Как мы видим, наличие выражения с переменной в основании влияет лишь на ОДЗ, а не на ход рассуждений. Кроме того, данное уравнение можно решать, не прибегая к нахождению ОДЗ, а просто в конце выполнить проверку.

2. Метод потенцирования.

Слайд 6.

Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.

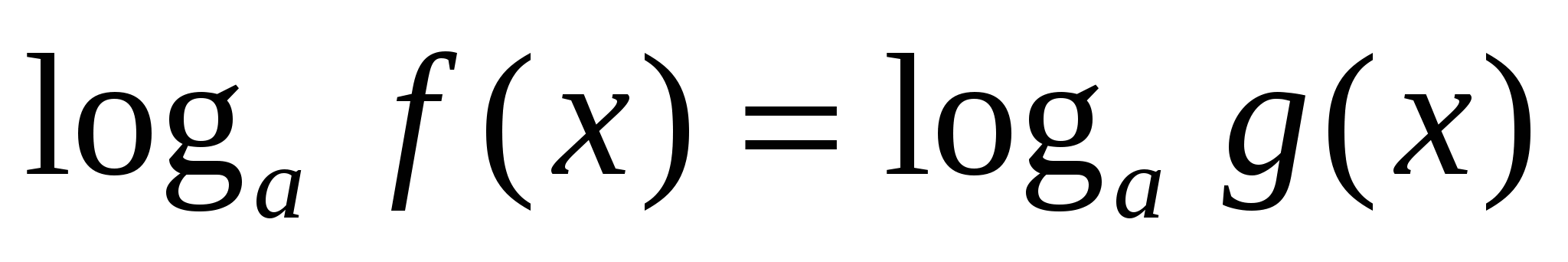
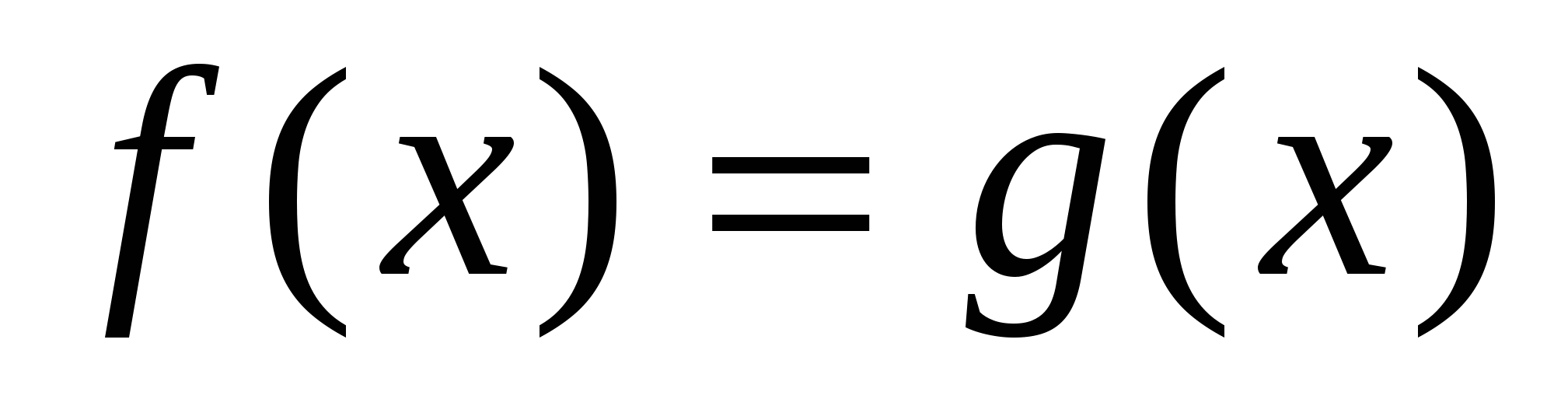, где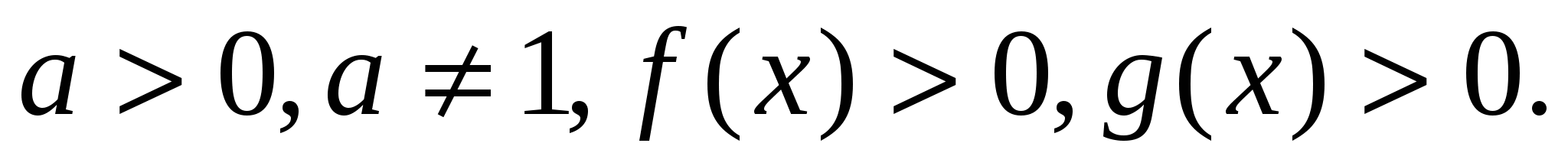

Пример 5: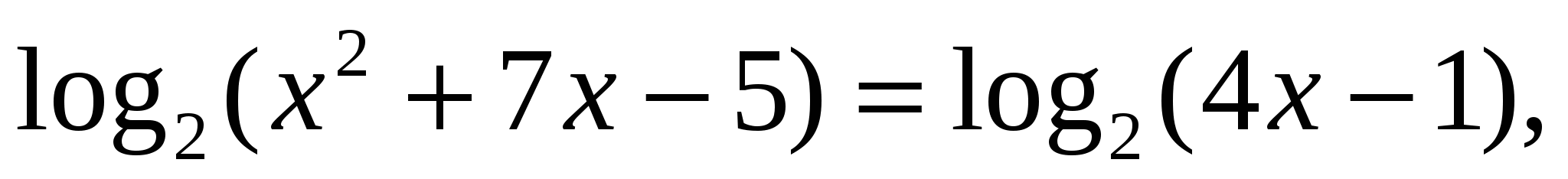

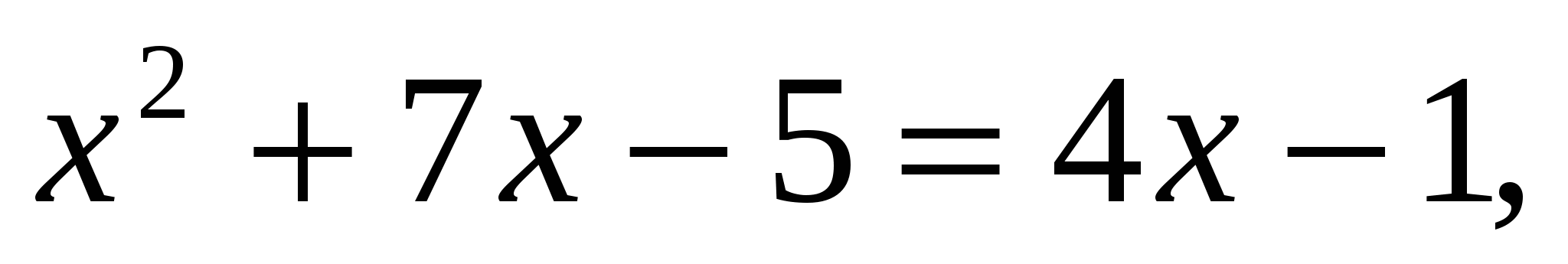
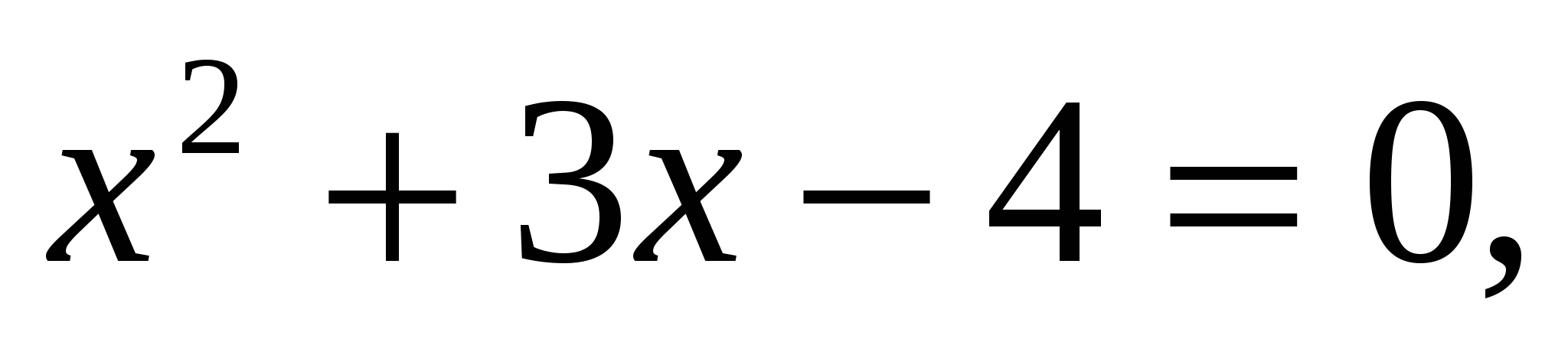
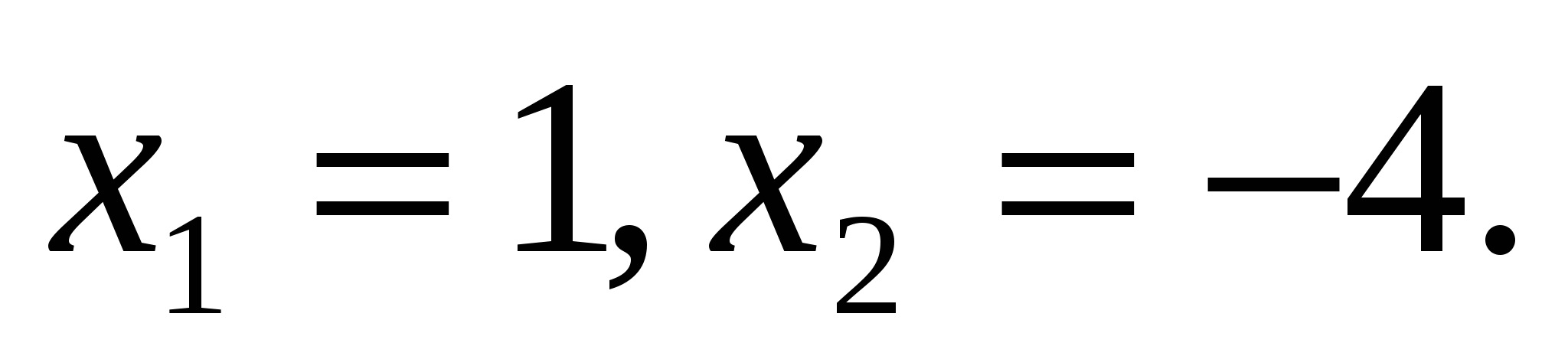
Проверка:

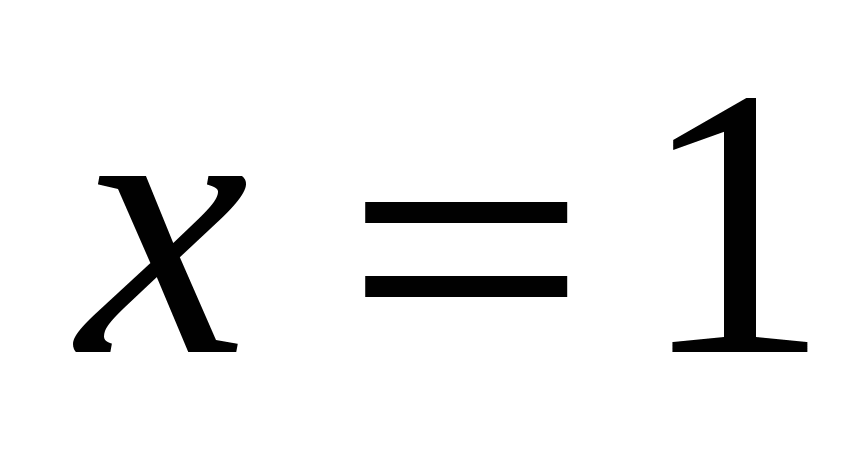
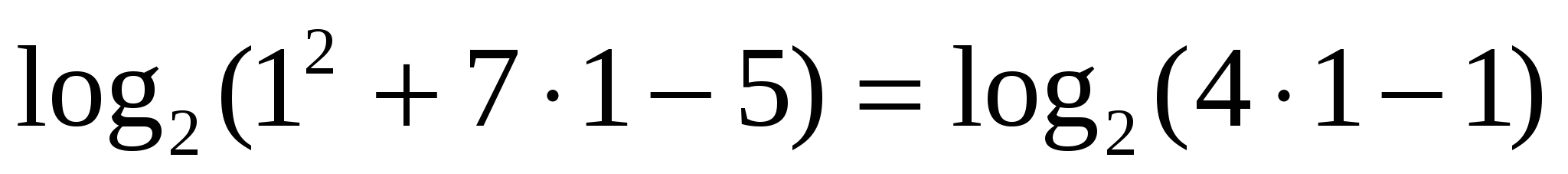
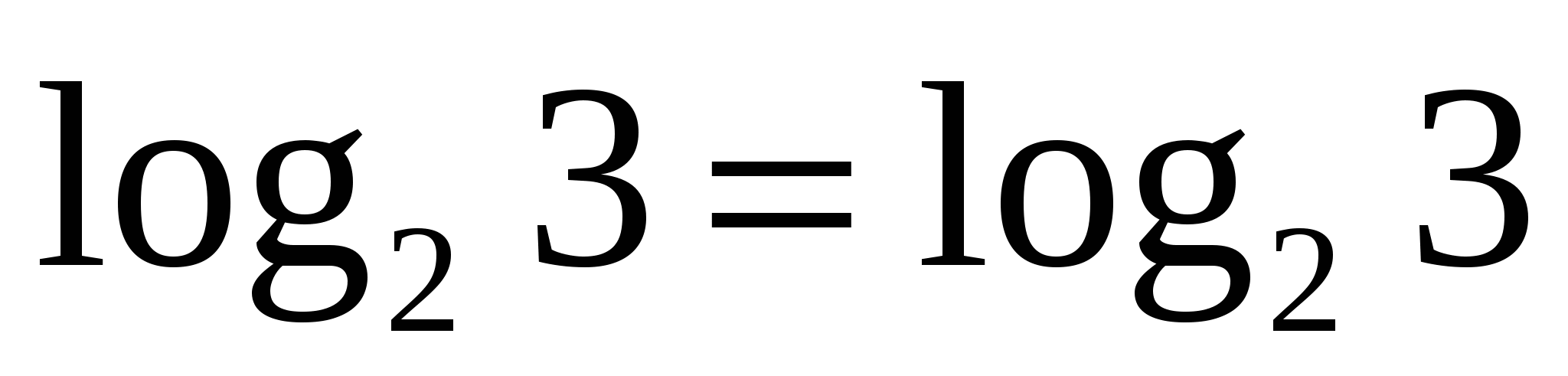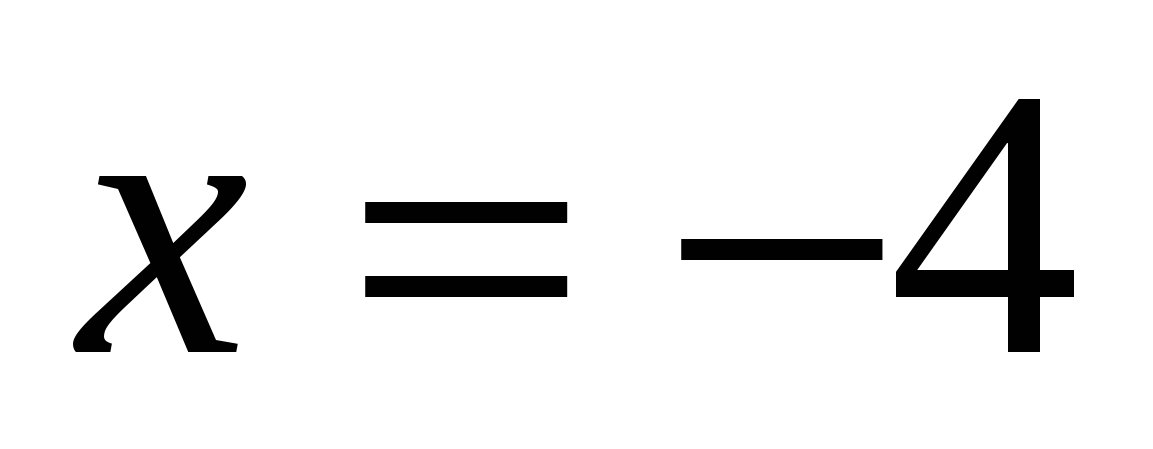
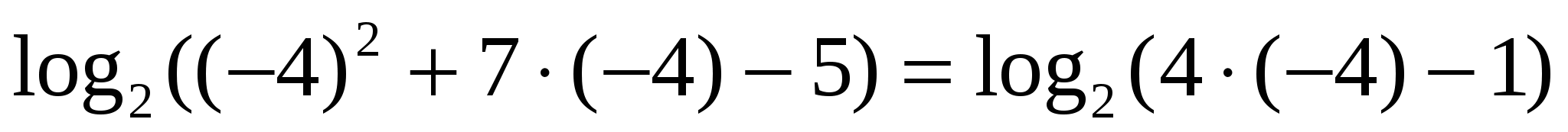
— верно.

— не верно.

Значит, только число 1 является решением исходного уравнения.

Ответ:1.

Слайд 7.

Если же в основании – выражение с переменной, то рассуждения не меняем! В этом случае уравнение будет иметь вид

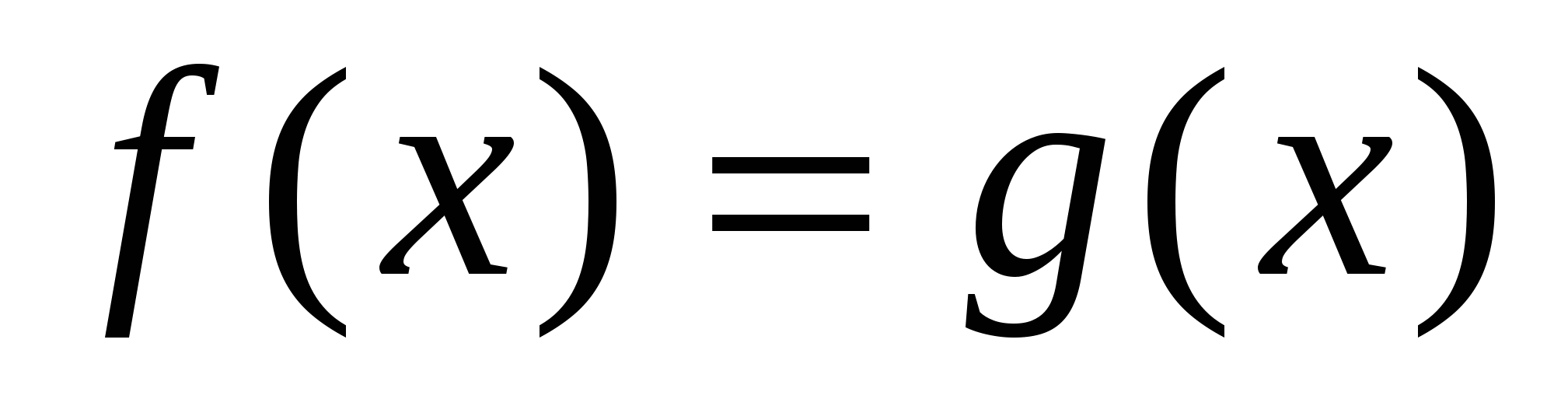, где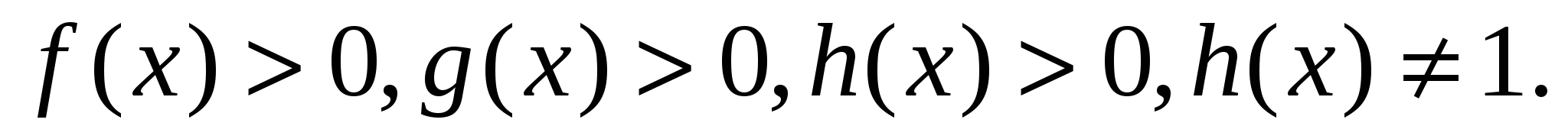

И пример такого уравнения можно разобрать на предыдущем примере 5.

Пример 6: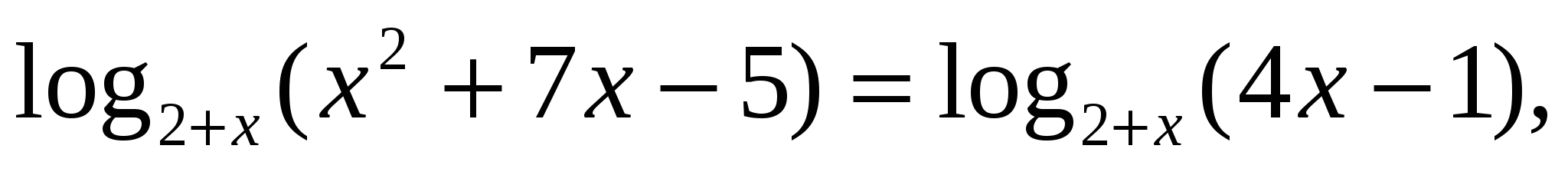

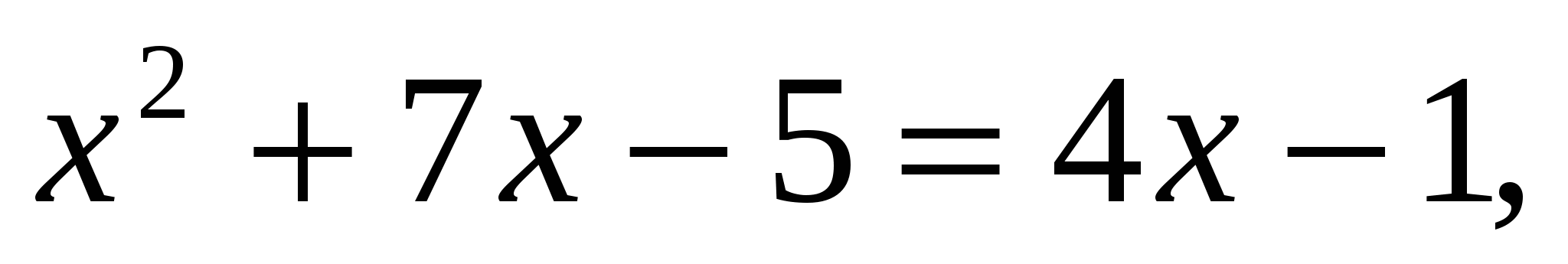
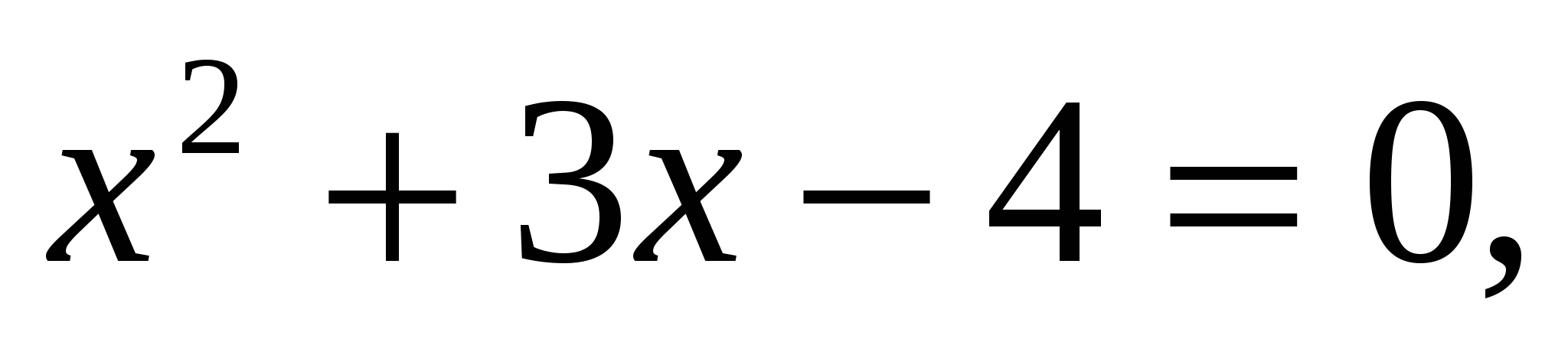
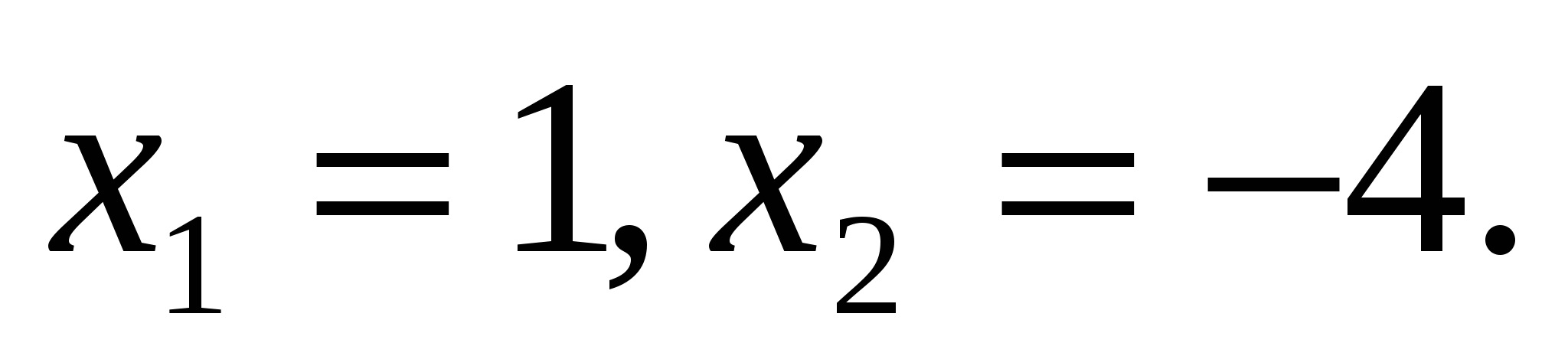
Проверка:

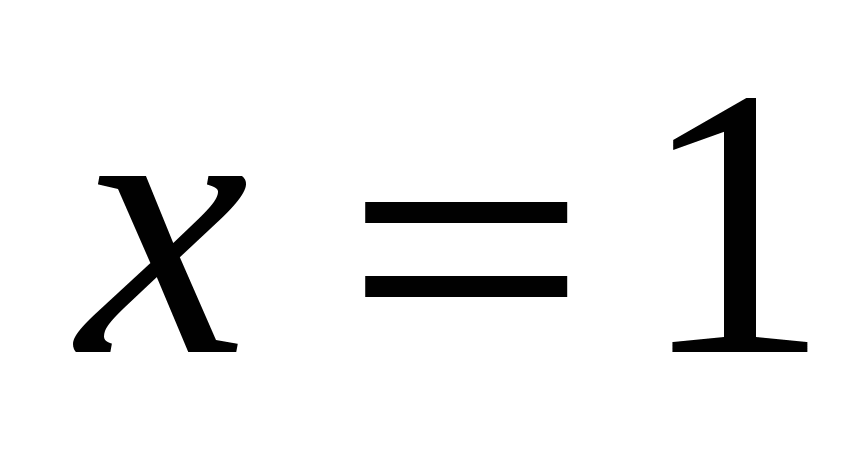
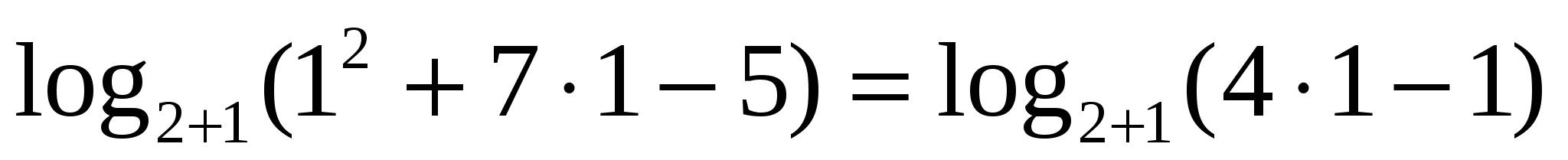
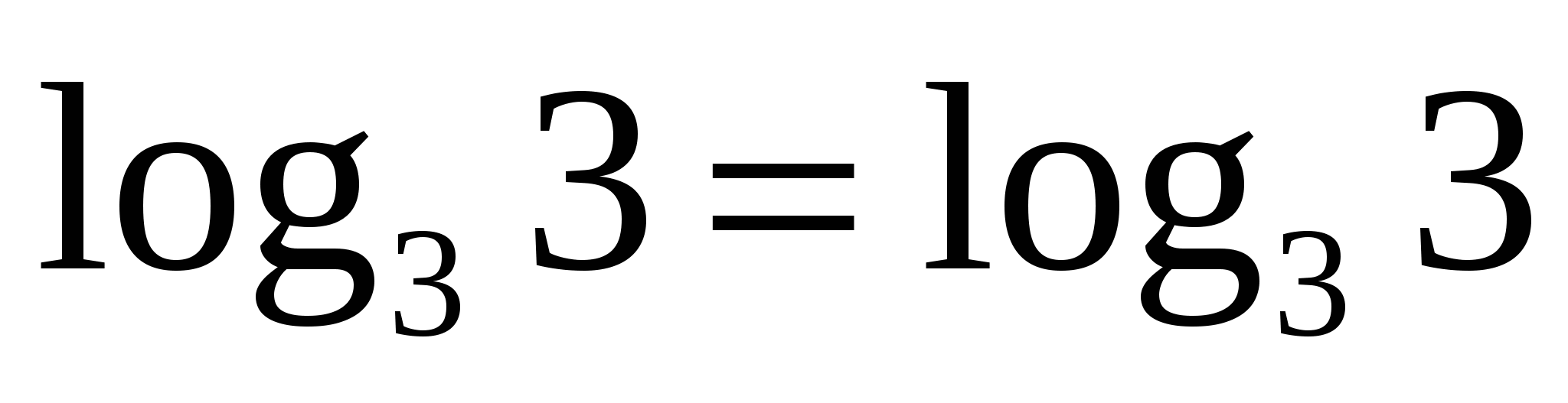
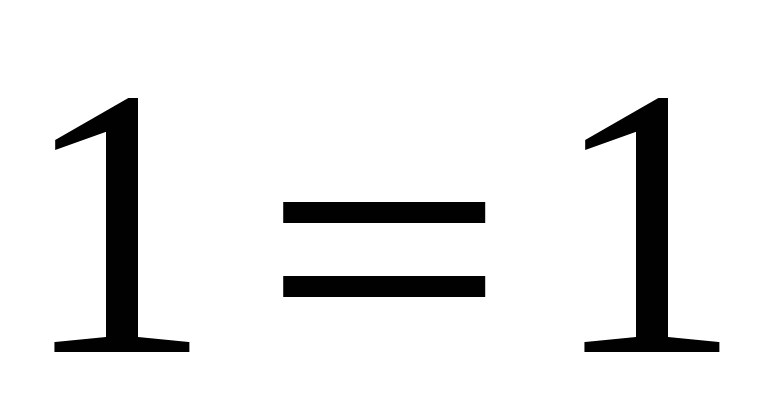— верно.

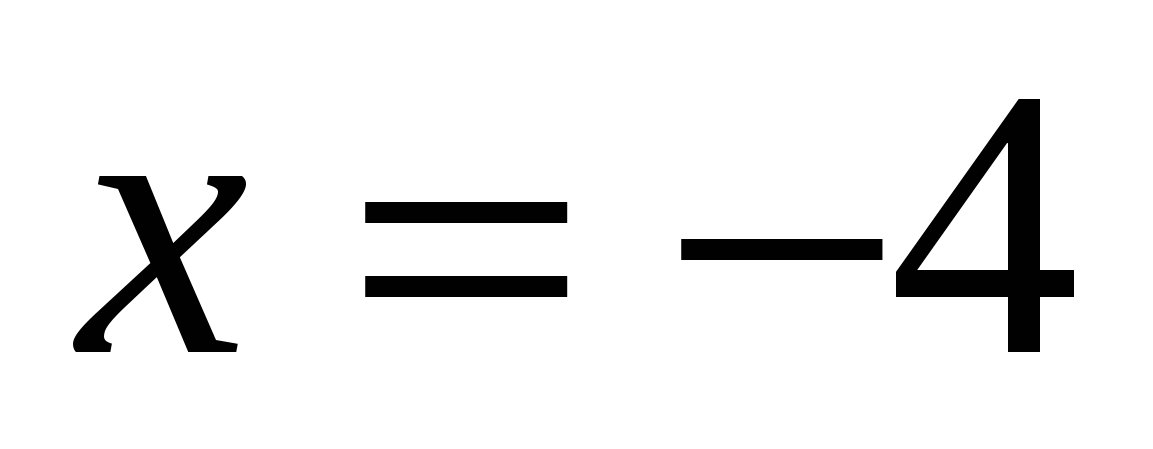
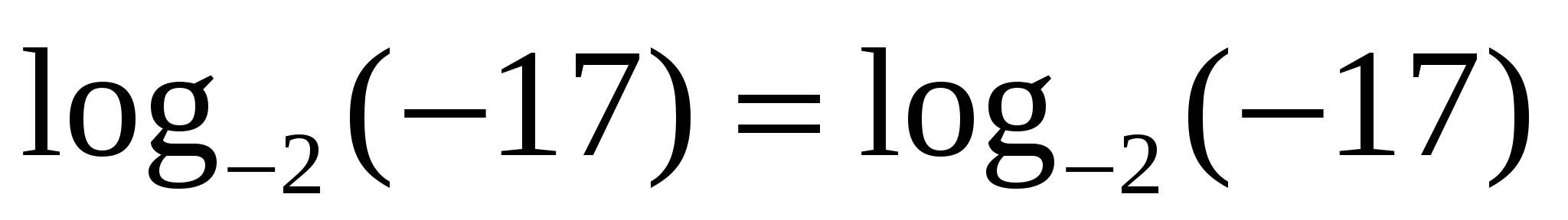— не верно.

Значит, только число 1 является решением исходного уравнения.

Ответ:1.

ОДЗ для данного уравнения выглядит следующим образом:

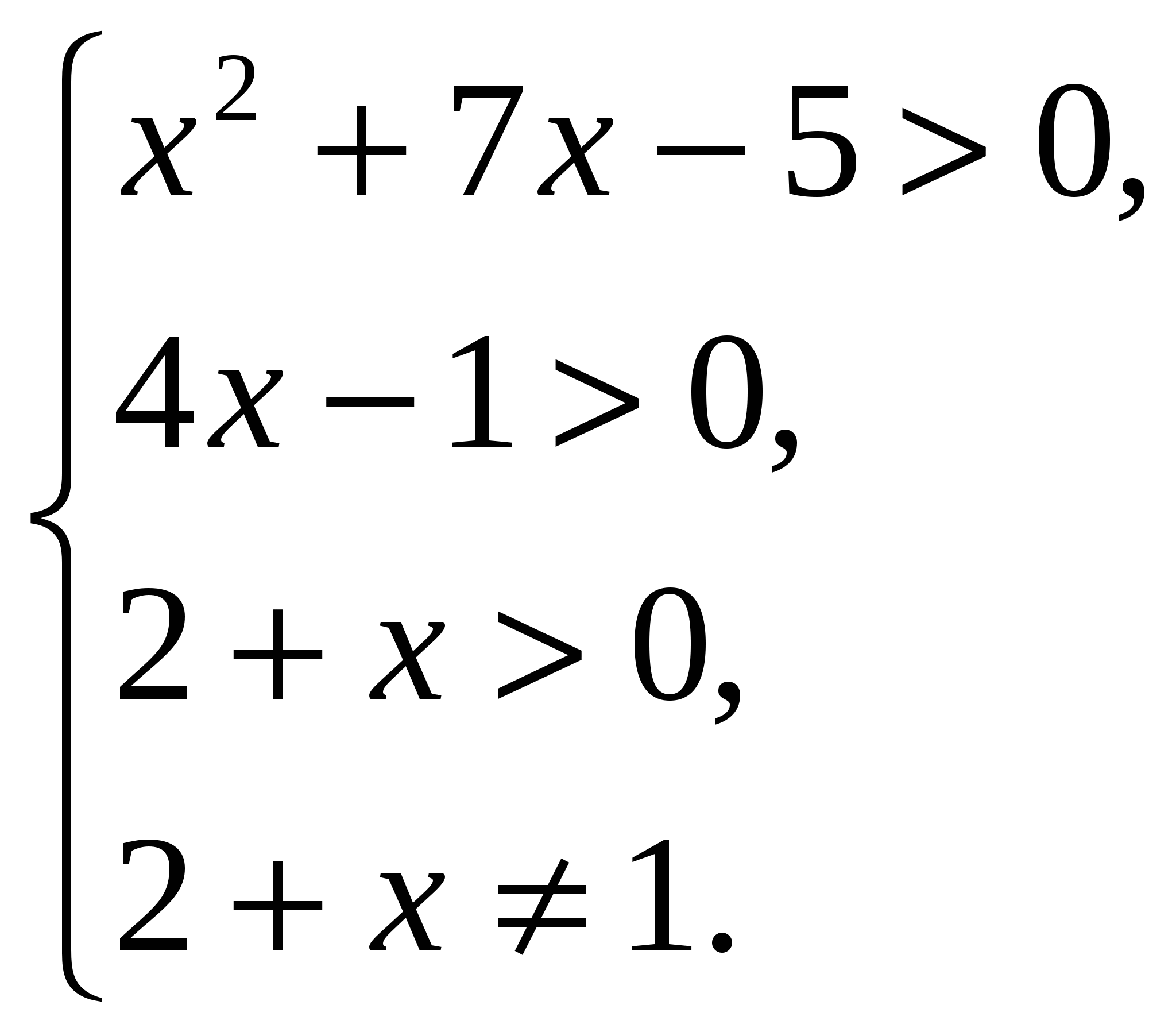
Мы видим, что в этом уравнении рациональнее выполнить проверку, а не искать ОДЗ. Но ещё раз повторюсь, что при решении неравенств ОДЗ находить придётся ОБЯЗАТЕЛЬНО.

Рассмотрим пример, который, на первый взгляд, не может относиться к данному типу уравнений.

Слайд 8.

Пример7:

Сделаем замену 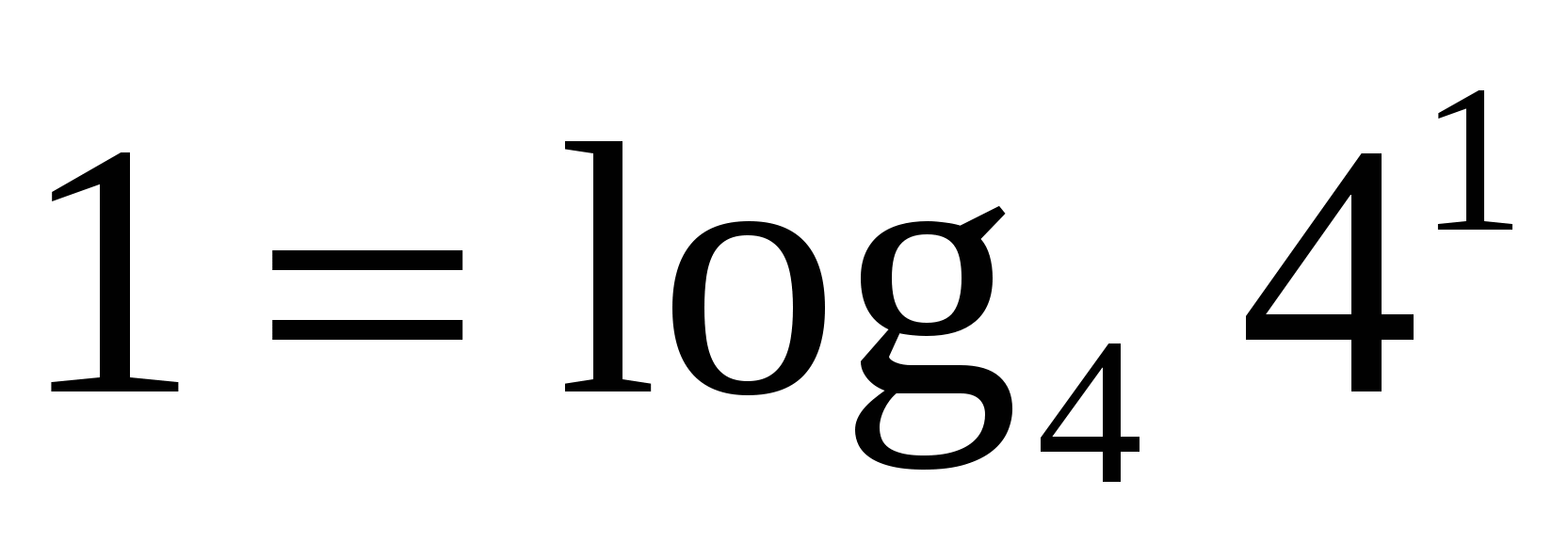, получим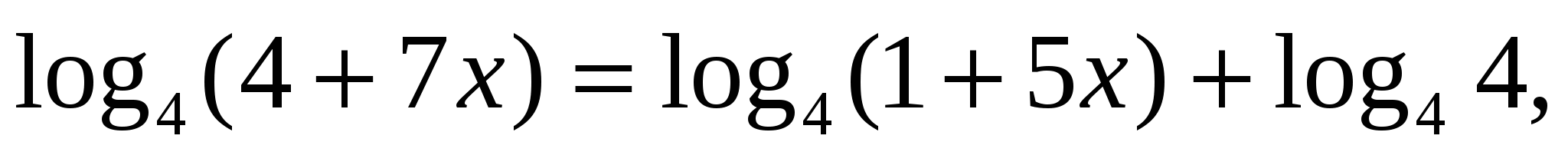

воспользовавшись свойством логарифма (сумма логарифмов равна логарифму произведения подлогарифмических выражений: 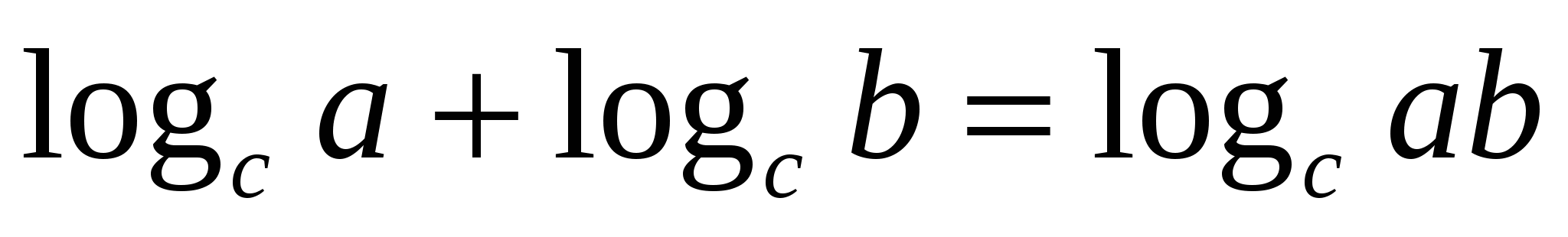), получим уравнение 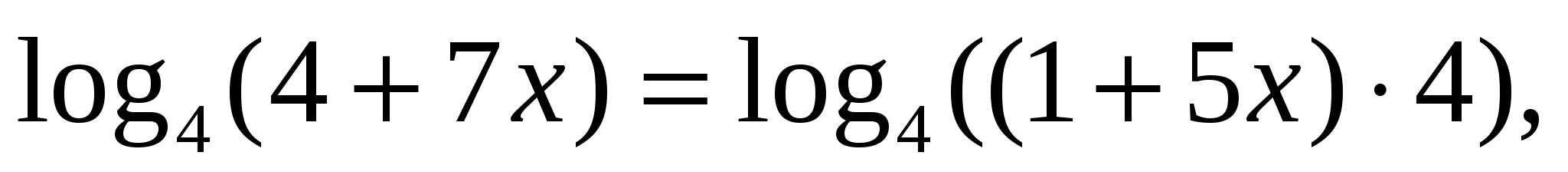которое в свою очередь замечательно решается методом потенцирования, т. е.

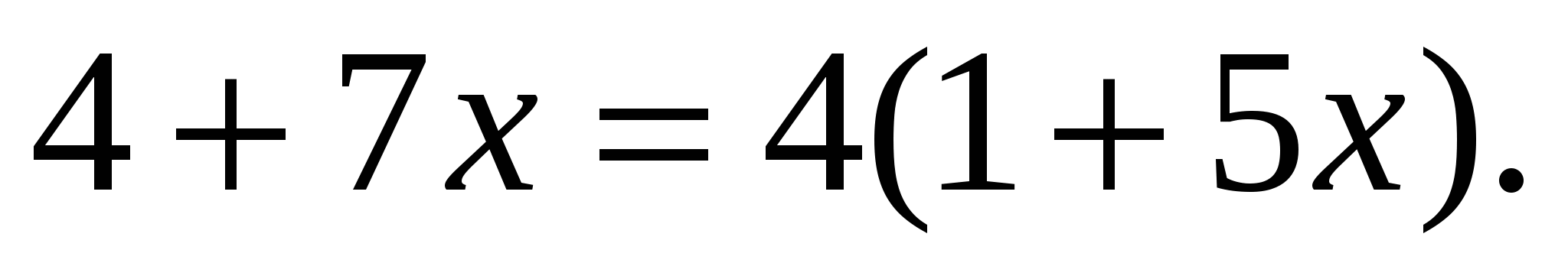А это линейное уравнение, решив которое, получим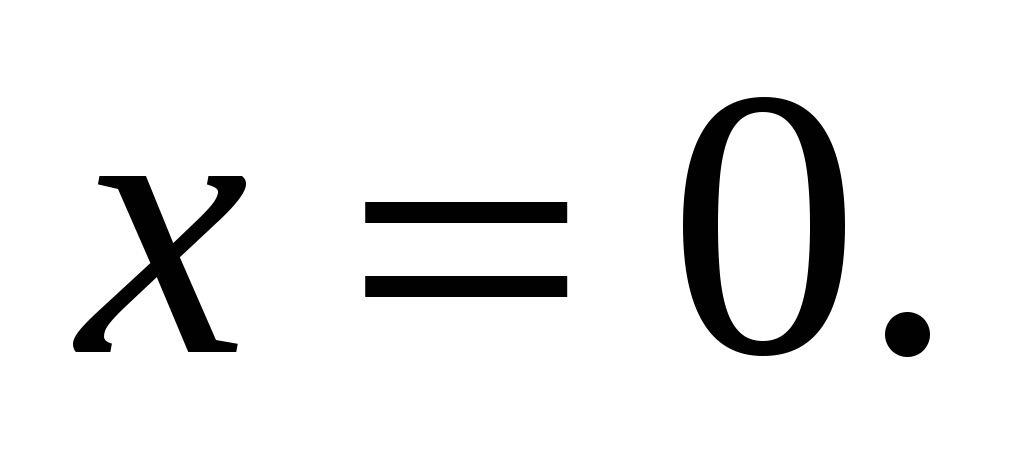

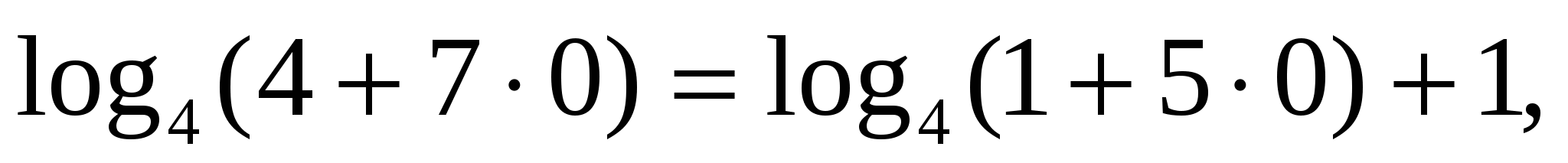
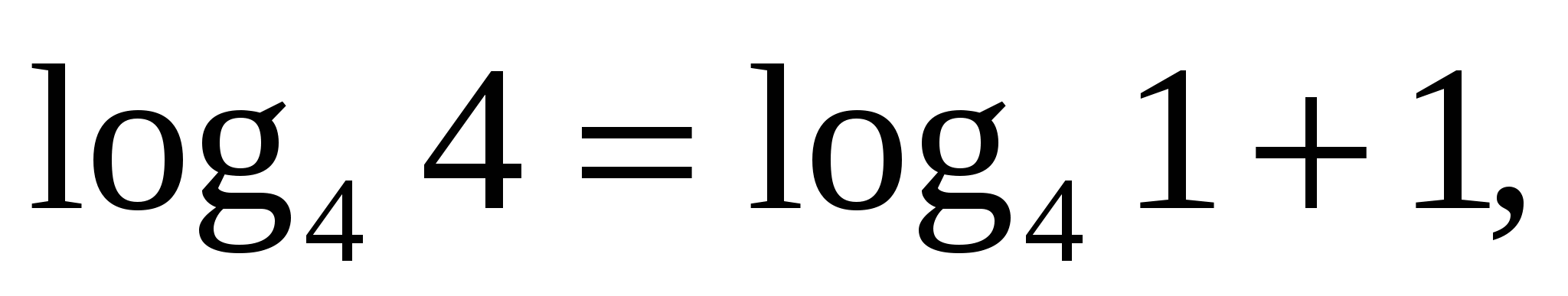
Проверка: 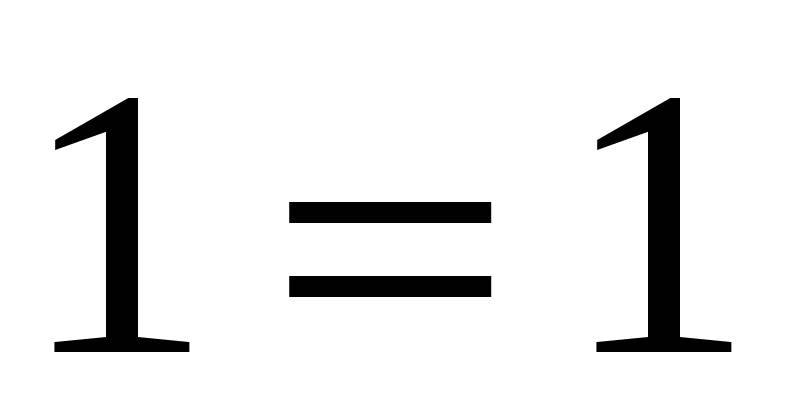— верно.

Ответ: 0.

Замечу, что часто перед применением какого-либо метода решений, необходимо преобразовать уравнение, применив различные свойства логарифмов. Предыдущий пример, тому подтверждение.

3. Метод подстановки.

Слайд 9.

Данный метод мы достаточно часто встречаем в математике, вспомните тригонометрические или показательные уравнения. Поэтому применение его при решении логарифмических уравнений я вам покажу на примере.

Пример 8: .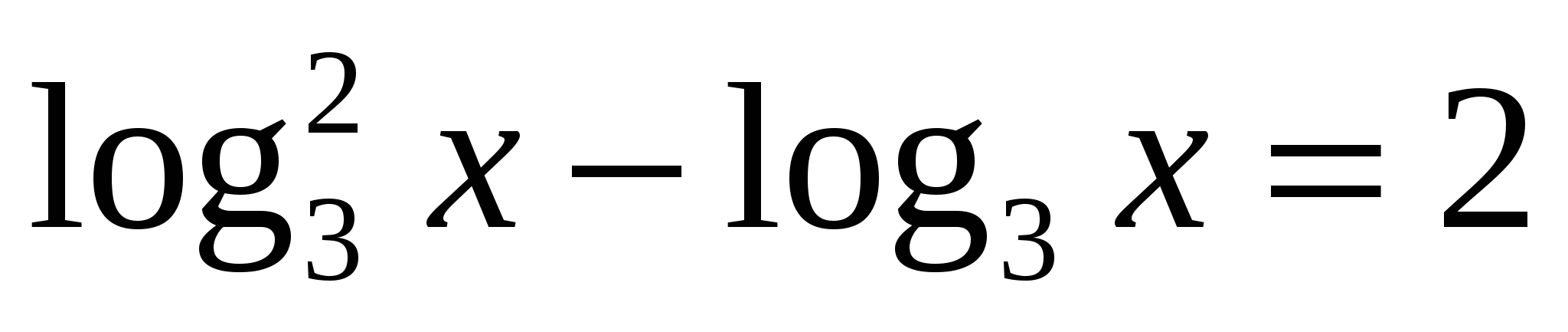

В этом уравнении рациональней найти ОДЗ: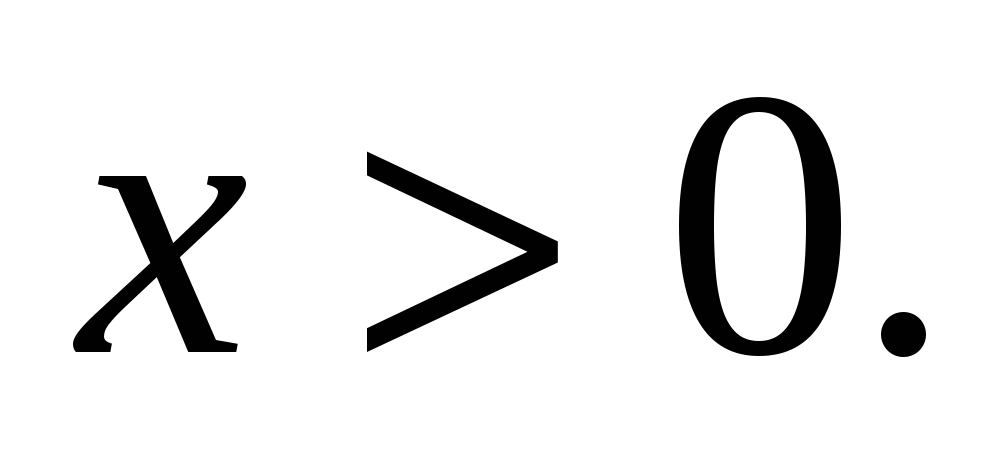

Пусть 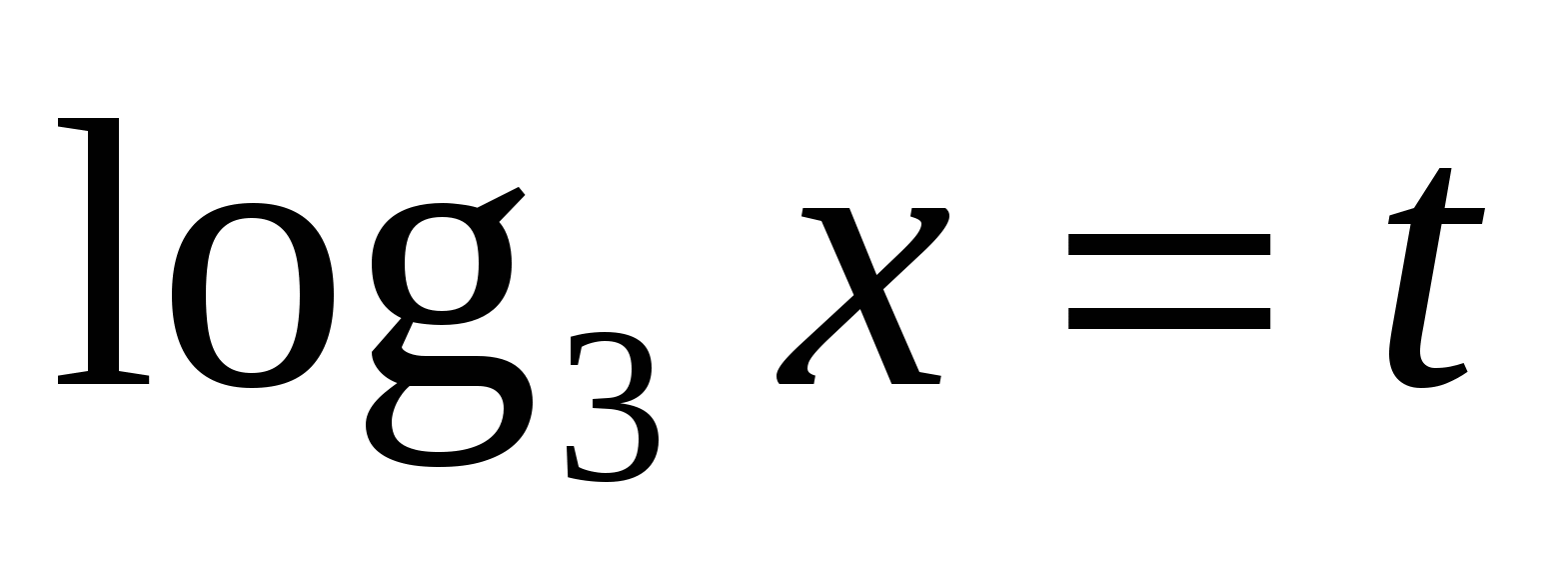, тогда уравнение примет вид

,

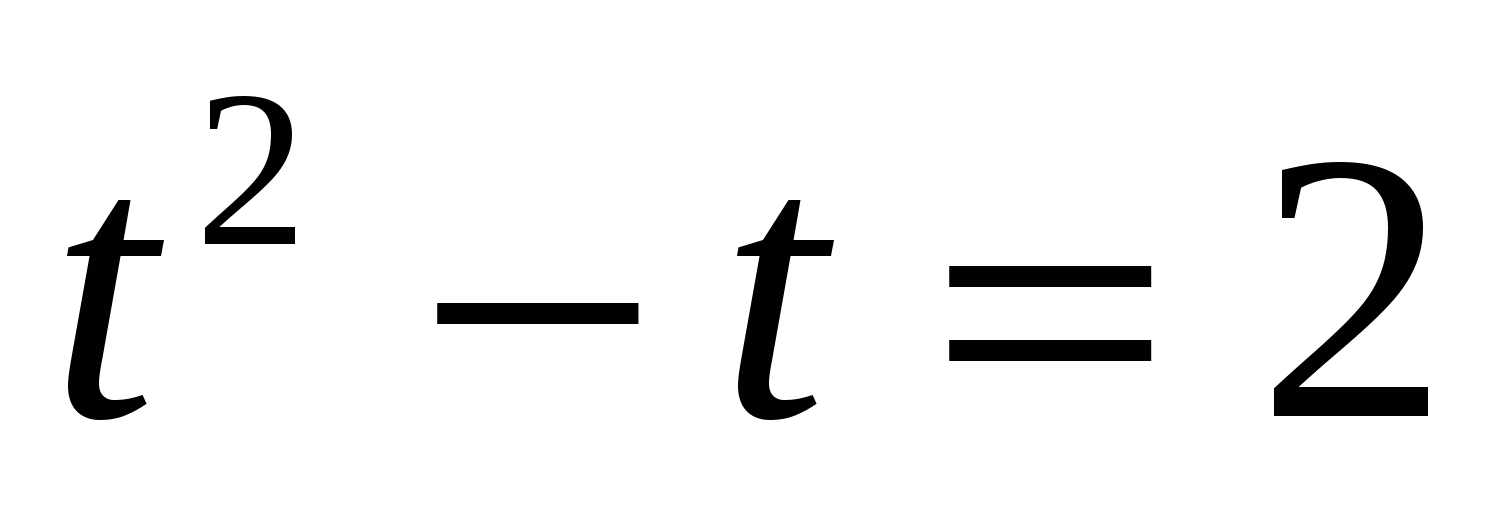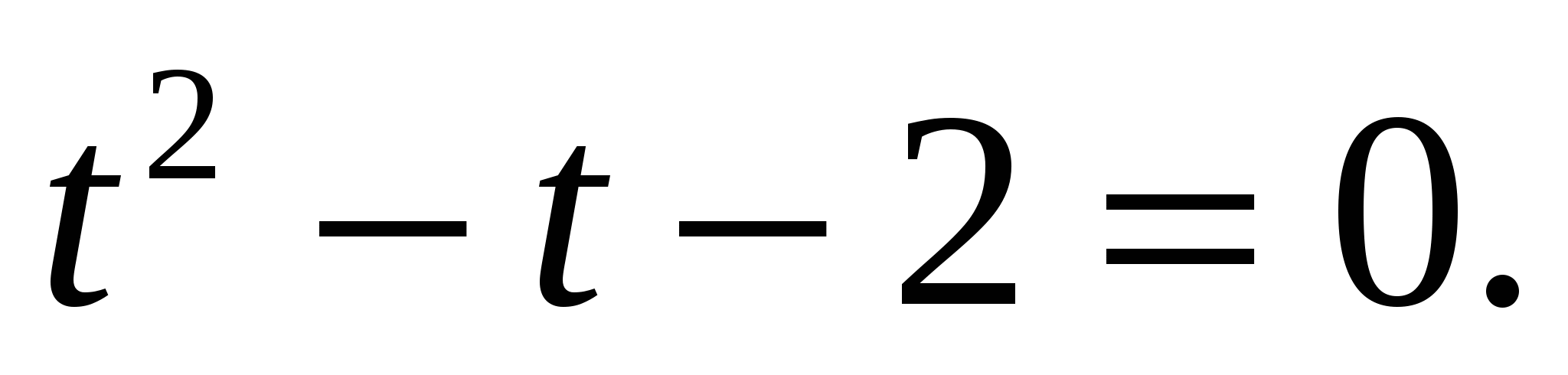
Значит или 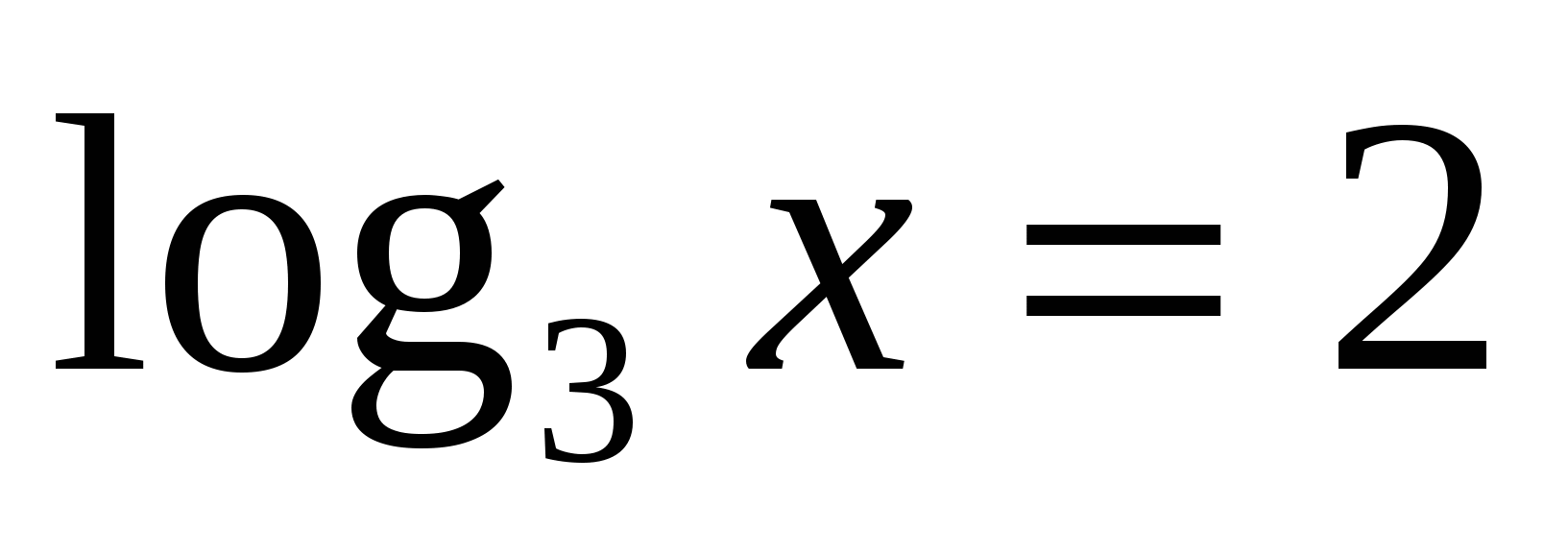. А это уравнения, которые мы решим, используя определение: 1)

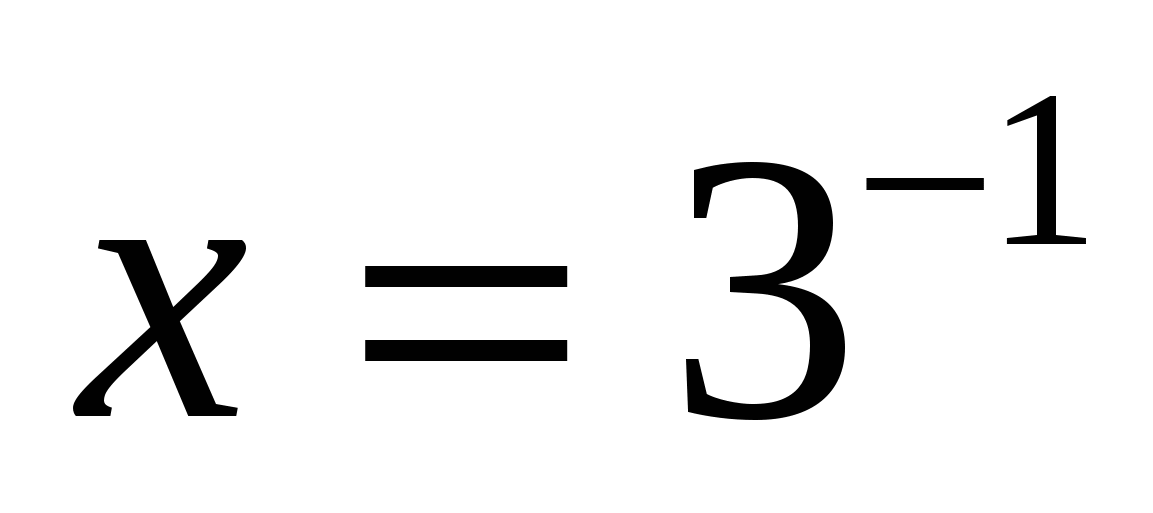
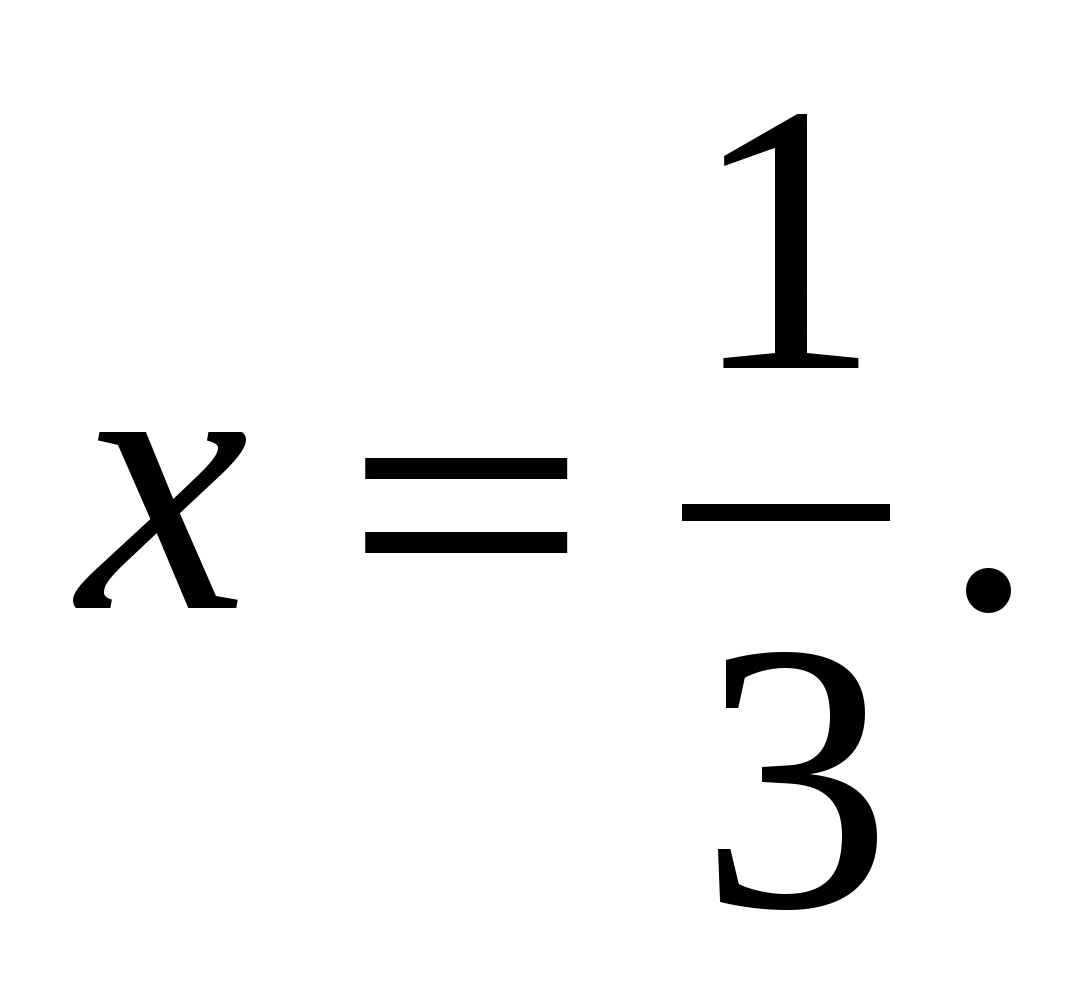
2)

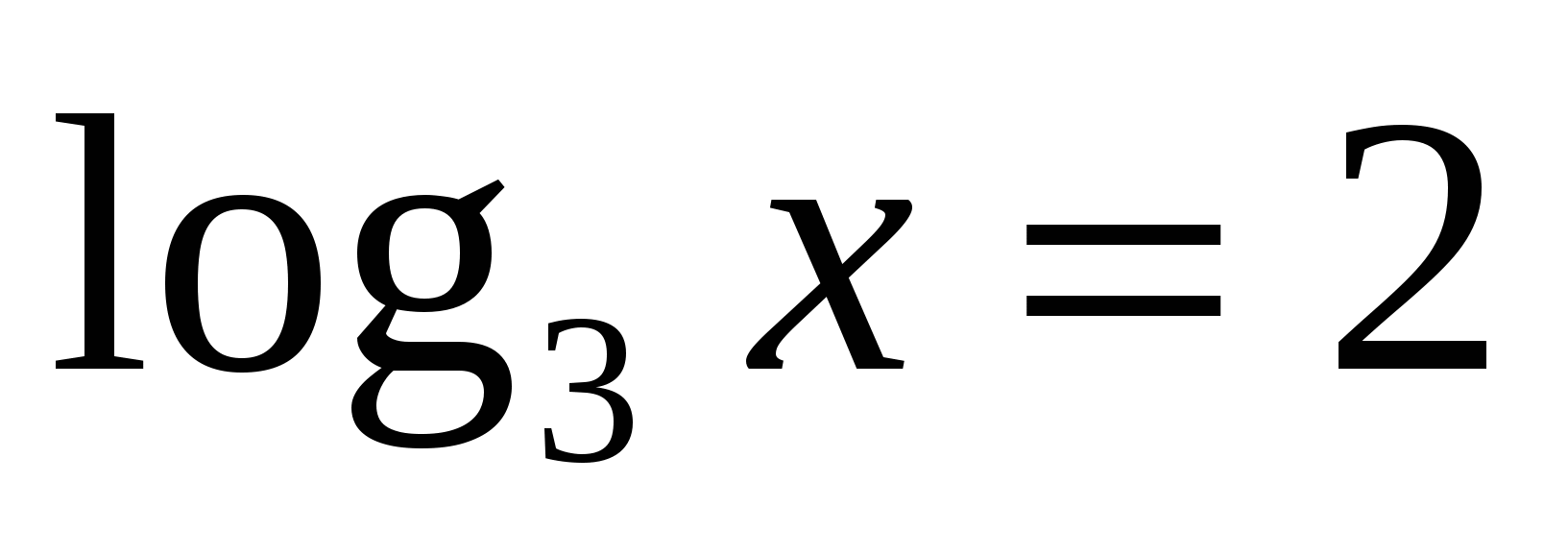
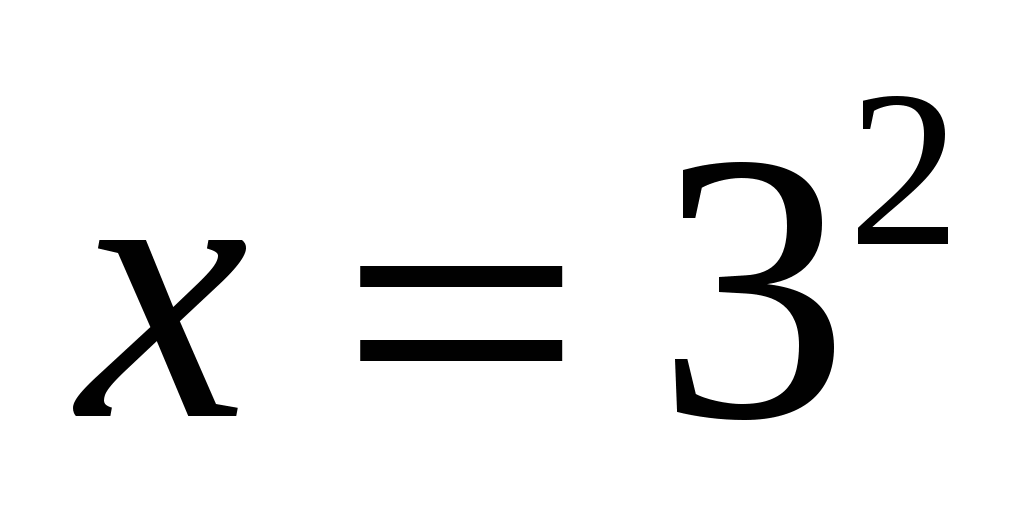
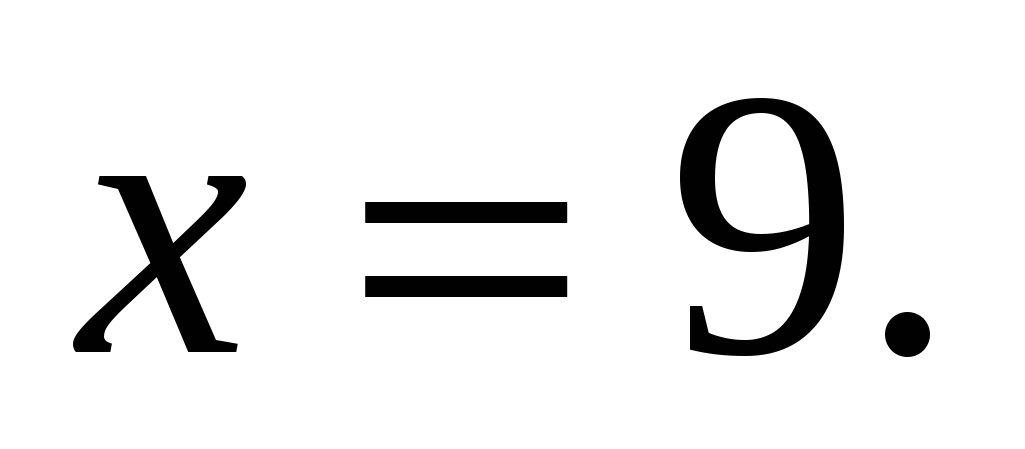
Мы видим, что оба корня удовлетворяют ОДЗ, значит оба числа являются решениями исходного уравнения.

Ответ: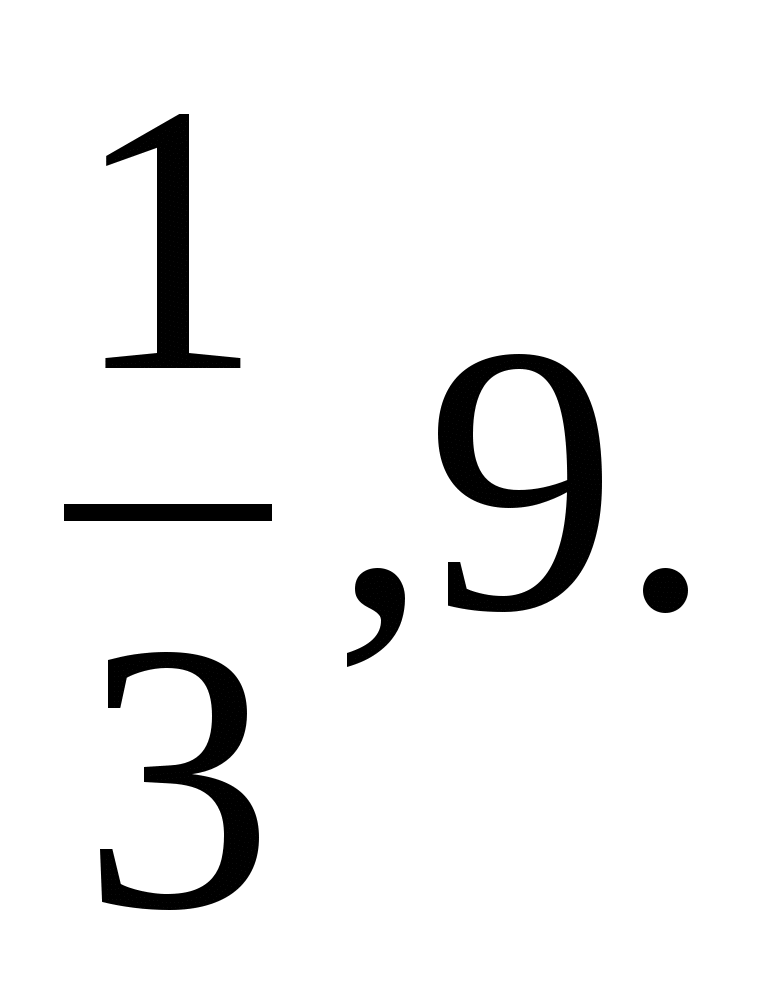

Слайд 10.

Если в основании логарифма лежит выражение с переменной, то уравнение в общем виде будет выглядеть следующим образом:

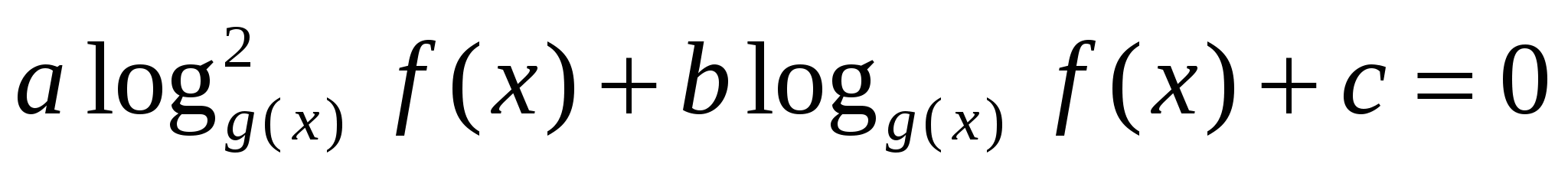, где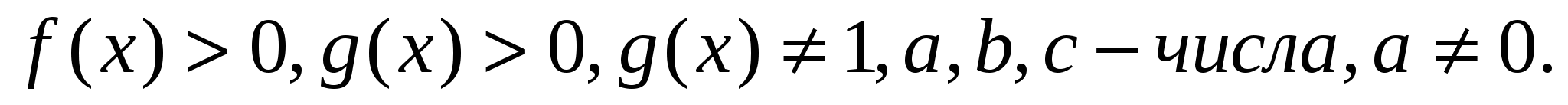

И опять, вы сами выбираете: ОДЗ или проверка.

Пример 9: .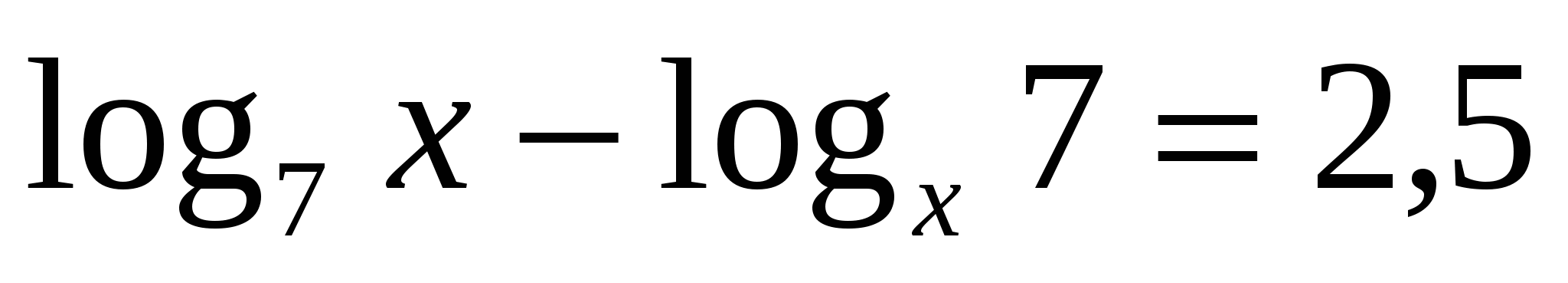

ОДЗ: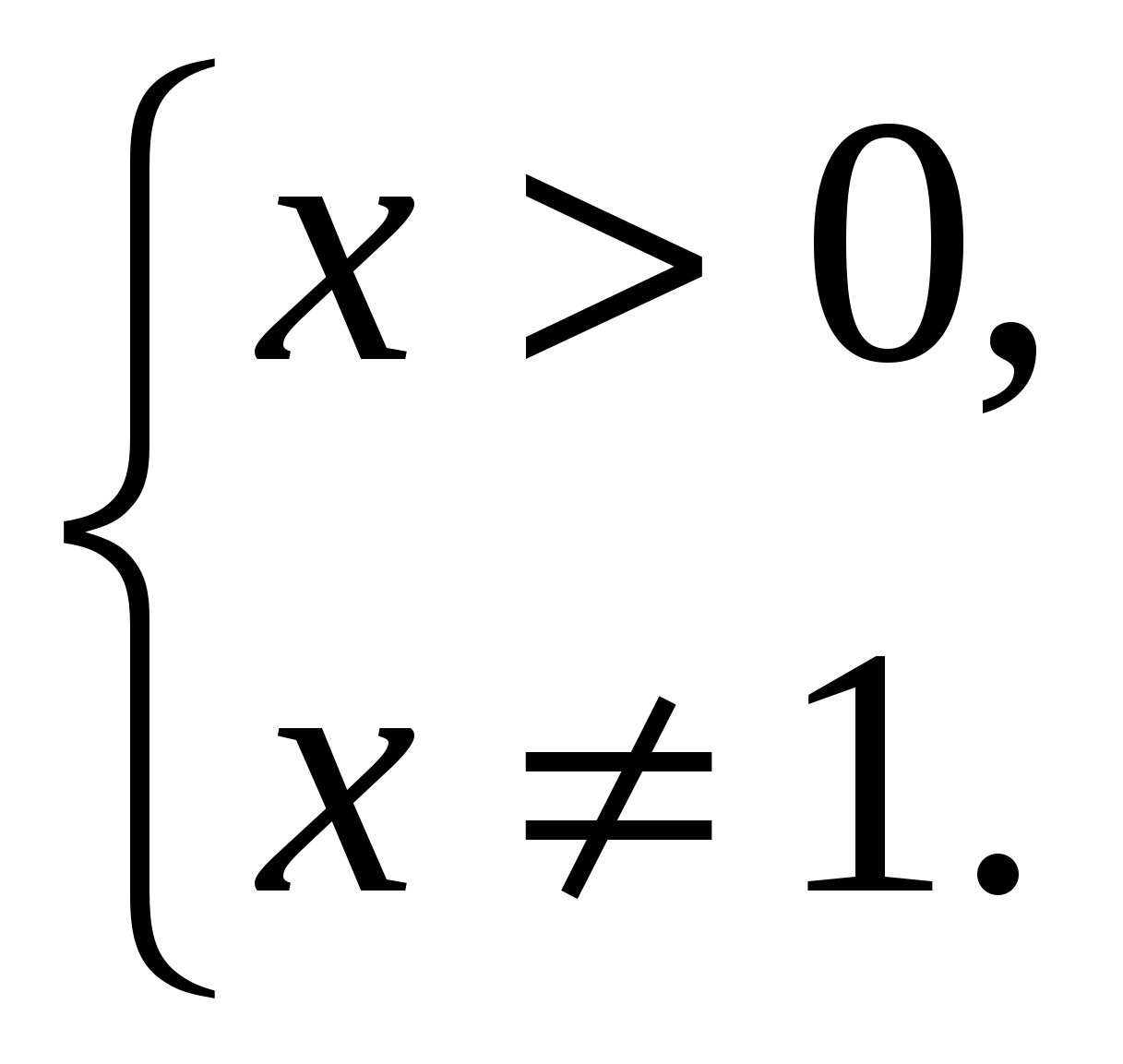

Приведём логарифмы к одному основанию – 7, пользуясь свойством перехода к новому основанию , получим:

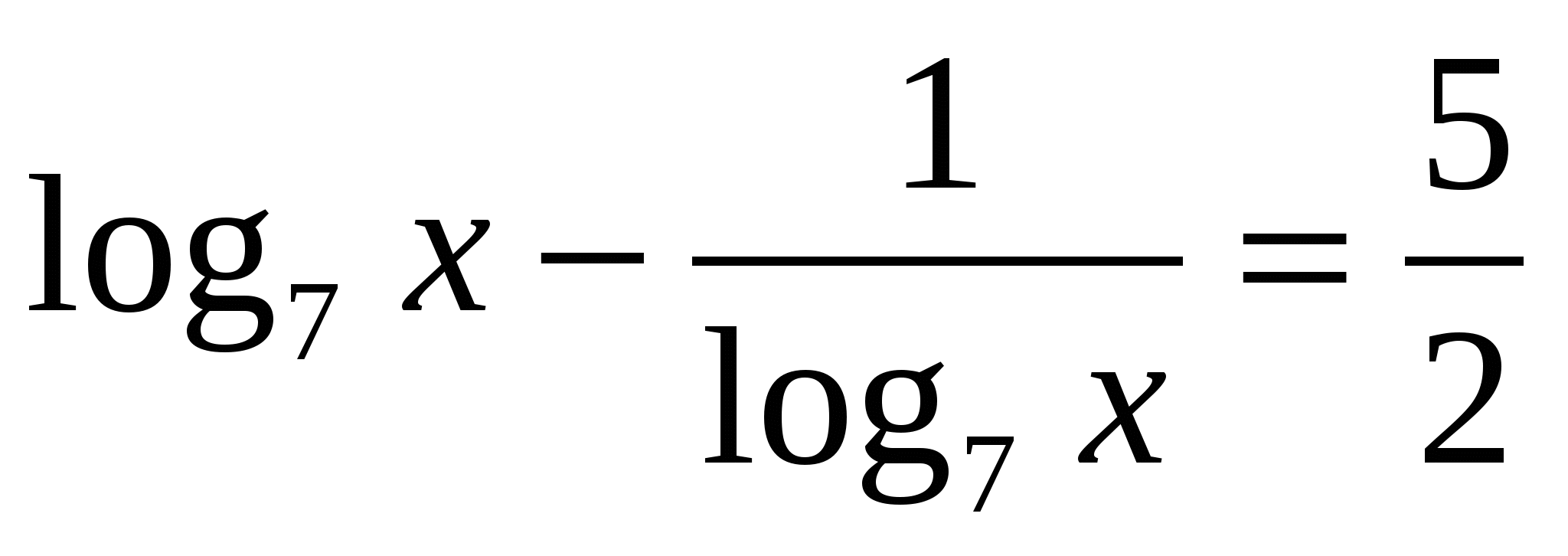, выполним подстановку 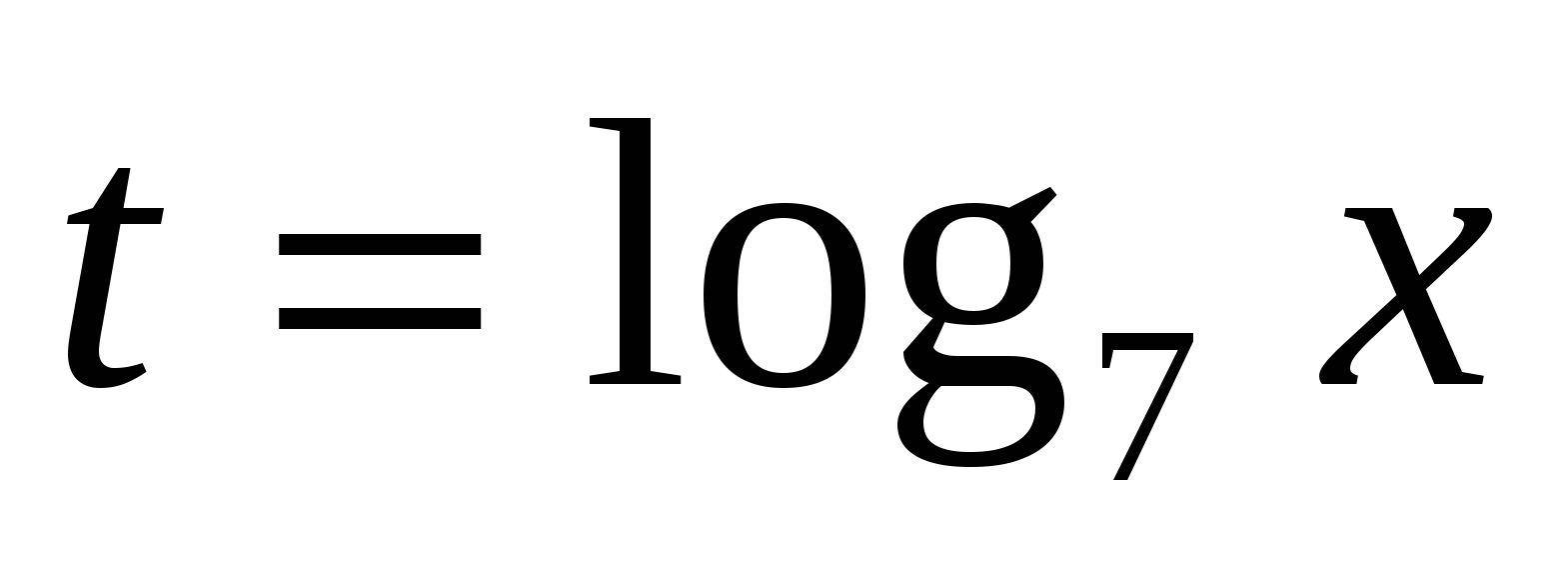, получим уравнение

,

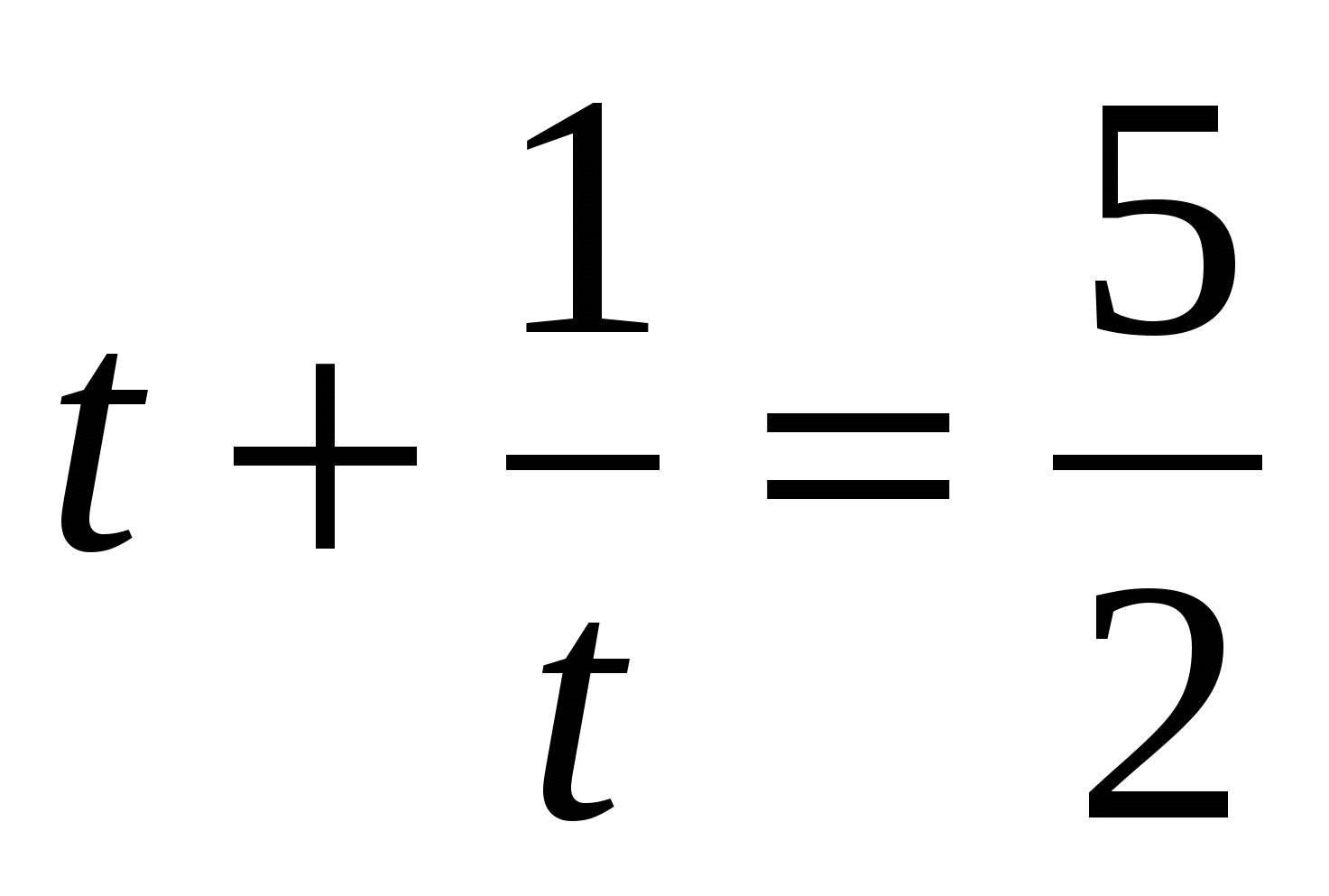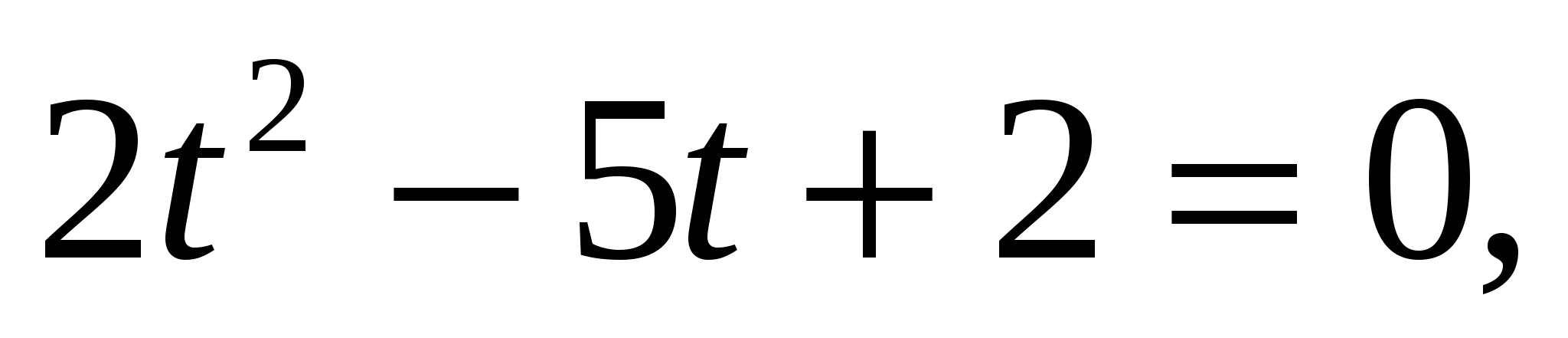
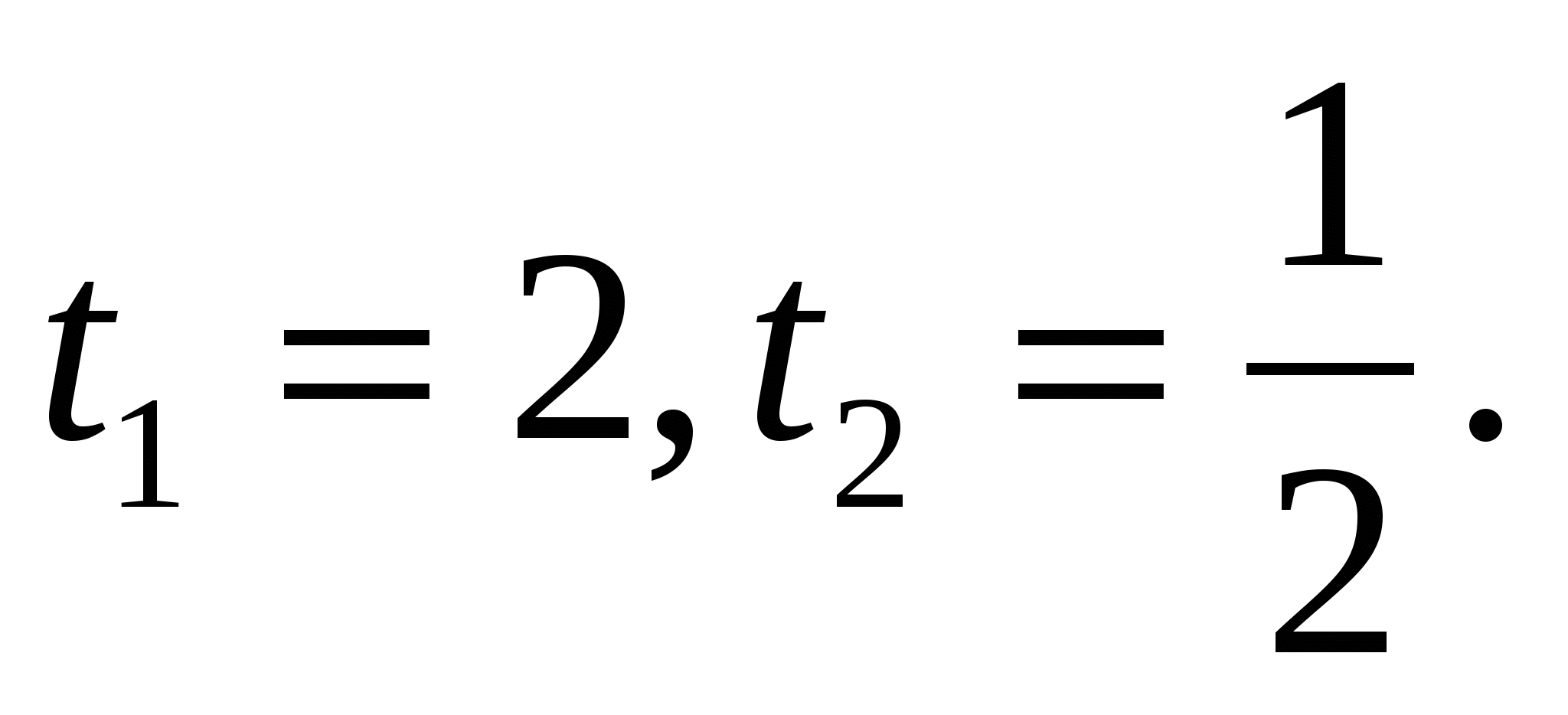
Значит, 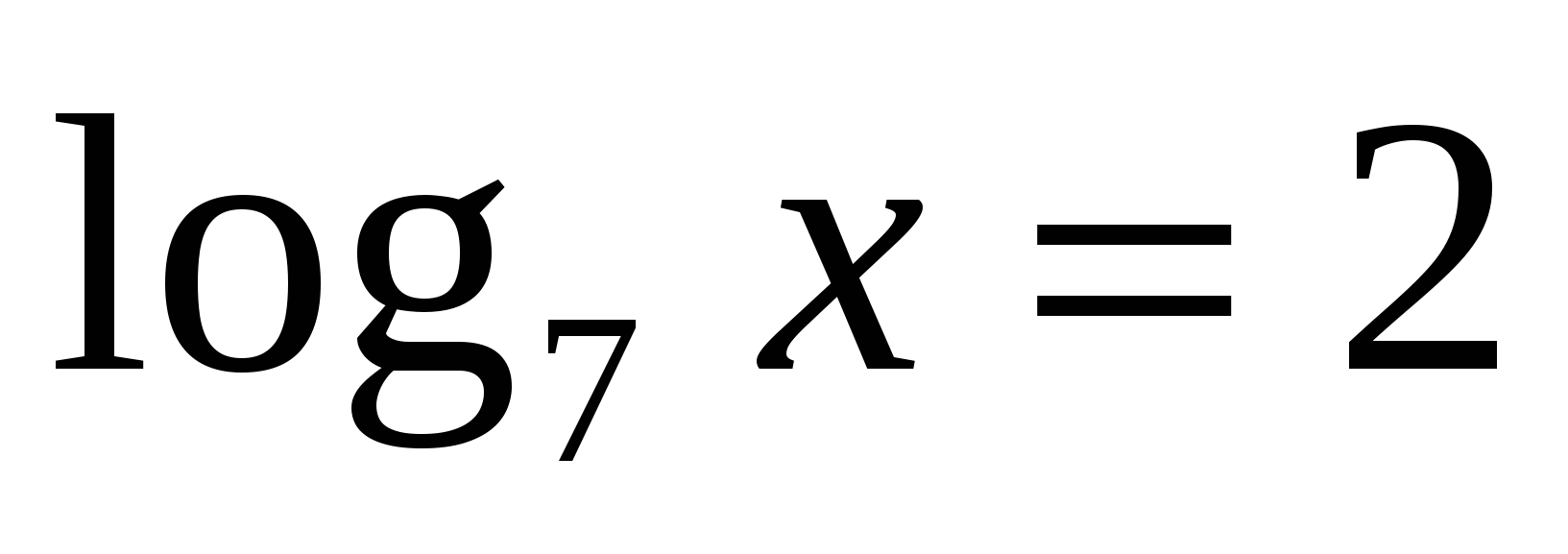или .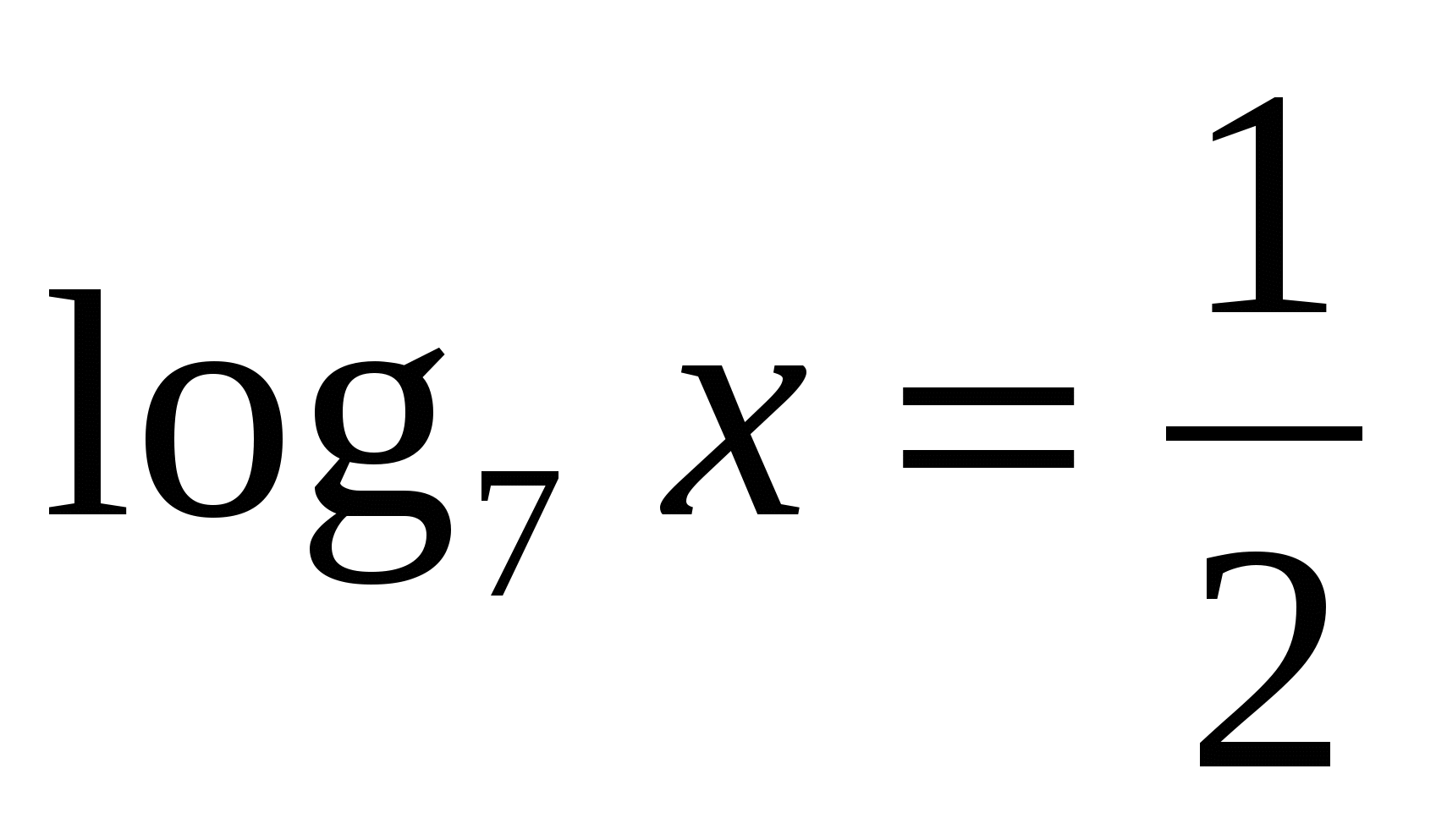

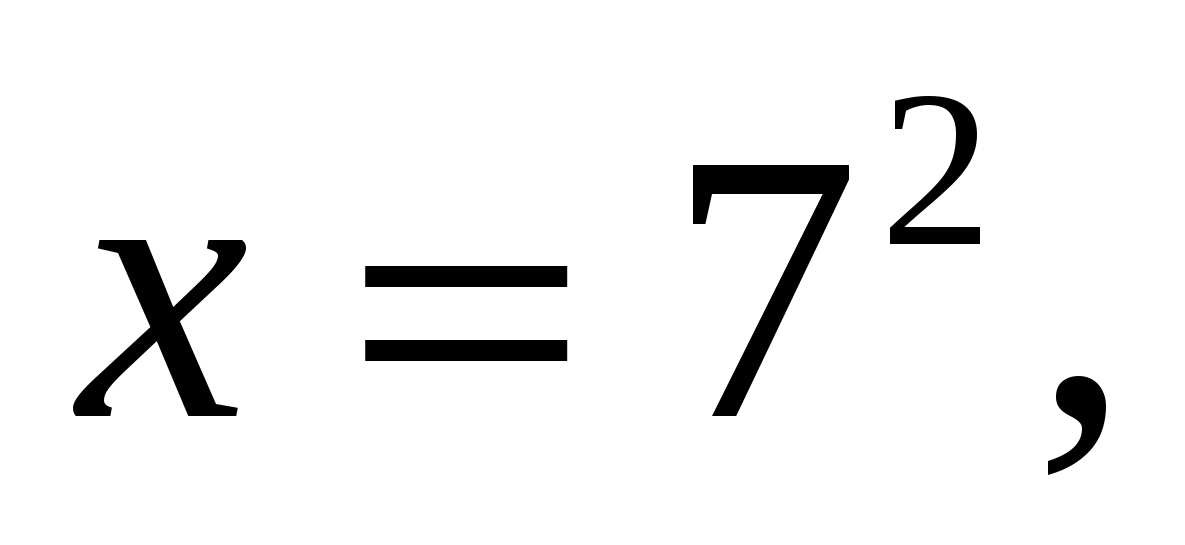
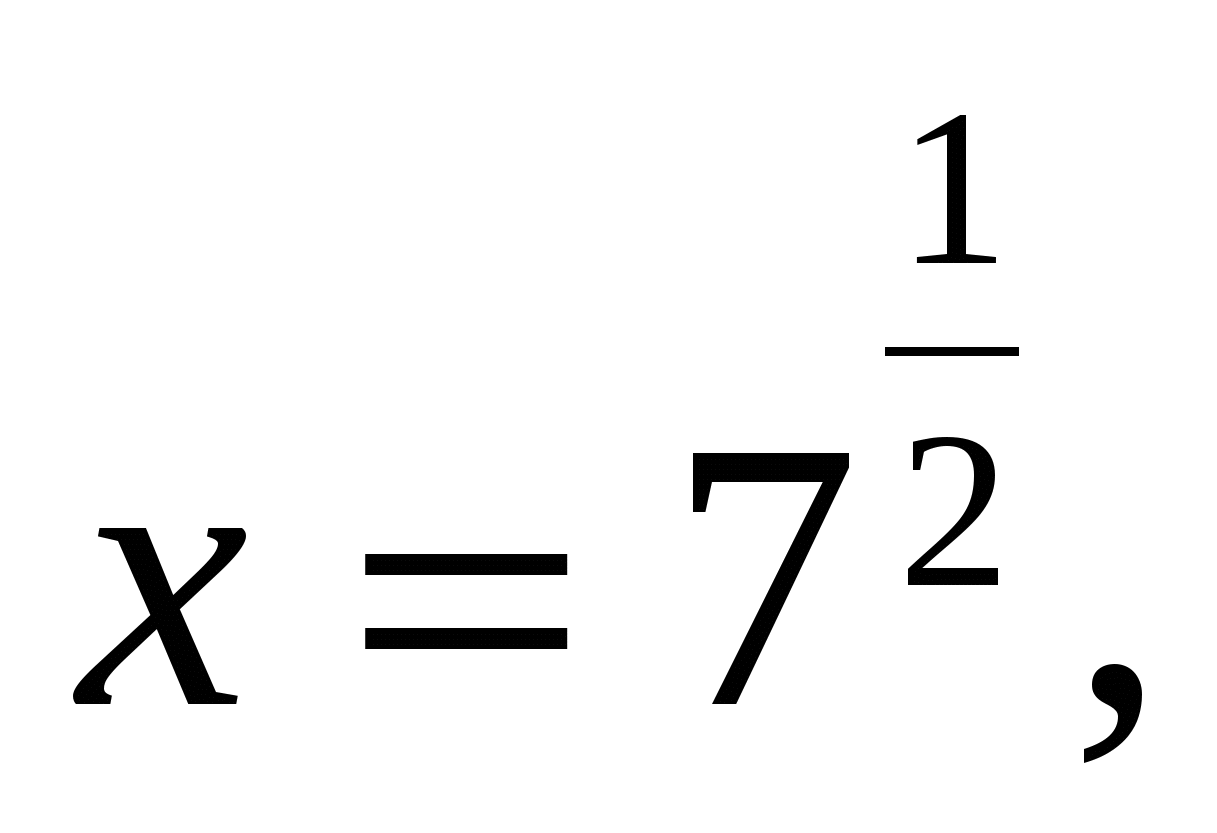
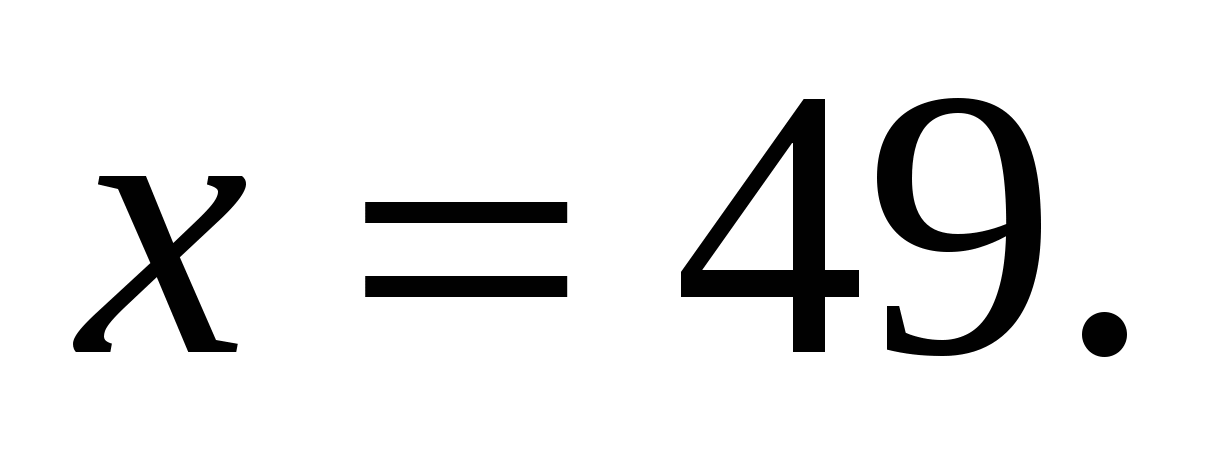
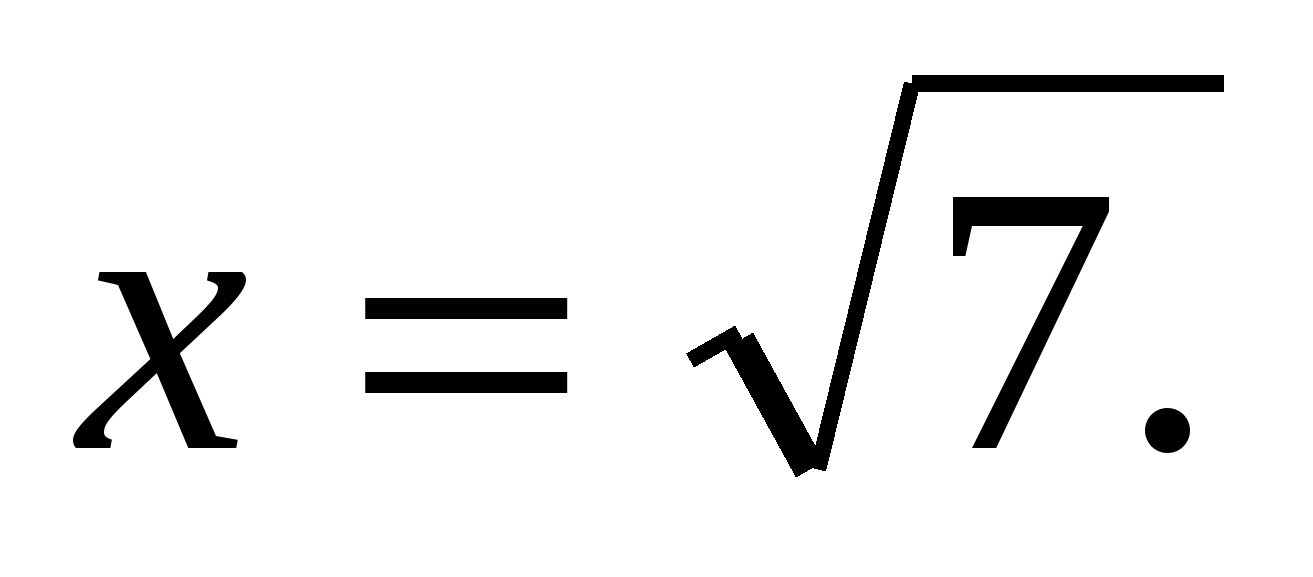
Оба числа удовлетворяют ОДЗ.

Ответ: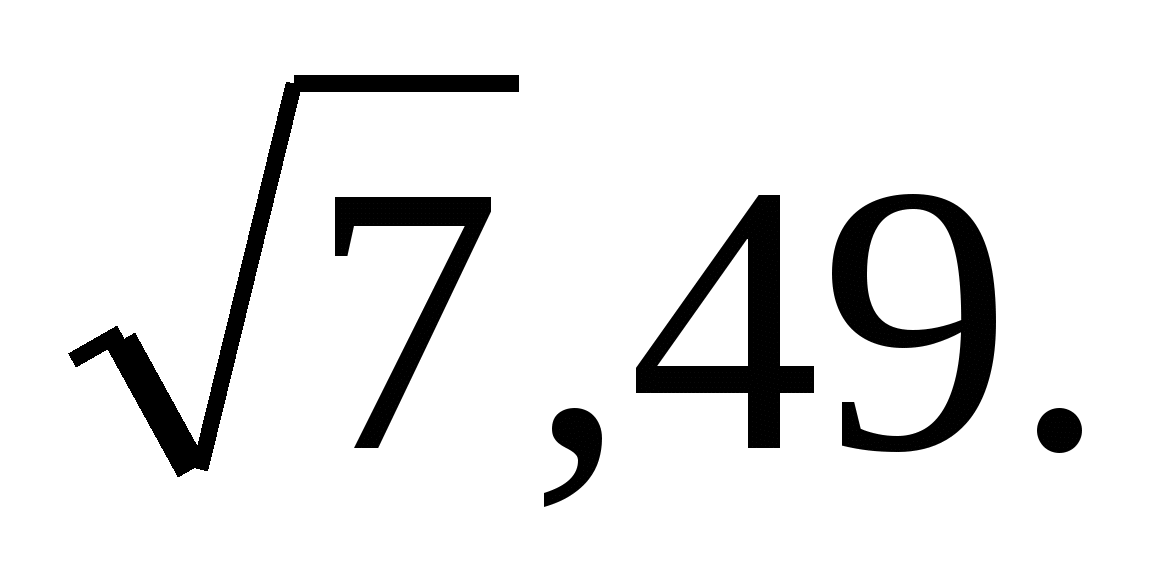

4. Метод логарифмирования.

Слайд 11.

Данный метод является «обратным» методу потенцирования, т. е. мы от уравнения без логарифмов переходим к уравнению, их содержащему.

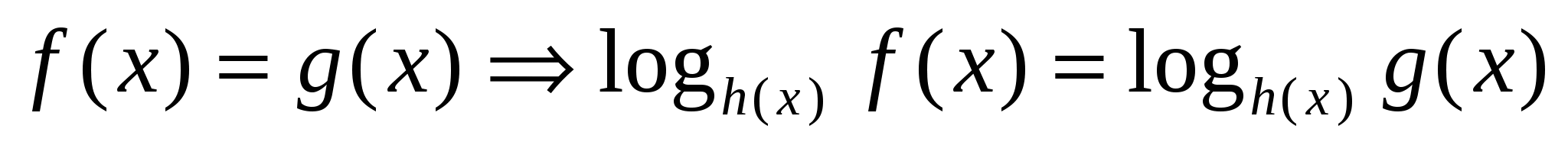, при этом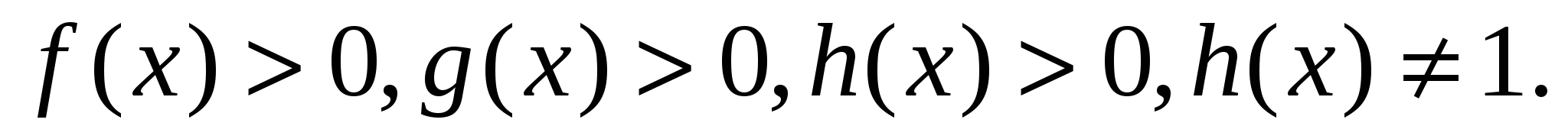

Этот метод обычно используется, если в уравнении есть показательные функции, логарифмы – в показателе. Рассмотрим этот метод на примере.

Пример 10:

ОДЗ: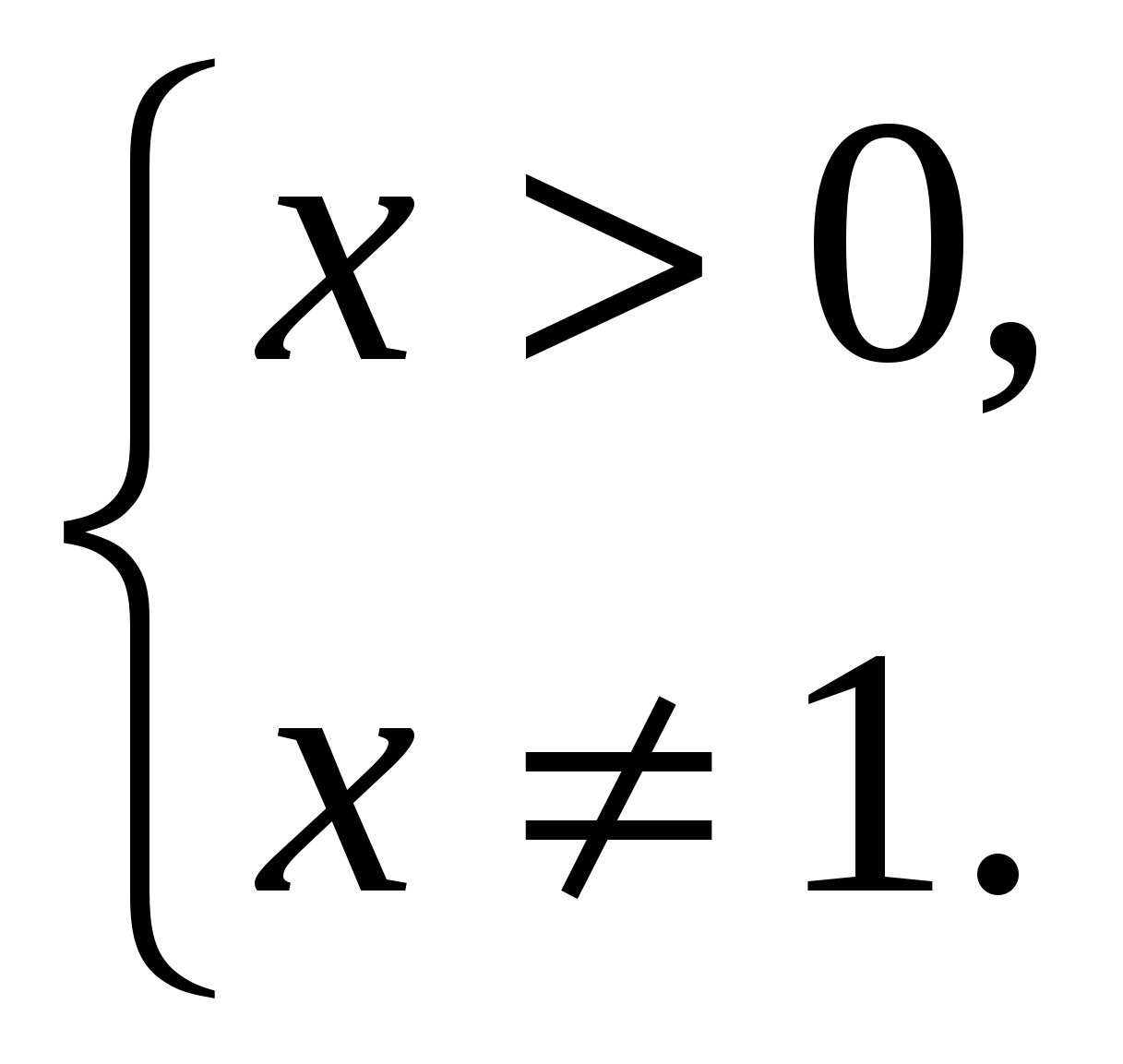

Прологарифмируем обе части уравнения по основанию 3:

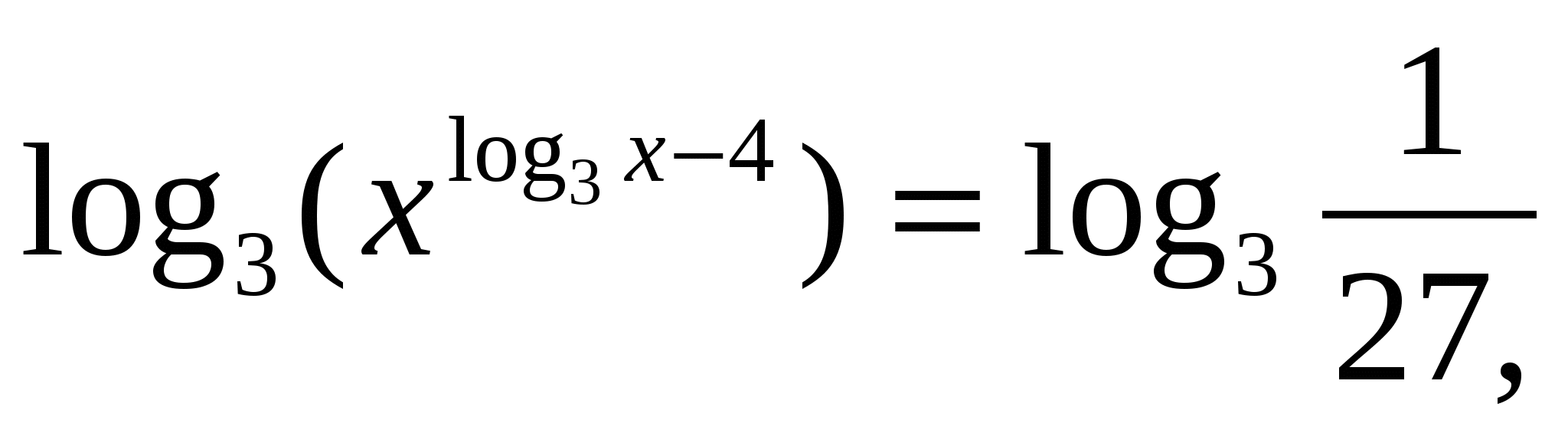а теперь воспользуемся свойством логарифмов 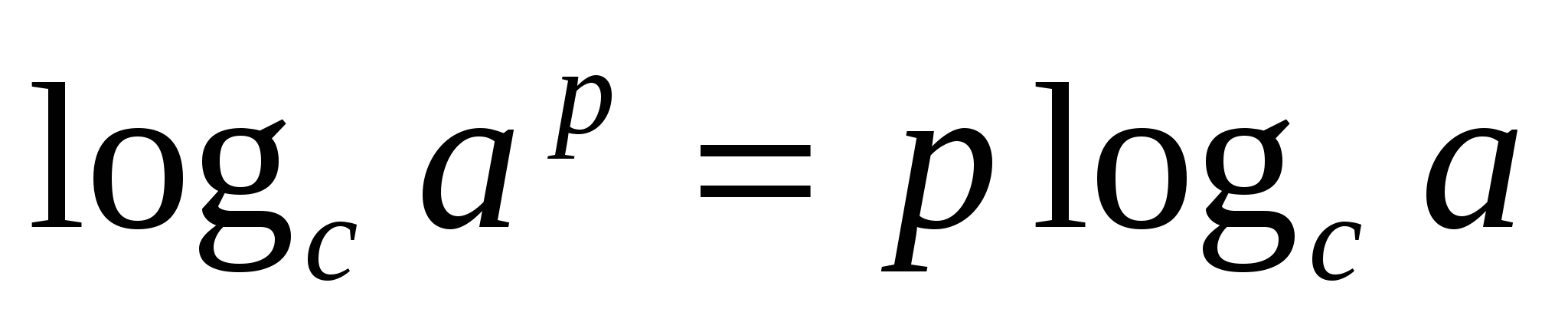, получим

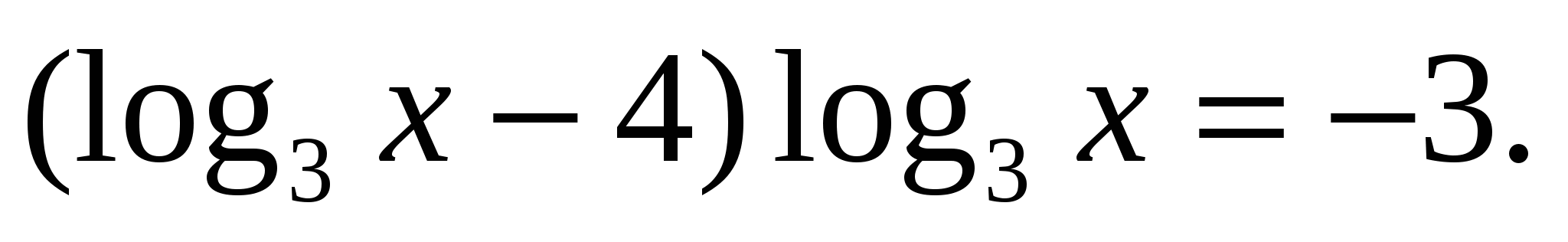
Выполним подстановку 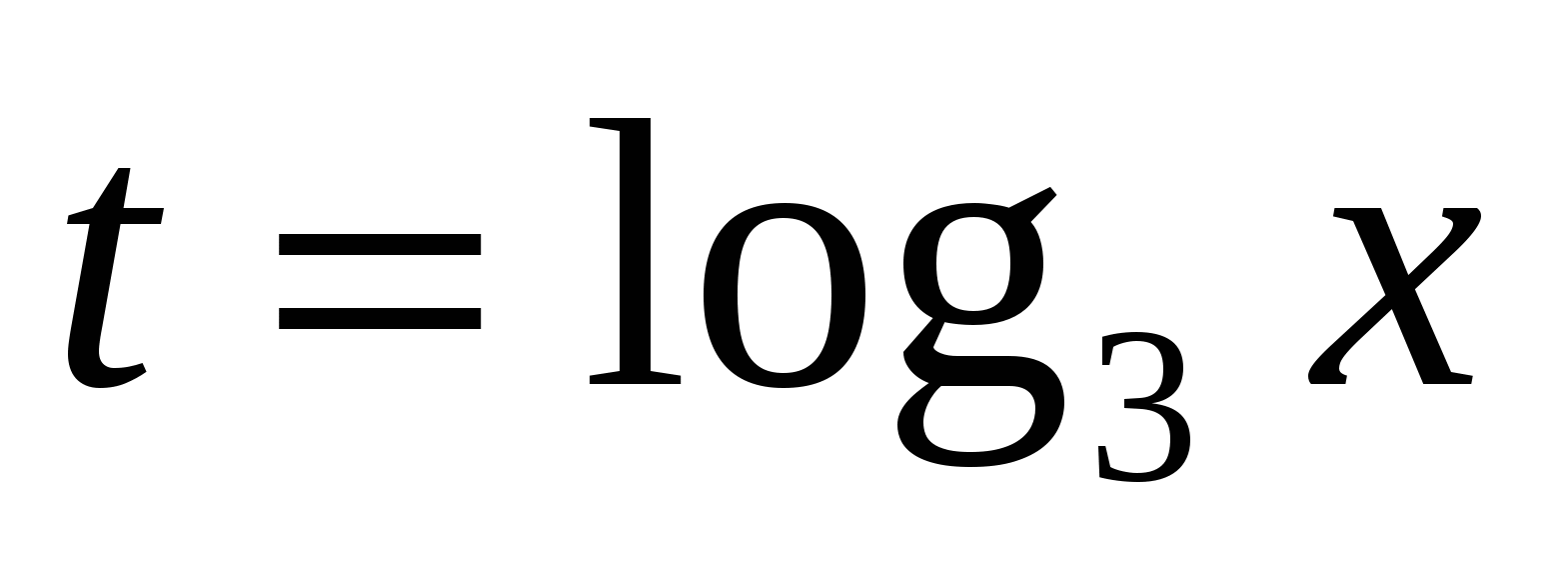, получим уравнение

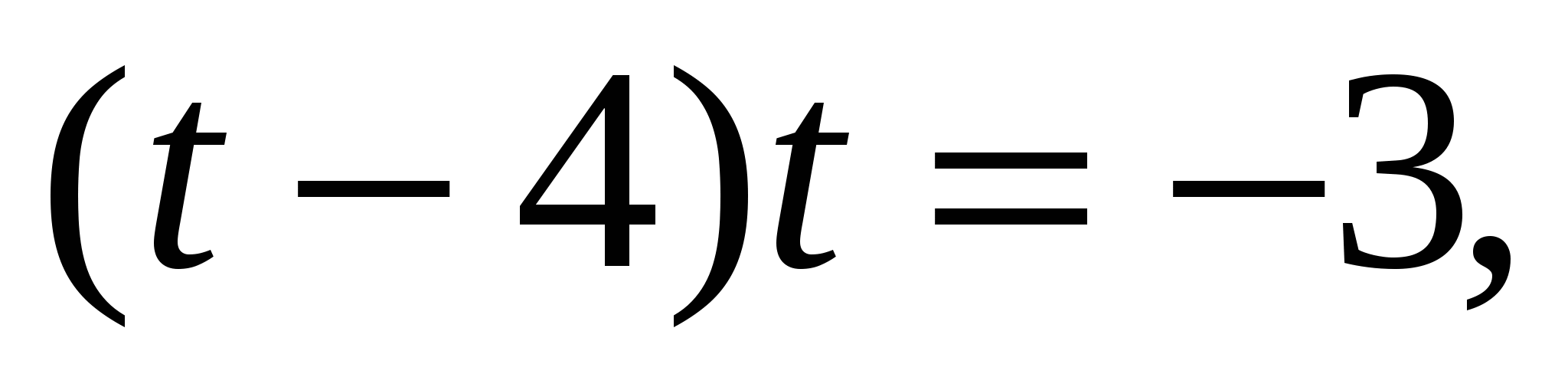
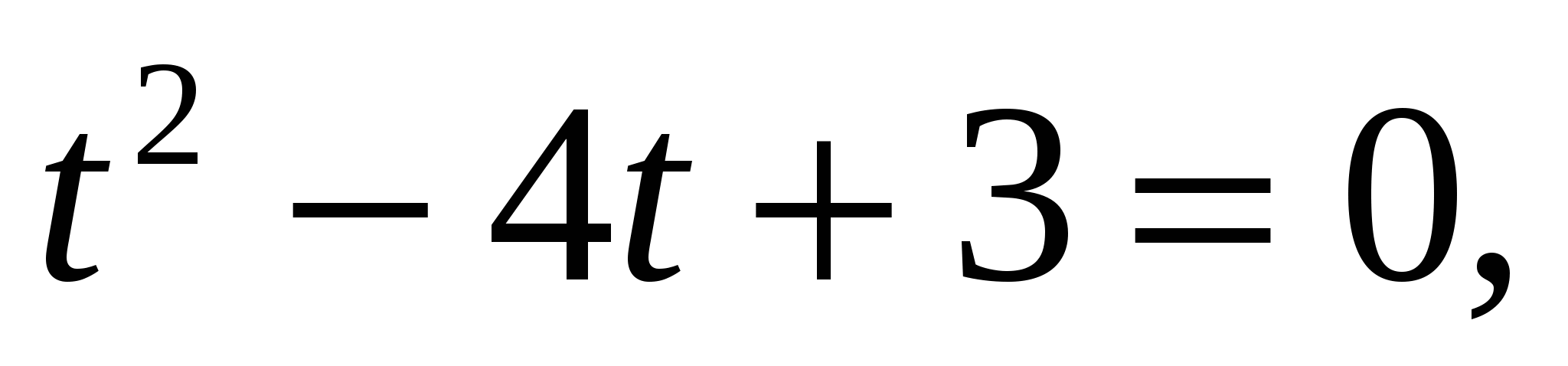
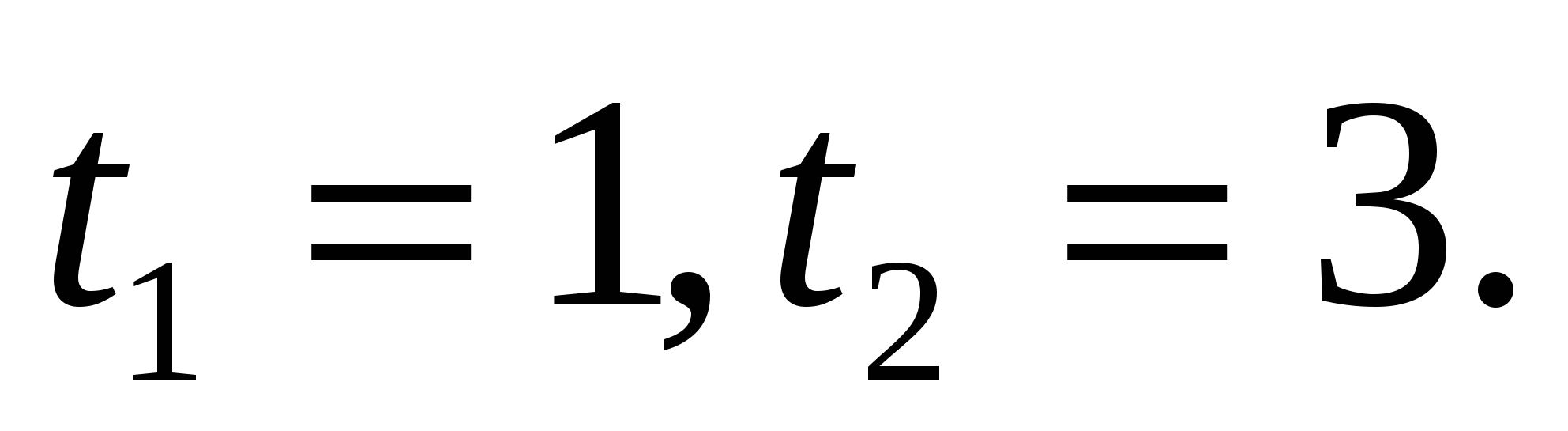
Значит, 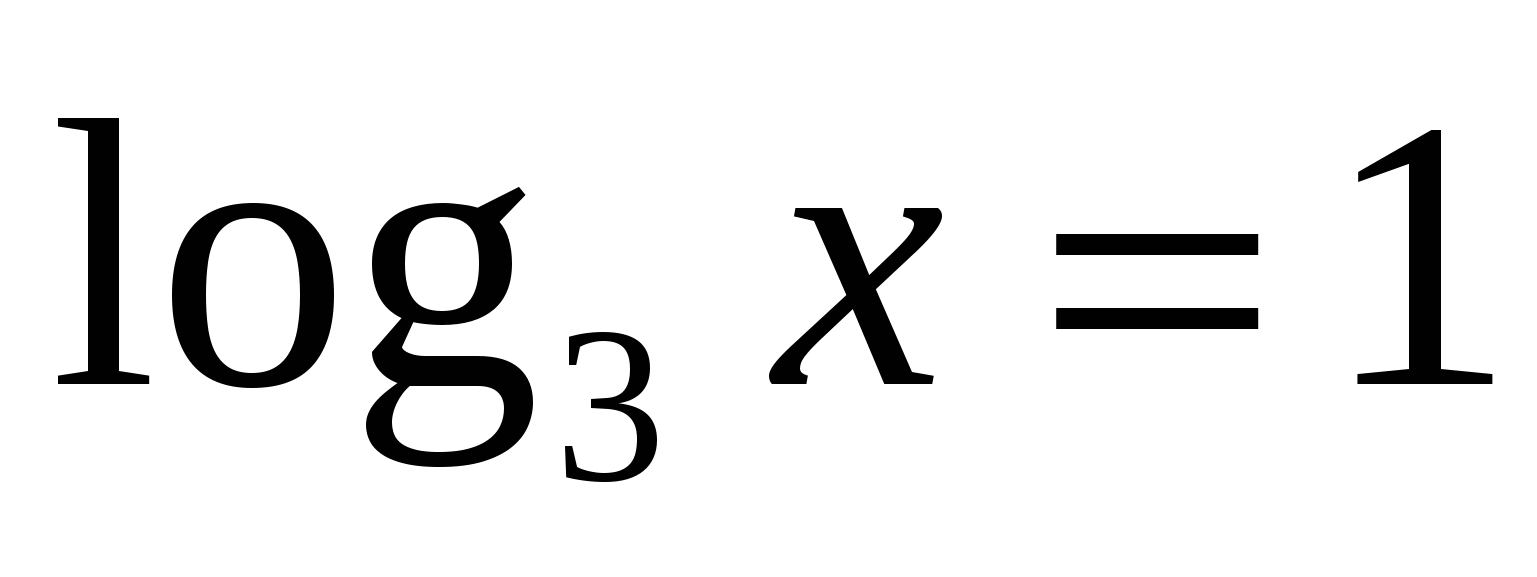или .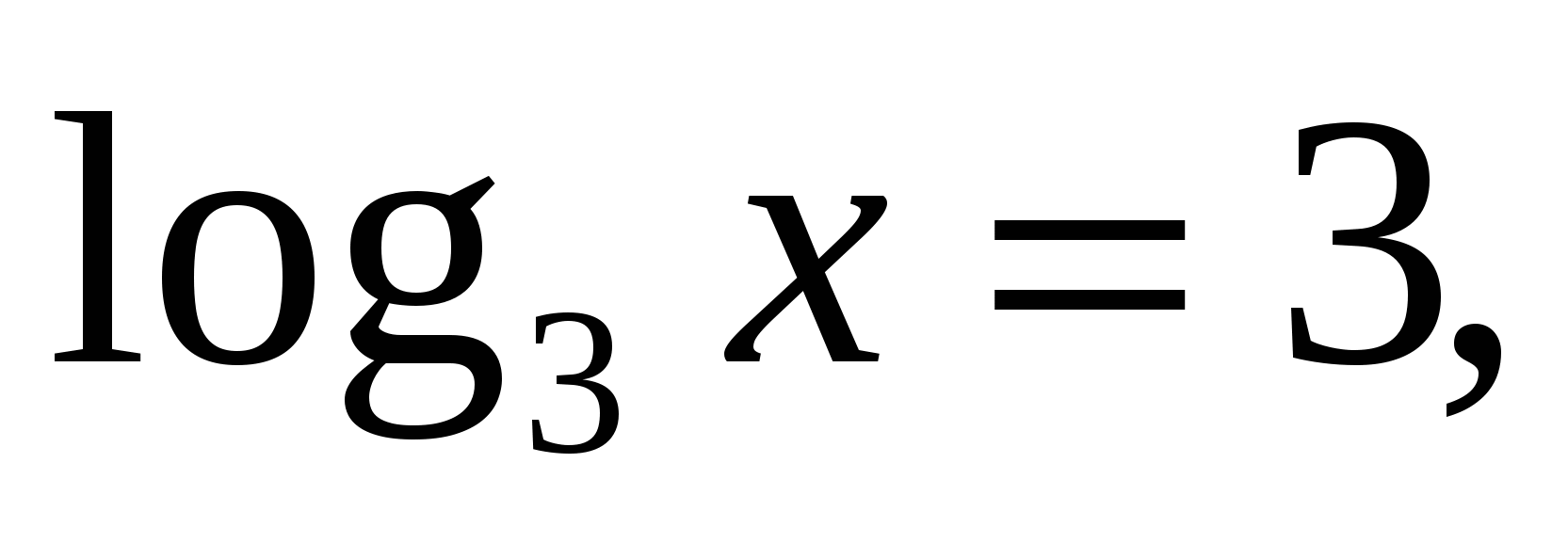

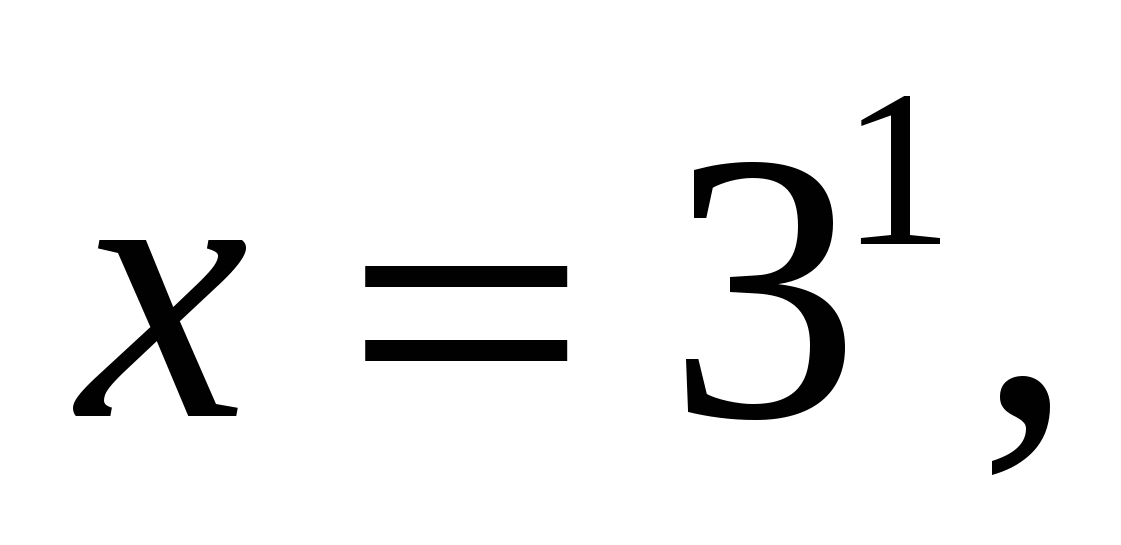
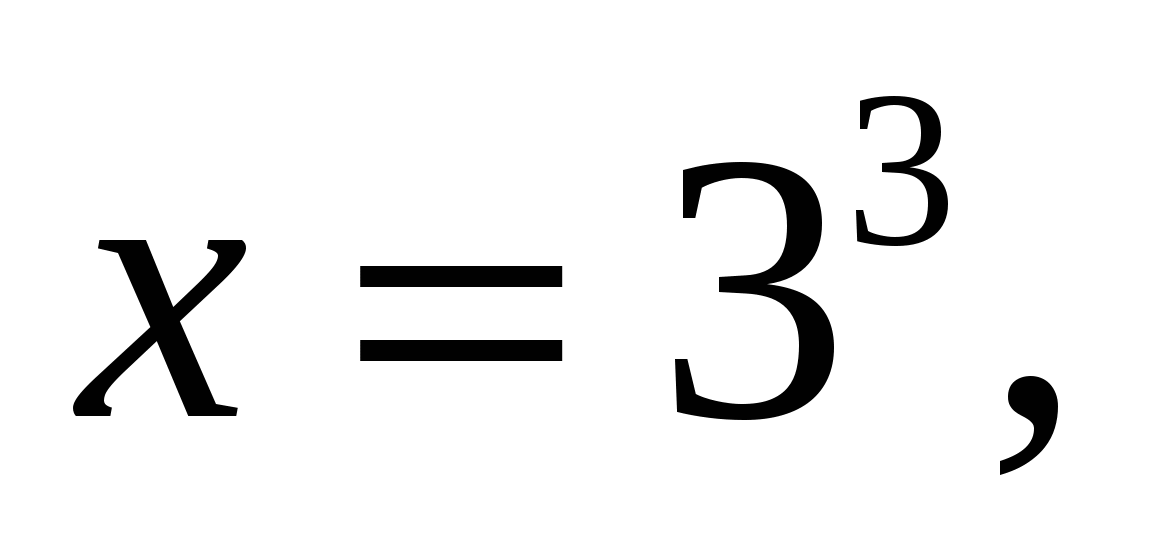
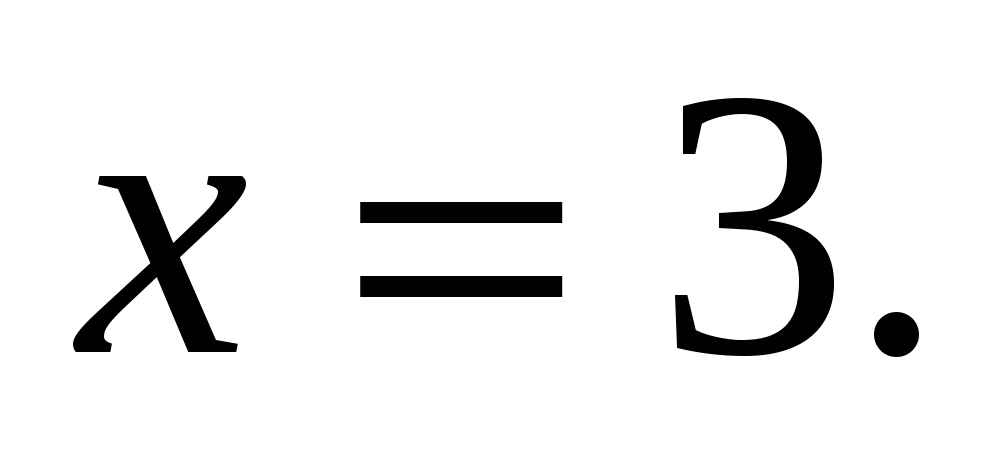
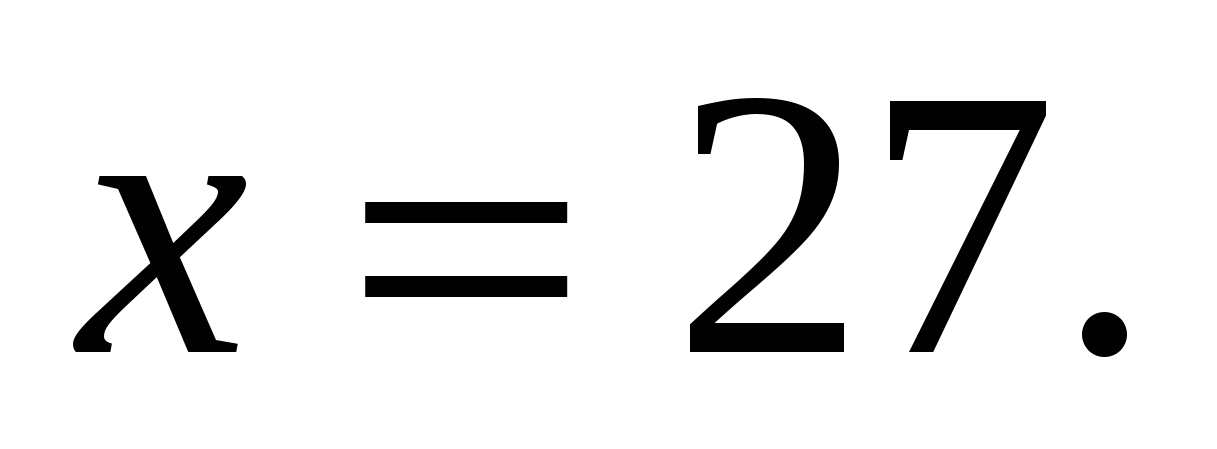
Оба числа удовлетворяют ОДЗ.

Ответ: 3, 27.

Этот пример показывает, что при решении логарифмических уравнений, возможна комбинация нескольких методов. А значит необходимо уметь пользоваться каждым из них. Научиться этому – теперь ваша задача.

Слайд 12.

Итак, сегодня мы с вами рассмотрели основные методы решения логарифмических уравнений:

1. На основании определения логарифма.

2. Метод потенцирования.

3. Метод постановки.

4. Метод логарифмирования.

Главным, по моему мнению, является метод, основанный на определении логарифма. Практически в каждом их других методов происходит «выход» на него. Кроме того, на примерах мы увидели, что все методы взаимосвязаны, в «чистом» виде при решении уравнений не используется ни один из них. Поэтому вам необходимо уметь пользоваться КАЖДЫМ!

Для отработки навыков решения логарифмических уравнений, я вам предлагаю следующее домашнее задание. Уравнения являются базовыми, т. е. решать их должен уметь решать каждый. Отмечу, что подборка сделана из открытого банка заданий для экзамена по математике ЕГЭ http://mathege.ru .

№ п/п

Уравнения

Комментарии

(даётся для слабых учащихся)

1

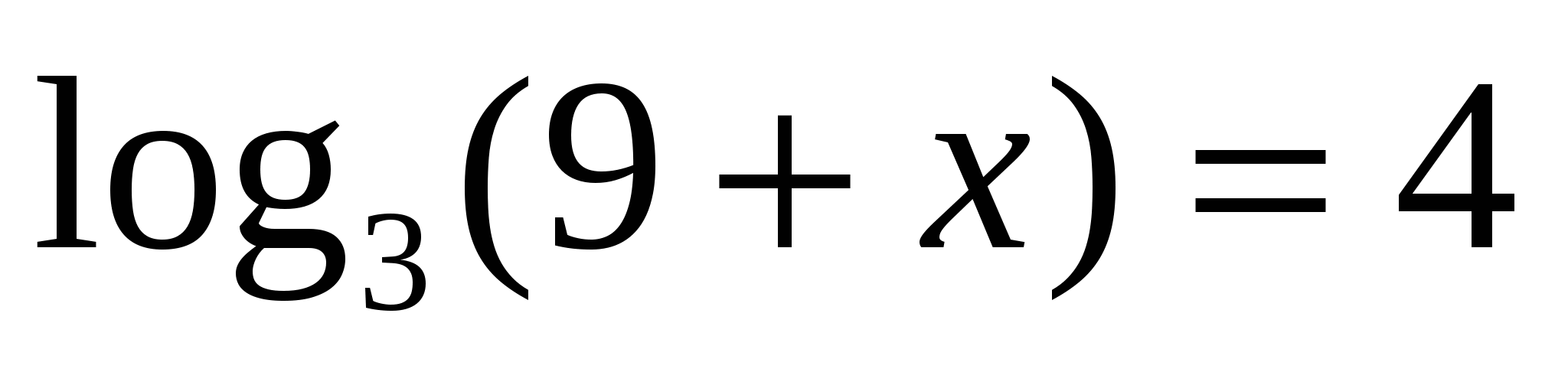
Пользуясь определением

2

Пользуясь определением

3

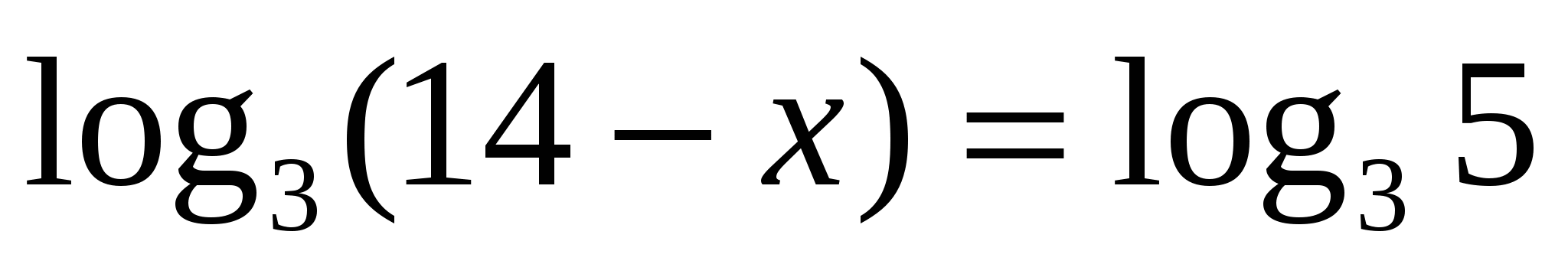
Потенциирование

4

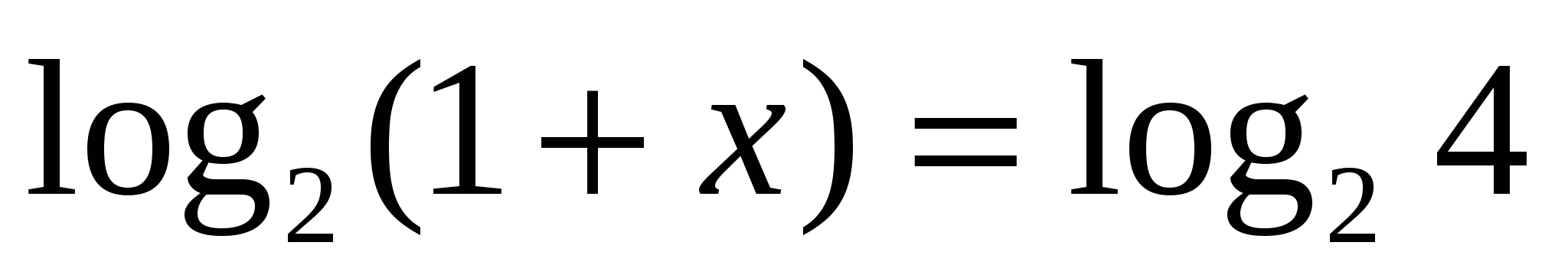
Потенциирование

5

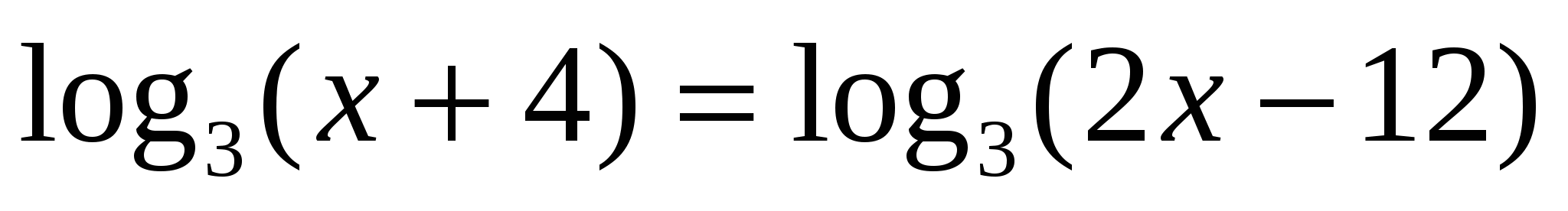
Потенциирование

6

Потенциирование

7

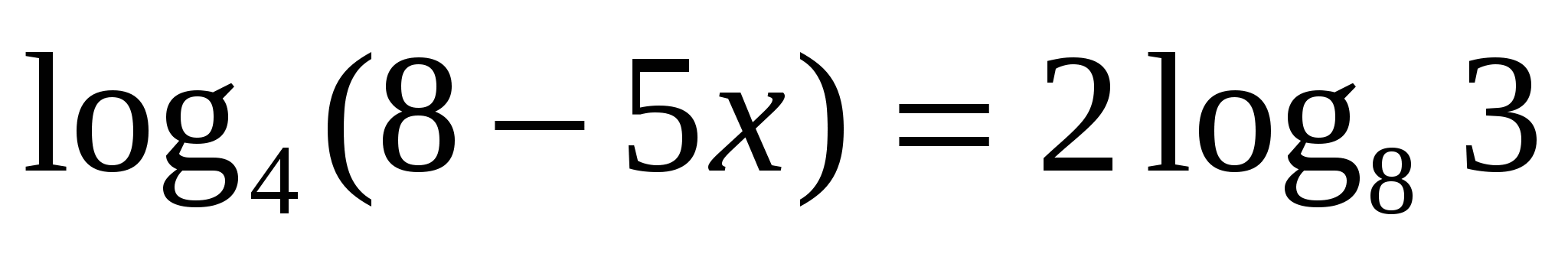
Применить свойства логарифмов и затем потенциировать

8

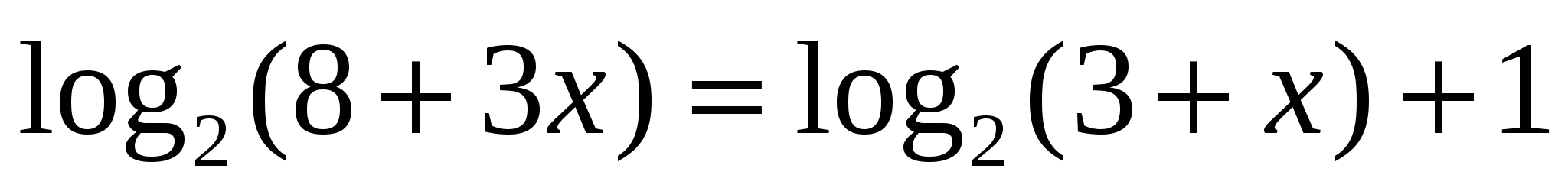
Применить свойства логарифмов и затем потенциировать

9

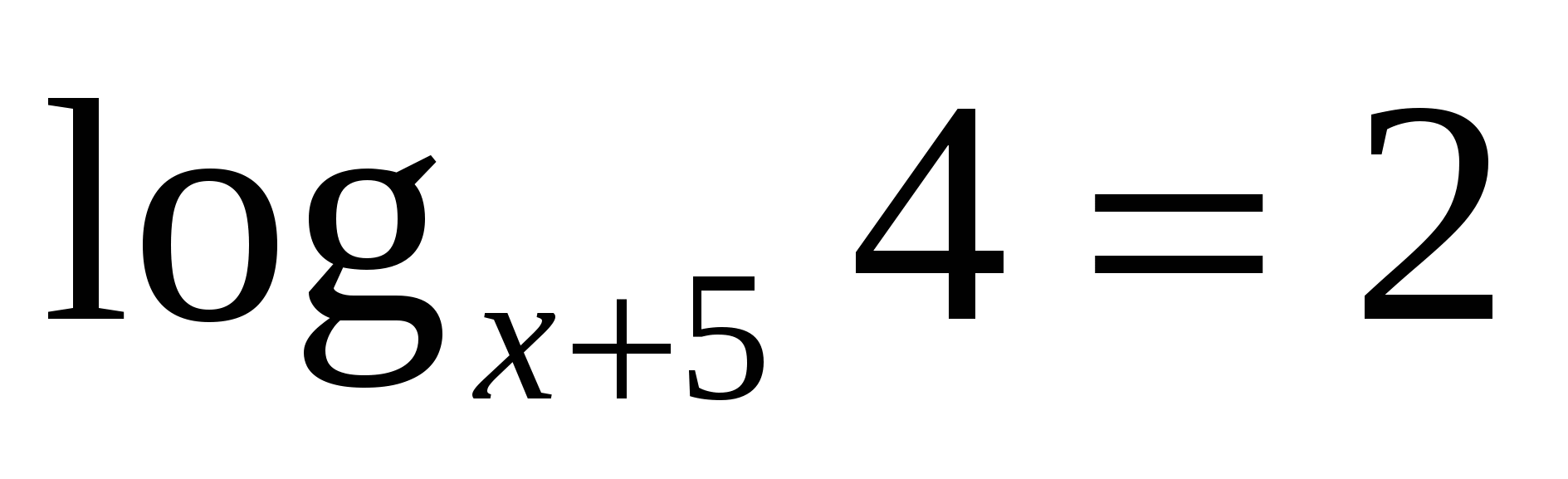
Пользуясь определением

10

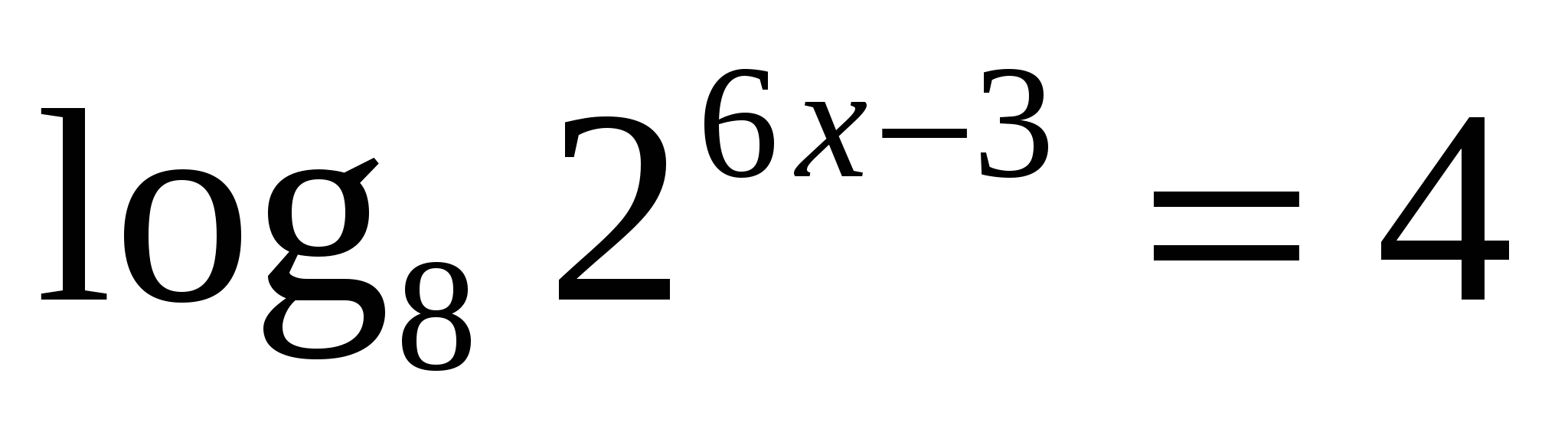
Пользуясь определением, выход на показательное уравнение

11

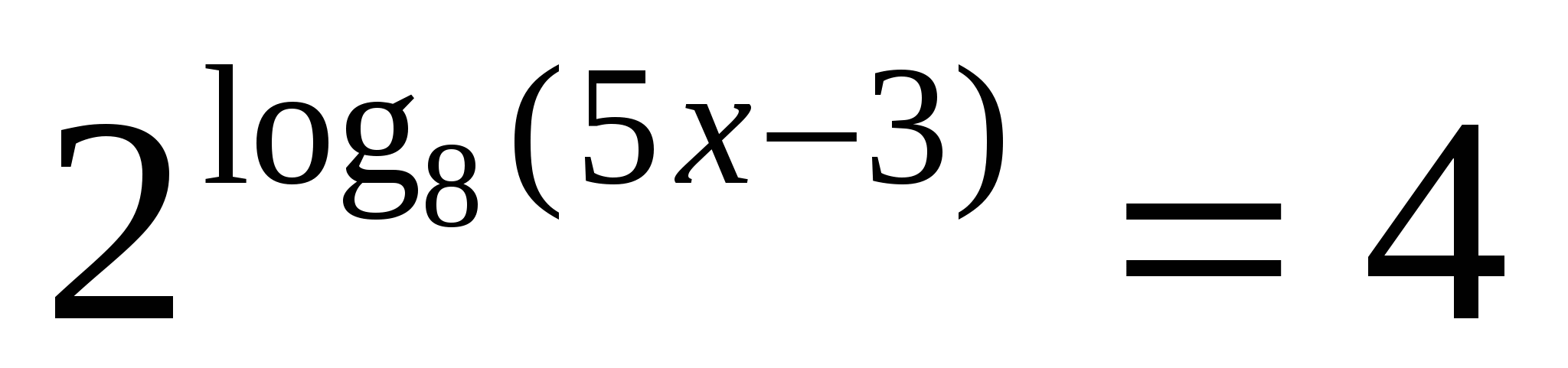
Показательное уравнение, выход на логарифмическое

Замечание: домашнее задание распечатано на листах для каждого ученика.

Слайд 13.

2, 3 урок

Решение задач по теме «Логарифмические уравнения». Зачёт.

Уравнения (примерные, зависит от математической подготовки учащихся).

Обязательный уровень

Повышенный уровень

1

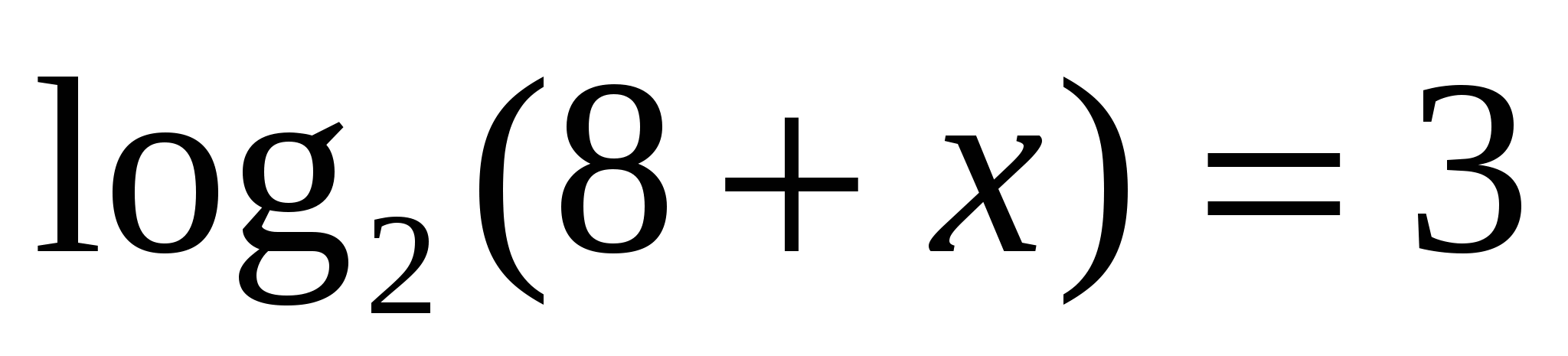
1

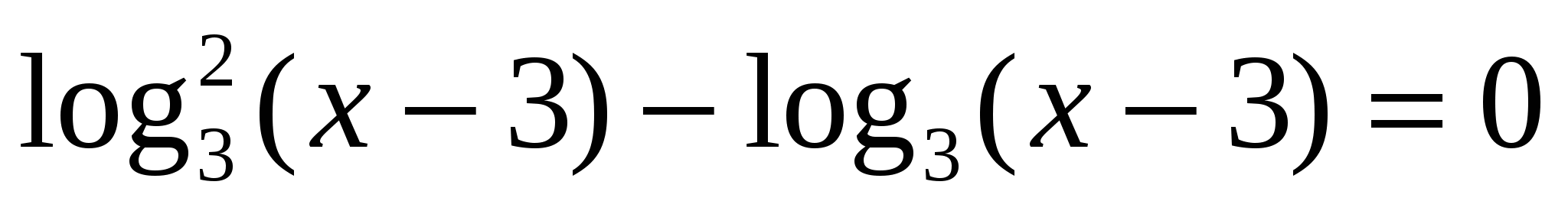
2

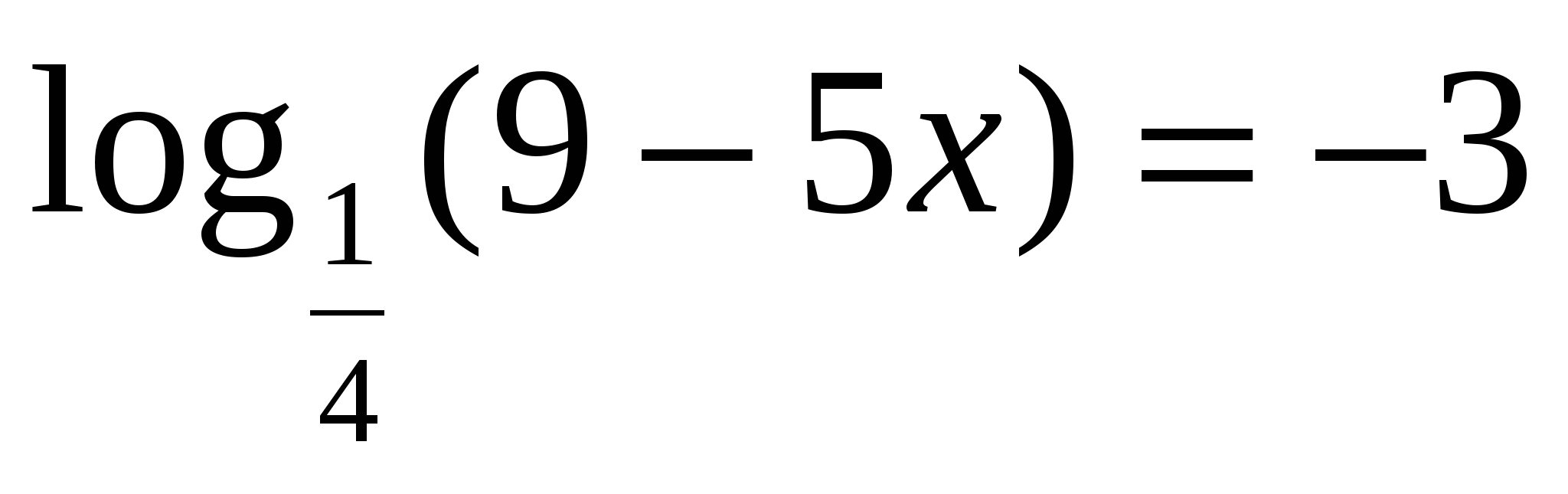
2

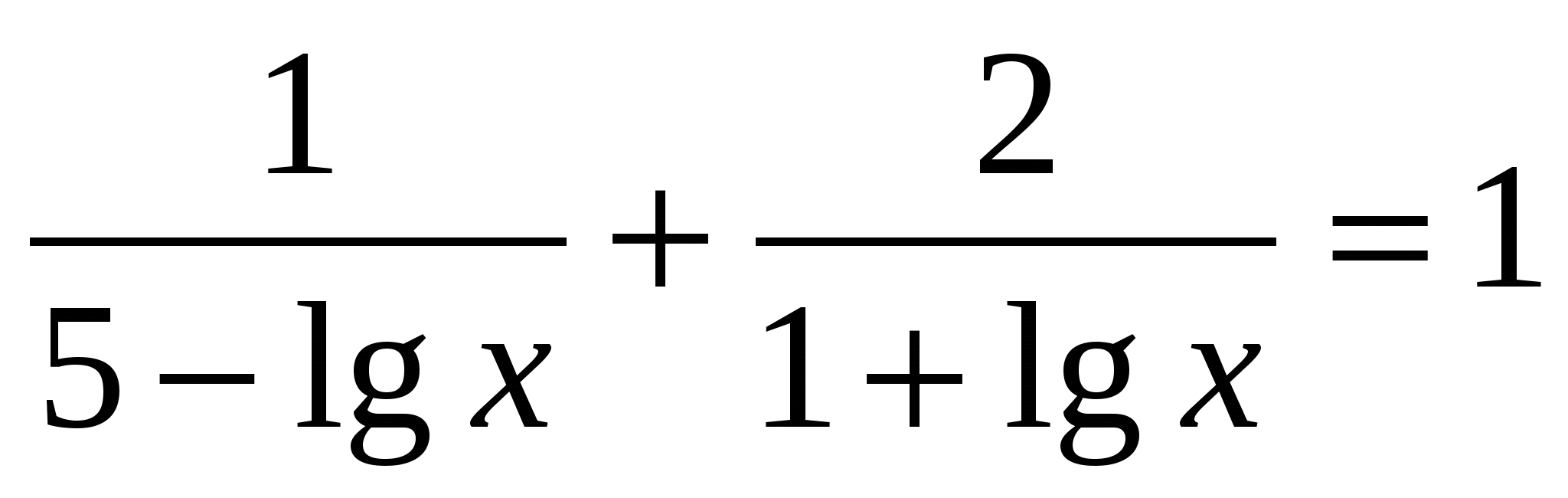
3

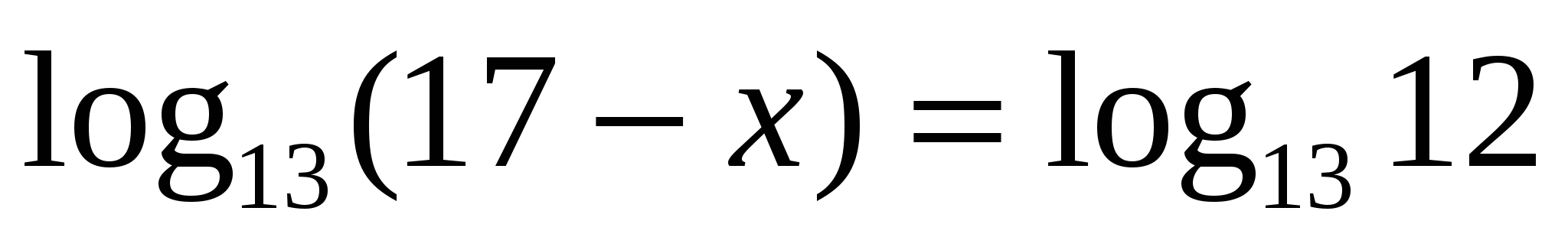
3

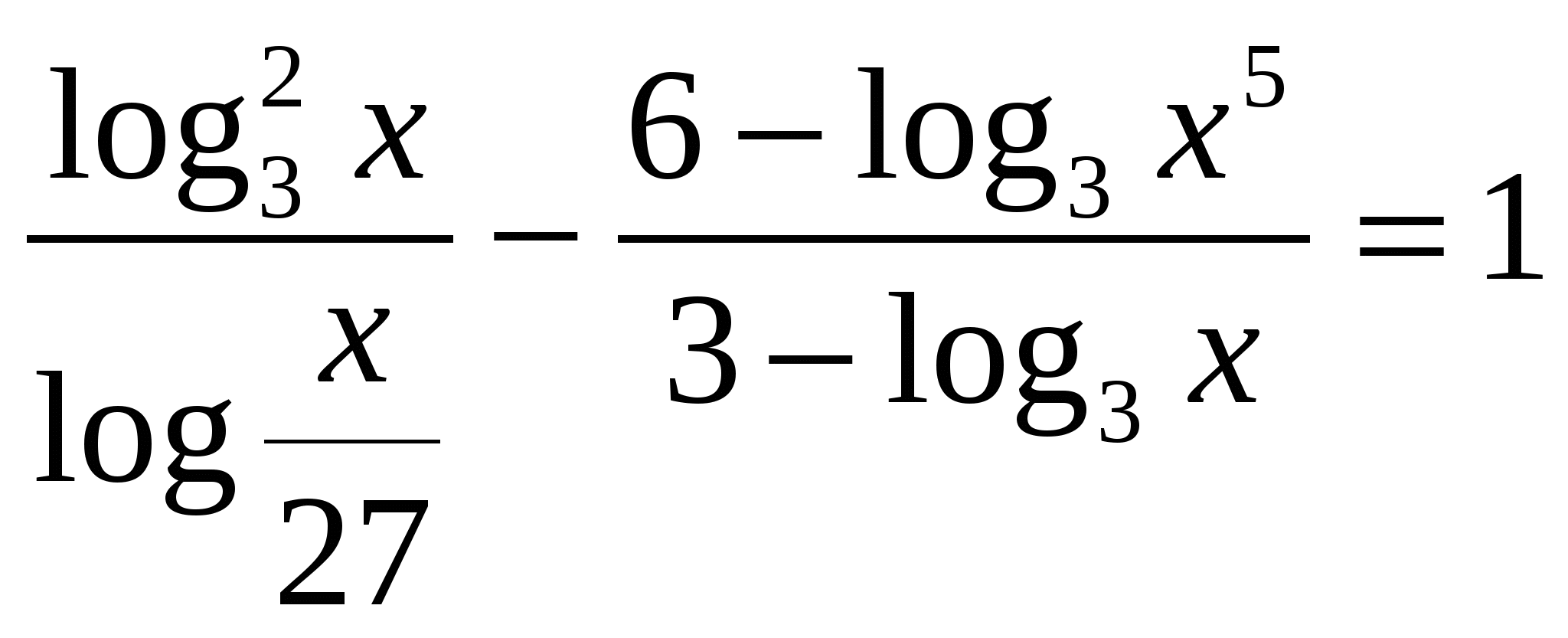
4

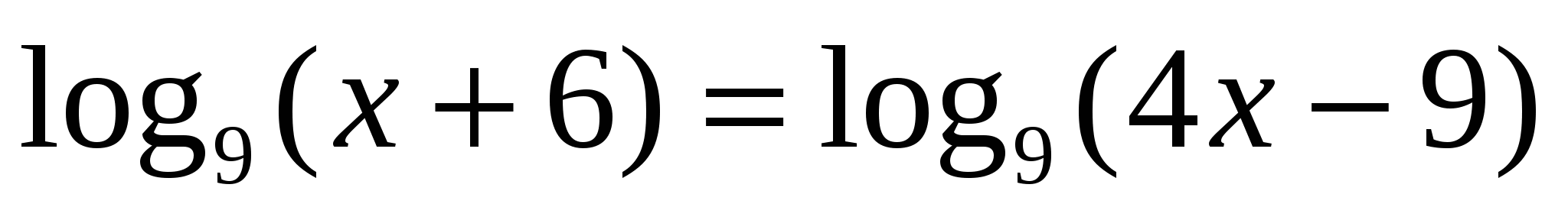
4

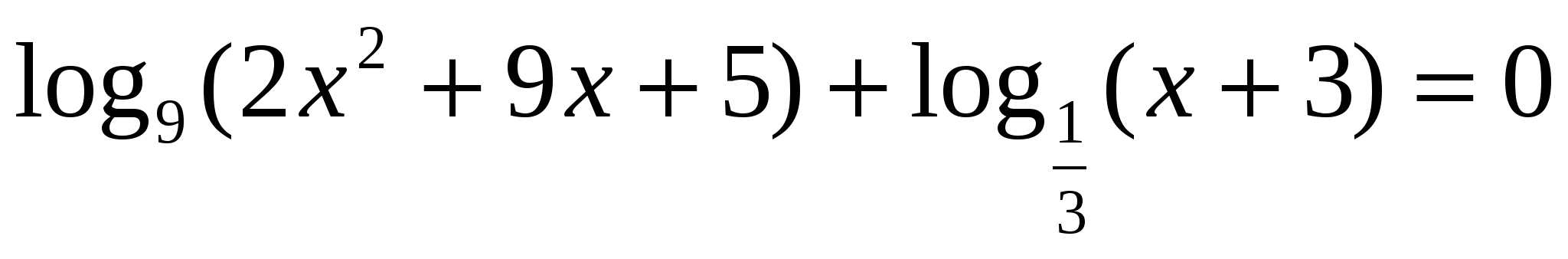
5

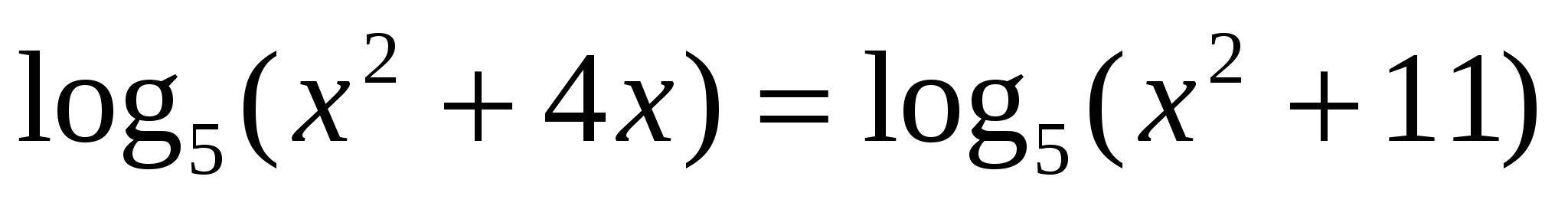
5

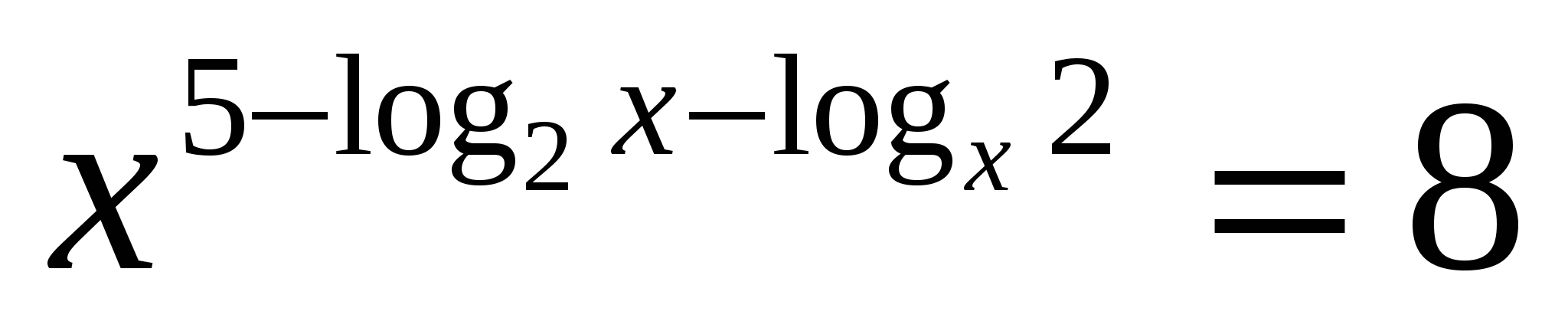
6

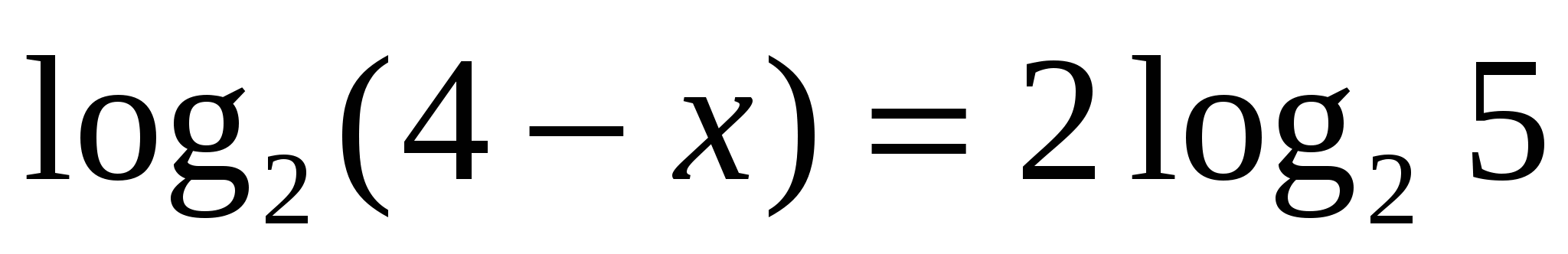
6

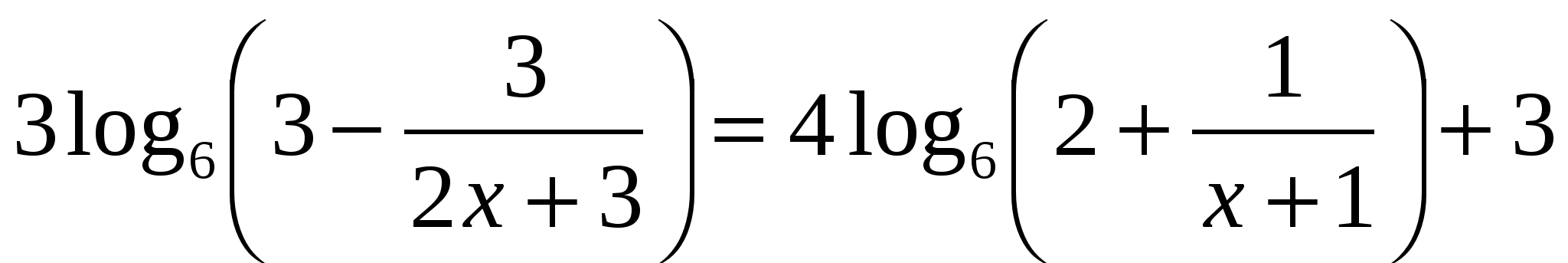
7

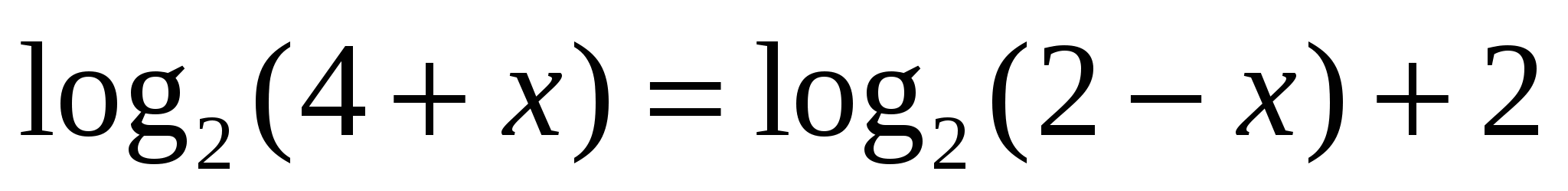
7

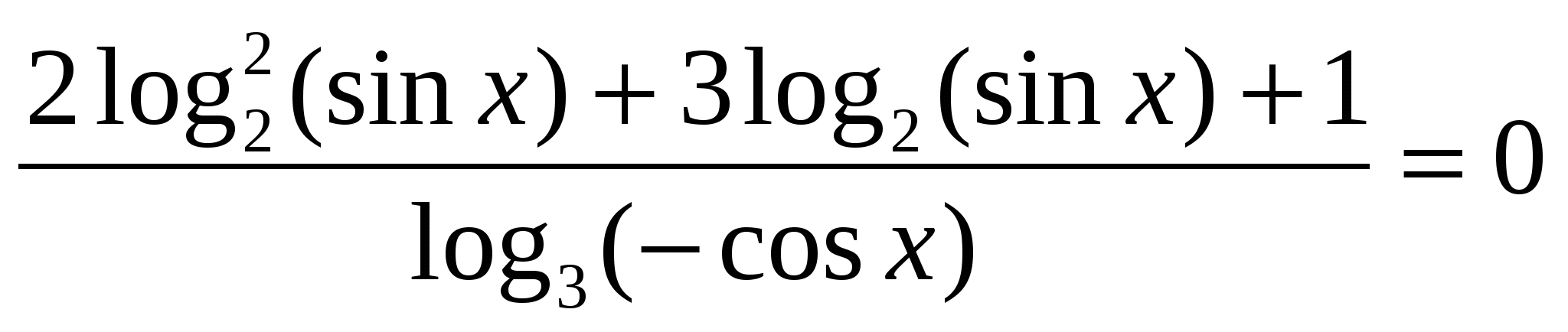
8

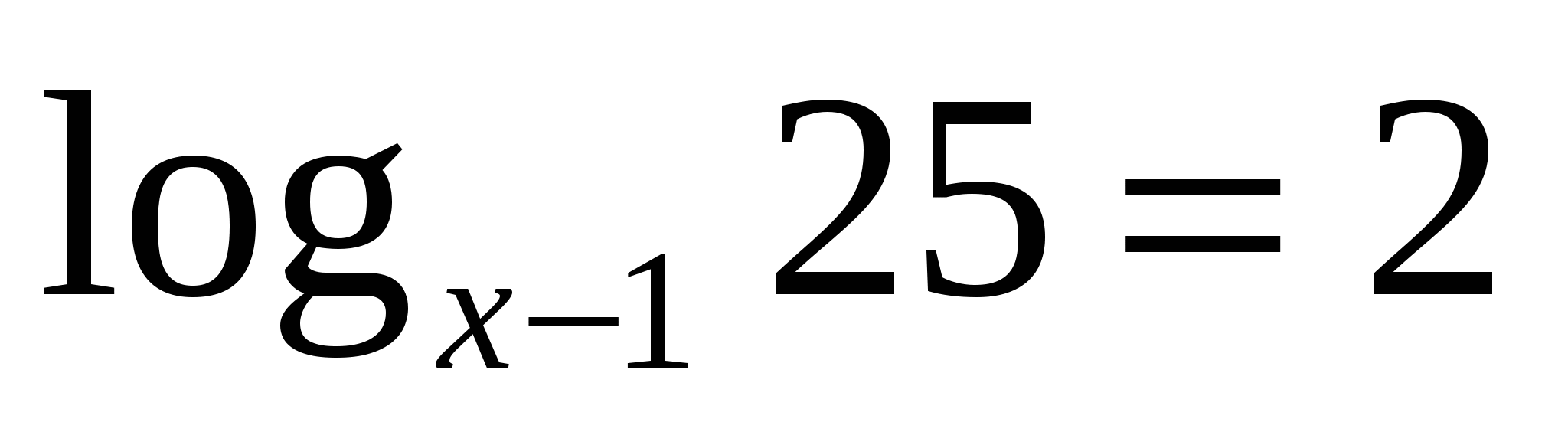
8

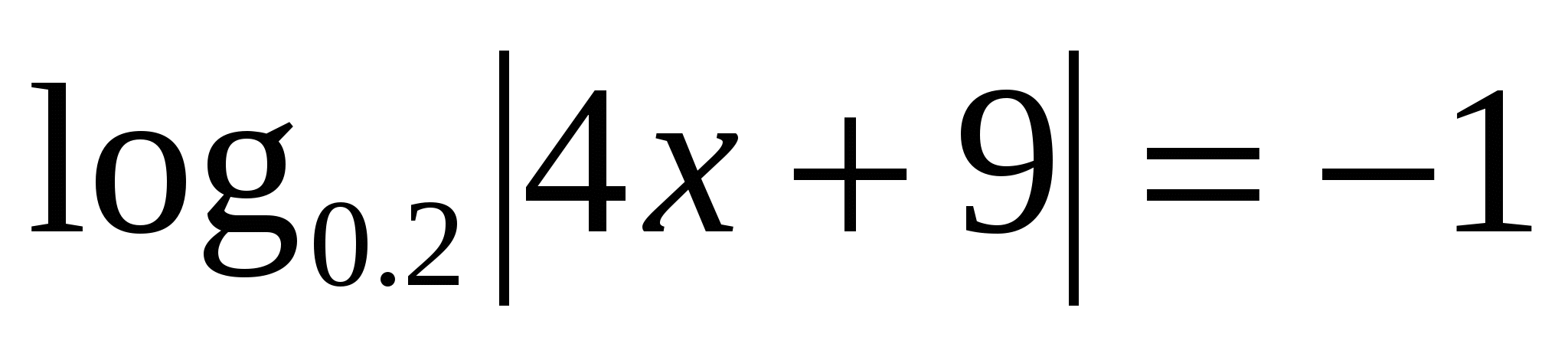
9

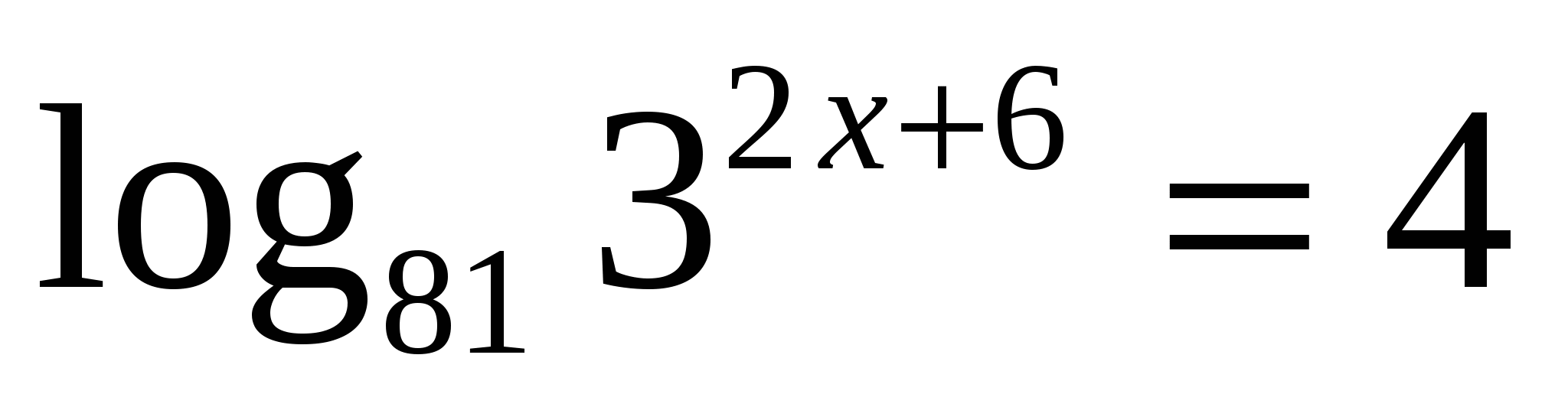
9

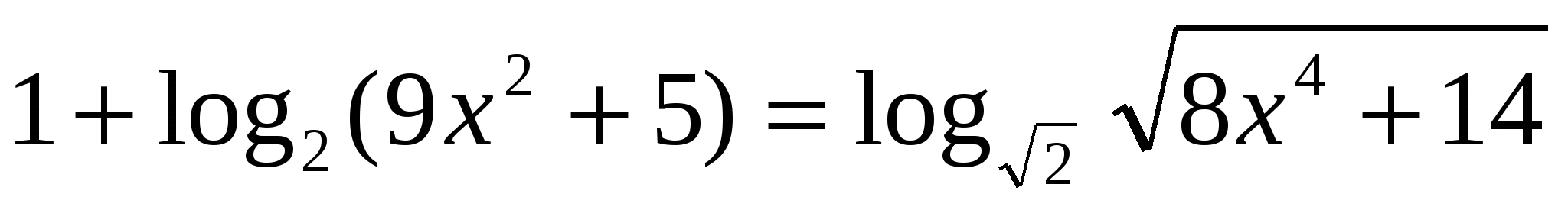. Найти все корни, принадлежащие отрезку 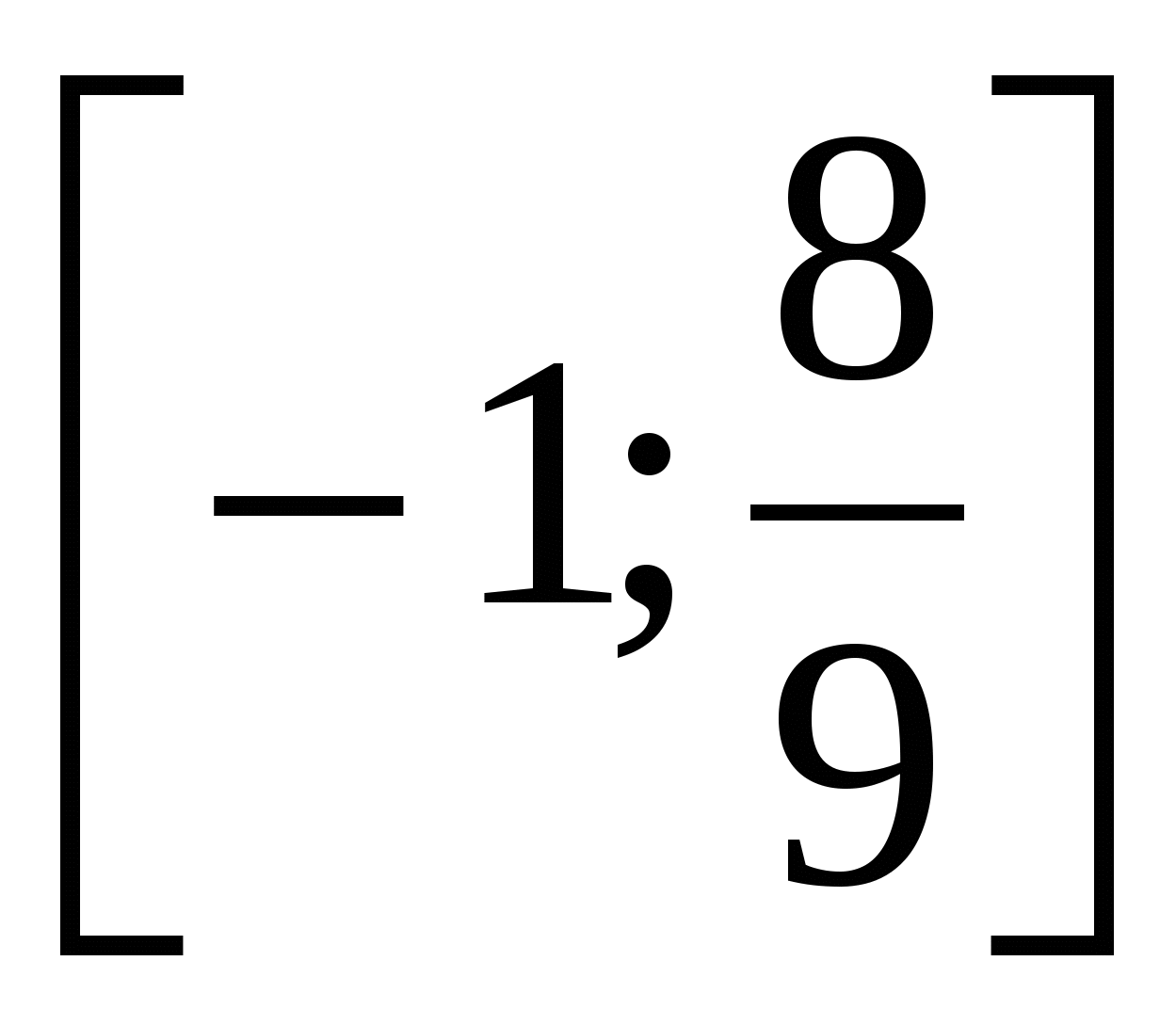. ЕГЭ, 2013

10

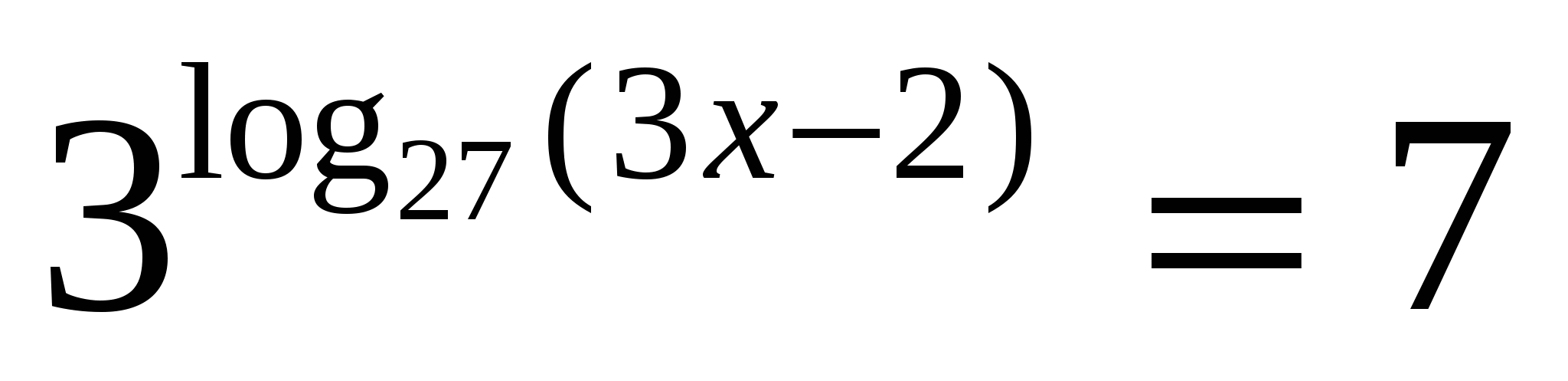
10

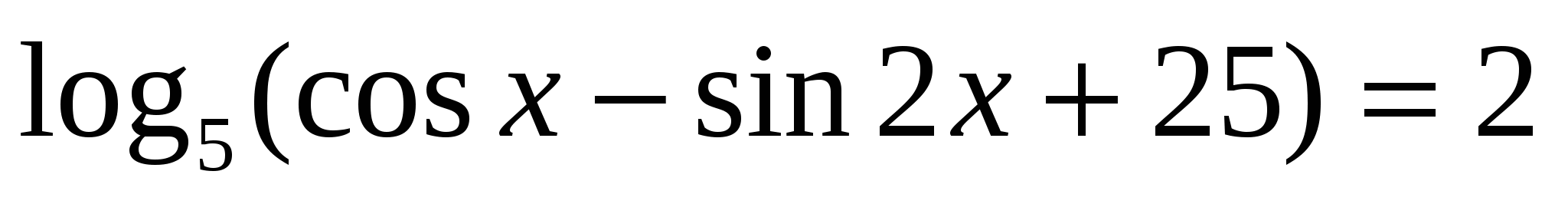. Найти все корни, принадлежащие отрезку 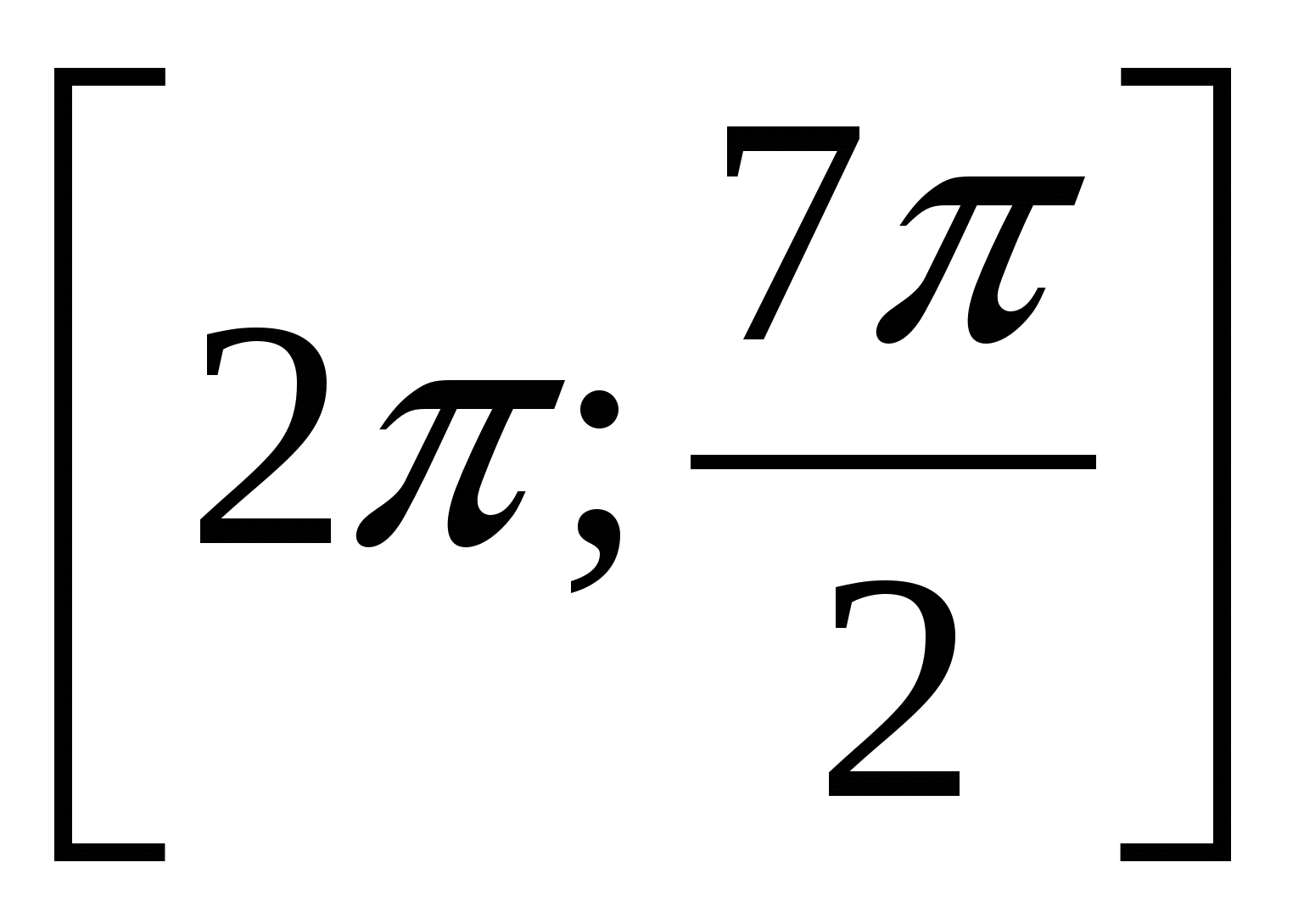. ЕГЭ, 2012.

11

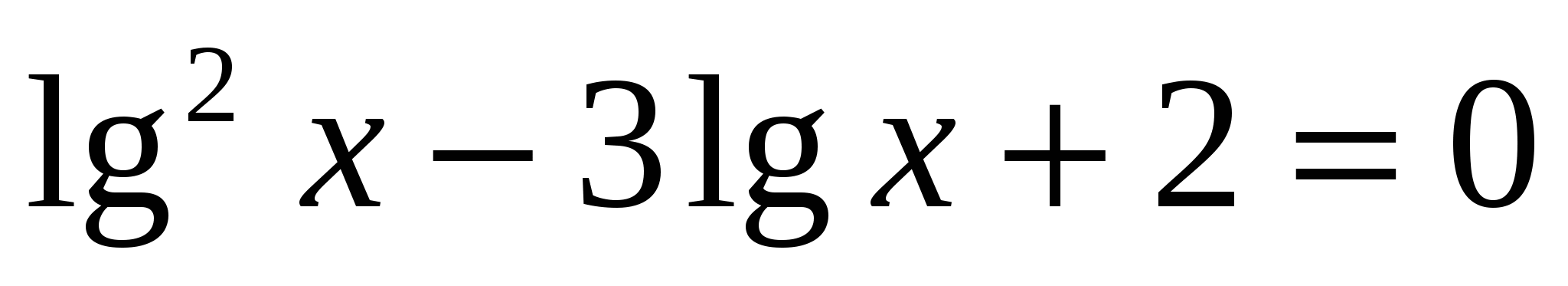
11

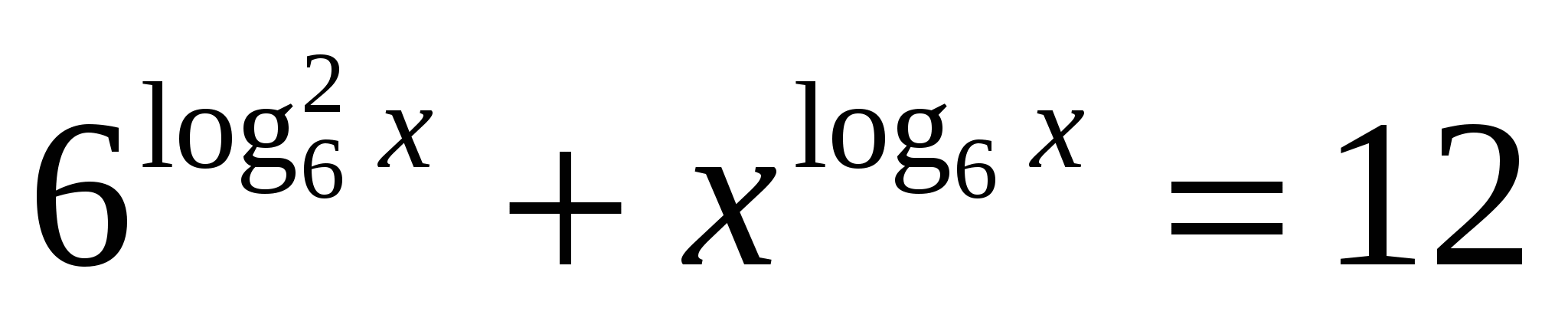
12

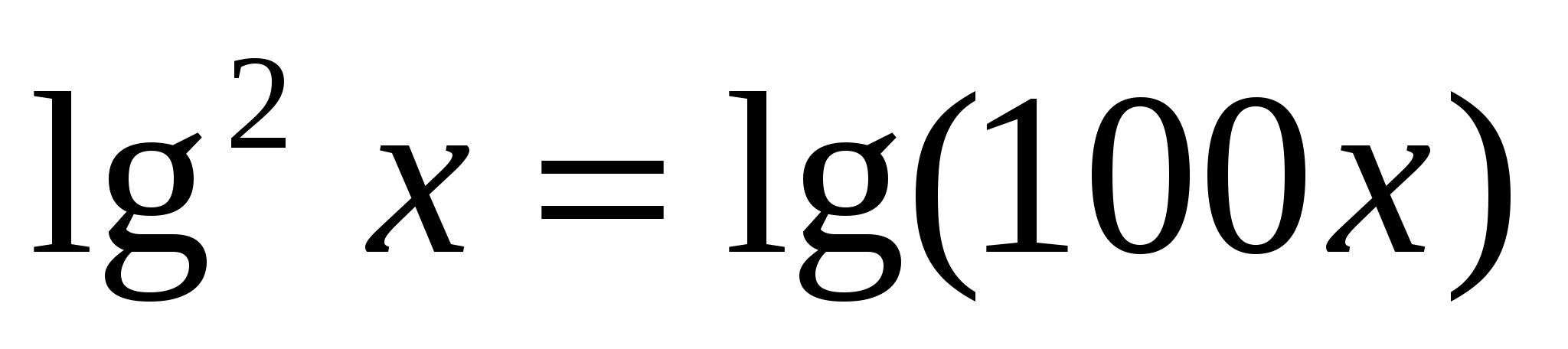
12

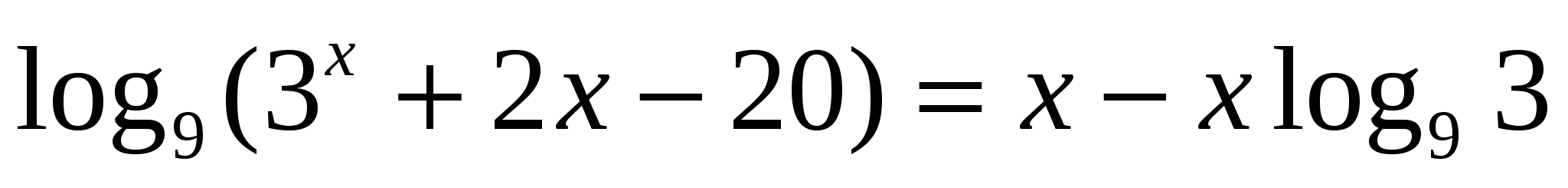
Подборка уравнений к уроку, зачёту проводится на сайтах www.fipi.ru , http://mathege.ru , http://mathus.ru/ , http://reshuege.ru/ , http://www.math.md/school/praktikum/logr/logr.html (Виртуальная школа юного математика).

Тест к зачёту.

№ п/п

Задание

Ответ

1

Обязательный уровень

Найдите корень уравнения .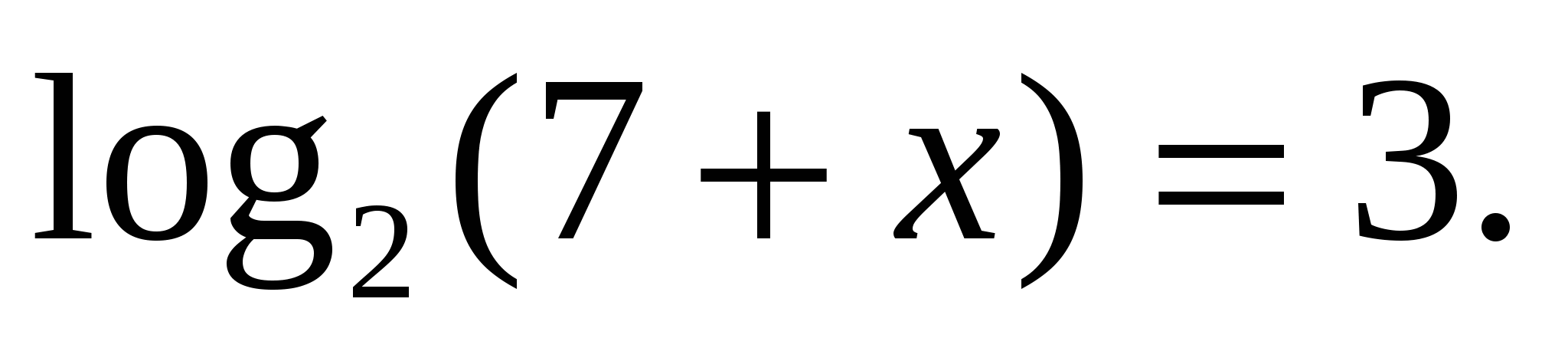

2

Найдите корень уравнения .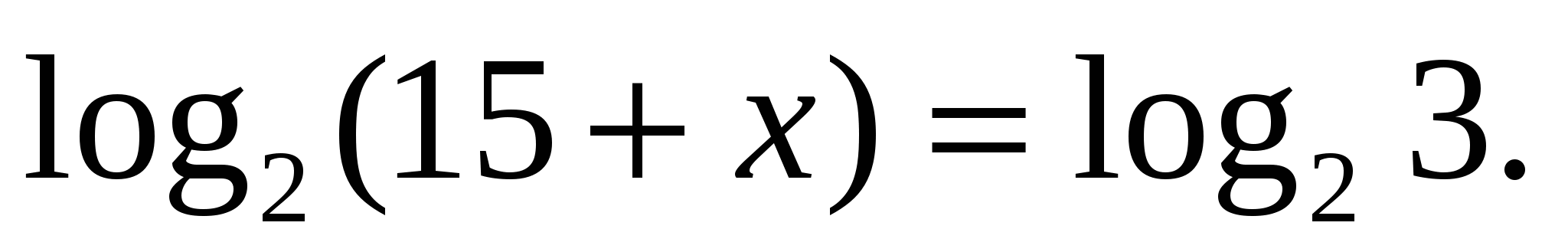

3

Найдите корень уравнения .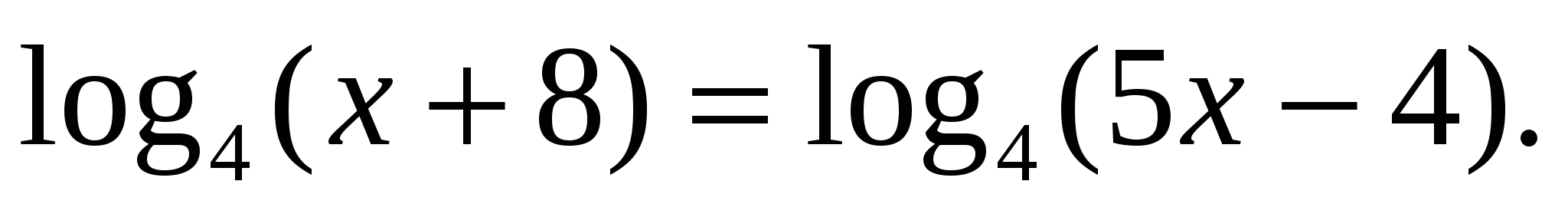

4

Найдите корень уравнения .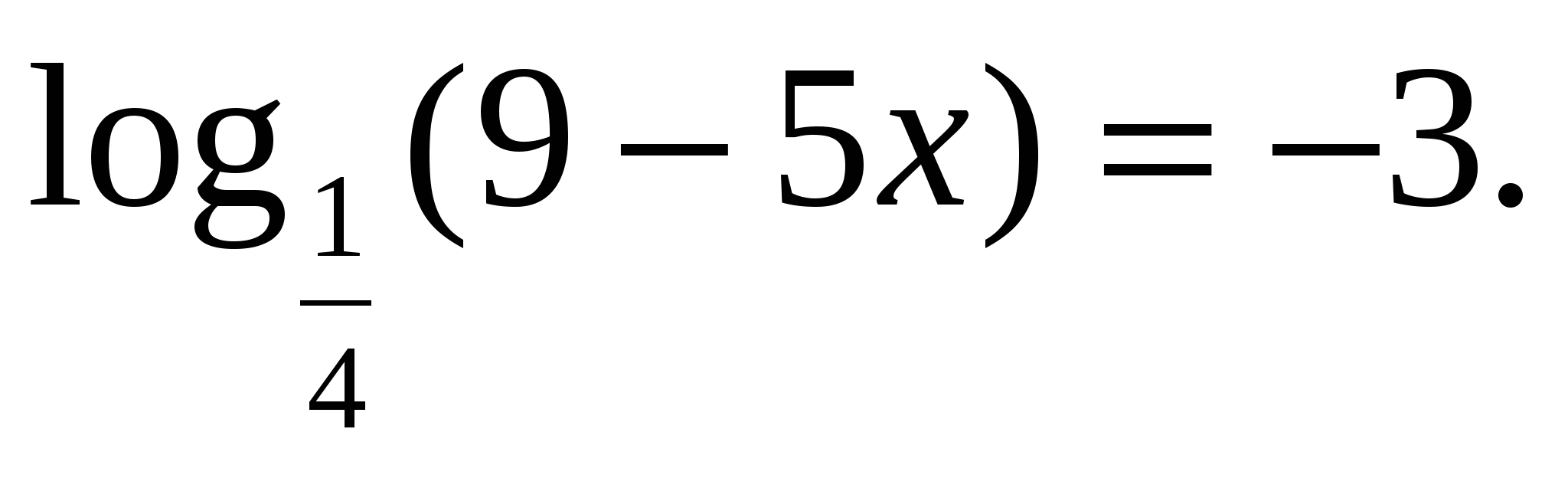

5

Найдите корень уравнения .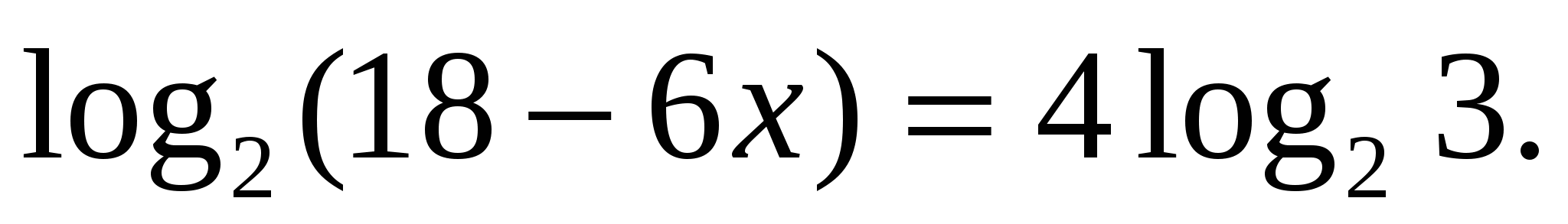

6

Найдите корень уравнения .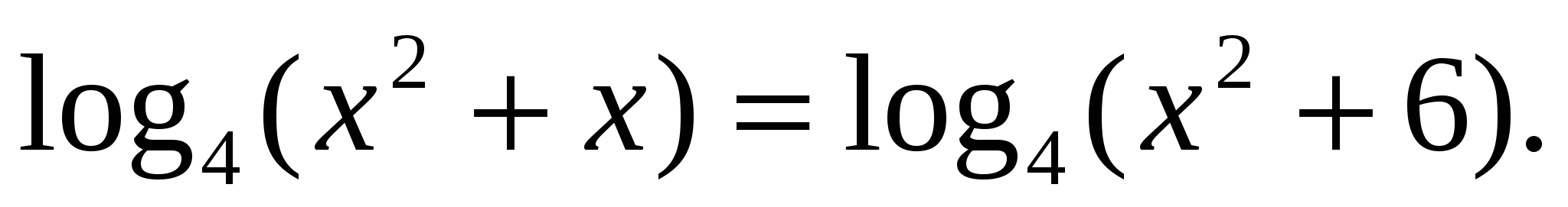

7

Найдите корень уравнения .

8

Найдите корень уравнения 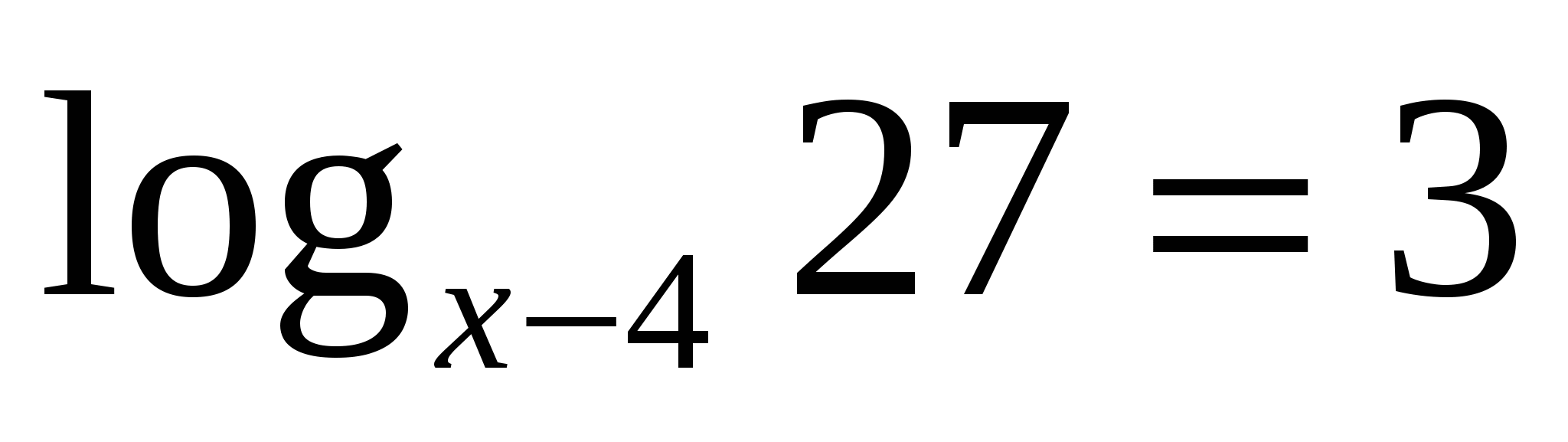. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

9

Найдите корень уравнения.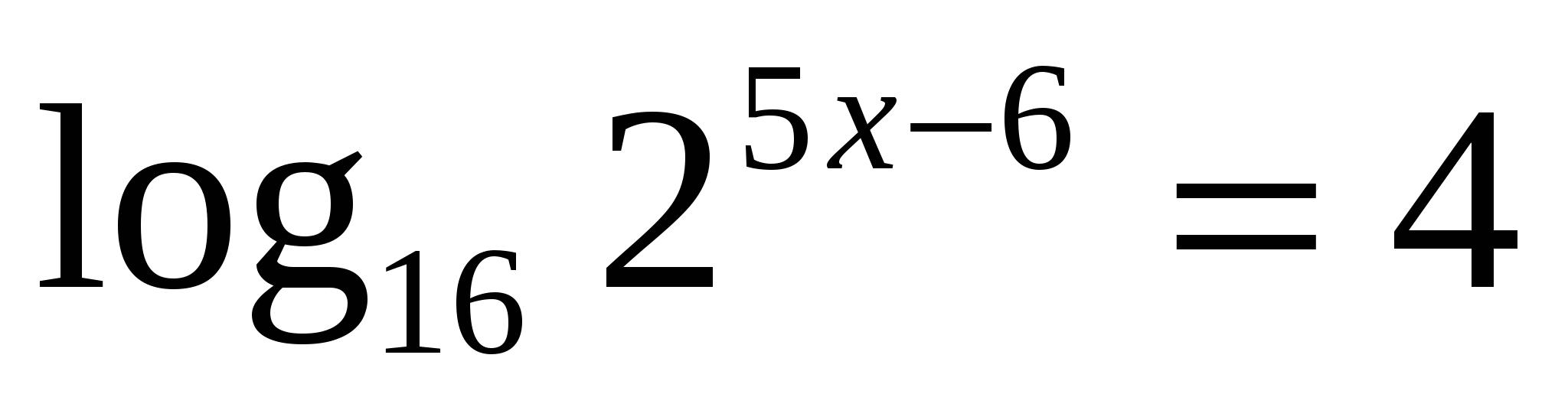

10

Найдите корень уравнения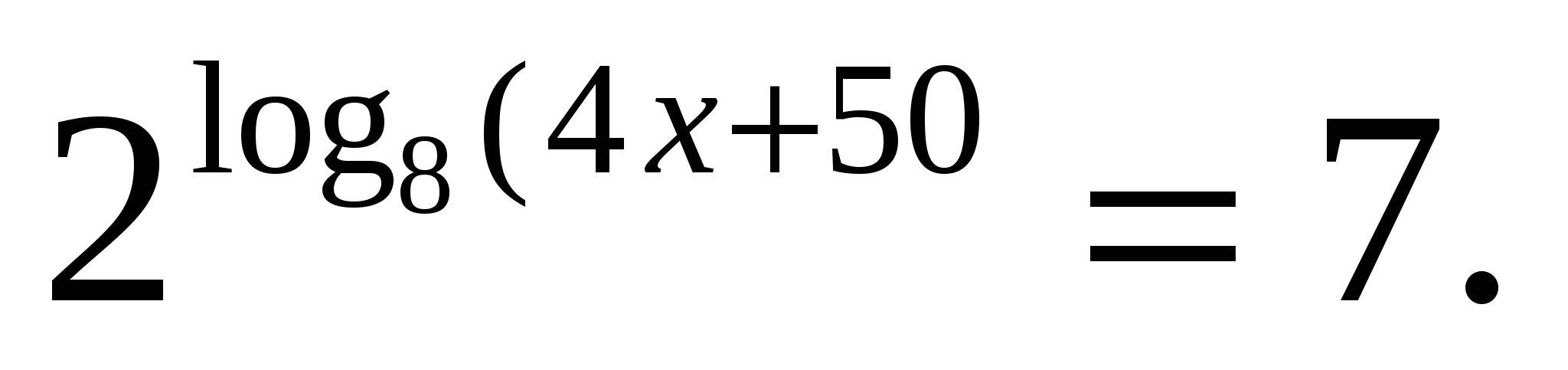 

11

Повышенный уровень

(решать по выбору)

Решить уравнение  log₂(5 + 3log₂(x — 3)) = 3.

Развёрнутое решение

12

Решить уравнение log_{2x + 1}(2x² — 8x + 15) = 2.

13

Решить уравнение 16^log₄^{(1 — 2x)} = 5x² — 5.

14

Решить уравнение 2log₃(x — 2) + log₃(x — 4)² = 0.

15

Решить уравнение log₂x + log₃x = 1.

16

Решить уравнение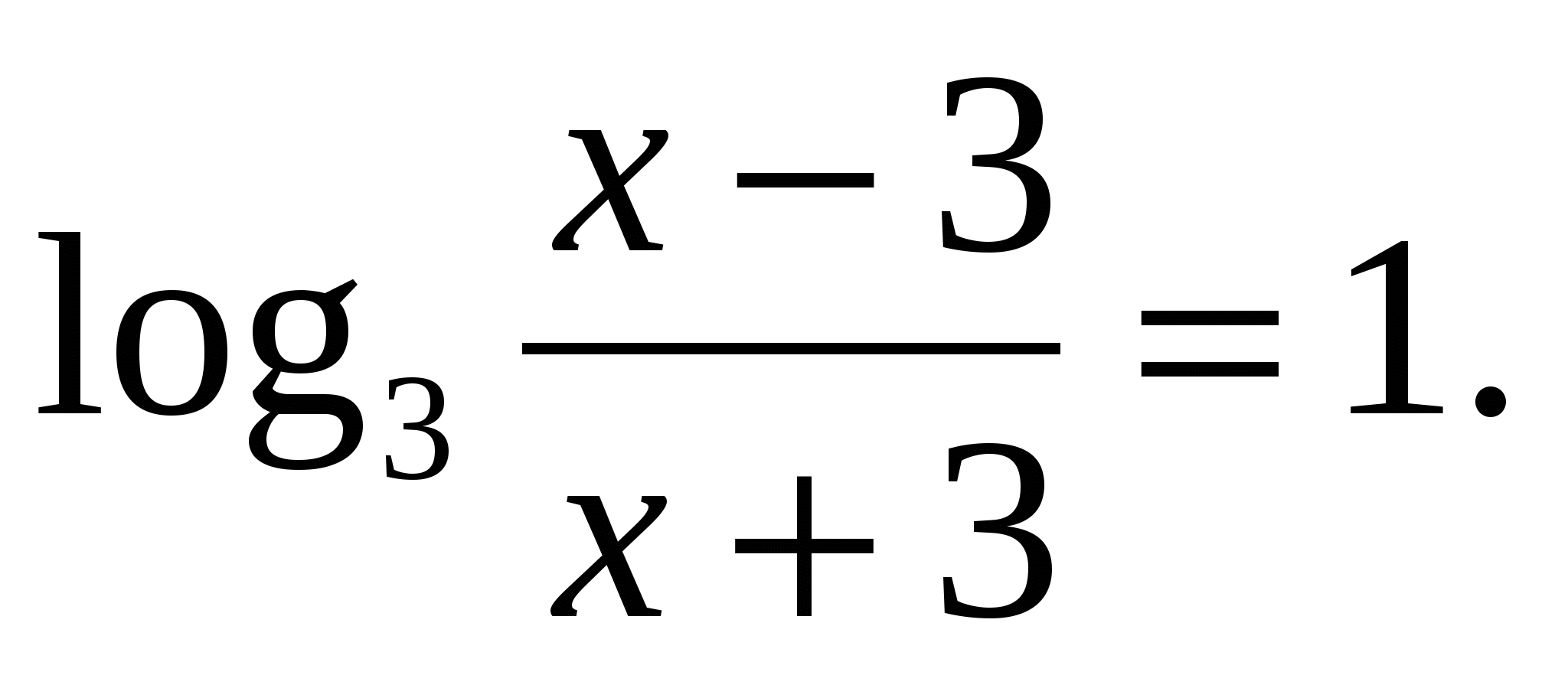

17

Решить уравнение .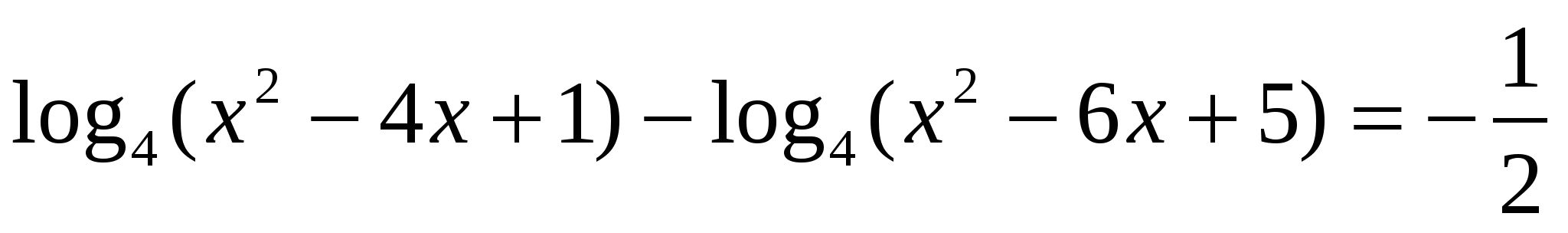

18

Решить уравнение 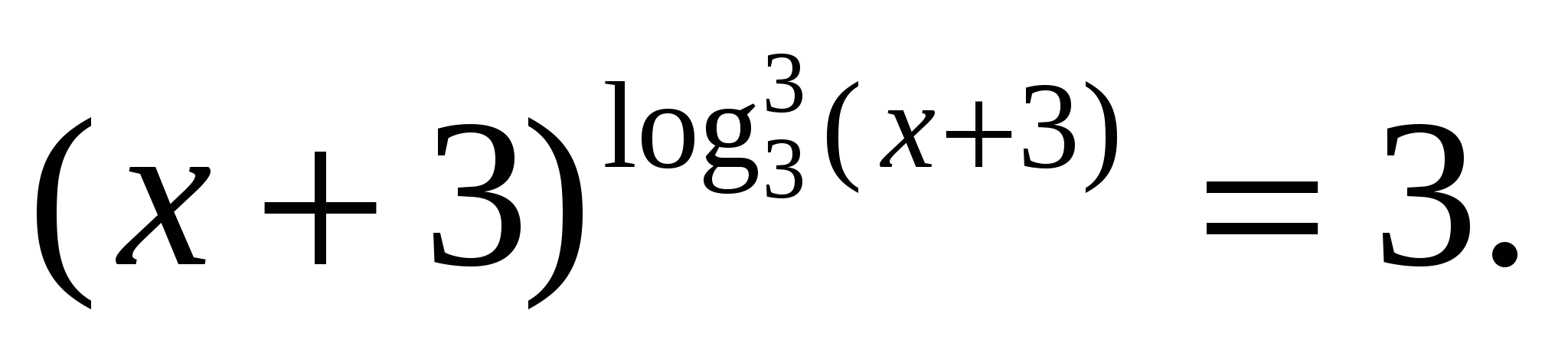Найти произведение корней.

Литература.

1. А.Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын, Б. М. Ивлев, С. И. Шварцбурд Алгебра и начала анализа 10-11 класс. — М.: Просвещение, 2005.

2. Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и другим формам выпускного и вступительного экзаменов/сост. Г. И. Ковалёва, Т. И. Бузулина, О. Л. Безрукова, Ю. А., Ю. А. Розка –Волгоград:Учитель, 2007.

3. С. А. Шестакова, П. И. Захаров. ЕГЭ 2013. Математика. Задача С1. Уравнения и системы уравнений. Под редакцией А. Л. Семёнова и И. В. Ященко — Москва, изд. МЦНМО, 2013.

4. Открытый банк заданий по математике http://mathege.ru.

5. Образовательный портал для подготовки к экзаменам Дмитрия Гущина: РЕШУ ЕГЭ по математике http://reshuege.ru/.

6. Сайт ФИПИ www.fipi.ru.

7. Сайт Виртуальная школа юного математика http://www.math.md/school/praktikum/logr/logr.html.

Методы решения логарифмических уравнений

Цели урока:

• образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;

• развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;

• воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку.

Технологии, используемые на уроке: педагогика сотрудничества, групповая технология, информацоинно-коммутативная технология.

«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь».

(французский математик, астроном

П.С. Лаплас)

Ход урока

I. Постановка цели урока.

Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.

Запишите в тетради тему урока: «Методы решения логарифмических уравнений». Приглашаю всех к сотрудничеству.

II. Актуализация опорных знаний.

Подготовимся к изучению темы урока. Каждое задание вы решаете и записываете ответ, условие можно не писать. Работайте в парах.

(Демонстрируется слайды с заданиями для устной работы).

1) При каких значениях х имеет смысл функция:

а)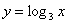

б)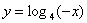 

в)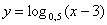

г)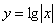

(По каждому слайду сверяются ответы и разбираются ошибки).

2) Совпадают ли графики функций?

а) y = x и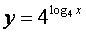  

б)  и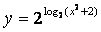

3) Перепишите равенства в виде логарифмических равенств:

 

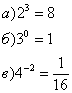
4) Запишите числа в виде логарифмов с основанием 2:

4 =

— 2 =

0,5 =

1 =

5) Вычислите: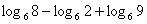

III. Ознакомление с новым материалом.

Демонстрируется на экране высказывание:

«Уравнение – это золотой ключ, открывающий все математические сезамы».
Современный польский математик С. Коваль.

Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).

Рассмотрим простейшее логарифмическое уравнение: log _аx = b

(где а>0, a ≠ 1 ). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.

Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х). Из определения логарифма сразу следует, что а^b является таким решением.

Запишите заголовок: Методы решения логарифмов.

1 метод. По определению логарифма.

Так решаются простейшие уравнения вида .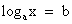

 

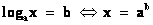
Решить уравнение :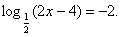

Как вы предлагаете его решать? (По определению логарифма).

Решение. 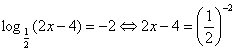, Отсюда 2х – 4 = 4; х = 4.

Ответ: 4.

В этом задании 2х – 4 > 0, так как 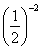> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.

2 метод. Потенцирование (переход от логарифма данного выражения к самому этому выражению).

Рассмотрим пример :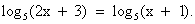

Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).

При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.

Решение 1. ОДЗ: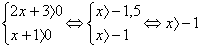

Потенцируем исходное уравнение 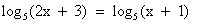, получим уравнение 2x + 3 = х + 1.

Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.

Можно решить это уравнение иначе – переходом к равносильной системе:

Уравнение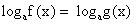

(Система содержит избыточное условие – одно из неравенств можно не рассматривать).

Решение 2. Уравнение 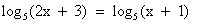 равносильно системе:

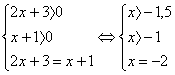
Эта система решений не имеет.

Есть еще один вариант решения – переход к следствию из данного уравнения. При неравносильных преобразованиях найденное решение необходимо проверить подстановкой в исходное уравнение.

Решение 3. .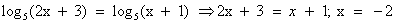

Сделаем проверку: 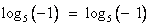неверно, так как не имеет смысла.

Ответ: корней нет.

Вопрос классу: Какое из этих трех решений вам больше всего понравилось? (Обсуждение способов).

Вы имеете право решать любым способом.

3. Введение новой переменной.

Рассмотрим пример. .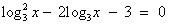

Что вы заметили? (Это квадратное уравнение относительно log3x).

Ваши предложения? (Ввести новую переменную)

Решение. ОДЗ: х > 0.

Пусть 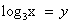, тогда уравнение примет вид: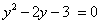. Дискриминант D > 0. Корни по теореме Виета:.

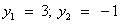Вернемся к замене: 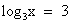или .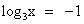

Решив простейшие логарифмические уравнения, получим:

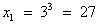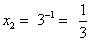; . Ответ: 27;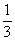

4. Логарифмирование обеих частей уравнения.

Решить уравнение:.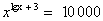

Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:

Применим свойство логарифма степени:

(lgx + 3) lgx =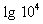

(lgx + 3) lgx = 4

Пусть lgx = y, тогда (у + 3)у = 4

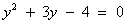, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.

Вернемся к замене, получим: lgx = -4,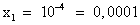; lgx = 1, .

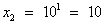Ответ: 0,0001; 10.

5. Приведение к одному основанию.

Решите уравнение: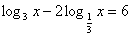

Решение: ОДЗ: х>0. Перейдем к основанию 3.

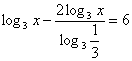  или ; .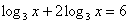

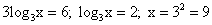Ответ: 9.

6. Функционально-графический метод.

Решить графически уравнение: 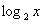= 3 – x.

Как вы предлагаете решать?

(Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков).

Посмотрите ваше решение на слайде.

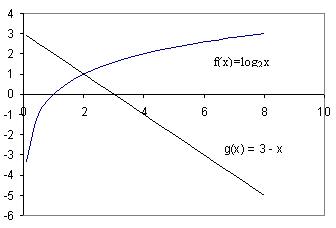
Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

В нашем случае функция 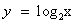возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .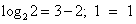

Ответ: 2.

IV. Первичное закрепление.

Демонстрируется высказывание:

«Правильному применению методов можно научиться,
только применяя их на различных примерах».
(Датский историк математики Г. Г. Цейтен)

Предложите метод решения уравнений:

1)

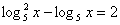
2)

3)

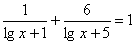
4)

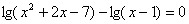
5)

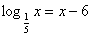
6)

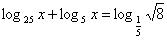
V. Домашнее задание.

Учебник для 10-11 классов общеобразовательных учреждений “Алгебра и начала анализа” Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др.

№340(1), №345(1, 3), №379(3), №391(1), №389(2) – 2 способа решения.

VI. Подведение итогов урока.

Какие методы решения логарифмических уравнений мы рассмотрели на уроке?

На следующих уроках рассмотрим более сложные уравнения. Для их решения пригодятся изученные методы.

Демонстрируется последний слайд:

«Что есть больше всего на свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого».
Фалес

Желаю всем достичь желаемого. Благодарю за сотрудничество и понимание.

Методы решения логарифмических уравнений

Алгебра 11 класс

Тема: « Методы решения логарифмических уравнений »

Цели урока:

• образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;

• развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;

• воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.

Тип урока: урок ознакомления с новым материалом.

«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь». 
Французский математик и астроном П.С. Лаплас

Ход урока

I. Постановка цели урока

Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.

Запишите в тетради тему урока: «Методы решения логарифмических уравнений». Приглашаю всех к сотрудничеству.

II. Актуализация опорных знаний

Подготовимся к изучению темы урока. Каждое задание вы решаете и записываете ответ, условие можно не писать. Работайте в парах.

1) При каких значениях х имеет смысл функция:

а)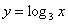 

б)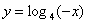 

в)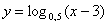 

д)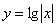 

(По каждому слайду сверяются ответы и разбираются ошибки)

2) Совпадают ли графики функций?

а) y = x и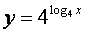  

б) 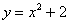 и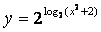 

3) Перепишите равенства в виде логарифмических равенств:

 

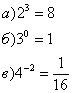
4) Запишите числа в виде логарифмов с основанием 2:

4 =

— 2 =

0,5 =

1 =

5) Вычислите: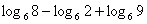 

6) Попытайтесь восстановить или дополнить недостающие элементы в данных равенствах.

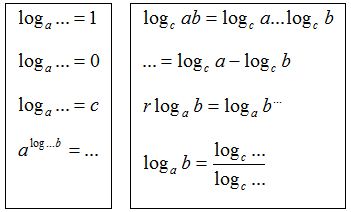
III. Ознакомление с новым материалом

Демонстрируется на экране высказывание:

«Уравнение – это золотой ключ, открывающий все математические сезамы».
Современный польский математик С. Коваль

Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).

Рассмотрим простейшее логарифмическое уравнение: log_а x = b (где а>0, a ≠ 1 ). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.

Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х). Из определения логарифма сразу следует, что а^в является таким решением.

Запишите заголовок: Методы решения логарифмических уравнений

1. По определению логарифма.

Так решаются простейшие уравнения вида .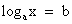

 

Рассмотрим № 514(а): Решить уравнение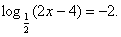 

Как вы предлагаете его решать? (По определению логарифма)

Решение. 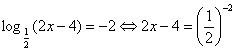, Отсюда 2х – 4 = 4; х = 4.

Ответ: 4.

В этом задании 2х – 4 > 0, так как 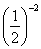> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.

2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).

Рассмотрим  №519(г): log₅(x²+8)-log₅(x+1)=3log₅ 2

Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).

При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.

Решение: ОДЗ:

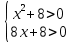
X²+8>0 лишнее неравенство

log₅(x²+8) =log₅ 2³+ log₅(x+1)

log₅(x²+8)= log₅ (8 x+8)

Потенцируем исходное уравнение 

x²+8= 8 x+8

получим уравнение x²+8= 8x+8

Решаем его: x²-8x=0

х=0, х=8

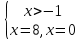
Ответ: 0; 8

В общем виде переходом к равносильной системе:

Уравнение 

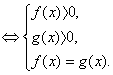
(Система содержит избыточное условие – одно из неравенств можно не рассматривать).

Вопрос классу: Какое из этих трех решений вам больше всего понравилось? (Обсуждение способов).

Вы имеете право решать любым способом.

3. Введение новой переменной.

Рассмотрим № 520(г). .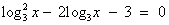

Что вы заметили? (Это квадратное уравнение относительно log3x) Ваши предложения? (Ввести новую переменную)

Решение. ОДЗ: х > 0.

Пусть 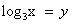, тогда уравнение примет вид: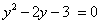. Дискриминант D > 0. Корни по теореме Виета:.

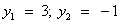Вернемся к замене: 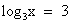или .

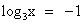Решив простейшие логарифмические уравнения, получим:

; .

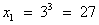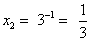Ответ: 27;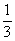 

4. Логарифмирование обеих частей уравнения.

Решить уравнение:.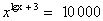

Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10:

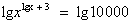. Применим свойство логарифма степени:

(lgx + 3) lgx =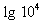

(lgx + 3) lgx = 4

Пусть lgx = y, тогда (у + 3)у = 4

, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.

Вернемся к замене, получим: lgx = -4,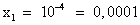; lgx = 1, .

Ответ: 0,0001; 10.

5. Приведение к одному основанию.

№ 523(в). Решите уравнение: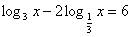 

Решение: ОДЗ: х>0. Перейдем к основанию 3.

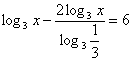 или ;.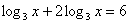

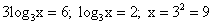Ответ: 9.

6. Функционально-графический метод.

№ 509(г). Решить графически уравнение: 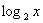= 3 – x.

Как вы предлагаете решать? (Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков).

Посмотрите ваше решение на слайде.

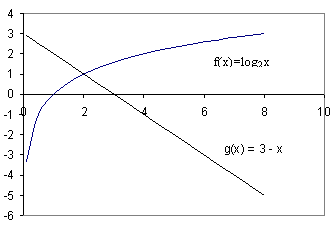
Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x)возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х.

Если корень имеется, то его можно угадать.

В нашем случае функция возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 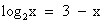имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как .

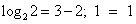Ответ: 2

«Правильному применению методов можно научиться,
только применяя их на различных примерах».
Датский историк математики Г. Г. Цейтен

IV. Домашнее задание

П. 39 рассмотреть пример 3, решить № 514(б), № 529(б), №520(б), №523(б)

V. Подведение итогов урока

Какие методы решения логарифмических уравнений мы рассмотрели на уроке?

На следующих уроках рассмотрим более сложные уравнения. Для их решения пригодятся изученные методы.

Демонстрируется последний слайд:

«Что есть больше всего на свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого».
Фалес

Желаю всем достичь желаемого. Благодарю за сотрудничество и понимание.

Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений. Теория.

Подготовка к ЕГЭ по математике

 

Эксперимент

 

Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений.

 

Теория

 

Конспект урока

На предыдущем уроке мы определили понятие логарифма, обсудили его основные свойства.

Сегодня мы поговорим о решении простейших логарифмических уравнений и видах логарифмических уравнений.

По аналогии с решением показательных уравнений мы воспользуемся свойствами логарифмической функции для решения логарифмических уравнений.

Рассмотрим логарифмическую функцию:

Рассмотрим её свойства:

1)   – это следует из определения логарифма (под логарифмом не может стоять отрицательное число или 0)

2)    Стоит отметить, что показательная и логарифмическая функции являются взаимно обратными. Поэтому область определения показательной функции совпадает с областью значения логарифмической и наоборот (более подробно о свойствах прямой и обратной функции мы поговорим в теме «Функции»).

3)  Точки пересечения с осями.

Ох (нули функции): 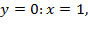 так как логарифм от 1 по любому основанию равен 0 (любое положительное число в 0 степени равно 1). Значит, график логарифмической функции проходит через точку

Оу:  – не существует, так как 0 не входит в область определения логарифмической функции.

4)   Функция не является ни чётной, ни нечётной (функция общего вида), так как область определения не симметрична относительно 0 (то есть, функция не определена при отрицательных значениях переменной).

Также функция не является периодической.

5)   При 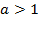 функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией).

При  функция монотонно убывает на всей области определения.

6)    Графики логарифмической функции пр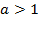и  и имеют вид:

Мы видим, что логарифмическая функция, как и показательная, является монотонной (монотонно возрастает при  и монотонно убывает при ).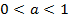

Это означает, что мы можем по аналогии с простейшими показательными уравнениями определить способ решения простейших логарифмических уравнений ():  Однако при этом необходимо помнить, что под логарифмом должно стоять положительное число. Таким образом, при решении логарифмических уравнений необходимо учитывать ОДЗ, а именно: проверять, что все подлогарифмические выражения, а также основания логарифмов являются положительными и основания не равны 1.

Однако можно избежать определения ОДЗ исходного уравнения, выполнив в конце проверку полученных результатов (поскольку мы не сужаем область поиска корней, а расширяем её). В большинстве случаев такой подход облегчает решение логарифмических уравнений.

Таким образом, для решения простейшего логарифмического уравнения достаточно привести обе части к одинаковому основанию, а затем приравнять подлогарифмические выражения.

Например:

Правда, в данном конкретном случае мы могли воспользоваться и определением логарифма:  Однако продемонстрированный метод более универсальный.

Любое более сложное логарифмическое уравнение решается «выливанием воды из чайника», то есть сведением его различными методами к простейшим.

 

1) Простейшие

2)  Простейшие с переменной в основании логарифма

3)  Простейшие с переменной и в основании, и под логарифмом

4)  Сводящиеся к простейшим с помощью использования свойств логарифмов

5)  Сводящиеся к квадратным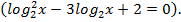

Системы логарифмических уравнений решаются по тем же принципам, что и системы показательных уравнений.

Самые простые системы логарифмических уравнений – это системы, в которых оба уравнения сводятся к простейшим. В дальнейшем получается обычная система из двух уравнений с двумя неизвестными, которая решается любым из удобных методов.

Пример такой системы: .

Ещё один важный тип систем логарифмических уравнений – это системы, которые сводятся к обычным с помощью замены. Пример такой системы: .

Также существуют системы логарифмических уравнений, которые решаются различными методами.

Более подробно о решении систем логарифмических уравнений мы поговорим в практической части урока.

На этом уроке мы с вами обсудили свойства логарифмической функции, научились решать простейшие логарифмические уравнения. Также мы узнали об основных видах логарифмических уравнений и их систем.

В практической части урока мы научимся решать различные логарифмические уравнения и их системы.

 

Полезные ссылки:

1)      Алгебра 11 класс: «Функция y=log_ax, ее свойства и график» 

2)      Алгебра 11 класс: «Функция y=log_ax, ее свойства и график (продолжение)» 

3)      Алгебра 11 класс: «Функция y=log_ax, ее свойства и график. Решение задач» 

4)      Алгебра 11 класс: «Логарифмические уравнения» 

5)      Алгебра 11 класс: «Решение логарифмических уравнений» 

6)      Алгебра 11 класс: «Решение логарифмических уравнений» 

Общие методы решения показательных и логарифмических уравнений

Урок обобщения материала по теме:

«Общие методы решения показательных

и логарифмических уравнений.

Комбинированные уравнения».

ЦЕЛЬ:  способствовать формированию у учащихся обобщенных

понятий, умения применить приемы обобщения, выделение

главного, переноса знаний в новую ситуацию,

• способствовать развитию творческих способностей учащихся путем решения нестандартных заданий

• побуждать учащихся к самоконтролю, самоанализу своей учебной деятельности

Оборудование:

• • тесты ЕГЭ 2005-2006,

  • контрольный тест,

  • плакаты «Обобщающие методы решений уравнений»,

  • индивидуальные карточки,

  • набор уравнений,

  • оценочный лист,

  • модель ракеты, ракушка.

Содержание урока

ЗНАНИЯ 

ОПОРНЫЕ

1. Показательная функция

2. Свойства степени с одинаковым основанием

3. Определение показательного уравнения

4. Логарифмическая функция и её свойства

5. Свойства логарифмов

6. Определение логарифмического уравнения

ОСНОВНЫЕ

1. методы решения показательных уравнений

2. методы решения логарифмических уравнений

3. Комбинированные уравнения

СПОСОБЫ ДЕЯТЕЛЬНОСТИ

1. Орг.момент.

2. Анализ содержания изученного материала:

а) проверка опорных знаний

б) анализ домашней работы

3. Обобщение и систематизация

а) методы решения уравнений

4. Контроль и самоконтроль: тестирование

5. Подведение итогов

6. Рефлексия

ХОД УРОКА

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

1. 1. Записать: число, классная работа.

   2. Закончи предложение:

— Равенство, содержащее неизвестное число, называется …

(уравнением)

— Значение неизвестного числа в уравнении называется …

(корнем)

— Решить уравнение, это значит …

(найти его корни или доказать, что их нет)

«Математика – это полёт» — говорил прославленный военный летчик Валерий Чкалов. Сегодня – 12 апреля, День космонавтики. На ВДНХ в Москве установлен памятник космонавтам (показать модель). Какую функцию он вам напоминает? (показательную).

Дать определение показательной функции и перечислить её свойства.

(показать ракушку)

Какая функция является исходной для данной спирали на ракушке?

(логарифмическая)

Дать определение логарифмической функции и перечислить её свойства.

— Уравнения, происходящие от данных функций называются …

(показательными, логарифмическими)

— А теперь сформулируйте тему сегодняшнего урока с учетом перечисленных понятий (учащиеся формулируют тему, учитель делает коррекцию, ученики записывают тему в тетрадях).

— Сегодня на уроке мы будем работать под известным латинским изречением:

«Rapetitio est mater studorum» («Повторение – мать учения»)

— Какова же цель нашего урока?

— Сегодня мы обобщим методы решения показательных, логарифмических и комбинированных уравнений, которые встречаются в заданиях ЕГЭ, проверим, как усвоен материал и над чем надо поработать.

1. 2. АНАЛИЗ ИЗУЧЕННОГО МАТЕРИАЛА

а) Задания по вариантам (по одному ученику у доски для проверки)

1 Вариант

1) Дать определение показательного уравнения

2) Записать свойства степеней с одинаковым основанием

2 Вариант

1) Дать определение логарифмического уравнения

2) Записать свойства логарифма

б) Дома было задание творческого характера. Учащимся надо было решить задания по карточкам и сделать классификацию методов решения.

Карточка 1. Показательные уравнения

№

Уравнение

Ответ

Метод решения

1

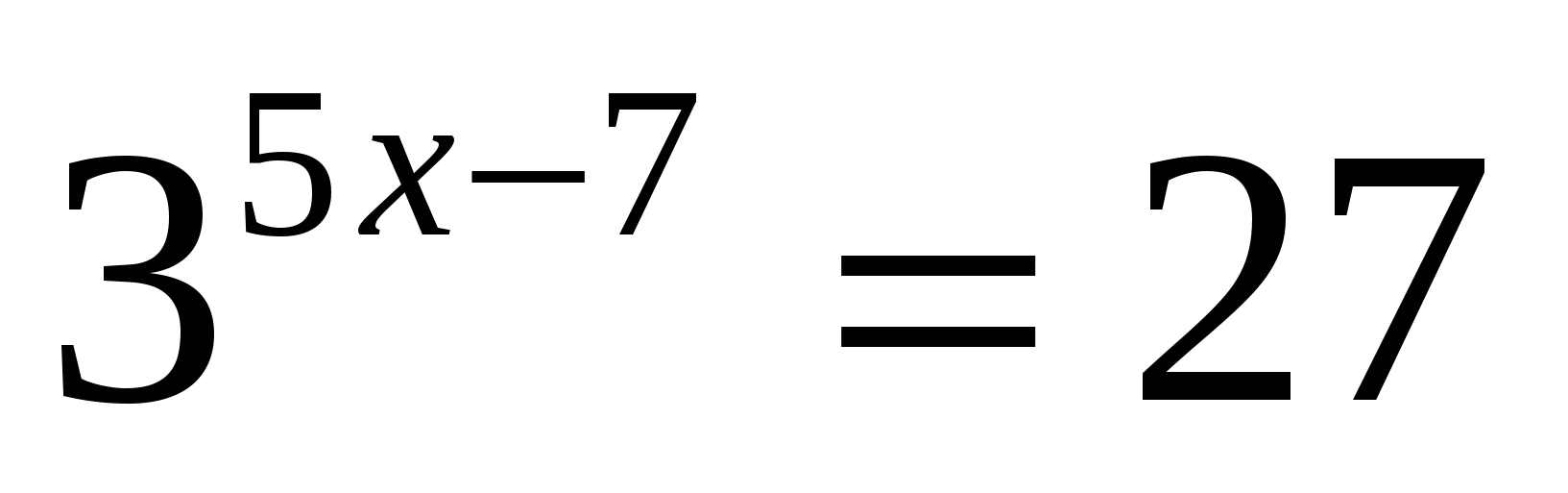
2

2

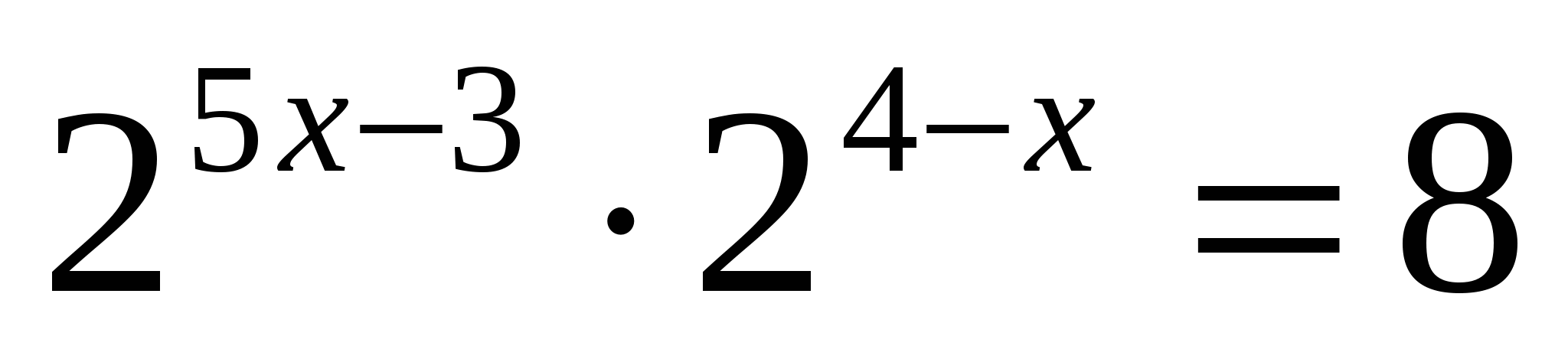
0,5

Свойства степеней с одинаковым основанием

3

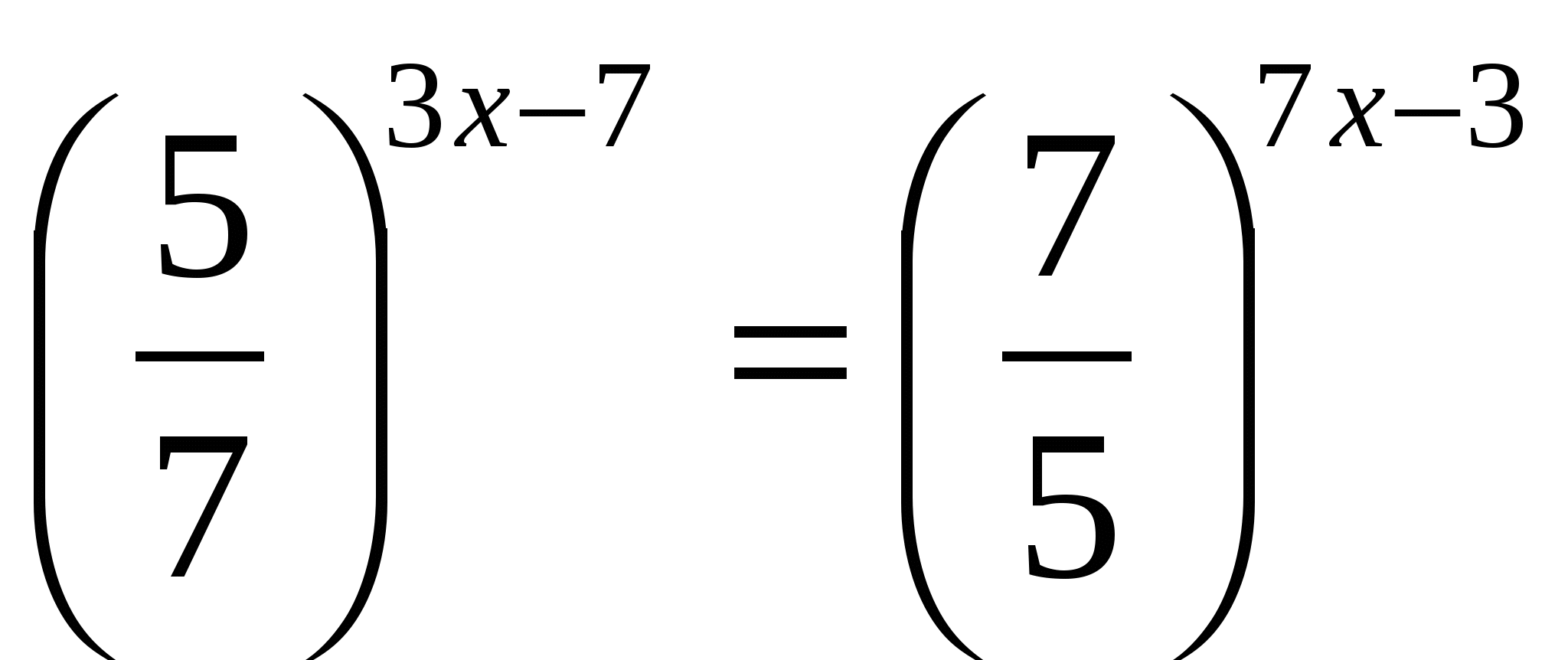
1

Определение степени с отрицательным показателем

4

2

Введение новой переменной

5

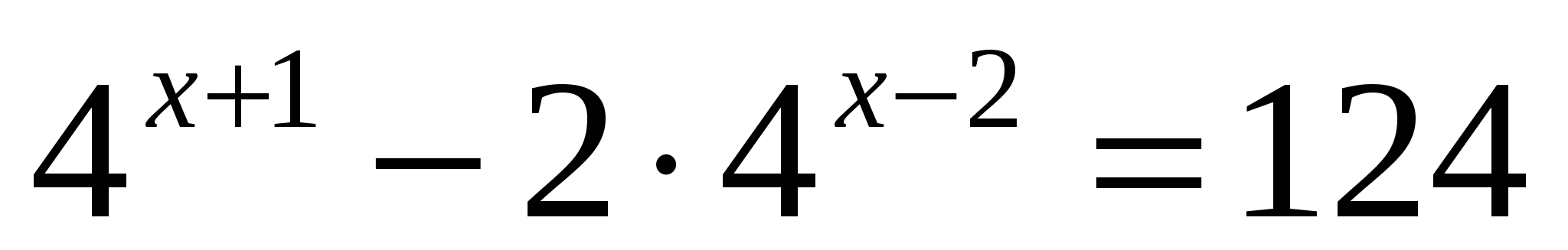
2,5

Вынесение общего множителя

6

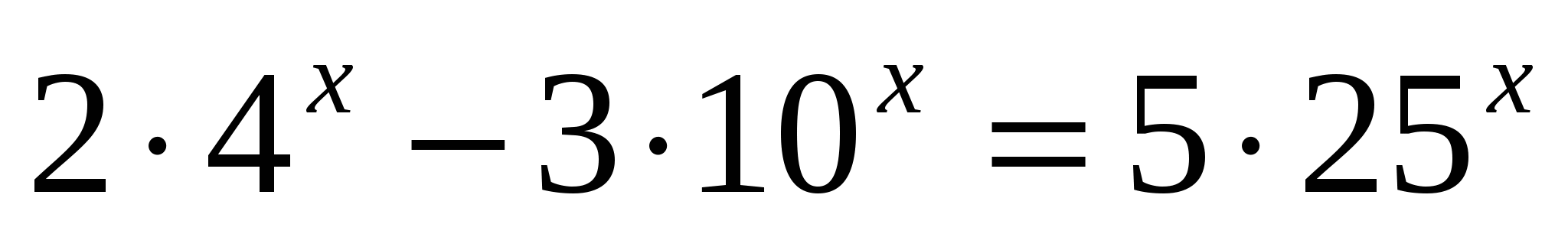
-1

Метод однородности

7

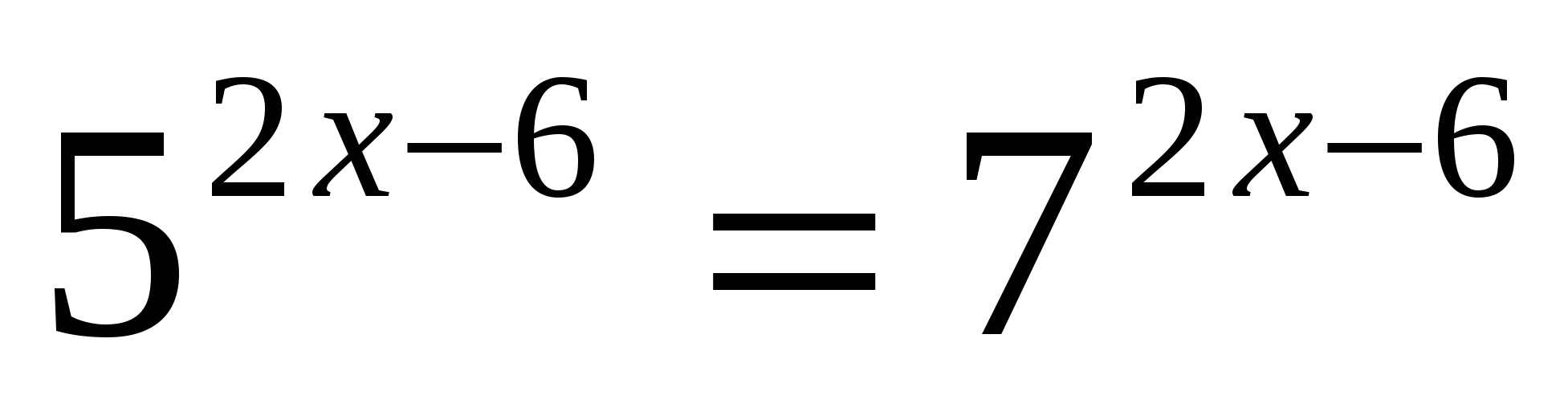
3

Деление на правую (левую) часть

8

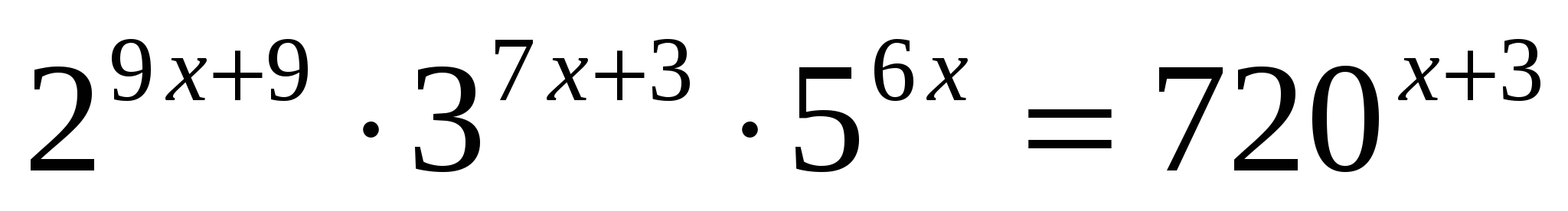
0,8

Разложение на простые множители

9

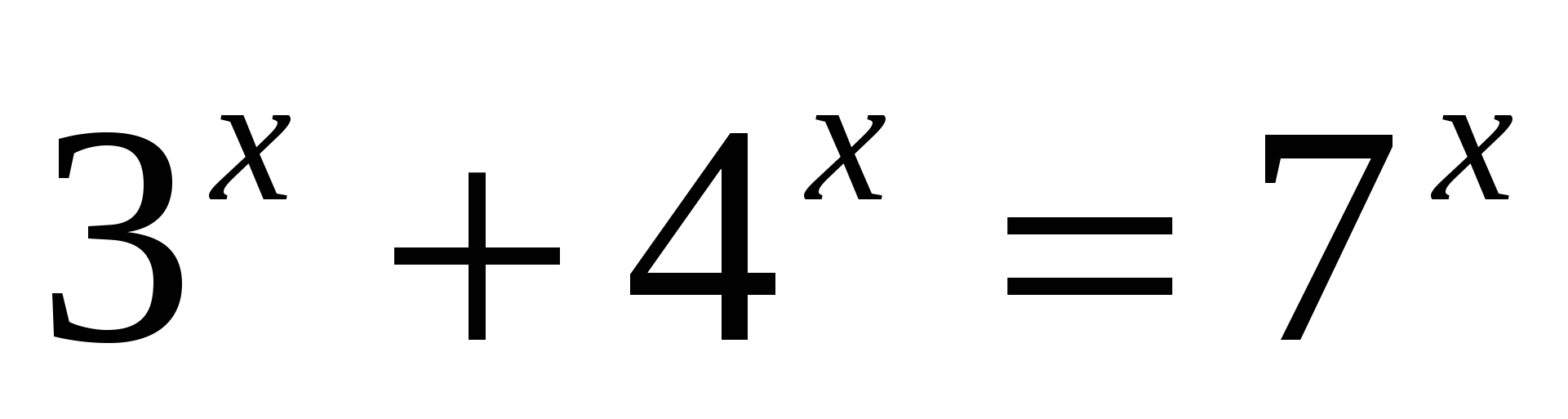
1

Использование монотонности функций

1. 2. ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ЗНАНИЙ

— Давайте остановимся на методах решения показательных уравнений. Сведем их в таблицу. Каким методом еще можно было бы решить последнее уравнение? (графическим).

(Вывешивается таблица методов решения и ряд уравнений)

Методы решения показательных уравнений

1.

2. Свойства степеней с одинаковым основанием

3. Использование определения степени с отрицательным показателем

4. Вынесение общего множителя

5. Метод введения новой переменной

6. Деление на правую (левую) часть

7. Метод однородности

8. Разложение на простые множители

9. Использование монотонности функции

10. Графический метод

1.

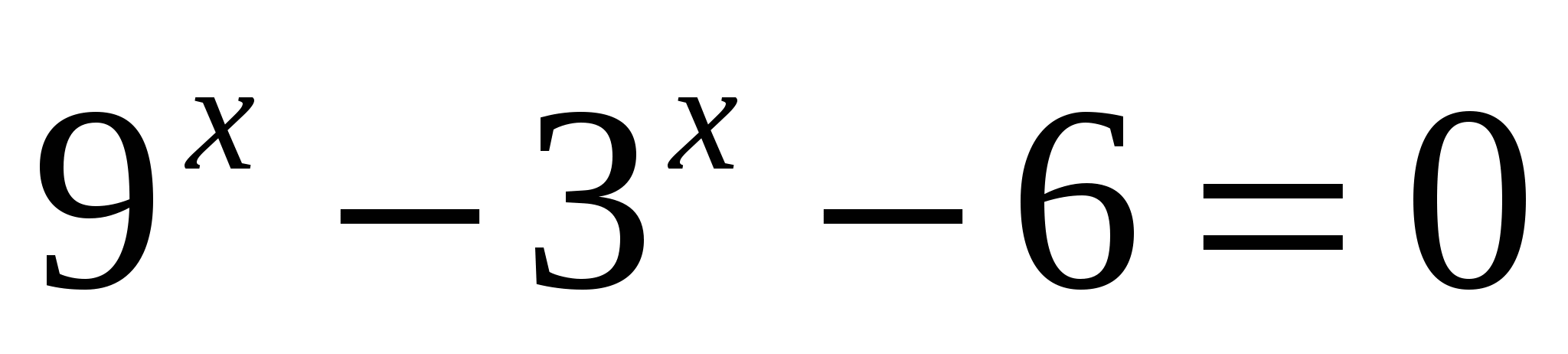
2.

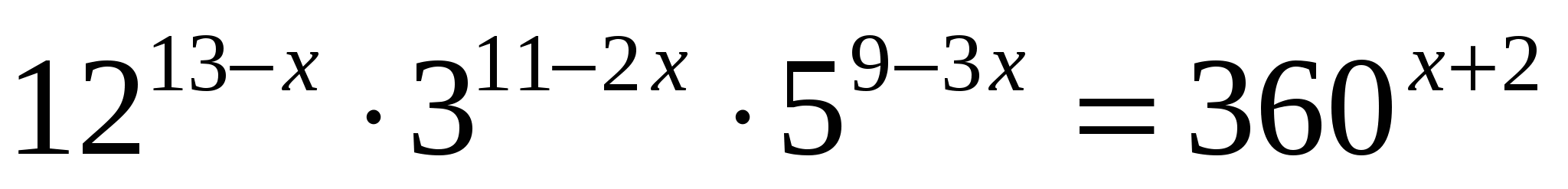
3.

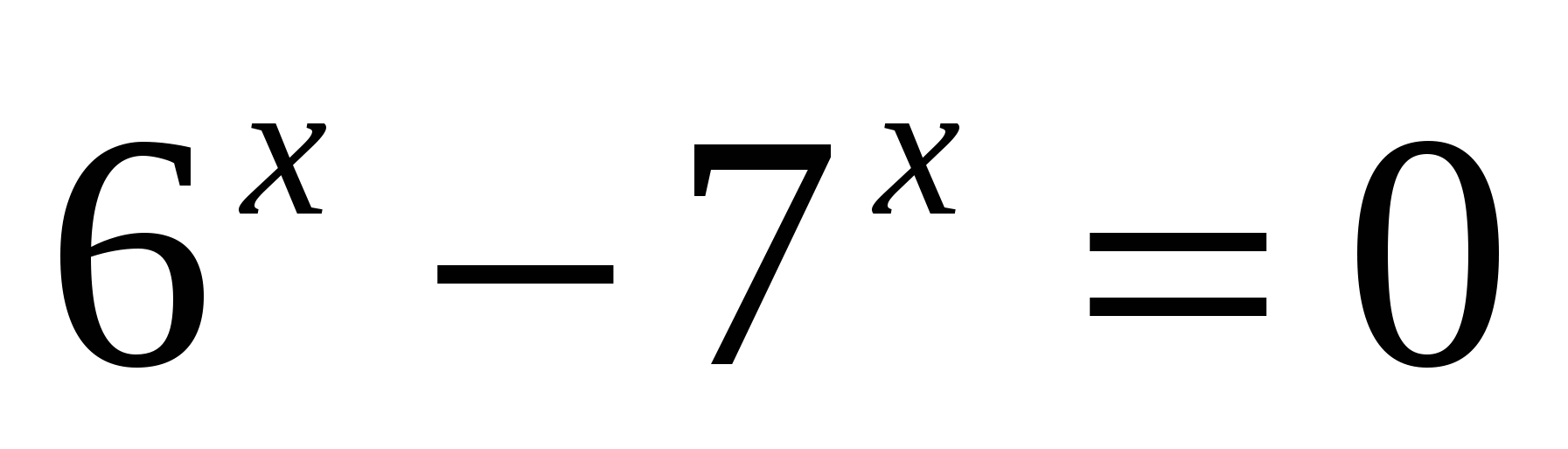
4.

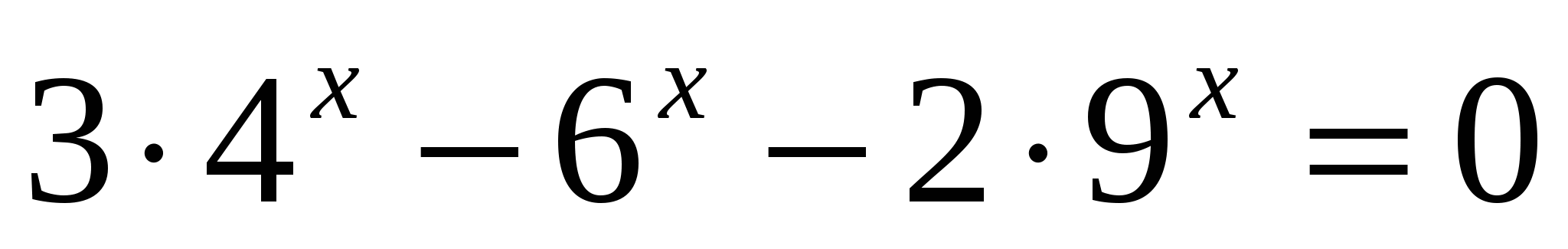
5.

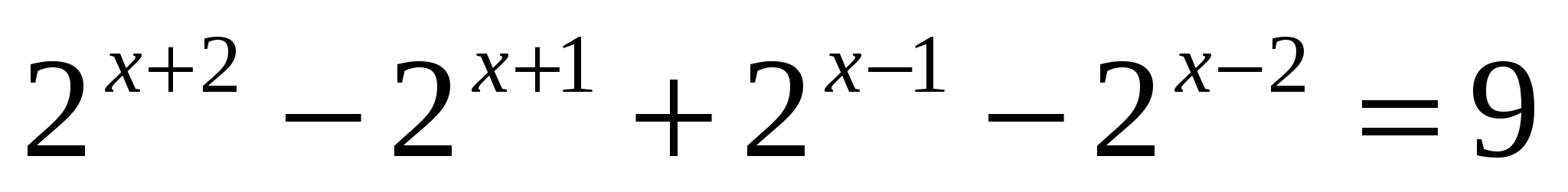
6.

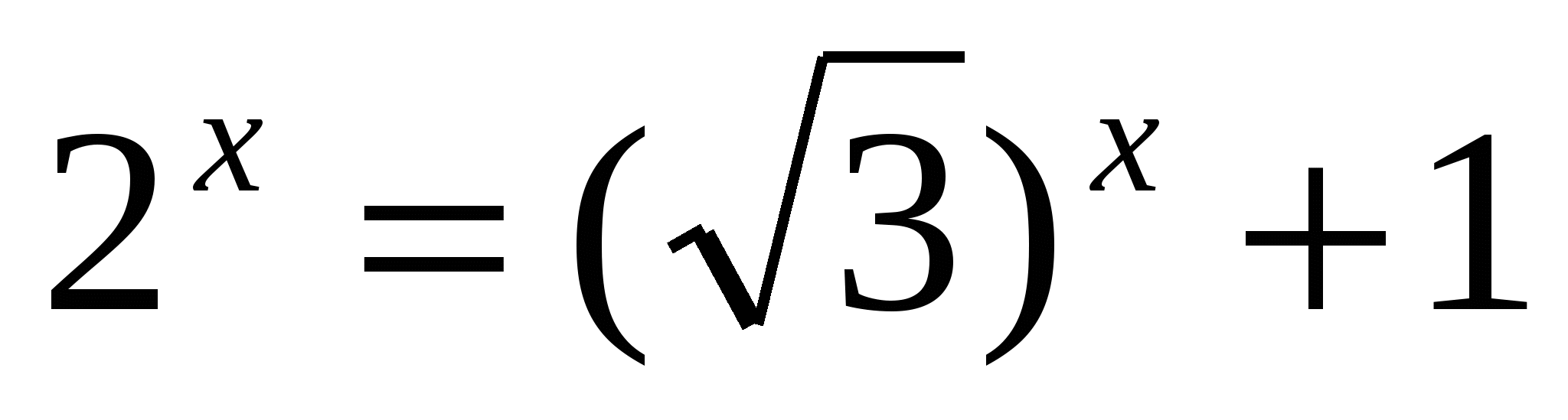
7.

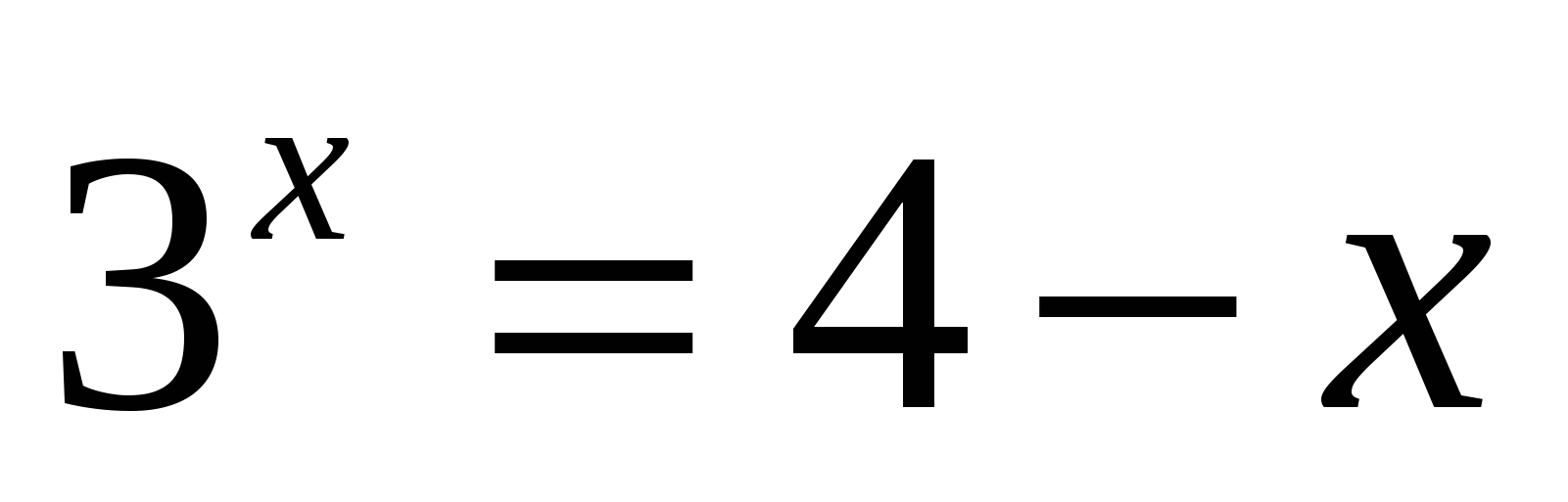
8.

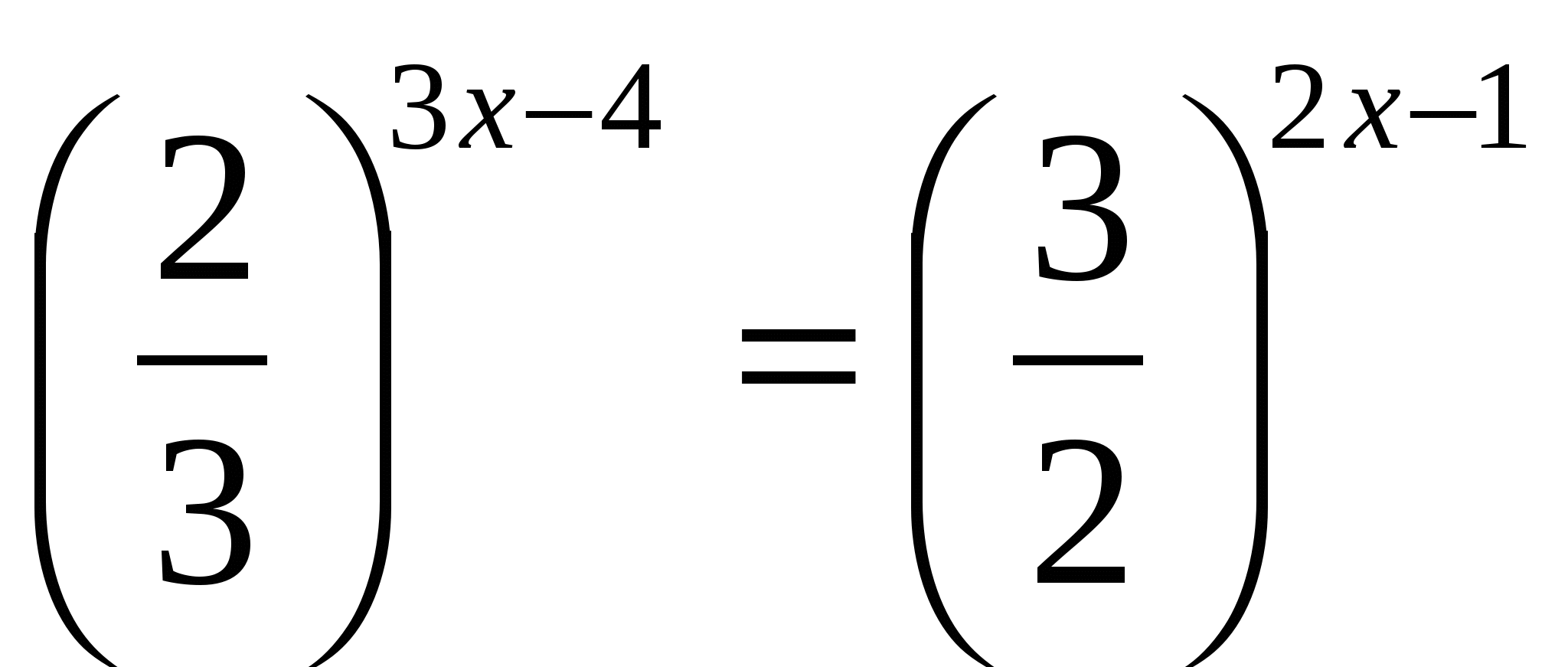
9.

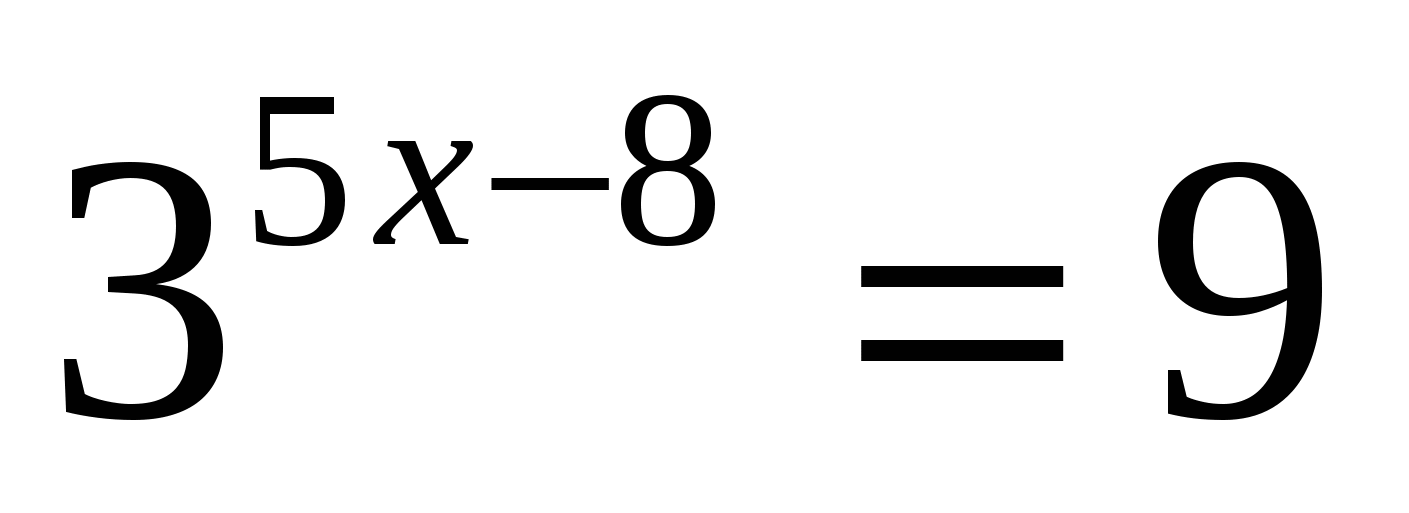
ВОПРОСЫ:

1. В чём заключается метод однородности?

2. Найдите ошибку?

; ; ; ;

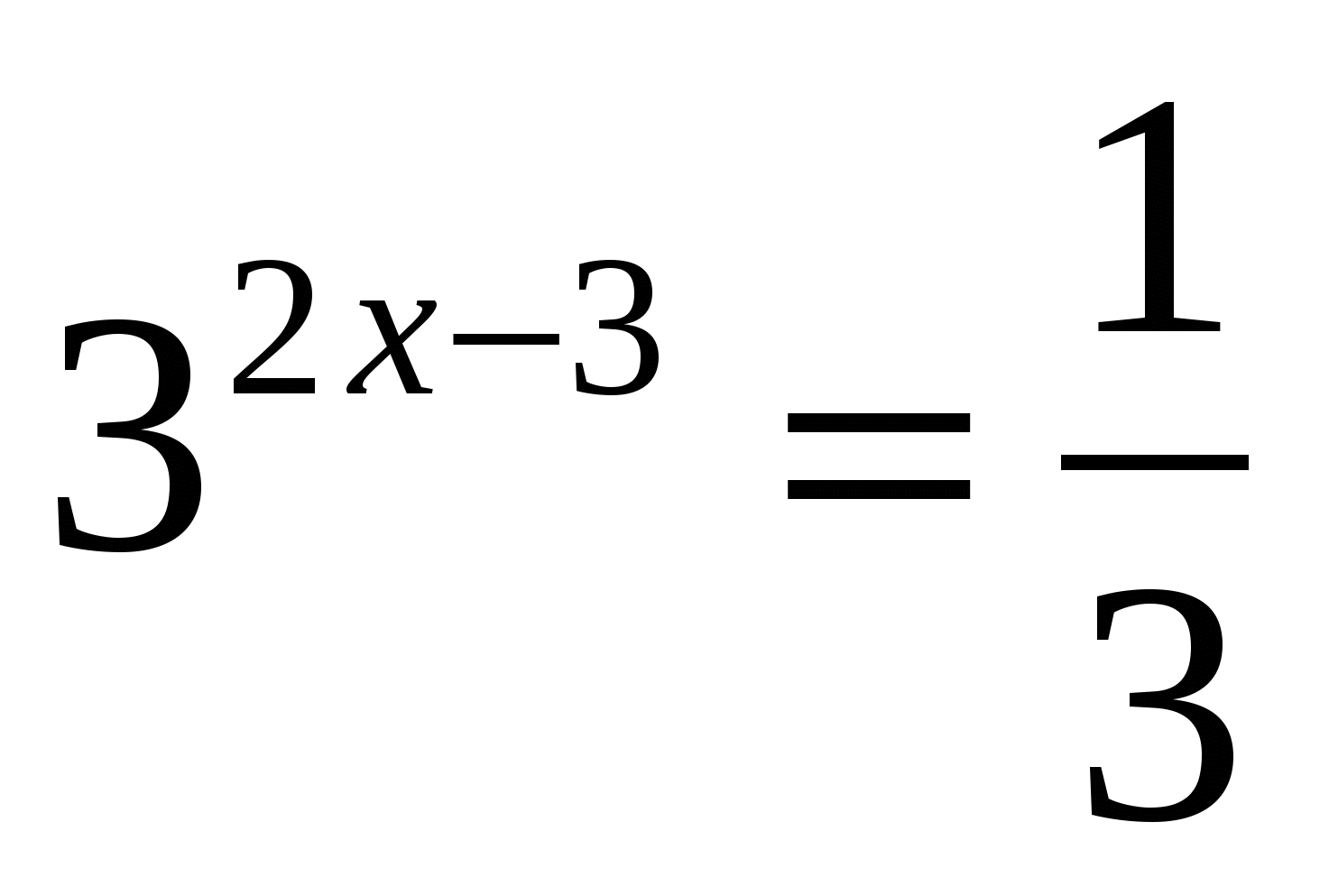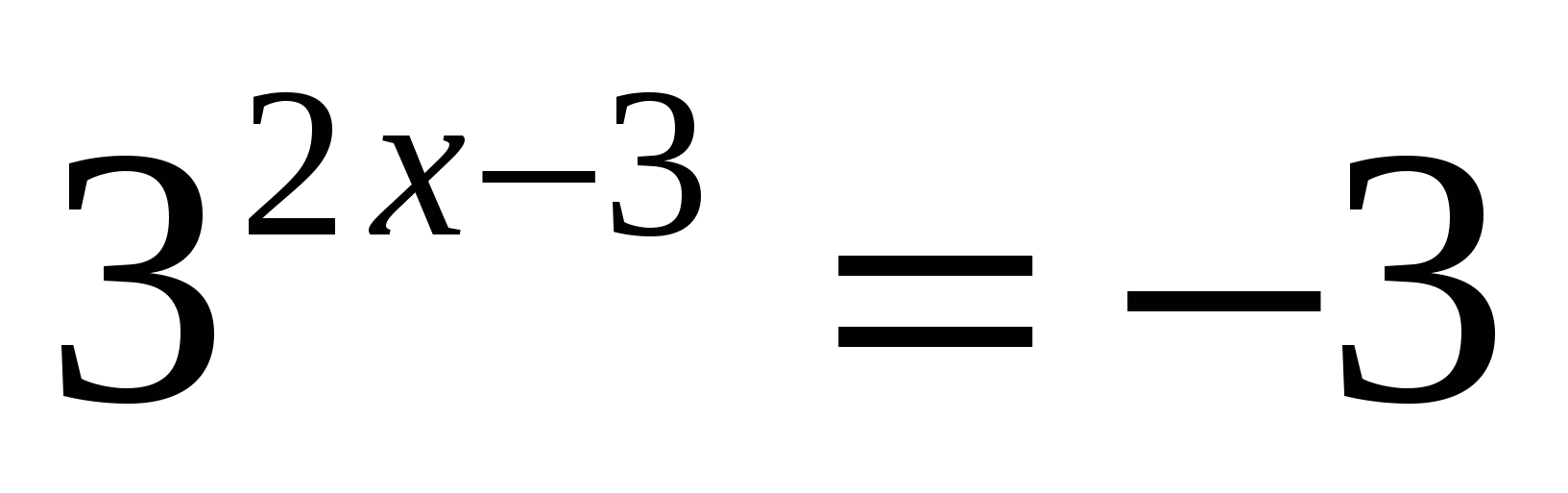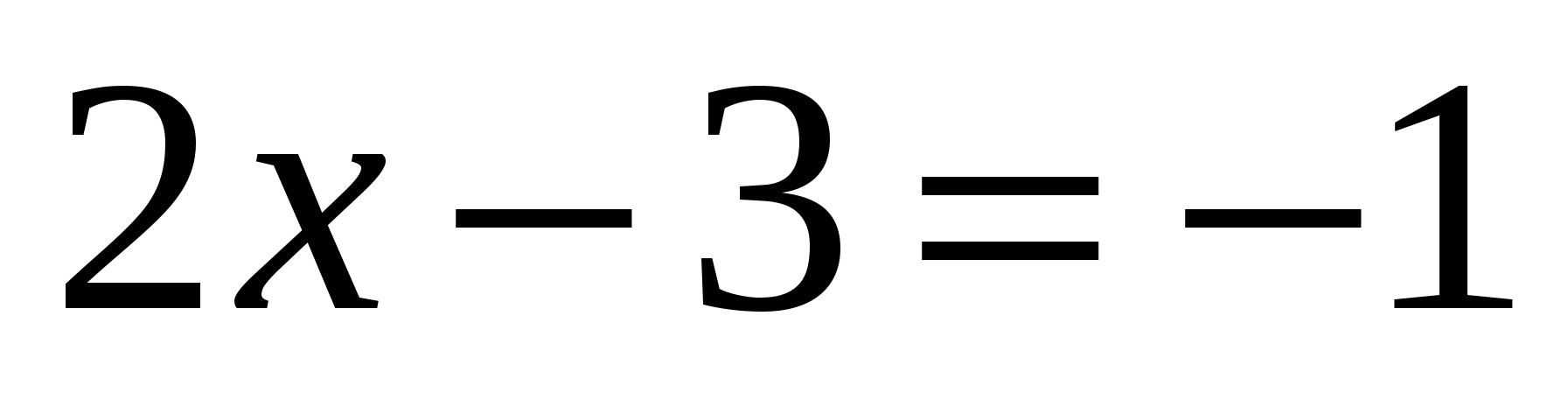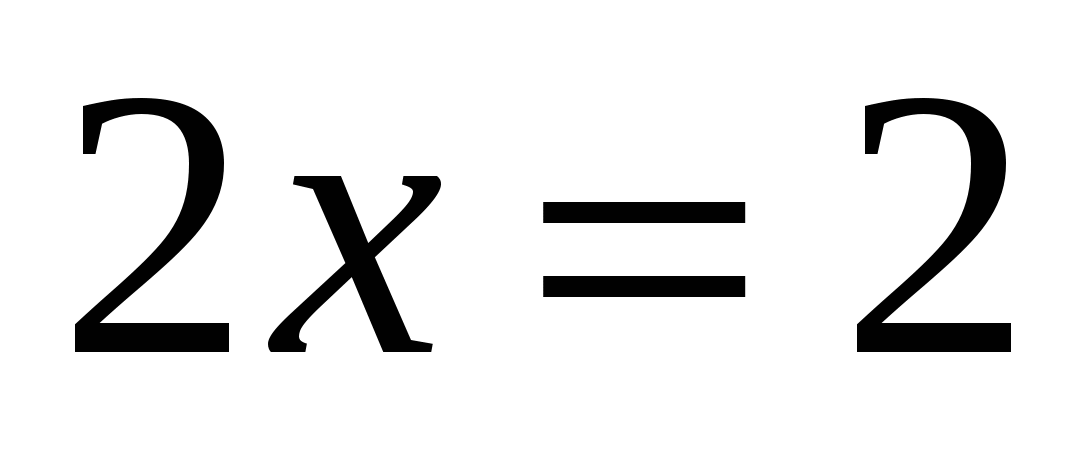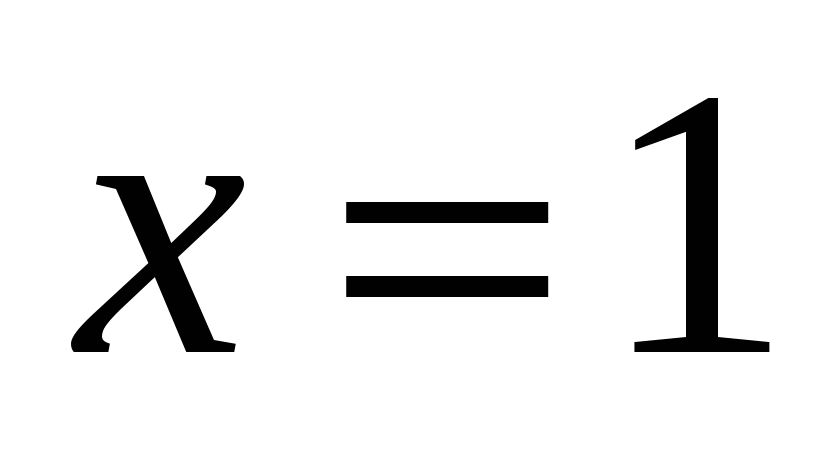
Карточка 2. Логарифмические уравнения

№

Уравнения

Ответ

Метод решения

1

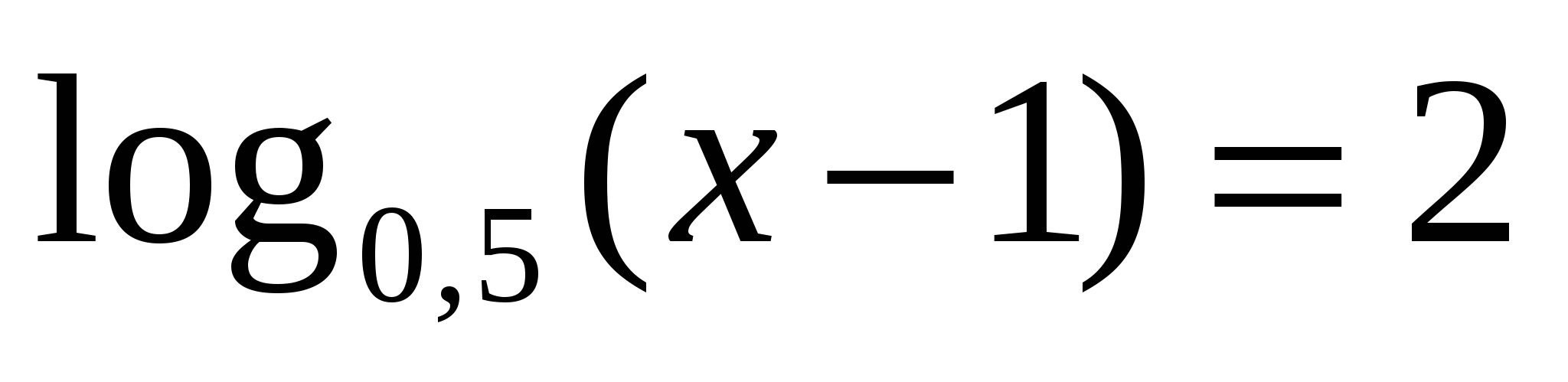
1,25

По определению логарифма

2

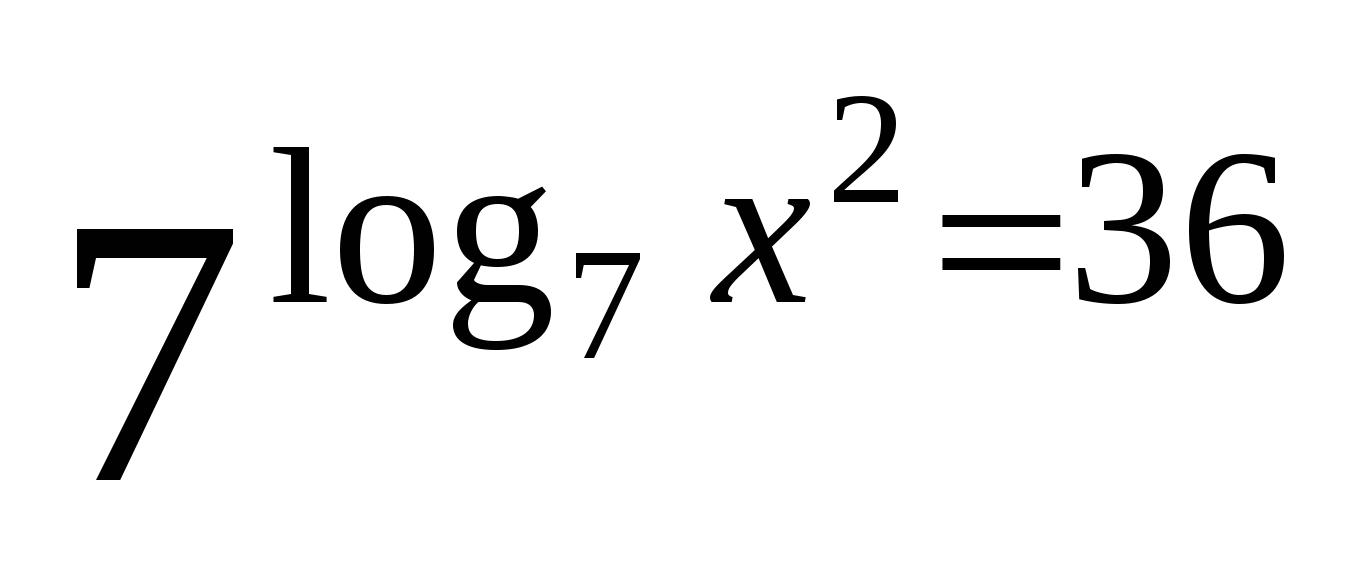
6

Использование основного логарифмического тождества

3

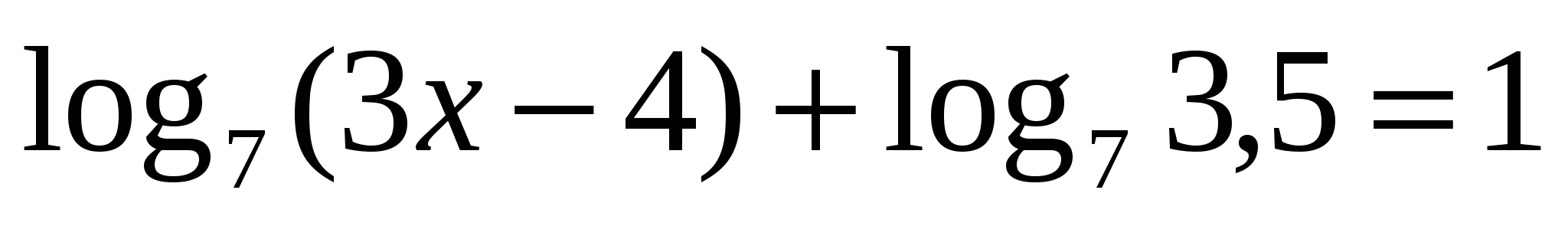
2

Свойства логарифмов

4

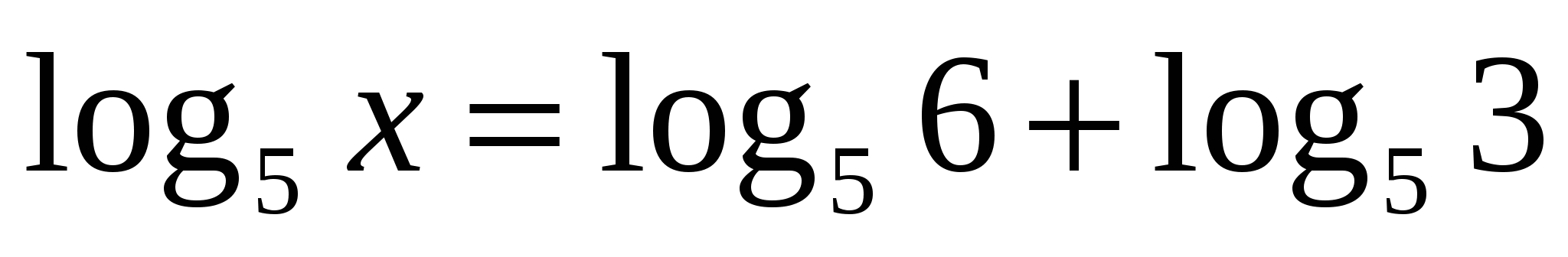
18

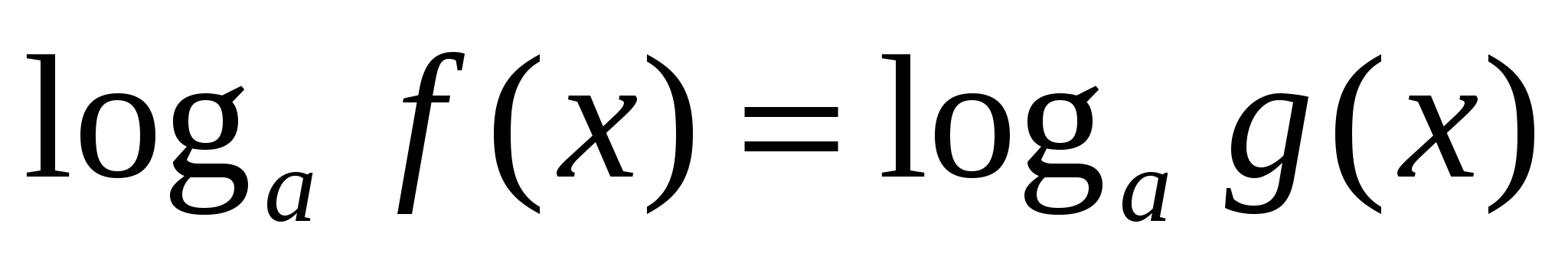(метод потенцирования)

5

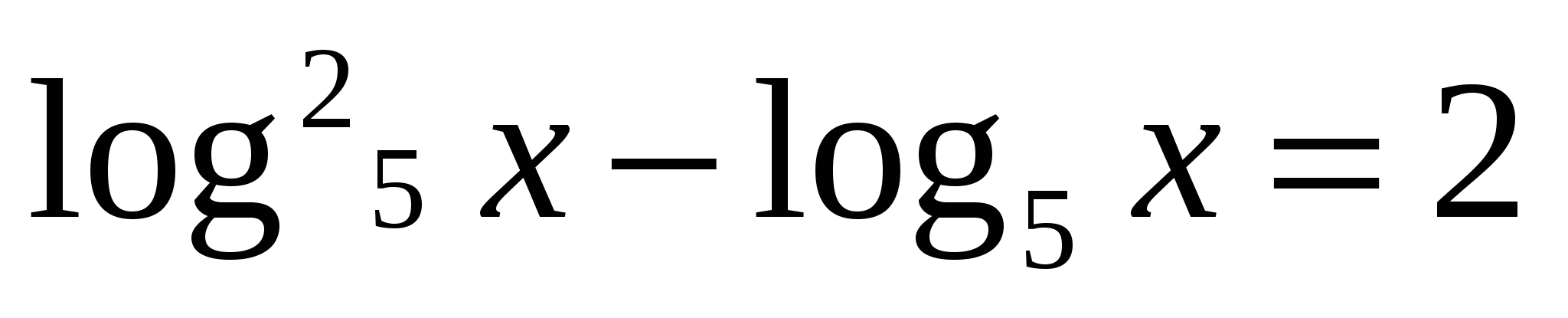
5;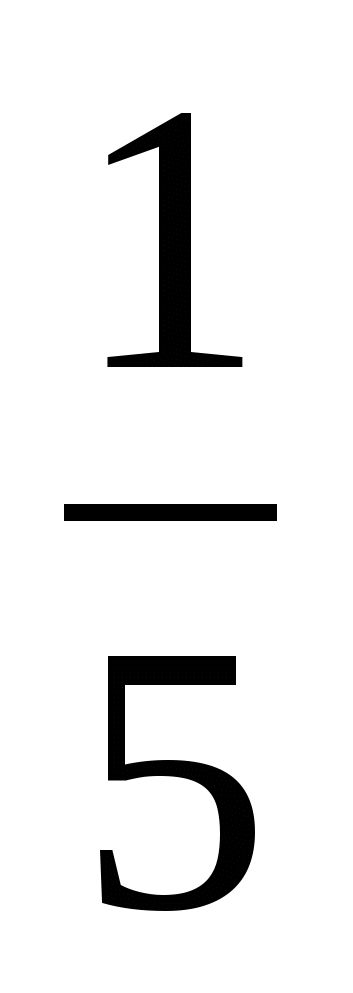

Введение новой переменной

6

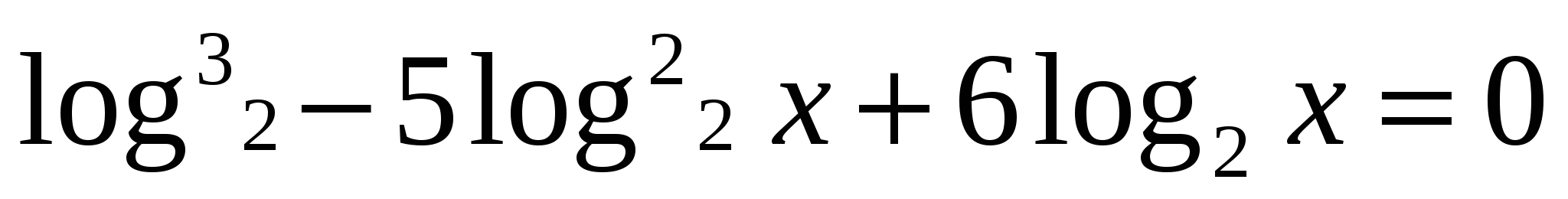
1; 2; 3

Разложение на множители

7

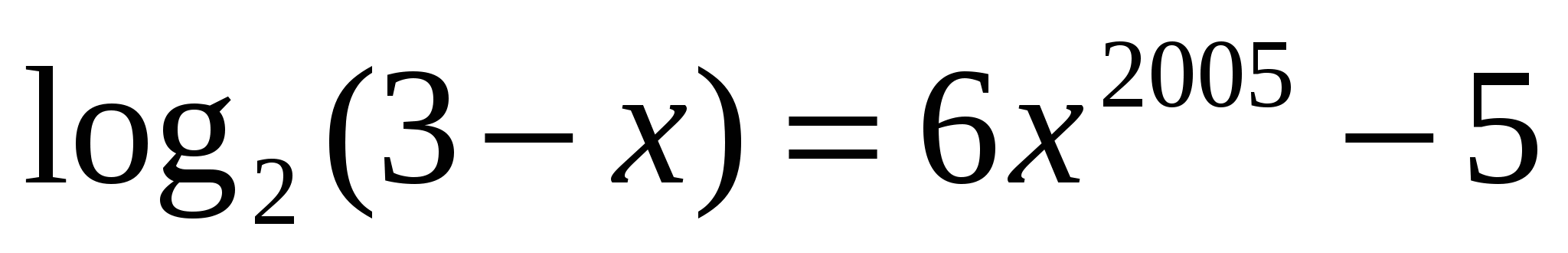
1

Функционально-графический метод

8

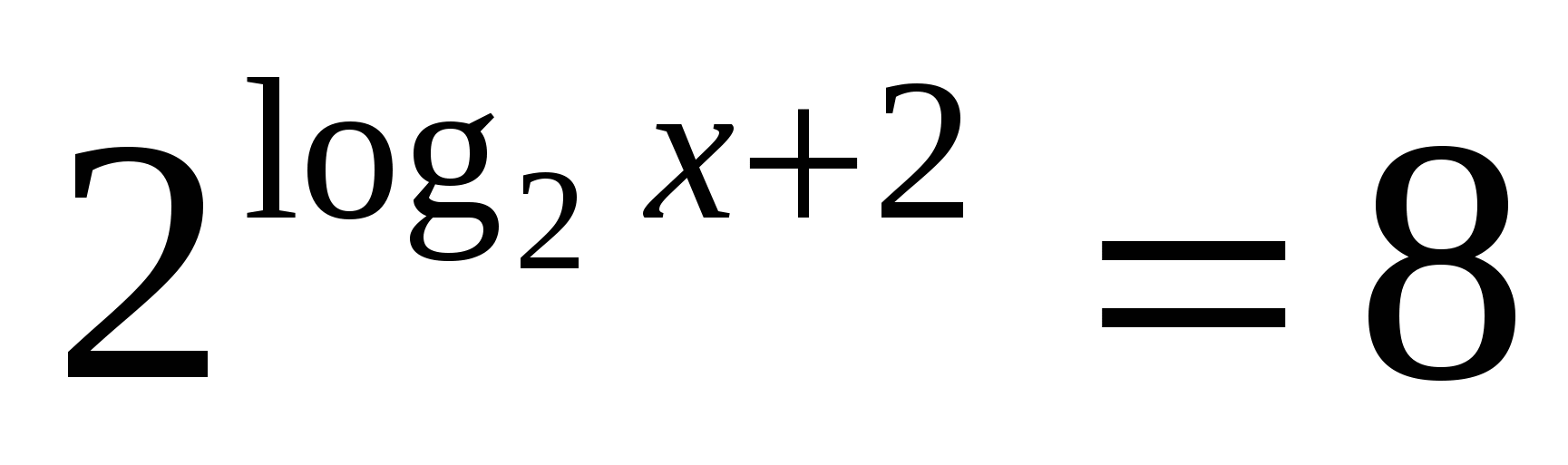
2;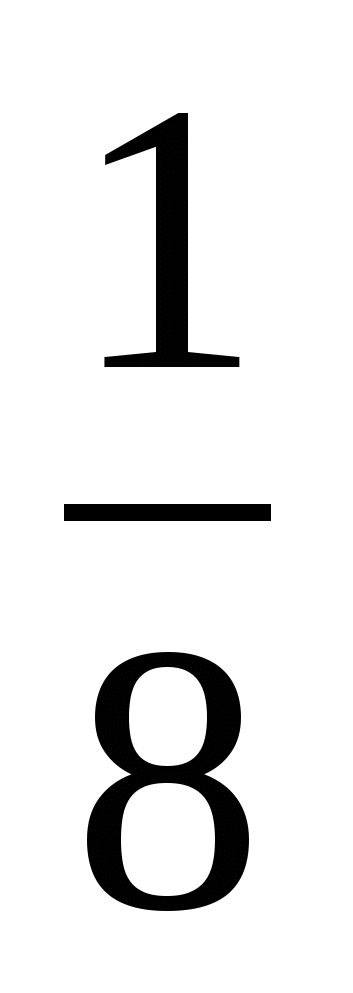

Метод логарифмирования

ВОПРОСЫ:

• Какое главное требование к решению логарифмических уравнений? (должна быть проверка или ОДЗ)

• Какой из методов не требует проверки?

• Когда используется функционально-графический метод? (когда в уравнение входят логарифмическая функция и любая другая (степенная, показательная, тригонометрическая, линейная).

Когда можно использовать метод логарифмирования? ( когда обе части положительные, тогда не будет потери корней)

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ + ЛОГАРИФМИЧЕСКИЕ образуют

КОМБИНИРОВАННЫЕ УРАВНЕНИЯ

Какое главное требование к решению комбинированных уравнений? (чтобы корни одного уравнения являлись одновременно корнями другого)

1. 2. КОНТРОЛЬ И САМОКОНТРОЛЬ

1. 2. 1. По тестам ЕГЭ 2005-2006 г. стр.10, вариант 2, задание В-7 решить уравнение :

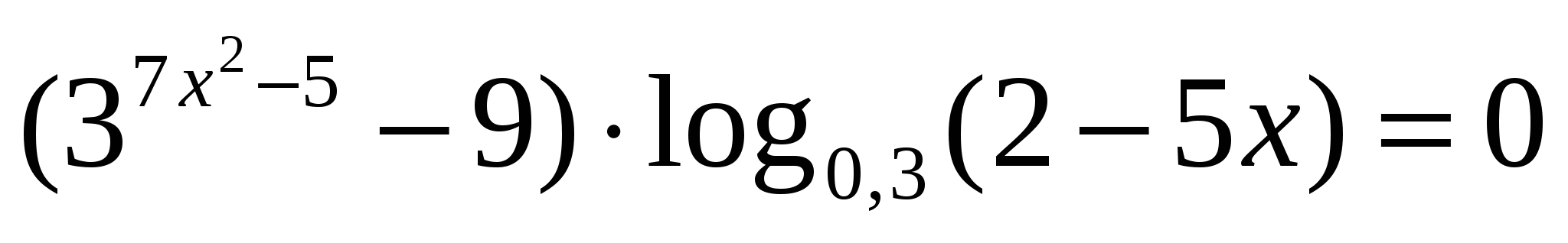
и указать наибольший корень.

Ответ: 0,2 (для проверки ученик решает на отвороте доски)

1. 2. 2. Задание по карточке: Найти произведение корней уравнения

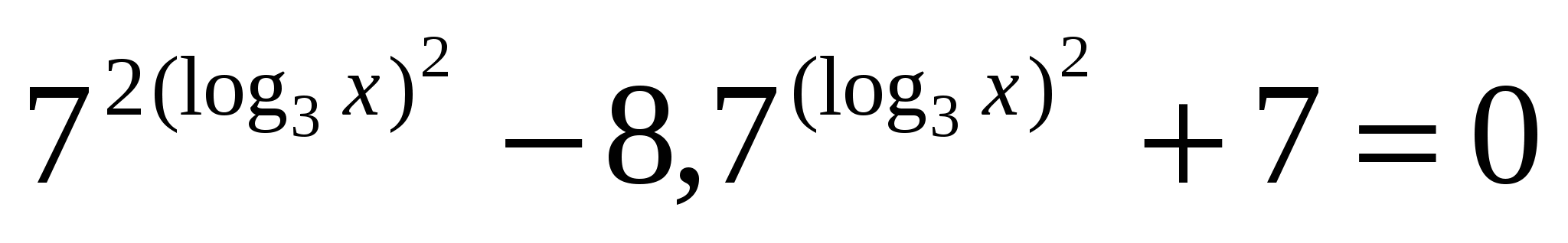
Ответ: корни 1; 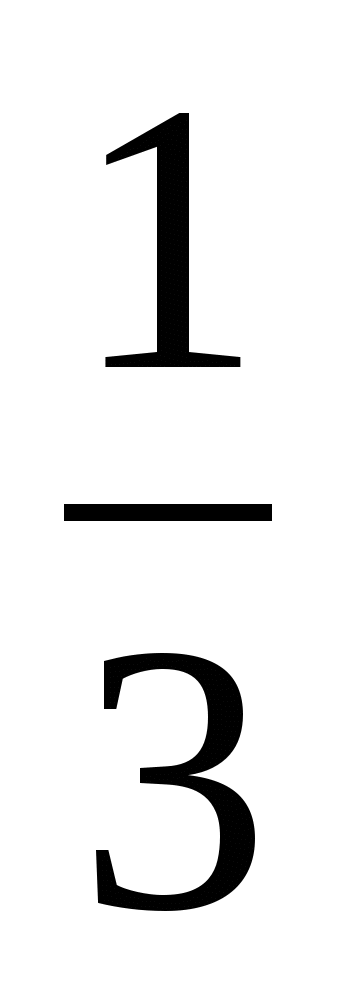; 3 произведение = 1

с) Работа с учебником: №175(г), страница 287.

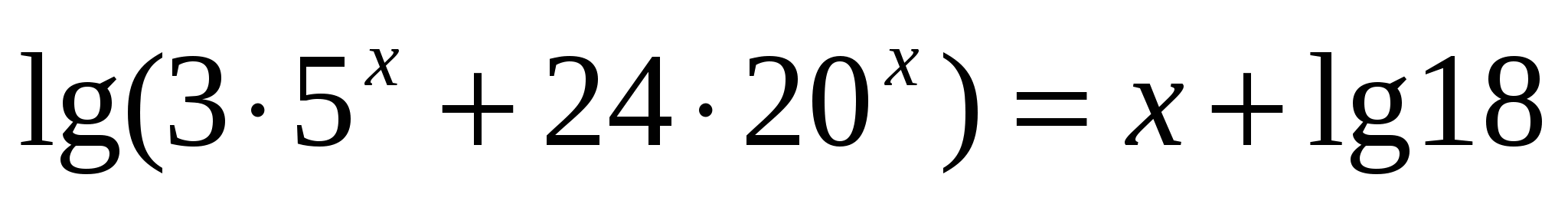
Ответ: -2 ; -1

d) Тестирование:

А1) Найти значение выражения:

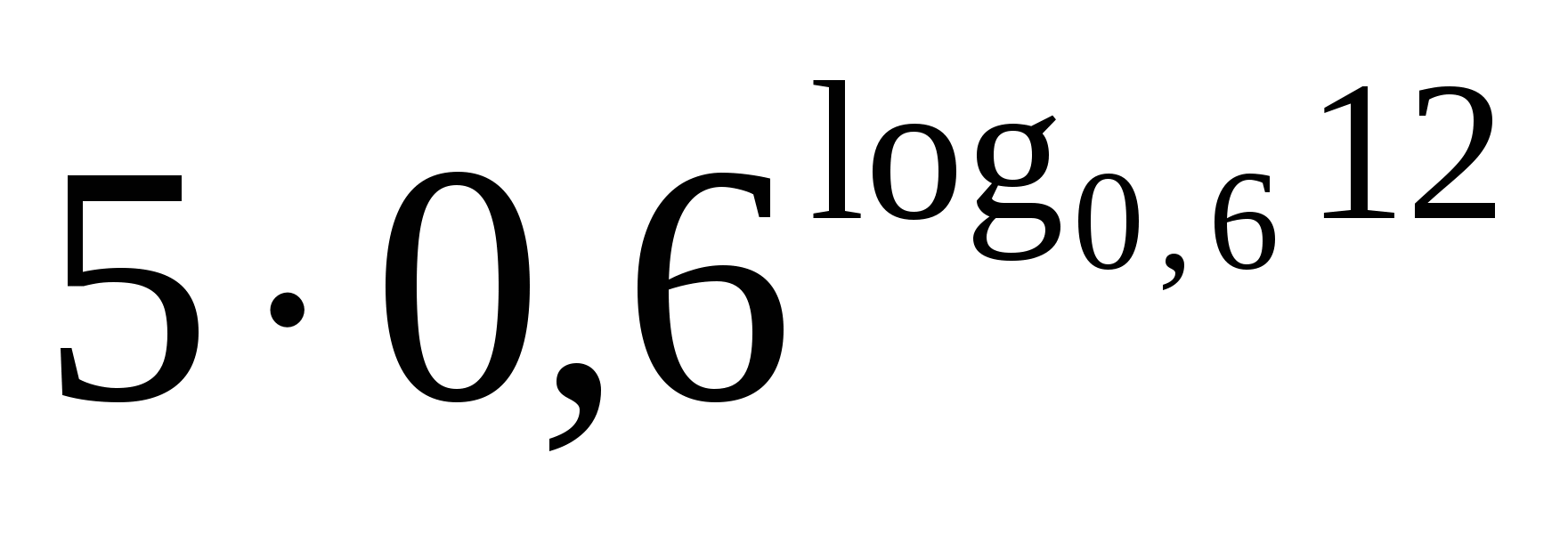
1) 100 2) 60 3) 3 4) 5

А2) Вычислить: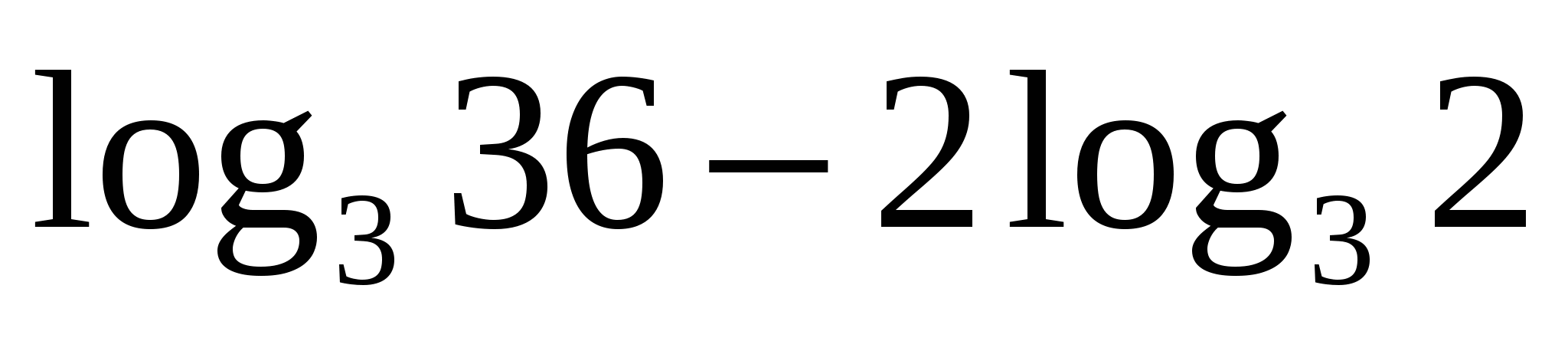

1) 18 2) 2 3) 0,5 4) 3

А3) Какое из чисел входит в множество значений функции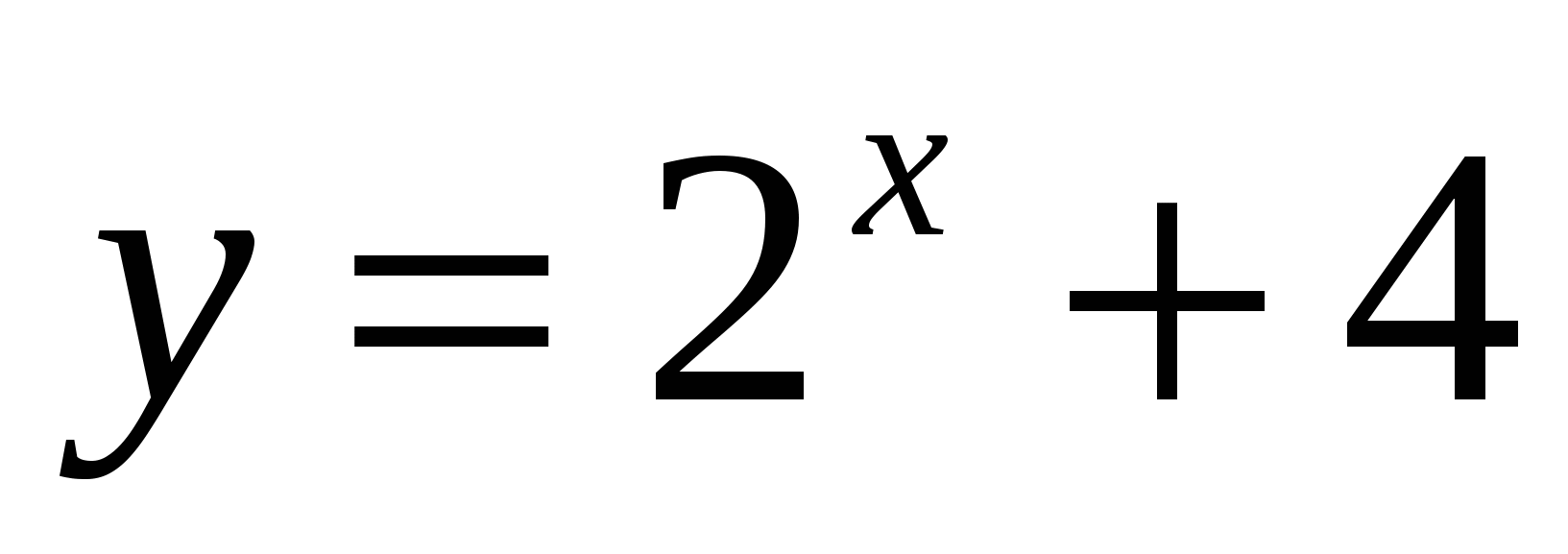

1) 5 2) 2 3) 3 4) 4

А4) Указать промежуток, содержащий корень уравнения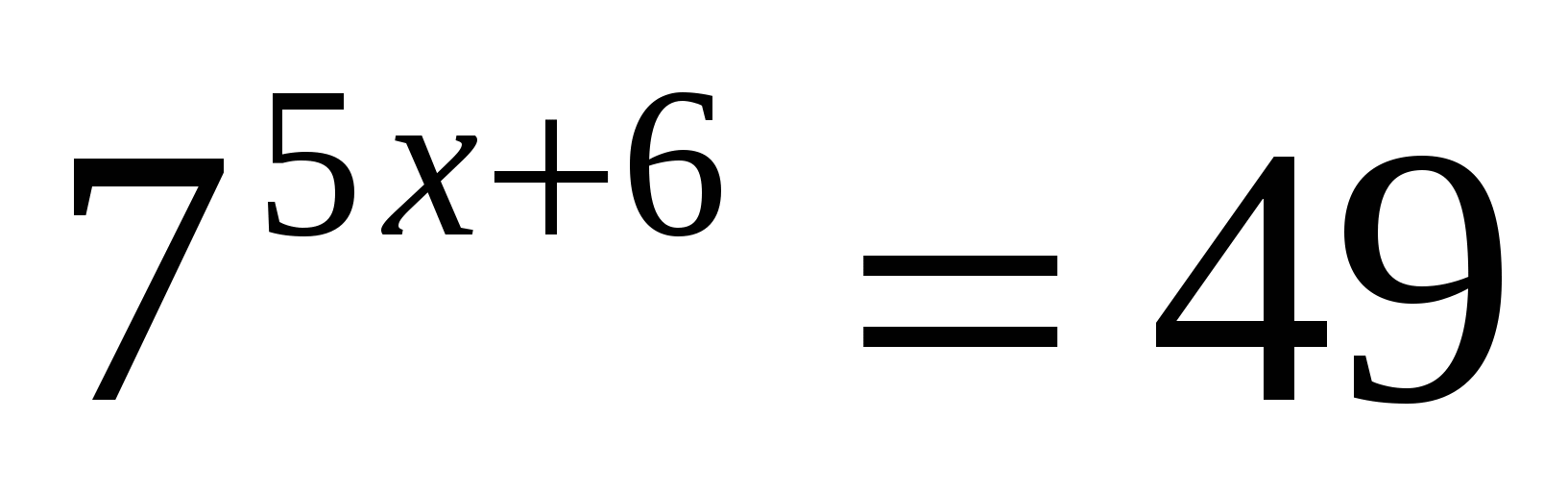

1) [- 4; — 1) 2) [ — 1; 0] 3) (0; 2) 4) [5 ; 9]

A5) Решить уравнение:

1) 9 2) 20 3) 1 4) 0

А6) Указать промежуток, которому принадлежит корень уравнения

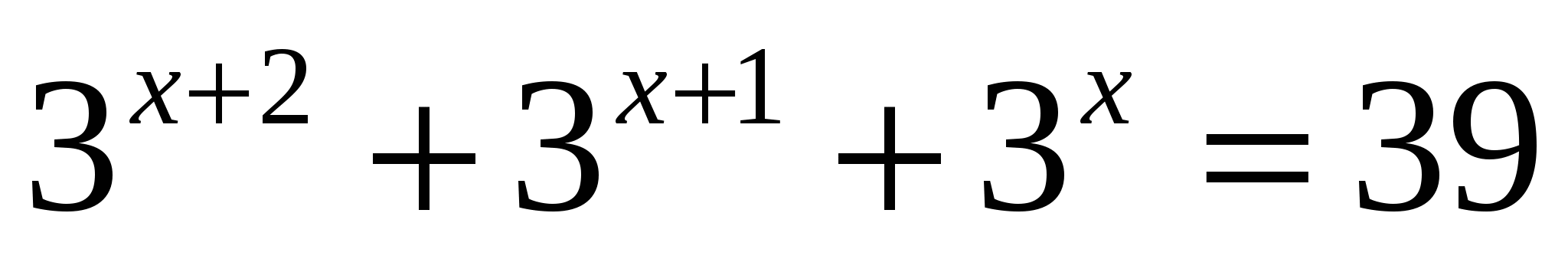
1) [ -2; 0] 2) [2 ; 4] 3) (4; 9) 4) (0; 2)

B1) Решить уравнение: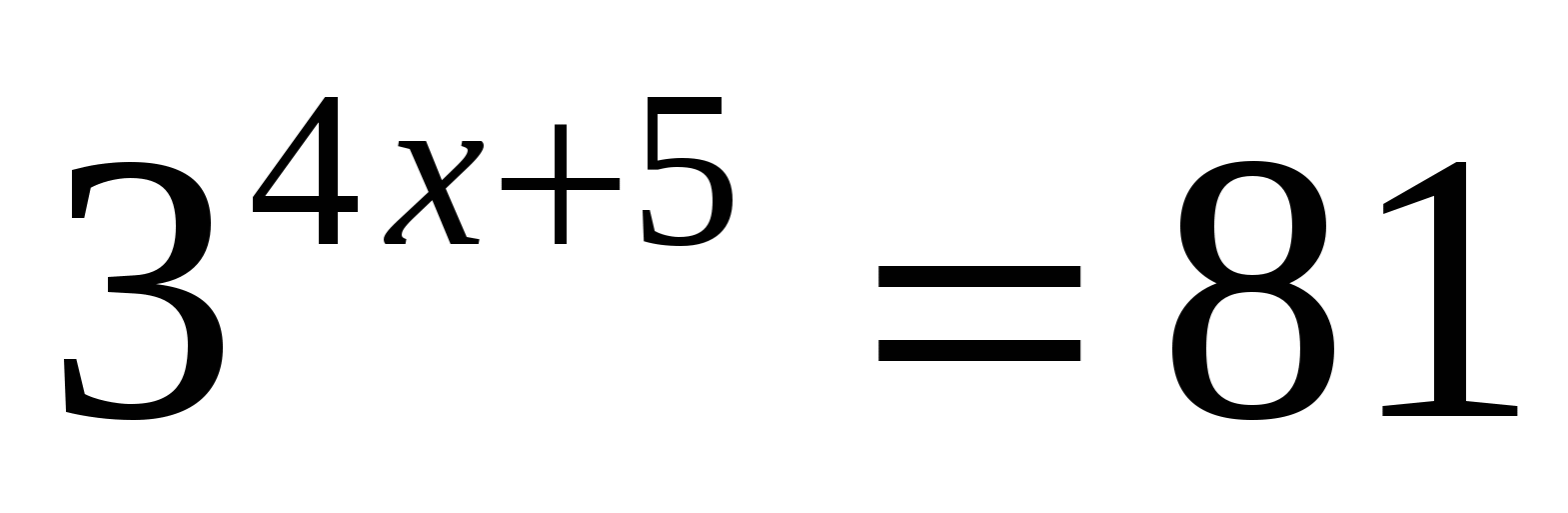

В2) Решить уравнение: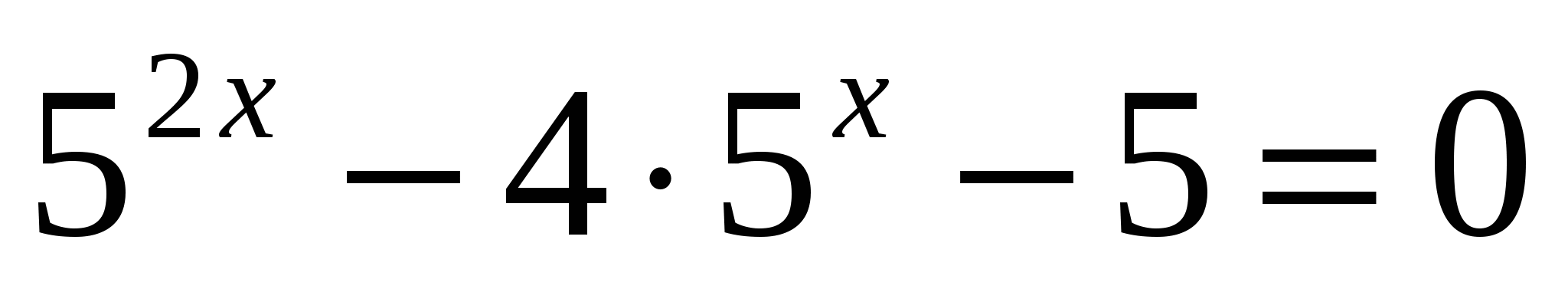

В3) Найти произведение корней уравнения: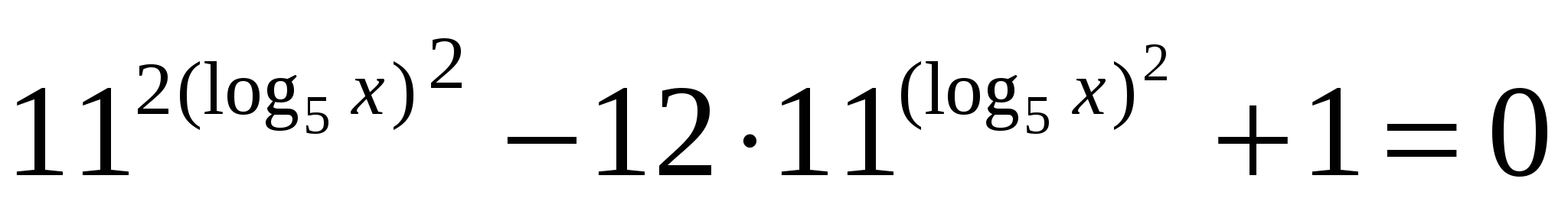

В4) Решить уравнение: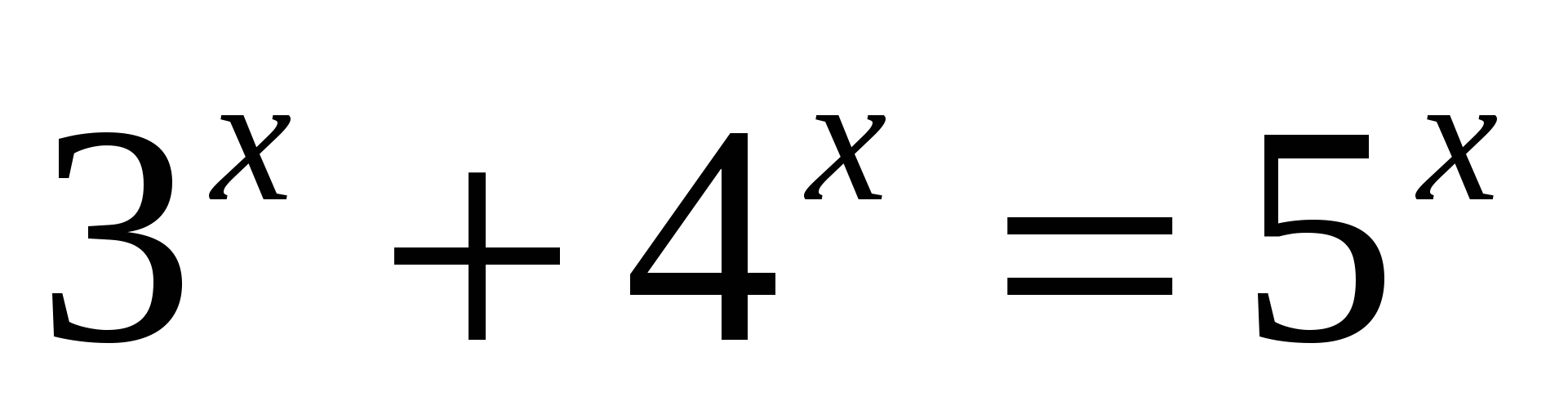

В5) Найти наименьший корень уравнения: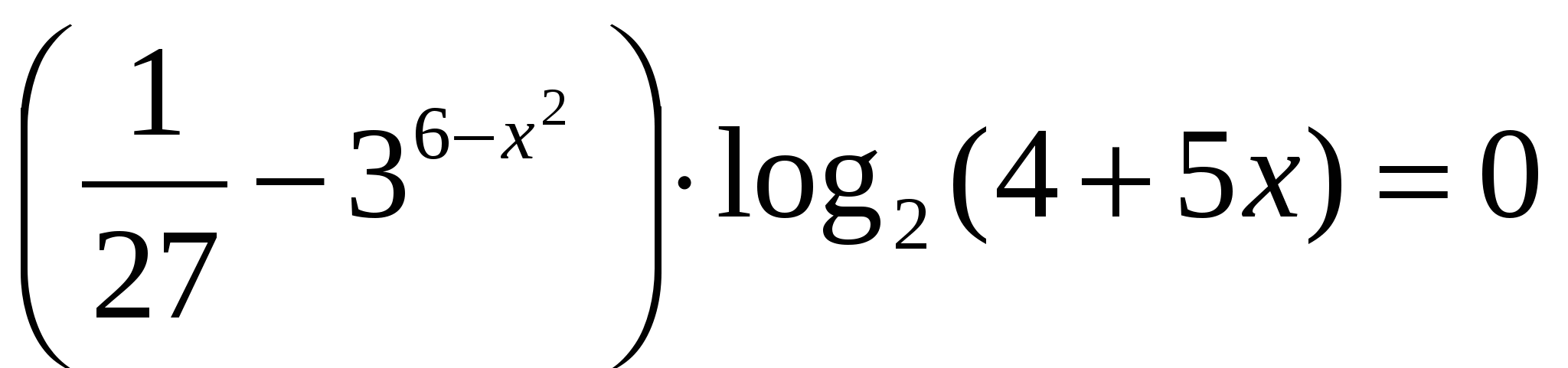

ОТВЕТЫ:

А1

А2

А3

А4

А5

А6

В1

В2

В3

В4

В5

4

2

1

2

2

4

-0,25

1

1

2

-0,6

Ответы ученики записывают в бланках ответов №1 образца ЕГЭ

Проверка результатов тестирования. Учащиеся оценивают себя, ставят оценки в оценочный лист.

V. ПОДВЕДЕНИЕ ИТОГОВ УРОКА

1. Чем мы сегодня занимались на уроке?

2. Дайте определение показательного и логарифмического уравнения.

3. Где в жизни мы встречаемся с показательной функцией? С логарифмической?

Есть такая поговорка: «Заруби себе на носу» На каком носу можно зарубить? (нос- это палочка для зарубок) Поэтому хотелось бы, чтобы и вы «зарубили себе на носу» общие методы решения показательных и логарифмических уравнений и смогли успешно справиться с ними на экзаменах.

Выставление оценок.

VI. РЕФЛЕКСИЯ.

У каждого человека есть свое уязвимое место. А как оно называется? (Ахиллесова пята).Скажите. какое уязвимое место у вас при решении данных уравнений. Над чем еще надо поработать? Каждый из вас выберет себе карточку для отработки заданий.

Спасибо за урок.