9. Механическая энергия, виды энергии. Работа и кинетическая энергия при поступательном и вращательном движении.
Энергия – скалярная физическая величина. Является мерой различных форм движения материи и различных видов взаимодействия.
Механическая энергия — это энергия, связанная с движением объекта или его положением. Она описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы.
Виды механической энергии: кинетическая (энергия движения) и потенциальная (энергия взаимодействия).
Кинетическая энергия: поступательного и вращательного движения.
Потенциальная энергия: упругого и гравитационного взаимодействия.
Потенциальная энергия гравитационного взаимодействия: у поверхности Земли и в общем случае.
Кинетическая энергия тела – функция механического состояния, зависящая от массы тела и скорости его движения.
Свойства кинетической энергии
1) Конечность, дифференцируемость, однозначность.
2) Кинетическая энергия не отрицательна.
3) Кинетическая энергия аддитивна.
4) Тело может передать кинетическую энергию другим телам посредством совершения работы.
5) Приращение кинетической энергии тела равно работе всех сил, действующих на тело.
Потенциальная энергия – функция механического состояния, зависящая от взаимного расположения тел в системе или их частей.
Свойства потенциальной энергии:
1) Конечность, непрерывность, дифференцируемость, однозначность.
2)Значение потенциальной энергии определяется с точностью до постоянной величины (const), которая зависит от выборов нулевого уровня. Потенциальная энергия может быть меньше нуля.
3) Потенциальная энергия может быть взаимной, причем сила взаимодействия между телами будет являться консервативной.
4) Убыль потенциальной энергии равна работе всех консервативных сил, действующих на тело.
5)Потенциальная энергия связана с консервативными силами.
Кинетическая энергия:
1. Поступательное
движение. В
этом случае все точки тела движутся с
одинаковыми скоростями, равными скорости
движения центра масс. То есть, для
любой точки 
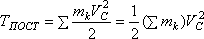
или
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
2. Вращательное
движение.
Если тело вращается вокруг какой-нибудь
оси Оz (см.
рис.46), то скорость любой его точки 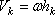 ,
где
,
где 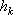
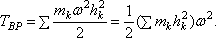
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
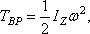
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
Работа силы равна изменению кинетической энергии.
10. Работа и потенциальная энергия. Свойства потенциальной энергии, ее связь с консервативной силой.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.
Работа силы упругости равна изменению потенциальной энергии пружины, взятому с противоположным знаком.
Свойства потенциальной энергии, ее связь с консервативной силой смотри в задании 9.
Механическая энергия
Механической энергией называют способность тела или системы тел совершать работу. Различают два вида механической энергии: кинетическая и потенциальная энергии.
Кинетическая энергия поступательного движения
Кинетическойназываетсяэнергия, обусловленная движением тела. Она измеряется работой, которую совершает равнодействующая сила, чтобы разогнать тело из состояния покоя до данной скорости.
Пусть тело массой mначинает двигаться под действием
равнодействующей силы .
Тогда элементарная работаdAравнаdA
.
Тогда элементарная работаdAравнаdA
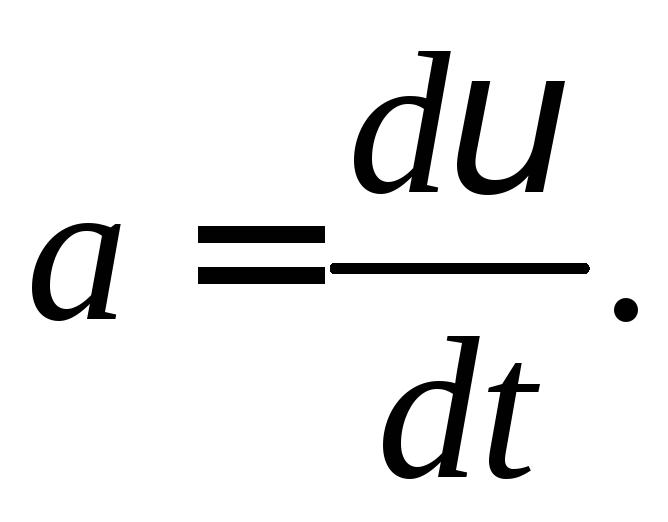 По второму закону НьютонаF = ma =
По второму закону НьютонаF = ma = 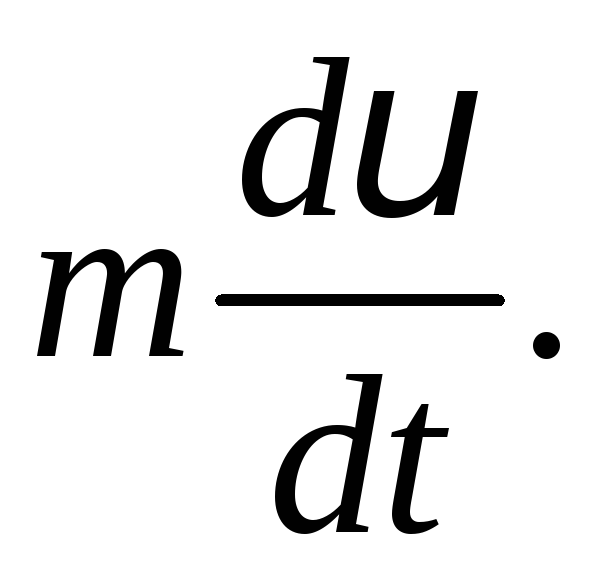 Поэтому
Поэтому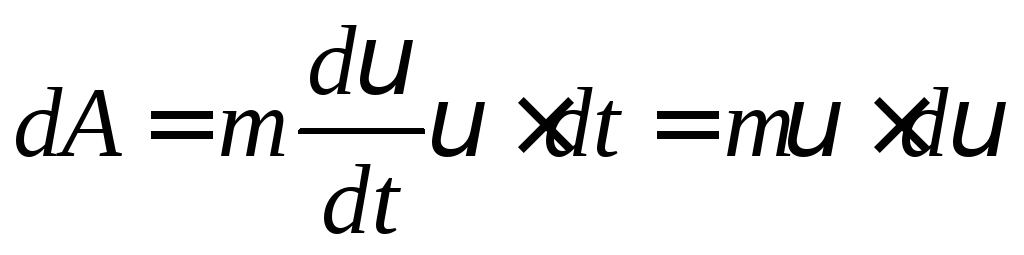 и полная работаАна путиlравна:
и полная работаАна путиlравна: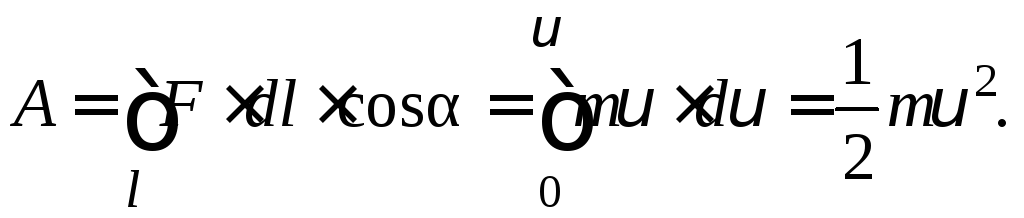 Согласно определению, Wk = A, поэтому
Согласно определению, Wk = A, поэтому 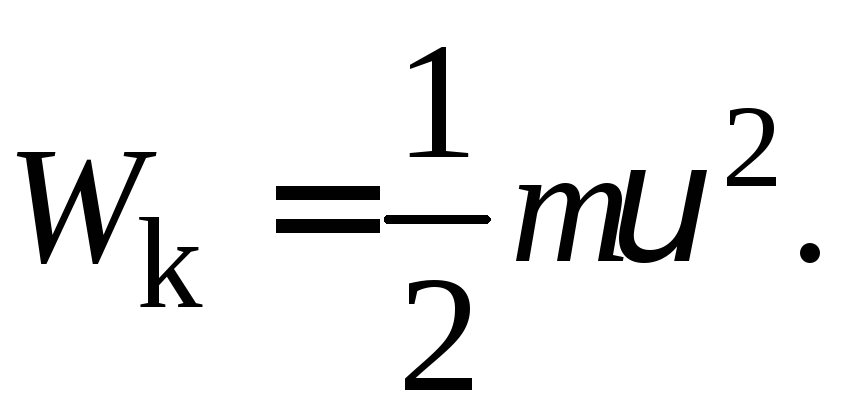 (6)
(6)
Из формулы (6) следует, что значение кинетической энергии зависит от выбора системы отсчёта, поскольку скорости тел в различных системах отсчёта различны.
Кинетическая энергия вращательного движения
Пусть тело с моментом инерции Izвращается относительно осиz с некоторой угловой скоростью. Тогда из формулы (6), пользуясь аналогией между поступательным и вращательным движениями, получаем:
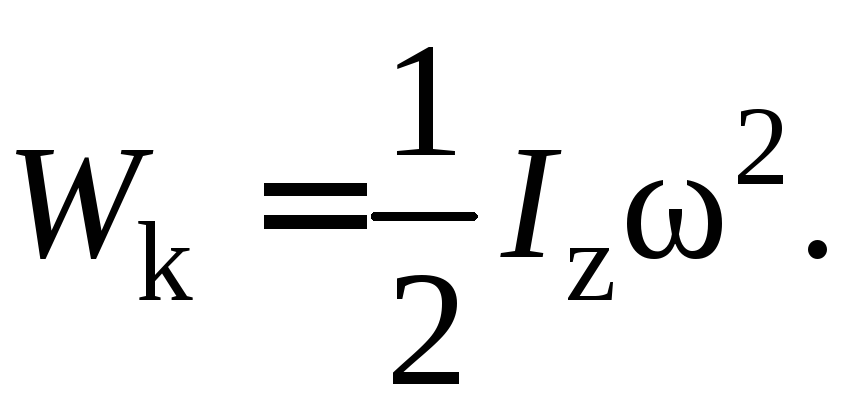 (7)
(7)
Теорема о кинетической энергии
Пусть тело массой т движется поступательно. Под действием
различных сил, приложенных к нему,
скорость тела изменяется от 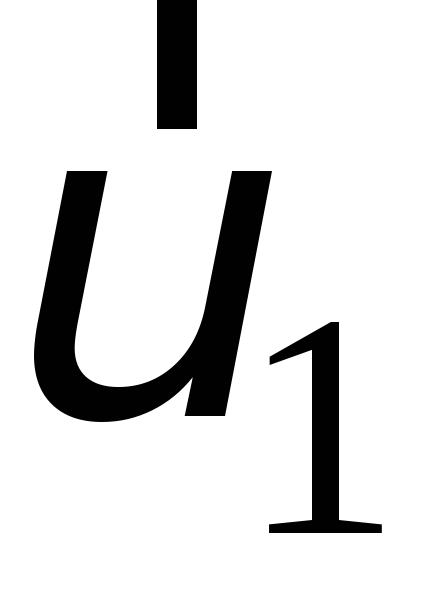 до
до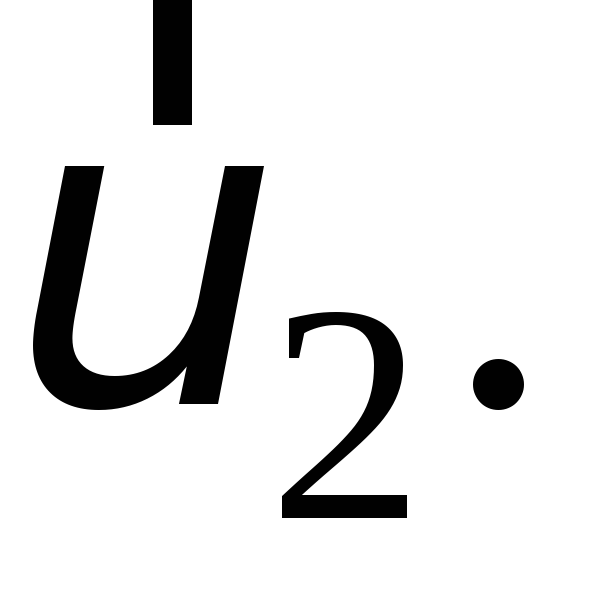 Тогда работаА этих сил равна
Тогда работаА этих сил равна
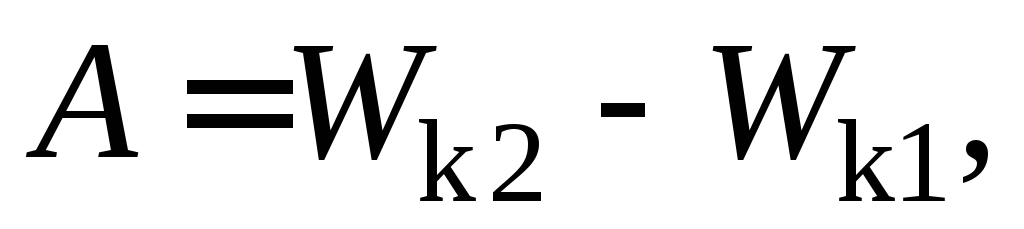
где Wk1иWk2—кинетическая энергия тела в начальном и конечном состоянии. Соотношение (8) называетсятеоремой о кинетической энергии.Его формулировка:работа всех сил, действующих на тело, равна изменению его кинетической энергии. Если тело одновременно участвует в поступательном и вращательном движениях, например, катится, то его кинетическая энергия равна сумме кинетической энергии при этих движениях.
Консервативные и неконсервативные силы
Если на тело в каждой точке пространства действует какая-нибудь сила, то совокупность этих сил называют силовым полем или полем. Существует два вида полей — потенциальные и непотенциальные (или вихревые). В потенциальных полях на тела, помещённые в них, действуют силы, зависящие только от координат тел. Эти силы получили название консервативных или потенциальных. Они обладают замечательным свойством:
работа консервативных сил не зависит от пути переноса тела и определяется только его начальным и конечным положением. Отсюда следует, что при движении тела по замкнутому пути (рис. 1) работа не совершается. Действительно, работа A на всём пути равна сумме работы A1B2, совершаемой на пути 1B2, и работы A2C1 на пути 2C1, т.е. А = A1B2 + A2C1. Но работа A2C1 = –A1C2, так как движение происходит в противоположном направлении и A1B2 = A1C2. Тогда А = A1B2 – A1C2 = 0, что и требовалось доказать. Равенство нулю работы по замкнутому пути можно записать в виде 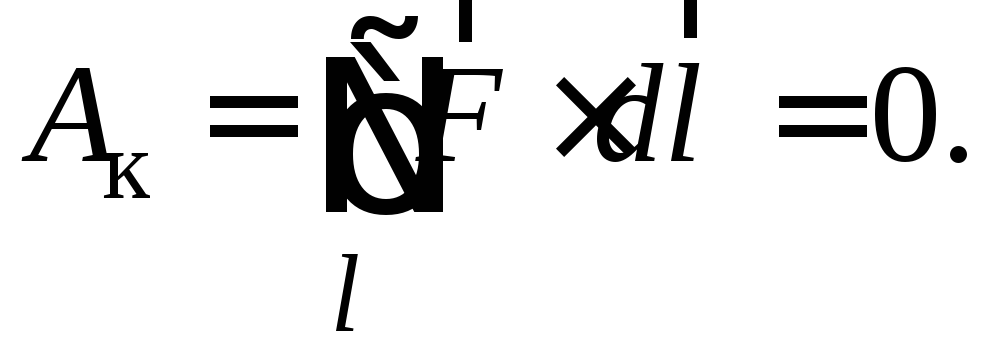 (9)
(9)
Значок «» на интеграле означает, что интегрирование производится по замкнутой кривой длиною
Р



1
B
C
2
ис. 1В макромире имеется всего лишь три вида потенциальных силгравитационная, упругая и электростатическая силы. К неконсервативным силам относятся силы трения, называемыедиссипативными. В этом случае направления силы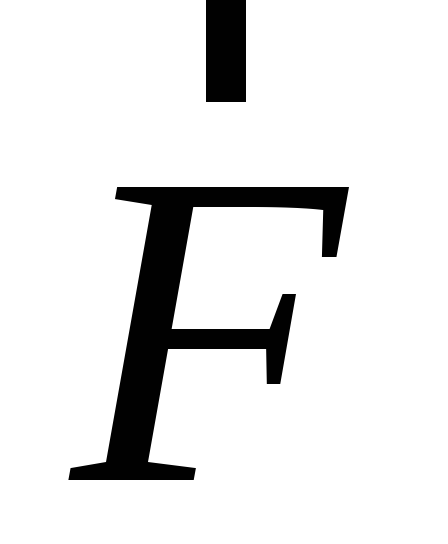 и
и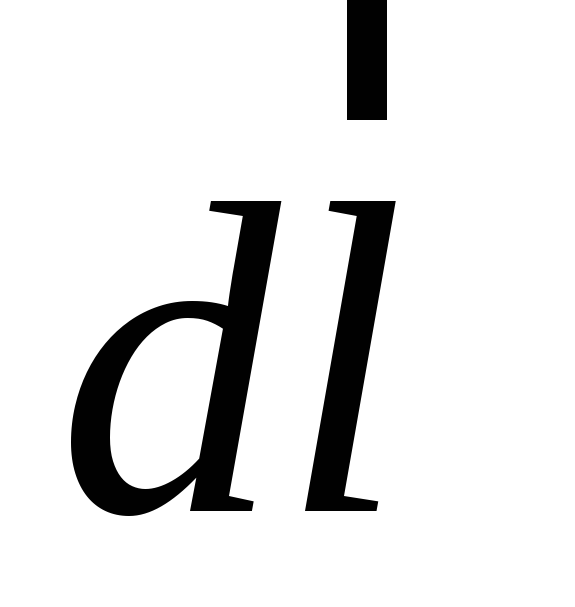 всегда противоположны. Поэтому работа
этих сил по любому пути отрицательная,
вследствие чего тело непрерывно теряет
кинетическую энергию.
всегда противоположны. Поэтому работа
этих сил по любому пути отрицательная,
вследствие чего тело непрерывно теряет
кинетическую энергию.Механическая энергия и ее виды :: SYL.ru
Цель этой статьи — раскрыть сущность понятия «механическая энергия». Физика широко использует это понятие как практически, так и теоретически.
Работа и энергия
Механическую работу можно определить, если известны сила, действующая на тело, и перемещение тела. Существует и другой способ для расчета механической работы. Рассмотрим пример:
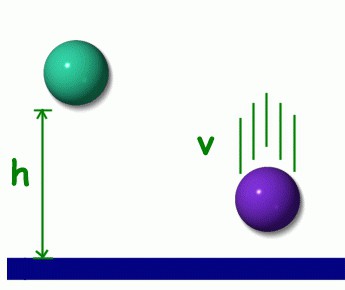
На рисунке изображено тело, которое может находиться в различных механических состояниях (I и II). Процесс перехода тела из состояния I в состояние II характеризуется механической работой, то есть при переходе из состояния I в состояние II тело может осуществить работу. При осуществлении работы меняется механическое состояние тела, а механическое состояние можно охарактеризовать одной физической величиной — энергией.
Энергия — это скалярная физическая величина всех форм движения материи и вариантов их взаимодействия.
Чему равна механическая энергия
Механической энергией называют скалярную физическую величину, которая определяет способность тела выполнять работу.
А = ∆Е
Поскольку энергия — это характеристика состояния системы в определенный момент времени, то работа — это характеристика процесса изменения состояния системы.
Энергия и работа обладают одинаковыми единицами измерения: [А] = [Е] = 1 Дж.
Виды механической энергии
Механическая свободная энергия делится на два вида: кинетическую и потенциальную.
Кинетическая энергия — это механическая энергия тела, которая определяется скоростью его движения.
Еk = 1/2mv2
Кинетическая энергия присуща подвижным телам. Останавливаясь, они выполняют механическую работу.
В различных системах отсчета скорости одного и того же тела в произвольный момент времени могут быть разными. Поэтому кинетическая энергия – относительная величина, она обуславливается выбором системы отсчета.

Если на тело во время движения действует сила (или одновременно несколько сил), кинетическая энергия тела меняется: тело ускоряется или останавливается. При этом работа силы или работа равнодействующей всех сил, которые приложены к телу, будет равняться разнице кинетических энергий:
A = Ek1 — Ek2 = ∆Еk
Этому утверждению и формуле дали название — теорема о кинетической энергии.
Потенциальной энергией именуют энергию, обусловленную взаимодействием между телами.
При падении тела массой m с высоты h сила притяжения выполняет работу. Поскольку работа и изменение энергии связаны уравнением, можно записать формулу для потенциальной энергии тела в поле силы тяжести:
Ep = mgh
В отличие от кинетической энергии Ek потенциальная Ep может иметь отрицательное значение, когда h<0 (например, тело, лежащее на дне колодца).
Еще одним видом механической потенциальной энергии является энергия деформации. Сжатая на расстояние x пружина с жесткостью k имеет потенциальную энергию (энергию деформации):
Ep = 1/2 kx2
Энергия деформации нашла широкое применение на практике (игрушки), в технике — автоматы, реле и другие.
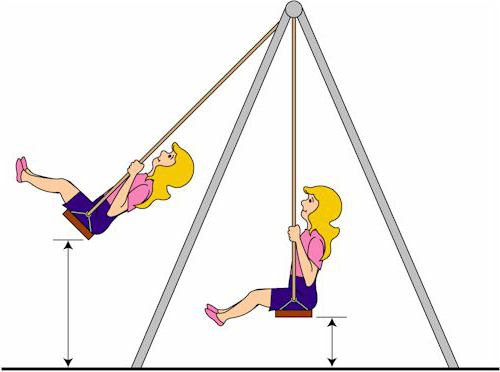
E = Ep + Ek
Полной механической энергией тела именуют сумму энергий: кинетической и потенциальной.
Закон сохранения механической энергии
Одни из самых точных опытов, которые провели в середине XIX века английский физик Джоуль и немецкий физик Майер, показали, что количество энергии в замкнутых системах остается неизменной. Она лишь переходит от одних тел к другим. Эти исследования помогли открыть закон сохранения энергии:
Полная механическая энергия изолированной системы тел остается постоянной при любых взаимодействиях тел между собой.
В отличие от импульса, который не имеет эквивалентной формы, энергия имеет много форм: механическую, тепловую, энергию молекулярного движения, электрическую энергию с силами взаимодействия зарядов и другие. Одна форма энергии может переходить в другую, например, в тепловую кинетическая энергия переходит в процессе торможения автомобиля. Если сил трения нет, и тепло не образуется, то полная механическая энергия не утрачивается, а остается постоянной в процессе движения или взаимодействия тел:
E = Ep + Ek = const
Когда действует сила трения между телами, тогда происходит уменьшение механической энергии, однако и в этом случае она не теряется бесследно, а переходит в тепловую (внутреннюю). Если над замкнутой системой выполняет работу внешняя сила, то происходит увеличение механической энергии на величину выполненной этой силой работы. Если же замкнутая система выполняет работу над внешними телами, тогда происходит сокращение механической энергии системы на величину выполненной ею работы.
Каждый вид энергии может превращаться полностью в произвольный иной вид энергии.
Урок 11. Лекция 11. Работа. Мощность. Энергия. Закон сохранения энергии
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
A = Fs cos α
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в
[1 Дж=1 Н·м]
Работа силы, совершаемая в единицу времени, называется мощностью.
Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
N=A/t
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Внесистемная единица мощности 1 л.с.=735 Вт
Связь между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα тогда N=(FScosα)/t, но S/t = v следовательно
N=Fvcos α
В технике используются единицы работы и мощности:
1 Вт·с = 1 Дж; 1Вт·ч = 3,6·103 Дж; 1кВт·ч = 3,6·106 Дж
Если тело способно совершить работу, то говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]
Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.
Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий
Е = Ек + Еp
Кинетическая энергия – это энергия тела, обусловленная его движением.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
Если тело движется со скоростью , то для его полной остановки необходимо совершить работу
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела.
Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй):
Ep = mgh
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией.
Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.
Е = Ек + Еp = const
Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
3. Работа и механическая энергия
3.1. Работа и мощность при поступательном и вращательном движениях
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Элементарной
работой силы  называется величина, равная скалярному
произведению силы на элементарное
перемещение
называется величина, равная скалярному
произведению силы на элементарное
перемещение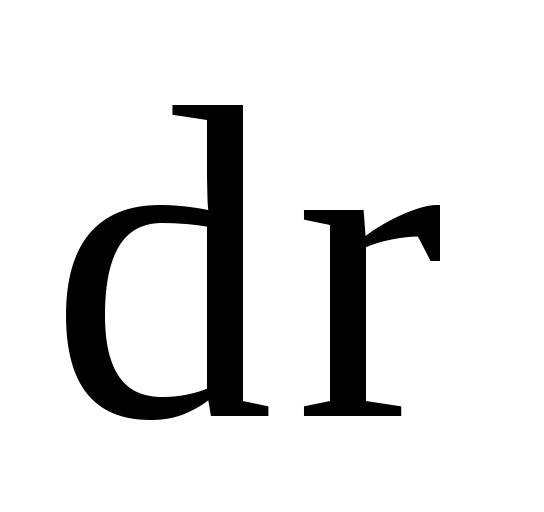 :
:
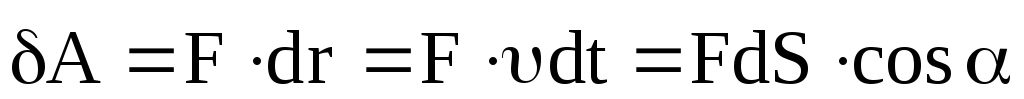 ,
,
где 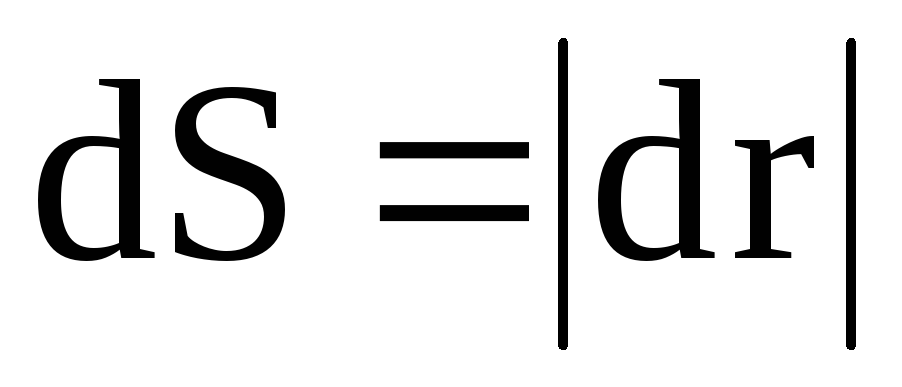 –
элементарный путь точки приложения
силы за время dt,
– угол между векторами
–
элементарный путь точки приложения
силы за время dt,
– угол между векторами  и
и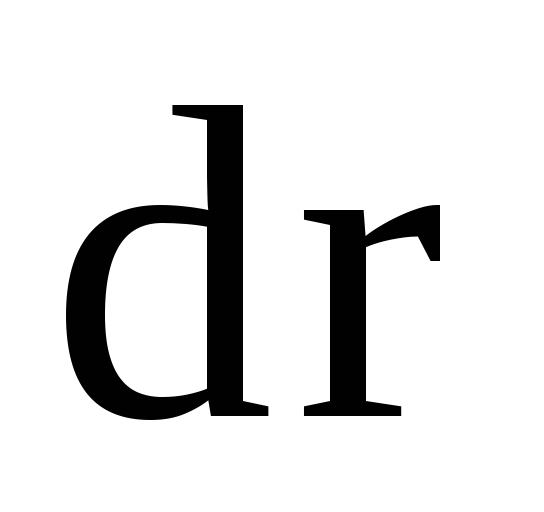 .
.
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
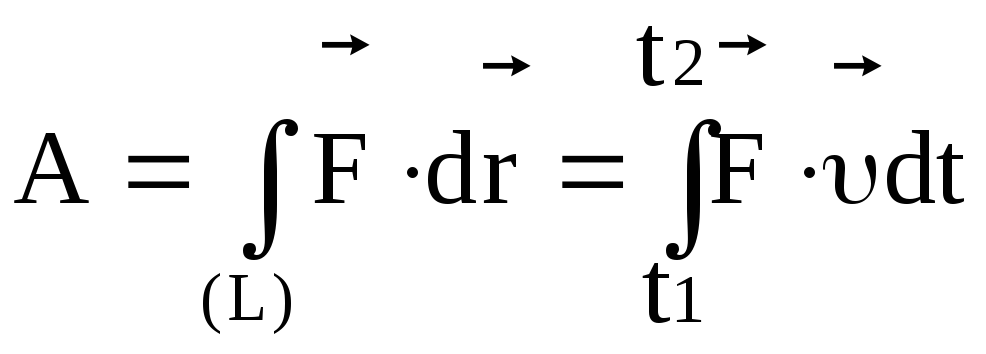 .
.
Если  =
const, то А=
=
const, то А=
 .
.
При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:
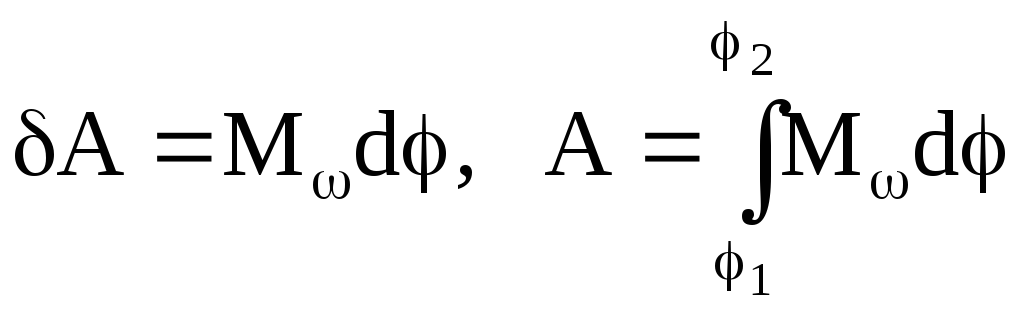 ,
,
если М = const, то А = М.
Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:
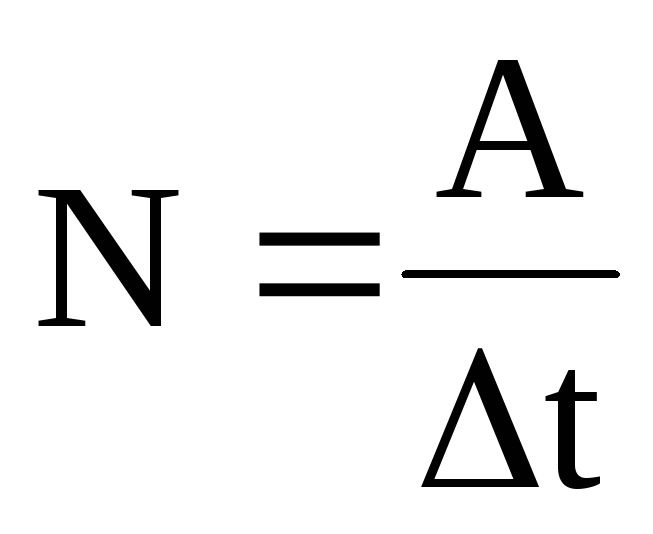 –средняя
мощность;
–средняя
мощность; 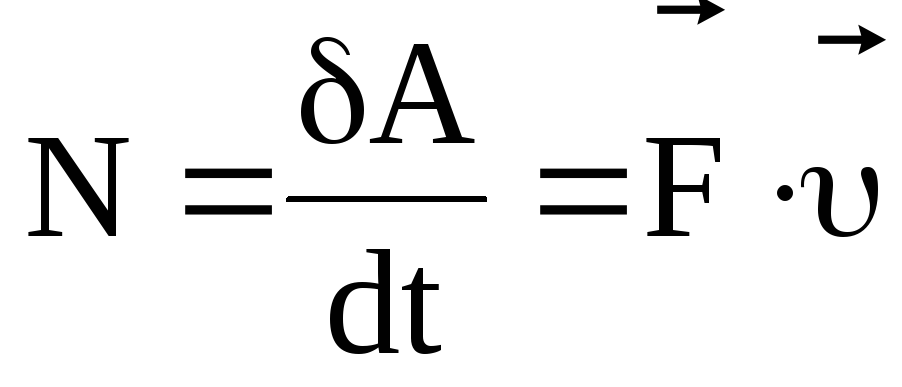 – мгновенная мощность.
– мгновенная мощность.
При вращательном движении мощность определяется следующим образом:
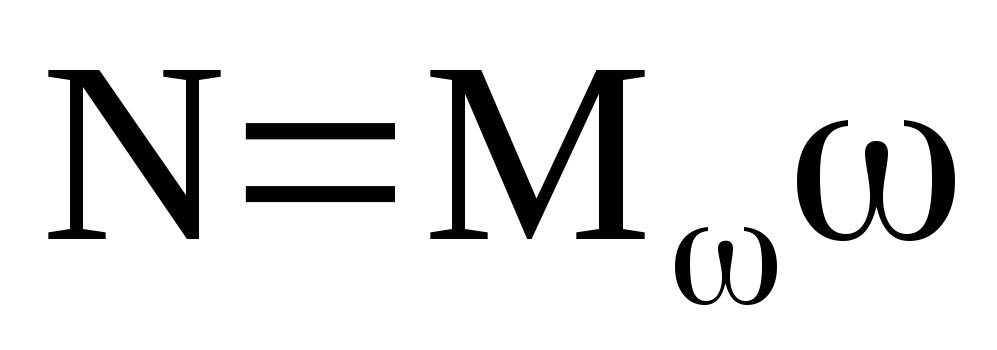 .
.
3.2. Консервативные и неконсервативные силы
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:
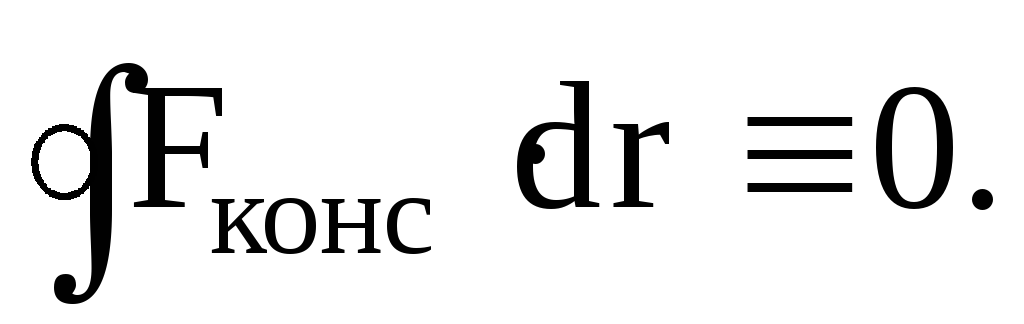
К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.
Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
3.3. Кинетическая энергия при поступательном и вращательном движениях
Кинетической энергией тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).
Кинетическая
энергия поступательного движения 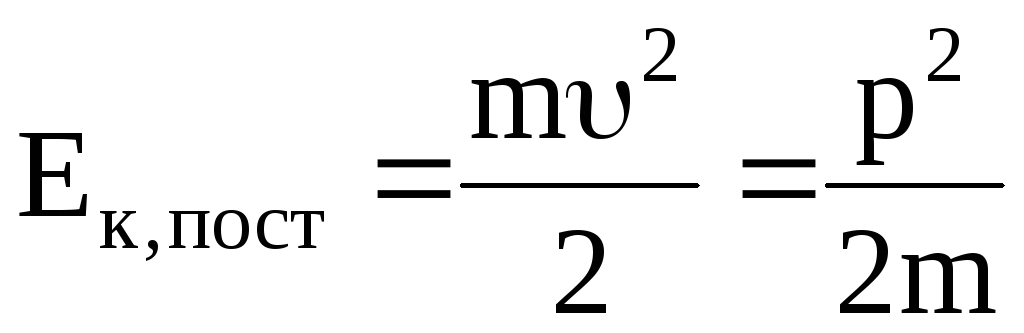 . Кинетическая энергия вращательного
движения
. Кинетическая энергия вращательного
движения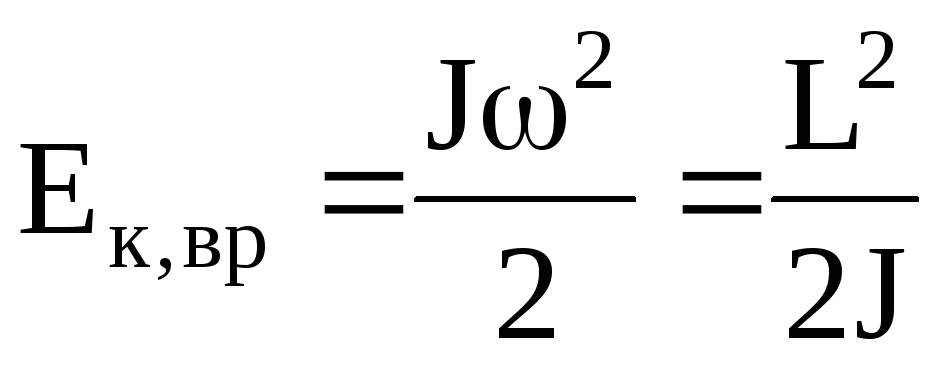 .
.
При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:
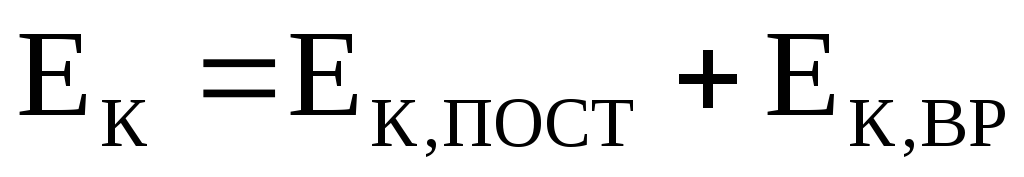 .
.
Свойства кинетической энергии.
1. Кинетическая энергия является конечной, однозначной, непрерывной функцией механического состояния системы.
2. Кинетическая энергия не отрицательна: ЕК 0.
3. Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.
4.
Приращение кинетической энергии тела
равно работе всех сил, действующих
на тело: 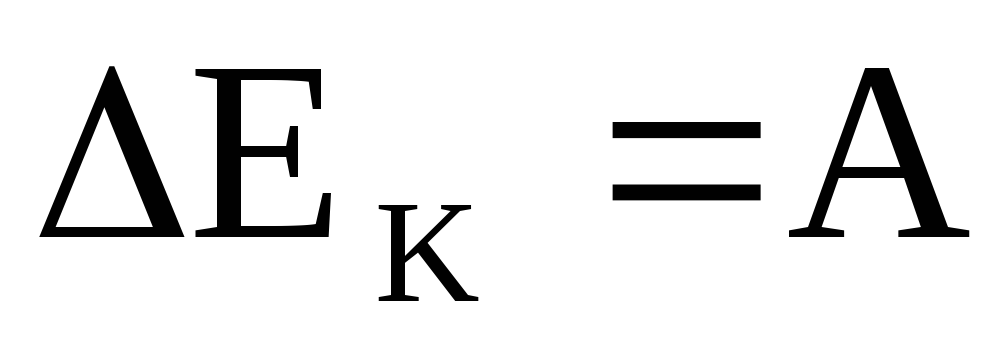 .
.
3.4. Потенциальная энергия
Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.
ЕП1 — ЕП2 = ЕП = А12конс,  .
.
Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.
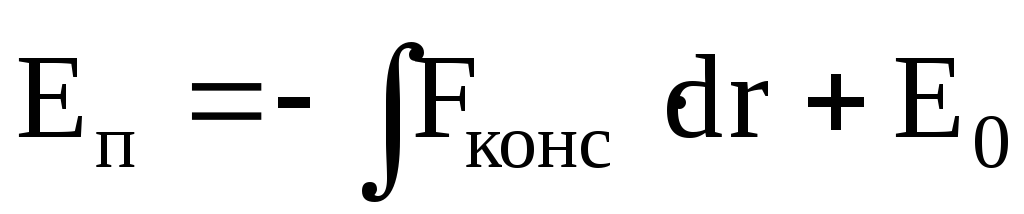 .
.
Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.
Свойства потенциальной энергии.
1. Потенциальная энергия является конечной, однозначной, непрерывной
функцией механического состояния системы.
2. Численное значение потенциальной энергии зависит от выбора уровня с
нулевой потенциальной энергией.
Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:
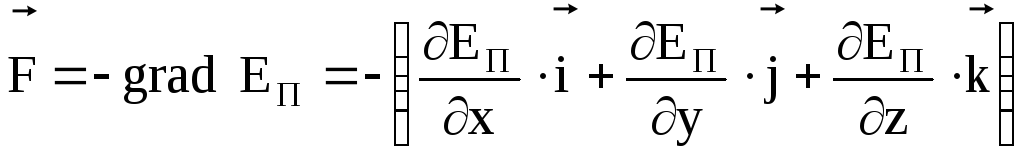 ,
,
причем 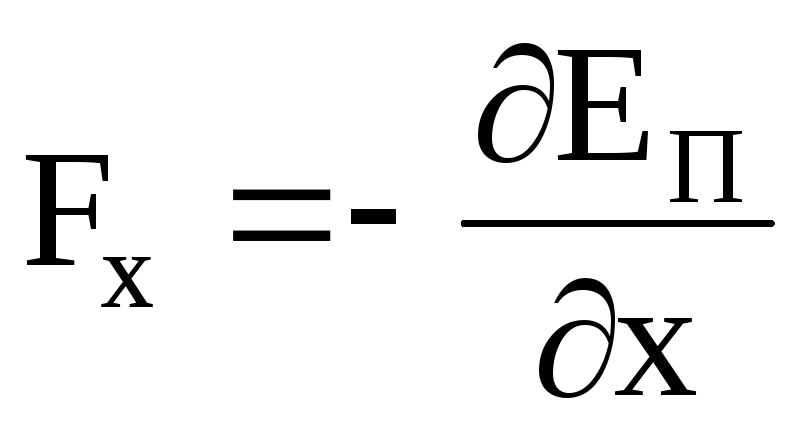 ,
,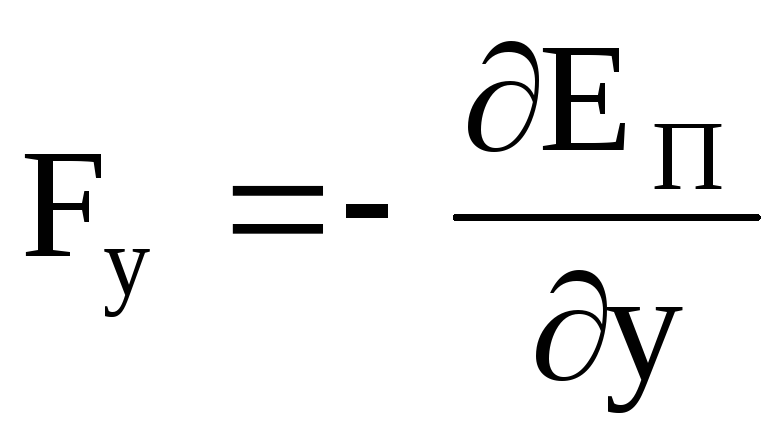 ,
,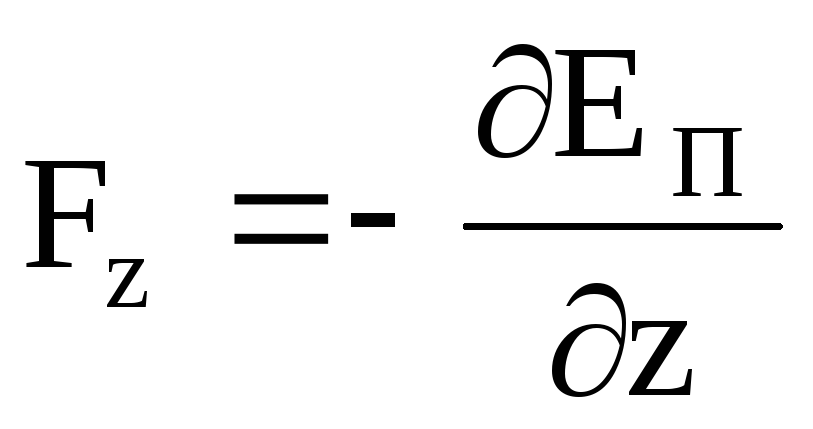 .
.
Примеры потенциальной энергии:
1) 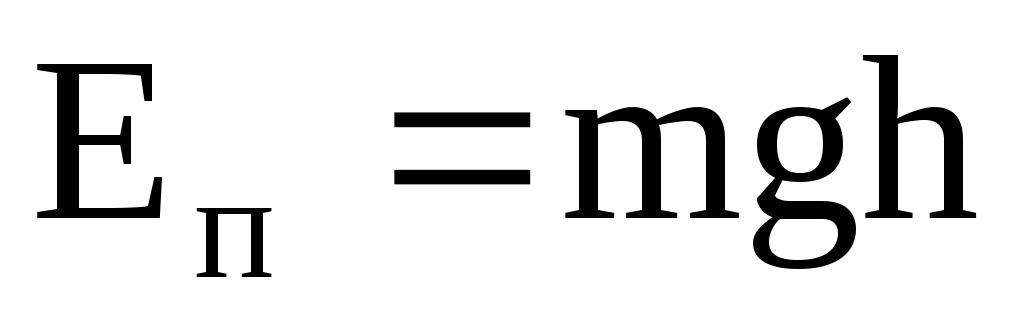 –
потенциальная энергия тела массой m,
поднятого на высоту h относительно
нулевого уровня энергии в поле силы
тяжести;
–
потенциальная энергия тела массой m,
поднятого на высоту h относительно
нулевого уровня энергии в поле силы
тяжести;
 –потенциальная
энергия упругого деформированного
тела, х
– деформация тела.
–потенциальная
энергия упругого деформированного
тела, х
– деформация тела.
4. Кинетическая и потенциальная энергия. Механическая работа и мощность. Консервативные и неконсервативные силы. Работа в поле этих сил. Закон сохранения энергии.
1.2.2 Законы сохранения
Запишем уравнение (1.24) в виде
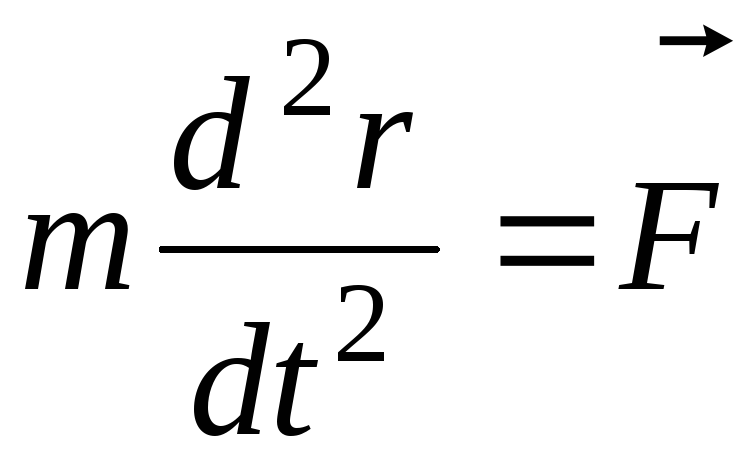 . (1.25)
. (1.25)
Выражение (2.25) представляет собой уравнение движения частицы. Если его проинтегрировать, то можно найти траекторию частицы r = r(t, F). Однако часто это не является необходимым. Оказывается, уравнения Ньютона обладают тем свойством, что некоторые величины, характеризующие движение частицы, остаются неизменными во все время движения. О таких величинах принято говорить, что они сохраняются. Их также называют интегралами движения. Знание интегралов движения позволяет получить ряд важных следствий без фактического решения уравнений движения. Получим некоторые сохраняющиеся величины.
Перепишем уравнение (1.25) в виде
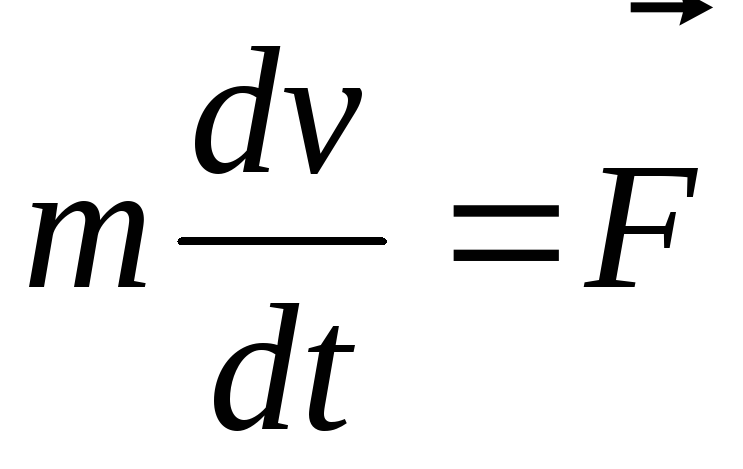 . (1.26)
. (1.26)
Величина 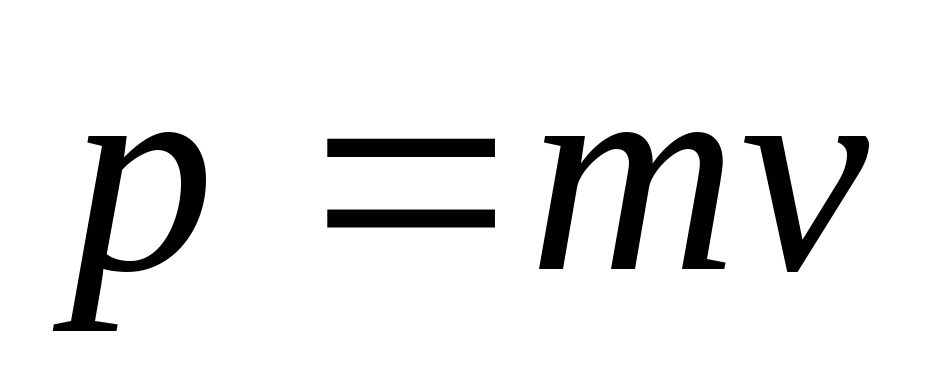 называется импульсом тела. Внеся
величинуm под знак
дифференциала в (1.26), закон Ньютона
можно записать в форме:
называется импульсом тела. Внеся
величинуm под знак
дифференциала в (1.26), закон Ньютона
можно записать в форме:
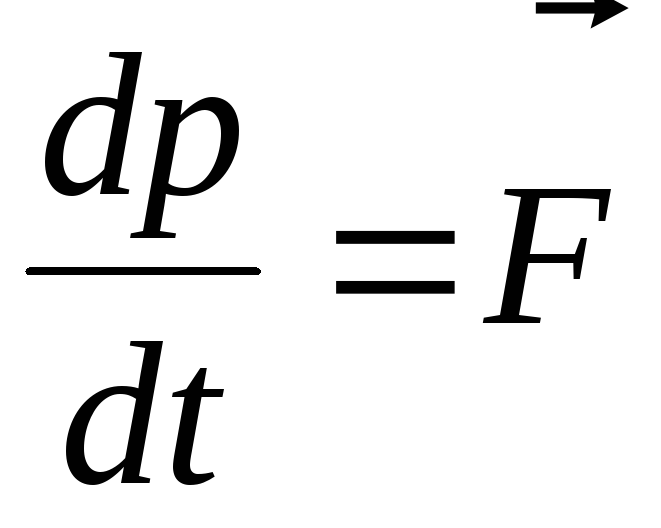 . (1.27)
. (1.27)
Физический смысл импульса становится очевидным, если уравнение (1.27) проинтегрировать на конечном интервале времени от 0 до t:
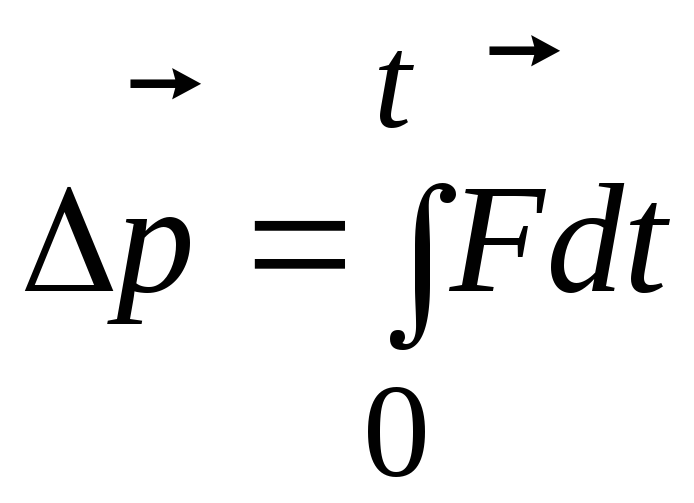 . (1.28)
. (1.28)
Изменение импульса служит мерой величины силы, действующей на тело в течение конечного промежутка времени. Численно величина импульса
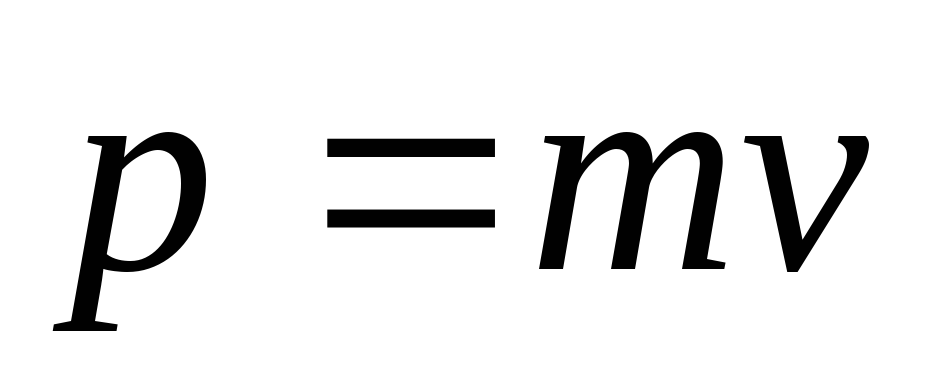 . (1.29)
. (1.29)
Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F=0; как видно из уравнений (1.26) или (1.27),
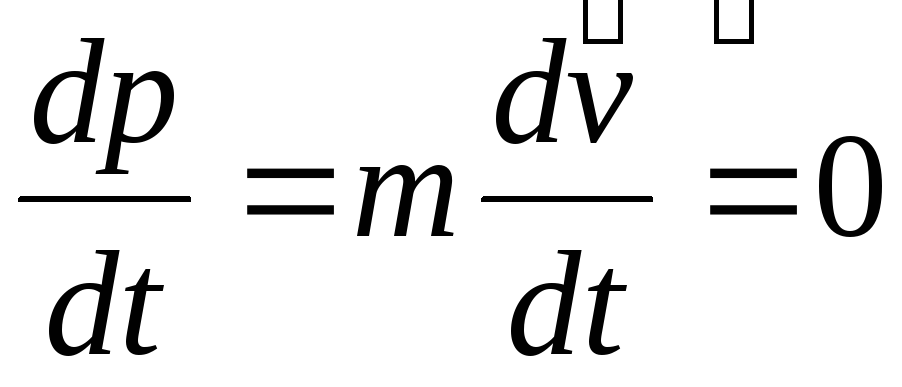
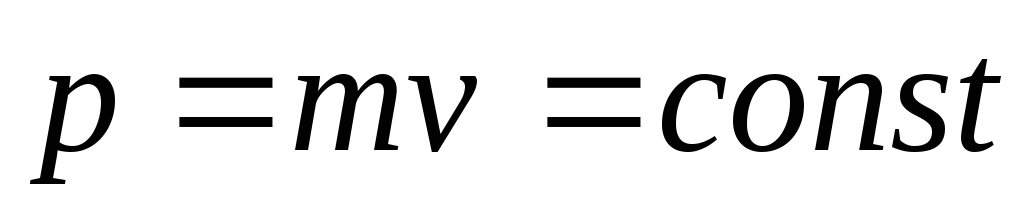 ,
т.е. величина , (1.30)
,
т.е. величина , (1.30)
остается постоянной во все время движения. Полученный результат представляет собой закон сохранения импульса, который имеет место как для одного тела, так и для системы тел в отсутствие внешних сил.
В отсутствие внешних сил сохраняется еще одна скалярная величина. Если умножить уравнение (1.26) одновременно слева и справа на вектор скорости, в левой части окажется производная от полного дифференциала, и уравнение примет вид
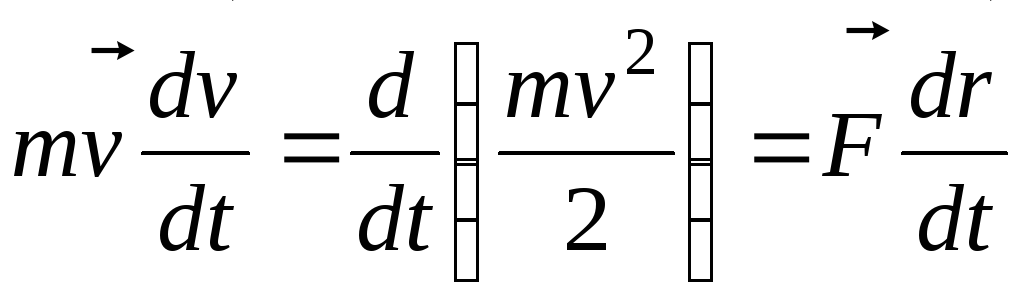 . (1.31)
. (1.31)
Пусть F = 0. Тогда постоянной во время движения является величина
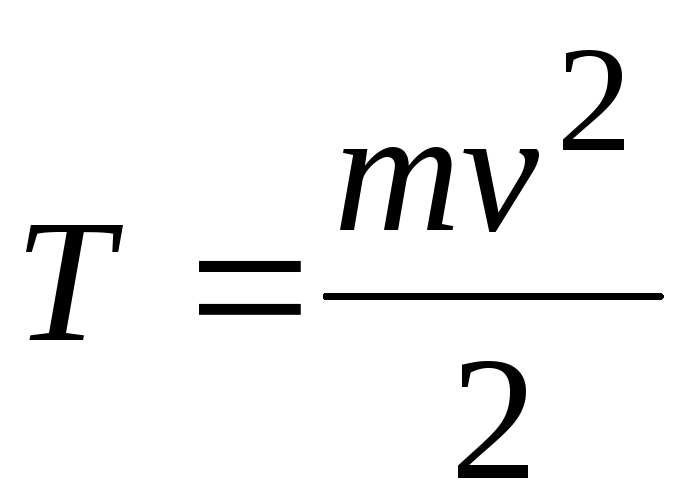 . (1.32)
. (1.32)
Она
называется кинетической энергией
частицы. При отсутствии внешних сил,
т. е. в замкнутой системе, сохраняется
кинетическая энергия как в случае
одного тела, так и для системы тел. Когда
на частицу действует внешняя сила F,
кинетическая энергия не остается
постоянной. В этом случае согласно
(1.31) приращение кинетической энергии
за время dt равно
скалярному произведению 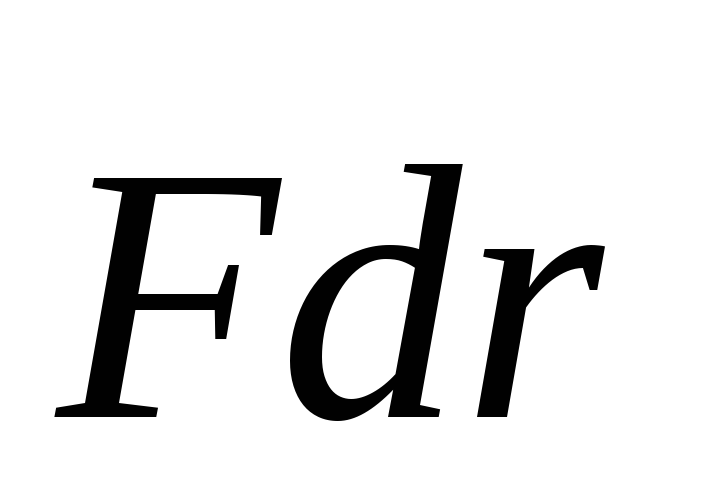 .
ВеличинаdA =
.
ВеличинаdA = 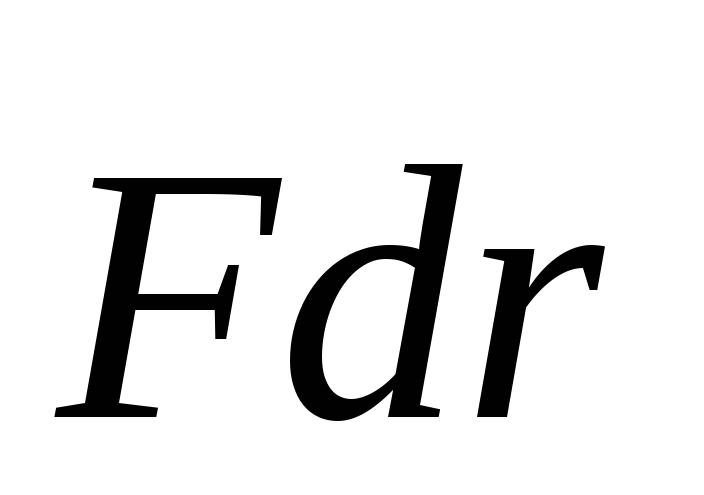 — это работа, совершаемая силойF на пути dr .
— это работа, совершаемая силойF на пути dr .
Проинтегрируем соотношение (1. 31) вдоль некоторой траектории от точки 1 до точки 2:
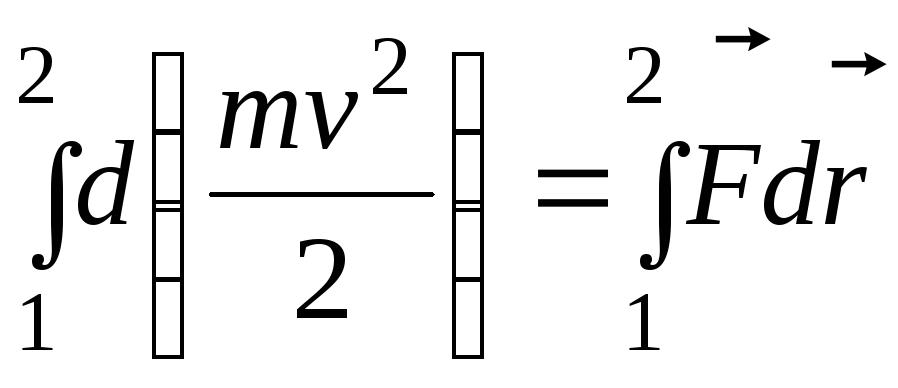 .
.
Левая часть представляет собой приращение кинетической энергии на пути между точками 1 и 2, а величина
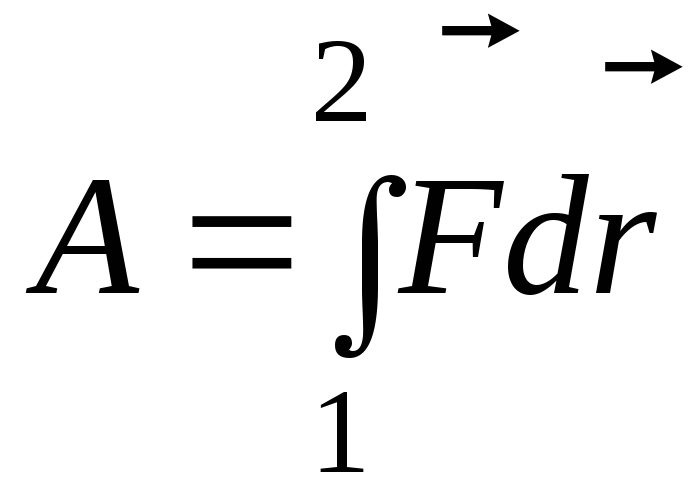 (1.33)
(1.33)
есть работа силы на пути 1—2.
Таким образом, работа сил, действующих на частицу, расходуется на изменение ее кинетической энергии:
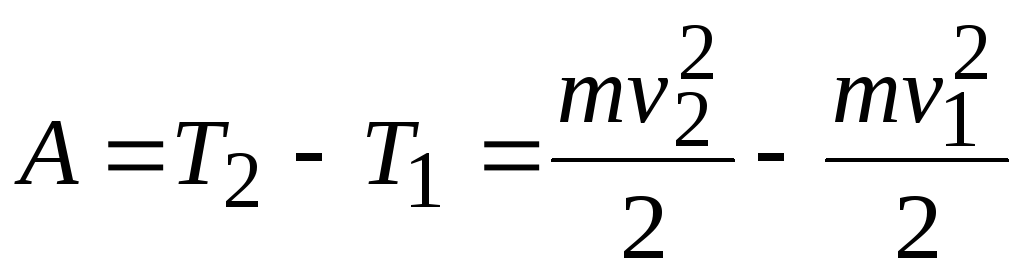 . (1.34)
. (1.34)
Соответственно, изменение кинетической энергии частицы служит мерой работы, произведенной над частицей.
Если частица в каждой точке пространства подвержена действию других тел, то говорят, что эта частица находится в поле сил. В случае силового поля действие силы распределено по всему пространству. Рассмотрим такое поле сил, действие которого на частицу зависит только от положения частицы в пространстве. Такое поле можно описать с помощью некоторой скалярной функции φ(r), зависящей, а соответствии со сказанным, только от координат. Это случай специального, но часто встречаемого в природе потенциального поля, а функция φ(r), характеризующая поле, является потенциалом поля. Сила связана с потенциалом в каждой точке соотношением
 , (1.35)
, (1.35)
где постоянная определяется свойствами частицы, взаимодействующей с полем сил.
Подставим соотношение (1.35) в (1.33) и опять проинтегрируем вдоль траектории от точки 1 до точки 2. Получим
T2 — T1 +const(φ2 — φ1) = О,
т.е. величина T2 +const·φ2 = T1 +const·φ1
остается постоянной при движении вдоль траектории. Таким образом, для частицы в потенциальном поле внешней силы сохраняется, т. е. является интегралом движения, величина
E = T+const·φ(r). (1.36)
Величина U = const·φ(r) называется потенциальной энергией частицы в поле φ(r), а выражение (1.36) представляет собой полную механическую энергию частицы
E = T + U.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Рассмотрим случай,
когда на
тело массой m действует
постоянная сила 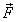 (она
может быть равнодействующей нескольких
сил) и
векторы силы
(она
может быть равнодействующей нескольких
сил) и
векторы силы 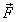 и
перемещения
и
перемещения 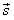 направлены
вдоль одной прямой в
одну сторону. В
этом случае
работу силы можно определить как A
= F∙s. Модуль
силы по второму закону Ньютона равен F
= m∙a, а
модуль перемещения s при
равноускоренном прямолинейном движении
связан с
модулями начальной
υ1 и
конечной υ2 скорости и
ускорения а выражением
направлены
вдоль одной прямой в
одну сторону. В
этом случае
работу силы можно определить как A
= F∙s. Модуль
силы по второму закону Ньютона равен F
= m∙a, а
модуль перемещения s при
равноускоренном прямолинейном движении
связан с
модулями начальной
υ1 и
конечной υ2 скорости и
ускорения а выражением
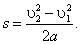
Отсюда для работы получаем
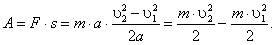
 (1)
(1)
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.
Кинетическая энергия обозначается буквой Ek.
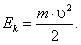 (2)
(2)
Тогда равенство (1) можно записать в таком виде:
A = Ek2 – Ek1. (3)
Теорема о кинетической энергии:
работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.
Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.
Если начальная скорость движения тела массой т равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:
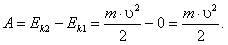 (4)
(4)
Физический смысл кинетической энергии:
кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Потенциальная энергия – это энергия взаимодействия тел.
Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Землигравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формытраектории.
При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторыедругие.
Силы, работа которых зависит от формы траектории, называются непотенциальными. При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.
Потенциальная энергия взаимодействия тела с Землей.
Найдем работу, совершаемую силой тяжести Fт при перемещении тела массой т вертикально вниз с высоты h1 над поверхностью Земли до высоты h2 (рис. 1).

Рис. 1.
Если разность h1 – h2 пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести Fт во время движения тела можно считать постоянной и равной mg.
Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна
A = F∙s = m∙g∙(hl – h2). (5)
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести Fт = m∙g совершает работу
A = m∙g∙s∙cos a = m∙g∙h, (6)
где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.
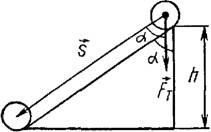
Рис. 2.
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотамиh’, h» и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:
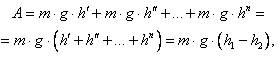 (7)
(7)
где h1 и h2 – высоты от поверхности Земли, на которых расположены соответственно точки В и С.
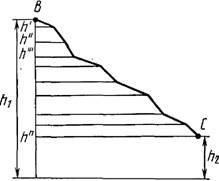
Рис. 3.
Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальноми конечном положениях.
При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.
Равенство (7) можно представить в таком виде:
A = – (m∙g∙h2 – m∙g∙hl). (8)
Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называютпотенциальной энергией взаимодействия тела и Земли.
Работа силы тяжести при перемещении тела массой т из точки, расположенной на высоте h2, в точку, расположенную на высоте h1 от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.
А= – (Ер2 – Ер1). (9)
Потенциальная энергия обозначается буквой Ер.
Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.
При таком выборе нулевого уровня потенциальная энергия Ер тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:
Ep = m∙g∙h. (10)
Физический смысл потенциальной энергии взаимодействия тела с Землей:
потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.
В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, таки отрицательной. Тело массой m, находящееся на высоте h, где h < h0 (h0 – нулевая высота), обладает отрицательной потенциальной энергией:
Еp = –m∙gh
Потенциальная энергия гравитационного взаимодействия
Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М, находящихся на расстоянии r одна от другой, равна
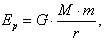 (11)
(11)
где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Еp = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей,где h – высота тела над поверхностью Земли, М3 – масса Земли, R3 – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.
 (12)
(12)
При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h « R3) равна
Еp = m∙g∙h,
где 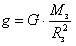 –
модуль ускорения свободного падения
вблизи поверхности Земли.
–
модуль ускорения свободного падения
вблизи поверхности Земли.
Потенциальная энергия упруго деформированного тела
Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x1 до конечного значения x2 (рис. 4, б, в).
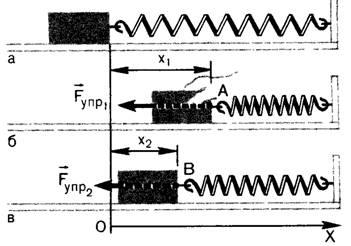
Рис. 4.
Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т. к. сила упругости линейно зависит от x) и умножить на модуль перемещения:
 (13)
(13)
где 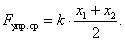 Отсюда
Отсюда
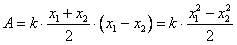
или
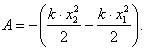 (14)
(14)
Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:
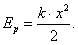 (15)
(15)
Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:
А = –(Ер2 – Ер1). (16)
Если x2 = 0 и x1 = х, то, как видно из формул (14) и (15),
Ер = А.
Тогда физический смысл потенциальной энергии деформированного тела
потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.
Механическая
работа —
физическая величина, равная произведению
модуля силы на модуль перемещения и
косинус угла между нимиA=Fscosα (см.
рис.). Работа — величина скалярная (число,
не вектор). Измеряется работа в джоулях
(Дж). 1 Дж — это работа, совершаемая силой
в 1 Н на перемещение 1 м. В зависимости
от направлений векторов силы (F) и
перемещения (S) механическая работа
может быть положительной, отрицательной
или равной нулю. Например, если
векторы  и
и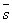 перпендикулярны,
то cos900 = 0 и A = 0. Мощность машины
или механизма — это отношение
совершенной работы ко времени, в течение
которого она совершена
перпендикулярны,
то cos900 = 0 и A = 0. Мощность машины
или механизма — это отношение
совершенной работы ко времени, в течение
которого она совершена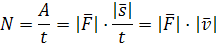 .
Измеряется мощность в ваттах (Вт), 1 Вт
= 1 Дж/с. Простые механизмы: наклонная
плоскость, рычаг, блок. Их действие
подчиняется«золотому правилу
механики»: во сколько раз выигрываем
в силе, во столько же раз проигрываем
в перемещении. (На практике совершаемая
с помощью механизма полная работа
всегда несколько больше полезной. Часть
работы совершается против силы трения
в механизме и перемещения его отдельных
частей. Например, применяя подвижный
блок, приходится дополнительно совершать
работу по поднятию самого блока, веревки
и по преодолению силы трения в оси
блока. Поэтому для любого механизма
полезная работа (AП) всегда меньше, чем
полная, затраченная (AЗ). По этой причине
КПД = AП/AЗ• 100% любого механизма не может
быть больше или хотя бы равен 100%).
.
Измеряется мощность в ваттах (Вт), 1 Вт
= 1 Дж/с. Простые механизмы: наклонная
плоскость, рычаг, блок. Их действие
подчиняется«золотому правилу
механики»: во сколько раз выигрываем
в силе, во столько же раз проигрываем
в перемещении. (На практике совершаемая
с помощью механизма полная работа
всегда несколько больше полезной. Часть
работы совершается против силы трения
в механизме и перемещения его отдельных
частей. Например, применяя подвижный
блок, приходится дополнительно совершать
работу по поднятию самого блока, веревки
и по преодолению силы трения в оси
блока. Поэтому для любого механизма
полезная работа (AП) всегда меньше, чем
полная, затраченная (AЗ). По этой причине
КПД = AП/AЗ• 100% любого механизма не может
быть больше или хотя бы равен 100%).
Мощность — Мощностью N называют величину, равную отношению работы А к промежутку времени t, в течение которого эта работа была совершена:
N=A/t (3.11)
Из формулы (3.11) следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.
Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):
N=Fvcosa.
(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V — мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cosa=1 и N=Fv. Из последней формулы следует, что
F=N/v и v=N/F.
Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.
Консервативные и неконсервативные силы |
Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек. К классу консервативных относятся, например, гравитационные силы, упругие, силы электростатического взаимодействия. Вычислим,
например, работу, которую совершает
сила тяжести при переходах частицы
разными путями из положения 1 в
положение 2 (рис. 6.2). Если этот переход
произошёл по вертикали, то работа
силы Теперь пусть та же частица переместится из 1 в 2 по пути 1-1’-2. Здесь промежуточная точка 1’ находится на высоте h3. Рис. 6.2 Полная работа будет складываться из работ силы тяжести на участках 1-1’ и 1’-2:
Работа силы тяжести на горизонтальном участке 1’-2 равна нулю, так как здесь вектор силы нормален перемещению. Мы вновь получили прежний результат, свидетельствующий о том, что работа силы тяжести не зависит от формы траектории. Этот вывод легко обобщается и на случай произвольной криволинейной траектории, соединяющей начальную и конечную точки пути. Гравитационная сила, сила упругости, кулоновская сила электростатического взаимодействия относятся к так называемым центральным силам. Центральными называются силы, направленные к одной и той же точке (либо от неё). Эта точка называется силовым центром. Величина центральной силы зависит только от расстояния до силового центра r (рис. 6.3). Рис. 6.3 Покажем, что все центральные силы консервативны. Вычислим работу центральной силы на участке 1-2 произвольной траектории (рис. 6.3). Элементарная
работа силы на участке
Здесь dSr = dSCosα
— проекция вектора перемещения dA = F(r)dr. Работа на конечном пути:
Так как по определению величина центральной силы есть функция только расстояния r, то значение определённого интеграла будет зависеть только от величин r1 и r2, и не будет зависеть от формы траектории. Можно дать иное определение консервативной силы. Рассмотрим
перемещение частицы из положения 1 в
положение 3 под действием консервативной
силы Рис. 6.4 Работа,
совершаемая при этом силой Теперь вычислим работу этой же силы на замкнутом пути 1-2-3-4-1. понятно, что её можно представить суммой работ на участках 1-2-3 и 3-4-1
При
этом Отсюда
можно заключить, что работа консервативной
силы по любому замкнутому пути равна
нулю Силы, работа которых на замкнутом пути не равна нулю, называются неконсервативными. К числу таких сил относятся, например, сила трения и сила вязкого сопротивления. Легко понять, что при движении частицы по замкнутому контуру работа подобных сил будет отрицательной. |
Тема 3. Работа. Кинетическая, потенциальная и полная энергия
Работа. Если на тело, движущееся прямолинейно,
действует постоянная сила 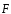 ,
которая составляет некоторый уголα с направлением перемещения
,
которая составляет некоторый уголα с направлением перемещения 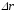 ,
то работа этой силы равна скалярному
произведению векторов
,
то работа этой силы равна скалярному
произведению векторов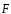 и
и 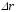 :
:
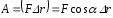 .
.
Для
переменной по величине и направлению
силы 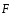 вводится понятиеэлементарной
работы
вводится понятиеэлементарной
работы  силы
силы на элементарном перемещении
на элементарном перемещении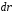 :
:
 ,
,
где α – угол между векторами 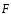 и
и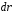 .
.
Работа А силы 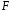 на участке траектории от точки1 до точки 2 равна алгебраической сумме элементарных
работ
на участке траектории от точки1 до точки 2 равна алгебраической сумме элементарных
работ 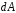 на отдельных элементарных участках
траектории, что приводит к интегралу:
на отдельных элементарных участках
траектории, что приводит к интегралу: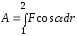 .
.
Кинетическая энергия – это механическая энергия движения тел.
Тело
массой m,
движущееся со скоростью 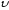 , обладает кинетической энергией:
, обладает кинетической энергией:
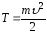 .
.
Потенциальная энергия – это механическая энергия системы тел, определяемая взаимным расположением тел или частей одного и того же тела относительно друг друга и характером сил взаимодействия между ними. Если взаимодействие тел таково, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то такие силы называются консервативными. Если же работа, совершаемая силой, зависит от выбора траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной. Примером такой силы является сила трения.
Полная
механическая энергия системы тел равна сумме кинетической и
потенциальной энергий, то есть 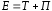 .
Если неконсервативные силы отсутствуют,
то полная механическая энергия системы
сохраняется:
.
Если неконсервативные силы отсутствуют,
то полная механическая энергия системы
сохраняется:
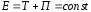 .
.
Таким образом, в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, что является законом сохранения полной механической энергии системы тел.
Тема 4. Момент инерции твердого тела. Теорема Штейнера
Моментом
инерции материальной точки массой m относительно некоторой оси вращения
называется физическая величина I,
равная произведению массы этой
материальной точки на квадрат расстояния  от этой точки до данной оси вращения:
от этой точки до данной оси вращения:
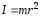 .
.
Для
того, чтобы найти момент
инерции твердого тела относительно некоторой оси вращения,
необходимо разбить это тело на элементарные
объемы так, чтобы каждый элементарный
объем можно было рассматривать как
материальную точку массой 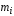 ,
находящуюся на определённом расстоянииот данной оси вращения. Тогдамомент
инерции твердого тела I равен сумме моментов
инерции всех n материальных точек массами
,
находящуюся на определённом расстоянииот данной оси вращения. Тогдамомент
инерции твердого тела I равен сумме моментов
инерции всех n материальных точек массами 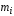 ,
на которые разбито это тело, или сумме
произведений масс материальных точек
,
на которые разбито это тело, или сумме
произведений масс материальных точек на квадраты расстояний
на квадраты расстояний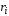 от этих материальных точек до
рассматриваемой оси:
от этих материальных точек до
рассматриваемой оси:
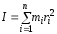 .
.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно оси, перпендикулярной основанию цилиндра и проходящей через его центр масс (рис. 4).
Разобьем
цилиндр на отдельные полые концентрические
цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним (r+dr).
Так как dr<<r ,
то считаем, что расстояние всех точек
полого цилиндра от оси равно r. Поэтому
момент инерции каждого полого
цилиндра можно Рис. 4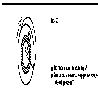
определить следующим образом:
dI=r2dm ,
где dm – масса элементарного полого цилиндра, равная rdV
(r — плотность материала, dV – объем полого цилиндра, равный 2prhdr).
Тогда момент инерциии элементарного полого цилиндра dI=2prhr3dr.
Следовательно, момент инерции сплошного цилиндра
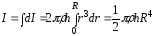 .
.
Так
как pR2h
— объем сплошного цилиндра, а prhR2— его
масса, то момент инерции сплошного
цилиндра: 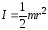 .
.
Теорема
Штейнера.
Если известен момент инерции тела  относительно оси ОО′,
проходящей через центр масс тела, то
момент инерции этого же тела относительно
другой оси
относительно оси ОО′,
проходящей через центр масс тела, то
момент инерции этого же тела относительно
другой оси 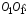 ,
параллельной оси ОО′,
равен сумме момента инерции
,
параллельной оси ОО′,
равен сумме момента инерции 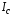 и произведения массыт данного тела на квадрат расстояния а между этими осями ОО′
и
и произведения массыт данного тела на квадрат расстояния а между этими осями ОО′
и 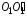 , то есть:
, то есть:
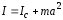 .
.
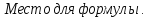
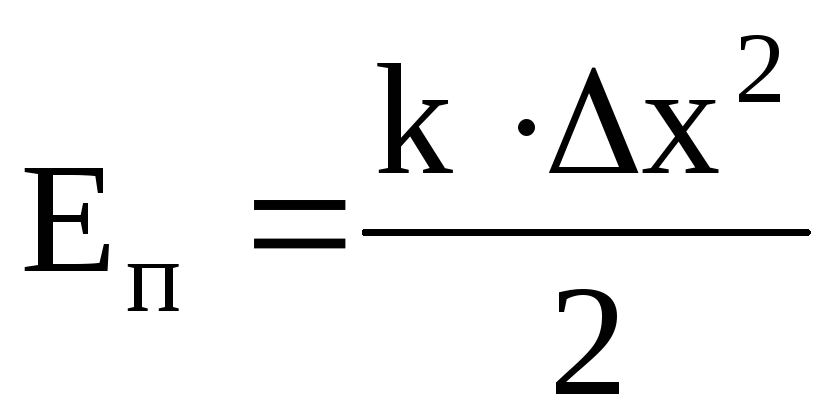 –потенциальная
энергия упругого деформированного
тела, х
– деформация тела.
–потенциальная
энергия упругого деформированного
тела, х
– деформация тела.
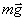 :
: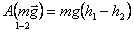 . (6.11)
. (6.11)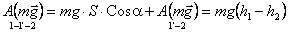 .
.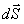 :
: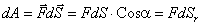 .
. на
направление силы
на
направление силы (или r).
Эта проекция представляет собой
изменение расстояния dr до
силового центра. Значит:
(или r).
Эта проекция представляет собой
изменение расстояния dr до
силового центра. Значит: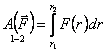 .
.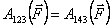 (рис.
6.4).
(рис.
6.4).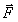 ,
не зависит формы от траектории, то
есть
,
не зависит формы от траектории, то
есть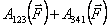 .
.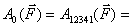

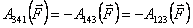 .
. .
.