Модуль действительного числа. Видеоурок. Алгебра 8 Класс

Тема: Действительные числа

Урок: Модуль действительного числа

Рассмотрим такое понятие, как модуль действительного числа, у него есть несколько определений.

Определение 1. Расстояние от точки на координатной прямой до нуля называется модулем числа, которое является координатой данной точки (рис. 1).

 

 

Рис. 1.

Пример 1. 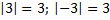. Заметим, что модули противоположных чисел равны и неотрицательны, т. к. это расстояние, а оно не может быть отрицательным, и расстояние от симметричных относительно нуля чисел до начала отсчета равны.

Определение 2. .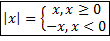

Пример 2. Рассмотрим одну из задач, поставленную в предыдущем примере для демонстрации равносильности введенных определений. 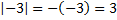, как видим, при отрицательном числе под знаком модуля добавление перед ним еще одного минуса обеспечивает неотрицательный результат, как и следует из определения модуля.

Следствие. Расстояние между двумя точками с координатами 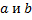 на координатной прямой можно найти следующим образом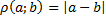

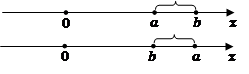
 в независимости от взаимного расположения точек (рис. 2).

 

 

 

Рис. 2.

1. Модуль любого числа неотрицателен

,

2. Модуль произведения – это произведение модулей

,

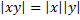3. Модуль частного – это частное модулей

,

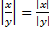4. 

,

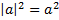
5. .

Пример 3. Решить уравнение .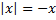

Решение. Воспользуемся вторым определением модуля: 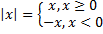 и запишем наше уравнение в виде системы уравнений при различных вариантах раскрытия модуля.

.

Ответ..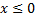

Пример 4. Решить уравнение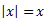 

.

Решение. Аналогично решению предыдущего примера получаем, что .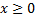

Ответ..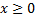

Пример 5. Решить уравнение .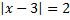

Решение. Решим через следствие из первого определения модуля: 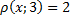. Изобразим это на числовой оси с учетом того, что искомый корень будет находиться на расстоянии 2 от точки 3 (рис. 3).

 

 

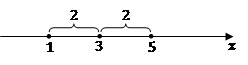
Рис. 3.

 Исходя из рисунка, получаем корни уравнения: 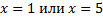, т. к. точки с такими координатами находятся на расстоянии 2 от точки 3, как то требуется в уравнении.

Ответ. .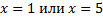

Пример 6. Решить уравнение .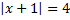

Решение. По сравнению с предыдущей задачей имеется только одно усложнение – это то, что нет полного сходства с формулировкой следствия о расстоянии между числами на координатной оси, т. к. под знаком модуля находится знак плюс, а не минус. Но привести к необходимому виду несложно, что мы и проделаем:

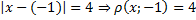. Изобразим это на числовой оси аналогично предыдущему решению (рис. 4).

 

 

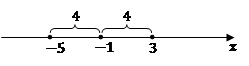
Рис. 4.

Корни уравнения .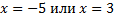

Ответ. .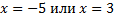

Пример 7. Решить уравнение .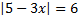

Решение. Это уравнение еще немного сложнее предыдущего, т. к. неизвестная находится на втором месте и со знаком минус, кроме того, она еще и с числовым множителем. Для решения первой проблемы воспользуемся одним из свойств модуля

 и получим:

.

Для решения второй проблемы выполним замену переменных: 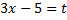, что приведет нас к простейшему уравнению 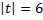. По второму определению модуля 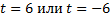. Подставим эти корни в уравнение замены и получим два линейных уравнения:

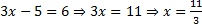 и .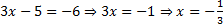

Ответ..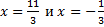

Довольно часто в ходе решения задач с корнями возникают модули, и следует обратить внимание, в каких ситуациях они возникают.

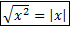
При первом взгляде на это тождество могут возникнуть вопросы: «зачем там модуль?» и «почему неверно тождество 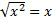?». Оказывается, что можно привести простой контрпример для второго вопроса: если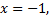

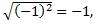то должно быть верно, чточто равносильно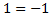, а это неверное тождество.

После этого может возникнуть вопрос: «а не решает ли проблему такое тождество 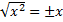», но и для этого предложения тоже есть контрпример. Еслито должно быть верно, что

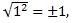
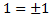что равносильно, а это неверное тождество.

Соответственно, если вспомнить, что квадратный корень из неотрицательного числа является неотрицательным числом, и значение модуля является неотрицательным, становится понятно, почему верно указанное выше утверждение:

.

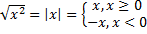Пример 8. Вычислить значение выражения .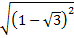

Решение. В подобных заданиях важно не избавиться бездумно сразу от корня, а воспользоваться указанным выше тождеством 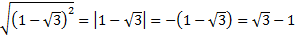, т. к.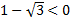

.

Ответ..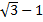

Пример 9.  Решить уравнение .

Решение. Заметим, что подкоренное выражение можно упростить с помощью формулы полного квадрата: . Аналогичные уравнения мы умеем решать и сводим данное уравнение к виду расстояния между точками на числовой оси   , и изображаем решение на рисунке 5.

 

 

 

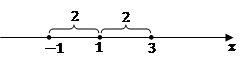
Рис. 5.

 Получаем корни уравнения .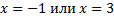

Ответ. .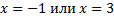

На сегодняшнем занятии мы основное внимание уделили геометрическому способу решения задач с модулями, однако существует еще достаточно много других подходов к решению, которые мы рассмотрим позже.

На следующем уроке мы поговорим о таком понятии, как возведение числа в отрицательную степень.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Мир уроков (Источник).

2. YouTube (Источник).

3. YouTube (Источник).

 

Домашнее задание

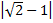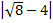1. Найдите: а) ; б) ; в) .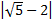

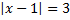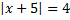2. Решите уравнение: а) ; б) ; в).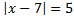

3. Упростите выражение: а) 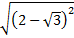; б) .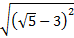

4. Упростите выражение , если .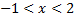

Урок алгебры в 8-м классе. Тема «Неравенства, содержащие модуль». Повторение

Цель урока: повторить различные способы решения неравенств с одной переменной и рассмотреть применение неравенств к решению задач и упражнений.

Ход урока

1. Организационный момент. Постановка цели.
2. Индивидуальная работа по карточкам (во время фронтального опроса).

1 карточка.

Решить неравенства:

1. 6x+2>9-x;

2. 2(x+3)-(x-8)<4.

2 карточка.

Решить неравенства:

1. ;

2. 5x+4>12-(x-3).

3 карточка.

Решить неравенства:

1. ;

4 карточка.

Решить неравенства:

1. x-4>12

2.

1. Фронтальный опрос
(используются слайды презентации учителя).

1.Что называется модулем числа а?

2.Решить неравенства

а)

б)

в)

г)

д)

3. на координатной плоскости изображены графики двух линейных функций. При каких x значения обеих функций одновременно положительны? Отрицательны?

Cм. Презентацию, слайды 3–5.

4.Самостоятельная работа (по вариантам)

Cм. Презентацию, слайд 6.

5. Актуализация опорных знаний.

Учитель. Очень часто при решении неравенств со знаком модуля возникает необходимость перейти либо к системе неравенств, либо к совокупности.

Вопросы?

1. Когда неравенство равносильно системе неравенств?
2. Когда число а является решением совокупности неравенств?

Экспресс-опрос (шесть человек работают у доски по карточкам, а в то же время остальные учащиеся работают со слайдом, на котором видно задание каждого ребенка, который стоит у доски).

Задание представлено в виде теста. По окончании решения необходимо выбрать правильный ответ, а букву, соответствующую этому варианту ответа, занести в соответствующую клетку кроссворда.

1 вариант.

2 вариант.

3 вариант.

4 вариант.

5 вариант.

6 вариант.

Итак, мы прочли Гарриот, это имя. Историческую справку о Гарриоте подготовил ученик.

Томас Гарриот (1560-1621)- английский математик. Родился в Оксфорде. Образование получил в Оксфордском университете. Переписывался с Галиллеем и Кеплером. Развивал алгебраическую символику, в частности, ввел знаки > и < , которые сразу были приняты. Гарриот пользовался для обозначений чисел строчными буквами алфавита, записывал уравнения в форме, близкой к современной. В этом отношении он шел дальше своего друга Франсуа Виета. Гарриот первый заметил, что число корней уравнения определяется его степенью и что левая часть уравнения должна разлагаться на такое же число линейных множителей. Гарриот строил уравнения по их корням.

Вопрос: какие существуют способы решения неравенств с одной переменной?

6. Решение задач и упражнений.

1.Задача. При каких значениях х точки графика функции лежат выше точек графика функции ?

Задача решается графическим способом.

2.Решить неравенство

Используется аналитический способ решения.

3.Найти допустимые значения переменной

7. Домашнее задание. Его необходимо выполнить в виде творческой работы:

1. Составить и решить по 2 неравенства со знаком модуля, решениями которых будут в одном случае система, а в другом- совокупность неравенств;
2. Придумать задачу, где применяется неравенство, а затем рассмотреть графический и аналитический способы решения этой задачи.

8. Сообщение учащегося из дополнительной литературы.

Учитель: Неравенства занимают важное место в курсе алгебры не только 8 класса, они встретятся нам и в 9 классе, и далее. Но уже сегодня, используя свойства известных нам неравенств, можно решать и более сложные задачи.

Ученик: напомним, что для любых двух действительных чисел а и b справедливо неравенство

(*)

Причем знак равенства достигается в том и только случае, когда

Решим задачу. Найти наименьшее значение функции

В силу неравенства (*)

Таким образом , причем знак равенства достигается только в том случае, когда х=0. Отсюда наименьшее значение функции равно 1 при х=0.

9. Итог урока. Оценки.

Учитель. Наш великий соотечественник Давидов Август Юльевич сказал: “Алгебра учит рассуждать о величинах. При этом она изображает их буквами и означает особыми знаками зависимость между ними”.

Вот этим сегодня мы и занимались на уроке.

Модуль числа. Решение уравнений и неравенств, содержащих модуль.

Модуль числа. Решение уравнений и неравенств, содержащих модуль.

Составила учитель математики

Привалова М.В.

1.Понятие модуля числа

Модулем действительного числа а называется само это число, если оно неотрицательное, и противоположное ему число, если данное число отрицательно.

| a | =

a, если a ≥ 0

-a , если a

Примеры:

• |3|=3
• |1/5|=1/5
• |-1|=-(-1)=1
• |-10|=-(-10)=10
• |0|=0

Из определения модуля следует:

Геометрический смысл модуля числа

|5|=|-5|= 5

A1

A

x

5

— 5

0

OA=OA

1

Модуль – расстояние от начала отсчета на координатной прямой до точки, изображающей число.

2.Уравнения, содержащие неизвестное под знаком модуля

Примеры:

а)|х|=7

б) |х+1|=3

в) |3х+2|=1 (в учебнике)

3.Неравенства, содержащие неизвестное под знаком модуля

|х| ≤ a

|х| ≥ a

Решение:

Решение:

x

x

-a

a

-a

a

— a ≤ х ≤ a

х ≤ -a ; x ≥ a

x ͼ [ -a; a ]

x ͼ (- ∞ ; -a ] U [a; + ∞ )

6 х 6 5. | 6 х+ 1 | 3. |х-6| — 2 -3 -1/2 -5 1 1″

Решите неравенства

4 . |х+5| ≥ 2

1. |х| 7

— 7

х+5 ≤-2 х+5 ≥2

x ≤ -2 -5 х ≥ 2-5

х ≤ -7 х ≥ -3

2. |х| 6

х 6

5. | 6 х+ 1 |

3. |х-6|

— 2

-3

-1/2

-5

1

Домашнее задание.

§10(учить), № (на доске)

Модуль числа.Уравнения и неравенства, содержашие модуль.

Цели: повторить понятие модуля числа; определить геометрический смысл модуля; научить решать уравнения, содержащие неизвестное под знаком модуля, научить решать неравенства, содержащие неизвестное под знаком модуля.

Просмотр содержимого документа
«Модуль числа.Уравнения и неравенства, содержашие модуль.»

Модуль числа. Решение уравнений и неравенств, содержащих модуль.

Составила учитель математики

Привалова М.В.

1.Понятие модуля числа

Модулем действительного числа а называется само это число, если оно неотрицательное, и противоположное ему число, если данное число отрицательно.

|a|=

a, если a ≥ 0

-a, если a

Примеры:

• |3|=3
• |1/5|=1/5
• |-1|=-(-1)=1
• |-10|=-(-10)=10
• |0|=0

Из определения модуля следует:

Геометрический смысл модуля числа

|5|=|-5|= 5

O

A1

A

x

-5

5

0

OA=OA

1

Модуль – расстояние от начала отсчета на координатной прямой до точки, изображающей число.

2.Уравнения, содержащие неизвестное под знаком модуля

Примеры:

а)|х|=7 (в учебнике)

б) |х+1|=3

в) |3х+2|=1 (в учебнике)

3.Неравенства, содержащие неизвестное под знаком модуля

|х| ≥ a

|х| ≤ a

Решение:

Решение:

x

x

a

-a

a

-a

-a≤ х ≤ a

х ≤ -a ; x ≥ a

x ͼ [ -a; a ]

x ͼ (- ∞ ; -a ] U [a; + ∞ )

6 х6 5. |6х+1| 3. |х-6| — 2 -3 -1/2 -5 1″

Решите неравенства

4 . |х+5| ≥ 2

1. |х| 7

-7

х+5≤-2 х+5≥2

x ≤ -2 -5 х ≥ 2-5

х ≤ -7 х ≥ -3

2. |х|6

х6

5. |6х+1|

3. |х-6|

— 2

-3

-1/2

-5

1

Домашнее задание.

§10(учить определения),

№ (на доске)

Презентации к урокам алгебры по теме «Модуль числа. Уравнения и неравенства, содержащие модуль»

Презентации содержат теоретический материал, изложенный в доступной для обучающихся форме, а также пошаговое решение уравнений и неравенств, содержищих неизвестное под знаком модуля. Материал может быть использован при проведении уроков повторения и обобщения знаний по теме, а также для самостоятельной работы обучающихся, пропустивших занятия в школе.

Просмотр содержимого презентации
«У — 1_Модуль числа. Уравнения, содержащие модуль»

|-а| = |а|

стр. 65 № 149

Что такое модуль?

4 ед.о.

4 ед.о.

В(-4)

О

А(4)

-4

1

0

4

Модуль числа — это расстояние от начала отсчета до точки, изображающей число.

Модуль – число положительное или нуль, так как расстояние между двумя точками не может быть отрицательным .

 

Модуль положительного числа и нуля равен

самому числу.

 

Модуль отрицательного числа равен числу,

противоположному данному.

 

10/24/19 Классная работа .

Модуль числа.

Уравнения,

содержащие модуль.

Ц е л ь — знакомство с решением уравнений, содержащих неизвестное под знаком модуля;

обучение выбору наиболее рациональных способов решения.

Л.С. Атанасян. Геометрия 10-11.

0 a 0 a = 0 a = 0 2 корня: = – a , a a 1 корень: х = 0 1 корень: х = 0 = a расстояние между двумя точками не может быть отрицательным расстояние между двумя точками не может быть отрицательным Нет корней Нет корней а ед.о. а ед.о. 0 х 0 х — a a х = 0″

Уравнения, содержащие модуль

│ х │= а

a 0

a 0

a = 0

a = 0

2 корня: = – a ,

a

a

1 корень: х = 0

1 корень: х = 0

= a

расстояние между двумя точками не может быть отрицательным

расстояние между двумя точками не может быть отрицательным

Нет корней

Нет корней

а ед.о.

а ед.о.

0

х

0

х

— a

a

х = 0

Модуль числа

№ 1. Решить уравнение: 1)

2

0

1

3

-2

х

-3

-1

Ответ: -3; 3.

Модуль числа

№ 1. Решить уравнение: 2)

х

4

5

2

0

-5

3

1

-4

-2

-3

-1

Ответ: -3; 7.

Модуль числа

№ 1. Решить уравнение: 3)

Модуль всегда число положительное или равное нулю, значит левая часть уравнения неотрицательна, а правая часть уравнения отрицательна.

Т.к. положительное число или нуль не может быть равным отрицательному, то данное уравнение корней не имеет.

Ответ: нет корней.

4) 2| x – 1| + 3 = 9 – | x – 1|,

2| x – 1| + | x – 1| = 9 – 3,

3| x – 1| = 6,

3

3

| x – 1| = 2,

1) Если x – 1 ≥ 0,то

x – 1 = 2,

2)Если x – 1

x – 1 = – 2,

x = 3

x = – 1

Ответ: -1; 3.

5) | x + 5| = x + 5,

По определению модуля решением уравнения будет

одновременное выполнение двух условий, поэтому

запишем две системы :

 

 

Решим первую систему:

 

 

 

Решение. Рассмотрим решение исходного уравнения

на трех промежутках, показанных на рисунке.

+

+

—

+

—

—

-5

1

 

 

 

 

— неверно

 

— неверно

решений нет

решений нет

х = -2

Ответ. -2

№ 2. Раскрыть модуль:

или

№ 3. Раскрыть модуль:

или

№ 4. Раскрыть модуль:

или

Закрепляем

стр. 65

№ 150(2; 4),

№ 151 (2; 4),

№ 152(2; 4),

№ 153(2; 4; 6)

Рефлексия

Домашнее задание

п. 10(1; 2),

№ 150(1; 3),

№ 151(1; 3),

№ 152(1; 3),

№ 153(1; 3)

Спасибо за работу на уроке!

Просмотр содержимого презентации
«У — 2_Модуль числа. Неравенства, содержащие модуль»

10/24/19 Классная работа .

Модуль числа.

Неравенства,

содержащие модуль.

Ц е л ь — знакомство с решением неравенств, содержащих неизвестное под знаком модуля;

обучение выбору наиболее эффективных способов решения задач.

Л.С. Атанасян. Геометрия 10-11.

0 а ед.о. а ед.о. — a a х 0       х  [ а; а ]   или или 2) │х – 2 │≤ 5 2 способ 1) │х │≤ 4 1 способ       + 2         Ответ: х  [; ]     Ответ: х  [; ]  «

Неравенства, содержащие модуль

1 .│х│≤ а, где а 0

а ед.о.

а ед.о.

— a

a

х

0

 

 

 

х  [ а; а ]

 

или

или

2) │х – 2 │≤ 5

2 способ

1) │х │≤ 4

1 способ

 

 

 

+ 2

 

 

 

 

Ответ: х  [; ]

 

 

Ответ: х  [; ]

 

0 8 ≤ 3 х ≤ 12   : 3 0   : 3 0     ≤ х ≤ 4       ≤ х ≤ 4     Ответ: х  [; ]»

3) │ 3 х – 2 │≤ 10

1 способ

2 способ

 

│ 3 х – 2 │≤ 10

 

10 ≤ 3 х – 2 ≤ 10

 

 

 

10+2 ≤ 3 х ≤ 10+2

 

 

: 3 0

8 ≤ 3 х ≤ 12

 

: 3 0

 

: 3 0

 

 

≤ х ≤ 4

 

 

 

≤ х ≤ 4

 

 

Ответ: х  [; ]

4) │ 7 – 5 х│≤ 22

22 ≤ 7 – 5 х ≤ 22

 

22 – 7 ≤ – 5 х ≤ 22 – 7

 

: (– 5)

29 ≤ – 5 х ≤ 15

 

≥ х ≥ 3

 

3 ≤ х ≤

 

Ответ: х  [

 

Неравенства, содержащие модуль

2 .│х│≤ 0

0 ед.о.

х

0

 

2) │ 6 х – 2 │≤ 0

1) │х + 17 │≤ 0

 

х + 17 = 0,

2

 

: 2  0

 

 

 

Ответ:

Ответ:

 

0 а ед.о. а ед.о. — a a х 0     х  ( а; а )     или или 1) │ 12 х│ 5   2) │ 5 4 х│ 11       11 5 4 х 11   11 5 4 х 11 5     : (– 4) 16 4 х 6     х   4 х ,     Ответ: х  (7; Ответ: х  (1,5;  «

Неравенства, содержащие модуль

3 .│х│  а, где а 0

а ед.о.

а ед.о.

— a

a

х

0

 

 

х  ( а; а )

 

 

или

или

1) │ 12 х│ 5

 

2) │ 5 4 х│ 11

 

 

 

11 5 4 х 11

 

11 5 4 х 11 5

 

 

: (– 4)

16 4 х 6

 

 

х

 

4 х ,

 

 

Ответ: х  (7;

Ответ: х  (1,5;

 

0 0 ед.о. х 0  «

Неравенства, содержащие модуль

 

4 .│х│  0, │х│  а, │х│а, где

а 0

0 ед.о.

х

0

 

0 а ед.о. а ед.о. — a a х 0     или или или х  ( − ∞ ; − а ]  [ а ; + ∞) 2) │ 3 х – 5 │≥ 4 1) │х │≥ 2   или 3 х – 5 ≥ 4 3 х – 5 ≤ – 4 3 х ≥ 4 + 5 3 х ≤ – 4 + 5, 3 х ≥ 9 3 х ≤ 1,   х ≥ 3   х ≤ Ответ: х  ( − ∞ ; − 2]  [2; + ∞) Ответ: х  ( − ∞ ; ]  [3; + ∞)  «

Неравенства, содержащие модуль

5 .│х│≥ а, где а 0

а ед.о.

а ед.о.

— a

a

х

0

 

 

или

или

или

х  ( − ∞ ; − а ]  [ а ; + ∞)

2) │ 3 х – 5 │≥ 4

1) │х │≥ 2

 

или 3 х – 5 ≥ 4

3 х – 5 ≤ – 4

3 х ≥ 4 + 5

3 х ≤ – 4 + 5,

3 х ≥ 9

3 х ≤ 1,

 

х ≥ 3

 

х ≤

Ответ: х  ( − ∞ ; − 2]  [2; + ∞)

Ответ: х  ( − ∞ ; ]  [3; + ∞)

 

а, где а 0 а ед.о. а ед.о. — a a х 0     или или или х  ( − ∞ ; − а )  ( а ; + ∞) │ 2 – 0 , 5 х│ 2 или 2 – 0,5 х 2 2 – 0 , 5 х 2 2 – 2 0,5 х 2 + 2 0 , 5 х , 0 0,5 х 4 0,5 х ∙ 10 0 0 х : 5 0 40 5 х х 0   Ответ: х  ( − ∞ ;  (8; + ∞) х 8 8″

Неравенства, содержащие модуль

6 .│х│ а, где а 0

а ед.о.

а ед.о.

— a

a

х

0

 

 

или

или

или

х  ( − ∞ ; − а )  ( а ; + ∞)

│ 2 – 0 , 5 х│ 2

или 2 – 0,5 х 2

2 – 0 , 5 х 2

2 – 2 0,5 х

2 + 2 0 , 5 х ,

0 0,5 х

4 0,5 х

∙ 10 0

0 х

: 5 0

40 5 х

х 0

 

Ответ: х  ( − ∞ ;  (8; + ∞)

х 8

8

0 х 0     или или или х  ( − ∞; 0)  (0; + ∞) х  0 │ 7 – 2 х│ 0 или 1 способ 2 способ или 7 – 2 х 0 7 – 2 х 0 7 – 2 х  0 7 2 х : 2 0 7 2 х : 2 0 : 2 7  2 х 3,5 х 3,5 3,5  х х 3,5 х 3,5 Ответ: х      Ответ: х  ( − ∞ ;  (3,5; + ∞)»

Неравенства, содержащие модуль

7 .│х│ 0

х

0

 

 

или

или

или

х  ( − ∞; 0)  (0; + ∞)

х  0

│ 7 – 2 х│ 0

или

1 способ

2 способ

или 7 – 2 х 0

7 – 2 х 0

7 – 2 х  0

7 2 х

: 2 0

7 2 х

: 2 0

: 2

7  2 х

3,5 х

3,5

3,5  х

х 3,5

х 3,5

Ответ: х 

 

 

Ответ: х  ( − ∞ ;  (3,5; + ∞)

Неравенства, содержащие модуль

8 .│х│≥ 0

х

0

 

или

или

 

или

х  ( − ∞; + ∞)

Закрепляем

стр. 65

№ 161(2; 4),

№ 162(2; 4),

№ 163(2; 4)

Рефлексия

Домашнее задание

п. 10(3), стр.60,

№ 157(1; 3),

№ 158(1; 3),

№ 159(1; 3),

№ 160(1; 3)

Спасибо за работу на уроке!

Модуль числа.Уравнения и неравенства, содержашие модуль.

Цели: повторить понятие модуля числа; определить геометрический смысл модуля; научить решать уравнения, содержащие неизвестное под знаком модуля, научить решать неравенства, содержащие неизвестное под знаком модуля.

Просмотр содержимого документа
«Модуль числа.Уравнения и неравенства, содержашие модуль.»

Модуль числа. Решение уравнений и неравенств, содержащих модуль.

Составила учитель математики

Привалова М.В.

1.Понятие модуля числа

Модулем действительного числа а называется само это число, если оно неотрицательное, и противоположное ему число, если данное число отрицательно.

|a|=

a, если a ≥ 0

-a, если a

Примеры:

• |3|=3
• |1/5|=1/5
• |-1|=-(-1)=1
• |-10|=-(-10)=10
• |0|=0

Из определения модуля следует:

Геометрический смысл модуля числа

|5|=|-5|= 5

O

A1

A

x

-5

5

0

OA=OA

1

Модуль – расстояние от начала отсчета на координатной прямой до точки, изображающей число.

2.Уравнения, содержащие неизвестное под знаком модуля

Примеры:

а)|х|=7 (в учебнике)

б) |х+1|=3

в) |3х+2|=1 (в учебнике)

3.Неравенства, содержащие неизвестное под знаком модуля

|х| ≥ a

|х| ≤ a

Решение:

Решение:

x

x

a

-a

a

-a

-a≤ х ≤ a

х ≤ -a ; x ≥ a

x ͼ [ -a; a ]

x ͼ (- ∞ ; -a ] U [a; + ∞ )

6 х6 5. |6х+1| 3. |х-6| — 2 -3 -1/2 -5 1″

Решите неравенства

4 . |х+5| ≥ 2

1. |х| 7

-7

х+5≤-2 х+5≥2

x ≤ -2 -5 х ≥ 2-5

х ≤ -7 х ≥ -3

2. |х|6

х6

5. |6х+1|

3. |х-6|

— 2

-3

-1/2

-5

1

Домашнее задание.

§10(учить определения),

№ (на доске)

План-конспект урока по алгебре (8 класс) на тему: «Использование геометрической интерпретации модуля для решения уравнений, содержащих знак абсолютной величины».

Конспект урока в восьмом классе по учебнику А.Г. Мордковича                       ( профильный уровень), по теме : «Алгебраические уравнения», 14 урок по теме, параграф № 37, « Уравнения с модулями».

                     Тема урока:

«Использование геометрической интерпретации модуля для решения уравнений, содержащих знак абсолютной величины».

                                                                                                                                                                         Урок разработан  учителем  

                                                                            высшей категории

                                                                            школы №74, г.Н.Новгорода

                                                                            Шаповаловой Еленой Владимировной.

Цели урока:- формирование умения применять геометрическую интерпретацию модуля при решении линейных уравнений;          осуществлять поиск решения задач синтетическим методом;                   учиться наблюдать и анализировать.

Тип урока: Изучение нового материала.

Структура урока:

1.Мотивационно-ориентировочный этап.

     1)  Повторение изученного материала;

     2)  Актуализация прежних знаний и способов действия;

     3)  Мотивация учебной деятельности;

     4)  Постановка целей и учебных задач урока, сообщение темы урока.

2. Операционно-познавательный этап.

1.  Ознакомление с новым материалом (формирование новых знаний и               способов решения)

3. Рефлексивно-оценочный этап.

1. Сопоставление целей и результатов урока;
2. Первичный контроль усвоения знаний;
3. Постановка домашнего задания;
4. Подведение итогов урока.

( к уроку прилагается презентация )

Содержание урока:

1этап урока.

            На доске записаны задания:

1) |х|=5;                 Сколько корней имеет данное уравнение?

                              Чем мы пользуемся при решении данного уравнения?

2)|х-3|=5.               Какие способы вы можете предложить для решения                                                                                                                     данного уравнения?

После устного ответа двое учеников решают уравнение графическим и аналитическим способами на доске.

|х-3|=5                                                         |х-3|=5

х-3=5               х-3=-5                                 у=|х-3|, сдвиг графика

х=8                   х=-2                                    у=|х| на 3 ед. вправо.

Ответ: х=8,х=-2.                                         У=5 –прямая || оси абсцисс.

3)Прочитать и объяснить словесную запись:

ρ(х;7)=2;               ρ(х;-5)=3

П.О.( предполагаемый ответ)Найти точки, которые находятся от точки 7 на расстоянии, равном 2 ед. отрезкам.

П.О.Найти точки, которые находятся от точки -5 на расстоянии, равном 3 ед. отрезкам.

Вопрос: В чем заключается геометрический смысл модуля?

П.О. Расстояние между точками на координатной прямой.

4)Записать аналитическую модель рисунка:

П.О. |х+6|=3

 5) |х-2|=3     Вопрос: в чем заключается смысл задания с                                 геометрической точки зрения?

П.О. Найти точки, которые находятся на расстоянии 3 ед. отрезков от точки 2.

Записать данное уравнение с помощью знака ρ и решить его.

Ρ(х;2)=3;                          х-2=3                 х-2=-3

                                          х=5                    х=-1

Вопрос:  как можно найти корни уравнения, используя координатную прямую?

6)Прочитайте данное уравнение  с помощью геометрического смысла модуля |х+5|=3, найдите его корни, используя координатную прямую.

П.О. Найти точки, которые находятся на расстоянии 3 ед. отрезков от точки -5.    

Ответ:   х=-2; х=-8.

7) |х-2|=|х+5|

Посмотрите внимательно на данное уравнение и попробуйте сами сформулировать задание с геометрической точки зрения.

П.О. Расстояние от х до -5 и 2 должно быть одинаковым.

Составьте план решения этого уравнения с помощью координатной прямой.

П.О.

а) найдем расстояние между точками -5 и 2.

    5+2=7.

б) т.к. х равноудалена от точек -5 и 2, найдем половину этого расстояния: 7/2=3,5

в) найдем координату точки: -5+3,5=-1,5 или 2-3,5=-1,5

Молодцы! Назовите способ, с помощью которого мы с вами решили данное уравнение. Как вы думаете, чем мы с вами будем заниматься сегодня на уроке? Попробуйте сами сформулировать тему сегодняшнего урока.

2 этап урока.   Учащиеся записывают в тетрадь тему урока:                         « Использование геометрической интерпретации модуля для решения уравнений.»

1).Посмотрите внимательно на следующее уравнение и прочитайте его с помощью геометрического смысла:

|х-1|+|х-2|=1

П.О. Левая часть есть сумма расстояний от точки х до 1 и 2.

         Правая часть показывает, что эта сумма равна 1.

Найдите расстояние между точками 2 и 1.

Оно равно 1. Следовательно, х может быть любым числом из отрезка [1;2].

Ответ: хЄ[1;2].

2).|х-1|+|х-2|=-1

Посмотрите внимательно на данное уравнение и дайте ответ.

П.О. Уравнение корней не имеет, т.к. сумма расстояний не может быть отрицательным числом.

 3).|х-1|+|х-2|=3. В чем заключается геометрический смысл данного                            уравнения?

П.О. Сумма расстояний от точки х до 1 и 2 равна 3.

Уравнение имеет 2 корня: х=0;х=3.

4).Аналогично рассуждая, решите сами следующее уравнение:

|х-3|+|х-7|=4

Ответ: хЄ[3;7].

5).|х-3|-|х-7|=4    В чем заключается геометрический смысл этого уравнения?

П.О. Разность расстояний от точки х до точек 3 и 7 равна 4.

Т.к. расстояние между 3 и 7 равно4, то ответом будет любое число, расположенное на координатной оси правее 7.

Ответ: хЄ[7;∞).

6).|х-7|-|х-3|=-4  (возможно учащиеся по аналогии с суммой скажут, что корней нет, но это неверный ответ , обязательно изобразить решение на координатной прямой).

Ответ: хЄ[7;∞).

7). |х-7|-|х-3|=4

Ответ: хЄ(-∞;3].

3 этап урока.  

Посмотрите внимательно на все решенные уравнения и попробуйте сделать вывод.

П.О. Сумма расстояний всегда положительна, а разность может принимать любое по знаку число.

Далее, с целью закрепления материала, учащиеся решают вместе с учениками, вызванными к доске задания:

1. |х-9|=3
2. |х-6|=|х+2|
3. |х-9|+|х-3|=6
4. |х-9|-|х-3|=6

и еще раз проговаривают схему решения данных уравнений

Подведем итог урока:

Что нового вы узнали сегодня на уроке?

Сколько способов решения уравнений, содержащих знак абсолютной величины,  вы знаете?

В чем заключается геометрический смысл модуля?

         Запишите в тетради задания на дом:

1. |х-13|=8
2. |х-28|=|х+14|
3. |х-10|+|х-36|=26
4. |х-18|-|х-12|=6
5. |х-18|-|х-12|=-6