Модуль
Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.\(|a|=\begin{cases} a, \;\; если \; a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\; a<0 \end{cases}\)
Второе название модуля – «абсолютное значение действительного числа».
Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:
— если подмодульное выражение положительно, модуль просто убирается. При этом само выражение не меняется.
— если же оно отрицательно, то при снятии модуля перед подмодульным выражением надо добавить знак «минус», чтобы сделать его положительным.
Об этом правиле нужно помнить при работе с более сложными выражениями или  4+1\)
4+1\)
Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).
Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):
\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)
Ответ: \(-10\)
Геометрическое определение модуля
\(|a|\) — это расстояние от \(0\) до числа \(a\) на числовой оси
Пример. Чему равен \(|5|\) и \(|-5|\)?
Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).
Значит ответ: \(|5|=5\), \(|-5|=5\).
Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.
Понимать легче второе определение, но практике удобнее использовать первое.
Решение простейших уравнений с модулем
Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности \( \left[ \begin{gathered}f= g\\ f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).
Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.
Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.
Пример.
 Решить уравнение:
Решить уравнение:|
\(|x-1|=3x\) |
Найдем ограничения уравнения. Запишем его немного правее от основного решения |
|
|
\(3x≥0\) |
Когда ограничение записано — можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений |
|
|
\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\) |
Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо» |
|
|
\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right. |
Приведем подобные слагаемые |
|
|
\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\) |
|
Поделим первое уравнение на \(-2\), второе на \(4\). |
|
\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\) |
|
Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ |
Ответ: \(\frac{1}{4}\)
Решение простейших неравенств с модулем
Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству \( -c< f< c\) , при условии, что \(c>0\).
Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!
Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).
Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).
А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.
Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
|
\(|3x-7|≤8\) |
\(|3x-11|≥11\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-8≤3x-7≤8\) \(|+7\) |
\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-1≤3x≤15\) |
\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(-\frac{1}{3}≤x≤5\) |
\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right. Задача 1. Построить графики функций y=|x| y=|x-1|. y=|x| Построим графики: y=|x-1| Это была простенькая задачка. Теперь то, что многих приводит в ужас. Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|. Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11. Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся. Вот ссылка, которая поможет вам проверить ваши построения: Общие сведения об уравненияхУравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач. С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии. В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно. Предварительные навыкиЧто такое уравнение?Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство. Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5. А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x, значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство. Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части. Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет Говорят, что число 2 является корнем или решением уравнения 3 + x = 5 Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство. Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет. Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы. Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части. Выразить одно через другоеИзучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также. Рассмотрим следующее выражение: 8 + 2 Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10 8 + 2 = 10 Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8. Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8: 2 = 10 − 8 Мы выразили число 2 из равенства 8 + 2 = 10. Как видно из примера, ничего сложного в этом нет. При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении. Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8. Данное равенство можно прочесть так: 2 есть 10 − 8 То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Число 2 есть разность числа 10 и числа 8 или Число 2 есть разница между числом 10 и числом 8. Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий. Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние: 8 + 2 = 10 Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2 8 = 10 − 2 Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние: 8 + 2 = 10 В этот раз выразим число 10. Но оказывается, что десятку выражать не нужно, поскольку она уже выражена. Достаточно поменять местами левую и правую часть, тогда получится то, что нам нужно: 10 = 8 + 2 Пример 2. Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить: 8 = 6 + 2 Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние: 8 − 2 = 6 Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6 2 = 8 − 6 Пример 3. Рассмотрим равенство 3 × 2 = 6 Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2 Вернем получившееся равенство в первоначальное состояние: 3 × 2 = 6 Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3 Пример 4. Рассмотрим равенство Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5 15 = 3 × 5 Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние: Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3 Правила нахождения неизвестныхРассмотрим несколько правил нахождения неизвестных. Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2. В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой. Чтобы выразить число 2, мы поступили следующим образом: 2 = 10 − 8 То есть из суммы 10 вычли слагаемое 8. Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x 8 + x = 10 В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10, а переменная x берет на себя роль так называемого неизвестного слагаемого Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10. Для нахождения неизвестного слагаемого предусмотрено следующее правило: Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10. Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8 2 = 10 − 8 А сейчас, чтобы найти неизвестное слагаемое x, мы должны из суммы 10 вычесть известное слагаемое 8: x = 10 − 8 Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x x = 2 Мы решили уравнение. Значение переменной x равно 2. Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно: В результате получается верное числовое равенство. Значит уравнение решено правильно. Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8. x + 2 = 10 В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. x = 10 − 2 x = 8 Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8. В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность Чтобы выразить число 8, мы поступили следующим образом: 8 = 6 + 2 То есть сложили разность 6 и вычитаемое 2. Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x x − 2 = 6 В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого Для нахождения неизвестного уменьшаемого предусмотрено следующее правило: Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6. А сейчас, чтобы найти неизвестное уменьшаемое x, мы должны к разности 6 прибавить вычитаемое 2 x = 6 + 2 Если вычислить правую часть, то можно узнать чему равна переменная x x = 8 Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x 8 − x = 6 В этом случае переменная x берет на себя роль неизвестного вычитаемого Для нахождения неизвестного вычитаемого предусмотрено следующее правило: Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6. А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6 x = 8 − 6 Вычисляем правую часть и находим значение x x = 2 Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3. В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение Чтобы выразить число 3 мы поступили следующим образом: То есть разделили произведение 6 на множитель 2. Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x x × 2 = 6 В этом случае переменная x берет на себя роль неизвестного множимого. Для нахождения неизвестного множимого предусмотрено следующее правило: Чтобы найти неизвестное множимое, нужно произведение разделить на множитель. Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6. Произведение 6 мы разделили на множитель 2. А сейчас для нахождения неизвестного множимого x, нужно произведение 6 разделить на множитель 2. Вычисление правой части позволяет нам найти значение переменной x x = 3 Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель: Чтобы найти неизвестный множитель, нужно произведение разделить на множимое. Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6. Тогда для получения числа 2 мы разделили произведение 6 на множимое 3. А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3. Вычисление правой части равенства позволяет узнать чему равно x x = 2 Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя: Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель. Например, решим уравнение 9 × x = 18. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9 Отсюда . Решим уравнение x × 3 = 27. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3 Отсюда . Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное. Чтобы выразить число 15 мы поступили следующим образом: 15 = 3 × 5 То есть умножили частное 3 на делитель 5. Теперь представим, что в равенстве вместо числа 15 располагается переменная x В этом случае переменная x берет на себя роль неизвестного делимого. Для нахождения неизвестного делимого предусмотрено следующее правило: Чтобы найти неизвестное делимое, нужно частное умножить на делитель. Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5. А сейчас, чтобы найти неизвестное делимое x, нужно частное 3 умножить на делитель 5 x = 3 × 5 Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x. x = 15 Теперь представим, что в равенстве вместо числа 5 располагается переменная x. В этом случае переменная x берет на себя роль неизвестного делителя. Для нахождения неизвестного делителя предусмотрено следующее правило: Чтобы найти неизвестный делитель, нужно делимое разделить на частное. Что мы и сделали, когда выражали число 5 из равенства . А сейчас, чтобы найти неизвестный делитель x, нужно делимое 15 разделить на частное 3 Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x. x = 5 Итак, для нахождения неизвестных мы изучили следующие правила:
КомпонентыКомпонентами мы будем называть числа и переменные, входящие в равенство Так, компонентами сложения являются слагаемые и сумма Компонентами вычитания являются уменьшаемое, вычитаемое и разность Компонентами умножения являются множимое, множитель и произведение Компонентами деления являются делимое, делитель и частное В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть. Пример 1. Найти корень уравнения 45 + x = 60 45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. x = 60 − 45 Вычислим правую часть, получим значение x равное 15 x = 15 Значит корень уравнения 45 + x = 60 равен 15. Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить. Пример 2. Решить уравнение Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма. При этом слагаемое 2x содержит переменную x. После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое: Теперь применяем правило нахождения неизвестного слагаемого. Вычислим правую часть получившегося уравнения: Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение При этом переменная x является не просто множителем, а неизвестным множителем Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое: Вычислим правую часть, получим значение переменной x Для проверки найденный корень отправим в исходное уравнение и подставим вместо x Получили верное числовое равенство. Значит уравнение решено правильно. Пример 3. Решить уравнение 3x + 9x + 16x = 56 Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить. Приведем подобные слагаемые в левой части данного уравнения: Имеем дело с компонентами умножения. Отсюда x равен 2 Равносильные уравненияВ предыдущем примере при решении уравнения 3x + 9x + 16x = 56, мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56. Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают. Уравнения называют равносильными, если их корни совпадают. Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2. Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56, а затем в уравнение 28x = 56, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Согласно порядку действий, в первую очередь выполняется умножение: Подставим корень 2 во второе уравнение 28x = 56 Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными. Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56, которое проще решать. Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает. Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному. и аналогично: Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному. Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число. Пример 1. Решить уравнение Вычтем из обеих частей уравнения число 10 Приведем подобные слагаемые в обеих частях: Получили уравнение 5x = 10. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 10 разделить на известный сомножитель 5. Отсюда . Вернемся к исходному уравнению и подставим вместо x найденное значение 2 Получили верное числовое равенство. Решая уравнение мы вычли из обеих частей уравнения число 10. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2 Пример 2. Решить уравнение 4(x + 3) = 16 Раскроем скобки в левой части равенства: Вычтем из обеих частей уравнения число 12 Приведем подобные слагаемые в обеих частях уравнения: В левой части останется 4x, а в правой части число 4
Получили уравнение 4x = 4. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 4 разделить на известный сомножитель 4 Отсюда Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно. Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12. Пример 3. Решить уравнение Раскроем скобки в левой части равенства: Прибавим к обеим частям уравнения число 8 Приведем подобные слагаемые в обеих частях уравнения: В левой части останется 2x, а в правой части число 9 В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5 Получили верное числовое равенство. Значит уравнение решено правильно. Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5 Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному. То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений. Рассмотрим следующее уравнение: Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство Получается верное равенство. Значит число 2 действительно является корнем уравнения . Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки. Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный: Получилось уравнение 12 = 9x − 3x. Приведем подобные слагаемые в правой части данного уравнения: Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Отсюда x = 2. Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными. На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число. Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x. Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием. Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12. В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом: Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения. Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число. Пример 1. Решить уравнение При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение. В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8: Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8 Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения: В результате останется простейшее уравнение Ну и нетрудно догадаться, что корень этого уравнения равен 4 Вернемся к исходному уравнению и подставим вместо x найденное значение 4 Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись: От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом: Пример 2. Решить уравнение Умнóжим обе части уравнения на 15 В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5 Перепишем то, что у нас осталось: Раскроем скобки в правой части уравнения: Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак: Приведем подобные слагаемые в обеих частях, получим Имеем дело с компонентами умножения. Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 5 Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15. Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x. Корень этого уравнения, как и уравнения равен 5. Значит эти уравнения равносильны. Пример 3. Решить уравнение Умнóжим обе части уравнения на 3 В левой части можно сократить две тройки, а правая часть будет равна 18 Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель: Отсюда Вернемся к исходному уравнению и подставим вместо x найденное значение 9 Получается верное числовое равенство. Пример 4. Решить уравнение Умнóжим обе части уравнения на 6 В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель: Сократим в обеих частях уравнениях то, что можно сократить: Перепишем то, что у нас осталось: Раскроем скобки в обеих частях уравнения: Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x, сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой: Приведем подобные слагаемые в обеих частях: Теперь найдем значение переменной x. Для этого разделим произведение 28 на известный сомножитель 7 Отсюда x = 4. Вернемся к исходному уравнению и подставим вместо x найденное значение 4 Получилось верное числовое равенство. Значит уравнение решено правильно. Пример 5. Решить уравнение Раскроем скобки в обеих частях уравнения там, где это можно: Умнóжим обе части уравнения на 15 Раскроем скобки в обеих частях уравнения: Сократим в обеих частях уравнения, то что можно сократить: Перепишем то, что у нас осталось: Раскроем скобки там, где это можно: Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные: Приведем подобные слагаемые в обеих частях уравнения: Найдём значение x В получившемся ответе можно выделить целую часть: Вернемся к исходному уравнению и подставим вместо x найденное значение Получается довольно громоздкое выражение. Воспользуемся переменными. Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B Найдем значение выражения, находящегося в переменной А. Значение переменной А равно . Теперь найдем значение переменной B. То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно Видим, что значение переменной B, как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно. Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить. Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42. Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Подставим найденное значение 2 вместо x в исходное уравнение: Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое: Выполним сокращение в каждом слагаемом: Перепишем то, что у нас осталось: Решим это уравнение, пользуясь известными тождественными преобразованиями: Получили корень 2. Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны. Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14, нам потребовалось разделить произведение 14 на известный сомножитель 7. Этим методом мы тоже будем пользоваться часто. Умножение на минус единицуЕсли обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному. Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1. Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать. Рассмотрим уравнение . Чему равен корень этого уравнения? Прибавим к обеим частям уравнения число 5 Приведем подобные слагаемые: А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . То есть минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом: Имеем дело с компонентами умножения. Чтобы найти х, нужно произведение −5 разделить на известный сомножитель −1. или разделить обе части уравнения на −1, что еще проще Итак, корень уравнения равен 5. Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице Получилось верное числовое равенство. Значит уравнение решено верно. Теперь попробуем умножить обе части уравнения на минус единицу: После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10 Корень этого уравнения, как и уравнения равен 5 Значит уравнения и равносильны. Пример 2. Решить уравнение В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1. Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками. Так, умножение уравнения на −1 можно записать подробно следующим образом: либо можно просто поменять знаки всех компонентов: Получится то же самое, но разница будет в том, что мы сэкономим себе время. Итак, умножив обе части уравнения на −1, мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3 Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали. Пример 3. Решить уравнение Умнóжим обе части уравнения на −1. Тогда все компоненты поменяют свои знаки на противоположные: Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые: Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые: Приравнивание к нулюНедавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному. А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего. В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Приведем подобные слагаемые в левой части: Прибавим к обеим частям 77, и разделим обе части на 7 Альтернатива правилам нахождения неизвестныхОчевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных. К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2 Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5 Уравнения вида мы решали выражая неизвестное слагаемое: Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак: Далее разделить обе части на 2 В левой части уравнения сократятся две двойки. Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее: В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения: Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме. Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится. Когда корней несколькоУравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9. В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9), которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй). То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю. x = 0 или x + 9 = 0 Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0. Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0. Несложно догадаться, что корень этого уравнения равен −9. Проверка показывает, что корень верный: −9 + 9 = 0 Пример 2. Решить уравнение Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2). А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2)). Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули: Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю: Когда корней бесконечно многоУравнение может иметь бесконечно много корней. Пример 1. Решить уравнение Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14. Это равенство будет получаться при любом x Пример 2. Решить уравнение Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x Когда корней нетСлучается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x, левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид Пусть Пример 2. Раскроем скобки в левой части равенства: Приведем подобные слагаемые: Видим, что левая часть не равна правой части. И так будет при любом значении y. Например, пусть y = 3. Буквенные уравненияУравнение может содержать не только числа с переменными, но и буквы. Например, формула нахождения скорости является буквенным уравнением: Данное уравнение описывает скорость движения тела при равноускоренном движении. Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s. Умнóжим обе части уравнения на t В правой части переменные t сократим на t и перепишем то, что у нас осталось: В получившемся уравнении левую и правую часть поменяем местами: У нас получилась формула нахождения расстояния, которую мы изучали ранее. Попробуем из уравнения определить время. Для этого нужно выразить переменную t. Умнóжим обе части уравнения на t В правой части переменные t сократим на t и перепишем то, что у нас осталось: В получившемся уравнении v × t = s обе части разделим на v В левой части переменные v сократим на v и перепишем то, что у нас осталось: У нас получилась формула определения времени, которую мы изучали ранее. Предположим, что скорость поезда равна 50 км/ч v = 50 км/ч А расстояние равно 100 км s = 100 км Тогда буквенное уравнение примет следующий вид Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t. Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t либо можно воспользоваться тождественными преобразованиями. Затем разделить обе части на 50 Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x Вычтем из обеих частей уравнения a Разделим обе части уравнения на b Теперь, если нам попадется уравнение вида a + bx = c, то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться. Решим уравнение 2 + 4x = 10. Оно похоже на буквенное уравнение a + bx = c. Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения: Видим, что второе решение намного проще и короче. Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0), поскольку деление на ноль на допускается. Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x Раскроем скобки в обеих частях уравнения Воспользуемся переносом слагаемых. Параметры, содержащие переменную x, сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой. В левой части вынесем за скобки множитель x Разделим обе части на выражение a − b В левой части числитель и знаменатель можно сократить на a − b. Так окончательно выразится переменная x Теперь, если нам попадется уравнение вида a(x − c) = b(x + d), то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Допустим нам дано уравнение 4(x − 3) = 2(x + 4). Оно похоже на уравнение a(x − c) = b(x + d). Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения: Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d. Это позволит нам не ошибиться при подстановке: Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0). Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю. Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d). В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части: Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x Приведем левую часть уравнения к общему знаменателю: Умнóжим обе части на a В левой части x вынесем за скобки Разделим обе части на выражение (1 − a) Линейные уравнения с одним неизвестнымРассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным. Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой». Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2(x + 3) = 16. Давайте решим его. Раскроем скобки в левой части уравнения, получим 2x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x, разделим произведение 10 на известный сомножитель 2. Отсюда x = 5. Уравнение 2(x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10, для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный». Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b. Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x. Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю. Если в линейном уравнении a = 0 и b = 0, то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0. При любом значении x левая часть будет равна правой части. Если в линейном уравнении a = 0 и b ≠ 0, то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5. Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти. Если в линейном уравнении a ≠ 0, и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3, и b равно какому-нибудь числу, скажем числу 6, то уравнение примет вид . Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0. Это то же самое уравнение, что и ax = b, но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0. Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде. В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным. Задания для самостоятельного решенияЗадание 1. Используя метод переноса слагаемого, решите следующее уравнение: Задание 2. Используя метод прибавления (или вычитания) числа к обеим частям, решите следующее уравнение: Задание 3. Решите уравнение: Задание 4. Решите уравнение: Задание 5. Решите уравнение: Задание 6. Решите уравнение: Задание 7. Решите уравнение: Задание 8. Решите уравнение: Задание 9. Решите уравнение: Задание 10. Решите уравнение: Задание 11. Решите уравнение: Задание 12. Решите уравнение: Задание 13. Решите уравнение: Задание 14. Решите уравнение: Задание 15. Решите уравнение: Задание 16. Решите уравнение: Задание 17. Решите уравнение: Задание 18. Решите уравнение: Задание 19. Решите уравнение: Задание 20. Решите уравнение: Задание 21. Решите уравнение: Задание 22. Решите уравнение: Задание 23. Решите уравнение: Задание 24. Решите уравнение: Задание 25. Решите уравнение: Задание 26. Решите уравнение: Задание 27. Решите уравнение: Задание 28. Решите уравнение: Задание 29. Решите уравнение: Задание 30. Решите уравнение: Задание 31. Решите уравнение: Задание 32. В следующем буквенном уравнении выразите переменную x: Задание 33. В следующем буквенном уравнении выразите переменную x: Задание 34. В следующем буквенном уравнении выразите переменную x: Задание 35. В следующем буквенном уравнении выразите переменную x: Задание 36. В следующем буквенном уравнении выразите переменную y: Задание 37. В следующем буквенном уравнении выразите переменную z: Понравился урок?
Возникло желание поддержать проект? Навигация по записямНатуральный логарифм, функция ln xПриведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел. Определение
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x. Исходя из определения, основанием натурального логарифма является число е: График натурального логарифма ln xГрафик функции y = ln x. График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x. Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения. При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ). При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция xa с положительным показателем степени a растет быстрее логарифма. Свойства натурального логарифмаОбласть определения, множество значений, экстремумы, возрастание, убываниеНатуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Значения ln x ln 1 = 0 Основные формулы натуральных логарифмов Формулы, вытекающие из определения обратной функции: Основное свойство логарифмов и его следствияФормула замены основания Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания: Обратная функцияОбратной для натурального логарифма является экспонента. Если , то Если , то . Производная ln x Производная натурального логарифма: Интеграл Интеграл вычисляется интегрированием по частям: Выражения через комплексные числа Рассмотрим функцию комплексной переменной z: Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией. Разложение в степенной ряд При имеет место разложение: Использованная литература: Автор: Олег Одинцов. Опубликовано: Изменено: Примеры вычисления полей в Python—ArcGIS ProВвод значений с клавиатуры – не единственный способ редактирования значений в таблице. В некоторых случаях вам может потребоваться выполнить математические вычисления для получения значения поля отдельной записи или даже всех записей. Можно выполнять как простые, так и сложные вычисления над всеми либо только выбранными записями. Кроме того, в полях атрибутивных таблиц можно вычислить длину, периметр и прочие геометрические свойства. В разделах ниже приводятся примеры использования калькулятора поля. Вычисления выполняются с помощью Python, SQL и Arcade. Этот раздел описывает примеры скриптов Python для Вычисления поля. Более подробно о выражениях Arcade, см. Руководство ArcGIS Arcade. Более подробно о выражениях SQL можно узнать в разделе Вычисление поля.
Простые вычисленияРяд вычислений можно производить, используя только короткое выражение. Примеры простых строчекСтроки поддерживаются несколькими строковыми функциями Python, в том числе capitalize, rstrip и replace. Сделать заглавной первую букву текста в поле CITY_NAME. Убрать все пробелы на концах строк в поле CITY_NAME . Заменить написание «california» на «California» в поле STATE_NAME. Доступ к символам в текстовом поле осуществляется путем индексации и разделения в Python. Индексация возвращает символы в индексном местоположении; разделение – группу символов. В следующей таблице предположим, что это строковое поле !fieldname! со значением «abcde».
Python также поддерживает форматирование строк с использованием метода format(). Скомбинировать поля FieldA и FieldB, разделенные двоеточием. Простые математические примерыPython предоставляет инструменты для обработки чисел. Python также поддерживает ряд числовых и математических функций, в том числе, math, cmath, decimal, random, itertools, functools и operator.
Вычислить объем сферы по заданному полю с радиусами. Прежние версии:В ArcGIS Pro используется Python 3, а в ArcGIS Desktop – Python 2. В Python 2 используются математические целые числа, то есть деление двух целочисленных значений всегда дает в результате целочисленное значение (3 / 2 = 1). В Python 3 при делении целочисленных значений результат будет числом с плавающей точкой (3 / 2 = 1.5). Встроенные функции PythonPython содержит ряд встроенных функций, включая max, min, round и sum. Вычисление максимального значения для каждой записи в списке полей. Вычисление суммы для каждой записи в списке полей. Использование блоков кодаС помощью выражений Python и параметра Блок кода вы можете сделать следующее:
Прежние версии:В ArcGIS Desktop инструмент Вычислить поле поддерживает типы выражений VB, PYTHON и PYTHON_9.3. Тип выражения VB, поддерживаемый в некоторых продуктах, не поддерживается в 64-битных продуктах, и в том числе в ArcGIS Pro. Ключевые слова PYTHON и PYTHON_9.3 все еще поддерживаются в ArcGIS Pro для сохранения обратной совместимости, но не указываются в списке выбора. Скрипты Python, использующие ключевые слова, продолжат работать корректно. Единственное различие между типом выражения Python 3 и устаревшим ключевым словом PYTHON_9.3 заключается в том, что Python 3 возвращает значения в полях данных как объекты Python datetime. Тип выражения Python 3 не связан с версией Python, установленной с ArcGIS Pro. Это просто исторически связанное с Python стороннее ключевое слово (после PYTHON и PYTHON_9.3). Функции Python задаются с помощью ключевого слова def, за которым идет имя функции и ее входные аргументы. Можно написать функцию Python, которая будет принимать любое число входных аргументов (в т.ч. их может и не быть). Значение возвращается из функции с помощью выражения return. Имя функции остаётся на ваш выбор (не используйте пробелы и не начинайте с цифр). Если функция с выражением return не возвращает значения, будет возвращено None. Помните, что отступы являются частью синтаксиса Python. Для определения каждого логического уровня используются четыре пробела. Приводите в соответствие начало и конец каждого блока, и будьте последовательны. Примеры кода – mathДля использования всех приведенных ниже математических примеров используйте тип выражения Python 3. Округлить значения поля до двух десятичных знаков. Используйте модуль math для конвертации метров в футы. Конвертация возводит в степень 2 и умножает на площадь. Вычисления полей с использованием логики PythonЛогические структуры могут быть включены в блок кода через выражения if, else и elif. Классифицировать на основании значений поля. Примеры кода – геометрияПомимо следующих примеров кода см. раздел Преобразование геометрических единиц, расположенный ниже, для получения дополнительной информации о преобразовании геометрических единиц. Вычислить площадь объекта. Вычислить максимальную x-координату объекта. Вычислить количество вершин объекта. Для точечного класса пространственных объектов сдвинуть x-координату каждой точки на 100. Информация о единицах измерения геометрииСвойства площади и длины в поле геометрии можно изменить с помощью типов единиц, обозначаемых знаком @.
Если данные хранятся в географической системе координат и поддерживаются линейные единицы (например, футы), вычисления длин будут конвертированы по геодезическому алгоритму. Внимание:Преобразование единиц площади в географическую систему координат даёт сомнительные результаты, так как десятичные градусы в разных частях глобуса имеют разную длину. Вычислить длину пространственного объекта в ярдах. Вычислить длину пространственного объекта в акрах. Геодезическая площадь и длина также может быть вычислена с помощью свойств geodesicArea и geodesicLength, с помощью символа @, следующего за ключевым словом единицы измерения. Вычисление геодезической длины пространственного объекта в ярдах. Вычисление геодезической площади пространственного объекта в акрах. Примеры кода – датыДату и время можно вычислить с помощью модулей datetime и time. Вычислить текущую дату. Вычислить текущие дату и время. Вычислить дату как 31 декабря 2000. Вычислить количество дней между текущей датой и значением в поле. Вычислить дату, прибавив 100 дней к значению даты в поле. Вычислить строку, представляющую дату, используя метод ctime в модуле datetime. В примере создается строка в формате: ‘Mon Feb 22 10:15:00 2021’. Вычислить день недели (например, воскресенье) для значения даты в поле. Вычислить отформатированную строку из поля даты, используя метод strftime модуля datetime и строку явного формата. В примере создается строка в формате: ’02/22/2021, 10:15:00′. Примеры кода – текстСтроковые вычисления могут выполняться с использованием различных шаблонов кодирования Python. Вернуть три самых правых символа. Заменить все вхождения заглавной буквы P на прописную p. Конкатенировать два поля, разделив их пробелом. Конвертация в нужный регистрВ этих примерах показаны различные способы конвертации слов таким образом, чтобы каждое слово начиналось с большой буквы, а остальные буквы были прописными. Регулярные выраженияМодуль Python re содержит операции сопоставления регулярных выражений, которые используются для сопоставления сложных примеров и правил замещения для строк. Замена St или St. перед новым словом в конце строки словом Street. Накопительные и последовательные вычисленияНакопительные и последовательные вычисления могут выполняться с использованием глобальных переменных. Вычислить последовательные идентификаторы ID или порядковые номера на основании интервала. Вычислить накопительные значения числового поля. Вычислить процентное приращение числового поля. Случайные значенияСлучайные значения можно получить с помощью модуля random. Используйте пакет numpy для вычисления случайных значений с плавающей точкой от 0.0 до 1.0. Используйте модуль random случайных чисел для вычисления случайных целочисленных значений от 0 до 10. Вычисление значений nullВ выражении Python пустые значения (null) можно вычислить, используя Python None. Следующее вычисление будет работать, только если поле может содержать нулевые значения. Используйте Python None для вычисления пустых значений. Связанные разделыОтзыв по этому разделу? Доказательства свойств модуля☰ Существуют следующие свойства модуля действительных чисел: 1) |a + b| ≤ |a| + |b|; 2) |ab| = |a| × |b|; 3) , a ≠ 0; 4) |a – b| ≥ |a| – |b|. Проведем доказательства, рассматривая различные случаи значений a и b. Доказательство 1) |a + b| ≤ |a| + |b|: Если a и b – положительные числа, то их модули совпадают с их значениями: |a| = a, |b| = b. Из этого следует, что |a + b| = |a| + |b|. Если a – отрицательное число, а b – положительное число, то выражение |a + b| можно записать как |b – a|. Выражение же |a| + |b| равно сумме абсолютных значений a и b, что больше, чем b – a. Поэтому |a + b| < |a| + |b|. Если b – отрицательное число, а a – положительное, то |a + b| принимает вид |a – b|, что также меньше суммы модулей |a| + |b|. Если a и b – отрицательные числа, то получим |–a – b|. Результат этого выражения равен |a + b| (т. к. |–a – b| = |–(a + b)| = |a + b|). Но уже было доказано, что |a + b| = |a| + |b|, следовательно и |–a – b| = |a| + |b|. Доказательство 2) |ab| = |a| × |b|: Доказательство 3) , a ≠ 0: Если a – положительное число, то |a| = a и, следовательно, доказываемое равенство верно, т. к. и правая и левая части равны 1/a. Если a – отрицательное число, то имеем . Взятие модуля в обоих выражениях приведет к делению единицы на абсолютное значение a. Значит эти выражения равны друг другу. Доказательство 4) |a – b| ≥ |a| – |b|: Если a и b – положительные числа, то их модули совпадают с самими числами. Поэтому |a – b| = |a| – |b|, потому что можно не брать модули вообще и тогда с двух сторон получим a – b. Если a – положительное число, а b – отрицательное, то выражение |a – b| примет вид |a + b|, что больше, чем |a| – |b|. Если a – отрицательное число, а b – положительное, то имеем |–a – b| = |–(a + b)| = |a + b|, что больше, чем |a| – |b|. ASUS ROG Strix XG43UQ: 43-дюймовый монитор для игровых консолейКонсольное направление — совсем новое для игровых мониторов, но в нем уже появляются очень интересные модели. Как, например, ASUS ROG Strix XG43UQ — с поддержкой режима [email protected] и технологии AMD FreeSync Premium Pro. от 52 299 грн Предложений: 6
ДизайнПри диагонали экрана в 43 дюйма ASUS XG43UQ выглядит скорее как некрупный телевизор: если его использовать как монитор для ПК, то он займет собой большую часть типичного компьютерного стола. Но при этом в его внешнем виде явно прослеживаются элементы дизайна, характерные для игровой линейки ASUS – ROG (Republic of Gamers). Дисплей обрамлен рельефной рамкой средней ширины (~14 мм сверху и по бокам и ~23 мм — снизу) из черного матового пластика, стоит он на металлической V-образной подставке с широко расставленными «ногами». Подставка позволяет регулировать лишь угол наклона экрана (-5..10°) — изменения высоты экрана над уровнем стола или его поворотов влево-вправо здесь нет. Подставка опирается на столешницу тремя дисками с прорезиненным низом, так что монитор сдвинуть с места оказывается очень нелегко (в том числе и благодаря его массе — целых 15 кг). При желании ASUS ROG Strix XG43UQ можно повесить на стену — ножка у него съемная, а на тыльной стороне есть VESA-совместимое крепление (100х100). Тыльная панель — из белого матового пластика, с рядом вентиляционных отверстий в верхней части и большим рельефным лого ROG справа. Разъемы разделены на две «группы», как это часто бывает в телевизорах: одна из них ориентирована вбок, другая — вниз. Первая предназначена для быстрого подключения устройств, здесь можно найти два порта HDMI 2.0, USB-концентратор на два порта USB 3.0 и два мини-джека — для наушников и микрофона. Вторая спрятана за декоративной крышкой, что предполагает более редкий доступ к разъемам; тут находятся два порта HDMI 2.1, один DisplayPort 1.4, разъем питания и порт micro-USB для подключения отдельного модуля, который высвечивает на поверхности стола логотип ROG.
МенюДля навигации по меню используется джойстик и три аппаратные кнопки, расположенные на боковой панели в правом нижнем углу, сразу над кнопкой питания. В основном меню первый пункт — игровой раздел Gaming: тут находятся видеорежимы GameVisual, управление овердрайвом и AMD FreeSync, высветление теней ShadowBoost, включение технологии повышения четкости EMLB и т.д. Далее идут два пункта настройки графики — Image и Color (яркость, контрастность, HDR, гамма, насыщенность, цветовая температура), после них — пункт с ручным выбором видеовхода. В разделе Lighting Effect — управление RGB-подсветкой и активация Aura Sync (синхронизация подсветки с другими устройствами ASUS), в MyFavorite можно переназначить «горячие клавиши» (по умолчанию им присвоены переключение видеовходов и вызов меню GameVisual). И в последнем разделе, System Setup, находятся системные настройки вроде параметров работы экранного меню, поведения индикатора активности, включения технологии DSC, вывода информации о текущем видеорежиме, сброса всех настроек на заводские установки и т.д.
ФункциональностьВ ASUS ROG Strix XG43UQ используется 10-битная 43-дюймовая VA-панель с разрешением 4K. Плотность пикселей составляет ~112,5 PPI, размер точки — 0,2451 мм. Если использовать его как очень большой компьютерный монитор и сидеть за ним на типичном расстоянии от экрана в полметра или чуть больше, при большом желании увидеть отдельные точки можно, хоть и с трудом; но уже с расстояния в метр разглядеть их получится только у игроков с очень острым зрением. Максимальная частота обновления экрана при подключении по DisplayPort составляет 144 Гц при разрешении 4K – причем благодаря технологии Display Stream Compression этого удается достичь при использовании одного входа DP 1.4 и без применения ухудшающей качество изображения цветовой субдескритизации. Впрочем, этот режим будет востребован только у компьютерных игроков, зато консольные геймеры наверняка оценят поддержку [email protected] Гц при подключении по HDMI 2.1 – именно этот режим востребован в консолях текущего поколения от Sony и Microsoft. Хоть игр с его поддержкой пока и не очень много, тем не менее, оценить все преимущества высокой частоты обновления при 4K-разрешении на консоли PlayStation 5 можно в таких проектах, как, например, ремастер обеих частей Nioh, Destiny 2, Borderlands 3 или Call of Duty: Black Ops Cold War. ASUS ROG Strix XG43UQ поддерживает технологию AMD FreeSync Premium Pro, которая согласовывает частоту обновления экрана с выводом кадров в игре, устраняя расслоение изображения в динамичных сценах и сохраняя при этом максимальную частоту обновления. Premium Pro – самая «продвинутая» версия AMD FreeSync, и для ее полноценной поддержки дисплей должен обладать рядом дополнительных характеристик (частота обновления не ниже 120 Гц при разрешении не ниже Full HD, полноценная поддержка HDR-режима, низкая задержка ввода как в SDR, так и в HDR, а также работоспособность FreeSync на низких частотах обновления). Яркость в этом мониторе регулируется с помощью изменения силы тока, ШИМ не применяется на всем диапазоне яркости, так что мерцания подсветки у него нет. В то время как обычные телевизоры не могут похвастаться высокой отзывчивостью — задержка ввода в десятки миллисекунд у них обычное дело, ASUS ROG Strix XG43UQ в этом плане демонстрирует результаты на уровне хорошего игрового десктопного монитора. При использовании овердрайва и технологии повышения четкости в динамике Extreme Low Motion Blur (ELMB) заявленное время отклика этого монитора составляет 1 мс (MPRT). Впрочем, один типичный «телевизионный» атрибут у этого монитора все-таки есть — пульт ДУ; учитывая, что ASUS ROG Strix XG43UQ в первую очередь ориентирован на консольный гейминг и, соответственно, стоять он скорее всего будет на месте телевизора в гостиной, пульт ДУ окажется явно не лишним.
Качество изображения ASUS ROG Strix XG43UQВ мониторе используется полуматовое покрытие экрана, которое почти полностью устраняет паразитные блики и отражения, при этом минимально страдает от кристаллического эффекта (легкая зернистость на однотонных участках изображения, заметная на обычных матовых дисплеях). Равномерность черного очень хорошая, каких-то заметных светлых пятен на черном фоне разглядеть не получается; глубина черного цвета, благодаря использованию VA-панели, также оказывается просто отличной: увидеть легкое свечение в темном помещении можно, лишь значительно подняв яркость экрана. Glow-эффект у ASUS ROG Strix XG43UQ также минимален, при отклонении в сторону свечение черных участков изображения практически отсутствует. Углы обзора весьма хороши как для VA-панели: при отклонении в сторону несколько снижается насыщенность цветов, появляется умеренный теплый оттенок, а черный фон становится светлее, из-за чего темная картинка «сереет», а контрастные сцены становятся менее насыщенными — в целом, типичное поведение экрана, изготовленного по этой технологии. Минимальная яркость довольно высокая: в зависимости от режима, она составляет 85-95 кд/м²; в полной темноте этот экран будет ощущаться довольно ярким даже в комнате со слабым освещением. Максимальная яркость в обычном режиме составляет 840 кд/м² (что интересно, заявленная в технических характеристиках оказывается ниже — «всего» 750 кд/м²), в HDR поднимается еще выше – вплоть до 1000 кд/м². Этот результат, наряду с остальными характеристиками панели, позволил монитору получить сертификацию VESA DisplayHDR1000. Статическая контрастность, в зависимости от видеорежима и настроек яркости, может достигать 3600:1, что является очень хорошим результатом даже по меркам VA-панелей. Дисплей обладает расширенным цветовым охватом, покрывающим 92% пространства DCI-P3 (84% Adobe RGB и 125% sRGB), благодаря чему он выдает очень яркие, насыщенные цвета. В меню GameVisual представлен почти десяток различных видеорежимов, как типичных для десктопных мониторов (Кино, Пейзаж, sRGB), так и предназначенных для различных игровых жанров (гонки, RTS/RPG, FPS, MOBA). Все они отличаются различными графическими установками, и в большинстве из них оказываются заблокированы те или иные параметры в экранном меню. Полный доступ к ручным регулировкам (и при этом максимально универсальные настройки по умолчанию) предлагает пользовательский режим — именно его мы бы и рекомендовали использовать как основной, особенно если вы планируете подстраивать под себя не только яркость. В нем экран демонстрирует полный цветовой охват, значение гаммы в настройках мы бы рекомендовали устанавливать в 2,5 (по результатам измерений в этом случае получается практически идеальное соответствие стандартному значению 2,2) или, если захочется чуть высветлить тени и проявить «прячущуюся» там информацию — в 2,2 (реальное значение при этом оказывается чуть ниже, 2,1). Режим «Пользовательский»: Цветовая температура при изменении яркости меняется очень слабо: при выборе пользовательского значения в соответствующем параметре от 5700K на минимальной яркости и до 6100K — на максимальной; если изображение при этом будет казаться чересчур теплым, лучше переключиться в режим Warm, в котором температура почти идеально соответствует стандартной, 6500K. Установки Normal и Cool выдают заметно более холодную температуру (7900K и 10100K, соответственно). Равномерность подсветки, как для экрана такой диагонали, оказывается достаточно хорошей: верхняя и нижняя части дисплея показывают на 8-13% меньшую яркость, чем центральная зона. А вот с равномерностью цветовой температуры ситуация несколько хуже: перепад между правой частью экрана и нижним левым углом оказывается в районе 10%. В режиме sRGB цветовой охват сужается до 91% sRGB (68% Adobe RGB, 70% DCI-P3). Кроме того, ASUS ROG Strix XG43UQ проходит заводскую калибровку режима sRGB, так что среднее значение deltaE в нем оказывается меньше единицы: это отличный результат, с такими характеристиками этот монитор вполне можно использовать не только для игр, но и для работы с графикой. Тут же стоит отметить, что в пользовательском режиме точность цветопередачи также очень высока и почти не отличается от этого. Режим sRGB: Плюсы: Отличное качество изображения; быстрая и отзывчивая панель; VESA DisplayHDR1000; AMD FreeSync Premium Pro; поддержка [email protected] Гц по HDMI 2.1 и [email protected] Гц по DisplayPort 1.4Минусы: Стоимость Вывод: ASUS ROG Strix XG43UQ — «консольный» игровой монитор в формате телевизора. Он демонстрирует отличное качество изображения и минимальную задержку ввода, на уровне десктопных игровых моделей, а поддержка видеорежима [email protected] Гц при подключении по HDMI 2.1 делает его отличным выбором для работы в связке с консолями Sony PlayStation 5 и Microsoft Xbox Series X. Единственное, что при желании можно записать ему в «минусы» — это высокую стоимость.Технические характеристики
Решение более простых абсолютных уравнений | PurplemathPurplemathКогда мы берем абсолютное значение числа, мы всегда получаем положительное число (или ноль). Независимо от того, был ли вход положительным или отрицательным (или нулевым), выход всегда положительный (или нулевой). Например, | 3 | = 3 и | –3 | = 3 тоже. Это свойство — положительное и отрицательное превращение в положительное — делает решение абсолютных уравнений немного сложным.Но как только вы усвоите «трюк», они не так уж и плохи. Начнем с простого: MathHelp.comЯ уже решил эту проблему в своем обсуждении выше: Значит, x должно быть равно 3 или равно –3. Но как мне решить эту проблему, если я, , не знаю ответа? Я буду использовать свойство положительного / отрицательного абсолютного значения, чтобы разделить уравнение на два случая, и я буду использовать тот факт, что знак «минус» в отрицательном случае означает «противоположный знак», а не «отрицательное число». Например, если у меня x = –6, то «- x » означает «противоположность x » или, в данном случае, — (- 6) = +6, положительное число.Знак «минус» в «- x » просто указывает на то, что я меняю знак на x . Это означает, что , а не , означает отрицательное число. Это различие очень важно! Каким бы ни было значение x , взятие абсолютного значения x делает его положительным. Поскольку значение x изначально могло быть положительным, а может быть отрицательным, я должен признать этот факт, когда удаляю столбцы абсолютного значения.Я делаю это, разбивая уравнение на два случая. Для этого упражнения это следующие случаи: а. Если значение x было неотрицательным (то есть, если оно было положительным или нулевым) для начала, то я могу вывести это значение из столбцов абсолютного значения, не меняя его знака, давая мне уравнение x = 3. г. Если значение x изначально было отрицательным, то я могу вывести это значение из столбцов абсолютного значения, изменив знак на x , получив уравнение — x = 3, которое решает как х = –3. Тогда мое решение — Кстати, мы можем проверить это решение графически. Когда мы пытаемся решить уравнение абсолютных значений | x | = 3, мы, по сути, приравниваем два линейных уравнения друг другу и находим, где они пересекаются. Например: Выше я построил график y 1 = | x | (синяя линия, которая выглядит как «V») и y 2 = 3 (зеленая горизонтальная линия).Эти два графика пересекаются при x = –3 и x = +3 (две красные точки). Если вы хотите проверить свои ответы на тесте (перед тем, как сдать его), может быть полезно подключить каждую сторону исходного уравнения абсолютного значения в ваш калькулятор как их собственные функции; затем спросите у калькулятора точки пересечения. Конечно, любое решение также можно проверить, вставив его обратно в исходное упражнение и подтвердив, что левая часть (LHS) уравнения упрощается до того же значения, что и правая часть (RHS). уравнение.Вот мой чек для приведенного выше уравнения: Если вы когда-нибудь сомневаетесь в своем решении уравнения, попробуйте построить график или попробуйте снова вставить свое решение в исходный вопрос. Проверяю свою работу всегда нормально! Шаг выше, где уравнение абсолютного значения было переформулировано в двух формах, одна со знаком «плюс», а другая со знаком «минус», дает нам удобный способ упростить ситуацию: когда мы изолировали абсолютное значение и перейти к снятию стержней, мы можем разделить уравнение на два случая; мы обозначим эти случаи, поставив «минус» на противоположной стороне уравнения (для одного случая) и «плюс» на противоположной стороне (для другого).Вот как это работает:
Абсолютное значение выделено в левой части уравнения, поэтому я уже настроил его, чтобы разделить уравнение на два случая. Чтобы очистить столбцы абсолютного значения, я должен разделить уравнение на два возможных случая, по одному для каждого случая, если содержимое столбцов абсолютного значения (то есть, если «аргумент» абсолютного значения) отрицательное, и если он неотрицательный (то есть положительный или нулевой).Для этого я создаю два новых уравнения, единственное различие между которыми — это знак в правой части. Сначала сделаю «минусовый» случай: x + 2 = –7 x + 2 = –7 x = –9 Теперь я займусь неотрицательным случаем, когда я могу просто опустить столбцы и решить: Теперь мне нужно проверить свои решения.Я сделаю это, вставив их обратно в исходное уравнение, поскольку оценщик не видит, как я проверяю графики на моем графическом калькуляторе. Оба решения проверяют, поэтому мой ответ:
Во-первых, я выделю часть уравнения, относящуюся к абсолютным значениям; то есть, я получу само выражение абсолютного значения с одной стороны от знака «равно», а все остальное — с другой стороны: | 2 x — 3 | — 4 = 3 | 2 x — 3 | = 7 Теперь я очищу столбцы абсолютных значений, разделив уравнение на два случая, по одному для каждого знака аргумента.Сначала сделаю отрицательный случай: 2 x — 3 = –7 2 x = –4 x = –2 А затем сделаю неотрицательный случай: 2 x — 3 = 7 2 x = 10 х = 5 Это упражнение не говорит мне о проверке, поэтому я не буду.(Но, если бы я хотел, я мог бы вставить «abs (2X – 3) –4» и «3» в свой калькулятор (как Y1 и Y2, соответственно), и увидеть, что точки пересечения были на моем x -значения.) Мой ответ: URL: https://www.purplemath.com/modules/solveabs.htm неравенств | Безграничная алгебраВведение в неравенствоНеравенства используются для демонстрации отношений между числами или выражениями. Цели обученияОбъясните, что представляет собой неравенство и как оно используется Основные выводыКлючевые моменты
Ключевые термины
В математике неравенства используются для сравнения относительного размера значений.Их можно использовать для сравнения целых чисел, переменных и различных других алгебраических выражений. Ниже приводится описание различных типов неравенств. Строгое неравенствоСтрогое неравенство — это отношение между двумя значениями, когда они различны. Точно так же, как в уравнениях используется знак равенства =, чтобы показать, что два значения равны, в неравенствах используются знаки, чтобы показать, что два значения не равны, и для описания их взаимосвязи. Символы строгого неравенства: [latex] <[/ latex] и [latex]> [/ latex]. Строгие неравенства отличаются от обозначения [latex] a \ neq b [/ latex], что означает, что a не равно [latex] b [/ latex]. Символ [latex] \ neq [/ latex] не говорит о том, что одно значение больше другого или даже о том, что их можно сравнить по размеру. В двух типах строгих неравенств [latex] a [/ latex] не равно [latex] b [/ latex]. Для сравнения размеров значений существует два типа отношений:
Значение этих символов можно легко запомнить, заметив, что «большая» сторона символа неравенства (открытая сторона) обращена к большему числу. «Меньшая» сторона символа (точка) обращена к меньшему числу. Указанные выше отношения можно показать на числовой прямой. Вспомните, что значения на числовой строке увеличиваются по мере продвижения вправо.Следовательно, следующее представляет отношение [латекс] a [/ латекс] меньше, чем [латекс] b [/ латекс]: [латекс] a[latex] a [/ latex] находится слева от [latex] b [/ latex] в этой числовой строке. и следующее демонстрирует, что [латекс] a [/ latex] больше, чем [latex] b [/ latex]: [латекс] a> b [/ латекс][latex] a [/ latex] находится справа от [latex] b [/ latex] в этой числовой строке. В целом обратите внимание, что:
Другое неравенствоВ отличие от строгого неравенства, существует два типа отношений неравенства, которые не являются строгими:
Неравенства с переменнымиВ дополнение к отображению взаимосвязей между целыми числами, неравенства могут использоваться для отображения взаимосвязей между переменными и целыми числами. Например, рассмотрим [латекс] x> 5 [/ латекс]. Это будет читаться как «[latex] x [/ latex] больше 5 ″ и означает, что неизвестная переменная [latex] x [/ latex] может иметь любое значение больше 5, но не 5 сама по себе.Для визуализации этого см. Числовую строку ниже: [латекс] x> 5 [/ латекс]Обратите внимание, что кружок над цифрой 5 не заполнен, что означает, что 5 не входит в возможные значения [latex] x [/ latex]. В качестве другого примера рассмотрим [латекс] x \ leq 3 [/ латекс]. Это будет читаться как «[latex] x [/ latex] меньше или равно 3 ″ и указывает, что неизвестная переменная [latex] x [/ latex] может иметь значение 3 или любое значение меньше 3. Для визуализации это, см. числовую строку ниже: [латекс] x \ leq 3 [/ латекс]Обратите внимание, что кружок над цифрой 3 закрашен, что означает, что 3 входит в возможные значения [latex] x [/ latex]. Неравенства демонстрируются раскрашиванием стрелки в соответствующем диапазоне числовой линии, чтобы указать возможные значения [latex] x [/ latex]. Обратите внимание, что открытый кружок используется, если неравенство строгое (т. Е. Для неравенств, использующих [latex]> [/ latex] или [latex] <[/ latex]), а закрашенный кружок используется, если неравенство не является строгим ( т.е. для неравенств, использующих [latex] \ geq [/ latex] или [latex] \ leq [/ latex]). Решение проблем с неравенствомНапомним, что уравнения могут использоваться для демонстрации равенства математических выражений, включающих различные операции (например: [latex] x + 5 = 9 [/ latex]).Точно так же неравенства можно использовать для демонстрации взаимосвязи между различными выражениями. Например, рассмотрим следующие неравенства:
Каждое из них представляет связь между двумя разными выражениями. Одно из полезных применений неравенств, подобных этому, — в задачах, связанных с максимальными или минимальными значениями. Пример 1У Джареда есть лодка, максимальная масса которой составляет 2500 фунтов. Он хочет взять на лодку как можно больше друзей и предполагает, что он и его друзья в среднем весят 160 фунтов. Сколько людей могут одновременно кататься на его лодке? Эту проблему можно смоделировать с помощью следующего неравенства: [латекс] 160n \ leq 2500 [/ латекс] где [latex] n [/ latex] — это количество людей, которые Джаред может взять на лодку. Чтобы понять, почему это так, рассмотрим левую часть неравенства.Он представляет собой общий вес [латексных] n [/ латексных] людей весом 160 фунтов каждый. Неравенство гласит, что общий вес Джареда и его друзей должен быть на меньше или равен максимальному весу 2500, что является пределом веса лодки. Есть шаги, которые можно выполнить, чтобы решить такое неравенство. На данный момент важно просто понять значение таких утверждений и случаев, в которых они могут быть применимы. Правила разрешения неравенствАрифметические операции могут использоваться для решения неравенств для всех возможных значений переменной. Цели обученияРешите неравенства, используя правила работы с ними Основные выводыКлючевые моменты
Ключевые термины
Операции с неравенствамиКогда вы выполняете алгебраические операции с неравенствами, важно проводить точно такие же операции с обеих сторон, чтобы сохранить истинность утверждения. Каждая арифметическая операция подчиняется определенным правилам: Сложение и вычитаниеЛюбое значение [латекс] c [/ латекс] может быть добавлено или вычтено из обеих сторон неравенства. То есть для любых действительных чисел [латекс] a [/ латекс], [латекс] b [/ латекс] и [латекс] c [/ латекс]:
Пока одна и та же стоимость добавляется или вычитается с обеих сторон, результирующее неравенство остается верным. Например, рассмотрим следующее неравенство: [латекс] 12 <15 [/ латекс] Давайте применим описанные выше правила, вычтя 3 с обеих сторон: [латекс] \ begin {align} 12 — 3 & <15 - 3 \\ 9 & <12 \ end {align} [/ latex] Это утверждение все еще верно. Умножение и делениеВ свойствах, связанных с умножением и делением, указано, что для любых действительных чисел [latex] a [/ latex], [latex] b [/ latex] и ненулевое [latex] c [/ latex]: Если [latex] c [/ latex] положительное значение, то умножение или деление на [latex] c [/ latex] не меняет неравенства:
Если [latex] c [/ latex] отрицательно, то умножение или деление на [latex] c [/ latex] меняет неравенство:
Обратите внимание, что умножение или деление неравенства на отрицательное число изменяет направление неравенства. Другими словами, символ больше становится символом меньше, и наоборот. Чтобы увидеть применение этих правил, рассмотрим следующее неравенство: [латекс] 5> -3 [/ латекс] Умножение обеих сторон на 3 дает: [латекс] \ begin {align} 5 (3) &> -3 (3) \\ 15 &> -9 \ end {align} [/ latex] Мы видим, что это верное утверждение, потому что 15 больше 9. Теперь умножьте то же неравенство на -3 (не забудьте изменить направление символа, потому что мы умножаем на отрицательное число): [латекс] \ begin {align} 5 (-3) & <-3 (-3) \\ -15 & <9 \ end {align} [/ latex] Это утверждение также верно. Это демонстрирует, насколько важно изменить направление символа «больше» или «меньше» при умножении или делении на отрицательное число. Устранение неравенствРешение неравенства, которое включает переменную, дает все возможные значения, которые может принимать переменная, которые делают неравенство истинным.Решение неравенства означает преобразование его таким образом, чтобы переменная находилась с одной стороны символа, а число или выражение — с другой. Часто для преобразования неравенства таким образом требуется несколько операций. Сложение и вычитаниеЧтобы увидеть, как правила сложения и вычитания применяются к решению неравенств, примите во внимание следующее: [латекс] x — 8 \ leq 17 [/ латекс] Сначала выделите [латекс] x [/ латекс]: [латекс] \ begin {align} x — 8 + 8 & \ leq 17 + 8 \\ x & \ leq 25 \ end {align} [/ latex] Следовательно, [латекс] x \ leq 25 [/ latex] является решением [латекса] x — 8 \ leq 17 [/ latex].Другими словами, [latex] x — 8 \ leq 17 [/ latex] истинно для любого значения [latex] x [/ latex], которое меньше или равно 25. Умножение и делениеЧтобы увидеть, как применяются правила умножения и деления, рассмотрим следующее неравенство: [латекс] 2x> 8 [/ латекс] Делим обе стороны на 2, получаем: [латекс] \ begin {align} \ dfrac {2x} {2} &> \ dfrac {8} {2} \\ x &> \ dfrac {8} {2} \\ x &> 4 \ end {align } [/ латекс] Таким образом, выражение [latex] x> 4 [/ latex] является решением для [latex] 2x> 8 [/ latex].Другими словами, [latex] 2x> 8 [/ latex] верно для любого значения [latex] x [/ latex] больше 4. Теперь рассмотрим другое неравенство: [латекс] — \ dfrac {y} {3} \ leq 7 [/ латекс] Из-за отрицательного знака мы должны умножить его на отрицательное число, чтобы найти [латекс] y [/ latex]. Это означает, что мы также должны изменить направление символа: [латекс] \ begin {align} \ displaystyle -3 \ left (- \ frac {y} {3} \ right) & \ geq -3 (7) \\ y & \ geq -3 (7) \\ y & \ geq -21 \ end {align} [/ латекс] Следовательно, решение [latex] — \ frac {y} {3} \ leq 7 [/ latex] — это [latex] y \ geq -21 [/ latex].Таким образом, данное утверждение верно для любого значения [latex] y [/ latex], большего или равного [latex] -21 [/ latex]. ПримерРешите следующее неравенство: [латекс] 3л — 17 \ geq 19 [/ латекс] Сначала прибавьте 17 к обеим сторонам: [латекс] \ begin {align} 3y — 17 + 17 & \ geq 19 + 17 \\ 3y & \ geq 36 \ end {align} [/ latex] Затем разделите обе стороны на 3: [латекс] \ begin {align} \ dfrac {3y} {3} & \ geq \ dfrac {36} {3} \\ y & \ geq \ dfrac {36} {3} \\ y & \ geq 12 \ конец {align} [/ latex] Особые соображенияОбратите внимание, что было бы проблематично, если бы мы попытались умножить или разделить обе части неравенства на неизвестную переменную.Если какая-либо переменная [latex] x [/ latex] неизвестна, мы не можем определить, имеет ли она положительное или отрицательное значение. Поскольку правила умножения или деления положительных и отрицательных чисел различаются, мы не можем следовать этому же правилу при умножении или делении неравенств на переменные. Однако переменные можно складывать или вычитать с обеих сторон неравенства. Сложные неравенстваСоставное неравенство включает в себя три выражения, а не два, но также может быть решено, чтобы найти возможные значения переменной. Цели обученияРешите сложное неравенство, уравновесив все три компонента неравенства Основные выводыКлючевые моменты
Ключевые термины
Определение сложных неравенствСложное неравенство имеет следующий вид: [латекс] a На самом деле здесь есть два утверждения. Первый оператор [латекс] a Составное неравенство [латекс] a Рассмотрим [латекс] 4 Указанное выше неравенство по числовой прямой. Аналогичным образом рассмотрим [латекс] -2 Указанное выше неравенство по числовой прямой. Теперь рассмотрим [латекс] 1 Утверждение [латекс] 1 Чтобы найти возможные значения [latex] x [/ latex], нам нужно получить [latex] x [/ latex] отдельно: [латекс] 1 — 6 [латекс] -5 Следовательно, мы находим, что если [latex] x [/ latex] — любое число строго между -5 и 2, утверждение [latex] 1 Решите [латекс] -3 <\ dfrac {-2x-7} {5} <7 [/ latex]. Умножьте каждую часть, чтобы удалить знаменатель из среднего выражения: [латекс] -3 \ cdot (5) <\ dfrac {-2x-7} {5} \ cdot (5) <7 \ cdot (5) [/ латекс] [латекс] -15 <-2x-7 <35 [/ латекс] Изолировать [латекс] х [/ латекс] в середине неравенства: [латекс] — 15 + 7 <-2x -7 + 7 <35 + 7 [/ латекс] [латекс] — 8 <-2x <42 [/ латекс] Теперь разделите каждую часть на -2 (и не забудьте изменить направление символа неравенства!): [латекс] \ displaystyle \ frac {-8} {- 2}> \ frac {-2x} {- 2}> \ frac {42} {- 2} [/ латекс] [латекс] 4> x> -21 [/ латекс] Наконец, принято (хотя и не обязательно) писать неравенство так, чтобы стрелки неравенства указывали влево (т.е., чтобы числа шли от наименьшего к наибольшему): [латекс] -21 Неравенства с абсолютными значениями можно решить, рассматривая абсолютное значение как расстояние от 0 до числа на числовой прямой. Решите неравенства с абсолютным значением Рассмотрим следующее неравенство, которое включает абсолютное значение: [латекс] | x | <10 [/ латекс] Зная, что решение [latex] \ left | x \ right | = 10 [/ latex] равно [latex] x = ± 10 [/ latex], многие студенты отвечают на этот вопрос [latex] x <± 10 [/ latex ].Однако это неверно. Вот два разных, но оба совершенно правильных подхода к решению этой проблемы. Какие номера работают? То есть, для каких чисел [латекс] \ left | x \ right | <10 [/ latex] верное утверждение? Давай попробуем. 4 работы. -4 тоже. 13 не работает. Как насчет -13? Нет: Если [латекс] x = -13 [/ латекс], то [латекс] \ left | x \ right | = 13 [/ latex], что не менее 10. Играя с числами таким образом, вы сможете убедить себя, что работающие числа должны быть где-то между -10 и 10.Это один из подходов к поиску ответа. Другой способ — представить абсолютное значение как расстояние от 0. [latex] \ left | 5 \ right | [/ latex] и [latex] \ left | -5 \ right | [/ latex] равны 5, потому что оба числа — 5 от 0. В данном случае [латекс] \ left | x \ right | <10 [/ latex] означает «расстояние между [latex] x [/ latex] и 0 меньше 10». Другими словами, вы находитесь в пределах 10 единиц от нуля в любом направлении.Еще раз делаем вывод, что ответ должен быть между -10 и 10. Этот ответ можно визуализировать в числовой строке, как показано ниже, в которой выделены все числа, абсолютное значение которых меньше 10. Решение для [латекса] \ left | x \ right | <10 [/ latex]: Все числа, абсолютное значение которых меньше 10. Нет необходимости использовать оба этих метода; используйте тот метод, который вам легче понять. К более сложным задачам абсолютного значения следует подходить так же, как к уравнениям с абсолютными значениями: алгебраически выделить абсолютное значение, а затем алгебраически решить для [латекс] x [/ латекс]. Например, рассмотрим следующее неравенство: [латекс] \ влево | 2x \ вправо | + 3> 8 [/ латекс] Трудно сразу представить себе значение этого абсолютного значения, не говоря уже о самом значении [latex] x [/ latex]. Необходимо сначала выделить неравенство: [латекс] \ begin {align} \ left | 2x \ right | + 3 — 3 &> 8 — 3 \\ \ left | 2x \ right | &> 8 \ end {align} [/ латекс] А теперь подумайте о числовой прямой. В этих терминах это утверждение означает, что выражение [latex] 2x [/ latex] должно находиться более чем в 8 разрядах от 0.Следовательно, оно должно быть больше 8 или меньше -8. Выражая это неравенствами, имеем: [латекс] 2x> 8 [/ латекс] или [латекс] 2x <-8 [/ латекс] Теперь у нас есть 2 отдельных неравенства. Если каждая из них решается отдельно для [latex] x [/ latex], мы увидим полный диапазон возможных значений [latex] x [/ latex]. Рассмотрим их самостоятельно. Первый: [латекс] \ begin {align} 2x &> 8 \\ \ dfrac {2x} {2} &> \ dfrac {8} {2} \\ x &> 4 \ end {align} [/ latex] Секунда: [латекс] \ begin {align} 2x & <-8 \\ \ dfrac {2x} {2} & <\ dfrac {-8} {2} \\ x & <-4 \ end {align} [/ latex ] Теперь у нас есть два диапазона решений исходного неравенства абсолютных значений: [латекс] x> 4 [/ латекс] и [латекс] x <-4 [/ латекс] Это также может быть визуально отображено в числовой строке: Решение для [латекса] \ left | 2x \ right | + 3> 8 [/ latex]: Решение — любое значение [latex] x [/ latex] меньше -4 или больше 4. Решите следующее неравенство: [латекс] \ влево | x-2 \ вправо | + 10> 7 [/ латекс] Во-первых, алгебраически выделите абсолютное значение: [латекс] \ begin {align} \ left | x-2 \ right | + 10-10 &> 7-10 \\ \ left | x-2 \ right | &> — 3 \ end {align} [/ латекс] А теперь подумайте: абсолютное значение выражения больше –3. Чему могло быть равно выражение? 2 работы. –2 тоже работает. И 0. И 7. И –10. Абсолютные значения всегда положительны, поэтому абсолютное значение чего-либо больше –3! Поэтому все числа работают. Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В этом мини-уроке мы узнаем об определении модульной функции, вычислении модуля для чисел, переменных и многочленов, а также о решаемых примерах и вопросах о модульной функции. Попробуйте калькулятор функции mod, чтобы найти модуль числа! Модуль функции, который также называется абсолютным значением функции, дает величину и абсолютное значение числа независимо от того, положительное или отрицательное число.Он всегда дает неотрицательное значение любого числа или переменной. Представляется как \ (\ begin {align} y = | x | \ end {align} \) или \ (\ begin {align} f (x) = | x | \ end {align} \) , где \ (\ begin {align} f: R \ rightarrow R \ end {align} \) и \ (\ begin {align} x \ in R \ end {align} \) \ (\ begin {align} | x | \ end {align} \) — это модуль \ (\ begin {align} x \ end {align} \), где \ (\ begin {align} x \ end { align} \) — неотрицательное число. Если \ (\ begin {align} x \ end {align} \) положительное значение, то \ (\ begin {align} f (x) \ end {align} \) будет иметь то же значение \ (\ begin {align } х \ конец {выравнивание} \).Если \ (\ begin {align} x \ end {align} \) отрицательно, то \ (\ begin {align} f (x) \ end {align} \) будет величиной \ (\ begin {align} х \ конец {выравнивание} \). Подводя итог вышеприведенным строкам, Это означает, что если значение \ (\ begin {align} x \ end {align} \) больше или равно 0, то функция модуля принимает фактическое значение, но если \ (\ begin {align} x \ end {align} \) меньше 0, тогда функция берет минус фактического значения ‘x’. Шаги по вычислению функций модуля приведены ниже. , если \ (\ begin {align} x = -3 \ end {align} \), то \ (\ begin {align} y = f (x) = f (-3) = — (-3) = 3 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) меньше 0 , если \ (\ begin {align} x = 4 \ end {align} \), то \ (\ begin {align} y = f (x) = f (4) = 4 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) больше 0 , если \ (\ begin {align} x = 0 \ end {align} \), то \ (\ begin {align} y = f (x) = f (0) = 0 \ end {align} \), здесь \ (\ begin {align} x \ end {align} \) равно 0 Подводя итог, можно сказать, что модуль отрицательного числа и положительного числа — это одно и то же число. Теперь давайте посмотрим, как построить график для функции модуля и найти ее домен и диапазон. Рассмотрим x как переменную, принимающую значения от -5 до 5 При вычислении модуля упругости для положительных значений ‘x’ линия на графике имеет вид ‘y = x’ , а для отрицательных значений «x» линия на графике имеет вид «y = -x». 2} \ end {align} \) Есть несколько других неотрицательных выражений, которые перечислены ниже.{2n} \ end {align} \) где \ (\ begin {align} n \ in Z \ end {align} \) \ (\ begin {align} y = 1 — sin \: x; y = 1 — cos \: x \: as \: sin \: x ≤1 \: и \: cos \: x ≤1 \ end { align} \) Signum функция определяется как математическая функция, которая дает знак действительного числа. Сигнум-функция выражается следующим образом. График сигнум-функции выглядит следующим образом. Комплексное число — это число, имеющее форму \ (\ begin {align} a + bi \ end {align} \), где ‘a’ и ‘b’ — действительные числа, а ‘i’ — мнимая единица.2} \ end {align} \) Функция модуля всегда возвращает неотрицательное число для всех действительных значений «x». Также некорректно приравнивать функцию модуля к отрицательному числу. \ (\ begin {align} | f (x) | = a; \: a> 0⇒f (x) = ± a \\ | f (x) | = a; \: a = 0⇒f (x ) = 0 \\ | f (x) | = a; a <0 \ end {align} \) Случай 1: (Если a> 0) Неравенство отрицательного числа \ (\ begin {align} | f (x) | Неравенство для положительного числа \ (\ begin {align} | f (x) |> a; a> 0 \ Rightarrow -a Случай 2: (Если <0) \ (\ begin {align} | f (x) | \ (\ begin {align} | f (x) |> a; a <0 \ Rightarrow \ end {align} \) - это действительно для всех реальных значений f (x). Если x, y — действительные переменные, то \ (\ begin {align} | -x | = | x | \ end {align} \) \ (\ begin {align} | x − y | = 0⇔x = y \ end {align} \) \ (\ begin {align} | x + y | ≤ | x | + | y | \ end {align} \) \ (\ begin {align} | x − y | ≥ || x | — | y || \ end {align} \) \ (\ begin {align} | xy | = | x | \ times | y | \ end {align} \) \ (\ begin {align} | \ dfrac {x} {y} | = \ dfrac {| x |} {| y |}; | y | \ neq 0 \ end {align} \) Теперь давайте рассмотрим некоторые решенные вопросы о модульных функциях, чтобы лучше понять их. Найдите модуль x для Раствор а) х = -4 \ (\ begin {align} | x | = | -4 | = — (-4) = 4 \ end {align} \) б) х = 6 \ (\ begin {align} | x | = | 6 | = 6 \ end {align} \) Для x = -4, \ (\ begin {align} | -4 | = 4 \ end {align} \) и для x = 6 \ (\ begin {align} | 6 | = 6 \ end {align} \) Решить \ (\ begin {align} | x + 3 | = 8 \ end {align} \) Раствор Сформируем два уравнения следующим образом. Корпус 1: Значение функции модуля отрицательное. \ (\ begin {align} | x + 3 | = 8 \ end {align} \) \ (\ begin {align} — | x + 3 | = 8 \ end {align} \) \ (\ begin {align} x + 3 = -8 \ end {align} \) \ (\ begin {align} x = -8 — 3 \ end {align} \) \ (\ begin {align} x = -11 \ end {align} \) Корпус 2: Значение функции модуля положительное. \ (\ begin {align} | x + 3 | = 8 \ end {align} \) \ (\ begin {align} x + 3 = 8 \ end {align} \) \ (\ begin {align} x = 8 — 3 \ end {align} \) \ (\ begin {align} x = 5 \ end {align} \) Следовательно, возможные значения x в модульной функции: \ (\ begin {align} x = 5, -11 \ end {align} \) Нарисуйте график для \ (\ begin {align} y = | x +2 | \ end {align} \) Раствор Согласно определению функции модуля, у нас есть \ (\ begin {align} y = | x + 2 | = x + 2, если \: x \ geq 1 \\ — 2 — x, если \: x <1 \ end {align} \) Изобразим таблицу с положительными и отрицательными значениями ‘x’. Построение графика с различными значениями \ (\ begin {align} x \ end {align} \) и \ (\ begin {align} -x \ end {align} \) мы получаем график для модуля функция, как показано ниже, Решить \ (\ begin {align} | 2x — 4 | = 5 — x \ end {align} \) Раствор Согласно определению функции модуля имеем В зависимости от функции модуля могут быть две возможности. Корпус 1: \ (\ begin {align} — | 2x — 4 | = 5 — x \ end {align} \) \ (\ begin {align} 2x — 4 = — (5 — x) \ end {align} \) \ (\ begin {align} 2x — 4 = -5 + x \ end {align} \) \ (\ begin {align} 2x — x & = -5 + 4 \\ x & = -1 \ end {align} \) Корпус 2: \ (\ begin {align} | 2x — 4 | = 5 — x \\ 2x — 4 = 5 — x \\ 2x + x = 5 + 4 \\ 3x = 9 \ x = 3 \ end {align} \) Урок был посвящен увлекательной концепции модульной функции, ее области и диапазона.Надеюсь, вам понравилось их изучать. Просматривая решенные примеры и решая неэффективные вопросы, вы получите больше знаний по предмету. Вы также можете попробовать калькулятор функции модуля, чтобы проверить модуль числа. В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению. Уравнение, которое дает модуль или величину данного числа, называется уравнением модуля. Обозначается как y = | x |. Модуль означает определение положительного или отрицательного числа. Применение модуля к неотрицательному и отрицательному числу всегда приводит к одному и тому же числу. Взяв отрицательные значения, такие как (-1, -2, -3), и положительные значения, такие как (1,2,3), в соответствии с данным уравнением модуля, мы можем нарисовать функцию модуля. Функция модуля используется для определения величины положительного или отрицательного числа. Модуль положительного числа положительный. Модуль отрицательного числа получается игнорированием знака минус. Таким образом, модуль всегда положителен. Производная функции модуля равна x / | x |. Диапазон функции модуля — это набор всех неотрицательных чисел или просто (0, бесконечность). | x | всегда положительный, независимо от того, начали ли мы с + x или -x. | y | всегда положительный, независимо от того, начали ли мы с + y или -y. Сложив или вычтя их без абсолютных значений, вы получите один из четырех возможных результатов: (+ x) + (+ y) или (+ x) + (-y) или (-x) + (+ y) или (-x) + (-y) Поскольку оба имеют одинаковый знак (xy> 0), это первое утверждение всегда верно, оно верно даже для x> y во втором утверждении.Но второе утверждение, | x | — | y | = | x — y | тогда xy <0 кажется ложным. Сначала разберемся со сложением … Мы будем использовать x = 3 и y = 10 для наших примеров: Оба отрицательные: -3 + (-10) = -13. Оба положительных: 3 + 10 = 13. Итак, пока оба числа имеют одинаковый знак (именно это означает xy> 0), ответ будет ± 13. Как только вы поместите это в абсолютное значение, оба результата будут положительными 13 и | x | + | y | = | x + y | Значение | -3 | + | -10 | = 3 + 10 = 13 (отдельные значения абс.) И | (-3) + (-10) | = | -13 | = 13 (объединены в один абс) (13 = 13, так что работает) | x | + | y | = | х + у | если оба числа имеют одинаковый знак (xy> 0) Здесь оба числа положительные: | 3 | + | 10 | = 3 + 10 = 13 и | 3 + 10 | = | 13 | = 13 (13 = 13 так работает) С другой стороны, если одно положительное, а другое отрицательное, вы, по сути, вычитаете. Например -3 + 10 = 7 или 3 + (-10) = -7 С разными знаками вы получите +7 или -7 в зависимости от порядка вычитания. Если вы поместите любой из этих результатов в абсолютное значение, вы получите ПОЛОЖИТЕЛЬНЫЙ 7. Все четыре случая с вычитанием, когда x Оба положительных: | 3 | — | 10 | = 3 — 10 = -7 и вместе внутри | 3-10 | = | -7 | = 7 (-7 ≠ 7 так не получится!) Оба отрицательных: | -3 | — | -10 | = 3 — 10 = -7 и вместе внутри | -3 — (-10) | = | 7 | = 7 (-7 ≠ 7 так не получится!) Различных знаков (xy <0): Негатив «3» и положительный «10»: | -3 | — | 10 | = 3 — 10 = -7 и вместе внутри | -3 — 10 | = | -13 | = 13 (-7 ≠ 13 так не получится!) «10» негр и «3» поз: | 3 | — | -10 | = 3 — 10 = -7 и вместе внутри | 3 — (-10) | = | 3 + 10 | = 13 (-7 ≠ 13 так не получится!) Второй, | x | — | y | = | x — y | когда xy <0, не работает ни в одном из четырех случаев, пока x (примечание: | x | — | y | может дать отрицательный результат (когда | x | <| y |), а | x - y | всегда будет положительным) Но если мы потребуем, чтобы x> y, так что теперь x = 10 и y = 3, мы имеем это: Обе позиции: | 10 | — | 3 | = 10 — 3 = 7 и | 10 — 3 | = | 7 | = 7 (7 = 7 так работает) Оба негатива: | -10 | — | -3 | = 10 — 3 = 7 и | -10 — (-3) | = | -10 + 3 | = | -7 | = 7 (7 = 7 так работает) «10» отрицательных и «3» положительных: | -10 | — | 3 | = 10 — 3 = 7 и | -10 — (+3) | = | -13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Положения «10» и отрицательные «3»: | 10 | — | — = 3 | = 10 — 3 = 7 и | 10 — (-3) | = | 10 + 3 | = | 13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Итак, вторая формулировка исходной задачи, вероятно, должна содержать xy> 0 AND x> y. Я нашел это в Интернете — истинное утверждение: | x-y |> | x | — | y | для xy <0. Это НЕРАВЕНСТВО истинно, УРАВНЕНИЕ во второй строке неверно. Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной.В большинстве случаев можно найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически с любым требуемым уровнем точности.
Кроме того, вы можете построить регионы, удовлетворяющие одному или нескольким неравенствам по двум переменным, четко видя, где происходят пересечения этих регионов. Вот несколько примеров неравенства: 2 х — 9> 0 х 2 — 3 х + 5 <= 0 | 5x — 1 | <> 5 х 3 + 1 <= 0 Команду Решить можно использовать для решения одного неравенства для одного
неизвестно на основной странице решения
или для одновременного решения системы многих неравенств в одном неизвестном на странице расширенного решения.2–5 <0 Другими словами, QuickMath попытается найти решения, удовлетворяющие сразу обоим неравенствам. Перейти на страницу решения Команда Plot из раздела Graphs построит график любого неравенства, связанного с
две переменные. Чтобы построить область, удовлетворяющую единственному неравенству
с участием x и y, перейдите к основному
страница построения неравенства, где вы можете ввести неравенство и указать
верхний и нижний пределы x и y, по которым вы хотите построить график
для.Продвинутый
Страница построения неравенства позволяет построить объединение или пересечение
до 8 регионов на одном графике. Вы можете контролировать такие вещи, как
или не показывать оси, где оси должны быть расположены и какой аспект
соотношение сюжета должно быть. Кроме того, у вас есть возможность показать каждый
отдельный регион самостоятельно. Уравнение говорит, что два выражения равны, а неравенство говорит
что одно выражение больше, больше или равно, меньше или
меньше или равно другому.Как и в случае с уравнениями, значение переменной для
что неравенство истинно, является решением неравенства, а множество всех
таких решений является множество решений неравенства. Два неравенства с
одинаковое множество решений являются эквивалентными неравенствами. Неравенства решаются с помощью
следующие свойства неравенства. СВОЙСТВА НЕРАВЕНСТВА Для действительных чисел a, b и c: (a) (Одно и то же число может быть добавлено к обеим сторонам неравенства без изменения
набор решений.) (Обе части неравенства можно умножить на одно и то же положительное число
без изменения набора раствора.) ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово
«умноженный» может быть заменен на «разделенный» на части (b) и (c) свойств
неравенства. Обратите особое внимание на часть (c): если обе стороны неравенства
умноженное на отрицательное число, направление символа неравенства должно быть
наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая
обе стороны на положительное число 2 дают все еще верное заявление. С другой стороны, начиная с — 3 <5 и
умножение обеих сторон на отрицательное число -2 дает истинный результат только в том случае, если
направление символа неравенства меняется на обратное. При умножении или делении обеих сторон неравенства на минус
числа, мы должны изменить направление символа неравенства, чтобы получить
эквивалентное неравенство. ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично
линейное уравнение. Линейное неравенство по одной переменной — это неравенство, которое можно записать в виде
форма Пример 1 Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 <
0, поменяйте направление символа неравенства на противоположное. Исходному неравенству удовлетворяет любое действительное число меньше 4.
множество решений можно записать как {x | x <4}. График множества решений показан на
Фигура 2.6, где скобки используются, чтобы показать, что 4 само по себе не принадлежит
к набору решений. Пример 2 Отныне решения всех неравенств будут записываться с интервалом
обозначение. Решить -2 <5 + 3m <20. Решение показано на Рисунке 2.8 Квадратичное неравенство — это неравенство, которое можно записать в виде Мы обсудим квадратичные неравенства в следующем разделе. Перейти на страницу графика неравенств CO-6: Применяйте основные концепции вероятности, случайной вариации и обычно используемых статистических распределений вероятностей. ЛО 6.22: Примените выборочное распределение выборочного среднего, как указано в Центральной предельной теореме (при необходимости). В частности, уметь идентифицировать необычные образцы из данной популяции. До сих пор мы обсуждали поведение статистической p-шляпы, доли выборки, относительно параметра p, доли генеральной совокупности (когда интересующая переменная является категориальной). Теперь мы переходим к исследованию поведения статистической шкалы x, выборочного среднего, по отношению к параметру μ (mu), генеральному среднему (когда интересующая переменная является количественной). Начнем с примера. Вес при рождении регистрируется для всех младенцев в городе. Средний вес при рождении составляет 3500 граммов, µ = mu = 3500 г. Если мы собираем множество случайных выборок по 9 младенцев за раз, как, по вашему мнению, будут вести себя выборочные средства? Здесь мы снова работаем со случайной величиной, поскольку случайные выборки будут иметь средства, которые непредсказуемо изменяются в краткосрочном периоде, но демонстрируют закономерности в долгосрочном периоде. Основываясь на нашей интуиции и на том, что мы узнали о поведении пропорций выборки, мы могли бы ожидать следующего относительно распределения выборочных средних: Центр : Некоторые средние образцы будут на низком уровне — скажем, 3000 граммов или около того — в то время как другие будут на высоком уровне, скажем, на 4000 граммов или около того.При повторной выборке мы можем ожидать, что случайные выборки будут иметь среднее значение в 3500 г. Другими словами, среднее значение выборки будет µ (мю), так же как среднее значение пропорции образца было p. Распространение : для больших выборок можно ожидать, что средние значения выборки не будут слишком сильно отклоняться от среднего значения генеральной совокупности, равного 3500. Выборка означает, что ниже 3000 или выше 4000 может вызвать удивление. Для меньших выборок мы были бы менее удивлены средними значениями выборки, которые немного варьируются от 3500.Другими словами, мы можем ожидать большей изменчивости средних значений выборки для меньших выборок. Таким образом, размер выборки снова будет играть роль в распределении показателей выборки, как мы наблюдали в отношении пропорций выборки. Форма : средние значения выборки, близкие к 3500, будут наиболее распространенными, а средние значения выборки, далеко от 3500 в любом направлении, постепенно менее вероятны. Другими словами, форма распределения средств выборки должна выпуклость в середине и сужение на концах, придавая ей некоторую нормальную форму.Это, опять же, то, что мы увидели, когда посмотрели на образцы пропорций. Комментарий: Давайте посмотрим на симуляцию: Результаты, полученные нами в ходе моделирования, неудивительны. Продвинутая теория вероятностей подтверждает это, утверждая следующее: Если повторяющиеся случайные выборки заданного размера n взяты из совокупности значений для количественной переменной, где среднее значение генеральной совокупности равно μ (мю), а стандартное отклонение генеральной совокупности равно σ (сигма), тогда среднее всех средних значений выборки (x -бар) — среднее значение μ (мю). Что касается разброса всех выборочных средних, теория определяет поведение гораздо точнее, чем утверждение, что для больших выборок разброс меньше. Фактически, стандартное отклонение всех средних значений выборки напрямую связано с размером выборки n, как указано ниже. Поскольку квадратный корень из размера выборки n появляется в знаменателе, стандартное отклонение действительно уменьшается с увеличением размера выборки. Давайте сравним и сопоставим то, что мы теперь знаем о выборочных распределениях для выборочных средних и выборочных пропорций. Теперь мы исследуем форму выборочного распределения выборочных средних. Когда мы обсуждали выборочное распределение пропорций выборки, мы сказали, что это распределение является приблизительно нормальным, если np ≥ 10 и n (1 — p) ≥ 10. Другими словами, у нас были рекомендации, основанные на размере выборки для определения условий в что мы могли бы использовать вычисления нормальной вероятности для пропорций выборки. Когда распределение выборочных средних станет примерно нормальным? Это зависит от размера выборки? Кажется разумным, что совокупность с нормальным распределением будет иметь выборочные средние, которые нормально распределены даже для очень маленьких выборок.Мы видели это в предыдущем моделировании с выборками размером 10. Что произойдет, если распределение переменной в генеральной совокупности сильно искажено? Имеют ли выборочные средства также искаженное распределение? Если мы возьмем действительно большие выборки, станут ли средние выборки распределенными более нормально? В следующем моделировании мы исследуем эти вопросы. Подводя итог, можно сказать, что распределение выборочных средних будет приблизительно нормальным, пока размер выборки достаточно велик.Это открытие, вероятно, является самым важным результатом, представленным на вводных курсах статистики. Формально она сформулирована как Центральная предельная теорема . Мы будем снова и снова полагаться на Центральную предельную теорему, чтобы производить вычисления нормальной вероятности, когда мы используем выборочные средства для того, чтобы делать выводы о среднем по генеральной совокупности. Теперь мы знаем, что можем сделать это, даже если распределение населения ненормальное. Какой большой размер выборки нам нужен, чтобы предположить, что выборочные средние будут нормально распределены? Что ж, это действительно зависит от распределения населения, как мы видели в моделировании.Общее практическое правило состоит в том, что выборки размером 30 или более будут иметь довольно нормальное распределение независимо от формы распределения переменной в генеральной совокупности. Комментарий: Прежде чем приступить к работе с примерами, давайте сравним и сопоставим то, что мы теперь знаем о выборочных распределениях для выборочных средних и выборочных пропорций. Размер домохозяйства в США составляет в среднем 2,6 человека и стандартное отклонение 1,4 человека. Должно быть ясно, что это распределение искажено вправо, поскольку наименьшее возможное значение — это домохозяйство из 1 человека, но самые большие домохозяйства действительно могут быть очень большими. (a) Какова вероятность того, что в случайно выбранном домохозяйстве более 3 человек? Здесь не следует использовать нормальное приближение, поскольку распределение размеров домохозяйств будет значительно смещено вправо. У нас недостаточно информации для решения этой проблемы. (b) Какова вероятность того, что средний размер случайной выборки из 10 домохозяйств больше трех? По любым меркам 10 — это небольшой размер выборки.Центральная предельная теорема не гарантирует, что среднее значение выборки, полученное из искаженной совокупности, будет приблизительно нормальным, если размер выборки не велик. (c) Какова вероятность того, что средний размер случайной выборки из 100 домохозяйств больше трех? Теперь мы можем применить центральную предельную теорему: даже несмотря на то, что распределение размера домохозяйства X искажено, распределение среднего размера домохозяйства по выборке (x-столбец) приблизительно нормально для большого размера выборки, такого как 100.Его среднее значение совпадает со средним значением генеральной совокупности, 2,6, а его стандартное отклонение — это стандартное отклонение генеральной совокупности, деленное на квадратный корень из размера выборки: Найти мы стандартизируем от 3 до z-значения, вычитая среднее значение и деля результат на стандартное отклонение (среднего по выборке). Затем мы можем найти вероятность с помощью стандартного обычного калькулятора или таблицы. Домохозяйства, состоящие из более чем 3 человек, конечно, довольно распространены, но было бы крайне необычно, если бы средний размер выборки из 100 домохозяйств был бы больше 3. Цель следующего упражнения — дать инструкции по нахождению выборочного распределения выборочного среднего (x-bar) и использовать его, чтобы узнать о вероятности получения определенных значений x-bar. math / -inf math / abs math / acos math / acosh math / asin math / asinh math / atan math / atan2 math / atanh math / cbrt math / ceil math / cos math / cosh math / e math / erf math / erfc math / exp math / exp2 math / expm1 math / floor math / gamma math / hypot math / inf math / int-max math / int-min math / int32-max math / int32-min math / log math / log10 math / log1p math / log2 math / nan math / next math / pi math / pow math / random math / rng math / rng-buffer math / rng-int math / rng-uniform math / round math / seedrandom math / sin math / sinh math / sqrt math / tan math / tanh math / trunc |
 \)
\) 2 или y=1/x. А как строить графики со знаком модуля?
2 или y=1/x. А как строить графики со знаком модуля? Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|). (Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1. 2 — |x| — 3|
2 — |x| — 3|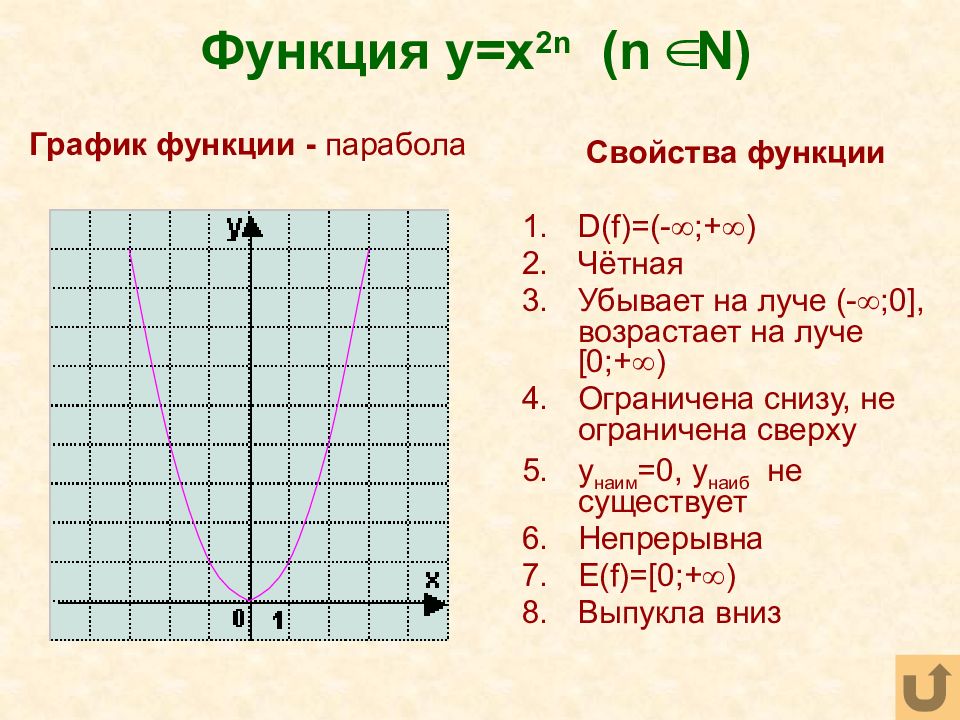
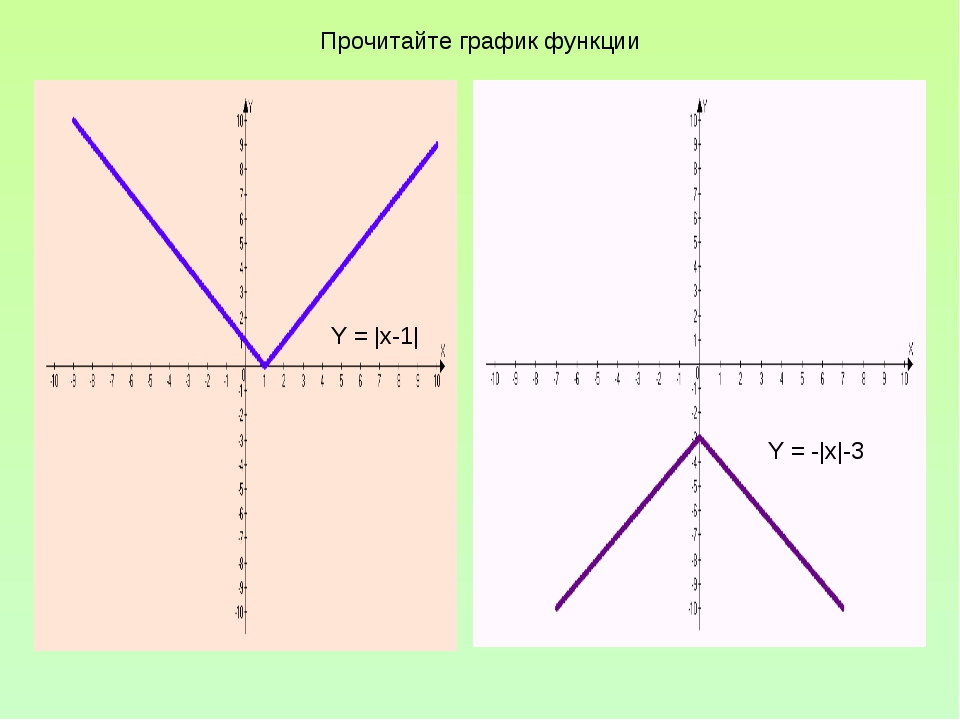
 К примеру, выразим число 2.
К примеру, выразим число 2. Тогда его можно будет прочитать следующим образом:
Тогда его можно будет прочитать следующим образом: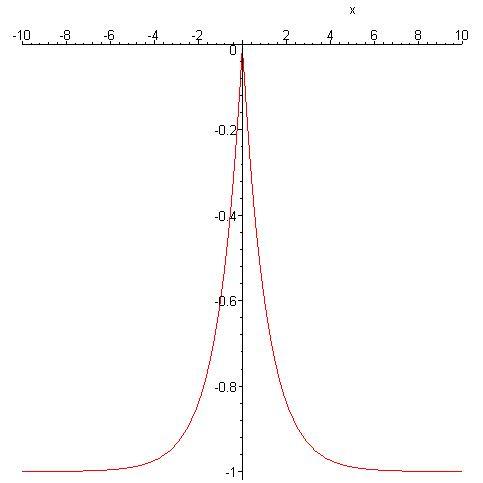 Рассмотрим равенство 8 − 2 = 6
Рассмотрим равенство 8 − 2 = 6 Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
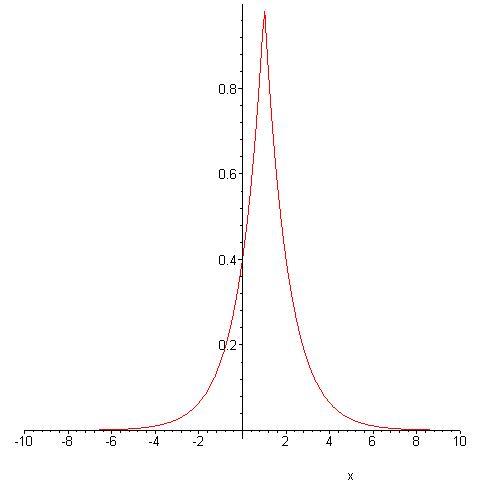 Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2
Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2 Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.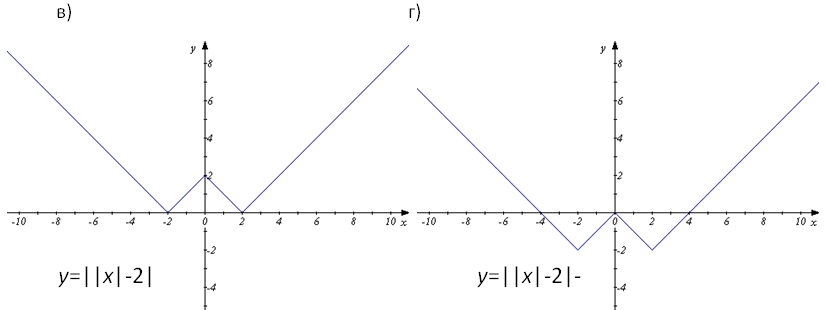
 Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.
Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.

 Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
 Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое: Вычитаем из суммы известное слагаемое:
Вычитаем из суммы известное слагаемое: 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое: Мы должны получить верные числовые равенства
Мы должны получить верные числовые равенства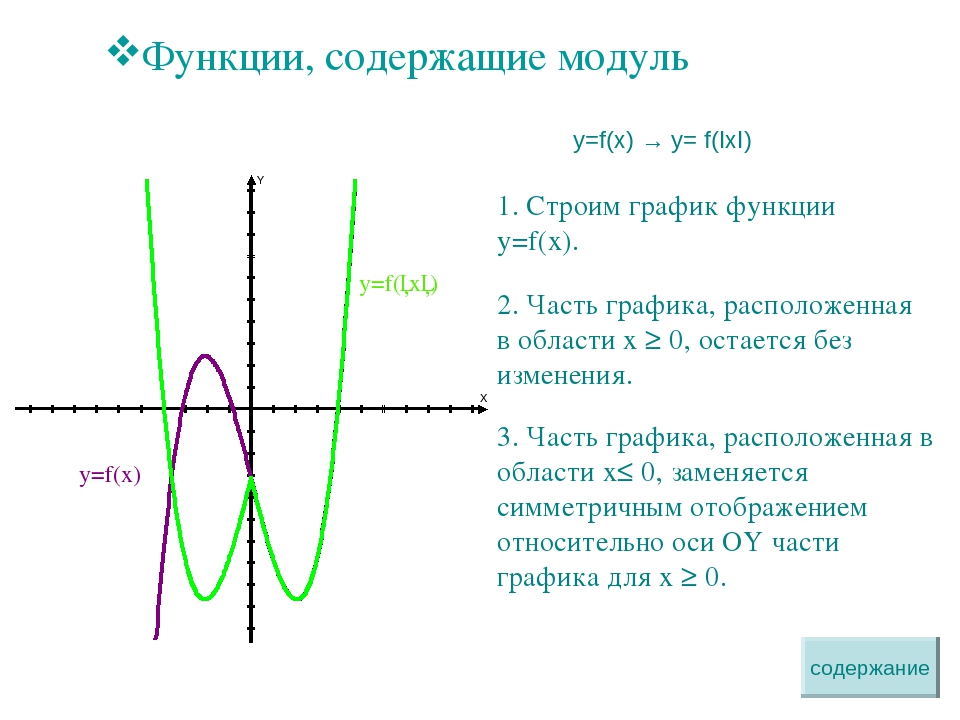
 Значит уравнение решено правильно.
Значит уравнение решено правильно. В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
 Найдём этот известный сомножитель:
Найдём этот известный сомножитель:

 Значит эти уравнения равносильны.
Значит эти уравнения равносильны. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель: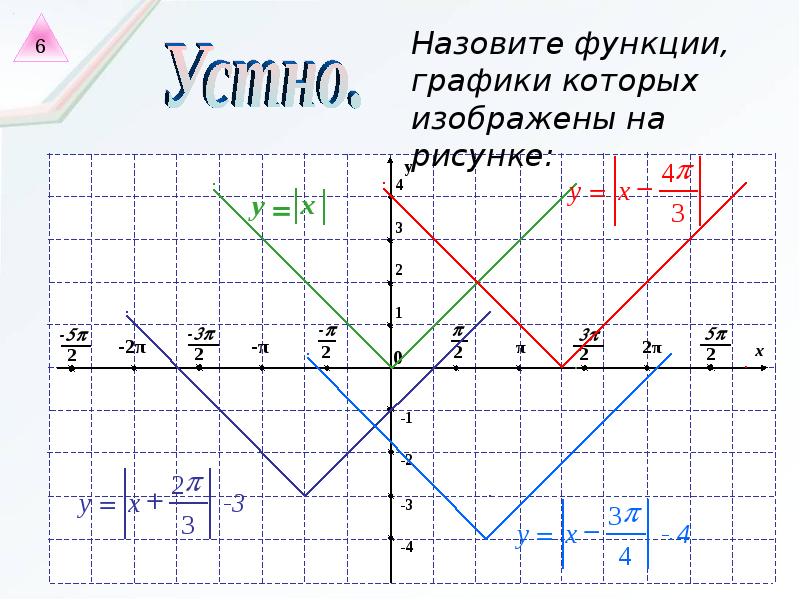 Значит уравнение решено правильно.
Значит уравнение решено правильно.
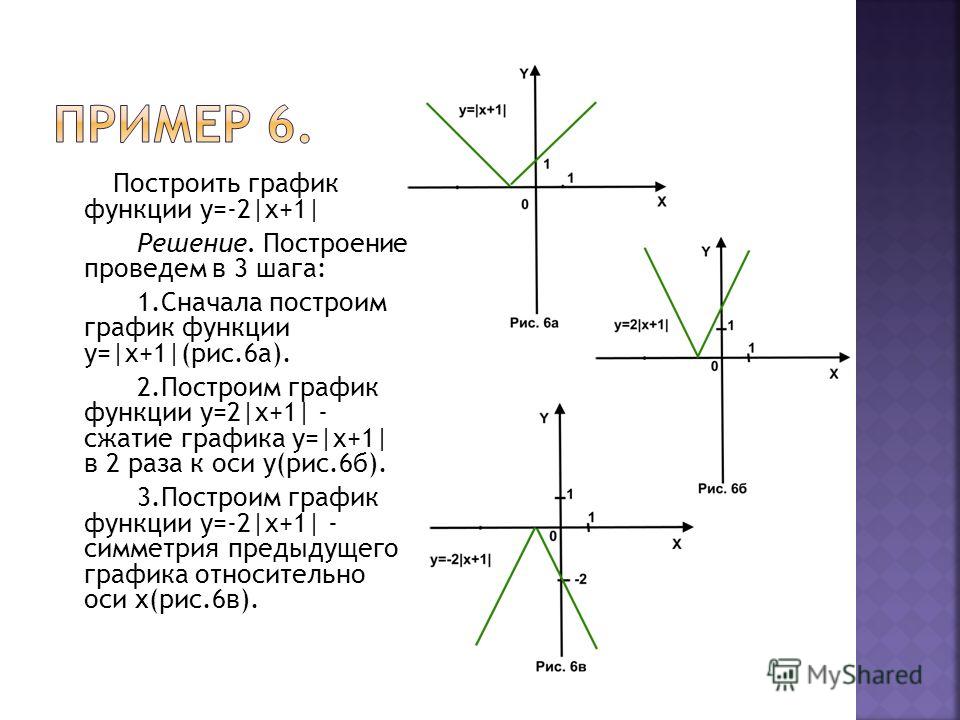 Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B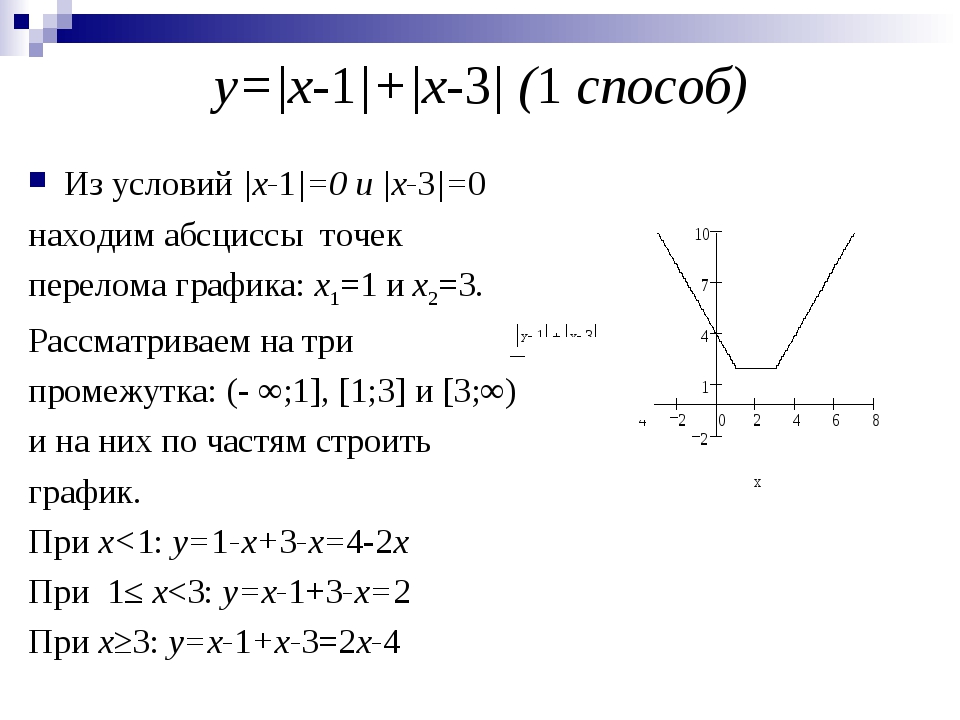 Далее выполняя известные тождественные преобразования, найдем значение x
Далее выполняя известные тождественные преобразования, найдем значение x Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7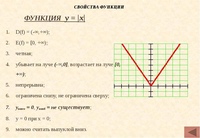 Это есть произведение минус единицы и переменной x
Это есть произведение минус единицы и переменной x

 Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Для этого перенесем все слагаемые из правой части в левую, изменив знаки: Правая часть будет равна 2. Отсюда .
Правая часть будет равна 2. Отсюда .
 То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
То есть подставив в такое уравнение любое число, мы получим верное числовое равенство. Решить уравнение
Решить уравнение 
 Сначала умножить обе части уравнения на t
Сначала умножить обе части уравнения на t