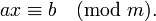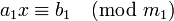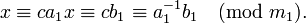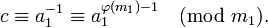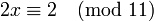Модуль — Википедия
Материал из Википедии — свободной энциклопедии
Страницы пространства имёнМодуль: находятся тутМодуль (от лат. modulus — «маленькая мера»):
- Модуль — функционально завершённый узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельный продукт. См. также: унификация.
- Модуль (космонавтика) — конструктивно законченная составная часть орбитального средства, предназначенная для реализации целевых, управляющих и/или обеспечивающих функций самостоятельно или в составе орбитального средства.
- Модуль (архитектура) — предварительно заданная величина, размер, кратным которому принимаются остальные размеры при разработке или при оценке проекта здания.
- Модуль — шаг сетки, основа композиции полос и разворотов в модульной системе вёрстки.
- Модуль — произведение длины между перпендикулярами, ширины и высоты борта судна в судостроении.
- Модуль (реклама) — размеры графики для печатной рекламы.
- Модуль зубчатого колеса — основной параметр зубчатой передачи.
- НТЦ «Модуль» — компания, учреждённая в 1990 году предприятиями НПО «Вымпел» и НИИ Радиоприборостроения.
- Информатика
- Модуль (программирование) — функционально законченный фрагмент программы, оформленный в виде отдельного файла с исходным кодом или поименованной непрерывной её части.
- Исполнимый модуль — файл, содержащий программу в виде, в котором она может быть исполнена компьютером.
- Объектный модуль — файл с промежуточным представлением отдельного модуля программы, полученный в результате обработки исходного кода компилятором.
- Модуль ядра — объект, содержащий код, который расширяет функциональность запущенного или т. н. базового ядра ОС.
- Математика
- Механика твёрдого тела
ru.wikipedia.org
МОДУЛЬ (в математике) — это… Что такое МОДУЛЬ (в математике)?
- МОДУЛЬ (в математике)
- МОДУЛЬ (в математике) МО́ДУЛЬ комплексного числа, см. Абсолютная величина (см. АБСОЛЮТНАЯ ВЕЛИЧИНА). Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab.
Энциклопедический словарь. 2009.
- МОДУЛЬ (в архитектуре)
- МОДУЛЬ (в радиоэлектронике)
Смотреть что такое «МОДУЛЬ (в математике)» в других словарях:
Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… … Словарь иностранных слов русского языка
Модуль (значения) — Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Модуль без кручения — Модуль без кручения модуль над кольцом без делителей нуля такой, что из равенства , где и , следует или . Примерами таких модулей (левых) являются само кольцо … Википедия
Модуль — I Модуль (от лат. modulus мера) в архитектуре, условная единица, принимаемая для координации размеров частей здания или комплекса. В архитектуре разных народов в зависимости от особенностей строительной техники и композиции зданий за М.… … Большая советская энциклопедия
Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
Модуль автоморфизма — Связать? Модуль автоморфизма вещественное положительное число, ставящееся в соответствие автоморфизму, локально компактной группы. Если такая группа и … Википедия
Модуль — I м. 1. Название некоторых коэффициентов, мерил каких либо величин (в точных науках). 2. Число, на которое нужно умножить логарифм одной системы при данном основании, чтобы получить логарифм другой системы при другом основании (в математике). II… … Современный толковый словарь русского языка Ефремовой
Модуль — I м. 1. Название некоторых коэффициентов, мерил каких либо величин (в точных науках). 2. Число, на которое нужно умножить логарифм одной системы при данном основании, чтобы получить логарифм другой системы при другом основании (в математике). II… … Современный толковый словарь русского языка Ефремовой
Ряд в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
dic.academic.ru
Модуль над кольцом — Википедия
Мо́дуль над кольцо́м
— одно из основных понятий в общей алгебре, являющееся обобщением двух алгебраических понятий — векторного пространства (фактически, векторное пространство — это модуль над полем), и абелевой группы (которая является модулем над кольцом целых чисел Z{\displaystyle \mathbb {Z} }).Понятие модуля лежит в основе коммутативной алгебры, которая играет важную роль в различных областях математики, таких как
В векторном пространстве множество скаляров образует поле и умножение на скаляр удовлетворяет нескольким аксиомам, таким как дистрибутивность умножения. В модуле же требуется только, чтобы скаляры образовывали кольцо (ассоциативное с единицей), аксиомы же остаются теми же самыми.
Значительная часть теории модулей состоит из попыток обобщить на них известные свойства векторных пространств, иногда для этого приходится ограничиваться модулями над «хорошо ведущими себя» кольцами, такими как области главных идеалов. Однако в целом модули устроены более сложно, чем векторные пространства. Например, не в каждом модуле можно выбрать базис, и даже те, в которых это возможно, могут иметь несколько базисов с различным числом элементов (в случае некоммутативного кольца).
Пусть R {\displaystyle R\ } — кольцо (как правило, считающееся коммутативным c единичным элементом 1∈R{\displaystyle 1\in R}). R{\displaystyle R}-модулем называется абелева группа M {\displaystyle M\ } с операцией умножения на элементы кольца R {\displaystyle R\ } :
- R×M→M,(r,m)↦rm,{\displaystyle R\times M\to M,\quad (r,m)\mapsto rm,}
которая удовлетворяет следующим условиям:
- 1) ∀m∈M,∀r1,r2∈R(r1r2)m=r1(r2m),{\displaystyle \forall m\in M,\,\forall r_{1},r_{2}\in R\quad (r_{1}r_{2})m=r_{1}(r_{2}m),}
- 2) ∀m∈M1m=m.{\displaystyle \forall m\in M\quad 1m=m.}
- 3) ∀m1,m2∈M,∀r∈Rr(m1+m2)=rm1+rm2,{\displaystyle \forall m_{1},m_{2}\in M,\,\forall r\in R\quad r(m_{1}+m_{2})=rm_{1}+rm_{2},}
- 4) ∀m∈M,∀r1,r2∈R(r1+r2)m=r1m+r2m.{\displaystyle \forall m\in M,\,\forall r_{1},r_{2}\in R\quad (r_{1}+r_{2})m=r_{1}m+r_{2}m.}
Примечание: В случае некоммутативного кольца такие модули часто называются левыми. Правыми модулями называют в этом случае такие объекты, у которых условие 1) заменено следующим:
∀m∈M,∀r1,r2∈R(r1r2)m=r2(r1m),{\displaystyle \forall m\in M,\,\forall r_{1},r_{2}\in R\quad (r_{1}r_{2})m=r_{2}(r_{1}m),}
что гораздо удобнее формулировать, записывая элемент кольца справа от элемента модуля m{\displaystyle m}:
∀m∈M,∀r1,r2∈Rm(r1r2)=(mr1)r2,{\displaystyle \forall m\in M,\,\forall r_{1},r_{2}\in R\quad m(r_{1}r_{2})=(mr_{1})r_{2},} отсюда и терминология.
В случае коммутативного кольца R {\displaystyle R\ } определения левого и правого модуля совпадают и их называют просто модулями.
Любое кольцо R {\displaystyle R\ } можно рассматривать как модуль над собой (в некоммутативном случае оно является также правым модулем над собой).
- ∀b∈B, r∈R :rb∈B{\displaystyle \forall b\in B,\ r\in R\ :rb\in B}.
Если кольцо R{\displaystyle R} рассматривать как левый модуль над собой, то его подмодули являются левыми идеалами, если кольцо рассматривать как правый модуль, то правыми идеалами, в коммутативном случае понятие левого и правого идеалов совпадают.
Гомоморфизмом или R{\displaystyle R}-гомоморфизмом R{\displaystyle R}-модулей A{\displaystyle A} и B{\displaystyle B} называется гомоморфизм групп ϕ:A→B{\displaystyle \phi :A\to B}, для которого выполнено дополнительное условие ϕ(ra)=rϕ(a)∀a∈A,r∈R{\displaystyle \phi (ra)=r\phi (a)\forall a\in A,r\in R}. Множество всех таких гомоморфизмов обозначают через HomR(A, B){\displaystyle Hom_{R}(A,\ B)}. На этом множестве можно ввести структуру абелевой группы, определяя 0, −{\displaystyle -} и +{\displaystyle +} следующими равенствами:
- 0a=0, (−ϕ)a=−(ϕa), (ϕ+ψ)a=ϕa+ψa{\displaystyle 0a=0,\ (-\phi )a=-(\phi a),\ (\phi +\psi )a=\phi a+\psi a}.
Если N{\displaystyle N} — подмодуль модуля M{\displaystyle M}, можно рассмотреть фактормодуль M/N{\displaystyle M/N} как множество классов эквивалентности элементов M{\displaystyle M}, определив отношение эквивалентности между элементами:
- a∼b{\displaystyle a\sim b} тогда и только тогда, когда b−a{\displaystyle b-a} принадлежит N{\displaystyle N}.
Элементы фактормодуля обычно обозначают как [a]={a+n:n∈N}=a+N{\displaystyle [a]=\{a+n:n\in N\}=a+N}. Операции сложения и умножения определяются формулами (a+N)+(b+N)=(a+b+N),r⋅(a+N)=(r⋅a+N){\displaystyle (a+N)+(b+N)=(a+b+N),r\cdot (a+N)=(r\cdot a+N)}.
Простейшие примеры модулей (конечные абелевы группы, то есть Z{\displaystyle \mathbb {Z} }-модули) появляются уже у Гаусса как группы классов бинарных квадратичных форм. Общее понятие модуля встречается впервые в 60—80-х гг. XIX века в работах Дедекинда и Кронекера, посвящённых арифметике полей алгебраических чисел и алгебраических функций. Проводившееся примерно в это же время исследование конечномерных ассоциативных алгебр, и в частности групповых алгебр конечных групп (Б. Пирс, Ф. Фробениус), привело к изучению идеалов некоторых некоммутативных колец. Первоначально теория модулей развивалась преимущественно как теория идеалов некоторого кольца. Лишь позднее в работах Э. Нётер и В. Крулля (W. Krull) было замечено, что многие результаты удобнее формулировать и доказывать в терминах произвольных модулей, а не только идеалов.
- Ван дер Варден Б. Л. Алгебра. — М.: Наука, 1975.
- Зарисский О., Самюэль П. Коммутативная алгебра. — М.: ИЛ, 1963. — Т. 1.
- Ленг С. Алгебра. — М.: Мир, 1967.
ru.wikipedia.org
Модуль числа – что это такое: что значит абсолютная величина
В школе на уроке математики каждый год ученики разбирают новые темы. 6 класс обычно изучает модуль числа – это важное понятие в математике, работа с которым встречается далее в алгебре и высшей математики. Очень важно изначально правильно понять объяснение термина и разобраться в этой теме, чтобы успешно проходить прочие темы.
Величины в математике
Для начала следует понимать, что абсолютная величина – это параметр в статистике (измеряется количественно), который характеризует изучаемое явление по его объему. При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:
- суммарные – подходят для группы единиц или полностью всей совокупности;
- индивидуальные – подходят только для работы с единицей некой совокупности.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Понятия широко используются в статистических измерениях, результатом которых являются показатели, характеризующие абсолютные размеры у каждой единицы некоего явления. Измеряются они в двух показателях: натуральном, т.е. физические единицы (шт., люди) и условно-натуральном. Модуль в математике является отображением данных показателей.


Модуль числа
Что такое модуль числа?
Важно! Данное определение «module» с латыни переводиться как «мера» и означает абсолютную величину любого натурального числа.

 Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.
Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.
Для того, чтобы определить данный показатель у числа, следует не учитывать его знак (минус, плюс), но при этом следует помнить то, что он никогда не может быть отрицательным. Данное значение на бумаге выделяется графически в виде квадратных скобок — |a|. При этом, математическое определение такое:
|х| = х, если х больше или равен нулю и -х, если меньше нуля.
Английский ученый Р. Котес был тем человеком, кто впервые применил данное понятие в математических расчетах. А вот К. Вейерштрасс, математик из Германии, придумал и ввел в использование графический символ.
Это интересно! Как разложить на множители квадратный трехчлен: формула
В геометрии module можно рассмотреть на примере координатной прямой, на которое нанесены 2 произвольные точки. Предположим, одна — А имеет значение 5, а вторая В — 6. При подробном изучении чертежа станет ясно, что расстояние от А до В – 5 единиц от нуля, т.е. начала координат, а точка В размещена от начала координат на 6 единиц. Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.
Полезное видео: что такое модуль действительного числа?
Свойства
Как у любого математического понятия, у module есть свои математические свойства:
- Он всегда положительный, поэтому модулем положительного значения будет оно само, например, модуль числа 6 и -6 равен 6. Математически это свойство можно записать как |a| = a, при a> 0;
- Показатели противоположных чисел равны между собой. Это свойство понятнее в геометрическом изложении, поскольку на прямой данные числа располагаются в разных местах, но при этом от начала отсчета их отделяет равное количество единиц. Математически это записывается так: |а| = |-а|;
- Модуль нуля равен нулю, при условии, что действительное число – это ноль. Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0;
- Если требуется найти модуль двух умножающихся цифр, стоит понимать, что он будет равен полученному произведению. Другими словами, произведение величин А и В = АВ, при условии, что они положительные или же отрицательные, и тогда произведение равняется -АВ. Графически это можно записать как |А*В| = |А| * |В|.
Это интересно! Считаем правильно: как находить процент от суммы и числа
Успешное решение уравнений с модулем зависит от знания данных свойств, которое поможет любому правильно вычислять и работать с данным показателем.


Свойства модуля
Важно! Показатель не может быть отрицательным, поскольку он определяет расстояние, которое всегда положительное.
В уравнениях
В случае работы и решения математических неравенств, в которых присутствует module, всегда необходимо помнить, что для получения итогового правильного результата следует раскрыть скобки, т.е. открыть знак module. Зачастую, в этом и есть смысл уравнения.
При этом стоит помнить, что:
- если в квадратных скобках записано выражение, его необходимо решить: |А + 5| = А + 5, при А больше или равным нулю и 5-А, в случае А меньше нуля;
- квадратные скобки чаще всего должны раскрываться независимо от значений переменной, например, если в скобках заключено выражение в квадрате, поскольку при раскрытии в любом случае будет положительное число.
Это интересно! Уроки математики: умножение на ноль — главное правило
Очень легко решаются уравнения с module путем занесения значений в систему координат, поскольку тогда легко увидеть визуально значения и их показатели.
Полезное видео: модуль действительного числа и его свойства
Вывод
Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.
Вконтакте
Одноклассники
Мой мир
znaniya.guru
Модуль числа в математике — что это такое, как раскрыть абсолютную величину, решение уравнений
 Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a|.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Это интересно: умножение на 0 правило для любого числа.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
 Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.- Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.
Графически это можно выразить следующим образом: |a| = OA.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
 Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
- Такое же правило распространяется и на показатель степени выражения.
Это интересно: что такое разность в математике?
Особенности решения уравнений с модулем
 Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5, если, А больше или равняется нулю.
5-А, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
tvercult.ru
Модульная арифметика — это… Что такое Модульная арифметика?
Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.
В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.
Определения
Говорят, что два целых числа a и b сравнимы по модулю натурального числа n, если при делении на n они дают одинаковые остатки.
Эквивалентные формулировки: a и b сравнимы по модулю n, если их разность a — b делится на n, или если a может быть представлено в виде a = b + kn, где k — некоторое целое число.
- Пример: 32 и −10 сравнимы по модулю 7, так как 32 = 7∙4 + 4, −10 = 7∙(-2) + 4.
Утверждение «a и b сравнимы по модулю n» записывается в виде:
Свойства
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
то
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример:  , однако, сократив на 2, мы получаем ошибочное сравнение:
, однако, сократив на 2, мы получаем ошибочное сравнение: 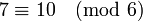 . Правила сокращения для сравнений следующие.
. Правила сокращения для сравнений следующие.
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
Другие свойства:
- Если
 и
и  , то
, то  , где m = [m1,m2].
, где m = [m1,m2]. - Если
 , то a, b сравнимы по любому модулю — делителю m.
, то a, b сравнимы по любому модулю — делителю m.
Классы вычетов
Множество всех чисел, сравнимых с a по модулю n называется классом вычетов a по модулю n, и обычно обозначается [a]n или 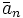 . Таким образом, сравнение
. Таким образом, сравнение 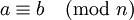 равносильно равенству классов вычетов [a]n = [b]n.
равносильно равенству классов вычетов [a]n = [b]n.
Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел 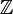 , то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается
, то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается 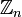 или
или 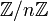 .
.
Операции сложения и умножения на 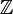 индуцируют соответствующие операции на множестве
индуцируют соответствующие операции на множестве 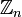 :
:
- [a]n + [b]n = [a + b]n
![[a]_n\cdot [b]_n=[a\cdot b]_n](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Относительно этих операций множество 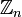 является конечным кольцом, а если n простое — конечным полем.
является конечным кольцом, а если n простое — конечным полем.
Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
- Если b не кратно d, то у сравнения нет решений.
- Если b кратно d, то у сравнения существует единственное решение по модулю m / d, или, что то же самое, d решений по модулю m. В этом случае в результате сокращения исходного сравнения на d получается сравнение:
где a1 = a / d, b1 = b / d и m1 = m / d являются целыми числами, причем a1 и m1 взаимно просты. Поэтому число a1 можно обратить по модулю m1, то есть найти такое число c, что 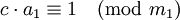 (другими словами,
(другими словами, 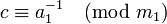 ). Теперь решение находится умножением полученного сравнения на c:
). Теперь решение находится умножением полученного сравнения на c:
Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Пример: решим уравнение 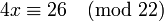 . Здесь d = 2, поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:
. Здесь d = 2, поэтому по модулю 22 сравнение имеет два решения. Заменим 26 на 4, сравнимое с ним по модулю 22, и затем сократим все 3 числа на 2:
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: 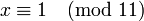 , эквивалентное двум решениям по модулю 22:
, эквивалентное двум решениям по модулю 22: 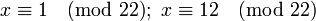 .
.
Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Ссылки
- Вейль А., Основы теории чисел, М.:Мир, 1972.
- Виленкин Н. Я., Сравнения и классы вычетов, Квант, № 10, 1978.
- Виноградов И. М., Основы теории чисел, М.: ГИТТЛ, 1952.
Wikimedia Foundation. 2010.
dic.academic.ru
Что такое модуль? И зачем он нужен в алгебре?
Модуль в математике, 1) Модуль (в математике) (или абсолютная величина) комплексного числа z = х + iy есть число (корень берётся со знаком плюс) . При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно Модуль (в математике) числа z. Модуль (в математике) допускает следующее геометрическое истолкование: комплексное число z = х + iy можно изобразить вектором, исходящим из начала прямоугольной системы координат и имеющим конец в точке с координатами (х, у) ; длина этого вектора и есть Модуль (в математике) комплексного числа z.
2) Модуль (в математике) перехода от системы логарифмов при основании а к системе логарифмов при основании b есть число М = 1/logab; для получения логарифмов чисел х при основании b, если известны логарифмы этих чисел при основании а, надо последние умножить на Модуль (в математике) перехода:
logbx = М logax.
Модуль (от лат. modulus — «маленькая мера» ) — составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь в целом.
Модуль (электроника) — функционально завершённый узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельный продукт. См. также: унификация.
Термальный модуль — комплект системы охлаждения компьютера.
Автономно управляемая часть космического корабля, например, модули МКС: Юнити, Коламбус, стыковочно-грузовой модуль и другие (см. таблицу: {{Модули МКС}}).
Модуль (программирование) — функционально законченный фрагмент программы.
Модульное обучение (педагогика) — законченный блок учебного материала.
Модуль (архитектура) — предварительно заданная велична, размер, кратным которому принимаются остальные размеры при разработке проекта здания или при оценке существующего.
Модуль (полиграфия) — предварительно заданная велична, основа модульной системы вёрстки.
Модуль (судостроение) — произведение длины между перпендикулярами, ширины и высоты борта.
Модуль (реклама) — размеры графики для печатной рекламы.
+1+2+3+4+5
otvet.mail.ru
 Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6. Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.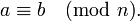

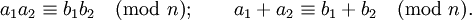
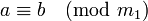 и
и 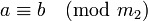 , то
, то 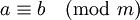 , где m = [m1,m2].
, где m = [m1,m2].![[a]_n\cdot [b]_n=[a\cdot b]_n](/800/600/https/dic.academic.ru/pictures/wiki/files/99/cb8dd8e51b2583aa2bcaa03446e485c3.png)