Вычисление целочисленного квадратного корня / Хабр

Возникла нужда проверить, является ли целое число квадратом, и если да, то вычислить корень. Причем хочется сделать это в целочисленной арифметике. Понятно, что можно реализовать метод Ньютона в целых числах, но он требует деления на каждом шаге. А нельзя ли по другому? Найти квадратный корень по модулю степени двойки, и проверить, а не будет ли он обычным квадратным корнем.

Можно ограничиться нечетными числами: для четного числа, если количество нулевых младших разрядов нечетно, то корня нет, а если четно, то можно сдвинуть число вправо, посчитать корень от нечетного, и сдвинуть обратно влево на половину от первоначального количества нулевых бит.

Для нечетного N и 2^k, k > 3, если N ≡ 1 mod 8, то есть 4 разных корня по модулю 2^k, а иначе корней нет. Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2^k — x, 2^k-1 + x и 2^k — 2^k-1 — x

Хочется что-то подобное вычислению обратного по модулю 2

k — удваивая количество верных бит за итерацию.

Пусть у нас уже есть корень x₀ из N по модулю 2^k: N — x₀² = 2^ka
И мы хотим найти x₁ = x₀ + 2^k-1y, такое чтобы в N — x₁² было больше младших нулевых бит.
N — (x₀ + 2^k-1y)² = 2^ka — 2^kx₀ * y — 2^2k-2y²
Поделим на 2^k: a — x₀ * y — 2^k-2y²
И приравняем к 0 по модулю 2^k-2: y = a * x₀^-1 mod 2^k-2
Получилии x₁ = x₀ + 2^k-1a * (x₀^-1 mod 2^k-2)

И окончательно x₁ = x₀ + (N — x₀²)/2 * (x₀^-1 mod 2^k-2)

Из k бит на следующей итерации получится 2(k-1) бит. Параллельно считаем на каждой итерации обратное к корню.

Тестовый код:

uint8_t sqr16(uint16_t n) {
  if (n % 8 != 1) return 0;
  uint16_t sqr = (n + 1) / 2;  //4 bit
  uint16_t inv = 2 - sqr;

  sqr += inv * (n-sqr*sqr)/2;   //6 bit
  inv *= 2 - sqr * inv;

  sqr += inv * (n-sqr*sqr)/2;  //10 bit
  //inv *= 2 - sqr * inv;

  if (sqr & 256)
    sqr = 0u - sqr;
  sqr = (uint8_t)sqr; // lowest root
  if (n == sqr*sqr) return sqr;
  return 0;
}

Добавив пару итераций, получим корень из uint_64

опять про квадратный корень — Ни о какой безапелляционности в моих высказываниях не может быть и речи! — ЖЖ

опять про квадратный корень [фев. 19, 2007|01:48 pm] Anatoly Vorobey Предположим, у нас есть какое-то (целое) число, например 2 или 25 или 234769 или любое другое. Обозначим его буквой N. Может быть, оно целый квадрат, т.е. квадрат другого натурального числа, например 9 это 3 в квадрате или 25 это 5 в квадрате. Тогда его квадратный корень — это целое число, как 3 или 5 в этих примерах. Если наше число N — не целый квадрат, то его квадратный корень не может быть целым числом. Но, может быть, его квадратный корень — какая-нибудь дробь вида 3/5 или что-нибудь такое. И третья возможность — это что квадратный корень из N — иррациональное число, которое нельзя записать как целую дробь. Так что всего с логической точки зрения у нас есть три возможных ситуации: 1) квадратный корень из N — целое число. 2) квадратный корень из N — дробное число. 3) квадратный корень из N — иррациональное число. Вот простое красивое доказательство того, что вторая ситуация — «дробное число» — не может случиться на самом деле. Поэтому из этого доказательства следует, что квадратный корень из 2, из 3, из 5, из 20, и вообще из любого числа, которое не целый квадрат — иррациональные числа. Ведь если мы исключили возможность номер два, то остаются только один и три; а все эти числа — 2, 3, 5, 20 и многие другие — не целые квадраты, то номер один тоже исключается, и их квадратные могут быть только иррациональными. Я попытаюсь написать это доказательство так, чтобы его могли понять читатели, которые не имеют никакого отношения к математике, и не учили ее со времем средней школы. Если вы такой читатель, и вам в этом доказательстве все понятно или наоборот что-то непонятно, то расскажите мне, пожалуйста, о своих впечатлениях и трудностях в комментариях. Итак, предположим, что есть такое N, которое не является целым квадратом, и что его квадратный корень можно записать как какую-то целую дробь A √N = --- B (запись √N означает «квадратный корень из N») Из всех возможных таких A/B (а их может быть много: ведь, например, 1/2 это то же самое, что 2/4 или 5/10) мы выберем такое A/B, в котором А самое меньшее по размеру («минимальное», говорят математики). Так что никакого другого A/B с тем же значением √N, в котором А еще меньше того, что мы выбрали, быть уже не может. Например, если бы нам надо было выбирать между возможными вариантами записать A/B как 2/5, 4/10 или 20/50, то мы выберем 2/5, потому что в этом варианте A меньше всех — равно 2 — и меньше варианта уже нету. Теперь возведем обе части в квадрат. Левая часть — квадратный корень из N — в квадрате будет просто N, а правую часть умножим саму на себя, ведь это и значит «возвести в квадрат»: A A N = --- * --- B B Перевернем одну из дробей и перенесем в левую часть. Или, говоря, другими словами, умножим обе части на B/A, и тогда в левой части прибавится B/A, а в правой части оно сократится с одной из двух копий A/B. N * B A ----- = --- A B Раз эти две дроби равны, то равны по отдельности их целые части и дробные части. Что такое дробная часть той дроби, что слева от знака равенства? Это какая-то дробь x --- A где x должно быть меньше A (иначе можно еще выделить целую часть). Соответственно дробная часть той дроби, что справа, это какое-то y/B, где y должно быть меньше B. Вместе получается x y --- = --- A B В этом равенстве мы можем перенести y влево, а A вправо, умножив сначала обе части на A, а потом поделив обе части на y: x y --- * A = --- * A A B Сокращаем A: y*A x = ----- B Делим на y: x y*A --- = --- y y*B и сокращаем y: x A --- = --- y B (мы можем это сделать, только если мы точно знаем, что y не равно 0, потому что на ноль делить нельзя. Но мы это точно знаем: ведь если y равно 0, это значит, что дробная часть A/B равна 0, т.е. исходный квадратный корень A/B целое число, но мы изначально предположили, что оно не целое) Сравнив это равенство с самым началом наших рассуждений, мы видим, что x √N = --- y причем, мы раньше видели, в этом равенстве x меньше нашего первоначального числительного A (потому что у нас была дробная часть x/A, в которой нельзя было выделить еще больше целой части). Но это противоречит тому, что мы написали о выборе A: А должно было быть самым меньшим из всех возможных способов представить √N в виде A/B. Исходя из этого допущения, мы тем не менее нашли какое-то еще меньшее число x, которое тоже подходит для этой цели, то есть пришли к противоречию. Раз мы неизбежно приходим к противоречию, исходя из предположения, что √N вообще можно представить как какое-то A/B, значит, это предположение неверно, и на самом деле такого не может быть. Что и требовалось доказать. Это доказательство приводят Conway & Guy в своей «Книге чисел» (The Book of Numbers). Comments: Страница 1 из 2 << [1] [2] >> From: maq 2007-02-19 12:04 pm (Link) А можно немножко не в тему спросить? Как выглядит график функции Y = A в степени X, если A отрицательное? То есть, скажем, -2 в квадрате это 4, а в кубе уже -8. Потом опять плюс, потом опять минус. А в дробных координатах где-то не существует (если внизу дроби чётное число), а где-то существует, если нечётное. Можно где-нибудь на такой график посмотреть? См. сегодняшнее рассуждение plover.com (markdominus) о геометрическом доказательстве иррациональности √2 (на самом деле это, конечно, красивая «геометризация» арифметич. док-ва) Именно оно подвигло меня на написание этой записи, косвенным путем. Сначала я хотел написать Марку письмо, и объяснить ему, что: 1) во-первых, это доказательство не придумали в 2000-м году, а оно существовало давно, в том числе в элементарных учебниках (см. например Proof 7 на этой странице). 2) во-вторых, оно действительно является очевидной геометризацией известного — хоть и далеко не так широко известного, как «стандартное» — арифметического доказательства 3) в-третьих, неверно называть его чисто геометрическим, потому что по сути своей оно содержит арифметический аргумент, апеллирующий к понятию «целое число», без которого чистая геометрия в ее древнегреческой версии вполне может обойтись 4) в-четвертых, по-видимому, неверно, что древние греки только случайно открыли «стандартное» доказательство, а не это, а это гораздо больше в их духе, потому что Марк не замечает того факта, что это доказательство глубоким образом опирается на принцип бесконечного спуска, которым, по-видимому, в явном виде древние греки не владели. Конечно, и «стандартное» доказательство на него опирается, но там эта зависимость вплетена в понятие «сокращение дробей», и необязательно понимать сам метод бесконечного спуска, достаточно «всего лишь» понимать сокращение дробей. Но, уже начав писать письмо Марку, я передумал, потому что вспомнил, что его отношение к критике, даже вполне дружелюбной, оставляет желать лучшего, по моему опыту, и что это вероятно будет бесполезным занятием. Раз уж я вспомнил эту тему, то решил попробовать записать как можно более понятным языком доказательство Конвея. Арифметическую версию доказательства про квадратный корень из двух я уже как-то приводил несколько месяцев назад, правда, она наверняка затерялась для почти всех читателей внутри длинного и утомительного логического рассуждения. (Удалённый комментарий) Я думаю, что вполне могу послужить подопытным кроликом, несмотря на когдатошнею степень — я честно забыла абсолютно всё. 1) мне было не очевидно, что B*N > A, и что мы можем выделить целую часть. 2) Мне были неочевидны переносы дробей — возможно и другим чайникам было бы проще если бы ты предлагал поделить и умножить обе части уровнения. Большое спасибо! 1) нам не нужно отдельно доказывать, что B*N > A — если вдруг нет, то пусть x = B*N, и вся дробь и есть дробная часть. 2) сейчас попробую дописать это, правда твоя. >Из всех возможных таких A/B (а их может быть много: ведь, например, 1/2 это то же самое, что 2/4 или 5/10) мы выберем такое A/B, в котором А самое меньшее по размеру Поскольку речь везде идет о целых, а не натуральных, такого А нет. From: avva 2007-02-19 05:20 pm Re: nitpicking (Link) Сознательно не хотел использовать незнакомое многим нематематическим читателям слово «натуральное», и поступился формальной корректностью. про перенос хотел только написать, а уже исправлено 🙂 Все равно спасибо 🙂 From: (Anonymous) 2007-02-19 06:40 pm (Link) Признаюсь честно, я засыпаю на ходу и не осилил, начиная с того момента, когда ввели х и у. Слишком много лишних слов, которые только путают Может потом вернусь, если вспомню Спасибо за честное мнение 🙂 если вернетесь и осилите, расскажите, как по-вашему было бы лучше объяснить. Спасибо, очень интересно. Получаю удовольствие от таких штучек. Собираюсь показать своим ученикам. Сама в универе хоть и училась, но из математики практически ничего. Так что если мне понятно — должно быть многим другим тоже. Попробую вернуться мысленно в школьные годы и посмотреть с той точки зрения… Так. Во-первых — и это моя основная проблема с традиционным изложением математики вообще — происходят какие-то манипуляции с формулами — но совсем непонятно почему именно эти, а не какие-то другие. 2) разложим обе части на простые множители. пусть в разложении x число 2 встречается m раз, а в разложении y — она встрачается n раз. Важно то, что разложение на простые множители единственно. (это проходят в школе точно) тогда в разложении левой части двойка будет встречаться 2m раз, а в разложении правой — 2n+1 раз Четное != нечетному. Противоречие. Теперь, если начать обобщать с двойки на произвольное целое число, то доказательство либо проходит — тогда корень остается иррациональным, либо нет — тогда (если чуть-чуть подумать) корень оказывается целым. Дробь ну никак выйти не может. Отсюда — если уже знать высшую математику — следует в частности, что иррациональность корня в поле напрямую связана с единственностью разложения на множители. Но это уже на любителя. Точно знаю, что школьнику это должно быть понятно, потому что в школе я это и придумал = )(разумеется, не первым) Где-то на этапе «Раз эти две дроби равны» хорошо было б подчеркнуть, что A>B, т. е. дроби >1 и можно выделить целую часть из A/B, а так как это равно NB/A, то можно и там выделить целую часть. А то как-то теряешься в самом конце: А что если х=А? В общем, всё как у Вирта — чем больше assert’ов, тем лучше 🙂 One more moment: For the non-mathematician the problem should be formulated sharply and interesting. For example, the following problems will probably not look to interesting 1) 🙂 In some area of mathematics we have cases a),b),c) let us prove that case b) is impossible. This looks like some technicality statement, and mathematics is so vast anyway …. 2) let us prove that sqrt(N) is irrational (baring full square). Most of non-mathimaticians don’t know what irrational means. And in mathematics there is plenty of weird terms, so what that something is called something ? And those who do remember irrational numbers, remember first of all sqrt(2), sqrt(3) (and pi). For them it is almost a tautology that square roots are irrational ! So I would have though that formulation of the problem like 3) Let us show that \sqrt{N} cannot be represented as (irreducable) ratio n/m *) is more interesting. Some may even be astonished (those who do not remember that there are irrational numbers). *) Caveat about ful squares have to be introduced somehow. Если в доказательстве больше 2-х ходов, оно начинает напоминать подозрительные манипуляции фокусника. From: 109 2007-02-20 08:50 am (Link) аплодисменты. мне тоже иногда приходится объяснять какие-то вещи, кажущиеся мне очевидными, гораздо подробнее, чем, казалось бы, нужно. когда я это делаю в устной форме, реакция собеседника подсказывает, когда нужно повторить, а когда можно двигаться вперёд. а когда я пишу, этого фидбэка нет, и меня всегда мучает страх «зациклиться», начать повторять одно и то же без продвижения вперёд. (Удалённый комментарий) Это кажется проще, но на деле пользуется единственностью разложения на простые множители, что вообще говоря намного более сложный результат, чем все «мое» доказательство. (Удалённый комментарий) Хм, я наверное чего-то не догоняю. Разве то, что возведение в квадрат несократимой дроби с неединичным знаменателем приведет к несократимой же дроби с неедиными знаментателем, не является достаточным рассуждением? Это рассуждение опирается на единственность разложения на простые множители, и вообще говоря будет неочевидно тем, кто его как следует не усвоил. From: (Anonymous) 2007-02-20 12:05 pm Интересно, (Link) а мировые константы иррациональны по отношению друг к другу? Не могу проверить, как придумать, ведь точных значений нет. (Удалённый комментарий) Страница 1 из 2 << [1] [2] >>

Определение арифметического корня натуральной степени.

Арифметический квадратный корень и его свойства

Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.

Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а .

Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.

Арифметический квадратный корень из числа а обозначается так: √а.

Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.

Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.

Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х , мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.

Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.

Квадратный корень из дроби

Вычислим . Заметим, что √25 = 5, √36 = 6, и проверим выполняется ли равенство .

Так как и , то равенство верно. Итак, .

Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .

Так как √а ≥0 и √b > 0, то .

По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.

Вычислить , по доказанной теореме .

Второй пример: Доказать, что , если а ≤ 0, b .

Еще примерчик: Вычислить .

.

Преобразование квадратных корней

Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:

Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;

Вычислить при х = 2. Непосредственная подстановка х = 2 в подкоренное выражение приводит к сложным вычислениям. Эти вычисления можно упростить, если вначале вынести из-под знака корня множители: . Подставив теперь х = 2, получим:.

Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а

Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)

Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)

Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.

Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:

Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt{a}$ и даже $\sqrt{a}$) и нечётной степени (всякие $\sqrt{a}$, $\sqrt{a}$ и т. {2}}=1$.

Кубические корни тоже часто встречаются — не надо их бояться:

\[\begin{align} & \sqrt{27}=3; \\ & \sqrt{-64}=-4; \\ & \sqrt{343}=7. \\ \end{align}\]

Ну, и парочка «экзотических примеров»:

\[\begin{align} & \sqrt{81}=3; \\ & \sqrt{-32}=-2. \\ \end{align}\]

Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!

А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.

Зачем вообще нужны корни?

Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?

Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:

\[\begin{align} & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end{align}\]

Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:

Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:

Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5 183 . Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.

После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?

Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. {n}}=a\]

Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.

Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:

\[\sqrt{2}=1,414213562…\]

Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:

\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]

Или вот ещё пример:

\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]

Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).

Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.

Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.

Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.

\[\begin{align} & \sqrt{2+\sqrt{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt{\sqrt{-32}}=\sqrt{-2}\approx -1,2599… \\ \end{align}\]

Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}$:

График квадратичной функции даёт два корня: положительный и отрицательный

Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку

С первым числом всё понятно — оно положительное, поэтому оно и есть корень:

Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)

В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y , т. {3}}$:

Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа

Из этого графика можно сделать два вывода:

1. Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
2. Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).

Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.

Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.

Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.

А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:

1. Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
2. А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.

Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.

Основные свойства и ограничения

У корней много странных свойств и ограничений — об этом будет отдельный урок. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.

Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.

Впрочем, все эти проблемы актуальны лишь для чётных показателей.

Вынесение минуса из-под знака корня

Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:

\[\sqrt{-a}=-\sqrt{a}\]

Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:

\[\begin{align} & \sqrt{-8}=-\sqrt{8}=-2; \\ & \sqrt{-27}\cdot \sqrt{-32}=-\sqrt{27}\cdot \left(-\sqrt{32} \right)= \\ & =\sqrt{27}\cdot \sqrt{32}= \\ & =3\cdot 2=6. \end{align}\]

Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.

И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!

Арифметический корень

Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?

А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.

Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.

Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:

Область поиска арифметического корня — неотрицательные числа

Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.

Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»

Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным.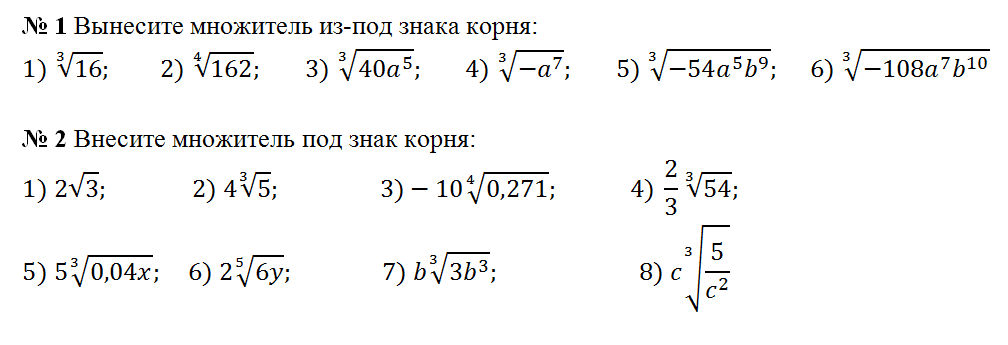 {2}}}=\sqrt{4} \gt 0. \\ \end{align}$

Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.

WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.

Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.

Алгебраический корень: для тех, кто хочет знать больше

Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]

Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:

1. Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
2. Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
3. Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.

Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.

Пример. Вычислите выражения:

\[\overline{\sqrt{4}};\quad \overline{\sqrt{-27}};\quad \overline{\sqrt{-16}}. \]

Решение. С первым выражением всё просто:

\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]

Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.

\[\overline{\sqrt{-27}}=\left\{ -3 \right\}\]

Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.

Наконец, последнее выражение:

\[\overline{\sqrt{-16}}=\varnothing \]

Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.

Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt{-16}$, и многие другие странные вещи.

Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».

Корнем степени n из действительного числа a , где n — натуральное число, называется такое действительное число x , n -ая степень которого равна a .

Корень степени n из числа a обозначается символом . Согласно этому определению .

Нахождение корня n -ой степени из числа a называется извлечением корня. Число а называется подкоренным числом (выражением), n — показателем корня. При нечетном n существует корень n -ой степени для любого действительного числа a . При четном n существует корень n -ой степени только для неотрицательного числаa . Чтобы устранить двузначность корня n -ой степени из числа a , вводится понятие арифметического корня n -ой степени из числа a .

Понятие арифметического корня степени N

Если и n — натуральное число, большее 1 , то существует, и только одно, неотрицательное число х , такое, что выполняется равенство . Это число х называется арифметическим корнем n -й степени из неотрицательного числа а и обозначается . Число а называется подкоренным числом, n — показателем корня.

Итак, согласно определению запись , где , означает, во-первых, что и, во-вторых, что , т.е. .

Понятие степени с рациональным показателем

Степень с натуральным показателем: пусть а — действительное число, а n — натуральное число, большее единицы, n -й степенью числа а называют произведение n множителей, каждый из которых равен а , т.е. . Число а — основание степени, n — показатель степени. Степень с нулевым показателем: полагают по определению, если , то . Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если и n — натуральное число, то . Степень с дробным показателем: полагают по определению, если и n — натуральное число, m — целое число, то .

Операции с корнями.

Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя:

Теперь формула a m: a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р. a 4: a 7 = a 4 — 7 = a -3 .

Если мы хотим, чтобы формула a m: a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а:

О выражениях, не имеющих смысла. Есть несколько таких выражений.

Случай 1.

Где a ≠ 0 , не существует.

В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0

Случай 2.

Любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.

Действительно,

Р е ш е н и е. Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует, что x – любое число; но принимая во внимание, что внашем случае x > 0 , ответом является x > 0 ;

3) при x

в этом случае нет решения. Таким образом, x > 0.

• Арифметическим корнем натуральной степени n>=2 из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень n получается число а. n = a*b.

Что и требовалось доказать. Значит свойство верно. Эти свойства очень часто придется использовать при упрощении выражений содержащих арифметические корни.

Решение квадратных уравнений путем извлечения квадратных корней

Пурпурная математика

Давайте еще раз посмотрим на последнюю проблему на предыдущей странице:

На предыдущей странице я решил это квадратное уравнение, разложив на множители разность квадратов в левой части уравнения, а затем приравняв каждый множитель к нулю, и т. д., и т. д.Решение было « x  = ± 2″. Однако —

Я также могу попытаться изолировать член квадрата переменной в левой части уравнения (то есть я могу попытаться получить член x ² сам по себе с одной стороны знака «равно»), переместив числовую часть (то есть 4) вправо, вот так:

Справка по математике.

ком

Когда я решаю уравнение, я знаю, что могу делать с этим уравнением все, что захочу , если я делаю то же самое с обеими частями этого уравнения . В левой части этого конкретного уравнения у меня есть x ² , и я хочу старый добрый x .Чтобы превратить x ² в x , я могу взять квадратный корень из каждой части уравнения, например:

х = ± 2

Тогда решение будет x  = ±2, точно так же, как это было, когда я решал разность квадратов на множители.

Зачем мне понадобился знак «±» (то есть «плюс-минус») перед 2, когда я извлекал квадратный корень из 4? Потому что я пытаюсь найти всех значений переменной, которые делают исходное утверждение верным, и это могло быть либо положительное 2, либо отрицательное 2, которое было возведено в квадрат, чтобы получить это 4 в исходном уравнении.

Эта двойственность похожа на то, что у меня было два множителя, один «плюс» и один «минус», когда я использовал формулу разности квадратов для решения того же уравнения на предыдущей странице.

---

«Нахождение решения уравнения» — это процесс, очень отличный от «вычисления квадратного корня из числа». При нахождении квадратного корня числа мы имеем дело исключительно с положительным значением. Почему? Потому что именно так определяется квадратный корень числа.Значение квадратного корня числа может быть только положительным, потому что именно так определяется «квадратный корень числа».

Решение уравнения, с другой стороны, то есть нахождение всех возможных значений переменной, которые могут работать в уравнении, отличается от простого вычисления выражения, которое уже определено как имеющее только одно значение.

Держите этих двоих прямо! Число с квадратным корнем имеет только одно значение, но уравнение с квадратным корнем имеет два из-за переменной.

---

В математике мы должны иметь возможность получить один и тот же ответ, независимо от того, какой правильный метод мы использовали для получения этого ответа. Итак, сравнение ответа, который я получил выше, с ответом, который я получил на предыдущей странице, подтверждает, что мы должны использовать «±» при извлечении квадратных корней для решения.

(Возможно, вы сомневаетесь в моей работе выше на шаге, где я извлек квадратный корень из любой части, потому что я поставил знак «±» только на одной стороне уравнения.Разве я не должен добавить этот символ к обеим частям уравнения? Типа, да. Но если бы я поставил его на обе стороны уравнения, действительно ли что-нибудь изменилось бы? Нет. Попробуйте все случаи, если не уверены.)

---

Преимущество этого процесса извлечения квадратного корня состоит в том, что он позволяет нам решать некоторые квадратные уравнения, которые мы не могли решить раньше, используя только факторинг. Например:

Этот квадрат имеет квадратную часть и числовую часть.Я начну с добавления числового члена к другой стороне уравнения (так что квадратная часть сама по себе), а затем я возьму квадратный корень из обеих сторон. Мне нужно не забыть упростить квадратный корень:

х ² – 50 = 0

х ² = 50

Тогда мое решение:

Хотя мы могли бы получить предыдущее целочисленное решение путем разложения на множители, мы никогда не смогли бы получить это радикальное решение путем разложения на множители.Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды методов позволяют нам находить решения дополнительных типов уравнений.

---

• Решить (

  x – 5) ² – 100 = 0,

Этот квадрат имеет квадратную часть и числовую часть. Я начну с добавления строго числового члена в правую часть уравнения, так что биномиальное выражение в квадрате, содержащее переменную, само по себе окажется в левой части.Затем я извлеку квадратный корень из обеих частей, помня «±» в числовой части, а затем упрощу:

.

( х – 5) ² – 100 = 0

( х – 5) ² = 100

х – 5 = ±10

х = 5 ± 10

x = 5 – 10 или x = 5 + 10

x = –5   или   x = 15

Это уравнение, после извлечения квадратного корня из любой части, не содержало радикалов.Благодаря этому я смог упростить свои результаты вплоть до простых значений. Мой ответ:

Предыдущее уравнение является примером уравнения, в котором небрежный учащийся пропустит «±» при решении и не поймет, как книга получила ответ « x  = –5, 15″.

Эти ученики имеют дурную привычку не утруждать себя написанием знака «±», пока не проверят свои ответы в конце учебника и вдруг не «вспомнят», что они «имели в виду» поставить там знак «±», когда они d берут квадратный корень из любой части уравнения.

Но эта «магия» работает только тогда, когда у вас есть ответ в конце (чтобы напомнить вам) и когда решение содержит радикалы (что случается не всегда). В остальных случаях «напоминания» не будет. Особенно в тестах ошибка пропуска «±» может быть смертельной. Не будь таким студентом. Всегда не забывайте вставлять «±».

Кстати, поскольку решение предыдущего уравнения состояло из целых чисел, это квадратное уравнение можно было бы решить также путем умножения квадрата, разложения на множители и т. д.:

( х – 5) ² – 100 = 0

х ² – 10 х + 25 – 100 = 0

х ² – 10 х – 75 = 0

( х – 15)( х + 5) = 0

х – 15 = 0, х + 5 = 0

х = 15, –5

---

• Решить (

  x – 2) ² – 12 = 0

Этот квадрат имеет квадратную часть и числовую часть. Я добавлю числовую часть на другую сторону, так что квадратная часть с переменной будет сама по себе. Затем я извлеку квадратный корень из обеих сторон, не забывая добавить «±» к числовой стороне, а затем упрощу:

.

( х – 2) ² – 12 = 0

( х – 2) ² = 12

Я больше не могу это упрощать. В моем ответе будут радикалы.Мое решение:

Это квадратное уравнение, в отличие от предыдущего, также нельзя было решить с помощью факторизации. Но как бы я решил ее, если бы они дали мне , а не квадратное выражение, уже представленное в виде «(часть квадрата) минус (часть числа)»? Это беспокойство приводит к следующей теме: решение путем заполнения квадрата.

---

URL-адрес: https://www. Purplemath.com/modules/solvquad2.htm

Квадратные и кубические корни

Чтобы найти кубический корень из числа, нужно найти некоторое число, которое при двукратном умножении само на себя дает исходное число. Другими словами, чтобы найти кубический корень из 8, вам нужно найти число, которое при двукратном умножении само на себя дает 8. Таким образом, кубический корень из 8 равен 2, потому что 2 × 2 × 2 = 8.Обратите внимание, что символом кубического корня является знак корня с маленькой тройкой (называемой индексом ) вверху и слева. Другие корни определяются аналогично и идентифицируются по заданному индексу. (В квадратном корне индекс два понимается и обычно не записывается.) Ниже приводится список первых одиннадцати совершенных (целых чисел) кубических корней.

Чтобы найти квадратный корень из числа, не являющегося полным квадратом, необходимо найти приблизительный ответ, используя процедуру, приведенную в примере.

.

Пример 1

Приблизительно .

Так как 6 ² = 36 и 7 ² = 49, то находится между и .

Следовательно, это значение между 6 и 7. Поскольку 42 находится примерно посередине между 36 и 49, вы можете ожидать, что оно будет близко к середине между 6 и 7, или примерно 6,5. Чтобы проверить эту оценку, 6,5 × 6,5 = 42,25, или около 42,

.

Квадратные корни несовершенных квадратов можно аппроксимировать, найти в таблицах или найти с помощью калькулятора. Вы можете иметь в виду эти два:

Упрощение квадратных корней

Иногда вам придется упростить квадратных корней или записать их в простейшей форме.В дробях можно сократить до . В квадратных корнях можно упростить до .

Существует два основных метода упрощения извлечения квадратного корня.

Метод 1: Разделите число под на два множителя, один из которых представляет собой максимально возможный правильный квадрат. (Совершенные квадраты 1, 4, 9, 16, 25, 36, 49, …)

Метод 2: Полностью разложите число под на простые множители, а затем упростите, выделив все множители, которые были парами.

Пример 2

Упростить .

В примере

, самый большой правильный квадрат легко увидеть, и метод 1, вероятно, является более быстрым методом.

Пример 3

Упростить .

В примере

, не столь очевидно, что самый большой правильный квадрат равен 144, поэтому метод 2, вероятно, является более быстрым методом.

Многие квадратные корни не могут быть упрощены, поскольку они уже имеют простейшую форму, например , , и .

Обратная функция квадратного корня

Чтобы найти обратную функцию квадратного корня, очень важно сначала набросать или построить график данной задачи, чтобы четко определить, каковы область и диапазон.Я буду использовать домен и диапазон исходной функции, чтобы описать домен и диапазон обратной функции, поменяв их местами. Если вам нужна дополнительная информация о том, что я имел в виду под «обменом домена и диапазона» между функцией и ее обратной функцией, см. мой предыдущий урок об этом.

---

Примеры нахождения обратной функции квадратного корня

Пример 1: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Каждый раз, когда я встречаю функцию квадратного корня с линейным членом внутри подкоренного символа, я всегда думаю о ней как о «половине параболы», нарисованной сбоку. Поскольку это положительный случай функции извлечения квадратного корня, я уверен, что ее диапазон будет становиться все более положительным, проще говоря, взлетать до положительной бесконечности.

Эта конкретная функция квадратного корня имеет этот график с указанными доменом и диапазоном.

С этого момента мне придется решать обратное алгебраически, следуя предложенным шагам.По сути, замените \color{red}f\left( x \right) на \color{red}y, поменяйте местами x и y в уравнении, найдите y, который вскоре будет заменен соответствующим обратным обозначением, и, наконец, укажите домен и диапазон.

Не забудьте использовать приемы решения радикальных уравнений, чтобы найти обратное. Возведение в квадрат или возведение во вторую степень члена квадратного корня должно устранить радикал. Тем не менее, вы должны сделать это для обеих сторон уравнения, чтобы сохранить его сбалансированным.

Убедитесь, что домен и диапазон обратной функции совпадают с исходной функцией.Они должны быть «напротив друг друга».

Размещение графиков исходной функции и обратной к ней на одной оси координат.

Видите ли вы их симметрию по линии y = x? См. зеленую пунктирную линию.

---

Пример 2: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Эта функция является «нижней половиной» параболы, поскольку функция квадратного корня отрицательна. Этот отрицательный символ просто замаскирован -1.2} = 1. Его домен и диапазон будут измененной «версией» исходной функции.

---

Пример 3: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Это график исходной функции, показывающий как ее домен, так и диапазон.

Определение диапазона обычно является сложной задачей. Лучший способ найти его — использовать график заданной функции с ее областью определения. Проанализируйте, как функция ведет себя вдоль оси y, рассматривая значения x из области.

Вот шаги, чтобы решить или найти обратную функцию квадратного корня.

Как видите, все очень просто. Убедитесь, что вы делаете это осторожно, чтобы избежать ненужных алгебраических ошибок.

---

Пример 4: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Эта функция представляет собой одну четвертую (четверть) круга с радиусом 3, расположенного в квадранте II. Другой способ его увидеть, это половина полукруга, расположенная над горизонтальной осью.

Я знаю, что он пройдет тест горизонтальной линии, потому что ни одна горизонтальная линия не будет пересекать его более одного раза. Это хороший кандидат на наличие обратной функции.

Опять же, я могу легко описать диапазон, потому что потратил время на его график. Что ж, я надеюсь, что вы осознаете важность наличия наглядного пособия, помогающего определить этот «неуловимый» диапазон.

Присутствие члена в квадрате внутри подкоренного символа говорит мне, что я применю операцию извлечения квадратного корня к обеим частям уравнения, чтобы найти обратное.Таким образом, у меня будет плюс или минус случай. Это ситуация, когда я приму решение о том, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу допустить, чтобы у вас было два ответа.

Как мне решить, какой из них выбрать? Ключевым моментом является рассмотрение домена и диапазона исходной функции. Я поменяю их местами, чтобы получить домен и диапазон обратной функции. Используйте эту информацию, чтобы сопоставить, какая из двух функций-кандидатов удовлетворяет требуемым условиям.

Хотя у них один и тот же домен, диапазон здесь является решающим! Диапазон говорит нам, что обратная функция имеет минимальное значение y = -3 и максимальное значение y = 0,

.

Случай положительного квадратного корня не соответствует этому условию, поскольку он имеет минимум при y = 0 и максимум при y = 3. Отрицательный случай должен быть очевидным выбором даже при дальнейшем анализе.

---

Пример 5: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Полезно посмотреть на график исходной функции, потому что мы можем легко определить ее домен и диапазон.

Отрицательный знак функции извлечения квадратного корня означает, что она находится ниже горизонтальной оси. Обратите внимание, что это похоже на пример 4. Это также четверть круга, но с радиусом 5. Домен заставляет четверть круга оставаться в квадранте IV.

Вот как мы алгебраически находим его обратное.

Вы выбрали правильную обратную функцию из двух возможных? Ответ – случай с положительным знаком.

---

Практика с рабочими листами

---

Вас также может заинтересовать:

Обратная матрица 2×2

Функция, обратная абсолютному значению

Обратная постоянная функция

Обратная экспоненциальная функция

Обратная линейная функция

Обратная логарифмическая функция

Обратная квадратичная функция

Обратная рациональная функция

Железо флоэмы ремоделирует развитие корней в ответ на аммоний как основной источник азота

isas был первоначально скринирован из библиотеки вставок Т-ДНК ²² с использованием прозрачных чашек Петри с освещенной светом средой для укоренения.Было обнаружено, что этот мутант представляет собой линию SALK_056696 со вставкой Т-ДНК во втором экзоне LPR2 (AT1G71040) (дополнительный рисунок 1a, b). qRT-PCR и иммуноблоттинг показали, что isas , скорее всего, является нокаутным мутантом LPR2 (дополнительная рис. 1c, d). Поскольку естественные почвы обычно обладают рН-буферной способностью, в нашем исследовании в среду для выращивания добавляли рН-буфер MES, если не указано иное. При выращивании на контрольной среде с NO ₃ ^— в качестве источника N корни isas морфологически не отличались от корней Col-0 дикого типа.Однако в среде с NH ₄ ⁺ в качестве источника азота мутанты isas показали лучший рост PR, чем проростки Col-0 (дополнительный рисунок 2).

Если не указано иное, мы использовали черный пластиковый лист для покрытия корней, чтобы исключить облучение светом в остальных исследованиях (дополнительный рисунок 3). В таких условиях затенения корней мутанты isas по-прежнему имели большее удлинение PR в источнике NH ₄ ⁺ -N, чем проростки Col-0 (рис.1а, б). Кроме того, другой мутант с инсерцией Т-ДНК, lpr2-1 (SALK_091930) ²³ , который также, вероятно, является нокаутным мутантом (дополнительный рисунок 1), имел аналогичный NH ₄ ⁺ -нечувствительный фенотип. Чувствительность NH ₄ ⁺ обоих мутантов lpr2 также исследовали в небуферизованных условиях, и оба мутанта постоянно демонстрировали лучший рост PR, чем проростки Col-0 в источнике NH ₄ ⁺ -N без MES. (Дополнительный рис.4). Эти результаты показывают, что ингибирующее действие NH ₄ ⁺ на рост PR может быть не связано с разрушением LPR2.

Рис. 1: LPR2-зависимое ингибирование роста первичных корней в среде Nh5+.

a Сравнение фенотипов Col-0 и isas , lpr2-1 , lpr1-1 и lpr1lpr2 . b Удлинение первичных корней. c Сравнение фенотипов Col-0, lpr2-1 и комплементарных линий (COM #7 и COM #15). d Количество клеток меристемы. e Количество клеток растяжения. f Длина первой дифференцированной клетки. г Длина зоны роста корня (удлинение плюс зона меристемы). b , d — g Представленные данные являются средним значением ± SD. Значения P < 0,05 указывают на значительные различия (двусторонний дисперсионный анализ с апостериорным тестом Тьюки HSD; n  = количество проростков). Четырехдневные проростки указанных генотипов переносили на среду NO ₃ ⁻ или NH ₄ ⁺ с 100 мкМ Fe и анализировали через 4 дня после переноса проростков.Каждый эксперимент был повторен независимо не менее трех раз с аналогичными результатами, и показан репрезентативный эксперимент.

LPR1 (AT1G23010) является близким паралогом LPR2 ²³ . Однако NH ₄ ⁺ -чувствительный PR-фенотип мутанта lpr1-1 не отличался от такового у проростков Col-0 (рис. 1а, б). Более того, двойные мутанты lpr1lpr2 не обладали большей нечувствительностью к NH ₄ ⁺ , чем одиночные мутанты lpr2 .Соответственно, чувствительность PR NH ₄ ⁺ была связана только с LPR2 , а не с LPR1 . Мы также создали трансформантов pLPR2::LPR2-YFP на фоне lpr2-1 . Эти линии комплементации (COM № 7 и COM № 15) имели умеренно более высокую экспрессию LPR2 и содержание LPR2, чем проростки Col-0 (дополнительная рис. 5), и полностью восстановили ингибирующее действие NH ₄ ⁺ на PR. рост (рис.1с). Эти результаты дополнительно демонстрируют, что LPR2 отвечает за чувствительность NH ₄ ⁺ PR.

Удлинение корня контролируется делением и дифференцировкой клеток вдоль продольной оси корня ²⁴ . Здесь мы показали, что количество меристематических клеток в PR проростков Col-0 и COM # 7 в источнике NH ₄ ⁺ -N было уменьшено примерно на 60% по сравнению с таковым в NO ₃ ^— -N, тогда как у мутантов lpr2-1 наблюдалось лишь незначительное снижение (рис.1г). Это указывает на то, что LPR2 ускоряет переход от клеточного деления к дифференцировке. Кроме того, как число элонгационных клеток, так и первая дифференцированная длина клеток в PR проростков Col-0 и COM#7 также значительно снижались под действием NH ₄ ⁺ , и такое снижение было явно уменьшено в lpr2-1. PR (рис. 1д, е). В результате в NH ₄ ⁺ мутанты lpr2-1 имели меньшую задержку роста в корневой зоне роста (меристема плюс зона удлинения), чем у проростков Col-0 и COM#7 (рис.1г). Следовательно, ингибирование роста PR в результате стресса NH ₄ ⁺ сильно зависит от LPR2 и инициируется ускоренным переходом от клеточного деления к дифференцировке в зоне меристемы с последующей ранней дифференцировкой удлиняющихся клеток.

LPR2 кодирует ферроксидазу клеточной стенки и незаменим для LPR1

Прогнозирование с помощью алгоритма SignalP 5.0 ²⁵ показало, что и LPR1, и LPR2 содержат предполагаемый секреторный сигнальный пептид в N-концевой области (дополнительная рис. 6). В соответствии с этим предсказанием конфокальный анализ трансформантов p35S::LPR2-GFP показал, что флуоресценция LPR2-GFP в основном локализуется в матриксе клеточной стенки (рис. 2a, b), что очень похоже на субклеточную локализацию LPR1 ²⁶ . Ранее было установлено, что LPR1 обладает ферроксидазной активностью, которая превращает Fe ²⁺ в Fe ^{3+, 26,27} . Как и ожидалось, рекомбинантный белок GST-LPR2 из Escherichia coli также обладал очевидной ферроксидазной активностью и проявлял типичную кинетику Михаэлиса-Ментен с K _m и V _max из 17.43 мкМ и 22,10 мкМ/мин/мг белка соответственно (рис. 2в, г).

Рис. 2: LPR2 представляет собой ферроксидазу клеточной стенки и незаменима для LPR1.

a Совместная флуоресцентная локализация LPR2-GFP и йодида пропидия в клетках корней p35S::LPR2-GFP . b Флуоресценция LPR2-GFP и FM4-64 в клетках корней p35S::LPR2-GFP после плазмолиза 0,8 М сорбита. Четырехдневные проростки переносили на среду NH ₄ ⁺ с 100 мкМ Fe, а конфокальный анализ проводили через 4 дня после переноса проростков. c Ферроксидазная активность рекомбинантного GST-LPR2. Анализ ферроксидазы с использованием 1 мкг очищенного белка GST-LPR2. Розовый цвет указывает на комплекс Fe ²⁺ -феррозин. Субстрат Fe ²⁺ добавляли в виде Fe(NH ₄ ) ₂ (SO ₄ ) ₂ · 6H ₂ O при начальной концентрации 50 мкМ. d Fe ²⁺ зависящая от концентрации (0–300  мкМ) ферроксидазная активность белка GST-LPR2. Представленные данные представляют собой среднее значение ± стандартное отклонение для трех биологических повторов. E , E , F Фенотип LPR2-1 Мутантные линии с промоутером LPR2-1 Специфика с LPR2, специфическими к тканям LPR1 ^CDS и LPR1 ^Genomic . Четырехдневные проростки указанных генотипов переносили на среду NO ₃ ⁻ или NH ₄ ⁺ с 100 мкМ Fe и анализировали через 4 дня после переноса проростков. Было проведено два ( c , d ) или три ( a , b , e , f ) независимых эксперимента с аналогичными результатами, и показан один репрезентативный эксперимент.

Принимая во внимание сходство LPR2 и LPR1 как в субклеточной локализации, так и в ферментативной реакции, мы исследовали, может ли LPR1 выполнять роль LPR2 в опосредовании чувствительности NH ₄ ⁺ . Мы использовали промотор LPR2 для ограничения сайта экспрессии LPR1 в мутанте lpr2-1 . Однако, хотя и PLPR2 :: LPR1 ^{CDS / LPR2-1} / PLPR2 :: LPR1 ^{Genomic / LPR2-1 Трансформанты имели сопоставимые или немного более высокие уровни экспрессии л. по сравнению с LPR2 в проростках Col-0 (дополнительный рис.7), они по-прежнему демонстрировали такой же рост PR, как и у проростков lpr2-1 в источнике NH ₄ + -N (рис. 2д, е). Следовательно, LPR2 незаменим для LPR1 в опосредовании чувствительности NH ₄ + , что может объяснить, почему только LPR2, а не LPR1 подавляет рост PR в присутствии NH ₄ + .}

Опосредованный LPR2 фенотип NH

₄ ⁺ -чувствительных PR зависит от действия Fe

Затем мы спросили, как LPR2 опосредует NH ₄ ⁺ чувствительность PR.Нарушение LPR2 не повлияло на уровень NH ₄ ⁺ в корнях (дополнительный рисунок 8), показывая, что LPR2-опосредованная чувствительность NH ₄ ⁺ не связана с накоплением NH ₄ ⁺ . Поскольку LPR2 является ферроксидазой, была исследована роль Fe в регуляции NH ₄ ⁺ чувствительности PR. Сначала мы выращивали проростки арабидопсиса на средах с различными дозами Fe. Дозы Fe ≤10 мкМ обеспечивали аналогичный рост PR Col-0 между источниками NH ₄ ⁺ — и NO ₃ ⁻ -N, тогда как ≥50 мкМ индуцировали явное дозозависимое ингибирование роста PR в источник NH ₄ ⁺ -N (дополнительный рис. 9 и рис. 3а). Напротив, добавление дефероксамина или феррозина, двух мощных хелаторов Fe, почти полностью восстановило рост PR проростков Col-0 в источнике NH ₄ ⁺ -N с 100   мкМ Fe (дополнительный рисунок 10). Ингибирующее действие NH ₄ ⁺ на рост корней растений риса также не было связано со снижением поступления Fe (дополнительный рисунок 11). Эти результаты показывают, что чувствительность корней к NH ₄ ⁺ сильно зависит от действия Fe.

Учитывая, что отсутствие железа (0 мкМ) и условия с высоким содержанием железа (≥200 мкМ) могут соответственно вызывать дефицит железа и избыток железа у арабидопсиса, мы использовали 10 и 100 мкМ Fe, определяемые как низкое содержание железа (Fe ^низкое ). и достаточное количество Fe (Fe ^suff ) соответственно в остальных оценках. Разница в чувствительности NH ₄ ⁺ между мутантами lpr2 и проростками Col-0 или COM#7 полностью исчезала, когда концентрация Fe снижалась с Fe ^suff до Fe ^low (рис. 3b), показывая, что LPR2-опосредованный NH ₄ ⁺ -чувствительный фенотип зависит от действия Fe.

Рис. 3: Fe-зависимое ингибирование роста первичных корней в среде Nh5+.

a Первичное удлинение корней проростков Col-0 в источнике NO ₃ ⁻ -N или NH ₄ ⁺ -N с различными дозами Fe. Центральная линия представляет собой среднее значение, а границы прямоугольника — стандартное отклонение; усы указывают минимальное и максимальное значения; n  = количество саженцев. Значения P <0,05 указывают на значительное взаимодействие между формой N и дозой Fe (двусторонний дисперсионный анализ с апостериорным тестом Тьюки HSD). b NH ₄ ⁺ — сравнение чувствительности Col-0, isas , lpr2-1 и линии комплементации COM#7 в Fe ^suff (100 µM1) и Fe 900 мкМ) условия. c Отложения Fe, указанные окрашиванием Perls/DAB в первичных корнях. d Крупный план отложения Fe в корневом стволе проростков Col-0, выращенных в среде Fe ^suff NH ₄ ⁺ .Ep epidermis, Co cortex, En endodermis, Pe перицикл, Ph флоэма, Xy ксилема. e Окрашивание Perls/DAB во флоэме первичных корней проростков Col-0, выращенных в среде Fe ^suff NH ₄ ⁺ . Красные и зеленые стрелки показывают отложения Fe на боковых клеточных стенках и ситовидных пластинках флоэмы соответственно. f Окрашивание промытым ацетоном Perls/DAB во флоэме первичных корней проростков Col-0, выращенных в среде Fe ^suff NH ₄ ⁺ .Окрашенные Perls/DAB корни промывали ацетоном в течение 3 часов. Четырехдневные проростки указанных генотипов переносили на среду NO ₃ ⁻ или NH ₄ ⁺ с различными дозами внесения Fe и анализировали через 4 сут после переноса проростков. Каждый эксперимент был повторен независимо три раза с аналогичными результатами, и показан репрезентативный эксперимент.

Кроме того, мы проверили, играет ли Fe роль в NH ₄ ⁺ чувствительности PR, когда источник N имеет высокое соотношение NH ₄ ⁺ /NO ₃ ⁻ (10:2). .Точно так же разница в ингибировании роста PR между мутантами lpr2 и проростками Col-0 при высоком соотношении NH ₄ ⁺ / NO ₃ ^— также устранялась за счет снижения добавки Fe (дополнительный рисунок 12). . Таким образом, Fe требуется для повторной формовки PR, когда NH ₄ ⁺ является единственным или преобладающим источником азота.

NH

₄ ⁺ индуцирует отложение Fe во флоэме

Сильная зависимость фенотипа NH ₄ ⁺ -чувствительных PR от Fe подняла вопрос о том, влияет ли NH 3 3 на стресс отложение в корнях.Мы использовали специфичную для Fe гистохимическую процедуру, окрашивание Perls/3,3′-диаминобензидином (DAB) ²⁸ , чтобы визуализировать распределение Fe в PR. Для проростков Col-0 и lpr1-1 с Fe ^suff источник NH ₄ ⁺ -N привел к массивному отложению Fe в корневом стволе по сравнению с NO ₃ ⁻ -N. источник (рис. 3c и дополнительный рис. 13a). Напротив, индуцированное NH ₄ ⁺ отложение Fe полностью устранялось либо разрушением LPR2 у мутантов lpr2-1 , либо обработкой Fe ^low у проростков Col-0.Линия комплементации COM#7 восстановила отложение Fe в корневой стеле в источнике NH ₄ ⁺ -N с Fe ^suff . Эти результаты показывают, что индуцированное NH ₄ ⁺ отложение Fe в корневом стволе зависит от LPR2, а также от достаточного поступления Fe. Примечательно, что эти соответствующие отложения Fe для различных генотипов и обработки дозами Fe отрицательно коррелировали с ростом PR в источнике NH ₄ ⁺ -N (рис. 3b), предполагая, что отложение Fe в корневой стеле определяет PR реакция роста на NH ₄ ⁺ стресс. Неожиданно, в присутствии либо NO ₃ ^— , либо NH ₄ ⁺ обработка Fe ^low привела к более высокому отложению Fe в нише корневых стволовых клеток (SCN) Col-0, lpr2. -1 и проростки COM#7 по сравнению с проростками, обработанными Fe (рис. 3c). Тем не менее, хотя отложение Fe не было обнаружено в SCN проростков lpr1lpr2 (дополнительная рис. 13b), этот двойной мутант демонстрировал аналогичную нечувствительность к NH ₄ ⁺ , что и мутант lpr2-1 (рис.1в), указывая на то, что чувствительность ФП NH ₄ ⁺ не зависит от отложения Fe в SCN.

Крупный план окрашенных Perls/DAB корней Col-0 при обработке Fe ^suff NH ₄ ⁺ показал, что наибольшее отложение Fe было в клетках флоэмы (рис. 3d). При большем увеличении обнаружено, что Fe в основном расположено на периферии ситовидных элементов (рис. 3д). Эта периферия, вероятно, является апопластом флоэмы, потому что LPR2, ответственный за это отложение Fe, является резидентным белком клеточной стенки. Поскольку сосудистую сеть флоэмы трудно подвергать плазмолизу методами осмотической дегидратации, для отмывки плазмалеммы использовали ацетон. Эта процедура не изменила отложение Fe на периферии ситовидных элементов (рис. 3f), обеспечивая дополнительную поддержку апопластного отложения Fe во флоэме.

Неожиданно источник NH ₄ ⁺ -N с Fe ^suff привел к сильному отложению Fe во всех типах клеток Col-0 PR в условиях облучения корней, что значительно отличалось от того, что наблюдалось при корневой -заштрихованные условия (дополнительный рис.14). Результат убедительно свидетельствует о том, что влияние искусственного освещения на корни нельзя игнорировать при изучении механизмов реакции роста корней на NH ₄ ⁺ , даже несмотря на то, что ингибирование роста корней NH ₄ ⁺ практически не зависит от световое облучение корней.

LPR2 распределяется в корневой стеле и активируется NH

₄ ⁺

NH ₄ ⁺ , индуцированное специфическим отложением Fe во флоэме, побудило нас проанализировать тканевое распределение pPR92L2 PR2: :LPR2-YFP/lpr2-1 трансформантов. LPR2-YFP был в основном распространен в корневом стеле, но его численность была ниже в источнике NO ₃ ⁻ -N. Флуоресценция LPR2-YFP увеличивалась в источнике NH ₄ ⁺ -N, при этом доза Fe мало влияла на этот ответ (рис. 4а). Неожиданно было обнаружено, что LPR2 повсеместно распределен по всей корневой стеле, за исключением ксилемы (рис. 4b), области, намного большей, чем область отложения Fe (т. е. флоэма). Это предполагает, что для специфичного отложения Fe во флоэме и ингибирования роста PR, индуцированного NH ₄ ⁺ , необходимы другие факторы.К сожалению, мы не смогли определить относительный(е) фактор(ы) в настоящем исследовании.

Рис. 4: Распределение LPR2 в корнях и его реакция на Nh5+.

a Экспрессия pLPR2::LPR2-YFP в первичных корнях линии комплементации COM#7. Корни контрастировали йодидом пропидия (фиолетовая флуоресценция) и анализировали на флуоресценцию YFP (зеленая). b Радиальный срез (вверху) и крупный план (внизу) экспрессии pLPR2::LPR2-YFP в корне проростка COM#7, выращенного в среде Fe ^suff NH ₄ ⁺ . c Экспрессия LPR2 в корнях Col-0. Относительные уровни экспрессии нормализовали до среднего геометрического экспрессии UBQ10 и EF1α . d , e Репрезентативные гели и относительные уровни белка в корнях Col-0. Относительные уровни LPR2 оценивали по отношению интенсивности сигнала LPR2 к интенсивности актина из того же образца. c , e Представленные данные представляют собой среднее ± ± стандартное отклонение для трех биологических повторов. P значений < 0.05 указывают на значительные различия (двусторонний дисперсионный анализ с апостериорным критерием HSD Тьюки). Четырехдневные проростки указанных генотипов были перенесены на среду NO ₃ ⁻ или NH ₄ ⁺ с Fe ^suff (100 мкМ) или Fe ^low (100 мкМ) и проанализированы 4 мкМ. дней после пересадки рассады. Каждый эксперимент был повторен независимо три раза с аналогичными результатами, и показан репрезентативный эксперимент. Распределение LPR1

в PR также исследовали в трансформантах pLPR1::LPR1-YFP / lpr1-1 .Обилие LPR1-YFP было ниже в присутствии любого источника азота, но оно в основном распределялось в SCN апикальной меристемы корня и немного распространялось на слои энтодермальных клеток (дополнительная рис. 15). Разница в тканевом распределении может быть другой частью объяснения того, почему LPR1 не играет роли в опосредовании NH ₄ ⁺ -чувствительного фенотипа, как это делает LPR2.

Также была исследована реакция LPR2 в корнях Col-0 на NH ₄ ⁺ .В соответствии с приведенным выше конфокальным результатом, либо экспрессия LPR2 , либо содержание LPR2 в корнях Col-0 показали увеличение при NH ₄ ⁺ по сравнению с NO ₃ ⁻ , что также не зависело от доза добавки Fe (рис. 4c–e). Следовательно, NH ₄ ⁺ , а не Fe активирует LPR2. Интересно, что хотя экспрессия LPR2 в линиях сверхэкспрессии p35S::LPR2-GFP была одинаковой между двумя источниками N, содержание LPR2-GFP в источнике NH ₄ ⁺ -N было выше, чем в NO ₃ ⁻ — источник N (дополнительный рис.16), что указывает на посттранскрипционную регуляцию LPR2. Стоит отметить, что, хотя LPR2 был слегка сверхэкспрессирован в линиях комплементации pLPR2::LPR2-YFP/lpr2-1 (дополнительная рис. 5), их PR имели аналогичный NH ₄ ⁺ -чувствительный фенотип, как и этот проростков Col-0 (рис. 1г). Кроме того, PR линий сверхэкспрессии p35S::LPR2-GFP также имели такую ​​же чувствительность NH ₄ ⁺ , что и PR Col-0 (дополнительная рис.17а). Эти результаты показывают, что усиленная часть LPR2 вносит небольшой вклад в чувствительность NH ₄ ⁺ , и дополнительно подтверждают, что, хотя LPR2 важен, для NH ₄ ⁺ -индуцированного PR также необходимы дополнительные факторы. ингибирование роста. Стоит отметить, что линии сверхэкспрессии p35S::LPR2-GFP показали нерегулярное отложение Fe в PR в источнике NH ₄ ⁺ -N (дополнительный рисунок 17b), что указывает на то, что NH ₄ ⁺ -индуцированное специфичное для флоэмы отложение Fe зависит от специфичного для стел распределения LPR2.

NH

₄ ⁺ -индуцированное отложение Fe вызывает выброс активных форм кислорода (АФК)

Чтобы понять, как LPR2-опосредованное отложение Fe ингибирует рост PR в источнике NH ₄ ⁺ -N, мы выполнили секвенирование всего транскриптома (RNA-seq) анализ экспрессии генов в корнях проростков Col-0 и lpr2-1 (дополнительные данные 1a). Надежность данных секвенирования РНК была подтверждена анализом qRT-PCR для экспрессии десяти случайно выбранных генов с разным содержанием (дополнительная рис.18). Поскольку обработка Fe ^{с низким содержанием} и разрушение LPR2 сходным образом уменьшали ингибирование роста PR в источнике NH ₄ ⁺ -N, мы провели скрининг дифференциально экспрессируемых генов (DEG) (-1 > log ₂ [кратное изменение] > 1; значение P <0,05) путем попарного сравнения содержания транскриптов либо между двумя обработками Fe, либо между lpr2-1 и Col-0 с обработкой Fe ^suff (дополнительные данные 1b–e). В источнике NO ₃ ^— -N было только 11 DEG между двумя обработками Fe для проростков Col-0 и 87 DEG между двумя генотипами, получившими обработку Fe ^suff (дополнительная рис.19а, б). Эти DEG вряд ли связаны с развитием PR, поскольку либо обработка Fe ^{с низким содержанием} , либо разрушение LPR2 мало влияли на рост PR в источнике NO ₃ ⁻ -N.

Впоследствии мы сосредоточились на ДЭГ в источнике NH ₄ ⁺ -N. Было 182 DEG (101 с повышенной экспрессией, 81 с пониженной активностью) между двумя обработками Fe для проростков Col-0 и 130 DEG (58 с повышенной активностью; 72 с пониженной активностью) между двумя генотипами, которые получали обработку Fe ^suff (рис.5а и дополнительный рисунок 19в, г). Однако в этих двух сравнениях мы не обнаружили каких-либо ДЭГ, о которых в настоящее время известно, что они связаны с токсичностью NH ₄ ⁺ (дополнительные данные 1f). Интересно, что соотношение перекрывающихся DEG в двух приведенных выше сравнениях было высоким (рис. 5a), а анализ обогащения Gene Ontology (GO) показал, что самый большой кластер в обоих сравнениях был связан с «реакцией на окислительный стресс» (рис. 5b). .

Рис. 5: Fe-зависимое ингибирование роста первичных корней под действием Nh5+ связано со всплеском активных форм кислорода (АФК).

a , b Диаграмма Венна и анализ обогащения онтологии генов дифференциально экспрессируемых генов (DEG), которые регулируются вверх и вниз в попарных сравнениях Col-0 Fe ^low против Col-0 Fe ^suff и lpr2-1 Fe ^suff по сравнению с Col-0 Fe ^suff в источнике NH ₄ ⁺ -N. Размер кружка представляет номера генов, а цвет представляет значение P -коррекция, рассчитанная с помощью гипергеометрических тестов и скорректированная для многократного тестирования с использованием FDR. Секвенирование РНК проводили с тремя биологическими повторами на линию и условие. c Визуализация АФК в первичных корнях проростков Col-0, lpr2-1 и линии комплементации COM#7 с помощью окрашивания H ₂ DCFDA. d Крупный план H ₂ Окрашивание DCFDA первичных корней проростков Col-0, выращенных в среде Fe ^suff NH ₄ ⁺ . e Совместная локализация ложного окрашивания H ₂ O ₂ и флуоресценция флоэмного маркера эскулина в первичных корнях проростков roGFP2-Orp1, выращенных на среде Fe ^suff NH ₄ + 9013. f , g Зависимость доза-реакция удлинения первичного корня проростков Col-0, построенная как функция концентрации поглотителей АФК. Показанные данные являются средним значением ± стандартное отклонение. n  = количество саженцев. Значения P < 0,05 указывают на значительные различия (однофакторный дисперсионный анализ с апостериорным тестом Тьюки HSD). ч Изображения воздействия 750 мкМ диметилтиомочевины (DMTU) и 200 мкМ 4-гидрокси-TEMPO (TEMPO) на проростки Col-0. Четырехдневные проростки указанных генотипов пересаживали на среду NO ₃ ⁻ или NH ₄ ⁺ с Fe ^suff (100 мкМ) или Fe ^low (10 мкМ) с или без указанные поглотители АФК.Анализы проводили через 4 дня после пересадки рассады. Эксперименты ( c – h ) были повторены независимо три раза с аналогичными результатами, и показаны репрезентативные данные из одного эксперимента.

Приведенные выше результаты побудили нас провести мониторинг образования АФК в корнях. Сначала мы гистологически визуализировали АФК с использованием 2′,7′-дихлордигидрофлуоресцеиндиацетата (H ₂ DCFDA), флуоресцентного индикатора АФК. Данные показали, что NH ₄ ⁺ приводили к четкому формированию АФК в корневом стволе, что зависело либо от действия LPR2, либо от достаточного количества железа (рис. 5в). Недавно было показано, что логометрический флуоресцентный репортерный белок roGFP2-Orp1 сообщает об уровне внутриклеточного H ₂ O ₂ ²⁹ . Из-за прохождения внеклеточного H ₂ O ₂ через плазматическую мембрану через аквапорины ^30,31 образование внеклеточного H ₂ O ₂ также может косвенно отражаться репортером roGFP2-Orp1 в соседнем ячейки ²⁹ . В соответствии с наблюдаемым образованием АФК репортер roGFP2-Orp1 показал, что NH ₄ ⁺ также вызвал всплеск H ₂ O ₂ в корневых стелах в условиях Fe ^suff (дополнительная рис.20). Крупный план окрашенных DCFDA корней H ₂ показал, что всплеск АФК, запускаемый NH ₄ ⁺ , в основном происходил во флоэме (рис. 5d) и напоминал картину NH ₄ ⁺ -индуцированное отложение Fe. Это открытие было дополнительно подтверждено репортером roGFP2-Orp1 в том, что накопление H ₂ O ₂ , вызванное NH ₄ ⁺ , хорошо перекрывалось маркером флоэмы эскулином (рис. 5e).

АФК действуют ниже по течению отложения Fe, чтобы опосредовать реакцию роста на NH

₄ ⁺

Приведенные выше результаты означают, что ремоделирование развития корней в ответ на стресс NH ₄ ⁺ может быть связано со всплеском РОС.Поэтому для проверки этого предположения использовались поглотители АФК. Неожиданно добавление аскорбиновой кислоты (ASA) или глутатиона (GSH) к среде NH ₄ ⁺ с Fe ^suff привело к большему ингибированию роста PR. Вероятно, это связано с тем, что либо ASA, либо GSH могут усиливать образование гидроксильных радикалов (·OH) — одного из наиболее вредных АФК — в условиях обогащения железом в результате реакций Фентона ³² . Мы также проверили действие йодида калия-акцептора H ₂ O ₂ , но это соединение показало высокую токсичность для растений в наших условиях роста, поскольку оно могло ингибировать рост PR даже в среде NO ₃ ^— . Таким образом, мы использовали другие более мягкие поглотители АФК, включая диметилтиомочевину (DMTU) и 4-гидрокси-TEMPO (TEMPO), чтобы противодействовать избыточному производству ROS. Применение любого из этих поглотителей к проросткам Col-0 мало влияло на рост PR в среде NO ₃ ^— с Fe ^suff (дополнительный рисунок 21), но значительно восстанавливало рост PR в NH ₄ ^{. +} среда с Fe ^и в зависимости от дозы (рис. 5f–h). Результат предполагает, что Fe-зависимое ингибирование роста PR в источнике NH ₄ ⁺ -N может быть связано с избыточным образованием АФК.

Мы также исследовали отложения Fe после обработки DMTU и TEMPO. Хотя рост PR проростков Col-0 в среде Fe ^suff NH ₄ ⁺ был восстановлен в присутствии поглотителей АФК, отложение Fe во флоэме корня все еще наблюдалось (дополнительная рис. 22). Следовательно, АФК, скорее всего, действуют ниже по течению от отложения Fe, реконструируя развитие корней в источнике NH ₄ ⁺ -N. Однако применение любого поглотителя АФК увеличивало расстояние между начальным участком NH ₄ ⁺ , индуцированным отложением Fe, и кончиком корня.Вероятно, это связано с улучшением развития зоны роста корней за счет поглотителей АФК.

NH

₄ ⁺ вызывает отложение каллозы во флоэме

Появляется все больше доказательств того, что АФК регулируют отложение каллозы ³³ . Поэтому мы исследовали образование каллозы с помощью окрашивания анилиновым синим (рис. 6а). Для проростков Col-0, обработанных Fe ^suff , источник NH ₄ ⁺ -N привел к массивному отложению каллозы в корневом стволе по сравнению с источником NO ₃ ^— -N.Это индуцированное NH ₄ ⁺ отложение каллозы было полностью подавлено либо разрушением LPR2 в проростках lpr2-1 , либо обработкой Fe ^low в проростках Col-0. Линия комплементации COM#7 вела себя подобно Col-0. Следовательно, NH ₄ ⁺ индуцирует отложение каллозы в корневой стеле LPR2- и Fe-зависимым образом. Кроме того, как крупный план, так и радиальный разрез корней Fe ^suff NH ₄ ⁺ Col-0 показали, что отложение каллозы в основном локализовано в двух полюсах корневой стелы (рис.6б).

Рис. 6: Fe-зависимое отложение каллозы во флоэме посредством активных форм кислорода (АФК) в ответ на Nh5+.

a Обнаружение каллозы в первичных корнях проростков Col-0, lpr2-1 и линии комплементации COM#7 с помощью окрашивания анилиновым синим. b Радиальный разрез (вверху) и крупный план (внизу) окрашивания анилиновым синим первичных корней проростков Col-0, выращенных в среде Fe ^suff NH ₄ ⁺ . c Флуоресцентная совместная локализация GFP-спорамина и окрашивания анилиновым синим в корнях pSUC2::GFP-спорамин . d поглотители АФК устраняли NH ₄ ⁺ -индуцированное отложение каллозы. Четырехдневные проростки указанных генотипов пересаживали на среду NO ₃ ⁻ или NH ₄ ⁺ с Fe ^suff (100 мкМ) или Fe ^low (10 мкМ) с или без указанный поглотитель АФК. Каждый эксперимент был повторен независимо три раза с аналогичными результатами, и показан репрезентативный эксперимент.

Чтобы определить тип клеток для этих двух полюсов, окрашивание анилиновым синим проводили в корнях трансформантов pSUC2::GFP-sporamin , в которых маркер GFP-спорамин был рестриктирован во флоэмных файлах, включая ситовидные элементы и клетки-компаньоны ³⁴ .Конфокальный анализ показал, что окрашивание анилиновым синим хорошо накладывалось на маркер GFP-спорамин в корнях, подвергнутых обработке Fe ^suff NH ₄ ⁺ , показывая, что NH ₄ ⁺ -зависимое отложение каллозы локализовано в флоэма (рис. 6c). При большом увеличении было обнаружено, что каллоза расположена на периферии ситовидных элементов (дополнительный рисунок 23), что поразительно похоже на локализацию отложений Fe.

Стоит отметить, что, хотя ни DMTU, ни TEMPO не отменили индуцированное NH ₄ ⁺ отложение Fe во флоэме корня (дополнительный рис.22), они существенно блокировали отложение каллозы во флоэме (рис. 6г). Следовательно, всплеск АФК действует после отложения Fe, вызывая отложение каллозы в ответ на стресс NH ₄ ⁺ .

Нарушение действия флоэмы отвечает за реакцию роста на NH

₄ ⁺

Поскольку отложение каллозы во флоэме может повлиять на действие флоэмы, для оценки воздействия40 2NH 9004 был использован флоэмомобильный зонд эскулин ³⁵ . 4 ⁺ воздействие на флоэму.Скорость транспорта флоэмы (PTV) определяли путем деления расстояния, пройденного эскулином между двумя метками, на прошедшее время ³⁶ . Данные показали, что NH ₄ ⁺ значительно ингибировал PTV в PR проростков Col-0 по сравнению с источником NO ₃ ⁻ -N в условиях Fe ^suff , тогда как любое нарушение LPR2 в lpr2 Мутанты -1 или обработка Fe ^low проростков Col-0 полностью устраняли это ингибирование. Линия комплементации COM#7 вела себя так же, как Col-0 (рис. 7а). Затем мы сосредоточились на разгрузке флоэмы. Как только эскулин был импортирован в кончик корня, были записаны отдельные изображения вместе с временем их получения ³⁷ . Как и ожидалось, NH ₄ ⁺ сильно останавливали выгрузку эскулина из флоэмы в зоне роста корня LPR2- и Fe-зависимым образом (рис. 7б). Эти результаты показывают, что NH ₄ ⁺ ухудшает функцию флоэмы посредством действия LPR2 и Fe.

Рис. 7: Ингибирование действия флоэмы и комплементация сахарозой роста первичного корня в среде Nh5+.

a , b Скорость транспорта флоэмы и выгрузка эскулина из флоэмы. Центральная линия представляет собой среднее значение, а границы прямоугольника — стандартное отклонение; усы указывают минимальное и максимальное значения. Значения P < 0,05 указывают на значительные различия (двусторонний ANOVA с апостериорным критерием HSD Тьюки, n  = 12 проростков на линию и условие). Четырехдневные проростки Col-0, lpr2-1 и комплементарной линии COM#7 переносили на среду NO ₃ ⁻ или NH ₄ ⁺ с Fe ^suff (100 мкМ ) или Fe ^low (10 мкМ) и анализировали через 4 дня после переноса рассады. c Реакция роста отделившихся первичных корней на локализованное поступление сахарозы. Показанные данные являются средним значением ± стандартное отклонение. Значения P < 0,05 указывают на значительные различия (двусторонний дисперсионный анализ с апостериорным критерием HSD Тьюки, n  = 16 отделенных первичных корней на линию и условие). Вставка: схема, изображающая анализ реакции роста отсоединенных первичных корней на локализованное снабжение сахарозой. У четырехдневных сеянцев вырезали корни (1  см). Отделенные корни затем переносили в вертикальную двухслойную агаровую систему со средой NO ₃ ^— или NH ₄ ⁺ с Fe ^suff или Fe ^low . Верхние слои обрабатывали различными дозами сахарозы, а нижние слои сахарозой не занимались. Анализы проводили через 3 дня после пересадки рассады. Каждый эксперимент был повторен независимо трижды с аналогичными результатами, и показан репрезентативный эксперимент.

Поскольку эскулин загружается во флоэму переносчиком сахарозы SUC2 ^35,38 , нарушение транспорта флоэмы и выгрузка эскулина отражают ингибирование поступления сахарозы в зону роста корней. Поэтому мы исследовали, связан ли LPR2-зависимый NH ₄ ⁺ -чувствительный фенотип с недостаточным выделением сахарозы в зону роста корней.Поскольку все вышеперечисленные тесты проводились с использованием сеянцев, подкормленных 1% сахарозой, нам сначала нужно было выяснить искусственный эффект от экзогенной сахарозы. Мутанты lpr2-1 по-прежнему демонстрировали лучший рост PR, чем проростки Col-0 на среде NH ₄ ⁺ , не содержащей сахарозы, хотя разница между ними была немного меньше по сравнению с таковой у растений, дополненных 1% сахарозы. (Дополнительный рис. 24). Таким образом, генотип-специфическая реакция роста на источник азота во многом зависит от нативных биологических процессов растений.

В последующих тестах мы использовали отдельные PR, чтобы исключить потенциальное влияние источника сахарозы побегов разных генотипов на рост их корней. Отделенные PR были перенесены в вертикальную двухслойную разделенную агаровую систему с отсутствием сахарозы в нижнем слое и присутствием различных доз сахарозы в верхнем слое (рис. 7c). При обработке без сахарозы отделенные PR почти полностью потеряли способность к росту независимо от источника азота и генотипа, что указывает на важность транспортируемой флоэмой сахарозы для поддержания роста корней.Для проростков Col-0 разница в росте отдельных PR между источниками NO ₃ ⁻ -N и NH ₄ ⁺ -N с Fe ^suff сильно зависела от дозы сахарозы: наиболее значимо при обработке 1% сахарозой, но оно уменьшалось при более низких дозах сахарозы, поскольку рост PR ингибировался в обоих источниках азота.