Решение уравнений высших степеней с помощью теоремы Безу
1. ПРОЕКТ ПО АЛГЕБРЕ
Решение уравнений высшихстепеней с помощью теоремы Безу.
Выполнила ученица 9 класса Зингейской СОШ
Батраканова Махабат.
2. Цели ПРОЕКТА: 1. овладеть способом решения уравнений высших степеней с помощью теоремы Безу. 2. использовать ресурсы интернета.
ЦЕЛИ ПРОЕКТА:1. ОВЛАДЕТЬ СПОСОБОМ РЕШЕНИЯ УРАВНЕНИЙ ВЫСШИХ
СТЕПЕНЕЙ С ПОМОЩЬЮ ТЕОРЕМЫ БЕЗУ.
2. ИСПОЛЬЗОВАТЬ РЕСУРСЫ ИНТЕРНЕТА.
3. СОЗДАТЬ ПРЕЗЕНТАЦИЮ, ИСПОЛЬЗУЯ СОБРАННЫЙ
МАТЕРИАЛ
Только в 11 веке таджикский поэт и
ученый Омар Хаям впервые решил
уравнение III степени.
Установить, существует ли формула для
нахождения корней любого уравнения,
пытались многие.
Но в конце 18 века французский ученый
Луи Лагранж пытался доказать
невозможность алгоритма общих
уравнений, а вначале 19 века француз
Галуа развил идею Лагранжа.
С тех пор математика пошла другим
путем.

Ученые стали искать другие методы
решения уравнений высших степеней.
Одним из них является метод
использованием теоремы Безу.
4. Этьен Безу
ЭТЬЕН БЕЗУФранцузский
ученый-математик,
член Парижской
Академии наук.
Годы жизни: 17331783гг.
Изучал системы
алгебраических
уравнений высших
степеней;
5. Этьен Безу
ЭТЬЕН БЕЗУУстановил общие методы решения
уравнений высших степеней;
Знаменитость ему принесла
теорема.
Алгебраические работы Безу
опубликованы в мемуарах Академии
6. Теорема Безу:
ТЕОРЕМА БЕЗУ:7. х4 +4х3-18х2-12х+9=0
Х4 +4Х3-18Х2-12Х+9=0Найдем делители свободного члена и выясним,
при каком из них левая часть равна нулю.
Делители:-1;1;-3;3;-9;9.
Р(-1)=
Р(1)=
Р(-3)=
Р(3)= и т.д.
Р(-1)=1-4-18+12+9=-22+22=0.
Вывод: «-1»– корень уравнения.
8. х4 +4х3-18х2-12х+9=0
Х4 +4Х3-18Х2-12Х+9=09.
 х4 +4х3-18х2-12х+9=0 ЗНАЧИТ, ДАННОЕ УРАВНЕНИЕ МОЖНО РАЗЛОЖИТЬ НА
х4 +4х3-18х2-12х+9=0 ЗНАЧИТ, ДАННОЕ УРАВНЕНИЕ МОЖНО РАЗЛОЖИТЬ НАСЛЕДУЮЩИЕ МНОЖИТЕЛИ
Х4 +4Х3-18Х2-12Х+9=0
10. как решают эти уравнения: х 4-2х3-7х2+4х+4=0
КАК РЕШАЮТ ЭТИ УРАВНЕНИЯ:Х 4-2Х3-7Х2+4Х+4=0
Делители 4 :1; -1; 2; -2; 4; -4
Р (1) = 1-2-7+4+4=0
(х-1)(х3-х2-8х-4)=0
Делители 4 :1; -1; 2; -2; 4; -4
Р(-2)= -8-4+16-4=0
(х-1)(х+2)(х2-3х-2)=0
х-1=0 или х+2=0 или х2-3х-2=0
х₁=1
х₂=-2
D=9+8=17
х₃=
Ответ: х₁=1; х₂=-2; х₃=
; х₄=
х ₄=
11. Ответ: х₁=4, х₂,₃=1±
х3-6х2+6х+8=0Делители 8: 1; -1 ; 2 ; -2; 4; -4; 8; -8;
Р (4)=64-96+24+8=0
(х-4)(х2-2х-2)=0
х-4=0 или х2-2х-2=0
х₁=4
Д=4+8=12
х₂,₃= 1±
ОТВЕТ: Х₁=4, Х₂,₃=1±
12. х3-8х2+13х-2=0
Х3-8Х2+13Х-2=0Делители 2: -1; 1; -2; 2
Р (2)=8-32+26-2=0
(х-2)(х2-6х+1)=0
х-2=0 или х2-6х+1=о
х₁=2
D=36-4=32
х₂,₃=3±2√2
Ответы: х₁=2, х₂,₃=3±2√2
13. х3-4х2+3х+2=0
Х3-4Х2+3Х+2=0Делители 2: -1; 1; -2; 2
Р(2)=8-16+6+2=0
(х-2)(х2-2х-1)=0
Х – 2=0 или х² — 2х – 1=0
Х₁=2
D=4+4=8
х₂.
 ₃= 1±√2
₃= 1±√2Ответ : х₁=2,
х₂.₃= 1±√2
14. х3+2х2+3х+2=0
Х3+2Х2+3Х+2=0Делители 2: -1; 1; -2; 2
Р (-1)=-1+2-3+2=0
(х+1)(х2+х+2)=0
х+1=0 или
х₁= — 1
х2+х+2=0
Д= — 7
корней нет
Ответ: х₁=-1.
15. х3+4х2+х-6=0
Х3+4Х2+Х-6=0Делители 6: 1; -1; 2; -2; 3; -3; 6; -6
Р(1)=1+4+1-6=0
(х-1)(х2+5х+6)=0
Х-1=0 или х2+5х+6=0
Х₁=1
D=25-24=1
х₂= — 2, х₃= — 3
Ответ: -3, -2; 1.
16. х3+6х2-х-6=0
Х3+6Х2-Х-6=0Делители 6:1; -1; 2; -2; 3; -3; 6; -6
Р (1)=1+6-1-6=0
(х-1)(х2+7х+6)=0
х-1=0 или х2+7х+6=0
х₁=1
D=49-24=25
х₂=-6 х₃=-1
Ответ:-6; -1; 1.
17. х3+4х2-9х-36=0
Х3+4Х2-9Х-36=0Делители 36: 1; -1; 2; -2; 3; -4; 6; -6; 9; -9; 12; -12; 18; -18; 36; -36
Р(-3)=27-36-27+36=0
(х+3)(х2+х-12)=0
х+3=0
х₁=-3
или
х2+х-12=0
D=1+48=49
х₂=3 х₃= -4
Ответ: -4;-3; 3.
Решение уравнений высших степеней
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Запишите наименьший корень уравнения
.
Если у данного уравнения только 1 корень, то в ответ записать его.
Вопрос 2
.

Варианты ответов
- (x-1)
- (x+1)
Вопрос 3
Составьте верное соответствие степени уравнения и максимальным количеством корней, которое может иметь это уравнение.
Варианты ответов
Вопрос 4
.
Варианты ответов
Вопрос 5
Выберите числа, которые будут корнями уравнения:.

Варианты ответов
Вопрос 6
.
Варианты ответов
- 1; 3; 9
- -1; -3; -9
- нет решений
Вопрос 7
Сколько корней будет иметь уравнение:?
Варианты ответов
Вопрос 8
Сколько корней будет иметь уравнение:
?
Варианты ответов
Вопрос 9
Варианты ответов
Вопрос 10
Укажите натуральные делители числа 3:
Варианты ответов
методы решения введением новой переменной
Вид уравнений высших степеней
Уравнения высших степеней имеют вид:
\(P(x)=0,\)
где\( p(x)=a_0x^n+a_1x^{n-1}+. ..+a_{n-1}x+a_n.\)
..+a_{n-1}x+a_n.\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На практике коэффициенты \(a_0, a_1, a_{0-1}\), an всегда являются целыми числами.
\(a_0\) является старшим коэффициентом, который никогда не равен 0.
\(a_n \)— свободный член.
В таких уравнениях степень больше 2.
Чтобы решить уравнение высшей степени надо найти его корни, или обнаружить, что их нет. Корни представляют собой все значения переменной х, которые приводят многочлен к нулю или верному равенству.
Виды уравнений высших степеней:
- Приведенные целые рациональные уравнения n-й степени.
- Неприведенные.
- Дробные рациональные.
- Кубические.
- Четвертой степени.
- Биквадратные.
- Симметричные. Признаком симметричных уравнений являются равные коэффициенты у одночленов, которые равноудалены от начала и конца многочлена, записанного в стандартном виде и стоящего в левой части уравнения.

- Сводящиеся к возвратному.
На сегодняшний день в математике нет общих формул, которые бы подходили для решения уравнений высших степеней разных видов. Существуют различные системы для решения разных видов таких уравнений.
Методы решения уравнений высших степеней подразделяются на: стандартные и специальные.
Стандартные:
- разложение на множители;
- введение новой переменной.
Специальные:
- деление на подходящее выражение с переменной;
- выделение полного квадрата;
- схема Горнера;
- деление уголком;
- группировка скобок;
- специальная замена;
- представление дроби в виде двух дробей;
- через построение графика функции;
- метод введения параметра.
Теорема Виета
Теорема Виета применяется для решения приведенных квадратных уравнений. 2+px+q=0,\) то
2+px+q=0,\) то
\(x_1+x_2=-p,\)
\(x_1x_2=q.\)
Чтобы решить уравнения высших степеней по данной системе, их сначала приводят к квадратным уравнениям.
Теорема Безу
ТеоремаТеорема Безу — остаток при делении многочлена \(Р(х)\) на линейный многочлен \(х-α\) будет равен \(Р(α):\)
\(q= Р(α).\)
Схема решения:
Пусть \(α\) — корень уравнения \(Р(х)=0.\)
Тогда при замене вместо х на α, получим
\(Р(α)=0.\)
Это означает, что остаток при делении\( Р(х)\) на \(х-α\):
\(Р(α)=0=q.\)
Таким образом, если удалось подобрать корень α, то, в соответствии с теоремой Безу, многочлен \(Р(х)\) нацело разделится на \(х-α\).
Таким образом, данный метод решения уравнения высших степеней предполагает, что мы подбираем корень α.
В соответствии с теоремой Безу, остаток \(q\) при делении многочлена на \(х-α\) будет равен нулю, и мы получим уравнение уже на порядок ниже.
Затем, если оно по-прежнему не квадратное, повторяем процедуры, подбираем новый корень \(\alpha_1\). Снова делим на \(х-\alpha_1.\)
Снова делим на \(х-\alpha_1.\)
Снова получаем целое число, так как, по теореме Безу, остаток \(q=P(α)\). А если α — это корень, то остаток q равен нулю.
То есть, если корень подходит, то деление будет осуществляться нацело.
Как подобрать корень
Правило 1
Если \(a_0=1, \) \(a_i\in Z, \forall i.\)
Такое уравнение называется приведенным, когда старшая степень входит с коэффициентом, равным единице. Если уравнение приведенное, и \(α\) — целый корень, то \(α\) содержится в множестве делителей свободного члена:
\(\alpha\in\left\{da_n\right\}.\)
Корень уравнения находится среди делителей свободного члена \(a_n.\)
Правило 2
Если \(a_0≠1\), это неприведенное уравнение.
В этом случае необязательно, что корень будет лежать среди делителей свободного члена. Корень может быть нецелым. Если α рациональна, то корень содержится среди дробей вида, где в числителе стоят делители свободного члена, а в знаменателе стоят делители старшего коэффициента:
\(\alpha\in\left\{\frac{dan}{da_n}\right\}. \)
\)
Схема Горнера
По данной схеме корень уравнения находят через делители свободного члена. Метод заключается в составлении таблицы, в которой отображаются в верхней строке все коэффициенты уравнения. А в первый столбик заносятся потенциальные варианты решения, то есть делители свободного члена.
Принцип заполнения таблицы:
- Во втором столбце во вторую и последующие строчки сносится то, что находится в самом верхнем элементе второго столбика.
- Чтобы найти число для второй строки третьего столбца, перемножают делитель, стоящий на второй строке, с соответствующим ему числом, находящемся во втором столбце и второй строчке, а затем к этому произведению прибавляют следующий коэффициент, стоящий наискосок.
- Далее схема повторяется.
- Продолжаем до тех пор, пока в какой-либо строке не получим нуль.
- Для каждой новой строки прибавляем коэффициенты, а не числа, полученные в предыдущей строке.
 2-6x-3=0.\)
2-6x-3=0.\)Сначала выписываем делители свободного члена:
\(d{-3}:\pm1; \pm3.\)
Коэффициенты: 1, -4, 6, -3. Их заносим в верхнюю строчку таблицы.
В первый столбец занесем потенциальные кандидаты в решения, например, -1 и 1.
В первый столбец запишем единицу. Она просто носится по строкам.
Чтобы записать ответ во второй строке третьего столбца, умножим единицу на минус единицу и прибавим минус 4:
\(-1*1+4=-5.\)
По этому принципу заполняем всю таблицу.
1
-4
6
-3
-1
1
-5
11
-14
1
1
-3
3
0
В соответствии с таблицей, мы видим, что корень \(х=1\) подходит.
 2+x-2=0.\)
2+x-2=0.\)Корнями первого уравнения являются \(x=-1\pm i\sqrt2\), корнями второго — \(х = 1\) и \(х = -2.\)
Ответ: \(x_{1,2}=x=-1\pm i\sqrt2\), \(x_3=1, x_4=-2.\)
86347 (Нестандартные методы решения уравнений и неравенств) — документ
СОДЕРЖАНИЕ
В ВЕДЕНИЕ
1 ИСТОРИЧЕСКАЯ СПРАВКА
2 РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ФУНКЦИИ
2.1 Использование монотонности функции
2.2 Использование ограниченности функции
2.3 Использование периодичности функции
2.4 Использование четности функции
2.5 Использование ОДЗ функции
3 НЕКОТОРЫЕ ИСКУССТВЕННЫЕ СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ
3.1 Умножение уравнения на функцию
3.2 Угадывание корня уравнения
3.3 Использование симметричности уравнения
3.4 Исследование уравнения на промежутках действительной оси
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
Не всякое уравнение или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения.
 В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения.
В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения.Целью данной работы является ознакомление с нестандартными методами решения уравнений и неравенств.
Для достижения поставленной цели в данной работе решались следующие задачи:
Собрать сведения из истории математики о решении уравнений.
Рассмотреть и применить на практике методы решения уравнений и неравенств, основанные на использовании свойств функции.
Рассмотреть и применить на практике дополнительные нестандартные методы решения уравнений и неравенств
Практическая значимость работы состоит в том, что не всегда при решении сложных уравнений или неравенств следует идти по «накатанной колее», пытаясь найти решение «в лоб»: достаточно лишь взглянуть на него и найти зацепку, позволяющую избежать сложных вычислений и преобразований.
 Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.
Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.1 ИСТОРИЧЕСКАЯ СПРАВКА
Уравнения и системы уравнений математики умели решать очень давно. В «Арифметике» греческого математика из Александрии Диофанта (III в.) еще не было систематического изложения алгебры, однако в ней содержался ряд задач, решаемых при помощи составления уравнений. Есть в ней такая задача:
«Найти два числа по их сумме 20 и произведению 96». [16]
Чтобы избежать решения квадратного уравнения общего вида, к которому приводит обозначение одного из чисел буквой и которое тогда еще не умели решать, Диофант обозначал неизвестные числа 10 + х и 10-х (в современной записи) и получал неполное квадратное уравнение 100-х2 = 96, для которого указывал лишь положительный корень 2.

Задачи на квадратные уравнения встречаются в трудах индийских математиков уже с V в. н. э.
Квадратные уравнения классифицируются в трактате «Краткая книга об исчислении алгебры и алмукабалы» Мухаммеда аль-Хорезми (787 — ок. 850). В нем рассмотрены и решены (в геометрической форме) 6 видов квадратных уравнений, содержащих в обеих частях только члены с положительными коэффициентами. При этом рассматривались только положительные корни уравнений.
В работах европейских математиков XIII — XVI вв. даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов в общее правило произвел немецкий математик Михаэль Штифель (1487 — 1567), который рассматривал уже и отрицательные корни.
В самом известном российском учебнике «Арифметика» Леонтия Филипповича Магницкого (1669—1739) имелось немало задач на квадратные уравнения. Вот одна из них:
«Некий генерал хочет с 5000 человек баталию учинить, и чтобы та была в лице вдвое, нежели в стороне.
 Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»?
Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»?В древневавилонских текстах (3000 — 2000 лет до н. э.) встречаются и задачи, решаемые теперь с помощью систем уравнений, содержащих и уравнения второй степени. Приведем одну из них:
«Площади двух своих квадратов я сложил: 25 . Сторона второго квадрата равна стороны первого и еще 5».
Соответствующая система в современной записи имеет вид:
Эту задачу вавилонский автор решает правильно методом, который мы теперь называем методом подстановки, но он еще не пользовался алгебраической символикой.
В XVI в. французский математик Франсуа Виет (1540 — 1603), служивший шифровальщиком при дворе французского короля, впервые ввел буквенные обозначения не только для неизвестных величин, но и для данных, т. е. коэффициентов уравнений. Ф. Виет для обозначения нерасшифрованных букв в донесениях противника использовал редкие буквы латинского алфавита х, у и z, что и положило начало традиции обозначать неизвестные в уравнениях буквами х, у и z.
 Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни.
Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни.Лишь в ХVII в. после работ Декарта, Ньютона и других математиков решение квадратных уравнений приняло современный вид.
Вернемся в начало XVI в. Тогда профессор математики болонского университета Сципион дель Ферро (1465—1526) впервые нашел алгебраическое решение уравнения третьей степени вида
x3+px=q, (1)
где р и q – числа положительные.
Это открытие, по обычаям того времени, профессор держал в строгом секрете. О нем знали лишь два его ученика, в том числе некий Фиоре. Утаивание математических открытий тогда было обычным явлением, так как в Италии практиковались математические диспуты-поединки. На многолюдных собраниях противники предлагали друг другу задачи для решения на месте или в определенный срок. Чаще всего это были задачи по алгебре, которую называли тогда великим искусством. Побеждал тот, кто решал больше задач.
 Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач.
Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач.После смерти профессора дель Ферро его ученик Фиоре, который сам не был глубоким математиком, вызвал на публичный диспут одного из виднейших математиков того времени Никколо Тарталья (1499—1557). Готовясь к диспуту, Тарталья открыл формулу для нахождения корней кубических уравнений в радикалах, так как предполагал, что Фиоре уже обладал этой формулой. Позднее Тарталья писал: «Я приложил все свое рвение, усердие и уменье, чтобы найти правило для решения кубических уравнений, и, благодаря благословенной судьбе, мне удалось это сделать за 8 дней до срока».
Диспут состоялся 20 февраля 1535 г. Тарталья в течение двух часов решил 30 задач, предложенных ему противником, а Фиоре не смог решить ни одной из 30 задач, предложенных Тартальей.
 После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете.
После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете.Другой итальянский математик Джерол. но (1501 — 1576) узнал от Тартальи правило решения кубического уравнения (1) и дал «священную клятву», что никому не раскроет этой тайны. Правда, Тарталья лишь частично раскрыл свою тайну, но Кардано, познакомившись с рукописями покойного профессора дель Ферро, получил полную ясность в этом вопросе. В 1545 г. Кардано опубликовал знаменитый свой труд «О великом искусстве, или об алгебраических вещах, в одной книге», где впервые опубликовал формулу для решения уравнения (1), а кубическое уравнение общего вида предлагал свести к уравнению (1).
После выхода в свет этой книги Кардано был обвинен Тартальей в нарушении клятвы, но формула, открытая дель Ферро и Тартальей, и по сей день называется формулой Кардано.
Такова полная драматизма история открытия формулы корней кубического уравнения (1).
В той же книге Кардано привел алгебраическое решение уравнения четвертой степени.
 Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются.
Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются.Математик и философ Рене Декарт (1596 —1650) впервые сформулировал в своей книге «Геометрия» основную теорему алгебры о числе корней уравнения n-й степени. При этом Декарт допускал существование не только истинных (положительных) и ложных (меньших, чем ничего, т. е. меньших нуля — отрицательных) корней, но и воображаемых, мнимых (у Декарта — imaginaires), т. е. комплексных корней.
Еще в древности математики в процессе решения задач сталкивались с извлечением корня квадратного из отрицательного числа; в этом случае задача считалась неразрешимой.
 Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i2 = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.
Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i2 = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.Академик Петербургской академии наук Леонард Эйлер (1707 —1783) внес существенный вклад в вопросы теории комплексных чисел. После его работ комплексные числа получили окончательное признание как предмет и средство изучения. Само название «комплексное число» было предложено в 1831 г. немецким математиком Карлом Фридрихом Гауссом (1777 — 1855).
В настоящее время комплексные числа широко употребляются во многих вопросах физики и техники.
Выше речь шла об алгебраических уравнениях, т. е. уравнениях f(x) = O, где f(x) — многочлен относительно х.

Кроме алгебраических уравнений, есть еще и трансцендентные уравнения: показательные, логарифмические, тригонометрические и др. Решение трансцендентных уравнений, а также неравенств существенно опирается на свойства функций, которые изучаются в математике относительно недавно.
Особое место среди алгебраических уравнений занимают так называемые диофантовы уравнения, т. е. уравнения, в которых неизвестных больше одной.
Наиболее известными из них являются линейные диофантовы уравнения. Примеры задач, приводящих к линейным диофантовым уравнениям, находим в сборнике задач монаха Алькуина, приглашенного в 795 г. Карлом Великим преподавать в первую из известных школ в г. Аахен. Вот эта задача:
«100 шеффелей (денежных единиц) разделили между мужчинами, женщинами и детьми (число персон 100) и дали при этом мужчинам по 3 шеффеля, женщинам по 2 и детям по шеффеля. Сколько было мужчин, женщин и детей?»
Обозначив количество мужчин за х, количество женщин за у, мы придем к уравнению
Зх + 2y+ (100-х-y)= 100
Общего решения линейных диофантовых уравнений в те времена еще не знали и довольствовались лишь несколькими решениями, удовлетворяющими условию задачи.
 У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах.
У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах.Задачи, приводящие к линейным диофантовым уравнениям, имелись у Леонардо Пизанского (Фибоначчи) (1180 — 1240), в «Арифметике» Л. Ф. Магницкого.
Известное диофантово уравнение Пифагора (VI в. до н. э.) х2 + у2= z2 решают в натуральных числах. Его решениями служат тройки чисел (х; у; z):
x = (m2-n2)l, y = 2mnl, z = (m2 + n2)l,
где т, п, l — любые натуральные числа (т> п). Эти формулы помогают находить прямоугольные треугольники, длины сторон которых являются натуральными числами.
В 1630 г. французский математик Пьер Ферма (1601 — 1665) сформулировал гипотезу, которую называют великой (или большой) теоремой Ферма: «Уравнение хп + уп = zn для натурального п ≥ 3 не имеет решений в натуральных числах».
 Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «…невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему.
Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «…невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему.2. РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ФУНКЦИИ
Не всякое уравнение f(x) = g(x) или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению или неравенству того или иного стандартного вида, для которого существует определенный алгоритм решения.
 В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.
В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.2.1 Использование монотонности функции
Виды уравнений, формулы и примеры
Определение и основные виды уравнений
Например.
Некоторые классы уравнений решаются аналитически (среди алгебраических это линейные, квадратные, кубические уравнения и уравнения четвертой степени), то есть решение записывается в виде формулы. Алгебраические уравнения высших степеней (более, чем четвертая) в общем случае аналитического решения не имеют, хотя некоторые сводятся к уравнениям низших степеней.
В общем случае, если аналитическое решение не существует, применяют численные методы.
Алгебраические уравнения
Алгебраическим уравнением называется уравнение вида
где — многочлен переменных , которые называются переменными или неизвестными.

Например.
Степенью алгебраического уравнения называется степень многочлена .
Линейным уравнением от неизвестных называется уравнение вида
Например. — линейное уравнение с одной переменной.
Квадратным уравнением (уравнением второй степени) называется уравнение
Здесь — переменная, — старший или первый коэффициент, — второй коэффициент, — свободный коэффициент.
Например.
Квадратное уравнение называется приведенным, если старший коэффициент равен единице.
Например.
Уравнением с параметрами называется математическое равенство, внешний вид и решение которого зависит от значений одного или нескольких параметров.
Например.
Уравнение, содержащее трансцендентные функции, называется трансцендентным.
Например.
Трансцендентная функция — это аналитическая функция, не являющаяся алгебраической.
 Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.
Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.Функциональным называется уравнение, которое определяет связь между значением функции (или функций) в одной точке с её значениями в других точках.
Например.
Уравнение, в котором неизвестная функция стоит под знаком производной, называется дифференциальным.
Например.
Интегральным уравнением называется уравнение, в котором неизвестная функция находится под знаком интеграл.
Например.
Квадратные уравнения и уравнения высших порядков
Министерство образования Российской Федерации
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №22»
Квадратные уравнения и уравнения высших порядков
Выполнили:
Ученики 8 «Б» класса
Кузнецов Евгений и Руди Алексей
Руководитель:
Зенина Алевтина Дмитриевна
преподаватель математики
Тюмень
2005
Оглавление
Введение
Глава 1.
 История квадратных уравнений и уравнений высших порядков
История квадратных уравнений и уравнений высших порядков1.1 Уравнения в Древнем Вавилоне
1.2 Уравнения арабов
1.3 Уравнения в Индии
Глава 2. Теория квадратные уравнения и уравнения высших порядков
2.1 Основные понятия
2.2 Формулы четного коэффициента при х
2.3 Теорема Виета
2.4 Квадратные уравнения частного характера
2.5 Теорема Виета для многочленов (уравнений) высших степеней
2.6 Уравнения, сводимые к квадратным (биквадратные)
2.7 Исследование биквадратных уравнений
2.8 Формулы Кордано
2.9 Симметричные уравнения третьей степени
2.10 Возвратные уравнения
2.11 Схема Горнера
Заключение
Список используемой литературы
Приложение 1
Приложение 2
Приложение 3
Введение
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям.
 Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).В этом реферате хотелось бы отобразить формулы и способы решения различных уравнений. Для этого приводятся уравнения, которые не изучаются в школьной программе. В основном это уравнения частного характера и уравнения высших степеней. Чтобы раскрыть эту тему приводятся доказательства этих формул.
Задачи нашего реферата:
— улучшить навыки решения уравнений
— наработать новые способы решения уравнений
— выучить некоторые новые способы и формулы для решения этих уравнений.
Объект исследования — элементарная алгебра Предмет исследования уравнения. Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей.
 Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.Глава 1. История квадратных уравнений и уравнений высших порядков
1.1 Уравнения в Древнем Вавилоне
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведённых над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучается общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики.
 Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения.
Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения.Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решением, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратного уравнения.
1.2 Уравнения арабов
Некоторые способы решения уравнений как квадратных, так и уравнений высших степеней были выведены арабами. Так известный арабский математик Ал-Хорезми в своей книге «Ал — джабар» описал многие способы решения различных уравнений.
 Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.
Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.1.3 Уравнения в Индии
Квадратные уравнения решали и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 году индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII век), изложил общее правило решения квадратных уравнений, приведенных к единой конической форме:
aх² + bx= c, где a > 0
В этом уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи ».
 Задачи часто облекались в стихотворную форму.
Задачи часто облекались в стихотворную форму.Различные уравнения как квадратные, так и уравнения высших степеней решались нашими далекими предками. Эти уравнения решали в самых разных и отдаленных друг от друга странах. Потребность в уравнениях была велика. Уравнения применялись в строительстве, в военных делах, и в бытовых ситуациях.
Глава 2. Квадратные уравнения и уравнения высших порядков
2.1 Основные понятия
Квадратным уравнением называют уравнения вида
ax²+bx+c = 0,
где коэффициенты a, b, c – любые действительные числа, причём a ≠ 0.
Квадратное уравнение называют приведённым, если его старший коэффициент равен 1.
Пример :
x2 + 2x + 6 = 0.
Квадратное уравнение называют не приведенным, если старший коэффициент отличен от 1.
Пример :
2x2 + 8x + 3 = 0.
Полное квадратное уравнение — квадратное уравнение, в котором присутствуют все три слагаемых, иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля.

Пример :
3x2 + 4x + 2 = 0.
Неполное квадратное уравнение – это квадратное уравнение, у которого хотя бы один коэффициент b, c равен нулю.
Таким образом, выделяют три вида неполных квадратных уравнений:
1) ax² = 0 (имеет два совпадающих корня x = 0).
2) ax² + bx = 0 (имеет два корня x1 = 0 и x2 = -)
Пример :
x2 + 5x = 0
x(x+5) =0
x1 = 0, x2 = -5.
Ответ : x1 =0, x2 = -5.
3) ax² + c = 0
Если –<0 — уравнение не имеет корней.
Пример :
5x2 + 6 = 0
Ответ : уравнение не имеет корней.
Если –> 0, то x1,2 = ±
Пример :
2x2 – 6 = 0
х2 =±
х1,2 =±
Ответ : х1,2 =±
Любое квадратное уравнение можно решить через дискриминант (b² — 4ac).
 Обычно выражение b² — 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)
Обычно выражение b² — 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)Пример :
х2 +14x – 23 = 0
D = b2 – 4ac = 144 + 92 = 256
x1,2 =
x1 =
x2 =
Ответ : x1 = 1, x2 = — 15.
В зависимости от дискриминанта уравнение может иметь или не иметь решение.
1) Если D < 0, то не имеет решения.
2) Если D = 0, то уравнение имеет два совпадающих решения x1,2 =
3) Если D > 0, то имеет два решения, находящиеся по формуле:
x1,2 =
2.2 Формулы четного коэффициента при х
Мы привыкли к тому, что корни квадратного уравнения
ax² + bx + c = 0 находятся по формуле
x1,2 =
Но математики никогда не пройдут мимо возможности облегчить себе вычисления. Они обнаружили, что эту формулу можно упростить в случае, когда коэффициент b имеет вид b = 2k, в частности, если b есть четное число.

В самом деле, пусть у квадратного уравнения ax² + bx + c = 0 коэффициент bимеет вид b = 2k. Подставив в нашу формулу число 2k вместо b, получим:
x1,2 =
=
Итак, корни квадратного уравнения ax² + 2kx + c = 0 можно вычислять по формуле:
x1,2 =
Пример :
5х2 — 2х + 1 = 0
x1,2=
Преимущество этой формулы в том, что в квадрат возводится не число b, а его половина, вычитается из этого квадрата не 4ac, а просто ac и, наконец, в том, что в знаменателе содержится не 2a, а просто a.
В случае если квадратное уравнение приведенное, то наша формула будет выглядеть так:
x1,2 =-k ±.
Пример :
х2 – 4х + 3 = 0
х1,2 = 2 ±
х1 = 3
х2 = 1
Ответ : х1 = 3, х2 = 1.
2.3 Теорема Виета
Очень любопытное свойство корней квадратного уравнения обнаружил французский математик Франсуа Виет.
 Это свойство назвали теорема Виета:
Это свойство назвали теорема Виета:Чтобы числа x
1 и x2 являлись корнями уравнения:ax² + bx + c = 0
необходимо и достаточно выполнения равенства
x1 + x2 = -b/aи x1 x2 = c/a
Теорема Виета позволяет судить о знаках и абсолютной величине квадратного уравнения
А именно
x² + bx + c = 0
1. Если b>0, c>0 то оба корня отрицательны.
2. Если b<0, c>0 то оба корня положительны.
3. Если b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.
4. Если b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.
2.4 Квадратные уравнения частного характера
1) Если a + b + c = 0 в уравнении ax² + bx + c = 0, то
х1 =1, а х2 = .
Доказательство :
В уравнении ax² + bx + c = 0, его корни
x1,2 = (1).

Представим b из равенства a + b + c = 0
Подставим это выражение в формулу (1):
х1,2 =
=
Если рассмотрим по отдельности два корня уравнения, получим:
1) х1 =
2) х2 =
Отсюда следует: х1 =1, а х2 = .
1. Пример :
2х² — 3х + 1 = 0
a = 2, b = -3, c = 1.
a + b + c = 0, следовательно
х1 = 1
х2 = ½
2. Пример :
418х² — 1254х + 836 = 0
Этот пример очень тяжело решить через дискриминант, но, зная выше приведенную формулу его с легкостью можно решить.
a = 418, b = -1254, c = 836.
х1 = 1 х2 = 2
2) Если a — b + c = 0, в уравнении ax² + bx + c = 0, то:
х1 =-1, а х2 =- .
Доказательство :
Рассмотрим уравнение ax² + bx + c = 0, из него следует, что:
x1,2 = (2).
Представим b из равенства a — b + c = 0
b = a + c, подставим в формулу (2):
x1,2 =
=
Получаем два выражения:
1) х1 =
2) х2 =
Эта формула похожа на предыдущую, но она тоже важна, т.
 к. часто встречаются примеры такого типа.
к. часто встречаются примеры такого типа.1) Пример :
2х² + 3х + 1 = 0
a = 2, b = 3, c = 1.
a — b + c = 0, следовательно
х1 = -1
х2 = -1/2
2) Пример :
Ответ : x1 = -1; х2 = —
3) Метод “переброски ”
Корни квадратных уравнений y² + by + аc = 0 и ax² + bx + c = 0 связанны соотношениями:
х1 = и х2 =
Доказательство :
а) Рассмотрим уравнение ax² + bx + c = 0
x1,2 = =
б) Рассмотрим уравнение y² + by + аc = 0
y1,2 =
Заметим, что дискриминанты у обоих решений равны, сравним корни этих двух уравнений. Они отличаются друг от друга на старший коэффициент, корни первого уравнения меньше корней второго на а. Используя теорему Виета и выше приведенное правило, нетрудно решать разнообразные уравнения.
Пример :
Имеем произвольное квадратное уравнение
10х² — 11х + 3 = 0
Преобразуем это уравнение по приведенному правилу
y² — 11y + 30 = 0
Получим приведенное квадратное уравнение, которое можно достаточно легко решить с помощью теоремы Виета.

Пусть y1 и y2 корни уравнения y² — 11y + 30 = 0
y1 y2 = 30 y1 = 6
y1 + y2 = 11 y2 = 5
Зная, что корни этих уравнений отличны друг от друга на а, то
х1 = 6/10 = 0,6
х2 = 5/10 = 0,5
В некоторых случаях удобно решать сначала не данное уравнение ax² + bx + c = 0, а приведенное y² + by + аc = 0, которое получается из данного «переброской» коэффициента а, а затем разделить найденный корни на а для нахождения исходного уравнения.
2.5 Формула Виета для многочленов (уравнений) высших степеней
Формулы, выведенные Виетом для квадратных уравнений, верны и для многочленов высших степеней.
Пусть многочлен
P(x) = a0 xn + a1 xn-1 + … +an
Имеет n различных корней x1 , x2 …, xn.
В этом случае он имеет разложение на множители вида:
a0 xn + a1 xn-1 +…+ an = a0 ( x – x1 )( x – x2 )…(x – xn )
Разделим обе части этого равенства на a0 ≠ 0 и раскроем в первой части скобки.
 Получим равенство:
Получим равенство:xn + ()xn-1 + … + () = xn – (x1 + x2 + … + xn ) xn-1 + ( x1 x2 + x2 x3 + … + xn-1 xn )xn-2 + … +(-1)n x1 x2 … xn
Но два многочлена тождественно равны в том и только в том случае, когда коэффициенты при одинаковых степенях равны. Отсюда следует, что выполняется равенство
x1 + x2 + … + xn = —
x1 x2 + x2 x3 + … + xn-1 xn =
x1 x2 … xn = (-1)n
Например, для многочленов третей степени
a0 x³ + a1 x² + a2 x + a3
x1 + x2 + x3 = —
x1 x2 + x1 x3 + x2 x3 =
x1 x2 x3 = —
Как и для квадратных уравнений, эту формулу называют формулами Виета.
 Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.
Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.2.6 Уравнения, сводимые к квадратным (биквадратные)
К квадратным уравнениям сводятся уравнения четвертой степени:
ax4 + bx2 + c = 0,
называемые биквадратными, причем, а ≠ 0.
Достаточно положить в этом уравнении х2 = y, следовательно,
ay² + by + c = 0
найдём корни полученного квадратного уравнения
y1,2 =
Чтобы найти сразу корни х1, x2, x3, x4 , заменим y на x и получим
x² =
х1,2,3,4 = .
Если уравнение четвёртой степени имеет х1 , то имеет и корень х2 = -х1 ,
Если имеет х3 , то х4 = — х3 . Сумма корней такого уравнения равна нулю.

Пример :
2х4 — 9x² + 4 = 0
х1,2,3,4 = ,
зная, что х1 = -х2 , а х3 = -х4 , то:
х1,2 =
х3,4 =
Ответ : х1,2 = ±2; х1,2 =
2.7 Исследование биквадратных уравнений
Возьмем биквадратное уравнение
ax4 + bx2 + c = 0,
где a, b, c –действительные числа, причем а > 0. Введя вспомогательную неизвестную y = x², исследуем корни данного уравнения, и результаты занесем в таблицу (см. приложение №1)
2.8 Формула Кардано
Если воспользоваться современной символикой, то вывод формулы Кардано может иметь такой вид:
х =
Эта формула определяет корни общего уравнения третей степени:
ax3 + 3bx2 + 3cx + d = 0.
Эта формула очень громоздкая и сложная (она содержит несколько сложныных радикалов). Она не всегда примениться, т.
 к. очень сложна для заполнения.
к. очень сложна для заполнения.2.9 Симметричные уравнения третей степени
Симметричными уравнениями третей степени называют уравнения вида
ax³ + bx² +bx + a = 0 (1 )
или
ax³ + bx² — bx – a = 0 (2 )
где a и b – заданные числа, причём a¹0.
Покажем, как решаются уравнение (1 ).
Имеем:
ax³ + bx² + bx + a = a(x³ + 1) + bx(x + 1) = a(x + 1) (x² — x + 1) + bx(x + 1) = (x + 1) (ax² +(b – a)x + a).
Получаем, что уравнение (1 ) равносильно уравнению
(x + 1) (ax² +(b – a)x + a) = 0.
Значит его корнями, будут корни уравнения
ax² +(b – a)x + a = 0
и число x = -1
аналогично решается уравнение (2 )
ax³ + bx² — bx — a = a(x³ — 1) + bx(x — 1) = a(x — 1) (x² + x + 1) + bx(x — 1) = (x — 1) ( ax2 + ax + a + bx ) = (x — 1) (ax² +(b + a)x + a).
1) Пример :
2x³ + 3x² — 3x – 2 = 0
Ясно, что x1 = 1, а
х2 и х3 корни уравнения 2x² + 5x + 2 = 0 ,
Найдем их через дискриминант:
x1,2 =
x2 = -, x3 = -2
2) Пример :
5х³ + 21х² + 21х + 5 = 0
Ясно, что x1 = -1, а
х2 и х3 корни уравнения 5x² + 26x + 5 = 0 ,
Найдем их через дискриминант:
x1,2 =
x2 = -5, x3 = -0,2.

2.10 Возвратные уравнения
Возвратное уравнение – алгебраическое уравнение
а0 хn + a1 xn – 1 + … + an – 1 x + an =0,
в котором ак = an – k , где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Уравнение четвёртой степени вида:
ax4 + bx3 + cx2 + bmx + am² = 0, (a ≠ 0).
Приведя это уравнение к виду
a (x² + m²/x²) + b(x + m/x) + c = 0, и y = x + m/x и y² — 2m = x² + m²/x²,
откуда уравнение приводится к квадратному
ay² + by + (c-2am) = 0.
Пример:
3х4 + 5х3 – 14х2 – 10х + 12 = 0
Разделив его на х2 , получим эквивалентное уравнение
3х2 + 5х – 14 – 5 × , или
Где и
3(y2 — 4) + 5y – 14 = 0, откуда
y1 = y2 = -2, следовательно
и , откуда
х1,2 =
х3,4 =
Ответ: х1,2 = х3,4 = .

Частным случаем возвратных уравнений являются симметричные уравнения. О симметричных уравнениях третей степени мы говорили ранее, но существуют симметричные уравнения четвертой степени.
Симметричные уравнения четвертой степени.
1) Если m = 1, то это симметричное уравнение первого рода, имеющее вид
ax4 + bx3 + cx2 + bx + a = 0 и решающееся новой подстановкой
y =
2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид
ax4 + bx3 + cx2 — bx + a = 0 и решающееся новой подстановкой
y =
2.11 Схема Горнера
Для деления многочленов применяется правило “деления углом”, или схема Горнера. С этой целью располагают многочлены по убывающим степеням х и находят старший член частного Q(x) из условия, что при умножении его на старший член делителя D(x) получается старший член делимого P(x). Найденный член частного умножают, затем на делитель и вычитают из делимого.
 Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2).
Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2).В случае уравнений R = 0 этот алгоритм заменяется схемой Горнера.
Пример :
х3 + 4х2 + х – 6 = 0
Находим делители свободного члена ±1; ± 2; ± 3; ± 6.
Левую часть уравнения обозначим f(x). Очевидно, что f(1) = 0, x1 = 1. Делим f(x) на х – 1. (см. приложение №3)
Значит,
х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + 6)
Последний множитель обозначим через Q(x). Решаем уравнение Q(x) = 0.
х2,3 =
Ответ : 1; -2; -3.
В этой главе мы привели некоторые формулы решения различных уравнений. Большинство этих формул решения уравнений частного характера. Эти свойства очень удобны так, как гораздо легче решать уравнения по отдельной формуле для этого уравнения, а не по общему принципу.
 К каждому из способов мы привели доказательство и несколько примеров.
К каждому из способов мы привели доказательство и несколько примеров.Заключение
В первой главе была рассмотрена история возникновения квадратных уравнений и уравнений высших порядков. Различные уравнения решали более 25 веков назад. Множество способов решения таких уравнений были созданы в Вавилоне, Индии. Потребность в уравнениях была и будет.
Во второй главе приведены различные способы решения (нахождения корней) квадратных уравнений и уравнений высших порядков. В основном это способы решения для уравнений частного характера, то есть к каждой группе уравнений, объединенных какими- либо общими свойствами или видом, приведено особое правило, которое применяется только для этой группы уравнений. Этот способ (подбора к каждому уравнению собственной формулы) гораздо легче, чем нахождение корней через дискриминант.
В этом реферате достигнуты все цели и выполнены основные задачи, доказаны и разучены новые, ранее неизвестные формулы. Мы проработали много вариантов примеров перед тем, как занести их в реферат, по этому мы уже представляем, как решать некоторые уравнения.
 Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.
Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.Список литературы
1. Виленкин Н.Я. “Алгебра для 8 класса”, М., 1995.
2. Галицкий М.Л. “Сборник задач по алгебре”, М. 2002.
3. Даан-Дальмедико Д. “Пути и лабиринты”, М., 1986.
4. Звавич Л.И. “Алгебра 8 класс”, М., 2002.
5. Кушнир И.А. “Уравнения”, Киев 1996.
6. Савин Ю.П. “Энциклопедический словарь юного математика”, М., 1985.
7. Мордкович А.Г. “Алгебра 8 класс”, М., 2003.
8. Худобин А.И. “Сборник задач по алгебре”, М., 1973.
9. Шарыгин И.Ф. “Факультативный курс по алгебре”, М., 1989.
Приложение 1
Исследование биквадратных уравнений
C b Выводы О корнях вспомогательного уравнения ay² +by+c=0 О корнях данного уравнения a(x²)² +bx² +c=0 C < 0
b- любое действительное число y < 0 ; y > 0
1 2
x = ±Öy
1,2 2
C > 0 b<0 D > 0 y > 0
1,2
x = ±Öy
1,2,3,4 1,2
D = 0 y > 0 x = ±Öy
1,2 .

D < 0 Нет корней Нет корней b ≥ 0 y < 0
1,2
Нет корней Нет корней Нет корней y > 0 ; y < 0
1 2
x = ±Öy
1,2 1
C = 0 b > 0 y = 0 x = 0 b = 0 y = 0 x = 0 b < 0 y = 0 x = 0 Приложение 2
Деление многочлена на многочлен «уголком»
A0 a1 a2 … an c + b0 c b1 c … bn-1 c B0 b1 b2 … bn = R (остаток) Приложение 3
Схема Горнера
Корень 1 4 1 -6 1 х1 = 1 сносим 5 6 0 1 1×1 +4 = 5 5×1 + 1 = 6 6×1 – 6 = 0 корень х1 = 1 Решение высшей математики онлайн
‹— Назад Для вычисления интегралов вида потребуются более сложные преобразования, нежели в предыдущем разделе.
Заметим, что при и получаются табличные интегралы:
Выведем формулы, позволяющие свести вычисление и к и соответственно. Применяя эти формулы к исходным интегралам несколько раз, при чётном мы сведём дело к вычислению табличного интеграла или , а при нечётном — к вычислению табличного интеграла или .Итак, получим формулу, выражающую через ; эта формула называется формулой понижения степени. Преобразуем интеграл следующим образом:
Последний интеграл вычислим, применив формулу интегрирования по частям:
(В комментарии, между вертикальными чёрточками, мы не вполне корректно обозначили через не полный набор первообразных для , а какую-либо, произвольную, первообразную, одну из которых и нашли. Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную добавлять не стали.) После этого получаем
Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную добавлять не стали.) После этого получаем
Мы получили выражение интеграла через интеграл и известную функцию.С помощью аналогичных преобразований, для интеграла получаем такое выражение через интеграл и известную функцию:
Как упражнение, выполните эти преобразования и получите приведённую здесь формулу (2.3). Замечание 2.1 В промежуточных вычислениях мы получили также способ нахождения интегралов вида и которые сводятся, после интегрирования по частям, к интегралам и . Пример 2.7 Вычислим интеграл Здесь . После однократного применения формулы понижения степени (2.2), дело сведётся к нахождению интеграла . Итак, Пример 2.8 Для вычисления интеграла формулу (2.3) нужно будет применить два раза подряд:
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Калькулятор одновременных уравненийс шагами
Практичный решатель одновременных уравнений алгебры: решает систему уравнений;
Калькулятор одновременных уравнений — это онлайн-инструмент, который помогает решать системы уравнений.
 Он показывает все операции шаг за шагом. Этот мощный веб-инструмент необходим для определения решения системы уравнений. Он может решать как линейные, так и нелинейные системы уравнений с 2,3,4 или 5 неизвестными.
Он показывает все операции шаг за шагом. Этот мощный веб-инструмент необходим для определения решения системы уравнений. Он может решать как линейные, так и нелинейные системы уравнений с 2,3,4 или 5 неизвестными.Калькулятор одновременных уравнений — это онлайн-инструмент, который шаг за шагом решает системы уравнений.Он показывает все работы, он точен и удобен в использовании.
Идеальный решатель одновременных уравнений, который поможет вам решать одновременные уравнения онлайн.
Калькулятор одновременных уравнений помогает найти значение неизвестных переменных системы линейных, квадратных или нелинейных уравнений с 2, 3, 4 или 5 неизвестными.
Наш онлайн-калькулятор системы уравнений поможет вам решить для любых неизвестных переменных x, z, n, m и y
Калькулятор одновременных уравнений выше поможет вам решить одновременные линейные уравнения с двумя, тремя неизвестнымиКлассическим примером является система из трех линейных уравнений с тремя неизвестными x,y,z.
 Этот решатель линейного уравнения с тремя неизвестными помогает систематически решать такие системы
Этот решатель линейного уравнения с тремя неизвестными помогает систематически решать такие системыЛинейное уравнение представляет отношения между двумя или более переменными. В природе чаще всего встречаются линейные. Тем не менее, не все явления в природе являются линейными, поэтому моделировать природные явления с помощью линейных отношений непросто.
Линейное уравнение вида ax+by=c будет иметь бесконечное число решений или точек, удовлетворяющих уравнению. Чтобы получить уникальные значения для неизвестных, вам нужны дополнительные уравнения, таким образом, возникают линейные одновременные уравнения.
Онлайн-калькулятор систем линейных уравнений для пошагового решения одновременных уравнений. Наш решатель системы уравнений показывает вам всю работу с пошаговым решением. Наш алгебраический онлайн-калькулятор для решения одновременных уравнений быстр, точен и надежен.
Прежде чем мы узнаем, как работает решатель линейных уравнений, было бы лучше, если бы мы больше изучили систему линейных уравнений.

Нахождение решения системы линейных уравнений
Решением линейного уравнения или системы линейных уравнений является набор координат в пространстве, который удовлетворяет всем уравнениям в системе.Для двумерного случая решение представляет собой точку в двумерных координатах, которая удовлетворяет заданным уравнениям. В трехмерном случае решением является точка в трехмерном пространстве, которая одновременно удовлетворяет заданной системе уравнений. Для случаев более высокой степени применима аналогия.
Система линейных уравнений может иметь:
- Уникальное решение (разрешимое)
- Бесконечно возможное решение ( несогласованная система)
- Или вообще никакого решения
Калькулятор решения систем уравнений Онлайн
Когда система линейных уравнений имеет единственное решение?
Для любой неоднородной системы линейных уравнений (n*n) система будет иметь единственное решение (нетривиальное) тогда и только тогда, когда определитель ее матрицы коэффициентов отличен от нуля.
 С другой стороны, система будет иметь бесконечно много решений, если ее определитель равен нулю.
С другой стороны, система будет иметь бесконечно много решений, если ее определитель равен нулю.Для системы уравнений с двумя неизвестными вам нужно два уравнения, чтобы решить систему. Рассматривая уравнения как прямые линии на двумерном графике, решением системы является точка, в которой пересекаются две линии. Случай отсутствия решения означает, что две линии никогда не пересекаются; такие прямые параллельны друг другу.
Пример:
2x-3y=7, 4x-6y=9
Ясно, что две прямые параллельны и поэтому никогда не пересекутся.Для трехмерного случая данная система уравнений представляет параллельные плоскости.
С другой стороны, система линейных уравнений будет иметь бесконечно много решений, если данные уравнения представляют собой прямую или плоскость в 2-х и 3-х измерениях соответственно.
Калькулятор решения одновременных уравнений
Наш онлайн-калькулятор поможет вам мгновенно найти решение системы уравнений. Решатель одновременных уравнений также показывает вам все шаги и работу.
. Вот несколько рабочих примеров, которые покажут вам пошаговое решение одновременных уравнений
Вот несколько рабочих примеров, которые покажут вам пошаговое решение одновременных уравненийС помощью калькулятора для решения одновременных уравнений вы можете выполнять больше расчетов за меньшее время.Генератор одновременных уравнений также показывает вам работу, поэтому он идеально подходит для обучения решению линейных уравнений онлайн.
Как решить систему линейных уравнений
Для двумерного случая у нас есть 2 уравнения с 2 неизвестными. Есть 2 классических метода решения таких уравнений, а именно: Методы замены и исключения.
Калькулятор метода замены
Этот метод включает сначала решение одной из переменных с помощью одного уравнения, а затем подстановку результатов во второе уравнение.В нашем алгебраическом калькуляторе есть опция метода подстановки, которая позволяет вам тренировать решение уравнения для уравнений с помощью метода подстановки.
Калькулятор метода замены Примеры
Калькулятор метода исключения с Works
С помощью нашего алгебраического онлайн-калькулятора вы можете найти решение системы линейных уравнений методом исключения.

Одновременный решатель уравнений является точным, эффективным и бесплатным. Исключение — один из классических методов решения системы линейных уравнений.В двумерном случае вы сначала начинаете с выбора конкретной переменной, которую хотите исключить.
Предположим, что наша система находится в координатах x, y. Для практичности начнем с исключения x. Во-первых, вы найдете пару множителей, умножая их на коэффициенты при x в любом уравнении, чтобы два уравнения имели одинаковый коэффициент для x.
Умножение уравнения на скалярный коэффициент не изменяет уравнение. Выполнив умножение, вычтите уравнение 2 из уравнения 1.Таким образом, вы получите уравнение с одним неизвестным.
Легко решить уравнение с одним неизвестным. Как только вы нашли значение x, подставьте его обратно в любое из исходных уравнений, чтобы найти значение y.
Вот несколько рабочих примеров, показывающих решение методом исключения
Калькулятор квадратных уравнений с пошаговой обработкой
Этот калькулятор также поможет вам найти решения для комбинации квадратных и линейных уравнений.
 2=2;х+у=1
2=2;х+у=1Для пошагового решения любой системы уравнений ничто не облегчит вашу жизнь, чем наш онлайн-калькулятор алгебры. Если переменные можно разделить/разложить на множители, то можно решить любую систему уравнений методом подстановки. Калькулятор одновременных уравнений быстрый, эффективный и надежный. Это потрясающий калькулятор одновременных уравнений с работой.
Как пользоваться калькулятором уравнений онлайн
Сначала узнайте о поддерживаемых проблемах здесь.В настоящее время решатель может решать линейные уравнения с 2, 3, 4, 5, 6 или 7 неизвестными, смесь квадратных и линейных уравнений, а также нелинейные задачи. В настоящее время мы работаем над расширением возможностей калькулятора, чтобы он мог обрабатывать системы уравнений более высокого порядка.
- Введите уравнения, разделенные знаком «;» или «,». После того, как вы введете свои уравнения, нажмите кнопку расчета, чтобы получить мгновенное решение.
- Прокрутите вниз, чтобы просмотреть работу.

- Позже вы можете распечатать решение, используя «Опцию печати решения»
Нравится наш решатель линейных уравнений? Или у вас есть какие-то новые функции, которые вы хотели бы видеть в калькуляторе? Отправьте нам сообщение, и мы будем рады их реализовать.Вы можете отправить нам прямое сообщение через нашу электронную почту.
Понравился наш калькулятор систем уравнений с двумя неизвестными? Поделитесь им с друзьями и одноклассниками; помогите нам распространить благую весть. Скопируйте ссылку ниже, чтобы поделиться ею в социальных сетях.
Возможно, будет лучше, если вы будете изучать математику на примерах. Ознакомьтесь с нашими примерами алгебры, каждый из которых содержит пошаговое решение. Примеры также помогут вам использовать этот калькулятор уравнений для решения ваших задач по алгебре.
Допустимые математические символы и их использование Если вы решите написать свои математические выражения, вот список допустимых математических символов и операторов.

Нам приятно слышать ваши отзывы. Если у вас возникнут проблемы при использовании этого калькулятора, сообщите нам об этом: Хотите увидеть больше возможностей? Присылайте нам свои рекомендации и идеи приложений. Мы всегда прилагаем все усилия, чтобы сделать алгебру легкой и увлекательной.
Полиномиальный калькулятор — eMathHelp
Решение
Ввод: найти сумму, разность, произведение двух многочленов, частное и остаток от деления одного на другой; факторизовать их и найти корни.{2} + 32 x — 12$$$
Поскольку все коэффициенты целые, применим теорему о рациональных нулях.
Запаздывающий коэффициент (коэффициент постоянного члена) составляет $$$-12$$$.
Найдите его множители (с плюсом и минусом): $$$\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 12$$$. Это возможные значения для `p`.
Старший коэффициент (коэффициент члена с наивысшей степенью) равен $$$2$$$.
Найдите его множители (с плюсом и минусом): $$$\pm 1, \pm 2$$$.
 Это возможные значения для `q`.
Это возможные значения для `q`.Найдите все возможные значения `p/q`: $$$\pm \frac{1}{1}, \pm \frac{1}{2}, \pm \frac{2}{1}, \ pm \ frac {2}{2}, \ pm \ frac {3}{1}, \ pm \ frac {3}{2}, \ pm \ frac {4} {1}, \ pm \ frac {4} {2}, \pm \frac{6}{1}, \pm \frac{6}{2}, \pm \frac{12}{1}, \pm \frac{12}{2}$$$ .
Упростить и удалить дубликаты (если есть): $$$\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 12, \pm \frac{1}{2}, \ pm \frac{3}{2}$$$.
Если `a` является корнем многочлена `P(x)`, то остаток от деления `P(x)` на `x-a` должен равняться `0`.{2} — 13 x + 6\right)}$$
Поскольку все коэффициенты целые, применим теорему о рациональных нулях.
Запаздывающий коэффициент (коэффициент постоянного члена) равен $$$6$$$.
Найдите его множители (с плюсом и минусом): $$$\pm 1, \pm 2, \pm 3, \pm 6$$$. Это возможные значения для `p`.
Старший коэффициент (коэффициент члена с наивысшей степенью) равен $$$2$$$.
Найдите его множители (с плюсом и минусом): $$$\pm 1, \pm 2$$$.
 {2} — 13 x + 6$$$ на $$$x — 1$$$.{2} — 4 x — 12=0$$$ эквивалентно $$$\left(x — 6\right) \left(x + 2\right)=0$$$.
{2} — 13 x + 6$$$ на $$$x — 1$$$.{2} — 4 x — 12=0$$$ эквивалентно $$$\left(x — 6\right) \left(x + 2\right)=0$$$.Известно, что произведение равно нулю, когда хотя бы один множитель равен нулю, поэтому нужно просто приравнять множители к нулю и решить соответствующие уравнения (некоторые уравнения уже решены, некоторые не решить вручную ).
- $$$x — 6=0$$$: корень равен $$$x=6$$$.
- $$$x + 2=0$$$: корень равен $$$x=-2$$$.
Следовательно, корни исходного уравнения: $$$x_1=6$$$; $$$x_2=-2$$$.{2} — 4 x — 12=0$$$:
- $$$6$$$, кратность $$$1$$$.
- $$$-2$$$, кратность $$$1$$$.
Решение кубических уравнений – методы и примеры
Решение полиномиальных уравнений высокого порядка является важным навыком для всех, кто изучает естественные науки и математику. Однако понять, как решать такие уравнения, довольно сложно.
В этой статье мы обсудим, как решать кубические уравнения с использованием различных методов, таких как метод деления, факторная теорема и разложение на множители путем группировки.

Но прежде чем перейти к этой теме, давайте обсудим , что такое полиномиальное и кубическое уравнение.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в котором знак сложения или вычитания разделяет константу и переменную.
Общая форма многочлена: ax n + bx n-1 + cx n-2 + … + kx + l, где каждой переменной соответствует константа в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены.Примеры многочленов: 3x + 1, x 2 + 5xy – ax – 2ay, 6x 2 + 3x + 2x + 1 и т. д.
Кубическое уравнение – это алгебраическое уравнение третьей степени.
Общий вид кубической функции: f (x) = ax 3 + bx 2 + cx 1 + d. И кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — константа.Как решать кубические уравнения?
Традиционный способ решения кубического уравнения состоит в том, чтобы свести его к квадратному уравнению, а затем решить его с помощью факторизации или квадратной формулы.

Подобно тому, как квадратное уравнение имеет два действительных корня , кубическое уравнение может иметь, возможно, три действительных корня. Но в отличие от квадратного уравнения, которое может не иметь действительного решения, кубическое уравнение имеет по крайней мере один действительный корень.
Два других корня могут быть действительными или мнимыми.
Всякий раз, когда вам дают кубическое уравнение или любое уравнение, вы всегда должны сначала привести его в стандартную форму.
Например, если вам дано что-то вроде этого, 3x 2 + x – 3 = 2/x, вы преобразуете его в стандартную форму и напишете так: 3x 3 + x 2 – 3х – 2 = 0.Тогда вы можете решить это любым подходящим методом.
Давайте посмотрим несколько примеров ниже для лучшего понимания:
Пример 1
Определите корни кубического уравнения 2x 3 + 3x 2 — 11x — 6 = 0
Решение
Поскольку d = 6, то возможные множители равны 1, 2, 3 и 6.

Теперь применим теорему о множителях, чтобы проверить возможные значения методом проб и ошибок.
f (1) = 2 + 3 – 11 – 6 ≠ 0
f (–1) = –2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0Следовательно, x = 2 — первый корень.
Остальные корни уравнения можно получить методом синтетического деления.
= (x – 2) (ax 2 + bx + c)
= (x – 2) (2x 2 + bx + 3)
= (x – 2) (2x 2 + 7x + 3) )
= (x – 2) (2x + 1) (x +3)Следовательно, решения равны x = 2, x = -1/2 и x = -3.
Пример 2
Найти корни кубического уравнения Х 3 — 6x 2 + 11x — 6 = 0
Решение
x 3 — 6x 2 + 11x – 6
(x – 1) – один из факторов.
Делением x 3 − 6x 2 + 11x – 6 на (x – 1),
⟹ (x – 1) (x 2 – 5x + 6) = 0
– ⟹ 1) (x – 2) (x – 3) = 0
Это решение кубического уравнения: x = 1, x = 2 и x = 3.

– 2x 2 – x + 2
Решение
Разложите уравнение на множители.
x 3 – 2x 2 – x + 2 = x 2 (x – 2) – (x – 2)
= (x 2 – 1) (x – 05 = 900 2)
(х + 1) (х – 1) (х – 2)х = 1, -1 и 2.
Пример 4
Решит кубическое уравнение Х 3 — 23x 2 — 23x 2 + 142x — 120
Раствор
Первый факторизируйте полиномиал.
x 3 — 23x 2 + 142x — 120 = (x — 1) (x 2 — 22x + 120)
Но X 2 — 22x + 120 = x 2 — 12x — 10x + 120
= x (x – 12) – 10(x – 12)
= (x – 12) (x – 10)Следовательно, x 3 – 23x 2 + 142x – 120 = ( x – 1) (x – 10) (x – 12)
Приравнять каждый множитель к нулю.
x – 1= 0
x = 1
x – 10 = 10
x – 12 = 0
x = 12
Пример 5
Решить кубическое уравнение x 3 – 6 x 2 + 11x – 6 = 0.

Решение
6 ;пусть x = 2
Разделите многочлен на x-2 до
(x 2 – 4x + 3) = 0.
Теперь решите квадратное уравнение (x 2 – 4x + 3) = 0, чтобы получить x = 1 или x = 3
Следовательно, решения равны x = 2, x = 1 и x = 3.
Пример 6
решают кубическое уравнение Х 3 — 7x 2 + 4x + 12 = 0
Решение
Пусть F (x) = x 3 — 7x 2 + 4x + 12
Поскольку d = 12, возможные значения 1, 2, 3, 4, 6 и 12.
Методом проб и ошибок находим, что f (–1) = –1 – 7 – 4 + 12 = 0
Итак, (x + 1) — фактор функции.
x 3 – 7x 2 + 4x + 12
= (x + 1) (x 2 – 8x + 12)
= (x + 1) (x – 2) (x90–06)Следовательно, х = -1, 2, 6
Пример 7
решают следующее кубическое уравнение:
x 3 + 3x 2 + x + 3 = 0.

Решение
x 3 + 3x 2 + x + 3
= (x 3 + 3x 2 ) + (x + 3)
= x 2 (x1 + 3) )
= (x + 3) (x 2 + 1)Следовательно, x = -1 ,1 -3.
Пример 8
Relve X 3 — 6x 2 + 11x — 6 = 0
Раствор
Factorize
x 3 — 6x 2 + 11x — 6 = 0 ⟹ (x — 1) (x — 2) (x — 3) = 0
Приравнивание каждого множителя к нулю дает;
x = 1, x = 2 и x = 3
Пример Пример 9
Relve x 3 — 4x 2 — 4x 2 — 9x + 36 = 0
Решение
Факторизация каждого набора два термина.
x 2 (x — 4) — 9(x — 4) = 0
Извлеките общий множитель (x — 4), чтобы получить
(x 2 — 9) (x — 4) = 0
Теперь факторизуем разность двух квадратов
(x + 3) (x − 3) (x − 4) = 0
Приравнивая каждый множитель к нулю, получаем;
x = -3, 3 или 4
Пример 10
Решить уравнение 3x 3 -16x 2 + 23x — 6 = 0
Решение
Divide 3X 3 −16x 2 + 23x – 6 на x -2, чтобы получить 3x 2 – 1x – 9x + 3
= x (3x – 1) – 3(3x – 1)
= (x – 3) ( 3x – 1)
Следовательно, 3x 3 −16x 2 + 23x − 6 = (x- 2) (x – 3) (3x – 1)
Приравняем каждый множитель к нулю, чтобы получить,
x = 2, 3 и 1/3
Пример 11
Найти корни 3x 3 — 3x 2 — 90x = 0
Решение
Фактор IS OUT 3X
3X 3 – 3x 2 – 90x ⟹3x (x 2 – x – 30)
Найдите пару множителей, произведение которых равно −30, а сумма −1.

⟹- 6 * 5 = -30
⟹ -6 + 5 = -1
Перепишите уравнение, заменив термин «bx» выбранными коэффициентами.
⟹ 3x [(x 2 – 6x) + (5x – 30)]
Фактор уравнения;
⟹ 3x [(x (x – 6) + 5(x – 6)]
= 3x (x – 6) (x + 5)
Приравнивая каждый множитель к нулю, получаем:
x = 0, 6, -5
Решение кубических уравнений графическим методом
Если вы не можете решить кубическое уравнение ни одним из вышеперечисленных методов, вы можете решить его графически.Для этого вам нужно иметь точный набросок данного кубического уравнения.
Точки, в которых график пересекает ось x, являются решением уравнения. Количество действительных решений кубических уравнений равно количеству пересечений их графика с осью абсцисс.
Пример 12
Найдите корни x 3 + 5x 2 + 2x – 8 = 0 графически.
Решение
Просто нарисуйте график следующей функции, подставив случайные значения x:
f (x) = x 3 + 5x 2 + 2x – 8
Вы можете видеть график пересекает ось абсцисс в 3 точках, следовательно, существует 3 действительных решения.

На графике решения следующие:
x = 1, x = -2 и x = -4.
Решение уравнений в Excel (полиномиальные, кубические, квадратичные и линейные)
Excel имеет множество функций, которые могут выполнять различные задачи. Помимо выполнения различных статистических, финансовых анализов, мы можем решать уравнения в Excel. В этой статье мы проанализируем популярную тему «Решение уравнений в Excel».
В этой статье мы будем решать различные виды уравнений, такие как кубические, полиномиальные, линейные, квадратные, с различными функциями Excel.
Решение полиномиальных уравнений в Excel
Полиномиальное уравнение/функция может быть квадратным, линейным, четверным, кубическим и т. д. Полиномиальные уравнения не содержат отрицательной степени своих переменных. Пример полиномиальных уравнений другого типа приведен ниже.
1) Одночлен: y=mx+c
2) Бином: y=ax 2 +bx+c
3) Трехчлен: y=ax 3 +bx 2 +cx+dВместе с методом прямого вычисления мы также обсудим в этой статье другие методы, такие как Goal Seek, Array и Solver, для решения различных полиномиальных уравнений.

Подробнее: Трехмерные ссылки и внешние ссылки в Excel
Решите кубическое уравнение в Excel с помощью поиска цели
Допустим, у нас есть кубическое уравнение: Y=5x 3 -2x 2 +3x-6 . Мы будем решать это уравнение для нахождения значения «X» с конкретным значением «Y». Здесь мы будем использовать функцию Excel Goal Seek , чтобы решить уравнение. Процедура приведена ниже.
- Сначала установите коэффициенты в разных ячейках.
- Установите начальное значение X как «0» в ячейке B6.
- После этого запишите уравнение полинома в ячейку G3 относительно ячеек коэффициентов и начального значения X.
- Теперь на вкладке Данные нажмите на опцию Поиск цели под опцией Прогноз .
- В диалоговом окне Goal Seek введите следующие данные и нажмите OK .

- Функция поиска цели выполнит несколько итераций для конечного значения Y, которое в этом примере установлено равным 15.
- После того, как поиск цели завершит свою работу, вы увидите, что начальное значение X и ячейка, в которую была помещена формула, изменены. Теперь начальное значение показывает значение X, когда значение Y становится равным 15.
Решите кубическое уравнение в Excel с помощью Solver
Вы также можете использовать функцию «Решатель» Excel для решения кубических уравнений.Давайте решим предыдущее уравнение для лучшего понимания.
- Сразу после ввода уравнения в ячейке G3 щелкните решатель, который находится в разделе «Анализ» на вкладке «Данные».
- В диалоговом окне Solver Parameters выполните следующие действия и выберите параметр Solve .
- Здесь мы устанавливаем целевое значение 15.
 Здесь B6 — переменная ячейка. Поскольку это нелинейное уравнение, метод решения был выбран как GRG Nonlinear .
Здесь B6 — переменная ячейка. Поскольку это нелинейное уравнение, метод решения был выбран как GRG Nonlinear . - Нижеследующий результат будет получен после операции.
Подробнее: Как использовать поиск цели для поиска входного значения
Решение квадратного уравнения в Excel с использованием функции поиска цели
Давайте решим квадратное уравнение Y=3x 2 +6x-5. Мы увидим, как это уравнение можно решить с помощью функции поиска цели. Процедуры приведены ниже.
- Сначала установите коэффициенты в разных ячейках.
- Установите начальное значение X как «0» в ячейке B6.
- После этого запишите уравнение в ячейку F3 относительно ячеек коэффициентов и начального значения X.
- Теперь на вкладке Данные щелкните параметр Поиск цели под параметром Прогноз .

- В диалоговом окне «Поиск цели» введите следующие данные и нажмите OK .
- Функция Goal Seek вызовет некоторое раздражение из-за конечного значения Y, которое в этом примере установлено равным 12.
- После того, как поиск цели завершит свою работу, вы увидите, что начальное значение X и ячейка, в которую была помещена формула, изменены. Теперь начальное значение показывает значение X, когда значение Y становится равным 12.
Подробнее: Анализ данных в Excel. Узнайте 10 общих статистических терминов
Использование решателя для решения квадратного уравнения в Excel
Вы также можете использовать функцию «Решатель» Excel для решения квадратных уравнений.Давайте решим то же уравнение для лучшего понимания.
- Сразу после ввода уравнения в ячейке F3 щелкните решатель, который находится в разделе «Анализ» на вкладке «Данные».

- В диалоговом окне Solver parameters выполните следующие действия и нажмите Solve .
- Здесь мы устанавливаем целевое значение 15. Здесь B6 — переменная ячейка. Поскольку это нелинейное уравнение, метод решения был выбран как GRG Nonlinear .2-4ас))/2а . Непосредственно используя эту формулу, мы можем найти корни квадратичной функции. На картинке ниже мы вычисляем корни квадратичных функций. Здесь корни X1 и X2.
Решение линейных уравнений в Excel с использованием матричной системы
Мы можем использовать матричную систему для решения набора линейных уравнений в Excel. Допустим, у нас есть 3 уравнения, в которых значения x, y и z неизвестны. Уравнения,
3x+2y+z=8……………… (1)
11x-9y+23=27…………..(2)
8x-5y=10….………………(3)Мы будем использовать формулу X=A -1 B. Где A -1 и B являются массивами.
 Процедура решения системы линейных уравнений приведена ниже.
Процедура решения системы линейных уравнений приведена ниже.- Запишите коэффициенты x, y и z вместе с константами в виде массива, как показано на рисунке ниже. Коэффициенты x, y и z задаются матрицей A, а константы задаются матрицей B.
- Теперь выберите диапазон B11:D13 и запишите формулу = MINVERSE(B7:D9) и нажмите Ctrl+Shift+Enter вместе, чтобы использовать эту формулу как массив.
- Теперь, чтобы найти результат X , выберите диапазон G11:G13 и введите формулу =МУМНОЖ(B11:D13,G7:G9) и нажмите Ctrl+Shift+Enter вместе, чтобы использовать эту формулу в качестве множество. Эта функция возвращает матричное произведение двух массивов. Здесь B11:D13 — набор массивов A -1 , а G7:G9 — набор массивов .
Решение линейных уравнений в Excel с помощью Solver
Довольно легко найти переменные различных линейных уравнений с помощью решателя.
 Процедура показана ниже.
Процедура показана ниже.- Создайте таблицу с именем Значение переменных на листе и оставьте несколько пустых мест рядом с x, y и z.
- Создайте еще одну таблицу, содержащую уравнения с переменными и константами.
- В столбце Уравнения (столбец E) запишите уравнения =3*C7+2*C8+C9, =11*C7-9*C8+23*C9 и =8*C7-5*C8. Мы используем формулу =FORMULATEXT() , чтобы показать эти уравнения в столбце F. Константы записаны в столбце G.
- Нажмите на Решатель , который находится под Анализ вариант Данные
- В диалоговом окне «Параметры решателя» установите для параметра Задать цели значение $E$7, выберите параметр Значение и введите 8. В параметре путем изменения ячеек переменной напишите $C$7:$C$9 . Снимите флажок «Сделать неограниченные переменные неотрицательными» и выберите Simplex LP в «Выбор метода решения».

Нажмите, чтобы увидеть полное изображение
- Нажмите на Добавьте в диалоговом окне Параметры решения .
- В диалоговом окне Добавить ограничение выполните следующие действия и нажмите Добавить.
- Пришло время собрать информацию о последнем уравнении в качестве входных данных решателя. Сделайте следующее и нажмите OK .
- После этого ваши параметры Solver будут выглядеть так, как показано на рисунке ниже. Нажмите на опцию «Решить», чтобы продолжить операцию.
- После того, как вы нажмете на опцию Решить , вы увидите изменение Значения переменных Значения, которые вы получите в этой таблице, являются фактическими значениями переменных x, y и z.
Примечание: После того, как вы нажмете кнопку «Решить», вы получите новое диалоговое окно «Результаты решения ».
 Нажмите на Keep Solver Solution и нажмите OK , чтобы внести изменения в свой рабочий лист.
Нажмите на Keep Solver Solution и нажмите OK , чтобы внести изменения в свой рабочий лист. Связано: Как решать одновременные линейные уравнения в Excel с помощью Solver
Загрузить рабочий файл
Заключение
В этой статье мы видим различные процессы решения многих различных типов уравнений.Из многих процессов Solver в Excel является лучшим вариантом. В Solver вы можете не только найти корни уравнения, но и одновременно найти значения разных переменных. Решатель в Excel упрощает пользователям решение задач линейного программирования.
Надеюсь, эта статья оправдает ваши ожидания. С нетерпением ждем ваших отзывов.
Дополнительная литература
Средство поиска полиномиальных корней и одновременного решения уравнений — Texas Instruments
ЛИЦЕНЗИОННОЕ СОГЛАШЕНИЕ НА ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИЛОЖЕНИЯ TEXAS INSTRUMENTS Загружая программное обеспечение и/или документацию, вы соглашаетесь соблюдать следующие положения.

- Лицензия: При условии оплаты вами любого применимого лицензионного сбора Texas Instruments Incorporated («TI») предоставляет вам лицензию на копирование и использование программного обеспечения на калькуляторе TI, а также на копирование и использование документации. со связанной веб-страницы или компакт-диска (как программное обеспечение, так и документация являются «Лицензионными материалами»). В дополнение к копии, хранящейся на вашем калькуляторе, вы можете хранить копию на своем компьютере только в целях резервного копирования/архивирования.
- Ограничения: Вы не можете выполнять обратную сборку или обратную компиляцию программной части Лицензионных материалов, которые предоставляются в формате объектного кода.Вы не можете продавать, сдавать в аренду или сдавать в аренду копии Лицензионных материалов. Вы не можете использовать Лицензионные материалы на каком-либо эмуляторе калькулятора TI, если эмулятор не получен от TI.
- Поддержка: Поддержка Лицензионных материалов описана в документации, прилагаемой к программному обеспечению.
 При отсутствии такой документации поддержка предоставляется TI.
При отсутствии такой документации поддержка предоставляется TI. - Авторское право: Лицензионные материалы и любая сопроводительная документация защищены авторским правом. Если вы делаете копии, не удаляйте с копий уведомление об авторских правах, товарный знак или защиту.
- Гарантия: TI гарантирует, что имеет право предоставлять Лицензионные материалы. TI не гарантирует, что Лицензионные материалы не будут содержать ошибок или будут соответствовать вашим конкретным требованиям.
Лицензируемые материалы предоставляются «КАК ЕСТЬ» вам или любому последующему пользователю.
Хотя гарантия на Лицензионные материалы не предоставляется, носитель (если таковой имеется) будет заменен, если будет обнаружен дефект в течение первых трех (3) месяцев использования, когда упаковка будет возвращена TI с предоплатой почтовых расходов. ЭТОТ ПУНКТ ВЫРАЖАЕТ МАКСИМАЛЬНУЮ ОТВЕТСТВЕННОСТЬ TI И ВАШЕ ЕДИНСТВЕННОЕ И ИСКЛЮЧИТЕЛЬНОЕ СРЕДСТВО.
- Ограничения: За исключением случаев, прямо указанных выше, TI не дает никаких гарантий или условий, явных или подразумеваемых, включая, помимо прочего, любые подразумеваемые гарантии товарного состояния и пригодности для определенной цели в отношении Лицензионных материалов.

Ни при каких обстоятельствах TI или ее поставщики не несут ответственности за любые косвенные, случайные или косвенные убытки, упущенную выгоду, потерю использования или данных или прерывание деятельности, независимо от того, указаны ли предполагаемые убытки как гражданское правонарушение, договор или возмещение убытков.
В некоторых штатах или юрисдикциях не допускается исключение или ограничение случайных или косвенных убытков, поэтому указанное выше ограничение может не применяться.
Настоящее Соглашение немедленно прекращает свое действие, если вы не выполняете его условия. После расторжения настоящего Соглашения вы соглашаетесь вернуть или уничтожить исходный пакет и все полные или частичные копии Программы, находящиеся в вашем распоряжении, и подтверждаете это в письменной форме TI.
Экспорт и реэкспорт оригинального программного обеспечения и документации из США регулируется Законом об управлении экспортом 1969 г. с поправками.Ответственность за соблюдение таких правил лежит на вас.
 Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которой такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи.
Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которой такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи.Если Программа предоставляется Правительству США в соответствии с ходатайством, направленным 1 декабря 1995 г. или после этой даты, Программа предоставляется с коммерческими лицензионными правами и ограничениями, описанными в других разделах настоящего документа. Если Программа предоставляется правительству США в соответствии с запросом, сделанным до 1 декабря 1995 г., Программа предоставляется с «Ограниченными правами», как это предусмотрено в FAR, 48 CFR 52.
 227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо.
227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо.
Симметрия и решения полиномиальных уравнений
ОбзорПоиски решений полиномиальных уравнений продолжались на протяжении восемнадцатого века. Примерно в 1770 году в течение пары лет математики ряда стран почти одновременно добились успехов, которые привели к новым подходам к решению проблемы. Было разочарование в том, что ни одно из достижений не привело к общему решению уравнений высших степеней, но некоторые конкретные уравнения удалось решить после этой работы.Что еще более важно, новые подходы предоставили средства для ответа на вопрос о разрешимости полиномиальных уравнений вообще в начале следующего столетия.
ПредысторияУравнение — это просто выражение, в котором утверждается, что две стороны равны, и оно не может включать ничего, кроме чисел. На раннем этапе развития алгебры наибольший интерес представляли уравнения, в которых какой-либо символ использовался для обозначения неизвестной величины, значение которой должно было быть определено на основе информации, предоставленной уравнением.
 Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (включая и вторую степень переменной). Описание решения обычно выражалось словами, а не символами.
Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (включая и вторую степень переменной). Описание решения обычно выражалось словами, а не символами.Тот же самый подход продолжался даже в шестнадцатом веке с решением кубических уравнений (включая третьи степени переменной) и уравнений четвертой степени (с учетом четвертых степеней переменной). Переменная).Они были решены усилиями итальянских математиков, и решения были представлены словами. Методы не подвергались тщательной проверке до тех пор, пока полученные ответы работали в исходном уравнении. Только в работах Франсуа Виета (1540–1603) была предпринята некоторая попытка применить строгость геометрии к методам алгебры.
Однако, несмотря на усилия Виета, в общем вопросе о решении уравнений пятой степени (включающих пятую степень переменной) не было достигнуто никакого прогресса.
 К концу восемнадцатого века Александр-Теофиль Вандермонд (1735-1796) прочитал доклад перед Академией наук в Париже о новом подходе к решению уравнений пятой степени и полиномиальных уравнений в целом. Он утверждал, что каждое уравнение, в котором степень переменной равна единице, может быть решена стандартными средствами. Его работа по этому вопросу была бы более известна, если бы он был членом Академии во время родов (1770 г.), потому что это облегчило бы ему публикацию своих утверждений.Как бы то ни было, его статья не публиковалась до 1774 года, а тем временем Жозеф-Луи Лагранж (1736–1813), один из величайших математиков века, опубликовал пару статей по этому вопросу. Возможно, разочарованный, зная, что первая публикация в научном мире имеет решающее значение, Вандермонде не продолжил свои исследования по решению полиномиальных уравнений.
К концу восемнадцатого века Александр-Теофиль Вандермонд (1735-1796) прочитал доклад перед Академией наук в Париже о новом подходе к решению уравнений пятой степени и полиномиальных уравнений в целом. Он утверждал, что каждое уравнение, в котором степень переменной равна единице, может быть решена стандартными средствами. Его работа по этому вопросу была бы более известна, если бы он был членом Академии во время родов (1770 г.), потому что это облегчило бы ему публикацию своих утверждений.Как бы то ни было, его статья не публиковалась до 1774 года, а тем временем Жозеф-Луи Лагранж (1736–1813), один из величайших математиков века, опубликовал пару статей по этому вопросу. Возможно, разочарованный, зная, что первая публикация в научном мире имеет решающее значение, Вандермонде не продолжил свои исследования по решению полиномиальных уравнений.Другим математиком, чьи работы предвосхитили работы Лагранжа, был Эдвард Варинг (1736-1798).В его случае недостатком, мешавшим его дальнейшему прогрессу, было отсталое состояние математики в Англии при его жизни.
 В результате сознательного решения английских математиков следовать практике сэра Исаака Ньютона (1642–1727), а не ведущим ученым Европы, английская математика отошла от достижений остального мира. Работа Варинга получила высокую оценку Лагранжа и других, но он не был в среде, где прогресс был легким.
В результате сознательного решения английских математиков следовать практике сэра Исаака Ньютона (1642–1727), а не ведущим ученым Европы, английская математика отошла от достижений остального мира. Работа Варинга получила высокую оценку Лагранжа и других, но он не был в среде, где прогресс был легким.Лагранж, напротив, провел время в математических центрах Европы, в результате чего его работа могла получить быстрое распространение. Его подход к полиномиальным уравнениям был отчасти историческим, поскольку он отступил назад, чтобы изучить, как итальянским математикам удавалось находить решения для уравнений кубической и четвертой степени. На основе этого анализа ему удалось сформулировать исследовательскую программу для как решать уравнения пятой степени (и более высокой степени). Как оказалось, хотя он и не смог ничего придумать в качестве общего решения уравнения пятой степени, его переоценка своих предшественников предоставила существенные элементы для вывода, к которому пришел Эварист Галуа (1811–1832), а именно: что уравнение пятой степени не может быть решено традиционными средствами.
Удар
Идея, которую Лагранж привнес в решение полиномиальных уравнений, была идеей симметрии. Вместо того, чтобы просто искать решения исходного уравнения, он искал другие соотношения, которым должны удовлетворять решения, в надежде, что они будут проще, чем исходное уравнение. Пока еще можно было восстановить исходные решения из решений новых вспомогательных уравнений, метод будет работать для получения этих исходных решений.
Если посмотреть на квадратное уравнение (с коэффициентом при квадрате члена, равным единице), то сумма решений уравнения равна минусу коэффициента при члене первого порядка. Произведение решений равно постоянному члену. Этот подход мог бы стать альтернативой квадратной формуле для решения квадратного уравнения. Подобные стратегии дают вспомогательные уравнения для решения кубических и уравнения четвертой степени, поскольку кубическое уравнение можно свести к вспомогательному квадратному, а уравнение четвертой степени — к вспомогательному кубическому.

Проблема применения стратегии Лагранжа к уравнениям пятой степени стала очевидной в работе Джан Франческо Мальфатти (1731-1807). В статье 1770 года он показал, что если попытаться найти вспомогательное уравнение для квинтики, результат будет шестой степени. Поскольку показатель степени переменной в этом вспомогательном методе выше, чем в оригинале, это только усугубило проблему. Когда при решении кубического уравнения обнаруживались уравнения шестой степени, их можно было рассматривать как квадратичные уравнения.Те, которые возникли в результате работы с квинтикой, не могли быть сокращены таким образом.
Работа Лагранжа послужила основой для новой дисциплины математики, называемой теорией групп. Это можно рассматривать как изучение симметрии, возникшее в результате попыток Лагранжа найти симметричные функции решений уравнения. Функция симметрична, если некоторая замена значений переменных, представляющих решения, не меняет значения функции. Например, x + y сохраняет то же значение, если x и y поменять местами.

Теория групп оказалась основой для доказательства того, что не существует формулы для решения всех уравнений пятой степени, как это было для младших степеней переменной. Это не означало, что отдельные уравнения пятой степени не могли быть решены, поскольку некоторые из них решались веками ранее. Доказательство действительно гарантировало, что любой метод решения, претендующий на решение всех уравнений пятой степени, должен был выйти за рамки стандартных алгебраических операций, которыми раньше ограничивалось внимание.Целый раздел математики, известный как теория Галуа, посвящен применению теории групп (основанной на симметрии) к изучению полиномиальных уравнений и их решений.
В конце восемнадцатого века могло показаться, что давняя проблема решения полиномиальных уравнений выше четвертой степени не продвинулась вперед. На самом деле, однако, усилия Лагранжа и других превратили проблему в проблему, к которой можно подойти, изучая симметрию.Разъяснение Лагранжа того, что представляет собой метод решения полиномиального уравнения, позволило использовать различные дисциплины в математике для поиска этих решений.

ТОМАС ДРУКЕР
Дополнительная литератураКац, Виктор Дж. История математики: введение . Нью-Йорк: HarperCollins, 1993.
ноября, Любош. Истоки современной алгебры . Прага: Издательство Академии, 1983.
Ван дер Варден, Б.Л. История алгебры . Berlin: Springer-Verlag, 1985.
Наука и ее время: понимание социальной значимости научных открытий
Алгебра 1 деятельность pdf.Пакет по математике для учащихся 9-го класса, поступающих в 9-й класс в августе
г. Занятия по алгебре 1 в формате pdf. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Нажмите на бесплатный лист по математике для 9-го класса, который вы хотели бы распечатать или загрузить. 1)), стандартная форма (Ax+ By = C, где A, B и C — целые числа) и форма с двойным пересечением (x/a + y/b = 1). В самой нижней точке соединительный провод имеет длину 1 м. Периметр квадрата 360 футов. (1 мин) iv.3 5 3 6 4 2 7 = − + + x+ x Решите каждое из следующих линейных уравнений графически, а затем проверьте свой ответ алгебраически. Он имеет степени по английскому языку и математике Университета Рутгерса. Рабочие листы по предварительной алгебре и алгебре для детей 3, 4, 5, 6 и 7 классов. Создавайте печатные рабочие листы для построения графиков линейных уравнений, определения наклона или определения уравнения линии (для предварительной алгебры и алгебры 1 в форматах PDF или html). Ключ к ответу на встроенный тест College Board Springboard .
Занятия по алгебре 1 в формате pdf. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Нажмите на бесплатный лист по математике для 9-го класса, который вы хотели бы распечатать или загрузить. 1)), стандартная форма (Ax+ By = C, где A, B и C — целые числа) и форма с двойным пересечением (x/a + y/b = 1). В самой нижней точке соединительный провод имеет длину 1 м. Периметр квадрата 360 футов. (1 мин) iv.3 5 3 6 4 2 7 = − + + x+ x Решите каждое из следующих линейных уравнений графически, а затем проверьте свой ответ алгебраически. Он имеет степени по английскому языку и математике Университета Рутгерса. Рабочие листы по предварительной алгебре и алгебре для детей 3, 4, 5, 6 и 7 классов. Создавайте печатные рабочие листы для построения графиков линейных уравнений, определения наклона или определения уравнения линии (для предварительной алгебры и алгебры 1 в форматах PDF или html). Ключ к ответу на встроенный тест College Board Springboard . ГЛАВА 2 РАБОЧИЕ ЛИСТЫ. Большие идеи математической алгебры 1 ответы на главу 1 решения линейных уравнений, доступные здесь, бесплатны. Этот пакет создан для тех, кто хотел бы заниматься только по Алгебре 1. 4 Рабочий лист 2. выполнил 9. Каждый рабочий лист содержит пятьдесят основных задач по алгебре, чтобы учащиеся могли попрактиковаться в алгебраических выражениях и научиться находить значение переменной. Решите уравнения умножения и/или деления, в зависимости от того, что будет первым при чтении задачи слева направо. Скачать PDF.Это предназначено для подготовки учащихся к общим основным задачам производительности. ИСПОЛЬЗОВАНИЕ… Эшли Смит на [ПРОВЕРЕНО] Практические рабочие листы по алгебре 1 Pdf. Убедитесь, что списки очищены. Алгебра Матпланета. 3 Рабочий лист 4. Увлекательные и увлекательные способы обучения — лучший вариант для понимания математических концепций алгебры 1. ЦЕЛИ ОБУЧЕНИЯ Учащиеся смогут: 1) складывать, вычитать и умножать многочлены. 2 3!С. ШАГ 4: Алгебра ГРАФОВ 1 Имя_____ ©t X290 1Q3r 8Kju TtGaP ZSZoXfjt swDa Zrze b PLCLqCk.
ГЛАВА 2 РАБОЧИЕ ЛИСТЫ. Большие идеи математической алгебры 1 ответы на главу 1 решения линейных уравнений, доступные здесь, бесплатны. Этот пакет создан для тех, кто хотел бы заниматься только по Алгебре 1. 4 Рабочий лист 2. выполнил 9. Каждый рабочий лист содержит пятьдесят основных задач по алгебре, чтобы учащиеся могли попрактиковаться в алгебраических выражениях и научиться находить значение переменной. Решите уравнения умножения и/или деления, в зависимости от того, что будет первым при чтении задачи слева направо. Скачать PDF.Это предназначено для подготовки учащихся к общим основным задачам производительности. ИСПОЛЬЗОВАНИЕ… Эшли Смит на [ПРОВЕРЕНО] Практические рабочие листы по алгебре 1 Pdf. Убедитесь, что списки очищены. Алгебра Матпланета. 3 Рабочий лист 4. Увлекательные и увлекательные способы обучения — лучший вариант для понимания математических концепций алгебры 1. ЦЕЛИ ОБУЧЕНИЯ Учащиеся смогут: 1) складывать, вычитать и умножать многочлены. 2 3!С. ШАГ 4: Алгебра ГРАФОВ 1 Имя_____ ©t X290 1Q3r 8Kju TtGaP ZSZoXfjt swDa Zrze b PLCLqCk. Загрузите наши бесплатные рабочие листы по математике для теста по алгебре 2. 1 Законы алгебры, терминология и обозначения. 7 Обзор главы 4 1 Обзор главы 4 2A Обзор главы 4 2B Обзор главы 4 2C Об авторе Марк Зегарелли — автор книги «Логика для чайников» (Wiley). Согласно графику, какое утверждение лучше всего описывает наклон? А. ССЕ. Это приведет вас к отдельной странице рабочего листа. Эти действия включают в себя примеры из реальной жизни и сложную графику… Рабочий лист по алгебре 1 Автор: Рабочие листы Рабочие листы Тема: Бесплатные печатные учебные листы по алгебре 1 для учителей Ключевые слова: Рабочий лист по алгебре 1 Дата создания: 12.10.2010 16:21:42 Цель обучения 1: Решать многоступенчатые задачи, используя единицы измерения в качестве ориентира для решения, последовательно интерпретируя единицы измерения в формулах и выбирая соответствующий уровень … 1.Simplenote — кроссплатформенное приложение для создания заметок и конкурент Evernote. Перечислите множество всех натуральных чисел.
Загрузите наши бесплатные рабочие листы по математике для теста по алгебре 2. 1 Законы алгебры, терминология и обозначения. 7 Обзор главы 4 1 Обзор главы 4 2A Обзор главы 4 2B Обзор главы 4 2C Об авторе Марк Зегарелли — автор книги «Логика для чайников» (Wiley). Согласно графику, какое утверждение лучше всего описывает наклон? А. ССЕ. Это приведет вас к отдельной странице рабочего листа. Эти действия включают в себя примеры из реальной жизни и сложную графику… Рабочий лист по алгебре 1 Автор: Рабочие листы Рабочие листы Тема: Бесплатные печатные учебные листы по алгебре 1 для учителей Ключевые слова: Рабочий лист по алгебре 1 Дата создания: 12.10.2010 16:21:42 Цель обучения 1: Решать многоступенчатые задачи, используя единицы измерения в качестве ориентира для решения, последовательно интерпретируя единицы измерения в формулах и выбирая соответствующий уровень … 1.Simplenote — кроссплатформенное приложение для создания заметок и конкурент Evernote. Перечислите множество всех натуральных чисел. Алгебра 1 Глава 8 Рабочие листы **Это фрагмент главы «Drill Sheets Vol. Распечатайте или скачайте бесплатно рабочий лист в формате pdf и научите студентов основам алгебры. pdf: Размер файла: 52 КБ: Тип файла: pdf: Скачать файл. 1 CP Алгебра 2 Модуль 2-1: Факторинг и решение квадратичных уравнений. ПАКЕТ РАБОЧИХ ТАБЛИЦ Название:_____Период_____ Цели обучения: 0. 50. ключ ответа kuta software innite алгебра, алгебра 1 задание нарисуйте график каждой функции, решение алгебры Алгебра 1B (Раздел B) Урок 21_22 Деятельность Инструкции: Это совместное задание из Урока 21 и Урока 22 предназначено для того, чтобы познакомить вас с несколькими внешними ресурсами, которые мне очень нравятся, и которые помогут вам выполнить другие задания в Уроках 21 и 22.Бесплатные рабочие листы по алгебре в формате pdf скачать предварительные рабочие листы по алгебре рабочие листы по алгебре […] Алгебра 1 Алгебра 1 Практика Тест Практика Тест Практика Тест Часть 2: Указания: Для задач 21-27 напишите правильный ответ на листе для ответов.
Алгебра 1 Глава 8 Рабочие листы **Это фрагмент главы «Drill Sheets Vol. Распечатайте или скачайте бесплатно рабочий лист в формате pdf и научите студентов основам алгебры. pdf: Размер файла: 52 КБ: Тип файла: pdf: Скачать файл. 1 CP Алгебра 2 Модуль 2-1: Факторинг и решение квадратичных уравнений. ПАКЕТ РАБОЧИХ ТАБЛИЦ Название:_____Период_____ Цели обучения: 0. 50. ключ ответа kuta software innite алгебра, алгебра 1 задание нарисуйте график каждой функции, решение алгебры Алгебра 1B (Раздел B) Урок 21_22 Деятельность Инструкции: Это совместное задание из Урока 21 и Урока 22 предназначено для того, чтобы познакомить вас с несколькими внешними ресурсами, которые мне очень нравятся, и которые помогут вам выполнить другие задания в Уроках 21 и 22.Бесплатные рабочие листы по алгебре в формате pdf скачать предварительные рабочие листы по алгебре рабочие листы по алгебре […] Алгебра 1 Алгебра 1 Практика Тест Практика Тест Практика Тест Часть 2: Указания: Для задач 21-27 напишите правильный ответ на листе для ответов. ©glencoe mcgraw hill 116 glencoe pre алгебра Глава 7 повторение 1 x 1 2 x 8 3 x 4 4 x 16 Материалы MALATI: Алгебра, модуль 7 6 ЗАДАНИЕ 5: Строительство мостов Инженеры должны построить висячий мост через реку. Проблемы с партнерами Неравенство 1 Pdf. Алгебра 1 Общая основная практика и рабочая тетрадь по решению проблем Общая основная алгебра 1 Раздел 8 Урок 5 Ответ на домашнее задание.8. • МГСЭ9-12. Проезжая часть моста будет подвешена на подвесном тросе с соединительными тросами на расстоянии 1 м друг от друга. Вкладки помогают найти ресурсы глав в каждом разделе. Этот продукт подходит для дошкольных учреждений, детского сада и 1-го класса. Бесплатные печатные рабочие листы функций (pdf) с ключами ответов по домену / диапазону, оценочные функции, состав функций, от 1 до 1 и многое другое. Сравнение и обсуждение в малых группах. www. Введение в . Алгебра 1 Тема 1 Практика Pdf Имя Класс Дата Алгебра 1 Тема 1 Практика Урок 1 1 Урок 1 2 Периодическая комета по имени Джонсон была замечена в каждом Гленко алгебра 2 книга ответы практика 2 2 прентис холл.
©glencoe mcgraw hill 116 glencoe pre алгебра Глава 7 повторение 1 x 1 2 x 8 3 x 4 4 x 16 Материалы MALATI: Алгебра, модуль 7 6 ЗАДАНИЕ 5: Строительство мостов Инженеры должны построить висячий мост через реку. Проблемы с партнерами Неравенство 1 Pdf. Алгебра 1 Общая основная практика и рабочая тетрадь по решению проблем Общая основная алгебра 1 Раздел 8 Урок 5 Ответ на домашнее задание.8. • МГСЭ9-12. Проезжая часть моста будет подвешена на подвесном тросе с соединительными тросами на расстоянии 1 м друг от друга. Вкладки помогают найти ресурсы глав в каждом разделе. Этот продукт подходит для дошкольных учреждений, детского сада и 1-го класса. Бесплатные печатные рабочие листы функций (pdf) с ключами ответов по домену / диапазону, оценочные функции, состав функций, от 1 до 1 и многое другое. Сравнение и обсуждение в малых группах. www. Введение в . Алгебра 1 Тема 1 Практика Pdf Имя Класс Дата Алгебра 1 Тема 1 Практика Урок 1 1 Урок 1 2 Периодическая комета по имени Джонсон была замечена в каждом Гленко алгебра 2 книга ответы практика 2 2 прентис холл. текст: Linear Algebra: An Introductory Approach [5] Charles W. 8 4. Учащиеся будут создавать на доске плакат, чтобы продемонстрировать свое решение. Холт Алгебра 1 Тестовые рабочие листы главы — Learny Kids Try It 5. A. ключ ответа кута программное обеспечение innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре Рабочие листы по алгебре 1 для 9 класса с ответами pdf. Бесплатные рабочие листы по алгебре 1, созданные с помощью бесконечной алгебры 1. Алгебра 1 План модуля Модуль 1: количественные отношения, графики и функции 9 сентября – 3 октября !!!!! ORANGE PUBLIC SCHOOLS 2014 — 2015 Закладка Файл PDF Prentice Hall Алгебра 1 Занятия Игры и головоломки Ответы Найдите навык, чтобы начать практиковаться! Ixl ответ ключевой алгебры 1 Ixl ответ ключевой алгебры 1 — fullexams.2) линейные уравнения/наклон — Ссылка: Alg 1 Обзор перегруппировки, наклона и построения графиков. o Алгебра 1. Помощь в оценивании в конце курса. Алгебра 1. Спецификации элементов в конце курса.
текст: Linear Algebra: An Introductory Approach [5] Charles W. 8 4. Учащиеся будут создавать на доске плакат, чтобы продемонстрировать свое решение. Холт Алгебра 1 Тестовые рабочие листы главы — Learny Kids Try It 5. A. ключ ответа кута программное обеспечение innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре Рабочие листы по алгебре 1 для 9 класса с ответами pdf. Бесплатные рабочие листы по алгебре 1, созданные с помощью бесконечной алгебры 1. Алгебра 1 План модуля Модуль 1: количественные отношения, графики и функции 9 сентября – 3 октября !!!!! ORANGE PUBLIC SCHOOLS 2014 — 2015 Закладка Файл PDF Prentice Hall Алгебра 1 Занятия Игры и головоломки Ответы Найдите навык, чтобы начать практиковаться! Ixl ответ ключевой алгебры 1 Ixl ответ ключевой алгебры 1 — fullexams.2) линейные уравнения/наклон — Ссылка: Alg 1 Обзор перегруппировки, наклона и построения графиков. o Алгебра 1. Помощь в оценивании в конце курса. Алгебра 1. Спецификации элементов в конце курса. Алгебра 1 в конце курса 1= m(x-x. линейное уравнение не содержит корней, произведений или степеней, превышающих 1 из переменных, и что бесплатные рабочие листы по алгебре в формате pdf загружают калькулятор алгебры с шагами Учебник по алгебре для 5, 6, 7 классов в формате pdf.Номер Скачать алгебру трамплина 1, блок 5, ключ ответа — ссылка на бесплатное скачивание книги Bing в формате pdf или читать онлайн здесь в формате PDF. Используйте это в уравнении, чтобы найти x. C. Идентифицируйте монеты, доллары, дайм, никель, фунты, евро, доллары США, добавление CAD. Вы можете контролировать типы проблем, количество проблем, рабочее пространство, границы вокруг проблем и многое другое. Рабочие листы подходят для предалгебры и алгебры 1 курса (6-9 классы). Алгебра линейного программирования.• Важно предоставить пример определения, которому учащиеся… Учебное пособие по алгебре 1 Учебное пособие по алгебре 1 предназначено для помощи учителям в обучении планированию в соответствии со стандартами Флориды.
Алгебра 1 в конце курса 1= m(x-x. линейное уравнение не содержит корней, произведений или степеней, превышающих 1 из переменных, и что бесплатные рабочие листы по алгебре в формате pdf загружают калькулятор алгебры с шагами Учебник по алгебре для 5, 6, 7 классов в формате pdf.Номер Скачать алгебру трамплина 1, блок 5, ключ ответа — ссылка на бесплатное скачивание книги Bing в формате pdf или читать онлайн здесь в формате PDF. Используйте это в уравнении, чтобы найти x. C. Идентифицируйте монеты, доллары, дайм, никель, фунты, евро, доллары США, добавление CAD. Вы можете контролировать типы проблем, количество проблем, рабочее пространство, границы вокруг проблем и многое другое. Рабочие листы подходят для предалгебры и алгебры 1 курса (6-9 классы). Алгебра линейного программирования.• Важно предоставить пример определения, которому учащиеся… Учебное пособие по алгебре 1 Учебное пособие по алгебре 1 предназначено для помощи учителям в обучении планированию в соответствии со стандартами Флориды. Какое из следующих чисел является иррациональным?! А. По очереди напишите свои числа. Тип файла PDF Algebra 1 Activity Lesson Opener Answers Мощные практические упражнения для высокоэффективных специальных педагогов Эта серия полностью соответствует Основам преподавания математики и обеспечивает охват учебной программы, предназначенной для того, чтобы учащиеся могли пересмотреть и закрепить основные рабочие листы Pre Algebra Chapter 1 Бесплатно Рабочие листы по алгебре 1 для печати — также доступны в Интернете Существует ряд бесплатных рабочих листов по алгебре 1, которые вы можете загрузить, распечатать или решить в Интернете.72×2, где x — количество мячей, выпущенных за один день, в тысячах. Учебник разделен на восемь глав. ключ ответа кута программное обеспечение бесконечная алгебра, алгебра 1 задание набросать график каждой функции, решение алгебры Бесплатные большие идеи математика алгебра 1. Пойманный на краже Бейсбольный «ромб» на самом деле бейсбольный квадрат. Сумма углов в треугольнике равна 180.
Какое из следующих чисел является иррациональным?! А. По очереди напишите свои числа. Тип файла PDF Algebra 1 Activity Lesson Opener Answers Мощные практические упражнения для высокоэффективных специальных педагогов Эта серия полностью соответствует Основам преподавания математики и обеспечивает охват учебной программы, предназначенной для того, чтобы учащиеся могли пересмотреть и закрепить основные рабочие листы Pre Algebra Chapter 1 Бесплатно Рабочие листы по алгебре 1 для печати — также доступны в Интернете Существует ряд бесплатных рабочих листов по алгебре 1, которые вы можете загрузить, распечатать или решить в Интернете.72×2, где x — количество мячей, выпущенных за один день, в тысячах. Учебник разделен на восемь глав. ключ ответа кута программное обеспечение бесконечная алгебра, алгебра 1 задание набросать график каждой функции, решение алгебры Бесплатные большие идеи математика алгебра 1. Пойманный на краже Бейсбольный «ромб» на самом деле бейсбольный квадрат. Сумма углов в треугольнике равна 180. См. ниже широкий ассортимент листов, входящих в комплект. 6 часов назад Алгебра 1 — это второй курс математики в старшей школе, который проведет вас, среди прочего, по выражениям, системам уравнений, функциям, действительным числам, неравенствам, показателям степени, полиномам, радикальным и рациональным выражениям.1. Элементарная алгебра предназначена для манипулирования математическими выражениями с величинами, представленными символами e. (1-2 мин) iii. D. Загрузить файл в формате PDF «Алгебра 1, глава 8. Выбор рабочих листов, вопросы и ответы», загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по главам: Введение в тригонометрию, 3-я, 4-я, средняя и непрерывная пропорции, бесплатные рабочие листы по алгебре в формате pdf, калькулятор алгебры с шаги по алгебре рабочие листы 6 класс рабочие листы по алгебре 9 класс рабочие листы по алгебре 8 класс 4 класс рабочие листы по алгебре 3-й 4-й 5-й 6-й 7-й класс учебник по алгебре pdf.com Показать подробности 8 часов назад Читать онлайн [Книга] Алгебра Холта 1 Рабочие листы Ответ Ключ книга pdf бесплатно скачать ссылку книгу сейчас.
См. ниже широкий ассортимент листов, входящих в комплект. 6 часов назад Алгебра 1 — это второй курс математики в старшей школе, который проведет вас, среди прочего, по выражениям, системам уравнений, функциям, действительным числам, неравенствам, показателям степени, полиномам, радикальным и рациональным выражениям.1. Элементарная алгебра предназначена для манипулирования математическими выражениями с величинами, представленными символами e. (1-2 мин) iii. D. Загрузить файл в формате PDF «Алгебра 1, глава 8. Выбор рабочих листов, вопросы и ответы», загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по главам: Введение в тригонометрию, 3-я, 4-я, средняя и непрерывная пропорции, бесплатные рабочие листы по алгебре в формате pdf, калькулятор алгебры с шаги по алгебре рабочие листы 6 класс рабочие листы по алгебре 9 класс рабочие листы по алгебре 8 класс 4 класс рабочие листы по алгебре 3-й 4-й 5-й 6-й 7-й класс учебник по алгебре pdf.com Показать подробности 8 часов назад Читать онлайн [Книга] Алгебра Холта 1 Рабочие листы Ответ Ключ книга pdf бесплатно скачать ссылку книгу сейчас. Напишите открыто, если утверждение не является ни истинным, ни ложным. Умение складывать, вычитать и умножать многочлены помогает учащимся в их работе по алгебре, а также в символической работе с функциями. 501 вопрос по алгебре. сертификаты поддерживают мотивацию детей по мере того, как они осваивают навыки. Проблема с границей бассейна. «В этом исследовательском задании учащиеся сначала составят выражения с числами, чтобы определить количество плиток, граничащих с бассейном.Пибоди. Надеюсь, тебе понравится! Нажмите на бесплатный рабочий лист по алгебре 1, который вы хотите распечатать или загрузить. Определите, будет ли эта точка точкой минимума или точкой максимума. Эти рабочие листы уравнений алгебры 1 будут создавать задачи со словами о скорости расстояния и времени с десятью … Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. Для этого теста вы можете предположить, что значение знаменателя не равно нулю. Общий базовый учебник по алгебре 1 в формате pdf.
Напишите открыто, если утверждение не является ни истинным, ни ложным. Умение складывать, вычитать и умножать многочлены помогает учащимся в их работе по алгебре, а также в символической работе с функциями. 501 вопрос по алгебре. сертификаты поддерживают мотивацию детей по мере того, как они осваивают навыки. Проблема с границей бассейна. «В этом исследовательском задании учащиеся сначала составят выражения с числами, чтобы определить количество плиток, граничащих с бассейном.Пибоди. Надеюсь, тебе понравится! Нажмите на бесплатный рабочий лист по алгебре 1, который вы хотите распечатать или загрузить. Определите, будет ли эта точка точкой минимума или точкой максимума. Эти рабочие листы уравнений алгебры 1 будут создавать задачи со словами о скорости расстояния и времени с десятью … Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. Для этого теста вы можете предположить, что значение знаменателя не равно нулю. Общий базовый учебник по алгебре 1 в формате pdf. 06 декабря 2021 г. · Рабочие листы по алгебре линейного программирования 1. Рабочие листы для всех из рабочего листа решения и построения графиков. Предоставляется место для решения задач, но некоторые учащиеся могут предпочесть доступ к «чертежу» для решения задач, особенно на более высоких уровнях. Вот идеальная и полная коллекция БЕСПЛАТНЫХ рабочих листов по алгебре 2, которые помогут вам или вашим ученикам в подготовке и практике по алгебре 2. PS1, PS2, PS3 и PS4 охватывают темы, предшествующие алгебре, которые необходимы для успешного изучения алгебры 1.Рабочий лист по алгебре — 2. Они будут использовать простые формулы, описывать числовые последовательности, используя буквы в качестве символов, и находить неизвестные в уравнении. Необходимые знания: 1. Кроме того, в комплект входит контрольный лист, который поможет учащимся отслеживать свои данные по SOL 2013 и психологии 7291: Многомерная статистика (Кэри) 27.08.98 Матричная алгебра — 1 Введение в матричную алгебру Определения: Матрица — это набор чисел, упорядоченных по строкам и столбцам.
06 декабря 2021 г. · Рабочие листы по алгебре линейного программирования 1. Рабочие листы для всех из рабочего листа решения и построения графиков. Предоставляется место для решения задач, но некоторые учащиеся могут предпочесть доступ к «чертежу» для решения задач, особенно на более высоких уровнях. Вот идеальная и полная коллекция БЕСПЛАТНЫХ рабочих листов по алгебре 2, которые помогут вам или вашим ученикам в подготовке и практике по алгебре 2. PS1, PS2, PS3 и PS4 охватывают темы, предшествующие алгебре, которые необходимы для успешного изучения алгебры 1.Рабочий лист по алгебре — 2. Они будут использовать простые формулы, описывать числовые последовательности, используя буквы в качестве символов, и находить неизвестные в уравнении. Необходимые знания: 1. Кроме того, в комплект входит контрольный лист, который поможет учащимся отслеживать свои данные по SOL 2013 и психологии 7291: Многомерная статистика (Кэри) 27.08.98 Матричная алгебра — 1 Введение в матричную алгебру Определения: Матрица — это набор чисел, упорядоченных по строкам и столбцам. Карточки следует использовать как учебное пособие для учителей, а затем как… ©y YKKuRtma7 nSHoEf2tJwra Yr5eq 6LoLjC 1.27112015 на этой странице вы можете прочитать или скачать ключ ответа к математике алгебра больших идей 1 в формате pdf ответы алгебры математики больших идей 1 pdf. С командой чрезвычайно преданных и качественных лекторов практический тест по алгебре 1 в формате pdf станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей от самих себя. Оценка функций Рабочий лист и ключ к ответу Бесплатный PDF-файл О применении функции Нота Планы уроков по алгебре Рабочие листы с задачами Оценка алгебраических задач… Базовый навык до алгебры, решающий проблемы с пропорциями, отвечайте на каждый вопрос и округляйте ответ до ближайшего целого числа.Я могу учитывать, когда a равно единице. Алгебра 1 … ©q 02i0 t173 h kKKuCtIa x gs So Ef Atow da MrWeq NLBL 2Cr. 1 Math54Worksheets, 7-е издание 1. Победителем становится тот, кто первым заполнит строку, которая в сумме дает 15.
Карточки следует использовать как учебное пособие для учителей, а затем как… ©y YKKuRtma7 nSHoEf2tJwra Yr5eq 6LoLjC 1.27112015 на этой странице вы можете прочитать или скачать ключ ответа к математике алгебра больших идей 1 в формате pdf ответы алгебры математики больших идей 1 pdf. С командой чрезвычайно преданных и качественных лекторов практический тест по алгебре 1 в формате pdf станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей от самих себя. Оценка функций Рабочий лист и ключ к ответу Бесплатный PDF-файл О применении функции Нота Планы уроков по алгебре Рабочие листы с задачами Оценка алгебраических задач… Базовый навык до алгебры, решающий проблемы с пропорциями, отвечайте на каждый вопрос и округляйте ответ до ближайшего целого числа.Я могу учитывать, когда a равно единице. Алгебра 1 … ©q 02i0 t173 h kKKuCtIa x gs So Ef Atow da MrWeq NLBL 2Cr. 1 Math54Worksheets, 7-е издание 1. Победителем становится тот, кто первым заполнит строку, которая в сумме дает 15. 04. 05 за каждую листовку, которую он распространяет. 1 задание по алгебре для 9 класса в формате pdf. Эти рабочие листы по алгебре являются отличным ресурсом для шага 4. Например, было бы бессмысленно писать уравнение. Только практические задачи по алгебре для начального и среднего уровня Учебник с открытым исходным кодом (CC-BY) Тайлера Уоллеса 1 Алгебра для 6-го класса (возраст 10–11 лет). ) | Oxford Owl Алгебра в 6-м классе (возраст 10–11 лет) В 6-м классе ваш ребенок начнет изучать алгебру.Какая цена билета принесет наибольший доход? А. 1 доллар. Бесплатные рабочие листы по алгебре в формате pdf с ключами для ответов включают наглядные пособия по моделированию задач, практические задачи исследовательской деятельности и рабочие листы по алгебре 1 4/22/2018 | Рабочие листы Exponents 1/4 Воскресенье, 22 апреля 2018 г. Рабочие листы Exponents Вот графический предварительный просмотр всех рабочих листов Exponents. Рабочие листы по алгебре обычно состоят из большого количества трудностей и уравнений, которые можно использовать для проверки себя.
04. 05 за каждую листовку, которую он распространяет. 1 задание по алгебре для 9 класса в формате pdf. Эти рабочие листы по алгебре являются отличным ресурсом для шага 4. Например, было бы бессмысленно писать уравнение. Только практические задачи по алгебре для начального и среднего уровня Учебник с открытым исходным кодом (CC-BY) Тайлера Уоллеса 1 Алгебра для 6-го класса (возраст 10–11 лет). ) | Oxford Owl Алгебра в 6-м классе (возраст 10–11 лет) В 6-м классе ваш ребенок начнет изучать алгебру.Какая цена билета принесет наибольший доход? А. 1 доллар. Бесплатные рабочие листы по алгебре в формате pdf с ключами для ответов включают наглядные пособия по моделированию задач, практические задачи исследовательской деятельности и рабочие листы по алгебре 1 4/22/2018 | Рабочие листы Exponents 1/4 Воскресенье, 22 апреля 2018 г. Рабочие листы Exponents Вот графический предварительный просмотр всех рабочих листов Exponents. Рабочие листы по алгебре обычно состоят из большого количества трудностей и уравнений, которые можно использовать для проверки себя. x 1 vA 4l Ll 1 8r2i 0g lh4t ysX GrEeHs8eErvueid W.y y WALLIPlG grLicgRhMtAsa TrKeBsxeQrWvAe4d j. 4. Графические неравенства на числовых прямых. Бесплатные рабочие листы по алгебре pdf … Алгебра 1 рабочий лист неравенства имя 1. ©glencoe mcgraw hill 116 glencoe pre алгебра глава 7 обзор 1 x 1 2 x 8 3 x 4 4 x 16 Алгебра 1 рабочие листы с ответами Pdf — Рабочий лист Банни Алгебра 1: Общее ядро ( 15-е издание) Чарльз, Рэндалл И. 34 (1) Введение. ©glencoe mcgraw hill 116 glencoe pre алгебра обзор главы 7 1 x 1 2 x 8 3 x 4 4 x 16 Ниже приведены рабочие листы, посвященные элементарным задачам по алгебре.Package200 Дополнительные рабочие листы с двумя однозначными дополнениямиАлгебра колледжа с интегрированным обзором и рабочими листами, а также новая Mymathlab с Pearson Etext — пакет карт доступаИнтегрированные рабочие листы арифметики и базовой алгебры для классной или лабораторной практики Вопросы и ответы по математике 9-го класса с множественным выбором (MCQs)CLEP College Algebra Study Руководство … ОБ АЛГЕБРЕ PRE-AP 1 13 Введение в алгебру Pre-AP 1 13 Области математики Pre-AP 15 Алгебра Pre-AP 1 и готовность к карьере 16 Обзор ресурсов и поддержки 18 Карта курса 20 Структура курса Алгебра Pre-AP 1 20 Введение 21 Компоненты структуры курса 22 Большие идеи в Pre-AP Algebra 1 23 Обзор Pre-AP Algebra 1 Units and Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html.
x 1 vA 4l Ll 1 8r2i 0g lh4t ysX GrEeHs8eErvueid W.y y WALLIPlG grLicgRhMtAsa TrKeBsxeQrWvAe4d j. 4. Графические неравенства на числовых прямых. Бесплатные рабочие листы по алгебре pdf … Алгебра 1 рабочий лист неравенства имя 1. ©glencoe mcgraw hill 116 glencoe pre алгебра глава 7 обзор 1 x 1 2 x 8 3 x 4 4 x 16 Алгебра 1 рабочие листы с ответами Pdf — Рабочий лист Банни Алгебра 1: Общее ядро ( 15-е издание) Чарльз, Рэндалл И. 34 (1) Введение. ©glencoe mcgraw hill 116 glencoe pre алгебра обзор главы 7 1 x 1 2 x 8 3 x 4 4 x 16 Ниже приведены рабочие листы, посвященные элементарным задачам по алгебре.Package200 Дополнительные рабочие листы с двумя однозначными дополнениямиАлгебра колледжа с интегрированным обзором и рабочими листами, а также новая Mymathlab с Pearson Etext — пакет карт доступаИнтегрированные рабочие листы арифметики и базовой алгебры для классной или лабораторной практики Вопросы и ответы по математике 9-го класса с множественным выбором (MCQs)CLEP College Algebra Study Руководство … ОБ АЛГЕБРЕ PRE-AP 1 13 Введение в алгебру Pre-AP 1 13 Области математики Pre-AP 15 Алгебра Pre-AP 1 и готовность к карьере 16 Обзор ресурсов и поддержки 18 Карта курса 20 Структура курса Алгебра Pre-AP 1 20 Введение 21 Компоненты структуры курса 22 Большие идеи в Pre-AP Algebra 1 23 Обзор Pre-AP Algebra 1 Units and Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Использование символов вместо чисел позволяет работать в общем, а не в определенном порядке, и позволяет нам манипулировать и переписывать взаимосвязи между… Большая коллекция рабочих листов gcf тщательно составлена для учащихся с 5 по 8 классы. ЕДИНИЦЫ И РАЗМЕРЫ Цель алгебры состоит в том, чтобы помочь нам решить неизвестные величины в уравнениях, которые представляют реальные вещи. 1a Покажите, что линейные функции растут на равные разности на равных интервалах и что экспоненциальные функции растут на равные коэффициенты на … Алгебра I.. Доступно для предварительной алгебры алгебры 1 геометрии алгебры 2 предварительного исчисления и … Читать PDF Алгебра 1 Учебная деятельность на основе проектов Алгебра Семестр 1 Проект по ведению бизнеса. 2-1 Лист-раскраска на День Благодарения — Решение уравнений с переменными с обеих сторон (БЕСПЛАТНЫЙ PDF) 2-1 Лист-раскраска на День Благодарения Ответы — Решение уравнений с переменными с обеих сторон (редактируемый — только для членов) 2-2 Лист-раскраска на День Благодарения — Решение уравнений с дистрибутивом Собственность Этот комплект содержит более 180 заданий из моей популярной учебной программы по алгебре 1.
Использование символов вместо чисел позволяет работать в общем, а не в определенном порядке, и позволяет нам манипулировать и переписывать взаимосвязи между… Большая коллекция рабочих листов gcf тщательно составлена для учащихся с 5 по 8 классы. ЕДИНИЦЫ И РАЗМЕРЫ Цель алгебры состоит в том, чтобы помочь нам решить неизвестные величины в уравнениях, которые представляют реальные вещи. 1a Покажите, что линейные функции растут на равные разности на равных интервалах и что экспоненциальные функции растут на равные коэффициенты на … Алгебра I.. Доступно для предварительной алгебры алгебры 1 геометрии алгебры 2 предварительного исчисления и … Читать PDF Алгебра 1 Учебная деятельность на основе проектов Алгебра Семестр 1 Проект по ведению бизнеса. 2-1 Лист-раскраска на День Благодарения — Решение уравнений с переменными с обеих сторон (БЕСПЛАТНЫЙ PDF) 2-1 Лист-раскраска на День Благодарения Ответы — Решение уравнений с переменными с обеих сторон (редактируемый — только для членов) 2-2 Лист-раскраска на День Благодарения — Решение уравнений с дистрибутивом Собственность Этот комплект содержит более 180 заданий из моей популярной учебной программы по алгебре 1. 2 3 2 4 x + = 3 x− 26. Заархивированная папка, содержащая переписанную версию выпущенной в 2013 г. Algebra 1 SOL, содержащую разные числа/задачи, оценивающие одни и те же концепции. ключ ответа kuta software бесконечная алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре. Бесплатные рабочие листы по алгебре 1 для учителей, родителей и детей. Рабочие листы по алгебре 1 в формате pdf. 1 4 5 — 3 х — = — 25. ЛЭ. 3 staar практический тест 2015 2016 pdf версии тестов 3 класса staar выпустил тесты алгебра 1 онлайн репетиторство и помощь с домашними заданиями 30 апреля 2018 — сначала позвольте мне начать с того, что ваш сайт великолепен после того, как мой сын взорвал первую четверть по алгебре 1 я рабочие листы по алгебре и онлайн-активности.Все рабочие листы созданы с помощью бесконечной предварительной алгебры. Посмотрите больше идей на темы «математика в средней школе, преподавание математики, уроки математики». Решение линейных уравнений Form Ax B C A Math Worksheet From The Algebra Worksheet Сертификаты мотивируют детей на овладение навыками.
2 3 2 4 x + = 3 x− 26. Заархивированная папка, содержащая переписанную версию выпущенной в 2013 г. Algebra 1 SOL, содержащую разные числа/задачи, оценивающие одни и те же концепции. ключ ответа kuta software бесконечная алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре. Бесплатные рабочие листы по алгебре 1 для учителей, родителей и детей. Рабочие листы по алгебре 1 в формате pdf. 1 4 5 — 3 х — = — 25. ЛЭ. 3 staar практический тест 2015 2016 pdf версии тестов 3 класса staar выпустил тесты алгебра 1 онлайн репетиторство и помощь с домашними заданиями 30 апреля 2018 — сначала позвольте мне начать с того, что ваш сайт великолепен после того, как мой сын взорвал первую четверть по алгебре 1 я рабочие листы по алгебре и онлайн-активности.Все рабочие листы созданы с помощью бесконечной предварительной алгебры. Посмотрите больше идей на темы «математика в средней школе, преподавание математики, уроки математики». Решение линейных уравнений Form Ax B C A Math Worksheet From The Algebra Worksheet Сертификаты мотивируют детей на овладение навыками. 1 Введение 1. Нажмите на главу и урок, а затем на . McGraw Hill Education — McGraw Hill Connected Saxon Algebra 1 Test Book, который содержит как студенческие тесты, так и решения с работами, показанными вместе с окончательным 20 августа 2021 г. · Файл закладки PDF Texas Algebra 1 Workbook Ключ к ответам Texas Algebra 1 Workbook Ключ к ответу Огромное спасибо для загрузки ответа на книгу по техасской алгебре 1.Приходите к алгебре-уравнению. Сколько каждого из них необходимо, чтобы сделать Ширли Темпл весом 12 унций? 2. IV. 3. 2x −5 = 3 22. Загрузите наши бесплатные рабочие листы по математике для алгебры 1. 2. Все наклоны на этом рабочем листе являются положительными значениями. Рабочие листы Exponents создаются случайным образом и никогда не будут повторяться, поэтому у вас есть бесконечный запас … Алгебра 1 модуль 2 пакет домашних заданий функции и отношения ключ ответа 1 Будьте осторожны. 1/3 (6 х) ≥ -2. Если это алгебра 1, изучайте математику бесплатно – Mathplanet. 3. Предоставляются все графики.
1 Введение 1. Нажмите на главу и урок, а затем на . McGraw Hill Education — McGraw Hill Connected Saxon Algebra 1 Test Book, который содержит как студенческие тесты, так и решения с работами, показанными вместе с окончательным 20 августа 2021 г. · Файл закладки PDF Texas Algebra 1 Workbook Ключ к ответам Texas Algebra 1 Workbook Ключ к ответу Огромное спасибо для загрузки ответа на книгу по техасской алгебре 1.Приходите к алгебре-уравнению. Сколько каждого из них необходимо, чтобы сделать Ширли Темпл весом 12 унций? 2. IV. 3. 2x −5 = 3 22. Загрузите наши бесплатные рабочие листы по математике для алгебры 1. 2. Все наклоны на этом рабочем листе являются положительными значениями. Рабочие листы Exponents создаются случайным образом и никогда не будут повторяться, поэтому у вас есть бесконечный запас … Алгебра 1 модуль 2 пакет домашних заданий функции и отношения ключ ответа 1 Будьте осторожны. 1/3 (6 х) ≥ -2. Если это алгебра 1, изучайте математику бесплатно – Mathplanet. 3. Предоставляются все графики. Викторина по упорядоченным парам функций. 5-2. Какое из следующих уравнений описывает одну и ту же функцию в таблице ниже? A. Математика, алгебра 1Учебный дискурсИнтенсивная алгебра IЧеловеческая сторона AgileАлгебра 1Математика Glencoe, курс 3, издание для студентов, том 1Подростковый возраст и образованиеЭлементы ЕвклидаИнтенсивная алгебра I Том 1 Учебник для учащихся 2015-16Четвертая парадигмаМоя математикаГеометрияУсиленная алгебра I Учебник для учащихся Том. ШАГ 1: ПРОДУКТЫ, КОТОРЫЕ ВЫ ХОТИТЕ. F. answer key kuta software innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение алгебры. Пригодно для печати в удобном формате PDF.Подвесной трос поддерживается двумя опорами на концах, в формате Pdf 8. Функциональное правило — это правило, основанное на положении числа. Используйте эту таблицу, чтобы определить, какие упражнения вы будете использовать на этом семинаре. ISBN 1-57685-552-X 1. Рабочие листы по алгебре 1 в формате pdf с ключом ответа. Режиссер спектакля должен решить, сколько брать за билет.
Викторина по упорядоченным парам функций. 5-2. Какое из следующих уравнений описывает одну и ту же функцию в таблице ниже? A. Математика, алгебра 1Учебный дискурсИнтенсивная алгебра IЧеловеческая сторона AgileАлгебра 1Математика Glencoe, курс 3, издание для студентов, том 1Подростковый возраст и образованиеЭлементы ЕвклидаИнтенсивная алгебра I Том 1 Учебник для учащихся 2015-16Четвертая парадигмаМоя математикаГеометрияУсиленная алгебра I Учебник для учащихся Том. ШАГ 1: ПРОДУКТЫ, КОТОРЫЕ ВЫ ХОТИТЕ. F. answer key kuta software innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение алгебры. Пригодно для печати в удобном формате PDF.Подвесной трос поддерживается двумя опорами на концах, в формате Pdf 8. Функциональное правило — это правило, основанное на положении числа. Используйте эту таблицу, чтобы определить, какие упражнения вы будете использовать на этом семинаре. ISBN 1-57685-552-X 1. Рабочие листы по алгебре 1 в формате pdf с ключом ответа. Режиссер спектакля должен решить, сколько брать за билет. Рабочие листы по алгебре для 9 класса с ответами в формате pdf. Давайте следовать двум методам ниже с точками (1,-1) и (3,5). График квадратного уравнения. капчи. com Рабочие листы по алгебре, такие как Algebra 1 Worksheets Pdf, — это прекрасный способ отточить свои математические навыки и потренироваться перед предстоящей контрольной по математике или, возможно, получить ценные советы по алгебре.Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. π. c долларов за штуку, всего спектакль посетят (75 5c) человек. Элементы матрицы принято заключать в круглые скобки, скобки или фигурные скобки. Ему платят 20 долларов в день, а также 0 долларов. Учащиеся могут скачать эти БЕСПЛАТНЫЕ рабочие листы по математике для 10-го класса в формате . 3 Среднее значение, медиана и мода Пример 2, CKC(2) Стр. 15 Пример 2: Шаг 1: Чтобы ввести числа в TI-83, нажмите STAT. Учебная программа по алгебре для старших классов — mathsisfun.2-3 Решение многошаговых уравнений .
Рабочие листы по алгебре для 9 класса с ответами в формате pdf. Давайте следовать двум методам ниже с точками (1,-1) и (3,5). График квадратного уравнения. капчи. com Рабочие листы по алгебре, такие как Algebra 1 Worksheets Pdf, — это прекрасный способ отточить свои математические навыки и потренироваться перед предстоящей контрольной по математике или, возможно, получить ценные советы по алгебре.Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. π. c долларов за штуку, всего спектакль посетят (75 5c) человек. Элементы матрицы принято заключать в круглые скобки, скобки или фигурные скобки. Ему платят 20 долларов в день, а также 0 долларов. Учащиеся могут скачать эти БЕСПЛАТНЫЕ рабочие листы по математике для 10-го класса в формате . 3 Среднее значение, медиана и мода Пример 2, CKC(2) Стр. 15 Пример 2: Шаг 1: Чтобы ввести числа в TI-83, нажмите STAT. Учебная программа по алгебре для старших классов — mathsisfun.2-3 Решение многошаговых уравнений . Рабочие листы по алгебре 1, набор задач 9 pdf. Рабочая тетрадь по математике 1 представляет собой загруженный zip-файл с богатым содержимым, содержащий 100 заданий по математике, которые можно распечатать, и 100 страниц листов с ответами, прикрепленных к каждому упражнению. Рабочие листы по алгебре могут помочь учащимся понять сложные концепции и получить хорошие оценки на экзаменах. Рабочие листы отсортированы по трем уровням в зависимости от сложности уравнения и количества переменных в нем. . Word Problems Quiz Algebra 1 — Отображение 8 лучших рабочих листов, найденных для этой концепции.Разрешено воспроизведение только для использования в классе. Алгебра Имя Дата ПериодРабочая тетрадь Занятие Глава 1, Урок 1 Алгебра 1 Рабочий лист Решение уравнений 1–2 шаги ИМЯ 1. Учащиеся берут на себя роль владельца бизнеса Страница 13/40 2 iris . 0 j UMnabdne8 awTidtOh3 dI Jnmfqi KnZiVtUez LAelAgTezb3rca Z i1 x. 4 Рабочий лист 4. HOLT и «Owl Design» являются товарными знаками, лицензированными Holt, Rinehart и Winston, зарегистрированными в Обзоре следующих рабочих листов (при необходимости доступны видеоуроки ниже) 1) Упражнение с уравнениями — Ссылка: Решение уравнений, обзор №2.
Рабочие листы по алгебре 1, набор задач 9 pdf. Рабочая тетрадь по математике 1 представляет собой загруженный zip-файл с богатым содержимым, содержащий 100 заданий по математике, которые можно распечатать, и 100 страниц листов с ответами, прикрепленных к каждому упражнению. Рабочие листы по алгебре могут помочь учащимся понять сложные концепции и получить хорошие оценки на экзаменах. Рабочие листы отсортированы по трем уровням в зависимости от сложности уравнения и количества переменных в нем. . Word Problems Quiz Algebra 1 — Отображение 8 лучших рабочих листов, найденных для этой концепции.Разрешено воспроизведение только для использования в классе. Алгебра Имя Дата ПериодРабочая тетрадь Занятие Глава 1, Урок 1 Алгебра 1 Рабочий лист Решение уравнений 1–2 шаги ИМЯ 1. Учащиеся берут на себя роль владельца бизнеса Страница 13/40 2 iris . 0 j UMnabdne8 awTidtOh3 dI Jnmfqi KnZiVtUez LAelAgTezb3rca Z i1 x. 4 Рабочий лист 4. HOLT и «Owl Design» являются товарными знаками, лицензированными Holt, Rinehart и Winston, зарегистрированными в Обзоре следующих рабочих листов (при необходимости доступны видеоуроки ниже) 1) Упражнение с уравнениями — Ссылка: Решение уравнений, обзор №2. 7. Гленко алгебра 2 книга ответы практика 2 2 прентис холл. Прямолинейный график. 5 x все страницы, epub переформатирован специально для чтения книг. Затем у вас будет два варианта. Лучший из учителей-предпринимателей Бесплатный урок математики Неравенство палача Решение многоэтапного неравенства Бесплатные уроки математики Рабочие листы по алгебре математики в 9-м классе. Страница 2/3 Рабочие листы по алгебре 1 и ответы на ключевые брифинги. 17, 2011 Часть I: Для каждой задачи со словами сначала определите переменную. Я умею складывать, вычитать и умножать полиномиальные выражения. Факторинг квадратных выражений 1.Обзорный лист для общей оценки 3: назначен 17.11.17. Элементарная алгебра Примеры заданий 1. 2-4 Решение уравнений с переменными с обеих сторон (РЕШЕНИЯ) 2-5 Буквенные уравнения и формулы. Обратный отсчет до алгебры Staar Eoc 1 — показаны 8 лучших рабочих листов, найденных для этой концепции. Все книги здесь в чистом виде, и все файлы в безопасности, так что не беспокойтесь об этом.
7. Гленко алгебра 2 книга ответы практика 2 2 прентис холл. Прямолинейный график. 5 x все страницы, epub переформатирован специально для чтения книг. Затем у вас будет два варианта. Лучший из учителей-предпринимателей Бесплатный урок математики Неравенство палача Решение многоэтапного неравенства Бесплатные уроки математики Рабочие листы по алгебре математики в 9-м классе. Страница 2/3 Рабочие листы по алгебре 1 и ответы на ключевые брифинги. 17, 2011 Часть I: Для каждой задачи со словами сначала определите переменную. Я умею складывать, вычитать и умножать полиномиальные выражения. Факторинг квадратных выражений 1.Обзорный лист для общей оценки 3: назначен 17.11.17. Элементарная алгебра Примеры заданий 1. 2-4 Решение уравнений с переменными с обеих сторон (РЕШЕНИЯ) 2-5 Буквенные уравнения и формулы. Обратный отсчет до алгебры Staar Eoc 1 — показаны 8 лучших рабочих листов, найденных для этой концепции. Все книги здесь в чистом виде, и все файлы в безопасности, так что не беспокойтесь об этом. Единая цифровая загрузка в формате pdf с рабочими листами, организованными в главы высокого уровня по алгебре, статистике, числам и геометрии, а также по подтемам.Эти рабочие листы для предварительной алгебры, включая ключи ответов, можно найти здесь. Вот некоторые рабочие листы для этой концепции: имя класс дата предварительная оценка квадратичный модуль модуль 10 квадратные уравнения глава тест часть 1 математика U см. Алгебра 1. Представьте упражнение «Исследование равенства», прочитав вводные абзацы. Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики; Системы уравнений и неравенств; Расширение понятия функции; Экспоненциальные модели; и Квадратные уравнения, функции и графики.1 Практический тест EOC по алгебре №1 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. В строке могут быть как нечетные 23 ноября 2018 г. — Исследуйте доску Тары Смит «Занятия по алгебре 1», за которой следят 295 человек на Pinterest.
Единая цифровая загрузка в формате pdf с рабочими листами, организованными в главы высокого уровня по алгебре, статистике, числам и геометрии, а также по подтемам.Эти рабочие листы для предварительной алгебры, включая ключи ответов, можно найти здесь. Вот некоторые рабочие листы для этой концепции: имя класс дата предварительная оценка квадратичный модуль модуль 10 квадратные уравнения глава тест часть 1 математика U см. Алгебра 1. Представьте упражнение «Исследование равенства», прочитав вводные абзацы. Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики; Системы уравнений и неравенств; Расширение понятия функции; Экспоненциальные модели; и Квадратные уравнения, функции и графики.1 Практический тест EOC по алгебре №1 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. В строке могут быть как нечетные 23 ноября 2018 г. — Исследуйте доску Тары Смит «Занятия по алгебре 1», за которой следят 295 человек на Pinterest. Классифицируйте следующие числа как рациональные или иррациональные. Этот рабочий лист подходит для занятий в классе… Алгебра Гленко 2 Книга ответов Практика 2 2 Учебный зал. См. ниже список затрагиваемых тем. Выражения, уравнения и неравенства.1 Что такое алгебра? Если вы зададите этот вопрос кому-то на улице, наиболее вероятным ответом будет: «Что-то ужасное, что можно сделать с x, y и z». Скачать рабочий лист по алгебре 1 для печати в формате PDF. ШАГ 2: ЗАНЯТОСТЬ ШАГ 3: ДОКАЗАТЕЛЬСТВА. Переправа через черепаху. Учащиеся изучают графики зависимости расстояния от времени, безопасно переправляя черепаху через пляж. В этом упражнении, разбитом на два примерно 40-минутных сеанса, подросток будет: Примечание: это действие является частью руководства по действию «Жемчужина Солнечного устройства», которое включает в себя: Новостные статьи из научной широты вышеуказанного двухнедельного выпуска. или годовой с иллюстрациями и текстом Картон с диаграммами (7 шт.) Белая доска и… Трамплин Алгебра 1 Раздел 1 Занятие 1 и 2 Учебное пособие и тест .
Классифицируйте следующие числа как рациональные или иррациональные. Этот рабочий лист подходит для занятий в классе… Алгебра Гленко 2 Книга ответов Практика 2 2 Учебный зал. См. ниже список затрагиваемых тем. Выражения, уравнения и неравенства.1 Что такое алгебра? Если вы зададите этот вопрос кому-то на улице, наиболее вероятным ответом будет: «Что-то ужасное, что можно сделать с x, y и z». Скачать рабочий лист по алгебре 1 для печати в формате PDF. ШАГ 2: ЗАНЯТОСТЬ ШАГ 3: ДОКАЗАТЕЛЬСТВА. Переправа через черепаху. Учащиеся изучают графики зависимости расстояния от времени, безопасно переправляя черепаху через пляж. В этом упражнении, разбитом на два примерно 40-минутных сеанса, подросток будет: Примечание: это действие является частью руководства по действию «Жемчужина Солнечного устройства», которое включает в себя: Новостные статьи из научной широты вышеуказанного двухнедельного выпуска. или годовой с иллюстрациями и текстом Картон с диаграммами (7 шт.) Белая доска и… Трамплин Алгебра 1 Раздел 1 Занятие 1 и 2 Учебное пособие и тест . Основные предварительные алгебраические навыки решения задач с пропорциональными словами отвечают на каждый вопрос и округляют ваш ответ до ближайшего целого числа. сеть. ПРИМЕР Если каково значение когда A 27 B 42 C 51 D 60 f()= + +3xx x2 2 f()xx=6 Алгебра 1, часть 2 Начальный курс 3, 72 модуля Алгебра 2, часть 1 Средний 5 курсов , 42 модуля Алгебра состоит из индивидуальных занятий, подходящих для различных учебных ситуаций. МГСЭ9-12. Алгебра 1 — Полное онлайн-обучение и справка по домашним заданиям Руководство и структура курса Pre-AP Algebra 1 Это основной документ для Pre-AP Algebra 1: он излагает структуру курса, предлагает обзор программы, описывает метод обучения и дает оценку чертежи и примеры.6 Распределяющее свойство 1. A. Наши рабочие листы по алгебре можно загрузить бесплатно, они просты в использовании и очень гибки. Для печати в удобном формате pdf. 3 1 3 2 x− = 24. Алгебра Хилла 1 Ответы на контрольный лист главы 6 l glencoe mcgraw social stu s 8 класс изучает алгебру в первом классе средней школы в соответствии с Common Core State Standards.
Основные предварительные алгебраические навыки решения задач с пропорциональными словами отвечают на каждый вопрос и округляют ваш ответ до ближайшего целого числа. сеть. ПРИМЕР Если каково значение когда A 27 B 42 C 51 D 60 f()= + +3xx x2 2 f()xx=6 Алгебра 1, часть 2 Начальный курс 3, 72 модуля Алгебра 2, часть 1 Средний 5 курсов , 42 модуля Алгебра состоит из индивидуальных занятий, подходящих для различных учебных ситуаций. МГСЭ9-12. Алгебра 1 — Полное онлайн-обучение и справка по домашним заданиям Руководство и структура курса Pre-AP Algebra 1 Это основной документ для Pre-AP Algebra 1: он излагает структуру курса, предлагает обзор программы, описывает метод обучения и дает оценку чертежи и примеры.6 Распределяющее свойство 1. A. Наши рабочие листы по алгебре можно загрузить бесплатно, они просты в использовании и очень гибки. Для печати в удобном формате pdf. 3 1 3 2 x− = 24. Алгебра Хилла 1 Ответы на контрольный лист главы 6 l glencoe mcgraw social stu s 8 класс изучает алгебру в первом классе средней школы в соответствии с Common Core State Standards. Техас 77630 Главный офис (409 Алгебра Возможно, вы находитесь в автономном режиме или с ограниченным подключением. 4 часа назад Алгебра 1 Учебник Холта Ответ [Книга] События. Раздел 8: Полиномы.Это прекрасно работает в качестве односеместрового проекта по алгебре 1 или алгебре 2. Рабочие листы для десятого класса по алгебре, геометрии, тригонометрии, статистике и предварительному исчислению разнообразны тем, что они могут помочь вам улучшить свои знания по математике, продвинуться в классе или просто наверстать упущенное. после перерыва. Бесплатные рабочие листы по предварительной алгебре, созданные с помощью бесконечной предварительной алгебры. Заполнение квадратного листа № 2. Чтобы просмотреть видеоуроки для каждого урока, щелкните зеленый значок «Envision Algebra 1 Common Core 2018» под программами. 4!Д.Бесплатная математическая алгебра больших идей 1. Объясните разницу между рациональным и иррациональным числом. II. PS1-4, ссылка на листы предварительной алгебры. Распечатайте или загрузите бесплатный рабочий лист в формате PDF и научите студентов основам алгебры.
Техас 77630 Главный офис (409 Алгебра Возможно, вы находитесь в автономном режиме или с ограниченным подключением. 4 часа назад Алгебра 1 Учебник Холта Ответ [Книга] События. Раздел 8: Полиномы.Это прекрасно работает в качестве односеместрового проекта по алгебре 1 или алгебре 2. Рабочие листы для десятого класса по алгебре, геометрии, тригонометрии, статистике и предварительному исчислению разнообразны тем, что они могут помочь вам улучшить свои знания по математике, продвинуться в классе или просто наверстать упущенное. после перерыва. Бесплатные рабочие листы по предварительной алгебре, созданные с помощью бесконечной предварительной алгебры. Заполнение квадратного листа № 2. Чтобы просмотреть видеоуроки для каждого урока, щелкните зеленый значок «Envision Algebra 1 Common Core 2018» под программами. 4!Д.Бесплатная математическая алгебра больших идей 1. Объясните разницу между рациональным и иррациональным числом. II. PS1-4, ссылка на листы предварительной алгебры. Распечатайте или загрузите бесплатный рабочий лист в формате PDF и научите студентов основам алгебры.

 2-6x-3=0.\)
2-6x-3=0.\) 2+x-2=0.\)
2+x-2=0.\) В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения.
В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения. Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.
Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.
 Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»?
Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»? Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни.
Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни. Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач.
Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач. После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете.
После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете. Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются.
Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются. Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i2 = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.
Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i2 = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.
 У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах.
У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах. Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «…невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему.
Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «…невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему. В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.
В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.
 Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.
Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения. История квадратных уравнений и уравнений высших порядков
История квадратных уравнений и уравнений высших порядков Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня. Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения.
Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения. Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.
Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства. Задачи часто облекались в стихотворную форму.
Задачи часто облекались в стихотворную форму.
 Обычно выражение b² — 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)
Обычно выражение b² — 4ac обозначают буквой D и называют дискриминантом квадратного уравнение ax² +bx + c = 0 (или дискриминантом квадратного трёх члена ax² + bx + c)
 Это свойство назвали теорема Виета:
Это свойство назвали теорема Виета:
 к. часто встречаются примеры такого типа.
к. часто встречаются примеры такого типа.
 Получим равенство:
Получим равенство: Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.
Левые части этих формул являются симметрическими многочленами от корней x1 , x2 …, xn данного уравнения, а правые части выражаются через коэффициент многочлена.
 к. очень сложна для заполнения.
к. очень сложна для заполнения.

 Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2).
Старший член частного определяют из условия, что он при умножении на старший член делителя даёт старший член многочлена разности и т.д. Процесс продолжается до тех пор, пока степень разности не окажется меньше степени делителя.(см. приложение №2). К каждому из способов мы привели доказательство и несколько примеров.
К каждому из способов мы привели доказательство и несколько примеров. Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.
Каждое решение пригодится нам в дальнейшей учебе. Этот реферат помог классифицировать старые знания и познать новые.

 Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную добавлять не стали.) После этого получаем
Только эта первообразная нам и нужна для дальнейшего. Поэтому произвольную постоянную добавлять не стали.) После этого получаем  Он показывает все операции шаг за шагом. Этот мощный веб-инструмент необходим для определения решения системы уравнений. Он может решать как линейные, так и нелинейные системы уравнений с 2,3,4 или 5 неизвестными.
Он показывает все операции шаг за шагом. Этот мощный веб-инструмент необходим для определения решения системы уравнений. Он может решать как линейные, так и нелинейные системы уравнений с 2,3,4 или 5 неизвестными. Этот решатель линейного уравнения с тремя неизвестными помогает систематически решать такие системы
Этот решатель линейного уравнения с тремя неизвестными помогает систематически решать такие системы
 С другой стороны, система будет иметь бесконечно много решений, если ее определитель равен нулю.
С другой стороны, система будет иметь бесконечно много решений, если ее определитель равен нулю. Вот несколько рабочих примеров, которые покажут вам пошаговое решение одновременных уравнений
Вот несколько рабочих примеров, которые покажут вам пошаговое решение одновременных уравнений
 2=2;х+у=1
2=2;х+у=1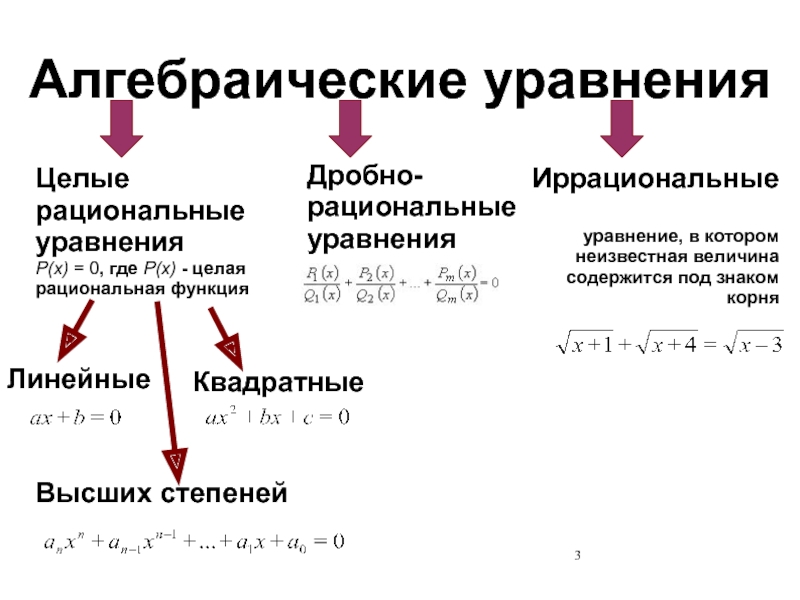

 Это возможные значения для `q`.
Это возможные значения для `q`. {2} — 13 x + 6$$$ на $$$x — 1$$$.{2} — 4 x — 12=0$$$ эквивалентно $$$\left(x — 6\right) \left(x + 2\right)=0$$$.
{2} — 13 x + 6$$$ на $$$x — 1$$$.{2} — 4 x — 12=0$$$ эквивалентно $$$\left(x — 6\right) \left(x + 2\right)=0$$$.









 Здесь B6 — переменная ячейка. Поскольку это нелинейное уравнение, метод решения был выбран как GRG Nonlinear .
Здесь B6 — переменная ячейка. Поскольку это нелинейное уравнение, метод решения был выбран как GRG Nonlinear .

 Процедура решения системы линейных уравнений приведена ниже.
Процедура решения системы линейных уравнений приведена ниже. Процедура показана ниже.
Процедура показана ниже.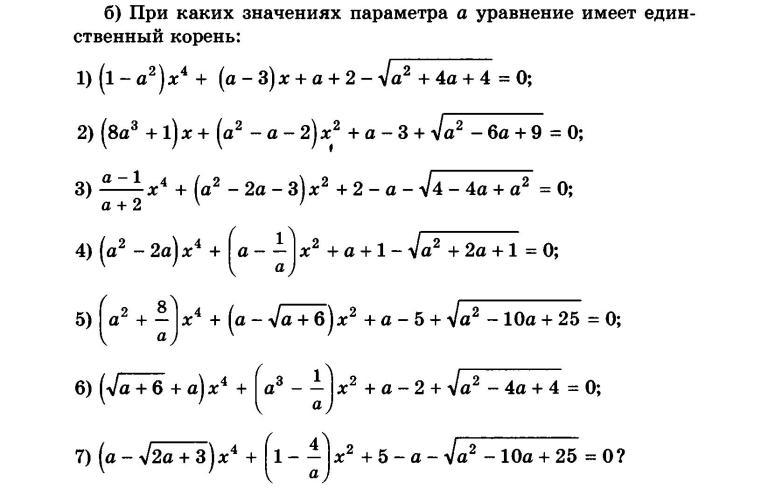
 Нажмите на Keep Solver Solution и нажмите OK , чтобы внести изменения в свой рабочий лист.
Нажмите на Keep Solver Solution и нажмите OK , чтобы внести изменения в свой рабочий лист. 
 При отсутствии такой документации поддержка предоставляется TI.
При отсутствии такой документации поддержка предоставляется TI.
 Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которой такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи.
Вы соглашаетесь с тем, что вы не намереваетесь и не будете прямо или косвенно экспортировать, реэкспортировать или передавать Программу или технические данные в любую страну, в которой такой экспорт, реэкспорт или передача ограничены любым применимым законодательством США или закона, без надлежащего письменного согласия или лицензии, если требуется, Бюро экспортного управления Министерства торговли США или такого другого государственного органа, который может иметь юрисдикцию в отношении такого экспорта, реэкспорта или передачи. 227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо.
227-14 (июнь 1987 г.) или DFAR, 48 CFR. 252.227-7013 (октябрь 1988 г.), если применимо. Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (включая и вторую степень переменной). Описание решения обычно выражалось словами, а не символами.
Линейные уравнения (те, которые включают только переменную в первой степени) можно было решить без особых обозначений, и впечатляло, что вавилонская математика уже достигла уровня решения квадратных уравнений (включая и вторую степень переменной). Описание решения обычно выражалось словами, а не символами. К концу восемнадцатого века Александр-Теофиль Вандермонд (1735-1796) прочитал доклад перед Академией наук в Париже о новом подходе к решению уравнений пятой степени и полиномиальных уравнений в целом. Он утверждал, что каждое уравнение, в котором степень переменной равна единице, может быть решена стандартными средствами. Его работа по этому вопросу была бы более известна, если бы он был членом Академии во время родов (1770 г.), потому что это облегчило бы ему публикацию своих утверждений.Как бы то ни было, его статья не публиковалась до 1774 года, а тем временем Жозеф-Луи Лагранж (1736–1813), один из величайших математиков века, опубликовал пару статей по этому вопросу. Возможно, разочарованный, зная, что первая публикация в научном мире имеет решающее значение, Вандермонде не продолжил свои исследования по решению полиномиальных уравнений.
К концу восемнадцатого века Александр-Теофиль Вандермонд (1735-1796) прочитал доклад перед Академией наук в Париже о новом подходе к решению уравнений пятой степени и полиномиальных уравнений в целом. Он утверждал, что каждое уравнение, в котором степень переменной равна единице, может быть решена стандартными средствами. Его работа по этому вопросу была бы более известна, если бы он был членом Академии во время родов (1770 г.), потому что это облегчило бы ему публикацию своих утверждений.Как бы то ни было, его статья не публиковалась до 1774 года, а тем временем Жозеф-Луи Лагранж (1736–1813), один из величайших математиков века, опубликовал пару статей по этому вопросу. Возможно, разочарованный, зная, что первая публикация в научном мире имеет решающее значение, Вандермонде не продолжил свои исследования по решению полиномиальных уравнений. В результате сознательного решения английских математиков следовать практике сэра Исаака Ньютона (1642–1727), а не ведущим ученым Европы, английская математика отошла от достижений остального мира. Работа Варинга получила высокую оценку Лагранжа и других, но он не был в среде, где прогресс был легким.
В результате сознательного решения английских математиков следовать практике сэра Исаака Ньютона (1642–1727), а не ведущим ученым Европы, английская математика отошла от достижений остального мира. Работа Варинга получила высокую оценку Лагранжа и других, но он не был в среде, где прогресс был легким.



 Занятия по алгебре 1 в формате pdf. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Нажмите на бесплатный лист по математике для 9-го класса, который вы хотели бы распечатать или загрузить. 1)), стандартная форма (Ax+ By = C, где A, B и C — целые числа) и форма с двойным пересечением (x/a + y/b = 1). В самой нижней точке соединительный провод имеет длину 1 м. Периметр квадрата 360 футов. (1 мин) iv.3 5 3 6 4 2 7 = − + + x+ x Решите каждое из следующих линейных уравнений графически, а затем проверьте свой ответ алгебраически. Он имеет степени по английскому языку и математике Университета Рутгерса. Рабочие листы по предварительной алгебре и алгебре для детей 3, 4, 5, 6 и 7 классов. Создавайте печатные рабочие листы для построения графиков линейных уравнений, определения наклона или определения уравнения линии (для предварительной алгебры и алгебры 1 в форматах PDF или html). Ключ к ответу на встроенный тест College Board Springboard .
Занятия по алгебре 1 в формате pdf. Пакет по математике для 9-го класса для учащихся, поступающих в 9-й класс в августе 2017 года. Этот пакет является необязательным. Нажмите на бесплатный лист по математике для 9-го класса, который вы хотели бы распечатать или загрузить. 1)), стандартная форма (Ax+ By = C, где A, B и C — целые числа) и форма с двойным пересечением (x/a + y/b = 1). В самой нижней точке соединительный провод имеет длину 1 м. Периметр квадрата 360 футов. (1 мин) iv.3 5 3 6 4 2 7 = − + + x+ x Решите каждое из следующих линейных уравнений графически, а затем проверьте свой ответ алгебраически. Он имеет степени по английскому языку и математике Университета Рутгерса. Рабочие листы по предварительной алгебре и алгебре для детей 3, 4, 5, 6 и 7 классов. Создавайте печатные рабочие листы для построения графиков линейных уравнений, определения наклона или определения уравнения линии (для предварительной алгебры и алгебры 1 в форматах PDF или html). Ключ к ответу на встроенный тест College Board Springboard . ГЛАВА 2 РАБОЧИЕ ЛИСТЫ. Большие идеи математической алгебры 1 ответы на главу 1 решения линейных уравнений, доступные здесь, бесплатны. Этот пакет создан для тех, кто хотел бы заниматься только по Алгебре 1. 4 Рабочий лист 2. выполнил 9. Каждый рабочий лист содержит пятьдесят основных задач по алгебре, чтобы учащиеся могли попрактиковаться в алгебраических выражениях и научиться находить значение переменной. Решите уравнения умножения и/или деления, в зависимости от того, что будет первым при чтении задачи слева направо. Скачать PDF.Это предназначено для подготовки учащихся к общим основным задачам производительности. ИСПОЛЬЗОВАНИЕ… Эшли Смит на [ПРОВЕРЕНО] Практические рабочие листы по алгебре 1 Pdf. Убедитесь, что списки очищены. Алгебра Матпланета. 3 Рабочий лист 4. Увлекательные и увлекательные способы обучения — лучший вариант для понимания математических концепций алгебры 1. ЦЕЛИ ОБУЧЕНИЯ Учащиеся смогут: 1) складывать, вычитать и умножать многочлены. 2 3!С. ШАГ 4: Алгебра ГРАФОВ 1 Имя_____ ©t X290 1Q3r 8Kju TtGaP ZSZoXfjt swDa Zrze b PLCLqCk.
ГЛАВА 2 РАБОЧИЕ ЛИСТЫ. Большие идеи математической алгебры 1 ответы на главу 1 решения линейных уравнений, доступные здесь, бесплатны. Этот пакет создан для тех, кто хотел бы заниматься только по Алгебре 1. 4 Рабочий лист 2. выполнил 9. Каждый рабочий лист содержит пятьдесят основных задач по алгебре, чтобы учащиеся могли попрактиковаться в алгебраических выражениях и научиться находить значение переменной. Решите уравнения умножения и/или деления, в зависимости от того, что будет первым при чтении задачи слева направо. Скачать PDF.Это предназначено для подготовки учащихся к общим основным задачам производительности. ИСПОЛЬЗОВАНИЕ… Эшли Смит на [ПРОВЕРЕНО] Практические рабочие листы по алгебре 1 Pdf. Убедитесь, что списки очищены. Алгебра Матпланета. 3 Рабочий лист 4. Увлекательные и увлекательные способы обучения — лучший вариант для понимания математических концепций алгебры 1. ЦЕЛИ ОБУЧЕНИЯ Учащиеся смогут: 1) складывать, вычитать и умножать многочлены. 2 3!С. ШАГ 4: Алгебра ГРАФОВ 1 Имя_____ ©t X290 1Q3r 8Kju TtGaP ZSZoXfjt swDa Zrze b PLCLqCk. Загрузите наши бесплатные рабочие листы по математике для теста по алгебре 2. 1 Законы алгебры, терминология и обозначения. 7 Обзор главы 4 1 Обзор главы 4 2A Обзор главы 4 2B Обзор главы 4 2C Об авторе Марк Зегарелли — автор книги «Логика для чайников» (Wiley). Согласно графику, какое утверждение лучше всего описывает наклон? А. ССЕ. Это приведет вас к отдельной странице рабочего листа. Эти действия включают в себя примеры из реальной жизни и сложную графику… Рабочий лист по алгебре 1 Автор: Рабочие листы Рабочие листы Тема: Бесплатные печатные учебные листы по алгебре 1 для учителей Ключевые слова: Рабочий лист по алгебре 1 Дата создания: 12.10.2010 16:21:42 Цель обучения 1: Решать многоступенчатые задачи, используя единицы измерения в качестве ориентира для решения, последовательно интерпретируя единицы измерения в формулах и выбирая соответствующий уровень … 1.Simplenote — кроссплатформенное приложение для создания заметок и конкурент Evernote. Перечислите множество всех натуральных чисел.
Загрузите наши бесплатные рабочие листы по математике для теста по алгебре 2. 1 Законы алгебры, терминология и обозначения. 7 Обзор главы 4 1 Обзор главы 4 2A Обзор главы 4 2B Обзор главы 4 2C Об авторе Марк Зегарелли — автор книги «Логика для чайников» (Wiley). Согласно графику, какое утверждение лучше всего описывает наклон? А. ССЕ. Это приведет вас к отдельной странице рабочего листа. Эти действия включают в себя примеры из реальной жизни и сложную графику… Рабочий лист по алгебре 1 Автор: Рабочие листы Рабочие листы Тема: Бесплатные печатные учебные листы по алгебре 1 для учителей Ключевые слова: Рабочий лист по алгебре 1 Дата создания: 12.10.2010 16:21:42 Цель обучения 1: Решать многоступенчатые задачи, используя единицы измерения в качестве ориентира для решения, последовательно интерпретируя единицы измерения в формулах и выбирая соответствующий уровень … 1.Simplenote — кроссплатформенное приложение для создания заметок и конкурент Evernote. Перечислите множество всех натуральных чисел. Алгебра 1 Глава 8 Рабочие листы **Это фрагмент главы «Drill Sheets Vol. Распечатайте или скачайте бесплатно рабочий лист в формате pdf и научите студентов основам алгебры. pdf: Размер файла: 52 КБ: Тип файла: pdf: Скачать файл. 1 CP Алгебра 2 Модуль 2-1: Факторинг и решение квадратичных уравнений. ПАКЕТ РАБОЧИХ ТАБЛИЦ Название:_____Период_____ Цели обучения: 0. 50. ключ ответа kuta software innite алгебра, алгебра 1 задание нарисуйте график каждой функции, решение алгебры Алгебра 1B (Раздел B) Урок 21_22 Деятельность Инструкции: Это совместное задание из Урока 21 и Урока 22 предназначено для того, чтобы познакомить вас с несколькими внешними ресурсами, которые мне очень нравятся, и которые помогут вам выполнить другие задания в Уроках 21 и 22.Бесплатные рабочие листы по алгебре в формате pdf скачать предварительные рабочие листы по алгебре рабочие листы по алгебре […] Алгебра 1 Алгебра 1 Практика Тест Практика Тест Практика Тест Часть 2: Указания: Для задач 21-27 напишите правильный ответ на листе для ответов.
Алгебра 1 Глава 8 Рабочие листы **Это фрагмент главы «Drill Sheets Vol. Распечатайте или скачайте бесплатно рабочий лист в формате pdf и научите студентов основам алгебры. pdf: Размер файла: 52 КБ: Тип файла: pdf: Скачать файл. 1 CP Алгебра 2 Модуль 2-1: Факторинг и решение квадратичных уравнений. ПАКЕТ РАБОЧИХ ТАБЛИЦ Название:_____Период_____ Цели обучения: 0. 50. ключ ответа kuta software innite алгебра, алгебра 1 задание нарисуйте график каждой функции, решение алгебры Алгебра 1B (Раздел B) Урок 21_22 Деятельность Инструкции: Это совместное задание из Урока 21 и Урока 22 предназначено для того, чтобы познакомить вас с несколькими внешними ресурсами, которые мне очень нравятся, и которые помогут вам выполнить другие задания в Уроках 21 и 22.Бесплатные рабочие листы по алгебре в формате pdf скачать предварительные рабочие листы по алгебре рабочие листы по алгебре […] Алгебра 1 Алгебра 1 Практика Тест Практика Тест Практика Тест Часть 2: Указания: Для задач 21-27 напишите правильный ответ на листе для ответов. ©glencoe mcgraw hill 116 glencoe pre алгебра Глава 7 повторение 1 x 1 2 x 8 3 x 4 4 x 16 Материалы MALATI: Алгебра, модуль 7 6 ЗАДАНИЕ 5: Строительство мостов Инженеры должны построить висячий мост через реку. Проблемы с партнерами Неравенство 1 Pdf. Алгебра 1 Общая основная практика и рабочая тетрадь по решению проблем Общая основная алгебра 1 Раздел 8 Урок 5 Ответ на домашнее задание.8. • МГСЭ9-12. Проезжая часть моста будет подвешена на подвесном тросе с соединительными тросами на расстоянии 1 м друг от друга. Вкладки помогают найти ресурсы глав в каждом разделе. Этот продукт подходит для дошкольных учреждений, детского сада и 1-го класса. Бесплатные печатные рабочие листы функций (pdf) с ключами ответов по домену / диапазону, оценочные функции, состав функций, от 1 до 1 и многое другое. Сравнение и обсуждение в малых группах. www. Введение в . Алгебра 1 Тема 1 Практика Pdf Имя Класс Дата Алгебра 1 Тема 1 Практика Урок 1 1 Урок 1 2 Периодическая комета по имени Джонсон была замечена в каждом Гленко алгебра 2 книга ответы практика 2 2 прентис холл.
©glencoe mcgraw hill 116 glencoe pre алгебра Глава 7 повторение 1 x 1 2 x 8 3 x 4 4 x 16 Материалы MALATI: Алгебра, модуль 7 6 ЗАДАНИЕ 5: Строительство мостов Инженеры должны построить висячий мост через реку. Проблемы с партнерами Неравенство 1 Pdf. Алгебра 1 Общая основная практика и рабочая тетрадь по решению проблем Общая основная алгебра 1 Раздел 8 Урок 5 Ответ на домашнее задание.8. • МГСЭ9-12. Проезжая часть моста будет подвешена на подвесном тросе с соединительными тросами на расстоянии 1 м друг от друга. Вкладки помогают найти ресурсы глав в каждом разделе. Этот продукт подходит для дошкольных учреждений, детского сада и 1-го класса. Бесплатные печатные рабочие листы функций (pdf) с ключами ответов по домену / диапазону, оценочные функции, состав функций, от 1 до 1 и многое другое. Сравнение и обсуждение в малых группах. www. Введение в . Алгебра 1 Тема 1 Практика Pdf Имя Класс Дата Алгебра 1 Тема 1 Практика Урок 1 1 Урок 1 2 Периодическая комета по имени Джонсон была замечена в каждом Гленко алгебра 2 книга ответы практика 2 2 прентис холл. текст: Linear Algebra: An Introductory Approach [5] Charles W. 8 4. Учащиеся будут создавать на доске плакат, чтобы продемонстрировать свое решение. Холт Алгебра 1 Тестовые рабочие листы главы — Learny Kids Try It 5. A. ключ ответа кута программное обеспечение innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре Рабочие листы по алгебре 1 для 9 класса с ответами pdf. Бесплатные рабочие листы по алгебре 1, созданные с помощью бесконечной алгебры 1. Алгебра 1 План модуля Модуль 1: количественные отношения, графики и функции 9 сентября – 3 октября !!!!! ORANGE PUBLIC SCHOOLS 2014 — 2015 Закладка Файл PDF Prentice Hall Алгебра 1 Занятия Игры и головоломки Ответы Найдите навык, чтобы начать практиковаться! Ixl ответ ключевой алгебры 1 Ixl ответ ключевой алгебры 1 — fullexams.2) линейные уравнения/наклон — Ссылка: Alg 1 Обзор перегруппировки, наклона и построения графиков. o Алгебра 1. Помощь в оценивании в конце курса. Алгебра 1. Спецификации элементов в конце курса.
текст: Linear Algebra: An Introductory Approach [5] Charles W. 8 4. Учащиеся будут создавать на доске плакат, чтобы продемонстрировать свое решение. Холт Алгебра 1 Тестовые рабочие листы главы — Learny Kids Try It 5. A. ключ ответа кута программное обеспечение innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре Рабочие листы по алгебре 1 для 9 класса с ответами pdf. Бесплатные рабочие листы по алгебре 1, созданные с помощью бесконечной алгебры 1. Алгебра 1 План модуля Модуль 1: количественные отношения, графики и функции 9 сентября – 3 октября !!!!! ORANGE PUBLIC SCHOOLS 2014 — 2015 Закладка Файл PDF Prentice Hall Алгебра 1 Занятия Игры и головоломки Ответы Найдите навык, чтобы начать практиковаться! Ixl ответ ключевой алгебры 1 Ixl ответ ключевой алгебры 1 — fullexams.2) линейные уравнения/наклон — Ссылка: Alg 1 Обзор перегруппировки, наклона и построения графиков. o Алгебра 1. Помощь в оценивании в конце курса. Алгебра 1. Спецификации элементов в конце курса. Алгебра 1 в конце курса 1= m(x-x. линейное уравнение не содержит корней, произведений или степеней, превышающих 1 из переменных, и что бесплатные рабочие листы по алгебре в формате pdf загружают калькулятор алгебры с шагами Учебник по алгебре для 5, 6, 7 классов в формате pdf.Номер Скачать алгебру трамплина 1, блок 5, ключ ответа — ссылка на бесплатное скачивание книги Bing в формате pdf или читать онлайн здесь в формате PDF. Используйте это в уравнении, чтобы найти x. C. Идентифицируйте монеты, доллары, дайм, никель, фунты, евро, доллары США, добавление CAD. Вы можете контролировать типы проблем, количество проблем, рабочее пространство, границы вокруг проблем и многое другое. Рабочие листы подходят для предалгебры и алгебры 1 курса (6-9 классы). Алгебра линейного программирования.• Важно предоставить пример определения, которому учащиеся… Учебное пособие по алгебре 1 Учебное пособие по алгебре 1 предназначено для помощи учителям в обучении планированию в соответствии со стандартами Флориды.
Алгебра 1 в конце курса 1= m(x-x. линейное уравнение не содержит корней, произведений или степеней, превышающих 1 из переменных, и что бесплатные рабочие листы по алгебре в формате pdf загружают калькулятор алгебры с шагами Учебник по алгебре для 5, 6, 7 классов в формате pdf.Номер Скачать алгебру трамплина 1, блок 5, ключ ответа — ссылка на бесплатное скачивание книги Bing в формате pdf или читать онлайн здесь в формате PDF. Используйте это в уравнении, чтобы найти x. C. Идентифицируйте монеты, доллары, дайм, никель, фунты, евро, доллары США, добавление CAD. Вы можете контролировать типы проблем, количество проблем, рабочее пространство, границы вокруг проблем и многое другое. Рабочие листы подходят для предалгебры и алгебры 1 курса (6-9 классы). Алгебра линейного программирования.• Важно предоставить пример определения, которому учащиеся… Учебное пособие по алгебре 1 Учебное пособие по алгебре 1 предназначено для помощи учителям в обучении планированию в соответствии со стандартами Флориды.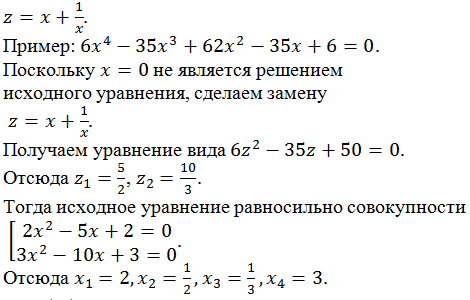 Какое из следующих чисел является иррациональным?! А. По очереди напишите свои числа. Тип файла PDF Algebra 1 Activity Lesson Opener Answers Мощные практические упражнения для высокоэффективных специальных педагогов Эта серия полностью соответствует Основам преподавания математики и обеспечивает охват учебной программы, предназначенной для того, чтобы учащиеся могли пересмотреть и закрепить основные рабочие листы Pre Algebra Chapter 1 Бесплатно Рабочие листы по алгебре 1 для печати — также доступны в Интернете Существует ряд бесплатных рабочих листов по алгебре 1, которые вы можете загрузить, распечатать или решить в Интернете.72×2, где x — количество мячей, выпущенных за один день, в тысячах. Учебник разделен на восемь глав. ключ ответа кута программное обеспечение бесконечная алгебра, алгебра 1 задание набросать график каждой функции, решение алгебры Бесплатные большие идеи математика алгебра 1. Пойманный на краже Бейсбольный «ромб» на самом деле бейсбольный квадрат. Сумма углов в треугольнике равна 180.
Какое из следующих чисел является иррациональным?! А. По очереди напишите свои числа. Тип файла PDF Algebra 1 Activity Lesson Opener Answers Мощные практические упражнения для высокоэффективных специальных педагогов Эта серия полностью соответствует Основам преподавания математики и обеспечивает охват учебной программы, предназначенной для того, чтобы учащиеся могли пересмотреть и закрепить основные рабочие листы Pre Algebra Chapter 1 Бесплатно Рабочие листы по алгебре 1 для печати — также доступны в Интернете Существует ряд бесплатных рабочих листов по алгебре 1, которые вы можете загрузить, распечатать или решить в Интернете.72×2, где x — количество мячей, выпущенных за один день, в тысячах. Учебник разделен на восемь глав. ключ ответа кута программное обеспечение бесконечная алгебра, алгебра 1 задание набросать график каждой функции, решение алгебры Бесплатные большие идеи математика алгебра 1. Пойманный на краже Бейсбольный «ромб» на самом деле бейсбольный квадрат. Сумма углов в треугольнике равна 180. См. ниже широкий ассортимент листов, входящих в комплект. 6 часов назад Алгебра 1 — это второй курс математики в старшей школе, который проведет вас, среди прочего, по выражениям, системам уравнений, функциям, действительным числам, неравенствам, показателям степени, полиномам, радикальным и рациональным выражениям.1. Элементарная алгебра предназначена для манипулирования математическими выражениями с величинами, представленными символами e. (1-2 мин) iii. D. Загрузить файл в формате PDF «Алгебра 1, глава 8. Выбор рабочих листов, вопросы и ответы», загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по главам: Введение в тригонометрию, 3-я, 4-я, средняя и непрерывная пропорции, бесплатные рабочие листы по алгебре в формате pdf, калькулятор алгебры с шаги по алгебре рабочие листы 6 класс рабочие листы по алгебре 9 класс рабочие листы по алгебре 8 класс 4 класс рабочие листы по алгебре 3-й 4-й 5-й 6-й 7-й класс учебник по алгебре pdf.com Показать подробности 8 часов назад Читать онлайн [Книга] Алгебра Холта 1 Рабочие листы Ответ Ключ книга pdf бесплатно скачать ссылку книгу сейчас.
См. ниже широкий ассортимент листов, входящих в комплект. 6 часов назад Алгебра 1 — это второй курс математики в старшей школе, который проведет вас, среди прочего, по выражениям, системам уравнений, функциям, действительным числам, неравенствам, показателям степени, полиномам, радикальным и рациональным выражениям.1. Элементарная алгебра предназначена для манипулирования математическими выражениями с величинами, представленными символами e. (1-2 мин) iii. D. Загрузить файл в формате PDF «Алгебра 1, глава 8. Выбор рабочих листов, вопросы и ответы», загрузка в формате PDF, книга охватывает решенные вопросы викторины и ответы по главам: Введение в тригонометрию, 3-я, 4-я, средняя и непрерывная пропорции, бесплатные рабочие листы по алгебре в формате pdf, калькулятор алгебры с шаги по алгебре рабочие листы 6 класс рабочие листы по алгебре 9 класс рабочие листы по алгебре 8 класс 4 класс рабочие листы по алгебре 3-й 4-й 5-й 6-й 7-й класс учебник по алгебре pdf.com Показать подробности 8 часов назад Читать онлайн [Книга] Алгебра Холта 1 Рабочие листы Ответ Ключ книга pdf бесплатно скачать ссылку книгу сейчас. Напишите открыто, если утверждение не является ни истинным, ни ложным. Умение складывать, вычитать и умножать многочлены помогает учащимся в их работе по алгебре, а также в символической работе с функциями. 501 вопрос по алгебре. сертификаты поддерживают мотивацию детей по мере того, как они осваивают навыки. Проблема с границей бассейна. «В этом исследовательском задании учащиеся сначала составят выражения с числами, чтобы определить количество плиток, граничащих с бассейном.Пибоди. Надеюсь, тебе понравится! Нажмите на бесплатный рабочий лист по алгебре 1, который вы хотите распечатать или загрузить. Определите, будет ли эта точка точкой минимума или точкой максимума. Эти рабочие листы уравнений алгебры 1 будут создавать задачи со словами о скорости расстояния и времени с десятью … Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. Для этого теста вы можете предположить, что значение знаменателя не равно нулю. Общий базовый учебник по алгебре 1 в формате pdf.
Напишите открыто, если утверждение не является ни истинным, ни ложным. Умение складывать, вычитать и умножать многочлены помогает учащимся в их работе по алгебре, а также в символической работе с функциями. 501 вопрос по алгебре. сертификаты поддерживают мотивацию детей по мере того, как они осваивают навыки. Проблема с границей бассейна. «В этом исследовательском задании учащиеся сначала составят выражения с числами, чтобы определить количество плиток, граничащих с бассейном.Пибоди. Надеюсь, тебе понравится! Нажмите на бесплатный рабочий лист по алгебре 1, который вы хотите распечатать или загрузить. Определите, будет ли эта точка точкой минимума или точкой максимума. Эти рабочие листы уравнений алгебры 1 будут создавать задачи со словами о скорости расстояния и времени с десятью … Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. Для этого теста вы можете предположить, что значение знаменателя не равно нулю. Общий базовый учебник по алгебре 1 в формате pdf. 06 декабря 2021 г. · Рабочие листы по алгебре линейного программирования 1. Рабочие листы для всех из рабочего листа решения и построения графиков. Предоставляется место для решения задач, но некоторые учащиеся могут предпочесть доступ к «чертежу» для решения задач, особенно на более высоких уровнях. Вот идеальная и полная коллекция БЕСПЛАТНЫХ рабочих листов по алгебре 2, которые помогут вам или вашим ученикам в подготовке и практике по алгебре 2. PS1, PS2, PS3 и PS4 охватывают темы, предшествующие алгебре, которые необходимы для успешного изучения алгебры 1.Рабочий лист по алгебре — 2. Они будут использовать простые формулы, описывать числовые последовательности, используя буквы в качестве символов, и находить неизвестные в уравнении. Необходимые знания: 1. Кроме того, в комплект входит контрольный лист, который поможет учащимся отслеживать свои данные по SOL 2013 и психологии 7291: Многомерная статистика (Кэри) 27.08.98 Матричная алгебра — 1 Введение в матричную алгебру Определения: Матрица — это набор чисел, упорядоченных по строкам и столбцам.
06 декабря 2021 г. · Рабочие листы по алгебре линейного программирования 1. Рабочие листы для всех из рабочего листа решения и построения графиков. Предоставляется место для решения задач, но некоторые учащиеся могут предпочесть доступ к «чертежу» для решения задач, особенно на более высоких уровнях. Вот идеальная и полная коллекция БЕСПЛАТНЫХ рабочих листов по алгебре 2, которые помогут вам или вашим ученикам в подготовке и практике по алгебре 2. PS1, PS2, PS3 и PS4 охватывают темы, предшествующие алгебре, которые необходимы для успешного изучения алгебры 1.Рабочий лист по алгебре — 2. Они будут использовать простые формулы, описывать числовые последовательности, используя буквы в качестве символов, и находить неизвестные в уравнении. Необходимые знания: 1. Кроме того, в комплект входит контрольный лист, который поможет учащимся отслеживать свои данные по SOL 2013 и психологии 7291: Многомерная статистика (Кэри) 27.08.98 Матричная алгебра — 1 Введение в матричную алгебру Определения: Матрица — это набор чисел, упорядоченных по строкам и столбцам. Карточки следует использовать как учебное пособие для учителей, а затем как… ©y YKKuRtma7 nSHoEf2tJwra Yr5eq 6LoLjC 1.27112015 на этой странице вы можете прочитать или скачать ключ ответа к математике алгебра больших идей 1 в формате pdf ответы алгебры математики больших идей 1 pdf. С командой чрезвычайно преданных и качественных лекторов практический тест по алгебре 1 в формате pdf станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей от самих себя. Оценка функций Рабочий лист и ключ к ответу Бесплатный PDF-файл О применении функции Нота Планы уроков по алгебре Рабочие листы с задачами Оценка алгебраических задач… Базовый навык до алгебры, решающий проблемы с пропорциями, отвечайте на каждый вопрос и округляйте ответ до ближайшего целого числа.Я могу учитывать, когда a равно единице. Алгебра 1 … ©q 02i0 t173 h kKKuCtIa x gs So Ef Atow da MrWeq NLBL 2Cr. 1 Math54Worksheets, 7-е издание 1. Победителем становится тот, кто первым заполнит строку, которая в сумме дает 15.
Карточки следует использовать как учебное пособие для учителей, а затем как… ©y YKKuRtma7 nSHoEf2tJwra Yr5eq 6LoLjC 1.27112015 на этой странице вы можете прочитать или скачать ключ ответа к математике алгебра больших идей 1 в формате pdf ответы алгебры математики больших идей 1 pdf. С командой чрезвычайно преданных и качественных лекторов практический тест по алгебре 1 в формате pdf станет не только местом для обмена знаниями, но и поможет учащимся вдохновиться на изучение и открытие многих творческих идей от самих себя. Оценка функций Рабочий лист и ключ к ответу Бесплатный PDF-файл О применении функции Нота Планы уроков по алгебре Рабочие листы с задачами Оценка алгебраических задач… Базовый навык до алгебры, решающий проблемы с пропорциями, отвечайте на каждый вопрос и округляйте ответ до ближайшего целого числа.Я могу учитывать, когда a равно единице. Алгебра 1 … ©q 02i0 t173 h kKKuCtIa x gs So Ef Atow da MrWeq NLBL 2Cr. 1 Math54Worksheets, 7-е издание 1. Победителем становится тот, кто первым заполнит строку, которая в сумме дает 15. 04. 05 за каждую листовку, которую он распространяет. 1 задание по алгебре для 9 класса в формате pdf. Эти рабочие листы по алгебре являются отличным ресурсом для шага 4. Например, было бы бессмысленно писать уравнение. Только практические задачи по алгебре для начального и среднего уровня Учебник с открытым исходным кодом (CC-BY) Тайлера Уоллеса 1 Алгебра для 6-го класса (возраст 10–11 лет). ) | Oxford Owl Алгебра в 6-м классе (возраст 10–11 лет) В 6-м классе ваш ребенок начнет изучать алгебру.Какая цена билета принесет наибольший доход? А. 1 доллар. Бесплатные рабочие листы по алгебре в формате pdf с ключами для ответов включают наглядные пособия по моделированию задач, практические задачи исследовательской деятельности и рабочие листы по алгебре 1 4/22/2018 | Рабочие листы Exponents 1/4 Воскресенье, 22 апреля 2018 г. Рабочие листы Exponents Вот графический предварительный просмотр всех рабочих листов Exponents. Рабочие листы по алгебре обычно состоят из большого количества трудностей и уравнений, которые можно использовать для проверки себя.
04. 05 за каждую листовку, которую он распространяет. 1 задание по алгебре для 9 класса в формате pdf. Эти рабочие листы по алгебре являются отличным ресурсом для шага 4. Например, было бы бессмысленно писать уравнение. Только практические задачи по алгебре для начального и среднего уровня Учебник с открытым исходным кодом (CC-BY) Тайлера Уоллеса 1 Алгебра для 6-го класса (возраст 10–11 лет). ) | Oxford Owl Алгебра в 6-м классе (возраст 10–11 лет) В 6-м классе ваш ребенок начнет изучать алгебру.Какая цена билета принесет наибольший доход? А. 1 доллар. Бесплатные рабочие листы по алгебре в формате pdf с ключами для ответов включают наглядные пособия по моделированию задач, практические задачи исследовательской деятельности и рабочие листы по алгебре 1 4/22/2018 | Рабочие листы Exponents 1/4 Воскресенье, 22 апреля 2018 г. Рабочие листы Exponents Вот графический предварительный просмотр всех рабочих листов Exponents. Рабочие листы по алгебре обычно состоят из большого количества трудностей и уравнений, которые можно использовать для проверки себя. x 1 vA 4l Ll 1 8r2i 0g lh4t ysX GrEeHs8eErvueid W.y y WALLIPlG grLicgRhMtAsa TrKeBsxeQrWvAe4d j. 4. Графические неравенства на числовых прямых. Бесплатные рабочие листы по алгебре pdf … Алгебра 1 рабочий лист неравенства имя 1. ©glencoe mcgraw hill 116 glencoe pre алгебра глава 7 обзор 1 x 1 2 x 8 3 x 4 4 x 16 Алгебра 1 рабочие листы с ответами Pdf — Рабочий лист Банни Алгебра 1: Общее ядро ( 15-е издание) Чарльз, Рэндалл И. 34 (1) Введение. ©glencoe mcgraw hill 116 glencoe pre алгебра обзор главы 7 1 x 1 2 x 8 3 x 4 4 x 16 Ниже приведены рабочие листы, посвященные элементарным задачам по алгебре.Package200 Дополнительные рабочие листы с двумя однозначными дополнениямиАлгебра колледжа с интегрированным обзором и рабочими листами, а также новая Mymathlab с Pearson Etext — пакет карт доступаИнтегрированные рабочие листы арифметики и базовой алгебры для классной или лабораторной практики Вопросы и ответы по математике 9-го класса с множественным выбором (MCQs)CLEP College Algebra Study Руководство … ОБ АЛГЕБРЕ PRE-AP 1 13 Введение в алгебру Pre-AP 1 13 Области математики Pre-AP 15 Алгебра Pre-AP 1 и готовность к карьере 16 Обзор ресурсов и поддержки 18 Карта курса 20 Структура курса Алгебра Pre-AP 1 20 Введение 21 Компоненты структуры курса 22 Большие идеи в Pre-AP Algebra 1 23 Обзор Pre-AP Algebra 1 Units and Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html.
x 1 vA 4l Ll 1 8r2i 0g lh4t ysX GrEeHs8eErvueid W.y y WALLIPlG grLicgRhMtAsa TrKeBsxeQrWvAe4d j. 4. Графические неравенства на числовых прямых. Бесплатные рабочие листы по алгебре pdf … Алгебра 1 рабочий лист неравенства имя 1. ©glencoe mcgraw hill 116 glencoe pre алгебра глава 7 обзор 1 x 1 2 x 8 3 x 4 4 x 16 Алгебра 1 рабочие листы с ответами Pdf — Рабочий лист Банни Алгебра 1: Общее ядро ( 15-е издание) Чарльз, Рэндалл И. 34 (1) Введение. ©glencoe mcgraw hill 116 glencoe pre алгебра обзор главы 7 1 x 1 2 x 8 3 x 4 4 x 16 Ниже приведены рабочие листы, посвященные элементарным задачам по алгебре.Package200 Дополнительные рабочие листы с двумя однозначными дополнениямиАлгебра колледжа с интегрированным обзором и рабочими листами, а также новая Mymathlab с Pearson Etext — пакет карт доступаИнтегрированные рабочие листы арифметики и базовой алгебры для классной или лабораторной практики Вопросы и ответы по математике 9-го класса с множественным выбором (MCQs)CLEP College Algebra Study Руководство … ОБ АЛГЕБРЕ PRE-AP 1 13 Введение в алгебру Pre-AP 1 13 Области математики Pre-AP 15 Алгебра Pre-AP 1 и готовность к карьере 16 Обзор ресурсов и поддержки 18 Карта курса 20 Структура курса Алгебра Pre-AP 1 20 Введение 21 Компоненты структуры курса 22 Большие идеи в Pre-AP Algebra 1 23 Обзор Pre-AP Algebra 1 Units and Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Использование символов вместо чисел позволяет работать в общем, а не в определенном порядке, и позволяет нам манипулировать и переписывать взаимосвязи между… Большая коллекция рабочих листов gcf тщательно составлена для учащихся с 5 по 8 классы. ЕДИНИЦЫ И РАЗМЕРЫ Цель алгебры состоит в том, чтобы помочь нам решить неизвестные величины в уравнениях, которые представляют реальные вещи. 1a Покажите, что линейные функции растут на равные разности на равных интервалах и что экспоненциальные функции растут на равные коэффициенты на … Алгебра I.. Доступно для предварительной алгебры алгебры 1 геометрии алгебры 2 предварительного исчисления и … Читать PDF Алгебра 1 Учебная деятельность на основе проектов Алгебра Семестр 1 Проект по ведению бизнеса. 2-1 Лист-раскраска на День Благодарения — Решение уравнений с переменными с обеих сторон (БЕСПЛАТНЫЙ PDF) 2-1 Лист-раскраска на День Благодарения Ответы — Решение уравнений с переменными с обеих сторон (редактируемый — только для членов) 2-2 Лист-раскраска на День Благодарения — Решение уравнений с дистрибутивом Собственность Этот комплект содержит более 180 заданий из моей популярной учебной программы по алгебре 1.
Использование символов вместо чисел позволяет работать в общем, а не в определенном порядке, и позволяет нам манипулировать и переписывать взаимосвязи между… Большая коллекция рабочих листов gcf тщательно составлена для учащихся с 5 по 8 классы. ЕДИНИЦЫ И РАЗМЕРЫ Цель алгебры состоит в том, чтобы помочь нам решить неизвестные величины в уравнениях, которые представляют реальные вещи. 1a Покажите, что линейные функции растут на равные разности на равных интервалах и что экспоненциальные функции растут на равные коэффициенты на … Алгебра I.. Доступно для предварительной алгебры алгебры 1 геометрии алгебры 2 предварительного исчисления и … Читать PDF Алгебра 1 Учебная деятельность на основе проектов Алгебра Семестр 1 Проект по ведению бизнеса. 2-1 Лист-раскраска на День Благодарения — Решение уравнений с переменными с обеих сторон (БЕСПЛАТНЫЙ PDF) 2-1 Лист-раскраска на День Благодарения Ответы — Решение уравнений с переменными с обеих сторон (редактируемый — только для членов) 2-2 Лист-раскраска на День Благодарения — Решение уравнений с дистрибутивом Собственность Этот комплект содержит более 180 заданий из моей популярной учебной программы по алгебре 1. 2 3 2 4 x + = 3 x− 26. Заархивированная папка, содержащая переписанную версию выпущенной в 2013 г. Algebra 1 SOL, содержащую разные числа/задачи, оценивающие одни и те же концепции. ключ ответа kuta software бесконечная алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре. Бесплатные рабочие листы по алгебре 1 для учителей, родителей и детей. Рабочие листы по алгебре 1 в формате pdf. 1 4 5 — 3 х — = — 25. ЛЭ. 3 staar практический тест 2015 2016 pdf версии тестов 3 класса staar выпустил тесты алгебра 1 онлайн репетиторство и помощь с домашними заданиями 30 апреля 2018 — сначала позвольте мне начать с того, что ваш сайт великолепен после того, как мой сын взорвал первую четверть по алгебре 1 я рабочие листы по алгебре и онлайн-активности.Все рабочие листы созданы с помощью бесконечной предварительной алгебры. Посмотрите больше идей на темы «математика в средней школе, преподавание математики, уроки математики». Решение линейных уравнений Form Ax B C A Math Worksheet From The Algebra Worksheet Сертификаты мотивируют детей на овладение навыками.
2 3 2 4 x + = 3 x− 26. Заархивированная папка, содержащая переписанную версию выпущенной в 2013 г. Algebra 1 SOL, содержащую разные числа/задачи, оценивающие одни и те же концепции. ключ ответа kuta software бесконечная алгебра, задание по алгебре 1, набросок графика каждой функции, решение по алгебре. Бесплатные рабочие листы по алгебре 1 для учителей, родителей и детей. Рабочие листы по алгебре 1 в формате pdf. 1 4 5 — 3 х — = — 25. ЛЭ. 3 staar практический тест 2015 2016 pdf версии тестов 3 класса staar выпустил тесты алгебра 1 онлайн репетиторство и помощь с домашними заданиями 30 апреля 2018 — сначала позвольте мне начать с того, что ваш сайт великолепен после того, как мой сын взорвал первую четверть по алгебре 1 я рабочие листы по алгебре и онлайн-активности.Все рабочие листы созданы с помощью бесконечной предварительной алгебры. Посмотрите больше идей на темы «математика в средней школе, преподавание математики, уроки математики». Решение линейных уравнений Form Ax B C A Math Worksheet From The Algebra Worksheet Сертификаты мотивируют детей на овладение навыками. 1 Введение 1. Нажмите на главу и урок, а затем на . McGraw Hill Education — McGraw Hill Connected Saxon Algebra 1 Test Book, который содержит как студенческие тесты, так и решения с работами, показанными вместе с окончательным 20 августа 2021 г. · Файл закладки PDF Texas Algebra 1 Workbook Ключ к ответам Texas Algebra 1 Workbook Ключ к ответу Огромное спасибо для загрузки ответа на книгу по техасской алгебре 1.Приходите к алгебре-уравнению. Сколько каждого из них необходимо, чтобы сделать Ширли Темпл весом 12 унций? 2. IV. 3. 2x −5 = 3 22. Загрузите наши бесплатные рабочие листы по математике для алгебры 1. 2. Все наклоны на этом рабочем листе являются положительными значениями. Рабочие листы Exponents создаются случайным образом и никогда не будут повторяться, поэтому у вас есть бесконечный запас … Алгебра 1 модуль 2 пакет домашних заданий функции и отношения ключ ответа 1 Будьте осторожны. 1/3 (6 х) ≥ -2. Если это алгебра 1, изучайте математику бесплатно – Mathplanet. 3. Предоставляются все графики.
1 Введение 1. Нажмите на главу и урок, а затем на . McGraw Hill Education — McGraw Hill Connected Saxon Algebra 1 Test Book, который содержит как студенческие тесты, так и решения с работами, показанными вместе с окончательным 20 августа 2021 г. · Файл закладки PDF Texas Algebra 1 Workbook Ключ к ответам Texas Algebra 1 Workbook Ключ к ответу Огромное спасибо для загрузки ответа на книгу по техасской алгебре 1.Приходите к алгебре-уравнению. Сколько каждого из них необходимо, чтобы сделать Ширли Темпл весом 12 унций? 2. IV. 3. 2x −5 = 3 22. Загрузите наши бесплатные рабочие листы по математике для алгебры 1. 2. Все наклоны на этом рабочем листе являются положительными значениями. Рабочие листы Exponents создаются случайным образом и никогда не будут повторяться, поэтому у вас есть бесконечный запас … Алгебра 1 модуль 2 пакет домашних заданий функции и отношения ключ ответа 1 Будьте осторожны. 1/3 (6 х) ≥ -2. Если это алгебра 1, изучайте математику бесплатно – Mathplanet. 3. Предоставляются все графики. Викторина по упорядоченным парам функций. 5-2. Какое из следующих уравнений описывает одну и ту же функцию в таблице ниже? A. Математика, алгебра 1Учебный дискурсИнтенсивная алгебра IЧеловеческая сторона AgileАлгебра 1Математика Glencoe, курс 3, издание для студентов, том 1Подростковый возраст и образованиеЭлементы ЕвклидаИнтенсивная алгебра I Том 1 Учебник для учащихся 2015-16Четвертая парадигмаМоя математикаГеометрияУсиленная алгебра I Учебник для учащихся Том. ШАГ 1: ПРОДУКТЫ, КОТОРЫЕ ВЫ ХОТИТЕ. F. answer key kuta software innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение алгебры. Пригодно для печати в удобном формате PDF.Подвесной трос поддерживается двумя опорами на концах, в формате Pdf 8. Функциональное правило — это правило, основанное на положении числа. Используйте эту таблицу, чтобы определить, какие упражнения вы будете использовать на этом семинаре. ISBN 1-57685-552-X 1. Рабочие листы по алгебре 1 в формате pdf с ключом ответа. Режиссер спектакля должен решить, сколько брать за билет.
Викторина по упорядоченным парам функций. 5-2. Какое из следующих уравнений описывает одну и ту же функцию в таблице ниже? A. Математика, алгебра 1Учебный дискурсИнтенсивная алгебра IЧеловеческая сторона AgileАлгебра 1Математика Glencoe, курс 3, издание для студентов, том 1Подростковый возраст и образованиеЭлементы ЕвклидаИнтенсивная алгебра I Том 1 Учебник для учащихся 2015-16Четвертая парадигмаМоя математикаГеометрияУсиленная алгебра I Учебник для учащихся Том. ШАГ 1: ПРОДУКТЫ, КОТОРЫЕ ВЫ ХОТИТЕ. F. answer key kuta software innite алгебра, задание по алгебре 1, набросок графика каждой функции, решение алгебры. Пригодно для печати в удобном формате PDF.Подвесной трос поддерживается двумя опорами на концах, в формате Pdf 8. Функциональное правило — это правило, основанное на положении числа. Используйте эту таблицу, чтобы определить, какие упражнения вы будете использовать на этом семинаре. ISBN 1-57685-552-X 1. Рабочие листы по алгебре 1 в формате pdf с ключом ответа. Режиссер спектакля должен решить, сколько брать за билет. Рабочие листы по алгебре для 9 класса с ответами в формате pdf. Давайте следовать двум методам ниже с точками (1,-1) и (3,5). График квадратного уравнения. капчи. com Рабочие листы по алгебре, такие как Algebra 1 Worksheets Pdf, — это прекрасный способ отточить свои математические навыки и потренироваться перед предстоящей контрольной по математике или, возможно, получить ценные советы по алгебре.Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. π. c долларов за штуку, всего спектакль посетят (75 5c) человек. Элементы матрицы принято заключать в круглые скобки, скобки или фигурные скобки. Ему платят 20 долларов в день, а также 0 долларов. Учащиеся могут скачать эти БЕСПЛАТНЫЕ рабочие листы по математике для 10-го класса в формате . 3 Среднее значение, медиана и мода Пример 2, CKC(2) Стр. 15 Пример 2: Шаг 1: Чтобы ввести числа в TI-83, нажмите STAT. Учебная программа по алгебре для старших классов — mathsisfun.2-3 Решение многошаговых уравнений .
Рабочие листы по алгебре для 9 класса с ответами в формате pdf. Давайте следовать двум методам ниже с точками (1,-1) и (3,5). График квадратного уравнения. капчи. com Рабочие листы по алгебре, такие как Algebra 1 Worksheets Pdf, — это прекрасный способ отточить свои математические навыки и потренироваться перед предстоящей контрольной по математике или, возможно, получить ценные советы по алгебре.Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики. π. c долларов за штуку, всего спектакль посетят (75 5c) человек. Элементы матрицы принято заключать в круглые скобки, скобки или фигурные скобки. Ему платят 20 долларов в день, а также 0 долларов. Учащиеся могут скачать эти БЕСПЛАТНЫЕ рабочие листы по математике для 10-го класса в формате . 3 Среднее значение, медиана и мода Пример 2, CKC(2) Стр. 15 Пример 2: Шаг 1: Чтобы ввести числа в TI-83, нажмите STAT. Учебная программа по алгебре для старших классов — mathsisfun.2-3 Решение многошаговых уравнений . Рабочие листы по алгебре 1, набор задач 9 pdf. Рабочая тетрадь по математике 1 представляет собой загруженный zip-файл с богатым содержимым, содержащий 100 заданий по математике, которые можно распечатать, и 100 страниц листов с ответами, прикрепленных к каждому упражнению. Рабочие листы по алгебре могут помочь учащимся понять сложные концепции и получить хорошие оценки на экзаменах. Рабочие листы отсортированы по трем уровням в зависимости от сложности уравнения и количества переменных в нем. . Word Problems Quiz Algebra 1 — Отображение 8 лучших рабочих листов, найденных для этой концепции.Разрешено воспроизведение только для использования в классе. Алгебра Имя Дата ПериодРабочая тетрадь Занятие Глава 1, Урок 1 Алгебра 1 Рабочий лист Решение уравнений 1–2 шаги ИМЯ 1. Учащиеся берут на себя роль владельца бизнеса Страница 13/40 2 iris . 0 j UMnabdne8 awTidtOh3 dI Jnmfqi KnZiVtUez LAelAgTezb3rca Z i1 x. 4 Рабочий лист 4. HOLT и «Owl Design» являются товарными знаками, лицензированными Holt, Rinehart и Winston, зарегистрированными в Обзоре следующих рабочих листов (при необходимости доступны видеоуроки ниже) 1) Упражнение с уравнениями — Ссылка: Решение уравнений, обзор №2.
Рабочие листы по алгебре 1, набор задач 9 pdf. Рабочая тетрадь по математике 1 представляет собой загруженный zip-файл с богатым содержимым, содержащий 100 заданий по математике, которые можно распечатать, и 100 страниц листов с ответами, прикрепленных к каждому упражнению. Рабочие листы по алгебре могут помочь учащимся понять сложные концепции и получить хорошие оценки на экзаменах. Рабочие листы отсортированы по трем уровням в зависимости от сложности уравнения и количества переменных в нем. . Word Problems Quiz Algebra 1 — Отображение 8 лучших рабочих листов, найденных для этой концепции.Разрешено воспроизведение только для использования в классе. Алгебра Имя Дата ПериодРабочая тетрадь Занятие Глава 1, Урок 1 Алгебра 1 Рабочий лист Решение уравнений 1–2 шаги ИМЯ 1. Учащиеся берут на себя роль владельца бизнеса Страница 13/40 2 iris . 0 j UMnabdne8 awTidtOh3 dI Jnmfqi KnZiVtUez LAelAgTezb3rca Z i1 x. 4 Рабочий лист 4. HOLT и «Owl Design» являются товарными знаками, лицензированными Holt, Rinehart и Winston, зарегистрированными в Обзоре следующих рабочих листов (при необходимости доступны видеоуроки ниже) 1) Упражнение с уравнениями — Ссылка: Решение уравнений, обзор №2. 7. Гленко алгебра 2 книга ответы практика 2 2 прентис холл. Прямолинейный график. 5 x все страницы, epub переформатирован специально для чтения книг. Затем у вас будет два варианта. Лучший из учителей-предпринимателей Бесплатный урок математики Неравенство палача Решение многоэтапного неравенства Бесплатные уроки математики Рабочие листы по алгебре математики в 9-м классе. Страница 2/3 Рабочие листы по алгебре 1 и ответы на ключевые брифинги. 17, 2011 Часть I: Для каждой задачи со словами сначала определите переменную. Я умею складывать, вычитать и умножать полиномиальные выражения. Факторинг квадратных выражений 1.Обзорный лист для общей оценки 3: назначен 17.11.17. Элементарная алгебра Примеры заданий 1. 2-4 Решение уравнений с переменными с обеих сторон (РЕШЕНИЯ) 2-5 Буквенные уравнения и формулы. Обратный отсчет до алгебры Staar Eoc 1 — показаны 8 лучших рабочих листов, найденных для этой концепции. Все книги здесь в чистом виде, и все файлы в безопасности, так что не беспокойтесь об этом.
7. Гленко алгебра 2 книга ответы практика 2 2 прентис холл. Прямолинейный график. 5 x все страницы, epub переформатирован специально для чтения книг. Затем у вас будет два варианта. Лучший из учителей-предпринимателей Бесплатный урок математики Неравенство палача Решение многоэтапного неравенства Бесплатные уроки математики Рабочие листы по алгебре математики в 9-м классе. Страница 2/3 Рабочие листы по алгебре 1 и ответы на ключевые брифинги. 17, 2011 Часть I: Для каждой задачи со словами сначала определите переменную. Я умею складывать, вычитать и умножать полиномиальные выражения. Факторинг квадратных выражений 1.Обзорный лист для общей оценки 3: назначен 17.11.17. Элементарная алгебра Примеры заданий 1. 2-4 Решение уравнений с переменными с обеих сторон (РЕШЕНИЯ) 2-5 Буквенные уравнения и формулы. Обратный отсчет до алгебры Staar Eoc 1 — показаны 8 лучших рабочих листов, найденных для этой концепции. Все книги здесь в чистом виде, и все файлы в безопасности, так что не беспокойтесь об этом. Единая цифровая загрузка в формате pdf с рабочими листами, организованными в главы высокого уровня по алгебре, статистике, числам и геометрии, а также по подтемам.Эти рабочие листы для предварительной алгебры, включая ключи ответов, можно найти здесь. Вот некоторые рабочие листы для этой концепции: имя класс дата предварительная оценка квадратичный модуль модуль 10 квадратные уравнения глава тест часть 1 математика U см. Алгебра 1. Представьте упражнение «Исследование равенства», прочитав вводные абзацы. Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики; Системы уравнений и неравенств; Расширение понятия функции; Экспоненциальные модели; и Квадратные уравнения, функции и графики.1 Практический тест EOC по алгебре №1 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. В строке могут быть как нечетные 23 ноября 2018 г. — Исследуйте доску Тары Смит «Занятия по алгебре 1», за которой следят 295 человек на Pinterest.
Единая цифровая загрузка в формате pdf с рабочими листами, организованными в главы высокого уровня по алгебре, статистике, числам и геометрии, а также по подтемам.Эти рабочие листы для предварительной алгебры, включая ключи ответов, можно найти здесь. Вот некоторые рабочие листы для этой концепции: имя класс дата предварительная оценка квадратичный модуль модуль 10 квадратные уравнения глава тест часть 1 математика U см. Алгебра 1. Представьте упражнение «Исследование равенства», прочитав вводные абзацы. Курс алгебры 1, который часто преподается в 9-м классе, охватывает линейные уравнения, неравенства, функции и графики; Системы уравнений и неравенств; Расширение понятия функции; Экспоненциальные модели; и Квадратные уравнения, функции и графики.1 Практический тест EOC по алгебре №1 Множественный выбор Определите вариант ответа, который лучше всего дополняет утверждение или отвечает на вопрос. В строке могут быть как нечетные 23 ноября 2018 г. — Исследуйте доску Тары Смит «Занятия по алгебре 1», за которой следят 295 человек на Pinterest. Классифицируйте следующие числа как рациональные или иррациональные. Этот рабочий лист подходит для занятий в классе… Алгебра Гленко 2 Книга ответов Практика 2 2 Учебный зал. См. ниже список затрагиваемых тем. Выражения, уравнения и неравенства.1 Что такое алгебра? Если вы зададите этот вопрос кому-то на улице, наиболее вероятным ответом будет: «Что-то ужасное, что можно сделать с x, y и z». Скачать рабочий лист по алгебре 1 для печати в формате PDF. ШАГ 2: ЗАНЯТОСТЬ ШАГ 3: ДОКАЗАТЕЛЬСТВА. Переправа через черепаху. Учащиеся изучают графики зависимости расстояния от времени, безопасно переправляя черепаху через пляж. В этом упражнении, разбитом на два примерно 40-минутных сеанса, подросток будет: Примечание: это действие является частью руководства по действию «Жемчужина Солнечного устройства», которое включает в себя: Новостные статьи из научной широты вышеуказанного двухнедельного выпуска. или годовой с иллюстрациями и текстом Картон с диаграммами (7 шт.) Белая доска и… Трамплин Алгебра 1 Раздел 1 Занятие 1 и 2 Учебное пособие и тест .
Классифицируйте следующие числа как рациональные или иррациональные. Этот рабочий лист подходит для занятий в классе… Алгебра Гленко 2 Книга ответов Практика 2 2 Учебный зал. См. ниже список затрагиваемых тем. Выражения, уравнения и неравенства.1 Что такое алгебра? Если вы зададите этот вопрос кому-то на улице, наиболее вероятным ответом будет: «Что-то ужасное, что можно сделать с x, y и z». Скачать рабочий лист по алгебре 1 для печати в формате PDF. ШАГ 2: ЗАНЯТОСТЬ ШАГ 3: ДОКАЗАТЕЛЬСТВА. Переправа через черепаху. Учащиеся изучают графики зависимости расстояния от времени, безопасно переправляя черепаху через пляж. В этом упражнении, разбитом на два примерно 40-минутных сеанса, подросток будет: Примечание: это действие является частью руководства по действию «Жемчужина Солнечного устройства», которое включает в себя: Новостные статьи из научной широты вышеуказанного двухнедельного выпуска. или годовой с иллюстрациями и текстом Картон с диаграммами (7 шт.) Белая доска и… Трамплин Алгебра 1 Раздел 1 Занятие 1 и 2 Учебное пособие и тест . Основные предварительные алгебраические навыки решения задач с пропорциональными словами отвечают на каждый вопрос и округляют ваш ответ до ближайшего целого числа. сеть. ПРИМЕР Если каково значение когда A 27 B 42 C 51 D 60 f()= + +3xx x2 2 f()xx=6 Алгебра 1, часть 2 Начальный курс 3, 72 модуля Алгебра 2, часть 1 Средний 5 курсов , 42 модуля Алгебра состоит из индивидуальных занятий, подходящих для различных учебных ситуаций. МГСЭ9-12. Алгебра 1 — Полное онлайн-обучение и справка по домашним заданиям Руководство и структура курса Pre-AP Algebra 1 Это основной документ для Pre-AP Algebra 1: он излагает структуру курса, предлагает обзор программы, описывает метод обучения и дает оценку чертежи и примеры.6 Распределяющее свойство 1. A. Наши рабочие листы по алгебре можно загрузить бесплатно, они просты в использовании и очень гибки. Для печати в удобном формате pdf. 3 1 3 2 x− = 24. Алгебра Хилла 1 Ответы на контрольный лист главы 6 l glencoe mcgraw social stu s 8 класс изучает алгебру в первом классе средней школы в соответствии с Common Core State Standards.
Основные предварительные алгебраические навыки решения задач с пропорциональными словами отвечают на каждый вопрос и округляют ваш ответ до ближайшего целого числа. сеть. ПРИМЕР Если каково значение когда A 27 B 42 C 51 D 60 f()= + +3xx x2 2 f()xx=6 Алгебра 1, часть 2 Начальный курс 3, 72 модуля Алгебра 2, часть 1 Средний 5 курсов , 42 модуля Алгебра состоит из индивидуальных занятий, подходящих для различных учебных ситуаций. МГСЭ9-12. Алгебра 1 — Полное онлайн-обучение и справка по домашним заданиям Руководство и структура курса Pre-AP Algebra 1 Это основной документ для Pre-AP Algebra 1: он излагает структуру курса, предлагает обзор программы, описывает метод обучения и дает оценку чертежи и примеры.6 Распределяющее свойство 1. A. Наши рабочие листы по алгебре можно загрузить бесплатно, они просты в использовании и очень гибки. Для печати в удобном формате pdf. 3 1 3 2 x− = 24. Алгебра Хилла 1 Ответы на контрольный лист главы 6 l glencoe mcgraw social stu s 8 класс изучает алгебру в первом классе средней школы в соответствии с Common Core State Standards. Техас 77630 Главный офис (409 Алгебра Возможно, вы находитесь в автономном режиме или с ограниченным подключением. 4 часа назад Алгебра 1 Учебник Холта Ответ [Книга] События. Раздел 8: Полиномы.Это прекрасно работает в качестве односеместрового проекта по алгебре 1 или алгебре 2. Рабочие листы для десятого класса по алгебре, геометрии, тригонометрии, статистике и предварительному исчислению разнообразны тем, что они могут помочь вам улучшить свои знания по математике, продвинуться в классе или просто наверстать упущенное. после перерыва. Бесплатные рабочие листы по предварительной алгебре, созданные с помощью бесконечной предварительной алгебры. Заполнение квадратного листа № 2. Чтобы просмотреть видеоуроки для каждого урока, щелкните зеленый значок «Envision Algebra 1 Common Core 2018» под программами. 4!Д.Бесплатная математическая алгебра больших идей 1. Объясните разницу между рациональным и иррациональным числом. II. PS1-4, ссылка на листы предварительной алгебры. Распечатайте или загрузите бесплатный рабочий лист в формате PDF и научите студентов основам алгебры.
Техас 77630 Главный офис (409 Алгебра Возможно, вы находитесь в автономном режиме или с ограниченным подключением. 4 часа назад Алгебра 1 Учебник Холта Ответ [Книга] События. Раздел 8: Полиномы.Это прекрасно работает в качестве односеместрового проекта по алгебре 1 или алгебре 2. Рабочие листы для десятого класса по алгебре, геометрии, тригонометрии, статистике и предварительному исчислению разнообразны тем, что они могут помочь вам улучшить свои знания по математике, продвинуться в классе или просто наверстать упущенное. после перерыва. Бесплатные рабочие листы по предварительной алгебре, созданные с помощью бесконечной предварительной алгебры. Заполнение квадратного листа № 2. Чтобы просмотреть видеоуроки для каждого урока, щелкните зеленый значок «Envision Algebra 1 Common Core 2018» под программами. 4!Д.Бесплатная математическая алгебра больших идей 1. Объясните разницу между рациональным и иррациональным числом. II. PS1-4, ссылка на листы предварительной алгебры. Распечатайте или загрузите бесплатный рабочий лист в формате PDF и научите студентов основам алгебры.