Обозначения физических величин

Величины
Наименование	Обозначение
Механические величины
Вес	G, P, W
Время	t
Высота	h
Давление	p
Диаметр	d
Длина	l
Длина пути	s
Импульс (количество движения)	p
Количество вещества	ν, n
Коэффицент жесткости (жесткость)	Ʀ
Коэффицент запаса прочности	Ʀ, n
Коэффицент полезного действия	η
Коэффицент трения качения	Ʀ
Коэффицент трения скольжения	μ, f
Масса	m
Масса атома	ma
Масса электрона	me
Механическое напряжение	σ
Модуль упругости (модуль Юнга)	E
Момент силы	M
Мощность	P, N
Объем, вместимость	V, ϑ
Период колебания	T
Плотность	ϱ
Площадь	A, S
Поверхностное натяжение	σ, γ
Постоянная гравитационная	G
Предел прочности	σпч
Работа	W, A, L
Радиус	r, R
Сила, сила тяжести	F, Q, R
Скорость линейная	ϑ
Скорость угловая	ώ
Толщина	d, δ
Ускорение линейное	a
Ускорение свободного падения	g
Частота	ν, f
Частота вращения	n
Ширина	b
Энергия	E, W
Энергия кинетитеская	EƦ
Энергия потенциальная	Ep
Акустические величины
Длина волны	λ
Звуковая мощность	P
Звуковая энергия	W
Интенсивность звука	I
Скорость звука	c
Частота	ν, f
Тепловые величины и величины молекулярной физики
Абсолютная влажность	a
Газовая постоянная (молярная)	R
Количество теплоты	Q
Коэффицент полезного действия	η
Относительная влажность	ϕ
Относительная молекулярная масса	Mr
Постоянная (число) Авогадро	NA
Постоянная Больцмана	Ʀ
Постоянная (число) Лошмидта	NL
Температура Кюри	TC
Температура па шкале Цельсия	t, ϴ
Температура термодинамическая (абсолютная температура)	T
Температурный коэффицент линейного расширения	a, ai
Температурный коффицент объемного расширения	β, av
Удельная теплоемкость	c
Удельная теплота парообразования	r
Удельная теплота плавления	λ
Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива)	q
Число молекул	N
Энергия внутренняя	U
Электрические и магнитные величины
Диэлектрическая проницаемость вакуума (электрическая постоянная)	Ԑo
Индуктивность	L
Коэффицент самоиндукции	L
Коэффицент трансформации	K
Магнитная индукция	B
Магнитная проницаемость вакуума (магнитная постоянная)	μo
Магнитный поток	Ф
Мощность электрической цепи	P
Напряженность магнитного поля	H
Напряженность электрического поля	E
Объемная плотность электрического заряда	ϱ
Относительная диэлектрическая проницаемость	Ԑr
Относительная магнитная проницаемость	μr
Плотность эенгии магнитного поля удельная	ωm
Плотность энергии электрического поля удельная	ωэ
Плотность заряда поверхностная	σ
Плотность электрического тока	J
Постоянная (число) Фарадея	F
Проницаемость диэлектрическая	ԑ
Работа выхода электрона	ϕ
Разность потенциалов	U
Сила тока	I
Температурный коэффицент электрического сопротивления	a
Удельная электрическая проводимость	γ
Удельное электрическое сопротивление	ϱ
Частота электрического тока	f, ν
Число виток обмотки	N, ω
Электрическая емкость	C
Электрическая индукция	D
Электрическая проводимость	G
Электрический момент диполя молекулы	p
Электрический заряд (количество электричества)	Q, q
Электрический потенциал	V, ω
Электрическое напряжение	U
Электрическое сопротивление	R, r
Электродвижущая сила	E, Ԑ
Электрохимический эквивалент	Ʀ
Энергия магнитного поля	Wm
Энергия электрического поля	Wэ
Энергия Электромагнитная	W
Оптические величины
Длина волны	λ
Освещенность	E
Период колебания	T
Плотность потока излучения	Ф
Показатель (коэффицент) преломления	n
Световой поток	Ф
Светасила объектива	f
Сила света	I
Скорость света	c
Увеличение линейное	β
Увеличение окуляра, микроскопа, лупы	Ѓ
Угол отражения луча	έ
Угол падения луча	ԑ
Фокусное расстояние	F
Частота колебаний	ν, f
Энергия излучения	Q, W
Энергия световая	Q
Величины атомной физики
Атомная масса относительная	Ar
Время полураспада	T1/2
Дефект массы	Δ
Заряд электрона	e
Масса атома	ma
Масса нейтрона	mn
Масса протона	mp
Масса электрона	me
Постоянная Планка	h, ħ
Радиус электрона	re
Величины ионизирующих излучений
Поглощеная доза излучения (доза излучения)	D
Мощность поглощенной дозы излучения	Ď
Активность нуклида в радиоактивном источнике	A

что такое n в физике? :: SYL.ru

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

• постоянная Авогадро;

• увеличение оптического прибора;

• концентрация вещества;

• число Дебая;

• полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

• показатель преломления, причем он может быть абсолютным или относительным;

• нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

• частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

N = А : t.

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро:

ν = N : N_А.

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

q = N × e.

Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:

ν = N : t.

Появляется буква «эн» в формуле для периода обращения:

Т = t : N.

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

n = с : v.

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n₂₁ = v₁ : v₂ = n₂ : n₁,

где n₁ и n₂ — абсолютные показатели преломления первой и второй среды, v₁ и v₂ — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n₂₁= sin α : sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Среда	Абсолютный показатель преломления
воздух	1,00029
лед	1,31
вода	1,33298
спирт этиловый	1,36
сахар	1,56
алмаз	2,419

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул. Как уже было сказано выше, N = А : t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000 : 600 = 20 000 Вт.

Ответ. Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с : v.

Решение. Из указанной формулы видно, что v = с : n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n₂₁= sin α: sin γ. А также: n = с : v.

Решение. В первой формуле n₂₁ — это отношение двух показателей преломления рассматриваемых веществ, то есть n₂ и n₁. Если записать вторую указанную формулу для предложенных сред, то получатся такие: n₁= с : v₁ и n₂ =с : v₂. Если составить отношение двух последних выражений, получится, что n₂₁ = v₁ : v₂. Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v₂ : v₁).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ. Значение угла преломления — 26º.

Задачи на период обращения

№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул. Период вращения и число оборотов связаны формулой Т = t : N.

Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600 : 5 = 720.

Ответ. Число оборотов лопастей мельницы равно 720.

№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула: частота ν = N : t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ. Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.

Обозначения в физике ℹ️ единицы измерения физических величин, таблица буквенных обозначений с пояснениями и примечаниями

Физическая величина	Символ	Единица измерения физической величины	Ед. изм. физ. вел.	Описание	Примечания
Сила тока	I	ампер	А	Протекающий в единицу времени заряд.
Плотность тока	j	ампер на квадратный метр	А/м2	Сила электрического тока, протекающего через элемент поверхности единичной площади.	Векторная величина
Электрический заряд	Q, q	кулон	Кл = (А·с)	Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.	экстенсивная, сохраняющаяся величина
Электрический дипольный момент	p	кулон-метр	Кл•м	Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей.
Поляризованность	P	кулон на квадратный метр	Кл/м2	Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве.
Напряжение	U	вольт	В	Изменение потенциальной энергии, приходящееся на единицу заряда.	скаляр
Потенциал, ЭДС	φ, σ	вольт	В	Работа сторонних сил (некулоновских) по перемещению заряда.
Напряженность электрического поля	E	вольт на метр	В/м	Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q
Электрическая емкость	C	фарад	Ф	Мера способности проводника накапливать электрический заряд
Электрическое сопротивление	R, r	ом	Ом = (м2·кг/(с3·А2))	сопротивление объекта прохождению электрического тока
Удельное электрическое сопротивление	ρ	ом-метр	Ом•м	Способность материала препятствовать прохождению электрического тока
Электрическая проводимость	G	сименс	См	Способность тела (среды) проводить электрический ток
Магнитная индукция	B	тесла	Тл	Векторная величина, являющаяся силовой характеристикой магнитного поля	Векторная величина
Магнитный поток	Ф	вебер	Вб = (кг/(с2·А))	Величина, учитывающая интенсивность магнитного поля и занимаемую им область.
Напряженность магнитного поля	H	ампер на метр	А/м	Разность вектора магнитной индукции B и вектора намагниченности M	Векторная величина
Магнитный момент	pm	ампер-квадратный метр	А•м2	Величина, характеризующая магнитные свойства вещества
Намагниченность	J	ампер на метр	А/м	Величина, характеризующая магнитное состояние макроскопического физического тела.	векторная величина
Индуктивность	L	генри	Гн	Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком
Электромагнитная энергия	N	джоуль	Дж = (кг·м2/с2)	Энергия, заключенная в электромагнитном поле
Объемная плотность энергии	w	джоуль на кубический метр	Дж/м3	Энергия электрического поля конденсатора
Активная мощность	P	ватт	Вт	Мощность в цепи переменного тока
Реактивная мощность	Q	вар	вар	Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока
Полная мощность	S	ватт-ампер	Вт•А	Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической

Постоянная Больцмана — Википедия

Материал из Википедии — свободной энциклопедии

Значения постоянной Больцмана в разных единицах

Численное значение	Единица
1,380 649⋅10−23	Дж·К−1[1]
1,380 649⋅10−16	эрг·К−1
8,617 333 262… ⋅10−5	эВ·К−1[2]

Постоя́нная Бо́льцмана (k{\displaystyle k} или kB{\displaystyle k_{\rm {B}}}) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её значение в Международной системе единиц СИ согласно изменениям определений основных единиц СИ точно равно

k=1,380649×10−23{\displaystyle k=1{,}380\,649\times 10^{-23}} Дж/К.

В системе единиц Планка постоянная Больцмана выбрана в качестве одной из основных единиц системы^[3].

Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, R=kNA{\displaystyle R=kN_{\mathrm {A} }}. Газовая постоянная более удобна, когда число частиц задано в молях.

В однородном идеальном газе, находящемся при абсолютной температуре T{\displaystyle T}, энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, kT/2{\displaystyle kT/2}. При комнатной температуре (300 К) эта энергия составляет 2,07×10−21{\displaystyle 2{,}07\times 10^{-21}} Дж, или 0,025851 эВ. В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 32kT{\displaystyle {\frac {3}{2}}kT}.

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона. В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы — 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Энтропия термодинамической системы определяется как величина, пропорциональная натуральному логарифму от числа различных микросостояний Z{\displaystyle Z}, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

S=kln⁡Z.{\displaystyle S=k\ln Z.}

Коэффициент пропорциональности k{\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими (Z{\displaystyle Z}) и макроскопическими состояниями (S{\displaystyle S}), выражает центральную идею статистической механики.

XXIV Генеральная конференция по мерам и весам, состоявшаяся 17—21 октября 2011 года, приняла резолюцию^[4], в которой, в частности, было предложено будущую ревизию Международной системы единиц произвести так, чтобы зафиксировать значение постоянной Больцмана, после чего она будет считаться определённой точно. В результате должно было выполняться точное равенство k = 1,380 6X⋅10⁻²³ Дж/К, где Х заменяет одну или более значащих цифр, которые должны были быть определены в дальнейшем на основании наиболее точных рекомендаций CODATA. Такая фиксация была связана со стремлением переопределить единицу термодинамической температуры кельвин, связав его величину со значением постоянной Больцмана.

Фи — Википедия

Материал из Википедии — свободной энциклопедии

Символы со сходным начертанием: ɸ · Ф · ф · ȹ ·  ·  · Փ · ቀ · Ⴔ

Буква греческого алфавита фи
Φφϕ
Изображения
	Φ: greek capital letter phi φ: greek small letter phi ϕ: greek phi symbol
Юникод	Φ: U+03A6 φ: U+03C6 ϕ: U+03D5
HTML-код	Φ‎:  или  φ‎:  или  ϕ‎:  или
UTF-16	Φ‎: 0x3A6 φ‎: 0x3C6 ϕ‎: 0x3D5
	Φ: %CE%A6 φ: %CF%86 ϕ: %CF%95
Мнемоника	Φ: Φ φ: φ

Φ, φ (название: фи, греч. φι, др.-греч. φῖ) — 21-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 500. От буквы фи произошла кириллическая буква Ф.

У строчной буквы начертание двоякое^[1]: φ и ϕ; орфографического значения различие не несёт (определяется, как правило, типом шрифта, так же, как варианты начертания букв эпсилон и каппа).

В древнейших вариантах греческого алфавита буква фи отсутствовала. В отличие от большинства других греческих букв, которые происходят от финикийских, φ не имеет финикийского прообраза, и её происхождение неясно.

В современном греческом языке буква φ обозначает глухой губно-зубной фрикатив^[en], [f]. В древнегреческом обозначала звук [pʰ], глухой билабиальный смычный согласный с придыханием, образовавшийся в протогреческом в результате оглушения придыхательных из [bʰ]; латинским алфавитом часто передаётся сочетанием «ph».

Прописная Φ[править | править код]

Строчная φ[править | править код]

• в географии, картографии, навигации — широта.

• в физике — угол поворота.

В Юникоде представлено несколько форм буквы фи:

В некоторых старых шрифтах, не совместимых со спецификацией Unicode 3.0 1998 года, символ U+03D5 (greek phi symbol) мог быть представлен «петлеобразным» символом φ{\displaystyle \varphi }^[2]. Это более не считается корректным. Символ U+03C6 (greek small letter phi) может быть представлен и «перечеркнутым» вариантом ϕ{\displaystyle \phi }, но предпочтительно — «петлеобразным» вариантом φ{\displaystyle \varphi }^[2].

HTML-мнемоники для прописной и строчной фи — это Φ и φ (Φ и φ, соответственно).

В LaTeX имеются математические символы \Phi, \phi и \varphi (Φ{\displaystyle \Phi }, ϕ{\displaystyle \phi } и φ{\displaystyle \varphi }, соответственно).

Формулы по физике

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t

Ускорение a=(υ—υ ₀)/t

Скорость при движении по окружности υ=2πR/Т

Центростремительное ускорение a=υ²/R

Связь периода с частотой ν=1/T=ω/2π

II закон Ньютона F=ma

Закон Гука Fy=-kx

Закон Всемирного тяготения F=G∙M∙m/R²

Вес тела, движущегося с ускорением а↑ Р=m(g+a)

Вес тела, движущегося с ускорением а↓ Р=m(g-a)

Сила трения Fтр=µN

Импульс тела p=mυ

Импульс силы Ft=∆p

Момент силы M=F∙ℓ

Потенциальная энергия тела, поднятого над землей Eп=mgh

Потенциальная энергия упруго деформированного тела Eп=kx²/2

Кинетическая энергия тела Ek=mυ²/2

Работа A=F∙S∙cosα

Мощность N=A/t=F∙υ

Коэффициент полезного действия η=Aп/Аз

Период колебаний математического маятника T=2π√ℓ/g

Период колебаний пружинного маятника T=2 π √m/k

Уравнение гармонических колебаний Х=Хmax∙cos ωt

Связь длины волны, ее скорости и периода λ= υТ

Количество вещества ν=N/ Na

Молярная масса М=m/ν

Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT

Основное уравнение МКТ P=nkT=1/3nm₀υ²

Закон Гей – Люссака (изобарный процесс) V/T =const

Закон Шарля (изохорный процесс) P/T =const

Относительная влажность φ=P/P₀∙100%

Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT

Работа газа A=P∙ΔV

Закон Бойля – Мариотта (изотермический процесс) PV=const

Количество теплоты при нагревании Q=Cm(T₂-T₁)

Количество теплоты при плавлении Q=λm

Количество теплоты при парообразовании Q=Lm

Количество теплоты при сгорании топлива Q=qm

Уравнение состояния идеального газа PV=m/M∙RT

Первый закон термодинамики ΔU=A+Q

КПД тепловых двигателей η= (Q₁ — Q₂)/ Q₁

КПД идеал. двигателей (цикл Карно) η= (Т₁ — Т₂)/ Т₁

Закон Кулона F=k∙q₁∙q₂/R²

Напряженность электрического поля E=F/q

Напряженность эл. поля точечного заряда E=k∙q/R²

Поверхностная плотность зарядов σ = q/S

Напряженность эл. поля бесконечной плоскости E=2πkσ

Диэлектрическая проницаемость ε=E₀/E

Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R

Потенциал φ=W/q

Потенциал точечного заряда φ=k∙q/R

Напряжение U=A/q

Для однородного электрического поля U=E∙d

Электроемкость C=q/U

Электроемкость плоского конденсатора C=S∙ε∙ε₀/d

Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2

Сила тока I=q/t

Сопротивление проводника R=ρ∙ℓ/S

Закон Ома для участка цепи I=U/R

Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R

Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R

Мощность электрического тока P=I∙U

Закон Джоуля-Ленца Q=I²Rt

Закон Ома для полной цепи I=ε/(R+r)

Ток короткого замыкания (R=0) I=ε/r

Вектор магнитной индукции B=Fmax/ℓ∙I

Сила Ампера Fa=IBℓsin α

Сила Лоренца Fл=Bqυsin α

Магнитный поток Ф=BSсos α Ф=LI

Закон электромагнитной индукции Ei=ΔФ/Δt

ЭДС индукции в движ проводнике Ei=Вℓυsinα

ЭДС самоиндукции Esi=-L∙ΔI/Δt

Энергия магнитного поля катушки Wм=LI²/2

Период колебаний кол. контура T=2π ∙√LC

Индуктивное сопротивление X_L=ωL=2πLν

Емкостное сопротивление Xc=1/ωC

Действующее значение силы тока Iд=Imax/√2,

Действующее значение напряжения Uд=Umax/√2

Полное сопротивление Z=√(Xc-X_L)²+R²

Эта — Википедия

Материал из Википедии — свободной энциклопедии

О баскской сепаратистской организации см. ЭТА. У этого термина существуют и другие значения, см. ETA. Буквы со сходным начертанием: H · Н · н · ዘ · ਮ Символы со сходным начертанием: ɳ · ŋ · Ƞ · ƞ · դ · ղ · ⴂ

Буква греческого алфавита эта
Ηη
Изображение
	Η: greek capital letter eta η: greek small letter eta
Юникод	Η: U+0397 η: U+03B7
HTML-код	Η‎:  или  η‎:  или
UTF-16	Η‎: 0x397 η‎: 0x3B7
	Η: %CE%97 η: %CE%B7
Мнемоника	Η: Η η: η

Η, η (название: э́та, греч. ήτα, др.-греч. ἦτα) — 7-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 8. Происходит от финикийской буквы 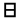 — хет. От буквы эта произошли латинская буква H и кириллическая И c Й. Новогреческое название — и́та (ήτα).

В современном греческом языке (новогреческий язык) эта буква произносится как закрытый передний гласный [i] и называется и́та. В древнегреческом языке она произносилась как долгий полуоткрытый передний гласный [ɛː]. Первоначально знак Η использовался для обозначения придыхания — глухого гортанного фрикатива [h]. В ионическом диалекте, где этот звук исчез к VI веку до н. э., буква стала использоваться для обозначения долгого [ɛː]. Когда ионический алфавит был принят в 403 до н. э. в Афинах, [ɛː] (ранее записывавшийся как Ε) стал также изображаться и как Η, отсюда современное использование^{[источник не указан 3106 дней]}.

В старославянской азбуке этой букве соответствовала буква «иже» («и восьмеричное»), в отличие от «і» («и десятеричного»), которой соответствовала греческая буква йота. Таким образом, с самого начала в кириллице было принято «новогреческое» произношение. В эпоху Возрождения в Европе два типа чтения буквы «эта» в древнегреческих текстах стали называться «рейхлиновым» ([i]) и «эразмовым» ([ɛː]) по именам известных современников, являвшихся сторонниками соответствующего типа чтения: Иоганна Рейхлина и Эразма Роттердамского^[1]:48.

Прописная Η[править | править код]

Строчная η[править | править код]

1. ↑ Иванова В.Ф. Кириллица и её постепенное изменение // Современный русский язык. Графика и орфография. — 2-е изд. — М.: Просвещение, 1976. — С. 43—51. — 288 с.