Проценты и пропорции
Напомним, что частное двух чисел называется отношением этих чисел. Равенство двух отношений называется пропорцией.
или 
, где 
и 
.
Числа
и 
называют крайними
членами пропорции, числа 
– средними
членами пропорции.Вспомним свойства пропорции.
1. Произведение крайних членов пропорции равно произведению средних:
если
, то 
.
2.
В пропорции, все члены которой не равны нулю, можно менять местами средние и
крайние члены, то есть если верна пропорция , то верными будут
и пропорции:
, 
.3.
Если произведение чисел 
и 
равно
произведению чисел 
и 
, причём 
,
, , то из этих чисел
можно составить пропорцию: .
Переменная
называется прямо
пропорциональной переменной 
, если 
, где 
.Зависимость,
выраженная формулой , где , называется прямой
пропорциональностью, а – коэффициентом
пропорциональности.
Прямая
пропорциональность переменных означает, что их отношение постоянно, то есть
зависимость между ними при 
выражена формулой:
Пусть
переменные и прямо
пропорциональны и пусть значениям 
и 
соответствуют
значения 
и 
.
Тогда,
если 
.Переменная
называется обратно
пропорциональной переменной , если 
, где – постоянная и .
Зависимость,
выраженная формулой
, называется обратной
пропорциональностью, а постоянная – коэффициентом
обратной пропорциональности.Обратная
пропорциональность переменных и означает, что их
произведение постоянно и не равно нулю, то есть зависимость между ними выражена
формулой:
.
Пусть
переменные
обратно
пропорциональные и пусть для значений и соответствующие
значения равны и .Тогда
для них верно равенство и
, или 
Также
напомним, что процентом числа называется его
сотая часть. Следовательно, само число составляет 
.
При
решении задач на проценты некоторая величина принимается за , а её часть –
величина – принимается за 
.
Из
этой пропорции определяют величину по
правилу нахождения неизвестного члена пропорции:
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание
первое. Найдите из пропорции 
.
Решение.
Задание второе. Разделите число 286 на части прямо пропорционально числам 2, 3, 8.
Решение.
Задание третье. Разделите число 286 на части обратно пропорционально числам 1, 2 и 3.
Решение.
Задание
четвёртое. Виноград содержит 
воды, а
полученный из него изюм содержит 
воды. Сколько
изюма получится из 
кг винограда?
Решение.
Задание
пятое. В парке 72 дерева – берёзы и клёны. Берёзы
составляют 
всех деревьев.
Сколько берёз надо ещё посадить в парке, чтобы они составляли 
всех деревьев?
Решение.
Задание шестое. Завод выпускал 852 изделия в месяц. В результате технического перевооружения он стал выпускать 1136 изделий в месяц. На сколько процентов увеличилась производительность завода?
Решение.
Задание
седьмое. В результате увеличения производительности труда на 
завод стал
выпускать 920 изделий в месяц. Сколько изделий в месяц выпускал завод ранее?
Решение.
Задание
восьмое. Завод выпускает 500 изделий в год. На сколько
изделий в год увеличится выпуск продукции, если производительность труда
увеличится на ?
Решение.
Задание
девятое. Цену товара сначала повысили на 
, а затем понизили
на столько же процентов. На сколько процентов уменьшилась первоначальная цена?
Решение.
videouroki.net
стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x. Получаем:
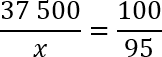
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
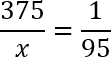
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
x = 375 · 95
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
x = 35 625
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
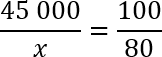
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
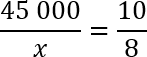
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x:
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
x = 4500 · 8
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Смотрите также:
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
- Задачи на проценты: считаем проценты с помощью пропорции
- Как решать квадратные уравнения
- Пробный ЕГЭ 2012. Вариант 11 (без логарифмов)
- Пробный ЕГЭ по математике 2015: 3 вариант
- Проценты в задачах на наибольшее-наименьшее значение используем пропорции
www.berdov.com
Зачёт по теме «Пропорции и проценты» Вариант 1 1. Выберите правильное определение: Пропорция — это… 2. Основное свойство пропорции: 3. Что называют процентом? 4. Как процент от числа? 5. Как называются числа a и b в пропорции x:a=b:y 6. Как перевести проценты в десятичную дробь? 7. Как найти неизвестный крайний член пропорции ? 8. Какие величины называют прямо пропорциональными? 9. Как узнать, сколько процентов одно число составляет от другого ? 10. Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? | Зачёт по теме «Пропорции и проценты» Вариант 2 1. Отношение двух чисел не изменится, если… 2. Чтобы найти неизвестный крайний член пропорции, нужно… А) произведение ее средних членов разделить на известный крайний; 3. Запишите определение отношения двух чисел. 4. Как называются числа x и y в пропорции x:a=b:y. 5. Как найти число по величине процента? 6. Какие величины называют обратно пропорциональными? 7. Как перевести десятичную дробь в проценты? 8. Как найти неизвестный средний член пропорции? 9. Какие член пропорций можно менять местами, чтобы получились новые верные пропорции? 10. Чему равен масштаб чертежа, если на нем детали уменьшена в 50 раз? |
infourok.ru
Отношение. Проценты. Пропорции — Мегаобучалка
Отношением числа x к числу y называется частное чисел x и y, то есть или х : у. Отношение означает во сколько раз x больше y, или какую часть числа y составляет число x.
Пропорцией называется равенство двух отношений, то есть .
а и y называются крайними членами, x и b называются средними членами пропорции.
Свойства пропорции.
· произведение крайних членов пропорции равно произведению её средних членов, то есть если , то .
· обратно: числа a,b,x,y составляют пропорцию , если .
· из пропорции вытекают пропорции , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
· чтобы найти неизвестный средний (крайний) член пропорции, надо произведение крайних (средних) членов разделить на известный средний (крайний) член пропорции
;
.
Процентом называется сотая часть какого-либо числа. Процент обозначается знаком % .
Чтобы число процентов выразить в виде дроби, достаточно число процентов разделить на сто.
Например: 125%=1,25; 2,3%=0,023.
Нахождение процентов данного числа. Чтобы найти а% от числа b, надо b умножить на а и разделить на 100.
Например: 30% от 60 составляют .
Нахождение числа по его процентам. Чтобы найти процентное отношение двух чисел a и b, надо отношение чисел умножить на 100%, то есть .
Например: при плановом задании 60 автомобилей в день завод выпускает 66 автомобилей. На сколько процентов выполнен план?
Решение: .
Целые числа
Два числа, отличающиеся друг от друга только знаком, называются противоположными числами: 1 и -1, 2 и -2, 15 и -15,…
Числа натуральные, им противоположные, а так же число нуль составляют множество целых чисел Z.
Множество натуральных чисел, дополненное нулем, называется множеством целых неотрицательных чисел.
Для целых чисел определены действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, причем сложение, вычитание и умножение выполняются всегда.
Рациональные числа
Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел Q. Любое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
На множестве рациональных чисел можно производить действия сложения, вычитания, умножения, деления (кроме деления на нуль).
Иррациональные числа
Иррациональным числом называют бесконечную десятичную непериодическую дробь. Множество таких дробей составляет множество иррациональных чисел I.
Например: 0,131331333125…;
π ≈ 3,14;
e ≈ 2,7;
и т.д.
Действительные числа
Объединение множества рациональных чисел и множества иррациональных чисел даёт множество действительных чисел, которое обозначается R.
megaobuchalka.ru
Онлайн урок проценты и пропорции.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
Дробь или обыкновенная дробь — это число вида m/n , где m — целое число, а n — натуральное число.
Любая обыкновенная дробь — это частное ее числителя и знаменателя. Разделив числитель на знаменатель, если такое деление возможно, мы получим запись обыкновенной дроби в виде десятичной.
Теперь выбери соответствия между картинками и определениями, которые мы только что повторили.
534 · 47674767 =534534 · 4767/4767 = 2 545 578/4767 = 4767
44/100 = 4,444/100 = 0,4444/100 = 22/50 = 11/25
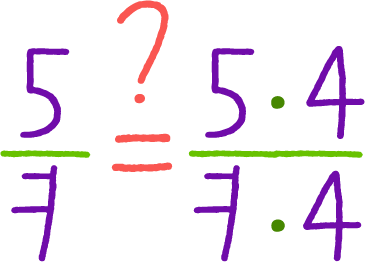
Эти дроби не равны.Эти дроби равны по основному свойству дроби: при умножении числителя и знаменателя дроби на одно и тоже число получаем дробь равную исходной.Эти дроби равны по основному свойству дроби: при умножении числителя и знаменателя дроби на одно и тоже число, отличное от нуля, получаем дробь равную исходной.
12/7 : 7/4 = 12 · 7/7 · 7 = 312/7 : 7/4 = 12 · 4/7 · 7
Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Проценты.
2. Пропорции.
myalfaschool.ru
Проценты | Формулы с примерами
Правила нахождения процентов
Формула
Свойства
Свойство 1
Свойство| Нахождение p% от числа a: умножить a на | p | ; |
| 100 |
23% от 53 равны 53 • 0,23 = 12,19;
131% от 19 равны 19 • 1,31 = 24,89;
Свойство 2
Свойство| Нахождение числа a, если его p% равны b: разделить b на | p | ; |
| 100 |
| Найти число, 16% которого равны 70: a = | 70 | = 437,5 = | 1 | ; |
| 0,16 | 5 |
| Найти число 175% которого равны 90: a = | 90 | = 51 | 1 | ; |
| 1,75 | 4 |
| Найти число 250% которого равны 100: a = | 100 | = 0,4. |
| 2,5 |
Свойство 3
Свойство Выражение в процентах частного двух чисел a и b (дроби): Пример| 15 : 20 = | 15 | • 100% = 75%. |
| 20 |
Свойство 4
Свойство Сколько процентов составляет число a от числа b: разделить a на b,полученную дробь записать в процентах: Пример Сколько процентов составляет число 30 от 60?
Процентное соотношение
Определение
Процентное соотношение представляет какую-либо часть от единицы
как часть от 100. Обозначение процентов: %.
1% = 1/100, одна сотая часть величины.
100% — это единица, или некоторое количество целиком.
50% = 50/100, т.е. половина от целого.
formula-xyz.ru
Урок математики «Решение задач на проценты и пропорции»
Министерство образования и науки
Краснодарского края
Государственное бюджетное профессиональное
образовательное учреждение
Краснодарского края
«Апшеронский техникум автомобильного транспорта и сервиса»
Методическая разработка
открытого урока по профессии «повар-кондитер»
по математике на тему:
«Решение задач на проценты и пропорции».
по калькуляции и учету на тему:
« Расчет норм закладки продуктов, используемых
для приготовления различных блюд в их различных вариантах (по категориям)».
Преподаватель:
Новичкова Н.И.
г. Апшеронск
Тема урока: «Лабораторно-практическая работа. Решение задач на пропорции и проценты.
Расчет норм закладки продуктов, используемых
для приготовления различных блюд в их различных вариантах (по категориям)».
Цель урока: образовательная – повторить понятия процента и пропорции, закрепить умножение десятичной дроби на натуральное число;
воспитательная — показать необходимость математических знаний в профессиональной деятельности;
развивающая-, развивать навыки вычислительной культуры учащихся.
Наглядные пособия к уроку: карточки устного счета, таблицы- плакаты, технологические карты, энциклопедический словарь юного математик, интерактивная доска, презентации..
.
Ход урока
1.Оргмомент. Организация учебного процесса, сообщение темы и цели урока. Цель нашего урока: показать, как математические знания применяются в профессии повар-кондитер. Одно из удовольствий человека – это вкусная еда, а для того чтобы ее приготовить, необходимо очень много знать и уметь. В первую очередь, необходимо уметь рассчитать расход продуктов при приготовлении блюд, а также уметь вычислять процент отходов при обработке продуктов, вести хозяйственный расчет, начислять заработную плату, делать калькуляцию блюд, для этого нужны такие математические понятие как проценты и порции, вычислительные навыки.
2. Устно: (карточки устного счета)
А | В | С | D | Е | |
1 | 0,7 | 1,3 | 1 2 | —3 4 | 7 12 |
2 | -0,4 | -3,2 | 2 3 | —4 5 | 3 1 20 |
3 | 1,5 | -4 | 5 4 | —2 3 | 11 20 |
4 | 0 | 2,5 | 4 5 | 1 -1 4 | 10 3 |
5 | -2 | 40 | 1 20 | —10 9 | 24 25 |
Вычислить: А1+ В1; А3+В3;
Б3 х В4; А2-С5;
А3+В4; Д2 х С3;
А3-В1; В5 х А5;
Д3+ С2; В3 х В2.
3. Историческая справка
(Энциклопедический словарь юного математика, показ слайда 1).
Проценты: (ученик)
Процентом называется сотая доля числа. Для чего нужны проценты и почему для этого введен специальный термин?
Прежде чем ответить на эти вопросы, попробуем ответить на другой: много ли соли в морской воде? Конечно, можно налить в ведро морскую воду, поставить его на огонь, и подождав, пока вся вода испарится, собрать и взвесить оставшуюся соль. Можно ли утверждать, что у другого человека получится столько же? Видимо, нет. Его ведро может оказаться больше или меньше, оно может быть налито более или менее полно; в результате, получится другое количество соли. Таким образом, наша мера солености морской воды оказалось неудачной. Возьмем другую меру – количество граммов соли на 1 кг раствора. Для этого нужно до кипячения взвесить раствор, а потом массу полученной соли разделить на массу раствора. Пусть масса раствора 8,4 кг, а масса соли 21 г. Тогда получаем ответ: 2,5 г соли на 1 кг раствора. Если опыт повторить, то получится почти такая же величина.
Проценты были известны индийцам еще в V веке. Это закономерно, так как в Индии с давних пор счет велся в десятичной системе счисления. В Европе десятичные дроби появились на тысячу лет позже, их ввел бельгийский ученый С. Стевин. В 1584 г. он впервые опубликовал таблицу процентов.
Введение процентов оказалось удобным не только для оценки содержания одного вещества в другом. В процентах стали измерять изменение производства товара, рост денежного дохода.
Со временем люди научились извлекать из вещества его компоненты, составляющие тысячные доли от массы самого вещества.
Пропорция (ученик)
Пропорцией называют равенство отношений двух или нескольких пар чисел или величин. Например, размеры модели машины или сооружения отличаются от размеров оригинала одним и тем же множителем, задающим масштаб модели.
Систематически пропорции начали изучать в Древней Греции. Сначала рассматривали лишь пропорции, составленные из натуральных чисел, и поэтому считали, что числа а, b, с,d образуют пропорцию. В этот период не различали пропорции, составленные из чисел. В IV веке до н.э. древнегреческий математик Евдокс дал определение пропорции, составленной из величин любой природы.
Древнегреческие математики превратили пропорции в весьма гибкий аппарат исследования. С их помощью решали задачи, которые в наши дни решают с помощью уравнений.
Роль теории пропорций заметно уменьшилась после того, как было осознано, что отношение величин является числом, а потому пропорция – это просто равенство чисел.
4. Повторение изученного материала
Учитель: «Итак, пропорция – это равенство двух отношений чисел». (Плакат на доске)
Крайние члены
8,6 : 2 = 17,2 : 4
Средние члены
Основное свойство пропорции: произведение крайних равно произведению средних, проверим это:
8,6 х 4 = 17,2 х 2
34,4 = 34,4
Решим пропорцию:
2,8: х = 5,6 : 4
Найдем х,
5,6 х х = 2,8 х 4
5,6 х = 11,2
х = 2
При расчете расхода продуктов для приготовления блюд нужно помнить, что и уметь переводить граммы в
1 кг = 1000г 1г = 0.001 кг 10 г =0,01 кг 100 = 0,1 кг |
Например: 350 г = 0,350 кг
18 г = 0,018 кг
5 г = 0,005 кг
750 г = 0,75 кг
5. Решение задач.
При решении задач на проценты очень важно правильно найти начальное число, от которого исчисляются проценты.
В тех случаях, когда в условиях задачи прямо не сказано, относительно какого числа следует вычислять проценты, его следует определить по содержанию задачи. Например, отходы при холодной обработке сырья, как правило, устанавливаются в процентах от массы брутто, и, следовательно, в этих случаях масса брутто является начальным числом.
Потери при тепловой обработке чаще всего устанавливаются от массы нетто, так как они получаются при варке или жарении продуктов, уже прошедших первичную обработку, здесь начальным числом следует считать массу нетто. (Показ слайда 2-8, запись в тетрадь)
Решение задач у доски.
Задача 1. Для приготовления блюда выделено 300 кг неочищенного картофеля (масса брутто). Определить массу отходов при его первичной обработке, если норма отходов установлена в 40% от массы брутто.
Решение
Данное в задаче число 300 кг является начальным, так как в процентах от него дается норма отходов. Оно содержит 100% масса отходов искомое число. Оно содержит 40%.
Данное число 300кг содержит 100%.
Искомое число X кг 40%
Составляем пропорцию:
300: 100=Х:40
Х=300х40 =120кг
100
Ответ: масса отходов 120кг.
Задача 2. Для приготовления блюд нужно израсходовать 180 кг очищенного картофеля (масса нетто). Сколько неочищенного картофеля (масса брутто) следует взять, если отходы при холодной обработке составляют 40% от массы брутто.
Решение
Начальным числом является масса брутто. Это искомое число. Оно содержит 100%. Данное число 180кг содержит 100%-40%=60% (так как масса нетто равна массе брутто за вычетом массы отходов)
180кг содержит 60%
Х кг 100%
Составляем пропорцию:
180 : 60 = Х : 100
Х = 180х100 =300кг
60
Ответ: масса брутто равна 300 кг
Задача 3. Масса картофеля (брутто) 300кг. Масса отходов при его обработке 120кг. Определите процент отходов.
Решение
Начальное число 300 кг, следует найти процент отходов, т.е. массу 120 кг выразить в %
300 кг – 100%
120 кг – х %
Решим пропорцию х = 120 кг х 100% = 40%
300 кг
Ответ: масса отходов соответствует 40 %
6. Самостоятельная работа
I Вариант
1. Взято для очистки 80 кг картофеля определите, каким должна быть масса отходов, если норма отходов установлена 30 % от массы брутто.
2. Масса очищенного картофеля 56 кг (масса нетто). Сколько было израсходовано неочищенного картофеля, если норма отходов 30 %?
3. При разделке свинины мясной выход составляет 86% отходы 13,5 кг. Определите массу отходов.
II Вариант
1. Взято для очистки 80 кг картофеля. Определите процент отходов при холодной обработке, если их масса 24 кг.
2. Масса разделанной говядины
180 кг. Сколько было израсходовано говядины (массой брутто), если норма отходов составляет 26%
3. Определить массу отходов, если переработали 120 кг моркови, отходы составляют 30 %.
7. Повторение.
При расчете количества продуктов на порцию блюда необходимо повторить умножение десятичной дроби на натуральное число.
Например:
Чтобы умножить десятичную дробь на натуральное число, нужно перемножить числа, не обращая внимание на запятую, затем в результате отделить запятой столько знаков, сколько их в десятичной дроби.
На примере одной технологической карты показать:
1) как рассчитать процент отходов
2) норму продуктов на 120 порций
3) цену одной порции.
8.Практическая работа
(Каждому ученику выдается технологическая карта из сборника рецептур).
Задание:
1. Рассчитать процент отхода каждого продукта
2. Рассчитать норму продуктов блюда на 120 порций (масса брутто)
3. Рассчитать цену 1 порции.
9. Итог урока. Подведение итогов, оценивание работ учащихся (показ слайда 9)
10.Литература:
1. Т.И. Перепятков «Калькуляция и учет» с.25-27
2. Энциклопедический словарь юного математика, — М., 1999.
3. Учебник, Математика 6/ под ред. Виленкина Н., М., 2009.
4. Сборник рецептур. Просвещение, 1990.
5. Дидактические материалы по математике, Просвещение, 2010.
Технологическая карта из сборника рецептур
88. Кекс «Весенний» (458)
Масса 100г
Наименование сырья | Массовая доля сухих веществ % | Расход сырья на 100 шт. готовых изделий г. | |
в натуре | в сухих веществах | ||
Мука пшеничная высшего сорта | 85,50 | 5592,0 | 4781,2 |
Сахар песок | 99,85 | 1594,0 | 1591,6 |
Масло сливочное | 84,00 | 1230,0 | 1033,2 |
Меланж | 27,00 | 1118,0 | 301,9 |
Дрожжи прессованные | 25,00 | 224,0 | 56,0 |
Соль | 96,50 | 16,8 | 16,2 |
Изюм | 80,00 | 559,0 | 447,2 |
Цукаты | 83,00 | 280,0 | 232,4 |
Ядра орехов сырые для обсыпки | 94,00 | 112,0 | 105,3 |
Пудра ванильная | 99,85 | 37,7 | 37,6 |
Пудра рафинадная | 99,85 | 112,0 | 11,8 |
8
videouroki.net