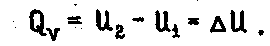лекция К

2. термохимия

Любая хим. реакция сопровождается поглощением или выделением теплоты — тепловым эффектом. Раздел ФХ, изучающий тепловые эффекты химических реакций называется ТЕРМОХИМИЕЙ. Термохимическими называют такие уравнения химической реакции, в которых наряду с формулами веществ, участвующих в реакции, указывается и тепловой эффект реакции

Пример Реакцию спиртового брожения глюкозы можно представить как:

С₆Н₁₂О₆→2С₂Н₅ОН+2СО₂; ΔН= -71,56 кДж/моль

где ΔН — тепловой эффект реакции в изобарно-изотермических условиях.

Тепловым эффектом хим. реакции называется теплота, выделяющаяся или поглощающаяся при реакции, если в системе: не совершается полезная работа, неизменны давление или объем системы, постоянство температуры до и после реакции, или иными словами реакция должна протекать в изобарно-изотермических или изохорно-изотермических условиях. Тепловой эффект обозначается как Q и измеряется в Дж/кмоль. Теплота экзотермических реакций считается положительной

(ΔH < 0 и ΔU < 0)., а эндотермических — отрицательной (ΔH > 0, ΔU > 0).

Закон Гесса

Определить тепловой эффект можно по закону Гесса, который формулируется как: при p=const или V=const тепловой эффект химической реакции зависит только от вида и состояния исходных веществ и продуктов реакции, но не зависит о пути перехода

Закон Гесса можно проиллюстрировать. Через и 2 обозначим исходное (до реакции) и конечное состояние (после реакции) системы. Процесс превращения исходных веществ в продукты можно осуществить: 1) непосредственно реакцией, тепловой эффект которой обозначим как

или 2) тремя реакциями, тепловые эффекты которых равны соответственно , , . Закон Гесса утверждает, что =+ +

Рассмотрим процесс горения углерода, его можно провести непосредственно или через две стадии:

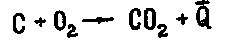2.1.1

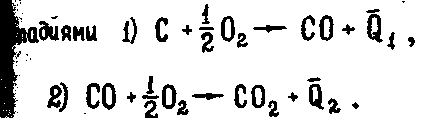2.1.2 и 2.1.3

Просуммировав (2.1.2) и (2.1.3), получим:

2.1.4

Из сопоставления (2.1.1) и (2.1.4) видно, что

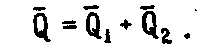2.1.5

Закон Гесса можно сформулировать по-иному: тепловой эффект реакции не зависит от пути процесса, а зависит от начального и конечного состояния системы. Из этой формулировки следует, что тепловой эффект реакции есть функция состояния, что противоречит первому закону термодинамики. Это объясняется тем, что закон Гесса справедлив только для частных случаев: для процессов, протекающих при постоянном объеме или давлении. Для этих процессов он легко выводится из первого закона термодинамики

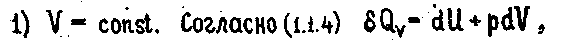
так как рdV=0, то δQv=dU откуда, проинтегрировав в пределах двух состояний, получим

2.1.6

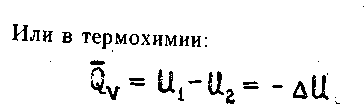2.1.7

Поскольку внутренняя энергия системы является функцией состояния, то и тепловой эффект реакции, протекающей при постоянном объеме, есть функция состояния.

Выражение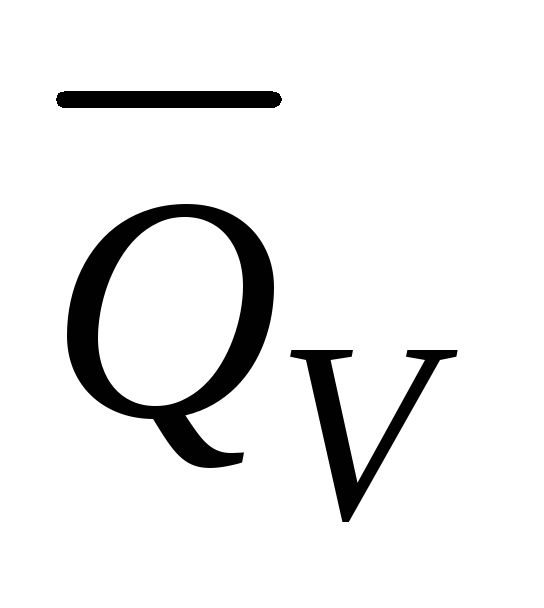

=-ΔU показывает, что причиной выделения теплоты при протекании химической реакции при V= соnst; является убыль внутренней энергии.

2) р = соnst

Выражение проинтегрируем в пределах двух состояний

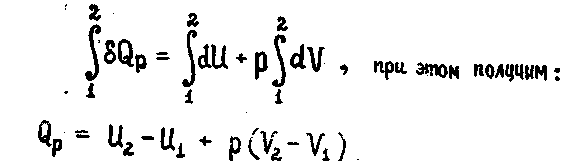2.1.8

Перейдем к термохимическим значениям

2.1.9 и 2.1.10

Сгруппируем члены относительно начального и конечного состояния системы

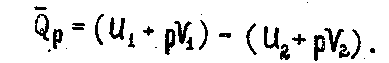2.1.11

Для расчета Qр надо знать, как измеряется функция U+pV. Эта функция называется энтальпией и обозначается буквой Н.

Термодинамическая теплота равна изменению энтальпии

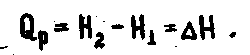2.1.12

Поскольку внутренняя энергия является функцией состояния, объем не зависит от пути процесса, а давление постоянное, то энтальпия также является функцией состояния и, следовательно, не зависит от пути процесса. Выражение Qp=-ΔН показывает, что причиной выделения теплоты при протекании реакции при постоянном давлении является убыль энтальпии системы.

Определение тепловых эффектов по теплоте образования, сгорания.

Расчет тепловых эффектов

Для определения теплового эффекта в термохимических уравнениях пользуются следствиями из закона Гесса. Таких следствий два.

1) Первое следствие формулируется как:

тепловой эффект хим. реакции равен разности теплоты образования продуктов реакции и теплоты образования исходных веществ, взятых в стехиометрических коэффициентах

Теплота образования — это кол-во теплоты, которое выделяется или поглощается при образовании одного киломоля соединения из составляющих его простых веществ.

Теплоты образования позволяют рассчитывать тепловой эффект реакции, не осуществляя опытов. В целях сопоставления и использования для расчетов, теплоты образования хим. соединений вычислены для стандартных условий (Т=298 К, р=1атм). Они называются стандартными теплотами образования и обозначаются ΔН°_обр или ΔН°_f,₂₉₈

Например, теплота образования хлорида натрия в станд. условиях равна тепловому эффекту реакции образования его из металлического натра и газообразного хлора, т.е.

Na+1/2Cl2→NaCl + 410,9 ΔН°_f ,₂₉₈ =-410.9 кДж

Представим это следствие в общем виде:

2.1.14

Тепловой эффект этой реакции для стандартных условий будет иметь вид

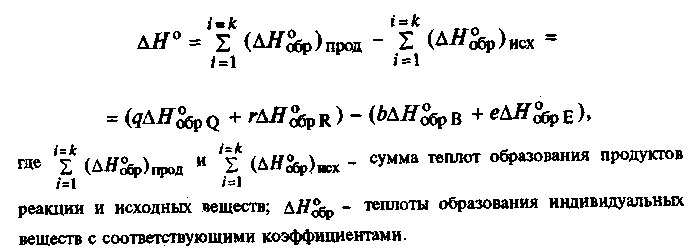2.1.15

Из равенств (2.1.14) и (2.1.15) следует, что тепловой эффект обратной реакции равен тепловому эффекту прямой реакции, взятой с противоположным знаком (в случае обратной реакции ее продукты становятся исходными веществами, а исходные вещества — продуктами реакции).

Теплота образования простых веществ, таких как Н₂, О₂ принята нулю. Значения ΔН°_f,₂₉₈ приводятся в справочных таблицах.

Например,

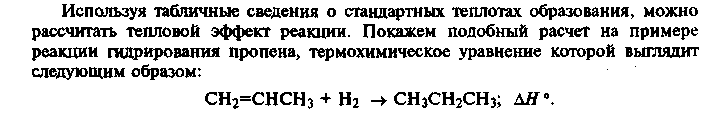
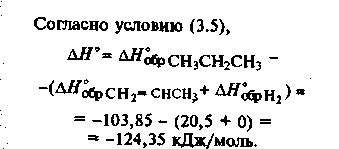
Итак, для расчетов тепловых эффектов реакции необходимо знать теплоты образования исходных веществ и продуктов реакции. Данные о теплоте образования экспериментально получают в калориметре (Зимон).

Определение тепловых эффектов по теплоте сгорания

Тепловой эффект реакции можно определить по теплоте сгорания веществ, участвующих в реакции. Для этой цели можно воспользоваться

2) вторым следствием из закона Гесса, которое формулируется следующим образом:

тепловой эффект химической реакции равен разности теплоты сгорания исходных веществ и теплоты сгорания продуктов реакции с учетом стехиометрических коэффициентов.

Теплота сгорания — это тепловой эффект реакции полного сгорания 1 моля вещ-ва при условии, что исходные вещества и продукты находятся в стандартных условиях. Обозначают ΔН°_с,₂₉₈

Аналогично уравн. 2.1.15 можно получить выражение для определения теплового эффекта реакции через теплоту сгорания:

2.1.16

Под теплотой сгорания подразумевают тепловой эффект реакции окисления данного соединения кислородом до образования высших оксидов элементов или соединений этих элементов.

Значения теплоты сгорания используют для определения тепловых эффектов реакций главным образом органических соединений. Теплота сгорания высших оксидов =0.

По известной теплоте сгорания можно определить теплоту образования. Покажем эту возможность на примере бензола, стандартная теплота сгорания которого составляет ΔН°

с,₂₉₈ = -3268 кДж/моль.

Термохимическое уравнение сгорания бензола выглядит следующим образом:

Теплоту сгорания, так же как и теплоту образования, измеряют при помощи калориметра.

Зависимость теплового эффекта реакции от температуры. Закон Кирхгофа.

Рассмотренные ранее расчеты тепловых эффектов на основе законов Гесса по теплотам образования и сгорания ограничены стандартными условиями. Для практических целей необходимо рассчитать тепловые эффекты для конкретных условий, отличных от стандартных..

Тепловые эффекты хим. реакций зависят не только от природы реагирующих веществ, но и от внешних условий, прежде всего от температуры. Зависимость тепловых эффектов от температуры можно установить термодинамически.

Ранее на основании закона Гесса, мы установили что

1. изменение теплоты при p=const выражается через изменение энтальпии .

2. тепловой эффект реакций, протекающих при V=const выражается как изменение внутренней энергии

Продифференцировав по температуре эти два уравнения, получим:

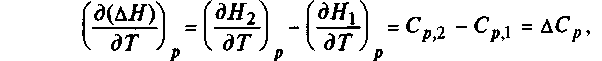2.1.17

2.1.18

где производная энтальпии по температуре — это теплоемкость при постоянном давлении, а производная внутренней энергии по температуре — теплоемкость при постоянном давлении

Уравнения (2.1.17) и (2.1.18) можно представить в несколько измененном виде:

Эта закономерность была установлена Кирхгофом. Закон Кирхгофа читается так: температурный коэффициент теплового эффекта равен приращению теплоемкости в результате протекания процесса.

Закон Кирхгофа в дифференциальной форме позволяет определить лишь изменение теплового эффекта с изменением температуры, а не величину самого теплового эффекта.

Чтобы найти значения теплового эффекта в зависимости от температуры, необходимо проинтегрировать уравнения 2.1.19 и 2.1.20 от Т до Т° (где Т и Т° — соответственно требуемая и стандартная температура), от ΔН до ΔН ° и от ΔU до ΔU° (где ΔН и ΔU — соответственно энтальпия и внутренняя энергия в условиях, отличающихся от стандартных). Интегрирование проводится для двух случаев: первого, когда ΔС_р = const и ΔС_v = const, и второго, когда ΔС_р ≠ const и ΔС_v ≠ const. После разделения переменных результаты интегрирования уравнений (2.1.19) и (2.1.20) в первом случае следующие:

2.1.21 и 2.1.22

Таким образом, для определения теплового эффекта ΔН или внутренней энергии ΔU при любой температуре Т, помимо теплоты процесса в стандартных условиях ΔН ° (или ΔU°), необходимо знать еще и изменение теплоемкости ΔС_р и ΔС_v.

Если учитывать зависимость теплоемкости от температуры (C_р = a + bT + cT²) то

2.1.23

После подставки (2.1.23) в (2.1.21, 2.1.22) и интегрирования получим расчетную формулу Кирхгофа:

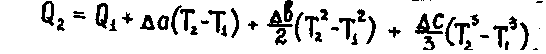2.1.24

Если бы взяли неопределенный интеграл от (2.1.21, 2.1.22), то получили бы:

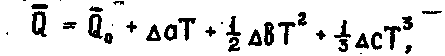2.1.25

где 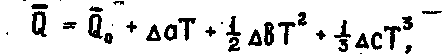— постоянная интегрирования, которую чаще всего определяют по стандартной теплоте химической реакции.

Итак закон Кирхгофа в интегральной форме дает возможность, не прибегая к эксперименту, рассчитывать тепловые эффекты при любой температуре по известному тепловому эффекту в стандартных условиях.

Понятие о теплоте сгорания — Справочник химика 21

    Еще одно важное для термохимии понятие — теплота сгорания. Теплота сгорания какого-либо вещества есть количество теплоты, которое выделяется при полном сгорании 1 моль вещества в токе кислорода. В частности, при сгорании органических веществ углерод окисляется до двуокиси углерода, водород — до воды и т. п. Например  [c.59]
    Следует четко разграничивать два различных термодинамических понятия — теплоту сгорания и энтальпию образования, хотя их численные значения в некоторых случаях могут совпадать так, например, стандартные теплоты сгорания углерода и водорода совпадают со стандартными теплотами образования СО2 и Н2О. Совпадение теплоты сгорания с теплотой образования вещества наблюдается в тех случаях, когда вещество представляет собой продукт сгорания входящих в него элементов, взятых в стандартных состояниях. [c.311]

    Закон Гесса и его следствия не могут быть использованы для расчета тепловых эффектов процессов, если мы не условимся, какой смысл вкладывать в понятия теплота образования и теплота сгорания вещества. [c.165]

    Закон Гесса и его следствия не могут быть использованы, если мы не условимся, какой смысл вкладываем в понятия теплота образования и теплота сгорания вещества. [c.12]

    Для сравнения разных видов топлива используют понятие условное топливо , которое имеет теплоту сгорания 29,3 МДж/кг. [c.121]

    Теплота сгорания твердого топлива в зависимости от его природы, метаморфизма, содержания влаги и золы может варьировать в довольно широких пределах. Когда сравниваются различные виды твердого топлива с учетом его применения в качестве источника тепловой энергии, очень часто используется понятие условное топливо. Это эталон, который условно принимается равным 29307 кДж/кг (7000 ккал/кг). [c.113]

    В ряде случаев для сравнения различных видов горючих применяется понятие условного топлива (у.т.) с теплотой сгорания 29,33 МДж/кг (по теплоте сгорания I т нефтяного топлива эквивалентна 1,4 -1,5 ту.т. [c.83]

    Объясните различив между следующими понятиями а) теплоемкость и теплота б) закон Гесса и первый закон термодинамики в) теплота образования и теплота сгорания г) теплота и тепловой эффект реакции. [c.81]

    Теплотой сгорания соединения называется тепловой эффект реакции полного сгорания 1 моль этого соединения до образования СОа, Н2О, N2 и других продуктов, которые специально указываются. Как и в случае теплот образования, пользуются понятиями стандартных теплот сгорания и таблицами этих величин. [c.72]

    Согласно идее Л. Полинга, на основе измерения неаддитивности какого-либо свойства молекулы (например, размера связи, теплоты сгорания, спектра, рефракции и др.) можно определить веса различных структур, а затем предсказать неаддитивность любого другого свойства. Так, Л. Полинг ввел понятие о двое-связности связей (доля участия двойной связи). В этане связь С—С на 100% одинарная, в этилене — на 100% двойная, в бензоле — на 50% одинарная, на 50% двойная. На основе этих и других привлекаемых соединений (например, графита) строится полуэмпирический график двоесвязность — расстояние между атомами, который позволяет потом по расстоянию определять двоесвязность любых молекул и, следовательно, их реакционную способность. [c.482]

    Для ТОГО, чтобы с помощью закона Гесса и его следствий можно было проводить расчет тепловых эффектов процессов, используют строго фиксированные понятия теплоты образования и теплоты сгорания, отнесенные к определенным условиям измерения этих величин. [c.177]

    На практике пользуются понятиями теплота образования и теплота сгорания . Эти понятия относятся к одному молю вещества. [c.88]

    На конкретных примерах поясните, что означают понятия тепловой эффект реакции , теплота образования и теплота сгорания . [c.93]

    Понятие связевая рефракция было введено в науку А. И. Бачинским [185] в 1918 г., когда он предложил рассчитывать молекулярную рефракцию (так же как и молекулярный объем, теплоту сгорания и т. п.) по связевым инкрементам. По Бачинскому, связевая рефракция [c.143]

    ТЕПЛОТА СГОРАНИЯ ГАЗА И ЕЕ ОПРЕДЕЛЕНИЕ Понятие о теплоте сгорания газов [c.64]

    X. т. использует понятия о типах термодинамич. систем (см. Гетерогенная система. Гомогенная система. Закрытая система, Изолированная система, Открытая система), параметрах состояния (см. Давление, Температура, Химический потенциал), термодинамич. ф-циях и термодинамических потенциалах (см., напр., Внутренняя энергия. Энтропия). В основе Х.т. лежат законы (начала) общей термодинамики. Первое начало термодинамики — закон сохранения энергаи дая термодинамич. системы, согласно к-рому работа может совершаться только за счет теплоты или к.-л. др. формы энергии. Оно является основой термохимии, изучения теплоемкостей в-в, тепловых эффектов реакций и физ.-хим процессов. Гесса закон позволяет определять тепловые эффекты расчетным путем, если известны теплоты образования каждого из в-в, участвующих в р-ции, или теплоты сгорания (для орг. соед.). Совр. термодинамич. справочники содержат данные о теплотах образования или теплотах сгорания неск. тысяч в-в, гто позволяет рассчитывать тепловые эффекты десятков тысяч хим. р-ций. Первое начало лежит в основе Кирхгофа уравнения, к-рое выражает зависимость теплового эффекта р-ции или физ.-хим. процесса ст т-ры и дает возможность рассчитать тепловой эффект процесса при любой т-ре, если известны теплоемкости в-в, участвующих в р-ции, и тепловой эффект при к.-л. одной т-ре. [c.236]

    Часто тепловой эффект реакции обозначают просто как теплоту реакции (теплоту сгорания, теплоту возгонки и т.д.). Правильнее употреблять понятие энтальпия реакции. Для любого химического вещества ири стандартных условиях характерно определенное значение некоторой величины, называемой энтальпией (Я), а тепловой эффект реакций выражают разницей энтальпий (АЯ) реагентов и продуктов реакции и называют энтальпией реакции. [c.40]

    Для ориентировочной оценки состава газа, получаемого при тех или иных условиях, часто использу

Химическая термодинамика использует понятия: 1) тепловой эффект реакции, 2) функция состояния, 3) функциональная

Условно принято, что энтропия совершенного кристалла при температуре абсолютного нуля равна
(*ответ*) нулю
 + 1
 — 1
 бесконечности
Установлено, что при переходе от газообразного состояния вещества к твердому его энтропия
(*ответ*) уменьшается
 стремится к бесконечности
 не изменяется
 увеличивается
Утверждение о том, что растворимость газа прямо пропорциональна его давлению над жидкостью, известно как
(*ответ*) закон Генри
 правило Марковникова
 закон Менделеева
 правило Хюккеля
Учет и оценку энергетических превращений, сопровождающих физические и химические процессы, изучает наука
(*ответ*) термодинамика
 кинетика
 термохимия
 молекулярная физика
Фаза — это: 1) часть системы, ограниченная со всех сторон физическими поверхностями раздела; 2) часть системы, не содержащая в своих пределах поверхности раздела; 3) часть системы, имеющая поверхность раздела
(*ответ*) 1 и 2
 только 3
 только 2
 только 1
Фазовая диаграмма: 1) представляет собой графическую зависимость давления от температуры; 2) указывает условия равновесия фаз; 3) определяет энергетику фазовых переходов
(*ответ*) 1 и 2
 только 3
 только 2
 только 1
Французский ученый Рауль установил, что для разбавленных растворов не электролитов повышение температуры кипения и понижение температуры замерзания
(*ответ*) пропорциональны концентрации раствора
 пропорциональны давлению паров воды
 определяются природой растворенного вещества
 зависят от температуры раствора
Функциями состояния идеального газа являются: 1) давление, 2) объем, 3) температура, 4) молярная масса
(*ответ*) 1, 2 и 3
 только 4
 только 2
 только 1
Химическая кинетика изучает: 1) тепловой эффект реакции, 2) скорость химической реакции, 3) механизм реакции
(*ответ*) 2 и 3
 только 3
 только 2
 только 1
Химическая реакция A + B ↔ C + D, при которой продукты реакции могут взаимодействовать между собой с образованием исходных веществ, называется
(*ответ*) обратимой
 колебательной
 сложной
 сопряженной
Химическая реакция, идущая в условиях постоянного давления, называется
(*ответ*) изобарной
 изоморфной
 изотопной
 изохорной
Химическая термодинамика и кинетика являются разделами науки
(*ответ*) физической химии
 химической физики
 молекулярной физики
 физики твердого тела
Химическая термодинамика использует понятия: 1) тепловой эффект реакции, 2) функция состояния, 3) функциональная группа, 4) энергия кристаллической решетки, 5) система
(*ответ*) 1, 2 и 5
 только 1
 2 и 3
 1 и 4

Тепловой эффект химической реакции — Википедия

Тепловой эффект химической реакции — изменение внутренней энергии ΔU{\displaystyle \Delta U} или энтальпии ΔH{\displaystyle \Delta H} системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления ,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции

Поясним приведённое выше определение теплового эффекта химической реакции. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[4]открытой однородной термодинамической системы^[5][6]:

dU=TdS−PdV+∑i=1kμidni,{\displaystyle dU=TdS-PdV+\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Фундаментальное уравнение Гиббса для внутренней энергии)

dH=TdS+VdP+∑i=1kμidni.{\displaystyle dH=TdS+VdP+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь T{\displaystyle T} — абсолютная температура, S{\displaystyle S} — энтропия, P{\displaystyle P} — давление, V{\displaystyle V} — объём, ni{\displaystyle n_{i}} — количество (или масса) i{\displaystyle i}-го составляющего систему вещества, μi{\displaystyle \mu _{i}} — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[7]квазистатического изохорного процесса (V=const{\displaystyle V=const})

dU=TdS+∑i=1kμidni;{\displaystyle dU=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i};}

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса (P=const{\displaystyle P=const})

dH=TdS+∑i=1kμidni.{\displaystyle dH=TdS+\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт изменения состава системы), но не происходит ни выделения/поглощения теплоты^[8], ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[9] (см. Неоднозначность понятий «теплота» и «работа») к отрытым системам не применима, и для них теплоту q{\displaystyle q} бесконечно малого квазистатического процесса полагают равной^[10][11]

q≡TdS.{\displaystyle q\equiv TdS.}

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса qV{\displaystyle q_{V}} равна

qV=dU−∑i=1kμidni,{\displaystyle q_{V}=dU-\sum _{i=1}^{k}\mu _{i}dn_{i},}

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса qP{\displaystyle q_{P}} равна

qP=dH−∑i=1kμidni.{\displaystyle q_{P}=dH-\sum _{i=1}^{k}\mu _{i}dn_{i}.}

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем химическую работу^{[12][13][14][15][16]} (работу изменения состава системы^[17]) ∑iμidni{\displaystyle \sum _{i}\mu _{i}dn_{i}} учитывать не требуется^[18][19], и выражения для теплот ещё более упрощаются:

qV=dU,{\displaystyle q_{V}=dU,}

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

qP=dH.{\displaystyle q_{P}=dH.}

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[18][19][20].

Тепловой эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определенных состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электрон, протоны, ионы, радикалы, атомарные простые вещества)^[21].

Теплота реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящий от условий её проведения.

Рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определенных температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[22] и находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Разность энтальпий ΔH{\displaystyle \Delta H} системы в конце и начале рассмотренного мысленного эксперимента и называют тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[23][24]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[25].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и тепловой эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[26].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[27][28][29][30]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[31], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции (ΔU<0{\displaystyle \Delta U<0} или ΔH<0{\displaystyle \Delta H<0}) считают отрицательным, эндотермической (ΔU>0{\displaystyle \Delta U>0} или ΔH>0{\displaystyle \Delta H>0}) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[32].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[32].

Стандартная энтальпия образования (стандартная теплота образования)

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[33]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[34], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[35] (или, несколько более точно, на стандартные условия^[36]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[37]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

ΔH(T2)=ΔH(T1)+∫12ΔCp(T1,T2)d(T).{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{2}{\Delta {C_{p}}(T_{1}{,}T_{2})d(T)}.}

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

ΔH(T2)=ΔH(T1)+∫1TφΔCp(T1,Tφ)d(T)+∫Tφ2ΔCp(Tφ,T2)d(T),{\displaystyle \Delta {H(T_{2})}=\Delta {H(T_{1})}+\int \limits _{1}^{T_{\varphi }}{\Delta {C_{p}}(T_{1}{,}T_{\varphi })d(T)}+\int \limits _{T_{\varphi }}^{2}{\Delta {C_{p}}(T_{\varphi }{,}T_{2})d(T)},}

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

См. также

Примечания

1. ↑ ^{1 2 3 4} БСЭ, 3-е изд., т. 25, 1976, с. 450.
2. ↑ ^{1 2} Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 16.
3. ↑ ^{1 2 3} Химическая энциклопедия, т. 4, 1995, с. 522—523.
4. ↑ Состояние простой термодинамической системы (газы и изотропные жидкости в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь) полностью задано её объёмом, давлением в системе и массами составляющих систему веществ.
5. ↑ Кубо Р., Термодинамика, 1970, с. 143.
6. ↑ Мюнстер А., Химическая термодинамика, 1971, с. 103.
7. ↑ Бесконечно малым (элементарным, инфинитезимальным) называют процесс, для которого разница между начальным и конечным состояниями системы бесконечно мала.
8. ↑ Под теплотой здесь подразумевается изменение энергии системы в результате теплопередачи через граничную поверхность (см. Теплота).
9. ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 8.
10. ↑ Базаров И. П., Термодинамика, 2010, с. 114.
11. ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 54.
12. ↑ Lebon G. e. a., Understanding Non-equilibrium Thermodynamics, 2008, p. 14.
13. ↑ Жариков В. А., Основы физической геохимии, 2005, с. 31.
14. ↑ Callen H. B., Thermodynamics and an Introduction to Thermostatistics, 1985, p. 36.
15. ↑ Сычёв В. В., Сложные термодинамические системы, 2009, с. 257.
16. ↑ Путилов К. А., Термодинамика, 1971, с. 125.
17. ↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, с. 11.
18. ↑ ^{1 2} Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 87.
19. ↑ ^{1 2} Бурдаков В. П. и др., Термодинамика, ч. 2, 2009, с. 10.
20. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 127.
21. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 128.
22. ↑ То, что конечное состояние может оказаться недостижимым в действительности, применительно к данному рассмотрению не имеет значения.
23. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 130.
24. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 24.
25. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 17.
26. ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 131.
27. ↑ Ляшков В. И., Теоретические основы теплотехники, 2015, с. 102.
28. ↑ Морачевский А. Г., Кохацкая М. С., Прикладная химическая термодинамика, 2008, с. 23.
29. ↑ Кнорре Д.Г. и др., Физическая химия, 1990, с. 245.
30. ↑ Никольский Б. П. и др., Физическая химия, 1987, с. 18.
31. ↑ До 1982 года ИЮПАК принимал в качестве стандартного давления 1 атм = 101325 Па; это следует учитывать при использовании данных из литературы, изданной ранее.
32. ↑ ^{1 2} Химический энциклопедический словарь, 1983, с. 563.
33. ↑ Курс физической химии // Под ред. Я. И. Герасимова. М.-Л.: Химия, 1964. — Т. 1. — С. 55.
34. ↑ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. p. 49. Electronic version.
35. ↑ Жуховицкий А. А., Шварцман Л. А. Физическая химия. — М.: Металлургия, 1976. — 544 с.
36. ↑ Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
37. ↑ Пригожин И., Дефэй Р. Химическая термодинамика = Chemical Thermodynamics / Перевод с англ. под ред. В. А. Михайлова. — Новосибирск: Наука, 1966. — 502 с.

Литература

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2^nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — DOI:10.1007/978-3-540-74252-4.
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с.
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Эткинс П. Физическая химия. — Москва. : Мир, 1980