График функции — это… Что такое График функции?
- График функции
Wikimedia Foundation. 2010.
Смотреть что такое «График функции» в других словарях:
график функции — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] график функции 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами, где x… … Справочник технического переводчика
График функции — [ graph of a function ] — 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами., где x — любая точка области определения этой функции,… … Экономико-математический словарь
график функции — ▲ изображение ↑ графический, функция (математическая) график изображение функции при помощи линии на плоскости. … грамма. номограмма. кардиограмма. эхограмма. диаграмма наглядное графическое изображение соотношения каких л. величин. круговая… … Идеографический словарь русского языка
график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых … Энциклопедический словарь
Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции … Большой Энциклопедический словарь
График — геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и… … Большая советская энциклопедия
График — График: График функции множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты соответствующими значениями функции . График деятель искусств, занимающийся графикой. График базальной… … Википедия
График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
dic.academic.ru
График функции — это… Что такое График функции?
- График функции
График функции [ graph of a function ] — 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x
,y) плоскости с прямоугольными координатами., где x — любая точка области определения этой функции, а y= f (x). Здесь дана функция одного переменного y=f(x), и область ее определения Е. Соответственно, график представляет собой той или иной формы кривую (прямую при линейной функции). Поэтому, кстати, часто говорят о «форме» функции: линейной, синусоидальной, параболической и др. Аналогично, если задана функция двух переменных z= f(x,y), то графиком является множество всех точек (x,y,z) пространства, где (x,y) любая точка области определения этой функции, а z= f(x,yВ обоих этих случаях график может быть отображен на бумаге (см. иллюстрации Г.5-Г.7). В случаях функции большего числа переменных приходится прибегать к использованию абстрактных многомерных (n — мерных) пространств.
Обычно графики строятся на основании таблиц, в которых указывается значение функции для каждого значения аргумента. Точность Г., построенного таким способом, зависит от того, насколько часто выбраны значения аргумента. Графики подвергаются разного рода преобразованиям, например, сжатию, параллельному переносу и т.п. Графики функций часто используются для приближенного решения уравнений, систем уравнений и неравенств.
Рис.Г.4 Графики линейных функций
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- График рассеивания
- Грационный период кредита
Смотреть что такое «График функции» в других словарях:
график функции — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] график функции 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами, где x… … Справочник технического переводчика
График функции — Для термина «График» см. другие значения. График функции множество точек, у которых абсциссы являются допустимыми значениями аргумента , а ординаты соответствующими значениями функции . Обычно рассматриваются графики вещественных… … Википедия
график функции — ▲ изображение ↑ графический, функция (математическая) график изображение функции при помощи линии на плоскости. … грамма. номограмма. кардиограмма. эхограмма. диаграмма наглядное графическое изображение соотношения каких л. величин. круговая… … Идеографический словарь русского языка
график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых … Энциклопедический словарь
Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции … Большой Энциклопедический словарь
График — геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и… … Большая советская энциклопедия
График — График: График функции множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты соответствующими значениями функции . График деятель искусств, занимающийся графикой. График базальной… … Википедия
График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
economic_mathematics.academic.ru
График функции — Википедия. Что такое График функции
Материал из Википедии — свободной энциклопедииГрафик функции — понятие в математике, которое даёт представление о геометрическом образе функции.
Наиболее наглядны графики вещественнозначных функций вещественного переменного.
В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:
- точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.
Таким образом, функция может быть адекватно описана своим графиком.
Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и тоже подмножество плоскости).
График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.
При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:
- Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}
В частности, при рассмотрении динамических систем, изображающая точка
- (t,f(t)){\displaystyle (t,f(t))},
представляет собою график решения соответствующего дифференциального уравнения.
Примеры
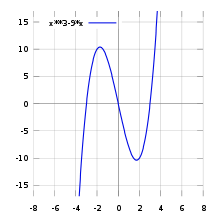 График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}
График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}- График кубического многочлена вещественной переменной
- f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}
- это множество
- {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.
- График функции
- f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}
- это множество из трёх точек {(1,a), (2,d), (3,c)}.
См. также
Литература
Ссылки
wiki.sc
1.2. Понятие функции
Для исследования различных явлений полезно знать, как изменение одних величин влияет на другие величины.
Понятие функции связано с установлением зависимости (связи) между двумя (несколькими) переменными величинами при их совместном изменении, или установлением зависимости между элементами двух (нескольких) множеств.
Определение.
Пусть даны две
переменные х и y с областями изменения Х и Y.
Переменная y называется функцией от х,
если по некоторому правилу или закону
каждому значению 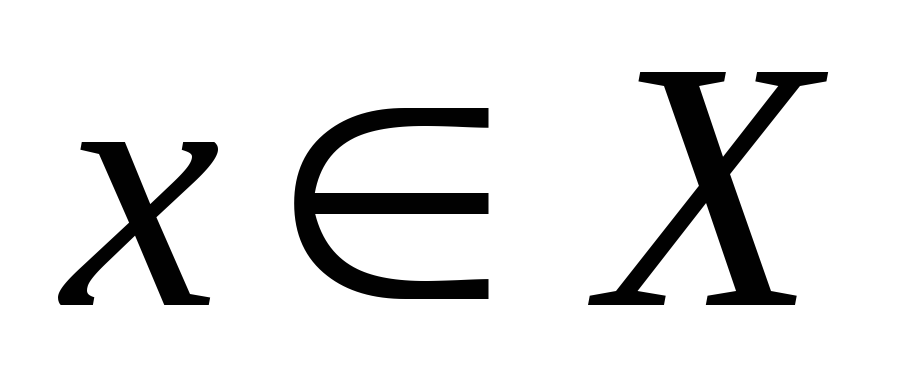 ставится в соответствие одно определенное
значение
ставится в соответствие одно определенное
значение .
.
Для указания этого
факта, что y есть функция от х,
пишут: 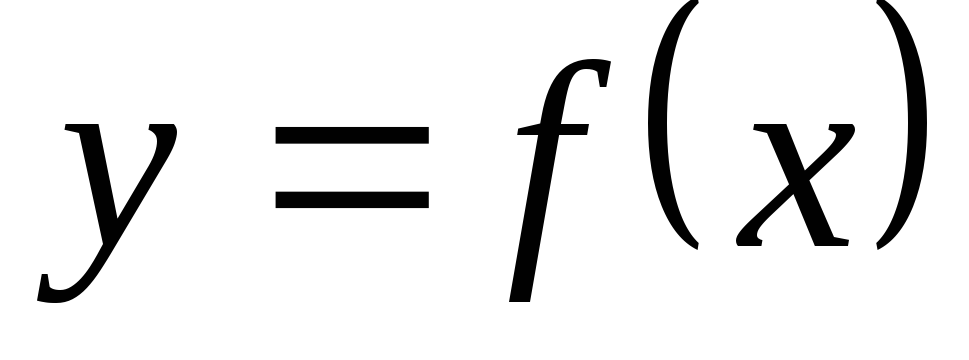 ,
,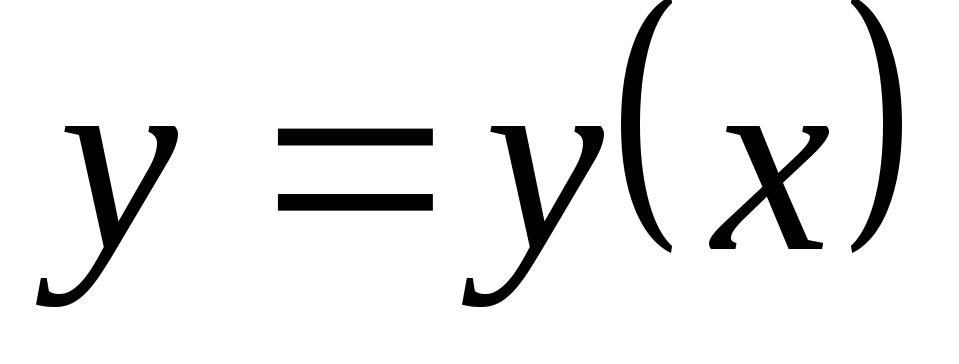 ,
,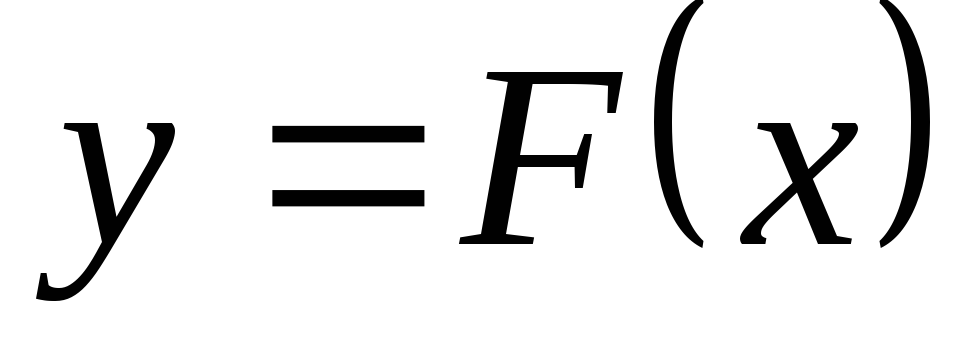 и т.п.
и т.п.
Можно также сказать,
что функция f отображает множество Х на множество Y.
Это обозначается так 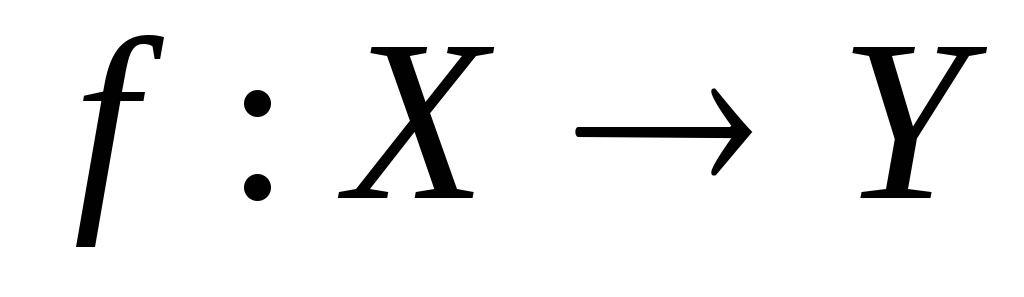 (рис.1.1).
(рис.1.1).
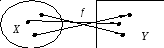
Рис. 1.1
Переменная х называется независимой переменной или аргументом.
Переменная y называется зависимой переменной или функцией.
Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.
1.3. Область определения и изменения функции
Определение.
Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения или областью существования этой функции.
Определение.
Множество Х называется областью
определения функции и обозначается 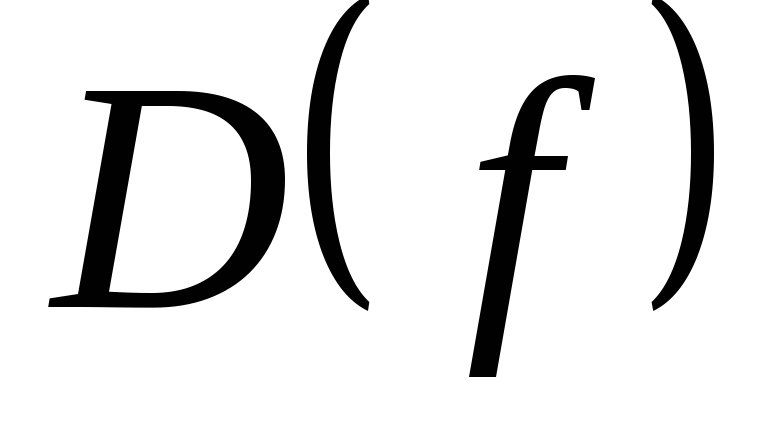 .
.
Обычно областью определения функции являются:
 ;
;
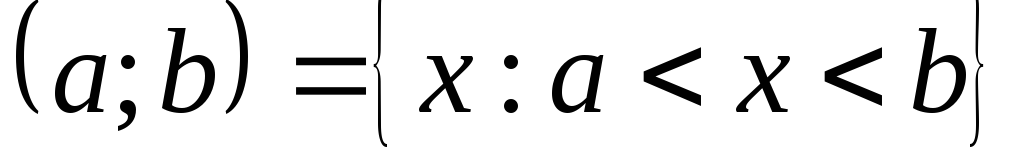 ;
;
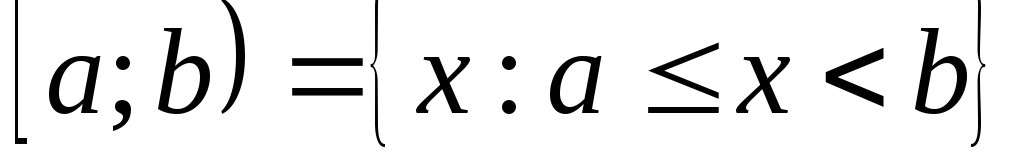 ;
;
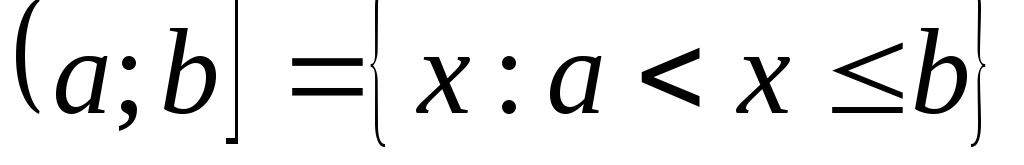 ;
;
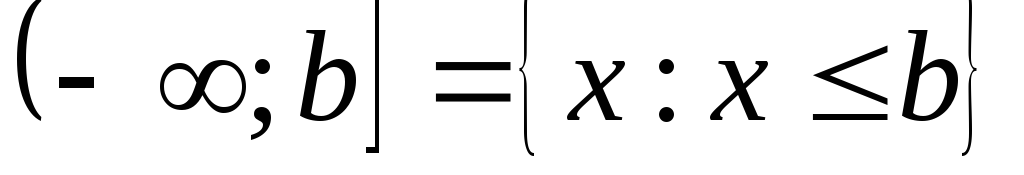 ;
; 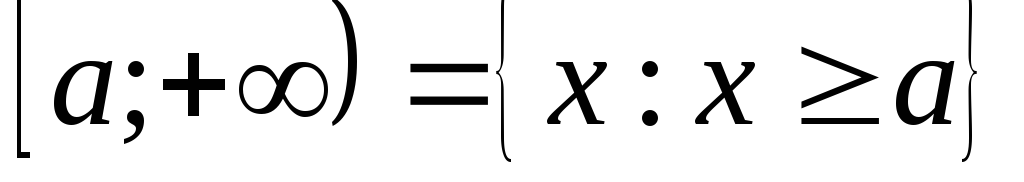 ;
;
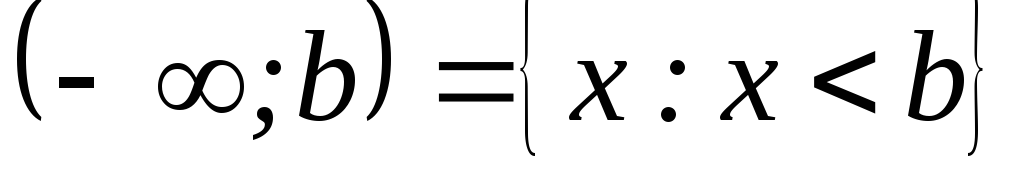 ;
; 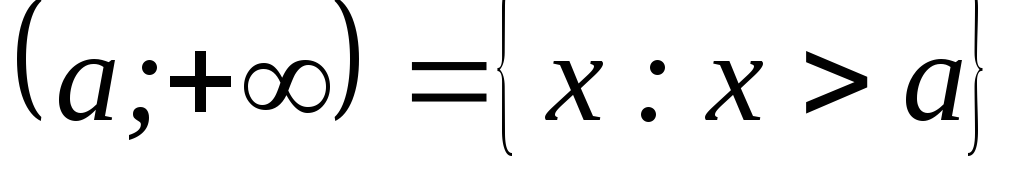 ;
;
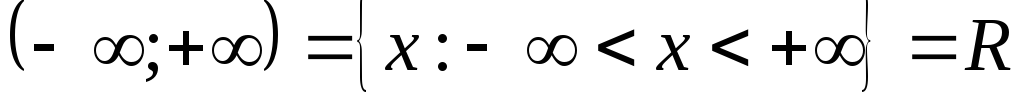 ,
,
где  ,
,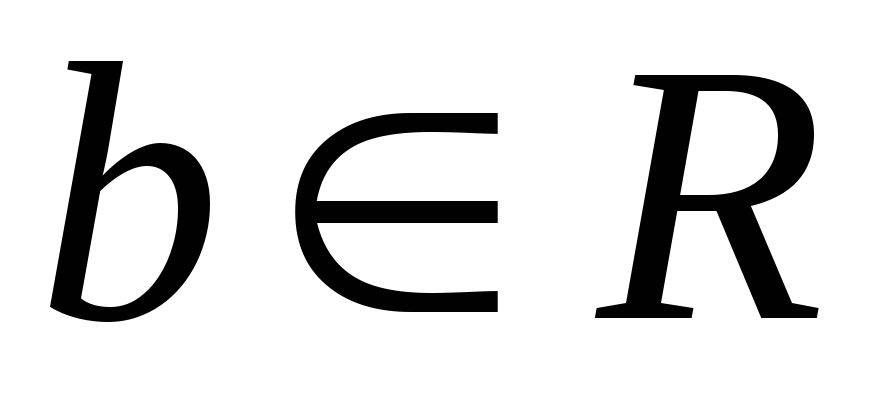 и
и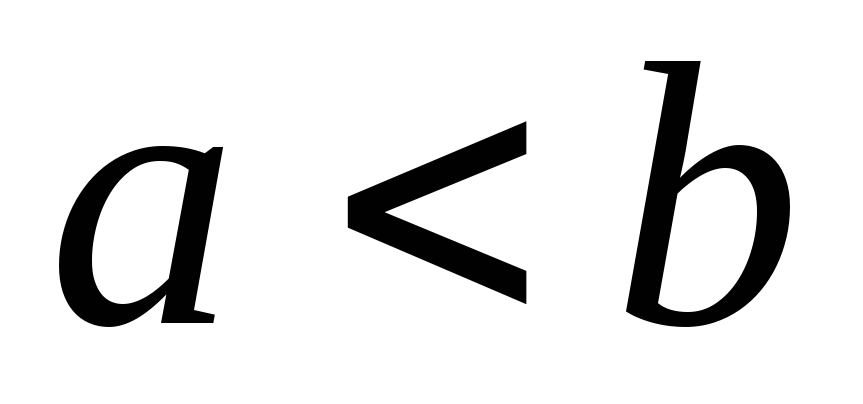 .
.
Например, для функций:
1) 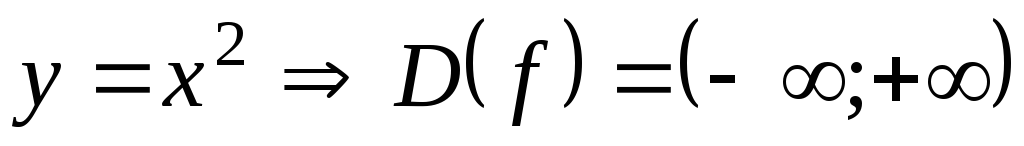 ;
;
2) 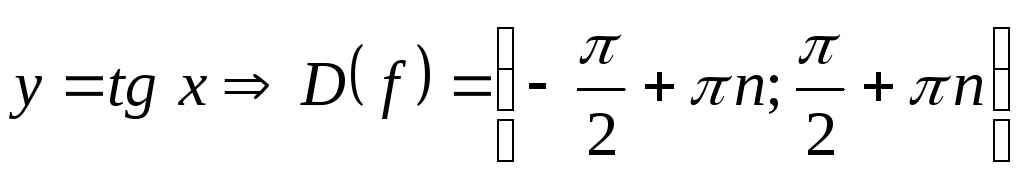 .
.
Область определения функции может состоять из одного или нескольких промежутков и из отдельных точек.
Определение.
Множество значений Y называется областью
изменения или областью значений функции, и
обозначается 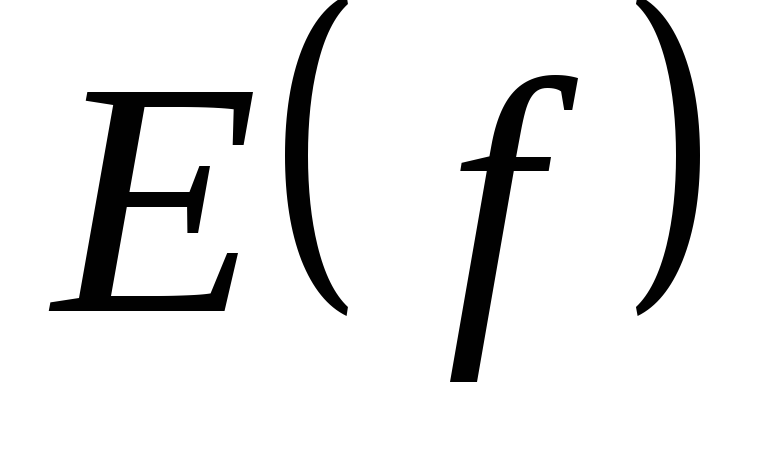 .
.
Область изменения функции (множество ее значений) определяется законом соответствия.
Например, для функций
1) 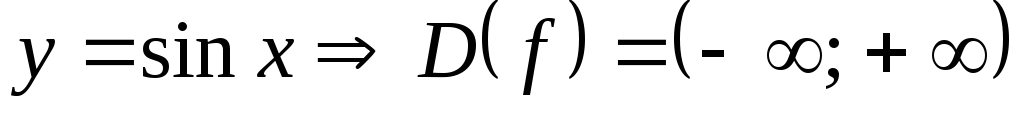 ;
;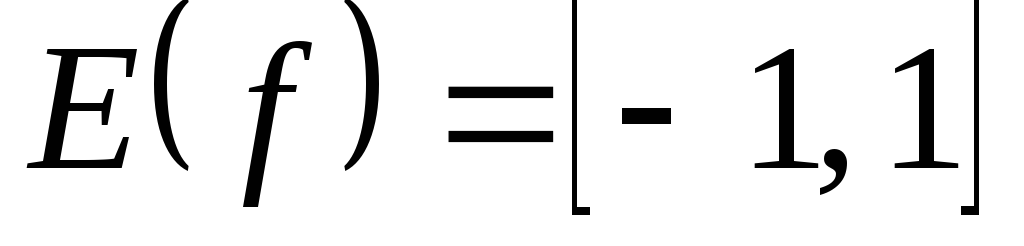 ;
;
2) 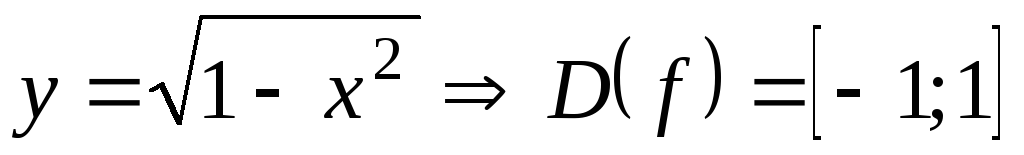 ;
;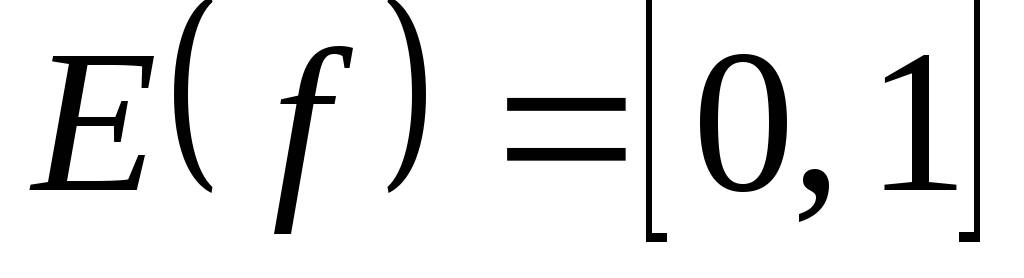 .
.
Определение.
Функция 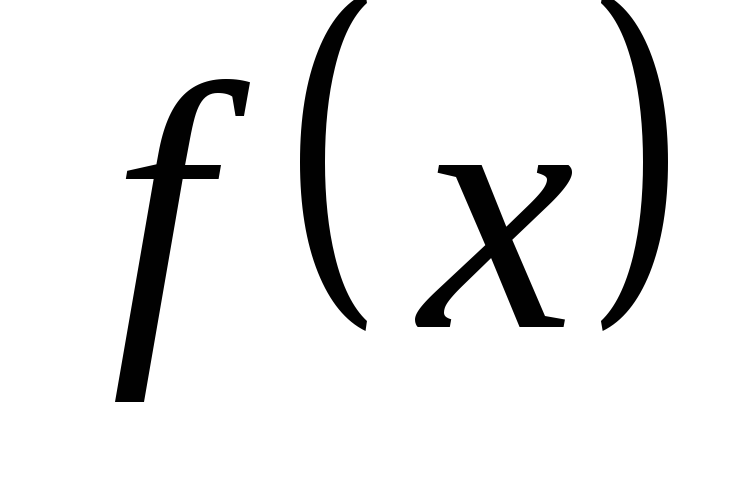 называетсячисловой функцией, если ее область определения
называетсячисловой функцией, если ее область определения 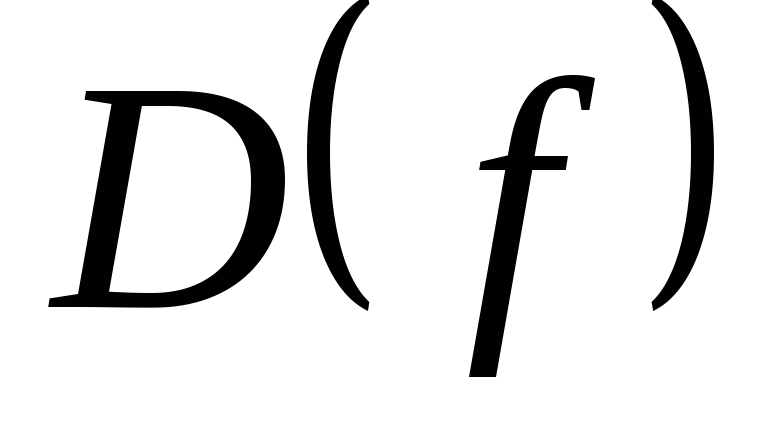 и множество значений
и множество значений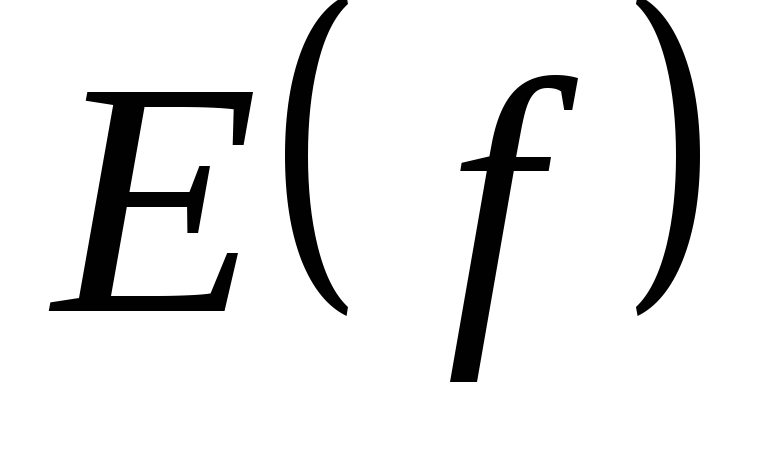 содержатся в множестве действительных
чиселR.
содержатся в множестве действительных
чиселR.
В дальнейшем будем
изучать лишь числовые функции. Частное
значение функции 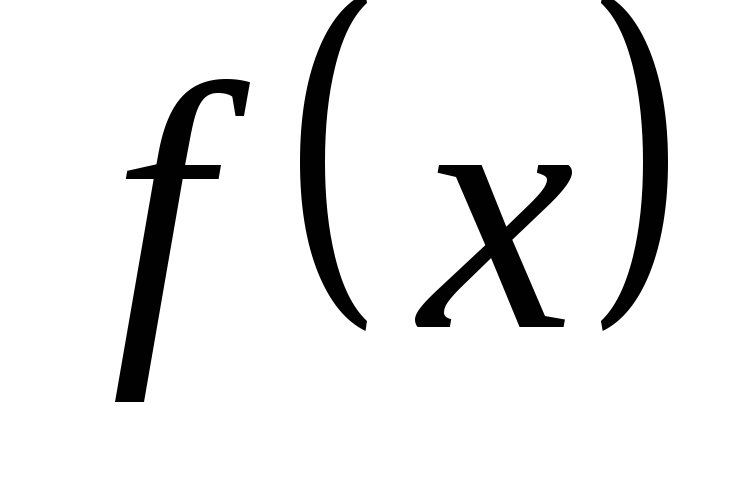 призаписывается так:
призаписывается так: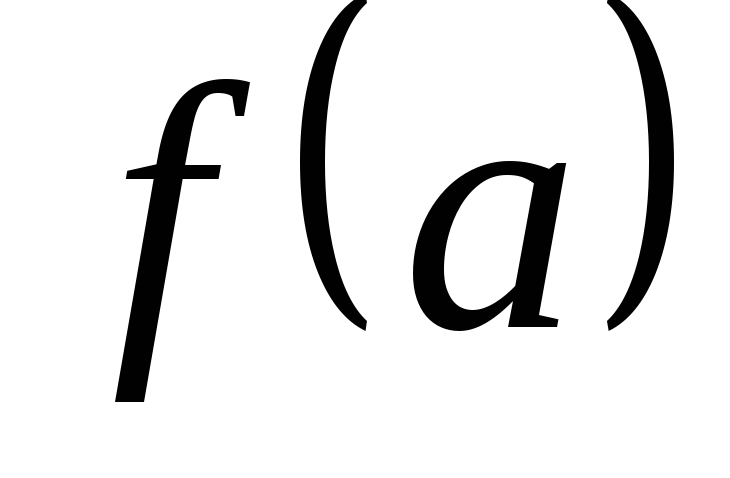 .
.
Например, если 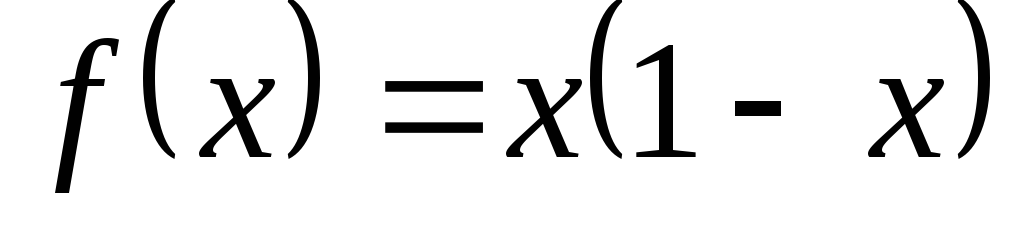 ,
то
,
то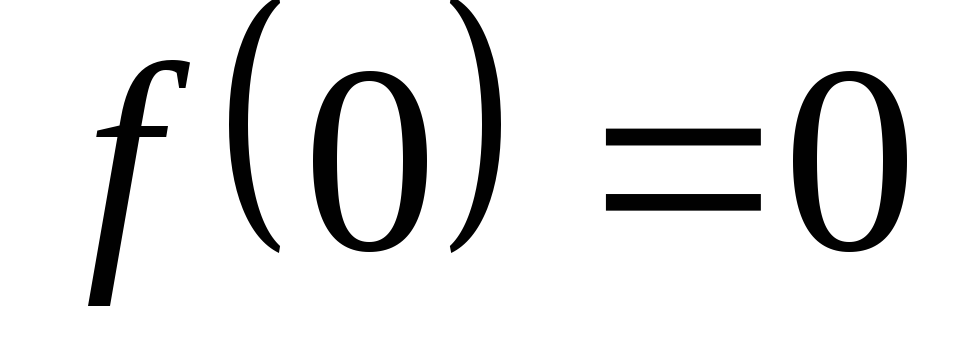 ,
,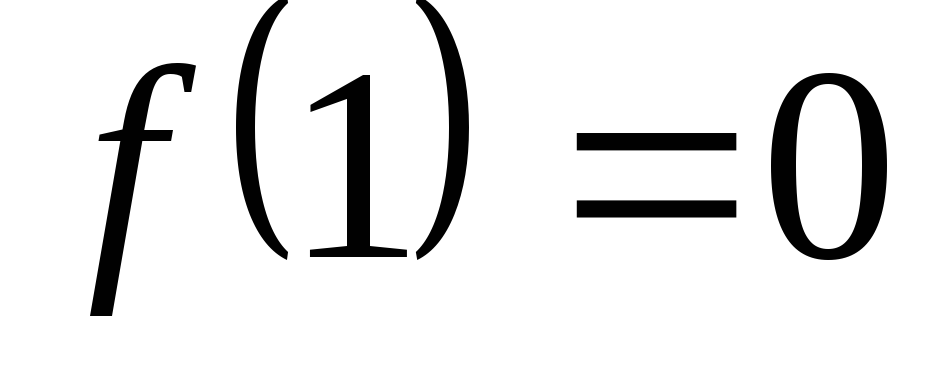 ,
,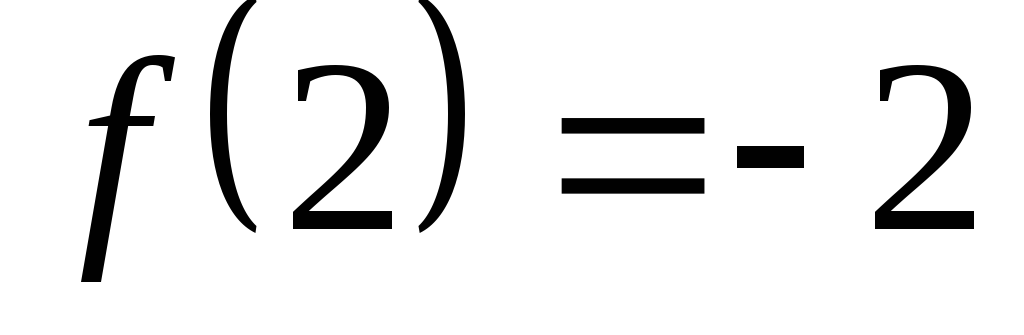 и т.п.
и т.п.
1.4. Последовательность
Определение.
Функция, определенная
на множестве натуральных чисел 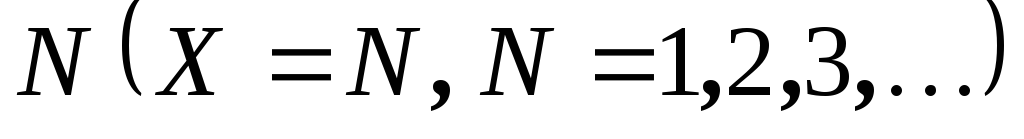 ,
называетсяпоследовательностью.
,
называетсяпоследовательностью.
Значения функции  т.е. элементы множества
т.е. элементы множества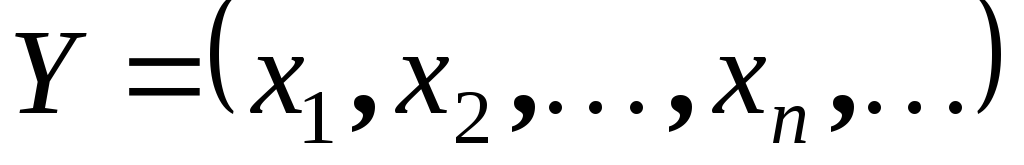 называются членами последовательности,
а
называются членами последовательности,
а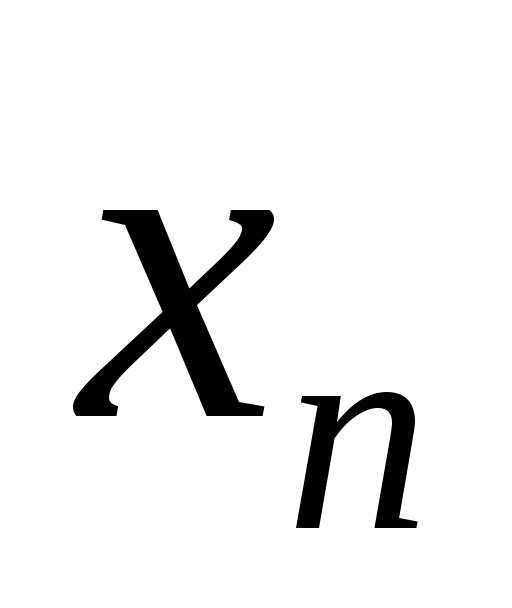 – общим членом последовательности.
– общим членом последовательности.
Последовательность
обычно обозначают через 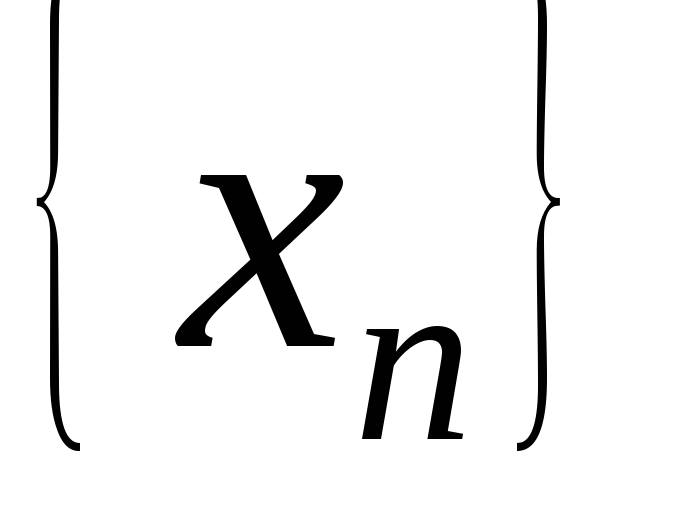 или
или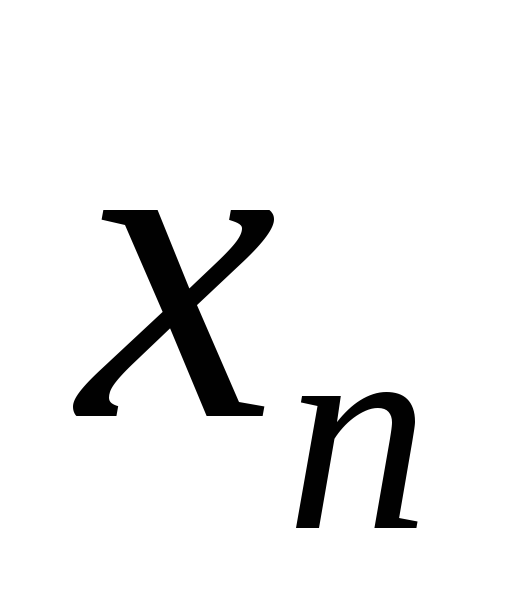 .
.
Например, 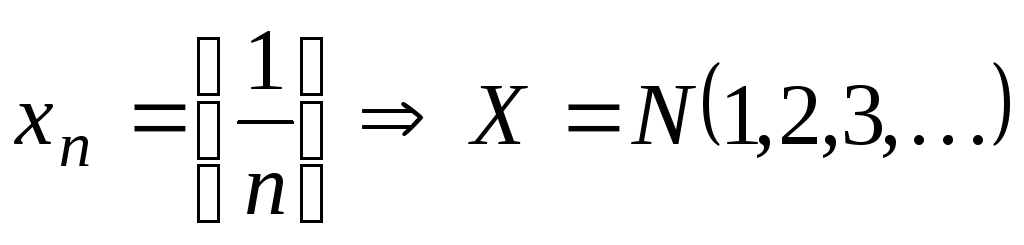 ;
;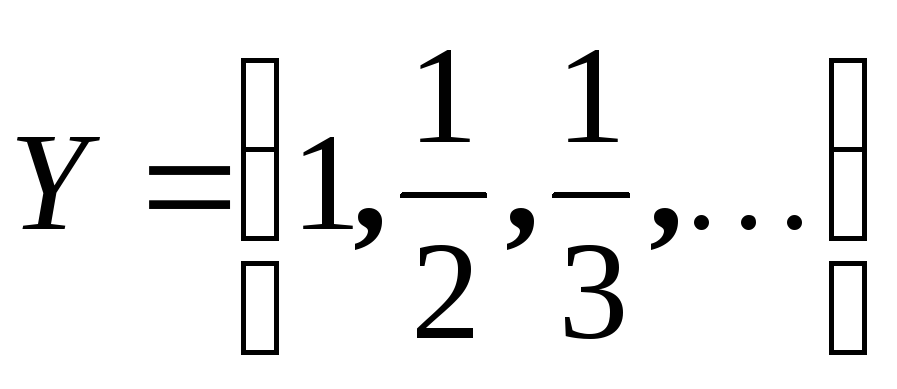 .
.
1.5. График функции
Для наглядного представления функции строят ее график.
Определение.
Графиком функции 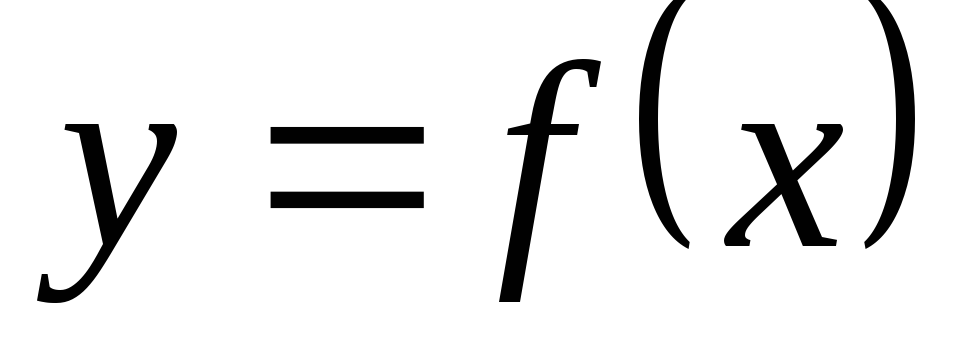 называется множество всех точек плоскости
называется множество всех точек плоскости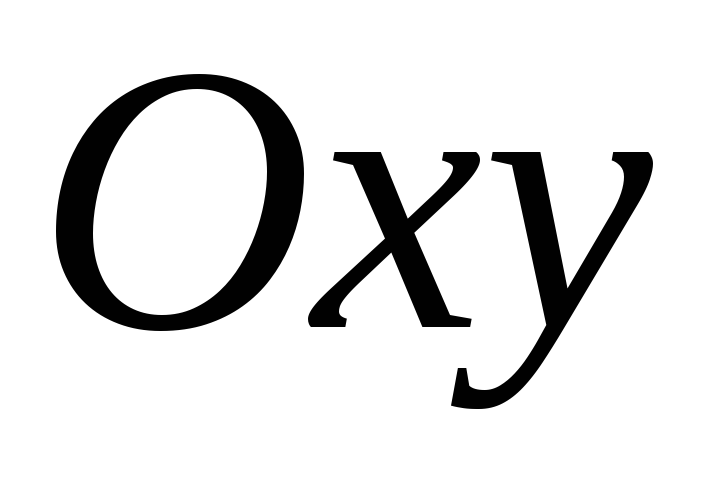 ,
для каждой из которыхх является значением аргумента,
а y – соответствующим значением функции.
,
для каждой из которыхх является значением аргумента,
а y – соответствующим значением функции.
Например, графиком
функции 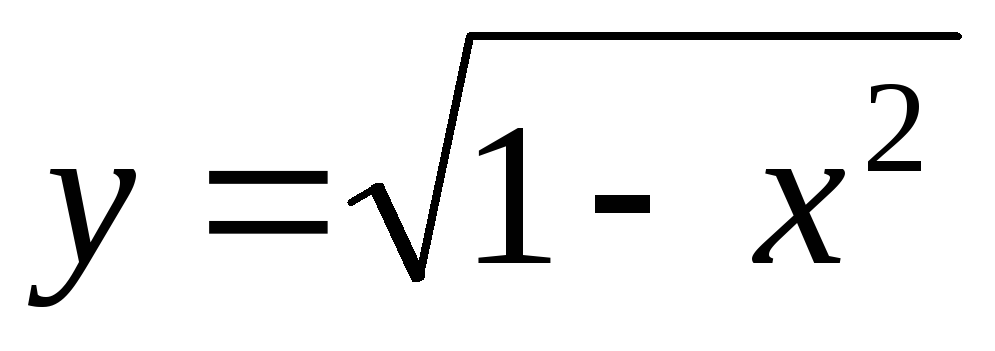 является верхняя полуокружность радиуса
является верхняя полуокружность радиуса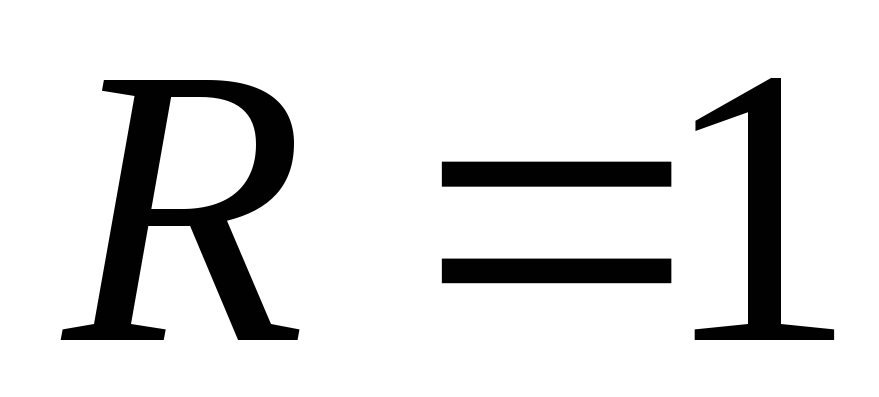 с центром в
с центром в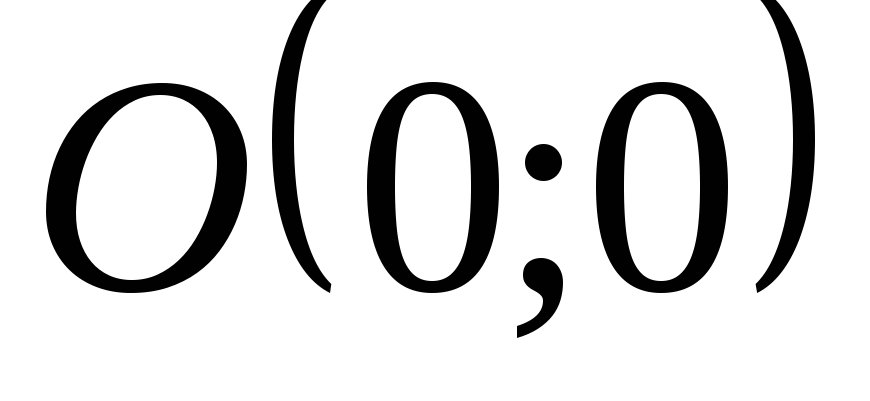 (рис. 1.2).
(рис. 1.2).
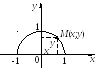
Рис. 1.2
1.6. Способы задания функции
Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции.
Существует три основных способа задания функции: аналитический, табличный и графический.
Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.
Например, 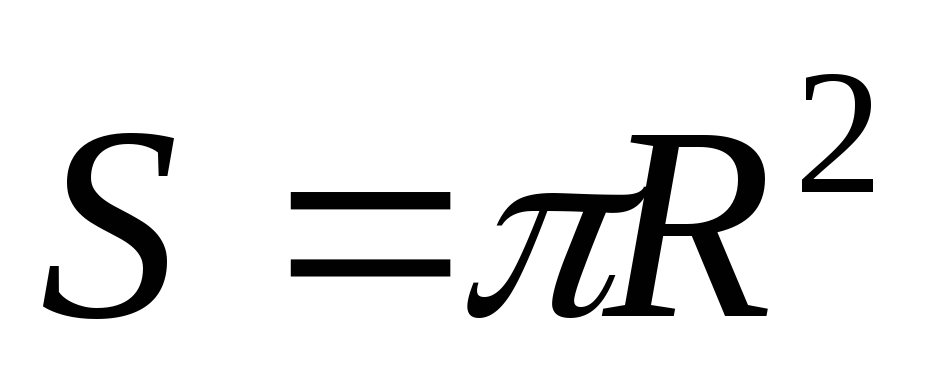 ;
;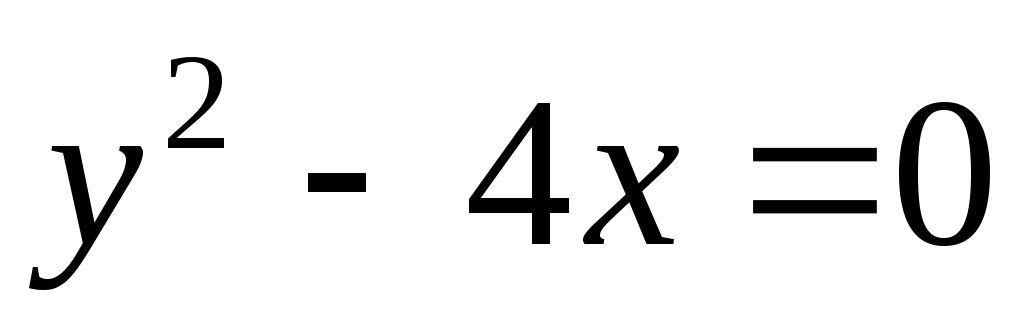 ;
;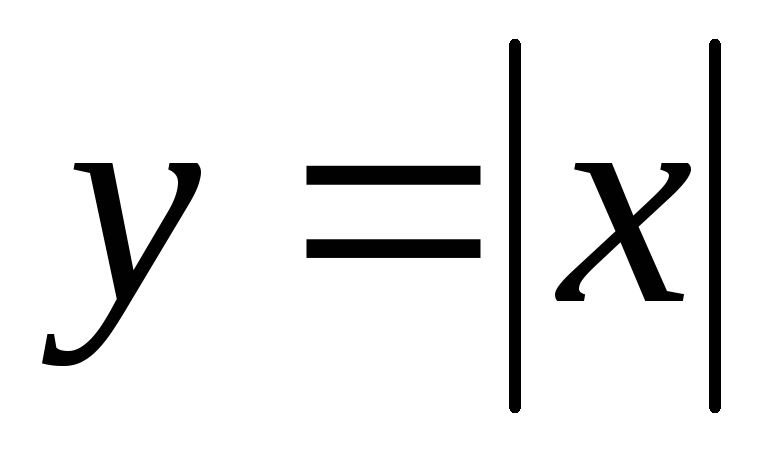 ,
где.
,
где.
Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию.
Табличный способпредусматривает задание таблицы, в
которой различным значениям аргумента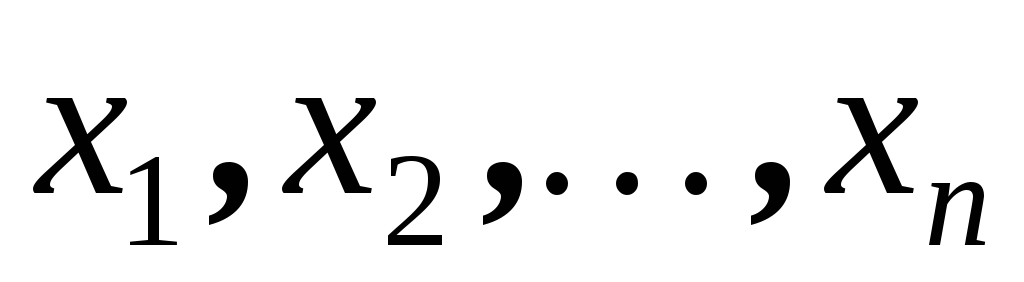 поставлены соответствующие значения
функции
поставлены соответствующие значения
функции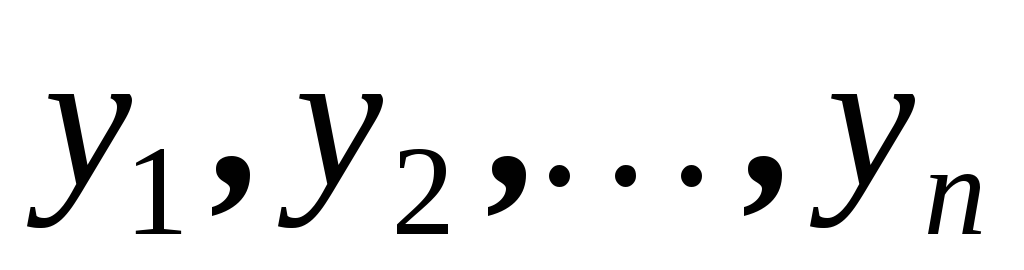 :
:
х | х1 | х2 | … | хn |
y | y1 | y2 | … | yn |
Такие таблицы составляются, например, по данным эксперимента; для облегчения вычислений с часто встречающимися функциями (таблицы логарифмов, таблицы тригонометрических функций и т.д.).
Графический способзадания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.
studfile.net
График функции Википедия
График функции — понятие в математике, которое даёт представление о геометрическом образе функции.
Наиболее наглядны графики вещественнозначных функций вещественного переменного.
В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:
- точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.
Таким образом, функция может быть адекватно описана своим графиком.
Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).
График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.
При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:
- Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}
В частности, при рассмотрении динамических систем, изображающая точка
- (t,f(t)){\displaystyle (t,f(t))},
представляет собою график решения соответствующего дифференциального уравнения.
Примеры
График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}- График кубического многочлена вещественной переменной
- f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}
- это множество
- {(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.
- График функции
- f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}
- это множество из трёх точек {(1,a), (2,d), (3,c)}.
См. также
Литература
Ссылки
wikiredia.ru
Значение словосочетания ГРАФИК ФУНКЦИИ. Что такое ГРАФИК ФУНКЦИИ?
График функции — понятие в математике, которое даёт представление о геометрическом образе функции.Наиболее наглядны графики вещественнозначных функций вещественного переменного.
В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:
точка
(
x
,
y
)
{\displaystyle (x,y)}
располагается (или находится) на графике функции
f
{\displaystyle f}
тогда и только тогда, когда
y
=
f
(
x
)
{\displaystyle y=f(x)}
.
Таким образом, функция может быть адекватно описана своим графиком.
Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и тоже подмножество плоскости).
График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.
При рассмотрении отображения произвольного вида
f
:
X
→
Y
{\displaystyle f:X\to Y}
, действующего из множества
X
{\displaystyle X}
в множество
Y
{\displaystyle Y}
, графиком функции называется следующее множество упорядоченных пар:
Γ
f
=
{
(
x
,
f
(
x
)
)
∈
X
×
Y
∣
x
∈
X
}
.
{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}
В частности, при рассмотрении динамических систем, изображающая точка
(
t
,
f
(
t
)
)
{\displaystyle (t,f(t))}
,
представляет собою график решения соответствующего дифференциального уравнения.
kartaslov.ru
график — это… Что такое график?
график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых … Энциклопедический словарь
ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции … Большой Энциклопедический словарь
ГРАФИК — (греч.). 1) чертеж для схематического изображения движение железно дор. поездов. 2) вообще изображение особым чертежом каких либо изменяющихся величин. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАФИК 1)… … Словарь иностранных слов русского языка
график — а, м. graphique, dessin graphique. 1. Чертеж хода поездов. Брокг. 18. Чертеж, употребляемый на в железнодорожной службе для наглядного изображения хода поездов, их взаимного расположения при движении и выяснения пропускной способности… … Исторический словарь галлицизмов русского языка
ГРАФИК — 1) расписание, определяющее последовательность выполнения действий, протекания событий во времени. Например, график движения поездов, график дежурств, график работы; 2) графическое изображение математической зависимости; математическая… … Экономический словарь
ГРАФИК — ГРАФИК, графика, муж. (от греч. graphikos письменный) (спец.). Диаграмма, чертеж, изображающий посредством кривых количественные зависимости различных процессов. График движения поездов. График изменения температуры воздуха. Толковый словарь… … Толковый словарь Ушакова
график — диаграмма, набросок, схема, кривая, чертёж, таблица; расписание, программа, план; табель, табуляграмма, гидрограф, годограф, синусоида, номограмма, эхограмма, ковер, рисовальщик, художник Словарь русских синонимов. график см. расписание Словарь… … Словарь синонимов
ГРАФИК — ГРАФИК, в математике наглядное представление зависимости между числами или величинами. Во многих графиках используется ДЕКАРТОВА СИСТЕМА КООРДИНАТ. Обычно оси чертят под прямым углом друг к другу и наносят на них шкалу переменных величин. На… … Научно-технический энциклопедический словарь
график — Чертеж, наглядно изображающий количественное соотношение и развитие взаимосвязанных процессов или явлений в виде кривой, прямой, ломаной линии, построенной в той или иной системе координат. [ГОСТ Р 7.0.3 2006] график [Лугинский Я. Н. и др. Англо… … Справочник технического переводчика
График — А. Изображение в виде кривой изменения функции при изменении аргумента для математической, физической или другой зависимости. Б. Таблица, расписание последовательности выполнения событий, действий. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ГРАФИК 1 — ГРАФИК 1, а, м. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
dic.academic.ru