3 Если $\overline{a} \neq \overline{0}$, то
4 Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.
5 $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$
6 $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$
7 $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$
Если векторы $\overline{a}$ и $\overline{b}$ заданы своими координатами: $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ , то их скалярное произведение вычисляется по формуле:
1Определение
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений
соответствующих координат. {\circ}$$
{\circ}$$
Читать дальше: векторное произведение векторов.
Савельев — Курс общей физики Том 1 — Механика — DJVU, страница 2
Перемещение точки. Векторы и скаляры Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают прямо- линейное движение, движение Троенвррия г по окружности, криволинейное движение и т. д. Пусть материальная точка (в дальнейшем мы для кратко- 1 стн будем говорить просто точка) переместилась вдоль некотоРвс.
3. рой траектории из точки 1 в точ- ку 2 (рис. 3). Расстояние от точки 1 до точки 2, отсчитанное вдоль траектории, пред. ставляет собой пройденный путь. Мы будем обозначать его буквой э. Отрезок прямой, проведенный из точки 1 в точку 2, называется перемещением. Обозначим его гиь Перемещение характеризуется, кроме своей величины (равной длине отрезка гм), также и направлением. Действительно, рассмотрим два одинаковых по величине перемещения гм н гм (рис. 4). Несмотря на равенство -длин этих отрезков, они явно представляют собой совершенно различные перемещения.
4). Несмотря на равенство -длин этих отрезков, они явно представляют собой совершенно различные перемещения.
Величины, подобные перемещению, подчиняются особому правилу сложении, которое можно уяснить на следующем примере. Пусть точка совершает последовательно два перемещевиш гм и гм (рис. 5). Суммой этих двух перемещений естественно назвать такое переме1х щенпе гэа, которое приводит к тому же результату, что и первые два перемещения вместе. Величины такого рода, как перемещение, т.
е. характеризующиеся численным значением и направлением, а также складывающиеся по правилу, показанному на рис. 5, называются векторами. К числу векторов принадлежат скорость, ускорение, сила и ряд других величин. Величины, для задания которых достаточно одного численного значения, называются скалярами. Примерами скаляров могут служить путь, время, масса и т. д. г Рис. 4. Векторы принято обозначать буквами жирного шриф- та. Например, вектор перемещения из точки 1 в точку 2 обозначается г1а.
Та же буква обычного шрифта озна- чает численное значение или, как говорят, модуль соот- ветствующего вектора ‘). Для обозначения модуля поль- зуются также символом вектора, заключенным между двумя вертикальными черточками. Таким образом, ] А ! = А = модулю вектора А, 1г,з!=г,а= модУлю вектоРа г,а. Модуль вектора — скаляр, причем всегда положи- тельныйй. На чертежах векторы изображаются в виде прямо- линейных отрезков со стрелкой на конце.
Для обозначения модуля поль- зуются также символом вектора, заключенным между двумя вертикальными черточками. Таким образом, ] А ! = А = модулю вектора А, 1г,з!=г,а= модУлю вектоРа г,а. Модуль вектора — скаляр, причем всегда положи- тельныйй. На чертежах векторы изображаются в виде прямо- линейных отрезков со стрелкой на конце.
Длина отрезка в устанонленном масштабе дает модуль вектора, а ука- занное стрелкой направление отрезка дает направление вектора. Показанная на рис. 5 операция сложения некторов символически записывается следующим образом: г~з+ газ= г~з. В При письме векторы обозначают буквами со стрелкой иад ними (например, Пэ), В этом случае та же буква без стрелки озна- чает модуль вектора. аз й 2. Некоторые сведения о векторах Векторы, направленные вдоль паранлельных прямых (в одну и ту же или в противоположные стороны), называютсн коллинеарными. Векторы, направления которых параллельны одной и той же плоскости, называются компланарными. Одинаковые по модулю коллинеарные векторы, направленные в одну и ту же сторону, считаются равными друг другу’). Равные по модулю коллн- неарные векторы, имеющие противоположные направления, считаются отличающимися друг от друга по знаку.
Равные по модулю коллн- неарные векторы, имеющие противоположные направления, считаются отличающимися друг от друга по знаку.
Так, 6 например, между векторами, изображенными на рис. 6, и их модулями имеются следующие соотношения: А=В; А= — С; В= — С; А=в-С нли )А)=!В!=~С1 Рис. 6. Рис. 7. несколько подробнее. Пусть нам даны два вектора А и В (рнс. 7,а). Чтобы получить результирующий век- ‘) Имеются в виду так называемые свободные векторы, т. е. векторы, которые могут быть отложены из любой точки пространства. Кроме свободных, бывают скальзяпгие векторы, начало которых может снользить по прямой, прохадяпьей через вентор, н связанные векторы, т. е, векторы, прилаженные к определенной тачке. Последние два вида векторов могут быть выражены через свободные векторы; па атой причине в основу векторного исчисления по.
ложена понятие свободного вектора, называемого обычно просто векторам. Сложение векторов. О том, как складываются два вектора в результирующий вектор, была уже речь в предыдущем параграфе. Рассмотрим теперь этот вопрос тор С, перенесем вектор В параллельно самому себе так, чтобы его начало оказалось совмещенным с концом вектора А’) (рис. 7,6). Тогда вектор С, проведенный из начала вектора А в конец вектора В, будет представлять собой результирующий вектор: С=А+ В.
Рассмотрим теперь этот вопрос тор С, перенесем вектор В параллельно самому себе так, чтобы его начало оказалось совмещенным с концом вектора А’) (рис. 7,6). Тогда вектор С, проведенный из начала вектора А в конец вектора В, будет представлять собой результирующий вектор: С=А+ В.
Можно, однако, осуществить построение несколько иным способом (рис. 7,в). Перенесем вектор В (или А) так, чтобы начала обоих векторов оказались совмещенными. Затем построим на векторах А и В параллелограмль Диагональ этого параллелограмма, очевидно, совпадает с вектором С, полученным по способу, показанному на рис. 7,6. По этой причине иногда говорят, что векторы складываются по правилу параллелограмма. Оба рассмотренных способа — 6) и в) — дают одинаковый результат. Однако в случае сложения более чем двух векторов способ 6) оказывается более простым и удобным.
Пусть даны векторы А, В, С и 0 (рис. 8). Перенесем векторы параллельно самим себе таким образом, б) в) Рис. 8. чтобы начало последующего вектора оказалось совмещенным с концом предыдущего.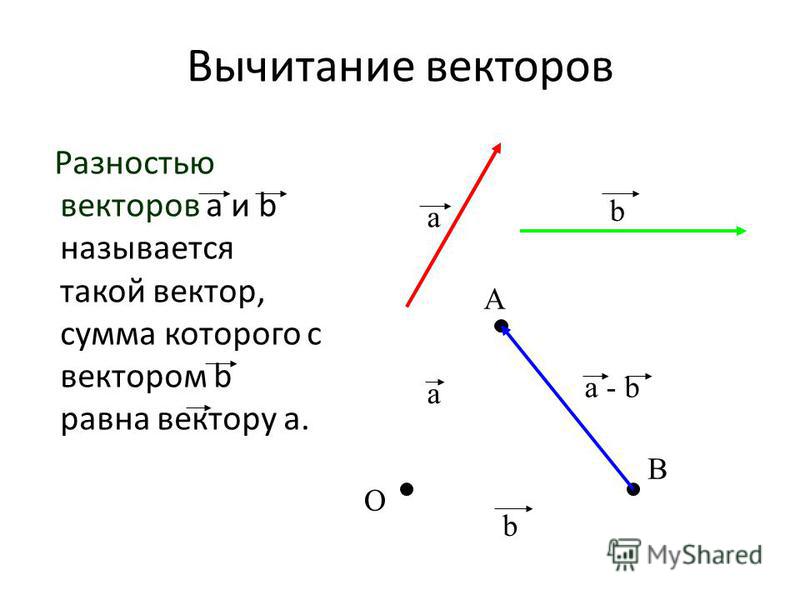 Получится ломаная линия. Результирующий вектор будет представлять собой вектор Е, проведенный из начала первого из слагаемых векторов А в конец последнего )). Легко убедиться в том, что результирующий вектор Е не завислп от последовательности, в которой складываются заданные векторы. г(а рис. 8, 6 показан случай Е = А + В + С + О, а на рис.
Получится ломаная линия. Результирующий вектор будет представлять собой вектор Е, проведенный из начала первого из слагаемых векторов А в конец последнего )). Легко убедиться в том, что результирующий вектор Е не завислп от последовательности, в которой складываются заданные векторы. г(а рис. 8, 6 показан случай Е = А + В + С + О, а на рис.
8,в — случай Е = л) + В + С + А. ‘) Такой перенос можно рассматривать как замену вектора В равным ему вектором, имеющим начало, совпадающее с концом вектора Аь Вычитание векторов, Разностью двух векторов А — В называется такой вектор С, который в сумме с векто- Ряс. иь Ряс. з. ром В дает вектор А (рис. 9). Поскольку разность А — В может быть представлена в виде А — В=А+( — В), вектор С = А — В можно получить, сложив вектор А с вектором, равным по величине вектору В, но имеющим противоположное ему направление. На рис.
! 0 сопоставлены сумма и разность векторов А н В. Разложение векторов иа,составляющие. М Каждый вектор А модг жно заменить несколькими векторами Аь Аг и т. д., которые в сум- А,, ме дают вектор А. $ В этом случае векторы Аь Аг и т.д. называкп- Ю ся составляющими векрис.
д., которые в сум- А,, ме дают вектор А. $ В этом случае векторы Аь Аг и т.д. называкп- Ю ся составляющими векрис.
!!. тора А. Саму операпню замены вектора А не- сколькими векторами называют разложением вектора А на составляющие. На рис. 11 показано разложение век- тора А на составляющие, имеющие направления пря- моугольных координатных осей, Символами А„, А„, А, обозначены составляющие вектора А по осям х, у и Проекция вектора иа ось. Пусть нам даны вектор А и некоторое направление в пространстве (ось), которое мы обозначим, например, буквой и (рис.
12). Проведем через начало и конец вектора А плоскости, перпендикулярные к направлению и. Точки 1′ и 2′, в которых пересекаются эти плоскости с осью и, называются проекциями начала и конца вектора А на ось н. Величина отрезка оси, заключенного между плоскостями, называется проекцией вектора А на направление (илн на ось) и. Проекция вектора — скаляр. Если направление от точки 1′ к точке 2′ совпадает с направлением и, проекция считается положительной; в противном случае проекция отрица- л 1 тельна.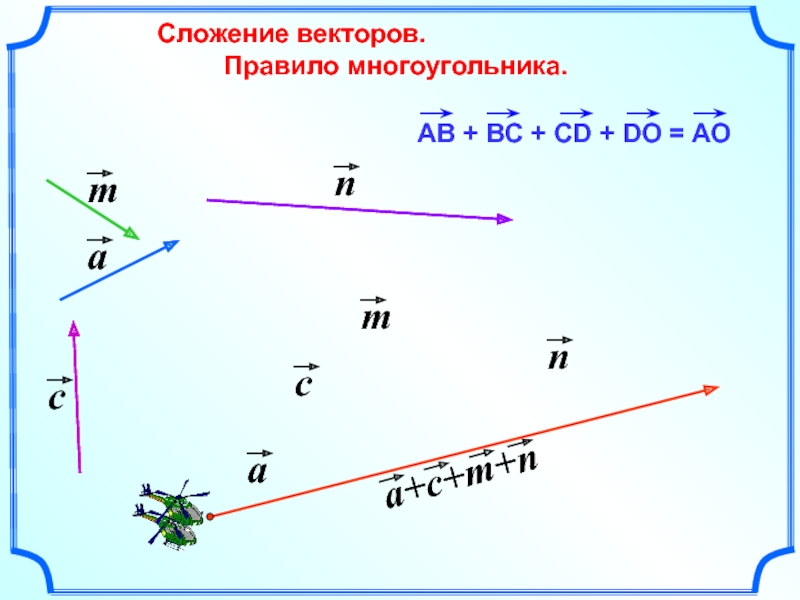
Проекция обозначается той же буквой, что и сам вектор, ‘ У с добавлением индекса, обозна- гз чающего то направление, на которое спроектирован вектор. Например, проекция вектора А на Рис. 12. направление а обозначается А„. Введем в рассмотрение угол <р, который образует вектор А с осью и (рис. 12).
Проекция Ав, очевидно, может быть вычислена следующим образом: А„= А соз <р, (2.1) где А — модуль вектора А. Если вектор образует с данным направлением острый угол, косинус этого угла положителен, проекция вектора также положительна. Если вектор образует с осью тупой угол, косинус этого угла отрицателен, проекция также отрицательна. Если вектор перпендикулярен к данной оси, проекция его равна нулю. На рис. 13 показаны проекции нескольких векторов на координатные оси к и у.
Для этих проекций имеют место следующие соотношении: А„=С )О, В„<0; А„=В„>О, С„<0. Если вектор А образует с осями х, у и г углы я, р и у, то его проекции будут равны: (2.2) 2 И. В. Савельев. т. 1 А =А сова, А„=Асозй, А,= А сову, Легко понять„что по ааданным проекциям вектора на три координатные оси может быть построен сам вектор. Следовательно, всякий вектор может быть определен тремя числами — проекциями его на оси координат. Напомним, что скаляр задаетсн одним числом.
т. 1 А =А сова, А„=Асозй, А,= А сову, Легко понять„что по ааданным проекциям вектора на три координатные оси может быть построен сам вектор. Следовательно, всякий вектор может быть определен тремя числами — проекциями его на оси координат. Напомним, что скаляр задаетсн одним числом.
У Рассмотрим сумму нескольких векторов Е = = А+ В+ С+Р (ркс. 14). Очевидно, что Ек=.йх+~.к+Се+ ~’х. (2.3) т. е. проекция суммы векторов на некоторое направление равна сумме проекций слагаемых векторов на т. же направление. !В Радиус-вектор. Радиусом-вектором тачки называется вектор, проведенный из начала координат в данную точку (рис. 15). Радиус-вектор г однозначно определяег положение точки в пространстве. Его проекции на координатные ося равны, как видно из рисунка, декартовым координатам точки: х» га р гд а (2.
4) Квадрат модуля вектора г равен сумме квадратов координат: г’= ха+уз+аз. (2.5) Умножение вектора ф на скаляр. В результате умножения вектора А на скаляр а получается новый вектор В, модуль которого в 1а~ раз боль* Рис.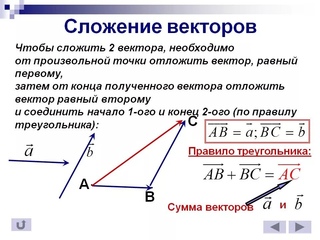 15. ше модуля вектора А, а направление совпадает с направлением А, если скаляр а положителен, и противоположно ему, если скаляр а отрицателен.
15. ше модуля вектора А, а направление совпадает с направлением А, если скаляр а положителен, и противоположно ему, если скаляр а отрицателен.
Сумма двух векторов. Законы сложения векторов. Сумма нескольких векторов. Правило параллелограмма. Вычитание векторов 9
Тема 24.
Сумма векторов. Разность векторов.
Рассмотрим пример. Пусть материальная точка переместилась из точки A в точку B, а затем из точки B в точку C. В результате этих перемещений, которые можно представить векторами AB⃗ и BC⃗, материальная точка переместилась из точки A в точку C. Поэтому результирующее перемещение можно представить вектором AC⃗. Поскольку перемещение из точки A в точку C складывается из перемещения из A в B и перемещения из B в C, то вектор AC⃗ естественно назвать суммой векторов AB⃗ и BC⃗:AC⃗=AB⃗+BC⃗.
Рассмотренный пример приводит нас к понятию суммы двух векторов.
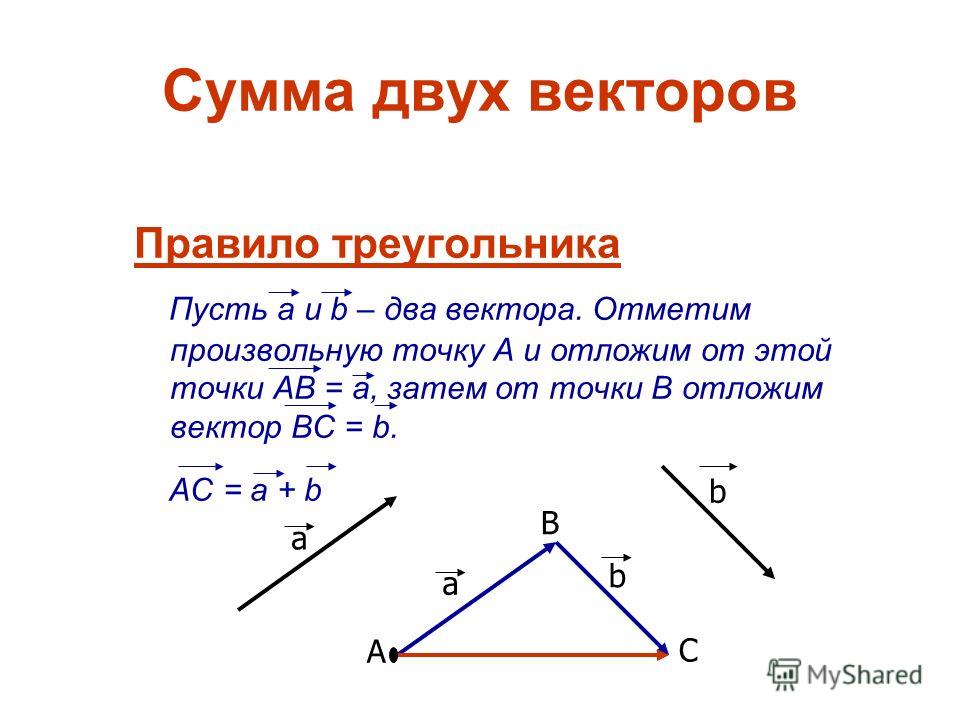
Пусть a⃗ и b⃗ – два вектора. Отметим произвольную точку A и отложим от этой точки вектор AB⃗ равный a⃗. Затем от точки B отложим вектор BC⃗, равный b⃗. Вектор AC⃗ называется суммой векторов a⃗ и b⃗. Это правило сложения векторов называется правилом треугольника. Рисунок это поясняет.
Сумма векторовa⃗ и b⃗ обозначается так: a⃗+b⃗.
Складывая по правилу треугольника произвольный вектор a⃗ с нулевым вектором, получаем, что для любого вектора a⃗ справедливо равенство
a⃗+0⃗=a⃗
Правило треугольника можно сформулировать также следующим образом: если
Это равенство справедливо для произвольных точек A, B и C, в частности, в том случае, когда две из них или даже все три совпадают.
Теорема
Для любых векторов a⃗,b⃗ и c⃗ справедливы равенства:
1. a⃗+b⃗=b⃗+a⃗ (переместительный закон).
a⃗+b⃗=b⃗+a⃗ (переместительный закон).
2. a⃗+b⃗+c⃗=a⃗+b⃗+c⃗ (сочетательный закон).
Докажем первое равенство. Рассмотрим случай, когда векторы a⃗ и b⃗ не коллинеарны. От произвольной точки A отложим векторы ABAD и на этих векторах построим параллелограмм ABCD. По правилу треугольника AC⃗=AB⃗+BC⃗=a⃗+b⃗. Аналогично AC⃗=AD⃗+DC⃗=b⃗+a⃗. Отсюда следует, что a⃗+b⃗=b⃗+a⃗.
При доказательстве первого свойства мы обосновали так называемое правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы a⃗ и b⃗, нужно отложить от какой-нибудь точки A векторы AB⃗=a⃗ и AD⃗=b⃗ и построить параллелограмм ABCD. Тогда вектор AC⃗ равен a⃗+b⃗. Правило параллелограмма часто используется в физике, например при сложении двух сил.
Сложение нескольких векторов производится следующим образом: первый вектор складывается со вторым, затем их сумма складывается с третьим вектором и т.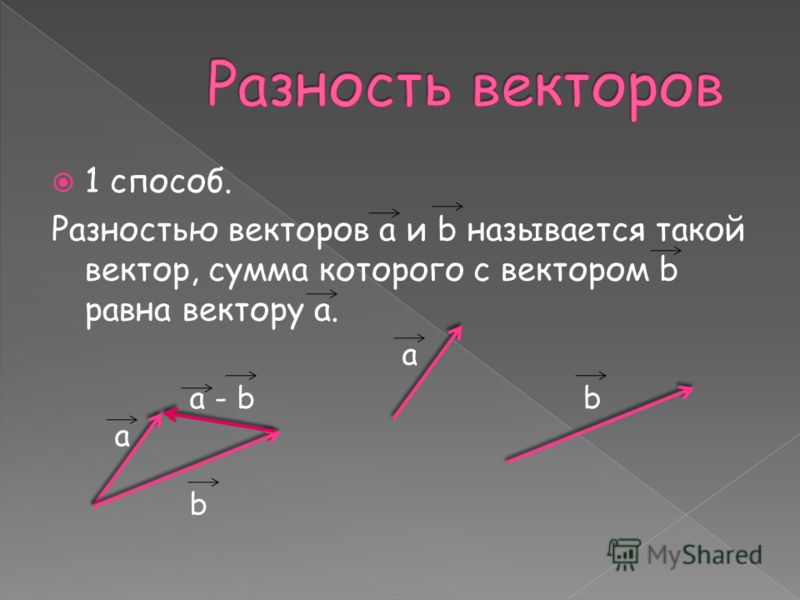 д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Например, от произвольной точки A отложен вектор AB⃗=a⃗, затем от точки B отложен вектор BC⃗=b⃗ и, наконец, от точки С отложен вектор CD⃗=c⃗. В результате получается вектор AD⃗=a⃗+b⃗+c⃗.
д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Например, от произвольной точки A отложен вектор AB⃗=a⃗, затем от точки B отложен вектор BC⃗=b⃗ и, наконец, от точки С отложен вектор CD⃗=c⃗. В результате получается вектор AD⃗=a⃗+b⃗+c⃗.
Аналогично можно построить сумму четырех, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется
Разностью векторов a⃗ и b⃗ называется такой вектор, сумма которого с вектором b⃗ равна вектору a⃗.
Разность векторов a⃗ и b⃗ обозначается так:a⃗-b⃗.
Рассмотрим задачу о построении двух векторов.
Даны векторы a⃗ и b⃗. Построить вектор a⃗-b⃗.
Отметим на плоскости произвольную точку O и отложим от этой точки векторы OA⃗=a⃗ и OB⃗=b⃗.
По правилу треугольника OB⃗+BA⃗=OA⃗ или b⃗+BA⃗=a⃗.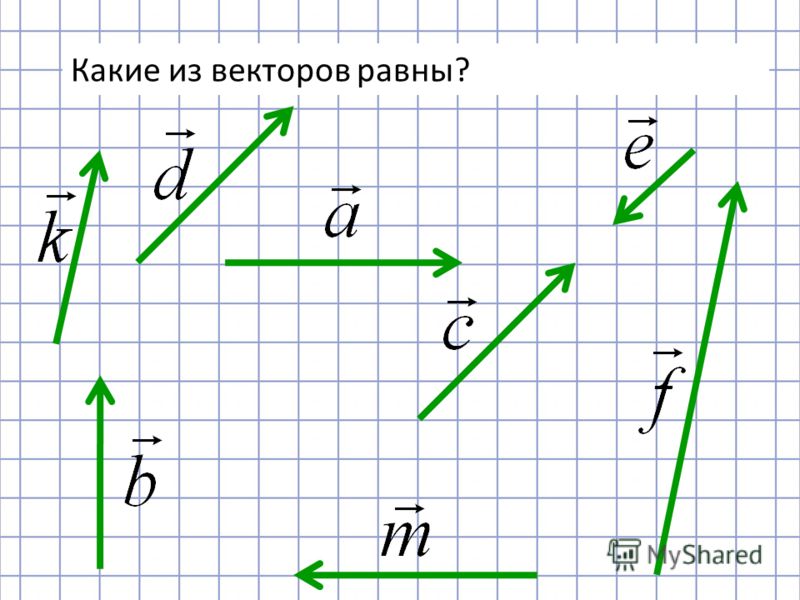 Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗. По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.
Таким образом, сумма векторов BA⃗ и b⃗ равна a⃗. По определению разности векторов это означает, что BA⃗=a⃗-b⃗, то есть вектор BA⃗ искомый.
Пусть a⃗ – произвольный ненулевой вектор. Вектор a1⃗ называется противоположным вектору a⃗, если векторы a⃗ и a1⃗ имеют равные длины и противоположно направлены.
Вектор, противоположный вектору a⃗, обозначается так: -a⃗. Очевидно, что a⃗+-a⃗=0⃗.
Теорема
Для любых векторов a⃗ и b⃗ справедливо равенство a⃗-b⃗=a⃗+-b⃗.
Сегодня мы научились складывать и вычитать векторы. Узнали правило треугольника, правило параллелограмма и правило многоугольника.
Скалярное произведение векторов
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:a · b = |a| · |b| cos α
Алгебраическая интерпретация.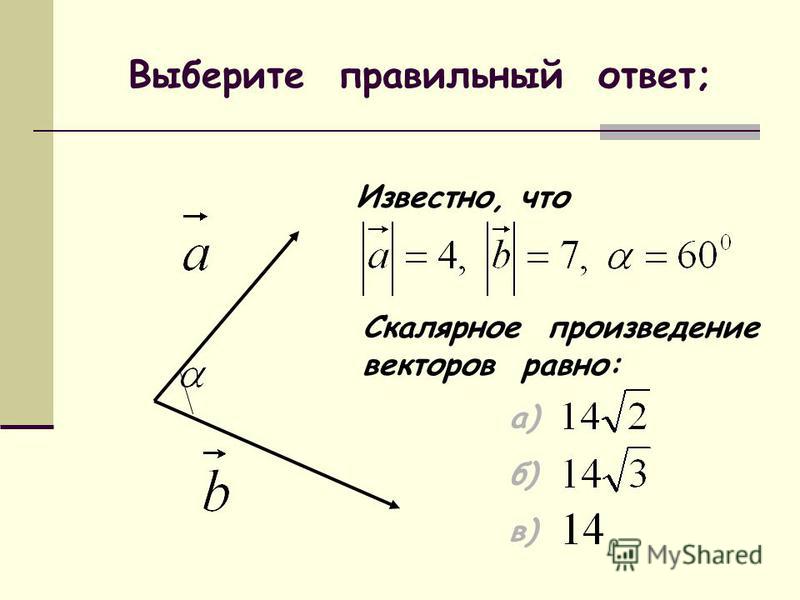 Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; a
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; . .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b == 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Решение: Запишем вектора a и b через ортонормированные базисные вектора
b = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.
Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
Глава 30. Линейные операции над векторами
Глава 30. Линейные операции над векторами
Суммой двух векторов и называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правильно треугольника). Построение суммы изображено на рис. 1.
Наряду с правилом треугольника часто
пользуются (равносильным ему) правилом
параллелограма: если векторы
и
приведены к
общему началу и на них построен параллелограмм,
то сумма
есть вектор, совпадающий с диагональю
этого паралеллограмма, идущей из общего начала
и
(рис. 2). Отсюда сразу следует, что
.
2). Отсюда сразу следует, что
.
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов , , , ).
Разность двух векторов и называется вектор, который в сумме с вектором составляет вектор . Если два вектора и приведены к общему началу, то разность их есть вектор, идущий из конца («вычитаемого») к концу («уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом , то другой обозначается символом . Легко видеть, что . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
Произведение
(или также
)
вектора
на число
называется
вектор, модуль которого равен произведению
модуля вектора
на модуль числа
; он параллелен
вектору
или лежит с ним на одной прямой и
направлен так же, как вектор
, если
—
число положительное, и противоположно вектору
,
если
— число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:
2). При умножении вектора на число его проекция умножается на то же число:
.
В частности, если
, ,
то
,
и
.
Если , то для любого числа
.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
, ,
является пропорциональность их координат:
.
Тройка векторов , , называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
1). Вектор лежит на оси Ох, вектор — на оси Оу, вектор — на оси Oz;
2). Каждый из векторов , , направлен по своей оси в положительную сторону;
3). Векторы , , единичные, то есть , , .
Каким бы ни был вектор , он всегда может быть разложен по базису , , , то есть может быть представлен в виде
;
коэффициенты этого разложения являются координатами вектора (то есть X, Y, Z суть проекции вектора на координатные оси).
| 761 | По данным векторам и построить
каждый из следующих векторов: 1). , 2). , 3). , 4).
. , 2). , 3). , 4).
. | |
| 762 | Даны =13, =19 и =24. Вычислить . | |
| 763 | Даны =11, =23 и =30. Определить . | |
| 764 | Векторы и взаимно перпендикулярны, причем =5, =12. Определить и . | |
| 765 | Векторы и образуют угол =600, причем=5 и =8. Определить и . | |
| 766 | Векторы и образуют угол =1200, причем =3 и =5. Определить и . | |
| 767 | Какому условию должны удовлетворять векторы и , чтобы имели место следующие соотношения: | |
767. 1 1 | ; | |
| 767.2 | ; | |
| 767.3 | . | |
| 768 | Какому условию должны удовлетворять векторы и , чтобы вектор делил пополам угол между векторами и . | |
| 769 | По данным векторам и построить каждый из следующих векторов: | |
| 769.1 | ; | |
| 769.2 | ; | |
769. 3 3 | ; | |
| 769.4 | . | |
| 770 | В треугольнике АВС вектор и вектор . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы , построить также векторы: | |
| 770.1 | ; | |
| 770.2 | ; | |
| 770.3 | ; | |
| 770.4 | ; | |
770. 5 5 | ; | |
| 770.6 | . | |
| 771 | Точка О является центром масс треугольника АВС. Доказать, что . | |
| 772 | В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его ребрами: , , , , . Построить векторы: | |
| 772.1 | ; | |
| 772.2 | ; | |
772. 3 3 | . | |
| 773 | В параллелепипеде ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с его ребрами: , , . Построить каждый из следующих векторов: | |
| 773.1 | ; | |
| 773.2 | ; | |
| 773.3 | ; | |
| 773.4 | ; | |
| 773.5 | . | |
| 774 | Три силы , , , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей , если известно, что =2Н, =10Н, =11Н. | |
| 775 | Даны два вектора ={3; -2; 6}, ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов: | |
| 775.1 | ; | |
| 775.2 | ; | |
| 775.3 | ; | |
775. 4 4 | ; | |
| 775.5 | ; | |
| 775.6 | . | |
| 776 | Проверить коллинеарность векторов ={2; -1; 3} и ={-6; 3; -9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 777 | Определить, при каких значениях , векторы и коллинеарны. | |
| 778 | Проверить, что
четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат
вершинами трапеции. | |
| 779 | Даны точки A(-1; 5; -10}, B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы и коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 780 | Найти орт вектора ={6; -2; -3}. | |
| 781 | Найти орт вектора ={3; 4; -12}. | |
| 782 | Определить модули суммы и разности векторов ={3; -5; 8} и ={-1; 1; -4}. | |
| 783 | Дано разложение
вектора по базису , , : . Определить
разложение по этому же базису вектора , параллельного
вектору и противоположного с ним
направления, при условии, что =75. Определить
разложение по этому же базису вектора , параллельного
вектору и противоположного с ним
направления, при условии, что =75. | |
| 784 | Два вектора ={2; -3; 6} и ={-1; 2; -2} приложены к одной точке. Определить координаты вектора направленного по биссектрисе угла между векторами и , при условии, что . | |
| 785 | Векторы ={2; 6; -4} и ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. | |
| 786 | Доказать, что если и
— какие угодно неколлинеарные
векторы, то всякий вектор, лежащих в их плоскости,
может быть представлен в виде . Доказать,
что числа и однозначно определяются векторами , и . Доказать,
что числа и однозначно определяются векторами , и . | |
| 787 | На плоскостиданы два вектора ={2; -3}, ={1; 2}. Найи разложение вектора ={9; 4} по базису , . | |
| 788 | На плоскости даны три вектора ={3; -2}, ={-2; 1}, ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других. | |
| 789 | Даны три вектора ={3; -1}, ={1; -2}, ={-1; 7}. Определить разложение вектора по базису , . | |
| 790 | Принимая в качестве
базиса векторы и , совпадающие
со сторонами треугольника АВС, опреедлить
разложение векторов, приложенных в вершинах
треугольника и совпадающие с его медианами. | |
| 791 | На плоскости даны етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить разложение векторов , , и , принимая в качестве базиса векторы и . | |
| 792 | Доказать, что если , , — какие угодно некомпланарные векторы, то всякий вектор пространства может быть представлен в виде . Доказать, что числа , , однознчно определяются векторами , , , . (Представление вектора в виде называется разложением его по базису , , . Числа , , называются коэффициентами этого разложения. | |
| 793 | Даны три вектора ={3; -2; 1}, ={-1; 1; -2}, ={2; 1; -3}. Найти разложение вектора ={11; -6; 5} по базису , , .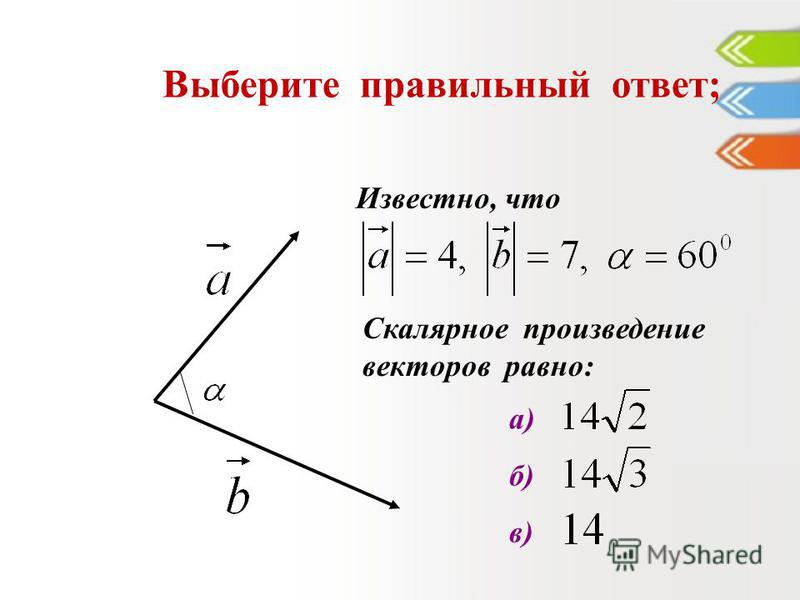 | |
| 794 | Даны четыре вектора ={2; 1; 0}, ={1; -2; 2}, ={2; 2; -1}, ={3; 7; -7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных. |
Дидактический материал по Геометрии 9 класс.
Самостоятельная работа 9кл урок 8
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с . Постройте векторы k+ с, k – p.
Постройте векторы k+ с, k – p.
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
1. Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Самостоятельная работа 9кл урок 8
Вариант 1
1. Начертите неколлинеарные вектора а, b, с . Постройте векторы а + с, с – b.
2. В равнобедренном треугольнике АВС точка В1 – середина основания АС.
а) Упростите выражение ВВ1 – АВ – В1С.
б) Найдите / ВВ1 – АВ – В1С / , если АВ=10см, ВВ1= 8см.
3. Найдите вектор РО – х = РМ
Самостоятельная работа 9кл урок 8
Вариант 2
1. Начертите неколлинеарные вектора p, k, с . Постройте векторы k+ с, k – p.
2. В равнобедренном треугольнике АВС , с основанием АВ проведена медиана СС1
а) Упростите выражение ВС1 – АС + АВ,
б) Найдите / ВС1— АС + АВ /, если АС=5см, АВ=6см.
3. Найдите вектор х – МА =РМ
Самостоятельная работа 9кл урок 10 стр 54
Вариант 1.
1. Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
Начертите вектор х такой что, /х /= 2см. Постройте векторы 3 х, -2 х, 1/2х,
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ= 2:1, О- точка пересечения диагоналей. Выразите векторы ОС и СК через векторы а=АВ, и b= АД.
Самостоятельная работа 9кл урок 10 стр 54
Вариант 2.
1. Начертите вектор а , абсолютная величина которого равна 3см. Постройте векторы 2а , -а, 1/3а.
2. В параллелограмме АВСД на стороне ВС взята точка Р так, что ВР:РС=3:1 , О- точка пересечения диагоналей . Выразите векторы АО и РА через векторы х=АВ и у=АД.
Урок 21 Геометрия 9кл
Самостоятельная работа
1 вариант
1.Окружность задана уравнением (х+5)2+(у-4)2=49.
а) Укажите центр окружности
б) Какие из точек А(2;4), В(1;3), С(-5;-3) лежат на данной окружности.
в) Найдите точку с абциссой -12 , лежащей на данной окружности.
2. Напишите уравнение окружности с центром С и радиусом r: если
а) С(-3;2), r= √ 3 . б) С(0;-6) , r= 4√5.
Самостоятельная работа 9 класс 27урок
Найдите sinA, если 1 вариант cosA= -1/3 2 вариант cosA=-1/4
2. Найдите cosA, если 1 вариант sinA= 2/5 2вариант sinA=-2/3
Проверьте, лежат ли на единичной окружности точки:
1 вариант В(7;3),С(0,5;0,5) 2 вариант С(2;3), В(-0,5;0,5)
4. Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен А. Найдите координаты точки М, если
1 вариант ОМ=8, <А=30° 2 вариант ОМ=10, <А=60°
Самостоятельная работа 9кл
По теме : Решение треугольников
1. Дано: △АВС , <А=450 , < С=150 , ВС= 4√6 .
Найти: АВ , АС , < В
2. Дано : △MNK , MN=6см , MK=10см, <M=1200.
Найти : NK , <N , <K.
3. Дано : △ ОРТ , ОР=24 , РТ=30, ОТ=36.
Найти: <О , <Р, <Т.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
1 вариант
1. Площадь параллелограмма равна 30V3 см2, а один из углов равен 600. Найдите его периметр, если длина одной из сторон равна 6см.
2. В треугольнике MNK MN=NK , MK=V2 , 0, MA- ,биссектриса. Найдите МА.
3. Стороны треугольника равны 8, 10 и 12см. Найдите угол, лежащий против меньшей стороны.
Самостоятельная работа 9 кл урок 33
Тема Решение треугольников
2 вариант
1. Площадь параллелограмма равна 40V2 см2 , а один из углов равен 450 . Найдите его периметр , если длина одной из сторон равна 10см.
2. В треугольнике СДЕ СМ- биссектриса , <ДСЕ=600 , МЕ= 3V2. Найдите СМ, если < СЕД =450.
3. Стороны треугольника равны 6, 9 и 10 см. Найдите угол , лежащий против большей стороны.
Самостоятельная работа 9кл. по геометрии
По теме Правильный многоугольник
1. Найдите углы правильного шестнадцатиугольника .
2. Каждый угол правильного многоугольника равен 1620 . Найдите число его сторон.
3. Чему равен внешний угол правильного восемнадцатиугольника .
4. Внешний угол правильного многоугольника равен 150.Найдите число его сторон.
5. Является ли равнобедренный треугольник с углом при вершине в 600 правильным.
6. Является ли ромб с равными диагоналями правильным четырехугольником .
Самостоятельная работа по геометрии 9кл
По теме Формулы для вычисления площади правильного многоугольника его стороны и радиуса вписанной окружности.
Вариант 1
1. Найдите углы правильного восемнадцатиугольника .
2. Угол правильного n-угольника равен 1080. Вычислите количество его сторон .
3. Сколько сторон имеет правильный вписанный многоугольник , если дуга описанной окружности , которую стягивает его сторона , равна 450.
Урок 44 9класс стр 228
Самостоятельная работа
1 вариант
1. Найдите длину окружности с радиусом 5см. Чему равна длина ее дуги с градусной мерой 360.
2. Длина окружности, описанной около квадрата , равна 12П см. Найдите длину окружности, вписанной в этот квадрат.
Урок 44 9класс стр 228
Самостоятельная работа
2 вариант
1. Найдите длину окружности с радиусом 9см. Чему равна длина ее дуги с градусной мерой 200.
2. Длина окружности , вписанной в правильный треугольник, равна 2√3 П см. Найдите длину окружности, описанной около этого треугольника.
Найдите длину окружности, описанной около этого треугольника.
Самостоятельная работа по геометрии 9кл.
По теме Площадь круга и кругового сектора урок 45
1. Найдите длины дуг , на которые разбивают окружность два радиуса . Угол между радиусами равен 1200, радиус окружности равен 6дм.
2. Найдите длину окружности , в которую вписан квадрат со стороной 5см.
Самостоятельная работа по геометрии 9кл
По теме Длина окружности . Площадь круга.
1 вариант
1. Длина окружности равна 8 П. Вычислите площадь круга , ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 6см. равна 300. Вычислите площадь кругового сектора , соответствующего этой дуге .
Самостоятельная работа по геометрии 9кл
По теме Длина окружности . Площадь круга.
2вариант
1. Длина окружности равна 10П . Вычислите площадь круга , ограниченного данной окружностью.
Длина окружности равна 10П . Вычислите площадь круга , ограниченного данной окружностью.
2. Градусная мера дуги окружности с радиусом 4см равна 450. Вычислите площадь кругового сектора , соответствующего этой дуге.
Самостоятельная работа 9кл урок 53
1 вариант
1.Дан четырехугольник АВСД. Постройте фигуру , симметричную данной:
а) относительно вершины Д б) относительно диагонали АС
2. Докажите , что при движении квадрат отображается в квадрат.
Самостоятельная работа 9кл урок 53
2 вариант
1. Дан четырехугольник АВСД. Постройте фигуру , симметричную данной:
а) относительно вершины А б) относительно диагонали ВД
2.Докажите , что при движении прямоугольник отображается на прямоугольник.
Самостоятельная работа
По геометрии 9кл ур.55
1. В прямоугольном треугольнике АВС ,СК-биссектриса , точки М и Н лежат на СК так , что М лежит между С и Н . Постройте образ треугольника АВС при параллельном переносе на вектор МН .
Постройте образ треугольника АВС при параллельном переносе на вектор МН .
2. Постройте образ треугольника АВС при параллельном переносе на вектор а.
3. Укажите координаты точек А1,В1, если известно , что они являются образами точек А(2;5) , В(-1;-3) при параллельном переносе на вектор а {-3;2}.
Самостоятельная работа
По геометрии 9кл ур.58
1.В результате параллельного переноса точка А(-1;3) переходит в точку А1 (2;4) , а точка В(1;-3) в точку В1.
2. При осевой симметрии относительно координатной оси Оу точка А переходит в точку А1 , а точка В в точку В1 . Найдите координаты точек А1 и В , если А(-2;5) , В1(-3;-8).
3. При центральной симметрии относительно начала координат четырехугольник АВСД
переходит в четырехугольник А1В1С1Д1. Найдите координаты точек А,В,С,Д, если
А1(-6;-1) ,В1(-5;-8), С1(-1;-6) ,Д1(0;0) .
4. В результате поворота вокруг начала координат точка А(4;0) перешла в точку А1(0;4). Найдите точку , в которую перейдет точка А в результате поворота на 300 , 450 ,1200 вокруг того же центра и в том же направления.
5. Какое наименьшее число вершин может иметь многоугольник , у которого есть две оси симметрии , пересекающиеся под углом 300.
Самостоятельная работа
Длина окружности и площадь круга
Вариант 1
1. Вычислите радиус окружности, длина которой равна сумме длины окружности с радиусом 9 см и длины дуги окружности с радиусом 20 см и центральным углом 18°.
Ответ: 10 см.
2. В круг вписан прямоугольный треугольник с катетами, равными 8 см и 15 см. Найдите разность площадей этих фигур.
Ответ:
3. В сектор с центральным углом 90° вписан круг так, что он касается радиусов и дуги. Найдите отношение площади сектора к площади круга.
Найдите отношение площади сектора к площади круга.
Ответ:
Вариант 2
1. Вычислите радиус окружности, длина которой равна разности длины окружности с радиусом 16 см и длины дуги окружности с радиусом 40 см и центральным углом 9°.
Ответ: 15 см.
2. В круг вписан прямоугольный треугольник с катетами, равными 5 см и 12 см. Найдите разность площадей этих фигур.
Ответ:
3. В сектор с центральным углом 120° вписан круг так, что он касается радиусов и дуги. Найдите отношение площади сектора к площади круга.
Ответ:
Решение треугольников
Вариант 1
А1. Найдите площадь равнобедренного △, если его боковая сторона равна 1 м, а угол при вершине равен 45о.
А2. В △ АВС АС = 0,59 дм, А = 40о, С = 35о. Вычислите ВС.
Вычислите ВС.
А3. Две стороны △ равны 1,3 и 42,5, < между ними 100о. Вычислите третью сторону △.
Самостоятельная работа 3.2
Решение треугольников
Вариант 2
А1. Найдите площадь равностороннего △ со стороной, равной 1 м.
А2. В △ АВС АС = 15,2 см, А = 25о, С = 80о. Вычислите ВС.
А3. Две стороны △ равны 27,4 и 16,3, < между ними 70о. Вычислите третью сторону △.
Самостоятельная работа Понятие вектора
Вариант 1
1. В выпуклом четырехугольнике ABCD точки K, L, M, N — середины сторон АВ, ВС, CD, DA соответственно. Установите связь между векторами
Ответ:
2. В прямоугольнике ABCD со сторонами АВ = 12 и AD = 10 точка К принадлежит АВ и АК : КВ = 1 : 2, точка L принадлежит CD и CL : LD = 1 : 3. Найдите величину
Ответ: 5√5.
3. В равностороннем треугольнике АВС со стороной а отрезок AD — медиана. Точка Е — середина отрезка BD. Найдите величину
Ответ:
Вариант 2
1. В выпуклом четырехугольнике ABCD точки K, L, M, N — середины сторон АВ, ВС, CD, DA соответственно. Установите связь между векторами
Ответ:
2. В прямоугольнике ABCD со сторонами АВ = 20 и AD = 12 точка К принадлежит АВ и АК : КВ = 2 : 3, точка L принадлежит CD и CL : LD = 1 : 4. Найдите величину
Ответ: 4√13.
3. В равностороннем треугольнике АВС со стороной а отрезок AD — медиана. Точка Е принадлежит BD и ВЕ : ED = 1 : 2. Найдите величину
Ответ:
Самостоятельная работа по теме векторы 9 класс
Вариант 1
На рисунке от точки А отложите вектор:
а) равный вектору а;
б) сонаправленный вектору b;
в) противоположно направленный вектору с.
с
А . а
b
АВСD – ромб. Равны ли векторы:
а) АВ и СD;
б) ВС и DА;
в) АВ и АD.
Самостоятельная работа
Вариант 2
На рисунке от точки В отложите вектор:
а) равный вектору b;
б) сонаправленный вектору с;
в) противоположно направленный вектору а.
B .
a
b
c
АВСD – квадрат. Равны ли векторы:
а) ВА и DС;
б) ВС и АD;
в) DА и DС.
Самостоятельная работа по теме «Векторы»
Вариант 1
1)Постройте векторы , такие, что векторы неколлинеарны. Постройте: а) б) в)
2)Точки M и N – середины сторон AB и AC △ ABC. Выразите через векторы а) , б) , в) г) , д) , где S – середина BC .
Самостоятельная работа по теме «Векторы»
Вариант 2
1)Постройте векторы , такие, что векторы неколлинеарны. Постройте: а) б) в) .
Постройте: а) б) в) .
2)Точка B1 – середина стороны AC △ ABC. Выразите через векторы а) , б) , в) г) , д) , где K – середина BB1 .
Сложение и вычитание векторов.
Вариант 1.
Постройте четыре попарно неколлинеарных вектора . Постройте а) по правилу треугольника б) по правилу параллелограмма
в) г) двумя способами д) е)
Сложение и вычитание векторов.
Вариант 2.
Постройте четыре попарно неколлинеарных вектора . Постройте а) по правилу треугольника б) по правилу параллелограмма
в) г) двумя способами д) е)
Координаты вектора.
Вариант 1
1.Даны векторы . а) Найдите координаты вектора . б) Запишите разложение вектора по единичным векторам . в) Найдите длину вектора . г) Найдите координаты вектора противоположного вектору .
2. Среди векторов найдите пары коллинеарных. 3. В параллелограмме ABCD . Точки M и N лежат на сторонах BC и СD соответственно так, что BM=MC, CN : ND=3 : 1. Найдите координаты вектора .
3. В параллелограмме ABCD . Точки M и N лежат на сторонах BC и СD соответственно так, что BM=MC, CN : ND=3 : 1. Найдите координаты вектора .
Координаты вектора. Вариант 2
1.Даны векторы . а) Найдите координаты вектора . б) Запишите разложение вектора по единичным векторам . в) Найдите длину вектора . г) Найдите координаты вектора противоположного вектору .
2. Среди векторов найдите пары коллинеарных. 3. В параллелограмме ABCD . Точки K и P лежат на сторонах AB и AD соответственно так, что AP=PD, AK : KB=2 : 1. Найдите координаты вектора .
Самостоятельная работа
Скалярное произведение векторов
Вариант 1
А1. Даны точки А(2; 4), В(5; 8), С(-7; -1), D(5; 8). Найдите скалярное произведение векторов .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 60о.
Самостоятельная работа
Скалярное произведение векторов
Вариант 2
А1. Даны точки А(2; 4), В(-1; 6), С(-4; -2), D(3; 2). Найдите скалярное произведение векторов и .
А2. Даны векторы . Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов, если , а угол между ними равен 30о.
Самостоятельная работа Простейшие задачи в координатах
Вариант 1
1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ACD. Найдите
Ответ:
2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (−3; 5) и В (6; 4).
Ответ: (1; 0) и (0; −9).
3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (0; 1), В (1; −4), С (5; 2).
Ответ: S = 13.
Вариант 2
1. Вершины треугольника АВС имеют координаты А (−4; 2), В (2; −8), С (10; 16). Отрезок AD — медиана треугольника АВС, а АЕ — медиана треугольника ABD. Найдите
Ответ:
2. На осях координат найдите точки, равноудаленные от концов отрезка АВ, если А (4; −3) и В (8; 1).
Ответ: (5; 0) и (0; 5).
3. Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты А (−4; 1), В (−2; 4), С (1; 2).
Ответ: S = 6,5.
Метод координат.
Вариант 1
1. Вершины треугольника ABC имеют координаты A(-5; 13), B(3; 5), C(-3; -1). Найдите: а) медиану, проведенную к стороне AC б) среднюю линию, параллельную стороне BC .
2. Четырехугольник ABCD задан координатами его вершин: A(1; 1), B(3; 5), C(9; -1), D(7; -5). а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
3) △MNK задан координатами своих вершин: M(2;N(0;0), K(3;. Найдите углы и площадь △.
Метод координат.
Вариант 2
1. Вершины треугольника ABC имеют координаты A(13; -5), B(5; 3), C(-1; -3). Найдите: а) медиану, проведенную к стороне AC б) среднюю линию, параллельную стороне BC
2. Четырехугольник ABCD задан координатами его вершин: A(-6; 1), B(2; 5), C(4; -1), D(-4; -5). а) Докажите, что ABCD -параллелограмм. б) Найдите координаты середины отрезка CO, где С – точка пересечения диагоналей.
3) Треугольник MNK задан координатами своих вершин: M(4;N(7;3), K(2;. Найдите углы и площадь треугольника.
Самостоятельная работа Уравнение окружности
Вариант1
1. Напишите уравнение окружности, которая проходит через точки А (−7; 8) и В (−3; −4). При этом хорда АВ является диаметром окружности.
При этом хорда АВ является диаметром окружности.
Ответ: (х + 5)2 + (у − 2)2 = 40.
2. Даны окружность, заданная уравнением х2 + у2 − 4х − 5 = 0, и точка А (5; 4). Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Ответ: (х − 5)2 + (у − 4)2 = 4.
3. В квадрат площадью S вписана окружность. Докажите, что сумма квадратов расстояний от любой точки окружности до вершин квадрата есть величина постоянная, и найдите эту величину.
Ответ: 3S.
Вариант 2
1. Напишите уравнение окружности, которая проходит через точки А (−5; 6) и В (−1; 4). При этом хорда АВ является диаметром окружности.
Ответ: (х + 3)2 + (у − 5)2 = 5.
2. Даны окружность, заданная уравнением х2 + у2 − 2у − 8 = 0, и точка А (4; 4). Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Ответ: (х − 4)2 + (у − 4)2 = 4.
3. Около квадрата площадью S описана окружность. Докажите, что сумма квадратов расстояний от любой точки окружности до вершин квадрата есть величина постоянная, и найдите эту величину.
Ответ: 4S.
Самостоятельная работа Уравнение прямой
Вариант1
1. Координаты вершин треугольника А (2; −6), В (4; 2) и С (0; −4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
Ответ: х + у − 1 = 0.
2. Найдите площадь треугольника, ограниченного прямыми, заданными уравнениями у − х = 0, у + х = 0 и у − 2х + 4 = 0.
Ответ: S = 16/3.
3. Прямая 2у + х − 4 = 0 пересекает окружность х2 + у2 = 5. Найдите длину хорды, которая отсекается этой окружностью на прямой.
Найдите длину хорды, которая отсекается этой окружностью на прямой.
Ответ: 6√5/5.
Вариант2
1. Координаты вершин треугольника А (4; −8), В (−2; 6) и С (2; 4). Напишите уравнение прямой, содержащей среднюю линию треугольника, которая параллельна стороне АС.
Ответ: 6х + у − 5 = 0.
2. Найдите площадь треугольника, ограниченного прямыми, заданными уравнениями у + х = 0, у − х = 0 и 2у − х + 6 = 0.
Ответ: S = 12.
3. Прямая у − 3х + 1 = 0 пересекает окружность х2 + у2 = 5. Найдите длину хорды, которая отсекается этой окружностью на прямой.
Ответ: 7√10/5.
Уравнение прямой. Уравнение окружности.
Вариант 1
1. а) Составьте уравнение прямой, проходящей через точки А(4;-1) и В(2;3). б) Лежат ли на этой прямой точки М(1;5) и N(-1;5). в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
2. Окружность задана уравнением . а) Найдите координаты центра окружности и ее радиус. б) Докажите, что отрезок АВ, где А(-1;-1), В(5;17), является хордой окружности. в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
Уравнение прямой. Уравнение окружности.
Вариант 2
1. а) Составьте уравнение прямой, проходящей через точки А(-1;3) и В(3;-5). б) Лежат ли на этой прямой точки М(4;9) и N(4;-7). в) Найдите точки пересечения этой прямой с осями координат. г) Найдите точку пересечения этой прямой и прямой . д) Докажите, что данная прямая параллельна прямой .
2. Окружность задана уравнением . а) Найдите координаты центра окружности и ее радиус. б) Докажите, что отрезок АВ, где А(3;-0), В(6;-1), является хордой окружности. в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
в) Выясните взаимное расположение окружности и прямой . г) Найдите расстояние от центра окружности до этой прямой.
Самостоятельная работа
Уравнение окружности. Уравнение прямой
Вариант 1
А1. Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(3;-5), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением . Напишите уравнения касательных к окружности, которые параллельны оси ординат.
_______________
Самостоятельная работа
Уравнение окружности. Уравнение прямой
Вариант 2
А1. Начертите окружность, заданную уравнением .
Начертите окружность, заданную уравнением .
А2. Запишите уравнение окружности с центром в точке С(-2;4), касающейся оси ординат.
А3. Прямая задана уравнением .
а) Начертите эту прямую.
б) Запишите координаты пересечения прямой с осями координат.
в) Найдите площадь треугольника, образованного осями координат и этой прямой.
________________
В1. Окружность задана уравнением . Напишите уравнения касательных к окружности, которые параллельны оси абсцисс.
Самостоятельная работа
Синус, косинус, тангенс угла
Вариант 1
А1. Стороны прямоугольного треугольника равны 3 см, 4 см и 5 см. Найдите косинус меньшего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Самостоятельная работа
Синус, косинус, тангенс угла
Вариант 2
А1. Стороны прямоугольного треугольника равны 5 см, 12 см и 13 см. Найдите тангенс большего острого угла этого треугольника.
Стороны прямоугольного треугольника равны 5 см, 12 см и 13 см. Найдите тангенс большего острого угла этого треугольника.
А2. Найдите .
А3. Найдите .
А4. Постройте угол
Самостоятельная работа синус, косинус и тангенс угла
Вариант 1
1. Известно, что tg α = − 5/12 и 90° < α < 180°. Найдите значение cos α.
Ответ: − 12/13.
2. Найдите значение выражения
Ответ: 4.
3. Упростите выражение
Ответ: 2.
Вариант 2
1. Известно, что tg α = − 15/8 и 90° < α < 180°. Найдите значение cos α.
Ответ: − 8/17.
2. Найдите значение выражения
Ответ: 6.
3. Упростите выражениеОтвет: −2.
Вписанная окружность — самостоятельная работа
1 вариант
1. Четырёхугольник АВСД описан около окружности. Найдите стороны ВС и АД, если АВ=7см, СД=11см, ВС в 2 раза меньше АД.
Четырёхугольник АВСД описан около окружности. Найдите стороны ВС и АД, если АВ=7см, СД=11см, ВС в 2 раза меньше АД.
2. В равносторонний △ со стороной 8см вписана окружность. Найдите радиус окружности.
Вписанная окружность — самостоятельная работа
2 вариант
1. Четырёхугольник АВСД описан около окружности. Найдите стороны АВ и СД, если ВС=6см, АД=9см, АВ в 2 раза больше СД.
2. В равносторонний △ вписана окружность радиусом 4см. Найдите сторону ∆.
Самостоятельная работа. Вписанная и описанная окружность
Вариант 1
1. Вокруг правильного шестиугольника описана окружность. В этот же шестиугольник вписана окружность. Найдите отношение радиусов этих окружностей.
Ответ: 2√3/3.
2. Вокруг одной и той же окружности описаны правильные треугольник и четырехугольник. Найдите отношение площадей этих фигур.
Найдите отношение площадей этих фигур.
Ответ: 3√3/4.
3. Сторона описанного правильного четырехугольника на 3 больше стороны правильного треугольника, вписанного в ту же окружность. Найдите сторону треугольника.
Ответ: 9 + 6√3.
Вариант 2
1. Вокруг правильного треугольника описана окружность. В этот же треугольник вписана окружность. Найдите отношение радиусов этих окружностей.
Ответ: 2.
2. Вокруг одной и той же окружности описаны правильные четырехугольник и шестиугольник. Найдите отношение площадей этих фигур.
Ответ: 2√3/3.
3. Сторона описанного правильного треугольника на 5 больше стороны правильного четырехугольника, вписанного в ту же окружность. Найдите сторону треугольника.
Ответ: 6 + √6.
Самостоятельная работа. Движение
Движение
Вариант1
1. Треугольник А1В1С1 симметричен треугольнику АВС с вершинами А (−1; 3), В (2; −4), С (4; 1) относительно точки D (7; −1). Найдите координаты вершин А1, В1, С1.
Ответ: А1 (15; −5), В1 (12; 2), С1 (10; −3).
2. Окружность задана уравнением (х + 3)2 + (у − 2)2 = 16. Она повернута на угол 90° против часовой стрелки относительно точки А (−2; 1). Напишите уравнение полученной окружности.
Ответ: (х + 3)2 + у2 = 16.
3. Найдите координаты точки, симметричной точке А (1; 7) относительно прямой, заданной уравнением у = х + 2.
Ответ: (5; 3).
Вариант2
1. Треугольник А1В1С1 симметричен треугольнику АВС с вершинами А (−4; 1), В (1; 3), С (3; −5) относительно точки D (5; −1). Найдите координаты вершин А1, В1, С1.
Найдите координаты вершин А1, В1, С1.
Ответ: А1 (14; −3), В1 (9; −5), С1 (7; 3).
2. Окружность задана уравнением (х + 2)2 + (у − 3)2 = 16. Она повернута на угол 90° по часовой стрелке относительно точки А (−1; 2). Напишите уравнение полученной окружности.
Ответ: х2 + (у − 3)2 = 16.
3. Найдите координаты точки, симметричной точке А (7; 2) относительно прямой, заданной уравнением у = −х + 3.
Ответ: (1; −4).
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
1 вариант
Мальчик прошел от дома по направлению на восток 800м. Затем завернул на север и прошел 600м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов.
 (Используйте таблицу тригонометрических функций)
(Используйте таблицу тригонометрических функций)
Горная железная дорога поднимается на 1 м на каждые 30м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах. В ответе укажите приближенное значение, выраженное целым числом.
Лестница имеет ступеньки, ширина которых30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выраженное целым числом.
С самолета радируют капитану рыболовецкого судна, что самолет находится над косяком рыбы на высоте 1000 м. С судна определяют, что угол, под которым виден самолет над горизонтом, равен 260. Используя таблицу тригонометрических функций, найдите расстояние от судна до косяка рыбы. В ответе укажите приближенное значение, выраженное целым числом.
Использую данные, приведенные на рисунке, найдите ширину АВ реки.

Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Девочка прошла от дома на запад 500 м. Затем повернула на север и прошла 300м. После этого она повернула на восток и прошла еще 100 м. Под каким углом к направлению на восток она должна идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций)
Человек, пройдя вверх по склону холма на 1000 м, поднялся на 90 м над плоскостью основания холма. Используйте таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выраженное целым числом.
Угол подъема лестница дачного домика равен 580. Используйте таблицу тригонометрических функций, найдите высоту ступенек лестницы, если ширина ступенек равна 20 см.

Самолет приближается к аэропорту А на высоте 8000м. Пилот имеет предписание производить снижение для посадки под постоянным углом 60. Используйте таблицу тригонометрических функций, найдите расстояние АВ от посадочной полосы до того места, над которым самолет должен начать снижение. В ответе укажите приближенное значение, выраженное целым числом метров.
Из окна, расположенного на высоте 15 м над поверхностью земли, нижний край дома, стоящего прямо на другой стороне улицы, виден под углом понижения 320. Найдите ширину улицы.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Грибник, войдя в лес, в течение двух часов шел в направлении на север, а затем с той же скоростью в течение полутора часов – на восток.
 Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Угол подъема дороги равен 70. Используя таблицу тригонометрических функций, найдите высоту, на которую поднимается пешеход, пройдя 200 м.
Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Используя таблицу тригонометрических функций, найдите угол между стропилами крыши и потолком.
Расстояние от наблюдателя до башни главного здания МГУ имени М.В.Ломаносова равно 150 м, а угол, под которым видно здание, равен 580. Используя таблицу тригонометрических функций, найдите высоту башни. В ответе укажите приближенное значение, выраженное целым числом метров.
Найдите расстояние между населенными пунктами А и В, расположенными на разных берегах реки, если расстояние между пунктами А и С, расположенными на одном берегу этой реки, равно 2 км, угол САВ равен 800, угол АСВ равен 700.
 В ответе укажите целое число метров
В ответе укажите целое число метров
.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол 600. Длина АС маятника 20 см. На сколько изменилась высота груза по сравнению с положением равновесия?
Пожарная лестница выдвинута на 50 м при предельном угле подъема 720. Используя таблицу тригонометрических функций, найдите высоту, которой достиг верхний конец лестницы, если ее нижний конец отстоит от поверхности земли на 1 м.
Длина балки, на которую опираются стропила крыши, равно 20 м. Используя таблицу тригонометрических функций, найдите высоту крыши, зная, что стропила с этой балкой образуют угол 240.

Расстояние от наблюдателя до башни главного здания МГУ имени М.В.Ломаносова равно 240 м, под каким углом видна эта башня с расстояния 200 м? В ответе укажите приближенное значение, выраженное целым числом градусов.
.
Использую данные, приведенные на рисунке, найдите ширину АВ озера. В ответе укажите целое число метров.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник в виде груза, подвешенного на нитке, отклонили от положения равновесия на угол 600. Длина АВ маятника 20 см. Используя таблицу тригонометрических функций, найдите расстояние СD от груза С до прямой АВ, проходящей через начальное положение маятника.
Используя таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб высотой 3 м, находящийся от наблюдателя на расстоянии 100 м.
 В ответе укажите целое число градусов.
В ответе укажите целое число градусов.
Из некоторой точки вершина горы видна под углом 300. При приближении к горе на 1000 м вершина стала видна под углом 450. Найдите приближенную высоту горы. В ответе укажите целое число метров.
Вершина радиомачты видна с расстояния 300 м от ее основания под углом 100. Используя таблицу тригонометрических функций, найдите высоту радиомачты.
Использую данные, приведенные на рисунке, найдите расстояние между населенными пунктами А и В, расположенными на разных берегах озера. В ответе укажите целое число метров.
Самостоятельная работа по теме
«Тригонометрические функции. Решение треугольников »
вариант
Маятник АВ длиной 50 см отклонили от положения равновесия на расстояние СD, равное 12 см.
 Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Телеграфный столб высотой 10 м находится на берегу реки. Верхний конец столба виден с другого под углом 200 к горизонту. Используя таблицу тригонометрических функций, найдите ширину реки.
Используя данные, указанные на рисунке, найдите расстояние от корабля К до берега АВ. В ответе укажите целое число метров.
Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите угол в градусах, под которым видна башня с расстояния 2000 м.
Подводная лодка, находясь впереди корабля, погрузилась в воду и пошла в направлении, перпендикулярном направлению на корабль со скоростью 30 км/ч. Под каким углом к направлению хода подводной лодки должен идти корабль со скоростью 60 км/ч, чтобы в некоторой точке пройти над подводной лодкой? Ответ укажите в градусах.

ОТВЕТЫ
Самостоятельная работа по теме
«Практическое применение подобия»
1 вариант
Используя данные, приведенные на рисунке, найдите расстояние АВ от лодки А до берега В
Для нахождения высоты египетской пирамиды недалеко от нее был установлен шест длиной 1,5 м. Его тень составила 1м. В тот же момент тень пирамиды была равна 96м. Чему равна высота пирамиды?
Какой должна быть ширина (Х) прямоугольной рамки для фотографии, указанной на рисунке, чтобы прямоугольники рамки и фотографии были подобны?
Самостоятельная работа по теме
«Практическое применение подобия»
2 вариант
Используя данные на рисунке , найдите высоту мачты АВ.

Чтобы изменить высоту дерева, ученик держит линейку в вертикальном положении на расстоянии вытянутой руки. Расстояние от глаз ученика дот линейки равно 60см. Часть линейки, закрывающая дерево, составляет 20 см. Расстояние от ученика до дерева равно 18 м. Чему равна высота дерева?
Строительный кирпич весит 4 кг. Сколько граммов весит игрушечный кирпич из того же материала, все размеры которого в 4 раза меньше?
Самостоятельная работа по теме
«Практическое применение подобия»
3 вариант
Используя данные, приведенные на рисунке, найдите ширину реки АВ.
Изображение дерева на фотопленке имеет высоту 15мм. Найдите высоту дерева, если расстояния от
объектива фотоаппарата до изображения и до дерева равны соответственно 50мм и 60мм.
3. Апельсин в два раза больше мандарина. Мандарин весит 40г. Считая их форму шарообразной и удельный вес одинаковым, найдите вес апельсина
ОТВЕТЫ
Векторы. Действия с векторами
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А — начало вектора, а точка В — его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора — это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Два вектора называются равными, если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными, если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными: вектора , и — коллинеарны.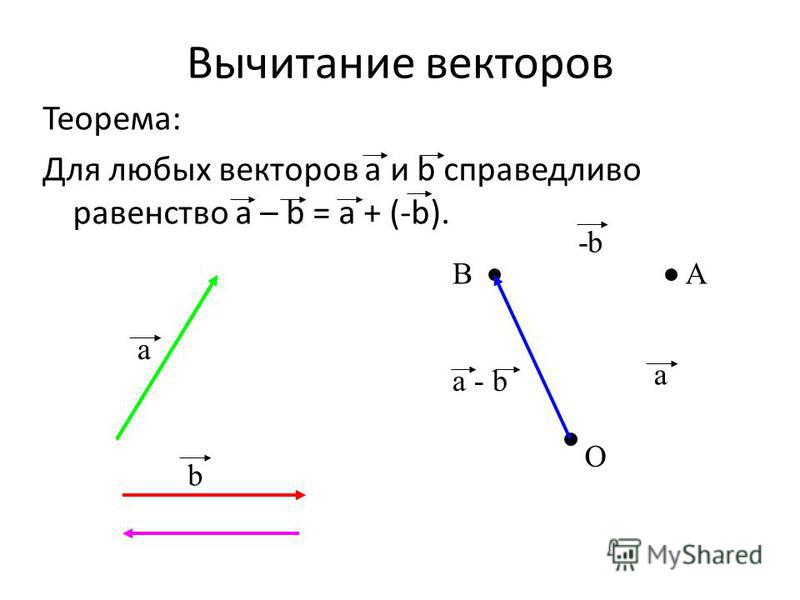
Произведением вектора на число называется вектор, сонаправленный вектору , если , и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
=k:
Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника.
Чтобы сложить два вектора по правилу параллелограмма, нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
:
Отсюда вытекает правило нахождения разности двух векторов: чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора ( то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки.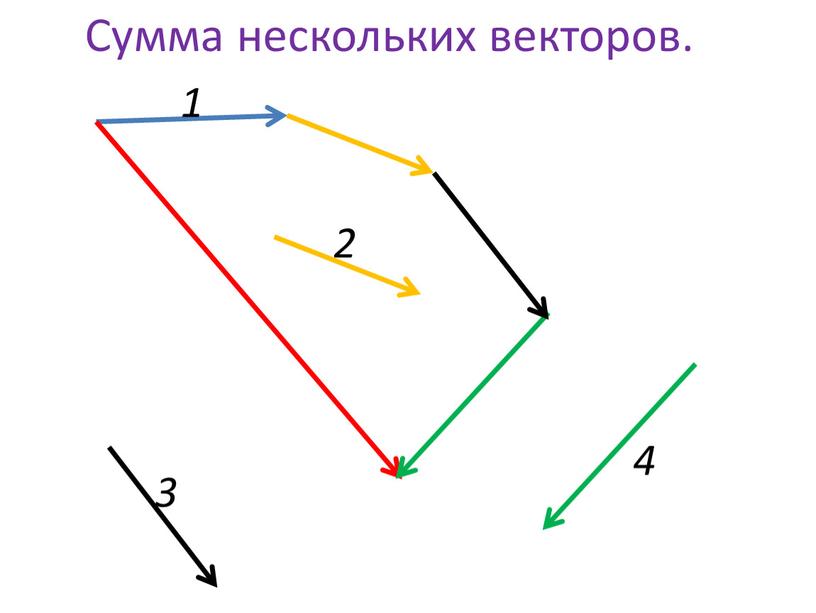 Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для подготовки к ЕГЭ по математике, а затем сверить све решение с ВИДЕОУРОКАМИ:
1. Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2. Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3. Задание 4 (№ 27711)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов и .
4. Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O.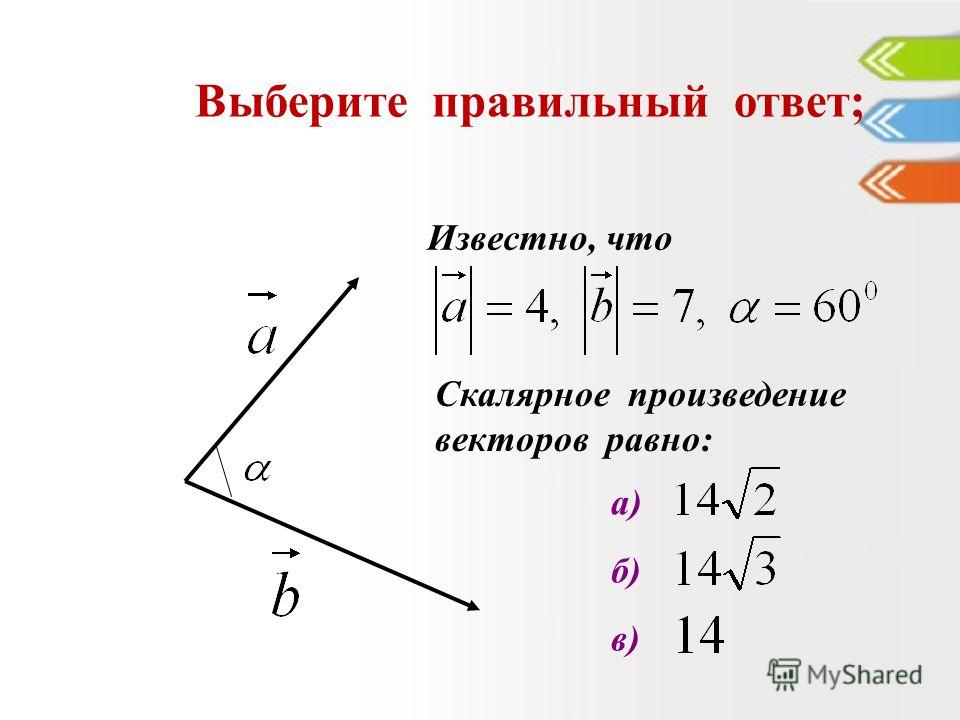 Найдите длину разности векторов и . (чертеж из предыдущей задачи).
Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5. Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6. Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7.Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
8.Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
9. Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10. Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — .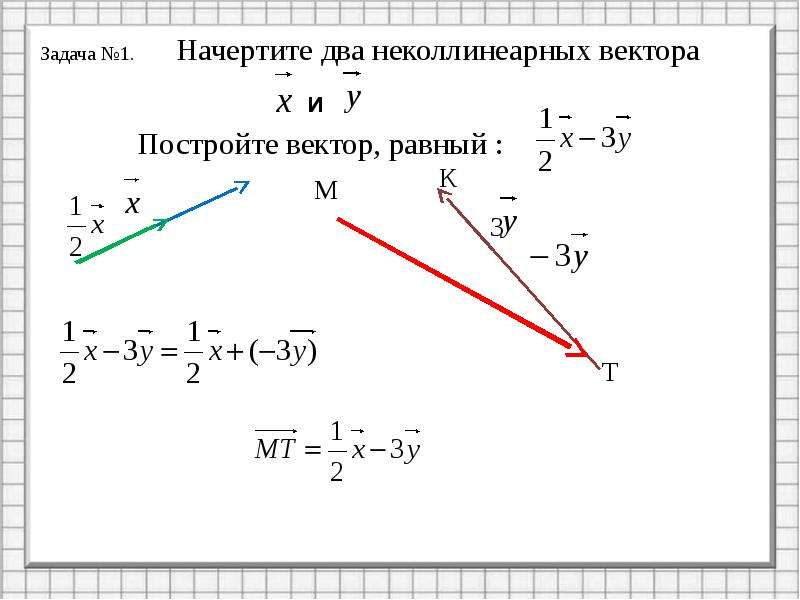 (чертеж из предыдущей задачи).
(чертеж из предыдущей задачи).
11.Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12. Задание 4 (№ 27720)
Стороны правильного треугольника ABC равны Найдите длину вектора +.
13. Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14. Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается.
 Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачатьFirefox
И.В. Фельдман, репетитор по математике.
Добавление компонентов (т. е. аналитический метод добавления векторов)
Ранее в этом уроке мы узнали, что векторы, ориентированные под прямым углом друг к другу, можно сложить, используя теорему Пифагора. Например, два вектора смещения с величиной и направлением 11 км, север и 11 км, восток можно сложить вместе, чтобы получить результирующий вектор, направленный как на север, так и на восток. Когда два вектора складываются «голова к хвосту», как показано ниже, в результате получается гипотенуза прямоугольного треугольника.Стороны прямоугольного треугольника имеют длины 11 км и 11 км. Результант можно определить с помощью теоремы Пифагора; его величина составляет 15,6 км. Решение показано под диаграммой.Этот пифагорейский подход полезен для сложения любых двух векторов, направленных под прямым углом друг к другу.
 У прямоугольного треугольника две стороны плюс гипотенуза; поэтому теорема Пифагора идеально подходит для сложения двух прямоугольных векторов. Но есть пределы полезности теоремы Пифагора при решении задач сложения векторов.Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой. Так что на первый взгляд может показаться, что нельзя использовать теорему Пифагора для определения равнодействующей при сложении трех или четырех векторов. Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу, например, при добавлении вектора севера и вектора востока. Но что делать, если два складываемых вектора не находятся под прямым углом друг к другу? Есть ли способ использовать математику для надежного определения результата для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию компонентов вектора (обсуждавшуюся ранее) и принципы разрешения векторов (обсуждавшиеся ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
У прямоугольного треугольника две стороны плюс гипотенуза; поэтому теорема Пифагора идеально подходит для сложения двух прямоугольных векторов. Но есть пределы полезности теоремы Пифагора при решении задач сложения векторов.Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой. Так что на первый взгляд может показаться, что нельзя использовать теорему Пифагора для определения равнодействующей при сложении трех или четырех векторов. Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу, например, при добавлении вектора севера и вектора востока. Но что делать, если два складываемых вектора не находятся под прямым углом друг к другу? Есть ли способ использовать математику для надежного определения результата для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию компонентов вектора (обсуждавшуюся ранее) и принципы разрешения векторов (обсуждавшиеся ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).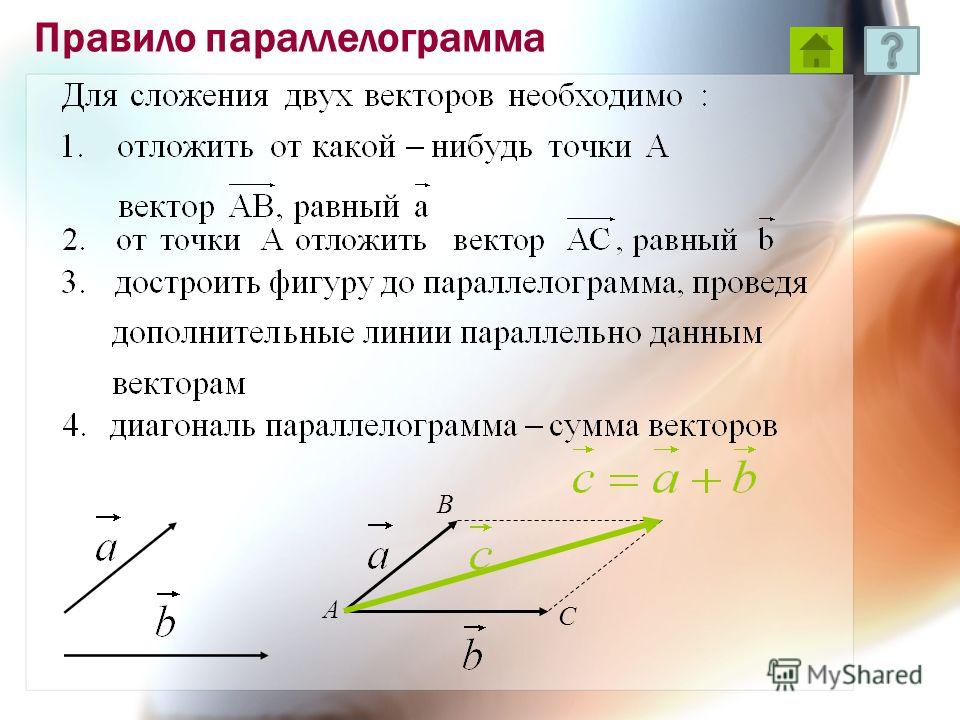
Добавление трех или более прямоугольных векторов
В качестве первого примера рассмотрим следующую задачу сложения векторов:Пример 1:
Студент проезжает на своей машине 6,0 км на север, затем поворачивает направо и 6,0 км на восток. Наконец, студент поворачивает налево и проезжает еще 2,0 км на север. Какова величина общего перемещения студента?
Как и любая задача в физике, успешное решение начинается с выработки мысленной картины ситуации.Построение диаграммы, подобной приведенной ниже, часто оказывается полезным в процессе визуализации. Если эти три вектора сложить вместе в прямом направлении, в результате получится вектор, который простирается от конца первого вектора (6,0 км, север, показано красным) до наконечника третьего вектора (2,0 км, Север, показан зеленым). Диаграмма сложения векторов головы к хвосту показана ниже. Как видно на диаграмме, результирующий вектор (нарисованный черным цветом) не является гипотенузой любого прямоугольного треугольника — по крайней мере, ни одного очевидного прямоугольного треугольника.
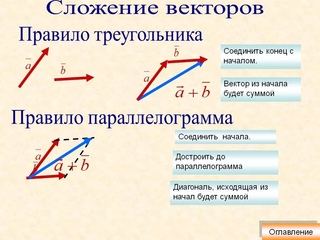 Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ: Да! Для этого необходимо изменить порядок добавления трех векторов. Векторы выше были нарисованы в том порядке, в котором они были заданы. Студент поехал на север, затем на восток и снова на север. Но если сложить три вектора в порядке 6,0 км, N + 2,0 км, N + 6,0 км, E, то диаграмма будет выглядеть так: После изменения порядка добавления трех векторов результирующий вектор теперь является гипотенузой прямоугольного треугольника.Длины перпендикулярных сторон прямоугольного треугольника равны 8,0 м, север (6,0 км + 2,0 км) и 6,0 км, восток. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ: Да! Для этого необходимо изменить порядок добавления трех векторов. Векторы выше были нарисованы в том порядке, в котором они были заданы. Студент поехал на север, затем на восток и снова на север. Но если сложить три вектора в порядке 6,0 км, N + 2,0 км, N + 6,0 км, E, то диаграмма будет выглядеть так: После изменения порядка добавления трех векторов результирующий вектор теперь является гипотенузой прямоугольного треугольника.Длины перпендикулярных сторон прямоугольного треугольника равны 8,0 м, север (6,0 км + 2,0 км) и 6,0 км, восток. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора. R 2 = (8,0 км) 2 + (6,0 км) 2
R 2 = 64,0 км 2 + 36,0 км 2
R 2 = 100,0 км 2
R = SQRT (100,0 км2)
R = 10,0 км
(SQRT указывает квадратный корень)
На приведенной выше первой диаграмме сложения векторов три вектора были добавлены в том порядке, в котором они управляются.
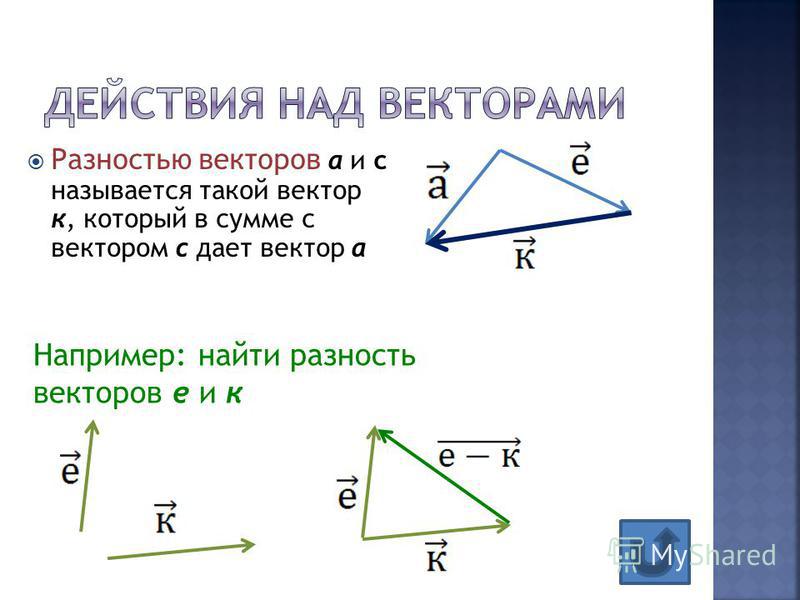 На второй диаграмме добавления векторов (сразу выше) порядок добавления векторов был изменен. Изменение порядка не повлияло на размер результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Сложение векторов A + B + C дает тот же результат, что и сложение векторов B + A + C или даже C + B + A . Пока все три вектора включены с их заданной величиной и направлением, результат будет одним и тем же.Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример задачи. Чтобы дополнительно проиллюстрировать стратегию, давайте рассмотрим ситуацию с добавлением векторов, описанную в примере 2 ниже.
На второй диаграмме добавления векторов (сразу выше) порядок добавления векторов был изменен. Изменение порядка не повлияло на размер результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Сложение векторов A + B + C дает тот же результат, что и сложение векторов B + A + C или даже C + B + A . Пока все три вектора включены с их заданной величиной и направлением, результат будет одним и тем же.Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример задачи. Чтобы дополнительно проиллюстрировать стратегию, давайте рассмотрим ситуацию с добавлением векторов, описанную в примере 2 ниже.
Пример 2:
Мак и Тош проводят лабораторию Vector Walk Lab . Начав у дверей своего кабинета физики, они проходят 2,0 метра на юг. Они поворачивают направо и идут 16.0 метров, запад. Они снова поворачивают направо и проходят 24 метра на север.Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения?
Графическое представление заданной проблемы поможет визуализировать происходящее. На приведенной ниже диаграмме показано такое представление.
Когда эти четыре вектора складываются вместе в режиме «голова к хвосту», в результате получается вектор, который простирается от хвоста первого вектора (2.0 м, юг, показано красным) до стрелки четвертого вектора (36,0 м, запад, показано зеленым). Диаграмма сложения векторов головы к хвосту показана ниже. Результирующий вектор (нарисованный черным цветом и помеченный R ) на приведенной выше диаграмме сложения векторов не является гипотенузой какого-либо сразу очевидного прямоугольного треугольника. Но, изменив порядок сложения этих четырех векторов, можно заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника. Например, путем добавления векторов в порядке 2.0 м, Ю + 24,0 м, С + 16,0 м, Ш + 36,0 м.
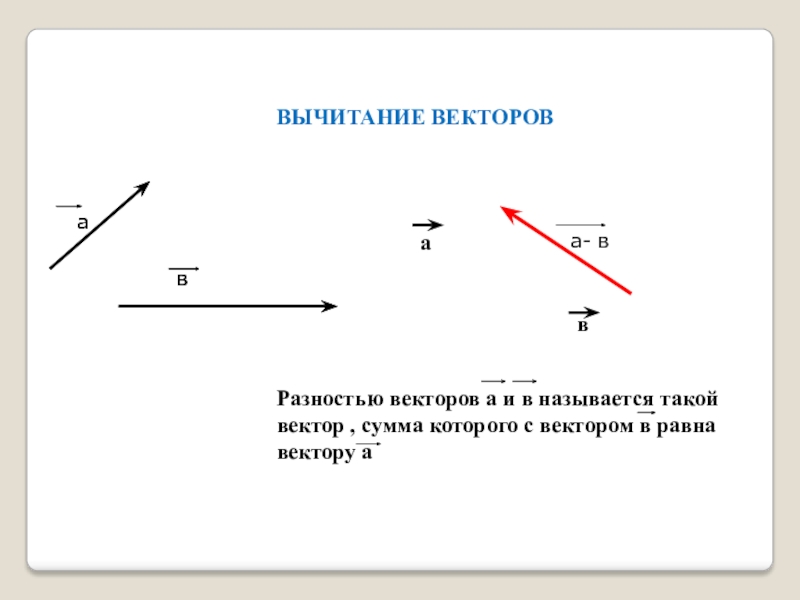 W, равнодействующая станет гипотенузой прямоугольного треугольника. Это показано на диаграмме сложения векторов ниже. После перестановки векторов результирующая теперь является гипотенузой прямоугольного треугольника, имеющего две перпендикулярные стороны с длинами 22,0 м на севере и 52,0 м на западе. 22,0 м, северная сторона является результатом сложения 2,0 м, юга и 24,0 м, северной стороны. 52,0 м, западная сторона – результат 16,0 м, западной и 36,0 м, западной стороны, сложенных вместе.Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
W, равнодействующая станет гипотенузой прямоугольного треугольника. Это показано на диаграмме сложения векторов ниже. После перестановки векторов результирующая теперь является гипотенузой прямоугольного треугольника, имеющего две перпендикулярные стороны с длинами 22,0 м на севере и 52,0 м на западе. 22,0 м, северная сторона является результатом сложения 2,0 м, юга и 24,0 м, северной стороны. 52,0 м, западная сторона – результат 16,0 м, западной и 36,0 м, западной стороны, сложенных вместе.Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора. R 2 = (22,0 м) 2 + (52,0 м) 2
R 2 = 484,0 м 2 + 2704,0 м 2
R 2 = 3188,0 м 2
R = SQRT (3188,0 м2 2 )
R = 56,5 м
(SQRT указывает квадратный корень)
Как видно из этих двух примеров, результат сложения трех или более прямоугольных векторов можно легко определить с помощью теоремы Пифагора.
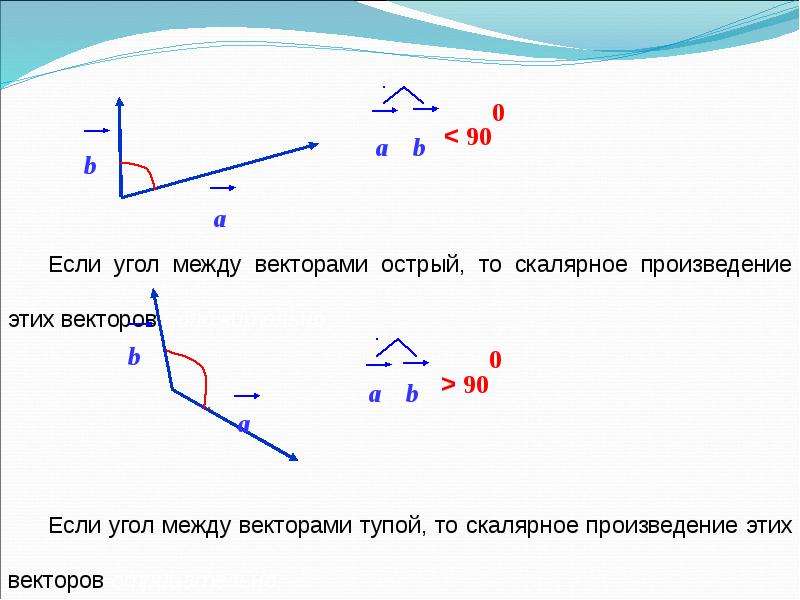 Это включает в себя добавление векторов в другом порядке.
Это включает в себя добавление векторов в другом порядке. SOH CAH TOA и направление векторов
Приведенное выше обсуждение объясняет метод определения величины равнодействующей для трех или более перпендикулярных векторов. Тема направления была проигнорирована в обсуждении. Теперь обратим внимание на способ определения направления результирующего вектора. В качестве беглого обзора вспомним, что ранее в этом уроке было введено соглашение для выражения направления вектора.Соглашение известно как соглашение против часовой стрелки от востока, часто сокращенно как соглашение CCW . Используя это соглашение, направление вектора часто выражается как угол поворота вектора против часовой стрелки вокруг его хвоста строго на восток.Чтобы начать наше обсуждение, вернемся к Примеру 1 выше, где мы попытались добавить три вектора: 6,0 км, N + 6,0 км, E + 2,0 км, N. В решении порядок сложения трех векторов переставили так, чтобы получился прямоугольный треугольник, а полученная гипотенуза треугольника.
 Треугольник перерисовывается справа. Обратите внимание, что угол в левом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью. Theta (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке, — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA помогает запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тета (Θ), и мы знаем длину стороны, противоположной тета (Θ) — 6.0 км — и длина стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже.
Треугольник перерисовывается справа. Обратите внимание, что угол в левом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью. Theta (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке, — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA помогает запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тета (Θ), и мы знаем длину стороны, противоположной тета (Θ) — 6.0 км — и длина стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже. Касательная(Θ) = Противоположная/Смежная
Тангенс(Θ) = 6,0/8,0
Тангенс(Θ) = 0,75
Θ = тангенс -1 (0,75)
Θ = 36. 869 …°
869 …°
Θ =37°
Проблема не решена после того, как вычислено значение тета (Θ). Эта угловая мера теперь должна использоваться для указания направления. Один из способов сделать это — просто указать, что направление равнодействующей — 37 ° к востоку от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Поскольку угол, который равнодействующая образует с востоком, является дополнением угла, который она образует с севером, мы могли бы выразить направление как 53° против часовой стрелки.
Теперь мы рассмотрим Пример 2 в качестве второго примера того, как использовать SOH CAH TOA для определения направления равнодействующей.В Примере 2 мы пытались определить величину 2,0 м. S + 16,0 м, W + 24,0 м, N + 36,0 м, W. Решение заключалось в переупорядочении сложения таким образом, чтобы результирующая была гипотенузой прямоугольного треугольника с известными сторонами. Прямоугольный треугольник показан ниже. Результат рисуется черным цветом.
 Еще раз обратите внимание, что угол в правом нижнем углу треугольника помечен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью.
Еще раз обратите внимание, что угол в правом нижнем углу треугольника помечен как тета (Θ). Тета (Θ) представляет собой угол, который вектор образует с северной осью. Theta (Θ) можно рассчитать с помощью функции тангенса.В этой задаче мы хотим определить угловую меру тета (Θ) и знаем длину стороны, противоположной тета (Θ) — 52,0 м — и длину стороны, прилегающей к углу тета (Θ) — 22,0 м. TOA SOH CAH TOA указывает, что тангенс любого угла представляет собой отношение длин стороны, противоположной стороне, примыкающей к этому углу. Таким образом, функция тангенса будет использоваться для вычисления угловой меры тета (Θ). Работа представлена ниже.
Касательная(Θ) = Противоположная/Смежная
Тангенс (Θ) = 52.0/22.0
Тангенс (Θ) = 2,3636 …
Θ = тангенс -1 (2,3636 …)
Θ = 67,067 …°
Θ = 67,1°
Проблема не решена после того, как вычислено значение тета (Θ). Эта угловая мера теперь должна использоваться для указания направления.
 Один из способов сделать это — просто указать, что направление равнодействующей — 67,1 ° к западу от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Северная ось повернута на 90° против часовой стрелки относительно востока, и этот вектор равен 67.1° против часовой стрелки мимо севера. Таким образом, направление против часовой стрелки равно 157,1° против часовой стрелки.
Один из способов сделать это — просто указать, что направление равнодействующей — 67,1 ° к западу от севера. В качестве альтернативы можно использовать соглашение против часовой стрелки. Северная ось повернута на 90° против часовой стрелки относительно востока, и этот вектор равен 67.1° против часовой стрелки мимо севера. Таким образом, направление против часовой стрелки равно 157,1° против часовой стрелки. Подводя итог, можно сказать, что направление вектора можно определить так же, как и всегда, — найдя угол поворота против часовой стрелки строго на восток. Поскольку равнодействующая является гипотенузой прямоугольного треугольника, это можно сделать, сначала найдя угол, который образует равнодействующая с одной из ближайших осей треугольника. После этого требуется немного подумать, чтобы связать угол с направлением.
Сложение неперпендикулярных векторов
Теперь рассмотрим ситуации, в которых два (или более) складываемых вектора не находятся под прямым углом друг к другу.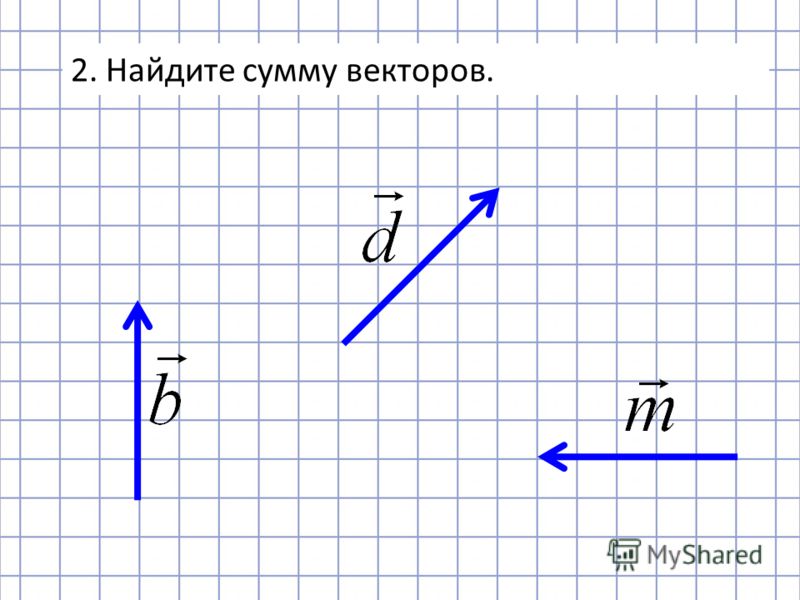 Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольного треугольника. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразоваться в другие векторы, образующие прямоугольный треугольник.Хитрость включает в себя понятие компонента вектора и процесс разрешения вектора.
Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольного треугольника. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразоваться в другие векторы, образующие прямоугольный треугольник.Хитрость включает в себя понятие компонента вектора и процесс разрешения вектора. Компонент вектора описывает действие вектора в заданном направлении. Любой вектор под углом состоит из двух компонентов; один направлен горизонтально, а другой направлен вертикально. Например, северо-западный вектор имеет северную составляющую и западную составляющую. Вместе эффект этих двух компонентов равен общему эффекту вектора под углом . В качестве примера рассмотрим самолет, который летит на северо-запад из аэропорта Чикаго О’Хара в направлении границы с Канадой.Вектор северо-западного смещения плоскости имеет две составляющие — северную и западную. При суммировании эти две составляющие равны общему смещению на северо-запад.
 Это показано на диаграмме ниже.
Это показано на диаграмме ниже. Северо-западный вектор имеет северную и западную компоненты, которые представлены как A x и A y . Можно сказать, что
А = А х + А у
Поэтому всякий раз, когда мы думаем о северо-западном векторе, мы можем думать вместо двух векторов — северного и западного.Два компонента A x + A y можно заменить на единственный вектор A в задаче.Теперь предположим, что ваша задача заключается в сложении двух неперпендикулярных векторов. Назовем векторы A и B . Вектор A — это вектор с неприятным углом , который не является ни горизонтальным, ни вертикальным. А вектор B — красивый, вежливый вектор, направленный горизонтально. Ситуация показана ниже.
Конечно противный вектор A имеет две составляющие — A x и A y . Эти два компонента вместе равны вектору A . То есть А = А х + А у .
Эти два компонента вместе равны вектору A . То есть А = А х + А у .
Чтобы увидеть, как этот процесс работает с реальной задачей сложения векторов, рассмотрим пример 3, показанный ниже.
Пример 3:
Макс играет полузащитника футбольной команды Юга.Во время одной из игр в прошлую пятницу вечером против New Greer Academy он сделал следующие движения после того, как мяч был снэпован на третьем дауне.Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и пробежал по полю на расстояние 4,8 метра в направлении 240° против часовой стрелки с востока (30° з.д. и ю.ш.), прежде чем, наконец, выбить ветер из широкого ресивера Нью Грир. Определите величину и направление общего смещения Макса.
Как обычно, решение начинается с диаграммы добавляемых векторов.
Для облегчения обсуждения три вектора были помечены как векторы A , B и C . Результатом является векторная сумма этих трех векторов; диаграмма сложения векторов головы к хвосту показывает, что результирующая направлена на юго-запад. Из трех добавленных векторов вектор C явно является неприятным вектором .Его направление не строго на юг и не строго на запад. Решение включает в себя разложение этого вектора на его компоненты.
Процесс разрешения векторов обсуждался ранее в этом уроке.
 Этот процесс включает в себя использование величины, функций синуса и косинуса для определения x- и y-компонент вектора. Вектор C образует угол 30° с южным направлением. Нарисовав прямоугольный треугольник с горизонтальными и вертикальными катетами и гипотенузой С, можно определить компоненты вектора С.Это показано на диаграмме ниже. Сторона, прилегающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C y . Таким образом, для определения C y используется функция косинуса. Сторона, противоположная углу 30°, является горизонтальной стороной; горизонтальная сторона представляет горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения южной составляющей, поскольку южная составляющая примыкает к углу 30°.Функция синуса используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30°.
Этот процесс включает в себя использование величины, функций синуса и косинуса для определения x- и y-компонент вектора. Вектор C образует угол 30° с южным направлением. Нарисовав прямоугольный треугольник с горизонтальными и вертикальными катетами и гипотенузой С, можно определить компоненты вектора С.Это показано на диаграмме ниже. Сторона, прилегающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C y . Таким образом, для определения C y используется функция косинуса. Сторона, противоположная углу 30°, является горизонтальной стороной; горизонтальная сторона представляет горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения южной составляющей, поскольку южная составляющая примыкает к углу 30°.Функция синуса используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30°. Работа представлена ниже.
Работа представлена ниже. Теперь наша задача сложения векторов была преобразована из сложения двух хороших векторов и одного неприятного вектора в сложение четырех хороших векторов.
Поскольку все векторы ориентированы вдоль обычных осей север-юг и восток-запад, их можно сложить в любом порядке, чтобы получить прямоугольный треугольник, гипотенуза которого является равнодействующей.Такая схема показана ниже.
Перпендикулярные стороны треугольника имеют длину 4,6 метра и 6,756 метра. Длина горизонтальной стороны (4,6 м) определялась путем сложения значений В (2,2 м) и С х (2,4 м). Длина вертикальной стороны (6,756… м) определялась путем сложения значений А (2,6 м) и С и (4,156… м). Результирующую величину (R) теперь можно определить с помощью теоремы Пифагора.
Р 2 = (6.756… м) 2 + (4,6 м) 2
R 2 = 45,655… м 2 + 21,16 м 2
R 2 = 66,815… м 2
R = SQRT(66,815… m 2 )
R = 8,174 … м
R = ~8,2 м
Направление равнодействующей можно определить, найдя угол, который образует равнодействующая с вектором север-юг или восток-запад.
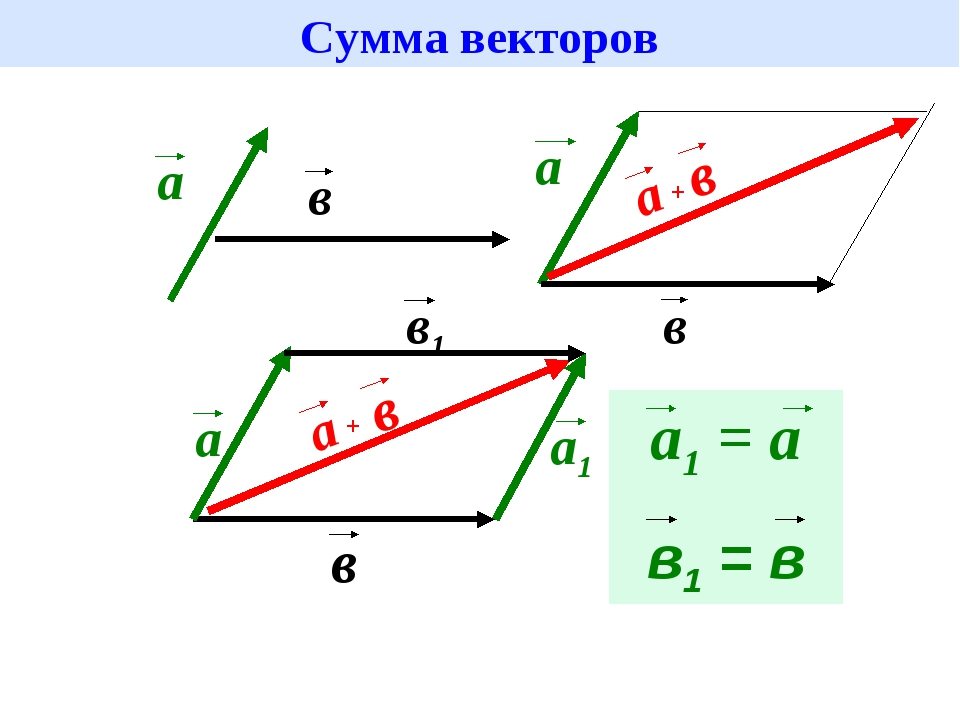 На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов.Этот угол тета представляет собой угол, который равнодействующая образует с западом. Его значение можно определить с помощью функции тангенса. Функция тангенса (как и в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. Это,
На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов.Этот угол тета представляет собой угол, который равнодействующая образует с западом. Его значение можно определить с помощью функции тангенса. Функция тангенса (как и в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. Это,тангенс(Θ) = (6,756… м)/(4,6 м) = 1,46889…
Используя функцию арктангенса, можно определить угол тета (Θ). На большинстве калькуляторов для этого используются кнопки 2nd-Tangent.
Θ = тангенс -1 (1.46889…) = 55,7536… °
Θ = ~56°
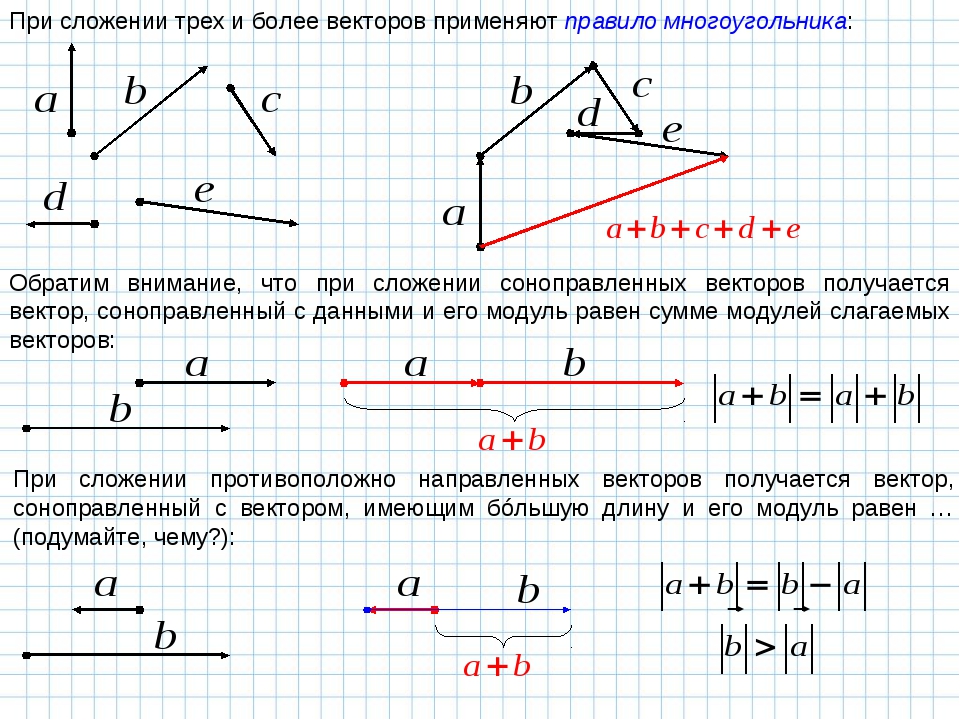
В примере 4 представлен последний пример того, как совместить разрешение векторов с добавлением векторов для добавления трех или более неперпендикулярных векторов.Поскольку этот пример включает в себя три особенно неприятных вектора , таблица будет использоваться для организации информации о величине и направлении компонентов. Использование таблицы — мудрая идея, когда проблемы усложняются.
Пример 4:
Кэмерон Пер (друзья зовут его Кэм) и Бакстер Натюр в походе. Начиная с домашней базы, они совершают следующие движения.A: 2,65 км, 140° против часовой стрелки
Определить величину и направление их общего смещения.
Б: 4.77 км, 252° против часовой стрелки
C: 3,18 км, 332° против часовой стрелки
Визуальное представление ситуации показано ниже.
Чтобы определить результат, три отдельных вектора разлагаются на горизонтальную и вертикальную составляющие.
 Информация об углах каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а перпендикулярные стороны ориентированы вдоль осей восток-запад и север-юг.Это показано на диаграмме ниже.
Информация об углах каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а перпендикулярные стороны ориентированы вдоль осей восток-запад и север-юг.Это показано на диаграмме ниже. Тригонометрические функции — синус, косинус и тангенс — затем используются для определения величины горизонтальной и вертикальной составляющих каждого вектора. Работа показана и организована в таблице ниже.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| А 2.65 км 140° против часовой стрелки | (2,65 км)•cos(40°) = 2,030… км, запад | (2,65 км)•sin(40°) = 1,703… км, север |
| Б 4,77 км 252° против часовой стрелки | (4,77 км)•sin(18°) = 1,474… км, запад | (4,77 км)•cos(18°) = 4,536… км, юг |
| С 3,18 км 332° против часовой стрелки | (3. 18 км)•cos(28°) 18 км)•cos(28°)= 2,808… км, восток | (3,18 км)•sin(28°) = 1,493… км, Юг |
| Сумма А+В+С | 0,696 км, Запад | 4,326 км, Юг |
Последняя строка приведенной выше таблицы представляет собой сумму всех компонентов Восток-Запад и сумму всех компонентов Север-Юг. Результат состоит из этих двух компонентов.Результирующая определяется путем сложения этих двух компонентов, чтобы сформировать прямоугольный треугольник с гипотенузой, равной равнодействующей. Обычно это включает сложение всех горизонтальных компонентов для определения общей длины горизонтальной стороны прямоугольного треугольника… и сложение всех вертикальных компонентов для определения общей длины вертикальной стороны прямоугольного треугольника. Это делается в приведенной выше таблице простым добавлением еще одной строки в таблицу для векторной суммы всех компонентов.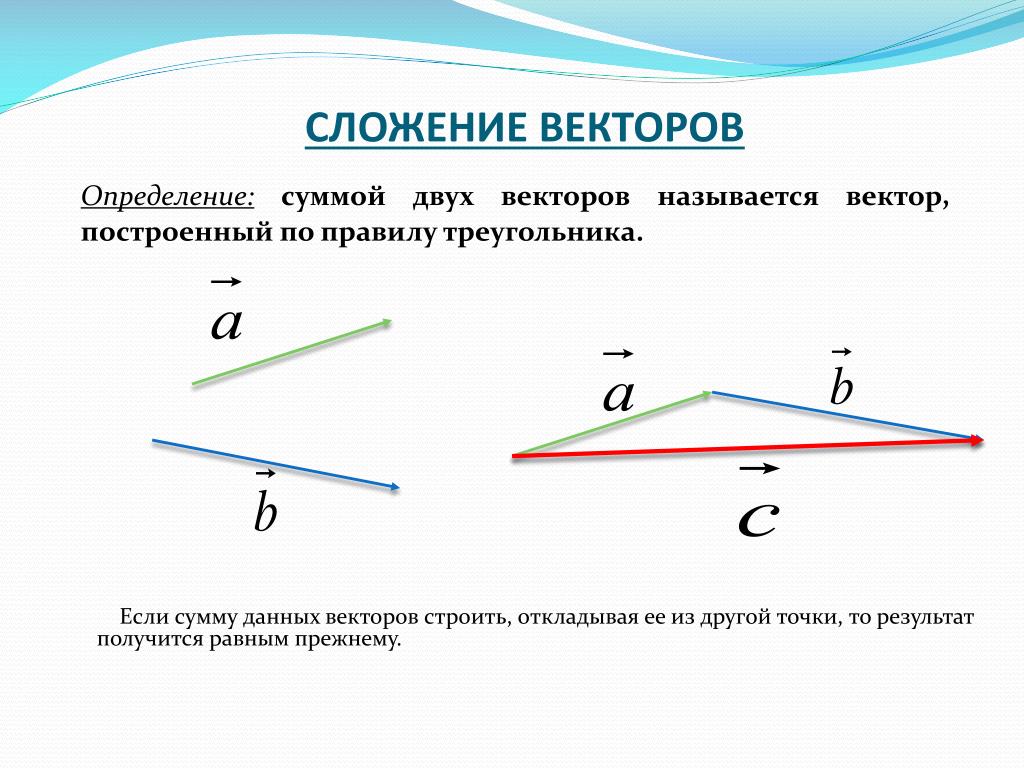 При сложении восточно-западных компонентов всех отдельных векторов необходимо учитывать, что восточный компонент и западный компонент будут складываться вместе как положительных и отрицательных . Некоторые студенты предпочитают думать об этом как о вычитании, а не о сложении. На самом деле это сложение — сложение векторов противоположного направления. Точно так же северный и южный компоненты также будут складываться как положительных и отрицательных .Как только нижняя строка точно определена, величину равнодействующей можно определить с помощью теоремы Пифагора.
При сложении восточно-западных компонентов всех отдельных векторов необходимо учитывать, что восточный компонент и западный компонент будут складываться вместе как положительных и отрицательных . Некоторые студенты предпочитают думать об этом как о вычитании, а не о сложении. На самом деле это сложение — сложение векторов противоположного направления. Точно так же северный и южный компоненты также будут складываться как положительных и отрицательных .Как только нижняя строка точно определена, величину равнодействующей можно определить с помощью теоремы Пифагора.
R 2 = (0,696 км) 2 + (4,326 км) 2
R 2 = 0,484 км 2 + 18,714 км 2
R 2 = 19,199 км 2
R = SQRT (19,199 км 2 )
R = ~4,38 км
Направление результирующего смещения можно определить, построив конечный треугольник из составляющих результирующего.
 Компоненты равнодействующей представляют собой просто сумму компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который образует результирующая с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:
Компоненты равнодействующей представляют собой просто сумму компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который образует результирующая с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:Тангенс(Θ) = противоположный/примыкающий
Тангенс (Θ) = (4,326 км)/(0,696 км)
Тангенс (Θ) = 6,216
Θ = тангенс -1 (6.216)
Θ = 80,9°
Эта угловая мера представляет собой угол поворота вектора к югу от строгого запада. Это будет сформулировано как 80,9 ° к югу от запада. Поскольку запад составляет 180 ° против часовой стрелки от востока, направление также может быть выражено против часовой стрелки (CCW) от востока как 260,9 °.
Таким образом, результатом нашего анализа является общее смещение 4,38 км с направлением 260,9° (против часовой стрелки).
Вопросы, которые были рассмотрены на этой странице:
- Как можно сложить три или более перпендикулярных вектора, чтобы получить равнодействующую?
- Как можно сложить два или более неперпендикулярных вектора, чтобы получить результат?
Мы хотели бы предложить … Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей интерактивной игры Name That Vector, нашей интерактивной игры с добавлением вектора или нашей интерактивной игры с угадыванием вектора.
 Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Поэкспериментируйте с виджетом ниже, а затем попробуйте решить задачи из раздела «Проверьте свое понимание», чтобы проверить свои навыки добавления векторов с использованием компонентов.
Практика! Виджет ниже вычисляет сумму трех векторов, если известны x- и y-компоненты.Используйте виджет, чтобы потренироваться и проверить проблему.Проверьте свое понимание Рассмотрим диаграмму ниже. На сетке представлены девять уникальных помеченных мест. Каждый квадрат на сетке представляет собой площадь 20 х 20 м. Вправо по сетке находится в восточном направлении и вверх по сетке в северном направлении. Используйте сетку, отвечая на следующие несколько вопросов.
1.
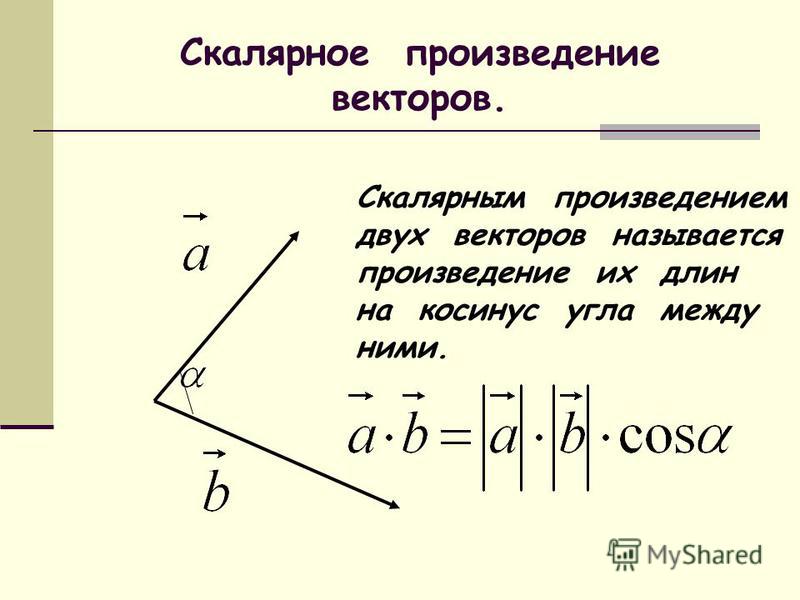 Предположим, что человек начинает с позиции А и идет к позиции Е, а затем к позиции G. Заполните приведенную ниже таблицу, указав компоненты восток-запад и север-юг отдельных этапов ходьбы и компоненты результирующего смещения. . Сделайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Предположим, что человек начинает с позиции А и идет к позиции Е, а затем к позиции G. Заполните приведенную ниже таблицу, указав компоненты восток-запад и север-юг отдельных этапов ходьбы и компоненты результирующего смещения. . Сделайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения. Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от А до Е | ||
| В-Г | ||
| Результат от А до G |
Величина результата: _________________________
Направление результата: _________________________
2. Используя ту же сетку, повторите измерения для прохождения от точки C к точке B и к точке F. Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Используя ту же сетку, повторите измерения для прохождения от точки C к точке B и к точке F. Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| С до В | ||
| от В до Ж | ||
| Результат C-F |
Величина результата: _________________________
Направление результата: _________________________
3.Наконец, используйте ту же сетку, чтобы повторить измерения для прогулки от точки I к точке B, к точке G и к точке H. Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующее смещение.
Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующее смещение.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от I до Б | ||
| от B до G | ||
| G-H | ||
| Результат от I до Н |
Величина результата: _________________________
Направление результата: _________________________
4.Во время своего недавнего похода в продуктовый магазин Клэр де Иль прошла 28 метров до конца прохода. Затем она повернула направо и прошла 12 м по концевому проходу. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг не являются фокусом.)
Затем она повернула направо и прошла 12 м по концевому проходу. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг не являются фокусом.)
5. В последнем матче прошлогоднего регулярного сезона команда South играла в New Greer Academy за титул чемпиона конференции.В последнем розыгрыше игры звездный квотербек Эйвери сделал рывок из схватки и отскочил назад (на север) на 8,0 ярда. Затем он пробежал боком (на запад) из кармана на 12,0 ярдов, прежде чем, наконец, бросить пас на 34,0 ярда прямо по полю (на юг) Кендаллу для победного в игре тачдауна. Определить величину и направление перемещения мяча.
6. Миа Андер выходит из парадной двери своего дома и идет по пути, показанному на схеме справа (не в масштабе).Прогулка состоит из четырех этапов со следующими величинами:
А = 46 м
В = 142 м
С = 78 м
Д = 89 м
Определите величину и направление результирующего смещения Мии.
 Рассмотрите возможность использования таблицы для организации ваших вычислений.
Рассмотрите возможность использования таблицы для организации ваших вычислений.
На рисунке показаны три вектора. Вектор \vec{A} имеет длину 37.\circ }} \right)j\\ \vec C &= 8,21\;i — 22,55\;j \конец{выравнивание*} {/экв}
Таким образом, сумма векторов A и B равна,
{экв}\начало{выравнивание*} \vec D &= \vec A + \vec C\\ \vec D &= 12,65\;i + 34,77\;j + 8,21\;i — 22,55\;j\\ \vec D &= 20,86\;i + 12,22\;j \конец{выравнивание*} {/экв}
Скалярное произведение векторов B и D равно,
{экв}\начало{выравнивание*} \vec B \cdot \vec D &= \vec B.\left( {\vec A + \vec C} \right)\\ \vec B \cdot \vec D &= \left( {59.\цирк } \конец{выравнивание*} {/экв}
Следовательно, вариант (а) является правильным ответом.
Сложение и вычитание векторов
Чтобы добавить или вычесть два вектора, добавьте или вычтите соответствующие компоненты.
Позволять
ты
→
знак равно
〈
ты
1
,
ты
2
〉
и
в
→
знак равно
〈
в
1
,
в
2
〉
быть два вектора.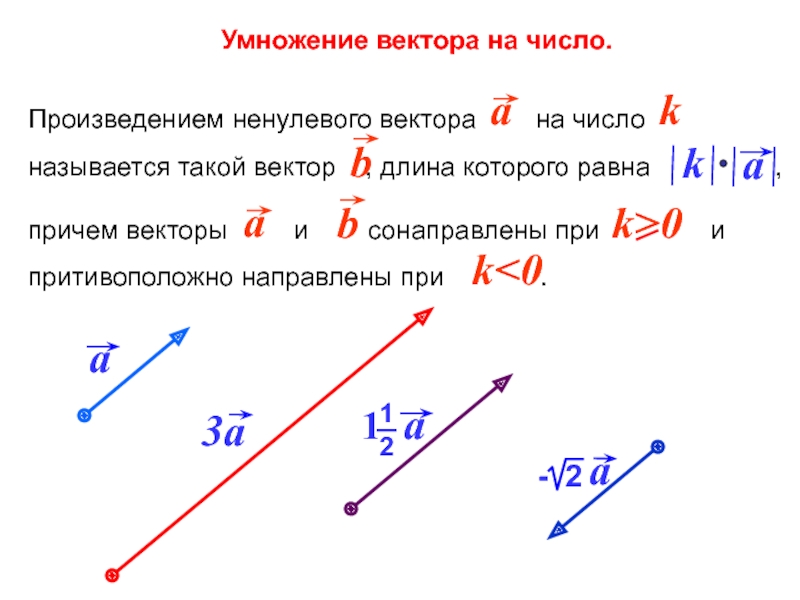
Тогда сумма ты → и в → это вектор
ты → + в → знак равно 〈 ты 1 + в 1 , ты 2 + в 2 〉
Разница ты → и в → является
ты → − в → знак равно ты → + ( − в → ) знак равно 〈 ты 1 − в 1 , ты 2 − в 2 〉
Сумма двух и более векторов называется равнодействующей. Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Результат двух векторов можно найти с помощью метод параллелограмма или метод треугольника .
Метод параллелограмма:
Нарисуйте векторы так, чтобы их начальные точки совпадали. Затем нарисуйте линии, чтобы сформировать полный параллелограмм. Диагональ из начальной точки в противоположную вершину параллелограмма является равнодействующей.
Добавление вектора:
- Поместите оба вектора ты → и в → в той же начальной точке.
- Завершите параллелограмм. Результирующий вектор ты → + в → является диагональю параллелограмма.
Вычитание векторов:
- Завершите параллелограмм.

- Проведите диагонали параллелограмма из начальной точки.
Метод треугольника:
Нарисуйте векторы один за другим, помещая начальную точку каждого последующего вектора в конечную точку предыдущего вектора.Затем проведите равнодействующую от начальной точки первого вектора до конечной точки последнего вектора. Этот метод также называют метод «голова к хвосту» .
Добавление вектора:
Вычитание векторов:
Пример:
Найди)
ты
→
+
в
→
и (б)
ты
→
−
в
→
если
ты
→
знак равно
〈
3
,
4
〉
и
в
→
знак равно
〈
5
,
−
1
〉
.
Подставить заданные значения ты 1 , ты 2 , в 1 и в 2 в определение сложения векторов.
ты → + в → знак равно 〈 ты 1 + в 1 , ты 2 + в 2 〉 знак равно 〈 3 + 5 , 4 + ( − 1 ) 〉 знак равно 〈 8 , 3 〉
Перепишите разницу
ты
→
−
в
→
как сумма
ты
→
+
(
−
в
→
)
. Нам нужно определить компоненты
−
в
→
.
Нам нужно определить компоненты
−
в
→
.
Напомним, что − в → является скалярным множителем − 1 раз в . Из определения скалярного умножения имеем:
− в → знак равно − 1 〈 в 1 , в 2 〉 знак равно − 1 〈 5 , − 1 〉 знак равно 〈 − 5 , 1 〉
Теперь добавьте компоненты
ты
→
и
−
в
→
.
ты → + ( − в → ) знак равно 〈 3 + ( − 5 ) , 4 + 1 〉 знак равно 〈 − 2 , 5 〉
Два вектора A и B на рисунке имеют равные величины 13.
 5 м и углы θ1 = 33° и θ2 = 110°. Как найти (a) компонент x и (b) компонент y их векторной суммы R , (c) величину R и (d) угол R ?
5 м и углы θ1 = 33° и θ2 = 110°. Как найти (a) компонент x и (b) компонент y их векторной суммы R , (c) величину R и (d) угол R ?У меня нет хорошего способа нарисовать схему, поэтому я попытаюсь провести вас по шагам по мере их появления.
Итак, идея здесь в том, что вы можете найти #x#-компоненту и #y#-компоненту векторной суммы , #R#, добавляя #x#-компоненты и #y#-компоненты соответственно, векторов #vec(a)# и #vec(b)#.
Для вектора #vec(a)# все довольно просто. Компонент #x# будет являться проекцией вектора на ось #x#, равной
.#a_x = a * cos(theta_1)#
Аналогично, компонент #y# будет проекцией вектора на ось #y#
#a_y = a * sin(theta_1)#
Для вектора #vec(b)# все немного сложнее. В частности, найти соответствующие углы будет немного сложно.@)#
Добавление вектора
Математика и наука были изобретены людьми для описания и
понимать окружающий мир. Заметим, что существуют некоторые величины и процессы в
наш мир, которые зависят от направления , в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению.
Математики и ученые называют количество
который зависит от направления векторной величины . Количество
которая не зависит от направления, называется скалярной величиной .А
векторное количество
имеет две характеристики: величину и направление . Когда
сравнение
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление.
Заметим, что существуют некоторые величины и процессы в
наш мир, которые зависят от направления , в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению.
Математики и ученые называют количество
который зависит от направления векторной величины . Количество
которая не зависит от направления, называется скалярной величиной .А
векторное количество
имеет две характеристики: величину и направление . Когда
сравнение
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление.
На этом слайде мы описываем метод сложения двух векторов. Сложение векторов — это один из аспектов большой векторной алгебры, которую мы изучаем. , а не будут представлены на этом сайте. Добавление вектора представлено здесь потому, что встречается довольно часто при изучении ракет и потому что он демонстрирует некоторые фундаментальные различия между векторы и скаляры.
Векторы обычно обозначаются на рисунках стрелкой. Длина стрелки указывает величину и
кончик стрелки указывает направление. Вектор
помечены буквой в алфавитном порядке
буква с линией сверху, чтобы отличить ее от скаляра.
Величину вектора будем обозначать символом |a| . Направление
будет измеряться углом фи относительно координаты
ось х .Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе
векторы! Они имеют величину и направление. Сначала ты
столкнуться с осями координат, когда вы учитесь строить графики. Так что у тебя есть
использовал векторы в течение некоторого времени, даже не подозревая об этом!
Длина стрелки указывает величину и
кончик стрелки указывает направление. Вектор
помечены буквой в алфавитном порядке
буква с линией сверху, чтобы отличить ее от скаляра.
Величину вектора будем обозначать символом |a| . Направление
будет измеряться углом фи относительно координаты
ось х .Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе
векторы! Они имеют величину и направление. Сначала ты
столкнуться с осями координат, когда вы учитесь строить графики. Так что у тебя есть
использовал векторы в течение некоторого времени, даже не подозревая об этом!
Если мы построим пунктирную линию от кончика вектора a идущий параллельно оси х, он пересекает ось у в том месте, где мы
этикетка ау .Точно так же линия от кончика вектора
параллельно оси Y пересекает ось X на x .
Величины x и ay называются
компоненты
вектора, и оба являются скалярными квантитами.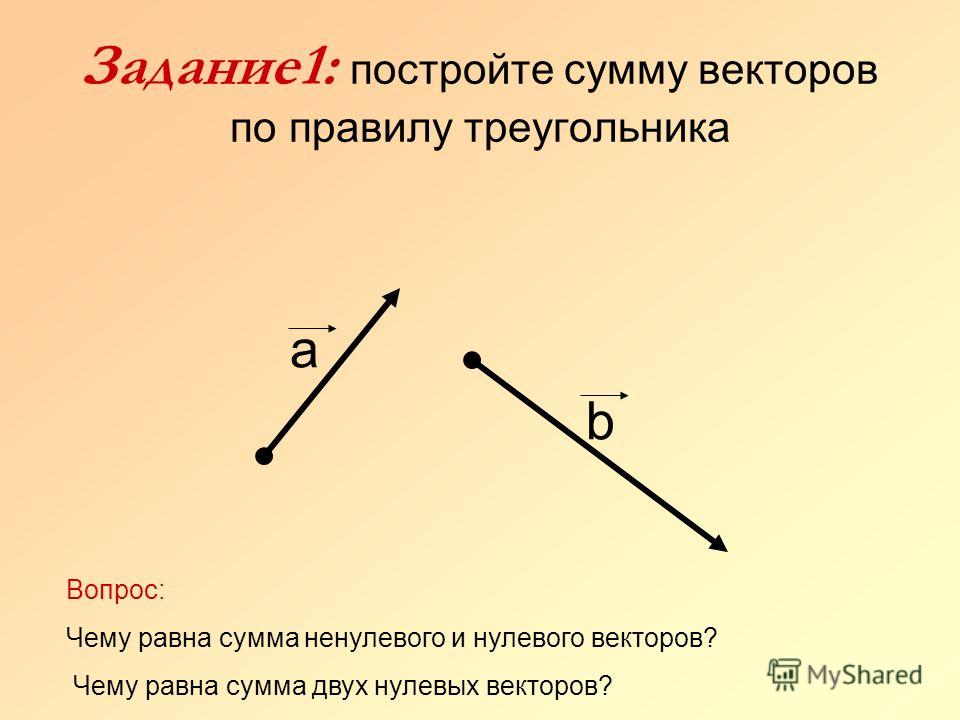
Чтобы добавить два вектора, a и b , мы сначала разбиваем каждый вектор на его компоненты, x и a , и bx и по , как показано на рисунке.Из правил, регулирующих равенство векторов, синий вектор b равен черному вектору b потому что он имеет одинаковую равную длину и одинаковое направление. Теперь, поскольку компоненты вектора и вектор b являются скалярами, мы можем добавить x-компонент для генерации x-компонент нового вектора c :
сх = топор + Ьх
Точно так же мы можем добавить y-компонентов :
су = ау + по
Новые компоненты cx и cy полностью определяют
новый вектор c , указав как величину, так и направление.Внимательно взглянув на диаграмму, мы видим, что сложение двух векторов дает
новый вектор, который равен , а не в направлении любого из
исходные векторы, величина которых равна , а не , равной сумме
величин исходных векторов.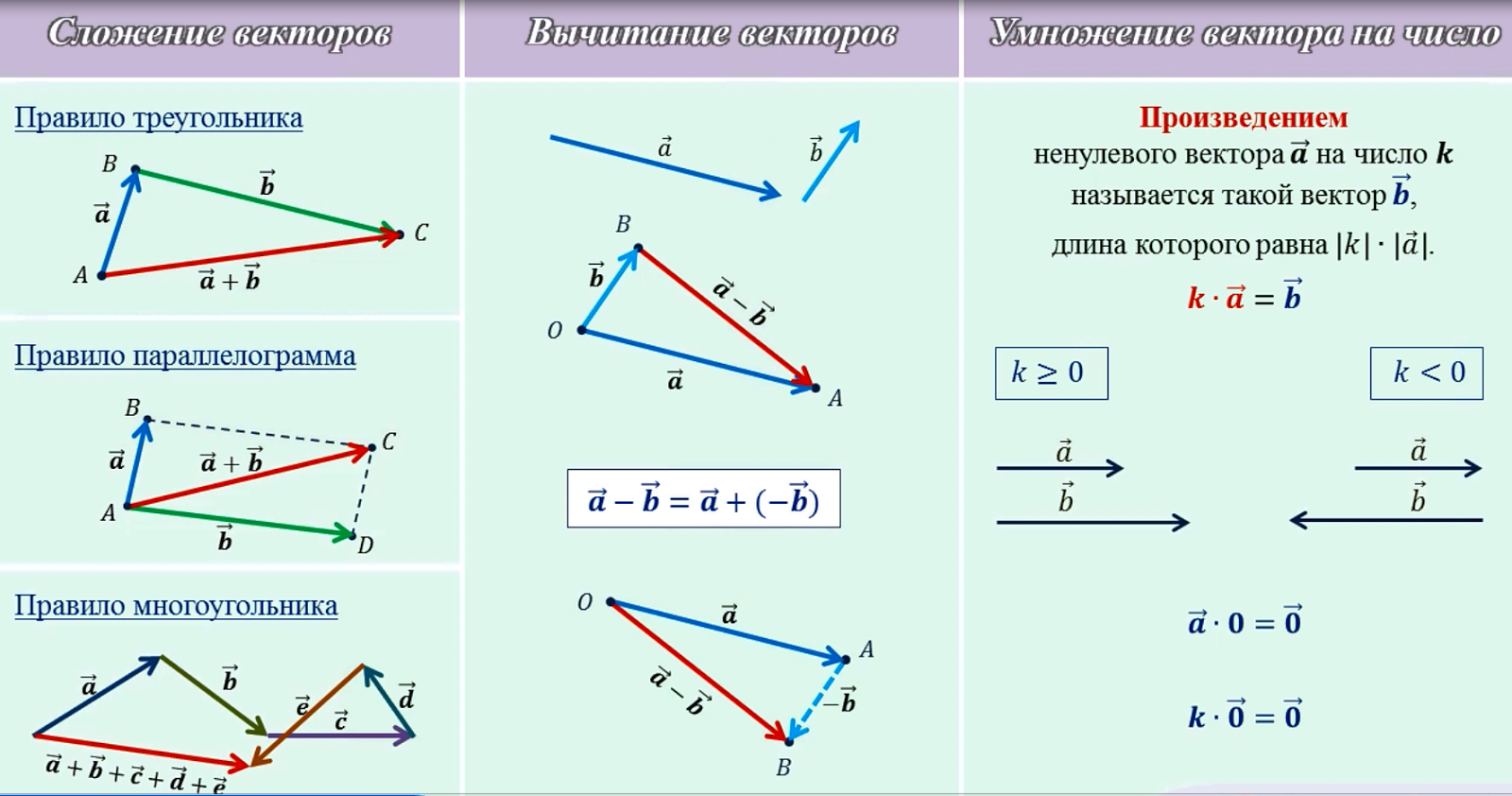 Векторная алгебра сильно отличается от скалярной алгебры, потому что она должна
учитывать как величину, так и направление.
Векторная алгебра сильно отличается от скалярной алгебры, потому что она должна
учитывать как величину, так и направление.
Примечание: На этом слайде для простоты мы разработали компоненты только в двух измерениях; имеются две оси координат.В действительности существуют три пространственных измерения и три компонента мира. все силы. Это важно для нашего вывода общие уравнения с движением для траекторий полета и для Навье-Стокса и уравнения Эйлера, которые описать силы и результирующее движение жидкостей в двигателе. Мы можем разбить очень сложные трехмерные векторные задачи на всего три скалярных уравнения.
Экскурсии с гидом
- Векторов:
- Ракетный перевод:
Деятельность:
Связанные сайты:
Rocket Index
Rocket Home
Руководство для начинающих Home
8.
 8: Векторы — Математика LibreTexts
8: Векторы — Математика LibreTextsПример \(\PageIndex{2B}\): демонстрация равенства двух векторов
Показать, что вектор \(\vec{v}\) с начальной точкой в \((5,−3)\) и конечной точкой в \((−1,2)\) равен вектору \(\vec{ u}\) с начальной точкой в \((−1,−3)\) и конечной точкой в \((−7,2)\). Нарисуйте вектор положения на той же сетке, что и \(\vec{v}\) и \(\vec{u}\). Затем найдите величину и направление каждого вектора.
Раствор
Как показано на рисунке \(\PageIndex{8}\), нарисуйте вектор \(\vec{v}\), начиная с начальной \((5,−3)\) и конечной точки \((−1,2 )\).Нарисуйте вектор \(\vec{u}\) с начальной точкой \((−1,−3)\) и конечной точкой \((−7,2)\). Найдите стандартное положение для каждого.
Затем найдите и зарисуйте вектор положения для \(\vec{v}\) и \(\vec{u}\). У нас есть
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7− (−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Поскольку векторы положения одинаковы, \(\vec{v}\) и \(\vec{u}\) совпадают.
Альтернативный способ проверки равенства векторов — показать, что величина и направление одинаковы для обоих векторов.{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39,8° \end{align*}\]
Однако мы видим, что вектор положения заканчивается во втором квадранте, поэтому мы добавляем \(180°\). Таким образом, направление равно \(−39,8°+180°=140,2°\).
Рисунок \(\PageIndex{8}\)
Косинусное сходство – обзор
4.5.1 Вычисление сходства между документами
Определим, как документы соотносятся друг с другом в нашем корпусе. Пусть T 1 9012 и T 2 — два вектора, соответственно, представляющие тему ассоциации документов D 1 и D 2 , где T 1 ( I ) и T 2 ( I ) , соответственно, количество терминов в D 1 и D 2 , которые связаны с темой I . Затем можно использовать сходство косина для получения меры документа сходства:
Затем можно использовать сходство косина для получения меры документа сходства:
σit1i * T2it1 * T2
здесь, ∥ T J ∥ обозначает норму вектора T J .
В текущем примере мы будем использовать строки матрицы res$document_sums в качестве списка признаков. Следовательно, два документа похожи, если они имеют сходное распределение тем. Следующие строки будут вычислять и выводить матрицу сходства для документов.
> mat <- t(as.matrix(res$document_sums)) %*% as.matrix(res$document_sums)
> d <- diag(mat)
> sim <- t(t(mat/ sqrt(d))/sqrt(d))
> sim[1:5, 1:5]
[,1] [,2] [,3] [,4] [,5]
[1 ,] 1.0000000 0.46389797 0.529169797 0.52916839 0.53162745 0.26788474
1 [2,] 0.4638980 1.00000000 0.846898028 0.
821 0.06361709[3,] 0.5291684 0.84688328 1.0000000000000000802892 0.07256801
[4,] 0.5316274 0.
821 0.821 0.821 0.97052892 1. 00000000 0.072
00000000 0.072[5,] 0.2678847 [5,] 0.2678847 0.06361709 0.07256801 0.072
1.0000000000Полученная матрица представляет собой симметричную матрицу, где вход в строке I и колонна J представляет собой мера сходства косинуса между документами D D D D i и d j . Чем больше записей, тем более похожи публикации с точки зрения тематических ассоциаций.Запись 1 указывает на идентичные публикации с точки зрения тематических ассоциаций.
В нашем примере документы 3 и 5 совершенно не похожи, а документы 2 и 3 чем-то похожи. На самом деле документ 3 относится к анализу дифференциальных уравнений в частных производных, а документ 5 обсуждает квантовую алгебру. Документ 2 в нашем корпусе представляет собой научную статью, в которой также обсуждается анализ дифференциальных уравнений в частных производных.
В качестве альтернативы можно использовать матрицу res$document_sums для вычисления расстояний между документами вместо косинусной меры сходства.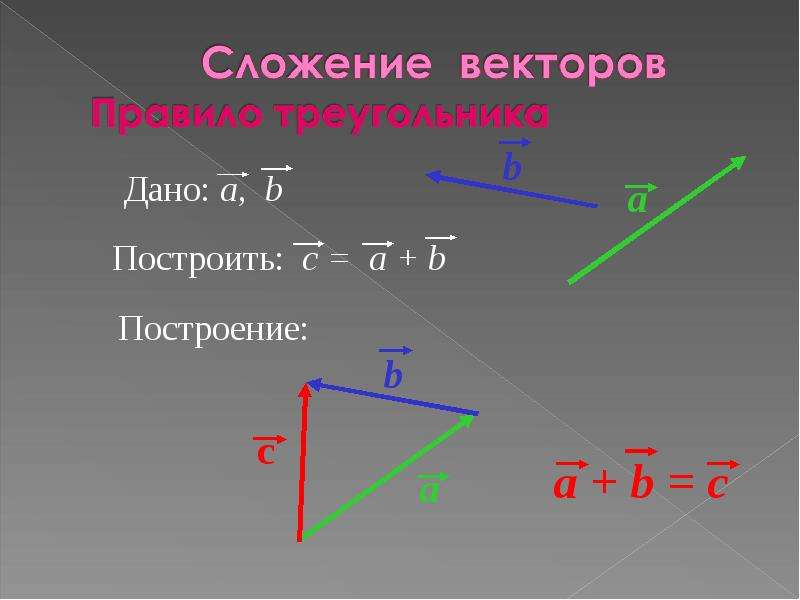 Функция dist в R позволяет это сделать.
Функция dist в R позволяет это сделать.
> AS.matrix (dist (t (res $ document_sums))) [1: 5, 1: 5]
1 2 3 4 5
1 0 0,00000 38.11824 41.96427 36.27671 50.45790
2 38.11824 0,00000 26.49528 11.00000 46.03260
3 41.96427 26.49528 0.00000 20.124528 0,00000 20.12461 57.50652
4 36.27671 11.00000 20.12461 0.00000 46.28175
5 50.45790 46.03260 57.50652 46.03260 57.50652 46.28175 0,00000
Ожидается, что расстояние между документами 2 и 3 является относительно небольшим по сравнению с другими значениями расстояния, которые отражают тот факт, что они несколько похоже.
Функция dist принимает множество аргументов, но самым важным из них является метод, используемый для вычисления расстояний. Это упрощает настройку метода расчета расстояния в соответствии с базовым набором данных и целями. Предусмотренные варианты: евклидов, который используется по умолчанию, максимальный, манхэттенский, канберрский, двоичный и метод расстояния Минковского.
 (Используйте таблицу тригонометрических функций)
(Используйте таблицу тригонометрических функций)

 Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.
Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? Используйте таблицу тригонометрических функций. В ответе укажите целое число градусов.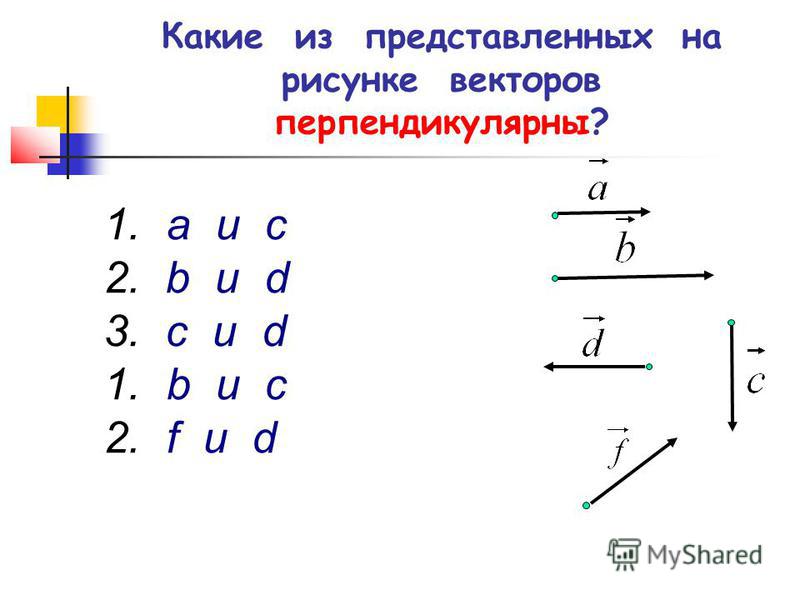 В ответе укажите целое число метров
В ответе укажите целое число метров
 В ответе укажите целое число градусов.
В ответе укажите целое число градусов. Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.
Используя таблицу тригонометрических функций, найдите угол, который образует новое положение Ас маятника с положением равновесия АВ.

 Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения?
Затем они поворачивают налево и проходят 36,0 метров на запад. Какова величина их общего смещения? Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и пробежал по полю на расстояние 4,8 метра в направлении 240° против часовой стрелки с востока (30° з.д. и ю.ш.), прежде чем, наконец, выбить ветер из широкого ресивера Нью Грир. Определите величину и направление общего смещения Макса.
Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и пробежал по полю на расстояние 4,8 метра в направлении 240° против часовой стрелки с востока (30° з.д. и ю.ш.), прежде чем, наконец, выбить ветер из широкого ресивера Нью Грир. Определите величину и направление общего смещения Макса.