Нахождения площади фигур формулы: Формулы площади. Площадь треугольника, квадрата, прямоугольника, ромба, параллелограмма, трапеции, круга, эллипса.

Posted on by alexxlab
2\cdot \text{ctg}(\frac{\pi}{n})$

n — число ребер(вершин).
$\pi=3,14159265359$

Содержание

Формулы площади и программы для расчета площадей

Содержание:

Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.


Формулы площади треугольника

1-ая формула

S — площадь треугольника

a, b — длины 2-х сторон треугольника

С — угол между сторонами a и b

2-ая формула

S — площадь треугольника

a — длина стороны треугольника

h — длина высоты, опущенной на сторону a

3-ья формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

p — полупериметр треугольника

4-ая формула

S — площадь треугольника

r — радиус вписанной окружности

p — полупериметр треугольника

5-ая формула

S — площадь треугольника

a, b, c — длины 3-х сторон треугольника

R — радиус описанной окружности

См. также: Программа для расчета площади треугольника.

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

S — площадь квадрата

a — длина стороны квадрата

d — длина диагонали квадрата

См. также: Программа для расчета площади квадрата.


Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

S — площадь прямоугольника

a — длина 1-ой стороны прямоугольника

b — длина 2-ой стороны прямоугольника

См. также: Программа для расчета площади прямоугольника.


Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

S — площадь параллелограмма

a — длина основания

h — длина высоты

См. также: Программа для расчета площади параллелограмма.

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

S — площадь трапеции

a — длина 1-ого основания

b — длина 2-ого основания

h — длина высоты трапеции

См. также: Программа для расчета площади трапеции.


Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

S — площадь ромба

a — длина основания ромба

h — длина высоты ромба

d1 — длина 1-ой диагонали

d2 — длина 2-ой диагонали

См. также: Программа для расчета площади ромба.


Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3. 1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

S — площадь круга

π — число пи (3.1415)

r — радиус круга

См. также: Программа для расчета площади круга.

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

S — площадь эллипса

π — число пи (3.1415)

a — длина большой полуоси

b — длина малой полуоси

См. также: Программа для расчета площади эллипса.

Слишком сложно?

Формулы площади не по зубам? Тебе ответит эксперт через 10 минут!

Площади геометрических фигур / math5school.ru

 

 

Треугольник

 

 

 

 

 

 

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

 

 

Треугольник

 

 

 

 

 

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. 

 

 

Треугольник

 

 

 

 

Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон. 

 

 

Треугольник 

 

 

 

 

Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла.  

 
 

 

 

Треугольник

 

 

 

 

 

 

Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов.

 
 

 

 

Треугольник 

 

 

 

 

 

Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника. 

 

 

Прямоугольный треугольник

 

 

 

 

 

Площадь прямоугольного треугольника равна половине произведения его катетов.  

 

 

Равнобедренный треугольник

 

 

 

 

 

 

Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания. 

 

 

Равносторонний треугольник 

 

 

 

 

 

Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх. 

 

 

Равносторонний треугольник  

 

 

 

 

Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх.  

 

 

 

Треугольник

 

 

 

 

 

Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности. 

 

 

Треугольник 

 

 

 

 

 

Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов.

 

 

 

Треугольник

 

 

 

 

 

Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник).

 
  

 

 

Треугольник 

 

 

 

 

 

 

Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника.

 

 

Прямоугольник

 

 

 

 

 

Площадь прямоугольника равна произведению двух соседних его сторон. 

 

 

Квадрат

 

 

 

 

Площадь квадрата равна квадрату его стороны. 

 

 

Квадрат

 

 

 

 

 

Площадь квадрата равна половине квадрата его диагонали.  

 

 

Параллелограмм

 

 

 

 

 

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне. 

 

 

Параллелограмм

 

 

 

 

 

Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними.  

 

Ромб

 

 

 

 

 

 

Площадь ромба равна произведению квадрата его стороны на синус одного из его углов.  

 

 

 

Ромб (дельтоид)

 

 

 

 

 

Площадь ромба (как и дельтоида) равна половине произведения его диагоналей. 

 

 

Трапеция

 

 

 

 

 

Площадь трапеции равна произведению полусуммы её оснований на высоту. 

 

 

Трапеция

 

 

 

 

 

 

Площадь трапеции равна произведению её средней линии на высоту. 

 

 

 

Выпуклый четырёхугольник

 

 

 

 

 

Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.   

 

 

Вписанный четырёхугольник

 

 

 

  

Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон. 

 

 

Круг

 

 

 

 

 

Площадь круга равна произведению числа «пи» на квадрат радиуса. 

 

 

Круг 

 

 

  

  

Площадь круга равна четверти произведения числа «пи» на квадрат диаметра. 

 

 

Круговой сектор

формулы для случаев градусной и радианной мер центральных углов

Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору.

 

 

Круговое кольцо

 

 

 

  

  

Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов. 
 

 

Круговое кольцо

 

 

  

  

Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров. 
 

 

Круговое кольцо

 

 

 

  

Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины.  

Площади фигур в геометрии — формулы с примерами

Содержание:

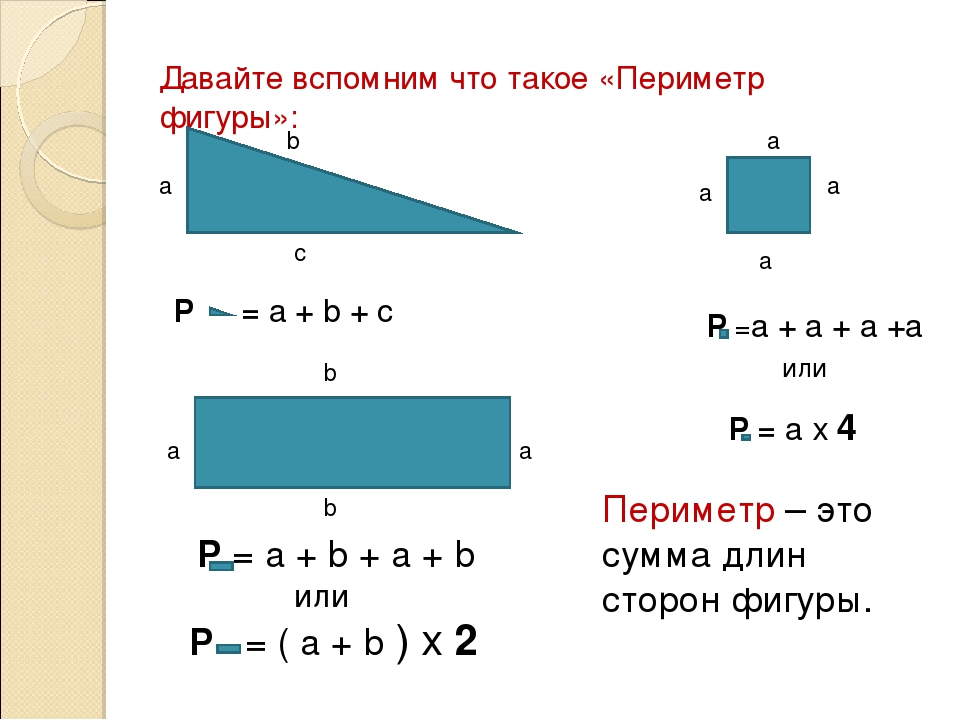
Аксиома равенства площадей: Площади конгруэнтных фигур равны.

Аксиома сложения площадей: Площадь фигуры, разделённой на части не имеющих общих внутренних точек, равна сумме площадей этих фигур.

Высота параллелограмма

Определение. Перпендикуляр, опушенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону, называется высотой параллелограмма. Если параллелограмм не ромб, то он имеет две высоты разной длины (на рисунке это BE и BF).

Практическая работа: Начертите на листе бумаги параллелограмм и его высоту. Разрежьте параллелограмм по высоте, как показано на рисунке, и приклейте к правой стороне. Выскажите своё мнение о полученной фигуре. Запишите формулу нахождения площади прямоугольника. Обобщите мнение о том, что такое площадь параллелограмма.

Так как длина стороны параллелограмма равна длине прямоугольника, а высота параллелограмма равна ширине прямоугольника, то площадь параллелограмма равна площади прямоугольника.

Площадь параллелограмма

Площадь параллелограмма равна произведения стороны и высоты, проведённой к данной стороне: или

Площадь треугольника

Площадь треугольника равна половине произведения стороны и высоты, проведённой к данной стороне,

Обозначим высоты, проведённые к сторонам соответственно как

Площадь прямоугольного треугольника равна половине произведения катетов.

Формула Герона для нахождения площади треугольника

Для треугольника со сторонами верна формула нахождения площади Эта формула называется формулой Герона. Здесь полупериметр треугольника:

Задача. Найдём площадь треугольника со сторонами 13 см, 14 см и 15 см. Дано:

По формуле Герона

Площадь трапеции

Высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.

Площадь трапеции равна произведению половине суммы оснований и высоты:

Площадь трапеции равна произведению средней линии и высоты:

Площадь ромба

1. Площадь ромба равна произведению стороны и высоты:

Отметим что высоты ромбы равны.

2. Площадь ромба равна половине произведения диагоналей:

3. Площадь любого произвольного выпуклого четырёхугольника, диагонали которого взаимно перпендикулярными равна t половине произведения диагоналей:

Площадь поверхности вращения

Определение 1. Пусть L – простая кривая на плоскости заданная явно в виде (см. § 30). Пусть функция y=y(x) — непрерывна и неотрицательна Разобьем отрезок [a b] на n частичных отрезков точками  и обозначим это разбиение  Пусть

— диаметр разбиения.

Пусть  точки на кривой Рассмотрим ломаную последовательно проходящую через точки При вращении кривой  вокруг оси Ох каждое звено  ломаной описывает поверхность
площадь которой  (боковая поверхность усеченного конуса).
— площадь всей поверхности.

Если ∃ предел при Δ → 0 площади  не зависящий от способа разбиения отрезка, то он называется площадью q поверхности вращения кривой L вокруг оси Ox .

Таким образом  (1)
 

Замечание. Пусть функция y=f(x) – непрерывно-дифференцируема на отрезке [a b] , тогда  – площадь боковой поверхности усеченного конуса; (по теореме Лагранжа (см. теорему 4 § 12)

Поэтому

Таким образом:

Где– дифференциал дуги. Формулы (2) и (3) приведены для кривых L, лежащих выше оси Ох. В общем случае верны формулы:

Если кривая L задана параметрически в виде

Для кривой L заданной в полярных координатах уравнением
 

Пример №1

– верхняя полуокружность радиуса R.

Найдем площадь поверхности при вращении вокруг оси Ох.
 

Решение.

, по формуле (2): 

 

Пример №2

– верхняя половина астроиды

Найдем 
 

Решение.


(см. пример 1 § 32). Пусть  тогда по формуле (6):

Поэтому площадь всей поверхности 
 

Пример №3

– лепесток лемнискаты, расположенный в первой четверти

Найдем 
 

Решение.


Площадь геометрической фигуры

Что такое площадь Площадь геометрической фигуры — это неотрицательная численная величина, которая характеризует размер этой фигуры.

Изначально, геометрия в Древней Греции (по-гречески «землемерие») занималась измерением площадей и объемов. Значительное число задач в области элементарной геометрии посвящено именно таким вопросам.

Общим методом нахождения площадей фигур в координатной плоскости является интегральное исчисление. Этими вопросами занимается математический анализ.
Для понимания применения универсального метода математического анализа для определения площади фигур можно привести следующие примеры вычисления площади:

  • Площадь фигуры, заключенная между графиком непрерывной функции на интервале [a,b] и осью абсцисс, равна определенному интегралу этой функции на том же интервале
  • Площадь фигуры, заключенная между графиками двух непрерывных функций на интервале [a,b] равна разности определенных интегралов этих функций на этом интервале

Или, с помощью формул это будет выглядеть следующим образом:

Как видно из рисунка и из формул, площадь фигуры, заключенной между графиком непрерывной функции f(x) и осью координат x на интервале [a,b] равна определенному интегралу этой функции [1].
Если же нам необходимо найти площадь фигуры, заключенной между графиками двух непрерывных функций — мы просто находим определенный интеграл для обоих функций и вычитаем площадь одной фигуры из площади другой. Разность площадей и даст нам искомую величину.

 С помощью интегрального исчисления также определяются площади поверхностей фигур и в полярных координатах (фигура, заключенная между двумя лучами) и в трехмерном пространстве.

Свойства площади фигур Площадь фигуры – это неотрицательная величина, числовое значение которой имеет следующие свойства:
  • Площадь фигуры является неотрицательной величиной
  • Равные фигуры имеют равные площади
  • Площадь фигуры равна сумме составляющих ее и не перекрывающих друг друга частей (свойство аддитивности).
  • Площадь квадрата со стороной, равной единице измерения, равна единице (свойство нормированности)
  • Площадь фигуры всегда больше площади ее части (свойство монотонности)

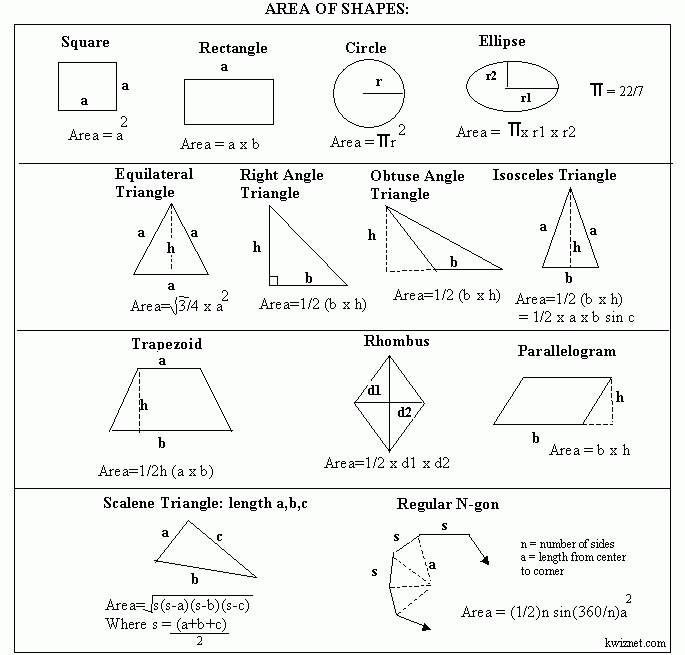
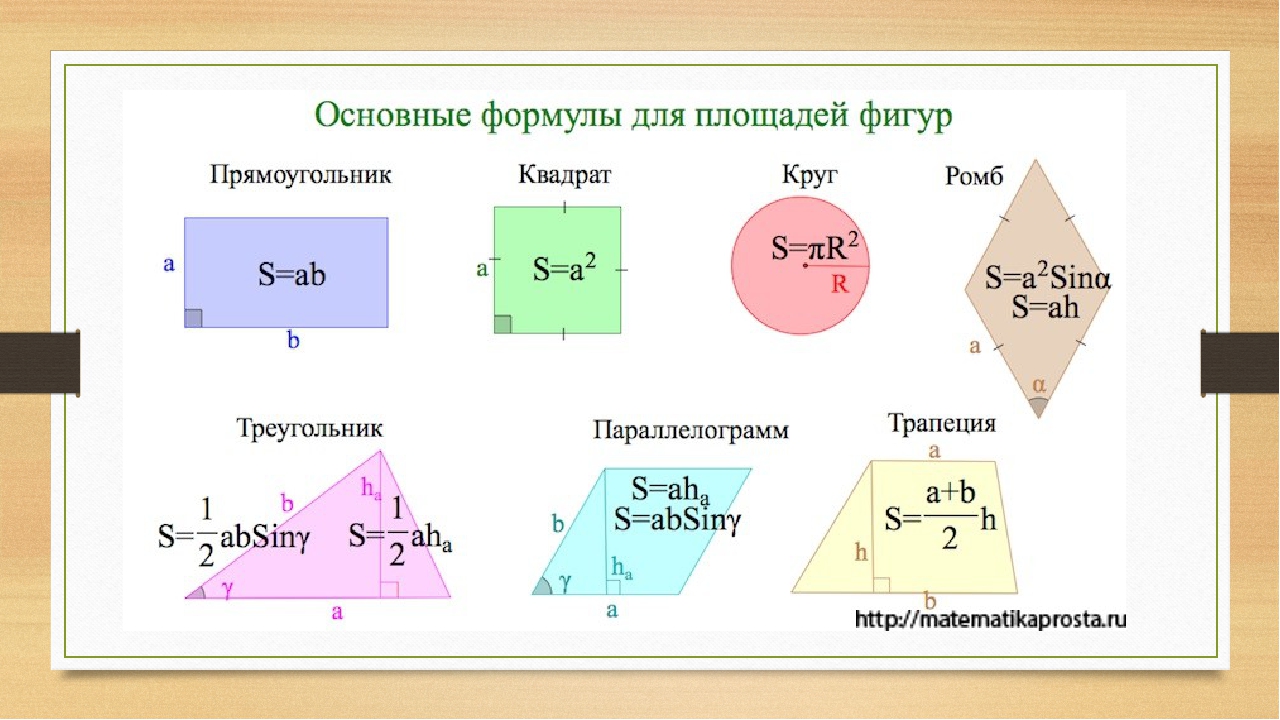
Формулы для нахождения площадей геометрических фигур

Площадь квадрата со стороной а

S=a2

См.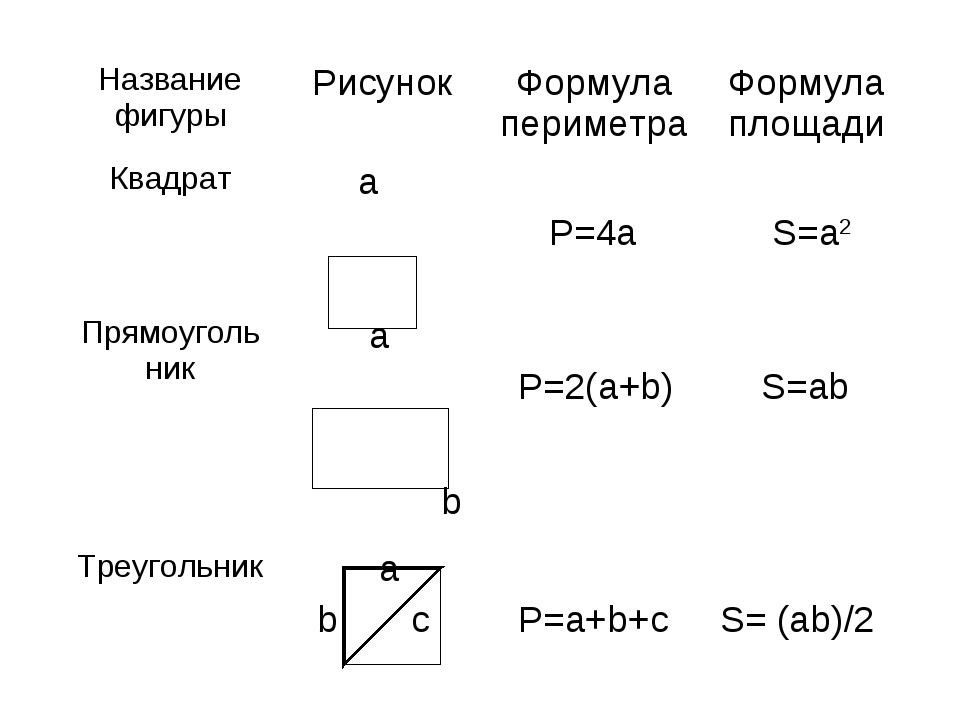 также — квадрат и площадь квадрата. Все формулы.

Площадь прямоугольника со сторонами а и b

S=ab

См. также Задачи про нахождение площади прямоугольника с пояснениями.

Площадь параллелограмма со сторонами а и b или с основанием а и высотой h

S=ah

S=ab*sin ∠ab

См. также свойства и площадь параллелограмма.

Площадь ромба со стороной а, углом между сторонами α, диагоналями d1, d2

S=ab*sinα

или

S=1/2 d1d2

См.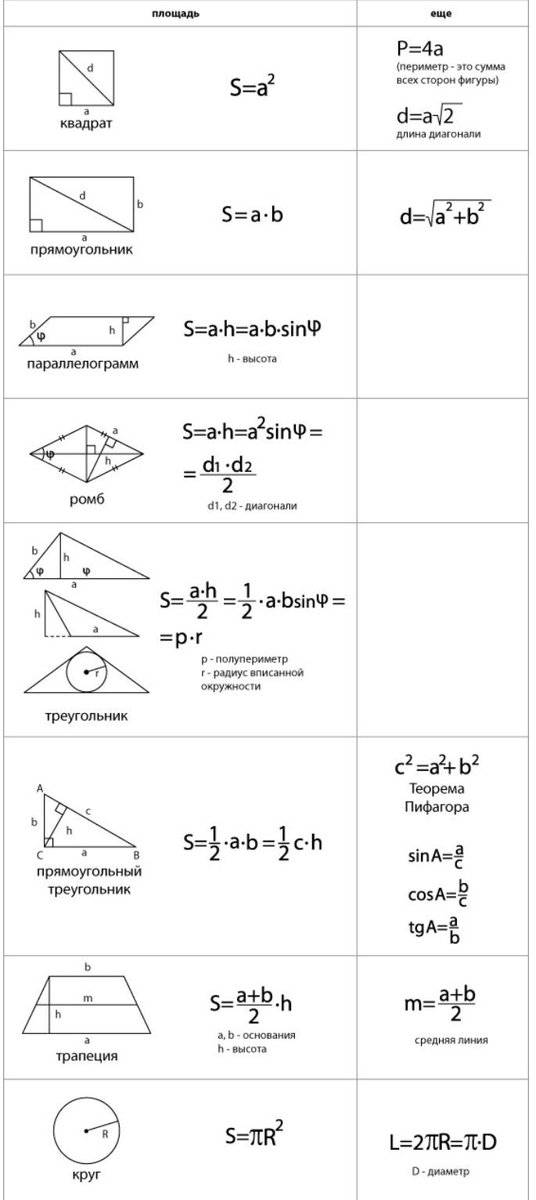 также Задачи о ромбе. 

Площадь треугольника с основанием а и высотой h

S=1/2 ah

См. также площадь треугольника (все формулы).

Площадь трапеции с основанием а, b и высотой h

S=(a+b)/2 * h

См. также свойства и площадь трапеции (все формулы).

Площадь круга

S=πR2

См. также Задачи про окружность.

 Биссектриса. Примеры решения задач | Описание курса | Окружность. Уравнение окружности 

   

3. Площадь фигур — Фигуры В Пространстве

 

   Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры.

    1. Площадь поверхности куба равна произведению квадрата длины его грани и числа шесть.

    Формула площади куба: 
    где 

S

 — площадь куба, 

            a

 — длина грани куба.

  

    2. Площадь призмы 


    Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы — сумма площадей ее боковых граней.

    

    Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

   

   

    3. Площадь прямоугольного  параллелепипеда 

Формула площади прямоугольного параллелепипеда:  

                                  S = 2(

a · b

 + 

a · h

 + 

b · h

)

    

    где 

S

 — площадь прямоугольного параллелепипеда, 

            a

 — длина, 

            b

 — ширина, 

            h

 — высота.

    4. Площадь пирамиды 


    Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней.

    Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

    Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметра оснований на апофему.

    5. Площадь цилиндра

    Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.

     Формула для вычисления площади боковой поверхности цилиндра: 

    Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.

    Формула для вычисления площади полной поверхности цилиндра: 

S = 2 

π R h

 + 2 

π R 

2

 = 2 

π R

(

R

 + 

h

)

    где 

S

 — площадь, 

            R

 — радиус цилиндра, 

            h

 — высота цилиндра, 

            π

= 3,141592

.

    6. Площадь конуса 

    Площадь боковой поверхности конуса равна произведению его радиуса и образующей, умноженному на число π . 

    Формула для вычисления площади боковой поверхности конуса: 

    Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.

Формула для вычисления площади полной поверхности конуса:

S = 

π R

2

 + 

π R l

 = 

π R

 (

R

 + 

l

)

    где 

S

 — площадь, 

            R

 — радиус основания конуса, 

            l

 — образующая конуса, 

            π

= 3,141592

.

    7. Площадь шара

    Площадь поверхности шара равна четырем его радиусам в квадрате, умноженным на число π.     Формула площади шара:     Площадь поверхности шара равна квадрату его диаметра, умноженного на число π.    Формула площади шара:     где 

V

 — площадь шара, 

           R

 — радиус шара, 

           D

 — диаметр шара, 

           π

= 3,141592

.

Разработка блока уроков по теме: «Площади фигур»

Блок уроков по теме “Площади фигур”.

Цели уроков:

1. Формирование понятие площади фигур.

2. Формирование навыков самостоятельной работы с учебником.

3. Формирование метода доказательства, заключающегося в введении новой фигуры, находящейся в известных связях с теми фигурами, отношение между которыми доказывается. Вывести формулы площадей простых фигур.

4. Формирование навыков применения знаний в новых ситуациях, видение изученной закономерности в различных ситуациях.

5. Формирование умений работать с задачей.

6. Систематизировать, расширять и углублять знания, умения и навыки учащихся, связанные с понятием плошали простых фигур и умения применять знания в новой ситуации.

7. Воспитывать доброжелательные отношения друг к другу.

Выслушивать мнения других и высказывать свою точку зрения.

Литература.

1. Атанасян Л. С. “Геометрия 7 – 9”

2. Карнацевич Л.С. “Изучение геометрии в 8 классе”. Москва. Просвещение, 1984 г.

3. Хамитов Р.Г. “Геометрия 7 – 9. Тест – обучающая программа”. Казань. 2000 г.

4. Окунев А.А. “Изучение геометрии в 8 классе”. Москва. Просвещение, 1996 г.

5. Макаров Ю.А. “Технология индивидуального обучения”. Сборник статей. Пермь. 19% г.

6. Рабинович Н.М. “Геометрия 7 – 9. Задачи на готовых чертежах”. Москва-Харьков, 1998 г.

7. Саранцев Г.И. “Упражнения в обучении математики”. Москва. Просвещение, 1995 г.

8. “Энциклопедический словарь юного математика”. Москва. Педагогика, 1989г.

9. Варданян С.С. “Задачи по планиметрии с практическим содержанием”. Москва. Педагогика. 1989 г.

10. Кукарцева Р.И. “500 задач по геометрии в рисунках и тестах. 7-9 класс.” Москва. Аквариум, 2001 г.

“Каждый должен сам овладеть навыками по усвоению знаний и делать это в присущем ему стиле”

С. Пейперт.

Сколько за последние годы появилось новых учебников, новых концепций, новых программ!

На данном этапе состояния математического образования одним из приоритетных направлений преподавания математики является изменение акцентов в учебной деятельности. Поэтому проблема самостоятельности, активности учащихся является одной ш центральных проблем обучения наших дней.

Обучение путем “делания” в 6-7 раз продуктивнее обучения путем “слушания”. (И. П. Подласый. Педагогика 1996 г.)

Возможности развития учащихся скрываются в специально отобранном содержании учебного материала, т.е. в познавательных заданиях, однако это лишь предпосылка для развития. Для того, чтобы обучение проявило свой развивающий эффект необходимо соблюдать универсальное условие: развиваемый ученик должен быть вовлечен в активную деятельность и общение. Это вытекает из того, что ученик в учебном процессе не только объект, но и субъект процесса собственного учения. Эффективность обучения зависит не только от характера предъявляемых заданий, но, прежде всего, от активности самого ученика. Специалисты считают, что при возможности выбора ученик может стать субъектом управления своей собственной деятельности и работе в зоне ближайшего развития.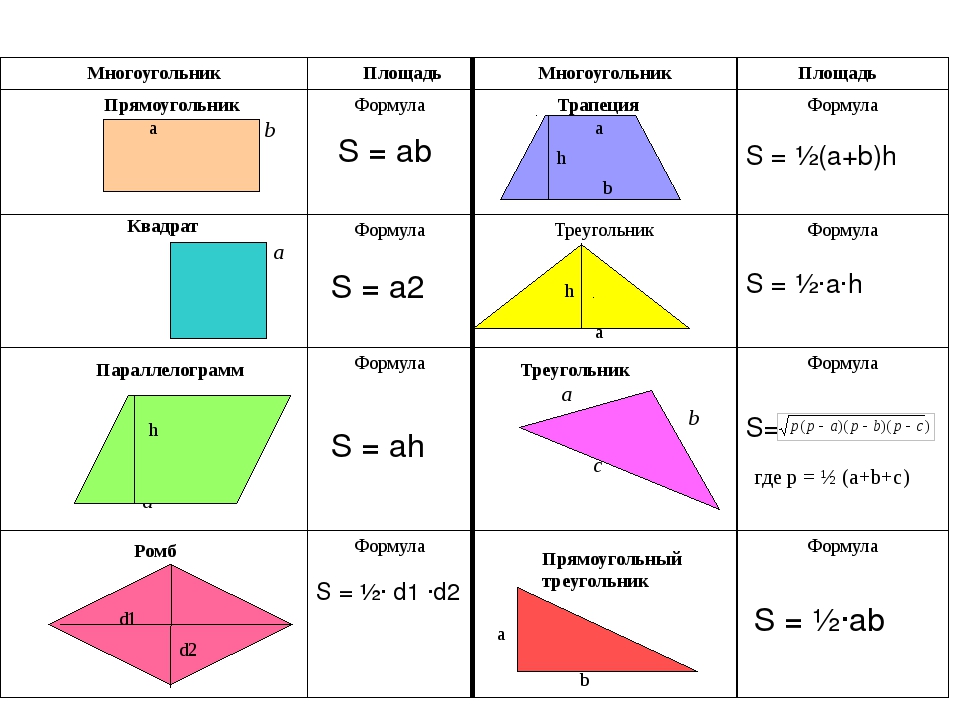

Пояснительная записка.

Много трудностей встречается в работе учителя математики. Если спросить школьников, какой предмет им нравится больше других, то вряд ли большинство из них назовут математику. Обычно ее скорее уважают, чем любят. Некоторые вопросы школьной математики учащимся кажутся недостаточно интересными, порой скучными.

Проверку домашнего задания и актуализацию прежних знаний в разных классах проводят по разному, в зависимости от эмоциональной и мотивационной настроенности учащихся к изучаемому материалу:

1) изучение и решение задачи или проблемы по требованию учителя;

2) изучение и решение задачи, вызвавшей удивление, интересной для учащихся;

3) учение для продвижения в жизни.

Школа призвана реализовывать и некоторые обязательные традиционные умения и навыки.

В начале урока выясняем все вопросы, возникшие у учащихся при подготовке домашнего задания. Если в классе подобраны слабые ученики, то домашнюю работу проверяем, предлагая по готовым чертежам найти площади изучаемых фигур, доказать теорему по готовому чертежу. Чаще группе таких учащихся предлагаем выполнить лабораторную работу, т.к. при выполнении лабораторных работ знания, полученные от пассивного созерцания, закрепляются при самостоятельной работе.

Более сильным ученикам предлагаем тесты, либо более трудные задачи.

Урок 1.

Тема: “Площадь многоугольника”.

– Начертите известные вам многоугольники. Перечислите их.

– С этого урока начинаем изучение площади многоугольников.

Понятие площади известно вам из повседневного опыта. Площади каких фигур, перечисленных вами, вы умеете находить?

Что такое площадь?

Площадью называется величина, характеризующая размер геометрической фигуры. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу. Древние греки умели правильно находить площади многоугольников. Когда каменщики определяют площадь прямоугольной стены дома они перемножают высота и ширину стены. Долгий был путь к нахождению формул, позволяющим найти площади любых фигур. В настоящее время существуют и механические приборы для вычисления площадей плоских фигур – так называемые планиметры.

– Что вы понимаете под выражением “измерение площади”?

– Какие формулы вы знаете для нахождение площадей простых фигур?

– Где вы применяете эти понятия в жизни?

– Что принято за единицу измерения площади?

– В каких единицах измеряется площадь? Рассмотрите рисунок. Найдите площадь фигуры.

Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно

было составить более простой многоугольник, площадь которого уже известна. О таких многоугольниках говорят, что они равносоставлены. Равносоставленные многоугольники имеют одинаковую площадь или. как говорят, равновелики.

Таким образом, для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:

1) Равновеликие фигуры имеют равные плошади.

2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей,

3) Площадь квадрата со стороной, равной единице измерения. равна единице.

Выполнить задачу.

Начертите квадрат и примите его за единицу измерения площадей. Далее начертите: а)квадрат. площадь которою выражается числом 4; б) прямоугольник, отличный от квадрата, площадь которого выражается числом 4: в) треугольник, площадь которого выражается числом 2.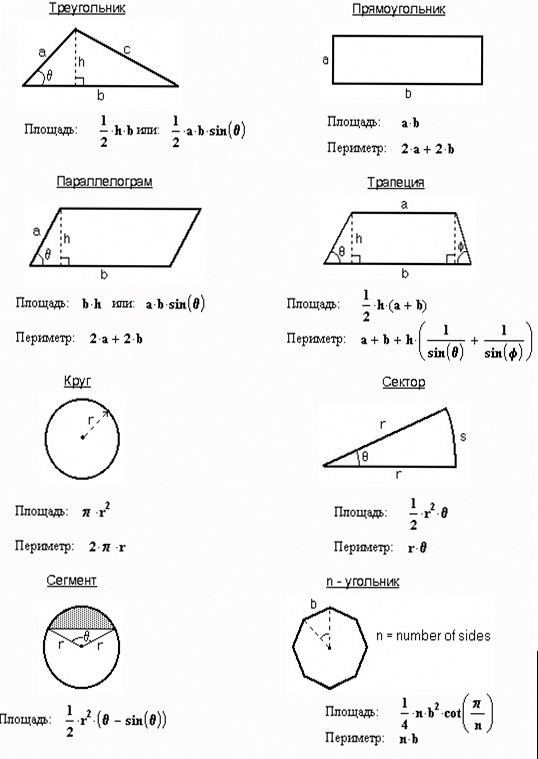

Домашнее задание: стр. 117 – 120 п.48. стр. 445, 446, 450 стр. 226

Урок №

2.

Тема: “Площадь прямоугольника”.

Так как вывод формулы для вычисления площади прямоугольника сопровождается довольно трудными для выполнения на доске рисунками, то учитель заранее изготавливает таблицу, в которой помещены рисунки и сделаны некоторые необходимые для доказательства записи.

Площадь прямоугольника.

1-й случай, а и b – конечные десятичные дроби (десятичных знаков не более n).

2-й случай, а и b – конечные или бесконечные десятичные дроби.

Доказываем, что площадь прямоугольника со сторонами а и b вычисляется по формуле S=ab. При рассмотрении первой части доказательства теоремы особое внимание следует уделить использованию свойств площади (равные квадраты имеют одинаковую площадь, площадь большого квадрата и прямоугольника равна сумме площадей содержащихся в них малых квадратов).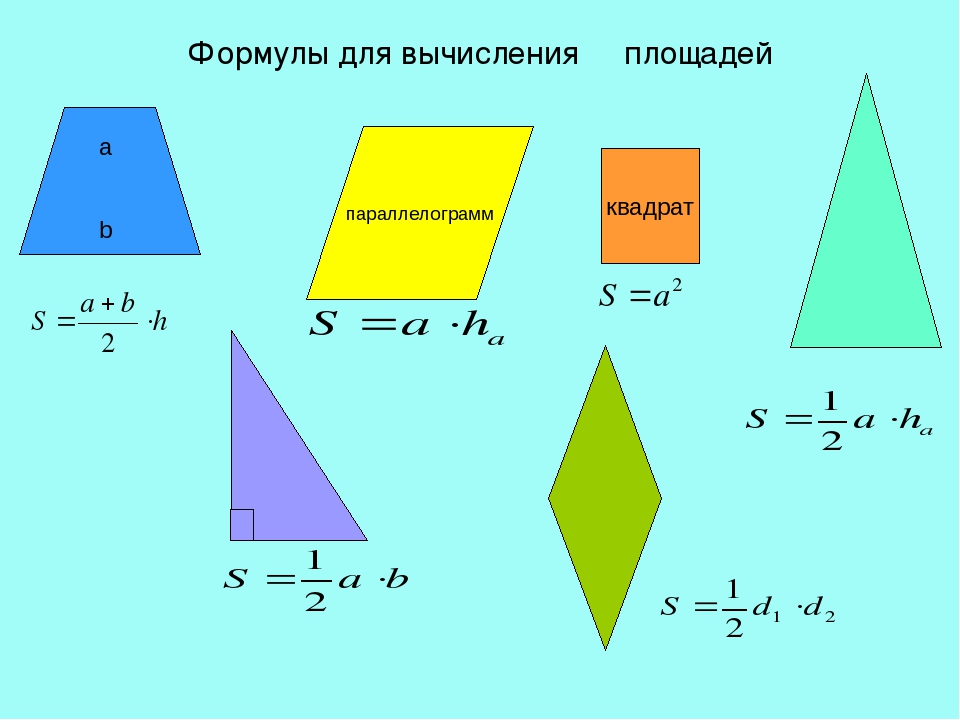

Следствие. Площадь квадрата равна квадрату его стороны.

Закрепление.

1. (Устно). В прямоугольнике стороны равны 3/4 см и 1.2 дм. Найдите площадь прямоугольника.

2. Как изменится площадь прямоугольника, если: 1) увеличить одну из его сторон в 3 раза; 2) увеличить каждую из его сторон в 2 раза?

3. Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?

Домашнее задание: вопросы 1,2, № 449, 452

Урок№3.

Тема: “Площадь прямоугольника”.

Проверка домашнего задания:

1) Как относятся площади прямоугольников, имеющие общее основание?

2) Квадрат и прямоугольник имеют равные площади. Чему равна сторона квадрата, если стороны прямоугольника 36 см и 25 см?

Затем слабым учащимся предлагаются лабораторные работы № 1 и

№2, а сильным – задачи с практическим содержанием (их можно

решать в любом порядке).

Лабораторная работа № I.

Тема: определение площади квадрата.

Цель работы: закрепление навыка определения площади квадрата.

Оборудование: линейки, квадраты.

Задание:

1. Определить сторону квадрата.

2. Записать формулу площади квадрата.

3. Записать результаты измерений и вычислений в таблицу

№ п/п

 Длина стороны квадрата Площадь квадрата

1

    

2

    

3

    

Лабораторная работа № 2.

Тема: определение площади прямоугольника.

Цель работы: закрепление навыка определения площади прям-ка

Оборудование: линейки, прямоугольники.

Задание:

4. Определить длину прямоугольника.

5. Определить ширину прямоугольника.

6. Записать результаты измерений и вычислений в таблицу.

№ п/п

 Длина

Прямоугольника

 Ширина прямоугольника Площадь прямоугольника

1

      

2

      

3

      

Задачи с практическим содержанием.

1) Каждый из двух равновеликих участков нужно обнести забором. Один участок имеет форму квадрата со стороной 80 м. а другой – форму прямоугольника, одна сторона которого раина 50 м. На какой забор потребуется больше материала и на сколько, если на каждые 12 м забора нужно 1 м2 пиломатериалов?

2) Колхозный сад имеет форму прямоугольника со сторонами 580 и 376 м. Сколько в нем яблонь, если на каждую яблоню приходится в среднем по 16 м2? Какую выручку дат сад после продажи яблок, если с 1 га собрано по 35 т яблок и каждая тонна продана в среднем по 450 р ?

3) Ребята решили пристроить к стене школы физкультурный зал прямоугольной формы. Оказалось, что кирпича у них хватит только на 100 м стены (по периметру трех новых стен). Зал должен быть как можно больше по площади. Что вы посоветуете ребятам? Какие размеры пристройки выбрать?

4) Новосел, решив выложить пол в квадратной кухне площадью 7,29 м2 квадратными разноцветными плитками, купил такой набор: 1 плитка со стороной 120 см. 3 плитки со стороной 90 см. 9 плиток со стороной 60 см и 2 плитки со стороной 30 см. Другой новосел для точно такой же кухни купил на I плитку больше со стороной 120 см, на 1 плитку меньше со стороной 90 см и на 1 плитку меньше со стороной 60 см. Кто из них поступил разумно?

После знакомства с задачами, желающие объяснить решение какой-либо задачи у доски, выходят и объясняют решение. Те, кто знает решение задач, выполняют эту работу самостоятельно и сдают тетради. Домашнее задание: Практическая работа.

1. Подсчитать, сколько требуется плиток кафеля для облицовки стен вашей кухни. Кафель размером 15×15. Подсчитайте стоимость материала.

2. Подсчитать количество рулонов обоев, необходимое для ремонта вашего зала. Сколько это будет стоить?

3. Найти интересную задачу на нахождение площади прямоугольника или квадрата

4. Повторить № 49, 50.

Урок №4.

Тема: “Площадь параллелограмма”.

1. Проверка домашнего задания.

2. Изучение нового материала.

Площадь какой фигуры вы уже умеете находить?

Начертите параллелограмм ABCD.

На этом уроке мы должны вывести формулу площади параллелограмм и научиться ее применять. Для этого нам необходимо найти высоту параллелограмма.

Постройте высоту параллелограмма: из вершины А опустите перпендикуляры АК на сторону ВС и AN на сторону DC.

Отрезок AN называется высотой параллелограмма, соответствующей сторонам АВ и DC. Отрезок АК называется высотой, соответствующей сторонам AD и ВС.

На доске предложены несколько чертежей. Назовите высоту параллелограмм и соответствующие ей стороны.

Подумайте, как можно разбить параллелограмм и составить из него фигуру, площадь которой вы умеете находить. После размышления предлагаем учащимся поделиться своими результатами своей деятельности.

Чаше предлагают частный случай.

Прочитайте пункт 54 стр.124 (Атанасян А.С.).

Как предлагает найти площадь параллелограмма автор.

Расскажите, как найти площадь, используя модель. Модель
представляет собой две равные трапеции АВСЕ, вырезанные из плотной бумаги или картона. На одной трапеции выделен красным цветом треугольник ADE, а на другой – треугольник BFC. При объяснении нового материала учитель может на одной модели загнуть треугольник BCF, а на другой – треугольник ADE.

После этого предложить учащимся прокомментировать нахождение площади каждой фигуры на рис. 1.

Затем вывешиваем таблицу № 1. (Без формул).

Как найти площадь параллелограмма, у которого известны стороны а и b и угол ? между ними? Предлагаем решить самостоятельно, затем выслушиваем решение. Заполняем таблицу маркером в ходе урока.

Решить №459. Ученик решает на откидной доске. Проверяем, выясняем все возникшие вопросы, заполняем таблицу (до конца).

Домашнее задание: 1) Как разделить участок, имеющий форму параллелограмма на две равновеликие части межой, проходящей через произвольную точку, которая задана на плане?

2) Выучить п.51 решить №464(а,б), 465.

Урок №5.

Тема: “Площадь треугольника”.

Проверка домашней работы. Выполнение лабораторных работ.

Лабораторная работа № 1. Тема: определение площади параллелограмма.

Цель работы: закрепить навыки учащихся по нахождению площади параллелограмма.

Оборудование: модели параллелограммов, линейка, карандаш.

Задание.

1. Измерить основание параллелограмма, провести высоту – и измерить ее.

2. Записать формулы для вычисления площади параллелограмма

и вычислить ее.

3. Результаты записать в таблицу:

№

Длина основания

Длина высоты

Площадь

1.

      

2.

      

3.

      

Лабораторная работа № 2. Тема: определение площади ромба.

Цель работы: закрепить навыки учащихся по нахождению площади ромба

Оборудование: модели ромбов, линейка, карандаш.

Задание.

4. Измерить основание ромба, провести высоту и измерить ее.

5. Записать формулы для вычисления площади ромба и вычислить ее.

6. Результаты записать в таблицу:

№

Длина основания

Длина высоты

Площадь

1.

 

 

 

2.

 

 

 

3.

 

 

 

Изучение нового материала.

Начертите остроугольный треугольник, проведите все его высоты. Начертите тупоугольный треугольник, проведите все его высоты. Начертите прямоугольный треугольник, проведите его высоту.

На этом уроке вам предстоит доказать формулу площади треугольника, используя при доказательстве ранее изученные формулы.

Рассмотрите любой треугольник. Подумайте, как получить формулу для нахождения площади треугольника. Выслушать предложения уч-ся.

Затем прочитать по учебнику стр. =l/2ha

Этот способ вычисления площади многоугольников был известен еще Евклиду, который жил более 2000 лет назад.

Запишите площадь каждого треугольника, которые вы чертили в начале урока.

Заполните полезную таблицу.

Решить № 21 (самостоятельно, выборочно взять тетради на проверку).

Найдите площадь треугольника, если известны стороны а, b, с.

Обсуждение задачи. Какую из известных формул мы можем использовать при решении? Если известны все стороны, можно ли найти стороны треугольника? Как?

1) По теореме косинусов находим Cos A

2) Из равенства Sin2A+Cos2A = 1 найдем Sin A

3) По формуле S=l/2bcSinA найдем площадь треугольника.

Домашнее задание: выучить п.52, №464, 465

Урок №6.

Тема: “Площадь треугольника”.

Проверка домашнего задания.

Решить задачу (самостоятельно, с последующим объяснением).

В треугольнике две стороны равны 2см и 4 см. Высота треугольника, проведенная на меньшую из данных сторон, равна 5 см. Что можно сказать о величине высоты, проведенной на большую сторону? Найдите эту высоту.

Самостоятельно № 36(2), проверить выборочно.

Задача: выразите площадь треугольника через его стороны а, b, с и радиус вписанной окружности r. Сделайте чертеж к задаче.

SСВА=SCOB+SBOA+SCOA

S=l/2ar+1/2br+l/2cr=l/2r(a+b+c)= =pr, где р – полупериметр треугольника ABC.

Результат заносим в полезную таблицу.

При изучении теоремы синусов доказали, что

SinA/a = SinB/b = SinC/c = 1/2R

где R – радиус описанной около треугольника окружности.

a=2RsinA.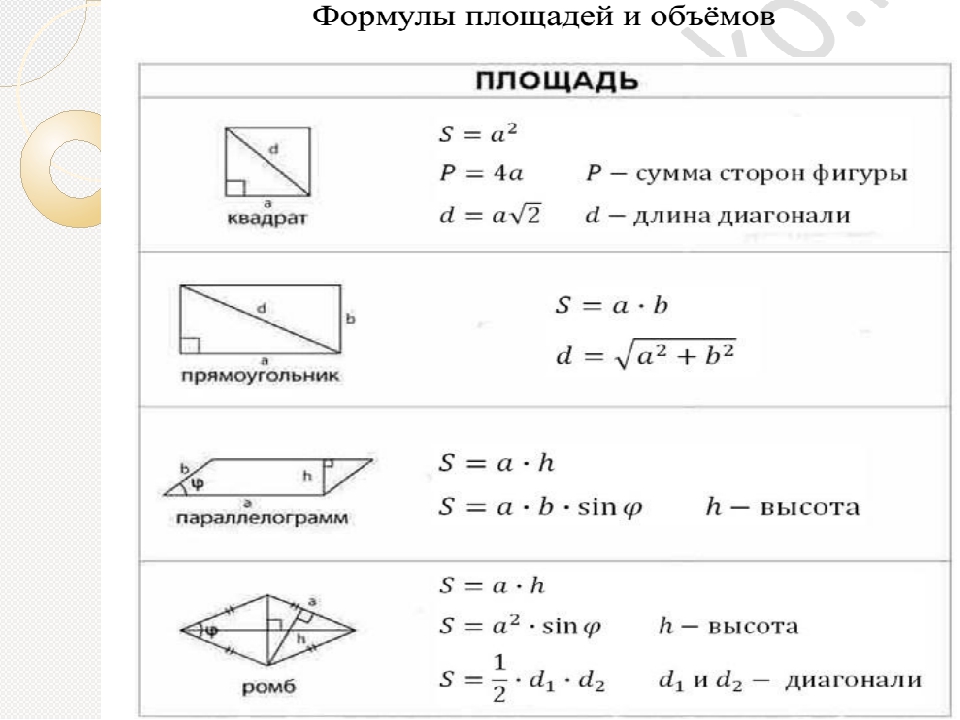 Выразите площадь треугольника через его стороны и радиус описанной окружности и формулу S=l/2bcSinA.

Т.к. SinA=a/2R, то abc/4R=S.

В заключении урока систематизировать знания уч-ся по теме “Площадь треугольника” с помощью таблицы. Необходимо выучить все формулы, знание их будут необходимы при дальнейшем обучении. Этой таблицей можно будет пользоваться в 11 классе при нахождении площадей поверхностей многогранников и их объемов.

Домашнее задание: индивидуальное.

Урок №7.

Тема: “Площадь трапеции”.

Проверка домашнего задания. Изучение нового материала.

Начертите 5 трапеций. Проведите высоту. Докажите, что площадь трапеции равна S=l/2(a+b)h.

S=ah-l/2(b-a)h = ah+(bh-ah)/2 = l/2ah+l/2bh = l/2h(a+b).

S=l/2bh+l/2ah=l/2h(b+a)

Предлагаем уч-ся поделиться своими находками.

Затем прочитать п. 126 стр.221.

Запишите площадь каждой трапеции, построенной в начале урока.

Разобрать по учебнику решение задачи № 40.

Решаем задачи.

1) Средняя линия трапеции равна 10 см, а высота 5 см. Найдите площадь трапеции.

2) Найдите площадь трапеции по данным, отмеченным на рисунках:

Домашнее задание: п.53; №480, 481.

На последующих уроках решаем задачи на нахождение площадей многоугольников.

Расчетная область | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Расчет площади формы или поверхности может быть полезен в повседневной жизни — например, вам может потребоваться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы засеять лужайку.

На этой странице описаны основные сведения, которые вам необходимо знать, чтобы понять и рассчитать площади общих форм, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади сеточным методом

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

Чтобы найти значение площади с использованием метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применяется к любой единице длины или расстояния.Например, вы можете использовать дюймы, метры, мили, футы и т. Д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному квадратному сантиметру.

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Есть 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике мы сокращаем «квадратные сантиметры» до 2 . 2 означает «квадрат».

Каждый квадрат сетки равен 1 см 2 .

Площадь большого квадрата 16см 2 .

Подсчет квадратов на сетке для определения площади работает для всех форм — если известны размеры сетки. Однако этот метод становится более сложным, когда формы не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не точно помещается на сетке.

Мы все еще можем вычислить площадь, считая квадраты сетки.

  • Имеется 25 квадратов полной сетки (заштрихованы синим цветом).
  • 10 квадратов полусетки (заштрихованы желтым цветом) — 10 полуквадратов равны 5 полным квадратам.
  • Также есть 1 четверть квадрата (заштрихована зеленым) — (или 0,25 целого квадрата).
  • Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.

Следовательно, площадь этого квадрата составляет 30,25 см 2 .

Вы также можете записать это как 30¼см 2 .

Хотя использование сетки и подсчет квадратов внутри фигуры — очень простой способ изучения концепций площади, он менее полезен для нахождения точных областей с более сложными формами, когда можно сложить много частей квадратов сетки.

Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Остальная часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сеток.

Площади простых четырехугольников:


квадратов, прямоугольников и параллелограммов

Простейшие (и наиболее часто используемые) вычисления площади выполняются для квадратов и прямоугольников.

Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Площадь прямоугольника = высота × ширина

Для квадрата вам нужно только найти длину одной из сторон (так как каждая сторона имеет одинаковую длину), а затем умножить это на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длину в квадрате.

Рекомендуется проверять, является ли фигура квадратом, измеряя две стороны. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измеряете, вы обнаруживаете, что на самом деле это прямоугольник.

Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах фокус состоит в том, чтобы разделить фигуру на несколько прямоугольников (или квадратов).Неважно, как вы разделите фигуру — любое из трех решений даст один и тот же ответ.

Для решений 1 и 2 необходимо создать две фигуры и сложить их площади, чтобы найти общую площадь.

Для решения 3 вы создаете большую форму (A) и вычитаете из нее меньшую форму (B), чтобы найти площадь.

Другая распространенная проблема — найти область границы — фигуры внутри другой фигуры.

В этом примере показана дорожка вокруг поля — ширина дорожки 2 метра.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете просмотреть путь как четыре отдельных прямоугольника, вычислить их размеры, а затем их площадь и, наконец, сложить области, чтобы получить итог.

Более быстрый способ — вычислить площадь всей формы и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из всей, оставив область пути.

  • Площадь всей формы составляет 16 м × 10 м = 160 м 2 .
  • Мы можем определить размеры средней секции, потому что знаем, что дорожка по краю имеет ширину 2 метра.
  • Ширина всей формы составляет 16 м, а ширина пути по всей форме — 4 м (2 м слева от формы и 2 м справа). 16 м — 4 м = 12 м
  • Проделаем то же самое для высоты: 10м — 2м — 2м = 6м
  • Итак, мы подсчитали, что средний прямоугольник имеет размер 12 × 6 м.
  • Таким образом, площадь среднего прямоугольника составляет: 12 м × 6 м = 72 м 2 .
  • Наконец, мы убираем область среднего прямоугольника из области всей формы. 160 — 72 = 88м 2 .

Площадь тропы 88м 2 .

Параллелограмм — это четырехсторонняя форма с двумя парами сторон равной длины — по определению прямоугольник является разновидностью параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехсторонних фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма рассчитывается так же, как и для прямоугольника (высота × ширина), но важно понимать, что высота означает не длину вертикальных (или отклоненных от вертикали) сторон, а расстояние между сторонами.

Из диаграммы вы можете видеть, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте себе воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

Расчет площади треугольников

Может быть полезно думать о треугольнике как о половине квадрата или параллелограмма.

Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:

Площадь треугольника = (высота × ширина) ÷ 2.

Другими словами, вы можете вычислить площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите свой ответ на 2.

Высота треугольника измеряется по прямой линии от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь рассчитана:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника составляет 4,5 см 2 .

В реальных ситуациях вы можете столкнуться с проблемой, требующей найти площадь треугольника, например:

Вы хотите покрасить фронтальный конец сарая. Вам нужно посетить магазин украшений только один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10 м 2 стены.Сколько краски нужно для покрытия торца фронтона?

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере измерения:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует дополнительных расчетов. Подумайте о здании как о двух формах: прямоугольнике и треугольнике.По имеющимся у вас измерениям вы можете рассчитать дополнительное измерение, необходимое для определения площади фронтона.

Размер D = 12,4 — 6,6

D = 5,8 м

Теперь вы можете определить площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2

Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64м 2

Сложите эти две области вместе, чтобы получить общую площадь:

76. 56 + 33,64 = 110,2 м 2

Как вы знаете, один литр краски покрывает 10 м 2 стены, поэтому мы можем рассчитать, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 л.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых канистрах, а результат — чуть больше 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но, если мы не будем разбавлять краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски.Это позволит учесть любые потери и оставить большую часть литра для подкраски позднее. И не забывайте, что если вам нужно нанести более одного слоя краски, вы должны умножить количество краски для одного слоя на количество необходимых слоев!

Области кругов

Чтобы рассчитать площадь круга, вам необходимо знать его диаметр или радиус .

Диаметр круга — это длина прямой линии от одной стороны круга до другой, проходящей через центральную точку круга.Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус круга — это длина прямой линии от центральной точки круга до его края. Радиус составляет половину диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности — важно измерять, используя прямую линию, проходящую через (диаметр) или заканчивающуюся в (радиусе) центром окружности.

На практике при измерении окружностей часто проще измерить диаметр, а затем разделить на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула:

Площадь круга = πR 2 .

Это означает:

π = Pi — постоянная, равная 3,142.

R = радиус окружности.

R 2 (радиус в квадрате) означает радиус × радиус.

Следовательно, круг с радиусом 5 см имеет площадь:

3,142 × 5 × 5 = 78,55 см 2 .

Круг диаметром 3 м имеет площадь:

Сначала прорабатываем радиус (3 м ÷ 2 = 1.5 м)

Затем примените формулу:

πR 2

3,142 × 1,5 × 1,5 = 7,0695.

Площадь круга диаметром 3 м составляет 7,0695 м 2 .

Заключительный пример

В этом примере используется большая часть содержимого этой страницы для решения простых задач с областями.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (номер записи: 376599).

Этот пример включает поиск передней части дома, деревянной решетчатой ​​части — исключая дверь и окна. Вам нужны следующие размеры:

A — 9,7 м B — 7,6 м
C — 8,8 м D — 4,5 м
E — 2,3 м F — 2,7 м
G — 1,2 м H — 1,0 м

Примечания:

  • Все размеры являются приблизительными.
  • Не стоит беспокоиться о границе вокруг дома — она ​​не учтена в измерениях.
  • Мы предполагаем, что все прямоугольные окна одинакового размера.
  • Размер круглого окна — это диаметр окна.
  • Размер двери включает ступеньки.

Какова площадь деревянной реечной части дома?

Работы и ответы ниже:

Ответы на приведенный выше пример

Сначала определите площадь основной формы дома — прямоугольника и треугольника, составляющих форму.

Главный прямоугольник (B × C) 7,6 × 8,8 = 66,88 м 2 .

Высота треугольника (A — B) 9,7 — 7,6 = 2,1.

Таким образом, площадь треугольника равна (2,1 × C) ÷ 2.
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .

Общая площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м 2 .

Затем проработайте площади окон и дверей, чтобы их можно было вычесть из всей площади.

Площадь двери и ступенек составляет (Д × В) 4,5 × 2,3 = 10,35 м 2 .

Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м 2 .

Есть пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м, поэтому радиус 0,5 м.

Используя πR 2 , обработайте площадь круглого окна: 3.142 × 0,5 × 0,5 =. 0,7855м 2 .

Затем сложите площади двери и окон.

(площадь двери) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из всей площади.

76,12 — 27,3355 = 48,7845

Площадь деревянного реечного фасада дома, и ответ на проблему: 48,7845м 2 .

Вы можете округлить ответ до 48.8м 2 или 49м 2 .

См. Нашу страницу на Оценка, приближение и округление .

Что такое площадь?

Площадь — это размер поверхности!

Пример:

Эти фигуры имеют одинаковую площадь 9:

.

Это помогает представить , сколько краски покроет форму.

Площадь простых форм

Для определенных форм существуют специальные формулы:

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = ш × в
ш = ширина
в = высота

Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :

Площадь = 5 × 3 = 15

Узнайте больше в Area of ​​Plane Shapes.

Площадь по подсчету квадратов

Мы также можем нанести фигуру на сетку и подсчитать количество квадратов:


Прямоугольник имеет площадь 15

Пример: когда каждый квадрат равен 1 метр со стороны, тогда площадь будет 15 м 2 (15 квадратных метров)

Квадратный метр и Квадратный метр

Базовая единица площади в метрической системе — квадратный метр , квадрат с каждой стороной по 1 метру:


1 квадратный метр

Будьте осторожны, говоря «квадратные метры», а не «квадратные метры»:

Существуют также «квадратные мм», «квадратные см» и т. Д., Подробнее см. В метрической зоне.

Примерная площадь по подсчету квадратов

Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.

В одну сторону:
  • больше чем половина квадрата считается как 1
  • меньше чем половина квадрата считается как 0

Как это:


Этот пятиугольник имеет площадь примерно 17

Или мы можем посчитать один квадрат, когда кажется, что
области в сумме составляют .

Пример: Здесь область, обозначенная « 4 », кажется равной примерно 1 целому квадрату (также для « 8 »):


Этот круг имеет площадь примерно 14

Но лучше всего использовать формулу (когда это возможно):

Пример: круг имеет радиус 2,1 метра:

Формула:

Площадь = π × r 2

Где:

Радиус 2.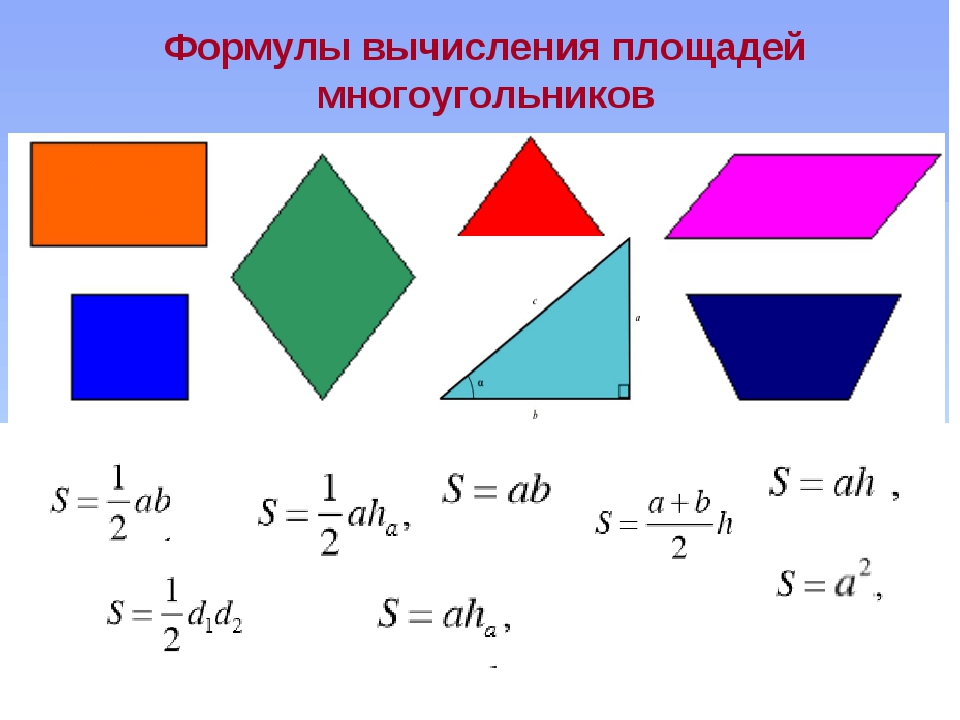 1м , итого:

Площадь = 3,1416 … × (2,1 м) 2

= 3,1416 … × (2,1 м × 2,1 м)

= 13,854 … м 2

Таким образом, круг имеет площадь 13,85 квадратных метров (с точностью до 2 знаков после запятой)

Область сложных форм

Иногда мы можем разбить фигуру на две или более простые формы:

Пример: Какова площадь этой формы?

Разобьем область на две части:

Часть А представляет собой квадрат:

Площадь A = a 2 = 20 м × 20 м = 400 м 2

Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2

Итак, общая площадь:

Площадь = Площадь A + Площадь B

Площадь = 400 м 2 + 140 м 2

Площадь = 540м 2

Площадь путем сложения треугольников

Мы также можем разбить фигуру на треугольники:

Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:

Затем рассчитайте каждую площадь (используя Area = ½b × h) и сложите их все.

Площадь по координатам

Когда мы знаем координаты каждой угловой точки, мы можем использовать метод «Площадь неправильных многоугольников».

Есть область многоугольника с помощью инструмента рисования, который тоже может помочь.

Площадь круга

Калькулятор

Введите радиус , диаметр, окружность или площадь круга, чтобы найти остальные три.Расчеты производятся «вживую»:

images / circle-dia-circ.js

Как посчитать площадь

Площадь круга:

или, если известен диаметр: A = (π / 4) × D 2

или, если вы знаете Окружность: A = C 2 / 4π

Пример: Какова площадь круга радиусом 3 м?

Радиус = r = 3

Площадь = π r 2

= π × 3 2

= 3.14159 … × (3 × 3)

= 28,27 м 2 (до 2 знаков после запятой)

Как помнить?


Чтобы помочь вам запомнить, подумайте «Пирог в квадрате»
(хотя пироги обычно круглые )

Сравнение круга с квадратом

Интересно сравнить площадь круга с квадратом:

Окружность имеет около 80% площади квадрата аналогичной ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%

Почему? Поскольку площадь квадрата равна w 2
, а площадь круга (π / 4) × w 2

Пример: сравните квадрат с кругом шириной 3 м

Площадь квадрата = w 2 = 3 2 = 9 м 2

Оценка площади круга = 80% площади квадрата = 80% от 9 = 7,2 м 2

Истинная площадь круга = (π / 4) × D 2 = (π / 4) × 3 2 = 7.07 м 2 (до 2 знаков после запятой)

Оценка 7,2 м 2 не за горами 7,07 м 2

Пример «Реальный мир»

Пример: Макс строит дом. Первый шаг — просверлить отверстия и залить их бетоном.

Отверстия шириной 0,4 м и глубиной 1 м , сколько бетона Макс должен заказывать для каждого отверстия?

Отверстия круглые (в поперечном сечении), так как высверливаются с помощью шнека.

Диаметр 0,4 м, значит Площадь:

A = (π / 4) × D 2

A = (3,14159 … / 4) × 0,4 2

A = 0,7854 … × 0,16

A = 0,126 м 2 (до 3 знаков после запятой)

А ямки глубиной 1 м, итак:

Объем = 0,126 м 2 × 1 м = 0,126 м 3

So Max должен заказать 0,126 кубометра бетона для заполнения каждой дыры.

Примечание: Макс мог иметь оценочной площади по:

  • 1.Расчет квадратного отверстия: 0,4 × 0,4 = 0,16 м 2
  • 2. Принимая 80% этого (примерный круг): 80% × 0,16 м 2 = 0,128 м 2
  • 3. А объем скважины глубиной 1 м составляет: 0,128 м 3

И кое-что интересное для вас:

См. Площадь круга по линиям

Площадь неправильных многоугольников

Введение

Я просто подумал, что поделюсь с вами умной техникой, которую когда-то использовал для определения площади общих многоугольников.

Многоугольник может быть правильным (все углы равны и все стороны равны) или неправильным

Обычный Нерегулярное

Пример многоугольника

Давайте используем этот многоугольник в качестве примера:

Координаты

Первый шаг — превратить каждую вершину (угол) в координату, как на графике:

Площадь под отрезком одной линии

Теперь для каждого линейного сегмента проработайте область до оси x .

Итак, как рассчитать каждую площадь?

Усредните две высоты, затем умножьте на ширину

Пример. Для фигуры, выделенной выше, мы берем две высоты (координаты «y» 2,28 и 4,71) и вычисляем среднюю высоту:

(2,28 + 4,71) / 2 = 3,495

Определите ширину (разница между координатами «x» 2,66 и 0,72)

2,66-0,72 = 1,94

Площадь ширина × высота:

1. 94 × 3,495 = 6,7803

Добавьте их всех

Теперь сложите их все!

Но фокус в том, чтобы складывать, когда они идут вперед (положительная ширина), и вычитать, когда они идут назад (отрицательная ширина).

Если вы всегда двигаетесь по многоугольнику по часовой стрелке и всегда вычитаете первую координату «x» из второй, это работает естественным образом, например:

из К
х y х y Средняя высота Ширина (+/-) Площадь (+/-)
0.72 2,28 2,66 4,71 3,495 1,94 6,7803
2,66 4,71 5 3,5 4,105 2,34 9. 6057
5 3,5 3,63 2,52 3,01 -1.37 -4.1237
3,63 2,52 4 1,6 2,06 0,37 0,7622
4 1,6 1,9 1 1,3 -2,1 -2,7300
1,9 1 0,72 2.28 1,64 -1,18 -1,9352
Всего: 8,3593

Вы также можете пойти в другом направлении. Если у вас есть отрицательная область, просто сделайте ее положительной.

А это выглядит так:

Вот и все! Площадь . 8 соток.3593

Инструмент Площадь многоугольника

Рад, что вы дочитали до этого места! Вы будете вознаграждены ссылкой на область инструмента рисования многоугольника, которая может сделать все это за вас. Он также допускает ввод координат вручную.

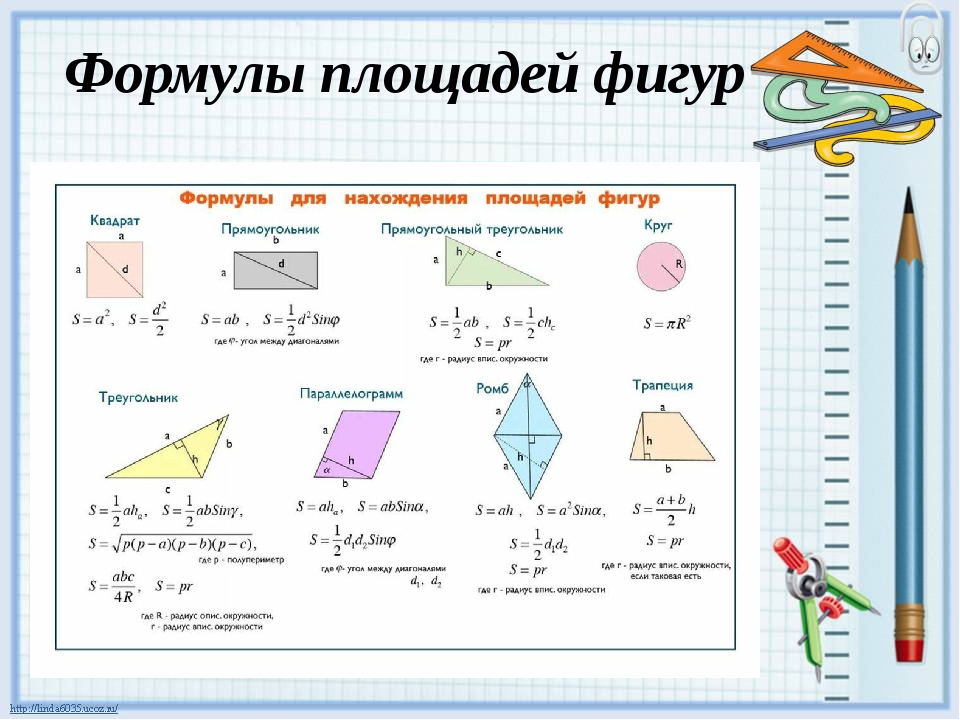
Формулы площади

( пи = = 3,141592 …)

Площадь Формулы

Примечание: «ab» означает «а» умножить на «б».»a

2 » означает «квадрат», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений. Примеры

квадрат = a 2

прямоугольник = ab

параллелограмм = bh

трапеция = h / 2 (b 1 + b 2 4)

9044

круг9000 pi r 2

эллипс = pi r 1 r 2

треугольник = , равная половине длины основания, умноженной на высоту треугольник

равносторонний треугольник =

треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C

треугольник даны a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)

правильный многоугольник = (1/2) n sin (360 ° / n) S 2
когда n = количество сторон и S = ​​длина от центра до угла

шт.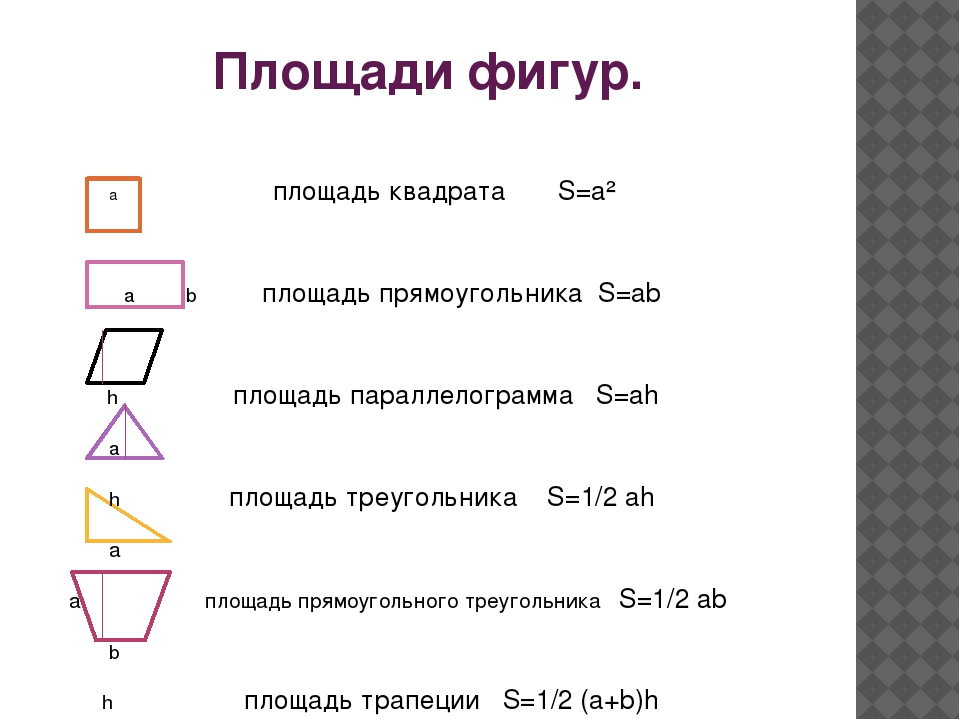

Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на этаж.

Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.

Если у квадрата одна сторона 4 дюйма, площадь будет равна 4 дюймам. 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в формате 2 .)

Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.

Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?

НЕ ПРАВИЛЬНО …. 4 раза 6 = 24

ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута.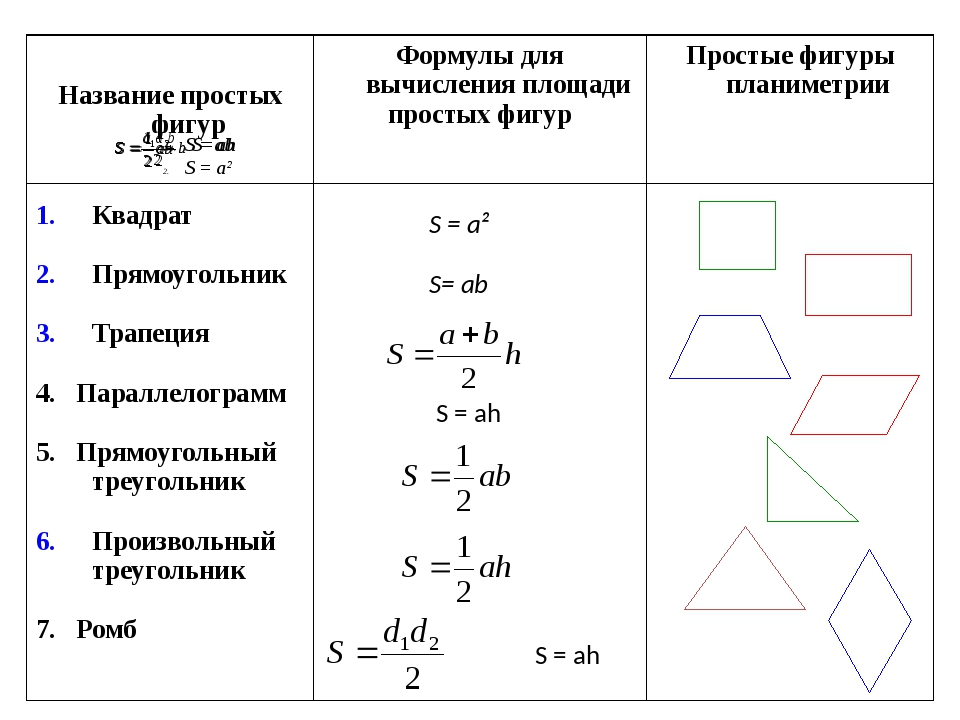 Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута 2 ).

Площадь нерегулярных фигур

Может показаться, что определить площадь прямоугольника легко, но что, если у фигуры более 4 сторон?

Обратите внимание, что у этой формы 8 сторон. Следовательно, мы могли бы назвать его восьмиугольником.

Однако заученная формула неправильного восьмиугольника в этой ситуации не очень поможет. Вместо этого разбейте фигуру на прямоугольники.

Затем вычислите площадь обоих прямоугольников и сложите их.

Площадь первого прямоугольника составляет 72 квадратных сантиметра, а площадь второго прямоугольника — 50 квадратных сантиметров.

Вместе 72 + 50 = 122 квадратных сантиметра.

Следовательно, площадь всей фигуры составляет 122 квадратных сантиметра.

Иногда сложение частей — самый простой метод. В других случаях вам может потребоваться другой подход. Посмотрите следующий пример.

Обратите внимание, что эта фигура выглядит как квадрат, в котором отсутствует часть.

В этом случае вычислите площадь квадрата и прямоугольника, а затем вычтите их.

A квадрат = s 2 A = bh

A = (30 дюймов) 2 A = (18 дюймов) (10 дюймов)

A = 900 дюймов 2 A = 180 дюймов 2

Площадь синего шестиугольника составляет 900 дюймов 2 — 180 дюймов 2 = 720 дюймов 2 .

Путем сложения или вычитания площадей прямоугольников можно вычислить площадь неправильной формы.Это не подойдет для всех неправильных фигур. Возможно, вам также придется использовать треугольники или другие формы.

Начните с разбивки этой фигуры на прямоугольники и треугольники. Есть несколько правильных способов сделать это. Вот один из возможных вариантов:

Затем используйте известные длины сторон, чтобы определить длины сторон, которые все еще необходимы для расчета площади трех частей.


Сюда мы добавили все части верхней длины. Затем мы можем вычесть это из 9 единиц, чтобы получить основание треугольника.

Теперь все основания и высоты помечены, чтобы можно было рассчитать площади.

A верхний прямоугольник = bh A большой прямоугольник = bh Треугольник = 1/2 bh

A = (3,5 единицы) (1,5 единицы) A = (5,5 единицы) (5,5 единицы) A = 1/2 (3,5 единицы) (4 единицы)

A = 5,25 единицы 2 A = 30,25 единицы 2 A = 7 единиц 2

Общая площадь = 5.25 единиц 2 + 30,25 единиц 2 + 7 единиц 2

Общая площадь = 42,5 единиц 2

Вот последний пример:

Представьте этот пример как треугольник с двумя удаленными прямоугольниками . Поскольку мы удаляем прямоугольники, площадь меньших прямоугольников нужно будет вычесть из общей площади треугольника.

A треугольник = 1/2 bh A верхний прямоугольник = bh A нижний прямоугольник = bh

A = 1/2 (18 мм) (13 мм) A = (5 мм) (3 мм) A = (7 мм) (2 мм)

A = 117 мм 2 A = 15 мм 2 A = 14 мм 2

Таким образом, общая площадь оранжевых цифр составляет:

117 мм 2 — 15 мм 2 — 14 мм 2 = 88 мм 2

Давайте рассмотрим

Когда вас попросят определить площадь неправильной фигуры, вы можете попробовать два основных метода. Оба они включают разбиение неправильных фигур на формы, с которыми вы можете работать. Как только вы это сделаете, вам нужно будет либо сложить площади частей вместе, либо вычесть недостающие части из целого.

9,5: Площадь и объем геометрических фигур и предметов

  1. Последнее обновление
  2. Сохранить как PDF
  1. Значение и обозначение для площади
  2. Формулы площади
  3. Нахождение областей некоторых общих геометрических фигур
  4. Значение и обозначение для объема
  5. Формулы объема
  6. Нахождение объемов некоторых общих геометрических объектов
  7. Упражнения
    1. Упражнения для Обзор

Цели обучения

  • знать значение и обозначения для площади
  • Знать формулы площади некоторых распространенных геометрических фигур
  • уметь найти площади некоторых общих геометрических фигур
  • знать значение и обозначения для тома
  • знать формулы объема для некоторых распространенных геометрических объектов
  • уметь находить объем некоторых обычных геометрических объектов

Нередко необходимо умножить одно номинальное число на другое. 2 \), или квадрат длины (квадрат длины), физически можно интерпретировать как площадь поверхности.

Площадь
Площадь поверхности — это количество квадратных единиц длины, содержащихся в поверхности.

Например, 3 кв. Дюйма означает, что 3 квадрата по 1 дюйм с каждой стороны можно точно разместить на некоторой поверхности. (Квадраты, возможно, придется разрезать и переставить так, чтобы они соответствовали форме поверхности.)

Рассмотрим площадь следующих геометрических фигур.

Формула площади

Мы можем определить площади этих геометрических фигур, используя следующие формулы.

Нахождение некоторых общих геометрических фигур

Образец набора A

Найдите площадь треугольника.

Решение

\ (\ begin {array} {rcl} {A_T} & = & {\ dfrac {1} {2} \ cdot b \ cdot h} \\ {} & = & {\ dfrac {1} {2} \ cdot 20 \ cdot 5 \ text {sq ft}} \\ {} & = & {10 \ cdot 6 \ text {sq ft}} \\ {} & = & {60 \ text {sq ft}} \\ { } & = & {60 \ text {ft} ^ 2} \ end {array} \)

Площадь этого треугольника составляет 60 квадратных футов, что часто записывается как 60 \ (\ text {ft} ^ 2 \).

Образец набора A

Найдите площадь прямоугольника.

Решение

Давайте сначала преобразуем 4 фута 2 дюйма в дюймы. Поскольку мы хотим преобразовать в дюймы, мы будем использовать дробную единицу \ (\ dfrac {\ text {12 дюймов}} {\ text {1 ft}} \), поскольку у нее есть дюймы в числителе. Затем

\ (\ begin {array} {rcl} {\ text {4 ft}} & = & {\ dfrac {\ text {4 ft}} {1} \ cdot \ dfrac {\ text {12 дюймов}} { \ text {1 ft}}} \\ {} & = & {\ dfrac {4 \ cancel {\ text {ft}}} {1} \ cdot \ dfrac {\ text {12 дюймов.}} {1 \ cancel {\ text {ft}}}} \\ {} & = & {\ text {48 дюймов}} \ end {array} \)

Таким образом, \ (\ text {4 фута 2 дюйма = 48 дюймов + 2 дюйма = 50 дюймов} \)

\ (\ begin {array} {rcl} {A_R} & = & {l \ cdot w} \\ {} & = & {\ text {50 дюймов} \ cdot \ text {8 дюймов}} \\ {} & = & {400 \ text {sq in.}} \ End {array} \)

Площадь этого прямоугольника 400 кв. Дюймов.

Образец набора A

Найдите площадь параллелограмма.

Решение

\ (\ begin {array} {rcl} {A_P} & = & {b \ cdot h} \\ {} & = & {\ text {10.3 см} \ cdot \ text {6.2 см}} \\ {} & = & {63.86 \ text {sq cm}} \ end {array} \)

Площадь параллелограмма 63,86 см2.

Образец набора A

Найдите площадь трапеции.

Решение

\ (\ begin {array} {rcl} {A_ {Trap}} & = & {\ dfrac {1} {2} \ cdot (b_1 + b_2) \ cdot h} \\ {} & = & {\ dfrac {1} {2} \ cdot (\ text {14,5 мм + 20,4 мм}) \ cdot (4,1 \ text {мм})} \\ {} & = & {\ dfrac {1} {2} \ cdot (\ текст {34.2} \\ {} & \ приблизительно & {(3.14) \ cdot (\ text {282,24 кв. Фута})} \\ {} & \ приблизительно & {888.23 \ text {sq ft}} \ end {array} \)

Площадь этого круга составляет примерно 886,23 кв. Фута.

Практический набор A

Найдите площадь каждой из следующих геометрических фигур.

Ответ

36 кв. См

Практический набор A

Ответ

37.503 кв. Мм

Практический набор A

Ответ

13,26 кв. Дюйма

Практический набор A

Ответ

367.5 кв. Миль

Практический набор A

Ответ

452,16 кв.футов

Практический набор A

Ответ

44.3 \), или кубическая единица длины (единица длины у.е.), физически можно интерпретировать как объем трехмерного объекта.

Объем
Объем объекта — это количество кубических единиц длины, содержащихся в объекте.

Например, 4 куб. Мм означает, что 4 куба, по 1 мм с каждой стороны, точно заполнят какой-нибудь трехмерный объект. (Кубики, возможно, придется разрезать и переставить, чтобы они соответствовали форме объекта.)

Формулы объема

Рисунок Формула объема Заявление
Прямоугольный цельный \ (\ begin {array} {rcl} {V_R} & = & {l \ cdot w \ cdot h} \\ {} & = & {\ text {(область базы)} \ cdot \ text {(высота )}} \ end {array} \) Объем прямоугольного твердого тела равен длине, умноженной на ширину, умноженной на высоту.2 \ cdot h} \\ {} & = & {\ text {(область основания)} \ cdot \ text {(высота)}} \ end {array} \) Объем конуса равен \ (\ dfrac {1} {3} \) умноженным на \ (\ pi \) квадрату радиуса, умноженному на высоту.

Поиск объемов некоторых общих геометрических объектов

Образец набора B

Найдите объем прямоугольного твердого тела. 2 \ cdot h} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.2 \ cdot \ text {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot (\ text {4 кв. Мм}) \ cdot \ текст {(5 мм)}} \\ {} & \ приблизительно & {(\ dfrac {1} {3}) \ cdot (3.14) \ cdot \ text {(20 у.е. мм)}} \\ {} & \ приблизительно & {20.9 \ overline {3} \ text {cu mm}} \\ {} & \ приблизительно & {\ text {20.93 cu mm}} \ end {array} \)

Объем этого конуса примерно 20,93 куб. Мм. Объем является приблизительным, потому что мы аппроксимировали \ (\ pi \) с 3,14.

Практический набор B

Найдите объем каждого геометрического объекта.Если требуется \ (\ pi \), округлите его до 3,14 и найдите приблизительный объем.

Ответ

21 куб. Дюйм

Практический набор B

Сфера

Ответ

904.32 куб. Футов

Практический набор B

Ответ

157 куб. М

Практический набор B

Ответ

0.00942 у.е. дюйм

Упражнения

Найдите каждое указанное измерение.

Упражнение \ (\ PageIndex {1} \)

Площадь

Ответ

16 кв.м

Упражнение \ (\ PageIndex {2} \)

Площадь

Упражнение \ (\ PageIndex {3} \)

Площадь

Ответ

1.21 кв. Мм

Упражнение \ (\ PageIndex {4} \)

Площадь

Упражнение \ (\ PageIndex {5} \)

Площадь

Ответ

18 кв. Дюймов

Упражнение \ (\ PageIndex {6} \)

Площадь

Упражнение \ (\ PageIndex {7} \)

Точная площадь

Ответ

\ ((60. 5 \ pi + 132) \ text {sq ft} \)

Упражнение \ (\ PageIndex {8} \)

Примерная площадь

Упражнение \ (\ PageIndex {9} \)

Площадь

Ответ

40,8 кв. Дюйма

Упражнение \ (\ PageIndex {10} \)

Площадь

Упражнение \ (\ PageIndex {11} \)

Примерная площадь

Ответ

31.0132 кв. Дюйм.

Упражнение \ (\ PageIndex {12} \)

Точная площадь

Упражнение \ (\ PageIndex {13} \)

Примерная площадь

Ответ

158,2874 кв. Мм

Упражнение \ (\ PageIndex {14} \)

Точная площадь

Упражнение \ (\ PageIndex {15} \)

Примерная площадь

Ответ

64. 2668 кв. Дюймов

Упражнение \ (\ PageIndex {16} \)

Площадь

Упражнение \ (\ PageIndex {17} \)

Примерная площадь

Ответ

43.96 кв.футов

Упражнение \ (\ PageIndex {18} \)

Объем

Упражнение \ (\ PageIndex {19} \)

Объем

Ответ

512 куб. См

Упражнение \ (\ PageIndex {20} \)

Точный объем

Упражнение \ (\ PageIndex {21} \)

Примерный объем

Ответ

11.49 куб.см

Упражнение \ (\ PageIndex {22} \)

Примерный объем

Упражнение \ (\ PageIndex {23} \)

Точный объем

Ответ

\ (\ dfrac {1024} {3} \ pi \ text {cu ft} \)

Упражнение \ (\ PageIndex {24} \)

Примерный объем

Упражнение \ (\ PageIndex {25} \)

Примерный объем

Ответ

22. 08 куб. Дюймов

Упражнение \ (\ PageIndex {26} \)

Примерный объем

Упражнения на повторение

Упражнение \ (\ PageIndex {27} \)

Сколько сотен в числе 23 426?

Ответ

4

Упражнение \ (\ PageIndex {28} \)

Перечислите все множители 32.

Упражнение \ (\ PageIndex {29} \)

Найдите значение \ (4 \ dfrac {3} {4} — 3 \ dfrac {5} {6} + 1 \ dfrac {2} {3} \).

Ответ

\ (\ dfrac {31} {12} = 2 \ dfrac {7} {12} = 2,58 \)

Упражнение \ (\ PageIndex {30} \)

Найдите значение \ (\ dfrac {5 + \ dfrac {1} {3}} {2 + \ dfrac {2} {15}} \).

Упражнение \ (\ PageIndex {31} \)

Найдите периметр.

Ответ

27,9 кв.м

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *