Пошаговый расчет площади картонной коробки

S =((A+B)*2+59)*(B+H+8)/1000000

где 59 – припуск на клеевой клапан и толщину гофрокартона, 8 – припуск на толщину гофрокартона.

S =((A+B)*2+69)*(B+H+16)/1000000

где 69 – припуск на клеевой клапан и толщину гофрокартона,16 – припуск на толщину гофрокартона.

Т. к. размеры подставляем в миллиметрах, то для получения площади в квадратных метрах делим полученное число на 1000000.

Если вам нужны коробки сложной конфигурации по индивидуальным размерам, наша компания «МС-ПАК» изготовит их на заказ. Технологи рассчитают площадь гофрокартона, необходимого для производства и его стоимость, а также посчитают итоговую цену тиража.

Площадь прямоугольника онлайн калькулятор

Чему равна площадь прямоугольника? 1. Необходимо знать длину и ширину прямоугольника. 2. Внесите значения сторон в графы ниже. 3. Нажмите кнопку рассчитать площадь прямоугольника!

Прямоугольник — это простая двухмерная геометрическая фигура. Все углы у него прямые, по этому он и называется прямоугольник. Стороны имеют разный размер, попарно, и обычно называются ширина и длина.

Формула площади прямоугольника — посчитать!

L * H = S чтобы найти площадь прямоугольника, необходимо перемножить ширину на длину. Другими словами её можно выразить так: площадь прямоугольника равна произведению сторон.

1. Приведём пример расчёта как найти площадь прямоугольника, стороны равны известным величинам, например ширина 4 см, длина 8 см.

Как найти площадь прямоугольника со сторонами 4 и 8 см: Решение простое! 4 х 8 = 32 см2. Чтобы решить такую простую задачу нужно вычислить произведение сторон прямоугольника или просто умножить ширину на длину, это и будет площадь!

2. Частным случаем прямоугольника является квадрат, это тот случай когда стороны у прямоугольника равны, в этом случае найти площадь квадрата можно по выше приведённой формуле.

Чему равна площадь прямоугольника?

Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений … не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!

Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором! О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.

Калькулятор расчёта площади комнаты, расчет площади пола и потолка

Приведу пример расчета пола или потолка комнаты (кухни) в квадратных метрах.

Формула расчета простая, S = a*b, где S — площадь, а и b — соответственно, длина и ширина комнаты.
В нашем примере (рисунка с обмерами) вместо маленьких букв длина — А и ширина — Б., и противоположенных стен — Г и В.

Чтобы рассчитать площадь комнаты по полу:

— если у нас длина комнаты 5 метра, а ширина 3 метров, тогда нам надо ( 5*3 = 15 кв.м.), в итоге получаем 15 кв.м. по полу

Воспользуйтесь нашим Калькулятором, чтобы расчитать площадь пола или потолка

Если вы не хотите в ручную рассчитывать площадь пола или вы, что то не поняли при описание расчетов, то вы можете воспользоваться нашим калькулятором и рассчитать площадь пола или потолка автоматически.

Для расчёта необходимо измерить в метрах длину, ширину комнаты и внести данные по порядку заполнив форму и вы автоматически получите расчет площади пола или потолка в квадратных метрах.

Калькулятор расчёта площади пола

Примечание:

Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 964 сантиметров, то в поля формы необходимо ввести значение 9.64.

Т.е. 2,6 — неправильно, 2.6 — правильно

Калькулятор рассчитывает не только площадь пола или потолка, данный калькулятор можно также использовать для расчёта площади любых других прямоугольных объектов у которых есть длина и ширина. В этом случае вместо ширины и длины комнаты вам необходимо подставить значения ширины и длины этих самых объектов (окна, двери и т.д.,) к примеру таких как площадь окон и дверей.

К примеру как можно проверить и расчитать в ручную площадь окон и дверей. :

— если у нас размеры окна ширина 1,6 метров, а высота 1,5 метров.
— а двери ширина 0,8 метров, а высота 2,05 метров.

Окно: (1,6*1,5)= 2,4 кв.м., в итоге окно получаем 2,4 кв.м.,

Чтобы рассчитать площадь комнаты по стенам: воспользуйтесь нашим Калькулятором, чтобы расчитать площадь стен

Источник: remont-otdelka-m.ru

Как найти площадь фигуры? Ответ на webmath.ru

Содержание:

Определения

Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.

Определение

Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.

Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.

Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.

Если фигура имеет площадь, то она называется квадрируемой.

Формулы площади основных геометрических фигур

Площадь треугольника

Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. То есть если известны длины двух сторон треугольника $ABC$, которые равны $a$ и $b$, а также угол $\alpha$ между этими сторонами, то искомая площадь:

$$\mathrm{S}_{\Delta A B C}=\frac{1}{2} a b \sin \alpha$$

Читать дальше: формулы площади треугольника и примеры решений →

Площадь круга

Чтобы найти площадь круга, надо найти произведение числа $\pi$ на квадрат радиуса этого круга, то есть

$$\mathrm{S}_{\kappa p}=\pi R^{2}$$

Читать дальше: формула площади круга и примеры решений →

Площадь квадрата

Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть

Читать дальше: формула площади квадрата и примеры решений →

Площадь прямоугольника

Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть

Читать дальше: формула площади прямоугольника и примеры решений →

Площадь параллелограмма

Чтобы найти площадь параллелограмма, нужно найти произведение стороны $a$ параллелограмма на высоту , проведенную к этой стороне, то есть

Читать дальше: формулы площади параллелограмма и примеры решений →

Площадь трапеции

Чтобы найти площадь трапеции, нужно длину средней линии умножить на длину высоты , опущенной к основанию:

Читать дальше: формулы площади трапеции и примеры решений →

Площадь ромба

Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:

Читать дальше: формулы площади ромба и примеры решений →

Площадь эллипса

Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число $\pi$, то есть

Читать дальше: формула площади эллипса и примеры решений →

Расчет площади многоугольника онлайн

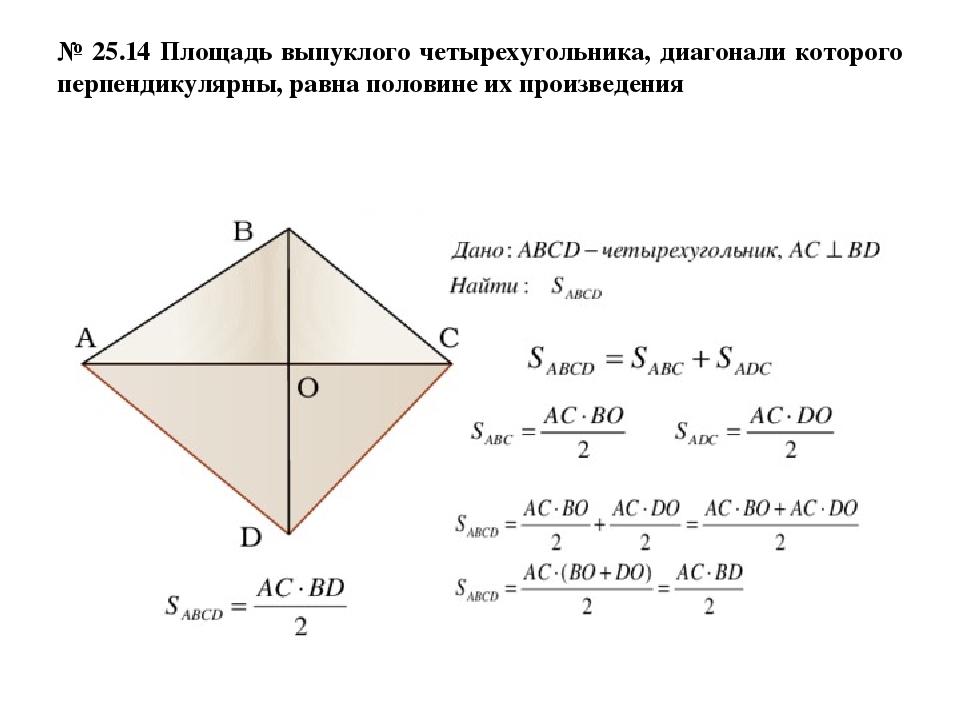
Калькулятор считает площадь многоугольника по введенным вами сторонами и диагоналям, главное чтобы диагонали делили многоугольник на несколько треугольников, которые в свою очередь не пересекались бы между собой.

И так, глядя на рисунок, можно сразу представить, что площадь данного многоугольника будет равна сумме площади трех треугольников, расположенных внутри многоугольника.

Для начала расчетов вам придется внимательно внести в таблицу значения сторон ваших треугольников.

Все остальное калькулятор сделает за вас. Пользуйтесь.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

Площадь поверхности тела | Онлайн калькулятор

В физиологии и медицине, площадь поверхности тела — это измеренная или рассчитанная поверхность человеческого тела. Для многих клинических целей площадь поверхности тела является лучшим показателем метаболического обмена, чем масса тела, поскольку она менее зависит от излишнего количества жировой ткани.

РассчитатьОчистить

Существует множество формул для расчета площади поверхности тела. Ниже представлены самые часто употребляемые.

Формула Дюбуа и Дюбуа:

ППТ = 0.007184 * вес (кг)^0.425 * рост (см)^0.725

Формула Дюбуа и Дюбуа (модификация):

ППТ =  (вес (кг)^0.425 * рост (см)^0.725)/139.2

Одной из часто использованных формул является формула Мостеллера, опубликованной в 1987:

ППТ =  √(вес (кг)* рост (см)/3600)

Формула Хейкока:

ППТ = 0. 024265 * вес (кг)^0.5378 * рост (см)^0.3964

Формула Гехана и Джорджа:

ППТ = 0.0235 * вес (кг)^0.51456 * рост (см)^0.42246

Формула Бойда:

ППТ = 0.0003207 * вес (г)^{(0.7285-0.0188log10вес(г))} * рост (см)^0.3

Формула Фудзимото:

ППТ = 0.008883 * вес (кг)^0.663 * рост (см)^0.444

Формула Такахира:

ППТ = 0.007241 * вес (кг)^0.725 * рост (см)^0.425

«Нормальное значение» обычно составляет 1,73 м² для взрослых.

Возраст	Значение
Новорождённый	0.25 м²
Ребёнок 2 года	0.5 м²
Ребёнок 9 лет	1.07 м²
Ребёнок 10 лет	1.14 м²
Ребёнок 12-13 лет	1. 33 м²
Для мужчин	1.9 м²
Для женщин	1.6 м²

Чему равна площадь круга (онлайн калькулятор)

 Одна из совершенных плоских фигур это круг. Ее совершенство выражается в какой-то законченности, простоте и прагматичности. В мире так много круглых предметов, которые между прочим были созданы исключительно природой, без участия человека. Скажем вы видели как падает капля любой жидкости на поверхность, пусть тот же дождь, когда он только начинается и мокрые капли хорошо видны!? Капли воды превращаются в круги, а их так много и они множатся до тех пор пока не покроют всю площадь вокруг нас… А да, кстати, о площади! Какая же интересно площадь у этих самых кругов? Как можно вычислить эту площадь, ведь она вроде как не очень просты по площади, там есть кривая, то есть этот самый контур, который является периметром круга.
 Давайте-ка разберемся со всем этим по порядку.

Круг как геометрическая фигура и из чего она состоит

 На самом деле, не смотря на то, что я так превозносил круг как совершенную фигуру, посчитать его площадь не так уж и просто. Ну это я к тому, что не так уж сразу и поймешь как это сделать. Мы привыкли считать площадь квадратами, прямоугольниками, в общем фигурами, у которых стороны перпендикулярны и параллельны.
 А здесь смотрите что, круг весь закругляется со всех сторон. И как к нему подступиться даже и не знаешь. Круги и чертят обычно циркулем, ставят в одной точке иглу циркуля и вокруг этой точки с выбранным размером (называется раствором) чертят контур круга. Но кругом является все пространство в площади ограниченной от точки центра, до нашей получившейся линии.

Отсюда наверное уже можно и придумать какое-то определение для круга.

Круг — это множество точек расположенных в объеме от центра круга, до его периметра.

При этом точки конечно же не должны накладываться одна на другую и второе, нас в этом объеме интересует именно характеристика площади. Однако как мы уже заметили, сразу к этой площади так не подступиться, надо бы попробовать как-то разложить на более простые фигуры, что мы и постараемся сейчас сделать.  

Раскладываем круг на более простые фигуры

 На само деле, площадь круга можно разбить на площади треугольников. Можно представить всю площадь в виде прямоугольных или равнобедренных треугольников, это не принципиально. Единственное, здесь не будет учитываться разность основания треугольника, которая представлена прямой и дуга окружности круга. По факту эта погрешность растворяется в том случае, если брать треугольники с минимальным основанием, то есть брать как можно больше треугольников в площади круга.  

Чем больше треугольников возьмем, тем более точно будет рассчитана площадь. То есть смысл этого в том, чтобы сумма всех оснований треугольников была равна периметру круга! Тогда этот вопрос с погрешностью будет закрыт.

 В этом случае остается воспользоваться простейшей формулой нахождения площади треугольника. Где в треугольнике R будет высотой, то есть R=H. Основание равно периметру круга, то есть π*R. Площадь же всех треугольников будет равна основание треугольника, умноженное на высоту и поделить все пополам. То есть (π*R*R)/2=π*R².

Как найти площадь круга  (формула)

Заметьте, по сути мы сами сейчас вывели формулу площади круга. Смотрите наши рассуждения выше.

Поэтому, если вы все поняли, как и что, то нас наверное можно по интеллекту древнегреческого математика Пифагора! Что же, из этой формулы теперь можно выводить и другие, то есть скажем выражая не через радиус, а через диаметр окружности. Это уже не принципиально!

Онлайн калькулятор нахождения площади круга

Калькулятор площади

Ниже приведены калькуляторы для оценки площади семи распространенных форм. Площадь более сложных форм обычно может быть получена путем разбивки их на агрегированные простые формы и суммирования их площадей. Этот калькулятор особенно полезен для оценки площади земельного участка.

Прямоугольник

Треугольник

Трапеция

Круг

Сектор

Эллипс

Параллелограмм

Площадь — это величина, которая описывает размер или размер двухмерной фигуры или фигуры на плоскости. Его можно визуализировать как количество краски, которое потребуется для покрытия поверхности, и оно является двумерным эквивалентом одномерной длины кривой и трехмерного объема твердого тела. Стандартная единица площади в Международной системе единиц (СИ) — квадратный метр, или м ² . Ниже приведены уравнения для некоторых из наиболее распространенных простых форм и примеры того, как рассчитывается площадь каждой из них.

Прямоугольник

Прямоугольник — это четырехугольник с четырьмя прямыми углами.Это одна из простейших форм, и для расчета ее площади необходимо лишь знать (или измерить) ее длину и ширину. Четырехугольник по определению — это многоугольник с четырьмя ребрами и вершинами. В случае прямоугольника длина обычно относится к двум более длинным краям четырехугольника, а ширина относится к более коротким из двух краев. Когда длина и ширина прямоугольника равны, форма представляет собой особый случай прямоугольника, называемый квадратом. Уравнение для расчета площади прямоугольника выглядит следующим образом:

площадь = длина × ширина

Фермер и его дочь — непроданная земля

Представьте, что фермер пытается продать участок земли совершенно прямоугольной формы.Поскольку у него есть несколько коров, которые он не хотел бы свободно резвиться, он огородил участок земли и знал точную длину и ширину каждого края. Фермер также живет в Соединенных Штатах и, не знаком с использованием единиц СИ, по-прежнему измеряет свой участок земли в футах. Стопа была определена как ровно 0,3048 метра в 1959 году после того, как она изменилась в течение длительного периода времени, поскольку исторически человеческое тело часто использовалось в качестве основы для единиц длины, и неудивительно, что оно было непостоянным в зависимости от времени и местоположения.Если не считать касательной, участок земли фермера имеет длину 220 футов и ширину 99 футов. Используя эту информацию:

площадь = 220 × 99 = 21780 кв. Футов

Земельный участок фермера площадью 21 780 квадратных футов равен половине акра, где акр определяется как площадь 1 цепи на 1 фарлонг, которая определяется чем-то другим, и так далее, и почему СИ сейчас существует. К несчастью для фермера, он живет в районе, где преобладают иностранные инвесторы с меньшим размером ноги, которые считали, что им следует получить больше квадратных футов за свои деньги, и его земля остается непроданной сегодня.

Треугольник

Существует множество уравнений для вычисления площади треугольника в зависимости от имеющейся информации. Как упоминалось в калькуляторе выше, используйте Калькулятор треугольников для получения дополнительных сведений и уравнений для расчета площади треугольника, а также для определения сторон треугольника с использованием любой доступной информации. Вкратце, уравнение, используемое в приведенном выше калькуляторе, известно как формула Герона (иногда называемая формулой Героя), относящаяся к герою Александрии, греческому математику и инженеру, которого некоторые считали величайшим экспериментатором древних времен. Формула выглядит следующим образом:

Фермер и его дочь — Triangle Daze

В этот момент, благодаря огромным усилиям и настойчивости, фермер, наконец, продал свой участок земли площадью 21 780 квадратных футов и решил использовать часть заработанных денег, чтобы построить бассейн для своей семьи. К несчастью для фермера, он не принимает во внимание тот факт, что одни только расходы на обслуживание бассейна в течение одного года, вероятно, могут покрыть посещение его детьми любого бассейна или аквапарка на долгие годы.Еще более печально для фермера, его 7-летняя дочь, которая недавно приехала в Египет через Дору-исследовательницу, влюбилась в треугольники и настаивает на том, чтобы бассейн был не только треугольной формы, но и необходимыми размерами. должна включать только цифру 7, чтобы обозначить ее возраст и увековечить этот момент ее жизни в форме треугольного бассейна. Как любящий отец, фермер соглашается на просьбу дочери и приступает к планированию строительства своего треугольного бассейна. Теперь фермер должен определить, есть ли у него на заднем дворе достаточно места для размещения бассейна. В то время как фермер начал больше узнавать об единицах СИ, он все еще испытывает дискомфорт от их использования и решает, что его единственный жизнеспособный вариант — построить бассейн в форме равностороннего треугольника со сторонами 77 футов в длину, поскольку любой другой вариант будет либо слишком большим, либо маленьким. Учитывая эти размеры, фермер определяет необходимую площадь следующим образом:

Поскольку наибольшее расстояние между любыми двумя точками равностороннего треугольника — это длина края треугольника, фермер резервирует края бассейна для плавания «кругов» в своем треугольном бассейне с максимальной длиной, примерно вдвое меньшей, чем у олимпийского. бассейн, но с двойной площадью — все под бдительными глазами правящей королевы бассейна, его дочери и неодобрительного взгляда его жены.

Трапеция

Трапеция — это простой выпуклый четырехугольник, у которого есть по крайней мере одна пара параллельных сторон. Свойство быть выпуклым означает, что угол трапеции не превышает 180 ° (в отличие от вогнутого четырехугольника), в то время как простота отражает то, что трапеции не самопересекаются, то есть две несмежные стороны не пересекаются. В трапеции параллельные стороны называются основаниями трапеции, а две другие стороны называются ногами.Существует больше различий и классификаций для разных типов трапеций, но их площади по-прежнему рассчитываются таким же образом с использованием следующего уравнения:

где b ₁ и b ₂ — базы. h — высота, или перпендикулярное расстояние между основаниями

Фермер и его дочь — Усилия по разгрому

Прошло два года с тех пор, как бассейн фермера был достроен, а его дочь выросла и повзрослела.Хотя ее любовь к треугольникам все еще сохраняется, она в конце концов пришла к осознанию того, что независимо от того, насколько хорошо она была «треугольной», сами по себе треугольники не могут заставить мир вращаться, и что мастерская Санты не может правдоподобно балансировать на Северном полюсе, если бы мир скорее пирамида, чем сфера. Постепенно она начала принимать другие формы в своей жизни и преследовала множество различных интересов — в настоящее время — фристайл BMX. Таким образом, ей требуется пандус, но, к сожалению для фермера, не просто пандус.Пандус должен состоять только из форм, которые можно сформировать из нескольких треугольников, поскольку, как и ее рэп-идол Б.о.Б., дочери фермера все еще трудно принять реальность искривленных поверхностей. Конечно, он должен использовать в своих измерениях только цифру 9, чтобы отразить ее возраст. Фермер решает, что его лучший вариант — построить пандус, состоящий из нескольких прямоугольников, при этом боковая поверхность пандуса имеет форму трапеции. По мере того, как фермер теперь привык к СИ, он может быть более креативным в использовании единиц и может построить пандус более разумного размера, соблюдая требования своей дочери.Он решает построить пандус с трапециевидной поверхностью высотой 9 футов, нижним основанием длиной 29,528 футов (9 м) и верхним основанием 9 футов. Площадь трапеции рассчитывается следующим образом:

Круг

Круг — это простая замкнутая форма, образованная множеством всех точек на плоскости, находящихся на заданном расстоянии от заданной центральной точки. Это расстояние от центра до любой точки окружности называется радиусом.Более подробную информацию о кругах можно найти на странице «Калькулятор круга», но для расчета площади необходимо только знать радиус и понимать, что значения в круге связаны математической константой π . Уравнение для вычисления площади круга выглядит следующим образом:

площадь = πr ²

Фермер и его дочь — Круг Ли (ж)

Прошло еще шесть лет, и его дочь превратилась в сильного, красивого, влиятельного, уверенного в себе 15-летнего неблагодарного человека, сосредоточенного исключительно на поиске внешнего подтверждения со стороны знакомых и незнакомцев в социальных сетях, при этом полностью игнорируя искреннюю поддержку со стороны ближайших родственников и друзей. .После спора с отцом по поводу чрезмерного использования социальных сетей, она решает использовать страх отца перед неизвестным и веру в сверхъестественное, чтобы разыграть его. Не зная, с чего начать, она ходит по городу, разговаривая с множеством незнакомцев, у каждого из которых, по-видимому, есть бесконечные источники мудрости и советов, где она узнает о кругах на полях и их связи с инопланетянами и неопознанными летающими объектами, а также о многих других темах, которые игнорируйте все научные и логические объяснения.Убедившись, наконец, в сферической природе Земли, удалив все свои прошлые публикации в социальных сетях, касающихся BoB, и расширив свою любовь к треугольникам до принятия других форм, она решает сделать основной круг на полях, состоящий из ряда концентрических кругов и хочет определить площадь, необходимую для создания кругов на полях с внешним радиусом 15 футов. Она делает это, используя следующее уравнение:

площадь = π × 15 ² = 706,858 кв. Футов

К несчастью для фермера, он не только напуган кругами на полях, которые появились в ту ночь, когда его дочь сказала ему, что она была на вечеринке со своими друзьями, что по какой-то странной причине не привело к лишним постам в Instagram (он был, конечно, первым последователем своей дочери), но количество «исследователей круга» и «цереологов», появившихся на его ферме, чтобы изучить и впоследствии подтвердить подлинность кругов на полях как инопланетной конструкции, стоило ему значительного ущерба для его посевов. .

Сектор

Сектор круга — это, по сути, часть круга, заключенного между двумя радиусами и дугой. Зная радиус и угол, площадь сектора можно вычислить, умножив площадь всего круга на отношение известного угла к 360 ° или 2π радианам, как показано в следующем уравнении:

или

Фермер и его дочь — разделение семьи

Фермер и его семья столкнулись с самой серьезной дилеммой на сегодняшний день. Прошел год, дочери фермера исполнилось 16 лет, и в рамках празднования ее дня рождения ее мать испекла ее любимый десерт — ежевичный пирог. К несчастью для дочери фермера, ежевичный пирог также является любимой едой их домашнего енота, Утконоса, о чем свидетельствует отсутствие пирога на 180 ° с явными признаками виновника в виде крошек, ведущих к чрезмерно увлеченному еноту. Изначально пирог легко можно было разделить между тремя людьми и одним енотом, но теперь половину пирога приходится делить между тремя людьми, поскольку огорченный, но пресыщенный Утконос наблюдает за ним издали.Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом:

площадь = 60 ° / 360 ° × π × 16 ² = 134,041 дюйм ²

В результате невнимательности Утконоса каждый получает на треть меньше, и дочь задумчиво вспоминает урок американской истории, где она узнала о битве при Аламо и изображении народного героя Дэви Крокетта и его шляпы из енотовидной шкуры.

Эллипс

Эллипс — это обобщенная форма круга и кривая на плоскости, где сумма расстояний от любой точки кривой до каждой из двух ее фокальных точек постоянна, как показано на рисунке ниже, где P равно любая точка эллипса, а F ₁ и F ₂ — это два фокусировки.

Когда F ₁ = F ₂ , полученный эллипс представляет собой круг. Большая полуось эллипса, как показано на рисунке, который является частью калькулятора, является самым длинным радиусом эллипса, а малая полуось — самым коротким.Большая и малая оси относятся к диаметрам, а не радиусам эллипса. Уравнение для вычисления площади эллипса аналогично уравнению для вычисления площади круга, с той лишь разницей, что используются два радиуса, а не один (поскольку фокусы находятся в одном месте для круга):

area = πab
, где a и b — мажор и малые полуоси

Фермер и его дочь — падение с орбиты

Прошло два года со времени таинственного исчезновения домашнего питомца, Утконоса, и случайного выигрыша пушистого аксессуара дочери фермера в школьной лотерее, которая помогла заполнить пустоту потери их любимого питомца. Дочке фермера сейчас 18, и она готова сбежать из сельской Монтаны, чтобы жить в колледже, полной свободы и распутства, и, конечно же, немного поучиться на стороне. К несчастью для дочери фермера, она росла в среде, наполненной позитивным подкреплением, и, следовательно, с менталитетом, что нужно «стрелять на луну, [поскольку] даже если вы промахнетесь, вы приземлитесь среди звезд», а также утверждение всех окружающих, что она может делать абсолютно все, что ей заблагорассудится! Таким образом, с ее неоптимальными оценками, отсутствием какой-либо внеклассной деятельности из-за ее бесчисленного множества различных интересов, отнимающих все ее свободное время, нулевого планирования и ее настойчивого стремления поступать только в самые лучшие из лучших университетов, шок, который возник, когда она не была принята ни в один из ведущих университетов, в которые она подавала документы, что вполне можно сравнить с ее метафорической посадкой в ​​глубоком космосе, надуванием, замерзанием и быстрым удушьем, когда она пропустила луну и приземлилась среди звезд. Наряду с легкими ее мечта стать астрофизиком была в конечном итоге нарушена, по крайней мере, на время, и ей пришлось вычислить эллиптическую площадь, необходимую в ее комнате, чтобы построить модель почти эллиптической орбиты Земли вокруг Солнца размером с человека. чтобы она могла с тоской смотреть на солнце в центре своей комнаты и его олицетворение ее сердца, пылающего страстью, но окруженного холодными просторами космоса, с далеким вращением Земли, насмешливо представляющим расстояние между ее мечтами и твердой землей .

площадь = π × 18 футов × 20 футов = 1130,97 кв. Футов

Параллелограмм

Параллелограмм — это простой четырехугольник, у которого есть две пары параллельных сторон, причем противоположные стороны и углы четырехугольника равны по длине и углам. Прямоугольники, ромбы и квадраты — это частные случаи параллелограммов. Помните, что классификация «простой» формы означает, что форма не является самопересекающейся. Параллелограмм можно разделить на прямоугольный треугольник и трапецию, которые в дальнейшем можно преобразовать в прямоугольник, что делает уравнение для вычисления площади параллелограмма по существу таким же, как и для вычисления прямоугольника. Однако вместо длины и ширины параллелограмм использует основание и высоту, где высота — это длина перпендикуляра между парой оснований. Основываясь на рисунке ниже, уравнение для расчета площади параллелограмма выглядит следующим образом:

площадь = b × h

Фермер и его дочь — Алмаз в небе

Прошло еще два года в жизни фермера и его семьи, и хотя его дочь была причиной сильного беспокойства, она наконец преодолела расстояние между пылающим солнцем, которое является ее сердцем, и Землей, на которой настаивает общество. она должна оставаться на земле.В результате борьбы, которая последовала за ее добровольной изоляцией, в окружении воображаемых, осуждающих глаз, предполагающих ее неудачу со всех сторон, дочь фермера вышла из-под натиска Земли подобно алмазу, сияя ярко и твердо в своей решимости. Несмотря на все недостатки, она решает, что у нее нет другого выбора, кроме как продержаться сквозь астероидное поле жизни в надежде, что конец сказки Диснея существует. Наконец-то, к счастью для дочери фермера и ее семьи, надежда действительно появилась, но не в виде Прекрасного Принца, а скорее как знак с предполагаемых небес.Несмотря на все ее метафорические размышления и невзгоды, связанные с космосом, почти становится правдоподобным, что дочь фермера каким-то образом повлияла на массивный восьмигранный алмазный астероид, падающий прямо, но безопасно на их сельхозугодья, что она интерпретирует как представление ее путешествия, становления и возможного возвращения домой. Дочь фермера приступает к измерению площади одного из ромбовидных лиц своего недавно найденного символа жизни:

площадь = 20 футов × 18 футов = 360 квадратных футов

К несчастью для дочери фермера, появление огромного алмаза привлекло внимание со всего мира, и после достаточного давления она уступает человеку внутри себя и продает алмаз, само изображение ее жизни и души, кому-либо. богатый коллекционер и продолжает жить остаток своей жизни в щедрых удовольствиях, отказываясь от своих убеждений и теряясь в черной дыре общества.

Единицы общего пользования

карту Google и найдите ее площадь

Вернитесь к этой карте радиуса здесь, просто сохраните эту ссылку

Введите адрес или увеличьте масштаб карты, затем щелкните начальную точку вашей фигуры.Продолжайте щелкать по внешнему краю фигуры, площадь которой вы хотите вычислить. По мере добавления точек площадь будет обновляться ниже и преобразовываться в акры, квадратные футы, метры, километры и мили. Он также покажет периметр формы. Этот инструмент полезен для определения приблизительной площади или участка земли, квадратного метра крыши или любого другого случая, когда вам нужно хорошо оценить площадь чего-либо. Если вы хотите, чтобы этот инструмент был на вашем веб-сайте, используйте наш инструмент для встраивания калькулятора площади или свяжитесь с нами для получения подробной информации.Чтобы вернуться к этой карте местности, воспользуйтесь ссылкой внизу страницы. .

— Измерьте площадь земельного участка

Самый простой способ измерить площадь земельного участка — начать с ввода адреса, связанного с земельным участком, площадь которого вам нужна. В сельской местности, где адрес может быть недоступен, вы можете ввести перекресток или даже координаты GPS точки на земле.Для GPS-координат обязательно введите широту, запятую и долготу, например. (41,87811, -87,629798). В любом случае это поместит маркер, который вы можете использовать в качестве ориентира для рисования области на карте. Когда вы закончите рисовать, калькулятор площади отобразит площадь фигуры над картой.

Как использовать инструмент калькулятора площади карт Google для измерения крыши

Обмерять периметр

Приложение для расчета площади

| FAQ

У нашей бесплатной учетной записи преподавателя есть доступ к панели управления, где можно создавать сеансы входа для студентов и управлять их сохраненными файлами.

Имя сеанса и сгенерированный пароль могут быть доступны всем учащимся, которые после входа в систему будут иметь полный доступ, за исключением возможности удалять файлы.

Регистрация разрешена только преподавателям аккредитованных школ и подлежит проверке, которая включает добавление «значка» SketchAndCalc на веб-сайт школы.

Этот значок необходим для подтверждения того, что преподаватель является действующим преподавателем аккредитованной школы.

Во время регистрации педагог назначит страницу школьного веб-сайта (например: www. school-homepage.edu/page1 ) в качестве предполагаемого местоположения значка, чтобы его можно было легко найти на наших серверах.

Затем будет отправлено электронное письмо с выбором значков с инструкциями.

Обычно проверка учетной записи занимает 24 часа, так как это выполняется вручную. После того, как регистрация будет одобрена и значок будет правильно размещен (например, в WordPress он будет добавлен как пользовательский HTML-код, а не встраиваемый), преподаватель сможет войти в систему на панели управления (Примечание: преподаватели не выбирают ‘студент’ на экране входа в систему) .

Сеансы входа в систему, созданные с панели инструментов, длятся 12 часов, но могут быть завершены в любое время. Просто введите имя сеанса и нажмите «Начать сеанс», чтобы сгенерировать случайный пароль, который вместе с именем сеанса может быть передан всем учащимся.

Чтобы войти в систему, студенты выбирают тумблер «студент» на экране входа в систему и вводят предоставленное имя сеанса и пароль.

Студенты могут экспортировать, распечатывать и сохранять файлы, созданные во время занятий. Преподаватели также могут просматривать все сохраненные файлы, созданные во время каждого занятия, на панели управления.

Параметры рисования глобально контролируются преподавателем с панели управления.

Если педагог увольняется из профессии или переходит в другую школу, его счет может быть закрыт. При закрытии учетной записи она преобразуется в учетную запись обычного пользователя, для чего требуется подписка или перерегистрация в новой школе.

Для начала нажмите «Зарегистрироваться» и выберите переключатель «Педагог».

Если у вас возникнут вопросы, обращайтесь сюда.

Калькулятор квадратных метров

Расчет площади прямоугольника

Использование калькулятора

Используйте этот калькулятор, чтобы найти квадратные метры, квадратные метры, квадратные метры или акры для здания, дома, сада или строительного объекта. Рассчитайте площадь в квадратных футах, ярдах, метрах и акрах для проектов ландшафта, пола, ковра или плитки, чтобы оценить площадь и количество материала, которое вам понадобится. Также рассчитайте стоимость материалов, когда вы вводите цену за квадратный фут, цену за квадратный ярд или цену за квадратный метр.

Цена вводится в поля, например, как
$ цена: 3.00 за: 1 квадратная единица: фут (ft²)
означает 3 доллара США за 1 квадратный фут.
или
$ Цена: 25.00 за: 1000 квадратная единица: фут (ft²)
, что означает 25 долларов США за 1000 квадратных футов.
и т.д ….

Если вы хотите рассчитать объем сыпучих материалов, таких как мульча или гравий, воспользуйтесь нашим калькулятор кубометров и кубометров.

Введите размеры в единицах США или метрических единицах. Вычислите площадь по вашим измерениям в дюймах (дюймах), футах (футах), ярдах (ярдах), миллиметрах (мм), сантиметрах (см) или метрах (м).Вы также можете ввести десятичные значения. Например, если у вас есть одно измерение, которое составляет 7 футов 3 дюйма, вы можете ввести его как 7,25 фута (3 дюйма / 12 дюймов = 0,25 фута). Если у вас размер 245 см, вы также можете ввести его как 2,45 м.

Как рассчитать квадратные метры

Квадратный метр — это площадь, выраженная в квадратных футах. Точно так же квадратный ярд — это площадь, выраженная в квадратных ярдах. Квадратные метры — тоже общепринятая мера площади.

Предположим, у вас есть прямоугольная область, такая как комната, и, например, вы хотите рассчитать площадь в квадратных футах для пола или ковра.

Прямоугольную площадь можно вычислить, измерив длину и ширину вашей области, а затем умножив эти два числа вместе, чтобы получить площадь в квадратных футах (футы ² ). Если у вас есть область необычной формы, например L-образная, разделите ее на квадратные или прямоугольные части и рассматривайте их как две отдельные области. Вычислите площадь каждой секции, затем сложите их и получите общую сумму. Если ваши измерения даны в разных единицах, например, в футах и ​​дюймах, вы можете сначала преобразовать эти значения в футы, а затем умножить их вместе, чтобы получить квадратные метры площади.

Мероприятие

• Измерьте стороны вашего участка

Преобразуйте все ваши измерения в футы

• Если вы измеряли в футах, перейдите к разделу «Рассчитать площадь в квадратных футах»
• Если вы измеряли в футах и ​​дюймах, разделите дюймы на 12 и прибавьте полученное значение к вашей стопе, чтобы получить общее количество футов
• Если вы измеряете в другой единице измерения, выполните следующие действия, чтобы преобразовать в футы
  — дюймы: разделите на 12, и это ваше измерение в футах.
  — ярды: умножьте на 3, и это ваше измерение в футах
  — сантиметры: умножить на 0.03281 конвертировать в футы
  — метры: умножьте на 3,281, чтобы преобразовать в футы

Вычислить площадь как квадратные метры

• Если вы измеряете площадь квадрата или прямоугольника, умножьте длину на ширину; Длина x Ширина = Площадь.
• Для других форм площади см. Формулы ниже, чтобы вычислить площадь (футы ² ) = квадратные метры.

Преобразование из квадратного дюйма, квадратного фута, квадратного ярда и квадратного метра

Вы можете, например, выполнить все свои измерения в дюймах или сантиметрах, вычислить площадь в квадратных дюймах или квадратных сантиметрах, а затем преобразовать окончательный ответ в нужные вам единицы, такие как квадратные футы или квадратные метры.

Для преобразования квадратных футов, ярдов и метров используйте следующие коэффициенты преобразования. Для других единиц используйте наш калькулятор для преобразование площади.

• квадратных футов в квадратных ярдов
  • умножьте футы ² на 0,11111, чтобы получить ярд ²
• квадратных футов в квадратных метров
  • умножить футы ² на 0.092903 получить м ²
• квадратных ярдов в квадратных футов
  • умножьте ярды ² на 9, чтобы получить ft ²
• квадратных ярдов в квадратных метров
  • умножьте yd ² на 0,836127, чтобы получить m ²
• квадратных метров в квадратных футов
  • умножить m ² на 10. 7639, чтобы получить ft ²
• квадратных метров в квадратных ярдов
  • умножьте m ² на 1,19599, чтобы получить yd ²

Формулы квадратных метров и изображения для различных областей

Площадь

Рассчитать площадь в квадратных футах для квадратная площадь

Площадь (футы ² ) = длина стороны x длина стороны

Площадь прямоугольника

Рассчитать площадь в квадратных футах для прямоугольная область

Площадь (футы ² ) = длина x ширина

Прямоугольная граница

Рассчитать площадь в квадратных футах для прямоугольная граница

Внутренняя площадь (футы ² ) = длина x ширина

Общая площадь (футов ² ) = (Длина + (2 x ширина границы)) x (Ширина + (2 x ширина границы))

Площадь (футы ² ) = Общая площадь — Внутренняя площадь

Площадь круга

Рассчитать площадь в квадратных футах для площадь круга

Площадь (футы ² ) = Pi x (Диаметр / 2) ^ 2

Pi = 3. 2

Площадь (футы ² ) = Внешняя область — Внутренняя область

Pi = 3.14

Очевидно, что граница круга и кольцо одинаковы, но измерены по-разному.

Площадь треугольника

Рассчитать площадь в квадратных футах для площадь треугольника

Площадь (футы ² ) = (1/4) x квадратный корень [(a + b + c) x (b + c-a) x (c + a-b) x (a + b-c)]

Площадь трапеции

Рассчитать площадь в квадратных футах для площадь трапеции

Площадь (футы ² ) = ((a + b) / 2) h

Калькулятор кругов

Форма круга

r = радиус
d = диаметр
C = окружность
A = площадь
π = пи = 3. 1415926535898
√ = квадратный корень

Использование калькулятора

Используйте этот калькулятор окружности, чтобы найти площадь, длину окружности, радиус или диаметр окружности. Учитывая любую одну переменную A, C, r или d круга, вы можете вычислить три других неизвестных.

Единицы: Обратите внимание, что единицы длины показаны для удобства.На расчеты они не влияют. Единицы измерения указывают порядок результатов, например футы, футы ² или футы ³ . Можно заменить любой другой базовый блок.

Формулы круга через Pi π, радиус r и диаметр d

Радиус и диаметр:

г = д / 2
d = 2r

Площадь круга:

A = πr ² = πd ² /4

Окружность круга:

С = 2πr = πd

Вычисления круга:

Используя приведенные выше формулы и дополнительные формулы, вы можете вычислить свойства данного круга для любой данной переменной. 2 \]

\ [C = 2 \ pi r \]

\ [d = 2r \]

Вычислить r, C и d | Учитывая A
Зная площадь круга, вычислите радиус, длину окружности и диаметр. Положив r, C и d через A, получим следующие уравнения:

\ [r = \ sqrt {\ frac {A} {\ pi}} \]

\ [C = 2 \ pi r = 2 \ pi \ sqrt {\ frac {A} {\ pi}} \]

\ [d = 2r = 2 \ sqrt {\ frac {A} {\ pi}} \]

Вычислить A, r и d | Учитывая C
По длине окружности вычислите радиус, площадь и диаметр.2} {4} \]

\ [C = 2 \ pi r = 2 \ pi \ frac {d} {2} = \ pi d \]

Калькулятор площади с использованием карт

Этот планиметр можно использовать для измерения замкнутой области определенной полилинии на карте.

[11 июля 2018] К сожалению, из-за значительного повышения цен на внутренние услуги мы больше не можем предлагать некоторые функции на этой странице.

Инструкции

Чтобы использовать инструмент калькулятора площади:

• Масштабируйте и перемещайте карту, чтобы найти интересующую область
• Щелкните карту, чтобы разместить вершины ломаной линии
• Щелкните столько раз, сколько необходимо, чтобы определить полилинию

Огражденная площадь будет выводиться в квадратных метрах и квадратных километрах

Вы можете нажать кнопку [Удалить последнюю точку], если вы допустили ошибку, или нажать [Очистить все] точки, чтобы удалить все точки с карты и начать заново.

Вы также можете изменить положение маркеров после того, как они были размещены на карте, перетащив их.

Чтобы нарисовать новую область, нажмите кнопку [Начать новую область] или нажмите Alt + n

Информация

Инструмент калькулятора площади позволяет определить площадь, заключенную внутри замкнутой полилинии, наложенной на карту.

Контрольные точки

Измерение озера Лох-Ней в Северной Ирландии. Сообщается, что площадь озера Лох-Ней составляет 388 км² [1], так что значение 380 823 442 м² не за горами.

Будущее использования и идеи

• Разрешить пользователю изменять цвет полилиний и заливку области (включая прозрачную)
• Разрешить сохранение области для дальнейшего использования
• Вариант экспорта в KML

История версий

• 17 июня 2015 г. Теперь при наведении курсора на маркеры отображаются широта и долгота.
• 18 декабря 2014 г. — Подсчитана общая площадь
• 23 марта 2014 г. — Добавлен выход гектаров
• 6 августа 2013 г. — Исправлена ​​ошибка с выводом периметра
• 21 февраля 2013 — Добавлен результат в квадратных футах
• 8 января 2012 г. — обновление до Google Maps API V3 и некоторые новые функции
• 20 июля 2010 — Добавлены перекрестия и возможность включения / выключения перекрестия
• 17 июня 2010 г. — добавлена ​​опция загрузки KML (бета)
• 2 июня 2010 г. — элемент управления масштабом перемещен в верхнюю часть карты, чтобы избежать конфликта с панелью поиска Google.
• 2 февраля 2010 г. — Добавлен вывод периметра в метрах и километрах
• 25 марта 2008 г. — добавлены перетаскиваемые маркеры, возможность щелкать внутри многоугольника и выводить данные в акрах.
• 26 июня 2007 г. — добавлен расчет базовой площади
• 24 июня 2007 г. — Страница создана

Вычислить площадь каждой формы онлайн бесплатно

Прямоугольник / Квадрат
Квадрат и прямоугольники — это четырехугольники с четырьмя прямыми углами. В случае квадрата все стороны равны, тогда как в прямоугольнике две стороны равны, две более длинные стороны называются длиной, а две меньшие стороны называются шириной. Уравнение для вычисления площади прямоугольника — площадь = длина X ширина. Это одна из наиболее часто используемых формул, особенно при строительстве зданий, окраске стен и облицовке полов.

Треугольник
Калькулятор площади помогает рассчитать площадь всех типов треугольников. Чаще всего для вычисления площади треугольника используется формула Герона или формула Героя, названная в честь известного греческого математика и инженера Героя Александрии. Формула записывается как:
Площадь = vs (s-l) (s-m) (s-n), здесь s — это полупериметр, а l, m, n — три стороны треугольника.

Трапеция
Четырехугольник, у которого одна пара параллельных сторон и две другие стороны не параллельны, называется трапецией.Две параллельные стороны называются основаниями трапеции, а другие стороны, которые не параллельны, называются ногами. Площадь трапеции рассчитывается по формуле — (b1 + b2) / 2Xh. Здесь b1 и b2 — длины оснований, а h — перпендикулярное расстояние между двумя параллельными линиями.

Круг
Простая замкнутая форма, в которой все точки на плоскости находятся на заданном расстоянии от заданной точки, центра, называется кругом. Расстояние от центра до внешнего края круга называется радиусом.Формула, по которой рассчитывается площадь круга, — Pir2, где Pi — универсальная постоянная, равная 3,14, а r — радиус. Вы также можете рассчитать площадь сектора круга. Сектор — это область, ограниченная двумя радиусами и дугой. Площадь сектора круга может быть рассчитана по формуле — (Q / 360º) × Pir2, где Q — угол между центром, измеренный в градусах.

Эллипс
Эллипс выглядит как круг, но не является кругом, а представляет собой группу всех точек на плоскости, расстояние от которых от двух фиксированных точек в сумме равно константе.В эллипсе у вас есть не один радиус, а два разных значения. Значения берутся от центра к двум разным краям эллипса, называемым большой и малой полуосями. Калькулятор рассчитывает площадь по формуле — Pi X a X b; здесь a и b — расстояния между двумя осями.

Параллелограмм
Параллелограмм — это четырехугольник, у которого два набора параллельных сторон; квадрат, прямоугольник и ромб — все параллелограммы. В отличие от квадрата или прямоугольника, калькулятор вычисляет площадь параллелограмма по формуле — высота основания X.Высота параллелограмма — это расстояние по перпендикуляру между двумя параллельными сторонами или основаниями.