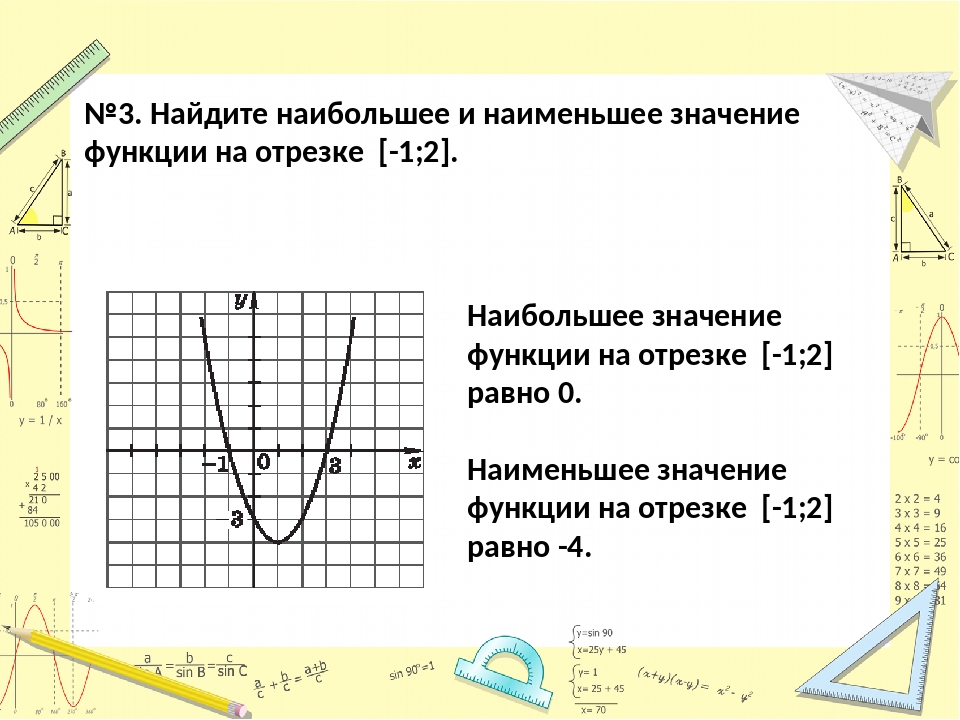
Наименьшее и наибольшее значение функции. Задачи
1.Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Значения функции в
концах отрезка.
1) y(0) = 0
y(4) = 43– 27 4 = – 44
3
-3
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(3) = 33– 27 3 = –54
Выбрать наименьшее из
полученных значений.
x = 3 [0; 4]
x = –3 [0; 4]
В 11
— 5 4
3
10 х
х
Выполнение этапов решения можно изменить, как вам удобно.
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
В 11
— 5 4
3
10 х
х
Другой способ решения
Этапы
1.
 Найти f /(x)
Найти f /(x)2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
3
-3
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
В 11
— 5 4
3
10 х
х
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.
2. Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
Значения функции в
концах отрезка.
1) y(0) = 4
y(-2) = (-2)3– 3 (-2) +4 = 2
1
-1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3×2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(-1) = (-1)3– 3 (-1) + 4 = 6
Выбрать наибольшее из
полученных значений.
x = 1 [-2; 0]
x = –1 [-2; 0]
В 11
6
3
10 х
3. Найдите наименьшее значение функции y = x3 – 2×2 + x +3
на отрезке [ 1; 4 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3×2 – 4x + 1= 3(x – 1)(x – 1 )
3
3×2 – 4x + 1 = 0
D=16–4*3*1=4
4+2
x1=
= 1 [1; 4]
6
4-2
1
= [1; 4]
x2=
6
3
y(1) = 3
В 11
3
3
10 х
х
x3
9x 7
4.
 Найдите наибольшее значение функции y
Найдите наибольшее значение функции y 3
на отрезке [ -3; 3 ]
3
( 3)
Значения функции в
у ( 3)
9( 3) 7 9 27 7 11
концах отрезка.
3
33
у (3) 9 3 7 9 27 7 25
3
2
Найдем критические
3
х
точки, которые
у/
9 х 2 9 ( х 3)( х 3)
3
принадлежат
заданному отрезку.
x = 3 [-3; 3]
x = –3 [-3; 3]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
y(-3) = -25
В 11
1 1
3
10 х
х
5. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
3
2
y x 3x 1
у(1) 1 3 1 1 1 3 1 1
3
2 2
у (9) 9 3 9 1 (3 ) 27 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.

3
х 3 0
3
3
/
у х 3
2
2
3 х 6 0
1
2
х 2
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Выбрать наибольшее из
полученных значений.
В 11
1
3
10 х
х
2
6. Найдите наименьшее значение функции y x х 3 x 1
3
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
y x 2 31x 1
х 21 3
x 1 1 1
у(1) 1 3y
1 x1
3
2 2
у (9) 9 3 9 13 (3 ) 27 1
y х 2 3x 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
1
Запишем функцию
3 в удобном
х 3 виде
0 2
для дифференцирования
3 2
3
/
у х 3
х 3 2
2
2
3 х 6 0
х 2
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
В 11
— 3
3
10 х
х
х 2 25
7. Найдите наименьшее значение функции y
х
на отрезке [-10; 1 ]
1
D(y): x = 0
y x 25
х
Значения функции в
1
2
концах отрезка.
х
25
у ( 10) 10 25
10 2,5 12,5
y
10
/
х
х
1
1
у (1) 1 25 26
2
1
х
y х 25
х
2
1
25
х
25
х
Найдем критические
у / 1 Запишем
25 функцию
1
в
2
2 удобном
2
точки, которые
х
хвиде
х
для
дифференцирования
принадлежат
( х 5)( х 5)
x = 5 [-10; 1]
заданному отрезку.
х2
x = –5 [-10; 1]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
x = 0 D(y)
1
у ( 5) 5 25
5 5 10
5
В 11
— 1 2 , 5
3
10 х
х
х 2 25
7.
 Найдите наименьшее значение функции y
Найдите наименьшее значение функции y х
на отрезке [-10; 1 ]
D(y): x = 0
Значения функции в
концах отрезка.
Можно решить задание,
применив формулу:
u u / v uv/
v2
v
/
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
В 11
— 1 2 , 5
3
10 х
х
36
y х
х
8. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
1
Значения функции в
концах отрезка.
/
1
1
2
х
х
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
D(y): x = 0
y x 36
х
Запишем функци
1
у (1) 1 36 37
удобном для
1
дифференциров
1
виде
у (9) 9 36 9 4 13
9
36 х 2 36
1
/
у 1 36 2 1 2
2
х
х
х
( х 6)( х 6)
x = 6 [ 1; 9]
х2
x = –6 [ 1; 9]
x = 0 D(y)
1
у (6) 6 36 6 6 12
6
В 11
3 7
3
10 х
х
9.
 Найдите наибольшее значение функции y 8 х e
Найдите наибольшее значение функции y 8 х eна отрезке [ 3; 10 ]
Значения функции в
концах отрезка.
uv u/ v uv/
x 7
5
у (3) (8 3)e 4
e
4
у(10) (8 10)e3 2e3
/
Найдем критические
принадлежат
заданному отрезку.
у / (8 х) / e x 7 (8 х)(e x 7 ) /
e x 7 (8 х)e x 7 e x 7 ( 1 8 х)
e
x 7
7
(7 х )
x = 7 [ 3; 10]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
1). Пер
меньш
знаме
5.
2). Вто
отрица
3). Зна
наибол
число
1
у(7) (8 7)e7 7 1e0 1
В 11
1
3
10 х
х
10. Найдите наименьшее значение функции y х 8 х 8 e
на отрезке [ 1; 7 ]
2
2 х
у(1) (1 8 8)e 1 e
Значения функции в
концах отрезка.
1
uv u v uv у(7) (49 56 8)e e5
Найдем критические у / ( х 2 8 х 8) / e 2 х ( х 2 8 х 8)( e 2 х ) /
/
/
точки, которые
принадлежат
заданному отрезку.

5
/
(2 х 8)e 2 х ( х 2 8 х 8)e 2 х ( 1)
e 2 х (2 х 8 х 2 8 х 8) e 2 х ( х 2 10 х 16)
e
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
2 х
( х 10 х 16) e
2
x = 2 [ 1; 7]
x = 8 [ 1; 7]
2 х
8
( х 8)( х 2)
Наименьшее число – 4, т.к.
первые два положительные.
1
у(2) (4 16 8)e0 4
В 11
— 4
2
3
10 х
х
м
ю
м
в
lnx
/
1
x
1. Найти f /(x)
y = 5ln(x+5) – 5x
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить значения
функции в критических
точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее.
11. Найдите наибольшее значение функции
y = ln(x+5)5 – 5x на отрезке [-4,5; 0]
1
5 x 20
у 5
5
5
х 5
х 5
х 5
5( x 4)
x = -4 [-4,5; 0]
х 5
/
y\
y
–
-4,5+ +
-5
-4
max
0
x
0
у ( 4) ln 15 5 ( 4)
0 20 20
В 11
2 0
3
10 х
х
Наибольшее
значение функция
будет принимать в
точке максимума.

Можно сэкономить
на вычислениях
значений функции в
концах отрезка.
12. Найдите наибольшее значение функции
1 5
y = ln(11x) – 11x + 9 на отрезке [
; ]
22 22
lnx 1x
/
1
1
1
/
у
(11х) 11
11 11 11
11х
11х
х
1 11x
1
1 5
[ 22 ; 22 ]
x=
11
х
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
22
y\
y
5
22
–
+
x
1
11
max
0
1
у ln 1 1 9 0 1 9 8
11
В 11
8
3
10 х
х
Наибольшее
значение функция
будет принимать в
точке максимума.
Можно сэкономить на
вычислениях
значений функции в
концах отрезка.
lnx
/
1. Найти f
/(x)
13. Найдите наименьшее значение функции
5 7
y = 2х2 – 5x + lnx – 3 на отрезке [
; ]
6 6
1
x
1
4( х 1)( х )
2
1
4
х
5
х
1
4
у / 4х 5
х
х
х
2.
 Найти
Найтикритические точки,
взять те, которые
принадлежат
данному отрезку.
x=1
y\
y
5
6
–
7
6
+
x
1
min
0
у 1 2 5 ln 1 3 2 8 6
В 11
— 6
3
10 х
х
[
5
6
; 76 ]
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить на
вычислениях
значений функции в
концах отрезка.
cosx – sinx
/
14. Найдите наибольшее значение функции
3
; 0
y = 7cosx +16x – 2 на отрезке
2
у 7 sin х 16
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
0
7 sin х 16 0
16
sin х
7
т.к. sin х [ 1;1]
Функция на всей области
определения возрастает.
Нетрудно догадаться,
что у / > 0.
Тогда наибольшее
значение функция будет
иметь в правом конце
отрезка, т.
 е. в точке х=0.
е. в точке х=0.3
3
3
у
7 cos
16
2 24 2
2
2
2
у 0 7 cos 0 16 0 2 7 2 5
В 11
5
3
10 х
х
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наибольшее.
sinx cosx
15. Найдите наибольшее значение функции
/
y = 10sinx –
у 10 cos х
/
1. Найти f
/(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
10 cos х
36
36
36
5
; 0
x + 7 на отрезке
6
Критических точек нет.
Тогда наибольшее
значение функция будет
принимать в одном из
концов отрезка.
36
cos х
10
т.к. cos х [ 1;1]
Можно было и раньше
догадаться, что
наибольшее значение
будет именно в левом
конце отрезка!
Как?
1
5
5 36 5
у
10 sin
7 10 30 7 32
2
6
6 6
Синус –нечетная функция
0
Формула приведения
5
5
1
у 0 sin
10 sin
7 7 Вsin
0 0
sin
sin
11 3 2
6
6
6
3
10 х
х
6
2
cosx – sinx
16.
 Найдите наименьшее значение функции
Найдите наименьшее значение функции/
у / 5 sin x 6
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3
у
2
y = 5cosx – 6x + 4 на отрезке
5 sin x 6 0
6
sin х
5
т.к. sin х [ 1;1]
0
3
5 cos
2
3
6
2
у 0 5 cos 0 0 4 9
В 11
9
3
10 х
Функция на всей области
определения убывает.
Нетрудно догадаться, что
у /
Тогда наименьшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
4 9 4
1
х
3
2 ; 0
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наименьшее.
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.

12 sin x 6 3 0
3
sin х
2
х ( 1)
у 12 cos 6 3 2 3 6 12
3
3
3
n
3
3
Но нам н
ВСЕ
стациона
точки.
Необходи
сделать в
значений
попадут в
заданный
n
у 12 cos 6 3 2 3 6 6 3
2
2
2
0 ; 2
у 0 12 cos 0 6 3 0 2 3 6 18 2 3
В 11
1 2
3
10 х
х
17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
y\
y
0
3
sin х
2
+
3
–
max
2
x
3
Убедимся, что данная точка
является точкой максимума на
заданном промежутке.
Значит, наибольшее значение
функция достигает именно в этой
точке.
Тогда значения функции в концах
отрезка можно не считать.
у 12 cos 6 3 2 3 6 12
3
3
3
В 11
1 2
3
10 х
х
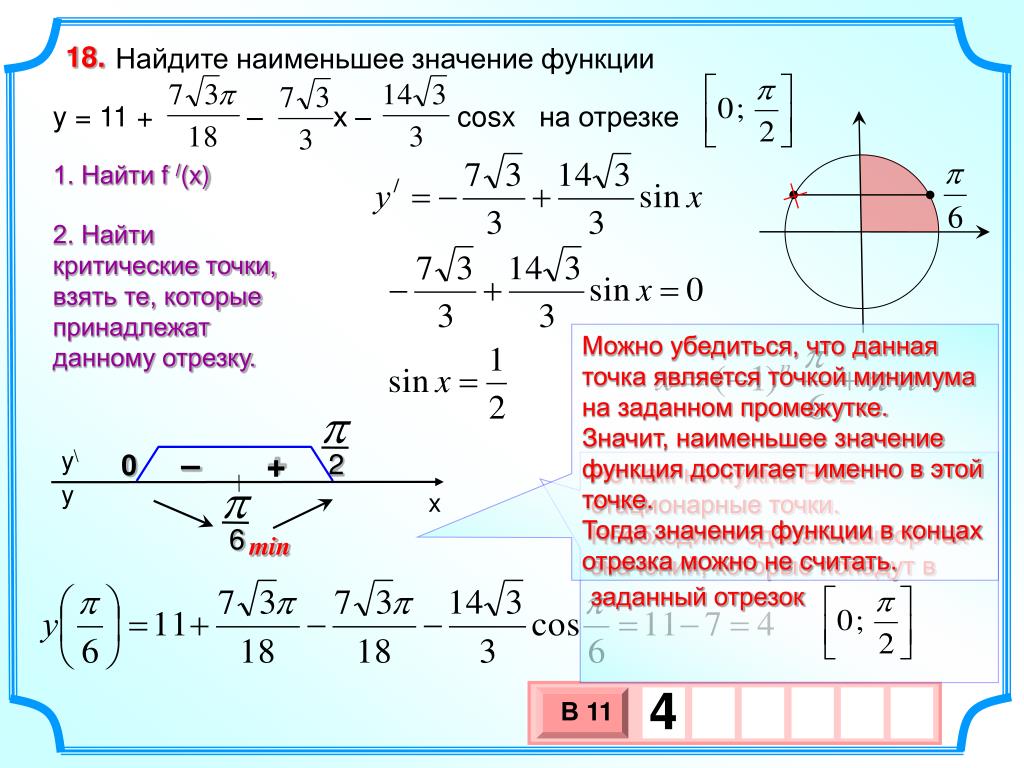
18. Найдите наименьшее значение функции
7 3
14 3
7 3
y = 11 +
–
х–
cosx на отрезке 0 ;
2
18
3
3
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
y\
y
0
–
7 3 14 3
у
sin x
6
3
3
7 3 14 3
sin x 0
3
3
Можно убедиться, что данная
1
n
точка
является
точкой
х ( 1)
минимума
n
sin x
на заданном промежутке.
6
2
/
+
6 min
2
x
Значит, наименьшее значение
функция
достигает
именно в этой
Но нам не
нужны ВСЕ
точке.
стационарные точки.
Тогда
значения
функции
в концах
Необходимо
сделать
выбор
тех
в
отрезка
можно
не считать.

значений,
которые
попадут
0
;
2
заданный
отрезок
7 3 7 3 14 3
у 11
cos 11 7 4
18
18
3
6
6
В 11
4
3
10 х
х
tgx
/
19. Найдите наименьшее значение функции
1
cos2x y = 4tgx – 4x – 4 + 5 на отрезке 4 ; 4
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 4
4
2
cos x
/
4
0
4
4 0
2
cos x
cos 2 x 1
Нам не нужны ВСЕ
у 4 5 1
4
у 4 5 9 2
4
у 0 0 0 5 5
4
стационарные точки.
Необходимо сделать выбор тех
значений, которые попадут в
3. Вычислим
значения функции
заданный
отрезок
в критических точках
;
и на концах отрезка.
4 4
4. Из вычисленных значений
сделаем выбор наименьшего.
В 11
1
3
10 х
х
tgx
/
20.
 Найдите наибольшее значение функции
Найдите наибольшее значение функции1
2
cos x y = 3tgx – 3x + 5 на отрезке 4 ; 0
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 3
3
2
cos x
/
0
3
3 0
2
cos x
cos 2 x 1
4
Нам не нужны ВСЕ
3. Вычислим значения функции в критическихстационарные
точках и на концах
точки.отрезка.
Необходимо сделать выбор тех
4. Из вычисленных значений сделаем выбор наибольшего.
значений, которые попадут в
-1
заданный отрезок
3 4 ; 0 3
у 3tg 3 5 3
5 2
4
4
4 0 4 4
у 0 3tg0 0 5 5
В 11
5
3
10 х
х
Решая задания на наибольшее и наименьшее значение
функции, я применяла различные способы. Если вы
решаете задания своим способом и всегда попадаете в
правильный ответ, не стоит переучиваться.
При использовании материалов сайта необходимо сделать
ссылку на сайт http://le-savchen.
 ucoz.ru
ucoz.ruЧто наименьшее наибольшее значение функции. Наибольшее и наименьшее значение функции
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти производную функции.
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.

- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x 3 – 18x 2 + 81x + 23 на отрезке .
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x 2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x 2 – 36x + 81 = 0, значит x 2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x 3 – 18x 2 + 81x + 23 = x (x -9) 2 +23:
- y (8) = 8 · (8-9) 2 +23 = 31;
- y (9) = 9 · (9-9) 2 +23 = 23;
- y (13) = 13 · (13-9) 2 +23 = 231.

Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции.
 Если точек максимума нет, то у функции нет наибольшего значения.
Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции.
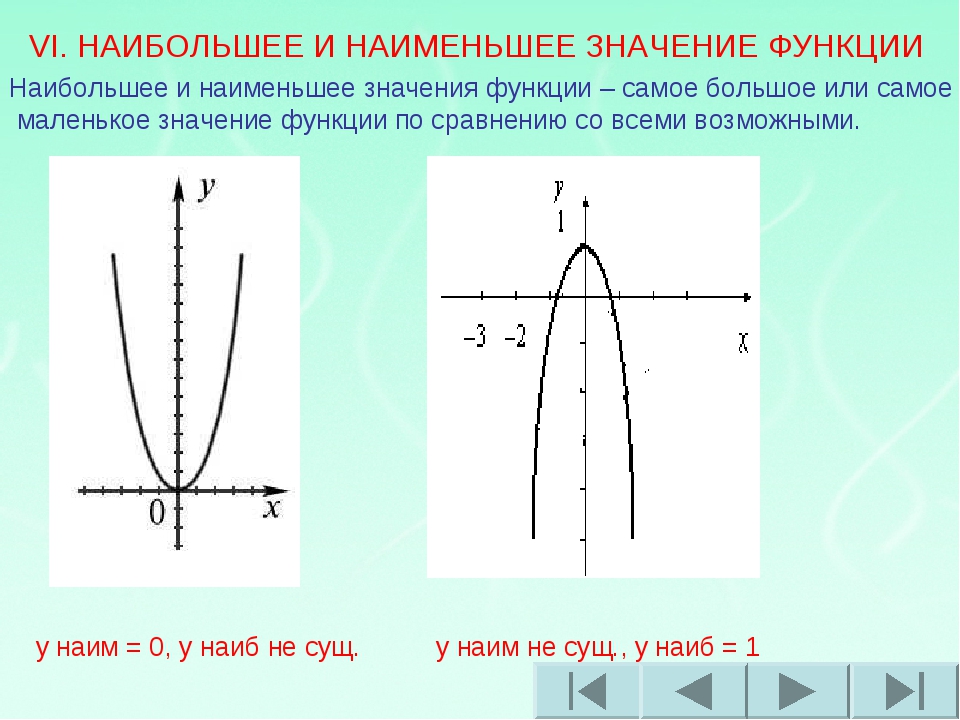
Наибольшим значением функции называется самое большее, наименьшим значением – самое меньшее из всех ее значений.
Функция может иметь только одно наибольшее и только одно наименьшее значение или может не иметь их совсем. Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
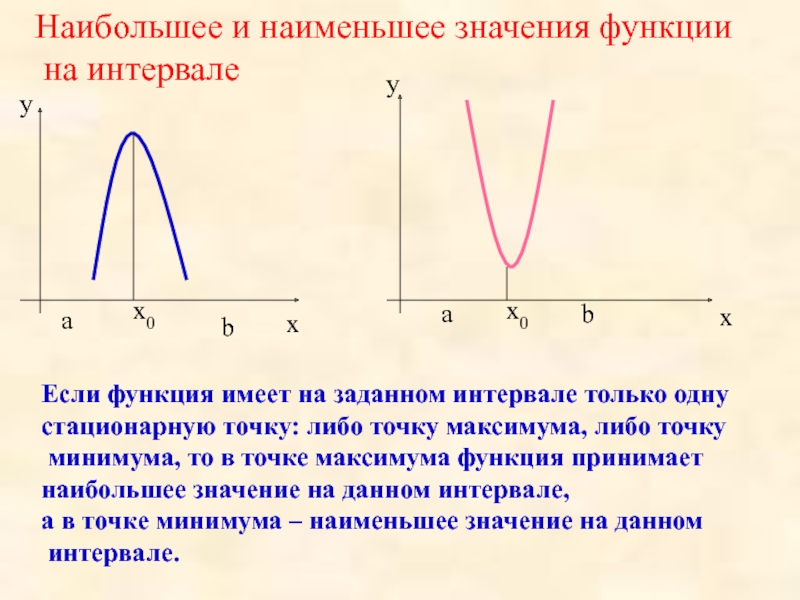
1) Если в некотором интервале (конечном или бесконечном) функция y=f(x) непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале.
2) Если функция f(x) непрерывна на некотором отрезке , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ее или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
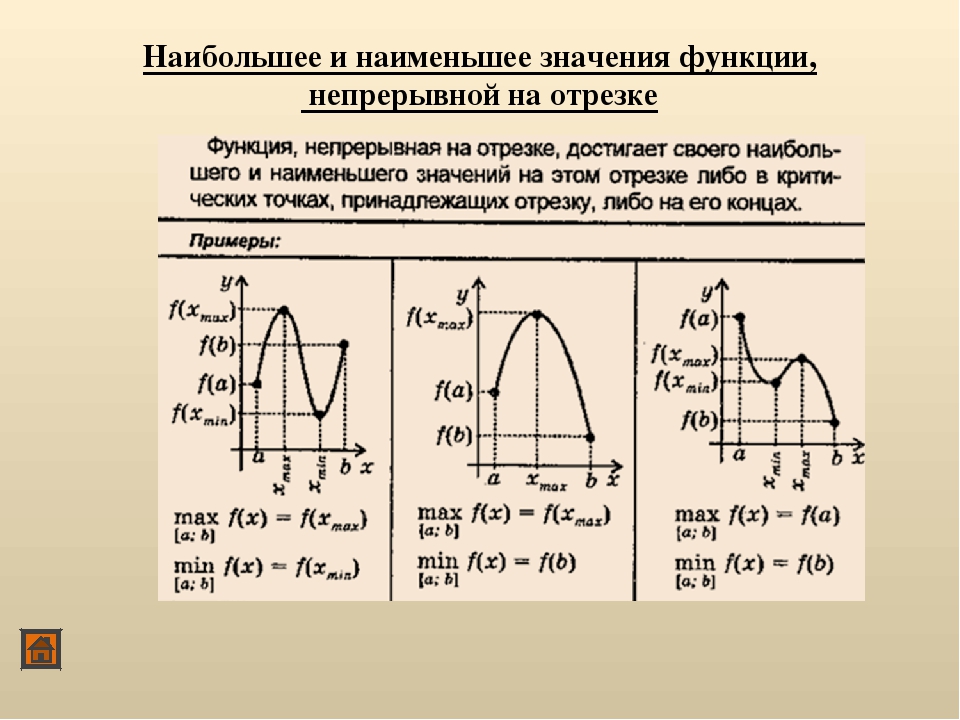
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную .
Найти производную .
2. Найти критические точки функции, в которых =0 или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее f наиб и наименьшее f наим.
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке Х. Для решения таких задач следует, исходя из условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную. Затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.
Пример. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л. воды, чтобы затраты на его лужение были наименьшими?
Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной. Обозначим через а дм – сторону основания, b дм – высоту резервуара. Тогда площадь S его поверхности равна
Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной. Обозначим через а дм – сторону основания, b дм – высоту резервуара. Тогда площадь S его поверхности равна
И
Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S (функция) и стороной основания а (аргумент). Исследуем функцию S на экстремум. Найдем первую производную , приравняем ее к нулю и решим полученное уравнение:
Отсюда а = 6. (а) > 0 при а > 6, (а)
Пример . Найти наибольшее и наименьшее значения функции на промежутке .
Решение : Заданная функция непрерывна на всей числовой оси. Производная функции
Производная при и при . Вычислим значения функции в этих точках:
.
Значения функции на концах заданного промежутка равны . Следовательно, наибольшее значение функции равно при , наименьшее значение функции равно при .
Вопросы для самопроверки
1. Сформулируйте правило Лопиталя для раскрытия неопределенностей вида . Перечислите различные типы неопределенностей, для раскрытия которых может быть использовано правило Лопиталя.
Сформулируйте правило Лопиталя для раскрытия неопределенностей вида . Перечислите различные типы неопределенностей, для раскрытия которых может быть использовано правило Лопиталя.
2. Сформулируйте признаки возрастания и убывания функции.
3. Дайте определение максимума и минимума функции.
4. Сформулируйте необходимое условие существования экстремума.
5. Какие значения аргумента (какие точки) называются критическими? Как найти эти точки?
6. Каковы достаточные признаки существования экстремума функции? Изложите схему исследования функции на экстремум с помощью первой производной.
7. Изложите схему исследования функции на экстремум с помощью второй производной.
8. Дайте определение выпуклости, вогнутости кривой.
9. Что называется точкой перегиба графика функции? Укажите способ нахождения этих точек.
10. Сформулируйте необходимый и достаточный признаки выпуклости и вогнутости кривой на заданном отрезке.
11. Дайте определение асимптоты кривой. 2 — 65. Даже ничего не считая становится очевидно, что в точке 100 функция имеет знак плюс. А значит и на промежутки от 1 до 100 она имеет знак плюс. При переходе через 1 (мы идем справа налево)функция сменит знак на минус. При переходе через точку 0 функция сохранит свой знак, так как это лишь граница отрезка, а не корень уравнения. При переходе через -1 функция опять сменит знак на плюс.
2 — 65. Даже ничего не считая становится очевидно, что в точке 100 функция имеет знак плюс. А значит и на промежутки от 1 до 100 она имеет знак плюс. При переходе через 1 (мы идем справа налево)функция сменит знак на минус. При переходе через точку 0 функция сохранит свой знак, так как это лишь граница отрезка, а не корень уравнения. При переходе через -1 функция опять сменит знак на плюс.
Из теории мы знаем, что там, где производная функции (а мы именно для нее это и чертили) меняет знак с плюса на минус (точка -1 в нашем случае) функция достигает своего локального максимума (y(-1)=44, как была посчитано ранее) на данном отрезке (это логически очень понятно, функция перестала возрастать, так как достигла своего максимума и начала убывать).
Соответственно, там где производная функции меняет знак с минуса на плюс , достигается локальный минимум функции . Да, да, мы также нашли точку локального минимума это 1, а y(1) — это минимальное значение функции на отрезке, допустим от -1 до +∞. Обратите огромное внимание, что это лишь ЛОКАЛЬНЫЙ МИНИМУМ, то есть минимум на определенном отрезке. Так как действительный (глобальный) минимум функция достигнет где-то там, в -∞.
Обратите огромное внимание, что это лишь ЛОКАЛЬНЫЙ МИНИМУМ, то есть минимум на определенном отрезке. Так как действительный (глобальный) минимум функция достигнет где-то там, в -∞.
На мой взгляд первый способ проще теоретически, а второй проще с точки зрения арифметических действий, но намного сложнее с точки зрения теории. Ведь иногда бывают случаи, когда функция не меняет знак при переходе через корень уравнения, да и вообще можно запутаться с этими локальными, глобальными максимумами и минимумами, хотя Вам так и так придется это хорошо освоить, если вы планируете поступать в технический ВУЗ (а для чего иначе сдавать профильное ЕГЭ и решать это задание). Но практика и только практика раз и навсегда научит Вас решать такие задачи. А тренироваться можете на нашем сайте. Вот .
Если появились какие-то вопросы, или что-то непонятно — обязательно спросите. Я с радостью Вам отвечу, и внесу изменения, дополнения в статью. Помните мы делаем этот сайт вместе!
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал (a ; b) , (a ; b ] , [ a ; b) , бесконечный интервал (a ; b) , (a ; b ] , [ a ; b) либо бесконечный промежуток — ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f (x) .
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1
Наибольшее значение функции y = f (x) на некотором промежутке x – это значение m a x y = f (x 0) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f (x) ≤ f (x 0) .
Определение 2
Наименьшее значение функции y = f (x) на некотором промежутке x – это значение m i n x ∈ X y = f (x 0) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f (x) ≥ f (x 0) .
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .
Определение 3
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (m a x y и m i n y) в стационарных точках, расположенных на отрезке [ — 6 ; 6 ] .
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ — 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.
Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале (- 6 ; 6) .
Если мы возьмем интервал [ 1 ; 6) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (- 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.
На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .
Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.

- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.
Пример 1
Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y » = x 3 + 4 x 2 » = x 3 + 4 » · x 2 — x 3 + 4 · x 2 » x 4 = = 3 x 2 · x 2 — (x 3 — 4) · 2 x x 4 = x 3 — 8 x 3
Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 — 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .
Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4:
y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4
Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – при x = 2 .
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3
Значит, m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
Ответ: Для отрезка [ 1 ; 4 ] — m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , для отрезка [ — 4 ; — 1 ] — m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
См. на рисунке:
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [ a ; b) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f (x) .

- Если интервал имеет вид (a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f (x) .
- Если интервал имеет вид (a ; b) , то нам надо вычислить односторонние пределы lim x → b — 0 f (x) , lim x → a + 0 f (x) .
- Если интервал имеет вид [ a ; + ∞) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f (x) .
- Если интервал выглядит как (- ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f (x) .
- Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f (x) и предел на минус бесконечности lim x → — ∞ f (x)
- Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f (x) , lim x → — ∞ f (x) .
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя.
 Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; + ∞) .
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · (- 6) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; — 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y » = 3 e 1 x 2 + x — 6 — 4 » = 3 · e 1 x 2 + x — 6 » = 3 · e 1 x 2 + x — 6 · 1 x 2 + x — 6 » = = 3 · e 1 x 2 + x — 6 · 1 » · x 2 + x — 6 — 1 · x 2 + x — 6 » (x 2 + x — 6) 2 = — 3 · (2 x + 1) · e 1 x 2 + x — 6 x 2 + x — 6 2
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = — 1 2 . Это стационарная точка, которая находится в интервалах (- 3 ; 1 ] и (- 3 ; 2) .
Вычислим значение функции при x = — 4 для промежутка (- ∞ ; — 4 ] , а также предел на минус бесконечности:
y (- 4) = 3 e 1 (- 4) 2 + (- 4) — 6 — 4 = 3 e 1 6 — 4 ≈ — 0 . 456 lim x → — ∞ 3 e 1 x 2 + x — 6 = 3 e 0 — 4 = — 1
Поскольку 3 e 1 6 — 4 > — 1 , значит, m a x y x ∈ (- ∞ ; — 4 ] = y (- 4) = 3 e 1 6 — 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение — 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к — 3 с левой стороны, мы получим только интервал значений:
lim x → — 3 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 — 0 3 e 1 (x + 3) (x — 3) — 4 = 3 e 1 (- 3 — 0 + 3) (- 3 — 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → — ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Значит, значения функции будут расположены в интервале — 1 ; + ∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = — 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:
Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e 4 25 — 4 ≈ — 1 . 444 y (1) = 3 e 1 1 2 + 1 — 6 — 4 ≈ — 1 . 644 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 — 3 + 0 + 3 (- 3 + 0 — 2) — 4 = = 3 e 1 (- 0) — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ (3 ; 1 ] = y — 1 2 = 3 e — 4 25 — 4 . Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Для интервала (- 3 ; 2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e — 4 25 — 4 ≈ — 1 . 444 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = — 4 lim x → 2 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 — 0 + 3) (2 — 0 — 2) — 4 = = 3 e 1 — 0 — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
Значит, m a x y x ∈ (- 3 ; 2) = y — 1 2 = 3 e — 4 25 — 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом — 4 .
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.
На промежутке (2 ; + ∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка — 1 ; + ∞ .
lim x → 2 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 + 0 + 3) (2 + 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 — 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = — 1 .
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word . Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f» 0 (x *) = 0 — это необходимое условие экстремума функции одной переменной, т.е.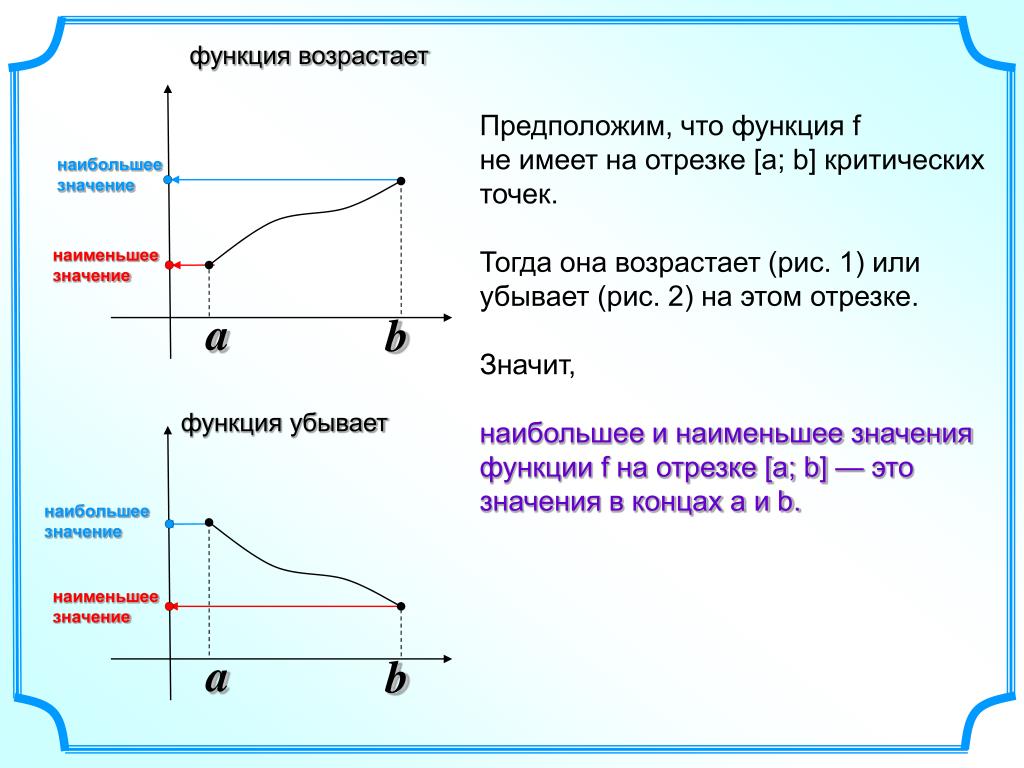 в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.
в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:F» 0 (x *) = 0
f»» 0 (x *) > 0
То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F» 0 (x *) = 0
f»» 0 (x *)
То точка x * — локальный (глобальный) максимум.
Пример №1
. Найти наибольшее и наименьшее значения функции:
на отрезке .
Решение.
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1
Пример №2
. С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
Пример №3
. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4
. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
Наименьшее значение функции f x. Наибольшее и наименьшее значение функции. Схема нахождения наибольшего и наименьшего значений функции $f(x)$ на отрезке $$
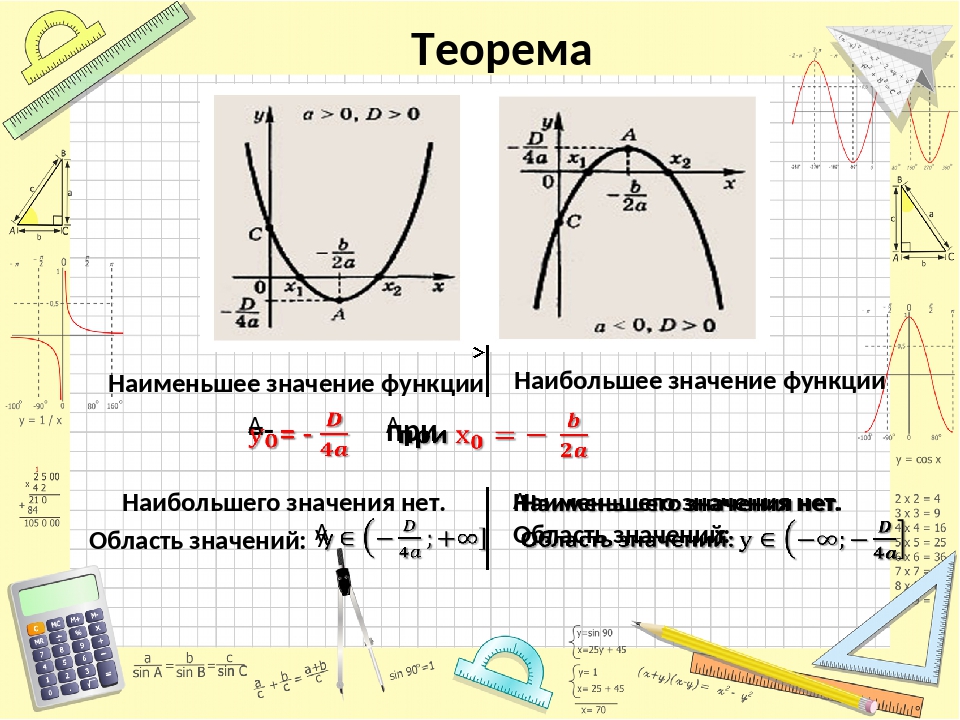
На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения. На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума функции. На правом рисунке — на концах отрезка.
Если функция y = f (x )
непрерывна на отрезке [a , b ]
,
то она достигает на этом отрезке наименьшего и наибольшего значений . Это, как
уже говорилось, может произойти либо в точках экстремума , либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции ,
непрерывной на отрезке [a , b ]
, нужно
вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее
и наибольшее.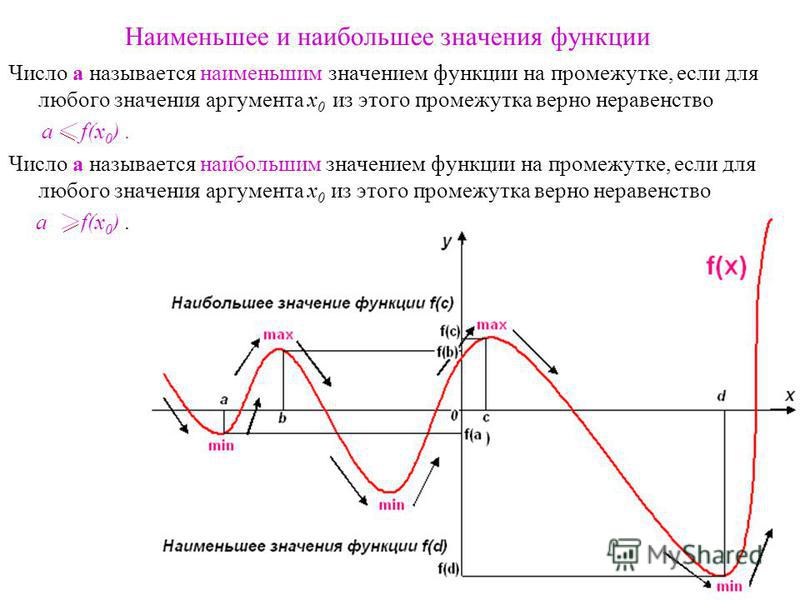
Пусть, например, требуется определить наибольшее значение функции f (x ) на отрезке [a , b ] . Для этого следует найти все её критические точки, лежащие на [a , b ] .
Критической точкой называется точка, в которой функция определена , а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f (a ) и f (b ) ). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a , b ] .
Аналогично решаются и задачи на нахождение наименьших значений функции .
Ищем наименьшее и наибольшее значения функции вместе
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2] .
Решение. Находим производную данной функции . Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо
следующее свойство непрерывных функций.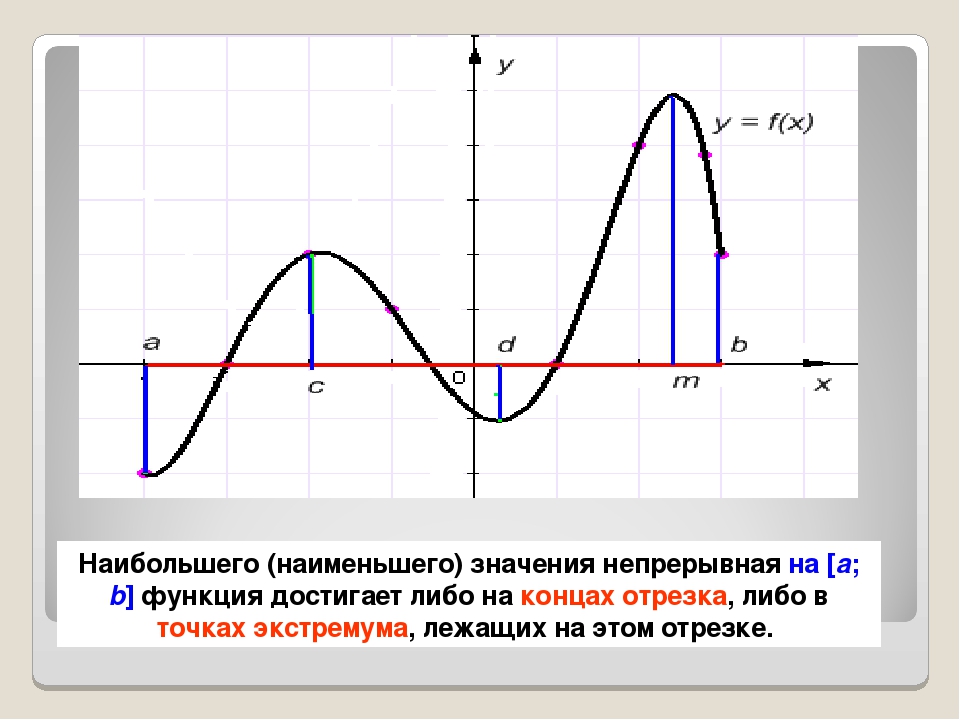
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных .
Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3] .
Решение. Находим производную данной функции как производную частного:
.
Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3] . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Сравниваем эти значения. Вывод: , равного -5/13, в точке и наибольшего значения , равного 1, в точке .
Продолжаем искать наименьшее и наибольшее значения функции вместе
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции
не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция —
многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами,
поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).
Поэтому в ход пойдут логарифм и тригонометрическая функция.
Но мы не ограничимся такими примерами,
поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).
Поэтому в ход пойдут логарифм и тригонометрическая функция.
Пример 8. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции как производную произведения :
Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Результат всех действий: функция достигает наименьшего значения , равного 0, в точке и в точке и наибольшего значения , равного e ² , в точке .
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных .
Пример 9. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции:
Приравниваем производную нулю:
Единственная критическая точку принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Вывод: функция достигает наименьшего значения , равного , в точке и наибольшего значения , равного , в точке .
В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.
Пример 10. Резервуар ёмкостью 4 ,
имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы
должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Каковы
должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S :
Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[ , причём
.
Приравниваем производную нулю ()
и находим критическую точку . Кроме того,
при производная не
существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума.
Итак, — единственная
критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём
вторую производную .
При вторая производная
больше нуля (). Значит, при
функция достигает
минимума . Поскольку
этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак,
сторона основания резервуара должна быть равна 2 м, а его высота .
Поскольку
этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак,
сторона основания резервуара должна быть равна 2 м, а его высота .
Для самопроверки при расчётах можно воспользоваться
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность .
Функция f (x ) называется монотонно возрастающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) x 2 ).
Функция f (x ) называется монотонно убывающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) > f (x 2 ).
Другими словами, для возрастающей функции чем больше x
, тем больше f
(x
). Для убывающей функции все наоборот: чем больше x
, тем меньше f
(x
).
Для убывающей функции все наоборот: чем больше x
, тем меньше f
(x
).
Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 0.
f (x ) = log a x (a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 0:
f (x ) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax 2 + bx + c . Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх (при a > 0) или вниз (a
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a
Наибольший интерес представляет именно вершина параболы , абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x 0 для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок в условии задачи отсутствует. Следовательно, вычислять f (a ) и f (b ) не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы x 0 , координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы y = ax 2 + bx + c и найти ее вершину по формуле: x 0 = −b /2a ;
- Найти значение исходной функции в этой точке: f
(x
0).
 Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Под корнем стоит квадратичная функция y = x 2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке x 0 = −3 функция y = x 2 + 6x + 13 принимает наименьшее значение.
Корень монотонно возрастает, значит x 0 — точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
y = log 2 (x 2 + 2x + 9)
Под логарифмом снова квадратичная функция: y
= x
2 + 2x
+ 9. График — парабола ветвями вверх, т.к. a
= 1 > 0.
График — парабола ветвями вверх, т.к. a
= 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке x 0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x — монотонная, поэтому:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = … = log 2 8 = 3
В показателе стоит квадратичная функция y = 1 − 4x − x 2 . Перепишем ее в нормальном виде: y = −x 2 − 4x + 1.
Очевидно, что график этой функции — парабола, ветви вниз (a = −1
x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x 0 = −2:
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: y = 3 − 2x − x 2 . Ее график — парабола, но ветви вниз, поскольку a = −1
Выписываем область допустимых значений (ОДЗ):
3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Теперь найдем вершину параболы:
x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1
Точка x 0 = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x 0 , а также на концах ОДЗ:
y (−3) = y (1) = 0
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
y = log 0,5 (6x − x 2 − 5)
Внутри логарифма стоит квадратичная функция y = 6x − x 2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5
Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.
Ищем вершину параболы:
x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: x 0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x 0:
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти производную функции.
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x 3 – 18x 2 + 81x + 23 на отрезке .
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.

- Производная функции равна: y’ = 3x 2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x 2 – 36x + 81 = 0, значит x 2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x 3 – 18x 2 + 81x + 23 = x (x -9) 2 +23:
- y (8) = 8 · (8-9) 2 +23 = 31;
- y (9) = 9 · (9-9) 2 +23 = 23;
- y (13) = 13 · (13-9) 2 +23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.

- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции.
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word
. Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f» 0 (x *) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:F» 0 (x *) = 0
f»» 0 (x *) > 0
То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F» 0 (x *) = 0
f»» 0 (x *)
То точка x * — локальный (глобальный) максимум.
Пример №1
. Найти наибольшее и наименьшее значения функции:
на отрезке .
Решение.
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1
Пример №2
. С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
Пример №3
. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4
. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами
и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.
Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: «Фракталы — это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».
То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией».
Максимальные и минимальные значения — Подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) больше на .
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше любого , чем любое .
Опять же, другие значения функции на самом деле могут быть меньше. При таком понимании мы отбросим термин «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производной при оценке как a или b — равен 0,
.f ‘ ( x ) = 0,
Более того, в точках непосредственно от осталось максимума — в точке C — наклон касательной положителен: f ‘ ( x ) > 0.В то время как в точках непосредственно на вправо — в точке D — наклон отрицателен: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на — .
Как минимум, f ‘ ( x ) меняет знак с − на + . Мы видим, что в точках E и F .
Мы также можем наблюдать, что в максимуме при A график вогнут вниз.(Тема 14 Precalculus.) Хотя, как минимум, на B он вогнут вверх.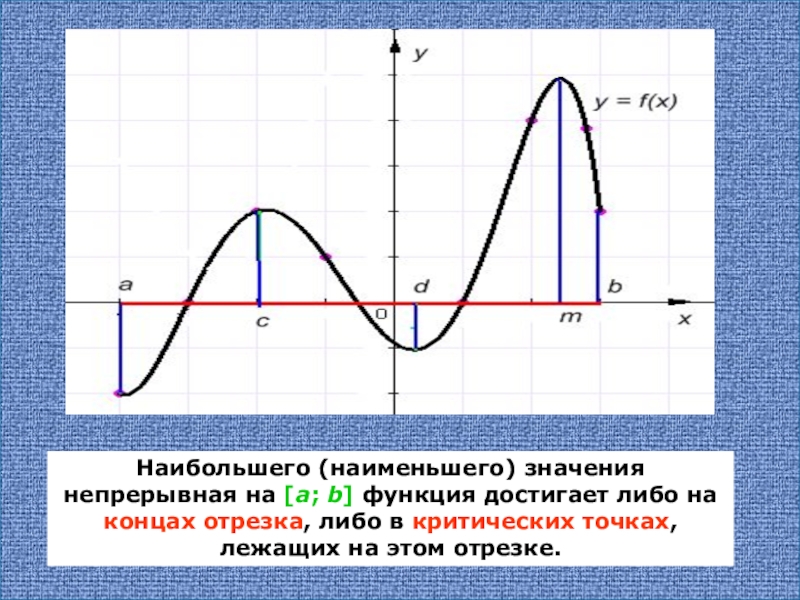
Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x .Критические значения — если они есть — будут решений от до f ‘ ( x ) = 0,
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x − 6 = 0 означает x = 3. (Урок 9 алгебры.)
x = 3 — единственное критическое значение. Это x координат точки поворота. Чтобы определить y -координат, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | х 2 − 6 х + 5 |
| f (3) | = | 3 2 − 6 · 3 + 5 |
| = | −4. | |
Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — это парабола, и мы видим, что точка поворота является минимумом.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но не всегда мы сможем посмотреть на график.Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с — на + . Это мы видим в точках E , B , F выше. Значение наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (урок 9) — скорость изменения наклона — равна положительной .
Опять же, вот f ( x ):
| f ( x ) | = | х 2 − 6 х + 5. |
| f ‘ ( x ) | = | 2 х − 6. |
| f » ( x ) | = | 2. |
f » оценивается при критическом значении 3 — f» (3) = 2 — положительный. Это говорит нам алгебраически, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение при x = a , если f ‘ ( a ) = 0
и f » ( a ) = положительное число.
Функция имеет максимальное значение при x = a if f ‘ ( a ) = 0
и f » ( a ) = отрицательное число.
В случае максимума наклон касательной равен уменьшению — он идет от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3,
Есть ли экстремальные значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Решение . f’ ( х ) = 6 х 2 — 18 х + 12 | = | 6( х 2 − 3 х + 2) |
| = | 6( х — 1)( х — 2) | |
| = | 0 | |
подразумевает:
x = 1 или x = 2.
(Урок 37 Алгебры.)
Это критические значения. Каждый из них определяет максимум или он определяет минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении.
| е ( х ) | = | 6 x 2 − 18 x + 12. |
| f » ( x ) | = | 12 х − 18. |
| ф» (1) | = | 12 — 18 = -6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум при x = 1,
.Чтобы найти y -координату — крайнее значение — в этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 − 9 x 2 + 12 x − 3 |
| f (1) | = | 2 − 9 + 12 − 3 |
| = | 2. | |
Максимум приходится на точку (1, 2).
Далее, определяет ли x = 2 максимум или минимум?
| ф » ( х ) | = | 12 х − 18. |
| ф» (2) | = | 24 — 18 = 6. |
Вторая производная положительна.Таким образом, функция имеет минимум при x = 2,
.Чтобы найти y -координату — экстремальное значение — в этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 − 9 x 2 + 12 x − 3. |
| f (2) | = | 16 − 36 + 24 − 3 |
| = | 1. | |
Минимум приходится на точку (2, 1).
Вот собственно график f ( x ):
Решения f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 3 .
Другой пример: y = sin x . Решения y» = 0 являются множителями π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы
у = х 2 — 8 х + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
у’ = 2 х — 8 = 0,
Отсюда следует, что x = 4. Это координата вершины x . Чтобы найти координату y , оцените y как x = 4:
Это координата вершины x . Чтобы найти координату y , оцените y как x = 4:
y = 4 2 − 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Исследуйте каждую функцию на наличие максимумов и минимумов.
а) y = x 3 − 3 x 2 + 2,
y’ = 3 x 2 — 6 x = 3 x ( x — 2) = 0 подразумевает
x = 0 или x = 2.
у» ( х ) = 6 х — 6.
г» (0) = -6.
Вторая производная отрицательна. Это означает, что максимальное значение составляет x = 0. Это максимальное значение равно
.г (0) = 2.
Далее,
у» (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что минимальное значение составляет x = 2.Это минимальное значение равно
Это означает, что минимальное значение составляет x = 2.Это минимальное значение равно
y (2) = 2 3 − 3 · 2 2 + 2 = 8 − 12 + 2 = −2.
b) y = −2 x 3 − 3 x 2 + 12 x + 10,
При x = 1 максимум y = 17.
При х = -2 есть минимум y = -10.
c) y = 2 x 3 + 3 x 2 + 12 x − 4,
Так как f’ ( x ) = 0 не имеет реальных решений, то нет и экстремальных значений.
г) y = 3 х 4 − 4 х 3 − 12 х 2 + 2,
При x = 0 максимальное значение составляет y = 2.
При x = -1 есть минимум y = -3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: teacher@themathpage.ком
Минимум и максимум Python: полное руководство
Функция Python max() используется для поиска наибольшего значения в списке значений. Функция Python min() используется для поиска наименьшего значения в списке. Список значений может содержать либо строки, либо числа.
Вы можете столкнуться с ситуацией, когда вам нужно найти минимальное или максимальное значение в списке или строке. Например, вы можете написать программу, которая находит самый дорогой автомобиль, проданный в вашем дилерском центре.Вот где на помощь приходят встроенные функции Python min() и max() .
В Python вы можете использовать min() и max() , чтобы найти наименьшее и наибольшее значение соответственно в списке или строке. В этом руководстве мы рассмотрим, как использовать методы min() и max() в Python, и рассмотрим несколько примеров каждого из них.
Функция Python min()
Функция Python min() возвращает наименьшее значение в списке элементов.min() можно использовать для поиска наименьшего числа в списке или первой строки, которая появилась бы в списке, если бы список был упорядочен в алфавитном порядке.
Вот синтаксис метода Python min() :
В этом синтаксисе метод min() принимает только один параметр: объект, минимальное значение которого вы хотите найти.
Мы также можем указать отдельные значения в качестве аргументов с помощью функции min():
Наибольшее значение из всех значений, которые мы указываем в качестве аргументов, возвращается, если вы решите указать отдельные значения.
81% участников заявили, что после посещения буткемпа они стали более уверенными в своих перспективах работы в сфере технологий. Подберите себе буткемп сегодня.
Найдите свой матч для буткемпаСредний выпускник буткемпа тратит менее шести месяцев на смену карьеры, от начала буткемпа до поиска своей первой работы.
Начните свою карьеру сегодняВы можете передать итерируемый объект, такой как список или кортеж списка, в качестве аргумента метода min(). Если итерируемый объект пуст, возникает ошибка ValueError:
.ValueError: аргумент max() является пустой последовательностью
Прочтите нашу статью «ValueError: аргумент max() является пустой последовательностью» (которая также относится к методу min()) для получения дополнительной информации.
мин Пример Python
Вот простой пример использования метода min() для поиска наименьшего значения в списке:
пример_список = [21, 22, 19, 14] печать (мин (example_list))
Наш код возвращает: 14 .
В первой строке нашего кода мы определяем список с именем example_list , в котором хранятся четыре значения. В следующей строке мы используем min() , чтобы найти наименьшее значение в этом списке и вывести это значение на консоль.
Давайте воспользуемся более подробным примером, чтобы показать этот метод в действии. Допустим, мы являемся владельцем кофейни и составили список потенциальных продавцов молока. Мы нашли шесть поставщиков и создали массив, в котором хранится цена за галлон, указанную нам каждым поставщиком.
Найдите свой тренировочный лагерь
- Карьера Карма подберет для вас лучшие технические учебные курсы
- Получите эксклюзивные стипендии и подготовительные курсы
Мы хотим найти самого дешевого поставщика в нашем списке, что мы можем сделать с помощью следующей программы:
supplier_quotes = [3.28, 3.27, 3.29, 3.30, 3.32, 3.26] print("Самая низкая цена $", min(supplier_quotes), " за галлон молока.")
Наш код возвращает наименьший элемент в нашей итерации:
Самая низкая цена — 3,26 доллара за галлон молока.
В первой строке нашего кода мы определяем список котировок поставщиков. Затем мы используем метод min() , чтобы найти наименьшее значение, и распечатываем сообщение с результатом этого метода. В этом случае самая низкая доступная цена составляла 3 доллара.26 за галлон молока.
Максимальная функция Python
Функция Python max() возвращает наибольшее значение в итерируемом объекте, таком как список. Если список содержит строки, max() возвращает последний элемент в алфавитном порядке.
Давайте посмотрим на синтаксис функции max() Python:
Вы видите, что можете указать отдельные значения, из которых будет выбрано наибольшее значение.
Мы также можем использовать этот синтаксис, когда мы передаем итерируемый объект в качестве аргумента:
Второй пример — наиболее распространенное использование max(). Этот код считывает содержимое указанного итерируемого объекта, например списка, и возвращает наибольшее значение в этом итерируемом объекте.
Этот код считывает содержимое указанного итерируемого объекта, например списка, и возвращает наибольшее значение в этом итерируемом объекте.
Передача пустого значения в качестве аргумента функции max() приведет к той же ошибке ValueError, которую мы обсуждали ранее.
max() Пример Python
Скажите, что мы — кофейня премиум-класса, и мы хотим платить премиальную цену за качественное молоко. Мы могли бы найти самую большую котировку, которую мы получили, используя следующий код:
supplier_quotes = [3.28, 3.27, 3.29, 3.30, 3.32, 3.26]
print("Самая дорогая цена $", max(supplier_quotes)) Наш код возвращает самый большой элемент в нашем списке:
«Карьерная карма вошла в мою жизнь, когда я больше всего в ней нуждалась, и быстро помогла мне попасть на буткемп. Через два месяца после выпуска я нашла работу своей мечты, которая соответствовала моим ценностям и целям в жизни!»
Венера, инженер-программист Rockbot
Найдите свой матч для буткемпаСамая дорогая цена — 3 доллара.32
Как видите, наш код почти идентичен коду в примере min() выше. Вместо min() мы использовали max() .
Метод max() просмотрел наш массив Python и вычислил максимальное значение в нашем списке. Затем наша программа вывела на консоль сообщение с этим значением.
Минимум и максимум Python со строками
В приведенных выше примерах мы использовали методы min() и max() для поиска наименьшего и наибольшего значений в списке.
Методы min() и max() также можно использовать для поиска наименьших и наибольших символов в строке. В этом случае наименьшее и наибольшее относятся к положению символа в алфавите.
Наименьший возможный символ — это заглавная буква A , поскольку в Python все заглавные буквы идут первыми. Наш самый большой символ — строчная буква z . (Чтобы узнать больше о системе заказов Python, ознакомьтесь с нашим руководством по методу Python ord(). )
)
Допустим, у нас есть строка, содержащая оценки каждого ученика пятого класса по математике. Мы хотим знать, какой был самый низкий класс. Чтобы вычислить самую низкую оценку, мы могли бы использовать функцию max() . Вот пример программы, выполняющей эту задачу:
. оценок = "AABABBACBAABCD"
print("Самая низкая оценка в классе была", max(grades)) Наш код возвращает:
Самая низкая оценка в классе была D
Наш код просматривает строку Python, чтобы найти наименьшее значение.В этом случае самой низкой оценкой была D, которую наша функция max() идентифицировала и вернула в наш код.
Когда вы работаете со строками и методами min() и max() , вы можете указать несколько параметров. Это позволяет найти наименьшую и наибольшую строку из нескольких значений.
Допустим, у вас есть три имени учащихся, и вы хотите узнать, какое из них стоит последним в алфавитном порядке. Вы можете сделать это, используя следующий код:
Вы можете сделать это, используя следующий код:
name_one = "Гарри"
name_two = "Ленни"
name_three = "Джерри"
print("Последним в алфавите стоит имя", max(name_one, name_two, name_three)) Наш код возвращает:
Последнее имя в алфавите — Ленни.
Метод max() принимал три параметра: name_one , name_two и name_three .Затем метод max() вычислил, какое из этих имен идет последним в алфавитном порядке, и вернул это имя программе.
Наконец, наш код напечатал сообщение с именем, которое стоит последним в алфавите.
Заключение
Часто, когда вы работаете со списками или строками, вам нужно найти самое низкое или самое высокое значение, которое появляется в этом списке или строке. Для этого можно использовать методы Python min() и max() .2=36. Наибольшее значение , происходит
в точках (целое положительное число или «бесконечно много»).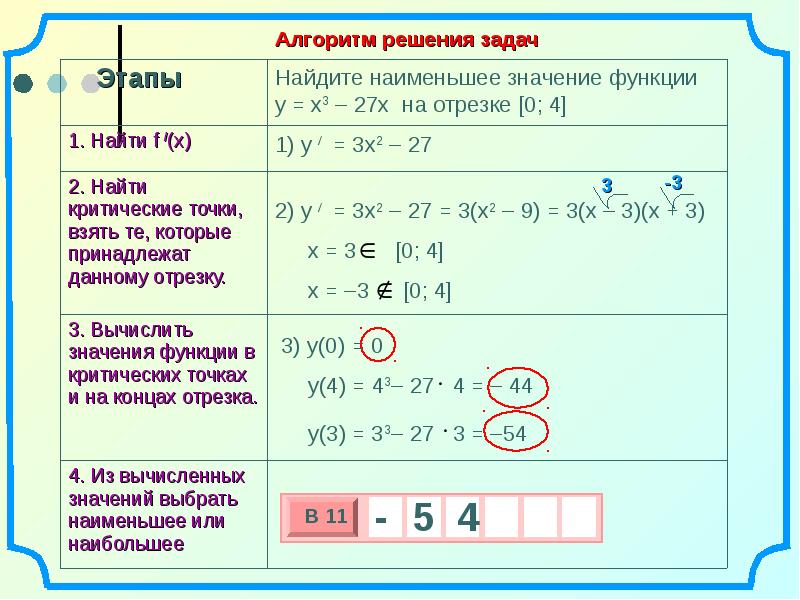 Наименьшее значение , встречающееся в точках
(целое положительное число или «бесконечно много»).
Наименьшее значение легко найти без вычислений!
Наименьшее значение , встречающееся в точках
(целое положительное число или «бесконечно много»).
Наименьшее значение легко найти без вычислений!
Стенограмма видео
100 из них действительно взлетят. Задача номер 11 здесь Функция Every задана часть. Действительно хорошо. Так что используйте ликер и бесплодие, чтобы найти много женщин Максимальное значение, вроде физической смерти, всего 30.Итак, шина пятая, как у Исаака, запятая. Отличный логистический палец ноги посмеялся я сказал ей касается две х запятая два пути кова. Так что мы будем аплодировать Потому что почему? Сделай это. А вот Durex, чего тут мало кроме как, дружище. Уходи, что хорошо, и сбежал туда. Но через это Итак, мы получим, почему вы, Курт Рассел, через запятую секса. Ну, ты низко кланяешься плюс-минус. Используя уравнение нити пистолета, X в квадрате плюс у в квадрате плюс шесть квадратов равно флирту. Таким образом, квадрат меньше бумажного квадрата плюс х класс Это было умно. Они должны были разобраться, что он идет, чтобы узнать Чрезмерный Кардо, Наше судно минус встревожено Третьим маршрутом или физическим лицом. Моя таинственная группа три на три. Хорошо. ВОЗ? Почему ты сказал, что нам нужно найти большие пробелы? Кто это был? Как бывший Зиглер тогда? Правильно. Мы также будем черными плюс-минус три понемногу. Три. И это тоже будет печатью на моей истории. Лучше. Три. Отец будет как восемь очков. Пилер доверился нашему большому позитиву в этом деле. Почему вы думаете или делаете, что все это заставило нас пройти через три на три.И это невероятно. Посылка три на три все противопоставлены три на три три на три кома швырнули три на три на этом я могу один будет это то что будет нужно я услышал три на три через три на три от я минус тренировался три на в точка X может быть отрицательной Райан через три на три Нам нужно было выяснить комбинации. Хорошо, хорошо три на три, и по умолчанию это работает. Оба моих конца выполнены. Они могли пройти маршрут три на три.
Они должны были разобраться, что он идет, чтобы узнать Чрезмерный Кардо, Наше судно минус встревожено Третьим маршрутом или физическим лицом. Моя таинственная группа три на три. Хорошо. ВОЗ? Почему ты сказал, что нам нужно найти большие пробелы? Кто это был? Как бывший Зиглер тогда? Правильно. Мы также будем черными плюс-минус три понемногу. Три. И это тоже будет печатью на моей истории. Лучше. Три. Отец будет как восемь очков. Пилер доверился нашему большому позитиву в этом деле. Почему вы думаете или делаете, что все это заставило нас пройти через три на три.И это невероятно. Посылка три на три все противопоставлены три на три три на три кома швырнули три на три на этом я могу один будет это то что будет нужно я услышал три на три через три на три от я минус тренировался три на в точка X может быть отрицательной Райан через три на три Нам нужно было выяснить комбинации. Хорошо, хорошо три на три, и по умолчанию это работает. Оба моих конца выполнены. Они могли пройти маршрут три на три. Подниматься. Мой Nestle, обученный втроем, выходит в онлайн-сортировку втроем.А в 50-й точке находятся Lexis. И я мог бы делать такие же выходы. Хм? Но ты возвращаешься таким. Вы можете написать оба. Это песчаный путь, как я не делаю. Я делаю. Почему три на три не приходят наши три на 30, мои абсолютные три на три. Они выглядят идеально. Тогда 6 долларов могут быть как захватывающий провал до минус 43 на три. Давай в мою ванную три на три запятая нажми маленькую три на три Тогда мы можем понравиться за деньги. Не потому ли, что минор через тренировку на троих Боже мой! Через торговлю через три запятых мой внутренний через три через три И только типа почему Х может быть отрицательным что у нас много работы но рано как Сможем ли мы пройти через это? Кроме того, вы не можете разбить ладно или три на три Кама Айна 33 на три Урок три на три Так что максимум годовой жарочный ресторан Benetto Готов? Так что, если максимальный реальный обмен назад на троих, обученный вверх, держите очередь, которая является Курто, один на три, Дорога три, И если Мэйбл будет нежной, минус, обученный, обученный целый куб, Вы просто идите Не обращайте внимания на нас на три Комната три.
Подниматься. Мой Nestle, обученный втроем, выходит в онлайн-сортировку втроем.А в 50-й точке находятся Lexis. И я мог бы делать такие же выходы. Хм? Но ты возвращаешься таким. Вы можете написать оба. Это песчаный путь, как я не делаю. Я делаю. Почему три на три не приходят наши три на 30, мои абсолютные три на три. Они выглядят идеально. Тогда 6 долларов могут быть как захватывающий провал до минус 43 на три. Давай в мою ванную три на три запятая нажми маленькую три на три Тогда мы можем понравиться за деньги. Не потому ли, что минор через тренировку на троих Боже мой! Через торговлю через три запятых мой внутренний через три через три И только типа почему Х может быть отрицательным что у нас много работы но рано как Сможем ли мы пройти через это? Кроме того, вы не можете разбить ладно или три на три Кама Айна 33 на три Урок три на три Так что максимум годовой жарочный ресторан Benetto Готов? Так что, если максимальный реальный обмен назад на троих, обученный вверх, держите очередь, которая является Курто, один на три, Дорога три, И если Мэйбл будет нежной, минус, обученный, обученный целый куб, Вы просто идите Не обращайте внимания на нас на три Комната три. Хорошо, так разработано, чтобы Спасибо. Спасибо
Хорошо, так разработано, чтобы Спасибо. Спасибо
MAX vs MAXA vs LARGE и MIN vs MINA vs SMALL Функции в Excel
Excel предоставляет функции для вычисления наибольшего или максимального значения в диапазоне, а также функции для вычисления наименьшего или минимального значения в диапазоне.
Первая функция, которую мы собираемся рассмотреть, это функция MAX. Эта функция возвращает наибольшее или максимальное значение из набора значений. Синтаксис функции MAX:
.Если используются ссылки, содержащие логические значения или текстовые представления чисел, то лучше всего использовать функцию MAXA.Функция MAXA также возвращает наибольшее значение из предоставленного списка значений, однако функция MAXA может включать числа, текстовые представления чисел и логические значения. Синтаксис функции MAXA:
. Функция НАИБОЛЬШИЙ возвращает k-е наибольшее значение в списке значений. Эту функцию можно использовать для возврата первого по величине значения (то же значение, которое вернула бы функция MAX), или второго по величине значения в наборе данных, или третьего по величине значения в наборе данных и так далее. Синтаксис функции НАИБОЛЬШИЙ:
Синтаксис функции НАИБОЛЬШИЙ:
Функция MIN возвращает наименьшее или минимальное значение набора значений. Синтаксис функции MIN:
.Если используются ссылки, содержащие логические значения, которые должны быть включены в фактическое вычисление, то лучше всего использовать функцию MINA. Функция MINA также возвращает наименьшее значение из предоставленного списка значений, однако функция MINA может включать числа, текстовые представления чисел и логические значения.Синтаксис функции MINA:
.Функция НАИМЕНЬШИЙ возвращает k-е наименьшее значение в списке значений. Эту функцию можно использовать для возврата наименьшего значения (того же значения, которое вернула бы функция MIN) или второго наименьшего значения в наборе данных или третьего наименьшего значения в наборе данных и так далее. Синтаксис функции МАЛЕНЬКИЙ:
. Итак, давайте начнем с нескольких простых примеров, чтобы проиллюстрировать, где использовать различные функции.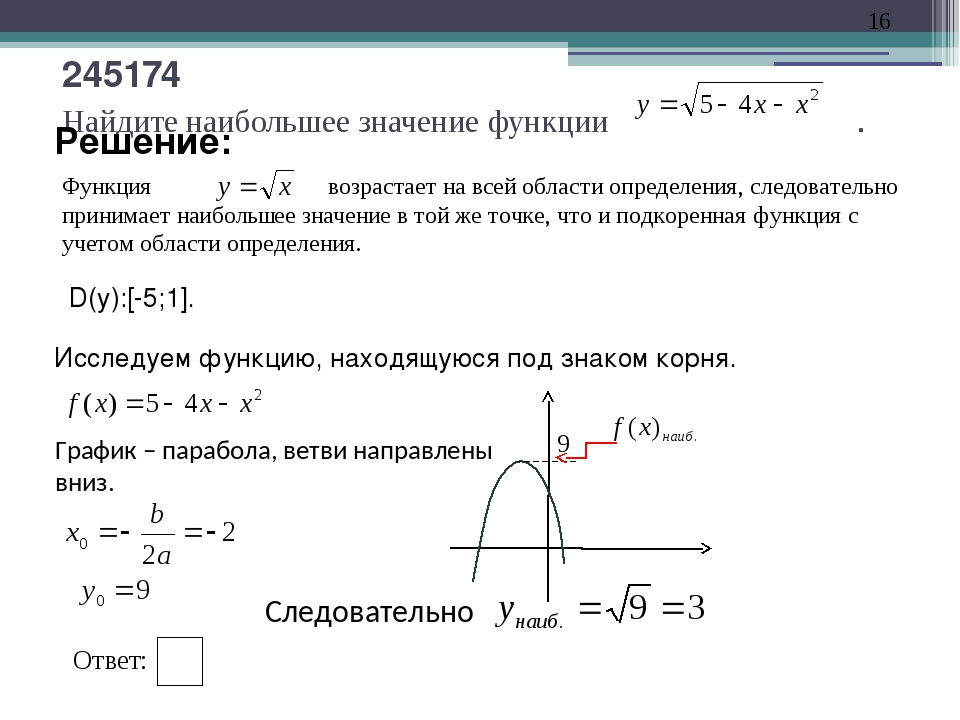
Функция МАКС
У нас есть список чисел в диапазоне ячеек A4: A50, и мы хотели бы увидеть значения, какое из которых является наибольшим или максимальным значением набора данных. Итак, для этой простой оценки мы можем использовать функцию MAX.
1) Итак, в ячейку С4 вводим следующую формулу:
=МАКС(А4: А50)
2) При нажатии CTRL-ENTER возвращается значение 1006,5.
3) Мы можем проверить это путем сортировки.
4) Выберите одну из ячеек в диапазоне и перейдите в «Данные»> «Сортировка и фильтр»> «Сортировать от большего к меньшему».
5) Затем значения сортируются от большего к меньшему, как показано ниже.
Подробнее: Как использовать функции Excel ОКРУГЛ, ОКРУГЛВВЕРХ, ОКРУГЛВНИЗ, ОКРУГЛ и ПОТОЛОК
Функция MAXA
У нас есть смешанный список значений (числа и логическое значение) в диапазоне ячеек A4: A8, и мы хотели бы увидеть значения, какое из них является наибольшим или максимальным значением набора данных. Итак, для этой оценки мы можем использовать функцию MAXA.
Итак, для этой оценки мы можем использовать функцию MAXA.
1) Итак, в ячейку С4 вводим следующую формулу:
=МАКС(А4: А8)
2) При нажатии CTRL-ENTER возвращается значение 1, поскольку логическое значение ИСТИНА читается как 1, и, таким образом, 1 (значение ИСТИНА) считается наибольшим из этого набора данных.
Функция БОЛЬШОЙ
У нас есть список чисел в диапазоне ячеек A4: A50, и мы хотели бы увидеть значения, которые являются наибольшими или максимальными значениями набора данных, используя функцию НАИБОЛЬШИЙ.Затем мы хотим увидеть второе по величине значение в наборе данных и четвертое по величине. Это тот же набор данных, который мы использовали в примере функции MAX.
1) Сначала мы хотим найти наибольшее или максимальное значение с помощью функции НАИБОЛЬШИЙ, поэтому в ячейке C4 мы вводим следующую формулу:
= НАИБОЛЬШИЙ(A4: A50, 1)
2) При нажатии CTRL-ENTER возвращается значение 1006,5. Это то же самое значение, которое возвращает функция MAX для набора данных.
Это то же самое значение, которое возвращает функция MAX для набора данных.
3) Теперь мы хотим найти второе по величине значение в наборе данных, используя функцию НАИБОЛЬШИЙ, поэтому в ячейке C5 мы вводим следующую формулу:
= НАИБОЛЬШИЙ (A4: A50, 2)
4) По нажатию CTRL-ENTER получаем значение 1004.5 возвращено, что является вторым по величине значением в наборе данных.
5) Теперь мы хотим найти четвертое по величине значение в наборе данных, используя функцию НАИБОЛЬШИЙ, поэтому в ячейке C6 мы вводим следующую формулу:
= НАИБОЛЬШИЙ (A4: A50, 4)
6) При нажатии CTRL-ENTER возвращается значение 1002, которое является четвертым по величине значением в наборе данных.
Функция МИН
У нас есть список чисел в диапазоне ячеек A4: A50, и мы хотели бы увидеть значения, какое из них является наименьшим или минимальным значением набора данных.Итак, для этой простой оценки мы можем использовать функцию MIN.
1) Итак, в ячейку С4 вводим следующую формулу:
= МИН (A4: A50)
2) При нажатии CTRL-ENTER возвращается значение 0,11.
Функция МИНА
У нас есть смешанный список значений (числа и логическое значение) в диапазоне ячеек A4: A8, и мы хотели бы увидеть значения, какое из них является наименьшим или минимальным значением набора данных.Итак, для этой оценки мы можем использовать функцию MINA.
1) Итак, в ячейку С4 вводим следующую формулу:
= МИНА (A4: A8)
2) При нажатии CTRL-ENTER возвращается значение 0, поскольку логическое значение FALSE читается как 0, и, таким образом, 0 (значение FALSE) оценивается как наименьшее из этого набора данных.
МАЛЕНЬКАЯ Функция
У нас есть список чисел в диапазоне ячеек A4: A50, и мы хотели бы увидеть значения, какое из них является наименьшим или минимальным значением набора данных с помощью функции МАЛЕНЬКИЙ. Затем мы хотим увидеть второе наименьшее значение в наборе данных и третье наименьшее значение. Это тот же набор данных, который мы использовали в примере функции MIN.
Затем мы хотим увидеть второе наименьшее значение в наборе данных и третье наименьшее значение. Это тот же набор данных, который мы использовали в примере функции MIN.
1) Сначала мы хотим найти наименьшее или минимальное значение с помощью функции МАЛЕНЬКИЙ, поэтому в ячейке C4 мы вводим следующую формулу:
= МАЛЕНЬКИЙ (A4: A50, 1)
2) При нажатии CTRL-ENTER возвращается значение 0,11. Это то же значение, которое возвращает функция MIN в наборе данных.
3) Теперь мы хотим найти второе наименьшее значение в наборе данных, используя функцию МАЛЕНЬКИЙ, поэтому в ячейке C5 мы вводим следующую формулу:
= МАЛЕНЬКИЙ (A4: A50, 2)
4) При нажатии CTRL-ENTER получаем значение 0.Возвращается 13, что является вторым наименьшим значением в наборе данных.
5) Теперь мы хотим найти третье наименьшее значение в наборе данных, используя функцию МАЛЕНЬКИЙ, поэтому в ячейке C6 мы вводим следующую формулу:
= МАЛЕНЬКИЙ (A4: A50, 3)
6) При нажатии CTRL-ENTER мы получаем возвращаемое значение 0,15, которое является третьим наименьшим значением в наборе данных.
Подробнее: Как использовать функцию Excel EDATE
Использование инструмента анализа данных для получения описательной статистики набора данных
Можно также получить минимальную, максимальную, среднюю и другую описательную статистику набора данных с помощью инструмента анализа данных.Вы также можете увидеть четвертое по величине значение или второе по величине значение, например, с помощью этого инструмента.
У нас есть диапазон чисел, и мы хотим получить полную описательную статистику для этого диапазона. Поэтому мы можем использовать инструмент анализа данных, чтобы сделать это.
1) Первым делом загрузите пакет инструментов анализа данных в Excel.
2) Затем перейдите в «Данные»> «Анализ»> «Анализ данных».
3) Выберите «Описательная статистика» и нажмите «ОК».
4) Выберите A4: A50 в качестве диапазона ввода, сгруппированного по столбцам. Выберите $E$4 в качестве выходного диапазона на том же листе. Проверьте сводную статистику, чтобы получить максимальную, минимальную и другую сводную статистику. Для K-го наибольшего значения поставьте 4, чтобы получить четвертое по величине значение набора данных. Для K-го наименьшего значения поставьте 2, чтобы получить второе наименьшее значение набора данных.
Выберите $E$4 в качестве выходного диапазона на том же листе. Проверьте сводную статистику, чтобы получить максимальную, минимальную и другую сводную статистику. Для K-го наибольшего значения поставьте 4, чтобы получить четвертое по величине значение набора данных. Для K-го наименьшего значения поставьте 2, чтобы получить второе наименьшее значение набора данных.
5) Нажмите «ОК».
6) Возвращается максимальное значение 1,275 и минимальное значение 0,082 для набора данных. Четвертое по величине значение 1.175 и второе наименьшее значение 0,085 из всего набора данных также предоставляется как часть описательной статистики.
Вот и все.
Перекрестный совет (использование этих функций в MS Word)
Можно также рассчитать MAX или MIN набора чисел в таблице Word. В нашей таблице Word ниже у нас есть два столбца, и мы хотели бы определить максимальное значение, используя функцию MAX в Word, для первого столбца и минимальное значение второго столбца, используя функцию MIN в Word.
1) Чтобы вычислить максимум для первого столбца, в заштрихованной синим цветом ячейке выберите Работа с таблицами>Макет>Данные>Формула.
2) Введите =MAX(ВЫШЕ) и выберите числовой формат, как показано ниже.
3) Возвращается максимальное значение для первого столбца, в данном случае 200.
4) Чтобы вычислить минимум для второго столбца, в заштрихованной оранжевым цветом ячейке выберите Работа с таблицами > Макет > Данные > Формула.
5) Введите =MIN(ВЫШЕ) и выберите числовой формат, как показано ниже.
6) Возвращается минимальное значение для второго столбца, в данном случае 20.
Заключение
Excel предоставляет несколько эффективных способов вычисления минимума или максимума набора данных. Стандартными функциями являются функции MIN и MAX. Однако существуют также функции MINA, MAXA, LARGE и SMALL, которые расширяют функциональность стандартных функций.Word также предоставляет способ расчета минимального и максимального значения в таблице, и можно использовать таблицу, ссылающуюся на номенклатуру в слове, для ссылки на ячейки или использовать номенклатуру ВЫШЕ, НИЖЕ, СЛЕВА в своих формулах таблицы слов.
Пожалуйста, не стесняйтесь комментировать и сообщать нам, какие из сводных статистических функций вы используете в своих электронных таблицах Excel или Word.
Подробнее…Скачать файлы
Макс-Макса-Большой-Мин-Мина-Малый
Пример слова
Функция Excel MAX — примеры формул для нахождения наибольшего значения
В этом учебном пособии объясняется функция MAX со множеством примеров формул, которые показывают, как найти наибольшее значение в Excel и выделить наибольшее число на листе.
MAX — одна из самых простых и простых в использовании функций Excel. Тем не менее, у него есть пара хитростей, знание которых даст вам большое преимущество. Скажите, как вы используете функцию MAX с условиями? Или как бы вы извлекли абсолютное наибольшее значение? В этом учебнике представлено более одного решения для этих и других связанных задач.
Функция Excel MAX
Функция МАКС в Excel возвращает наибольшее значение в указанном наборе данных.
Синтаксис следующий:
МАКС(число1, [число2], …)
Где число может быть представлено числовым значением, массивом, именованным диапазоном, ссылкой на ячейку или диапазон, содержащий числа.
Число1 требуется, число2 и последующие аргументы необязательны.
Функция MAX доступна во всех версиях Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2010, Excel 2007 и более ранних версиях.
Как сделать формулу MAX в Excel
Чтобы создать формулу MAX в ее простейшем виде, вы можете ввести числа непосредственно в список аргументов, например:
=МАКС(1, 2, 3)
На практике очень редкий случай, когда числа «зашиты» в код.По большей части вы будете иметь дело с диапазонами и ячейками.
Самый быстрый способ построить формулу Max, которая находит наибольшее значение в диапазоне, это:
- В ячейке введите =MAX(
- Выберите диапазон чисел с помощью мыши.

- Введите закрывающую скобку.
- Нажмите клавишу Enter, чтобы завершить формулу.
Например, чтобы вычислить наибольшее значение в диапазоне A1:A6, формула будет выглядеть следующим образом:
=МАКС(А1:А6)
Если ваши числа находятся в смежных строках или столбцах (как в этом примере), вы можете заставить Excel автоматически создать для вас формулу Max.Вот как:
- Выберите ячейки с вашими номерами.
- На вкладке Главная в группе Форматы щелкните Автосумма и выберите Макс. из раскрывающегося списка. (Или щелкните AutoSum > Max на вкладке Formulas в группе Function Library. )
Это вставит готовую к использованию формулу в ячейку под выбранным диапазоном, поэтому убедитесь, что под выбранным вами списком чисел есть хотя бы одна пустая ячейка:
5 вещей, которые нужно знать о функции MAX
Чтобы успешно использовать формулы Max на своих листах, запомните следующие простые факты:
- В текущих версиях Excel формула MAX может принимать до 255 аргументов.

- Если аргументы не содержат ни одного числа, функция MAX возвращает ноль.
- Если аргументы содержат одно или несколько значений ошибки, возвращается ошибка.
- Пустые ячейки игнорируются.
- Обрабатываются логические значения и текстовые представления чисел, указанные непосредственно в списке аргументов (ИСТИНА оценивается как 1, ЛОЖЬ оценивается как 0). В ссылках логические и текстовые значения игнорируются.
Как использовать функцию MAX в Excel – примеры формул
Ниже вы найдете несколько типичных случаев использования функции Excel MAX.Во многих случаях для одной и той же задачи существует несколько разных решений, поэтому я рекомендую вам протестировать все формулы, чтобы выбрать ту, которая лучше всего подходит для вашего типа данных.
Как найти максимальное значение в группе
Чтобы извлечь наибольшее число из группы чисел, укажите эту группу в функции MAX в качестве ссылки на диапазон. Диапазон может содержать любое количество строк и столбцов. Например, чтобы получить наибольшее значение в диапазоне C2:E7, используйте эту простую формулу:
Например, чтобы получить наибольшее значение в диапазоне C2:E7, используйте эту простую формулу:
=МАКС(C2:E7)
Найти наибольшее значение в несмежных ячейках или диапазонах
Чтобы создать формулу MAX для несмежных ячеек и диапазонов, необходимо включить ссылку на каждую отдельную ячейку и/или диапазон.Следующие шаги помогут вам сделать это быстро и безупречно:
- Начните вводить формулу Max в ячейку.
- После ввода открывающей скобки, удерживая нажатой клавишу Ctrl, выберите ячейки и диапазоны на листе.
- После выбора последнего элемента отпустите Ctrl и введите закрывающую скобку.
- Нажмите Enter.
Excel автоматически использует соответствующий синтаксис, и вы получите формулу, похожую на эту:
=МАКС(C5:E5, C9:E9)
Как показано на снимке экрана ниже, формула возвращает максимальное значение промежуточного итога из строк 5 и 9:
Как получить максимальную (последнюю) дату в Excel
Во внутренней системе Excel даты представляют собой не что иное, как порядковые номера, поэтому функция MAX обрабатывает их без заминок.
Например, чтобы найти последнюю дату доставки в C2:C7, сделайте обычную формулу Макса, которую вы использовали бы для чисел:
=МАКС.(C2:C7)
Функция MAX в Excel с условиями
Если вы хотите получить максимальное значение на основе условий, вы можете выбрать одну из нескольких формул. Чтобы убедиться, что все формулы возвращают одинаковый результат, мы проверим их на одном и том же наборе данных.
Задача : Имея предметы, перечисленные в B2:B15, и данные о продажах в C2:C15, мы стремимся найти самую высокую продажу для определенного предмета, введенного в F1 (см. снимок экрана в конце этого раздела).
Формула Excel МАКС ЕСЛИ
Если вы ищете формулу, которая работает во всех версиях Excel 2000 — Excel 2019, используйте функцию ЕСЛИ, чтобы проверить условие, а затем передайте полученный массив в функцию МАКС:
=МАКС(ЕСЛИ(B2:B15=F1, C2:C15))
Чтобы формула работала, необходимо одновременно нажать Ctrl + Shift + Enter, чтобы ввести ее как формулу массива. Если все сделано правильно, Excel заключит вашу формулу в {фигурные скобки}, что является визуальным признаком формулы массива.
Если все сделано правильно, Excel заключит вашу формулу в {фигурные скобки}, что является визуальным признаком формулы массива.
Также можно оценить несколько условий в одной формуле, и в следующем руководстве показано, как это сделать: МАКС. ЕСЛИ с несколькими условиями.
Формула MAX IF без массива
Если вам не нравится использовать формулы массива в ваших рабочих листах, объедините МАКС с функцией СУММПРОИЗВ, которая изначально обрабатывает массивы:
=СУММПРОИЗВ(МАКС((B2:B15=F1)*(C2:C15)))
Для получения дополнительной информации см. MAX IF без массива.
Функция MAXIFS
В Excel 2019 и Excel для Office 365 есть специальная функция MAXIFS, предназначенная для поиска наибольшего значения по 126 критериям.
В нашем случае есть только одно условие, поэтому формула проста:
=МАКСИФС(C2:C15, B2:B15, F1)
Подробное объяснение синтаксиса см. в разделе Excel MAXIFS с примерами формул.
На приведенном ниже снимке экрана показаны все 3 формулы в действии:
Получить максимальное значение без учета нулей
На самом деле это разновидность условного MAX, рассмотренного в предыдущем примере. Чтобы исключить нули, используйте логический оператор «не равно» и поместите выражение «<>0» либо в критерий MAXIFS, либо в логическую проверку MAXIFS.
Как вы понимаете, проверять это условие имеет смысл только в случае отрицательных чисел . Для положительных чисел эта проверка не нужна, поскольку любое положительное число больше нуля.
Чтобы попробовать, давайте найдем наименьшую скидку в диапазоне C2:C7. Поскольку все скидки представлены отрицательными числами, наименьшая скидка на самом деле является наибольшей величиной.
МАКС. ЕСЛИ
Обязательно нажмите Ctrl + Shift + Enter, чтобы правильно заполнить эту формулу массива:
=МАКС(ЕСЛИ(C2:C7<>0, C2:C7))
МАКСИФС
Это обычная формула, для которой достаточно обычного нажатия клавиши Enter.
=МАКСЕСЛИ(C2:C7,C2:C7,"<>0")
Найти наибольшее значение, игнорируя ошибки
Когда вы работаете с большим объемом данных, управляемых различными формулами, есть вероятность, что некоторые из ваших формул приведут к ошибкам, что приведет к тому, что формула MAX также вернет ошибку.
В качестве обходного пути можно использовать MAX IF вместе с ISERROR. Учитывая, что вы ищете в диапазоне A1:B5, формула принимает следующий вид:
=МАКС(ЕСЛИ(ЕОШИБКА(A1:B5)), "", A1:B5))
Чтобы упростить формулу, используйте функцию ЕСЛИОШИБКА вместо комбинации ЕСЛИ ОШИБКА.Это также сделает логику немного более очевидной — если есть ошибка в A1:B5, замените ее пустой строкой (»), а затем получите максимальное значение в диапазоне:
=МАКС(ЕСЛИОШИБКА(A1:B5, ""))
Ложкой дегтя является то, что вам нужно не забывать нажимать Ctrl + Shift + Enter, потому что это работает только как формула массива.
В Excel 2019 и Excel для Office 356 функция MAXIFS может быть решением, при условии, что ваш набор данных содержит хотя бы одно положительное число или нулевое значение:
=МАКСЕСЛИ(A1:B5,A1:B5,">=0")
Так как формула ищет наибольшее значение с условием «больше или равно 0», она не будет работать для набора данных, состоящего только из отрицательных чисел.
Все эти ограничения нехороши, и нам явно нужно лучшее решение. Идеально подходит функция АГРЕГАТ, которая может выполнять ряд операций и игнорировать значения ошибок:
=ОБЪЕДИНЕНИЕ(4, 6, A1:B5)
Число 4 в 1-м аргументе указывает на функцию MAX, число 6 во 2-м аргументе — на опцию «игнорировать ошибки», а A1:B5 — ваш целевой диапазон.
В идеальном случае все три формулы вернут один и тот же результат:
Как найти абсолютное максимальное значение в Excel
При работе с диапазоном положительных и отрицательных чисел иногда может потребоваться найти наибольшее абсолютное значение независимо от знака.
Первая идея, которая приходит на ум, состоит в том, чтобы получить абсолютные значения всех чисел в диапазоне с помощью функции ABS и передать их в MAX:
.{=МАКС(АБС( диапазон ))}
Это формула массива, поэтому не забудьте подтвердить ее сочетанием клавиш Ctrl + Shift + Enter. Еще одно предостережение заключается в том, что он работает только с числами и приводит к ошибке в случае нечисловых данных.
Не устраивает эта формула? Тогда давайте построим что-нибудь более жизнеспособное 🙂
Что, если мы найдем минимальное значение, перевернем или проигнорируем его знак, а затем оценим вместе со всеми другими числами? Да, это будет работать как обычная формула.В качестве дополнительного бонуса он отлично обрабатывает текстовые записи и ошибки:
С исходными номерами в A1:B5 формулы выглядят следующим образом.
Формула массива (завершается с помощью Ctrl + Shift + Enter):
=МАКС(АБС(А1:В5))
Обычная формула (заполняется клавишей Enter):
=МАКС(МАКС(A1:B5), -МИН(A1:B5))
или
=МАКС(МАКС(A1:B5), АБС(МИН(A1:B5)))
На снимке экрана ниже показаны результаты:
Возвращает максимальное абсолютное значение с сохранением знака
В некоторых ситуациях может возникнуть необходимость найти наибольшее абсолютное значение, но вернуть число с исходным знаком, а не абсолютное значение.
Предполагая, что числа находятся в ячейках A1:B5, вот формула для использования:
=ЕСЛИ(АБС(МАКС(A1:B5))>АБС(МИН(A1:B5)), МАКС(A1:B5), МИН(A1:B5))
Сложный на первый взгляд, логика довольно проста. Сначала вы находите наибольшее и наименьшее числа в диапазоне и сравниваете их абсолютные значения. Если абсолютное максимальное значение больше абсолютного минимального значения, возвращается максимальное число, в противном случае – минимальное число. Поскольку формула возвращает исходное, а не абсолютное значение, она сохраняет информацию о знаке:
Как выделить максимальное значение в Excel
В ситуации, когда вы хотите определить наибольшее число в исходном наборе данных, самый быстрый способ — выделить его с помощью условного форматирования Excel.Приведенные ниже примеры проведут вас через два разных сценария.
Выделить наибольшее число в диапазоне
Microsoft Excel имеет предопределенное правило для форматирования значений с самым высоким рейтингом, которое идеально подходит для наших нужд. Вот шаги для его применения:
Вот шаги для его применения:
- Выберите диапазон номеров (в нашем случае C2:C7).
- На вкладке Главная в группе Стили щелкните Условное форматирование > Новое правило .
- В диалоговом окне Новое правило форматирования выберите Форматировать только верхние или нижние ранговые значения .
- В нижней панели выберите Top из раскрывающегося списка и введите 1 в поле рядом с ним (это означает, что вы хотите выделить только одну ячейку, содержащую наибольшее значение).
- Нажмите кнопку Формат и выберите нужный формат.
- Дважды нажмите OK, чтобы закрыть оба окна.
Готово! Наибольшее значение в выбранном диапазоне выделяется автоматически. Если имеется более одного максимального значения (дубликатов), Excel выделит их все:
Выделить максимальное значение в каждой строке
Поскольку нет встроенного правила, позволяющего выделить наибольшее значение из каждой строки, вам придется настроить собственное правило на основе формулы MAX. Вот как:
Вот как:
- Выберите все строки, в которых вы хотите выделить максимальные значения (в данном примере C2:C7).
- На вкладке Главная в группе Стили щелкните Новое правило > Используйте формулу, чтобы определить, какие ячейки следует форматировать .
- В поле значений формата , где эта формула верна , введите следующую формулу:
=C2=МАКС($C2:$E2)Где C2 — крайняя левая ячейка, а $C2:$E2 — диапазон первой строки.Чтобы правило работало, обязательно зафиксируйте координаты столбца в диапазоне знаком $.
- Нажмите кнопку Формат и выберите нужный формат.
- Дважды нажмите OK.
Наконечник. Аналогичным образом можно выделить наибольшее значение в каждом столбце . Шаги точно такие же, за исключением того, что вы пишете формулу для диапазона первого столбца и фиксируете координаты строки: =C2=MAX(C$2:C$7)
Дополнительные сведения см.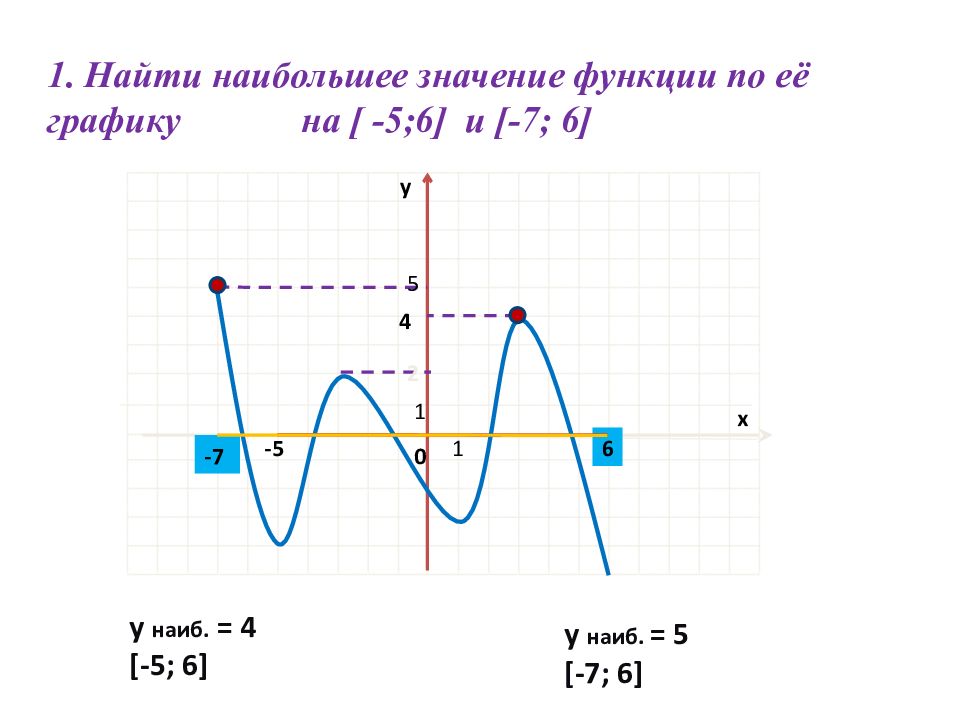 в разделе Как создать правило условного форматирования на основе формулы.
в разделе Как создать правило условного форматирования на основе формулы.
Функция Excel MAX не работает
MAX — одна из самых простых функций Excel. Если, вопреки всем ожиданиям, он работает неправильно, скорее всего, это одна из следующих проблем.
ФормулаMAX возвращает ноль
Если обычная формула MAX возвращает 0, даже если в указанном диапазоне есть более высокие числа, скорее всего, эти числа отформатированы как текст. Это особенно актуально, когда вы запускаете функцию MAX для данных, управляемых другими формулами.Вы можете проверить это с помощью функции ISNUMBER, например:
=IНОМЕР(A1)
Если приведенная выше формула возвращает ЛОЖЬ, значение в ячейке A1 не является числовым. Это означает, что вы должны устранять неполадки с исходными данными, а не с формулой MAX.
Формула MAX возвращает #N/A, #VALUE или другую ошибку
Пожалуйста, внимательно проверьте указанные ячейки. Если какая-либо из указанных ячеек содержит ошибку, формула MAX приведет к той же ошибке.


 Если точек максимума нет, то у функции нет наибольшего значения.
Если точек максимума нет, то у функции нет наибольшего значения.
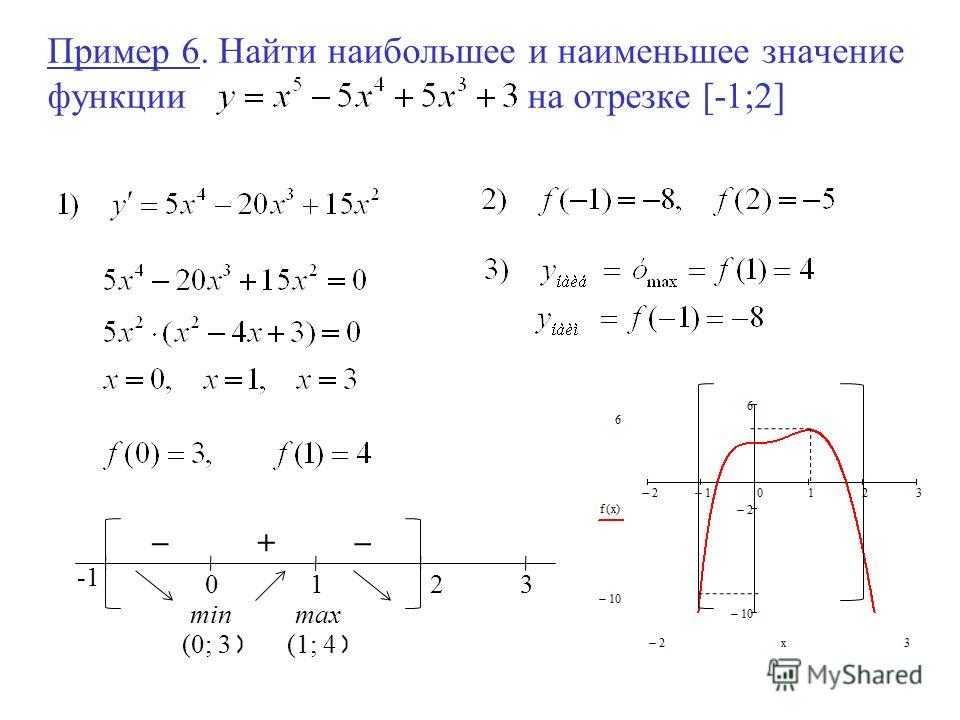

 Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала. Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.

 28, 3.27, 3.29, 3.30, 3.32, 3.26]
print("Самая низкая цена $", min(supplier_quotes), " за галлон молока.")
28, 3.27, 3.29, 3.30, 3.32, 3.26]
print("Самая низкая цена $", min(supplier_quotes), " за галлон молока.")  32
32 
