Нестандартные задачи по геометрии
Нестандартные задачи по геометрии
Николаев М.А. 11МБОУ Лицей № 40 при УлГУ
Гуськова А.Г. 11МБОУ Лицей № 40 при УлГУ
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение.
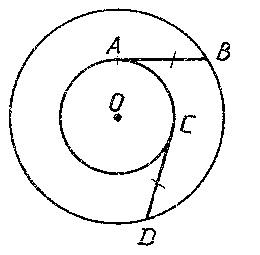
Для многих людей раздел математики — геометрия — кажется очень скучной, но, на самом деле, есть много интересных задач, любопытных и неожиданных. Я хочу познакомить вас с геометрическими загадками, представленными известным русским ученым Яковом Перельманом.
В век информационных технологий, мы не задумываемся о том, что отсутствие гаджетов и навигаторов может поставить проблемы, которые были давно решены, но могут возникнуть в форс-мажорных обстоятельствах. Например, если ты окажешься в лесу или в пустыне совсем без техники.
Забивая гвоздь, делая механическую работу, человек даже не понимает,почему целесообразно использовать определенную форму гвоздя при работе.
В данной работе я попробую рассмотреть эти вопросы на примерах придуманных мной задач.
Э ксперимент на площади Святого Марка.
Вот один опыт, произведенный в Венеции
на площади Св.Марка. Людям завязывали глаза,
ставили их на одном конце площади, напротив
собора, и предлагали до него дойти.
Казалось бы, надо пройти всего лишь 175 м. Но все же, ни один человек не дошел.
Почему? Давайте рассмотрим.
Площадь Святого Марка в Венеции.Поскольку обе половины тела человека развиты неодинаково: правая нога не равна левой по силе мускулов. Поэтому человек делает левой ногой более длинные шаги. (Рисунок № 5).
Представьте себе, что, занося левую ногу человек делает шаг на мм длиннее, чем правой. Тогда сделав попеременно каждой ногой 1000 шагов, человек опишет левой ногой на 1 м длинней, чем правой. На прямых параллельных путях это невозможно. Зато вполне осуществимо на окружностях.
Расстояние между линиями отпечатков правой и левой ноги при ходьбе равно примерно 10 см., т.е.0,1м. Когда человек описывает один полный круг, его правая нога проходит путь 2пR, а левая
2п (R + 0,1), где R– радиус этого круга в метрах. Разность
или 624мм, составились из разницы между длиною левого и правого шагов, повторённой столько
раз, сколько сделано было шагов.
Для участников этого опыта на площади Марка, мы можем установить наибольшую величину радиуса кругов, описанных ими при ходьбе. Действительно, т.к. ни один из них не дошел до фасада здания, то по стрелке АС = 41 м и хорде ВС, не превышающей 175 м, можно вычислить максимальный радиус дуги АВ. Он определяется изравенства:Откуда R, максимальный радиус, будет около 370 м. Зная это, мы из полученной ранее формулы Rx = 0,14 определяем наименьшую величину разности длины шагов: 370х = 0,14, откуда х = 0,4 мм. Итак, разница в длине правых и левых шагов у участников опыта не менее 0,4 мм.
Я думаю, что если по площади Св.Марка пройдёт манекенщица с завязанными глазами,
то она обязательно дойдет до собора. Т.к. походка по подиуму предполагает движение по
одной линии без отклонения левой ноги от правой .
3. ЗАДАЧА на круговое движение и её решение.
Папа рассказал сыну, что в незнакомом лесу люди ходят по кругу. Это происходит из-за того, что левая нога делает более длинный шаг, чем правая. Сын не поверил. Тогда они решили провести эксперимент. Арбитром позвали маму.
Они вышли в поле. Мама завязала им глаза и они отправились в разные стороны.
— у папы длина шага левой ноги больше, чем правой на 0,4мм, а у сына – на 0,3мм;
— скорость движения папы – 5 км\ч, а сына – 4 км\ч;
— длина шага папы – 0,7м, сына – 0,6м;
— отклонение левой ноги от линии движения у обоих – 0,1м
4. Свойства гвоздей в зависимости от площади поперечного
сечения
Какой гвоздь труднее вытащить: круглый, квадратный или треугольный – если они забиты одинаково глубоко и имеют одинаковую площадь поперечного сечения?
Конечно, крепче держится тот гвоздь, который соприкасается
с окружающим материалом по большей поверхности.
Мы знаем, что при равных площадях периметр квадрата
меньше периметра треугольника, а окружность меньше периметра квадрата.
Если сторону квадрата принять за единицу, то вычисление даёт для
этих трёх величин значения: 4,53; 4; 3,55.
Следовательно, крепче других должен держаться треугольный гвоздь.
5. Доказательство целесообразности применения круглых гвоздей относительно квадратных.
П– принять равным ~ 3,14
Рассмотрим сечение гвоздей при условии, что их площади равны.
Таким образом, силы трения при вбивании гвоздя, действующие на одинаковые по массе гвозди с разной геометрией, будут у круглого гвоздя меньше приблизительно на 12 %, чем у квадратного.
Кроме того, вследствие прямоугольной геометрии гвоздя будут возникать различные проблемы в зависимости от цели использования:
Углы гвоздя будут способствовать возникновению трещин в древесине, дополнительного напряжения металла в самом гвозде;
Прямоугольные гвозди будут чаще ломаться из-за разного расстояния от геометрического центра точки А до поверхности.
6.Выводы.
а) При движении в незнакомой местности, во избежание кругового движения, необходимо найти ориентиры, благодаря которым можно сохранять направление движения. Это могут быть и звезды, и мох на деревьях, и солнце…
б) Мы применяем гвозди с различными целями. Если необходимо что-то повесить на стену, берем круглый обычный гвоздь, но если нам необходимо закрепить висячую деталь, которая может раскачиваться, тогда лучше использовать квадратный гвоздь для повышения выносливости.
Целесообразность применения гвоздей с различной формой поперечного сечения зависит от отношения периметра к площади поперечного сечения.
7.Список литературы.
«За страницами учебника математики» Виленкин Н.Я., Депман И.Я.
«Занимательная геометрия между делом и шуткой». Перельман Я.И.
Своими руками – как сделать самому» 2009-2019. Гвозди и их применение. [Электронный ресурс] — //http//www.Kak-svoimi-rukami.com [дата обращения 20.02.2019]
Строительный справочник. Материалы-конструкции – технологии. [Электронный ресурс]-//http//www.NOVOSIBDOM.RU [дата обращения 21.02.2019]
Просмотров работы: 200
Нестандартные задачи по геометрии для учеников 10 класса
2.Отрезок пересекает плоскость, концы его отстоят от плоскости на расстояние 10 см и 3см .Найти расстояние от середины этого отрезка до плоскости
3. Определите высоту правильной четырехугольной пирамиды , если стороны ее оснований а и в а боковая поверхность равновелика сумме оснований.
4 Определите боковую поверхность правильной четырехугольной пирамиды, если сторона основания равна в и боковое ребро составляет с плоскостью основания угол в 30 градусов
5. Сторона основания правильной треугольной призмы равна в, а боковая поверхность равновелика сумме оснований. Определите объем призмы.
6. Высота конуса т. Угол между высотой и образующей равен 60 градусов. Найдите площадь сечения, проведенного через две взаимно перпендикулярные образующие.
7.Круговой сектор с углом в 60градусов и радиусом r вращается около одного из боковых радиусов .Определите объем пирамиды.
8.Высота правильной четырехугольной пирамиды в , а боковая грань образует с плоскостью основания угол в 30 градусов. Определите объем пирамиды.
9. Боковая поверхность усеченного конуса равна 4,а радиусы оснований l и d .Определите боковую поверхность полного конуса.
10.Площадь основания сегмента равна 64п, его сферическая поверхность-100п .Найдите объем пирамиды.
11.Найдите периметр основания правильной четырехугольной пирамиды, если ее высота равна 7см а апофема 8.5 см.
12.Найти боковую поверхность правильной шестиугольной усеченной пирамиды, стороны оснований который 14 дм и 7 дм и высота 3 дм
13. В конус, у которого радиус основания г, а образующая в, вписан шар. Определите длину линии, по которой поверхность шара касается боковой поверхности конуса.
14.Из точки вне плоскости проведен к этой плоскости перпендикуляр ,равный 14 см и наклонная ,равная 10 см. Найти проекцию перпендикуляра на наклонную.
Исследовательская работа «Решение задач по геометрии методом дополнительных построений»
Объект исследования: стереометрические задачи по геометрии
Предмет исследования: геометрия
Цель исследования: выявление способа, позволяющего решать задачи нетрадиционным методом.
Задачи:
Изучить литературу по теме исследования.
Проанализировать способы решения задач и выбрать более эффективный.
Для каждой фигуры найти рациональный метод построения.
Показать практическое применение данного метода.
Подобрать примеры для решения задач предложенным мной методом.
Содержание: стр.
Введение…………………………………………………………….. 3
Основная часть
Классификация дополнительных построений……………………4-21
Практическое применение приёма метода дополнительных построений………………………………………………………….22-30
Задачи на доказательство………………………………………….31-32
Задачи на вычисление………………………………………………33-35
Заключение…………………………………………………………..36
Список использованной литературы……………………………….37
Введение.
В геометрии существуют задачи к которым традиционные методы(методы геометрических треугольников, векторный метод, метод равных треугольников) или не применимы, или дают сложные и громоздкие решения. При решении задач такого вида помогает введение в чертёж дополнительных линий или проведение дополнительных построений. В таких задачах это единственный способ её решения. Так как чертёж данной в задаче фигуры можно достроить до фигуры другого типа, то всегда с многоугольной фигурой можно связать окружность и можно на чертеже выделить равные и подобные фигуры.
Суть данного метода дополнительных построений заключается в том, что чертёж и задача, на котором трудно заметить связь между данными и искомыми величинами, дополняется новыми элементами, после чего эти связи становятся очевидными.
Анализ решений задач показал, что для каждой фигуры существуют характерные признаки, которые можно классифицировать. Предлагаю классификацию, которую мне удалось выделить для некоторых фигур.
Классификация дополнительных построений.
Если в треугольнике задана медиана, то его можно достроить до параллелограмма, где основание медианы это точка пересечения диагоналей.
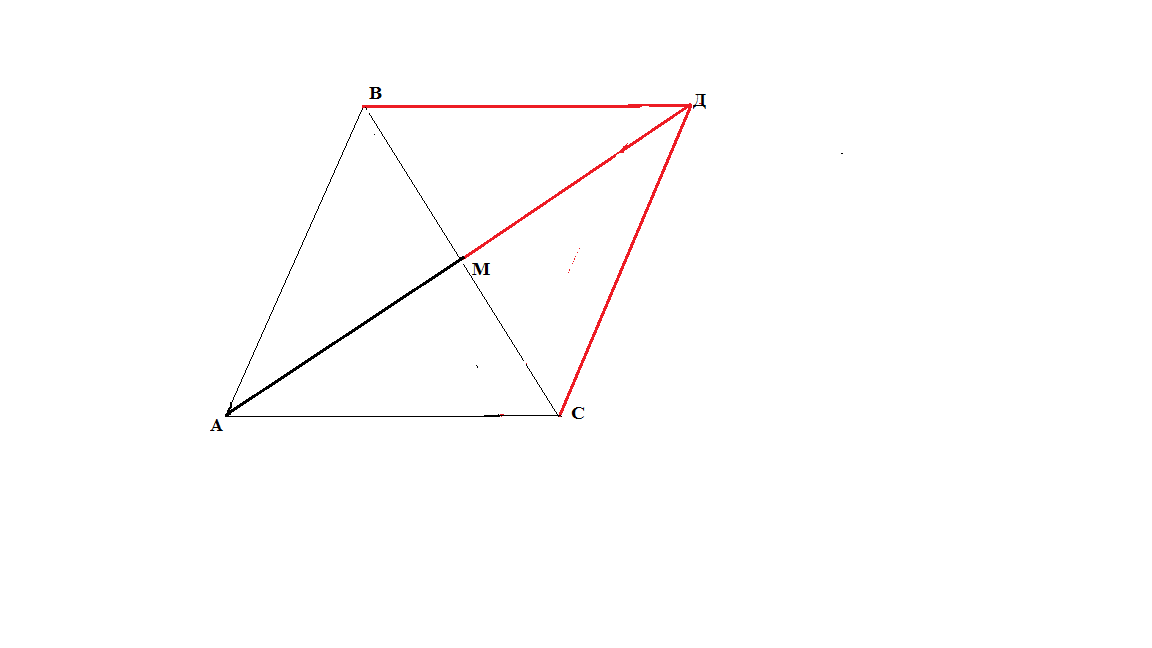
Если в треугольнике создан отрезок, соединяющий вершину с противоположной стороной, то через основание отрезка проводим прямую параллельную стороне треугольника.
МN ‖ АВ или прямую параллельную АС
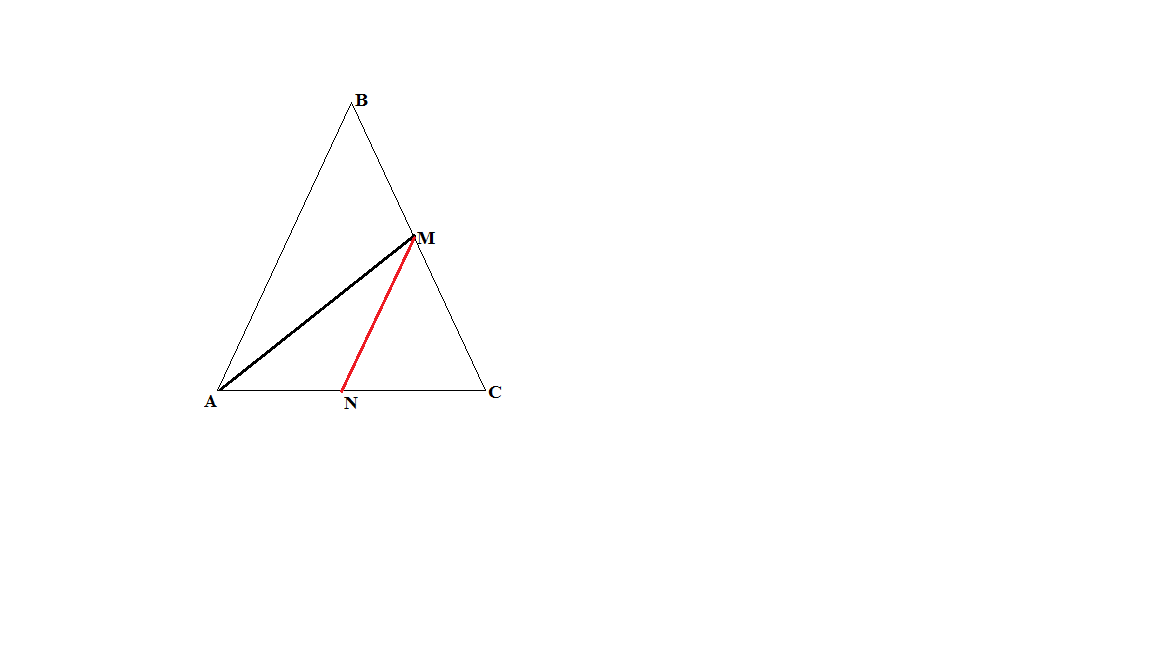 В результате данного построения получаются подобные треугольники ΔАВС~ ΔМNС или по теореме Фалеса получаются пропорциональные отрезки:
В результате данного построения получаются подобные треугольники ΔАВС~ ΔМNС или по теореме Фалеса получаются пропорциональные отрезки:
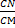 =
= 
что позволяет определить неизвестные стороны треугольника. Если АМ – медиана Δ АВС, тогда N всегда будет серединой отрезка АС.
Если в треугольнике задана медиана и отрезок, соединяющий вершину с противоположной стороной, то через основание медианы проводим прямую, параллельную данному отрезку.
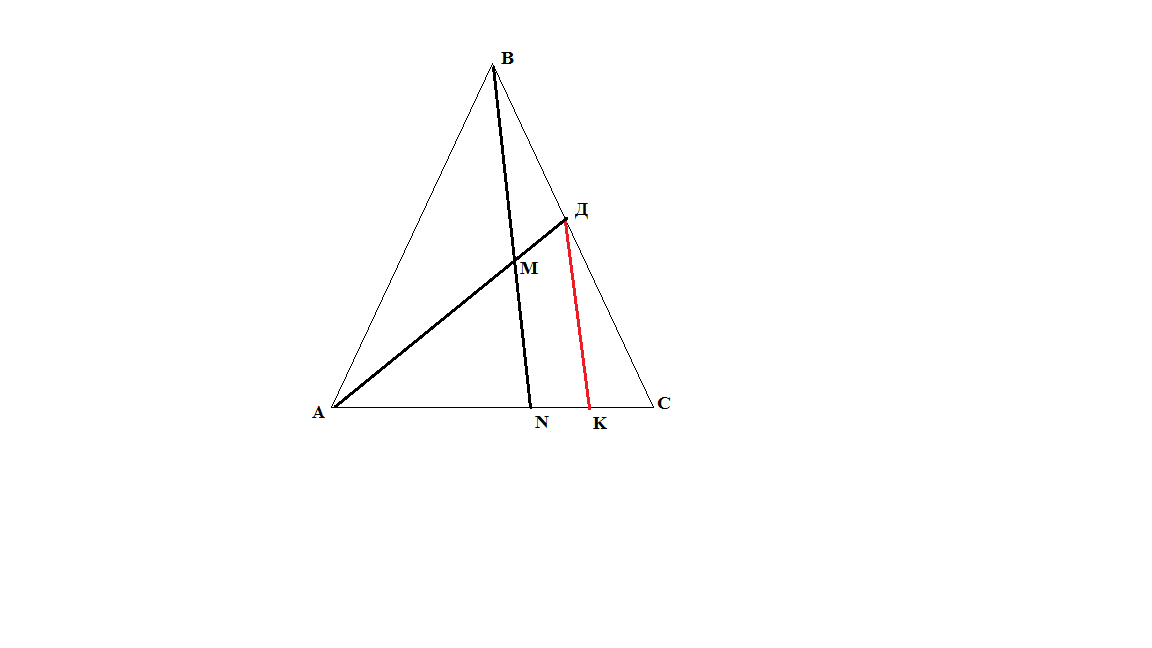
1) Δ АДК ~ Δ АМN
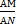 =
= 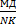
ДК – средняя линия Δ ВNС
3)NK= KC, К – середина NC
Если в треугольнике заданы два отрезка, проведённых из разных вершин, то проводится а) через основание одного отрезка прямая, параллельная другому отрезку
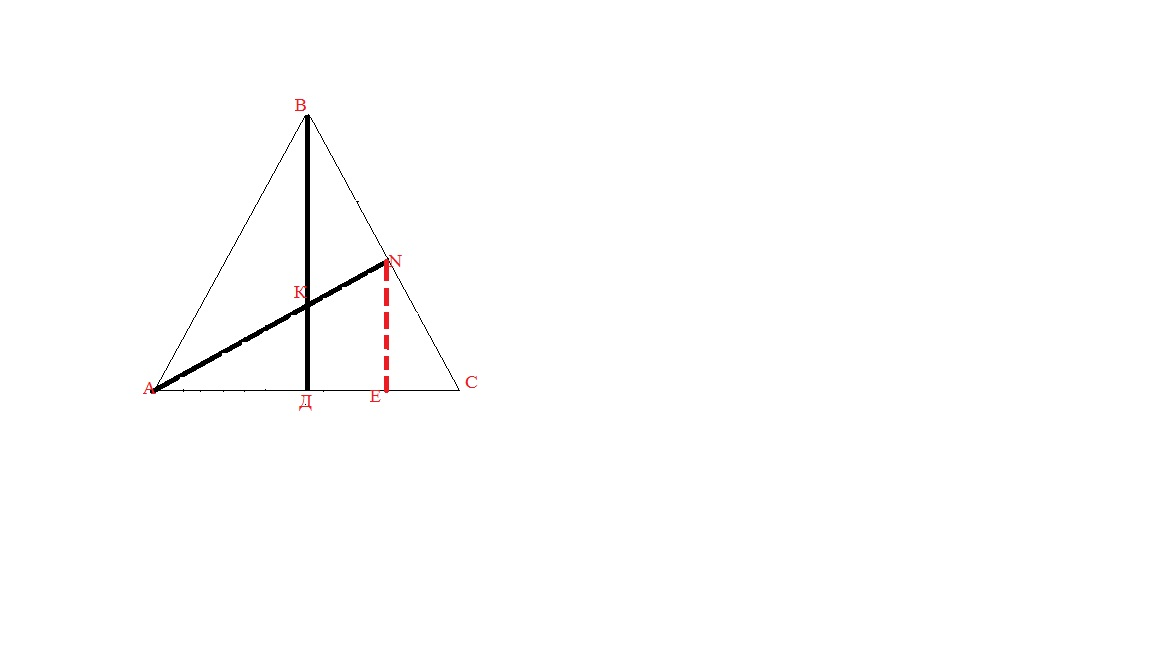
Δ АКД ~ Δ АNЕ
Δ NEC ~ Δ ВДС
б) прямая, проходящая через вершину треугольника параллельная стороне до пересечения с прямой, содержащей один из отрезков
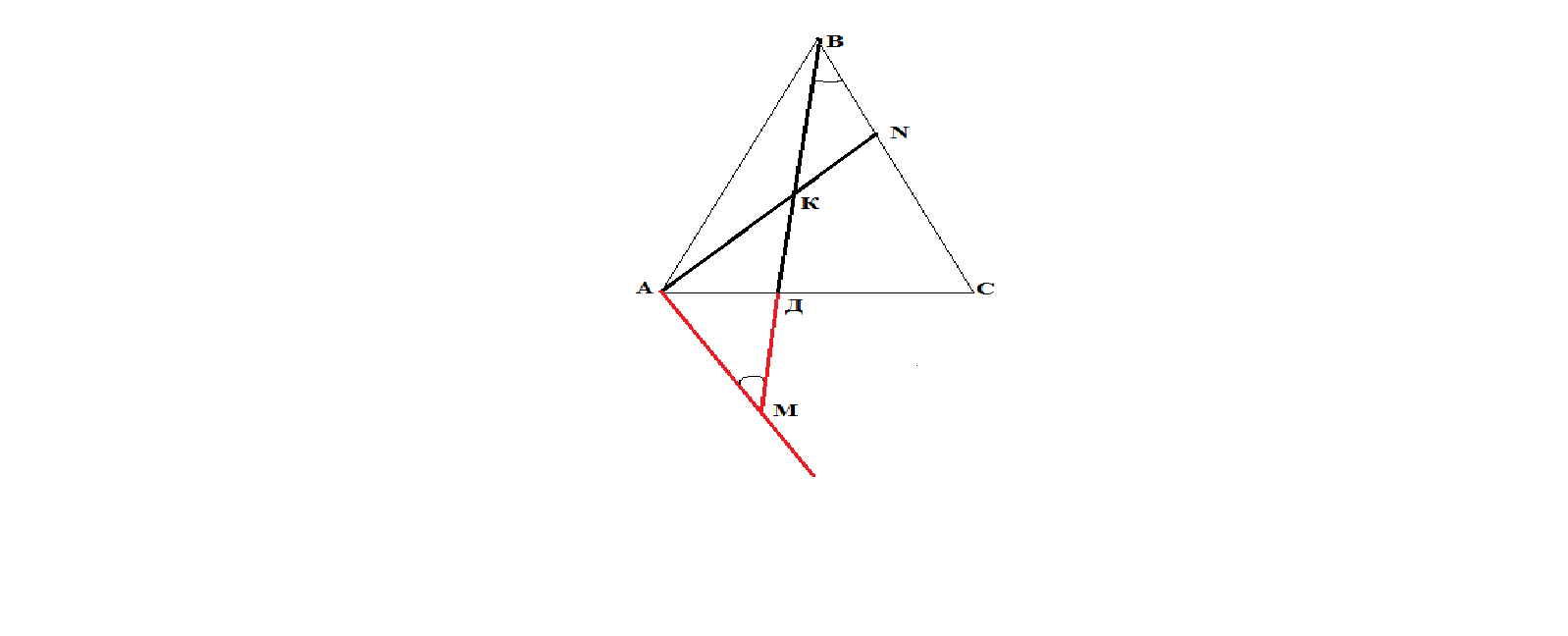
Если в треугольнике задан отрезок, проведённый из вершины до противоположной стороны и отрезок, соединяющий две другие стороны, но не параллелен его стороне, то данный отрезок продолжается в обе стороны до пересечения с продолжением третьей стороны и с прямой, параллельной этой стороне и проходящей через вершину, из которой выходит отрезок.
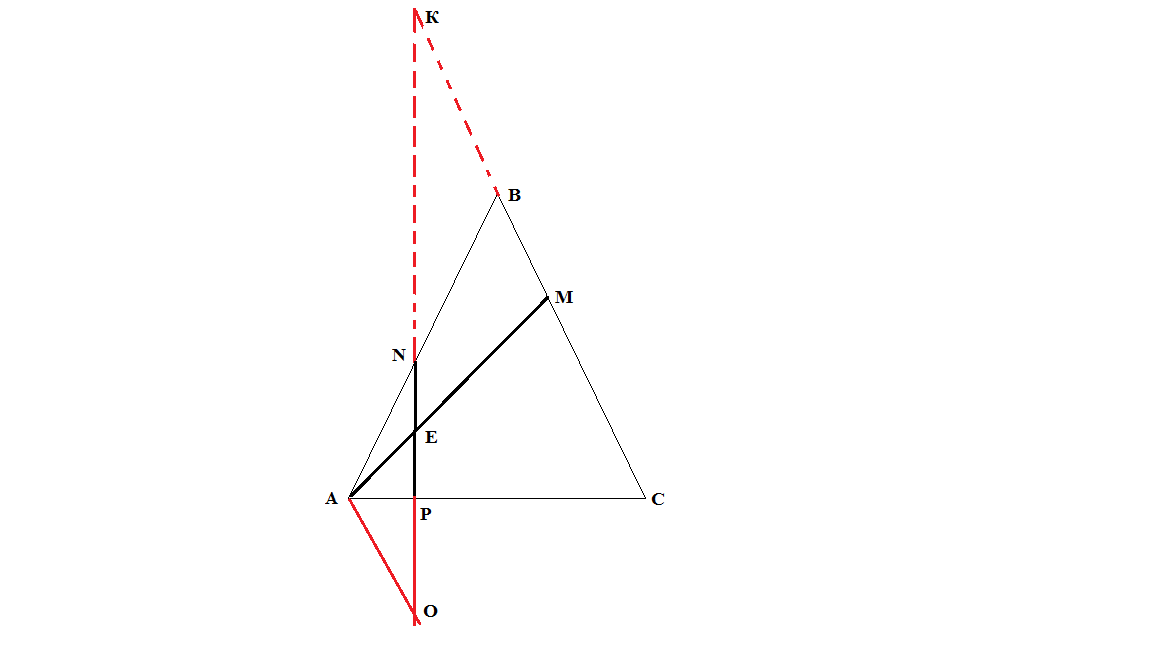
Δ ANP ~ Δ NBK
Δ ANO ~ Δ NBK
Δ AEO ~ Δ EMK
Если в треугольнике задан отрезок с концами на его сторонах и если продолжение этого отрезка пересекает прямую, содержащую третью сторону треугольника, то:
а) продолжаем отрезок до пресечения с прямой, проведённой через вершину треугольника параллельно третьей стороне.
б) проводим прямую, параллельную одной из сторон до пересечения с другой стороной.
а) 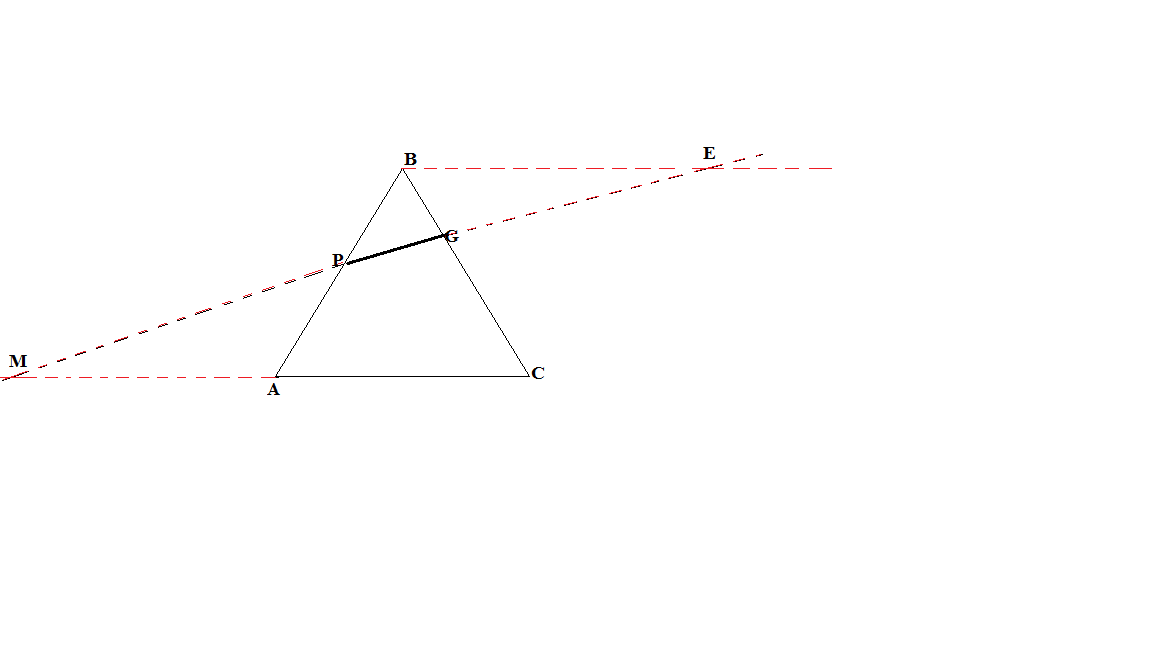
Δ МАР ~ Δ РВЕ
б) 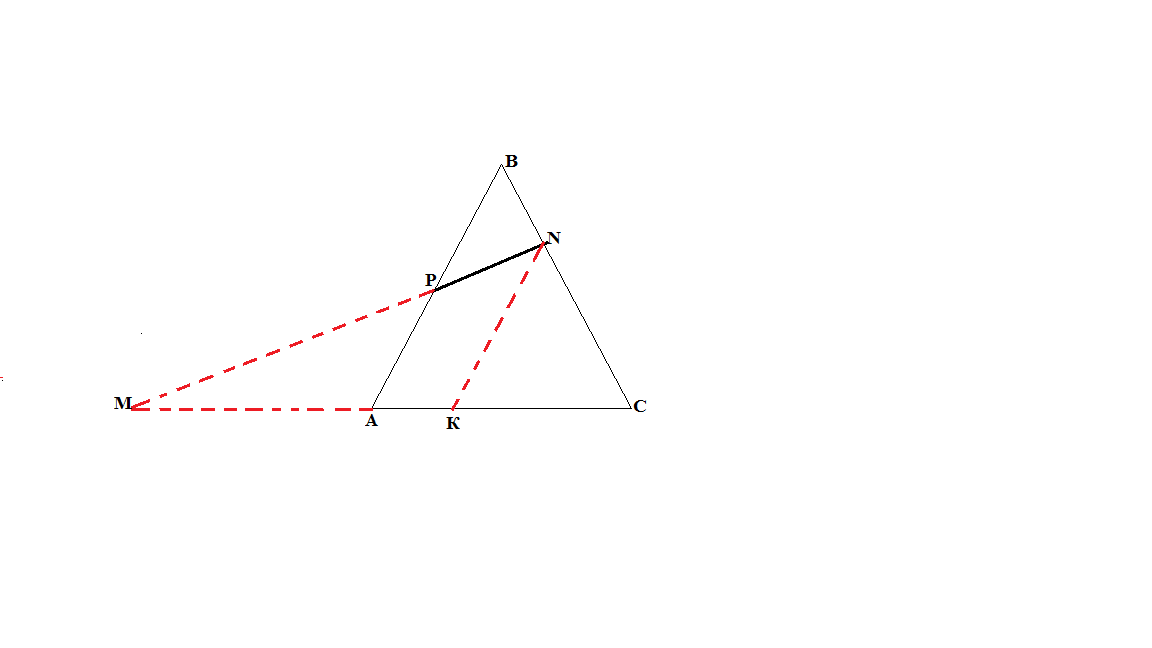
Δ МАР ~ Δ МNК
Δ АВС ~ Δ КNС
Если дан прямоугольный треугольник, то он достраивается до равнобедренного треугольника, в котором один из катетов данного треугольника становится высотой ( медианой и биссектрисой), а другой – половиной основания.
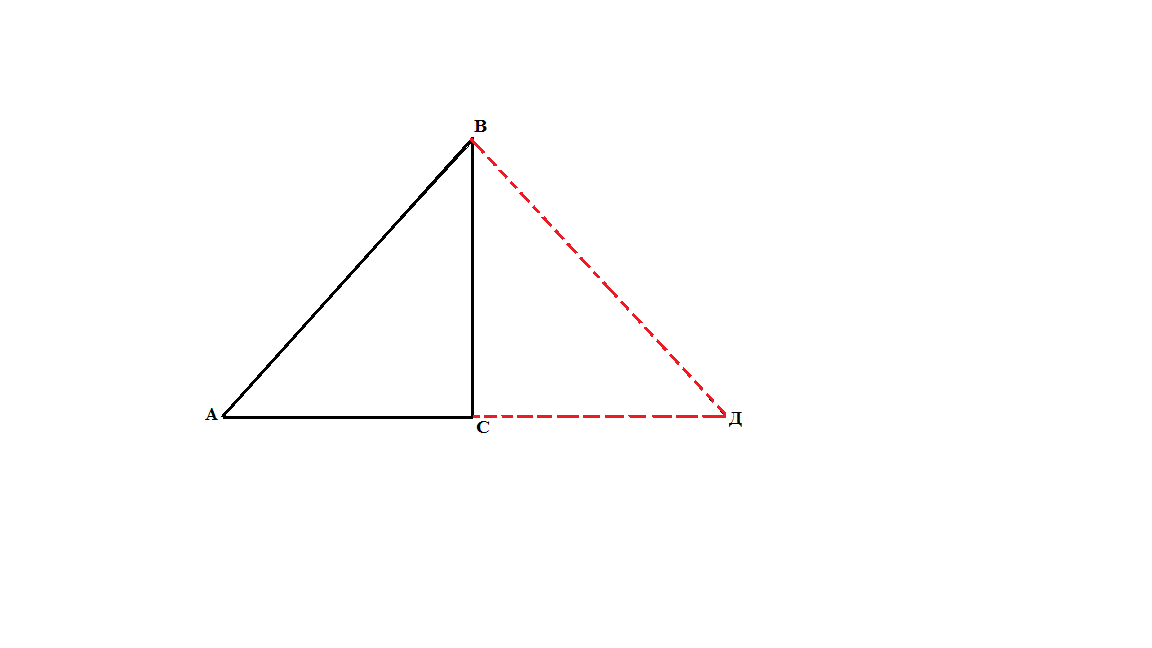
Если дана трапеция, то её диагональ или боковая сторона переносятся на вектор, определяемый одним из оснований.
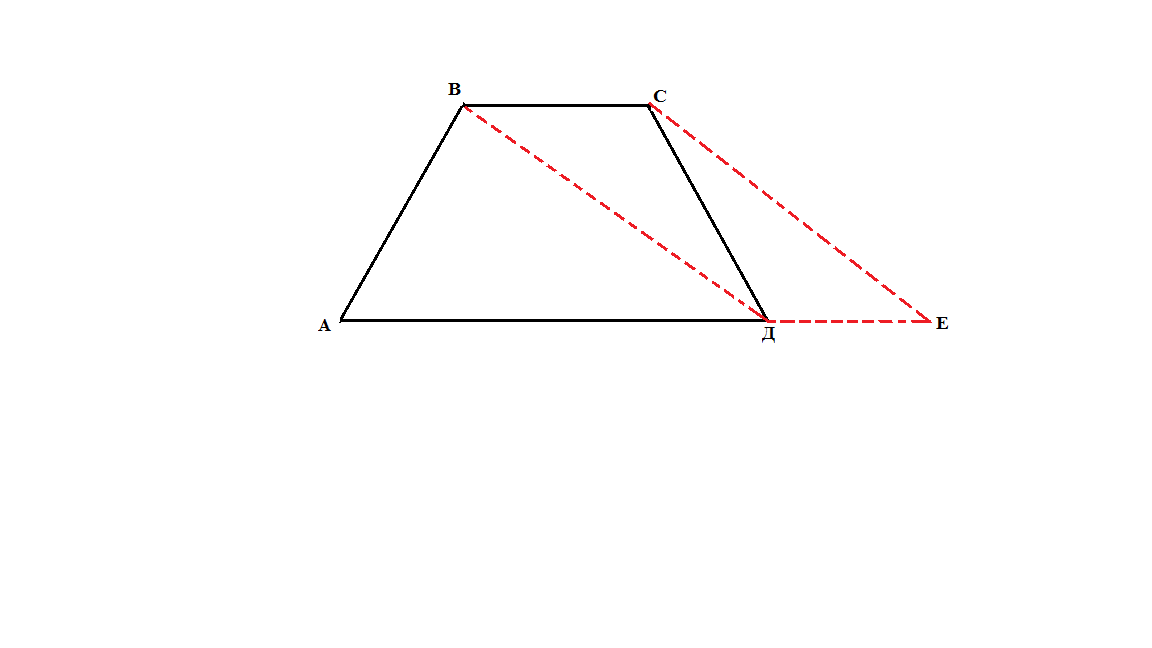
Если в треугольнике, параллелограмме или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится ромб, две стороны которого направлены по сторонам данной фигуры, а эта биссектриса является одной из диагоналей.
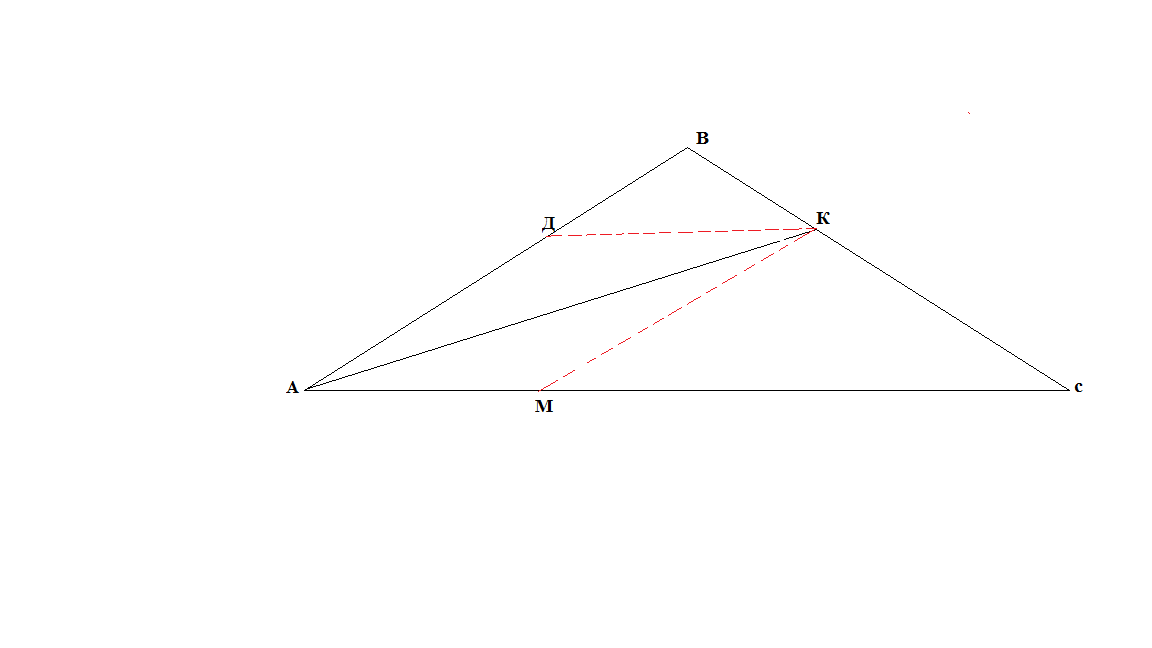
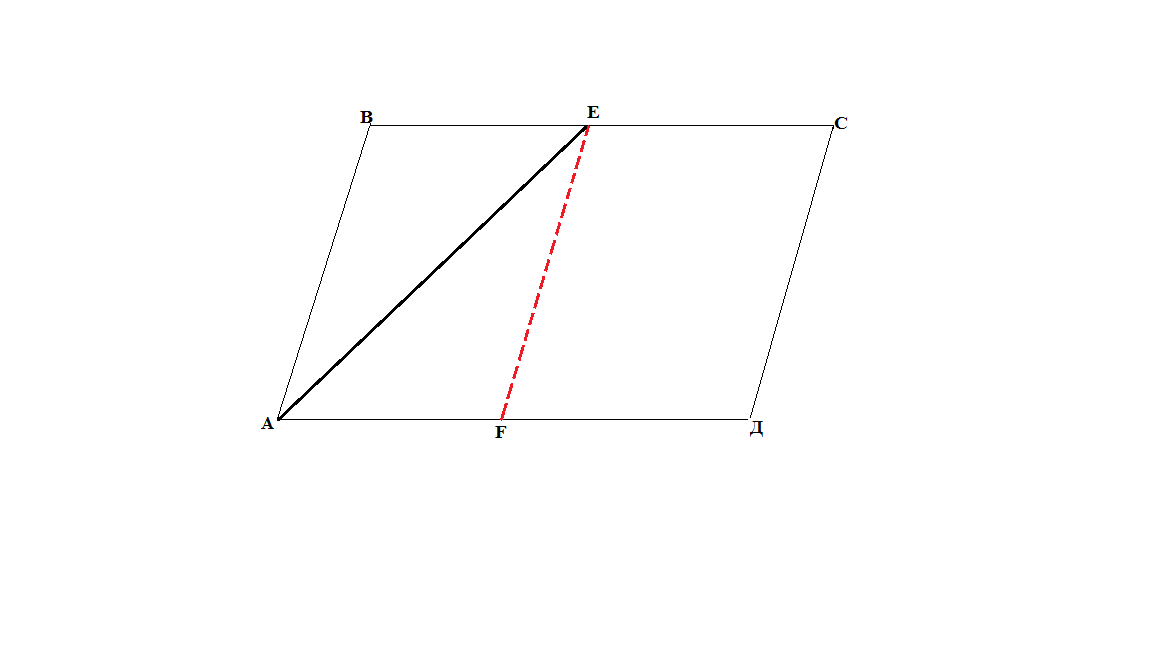
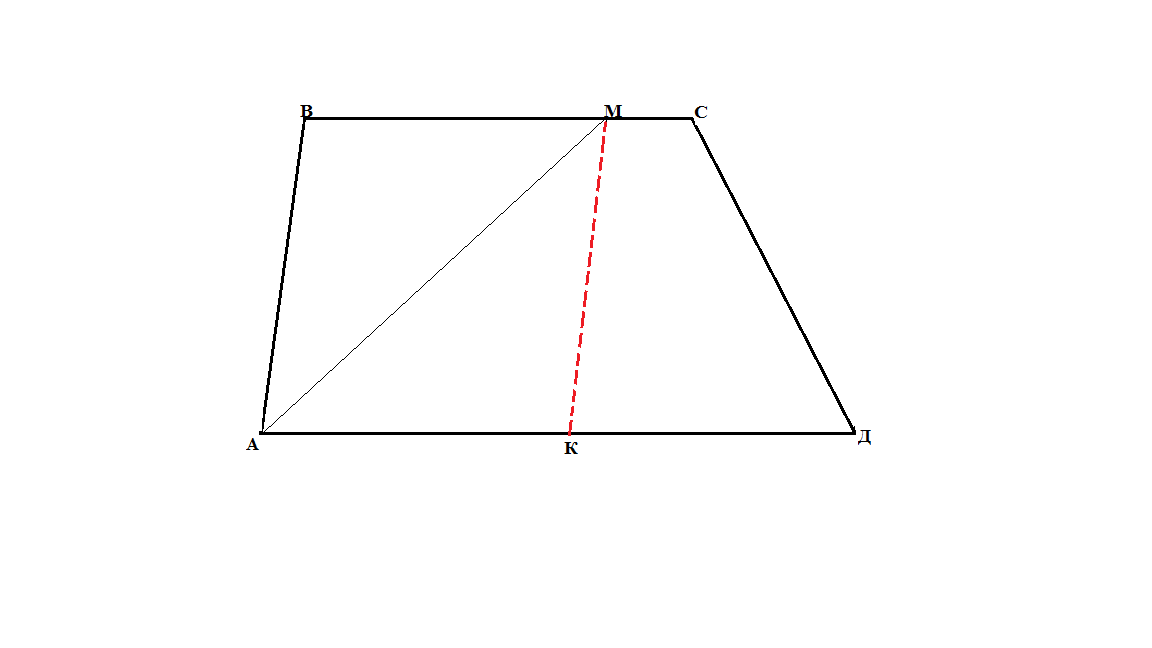
Если в треугольнике, параллелограмма или трапеции задана биссектриса одного из внутренних углов, то в чертёж вводится треугольник, одна из сторон которого содержит эту биссектрису, вторая совпадает со стороной исходной фигуры, а третья либо параллельна другой стороне этой фигуры, либо получается при её продолжении.
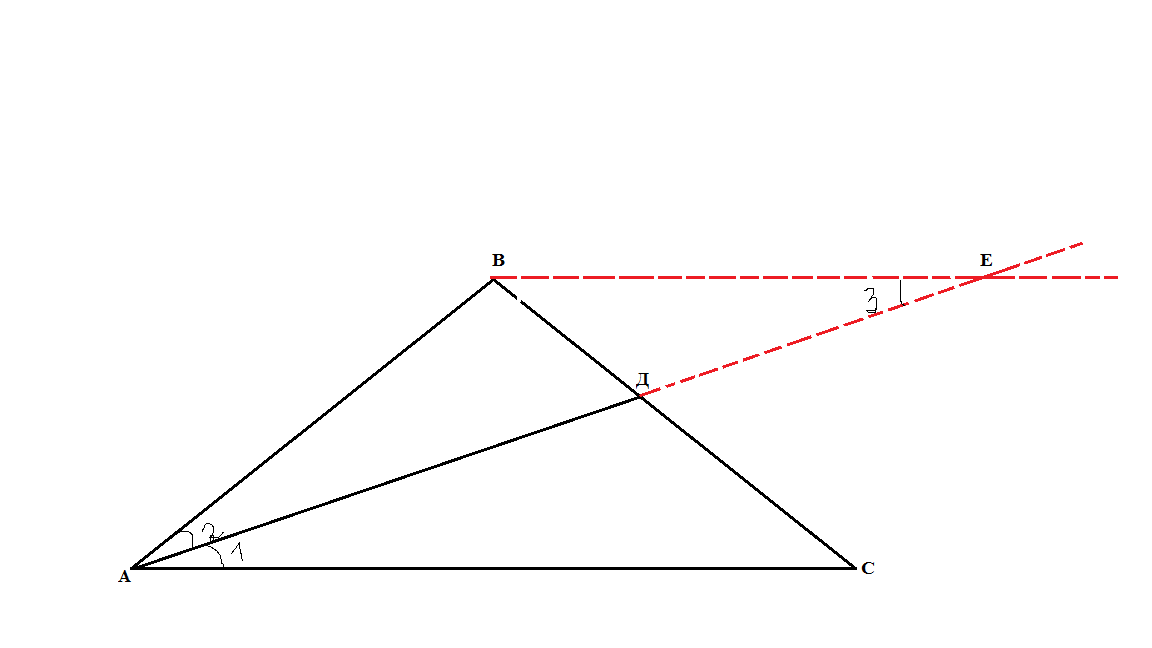
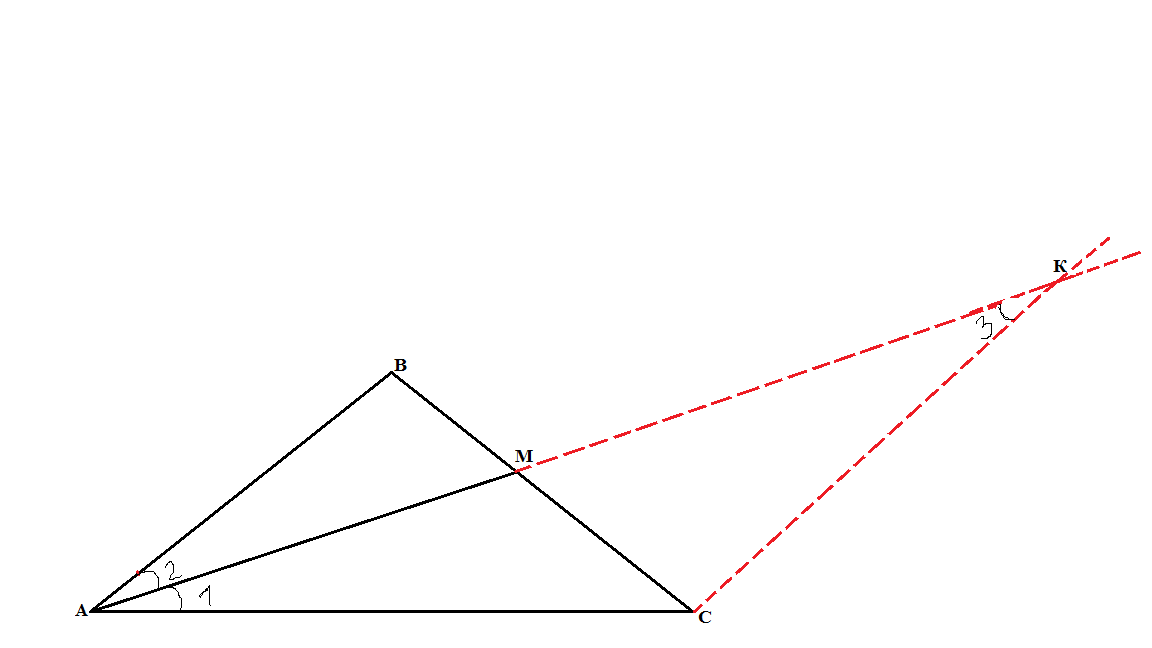
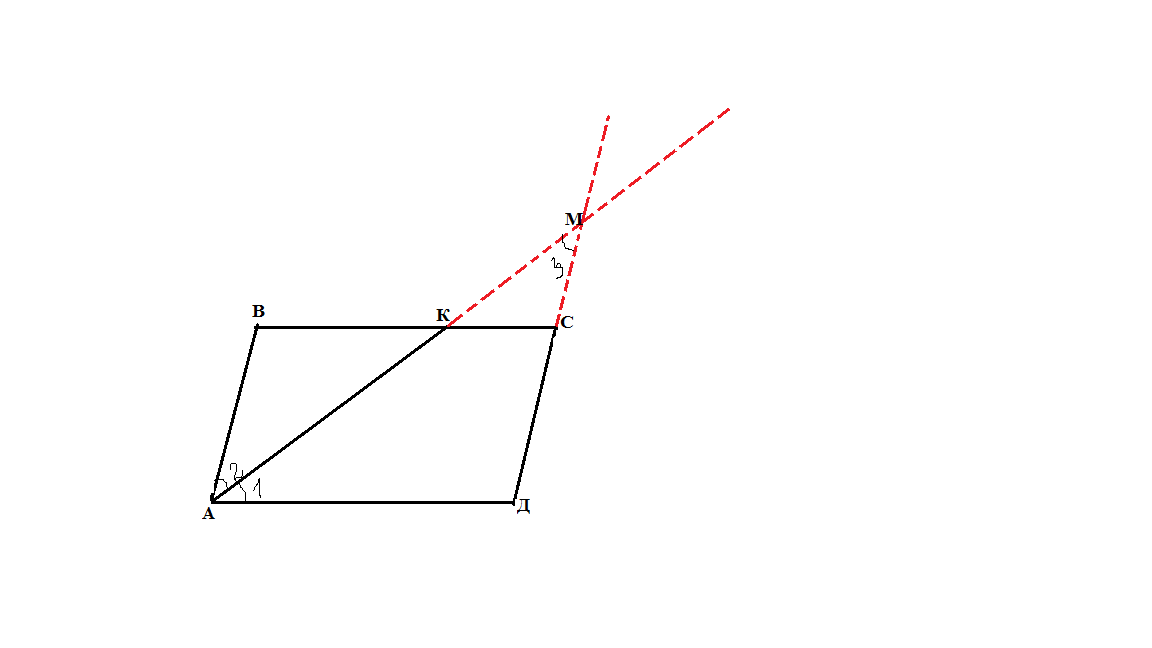
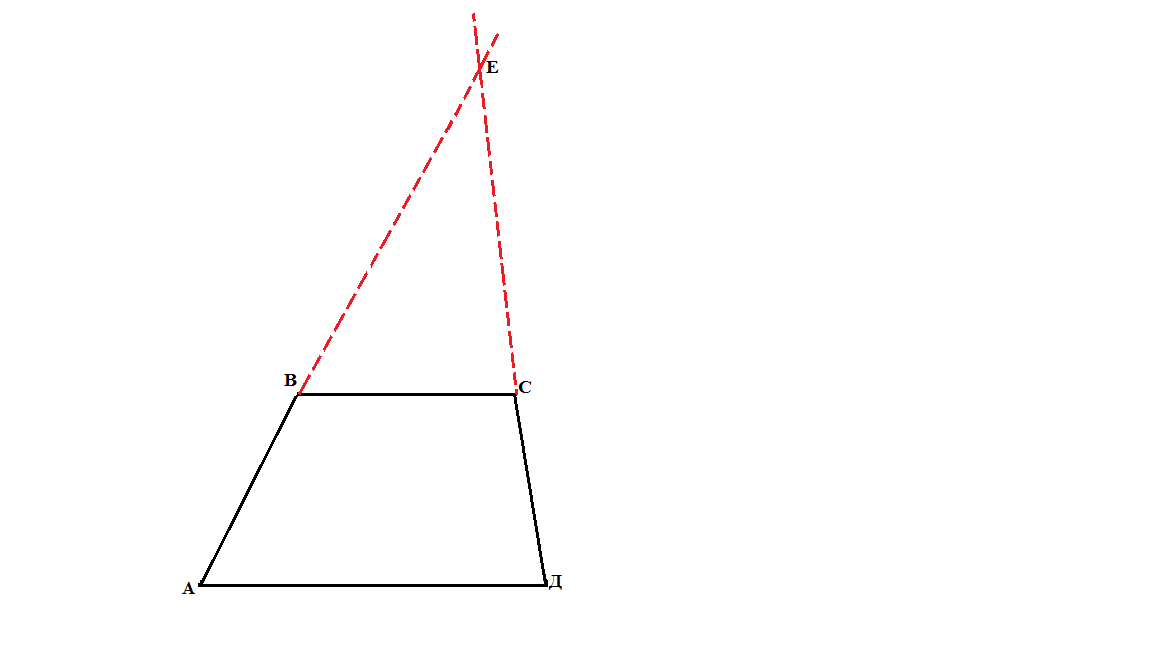
Если дана трапеция, то посредством продолжения боковых сторон она достраивается до треугольника.
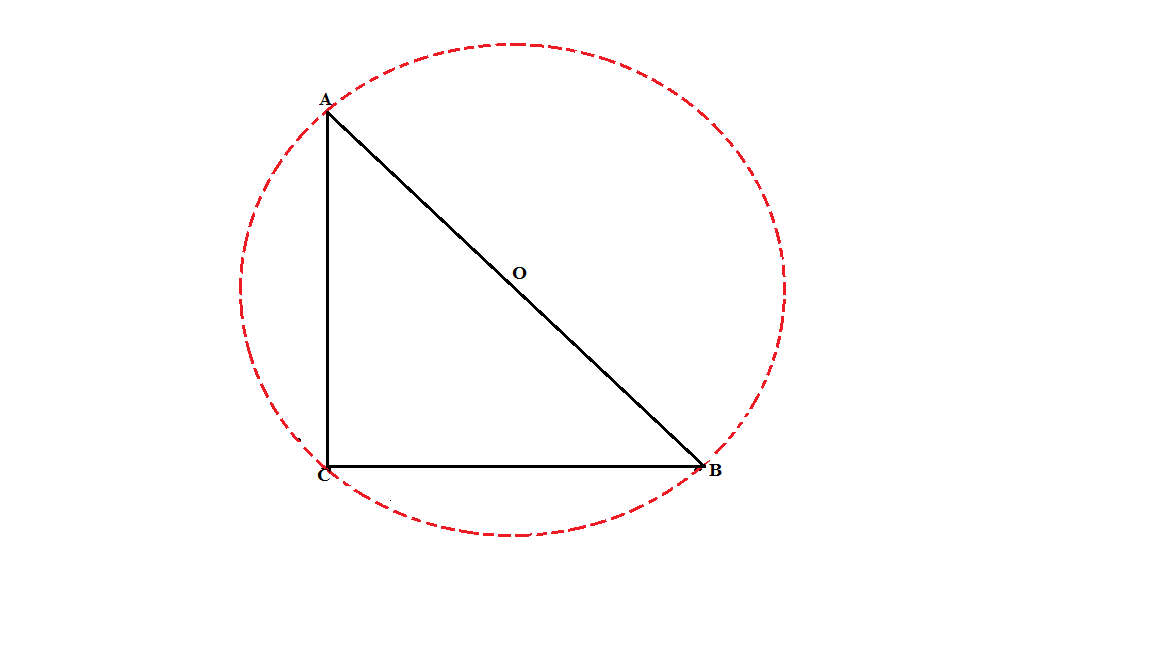
Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы.
Если дан четырёхугольник, у которого суммы противоположных углов равны, то вокруг него описывается окружность.
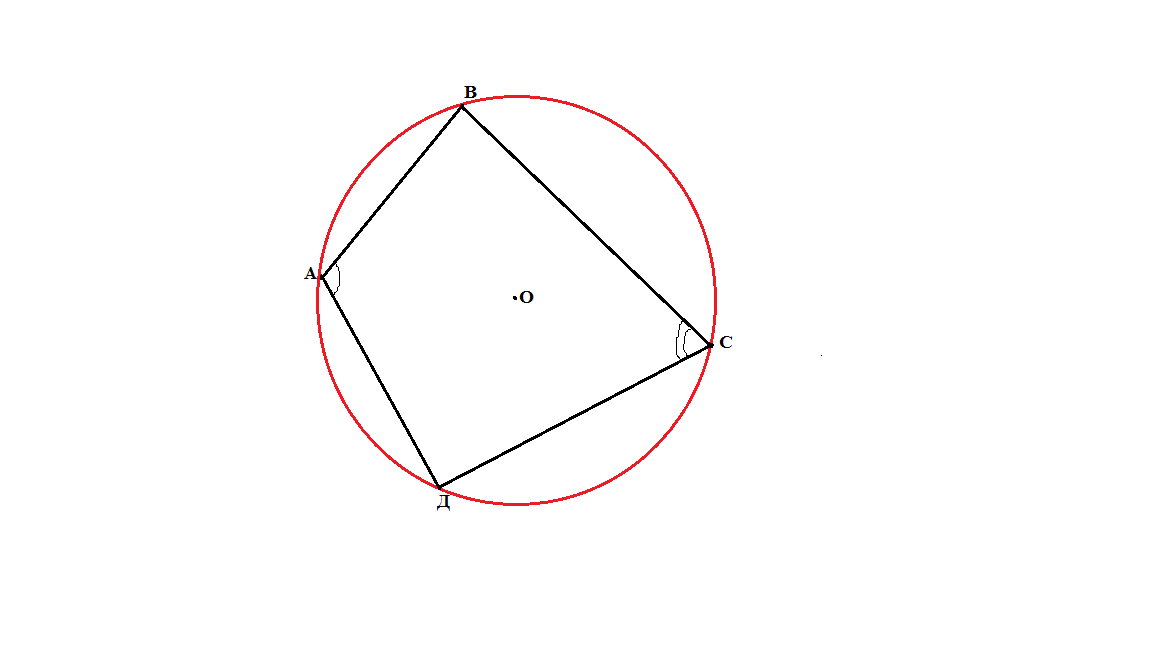
Если в треугольнике заданы биссектриса и медиана или биссектриса и серединный перпендикуляр, проведённые к одной и той же стороне, то около треугольника описывается окружность, а биссектриса продолжается до пересечения с нею.
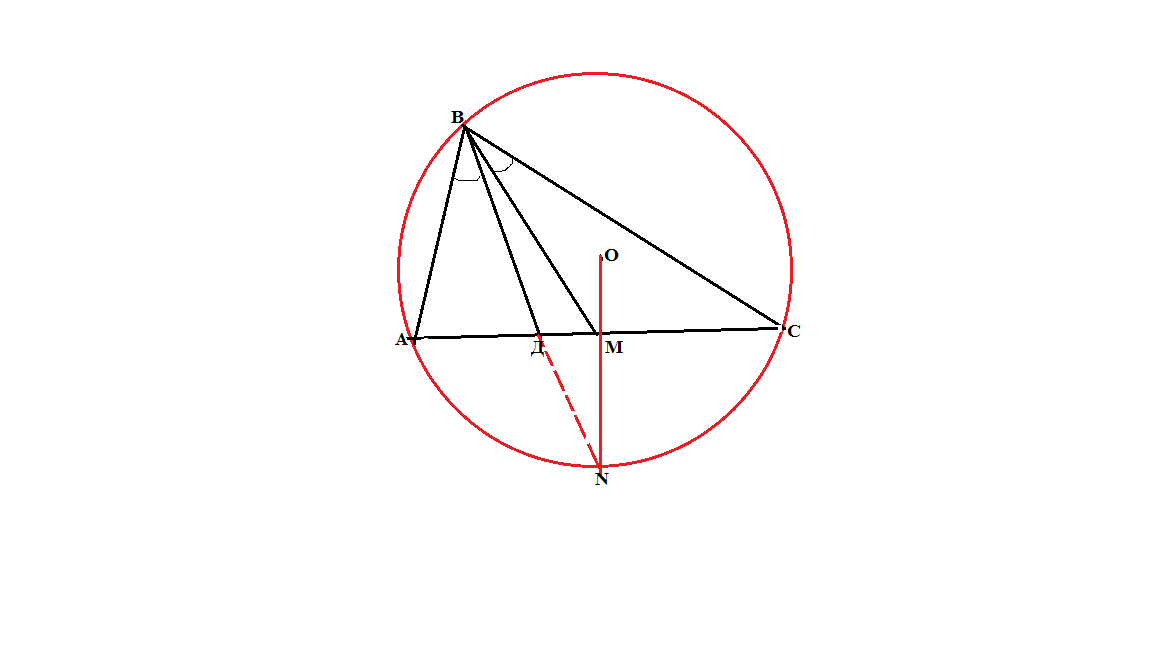
Если даны две окружности разных радиусов с общей касательной, то через центр меньшей окружности проводится прямая, параллельная данной касательной, до пересечения с радиусом большей окружности, идущим в точку касания, или с его продолжением.
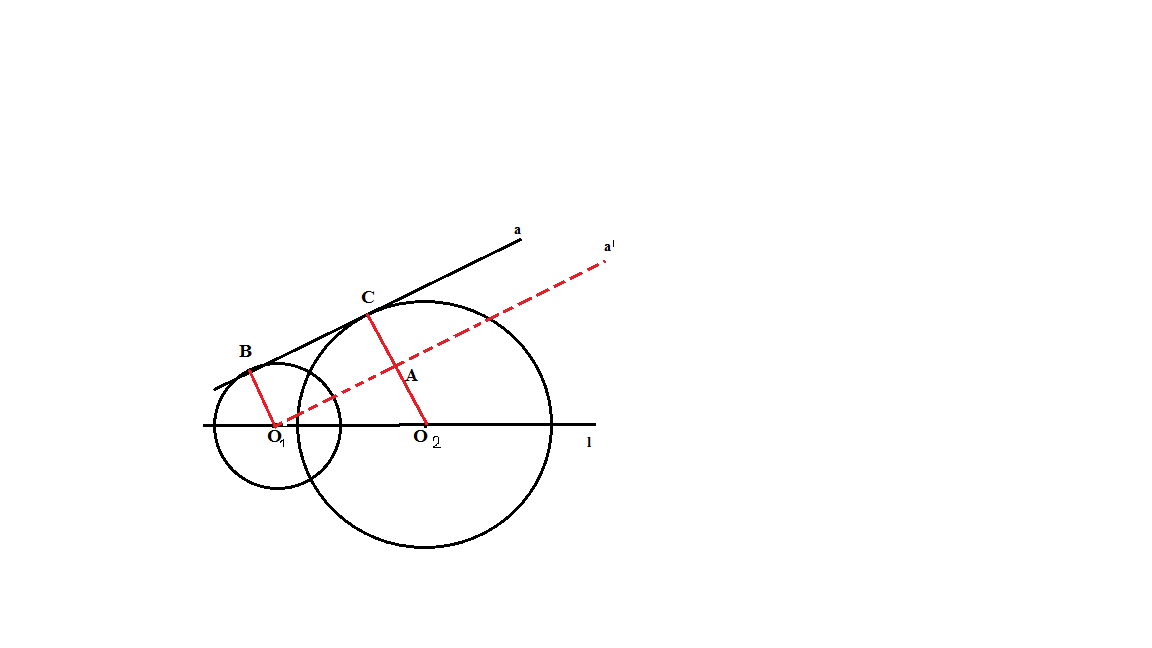
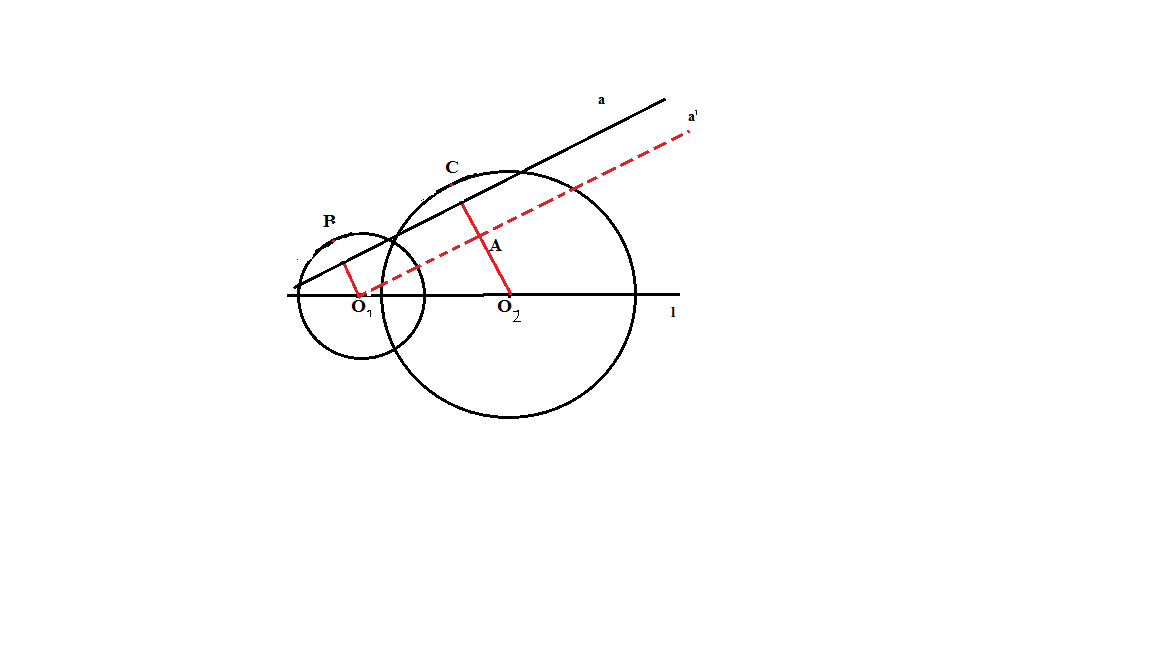
Если даны две окружности с общей внешней касательной, касающиеся друг друга внешним образом, то в рассмотрение вводится треугольник, вершинами которого служат три точки касания данных фигур.
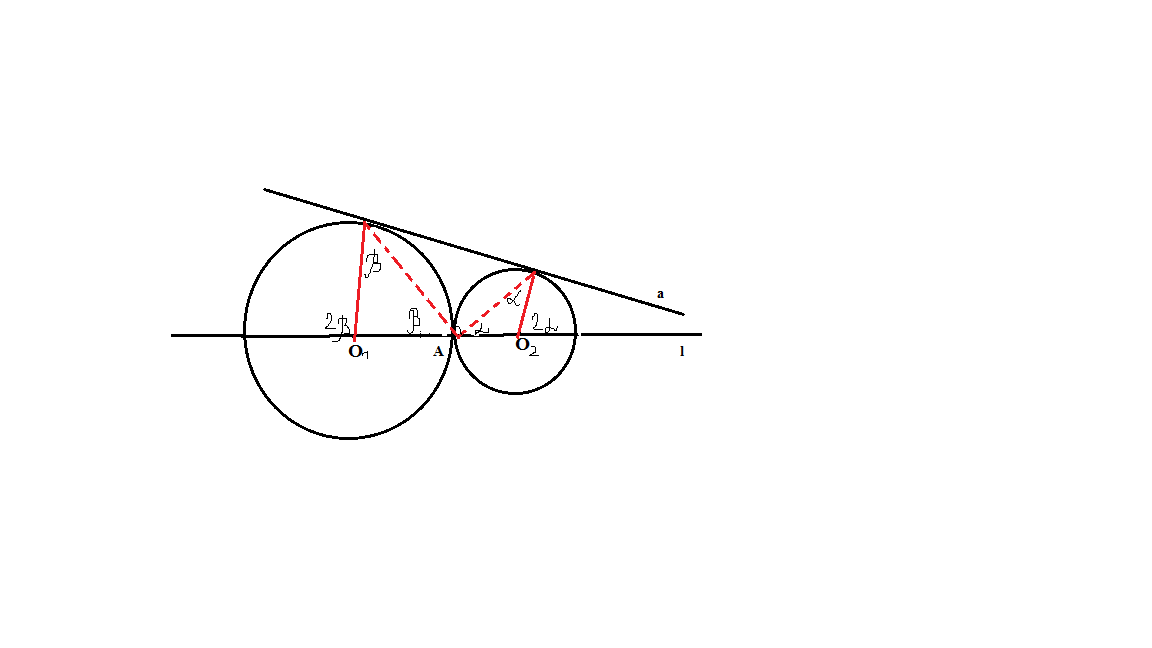
Практическое применение метода дополнительных построений.
Задача 1.
Две стороны треугольника равны 10см и 15см, угол между ними равен 600. Найти длину биссектрисы, проведённой из данного угла.
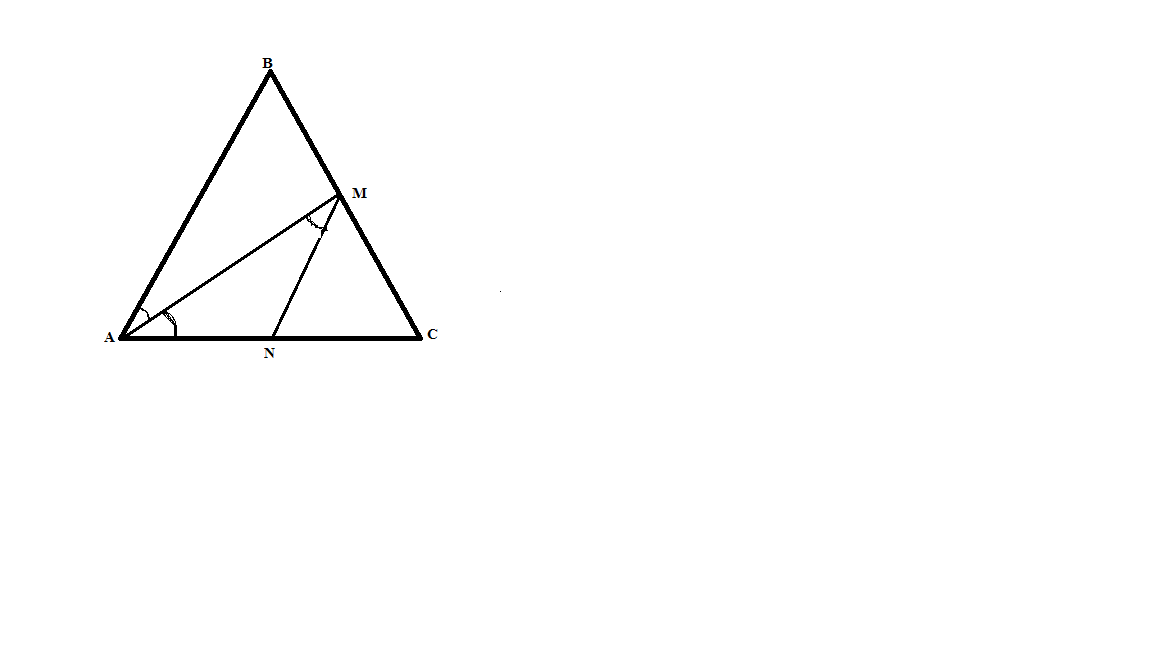
Дано: Δ АВС
АВ= 10см
АВ = 15см
< А = 600
Найти: АМ
Решение:
проведём MN ‖ АВ
< ВАМ = < MAN = < AMN = 300
Δ ANM – равнобедренный
AN = x, NC = 15 – x
Δ ABC ~ Δ NMC,
NC : АС = MN : АВ
(15 – х) : 15 = х : 10
10( 15 – х) = 15х
х = 6
AN = NC = 6
< ANM = 1800 – 600 =1200
По теореме косинусов:
АМ2 = AN2 + NM2 – 2 ∙ AN ∙ NM ∙ cos 1200
АМ2 = 36 + 36 – 2 ∙ 36 ∙ cos 1200
АМ2 = 72 + 2 ∙ 36 ∙ cos 600
АМ2 = 72 + 36 = 108
АМ = √108
Ответ: √108
Задача 2.
В треугольнике АВС высота АМ равна медиане BN. Найти < NBC.
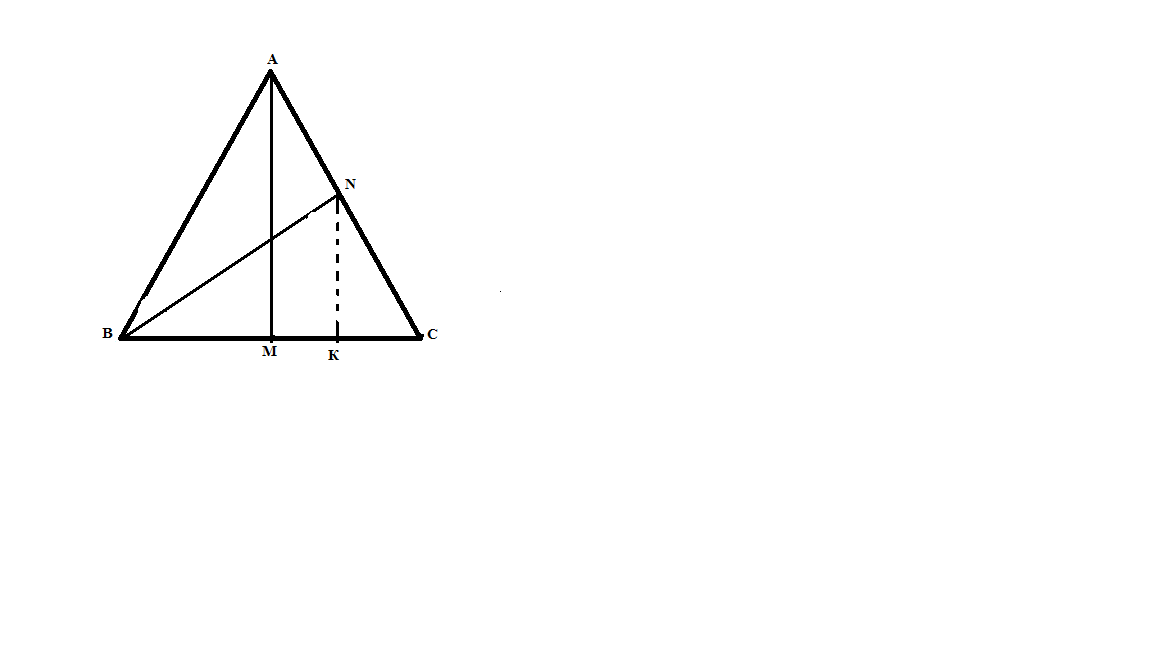
Дано: Δ АВС
АМ = BN
Найти: < NBC
Решение:
проведём NK ‖ AM
AN = NC, AM ‖ NK, тогда по теореме Фалеса МК = КС.
NK – средняя линия Δ АМС,
NK =  АМ
АМ
Δ BNK – прямоугольный
NK =  АМ =
АМ =  = BN
= BN
Катет, лежащий против угла в 300 равен половине гипотенузы
< NBC = 300
Ответ: 300
Задача 3.
Доказать, что если диагонали трапеции равны, то она равнобокая.
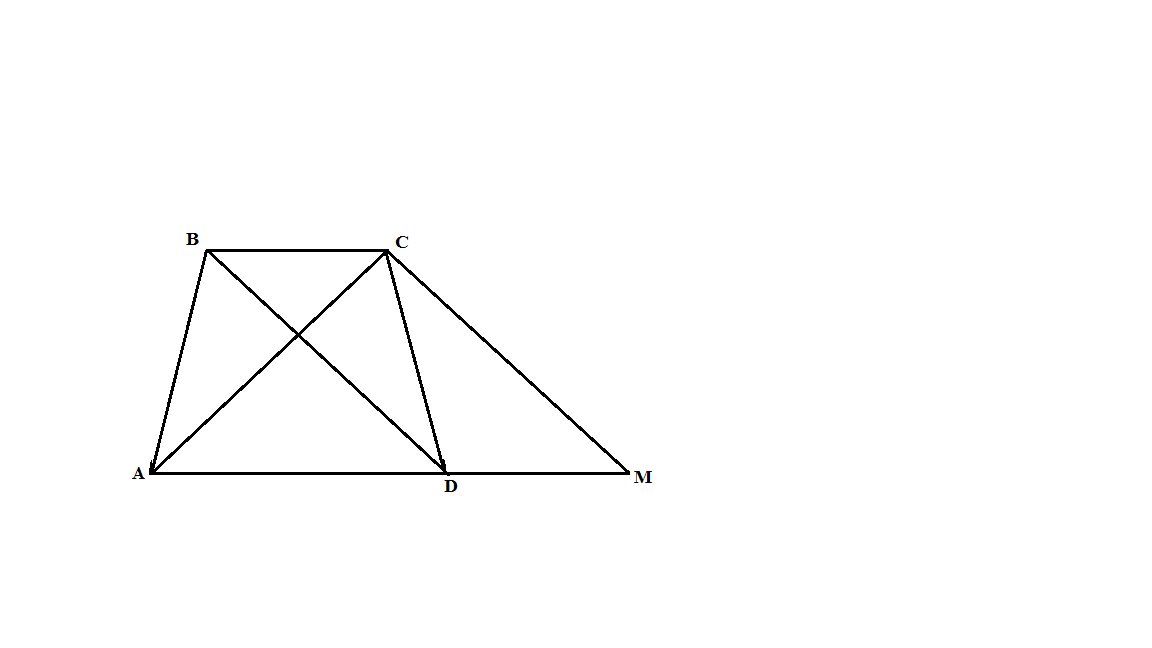
Дано: АBСD – трапеция
BD = AC
Доказать: АВ = СD
Доказательство:
BD ‖ CM, DC = DM
< BDA = < CMA как соответственные угла при параллельных прямых.
BD = CM, BD = AC, тогда АС = СМ,
Δ АСМ – равнобедренный,
< САМ = < СМА
Δ ABD = Δ DCA ( II признак равенства треугольников), тогда AB = CD,
ABCD – равнобокая трапеция.
Задача 4.
Биссектриса острого угла равнобокой трапеции делит боковую сторону на отрезки длиной 20см и 30см, считая от меньшего основания, которое равно 6см. Найти площадь трапеции.
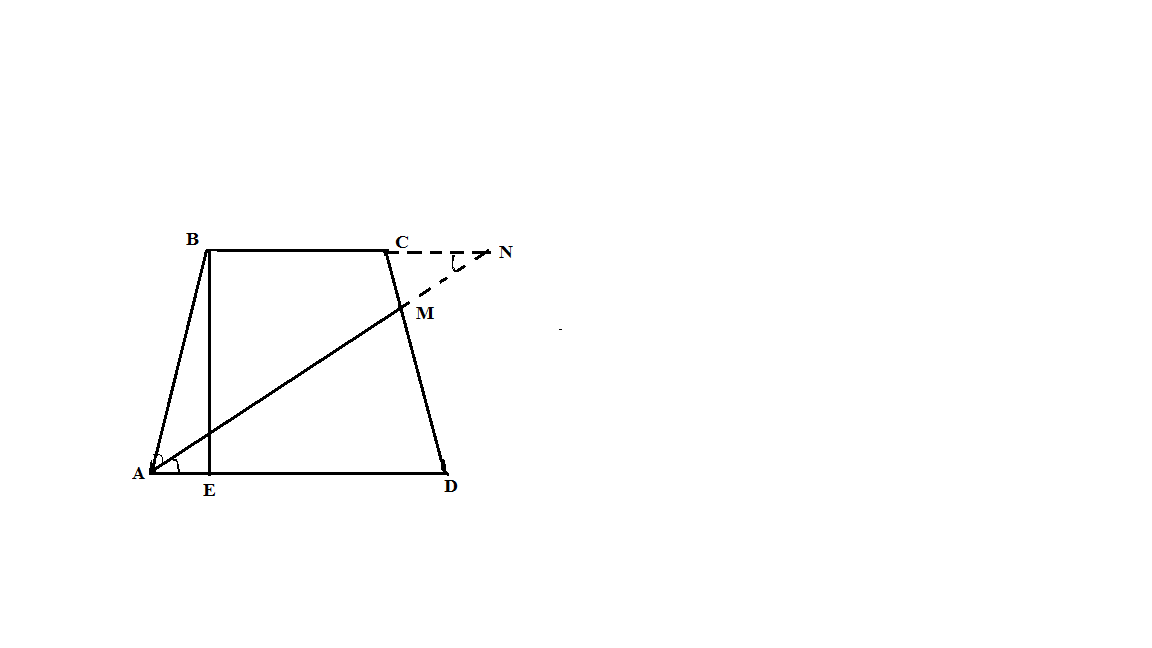
Дано: ABCD – трапеция
< ВАМ = < MAD
BC = 6 см
СМ = 20 см
MD = 30 см
Найти: S
Решение:
BN ‖ AD BN ∩ AN = N
Δ ABN – равнобедренный
< BAN = < BNA ( накрестлежащие, BN ‖ AD)
AB =BN = 50 см,
CN = BN – BC = 50 – 6 = 44 см
Δ AMD ~ Δ NCM
AD : 44 = 30 : 20
AD : CN = DM : СM
20 AD = 1320
AD = 66 cм
S =  ( AD + ВС) ∙ ВЕ
( AD + ВС) ∙ ВЕ
АЕ =  ( AD — ВС) = 30 см
( AD — ВС) = 30 см
Δ АЕВ – прямоугольный
ВЕ2 = АВ2 – АЕ2
ВЕ2 = 2500 – 900 = 1600
ВЕ = 40
S =  ( 66 + 6 ) ∙ 40 = 1440 см2
( 66 + 6 ) ∙ 40 = 1440 см2
Ответ: 1440 см2
Задача 5.
На стороне АВ треугольника АВС построен равносторонний треугольник АВD. Найти расстояние от центра этого треугольника до вершины С, если АВ = 5√3, < АВС = 1200.
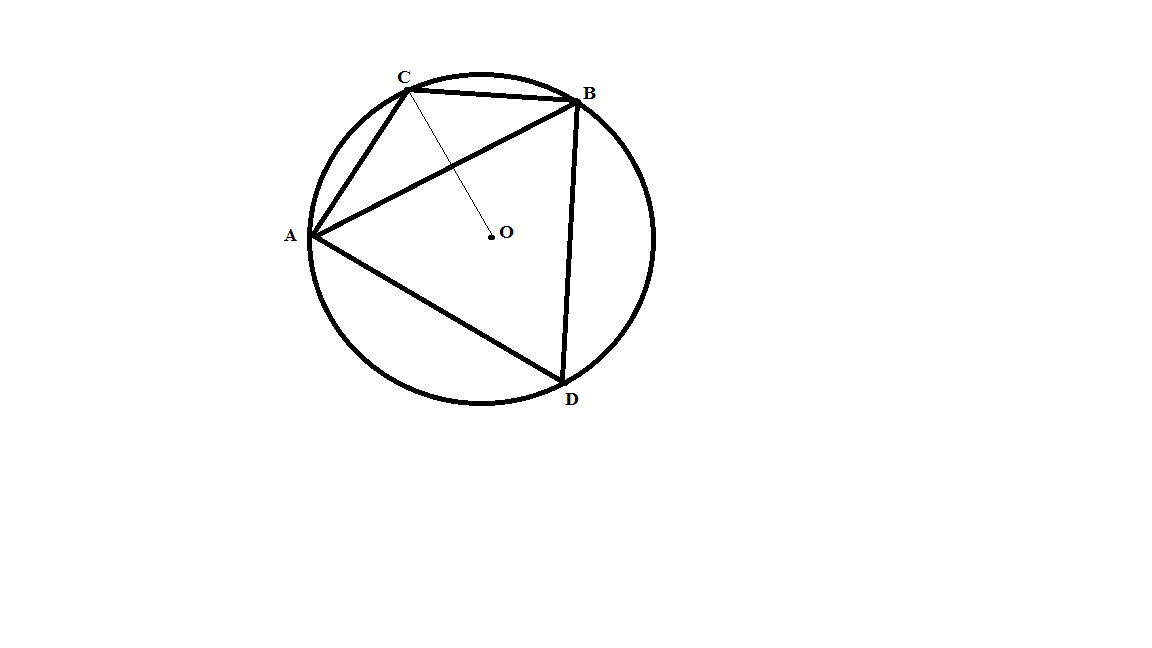
Дано: Δ АВС
AD = AB = BD
AB = 5√3
Найти: ОС
Решение:
Опишем около четырёхугольника ABCD окружность.
< С + < D = 1800 (сумма противолежащих углов)
< А + < В = 3600 – 1800 = 1800
Δ АВС – вписанный в окружность. ОС = R
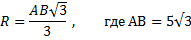
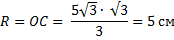 Ответ: 5 см
Ответ: 5 см
Задача 6.
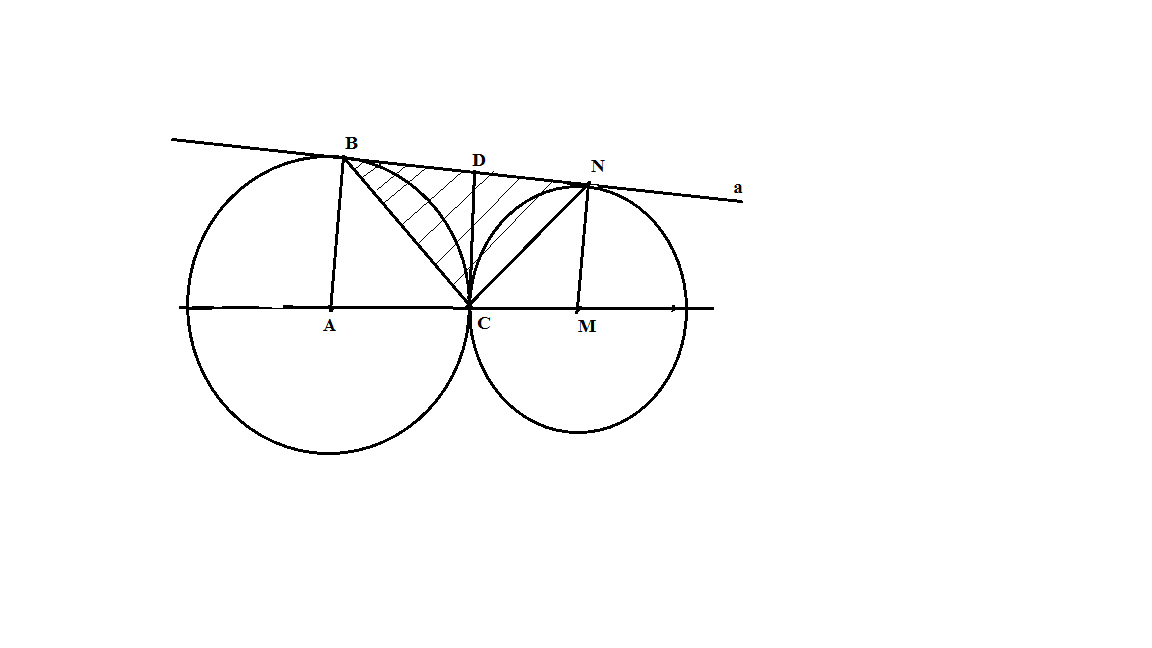
Даны две окружности, касающиеся между собой внешним образом в точке С. Прямая а касается обеих окружностей. Найти расстояние от точки С до общей касательной а данных окружностей, если известны их радиусы R1 = 10 см, R2 = 8см.
Дано: АВ = 10 см
MN = 8 см
Найти: CD
Решение:
а – касательная к окружностям АВ а, MN a, CD a
построим отрезки СВ и СN
Δ ВСN – прямоугольный, BN – гипотенуза, CD – высота, проведённая к гипотенузе
CD2 = BD ∙ DN
Так как AB ‖ CD ‖ MN, то по теореме Фалеса
BD : DN = AC : СМ
BD : DN = 5 : 4, BN = 2√АВ ∙ MN
BN = 2√10 ∙ 8 = 8√5
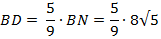
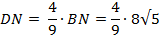
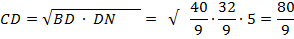
Ответ: 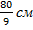
Задачи на доказательство.
Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине.
На сторонах АВ и ВС треугольника АВС построены вне его квадраты. Доказать, что отрезок, соединяющий вершины квадратов, в два раза больше медианы, проведённой из вершины В.
В треугольнике АВС луч, выходящий из вершины А, делит медиану ВВ1 в отношении 1: 2. Доказать, что этот луч делит противоположную сторону треугольника в отношении 1: 4.
Доказать, что если в прямоугольном треугольнике один острый угол равен 300, то противолежащий ему катет равен половине гипотенузы.
Катеты прямоугольного треугольника равны a и b. Доказать, что биссектриса прямого угла этого треугольника равна
 .
.Через середину О гипотенузы АВ прямоугольного треугольника АВС проведена прямая, перпендикулярная АВ, и на этой прямой в обе стороны от точки О отложены отрезки ОD и ОЕ, равные половине гипотенузы. Доказать, что [CD) и [CE) – биссектрисы внутреннего и внешнего углов треугольника АВС при вершине С.
Доказать, что прямая, соединяющая основания двух высот остроугольного треугольника, отсекает от него треугольник, подобный данному.
Точка D лежит на стороне АС правильного треугольника АВС, а точка Е – середина отрезка АD. Прямые, перпендикулярные сторонам АВ и ВС данного треугольника и проходящие соответственно через точки D и С, пересекаются в точке F. Доказать, что треугольник ВЕF прямоугольный с острыми углами 300 и 600.
Окружность радиусов R и r (R > r) касаются друг друга внешним образом. Доказать, что радиус третьей окружности, касающейся двух данных окружностей и их общей внешней касательной, равен

Две окружности радиусов R и r (R > r) касаются друг друга и сторон данного угла. Доказать, что радиус третьей окружности, касающейся сторон того же угла, центр которой находится в точке касания между собой двух данных окружностей, равен

Задачи на вычисление.
Найти площадь треугольника, если известно, что две стороны и медиана, выходящая из общей вершины этих сторон, имеют длины 3, 7 и 4 (соответственно).
В треугольнике длины двух сторон равны a и в. Известно, что медианы, проведённые к этим сторонам, перпендикулярны. Найти длину третьей стороны данного треугольника.
Найти площадь треугольника, медианы которого 12, 15 и 21.
В треугольнике известны длины двух сторон и медианы, выходящие из их общей вершины – 6 см, 8 см, 5 см соответственно. Найти косинусы углов, которые образует с этими сторонами данная медиана.
В треугольнике проведены высота ВВ1 и медиана СС1. Известно, что их точка пересечения О отстоит от стороны АС на расстоянии 1 см. найти сторону АВ, если |ВВ1| = 6 см, |СС1| = 5 см.
Точка В1 лежит на стороне АС треугольника АВС и делит её в отношении m :n, считая от вершины А. найти, в каком отношении медиана АА1 делит отрезок ВВ1.
Точки А1 и В1 делят стороны ВС и АС треугольника АВС в отношениях |ВА1| : |А1С| = 1 : p и |АВ1| : |В1С| = 1 : g. В каком отношении точка пересечения отрезков АА1 и ВВ1 делит каждую из них?
В треугольнике АВС точка С1 на стороне АВ и точка В1 на стороне АС расположены так, что |АС1| : |С1В| = 2: 3, |АВ1| : |В1С| = 4 : 5. Найти в каком отношении отрезок СС1 делит отрезок ВВ1.
Точка А1 взята на стороне АВ треугольника АВС так, что |АВ| = 3|АА1|. Точка С1 лежит на продолжении стороны АС за точку С и удовлетворяет условию: |АС1| = 2|АС|. Найти, в каком отношении прямая А1С1 делит сторону ВС данного треугольника.
Найти угол С треугольника АВС, если угол А равен 600, сторона АС вдвое меньше стороны АВ.
В прямоугольном треугольнике АВС с прямым углом С гипотенуза равна с. Найти катеты треугольника, если известно, что угол В равен 150.
В прямоугольном треугольнике высота, опущенная на гипотенузу, делит её на отрезки, разность которых равна одному из катетов треугольника. Найти величины острых углов данного треугольника.
Один из углов трапеции равен 300, а её боковые стороны пресекаются под прямым углом. Найти меньшую боковую сторону трапеции, если её средняя линия равнв 10 см, а одно из оснований равно 8 см.
Найти площадь трапеции с основаниями 7 и 11 и боковыми сторонами 4 и 6.
Основания трапеции равны 3 и 2, а диагонали – 4 и 3. Найти площадь трапеции.
Основания AD и ВС трапеции АВСD равны соответственно a и b (a > b). Найти длину отрезка MN, концы которого M и N делят боковые стороны АВ и СD а отношении |АМ| : |МВ| = |DN| : |NC| = 3 : 2.
Основание АD трапеции АВСD вдвое длиннее боковой стороны АВ и верхнего основания ВС. Диагональ АС равна а, боковая сторона СD равна b. Найти площадь трапеции.
В равнобедренном треугольнике АВС с основанием АС биссектриса АD пересекает высоту ВВ1 в точке О, причём |ВО| : |ОВ1| = 3 : 1. Найти, в каком отношении высота АА1 делит высоту ВВ1.
В параллелограмме АВСD точка D1 является серединой стороны АВ. Известно, что биссектриса СС1 угла С параллелограмма делит площадь треугольника АDD1 пополам. Найти длину стороны AD, если |CD| = 4.
Биссектриса острого угла равнобокой трапеции делит боковую сторону на отрезки длин 20 и 30, считая от меньшего основания, которое равно 6. Определить площадь трапеции.
Найти площадь трапеции, основания которой равны 2и 1, а углы, прилежащие к большему основанию, равны 300 и 600.
В прямоугольном треугольнике АВС с прямым углом С даны катеты: |АС| = 12, |ВС| = 8. Точка К – середина медианы BD. Найти длину отрезка СК.
В прямоугольном треугольнике медиана и биссектриса, проведённые из вершины прямого угла, образуют угол в 100. Найти острые углы данного треугольника.
Найти длину общей внешней касательной к двум окружностям радиусов R и r, если расстояние между их центрами равно а.
Две окружности касаются внешним образом и имеют общую касательную, отрезок которой равен 6√2 см. радиус большей окружности равен 4,5 см. найти радиус меньшей окружности.
Две окружности радиусов 1см и 3см касаются внешним образом. Найти расстояние от точки касания окружностей до их общей касательной.
Две окружности радиусов √2 и √5 пересекаются в точках P и Q. Расстояние между центрами окружностей равно 3. Через точку Р проведена секущая, отсекающая от данных окружностей равные хорды. Найти длины этих хорд.
Заключение.
Автор, тщательно проанализировав решение достаточно большого количества задач, в которых данные построения применяются прямо или косвенно, даёт квалификацию дополнительных построений, связанную с характерными признаками фигуры, исключающей метод геометрических преобразований, векторный метод и другие.
Список используемой литературы.
Готман Э.Г. Решение геометрических задач аналитическим способом. Москва. Просвещение 1989 г.
Киселёв А.П. Элементарная геометрия. Москва. Просвещение 1998 г.
Лысенко Ф.Ф. Подготовка к ЕГЭ 2010 – 2013г. Легион. Ростов на Дону.
Рахмист Р.Б. Методы решения геометрических задач. Москва 2003г.
Фирсов В.В. Избранные вопросы математики. Москва. Просвещение 2009г.
«Решение нестандартных геометрических задач повышенной трудности»
Внеурочное занятие
во 2 «Б» классе
МБОУ «СОШ №35»
г.Грозного
Тема: «Решение нестандартных геометрических задач повышенной трудности»

Учитель: Мадашева П.С.
Тема: Решение нестандартных геометрических задач повышенной трудности.
Тип занятия: общеметодологической направленности
Целевая направленность занятия:
— содержательная;
— деятельностная.
Цели для учителя:
Развитие регулятивных УУД: управление своей деятельностью, контроль и коррекция знаний, инициативность и самостоятельность.
Развитие коммуникативных УУД: формирование умения размышлять, ориентироваться в нестандартной ситуации, осуществлять перенос знаний, обосновывать полученные выводы.
Развитие универсальных логических действий, творческих способностей обучающихся.
Воспитание интереса, любви к математике.
Цели для ученика:
Понимание деятельностной единицы содержания образования;
умение ее применить в учебной, предметной задаче и реальной жизненной ситуации.
Ход занятия
Скажем, здравствуйте, руками!
Скажем, здравствуйте, глазами.
Скажем, здравствуйте, мы ртом,
Здравствуйте!
Стало здорово кругом
Математика пришла,
Занимай свои места,
Чтоб от безделья не зевать
Полезно голову ломать,
Прошу садиться.
Ребята у вас на столе лежат два кружочка с изображением мордашки.
Выберите мордашку по настроению.
Я рада, что большинство из вас выбрали улыбающуюся мордашку.
Значит у вас сейчас хорошее настроение.
Надеюсь, оно сохранится у вас до конца занятия.
Тем более, что занятие у нас сегодня необычное.
А сначала мы проведём маленькую разминку.
Разминка.
Не крутите пестрый глобус,
Не найдете вы на нем
Той страны, страны чудесной
В даль которой мы идем.
В той стране живут фигуры,
Линии, точки и тела.
Треугольники, квадраты,
Вот такие, брат, дела!
Пусть в эту страну не идут поезда,
Страна Геометрия
Рядом с нами всегда!
-Нас встречают жители этой страны – геометрические фигуры.
(Читают подготовленные ученики.)
1.Я-неведимка, в этом суть моя.
Меня всегда изображают
Прикосновеньем мела иль карандаша.
Но без меня и линий нет – одни движенья точки след.
2.Без начала и без края — линия Прямая.
Сейчас я вертикальна. Могу, однако же
Принять любой наклон,
Могу и лечь горизонтально.
3.Я сестра её родная-
Зовусь я линия Кривая.
4.Точки две поставь в тетрадь,
Чтоб потом нарисовать
Между ними под линеечку прямую.
И окажется, мой друг,
Что Отрезок вышел тут.
5.Кусок проволоки возьми
И его ты перегни.
Хочешь раз, а хочешь – два. Что же получилось?
Не прямая, не кривая – Ломаная линия.
6.Три вершинки, три угла,
Три сторонки – вот и Треугольник я!
7.Имею я четыре стороны,
И все они равны — и я Квадрат.
8.Четыре палочки сложил
Прямоугольник получил.
Прямоугольник квадрата длиннее.
Фигура попроще, чертите смелее.
9.А у меня число вершин
Лишь только стоит сосчитать.
Вот, например, когда их будет пять,
Пятиугольником меня должны принять.
Учитель: Мы от собравшихся гостей,
Достаточно узнали новостей.
Теперь легко ребятам изложить
Суть геометрии.
Прощайте,
Но только ваших свойств не забывайте! 
Сообщение темы (Слайд1)
Сегодня вместе со сказочными героями отправимся в путешествие по стране Геометрии.
Встреча с клубочком. Дети заблудились в лесу. (Слайд 2.
По лугу шли, клубок нашли,
За ним пошли.
Вперед, находочка, кати,
В любимый класс нас приведи!
II. Встреча с теремком
Ай, да терем, теремок!
Он не низок, невысок.
Если сможете, ребята,
Несколько задач решить,
Разрешат тогда зверята
Вас в ворота пропустить.
А задачи таковы
1) Игра «Угадай фигуру» (Слайд 4-7)
— Расставь 8 стульев у четырех стен комнат так, чтобы у каждой стены стояло по 3 стула. Расставь 9, потом 10, потом 11 стульев.
Проверка:
(Слайд 8)
Окна в доме открываются,
Звери в окнах появляются,
В лапках держат все задачки.
У кого ответ готов
На вопрос этих жильцов?
Игра «Танграмм» (Слайд 9)
(Слайд 13)

Хоть и тесно нам здесь жить,
Живем мы все дружно,
Умеем дружить.
И вам всем, ребятам,
Каждый желает,
Пусть ссор и обид
Класс ваш не знает.
Вас в ворота пропускаем,
Идти прямо предлагаем,
Вот по этому пути
Должны до леса вы дойти.
(Слайд 10)
III. Встреча с Красной Шапочкой
(Слайд 11)
Тропинка «Площадь задач»
Помогите-ка, ребята,
Волка мне перехитрить.
Но для этого вам надо
Задачу для меня решить.
Периметр фигуры вам надо найти,
Тогда до милой бабушки смогу я дойти
3см
2см 2 см
4см
3см 3см
4см

Физминутка

Сколько покажу кружков,
Столько выполни прыжков.
Приседаем столько раз,
Сколько кубиков у нас.
Сколько точек будет в круге,
Столько мы поднимем руки.
Сколько палочек прямых
Столько выполни наклонов
IV. Встреча с Незнайкой
(Слайд 12)
Повстречали дальше с вами
Мы Незнайку на пути.
Его вежливо спросили
Куда дальше нам идти.
Он помочь пообещал,
Но задание всем дал:
«Чтоб узнать о дальнейшем пути,
Должны вы по лесенке вверх пойти.
А там наверху в ответе примера
Указана будет дорога до сквера.
А в сквере вас ждет друг лучший мой.
Подскажет дорогу он к школе родной,
Где игры нас ждут среди лучших друзей.
Итак, смело вверх!
Ну, кто же быстрей?!
(Слайд 13)
Математическая эстафета (дети делятся на две команды) 
Путь открыт! Вперед, ребята!
V. Встреча с Буратино (у озера) (Слайд 18)
Мог бы вам помочь, ребята,
Только злющий Карабас
Спрятал здесь, в пруду, куда-то
Ключ от двери вашей в класс.
И только лягушка-квакушка одна
Поможет достать вам ключик со дна.
Ребята, задачку скорее решите,
Лягушку с пятеркой в ответе спросите.
Она вам поможет ключик достать,
Ответы к задачке скорей написать.
Все вместе мы в школу пойдем поскорей,
Чтоб встретить там много хороших друзей.
Наконец добрались в школу к вам
И расселись по местам.
А теперь всех, кто в пути
Дорогу нам помог найти,
Приглашаем поиграть

Ребята у вас на партах лежат конверты, давайте посмотрим что в них и попробуем составить из них какой ни будь предмет.
Что у вас получилось? ( Уч-ся собирают животных из геометрических фигур)
А теперь наше занятие подошло к концу .
Закончить путешествие настала нам пора.
Настала перемена. Вы рады, дети?
Да!
Элективный курс по математике на тему «Система подготовки к ЕГЭ по математике. Решение нестандартных задач по геометрии»
Элективный курс
«Система подготовки к ЕГЭ по математике. Решение нестандартных задач по геометрии»
11 класс
(34 часа)
2013-2014 учебный год
Учитель Гедровец Ж. Н.
Программа элективного курса
«Система подготовки к ЕГЭ по математике. Решение нестандартных задач по геометрии»
Учитель Гедровец Жанна Николаевна
2013-2014 учебный год
Элективный курс «Система подготовки к ЕГЭ по математике. Решение нестандартных задач по геометрии» разработан в рамках реализации концепции профильного обучения на старшей ступени общего образования и соответствует Государственному стандарту среднего образования по математике. При разработке данной программы учитывалось то, что элективный курс как компонент образования должен быть направлен на удовлетворение познавательных потребностей и интересов старшеклассников, на формирование у них новых видов познавательной и практической деятельности, которые характерны для традиционных учебных курсов.
Единый государственный экзамен по математике имеет свои сильные и слабые стороны. Чтобы минусы обратились в плюсы, учителю, который готовит школьников к экзамену, в первую очередь необходимо знание о формате и структуре ЕГЭ, особенностях процедуры его проведения. В 2009-2010 учебном году существенно изменилась структура и содержание ЕГЭ по математике. Нет части А, осталась часть В и часть С. Увеличилось количество заданий по геометрии.
Решение геометрических задач часто вызывает трудности у учащихся. Это в первую очередь связано с тем, что редко какая задача в геометрии может быть решена с использованием определенной формулы. При решении большинства задач не обойтись без привлечения разнообразных фактов теории доказательств тех или иных утверждений. Но и при хорошем знании теории приобрести навык в решении задач можно лишь решив достаточно много задач, начиная с простых и переходя к более сложным.
Цель курса:
Обобщение и систематизация теоретических и практических навыков при решении задач;
Ознакомление учащихся с некоторыми методами и приемами решения математических задач;
Формирование умения применять полученные знания при решении «нетипичных», нестандартных задач.
Умение выделить из общего количества задач опорные задачи;
Дополнить знания учащихся теоремами прикладного характера, областью применения которых являются задачи;
Расширить и углубить представления учащихся о приемах и методах решения математических задач;
Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования;
Развить интерес и положительную мотивацию изучения математики;
Структура курса представляет собой сеть логически законченных и содержательно взаимосвязанных тем, изучение которых обеспечит системность и практическую направленность знаний и умений учеников. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся различной степени подготовки. Все занятия направлены на расширение и углубление базового курса. Содержание курса можно варьировать с учетом склонностей, интересов и уровня подготовленности учеников.
Основной тип занятий — практикум. Для наиболее успешного усвоения материала планируются различные формы работы с учащимися: лекционно-семинарские занятия, групповые, индивидуальные формы работы. Для текущего контроля на каждом занятии учащимся рекомендуется серия заданий, часть которых выполняется в классе, а часть — дома самостоятельно. Изучение данного курса заканчивается проведением либо итоговой контрольной работы, либо теста.
В результате изучения курса учащиеся должны уметь:
Точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
Применять полученные знания при решении тестов по ЕГЭ;
Учебно-тематический план
№
Наименование тем курса
Всего часов
В том числе
Форма контроля
лекция
практика
1
Построения на плоскости
а)метод геометрических точек;
б) метод геометрических прямых;
3
1
2
тест
2
Треугольник:
а) замечательные точки и линии в треугольнике;
б) пропорциональные отрезки в треугольнике;
в) вписанная в треугольник и описанная окружность;
4
2
2
3
Окружность и круг.
Свойство дуг и хорд.
Углы, связанные с окружностью.
4
2
2
Зачетная работа
4
Средние геометрические и другие средние
2
1
1
5
Решение нестандартных задач по теме «Треугольник»
5
2
3
6
Метод подобия в задачах
5
1
4
Тест
7
Окружность
Взаимное расположение окружностей и общие касательные
4
1
3
8
Многоугольники
3
1
2
9
Площади
2
1
1
Тест
10
Итоговое занятие
2
1
1
Зачетная работа
ИТОГО:
34
13
21
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА:
И. Ф. Шарыгин «Факультативный курс по математике»;
Т. Дорофеев, М. Попов «Математика для поступающих в вузы»;
Л. С. Атанасян, В. Ф, Бутузов «Дополнительные главы к школьному учебнику»;
А. А. Прокофьев «Геометрия для поступающих в вузы»;
Энциклопедический словарь юного математика.-М.: Педагогика,1989.
Математика. Большой справочник для школьников и поступающих в вузы.-М.: Дрофа,1999.
Геометрический подход к баллистическим задачам
В серии статей на эту тему предложен интересный подход к решению задач кинематики, позволяющий решать их значительно проще. Некоторые задачи с помощью данного метода можно решить в одну строчку, в то время как другие можно решить только с его помощью.
Сначала немного теории.
Так как статья посвящена равноускоренному движению, то мы с вами будем использовать следующие формулы.
![Rendered by QuickLaTeX.com \[\vec{\upsilon}=\vec{\upsilon_0}+\vec{g}t\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2861b640c7942253599983212c211441_l3.png)
![Rendered by QuickLaTeX.com \[\vec{S}=\vec{\upsilon_0}t+\frac{\vec{g}t^2}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c3b025e0449f1f49e5b086900793b768_l3.png)
![Rendered by QuickLaTeX.com \[\pm 2gh=\upsilon^2-\upsilon_0^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8ab9517963e92fbcbdbc7aa7c54ef5c9_l3.png)
Здесь  – перепад высот, «минус» соответствует движению вверх, «плюс» – движению вниз. Формула хороша тем, что в ней отсутствует время
– перепад высот, «минус» соответствует движению вверх, «плюс» – движению вниз. Формула хороша тем, что в ней отсутствует время  . В общем виде формула записывается так:
. В общем виде формула записывается так:
![Rendered by QuickLaTeX.com \[2(\vec{g}\cdot \vec{S})=\upsilon^2-\upsilon_0^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-976554ab0987fbef37f8fb250ce636e4_l3.png)
Так как скалярное произведение равно  , а в нашем случае
, а в нашем случае  .
.

Рисунок 1
Последнюю формулу можно вывести из энергетических соображений:
![Rendered by QuickLaTeX.com \[(m\vec{g}\cdot \vec{S})=\frac{m\upsilon^2}{2}-\frac{m\upsilon_0^2}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-72f7b28f39b19313e71c78a77a7619ce_l3.png)
Наконец, нам понадобится еще формула
![Rendered by QuickLaTeX.com \[\vec{S}=\frac{\upsilon+\upsilon_0}{2}t\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b1fad35af01ea2a82d232ce2de083e16_l3.png)
При решении будем пользоваться векторными треугольниками. Выделяют два векторных треугольника: треугольник скоростей и треугольник перемещений.
Изобразим первый.

Рисунок 2
Вектор  направлен вниз. Сумма векторов
направлен вниз. Сумма векторов  и
и  в сумме дают вектор
в сумме дают вектор  . Проведем высоту в этом треугольнике. Тогда угол
. Проведем высоту в этом треугольнике. Тогда угол  – угол, под которым произведен бросок. Угол при вершине треугольника тогда будет равен
– угол, под которым произведен бросок. Угол при вершине треугольника тогда будет равен  . Достроим наш треугольник до параллелограмма. В параллелограмме диагонали делятся пополам точкой пересечения. Половина диагонали параллелограмма, таким образом, будет медианой треугольника. А длина этого вектора будет равна
. Достроим наш треугольник до параллелограмма. В параллелограмме диагонали делятся пополам точкой пересечения. Половина диагонали параллелограмма, таким образом, будет медианой треугольника. А длина этого вектора будет равна  . Этот вектор будет направлен вниз, если тело приземляется ниже точки броска. В случае же, если тело падает на тот же горизонтальный уровень, он будет направлен горизонтально и треугольник в этом случае равнобедренный,
. Этот вектор будет направлен вниз, если тело приземляется ниже точки броска. В случае же, если тело падает на тот же горизонтальный уровень, он будет направлен горизонтально и треугольник в этом случае равнобедренный,  . Если мы закидываем тело вверх, указанный вектор будет направлен вверх.
. Если мы закидываем тело вверх, указанный вектор будет направлен вверх.
Представим себе, что вектор  перпендикулярен
перпендикулярен  . Тогда указанный вектор (
. Тогда указанный вектор ( ) равен радиусу описанной окружности (из геометрии). Кроме того, в этом случае вектор
) равен радиусу описанной окружности (из геометрии). Кроме того, в этом случае вектор  направлен по биссектрисе угла между вектором перемещения и вертикалью. Это очень важный факт, который позволяет существенно упростить решение некоторых задач. Доказательство будет приведено ниже.
направлен по биссектрисе угла между вектором перемещения и вертикалью. Это очень важный факт, который позволяет существенно упростить решение некоторых задач. Доказательство будет приведено ниже.
Если говорить о площади этого треугольника, то она пропорциональна перемещению (дальности полета).
Теперь нарисуем второй треугольник -треугольник перемещений. Высота этого треугольника – не что иное, как дальность полета  .
.

Рисунок 3
Задача 1. С поверхности земли под углом  к горизонту выстрелила пушка. Через время
к горизонту выстрелила пушка. Через время  она поразила наземную цель. Определите дальность полета снаряда. Пушка и ее цель неподвижны и расположены на одном горизонтальном уровне. Сопротивлением воздуха пренебречь. Размеры пушки, снаряда и цели не учитывать.
она поразила наземную цель. Определите дальность полета снаряда. Пушка и ее цель неподвижны и расположены на одном горизонтальном уровне. Сопротивлением воздуха пренебречь. Размеры пушки, снаряда и цели не учитывать.
Первый способ решения. Введем систему координат, ось  направим горизонтально,
направим горизонтально,  – вертикально.
– вертикально.

Рисунок 4
Запишем уравнения по осям:
![Rendered by QuickLaTeX.com \[L=\upsilon_0 \cos{\alpha}\cdot \tau\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4d9d9fddad1a208eea5daef067967598_l3.png)
![Rendered by QuickLaTeX.com \[0=\upsilon_0 \sin{\alpha}\cdot \tau-\frac{gt^2}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-12a4a59d7606d46b76697b40077cbeae_l3.png)
Минус этого способа – два уравнения. Плюс – привычные нам оси.
Выражаем  :
:
![Rendered by QuickLaTeX.com \[\upsilon_0=\frac{g\tau}{2\sin{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8a8ad9b7eec52048a344cb4d0bc7be94_l3.png)
Подставим скорость в первое уравнение:
![Rendered by QuickLaTeX.com \[L=\frac{1}{2}g \tau^2 \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-120206d4b35eb7efe3ad1bd19709b2ee_l3.png)
Второй способ. Метод тоже аналитический. Выберем другие оси: выберем ось  , совпадающую с направлением скорости
, совпадающую с направлением скорости  , а ось
, а ось  – перпендикулярно ей.
– перпендикулярно ей.

Рисунок 5
Тогда в проекциях на эту ось  (проекция
(проекция  равна нулю):
равна нулю):
![Rendered by QuickLaTeX.com \[L\sin{\alpha}=0+\frac{1}{2}g \cos{\alpha}\tau^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-670e9c40a945a1933e8135fcc40922b0_l3.png)
![Rendered by QuickLaTeX.com \[L=\frac{1}{2}g \tau^2 \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-120206d4b35eb7efe3ad1bd19709b2ee_l3.png)
Третий способ. Нарисуем векторный треугольник перемещений.

Рисунок 6
Тогда в этом треугольнике
![Rendered by QuickLaTeX.com \[\operatorname{ctg}{\alpha}=\frac{L}{\frac{1}{2}g\tau^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9180b6261eda844e7fd53c947f99bc0b_l3.png)
![Rendered by QuickLaTeX.com \[L=\frac{1}{2}g \tau^2 \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-120206d4b35eb7efe3ad1bd19709b2ee_l3.png)
Ответ:  .
.
Задача 2. Мячик бросили со скоростью  под углом к горизонту. В полете он находился время
под углом к горизонту. В полете он находился время  . Чему равна дальность полета мячика, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
. Чему равна дальность полета мячика, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
Снова рисуем векторный треугольник перемещений.

Рисунок 7
По теореме Пифагора
![Rendered by QuickLaTeX.com \[L=\sqrt{\upsilon_0^2\tau^2-\frac{g^2\tau^4}{4}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b7e721b5493613c142657c76a267c7a1_l3.png)
Ответ:  .
.
Задача 3. С поверхности земли под углом к горизонту бросают камень со скоростью  . Какова максимальная дальность полета камня, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
. Какова максимальная дальность полета камня, если точки бросания и приземления находятся на одном горизонтальном уровне? Сопротивлением воздуха пренебречь.
По аналогии с задачей 2 запишем
![Rendered by QuickLaTeX.com \[L=\sqrt{\upsilon_0^2\tau^2-\frac{g^2\tau^4}{4}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b7e721b5493613c142657c76a267c7a1_l3.png)
Проанализируем выражение под корнем.  . Так как выражение под корнем – парабола, то
. Так как выражение под корнем – парабола, то
![Rendered by QuickLaTeX.com \[\tau_m^2=-\frac{b}{2a}=-\frac{\upsilon_0^2}{2g^2(\frac{1}{4})^2}=\frac{2\upsilon_0^2}{g^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9c079c911c38f0c991d6d586ca441de8_l3.png)
![Rendered by QuickLaTeX.com \[\tau_m=\frac{\upsilon_0}{g}\sqrt{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9770091a3b79eb45da25b034cbeb660b_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[L_{max}=\frac{\upsilon_0^2}{g}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-37b8bea6a967f962a6c3d777633aa29c_l3.png)
Ответ:  .
.
Задача 4. С обрыва под углом  к горизонту бросили камушек со скоростью
к горизонту бросили камушек со скоростью  м/с. Сколько времени камушек находился в полете, если его конечная скорость составила
м/с. Сколько времени камушек находился в полете, если его конечная скорость составила  м/с и была направлена под углом
м/с и была направлена под углом  к горизонту? Сопротивлением воздуха пренебречь.
к горизонту? Сопротивлением воздуха пренебречь.

Рисунок 8
Из того, что дано, заключаем, что конечная и начальная скорость перпендикулярны друг другу. Поэтому можно записать из треугольника скоростей
![Rendered by QuickLaTeX.com \[\upsilon_0^2+\upsilon^2=g^2t^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bb9f3489cc1ad5e6a06f99d92e6dd921_l3.png)
![Rendered by QuickLaTeX.com \[t=\frac{\sqrt{\upsilon_0^2+\upsilon^2}}{g}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-69b159e05f27730ee960717d3d148a78_l3.png)
Ответ: 
Задача 5. С обрыва под углом  к горизонту бросили камушек со скоростью
к горизонту бросили камушек со скоростью  м/с. Сколько времени камушек находился в полете, если его конечная скорость была направлена под углом
м/с. Сколько времени камушек находился в полете, если его конечная скорость была направлена под углом  к горизонту? Сопротивлением воздуха пренебречь.
к горизонту? Сопротивлением воздуха пренебречь.
Эта задача – вариант предыдущей. Из данных понимаем, что конечная и начальная скорость перпендикулярны друг другу. Мы в этой задаче не знаем конечную скорость, но знаем угол.
Поэтому можно записать из треугольника скоростей
![Rendered by QuickLaTeX.com \[\sin{\alpha}=\frac{\upsilon_0}{gt}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8878e64abcabe6ddef9a89753a8fced2_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[t=\frac{\upsilon_0}{g\sin{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8de7994bc55e2bf64839e12f59a61521_l3.png)
Ответ:  .
.
Задача 6. Камень бросили со скоростью  под углом
под углом  к горизонту. Чему равен модуль перемещения, если до места падения он летел время
к горизонту. Чему равен модуль перемещения, если до места падения он летел время  ? Сопротивление воздуха не учитывать.
? Сопротивление воздуха не учитывать.
Заметим, что нам не известно, на каком уровне упал камень: на том же самом или ниже.

Рисунок 9
Рассмотрим треугольник перемещений и применим для него теорему косинусов. Тогда
![Rendered by QuickLaTeX.com \[S=\sqrt{(\upsilon_0\tau)^2+\left(\frac{1}{2}g\tau^2\right)^2-2\upsilon_0\tau \cdot\frac{1}{2}g\tau^2\cdot \cos(90^{\circ}-\alpha)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-602e431e1d9899de1d1a8d43ca407e03_l3.png)
Это готовый ответ.
Задача 7. С крутого берега реки со скоростью  бросили камень под углом
бросили камень под углом  к горизонту. С какой скоростью он упал в воду, если до места падения он летел время
к горизонту. С какой скоростью он упал в воду, если до места падения он летел время  ? Сопротивление воздуха не учитывать.
? Сопротивление воздуха не учитывать.
В этой задаче мы также применим теорему косинусов для треугольника скоростей.

Рисунок 10
![Rendered by QuickLaTeX.com \[\upsilon=\sqrt{\upsilon_0^2+(g\tau)^2-2\upsilon_0g\tau\cos(90^{\circ}-\alpha)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2258b07c01b6c5f0f94cffaa5be84a6a_l3.png)
Ответ:  .
.
Конспект урока «Решение нестандартных задач по теме «Треугольник»
это открыть самому»
Д. Пойа
Учебный предмет: Геометрия 7 класс. Авторы: Л.С.Атанасян, В.Ф.Бутузов и др.
Форма учебной работы: классно – урочная.
Тип урока: урок комплексного применения знаний и умений
Тема: «Решение нестандартных задач по теме «Треугольник»
Цель: проверить, закрепить и совершенствовать знания учащихся по теме «Треугольник».
1) повторить и обобщить знания обучающихся по теме «Треугольник».
2) формировать умения находить равные треугольники на готовых чертежах;
1) доказывать равенство треугольников с использованием признаков равенства треугольников;
2)делать выводы о равенстве соответственных сторон и углов в равных треугольниках;
3) формировать математически грамотную речь обучающихся.
3) развивать способность применять изученный материал при решении нестандартных задач по данной теме.
1) развивать способность применять изученный материал при решении нестандартных задач по данной теме.
2) развивать логическое мышление, внимание, слуховую и зрительную память;
3) творческие способности, познавательную активность;
5) способствовать созданию условий для эффективной коммуникации, сотрудничества и работы в команде.
Дидактическое обеспечение: презентация к уроку, карточки с заданиями на повторение, с нестандартными задачами.
Методы обучения: эвристическая беседа, наглядные, практические, интерактивные.
Формы работы: групповая, парная и фронтальная.
Технологии: проблемного обучения, компьютерная и здоровьесберегающая, технология сотрудничества.
Межпредметные связи: история, биология, география, искусство.
— Здравствуйте ребята! Присаживайтесь! Меня зовут Терещенко Оксана Петровна, сегодня урок по геометрии проведу у вас я.
2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся
— Ребята, обратите внимание на слайд. Разгадайте зашифрованное слово.
— Ребята, на доске размещено дерево. Давайте создадим «Дерево знаний» в основание которого поместим слово «треугольник».
— Скажите: что мы знаем о треугольнике? (определение, элементы, свойства, признаки)
— Какие величины можем находить у фигуры? (периметр, площадь)
— Какие задания можем выполнять? (решать задачи, на доказательство, на нахождение некоторых элементов, на построение).
— Обратите внимание на слайд. В море на якоре стоит корабль. Необходимо найти расстояние от берега до корабля. Предложите варианты решения задачи. (Ответы детей).

— Ребята, а эта задача стандартная? (Нет)
— Какой будет тема нашего урока? (учитель открывает тему на доске)
— Запишите дату и тему урока на титульном листе своих тетрадей.
— Чтобы вы хотели узнать нового по этой теме? (дети говорят).
— Исходя из ваших пожеланий, можно сформулировать задачи сегодняшнего урока:
— узнать в каких источниках встречается первое упоминание о треугольнике;
— в каких сферах деятельности применяется тема «Треугольник»;
— научиться решать нестандартные задачи по теме.
— Треугольник – самая простая замкнутая прямолинейная фигура свойства, которой человек узнал еще в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни. Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. А древнегреческий ученый Платон считал, что вся «Поверхность состоит из треугольников».
3) Актуализация знаний
Интерактивный прием «Метеоритный дождь»
— Я предлагаю вам следующее задание. Используя теоретические знания по теме «Треугольник», восстановить утверждения.
1). Если в треугольнике две стороны равны, то треугольник называется ….
2). Отрезок, соединяющий вершину треугольника с … противоположной стороной, называется медианой треугольника.
3). Перпендикуляр, проведенный из вершины треугольника …, называют высотой треугольника.
4). Если три стороны одного треугольника … трем сторонам другого треугольника, то такие треугольники ….
5). Если сторона и … одного треугольника равны соответственно стороне и … другого треугольника, то такие треугольники равны.
6). Если … и угол между ними одного треугольника соответственно равны … ними другого треугольника, то такие треугольники равны.
7). В … треугольнике углы при основании равны.
8). Биссектриса … треугольника, проведенная к основанию, является медианой и высотой.
— Что мы повторили при выполнении этого задания? (Признаки равенства треугольников, понятия медианы, биссектрисы и высоты треугольника, свойства равнобедренного треугольника)
— При выполнении, каких заданий нам может пригодиться этот материал?
4) Первичное закрепление
— Давайте поработаем в парах. Найдите карточку № 1. На ней изображены треугольники. Выясните, верно, ли доказано равенство треугольников? Если нет, то исправьте ошибку.
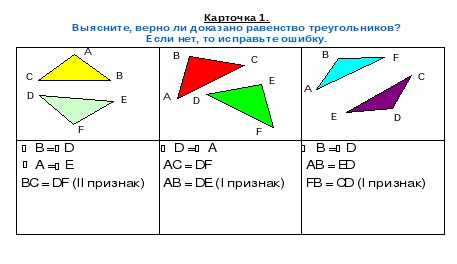
— Предлагаю проверить ваши выводы. (Ответы детей)
— Следующее задание предлагаю обсудить в группах, но прежде, ознакомьтесь с правилами:
Правила работы в группах:
1) работать должен каждый на результат;
2) один говорит, другие слушают;
3) свое несогласие высказывайте вежливо;
4) если не поняли задания, переспросите.
— Перед вами на карточке № 2 находятся чертежи. Какие точки достаточно на них соединить отрезками, чтобы получились равные треугольники? Определите, по какому признаку полученные треугольники будут равными?
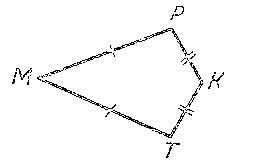
М
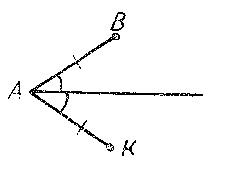
— Что мы повторили при выполнении этого задания? (Применение признаков равенства треугольников при решении задач на готовых чертежах).
— Ребята! Сейчас в своей работе вы использовали такой приём, как
доказательство. Эта форма работы вам ещё недостаточно известна. А до
VI века до н.э. с доказательством люди вообще были не знакомы. Первым учёным, который стал рассуждать, доказывать, был Фалес Милетский. Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя». Именно ему приписывают доказательство теоремы о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей.
— Вас впереди ждет серьезная работа, поэтому я предлагаю немного размяться.
Физкультминутка
— А теперь ребята встали! Плавно руки вверх подняли. В стороны, вперед, назад. Повернулись вправо, влево. Тихо сели и вновь за дело.
— Задачу Фалеса Милетского вы сможете решить, разобрав в группах, нестандартные задачи на применение признаков равенства треугольников, которые находятся на карточках. После обсуждения, вам необходимо представить устное решение. При работе в группах, помните о правилах.
5) Творческое применение и добывание знаний в новой ситуации (проблемные задания)
Интерактивный прием «Каждый учит каждого»
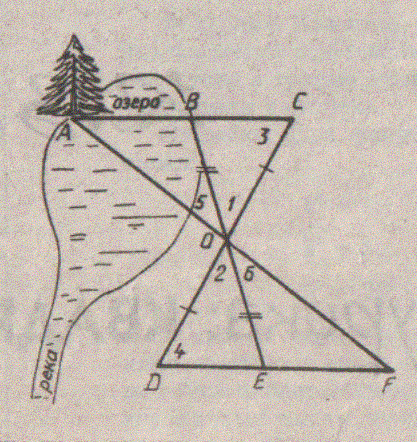
Задача 1.
При измерении длины озера отметили на местности точки А, В и С, а затем еще две точки D и К, так, чтобы точка С оказалась серединой отрезков АК и ВD. Измерив DК, получили 500 м и сделали вывод, что длина озера равна 500 м. Верно ли сделан вывод? Докажите.
— Представители групп, прокомментируйте решение.
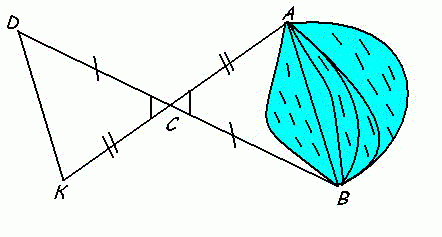
Задача 2.
Для нахождения расстояния от точки Д до дерева В на другой стороне реки отметили на местности точки О, С и А так, чтобы точка О была серединой отрезка СД и угол ДСА был бы равен углу ВДС. Наметив прямую AВ, проходящую через точку О, измерили одну из сторон треугольника ОСА и приняли ее длину за расстояние ВД. Какую сторону измерили? Докажите предположение.
— Представители групп, прокомментируйте решение.
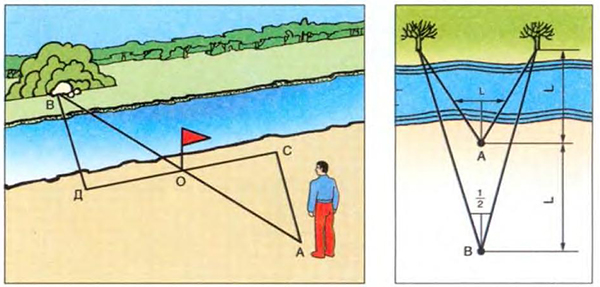
Задача 3.
На рисунке ОС=ОD, ОВ=ОЕ. Докажите, что ширина озера, отрезок АВ равен ЕF.
— Представители групп, прокомментируйте решение.
Задача 4.
От пункта А, расположенного на берегу, к пункту В, лежащему на острове, требуется провести телефонную связь. Как, не переплывая на остров, определить необходимое количество (длину) телефонного кабеля?


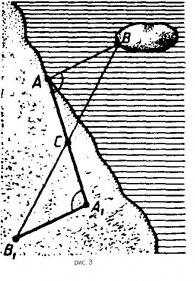
— Представители групп, прокомментируйте решение.
— Ребята, материал какой темы мы использовали при решении задач? (признаки равенства треугольников при решении нестандартных задач).
— Предлагаю вернуться к задаче Фалеса Милетского и решить ее, используя полученные знания.
— Как рассуждал ученый? (алгоритм решения)
— Сколько признаков равенства треугольников вы знаете? (три)
— В геометрии, на самом деле существует четыре признака равенства треугольников.
— Ребята, а может кто-нибудь из вас знает, как формулируется четвертый признак?
— Четвертый признак звучит так: «Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны».
— Попробуйте доказать данный признак в группах, используя условие и алгоритм. Для доказательства равенства треугольников, расположите их так, как показано на рисунке 2.
∆ АВС = ∆ А1В1С1.
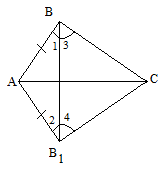 рис.2
рис.2
1. Рассмотрите треугольник ВАВ1 и докажите, что ے1 = ے2;
2. Рассмотрите треугольник ВСВ1, докажите равенство ے3 и ے4. Определите вид треугольника ВСВ1.
3. Докажите равенство треугольников АВС и
А1В1С1.
6) Рефлексия (подведение итогов занятия)
— Ребята, что нового или интересного вы узнали сегодня на уроке? Напишите на листочках и прикрепите их на «Дерево знаний».
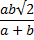 .
.