Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя
Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
О методе
При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.
- Записываем расширенную матрицу.
- Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду.

- Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.
Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.
В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!
Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.
На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .
Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.
Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!
(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)
Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!
Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .
Также очень часто определитель обозначают латинской буквой или греческой .
1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.
2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.
Начнем с определителя «два» на «два»
:ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.
Сразу рассмотрим пример:
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.
Начнем с двух простых способов
Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Теперь рассмотрим шесть нормальных способов для вычисления определителя
Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.
Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.
В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.
Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.
Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?
Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ .
Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)
Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:
1) Из матрицы знаков выписываем соответствующий знак:
2) Затем записываем сам элемент:
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:
Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).
Переходим ко второму элементу строки.
4) Из матрицы знаков выписываем соответствующий знак:
5) Затем записываем второй элемент:
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:
Ну и третий элемент первой строки. Никакой оригинальности:
Никакой оригинальности:
7) Из матрицы знаков выписываем соответствующий знак:
8) Записываем третий элемент:
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:
Оставшиеся четыре числа записываем в маленький определитель.
Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!
Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:
В следующем примере я раскрыл определитель по четвертому столбцу :
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.
Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .
БУДЬТЕ ВНИМАТЕЛЬНЫ!
Содержание
Введение…………………………………………………………………………………………….. 2
1. Постановка задачи………………………………………………………………………….. 3
2. Математические и алгоритмические основы решения задачи……………… 5
2.1 Определитель матрицы………………………………………………………………….. 5
2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6
2.3 Метод Гаусса для вычисления определителя……………………………………. 8
3. Функциональные модели и блок-схемы решения задачи…………………….. 9
Функциональные модели и блок-схемы решения задачи…………………….. 9
4. Программная реализация решения задачи………………………………………. 11
5. Пример выполнения программы…………………………………………………….. 16
Заключение………………………………………………………………………………………. 18
Список использованных источников и литературы……………………………… 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Вычислить определитель матрицы методом A исключения Гаусса.
.Приведем матрицу к диагональному виду методом Гаусса.
~.Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.Знак определяется количеством обменов строк, следовательно определитель матрицы
.2. Математические и алгоритмические основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать
или det A.Определение. Определителем квадратной матрицы
второго порядка называется число
.Определителем
квадратной матрицы порядка n,
, называется число — определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
2.2 Метод Гаусса для решения систем линейных уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
an1 x1 + an2 x2 + … + ann xn = bn
Выполним следующий алгоритм.
На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE «FLOAT:INITIAL-ELEMENT 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
Вычислим определитель методом Гаусса.
Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.
Идея метода состоит в следующем: пусть дан определитель третьего порядка
элементдолжен быть равен
,
для этого первую строку разделим на.
Получим определитель вида
(2)
Обнулим элементы, стоящие в первом
столбце, кроме первого. Для этого из
второй строки вычтем первую, умноженную
на
,
далее из третьей строки вычтем первую,
умноженную на.
Получим определитель вида
.
Обозначим его элементы буквой с, тогда
(3)
Теперь надо обнулить элемент
.
Элемент
должен быть равен
,
для этого вторую строку разделим на
.
Получим определитель вида
.
.
Обозначим его элементы буквой t, тогда
(4)
Вот мы привели определитель к треугольному
виду, теперь он равен
.
Разберем теперь это на конкретном примере.
Пример 4: Вычислить определительметодом Гаусса.
Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).
Получили
Из второй строки вычтем первую, умноженную
на 2, далее из третьей строки вычтем
первую, умноженную на 3. Получили
Получили —
§2.Матрицы Виды матриц
Определение 7: Если в матрицеmстрок иnстолбцов, то она
называетсяразмерностью mnи пишут
.
Определение 8: Если
,
то матрица называется квадратной.
Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).
Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.
Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.
Определение 12: Единичной матрицей
называется диагональная матрица, у
которой все элементы, стоящие на главной
диагонали равны единице.
Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.
Действиянад матрицами.
Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.
Пример 5:
Матрицы А и В равны, т.е.
Определение 15: Суммой (разностью)
матриц А и В называется такая матрица
С, у которой каждый элемент равен
.
Пример 6: Найти матрицу
,
если
Решение:
Cвойства сложения
А+В=В+А(переместительное)
2 0 А+О=А, где О-нулевая матрица
3 0 А+(В+С)=(А+В)+С (дистрибутивное)
4 0 А+(-А)=О, где – А противоположная матрица
(т.е. элементы имеют противоположные знаки)
Определение 16: Произведением матрицы
А на число
называется матрица, полученная из
данной умножением всех ее элементов на
число.
Пример 7:
Умножение матиц
Это действие распространяется на так
называемые согласованные матрицы.
Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.
Пример 8:
и
— согласованные
и
— несогласованные
и
несогласованные
Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.
Если матрица А имеет размерность
,
а матрица В
,
то
.
Пример 9: Умножить матрицы
Приведение определителя к треугольному виду
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами.
Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
Приемы вычисления определителей, зависящих от параметров [VMath]
§
Вспомогательная страница к разделу ОПРЕДЕЛИТЕЛЬ
Довольно часто на практике возникает необходимость вычислять определители, элементы которых зависят от параметров. Метод Гаусса оказывается не слишком приспособленным для такой задачи.
П
Пример. 2-{\color{Red} \alpha } -1 & {\color{Red} \alpha } +1
\end{array}
\right| \ .
$$
2-{\color{Red} \alpha } -1 & {\color{Red} \alpha } +1
\end{array}
\right| \ .
$$
Решение. Разложение по общей формуле даст величину этого определителя в виде полинома от $ {\color{Red} \alpha } $. С другой стороны, если для его вычисления мы попытаемся применить метод Гаусса, то на первом же шаге элементы преобразованного определителя окажутся дробно–рациональными функциями от параметра $ {\color{Red} \alpha } $. Понятно, что после приведения определителя к треугольному виду и перемножения стоящих на диагонали дробей мы, в конце концов, получим тот же ответ полиномиального вида, но сам факт, что для его получения потребовалось «выйти за пределы» множества полиномиальных функций не свидетельствует в пользу метода Гаусса… ♦
Универсальных методов вычисления подобных определителей (отличных, естественно, от определения) не существует. Успех во многом будет зависеть от искусства вычислителя. Здесь мы покажем несколько полезных приемов, которые иногда помогают.
Выделение линейных множителей
Этот прием основан на свойстве полиномиальности определителя как функции его элементов. Если элементы зависят — также полиномиально — от одного параметра, то можно попытаться определить линейные множители «полинома из ответа»: иногда из особенностей определителя очевидно при каких значениях параметра этот определитель обращается в нуль.
П
Пример. Вычислить определитель
$$\left|\begin{array}{ccccc} 1&1&1&\dots&1\\ 1&2-x&1&\dots&1\\ 1&1&3-x&\dots&1\\ \vdots& & &\ddots&\vdots\\ 1&1&1&\dots&n+1-x \end{array}\right|.$$
Решение. Ответом в этой задаче должен быть полином по $ x_{} $. Обозначим его $ F(x)_{} $ и попробуем догадаться какие корни он может иметь. Обратим внимание на структуру определителя. Если положить $ x=1_{} $, то вторая строка будет одинаковой с первой, на основании свойства
3 определителя, при этом значении $ x_{} $ будем иметь $ F(1)=0 $. Аналогично убеждаемся, что $ F(2)=0, \dots, F(n)=0 $. Итак, на основании теоремы Безу, имеем:
$$ F(x) \equiv F_1(x) (x-1)\times \dots \times (x-n) \ , $$
где через $ F_1(x) $ обозначен полином, являющийся частным от деления $ F(x)_{} $ на произведение линейных множителей. Оценим степень полинома $ F(x)_{} $. Очевидно, что при разложении определителя по общей формуле из определения, каждое слагаемое представляет произведение элементов определителя и будет полиномом по $ x_{} $. В каждом слагаемом максимально возможная степень может быть достигнута если каждый элемент в произведении будет иметь максимально возможную степень — в нашем случае равную $ 1_{} $. Отсюда с неизбежностью следует, что самым
«большим» по степени может быть только главный член определителя, т.е. произведение элементов его главной диагонали:
$$
F(x) \equiv 1\cdot (2-x)\times \dots \times (n+1-x) + \dots \ ,
$$
где многоточия скрывают все оставшиеся слагаемые полного разложения определителя и имеют степени меньшие степени выделенного слагаемого.
Аналогично убеждаемся, что $ F(2)=0, \dots, F(n)=0 $. Итак, на основании теоремы Безу, имеем:
$$ F(x) \equiv F_1(x) (x-1)\times \dots \times (x-n) \ , $$
где через $ F_1(x) $ обозначен полином, являющийся частным от деления $ F(x)_{} $ на произведение линейных множителей. Оценим степень полинома $ F(x)_{} $. Очевидно, что при разложении определителя по общей формуле из определения, каждое слагаемое представляет произведение элементов определителя и будет полиномом по $ x_{} $. В каждом слагаемом максимально возможная степень может быть достигнута если каждый элемент в произведении будет иметь максимально возможную степень — в нашем случае равную $ 1_{} $. Отсюда с неизбежностью следует, что самым
«большим» по степени может быть только главный член определителя, т.е. произведение элементов его главной диагонали:
$$
F(x) \equiv 1\cdot (2-x)\times \dots \times (n+1-x) + \dots \ ,
$$
где многоточия скрывают все оставшиеся слагаемые полного разложения определителя и имеют степени меньшие степени выделенного слагаемого. 2 \ . $$
2 \ . $$
♦
Метод рекуррентных соотношений
Основная идея метода заключается в том, что некоторые определители можно свести к вычислению определителей, имеющих аналогичный вид, но меньший порядок. Если удается установить вид этой зависимости в виде явной формулы, то эта формула — последовательным ее применением — позволит нам «спуститься» к определителям малых порядков.
П
Пример. Вычислить определитель
$$D_n=\left|\begin{array}{ccccc} a_1&x&x&\dots&x\\ x&a_2&x&\dots&x\\ x&x&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&a_n \end{array}\right|.$$
Решение. Представив элемент в правом нижнем углу в виде $ a_n=x+(a_n-x) $, можем определитель $ D_n $ разбить на сумму двух определителей:
$$D_n=\left|\begin{array}{ccccc}
a_1&x&x&\dots&x\\
x&a_2&x&\dots&x\\
x&x&a_3&\dots&x\\
\vdots&&&\ddots&\vdots\\
x&x&x&\dots&x
\end{array}\right|+\left|\begin{array}{ccccc}
a_1&x&x&\dots&0\\
x&a_2&x&\dots&0\\
x&x&a_3&\dots&0\\
\vdots&&&\ddots&\vdots\\
x&x&x&\dots&a_n-x
\end{array}\right|. $$
В первом определителе последний столбец вычтем из остальных, а второй определитель разложим по последнему столбцу:
$$D_n=x(a_1-x)(a_2-x)\times\dots\times(a_{n-1}-x)+(a_n-x)D_{n-1}\ .$$
Это и есть рекуррентное соотношение. Подставляя в него аналогичное выражение для
$ D_{n-1} $, найдем
$$\begin{array}{l}
D_n=x(a_1-x)(a_2-x)\times\dots\times(a_{n-1}-x)+\\
+x(a_1-x)(a_2-x)\times\dots\times(a_{n-2}-x)(a_n-x)+D_{n-2}(a_{n-1}-x)(a_n-x).
\end{array}$$
Повторяя то же рассуждение $ n-1 $ раз и замечая, что $ D_1=a_1=x+(a_1-x) $, найдем
$$\begin{array}{l}
D_n=x(a_1-x)(a_2-x)\dots(a_{n-1}-x)+x(a_1-x)\times\dots\times(a_{n-2}-x)(a_n-x)+\dots+\\
+x(a_2-x)\times\dots\times(a_n-x)+(a_1-x)(a_2-x)\times\dots\times(a_n-x)=\\
\displaystyle
=x(a_1-x)(a_2-x)\times\dots\times(a_n-x)\left( \frac{1}{x}+\frac{1}{a_1-x}+\dots+\frac{1}{a_n-x}\right).
\end{array}$$
$$
В первом определителе последний столбец вычтем из остальных, а второй определитель разложим по последнему столбцу:
$$D_n=x(a_1-x)(a_2-x)\times\dots\times(a_{n-1}-x)+(a_n-x)D_{n-1}\ .$$
Это и есть рекуррентное соотношение. Подставляя в него аналогичное выражение для
$ D_{n-1} $, найдем
$$\begin{array}{l}
D_n=x(a_1-x)(a_2-x)\times\dots\times(a_{n-1}-x)+\\
+x(a_1-x)(a_2-x)\times\dots\times(a_{n-2}-x)(a_n-x)+D_{n-2}(a_{n-1}-x)(a_n-x).
\end{array}$$
Повторяя то же рассуждение $ n-1 $ раз и замечая, что $ D_1=a_1=x+(a_1-x) $, найдем
$$\begin{array}{l}
D_n=x(a_1-x)(a_2-x)\dots(a_{n-1}-x)+x(a_1-x)\times\dots\times(a_{n-2}-x)(a_n-x)+\dots+\\
+x(a_2-x)\times\dots\times(a_n-x)+(a_1-x)(a_2-x)\times\dots\times(a_n-x)=\\
\displaystyle
=x(a_1-x)(a_2-x)\times\dots\times(a_n-x)\left( \frac{1}{x}+\frac{1}{a_1-x}+\dots+\frac{1}{a_n-x}\right).
\end{array}$$
♦
?
Вычислить определитель
$$\left|\begin{array}{ccccc}
a_1b_1&a_1b_2&a_1b_3&\dots&a_1b_n\\
a_1b_2&a_2b_2&a_2b_3&\dots&a_2b_n\\
a_1b_3&a_2b_3&a_3b_3&\dots&a_3b_n\\
\vdots&&&&\vdots\\
a_1b_n&a_2b_n&a_3b_n&\dots&a_nb_n
\end{array}\right|. {n-1}(a_{j+1}b_j-a_jb_{j+1}) $ .
{n-1}(a_{j+1}b_j-a_jb_{j+1}) $ .
П
Пример. Вычислить определитель
$$D_n=\left|\begin{array}{ccccc} a_1&x&x&\dots&x\\ y&a_2&x&\dots&x\\ y&y&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ y&y&y&\dots&a_n \end{array}\right|.$$
Решение начинается тем же приемом, что и в предыдущем примере:
$$ D_n= \left|\begin{array}{ccccc}
a_1&x&x&\dots&x\\
y&a_2&x&\dots&x\\
y&y&a_3&\dots&x\\
\vdots&&&\ddots&\vdots\\
y&y&y&\dots&x
\end{array}\right|+(a_n-x)D_{n-1}=x(a_1-y)(a_2-y)\times \dots \times (a_{n-1}-y)+(a_n-x)D_{n-1} \ .
$$
Можно было бы идти по проторенному пути и «разделывать» определитель $ D_{n-1} $ с использованием уже полученной формулы. Имеется, однако, более эффективный прием. Заметим, что начальный определитель симметричен относительно вхождения параметров $ x_{} $ и $ y_{} $, и эта симметрия должна проявляться в окончательном ответе. 2
\end{array}\right| \ .
$$
Но этот определитель — тот же определитель Вандермонда, только порядка меньшего исходного. Возвращая переменной $ x $ ее исходное значение, получаем рекуррентное соотношение:
$$ V(x_1,x_2,x_3,x_4)\equiv V(x_1,x_2,x_3) (x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$
Раскладываем определитель в правой части по той же схеме:
$$ V(x_1,x_2,x_3) \equiv \left|\begin{array}{ll}
1 &x_1\\
1 &x_2
\end{array}\right| (x_3-x_1)(x_3-x_2) \equiv (x_3-x_1)(x_3-x_2)(x_2-x_1) \ .
$$
Таким образом,
$$
V(x_1,x_2,x_3,x_4)=
$$
$$
=(x_2-x_1)(x_3-x_1)(x_3-x_2)(x_4-x_1)(x_4-x_2)(x_4-x_3) \ .
$$
А в общем случае получаем ответ
$$ V(x_1,\dots,x_n)= \prod_{1\le j < k \le n} (x_k-x_j)\ . $$
♦
2
\end{array}\right| \ .
$$
Но этот определитель — тот же определитель Вандермонда, только порядка меньшего исходного. Возвращая переменной $ x $ ее исходное значение, получаем рекуррентное соотношение:
$$ V(x_1,x_2,x_3,x_4)\equiv V(x_1,x_2,x_3) (x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$
Раскладываем определитель в правой части по той же схеме:
$$ V(x_1,x_2,x_3) \equiv \left|\begin{array}{ll}
1 &x_1\\
1 &x_2
\end{array}\right| (x_3-x_1)(x_3-x_2) \equiv (x_3-x_1)(x_3-x_2)(x_2-x_1) \ .
$$
Таким образом,
$$
V(x_1,x_2,x_3,x_4)=
$$
$$
=(x_2-x_1)(x_3-x_1)(x_3-x_2)(x_4-x_1)(x_4-x_2)(x_4-x_3) \ .
$$
А в общем случае получаем ответ
$$ V(x_1,\dots,x_n)= \prod_{1\le j < k \le n} (x_k-x_j)\ . $$
♦
Определитель трёхдиагональной матрицы
Более сложный пример применения метода дает задача вычисления определителя трехдиагональной матрицы, представленного в следующем виде (определитель Якоби):
$$
{\mathfrak J}_n =
\left|\begin{array}{ccccccc}
a_1 &b_1&0&0& \dots & 0 & 0\\
-c_2 &a_2&b_2&0& \dots & 0 & 0\\
0 &-c_3&a_3&b_3& \dots & 0 & 0\\
\vdots &&& &\ddots&& \vdots \\
0 &0&0&0& \dots & a_{n-1} & b_{n-1}\\
0 &0&0&0& \dots & -c_n & a_{n}
\end{array}\right|_{n\times n} \ . $$
Формальное вычисление этого определителя (в соответствии с определением) даст
полином по $ a_1,\dots,a_n,b_1,\dots,b_{n-1},c_2,\dots,c_n $, линейный
по каждой из этих переменных. Если разложить $ {\mathfrak J}_n $ по последней строке, то
получим:
$$
\begin{matrix}
{\mathfrak J}_n&=&a_n{\mathfrak J}_{n-1}+b_{n-1}c_n{\mathfrak J}_{n-2}
=a_n(a_{n-1}{\mathfrak J}_{n-2}+b_{n-2}c_{n-1}{\mathfrak J}_{n-3})+
b_{n-1}c_n{\mathfrak J}_{n-2}= \\
&=&(a_na_{n-1}+b_{n-1}c_n){\mathfrak J}_{n-2}+a_nb_{n-2}c_{n-1}{\mathfrak J}_{n-3}=
\dots
\end{matrix}
$$
$$
Формальное вычисление этого определителя (в соответствии с определением) даст
полином по $ a_1,\dots,a_n,b_1,\dots,b_{n-1},c_2,\dots,c_n $, линейный
по каждой из этих переменных. Если разложить $ {\mathfrak J}_n $ по последней строке, то
получим:
$$
\begin{matrix}
{\mathfrak J}_n&=&a_n{\mathfrak J}_{n-1}+b_{n-1}c_n{\mathfrak J}_{n-2}
=a_n(a_{n-1}{\mathfrak J}_{n-2}+b_{n-2}c_{n-1}{\mathfrak J}_{n-3})+
b_{n-1}c_n{\mathfrak J}_{n-2}= \\
&=&(a_na_{n-1}+b_{n-1}c_n){\mathfrak J}_{n-2}+a_nb_{n-2}c_{n-1}{\mathfrak J}_{n-3}=
\dots
\end{matrix}
$$
П
Пример.
$ {\mathfrak J}_2=a_1a_2+b_1c_2 $ , $ {\mathfrak J}_3=a_1a_2a_3+a_1b_2c_3+b_1c_2a_3 $, $$ {\mathfrak J}_5=a_1a_2a_3a_4a_5+b_1c_2a_3a_4a_5+a_1b_2c_3a_4a_5+a_1a_2b_3c_4a_5 +a_1a_2a_3b_4c_5+b_1c_2b_3c_4a_5+b_1c_2a_3b_4c_5+a_1b_2c_3b_4c_5 \ . $$
Т
Теорема. Значение $ {\mathfrak J}_n $ равно сумме главного члена $ a_1a_2\times \dots \times a_{n} $ и всевозможных произведений, получающихся из него заменой одной или нескольких пар соседних множителей $ a_ja_{j+1} $ на $ b_jc_{j+1} $.
Частный случай определителя Якоби — континуант: $$ Q_n(x_1,x_2,\dots,x_{n}) = \left|\begin{array}{ccccccc} x_1 &1&0&0& \dots & 0 & 0\\ -1 &x_2&1&0& \dots & 0 & 0\\ 0 &-1&x_3&1& \dots & 0 & 0\\ \vdots &&& &\ddots&&\vdots \\ 0 &0&0&0& \dots & x_{n-1} & 1\\ 0 &0&0&0& \dots & -1 & x_{n} \end{array}\right|_{n\times n} $$
Т
Теорема. Континуант равен сумме произведения $ x_1\cdot x_2 \times \dots \times x_n $ и всевозможных произведений, получающихся из него вычеркиванием пар соседних множителей (и добавлением $ 1 $ в случае четного $ n $).
П
Пример.
$$
\begin{array}{lcl}
Q_2(x_1,x_2)&=&x_1x_2+1 \ , \\
Q_3(x_1,x_2,x_3)&=& x_1x_2x_3+x_3+x_1 \ , \\
Q_6(x_1,x_2,x_3,x_4,x_5,x_6)&=&x_1x_2x_3x_4x_5x_6+\\
&&+x_3x_4x_5x_6
+x_1x_4x_5x_6+ x_1x_2x_5x_6+ x_1x_2x_3x_6+x_1x_2x_3x_4+ \\
&&+x_5x_6+x_1x_6+x_1x_2+x_1x_4+x_3x_4+x_3x_6+1 . \end{array}
$$
\end{array}
$$
Исследуем еще один частный случай определителя Якоби — при одинаковых элементах на диагоналях $$a_1=\dots=a_n = a, \ b_1=\dots=b_{n-1} = b, \ c_2=\dots=c_n = c \ ; $$ таким образом: $$ {\mathfrak J}_n= \left|\begin{array}{ccccccc} a &b&0&0& \dots & 0 & 0\\ c &a&b&0& \dots & 0 & 0\\ 0 &c&a&b& \dots & 0 & 0\\ \vdots &&& &\ddots&& \vdots \\ 0 &0&0&0& \dots & a & b\\ 0 &0&0&0& \dots & c & a \end{array}\right|_{n\times n} \ . $$ В этом случае уравнение, связывающее определители трех последовательных порядков, принимает вид: $$ {\mathfrak J}_n=a{\mathfrak J}_{n-1}-bc{\mathfrak J}_{n-2} \ .$$ Оно может быть решено применением общего приема решения линейного разностного уравнения.
П
Пример. Вычислить
$$
\left|\begin{array}{cccccc}
2 &2&0& \dots & 0 & 0\\
1 & 2 &2& \dots & 0 & 0\\
0 &1&2& \dots & 0 & 0\\
\vdots && \ddots &\ddots&& \vdots\\
0 &0&0& \dots & 2 & 2\\
0 &0&0& \dots & 1 & 2
\end{array}\right|_{n\times n} \ . n $ определителей.
n $ определителей.
Если при каждом разложении за первые слагаемые принимать числа $ a_i $, а за вторые — числа $ b_j $, то строки полученных определителей будут либо вида $ (a_i,a_i,\dots,a_i) $, либо вида $ (b_1,b_2,\dots,b_n) $. Две строки первого типа пропорциональны, а второго типа равны. При $ n>2 $ в каждый получившийся определитель попадут по крайней мере две строки одного типа, и он обратится в нуль. Таким образом, $$D_n=0 \ npu \ n>2,\ D_1=a_1+b_1,\quad D_2=\left|\begin{array}{cc} a_1&a_1\\ b_1&b_2 \end{array}\right|+\left|\begin{array}{cc} b_1&b_2\\ a_2&a_2 \end{array}\right|=(a_1-a_2)(b_2-b_1).$$
♦
?
Вычислить определитель методом представления его в виде суммы определителей
$$\left|\begin{array}{ccccc}
x_1&a_1b_2&a_1b_3&\dots&a_1b_n\\
a_2b_1&x_2&a_2b_3&\dots&a_2b_n\\
a_3b_1&a_3b_2&x_3&\dots&a_3b_n\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
a_nb_1&a_nb_2&a_nb_3&\dots&x_n
\end{array}\right|. {n-1} = \left| \begin{array}{llll}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} \\
\dots & & & \dots \\
s_{n-1}x-s_{n} & s_{n}x-s_{n+1} & \dots & s_{2n-2}x-s_{2n-1}
\end{array} \right|_{n\times n}
$$
при заданных числовых значениях $ s_0,s_1,\dots,s_{2n-1} $.
{n-1} = \left| \begin{array}{llll}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} \\
\dots & & & \dots \\
s_{n-1}x-s_{n} & s_{n}x-s_{n+1} & \dots & s_{2n-2}x-s_{2n-1}
\end{array} \right|_{n\times n}
$$
при заданных числовых значениях $ s_0,s_1,\dots,s_{2n-1} $.
Решение. Здесь каждый элемент определителя зависит от переменной $ x $. Как уже отмечалось в начале раздела, применение метода Гаусса к вычислению такого определителя неэффективно. Сформируем новый определитель порядка $ n+1 $, дополнив исходный одной строкой и одним столбцом:
$$
\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-1}x-s_{n } & s_{n}x-s_{n+1} & \dots & s_{2n-2}x-s_{2n-1}& 0 \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ . $$
Разложение нового определителя по последнему столбцу приведет к исходному определителю. С другой стороны, выполним элементарные преобразования нового определителя: прибавим последнюю строку к предпоследней:
$$
\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-1}x & s_{n}x & \dots & s_{2n-2}x& 1 \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
вынесем общий множитель:
$$
x\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
предпоследнюю строку прибавим к предыдущей:
$$
x\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-2}x & s_{n-1}x & \dots & s_{2n-3}x& 1/x \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
и снова вынесем общий множитель:
$$
x^2\left| \begin{array}{lllll}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-2} & s_{n-1} & \dots & s_{2n-3}& 1/x^2 \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ .
$$
Разложение нового определителя по последнему столбцу приведет к исходному определителю. С другой стороны, выполним элементарные преобразования нового определителя: прибавим последнюю строку к предпоследней:
$$
\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-1}x & s_{n}x & \dots & s_{2n-2}x& 1 \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
вынесем общий множитель:
$$
x\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
предпоследнюю строку прибавим к предыдущей:
$$
x\left| \begin{array}{llllc}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-2}x & s_{n-1}x & \dots & s_{2n-3}x& 1/x \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ ;
$$
и снова вынесем общий множитель:
$$
x^2\left| \begin{array}{lllll}
s_0x-s_1&s_1x-s_2&\dots& s_{n-1}x-s_{n} & 0 \\
s_1x-s_2&s_2x-s_3&\dots& s_{n}x-s_{n+1} & 0 \\
\dots & & & \dots & \dots \\
s_{n-2} & s_{n-1} & \dots & s_{2n-3}& 1/x^2 \\
s_{n-1} & s_{n} & \dots & s_{2n-2}& 1/x \\
s_n & s_{n+1} & \dots & s_{2n-1}& 1
\end{array} \right|_{(n+1)\times (n+1)} \ . {n}
\end{array} \right|_{(n+1)\times (n+1)} \ .
$$
Получившийся определитель имеет порядок больший исходного. Тем не менее, выражения его элементов стали проще с той точки зрения, что переменная оказалась «выметена на край» определителя. Если разложить теперь определитель по последнему столбцу, то коэффициентами при степенях $ x $ становятся числовые определители, для вычисления которых уже можно применять метод Гаусса.
♦
{n}
\end{array} \right|_{(n+1)\times (n+1)} \ .
$$
Получившийся определитель имеет порядок больший исходного. Тем не менее, выражения его элементов стали проще с той точки зрения, что переменная оказалась «выметена на край» определителя. Если разложить теперь определитель по последнему столбцу, то коэффициентами при степенях $ x $ становятся числовые определители, для вычисления которых уже можно применять метод Гаусса.
♦
Интерполяция
Для понимания материалов настоящего раздела рекомендуется ознакомиться с разделом «ИНТЕРПОЛЯЦИЯ». . Можно считать излагаемый ниже метод обобщением приведенного выше метода выделения линейных множителей: если матрица имеет полиномиальную зависимость от параметра (параметров), то угадать корни ее определителя — также полинома от этого параметра — удается не всегда, а вот его значения при конкретных величинах параметра (параметров) всегда можно вычислить. 8 $.
8 $.
Итак, неизвестный полином $ F(\alpha) $ имеет степень $ 8_{} $. Для его определения у нас имеется представление этого полинома в форме определителя. При этом считается, что числовые определители мы вычислять умеем. Будем искать полином $ F(\alpha) $ как решение задачи интерполяции. Зададим произвольные числовые значения для $ \alpha_{} $ — в количестве $ 9_{} $ штук (по числу коэффициентов полинома, требующих определения), вычислим соответствующие числовые определители, составим интерполяционную таблицу: $$ \begin{array}{c|cccc} \alpha & \alpha_1 & \alpha_2 & \dots & \alpha_9 \\ \hline F & \det A (\alpha_1) &\det A (\alpha_2) & \dots & \det A (\alpha_9) \end{array} $$ и вычислим $ F(\alpha) $ по одному из методов вычисления интерполяционного полинома.
На виду лежат два соображения:
1. имеет смысл в качестве чисел $ \alpha_j $ выбирать возможно минимальные по модулю;
2. 2-3\,\alpha-4 $.
2-3\,\alpha-4 $.
$$
B=\left(
\begin{array}{cccc}
1 &2 &2 &1 \\
2 &2 &2 & 0 \\
1 &2 &1 & 2 \\
1 & 2 & 2 & 1
\end{array}
\right) \ .
$$
Требуется выбрать по одному элементу из каждой строки и каждого столбца этой матрицы, так, чтобы получившаяся сумма стала максимальной:
$$
b_{1j_1}+b_{2j_2}+b_{3j_3}+b_{4j_4} \quad \mbox{ при различных } \quad \{ j_1,j_2,j_3,j_4\} \subset \{ 1,2,3,4 \} .
$$
Иными словами, после выбора какого-то кандидата в сумму, из матрицы вычеркиваются строка и столбец его содержащие, и дальнейший выбор осуществляется в оставшейся подматрице. Задача оказывается нетривиальной уже хотя бы потому, что «жадная стратегия» выбора — когда на каждом шаге выбирается максимальный из оставшихся элементов — не приводит к правильному ответу:
$$
B=\left(
\begin{array}{cc}
4 &3 \\
3 &1
\end{array}
\right) \quad \Rightarrow \quad 4+1 < 3 + 3 \ . 2} \prod_{0\le k < j \le 2n} \sin \frac{x_k-x_j}{2} \ .
$$
Рассматривается
☞
ЗДЕСЬ.
2} \prod_{0\le k < j \le 2n} \sin \frac{x_k-x_j}{2} \ .
$$
Рассматривается
☞
ЗДЕСЬ.
[1]. Микеладзе Ш.Е. Решение численных уравнений. Тбилиси.Мецниереба. 1965
algebra2/dets/special_cases.txt · Последние изменения: 2021/09/28 00:26 — au
Особенности вычисления определителя матрицы (Контрольная работа)
Содержание
Введение 2
1. Постановка задачи 3
2. Математические и алгоритмические основы решения задачи 5
2.1 Определитель матрицы 5
2.2 Метод Гаусса для решения систем линейных уравнений 6
2.3 Метод Гаусса для вычисления определителя 8
3. Функциональные модели и блок-схемы решения задачи 9
4. Программная реализация решения задачи 11
5. Пример
выполнения программы 16
Пример
выполнения программы 16
Заключение 18
Список использованных источников и литературы 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При
практическом решении системы линейных
уравнений методом Гаусса удобнее
приводить к ступенчатому виду не саму
систему уравнений, а расширенную матрицу
этой системы, выполняя элементарные
преобразования над ее строками. Последовательно получающиеся в ходе
преобразования матрицы обычно соединяют
знаком эквивалентности. Этот метод
(который также называют методом
последовательного исключения неизвестных)
известен в различных вариантах уже
более 2000 лет.
Последовательно получающиеся в ходе
преобразования матрицы обычно соединяют
знаком эквивалентности. Этот метод
(который также называют методом
последовательного исключения неизвестных)
известен в различных вариантах уже
более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Пример
1.
Вычислить определитель матрицы методом A исключения Гаусса.
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
~.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.
Знак определяется количеством обменов строк, следовательно определитель матрицы .
Пример 2.
Вычислить определитель матрицы методом A исключения Гаусса.
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
~.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.
Знак определяется количеством обменов строк, следовательно определитель матрицы .
2. Математические и алгоритмические
основы решения задачи
Математические и алгоритмические
основы решения задачи
2.1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать или det A.
Определение. Определителем квадратной матрицы
второго порядка называется число
.
Определителем
квадратной матрицы порядка n, , называется число
где — определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
2. 2
Метод Гаусса для решения систем линейных
уравнений
2
Метод Гаусса для решения систем линейных
уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
…
an1 x1 + an2 x2 + … + ann xn = bn
Выполним следующий алгоритм.
На
первом шаге найдём в первом столбце
наибольший по модулю элемент, поставим
уравнение с этим элементом на первую
строчку (обменяв две соответствующие
строки матрицы A и два соответствующих
элемента вектора B), а затем будем отнимать
это уравнение от всех остальных, чтобы
в первом столбце все элементы (кроме
первого) обратились в ноль. Например,
при прибавлении ко второй строке будем
домножать первую строку на -a21/a11, при
добавлении к третьей — на -a31/a11, и т. д.
д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
c11 x1 = d1
c22 x2 = d2
. ..
..
cnn xn = dn
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем
выполнять те же самые действия, что и
при решении системы линейных уравнений,
исключив только деление текущей строки
на a[i][i] (точнее, само деление можно
выполнять, но подразумевая, что число
выносится за знак определителя). Тогда
все операции, которые мы будем производить
с матрицей, не будут изменять величину
определителя матрицы, за исключением,
быть может, знака (мы только обмениваем
местами две строки, что меняет знак на
противоположный, или прибавляем одну
строку к другой, что не меняет величину
определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE :ELEMENT-TYPE ‘FLOAT :INITIAL-ELEMENT 0))
(SETQ T_ 1)
(SETQ DET 1)
(DO
((J 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(PROGN
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
(DO
(())
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
)
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
;МЕНЯЕМ J СТРОКУ И НАЙДЕННУЮ
(DO
((K 0))
((>= K SIZE))
(SETF (AREF R K) (AREF MATRIX J K))
(SETF (AREF MATRIX J K) (AREF MATRIX II K))
(SETF (AREF II K) (AREF R K))
(SETQ K (+ K 1))
)
)
)
;ПРЯМОЙ ХОД
;ПРИВЕДЕНИЕ К ТРЕУГОЛЬНОМУ ТИПУ
(DO
((I (+ J 1)))
((>= I SIZE))
;ЕСЛИ (AREF MATR I J)=0 ДЕЛАТЬ НИЧЕГО НЕ НАДО
(IF (/= (AREF MATRIX I J) 0)
(PROGN
(SETQ PAR (/ (AREF MATRIX I J) (AREF MATRIX J J)))
(DO
((JJ J))
((>= JJ SIZE))
(SETF (AREF MATRIX J JJ) (* (AREF MATRIX J JJ) PAR))
(SETF (AREF MATRIX I JJ) (- (AREF MATRIX I JJ) (AREF MATRIX J JJ)))
(SETF (AREF MATRIX J JJ) (/ (AREF MATRIX J JJ) PAR))
(SETQ JJ (+ JJ 1))
)
)
)
(SETQ I (+ I 1))
)
(SETQ J (+ J 1))
)
(IF (/= T_ 0)
(PROGN
(DO
((I 0))
((>= I SIZE))
(SETQ DET (* DET (AREF MATRIX I I)))
(SETQ I (+ I 1))
)
)
;ИНАЧЕ
(SETQ DET 0)
)
;ВОЗВРАЩАЕМ ОПРЕДЕЛИТЕЛЬ
DET
)
(SETQ N 0)
(SETQ
INPUT_STREAM (OPEN » D:\MATRIX. TXT» :DIRECTION :INPUT))
TXT» :DIRECTION :INPUT))
;РАЗМЕР МАТРИЦЫ
(SETF N (READ INPUT_STREAM))
(SETQ MATR (MAKE-ARRAY (LIST N N) :ELEMENT-TYPE ‘FLOAT :INITIAL-ELEMENT 0))
(SETF MATR (READ INPUT_STREAM))
(CLOSE INPUT_STREAM)
(SETQ DETERM (DETERMINANT MATR N))
;РЕЗУЛЬТАТ
(SETQ OUTPUT_STREAM (OPEN » D:\DETERMINANT.TXT» :DIRECTION :OUTPUT))
;ЗАПИСЫВАЕМ ОПРЕДЕЛИТЕЛЬ
(PRINT ‘DETERMINANT OUTPUT_STREAM)
(PRINT DETERM OUTPUT_STREAM)
;ЗАКРЫВАЕМ ФАЙЛ
(TERPRI OUTPUT_STREAM)
(CLOSE OUTPUT_STREAM)
5 Пример выполнения программы
Пример 1.
Рисунок 2 – Входные данные
Рисунок 3 – Выходные данные
Пример
2.
Рисунок 4 – Входные данные
Рисунок 5 – Выходные данные
Пример 3.
Рисунок 6 – Входные данные
Рисунок 7 – Выходные данные
Заключение
Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.
Итогом
работы можно считать созданную
функциональную модель для вычисления
определителя методом исключения Гаусса.
Созданная функциональная модель и ее
программная реализация могут служить
органической частью решения более
сложных задач.
Список использованных источников и литературы
Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.
Васильев, Ф.П. Численные методы решения экстремальных задач. [Текст] / Ф.П. Васильев – М.: Наука, 2002. C. 415.
Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.
Кнут, Д.Э. Искусство программирования. Основные алгоритмы [Текст] / Д.Э. Кнут. – М.: Вильямс, 2007. Т.1. – 712 с.
Метод Гаусса [Электронный ресурс] – Режим доступа: http://www.wikipedia.org/wiki/Метод_Гаусса.
Степанов, П.А. Функциональное программирование на языке Lisp. [Электронный ресурс] / П.А.Степанов, А.В. Бржезовский. – М.: ГУАП, 2003. С. 79.
Симанков, В.
 С. Основы функционального программирования
[Текст] / В.С. Симанков, Т.Т. Зангиев, И.В.
Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
С. Основы функционального программирования
[Текст] / В.С. Симанков, Т.Т. Зангиев, И.В.
Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.Хювенен Э. Мир Лиспа [Текст] / Э. Хювенен, Й. Сеппянен. – М.: Мир, 1990. – 460 с.
Исключение Гаусса — обзор
1.6 Централизаторы и нормализаторы
В этом разделе мы строим централизаторы и нормализаторы в алгебре Ли L. Мы также даем алгоритмы для вычисления базисов этих пространств. Для этого везде будем считать, что L имеет базис { x 1 ,…, x n } и структурные константы CijK относительно этого базиса (см. раздел 1.5).
Пусть S будет подмножеством L. Тогда множество
CLS=x∈L|xs=0foralls∈S
называется централизатором из S в L. Докажем, что C L6 S6 (
6 подалгебра L. Пусть x,y ∈ C L ( S ) и s ∈ S.
 Тогда по тождеству Якоби 0,
Тогда по тождеству Якоби 0,
, так что [ x,y ] ∈ C L ( S ) и C L ( S ) является подалгеброй 9005 L .
Легко видеть, что C L ( S ) равно централизатору K в L, , где K — подпространство, натянутое на 9000. В алгоритме построения централизатора предполагается, что вход является базисом { y 1 ,…, y t } подпространства K из L, , где
4 (1,00006) yl=yl ∑j=1nλljxj.
, то x = Σ I I I I I I I C L ( K ) если и только если [ x, y l ] = 0 для 1 ≤ l ≤ t. Это эквивалентно
∑i=1n∑j=1nλljCijkαi=0for1≤k≤nand1≤L≤t.
Отсюда следует, что мы имеем nt уравнений для n неизвестных α 1 ,… ,α n . Путем исключения Гаусса мы можем решить их; и поэтому мы находим алгоритм Централизатор для вычисления централизатора подпространства K из L.
Путем исключения Гаусса мы можем решить их; и поэтому мы находим алгоритм Централизатор для вычисления централизатора подпространства K из L.
. Имеем, что центр L является централизатором L в себе, т. е. C ( L ) — C L ( L ). Поскольку [ x,y ] = 0 для всех x ∈ C ( L ) и y ∈ L, немедленно, что C в L. Центр является ядром карты ad: L → End(L), т. е.
CL=x∈L|adx=0.
Итак, если мы изучаем структуру L через его сопряженную карту, то мы теряем «из виду» центр.
Если C ( L ) = L, , то L называется абелевым или коммутативным.
Алгоритм вычисления централизатора дает также алгоритм вычисления центра. В этом случае требование к элементу x = Σ I α I I I , принадлежащих к C ( L ) IS [ x, x j ] = 0 для 1 ≤ j ≤ n, , что сводится к
∑i=1nCijkαi=0for1≤j,k≤n.
Таким образом, мы имеем n 2 уравнений для n неизвестных α 1 ,… ,α n , которые можно решить методом исключения Гаусса. Это дает нам алгоритм Center.
Пусть V является подпространством L. Тогда множество
NLV=x∈L|xv∈Vforallv∈V
называется нормализатором V в том же
L. Как и для централизатора, мы можем доказать, что нормализатор
V в L является подалгеброй L. Если V оказывается подалгеброй L, , то V является идеалом в алгебре Ли N L ( V ).Теперь опишем алгоритм вычисления нормализатора. Пусть V будет подпространством L , натянутым на y 1 ,… ,y t , где y 1 равны y 1 . Тогда x = Σ I α I I I I — это элемент N L ( V ) Если и только если есть β лм для 1 ≤ л,м ≤ t такое, что
xyl=βl1y1+⋯+βltytforl=1,…,t.
Это составляет следующие линейные уравнения в переменных α i и β lm :
∑i=1n∑j=1nλljCijkαi−∑m=1tλmkβm=1tλmkβm=1tλmkβm т.
Снова методом исключения Гаусса мы можем решить эти уравнения. Однако значения β lm нас не интересуют, поэтому часть решения, соответствующую этим переменным, мы отбрасываем и находим базис N L ( V ) .Как следствие, у нас есть алгоритм Normalizer для вычисления нормализатора подпространства V из L.
…, x 5 } и таблица умножения
x1x4=x1,x1x5=−x2,x2x4=x2,x2x5=x1,x4x5=x3.
(Как обычно, мы перечисляем только продукты [ x i ,x j ] для i < j; , и мы опускаем те, которые равны 0.) Вычислим базис центра L. Пусть x=∑i=15αixi — произвольный элемент L. Тогда x ∈ C ( L ) тогда и только тогда, когда [ x i , x ] = 0 для 1 ≤ I ≤ 5. Так 0 = [ x 1 , x ] = α 4 , x 1 – α 5 , x 2 откуда следует, что α 4 = α 5 α 5 Тогда также [ x 2 , x ] = 0. Легко видеть, что [ x 3 , x ] = 0. От 0 = [ x 4 , x ] = α 1 , x 1 — α 2 , x 2 + α 5 , x 3 Мы вывод что α 1 = α 2 = α 5 = 0.Наконец [ x 5 , x ] = α 1 , x 1 — α 2 , x 1 — α 4 , X 3 , из которого α 1 = α = α 2 = α 4 = 0.
Так 0 = [ x 1 , x ] = α 4 , x 1 – α 5 , x 2 откуда следует, что α 4 = α 5 α 5 Тогда также [ x 2 , x ] = 0. Легко видеть, что [ x 3 , x ] = 0. От 0 = [ x 4 , x ] = α 1 , x 1 — α 2 , x 2 + α 5 , x 3 Мы вывод что α 1 = α 2 = α 5 = 0.Наконец [ x 5 , x ] = α 1 , x 1 — α 2 , x 1 — α 4 , X 3 , из которого α 1 = α = α 2 = α 4 = 0. Видно, что только α 3 могут быть ненулевыми. Отсюда следует, что C(L) натянуто на x 3 .
Видно, что только α 3 могут быть ненулевыми. Отсюда следует, что C(L) натянуто на x 3 .
Пусть V будет подпространством L , натянутым на x 1 . x 5 Пусть x=∑i=15αixi элемент L. Тогда x ∈ N L ( V ) тогда и только тогда, когда +дх5.
Первая из этих требований производит α 5 = 0 и A + α 4 = 0. Второй кипит до C — α 2 = 0 и α 1 = α 4 = 0. Следовательно, N L ( V ) натянуто на x 2 ,x 6 9 00013 9
%PDF-1.5 % 1 0 объект > эндообъект 4 0 объект (Предисловие) эндообъект 5 0 объект > эндообъект 8 0 объект (Линейные системы уравнений) эндообъект 9 0 объект > эндообъект 12 0 объект (1 Системы линейных уравнений) эндообъект 13 0 объект > эндообъект 16 0 объект (2 эквивалентные системы и элементарные операции с строками: метод исключения) эндообъект 17 0 объект > эндообъект 20 0 объект (3 решения линейных систем с использованием расширенных матриц) эндообъект 21 0 объект > эндообъект 24 0 объект (Форма 4 эшелонов и форма уменьшенного эшелона: исключение Гаусса) эндообъект 25 0 объект > эндообъект 28 0 объект (5 форм эшелона и решения для линейных систем) эндообъект 29 0 объект > эндообъект 32 0 объект (6 однородных систем линейных уравнений) эндообъект 33 0 объект > эндообъект 36 0 объект (Матрицы) эндообъект 37 0 объект > эндообъект 40 0 объект (7 матриц и матричные операции) эндообъект 41 0 объект > эндообъект 44 0 объект (8-матричное умножение) эндообъект 45 0 объект > эндообъект 48 0 объект (9 Обратная квадратная матрица) эндообъект 49 0 объект > эндообъект 52 0 объект (10 элементарных матриц) эндообъект 53 0 объект > эндообъект 56 0 объект (11 Нахождение A-1 с использованием элементарных матриц) эндообъект 57 0 объект > эндообъект 60 0 объект (Детерминанты) эндообъект 61 0 объект > эндообъект 64 0 объект (12 детерминант расширения кофактора) эндообъект 65 0 объект > эндообъект 68 0 объект (13 Оценка детерминантов путем сокращения строк) эндообъект 69 0 объект > эндообъект 72 0 объект (14 дополнительных свойств определителя) эндообъект 73 0 объект > эндообъект 76 0 объект (15 Поиск А-1 с использованием кофакторов) эндообъект 77 0 объект > эндообъект 80 0 объект (16 Применение детерминантов к системам: правило Крамера) эндообъект 81 0 объект > эндообъект 84 0 объект (Теория векторных пространств) эндообъект 85 0 объект > эндообъект 88 0 объект (17 векторных пространств и подпространств) эндообъект 89 0 объект > эндообъект 92 0 объект (18 Основ и Размер) эндообъект 93 0 объект > эндообъект 96 0 объект (Собственные значения и собственные векторы) эндообъект 97 0 объект > эндообъект 100 0 объект (19 Собственные значения квадратной матрицы) эндообъект 101 0 объект > эндообъект 104 0 объект (20 Нахождение собственных векторов и собственных пространств) эндообъект 105 0 объект > эндообъект 108 0 объект (21 Диагонализация матрицы) эндообъект 109 0 объект > эндообъект 112 0 объект (Линейные преобразования) эндообъект 113 0 объект > эндообъект 116 0 объект (22 Линейное преобразование: определение и элементарные свойства) эндообъект 117 0 объект > эндообъект 120 0 объект (23 Ядро и диапазон линейного преобразования) эндообъект 121 0 объект > эндообъект 124 0 объект (24 изоморфизма) эндообъект 125 0 объект > эндообъект 128 0 объект (Ключ ответа) эндообъект 129 0 объект > эндообъект 132 0 объект (Показатель) эндообъект 133 0 объект > эндообъект 136 0 объект > ручей xuMo0@
:Jb,q:Y+ ?akiA||%
(PDF) Определитель интервальной матрицы методом исключения Гаусса
ОПРЕДЕЛИТЕЛЬ ИНТЕРВАЛЬНОЙ МАТРИЦЫ. .. 31
.. 31
˜a22 = [3,2581,4,2419] ; ˜a23 = [−1,5,−0,5]
Сокращенная матрица: ,4,2419] [-1,5,-0,5]
[0,0] [-1,5,-0,5] [3,7,4,3]
Шаг 2: Элемент Pivot равен ˜m32 = [0,1179,0,4154] ˜a32 =˜
0; ˜a33 = [3,2256,
4,2411]. Следовательно, приведенная матрица имеет вид
˜
B=
[3.7,4.3] [−1.5,−0,5] [0,0]
[0,0] [3,2581,4,2419] [−1,5,−0,5]
[0,0] [0,0] [3,2256,4,2411]
.
Теперь определитель ˜
Bi является произведением элементов на его главной диагонали, и, следовательно, если мы вычислим определитель интервальной матрицы ˜
A прямым путем из определения, мы получим
|˜
A|=
[3,7,4,3] [−1,5,−0,5] [0,0]
[−1,5,−0,5] [3,7,4,3] [−1 .5,−0,5]
[0,0] [−1,5,−0,5] [3,7,4,3]
≈[44,178,75,822] + [−7,075,−0,925]
≈ 37.103,74.897]
Здесь мы видим, что m(|˜
A|) = m(|˜
B|) = 56. Отсюда по теореме (4) и (5)
Отсюда по теореме (4) и (5)
имеем |˜
A|≈ [38,8846,73,1159] .
Пример 7. Использование алгоритма удаления Gauss, FIE ND определитель
Интервальная матрица ~
A, где ~
a =
[4,6] [-1 ,1] [−1,1] [−1,1]
[−1,1] [−6,−4] [−1,1] [−1,1]
[−1,1] [−1,1] [9,11] [−1,1]
[−1,1] [−1,1] [−1,1] [−11,−9]
Шаг 1: Элемент Pivot равен ˜m21 = [−0.2333,0,2333]; ˜a21 =˜
0; ˜a22 =
[−6,2334, −3,7666]; ˜a23 = [−1,2334,1,2334]; ˜a24 = [−1,2334,1,2334].
Элемент Pivot равен ˜m31 = [−0,2333,0,2333]; ˜a31 =˜
0; ˜a32 = [−1,2334,1,2334];
˜a33 = [8,7666,11,2334]; ˜a34 = [−1,2334,1,2334].
Элемент Pivot равен ˜m41 = [−0,2334,0,2334]; ˜a41 =˜
0; ˜a42 = [−1,2334,1,2334];
˜a43 = [−1,2334,1,2334]; ˜a44 = [−11,2334, −8,7666]. Сокращенная матрица:
[4,6] [−1,1] [−1,1] [−1,1]
[0,0] [− 6. 2334,−3,7666] [−1,2334,1,2334] [−1,2334,1,2334]
2334,−3,7666] [−1,2334,1,2334] [−1,2334,1,2334]
[0,0] [−1,2334,1,2334] [8,7666,11,2334] [−1,2334,1,2334]
[0,0]04 [0,0] 1,2334,1,2334] [-1,2334,1,2334] [-11,2334,-8,7666]
.
Определитель матрицы методом прямого исключения Пример: Гауссовский: Autar Kaw
Наивное исключение Гаусса: Теория: Часть 1 из 2 [YOUTUBE 10:27] [СТЕНОК]
Наивное исключение Гаусса: теория: часть 2 из 2 [YOUTUBE 2:22] [СТЕНОК]
Наивный метод исключения Гаусса: Пример: Часть 1 из 2 (Выбывание вперед) [YOUTUBE 10:49] [СТЕНОК]
Наивный метод исключения Гаусса: Пример: часть 2 из 2 (обратная замена) [YOUTUBE 6:40] [СТЕНОК]
Подводные камни наивного исключения Гаусса Метод: [ЮТУБ 7:20] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: часть 1 из 3 [YOUTUBE 7:20] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: Часть 2 из 3 [YOUTUBE 7:40] [СТЕНОК]
Наивное исключение Гаусса: округление Проблемы с ошибками: Пример: часть 3 из 3 [YOUTUBE 8:07] [СТЕНОК]
Исключение по Гауссу с частичным Разворот: теория [YOUTUBE 10:39] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 1 из 3 (выбывание вперед) [YOUTUBE 7:15] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 2 из 3 (выбывание вперед) [YOUTUBE 10:08] [СТЕНОК]
Исключение по Гауссу с частичным Поворот: Пример: часть 3 из 3 (обратная замена) [YOUTUBE 6:18] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: ошибки округления Проблемы: пример: часть 1 из 3 [YOUTUBE 8:58] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: Проблемы с округлением: Пример: Часть 2 из 3 [YOUTUBE 8:17] [СТЕНОК]
Исключение по Гауссу с частичным Сводка: Проблемы с округлением: Пример: часть 3 из 3 [YOUTUBE 5:48] [СТЕНОК]
Определитель матрицы с использованием форварда Метод исключения: Фон [YOUTUBE 5:17] [СТЕНОК]
Определитель матрицы с использованием форварда Метод исключения: Пример [YOUTUBE 10:07] [СТЕНОК]
Нахождение обратной матрицы с использованием метода исключения Гаусса-Жордана и метода сопряженной матрицы | by Pollux Rey
Мы знаем, что
Если определитель матрицы коэффициентов A , det(A) , не равен нулю, то A 6 , имеет обратный. Если A имеет обратную и если мы умножим ее на приведенное выше уравнение, то получится, что
Если A имеет обратную и если мы умножим ее на приведенное выше уравнение, то получится, что
Это означает, что мы можем найти решение системы, используя обратную матрицу при условии, что B дано . В этой статье мы представим два метода его получения: Исключение Гаусса-Джордана и Метод сопряженных матриц .
Исключение Гаусса-Жордана
Выше мы видели, что когда A умножается на обратную ему матрицу, получается единичная матрица I (группа единиц на главной диагонали матрицы и с 0).{-1} . Что мы сделали ранее, так это увеличили A и B и использовали исключение Гаусса-Джордана, чтобы получить X . Это то, что мы также собираемся сделать здесь, мы сложим A и I вместе и уменьшим ряд, чтобы получить инверсию A .
Давайте сначала изложим некоторые термины.
Ранее мы упоминали, как получить определитель матрицы, но теперь мы углубимся в то, из чего состоит определитель.
Незначительный из матрицынесовершеннолетних матрицы , m_ {i, j} , это определяющий, полученный, когда вы игнорировали значения в I Th Row и j -й столбец вашей матрицы.
Кофактор матрицы
Кофактор матрицы , C_{i,j} , является минором со знаком . Это соответствует формуле
Определитель матрицы
Предположим, что у нас есть квадратная матрица
Определитель A равен
, если мы хотим расширить по i 9038 ряду. если мы хотим расширить по j -й столбец.Расширение C_{i,j} приведет к
или
. миноры и кофакторы матрицы
миноры и кофакторы матрицы
Сопряжение матрицы
Транспонирование матрицы кофакторов называется сопряжением матрицы — , то есть когда вы создаете новую матрицу, и значения этой матрицы являются кофакторами для каждого значение в старой матрице, затем вы помещаете значения первой строки результирующей матрицы в первый столбец и так далее.Математически говоря,
Как получить обратную матрицу для этого метода?
Рассмотрим произведение A и adj(A) ,
. Средний ряд в A и средняя колонна в B B
Единственный способ получить DET (A) , когда I = J .В противном случае он равен 0 (см. Разложение определителей Лапласа). Итак, если это так, то главная диагональ произведения A и adj(A) равна
, используя приведенное выше уравнение, мы получим
Итак, для этого метода, чтобы получить обратную матрицу, мы должны получить ее сопряженную и разделить ее на ее определитель.
8.5: Детерминанты и правило Крамера
В этом разделе мы сопоставляем каждой квадратной матрице \(A\) действительное число, называемое определителем матрицы \(A\), что в конечном итоге приведет нас к еще одному способу вычисления решение непротиворечивых независимых систем линейных уравнений.Определитель определяется рекурсивно, то есть мы определяем его для матриц \(1 \times 1\) и даем правило, по которому мы можем свести определители матриц \(n \times n\) к сумме определителей матриц \( (n-1) \times (n-1)\) матриц (подробнее о термине «рекурсивно» мы поговорим в разделе 9.1). Это означает, что мы сможем оценить определитель матрицы \(2 \times 2\) как сумму определителей матриц \(1 \times 1\); определитель матрицы \(3 \times 3\) как сумма определителей матриц \(2 \times 2\) и т.д.Чтобы объяснить, как мы возьмем матрицу \(n \times n\) и получим из нее \((n-1) \times (n-1)\), мы используем следующие обозначения.
Примечание \(\PageIndex{1}\)
Дана \(n \times n\) матрица \(A\), где \(n>1\), матрица \(A_{ij}\) равна \((n-1) \times (n- 1)\) матрица, образованная удалением \(i\)-й строки \(A\) и \(j\)-го столбца \(A\).
Например, используя приведенную ниже матрицу \(A\), мы найдем матрицу \(A_{23}\), удалив вторую строку и третий столбец матрицы \(A\).
\[ \begin{array}{ccc} A = \left[ \begin{array}{rr>{\columncolor[grey]{0.7}}r} 3 & 1 & 2 \\ 0 & -1 & 5 \ \ 2 & 1 & 4 \\ \end{массив} \right] & \xrightarrow{\text{Удалить \(R2\) и \(C3\)}} & A_{23} = \left[ \begin{массив }{rr} 3 & 1 \\ 2 & 1 \\ \end{массив} \right] \\ \end{массив}\]
Теперь мы можем определить определитель матрицы.
Определение \(\PageIndex{1}\): Определитель
Для заданной \(n \times n\) матрицы \(A\) определитель матрицы \(A\), обозначаемый \(\det(A)\), определяется следующим образом
- Если \(n=1\), то \(A = \left[ a_{11} \right]\) и \(\det(A) = \det\left( \left[ a_{11} \ справа] \справа) = а_{11}\).{1+n}\). Поскольку записи \(a_{11}\), \(a_{12}\) и так далее до \(a_{1n}\) составляют первую строку \(A\), мы говорим, что находим определитель \(A\) путем «расширения по первой строке».
 Позже в этом разделе мы разработаем формулу для \(\det(A)\), которая позволит нам найти его путем расширения по любой строке.
Позже в этом разделе мы разработаем формулу для \(\det(A)\), которая позволит нам найти его путем расширения по любой строке.Применяя Определение \ref{determinantdefn} к матрице \(A = \left[ \begin{array}{rr} 4 & -3 \\ 2 & 1 \\ \end{array} \right]\) мы получаем
\[ \begin{array}{rcl} \det(A) & = & \det \left( \left[ \begin{array}{rr} 4 & -3 \\ 2 & 1 \\ \end{array } \right] \right)\\ & = & 4\det\left(A_{11}\right) — (-3)\det\left(A_{12}\right)\\ & = & 4 \det ([1]) +3\det([2]) \\ & = & 4(1) + 3(2) \\ & = & 10 \\ \end{массив}\]
Для универсальной матрицы \(2 \times 2\) \(A = \left[ \begin{array}{cc} a & b \\ c & d \\ \end{array} \right]\) мы получаем
\[ \begin{array}{rcl} \det(A) & = & \det \left( \left[ \begin{array}{cc} a & b \\ c & d \\ \end{array} \right] \right)\\ & = & a \det\left(A_{11}\right) — b \det\left(A_{12}\right) \\ & = & a \det\left(\ left[ d \right]\right) — b \det\left(\left[c \right]\right) \\ & = & ad-bc \end{массив}\]
Эту формулу стоит запомнить
Примечание \(\PageIndex{1}\)
Для матрицы \(2 \times 2\),
\[ \det \left( \left[ \begin{array}{cc} a & b \\ c & d \\ \end{array} \right] \right) = ad-bc \]
Применение определения \ref{determinantdefn} к матрице \(3 \times 3\) \(A = \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-}2 \\ 0 & -1 & 5 \\ 2 & 1 & 4 \\ \end{array} \right]\) получаем
\[ \begin{array}{rcl} \det(A) & = & \det \left( \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-}2 \\ 0 & — 1 & 5 \\ 2 & 1 & 4 \\ \end{массив} \right] \right)\\ & = & 3\det\left(A_{11}\right) — 1\det\left(A_{ 12}\right) + 2\det\left(A_{13}\right) \\ & = & 3\det \left( \left[ \begin{array}{rr} -1 & 5 \\ 1 & 4 \\ \end{array} \right] \right) — \det \left( \left[ \begin{array}{rr} 0 & 5 \\ 2 & 4 \\ \end{array} \right] \right ) + 2 \det \left( \left[ \begin{array}{rr} 0 & -1 \\ 2 & 1 \\ \end{array} \right] \right) \\ & = & 3((- 1)(4) — (5)(1)) — ((0)(4)-(5)(2))+2((0)(1)-(-1)(2)) \\ & = & 3(-9)-(-10)+2(2) \\ & = & -13 \\ \end{массив} \]
Чтобы вычислить определитель матрицы \(4 \times 4\), мы должны были бы вычислить определители четырех матриц \(3 \times 3\), каждая из которых включает в себя нахождение определителей трех \(2 \times 2\) матрицы.
 Как видите, наш метод оценки определителей быстро выходит из-под контроля, и многие из вас могут потянуться за калькулятором. Существует некоторый математический аппарат, который может помочь нам в вычислении определителей, и мы представляем его здесь. Прежде чем мы сформулируем теорему, нам понадобится еще немного терминологии.
Как видите, наш метод оценки определителей быстро выходит из-под контроля, и многие из вас могут потянуться за калькулятором. Существует некоторый математический аппарат, который может помочь нам в вычислении определителей, и мы представляем его здесь. Прежде чем мы сформулируем теорему, нам понадобится еще немного терминологии.Примечание \(\PageIndex{1}\)
Пусть \(A\) — матрица \(n \times n\), а \(A_{ij}\) определено, как в определении \ref{Aijdefn}. \(ij\) из \(A\), обозначаемое \(M_{ij}\), определяется как \(M_{ij} = \det\left(A_{ij}\right)\).{1+n} \det\left(A_{1n}\right)\]
, что на языке кофакторов равно
.\[a_{11} C_{11} + a_{12}C_{12} + \ldots + a_{1n}C_{1n} \]
Теперь мы готовы сформулировать нашу основную теорему об определителях.
\(\PageIndex{1}\): Свойства определителя
Пусть \(A = \left[a_{ij}\right]_{n \times n}\). \index{определитель матрицы ! свойства} \index{matrix ! определитель! свойства}
- Определитель можно найти, разложив по любой строке.
 То есть для любого \(1 \leq k \leq n\), \[\det(A) = a_{k_1}C_{k_1} + a_{k_2}C_{k_2} + \ldots + a_{kn} C_{кн}\]
То есть для любого \(1 \leq k \leq n\), \[\det(A) = a_{k_1}C_{k_1} + a_{k_2}C_{k_2} + \ldots + a_{kn} C_{кн}\] - Если \(A’\) — матрица, полученная из \(A\) следующим образом:
- поменяв местами любые две строки, затем \(\det(A’)=-\det(A)\).
- замена строки ненулевым кратным (скажем, \(c\)) самой себе, тогда \(\det(A’)=c\det(A)\)
- замена строки самой собой и кратной другой строки, тогда \(\det(A’)=\det(A)\)
- Если \(A\) имеет две одинаковые строки или строку, состоящую из всех \(0\), то \(\det(A) = 0\).{-1}\right) = \dfrac{1}{\det(A)}\).
К сожалению, хотя мы можем легко \textit{демонстрировать} результаты теоремы \ref{determinantprops}, доказательства большинства этих свойств выходят за рамки этого текста. Мы могли бы доказать эти свойства для общих \(2 \times 2\) или даже \(3 \times 3\) матриц методом грубого перебора, но такой способ доказательства противоречит элегантности и симметричности определителя.
 Мы докажем те немногие свойства, которые сможем, после того, как разработаем еще несколько инструментов, таких как Принцип математической индукции в разделе \ref{Индукция} (для очень элегантной трактовки пройдите курс линейной алгебры.Там вы, скорее всего, увидите обращение с детерминантами, логически противоположное тому, что представлено здесь). В частности, определитель определяется как функция, которая переводит квадратную матрицу в действительное число и удовлетворяет некоторым свойствам теоремы \ref{determinantprops}. Из этой функции выводится формула для определителя.} А пока давайте продемонстрируем некоторые свойства, перечисленные в теореме \ref{determinantprops}, на матрице \(A\) ниже. (Другие будут обсуждаться в упражнениях.)
Мы докажем те немногие свойства, которые сможем, после того, как разработаем еще несколько инструментов, таких как Принцип математической индукции в разделе \ref{Индукция} (для очень элегантной трактовки пройдите курс линейной алгебры.Там вы, скорее всего, увидите обращение с детерминантами, логически противоположное тому, что представлено здесь). В частности, определитель определяется как функция, которая переводит квадратную матрицу в действительное число и удовлетворяет некоторым свойствам теоремы \ref{determinantprops}. Из этой функции выводится формула для определителя.} А пока давайте продемонстрируем некоторые свойства, перечисленные в теореме \ref{determinantprops}, на матрице \(A\) ниже. (Другие будут обсуждаться в упражнениях.)\[A = \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-} 2 \\ 0 & -1 & 5 \\ 2 & 1 & 4 \\ \end{array} \right ] \]
Мы нашли \(\det(A) = -13\) путем расширения по первой строке. Чтобы воспользоваться \(0\) во второй строке, мы используем теорему \ref{determinantprops}, чтобы найти \(\det(A) = -13\) путем расширения по этой строке.
 {i+j}\) перед минором в расширении определителя следует чередующемуся образцу.Ниже приведен шаблон для матриц \(2 \times 2\), \(3 \times 3\) и \(4 \times 4\), и он естественным образом распространяется на более высокие измерения.
{i+j}\) перед минором в расширении определителя следует чередующемуся образцу.Ниже приведен шаблон для матриц \(2 \times 2\), \(3 \times 3\) и \(4 \times 4\), и он естественным образом распространяется на более высокие измерения.\[ \begin{array}{ccc} \left[ \begin{array}{cc} + & — \\ — & + \\ \end{array} \right] & \qquad \left[ \begin{array }{ccc} + & — & + \\ — & + & — \\ + & — & + \end{array} \right] & \qquad \left[ \begin{array}{cccc} + & — & + & — \\ — & + & — & +\\ + & — & + & — \\ — & + & — & + \end{массив} \right] \end{массив} \]
Читатель, однако, предостерегается от чрезмерного толкования этих знаков.{i+j}\) в формуле; знак соответствующей записи, а также сам минор определяют конечный знак члена в разложении определителя.
Чтобы проиллюстрировать некоторые другие свойства теоремы \ref{determinantprops}, мы используем операции со строками для преобразования нашей матрицы \(3 \times 3\) \(A\) в верхнюю треугольную матрицу, отслеживая операции со строками, и пометить каждую последующую матрицу.
 \footnote{По сути, мы следуем алгоритму Гаусса-Жордана , но нас не заботит получение ведущих \(1\).}
\footnote{По сути, мы следуем алгоритму Гаусса-Жордана , но нас не заботит получение ведущих \(1\).}\[ \begin{array}{ccccc} \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-} 2 \\ 0 & -1 & 5 \\ 2 & 1 & 4 \\ \ конец {массив} \right] & \xrightarrow[\text{с \(-\frac{2}{3}R1+R3\)}]{\text{Заменить \(R3\)}} & \left[ \ begin{array}{rrr} 3 & 1 & \hphantom{-} 2 \\ 0 & -1 & 5 \\ 0 & \frac{1}{3} & \frac{8}{3} \\ \end {массив} \right] & \xrightarrow[\text{\)\frac{1}{3}R2+R3\)}]{\text{Заменить \(R3\) на}} & \left[ \begin{ array}{rrr} 3 & 1 & 2 \\ 0 & -1 & 5 \\ 0 & 0 & \frac{13}{3} \\ \end{array} \right] \\ A & & B & & C \\ \end{массив}\]
Теорема \ref{determinantprops} гарантирует нам, что \(\det(A) = \det(B) = \det(C)\), так как мы заменяем строку самой собой плюс кратное число другой строки, перемещаясь из одной матрицы в следующий.{-1} \\ \end{массив} \right] \end{массив}\]
Поскольку мы применяем наши допустимые операции со строками над \(A\), чтобы привести его к уменьшенной эшелонированной форме строк, определитель промежуточных матриц может отличаться от определителя \(A\) не более чем на \textit{ненулевое} кратное .
 Это означает, что если \(\det(A) \neq 0\), то определитель редуцированной ступенчатой формы \(A\) строки также должен быть отличен от нуля, что, согласно определению \ref{rowechelonform}, означает, что все элементы главной диагонали в сокращенной форме эшелона строк \(A\) должны быть \(1\).То есть редуцированная форма эшелона строк \(A\) есть \(I_{n}\), а \(A\) обратима. И наоборот, если \(A\) обратим, то \(A\) можно преобразовать в \(I_{n}\) с помощью операций со строками. Поскольку \(\det\left(I_{n}\right) = 1 \neq 0\), наша та же логика подразумевает \(\det(A) \neq 0\). По сути, мы установили, что определитель \textit{определяет}, является ли матрица \(A\) обратимой.\footnote{В разделе \ref{CramersRuleMatrixAdjoints} мы узнаем, что определители (в частности, кофакторы) глубоко связаны с обратным матрицы.}
Это означает, что если \(\det(A) \neq 0\), то определитель редуцированной ступенчатой формы \(A\) строки также должен быть отличен от нуля, что, согласно определению \ref{rowechelonform}, означает, что все элементы главной диагонали в сокращенной форме эшелона строк \(A\) должны быть \(1\).То есть редуцированная форма эшелона строк \(A\) есть \(I_{n}\), а \(A\) обратима. И наоборот, если \(A\) обратим, то \(A\) можно преобразовать в \(I_{n}\) с помощью операций со строками. Поскольку \(\det\left(I_{n}\right) = 1 \neq 0\), наша та же логика подразумевает \(\det(A) \neq 0\). По сути, мы установили, что определитель \textit{определяет}, является ли матрица \(A\) обратимой.\footnote{В разделе \ref{CramersRuleMatrixAdjoints} мы узнаем, что определители (в частности, кофакторы) глубоко связаны с обратным матрицы.}Стоит отметить, что когда мы впервые ввели понятие обратной матрицы, это было в контексте решения линейного матричного уравнения. По сути, мы пытались «поделить» обе части матричного уравнения \(AX = B\) на матрицу \(A\).
 Точно так же, как мы не можем разделить действительное число на \(0\), теорема \ref{determinantprops} говорит нам, что мы не можем «делить» на матрицу, \textit{детерминант} которой равен \(0\). Мы также знаем, что если матрица коэффициентов системы линейных уравнений обратима, то система непротиворечива и независима.Отсюда следует, что если определитель указанного коэффициента не равен нулю, то система непротиворечива и независима.
Точно так же, как мы не можем разделить действительное число на \(0\), теорема \ref{determinantprops} говорит нам, что мы не можем «делить» на матрицу, \textit{детерминант} которой равен \(0\). Мы также знаем, что если матрица коэффициентов системы линейных уравнений обратима, то система непротиворечива и независима.Отсюда следует, что если определитель указанного коэффициента не равен нулю, то система непротиворечива и независима.Правило Крамера и матричные сопряжения
В этом разделе мы вводим теорему, которая позволяет нам решать систему линейных уравнений только с помощью определителей. Как обычно, теорема формулируется в полной общности, используя пронумерованные неизвестные \(x_1\), \(x_2\) и т. д. вместо более привычных букв \(x\), \(y\), \(z \) и т. д. Доказательство общего случая лучше оставить курсу линейной алгебры.
\(\PageIndex{1}\): Правило Крамера
Предположим, что \(AX = B\) — матричная форма системы \(n\) линейных уравнений с \(n\) неизвестными, где \(A\) — матрица коэффициентов, \(X\) — неизвестные матрица, а \(В\) — постоянная матрица.
 Если \(\det(A) \neq 0\), то соответствующая система непротиворечива и независима, а решение для неизвестных \(x_1\), \(x_2\), \(\ldots x_{n}\) есть предоставлено:
Если \(\det(A) \neq 0\), то соответствующая система непротиворечива и независима, а решение для неизвестных \(x_1\), \(x_2\), \(\ldots x_{n}\) есть предоставлено:\[x_{j} = \dfrac{\det\left(A_{j}\right)}{\det(A)},\]
, где \(A_{j}\) — матрица \(A\), \(j\)-й столбец которой заменен константами из \(B\).
Другими словами, правило Крамера говорит нам, что мы можем найти решение для каждого неизвестного по одному, найдя отношение определителя \(A_{j}\) к определителю матрицы коэффициентов. Матрица \(A_{j}\) находится путем замены столбца в матрице коэффициентов, которая содержит коэффициенты \(x_{j}\) константами системы. Следующий пример конкретизирует этот метод.
Пример \(\PageIndex{1}\): Применение правила Крамера
Используйте правило Крамера для решения указанных неизвестных.
- Решить \(\left\{ \begin{array}{rcr} 2x_1 — 3x_2 & = & 4 \\ 5x_1 + x_2 & = & -2 \end{array} \right.\) для \(x_1\) и \(x_2\)
- Решите \(\left\{ \begin{array}{rcr} 2x — 3y + z & = & -1 \\ x-y+z & = & 1 \\ 3x-4z & = & 0 \end{array } \right.
 \) для \(z\).
\) для \(z\).
Решение
- Записав эту систему в матричной форме, мы находим \[ \begin{array}{ccc} A = \left[ \begin{array}{rr} 2 & -3 \\ 5 & 1 \\ \end{array} \right] & \qquad X = \left[ \begin{array}{r} x_1 \\ x_2 \\ \end{array} \right] & \qquad B = \left[ \begin{array}{r} 4 \\ -2 \\ \end{array} \right] \\ \end{array} \] Чтобы найти матрицу \(A_1\), мы удаляем столбец матрицы коэффициентов \(A\), который содержит коэффициенты из \(x_1\) и замените его соответствующими записями в \(B\).Точно так же мы заменяем столбец \(A\), который соответствует коэффициентам \(x_2\), с константами, чтобы сформировать матрицу \(A_2\). Это дает \[ \begin{array}{cc} A_1 = \left[ \begin{array}{rr} 4 & -3 \\ -2 & 1 \\ \end{array} \right] & \qquad A_2 = \left[ \begin{array}{rr} 2 & 4 \\ 5 & -2 \\ \end{array} \right] \\ \end{array} \] Вычисляя определители, получаем \(\det(A ) = 17\), \(\det\left(A_1\right) = -2\) и \(\det\left(A_2\right) = -24\), так что \[ \begin{array}{ куб.
 см} x_1 = \dfrac{\det\left(A_1\right)}{\det(A)} = -\dfrac{2}{17} & \qquad x_2} = \dfrac{\det\left(A_2\ right)}{\det(A)} = -\dfrac{24}{17} \\ \end{array} \] Читатель может проверить, что решением системы является \(\left(-\frac{2 }{17}, -\frac{24}{17}\right)\).
см} x_1 = \dfrac{\det\left(A_1\right)}{\det(A)} = -\dfrac{2}{17} & \qquad x_2} = \dfrac{\det\left(A_2\ right)}{\det(A)} = -\dfrac{24}{17} \\ \end{array} \] Читатель может проверить, что решением системы является \(\left(-\frac{2 }{17}, -\frac{24}{17}\right)\). - Чтобы использовать правило Крамера для нахождения \(z\), мы идентифицируем \(x_3\) как \(z\). У нас есть \[ \begin{array}{cccc} A = \left[ \begin{array}{rrr} 2 & -3 & 1 \\ 1 & -1 & 1 \\ 3 & 0 & -4 \end{ array} \right] & X = \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] & B = \left[ \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \right] & A_3 = A_{z} = \left[ \begin{array}{rrr} 2 & -3 & -1 \\ 1 & -1 & 1 \\ 3 & 0 & 0 \end{array} \right] \\ \end{array} \] Расширение как \(\det(A)\), так и \(\det\left(A_{z}\right)\) вдоль третьих строк (чтобы воспользоваться \(0\)) дает \[z = \dfrac{\det\left(A_{z}\right)}{\det(A)} = \dfrac{ -12}{-10} = \dfrac{6}{5} \] Читателю предлагается решить эту систему для \(x\) и \(y\) аналогичным образом и проверить ответ.

Наше последнее применение определителей — разработка альтернативного метода нахождения обратной матрицы.\footnote{Мы разрабатываем \textit{метод} в следующем обсуждении. Как и при обсуждении в разделе \ref{MatMethods}, когда мы разработали первый алгоритм для поиска обратных матриц, мы просим вас побаловать себя.} Давайте рассмотрим матрицу \(3 \times 3\) \(A\), которую мы так подробно изучено в разделе \ref{determinantdefnandprops}
\[A = \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-} 2 \\ 0 & -1 & 5 \\ 2 & 1 & 4 \\ \end{array} \right ]\]
С помощью различных методов мы нашли, что \(\det(A) = -13\).{-1}\), мы, по сути, решаем матричное уравнение \(AX = I_3\), где \(X = \left[ x_{ij} \right]_{3 \times 3}\) есть \( 3 \x 3\) матрица. Из-за того, как определено умножение матриц, первый столбец \(I_3\) является произведением \(A\) на первый столбец \(X\), второй столбец \(I_3\) является произведением \(A\) со вторым столбцом \(X\) и третьим столбцом \(I_3\) является произведением \(A\) с третьим столбцом \(X\).
 Другими словами, мы решаем три уравнения (читателю предлагается остановиться и хорошенько подумать).
Другими словами, мы решаем три уравнения (читателю предлагается остановиться и хорошенько подумать).\[\begin{array}{ccc} A\left[ \begin{array}{r} x_{11} \\ x_{21} \\ x_{31} \end{array} \right] = \left [ \begin{array}{r} 1 \\ 0 \\ 0 \end{массив} \right] & \qquad A\left[ \begin{array}{r} x_{12} \\ x_{22} \ \ x_{32} \end{массив} \right] = \left[ \begin{array}{r} 0 \\ 1 \\ 0 \end{массив} \right] & \qquad A\left[ \begin{ array}{r} x_{13} \\ x_{23} \\ x_{33} \end{массив} \right] = \left[ \begin{array}{r} 0 \\ 0 \\ 1 \end {массив} \right] \\ \end{массив}\]
Мы можем решить каждую из этих систем, используя правило Крамера.Ориентируясь на первую систему, имеем
\[ \begin{array}{ccc} A_1 = \left[ \begin{array}{rrr} 1 & 1 & \hphantom{-} 2 \\ 0 & -1 & 5 \\ 0 & 1 & 4 \ \ \end{array} \right] & A_2 = \left[ \begin{array}{rrr} 3 & 1 & 2 \\ 0 & 0 & 5 \\ 2 & 0 & 4 \\ \end{array} \ right] & A_3 = \left[ \begin{array}{rrr} 3 & 1 & \hphantom{-}1 \\ 0 & -1 & 0 \\ 2 & 1 & 0 \\ \end{array} \right ] \конец{массив} \]
Если мы расширим \(\det\left(A_1\right)\) по первой строке, мы получим
\[ \begin{array}{rcl} \det\left(A_1\right) & = & \det\left( \left[ \begin{array}{rr} -1 & 5 \\ 1 & 4 \\ \end{array} \right] \right) — \det\left( \left[ \begin{array}{rr} 0 & 5 \\ 0 & 4 \\ \end{array} \right] \right) + 2 \det\left( \left[ \begin{array}{rr} 0 & -1 \\ 0 & 1 \\ \end{array} \right] \right) \\ & = & \det\left( \ left[ \begin{array}{rr} -1 & 5 \\ 1 & 4 \\ \end{array} \right] \right) \end{array} \]
Удивительно, но это не что иное, как \(C_{11}\) кофактор \(A\).
 Читателю предлагается проверить это, а также утверждения о том, что \(\det\left(A_2\right) = C_{12}\) и \(\det\left(A_3\right) = C_{13}\ ).\footnote{Из солидного курса линейной алгебры вы узнаете, что свойства теоремы \ref{determinantprops} сохраняются одинаково хорошо, если слово «строка» заменить словом «столбец». В этом тексте мы не будем вдаваться в операции со столбцами, но они облегчают понимание того, что мы пытаемся сказать.} (Чтобы увидеть это, хотя это и кажется неестественным, разверните первую строку .) Правило Крамера говорит нам
Читателю предлагается проверить это, а также утверждения о том, что \(\det\left(A_2\right) = C_{12}\) и \(\det\left(A_3\right) = C_{13}\ ).\footnote{Из солидного курса линейной алгебры вы узнаете, что свойства теоремы \ref{determinantprops} сохраняются одинаково хорошо, если слово «строка» заменить словом «столбец». В этом тексте мы не будем вдаваться в операции со столбцами, но они облегчают понимание того, что мы пытаемся сказать.} (Чтобы увидеть это, хотя это и кажется неестественным, разверните первую строку .) Правило Крамера говорит нам\[\begin{array}{ccc} x_{11} = \dfrac{\det\left(A_1\right)}{\det(A)} = \dfrac{C_{11}}{\det(A )}, & x_{21} = \dfrac{\det\left(A_2\right)}{\det(A)} = \dfrac{C_{12}}{\det(A)}, & x_{31 } = \dfrac{\det\left(A_3\right)}{\det(A)} = \dfrac{C_{13}}{\det(A)} \end{массив} \]
Итак, первый столбец обратной матрицы \(X\):
\[ \left[ \begin{array}{r} x_{11} \\ x_{21} \\ x_{31} \end{массив} \right] = \left[ \begin{array}{r} \dfrac{C_{11}}{\det(A)} \\ \dfrac{C_{12}}{\det(A)} \\ \dfrac{C_{13}}{\det(A)} \ end{массив} \right] = \dfrac{1}{\det(A)} \left[ \begin{array}{r} C_{11} \\ C_{12} \\ C_{13} \end{ массив} \справа] \]
Обратите внимание на перестановку индексов, идущих от неизвестного к соответствующему кофактору \(A\).
 {-1} = \dfrac{1}{\det(A)} \left[ \begin{array}{ccc} C_{11} & C_{21} & C_{31} \\ C_ {12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \\ \end{массив} \right] = -\dfrac{1}{13} \ left[ \begin{array}{rrr} -9 & -2 & 7\\ 10 & 8 & -15 \\ 2 & -1 & -3 \\ \end{array} \right] = \left[ \begin {array}{rrr} \frac{9}{13} & \frac{2}{13} & -\frac{7}{13} \\ -\frac{10}{13} & -\frac{8 }{13} & \frac{15}{13} \\ -\frac{2}{13} & \frac{1}{13} & \frac{3}{13} \\ \end{массив} \ справа] \]
{-1} = \dfrac{1}{\det(A)} \left[ \begin{array}{ccc} C_{11} & C_{21} & C_{31} \\ C_ {12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \\ \end{массив} \right] = -\dfrac{1}{13} \ left[ \begin{array}{rrr} -9 & -2 & 7\\ 10 & 8 & -15 \\ 2 & -1 & -3 \\ \end{array} \right] = \left[ \begin {array}{rrr} \frac{9}{13} & \frac{2}{13} & -\frac{7}{13} \\ -\frac{10}{13} & -\frac{8 }{13} & \frac{15}{13} \\ -\frac{2}{13} & \frac{1}{13} & \frac{3}{13} \\ \end{массив} \ справа] \]Чтобы обобщить это на обратимые \(n \times n\) матрицы, нам понадобится другое определение и теорема.Наше определение дает специальное имя кофакторной матрице, а теорема говорит нам, как использовать ее вместе с \(\det(A)\) для нахождения обратной матрицы.
Определение \(\PageIndex{1}\): Matrix Adjoint
Пусть \(A\) — \(n \times n\) матрица, а \(C_{ij}\) обозначает \(ij\) сомножитель \(A\). -сопряженная матрица \(A\), обозначаемая \(\text{adj}(A)\), представляет собой матрицу, \(ij\)-элемент которой является \(ji\) кофактором \(A\), \(С_{дзи}\).
 Это
Это\[ \text{adj}(A) = \left[ \begin{array}{cccc} C_{11} & C_{21} & \ldots & C_{n1} \\ C_{12} & C_{22 } & \ldots & C_{n2} \\ \vdots & \vdots & & \vdots \\ C_{1n} & C_{2n} & \ldots & C_{nn} \\ \end{array} \right] \ ] \конец{определение}
Это новое обозначение значительно сокращает формулировку формулы, обратной матрице.{-1} = \dfrac{1}{ad-bc} \left[ \begin{array}{rr} d & -b \\ -c & a \\ \end{array} \right] \]
Доказательство теоремы \ref{adjointinverse}, как и многих других результатов в этом разделе, лучше оставить для курса линейной алгебры. В таком курсе вы не только получите более сложные методы доказательства, но и получите более широкую перспективу. Авторы уверяют вас, что настойчивость окупается. Если вы задержитесь на несколько семестров и пройдёте курс линейной алгебры, вы увидите, насколько хороши на самом деле все матричные вещи, несмотря на утомительные обозначения и море индексов.В рамках этого текста мы докажем несколько результатов, связанных с детерминантами, в разделе \ref{Индукция}, когда у нас будет хороший принцип математической индукции.
 А пока убедитесь, что вы разобрались в \textit{механике} матриц, и теория со временем придет.
А пока убедитесь, что вы разобрались в \textit{механике} матриц, и теория со временем придет.Авторы и авторство
- Карл Стиц, доктор философии. (Общественный колледж Лейкленда) и Джефф Зигер, доктор философии. (Общественный колледж округа Лорейн)
Gauss Jordan Исключение путем поворота
Gauss Jordan Исключение посредством поворотаСистема линейных уравнений может привести к матричной форме.Каждый уравнение становится строкой, и каждый переменная становится столбцом. Ан добавлен дополнительный столбец для справа. Система показаны линейные уравнения и результирующая матрица.
Система линейных уравнений…
3x + 2y - 4z = 3 2x + 3y + 3z = 15 5x - 3y + z = 14
становится расширенной матрицей…
х и г справа 3 2 -4 3 2 3 3 15 5 -3 1 14 Цель при решении системы уравнений состоит в том, чтобы по возможности привести расширенную матрицу к сокращенной ступенчато-строковой форме.

Существуют три элементарные операции со строками, которые можно использовать для размещения матрицы в редуцированная рядно-кулисная форма.
Каждое из требований редуцированной ступенчато-строковой матрицы может быть удовлетворено с помощью элементарной строки операции.
- Если есть строка, состоящая только из нулей, то она находится внизу матрицы.
Поменяйте местами две строки матрицы, чтобы переместить строку со всеми нулями вниз. - Первый ненулевой элемент любой строки равен единице.Этот элемент называется ведущим.
Умножить (разделить) строку на ненулевую константу, чтобы превратить первый ненулевой элемент в один. - Ведущий в любом ряду находится справа от ведущего в предыдущем ряду.
Умножить строку на ненулевую константу и добавить ее к другой строке, заменив эту строку. То Суть этой элементарной операции со строками состоит в том, чтобы превратить числа в нули. Делая числа под ведущими в ноль, он заставляет первый ненулевой элемент любой строки быть справа от ведущего предыдущего ряда.
- Все элементы выше и ниже ведущей единицы равны нулю.
Умножить строку на ненулевую константу и добавить ее к другой строке, заменив эту строку. То смысл этой элементарной операции со строками состоит в том, чтобы сделать числа равными нулю. Разница здесь что вы очищаете (обнуляете) элементы над ведущим, а не чуть ниже ведущий.
Что такое поворот?
Цель поворота — сделать элемент выше или ниже ведущего в ноль.
«Опорный элемент» или «опорный элемент» — это элемент в левой части матрицы. что вы хотите элементы выше и ниже равны нулю.
Обычно этот элемент равен единице. Если вы можете найти книгу, в которой упоминается поворот, они, как правило, сказать вам, что вы должны развернуться на один. Если ограничиться тремя элементарными рядами операций, то это верное утверждение.
Однако, если вы хотите объединить вторую и третью элементарные операции над строками, вы придумать еще одну операцию над строками (не элементарную, но все же допустимую).

- Вы можете умножить строку на ненулевую константу и добавить ее к ненулевому кратному другой строку, заменяя эту строку.
Ну и что? Если вам необходимо развернуться на одном, то вы должны иногда использовать второй элементарную операцию со строкой и разделить строку на ведущий элемент, чтобы сделать ее единицей. Деление приводит к дробям. Хотя дроби — ваши друзья, вы с меньшей вероятностью сделаете ошибку если вы их не используете.
В чем подвох? Если вы не будете ориентироваться на единицу, вы, вероятно, столкнетесь с большими числами.Большинство люди готовы работать с большими числами, чтобы избежать дробей.
Сводной процесс
Поворот работает, потому что общее кратное (не обязательно наименьшее) общее кратное) двух чисел всегда можно найти путем умножения два числа вместе. Возьмем пример, который у нас был раньше, и очистить первую колонку.
х и г справа 3 2 -4 3 2 3 3 15 5 -3 1 14 Полезные советы
- Хотя на один разворот не обязательно, но очень желательно.
 Поворот на единицу означает, что вы умножаете на 1 (что легко сделать).
Поворот на единицу означает, что вы умножаете на 1 (что легко сделать). - Поворачиваться по главной диагонали приятно, но не обязательно. Некоторым людям нравится начинать с верхнего левого угла и двигаться вниз к Нижний правый.
- Пока вы выполняете поворот только один раз для строки и столбца, столбцы, которые были очищены, останутся очищенными.
- Так как целью поворота является очистка столбца свода, выбор столбец, в котором уже есть нули, экономит время, потому что у вас нет чтобы изменить строку, содержащую ноль.
Выбор оси
- Выберите столбец с наибольшим количеством нулей.
- Использовать строку или столбец только один раз
- Повернуть на одну, если возможно
- Поворот на главной диагонали
- Никогда не поворачивайте на ноль
- Никогда не поворачивайте на правую сторону
Поскольку в первом ряду никого нет, у нас есть два варианта: Либо мы делим первую строку на три и работаем с дробями, или делаем поворот на три и получить большие числа.
 Это тот вариант, который я собираюсь использовать. я повернусь
на тройке R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.
Это тот вариант, который я собираюсь использовать. я повернусь
на тройке R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.х и г справа *3 2 -4 3 2 3 3 15 5 -3 1 14 Идея состоит в том, чтобы превратить числа в рамку (желтые) в ноль.Использование комбинированного операция строки (это не элементарная операция), это можно сделать по 3R 2 — 2R 1 → R 2 и 3R 3 — 5R 1 → R 3 .

Единственная неизменяемая строка — это строка, содержащая опорный элемент (элемент 3). Весь смысл процесса поворота состоит в том, чтобы сделать значения в прямоугольниках равными нулю. Перепишите сводную строку и очистите (обнулите) опорную колонку.
х и г справа *3 2 -4 3 0 0 Чтобы заменить значения в строке 2, каждый новый элемент получается путем умножения элемент заменяется во второй строке на 3 и вычитается в 2 раза элемент в первом строку из того же столбца, что и заменяемый элемент.

Чтобы выполнить поворот, поместите один палец на шарнир (обведен кружком). номер), и один палец на заменяемом элементе. Перемножьте эти два числа вместе. Теперь поместите один палец на цифре в рамке в той же строке, что и элемент, который вы замена и другого пальца в поворотном ряду и то же самое столбец как номер, который вы заменяете. Умножьте эти два числа вместе. Возьмите изделие с осью и вычесть произведение без опоры.
х и г справа *3 2 -4 3 2 3 3 15 5 -3 1 14 Чтобы заменить 3 в R 2 C 2 , вы должны взять 3(3) — 2(2) = 9 — 4 = 5.

Чтобы заменить 3 в R 2 C 3 , вы должны взять 3(3) — 2(-4) = 9 + 8 = 17.
Чтобы заменить 15 в R 2 C 4 , вы должны взять 3(15) — 2(3) = 45 — 6 = 39.
Чтобы заменить -3 в R 3 C 2 , вы должны взять 3(-3) — 5(2) = -9 — 10 = -19.
Чтобы заменить 1 в R 3 C 3 , вы должны взять 3(1) — 5(-4) = 3 + 20 = 23
Чтобы заменить 14 в R 3 C 4 , вы должны взять 3 (14) — 5 (3) = 42 — 15 = 27.
Вот как выглядит процесс.
х и г справа поворотный ряд, копия
3поворотный ряд, копия
2поворотный ряд, копия
-4поворотный ряд, копия
3поворотная стойка, прозрачная
03(3) — 2(2)
53(3) — 2(-4)
173(15) — 2(3)
39поворотная стойка, прозрачная
03(-3) — 5(2)
-193(1) — 5(-4)
233(14) — 5(3)
27Или, если убрать комментарии, то матрица после первого пивота выглядит так.

х и г справа 3 2 -4 3 0 5 17 39 0 -19 23 27 Пришло время повторить весь процесс.Проходим и выбираем другое место для разворота. Мы хотел бы, чтобы это было на главной диагонали, единице или имело нули в столбце. К сожалению, у нас не может быть ни того, ни другого. Но так как мы должны умножить все другие числа по оси, мы хотим, чтобы она была маленькой, поэтому мы будем поворачиваться на 5 в R 2 C 2 и убрать 2 и -19.

х и г справа 3 2 -4 3 0 *5 17 39 0 -19 23 27 Начните с копирования сводной строки (2-я строка) и очистки сводного столбца (2-я строка). столбец).Ранее очищенные столбцы останутся очищенными.
х и г справа 0 0 *5 17 39 0 0 Вот расчеты для нахождения следующего взаимодействия.
 Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.
Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.х и г справа 5(3) — 2(0)
15поворотная стойка, прозрачная
05(-4) — 2(17)
-545(3) — 2(39)
-63сводная строка, копия
0поворотный ряд, копия
5поворотный ряд, копия
17поворотный ряд, копия
39ранее очищенный
0поворотная стойка, прозрачная
05(23) + 19(17)
4385(27) + 19(39)
876И полученная матрица.

х и г справа 15 0 -54 -63 0 5 17 39 0 0 438 876 Обратите внимание, что все элементы в первой строке кратны 3 и все элементы в последней строке кратны 438.Мы разделим, чтобы уменьшить ряды.
х и г справа 5 0 -18 -21 0 5 17 39 0 0 1 2 Это дало нам дополнительное преимущество: 1 именно там, где мы хотим, чтобы оно было вращаться.
 Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите вашу ось и обведите остальные числа рамкой.
этот столбец, чтобы очистить.
Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите вашу ось и обведите остальные числа рамкой.
этот столбец, чтобы очистить.х и г справа 5 0 -18 -21 0 5 17 39 0 0 *1 2 Скопируйте вниз сводную строку и очистите сводную колонку.Ранее очищенные столбцы останется очищенным до тех пор, пока вы не выполните поворот в строке или столбце дважды.
х и г справа 0 0 0 0 0 0 *1 2 Обратите внимание, что с каждым разом нужно выполнять меньше вычислений.
 Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.
Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.х и г справа 1(5) +18(0)
5ранее очищенный
0поворотная стойка, прозрачная
01(-21) + 18(2)
15ранее очищенный
01(5) — 17(0)
5поворотная стойка, прозрачная
01(39) — 17(2)
5сводная строка, копия
0сводная строка, копия
0поворотный ряд, копия
1поворотный ряд, копия
2И полученная матрица.

х и г справа 5 0 0 15 0 5 0 5 0 0 1 2 Обратите внимание, что первая и вторая строки кратны 5, поэтому мы можем уменьшить их. ряды.
х и г справа 1 0 0 3 0 1 0 1 0 0 1 2 И окончательный ответ: x = 3, y = 1 и z = 2.
 Вы также можете написать это как
упорядоченная тройка {(3,1,2)}.
Вы также можете написать это как
упорядоченная тройка {(3,1,2)}.Надеюсь, вы заметили, что когда я работал над этим примером, я не следовал подсказкам Я дал. Это потому, что я хотел, чтобы вы увидели, что произойдет, если вы не развернетесь. на одном. Был один, на главной диагонали, в исходной матрице, и было бы лучше начать там.
Резюме
- Тщательно выбирайте поворотный элемент.
- Выбор столбца с нулями означает меньший поворот.
- Выбор единицы в качестве опорной уменьшает числа, упрощает умножение и оставляет ненулевые элементы в очищенном столбце одинаковые (менее поворотные)
- Поворот по главной диагонали означает, что вам не придется менять ряды, чтобы поместить матрицу в редуцированная рядно-кулисная форма.
- Не выполнять поворот на нуле.
- Не поворачивайте на правую сторону.
- Использовать строку или столбец только один раз
- Берем продукт с шарниром минус продукт без шарнира
Особые случаи
Если вы получили строку со всеми нулями, кроме правой части, то система не имеет решения.

- Определитель можно найти, разложив по любой строке.

 Для нахождения определителя нужно умножить все элементы на главной диагонали.
Для нахождения определителя нужно умножить все элементы на главной диагонали. С. Основы функционального программирования
[Текст] / В.С. Симанков, Т.Т. Зангиев, И.В.
Зайцев. – Краснодар: КубГТУ, 2002. – 160 с.
С. Основы функционального программирования
[Текст] / В.С. Симанков, Т.Т. Зангиев, И.В.
Зайцев. – Краснодар: КубГТУ, 2002. – 160 с. Позже в этом разделе мы разработаем формулу для \(\det(A)\), которая позволит нам найти его путем расширения по любой строке.
Позже в этом разделе мы разработаем формулу для \(\det(A)\), которая позволит нам найти его путем расширения по любой строке. Как видите, наш метод оценки определителей быстро выходит из-под контроля, и многие из вас могут потянуться за калькулятором. Существует некоторый математический аппарат, который может помочь нам в вычислении определителей, и мы представляем его здесь. Прежде чем мы сформулируем теорему, нам понадобится еще немного терминологии.
Как видите, наш метод оценки определителей быстро выходит из-под контроля, и многие из вас могут потянуться за калькулятором. Существует некоторый математический аппарат, который может помочь нам в вычислении определителей, и мы представляем его здесь. Прежде чем мы сформулируем теорему, нам понадобится еще немного терминологии. То есть для любого \(1 \leq k \leq n\), \[\det(A) = a_{k_1}C_{k_1} + a_{k_2}C_{k_2} + \ldots + a_{kn} C_{кн}\]
То есть для любого \(1 \leq k \leq n\), \[\det(A) = a_{k_1}C_{k_1} + a_{k_2}C_{k_2} + \ldots + a_{kn} C_{кн}\] Мы докажем те немногие свойства, которые сможем, после того, как разработаем еще несколько инструментов, таких как Принцип математической индукции в разделе \ref{Индукция} (для очень элегантной трактовки пройдите курс линейной алгебры.Там вы, скорее всего, увидите обращение с детерминантами, логически противоположное тому, что представлено здесь). В частности, определитель определяется как функция, которая переводит квадратную матрицу в действительное число и удовлетворяет некоторым свойствам теоремы \ref{determinantprops}. Из этой функции выводится формула для определителя.} А пока давайте продемонстрируем некоторые свойства, перечисленные в теореме \ref{determinantprops}, на матрице \(A\) ниже. (Другие будут обсуждаться в упражнениях.)
Мы докажем те немногие свойства, которые сможем, после того, как разработаем еще несколько инструментов, таких как Принцип математической индукции в разделе \ref{Индукция} (для очень элегантной трактовки пройдите курс линейной алгебры.Там вы, скорее всего, увидите обращение с детерминантами, логически противоположное тому, что представлено здесь). В частности, определитель определяется как функция, которая переводит квадратную матрицу в действительное число и удовлетворяет некоторым свойствам теоремы \ref{determinantprops}. Из этой функции выводится формула для определителя.} А пока давайте продемонстрируем некоторые свойства, перечисленные в теореме \ref{determinantprops}, на матрице \(A\) ниже. (Другие будут обсуждаться в упражнениях.) {i+j}\) перед минором в расширении определителя следует чередующемуся образцу.Ниже приведен шаблон для матриц \(2 \times 2\), \(3 \times 3\) и \(4 \times 4\), и он естественным образом распространяется на более высокие измерения.
{i+j}\) перед минором в расширении определителя следует чередующемуся образцу.Ниже приведен шаблон для матриц \(2 \times 2\), \(3 \times 3\) и \(4 \times 4\), и он естественным образом распространяется на более высокие измерения. \footnote{По сути, мы следуем алгоритму Гаусса-Жордана , но нас не заботит получение ведущих \(1\).}
\footnote{По сути, мы следуем алгоритму Гаусса-Жордана , но нас не заботит получение ведущих \(1\).} Это означает, что если \(\det(A) \neq 0\), то определитель редуцированной ступенчатой формы \(A\) строки также должен быть отличен от нуля, что, согласно определению \ref{rowechelonform}, означает, что все элементы главной диагонали в сокращенной форме эшелона строк \(A\) должны быть \(1\).То есть редуцированная форма эшелона строк \(A\) есть \(I_{n}\), а \(A\) обратима. И наоборот, если \(A\) обратим, то \(A\) можно преобразовать в \(I_{n}\) с помощью операций со строками. Поскольку \(\det\left(I_{n}\right) = 1 \neq 0\), наша та же логика подразумевает \(\det(A) \neq 0\). По сути, мы установили, что определитель \textit{определяет}, является ли матрица \(A\) обратимой.\footnote{В разделе \ref{CramersRuleMatrixAdjoints} мы узнаем, что определители (в частности, кофакторы) глубоко связаны с обратным матрицы.}
Это означает, что если \(\det(A) \neq 0\), то определитель редуцированной ступенчатой формы \(A\) строки также должен быть отличен от нуля, что, согласно определению \ref{rowechelonform}, означает, что все элементы главной диагонали в сокращенной форме эшелона строк \(A\) должны быть \(1\).То есть редуцированная форма эшелона строк \(A\) есть \(I_{n}\), а \(A\) обратима. И наоборот, если \(A\) обратим, то \(A\) можно преобразовать в \(I_{n}\) с помощью операций со строками. Поскольку \(\det\left(I_{n}\right) = 1 \neq 0\), наша та же логика подразумевает \(\det(A) \neq 0\). По сути, мы установили, что определитель \textit{определяет}, является ли матрица \(A\) обратимой.\footnote{В разделе \ref{CramersRuleMatrixAdjoints} мы узнаем, что определители (в частности, кофакторы) глубоко связаны с обратным матрицы.} Точно так же, как мы не можем разделить действительное число на \(0\), теорема \ref{determinantprops} говорит нам, что мы не можем «делить» на матрицу, \textit{детерминант} которой равен \(0\). Мы также знаем, что если матрица коэффициентов системы линейных уравнений обратима, то система непротиворечива и независима.Отсюда следует, что если определитель указанного коэффициента не равен нулю, то система непротиворечива и независима.
Точно так же, как мы не можем разделить действительное число на \(0\), теорема \ref{determinantprops} говорит нам, что мы не можем «делить» на матрицу, \textit{детерминант} которой равен \(0\). Мы также знаем, что если матрица коэффициентов системы линейных уравнений обратима, то система непротиворечива и независима.Отсюда следует, что если определитель указанного коэффициента не равен нулю, то система непротиворечива и независима. Если \(\det(A) \neq 0\), то соответствующая система непротиворечива и независима, а решение для неизвестных \(x_1\), \(x_2\), \(\ldots x_{n}\) есть предоставлено:
Если \(\det(A) \neq 0\), то соответствующая система непротиворечива и независима, а решение для неизвестных \(x_1\), \(x_2\), \(\ldots x_{n}\) есть предоставлено: \) для \(z\).
\) для \(z\).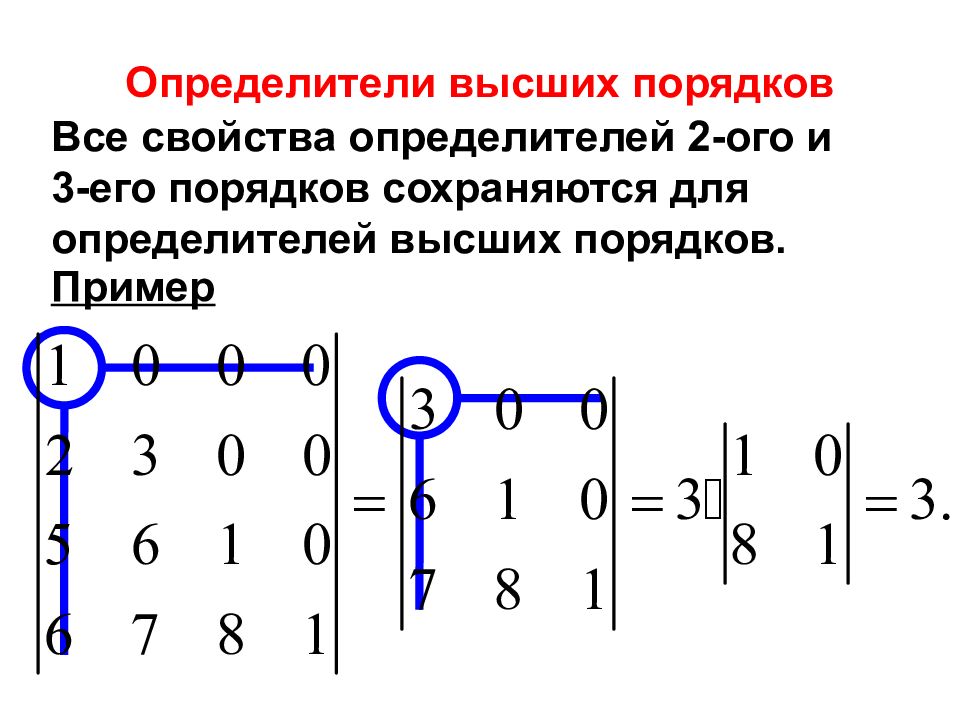 см} x_1 = \dfrac{\det\left(A_1\right)}{\det(A)} = -\dfrac{2}{17} & \qquad x_2} = \dfrac{\det\left(A_2\ right)}{\det(A)} = -\dfrac{24}{17} \\ \end{array} \] Читатель может проверить, что решением системы является \(\left(-\frac{2 }{17}, -\frac{24}{17}\right)\).
см} x_1 = \dfrac{\det\left(A_1\right)}{\det(A)} = -\dfrac{2}{17} & \qquad x_2} = \dfrac{\det\left(A_2\ right)}{\det(A)} = -\dfrac{24}{17} \\ \end{array} \] Читатель может проверить, что решением системы является \(\left(-\frac{2 }{17}, -\frac{24}{17}\right)\).
 Другими словами, мы решаем три уравнения (читателю предлагается остановиться и хорошенько подумать).
Другими словами, мы решаем три уравнения (читателю предлагается остановиться и хорошенько подумать). Читателю предлагается проверить это, а также утверждения о том, что \(\det\left(A_2\right) = C_{12}\) и \(\det\left(A_3\right) = C_{13}\ ).\footnote{Из солидного курса линейной алгебры вы узнаете, что свойства теоремы \ref{determinantprops} сохраняются одинаково хорошо, если слово «строка» заменить словом «столбец». В этом тексте мы не будем вдаваться в операции со столбцами, но они облегчают понимание того, что мы пытаемся сказать.} (Чтобы увидеть это, хотя это и кажется неестественным, разверните первую строку .) Правило Крамера говорит нам
Читателю предлагается проверить это, а также утверждения о том, что \(\det\left(A_2\right) = C_{12}\) и \(\det\left(A_3\right) = C_{13}\ ).\footnote{Из солидного курса линейной алгебры вы узнаете, что свойства теоремы \ref{determinantprops} сохраняются одинаково хорошо, если слово «строка» заменить словом «столбец». В этом тексте мы не будем вдаваться в операции со столбцами, но они облегчают понимание того, что мы пытаемся сказать.} (Чтобы увидеть это, хотя это и кажется неестественным, разверните первую строку .) Правило Крамера говорит нам {-1} = \dfrac{1}{\det(A)} \left[ \begin{array}{ccc} C_{11} & C_{21} & C_{31} \\ C_ {12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \\ \end{массив} \right] = -\dfrac{1}{13} \ left[ \begin{array}{rrr} -9 & -2 & 7\\ 10 & 8 & -15 \\ 2 & -1 & -3 \\ \end{array} \right] = \left[ \begin {array}{rrr} \frac{9}{13} & \frac{2}{13} & -\frac{7}{13} \\ -\frac{10}{13} & -\frac{8 }{13} & \frac{15}{13} \\ -\frac{2}{13} & \frac{1}{13} & \frac{3}{13} \\ \end{массив} \ справа] \]
{-1} = \dfrac{1}{\det(A)} \left[ \begin{array}{ccc} C_{11} & C_{21} & C_{31} \\ C_ {12} & C_{22} & C_{32} \\ C_{13} & C_{23} & C_{33} \\ \end{массив} \right] = -\dfrac{1}{13} \ left[ \begin{array}{rrr} -9 & -2 & 7\\ 10 & 8 & -15 \\ 2 & -1 & -3 \\ \end{array} \right] = \left[ \begin {array}{rrr} \frac{9}{13} & \frac{2}{13} & -\frac{7}{13} \\ -\frac{10}{13} & -\frac{8 }{13} & \frac{15}{13} \\ -\frac{2}{13} & \frac{1}{13} & \frac{3}{13} \\ \end{массив} \ справа] \] Это
Это А пока убедитесь, что вы разобрались в \textit{механике} матриц, и теория со временем придет.
А пока убедитесь, что вы разобрались в \textit{механике} матриц, и теория со временем придет.


 Поворот на единицу означает, что вы умножаете на 1 (что легко сделать).
Поворот на единицу означает, что вы умножаете на 1 (что легко сделать). Это тот вариант, который я собираюсь использовать. я повернусь
на тройке R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.
Это тот вариант, который я собираюсь использовать. я повернусь
на тройке R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.

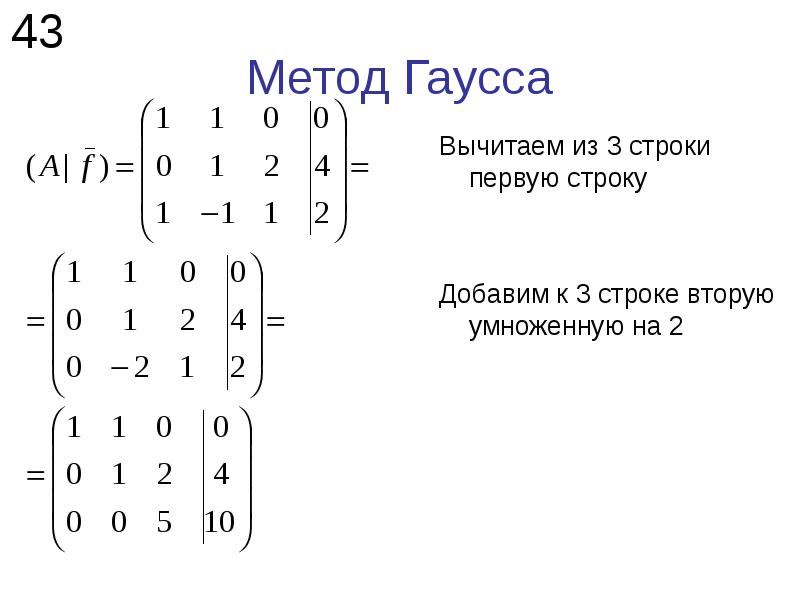


 Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.
Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.
 Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите вашу ось и обведите остальные числа рамкой.
этот столбец, чтобы очистить.
Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите вашу ось и обведите остальные числа рамкой.
этот столбец, чтобы очистить. Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.
Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.
 Вы также можете написать это как
упорядоченная тройка {(3,1,2)}.
Вы также можете написать это как
упорядоченная тройка {(3,1,2)}.