Вычисление площадей фигур, ограниченных заданными линиями
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃаb f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃаb f(x)dx.
Таким образом, S(G) = ʃаb f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃаb f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х3; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃаb f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х3,
{у = 1.
Таким образом, имеем х1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = SDACE – SDABE = ʃ12 x3 dx – 1 = x4/4|12 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃа
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫49 (√x – 2)dx = ∫49 √x dx –∫49 2dx = 2/3 x√х|49 – 2х|49 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у min = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х3 – 4х = 0 или х(х2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х1 = 0, х2 = 2, х3 = -2 (не подходит, т.к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ02 (x3 – 4x)dx|.
Имеем: ʃ02 (x3 – 4х)dx =(x4/4 – 4х2/2)|02= -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у0 = 2 · 22 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Гу = 2х2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х 2 – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:
xb = -b/2a;
xb = 2/4 = 1/2;
yb = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: SОAВD = SOABC – SADBC.
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле SADBC = 1/2 · DC · BC. Таким образом,
SADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
Далее:
SOABC = ʃ02(2x2 – 2х + 1)dx = (2x3/3 – 2х2/2 + х)|02 = 10/3 (кв. ед.).
Окончательно получим: SОAВ
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Вычислить площадь фигуры ПРИМЕРЫ
Вычислить площадь фигуры, ограниченной линиями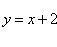
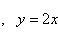
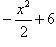 .
.Решение.
Находим точки пересечения заданных линий. Для этого решаем систему уравнений:
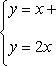
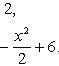
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
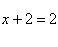
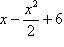 или
или
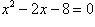
Находим: x1 = -2, x2 = 4.
Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
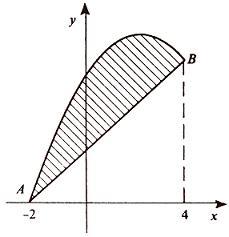
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
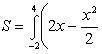
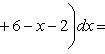
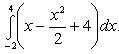
По формуле Ньютона-Лейбница находим:
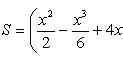
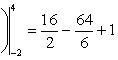
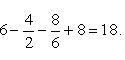
Найти
площадь области, ограниченной эллипсом 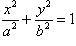 .
.
Решение.
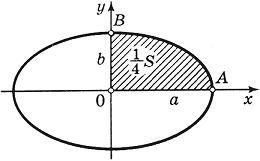
Из
уравнения эллипса для I
квадранта имеем 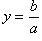
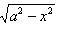 .
Отсюда
по формуле
.
Отсюда
по формуле 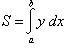 получаем
получаем
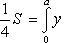
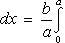
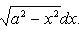
Применим подстановку x = a sin t, dx = a cos t dt. Новые пределы интегрирования t = α и t = β определяются из уравнений 0 = a sin t, a = a sin t. Можно положить α = 0 и β = π/2.
Находим одну четвертую искомой площади
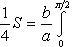
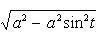
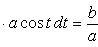
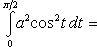
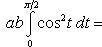
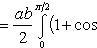
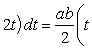
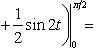
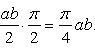
Отсюда S = πab.
Найти площадь фигуры, ограниченной линиями y = —x2 + x + 4 и y = —x + 1.
Решение.
Найдем точки пересечения линий y = —x2 + x + 4, y = —x + 1, приравнивая ординаты линий: —x2 + x + 4 = —x + 1 или x2 — 2x — 3 = 0. Находим корни x1 = -1, x2 = 3 и соответствующие им ординаты y1 = 2, y2 = -2.
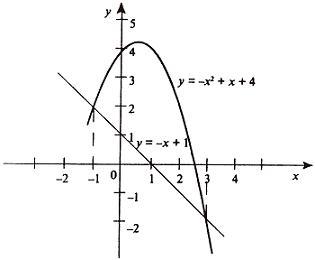
По формуле площади фигуры получаем
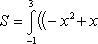
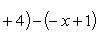
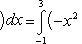
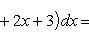
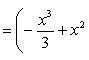
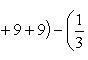
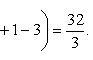
Определить площадь, ограниченную параболой y = x2 + 1 и прямой x + y = 3.
Решение.
Решая систему уравнений
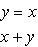
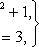
находим абсциссы точек пересечения x1 = -2 и x2 = 1.
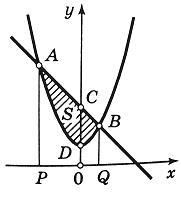
Полагая y2 =
3 — x и y1 = x2 +
1, на основании формулы 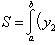
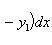 получаем
получаем
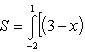
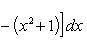
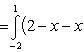
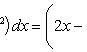
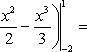
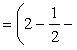
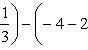
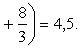
Вычислить площадь, заключенную внутри лемнискаты Бернулли r2 = a2cos 2φ.
Решение.
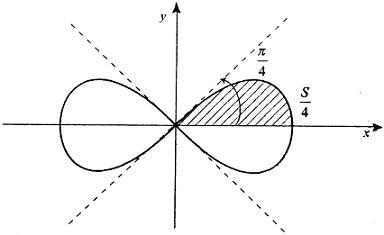
В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ1 = ʅ и φ2 = ʆ, выразится интегралом
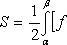
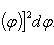
В силу симметрии кривой определяем сначала одну четвертую искомой площади
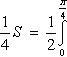
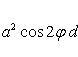
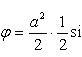
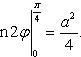
Следовательно, вся площадь равна S = a2.
Вычислить длину дуги астроиды x2/3 + y2/3 = a2/3.
Решение.
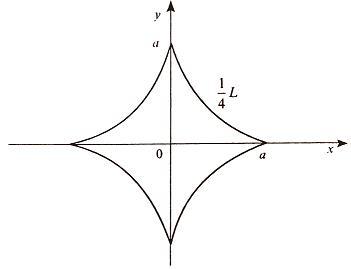
Запишем уравнение астроиды в виде
(x1/3)2 + (y1/3)2 = (a1/3)2.
Положим x1/3 = a1/3cos t, y1/3 = a1/3sin t.
Отсюда получаем параметрические уравнения астроиды
x = a cos3t, y = a sin3t, (*)
где 0 ≤ t ≤ 2π.
Ввиду симметрии кривой (*) достаточно найти одну четвертую часть длины дуги L, соответствующую изменению параметра t от 0 до π/2.
Получаем
dx = -3a cos2t sin t dt, dy = 3a sin2t cos t dt.
Отсюда находим
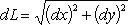
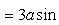
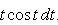
Интегрируя полученное выражение в пределах от 0 до π/2, получаем
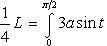
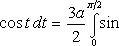
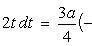
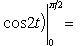
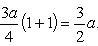
Отсюда L = 6a.
Найти площадь, ограниченную спиралью Архимеда r = aφ и двумя радиусами-векторами, которые соответствуют полярным углам φ1и φ2 (φ1 < φ2).
Решение.
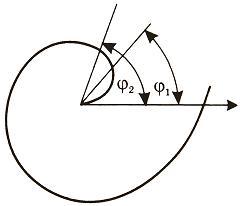
Площадь,
ограниченная кривой r = f(φ)
вычисляется по формуле 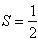
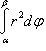 ,
где α и β —
пределы изменения полярного угла.
,
где α и β —
пределы изменения полярного угла.
Таким образом, получаем
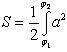
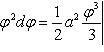
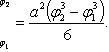 (*)
(*)
Из (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ1 = 0; φ2 = 2π):
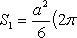
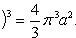
Аналогичным образом находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда (φ1 = 2π; φ2 = 4π):
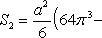
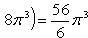
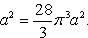
Искомая площадь равна разности этих площадей
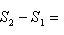
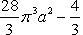
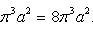
Вычислить объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной параболами y = x2 и x = y2.
Решение.
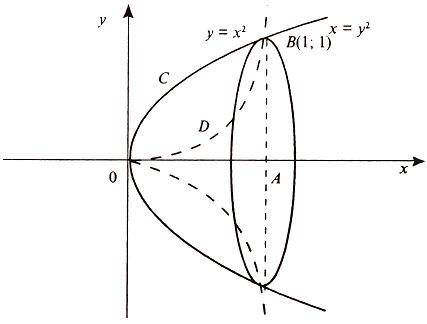
Решим систему уравнений
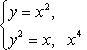
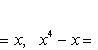
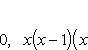
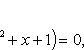
и получим x1 = 0, x2 = 1, y1 = 0, y2 = 1, откуда точки пересечения кривых O(0; 0), B(1; 1). Как видно на рисунке, искомый объем тела вращения равен разности двух объемов, образованных вращением вокруг оси Ox криволинейных трапеций OCBA и ODBA:
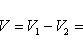
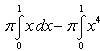
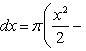
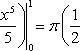
Вычислить площадь, ограниченную осью Ox и синусоидой y = sin x на отрезках: а) [0, π]; б) [0, 2π].
Решение.
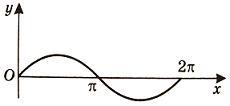
а)
На отрезке [0, π]
функция sin x сохраняет
знак, и поэтому по формуле 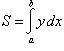 ,
полагая y =
sin x,
находим
,
полагая y =
sin x,
находим
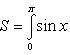
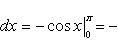
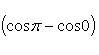
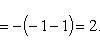
б) На отрезке [0, 2π], функция sin x меняет знак. Для корректного решения задачи, необходимо отрезок [0, 2π] разделить на два [0, π] и [π, 2π], в каждом из которых функция сохраняет знак.
По правилу знаков, на отрезке [π, 2π] площадь берется со знаком минус.
В итоге, искомая площадь равна
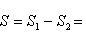
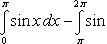
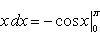
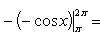
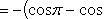

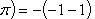
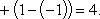
Определить
объем тела, ограниченного поверхностью,
полученной от вращения эллипса 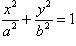 вокруг
большой оси a.
вокруг
большой оси a.
Решение.
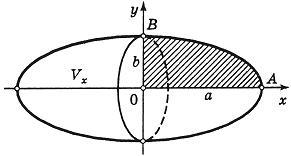
Учитывая, что эллипс симметричен относительно осей координат, то достаточно найти объем, образованный вращением вокруг оси Oxплощади OAB, равной одной четверти площади эллипса, и полученный результат удвоить.
Обозначим
объем тела вращения через Vx;
тогда на основании формулы 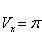
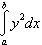 имеем
имеем 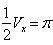
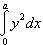 ,
где 0 и a —
абсциссы точек B и A.
Из уравнения эллипса находим
,
где 0 и a —
абсциссы точек B и A.
Из уравнения эллипса находим 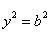
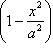 .
Отсюда
.
Отсюда
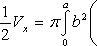
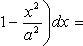
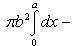
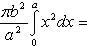
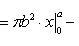
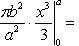
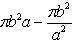
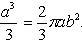
Таким
образом, искомый объем равен 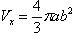 .
(При вращении эллипса вокруг малой
оси b,
объем тела равен
.
(При вращении эллипса вокруг малой
оси b,
объем тела равен 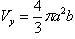 )
)
Найти площадь, ограниченную параболами y2 = 2px и x2 = 2py.
Решение.
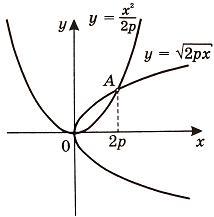
Сначала
найдем координаты точек пересечения
парабол, чтобы определить отрезок
интегрирования. Преобразуя исходные
уравнения, получаем 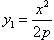 и
и 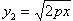 .
Приравнивая эти значения, получим
.
Приравнивая эти значения, получим 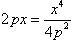 или x4 —
8p3x =
0.
или x4 —
8p3x =
0.
Отсюда
x4 — 8p3x = x(x3 — 8p3) = x(x — 2p)(x2 + 2px + 4p2) = 0.
Находим корни уравнений:
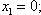
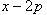
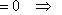
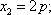
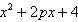
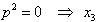
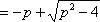
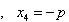
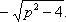
Учитывая то факт, что точка A пересечения парабол находится в первой четверти, то пределы интегрирования x = 0 и x = 2p.
Искомую площадь находим по формуле
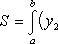
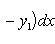
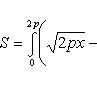
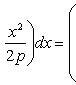
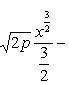
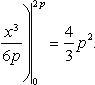
studfile.net
Вычисление площадей плоских фигур с помощью определённого интеграла
Рассмотрим постановку задачи о площади криволинейной трапеции.
Вычислить площадь криволинейной трапеции, ограниченной линиями (рис. 1).
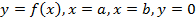 .
.
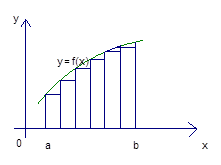
Рис. 1. Площадь криволинейной трапеции
Как мы пытались ее решить:
Первый способ.
Разбили отрезок 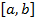 на
на 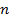 одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили
одинаковых отрезков, заменили искомую площадь площадью поступенчастой линии, легко ее сосчитали и получили приближенное решение нашей задачи. Далее устремили 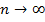 в пределе
в пределе 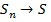 и
и
получили искомую площадь S. Ввели обозначение 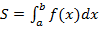 .
.
Это определенный интеграл. Вот таким образом мы пытались решить задачу. Мы знаем теперь, как приближенно ее решить, знаем обозначения для точного решения, но точного решения еще не знаем.
Затем мы получили точное решение задачи следующим образом: рис. 2:
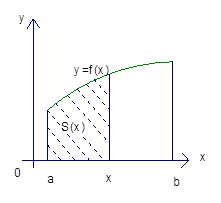
Рис. 2. Функция S (x)
Ввели функцию 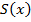 . Каждому
. Каждому 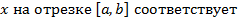 площадь под соответствующей частью кривой
площадь под соответствующей частью кривой 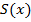 . Так, введенная функция удовлетворяет единственному закону, а именно:
. Так, введенная функция удовлетворяет единственному закону, а именно:
Каждому 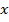 соответствует единственное значение
соответствует единственное значение 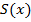 .
.
Мы доказали, что производная этой же функции 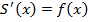 и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции
и доказали, что точная площадь вычисляется следующим образом. Надо найти любую первообразную от функции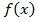 и взять приращение этих первообразных. То есть взять первообразную в точке
и взять приращение этих первообразных. То есть взять первообразную в точке 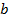 и отнять первообразную в точке
и отнять первообразную в точке 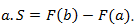 И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
И в результате мы получили формулу, которой мы будем пользоваться для вычисления площадей.
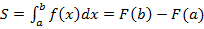 .
.
Методику нахождения площади рассмотрим сначала на относительно простом примере.
Пример 1.
Найти площадь фигуры, ограниченной линиями 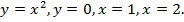
Решение.
Вот искомая площадь:
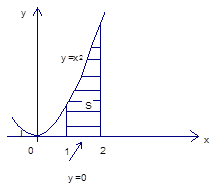
Рис. 3. Площадь
Вот формула:
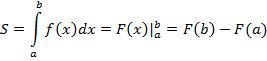
Это общая формула. Конкретно к нашему случаю она применима так:
Пределы интегрирования 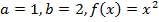 .
.
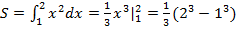 =
= .
.
Вычислили площадь криволинейной фигуры.
Ответ: 
В следующей задаче площадь искомой фигуры образовывается с помощью 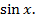 А именно:
А именно:
Найти площадь фигуры, ограниченной линиями 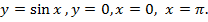
Решение.
Посмотрим, как выглядит фигура (рис. 4).
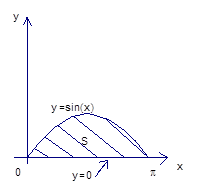
Рис. 4. Фигура, ограниченная линиями 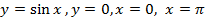
Формула та же самая: 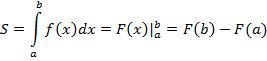
В нашем случае  . Итак, надо найти определенный интеграл
. Итак, надо найти определенный интеграл
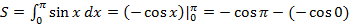 =-(-1)+1=1+1=2.
=-(-1)+1=1+1=2.
Искомая площадь найдена, и ответ получен.
Ответ: 2
Найти площадь фигуры, ограниченной линиями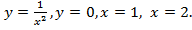
Решение.
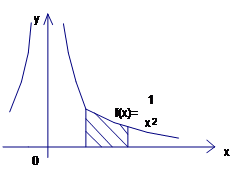
Рис. 5. Площадь фигуры, ограниченной линиями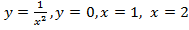
Формула для площади та же самая:
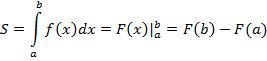
В нашем случае 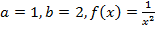 .
.
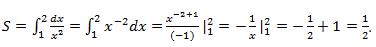
Ответ: 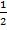
В следующем примере ищется площадь под параболой.
Найти площадь фигуры, ограниченной линиями 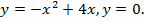
Решение.
Схематически изобразим параболу 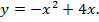 Корни
Корни 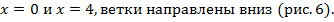
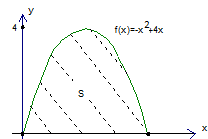
Рис. 6. Парабола 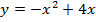
Применим известную формулу 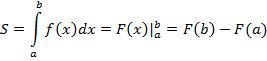
И применим ее для данной функции 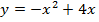 и пределов интегрирования
и пределов интегрирования
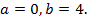
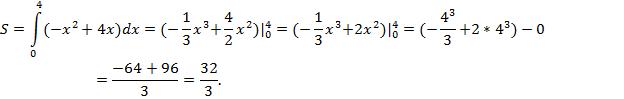
Искомая площадь найдена. 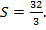
Ответ: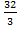
В предыдущих задачах площадь образовывалась с помощью разных кривых, но эта площадь находилась над осью 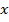 . В следующей задаче наоборот.
. В следующей задаче наоборот.
Найти площадь фигуры, ограниченной линиями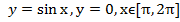 .
.
Решение.
Посмотрим, что это за фигура. График 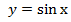 в пределах от Π до 2Π расположен под осью Ox (рис. 7).
в пределах от Π до 2Π расположен под осью Ox (рис. 7).
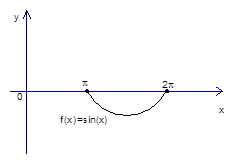
Рис. 7. График 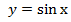 в пределах от Π до 2Π
в пределах от Π до 2Π
Ясно, что если возьмем определенный интеграл, то мы получим отрицательное число.
Вычисляем.
1. Сначала вычисляем определенный интеграл от π до 2π от подынтегральной функции 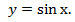
Надо найти первообразную.
По таблице первообразных: 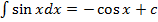 .
.
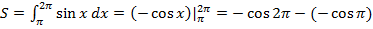 =-1-1=-2.
=-1-1=-2.
2. Для того чтобы найти площадь, надо взять модуль 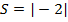 =2.
=2.
Ответ: 2.
Следующее усложнение – искомая площадь расположена между двумя кривыми.
А именно:
Найти площадь фигуры, ограниченной линиями (рис. 8)
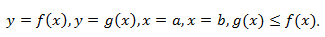
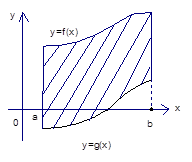
Рис. 8. Площадь фигуры, ограниченной линиями 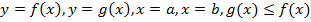
Решение.
Итак, площадь образуют 2 кривые, одна из них может находиться под осью 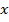 .
.
Каким образом мы будем решать эту задачу?
Во-первых, мы можем сдвинуть фигуру на такое положительное 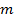 , что площадь находится над осью
, что площадь находится над осью 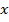 . Рис. 9.
. Рис. 9.
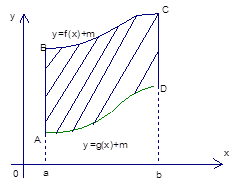
Рис. 9. Сдвиг фигуры
Затем мы возьмем соответствующий определенный интеграл и найдем площадь. Искомая площадь равна разности двух площадей.
Площадь под верхней кривой 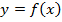 минус площадь под нижней кривой
минус площадь под нижней кривой 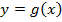 .
.
Каждую из площадей мы умеем находить.
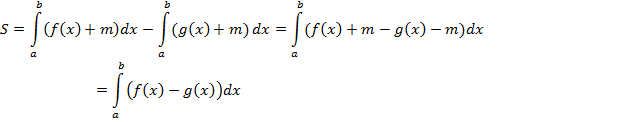
Таким образом, в общем виде была поставлена задача, в общем виде получен ответ.
Ответ: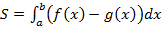
Обсудим и постановку задачи, и полученный важный результат.
Нам надо было найти площадь фигуры, ограниченной линиями
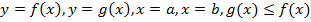 .
.
Мы использовали известный прием: эту площадь подняли на некоторое 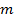 , и это
, и это  Так вот, эту площадь теперь можно считать без введения
Так вот, эту площадь теперь можно считать без введения 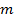 . Правило следующее:
. Правило следующее:
Площадь фигуры, ограниченной прямыми линиями 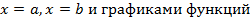
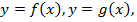 непрерывных на отрезке
непрерывных на отрезке 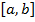 и таких, что для всех
и таких, что для всех 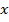 из отрезка
из отрезка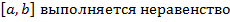
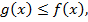 вычисляется по формуле, которую мы вывели:
вычисляется по формуле, которую мы вывели:
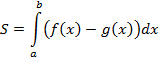
Рассмотрим первый конкретный пример на нахождение площади между двумя линиями.
Найти площадь фигуры, ограниченную линиями
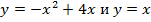 .
.
Решение. Для начала построим графики этих линий и поймем, где та площадь, которую нам надо искать.
График квадратичной функции – парабола. Корни – 0, 4, ветви вниз. График 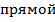
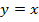 – биссектриса первого координатного угла. Вот площадь, которую надо найти:
– биссектриса первого координатного угла. Вот площадь, которую надо найти:
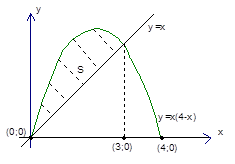
Рис. 10. Искомая площадь
Но для этого сначала надо найти точки пересечения и решить стандартную задачу.
1. Находим точки пересечения. Для этого решаем систему: 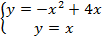 .
.
Отсюда получаем квадратное уравнение относительно 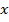 :
:
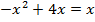
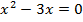
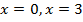
Мы нашли 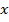 , то есть, пределы интегрирования. Это первое важное действие.
, то есть, пределы интегрирования. Это первое важное действие.
Теперь стандартное действие:
2. 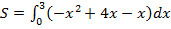 =
= 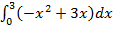 =(
=(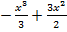 )
)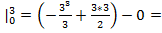
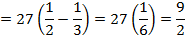
Искомая площадь равна 4,5
Ответ: 4,5
Во втором примере часть площади находится под осью 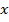 , но на методику это не влияет.
, но на методику это не влияет.
Пример 6.
Итак, требуется найти площадь фигуры, ограниченной линиями
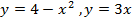
Решение.
Сначала построим графики, посмотрим, какую площадь нам нужно найти. Рис. 11.
Первая функция – парабола, ветви вниз. График второй функции – прямая линия.
Есть две точки пересечения, их придется найти, а именно взять пределы интегрирования, и тогда будем решать задачу по знакомому нам плану.
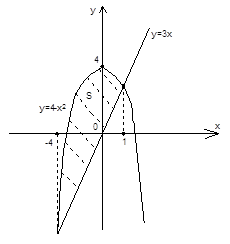
Рис. 11. Площадь фигуры, ограниченной линиями 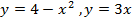
Первое действие – найти пределы интегрирования и второе – найти площадь.
Пределы интегрирования найдем из системы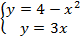 .
.
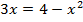
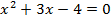
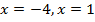
То есть, пределы интегрирования найдены.
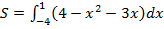 = (
= (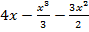 )
)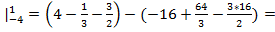
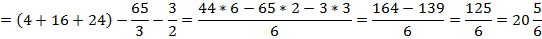
Ответ: 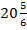
Итак, мы показали, каким образом можно вычислять площади плоских фигур с помощью определенного интеграла.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Ru.scribd.com (Источник).
- Math5you.ru (Источник).
- Dok.opredelim.com (Источник).
Домашнее задание
- Найти площадь фигуры, ограниченной линиями
 ,
,  ,
,  ,
,
- Найти площадь фигуры, ограниченной линиями

- Алгебра и начала анализа, Мордкович А.Г.: № 1030, 1033, 1037, 1038.
interneturok.ru
Вычислить площадь фигуры ограниченной линиями. Геометрический смысл определенного интеграла
Плоская фигура, ограниченная осью , прямыми и и графиком непрерывной на отрезке функции , которая не меняет знак на этом промежутке, называется криволинейной трапецией.
Площадь криволинейной трапеции численно равна определенному интегралу:
То есть, определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
На основании геометрического смысла определенного интеграла покоится целый класс задач на нахождение площадей фигур, ограниченных линиями.
100task.ru
Нахождение площади фигуры
Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y).
В разделе геометрический смысл определенного интеграла мы разобрались с нахождением площади криволинейной трапеции G. Вот полученные формулы:
 для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b],
для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b], для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].
для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].
Однако при решении задач на нахождение площади очень часто приходится иметь дело с более сложными фигурами.
В этой статье мы поговорим о вычислении площади фигур, границы которых заданы функциями в явном виде, то есть, как y=f(x) или x=g(y), и подробно разберем решение характерных примеров.
Навигация по странице.
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y).
Теорема.
Пусть
функции 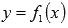 и
и 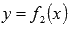 определены
и непрерывны на отрезке [a;b],
причем
определены
и непрерывны на отрезке [a;b],
причем 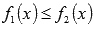 для
любого значения x из [a;b].
Тогда площадь
фигуры G,
ограниченной линиями x=a, x=b,
для
любого значения x из [a;b].
Тогда площадь
фигуры G,
ограниченной линиями x=a, x=b, 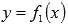 и
и 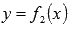 вычисляется
по формуле
вычисляется
по формуле 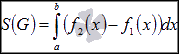 .
.
Аналогичная
формула справедлива для площади фигуры,
ограниченной линиями y=c,y=d, 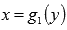 и
и 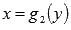 :
: 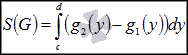 .
.
Доказательство.
Покажем справедливость формулы для трех случаев:
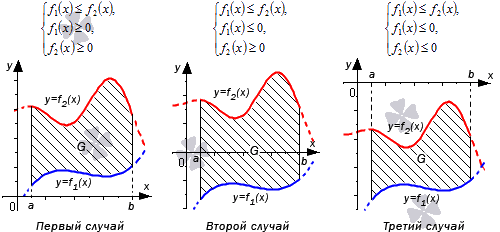
В
первом случае, когда обе функции
неотрицательные, в силу свойства
аддитивности площади сумма
площади исходной фигуры G и
криволинейной трапеции 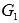 равна
площади фигуры
равна
площади фигуры 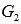 .
Следовательно,
.
Следовательно,
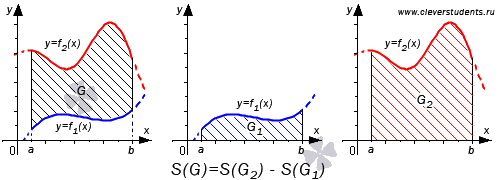
Поэтому, 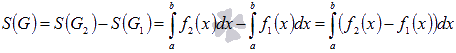 .
Последний переход возможен в силу
третьего свойства
определенного интеграла.
.
Последний переход возможен в силу
третьего свойства
определенного интеграла.
Аналогично,
во втором случае справедливо равенство 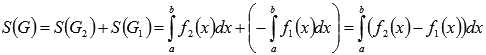 .
Вот
графическая иллюстрация:
.
Вот
графическая иллюстрация:
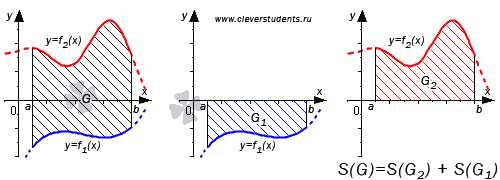
В
третьем случае, когда обе функции
неположительные, имеем 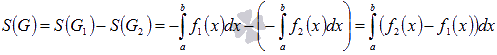 .
Проиллюстрируем
это:
.
Проиллюстрируем
это:
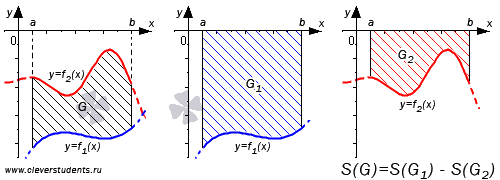
Теперь
можно переходить к общему случаю, когда
функции 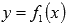 и
и 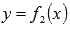 пересекают
ось Ox.
пересекают
ось Ox.
Обозначим
точки пересечения 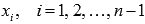 .
Эти точки разбивают отрезок [a; b]на n частей
.
Эти точки разбивают отрезок [a; b]на n частей 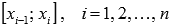 ,
где
,
где 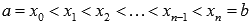 .
Фигуру Gможно
представить объединением фигур
.
Фигуру Gможно
представить объединением фигур 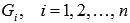 .
Очевидно, что на своем интервале
.
Очевидно, что на своем интервале 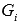 попадает
под один из трех рассмотренных ранее
случаев, поэтому их площади находятся
как
попадает
под один из трех рассмотренных ранее
случаев, поэтому их площади находятся
как 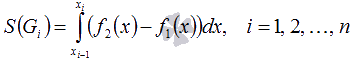
Следовательно, 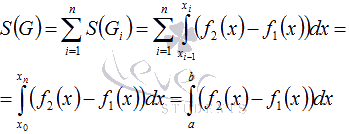
Последний переход справедлив в силу пятого свойства определенного интеграла.
Графическая
иллюстрация общего случая. 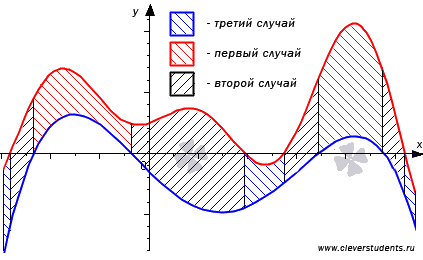
Таким
образом, формула 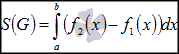 доказана.
доказана.
Пришло время перейти к решению примеров на нахождение площади фигур, ограниченных линиями y=f(x) и x=g(y).
К началу страницы
Примеры вычисления площади фигуры, ограниченной линиямиy=f(x) или x=g(y).
Решение каждой задачи будем начинать с построения фигуры на плоскости. Это нам позволит сложную фигуру представить как объединение более простых фигур. При затруднениях с построением обращайтесь к статьям: основные элементарные функции, их свойства и графики; геометрические преобразования графиков функций и исследование функции и построение графика.
Пример.
Вычислить
площадь фигуры, ограниченной параболой 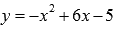 и
прямыми
и
прямыми 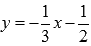 , x=1, x=4.
, x=1, x=4.
Решение.
Построим эти линии на плоскости.
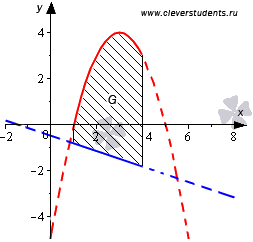
Всюду
на отрезке [1;4] график
параболы 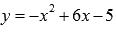 выше
прямой
выше
прямой 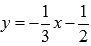 .
Поэтому, применяем полученную ранее
формулу для площади и вычисляем
определенный интеграл по формуле
Ньютона-Лейбница:
.
Поэтому, применяем полученную ранее
формулу для площади и вычисляем
определенный интеграл по формуле
Ньютона-Лейбница: 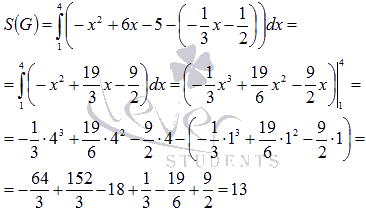
Немного усложним пример.
Пример.
Вычислить
площадь фигуры, ограниченной линиями 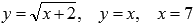 .
.
Решение.
В чем здесь отличие от предыдущих примеров? Ранее у нас всегда были две прямых, параллельных оси абсцисс, а сейчас только одна x=7. Сразу возникает вопрос: где взять второй предел интегрирования? Давайте для этого взглянем на чертеж.
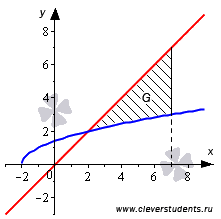
Стало
понятно, что нижним пределом интегрирования
при нахождении площади фигуры является
абсцисса точки пересечения графика
прямой y=x и
полу параболы 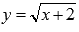 .
Эту абсциссу найдем из равенства:
.
Эту абсциссу найдем из равенства: 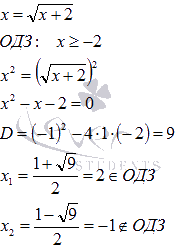
Следовательно, абсциссой точки пересечения является x=2.
Обратите внимание.
В
нашем примере и по чертежу видно, что
линии 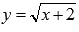 и y=x пересекаются
в точке(2;2) и
предыдущие вычисления кажутся излишними.
Но в других случаях все может быть не
так очевидно. Поэтому рекомендуем всегда
аналитически вычислять абсциссы и
ординаты точек пересечения линий.
и y=x пересекаются
в точке(2;2) и
предыдущие вычисления кажутся излишними.
Но в других случаях все может быть не
так очевидно. Поэтому рекомендуем всегда
аналитически вычислять абсциссы и
ординаты точек пересечения линий.
Очевидно,
график функции y=x расположен
выше графика функции 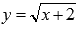 на
интервале [2;7].
Применяем формулу для вычисления
площади:
на
интервале [2;7].
Применяем формулу для вычисления
площади: 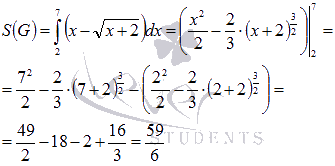
Еще усложним задание.
Пример.
Вычислить
площадь фигуры, ограниченной графиками
функций 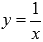 и
и 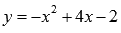 .
.
Решение.
Построим
график обратной пропорциональности 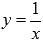 и
параболы
и
параболы 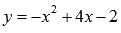 .
.
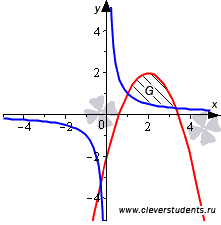
Прежде
чем применять формулу для нахождения
площади фигуры, нам нужно определиться
с пределами интегрирования. Для этого
найдем абсциссы точек пересечения
линий, приравняв выражения 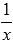 и
и 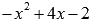 .
.
При
отличных от нуля значениях x равенство 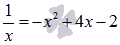 эквивалентно
уравнению третьей степени
эквивалентно
уравнению третьей степени 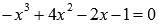 с
целыми коэффициентами. Можете обратиться
к разделу решение
кубических уравнений чтобы
вспомнить алгоритм его решения.
с
целыми коэффициентами. Можете обратиться
к разделу решение
кубических уравнений чтобы
вспомнить алгоритм его решения.
Легко
проверить, что x=1 является
корнем этого уравнения: 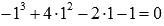 .
.
Разделив
выражение 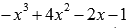 на
двучлен x-1,
имеем:
на
двучлен x-1,
имеем: 
Таким
образом, оставшиеся корни находятся из
уравнения 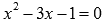 :
: 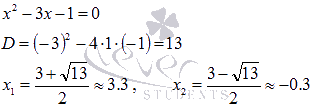
Теперь
из чертежа стало видно, что фигура G заключена
выше синей и ниже красной линии на
интервале 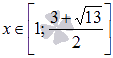 .
Таким образом, искомая площадь будет
равна
.
Таким образом, искомая площадь будет
равна 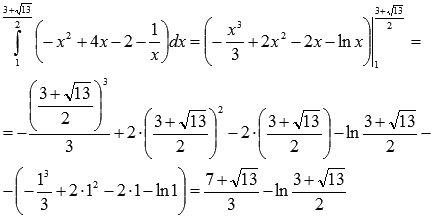
Рассмотрим еще один характерный пример.
Пример.
Вычислить
площадь фигуры, ограниченной кривыми 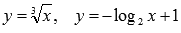 и
осью абсцисс.
и
осью абсцисс.
Решение.
Сделаем чертеж.
—
это обычная степенная функция с
показателем одна треть, график
функции 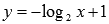 можно
получить из графика
можно
получить из графика 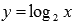 отобразив
его симметрично относительно оси абсцисс
и подняв на единицу вверх.
отобразив
его симметрично относительно оси абсцисс
и подняв на единицу вверх.
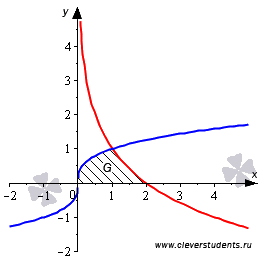
Найдем точки пересечения всех линий.
Ось абсцисс имеет уравнение y=0.
Графики
функций 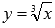 и y=0 пересекаются
в точке (0;0) так
как x=0 является
единственным действительным корнем
уравнения
и y=0 пересекаются
в точке (0;0) так
как x=0 является
единственным действительным корнем
уравнения 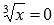 .
.
Графики
функций 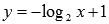 и y=0 пересекаются
в точке (2;0),
так как x=2является
единственным корнем уравнения
и y=0 пересекаются
в точке (2;0),
так как x=2является
единственным корнем уравнения 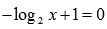 .
.
Графики
функций 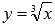 и
и 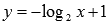 пересекаются
в точке (1;1),
так как x=1является
единственным корнем уравнения
пересекаются
в точке (1;1),
так как x=1является
единственным корнем уравнения 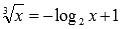 .
Это утверждение не совсем очевидно,
но
.
Это утверждение не совсем очевидно,
но 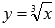 —
функция строго возрастающая, а
—
функция строго возрастающая, а 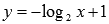 —
строго убывающая, поэтому, уравнение
—
строго убывающая, поэтому, уравнение 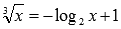 имеет
не более одного корня.
имеет
не более одного корня.
Как же действовать дальше? Здесь есть несколько вариантов.
Можно фигуру G представить суммой двух криволинейных трапеций. Первая фигура расположена выше оси абсцисс и ниже синей линии на отрезке
 ,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке
,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке  .
Следовательно,
искомая площадь будет равна
.
Следовательно,
искомая площадь будет равна  .
.Можно фигуру G представить разностью двух фигур. Первая фигура является криволинейной трапецией и расположена выше оси Ox и ниже синей линии на отрезке
 ,
вторая фигура расположена выше красной
и ниже синей линии на отрезке
,
вторая фигура расположена выше красной
и ниже синей линии на отрезке  .
В
этом случае площадь представляем как
.
В
этом случае площадь представляем как  .
.А можно фигуру G рассматривать на отрезке
 ,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.
,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.
Единственное
замечание: в этом случае для нахождения
площади придется использовать формулу
вида 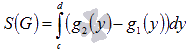 .
То есть, ограничивающие линии нужно
представить в виде функций от аргумента y.
Это сделать в нашем случае достаточно
легко. Разрешим уравнения
.
То есть, ограничивающие линии нужно
представить в виде функций от аргумента y.
Это сделать в нашем случае достаточно
легко. Разрешим уравнения 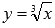 и
и 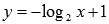 относительно x:
относительно x: 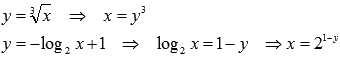
Таким
образом, искомая площадь равна 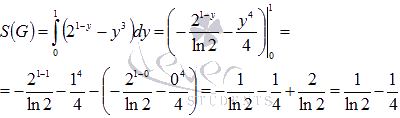
Мы бы пришли к этому же результату и в двух других случаях.
Можно переходить к последнему примеру.
Пример.
Вычислить
площадь плоской фигуры, ограниченной
линиями 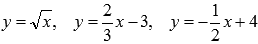 .
.
Решение.
С
построением этих линий проблем возникнуть
не должно. На чертеже красной линией
изображен график функции  ,
синей линией
,
синей линией 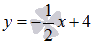 ,
а черной линией
,
а черной линией 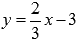 .
.
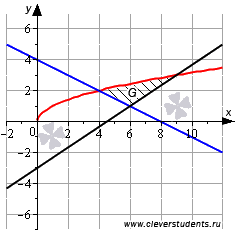
Определим точки пересечения линий.
Начнем
с графиков функций  и
и 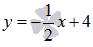 :
: 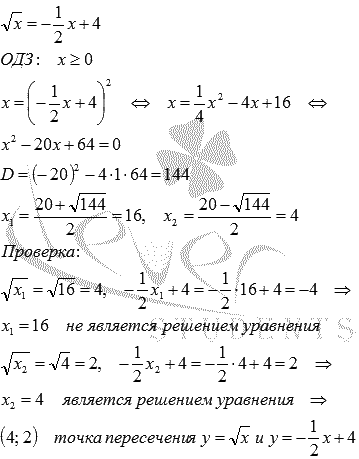
Найдем
точку пересечения графиков функций  и
и 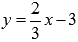 :
: 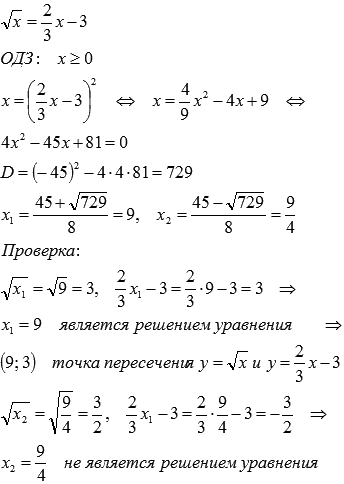
Осталось
найти точку пересечения прямых 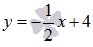 и
и 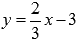 :
: 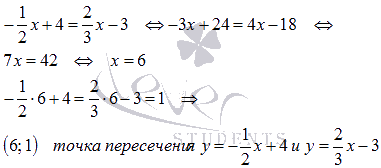
Дальше можно поступить двояко:
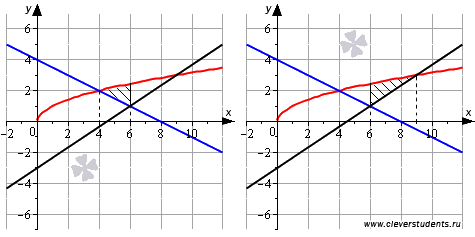
Тогда
площадь фигуры равна: 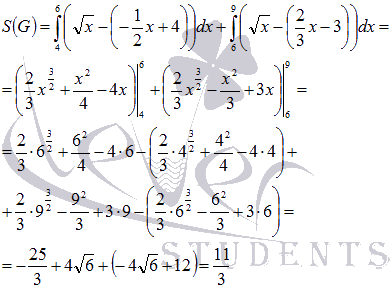
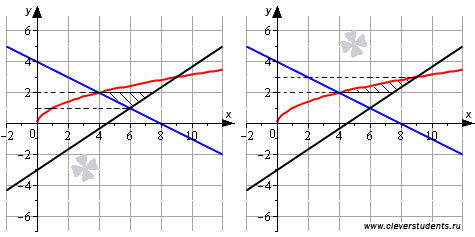
Для
этого случая, перед применением формулы
для вычисления площади фигуры, разрешим
уравнения линий относительно x: 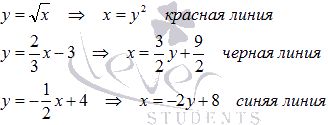
Таким
образом, площадь равна: 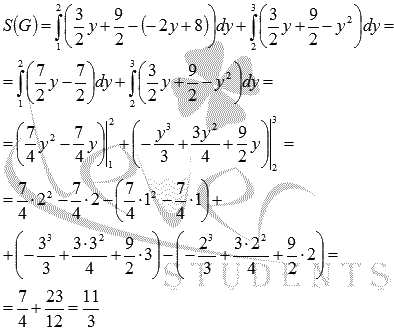
Как видите, значения совпадают.
К началу страницы
Подведем итог.
Мы разобрали все наиболее часто встречающиеся случаи нахождения площади фигуры, ограниченной явно заданными линиями. Для этого нужно уметь строить линии на плоскости, находить точки пересечения линий и применять формулу для нахождения площади, что подразумевает наличие навыков вычисления определенных интегралов.
studfile.net
Вычисление площадей плоских фигур с помощью интеграла
На этом уроке будем учиться вычислять площади плоских фигур, которые называются криволинейными трапециями.
Примеры таких фигур — на рисунке ниже.
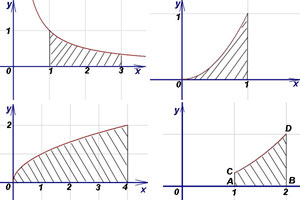
Для вычисления площади фигуры нам понадобятся:
- определённый интеграл от функции, задающей кривую, которая ограничивает криволинейную трапецию сверху (а если ограничивает снизу — то интеграл со знаком минус ;
- пределы интегрирования a и b, которые находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a, x = b.
А теперь всё это подробнее в более строгих определениях и формулах.
Фигуры, которые мы рассматриваем, ограничены осью абсцисс (Ox), отрезками прямых x = a, x = b и графиком непрерывной и неотрицательной функции y = f(x) для значений «икса», принадлежащих отрезку [a, b]. Боковые отрезки могут вырождаться в точки.
Определённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] (график функции расположен выше оси Ox) численно равен площади криволинейной трапеции с основанием [a, b], ограниченной сверху графиком функции y = f(x). В этом заключается геометрический смысл определённого интеграла.
Площадь s этой криволинейной трапеции может быть вычислена по формуле
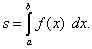 (1).
(1).
Если же f(x) ≤ 0 (график функции расположен ниже оси Ox), то площадь криволинейной трапеции может быть вычислена по формуле
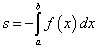 . (2)
. (2)
Есть ещё случаи, когда и верхняя, и нижняя границы фигуры — функции, соответственно y = f(x) и y = φ(x), то площадь такой фигуры вычисляется по формуле
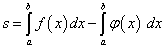 . (3)
. (3)
Начнём со случаев, когда площадь фигуры может быть вычислена по формуле (1).
Пример 1. Найти площадь фигуры, ограниченной графиком функции
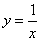 , осью абсцисс (Ox)
и прямыми x = 1, x = 3.
, осью абсцисс (Ox)
и прямыми x = 1, x = 3.
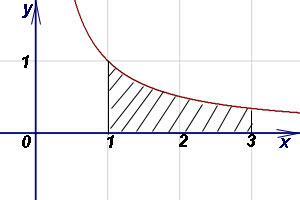
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции находим по формуле (1):
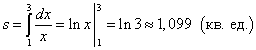 .
.
Пример 3. Найти площадь фигуры, ограниченной графиком функции
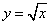 , осью абсцисс (Ox)
и прямой x = 4.
, осью абсцисс (Ox)
и прямой x = 4.
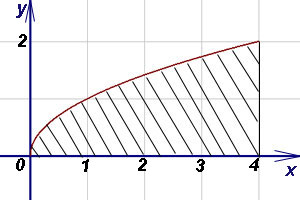
Решение. Фигура, соответствующая условию задачи — криволинейная трапеция, у которой левый отрезок выродился в
точку. Пределами интегрирования служат 0 и 4. Поскольку 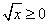 ,
по формуле (1) находим площадь криволинейной трапеции:
,
по формуле (1) находим площадь криволинейной трапеции:
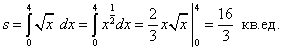 .
.
Пример 4. Найти площадь фигуры, ограниченной линиями
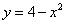 ,
,
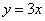 ,
,
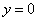 и
находящейся в 1-й четверти.
и
находящейся в 1-й четверти.
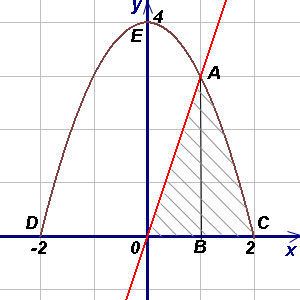
Решение. Чтобы воспользоваться формулой (1), представим площадь фигуры,
заданной условиями примера, в виде суммы площадей треугольника OAB и криволинейной
трапеции ABC. При вычислении площади треугольника OAB
пределами интегрирования служат абсциссы точек O и A, а для фигуры ABC —
абсциссы точек A и C (A является точкой пересечения прямой OA и
параболы, а C — точкой пересечения параболы с осью Ox).
Решая совместно (как систему) уравнения прямой и параболы, получим
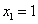 (абсциссу точки A) и
(абсциссу точки A) и 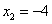 (абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично
получим
(абсциссу другой точки пересечения прямой и параболы, которая для решения не нужна). Аналогично
получим 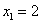 ,
,
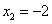 (абсциссы точек
C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
(абсциссы точек
C и D). Теперь у нас еть всё для нахождения площади фигуры. Находим:
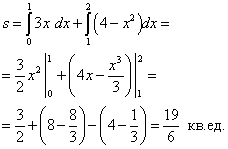
Пример 5. Найти площадь криволинейной трапеции ACDB,
если уравнение кривой CD 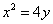 и абсциссы A и B соответственно 1 и 2.
и абсциссы A и B соответственно 1 и 2.
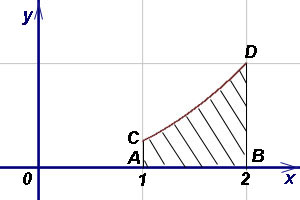
Решение. Выразим данное уравнение кривой через игрек:
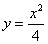 Площадь криволинейной
трапеции находим по формуле (1):
Площадь криволинейной
трапеции находим по формуле (1):
 .
.
Переходим к случаям, когда площадь фигуры может быть вычислена по формуле (2).
Пример 7. Найти площадь, заключённую между осью абсцисс (Ox) и двумя соседними волнами синусоиды.
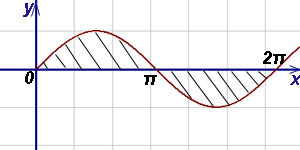
Решение. Площадь данной фигуры можем найти по формуле (2):
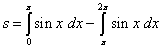 .
.
Найдём отдельно каждое слагаемое:
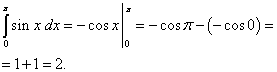 .
.
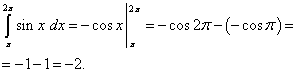 .
.
Окончательно находим площадь:
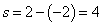 .
.
Пример 8. Найти площадь фигуры, заключённой между параболой
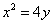 и кривой
и кривой
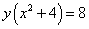 .
.
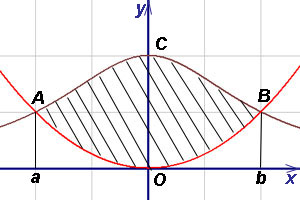
Решение. Выразим уравнения линий через игрек:
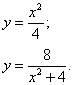
Площадь по формуле (2) получим как
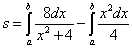 ,
,
где a и b — абсциссы точек A и B. Найдём их, решая совместно уравнения:
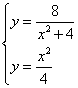
Отсюда
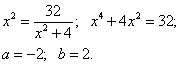
Окончательно находим площадь:
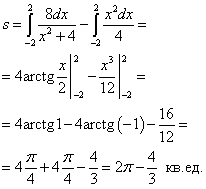
И, наконец, случаи, когда площадь фигуры может быть вычислена по формуле (3). Первый из этих примеров предлагается решить самостоятельно, а затем можно посмотреть правильное решение.

Начало темы «Интеграл»
function-x.ru
1. Вычисление площадей плоских фигур.
Если
плоская фигура ограничена прямыми 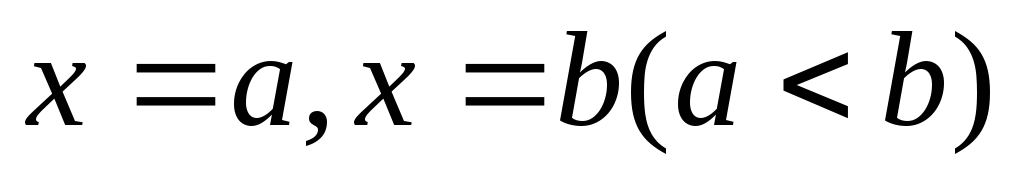 и
кривыми
и
кривыми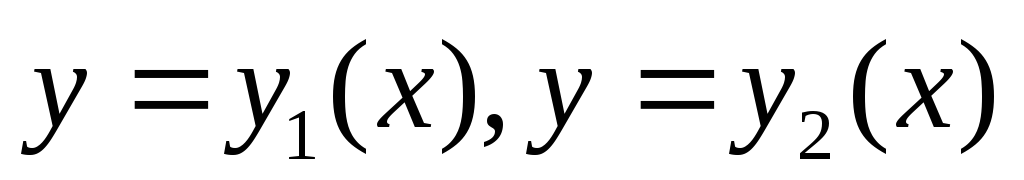 ,
причем,
,
причем,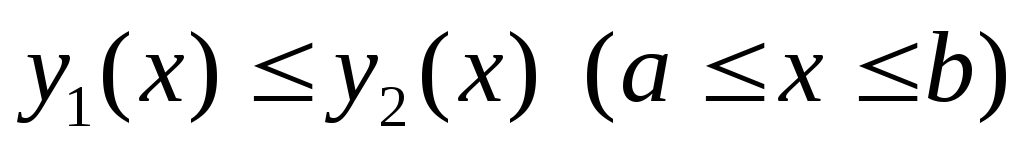 ,
то её площадь вычисляется по формуле
,
то её площадь вычисляется по формуле
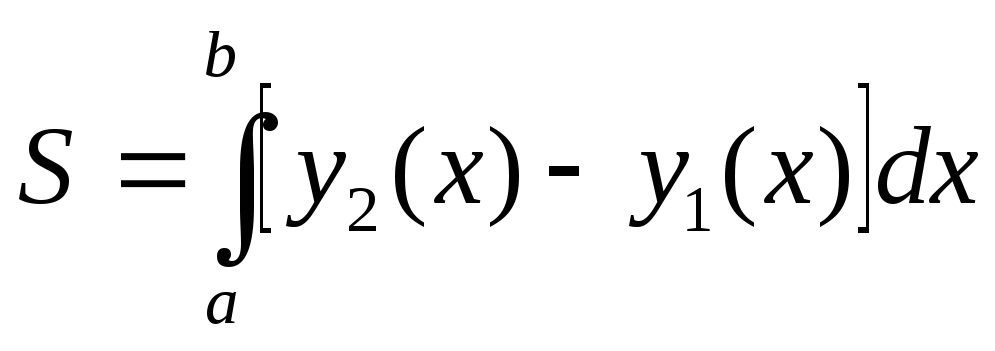 .
.
В
отдельных случаях левая граница 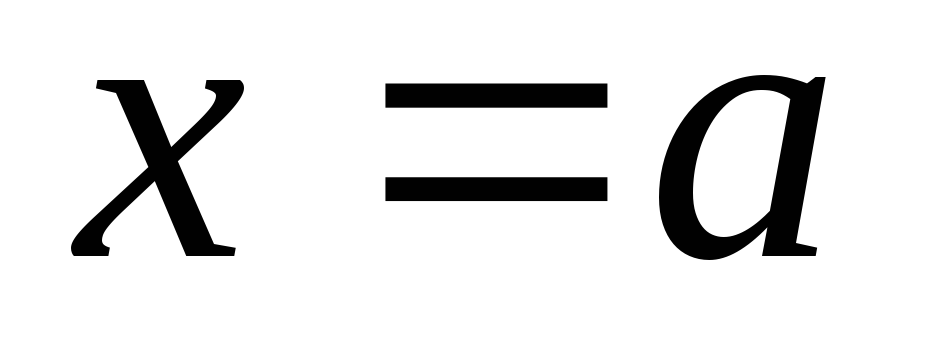 (или
правая граница
(или
правая граница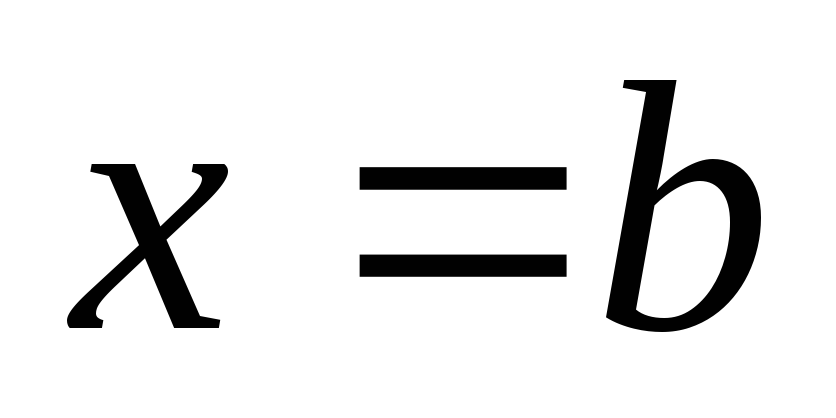 )
может выродиться в точку пересечения
кривых
)
может выродиться в точку пересечения
кривых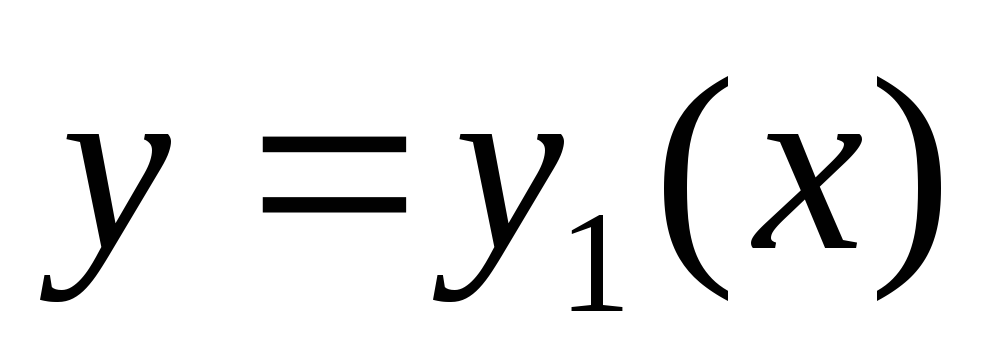 и
и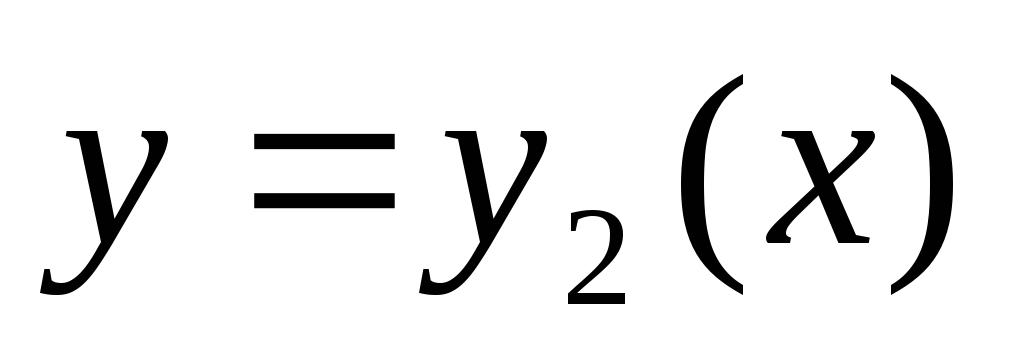 .
В этих случаях величины
.
В этих случаях величины и
и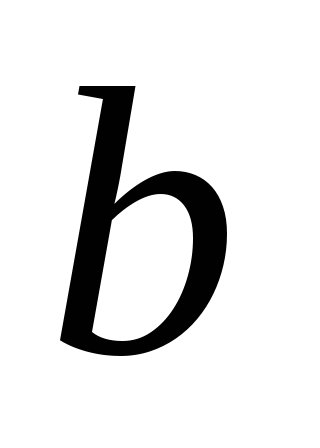 отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)
отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)
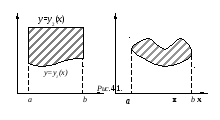
Если
граница фигуры задана параметрическими
уравнениями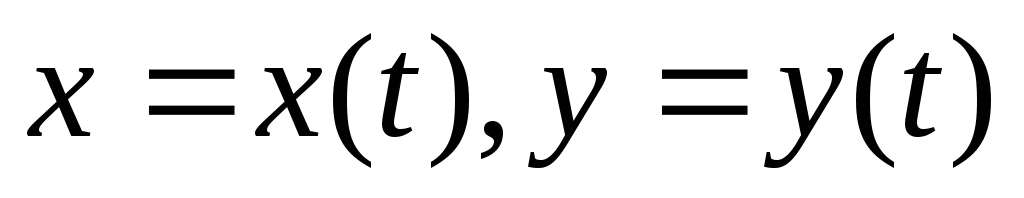 ,
то площадь фигуры вычисляется по одной
из трёх формул:
,
то площадь фигуры вычисляется по одной
из трёх формул:
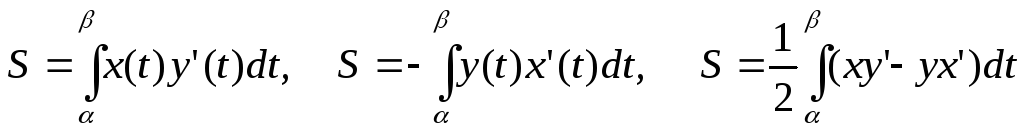 ,
,
где  и
и 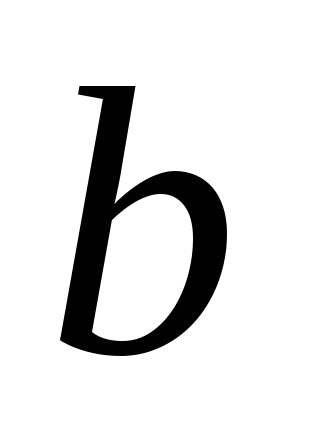 —
значения параметра
—
значения параметра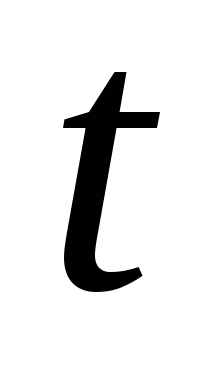 ,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
В
полярных координатах площадь сектора,
ограниченного дугой кривой 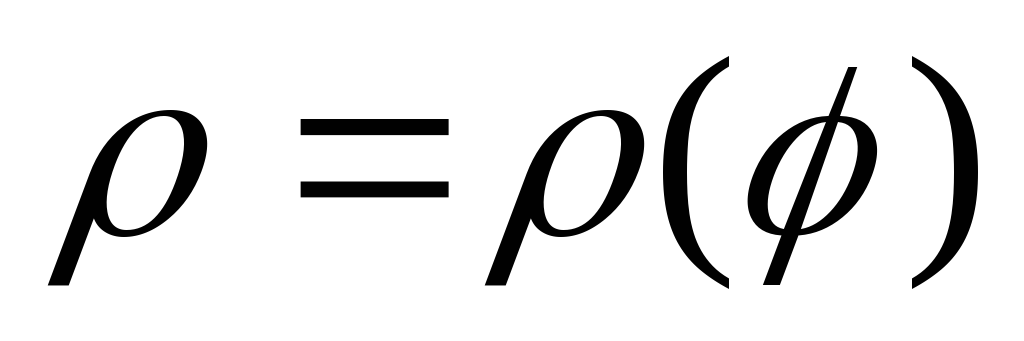 и
лучами
и
лучами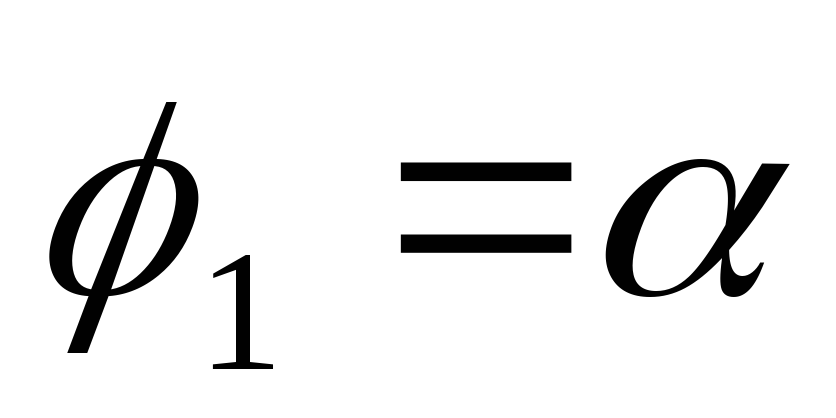 и
и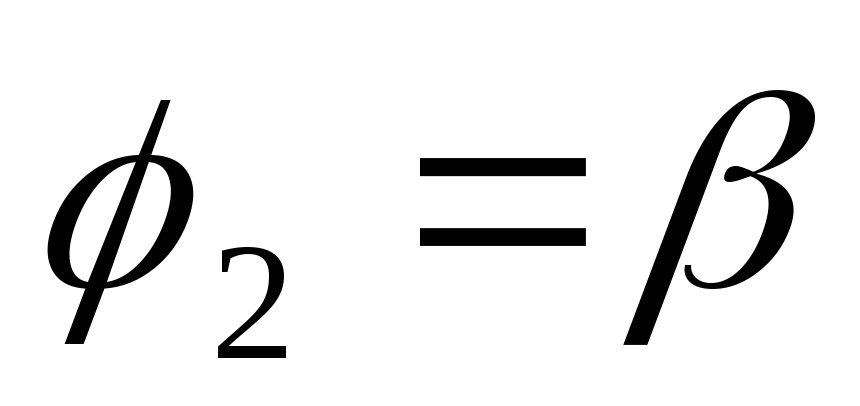 , выражается
формулой
, выражается
формулой
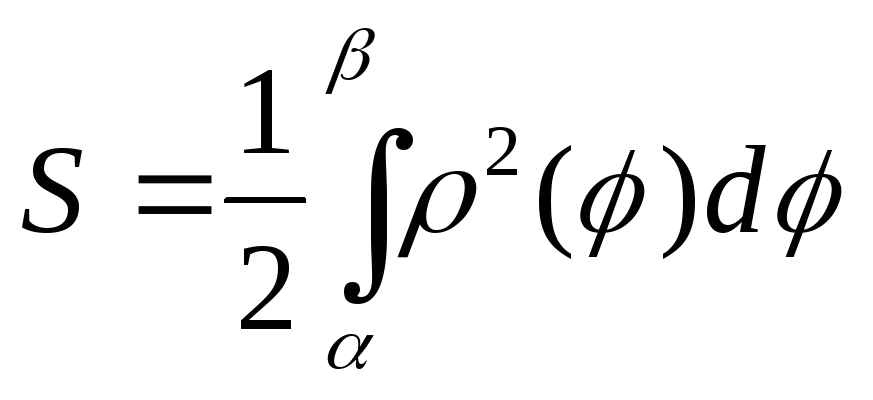 .
.
Пример.
Вычислить
площадь фигуры, ограниченной прямыми 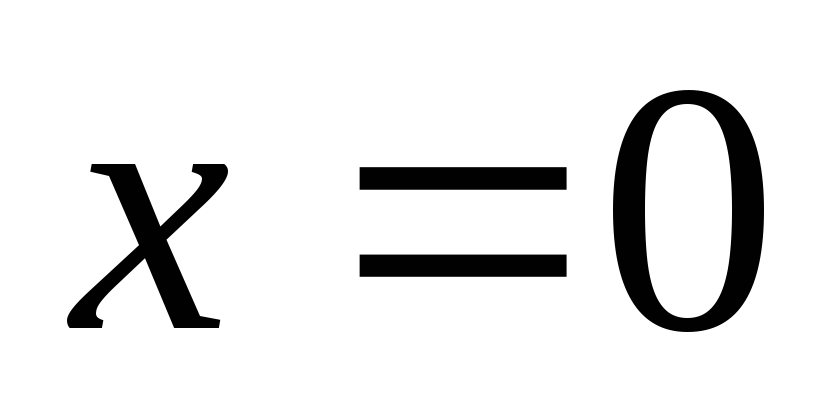 ,
,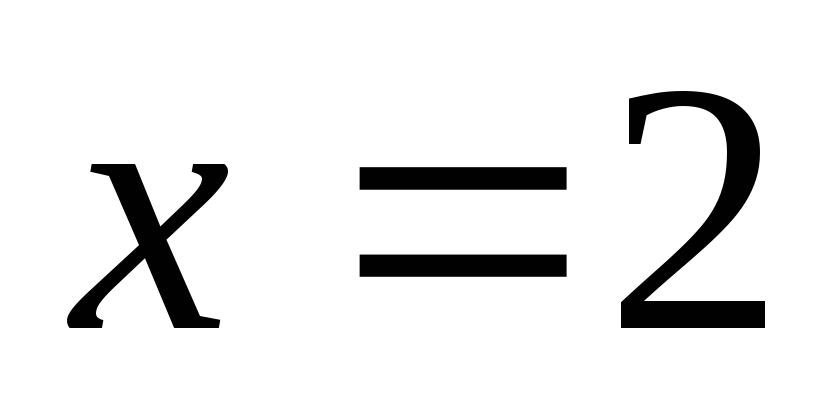 и кривыми
и кривыми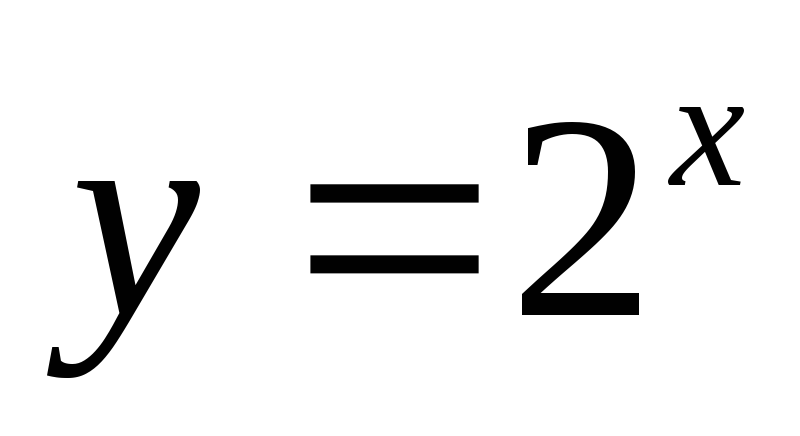 ,
,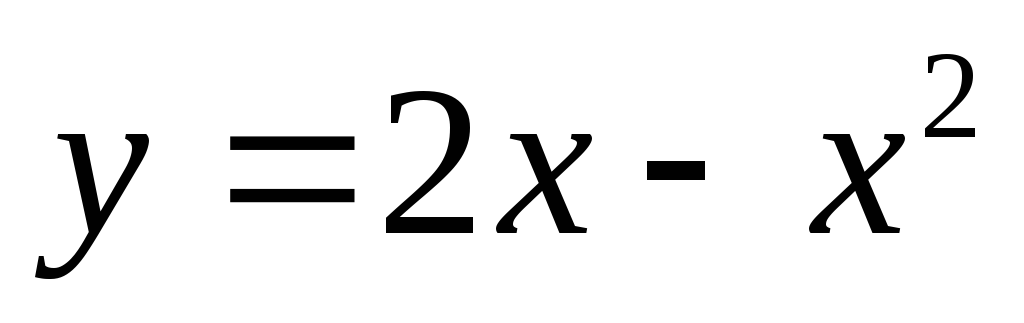 .
.
Решение.
Т ак
как максимум функции
ак
как максимум функции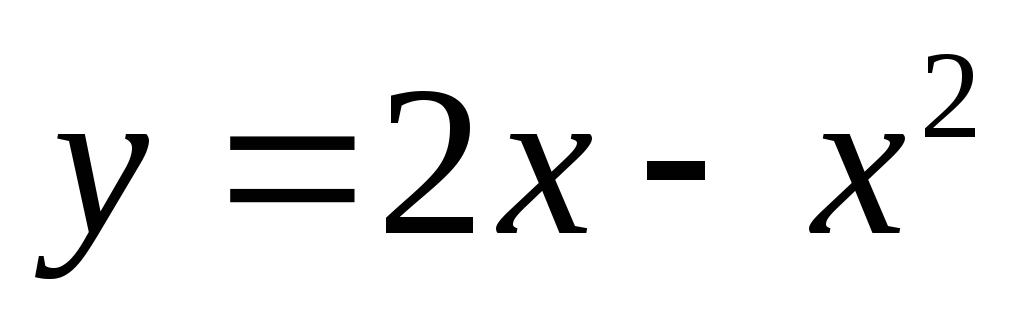 достигается
в точке
достигается
в точке 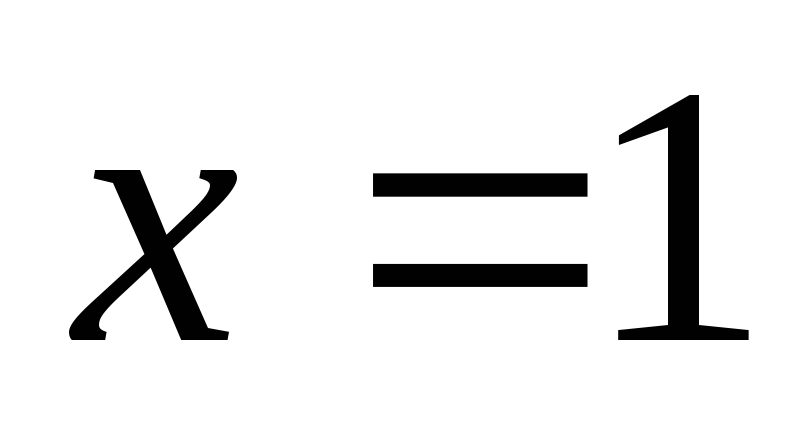 и равен 1, а функция
и равен 1, а функция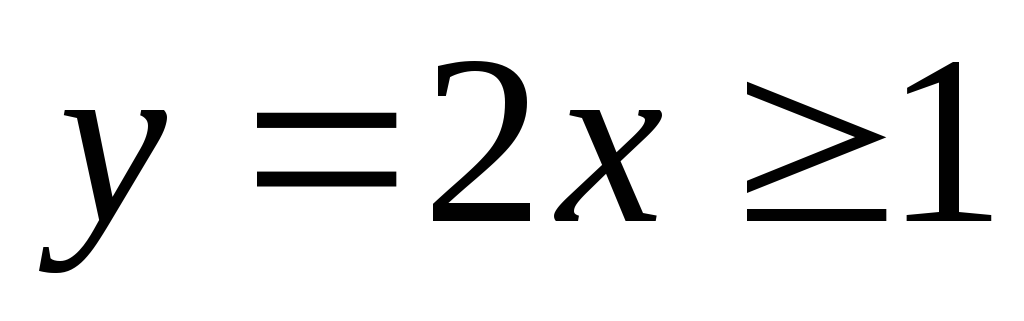 на отрезке
на отрезке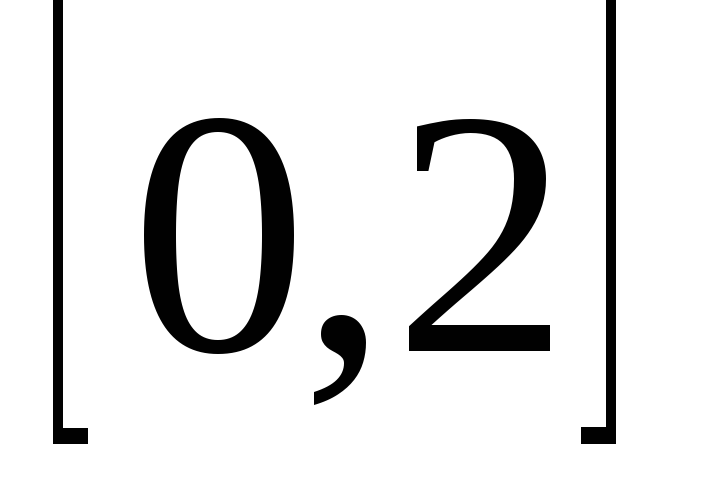 ,
то (см. рис. 4.2.)
,
то (см. рис. 4.2.)
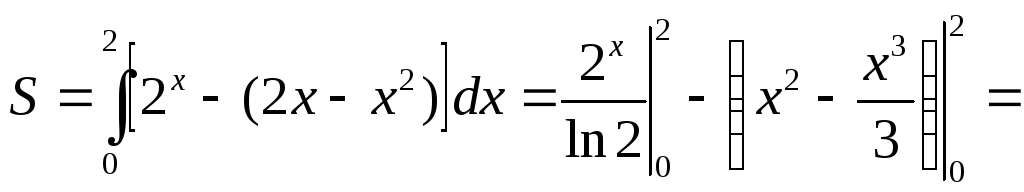
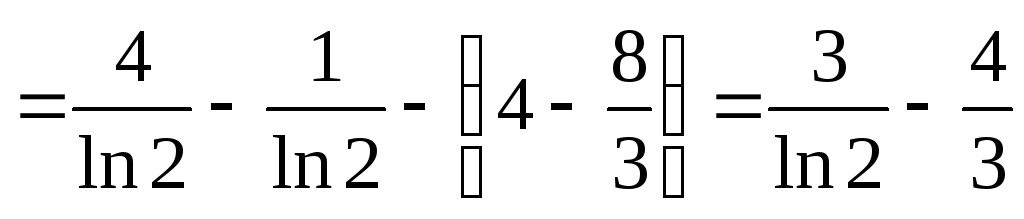 .
.
Пример.
Вычислить
площадь фигуры, ограниченной параболами 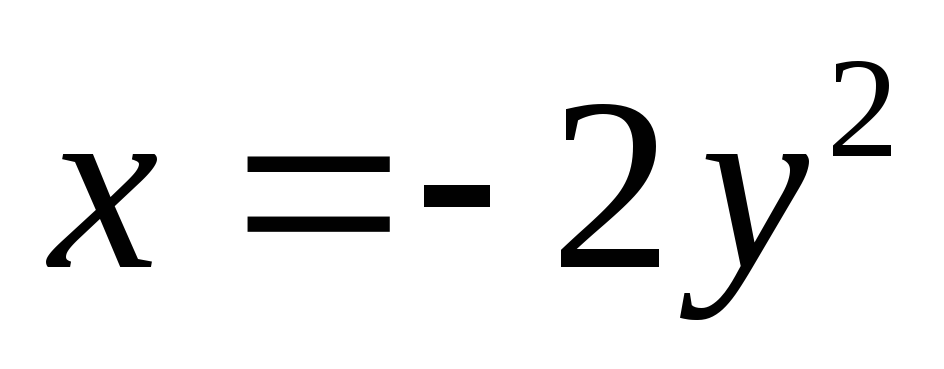 ,
,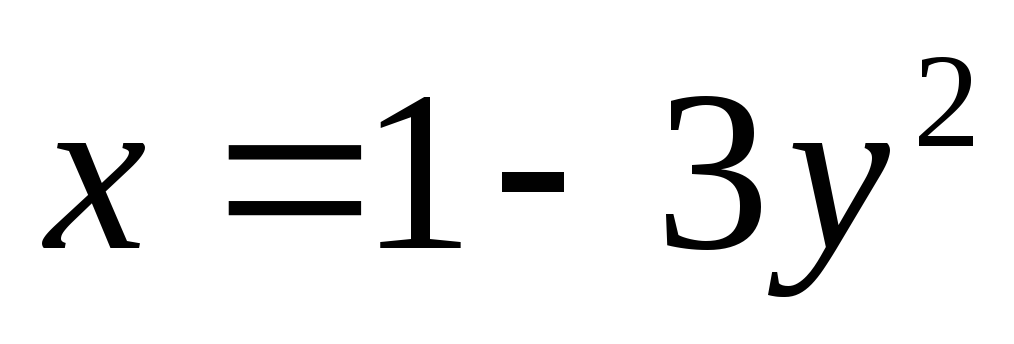 .
.
Р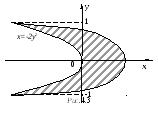 ешение.
ешение.
Решая систему уравнений
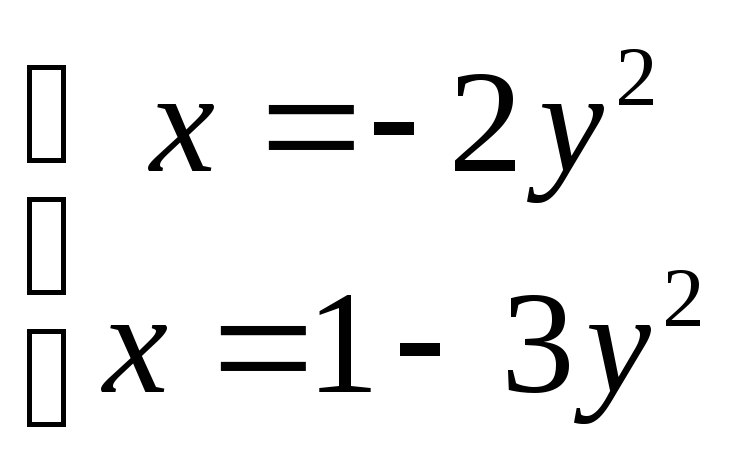
найдем
ординаты точек пересечения кривых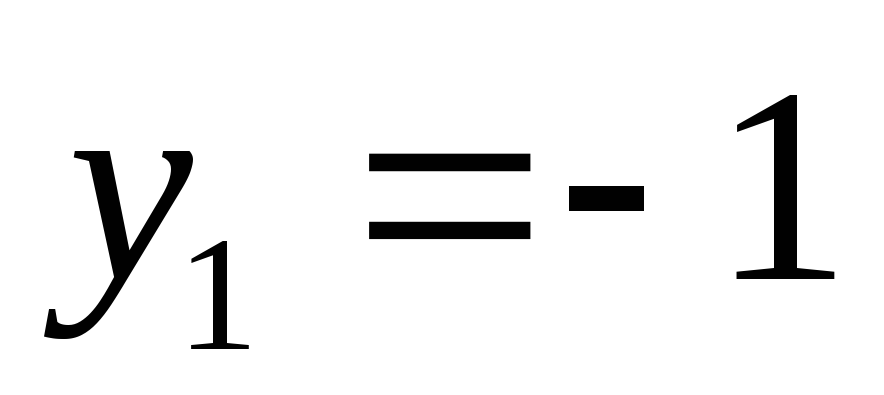 ,
,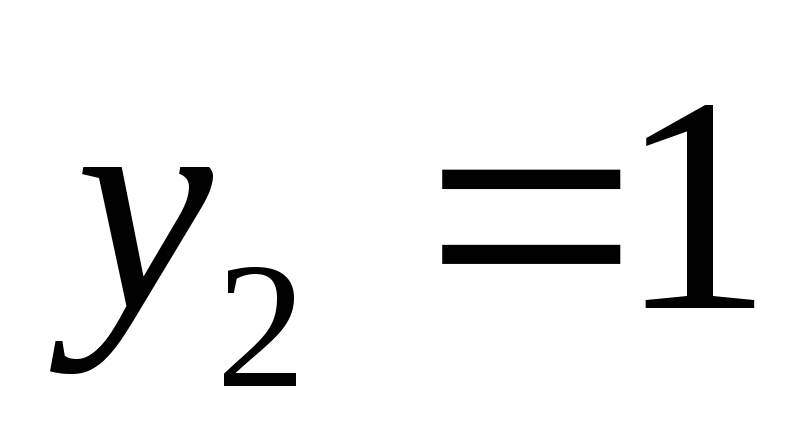 .
.
Так
как 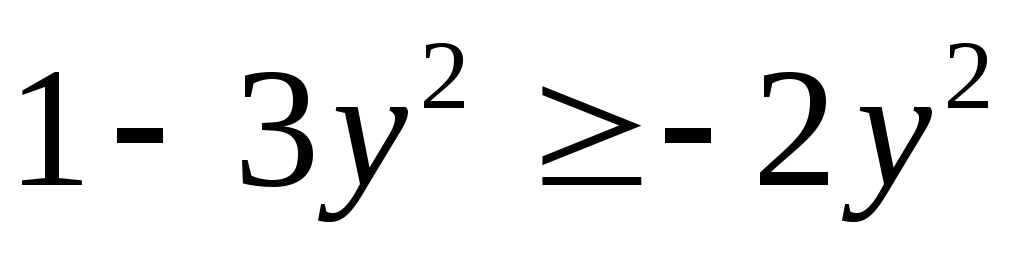 при
при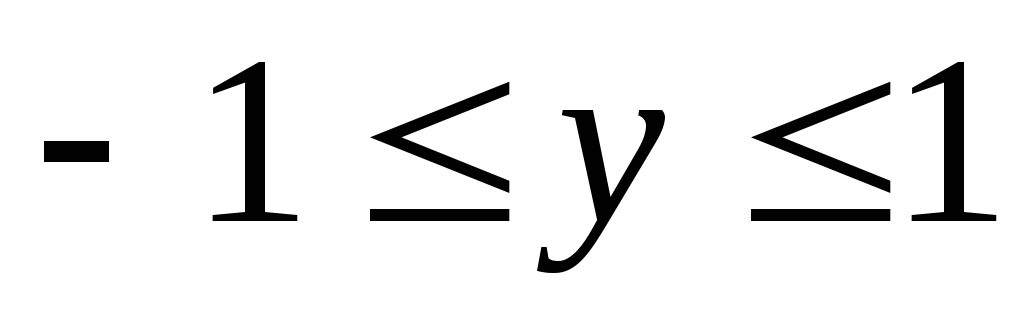 ,то
,то
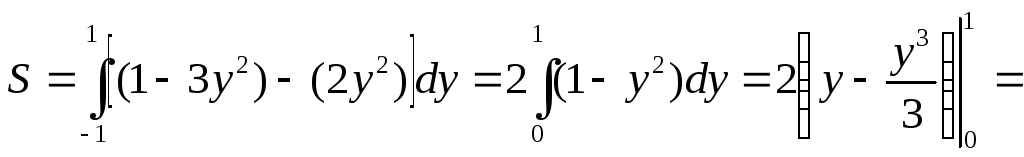
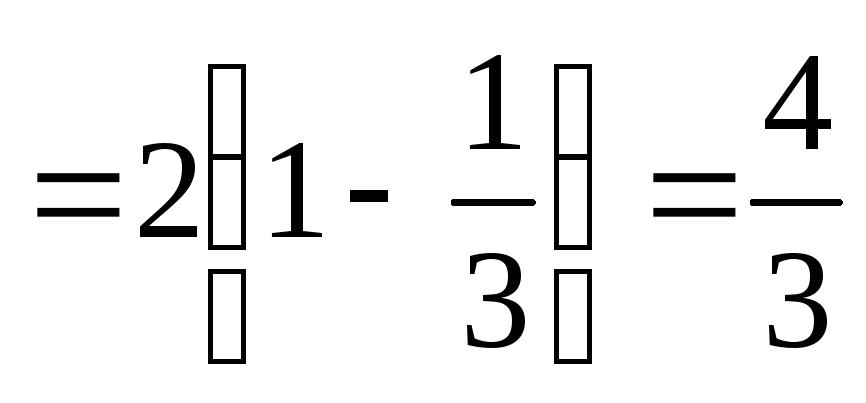 .
.
Пример.
Вычислить площадь фигуры, ограниченной эллипсом
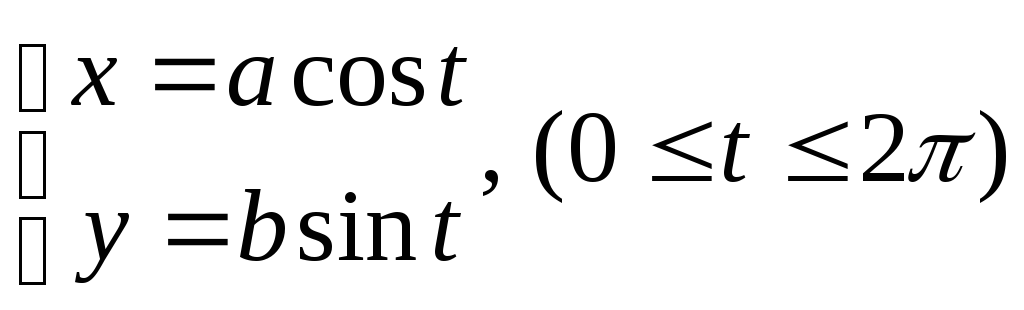
Решение.
Здесь удобно вычислить сначала
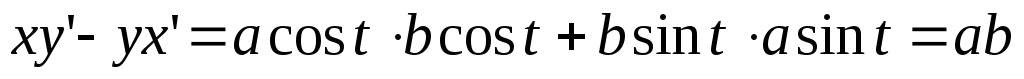 .
.
Отсюда
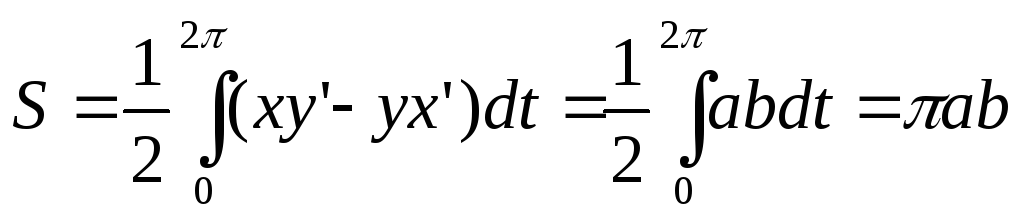
 .
.
Пример.
Найти
площадь фигуры, ограниченной
одним лепестком кривой 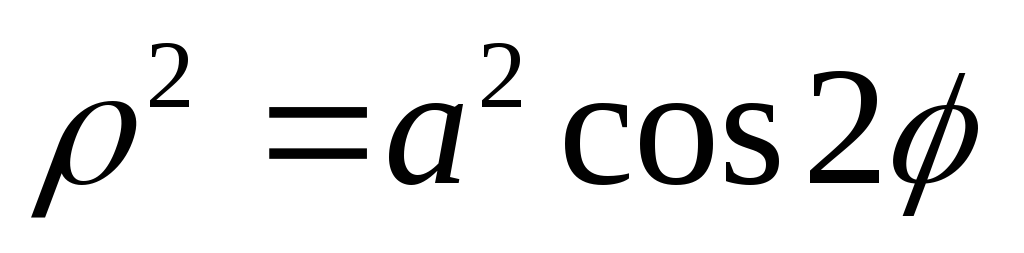 (лемниската).
(лемниската).
Решение.
Правая
часть уравнения кривой неотрицательна
при значениях  , для которых
, для которых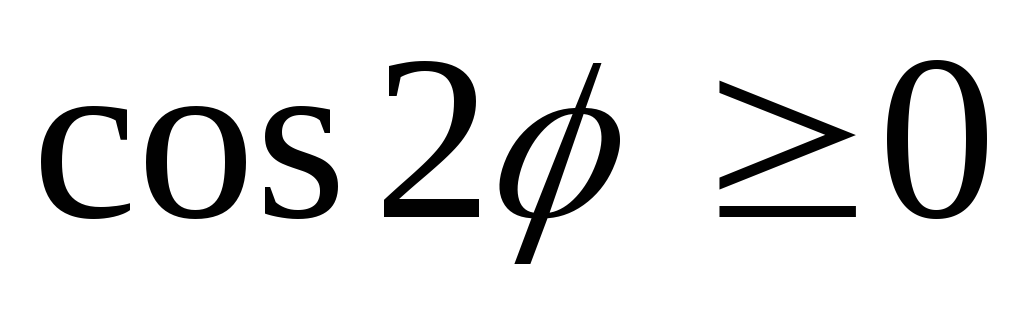 .
.
Поэтому первый лепесток лежит в угловом секторе, в котором
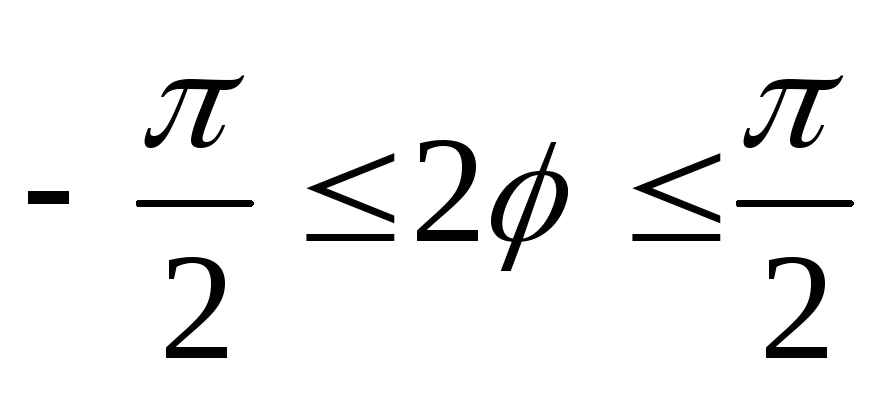 ,т.е.
,т.е. 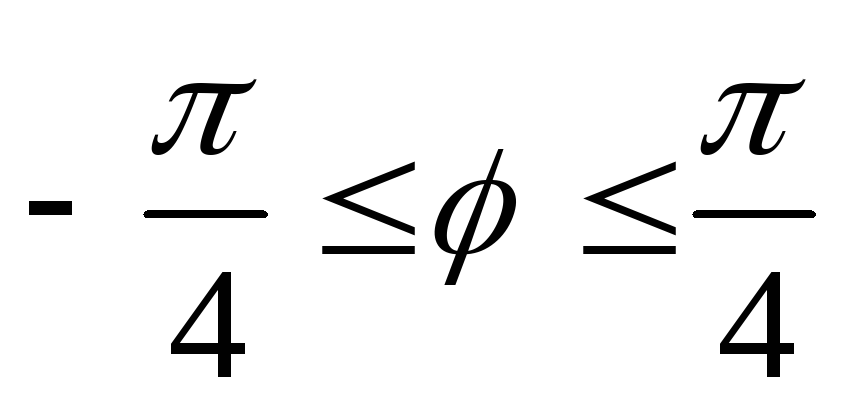 .
.
Следовательно,
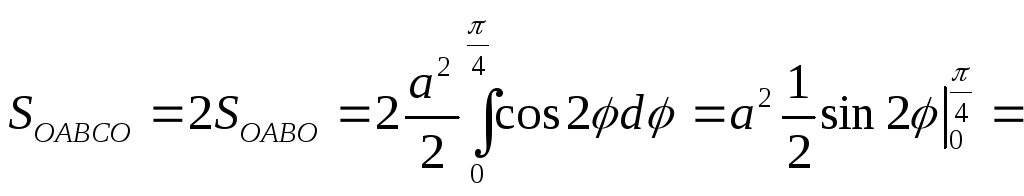
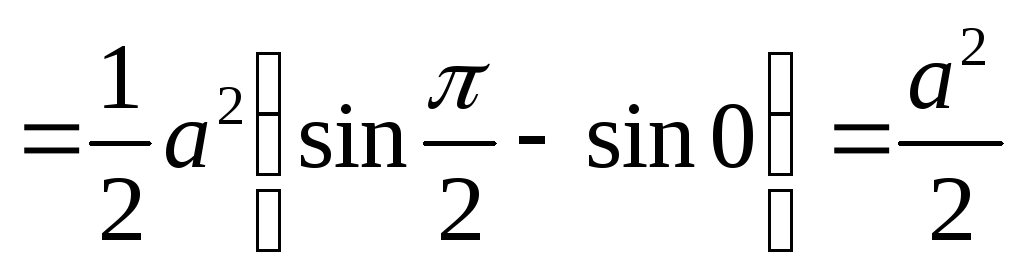 .
.
2. Вычисление длин дуг плоских кривых
Если
плоская кривая задана уравнением в
декартовых координатах 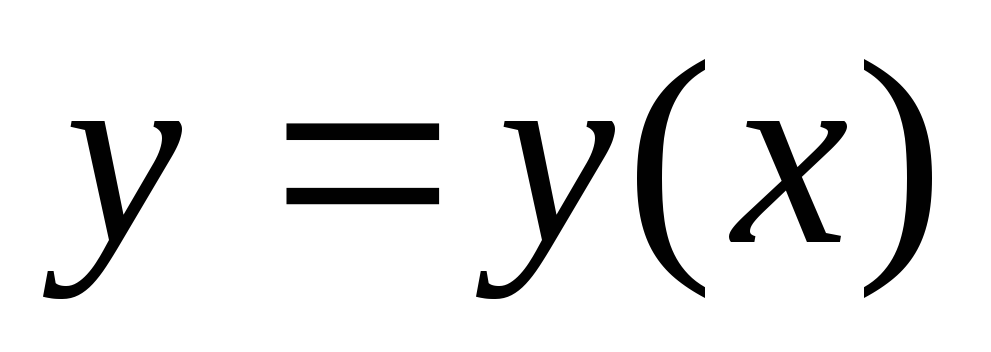 и производная
и производная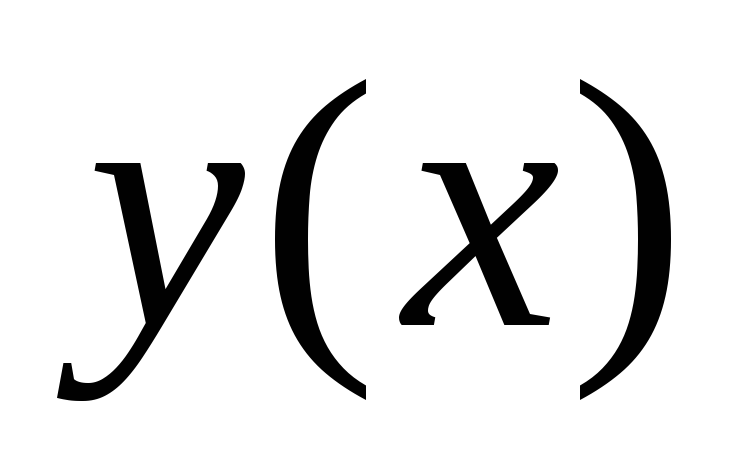 непрерывна,
то длина дуги этой кривой вычисляется
по формуле
непрерывна,
то длина дуги этой кривой вычисляется
по формуле
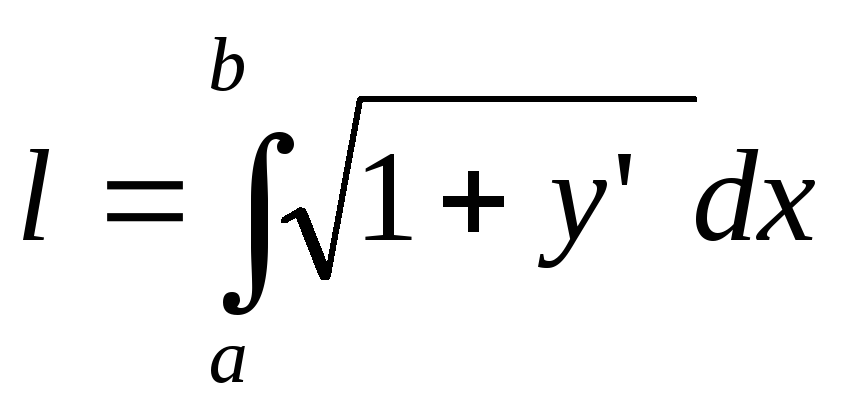 ,
,
где  и
и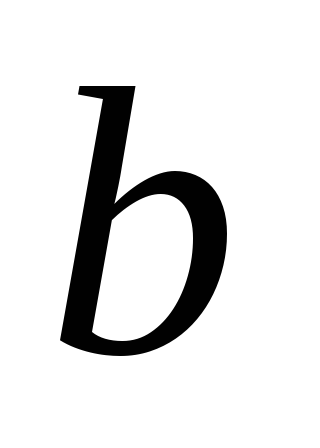 -абсциссы
концов данной дуги.
-абсциссы
концов данной дуги.
Если
кривая задана уравнениями в параметрической
форме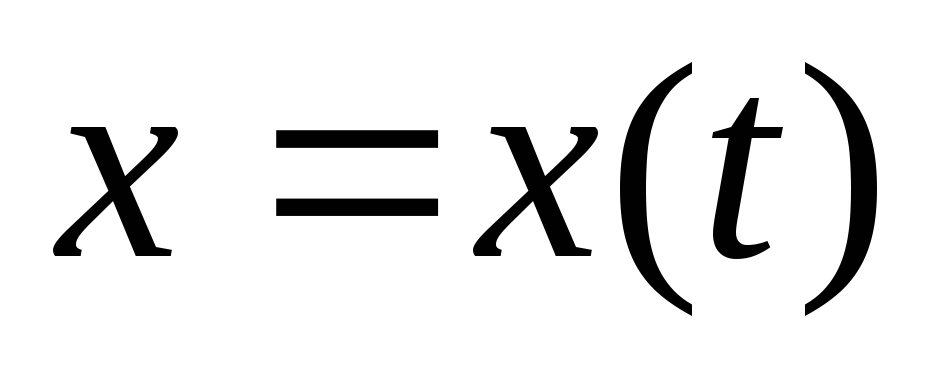 ,
,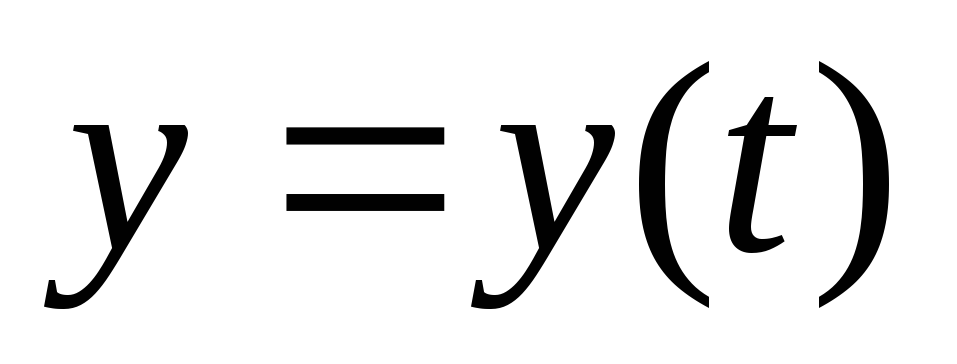 и производные
и производные 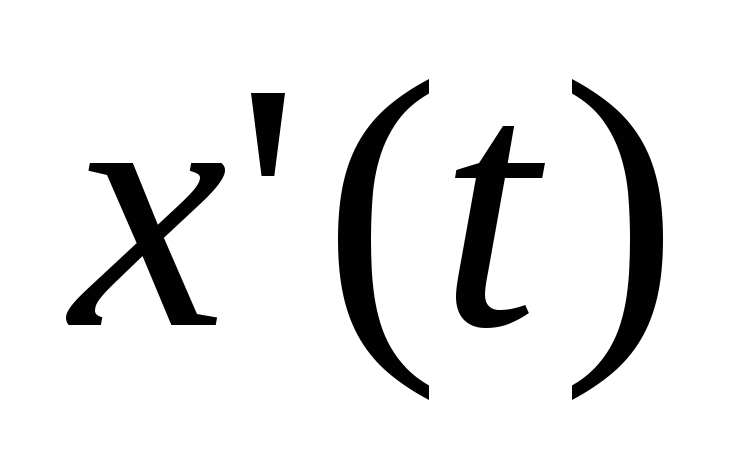 и
и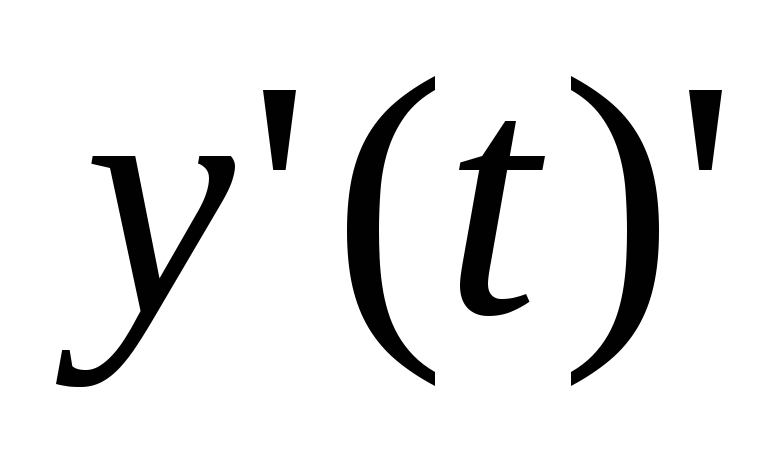 непрерывны
на отрезке
непрерывны
на отрезке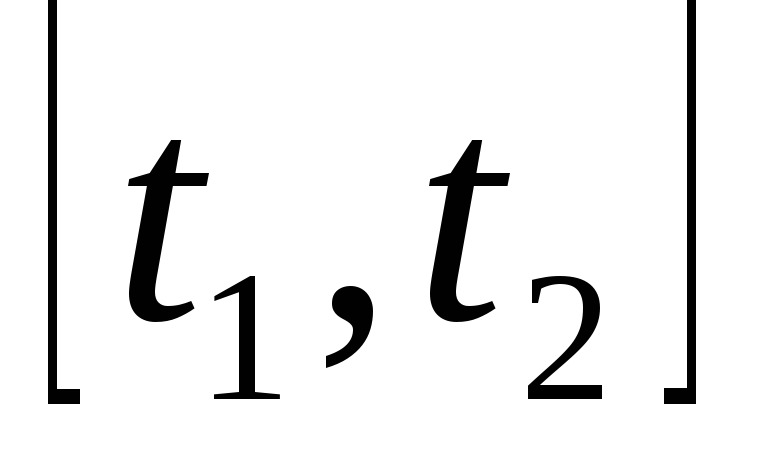 , то длина
дуги кривой выражается формулой
, то длина
дуги кривой выражается формулой
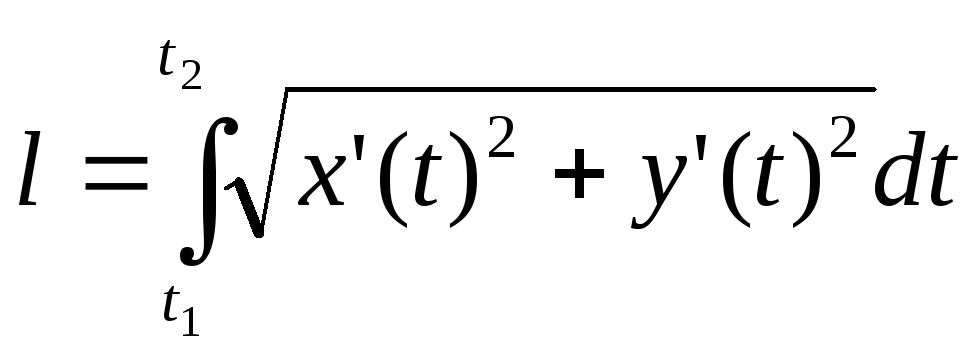 ,
,
где 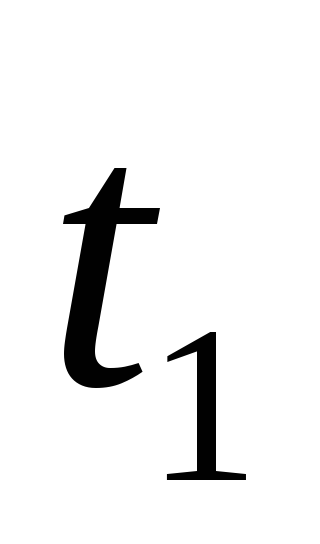 и
и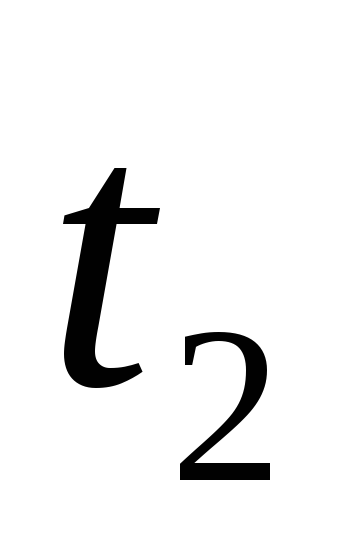 — значения параметра
— значения параметра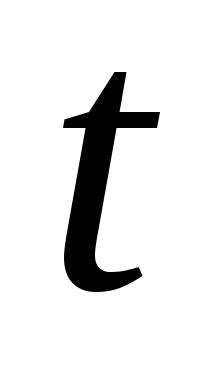 , соответствующие
концам дуги
, соответствующие
концам дуги 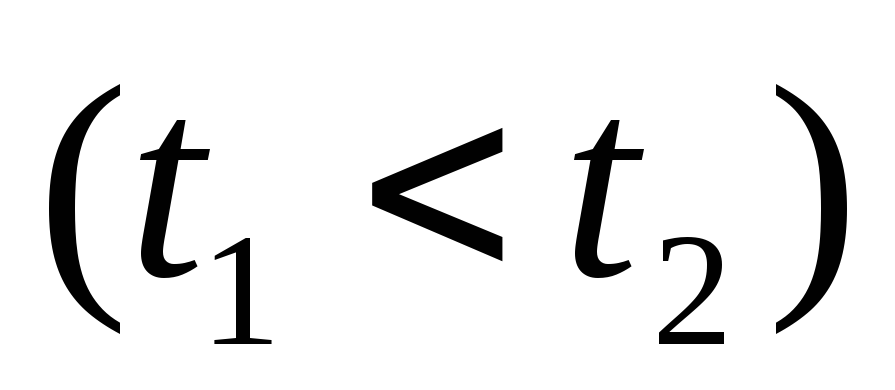 .
.
Если
кривая задана уравнением 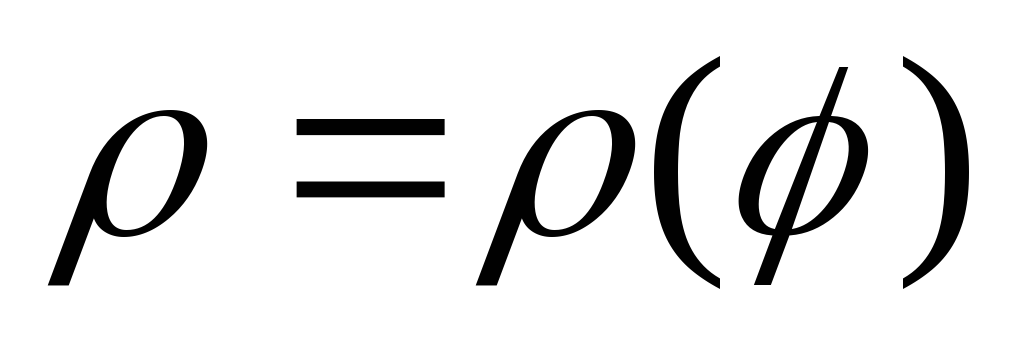 в
полярных координатах, то длина дуги
в
полярных координатах, то длина дуги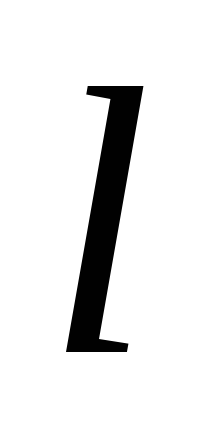 кривой выражается интегралом
кривой выражается интегралом
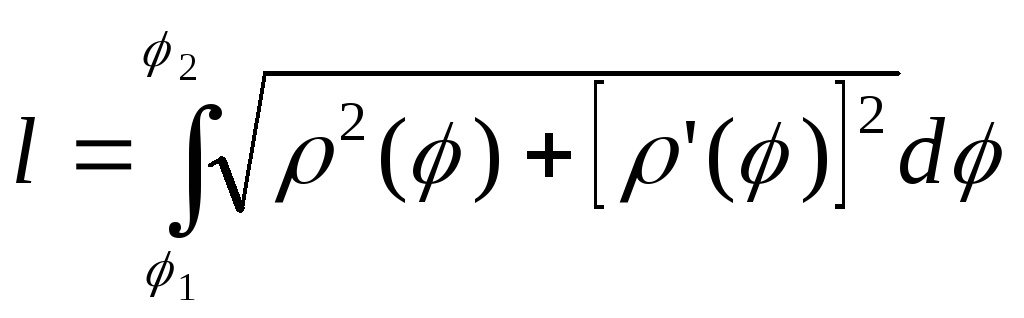 ,
,
где  и
и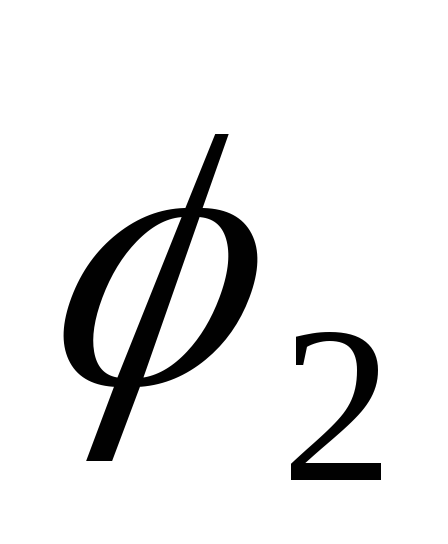 — значения полярного угла
— значения полярного угла в
концах дуги
в
концах дуги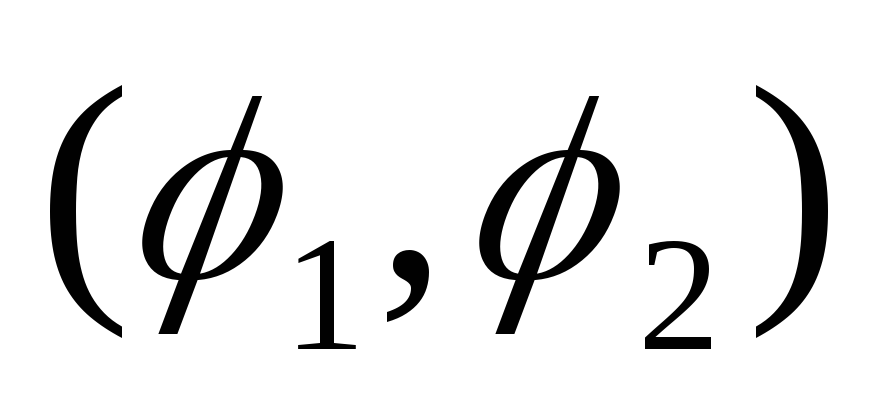 .
.
Пример.
Вычислить
длину дуги полукубической параболы 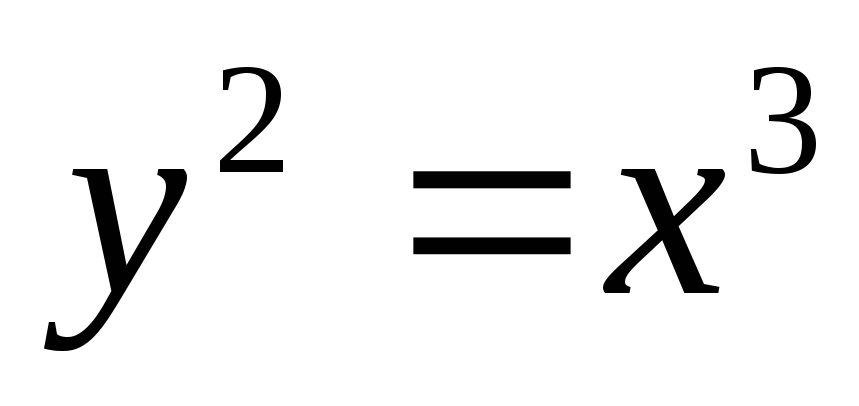 , заключенной
между точками
, заключенной
между точками 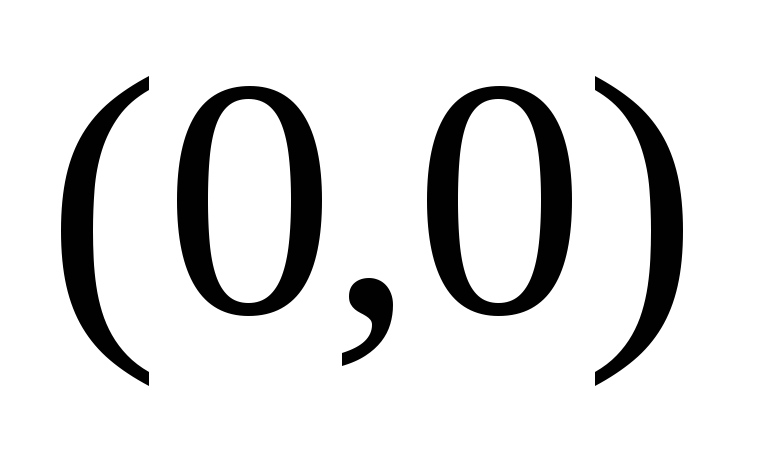 и
и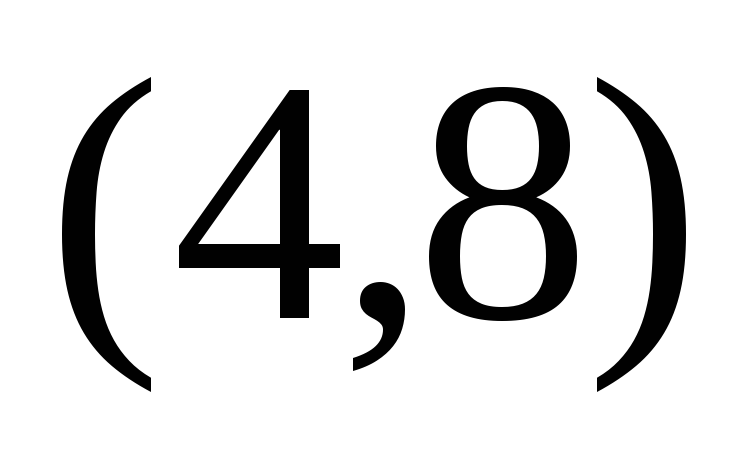 .
.
Р ешение.
ешение.
Функция 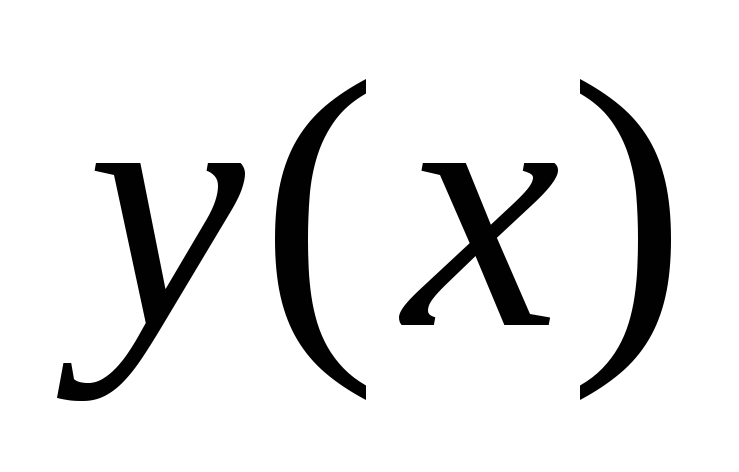 определена
при
определена
при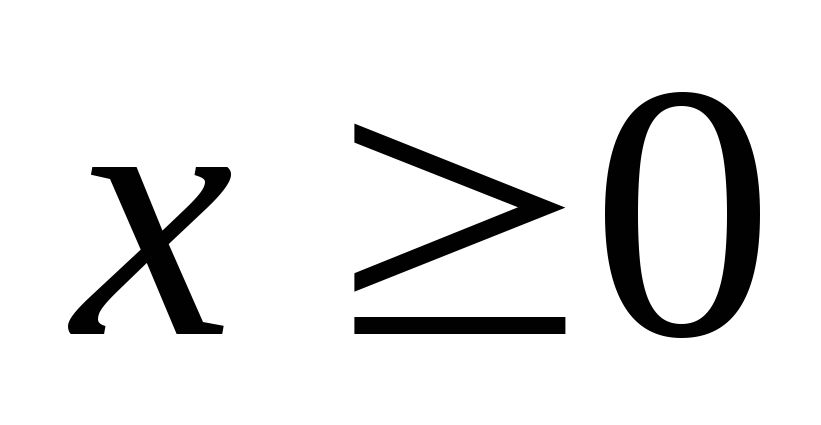 .
Поскольку данные точки
.
Поскольку данные точки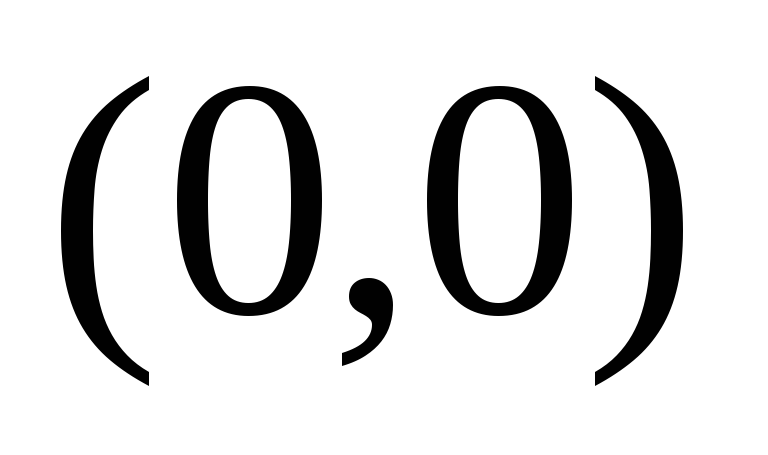 и
и 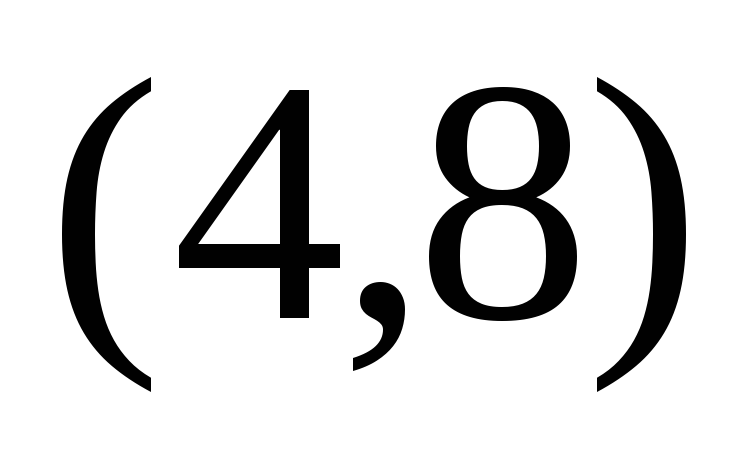 лежат в первой четверти, то
лежат в первой четверти, то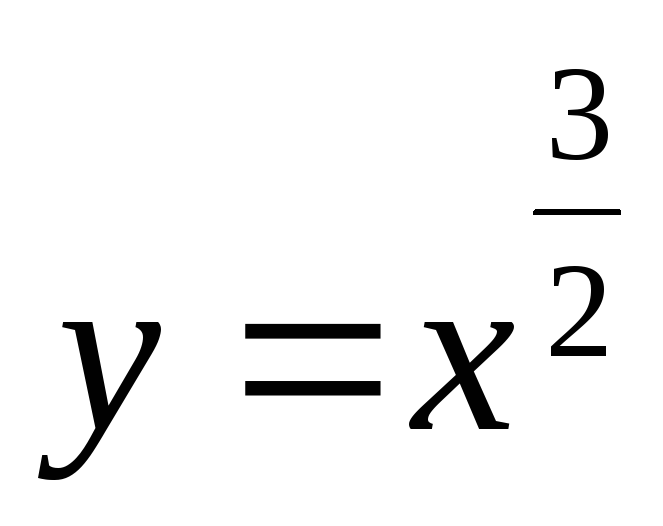 .
.
Отсюда
,
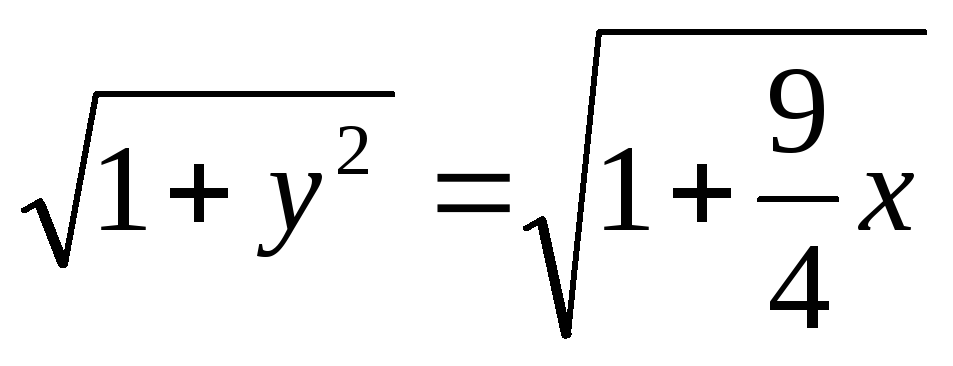 .
.
Следовательно,
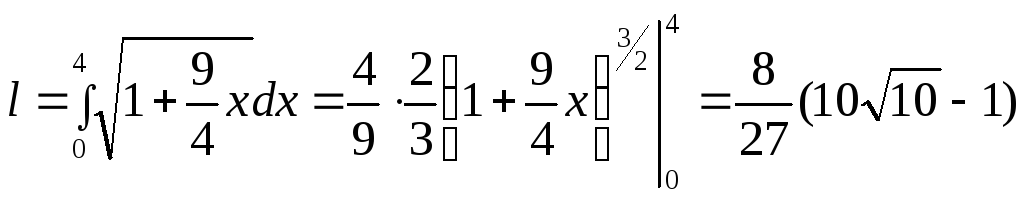 .
.
Пример.
Вычислить длину дуги развертки круга
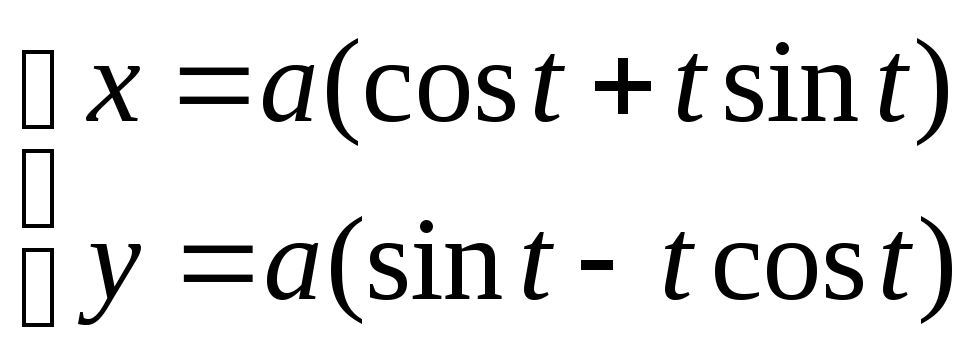 от
от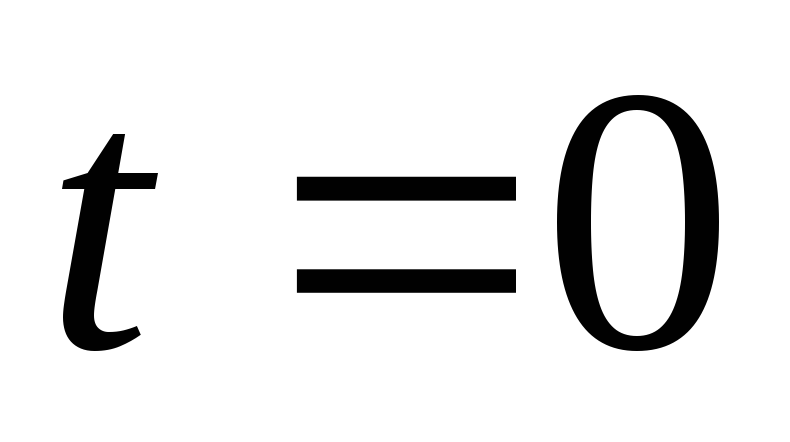 до
до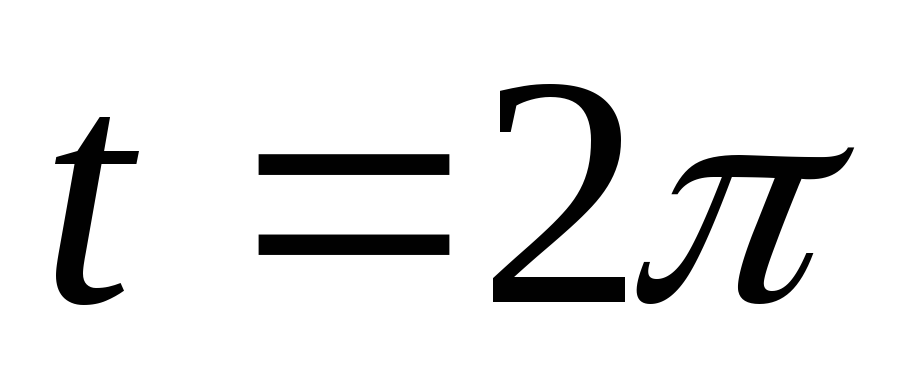 .
.
Решение.
Дифференцируя
по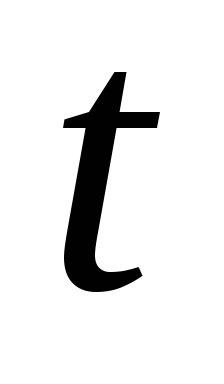 , получим
, получим
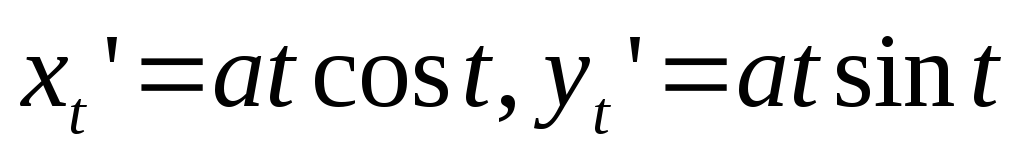 ,
,
откуда 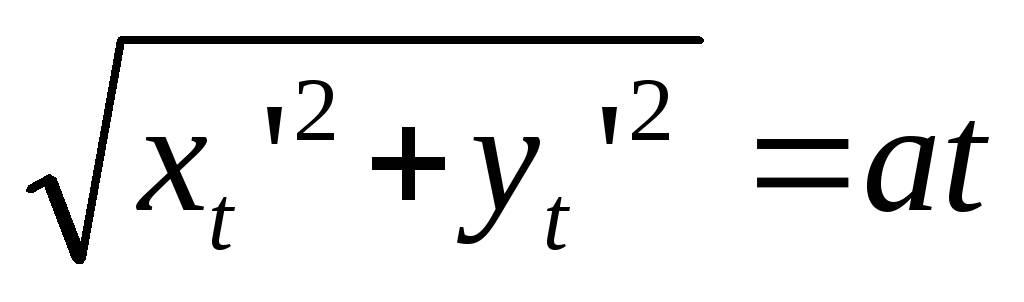 .
.
Следовательно,
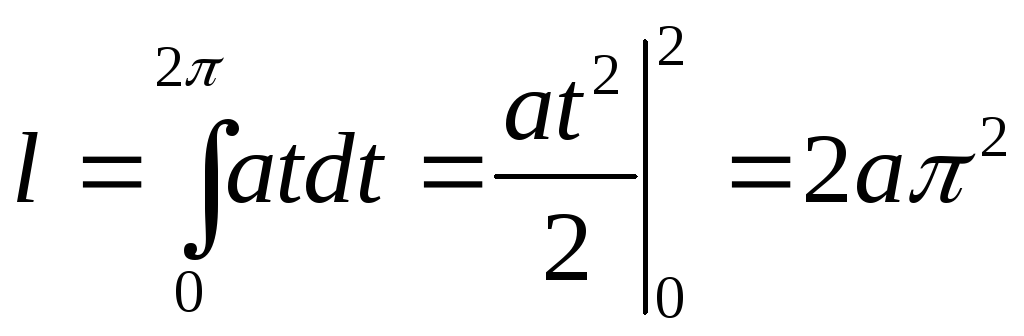 .
.
Пример.
Найти
длину первого витка архимедовой спирали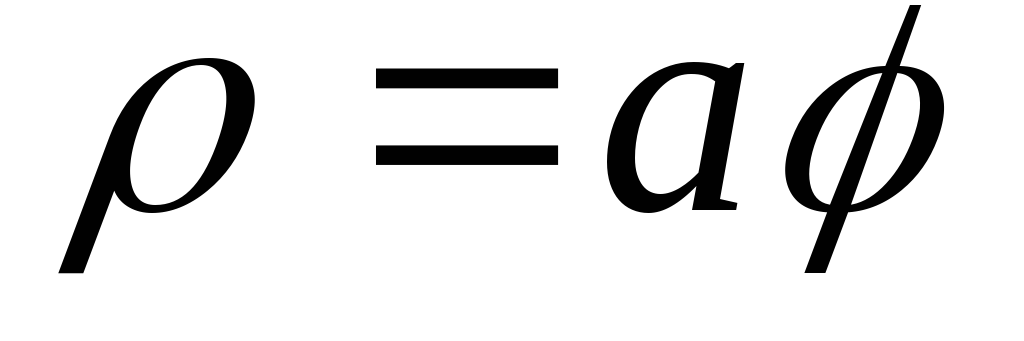 .
.
Решение.
Первый
виток архимедовой спирали образуется
при изменении полярного угла от 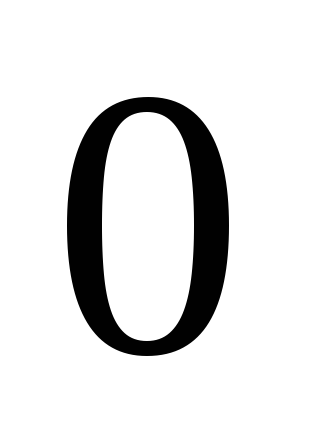 до
до .
Поэтому
.
Поэтому
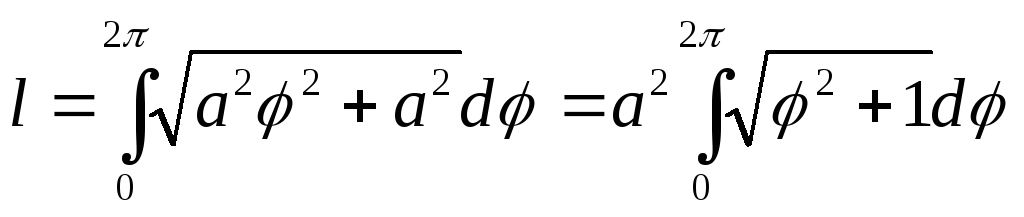 .
.
Вычислим
первообразную для функции 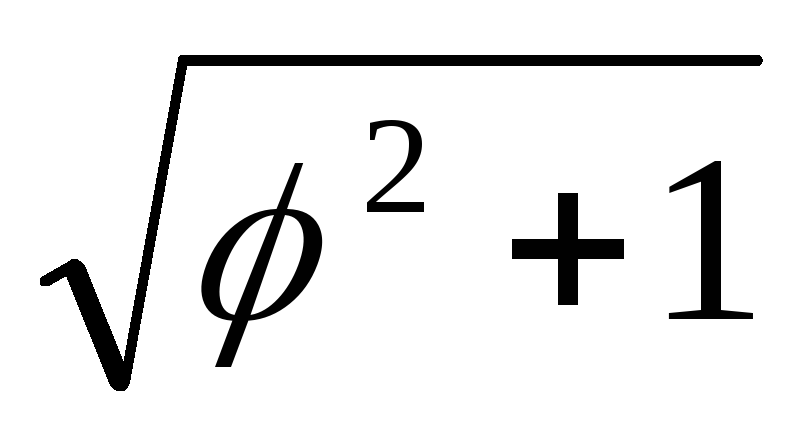 методом интегрирования по частям:
методом интегрирования по частям:
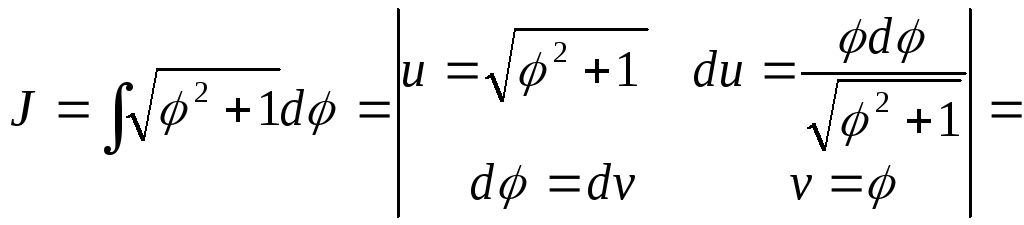
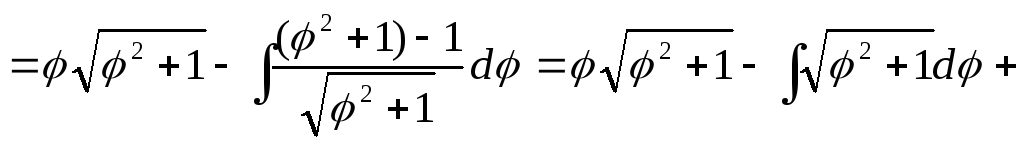
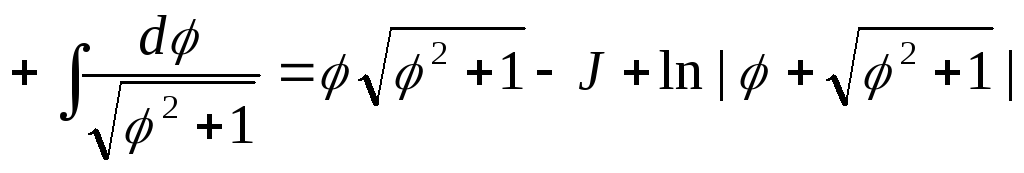 .
.
Откуда
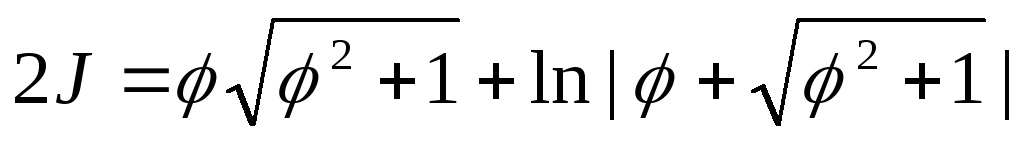 ,
,
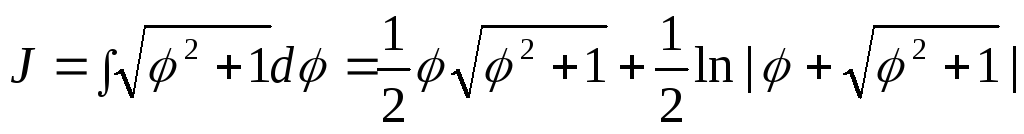 ,
,
и, следовательно,
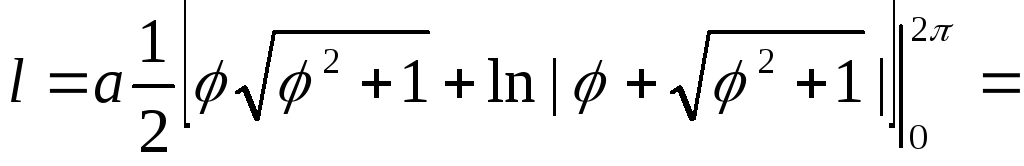
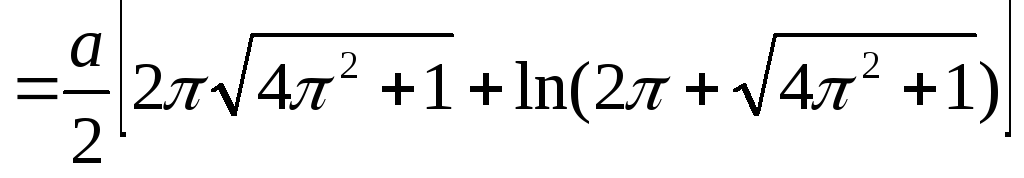 .
.
3. Вычисление объемов тел
Объем тела выражается интегралом
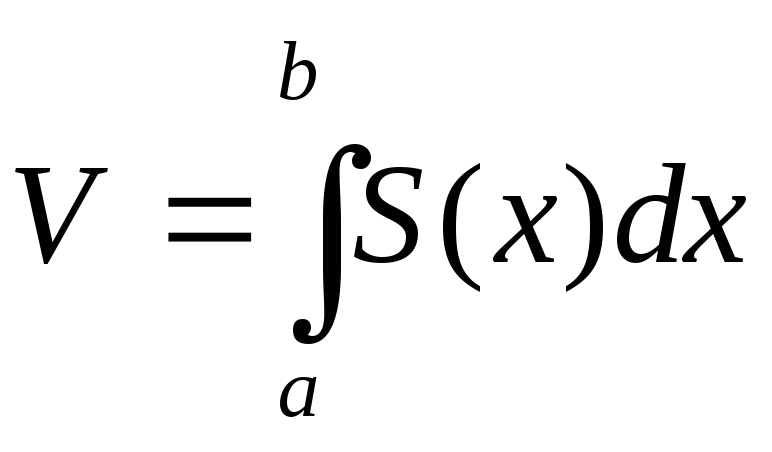 ,
,
где 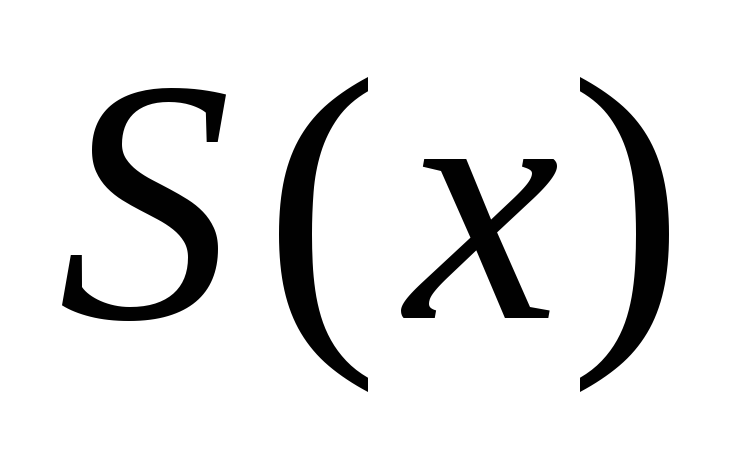 —
площадь сечения тела плоскостью,
перпендикулярной к оси
—
площадь сечения тела плоскостью,
перпендикулярной к оси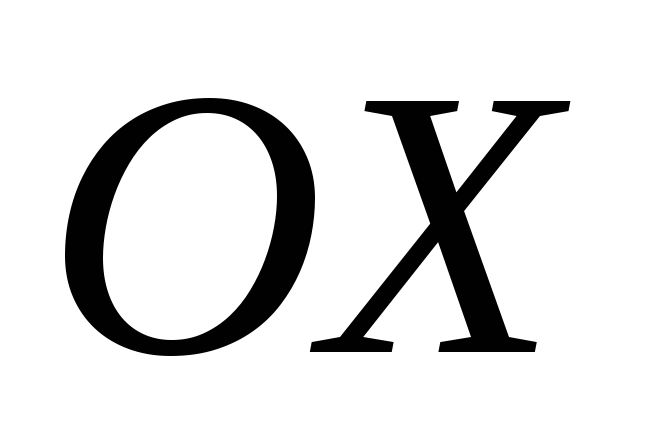 в точке с абсциссой
в точке с абсциссой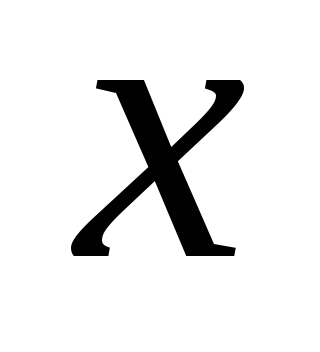 .
. и
и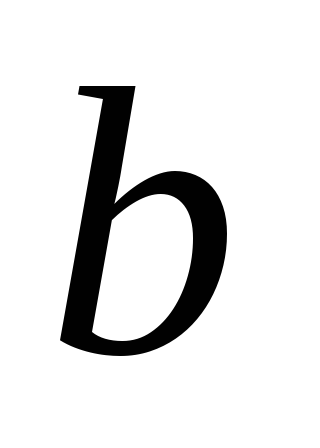 — левая и правая границы изменения
— левая и правая границы изменения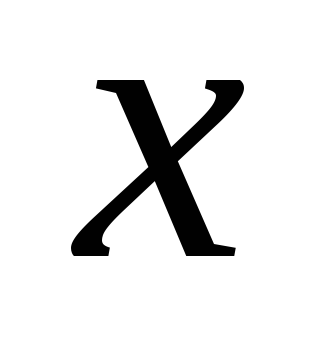 ,
,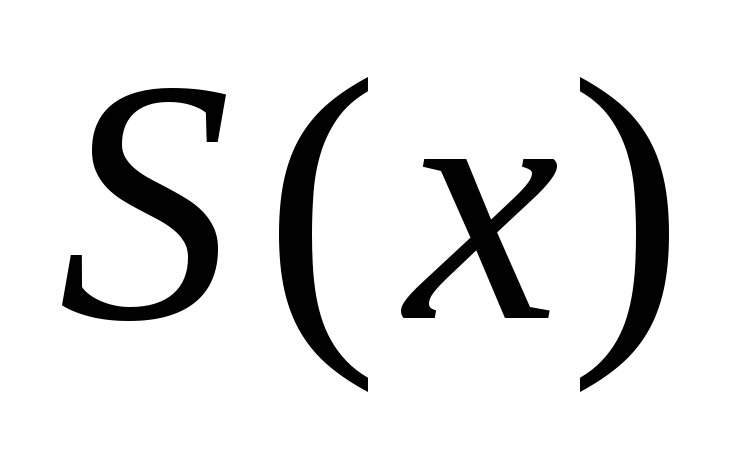 непрерывна
при
непрерывна
при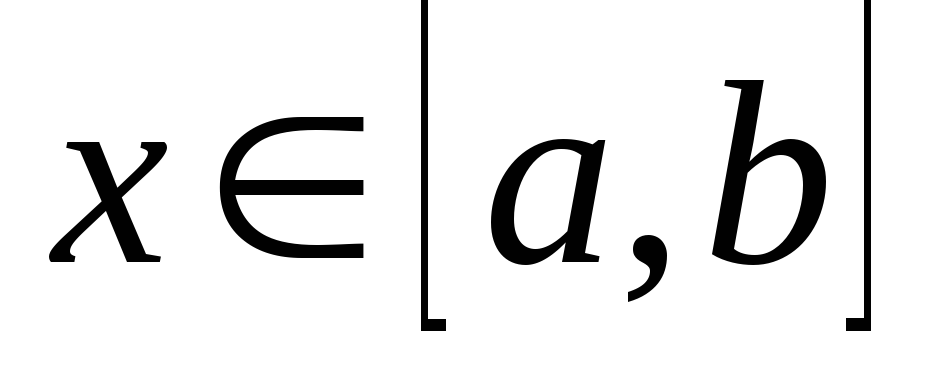 .
.
Объем
тела, образованного вращением вокруг
оси 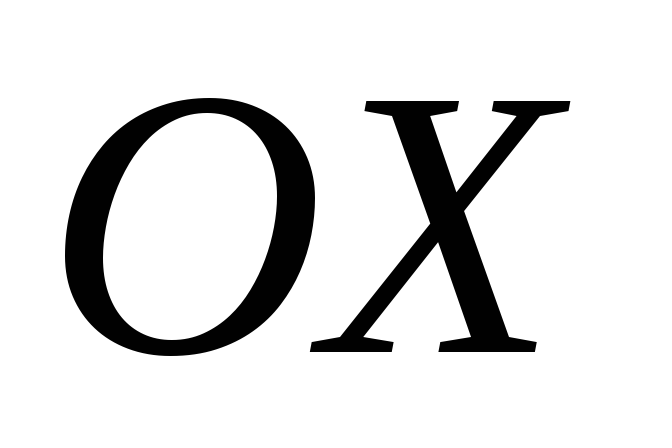 криволинейной трапеции, ограниченной
кривой
криволинейной трапеции, ограниченной
кривой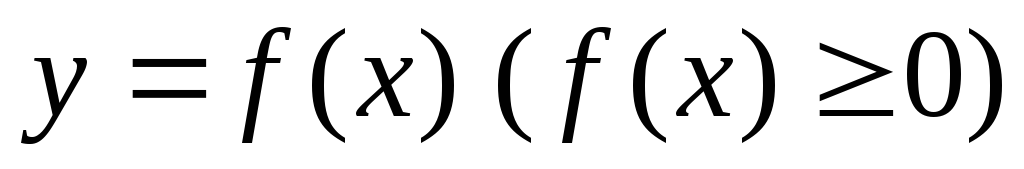 ,
осью абсцисс и прямыми
,
осью абсцисс и прямыми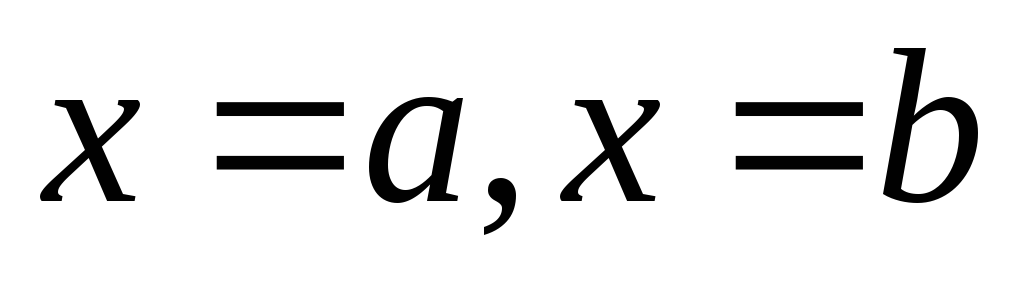 ,
,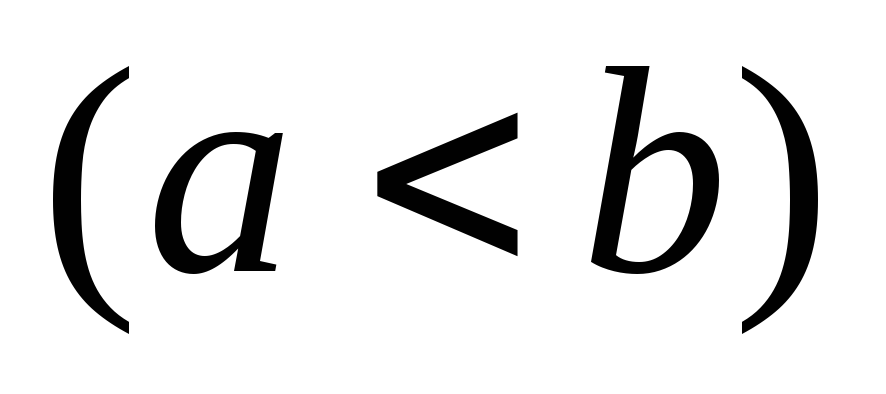 , выражается
интегралом
, выражается
интегралом
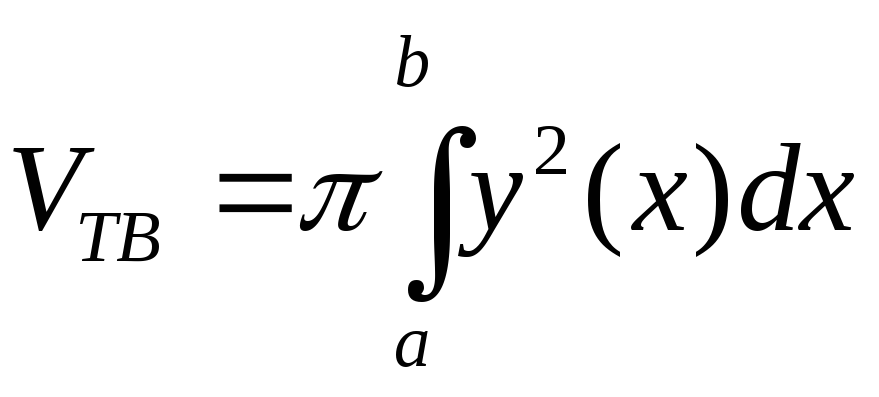 .
.
Объем
тела, образованного вращением вокруг
оси 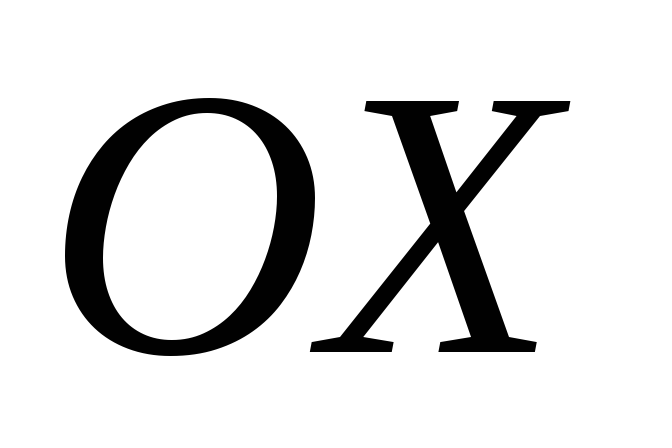 фигуры,
ограниченной кривыми
фигуры,
ограниченной кривыми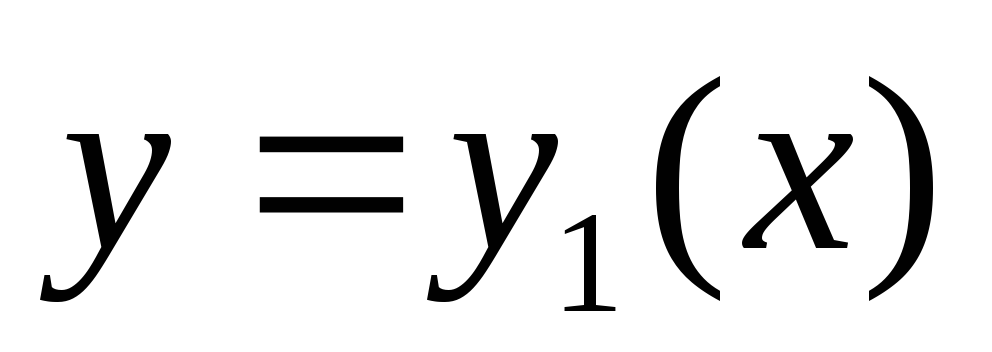 и
и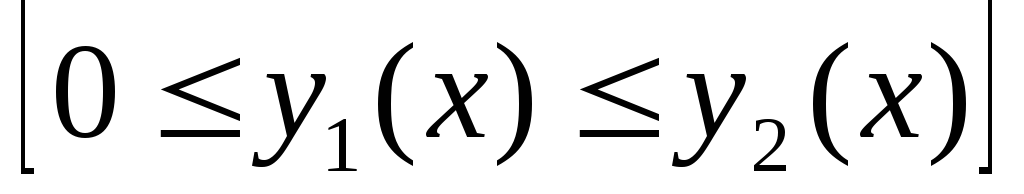 и прямыми
и прямыми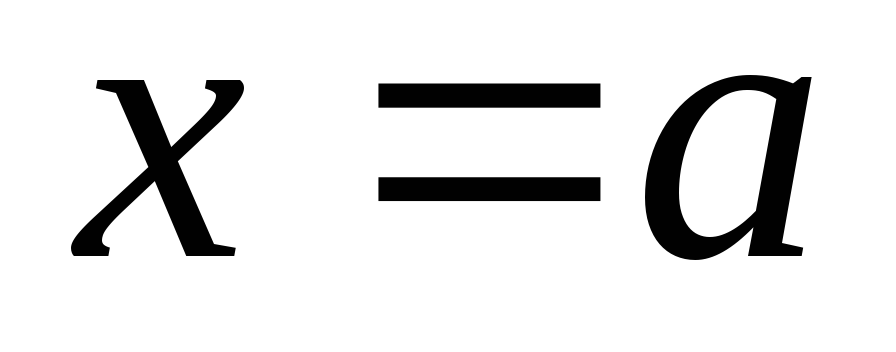 и
и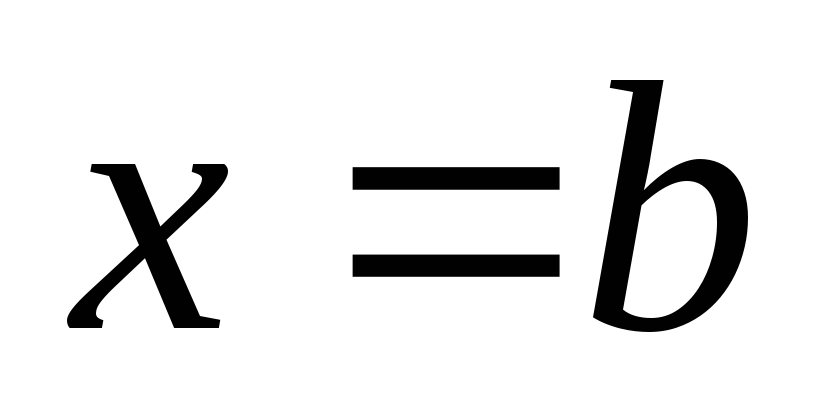 ,
выражается формулой
,
выражается формулой
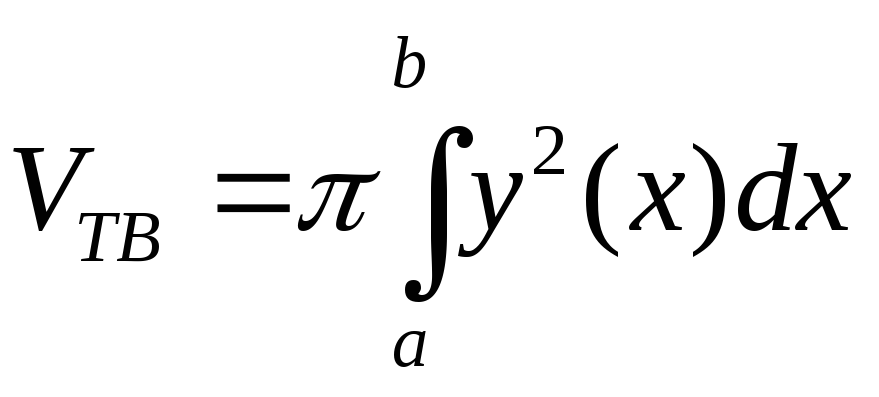 .
.
Если кривая задана параметрически или в полярных координатах, то следует сделать соответствующую замену переменной в указанных формулах.
Пример.
Найти объем эллипсоида
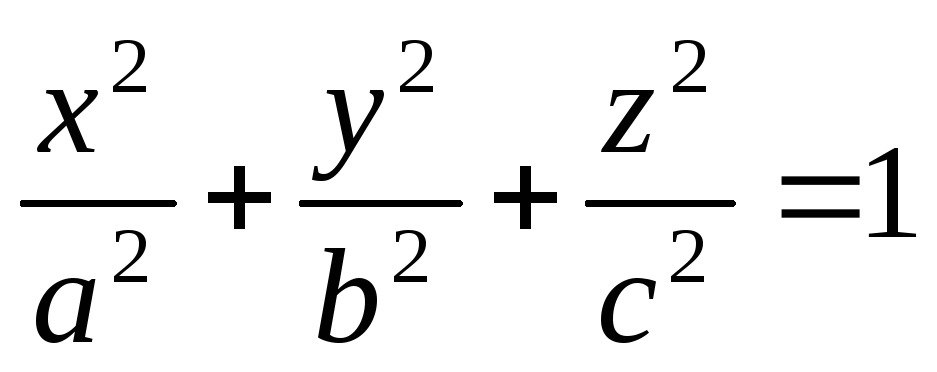 .
.
Р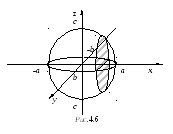 ешение.
ешение.
Сечение
эллипсоида плоскостью 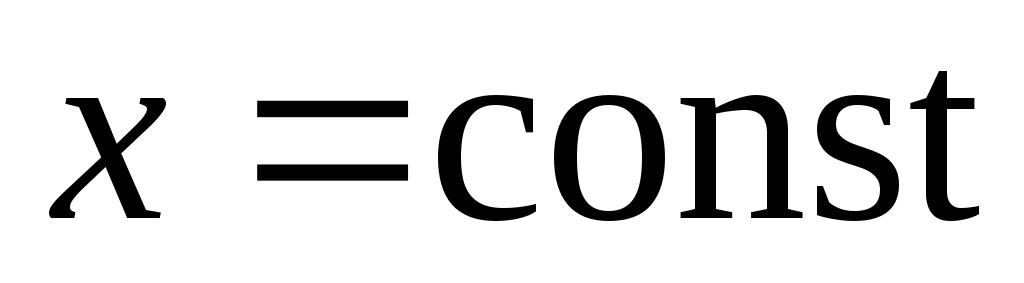 есть
эллипс
есть
эллипс

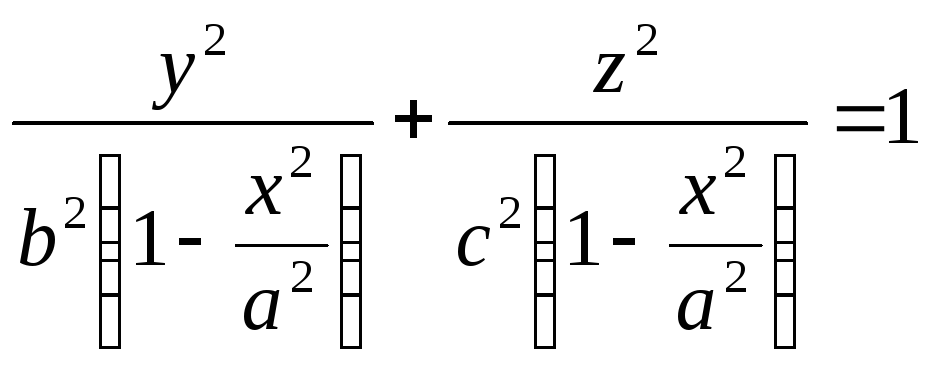
с
полуосями 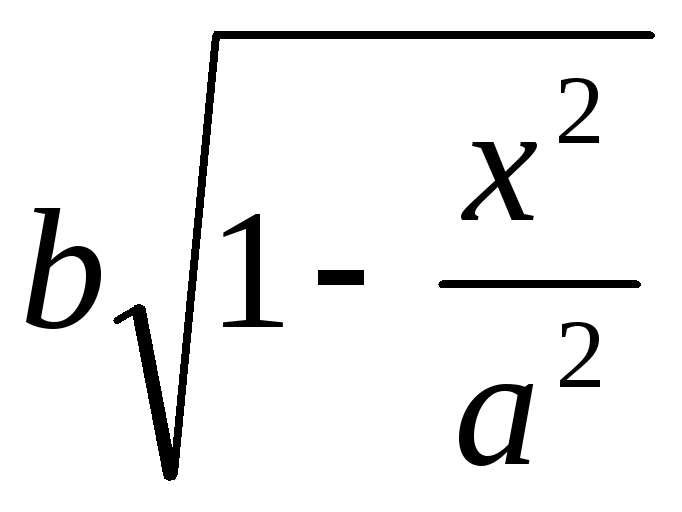 и
и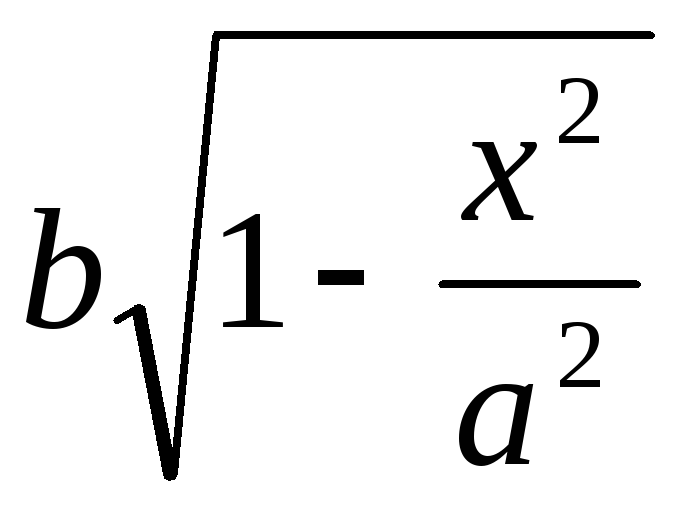 .
.
Следовательно площадь сечения
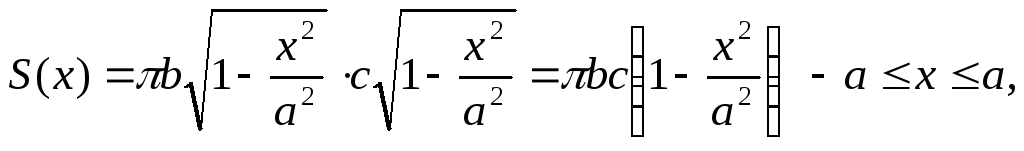
Поэтому объем эллипсоида
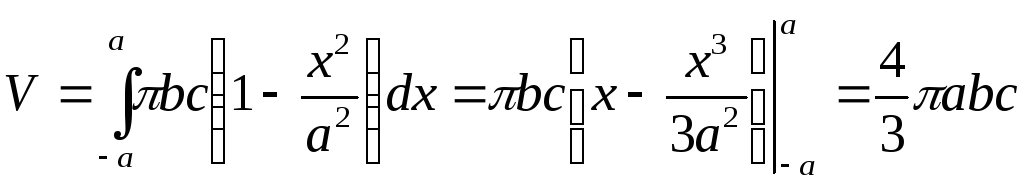 .
.
Положив,
в частности,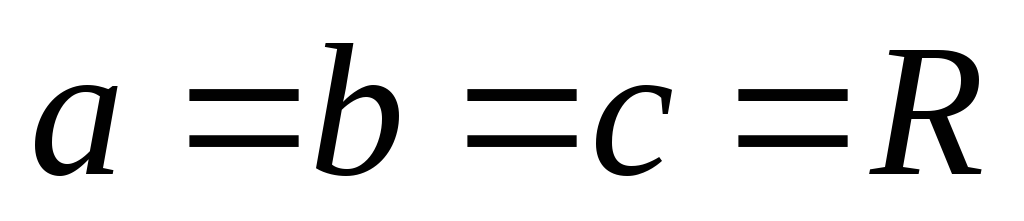 ,получим
объем шара
,получим
объем шара
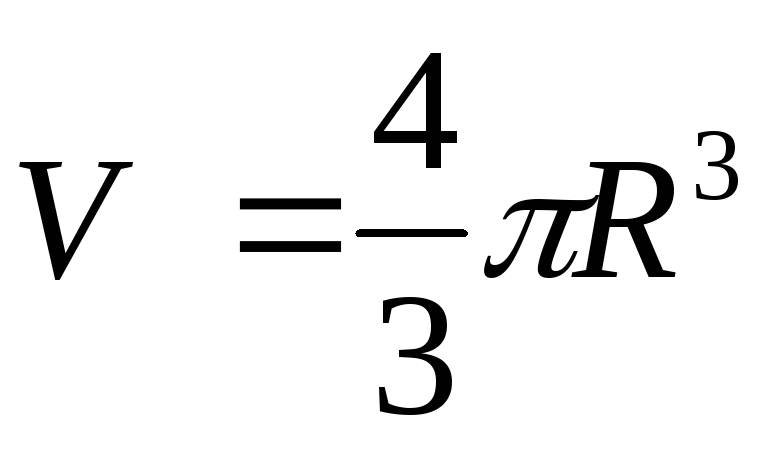 .
.
Пример.
Вычислить вокруг оси абсцисс объем тела, которое образуется при вращении одной арки циклоиды
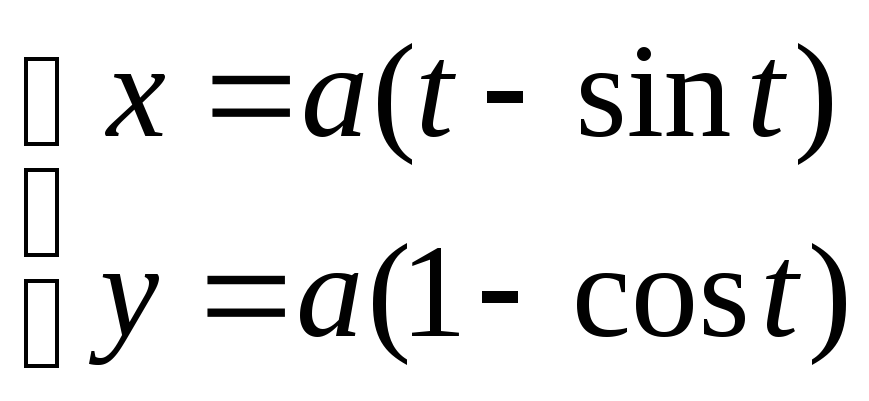
в округ
оси абсцисс.
округ
оси абсцисс.
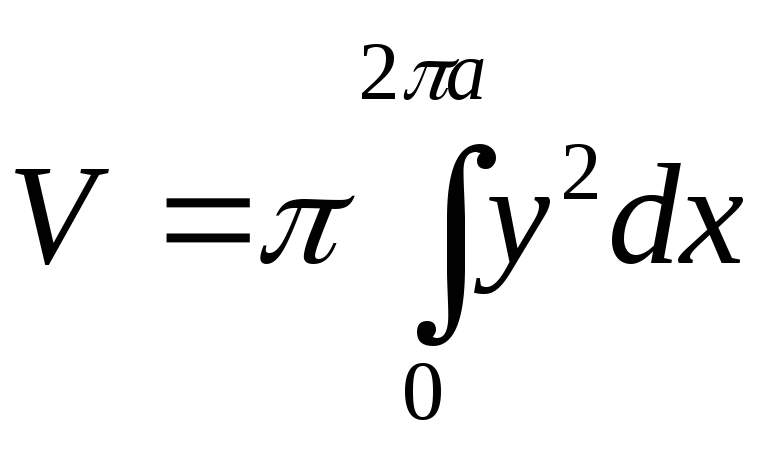
делаем замену переменной, полагая
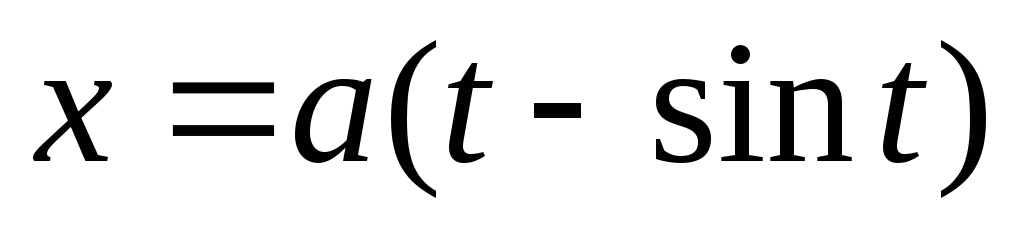 .
.
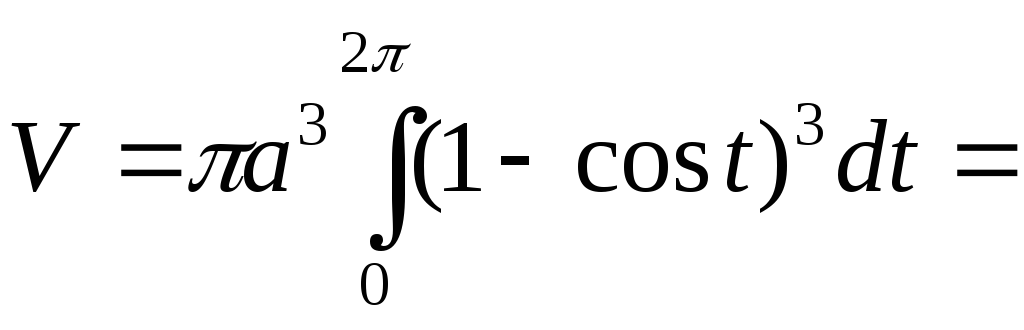
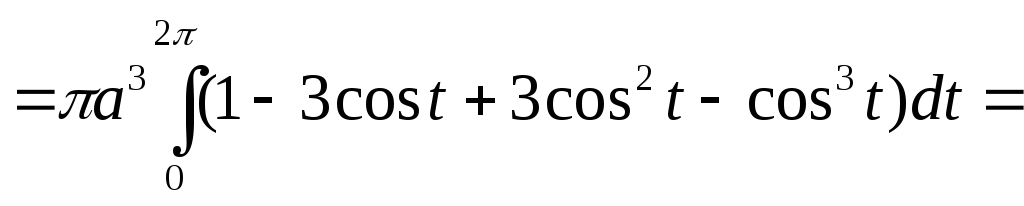
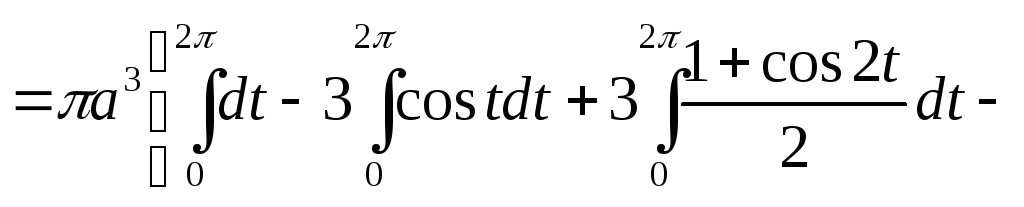
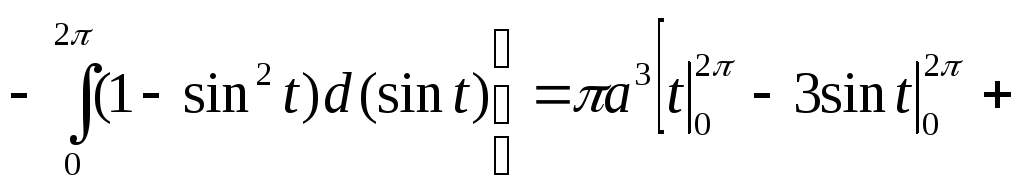
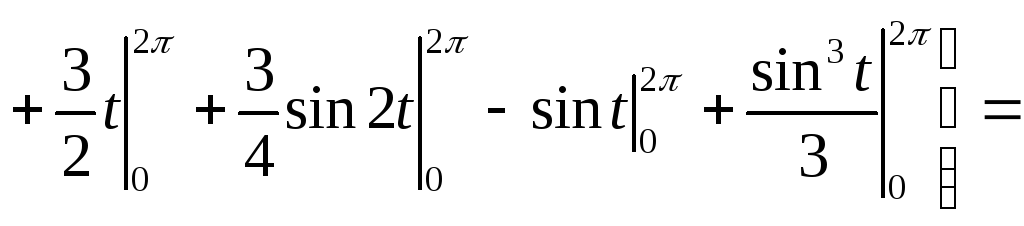
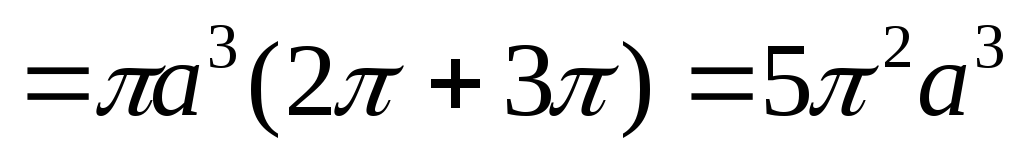 .
.
Контрольная работа №4 по теме
studfile.net
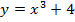 ,
, 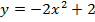 ,
, 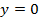 ,
,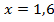
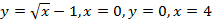
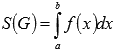 для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b],
для
непрерывной и неотрицательной
функции y=f(x) на
отрезке[a;b],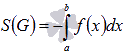 для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].
для
непрерывной и неположительной
функции y=f(x) на
отрезке[a;b].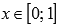 ,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке
,
вторая фигура расположена выше оси
абсцисс и ниже красной линии на отрезке 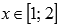 .
Следовательно,
искомая площадь будет равна
.
Следовательно,
искомая площадь будет равна 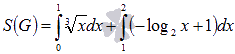 .
.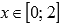 ,
вторая фигура расположена выше красной
и ниже синей линии на отрезке
,
вторая фигура расположена выше красной
и ниже синей линии на отрезке  .
В
этом случае площадь представляем как
.
В
этом случае площадь представляем как 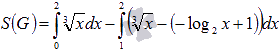 .
.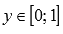 ,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.
,
заключенной правее синей линии и левее
красной. Вот
на этом варианте и остановимся.