1) координатных плоскостей; 2) осей координат; 3) начала координат.
Источник:  Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
Решебник
по
геометрии
за 10 класс (А.В. Погорелов, 2001 год),
задача №4
к главе «§18. Декартовы координаты и векторы в пространстве».
Все задачи >
Строим координатный параллелепипед как в задаче 3 и находим расстояния:
координаты данной точки, то есть (х; y; z) = (1; 2; -3).
2) Далее по теореме Пифагора имеем:
по теореме Пифагора. Так что
Так что расстояние до плоскостей: ху равно 3, yz равно 2, yz равно 1; расстояние до осей координат равно соответственно
, расстояние до начала координат равно ← 3. Дана точка А(1;2;3). Найдите основание перпендикуляров, опущенных из этой точки на координатные оси и координатные плоскости.5. В плоскости ху найдите точку D(x;y;0), равноудаленную от трех данных точек: А(0;1;-1), В(-1;0;1), С(0;-1;0). →- Вконтакте
5terka.com
Расстояние от точки до плоскости. Метод координат. Задание 14

В этой статье мы поговорим о том, как найти расстояние от точки до плоскости с помощью метода координат. О том как находить расстояние от точки до плоскости геометрическим способом, вы можете прочитать здесь.
Решим задачу: в единичном кубе  найдите расстояние от точки
найдите расстояние от точки  до плоскости
до плоскости  .
.

На этот раз давайте решим ее с помощью метода координат.
Сначала немного теории.
Рассстояние  от точки
от точки  до плоскости
до плоскости  вычисляется по такой формуле:
вычисляется по такой формуле:

Чтобы воспользоваться этой формулой, поместим наш куб в систему координат
: В нашей задаче роль точки
В нашей задаче роль точки  играет точка
играет точка  . То есть
. То есть  ,
,  ,
, 
Теперь наша задача найти коэффициенты  ,
,  ,
,  и
и  в уравнении
в уравнении  плоскости
плоскости 
Плоскость  определяется тремя точками
определяется тремя точками  ,
,  и
и  . Если мы координаты точек подставим в уравнение плоскости
. Если мы координаты точек подставим в уравнение плоскости 
Коэффициент  в уравнении плоскости мы можем принять равным 1.
в уравнении плоскости мы можем принять равным 1.
Чтобы найти коэффициенты  ,
,  и
и  , подставим координаты точек
, подставим координаты точек 
 и
и  в уравнение плоскости
в уравнение плоскости  . Получим систему уравнений:
. Получим систему уравнений:

Отсюда:  ,
,  ,
, 
Подставим координаты точки  и значения коэффициентов в формулу для расстояния:
и значения коэффициентов в формулу для расстояния:

Ответ: 
И.В. Фельдман, репетитор по математике.

ege-ok.ru
формулы, примеры, решения, формула расстояния между двумя точками
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Определение 1Расстояние между точками
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.

В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднит
zaochnik.com
Вычисление расстояния от точки до плоскости
Реферат
по алгебре и геометрии
Вычисление расстояния между линейными геометрическими объектами в пространстве
студента группы КБ-12
Никитченко Богдана
Вычисление расстояния от точки до плоскости
Первый способ
Расстояние от точки до плоскости находим по следующей формуле:
d= 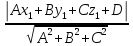 ,
где
,
где 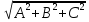 — длина вектора нормали N={A;B:C}
плоскости α, а число
— длина вектора нормали N={A;B:C}
плоскости α, а число 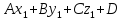 есть результат подстановки координат
точки M1(x1;
y1;
z1)
в левую часть общего уравнения плоскости.
есть результат подстановки координат
точки M1(x1;
y1;
z1)
в левую часть общего уравнения плоскости.
Пример ( Клетеник № 959(5)):
Вычислить расстояние d от точки M5(9;2;-2) до плоскости 12y-5z+5=0.
Решение:
N= {0; 12; -5}
d= 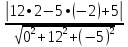 =
3
=
3
Ответ: 3
Второй способ
Составляем уравнение прямой L, которая проходит через точку М1 и перпендикулярна к плоскости α.
Находим координаты точки M0(x0; y0; z0) — точки пересечения прямой L и плоскости α.
Вычисляем
расстояние между точками M0 и М1
по формуле:
d=
M0M1 =
(x1-x0)2 +
(y1-y0)2 + (z1-z0)2
Пример ( Клетеник № 959(4)):
Вычислить расстояние d от точки M4(3;-6;7) до плоскости 4x-3z-1=0.
Решение:
L: 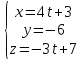

4(4t+3) -3(-3t+7) =0
16t +12 +9t -21-1=0
25t=10
t=0,4
x0= 4•0,4+3=4,6
y0= — 6
z0= -3•0,4+7=5,8
M0(4,6; -6; 5,8)
d= = 2
Ответ: 2
Вычисление расстояния между параллельными плоскостями
Первый способ
Выберем любую точку на первой плоскости.
Применим формулу расстояния от точки до плоскости.
d= 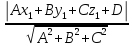
Пример (Клетеник № 964(5)):
Вычислить расстояние между параллельными плоскостями:
30x-32y+24z-75=0 15x-16y+12z-25=0
Решение:
Пусть y=0 и z=0. Тогда подставив эти значения в первое уравнение, получим
x=2,5.
Мы получили точку М(2,5; 0; 0) . Применим
формулу расстояния от точки до плоскости:
d=  =0,5
=0,5
Ответ: 0,5
Второй способ
Если плоскость α задана уравнением Ax + By + Cz + D1=0 , а плоскость β задана уравнением Ax + By + Cz + D2=0, то расстояние между параллельными плоскостями находим по следующей формуле:
d= 
Пример( Клетеник №964(6)):
Вычислить расстояние между параллельными плоскостями:
6x-18y-9z-28=0 4x-12y-6z-7=0
Решение:
Умножив
обе части второго уравнения на  ,
получим 6x-18y-9z-10,5=0.
,
получим 6x-18y-9z-10,5=0.
Применим
формулу: d= 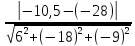 =
= 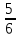
Ответ: 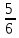
Вычисление расстояния от точки до прямой в пространстве
Первый способ
Определим
направляющий вектор прямой a
={ l;
m;
n}и
вычислим его длину по формуле
a
=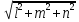




Найдем
координаты некоторой точки М0(x0;
y0;
z0),
лежащей на прямой a.
Вычислим координаты вектора M0M1={x1-x0;
y1-y0;
z1-z0},
найдем векторное произведение векторов
a
и
M0M1 и его длину.


Найдем расстояние от точки до прямой в пространстве по формуле:
d(M1;L)= 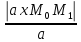



Пример (Клетеник №1063(1)):
Вычислить расстояние d от точки P(2; 3; -1) до прямой:
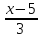 =
= 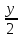 =
= 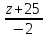
Решение:
a
= {3;
2; -2}
a
=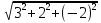 =
= 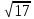

M0(5;
0; -25) M0P
= {-3; 3; 24}
a
x
M 0P
=  = 54i – 66j + 15k
= 54i – 66j + 15k 

a
x
M 0P
= 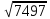 =21
=21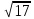

d=
21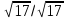 =21
=21
Ответ: 21
Второй способ
Составляем уравнение плоскости α , проходящей через данную точку М1(x1; y1; z1) перпендикулярно к данной прямой L.
Определяем координаты M0(x0; y0; z0) – точки пересечения прямой L и плоскости α .
Находим расстояние от точки М1до прямой L по формуле:
d=
(x1-x0)2 + (y1-y0)2 + (z1-z0)2
Пример(Клетеник №1063(2)):
Вычислить расстояние d от точки P(2; 3; -1) до прямой:
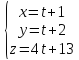
Решение:
Составим
уравнение плоскости, проходящей через
точку P(2;
3; -1) с вектором нормали a={1;
1; 4}.
(x-2) + (y-3) +4(z+1)=0
x+y+4z-1=0
Найдем точку пересечения прямой и плоскости
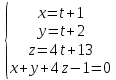
(t+1)+(t+2)+4(4t+13)-1=0
t+1+t+2+16t+52-1=0
18t=-54
t= -3
M0(-2; -1; 1) — точка пересечения прямой и плоскости.
d=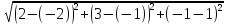 =6
=6
Ответ: 6
Вычисление расстояния между параллельными прямыми
Выберем на одной из прямых любую точку.
Применим формулу расстояния от точки до прямой:
d(M1;L)= 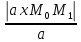



Пример(Клетеник № 1064):
Убедившись,
что прямые параллельны, вычислить
расстояние d
между ними. 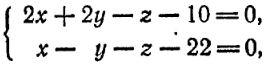
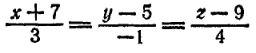

Решение:
Перейдем от общих уравнений прямой к каноническому.
Найдем точку M0(x0; y0; z0)
Пусть z0=0. Тогда подставим это значение в общие уравнения прямой.
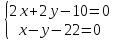
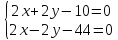
4x=54
x=13,5
y= -8,5
M0(13,5; -8,5; 0)
a1 =N1 x N2=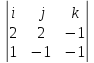 =
-3i+j-4k
=
-3i+j-4k




a 1={-3,1,-4} a 2={3,-1,4}
Векторы
a1и
a2 коллинеарны.
Следовательно прямые параллельны.

Из
уравнения второй прямой находим M1(-7;
5; 9).
M0M1={-20,5; 13,5; 9}
a1 x M0M1= =63i+109j-20k
=63i+109j-20k


a1 = 
a1 x M0M1 = 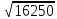


d= 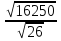 =25
=25
Ответ: 25
Вычисление расстояния между скрещивающимися прямыми
Расстояние
между скрещивающимися прямыми находим
по формуле: d(L1;L2)=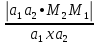 ,
где a1,a2 – направляющие
векторы прямых, M1,
M2–точки
на прямых L1 и L2.
,
где a1,a2 – направляющие
векторы прямых, M1,
M2–точки
на прямых L1 и L2. 






Если числитель равен нулю, то прямые пересекаются.
Пример (Клетеник №1083(3)):
Вычислить
кратчайшее расстояние между двумя
прямыми: 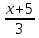 =
= 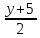 =
= 

Решение:
a1 x a2 = 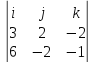 = -6i-9j-18k
= -6i-9j-18k

a1 x a2 =
21 

M1(-5;
-5; 1) M2(9;
0; 2)
M2M1={14; 5; 1}
a1 a2  M2M1 = -84 – 45 -18 =147
M2M1 = -84 – 45 -18 =147


d=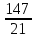 =7
=7
Ответ: 7
studfile.net
Расстояние от точки до плоскости
Поиск расстояния от точки до плоскости — частая задача, возникающая при решении различных задач аналитической геометрии, например, к этой задаче можно свести нахождение расстояния между двумя скрещивающимися прямыми или между прямой и параллельной ей плоскостью.
Рассмотрим плоскость $β$ и точку $M_0$ с координатами $(x_0;y_0; z_0)$, не принадлежащую плоскости $β$.
Определение 1
Кратчайшим расстоянием между точкой и плоскостью будет перпендикуляр, опущенный из точки $М_0$ на плоскость $β$.
Рисунок 1. Расстояние от точки, до плоскости. Автор24 — интернет-биржа студенческих работ
Ниже рассмотрено как найти расстояние от точки до плоскости координатным методом.
Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве
Перпендикуляр из точки $M_0$, пересекающийся с плоскостью $β$ в точке $M_1$ с координатами $(x_1;y_1; z_1)$, лежит на прямой, направляющим вектором которой является нормальный вектор плоскости $β$. При этом длина единичного вектора $n$ равна единице. Соответственно этому, расстояние от $β$ до точки $M_0$ составит:
$ρ= |\vec{n} \cdot \vec{M_1M_0}|\left(1\right)$, где $\vec{M_1M_0}$ — нормальный вектор плоскости $β$, а $\vec{n}$ — единичный нормальный вектор рассматриваемой плоскости.
В случае, когда уравнение плоскости задано в общем виде $Ax+ By + Cz + D=0$, координаты нормального вектора плоскости представляют собой коэффициенты уравнения $\{A;B;C\}$, а единичный нормальный вектор в этом случае имеет координаты, вычисляемые по следующему уравнению:
$\vec{n}= \frac{\{A;B;C\}}{\sqrt{A^2 + B^2 + C^2}}\left(2\right)$.
Теперь можно найти координаты нормального вектора $\vec{M_1M_0}$:
$\vec{M_0M_1}= \{x_0 – x_1;y_0-y_1;z_0-z_1\}\left(3\right)$.
Также выразим коэффициент $D$, используя координаты точки, лежащей в плоскости $β$:
$D= Ax_1+By_1+Cz_1$
Координаты единичного нормального вектора из равенства $(2)$ можно подставить в уравнение плоскости $β$, тогда мы имеем:
$ρ= \frac{|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|}{\sqrt{A^2+B^2+C^2}}= \frac{|Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|}{\sqrt{A^2+B^2+C^2}} = \frac{Ax_0+ By_0 + Cz_0 + D}{\sqrt{A^2+B^2+C^2}}\left(4\right)$
Равенство $(4)$ является формулой для нахождения расстояния от точки до плоскости в пространстве.
Общий алгоритм для нахождения расстояния от точки $M_0$ до плоскости
- Если уравнение плоскости задано не в общей форме, для начала необходимо привести его к общей.
- После этого необходимо выразить из общего уравнения плоскости нормальный вектор данной плоскости через точку $M_0$ и точку, принадлежащую заданной плоскости, для этого нужно воспользоваться равенством $(3)$.
- Следующий этап — поиск координат единичного нормального вектора плоскости по формуле $(2)$.
- Наконец, можно приступить к поиску расстояния от точки до плоскости, это осуществляется с помощью вычисления скалярного произведения векторов $\vec{n}$ и $\vec{M_1M_0}$.
Пример 1
Найдите расстояние от точки $M_0$, заданной координатами $(1;2;3)$ до плоскости $β$, заданной уравнением $5x+2y-z+3=0$
Воспользуемся формулой $(4)$:
$ρ=\frac{|5 \cdot 1 + 2 \cdot 2 -3 \cdot1+3|}{\sqrt{5^2 + 2^2 + (-1)^2}}=\frac{9}{\sqrt{30}}$.
spravochnick.ru