Уравнение прямой

Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

k = tg φ

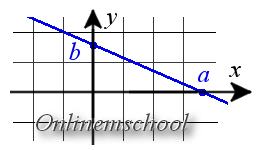
Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки M(x₁, y₁) и N(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂, то уравнение прямой можно найти, используя следующую формулу

x — x1	=	y — y1
x2 — x1		y2 — y1

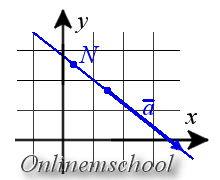
Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

x = l t + x₀y = m t + y₀

где N(x₀, y₀) — координаты точки лежащей на прямой, a = {l, m} — координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки N(x₀, y

0) лежащей на прямой и направляющего вектора a = {l; m} (l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу

Пример 1. Найти уравнение прямой проходящей через две точки M(1, 7) и N(2, 3).

Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки

x — 12 — 1 = y — 73 — 7

Упростив это уравнение получим каноническое уравнение прямой

x — 11 = y — 7-4

Выразим y через x и получим уравнение прямой с угловым коэффициентом

y — 7 = -4(x — 1)

y = -4x + 11

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 7} = {1; -4}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = -4t + 7

Пример 2. Найти уравнение прямой проходящей через две точки M(1, 3) и N(2, 3).

Решение.

Так как M_y — N_y = 0, то невозможно записать уравнение прямой проходящей через две точки.

Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN.

MN = {2 — 1; 3 — 3} = {1; 0}

Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой

x = t + 1y = 3

Уравнение прямой в пространстве

Уравнение прямой, проходящей через две различные точки в пространстве

Если прямая проходит через две точки M(x₁, y₁, z₁) и N(x₂, y₂, z₂), такие что x₁ ≠ x₂, y₁ ≠ y₂ и z₁ ≠ z₂, то уравнение прямой можно найти используя следующую формулу

x — x1	=	y — y1	=	z — z1
x 2 — x1		y2 — y1		z2 — z1

Параметрическое уравнение прямой в пространстве

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t + x0
	y = m t + y0
	z = n t + z0

где (x₀, y₀, z₀) — координаты точки лежащей на прямой, {l; m; n} — координаты направляющего вектора прямой.

Каноническое уравнение прямой в пространстве

Если известны координаты точки M(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x — x0	=	y — y0	=	z — z0
l		m		n

Прямая как линия пересечения двух плоскостей

Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений

	A1x + B1y + C1z + D1 = 0
	A2x + B2y + C2z + D2 = 0

при условии, что не имеет место равенство

A1	=	B1	=	C1	.
A2		B2		C2

ru.onlinemschool.com

Уравнение прямой, формулы и примеры

Прямая является одним из фундаментальных понятий геометрии.

Свойства прямой в евклидовой геометрии

1) через любую точку можно провести бесконечно много прямых;

2) через любые две несовпадающие точки можно провести единственную прямую;

3) две несовпадающие прямые на плоскости либо пересекаются в единственной точке, либо являются параллельными;

4) в трёхмерном пространстве существуют три варианта взаимного расположения двух прямых: прямые пересекаются; прямые параллельны; прямые скрещиваются.

Общее уравнение прямой

   

Здесь и — произвольные постоянные, причём коэффициенты и не равны нулю одновременно.

Например. .

Частные случаи расположения прямой

1. Если коэффициент , то прямая параллельна оси абсцисс.

   Например. .

2. В случае, когда постоянная , то прямая параллельна оси ординат.

   Например. .

3. Если , то прямая проходит через начало координат .

   Например. .

Для прямой (1), заданной общим уравнением, нормальный вектор имеет координаты

   

Уравнение прямой по точке и нормальному вектору

Если известно, что прямая проходит через точку и имеет нормальный вектор (2), то ее уравнение имеет вид:

   

Уравнение прямой с угловым коэффициентом

Если известно, что прямая проходит через точку и ее угловой коэффициент равен , то ее уравнение имеет вид:

   

Уравнение прямой в отрезках на осях

Если прямая пересекает ось в точке , а ось ординат — в точке , то ее уравнение

   

Нормальное уравнение прямой

   

где — длина перпендикуляра, опущенного на прямую из начала координат, — угол между положительным направлением оси и направлением этого перпендикуляра.

Если , то прямая проходит через начало координат.

Уравнение прямой, проходящей через две заданные несовпадающие точки

Если прямая проходит через две точки и , то она задается уравнением

   

или

   

Уравнение (4) называется еще каноническим уравнением прямой.

Уравнение прямой по точке и направляющему вектору

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Если прямая проходит через точку в направлении вектора , то ее уравнение

   

Параметрические уравнения прямой

   

Здесь — координаты направляющего вектора , — координаты точки (абсцисса и ордината соответственно), через которую проходит прямая, — параметр.

Уравнение прямой в полярных координатах

   

здесь — полярный радиус, — полярный угол.

ru.solverbook.com

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Уравнение прямой, проходящей через две точки − примеры и решения

Пример 1. Построить прямую, проходящую через точки A(2, 1, 1),

B(3, 1, -2).

Решение.

Уравнение прямой, проходящей через точки A(x₁, y₁, z₁) и B(x₂, y₂, z₂) имеет следующий вид:

Подставив координаты точек A и B в уравнение (1), получим:

или

(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

Ответ.

Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

Решение.

Уравнение прямой, проходящей через точки A(x

₁, y₁, z₁) и B(x₂, y₂, z₂) имеет следующий вид:

Подставив координаты точек A и B в уравнение (2), получим:

или

Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

Ответ.

Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

matworld.ru

Составить уравнение прямой | Треугольники

Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.

Пример 1.

Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).

Решение:

1 способ — составим уравнение прямой с угловым коэффициентом.

Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:

   

Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.

Таким образом, y= -2x+3 — искомое уравнение.

2 способ — составим общее уравнение прямой.

Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:

   

Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.

Умножив первое уравнение системы на -1 и сложив почленно со вторым:

   

получим: 5a-10b=0. Отсюда a=2b.

Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:

2bx+by-3b=0. Осталось разделить обе части на b:

2x+y-3=0.

Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:

y= -2x+3.

3 способ — составим уравнение прямой, проходящей через 2 точки.

Уравнение прямой, проходящей через две точки, имеет вид:

   

Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)

(то есть x₁= -3, y₁=9, x₂=2, y₂= -1):

   

и упростим:

   

По основному свойству пропорции

   

откуда 2x+y-3=0.

В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.

Замечание.

Если при подстановке координат заданных точек один из знаменателей уравнения

   

окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.

Пример 2.

Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).

Решение:

Подставляем  в уравнение прямой, проходящей через 2 точки, координаты точек C и D:

   

   

Пример 3.

Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).

Решение:

   

   

www.treugolniki.ru

Уравнение прямой на плоскости. Примеры решения типовых задач. Часть 2

Задача № 1. При каких значениях m и n прямая (m-3n-2)x+(2m+4n-1)y-3m+n-2=0 отсекает на оси Ox отрезок, равный 3 ед. масштаба, а на оси Oy отрезок, равный (-2).
Задача № 2. Через точку М (2;-1) провести прямую параллельно прямой 2x+3y=0.
Решение. Угловой коэффициент искомой прямой согласно условию параллельности должен быть равным угловому коэффициенту данной прямой: y=-2/3, k=-2/3.

Рис.1

Составим уравнение искомой прямой по формуле: y-y₁= k(x—x₁)
у+1=-2/3(х—2), Зу+3=—2х+4, 2х+3у—1=0.
Эту задачу можно решать и так.
Так как искомая прямая должна быть параллельна данной прямой, то A/2=B/3, или A:В=2:3.
Уравнение прямой будем искать в виде: 2х+Зy+С=0. С определим из условия, что прямая проходит через точку М (2; —1): 2·2+3·(-1)+c=0, c=3-4=-1, с=-1.
Следовательно, уравнение прямой будет 2х+3у-1=0.
Ответ: 2х+3у-1=0.
Решения этих двух задач подробно объясняются в следующем видео:

Задача № 3. Составить уравнения сторон треугольника, для которого точки А(—1; 2), В(3;-1) и С(0; 4) являются серединами сторон.
Решение этой задачи подробно изложено в следующем видео

Задача № 4.По какой линии должна двигаться точка, начальное положение которой определено координатами (3; 8), чтобы кратчайшим путем дойти до прямой х—2у — 2 = 0? В какой точке она достигнет этой прямой и как велик будет пройденный путь?
Решение этой задачи подробно изложено в следующем видео

Задача № 5. Точка М (-4; 5) является вершиной квадрата, диагональ которого лежит на прямой 7x-y+8=0. Составить уравнения сторон и второй диагонали этого квадрата.
Решение этой задачи подробно изложено в следующем видео

Задача № 6. Даны две смежные вершины А (2; 5) и В (5; 3) параллелограмма ABCD и точка М(-2; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.
Решение этой задачи подробно изложено в следующем видео

Задача № 7. Найти проекцию точки Р(—8; 12) на прямую, проходящую через точки А(2;-3) и В(-5; 1).
Решение этой задачи подробно изложено в следующем видео

Задача № 8. Через точку М (-2; 0) провести прямую, отсекающую на оси Оу отрезок, равный 6; через точку N (2;-1) провести вторую прямую, отсекающую на оси Оу отрезок, равный 5/3.
Решение этой задачи подробно изложено в следующем видео

Задача № 9. Составить уравнение прямой, проходящей через точку М(4;-1) и точку пересечения прямых х-2у+1=0 и у-1=0.
Задача № 10. Написать уравнение прямой, проходящей через точку пересечения прямых Зх-у+5=0 и 2х+3у+1=0 и параллельной прямой 7х-Зу+5=0.
Решения этих двух задач подробно объясняются в следующем видео:

Задача № 11. Через точку пересечения прямых 3x-у=0 и х+4у-2=0 провести прямую, перпендикулярную к прямой 2х+7у=0.
Решение этой задачи подробно изложено в следующем видео

math-helper.ru