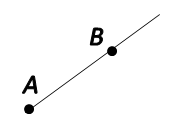
Отрезок. Длина и середина отрезка. Сравнение отрезков
Отрезок – это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка – это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок – это отрезок, длина которого принимается за единицу. Следовательно, длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

AB = 6 см.
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

- Длины равных отрезков равны.
Равные отрезки
Равные отрезки – это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример.
Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка – это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

CA < CB или CB > CA.
Если точка B окажется между точками C
и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB < CA.
Если точки A и B совпадут, то отрезки CA и CB равны:

CA = CB
Середина отрезка
Середина отрезка – это точка, делящая отрезок на две равные части.

Отрезок — Википедия
Материал из Википедии — свободной энциклопедии
Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля).
Отре́зком называются два близких понятия: в геометрии и математическом анализе.
Отрезок в геометрии
Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.
Направленный отрезок
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Отрезок числовой прямой
Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются
Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:
- [a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.
Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.
Стягивающаяся система сегментов
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.
Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.
Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если[2]
- каждый следующий отрезок содержится в предыдущем;
- ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}
- соответствующая последовательность длин отрезков бесконечно мала.
- limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
- ∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}
Этот факт следует из свойств монотонной последовательности.
См. также
Примечания
Разработка урока внеурочной деятельности «Отрезок. Обозначение отрезков, их сравнение»
Логика 3 класс
Тема: «Отрезок. Обозначение отрезков, их сравнение. Лучи. Ломаная, виды ломаных. Простые задачи на построение»
Цель:
познакомить ребят с историей возникновения луча, отрезка и ломаной;
научить ребят обозначать, измерять и сравнивать отрезки;
узнать, что такое ломаная и какие ее виды существуют;
рассмотреть простые задачи на построение;
способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;
содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность
Задачи:
— Продолжить формирование навыков контроля результатов деятельности.
— Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.
— Формирование логического, абстрактного, эвристического, системного мышления.
Оборудование: проектор, экран, компьютер, презентации
План.
Организационные моменты
История возникновения лучей, отрезков и ломаной.
Сказка о точке А и точке В
Однажды вечером Чистюлька стала искать Карандаша, но нигде не смогла его найти. Наконец, она увидела слабый огонёк в одном из шкафов. Заглянув туда, она удивилась, увидев небольшую комнату, где на кровати лежал её друг:
– Добрый вечер! Ты, я вижу, хорошо устроился, нарисовав себе тоже комнатку.
– Вечер не совсем добрый.
– Так- так… Что-то случилось?
– А ты не видишь?!
– Вижу, что ты весь замотался в шарф, ты что заболел? Простудился!
– Не простудился, а источился.
– Чего же проще, сейчас позову Точилку и закончатся все твои проблемы, а потом мы отправимся в наше новое путешествие. Подожди, я быстро.
– Не надо никуда идти, потому что Точилки нет, её взяла учительница домой, а сегодня выходной, так что она будет не скоро.
– Жаль, так хотелось увидеть точку А. Ладно, подождем. А что это такое,- она показала на сверток, что лежал на столе.
– Да это посылка какая-то.
– Давай откроем?
– Открывай.
Чистюлька открыла посылку:
– Смотри здесь какой-то диск.
– От кого?
– Ой, как здорово! Диск прислала геометрица А. Она как почувствовала, что мы хотим попутешествовать. На этом диске записана интересная история из ее жизни.
– Ура! Значит, сегодня мы отправляемся опять в путешествие по стране Геометрии.
– Да, только это путешествие будет воображаемым.
Чистюлька вставила диск в дисковод, и они услышали:
– Я точка А, привет всем, кто меня смотрит! Сегодня я расскажу, как подружилась с точкой В. Друзья смотрели рассказ, как увлекательный фильм.
Как-то утром точка А отправилась гулять. Идёт по прямой линии, а ей не видать конца, почему?
– Правильно, прямая линия не имеет ни начала, ни конца, — в один голос воскликнули Карандаш и Чистюлька, как будто подруга из страны Геометрии могла их услышать. А почему бы и нет?!
Остановилась точка А, подпрыгнула.. Вдруг кто-то говорит:
– Какой красивый луч получился!
Точка А удивилась, увидев точку красного цвета с жёлтым бантиком на голове:
– Ты кто?
– Я точка В, а ты кто?
– А я точка А.
– Замечательно! Давай дружить!? Мне так грустно и скучно одной. Я недавно появилась и многого не знаю.
– Я очень рада буду, если мы подружимся. А что ты говорила про луч?
– Как же, стоило тебе остановиться на линии, и
получился луч. Ведь ты знаешь определение луча!?
– Да, луч, но только не один, а два, потому что, если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.;
– Почему ты сошла с линии? — закричала точка В, — иди скорее сюда, будем рядом стоять.
Точка А подошла к новой знакомой, но встала чуть поодаль. Обе точки стояли на одной прямой, образовав новую геометрическую фигуру, которую вы уже знаете. Это…отрезок.
Точка А вспомнила определение отрезка и рассказала точке В, которая восторженно смотрела на точку А и запоминала каждое её слово.
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком.
– Как весело, что мы вместе! — воскликнула точка В и стала прыгать по прямой линии, но вдруг упала.
Точка А подняла новую знакомую:
– Ты не ушиблась?
– Нет, но я сломала твою линию.
– Ничего страшного, зато теперь у нас появилось две прямых линии.
Тут они увидели, как к ним навстречу двигается ещё одна точка. Она представилась, как точка С.
Точка С остановилась. Сразу же получился луч с началом в точке С. Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца.
Точки А, В и С встали рядом и протянули друг другу руки, как на рисунке, взявшись за руки втроём, и образовали новую линию, которая называется ломаная линия или ломаная. Это ломаная линия, которая состояла из… двух отрезков-звеньев.
Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку), отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой. Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой.
– А нельзя сделать ломаную линию из четырех звеньев?
– Какая ты еще маленькая, точка В, и многого не знаешь! А вы, друзья, знаете?
Друзья вздрогнули и поняли, что обращается точка А с диска к ним. Вот чудеса: она их слышит?! Чистюлька и Карандаш переглянулись и одновременно сказали:
–Нужно позвать другие точки.
А точки всегда рады поработать, их даже звать не пришлось, как только услышали, что они нужны, тут же появились. И точка Е, и точка D и другие.
Они стали радостно прыгать по прямой линии. Там, где они прыгнули, ломалась прямая линия. Каждая точка вставала на её конце и получалась ломаная линия.
– Сколько звеньев у этой линии?
Чистюлька стала считать вслух:
– 1, 2, 3…7.
А точка А продолжала на диске:
– Конечно, вы догадались — 7 звеньев-отрезков.
Точки спрашивают у точки В:
– Хочешь, мы покажем тебе фокус?
– Очень хочу, потому что люблю фокусы.
– Смотри…. — И точки взялись за руки.
– Ой, как интересно, ведь получился…?
– Треугольник — ура!
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник. Трехзвенная замкнутая ломаная линия — треугольник;. Треугольник — это геометрическая фигура, у которой 3 угла, 3 стороны и 3 вершины.
– Ведь это та же ломаная линия, только замкнутая. А можно мне к вам? — спросила точка В.
– Можно, только теперь будет другая фигура. Какая?
– Знаю, знаю, это четырехугольник. Четырехзвенная замкнутая ломаная линия — четырехугольник;. Определение про него такое: четырёхугольник — это многоугольник, у которого 4 стороны, 4 вершины и 4 угла.
– Ммм…
– Смотри, тебе на помощь спешит Линейка.
Линейка сказала:
– Принимайся, точка В, за дело.
– Какое дело?
– Измеряй стороны, а я буду тебе помогать. Посмотришь, что получится.
Точка В измеряла стороны на диске, а Чистюлька и Карандаш внимательно следили за её действиями. Они очень удивилась, потому что, оказалось, что, у этого четырехугольника противоположные стороны …одинаковые.
Затем точка В наложила прямой угол Линейки на каждый угол четырёхугольника и оказалось, что у него все углы прямые.
Можете сказать определение этой фигуры?
Прямоугольник — это четырёхугольник, у которого все углы прямые, а противоположные стороны равны.– Смотрите,- закричала точка В, — ещё один прямоугольник, но он какой- то необычный. Очень он похож на прямоугольник, но чем-то они различаются. И чем же?
Точка А сказала:
– Молодец, точка В, ты быстро соображаешь.
– Придется тебе, точка В, еще поработать.
Точка В проверила углы. Углы прямые, как у прямоугольника, а стороны… стороны-то у него оказались все одинаковые. И такой прямоугольник не просто прямоугольник, он называется квадрат. Точка В громко и чётко стала произносить определение квадрата.
Квадрат — это прямоугольник, у которого все стороны равны.
Точка А на диске с удовольствием поглядела на новую подругу.
– Как быстро ты всё запоминаешь, точка В.
– Мне с вами очень интересно и весело, — сказала точка В, — вы будете со мной дружить?
Точки хором воскликнули:
– Обязательно будем, потому что дружба — это самое главное на свете. Друг поможет тебе и в радости, и в горе, если, конечно, он – настоящий друг.
Диск закончил показывать историю знакомства точек. На экране монитора компьютера появилась точка А, внимательно посмотрела на друзей, подмигнула им.
– Так я познакомилась с точкой В,- закончила свое повествование точка А, — и с тех пор мы не расстаемся. До встречи, Карандаш и Чистюлька!
Чистюлька чуть не заплакала:
– Как жаль, что диск закончился, так не хочется расставаться с точкой А.
– Ничего, потерпи,- сказал Карандаш,- после моего выздоровления мы опять встретимся с ней и ее друзьями, а пока я нарисую тебе точку А и точку В. Смотри и любуйся.
Знакомство с элементами геометрических фигур.
Прямая
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Через две точки можно провести единственную прямую.
Две прямые могут пересекаться только в одной точке.
Через одну точку можно провести бесконечное множество прямых.
Способы обозначения прямых
Прямая a.
Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой.

Прямая АB.
Луч
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча естьначало, но нет конца.
Способы обозначения лучей
Луч c.
Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а вторая точка лежит на луче.

Луч AB.
Отрезок
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало, и конец.
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
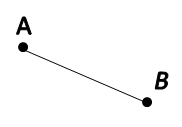
Отрезок AB.
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
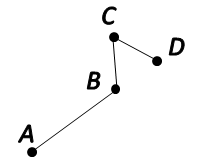
Ломаная ABCD.
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
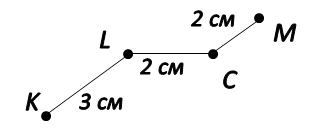
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см.
Ломаные бывают замкнутыми и незамкнутыми
Сказка о луче
В некотором царстве, в математическом государстве жили-были Прямая и Отрезок АВ. Прямая всегда убегала к своим друзьям, а отрезок не мог никуда идти. Потому что две точки загородили ему дорогу. Но вот один раз одна из точек захотела посмотреть, что твориться в математическом мире. Она выкатилась и покатилась. А Отрезок в то время думал, как же ему сдвинуться с места. И вот он дёрнулся с места и побежал. Так стал он счастливым лучом.
 \
\
Научить сравнивать отрезки и углы используя метод наложения.
Каждому из вас известно, что в окружающем нас мире встречаются предметы, которые имеют одинаковую форму и одинаковые размеры. Например, два одинаковых карандаша, два одинаковых автомобиля, два одинаковых будильника.
В геометрии две фигуры, имеющие одинаковую форму и одинаковые размеры, называют равными.
Давайте возьмём две фигуры F1 и F2 (рисунок 1), вырезанные из бумаги.

Рисунок 1.
Чтобы установить, равны они или нет, наложим одну фигуру на другую. Предположим, что наши фигуры совместились, тогда можем сказать, что они равны.
А вот некоторые фигуры P1 и P2 (рисунок 2).

Рисунок 2.
Если попробуем наложить их друг на друга эти две фигуры, то увидим, что их совместить невозможно, а, следовательно, они не равны.
Можем сделать следующий вывод:
Две геометрические фигуры называются равными, если их можно совместить наложением.
Поговорим, как сравнить два отрезка. Возьмём два произвольных отрезка (рисунок 3).

Рисунок 3.
Чтобы установить, равны данные отрезки или нет, наложим один отрезок на другой так, чтобы конец одного отрезка совместился с концом другого (рисунок 3). При этом совместятся и два других конца отрезков, а, следовательно, отрезки равны.
Теперь возьмём отрезок АВ и отрезок АС (рисунок 4), и наложим их друг на друга таким же образом. Видим, что отрезки не совместились полностью, а значит, они не равны.

Рисунок 4.
Из рисунка также видно, что отрезок АВ составляет часть отрезка АС, поэтому отрезок АВ меньше отрезка АС. Записывают это так: АВ < АС.
Поговорим о том, что же называют серединой отрезка. Рассмотрим отрезок АВ. Отметим на нём точку С, которая делит его на две равные части (рисунок 5). Таким образом, можно сказать, что точка С и есть середина отрезка АВ, т.е. отрезок АС равен отрезку АВ.

Рисунок 5.
Сформулируем определение:
Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.
Далее рассмотрим два неразвёрнутых угла: угол 1 и угол 2 (рисунок 6). Чтобы установить, равны они или нет, наложим один угол на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон.
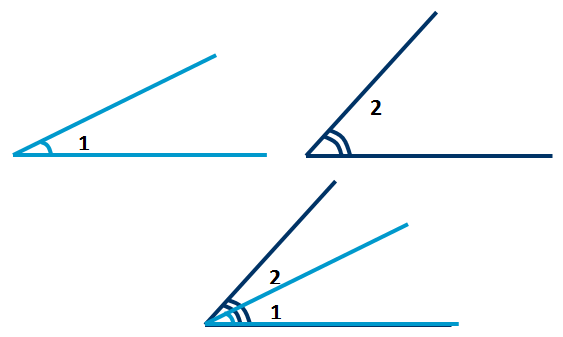
Рисунок 6.
Если две другие стороны также совместятся, то и углы полностью совместятся, а, значит, они равны. Но в нашем случае эти стороны не совместились, следовательно, наши углы не равны, и меньшим является угол, который составляет часть другого, а это угол 1.
Записываем это так: 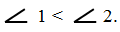
Возьмём неразвёрнутый угол АОС и развёрнутый угол ВОС (рисунок 7), наложим их друг на друга указанным выше способом (рисунок 8), то увидим, что неразвёрнутый угол составляет часть развёрнутого, а, следовательно, развёрнутый угол больше неразвёрнутого, т.е. угол ВОС больше угла АОС.
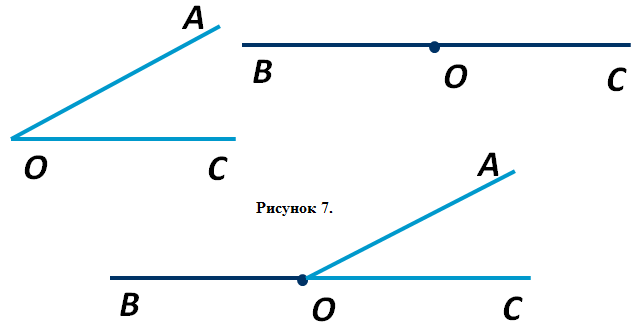
Рисунок 8.
Следует отметить, что любые два развёрнутых угла, очевидно, равны.
Научить деток сравнивать отрезки и углы по видеоуроку
Практическая работа.
Выполните задания:
Начертите несколько отрезков и обозначьте их
Измерьте длины ваших отрезков, сравните их
Начертите несколько лучей, назовите их
Нарисуйте несколько ломаных и обозначьте их
Измерьте длину ломанных
Итоги урока
Что вы сегодня узнали на уроке? Что больше всего запомнилось?
Домашнее задание.
Изобразить различные виды ломаных, назвать их, измерить их длину
Отрезок — Википедия. Что такое Отрезок
Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)
Отрезок AB (выделен красным)Отре́зком называются два близких понятия: в геометрии и математическом анализе.
Отрезок в геометрии
Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.
Направленный отрезок
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Отрезок числовой прямой
Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются внутренними точками отрезка[1].
Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:
- [a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.
Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.
Стягивающаяся система сегментов
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.
Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.
Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если[2]
- каждый следующий отрезок содержится в предыдущем;
- ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}
- соответствующая последовательность длин отрезков бесконечно мала.
- limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
- ∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}
Этот факт следует из свойств монотонной последовательности.
См. также
Примечания
Промежуток (математика) — Википедия
Промежуток[1], или более точно, промежуток числовой прямой — множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними[2]. С использованием логических символов, это определение можно записать так:
X⊂R{\displaystyle X\subset \mathbb {R} } — промежуток, если
- ∀x∀y∀z((x∈X)∧(z∈X)∧(x<y<z)⇒y∈X).{\displaystyle \forall x\forall y\forall z{\big (}(x\in X)\wedge (z\in X)\wedge (x<y<z)\Rightarrow y\in X{\big )}.}
В качестве примеров промежутков можно привести следующие множества:
- X1={x∈R:0⩽x⩽1},X2={x∈R:0⩽x<1},X3={x∈R:0<x⩽1},X4={x∈R:0<x<1},X5={x∈R:x>0},X6={x∈R:x<1},X7=R,X8=∅.{\displaystyle {\begin{aligned}X_{1}&=\{x\in \mathbb {R} \colon 0\leqslant x\leqslant 1\},&X_{2}&=\{x\in \mathbb {R} \colon 0\leqslant x<1\},&X_{3}&=\{x\in \mathbb {R} \colon 0<x\leqslant 1\},\\X_{4}&=\{x\in \mathbb {R} \colon 0<x<1\},&X_{5}&=\{x\in \mathbb {R} \colon x>0\},&X_{6}&=\{x\in \mathbb {R} \colon x<1\},\\X_{7}&=\mathbb {R} ,&X_{8}&=\varnothing .\end{aligned}}}
Конечный промежуток состоит из множества чисел, заключенных между двумя числами a{\displaystyle a} и b{\displaystyle b} — концами промежутка, которые сами могут быть включены в его состав, или нет[1].
Если a⩽b,a∈R,b∈R{\displaystyle a\leqslant b,a\in \mathbb {R} ,b\in \mathbb {R} }, то промежуток {x∈R:a⩽x⩽b}{\displaystyle \{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}} называется сегментом[3] или числовым отрезком, и обозначается [a,b]{\displaystyle [a,b]}:
- [a,b] =def {x∈R:a⩽x⩽b}.{\displaystyle [a,b]\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}.}
В случае a=b{\displaystyle a=b} отрезок состоит из одной точки.
Если a<b,a∈R,b∈R{\displaystyle a<b,a\in \mathbb {R} ,b\in \mathbb {R} }, то промежуток {x∈R:a<x<b}{\displaystyle \{x\in \mathbb {R} \colon a<x<b\}} называется интервалом и обозначается (a,b){\displaystyle (a,b)}:
- (a,b) =def {x∈R:a<x<b}.{\displaystyle (a,b)\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a<x<b\}.}
В средней школе для обозначения открытого промежутка вместо (a,b){\displaystyle (a,b)} иногда используют обозначение ]a,b[{\displaystyle ]a,b[}.
Промежутки
- [a,b) =def {x∈R:a⩽x<b},(a,b] =def {x∈R:a<x⩽b}{\displaystyle [a,b)\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a\leqslant x<b\},\quad (a,b]\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a<x\leqslant b\}}
называются полусегментами (не дополненными до сегмента) или полуинтервалами.
Длиной промежутка во всех случаях называется число b−a{\displaystyle b-a}.
Бесконечные промежутки
- {x∈R:x⩾a},{x∈R:x>a},{x∈R:x⩽b},{x∈R:x<b},R{\displaystyle \{x\in \mathbb {R} \colon x\geqslant a\},\quad \{x\in \mathbb {R} \colon x>a\},\quad \{x\in \mathbb {R} \colon x\leqslant b\},\quad \{x\in \mathbb {R} \colon x<b\},\quad \mathbb {R} }
не ограничены либо сверху, либо снизу каким-либо вещественным числом. В этом случае удобно считать, что у этих промежутков одним из концов, или обоими служат несобственные числа +∞,−∞{\displaystyle +\infty ,-\infty }, полагая, что для любого вещественного числа x∈R{\displaystyle x\in \mathbb {R} } справедливы неравенства x<+∞,x>−∞{\displaystyle x<+\infty ,x>-\infty }. Обозначения и наименования бесконечных промежутков аналогичны таковым для конечных промежутков. Например, выписанные выше бесконечные промежутки обозначаются соответственно
- [a,+∞),(a,+∞),(−∞,b],(−∞,b),(−∞,+∞).{\displaystyle [a,+\infty ),\quad (a,+\infty ),\quad (-\infty ,b],\quad (-\infty ,b),\quad (-\infty ,+\infty ).}
Пустое множество ∅{\displaystyle \varnothing } также является промежутком.
Промежутки расширенной числовой прямой[править | править код]
Множество вещественных чисел R{\displaystyle \mathbb {R} }, дополненное элементами +∞{\displaystyle +\infty } и −∞{\displaystyle -\infty }, называется расширенной числовой прямой и обозначается R¯{\displaystyle {\overline {\mathbb {R} }}}, то есть
- R¯=R∪{+∞}∪{−∞}{\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{+\infty \}\cup \{-\infty \}}
При этом для любого вещественного числа x∈R{\displaystyle x\in \mathbb {R} } по определению полагают выполненными неравенства
- −∞<x,x<+∞,−∞<+∞{\displaystyle -\infty <x,\quad x<+\infty ,\quad -\infty <+\infty }
Для расширенной числовой прямой также вводят понятия промежутков — отрезков, интервалов, полуинтервалов[1]. В отличие от соответствующих промежутков числовой прямой они могут содержать элементы ±∞{\displaystyle \pm \infty }. Например, (a,+∞]=(a,+∞)∪{+∞}{\displaystyle (a,+\infty ]=(a,+\infty )\cup {\{+\infty \}}}.
В русском языке слова промежуток и интервал соответствуют одному английскому слову interval. В англоязычной литературе[4] и в переводах иностранных книг, а также в некоторых других книгах на русском языке используется следующая терминология:
- [a,b]={x∈R:a⩽x⩽b}{\displaystyle [a,b]=\{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}} — замкнутый интервал (англ. closed interval),
- (a,b)={x∈R:a<x<b}{\displaystyle (a,b)=\{x\in \mathbb {R} \colon a<x<b\}} — открытый интервал (англ. open interval),
- [a,b)={x∈R:a⩽x<b}{\displaystyle [a,b)=\{x\in \mathbb {R} \colon a\leqslant x<b\}} — полуоткрытый (или полузамкнутый) интервал (англ. half-open interval/half-closed interval),
- (a,b]={x∈R:a<x⩽b}{\displaystyle (a,b]=\{x\in \mathbb {R} \colon a<x\leqslant b\}} — полуоткрытый (или полузамкнутый) интервал (англ. half-open interval/half-closed interval).
То есть, различные типы интервалов.
В более старой русскоязычной литературе[5] вместо «интервал» используется слово промежуток: замкнутый промежуток, открытый промежуток, полуоткрытый (или полузамкнутый) промежуток.
Однако, особенно в учебной литературе, где наибольшее количество теорем для функций на компактных множествах, для замкнутого промежутка предпочтительно иметь отдельное название в одно слово — сегмент[3] (термин «отрезок» имеет скорее геометрический оттенок, как и «промежуток числовой прямой»). В этом случае термин «интервал» закрепляется только за открытым промежутком.
См. также открытые и замкнутые множества.
Теорема о промежуточных значениях[править | править код]
Известная теорема Больцано — Коши о промежуточных значениях непрерывной функции гласит: образ любого промежутка при непрерывном отображении снова есть промежуток. Как следует из обобщения этой теоремы на случай произвольных топологических пространств, эта теорема — следствие того факта, что промежутки — в точности связные подмножества R{\displaystyle \mathbb {R} }. См. ниже связные множества.
Операции с промежутками[править | править код]
На практике промежуток нередко характеризует интервал возможных значений (приближённо) измеренной величины. На множестве таких промежутков можно определить арифметические операции. Тогда результату вычислений над величинами можно сопоставить соответствующие вычисления над их интервалами, задающие в итоге интервал возможных значений для результата.
Мера[править | править код]
Промежутки числовой прямой, прямоугольники на плоскости, прямоугольные параллелепипеды в пространстве и т. п. являются отправной точкой в теории меры, поскольку являются простейшими множествами, меру которых (длину, площадь, объем и т. п.) легко определить.
Связные множества[править | править код]
Обобщением промежутка числовой прямой является понятие связного топологического пространства. На числовой прямой всякое связное множество есть промежуток, и обратно, любой промежуток есть связное множество.
Также промежуток числовой прямой лежит в основе другого, более специального понятия линейной связности. Во множестве вещественных чисел R{\displaystyle \mathbb {R} }, а также в евклидовом пространстве Rn{\displaystyle \mathbb {R} ^{n}} произвольной размерности n{\displaystyle n} понятия связности и линейной связности совпадают.
Выпуклые множества[править | править код]
Другим обобщением понятия промежутка числовой прямой является понятие выпуклого множества.
Промежутки в частично упорядоченных множествах[править | править код]
В самом общем случае понятие промежутка можно ввести на любом множестве, на котором введено отношение порядка <{\displaystyle <}.
- ↑ 1 2 3 Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 64—65. — 704 с. — ISBN 5-7107-4119-1.
- ↑ В ряде источников описывается как интервал; например, см. Интервал // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2.
- ↑ 1 2 В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. I. — С. 53. — 672 с. — ISBN 5-482-00445-7.
- ↑ Гелбаум, Б., Олмстед, Дж. Контрпримеры в анализе = Counterexamples in Analysis. — М.: ЛКИ, 2007. — С. 17—18. — 258 с. — ISBN 978-5-382-00046-6.
- ↑ Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002. — Т. 1. — С. 35. — 416 с. — ISBN 5-9221-0196-X.