| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. | |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. |
|
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — корень квадратный | y = x1/2 | График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
|
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590… | |
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). Здесь пример для y = 2x (a = 2 > 1). |
|
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). |
|
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра |
|
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».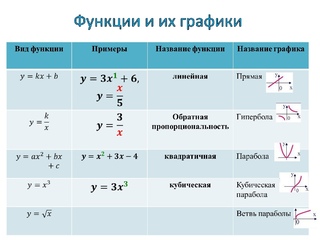 |
|
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности.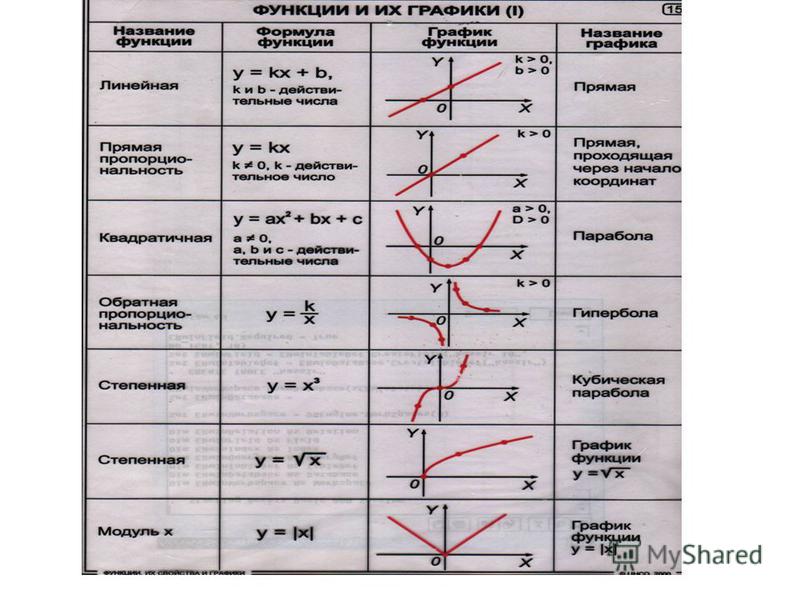 На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. |
|
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
|
| Степенная — корень квадратный | y = x1/2 | График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590. .. .. |
||
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). | |
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. |
|
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».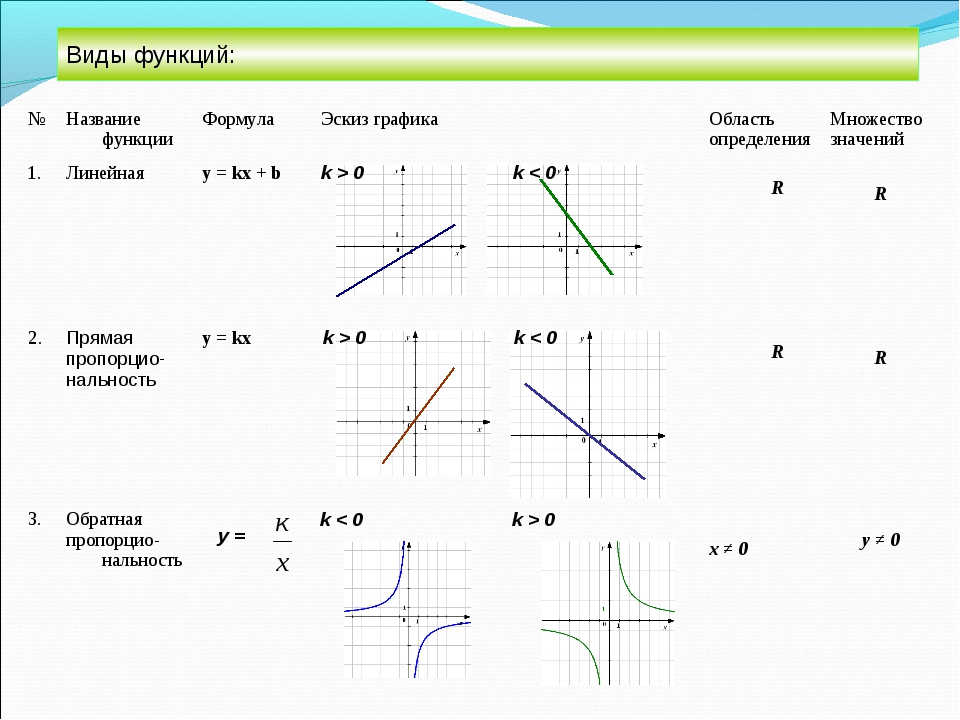 |
|
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Виды графиков и их формулы. Линейная функция
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f (x ) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции).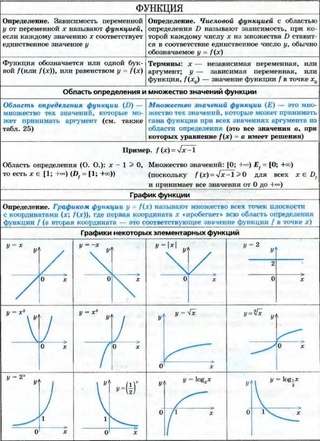 Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у . При этом одно и то же значение у может быть получено при различных х .
Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у . При этом одно и то же значение у может быть получено при различных х .
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х ), при которых функция определена, т.е. ее значение существует. Обозначается область определения D (y ). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е (у ).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f (x ) называют четной х
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f (x ) называют нечетной , если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х .
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида , и для них не выполняется ни одно из равенств или свойств приведенных выше.
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k
График квадратичной функции (Парабола)
График параболы задается квадратичной функцией:
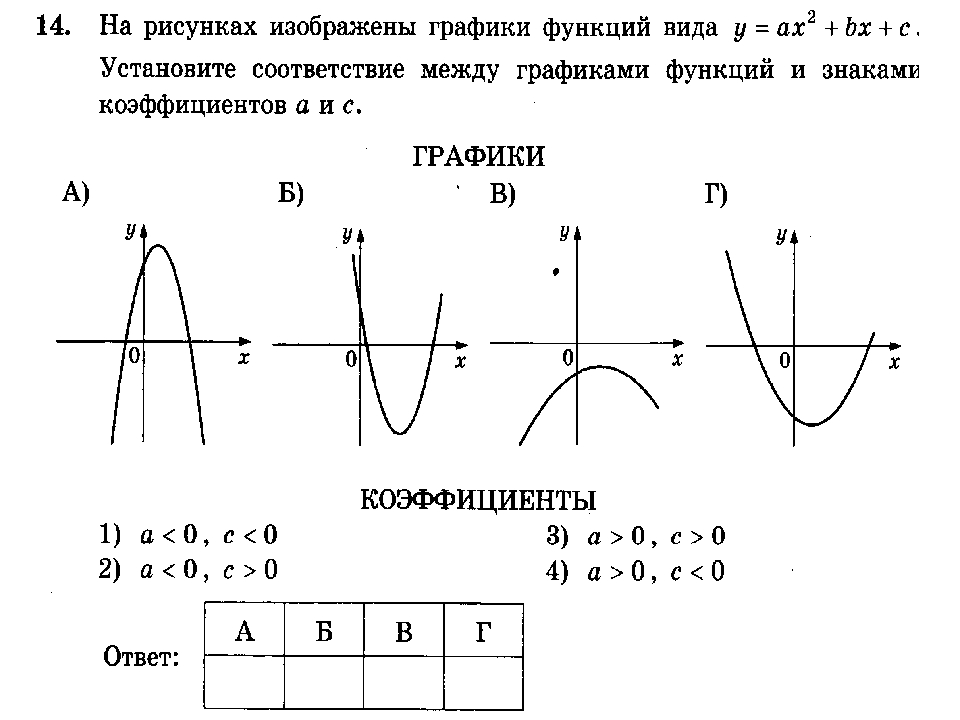
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x 1 ; 0) и (x 2 ; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x 0 ; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c ). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x 0 ; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c ). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax 2 + bx + c , то ветви параболы направлены вверх;
- если же a
Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a a > 0), значение квадратного трехчлена:
Графики других функций
Степенной функцией
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x | выглядит следующим образом:
Графики периодических (тригонометрических) функций
Функция у = f (x ) называется периодической , если существует такое, неравное нулю, число Т , что f (x + Т ) = f (x ), для любого х из области определения функции f (x ). Если функция f (x ) является периодической с периодом T , то функция:
Если функция f (x ) является периодической с периодом T , то функция:
где: A , k , b – постоянные числа, причем k не равно нулю, также периодическая с периодом T 1 , который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой :
График функции y = cosx называется косинусоидой . Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой . Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой . Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике .
 На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. - Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Национальный научно-исследовательский университет
Кафедра прикладной геологии
Реферат по высшей математике
На тему: «Основные элементарные функции,
их свойства и графики»
Выполнил:
Проверил:
преподаватель
Определение. Функция, заданная формулой у=а х (где а>0, а≠1), называется показательной функцией с основанием а.
Функция, заданная формулой у=а х (где а>0, а≠1), называется показательной функцией с основанием а.
Сформулируем основные свойства показательной функции:
1. Область определения — множество (R) всех действительных чисел.
2. Область значений — множество (R+) всех положительных действительных чисел.
3. При а > 1 функция возрастает на всей числовой прямой; при 0
4. Является функцией общего вида.
, на интервале xÎ [-3;3] , на интервале xÎ [-3;3]Функция вида у(х)=х n , где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).
Степенная функция у=х²
1. D(x)=R – функция определена на все числовой оси;
2. E(y)= и возрастает на промежутке
Степенная функция у=х³
1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:
2. D(x)=R – функция определена на все числовой оси;
3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;
4. При х=0 у=0 – функция проходит через начало координат O(0;0).
5. Функция возрастает на всей области определения.
6. Функция является нечетной (симметрична относительно начала координат).
, на интервале xÎ [-3;3]В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.
Степенная функция с целым отрицательным показателем:
Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:
1. D(x)=(-∞;0)U(0;∞) для любого n;
D(x)=(-∞;0)U(0;∞) для любого n;
2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;
3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.
4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.
5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.
, на интервале xÎ [-3;3]Степенная функция с дробным показателем
Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)
1. D(x) ÎR, если n – нечетное число и D(x)= , на интервале xÎ , на интервале xÎ [-3;3]
Логарифмическая функция у = log a x обладает следующими свойствами:
1. Область определения D(x)Î (0; + ∞).
Область определения D(x)Î (0; + ∞).
2. Область значений E(y) Î (- ∞; + ∞)
3. Функция ни четная, ни нечетная (общего вида).
4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0
График функции у = log a x может быть получен из графика функции у = а х с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 — для 0 ; на интервале xÎ ; на интервале xÎ
Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.
Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.
Функция y = sin (х).
1. Область определения D(x) ÎR.
2. Область значений E(y) Î [ — 1; 1].
3. Функция периодическая; основной период равен 2π.
4. Функция нечетная.
5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.
График функции у = sin (х) изображен на рисунке 11.
С задачей построения графика функции школьники сталкиваются в самом начале изучения алгебры и продолжают строить их из года в год. Начиная с графика линейной функции, для построения которой нужно знать всего две точки, к параболе, для которой нужно уже 6 точек, гиперболе и синусоиде. С каждым годом функции становятся все сложнее и построения их графиков уже невозможно выполнить по шаблону, необходимо проводить более сложные исследования, пользуясь производными и пределами.
Давайте разберемся, как найти график функции? Для этого начнем с самых простых функций, графики которых строятся по точкам, а потом рассмотрим план для построения более сложных функций.
Построение графика линейной функции
Для построения простейших графиков используют таблицу значений функции. Графиком линейной функции является прямая. Давайте попробуем найти точки графика функции y=4x+5.
- Для это возьмем два произвольных значения переменной x, подставим их поочередно в функцию, найдем значение переменной y и занесем все в таблицу.

- Возьмем значение x=0 и подставим в функцию вместо x — 0. Получим: y=4*0+5, то есть y=5 запишем это значение в таблицу под 0. Аналогично возьмем x=0 получим y=4*1+5, y=9.
- Теперь, чтобы построить график функции нужно нанести на координатную плоскость эти точки. Затем необходимо провести прямую.
Построение графика квадратичной функции
Квадратичная функция — это функция вида y=ax 2 +bx +c, где x-переменная, a,b,c — числа (a не равно 0). Например: y=x 2 , y=x 2 +5, y=(x-3) 2 , y=2x 2 +3x+5.
Для построения простейшей квадратичной функции y=x 2 обычно берут 5-7 точек. Возьмем значения для переменной x: -2, -1, 0, 1, 2 и найдем значения y также как и при построении первого графика.
График квадратичной функции называют параболой. После построения графиков функции у учеников появляются новые задачи, связанные с графиком.
Пример 1: найдите абсциссу точки графика функции y=x 2 , если ордината равна 9. Для решения задачи необходимо в функцию вместо y подставить ее значение 9. Получим 9=x 2 и решить это уравнение. x=3 и x=-3. Это можно увидеть и на графике функции.
Получим 9=x 2 и решить это уравнение. x=3 и x=-3. Это можно увидеть и на графике функции.
Исследование функции и построение ее графика
Для построения графиков более сложных функций необходимо выполнить несколько шагов, направленных на ее исследование. Для этого необходимо:
- Найти область определения функции. Область определения — это все значения которые может принимать переменная x. Из области определения следует исключить те точки, в которых знаменатель обращается в 0 или подкоренное выражение становится отрицательным.
- Установить четность или нечетность функции. Напомним, что четной является та функция, которая отвечает условию f(-x)=f(x). Ее график является симметричным относительно Оу. Функция будет нечетной, если она отвечает условию f(-x)=-f(x). В этом случае график симметричен относительно начала координат.
- Найти точки пересечения с осями координат. Для того, чтобы найти абсциссу точки пересечения с осью Ох, необходимо решить уравнение f(x)=0 (ордината при этом равна 0).
 Чтобы найти ординату точки пересечения с осью Оу, необходимо в функцию вместо переменной x подставить 0 (абсцисса равна 0).
Чтобы найти ординату точки пересечения с осью Оу, необходимо в функцию вместо переменной x подставить 0 (абсцисса равна 0). - Найти асимптоты функции. Асиптота — прямая, к которой график бесконечно приближается, но никогда ее не пересечет. Давайте разберемся, как найти асимптоты графика функции.
- Вертикальная асимптота прямая вида х=а
- Горизонтальная асимптота — прямая вида у=а
- Наклонная асимптота — прямая вида y=kx+b
- Найти точки экстремума функции, промежутки возрастания и убывания функции. Найдем точки экстремума функции. Для этого необходимо найти первую производную и приравнять ее к 0. Именно в этих точках функция может поменяться с возрастающей на убывающую. Определим знак производной на каждом интервале. Если производная положительна, то график функции возрастает, если отрицательна — убывает.
- Найти точки перегиба графика функции, промежутки выпуклости вверх и вниз.
Найти точки перегиба теперь проще простого. Нужно лишь найти вторую производную, затем приравнять ее к нулю. Следом находим знак второй производной на каждом интервале. Если положительный, то график функции выпуклый вниз, если отрицательна — вверх.
Нужно лишь найти вторую производную, затем приравнять ее к нулю. Следом находим знак второй производной на каждом интервале. Если положительный, то график функции выпуклый вниз, если отрицательна — вверх.
Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓
x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½
x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими.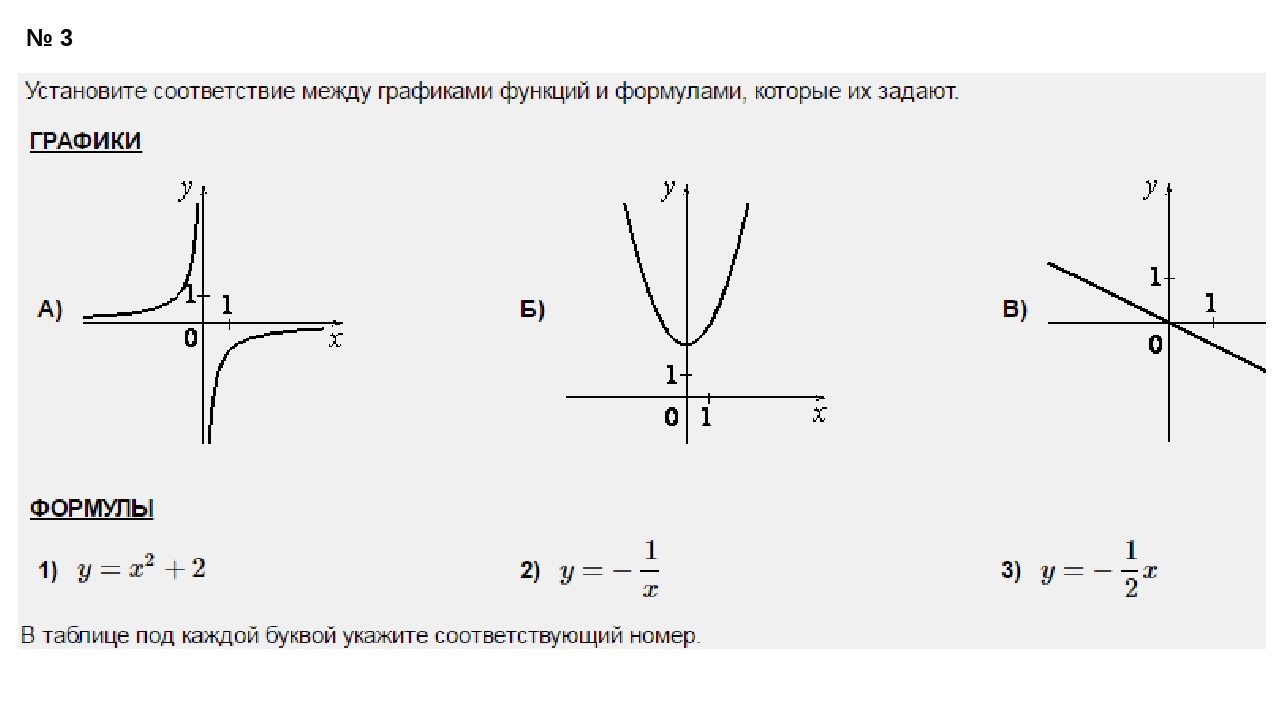 Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.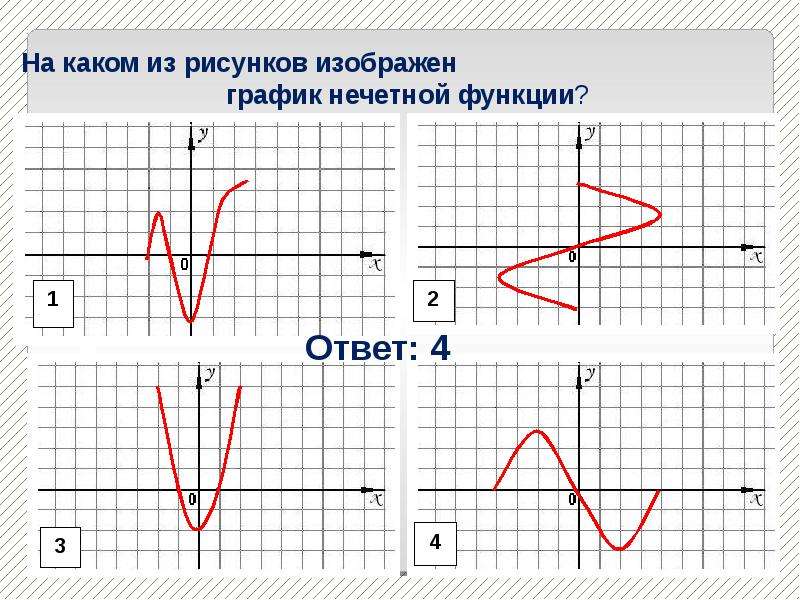
Если k 0
Если k>0 и b>0 , то график функции y=kx+b имеет вид:
Если k>0 и b , то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2
5.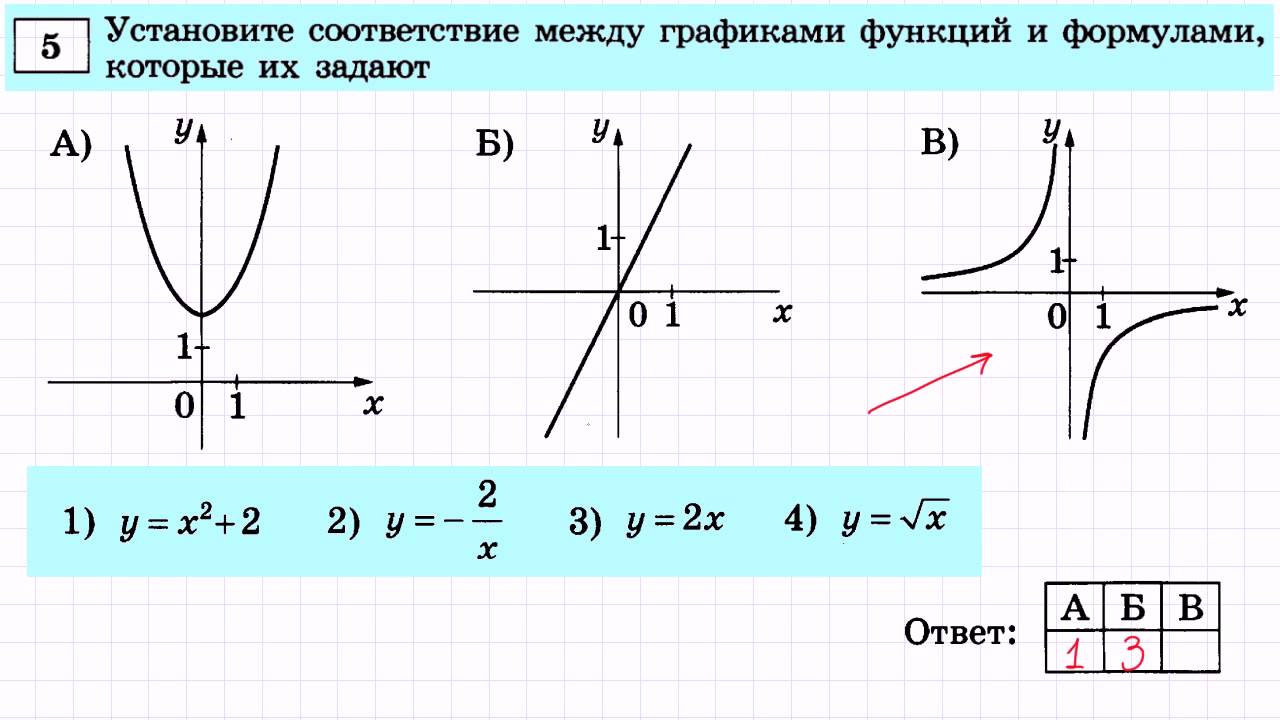 Условие перепендикулярности двух прямых:
Условие перепендикулярности двух прямых:
График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2
6. Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
|
СРОТКЛ |
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего. |
|
СРЗНАЧ |
Возвращает среднее арифметическое аргументов. |
|
СРЗНАЧА |
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ |
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию. |
|
Функция СРЗНАЧЕСЛИМН
|
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям. |
|
БЕТА.РАСП
|
Возвращает интегральную функцию бета-распределения. |
|
БЕТА.ОБР
|
Возвращает обратную интегральную функцию указанного бета-распределения. |
|
БИНОМ.РАСП
|
Возвращает отдельное значение вероятности биномиального распределения. |
|
БИНОМ. |
Возвращает вероятность пробного результата с помощью биномиального распределения. |
|
БИНОМ.ОБР
|
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему. |
|
ХИ2.РАСП
|
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.РАСП.ПХ
|
Возвращает одностороннюю вероятность распределения хи-квадрат. |
|
ХИ2.ОБР
|
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.ОБР.ПХ
|
Возвращает обратное значение односторонней вероятности распределения хи-квадрат. |
|
ХИ2.ТЕСТ
|
Возвращает тест на независимость. |
|
ДОВЕРИТ. |
Возвращает доверительный интервал для среднего значения по генеральной совокупности. |
|
ДОВЕРИТ.СТЬЮДЕНТ
|
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента. |
|
КОРРЕЛ |
Возвращает коэффициент корреляции между двумя множествами данных. |
|
СЧЁТ |
Подсчитывает количество чисел в списке аргументов. |
|
СЧЁТЗ |
Подсчитывает количество значений в списке аргументов. |
|
СЧИТАТЬПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне. |
|
СЧЁТЕСЛИ |
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию. |
|
Функция СЧЁТЕСЛИМН
|
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям. |
|
КОВАРИАЦИЯ.Г
|
Возвращает ковариацию, среднее произведений парных отклонений. |
|
КОВАРИАЦИЯ.В
|
Возвращает ковариацию выборки — среднее попарных произведений отклонений для всех точек данных в двух наборах данных. |
|
КВАДРОТКЛ |
Возвращает сумму квадратов отклонений. |
|
ЭКСП. |
Возвращает экспоненциальное распределение. |
|
F.РАСП
|
Возвращает F-распределение вероятности. |
|
F.РАСП.ПХ
|
Возвращает F-распределение вероятности. |
|
F.ОБР
|
Возвращает обратное значение для F-распределения вероятности. |
|
F.ОБР.ПХ
|
Возвращает обратное значение для F-распределения вероятности. |
|
F.ТЕСТ
|
Возвращает результат F-теста. |
|
ФИШЕР |
Возвращает преобразование Фишера. |
|
ФИШЕРОБР |
Возвращает обратное преобразование Фишера. |
|
ПРЕДСКАЗ |
Возвращает значение линейного тренда. Примечание. В Excel 2016 эта функция заменена функцией ПРЕДСКАЗ.ЛИНЕЙН из нового наборафункций прогнозирования. Однако эта функция по-прежнему доступна в целях обеспечения совместимости с предыдущими версиями. |
|
ПРЕДСКАЗ.ETS
|
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS). |
|
ПРЕДСКАЗ. |
Возвращает доверительный интервал для прогнозной величины на указанную дату. |
|
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ
|
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. |
|
ПРЕДСКАЗ.ETS.СТАТ
|
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда. |
|
ПРЕДСКАЗ. |
Возвращает будущее значение на основе существующих значений. |
|
ЧАСТОТА |
Возвращает распределение частот в виде вертикального массива. |
|
ГАММА
|
Возвращает значение функции гамма. |
|
ГАММА.РАСП
|
Возвращает гамма-распределение. |
|
ГАММА.ОБР
|
Возвращает обратное значение интегрального гамма-распределения. |
|
ГАММАНЛОГ |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАММАНЛОГ.ТОЧН
|
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАУСС
|
Возвращает значение на 0,5 меньше стандартного нормального распределения. |
|
СРГЕОМ |
Возвращает среднее геометрическое. |
|
РОСТ |
Возвращает значения в соответствии с экспоненциальным трендом. |
|
СРГАРМ |
Возвращает среднее гармоническое. |
|
ГИПЕРГЕОМ.РАСП |
Возвращает гипергеометрическое распределение. |
|
ОТРЕЗОК |
Возвращает отрезок, отсекаемый на оси линией линейной регрессии. |
|
ЭКСЦЕСС |
Возвращает эксцесс множества данных. |
|
НАИБОЛЬШИЙ |
Возвращает k-ое наибольшее значение в множестве данных. |
|
ЛИНЕЙН |
Возвращает параметры линейного тренда. |
|
ЛГРФПРИБЛ |
Возвращает параметры экспоненциального тренда. |
|
ЛОГНОРМ.РАСП
|
Возвращает интегральное логарифмическое нормальное распределение. |
|
ЛОГНОРМ.ОБР
|
Возвращает обратное значение интегрального логарифмического нормального распределения. |
|
МАКС |
Возвращает наибольшее значение в списке аргументов. |
|
МАКСА |
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения. |
|
Функция МАКСЕСЛИ
|
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек. |
|
МЕДИАНА |
Возвращает медиану заданных чисел. |
|
МИН |
Возвращает наименьшее значение в списке аргументов. |
|
МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения. |
|
Функция МИНЕСЛИ
|
Возвращает минимальное значение из заданных определенными условиями или критериями ячеек. |
|
МОДА.НСК
|
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных. |
|
МОДА.ОДН
|
Возвращает значение моды набора данных. |
|
ОТРБИНОМ.РАСП
|
Возвращает отрицательное биномиальное распределение. |
|
НОРМ.РАСП
|
Возвращает нормальное интегральное распределение. |
|
НОРМ.ОБР
|
Возвращает обратное значение нормального интегрального распределения. |
|
НОРМ.СТ.РАСП
|
Возвращает стандартное нормальное интегральное распределение. |
|
НОРМ.СТ.ОБР
|
Возвращает обратное значение стандартного нормального интегрального распределения. |
|
ПИРСОН |
Возвращает коэффициент корреляции Пирсона. |
|
ПРОЦЕНТИЛЬ. |
Возвращает k-ю процентиль значений в диапазоне, где k может принимать значения от 0 до 1, исключая границы. |
|
ПРОЦЕНТИЛЬ.ВКЛ
|
Возвращает k-ю процентиль для значений диапазона. |
|
ПРОЦЕНТРАНГ.ИСКЛ
|
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы). |
|
ПРОЦЕНТРАНГ.ВКЛ
|
Возвращает процентную норму значения в наборе данных. |
|
ПЕРЕСТ |
Возвращает количество перестановок для заданного числа объектов. |
|
ПЕРЕСТА
|
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов. |
|
ФИ
|
Возвращает значение функции плотности для стандартного нормального распределения. |
|
ПУАССОН. |
Возвращает распределение Пуассона. |
|
ВЕРОЯТНОСТЬ |
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов. |
|
КВАРТИЛЬ.ИСКЛ
|
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы. |
|
КВАРТИЛЬ.ВКЛ
|
Возвращает квартиль набора данных. |
|
РАНГ.СР
|
Возвращает ранг числа в списке чисел. |
|
РАНГ.РВ
|
Возвращает ранг числа в списке чисел. |
|
КВПИРСОН |
Возвращает квадрат коэффициента корреляции Пирсона. |
|
СКОС |
Возвращает асимметрию распределения. |
|
СКОС.Г
|
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего. |
|
НАКЛОН |
Возвращает наклон линии линейной регрессии. |
|
НАИМЕНЬШИЙ |
Возвращает k-ое наименьшее значение в множестве данных. |
|
НОРМАЛИЗАЦИЯ |
Возвращает нормализованное значение. |
|
СТАНДОТКЛОН.Г
|
Вычисляет стандартное отклонение по генеральной совокупности. |
|
СТАНДОТКЛОН.В
|
Оценивает стандартное отклонение по выборке. |
|
СТАНДОТКЛОНА |
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения. |
|
СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения. |
|
СТОШYX |
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. |
|
СТЬЮДРАСП
|
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.2Х
|
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ. |
Возвращает t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ОБР
|
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы. |
|
СТЬЮДЕНТ.ОБР.2Х
|
Возвращает обратное t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ТЕСТ
|
Возвращает вероятность, соответствующую проверке по критерию Стьюдента. |
|
ТЕНДЕНЦИЯ |
Возвращает значения в соответствии с линейным трендом. |
|
УРЕЗСРЕДНЕЕ |
Возвращает среднее внутренности множества данных. |
|
ДИСП.Г
|
Вычисляет дисперсию по генеральной совокупности. |
|
ДИСП.В
|
Оценивает дисперсию по выборке. |
|
ДИСПА |
Оценивает дисперсию по выборке, включая числа, текст и логические значения. |
|
ДИСПРА |
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения. |
|
ВЕЙБУЛЛ.РАСП
|
Возвращает распределение Вейбулла. |
|
Z. |
Возвращает одностороннее значение вероятности z-теста. |
Matplotlib. Урок2. Работа с инструментом pyplot
Практически все задачи, связанные с построением графиков, можно решить, используя возможности, которые предоставляет модуль pyplot. В рамках данного урока мы рассмотрим базовые возможности модуля для построения графиков.
Для того, чтобы запустить любой из примеров, продемонстрированных в первом уроке (“Matplolib. Урок 1. Быстрый старт), вам предварительно нужно было импортировать pyplot из библиотеки Matplolib. В настоящее время среди пользователей этого инструмента принято импорт производить следующим образом:
import matplotlib.pyplot as plt
Создатели Matplolib постарались сделать его похожим в использовании на MATLAB, так что если вы знакомы с последним, то разобраться с библиотекой будет проще.
Основным элементом изображения, которое строит pyplot является Фигура (Figure), на нее накладываются один или более графиков, осей, надписей и т.п. Для построения графика используется команда plot(). В самом минимальном варианте можно ее использовать без параметров:
import matplotlib.pyplot as plt %matplotlib inline plt.plot()
В результате будет выведено пустое поле:
Далее команду импорта и magic-команду для Jupyter (первая и вторая строки приведенной выше программы) мы использовать не будем.
Если в качестве параметра функции plot() передать список, то значения из этого списка будут отложены по оси ординат (ось y), а по оси абсцисс (ось x) будут отложены индексы элементов массива:
plt.plot([1, 7, 3, 5, 11, 1])
Для того, чтобы задать значения по осям x и y необходимо в plot() передать два списка:
plt.Текстовые надписи на графикеplot([1, 5, 10, 15, 20], [1, 7, 3, 5, 11])
Наиболее часто используемые текстовые надписи на графике это:
- наименование осей;
- наименование самого графика;
- текстовое примечание на поле с графиком;
- легенда.
Рассмотрим кратко данные элементы, более подробный рассказ о них будет в одном из ближайших уроков.
Наименование осейДля задания подписи оси x используется функция xlabel(), оси y – ylabel(). Разберемся с аргументами данных функций. Здесь и далее аргументы будем описывать следующим образом:
- Имя_аргумента: тип(ы)
Для функций xlabel()/ylabel() основными являются следующие аргументы:
- xlabel (или ylabel):str
- Текст подписи.
- labelpad : численное значение либо None; значение по умолчанию: None
- Расстояние между областью графика, включающую оси, и меткой.

- Расстояние между областью графика, включающую оси, и меткой.
Функции xlabel()/ylabel() принимают в качестве аргументов параметры конструктора класса matplotlib.text.Text, некоторые из них нам могут пригодиться:
- fontsize или size: число либо значение из списка: {‘xx-small’, ‘x-small’, ‘small’, ‘medium’, ‘large’, ‘x-large’, ‘xx-large’}.
- Размер шрифта.
- fontstyle: значение из списка: {‘normal’, ‘italic’, ‘oblique’}.
- fontweight: число в диапазоне от 0 до 1000 либо значение из списка: {‘ultralight’, ‘light’, ‘normal’, ‘regular’, ‘book’, ‘medium’, ‘roman’, ‘semibold’, ‘demibold’, ‘demi’, ‘bold’, ‘heavy’, ‘extra bold’, ‘black’}.
- Толщина шрифта.
- color: одни из доступных способов определения цвета см. Цвет линии.
Пример использования:
plt.xlabel('Day', fontsize=15, color='blue')Аргументов у этих функций довольно много и они позволяют достаточно тонко настроить внешний вид надписей. В рамках этого урока мы только начинаем знакомиться с инструментом pyplot поэтому не будем приводить весь список.
В рамках этого урока мы только начинаем знакомиться с инструментом pyplot поэтому не будем приводить весь список.
Для задания заголовка графика используется функция title():
plt.title('Chart price', fontsize=17)Из параметров отметим следующие:
- label: str
- Текст заголовка.
- loc: значение из набора {‘center‘, ‘left‘, ‘right‘}
- Выравнивание заголовка.
Для функции title() также доступны параметры конструктора класса matplotlib.text.Text, часть из них представлена в описании аргументов функций xlabel() / ylabel().
Текстовое примечаниеЗа размещение текста на поле графика отвечает функция text(), которой вначале передаются координаты позиции надписи, после этого – текст самой надписи.
plt.Легендаtext(1, 1, 'type: Steel')
Легенда будет размещена на графике, если вызвать функцию legend(), в рамках данного урока мы не будем рассматривать аргументы этой функции.
Разместим на уже знакомом нам графике необходимый набор подписей.
x = [1, 5, 10, 15, 20]
y = [1, 7, 3, 5, 11]
plt.plot(x, y, label='steel price')
plt.title('Chart price', fontsize=15)
plt.xlabel('Day', fontsize=12, color='blue')
plt.ylabel('Price', fontsize=12, color='blue')
plt.legend()
plt.grid(True)
plt.text(15, 4, 'grow up!')К перечисленным опциям мы добавили сетку, которая включается с помощью функции grid(True).
Работа с линейным графикомВ этом параграфе мы рассмотрим основные параметры и способы их задания для изменения внешнего вида линейного графика. Matplotlib предоставляет огромное количество инструментов для построения различных видов графиков. Так как наиболее часто встречающийся вид графика – это линейный, ему и уделим внимание. Необходимо помнить, что настройка графиков других видов, будет осуществляться сходным образом.
Необходимо помнить, что настройка графиков других видов, будет осуществляться сходным образом.
Параметры, которые отвечают за отображение графика можно задать непосредственно в самой функции plot():
plt.plot(x, y, color='red')
Либо воспользоваться функцией setp(), через которую можно модифицировать нужные параметры:
plt.setp( color='red', linewidth=1)Стиль линии графика
Стиль линии графика задается через параметр linestyle, который может принимать значения из приведенной ниже таблицы.
| Значение параметра | Описание |
| ‘-‘ или ‘solid’ | Непрерывная линия |
| ‘–‘ или ‘dashed’ | Штриховая линия |
| ‘-.’ или ‘dashdot’ | Штрихпунктирная линия |
| ‘:’ или ‘dotted’ | Пунктирная линия |
| ‘None’ или ‘ ‘ или ” | Не отображать линию |
Стиль линии можно передать сразу после указания списков с координатами без указания, что это параметр linewidth.
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] plt.plot(x, y, '--')
Либо можно воспользоваться функцией setp():
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] line = plt.plot(x, y) plt.setp(line, linestyle='--')
Результат будет тот же, что на рисунке выше.
Для того, чтобы вывести несколько графиков на одном поле необходимо передать соответствующие наборы значений в функцию plot(). Построим несколько наборов данных и выведем их с использованием различных стилей линии:
x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [i*1.2 + 1 for i in y1] y3 = [i*1.2 + 1 for i in y2] y4 = [i*1.2 + 1 for i in y3] plt.plot(x, y1, '-', x, y2, '--', x, y3, '-.', x, y4, ':')
Тот же результат можно получить, вызвав plot() для построения каждого графика по отдельности. Если вы хотите представить каждый график отдельно на своем поле, то используйте для этого subplot() (см. Размещение графиков на разных полях)
Размещение графиков на разных полях)
plt.plot(x, y1, '-') plt.plot(x, y2, '--') plt.plot(x, y3, '-.') plt.plot(x, y4, ':')Цвет линии
Задание цвета линии графика производится через параметр color (или c, если использовать сокращенный вариант). Значение может быть представлено в одном из следующих форматов:
- RGB или RGBA кортеж значений с плавающей точкой в диапазоне [0, 1] (пример: (0.1, 0.2, 0.3)
- RGB или RGBA значение в hex формате (пример: ‘#0a0a0a’)
- строковое представление числа с плавающей точкой в диапазоне [0, 1] (определяет цвет в шкале серого) (пример: ‘0.7’)
- символ из набора {‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’}
- имя цвета из палитры X11/CSS4
- цвет из палитры xkcd(https://xkcd.com/color/rgb/), должен начинаться с префикса ‘xkcd:’
- цвет из набора Tableau Color (палитра T10), должен начинаться с префикса ‘tab:’
Если цвет задается с помощью символа из набора {‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’}, то он может быть совмещен со стилем линии в рамках параметра fmt функции plot().
Например штриховая красная линия будет задаваться так: ‘–r’, а штрих пунктирная зеленая так ‘-.g’
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] plt.plot(x, y, '--r')Тип графика
До этого момента мы работали только с линейными графиками, функция plot() позволяет задать тип графика: линейный либо точечный, при этом для точечного графика можно указать соответствующий маркер. Приведем пару примеров:
plt.plot(x, y, 'ro')
plt.plot(x, y, 'bx')
Размер маркера можно менять, об этом более подробно будет рассмотрено в уроке, посвященном точечным графикам.
Размещение графиков на разных поляхСуществуют три основных подхода к размещению нескольких графиков на разных полях:
- использование функции subplot() для указания места размещения поля с графиком;
- использование функции subplots() для предварительного задания сетки, в которую будут укладываться поля;
- использование GridSpec, для более гибкого задания геометрии размещения полей с графиками в сетке.

В этом уроке будут рассмотрены первые два подхода.
Работа с функцией subplot()Самый простой способ представить графики в отдельных полях – это использовать функцию supplot() для задания их мест размещения. До этого момента мы не работали с Фигурой (Figure) напрямую, значения ее параметров, задаваемые по умолчанию, нас устраивали. Для решения текущей задачи придется один из параметров – размер подложки, задать вручную. За это отвечает аргумент figsize функции figure(), которому присваивается кортеж из двух float элементов, определяющих высоту и ширину подложки.
После задания размера, указывается местоположение, куда будет установлено поле с графиком с помощью функции subplot(). Чаще всего используют следующие варианты вызова subplot:
subplot(nrows, ncols, index)
- nrows: int
- Количество строк.
- ncols: int
- Количество столбцов.

- Количество столбцов.
- index: int
- Местоположение элемента.
subplot(pos)
- pos:int
- Позиция, в виде трехзначного числа, содержащего информацию о количестве строк, столбцов и индексе, например 212, означает подготовить разметку с двумя строками и одним столбцов, элемент вывести в первую позицию второй строки. Этот вариант можно использовать, если количество строк и столбцов сетки не более 10, в ином случае лучше обратиться к первому варианту.
Рассмотрим на примере работу с данными функциями:
# Исходный набор данных x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [i*1.2 + 1 for i in y1] y3 = [i*1.2 + 1 for i in y2] y4 = [i*1.2 + 1 for i in y3] # Настройка размеров подложки plt.figure(figsize=(12, 7)) # Вывод графиков plt.subplot(2, 2, 1) plt.plot(x, y1, '-') plt.subplot(2, 2, 2) plt.plot(x, y2, '--') plt.subplot(2, 2, 3) plt.plot(x, y3, '-.') plt.subplot(2, 2, 4) plt.plot(x, y4, ':')
Второй вариант использования subplot():
# Вывод графиков plt.subplot(221) plt.plot(x, y1, '-') plt.subplot(222) plt.plot(x, y2, '--') plt.subplot(223) plt.plot(x, y3, '-.') plt.subplot(224) plt.plot(x, y4, ':')Работа с функцией subplots()
Одно из неудобств использования последовательного вызова функций subplot() заключается в том, что каждый раз приходится указывать количество строк и столбцов сетки. Для того, чтобы этого избежать, можно воспользоваться функцией subplots(), из всех ее параметров, нас пока интересуют только первые два, через них передается количество строк и столбцов сетки. Функция subplots() возвращает два объекта, первый – это Figure, подложка, на которой будут размещены поля с графиками, второй – объект или массив объектов Axes, через которые можно получить полных доступ к настройке внешнего вида отображаемых элементов.
Решим задачу вывода четырех графиков с помощью функции subplots():
fig, axs = plt.subplots(2, 2, figsize=(12, 7)) axs[0, 0].plot(x, y1, '-') axs[0, 1].plot(x, y2, '--') axs[1, 0].plot(x, y3, '-.') axs[1, 1].plot(x, y4, ':')
Результат будет аналогичный тому, что приведен в разделе “Работа с функцией subplot()”.
P.S.Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Функции
по сравнению с отношениями (стр. Разделы: Функции и отношения, Домен и диапазон Есть разные взгляды на функции.Мы рассмотрим несколько. Но сначала нам нужно обсудить некоторую терминологию. «отношение»
это просто отношения между наборами информации. Подумайте обо всех людях
в одном из ваших классов, и подумайте об их росте. Соединение имен
и высота является отношением. В отношениях и функциях пары имен
а высоты «упорядочены», что означает, что сначала идет один, а другой
другое идет вторым.Другими словами, мы могли бы создать эту пару
так что либо ты даешь мне имя, а потом я даю тебе рост того человека,
а то ты дашь мне высоту, а я тебе имена всех людей
кто такие высокие. Набор всех
отправные точки
называется доменом, а множество всех конечных точек
называется «диапазон». Функция А это «хорошее» отношение. Так же, как и с членами вашего собственного семьи, у некоторых членов семьи парные отношения лучше вел себя лучше других.(Предупреждение: это означает, что хотя все функции отношения, так как они парная информация, не все отношения являются функциями. Функции — это подкласс отношений.) Когда мы говорим, что функция является «хорошим отношением», мы имеем в виду, что, учитывая начальное точка, мы точно знаем, куда идти; учитывая х , мы получаем только и ровно один y . Вернемся
к нашему отношению к вашим одноклассникам и их росту, и давайте предположим,
что домен — это набор всех высот. Отношение «рост указывает на имя» не очень хорошо себя ведет.Это не функция. Учитывая отношение ( x , y ) = (пять футов пять человек, имя), может быть шесть различных вариантов для y = «имя». Чтобы отношение было функция должна быть только и ровно один y , что соответствует данному x . Вот несколько фотографий этого:
В настоящее время Вы пытаетесь! «Тест вертикальной линии» Глядя на
эта функция наполняется графически, что, если бы у нас было отношение, состоящее
множества, состоящего всего из двух точек: {(2,
3), (2, –2)}? Мы уже знаем, что это не функция, так как х = 2 идет на каждое из y = 3 и y = –2.
Эта характеристика
нефункций было замечено не знаю кем и систематизировано в
«Тест вертикальной линии»: учитывая график отношения, если
можно нарисовать вертикальную линию, пересекающую график более чем в одном месте,
тогда отношение не является функцией.
В настоящее время Вы пытаетесь! «Есть это функция?» — Быстрый ответ без графика Подумай обо всем , отображающий , который вы сделали до сих пор. С другой рука, y 2 + 3 x = 6 не является функцией, потому что вы не можете решить для a уникальный y : То есть, да,
это решено для » y =» , но это не уникальный . Топ | 1 | 2 | Возвращение к индексу Далее >>
|
|
%PDF-1.3
%
929 0 объект
>
эндообъект
внешняя ссылка
929 57
0000000016 00000 н
0000001491 00000 н
0000001714 00000 н
0000001834 00000 н
0000001894 00000 н
0000001954 00000 н
0000002014 00000 н
0000002072 00000 н
0000002131 00000 н
0000002479 00000 н
0000002538 00000 н
0000002597 00000 н
0000002657 00000 н
0000002715 00000 н
0000002839 00000 н
0000002950 00000 н
0000003754 00000 н
0000004030 00000 н
0000004125 00000 н
0000004222 00000 н
0000004319 00000 н
0000004416 00000 н
0000004594 00000 н
0000005172 00000 н
0000005638 00000 н
0000005874 00000 н
0000006104 00000 н
0000006145 00000 н
0000006167 00000 н
0000006811 00000 н
0000007047 00000 н
0000007444 00000 н
0000007466 00000 н
0000007993 00000 н
0000008015 00000 н
0000008445 00000 н
0000008859 00000 н
0000009015 00000 н
0000009037 00000 н
0000009600 00000 н
0000009622 00000 н
0000010168 00000 н
0000010190 00000 н
0000010725 00000 н
0000010747 00000 н
0000011260 00000 н
0000011282 00000 н
0000011821 00000 н
0000014499 00000 н
0000014578 00000 н
0000053486 00000 н
0000077515 00000 н
0000077912 00000 н
0000088692 00000 н
0000097865 00000 н
0000003057 00000 н
0000003732 00000 н
трейлер
]
>>
startxref
0
%%EOF
930 0 объект
>
эндообъект
931 0 объект
[
932 0 Р 933 0 Р 934 0 Р 935 0 Р 936 0 Р 937 0 Р 938 0 Р 939 0 Р 940 0 Р
941 0 Р 942 0 Р 943 0 Р
]
эндообъект
932 0 объект
>
/Ф 946 0 Р
>>
эндообъект
933 0 объект
>
/Ф 947 0 Р
>>
эндообъект
934 0 объект
>
/Ф 948 0 Р
>>
эндообъект
935 0 объект
>
/Ф 5 0 Р
>>
эндообъект
936 0 объект
>
/Ф 10 0 Р
>>
эндообъект
937 0 объект
>
/Ф 14 0 Р
>>
эндообъект
938 0 объект
>
/Ф 21 0 Р
>>
эндообъект
939 0 объект
>
/Ф 22 0 Р
>>
эндообъект
940 0 объект
>
/Ф 949 0 Р
>>
эндообъект
941 0 объект
>
/Ф 6 0 Р
>>
эндообъект
942 0 объект
>
/Ф 45 0 Р
>>
эндообъект
943 0 объект
>
/Ф 35 0 Р
>>
эндообъект
944 0 объект
>
эндообъект
984 0 объект
>
ручей
Hb«`f`AXX8&040400800lql|y`mC,JL/’:e]H0>d+
T2Kp(Rr~9iBewa_»T},9z:69qiIʇ:xTf
,1NG&kx-kd»ШKu2I-W9l%a֧Ec
;s =Lr8aFN@.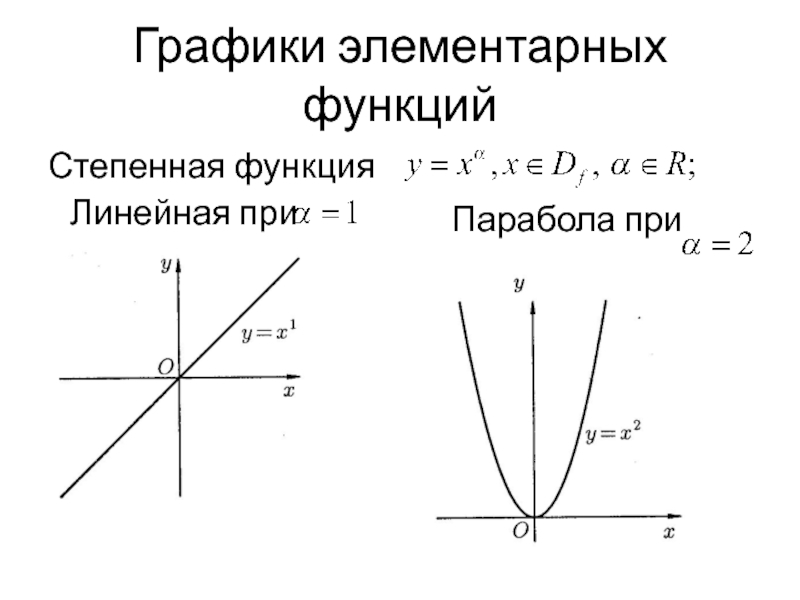 iVb3k)g0a?Cc/C3ho20.g’a6[yN13H 3(
iVb3k)g0a?Cc/C3ho20.g’a6[yN13H 3(
Функции SAT Math: линейные, квадратичные и алгебраические
ФункцииSAT имеют сомнительную честь быть одной из самых сложных тем в математическом разделе SAT. К счастью, это не потому, что задачи на функции сложнее решить, чем любую другую математическую задачу, а потому, что большинство студентов просто не занимались функциями так много, как другими математическими темами SAT.
Это означает, что разница между пропущенными пунктами в этой, казалось бы, сложной теме и достижением их является просто вопросом практики и ознакомления.А учитывая, что проблемы с функциями обычно возникают в среднем три-четыре раза за тест, вы сможете набрать еще несколько баллов по математике SAT, когда узнаете правила и работу функций.
Это будет вашим полным руководством по функциям SAT. Мы расскажем вам, что именно означают функции, как их использовать, манипулировать и идентифицировать, а также какие именно проблемы с функциями вы увидите на тесте SAT.
Что такое функции и как они работают?
Функции — это способ описания взаимосвязи между входными и выходными данными в форме графика или уравнения.2 + 2x − 4$
Функции всегда можно изобразить в виде графика, и разные виды функций будут давать разные графики. На стандартном координатном графике с осями $x$ и $y$ входом графика будет значение $x$, а выходом будет значение $y$.
Каждый вход (значение $x$) может производить только один выход, но один выход может иметь несколько входов. Другими словами, несколько входов могут давать один и тот же результат.
Один из способов запомнить это состоит в том, что вы можете иметь «многие к одному» (многие входы к одному выходу), но НЕ «один ко многим» (один вход ко многим выходам).
Это означает, что график функции может иметь потенциально много $x$-пересечений, но только один $y$-пересечение. (Почему? Потому что, когда на входе $x=0$, может быть только один выход или значение $y$. )
)
Функция с несколькими $x$ -перехватами.
Вы всегда можете проверить, является ли график функциональным графиком, используя это понимание входов и выходов. Если вы используете «тест вертикальной линии», вы можете увидеть, является ли график функцией или нет, поскольку график функции НЕ будет попадать более чем в одну точку на любой вертикальной линии.
Где бы мы ни рисовали вертикальную линию на нашей функции, она будет пересекаться с графиком максимум один раз.
Проверка вертикальной линии применяется ко всем типам функций, независимо от того, насколько «странными» они выглядят.
Даже «странно выглядящие» функции всегда проходят проверку вертикальной линией.
Но любой график, не прошедший тест вертикальной линии (пересекшийся с вертикальной линией более одного раза), автоматически НЕ является функцией.
Этот график НЕ является функцией, так как он не прошел тест вертикальной линии.
Слишком много препятствий на пути восхождения работает как для функций, так и для реальной жизни (то есть совсем не хорошо).
Функциональные термины и определения
Теперь, когда мы увидели, что делают функции, давайте поговорим о частях функции.
Функции представлены либо их уравнениями, их таблицами, либо их графиками (называемыми «графиком функции»).2+5$
$f$ — это имя функции
(Примечание: мы можем называть нашу функцию другими именами, кроме $f$. Эта функция называется $f$, но вы можете встретить функции, написанные как $h(x)$, $g(x)$, $r( x)$ или что-то еще.)
$(x)$ — это ввод
(Примечание: в этом случае входные данные называются $x$, но мы можем называть их как угодно. $f(q)$ или $f(\strawberries)$ — обе функции с входными данными $q$ и клубники, соответственно.2+5$
$f(3) = 9+5$
$f(3) = 14$
Итак, наша заказанная пара $(3, 14)$.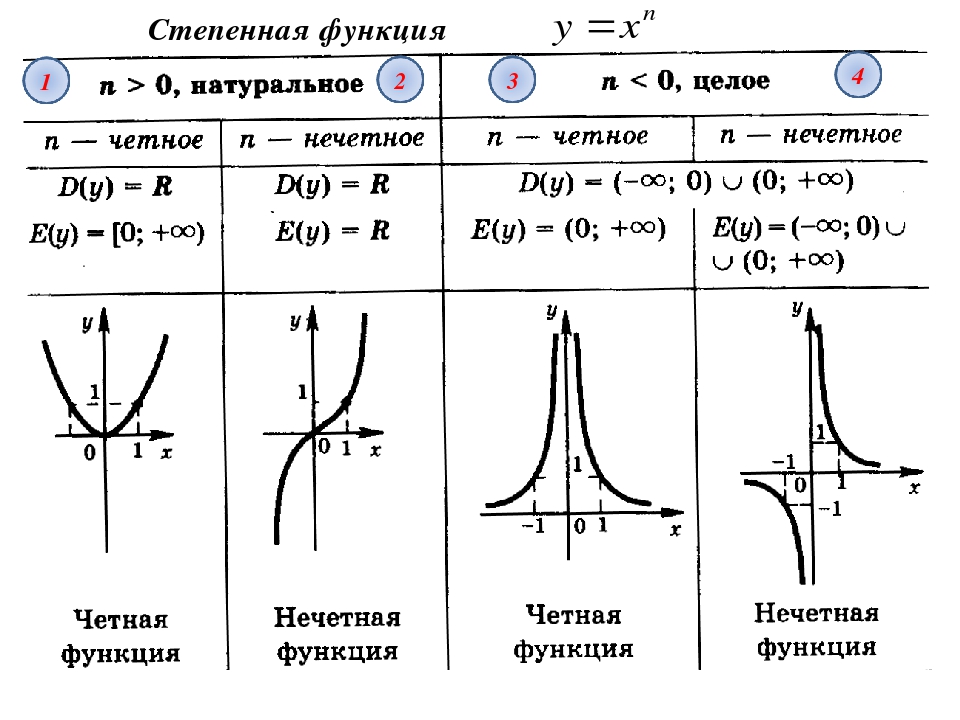
Упорядоченные пары также действуют как координаты , поэтому мы можем использовать их для построения графика нашей функции.
Теперь, когда мы понимаем наши функциональные ингредиенты, давайте посмотрим, как мы можем их соединить.
Различные типы функций
Ранее мы видели, что функции могут иметь всевозможные уравнения для своего вывода.2$ равно 9, значит, график не может быть прямой линией.
Примеры линейных функций:
$f(x) = x − 12$
$f(x) = 4$
$f(x) = 6x + 40$
Квадратичные функции
Квадратичная функция образует график параболы, что означает, что это график, изгибающийся либо вверх, либо вниз. Это также означает, что наша выходная переменная всегда будет равна в квадрате.
Причина, по которой наша переменная должна быть возведена в квадрат (не возведена в куб, не возведена в степень 1 и т. 2 + bx + c$
2 + bx + c$
Значение $\bi a$ говорит нам, как формируется парабола и в каком направлении она раскрывается.
положительных $\bi a$ дают нам параболу, которая открывается вверх.
отрицательное $\bi a$ дает нам параболу, которая открывается вниз.
большое $\bi a$ значение дает нам тощую параболу.
маленькое $\bi a$ значение дает нам широкую параболу.
Значение $\bi b$ сообщает нам, где находится вершина параболы, слева или справа от начала координат.
положительных $\bi b$ ставит вершину параболы слева от начала координат.
отрицательное $\bi b$ помещает вершину параболы справа от начала координат.
Значение $\bi c$ дает нам точку пересечения $y$ параболы.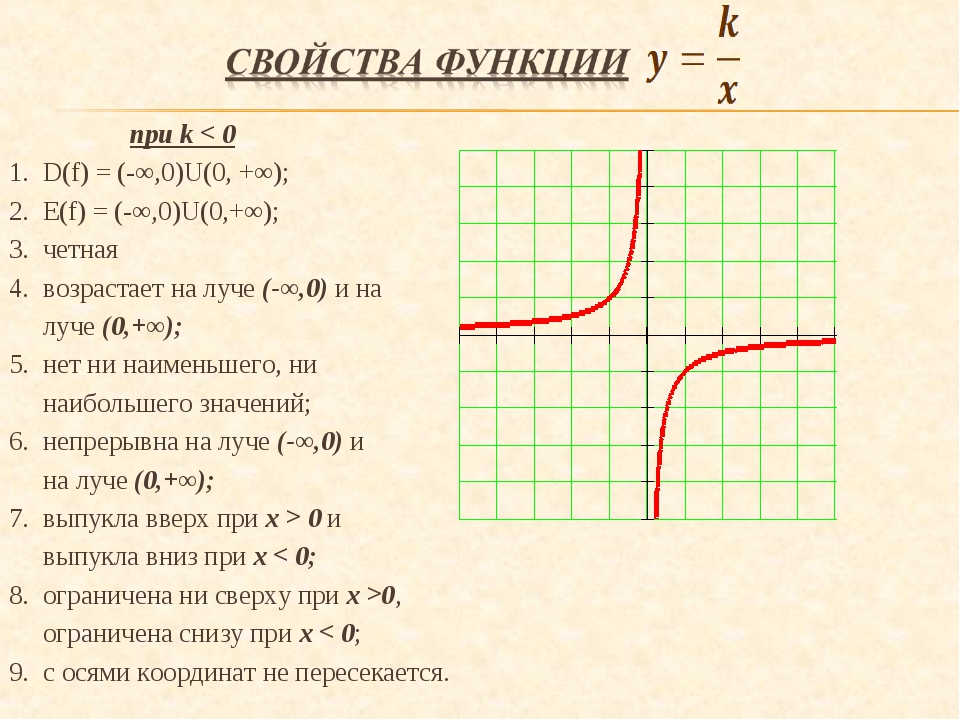 Это везде, где график достигает оси $y$ (и всегда будет только одна точка).
Это везде, где график достигает оси $y$ (и всегда будет только одна точка).
(Примечание: когда $b=0$, точка пересечения $y$ также будет точкой пересечения вершины параболы.)
Не волнуйтесь, если вам покажется, что сейчас слишком много для запоминания — с практикой понимание функциональных проблем и их компонентов станет второй натурой.
Готовы не просто читать о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Наша программа SAT, разработанная и написанная экспертами PrepScholar SAT , адаптируется к вашему уровню навыков по более чем 40 поднавыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.
Нажмите на кнопку ниже, чтобы попробовать!
Типичные проблемы с функциями
Проблемы с функциями SAT всегда будут проверять вас на то, правильно ли вы понимаете связь между входами и выходами. Эти вопросы обычно делятся на четыре типа вопросов:
Эти вопросы обычно делятся на четыре типа вопросов:
#1 : Функции с заданными уравнениями
#2 : Функции с графиками
#3 : Функции с таблицами
#4 : Вложенные функции
Между тремя категориями могут быть некоторые совпадения, но это основные темы, по которым вы будете тестироваться, когда речь заходит о функциях.Давайте посмотрим на некоторые реальные математические примеры SAT каждого типа.
Функциональные уравнения
Задача уравнения функции даст вам функцию в форме уравнения, а затем попросит вас использовать один или несколько входных данных, чтобы найти выход (или элементы выхода).
Чтобы найти конкретный выход, мы должны подставить заданный вход для $x$ в наше уравнение (выход).
Итак, если мы хотим найти $f(2)$ для уравнения $f(x) = x + 3$, мы должны подставить 2 вместо $x$.2 + 24$
$г(-4)= -16 + 24$
$г(-4)=8$
Наш окончательный ответ: А, 8.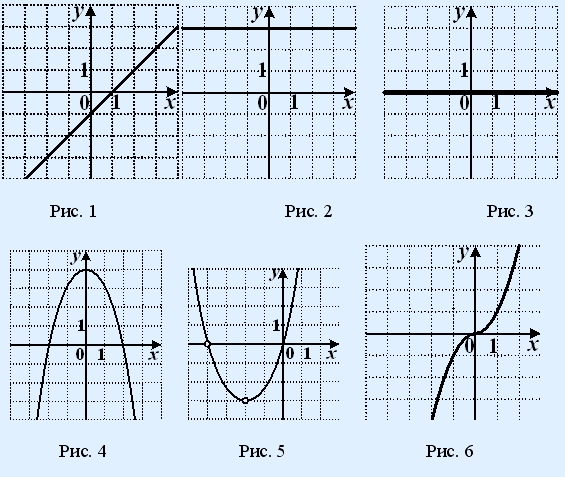
Графики функций
Вопрос о графике функции предоставит вам уже построенную функцию и задаст вам любое количество вопросов о ней.
Эти вопросы, как правило, требуют от вас определить конкретные элементы графика или найти уравнение функции на графике.
До тех пор, пока вы понимаете, что $x$ — это ваши входные данные, а ваше уравнение — ваши выходные данные, $y$, вопросы такого типа не будут такими сложными, как кажутся.
Минимальное значение функции соответствует $y$-координате точки на графике, где она является наименьшей по оси $y$.
Глядя на график, мы видим, что самая нижняя точка функции на оси $y$ приходится на $(-3,-2)$.
Поскольку мы ищем значение $x$, когда функция достигает минимума, нам нужна координата x, равная -3.
Итак, наш окончательный ответ: B, -3.
Таблицы функций
Третий способ увидеть функцию — это ее таблица.
Вам будет дана таблица значений как для входа, так и для выхода, а затем вам будет предложено либо найти уравнение функции, либо график функции.
Зачастую наилучшая стратегия для вопросов такого типа состоит в том, чтобы вставлять ответы, чтобы сделать нашу жизнь проще. Таким образом, нам не нужно на самом деле находить уравнение самостоятельно — мы можем просто проверить, какие варианты ответов соответствуют входным и выходным данным, указанным в нашей таблице.
Проверим вторую упорядоченную пару $(3,13)$ с каждым вариантом ответа.Для правильного ответа, когда мы подставим значение $x$ (3) в уравнение, мы получим правильное значение $y$ (13).
А) $f(x) = 2(3) +3 = 9$. Это уравнение неверно, так как 9 не равно 13.
Б) $f(x) =3(3) +2 = 1$. Это уравнение также неверно.
С) $f(x) = 4(3) +1=13$. Это матч! Это уравнение верно до сих пор.
D) $f(x)= 5(3)= 15$. Это уравнение также неверно.
Похоже, правильный вариант ответа — C, но давайте подставим первую и третью упорядоченные пары, чтобы убедиться в этом.
Для первой заказанной пары $(1,5)$:
$f(x) = 4(1) +1=5$ Верно!
За третью заказанную пару $(5,21)$
$f(x) = 4(5) +1=21$ Тоже верно!
Наш окончательный ответ C , $f(x) = 4x +1$
Вложенные функции
Последний тип функциональной проблемы, с которой вы можете столкнуться в SAT, называется «вложенной» функцией. По сути, это уравнение в уравнении.
По сути, это уравнение в уравнении.
Чтобы решить эти типы вопросов, подумайте о них с точки зрения вашего порядка операций.2 — 12x — 2
$
Поскольку $g(x)$ имеет самую глубокую вложенность, мы должны найти его выходные данные, прежде чем сможем найти $f(g(x−2))$.
Вместо числа для $x$ нам дается другое уравнение. Хотя это может выглядеть иначе, чем более ранние задачи, принцип точно такой же — заменить любые входные данные на переменную в выходном уравнении.
$g(x) = 3x + 4$
$г(х-2) = 3(х-2) + 4$
$ г(х-2) = 3х — 6 + 4$
$ г(х-2) = 3х — 2$
Итак, наш результат $g(x−2)$ равен $3x−2$.2 — 12х — 2$.
Функции внутри функций, сны внутри снов. Постарайтесь не потерять себя на этом пути.
Стратегии решения функциональных задач
Теперь, когда вы увидели все виды функциональных задач в действии, давайте рассмотрим некоторые советы и стратегии решения функциональных задач различных типов.
Для ясности мы разделили эти стратегии на несколько разделов — советы по всем функциональным проблемам и советы по функциональным проблемам по типам.Итак, давайте рассмотрим каждую стратегию.
Стратегии для всех функциональных проблем:
#1: Внимательно следите за всеми своими фигурами и записывайте все
Хотя это может показаться очевидным, в запале может быть слишком легко перепутать отрицательные и положительные значения или неправильно указать, какая часть вашей функции (или графика, или таблицы) является вашим входом, а какая выходом. Скобки имеют решающее значение.
Создатели SAT знают, как легко можно перепутать части ваших функциональных уравнений (особенно, когда ваши входные данные также являются уравнениями), поэтому внимательно следите за всеми движущимися частями и не пытайтесь функциональные проблемы в вашей голове.
#2: При необходимости используйте PIA и PIN-код
Как мы видели в нашей задаче с таблицей функций выше, использование стратегии подстановки ответов может сэкономить немало усилий и энергии. Вы также можете использовать метод подстановки собственных чисел, чтобы проверить точки на графиках функций, работать с любым уравнением функции переменной или работать с вложенными функциями с переменными.
Вы также можете использовать метод подстановки собственных чисел, чтобы проверить точки на графиках функций, работать с любым уравнением функции переменной или работать с вложенными функциями с переменными.
Например, давайте рассмотрим нашу предыдущую проблему с вложенной функцией с использованием PIN-кода.2 — 12x — 2
$
Если мы помним, как работают вложенные функции (мы всегда работаем наизнанку), то мы можем подставить собственное число для $x$ в функцию $g(x−2)$. Таким образом, нам не придется работать с переменными и вместо этого можно использовать реальные числа.
Допустим, $x$ есть функция $g(x−2)$, равная 5. (Почему 5? Почему бы и нет!)
Теперь $x−2$ будет равно $5−3$ или 3. Это означает, что $g(x−2)$ будет равно $g(3)$.
$ г(х-2) = 3х + 4$
г(3) = 3(3) + 4$
г(3) = 9 + 4$
$ г(3) = 13$
Теперь давайте подставим это число в качестве значения нашей функции $g(x−2)$ во вложенную функцию $f(g(x−2))$. 2 − 12(5) + 4$
2 − 12(5) + 4$
$9(25) − 60 + 4$
225 долларов − 60 + 4
долларов165$ + 4
$169
Это значение все еще слишком велико, но мы видим, что оно очень близко к окончательному ответу, который нам нужен. Просто просматривая наши варианты ответов, мы видим, что вариант ответа E — это точно такое же выражение, как вариант ответа D, за исключением конечного целочисленного значения. Если бы мы вычли 2 из 165 вместо прибавления 4 (как мы сделали с вариантом ответа D), мы получили бы окончательный ответ 163.2 — 12х — 2$.
#3: Практика, практика, практика
Наконец, единственный способ по-настоящему освоиться в любой математической теме — это попрактиковаться в решении как можно большего количества вопросов по этой теме. Если функции являются для вас слабой областью, обязательно поищите дополнительные практические вопросы.
Для функциональных графиков и таблиц:
#1: Начните с нахождения $\bi y$ -перехвата
Как правило, при работе с графиками функций и таблицами проще всего начать с нахождения точки пересечения по оси Y. Оттуда вы часто можете исключить несколько разных вариантов ответа, которые не соответствуют нашему графику или нашему уравнению (как мы делали в наших предыдущих примерах).
Оттуда вы часто можете исключить несколько разных вариантов ответа, которые не соответствуют нашему графику или нашему уравнению (как мы делали в наших предыдущих примерах).
Пересечение по оси Y почти всегда найти легче всего, так что это всегда хорошее место для начала.
#2: проверьте свое уравнение на нескольких упорядоченных парах
Всегда полезно найти две или более точек (упорядоченные пары) ваших функций и сравнить их с уравнением потенциальной функции.Иногда одна упорядоченная пара подходит для вашего графа, а вторая нет.
Вы должны сопоставить уравнение с графиком (или уравнение с таблицей), которое работает для каждой координатной точки/упорядоченной пары, а не только одной или двух.
Для функциональных уравнений и вложенных уравнений:
#1: Всегда работайте наизнанку
Вложенные функции могут выглядеть ужасными и сложными, но берите их по частям. Составьте уравнение в центре, а затем медленно стройте наружу, чтобы не перепутать какие-либо переменные или уравнения.
Составьте уравнение в центре, а затем медленно стройте наружу, чтобы не перепутать какие-либо переменные или уравнения.
№ 2: не забудьте ЗАПОЛНИТЬ
Для SAT довольно часто приходится возводить уравнение в квадрат. Это связано с тем, что многие учащиеся неправильно отвечают на вопросы такого типа и распределяют свои показатели степени вместо того, чтобы возводить в квадрат все выражение.
Если вы не будете должным образом FOIL, то вы получите эти вопросы неправильно. По возможности старайтесь не позволять себе терять очки из-за подобных ошибок по невнимательности.Например, предположим, что вы должны возвести выражение в квадрат.2 + 9$ но это неправильно . Не попадитесь в такую ловушку!)
Вы все прокачаны — пора сразиться с большим боссом и применить знания на деле!
Проверьте свои знания
Теперь давайте проверим ваши знания функций на реальных математических задачах SAT.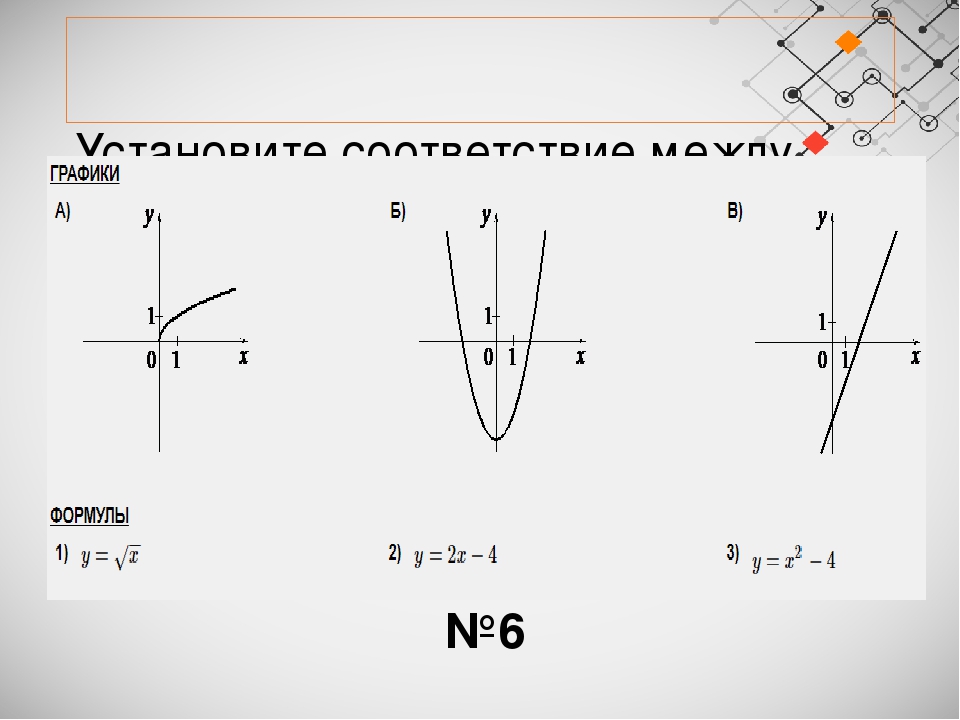
1. Пусть функция $f$ определена как $f(x)=5x-2a$, где $a$ — константа. Если $f(10)+f(5)=55$, какова стоимость $a$?
А) -5
Б) 0
С) 5
Г) 10
2. Функция $f$ удовлетворяет условию $f(2)=3$ и $f(3)=5$. Функция $g$ удовлетворяет условиям $g(3)=2$ и $g(5)=6$. Каково значение $f(g(3))$?
А) 2
Б) 3
С) 5
Г) 6
3.
4.
Ответы: C, B, A, D
Пояснения к ответу:
1. Как вы можете видеть здесь, нам дано наше уравнение, а также два входа и их объединенный вывод.Мы должны использовать это знание, чтобы найти элемент нашего вывода (в данном случае значение $a$.)
Итак, давайте найдем наши выходы для каждого заданного нами входа.
$f(x) = 5x − 2a$
$f(10) = 5(10) − 2a$
$f(10) = 50 − 2a$
и
$f(x) = 5x − 2a$
$f(5) = 5(5) − 2a$
$f(5) = 25 − 2a$
Теперь установим сумму двух наших выходов равной 55 (как было оговорено в вопросе).
50$ — 2а + 25 — 2а = 55$
75$ − 4a = 55$
$−4a = −20$
$a = 5$
Наш окончательный ответ C , $a=5$.
2. В вопросе сказано, что $g(3)=2$.
Чтобы найти значение $f(g(3))$, нам нужно заменить $g(3)$ на 2. Мы будем использовать это значение в уравнении $f(x)$.
Замена $g(3)$ на 2 дает нам $f(g(3))$ = $f(2)$.
Нам также сказали, что $f(2)=3$, значит, 3 — правильный ответ.
Наш окончательный ответ: B, 3.
3. Согласно нашим стратегиям, мы начнем с нахождения точки пересечения $y$.2−4x+4$
Это дало бы нам граф с точкой пересечения $y$ в точке +4 и вершиной, расположенной справа от оси $y$.
В процессе исключения у нас остался вариант ответа А. Но для перепроверки давайте проверим координатную точку на графике по формуле.
Мы уже знаем, что наше уравнение соответствует координатным точкам $(0, 2)$, так как это наш $y$-отрезок, но на графике есть еще несколько мест, которые совпадают с четными координатами.2+2$
4. Вместо того, чтобы использовать $x$ для ввода, в этой задаче мы использовали $t.$ Если вы очень привыкли использовать $f(x)$, это может показаться дезориентирующим, поэтому вы всегда можете переписать задачу используя $x$ вместо $t$.
В этом случае мы продолжим использовать $t$ просто для того, чтобы задача была систематизирована на странице.
Сначала найдем точку пересечения $y$.
Пересечение $y$ — это точка, в которой $x=0$, поэтому мы можем видеть, что это уже задано с первым набором чисел в таблице.Когда $t=0$, $f(t) = −1$
Таким образом, наш $y$-перехват равен -1, что означает, что мы можем автоматически исключить варианты ответов B, C и E.
Теперь давайте снова воспользуемся нашей стратегией подстановки чисел.
Наши варианты ответов находятся между A и D, поэтому давайте сначала проверим A со второй упорядоченной парой.
Наше потенциальное уравнение:
$f(t) = t − 1$
И наша заказанная пара:
$(1, 1)$
Итак, давайте сложим их вместе.
$f(t) = t − 1$
$f(1) = 1 − 1$
$f(1) = 0$
Это неверно, так как это означало бы, что наш вывод равен 0, когда наш ввод равен 1, и тем не менее упорядоченная пара говорит, что наш вывод будет 1, когда наш ввод равен 1.
Вариант ответа А неверный.
Методом исключения попробуем выбрать вариант ответа D.
Наше потенциальное уравнение:
$f(t) = 2t − 1$
И снова наша заказанная пара:
$(1, 1)$
Итак, давайте сложим их вместе.
$f(1) = 2(1) − 1$
$f(1) = 2 − 1$
$f(1) = 1$
Это соответствует вводу и выводу, которые нам даны в нашей упорядоченной паре.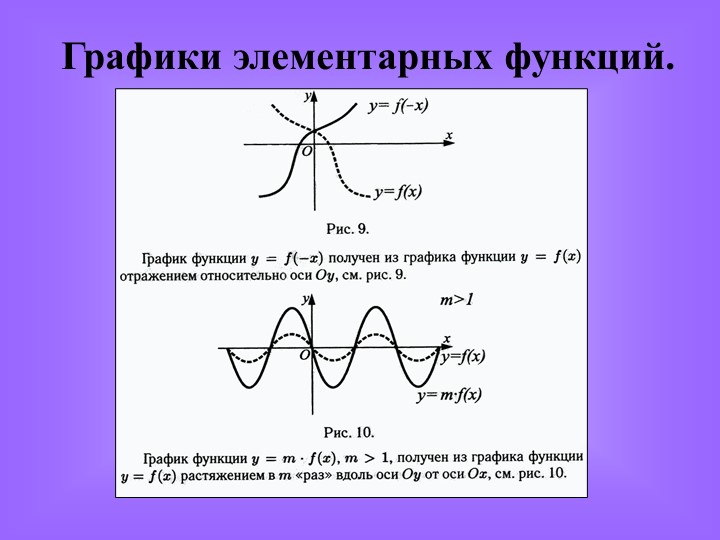 Вариант ответа D правильный.
Вариант ответа D правильный.
Наш окончательный ответ: D , $f(t) = 2t − 1$
Ты сделал это! Дай пять вокруг.
Вынос
Многие студенты мало что знают о функциях, но пусть такого рода вопросы не пугают и не сбивают вас с толку, когда вы видите их на SAT.Принципы, лежащие в основе функций, сводятся к простому вводу, выводу и подстановке значений. Тест будет пытаться замутить воду, когда сможет, но всегда помните, что эти вопросы кажутся более сложными, чем они есть на самом деле.
Хотя ошибиться с вашими знаками или переменными может быть легко, настоящие проблемы по своей сути просты. Так что будьте внимательны, перепроверяйте свою работу, и вскоре вы сможете решать проблемы с функциями без особых проблем.
Что дальше?
Говоря о квадратичных функциях, как у вас получается составлять квадрат? Узнайте, как и когда заполнить квадрат с помощью этого руководства.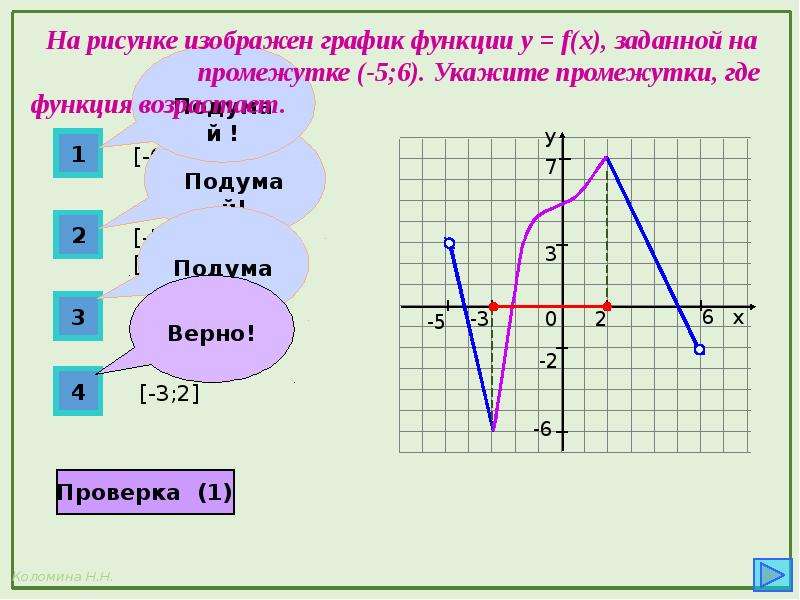
Фу! Знание своих функций означает знание значительной части математического раздела SAT (аплодисменты вам!), но есть еще много тем, которые нужно охватить. Взгляните на все темы, по которым вы будете тестироваться, в математическом разделе SAT, а затем просмотрите наши руководства по математике, чтобы просмотреть любую тему, в которой вы чувствуете себя заржавевшей. Не уверены в своих правилах экспоненты? Как насчет твоего понимания полигонов? Нужно пересмотреть склоны? Независимо от темы, мы вас охватили!
Нужна помощь по основам математики? Освежите свою память о распределительном свойстве, полных квадратах и о том, как найти среднее значение набора чисел здесь.
Думаете, вам нужен репетитор по математике? Ознакомьтесь с нашими руководствами о том, как найти репетитора, который наилучшим образом соответствует вашим потребностям (и вашему бюджету).
Не хватает времени на математический раздел SAT? Не беспокойтесь! У нас есть инструменты и стратегии, которые помогут вам выиграть время и увеличить количество очков.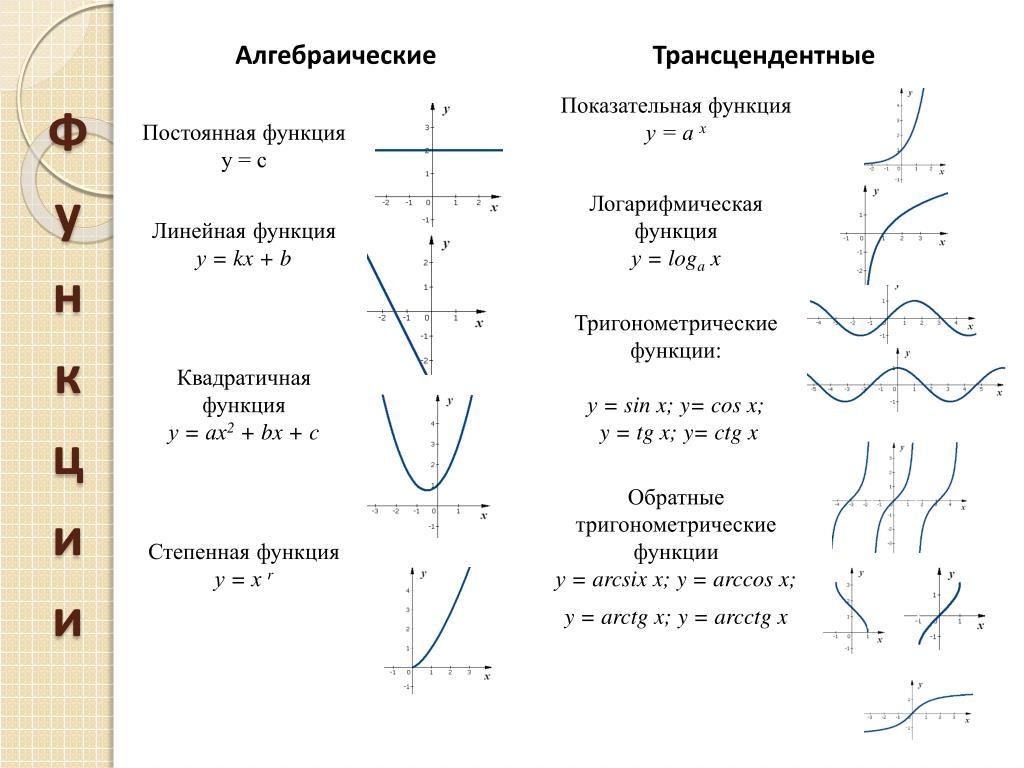
Пытаетесь набрать высший балл? Узнайте, как довести свой результат до максимума, из нашего руководства, написанного лучшим бомбардиром, чтобы получить 800 баллов по математике SAT.
Хотите улучшить свой результат SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег, если вы не улучшите свой результат SAT на 160 или более баллов.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравилось это руководство по математической стратегии, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно.Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
Ознакомьтесь с нашей 5-дневной бесплатной пробной версией:
%PDF-1.6
%
667 0 объект
>
эндообъект
233 0 объект
>
эндообъект
664 0 объект
>поток
2009-07-24T03:17:03+05:302009-07-24T03:12:35+05:302009-07-24T03:17:03+05:30Adobe Acrobat 8.12application/pdfuuid:6d6ffe25-20b4-8a45-b860 -efd8eb0e6f1duuid:564f6ba9-3f79-e345-9cd4-f44ca1c65537Adobe Acrobat 8.12 Плагин захвата бумаги конечный поток
эндообъект
650 0 объект
>
эндообъект
352 0 объект
>
эндообъект
353 0 объект
>
эндообъект
354 0 объект
>
эндообъект
651 0 объект
>
эндообъект
657 0 объект
>
эндообъект
658 0 объект
>
эндообъект
659 0 объект
>
эндообъект
660 0 объект
>
эндообъект
661 0 объект
>
эндообъект
662 0 объект
>
эндообъект
663 0 объект
>
эндообъект
197 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
201 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
205 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
209 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
213 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
217 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
221 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
225 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
229 0 объект
>/Шрифт>/ProcSet[/PDF/Text/ImageB]>>/Тип/Страница>>
эндообъект
1544 0 объект
>поток
HWiog[}Ed,,VA@ɔ@»mPW?OIι?+8~˻~YM~|ПJ n e!ZEs32E(Rw9DK:C’&’ un>9yϷɟ&N;FF]`W:-%Sx
*t9ϷYnѴPÃDё{Oyĥu/λ,.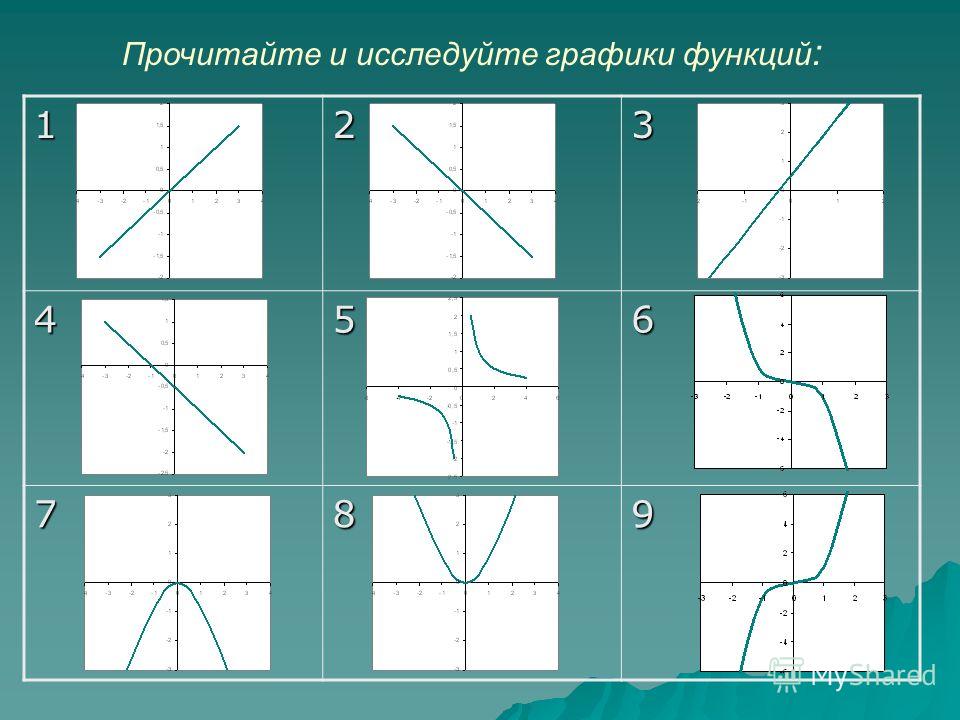 4$Xzz
@ʩ81s:rɌO}bT8F:hpBCY{f,J/mw}ѐuT»+CMYo&
4$Xzz
@ʩ81s:rɌO}bT8F:hpBCY{f,J/mw}ѐuT»+CMYo&
Полиномиальная функция — определение, формулы, типы, график
Полиномиальная функция — это самая простая, наиболее часто используемая и самая важная математическая функция. Эти функции представляют собой алгебраические выражения с определенными условиями. Они также охватывают большое количество функций. Для человека важно изучать и понимать полиномиальные функции из-за их обширных приложений.
В этой статье давайте узнаем об определении полиномиальных функций, их типах и графиках с решенными примерами.
Что такое полиномиальные функции?
В этой статье мы узнаем о различных аспектах полиномиальных функций. Polynomial состоит из двух слов: poly и nomial. «Полином» означает много, а «номинальный» означает термин, и, следовательно, когда они объединены, мы можем сказать, что полиномы — это «алгебраические выражения со многими терминами». Давайте продолжим и начнем с определения полиномиальных функций и их типов.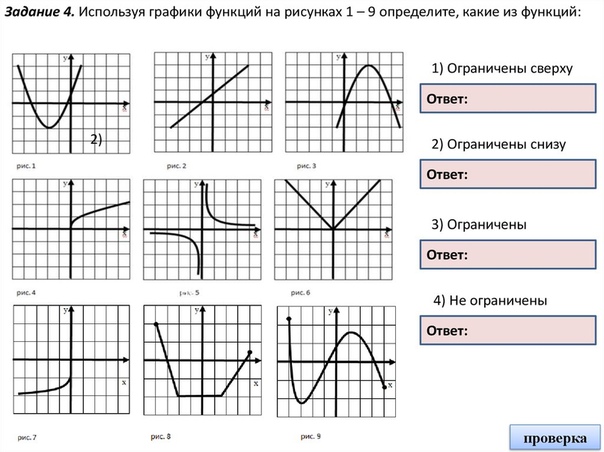
Определение полиномиальной функции
Полиномиальные функции — это выражения, которые могут содержать переменные различной степени, коэффициенты, положительные показатели и константы. Вот несколько примеров полиномиальных функций.
- f(x) = 3x 2 — 5
- г(х) = -7х 3 + (1/2) х — 7
- h(x) = 3x 4 + 7x 3 — 12x 2
Полиномиальная функция в стандартной форме
Полиномиальная функция в стандартной форме: f(x) = \(a_{n}\)x n + \(a_{n-1}\)x n-1 + … + \( а_{2}\)х 2 + \(а_{1}\)х + \(а_{0}\).Это алгебраическое выражение называется полиномиальной функцией от переменной x.
Здесь,
- \(a_{n}\), \(a_{n-1}\), … \(a_{0}\) — действительные числовые константы
- \(a_{n}\) не может быть равен нулю и называется старшим коэффициентом
- n — целое неотрицательное число
- Каждый показатель степени переменной в полиномиальной функции должен быть целым числом
Степень полиномиальной функции
Степень полиномиальной функции — это наивысшая степень переменной, в которую она возведена. Рассмотрим эту полиномиальную функцию f(x) = -7x 3 + 6x 2 + 11x – 19, наибольший найденный показатель степени равен 3 от -7x 3 . Это означает, что степень этого конкретного многочлена равна 3.
Рассмотрим эту полиномиальную функцию f(x) = -7x 3 + 6x 2 + 11x – 19, наибольший найденный показатель степени равен 3 от -7x 3 . Это означает, что степень этого конкретного многочлена равна 3.
Типы полиномиальных функций
Имя многочлена определяется количеством членов в нем. Три наиболее распространенных многочлена, с которыми мы обычно сталкиваемся, — это одночлены, двучлены и трехчлены.
- Мономы — это многочлены, содержащие только один член.Примеры: 15x 2 , 3b и 12y 4
- Биномы — это многочлены, содержащие только два члена. Примеры: x + y, 4x – 7 и 9x + 2
- Трехчлены — это многочлены, содержащие только три члена. Примеры: x 3 – 3 + 5x, z 4 + 45 + 3z и x 2 – 12x + 15
Кроме того, многочлены также классифицируются на основе их степеней. Четыре наиболее распространенных типа многочленов, которые используются в предварительном исчислении и алгебре, — это нулевая полиномиальная функция, линейная полиномиальная функция, квадратичная полиномиальная функция и кубическая полиномиальная функция.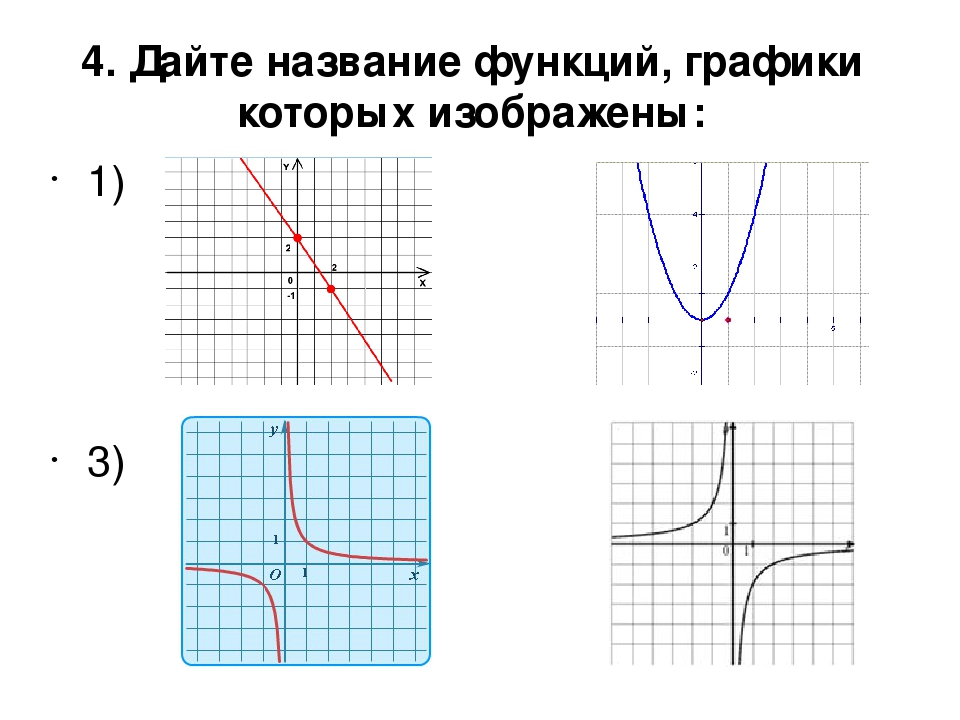
Нулевая полиномиальная функция
Нулевая полиномиальная функция имеет форму f(x) = 0, да, она просто содержит только 0 и никаких других членов или переменных. Поскольку здесь f(x) = константа, это постоянная функция.
Линейная полиномиальная функция
Линейная полиномиальная функция имеет степень 1. Она имеет вид f(x) = ax + b. Некоторые примеры линейной полиномиальной функции: f(x) = x + 3, f(x) = 25x + 4 и f(y) = 8y – 3,
Функция квадратичного полинома
Квадратичная полиномиальная функция имеет степень 2.Оно имеет вид f(x) = ax 2 + bx + c. Некоторые примеры квадратичной полиномиальной функции: f(m) = 5m 2 – 12m + 4, f(x) = 14x 2 – 6 и f(x) = x 2 + 4x.
Функция кубического полинома
Кубическая полиномиальная функция имеет степень 3. Она имеет вид f(x) = ax 3 + bx 2 + cx + d. Некоторые примеры функции кубического полинома: f(y) = 4y 3 , f(y) = 15y 3 – y 2 + 10 и f(a) = 3a + a 3 .
Как определить полиномиальную функцию?
Чтобы определить, является ли функция полиномиальной или нет, функцию необходимо проверить на выполнение определенных условий для показателей степени переменных. Эти условия следующие:
- Показатель степени переменной в функции в каждом члене должен быть только неотрицательным целым числом.
т. е. показатель степени переменной не должен быть дробью или отрицательным числом. - Переменная функции не должна находиться внутри корня i.д., он не должен содержать квадратных корней, кубических корней и т. д.
- Переменная не должна быть в знаменателе.
В таблице ниже показаны примеры и некоторые не примеры полиномиальных функций:
| Функции | Переменная | Экспонента | Полиномиальная функция или нет? |
|---|---|---|---|
| f(b) = 4b 2 – 6b + b 3 – 15 | б | 2 в б 2 ; 3 в б 3 | Да |
| f(x) = x 2/3 + 2x | х | 2/3 дюйма x 2/3 ; 1 в 2х | № |
| f(y) = 1/год 3 | г | -3 дюйма 1/год 3 | № |
Примечание: Помните, что коэффициенты могут быть дробями, отрицательными числами, 0 или положительными числами. Нам просто нужно позаботиться о показателях переменных, чтобы определить, является ли это полиномиальной функцией.
Нам просто нужно позаботиться о показателях переменных, чтобы определить, является ли это полиномиальной функцией.
График полиномиальной функции
Мы можем представить все полиномиальные функции в виде графика. Помните, что областью определения любой полиномиальной функции является множество всех действительных чисел. На приведенном ниже изображении показаны графики различных полиномиальных функций. Важным навыком в координатной геометрии является распознавание связи между уравнениями и их графиками.
- Линейная полиномиальная функция имеет форму y = ax + b и представляет собой прямую линию.
Чтобы узнать, как построить график линейной полиномиальной функции, нажмите здесь. - Квадратичная полиномиальная функция имеет форму y = ax 2 + bx + c и представляет собой параболу.
Чтобы узнать, как построить график квадратичной полиномиальной функции, нажмите здесь. - Кубическая полиномиальная функция имеет вид y = ax 3 + bx 2 + cx + d.

Чтобы узнать, как построить график кубической полиномиальной функции, нажмите здесь.
График полиномиальной функции
Чтобы построить график простой полиномиальной функции, мы обычно делаем таблицу значений с некоторыми случайными значениями x и соответствующими значениями f(x). Затем мы наносим точки из таблицы и соединяем их кривой. Нарисуем график квадратичной полиномиальной функции f(x) = x 2 .
| х | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f(x) = x 2 | 4 | 1 | 0 | 1 | 4 |
Построим точки и соединим их кривой (также продлим ее в обе стороны), чтобы получить график полиномиальной функции.
Если вам интересно узнать, как строить графики различных типов функций, нажмите здесь.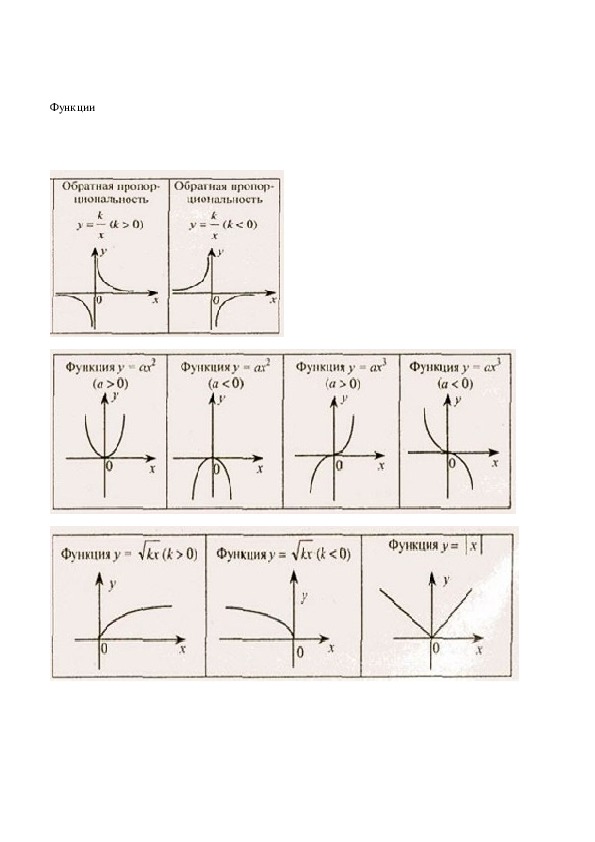
Нули полиномиальной функции
Нули (также известные как корни или точки пересечения по оси x) полиномиальной функции f(x) — это числа, удовлетворяющие уравнению f(x) = 0. Таким образом, чтобы найти нули полиномиальной функции f(x ):
Нули функции линейного полинома
Рассмотрим линейную полиномиальную функцию f(x) = 16x — 4.Чтобы найти его нули:
- Установить f(x) = 0
16х — 4 = 0 - Решите это.
16х = 4
х = 1/4
Таким образом, ноль f(x) равен 1/4.
Нули квадратичной полиномиальной функции
Рассмотрим квадратичную полиномиальную функцию f(x) = x 2 + 2x — 5. Чтобы найти ее нули:
- Установить f(x) = 0,
Тогда х 2 + 2х — 5 = 0, - Решите это.
Здесь а = 1, b = 2 и с = -5.
Воспользуемся квадратичной формулой, чтобы найти квадратные корни: x = [-b ± √(b 2 — 4ac)]/2a
х = [-2 ± √(2 2 — 4(1)(-5))]/(2)(1)
= [-2 ± √(4+20)]/2
= [-2 ± √(24)]/2
= [-2 ± 2√6]/2
= -1 ± √6
Следовательно, -1 + √6 и -1 -√6 являются нулями полиномиальной функции f(x).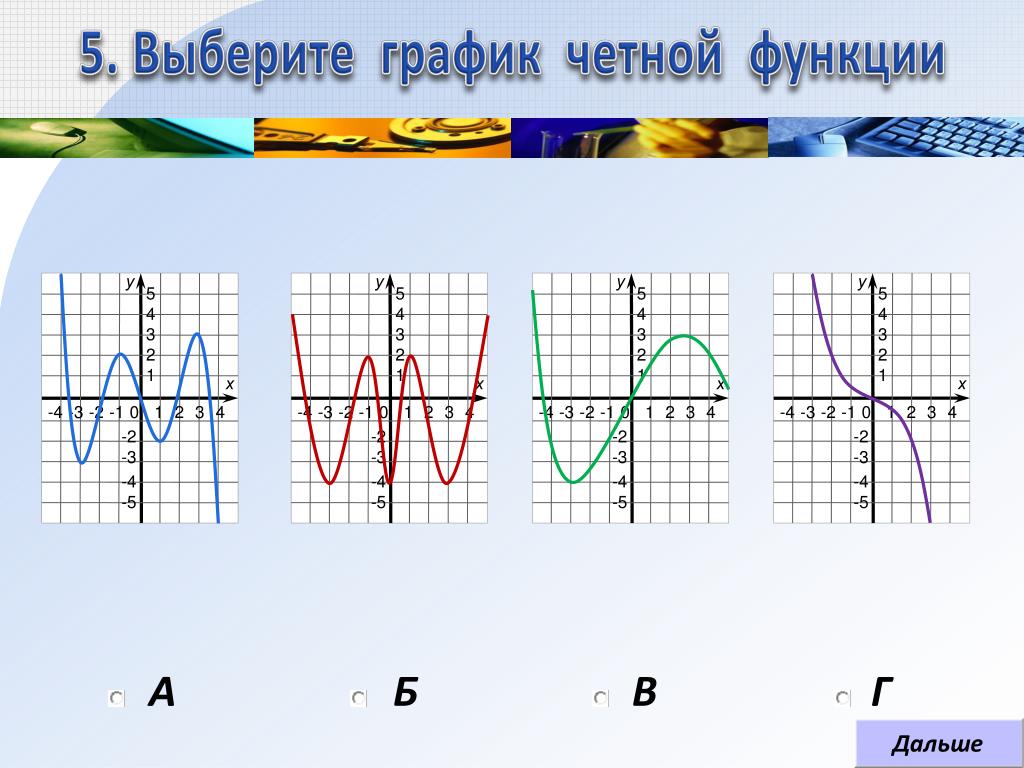 Помните, что иррациональные и комплексные корни полиномиальной функции всегда встречаются парами.
Помните, что иррациональные и комплексные корни полиномиальной функции всегда встречаются парами.
Нули функции кубического полинома
Нахождение нулей кубических многочленов такое же, как и у квадратных уравнений.Но чтобы сделать его намного проще, мы можем использовать некоторые из этих специальных продуктов:
Найдем нули функции кубического полинома f(y) = y 3 – 2y 2 – y + 2.
- Установить f(y) = 0,
у 3 – 2у 2 – у + 2 = 0, - Решите это.
у 2 (у – 2) – (у – 2) = 0
(у 2 – 1) (у – 2) = 0
(у + 1) (у – 1) (у – 2) = 0
у = 1, -1 и 2.
Следовательно, нули полиномиальной функции равны 1, -1 и 2.
Темы, связанные с полиномиальными функциями
Ознакомьтесь со следующими страницами, посвященными полиномиальным функциям:
Важные замечания по полиномиальным функциям
Вот несколько моментов, которые следует помнить при изучении полиномиальных функций:
- Степень полиномиальной функции определяется наибольшей степенью переменной, в которую она возведена.

- Постоянные функции являются полиномиальными функциями степени 0.
- Линейные функции — это полиномиальные функции степени 1.
- Квадратичные функции — это полиномиальные функции степени 2.
- Кубические функции — это полиномиальные функции степени 3.
Часто задаваемые вопросы о полиномиальной функции
Что такое полиномиальные функции?
Полиномиальные функции — это выражения, представляющие собой комбинацию переменных разной степени, ненулевых коэффициентов, положительных показателей (переменных) и констант.Например, f(b) = 4b 2 – 6 является полиномом от b и имеет степень 2.
Какие существуют типы полиномиальных функций?
Существуют различные типы полиномиальных функций, которые классифицируются на основе их степеней. Они:
- Нулевая полиномиальная функция (f(x) = 0; степень = 0)
- Постоянная функция (f(x) = k; степень = 0)
- Линейная полиномиальная функция (f(x) = ax + b; степень = 1)
- Квадратичная полиномиальная функция (f(x) = ax 2 + bx + c; степень = 2)
- Функция кубического полинома (f(x) = ax 3 + bx 2 + cx + d; степень = 3)
- Полиномиальная функция четвертой степени (f(x) = ax 4 + bx 3 + cx 2 + dx + e; степень = 4)
Что такое формула полиномиальной функции?
Вот формула полиномиальной функции: f(x) = \(a_{n}\)x n + \(a_{n-1}\)x n-1 + . .. + \(a_{2}\)x 2 + \(a_{1}\)x + \(a_{0}\). Вот,
.. + \(a_{2}\)x 2 + \(a_{1}\)x + \(a_{0}\). Вот,
- \(a_{n}\), \(a_{n-1}\), … \(a_{0}\) называются коэффициентами
- \(a_{n}\) не равно нулю
- n — целое неотрицательное число
- Показатель степени переменных должен быть неотрицательным и не дробным числом.
Как найти степень полиномиальной функции?
Степень полиномиальной функции определяется наибольшей степенью переменной, в которую она возведена.Рассмотрим полиномиальную функцию f(y) = -4y 3 + 6y 4 + 11y – 10, наибольший найденный показатель степени равен 4 от члена 6y 4 . Следовательно, степень этого конкретного полинома равна 4,
.Как найти количество корней полиномиальной функции?
Максимальное количество корней полиномиальной функции равно ее степени. Например:
- Линейная функция имеет один корень.
- Квадратичная функция имеет максимум 2 корня.
- Кубическая функция имеет максимум 3 корня.

Как найти нули полиномиальной функции?
Нули полиномиальной функции f(x) также известны как ее корни или x-отрезки. Вот шаги, чтобы найти их:
- Установите его равным нулю. т. е. f(x) = 0,
- Решите уравнение.
Каковы примеры полиномиальных функций?
Вот несколько примеров полиномиальной функции каждого типа:
- Постоянная функция.Например: у = 1
- Линейная полиномиальная функция. Например: 5 лет + 10
- Квадратичная полиномиальная функция. Например: 14x 2 + 2x – 6
- Функция кубического полинома. Например: 4 года 3 + 5 лет 2 + 2
- Полиномиальная функция четвертой степени. Например: 3 года 4 + 5
Обзор исчисления AP: функции и их графики — Блог Magoosh
В основе исчисления лежит концепция функций и их графиков. Все основные области исчисления, включая пределы , производные и интегралы , требуют твердого понимания функций. В этом обзоре мы рассмотрим, что вам нужно знать о функциях и их графиках, чтобы успешно сдать экзамены AP Calculus.
В этом обзоре мы рассмотрим, что вам нужно знать о функциях и их графиках, чтобы успешно сдать экзамены AP Calculus.
Основные понятия, касающиеся построения графиков и функций, включают:
- Вычисление функций
- Область и диапазон
- Графики (включая точки пересечения и асимптоты)
- Нахождение пределов и определение непрерывности на графике
- Увеличение, уменьшение и относительные экстремумы 913
- Вогнутость и точки перегиба
Функции и их графики
Начнем с основ.
По определению функция — это просто правило, которое назначает каждому входу x четко определенный выход y . Мы используем обозначение y = f ( x ), чтобы указать, что x — вход, y — выход, а f — имя функции.
В принципе на входе и выходе может быть что угодно: числа, векторы, символы, даже другие функции! Обычно в исчислении вход и выход являются действительными числами.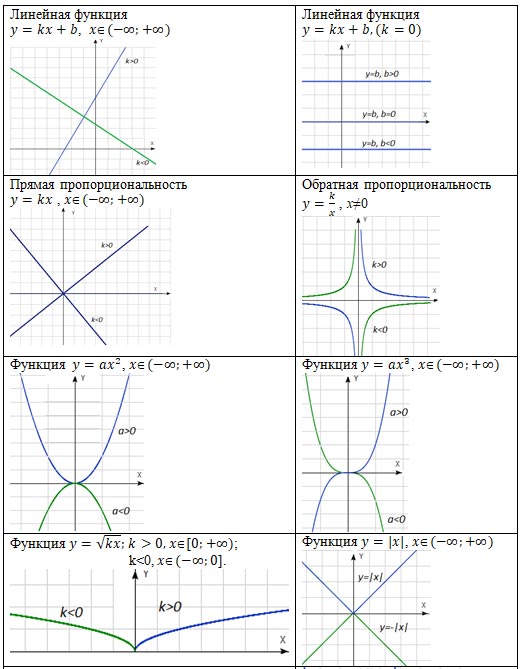
Функция F из X в Y. F(1) = d, F(2) = d и F(3) = c.
Обычно функция в исчислении определяется выражением, которое показывает, как вычислить результат на основе любого заданного входа. Например, функция возведения в квадрат f ( x ) = x 2 имеет входные данные x и выходные данные y = x 2 .
Оценка функций
Оценка функции на данном входе часто называется подключением .Продолжая наш пример, f ( x ) = x 2 , давайте посмотрим, как оценить f на различных входных данных.
- f (3) = 3 2 = 9.
- f (-1/5) = (-1/5) 2 = 1/25.
- ф ( с ) = с 2 .
- F ( C + ч + ч ) = ( C + H ) 2 = C 2 + 2 CH + ч 2 .

- , если г ( x ) = x — 12, потом г ( г ) = F ( x — 12) = x 2 – 24 x + 144.
Последний пример в списке иллюстрирует композицию двух функций, f и g . Понимание того, как работают композиции, поможет вам понять правило цепочки для производных и правило подстановки для интегралов.
Домен
Домен функции f ( x ) представляет собой набор всех входных значений ( x -значения) для функции.
Если не будет предоставлена дополнительная информация, мы ищем естественный домен , который является самым большим набором значений x , которые имеют смысл для функции.
Например, домен f ( x ) = x 2 представляет собой набор всех действительных чисел или (-∞, ∞) в интервальной записи.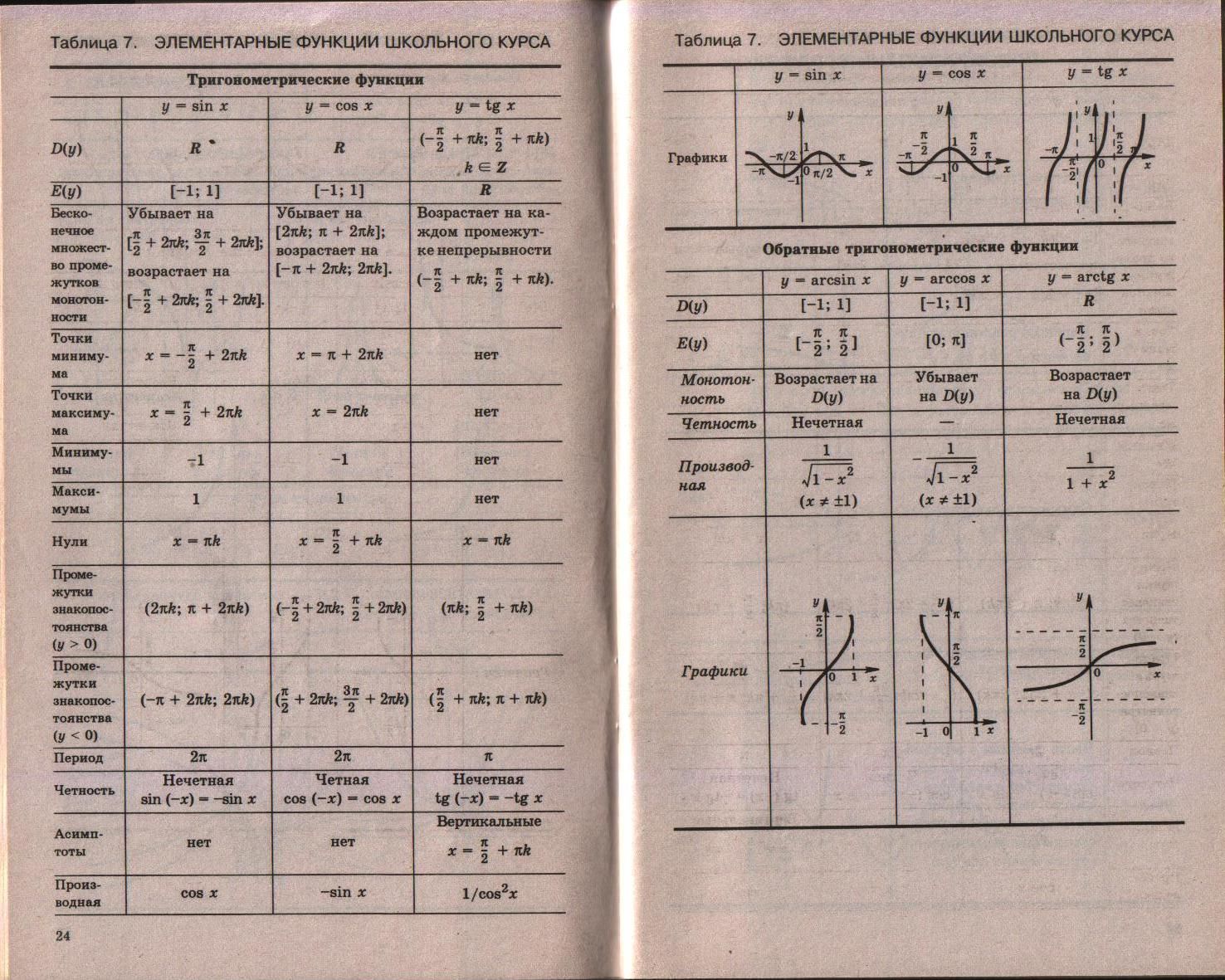 Любое действительное число вообще может служить входом для этой функции.
Любое действительное число вообще может служить входом для этой функции.
С другой стороны, область определения рациональной функции, такой как
, исключает любые значения x , для которых знаменатель равен нулю. Принимая во внимание нижнюю часть этого примера,, мы находим, что x = 5 и x = -2 должны быть исключены. Следовательно, домен равен: (-∞, -2) U (-2, 5) U (5, ∞).
Диапазон
Диапазон функции представляет собой набор всех выходных значений ( y -значения) для функции.
Поиск диапазона немного сложнее, чем поиск домена в целом. Это помогает сначала запомнить домены и диапазоны простых функций.
| Функция Домен | |||
|---|---|---|---|
| х 2 | (-∞, ∞) | [0, ∞) | |
| √ х | [ 0, ∞) | [0, ∞) | |
| 1/ x | (-∞, 0) U (0, ∞) | (-∞, 907 0) U (0, 0 061) U (0, 0 061) | |
| sin x | (-∞, ∞) | [-1, 1] | |
| COS x | (-∞, ∞) | [-1, 1] | |
| E x | (-∞, ∞) | (0, ∞) | |
| LN x | (0, ∞) | (∞) | (-∞, ∞) |
затем более сложный функции могут быть проанализированы с использованием свойств масштабирования и переводов.
Например, мы можем сделать вывод, что диапазон f ( x ) = ( x + 3) 2 – 7 равен (-7, ∞), потому что f – это просто перевод график x 2 на 7 единиц вниз (и 3 единицы влево, что не влияет на диапазон).
Вот хорошее напоминание о домене и диапазоне.
График
График функции f — это множество всех точек ( x , y ), которые удовлетворяют y =
x ().Другими словами, для каждого значения x подключитесь к функции, чтобы определить соответствующее значение y .Например, чтобы построить график f ( x ) = x 2 , оцените функцию в нескольких точках. Затем нанесите каждую точку ( x , x 2 ) на координатную плоскость и соедините точки плавной кривой.
Построение графика функции может занять много времени, но если вы работаете над разделом экзамена AP по исчислению, который позволяет использовать калькулятор, просто используйте функцию построения графика вашего калькулятора.
Точки пересечения и асимптоты
Точки пересечения и асимптоты являются важными функциями, которые помогают нам точно построить график функции. На самом деле, также полезно знать, как найти точки пересечения и асимптоты непосредственно на заданном графике.
Пересечения графика
Пересечение y функции f ( x ) является точкой пересечения графика с осью y . Там может быть только один. Просто подставьте x = 0, чтобы найти его.Но если 0 не находится в области определения функции, то у нее нет и -перехвата.
Точка пересечения x функции f ( x ) представляет собой любую точку, в которой график пересекает ось x . В отличие от перехвата х , для данного графа может быть много перехватов х . Чтобы их найти, установите f ( x ) = 0 и решите.
Асимптоты графика
Существует три типа асимптот.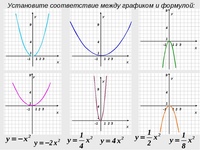
- Вертикальная асимптота для функции представляет собой вертикальную линию x = k , показывающую, где функция становится неограниченной.
- Горизонтальная асимптота для функции представляет собой горизонтальную линию, к которой график функции приближается, когда x приближается к ∞ или -∞.
- Наклонная асимптота для функции представляет собой наклонную линию, к которой функция приближается, когда x приближается к ∞ или -∞.
Пример
Ниже вы можете увидеть пример графика с помеченными точками пересечения и асимптотами.
Этот график имеет точку пересечения y в точке (0, 2), две точки пересечения x в точках (-2, 0) и (4, 0), вертикальную асимптоту в точке x = 2 и наклонная асимптота на y = (1/2) x .
Для получения дополнительной информации и примеров ознакомьтесь с этой статьей о горизонтальных асимптотах, вертикальных асимптотах и наклонных асимптотах.
Графики, пределы и непрерывность
На экзаменах AP по математическому анализу вам иногда нужно найти пределы на заданном графике.
Например, на графике ниже мы можем определить, что
Также видно, что вышеприведенный график непрерывен везде кроме при х = -1 (где есть вертикальная асимптота) и х = 2 (где предельное значение не равно значению функции). Таким образом, эта функция непрерывна на (∞, -1) U (-1, 2) U (2, ∞).
Для получения дополнительной информации ознакомьтесь с обзором экзамена AP: ограничения и преемственность.
Использование производных для анализа функций и их графиков
Часть того, что делает исчисление таким полезным, — это его способность анализировать поведение функций без использования графика в качестве ориентира.Используя производные (и вторые производные), можно определить:
- На каком интервале(ах) график увеличивается или уменьшается?
- Где находятся относительные экстремумы (относительные точки минимума и максимума)?
- На каком интервале(ах) график вогнут вверх или вниз?
- Где точки перегиба?
Ознакомьтесь с обзором экзамена AP по математическому анализу: анализ графиков, чтобы получить дополнительные разъяснения по этим более сложным темам.
Резюме
О функциях и их графиках нужно знать многое.Этот краткий обзор дает только основы. Теперь дело за вами, чтобы исследовать дальше!
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (вперёд!). Он получил степень бакалавра математики со степенью бакалавра компьютерных наук в Оберлинском колледже в 2002 году. Кроме того, Шон получил степень бакалавра.Мус. в том же году окончил Оберлинскую консерваторию по специальности «музыкальная композиция». Шон по-прежнему любит музыку — почти так же сильно, как математику! — и он (думает, что он) умеет играть на фортепиано, гитаре и басу. Шон преподавал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!
Посмотреть все сообщения
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Нажмите сюда, чтобы узнать больше!
Функции и линии — BUSI1915 — Основы бизнес-математики
7.1 Функции и обозначения функций
7.2 Домен и диапазон
7.3 Скорость изменения и поведение графиков
7.4 Линейные функции
7.5 Графики линейных функций
7.6 Моделирование с помощью линейных функций
7.7 Подгонка линейных моделей к данным
Что такое функция?
Мир природы полон взаимосвязей между изменяющимися величинами. Когда мы видим эти отношения, для нас естественно спросить: «Если я знаю одну величину, могу ли я тогда определить другую?» Это устанавливает идею входной величины, или независимой переменной, и соответствующей выходной величины, или зависимой переменной.Отсюда мы получаем понятие функциональной связи, в которой выход может быть определен из входа.
Для некоторых величин, таких как рост и возраст, между этими величинами, безусловно, существует взаимосвязь. Учитывая конкретного человека и любой возраст, достаточно легко определить его рост, но если бы мы попытались обратить эту зависимость и определить возраст по заданному росту, это было бы проблематично, поскольку большинство людей сохраняют один и тот же рост в течение многих лет.
Функция
Функция — это правило отношения между входной или независимой величиной и выходной или зависимой величиной, в которой каждое входное значение однозначно определяет одно выходное значение.Мы говорим, что «выход есть функция входа».
В приведенном выше примере роста и возраста рост зависит от возраста? Является ли возраст функцией роста?
Решение:
В приведенном выше примере с ростом и возрастом было бы правильно сказать, что рост является функцией возраста, поскольку каждый возраст однозначно определяет рост. Например, на мой 18-й день рождения у меня был ровно один рост 69 дюймов.
Однако возраст не является функцией роста, поскольку один входной рост может соответствовать более чем одному выходному возрасту.Например, для ввода роста 70 дюймов имеется более одного вывода возраста, так как я был 70 дюймов в возрасте 20 и 21 года.
В кафе меню состоит из блюд и их цен.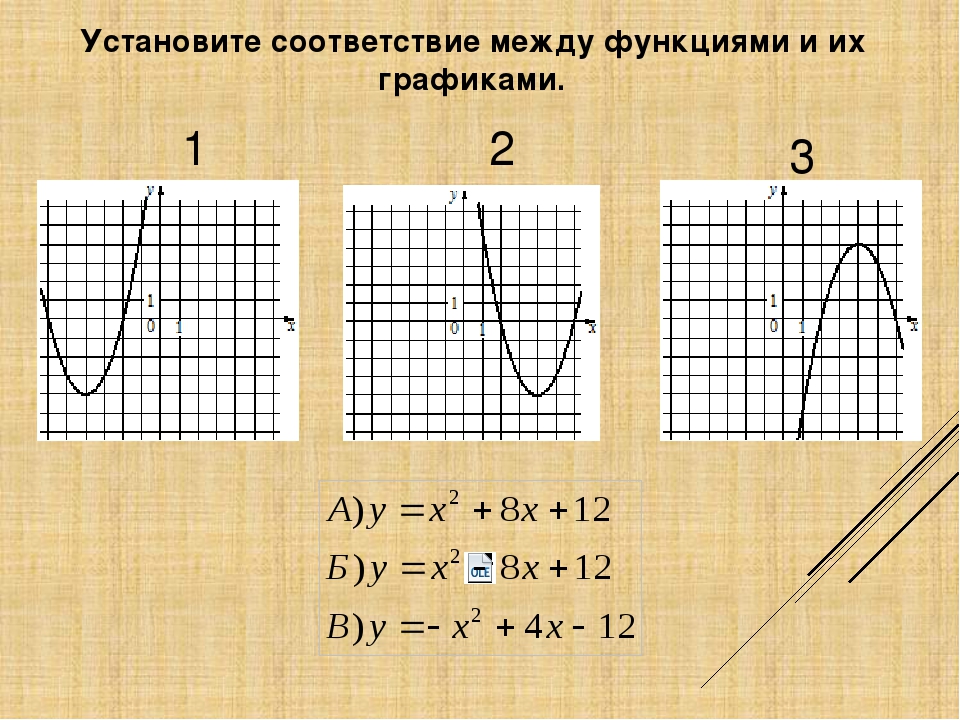 Является ли цена функцией товара? Является ли товар функцией цены?
Является ли цена функцией товара? Является ли товар функцией цены?
Решение:
Можно сказать, что цена является функцией предмета, поскольку каждый вход предмета имеет один выход цены, соответствующей ему. Мы не можем сказать, что предмет является функцией цены, поскольку два предмета могут иметь одинаковую цену.
Во многих классах общий процент, который вы зарабатываете на курсе, соответствует десятичному баллу. Является ли десятичный разряд функцией процента? Является ли процент функцией десятичной степени?
Решение:
Для любого заработанного процента будет связан десятичный разряд, поэтому мы можем сказать, что десятичный разряд является функцией процента. То есть, если вы введете процент, ваш результат будет десятичной оценкой. Процент может быть или не быть функцией десятичной оценки, в зависимости от схемы оценок учителя.В некоторых системах оценок существует диапазон процентов, соответствующих одному и тому же десятичному разряду.
Рассмотрим информацию о банковском счете.
1. Зависит ли ваш баланс от номера вашего банковского счета?
(Если вы вводите номер банковского счета, имеет ли смысл, что на выходе будет ваш баланс?)
2. Является ли номер вашего банковского счета функцией вашего баланса?
(Если вы вводите баланс, имеет ли смысл, что на выходе будет номер вашего банковского счета?)
Обозначение функции
Для упрощения написания выражений и уравнений, содержащих функции, часто используется упрощенная запись.Мы также используем описательные переменные, чтобы помочь нам запомнить значение величин в задаче.
Вместо того, чтобы писать «рост является функцией возраста», мы могли бы использовать описательную переменную для представления роста, а описательную переменную — для представления возраста.
«рост зависит от возраста»
, если мы назовем функцию, мы напишем
.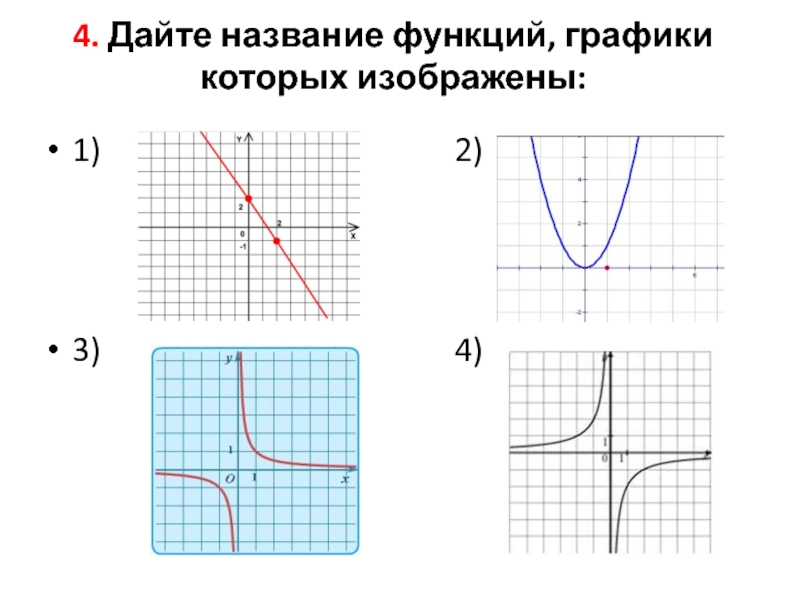
«от»
или проще
мы могли бы вместо этого назвать функцию h и написать
, который читается как «из .
Помните, что мы можем использовать любую переменную для имени функции; обозначение показывает нам, что зависит от . Значение « » необходимо подставить в функцию « », чтобы получить результат. Будьте внимательны – скобки указывают на то, что в функцию вводится возраст (Примечание: не путайте эти скобки с умножением!).
Обозначение функции
Выходные данные определяют функцию с именем . Это будет читаться как «выход — это вход».
Таблицы как функции
Функции могут быть представлены разными способами: словами (как мы это делали в последних нескольких примерах), таблицами значений, графиками или формулами.Представленный в виде таблицы, нам представлен список входных и выходных значений.
В некоторых случаях эти значения представляют все, что мы знаем об отношении, в то время как в других случаях таблица просто предоставляет нам несколько выбранных значений из более полного отношения.
Таблица 1: В этой таблице представлены входные данные, номер месяца (январь = 1, февраль = 2 и т. д.), а выходные данные — количество дней в этом месяце. Это представляет все, что мы знаем о месяцах и днях для данного года (это не високосный год)
| (ввод) Номер месяца, | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| (выход) Дни в месяце | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Таблица 2: В таблице ниже определена функция.Помните, что это обозначение говорит нам, что это имя функции, которая принимает входные данные n и дает выходные данные.
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
Таблица 3: В этой таблице представлен возраст детей в годах и их соответствующий рост.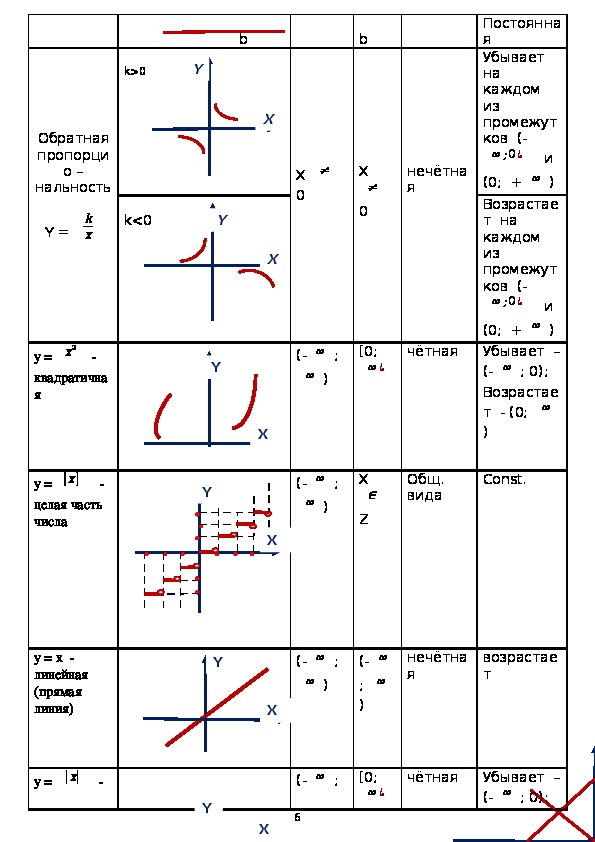 Это лишь некоторые из имеющихся данных о росте и возрасте детей.
Это лишь некоторые из имеющихся данных о росте и возрасте детей.
| (ввод) , возраст в годах | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| (выходной), высота в дюймах | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Какие из этих таблиц определяют функцию (если есть)?
| Ввод | Выход |
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
Решение:
Первая и вторая таблицы определяют функции.В обоих случаях каждый вход соответствует ровно одному выходу. Третья таблица не определяет функцию, поскольку входное значение 5 соответствует двум различным выходным значениям.
3. Если каждый заработанный процент перевести в однобуквенную оценку, будет ли это функцией?
Решение и оценка функций
Когда мы работаем с функциями, мы обычно делаем две вещи: вычисляем и решаю.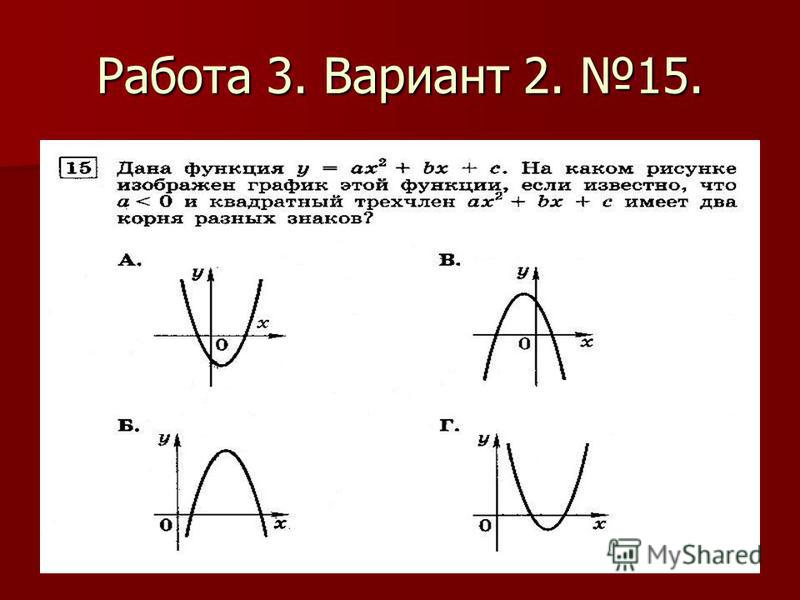 Вычисление функции — это то, что мы делаем, когда знаем входные данные и используем функцию для определения соответствующего выхода.Вычисление всегда будет давать один результат, поскольку каждый вход функции соответствует ровно одному выходу.
Вычисление функции — это то, что мы делаем, когда знаем входные данные и используем функцию для определения соответствующего выхода.Вычисление всегда будет давать один результат, поскольку каждый вход функции соответствует ровно одному выходу.
Решение уравнений с использованием функции — это то, что мы делаем, когда знаем результат и используем функцию для определения входных данных, которые будут давать этот результат. Решение функции может привести к нескольким решениям, поскольку разные входные данные могут привести к одному и тому же результату.
Используя показанную таблицу, где
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
а) Оценить
Решение:
Вычисление (читай: «из 3») означает, что нам нужно определить выходное значение , функции при заданном входном значении .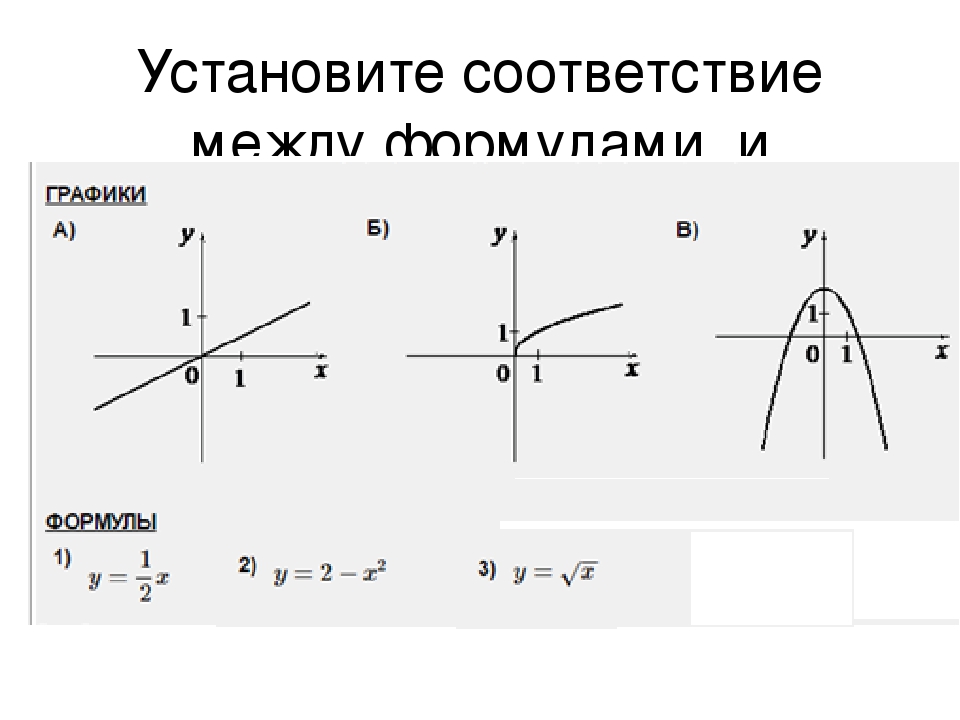 Глядя на таблицу, мы видим вывод, соответствующий is , что позволяет нам сделать вывод .
Глядя на таблицу, мы видим вывод, соответствующий is , что позволяет нам сделать вывод .
б) Решить
Решение:
Решение означает, что нам нужно определить, какие входные значения дают выходное значение 6. Глядя на таблицу, мы видим, что есть два решения: и . В частности:
- Когда мы вводим 2 в функцию g, наш результат равен . Другими словами, .
- Когда мы вводим 4 в функцию g, наш вывод также равен .Другими словами, .
4. Используя функцию из примера 7.1G, вычислите .
Графики как функции
Часто для определения функции можно использовать график зависимости. По соглашению графики обычно строятся с входным количеством по горизонтальной оси и выходным количеством по вертикали.
Наиболее распространенный график имеет вертикальную и горизонтальную оси, и мы говорим, что это функция , или когда функция называется .
Проверка вертикальной линии
Тест вертикальной линии — это удобный способ подумать о том, определяет ли график выход по вертикали как функцию входа по горизонтали.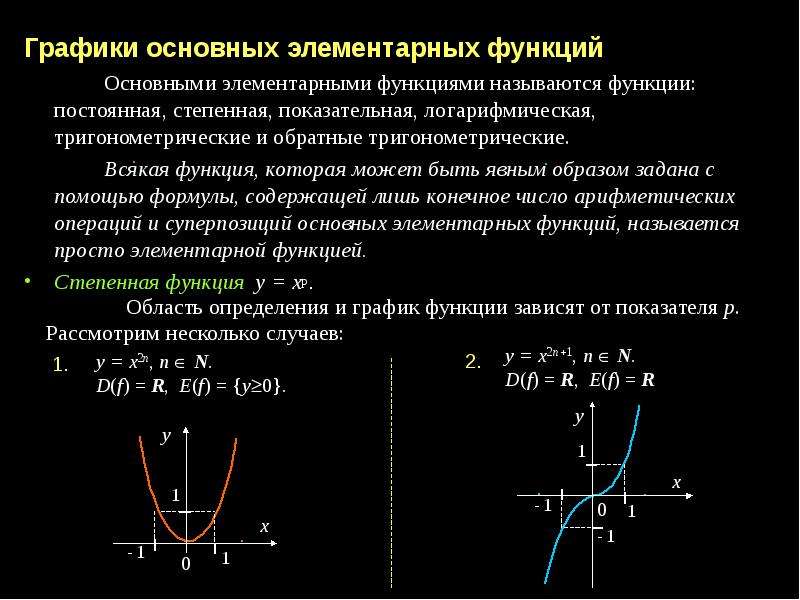 Представьте, что вы рисуете вертикальные линии на графике. Если любая вертикальная линия будет пересекать график более одного раза, то график не определяет только один вертикальный выход для каждого горизонтального входа.
Представьте, что вы рисуете вертикальные линии на графике. Если любая вертикальная линия будет пересекать график более одного раза, то график не определяет только один вертикальный выход для каждого горизонтального входа.
Для вычисления функции с помощью графика необходимо взять заданный вход и использовать график для поиска соответствующего выхода.Для решения функционального уравнения с помощью графика необходимо взять заданный выход и посмотреть на график, чтобы определить соответствующий вход.
5. Используя график из примера 7.1I, найдите f(x)=1.
Формулы как функции
Когда это возможно, очень удобно определять отношения с помощью формул. Если возможно выразить выход в виде формулы, включающей входную величину, то мы можем определить функцию.
Важно отметить, что не каждое отношение может быть выражено в виде функции с помощью формулы.
Обратите внимание, что важной особенностью уравнения, записанного в виде функции, является то, что выходное значение может быть определено непосредственно из входных данных путем выполнения вычислений — никаких дополнительных решений не требуется.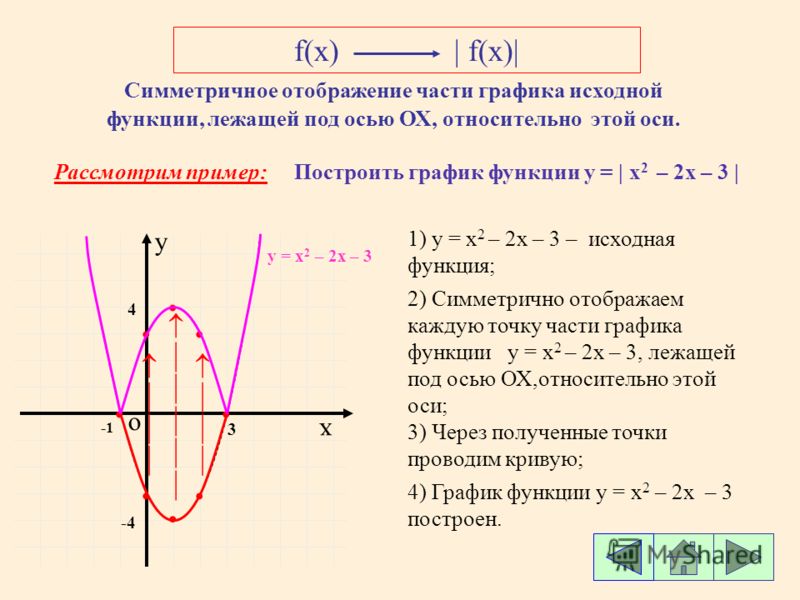 Это позволяет отношениям действовать как волшебный ящик, который принимает входные данные, обрабатывает их и возвращает выходные данные. Современные технологии и компьютеры полагаются на эти функциональные взаимосвязи, поскольку оценку функции можно запрограммировать в машине, тогда как решение задач является гораздо более сложной задачей.
Это позволяет отношениям действовать как волшебный ящик, который принимает входные данные, обрабатывает их и возвращает выходные данные. Современные технологии и компьютеры полагаются на эти функциональные взаимосвязи, поскольку оценку функции можно запрограммировать в машине, тогда как решение задач является гораздо более сложной задачей.
Как и в случае с таблицами и графиками, обычно вычисляются и решаются функции, использующие формулы. Для оценки потребуется заменить входную переменную в формуле предоставленным значением и выполнить расчет. Для решения потребуется заменить выходную переменную в формуле предоставленным значением и найти входные данные, которые дадут этот результат.
6. Учитывая функцию
а. Оценить
b. Решить
Ты попробуй… Ответы
- Да
- №
- Да, это функция
- или
- а.
б.
Раздел 7.
 1 Упражнения
1 Упражнения- Зависит ли рост конкретного человека от его возраста? Зависит ли возраст человека от его роста? Обоснуйте свои ответы.
- В кофейне меню состоит из блюд и их цен. Является ли цена функцией товара? Является ли товар функцией цены? Обоснуйте свои ответы.
- В Техническом университете Онтарио итоговая оценка, которую студент получает за курс, соответствует буквенной оценке (см. Технологический университет Онтарио – Оценка).Является ли буквенная оценка функцией процента, который студент может получить за курс? Является ли процент, который студент может получить за курс, функцией буквенной оценки? Оправдывать.
- Рассмотрите информацию о банковском счете.
- Является ли баланс счета функцией номера банковского счета? Оправдывать.
- Является ли номер банковского счета функцией баланса счета? Оправдывать.
- Введите нотацию функций по вашему выбору, используя имена переменных для представления функции, которая принимает в качестве входных данных название месяца и выдает в качестве выходных данных количество дней в этом месяце.
 Четко укажите, что представляет каждая переменная.
Четко укажите, что представляет каждая переменная. - Функция дает количество полицейских, , в городе в год . Что говорит нам?
- Какая из этих таблиц определяет функцию (если есть)? Оправдывать.
Ввод Выход -3 5 0 1 4 5
- Используя таблицу, показанную для:
1 2 3 4 5 8 6 7 6 8 - Оцените и интерпретируйте свой результат (опишите словами, что означает ответ).
- Решите и интерпретируйте результат.
- Оценить . Интерпретируйте свой результат.
- Решить . Интерпретируйте свой результат.
- Какой из этих графиков определяет функцию? Обоснуйте свои ответы.

- Учитывая показанный график,
- Вычислить .
- Решить .
- Оценить .
- Решить .
- Если возможно, выразите связь в виде функции.
- Рассмотрим отношение .Используйте это отношение, чтобы выразить следующие функции, если это возможно. Если это невозможно, обоснуйте почему.
- Экспресс как функция .
- Express в зависимости от .
- Учитывая функцию .
- Оценка .
- Решить .
- Учитывая функцию ,
- Оценка .
- Решить .
- Учитывая функцию
- Оценить
- Решить
Одна из наших главных целей в математике — смоделировать реальный мир с помощью математических функций.При этом важно помнить об ограничениях тех моделей, которые мы создаем.
В этой таблице показано соотношение между окружностью и высотой дерева по мере его роста.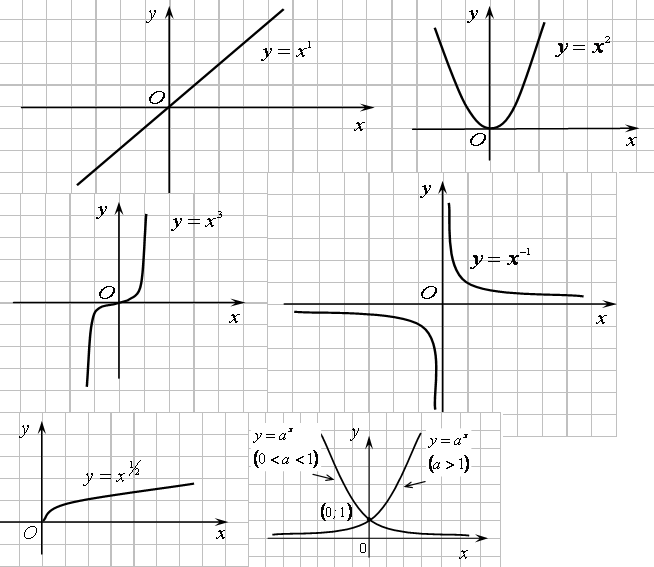
| Окружность, | 1,7 | 2,5 | 5,5 | 8,2 | 13,7 |
| Высота, | 24,5 | 31 | 45,2 | 54,6 | 92,1 |
Хотя между ними существует сильная связь, было бы, конечно, нелепо говорить о дереве с окружностью -3 фута или высотой 3000 футов.Когда мы определяем ограничения на входы и выходы функции, мы определяем домен и диапазон функции.
Домен и диапазон
Домен относится к набору возможных входных значений функции.
Диапазон относится к набору возможных выходных значений функции
При отправке письма через Почтовую службу США цена зависит от веса письма, как показано в таблице ниже.Определяем домен и диапазон.
Письма
| Вес не более | Цена |
| 1 унция | 0,44 $ |
| 2 унции | 0,61 $ |
| 3 унции | 0,78 $ |
| 4 унции | 0,95 $ |
Решение:
Предположим, что мы обозначаем вес письма через , а цену через , мы можем думать, что цена является функцией веса, .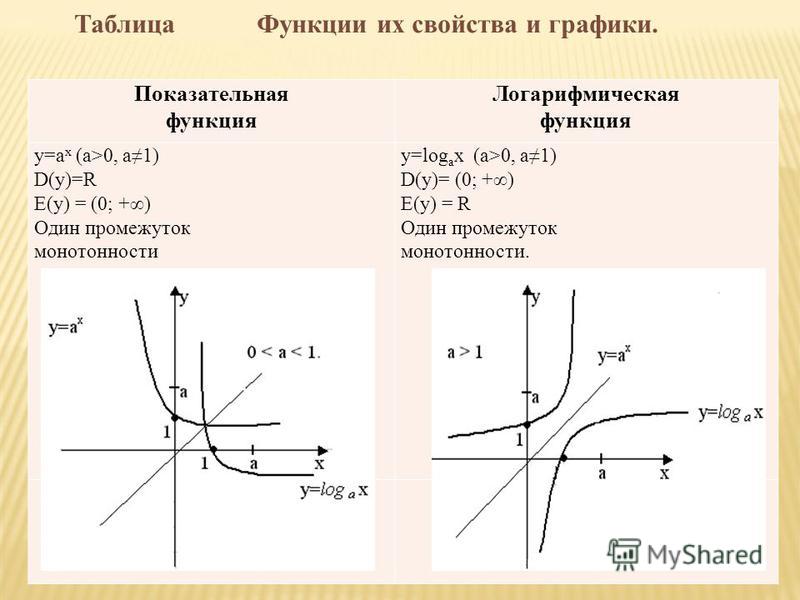 У нас есть то, что представляет собой цену за отправку письма веса.
У нас есть то, что представляет собой цену за отправку письма веса.
Поскольку приемлемые веса составляют 3,5 унции или меньше, а отрицательные веса и вес, равный нулю, не имеют смысла, домен будет равен или, в форме интервала, .
Поскольку возможные цены взяты из ограниченного набора значений, мы можем определить диапазон этой функции, только перечислив возможные значения. Мы используем скобки {…} для обозначения типа множества, составленного из списка значений. Таким образом, диапазон = {$0,44, $0.61, 0,78 долл. США, 0,95 долл. США}.
1. Население небольшого города в 1960 году составляло 100 человек. С тех пор население выросло до 1400 человек, зарегистрированных во время переписи 2010 года. Выберите описательные переменные для ввода и вывода и используйте нотацию интервала, чтобы записать домен и диапазон.
Обозначение
В предыдущих примерах мы использовали неравенства для описания области определения и диапазона функций. Это один из способов описания интервалов входных и выходных значений, но не единственный.Давайте уделим немного времени обсуждению обозначений домена и диапазона.
Это один из способов описания интервалов входных и выходных значений, но не единственный.Давайте уделим немного времени обсуждению обозначений домена и диапазона.
Использование неравенств, таких как , , и означает, что нас интересуют все значения между низкими и высокими значениями, включая высокие значения в этих примерах.
Однако иногда нас интересует конкретный список чисел, например, диапазон цен на отправку писем = 0,44 доллара США, 0,61 доллара США, 0,78 доллара США или 0,95 доллара США. Эти числа представляют набор конкретных значений: {0,44, 0,61, 0,78, 0,95}
Представление значений в виде набора или предоставление инструкций о том, как строится набор, приводит нас к другому типу нотации для описания домена и диапазона.
При описании диапазонов в нотации множества мы могли бы аналогичным образом написать что-то вроде , или, если бы у вывода была своя переменная, мы могли бы использовать ее. Таким образом, для нашего примера высоты дерева выше мы могли бы написать для диапазона .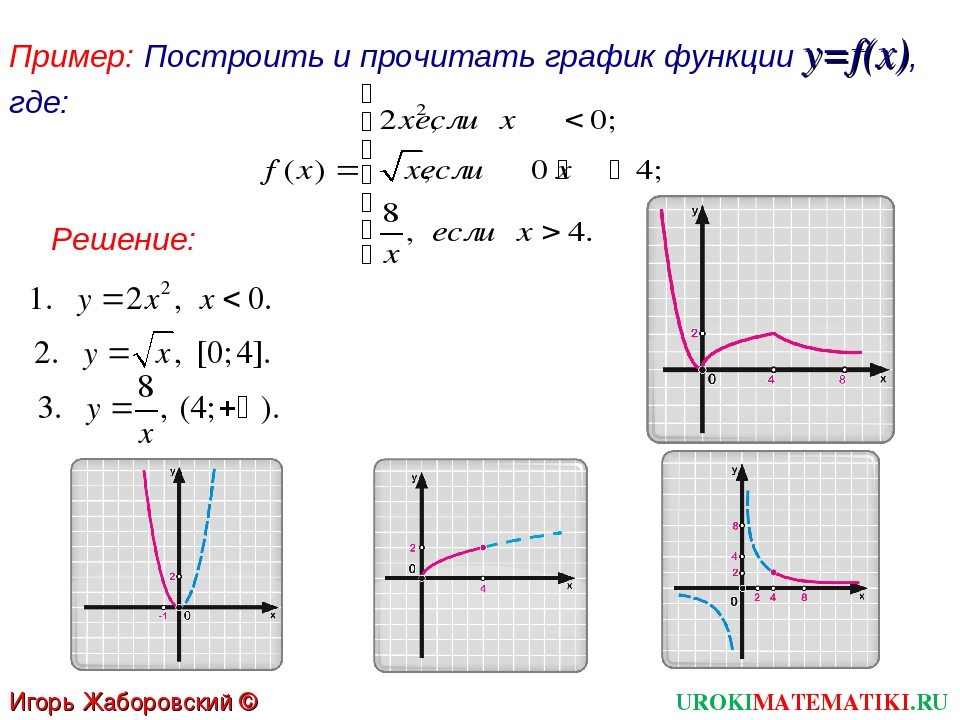 В нотации множества, если домен или диапазон не ограничены, мы могли бы написать {| является действительным числом} или , читаемым как «множество -значений, которое является элементом множества действительных чисел».
В нотации множества, если домен или диапазон не ограничены, мы могли бы написать {| является действительным числом} или , читаемым как «множество -значений, которое является элементом множества действительных чисел».
Более компактной альтернативой записи множества является интервальная запись , в которой интервалы значений обозначаются начальным и конечным значениями.Круглые круглые скобки используются для «строго меньше», а квадратные скобки используются для «меньше или равно». Поскольку бесконечность не является числом, мы не можем включить ее в интервал, поэтому мы всегда используем изогнутые скобки с и . Таблица ниже поможет вам увидеть, как неравенства соответствуют системе обозначений и обозначениям интервалов:
Чтобы объединить два интервала вместе, используя неравенства или систему обозначений, мы можем использовать слово «или». В записи интервалов мы используем символ объединения, чтобы объединить два несвязанных интервала вместе.
Опишите интервалы значений, показанные на линейном графике ниже, используя построитель наборов и обозначения интервалов.
Решение:
Чтобы описать значения , лежащие в интервалах, показанных выше, мы бы сказали: «является действительным числом, большим или равным 1 и меньшим или равным 3, или действительным числом, большим 5».
В виде неравенства это:
или
Обозначение в наборе:
или
В интервальной записи:
Помните при написании или чтении записи интервала:
- Использование квадратных скобок [ означает, что начальное значение включено в набор.
- Скобка ( означает, что начальное значение не включено в набор.
2. Учитывая следующий интервал, запишите его значение словами, нотацией построителя наборов и нотацией интервала.
Домен и диапазон из графиков
Мы также можем говорить о домене и диапазоне на основе графиков. Поскольку домен относится к набору возможных входных значений, домен графа состоит из всех входных значений, показанных на графике.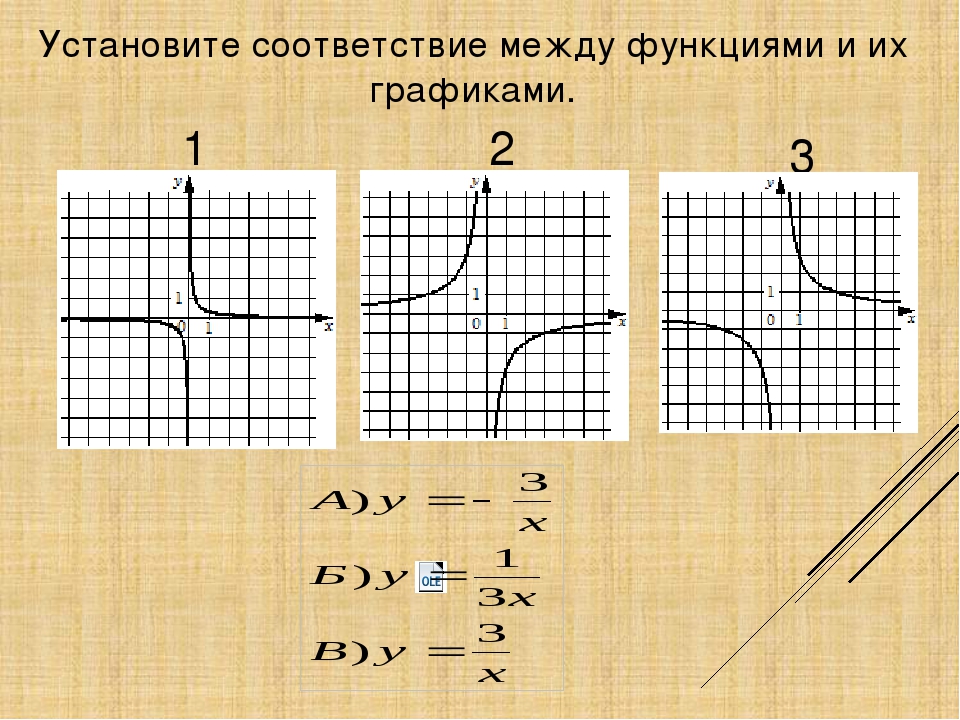 Помните, что входные значения почти всегда отображаются вдоль горизонтальной оси графика.Точно так же, поскольку диапазон — это набор возможных выходных значений, диапазон графика мы можем видеть из возможных значений вдоль вертикальной оси графика.
Помните, что входные значения почти всегда отображаются вдоль горизонтальной оси графика.Точно так же, поскольку диапазон — это набор возможных выходных значений, диапазон графика мы можем видеть из возможных значений вдоль вертикальной оси графика.
Будьте осторожны — если график выходит за пределы окна, в котором мы видим график, домен и диапазон могут быть больше, чем видимые значения.
Помните, что, как и в предыдущем примере, и не всегда являются входными и выходными переменными. Использование описательных переменных — важный инструмент для запоминания контекста проблемы.
3. Учитывая приведенный ниже график, запишите домен и диапазон в интервальной записи.
Домен и диапазон из формул
Большинство основных формул могут быть оценены на входе. Два общих ограничения:
- Квадратный корень из отрицательных значений не является действительным.
- Мы не можем делить на ноль.
Кусочные функции
Некоторые функции нельзя описать одной формулой.
Кусочная функция
Кусочная функция — это функция, в которой используемая формула зависит от области, в которой находятся входные данные.Мы обозначаем эту идею как:
Компания сотовой связи использует приведенную ниже функцию для определения стоимости в долларах за гигабайты передачи данных.
Найдите стоимость использования 1,5 гигабайт данных и стоимость использования 4 гигабайт данных.
Решение:
Чтобы определить стоимость использования 1,5 гигабайт данных, мы сначала смотрим, к какой части домена относятся наши входные данные. Поскольку 1.5 меньше 2, используем первую формулу, дающую .
Чтобы найти стоимость использования 4 гигабайт данных, мы видим, что введенное значение 4 больше, чем 2, поэтому воспользуемся второй формулой. .
Следовательно, стоимость использования 1,5 гигабайт данных составляет 25 долларов США, а стоимость использования 4 гигабайт данных — 45 долларов США.
Эскиз графика функции
Решение:
Мы можем представить график каждой функции, а затем ограничить график указанной областью.На концах области мы помещаем незакрашенные кружки, чтобы указать, где конечная точка не включена из-за строго меньшего неравенства, и замкнутый кружок, где конечная точка включена из-за неравенства меньше или равно -к неравенству. Первая и последняя части являются постоянными функциями, где выход одинаков для всех входов. Среднюю часть мы могли бы распознать как линию и построить график, оценив функцию на паре входов и соединив точки линией.
Теперь, когда у нас есть каждая часть по отдельности, мы объединяем их в один и тот же график.Когда первая и вторая части встречаются в точке , мы можем представить себе закрытую точку, заполняющую открытую точку. Поскольку на графике нет разрыва, точку показывать не нужно.
4. В Колледже Пирса в течение 2009-2010 учебного года стоимость обучения для жителей штата составляла 89,50 долларов США за кредит для первых 10 кредитов, 33 доллара США за кредит для кредитов 11-18, а для более чем 18 кредитов ставка составляет 73 доллара США за кредит. .
.
Напишите кусочно-определенную функцию для общей платы за обучение, , в Колледже Пирса в течение 2009-2010 гг. в зависимости от количества взятых кредитов, .Не забудьте рассмотреть разумный домен и диапазон.
Ты попробуй… Ответы
1. Домен: = годы
Диапазон: = население,
2. а. Значения, которые меньше или равны -2, или значения, которые больше или равны -1 и меньше 3
b.
с.
3. Домен: = годы
Диапазон: = население в миллионах,
4. Плата за обучение, , в зависимости от кредитов, .
Разумный домен должен состоять из целых чисел от 0 до (ответы могут отличаться), например.г.
Разумный диапазон должен быть $0 – (ответы могут отличаться), например.
Раздел 7.2 Упражнения
- Компания по хранению данных арендует место на сервере за фиксированную годовую плату в размере 150 долларов США и плату за хранение в размере 0,39 доллара США за ГБ менее чем за 1,8 петабайта в рамках годового контракта (один петабайт равен 1000 терабайтам, а один терабайт — 1000 ГБ).

- Напишите формулу для расчета общей стоимости аренды серверного пространства в зависимости от потребности в гигабайтах хранилища данных.
- Какова область применения этой функции?
- Каков диапазон этой функции?
- Найдите общую стоимость аренды места на сервере для 3 человек.5 терабайт дискового пространства.
- Определите, сколько места на сервере было арендовано по годовому контракту, если счет составлял 1203 доллара США.
- Компания по аренде автомобилей сдает автомобили за фиксированную плату в размере 20 долларов США и почасовую оплату в размере 10,25 долларов США. За сделанные, но отмененные бронирования взимается фиксированная плата. Политика компании гласит, что срок аренды не должен превышать 5 дней.
- Напишите формулу зависимости общей стоимости аренды автомобиля от количества часов аренды автомобиля.
- Какова область применения этой функции?
- Каков диапазон этой функции?
- Найдите общую стоимость аренды автомобиля на 2 дня и 7 часов.

- При принятии стратегических решений в производстве мы изучаем взаимосвязь между рыночным предложением товара и ценой товара. Предположим, что количество единиц, доступных по цене единицы определенного продукта, удовлетворяет следующему соотношению:
- Если возможно, выразите предложение как функцию цены, объясните, что это означает и почему это полезно.Если это невозможно, объясните, почему.
- Если возможно, выразите цену как функцию предложения, объясните, что это означает и почему это полезно. Если это невозможно, объясните, почему.
- Какова область определения функции предложения с точки зрения цены?
- Принимая стратегические решения о ценообразовании продукта, мы изучаем взаимосвязь между рыночным спросом на товар и ценой товара. Предположим, что рыночный спрос на количество единиц и цена единицы определенного продукта удовлетворяют следующему соотношению:
- Если возможно, выразите спрос как функцию цены, объясните, что это означает и почему это полезно.
 Если это невозможно, объясните, почему.
Если это невозможно, объясните, почему. - Если возможно, выразите цену как функцию спроса, объясните, что это означает и почему это полезно. Если это невозможно, объясните, почему.
- Какова область определения функции спроса с точки зрения цены?
- Какова область определения функции цены с точки зрения спроса?
- Если возможно, выразите спрос как функцию цены, объясните, что это означает и почему это полезно.
- Если выручка от продажи единиц определенного продукта и затраты на производство единиц того же продукта могут быть выражены как и ,
- Определите функцию прибыли по количеству единиц.
- Рассчитайте и интерпретируйте, что это значит.
- Рассчитайте и интерпретируйте, что это значит.
- Сколько единиц им нужно будет произвести и продать, чтобы выйти на безубыточность?
- Население Ошавы в 1960 году составляло 77 000 человек. С тех пор население выросло до 379 848 человек, зарегистрированных в ходе переписи 2016 года. Выберите описательные переменные для ввода и вывода и используйте нотацию интервала, чтобы записать домен и диапазон.

- Опишите домены
- Базовый тариф на передачу данных по телефону составляет 30 долларов в месяц.План включает в себя первые 2 ГБ бесплатно и взимает 10 долларов США за каждый дополнительный ГБ, до 8 ГБ общего использования, после чего взимается плата в размере 15 долларов США за каждый дополнительный ГБ. Если — объем используемых данных (в ГБ) и общая ежемесячная стоимость:
- Выразите в виде (кусочной) формулы.
- Определите независимые и зависимые переменные C.
- Определите домен и диапазон .
- График как функция для .
- Рассчитайте стоимость, если бы использовалось 9 ГБ.
- Опишите взаимосвязь, показанную на графике ниже, как функцию, и опишите ее область и диапазон в интервальной форме.
- Прирост населения: В таблице ниже указано население Канады по годам переписи (источник: Статистическое управление Канады).

Год переписи Население Канады (миллионы) 1991 27,3 1996 28,8 2001 30,0 2006 31,5 2011 33.5 2016 35,2 - Используя Microsoft Excel, найдите модель линейной регрессии, которая представляет численность населения Канады в миллионах по количеству лет, прошедших с 1991 года, и нарисуйте модель.
- Нарисуйте диаграмму рассеяния данных и начертите модель.
- Интерпретируйте наклон модели.
- Оцените численность населения Канады в 2003 г.
- Прогноз численности населения Канады в 2030 году.
Поскольку функции представляют, как выходная величина изменяется в зависимости от входной величины, естественно спросить о скорости, с которой изменяются значения функции.
Например, приведенная ниже функция дает среднюю стоимость галлона бензина в долларах после 2000 года.
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1.47 | 1,69 | 1,94 | 2,30 | 2,51 | 2,64 | 3,01 | 2,14 |
Если бы нас интересовало, как изменились цены на газ в период с 2002 по 2009 год, мы могли бы подсчитать, что стоимость галлона увеличилась с 1,47 до 2,14 доллара, то есть на 0,67 доллара. Хотя это интересно, было бы полезнее посмотреть, насколько изменилась цена за год . Вы, вероятно, заметили, что цена не меняется каждый год на одну и ту же величину, поэтому мы найдем среднюю скорость изменения за определенный период времени.
Цена на газ увеличилась на 0,67 доллара США с 2002 по 2009 год за 7 лет в среднем на доллары в год.
В среднем цена на газ увеличивалась примерно на 9,6 цента каждый год.
Скорость изменения
Скорость изменения описывает, как выходное количество изменяется по отношению к входному количеству. Единицы скорости изменения — это «единицы вывода на единицы ввода»
Некоторыми другими примерами скорости изменения могут быть такие величины, как:
- Популяция крыс увеличивается на 40 крыс в неделю
- Бариста зарабатывает 9 долларов в час (долларов в час)
- Фермер сажает 60 000 луковиц на акр
- Автомобиль может проехать 27 миль на одном галлоне
- Популяция серых китов уменьшается на 8 китов в год
- Сумма денег на вашем счету в колледже уменьшается на 4000 долларов в квартал
Средняя скорость изменения
Средняя скорость изменения между двумя входными значениями представляет собой общее изменение значений функции (выходных значений), деленное на изменение входных значений.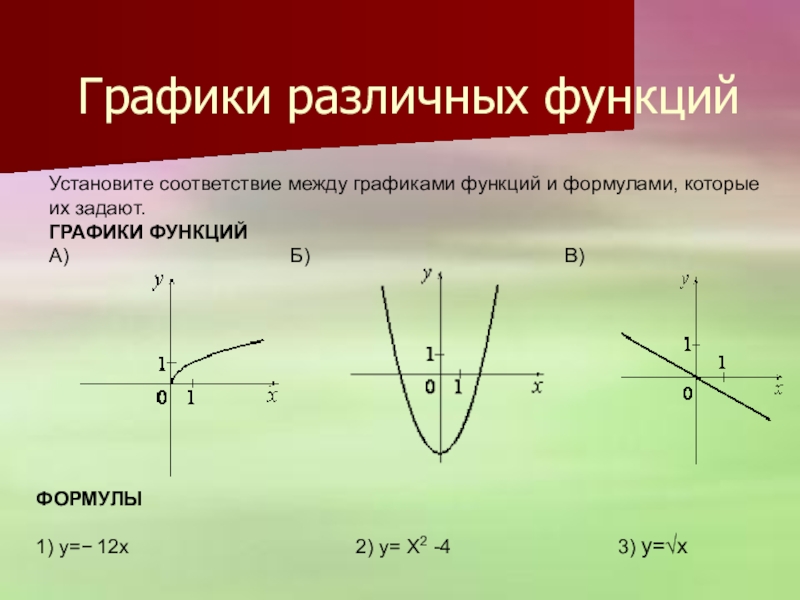
Средняя скорость изменения = =
Используя приведенную выше функцию стоимости газа, найдите среднюю скорость изменения между 2007 и 2009 годами.
Из таблицы видно, что в 2007 году стоимость газа составляла 2,64 доллара США. В 2009 году стоимость составляла 2,14 доллара.
Входные данные (годы) изменились на 2. Выходные данные изменились на 2,14 доллара США – 2,64 доллара США = -0,50.
Тогда средняя скорость изменения составит долларов в год
1. Используя ту же функцию стоимости газа, найдите среднюю скорость изменения между 2003 и 2008 годами
Обратите внимание, что в последнем примере изменение выходных данных было отрицательным, поскольку выходное значение функции уменьшилось.Соответственно, средняя скорость изменения отрицательна.
Во время поездки, забрав своего друга, который живет в 10 милях от вас, вы решаете записать свое расстояние от дома с течением времени. Найдите свою среднюю скорость за первые 6 часов.
| (часы) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (мили) | 10 | 55 | 90 | 153 | 214 | 240 | 292 | 300 |
Здесь ваша средняя скорость — это средняя скорость изменения.
Вы проехали 282 мили за 6 часов со средней скоростью = 47 миль в час
Мы можем более формально сформулировать вычисление средней скорости изменения, используя функциональную запись.
Средняя скорость изменения с использованием обозначения функций
Для данной функции средняя скорость изменения на интервале равна
Средняя скорость изменения =
Вычислить среднюю скорость изменения на интервале .
Мы можем начать с вычисления значений функции в каждой конечной точке интервала
Теперь вычисляем среднюю скорость изменения
Средняя скорость изменения =
2.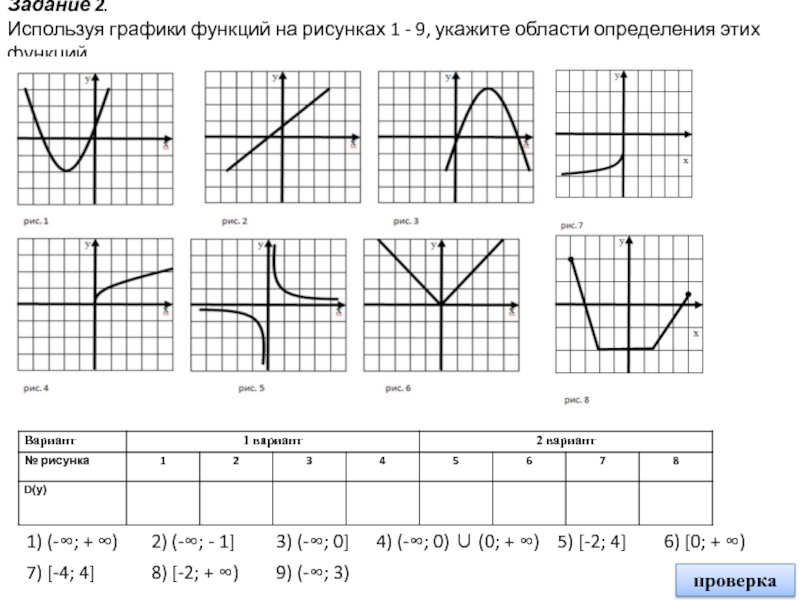 Найдите среднюю скорость изменения на интервале .
Найдите среднюю скорость изменения на интервале .
Магнитная сила между двумя магнитами, измеренная в ньютонах, связана с расстоянием между магнитами в сантиметрах по формуле . Найти среднюю скорость изменения силы, если расстояние между магнитами увеличить с 2 см до 6 см.
Мы вычисляем среднюю скорость изменения на интервале .
Средняя скорость изменения =
Оценка функции
Упрощение
Объединение членов числителя
Дальнейшее упрощение
Ньютона на сантиметр
Это говорит нам о том, что магнитная сила уменьшается в среднем на ньютоны на сантиметр в течение этого интервала.
Найдите среднюю скорость изменения на интервале . Ваш ответ будет выражением, включающим .
Используя формулу средней скорости изменения
Оценка функции
Упрощение
Дальнейшее упрощение и факторизация
Отмена общего множителя
Этот результат говорит нам о средней скорости изменения между и любой другой точкой. Например, на интервале средняя скорость изменения будет 5+3 = 8,
Например, на интервале средняя скорость изменения будет 5+3 = 8,
3. Найти среднюю скорость изменения на интервале .
Приложение для бизнеса
В бизнесе средняя скорость изменения связана с идеей предельных издержек, предельного дохода и предельной прибыли.
Предельные затраты/доход/прибыль
Предельные затраты обычно определяются как изменение общих затрат при увеличении количества произведенных изделий на единицу.Аналогично, предельный доход и предельная прибыль представляют собой изменение выручки и прибыли, если количество предметов увеличивается на единицу.
На практике предельные издержки обычно рассчитываются другим способом, с использованием методов исчисления, которые вы изучите в следующих курсах. Однако в этом курсе мы будем придерживаться расчета предельных издержек, рассматривая фактическое изменение общих издержек при увеличении объема производства на единицу.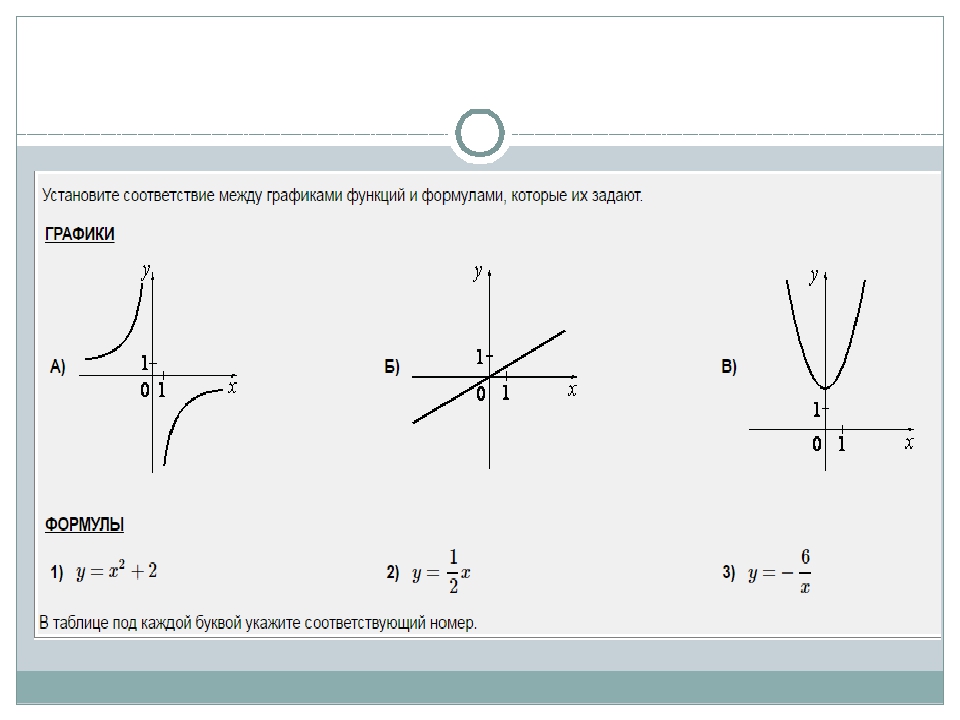
Компания определила, что общая стоимость производства товаров составляет .Найдите предельные издержки, если в настоящее время произведено 5000 изделий.
Мы хотим найти увеличение общих затрат при увеличении производства с 5000 до 5001 единиц. Это эквивалентно нахождению средней скорости изменения на интервале .
Общая стоимость при 5000 шт.:
Общая стоимость при 5001 шт.:
Предельные издержки равны
5535,89 – 5535,53 = 0,36 доллара США.
Другими словами, после производства 5000 изделий дополнительные затраты на производство 5001-го изделия составляют 0 долларов.36
Графическое представление функций
В рамках исследования того, как изменяются функции, интересно исследовать графическое поведение функций.
Увеличение/уменьшение
Функция равна , увеличивающей на интервале, если значения функции увеличиваются по мере увеличения входных данных. Формально функция возрастает, если для любых двух входных значений и в интервале с .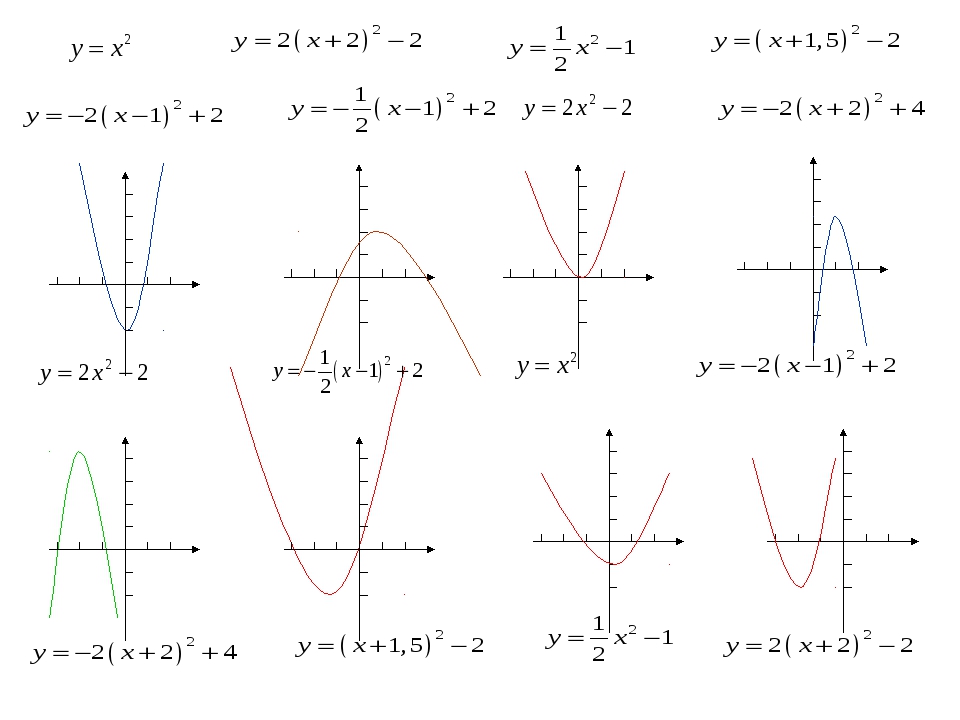 Средняя скорость изменения возрастающей функции равна 90 297 положительной 90 298 .
Средняя скорость изменения возрастающей функции равна 90 297 положительной 90 298 .
Функция является убывающей на интервале, если значения функции уменьшаются по мере увеличения входных данных. Более формально функция убывает, если для любых двух входных значений и в интервале с . Средняя скорость изменения убывающей функции равна минус .
Обратите внимание, что в последнем примере мы использовали открытые интервалы (интервалы, которые не включают конечные точки), поскольку функция не возрастает и не убывает при = 1, 3 или 4.
Локальные экстремумы
Точка, в которой функция изменяется с возрастающей на убывающую, называется локальным максимумом .
Точка, в которой функция меняется с убывающей на возрастающую, называется локальным минимумом .
Вместе локальные максимумы и минимумы называются локальными экстремумами или локальными экстремальными значениями функции.
4. Используйте график функции для оценки локальных экстремумов функции. Используйте их, чтобы определить интервалы, на которых функция увеличивается и уменьшается.
Подумай Ответы
1.= 0,264 доллара в год.
2. Средняя скорость изменения =
3.
4. Судя по графику, локальный максимум приходится на , а локальный минимум на . Функция возрастает по и убывает по .
Раздел 7.3 Упражнения
Вставьте сюда упражнения для повторения
Когда вы сядете в такси в Лас-Вегасе, счетчик сразу же покажет 3,30 доллара; это «сбрасываемый» заряд, когда таксометр активируется.После этой первоначальной платы таксометр будет добавлять 2,60 доллара за каждую милю, пройденную такси. В этом сценарии общая стоимость проезда на такси зависит от количества миль, пройденных в такси, и мы можем спросить, возможно ли смоделировать этот тип сценария с помощью функции. Используя описательные переменные, мы выбираем мили и стоимость в долларах как функцию миль: .
Используя описательные переменные, мы выбираем мили и стоимость в долларах как функцию миль: .
Мы точно знаем, что , так как скидка в размере 3,30 доллара США взимается независимо от того, сколько миль пройдено. Поскольку за каждую пройденную милю добавляется 2,60 доллара, тогда:
Если мы проедем вторую милю, еще 2 доллара.60 будет добавлено к стоимости:
Если мы проедем третью милю, к стоимости добавится еще 2,40 доллара:
Исходя из этого, мы можем проследить закономерность и сделать вывод, что если мили пройдены, потому что мы начинаем с снижения платы в размере 3,30 доллара, а затем за каждое увеличение мили мы добавляем 2,60 доллара.
Хорошо убедиться, что единицы измерения имеют смысл в этом уравнении. Плата за падение в размере 3,30 доллара США измеряется в долларах; плата в размере 2,60 доллара США измеряется в долларах за милю. Итак,
Если доллары за милю умножить на количество миль, результатом будет количество долларов, соответствующее единицам измерения 3. 30, и согласование желаемых единиц измерения для функции.
30, и согласование желаемых единиц измерения для функции.
Обратите внимание, что это уравнение состоит из двух величин. Во-первых, это фиксированная плата в размере 3,30 доллара США, которая не меняется в зависимости от стоимости ввода. Второй — стоимость 2,60 доллара за милю, что составляет 90 297 скорости изменения 90 298. В уравнении эта скорость изменения умножается на входное значение.
Глядя на эту же задачу в виде таблицы, мы также видим, что стоимость изменяется на 2,60 доллара США за каждое увеличение на 1 милю.
| 0 | 1 | 2 | 3 | |
| 3.30 | 5,90 | 8,50 | 11.10 |
Здесь важно отметить, что в этом уравнении скорость изменения постоянна ; на любом интервале скорость изменения одинакова.
Нарисовав это уравнение, мы видим, что фигура представляет собой линию, поэтому эти функции и получили свое название: линейные функции .
Когда количество миль равно нулю, стоимость составляет 3,30 доллара США, что соответствует точке (0, 3,30) на графике. Это вертикаль или перехват.График увеличивается по прямой линии слева направо, потому что стоимость каждой мили увеличивается на 2,40 доллара; этот показатель остается постоянным.
В этом примере вы видели стоимость такси, смоделированную словами, уравнением, таблицей и в графической форме. По возможности убедитесь, что вы можете связать эти четыре представления вместе, чтобы постоянно развивать свои навыки. Важно отметить, что вы не всегда сможете найти все 4 представления задачи, поэтому умение работать со всеми 4 формами очень важно.
Линейная функция
Линейная функция — это функция, график которой образует линию. Линейные функции всегда можно записать в виде
.или
Они эквивалентны, где:
— начальное или начальное значение функции (при вводе ), а
— постоянная скорость изменения функции
Многим людям нравится записывать линейные функции в форме, потому что это соответствует тому, как мы обычно говорим: «Выход начинается с и увеличивается со скоростью .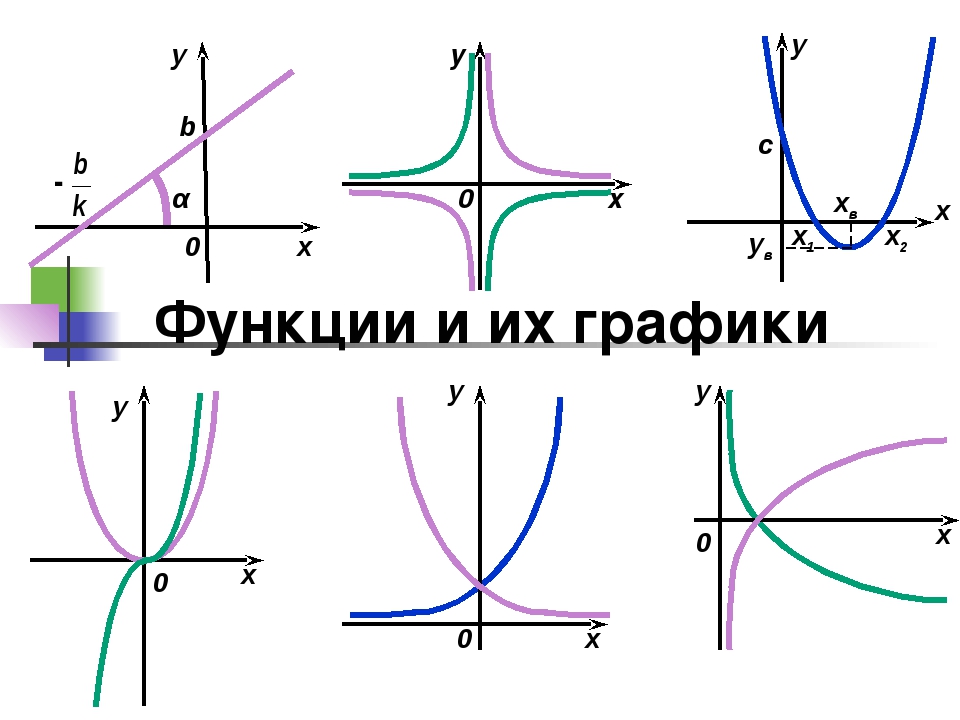
Только по этой причине мы будем использовать форму для многих примеров, но помните, что они эквивалентны и могут быть правильно написаны в обоих случаях.
Наклон и увеличение/уменьшение
— постоянная скорость изменения функции (также называемая наклоном). Наклон определяет, является ли функция возрастающей или убывающей функцией.
является функцией , увеличивающей , если
— это функция , уменьшающая , если
Если , скорость изменения равна нулю, а функция представляет собой просто горизонтальную линию, проходящую через точку , не возрастающую и не убывающую.
Чтобы начать производство новой модели нестандартных колес, компании необходимо приобрести новое оборудование на сумму 30 000 долларов США. Каждое изготовленное колесо обходится им в 40 долларов в виде расходных материалов и рабочей силы. Напишите формулу полной стоимости производства колес. Каковы будут их общие затраты в первый год, если они рассчитывают продать 240 колес?
Начальное значение этой функции равно 30 000, так как это затраты на запуск, поэтому
.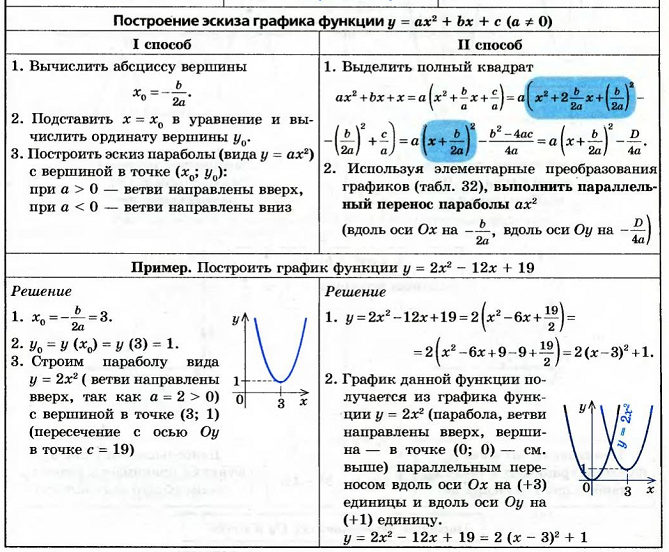 Стоимость увеличивается на 40 долларов за каждое изготовленное колесо, поэтому скорость изменения составляет 40 долларов за колесо.С этой информацией мы можем написать формулу:
Стоимость увеличивается на 40 долларов за каждое изготовленное колесо, поэтому скорость изменения составляет 40 долларов за колесо.С этой информацией мы можем написать формулу:
.
— возрастающая линейная функция.
С помощью этой формулы мы можем предсказать общую стоимость 240 колес:
.
Общая стоимость составит 39 600 долларов.
1. Если вы зарабатываете 30 000 долларов в год и тратите 29 000 долларов в год, напишите уравнение для суммы денег, которую вы сэкономите спустя годы, если вы начнете с нуля.
«Самое главное, тратьте меньше, чем зарабатываете!»
Расчет скорости изменения
Имея два значения для входа и , и два соответствующих значения для вывода, и , или набор точек и , если мы хотим найти линейную функцию, которая содержит обе точки, мы можем вычислить скорость изменения, :
Скорость изменения линейной функции также называется наклоном линии.
Примечание в обозначении функций и , поэтому мы могли бы эквивалентно написать
Население города увеличилось с 23 400 до 27 800 человек в период с 2002 по 2006 год. Найдите скорость изменения численности населения за этот промежуток времени.
Скорость изменения будет соотносить изменение численности населения с изменением во времени. Население увеличилось на человека за 4-летний временной интервал. Чтобы найти скорость изменения, число людей в год, население изменилось на:
= 1100 человек в год
Обратите внимание, что мы знали, что население увеличивается, поэтому мы ожидаем, что наше значение m будет положительным.Это быстрый способ проверить, является ли ваше значение разумным.
Давление в фунтах на квадратный дюйм (PSI) на дайвера зависит от их глубины ниже поверхности воды, в футах, согласно уравнению. Интерпретируйте компоненты этой функции.
Скорость изменения или наклон 0,434 будет иметь единицы
.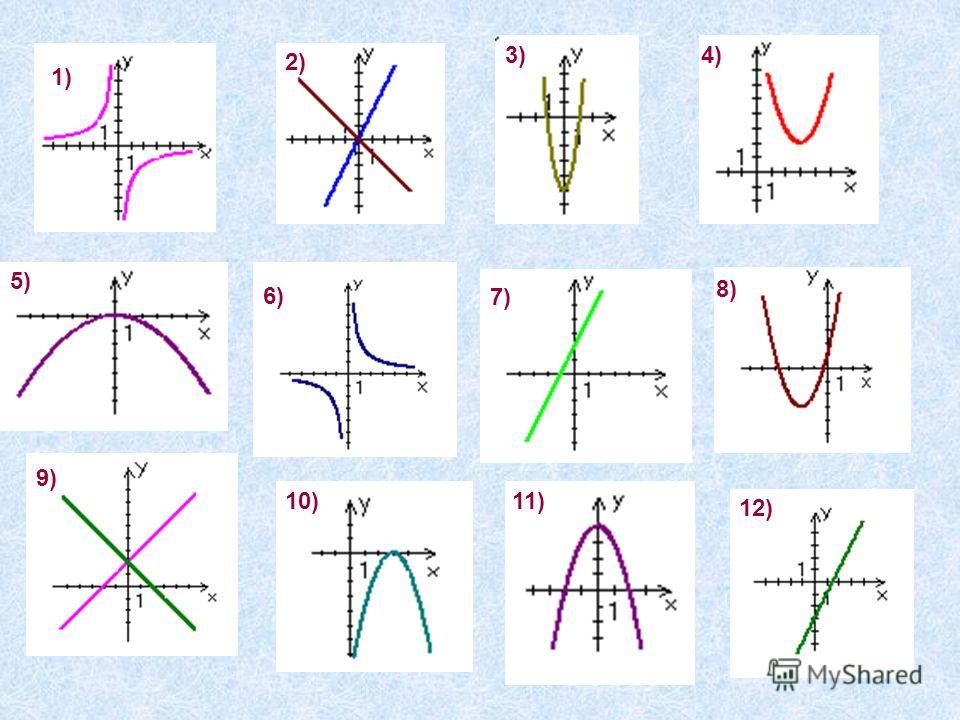
Это говорит нам о том, что давление на дайвера увеличивается на 0,434 фунтов на квадратный дюйм с увеличением глубины на каждый фут.
Начальное значение, 14.696, будут иметь те же единицы измерения, что и выходные данные, поэтому это говорит нам о том, что на глубине 0 футов давление на дайвера будет 14,696 фунтов на квадратный дюйм.
2. Учитывая две точки и , найдите скорость изменения. Эта функция возрастает или убывает?
Теперь мы можем найти скорость изменения для двух пар вход-выход и можем написать уравнение для линейной функции, когда у нас есть скорость изменения и начальное значение. Если у нас есть две пары вход-выход, и они не включают начальное значение функции, то нам придется решать ее.
Если – линейная функция, и , найдите уравнение для этой функции.
В примере 7.4C мы вычислили скорость изменения как . В этом случае мы не знаем начального значения, поэтому нам придется его найти. Используя скорость изменения, мы знаем, что уравнение будет иметь вид . Поскольку мы знаем значение функции при , мы можем оценить функцию при 3.
Используя скорость изменения, мы знаем, что уравнение будет иметь вид . Поскольку мы знаем значение функции при , мы можем оценить функцию при 3.
Поскольку мы это знаем, мы можем подставить слева
Это оставляет нам уравнение, которое мы можем решить для начального значения
Объединив это со значением скорости изменения, мы теперь можем написать формулу для этой функции:
Работая продавцом страховых услуг, Илья получает базовый оклад и комиссию с каждого нового полиса, поэтому недельный доход Ильи, , зависит от количества новых полисов, которые он продает в течение недели.На прошлой неделе он продал 3 новых полиса и заработал за неделю 760 долларов. За неделю до этого он продал 5 новых полисов и заработал 920 долларов. Найдите уравнение для и интерпретируйте значение компонентов уравнения.
Данная информация дает нам две пары ввода-вывода: и . Начнем с определения скорости изменения.
Отслеживание единиц измерения может помочь нам интерпретировать это количество. Доход увеличился на 160 долларов, когда количество полисов увеличилось на 2, поэтому скорость изменения составляет 80 долларов на полис; Илья получает комиссию в размере 80 долларов за каждый проданный полис в течение недели.
Доход увеличился на 160 долларов, когда количество полисов увеличилось на 2, поэтому скорость изменения составляет 80 долларов на полис; Илья получает комиссию в размере 80 долларов за каждый проданный полис в течение недели.
Затем мы можем найти начальное значение
тогда когда , , давая
это позволяет нам решить для
Это значение является начальным для функции. Это доход Ильи при , что означает, что новые полисы не продаются. Мы можем интерпретировать это как базовую зарплату Ильи за неделю, которая не зависит от количества проданных полисов.
Запись окончательного уравнения:
Наша окончательная интерпретация такова: базовая зарплата Ильи составляет 520 долларов в неделю, и он получает дополнительные 80 долларов комиссионных за каждый проданный полис каждую неделю.
3. Посмотрите на пример 7.4G:
Определите независимые и зависимые переменные.
Что такое разумный домен и диапазон?
4. Баланс на вашем платежном счете в колледже зависит от количества четвертей, которые вы посещаете. Объясните функцию словами. Сколько кварталов колледжа вы можете оплатить, пока этот счет не опустеет?
Баланс на вашем платежном счете в колледже зависит от количества четвертей, которые вы посещаете. Объясните функцию словами. Сколько кварталов колледжа вы можете оплатить, пока этот счет не опустеет?
Подумай Ответы
1. Каждый год экономится 1000 долларов.
2. ; Уменьшение, потому что
3. (количество проданных полисов) — независимая переменная.
(еженедельный доход как функция проданных полисов) — зависимая переменная.
Разумный домен: *
Разумный диапазон: *
* ответы могут различаться, если указано обоснование; 15 — это произвольный верхний предел, основанный на продаже 3 полисов в день при 5-дневной рабочей неделе, и 1740 долларов США соответствуют домену.
4. Ваш счет в колледже начинается с 20 000 долларов, и вы снимаете 4 000 долларов каждый квартал (или ваш счет содержит 20 000 долларов и уменьшается на 4 000 долларов каждый квартал.) Вы можете заплатить за 5 кварталов до того, как деньги на этом счете закончатся.
Раздел 7.4 Упражнения
- Сара хочет покататься на коньках на катке Super Skate. Она должна заплатить 7 долларов за вход и 1,25 доллара за каждую минуту пребывания на катке.
- Напишите уравнение для определения стоимости (C) в зависимости от количества минут (t), которые она провела на катке.
- Если у нее всего 43,25 доллара, найдите количество минут, которое она может провести на катке.
- Если вы зарабатываете 30 000 долларов в год и тратите 29 000 долларов в год, напишите сумму денег, которую вы сэкономите спустя годы, предполагая, что вы начинаете без денег.
- Баланс на вашем сберегательном счете после окончания средней школы зависит от количества семестров, которые вы посещаете. Объясните функцию словами и объясните значение каждого числа и символа в этом уравнении. Сколько триместров послесреднего образования вы можете оплатить, пока этот счет не опустеет?
- Менеджер местного рынка потратит в общей сложности 80 долларов на яблоки по 0,25 доллара за штуку и груши по 0,50 доллара за штуку.
 Запишите количество яблок, которые она может купить, как линейную функцию количества груш.Найдите наклон и интерпретируйте свой ответ. График функции.
Запишите количество яблок, которые она может купить, как линейную функцию количества груш.Найдите наклон и интерпретируйте свой ответ. График функции. - По цене 10 долларов за билет Вилли Уильямс и его команда Wranglers займут все 8000 мест в сборочном центре. Менеджер знает, что на каждый доллар повышения цены 500 билетов останутся непроданными.
- Запишите количество проданных билетов n как функцию цены билета p.
- Каковы пределы независимой переменной, если таковые имеются?
- При цене 2,28 доллара за бушель предложение ячменя составляет 7 500 миллионов бушелей, а спрос — 7 900 миллионов бушелей.При цене 2,37 доллара за бушель предложение составляет 7 900 миллионов бушелей, а спрос — 7 800 бушелей.
- Предполагая, что цена и предложение связаны линейно, определите цену с точки зрения предложения (уравнение цена-предложение ).
- Предполагая, что цена и спрос связаны линейно, определите цену с точки зрения спроса (уравнение цена-спрос ).

- Найдите точку равновесия (цена и количество единиц, для которых спрос и предложение равны).
- Нарисуйте уравнение цены-предложения, уравнение цены-спроса и точку равновесия в одной и той же системе координат.
Когда мы работаем с новой функцией, полезно знать как можно больше о функции: ее графике, где функция равна нулю, и любых других особенностях поведения функции.
При построении графика линейной функции существует два основных способа ее построения:
- Нанесение точек (не менее 2) и проведение линии через точки
- Использование начального значения (вывод при x = 0) и скорости изменения (наклон)
При использовании начального значения и скорости изменения на графике необходимо учитывать графическую интерпретацию этих значений.Помните, что начальное значение функции является выходом, когда вход равен нулю, поэтому в уравнении график включает точку . На графике это вертикальная точка пересечения — точка пересечения графика с вертикальной осью.
Для скорости изменения полезно вспомнить, что мы рассчитали это значение как
На графике линии это говорит нам о том, что если мы разделим разность по вертикали или подъем выходных данных функции на разность по горизонтали или пробег входных данных, мы получим скорость изменения, также называемую наклоном линия.
Обратите внимание, что это отношение одинаково независимо от того, какие две точки мы используем
Графическая интерпретация линейного уравнения
Графически, в уравнении
это точка пересечения по вертикали графика и говорит нам, что мы можем начать наш график с
это наклон линии и говорит нам, как далеко нужно подняться и бежать, чтобы добраться до следующей точки
Как только у нас будет хотя бы 2 точки, мы можем продолжить график линии влево и вправо.
1. Учтите, что наклон -2/3 также может быть записан как . С помощью найти другую точку на графике, имеющую отрицательное значение.
В значение определяет крутизну линии. При положительном значении график будет увеличиваться, а при отрицательном – уменьшаться. Глядя на некоторые примеры:
In действует как сдвиг по вертикали, перемещая график вверх и вниз, не влияя на наклон линии. Некоторые примеры:
В дополнение к пониманию основного поведения линейной функции (увеличение или уменьшение, распознавание наклона и вертикального пересечения) часто бывает полезно знать горизонтальное пересечение функции — где она пересекает горизонтальную ось.
Поиск горизонтального пересечения
Горизонтальная точка пересечения функции находится там, где график пересекает горизонтальную ось. Если функция имеет горизонтальную точку пересечения, вы всегда можете найти ее, решив .
Найдите точку пересечения .
Установка функции равной нулю, чтобы найти, какой ввод поместит нас на горизонтальную ось:
График пересекает горизонтальную ось в точке (6,0)
Есть два особых случая линий: горизонтальная линия и вертикальная линия.На горизонтальной линии, подобной показанной ниже, обратите внимание, что между любыми двумя точками изменение выходных параметров равно 0. В уравнении наклона числитель будет равен 0, в результате чего наклон будет равен 0. Используя наклон 0 в , уравнение упрощается до
Обратите внимание, что горизонтальная линия имеет точку пересечения по вертикали, но не имеет точки пересечения по горизонтали (если только это не линия ).
В случае вертикальной линии обратите внимание, что между любыми двумя точками изменение входных данных равно 0. В уравнении наклона знаменатель будет равен 0, и вы, возможно, помните, что мы не можем делить на 0; наклон вертикальной линии не определен.Вы также можете заметить, что вертикальная линия не является функцией. Чтобы написать уравнение вертикальной линии, мы просто пишем input=value, например.
Обратите внимание, что вертикальная линия имеет точку пересечения по горизонтали, но не имеет точки пересечения по вертикали (если только это не линия ).
Горизонтальные и вертикальные линии
Горизонтальные линии имеют уравнения вида
Вертикальные линии имеют уравнения вида
Напишите уравнение для горизонтальной линии, показанной выше.
Эта строка будет иметь уравнение
Напишите уравнение для вертикальной линии, показанной выше.
Эта строка будет иметь уравнение
Параллельные и перпендикулярные линии
Когда две линии наносятся вместе, линии будут параллельными , если они увеличиваются с одинаковой скоростью — если скорости изменения одинаковы. В этом случае графики никогда не пересекутся (если только они не будут одной и той же линией).
Параллельные линии
Две линии параллельны , если наклоны равны (или, если обе линии вертикальны).Другими словами, учитывая два линейных уравнения и
Линии будут параллельны, если
Если две линии не параллельны, еще одна интересная возможность состоит в том, что линии перпендикулярны, что означает, что линии образуют прямой угол (угол 90 градусов — прямой угол) в месте их пересечения. В этом случае наклоны при перемножении будут равны -1. Решение для одного наклона приводит нас к определению:
Перпендикулярные линии
Учитывая два линейных уравнения и
Линии будут перпендикулярными если , и так
Мы часто говорим, что наклон перпендикулярной линии является «отрицательной обратной величиной» наклона другой линии.
Найдите наклон линии, перпендикулярной прямой с:
а) наклоном 2.
б) наклоном -4.
c) наклон .
Если бы исходная линия имела наклон 2, наклон перпендикулярной линии был бы равен
.Если бы исходная линия имела наклон -4, наклон перпендикулярной линии был бы равен
.Если бы исходная линия имела наклон , наклон перпендикулярной линии был бы равен
2.Учитывая линию , найдите уравнение для линии, проходящей через это:
а) параллельно .
б) перпендикулярно .
Прямая проходит через точки и . Найдите уравнение перпендикуляра, проходящего через точку .
Из двух заданных точек на опорной линии мы можем вычислить наклон этой линии:
Перпендикулярная линия будет иметь наклон
Затем мы можем найти точку пересечения по вертикали, которая заставляет линию проходить через нужную точку:
затем в ,
Даю линию
Пересечение линий
Графики двух линий пересекутся, если они не параллельны.Они пересекутся в точке, удовлетворяющей обоим уравнениям. Чтобы найти эту точку, когда уравнения заданы как функции, мы можем решить для входного значения так, чтобы . Другими словами, мы можем установить формулы для линий равными и решить для входных данных, которые удовлетворяют уравнению.
Две параллельные линии также могут пересекаться, если они являются одной и той же линией. В этом случае они пересекаются в каждой точке прямых.
Нахождение пересечения позволяет нам ответить и на другие вопросы, например, определить, когда одна функция больше другой.
Подумай Ответы
1. Найден, начиная с вертикальной точки пересечения, поднимаясь на 2 единицы и 3 в отрицательном горизонтальном направлении. Вы могли бы также ответить: или и т. д.
2. Параллельно:
Перпендикулярно:
3. Дано
а. (0,5)
б. (5,0)
г. Уклон -1
д. Ни параллельно, ни перпендикулярно
e. Функция уменьшения
f. Учитывая функцию тождества, выполните вертикальное отражение (по оси) и сдвиньте вверх на 5 единиц.
Раздел 7.5 Упражнения
- Нарисуйте график следующей функции.
- Найдите точки пересечения – и – следующих прямых и начертите их на графике:
- Найдите наклон следующих линий и нарисуйте линии:
- Найдите уравнения прямых, проходящих через следующие точки, определите точки пересечения – и – и угол наклона для каждой из них и нарисуйте их графики.
- и
- и
- Рассмотрим точки и и линейную функцию, график которой проходит через них.
- Найдите наклон линии.
- Найдите форму пересечения наклона уравнения прямой.
- Запишите уравнение прямой в стандартной форме.
- График с использованием вертикальной точки пересечения и наклона. Используя тот факт, что наклон можно также записать как , найдите на графике точку с отрицательным значением .
- Рассмотрите график и определите для функции следующее:
- Вертикальные координаты пересечения
- Горизонтальные точки пересечения координат
- Склон
- Является ли функция возрастающей или убывающей (или ни той, ни другой)?
При моделировании сценариев с линейной функцией и решении задач, связанных с линейно изменяющимися величинами, мы обычно следуем тем же стратегиям решения проблем, что и для любого типа функции:
Стратегия решения проблем
- Определите изменяющиеся величины, а затем тщательно и четко определите описательные переменные для представления этих величин.При необходимости сделайте набросок изображения или определите систему координат.
- Внимательно прочитайте задачу, чтобы выявить важную информацию. Ищите информацию, дающую значения для переменных или значения для частей функциональной модели, таких как наклон и начальное значение.
- Внимательно прочитайте задачу, чтобы определить, что мы пытаемся найти, идентифицировать, решить или интерпретировать.
- Определите путь решения от предоставленной информации до того, что мы пытаемся найти. Часто это включает в себя проверку и отслеживание единиц, построение таблицы или даже поиск формулы для функции, используемой для моделирования проблемы.
- При необходимости найдите формулу функции.
- Решите или оцените, используя формулу, которую вы нашли для желаемых величин.
- Подумайте, разумен ли ваш ответ в данной ситуации и имеет ли он математический смысл.
- Четко изложите свой результат, используя соответствующие единицы измерения, и при необходимости отвечайте полными предложениями.
Компания приобрела новое офисное оборудование на сумму 120 000 долларов. Затем ожидайте, что стоимость обесценится (уменьшится) на 16 000 долларов в год.Найдите линейную модель для значения, затем найдите и интерпретируйте точку пересечения по горизонтали и определите разумную область и диапазон для этой функции.
В задаче есть две изменяющиеся величины: время и стоимость. Остаточная стоимость оборудования зависит от того, как долго оно находится в распоряжении компании. Мы можем определить наши переменные, включая единицы измерения.
Вывод: , оставшаяся стоимость, в долларах
Ввод: , время, в годах
Читая задачу, мы выделяем два важных значения.Первая, 120 000 долларов США, является начальной стоимостью для . Другое значение, по-видимому, представляет собой скорость изменения — единицы долларов в год соответствуют единицам нашей выходной переменной, деленной на нашу входную переменную. Стоимость обесценивается, поэтому вы должны признать, что оставшаяся стоимость уменьшается с каждым годом, а наклон является отрицательным.
Используя точку пересечения и наклон, представленные в задаче, мы можем написать уравнение:
Чтобы найти точку пересечения по горизонтали, мы устанавливаем выход равным нулю и решаем для входа:
Горизонтальное пересечение равно 7.5 лет. Поскольку это представляет собой входную стоимость, при которой выход будет равен нулю, интерпретируя это, мы могли бы сказать: оборудование не будет иметь никакой остаточной стоимости через 7,5 лет.
При моделировании любого сценария реальной жизни с помощью функций обычно существует ограниченная область, в которой эта модель будет действительна — практически ни одна тенденция не продолжается бесконечно. В этом случае говорить о входных значениях меньше нуля, конечно же, не имеет смысла. Эта модель также недействительна после горизонтального пересечения.
Домен представляет набор входных значений, поэтому разумным доменом для этой функции является . Диапазон представляет собой набор выходных значений, и значение начинается со 120 000 долларов США и заканчивается 0 долларов США через 7,5 лет, поэтому соответствующий диапазон равен .
Самое главное помнить, что домен и диапазон связаны друг с другом, и то, что вы решите, является наиболее подходящим для домена (независимая переменная), будет диктовать требования для диапазона (зависимая переменная).
Джамал выбирает между двумя транспортными компаниями.Первый, U-Haul, взимает авансовый платеж в размере 20 долларов, а затем 59 центов за милю. Второй, Budget, взимает авансовый сбор в размере 16 долларов, а затем 63 цента за милю. Когда U-Haul станет лучшим выбором для Джамала?
Двумя важными величинами в этой задаче являются стоимость и количество пройденных миль. Поскольку у нас есть две компании для рассмотрения, мы определим две функции:
Ввод: , миль
Выходы:
: стоимость в долларах за аренду у U-Haul
: стоимость в долларах за аренду у Budget
Если внимательно прочитать задачу, то окажется, что нам были даны первоначальная стоимость и скорость изменения для каждой компании.Поскольку наши результаты измеряются в долларах, а затраты на милю, указанные в задаче, указаны в центах, нам нужно будет преобразовать эти величины, чтобы они соответствовали нашим желаемым единицам: 0,59 доллара за милю для U-Haul и 0,63 доллара за милю для бюджета.
Глядя на то, что мы пытаемся найти, мы хотим знать, когда U-Haul будет лучшим выбором. Поскольку все, что нам нужно принять, это затраты, мы ищем, когда U-Haul будет стоить меньше, или когда . Путь решения приведет нас к тому, чтобы найти уравнения для двух функций, найти пересечение, а затем посмотреть, где функция меньше.Используя скорости изменения и начальные расходы, мы можем написать уравнения:
Эти графики показаны ниже с нарисованными пунктирными линиями.
Чтобы найти пересечение, приравняем уравнения и решим:
Это говорит нам о том, что стоимость двух компаний будет одинаковой, если будет пройдено 100 миль. Либо глядя на график, либо отмечая, что он растет более медленными темпами, мы можем сделать вывод, что U-Haul будет более дешевой ценой при пробеге более 100 миль.
Доход компании растет линейно. В 2012 году их выручка составила 1,45 миллиона долларов. К 2015 году выручка выросла до 1,81 миллиона долларов. Если эта тенденция сохранится,
a. Прогноз выручки в 2020 году
б. Когда выручка достигнет 3 миллионов долларов?
Двумя изменяющимися величинами являются доход и время. Хотя мы могли бы использовать фактическое значение года в качестве входной величины, это привело бы к очень уродливым уравнениям, поскольку точка пересечения по вертикали соответствовала бы году 0, более 2000 лет назад!
Чтобы сделать вещи немного лучше, а также облегчить нашу жизнь, мы определим наши входные данные как годы с 2012 года:
Входные данные: , годы с 2012 года
Выходные данные: , доход компании, в миллионах долларов
Задача дает нам две пары вход-выход.Преобразовав их в соответствии с нашими определенными переменными, 2012 год будет соответствовать , давая точку . Обратите внимание на то, что благодаря правильному выбору определения переменной мы «задали» себе вертикальную точку пересечения функции. 2015 год будет соответствовать , давая точку .
Чтобы предсказать численность населения в 2020 году (), нам потребуется уравнение для численности населения. Точно так же, чтобы найти, когда доход достигнет 3 миллионов долларов, нам нужно будет решить для входных данных, которые дадут выход, равный 3.В любом случае, нам нужно уравнение. Чтобы найти его, начнем с вычисления скорости изменения:
млн долларов в год
Поскольку мы уже знаем точку пересечения линии по вертикали, мы можем сразу написать уравнение:
Чтобы спрогнозировать выручку в 2020 году, мы оцениваем нашу функцию как
.Если тенденция сохранится, наша модель прогнозирует выручку в размере 2,41 млн долларов в 2020 году.
Чтобы найти, когда население достигнет 3 миллионов долларов, мы можем установить и решить для .
Наша модель предсказывает, что выручка достигнет 3 миллионов долларов США чуть менее чем через 13 лет после 2012 года или незадолго до 2025 года.
В бизнесе функции очень часто применяются для моделирования затрат, выручки и прибыли.
Стоимость, Доход, Прибыль
Когда компания производит q изделий, общая стоимость равна стоимости общих затрат на производство этих изделий. Общая стоимость включает как фиксированные затраты , которые представляют собой начальные затраты, такие как оборудование и здания, так и переменные затраты , которые зависят от количества произведенных изделий, таких как материалы и рабочая сила.
В самом простом случае Общая стоимость = (Постоянные затраты) + (Переменные затраты) ∙
Доход — это сумма денег, которую компания получает от продаж.
В самом простом случае Доход = (Доход на единицу товара) ∙
Прибыль — это сумма денег, которую приносит после расходов.
Прибыль = Доход – Затраты
Мы часто говорим о точке безубыточности . Это уровень производства, при котором выручка равна затратам или, что то же самое, прибыль равна нулю.Как правило, это минимальный уровень продаж, необходимый для получения компанией прибыли.
Технический стартап рассматривает возможность разработки и запуска нового мобильного приложения. Первоначальная разработка приложения будет стоить 300 000 долларов, а маркетинг и поддержка для каждого пользователя будут стоить 0,50 доллара. Хотя приложение будет бесплатным, по их оценкам, они смогут получать в среднем 2 доллара на пользователя от покупок в приложении. Сколько пользователей потребуется компании для безубыточности?
Начнем с моделирования затрат, выручки и прибыли.Пусть = количество пользователей.
Фиксированные (начальные) затраты составляют 300 000 долларов США, а переменные (за единицу) затраты составляют 0,50 долларов США на пользователя. Мы можем написать уравнение общей стоимости:
Доход составит 2 доллара США на пользователя, поэтому уравнение дохода будет таким:
Мы могли бы найти точку безубыточности, установив общие затраты равными выручке, что эквивалентно нахождению пересечения линий.
В качестве альтернативы мы могли бы сначала найти уравнение прибыли:
Точку безубыточности можно найти, установив прибыль равной нулю:
Чтобы выйти на уровень безубыточности, компании необходимо приобрести 200 000 пользователей.
1. Магазин пончиков оценивает свои фиксированные ежедневные расходы в 600 долларов. Если каждый пончик стоит около 0,05 доллара и продается по 0,60 доллара, сколько пончиков нужно продать, чтобы выйти в ноль?
В экономике существует модель определения цен на свободном рынке, которая утверждает, что спрос и предложение на продукт связаны с ценой. Отношение спроса показывает количество определенного продукта, которое потребители готовы купить по определенной цене.Обычно объем спроса на товар уменьшается, если цена увеличивается. Отношения предложения показывают количество товара, которое поставщики готовы произвести по определенной продажной цене. Как правило, спрос на предложение будет увеличиваться, если цена растет. Экономическая теория говорит, что спрос и предложение будут взаимодействовать, а точка пересечения будет равновесной ценой, или рыночной ценой, где количество спроса и предложения будет равным.
Спрос и предложение
Если это цена продукта, то
это объем спроса
это объем предложения
Кривая спроса является убывающей функцией, а кривая предложения — возрастающей функцией.
Пересечением кривых является равновесная цена и количество , также называемое рыночной ценой и количеством . Эта точка часто обозначается как , .
В последующих главах вы будете изучать нелинейные кривые спроса и предложения, но в этой главе мы сосредоточимся на линейных функциях спроса и предложения.
В большинстве книг по экономике вы встретите кривую спроса и предложения, написанную с ценой как входом и количеством как выходом, например .Однако графики спроса и предложения рисуются с ценой на вертикальной оси и количеством на горизонтальной. Чтобы избежать путаницы, большую часть времени в этом тексте мы вместо этого будем писать кривые спроса и предложения с ценой в качестве результата, чтобы соответствовать ее расположению на вертикальной оси.
При цене 2,50 доллара за галлон в определенном городе есть спрос на 42,5 тысячи галлонов газа и предложение 20 тысяч галлонов. При цене 3,50 доллара имеется спрос на 25,5 тысяч галлонов и предложение на 28 тысяч галлонов.Предполагая, что спрос и предложение линейны, найдите равновесную цену и количество.
Начнем с нахождения линейного уравнения для спроса и предложения. Мы будем использовать цену в долларах в качестве выходных данных и количество в тысячах галлонов в качестве входных данных.
На поставку у нас есть очки и .
Нахождение уклона:
Мы знаем, что уравнение будет выглядеть так, поэтому подставим
Уравнение предложения:
Для спроса у нас есть точки и .Используя аналогичный подход, мы можем найти уравнение спроса:
Чтобы найти равновесие, приравняем предложение к спросу:
Умножение на 8(17) = 136 для очистки дробей
Теперь находим
Чтобы найти равновесную цену, мы можем подставить это значение обратно в любое уравнение:
Равновесное количество газа составит 27,2 тысячи галлонов по цене 3 доллара.40.
2. Компания подсчитала, что при цене 140 долларов будет спрос на 4000 товаров, а при повышении цены на каждые 5 долларов спрос упадет на 200 товаров. Кривая предложения такова. Найдите равновесную цену и количество.
Подумай Ответы
1. Доход:
Безубыточность при количестве около 1091 пончика в день.
2. Спрос:
Предложение = Спрос при ,
Раздел 7.6 упражнений
- Компания приобрела новое офисное оборудование на сумму 120 000 долларов. Затем ожидайте, что стоимость обесценится (уменьшится) на 16 000 долларов в год. Найдите линейную модель стоимости оборудования спустя годы после покупки, затем найдите и интерпретируйте горизонтальную точку пересечения и определите разумную область и диапазон для этой функции.
- При цене 2,28 доллара за бушель предложение ячменя составляет 7 500 миллионов бушелей, а спрос — 7 900 миллионов бушелей. При цене 2,37 доллара за бушель предложение составляет 7 900 миллионов бушелей, а спрос — 7 800 бушелей.
- Предполагая, что цена и предложение связаны линейно, определите цену с точки зрения предложения (уравнение цена-предложение ).
- Предполагая, что цена и спрос связаны линейно, определите цену с точки зрения спроса (уравнение цена-спрос ).
- Найдите точку равновесия (цена и количество единиц, для которых спрос и предложение равны).
- Нарисуйте уравнение цены-предложения, уравнение цены-спроса и точку равновесия в одной и той же системе координат.
- Завод может производить 50 теннисных ракеток в день при общей дневной стоимости 3855 долларов и 60 теннисных ракеток в день при общей дневной стоимости 4245 долларов.
- Предполагая, что ежедневные затраты и производство связаны линейной зависимостью, найдите общие ежедневные затраты на производство теннисных ракеток.
- Интерпретируйте наклон и вертикальную точку пересечения этого уравнения стоимости.
- График общих ежедневных затрат на .
- Компания NewTech Wireless предлагает месячный тарифный план, в котором общая стоимость прямо пропорциональна количеству использованных минут.Учитывая, что общая ежемесячная стоимость использованных 100 минут составляет 45,00:
- Выразите стоимость в количестве использованных минут.
- Каковы домен и диапазон этой функции?
- Какова базовая стоимость плана и какова стоимость минуты?
- Нарисуйте график этой функции.
- Сколько будет стоить использование 400 минут в месяц?
- Если общая стоимость за месяц составила 40 долларов США, сколько минут было использовано?
- Охранная компания покупает новый фургон службы безопасности за 53 000 долларов США и предполагает, что через 5 лет его стоимость при обмене составит 28 000 долларов США.
- Найдите линейную модель амортизированной стоимости фургона по прошествии многих лет.
- Какова остаточная стоимость фургона через 3 года?
- Когда амортизированная стоимость упадет ниже 23 000 долларов?
- Производитель нового типа сковороды подсчитал, что ежемесячные фиксированные затраты составляют 83 000 долларов США, а переменные затраты — 7,35 долларов США на каждую произведенную сковороду. Кастрюли продаются дистрибьютору по цене 20 долларов США за кастрюлю. Ежемесячная производственная мощность составляет 20 000 единиц.
- Напишите функцию месячных затрат по количеству произведенных единиц. Определите его домен и диапазон и начертите его.
- Запишите функцию месячного дохода в виде количества произведенных единиц. Определите его домен и диапазон и начертите его.
- Напишите функцию месячной прибыли в виде количества произведенных единиц, предполагая, что все произведенные единицы проданы. Определите его домен и диапазон и начертите его.
- Какова будет их прибыль/убыток, если они будут работать на 25% мощности? На 75% мощности?
- Сколько единиц они должны произвести и продать в месяц, чтобы выйти на уровень безубыточности? Сколько процентов составляет производственная мощность? Какими должны быть продажи, чтобы выйти в ноль?
- Сколько единиц товара они должны произвести и продать в месяц, чтобы получить 100 000 долларов прибыли?
- Компания-производитель, заключившая контракт на поставку новой линии пивных бутылок, подсчитала, что производство 80 000 бутылок обойдется в 41 000 долларов, а производство 120 000 бутылок — в 59 000 долларов.Основываясь на анализе затрат на предыдущие производственные циклы, они определили, что линейная модель лучше всего отражает затраты на производство.
- Предполагая, что затраты и количество произведенных бутылок связаны линейной зависимостью, определите функцию затрат .
- Каковы фиксированные затраты в этой модели и каковы переменные затраты на бутылку?
В реальном мире вещи редко следуют тенденциям идеально. Когда мы ожидаем, что тренд будет вести себя линейно, или когда проверка предполагает, что тренд ведет себя линейно, часто желательно найти уравнение для аппроксимации данных.Поиск уравнения для аппроксимации данных помогает нам понять поведение данных и позволяет нам использовать линейную модель для прогнозирования данных внутри и вне диапазона данных.
В таблице ниже показано количество криков сверчка за 15 секунд и температура воздуха в градусах по Фаренгейту. Постройте эти данные и определите, кажутся ли данные линейно связанными.
| чирикает | 44 | 35 | 20.4 | 33 | 31 | 35 | 18,5 | 37 | 26 |
| Темп. | 80,5 | 70,5 | 57 | 66 | 68 | 72 | 52 | 73,5 | 53 |
При построении этих данных оказывается, что может существовать тенденция, и эта тенденция кажется примерно линейной, хотя, конечно, не идеальной.
Самый простой способ найти уравнение для аппроксимации этих данных — попытаться «на глазок» нарисовать линию, которая, кажется, довольно хорошо соответствует данным, а затем найти уравнение для этой линии на основе наклона и точки пересечения.
Из данных видно, что количество щебетов увеличивается с повышением температуры. Когда вы рассматриваете функцию для этих данных, вы должны знать, что вы смотрите на возрастающую функцию или функцию с положительным наклоном.
1. а. Какие описательные переменные вы бы выбрали для представления температуры и щебета?
б. Какая переменная является независимой, а какая зависимой?
с. Основываясь на этих данных и графике, каков разумный домен и диапазон?
д.Опираясь только на данные, это функция один к одному, поясните?
Затем это линейное уравнение можно использовать для аппроксимации решения различных вопросов, которые мы можем задать о тренде. Хотя данные не полностью соответствуют линейному уравнению, уравнение является нашим лучшим предположением о том, как отношения будут вести себя за пределами значений, для которых у нас есть данные. Однако есть разница между прогнозированием внутри домена и диапазона значений, для которых у нас есть данные, и вне этого домена и диапазона.
Интерполяция и экстраполяция
Интерполяция: Когда мы прогнозируем значение внутри домена и диапазона данных
Экстраполяция: Когда мы прогнозируем значение вне домена и диапазона данных
Для температуры как функции щебета в нашей нарисованной выше модели:
Интерполяция произойдет, если мы используем нашу модель для прогнозирования температуры, когда значения щебета находятся в диапазоне от 18,5 до 44.
Экстраполяция произошла бы, если бы мы использовали нашу модель для прогнозирования температуры, когда значения щебета меньше 18.5 или больше 44.
а) Будет ли предсказание температуры, когда сверчки стрекочут 30 раз за 15 секунд, интерполяцией или экстраполяцией? Сделайте прогноз и обсудите, является ли он разумным.
б) Будет ли предсказание количества стрекотаний сверчков под углом 40 градусов интерполяцией или экстраполяцией? Сделайте прогноз и обсудите, является ли он разумным.
С нашими данными по крикету количество чириканий в предоставленных данных варьировалось от 18,5 до 44. Предсказание 30 щебетов за 15 секунд находится внутри области наших данных, так что это будет интерполяция.Используя нашу модель:
градуса.
Судя по имеющимся у нас данным, это значение кажется разумным.
Значения температуры варьировались от 52 до 80,5. Прогнозирование количества щебетов под углом 40 градусов является экстраполяцией, поскольку 40 выходит за пределы наших данных. Используя нашу модель:
Согласно нашей модели, сверчки будут чирикать 8,33 раза за 15 секунд. Хотя это возможно, у нас нет оснований полагать, что наша модель действительна за пределами домена и диапазона.На самом деле, обычно сверчки перестают чирикать при температуре ниже 50 градусов.
Когда наша модель перестает применяться через какой-то момент, ее иногда называют разбивкой модели .
2. Какую температуру вы бы предсказали, если бы насчитали 20 чириканий за 15 секунд?
Подгоночные линии с технологией
Несмотря на то, что визуальный анализ линии работает достаточно хорошо, существуют статистические методы подбора линии к данным, которые минимизируют различия между значениями линии и данных.Этот метод называется регрессией наименьших квадратов и может быть рассчитан многими графическими калькуляторами, программами для работы с электронными таблицами, такими как Excel или Google Docs, статистическими программами и многими веб-калькуляторами.
Найдите линию регрессии методом наименьших квадратов, используя приведенные выше данные о крике крикета.
Используя ранее полученные данные о крике крикета, с помощью технологии мы получаем уравнение:
Обратите внимание, что эта линия очень похожа на уравнение, которое мы «на глазок» нарисовали, но должна лучше соответствовать данным.Обратите также внимание, что использование этого уравнения изменит наш прогноз температуры при прослушивании 30 чириков за 15 секунд с 66 градусов до:
.градуса.
Большинство калькуляторов и компьютерных программ также предоставляют вам коэффициент корреляции , меру того, насколько точно линия соответствует данным.
Коэффициент корреляции
Коэффициент корреляции представляет собой значение между -1 и 1.
r предполагает положительную (возрастающую) связь
предполагает отрицательную (убывающую) связь
Чем ближе значение к 0, тем больше разброс данных
Чем ближе значение к 1 или -1, тем меньше разброс данных
Коэффициент корреляции позволяет легко получить некоторое представление о том, насколько близко к линии падают данные.
Мы должны вычислять коэффициент корреляции только для данных, которые следуют линейному образцу; если данные демонстрируют нелинейный характер, коэффициент корреляции не имеет смысла. Чтобы понять взаимосвязь между значением и графиком данных, вот несколько больших наборов данных с их коэффициентами корреляции:
Примеры значений коэффициента корреляции
Рассчитайте коэффициент корреляции для наших данных по крикету.
Поскольку данные кажутся линейными, мы можем использовать технологию для расчета .Поскольку это значение очень близко к 1, оно предполагает сильную возрастающую линейную зависимость.
Потребление бензина в США неуклонно растет. Данные о потреблении с 1994 по 2004 год показаны ниже. Определите, является ли тренд линейным, и если да, найдите модель для данных. Используйте модель для прогнозирования потребления в 2008 г.
| Год | 94 | 95 | 96 | 97 | 98 | 99 | ’00 | 01 | 02 | 03 | 04 |
| Потребление (млрд галлонов) | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
Для упрощения введена новая входная переменная , представляющая годы с 1994 года.
Используя технологию, коэффициент корреляции был рассчитан равным 0,9965, что свидетельствует об очень сильном возрастающем линейном тренде.
Уравнение регрессии методом наименьших квадратов:
.
Использование этого для прогнозирования потребления в 2008 г. ,
миллиарда галлонов
Модель предсказывает, что в 2008 году будет потреблено 144,244 миллиарда галлонов бензина.
3. Используйте модель, созданную по технологии из примера 7.7F, для прогнозирования потребления газа в 2011 году.Это интерполяция или экстраполяция?
Подумай Ответы
1. а. T = температура, C = чириканье (ответы могут отличаться)
б. Независимый (щебетание), зависимый (температура)
c. Разумный домен, разумный диапазон (ответы могут отличаться)
d. НЕТ, это не один к одному, есть два разных выходных значения для 35 щебетов.
2. 54 градуса по Фаренгейту
3. 150,871 миллиарда галлонов, экстраполяция
Раздел 7.7 упражнений
Вставьте сюда упражнения для повторения
Раздел 7.1: Функции и обозначения функций
- Определение функции
- Вход (независимая переменная)
- Выход (зависимая переменная)
- Обозначение функции
- Описательные переменные
- Функции в словах, таблицах, графиках и формулах
- Проверка вертикальной линии
- Оценка функции при заданном входном значении
- Решение функции с заданным выходным значением
Раздел 7.2: Домен и диапазон
- Определение домена
- Определение диапазона
- Неравенства
- Обозначение интервала
- Набор обозначений построителя
- Домен и диапазон из графов
- Кусочно-определенные функции
Раздел 7.3. Скорость изменения и поведение графиков
- Скорость изменения
- Средняя скорость изменения
- Расчет средней скорости изменения с использованием обозначения функций
- Предельные затраты/выручка/прибыль
- Увеличение/уменьшение
- Локальные максимумы и минимумы (экстремумы)
Раздел 7.4: Линейные функции
- Определение линейной функции
- Структура линейной функции
- Функции возрастания и убывания
- Нахождение вертикального пересечения
- Определение наклона/скорости изменения,
- Интерпретация линейных функций
Раздел 7.5: Графики линейных функций
- Методы построения графиков линейных функций
- Другое название склона = подъем/спуск
- Горизонтальные пересечения
- Горизонтальные линии
- Вертикальные линии
- Параллельные линии
- Перпендикулярные линии
- Пересекающиеся линии
Раздел 7.6: Моделирование с помощью линейных функций
- Процесс решения проблем
1. Определите изменяющиеся величины, а затем тщательно и четко определите описательные переменные для представления этих величин. При необходимости сделайте набросок изображения или определите систему координат.
2. Внимательно прочитайте задачу, чтобы выявить важную информацию. Ищите информацию, дающую значения для переменных или значения для частей функциональной модели, таких как наклон и начальное значение.
3. Внимательно прочитайте задачу, чтобы определить, что мы пытаемся найти, идентифицировать, решить или интерпретировать.
4. Определите путь решения от предоставленной информации к тому, что мы пытаемся найти. Часто это включает в себя проверку и отслеживание единиц, построение таблицы или даже поиск формулы для функции, используемой для моделирования проблемы.
5. При необходимости найдите формулу функции.
6. Решите или оцените, используя формулу, которую вы нашли для желаемых величин.
7. Подумайте, разумен ли ваш ответ в данной ситуации и имеет ли он математический смысл.
8. Четко изложите свой результат, используя соответствующие единицы измерения, и при необходимости отвечайте полными предложениями. - Уравнения затрат, выручки, прибыли
- Спрос и предложение
- Равновесная цена и количество
Раздел 7.
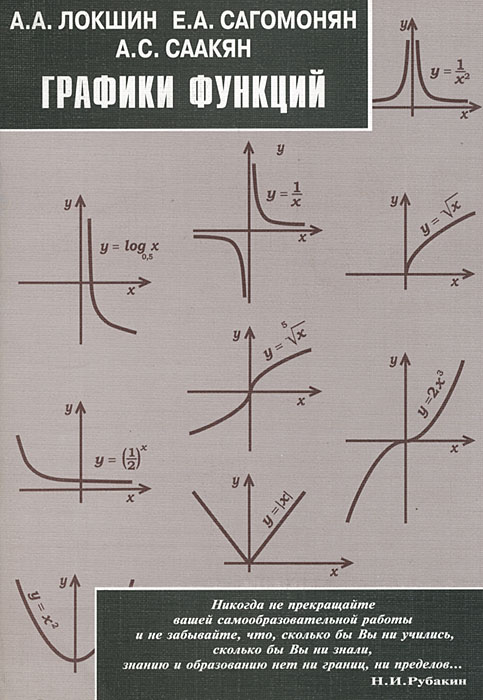 На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
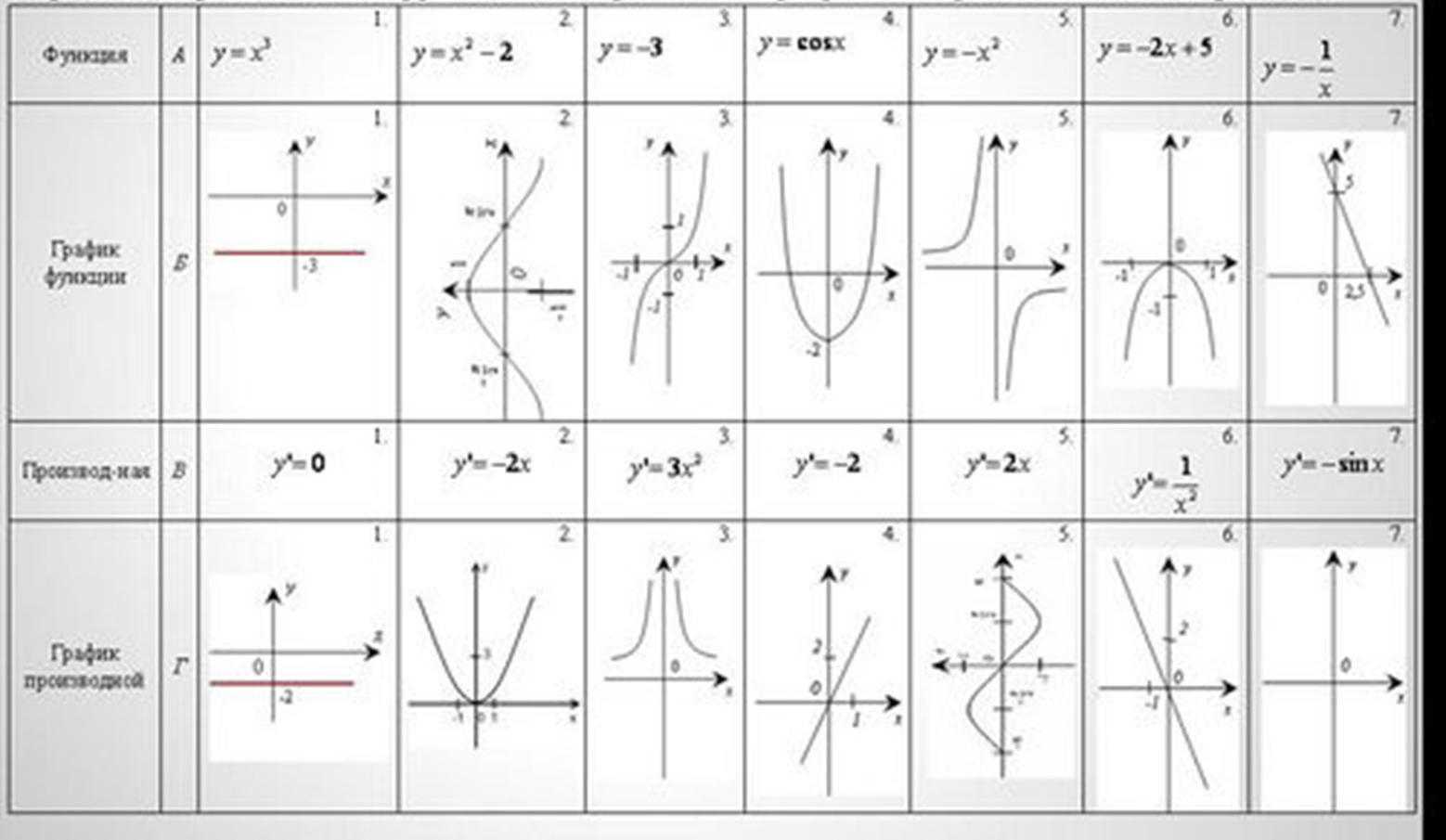
 Чтобы найти ординату точки пересечения с осью Оу, необходимо в функцию вместо переменной x подставить 0 (абсцисса равна 0).
Чтобы найти ординату точки пересечения с осью Оу, необходимо в функцию вместо переменной x подставить 0 (абсцисса равна 0).
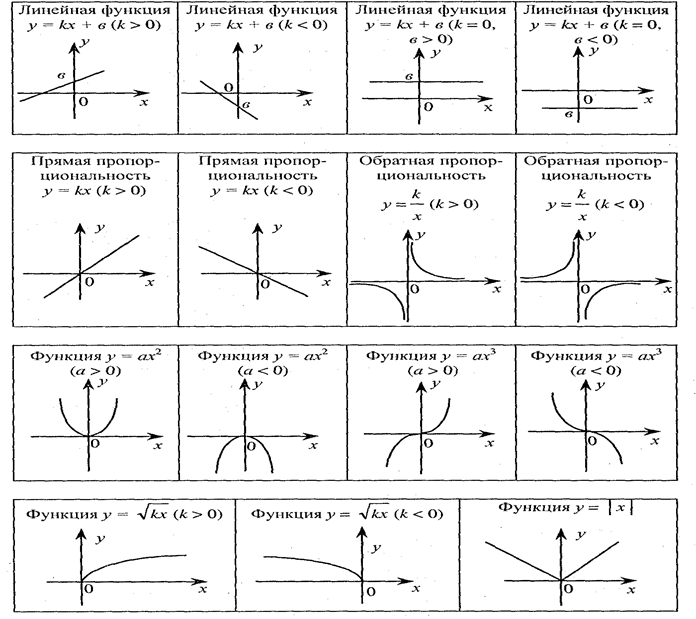
 РАСП.ДИАП
РАСП.ДИАП

 НОРМ
НОРМ

 РАСП
РАСП

 ЕTS.ДОВИНТЕРВАЛ
ЕTS.ДОВИНТЕРВАЛ
 ЛИНЕЙН
ЛИНЕЙН




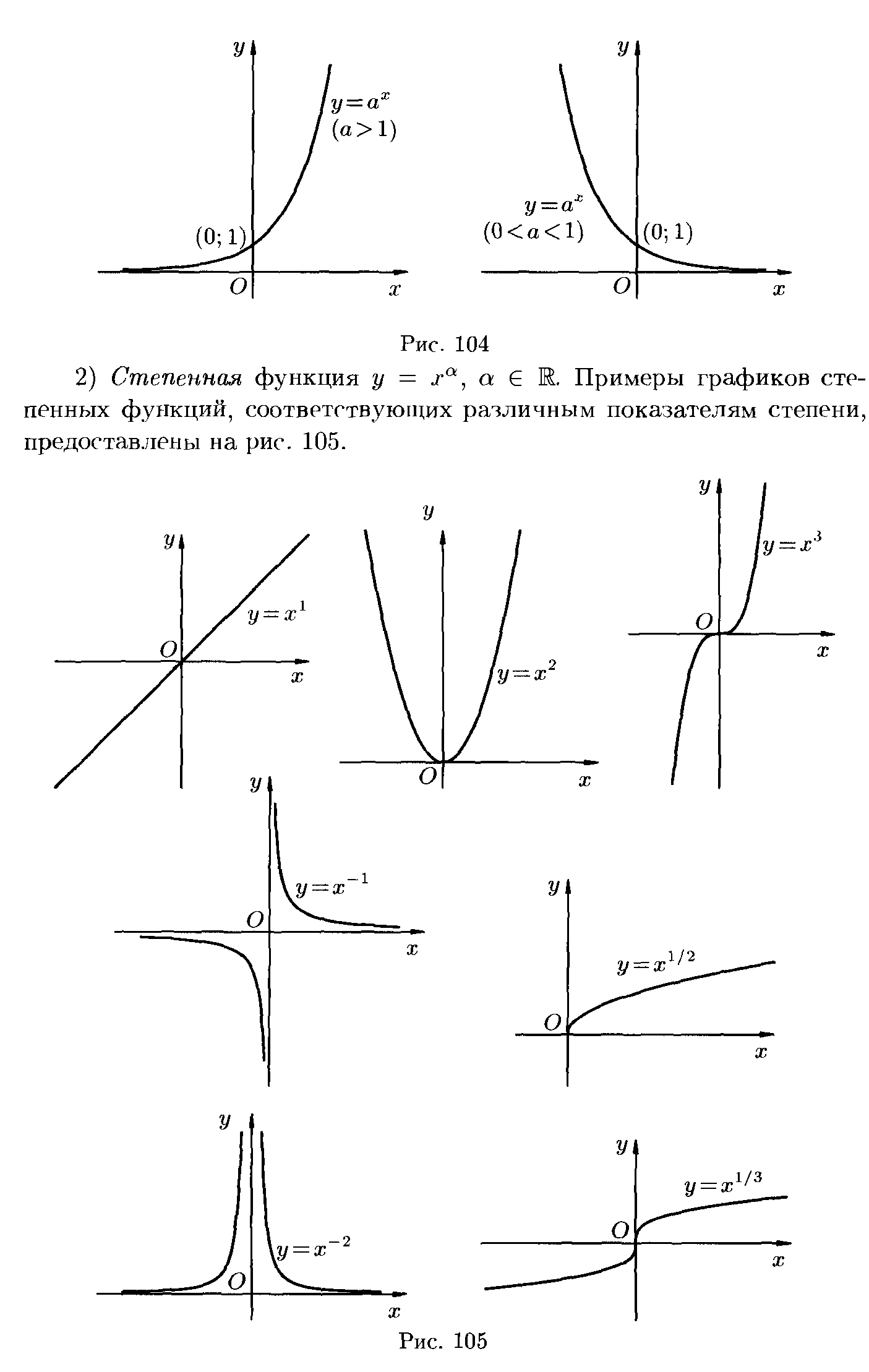
 ИСКЛ
ИСКЛ

 РАСП
РАСП
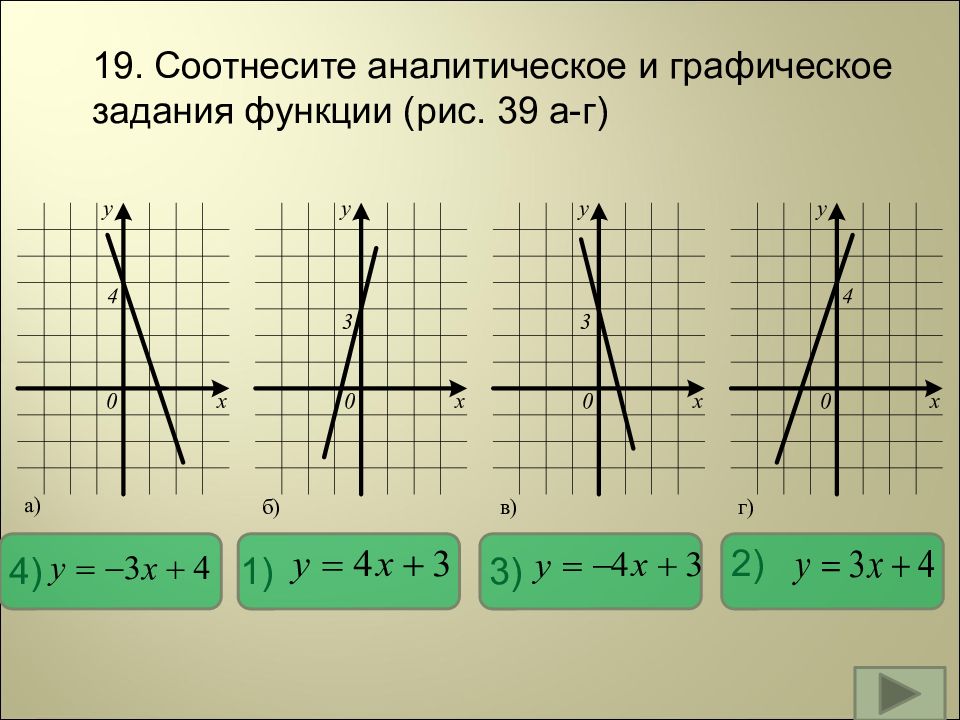

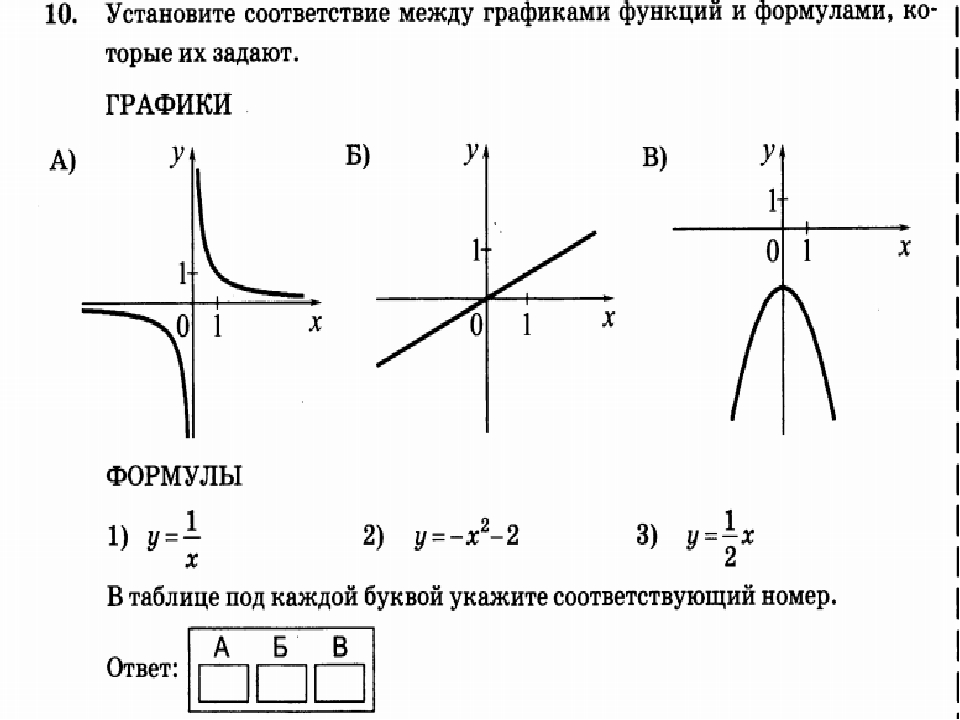

 РАСП.ПХ
РАСП.ПХ


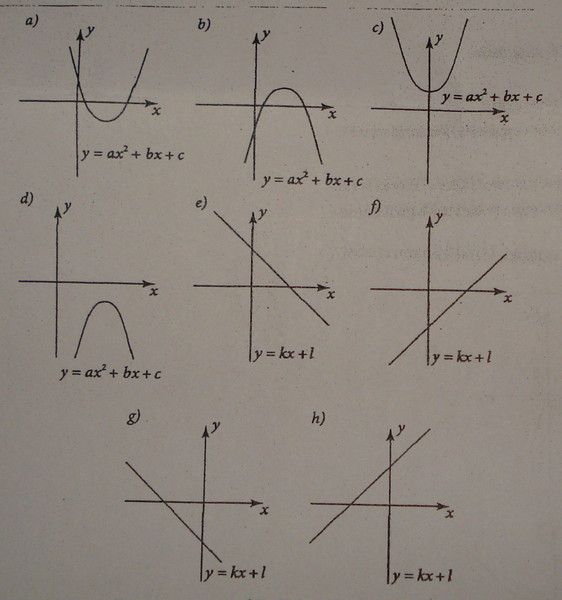 ТЕСТ
ТЕСТ
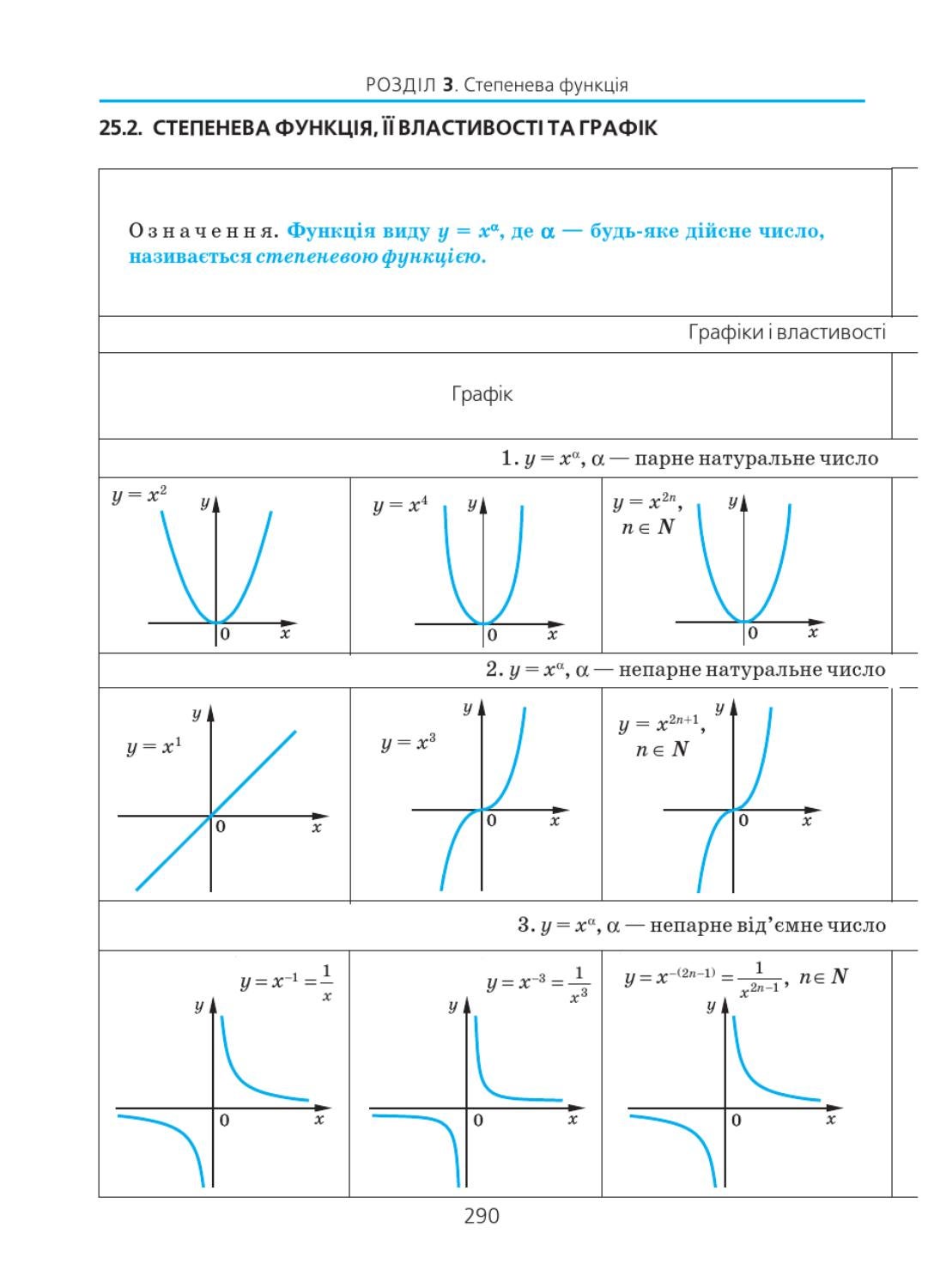 plot([1, 5, 10, 15, 20], [1, 7, 3, 5, 11])
plot([1, 5, 10, 15, 20], [1, 7, 3, 5, 11])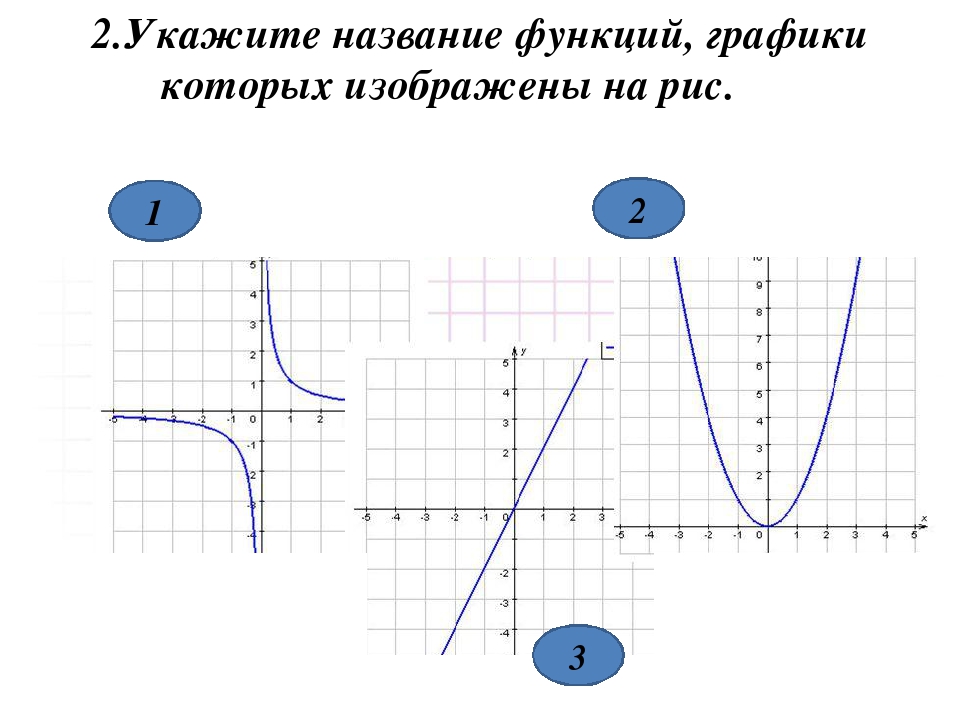
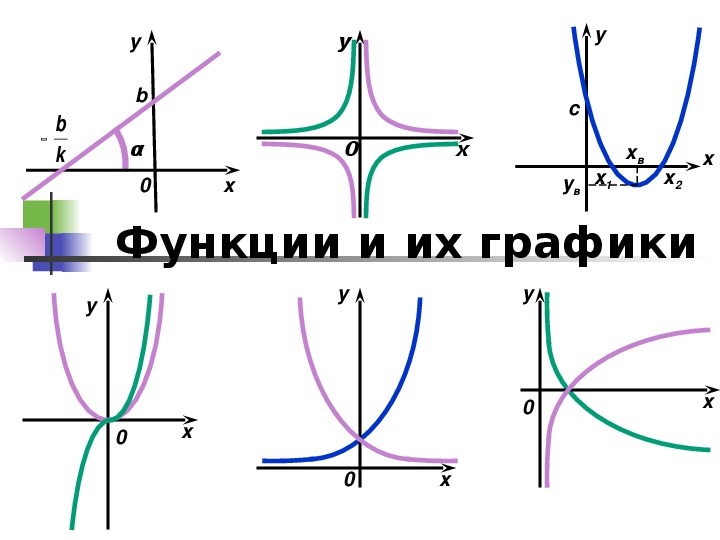 text(1, 1, 'type: Steel')
text(1, 1, 'type: Steel')
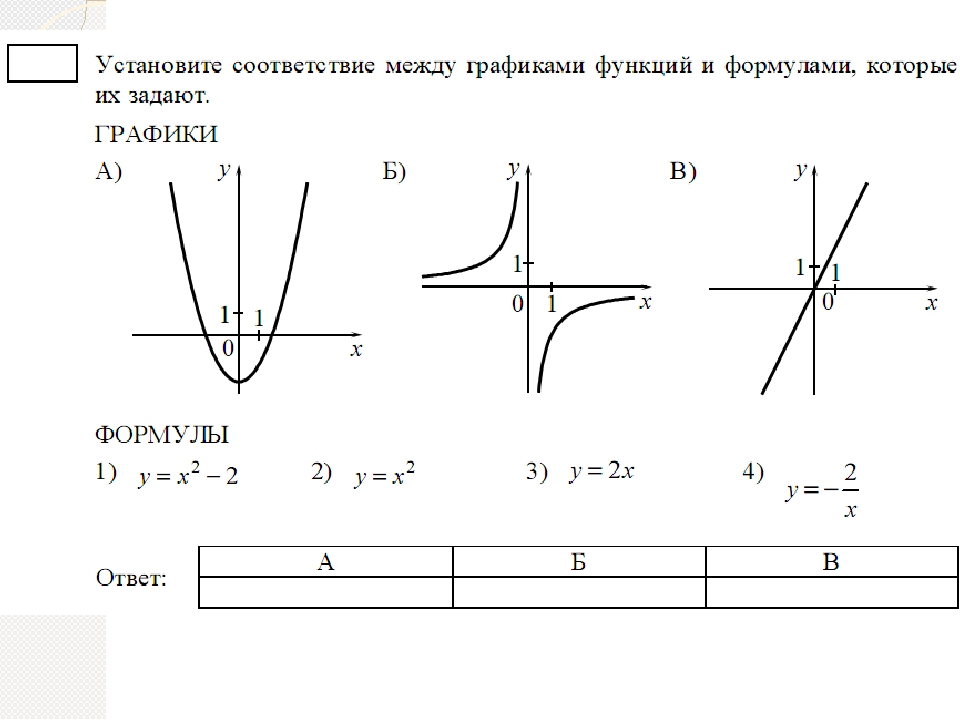
 plot(x, y4, ':')
plot(x, y4, ':') 1 из 2)
1 из 2) 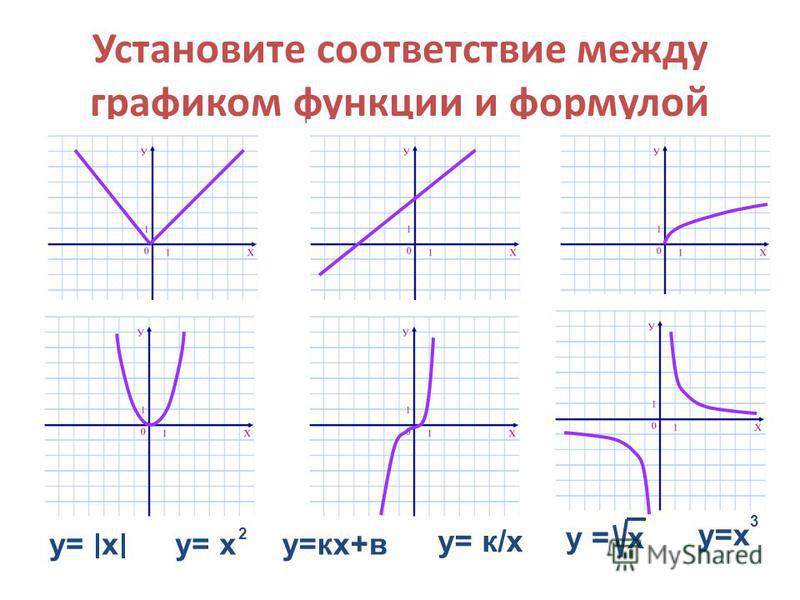 Домен — это то, с чего вы начинаете; в
диапазон — это то, что вы получите.Домен x ;
диапазон и .
(Я объясню больше об определении доменов и диапазонов позже.)
Домен — это то, с чего вы начинаете; в
диапазон — это то, что вы получите.Домен x ;
диапазон и .
(Я объясню больше об определении доменов и диапазонов позже.)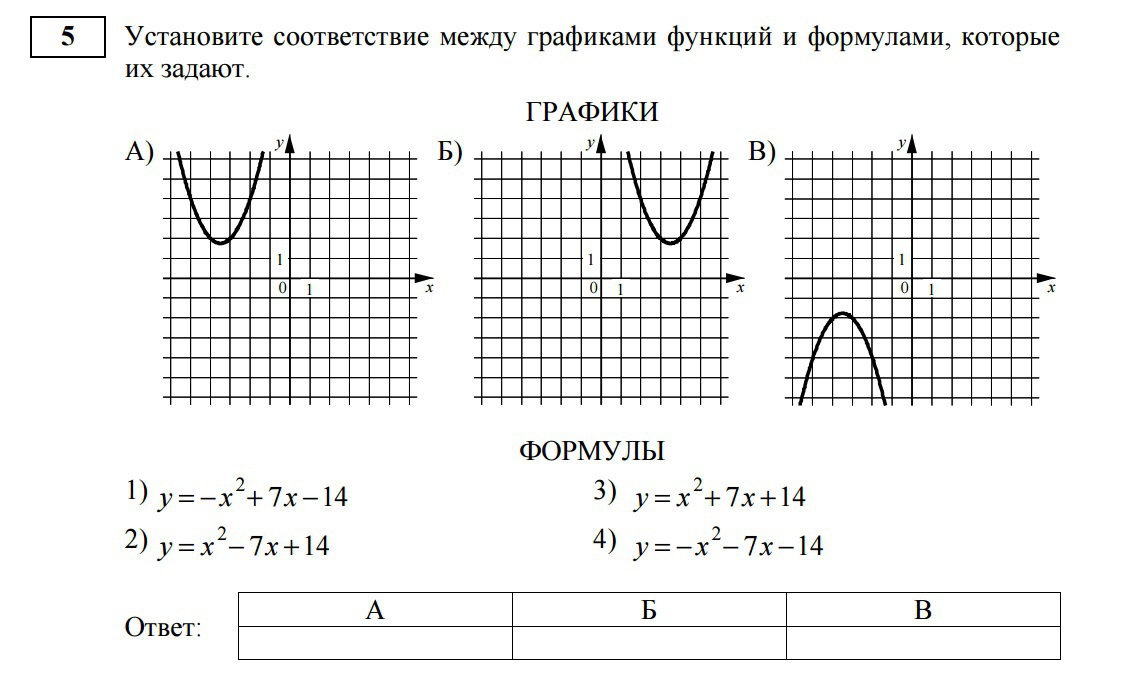 Предположим, что
в коридоре ждет доставщик пиццы. И вся доставка
парень знает, что пицца предназначена для ученика в вашем классе, который
пять футов пять дюймов. А теперь впусти парня. К кому он идет? Что, если никто
пять футов пять дюймов? Что, если в комнате шесть человек, которые
пять-пять? Они все должны платить? Что делать, если вы пять футов пять дюймов?
А что, если у вас закончились наличные? А аллергия на анчоусы? Ты все еще
на крючок? ак! Какой беспорядок!
Предположим, что
в коридоре ждет доставщик пиццы. И вся доставка
парень знает, что пицца предназначена для ученика в вашем классе, который
пять футов пять дюймов. А теперь впусти парня. К кому он идет? Что, если никто
пять футов пять дюймов? Что, если в комнате шесть человек, которые
пять-пять? Они все должны платить? Что делать, если вы пять футов пять дюймов?
А что, если у вас закончились наличные? А аллергия на анчоусы? Ты все еще
на крючок? ак! Какой беспорядок! 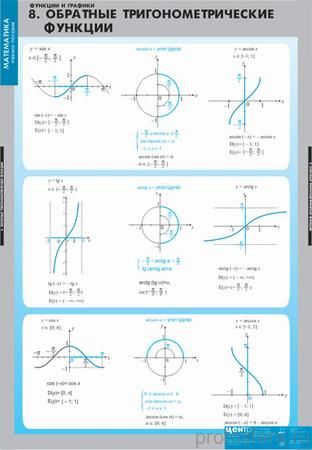 Вы можете сказать, проследив от каждого x до каждого y .
На каждые x приходится только один y ;
из каждого x выходит только одна стрелка.
Вы можете сказать, проследив от каждого x до каждого y .
На каждые x приходится только один y ;
из каждого x выходит только одна стрелка.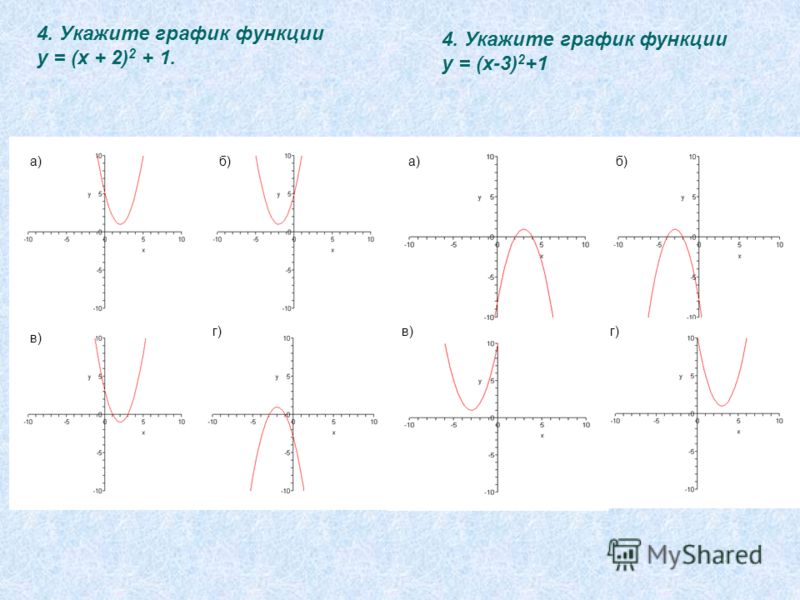 Итак, это отношение,
но это не функция.
Итак, это отношение,
но это не функция.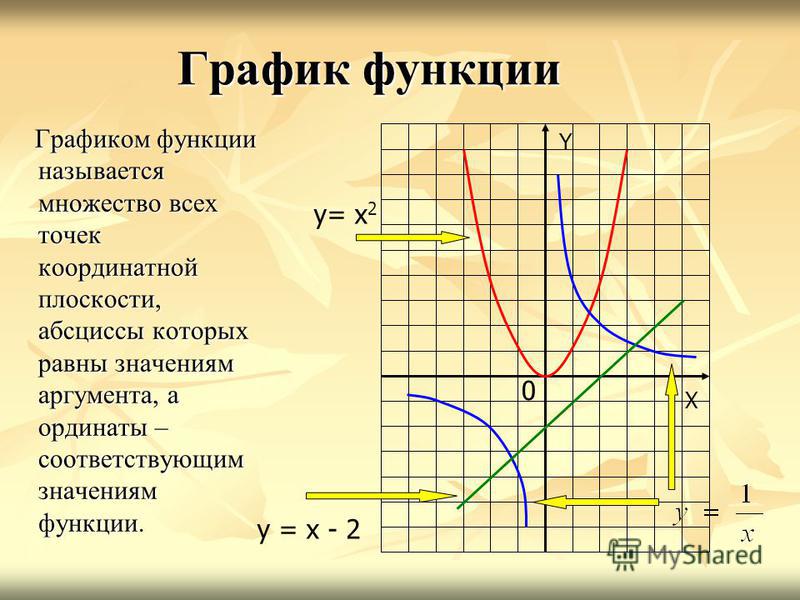 авторское право
© Элизабет Стапель 1999-2011 Все права защищены
авторское право
© Элизабет Стапель 1999-2011 Все права защищены Вот пара примеров:
Вот пара примеров: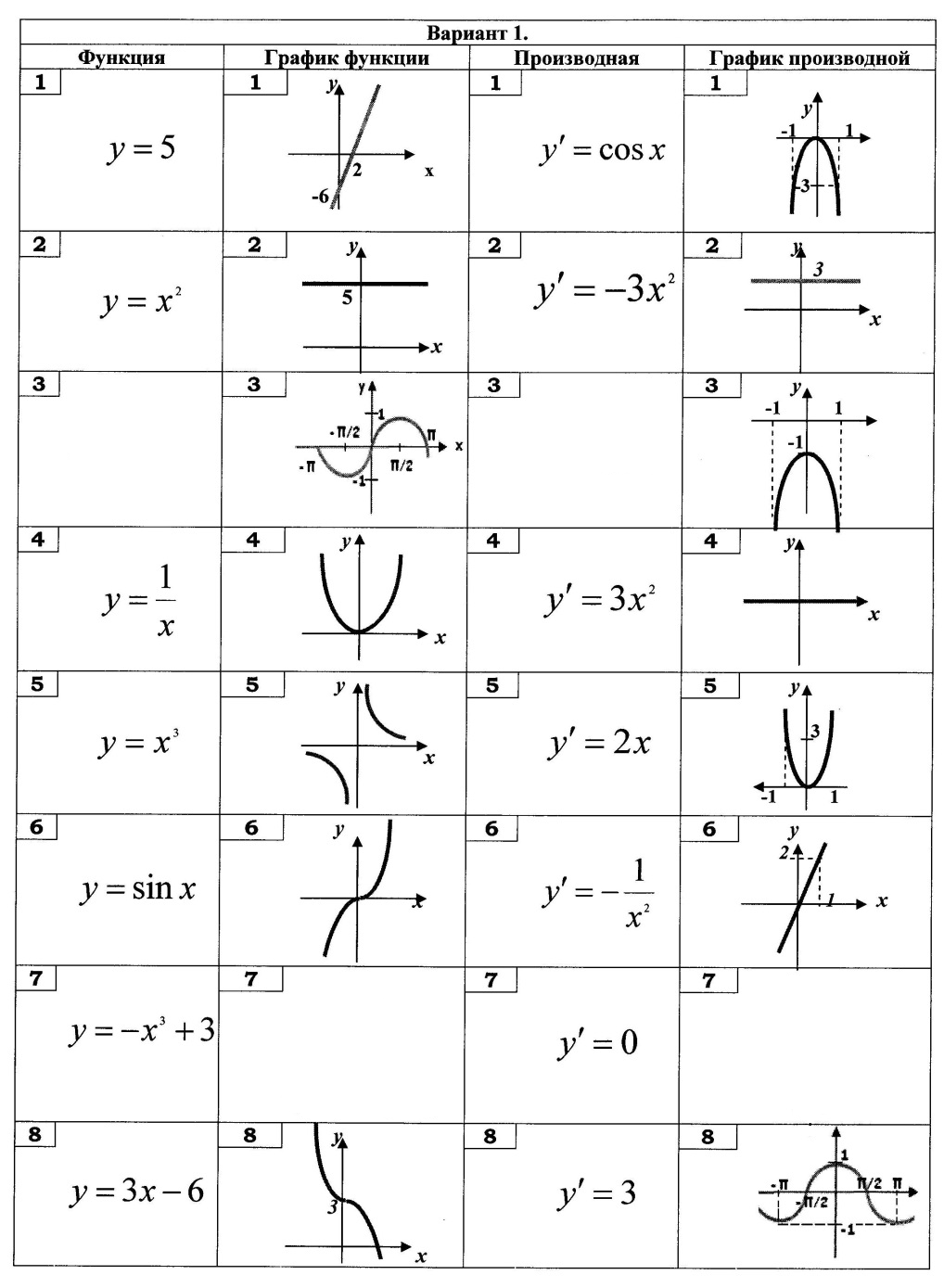 Самый простой способ — решить для « y =», сделать Т-диаграмму ,
выберите некоторые значения для x ,
решить для соответствующих значений y ,
нарисуйте свои точки и соедините точки, бла-бла-бла, бладда.Не только
это полезно для построения графиков, но эта методология дает еще один способ
идентифицирующих функций: если вы можете решить для « y =», то это функция. Другими словами, если вы можете ввести его в
ваш графический калькулятор, то это функция. Калькулятор может только
обрабатывать функции. Например, 2 y + 3 x = 6 — это функция, потому что вы можете найти y :
Самый простой способ — решить для « y =», сделать Т-диаграмму ,
выберите некоторые значения для x ,
решить для соответствующих значений y ,
нарисуйте свои точки и соедините точки, бла-бла-бла, бладда.Не только
это полезно для построения графиков, но эта методология дает еще один способ
идентифицирующих функций: если вы можете решить для « y =», то это функция. Другими словами, если вы можете ввести его в
ваш графический калькулятор, то это функция. Калькулятор может только
обрабатывать функции. Например, 2 y + 3 x = 6 — это функция, потому что вы можете найти y : Вы берете положительный квадрат
корень или минус? Кроме того, где клавиша «±» на вашем
графический калькулятор? Таким образом, в этом случае отношение не является функцией.
(Вы также можете проверить это, используя наше первое определение из приведенного выше. Подумайте
из « x = –1».
Тогда получаем y 2 – 3 = 6,
поэтому y 2 = 9, и тогда y может быть либо -3, либо +3. Тот
то есть, если бы мы построили стрелочную диаграмму, было бы две стрелки, исходящие из x = -1.)
Вы берете положительный квадрат
корень или минус? Кроме того, где клавиша «±» на вашем
графический калькулятор? Таким образом, в этом случае отношение не является функцией.
(Вы также можете проверить это, используя наше первое определение из приведенного выше. Подумайте
из « x = –1».
Тогда получаем y 2 – 3 = 6,
поэтому y 2 = 9, и тогда y может быть либо -3, либо +3. Тот
то есть, если бы мы построили стрелочную диаграмму, было бы две стрелки, исходящие из x = -1.) «Функции против отношений». Пурпурная математика . Доступно с
«Функции против отношений». Пурпурная математика . Доступно с 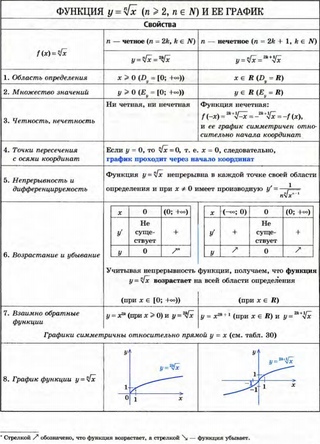

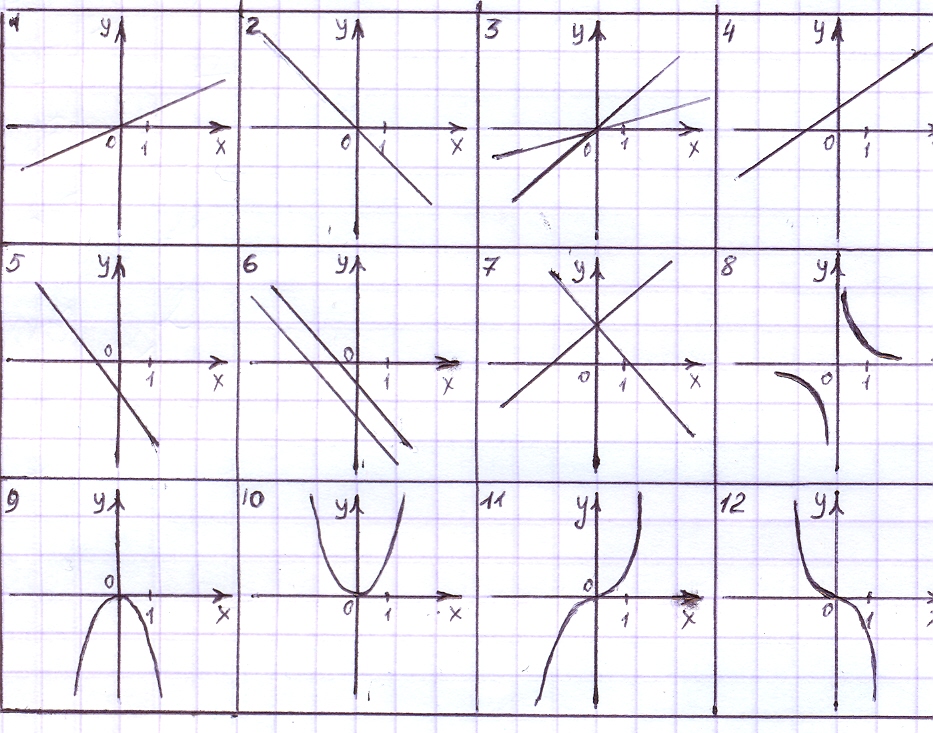
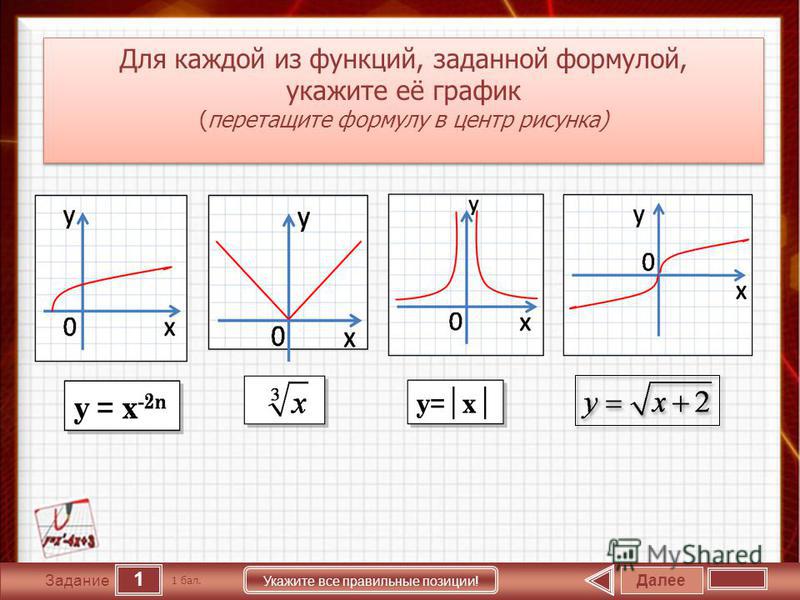
 Четко укажите, что представляет каждая переменная.
Четко укажите, что представляет каждая переменная.
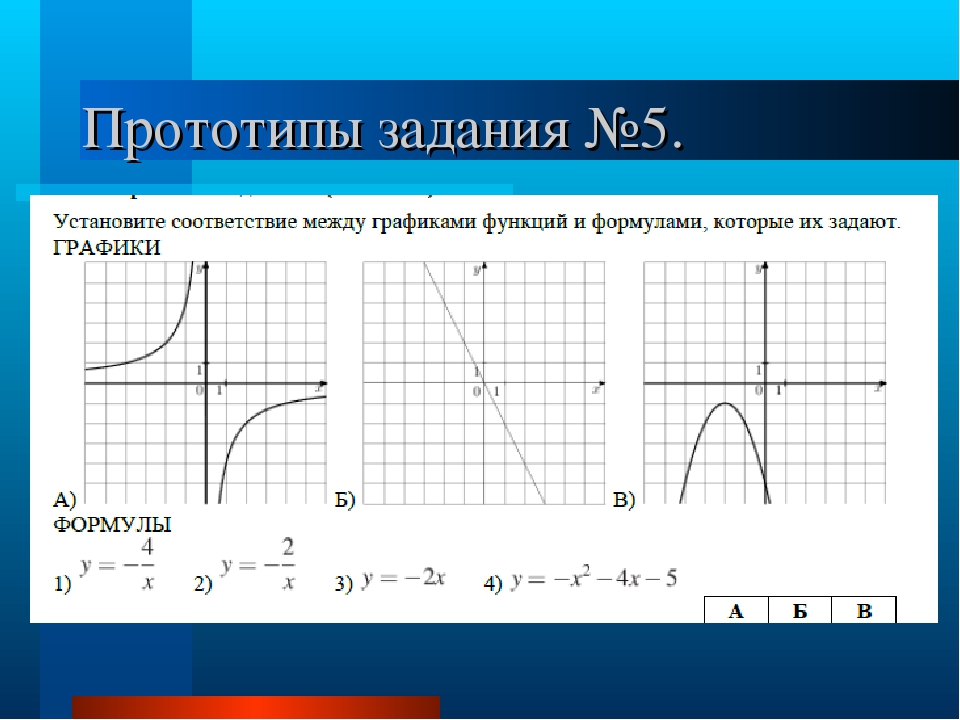

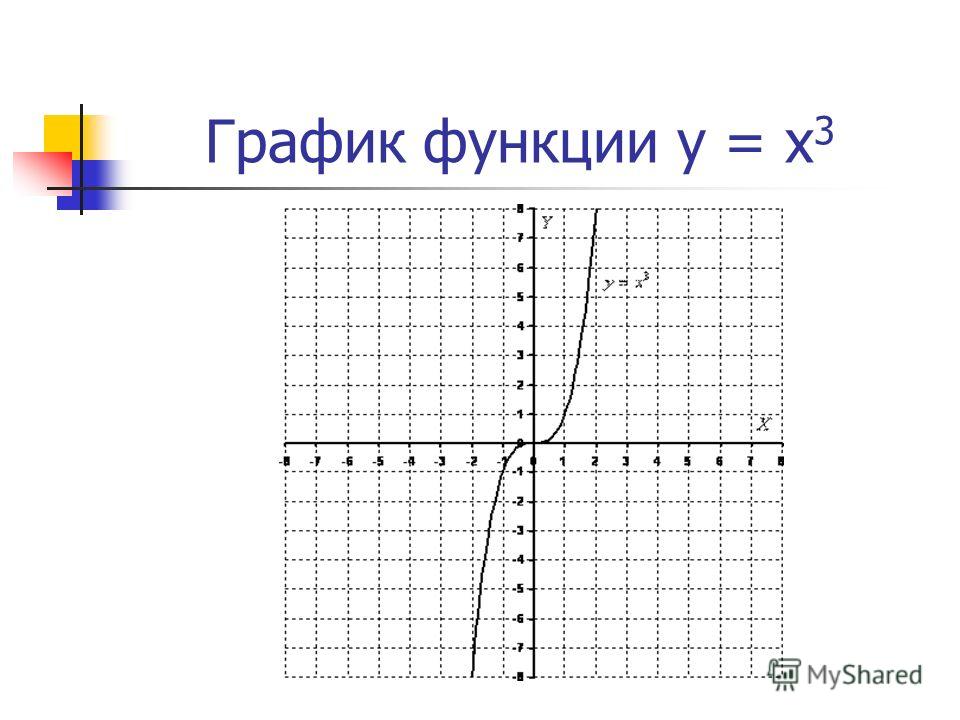 Если это невозможно, объясните, почему.
Если это невозможно, объясните, почему.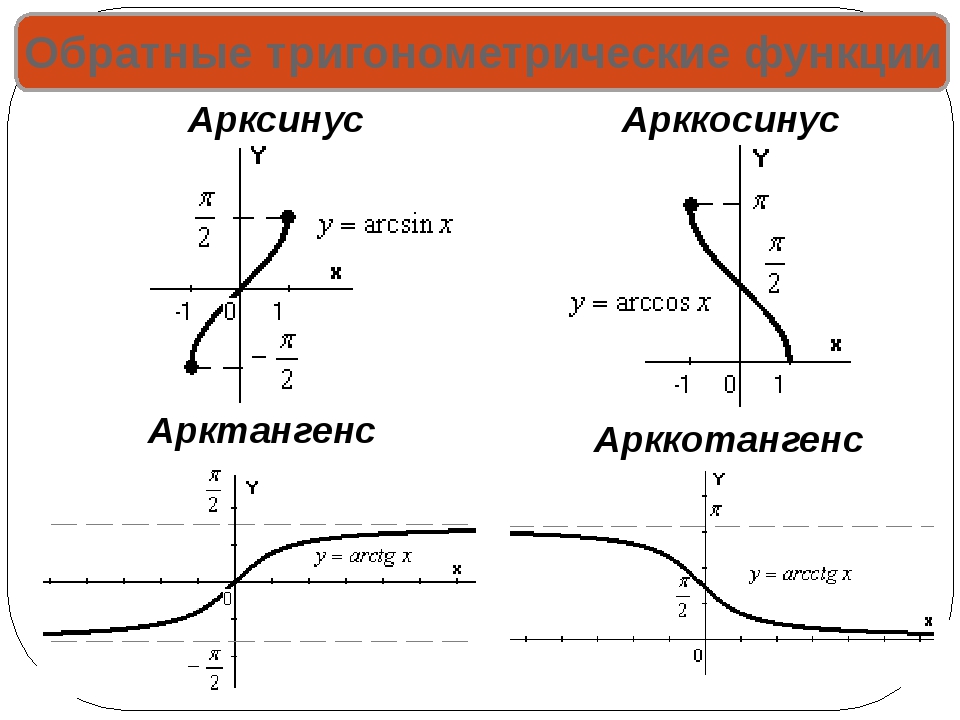

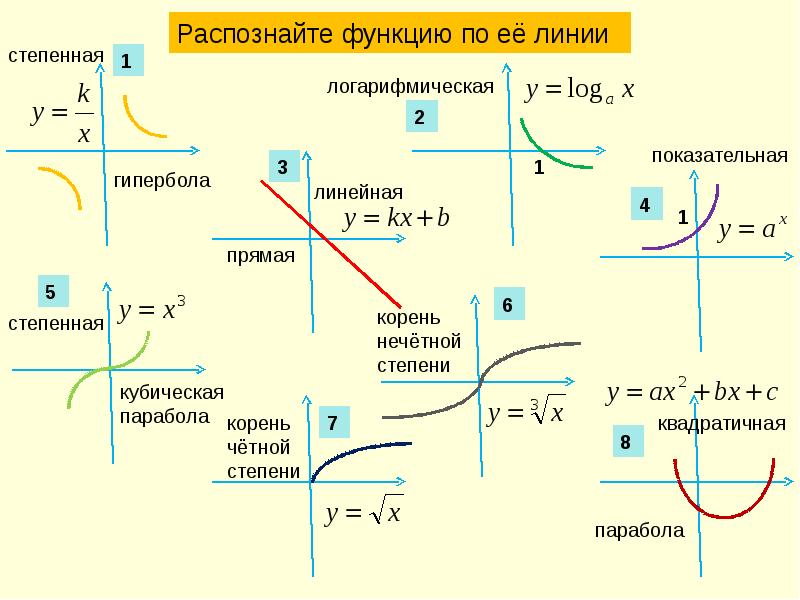 Запишите количество яблок, которые она может купить, как линейную функцию количества груш.Найдите наклон и интерпретируйте свой ответ. График функции.
Запишите количество яблок, которые она может купить, как линейную функцию количества груш.Найдите наклон и интерпретируйте свой ответ. График функции.