Свойства и функции логарифмической функции: Логарифмическая функция, её свойства и график — урок. Алгебра, 11 класс. — Детская игровая комната «Волшебный лес»

Posted on 25.12.197401.02.2022 by alexxlab

Содержание

Свойства показательной и логарифмической функции

Будем рассматривать логарифмические уравнения и неравенства (т.е. уравнения, содержащие логарифм, и неравенства с логарифмом), а также показательные уравнения и неравенства. Будут рассмотрены также уравнения и с логарифмом, и с экспонентой. Но прежде чем рассматривать методы решения логарифмических и показательных уравнений, а также неравенств нужно повторить некоторые свойства логарифма и экспоненты.

При решении уравнений и неравенств с логарифмическими и показательными функциями используют следующие свойства этих функций:

Свойства логарифмической функции:

log_aa = 1 ; log_aa^k= k ; log_a1 = 0
log_amⁿ = nlog_am (при четных значениях n правильнее было бы записать log_amⁿ = nlog_a| m |)
, и в частности
Основание логарифма а должно быть положительным числом, неравным 1; аргумент логарифмической функции n должен быть положительным числом.

Обратите Ваше внимание. Т.е. запись означает, что сначала берется логарифм от числа x по основанию а, а потом он возводится в квадрат. А запись log_ax² означает, что сначала вычисляется квадрат величины x, а потом вычисляется логарифм по основанию а.

Свойства показательной функции:

a¹ = a ; a⁰ = 1
a^{x + y} = a^xa^y
; в частности a^{x + 1} = a * a^y. А также
( a b )^x = a^xb^x. Свойство используется при разложении на множители, например 10^x= 2^x5^x.
, например 9^x= 3^2x= ( 3^x)². Свойство часто используется при заменах переменных.
; и в частности a^x = e^xlna.
Основание показательной функции a должно быть положительным; значение показательной функции всегда положительно.

Обратите Ваше внимание. К суммам и разностям двух показательных функций всегда можно применять формулы разложения на множители (разность квадратов, разность кубов, сумму кубов и т.д.)

Методическая разработка «Логарифмическая функция. Свойства и график»

Министерство образования и молодежной политики Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

«Чебоксарский техникум транспортных и строительных технологий»

(ГАПОУ «Чебоксарский техникум ТрансСтройТех»

Минобразования Чувашии)

Методическая разработка

ОДП. 01 Математика

«Логарифмическая функция. Свойства и график»

Разработал:

преподаватель математики

М.В. Дмитриева

Чебоксары – 2016

Оглавление

Пояснительная записка……………………………………………………………………………………………….….…3

Теоретическое обоснование и методическая реализация…………….……………………………..4-10

Заключение…………………………………………………………………………………………………………………….11

Список использованной и рекомендованной литературы………………………………………..………12

Приложения………………………………………………………………………………………………………….…………13

Пояснительная записка

Методическая разработка модуля занятия по дисциплине «Математика» на тему «Логарифмическая функция. Свойства и график» из раздела «Корни, степени и логарифмы» составлена на основе Рабочей программы по математике и календарно-тематического плана. Темы занятия взаимосвязаны содержанием, основными положениями.

Цель изучения данной темы узнать понятие логарифмической функции, изучить её основные свойства, научиться строить график логарифмической функции и научиться видеть логарифмическую спираль в окружающем нас мире.

Программный материал данного занятия базируется на знаниях математики. Методическая разработка модуля занятия составлена для проведения теоретических занятий по теме: «Логарифмическая функция. Свойства и график» –1 час. В процессе практического занятия студенты закрепляют полученные знания: определения функций, их свойства и графики, преобразования графиков, непрерывные и периодические функции, обратные функции и их графики, логарифмические функции.

Методическая разработка предназначена для оказания методической помощи студентам при изучении модуля занятий по теме «Логарифмическая функция. Свойства и график». В качестве внеаудиторной самостоятельной работы студенты могут подготовить с помощью дополнительных источников сообщение на тему, «Логарифмы и их применение в природе и технике», кроссворды и ребусы. Учебные знания и профессиональные компетенции, полученные при изучении темы «Логарифмические функции, их свойства и графики» будут применены при изучении следующих разделов: «Уравнения и неравенства» и «Начала математического анализа».

Дидактическая структура урока:

Тема: «Логарифмическая функция. Свойства и график»

Тип занятия: Комбинированный.

Цели занятия:

Образовательные – формирование знаний в усвоении понятия логарифмической функции, свойства логарифмической функции; применять графики при решении задач.

Развивающие – развитие мыслительных операций посредством конкретизации, развитие зрительной памяти, потребности к самообразованию, способствовать развитию познавательных процессов.

Воспитательные – воспитание познавательной активности, чувства ответственности, уважения друг к другу, взаимопонимания, уверенности в себе; воспитание культуры общения; воспитание сознательного отношения и заинтересованности к учебе.

Средства обучения:

— методическая разработка по теме;

— персональный компьютер;

— учебник Ш.А Алимов«Алгебра и начала анализа» 10-11 класс. Издательство «Просвещение».

Внутрипредметные связи: показательная функция и логарифмическая функция.

Межпредметные связи: алгебра и математический анализ.

Студент должен знать:

определение логарифмической функции;

свойства логарифмической функции;

график логарифмической функции.

Студент должен уметь:

выполнять преобразования выражений, содержащих логарифмы;

находить логарифм числа, применять свойства логарифмов при логарифмировании;

определять положение точки на графике по ее координатам и наоборот;

применять свойства логарифмической функции при построении графиков;

Выполнять преобразования графиков.

План занятия

1. Организационный момент (1 мин).

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся (1 мин).

3. Этап актуализации опорных знаний и умений (3 мин).

4. Проверка домашнего задания (2 мин).

5. Этап усвоения новых знаний (10 мин).

6. Этап закрепления новых знаний (15 мин).

7. Контроль усвоенного на уроке материала (10 мин).

8. Подведение итогов (2 мин).

9. Этап информирования учащихся о домашнем задании (1 мин).

Ход урока:

1. Организационный момент.

Включает в себя приветствие учителем класса, подготовку помещения к уроку, проверку отсутствующих.

2. Постановка целей и задач урока.

Сегодня мы с вами поговорим о понятии логарифмической функции, нарисуем график функции, изучим его свойства.

3. Этап актуализации опорных знаний и умений.

Проводится в форме фронтальной работы с классом.

Какую последнюю функцию мы изучали? Схематично изобразить на доске.

Дайте определение показательной функции.

Что является корнем показательного уравнения?

Дайте определение логарифма?

Назовите свойства логарифмов?

Назовите основное логарифмическое тождество?

4. Проверка домашнего задания.

Студенты открывают тетради и показывают решенные упражнения. Задают вопросы, которые возникли при выполнении домашнего задания.

5. Этап усвоения новых знаний.

Учитель: Открывайте тетради, записывайте сегодняшнее число и тему урока «Логарифмическая функция, ее свойства и график».

Учитель:

Определение: Логарифмической функцией называется функция вида

, где – заданное число, .

Рассмотрим построение графика данной функции на конкретном примере.

Построим графики функций и .

Примечание 1: Логарифмическая функция является обратной по отношению к показательной функции , где . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 1).

Рис. 1

Опираясь на определение логарифма и вид графиков, выявим свойства логарифмической функции:

1) Область определения: , т.к. по определению логарифма х>0.

2) Область значений функции: .

3) Логарифм единицы равен нулю, логарифм основания равен единице: , .

4) Функция , возрастает в промежутке (рис. 1).

5) Функция , убывают в промежутке (рис. 1).

6) Промежутки знакопостоянства:

Если , то при ; при ;

Если , то при при ;

Примечание 2: График любой логарифмической функции всегда проходит через точку (1; 0).

Теорема: Если , где , то .

6. Этап закрепления новых знаний.

Учитель: Решаем задания № 318 –№322 (нечётные) (§18Алимов Ш.А. «Алгебра и начала анализа» 10-11 класс).

№ 318

1) т.к функция возрастает.

3) , т.к функция убывает.

№ 319

1) , т.к и .

3) , т.к и .

№ 320

1) , т.к , , то .

3) , т.к 10> 1, , то .

№ 321

1)убывает

3)возрастает.

№ 322

7. Подведение итогов.

—Сегодня мы с вами хорошо поработали на уроке! Что нового вы узнали сегодня на уроке?

(Новый вид функции — логарифмическая функция)

— Сформулируйте определение логарифмической функции.

(Функцию y = logax, (a > 0, a ≠ 1) называют логарифмической функцией)

-Молодцы! Верно! Назовите свойства логарифмической функции.

(область определения функции, множество значений функции, монотонность, знакопостоянства)

8. Контроль усвоенного на уроке материала.

Учитель: Выясним, насколько хорошо вы усвоили тему «Логарифмическая функция. Свойства и график». Для этого напишем проверочную работу (Приложение 1). Работа состоит из четырех заданий, которые необходимо решить, применяя свойства логарифмической функции. На выполнение проверочной работы вам дается 10 минут.

9. Этап информирования учащихся о домашнем задании.

Запись на доске и в дневниках: Алимов Ш.А. «Алгебра и начала анализа» 10-11 класс. §18 №318 — №322 (четные)

Заключение

В ходе использования методической разработки мы добились всех поставленных целей и задач.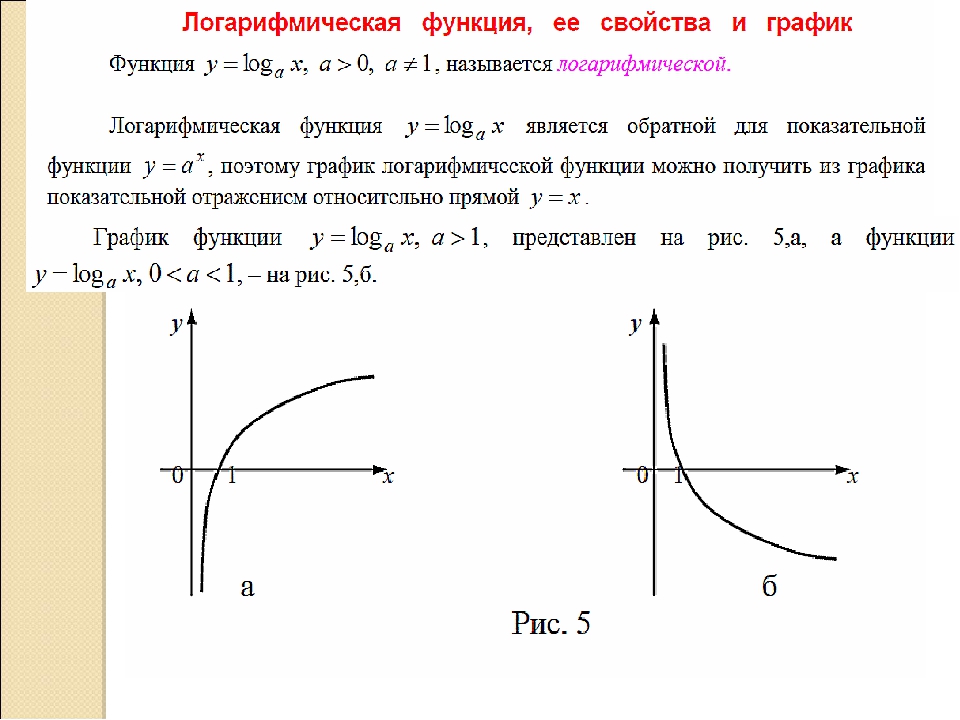 В данной методической разработке были рассмотрены все свойства логарифмической функции, благодаря которым студенты научились выполнять преобразования выражений, содержащих логарифмы и строить графики логарифмических функций. Выполнение практических задач способствует закреплению изученного материала, а контроль проверки знаний и умений поможет преподавателям и студентам выяснить насколько эффективной была их работа на уроке. Методическая разработка позволяет студентам получить интересную и познавательную информацию по теме, обобщить и систематизировать знания, применять свойства логарифмов и логарифмической функции при решении различных логарифмических уравнений и неравенств.

Список использованной и рекомендованной литературы

Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Фёдорова Н. Е., Шабунин М. И. под научным руководством академика Тихонова А. Н. Алгебра и начала математического анализа 10 — 11кл. – М. Просвещение, 2011.

Никольский С. М., Потапов М. К., Решетников Н. Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2006.

Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2005.

Лисичкин В. Т. Математика в задачах с решениями : учеб.пособие / В. Т. Лисичкин, И. Л. Соловейчик. — 3-е изд., стер. — СПб. [и др.] : Лань, 2011 (Архангельск). — 464 с.

Интернет-ресурсы:

http://school- collection.edu.ru – Электронный учебник «Математика в

школе, XXI век».

http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.

www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов.

Приложения

Вариант 1.

Вариант 2.

Критерии оценки:

Отметка «3» (удовлетворительно) ставится за любые 2 верно выполненных примера.

Отметка «4» (хорошо) ставится при верном выполнении любых 3 примеров.

Отметка «5» (отлично) ставится за все 4 верно выполненных примеров.

Логарифмическая функция: основные свойства и графики

Логарифмическая функция

Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а.

Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) — данная запись будет обозначать логарифм b по основанию а.

Основные свойства логарифмической функции:

1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.

2. Областью значения логарифмической функции будет являться все множество вещественных чисел.

3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a

4. График логарифмической функции всегда проходит через точку (1;0).

5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.

6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:

На следующем рисунке представлен график убывающей логарифмической функции — (0<a<1):

7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.

8. Функция не имеет точек максимума и минимума.

Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.

Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций.

Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 — 5*x).

Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+.

Тогда заданная функция будет определена для таких х, при которых 4 — 5*x>0. Решаем это неравенство и получаем x<0.8.

Таким образом, получается, что областью определения функции f(x) = log8(4 — 5*x) будет являться промежуток (-∞;0.8)

Логарифмическая функция: основные свойства и графики

«Логарифмическая функция, её свойства и график»

Практическое занятие № 66

«Логарифмическая функция, ее свойства и график»

Теоретический материал

Определение.

Логарифмом числа b>0 по основанию a>0, a ≠ 1 называется показатель степени, в которую надо возвести число a, чтобы получить число b.

Основные свойства логарифмов:

1⁰. log_a1=0, а>0, a ≠ 1;

2⁰. log_aа=1, а>0, a ≠ 1.

3°. log_а ху = log_ах + log_ау.

4°. log_а х/у = log_ах — log_ау.

5°. log_ах ^p = p · log_ах, для любого действительного p.

Основное логарифмическое тождество: а

log a b = b

Определение: Функцию, заданную формулой у=log_ax называют логарифмической с основанием а (а>0, а 1)

Основные свойства логарифмической функции:

1. Областью определения является все множество положительных действительных чисел.

2. Областью значения является все множество действительных чисел.

3. График логарифмической функции всегда проходит через точку (1;0).

4. Логарифмическая функция возрастает при а>1, и убывает при 0<а<1.

5. Функция не является четной или нечетной.

6. Функция не имеет точек максимума и минимума, в области определения непрерывна.

Задания практической работы

Задание №1 Построить графики функции у=log₂х, у=logх и описать их свойства

у=log₂х

Доп. точки:

х			1	2	4	8
у

1. D(f)=_______________________

2. E(f)= ______________________

3. Нули функции(точка пересечения с осью Ох)_________________________

4. Возрастание/убывание_____________________________________________

у=logх

Доп. точки:

х			1	2	4	8
у

1.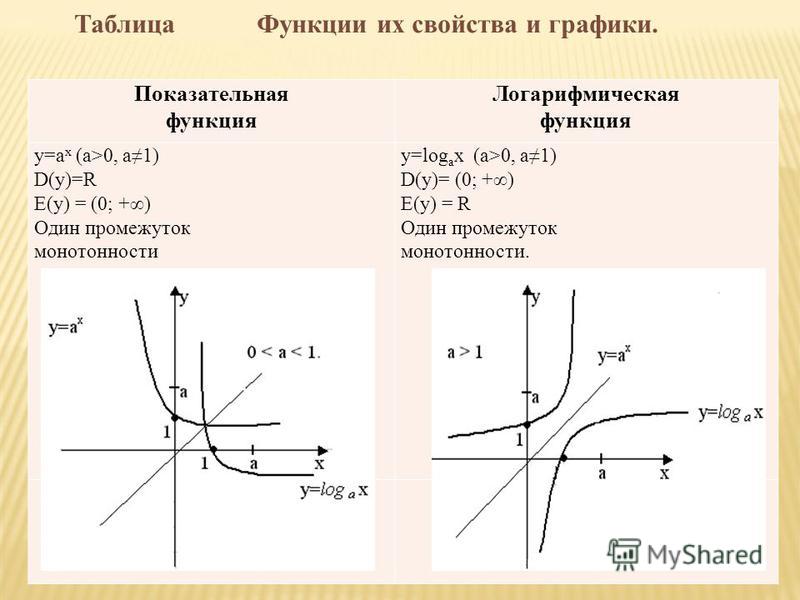 D(f)=_______________________

2. E(f)= ______________________

3. Нули функции(точка пересечения с осью Ох)_________________________

4. Возрастание/убывание_____________________________________________

Задание №2. Привести 3 примера возрастающей логарифмической функции

1._______________________________

2._______________________________

3._______________________________

Задание №3. Привести 3 примера убывающей логарифмической функции

1._______________________________

2._______________________________

3._______________________________

Логарифмические функции

Логарифмические функции обратны экспоненциальным функциям, и любая экспоненциальная функция может быть выражена в логарифмической форме. Точно так же все логарифмические функции можно переписать в экспоненциальной форме. Логарифмы действительно полезны, поскольку позволяют нам работать с очень большими числами, манипулируя числами гораздо более удобного размера.

Если бы x = 2 ^y нужно было решить для y , чтобы это можно было записать в функциональной форме, необходимо было бы ввести новое слово или символ.Если x = 2 ^y , то y = (степень по основанию 2) равно x . Слово логарифм, сокращенно log, введено, чтобы удовлетворить эту потребность.

y = (степень по основанию 2) равно x

Это уравнение переписывается как y = log ₂ x .

Это читается как « y равно логарифму x по основанию 2» или « y равно логарифму x по основанию 2».

Логарифмическая функция является функцией вида

, который читается как « y равно логарифму x , основание b » или « y равно логарифму, основание b , x ».

В обеих формах x > 0 и b > 0, b ≠ 1. На y ограничений нет.

Пример 1

Перепишите каждое показательное уравнение в его эквивалентной логарифмической форме.Решения следуют.

5 ² = 25

Пример 2

Перепишите каждое логарифмическое уравнение в эквивалентной ему экспоненциальной форме. Решения следуют.

журнал ₆ 36 = 2
бревно _а м = р

Пример 3

Решите следующие уравнения, если это возможно.

логарифм ₇ 49 = у
журнал _у 8 = 3
log ₄ у = –2
log ₃ (–9) = г

Это невозможно, так как 3 ^y всегда будет положительным результатом. Напомним, что логарифмы имеют только положительный домен; следовательно, -9 не находится в области логарифма.

При работе с логарифмами чаще всего используются основания 10 и e . (Буква e представляет собой иррациональное число, которое имеет множество применений в математике и естественных науках. Значение e приблизительно равно 2,718281828…) Логарифмическая база 10, log ₁₀ известна как десятичный логарифм и записывается как журнал, с не записанной базой, но понятой как 10.Логарифмическая база e , log _e известна как натуральный логарифм и записывается как пер.

Пример 5

Найдите следующие логарифмы.

журнал 100
журнал 10 000
журнал 0,1
п д
п д ²

1.

5 Экспоненциальные и логарифмические функции — Исчисление Том 1

Цели обучения

Определите форму экспоненциальной функции.
Объясните разницу между графиками и .
Осознайте значение числа.
Определите вид логарифмической функции.
Объясните связь между экспоненциальной и логарифмической функциями.
Опишите, как вычислить логарифм по другому основанию.
Определите гиперболические функции, их графики и основные тождества.

В этом разделе мы исследуем экспоненциальные и логарифмические функции. Мы используем свойства этих функций для решения уравнений, содержащих экспоненциальные или логарифмические члены, и изучаем значение и важность числа . Мы также определяем гиперболические и обратные гиперболические функции, которые включают комбинации экспоненциальных и логарифмических функций. (Обратите внимание, что мы представляем альтернативные определения экспоненциальных и логарифмических функций в главе «Приложения интегрирований» и доказываем, что функции обладают одинаковыми свойствами при любом определении. )

Экспоненциальные функции встречаются во многих приложениях. Одним из распространенных примеров является рост населения.

Например, если популяция начинается с особей, а затем растет с годовой скоростью , ее популяция через 1 год составляет

Его население через 2 года составляет

человек. .

В целом его население по прошествии лет составляет

человек. ,

, которая является экспоненциальной функцией. В более общем смысле, любая функция вида , где , является экспоненциальной функцией с основанием и показателем степени .Экспоненциальные функции имеют постоянные основания и переменные показатели. Обратите внимание, что функция вида для некоторой константы является не экспоненциальной, а степенной функцией.

Чтобы увидеть разницу между экспоненциальной функцией и степенной функцией, мы сравним функции и . На (рис.) мы видим, что оба и стремятся к бесконечности как . В конце концов, однако, становится больше и растет быстрее, чем . В обратном направлении, как , тогда как . Линия является горизонтальной асимптотой для .

На (Рисунок) мы построили оба графика и, чтобы показать, чем эти графики отличаются.

Вычисление экспоненциальных функций

Напомним свойства показателей: Если положительное целое число, то мы определяем (с факторами ). Если — отрицательное целое, то для некоторого положительного целого числа, и мы определяем. Кроме того, определяется как 1. Если рациональное число, то , где и целые числа и . Например, . Однако как определить, является ли число иррациональным? Например, что мы подразумеваем под ? Это слишком сложный вопрос, чтобы мы могли ответить на него прямо сейчас; однако мы можем сделать приближение.На (Рисунок) мы перечисляем некоторые рациональные числа, приближающиеся к , а также представлены значения для каждого рационального числа. Мы утверждаем, что если мы выбираем рациональные числа все ближе и ближе к , значения становятся все ближе и ближе к некоторому числу . Мы определяем это число как .

Значения для списка рациональных чисел, приближающиеся к
	1,4	1,41	1,414	1.4142	1.41421	1.414213
	2,639	2,65737	2,66475	2,665119	2,665138	2,665143

Бактериальный рост

Решение

Количество бактерий через 6 часов определяется бактериями. Количество бактерий через 10 часов определяется бактериями. Количество бактерий через 24 часа определяется бактериями.

Учитывая экспоненциальную функцию, оценить и .

Решение

Особый тип экспоненциальной функции часто используется в реальных приложениях. Чтобы описать это, рассмотрим следующий пример экспоненциального роста, который возникает из-за начисления процентов на сберегательный счет. Предположим, человек вкладывает доллары на сберегательный счет с годовой процентной ставкой, начисляемой ежегодно. Сумма денег через 1 год

Сумма денег через 2 года

В более общем случае сумма по прошествии лет составляет

. .

Если деньги начисляются 2 раза в год, сумма денег через полгода будет

Сумма денег через 1 год

Спустя годы сумма денег на счету

В более общем случае, если деньги начисляются несколько раз в год, сумма денег на счете по прошествии нескольких лет определяется функцией

Что происходит как ? Чтобы ответить на этот вопрос, допустим и напишем

и изучить поведение as с помощью таблицы значений ((Рисунок)).

The first row is labeled “m” and has the values “10; 100; 1000; 10,000; 100,000; 1,000,000”. The second row is labeled “(1 + (1/m)) to the power of m” and has the values “2.5937; 2.7048; 2.71692; 2.71815; 2.718268; 2.718280”.»>

Значения как
	10	100	1000	10 000	100 000	1 000 000
	2,5937	2,7048	2,71692	2,71815	2,718268	2,718280

Глядя на эту таблицу, кажется, что она приближается к числу между 2,7 и 2,8 как . На самом деле приближается к некоторому числу как .Звоним по этому номеру. С точностью до шести знаков после запятой,

Буква была впервые использована для обозначения этого числа швейцарским математиком Леонардом Эйлером в 1720-х годах. Хотя Эйлер не открыл это число, он показал много важных связей между логарифмическими и логарифмическими функциями. Мы до сих пор используем это обозначение в честь работы Эйлера, потому что оно появляется во многих областях математики и потому что мы можем использовать его во многих практических приложениях.

Возвращаясь к нашему примеру со сберегательным счетом, мы можем заключить, что если человек кладет доллары на счет с годовой процентной ставкой , непрерывно начисляемой, то .Эта функция может быть вам знакома. Поскольку в приложениях часто возникают функции с основанием, мы называем функцию естественной экспоненциальной функцией . Эта функция интересна не только из-за определения числа , но и, как будет показано далее, ее график имеет важное свойство.

Поскольку мы знаем, что увеличивается на . На (Рисунок) мы показываем график вместе с касательной к графику в . Мы дадим точное определение касательной в следующей главе; но неформально мы говорим, что касательная к графику at — это линия, проходящая через точку и имеющая тот же «наклон», что и в этой точке. Эта функция является единственной экспоненциальной функцией с касательной, у которой наклон равен 1. Как мы увидим далее в тексте, наличие этого свойства делает естественную экспоненциальную функцию самой простой экспоненциальной функцией для использования во многих случаях.

Рис. 3. График имеет касательную линию с наклоном 1 в точке .

Используя наше понимание экспоненциальных функций, мы можем обсудить их обратные функции, которые являются логарифмическими функциями. Они пригодятся, когда нам нужно рассмотреть любое явление, которое варьируется в широком диапазоне значений, например pH в химии или децибелы в уровне звука.

Экспоненциальная функция является однозначной, с доменом и диапазоном . Следовательно, у него есть обратная функция, называемая логарифмической функцией с основанием . Для любого логарифмическая функция с основанием, обозначенным , имеет область определения и область значений и удовлетворяет

если и только если .

Например,

Кроме того, поскольку и являются обратными функциями,

Наиболее часто используемой логарифмической функцией является функция . Поскольку в основе этой функции лежит натуральное число, она называется натуральным логарифмом .Здесь мы используем обозначение или для обозначения . Например,

Поскольку функции и обратны друг другу,

и их графики симметричны относительно прямой ((Рисунок)).

Рис. 4. Функции и обратны друг другу, поэтому их графики симметричны относительно прямой .

На этом сайте вы можете увидеть пример десятичной логарифмической шкалы.

В общем случае для любого основания функция симметрична относительно прямой с функцией . Используя этот факт и графики экспоненциальных функций, мы построили графики функций для нескольких значений ((Рисунок)).

Рисунок 5: Графики изображены для .

Прежде чем решать некоторые уравнения с экспоненциальными и логарифмическими функциями, давайте рассмотрим основные свойства логарифмов.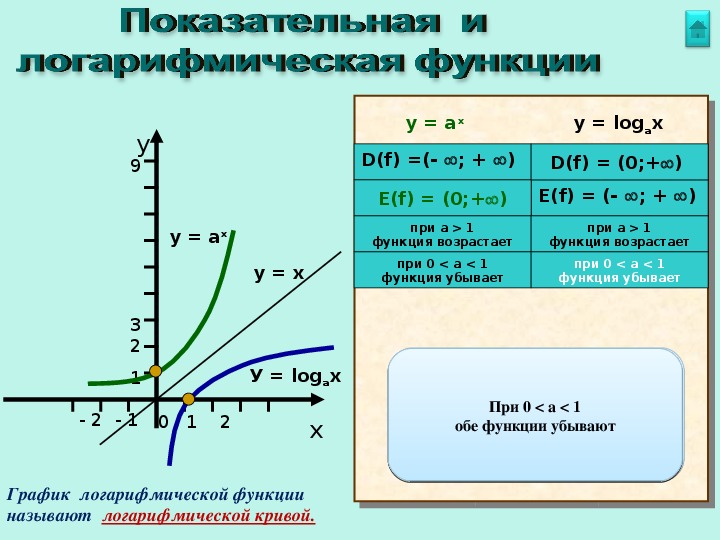

Правило: свойства логарифмов

Если , и любое действительное число, то

Решение уравнений с экспоненциальными функциями

Решите каждое из следующих уравнений для .

Решить .

Решение

Решение уравнений с логарифмическими функциями

Решите каждое из следующих уравнений для .

Решить .

Решение

Вычисляя логарифмическую функцию с помощью калькулятора, вы, возможно, заметили, что единственными вариантами являются либо log, называемый десятичным логарифмом , либо ln, натуральный логарифм. Однако экспоненциальные функции и логарифмические функции могут быть выражены в терминах любого желаемого основания. Если вам нужно использовать калькулятор для вычисления выражения с другим основанием, вы можете сначала применить формулы изменения основания. Используя эту замену базы, мы обычно записываем данную экспоненциальную или логарифмическую функцию в терминах натуральных экспоненциальных и натуральных логарифмических функций.

Доказательство

Для первой формулы замены основания мы начнем с использования свойства мощности логарифмических функций. Мы знаем это для любой базы . Следовательно,

Кроме того, мы знаем, что и являются обратными функциями. Следовательно,

Объединяя эти два последних равенства, заключаем, что .

Чтобы доказать второе свойство, покажем, что

Пусть , и . Мы это покажем. По определению логарифмических функций мы знаем, что и . Из предыдущих уравнений мы видим, что

Следовательно, . Поскольку экспоненциальные функции взаимно однозначны, мы можем заключить, что .

□

Замена базы

Используйте вычислительную утилиту для оценки с помощью представленной ранее формулы изменения базы.

Решение

Используйте второе уравнение с и :

Используйте формулу изменения базы и вычислительную утилиту для оценки .

Начало главы: Шкала Рихтера для землетрясений

Рисунок 6: (кредит: модификация работы Робба Ханнавакера, NPS)

В 1935 году Чарльз Рихтер разработал шкалу (теперь известную как шкала Рихтера ) для измерения магнитуды землетрясения. Шкала представляет собой логарифмическую шкалу с основанием 10, и ее можно описать следующим образом: рассмотрим одно землетрясение с магнитудой по шкале Рихтера и второе землетрясение с магнитудой по шкале Рихтера. Предположим, что означает, что землетрясение магнитудой сильнее, но насколько оно сильнее, чем другое землетрясение? Одним из способов измерения интенсивности землетрясения является использование сейсмографа для измерения амплитуды волн землетрясения.Если – амплитуда, измеренная для первого землетрясения, и – амплитуда, измеренная для второго землетрясения, то амплитуды и магнитуды двух землетрясений удовлетворяют следующему уравнению:

Рассмотрим землетрясение силой 8 баллов по шкале Рихтера и землетрясение силой 7 баллов по шкале Рихтера. Тогда

Следовательно,

, что подразумевает или . Так как это в 10 раз больше, мы говорим, что первое землетрясение в 10 раз сильнее, чем второе землетрясение.С другой стороны, если одно землетрясение оценивается в 8 баллов по шкале Рихтера, а другое — в 6 баллов, то относительная интенсивность двух землетрясений удовлетворяет уравнению

. .

Следовательно, . То есть первое землетрясение в 100 раз сильнее второго.

Как мы можем использовать логарифмические функции для сравнения относительной силы землетрясения силой 9 баллов в Японии в 2011 году с землетрясением силой 7,3 балла на Гаити в 2010 году?

Решение

Чтобы сравнить землетрясения в Японии и на Гаити, мы можем использовать приведенное ранее уравнение:

Следовательно, и делаем вывод, что землетрясение в Японии было примерно в 50 раз более интенсивным, чем землетрясение на Гаити.

Сравните относительную силу землетрясения магнитудой 8,4 с землетрясением магнитудой 7,4.

Землетрясение магнитудой 8,4 примерно в 10 раз сильнее, чем землетрясение магнитудой 7,4.

Гиперболические функции определяются в терминах определенных комбинаций и . Эти функции естественным образом возникают в различных инженерных и физических приложениях, в том числе при изучении волн на воде и колебаний упругих мембран.Другим распространенным использованием гиперболической функции является представление висячей цепи или троса, также известного как контактная сеть ((Рисунок)). Если ввести систему координат так, чтобы нижняя точка цепи лежала на оси -, мы можем описать высоту цепи в терминах гиперболической функции. Сначала определим гиперболические функции.

Рисунок 7. Форма нити шелка в паутине может быть описана в терминах гиперболической функции. Та же форма относится к цепи или кабелю, подвешенному к двум опорам только под собственным весом.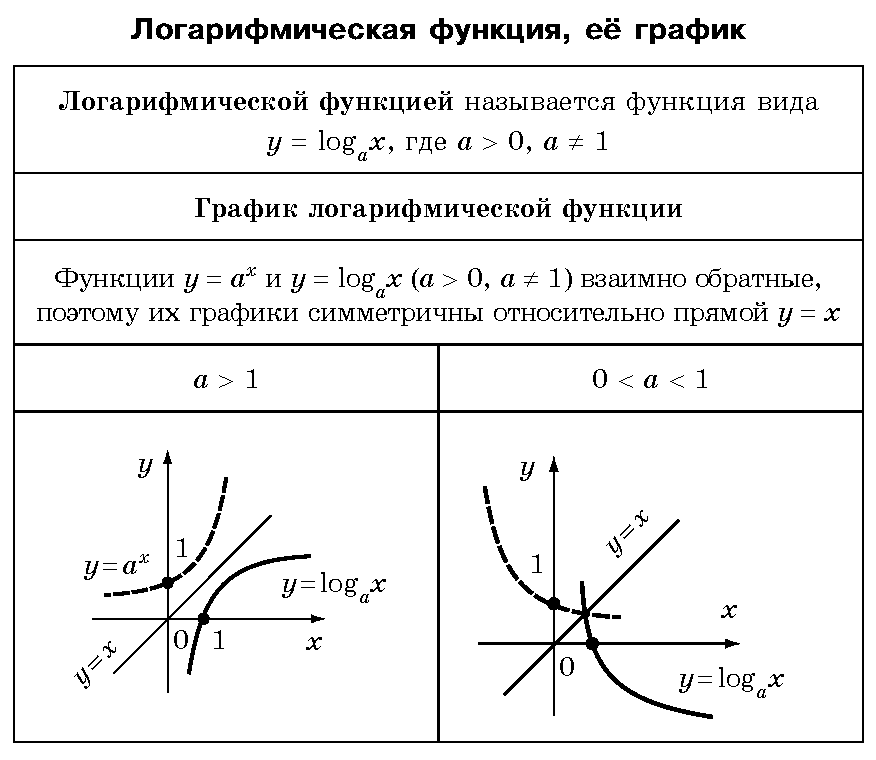

(кредит: «Мтпалей», Wikimedia Commons)

Определение

Гиперболический косинус

Гиперболический синус

Гиперболический тангенс

Гиперболический косеканс

Гиперболический секанс

Гиперболический котангенс

Имя cosh рифмуется со словом «черт возьми», тогда как имя sinh произносится как «cinch». Tanh , sech , csch и coth произносятся как «tanch», «seech», «coseech» и «cotanch» соответственно.

Используя определение и принципы физики, можно показать, что высота висячей цепи, такой как на (рис.), может быть описана функцией для определенных констант и .

Но почему эти функции называются гиперболическими функциями ? Чтобы ответить на этот вопрос, рассмотрим количество . Используя определение и , мы видим, что

Это тождество является аналогом тригонометрического тождества. Здесь при заданном значении точка лежит на единичной гиперболе ((Рисунок)).

Рис. 8. Единичная гипербола.

Обратные гиперболические функции

Из графиков гиперболических функций видно, что все они взаимно однозначны, кроме и . Если мы ограничим область определения этих двух функций интервалом , то все гиперболические функции будут взаимно однозначными, и мы сможем определить обратные гиперболические функции. Поскольку сами гиперболические функции включают экспоненциальные функции, обратные гиперболические функции включают логарифмические функции.

Определение

Обратные гиперболические функции

Давайте посмотрим, как вывести первое уравнение.Остальные следуют аналогично. Предполагать . Тогда и, по определению функции гиперболического синуса, . Следовательно,

Умножая это уравнение на , получаем

Это можно решить как квадратное уравнение с решением

Так как , единственное решение — это решение с положительным знаком. Применяя натуральный логарифм к обеим частям уравнения, мы заключаем, что

Вычисление обратных гиперболических функций

Оцените каждое из следующих выражений.

Решение

Оценить .

Решение

В следующих упражнениях оцените заданные экспоненциальные функции, как указано, с точностью до двух значащих цифр после запятой.

Решение

а. 125 б. 2,24 в. 9,74

Решение

а. 0,01 б. 10 000 с. 46.42

В следующих упражнениях сопоставьте экспоненциальное уравнение с правильным графиком.

5. 6. 7. 8. 9. 10.

Для следующих упражнений нарисуйте график экспоненциальной функции. Определите домен, диапазон и горизонтальную асимптоту.

11.

Решение

Домен: все действительные числа, Диапазон: , Горизонтальная асимптота в

12.

13.

Решение

Домен: все действительные числа, Диапазон: , Горизонтальная асимптота в

14.

15.

Решение

Домен: все действительные числа, Диапазон: , Горизонтальная асимптота в

16.

17.

Решение

Домен: все действительные числа, Диапазон: , Горизонтальная асимптота в

Для следующих упражнений запишите уравнение в эквивалентной экспоненциальной форме.

18.

19.

Решение

20.

21.

Решение

22.

23.

Решение

24.

25.

Решение

Для следующих упражнений запишите уравнение в эквивалентной логарифмической форме.

26.

27.

Решение

28.

29.

Решение

30.

31.

Решение

32.

33.

Решение

34.

35.

Решение

В следующих упражнениях используйте данные графики логарифмических функций, чтобы определить их область определения, диапазон и вертикальную асимптоту.

36.

38.

40.

В следующих упражнениях используйте свойства логарифмов, чтобы записать выражения в виде суммы, разности и/или произведения логарифмов.

42.

43.

Решение

44.

45.

Решение

46.

47.

Решение

Для следующих упражнений точно решите показательное уравнение.

48.

49.

Решение

50.

51.

Решение

52.

53.

Решение

54.

55.

Решение

Для следующих упражнений по возможности точно решите логарифмическое уравнение.

56.

57.

Решение

58.

59.

Решение

60.

61.

Решение

62.

63.

Решение

В следующих упражнениях используйте формулу замены основания и либо основание 10, либо основание для вычисления заданных выражений. Ответьте в точной форме и в приблизительной форме с округлением до четвертого знака после запятой.

64.

65.

Решение

66.

67.

Решение

68.

69.

Решение

70. Перепишите следующие выражения в терминах экспонент и упростите.

а.

б.

в.

д.

71. [T] Количество бактерий в культуре через несколько дней можно смоделировать с помощью функции . Найдите число бактерий, присутствующих через 15 дней.

Решение

72. [T] Спрос (в миллионах баррелей) на нефть в богатой нефтью стране определяется функцией , где — цена (в долларах) барреля нефти. Найдите объем спроса на нефть (с точностью до миллиона баррелей) при цене от 15 до 20 долларов.

73. [T] Накопленная сумма инвестиций в размере 100 000 долларов США, проценты по которым непрерывно начисляются в течение многих лет, определяется выражением . Найдите сумму, накопленную за 5 лет.

Решение

Приблизительно $131 653 накоплено за 5 лет.

74. [T] Инвестиции начисляются ежемесячно, ежеквартально или ежегодно и задаются функцией , где стоимость инвестиции в момент времени является первоначальным принципом инвестирования, годовая процентная ставка и количество раз, когда проценты начисляются в течение года.Учитывая годовую процентную ставку 3,5% и первоначальный принцип 100 000 долларов, найдите сумму, накопленную за 5 лет для процентов, которые начисляются а. ежедневно, б., ежемесячно, в. ежеквартально и д. ежегодно.

Решение

я. а. рН = 8 б. База II. а. pH = 3 б. Кислота 3. а. рН = 4 б. Кислота

76. [T] Йод-131 – радиоактивное вещество, распадающееся по функции , где – исходное количество навески вещества, выраженное в днях.Определите, сколько времени потребуется (с точностью до дня), чтобы 95% количества распалось.

78. [T] Сумма, накопленная после того, как 1000 долларов инвестируются на годы под процентную ставку 4%, моделируется функцией .

Найдите сумму, накопленную через 5 и 10 лет.
Определите, сколько времени потребуется, чтобы первоначальные инвестиции утроились.

79. [T] Известно, что колония бактерий, выращенная в лаборатории, удваивается в количестве за 12 часов.Предположим, что изначально присутствует 1000 бактерий.

Используйте экспоненциальную функцию для определения значения , которое представляет собой скорость роста бактерий. Округлите до четырех знаков после запятой.
Определите приблизительное время, необходимое для роста 200 000 бактерий.

Решение

а. б. часов

80. [T] Популяция кроликов в заповеднике удваивается каждые 6 месяцев. Предположим, первоначально было 120 кроликов.

Используйте экспоненциальную функцию для определения константы скорости роста.Округлите до четырех знаков после запятой.
Используйте функцию в части а. чтобы примерно определить, сколько времени потребуется, чтобы популяция кроликов достигла 3500 особей.

81. [T] Землетрясение 1906 года в Сан-Франциско имело магнитуду 8,3 балла по шкале Рихтера. В то же время в Японии землетрясение магнитудой 4,9 нанесло лишь незначительный ущерб. Примерно во сколько раз больше энергии было высвобождено при землетрясении в Сан-Франциско, чем при землетрясении в Японии?

Решение

Землетрясение в Сан-Франциско имело или в несколько раз большую энергию, чем землетрясение в Японии.

Функции десятичного логарифма

Логарифмическая функция является обратной экспоненциальной функции. Точно так же, как экспоненциальная функция имеет общие основания и естественную основу; логарифмические функции имеют общий логарифм и натуральный логарифм.

Это обсуждение будет сосредоточено на десятичных логарифмических функциях .

Общее десятичное логарифмическое уравнение:

ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ

y=loga x тогда и только тогда, когда x = a ^y

Где a > 0, a ≠ 90 и x0 > 3

При чтении loga x скажите: «логарифм по основанию a из x».

Некоторые примеры:

1. LOG10 100 = 2, потому что 10 ² = 100

2. Log3 81 = 4, потому что 3 ⁴ = 81

3. Log12 225 = 2, потому что 15 ² = 225

Обратите внимание, что в примерах основание журнала также является основанием соответствующего показателя степени. В приведенном выше примере 1 логарифмическая функция имеет логарифм по основанию 10, а соответствующая экспоненциальная функция имеет логарифм по основанию 10.

Если вы видите логарифм без основания, это означает логарифм по основанию 10 или log = log ₁₀ .Некоторые основные свойства логарифмических функций: Если logax=logay, то x = y Свойство «один к одному»

Свойство 4: loga ax=x и alogax=x Обратное свойство

Решим несколько простых логарифмических уравнений:

log x = 4

Шаг 1. Выберите наиболее подходящее свойство.

Свойства 1 и 2 не применяются, так как бревно не равно ни 0, ни 1. Свойство 3 не применяется, так как бревно не устанавливается равным бревну того же основания. Поэтому свойство 4 является наиболее подходящим.

Свойство 4 — обратное

Шаг 2. Примените свойство.

Помните, что log=log10. Поскольку журнал имеет основание 10, инверсия означает переписать обе стороны как показатели степени с основанием 10.

журнал х = 4 Оригинал

10 ^logx = 10 ⁴ Показатель степени 10

Шаг 3: Найдите x.

Свойство 4 утверждает, что alogax=x, поэтому левая часть становится x.

x = 10 ⁴ Применить свойство

х = 10 000 Оценивать

Пример 1: log3 x=log3 4x−9

Шаг 1. Выберите наиболее подходящее свойство.

Свойства 1 и 2 не применяются, так как бревно не равно ни 0, ни 1. Так как бревно устанавливается равным бревну того же основания. Свойство 3 является наиболее подходящим.

Свойство 3 — один к одному

Шаг 2. Примените свойство.

Свойство 3 утверждает, что если logax=logay, то x = y. Следовательно, х = 4х — 9.

х = 4х — 9 Применить свойство

Шаг 3: Найдите x.

-3x = -9 Вычесть 4x

х = 3 Разделить на -3

Пример 2: log3 3x=5

Шаг 1. Выберите наиболее подходящее свойство.

Свойство 4 — обратное

Шаг 2. Примените свойство.

Поскольку журнал имеет основание 3, инверсия означает переписать обе стороны как показатели степени с основанием 3.

log3 3x=5Исходный

3log33x=35Показатель степени 3

Шаг 3: Найдите x.

Свойство 4 утверждает, что alogax=x, поэтому левая часть становится x.

3 ^x = 3 ⁵ Применить свойство

x=2433 Поделить на 3

х = 81 Оценивать

Логарифмы

Цели: В этом разделе мы определяем логарифмическую функцию как обратная экспоненциальная функция.Свойства логарифмической функции которые обсудили. Графики различных логарифмических функций и их исследуются геометрические преобразования. После работы с этими материалами учащийся должен уметь

для обсуждения определения логарифмической функции;
для описания свойств и графиков логарифмических функций;
для распознавания графически и алгебраически геометрических преобразований логарифмические функции.

Модули:

Для начала следует вспомнить материал об обратных функциях.

Определение. Пусть a — положительное действительное число. Логарифм по основанию . f(x) = log _a (x) .

является обратной экспоненциальной функцией g(x) = a ^x .

Натуральный логарифм

f(x) = ln(x) .

является обратной экспоненциальной функцией g(x) = e ^x . Другими словами,

ln(x) = log _e (x) .

Комментарии:
- Область определения f(x) = log _a (x) состоит из всех положительных действительных чисел.
  Обсуждение.
- Диапазон f(x) = log _a (x) представляет собой совокупность всех действительных чисел.
  Обсуждение.
- log _a (a ^x ) = x и a ^{log _a (x)} = x . В частности, ln(e ^x ) = x и e ^ln(x) = x .
  Обсуждение.
- Если a, то f — убывающая функция, а если a > 1 , то f — убывающая функция. возрастающая функция.
  Обсуждение.
- Логарифмические функции удовлетворяют следующим свойствам:
  1. log _a (rs) = log _a (r) + log _a (s)
  2. log _a (r/s) = log _a (r) — log _a (s)
  3. log _a (r ^s ) = s log _a (r)
- Многие калькуляторы и компьютерные программы не имеют логарифмической функции log _a (x) , но имеют натуральный логарифм, ln(x) ; в этом случае полезно следующее тождество: log _a (x) = ln(x) / ln(a)
Примеры:
- Используйте эту записную книжку LiveMath для просмотра анимации показаны графики параметризованного семейства логарифмических функций.
- Записные книжки LiveMath для графического и символического изучения эффекта преобразования логарифмических функций.
- Java-апплет графически исследует эффект символьного преобразования логарифмических функций.

Экспоненциальные и логарифмические функции — Логарифмические функции

Вы собираетесь изучить самую важную концепцию решения экспоненциальных и логарифмических уравнений. Натуральный логарифм — очень удобный инструмент, который можно держать в вашем математическом наборе инструментов в этой главе.Натуральный логарифм не только является обратной функцией e ^x, но и непосредственно используется в последующих разделах для решения как экспоненциальных, так и логарифмических уравнений.

Вы посмотрите на графики функции натурального логарифма, потренируетесь в использовании свойств, а также оцените функции натурального логарифма на своем калькуляторе. Не думайте слишком много о том, чтобы шутить о натуральном бревне, мы уже знаем о них, но мы избавим вас от боли.

Натуральный логарифм, ln , представляет собой особый случай, когда у вас есть f ( x ) = log _e x . и — это основа! Если бы мы записали его длинным путем, это выглядело бы так: f ( x ) = log _{2.718281828…} x . В 1668 году какой-то умный парень по имени Николас Меркатор решил назвать это естественной логарифмической функцией. В 1600-х у нас не было блоггеров, у нас были лесорубы, также известные как старомодные ботаники.

Это эквивалентные заявления:

F ( x ) = log _E x
F ( x ) = LN ( x )

Обратите внимание, как основание логарифма равно e .Мы называем это естественным журналом, поэтому нам не нужно записывать log _e. Мы можем просто написать y = ln ( x ), и все поймут, что это означает. Наш маленький друг, e , хотел иметь свою собственную логарифмическую функцию. Какой парень!

Пример задачи

Постройте график естественной логарифмической функции и ее обратной функции.

Синяя кривая — это функция y = e ^x, а функция натурального логарифма y = ln ( x ) — красная кривая.Поскольку они инверсны, они в основном являются отражением этой воображаемой диагональной линии y = x .

Пример задачи

Используя свойства логарифмов (из нашего предыдущего раздела), перепишите эту функцию натурального логарифма как сумму или разность логарифмов:

Перепишите в виде сумм и разностей натуральных логарифмов.

Хорошо, давайте сделаем это поэтапно. Во-первых, поскольку это натуральный журнал, он следует тем же свойствам логарифмов (о которых мы узнали в предыдущем разделе).

Говоря об инверсиях, знаете ли вы, что мы можем применить инверсию натурального логарифма к экспоненциальной функции? Смотреть это волшебство:

E ^{ln x} = x
E

) = x

Проблема образца

оценка E ^{ln 9} .

Поскольку теперь мы знаем, что функция, обратная функции e , равна ln , решение:

e ^{ln 9} = 9.

Пример задачи

Оценка ln ( e ^1.9 ).

Easy Shmeazy. Ответ 1,9 благодаря нашему верному другу, обратному.

В последнем разделе, Графики логарифмических функций, мы упоминали, что вы можете преобразовать логарифм по определенному основанию в логарифм по основанию 10 с помощью простого трюка.

Запомните это…

y = log ₂ x

…то же самое, что и это:

которые помогут нам в этом в следующем разделе решить уравнения.Если у нас есть y = log ₃ x , мы можем преобразовать его в естественную логарифмическую функцию, которая некоторым людям нравится больше, чем работа с логами.

Натуральные журналы менее громоздки, и на вашем калькуляторе есть изящные маленькие кнопки, которые предназначены для ln , и вам не нужно беспокоиться о смене базы. Доставайте мюсли, мы будем естественными!

Пример задачи

Преобразуйте логарифм ₆ 100 в натуральный логарифм, а затем оцените (округлите до сотых).

Логарифмическая функция, определение, типы логарифмов, свойства, график логарифмов

Логарифмическая функция является важным средством математических вычислений. Логарифмы были открыты в 16 веке шотландским математиком, ученым и астрономом Джоном Нэпьером. Он имеет множество применений в астрономических и научных расчетах, связанных с огромными числами. Логарифмические функции тесно связаны с экспоненциальными функциями и часто рассматриваются как обратные экспоненциальной функции.Показательная функция a ^x = N преобразуется в логарифмическую функцию $log_aN = x$.

Логарифм любого числа X, если интерпретировать его как экспоненциальную форму, – это степень, до которой следует возвести основание логарифма, чтобы получить число X. Здесь мы будем стремиться узнать больше о логарифмических функциях, типах логарифмов, график логарифмической функции и свойства логарифмов.

Что такое логарифмические функции?

Логарифмическая функция получена из экспоненциальной функции.Некоторые значения нецелого показателя степени можно легко вычислить с помощью логарифмических функций. Найти значение x в экспоненциальных выражениях 2 ^x = 8, 2 ^x = 16 легко, но найти значение x в 2 ^x = 10 сложно. Здесь мы можем использовать логарифмические функции для преобразования 2 ^x = 10 в логарифмическую форму как $ log_210 = x$, а затем найти значение x. Логарифм подсчитывает количество вхождений основания в повторяющихся кратных числах.Формула преобразования экспоненциальной функции в логарифмическую выглядит следующим образом.

Показательная функция формы ^x = N может быть преобразована в логарифмическую функцию $ log_aN = x$. Логарифмы обычно рассчитываются по основанию 10, а логарифмическое значение любого числа можно найти с помощью таблицы логарифмов Нейпира. Логарифмы можно вычислять для положительных целых чисел, дробей, десятичных дробей, но нельзя вычислять для отрицательных значений.

График логарифмических функций

Область определения функции логарифма аналогична функции извлечения квадратного корня. Область логарифмической функции отложена по оси x, а диапазон отложен по оси y. Поскольку логарифм 1 по любому основанию ($\log_n1 = 0$) равен 0, логарифмическая функция при значении области значений, равном 1, пересекает ось x. Кроме того, логарифма нуля не существует, и, следовательно, график не проходит через начало координат.

Натуральные логарифмы и десятичные логарифмы

Логарифмы в целом делятся на два типа в зависимости от основания логарифмов. У нас есть натуральные логарифмы и десятичные логарифмы. Натуральные логарифмы — это логарифмы по основанию «е», а десятичные логарифмы — это логарифмы по основанию 10. Дальнейшие логарифмы можно вычислять по любому основанию, но часто они рассчитываются по основанию «е» или «10». Натуральные логарифмы записываются как $\log_ex $, а десятичные логарифмы записываются как $\log_{10}x$.{1.6.9} = 5\).

е = 2,718

$\log_eN = 2,303 ×\log_{10}N$

$\log_{10}N = 0,4343 × \log_eN$

Значение e = 2,718281828459, но часто записывается как e = 2,718. Также приведенные выше формулы помогают при взаимном преобразовании натуральных логарифмов и десятичных логарифмов.

Свойства логарифмических функций

Свойства логарифмических функций полезны при работе со сложными логарифмическими функциями.Все общие арифметические операции с числами преобразуются в другой набор операций с логарифмами. Произведение двух чисел, взятое внутри логарифмических функций, равно сумме логарифмических значений двух функций. Точно так же операции деления преобразуются в разность логарифмов двух чисел. Перечислим все свойства логарифмических функций в следующих пунктах.

логаб = лога + логб
loga/b = loga — logb
$log_b a = \frac{loga}{logb}$
логов ^x = х логарифмов
$log_1 а $ = 0
$log_a$ = 1

Производная логарифмических функций

Вывод логарифмической функции дает наклон касательной к кривой, представляющей логарифмическую функцию. Функции внутри логарифма могут быть простой переменной или тригонометрическим отношением. Производная, взятая для логарифмической функции, дает в качестве ответа обратную логарифмическую функцию. Формула производной логарифмической функции выглядит следующим образом.

д/дх. Логх = 1/х

Похожие темы:

Часто задаваемые вопросы о логарифмических функциях

Как решать логарифмические функции?

Логарифмическую функцию можно решить с помощью логарифмических формул.Произведение функций внутри логарифмов равно (logab = loga + logb) сумме двух логарифмических функций. Деление двух функций логарифмов (loga/b = loga — logb) заменено на разность функций логарифмов. Логарифмические функции также можно решить, придав им экспоненциальную форму.

Как построить график логарифмических функций?

График логарифмической функции y = log x можно получить, отложив значение logx по оси x и значение y по оси y. График logx не проходит через начало координат и похож на график квадратного корня.

Как связаны экспоненциальные и логарифмические функции?

Показательная функция формы ^x = N может быть преобразована в логарифмическую функцию $ log_aN = x$. Здесь экспоненциальная функция 2 ^x = 10 преобразуется в логарифмическую форму как $ log_210 = x$, чтобы найти значение x. Логарифм подсчитывает количество вхождений основания в повторяющихся кратных числах.

Как дифференцировать логарифмические функции?

Дифференцирование логарифмической функции приводит к обратной функции. Дифференциация logx равна 1/x. (d/dx .logx = 1//x). Кроме того, первообразная 1/x возвращает логарифмическую функцию.

Что такое диапазон логарифмических функций?

Диапазон логарифмической функции принимает все значения, включая положительные и отрицательные действительные числа. Таким образом, диапазон логарифмической функции находится в диапазоне от отрицательной бесконечности до положительной бесконечности.

Что такое область логарифмических функций?

Логарифмы могут быть вычислены для положительных целых чисел, дробей, десятичных дробей, но не могут быть вычислены для отрицательных значений. Следовательно, областью определения логарифмической функции является положительное действительное число.

Какая формула для логарифмических функций?

Следующие формулы полезны для работы и решения логарифмических функций.

логаб = лога + логб
loga/b = loga — logb
$log_b a = \frac{loga}{logb}$
логов ^x = х логарифмов

Для чего используются логарифмические функции?

Логарифмические функции имеют множество приложений в физике, технике, астрономии.Числовые измерения в астрономии включают в себя огромные числа с десятичными знаками и показателями степени. Огромные научные расчеты можно легко упростить и рассчитать с помощью логарифмических функций. Логарифмические функции помогают преобразовать произведение и деление чисел в сумму и разность чисел.

Логарифмические функции

Логарифмические функции

Алгебраическое представление

Как и экспонента, существенные свойства логарифма можно описать всего двумя параметрами .

Как и экспонента, параметр b называется основанием .

В отличие от экспоненты, параметр a не является точкой пересечения по оси Y! Действительно, члены этого базового семейства логарифмов не имеют y-пересечений. Чтобы раскрыть значение a , мы должны более внимательно рассмотреть обратную природу экспонент и логарифмов.

Напомним, что если e ^k = b , мы пишем k = log _e b (или k = ln (b) ).Мы используем одно и то же обозначение для любого основания. Таким образом, если b ^k = c , мы пишем k = log _b c .

Подробнее о записи журнала :

Уравнения y = b ^x и x = log _b y говорят об одном и том же.

Экспоненты и логарифмы — это просто разные способы выражения этой связи. Функция E(x) = b ^x запрашивает значение y, которое получается, когда b возводится в степень x.Функция L(x) = log _b x запрашивает показатель степени y, для которого b ^y дает результат x. Разница в том, какие из x и y вам даны и какие вы хотите найти? Что является входом, а что выходом?

Рассмотрим: 2 ³ = 8 , log ₂ 8 = 3 . Основание 2 . Е(3) = 8, L(8) = 3.

Это объясняет «зеркальное отображение» отношений между экспонентами и логарифмами с одним и тем же основанием. Если (x, y) – это пара вход-выход для одной функции, то (y, x) – это пара ввода-вывода для другой.

Это также помогает нам объяснить значение параметра a . Поскольку b ¹ = b , log _b (b) = 1 . То есть f(b) = a log _b b = a . Параметр a – это выход, когда вход является базовым. Красиво, но не очень полезно. ..

Лучше думать о a как о коэффициенте масштабирования , корректируя выходные данные log _b (x) вверх или вниз по мере увеличения или уменьшения a соответственно.

Законы логарифмов :

Поскольку основание логарифма на самом деле является замаскированным основанием экспоненты, мы сохраняем ограничение, данное для экспонент:

Основание b в логарифмической функции должно быть положительным.

Для экспонент это условие гарантировало, что выходные данные от b ^x всегда были положительными. Для логарифмов это ограничение, согласно которому входы всегда должны быть положительными. Логарифмы живут полностью справа от оси Y. Мы говорим, что у них есть ограниченный домен .

Как и в случае экспоненциальных функций, основание отвечает за скорость роста или убывания логарифмической функции.

Если 0, функция затухает по мере увеличения x.(Например, log _1/2 (1) > log _1/2 (2) > log _1/2 (3) .) Меньшие значения b приводят к более медленной скорости распада.
Если b > 1 , функция увеличивается на по мере увеличения x. (Например, log ₂ (1) log ₂ (2)

₂

Ключевым алгебраическим свойством логарифмических функций является следующее.

То есть умножение любого входного x на константу k приводит к добавлению постоянного интервала a log _b (k) к выходным данным.Это еще раз обратное экспоненциальному поведению, когда добавление постоянного интервала к входным данным приводит к умножению выходных данных на константу.

Свойство множителей входных данных, создающих одинаковые шаги вывода, является основой для многих логарифмических шкал, используемых в приложениях.