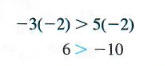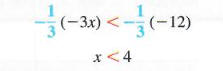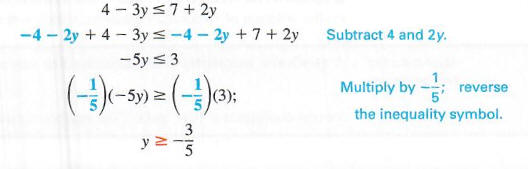Системы неравенств с двумя переменными: алгоритм графического решения, примеры
п.1. Алгоритм графического решения системы неравенств с двумя переменными
На входе система: \(\left\{ \begin{array}{ l } \mathrm{F(x,y) \lt 0} & \\ \mathrm{G(x,y \gt 0)} & \end{array}\right. \)
Шаг 1. Построить на координатной плоскости кривую F(x, y) = 0. Заштриховать область F(x, y) < 0.
Шаг 2. Построить на координатной плоскости кривую G(x, y) = 0. Заштриховать область G(x, y) > 0.
Шаг 3. Множество решений данной системы – это пересечение двух заштрихованных областей.
Системы с другими знаками сравнения (≤, ≥ и т.д.), а также системы с любым количеством неравенств решаются аналогично.
Например:
Найти на координатной плоскости множество решений системы неравенств: $$ \left\{ \begin{array}{ l } \mathrm{x^2+y^2\leq 9} & \\ \mathrm{x+y\gt 3} & \end{array}\right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит. |
п.2. Примеры
Пример 1. Найдите на координатной плоскости множество решений системы неравенств.
a) \( \left\{ \begin{array}{ l } \mathrm{x+y\geq 4} & \\ \mathrm{2x-y\leq 2} & \end{array}\right. \)
Выразим y(x) в явном виде
\( \left\{ \begin{array}{ l } \mathrm{y\geq -x+4} & \\ \mathrm{y\geq 2x-2} & \end{array}\right. \)
Строим прямые, заштриховываем области над ними, находим пересечение.
б) \( \left\{ \begin{array}{ l } \mathrm{y+x^2-6\leq 0} & \\ \mathrm{2y-x^2\geq 0} & \end{array}\right. \)
Выразим y(x) в явном виде
\( \left\{ \begin{array}{ l } \mathrm{y\leq -x^2+6} & \\ \mathrm{y\geq \frac{x^2}{2}} & \end{array}\right. \)
Строим параболы.
Заштриховываем область под первой параболой и над второй параболой.
Находим пересечение.
в) \( \left\{ \begin{array}{ l } \mathrm{y-\frac{6}{x}\leq 0} & \\ \mathrm{3x-2y\lt 0} & \end{array}\right. \)
Выразим y(x) в явном виде
\( \left\{ \begin{array}{ l } \mathrm{y\leq \frac{6}{x}} & \\ \mathrm{y\gt 1,5x} & \end{array}\right. \)
Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.
Находим пересечение.
г) \( \left\{ \begin{array}{ l } \mathrm{x^2+y^2\gt 4} & \\ \mathrm{x^2+y^2\leq 9} & \end{array}\right. \)
Строим окружности.
Заштриховываем области вне первой окружности и внутри второй.
Находим пересечение – кольцо.
Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:
\begin{gather*} \mathrm{ \frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-y_A}\Rightarrow\frac{x-2}{4-2}=\frac{y-3}{4-3}\Rightarrow x-2=2(y-3) }\\ \mathrm{ x-2y+4=0} \end{gather*}
\begin{gather*} \mathrm{ \frac{x-x_B}{x_C-x_B}=\frac{y-y_B}{y_C-y_B}\Rightarrow\frac{x-4}{3-4}=\frac{y-4}{0-4}\Rightarrow -4(x-4)=-(y-4) }\\ \mathrm{ 4x-y-12=0} \end{gather*}
\begin{gather*} \mathrm{ \frac{x-x_A}{x_C-x_A}=\frac{y-y_A}{y_C-y_A}\Rightarrow\frac{x-2}{3-2}=\frac{y-3}{0-3}\Rightarrow -2(x-2)=y-3 }\\ \mathrm{ 3x+y-9=0} \end{gather*}
Чтобы расставить знаки ≤, ≥, выбираем произвольную точку внутри треугольника, например D(3; 2), подставляем в полученные уравнения и получаем необходимые знаки:
Искомая система неравенств: \( \left\{ \begin{array}{ l } \mathrm{x-2y+4\geq 0} & \\ \mathrm{4x-y-12\leq 0} & \\ \mathrm{3x+y-9\geq 0} & \end{array}\right. \)
Разработка урока «Решение систем неравенств с двумя переменными» в 9 классе
Тема: Решение систем неравенств с двумя переменными
9 класс.
Цель урока: Обобщить пройденный материал. Научиться решать системы неравенств с двумя переменными. Разобрать решение неравенств, содержащие знак модуля у двух переменных. Продолжить формирование умений классифицировать, строить графики, находить решения неравенств.
Формирование УУД:
Познавательные: определять способы решения и обосновывать свое мнение;
анализировать задачу, ситуацию.
Регулятивные: выполнять самопроверку и самооценку выполнения учебного задания; умение планировать и осуществлять деятельность, направленную на решение проблем различного характера.
Коммуникативные: предлагать и обосновывать своё мнение.
Личностные: определять личностный смысл деятельности; осуществлять выбор в соответствии с задачей деятельности
Оборудование: Карточки для практических работ, проектор, презентация.
Тип урока: урок комплексного применения знаний, умений и навыков.
Структура урока
Организационный этап.
Устная работа.
Актуализация опорных знаний (тестовая работа)
Изучение новых знаний, необходимых для формирования умений.
Мотивация обучения.
Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
Домашнее задание.
Итоги урока. Рефлексия.
Эпиграф к уроку: «Дорогу осилит идущий,
Ход урока
1.Организационный этап. Здравствуйте, ребята. Сегодня у нас на уроке гости. Улыбнёмся гостям, друг другу, мне и начнём урок с хорошим настроением.
Сообщение темы и цели урока (читают учащиеся)
2.Устная работа.
Повторим основные приёмы и отличия.
Проанализируйте неравенства и скажите, в чём отличие первого неравенства от второго: х2 – 2х≥1; х2 – 2у≥ 1? ( В первом неравенстве одна переменная, во втором две).
Как изобразить решение таких неравенств? (на координатной прямой и координатной плоскости).
Какие особенности изображения решения строгого и нестрогого неравенства? (Строгое неравенство: ˃ , < пустые точки на прямой, пунктирная линия графика на плоскости
Нестрогое неравенство: ≥ , ≤ жирные точки на прямой, сплошная линия графика на плоскости)
Задание на повторение. Решить систему неравенств:
5х+1˃62х-4<3
0<4х+2≤6
х2-5х+4≤0
9-4х<0
y=kx+b, (x-х0)2+(y-у0)2=r2, y=a(x-m)2+n, у=a х2+bx+c, y=k/x, у = k х3 + b
соответствует: прямой, параболе, гиперболе, окружности, куб. параболе?
Что является решением неравенства с двумя переменными? (Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство)
Определите, является ли пара чисел (4,0), (1; 2) решением неравенства х2 – 2у≥ 1?
Алгоритм решения неравенства с двумя переменными. Решите неравенство.
Как найти множество решений неравенства?(Для изображения множества решений неравенства на координатной плоскости поступают следующим образом:
1. Строим график функции y = f(x), который разбивает плоскость на две области.
2. Выбираем на графике любую точку с координатами (х0,у0). Проводим в данной точке перпендикуляр к оси х. Выбираем точку с координатой у больше или меньше у0 в зависимости от знака неравенства или пробная точка. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – является область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.)
Вывод:- решением неравенства f(x,y)˃0, f(x,y)<0, f(x,y)≤0 f(x,y)≥0 называется упорядоченная пара чисел, которая превращает его в правильное числовое неравенство.
-графиком неравенства с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х, у), где каждая пара (х,у) является решением данного неравенства. Решением неравенства с двумя переменными будет внутренняя или внешняя область фигуры.)
3. Актуализация знаний.
Тренировочный блок:
№ 492 (а).
Р е ш е н и е
ху ≥ 0.
Произведение двух чисел является неотрицательным в том случае, если эти числа имеют одинаковые знаки. Значит, когда

Первой системе соответствует первая координатная четверть, а другой системе – третья координатная четверть. Множеством решений неравенства-объединение первой и третьей координатных четвертей, включая оси координат.
Разминка
Задание 1.На готовых шаблонах координатных плоскостей А-3 изобразите множество решений неравенства
х2 +у2 ≥25у ≤ — х2+1
у≥(х-1) 2
(х-1)2 +(у-2)2 ≤ 9
у ≥0
х ≤ 0
у≤-2
х ≥3
Решение неравенств (по слайдам 1-5 презентации)
Тестовая работа.
Определить неравенство по графику. (Задания на распознавание неравенств -3 мин)
Ответы:
1.22.3
3.2
4.3
5.1
Установить соответствие:
Предложенные ответыВаш ответ
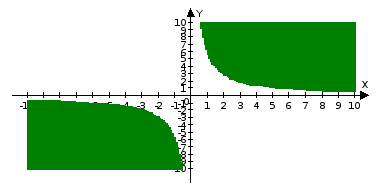
ху-6˃0
ху-6 ≥0
ху-6<0
ху-6≤0
1)
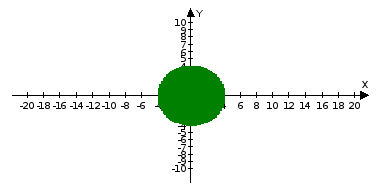
х2 +у2˃16
х2 +у2<16
х2 +у2≤16
х2 +у2≥16
2)
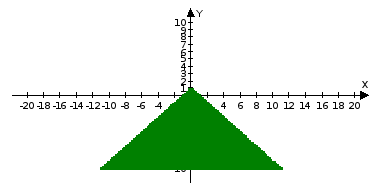
- у≤1-|х|
у< 1-|х|
у˃ 1-|х|
у≥ 1-|х|
3)
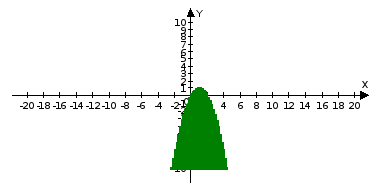
у≥ 2х-х2
у<2х-х2
у≤2х-х2
у˃2х-х2
4)
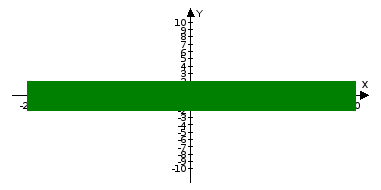
|у| ≤2
|х| ≤2
|у| ≥2
|х|≥2
5)
4. Изучение новых знаний, необходимых для формирования умений.
Подведение к новой теме:
1 задание (на листах А-4).
на предыдущем уроке вы нашли решение одного из неравенств с двумя переменными, в таком же формате решим ещё одно неравенство (задание в парах выполняют на файле, в который вложен чертёж координатной плоскости). А теперь найдём общее решение этих неравенств, т.е. решим систему неравенств.
Демонстрация работ
Алгоритм решения неравенств с двумя переменными:
1. Заменить знак неравенства на знак равенства.
2. Выразить переменную у через х.
3. Построить график полученного уравнения.
4. Выделить часть плоскости, соответствующую знаку неравенства.
Алгоритм решения систем неравенств с двумя переменными:
1. Решить каждое из неравенств системы отдельно.
2. Изобразить полученные решения на одной координатной плоскости.
3. Найти пересечение этих решений.
4. Общая часть этих решений и является решением данной системы неравенств.
№500(а,в)
1. Решение систем неравенств с использованием шаблонов (по слайдам презентации)
Разгрузочная пауза-лирическое отступление. Дания на протяжении почти 50 лет удерживает I место по показателям индекса благополучия и счастья. Датчане стараются во всём видеть хорошее и умеют получать радость от жизни и пользу. ХЮГГЕ! СЕКРЕТ ДАТСКОГО СЧАСТЬЯ! Мне бы хотелось чтобы РОССИЯ была на I месте всегда и во всём. Давайте поболеем за Россию: флаг (дети встают и садятся по очереди, получается волна, приветствуем Россию: хлопаем в ладоши (тук——тук——тук-тук-тук). В жизни всегда есть место подвигу. Вы его совершили. Надеюсь, что 40 минут урока дадут вам хороший позитив. Но России нужны хорошие инженеры и т.д. Знания собираются по капле — продолжаем работать.
5. Мотивация обучения. Формирование умений и навыков.
1задание. Решить систему неравенств используя шаблоны (на листах А-3):
х2+ у2<25х 2+ у2<9
y≥6/x
у≤х3
у≥ х2-4
х2+ (у+3)2<9
(х2+ у2—4)(х2+ у2-16) <0
у≤х+2
х≥ у2 -3
у≥х-3
х 2+у2 ≤16
Проверочная работа (задание по вариантам):
Дополнить неравенствами до систем по горизонтали:
I вариант: (у ≥ х2, у≤ 0, у ≥ 0, у ≤ — х2+3, х2+ у2≤ 9, х≤ 0)
II вариант: (у≤ — х2, у ≥0, у ≤ 0, у ≥ х2-3, х2+ у2≤ 4, х ≥ 0)
Решить систему неравенств (графики изобразить схематически с помощью шаблонов) 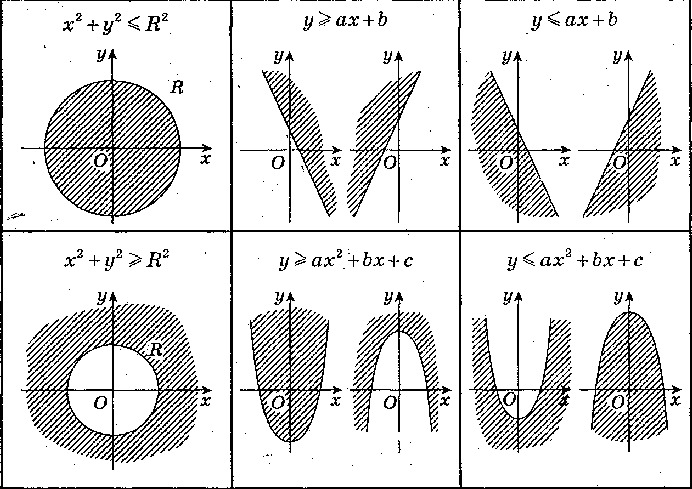
6. Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
2. Решение неравенств с модулем
Мотивация обучения.
Мы изучили решение неравенств, когда под знаком модуля находится одна из переменных например: у≥|х|, у| ≤|x|-1. Эти же рассуждения проведём для решения неравенств, в которых модуль содержится у двух переменных. Например | х | + | у | ≤ 1;
а) Изучение новых знаний, необходимых для формирования умений.
б) Изобразим на координатной плоскости фигуру, которую задает неравенство . Если пара (x0,y0) является решением неравенства, то каждая из пар (x0,-y0), (-x0,y0) и (-x0,-y0) также является его решением. Значит, искомая фигура симметрична относительно оси x и оси y. Изобразим сначала ее часть, расположенную в первой координатной четверти.
x+y=1
используя свойства симметрии, изобразим три остальные части. Полученная фигура представляет собой квадрат.
Алгоритм решения неравенств с двумя переменными, содержащие знак модуля
Построить график функции у=f(x,y) в первой координатной плоскости
Использовать преобразования графиков уравнений, связанных с модулем.
Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
Сделать вывод о решении неравенства
№ 556.
Р е ш е н и е
| х | + | у | ≤ 1;
| у | ≤ 1 – | х |.
Построим график уравнения | у | = 1 – | х |. Для этого нужно раскрыть знаки модуля.
Получим четыре случая:
1) х ≥ 0, у ≥ 0;у = 1 – х.
2) х ≥ 0, у < 0; –у = 1 – х; у = х – 1.
3) х < 0, у ≥ 0;у = 1 + x.
4) x < 0, y < 0;–у = 1 + х;у = –х – 1.
Объединяя все эти случаи, получим фигуру:
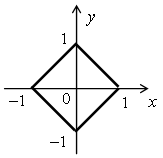
Данному неравенству удовлетворяет множество точек внутренней области этой фигуры.
Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
Изобразите на координатной плоскости множество решений неравенства:
х2 + у2-2|x|-2|y|+1≥0
Решение
Фигура симметрична относительно оси Х и оси Y.
1.Преобразуем неравенство к виду (|x|-1) 2+(|y|-1) 2≥1
2.Строим график уравнения , используя свойства модуля.
4. С помощью пробной точки устанавливаем решение неравенства.
7. Домашнее задание: Выучить теоретические факты, №498, 500 (б, г), инд. задание по карточкам
8. Рефлексия.
Вопросы:
– Что называется решением неравенства с двумя переменными?
– Чем отличается решение строгого неравенства от нестрогого? (линия функции пунктирная или сплошная)
– Как можно проверить правильно ли вы выбрали множество? (Правило пробной точки)
–Сколько решений может иметь система неравенств с двумя переменными?
– Как решить уравнение с модулем?
Давайте оценим себя, лист самооценки.
Заполнить таблицу, поставив в соответствующей графе «+».
ДА
Не очень хорошо
Не знаю
Уравнения графиков изученных функций
Как определить функцию, если она задана в нестандартном виде
Алгоритм преобразования графиков, связанных с модулем
Как выбирать пробную точку
Алгоритм решения неравенств с двумя переменными
Я умею:
Различать графики функций
Изображать график функции
Выполнять преобразование графиков, связанных с модулем
При помощи пробной точки устанавливать, являются ли ее координаты решением неравенства
Изображать решение неравенства с двумя неизвестными
Подсчитать в столбце «ДА» количество выставленных «+».
Критерии оценок:
9-10«5»
7-8
«4»
5-6
«3»
Меньше 5
«2»
Решение неравенств и систем неравенств с двумя переменными — Студопедия
Определение. Пусть 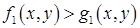 – неравенство, определенное на множестве
– неравенство, определенное на множестве  ;
; 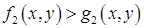 – неравенство, определенное на множестве
– неравенство, определенное на множестве  и т.д.
и т.д.  – неравенство, определенное на множестве
– неравенство, определенное на множестве 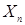 .
.
Конъюнкцию предикатов  ;
;  ; …;
; …; 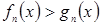 называют системой данных неравенств и записывают:
называют системой данных неравенств и записывают: 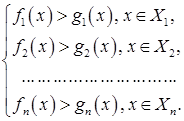
Аналогично определяют систему неравенств со знаками 

Областью определения системы неравенств с одной переменной называют множество  .
.
Значения переменной, при которой каждое неравенство системы обращается в верное числовое неравенство, называют решением системы неравенств.
Решить систему неравенств следовательно, найти все решения этой системы или установить, что их нет.
Множеством решений системы неравенств является пересечение множеств решений неравенств, образующих систему.
Две системы неравенств называются равносильными, если всякое решение одной из них является решением другой, и наоборот.
Если обе системы неравенств не имеют решений, то их тоже считают равносильными.
Решением неравенства с двумя переменными называют пару значений переменных, обращающую каждое неравенство в верное числовое неравенство.
Решением систем неравенств с двумя переменными является упорядоченная пара чисел, удовлетворяющая каждому неравенству системы.
Множество решений системы неравенств – это пересечение множеств решений всех неравенств, входящих в систему.
Поскольку пара действительных чисел  однозначно определяет точку координатной плоскости, то это дает возможность изобразить решение неравенства или системы неравенств с двумя переменными графически.
однозначно определяет точку координатной плоскости, то это дает возможность изобразить решение неравенства или системы неравенств с двумя переменными графически.
Теорема 5. В каждой из областей 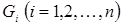 , на которые линия
, на которые линия 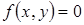 делит координатную плоскость, функция
делит координатную плоскость, функция  либо положительна, либо отрицательна.
либо положительна, либо отрицательна.
Каждое неравенство системы определяет некоторую область  плоскости
плоскости  , в которой лежит контрольная точка, в противном случае решением неравенства является область, не содержащая контрольную точку. В качестве контрольной точки удобно выбирать начало координат
, в которой лежит контрольная точка, в противном случае решением неравенства является область, не содержащая контрольную точку. В качестве контрольной точки удобно выбирать начало координат 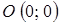 .
.
Пример. Найдем полуплоскость, определяемую неравенством  .
.
Решение. Построим прямую  .Данная прямая не проходит через начало координат. Следовательно, в качестве контрольной точки для решения неравенства
.Данная прямая не проходит через начало координат. Следовательно, в качестве контрольной точки для решения неравенства  целесообразно взять точку
целесообразно взять точку 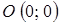 .
.
Подставим координаты точки 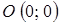 в неравенство, получим неверное числовое неравенство
в неравенство, получим неверное числовое неравенство  . Следовательно, точка
. Следовательно, точка 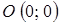 не принадлежит области решений неравенства. Другими словами, полуплоскость, определяемая неравенством, не содержит точку
не принадлежит области решений неравенства. Другими словами, полуплоскость, определяемая неравенством, не содержит точку 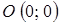 . На рисунке 14 искомая полуплоскость заштрихована.
. На рисунке 14 искомая полуплоскость заштрихована.
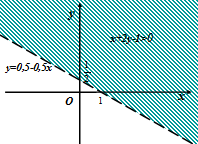 Рис.14
Рис.14
В общем случае множество решений системы неравенств представляет собой ограниченную или неограниченную область плоскости  , линию, точку, пустое множество.
, линию, точку, пустое множество.
Пример. Решим графически систему неравенств: 
Решение. Так как 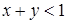 , то
, то 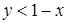 ; так как
; так как  , то
, то 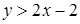 . Строим прямые
. Строим прямые  и
и  (Рис.15).
(Рис.15).
Множество решений неравенства 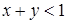 состоит из точек плоскости, лежащих под прямой
состоит из точек плоскости, лежащих под прямой  , а неравенство
, а неравенство  – из точек, лежащих над прямой
– из точек, лежащих над прямой  (Рис.15), то есть множество решений каждого из этих линейных неравенств есть полуплоскость.
(Рис.15), то есть множество решений каждого из этих линейных неравенств есть полуплоскость.
Графически решение данной системы неравенств есть пересечение полуплоскостей, не включая границу (Рис.15).
 Рис.15
Рис.15
Пример. Изобразим на координатной плоскости множество решений неравенства  .
.
Решение. Преобразуем неравенство к виду: 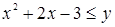 . Построим на координатной плоскости параболу
. Построим на координатной плоскости параболу 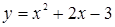 . Парабола разбивает плоскость на две области
. Парабола разбивает плоскость на две области 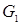 и
и 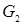 .
.  :
: 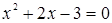 ;
;  ;
; 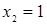 (Рис. 16).
(Рис. 16).
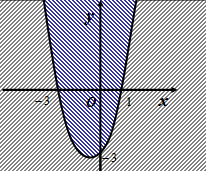
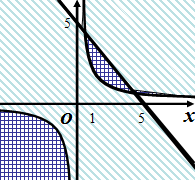
Рис.16 Рис.17
Решением неравенства является множество точек плоскости, лежащих выше параболы 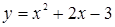 и поскольку неравенство
и поскольку неравенство 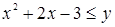 нестрогое, то в решение неравенства входит множество точек плоскости, лежащих на параболе
нестрогое, то в решение неравенства входит множество точек плоскости, лежащих на параболе 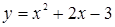 .
.
Решение данной системы неравенств представлено на рисунке 16.
Пример. Изобразим на координатной плоскости множество решений системы неравенств: 
Решение. 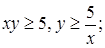
 ,
, 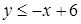 .
.
Геометрически, решением системы неравенств  ,
, 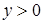 является множество точек первого координатного угла (Рис.17).
является множество точек первого координатного угла (Рис.17).
Решением неравенства  поскольку
поскольку  , является множество точек лежащих выше ветви гиперболы, служащей графиком функции
, является множество точек лежащих выше ветви гиперболы, служащей графиком функции 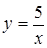 .
.
Решением неравенства  является множество точек, лежащих ниже прямой и на прямой, служащей графиком функции
является множество точек, лежащих ниже прямой и на прямой, служащей графиком функции 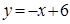 .
.
Решение данной системы неравенств представлено на рисунке 17.
Пример. Решим графически систему неравенств: 
Решение. Построим параболу 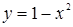 и прямую
и прямую  . Множество, заданное системой неравенств, состоит из точек, лежащих на параболе
. Множество, заданное системой неравенств, состоит из точек, лежащих на параболе 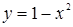 или под ней и одновременно на прямой
или под ней и одновременно на прямой  или над ней.
или над ней.
Решение данной системы неравенств представлено на рисунке 18.

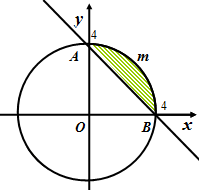
Рис.18 Рис.19
Пример. Решим графически систему двух неравенств: 
Решение. Решением первого неравенства являются точки полуплоскости с границей 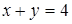 , включая эту прямую. Решением второго неравенства является внутренность круга с центром в начале координат и радиусом, равным
, включая эту прямую. Решением второго неравенства является внутренность круга с центром в начале координат и радиусом, равным  , включая точки окружности, которая является границей круга.
, включая точки окружности, которая является границей круга.
Решением системы неравенств является множество точек координатной плоскости, ограниченное дугой  окружности
окружности  и прямой
и прямой 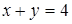 . Решение данной системы неравенств представлено на рисунке 19.
. Решение данной системы неравенств представлено на рисунке 19.
Уравнения и неравенства с двумя переменными. Алгебра, 11 класс: уроки, тесты, задания.
| 1. |
Выбор неравенства по рисунку
Сложность: лёгкое |
1 |
| 2. |
Выбор линейного неравенства по рисунку
Сложность: лёгкое |
1 |
| 3. |
Выбор рисунка по данному уравнению
Сложность: лёгкое |
1 |
| 4. |
Выбор и решение уравнения, если известна пара чисел
Сложность: лёгкое |
1 |
| 5. |
Уравнение в целых числах
Сложность: среднее |
3 |
| 6. |
Площадь фигуры
Сложность: среднее |
3 |
| 7. |
Назови уравнение по рисунку
Сложность: среднее |
3 |
| 8. |
Реши уравнение второй степени в целых числах
Сложность: сложное |
4 |
| 9. |
Текстовая задача
Сложность: сложное |
4 |
| 10. |
Построй график и найди площадь
Сложность: сложное |
4 |
| 11. |
Линейное уравнение с двумя неизвестными
Сложность: сложное |
2 |
Решение неравенств с двумя переменными
Решения неравенств с двумя переменными
Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию. Линейное неравенство с двумя переменными Неравенство, связывающее линейные выражения с двумя переменными. Набор решений — это область, определяющая половину плоскости. С другой стороны, есть набор решений, состоящий из области, определяющей половину плоскости.
Линейное уравнение | Линейное неравенство |
|---|---|
y = 32x + 3 | y≤32x + 3 |
Для неравенства линия определяет границу заштрихованной области.Это указывает на то, что любая упорядоченная пара в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться, что это так, выберите несколько контрольных точек — точку, не лежащую на границе линейного неравенства, используемую в качестве средства для определения, в какой полуплоскости лежат решения. и подставляем их в неравенство.
Контрольная точка | y≤32x + 3 |
(0, 0) | 0≤32 (0) + 30≤3 ✓ |
(2, 1) | 1≤32 (2) + 31≤3 + 31≤6 ✓ |
(−2, −1) | −1≤32 (−2) + 3−1≤ − 3 + 3−1≤0 ✓ |
Также мы можем видеть, что упорядоченные пары вне заштрихованной области не решают линейное неравенство.
Контрольная точка | y≤32x + 3 |
(−2, 3) | 3≤32 (−2) + 33≤ − 3 + 33≤0 ✗ |
График решения, установленного для линейного неравенства, всегда является областью.Однако граница не всегда может быть включена в этот набор. В предыдущем примере линия была частью набора решений из-за части «или равно» в инклюзивном неравенстве ≤. Если дано строгое неравенство <, мы использовали бы пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Неисключительная граница | Включая Граница |
|---|---|
y <32x + 3 | y≤32x + 3 |
Рассмотрим точку (0, 3) на границе; эта упорядоченная пара удовлетворяет линейному уравнению.Именно часть инклюзивного неравенства «или равно» делает упорядоченную пару частью множества решений.
y <32x + 3 | y≤32x + 3 |
3 <32 (0) +33 <0 + 33 <3 ✗ | 3≤32 (0) + 33≤0 + 33≤3 ✓ |
До сих пор мы видели примеры неравенства, которое было «меньше чем.”Теперь рассмотрим следующие графы с той же границей:
Больше, чем (вверху) | Меньше (ниже) |
|---|---|
y≥32x + 3 | y≤32x + 3 |
Учитывая приведенные выше графики, чего можно ожидать, если мы используем начало координат (0, 0) в качестве тестовой точки?
y≥32x + 3 | y≤32x + 3 |
0≥32 (0) + 30≥0 + 30≥3 ✗ | 0≤32 (0) + 30≤0 + 30≤3 ✓ |
Пример 1
Определите, является ли (2,12) решением 5x − 2y <10.
Решение:
Подставьте значения x и y в уравнение и посмотрите, получится ли истинное утверждение.
.Линейные неравенства в двух переменных
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma класса 12
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образцы документов CBSE чел для класса 12
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции CBSE
- Примечания к редакции
- CBSE Class
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE Дополнительные вопросы по математике для класса 10
- Дополнительные вопросы по науке, класс 10 по CBSE
- CBSE, класс
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Учебные решения
- CBSE Class
- Решения NCERT
- Решения NCERT для класса 11
- Решения NCERT для класса 11
- Примечания к редакции
- Примечания CBSE класса 7
Линейные системы с двумя переменными
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Системы уравнений Введение
- Линейные системы с тремя переменными
- Разделы
- Экспоненциальные и логарифмические функции
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Полная книга — Только проблемы
- Полная книга — Решения
- Текущая глава — Только проблемы
- Текущая глава — Решения
- Текущий раздел — Только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузок
- Полная книга
- Текущая глава
- Текущий раздел
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Общие графы
- Прямые, окружности и кусочные функции
- Параболы
- Эллипсы
- Гиперболы
- Разные функции
- Преобразования
- Симметрия
- Рациональные функции
- Полиномиальные функции
- Делительные многочлены
- Нули / корни многочленов
- Графические полиномы
- Нахождение нулей многочленов
- Частичные дроби
- Экспоненциальные и логарифмические функции
- Экспоненциальные функции
- Логарифмических функций
- Решение экспоненциальных уравнений
- Решение логарифмических уравнений
- Отборочные
Решайте неравенства и системы с помощью программы «Пошаговое решение математических задач»
Неравенства
Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной. В большинстве случаев можно найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически с любым требуемым уровнем точности. Кроме того, вы можете отобразить регионы, удовлетворяющие одному или нескольким неравенствам по двум переменным, четко видя, где происходят пересечения этих регионов.
Что такое неравенство?
Неравенства состоят из двух или более алгебраических выражений, соединенных символами неравенства. Символы неравенства:< менее > больше <= меньше или равно > = больше или равно ! = Или <> не равно Вот несколько примеров неравенства:
2 х — 9> 0
x 2 — 3 x + 5 <= 0
| 5x — 1 | <> 5
х 3 + 1 <= 0
Решить
Команду «Решить» можно использовать для решения одного неравенства для одного неизвестно на основной странице решения или для одновременного решения системы многих неравенств в одном неизвестном на странице расширенного решения.2–5 <0
Другими словами, QuickMath попытается найти решения, удовлетворяющие сразу обоим неравенствам.
Перейти на страницу решения
Участок
Команда Plot из раздела Graphs построит график любого неравенства, связанного с две переменные. Чтобы построить область, удовлетворяющую единственному неравенству с участием x и y, перейдите к основному страница построения неравенства, где вы можете ввести неравенство и указать верхний и нижний пределы x и y, по которым вы хотите построить график для.Продвинутый Страница построения неравенства позволяет вам построить объединение или пересечение до 8 регионов на одном графике. Вы можете контролировать такие вещи, как или не показывать оси, где оси должны быть расположены и какой аспект соотношение сюжета должно быть. Кроме того, у вас есть возможность показать каждый отдельный регион самостоятельно.
Уравнение говорит, что два выражения равны, а неравенство говорит что одно выражение больше, больше или равно, меньше или меньше или равно другому.Как и в случае с уравнениями, значение переменной для что неравенство истинно, является решением неравенства, а множество всех таких решений является множество решений неравенства. Два неравенства с одинаковое множество решений являются эквивалентными неравенствами. Неравенства решаются с помощью следующие свойства неравенства.
СВОЙСТВА НЕРАВЕНСТВА
Для действительных чисел a, b и c:
(a)

(Одно и то же число может быть добавлено к обеим сторонам неравенства без изменения набор решений.)
б)
(Обе части неравенства можно умножить на одно и то же положительное число без изменения набора раствора.)
(в)
(Обе части неравенства можно умножить на одно и то же отрицательное число без изменения множества решений, пока направление неравенства символ перевернут.)
Замена <на> приводит к эквивалентным свойствам.ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово «умноженный» может быть заменен на «разделенный» на части (b) и (c) свойств неравенства.
Обратите особое внимание на часть (c): если обе стороны неравенства умноженное на отрицательное число, направление символа неравенства должно быть наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая обе стороны на положительное число 2 дают

по-прежнему верное заявление. С другой стороны, начиная с — 3 <5 и умножение обеих сторон на отрицательное число -2 дает истинный результат, только если направление символа неравенства обратное.

Аналогичная ситуация возникает при делении обеих сторон на отрицательное число. В Резюмируя, можно сделать следующее заявление.При умножении или делении обеих сторон неравенства на минус числа, мы должны изменить направление символа неравенства, чтобы получить эквивалентное неравенство.
ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично линейное уравнение.
Линейное неравенство по одной переменной — это неравенство, которое можно записать в виде форма

, где a <> 0.Пример 1
Решите неравенство -3x + 5> -7.
Воспользуйтесь свойствами неравенства. Сложение — 5 с обеих сторон дает
Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 < 0, измените направление символа неравенства на противоположное.

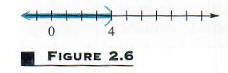
Исходному неравенству удовлетворяет любое действительное число меньше 4. множество решений можно записать {x | x <4}. График множества решений показан на Фигура 2.6, где скобки используются, чтобы показать, что 4 само по себе не принадлежит к набору решений.

Набор {x | x <4}, набор решений неравенства в Примере 1, является примером интервала. Упрощенное обозначение, называемое обозначением интервалов, используется для интервалы записи. В этих обозначениях интервал в примере 1 можно записать как (-oo, 4). Символ -oo не является действительным числом; он используется, чтобы показать, что интервал включает все действительные числа меньше 4.Интервал (-oo, 4) является примером открытый интервал, поскольку конечная точка, 4, не является частью интервала. Примеры другие наборы, записанные в интервальной записи, показаны ниже. Квадратная скобка - это используется, чтобы показать, что число является частью графика, а круглые скобки используются для указывают, что число не является частью графика. Когда два действительных числа a и b используются для записи интервала в следующей таблице, предполагается, что a <б.

Пример 2
Решите 4 — 3y <7 + 2y.Запишите решение в интервальной записи и на графике решение на числовой прямой. Напишите следующую серию эквивалентных неравенства.
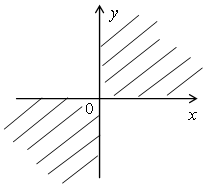
В нотации создателя множеств набор решений равен {y | y> = 3/5}, а в интервале обозначение множество решений (-3/5, oo). См. Рисунок 2.7 с графиком набора решений.

Отныне решения всех неравенств будут записываться с интервалом обозначение.
ТРЕХЧАСТНИЧНЫЕ НЕРАВЕНСТВА Неравенство -2 <5 + 3m <20 в следующем пример говорит, что 5 + 3м составляет от -2 до 20.Это неравенство можно решить используя расширение указанных выше свойств неравенства, работая со всеми три выражения одновременно.Решите -2 <5 + 3m <20.
Запишите эквивалентные неравенства следующим образом.

Решение показано на Рисунке 2.8

КВАДРАТИЧЕСКИЕ НЕРАВЕНСТВА Решение квадратичных неравенств зависит от решение квадратных уравнений.Квадратичное неравенство — это неравенство, которое можно записать в виде

Мы обсудим квадратичные неравенства в следующем разделе.
Перейти на страницу графика неравенств.
.
- 000 NC Книги
- BNAT 000 NC
- Классы