Тригонометрические неравенства и методы их решения

Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.

Методы решений неравенств:

1. Решение тригонометрических неравенств с помощью единичной окружности.
2. Графическое решение тригонометрических неравенств.
3. Решение неравенств методом интервалов.

При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:

I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.

II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.

Неравенство \(sinx>a\)

1. При \(|a|≥1\) неравенство \(sinx>a\) не имеет решений: \(x\in \varnothing\).
2. При \(a<−1\) решением неравенства \(sinx>a\) является любое действительное число: \(x\in \mathbb R\).
3. При \(−1≤a<1\) решение неравенства \(sinx>a\) выражается в виде \(arcsin a + 2\pi n < x < \pi -arcsin a + 2\pi n,\;n \in \mathbb{Z}\).

Неравенство \(sinx≥a\)

1. При \(|a|>1\) неравенство \(sinx\ge a\) не имеет решений: \(x\in \varnothing\).
2. При \(a\le−1\) решением неравенства \(sinx\ge a\) является любое действительное число: \(x\in \mathbb R\).
3. При \(-1<a<1\) решение неравенства \(sinx\ge a\) выражается в виде \(arcsin a + 2\pi n \le x \le \pi — arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
4. Случай \(a=1  \): \(x = \frac{\pi}2 +2\pi n,\;n \in \mathbb{Z}\).

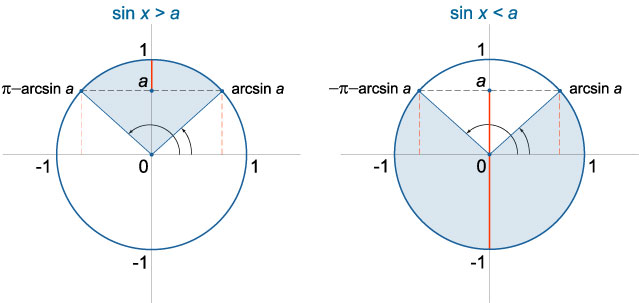
Неравенство \(sinx<a\)

1. При \(a>1\) решением неравенства \(sinx<a\) является любое действительное число: \(x\in \mathbb R\).\)
2. При \(a≤−1\) у неравенства \(sinx<a\) решений нет: \(x\in \varnothing\).\)
3. При \(-1<a\leq1\) решение неравенства \(sinx<a\) лежит в интервале \(-\pi — arcsin a + 2\pi n < x < arcsin a + 2\pi n,\;n \in \mathbb{Z}\).\)≤1\)

Неравенство \(sinx≤a\)

1. При \(a≥1\) решением неравенства \(sinx≤a\) является любое действительное число: \(x\in \mathbb R\).
2. При \(a<−1\) неравенство \(sinx≤a\) решений не имеет: \(x \in \varnothing\).
3. При \(-1<a<1\) решение нестрогого неравенства \(sinx≤a\) находится в интервале \(-\pi — arcsin a + 2\pi n \le x \le arcsin a + 2\pi n,\;n \in \mathbb{Z}\).
4. Случай \(a=−1\): \(x = -\frac{\pi}2 + 2\pi n,\;n \in \mathbb{Z}\).

Неравенство \(cosx>a\)

1. При \(a≥1\) неравенство \(cosx>a\) не имеет решений: \(x\in \varnothing\).
2. При \(a<−1\) решением неравенства \(cosx>a\) является любое действительное число: \(x\in \mathbb R\).
3. При \(−1≤a<1\) решение неравенства \(cosx>a\) имеет вид \(-arccos a + 2\pi n < x < arccos a + 2\pi n,\;n \in \mathbb{Z}\).

Неравенство \(cosx≥a\)

1. При \(a>1\) неравенство \(cosx≥a\) не имеет решений: \(x\in \varnothing\).
2. При \( a≤−1\) решением неравенства \(cosx≥a\) является любое действительное число: \(x\in \mathbb R\).
3. При \(-1<a<1\) решение неравенства \(cosx≥a\) имеет вид \(-arccos a + 2\pi n \le x \le arccos a + 2\pi n,\;n \in \mathbb{Z}\).
4. Случай \(a=1\): \(x = 2\pi n,\;n \in \mathbb{Z}\).

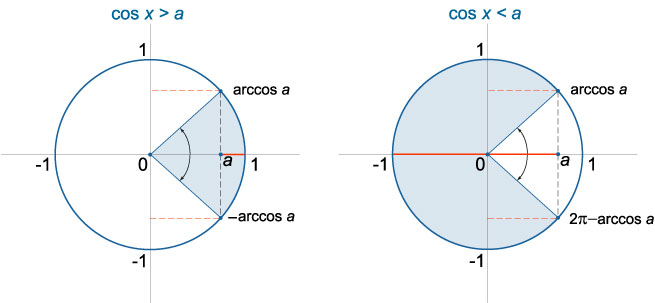
Неравенство \(cosx<a\)\)

1. При \(a>1\) неравенство \(cosx<a\) справедливо при любом действительном значении x: \(x\in \mathbb R\).\)
2. При \(a≤−1\) неравенство \(cosx<a\) не имеет решений: \(x\in \varnothing\).\)
3. При \(-1<a\leq1\) решение неравенства \(cosx<a\) записывается в виде \(arccos a + 2\pi n < x < 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\). \)≤1\)

Неравенство \(cosx≤a\)

1. При \(a≥1\) решением неравенства \(cosx≤a\) является любое действительное число: \(x\in \mathbb R\).
2. При \(a<−1\) неравенство \(cosx≤a\) не имеет решений: \(x\in \varnothing\).
3. При \(-1<a<1\) решение нестрогого неравенства \(cosx≤a\) записывается как \(arccos a + 2\pi n \le x \le 2\pi — arccos a + 2\pi n,\;n \in \mathbb{Z}\).
4. Случай \(a=−1\): \(x = \pi + 2\pi n,\;n \in \mathbb{Z}\).

Неравенство \(tgx>a\)

При любом действительном значении \(a\) решение строгого неравенства \(tgx>a\) имеет вид \(arctg a + \pi n < x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).

Неравенство \(tgx≥a\)

Для любого значения \(a\) решение неравенства \(tgx≥a\) выражается в виде \(arctg a + \pi n \le x < \frac{\pi}2 + \pi n,\;n \in \mathbb{Z}\).

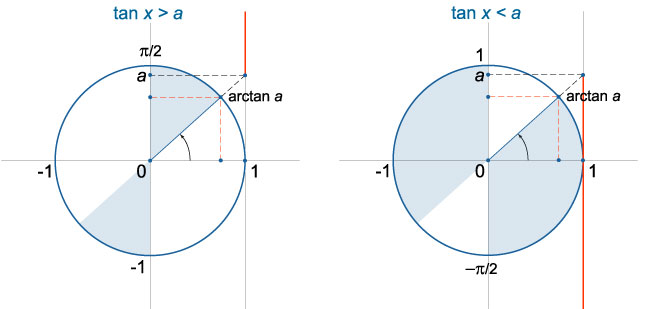
Неравенство \(tgx<a\)\)

Для любого значения \(a\) решение неравенства \(tgx<a\) записывается в виде \(-\frac{\pi}2 + \pi n < x < arctg a + \pi n,\;n \in \mathbb{Z}\).\)

Неравенство \(tgx≤a\)

При любом \(a\) неравенство \(tgx≤a\) имеет следующее решение: \(-\frac{\pi}2 + \pi n < x \le arctg a + \pi n,\;n \in \mathbb{Z}\).

Неравенство \(ctgx>a\)

При любом \(a\) решение неравенства \(ctgx>a\) имеет вид \(\pi n < x < arcctg a + \pi n,\;n \in \mathbb{Z}\).

Неравенство \(ctgx≥a \)

Нестрогое неравенство \(ctgx≥a\) имеет аналогичное решение \(\pi n < x \le arcctg a + \pi n,\;n \in \mathbb{Z}\).

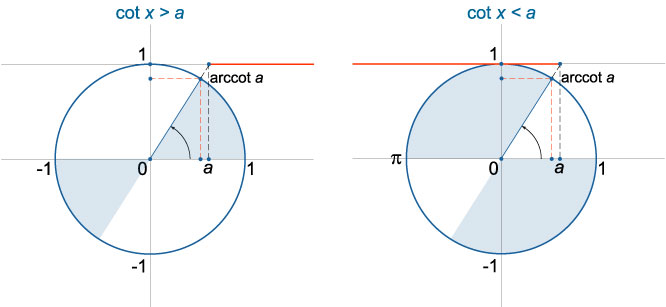
Неравенство \(ctgx<a\)\)

Для любого значения \(a\) решение неравенства \(ctgx<a\) лежит в открытом интервале \(arcctg a + \pi n < x < \pi + \pi n,\;n \in \mathbb{Z}\).\)

Неравенство \(ctgx≤a\)

При любом \(a\) решение нестрогого неравенства \(ctgx≤a\) находится в полуоткрытом интервале \(arcctg a + \pi n \le x < \pi + \pi n,\;n \in \mathbb{Z}\).

Пример. Решите неравенство: \(cosx>\frac12\).

Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.

Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(y=cosx \ и \ y=\frac12\). Выделим промежутки, на которых график функции косинус \(y=cosx\) расположен выше графика прямой \(y=\frac12\).

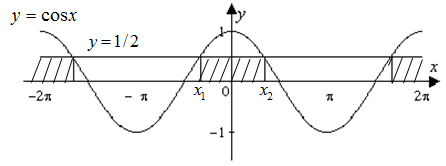
Найдем абсциссы точек \(x_1\ и \ x_2\) – точек пересечения графиков функций \(y=cosx\ и\ y=\frac12\), которые являются концами одного из промежутков, на котором выполняется указанное неравенство: \(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).

Учитывая, что косинус – функция периодическая, с периодом \(2\pi\), ответом будут значения x из промежутков \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).

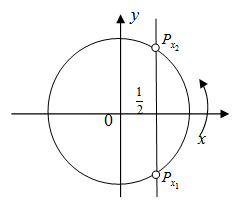
Второй способ. Построим единичную окружность и прямую \(x=\frac12\) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)

\(x_1=-arccos\frac12=-\frac{\pi}3; x_2=arccos\frac12=\frac{\pi}3\).

Учитывая периодичность косинуса, окончательно получим интервалы \((-\frac{\pi}3+2\pi k;\frac{\pi}3+2\pi k), \ k\in Z\).

Системы тригонометрических неравенств и методы их решения

Системы неравенств можно решать с помощью единичной окружности, придерживаясь следующего алгоритма:

1. Отметить на окружности решение первого неравенства.
2. Отметить решение второго неравенства.
3. Выделить общее решение (пересечение дуг).
4. Записать общее решение системы неравенств с учетом периода.

Пример 1. Ре­шите си­сте­му нера­венств: \(\begin{cases} sinx>-\frac{\sqrt2}2, \\ cosx\le\frac{\sqrt3}2. \\ \end{cases}\)

Решение: Решим про­стей­шие нера­вен­ства с по­мо­щью фор­мул общих ре­ше­ний: \(x\in (arcsina+2\pi n; \pi-arcsina+2\pi n), n\in Z \ и \\ x\in[arccosa+2\pi n; 2\pi-arccosa+2\pi n], n\in Z.\)

Для наших нера­венств имеем два про­ме­жут­ка ре­ше­ний:

\(1)\ x\in (arcsin(-\frac{\sqrt2}2)+2\pi n; \pi-arcsin(-\frac{\sqrt2}2)+2\pi n), n\in Z \Rightarrow \\ x\in(-\frac{\pi}4+2\pi n; \pi+\frac{\pi}4+2\pi n) \Rightarrow x\in(-\frac{\pi}4+2\pi n; \frac{5\pi}4+2\pi n), n\in Z. \)

\(2)\ x\in [arccos\frac{\sqrt3}2+2\pi n; 2\pi-arccos\frac{\sqrt3}2+2\pi n], n\in Z \Rightarrow \\x\in[\frac{\pi}6+2\pi n; 2\pi-\frac{\pi}6+2\pi n] \Rightarrow x\in[\frac{\pi}6+2\pi n; \frac{11\pi}6+2\pi n], n\in Z.\)

Для этих двух про­ме­жут­ков необ­хо­ди­мо ука­зать пе­ре­се­че­ние. Изоб­ра­зим это на три­го­но­мет­ри­че­ской окруж­но­сти:

Видно, что пе­ре­се­че­ни­ем об­ла­стей ре­ше­ний яв­ля­ет­ся про­ме­жу­ток:

\(x\in[\frac{\pi}6+2\pi n; \frac{5\pi}4+2\pi n), n\in Z\).

Про­ме­жу­ток \(x\in(-\frac{\pi}4+2\pi n; \frac{11\pi}6+2\pi n], n\in Z\) не яв­ля­ет­ся ча­стью ре­ше­ния, т. к. на самом деле здесь об­ла­сти не пе­ре­се­ка­ют­ся, по­сколь­ку лежат в раз­ных диа­па­зо­нах углов: от­ри­ца­тель­ном и по­ло­жи­тель­ном.

Об­ра­ти­те вни­ма­ние на то, что на­ча­ло про­ме­жут­ка ре­ше­ний вклю­ча­ет­ся, а конец ис­клю­ча­ет­ся.

Ответ: \(x\in[\frac{\pi}6+2\pi n; \frac{5\pi}4+2\pi n), n\in Z\).

Решение простейших тригонометрических неравенств

ТЕМА УРОКА: Решение простейших тригонометрических неравенств

Цель урока: показать алгоритм решения тригонометрических неравенств с использованием единичной окружности.

Задачи урока:

• Образовательные – обеспечить повторение и систематизацию материала темы; создать условия контроля усвоения знаний и умений;

• Развивающие – способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти;

• Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, мобильности, умения общаться, общей культуры.

Знания и навыки учащихся:
— знать алгоритм решения тригонометрических неравенств;

— уметь решать простейшие тригонометрические неравенства.

Оборудование: презентация к уроку, карточки с заданиями самостоятельной работы.

ХОД УРОКА:
1. Организационный момент (1 мин)

Девизом урока предлагаю слова Сухомлинского: « Сегодня – мы учимся вместе: я, ваш учитель и вы мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса».

2. Разминка. Диктант «Верно — неверно»

3. Повторение

Для каждого варианта — задания на слайде, продолжите каждую запись. Время выполнения 3 мин.

Давайте выполним взаимопроверку этой нашей работы, используя таблицу ответов на доске.

Критерий оценки: «5» — все 9 «+», «4» — 8 «+», «3» — 6-7 «+»

4. Актуализация знаний учащихся (8 мин)
Сегодня на уроке мы должны усвоить понятие тригонометрического неравенства и овладеть навыками решения таких неравенств.
– Давайте вначале вспомним, что такое единичная окружность, радианная мера угла и как связан угол поворота точки на единичной окружности с радианной мерой угла. (работа с презентацией)

Единичная окружность — это окружность с радиусом 1 и центром в начале координат.

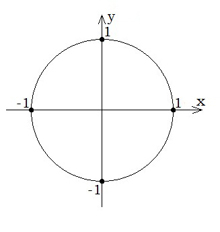
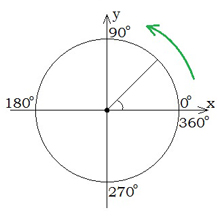
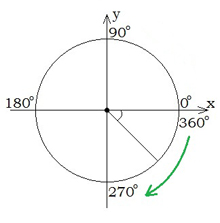
Угол, который образован положительным направлением оси OX и лучом OA, называется углом поворота. Важно запомнить, где находятся углы 0;  90;  180;  270;  360.

Если A перемещается против часовой стрелки, получаются положительные углы.

Если A перемещается по часовой стрелке, получаются отрицательные углы.

сos t – это абсцисса точки единичной окружности, sin t – ордината точки единичной окружности, t – угол поворота с координатами (1;0).
5 . Объяснение нового материала (17 мин)
Сегодня мы познакомимся с простейшими тригонометрическими неравенствами.
Определение.
Простейшими тригонометрическими неравенствами называют неравенства вида: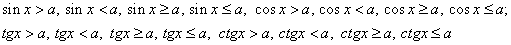

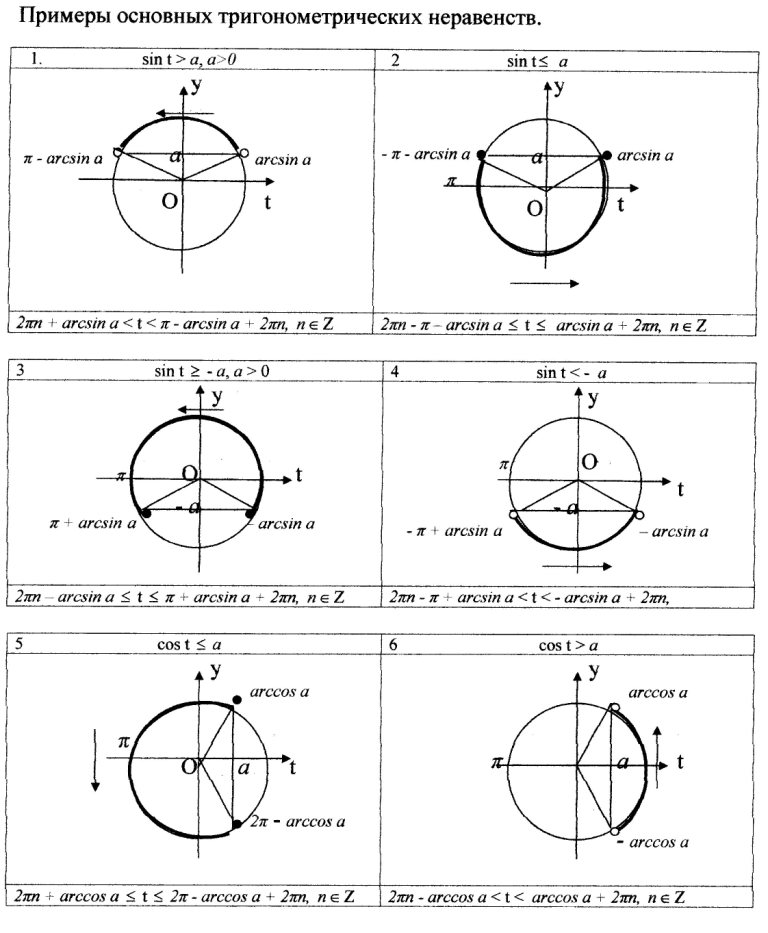
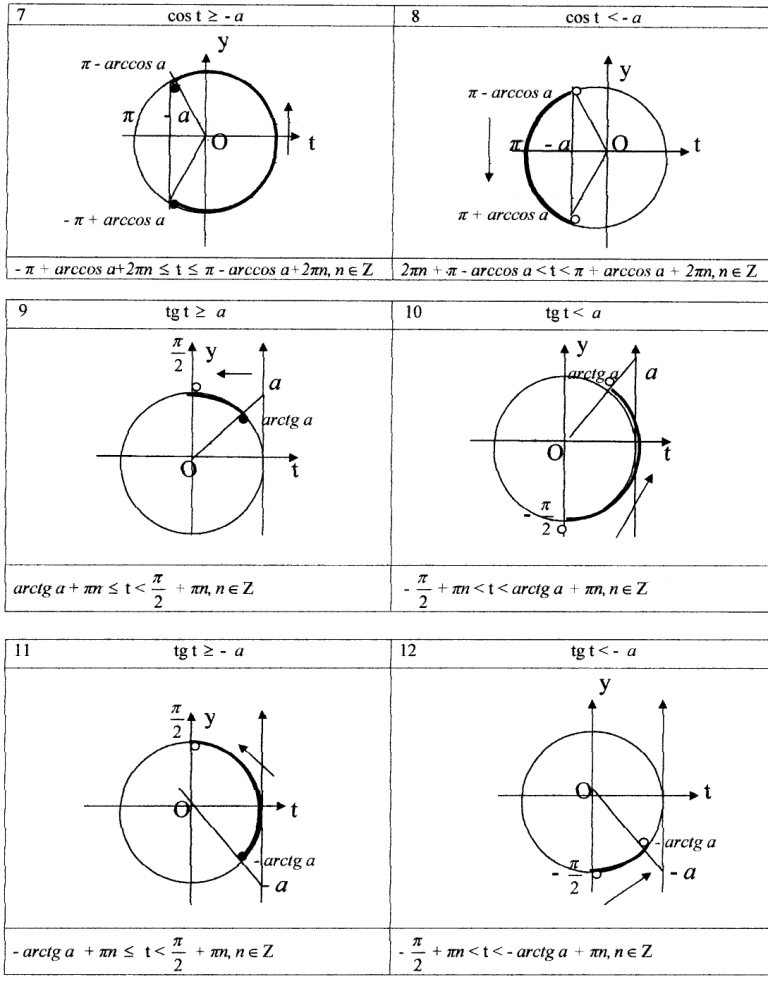
Как решить такие неравенств нам расскажут ребята (представление проектов учащимися с примерами). Определения и примеры учащиеся записывают в тетради.

В ходе выступления учащиеся объясняют решение неравенства, учитель дополняет рисунки на доске.
Алгоритм решения простейших тригонометрических неравенств дается после выступления учащихся. Все этапы решения неравенства учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения данной задачи.

Алгоритм решения тригонометрических неравенств с помощью единичной окружности:
1. На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции.
2. Провести через отмеченную точку прямую, пересекающую единичную окружность.
3. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства.
4. Выделить дугу окружности, на которой расположены решения неравенства.
5. Определить значения углов в начальной и конечной точках дуги окружности.
6. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.
Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые x = 1 и y = 1 соответственно, касающиеся тригонометрической окружности.
6. Практическая часть (12 мин)
Для отработки и закрепления теоретических знаний выполним небольшие задания. Каждый учащийся получает карточки с заданиями. Решив неравенства, нужно выбрать ответ и записать его номер.

7. Рефлексия деятельности на уроке
— Какая цель стояла перед нами?
— Назовите тему урока
— Получилось воспользоваться известным алгоритмом
— Проанализируйте свою работу на уроке.

8. Домашнее задание (2 мин)

Решите неравенство:

1. sin 3x

2. tg x — 1

3. cos 2x —

4. cos (x + ) <

5. sin x —

6. cos (3x — ) <

7. cos 2x

8. tg x —
   

9. Итог урока (2 мин)

Предлагаю закончить урок словами Я.А.Коменского: “ Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию ”.

                         

Решение простейших тригонометрических неравенств

Цели урока:

• повторить определения обратных тригонометрических функций,
• повторить решение простейших тригонометрических уравнений,
• научить решать простейшие тригонометрические неравенства.

Оборудование: проектор, компьютер, раздаточный материал.

Ход урока

Повторение. Обратные тригонометрические функции.

Вопросы классу.

1. Для какой функции существует функция обратная? Приведите пример функции, для которой существует обратная функция на всей области определения, не существует обратной функции на всей области определения.
2. Какая существует зависимость между областью определения и областью значений прямой и обратной функций?
3. Как располагаются в прямоугольной системе координат графики прямой и обратной функций?
4. Можно ли говорить о том, что тригонометрические функции на всей области определения имеют обратные функции? Обоснуйте свой ответ.

Далее даются определения обратных тригонометрических функций.

Определение 1. Арксинусом числа а называется такое число на отрезке , синус которого равен а.

Определение 2. Арккосинусом числа а называется такое число на отрезке [0; π], косинус которого равен а.

Определение 3.Арктангенсом числа а называется такое число на интервале , тангенс которого равен а.

Определение 4. Арккотангенсом числа а называется такое число из интервала (0; π), котангенс которого равен а.

Полезно задать учащимся несколько вопросов, которые помогут определить неформальное понимание определений.

Например.

1) Что означает запись y = аrcсоsх? Предполагаемый правильный ответ: по определению обратной тригонометрической функции это означает, что   и сosy = x

2) Правильно ли утверждение: “Арккосинус нуля равен 2πn?”.

3) Найдите .

Решение. Пусть . Тогда и . Применим основное тригонометрическое тождество sin²y + cos²y = 1. Найдем

Учащиеся должны увидеть, что на отрезке [0; π]  sin y ≥ 0 и правильным ответом будет .

4) у = arctgx. Если x ≥ 0, то, какому промежутку принадлежит у? А если х<0?

Повторение. Решение простейших тригонометрических уравнений.

Уравнение sinx = a (проектор, экран).

Множество решений уравнения имеет вид:

(рис.1,а для 0<a<1; рис 1,б для -1<a<0)

Рис. 1

Такая запись решения простейшего тригонометрического уравнения sinx = a удобна, когда проводится отбор корней. В основном же применятся следующая запись:

При решении уравнений вида sinx= 0, sinx=1, sinx= – 1 (частные случаи простейшего тригонометрического уравнения) мы пользуемся соответственно формулами: x=(рис2,а,б,в)

При  – уравнение решений не имеет.

Рис. 2

Изучение нового материала.

Решение простейших тригонометрических неравенств sin x < 0, sin x > 0

sin x ≤ 0, sin x ≥ 0

Учащимся предлагается воспользоваться карточкой № 1 (формат А-4) со следующим содержанием.

Карточка № 1.

Алгоритм решения тригонометрических неравенств.

1. На оси ординат единичной окружности отмечаем точку, соответствующую значению а (примерно).
2. Через полученную точку проводим прямую параллельно другой оси системы координат до пересечения с окружностью (Точки пересечения можно соединить с центром окружности).
3. На единичной окружности в точках пересечения записываем числа, соответствующие этим точкам.
4. Мысленно перемещаем нашу прямую параллельно оси координат в зависимости от значения а.
5. Выделяем штриховкой ту часть дуги единичной окружности, которую перемещающая прямая ее пересекает. Если неравенство строгое, то точки на концах дуги не заштриховываются (выколотые точки).
6. Записываем ответ.

Решение неравенства sinx>

Далее по алгоритму учитель на доске, а учащиеся на карточке проводят последовательные операции на единичных окружностях (рис. 3, а, б, в), рассматривая решение неравенства  sin x >

Рис. 3

Записывается ответ:

Уравнение cosx = a.

Учащимся предлагается работа по карточке № 2.

Карточка № 2.

(На карточке – пять единичных окружностей.)

Рис. 5

Учащиеся самостоятельно выполняют чертеж иллюстрирующий решение уравнения cosх = а для случая 0 < a < 1 (Рис. 4, а), для случая –1<a<0 (Рис. 4, б), для случая а = 0 (Рис. 5, а), для случая а = 1 (Рис. 5, б), для случая а = –1 (Рис. 5, в) и записывают решение уравнения для каждого из них по аналогии решения уравнения sinx = a.

Затем на экране высвечиваются чертежи соответствующие рисункам 4(а, б) и 5(а, б, в) с записью решения уравнения cosx = a.

Проводится обсуждение выполненной работы.

Решение неравенства соsx>

Решение неравенства проводится одним из учащихся на доске. Учащиеся на карточке при максимальной самостоятельности, используя рисунок, записывают решение данного неравенства (Рис. 6, а). При необходимости учитель оказывает помощь учащемуся у доски и учащимся класса. Закрепляется алгоритм решения неравенства.

Рис. 6

Ответ:

После решения этого неравенства учащимся предлагается самостоятельно решить неравенство (Рис. 6, б)

Ответ:

При проверке решений используется изображение на экране.

Уравнения tgx = a, ctgx = a

На экране высвечивается рисунок 7, а, б, по которому разбирается решение уравнений.

Здесь нужно заострить внимание учащихся на наличие двух дуг, симметричных относительно начала координат и в связи с этим на соответствующую запись ответа.

Рис. 7

Учитель у доски объясняет решение данных неравенств. Решение неравенств учащиеся оформляют в тетрадях. Целесообразно рассмотреть решение нестрогих неравенств, чтобы напомнить об области определения тангенса и котангенса, так как строгие неравенства не подчеркивают того, что тангенс и котангенс определены не для любого значения аргумента.

По результатам объяснения учителя учащиеся получают рисунок 8(а, б) с записью ответа.

Рис. 8

Рис. 9

Ответ:

Итог урока. Повторить алгоритм решения тригонометрических неравенств на каком либо примере учебника п.10 (А.Н.Колмогоров и др. Алгебра и начала математического анализа. 10 – Ф45 11-е классы: учебник для общеобразовательных учреждений с приложением на электронном носителе; под редакцией А.Н.Колмогорова. М.: Просвещение, 2009).

Домашнее задание: п.10, материал карточек.

Методическая разработка по теме «Тригонометрические неравенства и их системы»

Организационный момент

Основная часть

Занятие посвящено обобщению и систематизации знаний по теме «Решение тригонометрических неравенств и их систем». В ходе работы обобщим основные виды тригонометрических неравенств, систем неравенств и методы их решения, а также дополним наши знания применением тригонометрических неравенств в нестандартных ситуациях.

1. Обобщение решения простейших тригонометрических неравенств.

1. Актуализация знаний

1. Какие неравенства называются простейшими?

2. Приведите примеры простейших тригонометрических неравенств.

3. Чем можно пользоваться при решении тригонометрических неравенств?

Задание 1.

Необходимо напомнить алгоритм решения тригонометрических неравенств с помощью единичной окружности на конкретном примере.

Задание 2.

Необходимо напомнить алгоритм решения тригонометрических неравенств с помощью графика функции на конкретном примере.

1. Выполнение практических заданий.

Образцы карточек.

Карточка 1.

№1. Запишите все решения, соответствующие дуге, изображённой на рисунке.

а) б)

№2.Решите неравенство с помощью единичной окружности.

№3. Решите неравенство графически.

Карточка2.

№1. Запишите все решения, соответствующие дуге, изображённой на рисунке.

а) б)

№2.Решите неравенство с помощью единичной окружности.

№3. Решите неравенство графически.

2. Обобщение решения неравенств, сводящихся к простейшим.

Следующий тип неравенств, о которых пойдёт речь — это неравенства, сводящиеся к простейшим разными способами.

1. Актуализация знаний

1. Какими способами можно привести неравенство к простейшему виду? Приведите примеры таких неравенств.

Вспомним суть данного метода в ходе выполнения задания.

Задание. Решить неравенство

Учитель следит за решением, пошагово демонстрирует его с помощью презентации.

Мы повторили первый способ сведения неравенств к простейшему виду. Как ещё можно привести неравенство к простейшему виду?

Ещё раз обратим внимание на решение неравенств с использованием основных тригонометрических формул.

Учитель обсуждает решение неравенства с учениками, используя при этом презентацию.

* Вспомним, неравенства какого вида можно свести к простейшим введением вспомогательного угла?

* В чём состоит общий метод решения таких неравенств?

Задание. Решить неравенство

Учитель ведёт беседу с классом, на экране поэтапно появляется решение.

* Можно ли данное неравенство сразу решать введением вспомогательного угла?

* Можно ли каким-то образом преобразовать данное неравенство?

* Что для этого нужно сделать?

* Можно ли последнее неравенство решать введением вспомогательного угла?

* Что для этого нужно сделать?

* Какой вид имеет последнее неравенство?

* Ещё раз напомним решение данного типа неравенств.

* Решим данное неравенство.

2. Выполнение практических заданий.

(работа в группах)

Класс делится на 3-4 группы. Каждой группе даётся карточка заданий (на обороте указать фамилии участников группы). Группы выполняют задание, затем меняются решениями (I-II-III-IV-I) и проверяют работу друг друга (взаимоконтроль). Оценку заносят в рабочую карту с пометкой «в/к» (на обороте указать «Проверяли…»). Учитель затем перепроверяет решение и оценивание.

III. Обобщение методов решения неравенств с помощью замены переменной.

1. Актуализация знаний

1. В каком случае удобно использовать замену t=f(x), где f(x)- одна из тригонометрических функций?

2. В каком случае можно использовать замену t=sinx+cosx?

Повторим решение данного типа неравенств на конкретных примерах.

На доске записаны 3 неравенства. По желанию ученики поочерёдно выходят к доске и решают неравенства, комментируя каждый шаг. Остальные ученики записывают решения, стараясь делать самостоятельно.

Далее рассмотрим более сложное неравенство, которое также удобно решать заменой переменной.

Задание. Решить неравенство

cos2x-cos8x+cos6x<1.

Учитель ведёт беседу с классом, записывает решение на доске.

*Какие преобразования необходимо выполнить?

*Что замечаем далее?

*Можно ли в данный момент ввести новую переменную?

*Как можно сделать аргументы одинаковыми?

*Далее введём новую переменную . В результате получим неравенство

Решите самостоятельно последнее неравенство и найдите значения переменной t, удовлетворяющие неравенству.

*Возвращаясь к замене, решим полученные простейшие тригонометрические неравенства и запишем ответ.

IV. Обобщение решения тригонометрических неравенств методом интервалов.

Перед учениками и на доске — алгоритм решения неравенств методом интервалов.

Повторение данного метода проводим в ходе решения неравенства

Выполнение практических заданий.

Каждый ученик получает карточку с одним неравенством. Карточки разного уровня сложности. Например, сильные ученики решают неравенство методом интервалов, средние и слабые — введением новой переменной.

Работу оценивает учитель, оценку заносит в рабочую карту ученика.

V. Обобщение решения систем тригонометрических неравенств.

Задание. Необходимо напомнить алгоритм решения систем тригонометрических неравенств.

Далее работаем следующим образом: каждому ученику, в соответствии с вариантом, даются 3-4 карточки, на которых необходимо решить указанную систему неравенств. Выполнив задание первой карточки, необходимо отнести её на проверку (проверяет учитель или консультант (сильный ученик)). Если система решена верно, то её оставляют у проверяющего, приступают к решению задания следующей карточки. Если неверно, то карточка возвращается для исправления ошибки. Время работы ограничено-10 мин, поэтому ученики стараются выполнять задания быстро и по возможности правильно. По истечении времени работы, подводится итог:

4 верно выполненных задания — оценка «5»,

3 верно выполненных задания — оценка «4»,

2 верно выполненных задания — оценка «3»,

менее 2 выполненных заданий — оценка «2».

Оценка заносится в рабочую карту ученика.

3. Углубление знаний по теме

«Решение тригонометрических неравенств и их систем».

Заранее две группы учеников провели дополнительную исследовательскую работу. Первая группа изучала использование тригонометрических неравенств для нахождения области определения функций, вторая группа занималась решением неравенств смешанного типа. На специальном стенде ученики разместили решения различных заданий. Желающие могут ознакомиться. Далее ребята демонстрируют примеры решений неравенств указанных типов, используя подготовленные презентации.

4. Систематизация знаний

по теме

«Решение тригонометрических неравенств и их систем».

В ходе занятия мы обобщили знания о видах тригонометрических неравенств и их систем, способах их решения.

Кратко материал нашего урока можно представить в виде таблицы (см. приложение), которая будет являться своеобразной памяткой о видах тригонометрических неравенств, их систем и способах их решения.

Используя таблицу, ещё раз быстро повторим материал темы «Решение тригонометрических неравенств и их систем».

5) Заключение.

В качестве домашнего задания предлагается индивидуальная контрольная работа, анализ выполнения которой покажет степень усвоения материала данной темы каждым учеником.

—неравенства вида sinx>(<)a;cosx>(<)a;

tgx>(<)a;ctgx>(<)a.

— и др.

-тригонометрическим кругом или графиком тригонометрических функций.

— студент на примере неравенства рассказывает алгоритм решения неравенств с помощью единичной окружности, используя презентацию.

— ученик на примере неравенства рассказывает алгоритм решения неравенств с помощью графика функции, используя презентацию.

Ученики выполняют индивидуальную работу по карточкам. После выполнения работы самостоятельно себя оценивают, сравнивая свои решения с правильными решениями (правильные решения вместе с критерием оценки раздаются ученикам после выполнения работы или появляются на доске). Оценку заносят в рабочую карту урока.

а) С помощью замены переменной t=ax+b.

Н-р; неравенства вида

и др.

Ученики записывают решение в тетрадь. Один ученик с места комментирует решение:

1. Учитывая, что y=cost – чётная функция, запишем неравенство в виде

2. Пусть тогда неравенство примет вид -простейшее.

3. Воспользуемся алгоритмом решения простейших тригонометрических неравенств (проговаривает…).

4. Найдём значения переменной t, удовлетворяющие неравенству.

5. Вернёмся к переменной х и найдём её значения.

6. Запишем ответ.

б) С помощью основных тригонометрических формул.

Ученики ведут диалог с учителем, после обсуждения записывают решение в тетрадь.

— неравенства вида Аsinx+Bcosx>C, где А,В,С-данные числа и АВ

-Ученик, используя презентацию, рассказывает суть данного метода.

-нет, т.к. оно пока не имеет вид Аsinx+Bcosx>C.

-можно.

-перенести 1 в левую часть и применить формулы двойного угла: и

Тогда неравенство примет вид

;

или

— да.

— разделить обе части неравенства на

Тогда неравенство примет вид

Учтём, что

получим

— неравенство, сводящиеся к простейшему введением новой переменной.

— введём новую переменную , тогда неравенство примет вид

Далее ученики самостоятельно решают неравенство, затем проверяют себя по решению на экране.

Карточка 1.

Карточка 2.

Карточка 3.

Карточка 4.

-когда неравенство содержит одну и ту же тригонометрическую функцию одного и того же аргумента.

-когда в неравенство входят выражения sinx+cosx и sin2x.

Ученики участвуют в беседе, записывают решение в тетради.

-перенести –cos8x в правую часть неравенства и применить формулу суммы косинусов в левой части неравенства.

cos2x+cos6x<1+cos8x,

Тогда

-нет, т. к. аргументы косинусов различны.

-применить формулу косинуса двойного угла

Тогда неравенство примет вид

Ответ:

У доски один ученик решает данное неравенство, демонстрируя шаги алгоритма. Остальные ученики записывают решение в тетрадь.

1. Рассмотрим функцию

2.Найдём основной период Т функции:

3. Найдём нули функции f(x) на промежутке

Итак,

4. Найдём точки разрыва функции f(x) на промежутке

Итак,

5. Найденными точками разделим промежуток на части, в каждой из которых функция f(x) сохраняет свой знак:

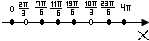
6. Определим знак функции в каждой части методом пробных точек:

7. Выберем те части, в которых выполняется исходное неравенство:

8. Учитывая периодичность функции, запишем ответ:

Ответ:

— ученик на примере системы неравенств рассказывает алгоритм решения систем тригонометрических неравенств, используя презентацию.

Задания для карточек.

I вариант

II вариант

1). Использование тригонометрических неравенств для нахождения области определения функции.

2) Неравенства смешанного типа.

Каждый ученик получает конспект урока в виде таблицы. Дома необходимо поработать с ним, переписав конспект в свою теоретическую тетрадь.

Домашняя контрольная работа

(примерное содержание одного из вариантов)

Простейшие тригонометрические неравенства | Формулы с примерами

sin x > a, | a |

Множество решений неравенства : x (arcsin a + 2?n; ? — arcsin a + 2?n), n Z

2. sin x

Множество решений неравенства: x (-? — arcsin a + 2?n; arcsin a + 2?n), n Z

3. cos x > a, | a |

Множество решений неравенства: x (-arccos a + 2?n; arccos a + 2?n), n Z

4. cos x

Множество решений неравенства: x (arccos a + 2?n; 2? — arccos a + 2?n), n Z

5. tg x > a, a R

Множество решений неравенства: x (arctg a + ?n; ?2 + ?n), n Z

6. tg x R

Множество решений неравенства: x (- ?2 + ?n; arctg a + ?n), n Z

7. ctg x > a, a R

Множество решений неравенства: x (?n; arcctg a + ?n), n Z

8. ctg x R

Множество решений неравенства: x (arcctg a + ?n; ? + ?n), n Z

Урок 53. Тригонометрические неравенства (факультативное занятие) | Поурочные планы по алгебре и начала анализа 10 класс

Урок 53. Тригонометрические неравенства (факультативное занятие)

09.07.2015 6506 0

---

Цель: рассмотреть способы решения тригонометрических неравенств.

Ход урока

I. Сообщение темы и цели урока

 

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

Решите уравнение:

Вариант 2

Решите уравнение:

 

III. Изучение нового материала

Решение тригонометрических неравенств (как и уравнений), как правило, сводится к решению простейших тригонометрических неравенств. Поэтому прежде всего остановимся на решении таких неравенств. Их удобно решать, используя единичную окружность.

Пример 1

Решим неравенство sin x > 1/2.

 

 

На единичной окружности по оси ординат отложим значение sin х = 1/2 и построим соответствующие углы   (углы откладываются против часовой стрелки и являются положительными). На рисунке видно, что неравенству sin х > 1/2 удовлетворяют значения  Учтем, что период функции синуса составляет 2π, и получим решение данного неравенства  или 

 

 

Пример 2

Решим неравенство 

 

 

На оси котангенсов для единичной окружности отложим значение  и построим соответствующий угол  Видно, что неравенству  удовлетворяют значения Учитывая период функции котангенса (равный π), получим решение данного неравенства:  или  где n ∈ Z.

В случае сложного аргумента тригонометрической функции рекомендуется обозначить его новой переменной, решить для него неравенство, а затем вернуться к старой неизвестной.

 

Пример 3

Решим неравенство 

 

 

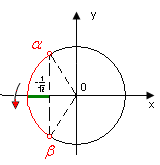
Обозначим аргумент косинуса  и получим простейшее тригонометрическое неравенство  Решим это неравенство. На единичной окружности по оси абсцисс отложим значение и построим соответствующие углы  Тогда неравенству  удовлетворяют значения  Учтем периодичность функции cos y и получим решения 

Теперь вернемся к старой неизвестной х и получим двойное линейное неравенство  Ко всем частям неравенства прибавим число π/6. Отсюда  Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:  или  где n ∈ Z.

Если неравенство не является простейшим, то используя преобразования, аналогичные тем, которые применялись для уравнений, сводим неравенство к простейшему.

 

Пример 4

Решим неравенство 

 

 

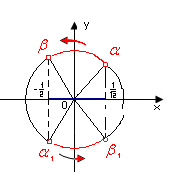
Введем новую переменную у = tg x и получим квадратное неравенство  Это неравенство имеет решение  Вернемся к старой неизвестной x и получим двойное неравенство  На единичной окружности по оси тангенсов отложим значения 1 и  и построим соответствующие углы  Тригонометрическому неравенству удовлетворяют значения  Учтем периодичность функции тангенса и получим решение данного неравенства:  или 

Также при решении тригонометрических неравенств можно использовать метод интервалов (который является универсальным для всех неравенств).

 

Пример 5

Решим неравенство 

 

 

На единичной окружности отметим значения х, при которых обращается в нуль числитель   (откуда ) и знаменатель sin 2х = 0 (тогда )   (откуда ) дроби. Определим знак этой дроби, например, при х = π/6 и получим:

 

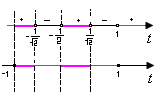
Учтем, что при переходе через отмеченные значения х знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Также учтем значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). Теперь легко выписать решения неравенства:  Учитывая, что через 2пn (где n ∈ Z) ситуация повторяется, выпишем решения данного неравенства: 

При наличии в неравенстве функций тангенса и котангенса удобно перейти к функциям синуса и косинуса и использовать рассмотренный метод интервалов.

 

Пример 6

Решим неравенство 

 

 

Учтем, что  и запишем неравенство в виде  Отметим на единичной окружности значения х, при которых обращается в нуль числитель sin x – cos x= 0 (откуда  и ) и знаменатель sin x cos x = 0 (тогда  и x = 2π) дроби. Определим знак данной дроби, например, при х = π/3 и получим:

Учтем, что при переходе через отмеченные значения x знак неравенства меняется на противоположный. Построим диаграмму знаков данной дроби. Учтем также значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). С учетом периодичности функций синуса и косинуса, входящих в неравенство, запишем окончательное решение данного неравенства  где n ∈ Z.

При использовании метода интервалов необходимо помнить, что тригонометрическое выражение может иметь кратные корни. При переходе через корень нечетной кратности знак выражения меняется на противоположный, при проходе через корень четной кратности знак сохраняется.

 

Пример 7

Решим неравенство 

 

 

На единичной окружности отметим значения x, при которых обращается в нуль числитель 2 sin x -1 = 0 (откуда ) и знаменатель   (тогда ). Учтем, что х = -π/6 — корень второй (четной) кратности и при переходе через него знак дроби не меняется. Определим знак выражения, например, при х = 0 и получим:  Построим диаграмму знаков данной дроби. Учтем значения х, при которых знаменатель дроби обращается в нуль (они отмечены кружками). С учетом периодичности функций, входящих в неравенство, запишем его решения: 

 

IV. Задание на уроке и на дом

Решите неравенство:

Ответы: 

 

V. Подведение итогов урока