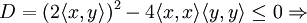Доказательство неравенства Коши
☰
Неравенство Коши было доказано французским математиком Огюстом Коши в первой половине XIX века. В сокращенном виде неравенство Коши утверждает, что среднее арифметическое неотрицательных чисел не меньше их среднего геометрического. В полном варианте в неравенство Коши также включаются среднее гармоническое и среднее квадратическое.
Среднее арифметическое — это сумма заданного количества чисел, деленная на количество чисел:
(x1 + x2 + x3 + … + xn) / n
Среднее геометрическое находится как извлечение корня в степени количества чисел, где подкоренное выражение — это произведение этих чисел:
n√( x1 * x2 * x3 * … * xn)
Таким образом, неравенство Коши утверждает, что
(x1 + x2 + x3 + … + xn) / n ≥ n
Для его доказательства упростим выражения, представив, что находим среднее арифметическое и среднее геометрическое только двух чисел: a и b. Доказательство неравенства для двух положительных чисел будет верно и для множества положительных чисел.
(a + b) / 2 ≥ √ab
В данном случае извлекается квадратный корень, так как находится среднее геометрическое только двух чисел.
Из свойств числовых неравенств известно, что если k – m в результате дает положительное число, то k > m; если числа одинаковы, то k = m. Значит, если доказать, что разность среднего арифметического и среднего геометрического есть положительное число (или равное нулю), то значит, будет доказано и само неравенство Коши.
Вычтем из среднего арифметического двух положительных чисел их среднее геометрическое:
(a + b) / 2 – √ab
Приведем к общему знаменателю:
(a + b) / 2 – 2√ab / 2
Многочлен a + b – 2√ab — это квадрат разности (√a – √b)2. Получаем:
(√a – √b)2 / 2
Квадрат любого числа есть число положительное или равное нулю (если a = b). Значит, в числителе будет неотрицательное значение. Знаменатель дроби также положителен. Значит, при вычитании из среднего арифметического среднего геометрического получилось неотрицательное значение. Таким образом, (a + b) / 2 ≥ √ab, что и требовалось доказать.
3.2. Неравенство Коши — Буняковского
Теорема
3.1. Для
любых векторов х, у евклидова
пространства 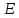 справедливо неравенство
Коши — Буняковского
справедливо неравенство
Коши — Буняковского
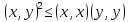 (3.1)
(3.1) При 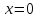 обе части неравенства (3.1) равны нулю
согласно свойству 3.3, значит, неравенство
выполняется. Отбрасывая этот очевидный
случай, будем считать, что
обе части неравенства (3.1) равны нулю
согласно свойству 3.3, значит, неравенство
выполняется. Отбрасывая этот очевидный
случай, будем считать, что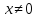 . Для
любого действительного числа
. Для
любого действительного числа 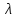 ,
в силу аксиомы г), выполняется неравенство
,
в силу аксиомы г), выполняется неравенство
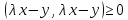 (3.2)
(3.2)
Преобразуем левую часть неравенства, используя аксиомы и свойства скалярного умножения:
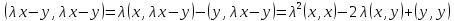
Мы
получили квадратный трехчлен относительно
параметра 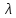 (коэффициент
(коэффициент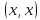 при
при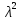 согласно аксиоме г) ненулевой, так как
согласно аксиоме г) ненулевой, так как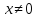 , неотрицательный
при всех действительных значениях
параметра. Следовательно, его дискриминант
равен нулю или отрицательный, т.е.
, неотрицательный
при всех действительных значениях
параметра. Следовательно, его дискриминант
равен нулю или отрицательный, т.е.
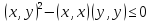
Что и требовалось доказать.
Доказательство неравенства Коши — Буняковского выглядит достаточно просто. Тем не менее это неравенство очень полезное. Применяя его в конкретных евклидовых пространствах, мы получаем некоторые хорошо известные в анализе и алгебре неравенства.
Пример
3.5. В
случае линейного
арифметического пространства 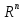 неравенство Коши — Буняковского
трансформируется в неравенство
Коши:
неравенство Коши — Буняковского
трансформируется в неравенство
Коши:
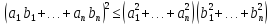
В
евклидовом пространстве  ,
скалярное произведение в котором
выражается определенным интегралом
(см. пример 3.4), неравенство Коши —
Буняковского превращается в неравенство Буняковского (называемое
также неравенством
Шварца):
,
скалярное произведение в котором
выражается определенным интегралом
(см. пример 3.4), неравенство Коши —
Буняковского превращается в неравенство Буняковского (называемое
также неравенством
Шварца):
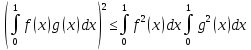
3.3. Нормированные пространства
В линейном пространстве обобщением понятия длины свободного вектора является норма. Длину вектора в линейном пространстве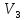 или
или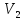 можно
рассматривать как функцию, определенную
на множестве
можно
рассматривать как функцию, определенную
на множестве 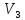 (соответственно
(соответственно 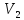 ), которая
каждому вектору ставит в соответствие
число — его длину. Норму вектора в
линейном пространстве иногда называют
длиной, имея в виду связь с аналогичным
термином векторной алгебры.
), которая
каждому вектору ставит в соответствие
число — его длину. Норму вектора в
линейном пространстве иногда называют
длиной, имея в виду связь с аналогичным
термином векторной алгебры. Определение
3.2. Функцию,
заданную на линейном пространстве 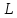 ,
которая каждому вектору
,
которая каждому вектору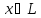
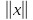 ,
называютнормой, если
она удовлетворяет следующим аксиомам
нормы:
,
называютнормой, если
она удовлетворяет следующим аксиомам
нормы: а) 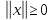 ,
причем равенство
,
причем равенство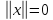 возможно только при
возможно только при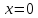 ;
;
б) 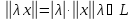 ;
;
в) 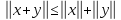 (неравенство
треугольника).
(неравенство
треугольника).
Евклидовы пространства и нормированные пространства представляют собой примеры линейных пространств с дополнительными структурами: скалярным умножением и нормой соответственно. Эти два понятия совершенно различны, однако, как утверждает следующая теорема, исходя из скалярного умножения в евклидовом пространстве можно задать норму и тем самым превратить евклидово пространство в нормированное.
Теорема 3.2. Всякое скалярное умножение в евклидовом пространстве определяет норму согласно формуле
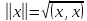 (3.3)
(3.3)
Отметим,
что, согласно аксиоме г) скалярного
умножения, 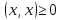
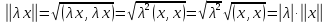
Остается проверить аксиому в) нормы, для чего мы воспользуемся неравенством Коши — Буняковского (3.1),
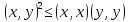 ,
,
которое можно записать в виде
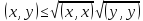
или, с учетом (3.3),
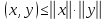
Используя это неравенство, получаем
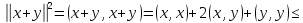
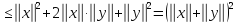
Что и требовалось доказать.
Введение нормы по формуле (3.3) опирается только на общие свойства скалярного умножения, вытекающие из его аксиом, и не связано со спецификой конкретного линейного пространства. Поэтому такую норму в евклидовом пространстве называют евклидовой или сферической нормой. Когда говорят, не уточняя, о норме в евклидовом пространстве, обычно имеют в виду именно эту норму.
Вовсе не обязательно, чтобы в евклидовом пространстве норма вводилась через скалярное произведение. Рассмотрим следующие примеры, показывающие другие часто используемые нормы, не связанные с каким-либо скалярным произведением.
Пример
3.6. В линейном
арифметическом пространстве 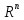 нормой
является функция
нормой
является функция 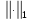 вида
вида
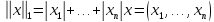
(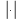 в
правой части обозначает модуль
действительного числа).
в
правой части обозначает модуль
действительного числа).
Легко убедиться, что аксиома а) нормы выполнена, так как величина
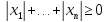 ,
причем она равна нулю тогда и только
тогда, когда все компоненты
,
причем она равна нулю тогда и только
тогда, когда все компоненты 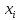 арифметического
вектора равны нулю.
арифметического
вектора равны нулю.
Так
же просто убедиться в верности аксиомы
б) нормы. Для проверки неравенства
треугольника (аксиома в) нормы) выберем
произвольные два вектора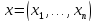 и
и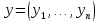 из
из 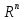 . Тогда
. Тогда
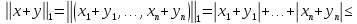
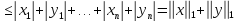
Приведенную
норму называют 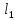 -нормой или октаэдрической
нормой.
-нормой или октаэдрической
нормой.
Пример 3.7. Функция
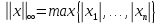
заданная
на векторах 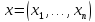 в
в 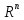 , также
является нормой в
, также
является нормой в 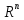 . Эту
норму называют
. Эту
норму называют 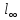 —нормой или кубической
Нормой.
—нормой или кубической
Нормой.
Как
и в предыдущем примере проверка аксиом
а) и б) нормы очевидна. Проверим неравенство
треугольника для произвольных векторов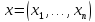 и
и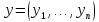 из
из 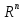 :
:
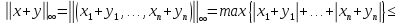
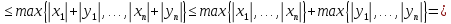
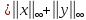
Нормы 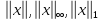 одного
и того же вектора х связаны
неравенствами
одного
и того же вектора х связаны
неравенствами
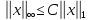 .
.
которые непосредственно вытекают из определений этих норм.
Пример
3.8. Множество S тех векторов х нормированного
пространства, которые удовлетворяют
равенству 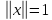 (единичных
векторов), называют единичной
сферой. Множество S зависит от линейного пространства и
однозначно определяет рассматриваемую
в нем норму. На рис. 3.1 изображен вид
единичной сферы для различных норм
двумерного линейного пространства
(конкретно линейного пространства
радиус-векторов точек плоскости):
евклидовой (рис. 3.1, а),
ок-таэдрической (рис. 3.1,6) и кубической
(рис. 3.1, в). В случае трехмерного линейного
пространства (линейного пространства
радиус-векторов) единичные сферы
указанных норм изображены на рис. 3.2. Мы
видим, что это сфера (рис. 3.2, а),
октаэдр (рис. 3.2, 6) и
куб (рис. 3.2, в).
Вид единичной сферы для этих норм и
послужил источником для их названий.
(единичных
векторов), называют единичной
сферой. Множество S зависит от линейного пространства и
однозначно определяет рассматриваемую
в нем норму. На рис. 3.1 изображен вид
единичной сферы для различных норм
двумерного линейного пространства
(конкретно линейного пространства
радиус-векторов точек плоскости):
евклидовой (рис. 3.1, а),
ок-таэдрической (рис. 3.1,6) и кубической
(рис. 3.1, в). В случае трехмерного линейного
пространства (линейного пространства
радиус-векторов) единичные сферы
указанных норм изображены на рис. 3.2. Мы
видим, что это сфера (рис. 3.2, а),
октаэдр (рис. 3.2, 6) и
куб (рис. 3.2, в).
Вид единичной сферы для этих норм и
послужил источником для их названий.
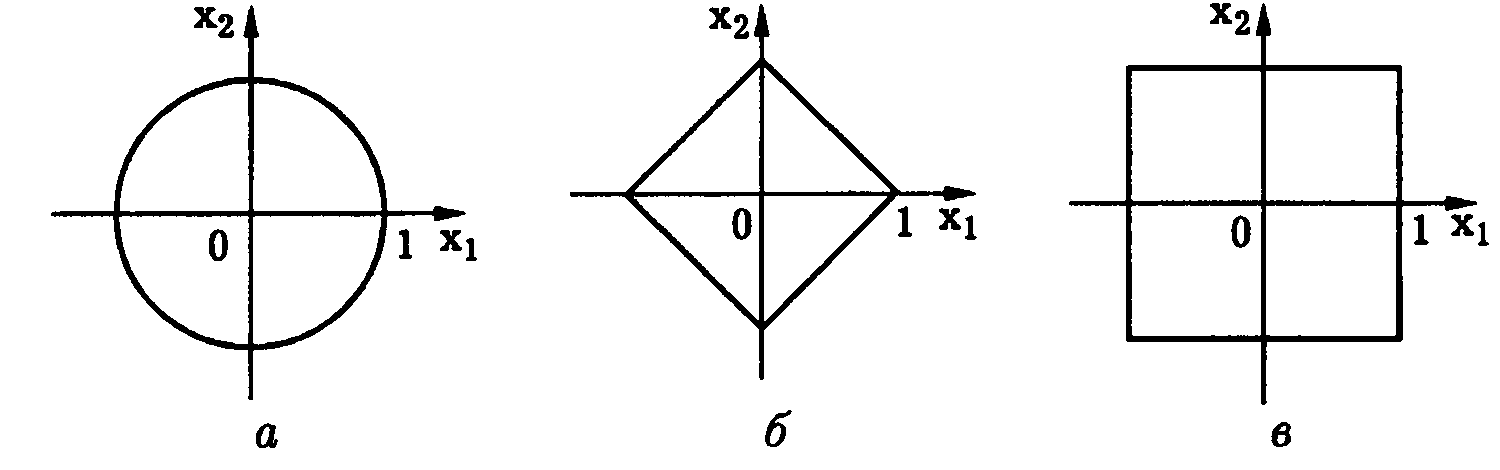
рис. 3.1
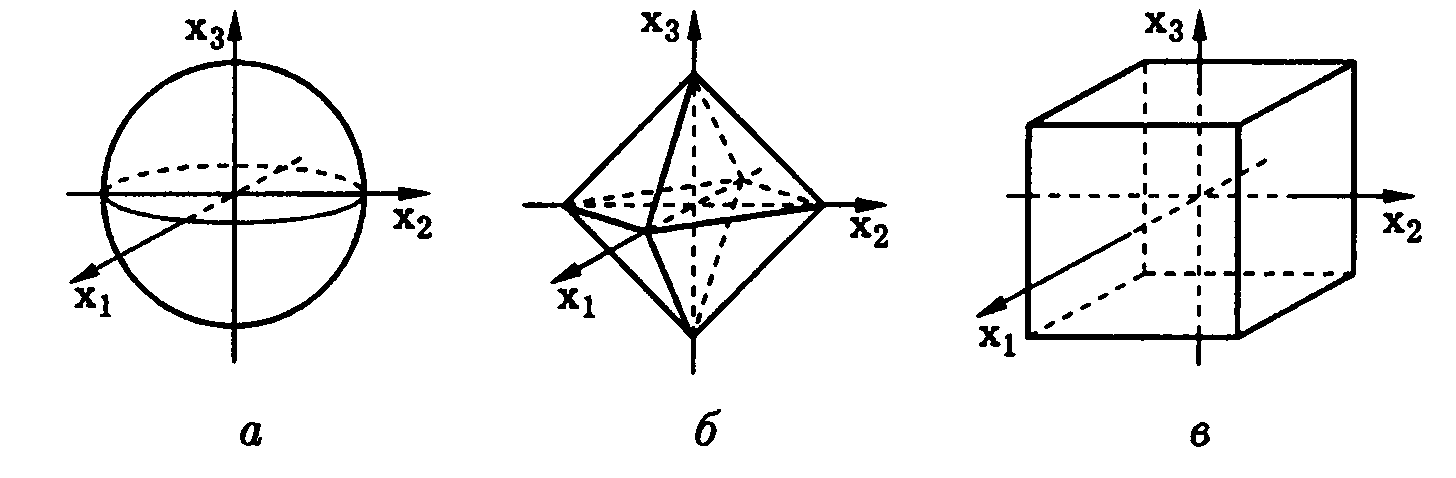
рис. 3.2
Неравенство Коши-Буняковского и его доказательство
Неравенство Коши-Буняковского и его следствие
Если наборы и рассматривать как координаты векторов -мерного евклидового пространства, то из неравенства Коши-Буняковского следует, что квадрат скалярного произведения двух векторов меньше либо равен произведению квадратов длин этих векторов
причем равенство достигается ли в том случае, когда векторы и коллинеарны.
Из неравенства Коши-Буняковского следует важное неравенство, которое называют неравенством треугольника:
длина стороны треугольника меньше длин суммы двух других сторон.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Перестановочное неравенство — Википедия
Перестановочное неравенство, или неравенство об одномонотонных последовательностях, или «транс-неравенство», утверждает, что скалярное произведение двух наборов чисел является максимальным возможным, если наборы одномонотонны (то есть оба одновременно неубывающие или одновременно невозврастающие), и минимально возможным, если наборы противоположной монотонности (то есть один неубывающий, другой невозврастающий).
Другими словами, если x1⩽x2⩽⋯⩽xn{\displaystyle x_{1}\leqslant x_{2}\leqslant \dots \leqslant x_{n}} и y1⩽y2⩽⋯⩽yn{\displaystyle y_{1}\leqslant y_{2}\leqslant \dots \leqslant y_{n}}, то для произвольной перестановки σ{\displaystyle \sigma } чисел {1,2,…,n}{\displaystyle \{1,2,\dots ,n\}} выполняется неравенство:
- x1yn+x2yn−1+⋯+xny1⩽x1yσ(1)+x2yσ(2)+⋯+xnyσ(n)⩽x1y1+x2y2+⋯+xnyn{\displaystyle x_{1}y_{n}+x_{2}y_{n-1}+\cdots +x_{n}y_{1}\leqslant x_{1}y_{\sigma (1)}+x_{2}y_{\sigma (2)}+\cdots +x_{n}y_{\sigma (n)}\leqslant x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}}
В частности, если yi=xi{\displaystyle y_{i}=x_{i}}, то x1xσ(1)+⋯+xnxσ(n)≤x12+…xn2{\displaystyle x_{1}x_{\sigma (1)}+\dots +x_{n}x_{\sigma (n)}\leq {x_{1}}^{2}+\dots {x_{n}}^{2}} независимо от упорядочивания x1,…,xn{\displaystyle x_{1},\dots ,x_{n}}.
Следствием перестановочного неравенства является неравенство Чебышёва для сумм.
Обозначим V(σ)=∑i=1nxiyσ(i){\displaystyle V(\sigma )=\sum \limits _{i=1}^{n}{x_{i}y_{\sigma (i)}}}. Для доказательства удобно несколько переформулировать утверждение:
- argmaxσ∈SnV(σ)=σ0{\displaystyle \arg \max \limits _{\sigma \in S_{n}}{V(\sigma )}=\sigma _{0}}
Здесь Sn{\displaystyle S_{n}} — множество всех возможных перестановок, а σ0: x↦x{\displaystyle \sigma _{0}:\ x\mapsto x} — тождественная перестановка.
Основная идея доказательства состоит в том, что если σ(i)>σ(j){\displaystyle \sigma (i)>\sigma (j)} для некоторых i<j{\displaystyle i<j}, то, поменяв местами значения σ(i){\displaystyle \sigma (i)} и σ(j){\displaystyle \sigma (j)}, мы не уменьшим значение суммы V(σ){\displaystyle V(\sigma )}.
Рассмотрим указанную сумму для некоторой перестановки σ≠σ0{\displaystyle \sigma \not =\sigma _{0}} и такой пары i,j{\displaystyle i,j}. Рассмотрим перестановку, образуемую из σ{\displaystyle \sigma } инверсий этой пары.
- σ′:x↦{σ(j),x=i,σ(i),x=j,σ(x),x∉{i,j}.{\displaystyle \sigma ‘:x\mapsto \left\{{\begin{matrix}\sigma (j),&x=i,\\\sigma (i),&x=j,\\\sigma (x),&x\not \in \{{i,j}\}.\end{matrix}}\right.}
По определению,
- V(σ′)=V(σ)−xiyσ(i)−xjyσ(j)+xiyσ(j)+xjyσ(i)=V(σ)+(xj−xi)(yσ(i)−yσ(j)){\displaystyle V(\sigma ‘)=V(\sigma )-x_{i}y_{\sigma (i)}-x_{j}y_{\sigma (j)}+x_{i}y_{\sigma (j)}+x_{j}y_{\sigma (i)}=V(\sigma )+(x_{j}-x_{i})(y_{\sigma (i)}-y_{\sigma (j)})}
Согласно выбору i,j{\displaystyle i,j} и предположению об упорядоченности x,y{\displaystyle x,y}, справедливо неравенство (xj−xi)(yσ(i)−yσ(j))≥0{\displaystyle (x_{j}-x_{i})(y_{\sigma (i)}-y_{\sigma (j)})\geq 0}, так что V(σ′)≥V(σ){\displaystyle V(\sigma ‘)\geq V(\sigma )}.
Следовательно, мы можем уменьшать число инверсий, не уменьшая значения V(σ){\displaystyle V(\sigma )}. В итоге такой процесс приведёт к превращению σ{\displaystyle \sigma } в σ0{\displaystyle \sigma _{0}}, так что V(σ)≤V(σ0){\displaystyle V(\sigma )\leq V(\sigma _{0})}.
Для нескольких перестановок[править | править код]
Пусть даны s{\displaystyle s} упорядоченных последовательностей x1(i)≤x2(i)≤⋯≤xn(i), i=1,…,s{\displaystyle x_{1}^{(i)}\leq x_{2}^{(i)}\leq \dots \leq x_{n}^{(i)},\ i=1,\dots ,s}. Обозначим V(σ1,…,σs)=xσ1(1)(1)xσ2(1)(2)…xσs(1)(s)+⋯+xσ1(n)(1)xσ2(n)(2)…xσs(n)(s){\displaystyle V(\sigma _{1},\dots ,\sigma _{s})=x_{\sigma _{1}(1)}^{(1)}x_{\sigma _{2}(1)}^{(2)}\dots x_{\sigma _{s}(1)}^{(s)}+\dots +x_{\sigma _{1}(n)}^{(1)}x_{\sigma _{2}(n)}^{(2)}\dots x_{\sigma _{s}(n)}^{(s)}}. Тождественную перестановку по-прежнему будет обозначать как σ0{\displaystyle \sigma _{0}}.
Тогда V(σ1,…,σs)≤V(σ0,…,σ0){\displaystyle V(\sigma _{1},\dots ,\sigma _{s})\leq V(\sigma _{0},\dots ,\sigma _{0})} для любого набора (σ1,…,σs){\displaystyle (\sigma _{1},\dots ,\sigma _{s})}.
Доказательство
Доказывается аналогично обычному перестановочному неравенству (частному случаю этого при s=2{\displaystyle s=2}).
Не ограничивая общности, будем предполагать, что σ1=σ0{\displaystyle \sigma _{1}=\sigma _{0}}, поскольку иначе можно просто умножить все перестановки на σ1−1{\displaystyle \sigma _{1}^{-1}}, не изменив значение суммы.
Если хотя бы одна из перестановок σ1,…,σs{\displaystyle \sigma _{1},\dots ,\sigma _{s}} отлична от σ0{\displaystyle \sigma _{0}}, то для неё (обозначим её σk{\displaystyle \sigma _{k}}) существуют i<j{\displaystyle i<j} такие, что σk(i)>σk(j){\displaystyle \sigma _{k}(i)>\sigma _{k}(j)}.
Тогда, если во всех перестановках σ{\displaystyle \sigma } из набора (σ1,…,σs){\displaystyle (\sigma _{1},\dots ,\sigma _{s})}, для которых \sigma (i) > \sigma (j), поменять местами значения σ(i){\displaystyle \sigma (i)} и σ(j){\displaystyle \sigma (j)}, то значение V{\displaystyle V} не уменьшиться, а общее количество инверрсий среди (σ1,…,σs){\displaystyle (\sigma _{1},\dots ,\sigma _{s})} станет меньше.
Производя такие действия нужное (конечное) количество раз, придём к набору (σ0,…,σ0){\displaystyle (\sigma _{0},\dots ,\sigma _{0})}, не уменьшив значение V{\displaystyle V}.
Для выпуклых функций[править | править код]
Идея доказательства через пошаговое исправление инверсий применима для более широкого класса случаев, чем просто для скалярного произведения.
Пусть f{\displaystyle f} — выпуклая функция, x{\displaystyle x} и y{\displaystyle y} упорядочены по неубыванию. Тогда
- f(x1+yσ(1))+⋯+f(xn+yσ(n))≤f(x1+y1)+…f(xn+yn){\displaystyle f(x_{1}+y_{\sigma (1)})+\dots +f(x_{n}+y_{\sigma (n)})\leq f(x_{1}+y_{1})+\dots f(x_{n}+y_{n})}
Доказательство
По определению выпуклой функции, если x1<x2, c>0{\displaystyle x_{1}<x_{2},\ c>0}, то f(x1+c)−f(x1)≤f(x2+c)−f(x2){\displaystyle f(x_{1}+c)-f(x_{1})\leq f(x_{2}+c)-f(x_{2})}, то есть f(x1+c)+f(x2)≤f(x1)+f(x2+c){\displaystyle f(x_{1}+c)+f(x_{2})\leq f(x_{1})+f(x_{2}+c)}. Подствляя c=c2−c1{\displaystyle c=c_{2}-c_{1}} и прибавляя к обоим x1,x2{\displaystyle x_{1},x_{2}} величину c1{\displaystyle c_{1}}, получаем f(x1+c2)+f(x2+c1)≤f(x1+c1)+f(x2+c2){\displaystyle f(x_{1}+c_{2})+f(x_{2}+c_{1})\leq f(x_{1}+c_{1})+f(x_{2}+c_{2})}. Иными словами, чем больше аргумент, тем больше изгиб функции вверх, и тем более ценнее для максимизации суммы прибавлять большее значение именно туда.
Как и в доказательстве обычного перестановочного неравенства, выберем i<j{\displaystyle i<j} такие, что σ(i)>σ(j){\displaystyle \sigma (i)>\sigma (j)}.
Тогда, как описано выше, f(xi+yσ(i))+f(xj+yσ(j))≤f(xi+yσ(j))+f(xj+yσ(i)){\displaystyle f(x_{i}+y_{\sigma (i)})+f(x_{j}+y_{\sigma (j)})\leq f(x_{i}+y_{\sigma (j)})+f(x_{j}+y_{\sigma (i)})}. Это позволяет провести индукцию, аналогичную обычному случаю.
Умножая все значения f{\displaystyle f} на −1{\displaystyle -1}, можно вывести аналогичное неравенство, но со знаком в другую сторону, для вогнутых функций.
Следствия[править | править код]
- при f(x)=ex{\displaystyle f(x)=e^{x}} (выпуклая функция): обычное перестановочное неравенство для наборов ex1,…,exn{\displaystyle e^{x_{1}},\dots ,e^{x_{n}}} и ey1,…,eyn{\displaystyle e^{y_{1}},\dots ,e^{y_{n}}}
- при f(x)=x2{\displaystyle f(x)=x^{2}} (выпуклая функция): ∑in(xi2+2xiyσ(i)+yσ(i)2)≤∑in(xi2+2xiyi+yi2){\displaystyle \sum \limits _{i}^{n}{(x_{i}^{2}+2x_{i}y_{\sigma (i)}+y_{\sigma (i)}^{2})}\leq \sum \limits _{i}^{n}{(x_{i}^{2}+2x_{i}y_{i}+y_{i}^{2})}}
После сокращения обеих частей на ∑i=1n(xi2+yi2){\displaystyle \sum \limits _{i=1}^{n}{(x_{i}^{2}+y_{i}^{2})}}, опять получаем обычное перестановочное неравенство.
- при f(x)=logx{\displaystyle f(x)=\log {x}} (вогнутая функция): ∑i=1nln(xi+yσ(i))≥∑i=1nln(xi+yi){\displaystyle \sum \limits _{i=1}^{n}{\ln(x_{i}+y_{\sigma (i)})}\geq \sum \limits _{i=1}^{n}{\ln(x_{i}+y_{i})}}
После взятия экспоненты от обеих частей: ∏i=1n(xi+yσ(i))≥∏i=1n(xi+yi){\displaystyle \prod _{i=1}^{n}{(x_{i}+y_{\sigma (i)})}\geq \prod _{i=1}^{n}{(x_{i}+y_{i})}};
- при f(x)=1x{\displaystyle f(x)={\frac {1}{x}}} (вогнутая функция): ∑i=1n1xi+yσ(i)≥∑i=1n1xi+yi{\displaystyle \sum \limits _{i=1}^{n}{\frac {1}{x_{i}+y_{\sigma (i)}}}\geq \sum \limits _{i=1}^{n}{\frac {1}{x_{i}+y_{i}}}}
Неудачные попытки обобщения[править | править код]
В 1946 году была опубликована (Scripta Mathematica 1946, 12(2), 164—169) попытка следующего обобщения неравенства:
Однако впоследствии оказалось, что уже при n=4{\displaystyle n=4} для этого неравенства существуют контрпримеры. Например,
- 0⋅0+1⋅1+2⋅10+3⋅2=27<31=0⋅2+1⋅1+2⋅0+3⋅10{\textstyle 0\cdot 0+1\cdot 1+2\cdot 10+3\cdot 2=27<31=0\cdot 2+1\cdot 1+2\cdot 0+3\cdot 10}
При n=3{\displaystyle n=3} это обобщение всегда верно.
Перестановочное неравенство интересно тем, что позволяет интуитивно объединить общей основой внешне совершенно непохожие, но очень много применяемые в разных областях математики числовые неравенства.
В этом разделе мы будем рассматривать наборы чисел длины n{\displaystyle n} и подразумевать, что обозначение xi{\displaystyle x_{i}} при i>n{\displaystyle i>n} обозначает xi−n{\displaystyle x_{i-n}}, то есть индексы зациклены.
Неравенство Коши — Буняковского[править | править код]
Согласно перестановочному неравенство, для любого k{\displaystyle k} выполняется ∑i=0n−1aiai+k]≤∑i=0n−1ai2{\displaystyle \sum \limits _{i=0}^{n-1}{a_{i}a_{i+k}]}\leq \sum \limits _{i=0}^{n-1}{a_{i}^{2}}}.
Из этого можно вывести важный частный случай неравенства Коши-Буняковского:
(∑i=0n−1ai)2=∑i=0n−1∑j=0n−1aiaj=∑i=0n−1∑j=0n−1aiai+j≤∑j=0n−1∑i=1nai2=n∑i=1nai2{\displaystyle \left({\sum \limits _{i=0}^{n-1}{a_{i}}}\right)^{2}=\sum \limits _{i=0}^{n-1}\sum \limits _{j=0}^{n-1}{a_{i}a_{j}}=\sum \limits _{i=0}^{n-1}\sum \limits _{j=0}^{n-1}{a_{i}a_{i+j}}\leq \sum \limits _{j=0}^{n-1}{\sum \limits _{i=1}^{n}{a_{i}^{2}}}=n\sum \limits _{i=1}^{n}{a_{i}^{2}}}
Аналогично, разбивая сумму на nk−1{\displaystyle n^{k-1}} частей по всем возможным (k−1){\displaystyle (k-1)}-мерным сдвигам индексов и используя обобщение на несколько перестановок, можно вывести более общее неравенство для целых k{\displaystyle k}:
(∑i=0n−1ai)k≤nk−1∑i=0n−1aik{\displaystyle \left({\sum \limits _{i=0}^{n-1}{a_{i}}}\right)^{k}\leq n^{k-1}\sum \limits _{i=0}^{n-1}{a_{i}^{k}}}
Общее неравенство Коши-Буняковского[
Неравенство Шварца — это… Что такое Неравенство Шварца?
- Неравенство Шварца
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца, хотя работы Шварца (нем.) на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть дано линейное пространство L со скалярным произведением
 . Пусть
. Пусть  — норма, порождённая скалярным произведением, то есть
— норма, порождённая скалярным произведением, то есть  . Тогда для любых
. Тогда для любых  имеем
имеем ,
,
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что
 , где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.
, где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.В общем случае

Примеры
 ,
,
- где
 обозначает комплексное сопряжение yk.
обозначает комплексное сопряжение yk.
 .
.
![\mathrm{cov}^2(X,Y) \le \mathrm{D}[X] \cdot \mathrm{D}[Y]](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) ,
,
- где cov обозначает ковариацию, а D дисперсию.
Доказательство
Значит дискриминант многочлена
 неположительный, то есть
неположительный, то есть
 .
.
Литература
- ↑ Bounjakowsky W., «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.
Wikimedia Foundation. 2010.
- Неравенство Чёбышева
- Неравенство Шнирельмана
Смотреть что такое «Неравенство Шварца» в других словарях:
Неравенство Коши — Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши … … Википедия
Неравенство Коши — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Буняковского — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Неравенство Коши-Буняковского — связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
Неравенство Коши—Буняковского — связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского иногда, особенно в иностранной… … Википедия
ШВАРЦА ЛЕММА — если функция f(z) регулярна в круге E={|z|<1 }, f(0)=0 и в E, то при справедливы неравенства причем знаки равенства в них (в первом из неравенств (1) при имеют место только в случае, когда где действительная постоянная (классическая форма Ш. л … Математическая энциклопедия
БУНЯКОВСКОГО НЕРАВЕНСТВО — неравенство математич. анализа; для функций j(x).и g(x), интегрируемых с квадратом, установлено В. Я. Буняковским [1]. Это неравенство аналогично алгебраич. неравенству Коши: Иногда Б. н. наз. неравенством Шварца (по имени Г. А. Шварца; Н. A.… … Математическая энциклопедия
Буняковского неравенство — Неравенство Коши Буняковского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением. Неравенство Коши Буняковского… … Википедия
Буняковского неравенство — одно из важнейших неравенств математического анализа, утверждающее, что установлено В. Я. Буняковским (См. Буняковский). Это неравенство аналогично элементарному алгебраическому Коши неравенству (См. Коши неравенство):… … Большая советская энциклопедия
Обнаружение с использованием оптимальной фильтрации — Содержание 1 5.6. Обнаружение с использованием оптимальной фильтрации 1.1 5 … Википедия
Неравенство Коши — Буняковского — это… Что такое Неравенство Коши — Буняковского?
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в линейном пространстве. Это неравенство эквивалентно неравенству треугольника для нормы в пространстве со скалярным произведением.
Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца, хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.
Формулировка
Пусть дано линейное пространство L со скалярным произведением . Пусть — норма, порождённая скалярным произведением, то есть . Тогда для любых имеем:
причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).
Комментарии
В конечномерном случае можно заметить, что , где — площадь параллелограмма, натянутого на векторы x и y.
В общем случае:
Примеры
где обозначает комплексное сопряжение yk.
- где cov обозначает ковариацию, а D — дисперсию.
Доказательство
Значит дискриминант многочлена неположительный, то есть
Следовательно,
Литература
Примечания
- ↑ Bounjakowsky W. «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.
Обсуждение:Неравенство Коши — Буняковского — Википедия
Материал из Википедии — свободной энциклопедии
Коши, Шварц или Буняковский?[править код]
A кто может объяснить какое отношение к этому неравенству имеет Коши? —Tosha 06:18, 10 Май 2005 (UTC)
В немецкой статье про Буняковского написано, что его работа на 50 лет старше работы Шварца. А здесь стоит 25 лет —Василий 20:03, 22 декабря 2005 (UTC)
‘современная иллюстрированная энциклопедия. математика. информатика’ [м.:зао’росмэн-пресс’ м34 2007] гл.редактор и автор проекта профессор мгу а.п.горкин, науч. редактор профессор независимого московского университета в.в.прасолов: ‘установлено в.я. буняковским в 1859г. и независимо г.шварцем в 1884г.’ 81.200.20.180 11:04, 18 июня 2008 (UTC)
- Неравенство Коши — Шварца (называемое в отечественной литературе неравенством Коши — Буняковского) есть частный случай неравенства Гельдера. Это указано в источнике: Г. Корн и Т. Корн. Справочник по математике для научных работников. М., «Наука», 1978; стр. 129 (гл. 4, п. 4.6-19). Таким образом, именование формулы — лишь вопрос терминологии. Но источники имеются. —Владимир 18:10, 17 ноября 2010 (UTC)
Гильбертовость не нужна,[править код]
нужно лишь скалярное произведение и норма порождённая им. Полнота нигде не требуется. ПБХ 04:59, 2 июня 2006 (UTC)
в неравенстве для l2{\displaystyle l^{2}} знаки модуля были не там, где надо. ПБХ 15:26, 2 июня 2006 (UTC)
Вопрос: неравенство между средним арифметическим и средним геометрическим — это что, частный случай данного неравенства? Не вижу никакой связи. Между тем по ссылке в указанной статье написано, что именно это неравенство Коши опубликовал в 1821 году… Qwertic 11:22, 30 января 2007 (UTC)
- Похоже это довольно большая книжка была — учебник по матанализу, там скорее всего много разного было. Ссылка на саму книжку есть на английской странице по неравенство между средним арифметическим и средним геометрическим Mir76 14:06, 30 января 2007 (UTC).
‘современная иллюстрированная энциклопедия. математика. информатика’ [м.:зао’росмэн-пресс’ м34 2007] гл.редактор и автор проекта профессор мгу а.п.горкин, науч. редактор профессор независимого московского университета в.в.прасолов: нер-во коши-буняковского равносильно алгебраическому нер-ву a1b1 + .. + anbn <= sqrt((a1)^2 + .. + (an)^2) * sqrt((b1)^2 + (bn)^2) доказанному о.л.коши в 1821г. извините за такой стиль записи: ai — a с индексом i, <= — меньше, либо равно, sqrt(a) — арифметический корень из а, (аi)^2 — ai в квадрате. 81.200.20.180 11:14, 18 июня 2008 (UTC)
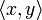 . Пусть
. Пусть  — норма, порождённая скалярным произведением, то есть
— норма, порождённая скалярным произведением, то есть  . Тогда для любых
. Тогда для любых  имеем
имеем ,
,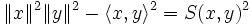 , где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.
, где S(x,y) — площадь параллелограмма, натянутого на векторы x и y.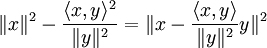
 ,
, обозначает комплексное сопряжение yk.
обозначает комплексное сопряжение yk. .
.![\mathrm{cov}^2(X,Y) \le \mathrm{D}[X] \cdot \mathrm{D}[Y]](/800/600/https/dic.academic.ru/pictures/wiki/files/50/2c7bab23479cb2caeabdbf2145b2b634.png) ,
,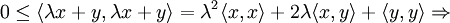
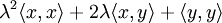 неположительный, то есть
неположительный, то есть