Неравенство Коши — Буняковского — Википедия

Материал из Википедии — свободной энциклопедии

Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом или гильбертовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.

Неравенство Коши — Буняковского иногда, особенно в иностранной литературе, называют неравенством Шварца и неравенством Коши — Буняковского — Шварца, хотя работы Шварца на эту тему появились только спустя 25 лет после работ Буняковского^[1]. Конечномерный случай этого неравенства называется неравенством Коши и был доказан Коши в 1821 году.

Пусть дано линейное пространство L{\displaystyle L} со скалярным произведением ⟨x,y⟩{\displaystyle \langle x,\;y\rangle }. Пусть ‖x‖{\displaystyle \|x\|} — норма, порождённая скалярным произведением, то есть ‖x‖≡⟨x,x⟩,∀x∈L{\displaystyle \|x\|\equiv {\sqrt {\langle x,\;x\rangle }},\;\forall x\in L}. Тогда для любых x,y∈L{\displaystyle x,\;y\in L} имеем:

|⟨x,y⟩|⩽‖x‖⋅‖y‖,{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|,}

причём равенство достигается тогда и только тогда, когда векторы x{\displaystyle x} и y{\displaystyle y} пропорциональны (коллинеарны).

Комментарии[править | править код]

В конечномерном случае можно заметить, что ‖x‖2‖y‖2−⟨x,y⟩2=S(x,y)2{\displaystyle \|x\|^{2}\|y\|^{2}-\langle x,\;y\rangle ^{2}=S(x,\;y)^{2}}, где S(x,y){\displaystyle S(x,\;y)} — площадь параллелограмма, натянутого на векторы x{\displaystyle x} и y{\displaystyle y}.

В общем случае:

‖x‖2−⟨x,y⟩2‖y‖2=‖x−⟨x,y⟩‖y‖2y‖2.{\displaystyle \|x\|^{2}-{\frac {\langle x,\;y\rangle ^{2}}{\|y\|^{2}}}=\left\|x-{\frac {\langle x,\;y\rangle }{\|y\|^{2}}}y\right\|^{2}.}

• Важным частным случаем, часто использующимся в теории чисел, является случай, когда один из векторов полностью состоит из единиц:

(∑i=1nai)2≤(∑i=1n1)∑i=1nai2=n∑i=1nai2{\displaystyle \left({\sum \limits _{i=1}^{n}{a_{i}}}\right)^{2}\leq \left({\sum \limits _{i=1}^{n}{1}}\right)\sum \limits _{i=1}^{n}{{a_{i}}^{2}}=n\sum \limits _{i=1}^{n}{{a_{i}}^{2}}}

|∑k=1∞xky¯k|2⩽(∑k=1∞|xk|2)⋅(∑k=1∞|yk|2),{\displaystyle \left|\sum \limits _{k=1}^{\infty }x_{k}{\bar {y}}_{k}\right|^{2}\leqslant \left(\sum _{k=1}^{\infty }|x_{k}|^{2}\right)\cdot \left(\sum _{k=1}^{\infty }|y_{k}|^{2}\right),}

где y¯k{\displaystyle {\bar {y}}_{k}} обозначает комплексное сопряжение yk{\displaystyle y_{k}}.

|∫Xf(x)g(x)¯μ(dx)|2⩽(∫X|f(x)|2μ(dx))⋅(∫X|g(x)|2μ(dx)).{\displaystyle \left|\int \limits _{X}f(x){\overline {g(x)}}\,\mu (dx)\right|^{2}\leqslant \left(\int \limits _{X}\left|f(x)\right|^{2}\,\mu (dx)\right)\cdot \left(\int \limits _{X}\left|g(x)\right|^{2}\,\mu (dx)\right).}

• В пространстве случайных величин с конечным вторым моментом L2(Ω,F,P){\displaystyle L^{2}(\Omega ,\;{\mathcal {F}},\;\mathbb {P} )} неравенство Коши — Буняковского имеет вид:

  cov2(X,Y)⩽D[X]⋅D[Y],{\displaystyle \mathrm {cov} ^{2}(X,\;Y)\leqslant \mathrm {D} [X]\cdot \mathrm {D} [Y],}

где cov{\displaystyle \mathrm {cov} } обозначает ковариацию, а D{\displaystyle \mathrm {D} } — дисперсию.

• Для двух независимых случайных величин ξ{\displaystyle \xi } и η{\displaystyle \eta } неравенство Коши — Буняковского имеет вид:

  [M(η⋅ξ)]2⩽M[η2⋅ξ2]=Mη2⋅Mξ2.{\displaystyle \left[\mathbf {M} (\eta \cdot \xi )\right]^{2}\leqslant \mathbf {M} \left[\eta ^{2}\cdot \xi ^{2}\right]=\mathbf {M} \eta ^{2}\cdot \mathbf {M} \xi ^{2}.}

• Если ⟨x,y⟩∈R,{\displaystyle \langle x,y\rangle \in \mathbb {R} ,} то ∀λ∈R{\displaystyle \forall \lambda \in \mathbb {R} } верно следующее

0⩽⟨λx+y,λx+y⟩=λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩.{\displaystyle 0\leqslant \langle \lambda x+y,\;\lambda x+y\rangle =\lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle .}

Значит, дискриминант многочлена λ2⟨x,x⟩+2λ⟨x,y⟩+⟨y,y⟩{\displaystyle \lambda ^{2}\langle x,\;x\rangle +2\lambda \langle x,\;y\rangle +\langle y,\;y\rangle } неположительный, то есть

D=4(⟨x,y⟩)2−4⟨x,x⟩⟨y,y⟩⩽0.{\displaystyle D=4(\langle x,\;y\rangle )^{2}-4\langle x,\;x\rangle \langle y,\;y\rangle \leqslant 0.}

Следовательно,

|⟨x,y⟩|⩽‖x‖⋅‖y‖.{\displaystyle |\langle x,\;y\rangle |\leqslant \|x\|\cdot \|y\|.}

• Если Im⁡⟨x,y⟩≠0,{\displaystyle \operatorname {Im} \langle x,y\rangle \neq 0,} то представим скалярное произведение в тригонометрическом виде ⟨x,y⟩=reiϕ.{\displaystyle \langle x,y\rangle =re^{i\phi }.}

Определим вектор z=e−iϕx.{\displaystyle z=e^{-i\phi }x.} Тогда

⟨z,y⟩=e−iϕ⟨x,y⟩=r=|⟨x,y⟩|∈R{\displaystyle \langle z,y\rangle =e^{-i\phi }\langle x,y\rangle =r=\left|\langle x,y\rangle \right|\in \mathbb {R} } и

⟨z,z⟩=e−iϕ⟨x,e−iϕx⟩=e−iϕeiϕ⟨x,x⟩=⟨x,x⟩.{\displaystyle \langle z,z\rangle =e^{-i\phi }\langle x,e^{-i\phi }x\rangle =e^{-i\phi }e^{i\phi }\langle x,x\rangle =\langle x,x\rangle .}

К скалярному произведению ⟨z,y⟩∈R{\displaystyle \langle z,y\rangle \in \mathbb {R} } применим результат первого пункта доказательства.

|⟨x,y⟩|=r=⟨z,y⟩⩽‖z‖⋅‖y‖=‖x‖⋅‖y‖.{\displaystyle \left|\langle x,y\rangle \right|=r=\langle z,y\rangle \leqslant \|z\|\cdot \|y\|=\|x\|\cdot \|y\|.}

1. ↑ Bounjakowsky W. «Mémoires de l’Académie des sciences de St-Pétersbourg. 7 série», 1859, t. 1, № 9.

Неравенство Коши-Буняковского

Математика заключает в себе не только истину, но и высочайшую красоту…

Английский философ, математик  Бертран Рассел

    К числу известных в математике числовых неравенств относится неравенство Коши – Буняковского, названного в честь французского математика, механика Огюстена Луи Коши (1789 – 1857) и русского математика Виктора Яковлевича Буняковского (1804 – 1889).

    Как и неравенство Коши, данное неравенство применяется во многих разделах школьной математики, в частности, при доказательстве неравенств и при решении некоторых уравнений повышенной сложности.

Основные определения

     Для произвольных действительных чисел и  выполняется неравенство

,               (1)

где  . Причем равенство в (1) достигается в том и только в том случае, когда числа    и   пропорциональны, т.е. существует константа такая, что  для всех    выполняется равенство   .

Рассмотрим два метода доказательства неравенства (1).

    Метод 1. Для произвольного действительного    выполняется очевидное неравенство   

.

Отсюда после раскрытия скобок получаем квадратное неравенство относительно переменной     вида

    

Поскольку квадратный трехчлен при любом значении принимает неотрицательные значения, то его дискриминант меньше или равен 0, т.е.

.

Отсюда следует справедливость неравенства (1).

     Метод 2. Пусть в  мерном евклидовом пространстве заданы два вектора:    и  , где  .

Скалярное произведение векторов и обозначается как . Для вычисления   используют следующие две формулы: 

  и   , 

 где длина вектора , длина вектора и угол, образованный векторами и .  Отсюда следует, что 

.               (2)

Так как  , и  , то из (2) получаем    

.

Отсюда вытекает справедливость неравенства (1). Кстати, в данной интерпретации равенство в (1) достигается тогда и только тогда, когда векторы   и являются коллинеарными.

   

Рассмотрим применение неравенства Коши – Буняковского при доказательстве неравенств и при решении непростых уравнений.

Доказательство неравенств

Пример 1. Доказать неравенство

.               (3) 

Доказательство. Принимая во внимание формулу (1) можно записать

 

Неравенство (3) доказано.

 

Пример 2. Доказать неравенство 

,               (4)

где  

Доказательство. Так как то

Применим к выражению     неравенство (1) и получим

.

Неравенство (4) доказано.

  

Пример 3. Доказать, что  .                                   

Доказательство.  На основе применения неравенства (1) можно записать, что

.

Так как  ,  то    

или  .

Неравенство доказано.

Примечание. По аналогии можно доказать, например, что.

 

Пример 4. Доказать, что

                                       .               (5)                                

Доказательство.  Согласно неравенству (1), здесь имеем

   или

.               (6)

Так как   

или     ,  то  .                                         

Отсюда и из неравенства (6) следует требуемое неравенство (5).

  

Пример 5. Доказать, что

.               (7)                               

Доказательство.  Обозначим 

и воспользуемся неравенством (1). Тогда

Так как   , то отсюда следует  .

Двойное неравенство (7) доказано.

Примечание.  Нижняя и верхняя оценки выражения    являются  достижимыми, поскольку 

,

.

Перейдем к рассмотрению уравнений, решение которых связано с применением неравенства (1).

 

Решение уравнений

Пример 6. Решить уравнение

.               (16)

Решение. Область допустимых значений переменной    в уравнении (16) образует отрезок  .

Если к левой части уравнения (16) применить неравенство Коши – Буняковского (1), то получим

 или .

Отсюда и из уравнения (16) следует, что примененное неравенство (1) превратилось в равенство. В этой связи можно записать: 

,  ,  ,  .

Так как  , то является единственным корнем уравнения (16).

Ответ:  .

 

Пример 7. Решить уравнение 

.               (17)

Решение.  Применим к уравнению (17) неравенство (1) и получим 

,  

  или    

.               (18)

Преобразуем неравенство (18) следующим образом:

,     или

.               (19)

Так как    и  , то   из  неравенства (19) следует, что   .

Подставим значение в уравнение (17) и убедимся, что это значение является его корнем.

Ответ:  .    

Пример 8. Определить объем прямоугольного параллелепипеда, если его размеры   связаны между собой соотношением   ,  а  его диагональ    равна  .                                       

Решение. Так как является диагональю прямоугольного параллелепипеда, то  . Если к выражению  применить неравенство (1), то

  или  .

Однако    и  , то  .     Отсюда следует, что примененное неравенство (1) обратилось в равенство и поэтому     или    

В таком случае уравнение принимает вид

  или  .

Так как   и объем параллелепипеда ,  то  

.

Ответ:   .

    Более подробно с вопросами применения неравенства Коши – Буняковского при решении задач школьной математики можно ознакомиться посредством изучения учебных пособий, приведенных в списке рекомендованной литературы.

Рекомендуемая литература

1.  Кушнир А.И. Шедевры школьной математики (задачи и решения в двух книгах). – Киев: Астарта, книга 1, 1995. – 576 с.

2. Супрун В.П. Математика для старшеклассников: задачи повышенной сложности. – М.: КД «Либроком» / URSS, 2017. – 200 с.

3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS, 2017. – 296 с.

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Неравенство между средним арифметическим и средним геометрическим — Википедия

Неравенство Коши (неравенство о средних) гласит, что для любых неотрицательных чисел x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}} верно неравенство:

x¯kvadr⩾x¯arithm⩾x¯geom⩾x¯garmon,{\displaystyle {\bar {x}}_{\mathrm {kvadr} }\geqslant {\bar {x}}_{\mathrm {arithm} }\geqslant {\bar {x}}_{\mathrm {geom} }\geqslant {\bar {x}}_{\mathrm {garmon} },}

причем равенство достигается тогда и только тогда, когда x1=x2=…=xn{\displaystyle x_{1}=x_{2}=\ldots =x_{n}}.

Выражение

x¯arithm=1n∑i=1nxi=x1+x2+…+xnn{\displaystyle {\bar {x}}_{\mathrm {arithm} }={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}={\frac {x_{1}+x_{2}+\ldots +x_{n}}{n}}}

называется средним арифметическим чисел x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}}.

Выражение

x¯geom=∏i=1nxin=x1⋅x2⋅…⋅xnn{\displaystyle {\bar {x}}_{\mathrm {geom} }={\sqrt[{n}]{\prod _{i=1}^{n}{x_{i}}}}={\sqrt[{n}]{x_{1}\cdot x_{2}\cdot \ldots \cdot x_{n}}}}

называется средним геометрическим чисел x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}}.

Выражение

x¯garmon=n∑i=1n1xi=n1x1+1×2+…+1xn{\displaystyle {\bar {x}}_{\mathrm {garmon} }={\frac {n}{\sum _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\ldots +{\frac {1}{x_{n}}}}}}

называется средним гармоническим чисел x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}}.

Выражение

x¯kvadr=1n∑i=1nxi2=x12+x22+…+xn2n{\displaystyle {\bar {x}}_{\mathrm {kvadr} }={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}{x_{i}^{2}}}}={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\ldots +x_{n}^{2}}{n}}}}

называется средним квадратическим чисел x1,x2,…,xn{\displaystyle x_{1},x_{2},\dots ,x_{n}}.

Одно из доказательств этого неравенства было опубликовано Коши в его учебнике по математическому анализу в 1821 году^[1].

При n=2.[править | править код]

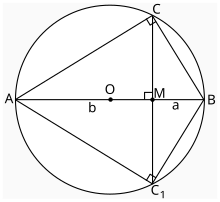
Количество доказательств этого неравенства на данный момент сравнимо, наверное, только с количеством доказательств теоремы Пифагора. Приведем красивое геометрическое доказательство для случая n=2{\displaystyle n=2}. Пускай нам даны два отрезка длины a{\displaystyle a} и b{\displaystyle b}. Тогда построим окружность диаметром a+b{\displaystyle a+b} (см. рис. 1). От одного из концов диаметра отметим точку M{\displaystyle M} на расстоянии a{\displaystyle a}. Проведем через эту точку перпендикуляр к диаметру; полученная прямая пересечет окружность в двух точках, C{\displaystyle C} и C1{\displaystyle C_{1}}. Рассмотрим полученную хорду. Треугольник ABC{\displaystyle ABC} прямоугольный, так как угол C{\displaystyle C} — вписанный в окружность и опирающийся на её диаметр, а значит, прямой. Итак, CM{\displaystyle CM} — высота треугольника ABC{\displaystyle ABC}, а высота в прямоугольном треугольнике есть среднее геометрическое двух сегментов гипотенузы. Значит, CM=ab{\displaystyle CM={\sqrt {ab}}}. Аналогично, из треугольника ABC1{\displaystyle ABC_{1}} получаем, что C1M=ab{\displaystyle C_{1}M={\sqrt {ab}}}, поэтому CC1=2CM=2C1M=2ab{\displaystyle CC_{1}=2CM=2C_{1}M=2{\sqrt {ab}}}. Так как CC1{\displaystyle CC_{1}} — хорда окружности с диаметром a+b{\displaystyle a+b}, а хорда не превосходит диаметра, то получаем, что 2ab⩽a+b{\displaystyle 2{\sqrt {ab}}\leqslant a+b}, или же ab⩽a+b2{\displaystyle {\sqrt {ab}}\leqslant {\frac {a+b}{2}}}. Заметим, что равенство будет тогда, когда хорда будет совпадать с диаметром, то есть при a=b{\displaystyle a=b}.

Обобщенное неравенство.[править | править код]

x1x2…xnn⩽x1+x2+…+xnn{\displaystyle {\sqrt[{n}]{x_{1}x_{2}…x_{n}}}\leqslant {\frac {x_{1}+x_{2}+…+x_{n}}{n}}}

Поделим обе части неравенства на x1x2…xnn{\displaystyle {\sqrt[{n}]{x_{1}x_{2}…x_{n}}}} и произведем замену yi=xix1x2…xnn{\displaystyle y_{i}={\frac {x_{i}}{\sqrt[{n}]{x_{1}x_{2}…x_{n}}}}}. Тогда, при условияхy1>0,y2>0,…,yn>0;y1y2…yn=1{\displaystyle y_{1}>0,y_{2}>0,…,y_{n}>0;\quad y_{1}y_{2}…y_{n}=1}необходимо доказать, что 1⩽y1+y2+…+ynn{\displaystyle 1\leqslant {\frac {y_{1}+y_{2}+…+y_{n}}{n}}}(1).

Воспользуемся методом математической индукции.

Нужно доказать, что если m1>0,m2>0,…,mn+1>0;m1m2…mn+1=1{\displaystyle m_{1}>0,m_{2}>0,…,m_{n+1}>0;\quad m_{1}m_{2}…m_{n+1}=1}, то m1+m2+…+mn+1≥n+1{\displaystyle m_{1}+m_{2}+…+m_{n+1}\geq n+1}. Воспользуемся неравенством (1), которое по предположению индукции считаем доказанным для n. Пусть y1=m1,y2=m2,…,yn=mnmn+1{\displaystyle y_{1}=m_{1},y_{2}=m_{2},…,y_{n}=m_{n}m_{n+1}}. Тогда выполнены оба условия y1>0,y2>0,…,yn>0;y1y2…yn=1{\displaystyle y_{1}>0,y_{2}>0,…,y_{n}>0;\quad y_{1}y_{2}…y_{n}=1} и предполагается доказанным неравенство y1+y2+…+yn≥n{\displaystyle y_{1}+y_{2}+…+y_{n}\geq n}или m1+m2+…+mnmn+1≥n{\displaystyle m_{1}+m_{2}+…+m_{n}m_{n+1}\geq n}. Теперь заменим mnmn+1{\displaystyle m_{n}m_{n+1}}на mn+mn+1{\displaystyle m_{n}+m_{n+1}}. Это возможно сделать в силу того, что mn+mn+1≥mnmn+1+1{\displaystyle m_{n}+m_{n+1}\geq m_{n}m_{n+1}+1} или mn+mn+1−mnmn+1−1≥0{\displaystyle m_{n}+m_{n+1}-m_{n}m_{n+1}-1\geq 0}, что, очевидно выполняется, так как mn(mn+1−1)−(1−mn+1)=(mn−1)(1−mn+1)≥0{\displaystyle m_{n}(m_{n+1}-1)-(1-m_{n+1})=(m_{n}-1)(1-m_{n+1})\geq 0}. Таким образом, неравенство доказано.

Эпизод с доказательством, что среднее арифметическое больше среднего геометрического, присутствует в одной из сцен кинофильма «Сердца четырёх» 1941 года.

Неравенство Коши в задачах на оптимизацию

Предлагаю решение нескольких задач на оптимальный выбор, в ходе которого потребовалось использование неравенства Коши.

Вообще формулировка этого замечательного неравенства звучит так: «Среднее арифметическое любых двух неотрицательных чисел и не меньше их среднего геометрического, причем равенство достигается только при ».

Неравенство Коши можно записать по-разному:

   

   

   

Причем равенство достигается только при .

   

Задача 1. Требуется изготовить бак с крышкой объемом 0,25 м, имеющий квадратное основание. Сварка швов производится по всему периметру основания и одному боковому ребру. Стоимость сварки составляет 10 руб/м, а стоимость жести – 20 руб/м. Необходимо выяснить размеры бака, при которых его стоимость будет наименьшей.

Пусть сторона основания бака , а высота . Тогда площадь его поверхности можно вычислить так: дно , такая же крышка, боковая поверхность . Если выразить высоту как , то полная площадь поверхности равна

   

Стоимость жести, следовательно, будет

   

Теперь швы. Их общая длина . Стоимость швов будет

   

Общая стоимость бака сложится из стоимости жести и швов:

   

Эту-то функцию нам надо минимизировать. Перепишем иначе:

   

С применением теоремы Коши минимизируем сумму первых двух слагаемых:  если произведение двух положительных переменных постоянно, то сумма их имеет наименьшее значение при выполнении равенства:

   

Тогда

   

   

Если обозначить , то

   

Или

   

   

   

Вернемся к основной переменной:

   

   

Тогда

   

Исследование минимума суммы вторых двух слагаемых (либо с помощью неравенства Коши, либо с помощью производной) дает большее значение .

Ответ: м, .

 

Задача 2. Химический комбинат получил заказ на изготовление этилового спирта, соляной кислоты и дистиллированной воды. Для готовой продукции потребовалась 21 железнодорожная цистерна. При перекачивании были использованы три специализированных насоса: сначала первый насос заполнил четыре цистерны этиловым спиртом, затем второй насос заполнил шестнадцать цистерн соляной кислотой и в завершение третий насос заполнил одну цистерну дистиллированной водой. Найдите минимально возможное время, затраченное на перекачивание всей продукции, если известно, что суммарная производительность всех трёх насосов равна семи цистернам в сутки.

Решение Инны Фельдман.

Пусть производительность первого насоса цистерн в сутки, второго – цистерн в сутки, третьего – цистерн в сутки.

Тогда время работы первого насоса равно дней, второго – дней, третьего –   дней.

Нам надо минимизировать следующую сумму:

   

При условии

Перемножим уравнения:

   

Раскрываем скобки:

   

Или

   

Сумма двух слагаемых согласно неравенству Коши больше или равна 16, двух слагаемых – больше или равна 4, слагаемых –  больше или равна 8. Тогда, подставив минимальные значения 16, 4 и 8, получим:

   

   

Тогда , если

   

Или

   

   

   

   

Тогда , , .

Ответ: 7 дней.

 

Задача 3. Требуется разместить на земле участок площадью 3400 м, который состоит из трёх прямоугольных частей и имеет форму многоугольника ABCDFGHM, изображённого на рисунке, где  м,  м,  м и  м. Найдите наименьшее значение периметра такого участка и какие-либо значения длин ,  и , при которых периметр является наименьшим.

К задаче 3

Площадь участка равна , а его периметр равен периметру Р прямоугольника  . Обозначим , ;  и . Тогда

   

   

Следовательно,

   

Тогда

   

Применим неравенство Коши:

   

   

Равенство достигается при .

Тогда .

Следовательно, периметр

   

Такое значение достигается при . Действительно, площадь квадрата тогда 4900, площадь участка 3400, площадь дана и равна 300 – тогда на площадь приходится 1200, и .

Ответ: м, , , .

 

1.1 Средние величины. Классические неравенства. Неравенство Коши

Тема: Обучение доказательству неравенств в курсе основной школы

СОДЕРЖАНИЕ

ГЛАВА І. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1 Средние величины. Классические неравенства. Неравенство Коши

1.2 Доказательство неравенств методом «от противного»

1.3 Доказательство неравенств методом математической индукции

ГЛАВА ІІ. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1 Неравенство Коши – Буняковского

2.2 Решение уравнений с помощью замечательных неравенств

2.3 Использование неравенства Коши-Буняковского при решении тригонометрических уравнений

2.4 Использование классических неравенств при решении задач с параметрами

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

«…Основные результаты математики

чаще выражаются неравенствами,

а не равенствами»

Р. Беллман

«Введение в неравенства»

неравенство коши тригонометрический математический

В современной математике неравенства играют огромную роль. Неравенствам отводится центральное место в линейном и нелинейном программирование, теории игр, исследовании операций, теории информации и кодирования, при нахождении максимального или минимального значения функции, при оценке любой величины сверху или снизу, имеют целью также доказательства неравенства. Роль и актуальность этой темы трудно переоценить.

Изучая неравенства, преследуется цель развития у детей мыслительных навыков, умения обобщать и конкретизировать, иметь представление об аксиоматической основе любой теории как системе знаний.

Наиболее широко подойти к раскрытию теории неравенств можно с помощью разработки элективных курсов и курсов по выбору для школьников старших классов. На подобных занятиях укладываются как теоретические вопросы тематики неравенств, так и их приложения. В зависимости от индивидуальных особенностей учащихся педагог должен производить отбор материала для изучения, продумывать формы и методы работы на занятиях, а также тематику самостоятельных заданий. Элективный курс, посвященный вопросам доказательства неравенств, может идти в нескольких направлениях.

При доказательстве неравенств классическими методами отсутствует аналитическая составляющая и необходимо изобретать нестандартные преобразования, которые не имеют полной классификации. То есть не исследуются функции, участвующие в неравенстве, появляются все новые дополнительные преобразования, без которых применение классических неравенств невозможно. Это касается классических неравенств, таких как неравенство Коши, неравенство Коши-Буняковского (Коши-Шварца), транснеравенство, неравенство Чебышева, неравенство Мюрхеда, неравенство Караматы, неравенство Гельдера, неравенство Йенсена, неравенство Шура.

В современной литературе можно найти множество специальных подборок задач из различных олимпиад, показывающих применения этих неравенств. Существуют специальные методики, которые должны помочь учащимся догадаться до необходимой комбинации классических неравенств. Есть метод баланса коэффициентов, который используется для применения неравенства Коши, неравенства Коши-Шварца, неравенства Гельдера.

Изучение доказательств неравенств в школе предваряет изучение функций, поскольку исторически понятие функции возникло позднее. Пропедевтика понятия неравенства начинается еще в начальной школе, изучение основного содержания темы происходит на основной ступени, а углубление, обобщение и систематизация изученного – в старших классах.

С первыми примерами функциональных зависимостей учащиеся сталкиваются в основной школе. Более глубокое изучение функциональной линии реализуется в курсе начал анализа. Именно тематика неравенств в средней школе представляет хорошие условия для развития учащихся и формирования их интеллектуальных качеств.

Тесную историческую связь понятий неравенства и функции отмечает А. Н. Земляков. Задачи на максимум и минимум. Теорема Ферма и теория чисел элективного курса «Мир, математика, математики (историческая реконструкция элементарной алгебры и математического анализа)», отмечает, что такая характеристика функции посредством неравенства, как ее наибольшее/ наименьшее значение, относится по своей сути не к алгебре или геометрии, а к математическому анализу. «Сначала понятие наибольшего/наименьшего значения не отделяется от алгебры. Шажок в сторону анализа делает И. Кеплер со своей знаменитой наилучшей австрийской бочкой … А дальше «вступает в игру» Пьер Ферма, придумавший «метод отыскания наибольших и наименьших значений», от которого всего два шага до методов собственно математического анализа».

Неравенства, представляя аппарат элементарной математики, упрощают изучение математического анализа, позволяя осуществить переход ко многим его понятиям (свойства функции, предел и др.). Далее неравенства продолжают активно взаимодействовать с функциональной линией курса математики, допуская с ней множество интеграций. Тематика неравенств не теряет свойства с, поскольку позволяет обнаруживать и воплощать разнообразные идеи исследований. Такой подход к изучению неравенств дает возможность «выйти» на изучение современных разделов математики еще в школе, предваряя изменения содержания общего математического образования.

Научно-образовательный потенциал неравенств проявляется в общем развивающем воздействии данной тематики на личность школьника. Освоение неравенств требует от учащихся совершения аналитических и синтетических рассуждений, умений сравнивать, классифицировать, обобщать, конкретизировать, действовать по аналогии, производить индуктивные и дедуктивные умозаключения. Проблемы реализации математических исследований школьников могут продуктивно решаться обращением к неравенствам.

Во-первых, тематика неравенств позволяет вписать в решение отдельной математической задачи (или совокупности задач), что повлечет обращение к необходимым математическим методам.

Во-вторых, проблема исследования может оказаться полезной при подготовке учащегося к предметной олимпиаде или итоговой аттестации за курс общеобразовательной школы (проекты, посвященные истории математики, симметрии, золотому сечению, фракталам и т. п. далеко не всегда могут этим «похвастаться»).

В-третьих, работа по тематике неравенств сопряжена с изучением не только популярных, но и научных источников литературы. Это позволит стимулировать формирование общих приемов мыслительной деятельности учащегося. Цель исследовательской деятельности школьников – не столько добиться собственно научных результатов, сколько получить основные представления о методах исследования, научиться системной, целенаправленной работе над темой, логике построения материала и получению аргументированных выводов. Организация процесса исследования приобретет для учащихся огромную ценность.

Существует немало любопытных фактов из теории неравенств, которые могут заинтересовать учащихся и послужить идеей исследовательского проекта. В частности, неравенство Коши, связывающее среднее арифметическое и среднее геометрическое положительных чисел, является примером задачи, решенной почти два века назад, но до сих пор занимающей умы многих ученых. Известно более ста различных доказательств упомянутого неравенства. Это не является препятствием для публикации все новых способов обоснования знаменитого соотношения. Изучению и применению доказательств неравенств посвящена данная работа.

ГЛАВА І. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Главным неравенством в области действительных чисел является неравенство х²  0. Из него следуют другие, известные и употребительные неравенства, первым из которых является неравенство Коши или, как его называют, неравенство о средних:

Доказывается просто: , поскольку a+b0, значит неравенство можно возводить в квадрат:

(a + b)²  4ab,

a² + 2ab + b²  4ab,

a² + 2ab + b² –4ab  0,

a² – 2ab + b²  0

(a – b)²  0.

Полученное неравенство верно для любых a, b, и в том числе при положительных. Итак, исходное неравенство верно для любых a, b  0.

Пусть даны положительные числа произведение которых равно 1. Тогда справедливо неравенство причем равенство выполняется при .

Пусть даны положительные числа . Тогда справедливо неравенство

Это неравенство французского математика О. Л. Коши, установленное в 1821г., причем равенство имеет место лишь в случае, когда .

Частный случай этого неравенства известен как неравенство между средним арифметическим и средним геометрическим.

Для > 0 среднее геометрическое двух чисел не превосходит их среднего арифметического ≤ .

Пример 1. Доказать, что если ab, то

Доказательство: Имеем

Так как ab, то , причем знак равенства имеет место при a=b. Таким образом, разность неотрицательна и неравенство доказано.

Пример 2. Доказать, что для любых чисел a, b и c имеет место неравенство

Доказательство: выберем неравенства

, ,

Сложим эти неравенства, а затем разделим обе части полученного неравенства на два, получим нужное неравенство.

Пример 3. Доказать, что для любых неотрицательных чисел a, b, c, d имеет место неравенство

Доказательство: Воспользуемся неравенствами Коши

и

Тогда получим:

1.2 Доказательство неравенств методом «от противного»

Метод доказательства «от противного» высказывания «из А следует В» применяют в следующей форме: считают истинным высказывание «не выполняется В» и пытаются вывести отсюда справедливость высказывания «не выполняется А». Если это удается, то получается противоречие, из которого следует, что предположение о неверности А – ошибочно. Покажем, как этот метод применяется при доказательстве неравенств.

Пример 4. Доказать, что для любого числа а выполняется неравенство

Доказательство: Предположим противное, что для некоторого числа а рассматриваемое неравенство неверно, то есть имеет место неравенство:

Умножим обе части неравенства на положительное число , при этом знак неравенства не изменится:

.

Из обеих частей неравенства можно вычесть выражение

2+. После преобразований правой части получим:

Последнее неравенство не выполняется ни при каком значении а, правая часть неравенства не может принимать отрицательные значения. Полученное противоречие доказывает верность исходного неравенства.

1.3 Доказательство неравенств методом математической индукции

Доказательство неравенств методом математической индукции проводится по следующей схеме:

1. Проверяется неравенство для некоторого начального значения n, например, для n=1.

2. Предполагается, что неравенство выполняется для n=k.

3. Доказывается, что тогда неравенство выполняется для n=k+1.

Пример 5. Доказать, что если n = 2, 3, 4,…, то

Доказательство:

1. При n = 2 неравенство верно:

2. Предположим, что неравенство выполняется для n=k, то есть

3. Докажем, что тогда неравенство выполняется для n=k+1, то есть

для всех значений k>1.

Согласно принципу математической индукции, можно сделать вывод о том, что неравенство выполняется при всех значениях n = 2, 3, 4,….

Неравенство для среднего арифметического и среднего геометрического n неотрицательных чисел

Если — любые неотрицательные числа, то

Равенство имеет место при .

Задача 1. Доказать, что для любых двух положительных чисел a и b выполнено неравенство .

Доказательство:

І способ

;

ІІ способ:

+1>0.

Среднее гармоническое двух положительных чисел a и b равно отношению удвоенного произведения этих чисел к их сумме.

Если среднее гармоническое положительных чисел a и b обозначить буквой h, то можно записать:

Величина, обратная среднему гармоническому a и b, есть среднее арифметическое величин, обратных a и b.

Докажем, что

Данное неравенство верно для положительных чисел a и b.

Заметим, что

Следовательно имеет место неравенство:

.

В математике используется понятие среднего квадратичного:

для двух положительных чисел a и b среднее квадратичное равно

Покажем, что

Для любых положительных и всегда будет выполняться неравенство:

Все приведённые средние значения связаны неравенствами:

для любых a, b > 0.

При этом знак равенства достигается лишь в том случае, когда a=b.

ГЛАВА ІІ. ПРАКТИЧЕСКАЯ ЧАСТЬ

Неравенство Коши | Социальная сеть работников образования

li{counter-increment:lst-ctn-kix_list_1-7}#doc4881832 .lst-kix_list_1-3>li:before{content:»» counter(lst-ctn-kix_list_1-3,decimal) «. «}#doc4881832 .lst-kix_list_1-1>li:before{content:»» counter(lst-ctn-kix_list_1-1,lower-latin) «. «}#doc4881832 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc4881832 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc4881832 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc4881832 .lst-kix_list_1-2>li:before{content:»» counter(lst-ctn-kix_list_1-2,lower-roman) «. «}#doc4881832 .lst-kix_list_1-5>li:before{content:»» counter(lst-ctn-kix_list_1-5,lower-roman) «. «}#doc4881832 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc4881832 .lst-kix_list_1-8>li{counter-increment:lst-ctn-kix_list_1-8}#doc4881832 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc4881832 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc4881832 .lst-kix_list_1-2>li{counter-increment:lst-ctn-kix_list_1-2}#doc4881832 .lst-kix_list_1-4>li:before{content:»» counter(lst-ctn-kix_list_1-4,lower-latin) «. «}#doc4881832 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc4881832 ol.lst-kix_list_1-7{list-style-type:none}#doc4881832 ol.lst-kix_list_1-8{list-style-type:none}#doc4881832 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc4881832 .lst-kix_list_1-6>li:before{content:»» counter(lst-ctn-kix_list_1-6,decimal) «. «}#doc4881832 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc4881832 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc4881832 .lst-kix_list_1-5>li{counter-increment:lst-ctn-kix_list_1-5}#doc4881832 .lst-kix_list_1-7>li:before{content:»» counter(lst-ctn-kix_list_1-7,lower-latin) «. «}#doc4881832 .lst-kix_list_1-0>li:before{content:»» counter(lst-ctn-kix_list_1-0,decimal) «. «}#doc4881832 ol.lst-kix_list_1-8.start{counter-reset:lst-ctn-kix_list_1-8 0}#doc4881832 .lst-kix_list_1-8>li:before{content:»» counter(lst-ctn-kix_list_1-8,lower-roman) «. «}#doc4881832 ol.lst-kix_list_1-2{list-style-type:none}#doc4881832 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc4881832 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc4881832 ol.lst-kix_list_1-1{list-style-type:none}#doc4881832 ol.lst-kix_list_1-0{list-style-type:none}#doc4881832 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc4881832 ol.lst-kix_list_1-6{list-style-type:none}#doc4881832 ol.lst-kix_list_1-5{list-style-type:none}#doc4881832 ol.lst-kix_list_1-4{list-style-type:none}#doc4881832 ol.lst-kix_list_1-3{list-style-type:none}#doc4881832 ol{margin:0;padding:0}#doc4881832 .c2{line-height:1.0;padding-top:5pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc4881832 .c6{line-height:1.0;padding-top:0pt;text-align:justify;direction:ltr;padding-bottom:0pt}#doc4881832 .c0{vertical-align:super;font-size:14pt;font-style:italic;font-family:»Times New Roman»}#doc4881832 .c3{vertical-align:baseline;font-size:14pt;font-style:italic;font-family:»Times New Roman»}#doc4881832 .c8{line-height:1.0;padding-top:0pt;direction:ltr;padding-bottom:0pt}#doc4881832 .c1{vertical-align:sub;font-size:14pt;font-style:italic;font-family:»Times New Roman»}#doc4881832 .c12{vertical-align:super;font-size:14pt;font-family:»Times New Roman»}#doc4881832 .c5{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»}#doc4881832 .c13{vertical-align:baseline;font-size:16pt;font-family:»Times New Roman»}#doc4881832 .c10{vertical-align:sub;font-size:14pt;font-family:»Times New Roman»}#doc4881832 .c14{max-width:467.7pt;background-color:#ffffff;padding:56.7pt 42.5pt 56.7pt 85pt}#doc4881832 .c7{font-weight:bold}#doc4881832 .c9{margin-right:-1.1pt}#doc4881832 .c11{color:#000000}#doc4881832 .c4{height:11pt}#doc4881832 .c15{margin-left:18pt}#doc4881832 .title{padding-top:24pt;line-height:1.15;text-align:left;color:#000000;font-size:36pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt}#doc4881832 .subtitle{padding-top:18pt;line-height:1.15;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:»Georgia»;padding-bottom:4pt}#doc4881832 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc4881832 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc4881832 h2{padding-top:24pt;line-height:1.15;text-align:left;color:#000000;font-size:24pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt}#doc4881832 h3{padding-top:18pt;line-height:1.15;text-align:left;color:#000000;font-size:18pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt}#doc4881832 h4{padding-top:14pt;line-height:1.15;text-align:left;color:#000000;font-size:14pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt}#doc4881832 h5{padding-top:12pt;line-height:1.15;text-align:left;color:#000000;font-size:12pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4881832 h5{padding-top:11pt;line-height:1.15;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4881832 h6{padding-top:10pt;line-height:1.15;text-align:left;color:#000000;font-size:10pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt}#doc4881832 ]]>

НЕРАВЕНСТВО КОШИ

Введение

                                                       «Основные результаты математики

                                                        чаще выражаются         неравенствами,

                                                        а не равенствами».

                                                        Э.Беккенбах, Р.Беллман.

     1. Неравенства играют фундаментальную роль в большинстве разделов современной математики, без них не может обойтись ни физика, ни математическая статистика, ни экономика. Не обойтись без них ни химии, ни астрономии. Теория вероятностей, математическая статистика, финансовая математика, экономика — все эти взаимопроникающие и обобщающие друг друга науки и в формулировках основных своих законов, и в методах их получения, и в приложениях постоянно используют неравенства. Неравенства участвуют в получении и обосновании многих важных математических результатов, помогающих разобраться в законах и методах математической системы и экономики.

     С помощью классических неравенств во многих случаях можно осуществить исследования на максимум и минимум целого ряда функций без обращения к нахождению и исследованию их производных (тем более, что производная исследуемой функции может отсутствовать).

     Задачи, относящиеся к наибольшим и наименьшим значениям или задачи на максимум и минимум более привлекательны, чем другие математические задачи и это имеет простые причины. У каждого из нас есть свои личные задачи. Эти задачи очень часто являются своего рода задачами на максимум или минимум. Мы хотим получить определенный предмет за наиболее низкую возможную цену, или наибольший возможный эффект при определенном усилии, или максимальную работу, произведенную за данное время, и конечно, хотим как можно меньше рисковать. Математические задачи на максимум привлекательны потому, что они идеализируют наши повседневные задачи.

     То, что подобные задачи на оптимизацию встречались еще в глубокой древности, донесли до нас мифы Древней Греции и Рима. Вот один из таких мифов, наполовину древнегреческий, наполовину древнеримский. Дочь царя Тира, Дидона, жена жреца храма Геракла Акербаса вынуждена была бежать из Финикии, в Северную Африку. Причина бегства — ее брат, Пигмалион, позаривщийся на богатства ее мужа и убивший его. Многочисленные сокровища мужа и (видимо поэтому) многочисленные спутники Дидоны нуждались в пристанище. Чтобы обрести его беглянка купила у берберийского царя Ярба землю, причем по условию она в обмен на немалые сокровища могла взять ровно столько земли, сколько покроет одна бычья шкура. Чтобы выполнить это условие и получить достаточно большую территорию, Дидона разрезала шкуру на тонкие ремни ,сделала из них длинную веревку и «окружила» ею изрядный кусок земли, естественно, круглой формы, на котором основала Карфаген.

     Задача, которую решила Дидона, может быть сформулирована так: найти замкнутую кривую заданной длины, ограничивающую часть плоскости с максимальной площадью. Задачи типа задачи Дидоны называются в математике изопериметрическими задачами (от греческого слова isos — равный и perimetrio — измеряю вокруг).

     2. Неравенство Коши, его частные случаи.

     Одно из самых известных замечательных неравенств — это соотношение между средним арифметическим и средним геометрическим нескольких действительных неотрицательных чисел, опубликованное в 1821 году французским математиком Агюстеном Луи Коши и ставшее столь популярным, что для него к настоящему времени найдены десятки доказательств и сотни применений.

   

     2.1. «Школьный» вариант неравенства Коши.

Докажите, что для любых неотрицательных a и b справедливо неравенство

                                    (a  + b) / 2  ≥ √ ab,      

причем равенство имеет место тогда и только тогда, когда a=b.

     Решение. Составим и преобразуем разность между левой и правой частями доказываемого равенства, а затем сравним эту разность с 0:

                        a+b/2-√ab=(a-2√ab + b)/2=1/2(√a-√b)²≥0,

что и доказывает исследуемое неравенство, а также дает условие реализации этого соотношения в варианте равенства, а именно, когда a=b.

     2.2. Докажите, что для любых неотрицательных a, b, c, d справедливо неравенство (неравенство Коши для четырех переменных):

                                        (a+b+c+d)/4≥4√abcd¸

при чем это соотношение реализуется в варианте равенства только если a=b=c=d.

     Решение. (a+b+c+d)/4=((a+b)/2+(c+d)/2)/2≥(√ab+√cd)/2≥√√ab·√cd=4√abcd¸

причем равенство имеет место тогда и только тогда, когда одновременно выполняются три условия: (a+b)/2=√ab; (c+d)/2=√cd; √ab=√cd¸ т.е. когда  a=b=c=d. Доказательство завершено.

     2.3.Теорема. Неравенство Коши для произвольного числа параметров.

     Для любых действительных неотрицательных чисел x1, х2, …, хn справедливо следующее неравенство (x1+ х2+ …+ хn)/n ≥ n √ x1 · х2 ·  … ·  хn

причем равенство имеет место тогда и только тогда, когда x1= х2= …= хn

Левая часть написанного выше неравенства называется средним арифметическим величин x1, х2, …, хn, а правая часть средним геометрическим. Иногда теорему называют «теоремой о среднем арифметическом и среднем геометрическом «, или короче «теоремой о средних».

Другие варианты записи неравенства Коши:

а)  ((x+, х2+ …+ хn)/n)n  ≥  x1 · х2 ·  … ·  хn 

б)  (x1 + х2 + … + хn)n  ≥ nn · x1 · х2 ·  … ·  хn

    2.4.  Неравенство Коши — Буняковского.

     Теорема 1. Для любых действительных чисел a1, a2¸ …, аn, b1, b2¸ …, bn             (n — любое натуральное число, больше 1) справедливо следующее неравенство 

(a1b1+a2b2+…+аnbn)²≤(a1²+ a2²+…+ an²)(b1²+ b2²+…+ bn²) или a1b1+a2b2+…+аnbn ≤√ a1²+ a2²+…+ a2n · √ b1²+ b2²+…+ bn² ,  именуемое неравенством Коши — Буняковского, причем данное соотношение реализуется в варианте равенства тогда и только тогда, когда выполняются условия   b1/а1= b2/а2=…= bn/аn.

     Доказательство.

1. Пусть  а1=а2=…= аn=0 и утверждения теоремы 1 очевидно справедливы.

2. Пусть теперь хотя бы одно из чисел  а1, а2,… аn отлично от нуля. Введем тогда следующие обозначения: А= a1²+ a2²+…+ an²>0, С=b1²+ b2²+…+ bn², В= a1b1+a2b2+…+аnbn, позволяющие записать изучаемое неравенство в следующем виде В2 ≥ АС. Очевидно, что ему будет равносильно неравенство (2В)2 – 4АС ≤ 0, что подсказывает ввести в рассмотрение следующую вспомогательную функцию f(x)=Ax2 + 2Bx+C,  xєR. Легко видеть, что f(x)=Ax2 + 2Bx+C= (a1²+ a2²+…+ an)х2+2(a1b1+a2b2+…+аnbn)х+(b1²+ b2²+…+ bn²)=( a1х+b1)2 +… +( аnх+bn)2, т.е. при любом х значение этой квадратичной функции (с положительным коэффициентом при х2) неотрицательно, а это означает, что дискриминант рассматриваемого трехчлена меньше или равен нулю, т.е. D=4В2-4АС≤0, а значит, В2≤А·С, иначе говоря, для любых действительных чисел а1, а2,… аn , b1, b2, …,bn  справедливо неравенство Коши-Буняковского: (a1b1+a2b2+…+аnbn)2≤(a1²+ a2²+…+ an)(b1²+ b2²+…+ bn²), причем равенство в полученном соотношении достигается тогда и только тогда, когда D=0, т.е. когда график функции f(x) касается оси ОХ, а значит, уравнение   Ax2 + 2Bx+C=0 имеет ровно один корень, т.е. когда следующая система уравнений совместна:

                        a1х+b1=0,

                        аnх+bn=0,  

т.е. когда  b1 / a1 = b2 / a2 =…= bn / аn . Теорема доказана.

       3.Свойство монотонности среднего степенного.

Сα(а) =(( a1α+ a2α+…+ anα)/п)1/α  – среднее  степенное  порядка α              положительных чисел а1, а2,… аn. Для действительных α и β,                                   таких, что   α ≤ β имеет место неравенство (свойство монотонности) Сα(а) ≤ Сβ(а).

   4. Теоремы о постоянной сумме и постоянном произведении.

     Теорема 1. Если сумма двух положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда оба сомножителя принимают одинаковые значения.

     Доказательство. Пусть х и у — положительные переменные величины и пусть х+у=с, где с — постоянная величина.

      Применяя неравенство о среднем арифметическом и среднем геометрическом, получим: (х+у)/2≥√ху или с/2≥√ху                              или, наконец,

                  ху≤c²/4.

Отсюда видно, что наибольшее значение произведения ху равно  c²/4            и получается оно при х=у.

     Теорема 2. Если сумма n положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда все эти переменные принимают одинаковые значения.

     Доказательство. Пусть x1, х2,…,хn — положительные переменные величины и пусть  x1 + х2 + … + хn=с, где с постоянна. По теореме Коши о среднем арифметическом и среднем геометрическом имеем:  

             ( x1 + х2 + … + хn)/ n ≥ n√ x1, х2,…,хn .

      Отсюда   x1 х2…хn≤(с/п)п , здесь знак равенства имеет место тогда и только тогда, когда x1 = х2 = … = хn. Следовательно, наибольшее значение произведения  x1 х2…хn равно (с/п)п  и получается оно при   x1 = х2 = … = хn . Теорема доказана.

     Теорема 3. Если произведение переменных x1, х2,…,хn            постоянно, то их сумма  x1 + х2 + … + хn  принимает наименьшее значение при x1 = х2 = … = хn .

     5. Решение задач.

     5.1. Задачи на наименьшее и наибольшее значение функции.

     Задача 1. Найти наибольшее значение функции  f(x)=х4 (32- х4).

     Решение. Заметим, что при х‹4√32 множители х4 и 32-х4 положительны, а их сумма является величиной постоянной. По теореме 1 наибольшее значение данной функции получим при условии, что

           х4= 32- х4,

          2х4= 32, 

          х4=16,

          х=2.

     При х=2  f(x)=24 (32- 24)= 16·16=256.

     Ответ: 256.

     Задача 2. Найти наибольшее значение функции f(x) =√х-2 + +√16-х.

Если  f(x)≥ 0 и не удается найти наибольшее и наименьшее значение f(x), то в некоторых случаях задачу можно решить путем отыскания наибольшего или наименьшего значения функции [f(x)]2 т.е. квадрата данной функции.

     Решение.             х-2 ≥ 0,                     х ≥ 2,

                                  16-х≥0;                   х ≤ 16;                   2 ≤ х≤ 16.

     Функция f(x) определена для значений х, удовлетворяющих неравенству

                2 ≤ х≤ 16.

     При х=2 и х=16 функция обращается в нуль, а при всех значениях х, заключенных между 2 и 16, она положительна.

     Найдем наибольшее значение квадрата данной функции, т.е. функции 14+2√ (х-2)(16-х).

     Множители  (х-2) и (16-х) положительны и в сумме дают 14, т.е. постоянную величину. Следовательно, наименьшее значение получится при условии    х-2=16-х,

                        2х=18,

                        х=9.

      Наибольшее значение квадрата данной функции равно

14+2√ (9-2)(16-9)=14+2√49=28, а наибольшее значение самой данной функции будет равно √28.

     Ответ: √28.

     Задача 3. На гиперболе у=2/х найдите точки, ближайшие к началу координат.

 

 

 

   Решение. ООФ: х≠0. Функция у=2/х – нечетная, искомых точек будет две.

   Пусть кротчайшее (наименьшее) расстояние от О(0;0) до точек гиперболы М(х;у) и М1(х1;у1) будет равно d.

     Тогда d=√х2+у2, где у=2/х,

               d=√х2+4/х2.

               х2+4/х2≥2 √х2∙4/х2,

               х2+4/х2≥4,

               √х2+4/х2≥2,

               d≥2.

Очевидно, что dнаим.=2, если х2=4/х2, х4=4, х1=√2,

                                                                        х2=-√2.

Имеем:  х=√2,      и       х=-√2,    

               у=√2.               у=-√2.    

        Ответ: М1 (√2;√2), М2 (-√2;-√2).

     5.2. Задачи на экстремумы.

     Задача 4. Найдите экстремумы функции у=х4-4х3+4х2.

     Решение. О.О.Ф.: х — любое действительное число.

у=х2(х2-4х+4)=х2(х-2)2=х·х(2-х)(2-х)

у=0, если х=0; 2.

При 0 ≤ х ≤ 2, 2 – х ≥ 0, поэтому можно записать

            (х+х+2-х+2-х)/4 ≥4√ х2 (2-х)2 ,

            4√ х2 (2-х)2 ≤ 1,

            х2 (2-х)2 ≤ 1,

            у ≤ 1.

Находим уmax = 1 при х = 2-х, х = 1.

                 уmin = 0 при х = 0; 2.

     Задача 5. Найдите экстремальное значение функции  у = х2- х3.

     Решение. D(y) = R (ООФ: х-любое действительное число).

У = х2-х3 = х2(1-х) = 1/2х2(2-2х ).

Используем неравенство Коши:

х+х+2-2х/3≥3√х∙х(2-2х),

откуда 3√х2(2-2х)≤2/3

             х2(2-2х)≤8/27,

             2х2(1-х)≤8/27,

             2у≤8/27,

             у≤4/27.

Отсюда можно сделать вывод: уmax= 4/27 при х = 2-2х, т.е. при х = 2/3.

     Ответ:ymax= 4/27.

     

     5.3. Использование  свойство  монотонности  среднего   степенного.

     

     Задача 6. Найти наибольшее и наименьшее значение функции

У = (1+х) n +(1-х)n на [-1;1].

     Решение. Воспользовавшись свойством монотонности среднего степенного, получим:

(((1+х) n+(1-х) n)/2)1/ n≥((1+х)+(1-х))/2=1.

Значит уmin= 2.

При х = 0.

     Для нахождения наибольшего значения функции воспользуемся очевидными неравенствами:

((1+х)/2) n≤(1+х) и ((1-х)/2) n≤(1-х) (так как по условию 0≤(1+х) и 0≤(1-х)≤1). Сложив эти неравенства, получим:

                                    ymax= 2 n.

   

     Задача 7. Точка М лежит внутри треугольника, АВС — расстояние от М до стороны треугольника, НКР – соответствующие высоты. Найдите наименьшее значение выражения:

(А/Н)α+(В/К)α +(С/Р)α  при α≥1.

     Решение. Имеем 2S=aA+bB+cC=aH=bК=сР, где S – площадь треугольника. Разделим обе части равенства aA+bB+cC=aH на аН:

А/Н+ (b/a)(В/Н)+(с/а)(С/Н)=1, так как (b/a)=(Н/К) и (с/а)=(Н/К), то А/Н+В/К+С/Р=1.

     В сумме свойства монотонности среднего степенного, получаем:

(А/Н)α+(В/К)α +(С/Р)α ≥3(⅓)α=1/3α-1 при α≥1.

Значит, наименьшее значение данного выражения равно 1/3α-1.

   

     5.4. Применение неравенства Коши – Буняковского.

     

    Задача 8. Найдите наименьшее и наибольшее значения функции u = х1у1+х2у2+…+хnуn, если известно, что х12+х22+…+хn2≤а2, у12+у22+…+уn2≤b2, где а,b – положительные числа .

     Решение. В силу неравенства Коши – Буняковского

(х1у1+х2у2+…+хnуn)2≤(х12+х22+…+хn2 )∙( у12+у22+…+уn2) или u2≤a2b2, откуда — ab≤u≤ab.  Значит, umin=-ab, umax=ab.

         

     5.5 Геометрические задачи на максимумы и минимумы.

     

    Задача 9. Дана плоскость поверхности ящика; найдите максимум его объема.

     Решение. Ящик – прямоугольный параллелепипед. Пусть а,b,c – длины трех ребер ящика, выходящие из одной и той же вершины, S – площадь поверхности, V – объем.

     Очевидно, S=2(аb+ac+bc), V=abc. Заметим, что аb+ac+bc = S/2, аb∙ac∙bc = V2.

      По теореме о средних V2=(abc)‹(( аb+ac+bc)/3)3=(S/6)3, если не выполняется равенство  аb=ac=bc, или a=b=c.

     Иначе говоря, V‹(S/6)3/2, если ящик не являлся кубом, когда осуществляется равенство. Результат можно выразить в двух различных (хотя по существу эквивалентных) формах:  

1) из всех ящиков с данной площадью поверхности куб имеет наибольший объем;

2) всех ящиков с данным объемом куб имеет наименьшую площадь поверхности.

     Задача 10. Найдите среди всех треугольников с заданным периметром тот, чья площадь наибольшая.

     Решение. Если обозначим стороны произвольного треугольника символами x, y и z, то по условию 0‹х‹у+z, 0‹у‹х+z, 0‹z‹х+у и х+у+z=2р, где фиксированное число р›0. Требуется определить наибольшее значение выражения S=√р(р-а)(р-b)(р-с)=√р∙√(р-а)(р-b)(р-с). Неравенство Коши немедленно дает 3√(р-а)(р-b)(р-с)≤((р-а)+(р-b)+(р-с))/3=р/3, т.е. S≤√р∙√(р/3)3=р2/3√3, причем равенство достигается тогда и только тогда, когда р-а=р-b=р-с, т.е. для равностороннего треугольника.  

   

     Задача 11. Из гранита нужно вырубить постамент в форме прямоугольного параллелепипеда, высота которого должна быть равна диагонали основания, а площадь основания должна быть равна 4м2. При каких длинах сторон основания площадь поверхности постамента будет наименьшей?

                                                  

      Решение. Обозначим символами х и у длины (в метрах) сторон прямоугольника, лежащего в основании постамента. Тогда высота постамента h=√х2+у2, а площадь поверхности S=2(х+у)√ х2+у2+8, причем ху=4 и х,у — положительные числа. Так как х∙у=4, х›0, у›0, то неравенство Коши дает, что х+у≥2√ху=4, а х2+у2≥2ху=8, т.е. √х2+у2≥√8.  Следовательно,  S≥8+16√2 (м2),  причем  равенство, очевидно, достигается при х=у=2. 

      6. Заключение. Я показала не традиционный способ решения целого ряда задач на нахождение экстремумов функции с помощью замечательного неравенства Коши. Такой способ является удобным и во многих случаях более простым и быстрым решением задач на максимум и минимум без обращения к нахождению к производной данной функции.

1. Введение.

     2. Неравенство Коши, его частные случаи.

     3.Свойство монотонности среднего степенного.

     4. Теоремы о постоянной сумме и постоянном произведении.

     5. Решение задач.

     6. Заключение.

     7. Список литературы.

7. Список литературы.

1. В. К. Смышляев. Практикум по решению задач школьной математики. Просвещение, 1978.

2.  Д. Пойа. Математика и правдоподобные размышления. Наука, 1975.

3. С. И. Туманов. Поиски решения задачи. Просвещение, 1967.

4. А. В. Ефремов, М. А. Ефремов, С. А. Загидуллина. Особые применения решения экстремальных задач. Магариф, 2003.

5. С. А. Гомонов. Замечательные неравенства: способы получения и примеры применения. Дрофа, 2005.

Неравенства Коши

Неравенства Коши

Введение

Коши Огюстен Луи (1789—1857) — знаменитый французский математик. Доказал ряд замечательных теорем в области анализа, теории функций комплексного переменного, теории дифференциальных уравнений и т. д. Большая заслуга Коши — разработка курса анализа, в котором, в частности, он предложил ставшие классическими определения предела, непрерывности функции и т. п.

Решительный шаг к созданию прочного фундамента анализа был сделан в 20-е годы прошлого века французским математиком О. Коши (1789—1857), предложившим точные определения пределов функции и последовательности и на их основе доказавшим многие фундаментальные теоремы анализа. Несколько раньше (1821 г.) определения предела и непрерывности, целый ряд других замечательных результатов (в том числе знаменитый пример функции, непрерывной на промежутке, но не имеющей производной ни в одной его точке) получил чешский математик Б. Больцано (1781 —1848), но его работы стали известны много позднее.

Определение предела функции по Коши формулируется так: «Число А называется пределом функции f (х) при х, стремящемся к а (т.е. 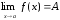), если для любого числа 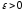можно подобрать такое числ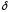о >0, что 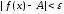для всех х, удовлетворяющих неравенству

0< | x—а |< ».

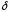Опираясь на это определение, уже нетрудно дать определение непрерывности в точке: функция f непрерывна в точке x0 если

limf(x)=f(x0)

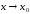
Формулировка определения предела последовательности такова: «Число А является пределом последовательности если для любого 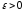существует номер N, такой, что при всех n>N верно неравенство

| ».

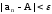О. Л. Коши внес также большой вклад в развитие математического анализа. О. Л. Коши хорошо известен каждому человеку, изучавшему математический анализ своими результатами в области математического анализа.

1. Множества в Евклидовом Пространстве

1.1 Основные метрические понятия

п.1 Угол между векторами. Угол между парой векторов x и y мы будем называть тот угол (в пределах от 0 до 1800), косинус которого равен отношению .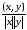

Чтобы это определение можно было применить в общем евклидовом пространстве, необходимо доказать, что указанное отношение по абсолютной величине не превосходит единицы, каковы бы ни были векторы x и y.

Для доказательства этого утверждения рассмотрим векторы 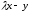, где 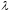– вещественное число. В силу аксиомы о положительно определенной форме скалярного произведения векторов при любом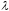

.

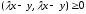Используя формулу

,

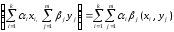мы можем написать это неравенство в виде

.

В левой части неравенства стоит квадратный трехчлен относительно 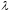с постоянными коэффициентами. Трехчлен этот не может иметь различных вещественных корней, так как тогда он не мог бы сохранять знака для всех значений 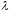. Поэтому дискриминант 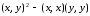этого трехчлена не может быть положительным. Следовательно,

,

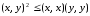откуда ,извлекая квадратный корень, получаем

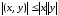, (1)

что и требовалось.

Неравенство (1) называют неравенством Коши–Буняковского.

Примеры.

а) В пространстве V3 неравенство Коши–Буняковского, очевидно, вытекает из самого определения скалярного произведения как произведение длин векторов и косинуса угла между ними.

б) В пространстве Rn неравенство Коши–Буняковского имеет вид

;

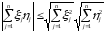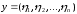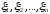оно справедливо для любой пары векторов и или, что-то же самое, для любых двух систем вещественных чисел и .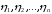

в) В пространстве R2(a,b) неравенство Коши–Буняковского имеет вид

.

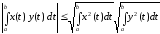Рассмотрим более подробно неравенство Коши в пространстве Rn. Для начала дадим определение n–мерного евклидового пространства Rn..

Def. n–мерное точечное пространство, в котором расстояние между точками определено по данной формуле

,

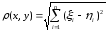называется n–мерным евклидовым пространством и обозначается Rn.

Ясно, что 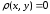тогда и только тогда, когда x = y, т. е. когда 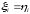при всех i = 1, 2, …,n. Также ясно, что

.

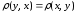Докажем, что для любых трех точек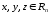

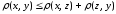(2)

Это неравенство в двумерном или трехмерном пространстве выражает тот элементарный геометрический факт, что сумма двух сторон треугольника не меньше третьей стороны*, и потому называется неравенством треугольника. Также данное неравенство является одним из аксиом метрического пространства и называется аксиомой треугольника

Предварительно установим важное неравенство Коши

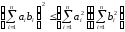, (3)

справедливо для любых вещественных чисел ai и bi. Простое доказательство этого неравенства основывается на следующем замечании: если квадратный трехчлен Ax2+2Bx+C с вещественными коэффициентами неотрицателен при всех вещественных x, то его дискриминант 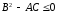*. Составим вспомогательную функцию 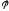от вещественной переменной x, сводящуюся к квадратному трехчлену:

,

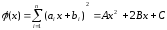где

Из определения 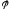видно, что 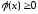при всех x.

Тогда, на основании предыдущего замечания,

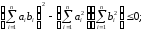
это и есть иначе записанное неравенство Коши.

Далее из неравенства (3) выведем еще одно неравенство

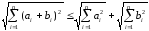(4)

(ai и bi – любые вещественные числа), которое тоже называют неравенством Коши.

Для доказательства неравенства (4) извлечем квадратные корни из обеих частей неравенства (3), затем удвоив обе части полученного нового неравенства и прибавим к ним выражение 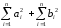. В результате получим

Это неравенство можно переписать и так:

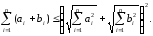
Извлекая, квадратные корни из обеих частей последнего неравенства, получим (4).

Теперь уже легко доказать неравенство треугольника (2). Пусть

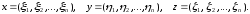
Полагая в неравенстве (4)

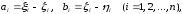
мы получим неравенство (2).

Теперь приведем некоторые примеры метрических пространств.

Пусть множество l состоит из всех бесконечных числовых последовательностей 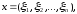удовлетворяющих условию

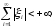
Таким образом, l – метрическое пространство

Обозначим через l2 множества всех таких последовательностей 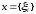вещественных чисел, для которых 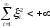, и положим

.

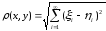Прежде всего нужно проверить, что 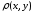конечно (т. е. что ря в правой части сходится) для любых x и y из l2. А для этого сначала покажем, что неравенство Коши (4) справедливо и для бесконечных последовательностей чисел ai и bi (i=1, 2, …). Действительно, беря произвольное натуральное n, запишем неравенство (4), а затем перейдем в нем к пределу при 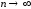. Получим неравенство

, (5)

которое мы будем называть неравенством Коши для бесконечных последовательностей. Аналогичным образом из неравенства (3) выводится и другое неравенство Коши для бесконечных последовательностей:

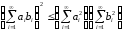. (6)

Из неравенства (5), в частности, следует, что есл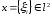и

и ,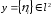

то и последовательность

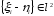, т.е. .

Теперь проверка выполнения в l2 аксиом метрического пространства может быть произведена совершенно так же, как это сделано для Rn.

Пространство l2 иногда называют бесконечномерным евклидовым пространством.

п.2 Неравенство треугольника. Если x и y –произвольные векторы, то по аналогии с элементарной геометрии вектор x+y естественно называть третьей стороной треугольника, построенного на векторах x и y. Используя неравенство Коши–Буняковского, мы получаем

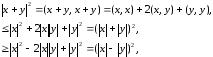
или

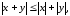(7)

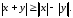(8)

Неравенства (7)–(8) называются неравенствами треугольника. Геометрически они означают, что длина любой стороны всякого треугольника не больше, чем сумма длин двух других сторон, и не меньше, чем абсолютная величина разности длин этих сторон.

2. Комплексные пространства со скалярным произведением

2.1 Скалярное произведение (Основные метрические понятия)

коши скалярный математический евклидовый

п.3 Неравенство Коши–Буняковского. Для любых двух векторов x, y из C имеет место неравенство

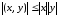, (9)

Доказательство проводится по той же схеме, что и в вещественном случае (п.1), но с некоторой осторожностью обращения с комплексными числами. Если (x, y)=0, неравенство (9) очевидно. При (x, y)0 замечаем, что

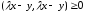
при любом комплексном 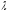. Раскрываем скобки, находим

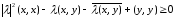. (10)

Будем считать, что 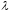изменяется по прямой 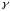, симметричной относительно вещественной оси с прямой, определяемой комплексным числом (x, y), так что

,

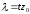где t вещественно, а zo–единичный вектор, определяющий направление прямой ,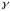

.

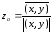Тогда

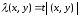
есть вещественное число, так что

.

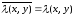Неравенство (10) преобразуется к виду

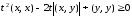. (11)

Теперь та же аргументация, что и в (п.1), приводит нас к искомому неравенству (9).

Если в неравенстве(9) стоит знак равенства, то трехчлен в левой части (11) имеем один вещественный корень to. Заменяя tzo на 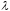, мы получаем, что трехчлен в левой части (10) имеет корень 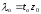, откуда

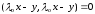
и

,

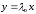так что векторы x и y отличаются лишь (комплексным) множителем.

п.4 Неравенство треугольника. Если x и y – два вектора в унитарном пространстве C, то по неравенству Коши–Буняковского (п.3)

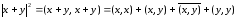
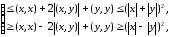
откуда

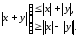(12)

Неравенства (12), как и в вещественном случае, называют неравенствами треугольника.

Список литературы

1. Вулих Б. З. Краткий курс теории функций вещественной переменной. М.,1973. – 350 с.

2. Коровкин П. П. Неравенства. М., 1983. – 56 с.

3. Шилов Г.Е. Математический анализ (конечномерные линейные пространства). М.,1969 г., 432 с.

4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том 2 М., 1966 г., 800с.