Несобственный интеграл — это… Что такое Несобственный интеграл?
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
- Предел a или b (или оба предела) являются бесконечными;
- Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Несобственные интегралы I рода
Пусть определена и непрерывна на множестве от и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
- Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
Пусть определена и непрерывна на множестве от и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае называется сходящимся.
- Если не существует конечного ( или ), то интеграл называется расходящимся к , или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные интегралы II рода
Пусть определена на , терпит бесконечный разрыв в точке x=a и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Пусть определена на , терпит бесконечный разрыв при x=b и . Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Если функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой:
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
Пример
Отдельный случай
Пусть функция определена на всей числовой оси и имеет разрыв в точках .
Тогда можно найти несобственный интеграл
Критерий Коши
1. Пусть определена на множестве от и .
- Тогда сходится
2. Пусть определена на и .
- Тогда сходится
Абсолютная сходимость
Интеграл называется абсолютно сходящимся, если сходится.
Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл называется условно сходящимся, если сходится, а расходится.
См. также
Список используемой литературы
Дмитрий Письменный Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
Несобственный интеграл — Википедия
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
- Область интегрирования является бесконечной. Например, является бесконечным промежутком [a,+∞){\displaystyle [a,+\infty )}.
- Функция f(x){\displaystyle f(x)} является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал [a,b]{\displaystyle [a,b]} конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.
Несобственные интегралы I рода
Несобственный интеграл первого родаПусть f(x){\displaystyle f(x)} определена и непрерывна на интервале [a,+∞){\displaystyle [a,+\infty )} и ∀A>a ∃∫aAf(x)dx{\displaystyle \forall A>a\ \exists \int \limits _{a}^{A}f(x)dx}. Тогда:
- Если ∃limA→+∞∫aAf(x)dx=I∈R{\displaystyle \exists \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫a+∞f(x)dx{\displaystyle I=\int \limits _{a}^{+\infty }f(x)dx} называется сходящимся.
- Если не существует конечного limA→+∞∫aAf(x)dx{\displaystyle \lim _{A\to +\infty }\int \limits _{a}^{A}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫a+∞f(x)dx{\displaystyle \int \limits _{a}^{+\infty }f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена и непрерывна на множестве от (−∞,b]{\displaystyle (-\infty ,b]} и ∀B<b⇒∃∫Bbf(x)dx{\displaystyle \forall B<b\Rightarrow \exists \int \limits _{B}^{b}f(x)dx}. Тогда:
- Если ∃limB→−∞∫Bbf(x)dx=I∈R{\displaystyle \exists \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx=I\in \mathbb {R} }, то используется обозначение I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} и интеграл называется несобственным интегралом Римана первого рода. В этом случае I=∫−∞bf(x)dx{\displaystyle I=\int \limits _{-\infty }^{b}f(x)dx} называется сходящимся.
- Если не существует конечного limB→−∞∫Bbf(x)dx{\displaystyle \lim _{B\to -\infty }\int \limits _{B}^{b}f(x)dx} (±∞{\displaystyle \pm \infty } или ∄{\displaystyle \nexists }), то интеграл ∫−∞bf(x)dx{\displaystyle \int \limits _{-\infty }^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
∫−∞+∞f(x)dx=∫−∞cf(x)dx+∫c+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{c}f(x)dx+\int \limits _{c}^{+\infty }f(x)dx}, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
∫−∞−11x2dx=lima→−∞∫a−11x2dx=lima→−∞−1x|a−1=1+lima→−∞1a=1+0=1{\displaystyle \int \limits _{-\infty }^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }\int \limits _{a}^{-1}{1 \over x^{2}}dx=\lim _{a\to -\infty }{\Bigl .}-{\frac {1}{x}}{\Bigr |}_{a}^{-1}=1+\lim _{a\to -\infty }{\frac {1}{a}}=1+0=1}
Несобственные интегралы II рода
Несобственный интеграл Римана второго родаПусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]}, терпит бесконечный разрыв в точке x = a и ∀δ>0⇒∃∫a+δbf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Пусть f(x){\displaystyle f(x)} определена на [a,b){\displaystyle [a,b)} , терпит бесконечный разрыв при x = b и ∀δ>0⇒∃∫ab−δf(x)dx=I(δ){\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a}^{b-\delta }f(x)dx={\mathcal {I}}(\delta )}. Тогда:
- Если ∃limδ→0+0I(δ)=I∈R{\displaystyle \exists \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=I\in \mathbb {R} }, то используется обозначение I=∫abf(x)dx{\displaystyle I=\int \limits _{a}^{b}f(x)dx} и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
- Если limδ→0+0I(δ)=∞(±∞{\displaystyle \lim _{\delta \to 0+0}{\mathcal {I}}(\delta )=\infty \;(\pm \infty } или ∄){\displaystyle \nexists )}, то обозначение сохраняется, а I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} называется расходящимся к «∞{\displaystyle \infty }», «±∞{\displaystyle \pm \infty }», или просто расходящимся.
Если функция f(x){\displaystyle f(x)} терпит разрыв во внутренней точке c{\displaystyle c} отрезка [a;b]{\displaystyle [a;b]}, то несобственный интеграл второго рода определяется формулой:
∫abf(x)dx=∫acf(x)dx+∫cbf(x)dx.{\displaystyle \int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx.}
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.
Пример
∫01dxx=limδ→0+0ln|x||0+δ1=0−limδ→0+0lnδ=+∞{\displaystyle \int \limits _{0}^{1}{dx \over x}=\lim _{\delta \to 0+0}{\Bigl .}\ln |x|{\Bigr |}_{0+\delta }^{1}=0-\lim _{\delta \to 0+0}\ln \delta =+\infty }
Отдельный случай
Пусть функция f(x){\displaystyle f(x)} определена на всей числовой оси и имеет разрыв в точках x1,x2,…,xk{\displaystyle x_{1},x_{2},\dots ,x_{k}}.
Тогда можно найти несобственный интеграл ∫−∞+∞f(x)dx=∫−∞x1f(x)dx+∑j=1k−1∫xjxj+1f(x)dx+∫xk+∞f(x)dx{\displaystyle \int \limits _{-\infty }^{+\infty }f(x)dx=\int \limits _{-\infty }^{x_{1}}f(x)dx+\sum _{j=1}^{k-1}{\int \limits _{x_{j}}^{x_{j+1}}f(x)dx}+\int \limits _{x_{k}}^{+\infty }f(x)dx}
Критерий Коши́
1. Пусть f(x){\displaystyle f(x)} определена на множестве от [a,+∞){\displaystyle [a,+\infty )} и ∀A>a⇒∃∫aAf(x)dx=I{\displaystyle \forall A>a\Rightarrow \exists \int \limits _{a}^{A}f(x)dx={\mathcal {I}}}.
- Тогда I=∫a+∞f(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{+\infty }f(x)dx} сходится ⇔∀ε>0⇒∃A(ε)>a:∀(A2>A1>A)⇒|∫A1A2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists A(\varepsilon )>a:\forall (A_{2}>A_{1}>A)\Rightarrow \left|\,\int \limits _{A_{1}}^{A_{2}}f(x)dx\right|<\varepsilon }
2. Пусть f(x){\displaystyle f(x)} определена на (a,b]{\displaystyle (a,b]} и ∀δ>0⇒∃∫a+δbf(x)dx=I{\displaystyle \forall \delta >0\Rightarrow \exists \int \limits _{a+\delta }^{b}f(x)dx={\mathcal {I}}}.
- Тогда I=∫abf(x)dx{\displaystyle {\mathcal {I}}=\int \limits _{a}^{b}f(x)dx} сходится ⇔∀ε>0⇒∃δ(ε)>0:∀(0<δ1<δ2<δ)⇒|∫a+δ1a+δ2f(x)dx|<ε{\displaystyle \Leftrightarrow \forall \varepsilon >0\Rightarrow \exists \delta (\varepsilon )>0:\forall (0<\delta _{1}<\delta _{2}<\delta )\Rightarrow \left|\,\int \limits _{a+\delta _{1}}^{a+\delta _{2}}f(x)dx\right|<\varepsilon }
Абсолютная сходимость
Интеграл ∫a+∞f(x)dx (∫abf(x)dx){\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ \left(\int \limits _{a}^{b}f(x)dx\right)} называется абсолютно сходящимся, если ∫a+∞|f(x)|dx (∫ab|f(x)|dx){\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ \left(\int \limits _{a}^{b}|f(x)|dx\right)}сходится.
Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } называется условно сходящимся, если ∫a+∞f(x)dx {\displaystyle \int \limits _{a}^{+\infty }f(x)dx\ \ } сходится, а ∫a+∞|f(x)|dx {\displaystyle \int \limits _{a}^{+\infty }|f(x)|dx\ \ } расходится.
См. также
Литература
Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.
Несобственные интегралы с бесконечными пределами интегрирования
Пусть
функция 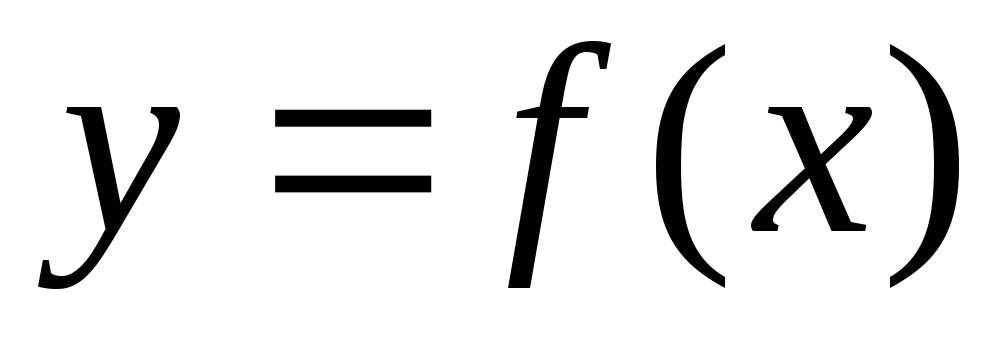 определена и интегрируема на произвольном
обрезке
определена и интегрируема на произвольном
обрезке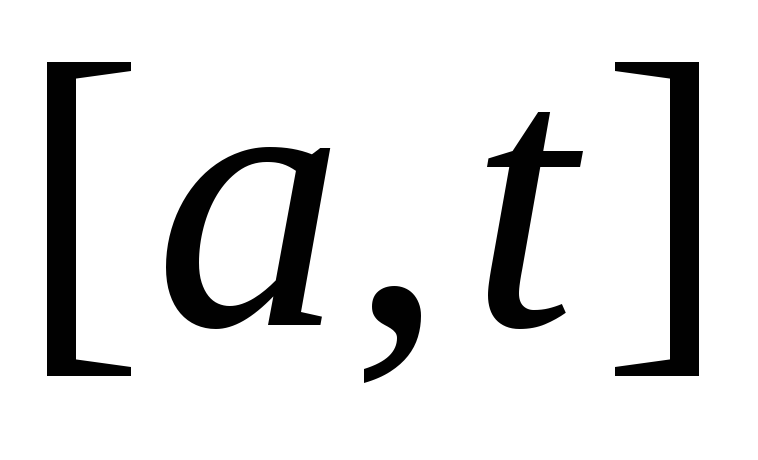 ,
т.е. функция
,
т.е. функция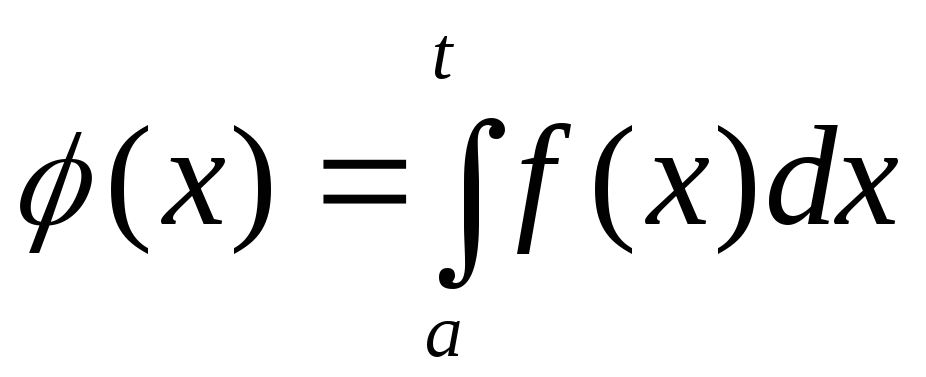 определена для произвольного
определена для произвольного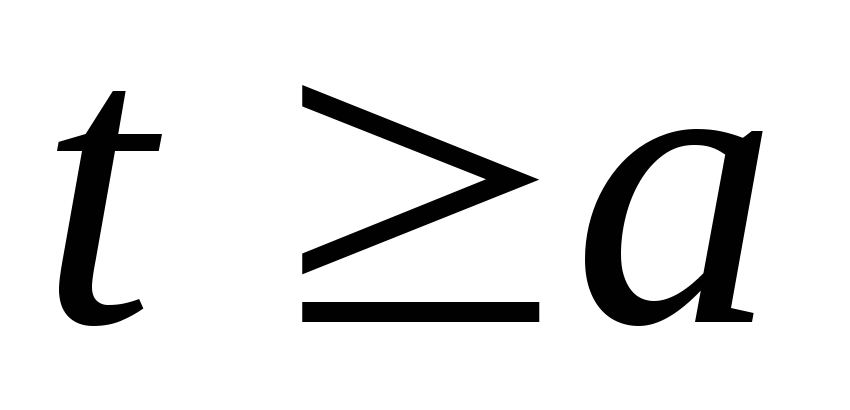 .
.
Несобственным
интегралом с бесконечным верхним
пределом 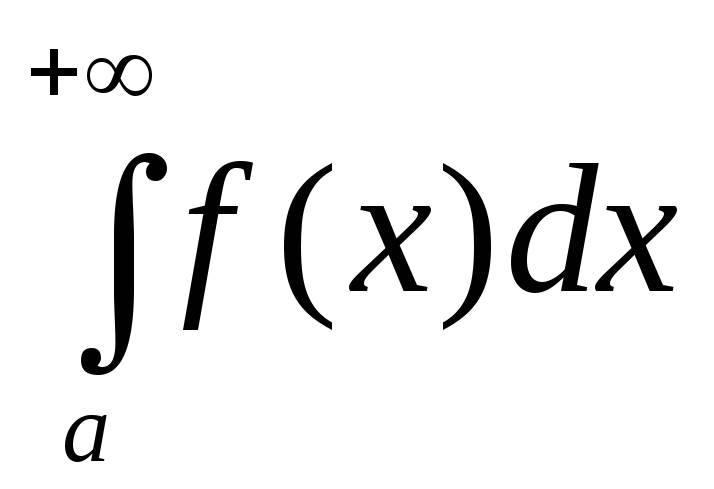 от непрерывной функции
от непрерывной функции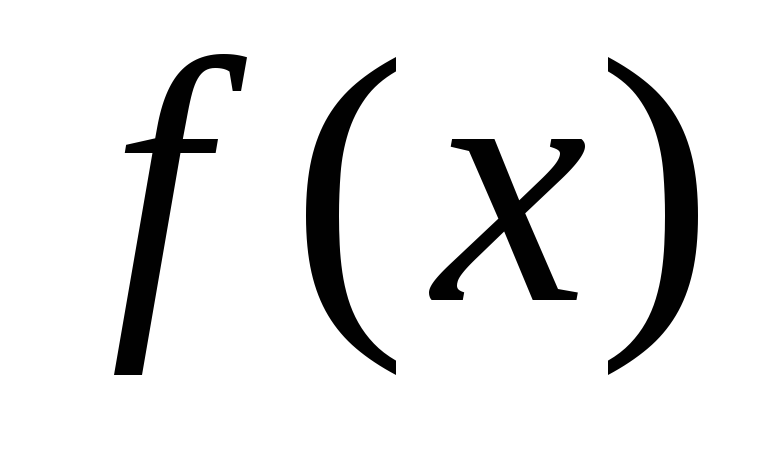 на полуинтервале
на полуинтервале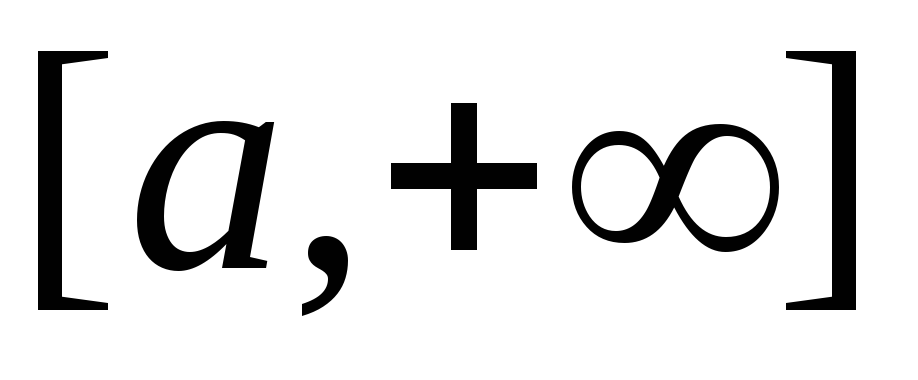 называется предел интеграла
называется предел интеграла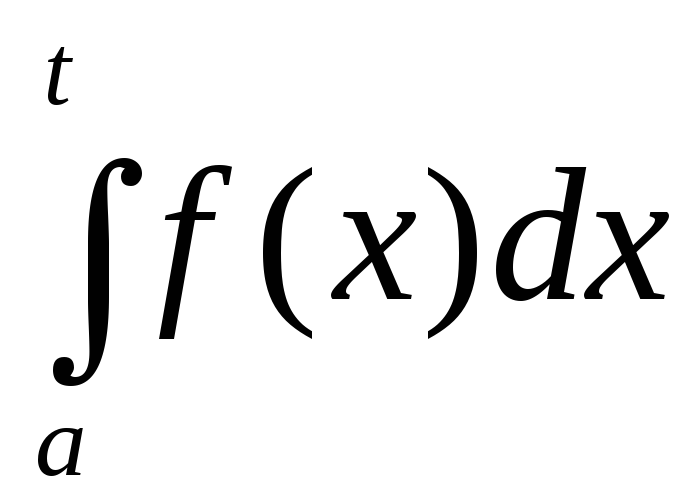 при
при стремящемся к
стремящемся к ,
т.е.
,
т.е.
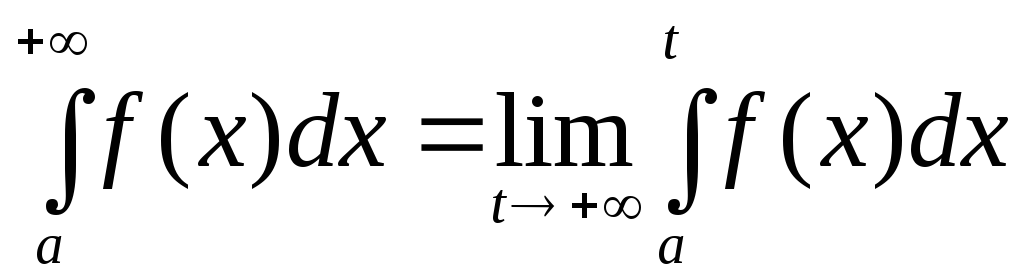 .
.
Если этот предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся.
При работе с несобственными интегралами выделяют 2 задачи:
исследование вопроса о сходимости заданного несобственного интеграла;
вычисление значения интеграла в случае, если последний сходится.
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.
Пример. Вычислить 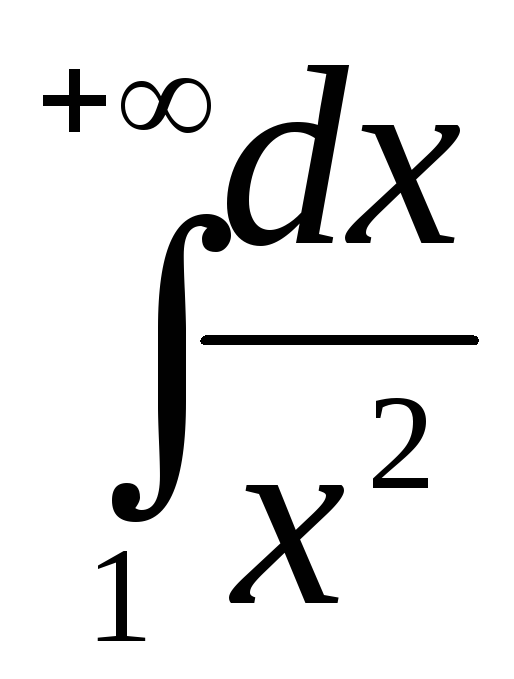 .
.
Аналогично определяется несобственный интеграл от непрерывной функции с бесконечным нижним пределом интегрирования, а именно
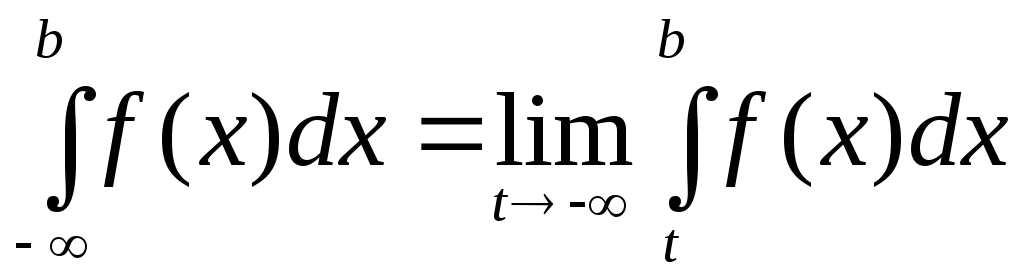 .
.
Несобственный
интеграл с двумя бесконечными пределами интегрирования имеет вид: 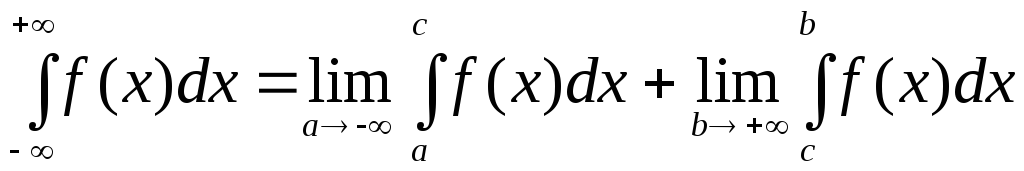 ,
где
,
где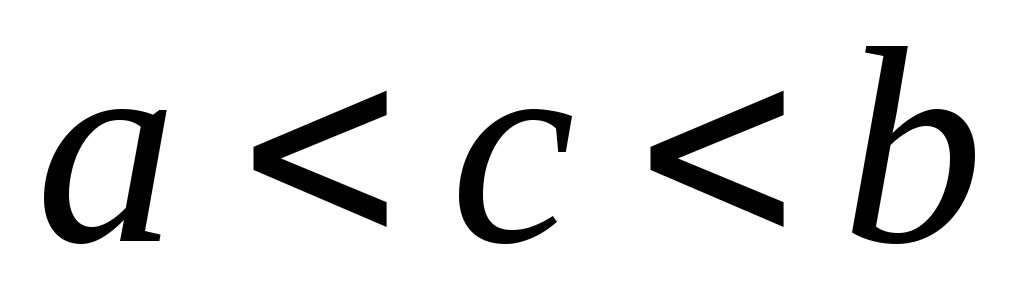 .
.
Пример. Вычислить 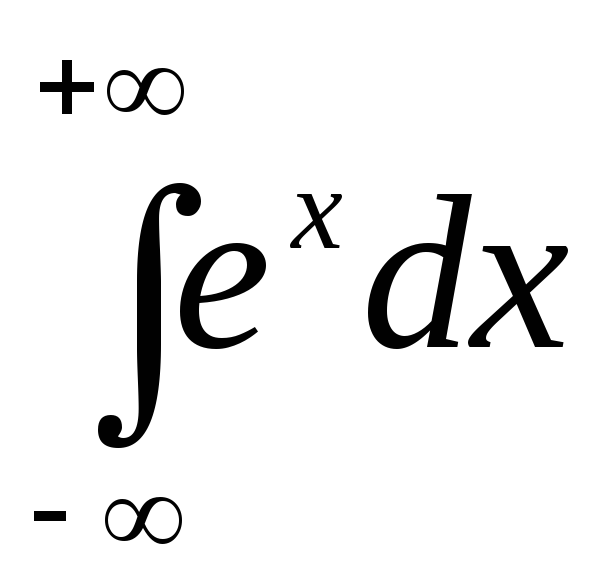 .
.
Задания для самостоятельной работы.
Найти интегралы:
Найти определенные интегралы:
Вычислить площадь фигуры, ограниченную линиями:
 .
. .
. .
. .
.
Вычислить интегралы или установить их расходимость:
13
§12. Несобственный интеграл второго рода.
y
Как уже отмечалось выше для неограниченной на отрезке [a, b] ф-и интеграл Римана смысла не имеет. Обобщим понятие определенного интеграла на ф-ю f(x) неограниченную на полуинтервале [a, b), но ограниченную и интегрируемую на любом отрезке [a, b-ε], 0<ε<a. Рассмотрим ф-ю F(ε)=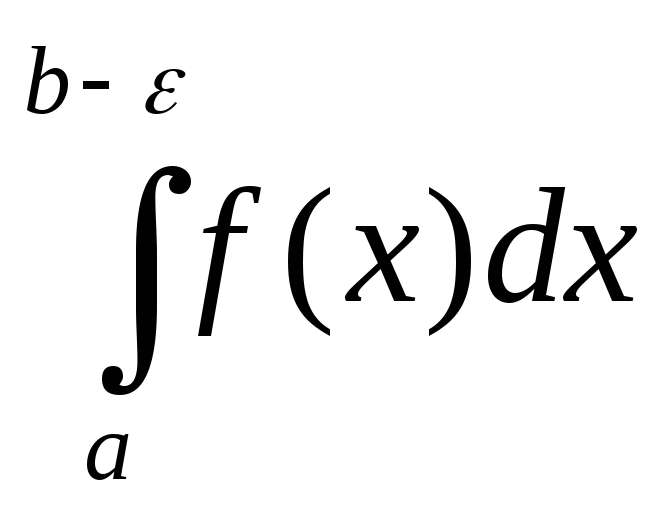 .(1)
.(1)Перейдем в (1) формально к пределу при ε→0
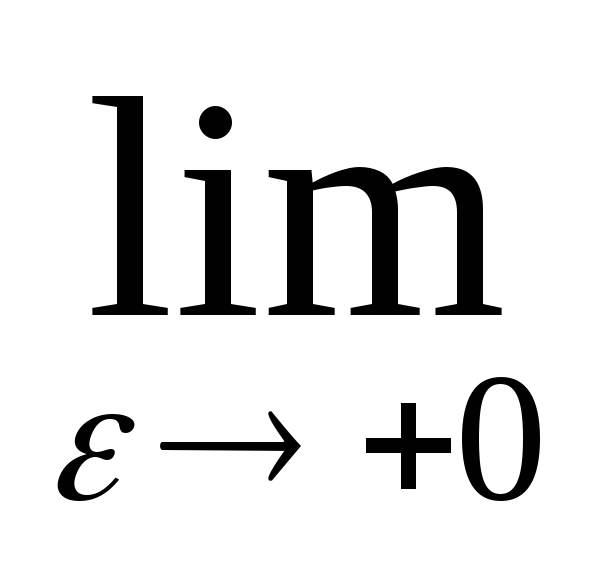 F(ε)=
F(ε)= 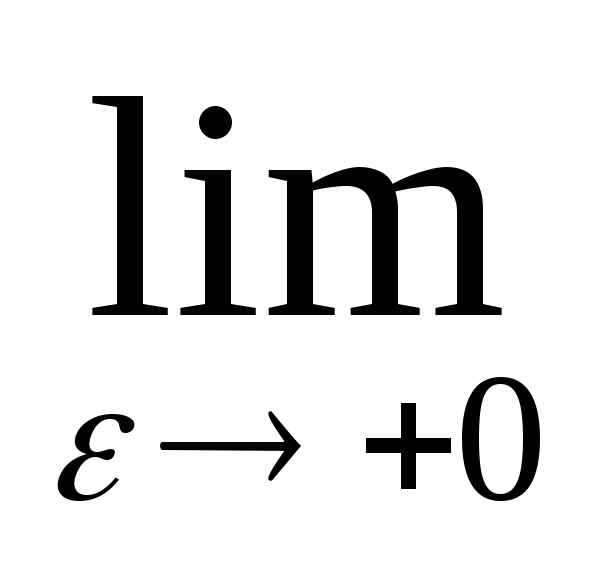
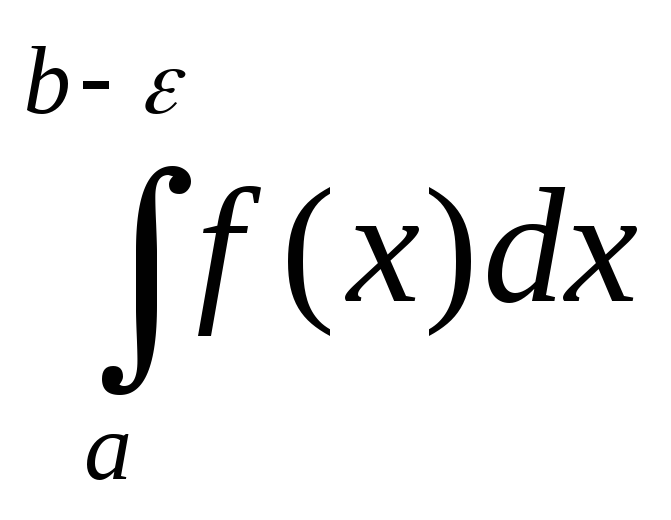 =
=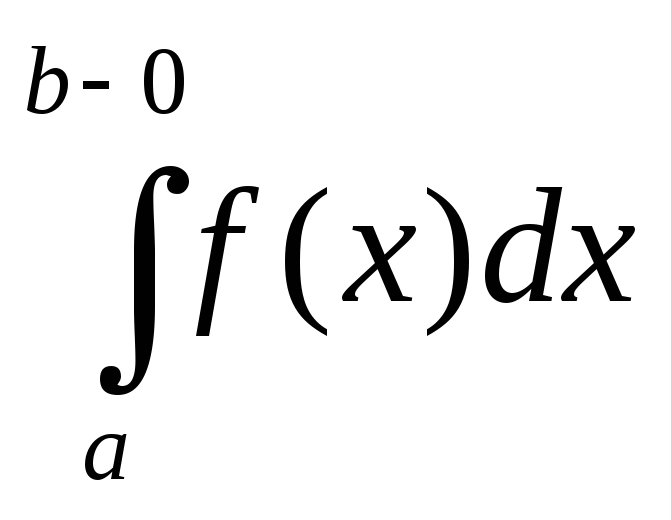 .(2).
.(2).Символ 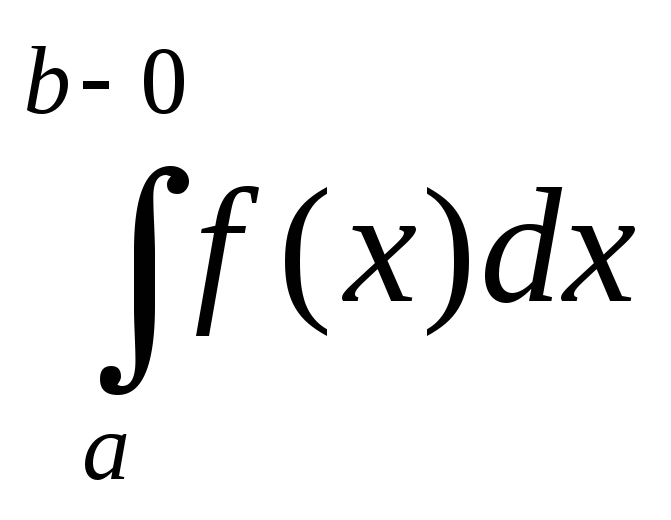 =
=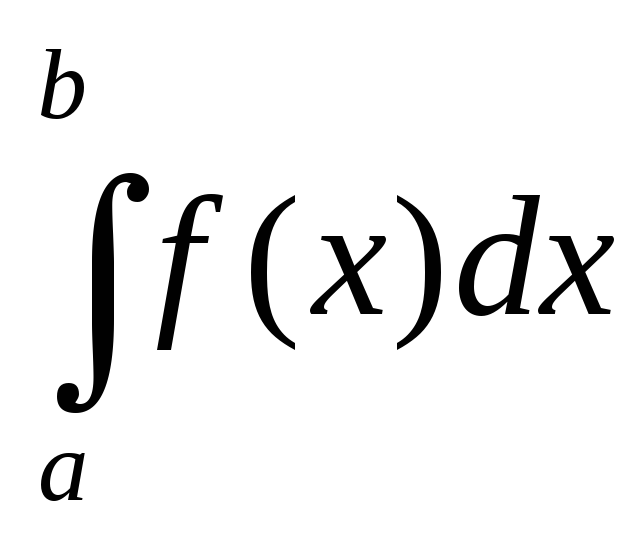 называют несобственным интегралом 2-го
рода. При этом, если предел (1) конечный,
то несобственный интеграл 2-го рода
называют сходящимся. Если предел
бесконечный или не сущ., то расходящимся.
Точкуx=b
называют особой.
называют несобственным интегралом 2-го
рода. При этом, если предел (1) конечный,
то несобственный интеграл 2-го рода
называют сходящимся. Если предел
бесконечный или не сущ., то расходящимся.
Точкуx=b
называют особой.
Аналогично определяются несобственные интегралы 2-го рода, если особой точкой является левый конец отрезка [a, b] или внутренняя точка x=c отрезка [a, b].
=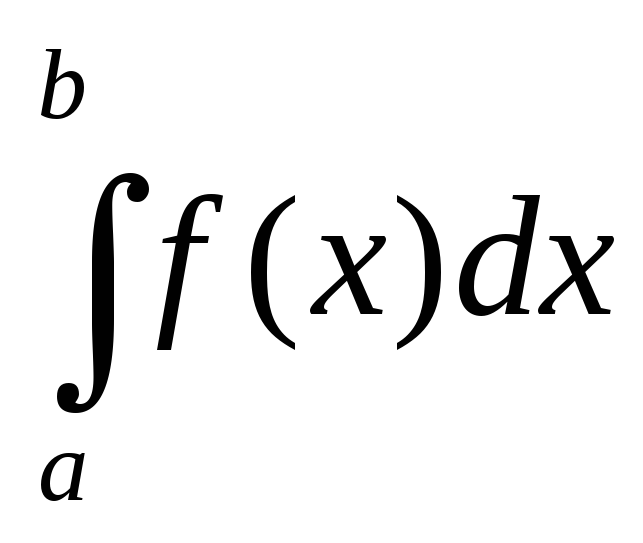 =
=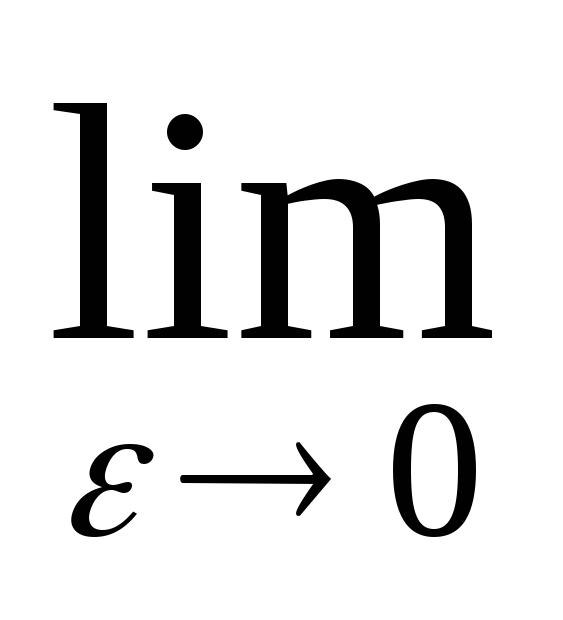
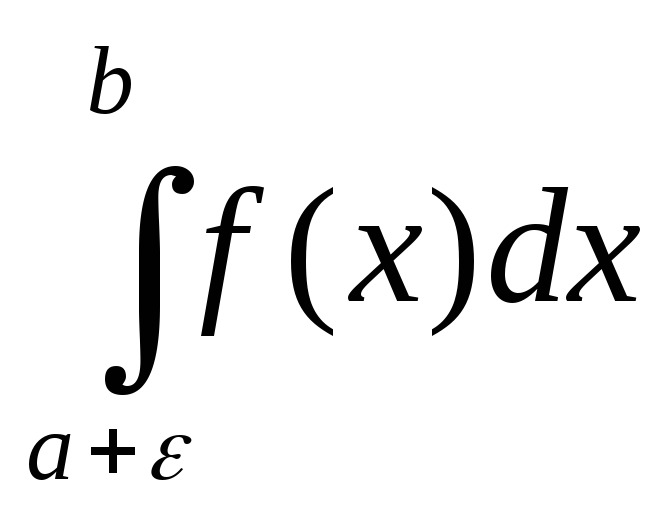 ,
,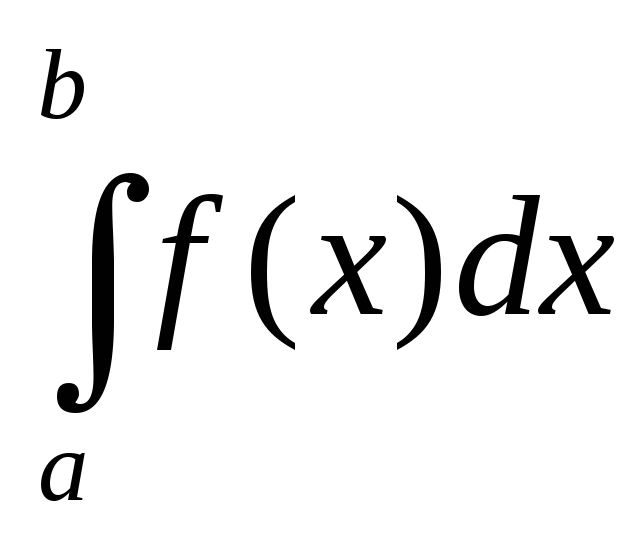 =
=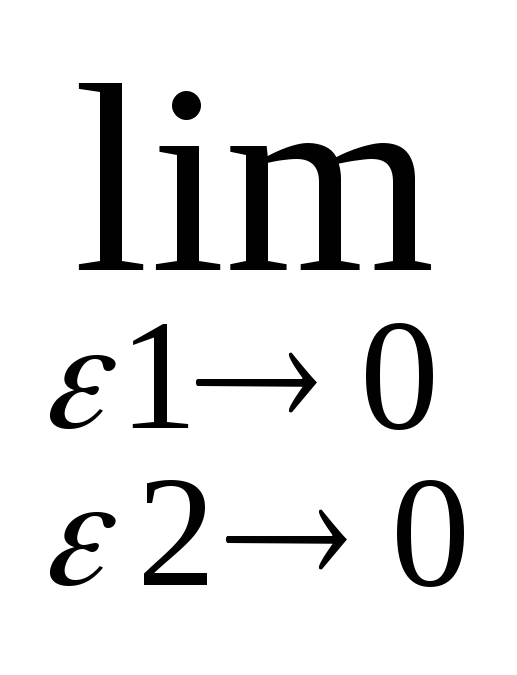 (
(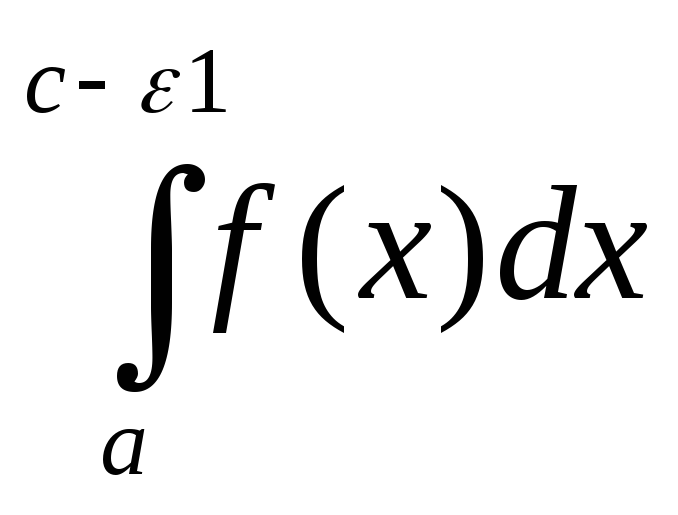 +
+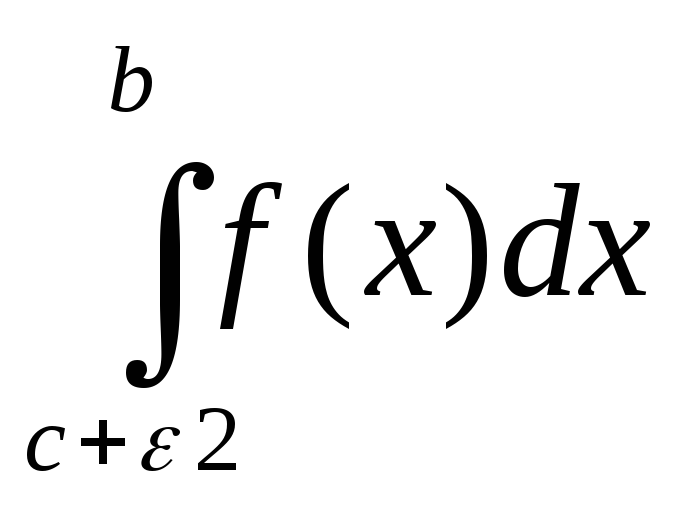 ).(3)
).(3)
Величины ε1 и ε2 →0 независимо друг от друга.
Пример
1. Исследовать
на сходимость интеграл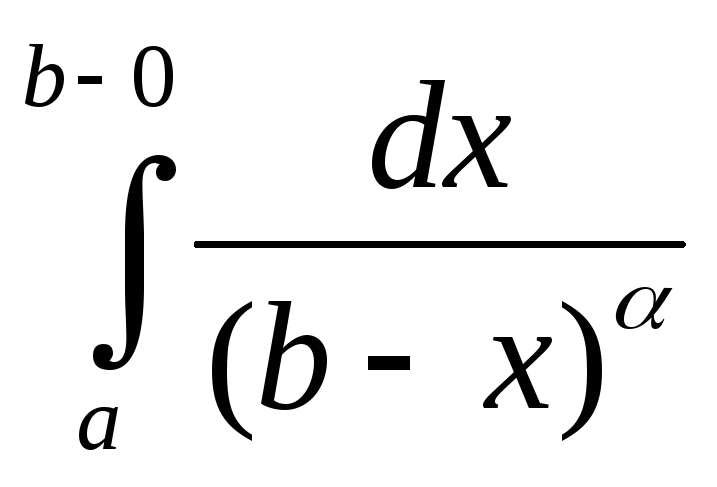 .
.
Решение. Пусть α=1. Тогда 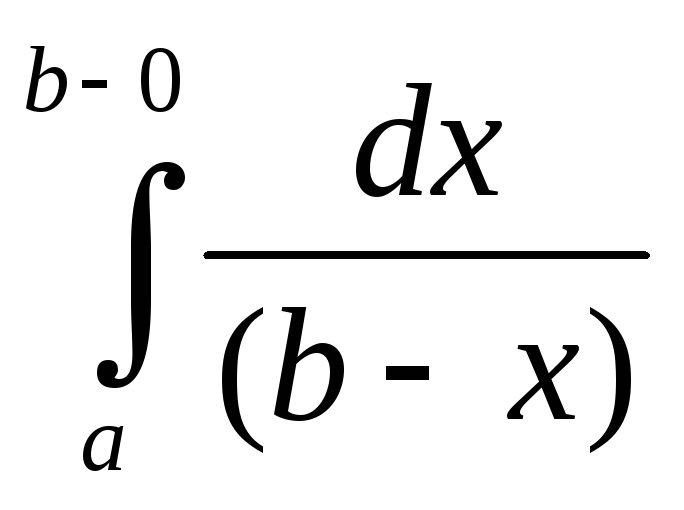 =
=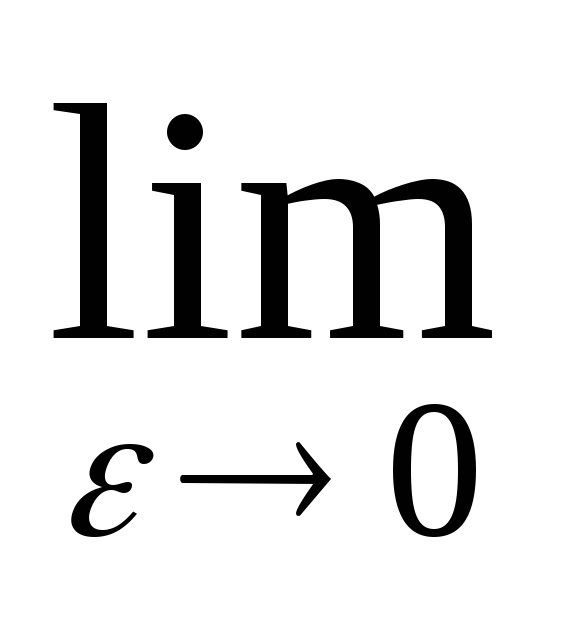
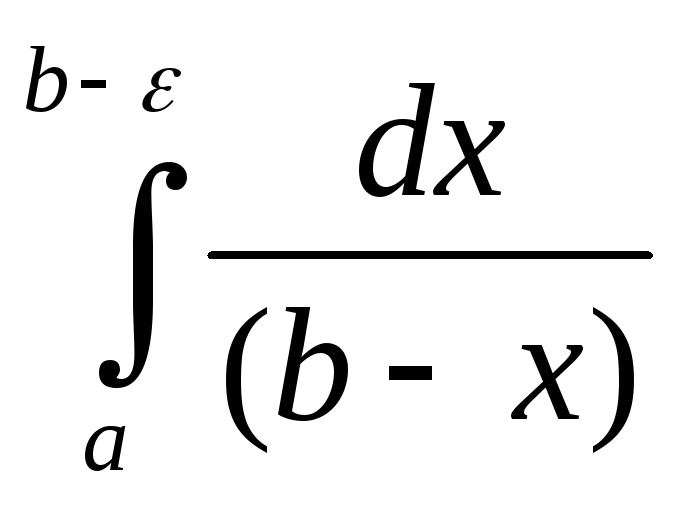 =-
=-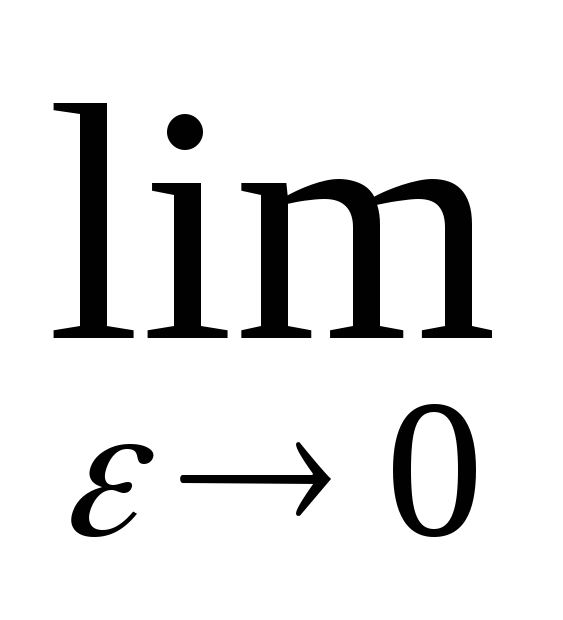 ln(b-x)
ln(b-x) 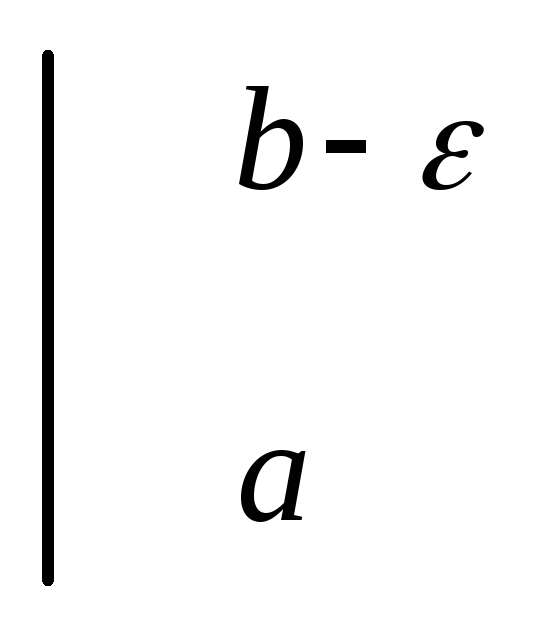 =
=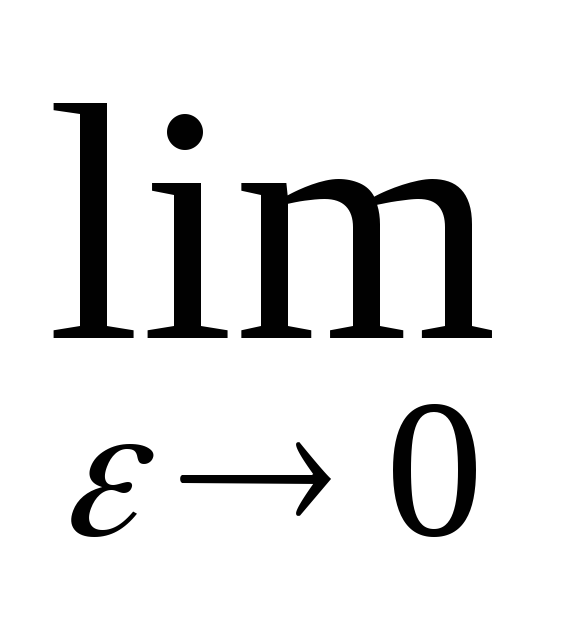 (ln(b-a)-lnε)=∞
=> ряд расходится.
(ln(b-a)-lnε)=∞
=> ряд расходится.Пусть
α≠1. Тогда 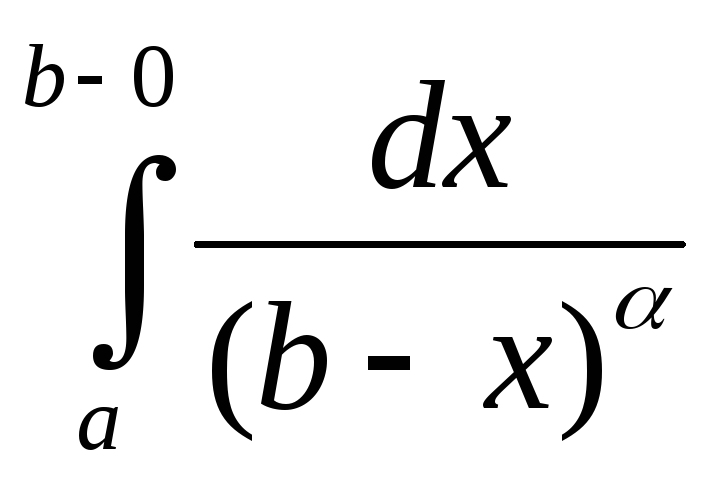 =
=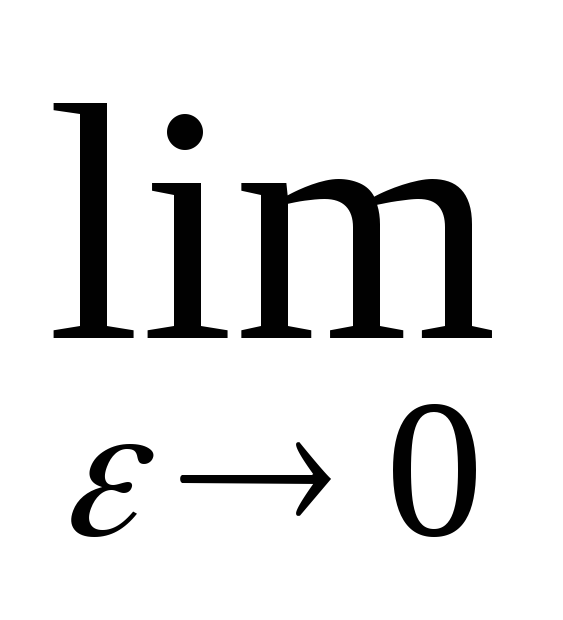
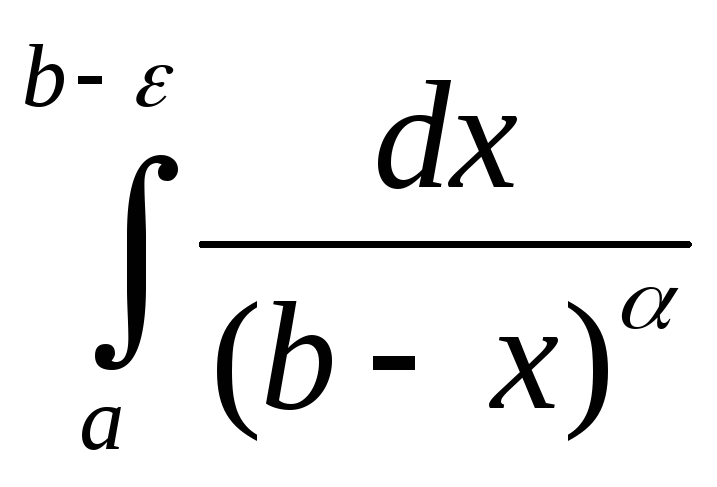 =
=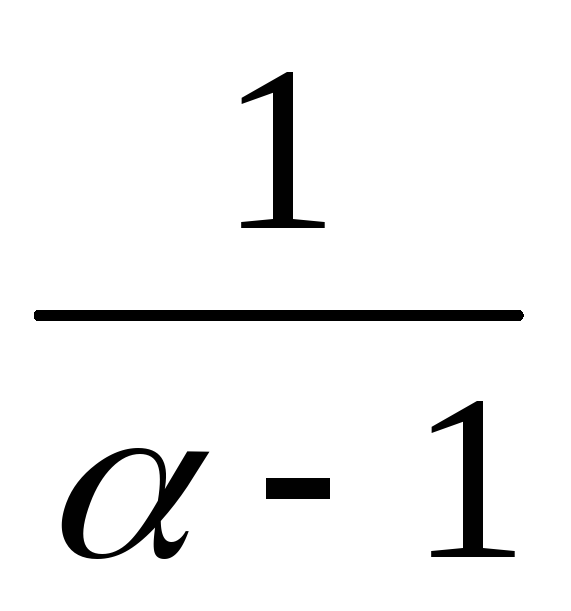
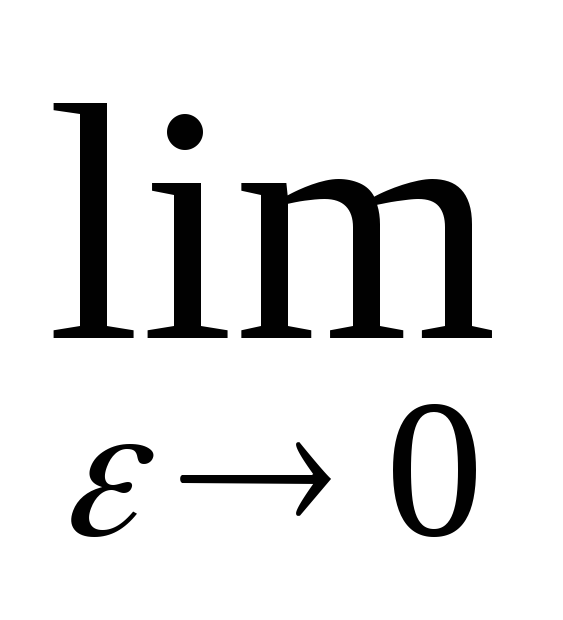
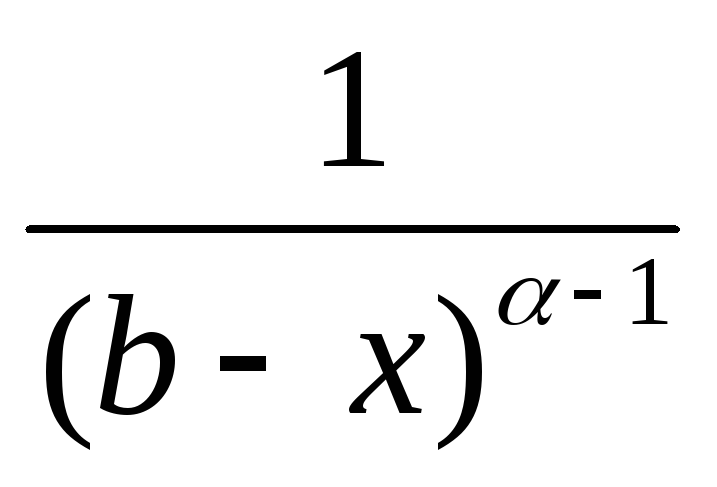
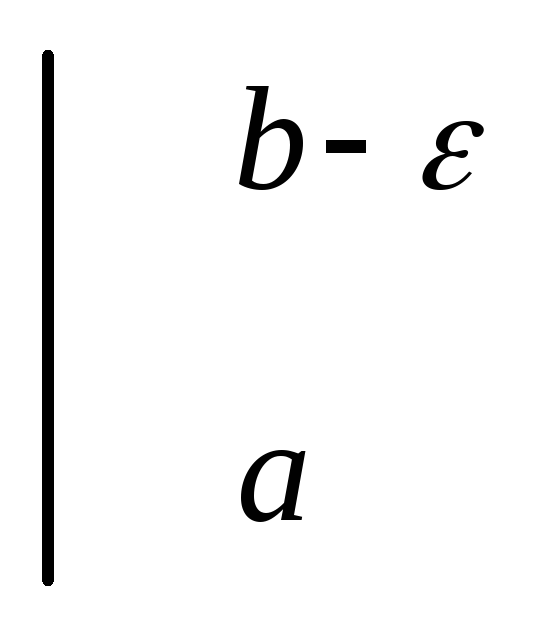 =
=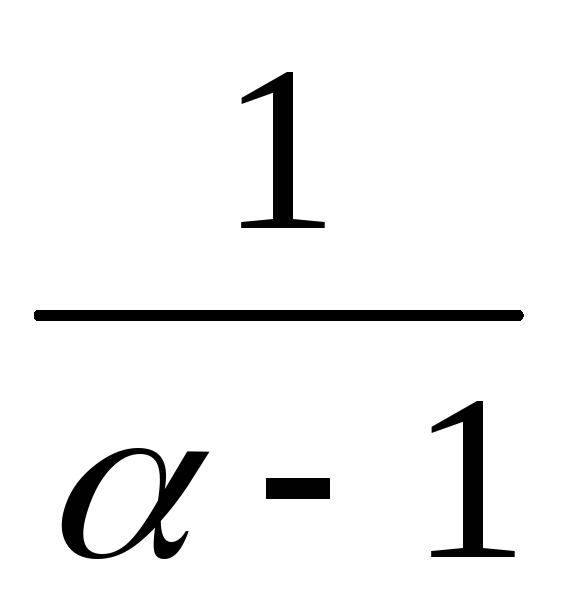
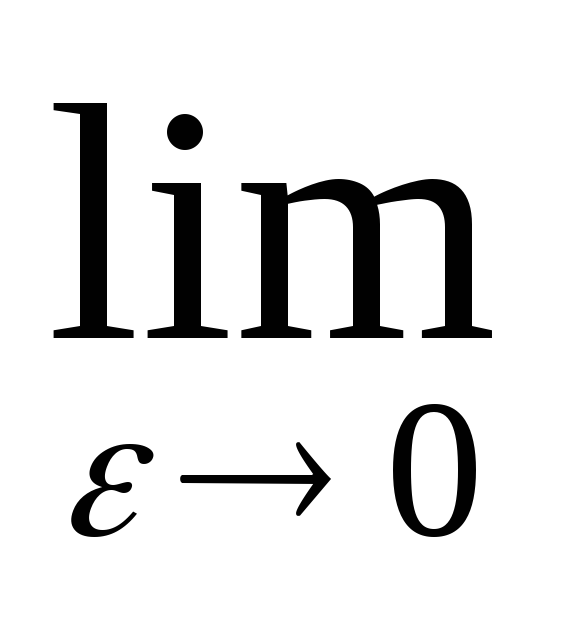 (
(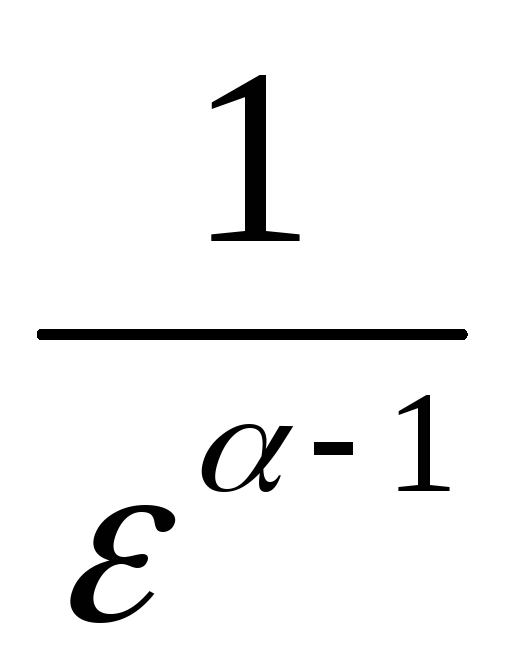 —
—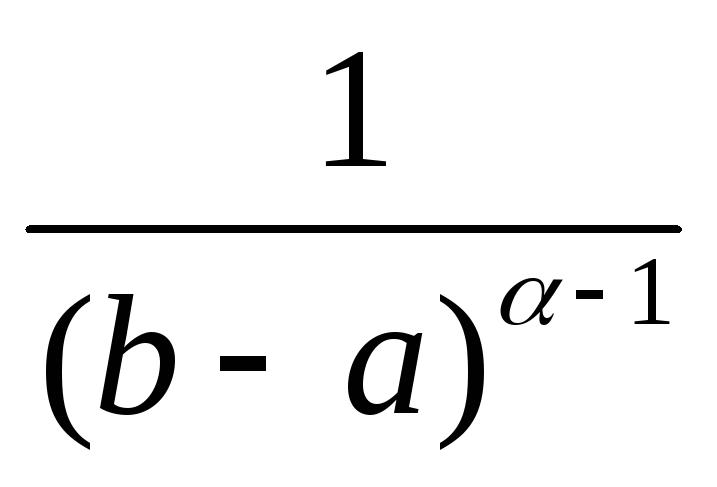 )
=> Сходится, если α<1. Расходится, если
α>1.
)
=> Сходится, если α<1. Расходится, если
α>1.Вывод: при α<1 интеграл сходится, при α≥1 интеграл расходится.
При некоторых ограничениях на ф-ю f(x) несобственный интеграл 2-го рода сводится к несобственному интегралу 1-го рода.
Пусть
f(x)
непрерывна на [a,
b)
и b
– особая точка. В интеграле 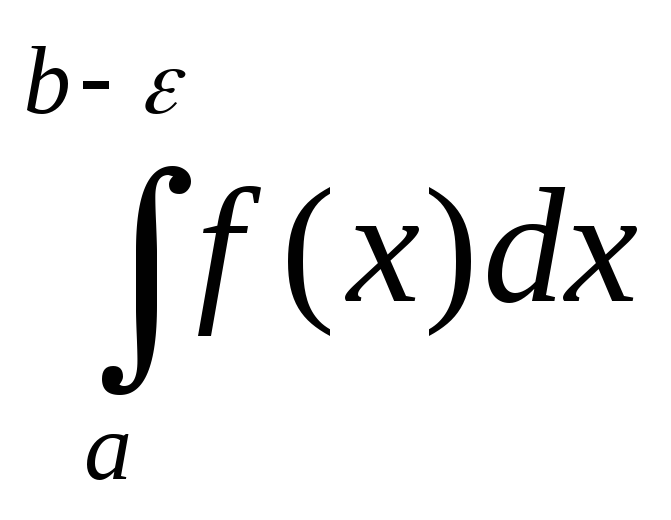 сделаем замену.
сделаем замену.
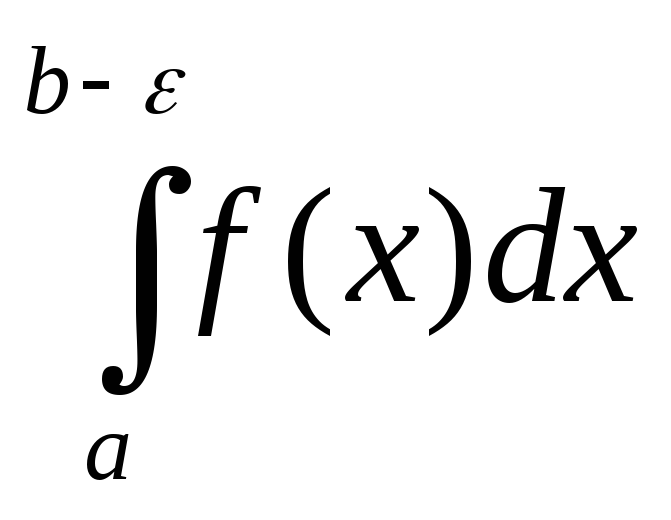 =
=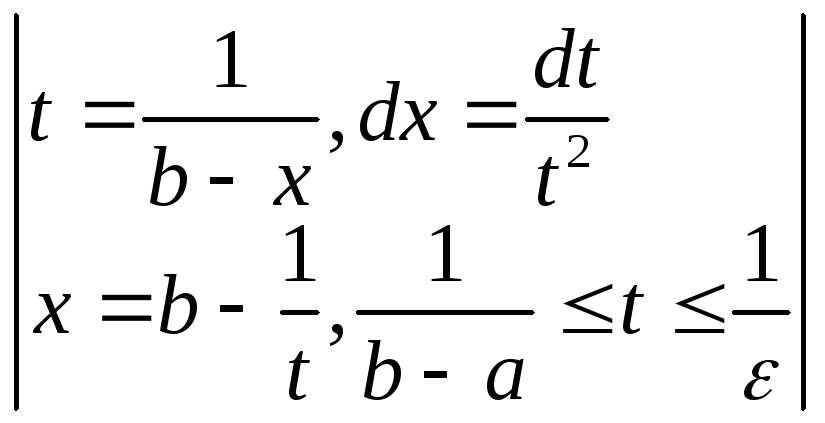 =
=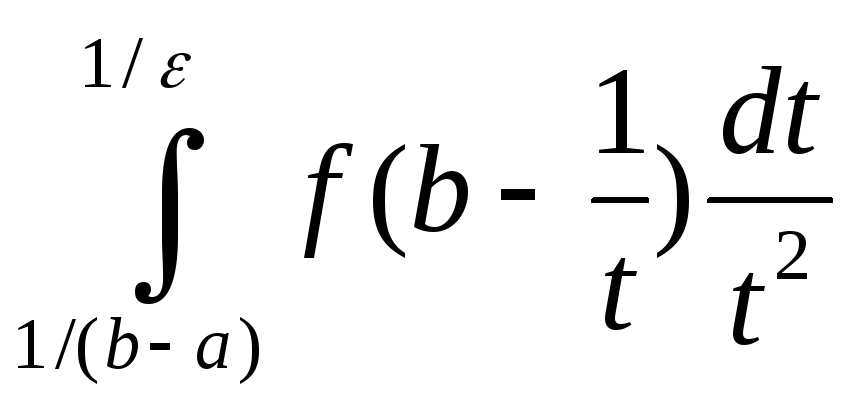 .(4)
.(4)Перейдем в (4) к пределу при ε→+0. Получим
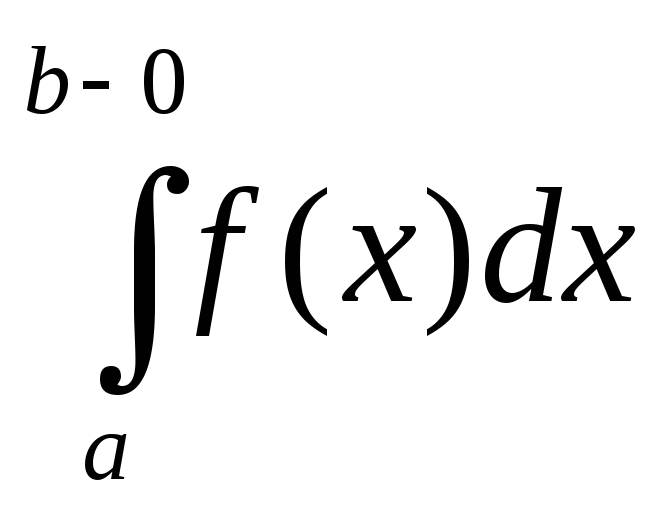 =
=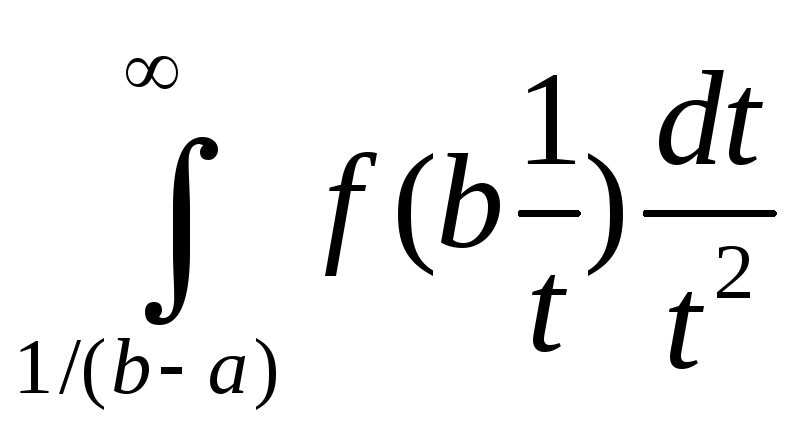 .(5)
.(5)
Таким образом данная замена переводит несобственный интеграл 2-го рода в несобсвенный интеграл 1-го рода. Ясно, что если интеграл в левой части (5) существует, то существует и интеграл в правой части (5), и наоборот. Все признаки сходимости, доказанные для несобственного интеграла 1-го рода, справедливы (с нек. исправлениями) и для интеграла 2-го рода. Правила интегрирования также остаются прежними.
Пример 2. Вычислить несобственный интеграл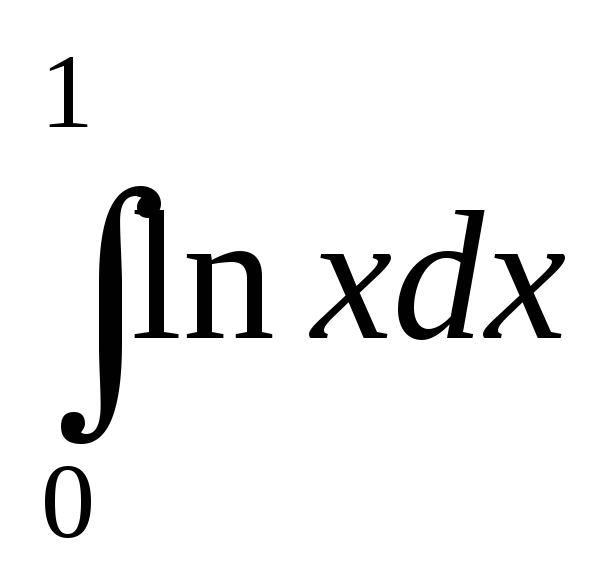 .
.Согласно
(2) имеем 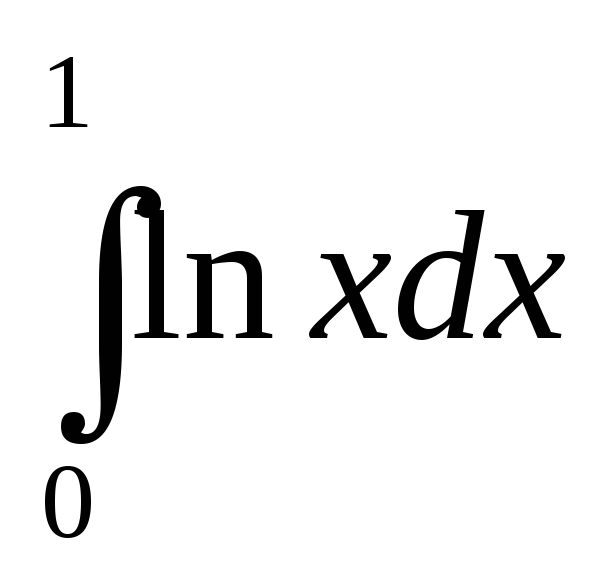 =
=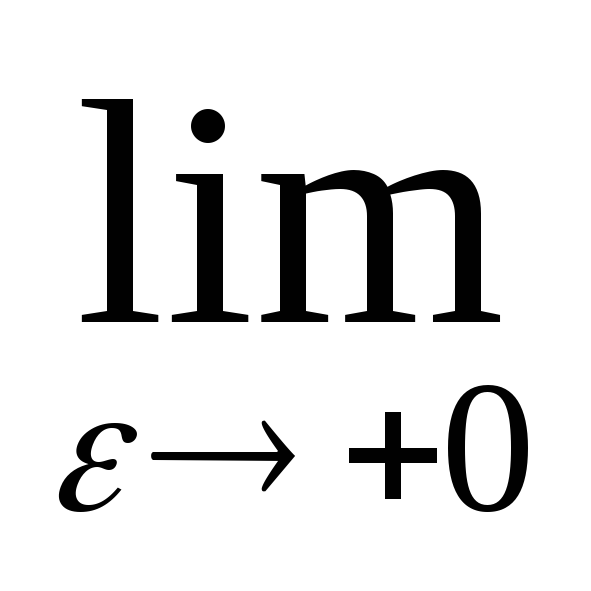
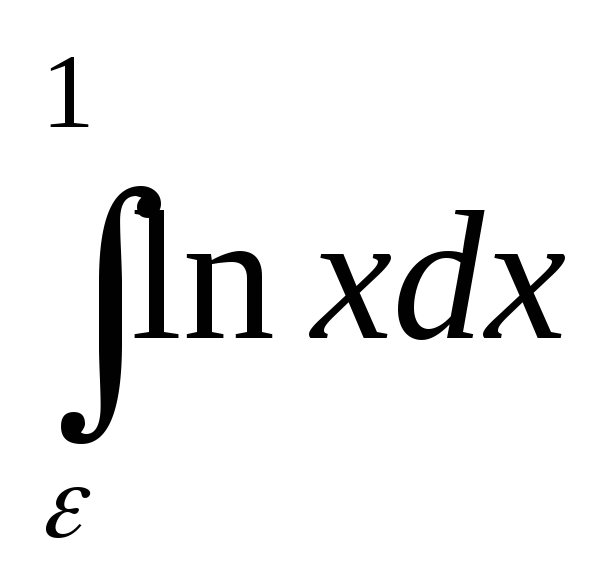 =
=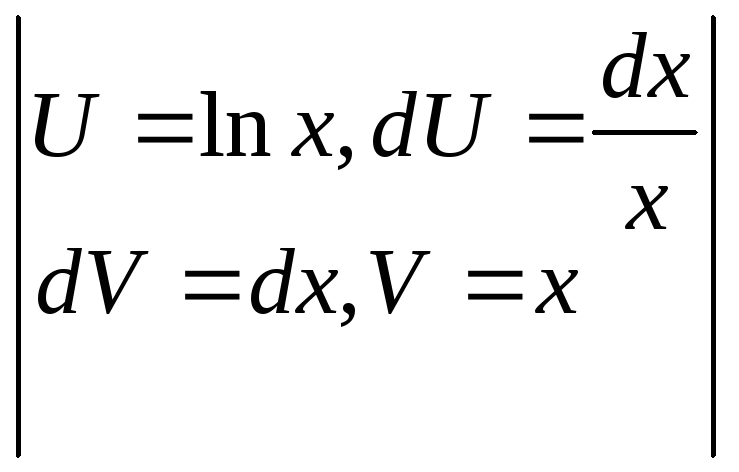 =
=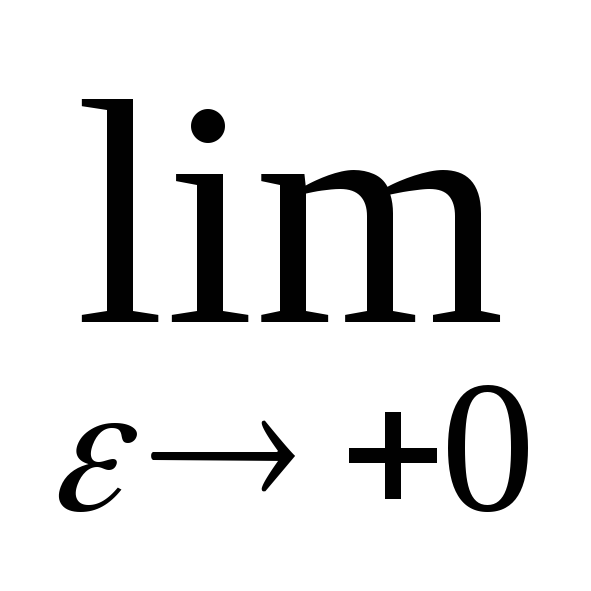 (xlnx-x)
(xlnx-x) 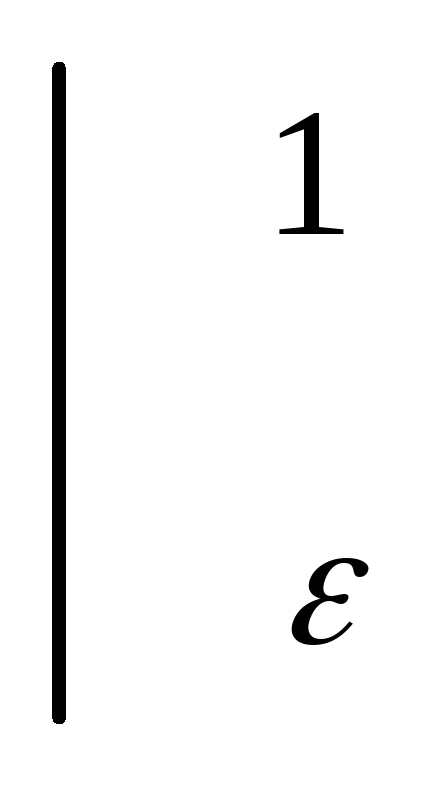 =
=
=
=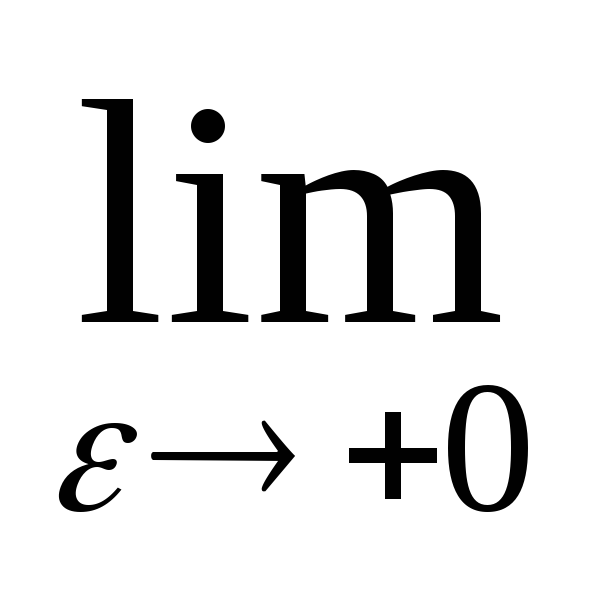 (-1-εlnε+ε)=-1-
(-1-εlnε+ε)=-1-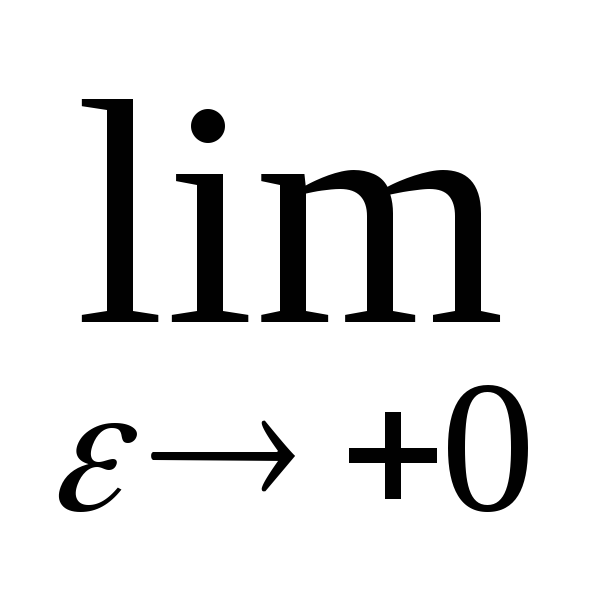
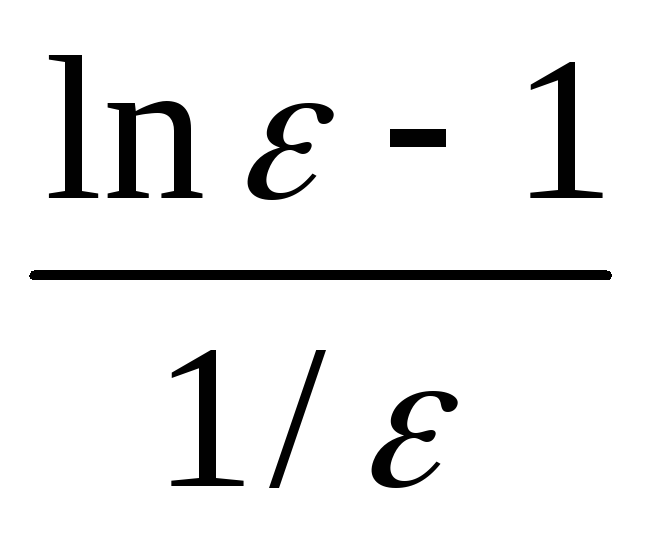
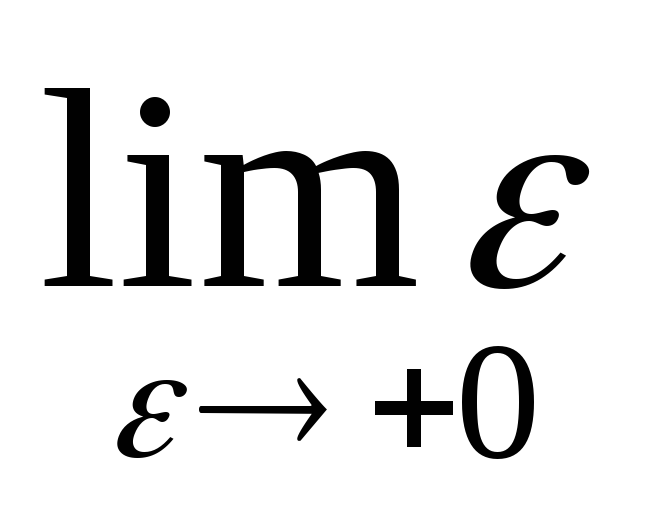 =-1.
=-1.Пример
3. Исследовать
на сходимость интеграл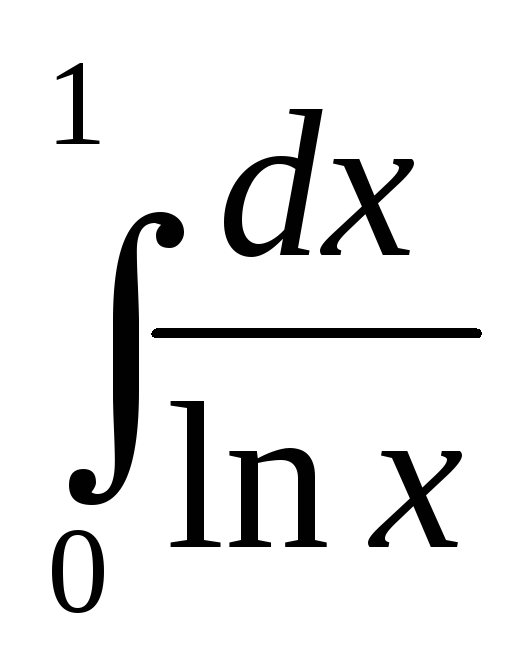 .
.
Доопределим
подыинтегральную ф-ю в точке x=0,
т.е. положим 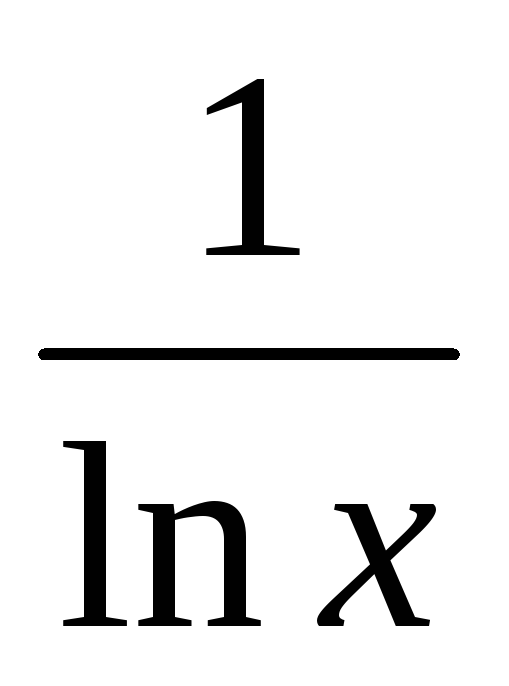
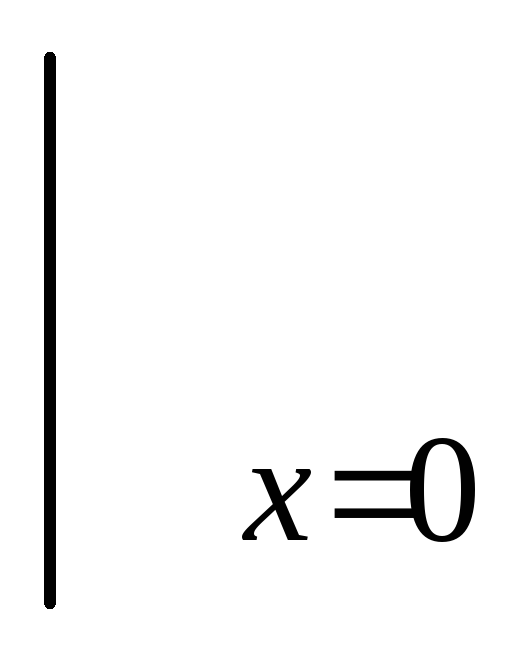 =0.
Особой точкой являетсяx=1.
Найдем предел
=0.
Особой точкой являетсяx=1.
Найдем предел 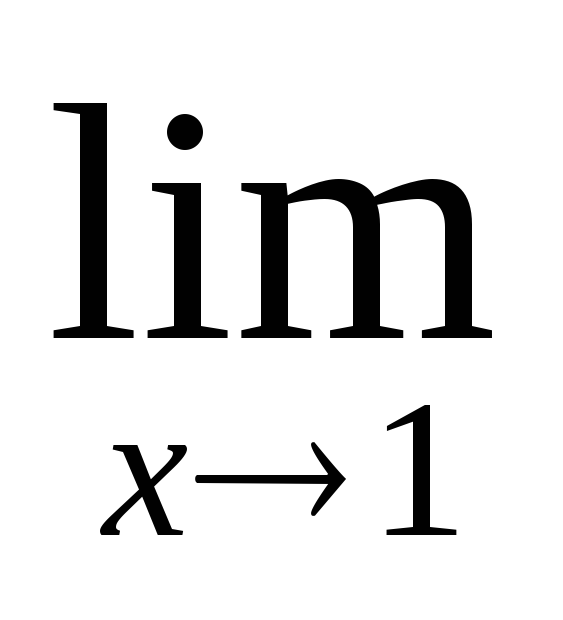
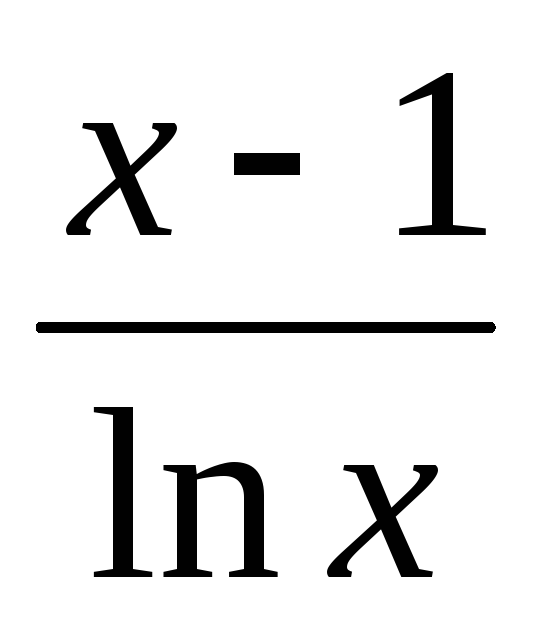 =
=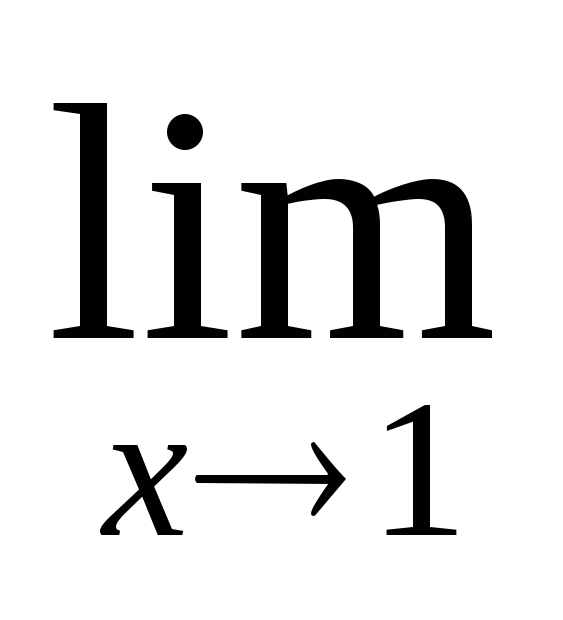 x=1.
Это означает эквивалентность функций
в точке x=1,
т.е.
x=1.
Это означает эквивалентность функций
в точке x=1,
т.е.  ~
~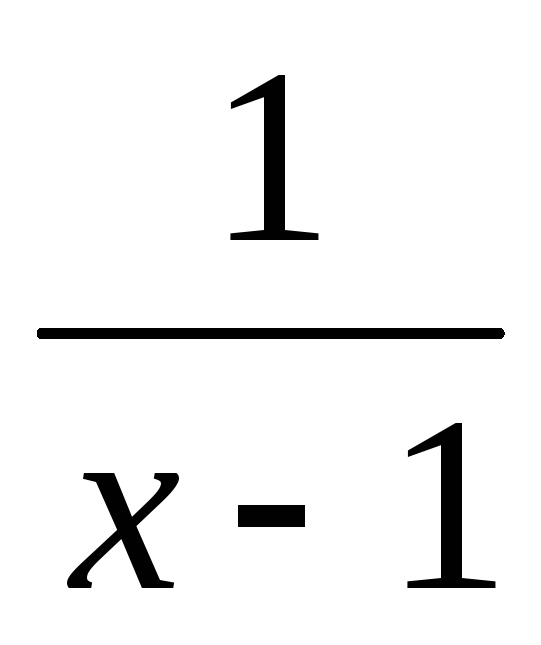 приx→1.
Согласно предельному признаку сравнения
интеграла
приx→1.
Согласно предельному признаку сравнения
интеграла 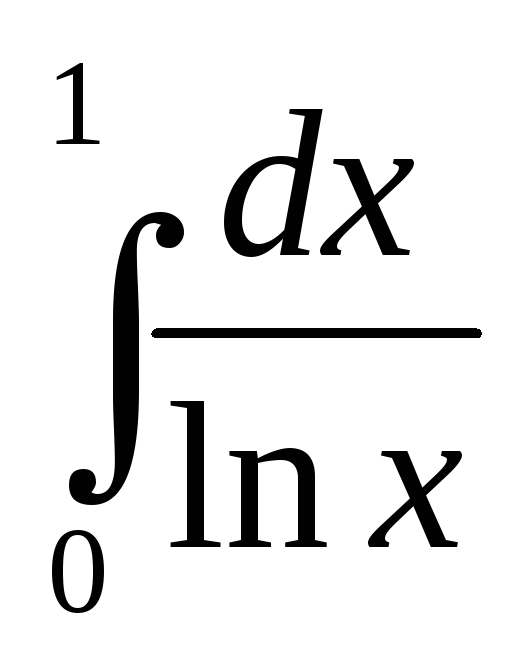 и
и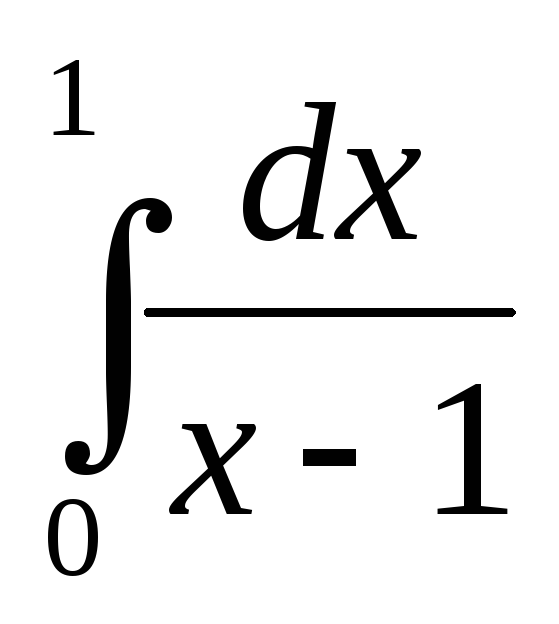 ведут себя одинаково. Но интеграл
ведут себя одинаково. Но интеграл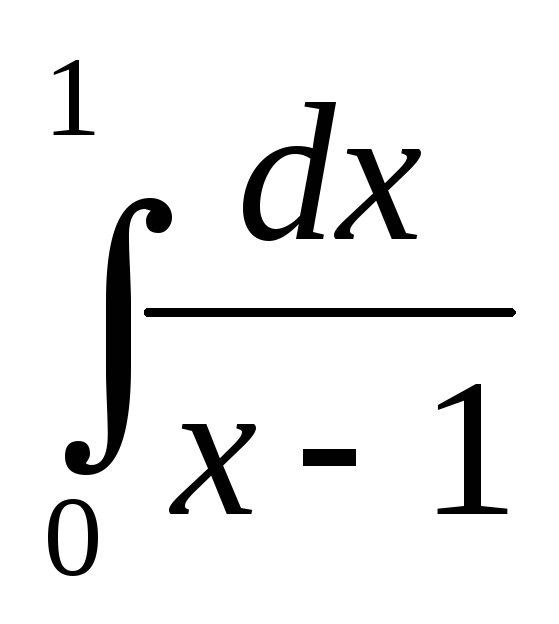 расходится (см. пр. 1), => и данный интеграл
расходится.
расходится (см. пр. 1), => и данный интеграл
расходится.
П 18. Главное значение несобственного интеграла.
Пусть ф-я f(x) определена на всей числовой оси и интегрируема на любом конечном отрезке числовой оси. Тогда
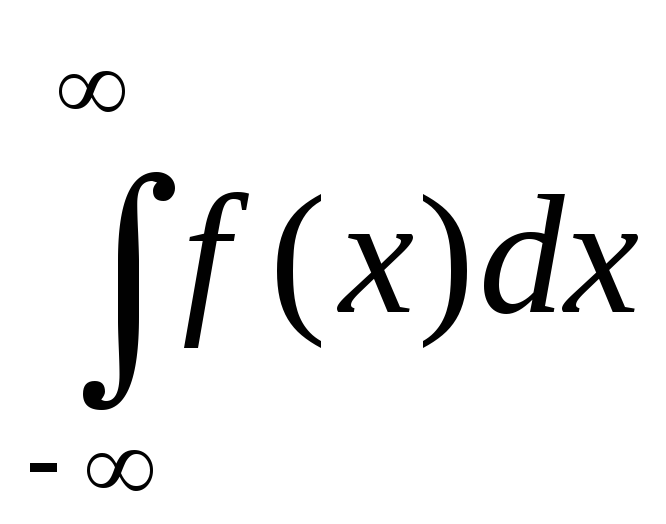 =
=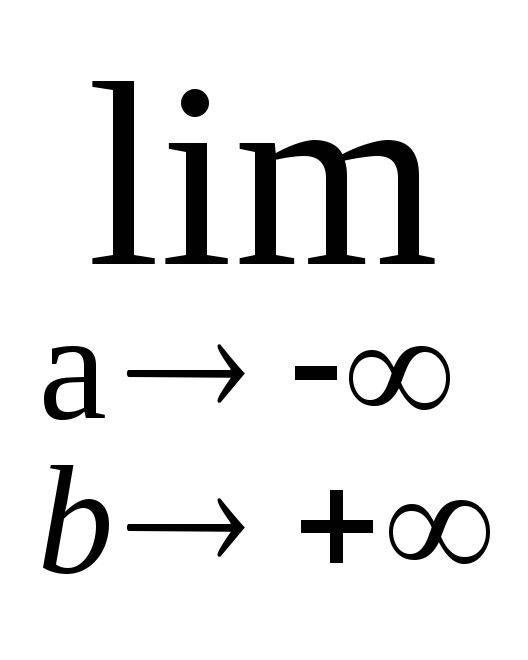 (1) –
(1) –
несобственный
интеграл 1-го рода. Напомним, что a
и b
стремятся к ∞ независимо друг от друга.
Положим теперь b=-a.
Если существует предел 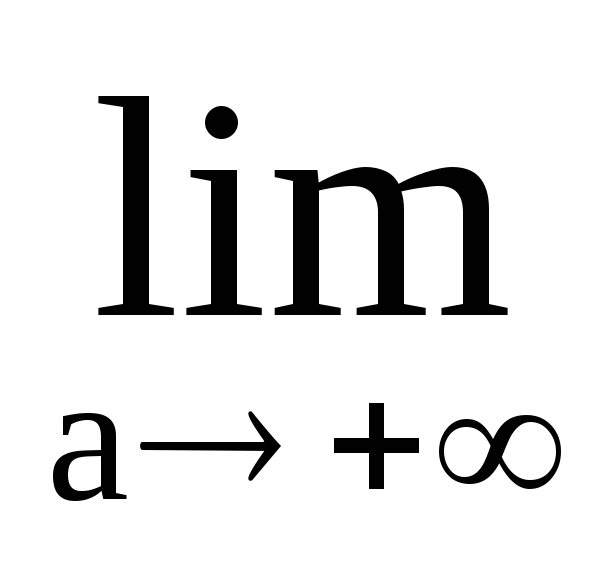
 ,
то говорят, что несобственный интеграл
сходится по Коши, а его значение называют
главным значением несобственного
интеграла по Коши и обозначают
,
то говорят, что несобственный интеграл
сходится по Коши, а его значение называют
главным значением несобственного
интеграла по Коши и обозначают
V.P.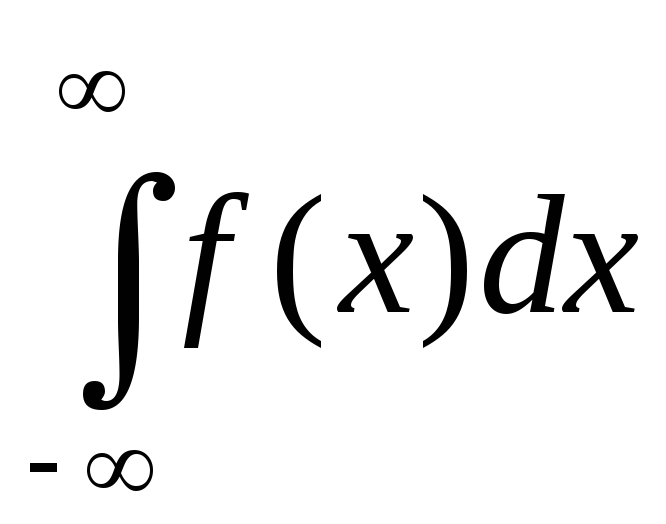 =
=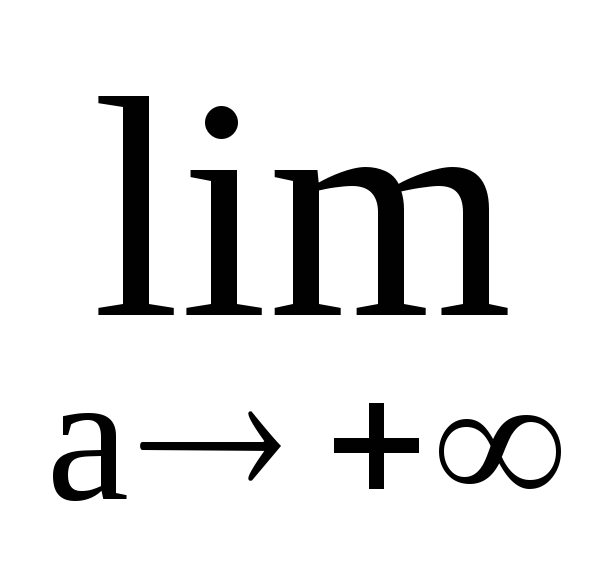
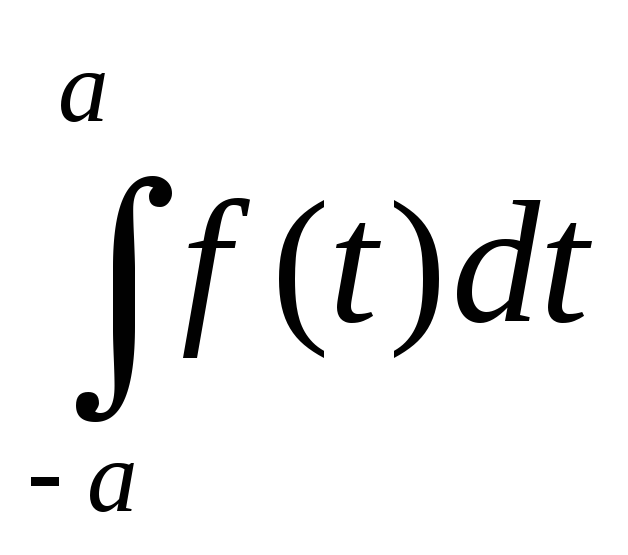 .(2)
.(2)
Ясно, что если интеграл (1) сходится, то он сходится к этому же значению по Коши. Однако интеграл (1) может расходится, но иметь главное значение по Коши.
Пример
1. 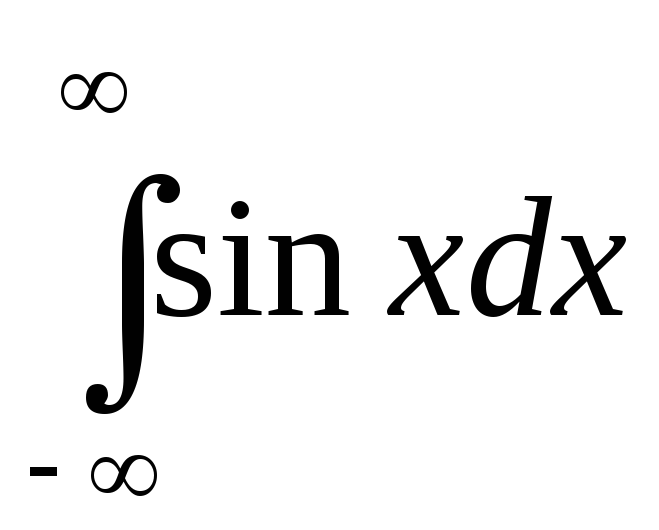 — расходится (см. пр.2 §9). Найдем его
главное значение.
— расходится (см. пр.2 §9). Найдем его
главное значение.
V.P.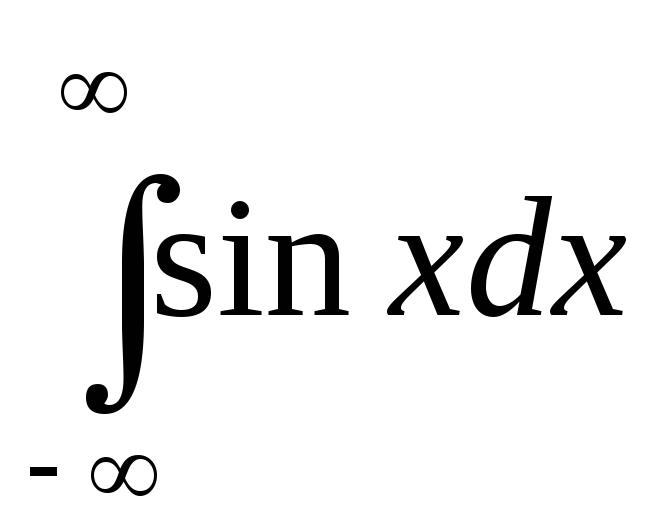 =
=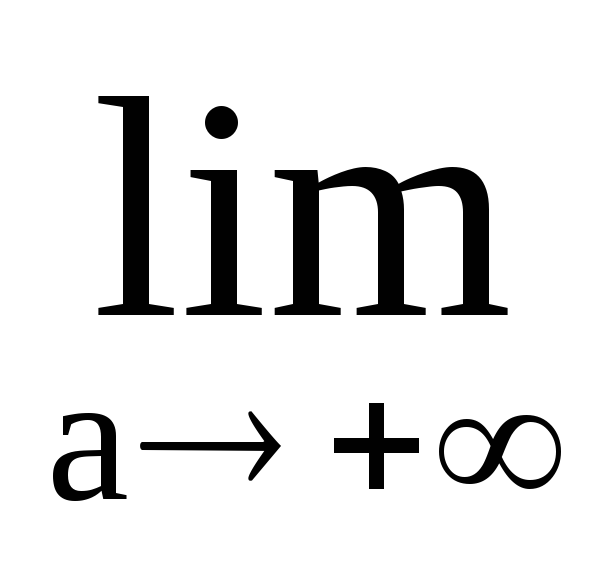
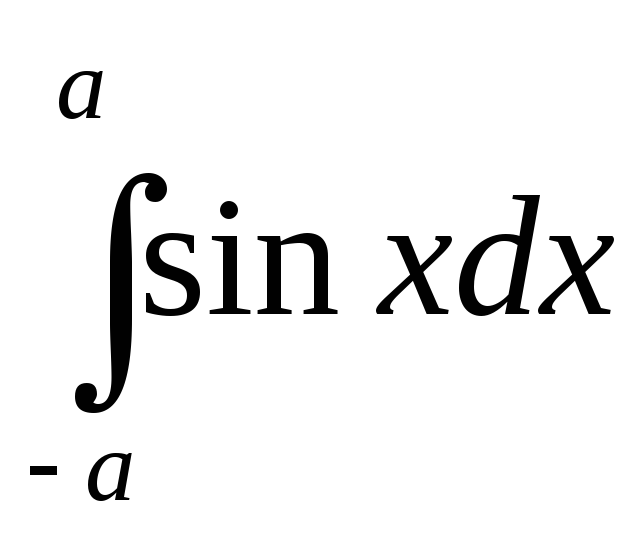 =-
=-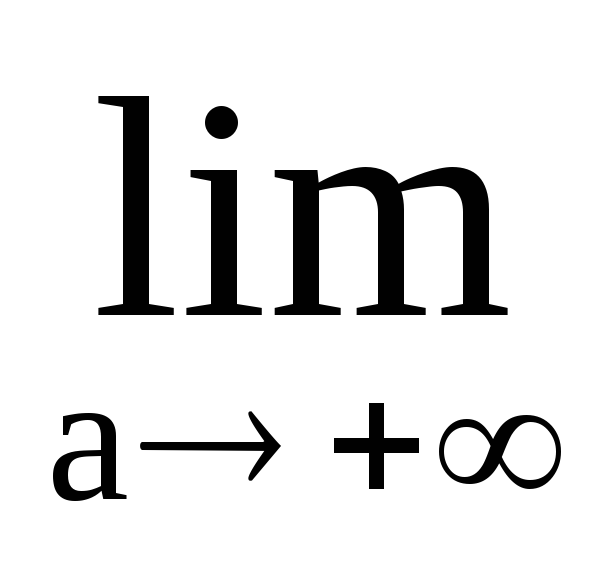 (cosa-cos(-a))=0.
(cosa-cos(-a))=0.
Теорема 1. Если ф-я f(x) нечетная и интегрируема по Риману на любом конечном отрезке, то ее главное значение равно нулю.
Док-во. 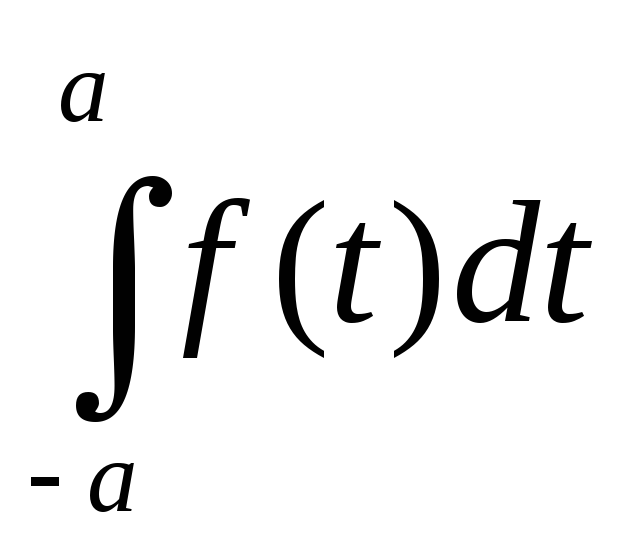 =
=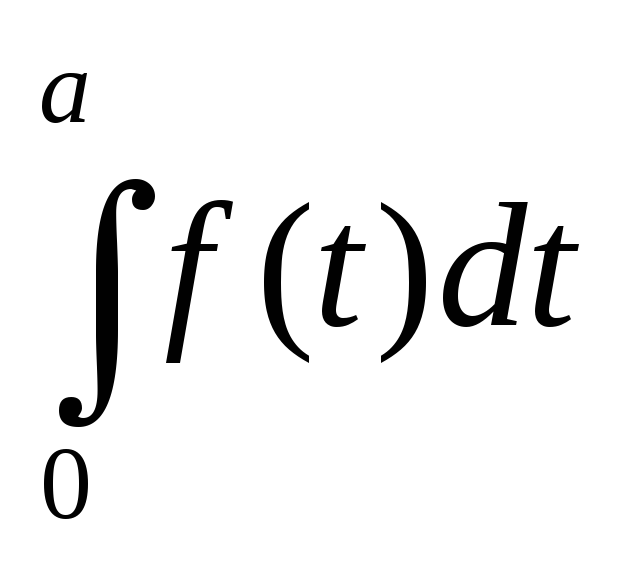 +
+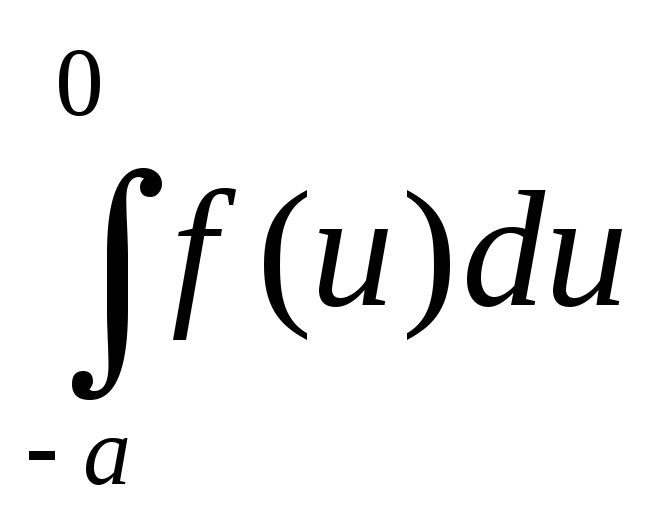 =
=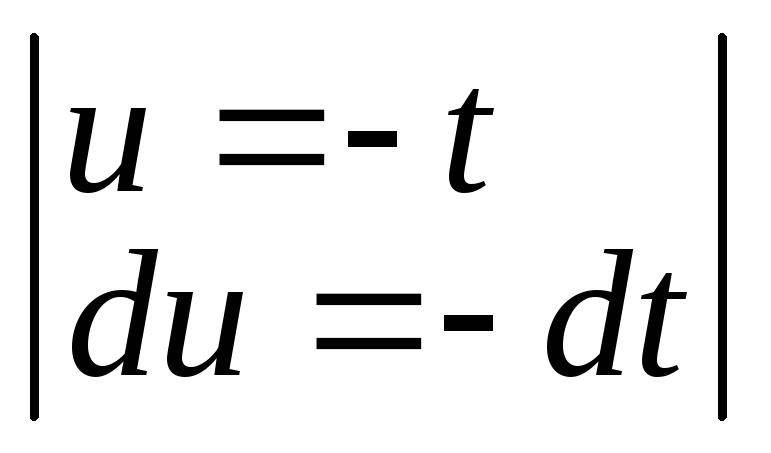 =
=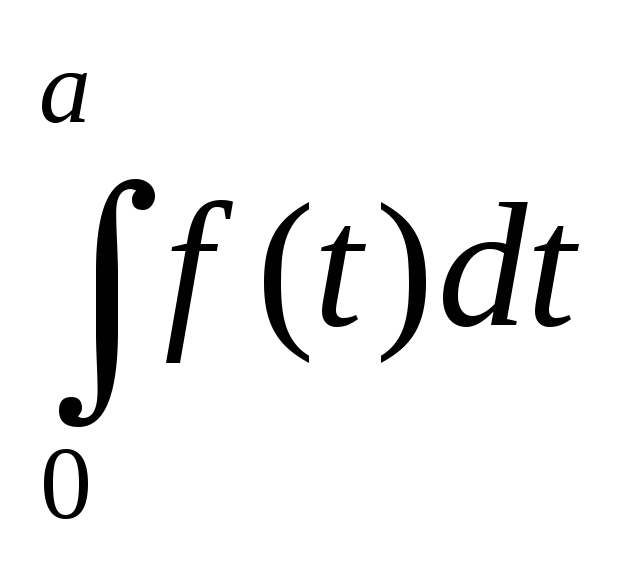 —
—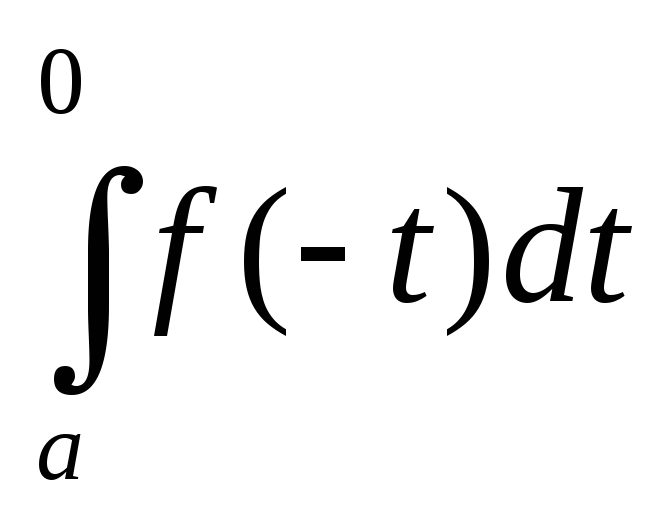 =
=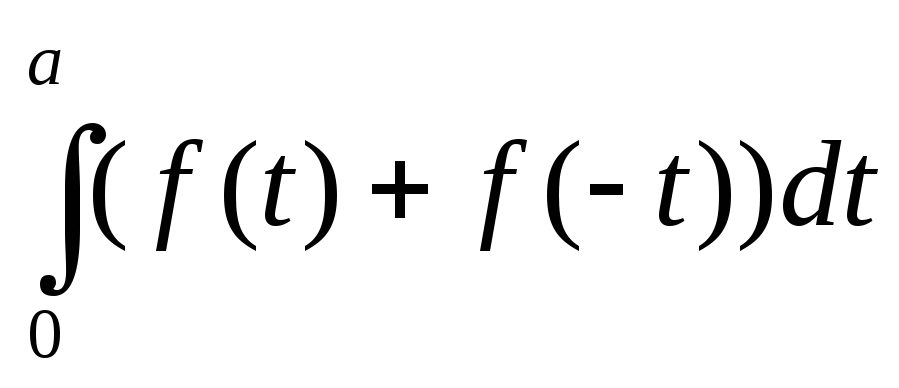 =0,
т.к.f(t)
нечетная V.P.
=0,
т.к.f(t)
нечетная V.P.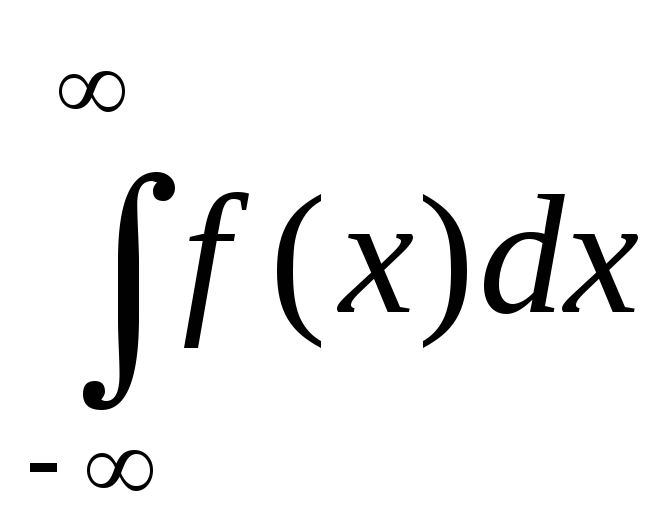 =
=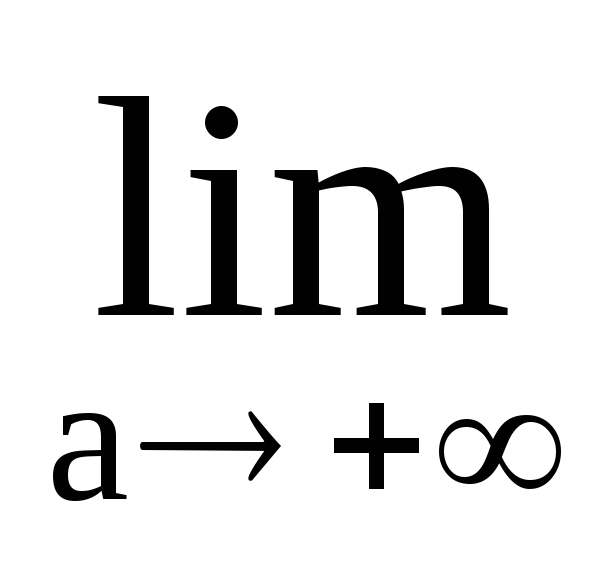
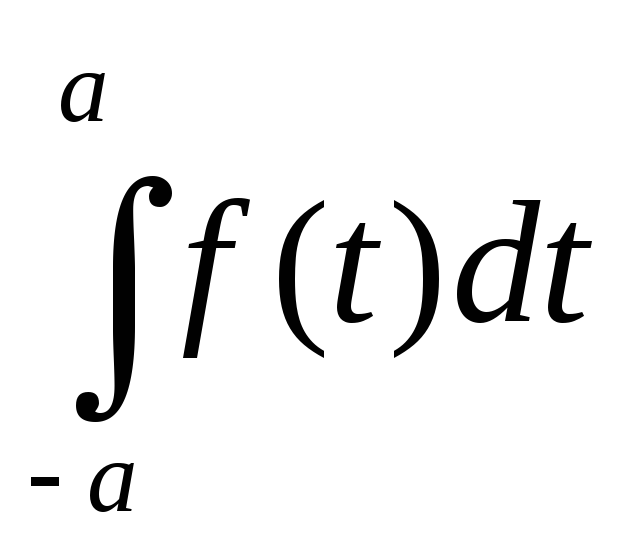 =0.
Теорема доказана.
=0.
Теорема доказана.
Если любая особая точка c внутренняя для отрезка [a, b], то главное значение интеграла по Коши можно ввести и для несобственного интеграла 2-го рода.
V.P.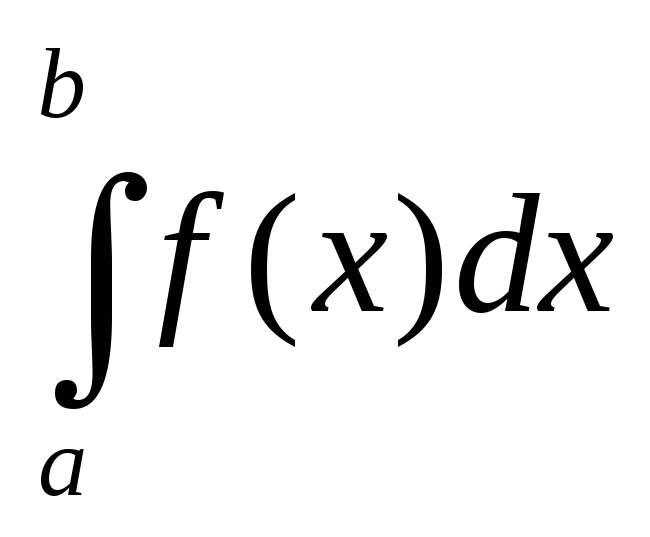 =
=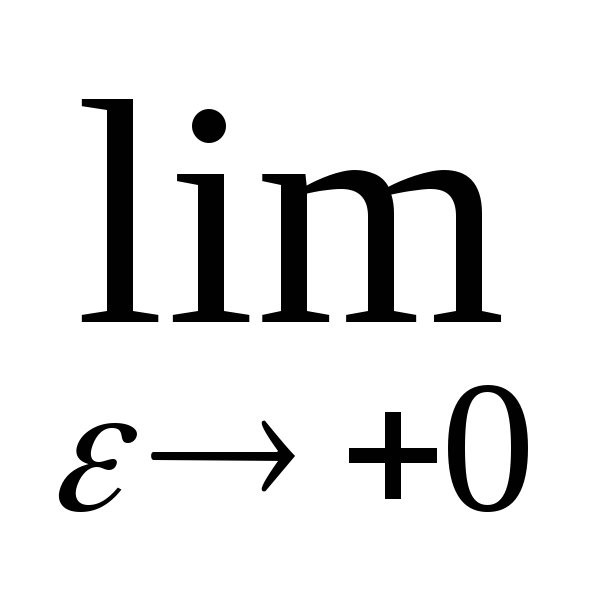 (
(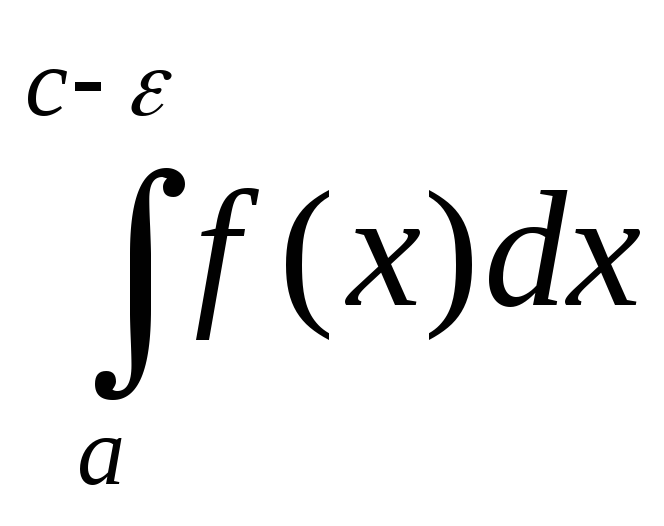 +
+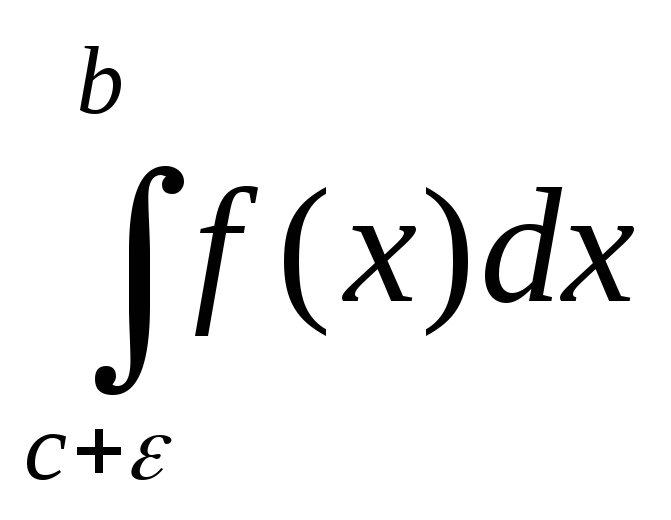 ).(3)
).(3)
Пример
2. Интеграл 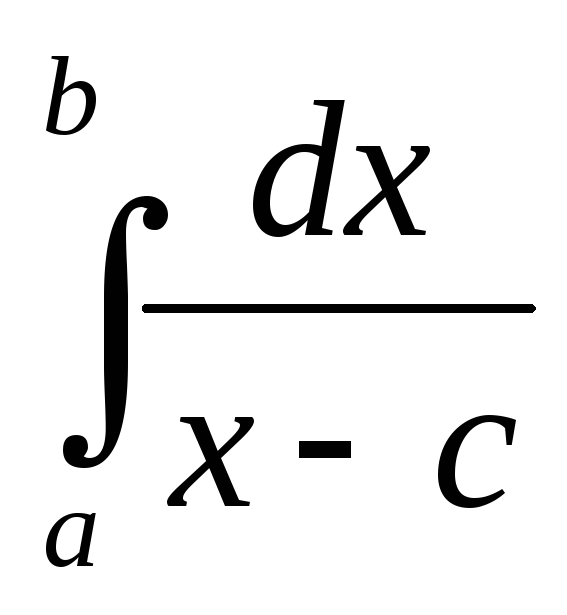 ,a<c<b
расходится (см. пр.1 §12). Найдем его главное
значение.
V.P.
,a<c<b
расходится (см. пр.1 §12). Найдем его главное
значение.
V.P.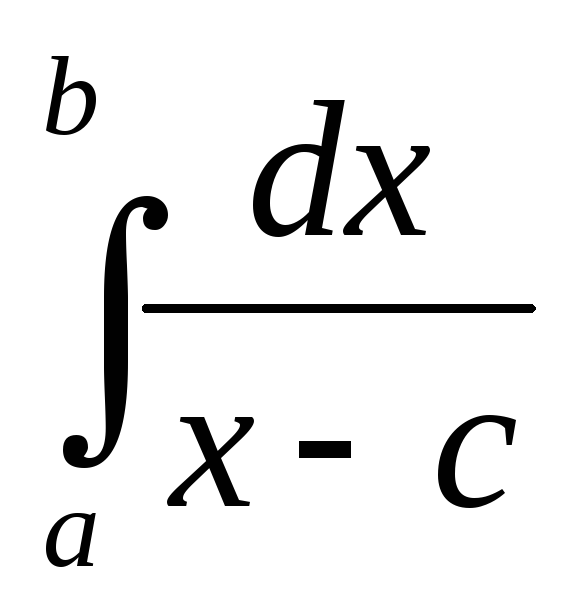 =
=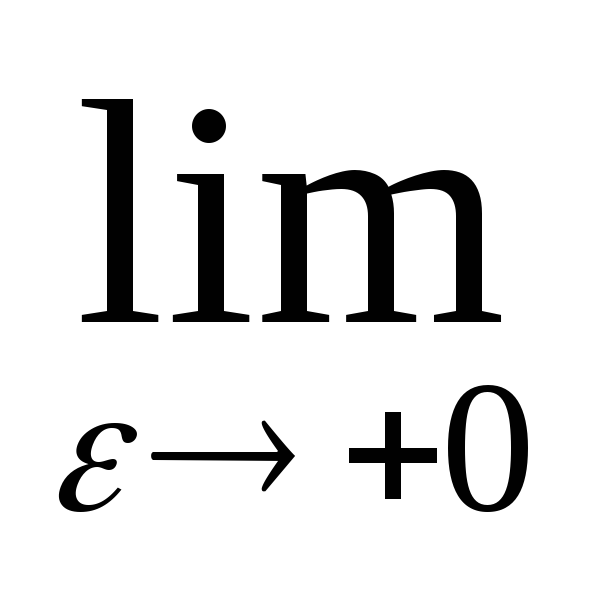 (
(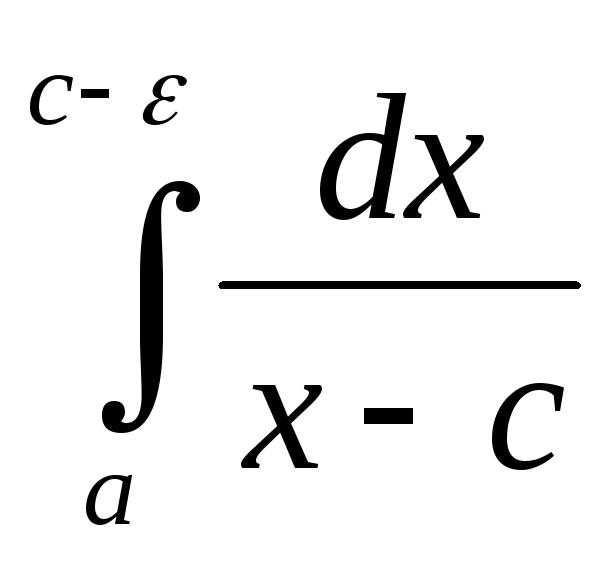 +
+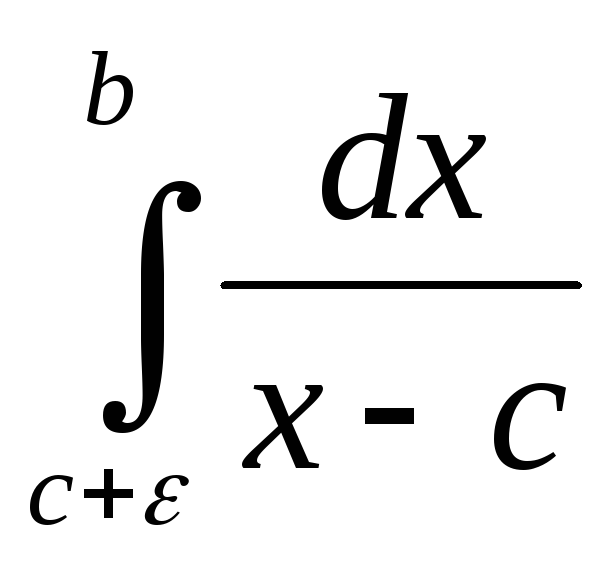 )=
)=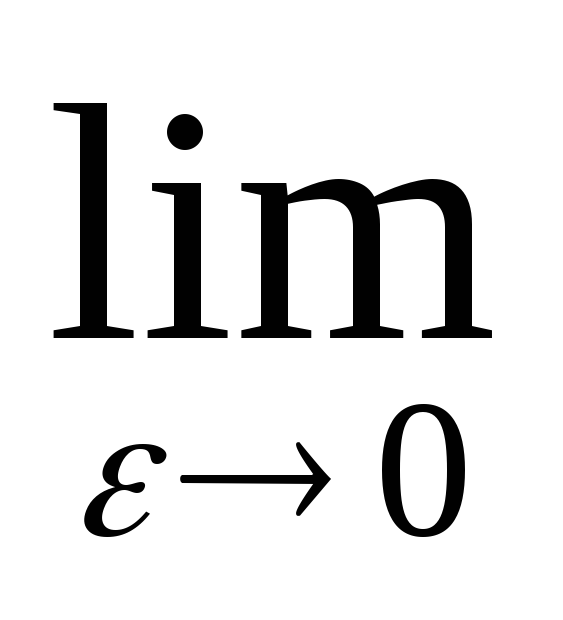 (ln|x-c|
(ln|x-c| +ln|x-c|
+ln|x-c|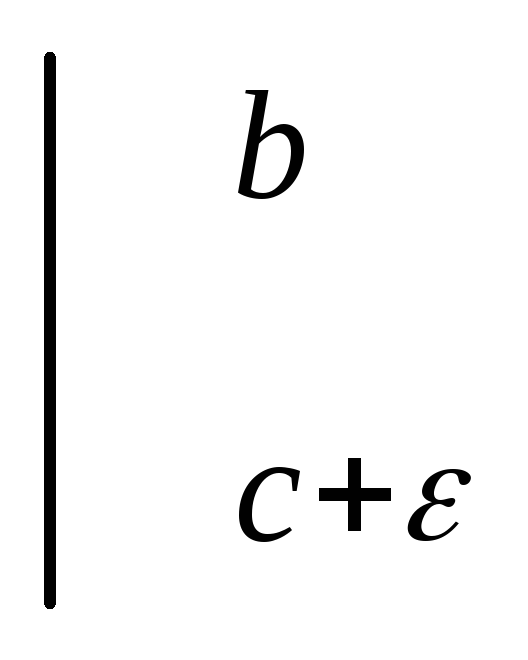 )=
)=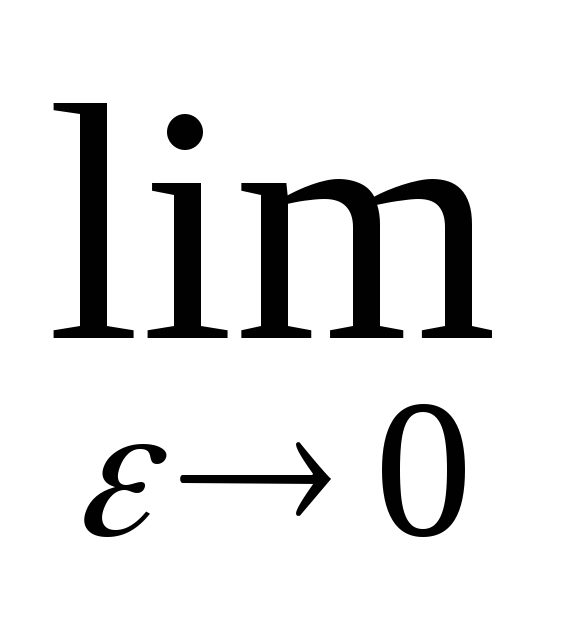 (lnε-ln|a-c|+ln(b-c)-lnε)=
(lnε-ln|a-c|+ln(b-c)-lnε)= 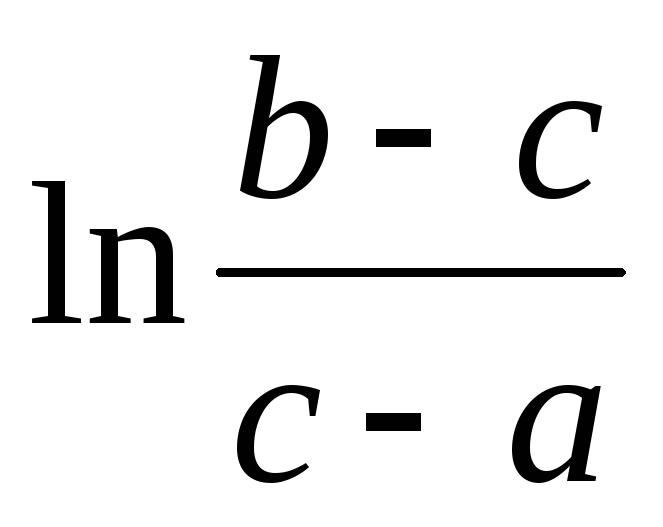 .
.
Пример
3. Интеграл 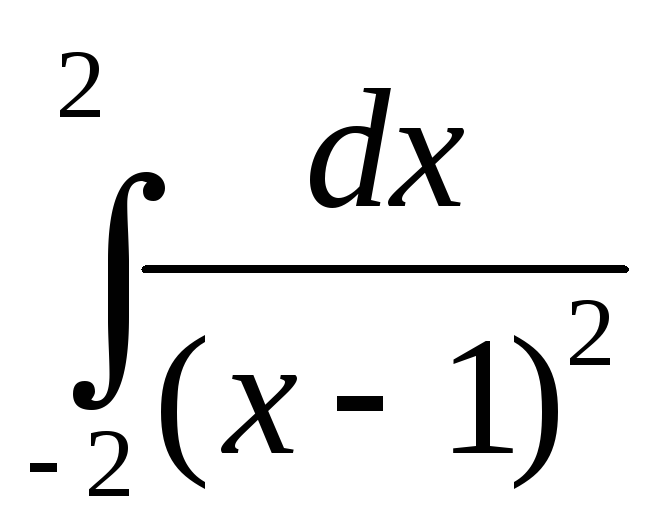 расходится. Найдем его главное значение.V.P.
расходится. Найдем его главное значение.V.P.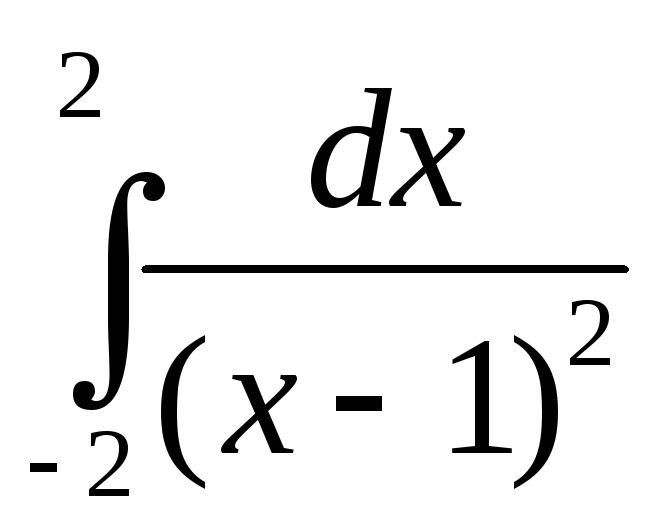 =
= 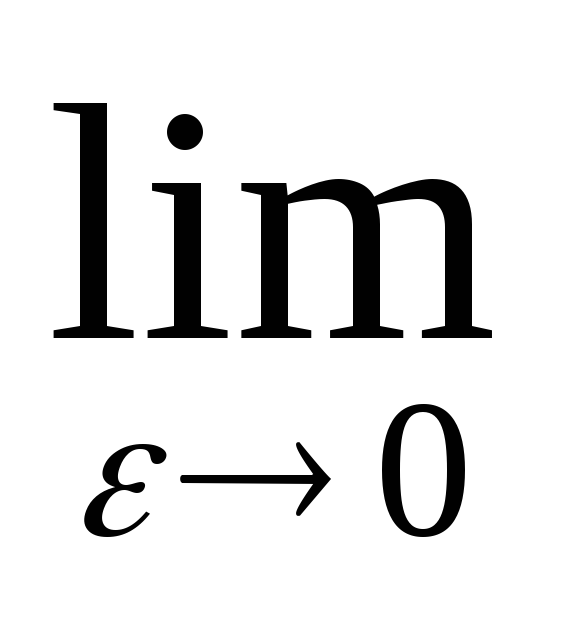 (
(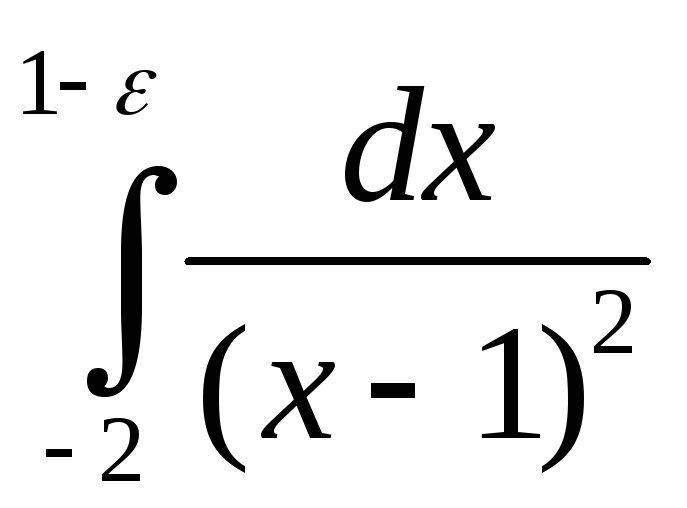 +
+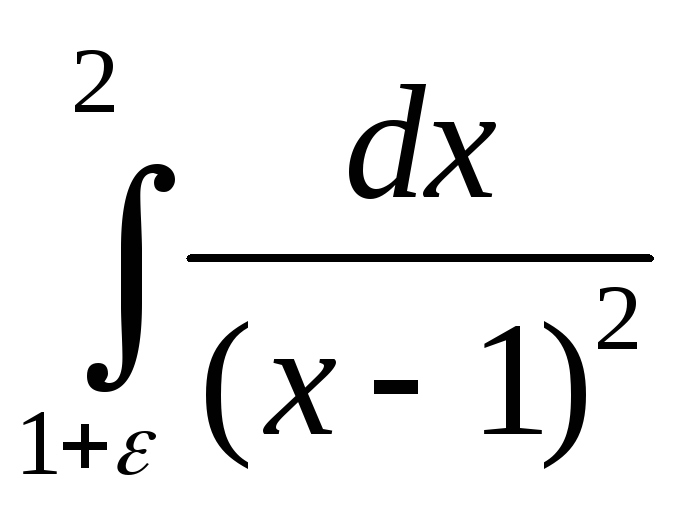 )=-
)=-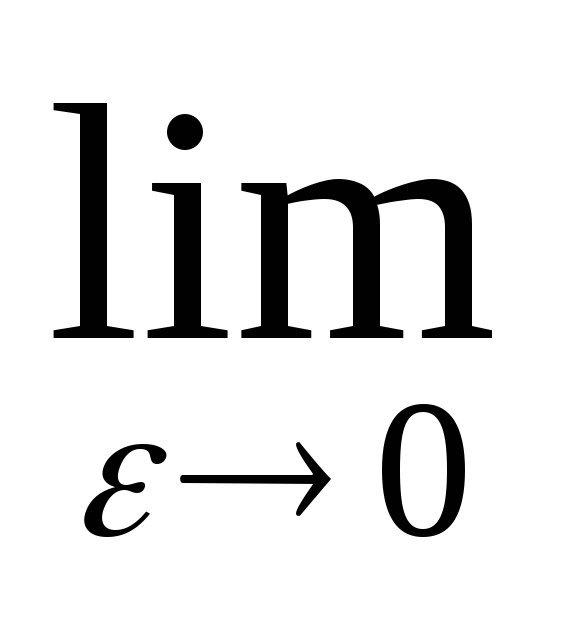 (
(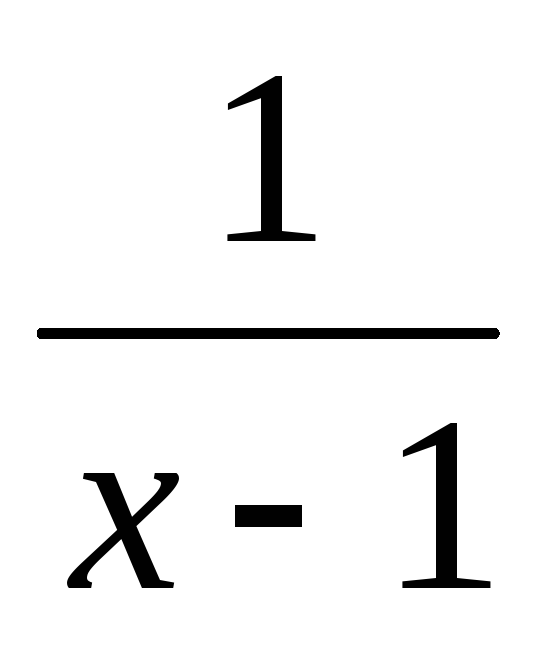
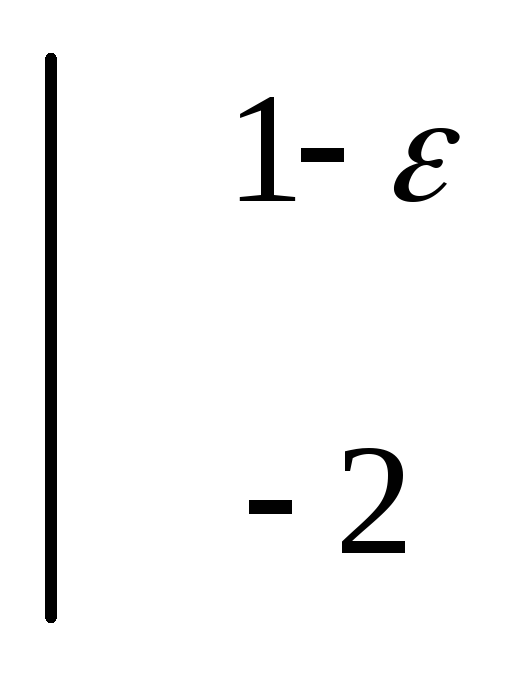 +
+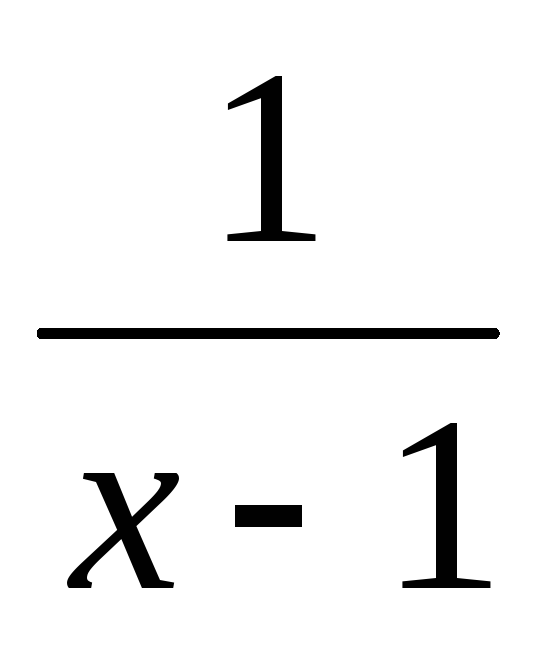
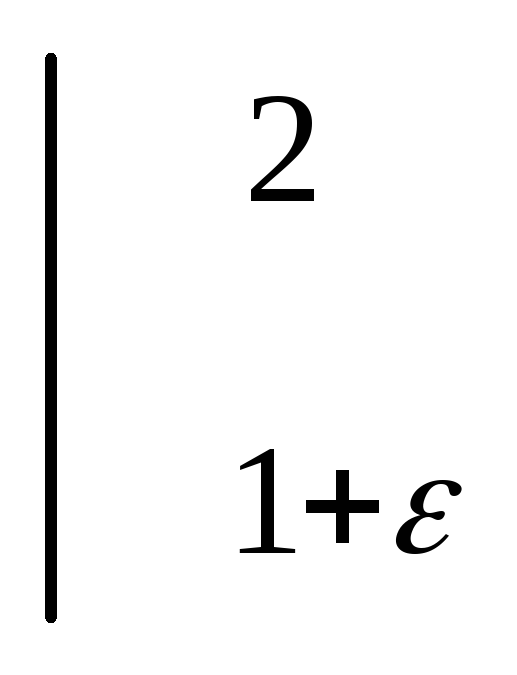 )=-
)=-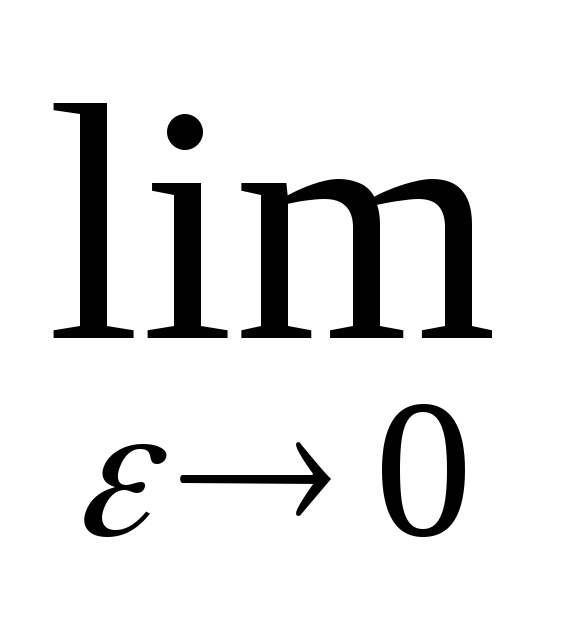 (-
(-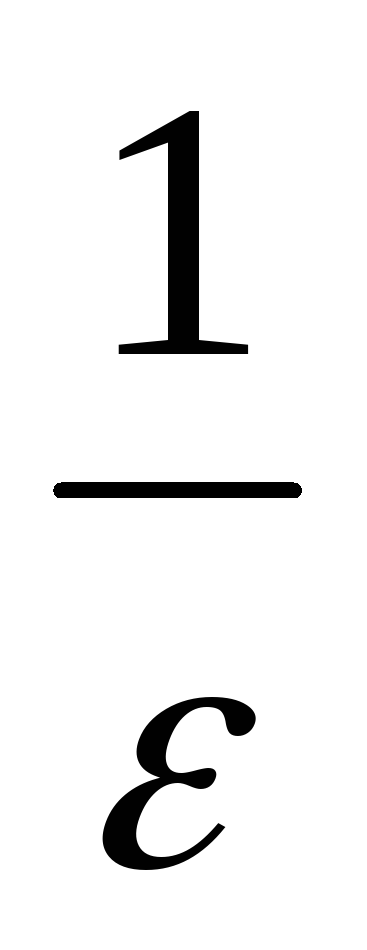 +
+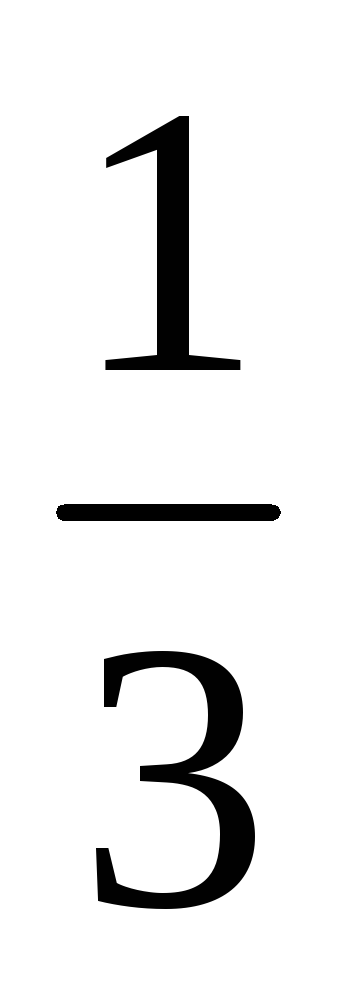 +1-
+1-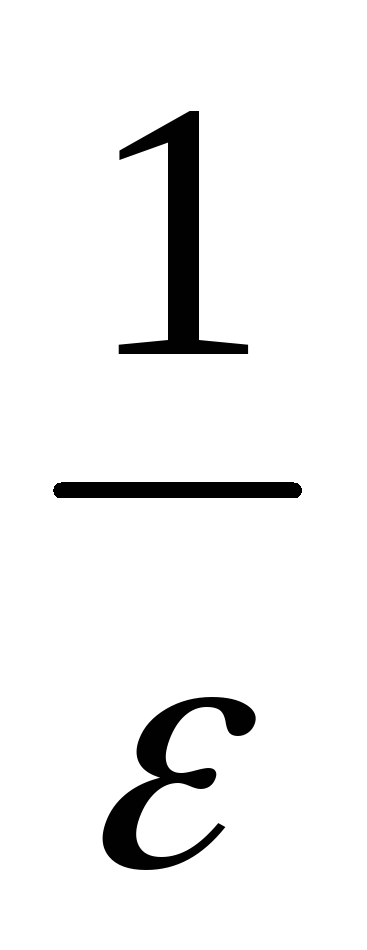 )=-∞.
Главное значение данного интеграла не
существует.
)=-∞.
Главное значение данного интеграла не
существует.
23
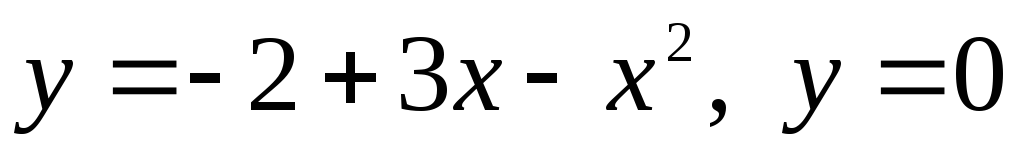 .
.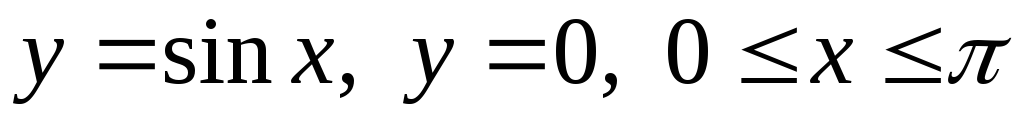 .
.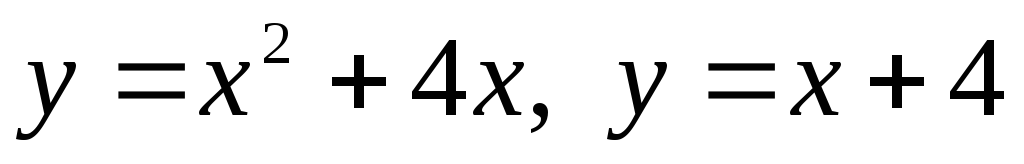 .
.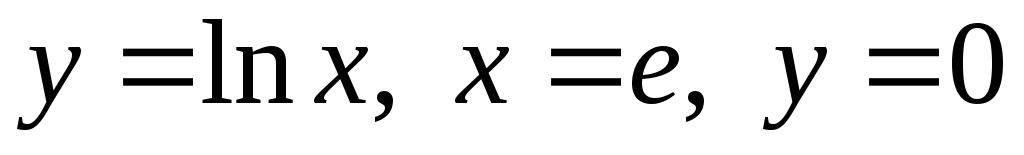 .
.