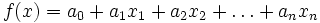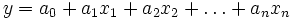Нули функции | Алгебра
Что такое нули функции? Как определить нули функции аналитически и по графику?
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
1) Найти нули линейной функции y=3x+15.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
3)Найти нули функции
Решение:
Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)
x ∈ (-∞; -1)U(-1; 1)U(1;∞).
Решаем уравнение
Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.
Ответ: x=-4.
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Если график не пересекает ось Ox, функция не имеет нулей.
Например,
функция, график которой изображен на рисунке,имеет четыре нуля —
В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.
www.algebraclass.ru
Линейная функция, ее свойства и график
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k>0, то график наклонен вправо. Причем, чем больше значение k, тем круче идет прямая.
если kКоэффициент b отвечает за сдвиг графика вдоль оси OY:
если b>0, то график функции y = kx + b получается из графика функции y = kx сдвигом на b единиц вверх вдоль оси OY
если b
Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) ky = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b
Подведем итоги в виде таблицы:
spishy-u-antoshki.ru
Математика. Нули функции + примеры + инструкция
Нули функции — это значения аргумента, при которых функция равна нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
Инструкция
1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк. 2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x).
3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений. 4. Рассматривая функцию с выражением под корнем четной степени, примите за область определения все доводы х, значения которых не обращают подкоренное выражение в негативное число (напротив функция не имеет смысла). Уточните, попадают ли обнаруженные нули функции в определенную область допустимых значений х. 5. Знаменатель дроби не может обращаться в нуль, следственно исключите те доводы х, которые приводят к такому итогу. Для логарифмических величин следует рассматривать лишь те значения довода, при которых само выражение огромнее нуля. Нули функции, обращающие подлогарифмическое выражение в нуль либо негативное число, обязаны быть отброшены из финального итога.Нулями функции называются значение абсциссы, при котором значение функции равно нулю.
Если функция задана своим уравнением, то нулями функции будут решения уравнения . Если задан график функции , то нули функции — это значения , в которых график пересекает ось абсцисс.
Примеры нахождения нулей функции
ПРИМЕР 1
multiurok.ru
2. Свойства линейной функции и
Напоминание:
Определение. Линейной
называется функция вида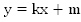 ,
где
,
где
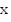 —
независимая переменная,
аргумент;
—
независимая переменная,
аргумент;
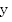 —
зависимая переменная,
функция;
—
зависимая переменная,
функция;
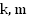 —
константы.
—
константы.
Примеры.
а.  ,
(естественная область
определения).
,
(естественная область
определения).
б. 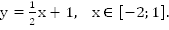
3. Анализ свойств конкретных линейных функций
а.
Функция  (см.
Рис.1).
(см.
Рис.1).
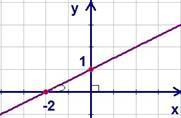
Рис.
1. График функции 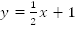
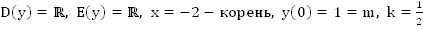 .
.
 .
.
 .
.
Монотонно возрастает, непрерывна, не ограничена.
График иллюстрирует свойства.
б.
Функция 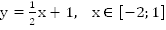 (см.
Рис.2).
(см.
Рис.2).
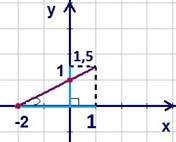
Рис.
2. График функции 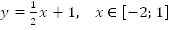
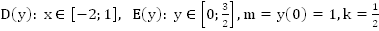 .
.
Монотонно возрастает, непрерывна, ограничена.
График иллюстрирует свойства.
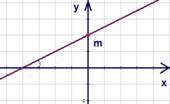
Задача на определение знаков
По
графику функции определить
знаки  и
и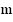 .
.
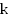 –
угловой
коэффициент;
–
угловой
коэффициент; 
 .
. 
Ответ: 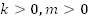 .
.
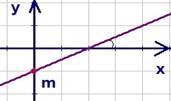
Ответ:  .
.
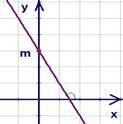
Ответ:  .
.
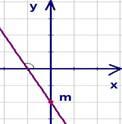
Ответ:  .
.
Задача о нахождении уравнения прямой, проходящей через две заданные точки
Найти
уравнение прямой 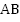 ,
если
,
если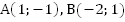 .
.
Решение. График прямой на Рис. 4.
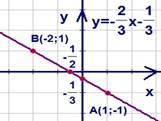
Рис.
4. График функции 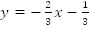 .
.

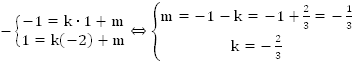 .
.
Ответ: 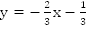 .
.
Взаимное расположение прямых
(1)  и
и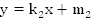 (2).
(2).
1. 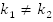 (прямые
пересекаются) (см. Рис. 5).
(прямые
пересекаются) (см. Рис. 5).
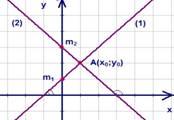
Рис. 5.
2. 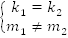 (прямые
параллельны) (см. Рис. 6)
(прямые
параллельны) (см. Рис. 6)
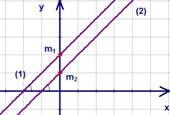
Рис. 6.
3. 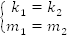 (прямые
совпадают) (см. Рис. 7)
(прямые
совпадают) (см. Рис. 7)

Рис. 7.
8. Определение числа решений системы
Определить число решений системы.
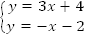
Ответ: одно решение
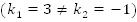
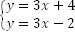
Ответ: решений нет
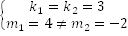
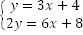
Ответ: бесчисленное множество решений
9. Свойства линейной функции
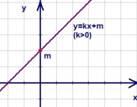
Рис.
8. График функции 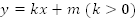
Рис.
9. График функции 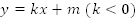
1. 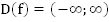 ;
;
2.
Возрастает, если 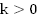 ;
убывает, если
;
убывает, если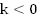 ;
;
3. Не ограничена ни снизу, ни сверху;
4. Нет ни наибольшего, ни наименьшего значений;
5. Функция непрерывна;
6. 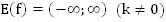 ;
;
7. О выпуклости говорить нет смысла.
10. Функция и её свойства
Графиком
функции 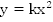 является
парабола с вершиной в
начале координат и с
ветвями, направленными
вверх (см. Рис. 10), если
является
парабола с вершиной в
начале координат и с
ветвями, направленными
вверх (см. Рис. 10), если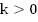 ,
и вниз (см. Рис. 11), если
,
и вниз (см. Рис. 11), если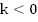 .
.
Свойства
функции  :
:
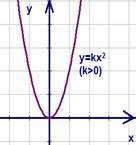
Рис.
10. График функции 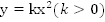
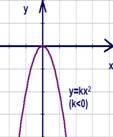
Рис.
11. График функции 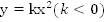
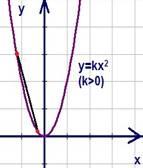
Рис.
12. График функции 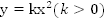
а.
для случая 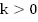 (см.
Рис. 12).
(см.
Рис. 12).
1. 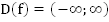 ;
;
2.
Убывает на 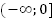 ;
возрастает на
;
возрастает на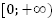 ;
;
3. Ограничена снизу, но не ограничена сверху;
4. 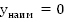 ,
,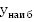 не
существует;
не
существует;
5. Непрерывна;
6. 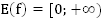 ;
;
7. Выпукла вниз.
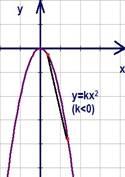
Рис.
13. График функции 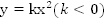
б.
для случая 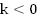 (см.
Рис. 13).
(см.
Рис. 13).
1.  ;
;
2.
Возрастает на луче 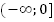 ;
убывает на луче
;
убывает на луче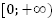 ;
;
3. Не ограничена снизу, но ограничена сверху;
4. 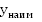 не
существует,
не
существует,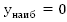 ;
;
5. Непрерывна;
6. 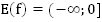 ;
;
7. Выпукла вверх.
11. Задача
Доказать
возрастание функции 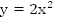 при
при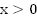 .
.
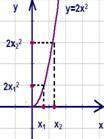
Рис.
14. График функции 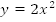
Доказательство. Так
как 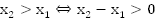 ,
то есть
,
то есть
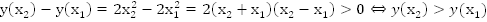 для
всех
для
всех 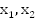 из
множества
из
множества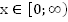 .
.
Степенная функция с четным показателем степени её свойства и график
Мы
уже знакомы с функцией Теперь
познакомимся состепенной
функцией вида 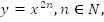 изучим
свойства и графики таких
функций.
изучим
свойства и графики таких
функций.
Изучение свойств функции
Рассмотрим
функцию 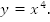
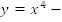 четная
функция,
четная
функция, 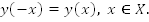
График симметричен относительно оси y.
Рассмотрим
график функции 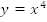 при
при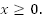 Построим
график по таблице значений
функции (Рис. 1).
Построим
график по таблице значений
функции (Рис. 1).
x | 0 | 1 | | 2 |
|
y | 0 | 1 | | 16 | |

Симметрично
отобразим график относительно
оси y,
и получим график функции
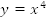 (Рис.
2).
(Рис.
2).
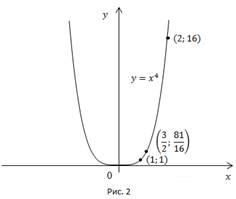
Прочтем полученный график.
1. 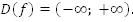
2. Функция четная.
3.
Убывает при 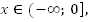 возрастает
при
возрастает
при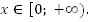
4. Функция ограничена снизу и не ограничена сверху.
5. 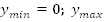 не
существует.
не
существует.
6. Функция непрерывна.
7.
Область значений: 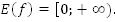
8. Функция выпукла вниз. Это значит, что если мы соединим отрезком две точки на графике, то график будет расположен под этим отрезком.
studfile.net
Линейная функция, её свойства и график. — МегаЛекции
Понятие числовой функции. Способы задания функции. Свойства функций.
Числовая функция — функция, которая действует из одного числового пространства (множества) в другое числовое пространство (множество).
Три главных способа задания функции: аналитический, табличный и графический.
1. Аналитический.
Способ задания функции при помощи формулы называется аналитическим. Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции.
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции.
Функция у=f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями.

Свойства функции, которые необходимо учитывать при построении её графика:
1)Область определения функции.
Область определения функции, то есть те значения, которые может принимать аргумент х функции F =y (x).
2) Промежутки возрастания и убывания функции.
Функция называется возрастающей на рассматриваемом промежутке, если большему значению аргумента соответствует большее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х1 и х2, причём х1 > х2, то у(х1) > у(х2).
Функция называется убывающей на рассматриваемом промежутке, если большему значению аргумента соответствует меньшее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х1 и х2, причём х1 < х2, то у(х1) < у(х2).
3) Нули функции.
Точки, в которых функция F = y (x) пересекает ось абсцисс (они получаются, если решить уравнение у(х) = 0) и называются нулями функции.
4)Чётность и нечётность функции.
Функция называется чётной, если для всех значений аргумента из области определения
у(-х) = у(х).
График чётной функции симметричен относительно оси ординат.
Функция называется нечётной, если для всех значений аргумента из области определения
у(-х) = -у(х).
График чётной функции симметричен относительно начала координат.
Многие функции не являются ни чётными, ни нечётными.
5)Периодичность функции.
Функция называется периодической, если существует такое число Р, что для всех значений аргумента из области определения
у(х + Р) = у(х).
Линейная функция, её свойства и график.
Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел.
k – угловой коэффициент (действительное число)
b – свободный член (действительное число)
x – независимая переменная.
· В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).
· Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.
o Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
o Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось.
Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание. Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) k < 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b < 0; y = kx + b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k < 0, следовательно y = kx + b убывает на всей области определения.
| 8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b. | 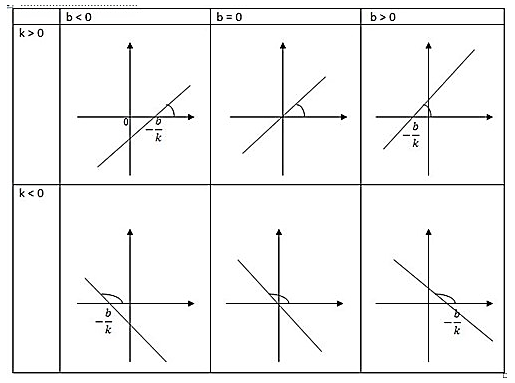 |
11. Функция у = ах2 + bх + с, её свойства и график.
| Функция у = ах2 + bх + с (а, b, с — постоянные величины, а ≠ 0) называется квадратичной. В простейшем случае у = ах2 (b = с = 0) график есть кривая линия, проходящая через начало координат. Кривая, служащая графиком функции у = ах2, есть парабола. Каждая парабола имеет ось симметрии, называемую осью параболы. Точка О пересечения параболы с ее осью называется вершиной параболы. |
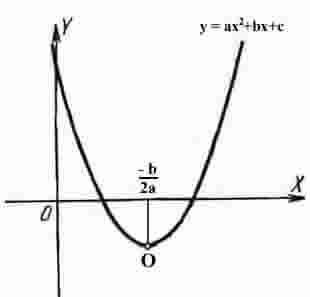 |
| График можно строить по следующей схеме:
1) Находим координаты вершины параболы х0 = -b/2a; у0 = у(х0).
2) Строим еще несколько точек, которые принадлежат параболе, при построении можно использовать симметрии параболы относительно прямой х = -b/2a.
3) Соединяем обозначены точки плавной линией.
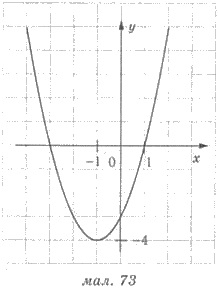
Пример. Построить график функции в = х2 + 2х — 3.
Решения. Графиком функции является парабола, ветви которой направлены вверх. Абсцисса вершины параболы х0 = 2/(2 ∙1) = -1, ее ординаты y(-1) = (1)2 + 2(-1) — 3 = -4.
Итак, вершина параболы — точка (-1; -4). Составим таблицу значений для нескольких точек, которые размещены справа от оси симметрии параболы — прямой х = -1.
Обозначим точки, координаты которых записанные в таблице, и точки, симметричные им относительно прямой х = -1. Соединяем точки плавной линией и получим график функции у = х2 + 2х — 3 (рис. 73).
|
Свойства функции.

Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Функция, область определения, множество значений, четность, периодичность, график, монотонность: возрастание, убывание, нули. Тесты
Тестирование онлайн
Понятие функции
Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.
Обозначение:
Переменную x называют независимой переменной или аргументом, а переменную y — зависимой. Говорят, что y является функцией от x. Значение y, соответствующее заданному значению x, называют значением функции.
Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Обозначения:
D(f) — значения аргумента. E(f) — значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.
Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Если некоторому значению x=x0 соответствуют несколько значений (а не одно) y, то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.
Способы задания функции
1) Функция может быть задана аналитически в виде формулы. Например,
2) Функция может быть задана таблицей из множества пар (x; y).
3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «взбираться» вверх по графику.
Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы «скатываться» вниз по графику.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Нули функции и промежутки знакопостоянства
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.
Такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
Четные и нечетные функции
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
Периодические функции
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T — это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
fizmat.by
Нелинейная функция — это… Что такое Нелинейная функция?
Примеры линейных функций.
Линейная функция — функция вида
- f(x) = kx + b.
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.
- Частный случай
 линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от
линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от  — неоднородных линейных функций.
— неоднородных линейных функций.
Свойства
- k является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.
- При k > 0, прямая образует острый угол с осью абсцисс.
- При k < 0, прямая образует тупой угол с осью абсцисс.
- При k = 0, прямая параллельна оси абсцисс
- b является показателем ординаты точки пересечения прямой с осью ординат.
- При b = 0, прямая проходит через начало координат.
Линейная функция нескольких переменных
Линейная функция n переменных 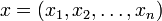 — функция вида
— функция вида
где 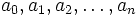 — некоторые фиксированные числа. Областью определения линейной функции является всё n-мерное пространство переменных
— некоторые фиксированные числа. Областью определения линейной функции является всё n-мерное пространство переменных 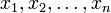 вещественных или комплексных. При a0 = 0 линейная функция называется однородной, или линейной формой.
вещественных или комплексных. При a0 = 0 линейная функция называется однородной, или линейной формой.
Если все переменные 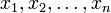 и коэффициенты
и коэффициенты 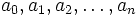 — вещественные числа, то графиком линейной функции в (n + 1)-мерном пространстве переменных
— вещественные числа, то графиком линейной функции в (n + 1)-мерном пространстве переменных 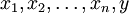 является n-мерная гиперплоскость
является n-мерная гиперплоскость
в частности при n = 1 — прямая линия на плоскости.
Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X над некоторым полем k в это поле, то есть для такого отображения 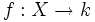 , что для любых элементов
, что для любых элементов 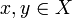 и любых
и любых 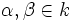 справедливо равенство
справедливо равенство
- f(αx + βy) = αf(x) + βf(y)
причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Нелинейные функции
Для функций, не являющихся линейными (то есть достаточно произвольных), когда хотят подчеркнуть некие свойства, употребляют термин нелинейные функции. Обычно это происходит, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
В ряде случаев этот термин может применяться и к зависимостям f = kx + b, где 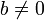 , то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае
, то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае 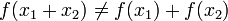 и
и 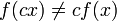 . Например, нелинейной зависимостью считают σ(τ) для материала с упрочнением (см. теория пластичности).
. Например, нелинейной зависимостью считают σ(τ) для материала с упрочнением (см. теория пластичности).
См. также
- Логарифмический рост
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru


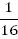

 .
.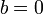 линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от
линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от