Площадь равнобедренного треугольника
В данном уроке размещены формулы и задачи на нахождение площади равнобедренного треугольника. Формулы снабжены пояснениями и комментариями. На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
См. также:
Буквенные обозначения сторон и углов на приведенном рисунке соответствуют обозначениям, которые указаны в формулах. Таким образом, это поможет Вам сопоставить их с элементами равнобедренного треугольника. Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Формула площади равнобедренного треугольника
Далее приведены формулы нахождения площади равнобедренного треугольника: через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.- Площадь равнобедренного треугольника можно найти, зная его сторону и основание. Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Пример использования такой формулы приведен на примере решения задачи ниже. - Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна a * sin β. Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника (Пояснение: полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 - Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине.
Строго говоря, зная один из углов равнобедренного треугольника, можно найти и остальные, поэтому применение данной или предыдущей формулы — вопрос вкуса (кстати, поэтому можно запомнить только одну из них).
У третьей формулы также есть еще одна интересная особенность — произведение a sin α даст нам длину высоты, опущенной на основание. В результате мы получим простую и очевидную формулу 5. - Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны) как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами. Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
- Разумеется, площадь равнобедренного треугольника можно найти, опустив высоту из вершины на основание, в результате чего получится два прямоугольных треугольника. Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
- Эта формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора. Для этого выразим высоту из предыдущей формулы, которая одновременно, является катетом прямоугольного треугольника, образованного боковой стороной, половиной его основания и высотой, через теорему Пифагора. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Кстати, самые сообразительные могут увидеть, что если в Формуле 1 раскрыть скобки, то она превратиться в Формулу 6. Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
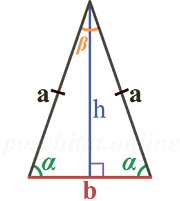
Обозначения, которые были применены в формулах на рисунке:
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основании
β — величина угла между равными сторонами треугольника и противолежащего его основанию
h — длина высоты, опущенная из вершины равнобедренного треугольника на основание
Важно. Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
См. также: другие формулы и свойства равнобедренного треугольника
Примечание. Это часть урока с задачами по геометрии (раздел площадь равнобедренного треугольника). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение
.Задача
Боковая сторона равнобедренного треугольника равна 13 см, а основание равно 10 см. Найдите площадь равнобедренного треугольника.
Решение.
1-й способ. Применим формулу Герона. Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
где а — длина боковых сторон, а b — длина основания.
Подставив значения длин сторон треугольника из условия задачи, получим:
S = 1/2 * 10 * √ ((13 + 5 )( 13 — 5 )) = 5 √ (18 * 8) = 60 см2
2-й способ. Применим теорему Пифагора
Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна
AK = AC / 2 = 10 / 2 = 5 см .
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник ABK. В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Соответственно, высота будет равна:h = √ ( 132 — 52 ) = √144 = 12 см
Площадь исходного равнобедренного треугольника ABC будет равна площади двух прямоугольных треугольников ABK и CBK, образованных боковыми сторонами, высотой и половинами основания равнобедренного треугольника. Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Площадь равнобедренного треугольника — формула, пример расчета, калькулятор
Равнобедренным треугольником называется фигура с двумя равными сторонами. В этом случае третья сторона считается основанием, а равные стороны – боковыми. Если все стороны треугольника равны, то он считается правильным. Правильный треугольник также является равнобедренным.
Если все стороны треугольника равны, то он считается правильным. Правильный треугольник также является равнобедренным.
Равнобедренный треугольник отличается следующими свойствами:
- Углы (α) при основании равны;
- Биссектрисы, медианы и высоты, исходящие из этих углов также равны между собой;
- Центры описанной и вписанной окружности лежат на одной прямой;
- Биссектриса, медиана и высота, проведенные из угла β к основанию b, равны между собой.
Существует множество способов нахождения площади равнобедренного треугольника. Для начала рассмотрим классический метод, для которого потребуется высота и основание. Зная эти параметры можно применить формулу площади равнобедренного треугольника:

То есть площадь равнобедренного треугольника равняется произведению высоты на половину длины основания.
 Рассмотрим пример расчета площади равнобедренного треугольника.
Рассмотрим пример расчета площади равнобедренного треугольника.Задача: дан треугольник, в котором основание равно 4 см, а высота 6 см. Найдите площадь.
Подставляем данные в формулу:

Площадь треугольника равняется 12 кв. см
Также найти площадь можно по формуле площади через три стороны, или как еще говорят – формуле Герона. Во многих случаях это значение находится через радиус вписанной окружности.
Найти площадь фигуры через стороны, применив метод Герона, можно по этой формуле.

Это выражение можно преобразовать в сокращенную формулу:

 Рассмотрим на примере.
Рассмотрим на примере.В равнобедренном треугольнике основание b= 3 см, а сторона a= 6 см. Подставим значения в формулу:

или
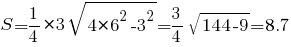
Зная стороны, мы легко определили, что S = 8,7 кв. см
Для вычислений можно использовать две равные стороны и угол между ними.

 И снова смотрим пример:
И снова смотрим пример:Стороны a = 6 см., а угол между ними 45°. По таблице синусов синус 45° равен 0.7071.
Рассчитываем площадь:
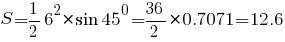
Площадь такого равнобедренного треугольника будет равна 12,6 квадратных сантиметра
Площадь равнобедренного треугольника | Треугольники
Как найти площадь равнобедренного треугольника? Это можно сделать с помощью любой из формул для площади треугольника. Свойства равнобедренного треугольника эти формулы могут несколько видоизменить.
I. Площадь треугольника равна половине произведения стороны на проведенную к этой стороне высоту.
В равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой. Поэтому FC=1/2 BC, то есть
Этот факт стоит использовать, например, если нужно найти площадь равнобедренного треугольника, и известны его боковая сторона и высота, проведенная к основанию. В этом случае из прямоугольного треугольника треугольника AFC по теореме Пифагора найдем FC,
а затем сразу же — площадь
II. Площадь треугольника равна половине произведения двух сторон на синус угла между ними.
III. Площадь треугольника по трем сторонам ищут по формуле Герона. Поскольку в равнобедренном треугольнике две стороны равны, формула Герона для равнобедренного треугольника приобретает вид:
Полупериметр
поэтому
Специально запоминать эту формулу не нужно — практически, это формула из пункта I.
IV. Площадь треугольника через радиус вписанной окружности равна произведению радиуса на полупериметр.
Для равнобедренного треугольника
V. Площадь треугольника через радиус описанной окружности для равнобедренного треугольника приобретает вид:
Вычислить площадь равнобедренного треугольника | FIFAFAQ.ru
Онлайн калькулятор
Чтобы вычислить площадь равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длина основания (b) и высота (h)
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и длину основания (b)
Введите их в соответствующие поля и узнаете площадь равнобедренного треугольника (S).
Как посчитать площадь равнобедренного треугольника зная длину основания и высоту
Чему равна площадь равнобедренного треугольника если длина основания , а длина высоты
Какова площадь равнобедренного треугольника (S) если известны длина основания (b) и высота (h)?
Формула
Пример
Если основание b = 5 см, а высота h = 10 см, то:
S = ½⋅5⋅10 = 50/2 = 25 см 2
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между ними (β)
Чему равна площадь равнобедренного треугольника если длина сторон , а угол между ними
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между ними (β)?
Формула
Пример
Если сторона а = 10 см, а ∠β = 30°, то:
S = ½⋅10 2 ⋅sin30° = ½ ⋅100⋅0.5= 50/2 = 25 см 2
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между стороной и основанием (α)
Чему равна площадь равнобедренного треугольника если длина сторон , а угол
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между стороной и основанием (α)?
Формула
Пример
Если сторона а = 10 см, а ∠α = 75°, то:
S = ½⋅10 2 ⋅sin(180-2⋅75)° = ½ ⋅100⋅0.5 = 50/2 = 25 см 2
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и длину основания (b)
Чему равна площадь равнобедренного треугольника если длина сторон , а длина основания
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и длина основания (b)?
Формула
Пример
Если сторона а = 10 см, а основание b = 5, то:
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Онлайн калькулятор – площадь равнобедренного треугольника
Какие размеры треугольника известны:
Основание и высота Основание и сторона
Решение
Теория
Треугольник – это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.
Треугольники бывают прямоугольный, равнобедренный, равносторонний.
Равнобедренный треугольник – это треугольник у которого две стороны равны. Эти равные стороны называют боковыми, а третью сторону равнобедренного треугольника называют основанием.
Формула площади равнобедренного треугольника
Чтобы посчитать площадь равнобедренного треугольника, необходимо знать размеры двух сторон треугольника.
Площадь равнобедренного треугольника расчитывается по формуле: