Кинематика — Википедия
Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.
Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.
Долгое время понятия о кинематике были основаны на работах Аристотеля, в которых утверждалось, что скорость падения пропорциональна весу тела, а движение в отсутствие сил невозможно. Только в конце XVI века этим вопросом подробно занялся Галилео Галилей. Изучая свободное падение (знаменитые опыты на Пизанской башне) и инерцию тел, он доказал неправильность идей Аристотеля. Итоги своей работы по данной теме он изложил в книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению»[1].
Рождением современной кинематики можно считать выступление Пьера Вариньона перед Французской Академией наук 20 января 1700 года. Тогда впервые были даны понятия скорости и ускорения в дифференциальном виде.
В XVIII веке Ампер первый использовал вариационное исчисление в кинематике.
После создания СТО, показывающей, что время и пространство не абсолютны и скорость имеет принципиальное ограничение, кинематика вошла в новый этап развития в рамках релятивистской механики (см. Релятивистская кинематика).
Главной задачей кинематики является математическое (уравнениями, графиками, таблицами и т. п.) определение положения и характеристик движения точек или тел во времени. Любое движение рассматривается в определённой системе отсчёта. Также кинематика занимается изучением составных движений (движений в двух взаимно перемещающихся системах отсчёта).
Положение точки (или тела) относительно заданной системы отсчёта определяется некоторым количеством взаимно независимых функций координат:
- p1=f1(t){\displaystyle p_{1}=f_{1}(t)}
- p2=f2(t){\displaystyle p_{2}=f_{2}(t)}
- ⋮{\displaystyle \vdots }
- pn=fn(t){\displaystyle p_{\mathrm {n} }=f_{\mathrm {n} }(t)},
где n{\displaystyle n} определяется количеством степеней свободы. Так как точка не может быть в нескольких местах одновременно, все функции fi(t){\displaystyle f_{i}(t)} должны быть однозначными. Также в классической механике выдвигается требование их дифференцируемости на промежутках. Производные этих функций определяют скорость тела[2].
Скорость движения определяется как производная координат по времени:
- v1=dp1(t)dt{\displaystyle v_{1}={\frac {dp_{1}(t)}{dt}}}
- v2=dp2(t)dt{\displaystyle v_{2}={\frac {dp_{2}(t)}{dt}}}
- ⋮{\displaystyle \vdots }
- vn=dpn(t)dt{\displaystyle v_{n}={\frac {dp_{n}(t)}{dt}}}
- v→=v1τ→1+v2τ→2+….+vnτ→n{\displaystyle {\vec {v}}=v_{1}{\vec {\tau }}_{1}+v_{2}{\vec {\tau }}_{2}+….+v_{n}{\vec {\tau }}_{n}},
где τ→i{\displaystyle {\vec {\tau }}_{i}} — единичные векторы, направленные вдоль соответствующих координат.
Ускорение определяется как производная скорости по времени:
- a→=dv→(t)dt{\displaystyle {\vec {a}}={d{{\vec {v}}(t)} \over dt}}
Следовательно, характер движения можно определить, зная зависимость скорости и ускорения от времени. А если кроме этого известны ещё и значения скорости/координат в определённый момент времени, то движение полностью задано.
Деление кинематики по типам объекта исследования[править | править код]
В зависимости от свойств изучаемого объекта, кинематика делится на кинематику точки, кинематику твёрдого тела, кинематику деформируемого тела, кинематику газа, кинематику жидкости и т. д.
Кинематика точки[править | править код]
Основная статья: Кинематика точки
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
- Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
- a→=0{\displaystyle {\vec {a}}=0}
- v→=const{\displaystyle {\vec {v}}=\mathrm {c} onst}
- p1(t)=p1(0)+v1t{\displaystyle p_{1}(t)=p_{1}(0)+v_{1}t}
- p2(t)=p2(0)+v2t{\displaystyle p_{2}(t)=p_{2}(0)+v_{2}t}
- …{\displaystyle \dots }
- pn(t)=pn(0)+vnt{\displaystyle p_{n}(t)=p_{n}(0)+v_{n}t}
- s=∣v→∣(t1−t2){\displaystyle s=\mid {\vec {v}}\mid (t_{1}-t_{2})},
где s{\displaystyle s} — длина пути траектории за промежуток времени от t2{\displaystyle t_{2}} до t1{\displaystyle t_{1}}, v1,v2,…,vn{\displaystyle v_{1},v_{2},\dots ,v_{n}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси координат.
- Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).
- a→=const{\displaystyle {\vec {a}}=\mathrm {c} onst}
- v→(t)=v→(0)+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}(0)+{\vec {a}}t}
- p1(t)=p1(0)+v1(0)t+a1t22{\displaystyle p_{1}(t)=p_{1}(0)+v_{1}(0)t+{\frac {a_{1}t^{2}}{2}}}
- p2(t)=p2(0)+v2(0)t+a2t22{\displaystyle p_{2}(t)=p_{2}(0)+v_{2}(0)t+{\frac {a_{2}t^{2}}{2}}}
- …{\displaystyle \dots }
- pn(t)=pn(0)+vn(0)t+ant22{\displaystyle p_{n}(t)=p_{n}(0)+v_{n}(0)t+{\frac {a_{n}t^{2}}{2}}}
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt},
где s{\displaystyle s} — длина пути траектории за промежуток времени от t2{\displaystyle t_{2}} до t1{\displaystyle t_{1}}, v1,v2,…,vn{\displaystyle v_{1},v_{2},\dots ,v_{n}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси координат, a1,a2,…,an{\displaystyle a_{1},a_{2},\dots ,a_{n}} — проекции a→{\displaystyle {\vec {a}}} на соответствующие оси координат.
- Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
- a→⊥v→{\displaystyle {\vec {a}}\perp {\vec {v}}}
- ∣a→∣=∣v→∣2R{\displaystyle \mid {\vec {a}}\mid ={\frac {{\mid {\vec {v}}\mid }^{2}}{R}}}
- s=∣v→∣(t1−t2){\displaystyle s=\mid {\vec {v}}\mid (t_{1}-t_{2})},
где R{\displaystyle R} — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
- y=Rsin(∣v→∣Rt+arcsin(y(0)R)){\displaystyle y=R\sin {\Bigg (}{\frac {\mid {\vec {v}}\mid }{R}}t+\arcsin {\Big (}{\frac {y(0)}{R}}{\Big )}{\Bigg )}}
- x=Rcos(∣v→∣Rt+arccos(x(0)R)){\displaystyle x=R\cos {\Bigg (}{\frac {\mid {\vec {v}}\mid }{R}}t+\arccos {\Big (}{\frac {x(0)}{R}}{\Big )}{\Bigg )}}
- z=0{\displaystyle z=0}
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
- a→=const{\displaystyle {\vec {a}}=\mathrm {c} onst}
- v→(t)=v→(0)+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}(0)+{\vec {a}}t}
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt}
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
- y(t)=y(0)+vy(0)t+∣a→∣t22{\displaystyle y(t)=y(0)+v_{y}(0)t+{\frac {\mid {\vec {a}}\mid t^{2}}{2}}}
- x(t)=x(0)+vx(0)t{\displaystyle x(t)=x(0)+v_{x}(0)t}
- z=0{\displaystyle z=0},
где vy{\displaystyle v_{y}} и vx{\displaystyle v_{x}} — проекции v→{\displaystyle {\vec {v}}} на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
- Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.
- В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
- s=∫t1t2∣v→(t)∣dt{\displaystyle s=\int \limits _{t_{1}}^{t_{2}}\mid {\vec {v}}(t)\mid dt}
Кинематика твёрдого тела[править | править код]
Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:
- v→B=v→A+ω→×AB→{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\vec {\omega }}\times {\vec {AB}}},
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела.
Кинематика деформируемого тела, Кинематика жидкости[править | править код]
Основные статьи: Кинематика деформируемого тела, Кинематика жидкости
Кинематика деформируемого тела и кинематика жидкости относятся к кинематике непрерывной среды.
Кинематика газа[править | править код]
Кинематика газа изучает деление газа на скопления при движении и описывает движение этих скоплений. В рамках кинематики газа описываются не только основные параметры движения, но и типы движения газа.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. — М.: Изд-во Физического факультета МГУ, 1997.
- Матвеев А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Павленко Ю. Г. Лекции по теоретической механике. — М.: ФИЗМАТЛИТ, 2002. — 392 с.
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560с.
- Стрелков С. П. Механика. — М.: Наука, 1975.
- Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов (4-е изд.). — М.: Наука, 1968.
основные формулы с пояснениями или определения по физике в 10 классе, какие законы динамики или механики для ЕГЭ
Описать можно все что угодно: картину в галерее, уличного хулигана в кабинете участкового и даже свои душевные переживания на приеме у психотерапевта. Достаточно вооружиться бумагой, ручкой и вперед.
Но что необходимо, чтобы описать движение? На этот вопрос нам поможет ответить кинематика, раздел механики, который как раз и занимается описанием механического движения.
Физика простыми словами | Кинематика
Как описать движение?
Давайте разберемся с терминологией и введем основные понятия, без которых нам никак не обойтись. Итак, движением мы будем называть любое изменение положения тела в пространстве с течением времени.
К слову сразу отметим, что время в физике принято мерить секундами, а само движущееся тело не всегда рассматривается целиком. Зачастую его размерами и формой можно пренебречь и рассматривать как точку, имеющую массу.
В механике вы можете услышать такие понятия как точечное тело или материальная точка. Так вот знайте, речь идет как раз об этом.
К примеру, какие бы габариты не имела ваша машина, если вы едете по трасе из Ростова в Москву, то она в любом случае очень мала в сравнении с расстоянием, а значит мы можем рассматривать её как материальную точку. А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.
Положение тела или материальной точки в пространстве рассматривается с помощью системы координат, за начало которой мы принимаем тело отсчета, относительно которого происходит движение. В зависимости от сложности этого движения мы можем иметь дело с одномерным, двухмерным, или трехмерным пространством.
Соответственно, наша система координат может иметь одну, две или три оси. Как правило трехмерные пространства в школьной физике практически не встречаются, поэтому мы ограничимся двухмерным с координатными осями х и у.
Чтобы определить координаты нашей материальной точки, необходимо построить её проекции на соответствующие координатные оси, опустив на них перпендикуляры.
Теперь если наблюдая за движущейся материальной точкой, построить линию, по которой она движется, мы получим траекторию движения. Измерив длину траектории можно определить пройденный путь, а если построить вектор, соединяющий начальное и конечное положение точки, это будет перемещение.
Так как единицей длинны в международной системе единиц был принят метр, то путь, пройденный телом, и длина вектора перемещения, или, как еще говорят, его модуль, так же будут измерятся в метрах. Отметим, что модуль перемещения всегда будет меньше, ну или в крайнем случае равен пути, но никак не больше.
Все просто, вектора кривыми не бывают, и перемещение не является исключением. А вот что касается траектории, то её мы можем гнуть как угодно.
Исходя из этого, можно выделить два вида механического движения: прямолинейное — когда траектория прямая линия и криволинейное — когда тело движется по кривой, ну, к примеру, параболе или окружности.
Прямолинейное движение
Давайте представим, что мы едем в автобусе, а для простоты будем считать, что траектория нашего движения — прямая линия. Если разделить весь путь (s), который мы проедем на затраченное время (t), мы получим скорость (v). То есть величину, которая характеризует быстроту движения. Измеряется она в метрах в секунду м/с.
v=s/t
Так как движение относительно, то относительной будет и скорость. К примеру, если наш автобус едет со скоростью v1, ну скажем, равной 20 м/с, а мы, находясь в автобусе, идем в направлении водителя со скоростью v2, равной 1 м/с, то наша скорость относительно дороги будет определятся как сумма двух этих скоростей. То есть 21 м/с.
v=v1+v2
Ну а если мы будем идти от водителя, то наша скорость относительно дороги будет уже равна 19 м/с. И казалось бы, ничего не поменялось, и значения скоростей v1 и v2 остались прежними, но изменилось направление нашего движения, а значит, чтобы найти скорость, с которой мы движемся относительно дороги, нам нужно вычесть v2 из v1 .
v=v1-v2
В рассмотренных примерах мы условно принимали движение как равномерное, то есть движение с постоянной скоростью. Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.
Да и у нас не получится ходить по нему с постоянной скоростью, тем более если ехать в час пик, когда автобус забит под завязку. В реальности движение будет неравномерным, и скорость будет постоянно меняться.
При неравномерном движении отношение всего пройденного пути ко времени называется средней скоростью.
vср=s/t
И хотя в некоторых случаях она бывает очень удобна, но все же не всегда приемлема при описании движения. Думаю, будет очень трудно доказать сотруднику гос автоинспекции, остановившему вас за превышение скорости, что ваша средняя скорость на всем пути была в пределах нормы.
Тут речь пойдет о мгновенной скорости, или скорости в какой-то определенный момент времени. Если посмотреть на спидометр движущегося автомобиля, то мы как раз её увидим.
И стоит нам по сильнее нажать на педаль газа, как в то же мгновение стрелка спидометра начинает ползти вверх, оповещая нас об изменении скорости.
И здесь необходимо ввести понятие ускорения, величины, которая будет характеризовать изменение скорости движения за какой то промежуток времени (t). Её принято обозначать маленькой буквой a и измерять в м/с2.
а=(V-V0)/t
Ускорение, так же как и скорость, величина векторная, а значит будет иметь свое направление. Причем, если направление вектора ускорения будет совпадать с направлением скорости, то скорость будет возрастать.
Такое движение называют ускоренным. И напротив, снижение скорости, при замедленном движении, будет свидетельствовать о том что вектора ускорения и скорости смотрят в разные стороны. Выразим скорость и перемещение для движения с ускорением:
Если объединить эти уравнения в одно, мы получим формулу разности квадратов скоростей :
Итак, мы ввели основные понятия и величины кинематики и вывели основные уравнения, связывающие их. Но для простоты мы брали прямолинейное движение.
Если же говорить о движении по кривой, то нам придется уже рассматривать его в двухмерном или даже трехмерном пространстве.
Для этого необходимо будет построить проекции векторов скорости, перемещения и ускорения на соответствующие координатные оси, а при работе с проекциями мы опять получим уже знакомые уравнения для прямолинейного движения, которые примут следующий вид:
- Sx= V0x t +(axt2) /2
Sy= V0у t +(aуt2) /2
vx=v0x+axt
vy=v0y+ayt
Или для определения координат движущейся материальной точки:
- x= x 0 + V0x t +(axt2) /2
y= y 0 + V0у t +(aуt2) /2
Где х0, у0 — координаты начального положения точки в пространстве, а х, у — координаты её конечного положения.
Для описания движения в трехмерном пространстве у нас добавится третья ось z, и, соответственно, проекции скорости, ускорения и перемещения на эту ось.
Принцип разложения движения на простые составляющие лежит в основе многих устройств. Так первые компьютерные мыши были оснащены шариком, вращение которого приводило во вращение два перпендикулярно расположенных друг к другу колесика со специальными датчиками, они то и раскладывали сложные движения мыши на горизонтальные и вертикальные составляющие.
Стоило одному из этих колесиков покрыться толстым слоем грязи, как оно переставало вращаться, и указатель на экране начинал двигаться только по прямой, горизонтальной или вертикальной.
Современные оптические мыши лишены этого недостатка, так как в них шарик и колесики, заменены на лазерные датчики, но тем не менее принцип разложения движения они унаследовали от своих прародительниц.
Источник: https://physicsline.ru/teoriya/fizika-prostymi-slovami/fizika-prostymi-slovami-kinematika/
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:

Также давайте вспомним движение по кругу:

Медленно, но уверенно мы перешли более сложной теме – к динамике:

Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:

После статики можно рассмотреть и гидростатику:

Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:

Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:

Теперь можно смело переходить к молекулярной физике:

Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:

Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

- Переходим к постоянному электрическому току:
- Далее добавляем формулы по теме: “Магнитное поле электрического тока”
- Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
- Ну и, конечно, куда же без электромагнитных колебаний:
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
Источник: https://NauchnieStati.ru/spravka/bolee-50-osnovnyh-formul-po-fizike/
Кинематика твёрдого тела — Википедия
Материал из Википедии — свободной энциклопедии
Кинема́тика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.
Аддитивность угловой скорости[править | править код]
Если тело вращается с угловой скоростью ω0→{\displaystyle {\vec {\omega _{0}}}} в системе отсчёта O′{\displaystyle O’}, а эта система отсчёта, в свою очередь, вращается относительно системы отсчёта O{\displaystyle O} с угловой скоростью ωO′→{\displaystyle {\vec {\omega _{O’}}}}, то это тело вращается относительно O{\displaystyle O} с угловой скоростью
- ω→=ωO′→+ω0→{\displaystyle {\vec {\omega }}={\vec {\omega _{O’}}}+{\vec {\omega _{0}}}}
Дифференцирование по времени[править | править код]
Вращающееся тело — неинерциальная система отсчёта. Поэтому оператор дифференцирования по времени для векторов, определённых в покоящейся системе координат O{\displaystyle O}, связан с оператором дифференцирования по времени для векторов, определённых в системе координат на вращающемся теле O′{\displaystyle O’}, соотношением:
- ddtO=ddtO′+ω→O′×{\displaystyle {\frac {d}{dt_{O}}}={\frac {d}{dt_{O’}}}+{\vec {\omega }}_{O’}\times },
где «×{\displaystyle \times }» — векторное произведение.
Формула Эйлера[править | править код]
Формула Эйлера связывает скорости двух точек твёрдого тела:
- v→B=v→A+ω→×AB→,{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\vec {\omega }}\times {\vec {AB}},}
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела.
Выводится эта формула путём дифференцирования формулы r→B=r→A+AB→{\displaystyle {\vec {r}}_{B}={\vec {r}}_{A}+{\vec {AB}}} по времени с учётом замены оператора для неинерциальной системы отсчёта (см. выше). Путём повторного дифференцирования можно получить связь ускорений двух точек:
- a→B=a→A+ω→×(ω→×AB→)+ε→×AB→,{\displaystyle {\vec {a}}_{B}={\vec {a}}_{A}+{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {AB}})+{\vec {\varepsilon }}\times {\vec {AB}},}
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела, а ε→{\displaystyle {\vec {\varepsilon }}} — вектор углового ускорения тела.
Второе слагаемое называется центростремительным ускорением.
Ускорение Кориолиса[править | править код]
Ускорение точки B (в покоящейся системе координат), движущейся по поверхности вращающегося тела равно
- a→=a→B+[ε→×r→B]+[ω→×[ω→×r→B]]+2[ω→×v→B],{\displaystyle {\vec {a}}={\vec {a}}_{B}+\left[{\vec {\varepsilon }}\times {\vec {r}}_{B}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {r}}_{B}\right]\right]+2\left[{\vec {\omega }}\times {\vec {v}}_{B}\right],}
где r→B=r→B(t){\displaystyle {\vec {r}}_{B}={\vec {r}}_{B}(t)} — радиус-вектор точки В в системе координат на вращающемся теле. Последнее слагаемое и будет кориолисовым ускорением.
основана на формуле сложения скоростей:
- v→a=v→r+v→e{\displaystyle {\vec {v}}^{\,a}={\vec {v}}^{\,r}+{\vec {v}}^{\,e}}.
Раздел «Кинематика» теоретической механики — Лекции и примеры решения задач технической механики
Кинематика — это раздел теоретической механики, в котором изучается движение механических систем с геометрической точки зрения, без учета причин (сил), вызывающих это движение и изменение движения.
Положение тела, его движение в пространстве может быть определено относительно другого неизменяемого тела. С ним связывают выбранную систему отсчёта — систему координат, в которой и определяют параметры движения.
Установление способов, с помощью которых может быть задано движение точек или тел по отношению к выбранной системе отсчёта, позволит определить кинематические характеристики движения (траектории точек, их скорости, ускорения, угловые параметры тел.)
Движение любой механической системы относительно выбранной системы отсчёта будет известно, если известно движение каждой точки этой системы. Поэтому изучение раздела «Кинематика» начинается с темы «Кинематика точки», далее рассматривается тема «Кинематика твёрдого тела».
Данное учебно-методическое пособие поможет студентам при выполнении контрольных работ по разделу «Кинематика».
В пособии кратко изложена теория, даны основные формулы, приведены примеры решения типовых задач.
Краткость изложения теории предполагает предварительное изучение курса по учебникам, в которых даны подробные обоснования определений, выводы, доказательства теорем.
Методическое пособие может быть рекомендовано и на практических занятиях и при выполнении расчётно-графических работ.
Содержание
- Кинематика точки
- Способы задания закона движения точки
- Векторный
- Координатный
- Естественный
- Кинематика твердого тела
- Поступательное движение
- Вращательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Угловая скорость и угловое ускорение
- Скорости и ускорения точек вращающегося твердого тела
- Передаточные механизмы
- Плоскопараллельное движение твердого тела
- Определение скоростей точек в плоскопараллельном движении
- Теорема о скоростях точек в ППД
- Следствие из теоремы о скоростях точек
- Мгновенный центр скоростей
- Определение МЦС
- Ускорение точки в плоскопараллельном движении
- Мгновенный центр ускорений
- Частные случаи МЦУ
- Сложное движение точки
- Определение скоростей и ускорений точек в сложном движении
- Ускорение Кориолиса
- Сферическое движение
- Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
- Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
- Скорости и ускорения точек при вращении тела вокруг неподвижной точки
Кинематика поступательного движения
При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.
Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.
Линию, по которой движется материальная точка в пространстве, называют траекторией.
Перемещениемматериальной точки за некоторый промежуток времени называется вектор перемещения∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.
Скоростьматериальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета.Вектор ускоренияхарактеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.
Кинематика вращательного движения.
Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся _по окружностям, центры которых лежат на одной прямой (ось вращения).
Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости .
Cвязь кинематических величин поступательного и вращательного движения.
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате sсоответствует уголφ , линейной скоростиv— угловая скоростьw, линейному (касательному) ускорениюа— угловое ускорениеε. Сравнительные параметры движения:
Поступательное движение | Вращательное движение | ||||
Перемещение | S | Угловое перемещение | φ | ||
Линейная скорость |
| Угловая скорость |
| ||
Ускорение |
| Угловое ускорение |
| ||
Масса | m | Момент инерции | I | ||
Импульс |
| Момент импульса |
| ||
Сила | F | Момент силы | M | ||
Таблицу можно продолжать и далее.
Работа:
|
|
Кинетическая энергия
|
|
Выражения для вращательного движения напоминают соответствующие выражения поступательного движения. Они получаются из последних формальной заменой m → I , v → w , p → L
Выражения имеют не просто формальное сходство. Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.

Представленная таблица не может претендовать на всю полноту охвата аналогичных значений. Для вращательного и поступательного движений формулируются и аналогичные законы:
Закон сохранения импульса (ЗСИ)
| Закон сохранения момента импульса (ЗСМИ)
|
Эти законы формулируются следующим образом:
«Если геометрическая сумма внешних сил, действующих на систему, равна нулю, то импульс системы сохраняется, т.е. не меняется со временем. В частности, это имеет место, когда система замкнута» | «Если момент внешних сил относительно неподвижного начала Оравен нулю, то момент импульса системы относительно того же начала остается постоянным во времени» |
[Д.В.Сивухин. Общий Курс Физики. т.I Механика] | |
Динамика поступательного движения. Законы Ньютона.
Первый закон Ньютона:существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.Такие системы отсчета называются инерциальными.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй закон Ньютона–основной закон динамики поступательного движения –отвечает на вопрос, как изменяется механическое движение тела под действием приложенной к нему силы:если на тело действует сила, то это тело приобретает ускорение, прямо пропорциональное действующей силе и обратно пропорциональное массе данного тела:
 .
.
В том случае, если на тела действует не
одна, а несколько сил, то приведенная в
этой формуле сила 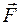 является
равнодействующей всех действующих на
это тело сил и определяется их векторной
суммой.
является
равнодействующей всех действующих на
это тело сил и определяется их векторной
суммой.
Из уравнения второго закона Ньютона
следует: 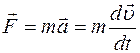 .
.
В случае неизменности массы тела можно записать:
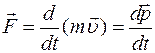 ,
где
,
где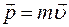 .
.
Вектор  называетсяимпульсом (иликоличеством
движения)тела.
называетсяимпульсом (иликоличеством
движения)тела.
Отсюда следует иная формулировка второго закона Ньютона, называемая формулировкой в дифференциальном виде, а именно: скорость изменения импульса тела равна силе, действующей на этр тело,то есть
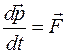 .
.
В том случае, если на тела действует не
одна, а несколько сил, то приведенная в
этой формуле сила 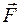 является
равнодействующей всех действующих на
это тело сил и определяется их векторной
суммой.
является
равнодействующей всех действующих на
это тело сил и определяется их векторной
суммой.
Третий закон Ньютонаопределяет
взаимодействие между материальными
точками:если первая материальной
точка действует на вторую с силой 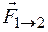 ,
то вторая точка действует на первую с
силой
,
то вторая точка действует на первую с
силой 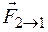 ,
по модулю равной, а по направлению
противоположной силе
,
по модулю равной, а по направлению
противоположной силе  (силы
(силы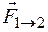 и
и 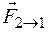 направлены
по прямой, соединяющей взаимодействующие
точки).
направлены
по прямой, соединяющей взаимодействующие
точки).
Импульс системы тел.Если
принять, что импульс системы, состоящей
изn тел, можно определить, как
векторную сумму импульсов всех n тел,
то есть ,
то из третьего закона Ньютона при условии
отсутствия внешних сил (то есть, для
замкнутой системы) следует:
,
то из третьего закона Ньютона при условии
отсутствия внешних сил (то есть, для
замкнутой системы) следует:
 ,
т.е.
,
т.е.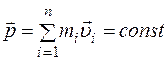 .
.
Таким образом, импульс замкнутой системы тел не изменяется с течением времени, что являетсязаконом сохранения импульса.
Закон сохранения импульса. Реактивное движение.
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
Реактивное движение — это движение, которое возникает при отделении от тела некоторой его части с определенной скоростью.
Реактивное движение, например, выполняет ракета. Особенностью этого движения является то, что тело может ускоряться и тормозить без какой-либо внешней взаимодействия с другими телами. Продукты сгорания при вылет получают относительно ракеты некоторую скорость. Согласно закону сохранения импульса, сама ракета получает такой же импульс, как и газ, но направлен в другую сторону. Закон сохранения импульса нужен для расчета скорости ракеты.
Энергия и работа при поступательном движении.
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.
Элементарной работой силы 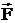 называется
величина, равная скалярному произведению
силы на элементарное перемещение
называется
величина, равная скалярному произведению
силы на элементарное перемещение :
:
 ,
,
где 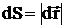 –
элементарный путь точки приложения
силы за время dt,
– угол между векторами
–
элементарный путь точки приложения
силы за время dt,
– угол между векторами 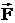 и
и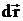 .
.
Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:
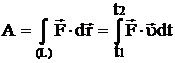 .
.
Кинетической энергиейтела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).
Кинетическая энергия поступательного движения
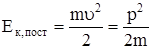 .
.
Закон сохранения энергии.
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени
Другими словами, энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую.
Связь силы и потенциальной энергии в консервативной системе.
-Осуществляется по следующей позиции
Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком «минус» (работа совершается за счет убыли потенциальной энергии).
Потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.

Для консервативных сил
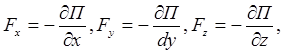 или
в векторном виде
или
в векторном виде 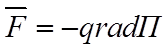 .
.
 —
градиент скаляра П (
—
градиент скаляра П (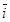 ,
,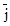 ,
, —
единичные векторы координатных осей).
—
единичные векторы координатных осей).
Потенциальная
энергия тела массой 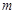 на
высоте
на
высоте 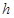 вычисляется
по формуле .
вычисляется
по формуле .
Потенциальная энергия упруго деформированного тела (пружины):

Типы сил. Упругие силы. Потенциальная энергия упругодеформированного тела
В природе существует четыре типа сил: гравитационные, электромагнитные, ядерные и слабые.
Гравитационные силы, или силы тяготения, действуют между всеми телами. Но эти силы заметны, если хотя бы одно из тел имеет размеры, соизмеримые с размерами планет. Силы притяжения между обычными телами настолько малы, что ими можно пренебречь. Поэтому гравитационными можно считать силы взаимодействия между планетами, а также между планетами и Солнцем или другими телами, имеющими очень большую массу. Это могут быть звёзды, спутники планет и т.п.
Электромагнитные силы действуют между телами, имеющими электрический заряд.
Ядерные силы (сильные) являются самыми мощными в природе. Они действуют внутри ядер атомов на расстояниях 10-13 см.
Слабые силы, как и ядерные, действуют на малых расстояниях порядка 10-15 см. В результате их действия происходят процессы внутри ядра.
-Упругие Силы
Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости.
При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются.
— Деформированное упругое тело(например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины.
Гравитационные силы. Потенциальная энергия гравитационного взаимодействия.
Все тела в природе взаимно притягиваются друг к другу. Впервые Ньютон доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения (гравитационная сила), действующая между любыми телами Вселенной.
Гравитационные силы — это силы центральные, т. е. они направлены вдоль прямой, соединяющей взаимодействующие материальные точки.
Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это поле, наряду с другими полями и веществом, является одной из форм материи.
С каждым телом неразрывно связано гравитационное поле, проявляющееся в том, что на помещенную в поле материальную точку действует гравитационная сила, пропорциональная массе этой точки.
Кинематика вращательного движения
Пусть некоторая
точка движется по окружности радиуса r.
Изменение положения точки в пространстве
за промежуток времени t определяется углом поворота  (рис. 3). Элементарный поворот на угол
(рис. 3). Элементарный поворот на угол можно рассматривать как вектор
можно рассматривать как вектор . Модуль вектора
. Модуль вектора  равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия правого винта, головка
которого вращается в направлении
движения точки по окружности, т.е.
подчиняется правилу правого винта.
равен углу поворота, а его направление
совпадает с направлением поступательного
движения острия правого винта, головка
которого вращается в направлении
движения точки по окружности, т.е.
подчиняется правилу правого винта.
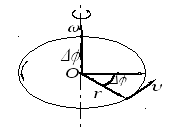
Рис. 3
Угловой скоростью  называется векторная величина, равная
пределу отношения угла поворота
называется векторная величина, равная
пределу отношения угла поворота к промежутку времениt,
за который этот поворот произошел, при
стремлении t к нулю:
к промежутку времениt,
за который этот поворот произошел, при
стремлении t к нулю:
 ,
,
где  – первая производная от функции угла
поворота
– первая производная от функции угла
поворота 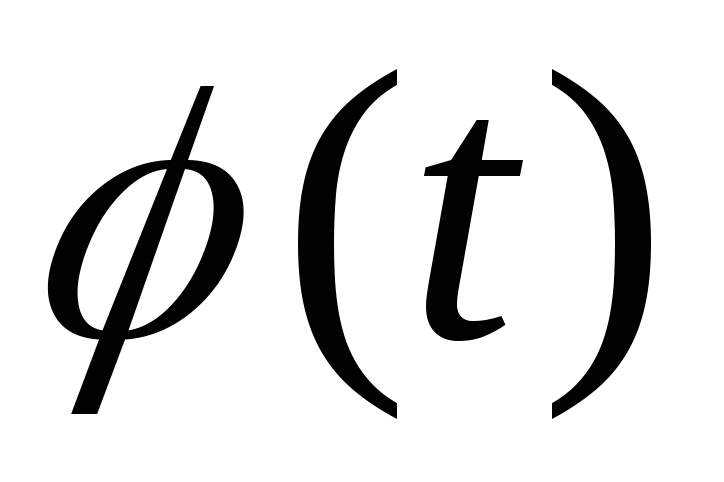 радиус-вектора
радиус-вектора  по времени t.
Эту производную принято обозначать,
как
по времени t.
Эту производную принято обозначать,
как  .
.
Вектор  направлен вдоль оси вращения в
соответствии с правилом правого винта
(рис. 3).
направлен вдоль оси вращения в
соответствии с правилом правого винта
(рис. 3).
Угловым ускорением 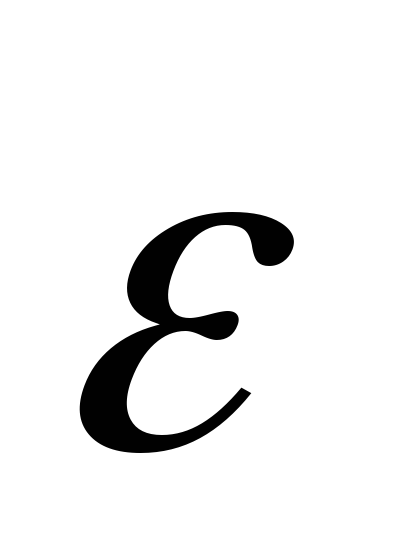 называется векторная величина, равная
пределу отношения изменения угловой
скорости
называется векторная величина, равная
пределу отношения изменения угловой
скорости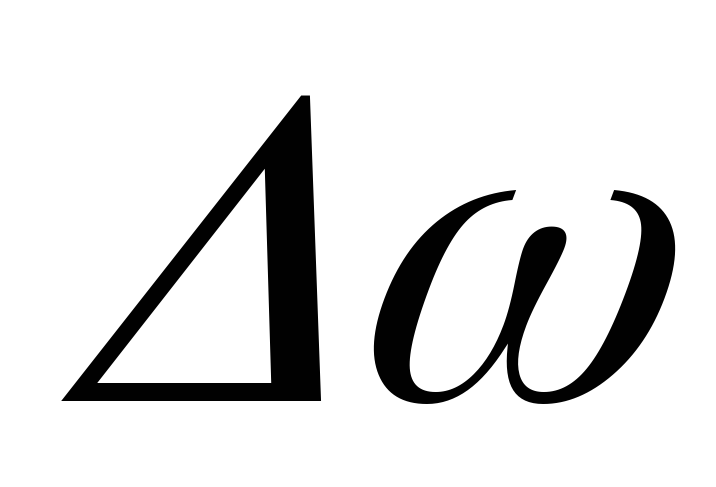 к промежутку времениt,
за который это изменение произошло, при
стремлении t к нулю:
к промежутку времениt,
за который это изменение произошло, при
стремлении t к нулю:
 ,
,
где  – первая производная от функции
– первая производная от функции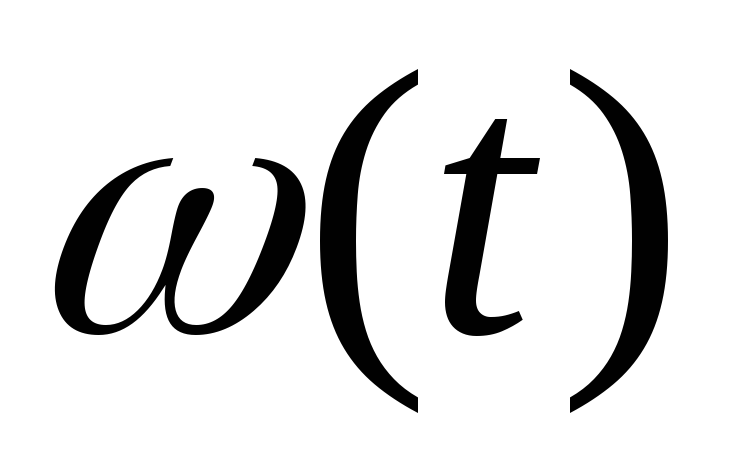 по времени t,
по времени t,
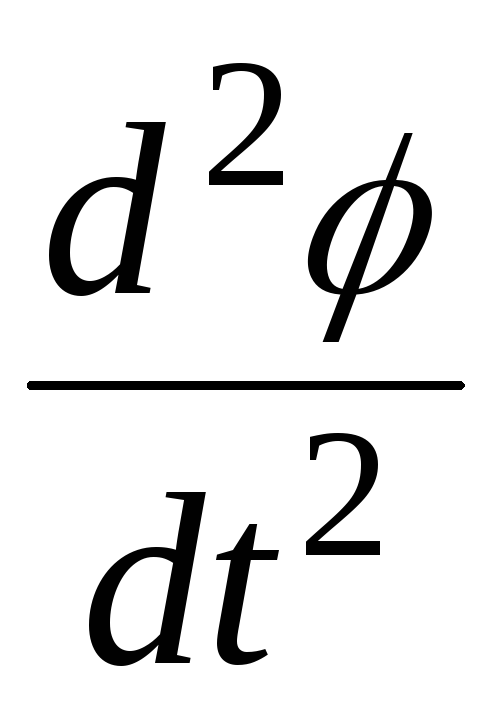 –вторая производная
от функции
–вторая производная
от функции  по времени t.
по времени t.
Эти производные
принято
обозначать соответственно в виде:  и
и .
.
Вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном вращении направление вектора  совпадает с направлением вектора угловой
скорости
совпадает с направлением вектора угловой
скорости ,
а при замедленном – противоположно
ему.
,
а при замедленном – противоположно
ему.
Кинематические
параметры поступательного и вращательного
движения связаны между собой. Связь
скорости  и угловой скорости
и угловой скорости (см. рис. 3) определяется следующим
образом:
(см. рис. 3) определяется следующим
образом: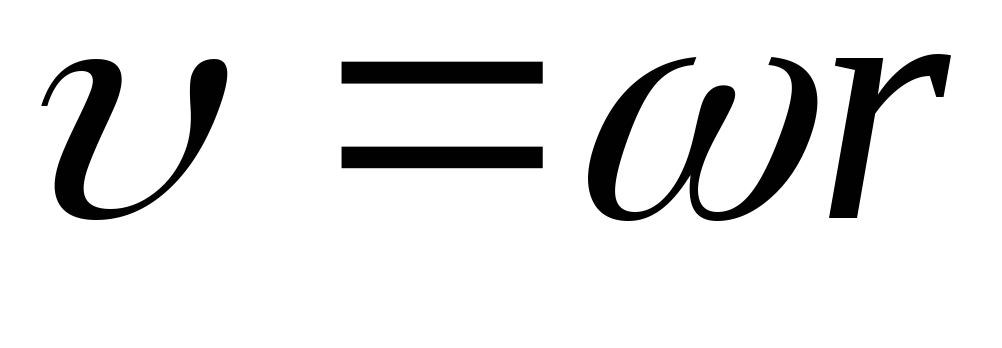 .
.
В векторном виде
эту связь для векторов  и
и можно записать с помощью векторного
произведения:
можно записать с помощью векторного
произведения: .
.
Ускорение а также можно выразить через угловые
параметры, разложив ускорение а на две составляющие  и
и ,
то есть:
,
то есть: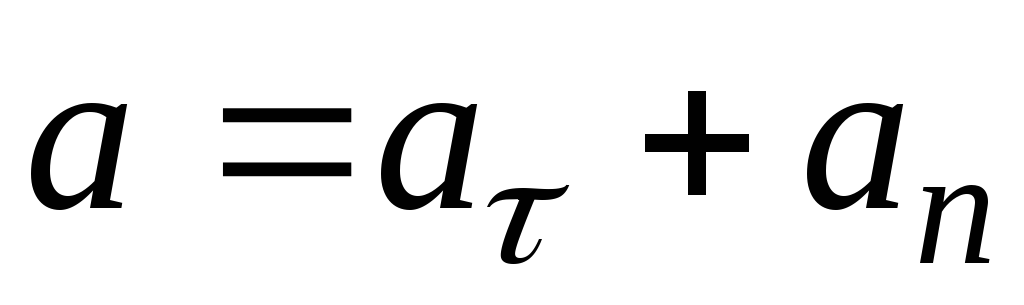 .
.
Тангенциальная
составляющая 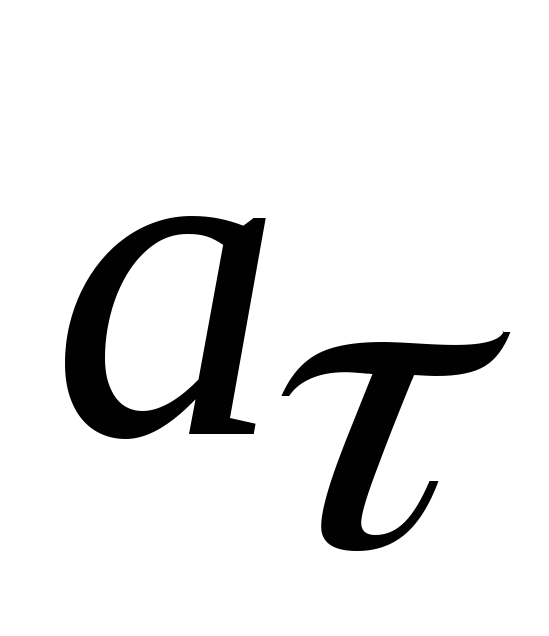 выражается через угловое ускорение
выражается через угловое ускорение :
:
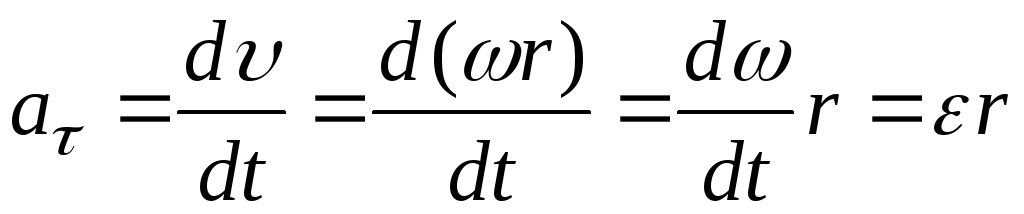 ,
,
а нормальная
составляющая 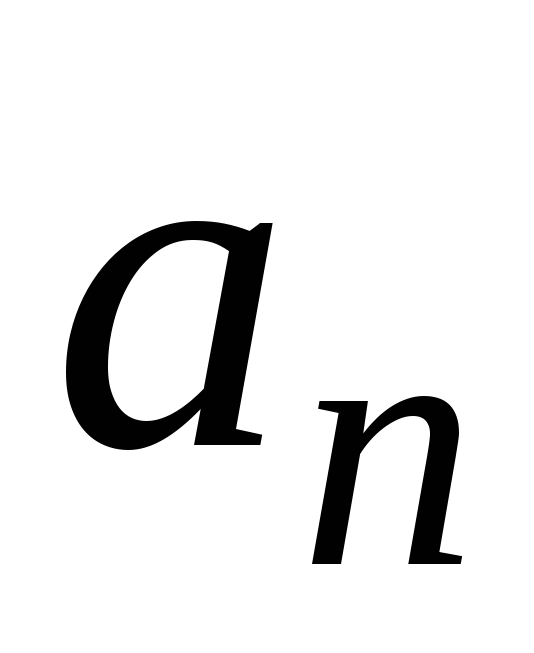 – через угловую скорость
– через угловую скорость :
:
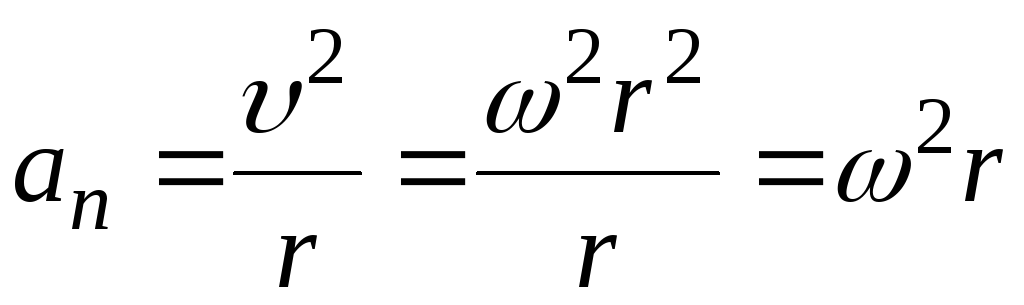 .
.
Тогда ускорение:  .
.
При равномерном
вращении угловая скорость  не изменяется. В этом случае вращение
можно характеризоватьпериодом вращения T , то есть временем, за которое точка
совершает один полный оборот.
не изменяется. В этом случае вращение
можно характеризоватьпериодом вращения T , то есть временем, за которое точка
совершает один полный оборот.
Угловая скорость равномерного вращения связана с периодом вращения:
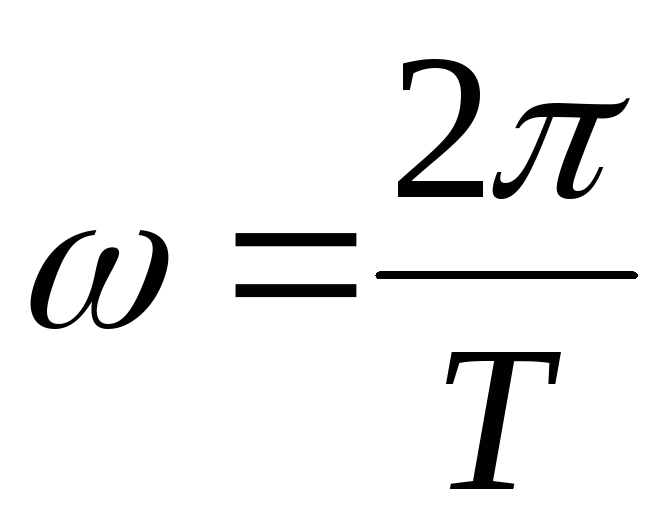 .
.
Частотой вращения n называется число полных оборотов, совершаемых телом в единицу времени. При равномерном вращении:
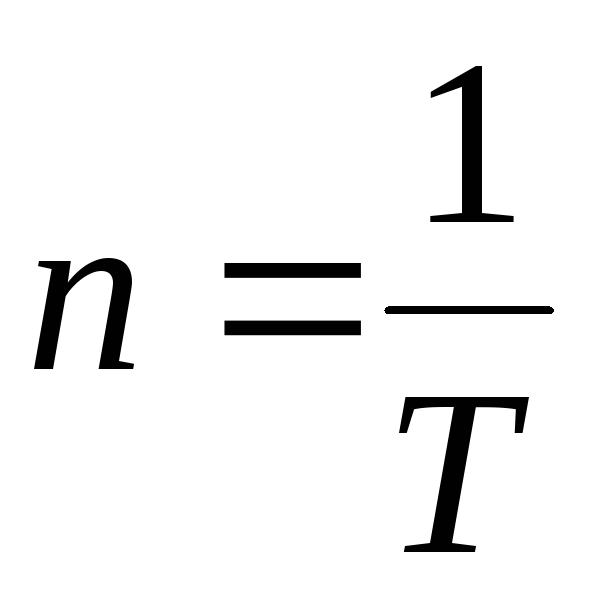 ,
откуда
,
откуда 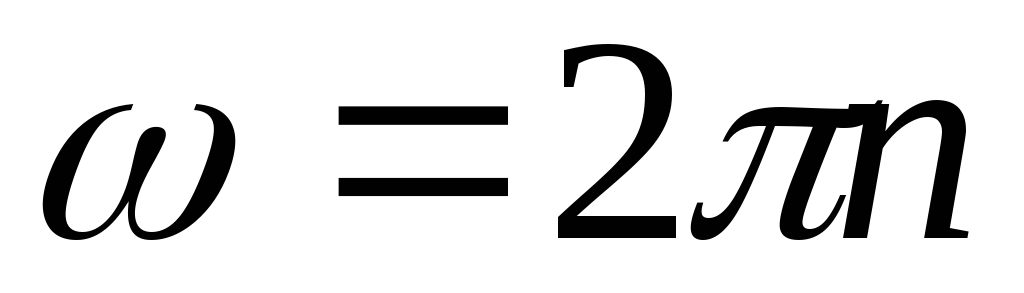 .
.
Тема 2. Динамика поступательного движения. Законы Ньютона
Первый закон Ньютона: существуют такие системы отсчета, в которых всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Такие системы отсчета называются инерциальными.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение тела под действием приложенной к нему силы: если на тело действует сила, то это тело приобретает ускорение, прямо пропорциональное действующей силе и обратно пропорциональное массе данного тела:
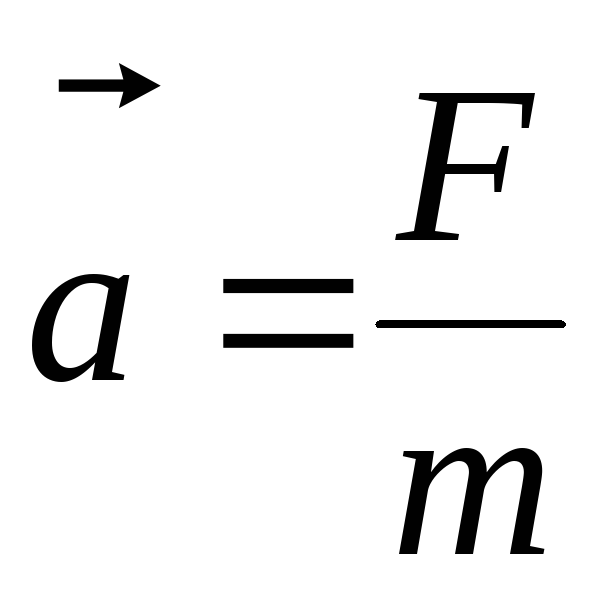 .
.
В том случае, если
на тела действует не одна, а несколько
сил, то приведенная в этой формуле сила  является равнодействующей всех
действующих на это тело сил и определяется
их векторной суммой.
является равнодействующей всех
действующих на это тело сил и определяется
их векторной суммой.
Из уравнения второго закона Ньютона следует:
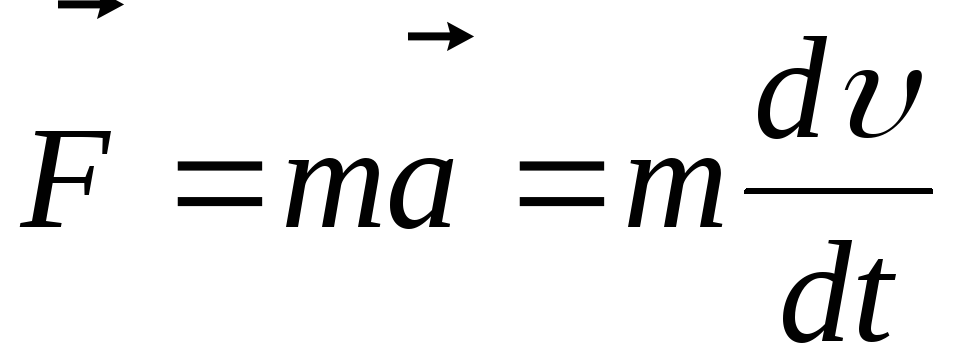 .
.
В случае неизменности массы тела можно записать:
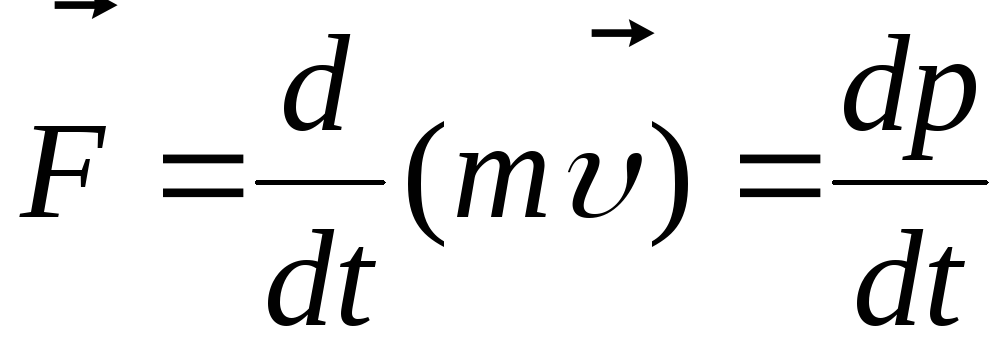 ,
где
,
где 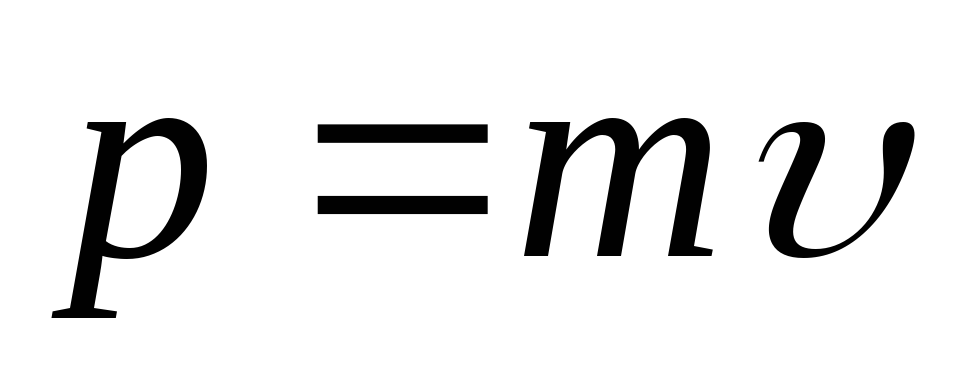 .
.
Вектор 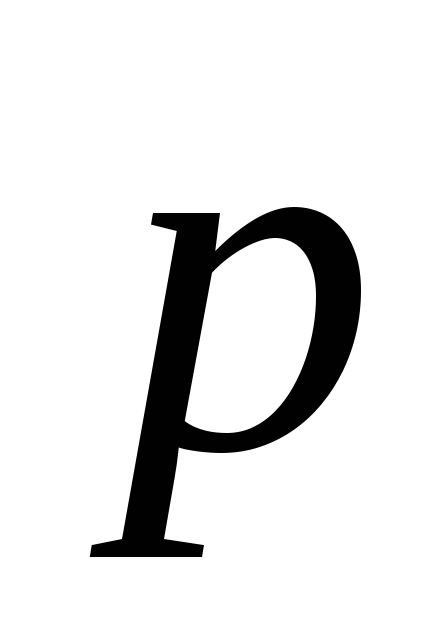 называетсяимпульсом
(или количеством движения) тела.
называетсяимпульсом
(или количеством движения) тела.
Отсюда следует иная формулировка второго закона Ньютона, называемая формулировкой в дифференциальном виде, а именно: скорость изменения импульса тела равна силе, действующей на этр тело, то есть
 .
.
В том случае, если
на тела действует не одна, а несколько
сил, то приведенная в этой формуле сила  является равнодействующей всех
действующих на это тело сил и определяется
их векторной суммой.
является равнодействующей всех
действующих на это тело сил и определяется
их векторной суммой.
Третий закон
Ньютона определяет
взаимодействие между материальными
точками: если
первая материальной точка действует
на вторую с силой  ,
то вторая точка действует на первую с
силой
,
то вторая точка действует на первую с
силой 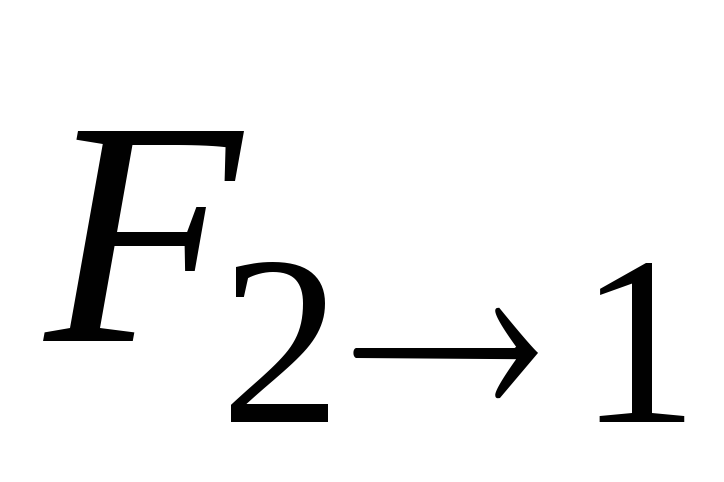 , по
модулю равной, а по направлению
противоположной силе
, по
модулю равной, а по направлению
противоположной силе 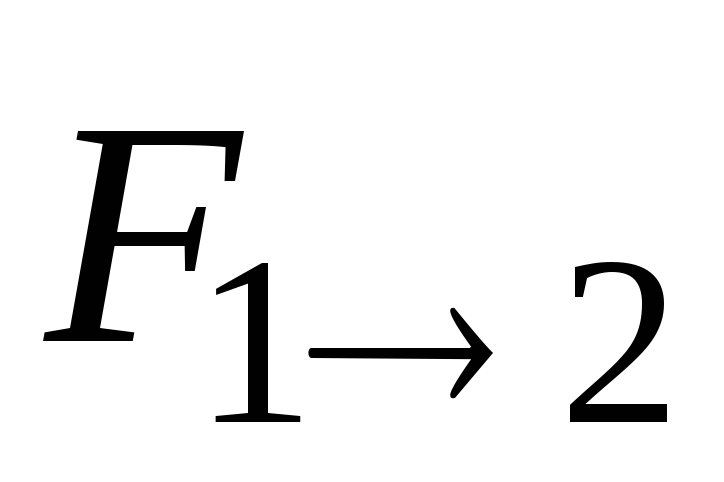 (силы
(силы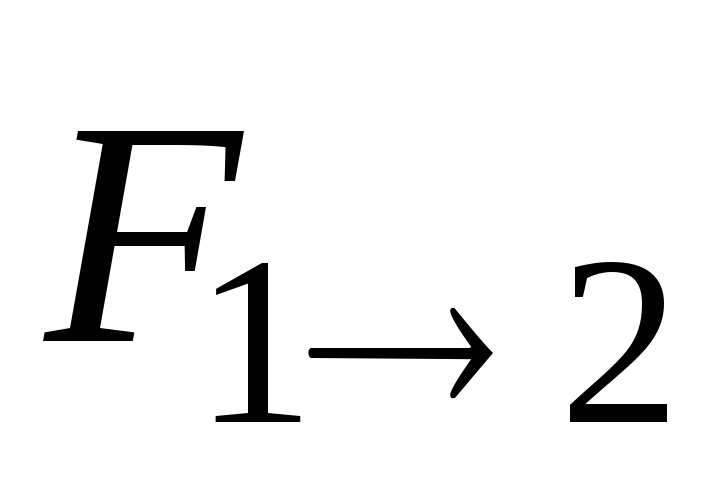 и
и  направлены
по прямой, соединяющей взаимодействующие
точки).
направлены
по прямой, соединяющей взаимодействующие
точки).
Импульс системы
тел. Если
принять, что импульс системы, состоящей
из n тел, можно
определить, как векторную сумму импульсов
всех n тел, то есть  ,
то из третьего закона Ньютона при условии
отсутствия внешних сил (то есть, для
замкнутой системы) следует:
,
то из третьего закона Ньютона при условии
отсутствия внешних сил (то есть, для
замкнутой системы) следует:
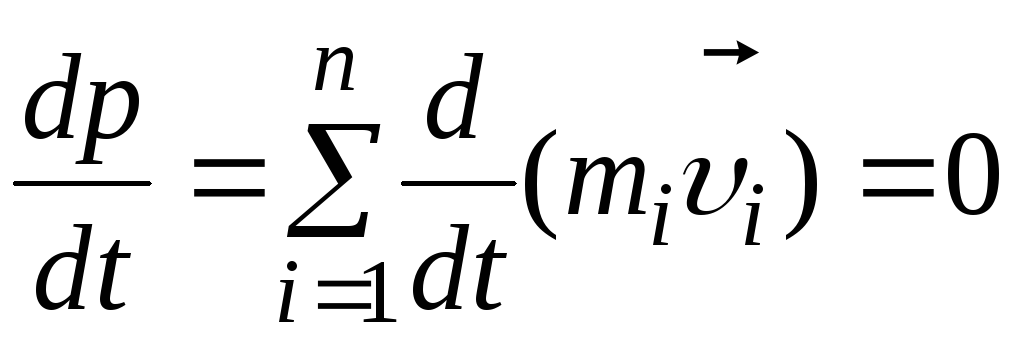 ,
т.е.
,
т.е.  .
.
Таким образом, импульс замкнутой системы тел не изменяется с течением времени, что является законом сохранения импульса.

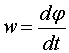
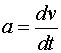
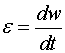
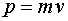

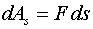
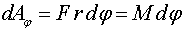
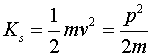

 ,при Fвнеш = 0
,при Fвнеш = 0
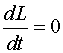 ,
при Mвнеш = 0
,
при Mвнеш = 0