Ромбододекаэдр — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 марта 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 марта 2019; проверки требует 1 правка. Развёртка ромбододекаэдра

Ромбододека́эдр (от «ромб», др.-греч. δώδεκᾰ «двенадцать» и ἕδρα «сиденье») — двенадцатигранник, составленный из одинаковых ромбов. У ромбододекаэдра 14 вершин, 6 из которых являются вершинами меньших углов 4 ромбов, а 8 — вершинами 3 ромбов при их больших углах. Острый угол каждого ромба arccos⁡13≈70,53∘{\displaystyle \arccos {\frac {1}{3}}\approx 70{,}53^{\circ }}, а тупой ≈109,47∘{\displaystyle \approx 109{,}47^{\circ }}. Другими словами: отношение большей диагонали ромба к меньшей равно 2{\displaystyle {\sqrt {2}}}. Одинаковыми ромбододекаэдрами можно заполнить трёхмерное пространство без промежутков и наложений. Взаимное расположение плоскостей граней ромбододекаэдра называется ромбическим (при октаэдрической симметрии) (и также называется положение самих граней). Такое же положение имеют, например, 12 из 18 квадратных граней ромбокубооктаэдра.

Ромбододекаэдр можно собрать из двух равных кубов, разрезав один из них на 6 одинаковых пирамид, квадратные основания которых — 6 граней куба, а вершины совпадают с его центром, и затем приложив эти пирамиды к 6 граням другого куба.

Площадь и объём ромбододекаэдра вычисляется по формулам:

S=82a2≈11,3137085a2{\displaystyle S=8{\sqrt {2}}a^{2}\approx 11{,}3137085a^{2}}

V=1693a3≈3,07920144a3{\displaystyle V={\frac {16}{9}}{\sqrt {3}}a^{3}\approx 3{,}07920144a^{3}}

шар, куб, пирамида, призма, тетраэдр

Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.

Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a³ и S = 6*a², соответственно.

Фигура пирамида

Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a²*h/3 и S = 2*a*√(h²+a²/4) + a², соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a^3*√2/12 и S = √3*a², где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH₄, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма — это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a²*h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r², а объем шара можно вычислить по формуле: V = 4*pi*r³/3, где pi — число пи (3,14), r — радиус сферы (шара).

Как сделать ромб из бумаги (оригами) поэтапно

Распечатать Спасибо, отличный урок +2

В оригами очень часто приходиться сталкиваться с такой базовой фигурой, как ромб. Из него далее можно создать немало интересных поделок, которые вызовут восторг и радость у любого ребенка. К ним относятся верблюд, аист, пальма и т. д.

Так как эта фигура встречается часто, то делать ее безусловно легко и справиться с этим даже дошкольник. Как и для любой поделки вам понадобиться лист бумаги квадратной формы. Для удобства можно взять стикер и первую заготовку сделать именно из него. Повторяйте шаг за шагом и уже на шестом этапе у вас получиться красивый и аккуратный ромб из бумаги в технике оригами.

Необходимые материалы:

• Лист бумаги любого цвета квадратной формы

Поэтапный фото урок:

Берем наш квадратный лист бумаги и помещаем его к нам углом. Берем пальцами за правый боковой уголок и складываем эту сторону на левый бок.

Теперь можно пройтись по сгибу и затем раскрыть заготовку.

Берем за правый нижний угол и сгибаем его прямо к середине, а именно – к центральному сгибу.

Теперь можно согнуть и левый нижний уголок к этому центральному сгибу. Такая фигура является базовой формой в оригами и называют ее «Воздушным змеем». Однако, мы продолжим изготавливать из бумаги ромб. Поэтому перейдем к следующему этапу.

Переворачиваем заготовку и сгибаем поочередно нижние уголки к центру.

Переворачиваем и получаем вот такую замечательную фигуру под названием ромб. Ромб из цветной бумаги в технике оригами готов! Можно его сохранить в качестве заготовки для другой более интересной и сложной поделки.

Узор ромбы спицами — подборка схем и видеоуроков

Сложно назвать хотя бы несколько узоров, которые по популярности могли бы конкурировать с королевской косой или плетенкой. «Ромбы» — приятное исключение. Этот узор вписывается практически в любое изделие, но нужно ответственно подходить к выбору его модификации. В этом материале мы представили для вас самые используемые варианты его выполнения.

Навигация по статье

Схемы

Объемные ромбы

Самый популярный вариант. Используется при вязании почти всех теплых вещей: пуловеров и джемперов, пледов, снудов, кардиганов. Сравнительно прост в выполнении.

Большие объемные ромбы спицами

Раппорт узора обозначен надписью MS и составляет 12 петель. В схеме показаны только лицевые ряды. Изнаночные ряды вяжутся по рисунку.

Схема к первому варианту вязания узора «Ромбы»

Ромбы с дырочками

Отличный вариант для летних вещей. Результат вязания, подобный полотну на фото, можно получить при использовании пряжи из хлопка или вискозы. Дырочки получаются путем выполнения накидов. Этот вариант вязания ромбов потребует значительно больше терпения, чем предыдущий.

Узор «Ромбы» с дырочками

Раппорт узора — 24 петли. В схеме показаны только лицевые ряды. Изнаночные ряды вяжутся по рисунку.

Схема к узору «Ромбы» с дырочками

Рельефные ромбы

Раппорт узора — 10 петель. Рельефные ромбы получаются путем комбинирования лицевых и изнаночных петель. В данном варианте узора не требуется дополнительная спица — все предельно просто.

На схеме указаны только лицевые ряды. Изнаночные (четные) ряды всегда вяжутся по рисунку.

Рельефные ромбы, связанные спицами

Схема вязания рельефных ромбов

Видеоуроки

Малые ромбы

Один из вариантов вязания узора «Ромбы» спицами. За счет сравнительно небольшого размера подойдет для детских вещей, на которых просто нет места для более крупного узора. Будет хорошо смотреться на джемперах, шарфах и любых других зимних вещах.

Большие ромбы

Крупный узор, использующийся преимущественно в вещах для взрослых. Например, при вязании мужских пуловеров. Может использоваться как вставка в детских вещах, иногда встречается в схемах вязания кардиганов и даже пледов. При выборе тонкой пряжи размеры ромбов значительно уменьшаются, что дает рукодельницам более широкий спектр вариантов использования.

Необычные ромбы

Вариант узора «Ромбы» спицами, не имеющий ничего общего с объемными узорами. Ромбы получаются путем своеобразного комбинирования лицевых и изнаночных петель. Полотно получается не только оригинальным, но и невероятно теплым. Размер самих ромбов может быть увеличен за счет добавления дополнительных петель в каждый мотив.

Развёртки геометрических фигур

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура – ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

Золотой ромб — Википедия

Материал из Википедии — свободной энциклопедии

Золото́й ромб — ромб, чьи диагонали относятся друг к другу как φ{\displaystyle \varphi }, где φ≈1,618{\displaystyle \varphi \approx 1,618} (золотое сечение).

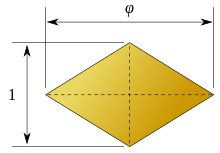
Углы золотого ромба равны:

• Острые углы: 2arctan⁡1φ=arctan⁡2≈63,43495{\displaystyle 2\arctan {\frac {1}{\varphi }}=\arctan 2\approx 63,43495}°
• Тупые углы: 2arctan⁡φ=arctan⁡1+arctan⁡3≈116,56505{\displaystyle 2\arctan \varphi =\arctan 1+\arctan 3\approx 116,56505}°, которые совпадают с двугранным углом додекаэдра.

Отношение стороны золотого ромба к его короткой диагонали равно 121+φ2=1410+25≈0.95106{\displaystyle {\frac {1}{2}}{\sqrt {1+\varphi ^{2}}}={\frac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}\approx 0.95106}.

Длины диагоналей золотого ромба с длиной стороной 1 равны:

p=2+2510+25≈1.70130{\displaystyle p={\frac {2+2{\sqrt {5}}}{\sqrt {10+2{\sqrt {5}}}}}\approx 1.70130}

q=410+25≈1.05146{\displaystyle q={\frac {4}{\sqrt {10+2{\sqrt {5}}}}}\approx 1.05146}

Радиус вписанной окружности золотого ромба равен pφ2(5+5){\displaystyle {\frac {p\varphi }{\sqrt {2(5+{\sqrt {5}})}}}}.

Площадь золотого ромба равна p21+5{\displaystyle {\frac {p^{2}}{1+{\sqrt {5}}}}}.^[1]

Золотой прямоугольник может быть описан вокруг золотого ромба

1. ↑ Weisstein, Eric W. Golden Rhombus (англ.). mathworld.wolfram.com. Дата обращения 29 декабря 2016.

Плетением «двойной ромб»: особенности плетения

Изделия из золота имеют очень большую популярность. Такие украшения любят и мужчины, и женщины, и юные, и зрелые. Почти на каждом можно увидеть цепочку, у которой узоры бывают очень разнообразными. Одним из самых популярных считается плетение «двойной ромб». Оно представляет собой ромбы, которые сделанные с острыми углами и переплетены в два слоя. За счет этого изделие получается более прочным.

Технология изготовления

Методика изготовления таких цепочек довольно простая. Из металла отливают небольшие ромбики, после чего их соединяют и спаивают. После этих процедур получается очень красивое плетение, оно легкое в исполнение, но в то же время выглядит очень богато и нарядно. Если рассматривать предпочтения людей, то дамы выбирают золотую цепочку с двойным ромбом в более упрощенном варианте. Она должна быть не слишком толстой и тяжелой. Мужчины же, наоборот, хотят цепочку потяжелее и, возможно, даже с тройным переплетением ромбов. Их делают более широкими, чтобы изделие выглядело массивнее.

Виды двойного ромба

В продаже готовое изделие из золота или серебра можно увидеть в нескольких вариантах:

1. Ромб с закругленными углами. Двойное плетение больше напоминает цветочную композицию.
2. Перевернутый квадрат. Это изделие имеет большой объем и выглядит тяжелее.
3. Традиционный ромб. Он слегка вытянут. Этот вариант самый распространенный.

Отличительные признаки

Цепочки из золота, которые имеют простое плетение из ромбов, в основном изготавливают при помощи станка, а двойной ромб можно сделать только при помощи специальной машины. Основа плетения состоит в том, что в два кольца добавляется третье, после чего узор получается объемным и отличительным от других. После сбора всех ромбов цепочку отправляют под пресс, где она приобретает плоскую форму и все части выравниваются и получаются одинаковыми.

Но на этом процесс изготовления цепочки не заканчивается. Сплюснутые грани колец, которые находятся на самом краю, дополняют некими надрезами, а для того, чтобы изделие имело законченный вид, ювелиру предстоит еще ручная филировка. После чего украшение покрывают гальваническим составом. Он представляет собой сплав золота с другими добавками.

В основном, чтобы сделать украшение с плетением «двойной ромб», берут золото 585 пробы, а серебро 925 или же позолоченное серебро. А чтобы с него не так быстро стерся гальванический слой, серебро нужно обязательно покрывать золотым сплавом.

Дополнительные аксессуары

Если вы зашли в ювелирный магазин, то вы должны заметить в продаже наборы, которые представляют собой некую композицию из различных аксессуаров. Их можно подбирать под различный наряд, а если будет небольшая подвеска с красивым кулоном, которая зачастую идет в паре с серьгами и браслетом, то такой наборчик будет отличным дополнением к вечернему платью. Цепочку с плетением «двойной ромб» могут дополнять такие украшения:

1. Подвеска, которая имеет не очень большую длину.
2. Кулон, который сочетается с большим камнем.
3. Кулоны, на другой стороне которых имеются именные надписи.
4. Узоры или же орнаменты, которые могут быть представлены в виде длинных подвесок.

В основном самыми эффектными считаются изделия, изготовленные из золота, но они могут быть и из другого материала. Золотая цепочка с плетением «двойной ромб» выглядит очень прочно, а если изделие из серебра, то красив будет и одинарный вариант.

Плюсы изделия

У изделия плетения «двойной ромб» есть несколько положительных моментов, о которых сейчас и пойдет речь.

1. Прочность. Эти цепочки или браслеты не так легко порвать, именно поэтому плетение предпочитает большинство покупателей.
2. Много вариаций изделия. У такого вида плетения достаточно много техник и видов, поэтому выбор таких изделий достаточно велик. Каждый человек может выбрать себе изделие по вкусу.
3. Универсальность. Изделия с плетением «двойной ромб» могут подходить под любой стиль и образ, они будут красиво смотреться с праздничной одеждой и со строгим офисным костюмом.

Отзывы

Изделия из золота любят очень многие люди. Предпочтения у всех самые разные — так же, как и отзывы. Если же говорить именно о плетении «двойной ромб», то о нем в основном отзывы положительные. Объемный рисунок, который создают ромбы, не оставит никого равнодушным. Еще одни существенный плюс украшений — многообразие вариантов плетения. Ювелир может создать и строгую классическую, и нарядную, экстравагантную вещь.

О цепочках, также как и о браслетах, в основном, говорят, что они на теле выглядят очень красиво. Многие называют это плетение классическим: именно оно никогда не выйдет из моды и будет всегда на пике популярности.

Отмечают покупатели и то, что прочность изделия очень велика. Также оно очень удобное, не царапает и не создает никакого дискомфорта коже. Если вам сказали, что с таким плетение бывают только мужские цепочки из золота, знайте, что выбор зависит только от вашего предпочтения. Разные люди могут ходить с таким изделием, так как они подходят абсолютно всем.