Область определения прямой функции: Как найти область определения функции?

Posted on by alexxlab
Линейная функция — область определения и значения. Свойства, примеры и график

Функцию, которую можно задать формулой вида y = kx + b, где  k и b — некоторые числа, х — независимая переменная, называют линейной. Рассмотрим несколько примеров.

В бассейне было 200 л. воды. В течении t мин. в бассейн каждую минуту поступало 80 л. воды. Тогда объем V воды в бассейне вычисляется по формуле: V = 80t + 200, где t ≥ 0. Эта формула задает функциональную зависимость переменной V от переменной t.

Первая бригада собрала 25 ящиков яблок; каждый рабочий второй бригады собрал по 2 ящика. Пусть во второй бригаде было х рабочих. Обозначим число всех ящиков, собранных двумя бригадами, буквой y. Тогда зависимость переменной y от переменной х выражается формулой y = 2x + 25, где х — натуральное число. Важно заметить, что областью определения линейной функции являются все действительные числа.

Содержание

График линейной функции

Построим график функции y = -2x + 1.

Первым делом составим таблицу значений этой функции для некоторых значений аргумента.

  х  -3  -2  -1  0  1  2  3
  y  7  5  3  1  -1  -3  -5

Точки А(-3;7), В(-2;5), С(-1;3), Е(0;1), Т(1;-1), М(2;-3), К(3;-5) принадлежат искомому графику.

Все эти точки лежат на одной прямой, которая и является графиком функции y = -2x + 1.

Заметим, что вертикальная прямая, т. е. прямая перпендикулярная оси абсцисс не может служить графиком функции. Поскольку прямая однозначно задается любыми двумя своими точками, то то для построения графика линейной функции достаточно выбрать два произвольных значения аргумента и составить таблицу значений функции, имеющую лишь два столбца.  Рассмотрим пример.

Построим график функции y = — 3x + 2, составим таблицу значений данной функции для двух произвольных значений аргумента.

  х  0  1
  y  2  -1

Отметим на координатной плоскости точки (0;2) и (1;-1) и проведём через них прямую линию.

Эта прямая является графиком линейной функции y = — 3x + 2.

В формуле y = kx + b, задающей линейную функцию, не исключены случаи, когда k = 0 или b = 0. Рассмотрим случай, когда b = 0 и k ≠ 0. Тогда формула приобретает вид y = kx. Отсюда для всех не равных нулю значений аргумента можно записать, что y/x = k. Эта формула показывает, что для функции 

y = kx при x ≠ 0 отношение соответствующих значений зависимой и независимой переменных остается постоянным и равно k. Такую зависимость называют прямой прямой пропорциональностью. Поэтому линейную функцию, которую задают формулой y = kx, где k ≠ 0, называют прямой пропорциональностью.                 Функции y = 2x, y = x, y = — x, y = —1/3x — примеры прямых пропорциональностей. Поскольку прямая пропорциональность — частный случай линейной функции, то её график — прямая. Особенностью является то, что эта прямая при любом значении k проходит через точку О(0;0). Действительно, если в формуле y = kx предположить что x = 0, то получим y = 0. Поэтому для построения графика прямой пропорциональности достаточно указать какую-нибудь точку графика, отличающуюся от начала координат, и провести прямую через эту точку и начало координат О(0;0). Для примера изобразим графики прямых пропорциональностей которые приводились выше.

Рассмотрим еще один частный случай линейной функции. В формуле y = kx + b предположим k = 0. Получим y = b. Ясно, что в этом случае значения функции будут оставаться неизменными при любых изменениях значений аргумента. Рассмотрим пример, построим график функции y = 2. Как и для построения графика любой линейной функции, нужно знать две принадлежащие ему точки. Эти точки будут иметь одинаковые ординаты, равные 2. Их абсциссы выберем произвольно, например равные -2 и 0. Остается провести прямую через точки А(-2;2) и В(0;2), эта прямая будет параллельна оси абсцисс.

Важно, графиком функции y = 0 является ось абсцисс. Графиком функции y = b, где b ≠ 0, является прямая, параллельная оси абсцисс.

Рассмотрим пример, задайте формулой линейную функцию, график которой изображен на рисунке ниже.

График данной функции пересекает ось ординат в точке (0;4). Подставив координаты этой точки в формулу y = kx + b, получаем 4 = k0 + b, откуда b = 4. Так как данный график пересекает ось абсцисс в точке (3;0), то подставив её координаты в формулу y = kx + 4, получим: 3k + 4 = 0, k = —4/3. в ответе получаем уравнение y = -4/3x + 4.

 

Автор публикации

не в сети 1 неделя

Юрий

0 Комментарии: 3Публикации: 87Регистрация: 04-09-2015

Область определения функции | Онлайн калькулятор

Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.

Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.

Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)

3.1.1 Функция, область определения функции

Видеоурок: Функция. Область определения и область значений функции

Лекция: Функция, область определения функции

Функция — это некая модель, которая описывает зависимость независимой величины «х» от «у». «х» — это произвольная величина, которая еще называется аргументом, переменной, которая влияет на значение функции «у».

Функция обозначается следующим образом: y = f(x).

Значения, которые может принимать аргумент для конкретной функции, называются областью определения функции (D(f)). 

То есть на конкретном промежутке функция может существовать. Значения, которые может принимать функция для конкретной области определения, называются областью значения функции (E(f)). То есть, иными слова, D(f) — это значение аргумента, а E(f) — значение функции.

Графиком любой функции называется множество точек на координатной плоскости, которые соответствуют функциональной зависимости.

 

Обратите внимание, функцией и графиком функции называется только та зависимость, в которой одному значению аргумента соответствует единственное значение функции.

Область определения функции зависит от знаний свойств функций.

Например, областью значения выражения, стоящего под знаком корня, не может быть отрицательным, а значение выражения, которое стоит в знаменателе, не может равняться нулю.

Рассмотрим область определения функции на конкретных примерах:

1. Функция: 

Данная функция называется гиперболой.

Данная функция существует при всех «х», кроме х = 0, значит, D(f) = (-∞; 0) и (0; ∞).

2. Функция:


 

Данная функция называется параболой.

Данная функция существует при всех «х», значит, D(f) = (-∞; ∞).

3. Функция:

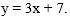
Данная функция называется линейной.

Данная функция существует при всех «х», значит, D(f) = (-∞; ∞).

4. Функция

 

Данная функция имеет вид ветви параболы.

Данная функция существует при неотрицательных «х», значит, D(f) = [0; ∞).

Область определения функции — Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Определение

Если на множестве X {\displaystyle X} задана функция, которая отображает множество X {\displaystyle X} в другое множество, то множество X {\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f\colon X\to Y} , то

  • множество X {\displaystyle X} называется областью определения[1] или областью задания[2] функции f {\displaystyle f} и обозначается D ( f ) {\displaystyle D(f)} или d o m f {\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматривают функции, определенные на подмножестве D {\displaystyle D} некоторого множества X {\displaystyle X} . В этом случае множество X {\displaystyle X} иногда называют областью отправления функции f {\displaystyle f} [3].

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

  • вещественнозначные функции вещественного переменного — это функции вида f : R → R {\displaystyle f\colon \mathbb {R} \to \mathbb {R} } ;
  • а также комплекснозначные функции комплексного переменного вида f : C → C {\displaystyle f\colon \mathbb {C} \to \mathbb {C} } ,

где R {\displaystyle \mathbb {R} } и C {\displaystyle \mathbb {C} }  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f ( x ) = x {\displaystyle f(x)=x} совпадает с областью отправления ( R {\displaystyle \mathbb {R} } или C {\displaystyle \mathbb {C} } ).

Гармоническая функция

Область определения функции f ( x ) = 1 / x {\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:

d o m f = C ∖ { 0 } {\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}} ,

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции

Область определения функции вида

f ( x ) = a 0 + a 1 x + ⋯ + a m x m b 0 + b 1 x + ⋯ + b n x n {\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b 0 + b 1 x + ⋯ + b n x n = 0 {\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0} .

Эти точки называются полюсами функции f {\displaystyle f} .

Так, например, f ( x ) = 2 x x 2 − 4 {\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x 2 − 4 ≠ 0 {\displaystyle x^{2}-4\neq 0} . Таким образом d o m f {\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F = { f ∣ f : X → R } {\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}}  — семейство отображений из множества X {\displaystyle X} в множество R {\displaystyle \mathbb {R} } . Тогда можно определить отображение вида F : F → R {\displaystyle F\colon \mathbb {F} \to \mathbb {R} } . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x 0 ∈   X {\displaystyle x_{0}\in ~X} , то можно определить функцию F ( f ) = f ( x 0 ) {\displaystyle F(f)=f(x_{0})} , которая принимает в «точке» f {\displaystyle f} то же значение, что и сама функция f {\displaystyle f} в точке x 0 {\displaystyle x_{0}} .

См. также

Примечания

Литература

  • Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
  • Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
  • И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
  • А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
  • Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
  • В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
  • Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65 — 69. — 528 с.
  • А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — Вып. 1. — С. 27-36. — ISSN 0130-2221.

Область определения функции — Википедия

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Определение

Если на множестве X {\displaystyle X} задана функция, которая отображает множество X {\displaystyle X} в другое множество, то множество X {\displaystyle X} называется областью определения или областью задания функции.

Более формально, если задана функция f {\displaystyle f} , которая отображает множество X {\displaystyle X} в Y {\displaystyle Y} , то есть: f : X → Y {\displaystyle f\colon X\to Y} , то

  • множество X {\displaystyle X} называется областью определения[1] или областью задания[2] функции f {\displaystyle f} и обозначается D ( f ) {\displaystyle D(f)} или d o m f {\displaystyle \mathrm {dom} \,f} (от англ. domain — «область»).

Иногда рассматривают функции, определенные на подмножестве D {\displaystyle D} некоторого множества X {\displaystyle X} . В этом случае множество X {\displaystyle X} иногда называют областью отправления функции f {\displaystyle f} [3].

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

  • вещественнозначные функции вещественного переменного — это функции вида f : R → R {\displaystyle f\colon \mathbb {R} \to \mathbb {R} } ;
  • а также комплекснозначные функции комплексного переменного вида f : C → C {\displaystyle f\colon \mathbb {C} \to \mathbb {C} } ,

где R {\displaystyle \mathbb {R} } и C {\displaystyle \mathbb {C} }  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции f ( x ) = x {\displaystyle f(x)=x} совпадает с областью отправления ( R {\displaystyle \mathbb {R} } или C {\displaystyle \mathbb {C} } ).

Гармоническая функция

Область определения функции f ( x ) = 1 / x {\displaystyle f(x)=1/x} представляет собой комплексную плоскость без нуля:

d o m f = C ∖ { 0 } {\displaystyle \mathrm {dom} \,f=\mathbb {C} \setminus \{0\}} ,

поскольку формула не задаёт значение функции в нуле каким-нибудь числом, что требуется в формулировке понятия функции. Область отправления представляет собой всю комплексную плоскость.

Дробно-рациональные функции

Область определения функции вида

f ( x ) = a 0 + a 1 x + ⋯ + a m x m b 0 + b 1 x + ⋯ + b n x n {\displaystyle f(x)={\frac {a_{0}+a_{1}x+\dots +a_{m}x^{m}}{b_{0}+b_{1}x+\dots +b_{n}x^{n}}}}

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

b 0 + b 1 x + ⋯ + b n x n = 0 {\displaystyle b_{0}+b_{1}x+\dots +b_{n}x^{n}=0} .

Эти точки называются полюсами функции f {\displaystyle f} .

Так, например, f ( x ) = 2 x x 2 − 4 {\displaystyle f(x)={\frac {2x}{x^{2}-4}}} определен на всех точках, где знаменатель не обращается в ноль, то есть, где x 2 − 4 ≠ 0 {\displaystyle x^{2}-4\neq 0} . Таким образом d o m f {\displaystyle \mathrm {dom} \,f} является множеством всех действительных (или комплексных) чисел кроме 2 и -2.

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть F = { f ∣ f : X → R } {\displaystyle \mathbb {F} =\{f\mid f\colon X\to \mathbb {R} \}}  — семейство отображений из множества X {\displaystyle X} в множество R {\displaystyle \mathbb {R} } . Тогда можно определить отображение вида F : F → R {\displaystyle F\colon \mathbb {F} \to \mathbb {R} } . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку x 0 ∈   X {\displaystyle x_{0}\in ~X} , то можно определить функцию F ( f ) = f ( x 0 ) {\displaystyle F(f)=f(x_{0})} , которая принимает в «точке» f {\displaystyle f} то же значение, что и сама функция f {\displaystyle f} в точке x 0 {\displaystyle x_{0}} .

См. также

Примечания

Литература

  • Функция, математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
  • Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
  • И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
  • А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
  • Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
  • В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
  • Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 65 — 69. — 528 с.
  • А. Н. Колмогоров. «Что такое функция» // «Квант». — М.: «Наука», 1970. — Вып. 1. — С. 27-36. — ISSN 0130-2221.
Понятие функции. Область определения функции. Способы задания функции (стр. 1 из 2)

ИНСТИТУТ БИЗНЕСА, ПРАВА И ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИЙ

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

МАТЕМАТИКА

на тему

Понятие функции. Область определения функции.

Способы задания функции

Выполнил: Мальский Эдуард Александрович,

студент 2 курса

юридического факультета

заочного отделения

группа 25-ЮЗП

Преподаватель:

Оценка:_______________

Подпись преподавателя:_______________

2004 г.

Оглавление

контрольной работы по дисциплине «Математика»

на тему «Понятие функции. Область определения функции.

Способы задания функции»

Введение……………………………………………………………………………3

1. Функция и её свойства……………………………………………………..4

2. Способы задания функции…………………………………………………..5

3. Виды функций и их свойства………………………………………………6

Заключение……………………………………………………………………….11

Список использованной литературы……………………………………………12

Введение.

Функция — одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции — теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Раздел 1. Функция и её свойства.

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у, соответствующее заданному значению х.

Область определения функции- все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)

Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)

Возрастающая функция- если для любых х1и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)

Убывающая функция- если для любых х1и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)

Раздел 2. Способы задания функции.

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)- с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Раздел 2. Виды функций и их свойства.

1) Постоянная функция- функция, заданная формулой у=b, где b—некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число kназывается коэффициентом пропорциональности.

Cвойства функции y=kx:

1. Область определения функции- множество всех действительных чисел

2. y=kx — нечетная функция

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

3)Линейная функция- функция, которая задана формулой y=kx+b, где kиb—действительные числа. Если в частности,

k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.

Свойства функции y=kx+b:

1. Область определения- множество всех действительных чисел

2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.

3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой

Графиком функции является прямая.

4)Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности.

Свойства функции y=k/x:

1. Область определения- множество всех действительных чисел кроме нуля

2. y=k/x— нечетная функция

3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).

Графиком функции является гипербола.

5)Функция y=x2

Свойства функции y=x2:

1. Область определения- вся числовая прямая

2. y=x2— четная функция

3. На промежутке [0;+¥) функция возрастает

4. На промежутке (-¥;0] функция убывает

Графиком функции является парабола.

6)Функция y=x3

Свойства функции y=x3:

1. Область определения- вся числовая прямая

2. y=x3—нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой y=xn, где n— натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x

2; y=x3. Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8… В этом случае функция y=xnобладает теми же свойствами, что и функция y=x2. График функции напоминает параболу y=x2, только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем “теснее прижимаются” к оси Х, чем больше n.

Пусть n- произвольное нечетное число, большее трех: 5,7,9… В этом случае функция y=xnобладает теми же свойствами, что и функция y=x3. График функции напоминает кубическую параболу.

8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y=x—n, где n— натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.

Пусть n- нечетное число, большее единицы: 3,5,7… В этом случае функция y=x—nобладает в основном теми же свойствами, что и функция y=1/х.

Пусть n- четное число, например n=2.

Свойства функции y=x-2:

1. Функция определена при всех x¹0

2. y=x-2 — четная функция

3. Функция убывает на (0;+¥) и возрастает на (-¥;0).

Теми же свойствами обладают любые функции при четном n, большем двух.

9)Функция y=Öх

Свойства функции y=Öх:

1. Область определения — луч [0;+¥).

2. Функция y=Öх — общего вида

3. Функция возрастает на луче [0;+¥).

10)Функция y=3Öх

Свойства функции y=3Öх:

1. Область определения- вся числовая прямая

2. Функция y=3Öх нечетна.

3. Функция возрастает на всей числовой прямой.

11)Функция y=nÖх

При четном n функция обладает теми же свойствами, что и функция y=Öх. При нечетном n функция y=nÖх обладает теми же свойствами, что и функция y=3Öх.

12)Степенная функция с положительным дробным показателем- функция, заданная формулой y=xr, где r— положительная несократимая дробь.

Свойства функции y=xr:

1. Область определения- луч [0;+¥).

2. Функция общего вида

3. Функция возрастает на [0;+¥).

На рисунке изображен график функции y=x5/2. Он заключен между графиками функций y=x2 и y=x3, заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y=xr, где r>1.

На рисунке изображен график функции y=x2/3. Подобный вид имеет график любой степенной функции y=xr , где 0<r<1

13)Степенная функция с отрицательным дробным показателем-функция, заданная формулой y=x—r, где r— положительная несократимая дробь.

Свойства функции y=x—r:

1. Обл. определения -промежуток (0;+¥)

2. Функция общего вида

3. Функция убывает на (0;+¥)

14)Обратная функция

Если функция y=f(x) такова, что для любого ее значения yo уравнениеf(x)=yo имеет относительно х единственный корень, то говорят, что функция fобратима.

Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.

Область значений функции


Всем здравствуйте! Тренируемся находить область значений функции! Кто еще не понял, что такое область определения (а она нам тоже понадобится непременно), тому сюда.

Что же такое область значений функции? Это та “часть” оси ординат, та область, где можно наткнуться на какие-либо точки, принадлежащие функции. То есть можно сказать, что если область значений найдена, то все точки функции находятся в ней, не выше и не ниже. Это почти тоже самое, что и область определения, только теперь это “область определения по оси ординат”. Здесь никаких особых ограничений нет, поэтому, чтобы найти область значений, нужно иметь представление об элементарных функциях – например, как выглядят парабола или гипербола, как определить, направлены ли ветви параболы вверх или вниз и т.п. Все это рассказано и показано здесь.

Ну, поехали!

Примеры.

1. Найдите область значений функции

Решение: функция – квадратичная, представляет собой параболу с положительным старшим коэффициентом, ветви направлены вверх. Понятно тогда, что весь график располагается выше координаты своей вершины (вершина – самая низшая точка). Ордината вершины: , тогда .

 

2. Найдите область значений функции

Решение: область определения функции ( ] [).

В точках (-7) и (3) двучлен обращается в ноль. Поскольку результат извлечения корня – величина положительная, то вся функция располагается выше оси абсцисс, и ее область значений [)

 

3. Найти область значений функции

Область определения – вся числовая ось, кроме ноля. Можем подставить любое число из области определения, при этом функция всегда отрицательна.

Из графика также видно, что

4. Найти область значений функции:

Решение. Область определения:


На концах отрезка функция принимает значение 1, под корнем имеем квадратный двучлен, наибольшее значение он принимает в вершине, при , значит, функция будет принимать в этой точке наименьшее значение.

Подставив 1, получаем

Ответ:

5. Найдите область значений функции:

Очевидно, что график данной функции может быть получен из графика обычной параболы , область значений которой легко найти: ветви направлены вверх, поэтому низшая точка – вершина параболы. Однако заметим также, что если аргумент функции под знаком модуля, то график такой функции может быть построен с помощью отражения части  графика, лежащей в правой вертикальной полуплоскости, в левую полуплоскость(см. рисунок). Тогда от нашей параболы останется только часть, лежащая правее оси ординат, и именно она будет отражена относительно оси y, и тогда низшей точкой окажется та, в которой график пересечет ось ординат, а это – значение свободного члена (коэффициента с), который у нас равен (-6).

Область значений нашей функции [)

6. Найдите область значений функции:

Очевидно, что график данной функции может быть получен из графика обычной параболы . Так как все выражение находится под знаком модуля, то для  того, чтобы построить такой график, нужно отразить всю часть графика, расположенную ниже оси х, вверх, поэтому [).

 

 

 

 

 

 

 

7. Найдите область значений функции:

Данная функция получена преобразованием обычной гиперболы. Данная функция не существует при , или .  При  второе слагаемое обращается в ноль, и функция стремится к  значению , причем можно заметить, что при положительных больших значениях х данная функция приближается к 2 снизу, а при отрицательных  – сверху.

Ответ:

 

8. Найти область значений функции:

Решение. Область определения:

При  функция принимает наибольшее значение ,

При x, стремящемся к бесконечности, функция стремится к нулю. Но мы запишем область значений от меньшего к большему:

Ответ: (]


прямая функция | Документация R

Прямые оценки.

Эта функция вычисляет прямые оценки средних по домену.

Ключевые слова
метод
Использование 
  прямой (y, dom, sweight, domsize, data, replace = FALSE)
Аргументы
и

вектор, указывающий отдельные значения переменной, для которой мы хотим оценить доменное значение.

дом

вектор или коэффициент (такого же размера, как и ) с кодами доменов.

Sweight

необязательный вектор (такого же размера, как и ) с весами выборки. Когда этот аргумент не включен, по умолчанию оценщики получены при простой случайной выборке (SRS).

Доминик

D * 2 фрейм данных с кодами доменов в первом столбце и соответствующими размерами совокупности доменов во втором столбце.Этот аргумент не требуется, если Sweight не включен и replace = TRUE (SRS с заменой).

данных

необязательный фрейм данных, содержащий переменные, названные y , dom и sweight . По умолчанию переменные берутся из среды, из которой вызывается прямой .

заменяет
Логическая переменная

со значением по умолчанию ЛОЖЬ для случайной выборки без замены в каждом домене. и ИСТИНА для случайной выборки с заменой в каждом домене.

Значение

Функция возвращает фрейм данных размером D * 5 со следующими столбцами:

Домен
Доменные коды

в порядке возрастания.

SampSize

доменных размеров.

Прямая

Прямые оценки доменных средних переменных и .

SD

оцененные стандартные отклонения прямых оценок доменов.Если дизайн выборки — выборка SRS или Пуассона, оценочные отклонения несмещены. В противном случае оцениваемые дисперсии получаются в приближении, согласно которому вероятности включения второго порядка являются произведением вероятностей включения первого порядка.

CV

абсолютное значение процентных коэффициентов вариации прямых оценок доменов.

Случаи со значениями NA в y, dom или sweight игнорируются. %% …

Отзывы

— Cochran, W.Г. (1977). Методы отбора проб. Вилли, Нью-Йорк.

— Рао, J.N.K. (2003). Оценка малых площадей. Вилли, Лондон.

— Sarndal C.E., Swensson B. and Wretman J. (1992). Выборочный опрос с помощью модели. Springer-Verlag.

См. Также

pssynt для постстратифицированной синтетической оценки, ssd для зависимой от размера выборки оценки.

В случае, если дизайн выборки известен, см. Пакеты опрос или выборка для более точной оценки дисперсии.

Псевдонимы
Примеры 
  # НЕ РАБОТАЕТ {
# Загрузка набора данных с синтетическими данными о доходах для провинций (доменов)
Данные (incomedata)

# Загрузка численности населения провинций
Данные (sizeprov)

# Вычислите прямую оценку среднего дохода Хорвица-Томпсона для каждого
# Провинция в случайной выборке без замены внутри каждой провинции.
result1 <- direct (y = доход, dom = prov, sweight = вес,
                   domsize = sizeprov [, 2: 3], data =comedata)
result1

# То же самое, но с использованием меток провинций в качестве кодов доменов
результат2 <- прямой (у = доходные данные $ доход, дом = доходные данные $ провлаб,
                  Sweight = доходность данных $ вес, domsize = sizeprov [, c (1,3)])
result2

# То же самое, под СГД без замены внутри каждой провинции.result3 <- direct (y = доход, dom = provlab, domsize = sizeprov [, c (1,3)],
                  Данные = incomedata)
result3

# Вычислить прямую оценку среднего дохода для каждой провинции
# под SRS с заменой в каждой провинции
результат4 ​​<- прямой (у = доход, дом = провлаб, данные = доходданные, заменить = ИСТИНА)
result4
#}
Документация воспроизведена из пакета sae, версия 1.3, Лицензия: GPL-2

Примеры сообщества

Похоже, еще нет примеров.

,

Направляющая Функция Управления

НАПРАВЛЕНИЕ считается процессом, в котором руководители инструктируют, направляют и контролируют работу работников для достижения заранее определенных целей. Говорят, что руководство является сердцем процесса управления. Планирование, организация, укомплектование персоналом не имеют значения, если не выполняется функция направления.

Направление инициирует действие, и отсюда начинается настоящая работа. Говорят, что направление состоит из человеческих факторов.Говоря простыми словами, это можно описать как руководство для рабочих, выполняющих работу. Говорят, что в области управления руководство - это все те действия, которые призваны поощрять подчиненных работать эффективно и результативно. По словам Человека, «Управление состоит из процесса или техники, с помощью которой могут быть изданы инструкции, а операции могут выполняться в соответствии с первоначальным планом». Таким образом, «Управление» является функцией руководства, вдохновления, контроля и инструктирования людей по достижению целей организации.

Направление

имеет следующие характеристики:

  1. Pervasive Function - Направление требуется на всех уровнях организации. Каждый менеджер обеспечивает руководство и вдохновение для своих подчиненных.
  2. Непрерывная деятельность - Направление - это непрерывная деятельность, поскольку она непрерывна на протяжении всей жизни организации.
  3. Человеческий фактор - Функция управления связана с подчиненными и, следовательно, связана с человеческим фактором.Поскольку человеческий фактор сложен, а поведение непредсказуемо, функция направления становится важной.
  4. Творческая деятельность - Функция направления помогает преобразовывать планы в результаты. Без этой функции люди становятся неактивными, а физические ресурсы не имеют смысла.
  5. Исполнительная функция - Функция направления выполняется всеми менеджерами и руководителями на всех уровнях в течение всей работы предприятия, подчиненный получает инструкции только от своего начальника.
  6. Функция делегата - Предполагается, что руководство является функцией, касающейся людей. Поведение человека непредсказуемо по своей природе и обусловливает поведение людей по отношению к целям предприятия - вот что делает исполнительная власть в этой функции. Следовательно, это называется деликатностью в отношении поведения человека.



Авторство / Ссылка - Об авторе (авторах)

Статья написана «Prachi Juneja» и рецензирована Руководства по изучению управления содержанием.Команда MSG Content состоит из опытных преподавателей, специалистов и экспертов по предметам. Мы являемся сертифицированным образовательным учреждением в соответствии с ISO 2001: 2015. Чтобы узнать больше, нажмите О нас. Использование этого материала бесплатно в учебных и образовательных целях. Пожалуйста, укажите авторство использованного контента, включая ссылки на ManagementStudyGuide.com и URL страницы контента.


,

функций: домен и диапазон | Purplemath

Purplemath

Вернемся к теме доменов и диапазонов.

Когда функции будут впервые представлены, вы, вероятно, будете иметь некоторые упрощенные «функции» и отношения, с которыми вам придется иметь дело, обычно это просто наборы точек. Это не будут ужасно полезные или интересные функции и отношения, но ваш текст хочет, чтобы вы поняли, что такое область и диапазон функции.Небольшие наборы точек - это, как правило, самые простые виды отношений, поэтому ваша книга начинается с них.

Например:

MathHelp.com

Domain and Range on MathHelp.com
  • Укажите домен и диапазон следующего отношения.Является ли отношение функцией?

{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}

Приведенный выше список точек, представляющих собой связь между определенными х и определенными х , является взаимосвязью. Домен - все значения x , а диапазон - все значения y . Чтобы дать домен и диапазон, я просто перечисляю значения без дублирования:

Домен

: {2, 3, 4, 6}

Диапазон

: {–3, –1, 3, 6}

(обычно перечислять эти значения в числовом порядке, но это , а не ).Наборы называются «неупорядоченными списками», так что вы можете перечислять номера в любом порядке. Только не дублируйте: технически, повторы хороши в наборах, но большинство преподавателей рассчитывают на это.)

Хотя данный набор действительно представляет отношение (поскольку x и y связаны друг с другом), набор, который они мне дали, содержит две точки с одинаковым значением x : (2, –3) и (2, 3).Поскольку x = 2 дает мне два возможных пункта назначения (то есть два возможных значения y ), то это отношение не является функцией.

Обратите внимание, что все, что мне нужно было сделать, чтобы проверить, является ли отношение функцией, - это найти дубликаты x -значений. Если вы обнаружите дубликаты значений x , то различные значения y означают, что у вас нет функции. Помните: чтобы отношение было функцией, каждое значение x должно быть равно одному, и только одному значению , y .

  • Укажите домен и диапазон следующего отношения. Является ли отношение функцией?

{(–3,5), (–2,5), (–1,5), (0,5), (1,5), (2,5)}

Я просто перечислю x значений для домена и y значений для диапазона:

Домен

: {–3, –2, –1, 0, 1, 2}

Диапазон

: {5}

Это еще один пример «скучной» функции, такой же, как пример на предыдущей странице: каждое последнее значение x переходит в точно такое же значение y .Но каждое значение x отличается, так что, пока скучно,

это отношение действительно функция.

Фактически, эти точки лежат на горизонтальной линии y = 5.

Кстати, имя для набора, содержащего только один элемент, например, «диапазон», установленный выше, - «синглтон». Таким образом, диапазон также может быть указан как «синглтон 5»

Существует еще один случай для нахождения домена и диапазона функций.Они дадут вам функцию и попросят найти домен (и, возможно, диапазон). Я только когда-либо видел (или даже могу думать о) две вещи на этом этапе вашей математической карьеры, которые вы должны будете проверить, чтобы определить область функции, которую они вам дадут, и эти две вещи являются знаменателями и квадратные корни.

  • Определить область и диапазон заданной функции:

Домен - это все значения, которые разрешено принимать x .Единственная проблема, которую я имею с этой функцией, заключается в том, что мне нужно быть осторожным, чтобы не делить на ноль. Таким образом, единственные значения, которые x не могут принять, - это те, которые вызывают деление на ноль. Поэтому я установлю знаменатель равным нулю и решу; мой домен будет всем остальным.

x 2 - x - 2 = 0

( x - 2) ( x + 1) = 0

x = 2 или x = –1

Тогда домен «все x не равен –1 или 2».

Диапазон немного сложнее, поэтому они могут не просить об этом. В целом, однако, они захотят, чтобы вы нарисовали график функции и нашли диапазон на картинке. В этом случае:

Как видно из моего рисунка, график «охватывает» все значения и ; то есть график будет идти так низко, как мне нравится, а также будет идти так высоко, как мне нравится. Для любой точки на оси и , независимо от того, как высоко, так и низко, я могу перейти из этой точки вправо или влево, и, в конце концов, я пересечу график.Поскольку график в конечном итоге охватит все возможные значения y , то:

диапазон "все действительные числа".

  • Определить область и диапазон заданной функции:

Домен - это все значения, которые могут принимать x .Единственная проблема, которую я имею с этой функцией, состоит в том, что у меня не может быть отрицательного в квадратном корне. Так что я установлю внутренности больше или равными нулю и решу. Результатом будет мой домен:

–2 x + 3 ≥ 0

–2 x ≥ –3

2 x ≤ 3

x ≤ 3/2 = 1,5

Тогда домен «все x ≤ 3/2».

Диапазон требует графика. Мне нужно быть осторожным при отображении радикалов:

График начинается с y = 0 и оттуда идет вниз (влево). Хотя график снижается очень медленно, я знаю, что, в конце концов, я могу пойти настолько низко, насколько захочу (выбрав достаточно большой размер x ). Кроме того, из моего опыта работы с графиками я знаю, что график никогда не начнет возвращаться. Тогда:

диапазон «все и ≤ 0».

Партнерская

Algebra Tutors
  • Определить область и диапазон заданной функции:

y = - x 4 + 4

Это просто многочлен сорта с садом.Здесь нет знаменателей (поэтому нет проблем с делением на ноль) и нет радикалов (поэтому нет проблем с квадратным корнем из отрицательных значений). С полиномом проблем нет. Нет значений, которые я не могу подключить для x . Когда у меня есть полином, ответ для домена будет , всегда :

Диапазон будет варьироваться от полинома до полинома, и они, вероятно, даже не спросят, но когда они это сделают, я смотрю на картинку:

График поднимается только до y = 4, но он идет так низко, как мне нравится.Тогда:

Диапазон «все и ≤ 4».

URL: https://www.purplemath.com/modules/fcns2.htm

,

Область и диапазон логарифмических функций

В этом разделе вы узнаете, как найти область и диапазон логарифмических функций.

В приведенной ниже таблице приведены область и диапазон различных логарифмических функций.

Наименование частей логарифма

Обычно логарифм состоит из трех частей.

Давайте рассмотрим названия этих трех частей с примером.

log 10 A = B

В приведенной выше логарифмической функции

10 называется Base

A называется Аргумент

B называется Ответ

Факт, который нужно знать о области функций логарифма

Очень важный факт, который мы должны знать о области логарифма для любой базы:

«Логарифмическая функция определяется только для положительных значений аргумента»

Например, если логарифмическая функция равна

y = log 10 x,

, затем домен

x> 0 или (0, + ∞)

Домен y = log₁ ₀ (x)

В логарифмической функции

y = log 10 (x),

аргумент «x».

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения х должны быть больше нуля.

Таким образом, область вышеуказанной логарифмической функции равна

x> 0 или (0, + ∞)

Домен y = log₁ ₀ (x + a)

В логарифмической функции

y = log 10 (x + a),

аргумент «x + a».

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения 'x + a' должны быть больше нуля.

Затем,

x + a> 0

Вычтите «a» с каждой стороны.

x> -a

Таким образом, область вышеуказанной логарифмической функции равна

x> -a или (-a, + ∞)

Домен y = log₁ ₀ (x-a)

В логарифмической функции

y = log 10 (x-a),

аргумент «x-a».

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения 'x-a' должны быть больше нуля.

Затем,

x - a> 0

Добавьте «a» с каждой стороны.

x> a

Следовательно, область вышеуказанной логарифмической функции равна

x> a или (a, + ∞)

Домен y = log₁ k (kx)

В логарифмической функции

y = log 10 (kx),

аргумент «kx».

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения 'kx' должны быть больше нуля.

Затем,

kx> 0

Разделите каждую сторону на 'k'.

x> 0

Следовательно, область вышеуказанной логарифмической функции равна

x> 0 или (0, + ∞)

Домен y = log₁ k (kx + a)

В логарифмической функции

y = log 10 (kx + a),

аргументом является 'kx + a'.

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения 'kx + a' должны быть больше нуля.

Затем,

kx + a> 0

Вычтите «a» с каждой стороны.

kx> -a

Разделить каждую сторону на k.

x> -a / k

Таким образом, область вышеуказанной логарифмической функции равна

x> -a / k или (-a / k, + ∞)

Домен y = log₁ k (kx-a)

В логарифмической функции

y = log 10 (kx-a),

аргументом является 'kx-a'.

Из факта, объясненного выше, аргумент всегда должен быть положительным значением.

Итак, значения 'kx-a' должны быть больше нуля.

Затем,

kx - a> 0

Добавьте 'a' с каждой стороны.

kx> a

Разделите каждую сторону на k.

x> a / k

Следовательно, область вышеуказанной логарифмической функции равна

x> a / k или (a / k, + ∞)

Еще кое-что о области логарифмических функций

Давайте рассмотрим логарифмические функции, которые описаны выше.

y = log 10 (x)

y = log 10 (x + a)

y = log 10 (xa)

y = log 10 (kx)

y = log 10 (kx + a)

y = log 10 (kx-a)

Домен уже объяснен для всех вышеупомянутых логарифмических функций с основанием ' 10' .

В случае, если основание не равно «10» для вышеуказанных логарифмических функций, домен останется неизменным.

Например, в логарифмической функции

y = log 10 (x),

вместо базы '10', если есть какая-то другая база, домен останется таким же. Это

x> 0 или (0, + ∞)

Диапазон логарифмических функций

В приведенной ниже таблице поясняется диапазон y = log 10 (x).

То есть

"Все вещественные числа"

Здесь мы можем подумать, что если основание не равно 10, каков может быть диапазон логарифмических функций?

Какую бы базу мы не использовали для логарифмической функции, диапазон всегда равен

«Все действительные числа»

Для базы, отличной от «10», мы можем определить диапазон логарифмической функции таким же образом, как описано выше для база «10».

Помимо материалов, приведенных в этом разделе, если вам нужны другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Вы также можете посетить следующие веб-страницы по различным материалам по математике.

ПРОБЛЕМЫ СЛОВА

Словесные задачи HCF и LCM

Задачи со словами в простых уравнениях

Задачи в области линейных уравнений

Задачи в словах по квадратным уравнениям

Задачи в алгебре

Проблемы со словами в поездах

Проблемы со словами в области и по периметру

Проблемы со словами при прямом и обратном изменении

Проблемы со словами в цене за единицу

Проблемы со словами в цене за единицу

Слово задачи по сравнению ставок

Преобразование словесных задач в обычных единицах

Преобразование словесных задач в метрических единицах

Задачи со словами по простым интересам

Задачи со словами по сложным процентам

Задачи со словами по типам ngles

Проблемы с дополнительными и дополнительными углами слов

Проблемы с двойными фактами

Проблемы с тригонометрическими словами

Проблемы с процентами в словах

Проблемы со словами о прибылях и убытках

Уценка и разметка задачи

задачи о десятичном слове

задачи о слове на дроби

задачи о слове на смешанных дробях

задачи с одним уравнением в слове задачи

проблемы о линейных неравенствах слова

слово и пропорции задачи

Проблемы со временем и работой

Проблемы со словами на множествах и диаграммах Венна

Проблемы со словами в возрасте

Проблемы со словами в теореме Пифагора

Процент числа oblems

Задачи на слово с постоянной скоростью

Задачи на слово на средней скорости

Задачи на слово на сумму углов треугольника составляет 180 градусов

ДРУГИЕ ТЕМЫ

Сочетания прибылей и убытков

Сокращения в процентах

Ярлыки временного стола

Сокращения времени, скорости и расстояния

Сокращения соотношений и пропорций

Область и диапазон рациональных функций

Домен и диапазон функции с отверстиями

Построение рациональных функций с графиками

Построение рациональных функций с отверстиями

Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

Поиск квадратного корня с помощью длинных чисел зрение

л.Метод CM для решения задач времени и работы

Перевод словесных задач в алгебраические выражения

Остаток при делении 2-й степени 256 на 17

Остаток при делении 17-й степени 23 на 16

Сумма всех трехзначных чисел, кратных 6

Сумма всех трехзначных чисел, кратных 7

Сумма всех трехзначных чисел, кратных 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Обучение не для оценки, это процесс для понимания концепции.

Мы твердо верим, что глубокое понимание концепции имеет значение. Наша конечная цель всегда состоит в том, чтобы студенты глубже поняли концепцию.

Наши студенты всегда получают оценки только благодаря пониманию концепции.

Мы являемся экспертами в SCAT (математика и английский), SAT (математический английский), ACT (математика и английский), SAT Level 1 & 2 (предметные тесты), исчисление, предварительное исчисление и многое другое.

Для онлайн-классов, пожалуйста, свяжитесь:

WhatsApp: + 91-

37004

Skype ID: rams_tpt

,

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *